{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
" "
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [],
"source": [
"%matplotlib inline\n",
"import matplotlib as mpl\n",
"import matplotlib.pyplot as plt\n",
"import numpy as np\n",
"import scipy as scipy\n",
"import scipy.special as sp\n",
"import pandas as pd\n",
"\n",
"import time"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [],
"source": [
"colors = [\"xkcd:dusty blue\", \"xkcd:dark peach\", \"xkcd:dark seafoam green\", \n",
" \"xkcd:dusty purple\",\"xkcd:watermelon\", \"xkcd:dusky blue\", \"xkcd:amber\", \n",
" \"xkcd:purplish\", \"xkcd:dark teal\", \"xkcd:orange\", \"xkcd:slate\"]\n",
"\n",
"plt.style.use('ggplot')\n",
"plt.rcParams['font.family'] = 'sans-serif'\n",
"plt.rcParams['font.serif'] = 'Ubuntu'\n",
"plt.rcParams['font.monospace'] = 'Ubuntu Mono'\n",
"plt.rcParams['font.size'] = 10\n",
"plt.rcParams['axes.labelsize'] = 10\n",
"plt.rcParams['axes.labelweight'] = 'bold'\n",
"plt.rcParams['axes.titlesize'] = 10\n",
"plt.rcParams['xtick.labelsize'] = 8\n",
"plt.rcParams['ytick.labelsize'] = 8\n",
"plt.rcParams['legend.fontsize'] = 10\n",
"plt.rcParams['figure.titlesize'] = 12\n",
"plt.rcParams['image.cmap'] = 'jet'\n",
"plt.rcParams['image.interpolation'] = 'none'\n",
"plt.rcParams['figure.figsize'] = (16, 8)\n",
"plt.rcParams['lines.linewidth'] = 2\n",
"plt.rcParams['lines.markersize'] = 8"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [],
"source": [
"import urllib.request\n",
"\n",
"filepath = \"../dataset/\"\n",
"url = \"https://tvml.github.io/ml2425/dataset/\"\n",
"\n",
"def get_file(filename, local):\n",
" #IS_COLAB = ('google.colab' in str(get_ipython()))\n",
" if local:\n",
" urllib.request.urlretrieve (url+filename, filename)\n",
" return filename\n",
" else:\n",
" return filepath+filename"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [],
"source": [
"def plot_ds(data,m=None,q=None):\n",
" fig = plt.figure(figsize=(16,8))\n",
" minx, maxx = min(data.x1), max(data.x1)\n",
" deltax = .1*(maxx-minx)\n",
" x = np.linspace(minx-deltax,maxx+deltax,1000)\n",
" ax = fig.gca()\n",
" ax.scatter(data[data.t==0].x1, data[data.t==0].x2, s=40, edgecolor='k', alpha=.7)\n",
" ax.scatter(data[data.t==1].x1, data[data.t==1].x2, s=40, edgecolor='k', alpha=.7)\n",
" if m:\n",
" ax.plot(x, m*x+q, lw=2, color=colors[5])\n",
" plt.xlabel('$x_1$', fontsize=12)\n",
" plt.ylabel('$x_2$', fontsize=12)\n",
" plt.xticks(fontsize=10)\n",
" plt.yticks(fontsize=10)\n",
" plt.title('Dataset', fontsize=12)\n",
" plt.show()"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [],
"source": [
"def plot_1(cost_history, m, q, low=0, high=None, step=1):\n",
" if high is None:\n",
" high = m.shape[0]\n",
" idx = range(low,high,step)\n",
" ch = cost_history[idx]\n",
" th1 = m[idx]\n",
" th0 = q[idx]\n",
" fig = plt.figure(figsize=(12,6))\n",
" ax = fig.add_subplot(1,1,1)\n",
" minx, maxx, miny, maxy = 0, len(ch), ch.min(), ch.max()\n",
" deltay, deltax = .1*(maxy-miny), .1*(maxx-minx)\n",
" miny, maxy, minx, maxx = miny - deltay, maxy + deltay, minx - deltax, maxx + deltax\n",
" ax.plot(range(len(ch)), ch, alpha=1, color=colors[0], linewidth=2)\n",
" plt.xlabel('iterations')\n",
" plt.ylabel('cost')\n",
" plt.xlim(minx,maxx)\n",
" plt.ylim(miny,maxy)\n",
" ax.xaxis.set_major_formatter(mpl.ticker.FuncFormatter(lambda x, pos: '{:0.0f}'.format(x*step+low)))\n",
" plt.xticks(fontsize=8)\n",
" plt.yticks(fontsize=8)\n",
" ax.set_yticklabels([]) \n",
" plt.tight_layout()\n",
" plt.show()"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [],
"source": [
"def plot_2(cost_history, m, q, low=0, high=None, step=1):\n",
" if high is None:\n",
" high = m.shape[0]\n",
" idx = range(low, high ,step)\n",
" ch = cost_history[idx]\n",
" th1 = m[idx]\n",
" th0 = q[idx]\n",
" fig = plt.figure(figsize=(12,6))\n",
" ax = fig.add_subplot(1,1,1)\n",
" minx, maxx, miny, maxy = th0.min(), th0.max(), th1.min(), th1.max()\n",
" deltay, deltax = .1*(maxy-miny), .1*(maxx-minx)\n",
" miny, maxy = miny - deltay, maxy + deltay\n",
" miny, maxy, minx, maxx = miny - deltay, maxy + deltay, minx - deltax, maxx + deltax\n",
" ax.plot(th0, th1, alpha=1, color=colors[1], linewidth=2, zorder=1)\n",
" ax.scatter(th0[-1],th1[-1], color=colors[5], marker='o', s=40, zorder=2)\n",
" plt.xlabel(r'$x_1$')\n",
" plt.ylabel(r'$x_2$')\n",
" plt.xlim(minx,maxx)\n",
" plt.ylim(miny,maxy)\n",
" plt.xticks(fontsize=8)\n",
" plt.yticks(fontsize=8)\n",
" ax.grid(True)\n",
" ax.set_xticklabels([]) \n",
" ax.set_yticklabels([]) \n",
" plt.tight_layout()\n",
" plt.show()"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [],
"source": [
"def plot_all(cost_history, m, q, low=0, high=None, step=1):\n",
" if high is None:\n",
" high = m.shape[0]\n",
" idx = range(low,high,step)\n",
" ch = cost_history[idx]\n",
" th1 = m[idx]\n",
" th0 = q[idx]\n",
" fig = plt.figure(figsize=(18,6))\n",
" ax = fig.add_subplot(1,2,1)\n",
" minx, maxx, miny, maxy = 0, len(ch), ch.min(), ch.max()\n",
" deltay, deltax = .1*(maxy-miny), .1*(maxx-minx)\n",
" miny, maxy, minx, maxx = miny - deltay, maxy + deltay, minx - deltax, maxx + deltax\n",
" ax.plot(range(len(ch)), ch, alpha=1, color=colors[0], linewidth=2)\n",
" plt.xlabel('iterations')\n",
" plt.ylabel('cost')\n",
" plt.xlim(minx,maxx)\n",
" plt.ylim(miny,maxy)\n",
" ax.xaxis.set_major_formatter(mpl.ticker.FuncFormatter(lambda x, pos: '{:0.0f}'.format(x*step+low)))\n",
" plt.xticks(fontsize=8)\n",
" plt.yticks(fontsize=8)\n",
" ax = fig.add_subplot(1,2,2)\n",
" minx, maxx, miny, maxy = th0.min(), th0.max(), th1.min(), th1.max()\n",
" deltay, deltax = .1*(maxy-miny), .1*(maxx-minx)\n",
" miny, maxy = miny - deltay, maxy + deltay\n",
" miny, maxy, minx, maxx = miny - deltay, maxy + deltay, minx - deltax, maxx + deltax\n",
" ax.plot(th0, th1, alpha=1, color=colors[1], linewidth=2, zorder=1)\n",
" ax.scatter(th0[-1],th1[-1], color=colors[5], marker='o', s=40, zorder=2)\n",
" plt.xlabel(r'$m$')\n",
" plt.ylabel(r'$q$')\n",
" plt.xlim(minx,maxx)\n",
" plt.ylim(miny,maxy)\n",
" plt.xticks(fontsize=8)\n",
" plt.yticks(fontsize=8)\n",
" plt.tight_layout()\n",
" plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Rischio e minimizzazione\n",
"Dato un qualunque algoritmo che fornisce per ogni valore di input $x$ una previsione $f(x)$, la qualità delle previsioni fornite dall'algoritmo può essere definita per mezzo di una *funzione di costo* (loss function) $L(x_1, x_2)$, dove $x_1$ è il valore predetto dal modello e $x_2$ è il valore corretto associato a $x$ . Sostanzialmente, il valore della funzione di costo $L(f(x),y)$ misura quindi quanto \"costa\" (secondo il modello di costo indotto dalla funzione stessa) prevedere, dato $x$, il valore $f(x)$ invece del valore corretto $y$.\n",
"\n",
"Dato che evidentemente il costo è dipendente dalla coppia di valori $x,y$, una valutazione complessiva della qualità delle predizioni dell'algoritmo potrà essere fornita considerando il valore atteso della funzione di costo al variare di $x$ e $y$, nell'ipotesi di una (densità di) distribuzione di probabilità congiunta di tali valori $p(x,y)$. La distribuzione $p(x,y)$ ci fornisce quindi la probabilità che il prossimo punto su cui effettuare la predizione sia $x$ e che il valore corretto da predire sia $y$. Si noti che non si fa l'ipotesi che due diverse occorrenze di $x$ siano associate allo stesso valore di $y$: non si assume quindi una relazione funzionale, seppure sconosciuta, tra $x$ e $y$, ma solo una relazione in probabilità $p(y\\mid x)$. \n",
"Questo permette di considerare la presenza di rumore nelle osservazioni effettuate.\n",
"\n",
"Da quanto detto, indicando con $D_x$ e $D_y$ i domini di definizione di $x$ e $y$, e assunta una distribuzione $p(x,y)$ che fornisce un modello statistico del contesto in cui si intende effettuare le predizioni, la qualità di un algoritmo di previsione che calcola la funzione $f(x)$ sarà data dal *rischio*\n",
"$$\n",
"\\mathcal{R}(f)=\\mathbb{E}_p[L(f(x),y)]=\\int_{D_x}\\int_{D_y} L(f(x),y)p(x,y)dxdy\n",
"$$\n",
"\n",
"Il rischio di dice quindi quanto ci aspettiamo che ci costi prevedere $f(x)$, assumendo che:\n",
"\n",
"1. $x$ sia estratto a caso dalla distribuzione marginale\n",
" $$\n",
" p(x)=\\int_{D_y} p(x,y)dy\n",
" $$\n",
"\n",
"2. il relativo valore corretto da predire sia estratto a caso dalla distribuzione condizionata \n",
"$$\n",
"p(y\\mid x)=\\frac{p(x,y)}{p(x)}\n",
"$$\n",
"\n",
"3. il costo sia rappresentato dalla funzione $L(x_1,x_2)$"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### Esempio\n",
"\n",
"Consideriamo il caso in cui vogliamo effettuare previsioni sulla possibilità di pioggia in giornata, date le condizioni del cielo al mattino, assumendo che le possibili osservazioni siano \"sereno\" (S), \"nuvoloso\" (N), \"coperto\" (C), e che le previsioni siano \"pioggia\" (T) e \"non pioggia\" (F). La funzione di costo, sarà allora del tipo $L:\\{T,F\\}^2\\mapsto\\mathbb{R}$\n",
"\n",
"La definizione di una particolare funzione di costo è legata alla valutazione delle priorità dell'utente. Nel caso specifico, se si valuta allo stesso modo \"sgradevole\" uscire con l'ombrello (per una previsione T) senza poi doverlo usare che bagnarsi per la pioggia non avendo preso l'ombrello (per una previsione F) allora la funzione di costo risulta $L_1(y,t)$, definita dalla tabella seguente\n",
"\n",
"| $x_1$/$x_2$ | T | F |\n",
"| :---------: | :--: | :--: |\n",
"| T | 0 | 1 |\n",
"| F | 1 | 0 |\n",
"\n",
"Se invece reputiamo molto più sgradevole bagnarci per non aver preso l'ombrello rispetto a prendere l'ombrello stesso inutilmente, allora la funzione di costo $L_2(y,t)$, potrà essere definita come\n",
"\n",
"| $x_1$/$x_2$ | T | F |\n",
"| :---------: | :--: | :--: |\n",
"| T | 0 | 1 |\n",
"| F | 25 | 0 |\n",
"\n",
"Se facciamo l'ipotesi che la distribuzione congiunta su $\\{S,N,C\\}\\times\\{T,F\\}$ sia \n",
"\n",
"| $x$/$y$ | T | F |\n",
"| :-----: | :--: | :--: |\n",
"| S | .05 | .2 |\n",
"| N | .25 | .25 |\n",
"| C | .2 | .05 |\n",
"\n",
"e consideriamo due possibili funzioni predittive $f_1(x)$ e $f_2(x)$\n",
"\n",
"\n",
"| $x$ | $f_1(x)$ | $f_2(x)$ |\n",
"| :--: | :--------------------: | :------: |\n",
"| S | F | F |\n",
"| N | F | T |\n",
"| C | T | T |\n",
"\n",
"\n",
"possiamo verificare che nel caso in cui la funzione di costo sia $L_1$ allora il rischio nei due casi è $\\mathcal{R}(f_1)=0.65$ e $\\mathcal{R}(f_2)=0.4$ per cui $f_2$ è preferibile a $f_1$. Al contrario, se la funzione di costo è $L_2$, allora risulta $\\mathcal{R}(f_1)=1.55$ e $\\mathcal{R}(f_2)=7.55$, per cui, al contrario, $f_1$ è preferibile a $f_2$.\n",
"\n",
"Come si vede, quindi, la scelta tra $f_1(x)$ e $f_2(x)$ è dipendente dalla funzione di costo adottata e dalla distribuzione $p(x,y)$ che invece è data e, tra l'altro, sconosciuta. Quindi, una diversa distribuzione potrebbe portare a conclusioni diverse anche considerando una stessa funzione di costo: se ad esempio si fa riferimento alla funzione di costo $L_1$, allora la distribuzione congiunta\n",
"\n",
"| $x$/$y$ | T | F |\n",
"| :-----: | :--: | :--: |\n",
"| S | .05 | .05 |\n",
"| N | .05 | .4 |\n",
"| C | .05 | .4 |\n",
"\n",
"determina dei valori di rischio $\\mathcal{R}(f_1)=0.6$ e $\\mathcal{R}(f_2)=0.9$, rendendo ora $f_1$ preferibile a $f_2$.\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Rischio empirico\n",
"Dato che la distribuzione reale $p(x,y)$ è sconosciuta per ipotesi (se così non fosse potremmo sempre effettuare predizioni utilizzando la distribuzione condizionata reale $p(y\\mid x)$) il calcolo del rischio reale è impossibile ed è necessario effettuare delle approssimazioni, sulla base dei dati disponibili. In particolare, possiamo applicare il metodo standard di utilizzando la media aritmetica su un campione come stimatore del valore atteso, e considerare il *rischio empirico* (empirical risk) calcolato effettuando l'operazione di media sul campione offerto dai dati disponibili nel training set $X=\\{(x_1,y_1),\\ldots,(x_n,y_n)\\}$\n",
"\n",
"$$\n",
"\\overline{\\mathcal{R}}(f; X)=\\overline{L}(f(x), y; X)=\\frac{1}{n}\\sum_{i=1}^nL(f(x_i),y_i)\n",
"$$\n",
"\n",
"La funzione utilizzata per le predizioni sarà allora quella che, nell'insieme di funzioni considerato, minimizza il rischio empirico\n",
"\n",
"$$\n",
"f^*=\\underset{f\\in F}{\\mathrm{argmin}}\\;\\overline{\\mathcal{R}}(f;X)\n",
"$$\n",
"\n",
"Si noti che, in effetti, il rischio empirico dipende sia dai dati in $X$ che dalla funzione $f$: in questo senso è una funzione rispetto a $X$ e un funzionale rispetto a $f$. La ricerca di $f^*$ comporta quindi una minimizzazione funzionale del rischio empirico. In generale, tale situazione viene semplificata limitando la ricerca all'interno di classi di funzioni definite da coefficienti: in questo modo, il rischio empirico può essere espresso come funzione dei coefficienti della funzione (oltre che di $X$) e la minimizzazione è una normale minimizzazione di funzione. \n",
"\n",
"Chiaramente, la speranza è che minimizzare il rischio empirico dia risultati simili a quelli che si otterrebbero minimizzando il rischio reale. Ciò dipende, in generale, da quattro fattori:\n",
"\n",
"- La dimensione del training set $X$. Al crescere della quantità di dati, $\\overline{\\mathcal{R}}(f; X)$ tende a $\\mathcal{R}(f)$ per ogni funzione $f$\n",
"- La distribuzione reale $p(x,y)$. Maggiore è la sua complessità, maggiore è la quantità di dati necessari per averne una buona approssimazione.\n",
"- La funzione di costo $L$, che può creare problemi se assegna costi molto elevati in situazioni particolari e poco probabili\n",
"- L'insieme $F$ delle funzioni considerate. Se la sua dimensione è elevata, e le funzioni hanno una struttura complessa, una maggior quantità di dati risulta necessaria per avere una buona approssimazione.\n",
"Al tempo stesso, considerare un insieme piccolo di funzioni semplici rende sì la minimizzazione del rischio implicito su $F$ una buona approssimazione del minimo rischio reale su $F$ stesso, ma al tempo stesso comporta che tale minimo possa essere molto peggiore di quello ottenibile considerando classi più ampie di funzioni.#### Rischio empirico\n",
"Dato che la distribuzione reale $p(\\mathbf{x},t)$ è sconosciuta per ipotesi (se così non fosse potremmo sempre effettuare predizioni utilizzando la distribuzione condizionata reale $p(t\\mid \\mathbf{x})$) il calcolo del rischio reale è impossibile ed è necessario effettuare delle approssimazioni, sulla base dei dati disponibili. In particolare, possiamo applicare il metodo standard di utilizzando la media aritmetica su un campione come stimatore del valore atteso, e considerare il *rischio empirico* (empirical risk) calcolato effettuando l'operazione di media sul campione offerto dai dati disponibili nel training set $X=\\{(\\mathbf{x}_1,t_1),\\ldots,(\\mathbf{x}_n,t_n)\\}$\n",
"\n",
"$$\n",
"\\overline{\\mathcal{R}}(f; X)=\\frac{1}{n}\\sum_{i=1}^nL(f(x_i),y_i)\n",
"$$\n",
"\n",
"La funzione utilizzata per le predizioni sarà allora quella che, nell'insieme di funzioni considerato, minimizza il rischio empirico\n",
"\n",
"$$\n",
"f^*=\\underset{f\\in F}{\\mathrm{argmin}}\\;\\overline{\\mathcal{R}}(f;X)\n",
"$$\n",
"\n",
"Si noti che, in effetti, il rischio empirico dipende sia dai dati in $X$ che dalla funzione $f$: in questo senso è una funzione rispetto a $X$ e un funzionale rispetto a $f$. La ricerca di $f^*$ comporta quindi una minimizzazione funzionale del rischio empirico. In generale, tale situazione viene semplificata limitando la ricerca all'interno di classi di funzioni definite da coefficienti: in questo modo, il rischio empirico può essere espresso come funzione dei coefficienti della funzione (oltre che di $X$) e la minimizzazione è una normale minimizzazione di funzione. \n",
"\n",
"Chiaramente, la speranza è che minimizzare il rischio empirico dia risultati simili a quelli che si otterrebbero minimizzando il rischio reale. Ciò dipende, in generale, da quattro fattori:\n",
"\n",
"- La dimensione del training set $X$. Al crescere della quantità di dati, $\\overline{\\mathcal{R}}(f; X)$ tende a $\\mathcal{R}(f)$ per ogni funzione $f$\n",
"- La distribuzione reale $p(\\mathbf{x},t)$. Maggiore è la sua complessità, maggiore è la quantità di dati necessari per averne una buona approssimazione.\n",
"- La funzione di costo $L$, che può creare problemi se assegna costi molto elevati in situazioni particolari e poco probabili\n",
"- L'insieme $F$ delle funzioni considerate. Se la sua dimensione è elevata, e le funzioni hanno una struttura complessa, una maggior quantità di dati risulta necessaria per avere una buona approssimazione.\n",
"Al tempo stesso, considerare un insieme piccolo di funzioni semplici rende sì la minimizzazione del rischio implicito su $F$ una buona approssimazione del minimo rischio reale su $F$ stesso, ma al tempo stesso comporta che tale minimo possa essere molto peggiore di quello ottenibile considerando classi più ampie di funzioni."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Minimizzazione della funzione di rischio\n",
"\n",
"In generale, l'insieme $F$ delle funzioni è definito in modo parametrico $F=\\{f(\\mathbf{x};\\theta)\\}$ dove $\\theta\\in D_\\theta$ è un coefficiente (tipicamente multidimensionale) che determina, all'interno della classe $F$ (definita tipicamente in termini ''strutturali'', con la definizione di $f$) la particolare funzione utilizzata. Un esempio tipico è offerto dalla *regressione lineare*, in cui si vuole prevedere il valore di un attributo $y$ con dominio $R$ sulla base dei valori di altri $m$ attributi $\\mathbf{x}=(x_1,\\ldots, x_m)$ (che assumiamo per semplicità in $R$ anch'essi): nella regressione lineare, l'insieme delle possibili funzioni $f:R^m\\mapsto R$ è limitato alle sole funzioni lineari $f_\\mathbf{w}(\\mathbf{x})=w_0+w_1x_1+\\ldots+w_mx_m$, e il parametro $\\theta$ corrisponde al vettore $\\mathbf{w}=(w_0,\\ldots,w_m)$ dei coefficienti.\n",
"\n",
"In questo caso, il rischio empirico, fissata la famiglia $F$ di funzioni, può essere ora inteso come funzione di $\\theta$\n",
"$$\n",
"\\overline{\\mathcal{R}}(\\theta; X)=\\frac{1}{n}\\sum_{i=1}^nL(f(\\mathbf{x}_i;\\theta),t_i)\\hspace{2cm}f\\in F\n",
"$$\n",
"e la minimizzazione del rischio empirico può essere effettuata rispetto a $\\theta$\n",
"$$\n",
"\\theta^*=\\underset{\\theta\\in D_\\theta}{\\mathrm{argmin}}\\;\\overline{\\mathcal{R}}(\\theta;X)\n",
"$$\n",
"da cui deriva la funzione ottima (nella famiglia $F$) $f^*=f(\\mathbf{x};\\theta^*)$\n",
"\n",
"la minimizzazione della funzione di rischio avrà luogo nel dominio di definizione $D_\\theta$ di $\\theta$, e potrà essere effettuata in modi diversi, in dipendenza della situazione e di considerazioni di efficienza di calcolo e di qualità delle soluzioni derivate."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Ricerca analitica dell'ottimo\n",
"Se il problema si pone in termini di minimizzazione *senza vincoli*, e quindi all'interno di $R^m$, un primo approccio è quello standard dell'analisi di funzioni, consistente nella ricerca di valori $\\overline\\theta$ di $\\theta$ per i quali si annullano tutte le derivate parziali $\\frac{\\partial \\overline{\\mathcal{R}}(\\theta; X)}{\\partial \\theta_i}$, tale cioè che, se indichiamo con $m$ la dimensione (numero delle componenti) di $\\theta$, il sistema su $m$ incognite definito dalle $m$ equazioni \n",
"$$\n",
"\\frac{\\partial \\overline{\\mathcal{R}}(\\theta; X)}{\\partial \\theta_i}\\Bigr|_{\\theta=\\overline\\theta}=0\\hspace{2cm} i=1,\\ldots,m\n",
"$$\n",
"risulta soddisfatto. La soluzione analitica di questo sistema risulta tipicamente ardua o impossibile, per cui vengono spesso adottate tecniche di tipo numerico.\n",
"\n",
"La stessa condizione può essere espressa, in modo vettoriale, ponendo il *gradiente* pari a $0$.\n",
"$$\n",
"\\nabla_\\theta\\overline{\\mathcal{R}}(\\theta; X)=0\n",
"$$\n",
"Si ricorda che, data una funzione $f(x_1,x_2,\\ldots,x_d)$, il gradiente $\\nabla f$ di $f$ è il vettore $d$-dimensionale delle derivate di $f$ rispetto alle variabili $x_1,\\ldots, x_d$: il vettore cioè tale che $[\\nabla f]_i=\\frac{\\partial f}{\\partial x_i}$.\n",
"\n",
"Come si può osservare, in questo modo il metodo consente di raggiungere un valore di $\\theta$ per il quale il gradiente risulta nullo, e quindi un ottimo locale o un punto di sella della funzione di costo. Tipicamente, il rischio di ottenere un valore di $\\theta$ che non corrisponde a un minimo (in particolare globale) viene limitato mediante vari accorgimenti (scelta della funzione $\\overline{\\mathcal{R}}$, scelta del metodo di calcolo)."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### Gradient descent\n",
"\n",
"La discesa del gradiente (*gradient descent*) è una delle tecniche di ottimizzazione più popolari, in particolare nel settore del Machine Learning e delle Reti Neurali. La tecnica consiste nel minimizzare una funzione obiettivo $J(\\theta)$ definita sui parametri $\\theta\\in\\mathbb{R}^d$ del modello mediante aggiornamenti successivi del valore di $\\theta$ (a partire da un valore iniziale $\\theta^{(0)}$) nella direzione opposta a quella del valore attuale del gradiente $J'(\\theta)=\\nabla J(\\theta)$. Un parametro $\\eta$, detto *learning rate* determina la scala degli aggiornamenti effettuati, e quindi la dimensione dei passi effettuati nella direzione di un minimo locale.\n",
"\n",
"Possiamo interpretare la tecnica come il muoversi sulla superficie della funzione $J(\\theta)$ seguendo sempre la direzione di massima pendenza verso il basso, fino a raggiungere un punto da cui è impossibile scendere ulteriormente. Il metodo è detto del *primo ordine* in quanto richiede il calcolo delle derivate prime della funzione da ottimizzare."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### Varianti di discesa del gradiente\n",
"In molti casi, e sempre nell'ambito del ML, la funzione obiettivo corrisponde all'applicazione di una funzione di costo (*loss function*), predefinita e dipendente dal modello adottato, su un insieme dato di elementi di un dataset $X=(\\mathbf{x}_1,\\ldots, \\mathbf{x}_n)$ (che nel caso di apprendimento supervisionato è un insieme di coppie $X=((\\mathbf{x}_1,t_1),\\ldots,(\\mathbf{x}_n,t_n))$): indichiamo tale funzione come $J(\\theta; X)$: si noti che, fissata la funzione di costo $J$ e il dataset $X$, il risultato è funzione dei parametri $\\theta$. \n",
"\n",
"Questo corrisponde all'approssimazione del *rischio* \n",
"\n",
"$$\n",
"\\mathcal{R}(\\theta)=\\int J(\\theta,\\mathbf{x})p(\\mathbf{x})d\\mathbf{x}=E_{p}[\\theta]\n",
"$$\n",
"\n",
"In generale, la funzione di costo è definita in modo additivo rispetto agli elementi di $X$ (il costo relativo all'insieme $X$ è pari alla somma dei costi relativi ai suoi elementi), per cui il valore risulta $J(\\theta;X)=\\sum_{i=1}^nJ(\\theta;\\mathbf{x}_i)$, o preferibilmente, per evitare una eccessiva dipendenza dal numero di elementi, come media \n",
"$$\n",
"J(\\theta;X)=\\frac{1}{n}\\sum_{i=1}^nJ(\\theta;\\mathbf{x}_i)\n",
"$$ \n",
"Si noti che, per le proprietà dell'operazione di derivazione, da questa ipotesi deriva l'additività anche del gradiente, per cui \n",
"$$\n",
"J'(\\theta; X)=\\sum_{i=1}^nJ'(\\theta;\\mathbf{x}_i)\n",
"$$ \n",
"o \n",
"$$\n",
"J'(\\theta;X)=\\frac{1}{n}\\sum_{i=1}^nJ'(\\theta;\\mathbf{x}_i)\n",
"$$\n",
"\n",
"Possiamo allora identificare tre varianti del metodo, che differiscono tra loro per la quantità di elementi di $X$ utilizzati, ad ogni passo, per calcolare il gradiente della funzione obiettivo. Una quantità maggiore di dati utilizzati aumenta l'accuratezza dell'aggiornamento, ma anche il tempo necessario per effettuare l'aggiornamento stesso (in particolare, per valutare il gradiente per il valore attuale di $\\theta$)."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### Batch gradient descent\n",
"\n",
"In questo caso, il gradiente è valutato, ogni volta, considerando tutti gli elementi nel training set $X$. Quindi si ha che al passo $k$-esimo viene eseguito l'aggiornamento\n",
"\n",
"$$\n",
"\\theta^{(k+1)}=\\theta^{(k)}-\\eta\\sum_{i=1}^nJ'(\\theta^{(k)};\\mathbf{x}_i)\n",
"$$\n",
"\n",
" o anche, per i singoli coefficienti\n",
"\n",
"$$\n",
"\\theta_j^{(k+1)}=\\theta_j^{(k)}-\\eta\\sum_{i=1}^n\\frac{\\partial J(\\theta;\\mathbf{x}_i)}{\\partial\\theta_j}\\Bigr\\vert_{\\small\\theta=\\theta^{(k)}}\n",
"$$\n",
"\n",
"Dato che si richiede quindi, ad ogni iterazione, la valutazione del gradiente (con il valore attuale $\\theta^{(k)}$ di tutti i coefficienti) su tutti gli elementi di $X$, questa soluzione tende ad essere molto lenta, soprattutto in presenza di dataset di dimensioni molto estese, come nel caso di reti neurali complesse e deep learning. Inoltre, l'approccio diventa del tutto impraticabile se il dataset è talmente esteso da non entrare neanche in memoria.\n",
"\n",
"In termini di codice, il metodo batch gradient descent si presenta come:\n",
"\n",
"```python\n",
"for i in range(n_epochs):\n",
" g = 0\n",
" for k in range(dataset_size):\n",
" g = g+evaluate_gradient(loss_function, theta, X[k])\n",
" theta = theta-eta*g\n",
"```\n",
"Il ciclo viene eseguito un numero di volte pari al numero di epoche, dove per *epoca* si intende una iterazione su tutti gli\n",
"elementi di $X$. Di conseguenza, la valutazione di $\\theta$ viene aggiornata un numero di volte pari al numero di epoche. Il\n",
"metodo batch gradient descent converge certamente al minimo globale se la funzione $J(\\theta)$ è convessa, mentre altrimenti\n",
"converge a un minimo locale.\n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### Esempio\n",
"Applichiamo le considerazioni a un semplice problema di classificazione su un dataset bidimensionale, riportato graficamente di seguito.\n"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA7sAAAHzCAYAAADhDgreAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAABEK0lEQVR4nO3de3TUd53H/9c3M0AyM5ArgQ2XU6FluRe6SVsJNUAD5Qy2i23EUsn+1N3FLj1qde2vsFXQIpZeOO2vlm71qFXTXW0Xejmuszam0HQbrR1KYkowWry0WlpjCKEkIchkvr8/YmYJSSAhM/O9PR/neI6ZzJA3+ZB0Xt/v+/P+GKZpmgIAAAAAwEUyrC4AAAAAAIBkI+wCAAAAAFyHsAsAAAAAcB3CLgAAAADAdQi7AAAAAADXIewCAAAAAFyHsAsAAAAAcB3CLgAAaXbJJZcoKytL48ePV05OjpYsWaLHHntM8Xj8gq/9/e9/L8MwFIvFUlpjur4OAACpQtgFAMACP/zhD3Xy5Em9+eab2rx5s+6991794z/+o9VlAQDgGoRdAAAslJ2drRtuuEFPPvmkvvvd7+rQoUP60Y9+pMWLF2vChAmaNm2avvSlLyWe/4EPfECSlJOTo1AopJ/97Gf6zW9+oxUrVig/P18FBQX66Ec/qvb29sRr7r33Xk2ZMkXjx4/X3/7t3+qFF16QJMXjce3cuVMzZ85Ufn6+1q1bp7a2tiG/DgAATkLYBQDABq688kpNnTpV//u//6tgMKjvfe97am9v149+9CP9+7//u5599llJ0ksvvSRJam9vV0dHh97//vfLNE1t2bJFR48e1S9/+Uv94Q9/SATkX/3qV3rkkUcUjUZ18uRJPf/887rkkkskSV/72tf07LPPqra2VkePHlVubq5uu+22Ib8OAABOQtgFAMAmioqK1NbWpmXLlmnBggXKyMjQwoULtX79etXW1g75uksvvVQrV67UuHHjNHHiRH3uc59LPN/n8+n06dM6fPiwzpw5o0suuUQzZ86UJD322GPasWOHpk6dqnHjxulLX/qS9uzZwz5dAIArEHYBALCJt99+W3l5efr5z3+u5cuXa+LEicrOztZjjz2m1tbWIV/3pz/9STfffLOmTJmiCRMmaMOGDYnnX3rppXrooYf0pS99SYWFhbr55pt19OhRSdKbb76pD33oQ8rJyVFOTo7mzJkjn8+nP/3pT2n5+wIAkEqEXQAAbCAajertt9/W0qVLdcstt+iGG27QH/7wB504cUK33nqrTNOUJBmGMeC1//Zv/ybDMPT666/rvffe0xNPPJF4viTdcsstevnll/Xmm2/KMAzdeeedkqRp06bpf/7nf9Te3p74X3d3t6ZMmTLo1wEAwEkIuwAAWOi9997Tf//3f+vmm2/Whg0btGDBAp08eVJ5eXnKzMzUq6++qv/8z/9MPH/ixInKyMjQb3/728RjJ0+eVCgUUnZ2tt5++23df//9ic/96le/0r59+3T69GllZmYqKytLGRm9//m/9dZbddddd+nNN9+UJP35z3/Wc889N+TXAQDASQi7AABY4Prrr9f48eM1bdo07dixQ5/73Of0+OOPS5IeffRRbd26VePHj9fdd9+tdevWJV4XCAR01113qbS0VDk5OXrllVe0bds2HTx4UNnZ2VqzZo1uvPHGxPNPnz6tzZs3q6CgQJMnT1ZLS4vuueceSdJnPvMZ3XDDDVq1apXGjx+vq6++Wj//+c+H/DoAADiJYZ7d5wQAAAAAgAtwZxcAAAAA4DqEXQAAAACA6xB2AQAAAACuQ9gFAAAAALgOYRcAAAAA4DqEXQAAAACA6/itLiAdjh49anUJSIGCggK1trZaXQZSjHX2BtbZG1hnb2CdvYF19gYnrHNRUdGQn+POLgAAAADAdQi7AAAAAADXIewCAAAAAFyHsAsAAAAAcB3CLgAAAADAdQi7AAAAAADXIewCAAAAAFyHsAsAAAAAcB1/ur/go48+qoMHDyo7O1u7du2SJD311FN64YUXNGHCBEnS+vXrdcUVVwx4bUNDgx5//HHF43Fde+21Wrt2bTpLBwAAAAA4RNrD7rJly7R69Wrt3r273+Nr1qzRDTfcMOTr4vG4vvWtb+kLX/iC8vPztWXLFhUXF2vq1KmpLhkAAAAA4DBpb2OeO3euQqHQiF935MgRTZ48WZMmTZLf79eSJUsUjUZTUCEAAAAAwOnSfmd3KM8//7xeeuklzZgxQ//wD/8wIBC3tbUpPz8/8XF+fr7eeOONdJcJAAAAAHAAW4TdVatWqaKiQpL05JNP6nvf+542bdp00X9eTU2NampqJEk7d+5UQUFBUuqEvfj9ftbWA1hnb2CdvYF19gbW2RtYZ29w+jrbIuzm5OQk/v+1116re++9d8Bz8vLydOzYscTHx44dU15e3qB/Xnl5ucrLyxMft7a2Jq9Y2EZBQQFr6wGsszewzt7AOnsD6+wNrLM3OGGdi4qKhvycLY4eOn78eOL/v/rqq5o2bdqA58ycOVPvvPOOWlpaFIvF9NOf/lTFxcXpLBMAAAAA4BBpv7P70EMP6fDhwzp58qRuvfVWrVu3Tk1NTfr9738vwzA0ceJEbdy4UVLvPt2vf/3r2rJli3w+nz7xiU9ox44disfjWr58+aChGAAAYDiaGur1+vMRjTnVoTNZIS24Lqx5ixZbXRYAIEkM0zRNq4tItaNHj1pdAlLACW0VGD3W2RtYZ2+w0zo3NdTr3T1VKivMkWEYMk1TtS3tmlxRSeAdJTutM1KHdfYGJ6yz7duYAQAA0ulQdSQRdCXJMAyVFeboUHXE4soAAMlC2AUAAJ7j7+pIBN0+hmHI39VpUUUAgGQj7AIAAM+JBUI6dyeXaZqKBYIWVQQASDbCLgAA8Jz5q8KqbWlPBN6+PbvzV4UtrgwAkCy2OGcXAAAgnfqGUO2tjsjf1alYIKj5DKcCAFch7AIAAE+at2gx4RYAXIw2ZgAAAACA6xB2AQAAAACuQ9gFAAAAALgOYRcAAAAA4DqEXQAAAACA6xB2AQAAAACuQ9gFAAAAALgO5+wCAICka2qo1+vPRzTmVIfOZIW04LqwyspXWl0WAMBDCLsAACCpmhrq9e6eKlUU5sgIBGSaPardU6VfZGdryvtmWF0eAMAjaGMGAABJdag6orLCHBmGIUkyDENlhTk68MNnLK4MAOAlhF0AAJBU/q6ORNDtYxiGfJ0dFlUEAPAiwi4AAEiqWCAk0zT7PWaapnqCIYsqAgB4EWEXAAAk1fxVYdW2tCcCr2maqm1pV/H1H7K4MgCAlzCgCgAADNtgU5bnLVrc7zl9H++tjsjf1alYIKj5FZW6vORKtba2WlE2AMCDCLsAAGBYhpqyLGnQwHvuY7CH4VywAAA3oI0ZAAAMy1BTlg9VRyyuDMOVuGCR1aO1+QFVZPXo3T1Vamqot7o0AEg6wi4AABiWoaYs+7s6LaoII8UFCwBeQtgFAADDMtSU5VggaFFFGCkuWADwEsIuAAAYlqGmLM9fFba4MgwXFywAeAlhFwAADMu8RYs1uaJSe7t9evbYKe3t9mlyRSXDjRyECxYAvIRpzAAAYNiYsuxsQx0LxZoCcCPCLgAAgIdwwQKAV9DGDAAAAABwHcIuAAAAAMB1CLsAAAAAANch7AIAAAAAXIcBVQAAAPCMpoZ6vf58RGNOdehMVkgLrgszsAtwKcIuAAAAPKGpoV7v7qlSRWGOjEBAptmj2j1VkkTgBVyINmYAAAB4wqHqiMoKc2QYhiTJMAyVFeboUHXE4soApAJhFwAAAJ7g7+pIBN0+hmHI39VpUUUAUomwCwAAAE+IBUIyTbPfY6ZpKhYIWlQRgFQi7AIAAMAT5q8Kq7alPRF4TdNUbUu75q8KW1wZgFRgQBUAAAA8oW8I1d7qiPxdnYoFgppfUclwKsClCLsAAADwjHmLFhNuAY+gjRkAAAAA4DqEXQAAAACA69DGDAAAYHNNDfV6/fmIxpzq0JmskBZcF6YVFwAugLALAABgY00N9Xp3T5UqCnNkBAIyzR7V7qmSJAIvhsQFEoCwCwAAYGuHqiO6qTBHhmFIkgzDUFlhjvZWRwgvSeSmcMgFEqAXe3YBAABszN/VkQi6fQzDkL+r06KK3CcRDrN6tDY/oIqsHr27p0pNDfVWl3ZRDlVHVDbIBZJD1RGLKwPSK613dh999FEdPHhQ2dnZ2rVrlySpqqpKr732mvx+vyZNmqRNmzYpGAwOeO1tt92mzMxMZWRkyOfzaefOneksHQAAwBKxQEim2dMv8JqmqVhg4PslXBy33T33d3XIyAr0e4wLJPCitIbdZcuWafXq1dq9e3fisYULF+qWW26Rz+fTE088oWeeeUYbNmwY9PXbtm3ThAkT0lUuAACA5eavCqt2T1XiTp1pmqptadf8ikqrS3MNt4VDLpAAvdIadufOnauWlpZ+j11++eWJ/z9r1iy98sor6SwJAAAgwY77Nvu+/t7qiPxdnYoFgppfUWl5XW7itnDIBRKgl60GVO3bt09LliwZ8vM7duyQJK1cuVLl5eXpKgsAAHiAnYf6zFu02PIa3Mxt4ZALJEAv24Tdp59+Wj6fT9dcc82gn9++fbvy8vJ04sQJfeUrX1FRUZHmzp076HNrampUU1MjSdq5c6cKCgpSVjes4/f7WVsPYJ29gXX2Bruv85GX9ulDUwv73d1bObVQz7y0T2XlKy2szFnsvs6DKStfqV9kZ+tHP3xGvo4O9QRDKv7HDbq85EqrS7toZeUrU/rv1onrjJFz+jrbIuy++OKLeu2117R169YB0wb75OXlSZKys7NVUlKiI0eODBl2y8vL+935bW1tTX7RsFxBQQFr6wGsszewzt5g93WOtbXqTH5gkMffs3XddmP3dR7KlPfN0JRP/2u/x5z490gXp64zRsYJ61xUVDTk5ywPuw0NDXruuef05S9/WePGjRv0Od3d3TJNU1lZWeru7lZjY6MqKirSXCkAAHCrpoZ6Hf5ls+K+mGIZPi2YPk1z/qbQ0fs2AcDr0hp2H3roIR0+fFgnT57UrbfeqnXr1umZZ55RLBbT9u3bJUmXXXaZNm7cqLa2Nn3961/Xli1bdOLECT3wwAOSpJ6eHi1dulSLFi1KZ+kAAMCl+vbqfmrBDJ1+523ljfWr9q03ZcpUS8ZYx+7bBACvM0zTNK0uItWOHj1qdQlIASe0VWD0WGdvYJ29wa7r/OR9O3RTZu8k3o73Tui9P7fIiMX0ndZT+tDmrQz1GSG7rjOSi3X2Biess63bmAHAq+x4xAngRWefsRqakK3QhGxJ0pyCU/xMAoCDEXYBwAJ2PuIE8Bq3nbEKAOhF2AUACxyqjuimv57nKEmGYaisMEd7qyOEXSDNknXGKt0aAGAvhF0AsMDZbZN9DMOQv6vToooA7+oLpHurI/J3dSoWCGp+ReWIgirdGgBgP4RdALAAbZOAvcxbtHhUoZRuDQCwnwyrCwAAL5q/Kqzalnb1DcRPtE2uCltcGYCL4e/q6HfxSqJbAwCsxp1dALBAMtomAdgH3RoAYD+EXQCwyGjbJgHYR7KGXAEAkoewCwBAEjCJ19vo1gAA+yHsAgAwSkzihUS3BgDYDQOqAAAYpUPVkUT7qvR/k3gPVUcsrgwAAO8i7AIAMEpM4gUAwH5oYwYAYJSYxAuk13D2yLOPHgBhFwBgK4O9QZVk6zetTOIF0mc4e+TZRw9AIuwCAGxksDeo//nY/6cJY/2quHS6bd+0MokXSJ9D1RHdNMge+b3VkcTP3HCeA8D9CLsAANsY7A3qmJPtuqJgvO3ftDKJF0gPf1eHjKxAv8fO3SM/nOcAcD8GVAEAbGOwQU9jzB754vF+j/GmFfCu3j3yZr/Hzt0jP5znAHA/wi4AwDYGe4N6xvCpJ6P/f6540wp41/xVYdW2tCd+VyT2yK8Kj+g5ANyPNmYAwHmlc6LpYIOezozP0UHTryLTZPgTgGHtkWcfPQCJsAsAOI90TzQd7A3q3936mQGP8aYV8Lbh7JFnHz0Awi4AYEhWTDQd6g0qb1oBAMBIsGcXADCkwQZGMRwKAAA4AWEXADAkJpoCAACnIuwCAIbERFMAAOBU7NkFAAyJiaZAf+mcTg4AGB3CLgDgvNww0ZSAYn9OWKPhTid3wt8FALyAsAsAcLV0H5+EkXPKGg1nOrlT/i4A4AXs2QUAuNqh6ojKBgkoh6ojFleGPk5Zo+FMJ3fK3wUAvICwCwBwNY5Psj+nrNFwppM75e8CAF5A2AUAuBrHJ9mfU9ZoONPJnfJ3AQAvIOwCAFyN45PszylrNG/RYk2uqNTebp+ePXZKe7t9mnzOdHKn/F0AwAsYUAUAcDU3H5/klqm/TlqjC00nd9LfBQDcjrALAHA9NxyfdC63Tf110xrZ4e/ilgshADAatDEDAOBATP3FUBIXQrJ6tDY/oIqsHr27p0pNDfVWlwYAaUXYBQDAgZj6i6FwIQQAetHGDACQRNuj0/RO/e3pF3iZ+gvprxdCsgL9HuNCCAAv4s4uAIC2Rwdi6i+GwvFHANCLsAsAoO3RgYZzDA68iQshANCLNmYAAG2PDmWHqb+DoSXeWhx/BAC9CLsAAPZ/ImnOdyRSWflKi6vzDrteCAGAdCLsAgB62x73VCVamRNtjxWVVpdmS1bfubT665/PoeqIbhqkJX5vdYSwCwBIK8IuAIC2xxE4353LdHy/rP76F0JLPGAPdr4oBqQLYRcAIIm2x+E6353LdHz/rP76F0JLPGA9u18UA9KFacwAAIyAv6ujX5CT0nvn0uqvfyFMAgasx4R9oBd3dgEAGAGr71xa/fUvhJZ4wHpsJwB6EXYBABgBq4d5Wf31h4OWeMBadr8oBqQLYRcAgBGw+s6l1V8fgP054aIYkA5pD7uPPvqoDh48qOzsbO3atUuS1NHRoQcffFB//vOfNXHiRH32s59VKBQa8NoXX3xRTz/9tCTpxhtv1LJly9JZOgAAkqy/c2n11wdgb1wUA3qlPewuW7ZMq1ev1u7duxOPPfvss1qwYIHWrl2rZ599Vs8++6w2bNjQ73UdHR3as2ePdu7cKUnavHmziouLBw3FAAAAgJdxUQywYBrz3LlzBwTUaDSqsrIySVJZWZmi0eiA1zU0NGjhwoUKhUIKhUJauHChGhoa0lEyAAAAAMBhbLFn98SJE8rNzZUk5eTk6MSJEwOe09bWpvz8/MTHeXl5amtrG/TPq6mpUU1NjSRp586dKigoSEHVsJrf72dtPYB19gbW2Ru8uM6/iL6q6A+fkb/zpGLB8Sq5/kO6vORKq8tKKS+usxexzt7g9HW2Rdg9m2EYA84PHKny8nKVl5cnPm5tbR1tWbChgoIC1tYDWGdvYJ29wWvr3NRQr3f3VOmDhTkyQj6ZZqdqv/WI2k+4e++k19bZq1hnb3DCOhcVFQ35ubS3MQ8mOztbx48flyQdP35cEyZMGPCcvLw8HTt2LPFxW1ub8vLy0lYjAADASByqjiSm4Uq9F/TLCnN0qDpicWUA4A22uLNbXFys2tparV27VrW1tSopKRnwnEWLFun73/++Ojo6JEm/+MUvdMstt6S7VAAAYDNNDfV6/fmIxpzq0JmskBZcF7bFnVN/V4eMrEC/xwzDkL+r06KKAMBb0h52H3roIR0+fFgnT57UrbfeqnXr1mnt2rV68MEHtW/fvsTRQ5L0m9/8Rj/5yU906623KhQK6aabbtKWLVskSRUVFUxiBgDA4/pahSsKc2QEAjLNHtXuqZIkywNvLBCSafb0255lmqZigaCFVQGAdximaZpWF5FqR48etboEpIAT9hBg9Fhnb2CdvSEV6/zkfTt0U+bAQLm326eP/L93JfVrjVRfEO9rZTZNU7Ut7Zrs8vNO+Xn2BtbZG5ywzufbs2uLNmYAAICLYedW4b5Au7c6In9Xp2KBoOa7POimQ6rb1u3aFg9g5Ai7AFyDNyiA9wy3Vdiq3w/zFi0e9Ovw++ripLpt3c5t8QBGzhbTmAFgtBJvULJ6tDY/oIqsHr27p0pNDfVWlwYgheavCqu2pV19u7L6WoXnrwonnmO33w92q8dJUj3hmgnagLsQdgG4Am9QAG+at2ixJldUam+3T88eO6W93b4Be2Lt9vvBbvU4ib+ro99dfCm5beup/vMBpBdtzABcwc779gCk1lCtwn3s9vvBbvU4SaonXDNBG3AX7uwCcIXeNyj9h8vzBgWAZL/fD3arx0mG07Zu5z8fQHpxZxeAK8xfFVbtIEd8zK+otLo0ABZLx++HkQyc4vfVxUvVhOuz1+9Pp+M69NYxTQ0FmaANOBxhF4ArcMQHgKGk+vfDSCf48vtqdC7Utj5SA9YvL6v3POS1H2ZNAIcj7AJwjWS/AQLgHqn8/XCoOqKbBhk4tbc6MuTX5PeVfVzM+gFwBvbsAgAAjAITfJ2N9QPci7ALAAAwCgyccjbWD3Av2pgBeNpIhsrAfVh/JAMDp5yN9QPci7ALwLNGOlQG7sL6p8fZFxR8eQW67AMrXPf9ZeCUs7F+gHsRdgF4FkNJvI31T71zLyiMGXNGP3HpBQUGTjkb6we4E3t2AXgWQ0m8jfVPvUPVkURrqPR/FxQOVUcsrgwA4AWEXQCexVASb2P9U48LCgAAKxF2AXjW/FVh1ba0JwJPYijJqrDFlSEdWP/U44ICAMBK7NkF4FkMJfE21j/1mHILALASYReApzGUxNtY/9Q694KCPy+gS7mgAABIE8IuAABImbMvKBQUFKi1tTVpfzbnJAMAzoewCwAAHIdzkgEAF8KAKgAA4DgcawQAuBDCLgAAcByONQIAXAhhFwAAOA7HGgEALoSwCwAAHIdzkgEAF8KAKgAA4DickwwAuBDCLgAAcCTOSQaA1KlvbNK+A4fU2nlaIV9c4aUlWrxwntVljQhhFwAAAACQUN/YpKq6Zk1aWKbgmTOKm6aq6qKS5KjAy55dAAAAAEBCpO6AcmeX9DveLXd2iSJ1ByyubGS4swsAAJBG9Y1NirwcVUdPhmNbAwG4W0fMUHCQ4906Y8YQr7Anwi4AAECa9LUG5s5ZoaBhOLY1EIC7hfym4oMc7xb0m0O8wp5oYwYAAEgTt7QGAnC3cGmxjjdH+x3vdrw5qnBpscWVjQx3dgEAANLELa2BANytr9Nk32u1OtFxWkG/qcrSYsd1oBB2AQAA0qSvNdA4K/A6sTUQgPstXjhPK1eUqbW11epSLhphFwAAG2tqqNfrz0c05lSHzmSFtOC6MGfLOli4tFhVddFEK3Nfa2Clw1oDAcAJCLsAANhUU0O93t1TpYrCHBmBgEyzR7V7qiSJwOtQfS2Akbr96owZjm0NBAAnIOwCAGBTh6ojuqkwp98wo7LCHO2tjhB2HWzxwnmEWwBIA6YxAwBgU/6ujn57O6XewOvv6rSoIgAAnIOwCwCATcUCocSxD31M01QsELSoIgAAnIOwCwCATc1fFVZtS3u/cw5rW9o1f1XY4soAALA/9uwCAGBTffty91ZH5O/qVCwQ1PyKSvbrAgAwDIRdAABsbN6ixYRbABdU39ikyMtRdfRkKOSLK7y0hEFo8DzCLgAAAOBg9Y1NqqprVu6cFQoahuKmqaq6qCQReOFp7NkFAAAAHCxSd0C5s0v6HVOWO7tEkboDFlcGWIuwCwAAADhYR8wY9JiyzpgxxCsAb6CNGQAAAEnzi+ir+t+nvq8xpzp0JiukBdeF2XeeYiG/qbhp9gu8pmkq6DfP8yrA/WwRdo8ePaoHH3ww8XFLS4vWrVunNWvWJB5ramrSfffdp8LCQknSVVddpYqKirTXCgAAgME1NdTr2HNPqiI3ICMQkGn2qHZPlSQReFMoXFqsqrpoopXZNE0db46qsrTY6tIAS9ki7BYVFen++++XJMXjcX3yk5/UlVdeOeB5c+bM0ebNm9NdHgAAAIbhUHVE6yfl6MyZM5J6W2nLCnO0tzpC2E2hviFUkbr96owZCvpNVZYWM5wKnmeLsHu2119/XZMnT9bEiROtLgUAAAAj4O/qkJGd0+8xwzDk7+q0piAPWbxwHuEWOIftwm5dXZ1KS0sH/dyvf/1r3XHHHcrNzVVlZaWmTZs26PNqampUU1MjSdq5c6cKCgpSVi+s4/f7WVsPYJ29gXX2BtbZ/fx5BTIU09ixYxOPmaYpf16AtXcZfp69wenrbJimaZud67FYTJ/85Ce1a9cu5eTk9PtcV1eXMjIylJmZqYMHD+o73/mOHn744WH9uUePHk1BtbBaQUGBWltbrS4DKcY6ewPr7A2ss/v17dldkhtI7B2tbWnX5IpK2phdhp9nb3DCOhcVFQ35OVsdPVRfX6/3ve99A4KuJAUCAWVmZkqSrrjiCvX09Oi9995Lc4UAAAAYyrxFizXzHzZqb7dPzx47pb3dPoIuAMvYqo35fC3M7e3tys7OlmEYOnLkiOLxuMaPH5/mCgEAAHA+l5dcqSnvm2F1GQBgn7Db3d2txsZGbdy4MfFYdXW1JGnVqlV65ZVXVF1dLZ/Pp7Fjx+r2228fcHg2AAAAAACSjcJuZmamvv3tb/d7bNWqVYn/v3r1aq1evTrdZQGAozU11Ov15yMac6pDZ7JCWnBdmHZCAADgCbYJuwCA5GpqqNe7e6pUUZgjIxCQafaodk+VJBF4AQCA6xF2AcClDlVHdFNhTmLLh2EYKivM0d7qCGEXGKH6xiZFXo6qoydDIV9c4aUlnGkKADZH2AUAl/J3dcjICvR7zDAM+bs6LaoIcKb6xiZV1TUrd84KBQ1DcdNUVV1Ukgi8AGBjtjp6CACQPLFASOcepW6apmKBoEUVAc4UqTug3Nkl/bokcmeXKFJ3wOLKAADnw51dAHCp+avCqt1TpbK/tjKbpqnalnbNr6i0ujTAUTpihoLnnABhGIY6Y84/FYL2bABuRtgFHIg3JxiOvn25e6sj8nd1KhYIan5FJft1gREK+U3FTbPfkYemaSroN8/zKvujPRuA2xF2AYfhzQlGYt6ixYRbOI7dLuiFS4tVVRdNtDKbpqnjzVFVlhZbVlMy9LZnLx+kPXs//z0B4AqEXcBheHMCwM3seEGv7+tG6varM2Yo6DdVWVrs+N+5bm7PBgCJsAs4Dm9OALiZXS/oLV44z/Hh9lxubc8GgD5MYwYcJuQ3B52wy5sTAG7QETP6hS+JC3qpEi4t1vHmaOK/KX3t2WGHt2cDQB/u7AIO49a9YwAgcbcxndzang0AfQi7gMPw5gSAm3FBL73c2J4NAH0Iu4AD8eYEGJ2mhnq9/nxEY0516ExWSAuuCzO12ia4oAcASBbCLgDAU5oa6vXunipVFObICARkmj2q3VMlSQRem+CCHgAgGQi7AABPOVQd0U2FOf2m/ZYV5mhvdYSwCwA4L7udA47zI+wCADzF39UhIyvQ7zHDMOTv6rSoIgCAE9jxHHCcH0cPAQA8JRYIDXp8VywQtKgiAIAT9J4DXjLIOeAHLK4MQyHsAgA8Zf6qsGpb2vudLVrb0q75q8IWVwYAsDPOAXce2pgBAJ7Sty93b3VE/q5OxQJBza+oZL8uAOC8OAfceQi7AADPmbdoMeEWADAinAPuPIRdAAAAALgAzgF3HsIuAABIusGO51i5oszqsgBgVDgH3FkIuwAAIKmGOp4jOydbM6ZPtbo8pBFnkgKwEmEXACzW1FCv15+PaMypDp3JCmnBdWH2k8LReo/nWD7geI5nXqjTv378IxZXh3ThTFIAVuPoIQCwUFNDvd7dU6WKrB6tzQ+oIqtH7+6pUlNDvdWlARdtqOM5Os5YVBAswZmkAKxG2AUACx2qjqisMKffm8Gywhwdqo5YXBlw8UJ+M3GOcR/TNBUaY1FBsARnkgKwGm3MAGAhf1eHjKxAv8cMw5C/q9OiioDRG+p4jo+uKU3L12efqD1wJikAqxF2AcBCsUBIptkz4M1gLBC0sCpgdIY6nuPKKxaptbU1pV+bfaL2wZmkAKw2rLAbj8cVjUZlGIaKi4uVkdHb/fyzn/1M73//+1NaIAC42fxVYdXuqUq0MpumqdqWds2vqLS6NGBUrDqeY6jhWJG6/YTdNONMUgBWG1bYfeSRR1RQUCC/368f/vCHuu222zR58mRVV1cTdgFgFPqmLu+tjsjf1alYIKj5FZVMYwYuUkfMUJB9orbBmaQArDSssNvW1qZPf/rTkqTly5frkUce0Yc//OGUFgYAXjFv0WLCrUuwV9R67BO1Vn1jk/YdOKTWztP8DACw3LDCbiwW05kzZzRmzBhNnDhRmzdv1kMPPaS33nor1fUBAOAI7BW1B/aJWqfvZ2DSwjIFz5zhZwCA5c4bdnt6euTz+fSxj31MnZ2dysnJkSRlZWXpzjvv1Msvv5yOGgEAsD32itoD+0Stw88AALs5b9j96le/qjvuuEOXXnrpgM9lZGToAx/4QMoKAwDASdgrah/sE7UGPwMA7CbjfJ+85JJL9MUvflFtbW2Jxw4fPqytW7emvDAAAJwk5Ddlmv33hbJXFF7CzwAAuzlv2K2srNTKlSv1xS9+UXV1ddq+fbsefPBBlZSUpKs+AAAcIVxarOPN0cSb/b69omH2isIj+BkAYDcXHFA1a9YsBQIBPfzwwyorK9Odd96psWPHpqM2AAAcg72i8Lq+f+v7XqvViY7T/AykEJPfgeE5b9i9//77dfjwYa1Zs0br1q3TN7/5TR06dEhXXHFFuuoDAMAx2CsKr1u8cJ5WrihTa2ur1aW4FpPfgeE7b9j9m7/5G/3Lv/yLQqGQJGnSpEm699571dLSotWrV6elQAAAAAC9mHoNDN959+xu2LAhEXQlafr06dq+fbteeOGFlBcGAAAAoL+OmJEIun2Yeg0M7rxhdzB5eXm6++67U1ELAAAAgPNg6jUwfCMOu5KUlZWV7DoAAAAAXABTr4Hhu+A0ZgAAAAD2wOR3YPgIuwAAAICDMPkdGJ6LamMGAAAAAMDOCLsAAAAAANexVRvzbbfdpszMTGVkZMjn82nnzp39Pm+aph5//HHV19dr3Lhx2rRpk2bMmGFRtQAAAPC6+sYmRV6OqqMnQyFfXOGlJZ5tMeZ7AbuxVdiVpG3btmnChAmDfq6+vl7vvvuuHn74Yb3xxhv65je/qa9+9atprhAAAADpZscgVd/YpKq6ZuXOWaGgYShumqqqi0qS5bWlG98L2JGj2pgPHDigD3zgAzIMQ7NmzVJnZ6eOHz9udVkAAABIob4gFZ+zQsEFyxWfs0JVdc2qb2yytK5I3QHlzi6RYRiSJMMwlDu7RJG6A5bWZQW+F7Aj293Z3bFjhyRp5cqVKi8v7/e5trY2FRQUJD7Oz89XW1ubcnNz+z2vpqZGNTU1kqSdO3f2ew3cw+/3s7YewDp7A+vsDayzN6Rinfe9dkiTFpYlgpQkTVpYqn2v1WrlirKkfq2ROOPLVGDcuAGPn/Jluv7f+rnr7OXvhZs5/fe2rcLu9u3blZeXpxMnTugrX/mKioqKNHfu3BH/OeXl5f2CcmtrazLLhE0UFBSwth7AOnsD6+wNrLM3pGKdWztOK3jmzIDHT3SctvTf1Jiebp0+fbpfCDdNU/6ebtf/Wz93nb38vXAzJ/zeLioqGvJztmpjzsvLkyRlZ2erpKRER44cGfD5s7/Zx44dS7wGAAAA7hTymzJNs99jpmkq6DeHeEV6hEuLdbw5mqjNNE0db44qXFpsaV1W4HsBO7LNnd3u7m6ZpqmsrCx1d3ersbFRFRUV/Z5TXFysH//4xyotLdUbb7yhQCAwoIUZAAA3s+OQHiDVwqXFqqqLJvaE9gWpSouDVN/PXqRuvzpjhoJ+U5WlxZ78meR7ATuyTdg9ceKEHnjgAUlST0+Pli5dqkWLFqm6ulqStGrVKi1evFgHDx7Upz/9aY0dO1abNm2ysmQAANKKaafwKjsHqcUL59miDjvgewG7Mcxze0Jc6OjRo1aXgBRwwh4CjB7rPDQ33eFjnYdnx79/V/HZywfsicto3q+7/uX/sbCy4WGdvYF19gbW2RucsM7n27Nrmzu7AIDh4w6fN3XEDAXPCrpS7/EenTFjiFcAAOBdthpQBQAYHs4z9Ca7DukBAMCOCLsA4EAdMaNfK6vEHT4vYNopAADDRxszADhQyG8qbpoD9m5yh8/d7DykBwAAuyHsAoAD2fUYDqQe004BABgewi4AOBB3+Ppz02RqAACQHIRdAHAo7vD1YjI1AAAYDAOqAACOxmRqAAAwGMIuAMDRmEwNAAAGQ9gFADgaZ88CAIDBEHYBAI7G2bMAAGAwDKgCADha3xCq7z23V7/98wn1nDmtmYU5kmZbWhcAALAWYRcA4ApGwXQVL/2/c4eZyAwAgLfRxgwAcDwmMgMAgHNxZxcA4HgdMUNBF09krm9sUuTlqDp6MhTyxRVeWsIdawAALoCwCwBwvJDfVNw0+x1B5JaJzPWNTaqqa1bunBUKGobitGgDADAstDEDABzPzROZadEGAODicGcXAOAK8dY3deCZQ4r/pVszJufqYzeuccWdT7e3aAMAkCqEXQCAo/W1+eYvrVDBXycxH2+OWl1W0ri5RRsAgFSijRkA4Ghub/N1c4s2AACpxJ1dAICjub3Nt68VO1K3X50xQ0G/qcrSYle0aAMAkEqEXQCAo3mhzXfxwnmEWwAARog2ZgCAo9HmCwAABsOdXQCAo9HmCwAABkPYBQA4Hm2+uBj1jU2KvBxVR0+GQr64wktL+HcEAC5C2AUAAJ7Td2RV7pwVChqG4qapqrreI6sIvADgDuzZBQAAnuP2I6sAAIRdAADgQR0xo98Eb8ldR1YBAAi7AADAg0J+MzHBu4/bjqwCAK9jzy4AADbAsKT0CpcWq6oummhl7juyqpIjqwDANQi7AABYjGFJ6ceRVcDInHtBbv0HyzVj+lSrywLOi7ALAIDFeoclLR9kWNJ+wlcKcWQVMDyDXZD7RnW9PnLlCX6GYGuEXQAALNYRMxRkWBIwAO399jDoBbk5JYrUPc96wNYIuwAAWCzkNxU3zX7TgRmWBK+jvd8+uCAHp2IaMwAAFguXFut4czQxHbhvWFKYYUnwMM5Ctg+ml8OpuLMLAIDFGJYEDMTdRPsYdHr5L6P6CBfkYHOEXQAAbIBhSUB/tPfbx2AX5DauuZZpzLA9wi4AAABsh7OQ7eXcC3IFBQVqbW21sCLgwgi7AABgUEzChZVo7wcwWoRdAAAwAJNwYQe09wMYDaYxAwCAAZiECwBwOsIuAAAYoCNm9BsMJDEJFwDgLLQxAwCAAS52Ei77fAEAdkHYBZASvOEFnO1iJuGyz9c5+B0NwAsIuwCSjje8gPNdzCTc3n2+ywfZ57ufn30b4Xc0AK8g7AJIOt7wAu4w0km4HTFDQfb5pkyy7sbyOxqAV9gi7La2tmr37t1qb2+XYRgqLy9XOBzu95ympibdd999KiwslCRdddVVqqiosKJcABfAG17Amy52ny8uLJl3Y/kdDcArbBF2fT6fKisrNWPGDJ06dUqbN2/WwoULNXXq1H7PmzNnjjZv3mxRlQCGize8gDddzD5fDE8y78byOxqAV9ji6KHc3FzNmDFDkpSVlaUpU6aora3N4qoAXKxwabGON0dlmr1vnPre8IZ5wwu42uKF81RZOlsZzfvV9fp+ZTTvV2XpbFpjkyCZR0HxOxqAV9jizu7ZWlpa9Lvf/U6XXnrpgM/9+te/1h133KHc3FxVVlZq2rRpFlQI4EIuZrANAHcY6T5fDE8y78byOxqAVxhm32U9G+ju7ta2bdt044036qqrrur3ua6uLmVkZCgzM1MHDx7Ud77zHT388MOD/jk1NTWqqamRJO3cuVN/+ctfUl470s/v9ysWi1ldBlKMdfYG1tkbWOeL9+rBBn2jul65c85qEf9lVBtXLdaVVyyyurx+WGdvYJ29wQnrPHbs2CE/Z5uwG4vFdO+99+ryyy/XBz/4wQs+/7bbbtM999yjCRMmXPC5R48eTUaJsJmCggK1trZaXQZSjHX2BtbZG1jn0alvbFKk7kDibmzYpndjWWdvYJ29wQnrXFRUNOTnbNHGbJqmHnvsMU2ZMmXIoNve3q7s7GwZhqEjR44oHo9r/Pjxaa4UAADAGrSIA8DI2CLs/upXv9JLL72k6dOn64477pAkrV+/PnEVYdWqVXrllVdUXV0tn8+nsWPH6vbbbx8wqAEAAAAAAMkmYXf27Nl66qmnzvuc1atXa/Xq1WmqCAAAAG5R39ikyMtRdfRkKOSLK7y0hLvkgAfYIuwCAAAAqVDf2KSqumblzlmhoGEobpqqqotKEoEXcDlbnLMLAAAApEKk7oByZ5cktr8ZhqHc2SWK1B2wuDIAqUbYBQAAgGt1xIwBc14Mw1BnjNkvgNvRxgwAAJAk7A21n5DfVNw0+wVe0zQV9Nvi9E0AKcSdXQAAgCTo2xsan7NCwQXLFZ+zQlV1zapvbLK6NE8LlxbreHNUptkbbk3T1PHmqMKlxRZXBiDVuLMLAACQBL17Q5cPsjd0P3d3LdT3vY/U7VdnzFDQb6qytJg1ATyAsAsAAJAEHTFDQfaG2tLihfMIt4AH0cYMAACQBCG/mWiV7cPeUACwDmEXAAAgCdgbCgD2QhszACApmEILr2NvKADYC2EXADBqfVNoc+esUNAwFDdNVdVFJYk3+vAU9oYCgH3QxgwAGLXeKbQlg0yhPWBxZQAAwKu4swsAGDWm0ALuxjYFAE5E2AUAjFrIbypumok7uxJTaAG3YJsCAKeijRkAMGpMoQXci20KAJyKO7sAgFFjCi3gXmxTAOBUhF0AQFIwhRZwJ7YpAHAq2pgBAAAwJLYpAHAq7uwCAABgSGxTAOBUhF0AAACcF9sUADgRYRcAgEFwrigAAM5G2AUA4BycKwoAgPMxoAoAgHNwrigAAM5H2AUA4BwdMaPfMSsS54oCAOA0hF0AAM4R8puJY1b6cK4oAADOQtgFAOAcnCsKAIDzMaAKAIBzcK6ofTAVGwBwsQi7AAAMgnNFrcdUbADAaNDGDAAAbImp2ACA0SDsAgAAW2IqNgBgNAi7AADAlpiKDQAYDcIuAACwJaZiAwBGgwFVAADAlpiKDQAYDcIuAACwLaZiAwAuFm3MAAAAAADX4c4uAAAAbKO+sUmRl6Pq6MlQyBdXeGkJd/cBXBTCLgC4EG8WAThRfWOTquqalTtnhYKGobhpqqouKkn8DgMwYoRdAHAZ3ixipLg4AruI1B1Q7uzlifOVDcNQ7uwSRer2828SwIgRdgHAZXiziJHg4gjspCNmKPjX3119DMNQZ8wY4hUAMDQGVAGAy3TEjETQ7cObRQyl9+JIySAXRw5YXBm8KOQ3E+cq9zFNU0G/OcQrAGBohF0AcBneLGIkuDgCOwmXFut4czTxO8w0TR1vjipcWmxxZQCciDZmAHCZcGmxquqiibt1fW8WK3mziEGE/Kbiptkv8HJxBFbpa52P1O1XZ8xQ0G+qsrSYlnoAF4WwCwAuw5tFjAQXR2A3ixfO4/cVgKQg7AKAC/FmEcPFxREAgFsRdgGMGseWAM7GxREAgBsRdgGMCseWAEgGLpoBAJLNVmG3oaFBjz/+uOLxuK699lqtXbu23+fPnDmjRx55RL/97W81fvx43X777SosLLSmWACSONMVwOhx0QwAkAq2CbvxeFzf+ta39IUvfEH5+fnasmWLiouLNXXq1MRz9u3bp2AwqK997Wuqq6vTf/zHf+izn/2shVUD6IgZCnr02BLuRAHJwUUzAEAq2Oac3SNHjmjy5MmaNGmS/H6/lixZomg02u85Bw4c0LJlyyRJV199tQ4dOjTgLEkA6eXVM1377kTF56xQcMFyxeesUFVds+obm6wuDXAczvoFAKSCbcJuW1ub8vPzEx/n5+erra1tyOf4fD4FAgGdPHkyrXUC6C9cWqzjzdFE4O07tiTs8mNLeu9ElQxyJ+qAxZUBzuPVi2YAgNSyTRtzMtXU1KimpkaStHPnThUUFFhcEVLB7/eztjawckWZsnOy9cwLdeo4I4XGSB9dU6orr1iUlD/frut8xpepwLhxAx4/5cu0Zb12Z9d1RnINtc7r11yrb1TXK3fOWWf9/jKqjWuu5d+FA/Hz7A2sszc4fZ1tE3bz8vJ07NixxMfHjh1TXl7eoM/Jz89XT0+Purq6NH78+AF/Vnl5ucrLyxMft7a2pq5wWKagoIC1tYkZ06fqXz/+kX6PJWtt7LrOY3q6dfr06X6tl6Zpyt/Tbct67c6u64zkGmqdZ0yfqo9ceUKRuucTZ/1+pLRYM6ZP5d+FA/Hz7A2sszc4YZ2LioqG/Jxtwu7MmTP1zjvvqKWlRXl5efrpT3+qT3/60/2e83d/93d68cUXNWvWLL3yyiuaN2/egD0+AJAO4dJiVdVFE63Mfe3blS5v3wZShbN+AQDJZpuw6/P59IlPfEI7duxQPB7X8uXLNW3aND355JOaOXOmiouLtWLFCj3yyCP61Kc+pVAopNtvv93qsgF4VN+b8kjd/sSdqMrSYt6sAwAA2IRhemCc8dGjR60uASnghLYKjB7r7A2sszewzt7AOnsD6+wNTljn87Ux22YaMwAAAAAAyULYBQAAAAC4DmEXAAAAAOA6hF0AAAAAgOvYZhozANhdfWOTIi9H1dGToZAvrvDSEqYvAwAA2BRhFwCGob6xSVV1zcqds0JBw1DcNFVVF5UkAi8AAIAN0cYMAMMQqTug3NklMgxDkmQYhnJnlyhSd8DiygAAADAYwi4ADENHzEgE3T6GYagzZgzxCgAAAFiJNmYAGIaQ31TcNPsFXtM0FfSbFlYFuA974wEAycKdXQAYhnBpsY43R2WaveHWNE0db44qXFpscWWAe/TtjY/PWaHgguWKz1mhqrpm1Tc2WV0aAMCBuLMLAMPQd2cpUrdfnTFDQb+pytJi7jgBSdS7N375IHvj9/OzBgAYMcIuAAzT4oXzeMMNpFBHzFCQvfEAgCShjRkAANhCyG8mtgr0YW88AOBiEXYBAIAtsDceAJBMtDEDAABbYG88ACCZCLsAAMA22BsPAEgW2pgBAAAAAK5D2AUAAAAAuA5hFwAAAADgOoRdAAAAAIDrEHYBAAAAAK5D2AUAAAAAuA5hFwAAAADgOoRdAAAAAIDr+K0uAACAVKhvbFLk5ag6ejIU8sUVXlqixQvnWV0WAABIE8IuAMB16hubVFXXrNw5KxQ0DMVNU1V1UUki8AIA4BG0MQMAXCdSd0C5s0tkGIYkyTAM5c4uUaTugMWVAQCAdOHOrkVorwOA1OmIGQr+Nej2MQxDnTFjiFcAAAC3IexagPY6AEitkN9U3DQTd3YlyTRNBf2mhVUBAIB0IuxaoLe9bvkg7XX7CbsAkATh0mJV1UUTrcymaep4c1SVpcVWl5Y0dAgBAHB+hF0L0F4HAKlxdgCMt7eqtfY3CuZPVtBvqrK02DVhkA4hAAAujLBrAdrrACD5zg2Agb/ezf1w6WzXBUA6hAAAuDCmMVsgXFqs481RmWZvuO1rrwu7qL0OANLNSxOYO2JGvwumEh1CAACcizu7Fui76h6p26/OmOG69joAsIKXtojQIQQAwIURdi2yeOE8wi0AJJGXAqAXBnABADBahF0AgCt4KQDSIQQAwIURdgEAruC1AEiHEAAA50fYBQC4BgEQAAD0YRozAAAAAMB1CLsAAAAAANehjRkAgHPUNzYp8nJUHT0ZCvniCi8toT0aAACHIewCAHCW+sYmVdU1K3fOCgUNQ3HTVFVdVJIIvAAAOAhtzAAAnCVSdyBxfJEkGYah3NklitQdsLgyAAAwEoRdAADO0hEzEkG3j2EY6owZQ7wCAADYEWEXAICzhPymTNPs95hpmgr6zSFeAQAA7Ig9uwDgMgxXGp1wabGq6qKJVmbTNHW8OarK0mKrSwMAACNgeditqqrSa6+9Jr/fr0mTJmnTpk0KBoMDnnfbbbcpMzNTGRkZ8vl82rlzpwXVAoC9MVxp9Pq+T5G6/eqMGQr6TVWWFvP9AwDAYSwPuwsXLtQtt9win8+nJ554Qs8884w2bNgw6HO3bdumCRMmpLlCAHCO3uFKywcZrrSfsDYCixfO4/sFAIDDWb5n9/LLL5fP55MkzZo1S21tbRZXBADOxXAlAACAXpbf2T3bvn37tGTJkiE/v2PHDknSypUrVV5enq6yAMAxQn5TcdPsF3gZrgQAALzIMM8dOZkC27dvV3t7+4DHb775ZpWUlEiSnn76af3mN7/R5z//+QF3JSSpra1NeXl5OnHihL7yla/o4x//uObOnTvo16upqVFNTY0kaefOnfrLX/6SvL8MbMPv9ysWi1ldBlKMdR6ZVw826BvV9cqdc9ZwpV9GtXHVYl15xSKryxsS6+wNrLM3sM7ewDp7gxPWeezYsUN+Li1h90JefPFF/eQnP9HWrVs1bty4Cz7/qaeeUmZmpm644YZh/flHjx4dbYmwoYKCArW2tlpdBlKMdR65+sYmReoOJIYrhR0wXIl19gbW2RtYZ29gnb3BCetcVFQ05Ocsb2NuaGjQc889py9/+ctDBt3u7m6ZpqmsrCx1d3ersbFRFRUVaa4UAJyB4UoAAAA2CLvf+ta3FIvFtH37dknSZZddpo0bN6qtrU1f//rXtWXLFp04cUIPPPCAJKmnp0dLly7VokWLLKwaAAAAAGBntmhjTjXamN3JCW0VGD3W2RtYZ29gnb2BdfYG1tkbnLDO52tjtvzoIQAAAAAAko2wCwAAAABwHcIuAAAAAMB1CLsAAAAAANch7AIAAAAAXIewCwAAAABwHcIuAAAAAMB1/FYXAABwn/rGJkVejqqjJ0MhX1zhpSVavHCe1WUBAAAPIewCAJKqvrFJVXXNyp2zQkHDUNw0VVUXlSQCLwAASBvamAEASRWpO6Dc2SUyDEOSZBiGcmeXKFJ3wOLKAACAlxB2AQBJ1REzEkG3j2EY6owZQ7wCAAAg+Qi7AICkCvlNmabZ7zHTNBX0m0O8AgAAIPkIuwCApAqXFut4czQReE3T1PHmqMKlxRZXBgAAvIQBVQCApOobQhWp26/OmKGg31RlaTHDqQAAQFoRdgEASbd44TzCLQAAsBRtzAAAAAAA1yHsAgAAAABch7ALAAAAAHAdwi4AAAAAwHUIuwAAAAAA1yHsAgAAAABch7ALAAAAAHAdwi4AAAAAwHUIuwAAAAAA1yHsAgAAAABch7ALAAAAAHAdwi4AAAAAwHUIuwAAAAAA1yHsAgAAAABch7ALAAAAAHAdwzRN0+oiAAAAAABIJu7swrE2b95sdQlIA9bZG1hnb2CdvYF19gbW2Rucvs6EXQAAAACA6xB2AQAAAACuQ9iFY5WXl1tdAtKAdfYG1tkbWGdvYJ29gXX2BqevMwOqAAAAAACuw51dAAAAAIDr+K0uALhYP/jBD3TgwAEZhqHs7Gxt2rRJeXl5VpeFJKuqqtJrr70mv9+vSZMmadOmTQoGg1aXhST72c9+pv/6r//S22+/ra9+9auaOXOm1SUhiRoaGvT4448rHo/r2muv1dq1a60uCSnw6KOP6uDBg8rOztauXbusLgcp0Nraqt27d6u9vV2GYai8vFzhcNjqspBkf/nLX7Rt2zbFYjH19PTo6quv1rp166wu66LQxgzH6urqUiAQkCRFIhH98Y9/1MaNGy2uCsn2i1/8QvPnz5fP59MTTzwhSdqwYYPFVSHZ/vjHPyojI0Pf+MY3VFlZSdh1kXg8rs985jP6whe+oPz8fG3ZskWf+cxnNHXqVKtLQ5IdPnxYmZmZ2r17N2HXpY4fP67jx49rxowZOnXqlDZv3qw77riDn2eXMU1Tp0+fVmZmpmKxmLZu3aqPfexjmjVrltWljRhtzHCsvqArSadPn5ZhGBZWg1S5/PLL5fP5JEmzZs1SW1ubxRUhFaZOnaqioiKry0AKHDlyRJMnT9akSZPk9/u1ZMkSRaNRq8tCCsydO1ehUMjqMpBCubm5mjFjhiQpKytLU6ZM4b/LLmQYhjIzMyVJPT096unpcez7bNqY4Wjf//739dJLLykQCGjbtm1Wl4MU27dvn5YsWWJ1GQBGoK2tTfn5+YmP8/Pz9cYbb1hYEYBkaGlp0e9+9ztdeumlVpeCFIjH47rzzjv17rvv6rrrrtNll11mdUkXhbALW9u+fbva29sHPH7zzTerpKRE69ev1/r16/XMM8/oxz/+sWP3E3jdhdZZkp5++mn5fD5dc801aa4OyTKcdQYA2F93d7d27dqlj33sY/067eAeGRkZuv/++9XZ2akHHnhAb731lqZPn251WSNG2IWtffGLXxzW86655hrdc889hF2HutA6v/jii3rttde0detWx7bRYPg/z3CXvLw8HTt2LPHxsWPHGCYIOFgsFtOuXbt0zTXX6KqrrrK6HKRYMBjUvHnz1NDQ4Miwy55dONY777yT+P/RaJT9fi7V0NCg5557TnfeeafGjRtndTkARmjmzJl655131NLSolgspp/+9KcqLi62uiwAF8E0TT322GOaMmWKPvjBD1pdDlLkvffeU2dnp6TeycyNjY2aMmWKxVVdHKYxw7EeeOABvfPOOzIMQwUFBdq4cSN3C1zoU5/6lGKxWGLoyWWXXcbUbRd69dVX9e1vf1vvvfeegsGgLrnkEt11111Wl4UkOXjwoL773e8qHo9r+fLluvHGG60uCSnw0EMP6fDhwzp58qSys7O1bt06rVixwuqykETNzc3aunWrpk+fnui0Wr9+va644gqLK0Myvfnmm9q9e7fi8bhM09T73/9+VVRUWF3WRSHsAgAAAABchzZmAAAAAIDrEHYBAAAAAK5D2AUAAAAAuA5hFwAAAADgOoRdAAAAAIDrEHYBAAAAAK5D2AUAwKGeeOIJ3XfffYmPq6qqdPfddysWi1lYFQAA9kDYBQDAof7+7/9eTU1N+t3vfqfq6mo1NDTo85//vPx+v9WlAQBgOcM0TdPqIgAAwMV56qmn9Oqrr6qrq0t33323CgoK1NXVpe3bt+uPf/yjduzYoenTp1tdJgAAacedXQAAHOx973uf3nrrLd1yyy0qKCiQJI0dO1ZbtmzR1VdfbXF1AABYh7ALAIBDvfXWW/rmN7+psrIy7d+/P/G43+/XhAkTLKwMAADrEXYBAHCgtrY23Xvvvfrnf/5n/dM//ZPeeustNTU1WV0WAAC2QdgFAMBhurq6dM8992jNmjUqLi7WuHHjdP311+sHP/iB1aUBAGAbDKgCAMCldu/ereuvv54BVQAATyLsAgDgQvfcc49+//vfq6CgQCtXrtSyZcusLgkAgLQi7AIAAAAAXIc9uwAAAAAA1yHsAgAAAABch7ALAAAAAHAdwi4AAAAAwHUIuwAAAAAA1yHsAgAAAABch7ALAAAAAHAdwi4AAAAAwHUIuwAAAAAA1/n/AUlQYQ7XtAxKAAAAAElFTkSuQmCC",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"data = pd.read_csv(get_file(\"testSet.txt\", local=False), \\\n",
" delim_whitespace=True, header=None, names=['x1','x2','t'])\n",
"plot_ds(data)"
]
},
{
"cell_type": "code",
"execution_count": 29,
"metadata": {},
"outputs": [],
"source": [
"n = len(data)\n",
"nfeatures = len(data.columns)-1\n",
"\n",
"X = np.array(data[['x1','x2']])\n",
"t = np.array(data['t']).reshape(-1,1)\n",
"X = np.column_stack((np.ones(n), X))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n",
"Il metodo considerato per la classificazione è la *logistic regression*, che determina un iperpiano (retta, in questo caso) di separazione minimizzando rispetto al vettore $\\theta$ dei coefficienti dell'equazione dell'iperpiano (3 in questo caso) il rischio empirico sul dataset associato alla funzione di costo *cross-entropy*, per la quale il costo associato a un singolo elemento $\\mathbf{x}=(x_1,\\ldots,x_d)$ è\n",
"\n",
"$$ J(\\theta, \\mathbf{x})=-\\left(t\\log y + (1-t)\\log (1-y)\\right) $$\n",
"dove $t$ è il valore *target* è il valore $0/1$ della classe dell'elemento e $y\\in (0,1)$ è il valore predetto dal modello, definito come \n",
"$$\n",
"y = f(\\mathbf{x}; \\theta) = \\sigma\\left(\\sum_{i=1}^d\\theta_ix_i+\\theta_0\\right) = \\frac{1}{1+e^{-(\\sum_{i=1}^d\\theta_ix_i+\\theta_0)}}\n",
"$$"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {},
"outputs": [],
"source": [
"def f(theta, X):\n",
" return sp.expit(np.dot(X, theta)).reshape(-1,1)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Il rischio empirico associato all'intero dataset può essere allora definito come la corrispondente media\n",
"$$\n",
"J(\\theta, X)=\\frac{1}{n}\\sum_{i=1}^n \\left(t_i\\log f(\\mathbf{x}_i;\\theta) -(1-t_i)\\log (1-f(\\mathbf{x}_i;\\theta))\\right)\n",
"$$"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {},
"outputs": [],
"source": [
"def approx_zero(v):\n",
" eps = 1e-50\n",
" v[v"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plot_all(cost_history, m, q)"
]
},
{
"cell_type": "code",
"execution_count": 30,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA1gAAAGoCAYAAABbkkSYAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAAAvLklEQVR4nO3deYzd90Hv/c9ZZh+Pl4zjJc7qxEmT1E1abkpJGjZT0gIFwdNWQFiqR6BbVJGH6hEgoYaoARF0H0AIChfupbS9VBWhLbRUQFPTNpSmlLQhq5M6S+PEcWJ7PN5mX855/pjF4yWeSXI8Z5nXS7LmzO9sX0++neTd7+98f4VqtVoNAAAAr1mx3gMAAABoFQILAACgRgQWAABAjQgsAACAGhFYAAAANSKwAAAAaqRcjzfdt29fPd62YfX392dgYKDew6CBmSOcjfnBYswRFmOOsBhz5HSbN28+43ErWAAAADUisAAAAGpEYAEAANSIwAIAAKgRgQUAAFAjAgsAAKBGBBYAAECNCCwAAIAaEVgAAAA1IrAAAABqRGABAADUiMACAACoEYEFAABQIwILAACgRgQWAABAjQgsAACAGhFYAAAANSKwAAAAakRgAQAA1IjAAgAAqBGBBQAAUCMCCwAAoEYEFgAAQI0ILAAAgBoRWAAAADUisAAAAGpEYAEAANSIwAIAAKgRgQUAAFAj5XoPYCV7ZM9g/v4b38l3bducd1y3qd7DAQAAXiMrWHU0NV3J8dHJjIxN1nsoAABADQisOioWC0mS6Wq1ziMBAABqQWDVUWGmr1KpCCwAAGgFAquOirOFVbGCBQAALUFg1dFcYFUFFgAAtIRl2UVw586d2blzZ5LkrrvuSn9//3K8bcNbfWw6SVKtxs+EsyqXy+YIL8v8YDHmCIsxR1iMObJ0yxJYO3bsyI4dO+a/HxgYWI63bXhDx48nmdlN0M+Es+nv7zdHeFnmB4sxR1iMOcJizJHTbd68+YzHnSJYR3O7CPoMFgAAtAaBVUezfeUzWAAA0CIEVh0V5nYRtE07AAC0BIFVR7ZpBwCA1iKw6khgAQBAaxFYdVSc/elPO0UQAABagsCqo4ILDQMAQEsRWHU0f4pgpc4DAQAAakJg1dHcNu0+gwUAAK1BYNXR3ArWtCUsAABoCQKrjkql2cCatoIFAACtQGDVUbk08+OfnJ6u80gAAIBaEFh11DYfWE4RBACAViCw6qg8eyGsySmBBQAArUBg1dHcZ7CmpiuuhQUAAC1AYNVRsVBIaXav9qmKwAIAgGYnsOpsbqOLKZ/DAgCApiew6qy84DRBAACguQmsOmubX8FyiiAAADQ7gVVnczsJWsECAIDmJ7DqbO4UQdfCAgCA5iew6qzsFEEAAGgZAqvO5gOrYgULAACancCqM7sIAgBA6xBYdWYXQQAAaB0Cq85KdhEEAICWIbDqrM0uggAA0DIEVp3ZRRAAAFqHwKozuwgCAEDrEFh1ZhdBAABoHQKrzuwiCAAArUNg1ZldBAEAoHUIrDqziyAAALQOgVVndhEEAIDWIbDqzC6CAADQOgRWndlFEAAAWofAqrMTuwgKLAAAaHYCq85O7CLoM1gAANDsBFad2UUQAABah8Cqs7JTBAEAoGUIrDo7sYugUwQBAKDZCaw6s4IFAACtQ2DVWZtt2gEAoGUIrDqziyAAALQOgVVnroMFAACtQ2DVWdk27QAA0DIEVp2dWMFyiiAAADQ7gVVn5fLMP4LJ6UqqVZEFAADNTGDVWbFQWLBVu8ACAIBmJrAaQEdbKUkyMTVd55EAAACvhcBqAG0LThMEAACal8BqAO3lmRWsySmBBQAAzUxgNYC5UwStYAEAQHMTWA2grTz3GSyBBQAAzUxgNYD5UwStYAEAQFMTWA1g/hRBK1gAANDUBFYDaLOCBQAALUFgNQC7CAIAQGsQWA2gffY6WC40DAAAzU1gNYB227QDAEBLKC/Hm+zcuTM7d+5Mktx1113p7+9fjrdtGp3tg0mSto4uPxvOqFwumxu8LPODxZgjLMYcYTHmyNItS2Dt2LEjO3bsmP9+YGBgOd62aZSLhSTJ0WPH/Ww4o/7+fnODl2V+sBhzhMWYIyzGHDnd5s2bz3jcKYINYO4UQRcaBgCA5iawGoALDQMAQGsQWA3ANu0AANAaBFYDaG+b+cdgBQsAAJqbwGoAVrAAAKA1CKwGMBdYLjQMAADNTWA1ABcaBgCA1iCwGoBTBAEAoDUIrAZgm3YAAGgNAqsBzJ8iaAULAACamsBqAO3lmX8MEwILAACamsBqAE4RBACA1iCwGkC5VEyhkExXqqlUqvUeDgAA8CoJrAZQKBTSVpo7TdC1sAAAoFkJrAZx4mLDThMEAIBmJbAaREebjS4AAKDZCawGMbeCNe4UQQAAaFoCq0F0zF4La2JSYAEAQLMSWA1i7lpY404RBACApiWwGoQVLAAAaH4Cq0GcWMESWAAA0KwEVoPomNumfdIpggAA0KwEVoNob7OCBQAAzU5gNYh2K1gAAND0BFaD6HAdLAAAaHoCq0F0zJ4iOCGwAACgaQmsBjF3iuC4UwQBAKBpCawGMX8dLCtYAADQtARWg5i/DpYLDQMAQNMSWA3ixAqWUwQBAKBZCawGceIzWFawAACgWQmsBnFiF0ErWAAA0KwEVoOYv9CwTS4AAKBpCawGcWKTi0qq1WqdRwMAALwaAqtBlEvFlIqFVKrVTFcEFgAANCOB1UBs1Q4AAM1NYDWQua3ax30OCwAAmpLAaiAd81u120kQAACakcBqIJ3tM4E1NjFV55EAAACvhsBqIHOnCI75DBYAADQlgdVAuuZXsAQWAAA0I4HVQDrbykmsYAEAQLMSWA3EKYIAANDcBFYDsckFAAA0N4HVQHwGCwAAmpvAaiBOEQQAgOYmsBqITS4AAKC5CawGMneK4LjAAgCApiSwGsj8KYI2uQAAgKYksBrI3C6Coza5AACApiSwGkhnm1MEAQCgmQmsBtLZfmKTi2q1WufRAAAAr5TAaiBtpWJKxUKmK9VMVQQWAAA0G4HVYDptdAEAAE1LYDWYuY0uxmx0AQAATUdgNRgXGwYAgOYlsBrM/AqWwAIAgKYjsBrM3GewRn0GCwAAmo7AajDdHTOnCI6OW8ECAIBmI7AazFxgjVjBAgCAplNejjfZuXNndu7cmSS566670t/fvxxv2zTK5fL8z6R/7ZEkLybFNj8n5i2cI3Aq84PFmCMsxhxhMebI0i1LYO3YsSM7duyY/35gYGA53rZp9Pf3z/9MqlPjSZJDR477OTFv4RyBU5kfLMYcYTHmCIsxR063efPmMx53imCDcYogAAA0L4HVYOYDa1xgAQBAsxFYDaarXWABAECzElgNprvDdbAAAKBZCawG090+dx0sgQUAAM1GYDWYjrZSioVkfKqSqelKvYcDAAC8AgKrwRQKhXTNbnThNEEAAGguAqsBdc9vdDFd55EAAACvhMBqQK6FBQAAzUlgNaC5wLLRBQAANBeB1YBcCwsAAJqTwGpAcytYwwILAACaisBqQPOfwRqfrPNIAACAV0JgNaDezrYkydCYFSwAAGgmAqsBzQXW8JgVLAAAaCYCqwH1ds6cIjgksAAAoKkIrAZ04hRBgQUAAM1EYDWgnvlTBH0GCwAAmonAakBd7aUUC4WMTU5narpS7+EAAABLtKTAes973pP77rtv/vsHHnggt9122zkb1EpXKBR8DgsAAJpQ+Wx3DgwM5MCBA0mSvXv3ZteuXUmSBx98MPv37z/3o1vBejrbcmx0MkNjU1nT01Hv4QAAAEtw1sD68pe/nE996lNJkk9/+tP59Kc/PX/fBRdccG5HtsLZqh0AAJrPWQPr8ssvz9ve9rbcc8892b59ezZt2pQk6e3tzU033bQsA1ypnCIIAADN56yBdf311+f666/P1q1bc80112T9+vVJkkqlkmLR/hjnUo+t2gEAoOksqZKef/75fPnLX87g4GDe97735ed+7ufypS996VyPbUXrtVU7AAA0nSUF1r//+7+np6cnX/va1zI1NZVNmzblM5/5zLke24rmFEEAAGg+SwqsoaGhrFq1Kt/5zndy8803553vfGcOHz58rse2os2dInh8VGABAECzWFJg9ff355Of/GTuv//+bN26NUNDQ+nt7T3XY1vRVne3J0mOj07UeSQAAMBSLSmwfvZnfza9vb25/vrrc8MNN2RgYCBvfvObz/XYVrS+rpnAOjpiBQsAAJrFWXcRnHPDDTfkTW96U1588cW89NJLufXWW+0ieI71drWlkJnrYE1XqikVC/UeEgAAsIglBdbevXvzP/7H/8hLL72UJNm4cWN+/dd/3cWGz6FSsZDerrYcH53M0OhkVve013tIAADAIpa0DPVXf/VXOXz4cG688cbceOONOXLkSD7ykY+c67GteHOnCR7zOSwAAGgKS1rBeuaZZ/IzP/MzueWWW5Ik//Iv/5JPfvKT53RgJH3dbXlhMDk6MpEL6z0YAABgUUtawert7c3DDz+c/fv3Z//+/Xn44YftIrgM+mZ3Ejw2YgULAACawZJWsH7gB34gd999d771rW/NH3vPe95zzgbFjBOnCNpJEAAAmsGSAuvmm2/O6tWr8/DDDydJ3vCGN2T79u3ndGAkq7tnLjZsBQsAAJrDkk4RvPPOOzMwMJAPfOAD+cAHPpCDBw/md37nd8712Fa8+VMEbXIBAABNYUmBNTg4mPPPP3/++/Xr1+fQoUPnbFDMmD9F0MWGAQCgKSzpFMENGzbkH//xH7Nu3bpUq9V8/vOfz4YNG8712Fa8PqcIAgBAU1lSYP34j/94PvzhD+f3fu/35o+9//3vP2eDYkZPZ1uKhUKGx6cyOVVJW3lJC44AAECdLHmTi/7+/jzwwANJkje+8Y25+uqrz+nASIqFQlb3tOfw0HiODI9n/equeg8JAAA4iyUFVpJcffXVoqoO1s4G1mGBBQAADc85Zw1ubW9HkuTwkM9hAQBAoxNYDW5tz2xgDY/XeSQAAMBiBFaDO7GCJbAAAKDRCawGt2Z2BeuIFSwAAGh4AqvBre2dudiwFSwAAGh8AqvBza1gHR2ZyHSlWufRAAAAZyOwGlxbqZhVXW2pVJNjI3YSBACARiawmsBan8MCAICmILCawNxOgoM+hwUAAA1NYDWB81bNBNah42N1HgkAAHA2AqsJ9K/qTJIMHBNYAADQyARWE+jvE1gAANAMBFYTmA+s42OpVm3VDgAAjUpgNYHezrZ0tJUyOjGdkfGpeg8HAAB4GQKrCRQKhfnPYR10miAAADQsgdUk+vtmdhIcsJMgAAA0LIHVJPpXdSVJDlnBAgCAhiWwmoSdBAEAoPGVl+NNdu7cmZ07dyZJ7rrrrvT39y/H2zaNcrm86M9k63gxydM5PDLl57cCLWWOsHKZHyzGHGEx5giLMUeWblkCa8eOHdmxY8f89wMDA8vxtk2jv79/0Z9JR2Z2D9x36HgOHDyYYqGwHEOjQSxljrBymR8sxhxhMeYIizFHTrd58+YzHneKYJPo7iinr6stk9OVDB4fr/dwAACAMxBYTWTDmu4kyf4jI3UeCQAAcCYCq4lsXDOzk+BLR0brPBIAAOBMBFYT2bjWChYAADQygdVENljBAgCAhiawmsiG1TOBdeDoaKYr1TqPBgAAOJXAaiKd7eWs6WnPdKWaQ8ddcBgAABqNwGoyG2d3EnzpsM9hAQBAoxFYTWbzupnA2ntouM4jAQAATiWwmsyW83qTJC8MCiwAAGg0AqvJbDmvJ8nMCla1aqMLAABoJAKryazpaU93Rzkj41M5MjxR7+EAAAALCKwmUygUTlrFAgAAGofAakInAmuoziMBAAAWElhN6AIrWAAA0JAEVhOy0QUAADQmgdWE1vZ0ZFVXW0bGp3Lw2Fi9hwMAAMwSWE2oUCjkkvNXJUmePXC8zqMBAADmCKwmdanAAgCAhiOwmpQVLAAAaDwCq0ltXtedtnIxB4+NZWhsst7DAQAAIrCaVqlYzEX9vUmsYgEAQKMQWE3skvUzpwl+Z7/AAgCARiCwmtjlm/qSJE++eLTOIwEAABKB1dQuPn9VyqVCXjw8kuOjE/UeDgAArHgCq4m1lYq5bMPMKtZTLx6r82gAAACB1eSu2LQ6idMEAQCgEQisJnfF5pnA2r3vaKrVap1HAwAAK5vAanKb1nanp7OcoyMTOXhsrN7DAQCAFU1gNblioZBtm9ckSXY9f7i+gwEAgBVOYLWAay5cm0RgAQBAvQmsFnDl5tUpFQt59uDxDI1N1ns4AACwYgmsFtDZXs7WjX2pVpPHrWIBAEDdCKwWMXea4GMCCwAA6kZgtYirZwNr976jmZicrvNoAABgZRJYLWJNT0cuXt+byemKVSwAAKgTgdVCrr+0P0nyX98ZqPNIAABgZRJYLWT7JetSLCTffuFohu0mCAAAy05gtZBVXe25fNPqVKrVPLxnsN7DAQCAFUdgtZjrL5s9TfAZpwkCAMByE1gt5tqL1qW9XMx3DhzPgaOj9R4OAACsKAKrxXS2lXLd7GYX39h9oM6jAQCAlUVgtaDv3nZ+kuSbTx/M5HSlzqMBAICVQ2C1oC3n9eSCdd0ZGZ/Koza7AACAZSOwWlChUMibt21Iktz37f11Hg0AAKwcAqtFXX9ZfzrbSnn2wPE8d/B4vYcDAAArgsBqUZ1tpbzlyplVrHsfe7HOowEAgJVBYLWwG6/amFKxkEeeG8yh42P1Hg4AALQ8gdXCVve057pLz0u1mnx1l1UsAAA41wRWi/veazYnmbkm1tHhiTqPBgAAWpvAanGb1nZn+8XrMlWp5l8feaHewwEAgJYmsFaAt123JYUk//nkgRweGq/3cAAAoGUJrBVgw5ruXHdZf6Yr1Xzxob31Hg4AALQsgbVC/NAbLkixkHzz6YPZNzhc7+EAAEBLElgrxPq+rnzPVRtTrSafu39PqtVqvYcEAAAtR2CtID/0hi3p7ijn6ZeO5dHnDtd7OAAA0HIE1grS3VHOD1+3JUny+W/uycTUdJ1HBAAArUVgrTBv3rYhG9d2Z3BoPPc8aMMLAACoJYG1wpSKhbzrLZelUEj+bdeLeX5gqN5DAgCAliGwVqCL1vfmra/blGo1ufu+ZzI1Xan3kAAAoCUUqsuwndzOnTuzc+fOJMldd92ViYmJc/2WTaVcLmdqampZ33N8cjof/Ni9OXh0JD/65svzUzddtazvzytTjzlC8zA/WIw5wmLMERZjjpyuvb39jMeXJbBOtW/fvuV+y4bW39+fgYGBZX/fZ146lv95z66kmvzy216XyzetXvYxsDT1miM0B/ODxZgjLMYcYTHmyOk2b958xuNOEVzBLtvYlx/cfkGqST751acyPDZZ7yEBAEBTE1gr3I7tW3LJ+atybHQyf/u1p1NxAWIAAHjVBNYKVyoW8jNvvTxd7aU8vvdI7vkvW7cDAMCrJbDI2t6O3Pq9V6RQSP71kRfy0LOH6j0kAABoSgKLJMm2zWvyY991cZLkb//96ew9NFznEQEAQPMRWMy76XUb811b12dyupK/2vlEBo6N1XtIAADQVAQW8wqFQn7qLZfmik2rMzQ2mf/1xcdzbNQ1ywAAYKkEFicpl4r5+e/fli3n9WRwaDz/+4tPZGTcReUAAGApBBan6Wwr5f/ecVXW93XmxcMj+ct7drlGFgAALIHA4ox6O9vyy297XfpXdeaFwZH8xT2PZ0hkAQDAWQksXtaano7891uunl/J+p9f2JUjw+P1HhYAADQsgcVZre5uz3+/5epsWN2V/UdG86f/9FhePDxS72EBAEBDElgsqq+rPe+75epccv6qHB2ZyJ/982N56sWj9R4WAAA0HIHFkvTMfiZr+8XrMjY5nf+984nc98RLqVar9R4aAAA0DIHFkrWVivnZ770iN1+9KdOVav7+G8/m7q89k8mpSr2HBgAADUFg8YoUC4X82H+7OD/z1svTVirmm08fzIf/+bEcOj5W76EBAEDdCSxelesv68/733FN1vV25IXB4fzR5x7O/U8dcMogAAArmsDiVdu8rie3/ejrs/3idRmfquTurz2Tv7n3yYyMT9V7aAAAUBcCi9eku6OcW7/3irznxq3pKBfz8J7B/MFnH8rDew5ZzQIAYMURWLxmhUIh33X5+vw/P7Y9F6/vzbHRyfyfrzyZj315twsTAwCwoggsaqa/rzO/css1+Yk3X5KOtlIee/5w/r/PPpyv7nox0xU7DQIA0PoEFjVVLBZy41Ub8//++PZcc+HajE9O53P378kffPbh7Hr+sNMGAQBoaQKLc2JNT0d+8QeuzHt/4Mqs7+vMwWNj+esvfTv/64tPZN/gcL2HBwAA50S53gOgtV194dps27w6X//2/nzxob158sWj+aN/fCTbL16Xt123JRvWdNd7iAAAUDMCi3OuXCrmrVdvyhsv68/Oh1/If3x7fx7eM5hH9gzmukvPy443bMn5q7vqPUwAAHjNBBbLpqezLT9+wyX5vms2518feSH/+eSB/Nd3DuXB7xzKNRetzfdeszmXnL+q3sMEAIBXTWCx7Fb3tOcnv/vSfP+1M6H1zacO5tHnDufR5w7n4vW9+d5rNueaC9emWCzUe6gAAPCKCCzqZm1vR/6vt1yWt123JV97/KV8/dv7s+fgUD7+ld1Z29uR7952fv7b5euzqqu93kMFAIAlEVjUXV9Xe97+xovyA6+/IPc/dSBf3fVSBofG888PPJ97Htybay9al7dcuSGXbViVQsGqFgAAjUtg0TA62kq56XWb8j1XbszufUfy9d0H8vjew3no2UN56NlD6V/VmTdu7c8bL+vPeas66z1cAAA4jcCi4RSLhVy1ZW2u2rI2R4bH843dB/KfTx7IwPGx3PPg3tzz4N5ccv6qvPGy/rzhkvPS3WEaAwDQGPyXKQ1tTU9Hfvj6C/NDb9iSJ188mgeeGcgjzw3m2QPH8+yB4/nsfz6byzf15fUXnZdrLlqb3s62eg8ZAIAVTGDRFIrFQq68YE2uvGBNfnJyOo8+N5hvPT2Qp146mm+/MPPn0/+RXLahL6+/aF2uvWhdVvfYHAMAgOUlsGg6HW2lvGnr+rxp6/oMjU3msecO55HnDuWpF4/l6Zdm/vzDfz6bzeu6c9UFa3LVBWty0fpVKdn2HQCAc0xg0dR6O9vy5m3n583bzs/oxFR2PX84j+wZzO59R7NvcCT7BkfypUf2pau9lG2bV+fKC9Zk2+Y1Wd1tdQsAgNoTWLSMrvby/MrW5HQlz7x0LE+8cCRPvHAkA8fG8tCzg3no2cEkyfq+zmzd2JfLN63O1g196e3y2S0AAF47gUVLaisV5z+z9eNJBo6N5YkXjuTbLxzJM/uP5eCxsRw8Npb/2H0gSbJhTVcu39iXyzb05eLzV1nhAgDgVRFYrAj9fZ25qW9jbnrdxkxXKnl+YHj+81rPHjie/UdGs//IaL72xP4kyZqe9lyyflUuPr83F69flc3rulMqFuv8twAAoNEJLFacUrGYS85flUvOX5Uf3H5BpqYreW5gKE+/dCzf2X88zw8M5cjwRB4cPpQHnz2UZGZF7ML+nlzY35st5/XkgvN6ct6qzhQLNs4AAOAEgcWKVy4Vc9mGmdMDk6RSqWb/0dHsOThzra3nDg7l4LGxPLP/eJ7Zf3z+eZ1tpWxe150t552Irv4+0QUAsJIJLDhFsVjIprXd2bS2O9+9bUOSZHhsMnsODmXvoaHsPTScFw4N59jo5GnR1VEuZsPa7mxa052Na7uycU13Nq7tdgFkAIAVQmDBEvR0tuXqC9fm6gvXzh87NjKRFwaH54Nr76HhHB2ZyHMHh/LcwaGTnt/b2TYfXJvWdmfDmq6s7+tKd4f/CQIAtBL/dQevUl93e/q62/O6LSeia2hsMi8dHslLR0by4uHRvHRkJPsPj2RobDJPvTiZp148dtJr9HSWc35fV9av7sz6vq6s7+vM+tVdOW9Vh001AACakMCCGurtbMvlm1bn8k2r549VqtUcGR7PS7PB9dLhkew/OpqDx8YyPDaV74wdz3cOHD/pdYqFZN2qzqzv60z/qs5ctPF4OopTWdfbmXW9HWkriy8AgEYksOAcKxYKs2HUedIphpVqNcdGJnLg6FgOHhvNwbmvx8ZyZGg8A8fGMnBsbObBj7900mv2dbXlvFWdWbeqI+t6O7JuVWfOm/26qqvNRhsAAHUisKBOioVC1vR0ZE1PR7ZtXn3SfZNTlQwcH8vBo6M5NDSekcnkhYNHMzg0lsNDEzk2Opljo5OnrXwlSalYSF93e9b2tGd1T8fM1+722fea+drVXkpBhAEA1JzAggbUVi7O72SYJP39/RkYGEiSTFeqOToynsHj4zl0fDyDQ2Mzt2e/Do9P5fDQeA4PjSc5PcCSmd0OVy8Irr7utvR1taevq23ms2Vd7entakupKMIAAF4JgQVNplQ8ccrh5ZtOv39iajpHhydyZGQiR4bGZ74OT+TI8Pj81/GpSg4cHc2Bo6Mv+z6FzOyeOB9f3W1ZdVKEzXzf29WWtpLPhAEAJAILWk57uZT1q7uyfnXXGe+vVqsZnZjOkeHxHB2ZyOGh8Rwfncyx0YkcGznxdXhsMkOzf/Zl5Kzv2dFWSm9nOb2dbfN/ehZ+3zV3vJzuDitjAEDrEliwwhQKhXR3lNPdUc7mdT0v+7jpSjVD8+E187mv46dE2PHRiQyPT2V8cjrjk9M5dHx88fdP0tVRPim4ujvK6Zkd08I/PR3ldHWU091eTtkqGQDQBAQWcEalYiGre9qzuqf9rI+rVqsZm5zO0OjcitfU/MrX0Ohkhsdnj83ePzI+Nf/nwNGlj6ejrZTu9tJJQda1IMy6Osrpaiulq72czvaZr13tpbS3leyqCAAsG4EFvCaFQmE2Zsove1riQtOVakbGT4TYwuAaGZ/K8Pjpx0YmTqySHR6eeIXjSzrbSumcDa6u9nI6204EWOf81zMcayuno63oos8AwJIJLGBZlYqFrOpqz6qus6+MLVSpVjM+OZ3hsamMTkxl+KQAmw2yiemMTUxlbGI6oxNTGZ39fnyqktGJ6YxOTOfwqxxzuVhIR3spHeWZEOsol9LRVkpn28zXhX9mjhVPun/h45zqCACtTWABDa+4YJXslZquVGfCa3J6PrpGT4mwmfumTrt/btVsqlLN1NhUhjP1mv8upWJhPrbay8W0l4vpKJfSXp79vq144vaCrx0nHZ+9PXts1eR0qtWqa5sBQAMQWEBLKxUL6elsS09n26t6frVazeR0ZTa2Khmbja65Py/7/dR0xiamMz5VyfjsStrYxPTsKZIzq2+1VMjM9dNOhNrJMdZWmrldLhXTVirOPnbmdrl04nbbqV9POVYuFX2mDQDOQmABnEWhUJiNllJWLf4Rs7OqVquZqlTnY2xiqpKJqZmv45PTmTzl+5n7Txyb/7rgueNTlUxOV2afO/PnXCuXCrPBNhNu5XIxbaXCie9LJ8dbuVSYD7tyqZBy8fTjpWLhjI8vzb5XuThzW9wB0OgEFsAyKRQKaZsNht5XuaJ2Jv39/Tlw4GAmpmcjbPL0KJucC7HpBbdP+ToxVcnU9Nzt6UxOVzM1NXd75vjUdHX2z8wpl8utVCzMR9hceM0FWfmUgGs7w/HS3NdiYf61Tr1dLhZSmr8995xCSrPPK5dmbs88bib6nJ4JwByBBdACisVCOoszG2rkNa60nU2lWp2JsLPG2Yn7pqZn/1Sqs7ers6G28NhcuM1G3BmOzz1+ulLNdGU645Pn7u/4ShUyE36lUwKtPBtupdkIPPX2XLydHG6FlArFFOefOxNwpWLhpGPz38/fV3zZ+0rFQoodozk+OpFSccFrF2YeB0BtCSwAlqy44JTJ5VapzgTWmaJsurIg3OairLIg2mYfMzVdzXSlMvt15vbca05XqrMRt+D++bBb+JyF31dSqWbmvSrLv6L3WhWSk2PupDArvux9p8decT7YioXMh2HxlK+l2fsLhcIZHpMFjznTc3Pa8dLs6mGxmAXvf/pj5l7bSiOwHAQWAE2hWCikOHtqYCOpVKqZrp6ItOm5iFsQbtOnRNpUpTL7uBO3pyonHlupnIi5ubCce42Xu29uHCfdP/ucaqGQyanp0+6rJvPfrwSFQk4Jr9kQK+Rl4uz0qJt/jcKJ24W51ygUUiguuL3g+KLPLZ7yOqeM65U892zjmLs9F6Zzx9qGxzM8Nvmy4xCnsHSFarV6zn+r7ty5Mzt37kyS3HXXXZmYeGUXCm115XI5U1O13VGM1mKOcDbmB4t5uTkyF2BTs6t1C1f1Fn6/2P1zq4DV6pljrzL7mEr15PBb+LiF9y3l8ScdX/jcU19nweN59eZWOwuFE1FamIu/BfedHH8nf3+m22d8TLGQQgonR2AW3HfKexaX9B4nQrEwF7zJyZF66nuc7fmz95/08zjl+NxrFRf8XQoL/y6zj8nc83Pq3yHzjz3T321u/Kc9p1A46b7igucvvO+V8u+a07W3n/manssSWKfat2/fcr9lQ+vv78/AwEC9h0EDM0c4G/ODxZgjM7t4Vqszp5qeGnaVyolTUCsLj1dzUrRVqyeOV+cfl/nj869/ynstfMySn1s55fFzt89w/OWfu/C+E8890ziTwnzEnnrf8v+XIsvh5IA7JcySk8KukJnPlv7aj177qi970oo2b958xuNOEQQAWt78/8ufQrL8HyFseGeL8OopsTUfdsmC46c8JjPhWs3cc0593sLXOuU98jLHqwtf7/QxVXPqGM/8uqc9b8HrnvH5p73u3HNmovX058693ynfL3zeKeM+8fX0MZ358S93+2yPO/F6mbsvCw6cuMFrJLAAAHhZJ8UpLeG0iJuLx5k7T4u9SqpZu3ZdJkeP13nkzUFgAQDACjIXzXkF0by2tzMDY0PnbEytpLG2YgIAAGhiAgsAAKBGBBYAAECNCCwAAIAaEVgAAAA1IrAAAABqRGABAADUiMACAACoEYEFAABQIwILAACgRgQWAABAjQgsAACAGhFYAAAANSKwAAAAakRgAQAA1IjAAgAAqBGBBQAAUCMCCwAAoEYEFgAAQI0ILAAAgBoRWAAAADUisAAAAGpEYAEAANSIwAIAAKgRgQUAAFAjAgsAAKBGBBYAAECNCCwAAIAaEVgAAAA1UqhWq9V6DwIAAKAVWMFqAL/5m79Z7yHQ4MwRzsb8YDHmCIsxR1iMObJ0AgsAAKBGBBYAAECNCKwGsGPHjnoPgQZnjnA25geLMUdYjDnCYsyRpbPJBQAAQI1YwQIAAKgRgQUAAFAj5XoPYKX76Ec/mmeeeSaXXnpp3vve99Z7OCyzJ598Mh/72MdSKBSydevW/OIv/mI+97nP5f7778/69evzK7/yKymXy0s+Ruv6/Oc/n2984xu58847z/h7Y6nHaE333ntv7r333lQqlfzqr/5qPve5z5kjzBsfH88f/uEfZnx8PN3d3fm1X/u1fOITnzBHVrjBwcH8/u//fvbu3ZuPf/zjKZVKr+nfL+bKCVaw6uiZZ57J2NhYPvShD2VqaipPPfVUvYfEMlu/fn1uv/323HnnnTl27Fh27dqVxx57LHfeeWcuuuii3H///Tl69OiSjtG6Jicn8+yzzyY58++NpR6jNQ0ODmbXrl25/fbbc8cdd+TIkSPmCCd58MEHc8UVV+SOO+7I5Zdfnn/4h38wR0hvb28++MEP5oorrkjy2v79Yq6czP/lXUdPPvlktm/fniR5/etfn927d+fyyy+v86hYTmvWrJm/XSqV8vzzz+fqq69Okmzfvj1f/epX09HRsaRjb3nLW5Z9/CyPL33pS/m+7/u+/O3f/u0Zf2+USqUlHfP7pTU9+OCDqVQq+dCHPpQtW7Zk8+bN5ggn2bBhQ5588skkyfDwcLq6uswR0t7envb29vnvX8u/X8yVk1nBqqPh4eF0d3cnSbq7uzMyMlLnEVEve/bsybFjx9LT05Ourq4kM3NieHg4IyMjSzpGa5qamspjjz2Wa6+9NsmZf28s9Rit6ejRo5mamsrtt9+e9vb2jIyMmCOcZNOmTXnyySfzgQ98IM8880yKxaI5wmley79fzJWTCaw6WjgBR0dH5ycmK8vQ0FA+8pGP5H3ve1+6u7szOjqaJBkZGUlPT8+Sj9Ga/u3f/i033XTT/Pdn+r2x1GO0pu7u7vkV7bkQN0dY6N57782b3vSm/OEf/mGuv/76TE9PmyOc5rX8+8VcOZnAqqNt27bl0UcfTZI88sgj2bZtW51HxHKbnp7On/zJn+Tnfu7nsmbNmmzdujW7du1KMjMnrrjiiiUfozXt27cvX/ziF/O7v/u72bt3b44fP37a740z/S7x+2XluPLKK7Nnz54kmf+snjnCQtVqNb29vUmSvr6+JOYIp1vqHDBXFiew6uiyyy5LW1tbbr/99hSLxRV9rupK9fWvfz1PPfVU/uZv/iZ33HFH9u/fn9e97nX54Ac/mGeffTY33HBDVq9evaRjtKZbb701v/Vbv5Xf+q3fypYtW/Kud73rtN8bZ/pd4vfLynHJJZekvb09d9xxR55++um8853vNEc4yU033ZSvf/3rueOOO/LVr341b3/7280RMjU1lTvvvDN79uzJ7/7u72Z6evpVzwtz5WSFarVarfcgAAAAWoEVLAAAgBoRWAAAADUisAAAAGpEYAEAANSIwAIAAKgRgQXAsjhw4EDe/e5356677soDDzyQu+++OwcOHKj5++zduzd33313HnvssfljH/7wh/Pud787Tz/9dM3fDwAWKtd7AACsDH19fbntttuybt263HffffnCF76Qa665Jueff/4rep3p6emUSqWXvX/v3r351Kc+lSS55pprkiRve9vbct1112XDhg2v/i8AAEvgOlgALIsDBw7k/e9/fzo6OjI+Pn7SfXfffXd2796dj33sY3nuueeybt26vOtd78pNN900/7xt27alo6Mjzz33XP7gD/4gv/M7v5MXX3wxSXLppZfml37pl9LR0ZH3v//9J732b//2b+crX/lK7r333vze7/1etm7dmp07d+Zzn/tcDh8+nC1btuQXfuEXctVVV+UrX/lK/uzP/izf8z3fkxdeeCEDAwN517velXe84x3Zt29f/vRP/zR79uxJe3t7LrzwwnzoQx9atp8fAM3BKYIALKurr746b3jDG5IkP/VTP5XbbrstQ0NDueuuuzIyMpKf/MmfzPr16/Mnf/InefbZZ+eft3v37lx66aV5z3vek0KhkBtuuCHvfe978xM/8RPZs2dPPvrRj6avry/veMc7kiRvfvObc9ttt2XLli0nvf+jjz6av/zLv0xfX19+/ud/PgMDA/n93//9HD9+fP4xjz32WH7wB38wSfKJT3wiU1NT+cIXvpCnn346t956a376p386/f395/gnBUAzcoogAMuqUChk48aNeeihh3LttdfmmmuuyQMPPJChoaEMDQ3lk5/85PxjH3300dxwww1JZlapbr311iTJ4OBgHnrooezevTtzJ2I899xz6ezszFVXXZV/+qd/yoUXXpgbb7zxtPd/4IEHkiTvfve7s3379gwMDOTv//7v8+STT84/5vu///tzyy235Fvf+lYeeuihHDlyJJs2bUq1Ws1//dd/ZevWrfMhBwALCSwAll2hUDjj8Ztvvjk333zz/PcLP5+1du3a+dv//M//nG9/+9v5kR/5kVx//fX58z//84yOjtZsLL29vUky/1mvSqWSW265JRdccEF27dqVb37zm/nMZz6TP/qjP8rmzZtf1fsC0JqcIgjAsuvp6UmS/Md//EceeOCBbNu2Lb29vXnooYeyb9++PP/88/nsZz+bwcHBs77O8PBwdu3alUOHDs0fm4ujJ554Il/72tcyMTFx0nPe+MY3Jkn+7u/+Ll/84hfzpS99KT09PbniiivO+l733HNPdu/enY0bN2bDhg2pVqs5cuTIK/2rA9DiBBYAy+6tb31rLrjggtxzzz3567/+6/T29uY3f/M3s3HjxnziE5/IZz7zmbS3t2f9+vVnfP7b3/72bN26Nffdd18GBwdz4YUXzt931VVX5fWvf30ef/zx/PEf//FJn61KkmuvvTa//Mu/nKNHj+bjH/94zjvvvPzGb/xGVq1addYxt7W15Stf+Ur+4i/+Io8//nh++Id/OFddddVr/2EA0FLsIggAAFAjVrAAAABqRGABAADUiMACAACoEYEFAABQIwILAACgRgQWAABAjQgsAACAGvn/AfMp6izwDZjFAAAAAElFTkSuQmCC",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plot_1(cost_history, m, q)"
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA1gAAAGoCAYAAABbkkSYAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAAA0YElEQVR4nO3daXBe133n+d+592IlwBXcwA3cSZAE90WkdlISJfeM23ZlkrF7lIx7UtOemu7Jm1RSmcpWlRdKVVyZSnd1eronTlV3x84kbU+nY2uFKImkuC8gQHDfF3ADSIIAQSz33DMvLkVKNCVxuXjOg+f5fqpYoo8gPX8fySS+fu5zjnHOOQEAAAAAnlrgewAAAAAAKBQEFgAAAABkhMACAAAAgIwQWAAAAACQEQILAAAAADJCYAEAAABARiKfL97W1ubz5fNGTU2N2tvbfY9RVNhzP9j33GPP/WDf/WDfc48994N99+PBfa+trX3o1/EOFgAAAABkhMACAAAAgIwQWAAAAACQEQILAAAAADJCYAEAAABARggsAAAAAMgIgQUAAAAAGSGwAAAAACAjBBYAAAAAZITAAgAAAICMEFgAAAAAkBECCwAAAAAyQmABAAAAQEYILAAAAADICIEFAAAAABkhsAAAAAAgIwQWAAAAAGSEwAIAAACAjBBYAAAAAJARAgsAAAAAMkJgAQAAAEBGCCwAAAAAyAiBBQAAAAAZIbAAAAAAICMEFgAAAABkhMACAAAAgIwQWAAAAACQEQILAAAAADJCYAEAAABARggsAAAAAMgIgQUAAAAAGSGwAAAAACAjBBYAAAAAZITAAgAAAICMEFgAAAAAkBECCwAAAAAyQmABAAAAQEYILAAAAADICIEFAAAAABkhsAAAAAAgIwQWAAAAAGSEwAIAAACAjBBYAAAAAJARAgsAAAAAMkJgAQAAAEBGCCwAAAAAyAiBBQAAAAAZIbAAAAAAICMEFgAAAABkhMACAAAAgIwY55zL1Ys1NjaqsbFRkvTWW2+pv78/Vy+d16IoUhzHvscoKuy5H+x77rHnfrDvfrDvucee+8G++/HgvpeWlj7063IaWA9qa2vz9dJ5paamRu3t7b7HKCrsuR/se+6x536w736w77nHnvvBvvvx4L7X1tY+9OuiXA0EAAAAPC3nEimOpbhfigfk4oH055+9Z2DM3a80UhTJlJRJJaVSSZlMEHqbG8WDwAIAAIB3Lkmkni657htyXXd/3L4l3emW670t3bmd/rG3R9ITPoAVRlJ5pUzlcJmKKqlyuExltczw0TIjxsiMqJHKh8ncizTg8RFYAAAAyBk30Cd346rczavpHz/70X1TSuyj/U2ikns/TFSa/twE99/Fkkt/bmO5gT5poF8a6JNsLN2+JXf71pcnWkmZzMixMmNqFdTUytTUyoyeIFPy8M/bAA8isAAAADAoXF+P3LWLSq5dlLt2QUn7Ranrxpf/BRVVMtWjZKpGylSPkoaNkKmokqkYJpV/9sfKJ3rUzzknxQNS7225ni65nq70HbPbnXK3rsvd6pDrbJf6e+WuXUjn/ewvNkZmzEQFE+pkJk5XMHF6+g4Y8BAEFgAAAJ6ac4nc9Styl84ouXxGybXz0q3rv/yFQSgzskZm5HiZUePu/6gePajvEhlj7n4WqzSNt4f+d3BpgN24oqT9klxHm1x7W/oOW3ubbHubdHBb+vcbNU7BlLkKps6TmTBNJuTbaqT4NwEAAACPzSVW/RdPKj7cJHfptJLLZ6T+3i9+URilj9jVTFIwdrLM2Enp43d5etiEMSZ9F62iSkHtzHvrbqBf7up5JZdPK7l0Ru7KWbkbV2VvXJVt3iKVlCmYPFvBjIUKps1PD9ZA0SKwAAAA8EjcretKLhxTcv64krYTutbf98UvqBqpYEJd+gjd+Ckyo8bnbUw9DlNSKjNppoJJaXQ5a+WunFVy7oiSc0fTd7xOH1Ry+qAUlSiYNl/BzMUKpsyRiUo8T49cI7AAAADwUC4eUHLhuJILx+XOH5O71fGFPx+NHq9k/DQFE6YrmFj3pY/eFRoThjK1MxTUzpDWvCHXdV3J2cOyJ5rT8DrZrORks1RWqXDOUgXzVysYNc732MgRAgsAAAD3uDu3lZw7rOTMISUXjqcHQ3ymtDx9FO7uj7HTZ3PhrSRTPVrhwnUKF66T67ohe7JZyYkmuY5Lsi2fyrZ8KjOhTuH81QpmLuLzWgWOf7oAAABFznV2yJ49pOR0q9yVs5877lwyYycrmDovfdxt7KSCeORvMJnqUYqWvCAteUHJtQuyh3elsXX5jOLLZ6Sd7yhctFbh/NUyZRW+x8UgILAAAACKkOu6KXvygJKTzXLtF+//iSCUmTRTYV29grr5MsNG+BtyiAvGTlYwdrLcmm8oOdEk27pN7voV2Z3vyu7bpHDeKoUNz8lUsceFhMACAAAoEq6nS8mp5nufFbqnpCx9l6quXsGUuTJl5f6GLECmtExh/WoF81fJnT+muHmL3MUTsi1bZQ/tUDh/lcKlL8lUVvseFRkgsAAAAAqY6+9VcqpF9niT3KVT9x//i0oUTJ2vYFZDGlWcdjfojDEyU+eqdOpcJe0XZfd/kgbvwW2yR3YrrH9G4ZLnucR4iCOwAAAACoxzidzFU7LH9qZHh392UEUQKpg6R8GsxdzX5FlQM0nBK99V0vGS7J4PlJw5JNu8WfbIToVLX1a4aB2HYQxR/FMDAAAoEElnu5Kje2WP75O6O++tm4nTFc5ZpmD6Qg5WyDPBmIkKXntTybULine/L3f+mOzOd2QP71S05g0FdQvSC5AxZBBYAAAAQ5gb6E8fMzuyW+7y5z5XVT1K4ZxlCucskxk+xt+AeCTB2MkqfeP7Ss4fU7z953I3rip+/z/L1M5Q9Ow3FYwa73tEPCICCwAAYAhKblxRcmin7LF9Un9vuhiVKpixUOHc5TITp8uYwO+QeGzBlDkqmfR/KDm8S/GeD+TaTmngv/yFwiUvpAdh8Fm5vEdgAQAADBHOxkpOHZQ9tEPu8pl762bs5PSUupkNfK6qAJggVLjgGQWzFive+Z6Swztl921ScrJZ0XPfkmpqfI+Ir0BgAQAA5Lmks13JoV2yx/ZIvT3pYkmpgllLFdavUlAzye+AGBSmrFIlz39Lyeylirf8TO7GVQ38/D/oxoWjcsvWE9N5isACAADIQ84lcuePKz74qdz5Y/fWzZiJCuvXKJi1RKaUb7CLQTCxTiXf+VeyBz6R3btJPU2bpVMHVfLS/6BgQp3v8fAAAgsAACCPuIE+JUf3ybZuk7t5LV0MIwWzFiusXyMzdjKnyhUhE0aKlq1XULdA+uSnGrh6XgP/7f9WuPgFhSs2cKR7HuGfBAAAQB5wtzpkW7fLHtlz/9CKYSMULnhG4fyVMuXD/A6IvBCMnqAx3/8/deXdv03f0Wr6WMn5oyp55XsyI/hsVj4gsAAAADxxzsm1nZI9+KmSM4clOUmSmTBN4cJ1CqYvkAlCv0Mi75gwUrR6o4Jp8zXw0f8r13FJ/T/914pe+I7CmQ2+xyt6BBYAAECOucSmpwEe+ESuvS1dDEIFMxsULlqnYOxkvwNiSAgmTFPpt/+V4s0/VXKqRXHjj5VcOq3omW/wyKBH7DwAAECOuIF+2SO7ZVu2Sl030sWKKoX1axTWr5aprPY7IIYcU1auaMN3lbRuU7z9bSWt2zVw9bxKXv1nMlUjfY9XlAgsAACAQebudMse3Cbbul3quyNJMiNqFDY8p2DOMi6PxVMxxihcuE5m3FQNNP5Y7toF9f/s36jk1f9JwYRpvscrOgQWAADAIEk622UPbFFybK9kY0mSGT9V4eLnFUyrlwkCzxOikATjpqj02/+7Bj74sVzbSQ38479X9Py3FM5d4Xu0okJgAQAAZCy5ej493e30IX12cEUwbb7CJS9wbxEGlSkfppI3vq94+8+VtG5X/PF/kbt+WeHqNwj6HCGwAAAAMuCck7t0WvG+TXIXT6SLQahgzlKFDc8rGDXO74AoGiYMVfLsN2VHT1D86T/INm+Vu3VD0fpf43HUHCCwAAAAnoJzTu78McX7P5K7fCZdLClTuGBN+rmYYcO9zofiFdavlhlZo4H3/pOSM60a+MVfqWTjmzJllb5HK2gEFgAAwBNwLlFy5rDsvk1y7RfTxbIKhYvWKVy4lm9ikReC2pkq+ea/0MDbP5K7fEYD//DvVPLG9zlhcBARWAAAAI/BJYmSU82y+z6Su3ElXayoUtjwnML6NTKlZX4HBB4QjJ6g0n/6v6WRdeOq+v/rv1XJN/4XHlsdJAQWAADAI3DWKjm+T7bpE7nO9nRx2AhFS55XMG8Vn21BXjNVI9N3st79j+k7Wf/471XyT35TwejxvkcrOAQWAADAV/gsrOJ9m+5fDjx8jKIlL6R3WIV8O4WhwZRVquSN72vgvf8od/HE3cj65wrG1PoeraDwKwIAAMBDuMQqObZf8f5N0q3rkiQzcqzCZS8rmNkgE4SeJwQenykpVcnGX9fA+/9J7vwxDfzj/6OSb/xzBWMn+R6tYBBYAAAAn+MSq+R4U/qO1a0OSZ+F1fq7YcVdQhjaTFSiktfeVPzB3yg5ezg9XfC//195XDAjBBYAAIDuhtWJA+mpgHc/Y2VG1KRhNWsxYYWCYsJI0SvfU/z+f1Zy7ogGfvFXKv3mv5AZPtr3aEMegQUAAIqaSxIlJw/I7v3w/uEVw8coWv6ygllLeBQQBeuzyBp4+0dyl06r/7PIqqz2PdqQRmABAICidO+49b0fyt28li5Wj1a07GUFc5YSVigKJipJP5P1j/9Brv1i+rjgN3/AdQNPgcACAABFxTmn5Eyr7O4P7t9jVT0qDavZy2RCwgrFxZSWq+SN/1kD//Dv5K5fVvzhTxS99iaPxT4hAgsAABQF55zcxROKd70nd+1Culg18u47Vhy3juJmKqpU8vpvqP//+7dKzh2R3fm2omf+ie+xhiR+JQEAAAUvuXxW8e735NpOpQsVVWlYzV9FWAF3mRE1Knn1n2ngF38l27xVZtR4hfNW+h5ryOFXFAAAULCSjjbZXe8rOXckXSirULjkBYUL1sqUlPodDshDQe0MRc/9U8Wf/FTx1n+QqZmkoIaLiB8HgQUAAApOcvOa7J5GJScPpAtRqcKGZxU2PCdTVuF3OCDPhfNWKrl6XsnhXYobf6ySb/9LDr14DAQWAAAoGK77puK9Hyo5uldyiRSEChesUbj0JZmKKt/jAUNGtPa/08CVc9p/vleb/q+fq6d0hKqGlerVZ2dp6Xze0foqBBYAABjy3J1u3fygUf17PpISK5lAwbyVipatl6ke6Xs8YMgxUYla6jbqxwea1ZUEkrokSW1Xu6Vvi8j6CgQWAAAYslx/r+yBzbLNW9Uf90uSgpmLFa7YoGDkWM/TAUNbY9NVdSUlX1jrut2n97eeILC+AoEFAACGHGdj2UM7ZPd9JPXeliSVz2qQXfwiH8gHMtJ9u//h6z0PX0eKwAIAAEOGc4mSE82Kd78vdV2XJJkJdYpWv64xC5ervb3d84RA4aga9vCTNqsqOYHzqxBYAABgSEjOH1O88x25jkuSJDNqnMJVGxVMmy9jjOfpgMLz6rOz1Ha1W123++6tVQ8r06vPzvI4Vf4jsAAAQF5Lrl1QvPNduYsn0oVhIxSteEXBnGUyQeB3OKCALZ1fK31ben/rCXX39KuqklMEHwWBBQAA8pLr7FC8+/37d1mVlitc+pLChWtlopKv/osBZGLp/FqC6jERWAAAIK+4O92y+zbJHtqZHrkeRgoXrlW45EWZ8krf4wHAVyKwAABAXnADfbLNW2QPbJYG+iUZBXOXK1rxikzVSN/jAcAjIbAAAIBXzlolR3Yr3tso3emWJAVT5ylcvVHB6AmepwOAx0NgAQAAL5xzSk61yO56T+5WhyTJjJuqaPVGBbUzPE8HAE+GwAIAADmXtJ1Kj1y/el6SZEbUpEeuT1/AkesAhjQCCwAA5Exy85rszneUnDmULlRWK1q+QcG8FTJB6Hc4AMgAgQUAAAadu3Nbdt+Hsod2SEkiRaUKl7ygsOE5mZJS3+MBQGYILAAAMGicjWUPbpPdt0nq75WMUTBvlaIVG2SGDfc9HgBkjsACAACZc84pOdmseNe7UtcNSZKZPEfRmjcUjOFkQACFi8ACAACZSi6fVbz9F3JXz0mSzOjxitZ8Q8GUOZ4nA4DBR2ABAIBMuM4OxbveVXKqJV2oqFK08lUFc1fIBIHf4QAgRwgsAADwVFxfj+y+TbIHt0uJlaIShQ3PKVz8gkxpme/xACCnCCwAAPBEnI1lD+2Q3btJ6uuRZBTMWaZo5WsyVSN8jwcAXhBYAADgsTjnlJxpld3xjtytDkmSqZ2h6JlvKKiZ5Hk6APCLwAIAAI8suXo+PcDi8hlJkhk5VuGaNxRMnSdjjN/hACAPGOecy9WLNTY2qrGxUZL01ltvqb+/P1cvndeiKFIcx77HKCrsuR/se+6x534U4r7HnR269dHPdKd1pyQpqKxS9XPf1LClz8mE+fH/1xbivuc79twP9t2PB/e9tPThl6TnNLAe1NbW5uul80pNTY3a29t9j1FU2HM/2PfcY8/9KKR9d329sk0fy7ZslWwshZHCResULnlJpqzc93hfUEj7PlSw536w7348uO+1tbUP/br8+L+cAABAXnGJVXJ4t+I9H0i9tyVJwazFila9JlM92vN0AJC/CCwAAHCPc07JuSOyO96Wu3lNkmQm1KUHWIyb4nk6AMh/BBYAAJAkJe1t6QEWbSclSWb4GIWrX1cwfQEHWADAIyKwAAAocu52p+Jd7ys5tk+Sk8oqFC5br3DBmrw5wAIAhgp+1QQAoEi5gT7Zpk9km7dI8YAUhAoXPKNw2csy5ZW+xwOAIYnAAgCgyLgkUXJ0T3qARU+XJCmYsUjRqo0yI8Z4ng4AhjYCCwCAIpKcP6Z4x9ty1y9Lksy4KekBFhPq/A4GAAWCwAIAoAgk1y+nYXX+WLpQPUrRqo0KZjZwgAUAZIjAAgCggLmeLsW7P1BydLfknFRapnDpywoXrpWJSnyPBwAFh8ACAKAAuYF+2ZYtsk2fSAP9kgkULFijaPkGmYphvscDgIJFYAEAUECcS5Qc269493vS7VuSpGDafIVr3lAwcqzn6QCg8BFYAAAUiOTiScU7fiHX3iZJMjWTFD3zhoLamZ4nA4DiQWABADDEJTeuyu58R8nZw+nCsBGKVr2mYPYSGRP4HQ4AigyBBQDAEOXudCve+6GSQzsll0glpQqXvKhw0bMyJaW+xwOAokRgAQAwxLh4QPbgp7L7P5L6+yRjFMxfpWjFKzKV1b7HA4CiRmABADBEOOeUnDygeOe7UvdNSVIwZW56gMXo8X6HAwBIIrAAABgSkktn0gMsrp6XJJnRExQ98w0Fk2d7ngwA8HkEFgAAecx1tive+Y6S063pQmW1opWvKpizXCbgAAsAyDcEFgAAecj19sju+1C2dYeUWCkqUdjwvMIlz8uUlPkeDwDwJQgsAADyiLOxbOt22X2bpL47koyCucsVrXxVZtgI3+MBAL4GgQUAQB5wzik5fTA9wOJWhyTJTJqlaM0bCmpqPU8HAHhUBBYAAJ4lV86lB1hcPitJMiPHpScDTp0rY4zn6QAAj4PAAgDAE9d1XfHO95ScPJAulA9TtPIVBfNWygSh3+EAAE+EwAIAIMdcX6/s/o9kD34q2VgKI4WLnlW49EWZ0nLf4wEAngKBBQBAjjhrlRzepXhvo9R7W5IUzFqiaNVGmeqRfocDAGSCwAIAYJA555ScPSy78x25m9ckSWZCXXpR8LgpnqcDAGSJwAIAYBAl1y4o3vG2XNspSZIZUaNw9esK6uo5wAIAChCBBQDAIHBdNxXvfk/J8f3pQlmlwuXrFdavlgn57RcAChW/wgMAkCHX36vOj36m/p3vpwdYBKHCResULn1JpqzC93gAgEFGYAEAkAFnrZIjuxTvaVT/ZwdYzFysaPVrMtWjPU8HAMgVAgsAgKfwsAMsSqfMllv+ioLxUz1PBwDINQILAIAn9EsHWAwfo3D166pZ+YI6Ojo8TwcA8IHAAgDgMbnum4p3ffkBFpwOCADFi8ACAOARuf5e2f0fy7Zs5QALAMBDEVgAAHwNl1glh3cr3vOB9PkDLFa9JjOcAywAAPcRWAAAfImHHWBhJkxTtOYbHGABAHgoAgsAgIdIrl1UvOMXv3SARTB9AZ+xAgB8KQILAIDPefgBFi8rrF8jE/LbJgDgq/E7BQAAunuARdMnss1b7h9gsXCdwmUvypRV+h4PADBEEFgAgKLmEqvkyG7FexqlO92SpGBmw90DLMZ4ng4AMNQQWACAouScU3LuiOyOtznAAgCQGQILAFB0kvaLirffP8BCw8coWr1RwfSFHGABAHgqBBYAoGi47puKd7+v5Nh+SY4DLAAAmeN3EwBAwXN9vbJNH8u2bP3cARZrFS57iQMsAACZIrAAAAXL2Vj20E7ZfR9KvT2SpGBGg6LVHGABABgcBBYAoOA455ScalG8613p1nVJkpk4XdHq1znAAgAwqAgsAEBBSdpOKd7xtty1C5IkM3KcwtUbFUybzwEWAIBBR2ABAApCcv2K7M53lJw7ki5UVita8YqCuctlgtDvcACAokFgAQCGNHf7luI9Hyg5ukdyTiopVbj4BYUNz8mUlPoeDwBQZAgsAMCQ5Pp7ZQ9slm3eIsUDkgkU1K9WtHy9TGW17/EAAEWKwAIADCnOWiWHdyne2yj13pYkBdMXKFy1UcHIsZ6nAwAUOwILADAkOOeUnD4ou+s9uc52SZIZP03RmjcUTJjmeToAAFIEFgAg7yWXz6QnA145J0kyI2oUrn5dQV09JwMCAPIKgQUAyFvJzWuyO99VcqY1XaioUrR8g4J5K2VCTgYEAOQfAgsAkHdcT5fivR8qObxLcokUlShseF7h4udlSst8jwcAwJcisAAAecMN9Mk2b5Ft2izF/ZIxCuavUrR8g8yw4b7HAwDgaxFYAADvXGKVHNmTngzY0yVJCqbNTz9nNWqc5+kAAHh0BBYAwJt7JwPufl/u5jVJkhk3RdHq1xXUzvA8HQAAj4/AAgB4kbSdVLzzXbmr5yVJZvgYhateUzBjEScDAgCGLAILAJBTSUeb7M73lJw/mi5wMiAAoIAQWACAnHC3rive84GS402SnFRSpnDJ8woXPStTwsmAAIDCQGABAAaVu9Mtu2+T7KGdUmKlIFS4YI3CpS/JVFT5Hg8AgEwRWACAQZEeub5V9sBmaaBPklEwe6mila/IVI/2PR4AAIOCwAIAZMrZWMnh3Yr3fSjd6ZYkBVPnKly1UcGYiZ6nAwBgcBFYAIBMOJcoOdmiePf70q0OSRy5DgAoPgQWAOCpJReOp0eut1+UJJmRY9Mj1+sWcOQ6AKCoEFgAgCeWXLuQhtXFE+lC5XBFKzYomLtcJuDIdQBA8THOOZerF2tsbFRjY6Mk6a233lJ/f3+uXjqvRVGkOI59j1FU2HM/2PfcG6w9j69f0a1P/qvuHNotSTJlFape+4aGrXxZAUeu8++6J+x77rHnfrDvfjy476WlpQ/9ukcOrObmZm3btk0bN25UXV2dGhsbtWHDhqcasq2t7an++kJRU1Oj9vZ232MUFfbcD/Y997Lec9fTpXjvh0qO7JKSRAojhQvXKlzyokx5ZWavM9Tx77of7Hvused+sO9+PLjvtbW1D/26R35EcNOmTfrN3/xN/fSnP1V3d7fOnDnz1EMCAIYG198re2CzbPNWKe6XjFEwd4WiFRtkqkb6Hg8AgLzxyIFVUVGhYcOG6c0339Tf/M3f6OTJk4M5FwAgD7h4QLZ1u2zTx1JvjyQpqKtPD7AYNd7vcAAA5KFHDqxly5bd+/n3vvc9vfPOO4MyEADAP2etkqN70rusbt+SJJkJdYpWb1Qwoc7vcAAA5LGvDay//uu/1m/8xm9o5cqVX1h//fXXB20oAIAfn91lZfd8INeZPmduxkxMLwmeMocj1wEA+BrB131BRUWF/vRP/1R9fX2SpKamJv3+7//+oA8GAMgd55zsuSMa+Om/VvzhT+Q622VG1Cha/z+q5Dv/UuHUucQVAACP4Gvfwfq1X/s1bd26VX/0R3+kKIpUXl6u7373u7mYDQCQA8mlM4p3vSt3+Uy6MGy4ouUbFMxZLhNylxUAAI/jawOrpaVFH374ocrKynTjxg394Ac/+NIjCQEAQ0fS3ia76z0l54+mC+WVCpe+pLB+jUxU4nc4AACGqK8NrJ/97Gf61V/9Vc2bN0/nzp3Tn//5n+vXf/3XtXDhwlzMBwDIWHLzmuyeD5ScbE4XSkoVNjynsOE5mdJyv8MBADDEfW1g/eEf/uG9n0+dOlW/93u/px/+8If6kz/5k0EdDACQLdfdqXhvo5KjeyV395Lg+jUKl74oU1HlezwAAArCIx/T/plRo0bpD/7gDwZjFgDAIHB3bss2fSTbukOysWQCBfNWKlq+nkuCAQDI2GMHliSVlpZmPQcAIGOuv0+3Nv839e94TxpIT4INZjQoXPmKgpFjPU8HAEBheqLAAgDkLxcPyB7aIbv/Y/X33pYkmSlzFK18TcHYSZ6nAwCgsBFYAFAgnLVKju1VvPdD6XanJKl08ky5pesV1M7wPB0AAMWBwAKAIc4liZITBxTvbZRudUiSzOgJCldtVM2ydero6PA8IQAAxYPAAoAhyrlEyamDsnsa5W5elSSZETUKV2xQMLNBxgQyxnieEgCA4kJgAcAQ45xTcu6I7O735ToupYvVoxQtX69g9lKZIPQ7IAAARYzAAoAhwjknd/GE4t3vy109ny5WDle0/GUFc1fIhPySDgCAb/xuDABDQHLpdBpWl06nCxVVCpe8qLB+tUxU4nc4AABwD4EFAHksuXpe8e4P5C4cSxfKKhQufkHhwmdkSsr8DgcAAH4JgQUAeSjpuCS75wMlZw6lCyVlChueVbjoOZmycr/DAQCAL0VgAUAeSW5cld3bqORkc7oQlShcuFbh4udlyof5HQ4AAHwtAgsA8oC71aF474dKju+XnJOCUGH9GoVLX5SprPY9HgAAeEQEFgB45Lo7Fe/bpOTobilJpCBQMG+VomUvyVSN9D0eAAB4TAQWAHjgerpk938se3inZGPJGAVzlilavl5m+Bjf4wEAgCdEYAFADrne27IHNsse3CbFA5KkYEaDwhUbFIwa53k6AADwtAgsAMgB19cj27xVtuVTaaBPkhRMm69w5SsKxtR6ng4AAGSFwAKAQeT6emVbtsq2bJX6eyVJZvJsRStfVTBuiufpAABA1ggsABgErr9XtuVT2eYt98OqdqaiFa8omFjndzgAADBoCCwAyJDr75M9uC0Nq74eSZKpnaFo+QYFtTM8TwcAAAYbgQUAGXADfbKt22UPbJZ674bVhLr0HatJMz1PBwAAcoXAAoCn4Ab6ZQ/tkG36ROq9LUky46cpWvGKzKSZMsZ4nhAAAOQSgQUAT8AN9Mse3pmG1Z1uSZIZN1XRig0yk2cTVgAAFCkCCwAeg4sH7odVT5ckyYydrHDFKwqmzCGsAAAocgQWADwCFw8oObJL8f6P74dVzaQ0rKbOJawAAIAkAgsAvpKzsZIjuxXv/0i6fUuSZGpqFS7foGDafMIKAAB8AYEFAA/hbKzk6J40rLo7JUlm9IT0Hau6esIKAAA8FIEFAJ/j4oG7YfWxdPuzsBqfvmM1fYGMCfwOCAAA8hqBBQD63Gesmj65/yjg6PEKl61XMGMhYQUAAB4JgQWgqD30VMDRExQuX887VgAA4LERWACK0kPvsRozMQ2runrCCgAAPBECC0BRcQP9sq3bZZu33A+rmklpWHEqIAAAeEoEFoCi4Ab60rA6sEXqvS3p7gXByzdwjxUAAMgMgQWgoLn+XtmD22Vbtki9PZIkM25KGlZT5hBWAAAgUwQWgILk+nplD34q27JV6rsjSTLjpylavl5m8mzCCgAADAoCC0BBcX13ZFvuhlV/ryTJTKhTtHyDzKSZhBUAABhUBBaAguB6e2Rbtsoe/FTq75MkmYnT07CqnUFYAQCAnCCwAAxprve2bPNW2YPbpIG7YVU7U9Hy9QpqZ3ieDgAAFBsCC8CQ5Hq6ZA9skT20Q4r7JUlm0ixFyzcomFjndzgAAFC0CCwAQ4rruqn4wCdKjuyWbCxJMlPmKFq2XsGEaZ6nAwAAxY7AAjAkuM4OxU0fKzm2T0qsJCmoW6Bw2UsKxk72PB0AAECKwAKQ15IbV2T3faTk5AHJOckYBbMWK1z6koLRE3yPBwAA8AUEFoC8lLRfTMPq9MF0IQgUzFmucOmLCkbUeJ0NAADgyxBYAPJKcvms7P5NSs4dTRfCSMHcFYqWvCBTPcrvcAAAAF+DwALgnXNOru2U4n2b5NpOpotRicL61QobnpcZNtzvgAAAAI+IwALgjXNOyfmjsvs2yV05ly6WlilcsFbhomdlKob5HRAAAOAxEVgAcs65RMnpQ7L7N8m1t6WL5ZUKF61TuGCtTFmF3wEBAACeEIEFIGdcYmWP75fd/5HcjavpYkWVwsXPK6xfLVNS5ndAAACAp0RgARh0zsZKju/XlebNsjeupYtVIxQtflHBvBUyUYnfAQEAADJCYAEYNC4eUHJkj+IDH0vdneni8DGKlr6oYPZSmZBfggAAQGHhuxsAmXN9vbKHdsi2bJXudEuSzKhxGvn8N3V7XJ1MEHqeEAAAYHAQWAAy43q6ZFs+lT20XervkySZmkkKl76kYHq9KseOU097u+cpAQAABg+BBeCpua7rips2Kzm6R7KxJMnUzlC05EWZybNljPE8IQAAQG4QWACeWHL9smzTJ0pOHJBcIkkK6uoVLnlRwfipnqcDAADIPQILwGNLLp+VbfpYydnD6YIJFMxemobV6PF+hwMAAPCIwALwSJxzcheOK97/kdyl0+liGCmYt1LR4udkqkf7HRAAACAPEFgAvpJLEiWnD8o2fSzX3pYulpYrXPCMwkXrZCqq/A4IAACQRwgsAA/lbKzk2D7ZA5vlOu+e/FdRpbDhWYXz18iUlfsdEAAAIA8Z55zL1Ys1NjaqsbFRkvTWW2+pv78/Vy+d16IoUhzHvscoKuz5l0v6e3V7/2Z173hfSfdNSVI4skbVazaqcvE6majkif/e7Hvused+sO9+sO+5x577wb778eC+l5aWPvTrchpYD2pra/P10nmlpqZG7dwNlFPs+S9zvbdlW7bJtm6T+u5IkszoCenBFTMXZXI5MPuee+y5H+y7H+x77rHnfrDvfjy477W1tQ/9Oh4RBIqc674p27xF9vAuKR6QJJnx0xQufVHB1HncYQUAAPAYCCygSCU3r6VHrR9vkhIrSQqmzE3DauJ0r7MBAAAMVQQWUGSSaxdk93+s5HSrJCcZo2BmQ/ooYM3D3+oGAADAoyGwgCJw7w6rA5vlLp5IF4NQwdzlihY/LzOixu+AAAAABYLAAgqYS6ySky2yBz6R67iULpaUKpy/RmHDszLDhvsdEAAAoMAQWEABcgP9So7uVnxgi3T3qHVVVClc9KzC+tUyZRVe5wMAAChUBBZQQNydbtmD22Vbt0t9PZIkM6JG4eLnFcxe+lR3WAEAAODrEVhAAXCdHYqbtyg5ukey6QV4ZtxUhUteUFA3X8YEnicEAAAoDgQWMIQl1y7INm1WcrpFuntneDB1nsIlL8pMmMYdVgAAADlGYAFDzL0TAZs+kWs7mS4GoYLZS9JHAUeP9zsgAABAESOwgCHCWavkVLNs0ydy1y+niyVlCuevVrhonUzVCL8DAgAAgMAC8p0b6JM9slu2eev9EwErqxUuWqdwPicCAgAA5BMCC8hTrqdLtvWzEwHvSJLMyLH3TwQM+Z8vAABAvuE7NCDPJDeuyDZvUXJsv5RYSZIZf/dEwGmcCAgAAJDPCCwgDzjn5C6dkj2wRcm5I3dXjYK6eoUNzyuYWOdzPAAAADwiAgvwyFmr5HSL7IEtcu0X08UwUjB3ucJFzyoYOdbvgAAAAHgsBBbggevvkz2yS7bl0/sHV5QPU7jwGYX1a2QqqrzOBwAAgCdDYAE55Lo7ZQ9+Knt4l9TfK0kyI2oUNjynYM4ymajE84QAAAB4GgQWkANJR1v6+aqTB6QkkSSZidPTsJo2j4MrAAAACgSBBQwS55zcheOKm7fIXTieLhqjYEaDwsXPKRg3xe+AAAAAyByBBWTM2VjJiQOyzVvkrl9OF6NShfNWKFz0rMzw0X4HBAAAwKAhsICMuL47sod3yrZsk3pupYuV1QoXrlNYv0qmrNLvgAAAABh0BBbwlNytDtmWT2WP7pEG+iVJZtT49DHAWUtkQv5nBgAAUCz4zg94As45uctnZZu3KDlzSJKTJJlJsxQ1PCczZY6MMX6HBAAAQM4RWMBjuHcxcPNWuWsX0sUgVDBrcXoxcE2t3wEBAADgFYEFPALX1yN7eLfswW3S7c50sbxSYf2a9GLgYcP9DggAAIC8QGABX8F1titu+VTJ0b1SfPfzVSPHpu9WzV4qU1LqeUIAAADkEwILeIBzTu7SadmWrUrOHNbnP18VNjynYMpsLgYGAADAQxFYwF3OxkpOtsi2bJVrv5guBqGC2UvTd6zGTPA7IAAAAPIegYWi53p70vurDm6/f39V+TCFC+5+vqqy2u+AAAAAGDIILBSt5OY12ZZPlRzbK8UDkiQzalz6GOCsJTJRiecJAQAAMNQQWCgqzjm5tlPq+PDHGjjRfG/dTJ6jqOFZmcmzub8KAAAAT4zAQlFIP191IL2/quOSBiQpjBTMXqawYZ2CUeN9jwgAAIACQGChoLmeLtlDO2QP7ZTudKeLFVWqXrlefXWLZCqq/A4IAACAgkJgoSAl1y6kn6862SwlVpJkRk9Q2PCsgllLNHz8BLW3t3ueEgAAAIWGwELBcIlVcrpV9uA2uctn7q4aBXX1Chetk5k4g89XAQAAYFARWBjyXG+P7JFdsq3bpe7OdLG0XOG8FQoXrJUZPtrvgAAAACgaBBaGrOTGFdmWbUqO77t/zPqIGoUL1ymYu0ympMzzhAAAACg2BBaGFOcSJeeOyR78VO7C8XvrZvIchYvWKZgyW8YEHicEAABAMSOwMCS4/j4lx/bItmyTu9WRLkYlCuYsV7hwrYJR4/wOCAAAAIjAQp5znR2yrdtkj+6R+vvSxaqRCheuVThvhUxZpd8BAQAAgM8hsJB3nHNybSfTY9bPHpHkJElm4vT081V182WC0O+QAAAAwEMQWMgbLh5Qcnx/+vmq61fSxSBUMGuJwkVrFdRM8jsgAAAA8DUILHjnujtlW7fLHtkl9faki5XVCuvXKKxfLVNR5XdAAAAA4BERWPDCOSd36bRs63Ylp1sll0iSzNjJ6WOAMxfJhPzrCQAAgKGF72CRU26gT8nxJtnWbfcfAzSBghkNChetkxk/VcYYv0MCAAAAT4jAQk4kN68pad0he+xzpwFWVCmcv1ph/SqZYSP8DggAAABkgMDCoHFJouT8UdmD2+UuHLu3biZMU7jgGQXTF/IYIAAAAAoK390ic663R/boHtnWHVLX9XQxjBTMXpKGFacBAgAAoEARWMhM0n5R9uB2JSeaJBuni9WjFS5Yo3DuCplyLgUGAABAYSOw8FScjZWcPpg+Bnjl7L11M2WOwgVrFUyZIxMEHicEAAAAcofAwhNxtztlD+2SPbxTutOdLpaWK5y7XEH9GgUjx/odEAAAAPCAwMIj+9K7q0aPT9+tmr1EpqTM85QAAACAPwQWvpYb6FdyfL9s63a565fTRRMomLFI4YJnZCZO5+4qAAAAQAQWvoLrbJdt3SF7dI/U35suVlQpnL9K4fzVMlXcXQUAAAB8HoGFL3AuUXLumGzrNrnzn7u7avzU9DHAGdxdBQAAAHwZvlOGpM/dXXVoh3Trc3dXzVqc3l01drLfAQEAAIAhgMAqckl7m2zrNiUnDkjxQLpYPUph/RqF81bIlA/zOyAAAAAwhBBYRSi9u6o1fQzw8ufurpo8O323auo87q4CAAAAngCBVUTc7Vuyh3fKHt4l9XSli6VlCuesULCAu6sAAACAp0VgFTjnnNzls+ljgKcPSsndu6tGjVe48BkFs5dydxUAAACQEQKrQLmBfiUnmmQPbvvi3VXTFypc+IzMxBncXQUAAABkjMAqMK6zXfbQDtkjD9xdNW+lwvrVMlUjvc4HAAAAFDICqwA4lyg5f1xJ6zYl545JcpIkM25q+hjgjEXcXQUAAADkAN91D2Gur0f26F7Z1h3SrY50MYwUzFychhV3VwEAAAA5RWANQUlHm+zBHUpO7L9/d1XVSIULnlE4d4VMBXdXAQAAAD4QWEOEs1bJmdb00IrLZ+6tc3cVAAAAkD+Mc87l6sUaGxvV2NgoSXrrrbfU39+fq5fOa1EUKY7jh/4523VTt/dv1u39nyjp7pQkmdJyVTas1bDlL6mkZmIuRy0YX7XnGDzse+6x536w736w77nHnvvBvvvx4L6XlpY+9OtyGlgPamtr8/XSeaWmpkbt7e33/rNzTu7KWdmD25Wcbrl/d9XIcXfvrlomU8rdVU/jwT1HbrDvucee+8G++8G+5x577gf77seD+15bW/vQr+MRwTxy7+6q1u1yHZfSRWMUTF+gcMFamVrurgIAAADyGYGVB+IbVxVvf0f26B6p7066WD5M4fxVCuevlqke6XU+AAAAAI+GwPLMOaeOv/s3su3p45Jm3JT00IoZi2SiEs/TAQAAAHgcBJZnxhhVrVyvWydb07AaN8X3SAAAAACeEIGVB4Yte0F3pi7wPQYAAACAp8TFSQAAAACQEQILAAAAADJCYAEAAABARggsAAAAAMgIgQUAAAAAGSGwAAAAACAjBBYAAAAAZITAAgAAAICMEFgAAAAAkBECCwAAAAAyQmABAAAAQEYILAAAAADICIEFAAAAABkhsAAAAAAgIwQWAAAAAGSEwAIAAACAjBBYAAAAAJARAgsAAAAAMkJgAQAAAEBGCCwAAAAAyAiBBQAAAAAZIbAAAAAAICMEFgAAAABkhMACAAAAgIwQWAAAAACQEQILAAAAADJCYAEAAABARggsAAAAAMgIgQUAAAAAGSGwAAAAACAjBBYAAAAAZITAAgAAAICMEFgAAAAAkBECCwAAAAAyQmABAAAAQEYILAAAAADICIEFAAAAABkhsAAAAAAgIwQWAAAAAGSEwAIAAACAjBBYAAAAAJARAgsAAAAAMkJgAQAAAEBGCCwAAAAAyAiBBQAAAAAZIbAAAAAAICMEFgAAAABkhMACAAAAgIwQWAAAAACQEQILAAAAADJCYAEAAABARggsAAAAAMgIgQUAAAAAGTHOOed7CAAAAAAoBLyDlQd+93d/1/cIRYc994N9zz323A/23Q/2PffYcz/Ydz8edd8JLAAAAADICIEFAAAAABkhsPLAhg0bfI9QdNhzP9j33GPP/WDf/WDfc48994N99+NR951DLgAAAAAgI7yDBQAAAAAZIbAAAAAAICMEFgAAAABkhMACAAAAgIwQWAAAAACQEQILAAAAADJCYAEAAABARggsAAAAAMgIgQUAKAh//Md/rObmZknS3/7t3+pHP/qR54kAAMUo8j0AAABZ+JVf+RX93d/9nTo7O3X69Gn9zu/8ju+RAABFiHewAAAFob6+Xs45/fznP9dv/dZvKQgCXblyRX/5l3+pH/7wh77HAwAUCQILAFAQzp07p5s3byqKIlVUVEiSxo8frx/84AeeJwMAFBMCCwAw5N24cUN/8Rd/od/+7d9WeXm5mpqafI8EAChSBBYAYEjr6+vTn/3Zn+nNN9/U5MmT9Z3vfEd///d/73ssAECRMs4553sIAAAGQ1dXl37yk5+opaVFL7/8sr71rW/5HgkAUOAILAAAAADICI8IAgAAAEBGCCwAAAAAyAiBBQAAAAAZIbAAAAAAICMEFgAAAABkhMACAAAAgIwQWAAAAACQEQILAAAAADLy/wPfRPZeTks5IgAAAABJRU5ErkJggg==",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plot_2(cost_history, m, q)"
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {},
"outputs": [],
"source": [
"#m_star = 0.62595499\n",
"#q_star = 7.3662299\n",
"d = lambda i: np.sqrt((m_star-m[i])**2+(q_star-q[i])**2)"
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {},
"outputs": [],
"source": [
"def near_opt(m, min_dist=1e-1, ge_per_step=1):\n",
" dist = np.array([d(i) for i in range(len(m))])\n",
" near = np.where(dist0:\n",
" ll = np.min(near[0])\n",
" print(f\"{ll} passi e {ll*ge_per_step} gradienti calcolati per arrivare a distanza minore o uguale di {min_dist} dall'ottimo\")\n",
" else:\n",
" print(f\"in {len(m)} passi e {(len(m))*ge_per_step} gradienti calcolati non raggiunge un punto a distanza minore o uguale di {min_dist} dall'ottimo\")"
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"3767 passi e 376700 gradienti calcolati per arrivare a distanza minore o uguale di 0.1 dall'ottimo\n"
]
}
],
"source": [
"near_opt(m, min_dist=1e-1, ge_per_step=n)"
]
},
{
"cell_type": "code",
"execution_count": 31,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA7sAAAHzCAYAAADhDgreAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAABS30lEQVR4nO3de3Rb5Z3v/8+2FMeWFF9kxQ65HZoAk5AQEmpTitOGhBCyTMvQ4kkhxbPazgzDgXUYpqcsktMW2tKUUMqvLAoM7YKhUzNn2p5wW5zqDG6aEAa3DA6xJ8Q0lNAWWgIxsmwn8iWxpP37w5Zi+e7Y0t7aer/WYimWpfixHjvos5/v830M0zRNAQAAAADgIHlWDwAAAAAAgJlG2AUAAAAAOA5hFwAAAADgOIRdAAAAAIDjEHYBAAAAAI5D2AUAAAAAOA5hFwAAAADgOIRdAAAy7Oyzz1ZhYaHmzJmjkpISXXrppXr00UcVj8cnfO4f//hHGYahaDSa1jFm6usAAJAuhF0AACzw/PPP68SJE3rnnXe0bds23Xvvvfqbv/kbq4cFAIBjEHYBALBQcXGxrr76av3sZz/Tv/zLv+jQoUP6xS9+oTVr1qioqEiLFi3SN77xjeTjP/nJT0qSSkpK5PP59Jvf/EZvv/22NmzYoLKyMgUCAX3+859XZ2dn8jn33nuvFixYoDlz5ugv/uIv9Ktf/UqSFI/HtXPnTi1dulRlZWXasmWLwuHwmF8HAIBsQtgFAMAGLr74Yi1cuFD/8R//Ia/Xq5/85Cfq7OzUL37xC/3TP/2Tnn32WUnSSy+9JEnq7OxUJBLRxz/+cZmmqe3bt+vo0aP67W9/qz/96U/JgPzmm2/qoYceUlNTk06cOKEXXnhBZ599tiTpBz/4gZ599lnt27dPR48eVWlpqW655ZYxvw4AANmEsAsAgE3Mnz9f4XBYl112mS644ALl5eVp1apVuv7667Vv374xn3fOOefoiiuu0OzZszV37lx9+ctfTj7e5XLp5MmTeuONN9Tf36+zzz5bS5culSQ9+uij2rFjhxYuXKjZs2frG9/4hnbt2sU+XQCAIxB2AQCwiffee09+v1//+Z//qfXr12vu3LkqLi7Wo48+qlAoNObzjh07puuuu04LFixQUVGRbrjhhuTjzznnHD3wwAP6xje+ofLycl133XU6evSoJOmdd97RZz7zGZWUlKikpETLly+Xy+XSsWPHMvL9AgCQToRdAABsoKmpSe+9957Wrl2rrVu36uqrr9af/vQndXV16aabbpJpmpIkwzBGPPd//a//JcMw9Prrr+v48eN68sknk4+XpK1bt+rll1/WO++8I8MwdMcdd0iSFi1apP/3//6fOjs7k//19fVpwYIFo34dAACyCWEXAAALHT9+XP/3//5fXXfddbrhhht0wQUX6MSJE/L7/SooKNCrr76q//2//3fy8XPnzlVeXp5+//vfJ+87ceKEfD6fiouL9d577+m+++5Lfu7NN9/Unj17dPLkSRUUFKiwsFB5eQP/+7/pppv01a9+Ve+8844k6cMPP9Rzzz035tcBACCbEHYBALDApz/9ac2ZM0eLFi3Sjh079OUvf1lPPPGEJOmRRx7RnXfeqTlz5uhb3/qWtmzZknyex+PRV7/6VVVXV6ukpESvvPKK7rrrLh04cEDFxcW66qqr9NnPfjb5+JMnT2rbtm0KBAKaN2+e2tradM8990iS/uEf/kFXX321Nm3apDlz5uiSSy7Rf/7nf475dQAAyCaGObTOCQAAAAAAB2BlFwAAAADgOIRdAAAAAIDjEHYBAAAAAI5D2AUAAAAAOA5hFwAAAADgOIRdAAAAAIDjuK0eQCYcPXrU6iHYUiAQUCgUsnoYGIZ5sSfmxZ6YF/thTuyJebEn5sV+mBN7Gm9e5s+fP+bzWNkFAAAAADgOYRcAAAAA4DiEXQAAAACA4xB2AQAAAACOQ9gFAAAAADgOYRcAAAAA4DiEXQAAAACA4xB2AQAAAACO4870F3zkkUd04MABFRcX6/7775ck/fznP9evfvUrFRUVSZKuv/56XXTRRSOe29LSoieeeELxeFyXX365rrnmmkwOHQAAAACQJTIedi+77DJt3rxZDz/8cMr9V111la6++uoxnxePx/X444/ra1/7msrKyrR9+3ZVVlZq4cKF6R4yAAAAACDLZLyM+fzzz5fP55vy844cOaJ58+apoqJCbrdbl156qZqamtIwQgAAAABAtsv4yu5YXnjhBb300ktasmSJ/vqv/3pEIA6HwyorK0t+XFZWprfeeivTwwQAAAAAZAFbhN1NmzaptrZWkvSzn/1MP/nJT3TzzTef8d+3e/du7d69W5K0c+dOBQKBGRmn07jdbl4bG2Je7Il5sSfmxX6YE3tiXuyJebEf5sSeznRebBF2S0pKkn++/PLLde+99454jN/vV3t7e/Lj9vZ2+f3+Uf++jRs3auPGjcmPQ6HQzA3WQQKBAK+NDTEv9sS82BPzYj/MiT0xL/bEvNgPc2JP483L/Pnzx3yeLY4e6ujoSP751Vdf1aJFi0Y8ZunSpXr//ffV1tamaDSqX//616qsrMzkMAEAAAAAWSLjK7sPPPCA3njjDZ04cUI33XSTtmzZotbWVv3xj3+UYRiaO3eubrzxRkkD+3R/+MMfavv27XK5XPrSl76kHTt2KB6Pa/369aOGYgAAkHtaW5r1+gtBzeqNqL/QpwuurNGK1WusHhYAwEIZD7u33XbbiPs2bNgw6mP9fr+2b9+e/Piiiy4a9fxdAACQu1pbmvXBrnrVlpfI8HhkmjHt21UvSQReAMhhtihjBgAAOFOHGoJaV14iwzAkSYZhaF15iQ41BC0eGQDASoRdAACQ1dw9kWTQTTAMQ+6ebotGBACwA8IuAADIalGPT6ZpptxnmqaiHq9FIwIA2AFhFwAAZLWVm2q0r60zGXhN09S+tk6t3FRj8cgAAFayxTm7AAAAZyrRhOqphqDcPd2KerxaWVtHcyoAyHGEXQAAkPVWrF5DuAUApKCMGQAAAADgOIRdAAAAAIDjEHYBAAAAAI5D2AUAAAAAOA5hFwAAAADgOIRdAAAAAIDjEHYBAAAAAI7DObsAAOCMtbY06/UXgprVG1F/oU+f2HK9FnxkidXDAgCAlV0AAHBmWlua9cGuetUWxnRNmUe1hTG9/ZMfqbWl2eqhAQBA2AUAAGfmUENQ68pLZBiGJMkwDF1WUaJDDUGLRwYAAGEXAACcIXdPJBl0EwzDkLun26IRAQBwGmEXAACckajHJ9M0U+4zTVNRj9eiEQEAcBphFwAAnJGVm2q0r60zGXhN09SLxzq1clONxSMDAIBuzAAAYBzDuy1fcGWNVqxeI0nJ26cagnL3dCvq8WrtX99IN2YAgC0QdgEAwKiS3ZbLS2R4PDLNmPbtqpeklMCb+LMkBQIBhUIhS8brJONdZAAATA5lzAAAYFSjdVteV0635XQb7UinD3bVc6QTAEwRYRcAAIyKbsvW4CIDAMwMwi4AABgV3ZatwUUGAJgZhF0AADCq0bot72uj23K6cZEBAGYGYRcAAIxqxeo1mldbp6f6XHq2vVdP9bk0r7aORklpxkUGAJgZdGMGAABjGt5tGek32pFOK7nIAABTRtgFAACwGS4yAMD0UcYMAAAAAHAcwi4AAAAAwHEIuwAAAAAAxyHsAgAAAAAchwZVAAAASLvWlma9/kJQs3oj6i/06YIra2jCBSCtCLsAAABIq9aWZn2wq1615SUyPB6ZZkz7dtVLEoEXQNpQxgwAAIC0OtQQ1LryEhmGIUkyDEPrykt0qCFo8cgAOBlhFwAAAGnl7okkg26CYRhy93RbNCIAuYCwCwAAgLSKenwyTTPlPtM0FfV4LRoRgFxA2AUAAEBardxUo31tncnAa5qm9rV1auWmGotHBsDJaFAFAACAtEo0oXqqISh3T7eiHq9W1tbRnApAWhF2AQAAkHYrVq8h3ALIKMqYAQAAAACOQ9gFAAAAADgOZcwAAAAzrLWlWa+/ENSs3oj6C3264MoaSngBIMMIuwAAADOotaVZH+yqV215iQyPR6YZ075d9ZJE4M1yXMQAsgthFwAAYAYdagjq2vISGYYhSTIMQ+vKS/RUQ5BgNIpsCZBcxACyD3t2AQAAZpC7J5IMugmGYcjd023RiOwrGSALY7qmzKPawpg+2FWv1pZmq4c2wqGGoNaNchHjUEPQ4pEBGEtGV3YfeeQRHThwQMXFxbr//vslSfX19XrttdfkdrtVUVGhm2++WV6vd8Rzb7nlFhUUFCgvL08ul0s7d+7M5NABAAAmJerxyTRjKYHXNE1FPSPf3+S6bFoFd/dEZBR6Uu7jIgZgbxkNu5dddpk2b96shx9+OHnfqlWrtHXrVrlcLj355JN65plndMMNN4z6/LvuuktFRUWZGi4AAMCUrdxUo3276pOrgKZpal9bp1bW1lk9NNvJpgDJRQwg+2Q07J5//vlqa2tLue/CCy9M/vm8887TK6+8kskhAQAAB7JyH2ji6zzVEJS7p1tRj1cra+tst1JpB9kUILmIAWQfWzWo2rNnjy699NIxP79jxw5J0hVXXKGNGzdmalgAACCL2KGR0IrVawi3k5BNAZKLGED2MUzTNDP5Bdva2nTvvfcm9+wmPP3003r77bf1la98ZURTB0kKh8Py+/3q6urSt7/9bX3xi1/U+eefP+rX2L17t3bv3i1J2rlzp06dOjXz34gDuN1uRaNRq4eBYZgXe2Je7Il5sR87zMnjd27XZ/L7R6wWPnNqlv7mW/dYODLr2GFexvJfTa9q//PPyNUdUczrU+WnP6MLqy62elgZYed5yVXMiT2NNy/5+fljPy9dA5qKF198Ua+99pruvPPOUYOuJPn9fklScXGxqqqqdOTIkTHD7saNG1NWfkOh0MwP2gECgQCvjQ0xL/bEvNgT82I/dpiTaDik/jLPKPcft3xsVrHDvIxlwUeWaMGt/zPlPruOdabZeV5yFXNiT+PNy/z588d8nuVht6WlRc8995y++c1vavbs2aM+pq+vT6ZpqrCwUH19fTp48KBqa2szPFIAAJAN/hzp0c/e+q3yzZj681y6YPEiLZs315b7QAEA6ZPRsPvAAw/ojTfe0IkTJ3TTTTdpy5YteuaZZxSNRnX33XdLks4991zdeOONCofD+uEPf6jt27erq6tL3/ve9yRJsVhMa9eu1erVqzM5dAAAkAVaW5r1305165Li2QoU5Eumqb3vvqMD4RP66E3/YPXwAAAZlNGwe9ttt424b8OGDaM+1u/3a/v27ZKkiooK3XfffekcGgAAcIBDDUFde85idZ84rvc/bFNeLK6/KCvWkdmlNBICgBxjeRkzACB9rDx+BbBC4txWX1GxfEXFyfvL23stHBUAwAqEXQBwKDscvwJkWjad2woASC/CLgA41KGGoK4dPLtSkgzD0LryEj3VECTswrGmc24rlRAA4CyEXQBwqEQ551CGYcjd023RiID0S4TTpxqCcvd0K+rxamVt3YShlUoIAHAewi4AOBTlnMhVK1avmXJApRICAJwnz+oBAADSY+WmGu1r65RpmpJ0upxzU43FIwPsx90TSbkwJFEJAQDZjpVdAHCoMy3nBHIRlRAA4DyEXQBwsDMp5wRy0XQaWwEA7ImwCwBAGtHhNztQCQEAzkPYBQAgTejwm12ohAAAZ6FBFQAAaXKoIZgsi5VOd/g91BC0eGQAADgfYRcAgDShwy8AANahjBkAgDShwy+cbLz96OxVB2AHhF0AQNYb/sba95GlivzhbcvfaNPhF0413n50SexVB2ALhF0AQFYb/qb7jfff1xu7XtbmVedrTlmJpW+06fALpzrUENS1o+xHf2pwP/pYn+NnH0AmEXYBAFlt+Jvu1nf/rGsXlOmD0IeaU1xi+RttOvzCidw9ERmFnpT7Tu9HN8f5HABkDg2qAABZbXgTKHc8pjzDUF4slryPN9rAzBrYj26m3JfYjz7e5wAgkwi7AICsNvyNdTTPpbhpKu5yJe/jjTYws1ZuqtG+ts7k715yP/qmmnE/BwCZRBkzACAj0tWddXgTqBWLF+rpI2/rylXnSxJNoYA0mMx+dPaqA7AaYRcAkHbjdW6d7hvgEW+6S86St3atXvjj23K380YbSJfx9qOzVx2AHRB2AQBpN17n1pl4Q8wbawAAMBx7dgEAaTe8iZRE0ygAAJBehF0AQNrRnRUAAGQaYRcAkHZ0ZwUAAJnGnl0AQNpNpnMrkCnp6gwOALAXwi4AICOyoYkUISh97PLaTtQZ3C7jBABMH2EXAACl93ikXGen13a8zuCSbDNOAMD0sWcXAAANhKB1o4SgQ4MhCGfOTq/teJ3B7TROAMD0EXYBABDHI6WTnV7b8TqD22mcAIDpI+wCACCOR0onO72243UGt9M4AQDTR9gFAEAcj5ROdnptV6xeo3m1dXqqz6Vn23v1VJ9L8wY7g9tpnACA6aNBFQAAys7jkbKlc7DdXtuxOoPbbZwAgOkh7AIAMCgbjkdKsFOH48nIltc20+PMlgsWAJCNKGMGACAL0Tk4+yUvWBTGdE2ZR7WFMX2wq16tLc1WDw0AHIGwCwBAFqJzcPbjggUApBdlzACAGUVZZmYMdA6OpQReOgdnF3dPREahJ+U+LlgAwMxhZRcAMGMoy8wcOgdnP446AoD0IuwCAGYMZZmZM94ROsgOXLAAgPSijBkAMGMoy8wsqzscj1ayvm7jFZaNJ9tw1BEApBdhFwAwY9hHmjvGOvrov4qLteAjS6weXtaw+oIFADgZYRcAMGNWbqrRvl31yVLmZFlmbZ3VQ8uITDbnsroR2KGGoK4dpWT9F88/owW3/s+MjQMAgLEQdgEAMyaXyzLHWumUNOPffya/1ljGKll3RSIZ+fpApll9gQnA1BF2AQAzKlfLMsda6XyqITjjr0cmv9ZYxipZj3l9Gfn6QCbZ4QITgKmjGzMAADPA3RNJCX5S+ppzZfJrjWWsTsKVn/5MxsYAZAqd5oHsxMouAAAzIJPNuezQCGyskvULqy5WKBTK2DiATKDTPJCdCLsAAMyATDbnsksjsFwtWUfuscMFJgBTR9gFAGAGZLI5Vy43AgOsYJcLTACmJuNh95FHHtGBAwdUXFys+++/X5IUiUT0/e9/Xx9++KHmzp2rf/zHf5TPN7LBxYsvvqinn35akvTZz35Wl112WSaHDgDAuDK50smqKpA5XGACslPGw+5ll12mzZs36+GHH07e9+yzz+qCCy7QNddco2effVbPPvusbrjhhpTnRSIR7dq1Szt37pQkbdu2TZWVlaOGYgAAAGAmcYEJyD4Z78Z8/vnnjwioTU1NWrdunSRp3bp1ampqGvG8lpYWrVq1Sj6fTz6fT6tWrVJLS0smhgwAAAAAyDK22LPb1dWl0tJSSVJJSYm6urpGPCYcDqusrCz5sd/vVzgcHvXv2717t3bv3i1J2rlzpwKBQBpGnf3cbjevjQ0xL/bEvNgT82I/TpqT/2p6VU3PPyN39wlFvXNU9enP6MKqi60e1hlx0rw4CfNiP8yJPZ3pvNgi7A5lGMaIswOnauPGjdq4cWPyY45AGF0gEOC1sSHmxZ6YF3tiXuzHKXPS2tKsD3bV61PlJTJ8Lplmt/Y9/pA6u7Jzn6ZT5sVpmBf7YU7sabx5mT9//pjPy3gZ82iKi4vV0dEhSero6FBRUdGIx/j9frW3tyc/DofD8vv9GRsjAADIHYcagsnOu9LAxfh15SU61BC0eGQAgMmyxcpuZWWl9u3bp2uuuUb79u1TVVXViMesXr1a//Zv/6ZIJCJJ+q//+i9t3bo100MFAAAZ0NrSrNdfCGpWb0T9hT5dcGVNRldU3T0RGYWelPsMw5C7pztjYwAATE/Gw+4DDzygN954QydOnNBNN92kLVu26JprrtH3v/997dmzJ3n0kCS9/fbb+uUvf6mbbrpJPp9P1157rbZv3y5Jqq2tpRMzAAAOlCghri0vkeHxyDRj2rerXpIyFnijHp9MM5aytco0TUU93ox8fQCwC9M0p73N1CoZD7u33XbbqPffeeedI+5bunSpli5dmvx4w4YN2rBhQ7qGBgAAbOBQQ1DXjlJC/FRDMGNhd+WmGu3bVZ8sZTZNU/vaOrWyti4jXx8AMikeN9Xe2aO29m4da4/oWHtk4M+hiAoLZunrN19m9RDPiC3KmAEAABLsUEKcCNVPNQTl7ulW1OPVytrsbE6VDjNdZm512TqQC+JxU6HOHrW1R3Qs1K228OlA+2FHt2Ixc9Tnzc53Z+3qLmEXAGYIb9aAmTGZEuJM/L6tWL1mxN/J7/nMl5nboWwdcIpYLK72rl61hSI6NrhK29Y+8OfQOIFWkkqKClRR5lN5mXfEbTYGXYmwCwAzgjdrwMyZqITYqt83fs8HzHSZuR3K1oFsEovFh5Ucd0860JYWFai8zKeKMm/KbXmZV7PznRcNnfcdAYAFeLMGzJyJSoit+n3j93zATJeZ26FsHbCbRKBNBtnBsuNjoYhCHT2KxccPtMmV2YBP5f6B27l+Zwba8eTWdwsAacKbNWBmjVZCnGDV7xu/5wNmulM1na+Rq2Kx+OAe2oF9s21Dyo4nDLTFharwe1UeSF2lzcVAOx5eCQCYAbxZAzLHqt83fs8HzHSnajpfw8miiRXalDA7cNs+mUA7rNy4osynuX4PgXaSeJUAYAbwZg3InHT8vk2m8RS/5wNmqlP10Nf82Mm4Dr3broU+L52vkXWisbjaO3pG7J9tm0Sg9RcXpjaECvhU7h/4c/4sVwa/C2ci7ALADOCYEiBzZvr3bbKNp/g9P228MvPJGPGa+wu1r61T8675q5x8PWF/IwJtKKJj4YHbUGeP4hME2pQwOxhu5/oJtOlG2AWAGTLdN38AJm8mf9+m0niK3/OZQbMv2FE0Ftd7xzr15pEPRpQdjxdoDUMqKykctcsxgdZahF0AAJDTaDyVebzmsEo0Gleos3ugu/GwsuP2qQbawU7H5X6vZhFobYmwCwAAchqNpzKP1xzpFI3G9WFH94iGUG2D59CaY1QcG4ZUXuZToLRQ5X6fKgKDZ9ASaLMWYRcALDCZZjiwB+bK+Wg8lXm85piuRKBNhtlQRG3hgdv2zp5xA22g1JPaFGrwdq7fq7PmVSgUCmX2m0HaEHYBIMMm2wwH1mOuJmfoBQGXP6BzP7khq14fGk9lHq85JqM/GlMo3KNj4YjaQsOO7ZlEoB0eZivKfAr4PZrlZoU2VxB2ASDDaMySPZiriQ2/IDBrVr9+mYUXBGg8lXm85pAGAu2H4YGS4xHn0E410Aa8qvATaHEaYRcAMozGLNmDuZoYFwQATCQRaJPNoELdagsP3Ia7JhFoBxtBDT22J1BKoMXECLsAkGE0ZskezNXEuCAAQJL6+2NqC3cn980OXaWdKNDO9XtH30Nb6pXbnZfZbwSOQtgFgAyjMUv2YK4mxgUBIHckA+2wI3va2iMKd/VOGGiHn0FbEfAqUEKgRfoQdgEgw2jMkj2Yq4lxQQBwllED7WDZ8XiBNi/P0NzhXY4Hy44JtLAKYRcALEBjluzBXI1v+AUBt9+jc7ggANjaqf7EHtohx/YMlh13HJ9EoA34VOH3DtwOhtuyEg+BFrZD2AUAANMy9IJAIBCY9hmVnG0MTN+p/thAh+NwZMQe2gkDrd+TWm6cCLSlHrldBFpkD8IuAACwDc42BiYvEWgHQmzqPtqOrt4xn5cItCPOoQ0MrtASaOEQhF0AAGAbHGUEpDp5Kpp6bE97t9pCER0Ljx9oXXmGAqWJFdrUPbQEWuQKwi4AALANjjJCLkoG2lBkxNE9Hcf7xnxeItAOnEM70N04UXZcVuKRi0CLHEfYBQAAtsFRRnCqk6eiA3tohx7Xc/yU3vugY+JAO+zYnsRKLYEWGB9hFwAA2AZHGSGbJQJtssvxkNvO8QKty9DcUu/pUuMhq7RlxYUEWuAMEXYBAIBtcLYx7O7kqeiQ/bNDju4Jd08q0Cb2zVaU+XTuR+arYFZMfgItkBaEXQAAYCucbQyr9Z2Mqi2caAQV0bHQ6fLjrhPjB9pyv3fYsT2nS47z8oyUx8/EUV2YOc0HW7Vn/yGFuk/K54qrZm2V1qxaYfWwMA2EXQAAAOScvpNRtQ0pMx66Wtt14uSYz3O78kY5tmeg7NhfPDLQIjs0H2xVfeNhVaxaJ29/v+KmqfrGJkki8GYxwi4AAAAcqfdkvz5s7x5ZdjypQDvYFCrgU4V/8LaMQOtUwcb9Kl22PuXYs9JlVQo27iXsZjHCLgAAwCQ0H2xV8OUmRWJ5lDjaSO/J/pR9s0OP7TkemUSgDaSWG1eU+eQvLiTQ5phI1JDXSJ1zwzDUHeXnIJsRdgEAACaQKHEsXb5BXsOgxDHDevv6Ry03bmvvHj/QuvMG99AOKTce3EtLoMVQPrepuGmm3Geaprxuc4xnIBsQdgEAACZAiWP6jRloQ9063j1xoE3dQzvQ9bi0iECLyamprlR9Y5MqVlVLGgi6HYebVFddafHIMB2EXQAAgAlQ4jgzevv6RxzXkyg7Hi/Qzkqu0A6eP+v3JY/wIdBiJiQuWu15bZ+6IifldZuqq67kYlaWI+wCAABMIFHiaAwJvJQ4jq6nr39gVTY0sinUie5TYz4vGWgDqcf2VJR5VUKgRQasWbVCV2xYx3FQDkLYBQAgC7S2NOv1F4Ka1RtRf6FPF1xZw1m0GZQocSxdViXDMHK+xLGnrz+lEVTbkNLjCQPt8HJjAi2ANCHsAgBgc60tzfpgV71qy0tkeDwyzZj27aqXJAJvhiRKGYONe9UdNXKixLGn95SOJcNsd0r5caRn4kCbXJ0dUnZcMqeAQAsgYwi7AADY3KGGoK4tL0lpjrSuvERPNQQJuxm0ZtUKx4XblEAb6taxcERtoYFV2vECbf4sl8rLvAONoQK+lG7HBFoAdkHYBQDA5tw9ERmFnpT7DMOQu6fbohEhm3T3nlLHHz/Um0f+PKLseDKBdkSX4zKfSooKUvYvA4AdEXYBALC5qMcn04yNaI4U9XgtHBXspLv31LA9tKdvpxpoE38m0ALIdoRdAABsbuWmGu3bVa91g6XMpmlqX1unVtbWWT00ZFCk51RKI6jkbSii7t7+MZ+XP8ulBRXF8hcXDCs59qpkDoEWgHMRdgEAsLnEvtynGoJy93Qr6vFqZW0d+3UdKNJzaoxzaMcPtLPzXalNoYYc3VM8Z7bmzp3LcSoAcg5hFwCALLBi9RrCrUNEek4OrMqGRq7SThRoR9s/Wz4YaFmhnXnNB1sVfLlJkViefK64atZWOa5JGeBkhF0AAIAZZJrmYMlx94hV2okDrTt1dTbgU8Vgx+MiH4E2k5oPtqq+8bBKl2+Q1zAUN03VNzZJEoEXyBKEXQAAgClKBNqUMDsk3Pb0TRBok2fPng62FWUEWjsJNu5X6bL1KUd+lS6rUrBxL2EXyBKEXQAAgFGYpqkT3afUFo7oWCi13HiygXa0smMCbXaIRA15h82TYRjqjjJ3QLYg7AIAgJyVDLSDQXb4sT294wTagtnukWE24FO532urQNva0qy3XtqjWDik/kKfLriyhv3fk+Bzm4qb5ogjv7xu08JRAZgKW4Tdo0eP6vvf/37y47a2Nm3ZskVXXXVV8r7W1lZ997vfVXl5uSTpYx/7mGprazM+VgAAkF1SA23kdHOocPekA21yH23gdJfjOd582wTasbS2NOuDXfX67MJy9Zd5ZJox7dtVL0kE3gnUVFeqvrFJpcuqkkd+dRxuUl11pdVDAzBJtgi78+fP13333SdJisfj+vu//3tdfPHFIx63fPlybdu2LdPDAwAANpcItAMrsiPLjntPRsd8buFsd7IRVHng9P7Z8iwJtOM51BDUtYPnM0sDZbjrykv0VEOQsDuBxL7cYONedUcNed2m6qor2a8LZBFbhN2hXn/9dc2bN09z5861eigAAMBGTNPU8cjJIWfPni43nnSgHVJ2nFitzfZAOx53T0RGoSflPsMw5O7ptmhE2WXNqhWEWyCL2S7sNjY2qrq6etTP/e53v9Ptt9+u0tJS1dXVadGiRaM+bvfu3dq9e7ckaefOnQoEAmkbbzZzu928NjbEvNgT82JPzIv9THdOTNNU54levX/suN7/8LiOHutKuR2v5NhbmK+zyot0Vnmx5pcX6azyIs0vL9ZZ5UUq8hU4NtCOx+0PaNasfuUZhvLz8yUNvMZuv4ffHRvg3zD7YU7s6UznxTBN0za77KPRqP7+7/9e999/v0pKSlI+19PTo7y8PBUUFOjAgQP68Y9/rAcffHBSf+/Ro0fTMNrsFwgEFAqFrB4GhmFe7Il5sSfmxX4mMyeJFdpjQ8qMj4W61RYeWKXtG2+FtmDWkDLjwYZQgx/7PM5doT1TiT27VywsV39/v0zT1L62Ts2rraOM2Qb4N8x+mBN7Gm9e5s+fP+bzbLWy29zcrI985CMjgq4keTynS3AuuugiPf744zp+/LiKiooyOEIAADAZyUCbaAQVGhJs27t18tTYgdZTMCvZ1XhomC0v8xJopygRaJ95aY+i4eOKerxaSdAFkCNsFXbHK2Hu7OxUcXGxDMPQkSNHFI/HNWfOnAyPEAAAJJimqa4TJ5Ndjtvau9Vxol9/fj88YaD1Fs4a7GrsPX072BzK55mdwe/C+VasXqN1G69gtQpAzrFN2O3r69PBgwd14403Ju9raGiQJG3atEmvvPKKGhoa5HK5lJ+fr9tuu40ruwAApFki0Ca7HLendjk+eSo25nOTgXaUVVqfJz+D3wUAIBfZJuwWFBTon//5n1Pu27RpU/LPmzdv1ubNmzM9LADAMK0tzXr9haBm9UbUX+jTBVfWUBKZ5QaaQvWldDc+FoqoLTy5QDsQYgdWZZeefZY8+XGVE2gBABazTdgFANhfotlNbXmJDI9HphnTvl31kkTgtblkoA1161g4MuLonlP9Ywdanyc/Zd9s4na0QEtzFwCAXRB2AQCTdqghqGvLS5LbSAzD0LryEj3VECTs2oBpmuo8fnqFNrlKO8lAe3r/bGqnY2+hc1Zomw+2KvhykyKxPPlccdWsreIcVQBwKMIuAGDS3D0RGYWelPsMw5C7p9uiEeWeeDxRchwZpeR4koE24FOF36fywOlVWicF2rE0H2xVfeNhlS7fIK9hKG6aqm9skiQCLwA4EGEXADBpUY9PphlLaRBomqaiHq+Fo3KeRKAdCLGDZ9AONoX6MDyJQDvsuJ5cCrTjCTbuV+my9SmVCaXLqhRs3EvYBQAHIuwCACZt5aYa7dtVr3WDpcymaWpfW6dW1tZZPbSsE4+b6jzeq2NDm0IN3k4UaOd484cd25MItV55cjzQjicSNeQddpKDYRjqjtr7dAdKrwHgzBB2AaQdb9ScI7Ev96mGoNw93Yp6vFpZW8d+3TGMDLSDR/YMlh33R+NjPneON3/YyqxPFQGvyv0E2jPlc5uKm+aIygSv27RwVOOj9BoAzhxhF0Ba8UbNeVasXkO4HSIeN9VxvHfI3tnTZccTBdoi7+zTjaCGnENbXuaTp2BWBr+LzLHy4ldNdaXqG5tUuqwqWZnQcbhJddWVGfn6Z4LSawA4c4RdAGnFGzU4QSLQDj+u59hgoI1OFGgDQ1ZnB1dq55Z5HRtox2L1xa/E1wg27lV31JDXbaquutLW/xZla+k1ANgBYRdAWvFGDdkiHjcV7uo9XWo8pNvxhIHWNzu13HhIU6jCHAu047HDxa81q1bYOtwOl42l1wBgF4RdAGnFGzXYSSLQpjaEGig7/rBj4kCbcv6s//QtgXZyuPg1ddlYeg0AdkHYBZBWvFFDpg0E2p5kI6hj4cHbwS7H0djYgbZ4zmyV+wcbQQ3pclxe5lXhbALtdHHxa+qysfQaAOyCsAsgrXijhnRIBNo/tfXpyO+PpqzUfhjumTDQjuhyXObVXAJt2nHx68xkW+k1ANgFYRdA2vFGDWciHjfV3tmTWm48uJd24kBbcPoM2oBXFX6fygdLjgtmT+5/fa0tzXr9haBm9UbUX+jTBVfW0IV6mrj4BQDIJMIuAMAyiUCbuod24AifDzu6FYuNXd5aUlSgBRUl8henNoeaSqAdS2tLsz7YVa/a8hIZHo9MM6Z9u+olicA7TVz8AgBkCmEXAJBWsVhc7Ykux6HuwXNoB0LtZAJtasnx6dvZ+W4FAgGFQqEZH/OhhqCuLS9J6Rq8rrxETzUECbsAMAYrz9EGRkPYBQBMWywWTyk5Pn10T7dCEwTa0qKC5L7ZobeJQGsFd09ERqEn5T7DMOTu6bZkPABgd1afow2MhrALAJiUEYF2yCptqKNHsfj4gXa0Y3vm+q0LtOOJenwyzdiIrsFRj9fCUQGAfdnhHG1gOPu9wwAAWCYWiyuUCLSDpcaTDrTFharwe1UeSF2ltWugHc/KTTXat6te6wZLmU3T1L62Tq2srbN6aABgS5yjDTvKrncfAIBpiw6u0CbC7NDmUO2TCbTDyo0rynya6/dkXaAdT2Jf7lMNQbl7uhX1eLWyto79ugAwBs7Rhh05550JACApGourvaNnxP7ZtkkEWn9xYWpDqIBP5f6BP+fPcmXwu7DWitVrCLcAMEmcow07IuwCQJYaEWhDER0LD9yGOnsUnyDQpoTZwXA7159bgRYAMDM4Rxt2RNgFABuLxuIKdXSn7KFNlB2PF2gNQyorKVS536eKQGrZMYEWM2n4USPXf2qjlixeaPWwAFiAc7RhN4RdALBYNBpXqLN7oLvxsLLj9skE2tGO7fF7NYtAizQb7aiRHzU063MXd/GG16Y4BxVALiHsAkAGRKNxfZhYoW1PXaGdONB6RtlD651SoG1tadbrLwQ1qzei/kKfLriyhv2omLZRjxpZXqVg4wsEKBviHFQAuYawCwAzJBFok2E2FFFbeOC2vbNH5hhbaBOBtiLgHVF2PLd0+iu0rS3N+mBXvWrLS2R4PDLNmPbtqpckAi+mhaNGsgvnoALINYRdAJiCaDSuD8PdOhaOqC007NieCQJtoNRzenV28LZ88BzaWe70lRwfagjq2sHzYgfGYmhdeYmeaggSdjEtHDWSXbg4ASDXEHYBYJj+aEyhcE9KkO04fkp//qBj6oE24FWF36eA35PWQDsed09ERqFn2FgNuXu6LRkPnGPUo0Z+26TPpeGoEfaaTh8XJwDkGsIugJzUH43pw/DYe2gnDLSD+2aTx/ZYHGjHE/X4ZJqxEW9wox6vhaOCE4x21MiNV10+492Y2Ws6MzgHFUCumVTYjcfjampqkmEYqqysVF5eniTpN7/5jT7+8Y+ndYAAcKb6+2ODe2gHuxuHutUWHrgNd40faOf6vSnlxud+ZL4KZsU0t9Qrtzsvs9/INK3cVKN9u+q1brCU2TRN7Wvr1MraOquHBgcYftRIIBBQKBSa0a/BXtOZwTmoAHLNpMLuQw89pEAgILfbreeff1633HKL5s2bp4aGBsIuAEv198fUFu5ONoIaukI7mUA7/MieioBXgZKRgTYdb+AzJbEv96mGoNw93Yp6vFpZW8d+XWQN9prOHM5BBZBLJhV2w+Gwbr31VknS+vXr9dBDD+mv/uqv0jowAEhIBtphZ9C2tUcU7uodM9Dm5RmaWzrKsT1lowdaJ1uxeg3h1kLsN50e9ppOT/PBVu3Zf0ih7pP8/AHIKZMKu9FoVP39/Zo1a5bmzp2rbdu26YEHHtC7776b7vEByBGn+gf20KYc25NsDjWJQBvwqcLvHbgdDLdlJZ6cCrSwJ/abTh97Tc9c4uevYtU6efv7+fkDkFPGDbuxWEwul0tf+MIX1N3drZKSEklSYWGh7rjjDr388suZGCMAhzjVH1Nbe2LfbGrJ8YSB1u9JLTdOBNpSj9wuAi3si/2m08de0zPHzx+AXDZu2P3Od76j22+/Xeecc86Iz+Xl5emTn/xk2gYGIDslAu1AiE0tO+7o6h3zeYlAO/wc2orA4AotgRZZiv2mM4O9pmeGnz8AuWzcsHv22Wfr61//urZv3y6/3y9JeuONN/TTn/5U3/rWtzIyQAD2c/JUdLDkeMj+2VBEx8LjB1pXnqFAaWKFNnUPLYEWTsV+U1gp8fM3FD9/AHLFuGG3rq5ODQ0N+vrXv66tW7dqz549evfdd3X11VdnanwALJIMtKHIiE7HHcf7xnxeItAOnEM70N04UXbsJ9AiB7HfFFZK/PxVrKqWJH7+AOSUCRtUnXfeefJ4PHrwwQe1bt063XHHHcrPz8/E2ACk2clT0YE9tKN0OZ4w0A47tiexUltW4pGLQAsksd8UVkr8nO15bZ+6Iif5+ZsAndMBZxk37N5333164403dNVVV2nLli167LHHdOjQIV100UWZGh+AaUoE2mSX4yG3neMFWpehQOnQQDvYHCrgU1lxIYEWmAL2m8JKa1at0BUb1mXtWeGZQud0wHnGDbtnnXWW/vt//+/y+XySpIqKCt17771qa2vT5s2bMzJAABM7eSo6ZGV2yNE94e4JA+3cUu/pvbNDyo4JtACAXELnasB5xg27N9xwQ8rHixcv1t1336177rmHsAtkWN/JqNrCiUZQER0LnS477joxcaBNNIIa2u3YT6AFAEASnasBJ5pwz+5wfr+fTsxAmvSdjOr3f2rX7468p2PD9tGOF2jdrryUY3uGdjsuK/EoL4//UQMAMB46pwPOM+WwK0mFhYUzPQ4gZ/Se7NeH7d0jy47bI+o6cXLM5w0EWm9y32yFf/C2zCt/MYEWAIDpoHM64DxnFHYBjK/3ZP9gl+NEQ6jBsuPwxIH2rPIilZUUpJ5FO1hyTKAFACA96JwOOA9hFzhDiUA72jm0xyPjBFp3nsr93iH7Z33Jjsf+4kKVl8+lYyYAABagczrgLIRdYBy9ff3JAJtSdhzq1vHuiQPt0JXZRMfj0iJWaAEAAIB0I+wi500n0Fb4B5tBBbyDx/YMhFoCLQAAAGAtW4XdW265RQUFBcrLy5PL5dLOnTtTPm+app544gk1Nzdr9uzZuvnmm7VkyRKLRots0tPXf3rf7LCmUCe6T435vFmJkuPA6VLjisGy4xICLQAAGdN8sFXBl5sUieXJ54qrZm2Vo0qOnf79AVawVdiVpLvuuktFRUWjfq65uVkffPCBHnzwQb311lt67LHH9J3vfCfDI4Rd9fT1p+ybbRuyUjthoB1ebkygBQBgBKsCWfPBVtU3Hlbp8g3yGobipqn6xiZJckQgdPr3B1jFdmF3PPv379cnP/lJGYah8847T93d3ero6FBpaanVQ0OG9PSe0rFkmB1yG4oo0jNxoE2uzg4pOy6ZU0CgBQBgAlYGsmDjfpUuW588A9cwDJUuq1Kwca8jwqDTvz/AKrYLuzt27JAkXXHFFdq4cWPK58LhsAKBQPLjsrIyhcPhEWF39+7d2r17tyRp586dKc/BaW6325avTaTnpN5vO66jbV16v+243m/r0tG243q/7biOR/rGfF7+LJfOKi/WWeVFml9epLPKiwdvi+Qv9mZNoLXrvOQ65sWemBf7YU7saSbmZc9rh1Sxal0ykElSxapq7Xltn67YsG66QxxXv6tAntmzR9zf6yrI6p+3xLw49fvLRvwbZk9nOi+2Crt33323/H6/urq69O1vf1vz58/X+eefP+W/Z+PGjSlBmWNcRhcIBCx7bbp7T50+tmdY2fF4K7T5s1wjyo0Tt8VjrdDG+hQOjx2S7cbKecHYmBd7Yl7shzmxp5mYl1DkpLz9/SPu74qcTPucz4r16eTJkylB2zRNuWN9Wf3zlpgXp35/2Yh/w+xpvHmZP3/+mM+zVdj1+/2SpOLiYlVVVenIkSMpYdfv96d8k+3t7cnnwH66e08NC7Onb6caaBN/LikqSPkfAQAAyAyf21TcNEcEMq/bTPvXrqmuVH1jk0qXVckwDJmmqY7DTaqrrkz7184Ep39/gFVsE3b7+vpkmqYKCwvV19engwcPqra2NuUxlZWV+vd//3dVV1frrbfeksfjYb+uxSI9p1IaQSVvQxF19468+pswItAGfKrw+1Qe8KpkDoEWAMZD11ZYwcpAlvj5DjbuVXfUkNdtqq660jE/907//gCr2CbsdnV16Xvf+54kKRaLae3atVq9erUaGhokSZs2bdKaNWt04MAB3XrrrcrPz9fNN99s5ZBzRqTnVEojqLZwovx4/EA7O9810OXY702eP5tcoSXQAsAZoWsrrGJ1IFuzaoWjf8ad/v0BVrBN2K2oqNB999034v5NmzYl/2wYhv72b/82k8PKGZGekwOrsqGRq7STCbSnz6A9fRZt8ZzZBFogC7FqaG90bYWVCGQAsoltwi7SyzTNwT20p4NsV6Rf7x4NTyrQjtYQqpxACzgOq4b2F4ka8g77d9cwDHVH+bcYAIChCLsOYprm4B7a7lHLjnv6xgu07iFnz55epa0o86nIR6AFcgWrhvZnZZMgAACyCWE3yyQCbUqYHRJuJxNoE6uz55x9lgrz4wRaAEmsGtofXVsBAJgcwq4NmaapE92n1BaOpJQdJ257xwm0BbPdI0uOAwNNooYHWs4RAzAcq4b2Z3WTIAAAsgVh10LHIyeTAXb4ObSTCbTJZlCB002h5njzWaEFcMZYNcwONAkCAGBihF0L/X8/btS7R7tG/VzhbLfKAz5V+L0Dt0OaQhFoAaRLLqwa0m0aAIDcQNi10H+bXyLDMFLKjhOrtQRaAFZx8qoh3aYBAMgdhF0LffGzF1k9BADIKXSbBgAgd+RZPQAAADIlEjVGVM3QbRoAAGci7AIAcobPbco0UztL020aAABnIuwCAHJGTXWlOg43JQNvott0Dd2mAQBwHPbsAgByRmJf7k+ee0q//7BLsf6TWlpeImmZpeMCAAAzj7ALAMg5RmCxKteePkuYjswAADgPZcwAgJwy0JG5apSOzPstHhkAAJhJrOwCAHJKJGrIm6UdmZsPtir4cpMisTz5XHHVrK1iNRoAgDEQdgEAOcXnNhU3zZQjiLKhI3PzwVbVNx5W6fIN8hqG4pRfAwAwLsqYAQA5JVs7MlN+DQDA1LCyCwDIOfHQO9r/zCHFT/VpybxSfeGzV9l+dTSby68BALACYRcAkDMSpcBla2sVGOzE3HG4yephTUq2ll8DAGAVypgBADkjm0uBs7X8GgAAq7CyCwDIGdlcCpwosw427lV31JDXbaquutL25dcAAFiFsAsAyBnZXgq8ZtUKwi0AAJNEGTMAIGdQCgwAQO5gZRcAkDMoBQYAIHcQdgEAOYVSYGdqPtiq4MtNisTy5HPFVbO2inkGgBxH2AUAAFktcaRU6fIN8hqG4qap+saBI6UIvACQu9izCwAAslo2HykFAEgfwi4AAMhqkaiR0mFbyp4jpQAA6UPYBQAAWc3nNpMdthOy6UgpAEB6sGcXAACbodnS1NRUV6q+sSlZypw4UqqOI6UAIKcRdgEAsBGaLU0dR0ohWwy/kHX9pzZqyeKFVg8LcCzCLgAANjLQbGn9KM2W9hLexsGRUrC70S5k/aihWZ+7uIufXSBNCLsAANhIJGrIS7Ml2Ayl9dM36oWs5VUKNr7AawmkCWEXAAAb8blNxU0zpbswzZZgJUrrZwYXsoDMoxszAAA2UlNdqY7DTcnuwolmSzU0W4JFOMd4ZtA1HMg8VnYBALARmi3BbliRnBmjdg3/bZM+x4UsIG0IuwAA2AzNlmAnlNbPjNEuZN141eV0YwbSiLALAACAMXGO8cwZfiErEAgoFApZOCLA2Qi7AABAEh13MTpK6wFkK8IuAACg4y7GRWk9gGxEN2YAAEDHXQCA4xB2AQCAIlEjpQGRRMddAEB2o4wZAABMueMu+3sBAHZH2AWQM3hzDoxtKh13x9vfe8WGdZkeuiPx7xUATB9hF0BOoPkOML6pdNwd2N+7fpT9vXsJuzOAf68AYGYQdgHkhPHenPPmERgw2Y67kaghL/t7J3Smq7P8ewUAM8MWYTcUCunhhx9WZ2enDMPQxo0bVVNTk/KY1tZWffe731V5ebkk6WMf+5hqa2utGC6ALMSbc2DmTHV/by6azuos/14BwMywRdh1uVyqq6vTkiVL1Nvbq23btmnVqlVauHBhyuOWL1+ubdu2WTRKANmMN+fAzJnK/t5cNZ3VWf69AoCZYYujh0pLS7VkyRJJUmFhoRYsWKBwOGzxqAA4SU11pToON8k0B94sJt6c1/DmHJiyNatWqK56mfIO71XP63uVd3iv6qqXUWI7xHSOcuLfKwCYGbZY2R2qra1Nf/jDH3TOOeeM+Nzvfvc73X777SotLVVdXZ0WLVpkwQgBZKOpNN8BMLHJ7u/NVdNZneXfKwCYGYaZuGxoA319fbrrrrv02c9+Vh/72MdSPtfT06O8vDwVFBTowIED+vGPf6wHH3xw1L9n9+7d2r17tyRp586dOnXqVNrHno3cbrei0ajVw8AwzIs9MS/2xLzYD3My4NUDLfpRQ7NKlw8p9f5tk27ctEYXX7Q64+NhXuyJebEf5sSexpuX/Pz8MZ9nm7AbjUZ177336sILL9SnPvWpCR9/yy236J577lFRUdGEjz169OhMDNFxAoGAQqGQ1cPAMMyLPTEv9sS82A9zclrzwVYFG/cnV2drLFydZV7siXmxH+bEnsabl/nz54/5PFuUMZumqUcffVQLFiwYM+h2dnaquLhYhmHoyJEjisfjmjNnToZHCgAAMDmUegOAtWwRdt9880299NJLWrx4sW6//XZJ0vXXX59M75s2bdIrr7yihoYGuVwu5efn67bbbhvR+AEAAAAAAMkmYXfZsmX6+c9/Pu5jNm/erM2bN2doRAAAAJiu5oOtCr7cpEgsTz5XXDVrq1jtBpAxtgi7AAAAcJbmg62qbzys0uUb5DUMxU1T9Y1NkkTgBZARtjhnFwAAAM4SbNyv0mVVyW1nhmGodFmVgo37LR4ZgFxB2AUAAMCMi0SNEf1VDMNQd5SeKwAygzJmAACAQewxnTk+t6m4aaYEXtM05XXb4tRLADmAlV0AAACd3mMaX75B3gvWK758g+obD6v5YKvVQ8tKNdWV6jjcJNMcCLemaarjcJNqqistHhmAXMHKLgAAgBJ7TNePssd0L6u7ZyDxmgUb96o7asjrNlVXXclrCSBjCLsAAAAa2GPqZY/pjFqzagXhFoBlKGMGAADQwB7TRMltAntMASB7EXYBAADEHlMAcBrKmAEAtkAXXFiNPaYA4CyEXQCA5RJdcEuXb5DXMBQ3TdU3NkkSQQMZxR5TAHAOypgBAJYb6IJbNUoX3P0WjwwAAGQrVnYBAJajCy5w5tgCAACjI+wCACznc5uKm2ZyZVeiCy4wGWwBAICxUcYMALAcXXCBM8MWAAAYGyu7AADL0QUXODNsAQCAsRF2AQC2QBdcYOrYAgAAY6OMGQAAIEuxBQAAxsbKLgAAQJZiCwAAjI2wCwAAkMXYAgAAoyPsAgAwRZxrCgCA/RF2AQCYAs41BQAgO9CgCgCAKeBcUwAAsgNhFwCAKYhEjZRjXiTONQUAwI4IuwAATIHPbSaPeUngXFMAAOyHsAsAwBRwrikAANmBBlUAAEwB55rOHLpaAwDSibALAMAUca7p9NHVGgCQbpQxAwCAjKOrNQAg3Qi7AAAg4+hqDQBIN8IuAADIOLpaAwDSjbALAAAyjq7WAIB0o0EVAADIOLpaAwDSjbALAAAsQVdrAEA6UcYMAAAAAHAcVnYBAAAwQvPBVgVfblIkliefK66atVWsxAPIKoRdAMCk8MYXyB3NB1tV33hYpcs3yGsYipum6hubJInfewBZg7ALAJgQb3ydh4sXGE+wcb9Kl61PnoVsGIZKl1Up2LiXnxMAWYOwCwCYEG98nYWLF5hIJGrIO/j7nmAYhrqjxhjPAAD7oUEVAGBCkaiRDLoJvPHNXgMXL6pGuXix3+KRwS58bjN5BnKCaZryus0xngEA9kPYBQBMiDe+zsLFC0ykprpSHYebkr/3pmmq43CTaqorLR4ZAEweZcwAgAnVVFeqvrEpuRqYeONbxxvfrORzm4qbZkrg5eIFhkqUswcb96o7asjrNlVXXUmZO4CsQtgFAEyIN77OwsULTMaaVSv4HQeQ1Qi7AIBJ4Y2vc3DxAgCQCwi7AByLo1WAsXHxAgDgdIRdAI7E0SqAvXDxCQCQabYKuy0tLXriiScUj8d1+eWX65prrkn5fH9/vx566CH9/ve/15w5c3TbbbepvLzcmsECsDXOhQXsg4tPAAAr2CbsxuNxPf744/ra176msrIybd++XZWVlVq4cGHyMXv27JHX69UPfvADNTY26l//9V/1j//4jxaOGoBdRaKGvA47WoWVMWQrLj4BAKxgm3N2jxw5onnz5qmiokJut1uXXnqpmpqaUh6zf/9+XXbZZZKkSy65RIcOHRpx7iMASM47FzaxMhZfvkHeC9YrvnyD6hsPq/lgq9VDAybEub4AACvYJuyGw2GVlZUlPy4rK1M4HB7zMS6XSx6PRydOnMjoOAFkh5rqSnUcbkoG3sTRKjVZerTKwMpY1SgrY/stHhkwMaddfAIAZAfblDHPpN27d2v37t2SpJ07dyoQCFg8Intyu928NjbEvMyMKzasU3FJsZ75VaMi/ZJvlvT5q6p18UWrz+jvs3pe+l0F8syePeL+XldBTv+8WD0vGGm0Obn+qsv1o4ZmlS4fcq7vb5t041WXM38Zwu+KPTEv9sOc2NOZzottwq7f71d7e3vy4/b2dvn9/lEfU1ZWplgspp6eHs2ZM2fE37Vx40Zt3Lgx+XEoFErfwLNYIBDgtbEh5mXmLFm8UP/zi59Lue9MX1ur52VWrE8nT55MKQU1TVPuWF9O/7xYPS8YabQ5WbJ4oT53cZeCjS8kz/X9XHWllixeyPxlCL8r9sS82A9zYk/jzcv8+fPHfJ5twu7SpUv1/vvvq62tTX6/X7/+9a916623pjzmox/9qF588UWdd955euWVV7RixYoRe4AAwIlqqitV39iULGVOlGXXZWlZNnIP5/oCADLNNmHX5XLpS1/6knbs2KF4PK7169dr0aJF+tnPfqalS5eqsrJSGzZs0EMPPaT/8T/+h3w+n2677Tarhw0AGZEICcHGvcmVsbrqSsIDAADAGGwTdiXpoosu0kUXXZRy3+c+d7oEMT8/X1/+8pczPSwAsAVWxgAAACbPNt2YAQAAAACYKYRdAAAAAIDjEHYBAAAAAI5D2AUAAAAAOI6tGlQBAE5rPtiq4MtNisTy5HPFVbO2igZVAAAAk0TYBQAbaj7YqvrGwypdvkFew1DcNFXf2CRJBF4AAIBJoIwZAGwo2LhfpcuqZBiGJMkwDJUuq1Kwcb/FIwMAAMgOhF0AsKFI1EgG3QTDMNQdNcZ4BgAAAIaijBkAbMjnNhU3zZTAa5qmvG7TwlEB08M+dABAJrGyCwA2VFNdqY7DTTLNgXBrmqY6DjepprrS4pEBZyaxDz2+fIO8F6xXfPkG1TceVvPBVquHBgBwKFZ2AcCGEqtdwca96o4a8rpN1VVXsgqGrDWwD339KPvQ9/JzDQBIC8IuANjUmlUrCAFwjEjUkJd96ACADKKMGQAApJ3PbSbL8hPYhw4ASCfCLgAASDv2oQMAMo0yZgAAkHbsQwcAZBphFwAAZAT70AEAmUQZMwAAAADAcQi7AAAAAADHIewCAAAAAByHsAsAAAAAcBzCLgAAAADAcQi7AAAAAADHIewCAAAAAByHsAsAAAAAcBy31QMAAMBKzQdbFXy5SZFYnnyuuGrWVmnNqhVWDwsAAEwTYRcAkLOaD7aqvvGwSpdvkNcwFDdN1Tc2SRKBFwCALEcZMwAgZwUb96t0WZUMw5AkGYah0mVVCjbut3hkAABguljZhS1QRgjACpGoIe9g0E0wDEPdUWOMZwAAgGxB2IXlKCMEYBWf21TcNJMru5Jkmqa8btPCUQEAgJlA2IXlBsoI149SRriXsAsgrWqqK1Xf2JQsZTZNUx2Hm1RXXWn10CaFqhgAAMZG2IXlKCMEkGlDQ2K8M6TQvrflLZsnr9tUXXVlVgRGqmIAABgfYReWo4wQQCYND4mewdXcv6pellUhkaoYAADGRzdmWK6mulIdh5tkmgPhNlFGWJMlZYQAsotTOjBHokbKRUKJqhgAAIZiZReWS6xABBv3qjtqZFUZIYDs45StE1TFAAAwPsIubGHNqhWEWwAZ4ZSQmO3NtQAASDfCLgAgpzglJFIVAwDA+Ai7AICc4qSQSFUMAABjI+wCAHIOIREAAOejGzMAAAAAwHEIuwAAAAAAx6GMGQCAKWo+2Krgy02KxPLkc8VVs7aKsmgAAGyGsAsAwBQ0H2xVfeNhlS7fIK9hKG6aqm9skiQCLwAANkIZMwAAUxBs3J88tkiSDMNQ6bIqBRv3WzwyAAAwFGEXAIApiESNZNBNMAxD3VFjjGcAAAArEHYBAJgCn9uUaZop95mmKa/bHOMZAADACuzZBQBMiIZMp9VUV6q+sSlZymyapjoON6muutLqoQEAgCEsD7v19fV67bXX5Ha7VVFRoZtvvller3fE42655RYVFBQoLy9PLpdLO3futGC0AJB7aMiUKvE9Bxv3qjtqyOs2VVddmZOvBQAAdmZ52F21apW2bt0ql8ulJ598Us8884xuuOGGUR971113qaioKMMjBIDcNtCQaf0oDZn25mzAW7NqRc5+7wAAZAvL9+xeeOGFcrlckqTzzjtP4XDY4hEBAIaiIRMAAMhGlq/sDrVnzx5deumlY35+x44dkqQrrrhCGzduzNSwACCn+dym4qaZEnhpyAQAAOzOMIe3lEyDu+++W52dnSPuv+6661RVVSVJevrpp/X222/rK1/5yogVBEkKh8Py+/3q6urSt7/9bX3xi1/U+eefP+rX2717t3bv3i1J2rlzp06dOjVz34yDuN1uRaNRq4eBYZgXe8rleXn1QIt+1NCs0uVDGjL9tkk3blqjiy9abenYcnle7Io5sSfmxZ6YF/thTuxpvHnJz88f83kZCbsTefHFF/XLX/5Sd955p2bPnj3h43/+85+roKBAV1999aT+/qNHj053iI4UCAQUCoWsHgaGYV7sKdfnpflgq4KN+5MNmWps0pAp1+fFjpgTe2Je7Il5sR/mxJ7Gm5f58+eP+TzLy5hbWlr03HPP6Zvf/OaYQbevr0+maaqwsFB9fX06ePCgamtrMzxSAMhdNGQCAADZxvKw+/jjjysajeruu++WJJ177rm68cYbFQ6H9cMf/lDbt29XV1eXvve970mSYrGY1q5dq9WrV1s4agAAAACAnVkedn/wgx+Mer/f79f27dslSRUVFbrvvvsyOSwAAAAAQBaz/OghAAAAAABmGmEXAAAAAOA4hF0AAAAAgOMQdgEAAAAAjkPYBQAAAAA4DmEXAAAAAOA4hF0AAAAAgONYfs4uAADDNR9sVfDlJkViefK54qpZW6U1q1ZYPSwAAJBFCLsAAFtpPtiq+sbDKl2+QV7DUNw0Vd/YJEkEXgAAMGmUMQMAbCXYuF+ly6pkGIYkyTAMlS6rUrBxv8UjAwAA2YSwCwCwlUjUSAbdBMMw1B01xngGAADASIRdAICt+NymTNNMuc80TXnd5hjPAAAAGImwCwCwlZrqSnUcbkoGXtM01XG4STXVlRaPDAAAZBMaVAEAbCXRhCrYuFfdUUNet6m66kqaUwEAgCkh7AIAbGfNqhWEWwAAMC2UMQMAAAAAHIewCwAAAABwHMIuAAAAAMBxCLsAAAAAAMch7AIAAAAAHIewCwAAAABwHMIuAAAAAMBxCLsAAAAAAMch7AIAAAAAHIewCwAAAABwHMIuAAAAAMBxCLsAAAAAAMch7AIAAAAAHIewCwAAAABwHMIuAAAAAMBxDNM0TasHAQAAAADATGJlN4dt27bN6iFgFMyLPTEv9sS82A9zYk/Miz0xL/bDnNjTmc4LYRcAAAAA4DiEXQAAAACA4xB2c9jGjRutHgJGwbzYE/NiT8yL/TAn9sS82BPzYj/MiT2d6bzQoAoAAAAA4Dis7AIAAAAAHMdt9QBgD88//7zq6+v12GOPqaioyOrh5Lyf/vSn2r9/vwzDUHFxsW6++Wb5/X6rh5Xz6uvr9dprr8ntdquiokI333yzvF6v1cPKab/5zW/0f/7P/9F7772n73znO1q6dKnVQ8ppLS0teuKJJxSPx3X55ZfrmmuusXpIOe+RRx7RgQMHVFxcrPvvv9/q4UBSKBTSww8/rM7OThmGoY0bN6qmpsbqYeW8U6dO6a677lI0GlUsFtMll1yiLVu2WD0sSIrH49q2bZv8fv+UuzITdqFQKKSDBw8qEAhYPRQMuvrqq3XddddJkoLBoHbt2qUbb7zR4lFh1apV2rp1q1wul5588kk988wzuuGGG6weVk5btGiRvvKVr+hHP/qR1UPJefF4XI8//ri+9rWvqaysTNu3b1dlZaUWLlxo9dBy2mWXXabNmzfr4YcftnooGORyuVRXV6clS5aot7dX27Zt06pVq/hdsdisWbN01113qaCgQNFoVHfeeadWr16t8847z+qh5bxgMKgFCxaot7d3ys+ljBn6l3/5F33+85+XYRhWDwWDPB5P8s8nT55kbmziwgsvlMvlkiSdd955CofDFo8ICxcu1Pz5860eBiQdOXJE8+bNU0VFhdxuty699FI1NTVZPaycd/7558vn81k9DAxRWlqqJUuWSJIKCwu1YMEC/n9iA4ZhqKCgQJIUi8UUi8V4/2UD7e3tOnDggC6//PIzej4ruzmuqalJfr9fZ599ttVDwTD/9m//ppdeekkej0d33XWX1cPBMHv27NGll15q9TAA2wiHwyorK0t+XFZWprfeesvCEQH219bWpj/84Q8655xzrB4KNFChcscdd+iDDz7QlVdeqXPPPdfqIeW8H//4x7rhhhvOaFVXIuzmhLvvvludnZ0j7r/uuuv0zDPP6Gtf+1rmB4Vx56WqqkrXX3+9rr/+ej3zzDP693//d/aNZMhE8yJJTz/9tFwulz7xiU9keHS5aTJzAgDZpq+vT/fff7++8IUvpFR0wTp5eXm677771N3dre9973t69913tXjxYquHlbNee+01FRcXa8mSJWptbT2jv4OwmwO+/vWvj3r/u+++q7a2Nt1+++2SBsoE7rjjDt1zzz0qKSnJ4Ahz01jzMtwnPvEJ3XPPPYTdDJloXl588UW99tpruvPOOylvypDJ/q7AWn6/X+3t7cmP29vbaawHjCEajer+++/XJz7xCX3sYx+zejgYxuv1asWKFWppaSHsWujNN9/U/v371dzcrFOnTqm3t1cPPvigbr311kn/HYTdHLZ48WI99thjyY9vueUW3XPPPXRjtoH3339fZ511lqSBUnP2JNpDS0uLnnvuOX3zm9/U7NmzrR4OYCtLly7V+++/r7a2Nvn9fv3617+e0hsSIFeYpqlHH31UCxYs0Kc+9Smrh4NBx48fl8vlktfr1alTp3Tw4EH95V/+pdXDymlbt27V1q1bJUmtra16/vnnp/z/FcIuYEP/+q//qvfff1+GYSgQCNCJ2SYef/xxRaNR3X333ZKkc889l7mx2Kuvvqp//ud/1vHjx7Vz506dffbZ+upXv2r1sHKSy+XSl770Je3YsUPxeFzr16/XokWLrB5WznvggQf0xhtv6MSJE7rpppu0ZcsWbdiwweph5bQ333xTL730khYvXpysrrv++ut10UUXWTyy3NbR0aGHH35Y8Xhcpmnq4x//uD760Y9aPSxMk2Gapmn1IAAAAAAAmEkcPQQAAAAAcBzCLgAAAADAcQi7AAAAAADHIewCAAAAAByHsAsAAAAAcBzCLgAAAADAcQi7AABkqSeffFLf/e53kx/X19frW9/6lqLRqIWjAgDAHgi7AABkqb/8y79Ua2ur/vCHP6ihoUEtLS36yle+IrfbbfXQAACwnGGapmn1IAAAwJn5+c9/rldffVU9PT361re+pUAgoJ6eHt19993685//rB07dmjx4sVWDxMAgIxjZRcAgCz2kY98RO+++662bt2qQCAgScrPz9f27dt1ySWXWDw6AACsQ9gFACBLvfvuu3rssce0bt067d27N3m/2+1WUVGRhSMDAMB6hF0AALJQOBzWvffeq7/7u7/T3/7t3+rdd99Va2ur1cMCAMA2CLsAAGSZnp4e3XPPPbrqqqtUWVmp2bNn69Of/rR++tOfWj00AABsgwZVAAA41MMPP6xPf/rTNKgCAOQkwi4AAA50zz336I9//KMCgYCuuOIKXXbZZVYPCQCAjCLsAgAAAAAchz27AAAAAADHIewCAAAAAByHsAsAAAAAcBzCLgAAAADAcQi7AAAAAADHIewCAAAAAByHsAsAAAAAcBzCLgAAAADAcQi7AAAAAADH+f8BegkpDTe4mNwAAAAASUVORK5CYII=",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plot_ds(data,m_star,q_star)"
]
},
{
"cell_type": "code",
"execution_count": 32,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Valore della funzione loss per la soluzione: 0.0974\n"
]
}
],
"source": [
"print(f'Valore della funzione loss per la soluzione: {cost_history[-1][0]:.4f}')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Stochastic gradient descent\n",
"\n",
"Nella stochastic gradient descent, a differenza del caso precedente, la valutazione del gradiente effettuata ad ogni iterazione fa riferimento a un solo elemento $\\mathbf{x}_i$ del training set. Quindi si ha \n",
"\n",
"$$\n",
"\\theta^{(k+1)}=\\theta^{(k)}-\\eta J'(\\theta^{(k)};\\mathbf{x}_i)\n",
"$$\n",
"\n",
"e, per i singoli coefficienti,\n",
"\n",
"$$\n",
"\\theta_j^{(k+1)}=\\theta_j^{(k)}-\\eta\\frac{\\partial J(\\theta;\\mathbf{x}_i)}{\\partial\\theta_j}\\LARGE\\vert_{\\small\\theta=\\theta^{(k)}}\n",
"$$\n",
"\n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"La discesa del gradiente batch valuta il gradiente per tutti gli elementi, anche quelli simili tra loro, a ogni iterazione,\n",
"eseguendo così un insieme ridondante di operazioni. SGD risolve questo problema effettuando una sola valutazione, e quindi\n",
"operando in modo più veloce.\n",
"\n",
"Al tempo stesso, però, mentre i valori della funzione di costo nel caso di BGD decrescono con regolarità verso il minimo locale,\n",
"applicando SGD si riscontra un andamento molto più irregolare, con fluttuazione della funzione di costo intorno a un trend\n",
"complessivo di decrescita, ma con incrementi locali anche significativi. Questo da un lato può non risultare negativo, in quanto\n",
"le oscillazioni locali posso consentire di uscire dall'intorno di un minimo locale, proseguendo la ricerca di nuovi minimi. Al\n",
"tempo stesso, l'oscillazione locale rende difficile la convergenza finale verso il minimo.\n",
"\n",
"Questa oscillazione si riscontra anche nell'andamento dei valori dei coefficienti. Si noti comunque che, considerando la sequenza dei valori della funzione di costo assunti al termine di ogni *epoca* (sequenza\n",
"delle iterazioni che considerano tutti gli elementi del dataset), emerge la tendenza di decrescita di fondo. \n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"In termini di codice, il metodo stochastic gradient descent si presenta come:\n",
"\n",
"```python\n",
"for i in range(n_epochs):\n",
" np.random.shuffle(data)\n",
" for k in range(dataset_size):\n",
" g = evaluate_gradient(loss_function, theta, X[k])\n",
" theta = theta-eta*g\n",
"```\n",
"\n",
"\n",
"Nel caso della logistic regression, l'aggiornamento a ogni iterazione risulta quindi\n",
"\n",
"\\begin{align*}\n",
"\\theta_j^{(k+1)}&=\\theta_j^{(k)}+\\eta(t_i-f(\\mathbf{x}_i;\\theta^{(k)}))x_{ij}\\hspace{1cm}j=1,\\ldots,d\\\\\n",
"\\theta_0^{(k+1)}&=\\theta_0^{(k)}+\\eta(t_i-f(\\mathbf{x}_i;\\theta^{(k)}))\n",
"\\end{align*}"
]
},
{
"cell_type": "code",
"execution_count": 52,
"metadata": {},
"outputs": [],
"source": [
"def stochastic_gd(X, t, eta = 0.01, epochs = 1000):\n",
" theta = np.zeros(nfeatures+1).reshape(-1,1)\n",
" theta_history = []\n",
" cost_history = []\n",
" for j in range(epochs):\n",
" for i in range(n):\n",
" delta = - eta * gradient(theta,X[i,:].reshape(1,-1),t[i])\n",
" theta = theta + delta\n",
" #e = (t[i] - f(theta, X[i,:]))[0]\n",
" #theta = theta + eta * e * X[i,:].reshape(-1,1)\n",
" theta_history.append(theta)\n",
" cost_history.append(cost(theta, X, t))\n",
" theta_history = np.array(theta_history).reshape(-1,3)\n",
" cost_history = np.array(cost_history).reshape(-1,1)\n",
" m = -theta_history[:,1]/theta_history[:,2]\n",
" q = -theta_history[:,0]/theta_history[:,2]\n",
" return cost_history, theta_history, m, q"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Applicando il metodo è necessario ancora specificare il valore di $\\theta$ e il numero di epoche. Per la struttura dell'algoritmo, si avranno allora un numero di iterazioni pari al numero di epoche moltiplicato per la dimensione $n$ del dataset."
]
},
{
"cell_type": "code",
"execution_count": 53,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"tempo di esecuzione: 1.720 secondi\n",
"50000 passi\n",
"50000 gradienti calcolati\n"
]
}
],
"source": [
"start_time = time.time()\n",
"cost_history, theta_history, m, q = stochastic_gd(X, t, eta = 0.01, epochs = 500)\n",
"print(f\"tempo di esecuzione: {time.time()-start_time: 4.3f} secondi\")\n",
"print(f\"{len(m)} passi\")\n",
"print(f\"{len(m)} gradienti calcolati\")"
]
},
{
"cell_type": "code",
"execution_count": 54,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABQgAAAGoCAYAAAAKMwiTAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAAC7sElEQVR4nOz9d3Rc933n/z9vmUElCJIgCYINbGAnxV7VoUKJsh3GKyf22mvZXudkN5usk/PN8W/3a+/32Mk3ysb5buKyWVuOYyvuRY6sRomQqMLexN4J9g6C6MDM3PL742IGAAGQIAlw5gKvxzk+Ju69M3hfXIHlhffn8zZ83/cRERERERERERGRAclMdwEiIiIiIiIiIiKSPgoIRUREREREREREBjAFhCIiIiIiIiIiIgOYAkIREREREREREZEBTAGhiIiIiIiIiIjIAKaAUEREREREREREZACz011AT124cCHdJdyVoqIiqqqq0l2GoGeRSfQsMoeeRebQs8gc/eVZlJSUpLuEPhH2vxtmkv7y3/pAomcWLnpe4aNnFj56Zj3X3d8N1UEoIiIiIiIiIiIygCkgFBERERERERERGcAUEIqIiIiIiIiIiAxgCghFREREREREREQGMAWEIiIiIiIiIiIiA5gCQhERERERERERkQFMAaGIiIiIiIiIiMgApoBQRERERERERERkAFNAKCIiIiIiIiIiMoApIBQRERERERERERnAFBCKiIiIiIiIiIgMYAoIRUREREREREREBjAFhCIiIiIiIiIiIgOYAkIREREREREREZEBTAGhiIiIiIiIiIjIAKaAUEREREREREREZABTQCgiIiIiIiIiIjKAKSAUEREREREREREZwBQQioiIiIiIiIiIDGAKCEVERERERERERAYwBYQiIiIiIiIiIiIDmAJCERERERERERGRAUwBoYiIiIiIiIiIyACmgFBERERERERERGQAU0AoIiIiIiIiIiIygCkgFBERERERERERGcAUEIqIiIiIiIiIiAxgdroLEBEREZH+78yZM3zve9/DNE2Ki4v54z/+YwzDSJ174YUXAPjCF77A+PHj01mqiIiIyICjDkIRERER6XMlJSX81V/9FV/72tcAOHHiROrcL37xC/7sz/6ML33pS/ziF79IV4kiIiIiA5YCwgzy/oGL/O83DpBwvHSXIiIiItKrbNvu8OuioqLUx42NjRQVFTF06FAaGxvTUZ6IiIjIgKYlxhlkx4mrXLzexIXrjYwfPijd5YiIiIj0qh07dvCzn/2M4uJi8vPzU8d937/laysqKqioqADg+eef7xAwyt25MbCVzKdnFi56XuGjZxY+emZ3TwFhBok7LoA6CEVERKRfWrhwIQsXLuQHP/gBu3btYvHixZ2uSe5LeKPy8nLKy8tTH1dVVfVZnQNNUVGRvp4ho2cWLnpe4aNnFj56Zj1XUlLS5XEFhBkk3hoMxhUQioiISD+TSCSIRCIA5OTkEI1GU+fy8/O5du0ahmGQk5OTrhJFREREBiwFhBkknmjtIHQVEIqIiEj/snv3bl599VUARo0axbhx43jppZdYs2YNzz77LP/wD/8AwOc///k0VikiIiIyMCkgzBC+76c6B7XEWERERPqbRYsWsWjRog7H1qxZA8D48eP5+te/no6yRERERARNMc4YjuuT3J47uRehiIiIiIiIiIhIX1NAmCHah4JaYiwiIiIiIiIiIveKAsIM0X4wiYaUiIiIiIiIiIjIvaKAMEPEEu06CBUQioiIiIiIiIjIPaKAMEO07xrUEmMREREREREREblXFBBmiPZ7EGqJsYiIiIiIiIiI3CsKCDNEhw5CTTEWEREREREREZF7RAFhhlAHoYiIiIiIiIiIpIMCwgyhPQhFRERERERERCQdFBBmiPYdhJpiLCIiIiIiIiIi94oCwgyhDkIREREREREREUkHBYQZIp5oCwW1B6GIiIiIiIiIiNwrCggzRKzDEmNNMRYRERERERERkXtDAWGGaN81GNcSYxERERERERERuUcUEGYIDSkREREREREREZF0UECYIToMKXE8fN9PYzUiIiIiIiIiIjJQKCDMEPFEWwehDzieAkIRERERERERkXTzWxrxG2rTXUafstNdgARunFyccDwilvJbEREREREREZF08GPNuLvfw92/EYDoZ/8HhtU/o7T+eVchFL9hcnHC8SArTcWIiIiIiIiIiAxQvpPAPbgFd9d6iDUBYJbNB7P/NnIpIMwQyQ5C0wDPh7jr3uIVIiIiIiIiIiLSW3zPwzv+Ic72ddBQA4AxtBh7+TOYoyelt7g+poAwQyQDwtysCA0tCU0yFhERERERERG5B3zfxzt7BHfrWvzqS8HB7DzsRY9jTluE0Y87B5MUEGaIWOsS4/xsm4aWRKc9CUVEREREREREpHd5l8/gbH0D/+LJ4IBpYs1ajjX/UYysnPQWdw8pIMwAnu+nOgZzs4JHknAVEIqIiIiIiIiI9AWv5irutjfxTu5PHTPHTcNa9jRm4fA0VpYeCggzgNMaDkYsk6yIBaAlxiIiIiIiIiIivcxvrMPZ+Tbe4e3gB9mLUTgCe/lqzLFlaa4ufRQQZoDkcuJoxCRima3HNKRERERERERERKQ3+LEW3D3v4e7bAE4iOBjNxlr4GNaMpRiWld4C00wBYQZI7j8YtS0idhAQqoNQREREREREROTu+K6De2AL7ofvQEtTcNAwMGcsxV5YjpGdl94CM4QCwgyQ6iC0TaJ26xJj7UEoIiIiIiIiInJHfN/DO7YHZ8dbUH89ddwYPTlYTjy0OI3VZR4FhBkgnuogbL/EWAGhiIiIiIiIiMjt8H0f/+xRnG1r8a9dTB03CoYFA0jGT8cwjDRWmJkUEGaAtg5Ci2hyibE6CEVEREREREREesy7chZn6xv4FyrbDkaysOY/gjV7BYalGKw7ffqV+eEPf0hlZSUTJkzgueeeSx3/h3/4B2pqakgkEsTjcf7u7/6uL8vIePFE0EGYpT0IRURERERERERui1N9mcS6X+BV7m131MCcthB70eMYuYPSVltY9FlAWFlZSUtLC1/72td44YUXOH78OJMnTwbgv/7X/wrAtm3bqKysvMm7DAzt9yDUEmMRERERERERkVvzm+pxdr7N5cPbwXNTx43iUuwVz2AWjU5jdeHSZwHhsWPHmDNnDgCzZ8/m6NGjqYAwadu2bTz11FNdvr6iooKKigoAnn/+eYqKivqq1HvCtu1u7yF6oRGAQfm5DC0sAMC0I6G/50x1s2ch95aeRebQs8gcehaZQ89CREREJDP58RbcPR/g7v0AnHjbifxC7KVPYU6crX0Gb1OfBYSNjY2MHDkSgNzcXM6dO9fhvOM4nDlzhokTJ3b5+vLycsrLy1MfV1VV9VWp90RRUVG391BdUweA7yaItTQDUN/YFPp7zlQ3exZyb+lZZA49i8yhZ5E5+suzKCkpSXcJIiIiIr3Cdx28Q1txdr4DLY2p40Ykinnfg1hzHsCwI2msMLz6LCDMzc2lqakJgObmZnJzczucP3jwIDNmzOirTx8qXS0x1h6EIiIiIiIiIiLg+x7eib0429+CuuoO58wp8xjx5Ce5Hne7ebX0hNlXb1xWVsb+/fsB2LdvH2VlZR3Ob9u2jcWLF/fVpw+VWOuQkvZTjLUHoYiIiIiIiIgMdN65YyRe+jbO2z/vEA4aI8YS+dh/IvLIJ7AKhqSxwv6hzzoIJ06cSCQS4atf/SqlpaUUFRXx0ksvsWbNGnzf5+jRo3zuc5/rq08fKh06CFsDQsdVQCgiIiL9x7Fjx/jRj36EYRhMmjSJz372s6lzv/zlL9m+fTt5eXksXLiQ1atXp69QERERyQje1XM4W9finz/e8URuAfaSVZhT5mIYfdb3NuD0WUAI8Nxzz3X4eM2aNQAYhsH//J//sy8/dajEHXUQioiISP82fPhwvvrVrxKNRvnmN7/JmTNnGDduXOr8pz/96dSAOxERERm4/NprONvfwjuxp+MJy8aa+wDWfQ9iRLLSU1w/1qcBofRMxz0ILQASrtbOi4iISP9RWFiY+rVlWZhmx5/4/+QnP+Hll1/m05/+NKWlpfe2OBEREUk7v7kBZ+fbeIe2gtexacqcOBt76SqMQUPTVF3/p4AwAyQ7CLMiFhHbaD2mDkIRERHpf06fPk1dXR1jxoxJHXvqqad49tlnuXjxIv/0T//E1772tU6vq6iooKKiAoDnn3+eoqKie1Zzf2fbtr6eIaNnFi56XuGjZ3ZvebEWGra+RcPWN/HjsQ7nIiPHMfjxPyBrXFk3rw7omd09BYQZoH0HYTTZQaiAUERERPqZhoYGfvCDH/ClL32pw/H8/HwARo0a1e1ry8vLKS8vT31cVVXVN0UOQEVFRfp6hoyeWbjoeYWPntm94bsO3qHtOLvehuaGjidz8rEXP4FRtoB606T+Fs9Dz6znSkpKujyugDADxFNTjNuGlMQ1pERERET6Edd1+da3vsWnP/3pDsuNAZqamsjNzaWurg5X26yIiIj0a77v4Z3Yh7P9Lai71vGkaWHNXoE1/xGMaHZ6ChygFBBmgLYOQouIFQSECcfD930Mw0hnaSIiIiK9YvPmzRw/fpwf//jHAHzyk59kw4YNfO5zn+PHP/4xZ8+exfM8PvWpT6W5UhEREekr3vnjwWTiq+c6nTNLZ2AvfQpjsJYKp4MCwgyQmmIcMTFNA9s0cDwfx/VTexKKiIiIhNnKlStZuXJlh2NlZcF+Ql/84hfTUZKIiIjcI17VhSAYPHe00zljyEjs5asxx0xJQ2WSpIAwA8TadRACRGwTJ+4Sd9zUkmMRERERERERkTDx66pxtr+Fd3x355NZudiLHsOcvhjDtO55bdKRAsIMkOogbA0Do7ZFc9wloX0IRURERERERCRk/OYG3F3rcQ9uAe+G/YUNE2vmUqwF5RjZuekpUDpRQJhmXutSYgNS+w8muwY1yVhEREREREREwsJPxHH3fYC7+31IxDqdN8aUBcuJh4xIQ3VyMwoI0yw5rThim6mBJMmgUJOMRURERERERCTT+a6Ld2Q7zs63oam+03ljcBHWstWY46ZqGGuGUkCYZm3Li9vW26uDUEREREREREQyne/7eCf34257E7+2qvMF0WysBY9izVyGYSmCymR6OmkWTyQHlLQNI4kmOwgVEIqIiIiIiIhIBvIunAgmE1852/mkYWBOW4y96DGMnPx7X5zcNgWEaZbqIIx01UHodvkaEREREREREZF08K5dxN26Fu/skS7PGyUTsZc/gzls1D2uTO6GAsI0S3YJduggTAaE2oNQRERERERERDKAX1+Ns30d3rHdgN/5gkFDsZc+hTlhpvYZDCEFhGmW7CDMar8HoWW1nlNAKCIiIiIiIiLp4zc34n64HvfAZvC6WOloR7HmP4w1eyWGHbn3BUqvUECYZrEu9iDUkBIRERERERERSSc/EcfdtxF3z7sQj3V5jVm2AHvxExh5Bfe2OOl1CgjTrG2KceclxnEtMRYRERERERGRe8j3XLwjO3F2rIOm+uCgHQHHIbm02Bg5Hnv5aswRY9NXqPQqBYRp1rYHYVdDSsIXEMYSLr/bfpoFE4uYWKyfIIiIiIiIiIiEge/7eKcO4G57E7/manAwOw/woaUp+DhvMPbSVZiT5mqfwX5GAWGadTWkJGIlh5SEb4rx0Qu1bDt2hYaWhAJCERERERERkRDwLlTibF2Lf+VMcCB3EEYkC7+hBlwH7AjW3Aew5j6IEYmmtVbpGwoI0yy1xDjS1kEYDXEHYUvc6fD/IiIiIiIiIpKZvOpLuFvX4p05HBzIzsMoGIZfdw2/tgoAc/Jc7CWrMPIL01eo9DkFhGnW1R6EYZ5iHGu9nzDWLiIiIiIiIjIQ+PU1ODvW4R3dBfgQiWIWT8BvqEl1ERpFo7FXPINZXJrWWuXeUECYZvFE5z0Iw91BGASEsUT4lkeLiIiIiIiI9Gd+SxPuh+/iHtgULB02TcxxM/CdON7ZI8FFuYOwFz+BWTYfwzBv/obSbyggTLMu9yAM8RTjZAehAkIRERERERGRzOA7Cdz9G3E/fBfiLQCYpTMgmoNXuRecBJgW1pz7seY9jBHNSm/Bcs8pIEyz5BLjrHZ7EKaGlIS4g1BLjEVERERERETSy/dcvKO7cHasg8Y6AIzRkzGHj8Y9vgcaagAwJ8zEXvoURsGwNFYr6aSAMM266iBM/joZHoZJrPV+Yo6L7/saey4iIiIiIiJyj/m+j3f6IO7WN/FrrgBgFJVgTpqLd+Yw7u73gmNDi7GXP4M5elI6y5UMoIAwzbocUtK6H2EijEuMWzsIfT+ov/3eiiIiIiIiIiLSt7xLp3C2vIF/+XRwYNBQrFnL8a8HE4vBh+w87EWPY05bhGFqn0FRQJh2bR2E/WNISaxd12Ms4SogFBEREREREbkHvOuXcbeuxTt9KDiQnYd134Pgurg71kEiBqaJNWsF1vxHMbJy0luwZBQFhGnWZQdhcg/CEHYQJvcgBIglPAbp9xsRERERERGRPuM31OLsWId3dGewnM+OYs1ZiVE4HHdHBX7dNQDMcdOwlj2NWTg8zRVLJlJAmGZddRCmphiHvYMwhHsoioiIiIiIiISBH2vC3f0e7r6N4DpgmpjTl2BNmIWz+138Xe8AYBSOwF6+GnNsWZorlkymgDDNYonOHYTRfjDFGCCeUEAoIiIiIiIi0pt8J4F7YDPuh+sh1gyAOXE21pz7cY99SOL1H4DvQTQba+FjWDOWYlja/ktuTgFhmqU6CCNt36y23bbE2PN9zBBNAr5xD0IRERERERERuXu+5+Ed24WzYx001AJglEzEXvQE3tVzJN74lyAwNAzMmcuwF5ZjZOeluWoJCwWEaeR6Pq7nYxhgm20hoGkY2JaB4/o4IZoE7Hp+h67HWAg7IEVEREREREQyie/7eGcO425di3/9MgDG0GLsJavAMHDe+w1+zZXg+OjJwXLiocXpLFlCSAFhGiUHlGTZFsYNXYJR28JxHRJOeALC+A17DqqDUEREREREROTOeZdO42x9A//SqeBAfiH2oicwho/G3fI63pnDwfGCYdjLnsIcP6NTviDSEwoI0yieSA4oMTudS04yjjseYWkIbr//IHQODEVERERERETk1rzrV3C3vYl36kBwIDsXa94jWFPuw939Ls57vwLPg0gW1vxHsGavwLAU8cid0389aZQM0LrqEIy224cwLG7sGIwlwlO7iIiIiIiISLr5jbU4O97GO7IdfB/sCNbslVhz7ser3Ef8l/8LWhoBA3PawqCbMHdQusuWfkABYRolB5REuuogtMM3ybilU0CoDkIRERERERGRW/Fjzbi738PdvxGcBBgm5vTF2Asexa+9SuLVF/CvXQTAKC7FXv4M5vDRaa5a+hMFhGnU1kF4kyXGoe4gVEAoIiIiIiIi0h3fSeAe3IK7az3EmgAwJ8zCWvwEhmnibHwZ72TrMuP8QuylT2FOnK19BqXXKSBMo2QHYVak8xLjtg7C8IRsnQLCENUuIiIiIiIicq/4nod3/EOc7eugoQYAY9QE7CWrMIaMxP1wPe7eD8Bzg2XG8x7CmvMAhh1Ja93SfykgTKPYTToIo1YQGsZDtMQ4GRBGbZO444WqdhEREREREZG+5vs+3tkjuFvX4ldfAsAYOhJrySrMsWV4R3eReOtfoakeAHPKPOwlT2LkDU5n2TIAKCBMo2SA1tWQkjDuQZgMPAtyo1TVtWiJsYiIiIiIiEgr7/IZnK1v4F88GRzIL8Re9Bjm5Hn4V86S+O3/xr96DgBjxNhgn8GR49JYsQwkCgjTKJ64SQdhCKcYt8RbA8KciAJCEREREREREcCruYq7/S28yn3BgaxcrPkPY81YCi2NOOt/gXd8T3AutwB7ySrMKXMxjM5ZgUhfUUCYRjftIEwOKQljB2FOtPXj8NQuIiIifevYsWP86Ec/wjAMJk2axGc/+9nUuerqar71rW+RSCR49tlnmTNnTvoKFRER6SV+Yx3OrrfxDm0H3wPLxpq9Euu+B8G0gqnFe94LphZbNtbcB7DuexAjkpXu0mUAUkCYRqkpxpEuphiHcEhJqoMwNwgI4+ogFBERkVbDhw/nq1/9KtFolG9+85ucOXOGceOCZVP/9m//xic+8QlKS0t5/vnnFRCKiEio+fEW3D3vB0NGnAQYBua0RdgLyyG3AO/EXpytr0NDLQDmxNnYS1dhDBqa5splIFNAmEY36yBMLjGOh2iJcbJjsCA3mKqkJcYiIiKSVFhYmPq1ZVmYZtsPSM+ePcvUqVMxDIPs7GyamprIzc1NQ5UiIiJ3zncd3INbcHeth5ZGAMzSGViLn8QcMgLv6jmcip/iXzoNgFFUgr1sNWbJxHSWLQIoIEyrtoCwiw5CK4RDSuI3LjFWQCgiIiIdnT59mrq6OsaMGZM65nkehmEAkJub22VAWFFRQUVFBQDPP/88RUVF967ofs62bX09Q0bPLFz0vMLndp+Z73s0H9hG3bv/hltbBUB07BQKHvl9ssZMxm2opW79S8T2bgJ8zLxBFDy0htw5KzBM7TPYG/R9dvcUEKZRaolxVwFha1dhqALC1vsZlBPBMMBxfVzPxzKNNFcmIiIimaChoYEf/OAHfOlLX+pwPBkOAjQ3N3fZPVheXk55eXnq46qqqr4rdIApKirS1zNk9MzCRc8rfHr6zHzfxz93LJhMfO0iAMaQEViLn4Tx06lzHdx1v8b98B1IxMG0sGavwJr/CM3RbJqrq/v6VgYMfZ/1XElJSZfHFRCmUbKDMOsmS4zDOMU4K2KRZVu0JFzijktOVP+ZiYiIDHSu6/Ktb32LT3/60x2WGwOMGzeOo0ePMm7cuG4DQhERkUziXT2Hs+UN/AsnggN5g7EXPoZZNh8MA+/UAZzNr0N9EAKapTOwlz6FMVhdbpKZlNykUXKPvpstMQ7jFOPsiEXUNmlJuMQSCghFREQENm/ezPHjx/nxj38MwCc/+Uk2bNjA5z73OT760Y/y7W9/m3g8zrPPPpvmSkVERLrn11bhbHsLr3JvcCCajTXvYaxZyzHsCN61izibXsG/UAmAMWQk9vLVmGOmpLFqkVtTcpNGiZsMKWmbYhyegLBDB2HEguYEsUR46hcREZG+s3LlSlauXNnhWFlZGQDDhg3jf/yP/5GOskRERHrEb6rH2fk23uFt4Hlg2VizVmDNexAjKxe/uYHEpleD874PWbnYix7DnL4Yw+z8b36RTKOAMI1SexBGOncQtk0xDs+gj/YdhFmR4DdATTIWERERERGRsPLjMdw97+Pu/QCcOBgG5tSF2AvLMfIL8V0HZ+8HuDvfhngLGCbWrGVYC8oxsrVlhoSHAsI0it+0gzBcQ0pczyfheBhG0P2YDAjjmmQsIiIiIiIiIeO7Dt6hrTg734GWRgDM8dOxFj+JOXQkAO6Zw7ibXsVvnVxsjCnDXv405pCRaatb5E4pIEyjm+1BGA3ZHoTJIDDLtjAMI3VPLeogFBERERERkZDwfY+mA9uIv/NrqAsGjBgjx2MvWYU5qhQA7/oVnM2v4p89GpwfXIS1bDXmuKkYhpGu0kXuigLCNLp5B2G4phi333+w/f+HJeAUERERERGRgc07dwxn61quV50HwCgcjrXkSczxMzAMAz/WhLujAvfAFvC9YEDJgkexZi7DsBSvSLjpv+A0agsIu59iHJYlxsluyOxkQGhrD0IRERERERHJfN7V8zjb1uKfOwaAmV+IOf8RzKkLMEwL33NxD27D2bEOWpqCfQinL8Fe9BhGTn6aqxfpHQoI08RxPTzfxzQMbKv7ISWh6SBMdN1BGNaA0PN84o5LdlTfIiIiIiIiIv2RX3cNZ/tbeMf3BAei2Vj3PcSIh56hurYeaO0q3PwqfvVlAIySidjLV2MOK0lX2SJ9QulHmiS7B7O6mGAMbUuMwzLkI3ZDQJiczByW+m/0r+8d49iFGv7bx+eTm6VvExERERERkf7Cb27A3fUO7sGt4LlgWlizlmPNewgjOw8zkoVfexJny+t4pw4GLxo0FHvpU5gTZmqfQemXlHykSTI462r/QSDVVei4fqrTMJPdGBC2LTEORwfkjc5fayDmeFyrbyE3Sy3jIiIiIiIiYecnYrh7P8Dd8z4k4oCBWTYfe+FjGIOGBNfEW6h9+1fEt1UE4aEdxZr/MNbslRh2JL03INKHFBCmyc32HwQwDYOIZZJwPRzHIxrpOkjMFJ32IEwuMQ5pB2FyybSmMIuIiIiIiISb77p4h7fh7HwbmhsAMMdNw1r8JOaw4uAaz8M7uhNn25vEk9eULcBe/ARGXkHaahe5VxQQpklbB2HXASEEy4wTrkfczfyAsD/tQej7fqru5HRmERERERERCRff9/Eq9+FuexO/7hoAxoix2EtWYZZMTF3nXTyJs+kV/KoLAETHTMJf9CTmiLFpqVskHRQQpkk8kewg7D74i9omTbFwTDK+sYMwGXzGQ7jEOO54eH7w67B2QIqIiIiIiAxk3vnjOFvX4l89B4AxuCjoGGy3h6Bffx1nyxt4lXuDF+UNxl66iqIlj3Lt2rV0lS6SFgoI0yTVQdjNkBKAiJUc9JH5IVtbB6HZ+v/hXWLcvmswpg5CERERERGR0PCqLgTB4LmjwYHcQdgLyjGnLcQwg3+n+ok47u53g70IXQfsCNbcB7DmPogRiWoIiQxICgjTJOb0rIMQIOFmfkjV/ZCSzK/9Ru33HdQehCIiIiIiIpnPr6vG2f4W3vHdwYFoFtbch7Bmr8CIRINrfA/v2B6cbW9AYx0A5uS52EtWYeQXpqdwkQyhgDBNerIHYXKScZiWGLftQWh2OB4mLQkn9esw1i8iIiIiIjJQ+M2NuLvewT24JZg6bFpYM5dhzXsYIycvdZ135SzOxlfwr5wBwCgajb3iGczi0jRVLpJZFBCmSbxHHYRWh2szWax1r8Ebh5SEofYbtV9irA5CERERERGRzOMn4rj7NuDufg8SMcDAnDIPe9FjGIOGtl3XWIuzdS3esQ+DA7mDsBc/gVk2H8PovmFHZKBRQJgmbQHhzacYAyTczA/Zkl13bUNK+scS4zDWLyIiIiIi0l/5rot3ZAfOzgpoqgfAHDsVa8kTmMNK2q5zErh7P8D9cD04iaCzcM79QWdhNCtd5YtkLAWE94jv+x0+jieSS4xv0kEYqiXGN3YQti4xdlx83w/VJq8t8bYlxuogFBERERERST/f9/FO7sfd9iZ+bRUAxvAx2EtWYY6e1PG6yn04W16HhhoAzAkzsZc+hVEwLB2li4SCAsJ7YP+ZaravP87vLxlHQW6wOertdBCGYZluclpxsoPQMk1s08DxfBKud9MgNNOog1BERERERCRzeBcqcba+gX/lLABGwTCsxU9gTpzdoRnFqzqPs+lV/Isng+uGFmMvf6ZDgCgiXVNA2Mc8z+eNXWe4UtvCmSu1/MHKSUwdXdijISVhmmKc3Lcv2UGY/LUTc4gnQhYQxhUQioiIiIiIpJt37SLutrV4Z44EB3LysReUY05bhGG1/RvTb6oPJhgf3gH4kJ2Hvejx4DpT+wyK9IQCwj5mmgZ/9PgMfrP1DAfPVPH9isM8PKskFUJFI90HZ2HuIITg3hpjDi0Jl/ycSLpKu23tOwi1xFhEREREROTe8uuv4+xYh3f0Q8CHSBRr7oNYc1ZiRNr2D/RdB3f/JtydbweDSkwTa+YKrAWPYmTlpO8GREJIAeE9UJAb5S9+fwm/encvb+4+y/r9F1Lnsm7SWRdp/YlIpu9B6Ho+CcfDMNpCTWg/yThcIVtzuz0I1UEoIiIiIiJyb/gtjbgfrsfdvxk8NxgsMmMJ1vxHMHLy267zfbzTh3A3v4Zfdw0Ac9xUrGWrMQuHp6t8kVBTQHiPmKbBo3NGM3HkIH7y/nFqm+JA/9iDMBkAZtlWh/0fsuzkoJLMrv9GMXUQioiIiIiI3DN+Io67fyPu7nchHgPAnHwf9qLHOg0W8aovBfsMnj8OgFE4HHvZasxxU+912SL9igLCe2zCyAK+9MxsXtpyktNXGygZmtvttakpxm5mB2xd7T/Y/uOwdeG134Mw4Xi4no9lhmcKs4iIiIiISBj4not3ZCfOjgpoqgPAGDMFe8mTmEWjO17b0oizowLv4FbwPYhmYy18DGvG0g77EYrInVFAmAZ52RE+/VAZvu936Li7UbKDMNOXGCcDwOwbAsLkYJJ42ALCG+qNOy45UX2riIiIiIiI9Abf9/FOHcDd9iZ+zVUAjKLRQTA4ZkrHa10X9+AW3J0VEGsGw8CcsRR74WMYOXnpKF+kX1LqkUY3CwchPFOMk4Fa5w7C1iXGYQsI426njxUQioiIiIiI3D3v4kmcLW/gXzkTHCgYir3oCcxJszGMjltweWePBsuJa64AYIyejL18NebQ4ntdtki/p9Qjg0WscOxBGOsuIGztIAzbHoTNiWBISW6WTVPMCV3AKSIiIiIikmm86ku4W9finTkcHMjOw15Qjjl9EYbVMZrwaq7ibn6t7dqCYdjLnsIcP+OWjTYicmf6NCD84Q9/SGVlJRMmTOC5555LHW9oaOB73/se9fX1zJ49mzVr1vRlGaEVscMxxbjbgDCkexDGWjsIB+dGaYo5GlQiIiIiIiJyh/yGGpwd6/CO7gLfBzuKNfcBrDn3Y0SzOl4ba8bd9Tbu/k3geRDJwpr/CNbsFZ1CRBHpXX32HVZZWUlLSwtf+9rXeOGFFzh+/DiTJ08G4Fe/+hWf+MQnGD169C3eZWBLLjGOZ/iQku72IEwGhMkpx2HguB6O52MaBvnZESB8AaeIiIiIiEi6+S1NuLvfDcI+1wHTDPYOnP8IRu6gjtd6Ht7h7Tjb34KWRsDAnLYQe9ETna4Vkb7RZwHhsWPHmDNnDgCzZ8/m6NGjqYDw7Nmz/Pa3v+XatWv84R/+IWVlZZ1eX1FRQUVFBQDPP/88RUVFfVXqPWHb9m3fQ5MXBFQ+Rkbfv3UmmDZVWJDXoc6hhfUAGFY0o+q/2bOoa4oBwfLigvwcoJZodm5G1d+f3Mn3hfQNPYvMoWeROfQsREREbp/vJHD3b8T98F2ItwBgTpqDvehxjMGd/1z1LpwI9hm8dhEAo7gUe/kzmMPVUCRyL/VZQNjY2MjIkSMByM3N5dy5c6lzR44c4W//9m/Jz8/n7//+7/n617/e6fXl5eWUl5enPq6qquqrUu+JoqKi276HxvpmAJpbEhl9/9XXg4DQdzrWmYgF9dfWN2ZU/Td7FlfrgpqjtonhBZ2DV6trqKqK3rP6BpI7+b6QvqFnkTn0LDJHf3kWJSUl6S5BREQGAN9z8Y7uwtmxDhqDfyMaJZOwl67CHD6m8/V11ThbXsc7uT84kF+IvfQpzImztc+gSBr0WUCYm5tLU1MTAM3NzeTm5qbOlZSUMGZM8BuEaZpdvl4gklxifIdLdOua4hgGDMrp23CrbYpxx2eZ2oMwREuMkxOMc6IW2dFw7qEoIiIiIiJyr/i+j3f6EO62tfjXW6cNDxuFvWQVxpgpncI+Px7D/XA97r4NwdJjO4I17yGsOQ9g2JE03IGIQB8GhGVlZVRUVLB8+XL27dvHQw89lDo3atQorl+/Tk5ODq6r8KU7ySnGidvcg7Al4fL23nN8cPAStmnw2UemMnnU4L4oEbjZFGOzw/kwaH8vySnMGlIiIiIiIiLSmXfpFM7WN/AvnQ4ODBqKvehxzMlzMIyODSS+7+Ed/RBn21poCrajMqfMw17yJEZe3/17VUR6ps8CwokTJxKJRPjqV79KaWkpRUVFvPTSS6xZs4Znn32Wf/zHfyQej/Pxj3+8r0oIvehtTjH2fJ8PK6t4becZ6psTALiez/crDvOpB6Ywe/zQPqmzu4AwGsIpxs2tHYTZUZssdRCKiIiIiIh04l2/jLvtTbxTB4MD2XnBtOEZS7qcNuxdOo2z6RX8q8HWY8aIscE+gyPH3cuyReQm+nRO+HPPPdfh4zVr1gAwZswY/p//5//py0/dL9hW0IrteD6e52OaXe/D4LgelZfreWv3WU5fbQBgXFE+H108nl2VVWw8fJl/fe8ov790IkvKRvR6nbFEEGB2P8U4s6cwt9eScIDgXpL3ow5CERERERER8BtqcXauwzuyE3w/WB48536suQ9gRLO7uL4GZ+tavOO7gwO5BdhLnsSccl+nDkMRSa8+DQjl7hiGQcQ2STgeCdcjywwCK9fzOXetgROX6jh+sY6TV+pwXB+A/OwITy8Yx/xJRZiGwdiifHKzIqzbc45fb66kKZbgoVklvbrpazJU67zEOHwdeO33IEztoRgPT/0iIiIiIiK9zY814e5+D3ffxmDfQMPEnLEEe8GjGLmDOl+fiOPueR93z3vgJMCygyBx3kMYkax7fwMicksKCDNc1AoCwvPVjVysbuLoxVoqL9V16morHpLLzLFDeGjmKLKjbY/VMAwev28Medk2L289xeu7zhJ3PJ6YN7bXakx1EEZv7CBs3YMwTENKWr+u2RFbHYQiIiK9qLq6mr/927/l3LlzvPjii1hW298bvvOd73D+/Hmi0Sjl5eWsXLkyjZWKiEiS7yRwD2zG/XA9xJoBMCfOxlr0OGbh8M7X+z7eib04W1+HhtrU9fbSVRiD+mbLKxHpHQoIM1zENiEG/7T2YIfjRQXZTC4uYPKowUwqLiA/++bTnlZMKyY3avOzDcd5Z995Hpg5ipxo7zz+1B6Edv/pIMxq30EYovpFREQyVX5+Pl/5ylf4xje+0eX5P/3TP6W4uPgeVyUiIl3xPQ/v2C6cHetSQZ9RMhF7ySrMEV03m3hXzwX7DLYOLDGGjQr2GSyZeM/qFpE7p4Aww40szKGmMU5ets2UUYMpGzWYyaMGMyT/9tuy500sYsvRy1RerufohVrmlg7rlRpbuhlSErFNDMBxfVzPx+pmD8VM0tZBqD0IRUREelM0GiUajXZ5zjAMvv3tb5Ofn8/nP/95hg/v3JUiIiJ9z/d9vDOHcbeuxb9+GQBjaDH2klUYY8u63KrKb6rH2bYW78guwIec/GCS8dSFGKb2GRQJCwWEGe4zD5ZR2xxn2KBszF7YN3Da6EIqL9dz+FxNrwWEsXahWnuGYRCNWMQSLnHH7bWOxb7UEg/2U8zpBx2Enudz8Nx1JowYRN4tOkxFRETS6TOf+Qz5+fkcPnyYF198kb/4i7/odE1FRQUVFRUAPP/88xQVFd3rMvst27b19QwZPbNwCcvzip8/Qe07v8E5cxQAa/AwCh78GDmzlnQ5UMR3EjRsW0f9xtfw4zEwLfIXlzNoxdOY2bn3uvxeFZZnJm30zO5e5ic2A1w0YjE8ktNr7zd9zBBe33WWw+dr8Hz/rkNH1/NJuB6G0boc+gZZtkks4RJLhCQg7KKDMKwB4ZELNfxo/VGWlI3g48vU1i8iIpkrPz8fgGnTpvGTn/yky2vKy8spLy9PfVxVVXVPahsIioqK9PUMGT2zcMn05+Vdv4K77U28UweCA9m5WPMewZq5lCbLpuladYfrfd/HO3UAZ/PrUB+cM8dPx1r2NInBRVQ3NEFD072+jV6V6c9MOtMz67mSkpIuj2d+YiO9amRhDoV5UWoa45y/1sjYovy7er/2+w921W6eFbGgOUHc8e7q89wrqeXSUZusaLiXGNc0xgGobf1/ERGRTNXU1ERubi4XLlwgLy8v3eWIiAwIfmMdzo4KvCM7wPfAjmDNXok190GMrOwuX+NduxjsM3ihEgBjyEjs5asxx0y5l6WLSB9QQDjAGIbBtNGFbDl6hcPna3ovILxheXFS2JbpJoeU5EQsbNPANAxcz8dxPWwrXPtnNLcul07+v4iISDo5jsPf/M3fcPr0af76r/+aj3/84xw+fJg1a9bwzW9+k8bGRgzD4Atf+EK6SxUR6df8WAvunvdw920AJwGGiTl9MfaCcoy8gq5f09yAs30d3uFt4PuQlYu98DHMGYsxzK7/LSgi4aKAcACaPmZIEBCeq+GxuWPu6r26238wKdq67Dg8AWEQpmVHg47I7KhFU8whlnBDGxCGtQNSRET6F9u2+cpXvtLh2IwZMwD48pe/nI6SREQGFN91cA9sxt21HmLBEmBzwkysRU9gDhlx89fsfBviLWCYWLOWYS0oxwj5PoMi0pECwgFocnEBlmlwtqqBhpYE+XcxwKK7CcZJoesgvCHwzIoEAWFLwg3doI/m1m7IsHztRURERESk9/meh3d8N872t6ChBgBj1ATsJaswR47r9nXumcO4m17Frw32dTPGlGEvfxpzyMh7UbaI3GMKCAegaMRiUnEBRy/UcuR8DQsmDb/j97rlEmM7OB6GPQg9zyfueBgEXyNou68wduEluyGTy6ZFRERERGTg8H0fd8/7uFvfSB0zho7EWrwKc9zULveQh2BoibP5VfyzwTRjY3AR1rLVN32NiISfAsIBatroQo5eqOXwuT4OCEMUsLXvhkxOdw7zJOP2HYS9MbFaRERERETCwa3ch7Ou41R4+6F/hzllHobZ9dZJfqwJd8fbuAc3g+dBNBtrwaNYM5dhWIoORPo7fZcPUNPHDOF3209z5EINrudjmXcWHt1yD8JI8IdP3Mn8gK0l0bb/YFK4A8LgfnyC+nOi+nYXEREREenPvEunSbz8T52ORz/zf2PkdD2g0vdcvEPbcHasg5YmMAzM6UuwFz3W7WtEpP9RYjBAFRVkU1SQTVVdC2eqGpgwYtAtX1NV10J+TqRDGNif9iBMLsVtf39ZrQFnGJfpNreruSWugFBEREREpL/ya68R//nfdToeWfUc5rip3b7OO3ccZ/Mr+NWXATBKJmIvX405rKTPahWRzKTEYACbNrqQDXWXOHzu+i0DwvcPXOSVHaeZMmowX3x8eur4rToIk3sQxhKZvwdhKiBsF6RlRYJfx0LQAXmjZAchhGOJt4iIiIiI3B6/pYn4L/4eWho7HLfmPYy18LHulxPXVuFseR3v1MHgwKCh2EufwpwwU/sMigxQCggHsGmjC9lw6BKHztWwan7X06s83+e1HWd4/+BFAI5drKWmMUZhXhbQvoOw6z94onZwPAwB240TjNv/OmwdhL7vd6i5pV1YKCIiIiIi4eY7CRKvfR//0ukOx40R44g8+ZnulxPHW3B3rcfdtwE8F+wo1vyHsWavxLAj96J0EclQCggHsEnFBURsk4vXm6htjDM4L9rhvON6/HLjCT48eQ3TMBg2KIurdS3sOVXNgzNHAT0fUhIPQQdbVwFhmJZIt5dwPVzPT32sDkIRERERkfDzfQ/n/ZfwDu/odC7y0T/GLB7f9es8D+/oTpxtb0JzAwBm2QLsxU9g5BX0ac0iEg4KCAcw2zKZMmowB89e5/D5GpaUjUida4k7vPjuMY5drCXLNvn0Q2W0JFx+/N4x9pysuu2AMBxLjDsPKQlrQNh8Q8dj2DogRURERESkje/7uLvfw922ttM5e8UzmDOWYphd/5vMu3gSZ9Or+FXnATBGjsNe/gzmiLF9WrOIhIsCwgFu2uhCDp69zjv7znPw7HXirkvC8ahpjFPbFCc/O8Lny6cxZlgeccclapucvdbItfoWhg3KTgV/3e5BmAzYwrTEuIspxmHrwLtxSXGzlhiLiIiIiISSe2IvTsVPOx03p8zDXvoURm7X+8n79ddxtryBV7k3OJA3GHvJKszJc7XPoIh0ooBwgJs+phDTMKhuiFHdEOtwrqggmy+UT2PYoGwAorbFjLFD2H3yGntOXeOR2aNpSQTBU7cdhMk9CEMQsLVNMW77tkiGhWGov72mGzsIQ1a/iIiIiMhA5106TeLlf+p03BhchP3gxzFHlXb5Oj8Rx939Lu6e98F1wI5gzX0Aa+6DGJFol68REVFAOMAV5mXxJ0/N5Fp9CxHLJGKbRGyLqGUysjAH2+o4fGRu6TB2n7zG7pNBQJjqIIzeYg/CMHUQtt+DsDXgDFvAdmMHoZYYi4iIiIiEg197jfjP/67Lc9byZ7Bmdr2c2Pc9vGN7cLa9AY11AJiT5mIvWYUxqLAvSxaRfkABoTC2KJ+xRV1PubrRtNGFZEcsLl5v4kptc9sehHbXAWHUDvkehNHgWyRsHYSd9iAMWf0iIiIiIgON39JI/Od/D7GmTudutZzYu3IWZ+Mr+FfOAGAUjQ72Jiwu7cuSRaQfUUAot8W2TGaOG8LOE1XsPnktFTxl3aKDMAwBW1cdhGHdgzC552BWxCKWcDt1FIqIiIiISGbwXYfEKy/gXz7d6ZwxtBh7xUcwSyZ2/drGWpyta/GOfRgcyB2EvegJzKnzMQyzy9eIiHRFAaHctvsmFLHzRBV7Tl1LBX/Z3XQQZkWCP5Tijovv+xm9GW5qD8Jo27dFsv4wBJztJe9lSF6USzXNoQs4RURERET6O9/3cN79Dd7RnZ1PRrKwFj6GNWtZ18uJnQTu3g9wP1wPTgJMC2vO/VjzHsaIZt2D6kWkv1FAKLdtyqgCcrNsrtQ2A2AYELG7/umUZZrYpoHj+TiuT8TO4ICwyynGYV1iHHQMDsnPCgJC7UEoIiIiIpIxnA/fxd22tstz5uT7guXEeQWdzvm+j1e5D2fL69BQE1xfOhN72VMYBcP6smQR6ed61HP8iU98gk2bNqU+3rVrF3/2Z3/WZ0VJZrNMk9njhqY+zrKtm3YGRpPLjDN8UElqD8L2Q0oibUNKfN9PS113IhkQFuYFPz1sDlnAKSIiIiLSH7nH9xD77pe7DAeNISOJPPNFIo/+QZfhoFd1nsQr38Op+Ck01GAMLSay+j8SeeLTCgdF5K7dtIOwqqqKK1euAHDu3DkOHjwIwO7du7l8+XLfVycZ674Jw9h6LPhvIyvS9fLipKyIRVPMIZZwyc+O3Ivy7khXexBapoltGTiuT8LxUmFnpksOKRmaHwSE2oNQRERERCR9vEunSLz8f7o+GYkGy4lnLsewulhO3FSPs/0tvMM7AB+y87AXPY45bRGGqX0GRaR33DQgXL9+Pb/+9a8B+M1vfsNvfvOb1LnRo0f3bWWS0SaOLCA/O0JDS6JDoNaVLDvz9/Hzfb/LJcYQLDNucBO0OG6IAsK2JcaAlhiLiIiIiPQx3/fxa65iFAzFsIJ/avu1VZz/7pe7fc1NlxO7Du7+Tbg734ZEDEwTa+YKrAWPYmTl9Nl9iMjAdNOAcPLkyTz++OO89dZbzJkzh1GjRgGQn5/PypUr70mBkplM02Bu6VA2Hr7cow5CgJjj3fbncT2fK7XNFBfm9OmAk5jj4fvBXorWDT+Fy45YNLQkiMVdCMmfw8lAsDAvCgThrOf7mBk8JEZEREREJKy8y2dwtryOf+kU1pwHsOY9SPxnfwfxli6vN4aMwF75UcySSZ3O+b6Pd/oQ7ubX8OuuAWCOm4q1bDVm4fA+vQ8RGbhuGhDOmzePefPmMWnSJGbOnMnw4cFvRp7nYaqVecBbOHkEW45eoXhI7k2vi7ZOOI7fZgdhVV0LP/3gGGerGpk/sYhPrJzUZwFXLN55eXFS+30IwyLZQZibZZNlm8Qcj3jC7TChWURERERE7o5fW4Wz7U28yn3BAcvG3fs+7t73u35BJIq1oBxr1ooulxN71ZdxNr+Kf+4YAEbhcOxlqzHHTe2rWxARAXo4xfjs2bNcuXKF8vJy/vt//+/U1dXx+c9/nkceeaSv65MMNmZYHl9ecx95t9hXMNVB2MOAzfd9dhy/yr9tO0W8tetwV2UVUdtkzdIJfdJJ2JLoPKAk6XbrzwTJPQhzojZZEYuY49GigFBEREREpFf4zQ04O9/GO7QVvHYrpdzu9/42J80Npg3nDe78fi2NODsq8A5uBd+DaHawL+GMpV0GiSIiva1HacGGDRv4yEc+wsaNG3Ech1GjRvHSSy8pIJTUlNybSXbg9WSKcVPM4TebK9l7uhqAuaVDmVtaxE/fP8aWo1fIilg8vWBcr4eEyUDtxv0HIdiDEMLTQej7foeJzNlRm7rmRLDsOC/NxYmIiIiIhJifiOPu24C7+71gX8AesIcVYyxbjTl6cuf3c128Q1twdlRArBkMA3PGUuyFj2Hk6C/vInLv9CggbGhoYNCgQezevZsHHniA8ePH893vfreva5N+IrnEOJboeg9Cx/U4fbWBYxdr2XH8KrVNcbJsk48tncCCiUUYhsFnHi7jh+8c5b0DF8mKWDw2d0yv1tg2wbjzt0RWNFwdhDHHw2vdT9G2zFTo2RyS+kVEJH3+y3/5L4wdO5bS0lLGjRtHaWkpxcXF6S5LRCTtfM/FO7ITZ8c6aKrv2YvsKNaCRxnx8Ee5dr2m02nv7FGcTa/i11wBwBg9GXv5asyh+n1XRO69HgWERUVF/OxnP6OhoYE//uM/pqamhvz8/L6uTfqJ5LLdeLsOwoaWBDtPVHHsYg2Vl+tJtBtgMm54Pn+4cjJFBdmpY9PHDOGTD0zmJ+8f463d58iyLR6YOarXakyGfzlddBCGYQpze8nuwdzW5cTJr3/yeNhsPHyJs1UNPLui7/agFBGRwKJFi3Ach8LCQvbu3cu3v/1tBg0axNChQxk/fjxf/OIX012iiEif8l0HEnGM7GCf9dTAkG1r8a9fufmLo1kQD7oKzYlzsJc9jZE/ODXROMmruYq7+TW8M4eDAwXDsJc9hTl+Rp8OZhQRuZkeBYSf+tSn+NWvfsWUKVNYvHgxP/3pT1myZElf1yb9RLRdwHatvoX3D1xk+/GrJNy2ULC4MIcpowYzpWQwZSWFWGbnPxjnlg4jnnD55aZKXtlxmhGFOUwbXdgrNSbDs64mMic78MKyxPjG5dLJ0DM52Ths1u+7QG1TnIdnjWZkYUjGSIuIhNTevXv5xje+kfr44YcfZtu2bTz55JOcPn06jZWJiPQt3/Pwju3C2fYWxJuJ/uFf4jfUBJOJL5686WuNwuH4NVchHguGiqz4COaYKZ0/R6wZd9fbuPs3g+dCJAtr/iNYs1d0ChFFRO61Hv0utHjxYhYsWMDFixe5dOkS//7f/3tNMZYeS4Zu245dZf3+C/h+cHz6mELum1DE5FEFFOREe/Rei6aMoLohRsXe82w9eqXXAsKe7EEYlg7C5ATjnFQHYbj2ULxRU+v9NIe0A1JEJEwGDRrEqVOnKC0tBWDKlCl873vf41Of+hTDhg1Lb3EiIn3EO3csCAKvXQwOZOfivP8S3ulDN32dMXoy/uUzQThoR7AWPIo1e2WnsM/3PNyDW3G2vwUtjYCBOW0h9qInMHIH9dFdiYjcnh4FhOfOnePv/u7vuHTpEgDFxcX85V/+JaNHj+7T4qR/SAaEDS0JLNNg3sQiHpw5iuIhuXf0fkvKRlCx9zyHz18PJvN20fV3u266B2EkbEuMOy6XTnVAhjBgc1wvtfw8jPWLiITNH/3RH/Htb3+bMWPGUFpayvnz54lGe/ZDPBGRTOe7Dt7Zo5gjx2Pk5OFVX8Ld8gbe2SMdL2xpvmk4aE6ei191Af/88eDjibNblxMXdrrWu3CCq7/9Ds6VswAYxaXYy5/BHK5/S4tIZulRQPjP//zPXL9+nRUrVgCwc+dOfvCDH/CVr3ylT4uT/mHKqMFMHDmIMcPyuX9GcY8mH99MYV4WE0YM4uSVeg6evc78iUV3XeONoVp7yYAzLB14yY677Bv3IAxJ/e01tQsFm0O6RFpEJEyKi4v52te+xvbt2zl58iTFxcU8++yz6S5LROSuBPsIHsTd8gZ+bRXm2KmQNxjvyHZSy5s6vqLL9zGnzAPXxTu+BwBjcFGwnHhsWed3qKvG2fI63sn9wYH8QuylT2FOnK19BkUkI/UoIKysrOSTn/wkTz75JABr167lZz/7WZ8WJv3HkPws/vjJmb36nnNLh3HySj17Tl3rnYAw0RqqdbUHYXKJbkgCqrYhJckOwqD+MAZszbH2AaE6CEVE7gXTNFmyZIn2mxaR0PJbGnF3vo135SzWvIdx937QYR/BTh2Dt2COm4YxqhR35zvgxIPlxPMfwZpzf+flxPEY7ofrcfdtANcBO8Kg5U8Rm7IQw470yv2JiPSFHgWE+fn57N27l3nz5gHBBtaaYizpNHv8UF7edooj52tojjup/fbuVDL8y+qyg7B1ibETjoCtbT/F1g7CkA1Zaa+pXagZxoBTRERERPqWX18Dvod7cj/uvo0YOfn4ddcg3gKA8+aLd/zexpARWEuewt3yemrisDlhJvayZzAGFXasw/fwjn6Is20tNNUH106Zh734SQpKJ1FVVXXHdYiI3As9SlUeeeQRfvnLX7Jz587UsU984hN9VpTIrRTkRplYXMCJS3UcOHOdhZOH39X73WwPwmRXYSwkAVXbkJLWDsJIePcgVAehiIiIiNzIb6wLlu8e393Fudq7/wSGSeT3/jPu3vdx1v4wOFQwLFhOPG5qp8u9S6dxNr2Cf/VccO2IscE+gyPH3X0tIiL3SI8CwgceeIDBgwezd+9eAObOncucOXP6tDCRW5lbOowTl+rYc+ra3QeEN92DMFxTgNvuxW79f6vD8TBpimkPQhEREREJ+E4Cd/d7uDsr+uxzRH7/T/HOHyfxynch0bqceN7DWHMf6LycuKEGZ+vatqAytwB7yZOYU+7DMMw+q1FEpC/0KCD8+te/zvLly/nzP/9zAH7+85/zV3/1V/zjP/5jnxYncjOzxw3lt1tPcvRCLU0xh9ysO19mHEt1EN5kiXFIAsLm1JCSZAdhuALO9tp3DYaxA1JERERE7p7v+3iV+3AqftpnnyPy9OfBNHHe+Tn+9SsAmKUzsJevxhg0tGM9iTjunvdx97wHTgIsG2vO/VjzHsKI3N1ARhGRdOlRolJdXc2IESNSHw8fPpxr1671WVEiPZGfE2Fy8WCOXaxl/5lqFk8ZcesXEfwF40bNrUNKutqDMLXEOCQBW/MNHYSpPQhDGLC17yBsCmH9IiIiInJ3vKrzJF77Z2hp6pP3tx/8OObYso5LlguGYa94BmvctA7X+r6Pd2IvztbXoSFYymxOnI29dFWnEFFEJGx6FBCOHDmSV155haFDh+L7Pq+++iojR47s69pEbmlu6TCOXaxl98lrtwwIHdfjV5sqOXJhJ3+yaiZFBdmpc6lluV3sQRhNBoSOh+f5mKbRi3fQ+9r2IGwNCCPhHVLSsYMwfPWLiEib6upq/vZv/5Zz587x4osvYlltP5Q7c+YML7zwAgBf+MIXGD9+fLrKFJEM4TfV43zwW7xTB/vk/a15D2MtKMc9sIn4L/4eErGgEzC5nPiGicPe1XPBPoOXTgNgDBsV7DNYMrFP6hMRudd6FBB+9KMf5Tvf+Q5/8zd/kzr2J3/yJ31WlEhPzRo3hJe2GJy4VEtDS4L87EiX1yVcj3999yiHztUAsPXYZZ5eMD51zvV8LNPAtjqHf6ZhkBWxiCVcYo571xOT+1rzDfsptp9i7Ps+hpHZAWd7TRpSIiLSb+Tn5/OVr3yFb3zjG53O/eIXv+DP/uzPME2T73//+/zlX/5lGioUkUzguw7unvdwt6/rk/c3x07FfvI/4F86ReKlb+JXXw6Oj5+OvfwZjIIblhM31eNsW4t3ZBfgQ04+9qLHMacuxDC1z6CI9B89HlJSVFTErl27AJg/fz4zZszo08JEeiIvO8KUkgKOnK9l3+lqlk3t3NkaT7j8cP1Rjl2sJWKbJByPXSeqWDVvHKZppJbeZkesbsOzLNsMAsJE5geELTd0EFqmmbrvmON1uc9ipmq/rFhDSkREwi0ajRKNRrs819jYSFFRUerXXamoqKCiIhhM8Pzzz6eul7tn27a+niHTH5+Z7/u0HPmQ6t/87z77HKP+8jv4sRZq3/4Vzfu3AGAVDmfw439AzpS5HetxEjRsq6B+46v48RiYFvmLyxm04mnM7Nzb+rz98Xn1d3pm4aNndvd6nHTMmDFDoaBkpLmlwzhyvpY9p651CghbEi4/qDjMySv15GdH+OLj0/nX945ztbaJ45fqKCsZnFp6m93F/oNJ2VGLuuZExu9D6Pl+ailuVrsgMCdikXA8WuJOqALC5ljb17s57oSuA1JERHqmq/2Bb1ReXk55eXnq46qqqr4saUApKirS1zNk+tsz865dJPH6D6Cpvk/eP/rv/xvk5HFlwxu4O9ZBvHU58X0PYd33II12hMbWr6fv+3inDuBseR3qqoGgu9Ba9jSJwUVUNzRBw+3th9jfntdAoGcWPnpmPVdSUtLl8cxuhRLpgZljh2KZJ6m8XMeGQxfJsi0itoltmazfd4EzVQ0Mzo3yxcenM2JwDstnjOblzcfYeeJqEBDGu59gnJQVkn38YgkXn6Beq91eiWEJOG/UvoPQ9wldB6SIiNw+/SBIZODwmxtwNryMV7mvT94/8sx/xCyZhHfxFM7rP8CvvgSAOW4a9opnMAqGdbjeu3Yx2GfwQiUAxpCR2MtXY46Z0if1iYhkEgWEEnq5WTZTSwo5eO46L2873en8kPws/ujx6QwbFAwlWT5jDC9vPsb+M9XEEm67DsLuvx2yQjLJuG1ASccQLbt1+ErYlukm9yC0TQPH82mOhasDUkREeiY/P59r165hGAY5OTnpLkdE+pjvOrj7NuBuXdsn72/Nexh78RP4TfUk1v8S72iwVRaDhmIvX41V2nFlnN/cgLNjHd6hbcFPpbNysRc+hjljMYapv3uKyMCggFD6hY8sHs/wwdnEEi4J1yPheCRcj9wsmyfnjaUwLyt17YjCPMYPz+f01Qb2n6kmarcO87hJ8BSWScBtA0o6fmu3H1QSFp7vpwLPIflZXK1roTnuMISsW7xSREQykeM4/M3f/A2nT5/mr//6r/n4xz/O4cOHWbNmDc8++yz/8A//AMDnP//59BYqIn3G932804dw3nyxbz7BoCFEn/1zME3c/Rtxtr/Vtpx47oNY8x7qMJ3Yd13cA5txd1ZAvAUME2vWMqwF5Ri3uc+giEjYKSCUfmHYoGxWLxzf4+sXTBrO6asN7DxRxbwJwdKCm+1BmOogzPAOvJZuOwitDufDIJZwgx/g2ib52RGu1rWkloOLiEj42LbNV77ylQ7Hkvtbjx8/nq9//evpKEtE7hGv+hKJN/4FGmr75P0jn/gLzMLheJdO4Wx4Gf/aRQDMcVOxl38EY3DH5cTumcO4m1/Dr7kKgDGmDHv505hDOg89FBEZCBQQyoA0t3QYL287xfGLtZQMDX462JMOwpiT2QFVsoPwxuXSyY/D1EGYWi6dZafC2+YQBZwiIiIiAn5zI86m3+Ed39Mn728/9O8wy+ZDSyOJ9b/CO7ozOJFfiL3iI5jjp3fY29S7fgVn86v4Z48CYAwuwlq2GnPcVO2BKiIDmgJCGZBys2xmjB3CvtPV7Dge/NQwuU9fV1JDSjK8g637PQjDUX97TbG25dLJJdNh20NRREREZKDyXRd3/0bcLa/3yfubU+ZhL38Gotl4B7bgbH8zWCZsWlj3PYh130MYkWhbPbEm3B1v4x7cDJ4H0SysBeVYM5dhWPpnsYiIfieUAWvBxCL2na6msXUQxs2WGIdlD8KWW+1BGKKALTmgJDerfUCoDkIRERGRTOeeOYzzxg/75s1z8ok8/u8xi0vxLp3G2fgyftUFAIyxZUHX4OCi1OW+5+Id2oazYx20NAEG5vTF2Isex8jJ75saRURCSAGhDFhTRxeSm2Wngqge7UGY4QFhUzcdhDmpISXhCdjauiHtVP3qIBQRERHJXN71KyTW/hDqqvvk/a0lq7Bmr4R4M4l3f413ZEdwIr8Qe/kzmKUzOi4nPnccZ/Mr+NWXATBKJmIvX405rKRP6hMRCTMFhDJg2ZbJvAnD2Hg4+AvDzfYgvJuA0Pd9dlZWkWVbzB4/9M6K7aFuOwgj4Vuiqw5CERERkXDwW5pwNr2Cd+zDPnl/c9w07JUfgbzCoBtw29q25cRzH8Ca93DH5cS1VThbXsc7dTA4MGgI9tKnMCfM0j6DIiLdUEAoA9r8icN7FBDe6RJjx/X41aZKdlVWAfCpByZz34SiW7zqziUDtBu7IVNLjDO8A7K95L3kZlntOggVEIqIiIhkCt9zcQ9sxt30at98gtwC7BXPYE6YhX/lLM5bP8GvOg+AMWZKsJy4cHhbPfEW3F3rcfdtAM8FO4o1/2Gs2Ssx7Ejf1Cgi0k8oIJQBbWxRHiMG53CltpmC3Gi3191JB2FjS4IX3z1K5eV6LNPA9Xx+sfEEQ/OzGDd80F3X3pXmbjsIk3sQhidgS3YQ5kTttinMIeqAbK+hJcGrO06zYloxY4u0142IiIjcG7sOXmDdxuM0NMbJz4vy+MrJzJve8+W1vu/jnTmMf+5YMPQjryB1zjt7lMTrP+iLssEwsGYux1r0GLgOzvu/wTucXE48GHvZM5gTZqa6AX3Pwzu6E2fbm9DcAIBZNh978ZMdahYRke4pIJQBzTAMPvtwGReuN1EyNK/b65IdeD0NCK/WNfODt49QVddCQU6Ezz06jc1HL7P16BX+5Z2j/OnTsxiSn9Ur99BeS3dTjJMBWyg7CG1ys8LdQXjgTDU7T1Th+/CH909OdzkiIiIyAOw6eIEf/XY39Y2x1LELVxpgDbcMCX3PxTuxF3f3u2379w0fjVW2AK/mKs6bL+LXXO2Tuo3hY7Dv/xjGsBK8w9uC0C/WHCwnnnM/1vxHOiwn9i6exNn0altn4chxwX6EI8b2SX0iIv2VAkIZ8IYPzmH44JybXpPVwyXGrudz9EINP99wgqaYQ8nQXD73yDQG50X5vSWlXKtv4fjFOv7lnSP8p1Uzb7qs+U4kOwizu+0gDE9A2BQLas1t10EYpj0U22toCYLNZFekiIiISF9bt/F4h3AQoL4xxlsbjncbEPpOAnf/Jtytb7QdbN3nzxw7reNgkN4WycJe/DjmjGX4VedJ/Nv/xr96DuhmOXH9dZwtb+BV7g0O5A3GXrIKc/Jc7TMoInIHFBCK9EB2aomx1+lcQ0uCI+drOHyuhiMXalIh1vQxhXzqgSmpcNEyTT79YBnffn0/F6838dP3j/HZh6dimr33F5hU190NAWFOiPcgzMmyQ78HYTIYbApp/SIiIhIufkMN9deud3muoSne+fpYC+6uCty9Gzqdi6z5E/yLp4i/+PVerzPJnDgbe/lqsGycD/4N7/B2wA9Cv+WrOwwX8RNx3N3v4u55H1wH7EgwqGTugx06C0VE5PYoIBTpgbYOwiDg8X2fI+dreO/gRU5crMNvd23RoGzmTyri0dmjO4V/uVk2n3t0Gt96fT+HztXw+q4zrF44vtfqbOsg7GZISdzB9/1Q/FQ1NcU42n6KcXgCzvYaYwkAmtVBKCIiIn3M2f0e7tY3yItNBzrvv5ffbt9tv7khmD58fE+n64yiEuzFT5L49T/2XbGDhmCv/Cjm2DK8Q9tblxM3gWlizXmgdTlxsC2P7/t4x3fjbH0DGusAMCfNxV6yCmNQYd/VKCIyQCggFOmBiGViGuC4PtuPXeH9Q5e4dL0JAMs0mFRcwLTRhUwbU8jwgpsvVy4qyOY/PFTGd986yAcHL/HAjFE3HZDSU67nE0u4GLQFmkmWaRKxTBKuR8LxiPby0ua+0NZBaJEVsTAI9oB0PR+rF7su74VUB6ECQhEREekDvpMg/s9f6XDs0UEXueTkUu+2/ZNvUF4Wj6+cjF9fTWL9r/Avnuzy/ezHPoW7s6LvhpC0CwD965dJ/LbdcuKSSUFoOGRE6nLvylmcja/gXzkTXFM0OphuXFzaN/WJiAxACghFesAwDLIiFs1xl19uqgSgICfCyhmjWFo2otPU4FuZWFzA9DFDOHD2OjtOXOWR2aPvusbkAJXsqIXZRYdgdtQi0ezRnHBDERC27yA0DYPsaPD1jyVccrPC9VtX8l6aQ9TBKSIiIpnPb27Eu3oO541/6XRu/oMLsXOms27jCRqa4uTnRnls7nBmfPhj4u9Xd/2Gpok5dSHOup/0Wc1G8Xjs+38PI3cQzubX8A5tA3zILQiWE0+c3bacuLEOZ9tavKO7ghfnDsJe9ATm1PkYhtlnNYqIDETh+le2SBoNzsuiOd7EiME5PDRzFPMmFmFbd/4Xk6VlIzhw9jpbj17hoVklXYZ6tyPZcXfjgJKk7IhFfXOClrjL4Ny7+lR9znE94o6HabR1Q2ZHbZrjLk0xJ7QBoecHQW53z0hERESkJ3zXIfa9/wZ+5/2xASIf/1PMYSXMB+bPGI136TSJl/8PfOh3eT2ANXsl7r4NrYFdL7LsYK/ArFzspaswyxbgHdlBYttaaGldTjz7fqz5j2JEW5cTOwncvR/gfvguOPG2CcbzHk5dIyIivUv/ShXpof/wUBk1jTEmFhfcdZgHUFZSyJC8KNUNMY5dqGXq6MK7er/k/ny50a67A1P7ECYyf5lranlx1E79BDk3anGdcNR/o8Z2S4ub4o4CQhEREblj3qVTXPju/+nynDluGvZjn8KwI8GefWeO4Kz94c3fMDsPWhpx93UeUHI3jIJh+HXXwHUwy+ZjL30Kv6GGxMv/hH/lbHBNycTW5cQjgdZ9Bk/ux9n8GjTUBPdUOhN72VMYBcN6tT4REelI/0oV6aGigmyKCrJ77f1M02DxlBG8ufscW49dueuAsOWWHYR263WZP+ijKdYadrbrFMwO6aASz/M7DCdpjrmQn8aCREREJHS82ioSP//GTa+JPPU5zLFl+J6He3Qnzvpf3fqNc/KhuaGXqgyY46bhnTmMX3cNo3A49v0fwxg6Cmf7W3gHtxIsJx6EvWw15qQ5qR8Ge1UXcDa9ktoX0RhajL38GczRk3q1PhER6ZoCQpE0WjRlBOv2nOPAmevUNccpyLnzYSVNqa67rjsIc1IdhJkfsLUNKGn7LSpZf9gmATfHnQ5TrpPPSURERKQnnF1v425f1/0FdoToJ78M0azUBOMe68Vw0Jw4G+/8Cbwzh8GyseY9jDX3Abzju0ms+ym0NAbLiWetxFpQ3racuLkBZ9tbeIe3Az5k52Evehxz2iIMU/sMiojcKwoIRdJocG60bVjJ8bsbVpLsDOxuYEpqiXEIAqr2A0qSckLaQXjj5GJNMhYREZGeCCYTfxXoft9Ae8VHMKcuwN2xDndv7y4R7imjuBQ8D69yX/Dx6MnY938M4jESr7zQNnl41ATslR/DHNq6nNh1cPdvwt31NsRjQXg4cwXWgkcxsnLSci8iIgOZAkKRNLvdYSXXG2L8enMls8cPZWnZyNTxtiEl3exBGAlPwNbUZQdhsv5wBWyNCghFRESkh7wzR0i88S8YQ0bgX79y02sjv/efcfd+gLPxd/eouhsZmJPm4J3cB54HOfnBFOKxZTjb1+Ed3AJ+63LipU9jTp6LYRjBPoOnD+Fufi3YoxAwx03FWvo05pARaboXERFRQCiSZmUlhRS2Dis5frGWspLCbq+ta4rzvbcOUVXfwtmqBhZMHE7EDpZeNPe0gzAMS4xTHYRtYWey/rAFhDcGgmGrX0RERPqe7/s4b/0r3qmDwcc3CQeN0ZOxfY/Eb79zr8rrxJwyD+/SKbwTewADc8YS7EVP4J0+SPznfx8sJzZMrNkrsBaWY0SDfby96ss4m1/FP3csuJfC4VjLVmONm5q2exERkYACQpE0Sw4reWv3ObYevdJtQNjQkkiFgxAEgvvPVDNvYhHQtnS424AwklxinPkBYVcdhLlaYiwiIiL9kN/cQPzFv+r59eePk+jDem7GGFMGnot37MPg46HF2A+sAcsmsfZH+JdPB8eLS4PlxMOKg5pbGnF2VARDSnwPotlYC8uxZizDsLpe/SIiIveWAkKRDLB48ggq9pxjfzfDSprjDt9fd4jLtc2MLMxhbukw3tp9jm3HrqQCwrYOwu6WGCc7CDM/oGpOTjGOtp9iHJ49FNtrjAV/hY/YJgnHUwehiIjIAOfHWiAaxTBM3BN7cSp+mu6Sbi2/ELNoNN7545CIgR3BWvgYVtkC3F1v4x7YHCwnzskPlhNPuS9YTuy6eIe24OyogFgzGAbmjKXYCx/DyMlL912JiEg7CghFMsDgvLZhJe/tv8jK6cUMzo1imgaxhMs/VxzmfHUTRYOy+eJj04nYJu/sO8/xS3Vcq29h2KDstsm/3S4xDo6HtYMw7ENKigZlc/F6E02xcNUvIiIivcP3POL/+lfQ0oQ5bRF+bRX+xZPpLuuWjLFl0FiLd+oAAOb46dgrPoJ3sZL4r/5XMAnZMLBmrcBa+BhGVuty4rNHcTa9il8TLJc2Rk/GXrY61VUoIiKZpU8Dwh/+8IdUVlYyYcIEnnvuudTx73znO5w/f55oNEp5eTkrV67syzJEQmFJ67CS9w9e5P2DF7FMg6H5Wfg+VNW3UJgX5YuPT6cgN+gunDN+GLsqq9h+7CpPzh+bCs66HVISyj0I2wWEWeEeUlJUEASEYatfRERE7p5fW0X8599Ifewd3p7GanrGGDICcgYF+wX6PuQNxl7xEYyCoSTe+QX+pVPBdcWl2Cs/ijlsFABezVXcza/hnTkcvFHBMOxlT2GOn4Fxi2F8IiKSPn0WEFZWVtLS0sLXvvY1XnjhBY4fP87kyZNT5//0T/+U4mL99EgkaeroQh6eVcLJK/Vcq2+hvjnB1bpgv8GCnAh/9PgMhuRnpa5fPGUEuyqr2HHiKo/fN+bWHYSR8CzRTXYQ5rbvIIwkh5RkfsDZXvsOwvYfi4iIyMDg7t+UxknDdyASxRg+Br/mKly/EnQHzl6JNfd+3N3v46z7SbCPYE4+9tKnMKfMC5YTx5qD5cb7N4PnQiQLa/4jWLNXYFhauCYikun67HfqY8eOMWfOHABmz57N0aNHUwGhYRh8+9vfJj8/n89//vMMHz680+srKiqoqKgA4Pnnn6eoqKivSr0nbNsO/T30F5n8LD7zRNv3QizhUFXbTHV9MxNHFZKX3XFfwmHDhvHS1lNcqWniYoNH3PEBGF08nKGDcjq9t2MFAVXcJWPuv7tnkbyXkpFFFA0bBICV1QxAzPEypv6eSHjBlL7SkiLYf4GWRGbWn8nfFwONnkXm0LMQkbvhOwkSv/0OfvWldJfSY8bQYjAM/AuVwccjxmLf/zH86svEf/OtdsuJl7cuJ87B9zzcQ9twtr8VTC/GwJy2EHvRExi5g9J7QyIi0mN9FhA2NjYycuRIAHJzczl37lzq3Gc+8xny8/M5fPgwL774In/xF3/R6fXl5eWUl5enPq6qquqrUu+JoqKi0N9DfxGmZ5EFjBpk0txQR3ND5/MLJg7jjV1NVOw8QWNLHIDmhjqqYo2drm1pDoZlNLbEM+b+u3sW9U0xAGJN9VT5wa/jTtA5mEn190RNQxBsZhtB52Cm1h+m74v+Ts8ic/SXZ1FSUpLuEkT6NT/WhH/9KsbIcakltF71ZRK/+l9pruw2ZOdhFAwNwkwnAdEs7MVPYhSPx9nwu7blxCPHB8uJi4LfV7wLJ4J9Bq9dDM4Xl2IvfwZz+Oh03YmIiNyhPgsIc3NzaWpqAqC5uZnc3NzUufz8fACmTZvGT37yk74qQaTfWzBpOG9+eJaDZ6/j+T6mAVHb7PLatinALr7vZ+weML7vd7lcOmKZWKaB4/okXI+I1fV9ZpqmliCYHZKfhWlA3PFwXA87JPWLiIhI97wLlSTe/hk01RP5vf8Mw8fg7t+Eu+mVdJfWY8bQYvx4M/6VswCYk+ZgLXwM7+BWnI2vBMuJs/OC5cRl8zAME7+uGmfL63gn9wdvkl8YnJ84O2P/jikiIjfXZwFhWVkZFRUVLF++nH379vHQQw+lzjU1NZGbm8uFCxfIy9N4e5E7NTg3yrTRQzh47joQTCru7i9ltmVimwaOFwRsUbvrYSbdaYo5HL1Qw8yxQ4l0E0L2hljCxfODoLN9iGYYBtlRi8YWh+a4QyQnepN3yQy+76f2HMzLtsnJsmlscWiKOxSEoP4b7T11jWsNMR6epW4kEREZ2Hzfw/1wPe6OCvB9jBFjMfIGk3j5/+BfPp3u8nomJx8jK7dtCXTBUCIrPoofayLxyvegqR4MA3PmMuxFjwXXJmI4H76Lu/cDcB2wI1j3PYQ19wEMO5Le+xERkbvSZwHhxIkTiUQifPWrX6W0tJSioiJeeukl1qxZwze/+U0aGxsxDIMvfOELfVWCyICwaMrwVECY080E46TsqE1DS4KWuHtbAWFdc5zvvnmIK7XNzB4/lE8/OKXPfjqcHELSfkBJUm40CNha4i4FnbdZzDhxx8PxfGzLIGpbqfqbY+Go/0YvbztFXXOC+ROKGJwXvoBTRESkN/jNDcEU33PBPsNm6UysGUuI//j/TXNlPWRakF8ILQ34NVfAtLDmPoA5YSbO5tfwL54EwBg5rnU58eggED2yE2fb2iA4BMwp84JlyPmD03gzIiLSW/p0nNRzzz3X4eM1a9YA8OUvf7kvP63IgDJ9TCH52REaWhLdTjBOyo5aQUCYcCno4fvXNcX57lsHuVIbTFTed7qaDw5e4oGZo+6y8q4lO+66upfkMunmEExihrZ7ycsKfqKe0xp6NoWk/vY836e+dbl0Q0tCAaGIiAxI7ZcUA1izVkA0i8TrP0hzZT2Ukw+GAXXXADBGTcBesgqvci+J3/7vtuXES1ZhTp2PYZh4l07jbHoF/2qwp7wxYmywz+DIcem8ExER6WWaNy8ScpZpsmjycNbvv5AK0LqTHUnuQ9izgKq2MQgHr9a1MGpILiumjeTXm0/y2s4zjB2ez4QRvT+ZLhmeddVBmAwNk12Gma4x1vFecpP1x8IXEDbHHPxguDSNsUR6ixEREbnHgiXF7+LuWAe+H0zynfsA3oWT+FfO9MnnNMdPx7t4EuItd/9mlg1ZOdDSBJ4L2bnYS54Cyybx1r+2Bp4G5oyl2Isex8jOxW+oJbH1Dbzju4P3yC3AXvIk5pT7MAztpSwi0t8oIBTpB1ZMK6bych0LJg2/6XVtHXi3DthqGmN8981DVNW3UDI0ly8+Np287AhXalt4/+BFfvzuUb70zBzyc3p3v5nmm3QQ5oQsYGtqDdLyWgPCMHcQNrb7mjeF5OsvIiLSE34ihhHJ6v78DUuKsSOYk+bi7n6vbwrKC5bseqcP9c77ZeUEoWByafDUBVhlC3B2VuBfqARauwJXfhRz+Bj8RBxnZ0Vwf04CLBtrzv1Y8x666ddJRETCTQGhSD8wOC/Knzw165bXZUeCb/mWRPcBYcLxOHaxlt9tP8W1+hijh+byH1vDQYCnFozlbFUDJ6/U85MPjvEfy6djmr23H2FbB2HnbsickC4x7g8dhI0tbV2DjSGsX0RE5Ea+6+Bs/B3eoe3Y5X+INWlOp2uCJcU/h6a64EA0G6NwON6RHX1XWGNt77yPaQWdg7FmAIzCEVhLn8K/UEnite+D57V2Eq7CnLoAMHCP78HZ+jo0BDWYE2djL12FMWho79QkIiIZSwGhyACSDNhabuggbGhJcOjcdQ6cuc7Ri7UkHA+AMcPy+I+PTe+w3NcyTT714BT+4ZV9HL9Yx1t7zvHkvLG9VmNPOghvFnBmkk5LjFtDzzB24DW0qINQRET6D7+pnsS6H+NfOg2miZHXcdBGpyXFbSfwr5y9x9XeAcsOAsBELOgAnP8oRv5gnPdfag07DcwZS7AXPYGRnYt39Vywz+ClYAKzMWxUsM9gycT03oeIiNwzCghFBpDUHoStAdvpq/W8f+Ai+85Ud/i775hhecwYO4SV04u7DOoG50b55AOTeWHdId7ee54powYzqbinY09u7uZ7EIYrYLtxSEnynsJSf3vt9x0MY/0ikhl++MMfUllZyYQJEzoMs/vOd77D+fPniUajlJeXs3LlyjRWKf2dd/UciTf/NejUM03s8k9iFo9Pne+0pLi9RKzX67FmrwDfx92/qXfe0DDADf6sNsaUYc1ajrv3A/wLJ4Jjw8dg3/+xYDlxUz2Jd3+Fd2QX4AcDShY/gTl1IYapfQZFRAYSBYQiA0hyD8KjF2rYd/oap682AGAaBlNKCpg5dggzxg6hMO/W+8tMGTWYR2aP5u2951m35xyTimf0So1NsSC87HqKcWsHYUiGlNy4xLhtyEr4ArbGdh2EWmIsIneisrKSlpYWvva1r/HCCy9w/PhxJk+enDr/p3/6pxQXF6exQhkI3GO7cd77dRCgGSb2o3+INaFtm5ZOS4r7mDl2Ku6+jb37pr4PuYOwFz2OX3MV560Xg27CrNxgyMi0heB5OLvfxd31DiTiYFpYs1ZgzX8EIyu7d+sREZFQUEAoMoAk9yA8eiHYVyYnarG0bCQrphUzOC962+/34MxRbDx0iROX6jh1pZ7SXphq3NyDDsKwBGzJfftys5NLjEM8pKT9HoQtmmIsIrfv2LFjzJkT7PE2e/Zsjh49mgoIDcPg29/+Nvn5+Xz+859n+PDOQ7cqKiqoqKgA4Pnnn6eoqOjeFd/P2bbd77+evudR9+5LxDavDQ4YJkPX/BE50xYE532Phk1vUPfev3VcUtwHcqYvpPlQsIehd/ZIL7+7Qd6Ch4iMHEvdB6/g1V8HDHLnPUDBQ2swc/JoOfIhtW//CrfmKgDZU+YyuPxZ7KEje7kWSRoI32P9jZ5Z+OiZ3T0FhCIDSPGQXACGDcri/hmjWDhpOFmRzsNAeionarN82kje2XeBd/ad53OPTrvrGpt6MsU4JB2Ejaklxh07CMO4RLdBU4xF5C41NjYycmQQQOTm5nLu3LnUuc985jPk5+dz+PBhXnzxRf7iL/6i0+vLy8spLy9PfVxVVdX3RQ8QRUVF/frr6ceacd7+eVsYZ5jYj/4BjUXjaayquvmS4j6QDAd7mzFsFNac+2k6ugt/5/rg2PAx2Cs/ijtiLNfOngz2GUxOLh4yAnv5M/hjplDjAf34v4F06+/fY/2Rnln46Jn1XElJSZfHFRCKDCBlJYP5yrPzyc+K9Nrk4funj+KDg5c4dK6GC9WNlAzNu6v3u3FZbnthW6LbdENAmLynsASc7bXvGlRAKCJ3Ijc3l6amJgCam5vJzc1NncvPzwdg2rRp/OQnP0lLfdI/edev4Lz5In5t6z8aW8PB5MTie72kmKxciDX17nvaUax5D0IshvPeb8BzISsHe/GTmNMWQayJxAe/xTu0LeiOzMrFXvgY5ozFGOad/6BYRET6FwWEIgNMQc7tLyW+mfycCEvKRrDh0CXW77/Apx6Y0uPX+l0s4WlbYtz5L6zdTWHOVG1hZ+uQkhB3EDZqirGI3KWysjIqKipYvnw5+/bt46GHHkqda2pqIjc3lwsXLpCXd3c/aJL+Ifl3BMO48x9ouqcP47zzM4i3DhYxDOxHPoE1aU4wpXj3e7jb37q7JcV2BJzb2Hqjl8NBs3QGxqiJuPs+gIZgCxlz2iLsxU9CNBt3/ybcnRUQbwHDxJq1DGtBOUZ27i3eWUREBhoFhCJy1x6cOYpNhy+z59Q1nrhvLEUFN9/c2vN9frnxBMcufsifrJrBkPy2oSjNPVhiHJY9/DoNKclq20PR833Mu/hHz73WfopxS8LF9TwsTTcUkdswceJEIpEIX/3qVyktLaWoqIiXXnqJNWvW8M1vfpPGxkYMw+ALX/hCukuVNPNbGkms/RH4PpGP/afbDgl93w/Cv21vAq3hn2FgP/IHWJPnti4p/iX+uaN3X+xNwsHIs1/CKBwBjXXEf/I3d/+52rEKhsKMpXjnjuFtfhUAo2g09sqPYo4ch3vmMO7m1/Bb9xk0xkzBXr4ac4j2GRQRka4pIBSRu1aYl8WCSUVsP36Vd/df4OPLJ970+ld3nGbniWCpz8bDl1i9cDwArucRczxMA7K72BsxO9VB6OD7/l11FfQ11/NoSbgYRlvdlmmSFbGIJVxiCbfLEDRTJTsII7ZJwvFoijkM6uVuVBHp/5577rkOH69ZswaAL3/5y+koRzKQH2sm8doP8KvOYxSOuP1wMBHHee83eCf2tB00DOyHP4E1ee49WVIcefrzmGOm4DsJ3L0fBJOCe4thYk5fTHZeHo3b3gyWE0ezg+XE0xfj11YRf/0H+GeD8NMYXIS17GnMcdMy+u9NIiKSfuH516mIZLSHZ5Ww4/hVdpy4ymNzx3Q7FfmDgxf54OAlDCNY0bP9+FWenDcW2zJpjgVLh3Oidpd/ibUtMxVQxR3vrgas9LVU92DU7tApmBMNAsLmmBOagDCecEm4HrZlUJgb5WpdiwJCERHpdX48RuL1f8GvOg+Aff/Hbu/19TUk3noRv+pC20HDwH74WczJc3A+XH/3S4p7wNmxDuPoLrwLJ6Dx1kGkff/v4R7ZgX/l7E2vM0aMwxw7BffIThobagAwpy0MlhObJu7m13APbgbPg2gW1oJyrJnLMKxw/H1DRETSS39aiEivGD44hzmlQ9lzqpr3Dl7gI4tKO12z9/Q1Xtl+GoA/WDmZDYevcPZqHXtPVzN/YlFq6XBOFwNKknIiFgnHoznuZHRAmOy4u3HYSm6WTU1jnKa4w9B0FHYHGlqXF+dnR1L3035PQhERkbvlJ+Ik3vgX/CtnADBnLMEsufmKhPa8iydJvPVjaGlsO2gY2A89izlmConXf3hHS4qNohLM4gkYQ4bjntibmgDcSTQ72OcP8C+fwb985pbvHf3Ul3EPb8fZ+LugE7DbC7Oxpi3Cq76Eu/NtACIjx8HSpzFGjME7tB1nx1vQ0gQYmNMXYy96HCMn/3ZvV0REBjAFhCLSax6eNZo9p6rZcvQKJUPzmDSyILW/4Mkr9fzs/eP4wKr5Y5k/sYhIVg4vVuxjy5HLQUDYruuuOzlZNnXNCZrjLoUZvI99d9OYwzioJBkG5mVFyGsduNIYovpFRCSz+U6CxJsv4l86FRzIH4y9ZFWPX+8e3Iqz8eWgcy7FwH7o32EMKiT+62/e0ZLi6Ce/DPmD8Q5tw/ngtze/ON4CpnlDDV2z5j2MX19N/DffbA31umeWzoDsPNz9m9qWEy96guEPPM3VvdtI/Oab+NWXATBKJgb7DA4r6fE9ioiIJCkgFJFeM3pYHtPHFHLoXA2/2HACgCF5USYWF3DoXA2O57O0bAQPzwr+4rp0+mh+8d5BTl6p5+L1ptQE45wuJhgnJZflNmf4oJJkgJYM1JKSgWFzSCYxAzS2BB2Eedk2ednhCzhFRCRz+a6Ds+7H+OePp45F7l+DEb35wLPUaze9indwS3DAMMH3CMLB38dvrMV599etx3rOGFsWdB2++8vuOwYBo3A4RvF4zKIxGEUl+DVXcXa9DXXVN31/98P1t66hYBjG2DK804cguZy4bAH20lUQj1H9m38icfTD4OJBQ7CXPoU5YZb2GRQRkTumgFBEetWnHpjClqNXqLxUx8krdVxvjKcGkkwfU8jHlkxI/eU1J2ozf2IRm49cZsuRy4wbHiyFuWkHYevAj+YMD6i66yDMCWEHYUMy7Gy3xLgp1v3UxkzXHA/P/o8iIv2Z77o4FT/DO3Mkdcwsm485buqtX9vcQGLdT/AvngTLxigYhn/9MmBgLXgU9/jeO55S7J89inv25q+Nfur/h5E/GADvwgmcjb/Dv3ru1m9u2RjDx7R1S97ItDAnzsZvqsc7sBkAY9go7JUfxRhajLtrPe6+DUE3oR3Fmv8w1uyVGHak6/cTERHpIf0LSUR6VVbE4sGZo3hw5ig8z+diTROVl+poijk8PKsEy+z4k+1lU0ey+chldlZWUZAbDL24MVRrL9VBmMjsDrxkgJbsuEtqC9jCExAmlxjnZ9ltexCGqP72jl2s5YW3DvGRxeNZOX1UussRERmwfM/DWf8LvFMH2g7m5GMvW33L13pVF0i8+WLQWZc7CLO4FK9yX3AybxDu7nfB7f0/p6xlT+Md34N/9RyJd36OvXw17vZ1eGcO3/R1xpARmGPKMMeW4cdbcDa/1vV1I8Zh5BcG95JaTvw45vTFeMc+DPZYbG4AIHfOcpw5D2HkFfT6fYqIyMCkgFBE+oxpGowemsfood1vFjhqSC6lIwZx6ko9W44Ge+jcrLsr2UHYcodLjK/UNhO1TQrzsu7o9T3V2F0HYVY4lki317bEOEJeCAPO9s5WNeADZ642wPR0VyMiMjD5vofz3q/xTuztcNxe+TGM7NybvtY9sRfn3V+Bk8AYMRazuBR37wdtF/RganAnrfv6eZdP4R3f0/l8wVCia/4LRlYO/qQ5xH/8N/gXT5L4zbe6fUtz3DTM0hmYY8owBhXiN9bhbHqlLchsLzsPs2Qi3tVzbUNayuZjL1mFX3uNxL/9U2qyszFyHPbyZxgyYx5VVVW3f68iIiLdUEAoImm3tGwEp67UU9MYB27eQZidWqJ7+x2EB89e54frj5AdsfjSM3NSA1T6QlNqD8J+MKSkXTdkbsiHlDQ0B/cS1vpFRMLO932cD/4N7+gusCPBvoGJGObE2VgTZ93kdR7u9nWp/fvMsvkYhSNwt63t0ee1n/gM5vAxxH/8/6aOGSPHESn/FH4ihvPur1PhXHuRpz+POWZKUEOsBffAlpt/nlWfxRw9BcOy2uo+uBVn6xupKcftGSUTwXVSwaExtDgISvMLg0AxGaLmBYNbzMlztc+giIj0CQWEIpJ2c0qH8bvtp1OhWU4PlhjfbgfhqSv1/Pi9Y/h+MCDk5xuO80ePz8A0++Yv2W17EHbcEyg5gCVMAWFDuynGYVwi3V59azdksitSRETuHd/3cTe9gndoG1g25sTZQVCYlYu94iPdvy7egvP2z4OlvIaJtewpqK/pUThoLV+NPXsl3rULJF77fnDQtLAWPY41ewXunvdxt7/V+YWGgbXoCdxTB3H3bsCvr8avqw6W/t7INIM9CXMHtdXcWId3+TTuvo1d7zdYMAxj0JDgnOtANAtr4eNYZQtw976Pu+f94LgdwZr7ANbcBzEi0Vver4iIyJ1SQCgiaRexTBZNHs57By4CPRxSchtTgC/XNPMv7xwh4XrMmzCM45fqqLxcz7sHLvDI7NF3V3w3ultinBuSKczttZ9i3NYBGc6AraH1XpKhp4iI3Bu+7+NufQN3/yYwLez7P4az6VUA7OWrO4Rr7Xm1VThrX8SvuQJZOUTKP4m7b+Mt9/0jK5fIk5/BGDkOZ+8HuFvXgudiDC7CWrIKv76a+Pf/75sV3KMAMvLsn2MUDsevuYp3+hDepVN4l051P8nYjmAUjcavv56a3GxOmYe9ZBXehRPEf/X/pZZJm5PmYi9ZhTGo8JZ1iIiI3C0FhCKSEZaWjUwFhD3pIOxpwFbbGOf7FYdoijnMGDOET6yczLGLtfxzxWHe/PAcU0YNZmxR/t3fwA1SQ0puDAiTHXi3EXCmWzLszM+OkB2xOhwLm2Qw2BhL4Pu+lmmJiNwj7o6KoCvONLEf+xTekR0Qb8EcNxVzyryuX3P6MM47P4d4C8aQkdgPfRznnV/g13bce88oHI4xejLesV0Qj0HuIOzlz+BXnSfx8v/pcK1fW4Xz1r/euuDsXKzJ9+G7Lt6hrZ1OW0tWBTVufQPv8mloaep4QSQKdjQ1VCSocwSYRqqj0Bg6EnvFR8GOkHjrx6klzkbRaOzlz2COKr11nSIiIr1EAaGIZISigmwWThrOkQs1FBfmdHtdWwfhrQOq5rjD9ysOUdMYZ/zwfD714GQs02Da6EJWTi9mw6FL/PSD43xp9WyircFXb+l2SEky4AxRwJbqIMyyyWr9OjXHnFAGbMk9CB3XJ+54qfsREZG+43y4HnfX22AY2I/8QbDn3qmDEMnCvv/3Ov1Z4jfW4mx6Da+ydf+9SBRj0BASv/1Oh+usWSswpy2CRIzE6z+ARCw40VSPU/HTHtdnjJmCPf8RjIJhuPs24u55DwwT98TeDgFf2ye2cbe+0fFY7iDM4gmYo8ZjDCvBq9yPe2BzcC4rFyOvIAg2XQciWVgLH8OaMAtnx1vBMmsIpjgvfhJz6nwMw+xx/SIiIr1BAaGIZIx/t2IiBtw0dGrrIOy+A6+6oYUDZ66z7dgVLtU0M2JwNs89MpWo3RYGPbVgHMcv1nKpppnfbT/Nx5dP7LX78H0/FQB2WmIcsj38XM+jOe5iGEFnp2kYZEUsYgmXloR704nTmcbz/NTAFQi6CBUQioj0LWfvB7jb3gQM7IeexSyZRPyX/x8A9tKnMPILU9f6rou7fyPuzgpIxNveJBHvsKTYKJlI5KnPYVjBn0GJDS+3hYNdsGYtxz1zBOqudThuls3HXvo0Rk5e27WzVwQBYVfBYJLrYAwZgVFcitn6PwYNwTAM3FMHSLzzc2ioBcOAgmEQb8GvvhR8zsn3YS96HPf47uDr4MSDPRHnrMSa9zBGNPsWX1EREZG+EZ5/2YlIv2f2oButuw7Cq7XN7D51jQNnqjlf3bbMpzAvyhfKp5OX3XFYSMQy+eQDU/jmq/vYeuwKU0cXMnv80F64C2hJuHg+ZEUsbKtjB0DUNrFMg4TrkXA9IlZmdwi074RMPp/cLJtYwqWxxQlVQNgUd/D9to8bWxyG9v7qchERaeUe2Iy7+TUA7AfXYJXNI/H2z6GlEaNkIub0RalrvQuVOO+/1Gn58I3sFR/FmrWs47GFj+GNngSNdTjb3wqmBZsW1tJVmENGpj5nSm4BkYf/XWo6MYDvOjgbfod3eFuXn9cYOR6zuBSjeDxm8XiM7LwO5/2GGhIbfxd0RgJk5YJtp0JJY8hI7JUfwW9pIv7K96ChBgCzdGYQlA4edtP7FhER6Wvh+ZediAht+xO2xF08z+fw+Ro2HLrEsYu1qWuybJNpYwqZNW4o08YMSe2bd6NRQ3J5asE4frf9NC9tOcmUUQVk90Lg1djSdfcgBN2ROVGbhpYEzTGHSG5mTyRM3kt+u2nMeVk21xtirfsshqfTIbm8OPWxJhmLiPQZ9/B2nA0vA62h3rRFuKcP4R3fDXaEyAO/j2GYeFXnSfzmW53fwLQwS2eC7+KdPND6Ph/pFA4CEM3Gr60KphF7XhDG3f97uEd3kWgdhJJkzX0Aa0F5aiKw73m4e95r7XLsyLrvIcxxUzGGj8GwI53OB693cfdvwt2+LtUNSDQ7CCljTRCJYi18DLO4FGfL6/gXTwJgDC3GXr4ac/Tknn5JRURE+pQCQhEJlayIhUHQpfe3v91NdUOwpChimcwtHcac0qFMHjW4x515K6YXs+fUNU5fbaBi73lWLxx/1zUmlw/fOKAkKTfLoqElQVPMoSDjA8K2CcZJyeAzbINKbgwEw1a/iEhYuMd247z3EgDWsqexZi3DjzXjvP/b4NjCx4LpxD//u06vNQYXYc5cijVlHl7lfpwPgtfYK57BmrW80/V+Qw2J9b/Ev1AZvPes5RijJpB4+6fBNGDTAi/YlsScPBd76VPB63wf7/hunHd+0fEN8wYT/b3/jJFXcMv79C6fwfngt/jXgiFr2FHAT3UrmpPnYs19EPfAFhKbXw/OZediL3occ9oiDFPbXIiISOZQQCgioWIaBtlRi+a4S3VDjKH5WSyfNpJFk0d02bHXk/f76OJSvvnafjYcusSSshEML+h+SEpPJCcYd1dPclluUw8nMadTMkRrv0Q7bPsoJnUKCNVBKCLS69zKfTjrfwn4WIuewJ5zPwDOltehqS64Zt+GILxrxygej71sddCtZxi4B7emwkFr+WqsWSs6f64Te3Hefyno1svJx176NN7ZI7jrfhK854ix2A99HEyLxM+/gXfyAH5LI371JRKvvNDp/SLP/jnmkBE3vT/f86C+GmfvBryDWwEfMMA0gw5CgmnF9vLVeNWXSLzy3WCysmlizVyOteBRjKzc2/mSioiI3BMKCEUkdO6fMYrz1xpZPGUE00YXYpp3N0l3bFE+CycNZ8eJq7y64wzPPTK1x6/1fL/T3ondTTBOSh4PwyTjhnYTjJPy+k1AGK76RUQynXvqIM7bPwPfw5r/CPb8h4MlvFtewzu8ve3CG8LB6B/+XxgFbXvwuYe2tYWDy1Zjz17Z4Xo/HsPZ+Du8ozsBMMdNwxxbhrP51aB7zzCDKcHJ5ci+hzF8DP7Vc8R/9PVOdUee+SJmScdhZb7r4Ndew6+5gn+99X81V/BrrgaTiDteHXQp2tEgACwYhrPhZfzW/QfNcVOxlj59y/BRREQknRQQikjoPDZ3TK+/56r5Y9l3+hoHz17n6IUaykoKb/mak1fq+Ze3D7N4yogOS5NvvcQ4RB2ELV11EAa/DtsS3YbmoN7BuVFqm+IdJhqLiMid830fL7nnoOdhzXkAa/pinB3rcPdvglhz6lpz3FS8C5XgJGDQUKIf+SOM/MGp8+6pg0FXIIBhBlON930Ang++1+V0Ye/M4Q5TjvE93O1v4m7vvK9ge/ajf4g5fjp+zVXcYx92DAJrrwWfryt5BcE9OW1/jpiT5mBNXYiz9wP8rW8E5RcOx1q2Gmtcz3/wKCIiki4KCEVEgILcKI/MGc0bu87yu+2n+dIzg7Fu0pl4vSHGi+uP0hx32XjoEg/NKiE/u2NwdsslxjG3l++i9yWX4eZn958OwpGFOUFAqA5CEZG75rc04rz3Et6pYJAIg4bi11wm/tO/pcPoeCD6B/8XiQ9+GwRreYOJrv5Ch3AQwL9+pd0HHtRfv/2iDBOM5LLfrn8YZIwpw9m2Ft7+OcEy4U5XQMFQzMIRGENa/1c4AiJR3B0VeCf3B1cVDg/2VLx4ksQbPwxqjmZjLSzHmrEMw9I+gyIiEg4KCEVEWt0/YxRbj17hck0zW45eZsW04i6vizsuP1p/hIaWBIYBjuez9egVHp0zGmgLznKzup54mFpiHIYOwlhyiXFXexCGqwOvvl1AePRCraYYi4jcJe/8CRLrf9FxyXB9NV59dTAcJC8fGmrBMIh89I9xNr2Cf/445OQTWf0FjIKhnd7Tuu9BrImz8T0XTBPDMPAbakms/yU01ABgjJ4MLY2p4SBGySQiD/4+DCrEMIIhZV7NVdxtb6aCPLJywY5AYy0A/rmjwXHTxCgY3hYCtgaBRuHwDpOLfdfB3bsBd9fbQehoR7HmPQy2HSyHjjWDYWDOWIq98DGMnLxe/mqLiIj0LQWEIiKtIpbJ6oXjefHdo7y1+xzzJhR16gL0fZ9fbqzkfHUTwwZl8eS8sfzk/eNsPnKZh2aNwjLNVHDW7RLjaHg68NqWGHcxxThkHXjJQLC4MNgcPmxLpEVEMoXvurjb3sTd+36nc8bgIszpi7EmzSHx2j/jA9ac+3H3vBcsA87OJbL6C5iFw7t8b8MwYPAwkj387tEPcTb8GyRikFtA5OF/h7N1bRAOZuViL1+NOWVe8DrAb6zD2fl2sOeh74EdwZq9Emvug2BZuB+uB8vCKBwZhIEFw27Z5eedO4az8XfB/oOAOXE25tgy3L0fpDoejdGTsZetxhzW9Q8XRUREMp0CQhGRdmaNG8Kk4gJOXKrjJ+8f45HZo5kwclBqEMn6/RfYc+oaWbbJZx+eysjCHNbtOceV2hb2n7nO3NJht15iHKYhJV1MMU6GhWEL2Bqag4BwxOBgSnWYpxiv23OOmsY4H182IfWPYhGRe8G7eo7ES9/ueNAwMCfNxZq+GGNU8PuSs3Utfs1VjMFF+HXVeCcPQDSbyNOfxxx66xDNjzXjbHgZ7/huAMwJM7EfWIORnQc73wbAvv9jWJPmtF7fgrvnvWBCspMIapq2GHthOUZeQep97UWP9/he/YZanM2v4lXuC25zcBHW7BV4Z47gvPeb4KKCYdjLnsIcP0O/H4uISKgpIBQRaccwDD6yaDzfen0/Ry/UcvRCLUPyosybWMSQ/CzW7jqLAfzh/ZMpHhJ0oq2YVsxvt55i46FLzC0d1jakJLu7DsKgUyEcQ0pa9yDscolx5tffXrKDcMTgHAwDmuMurudhmWaaK7s9vu/zzr7zOK7P4/eNYXBuNN0licgA4qz/ZYePrWVPY02Z32FJrXf1PO6e1u5C0wyW+UaiRJ76HGbR6Ft+Du/iSRLv/CJYUmxHsVc8gzl1YSqAM0dNwL10Cv/KOfzSGbgHtuB++A60NAXnS2diLX7ijqcG+66Du28j7s63wYkHXYizVoATx9n0ajCxOJKFNf8RrNkrMCz9k0pERMJPf5qJiNygZGgef/6ROew4fpVdlVVcb4zzzr4LqfNPzhvLzHFt+yYtmDScN3ad5eSVes5fa0wtve2ugzA3JB2Evu93s8Q4CAvDFBDGEy5xx8M2DXKiFrlRm8aYQ1PMYVBOuAK2loSL4wYb6je0JBQQisg9Zc1YhntwSxDAjZ/eqWvOdx2cd3+VmgDsX78CdoTIk5/FHDnupu/tuy7urreDZcC+jzF8DPajf4A5uKjDdWZxKS7g7n0ft3Jv296ExaXYS1ZhFo+/4/vzzh3H2fhy23Li0pkYQ0fiHtwKLY2AgTltIfaiJzByB93x5xEREck0CghFRLowvCCHVfPH8cS8sZy8XMeuyir2n7nOzLFDeGR2SYdrsyLW/7+9Ow+Pq7zv/v8+Z2a0jEarJWuzJVmyZHk3mJhgY2NAECChJSQ4IaUJZOnzpE3jpL8+ba6rjUNw84Nc/ZWSpm2ehDyBkPCkLGELuwW1MZiYxfsq2bJWW5a1SzNaZuac3x+jGVu2JMu2ZGmkz+u6uJBmzszcR7eO5Pnoe99fPjE3g60HG3nvUON5m5SElxhfbAXh0cYO3j/cxC1XzCY9Ke6inmM0ev1BLNsm1uXA6ThdZRfrNHGYBv6ghT9g4XJO/gq87oF9IT3xLgzDICHOhbcvgLc3+gLCrp7TS6O7e6J3mbSIRCfHomtwLLpm2PuDu7ZgtzaevsF04PrUlzFzCkd8XrujGf/bT2E31QEGjiuux7G87Jz9AW3bxvb3nb6hux0jLRPHilsw80ovepmv7e0gsO0VrKo9wMBeioWLsWoPRTo0G1kFOFfejplx/ipIERGRaKOAUERkBKZhUJSVTFFWMnetHP64laVZvHuwkR1VzQQtG4dpEDtMcHYpTUoa23w89tZh+gIWLV29fOu2RTjM8dnzKLwk9+xmK4ZhkBDrpLPHj7fPT4ozdlxefyx194S+1p6BvRTD5xSNnYwHBYRROH4RmbpsbyfBHW8Pus15059hzioe/jG2jXX4IwLv/SG0nNeTjOv6LwwZKFpNdQS2v4Z9vCpym1l8Bc61d2Fc5HYRQy0nNudeAb7OUCUjgCcF5ydvwyxcrH0GRURkylJAKCIyBtKT4iidlcLB+nYgtIx4uDcRcQMBYW9/qELPHOWbDW+vn8feDoWDBlDf4mXL/uPcsHh8KhmGWl4c5o4EhAFSEqIgIAzvpRgOCAf+H22NVgC6evojH3dHWSdpEZnibCu0P98ZAttexm44EqruyykctF+f3esj8M5zoT0KAbNoCc7Vn8WIjR/0HFZHM8EP3og0CyE2Hvp6ADASkqGnGzsYwA76IRCAYAACfuxgAIL+yOcEA6HbBj4m6MeqrcBuH+hEPKsYI96DVbkjdL/ThWPZWhxL12A4h14VICIiMlUoIBQRGSOrSrMGBYTDcZgGcS4Hvf4gvf3BEY8NC1oWv9lSSWt3H7NmJFC2JJfH/7uCN3fVs2BWaqRhyljynhWqnSnaGpWcHRB6wp2Yo7AC78wKwmgcv4hMXcFj+09/YpihIK+rleC+bQT3bQNnDOasYsz8UnC4CGx/Fbyd4IrFee2fYhZfMeiPa7avi8DHb2Ed+gAsCxxOHItX4Vh2HVbDUQKbniS4azPBXZsvbeBJMzBnzsI6XoXt6wLAnLsM59W3YniSL+25RUREooQCQhGRMVKck0xGUhynOnvPWZZ7Nnesk15/EF9fYFQB4Ysf1HC0sZPEeBf3Xj+P5IQYri6eyfbKJp567+i4LDUOV9clDLGXYrQ1KokEhPGhr3X4nKKzglBLjEVk8gke2E5w2x8AcK65E8f8FdiWhX2qHqvmIFbtIeyWE1jV+yN7+oU5134ec86iSDho9/cS3P0OwT1bQ9V+xkBjkOU3RQI7c1YxRloWdnc7OF3gcIaqEwc+Dn3uAqcTHGfcFr5/4Ha7sxW7sRrryG4AjJmzQ/sMnqehioiIyFSjgFBEZIyYhsGq+Vm8sL36vMtu42OcQB89o2hU8v7hk7x/+CRO0+De60tITgg11fjMVXkcPt4+bkuNw9VpQy0xDgeg0VLBFm7mcXqJcXSN/0wKCEVksglW7CCw9QUAHCtvxzF/BQCGaWJk5oXCthWfwu5ux6o9ROD9V0LB34DApifBnRRahpyYQnDvewMdg8EsWBDqmJyaOeg1jZg4Yu76zkWP2e7uILD9Nawju0I3uBNxXn3LQBXj5G++JSIiMtYUEIqIjKFrSjKJcZrMzRp5SdL5lujats3xVh97alrYvO8EAJ9fWUheRmLkmLgYJ3etLOTRTYfGZalxd2QPwuhfYtw1zB6E0biH35mhoLoYi8hECx7dQ2DzM4CN4+pbcC5eNeyxhicFx4JPYmTMwv/cvwNgzr8aq/YgeDtDS4nDx2bm4/zkrZhZBWM6XtvfT3DPOwR3bQmFlA4njiWrcVyxFsM1+ffUFRERGS8KCEVExpBpGnxi7szzHueOdQAMqiC0bZvqU93sq2llb20rbd19kfvWLspmeVHGOc9TkpMybkuNvX0DodoQS6CjLSA8p0lJuAKyL/oCtsFNSqJv/CIydQSrDxB4+7/AtnEsvxHnsrWjepwRExf6IDEN15rPYtt3hJYf1x7EbmvCLFqKmT9/TDsG27aNdXRPaN/D7g4AzMLFoX0Gk9LG7HVERESilQJCEZEJEB9zOmDr7vHz0dFTbK9oormrN3JMYryLRXlpLMlPoygradjnOnOp8dt7G7hp6awxGaN3hArCyBLdqAkIQ+P0xIeblAzsQRiFFYRnLjHu6vVj2/aYvokWERkNq74ytDTYsnAsXYNjednoHxwOCPtDv/MMw8BIz8FMzxmHkYJ1qp7Atj9gN9aEXm9GdmifwZzCcXk9ERGRaKSAUERkAoQr8LbsP8FLH9YQtGwAkt0xLC2YweL8NPIyPJijCH7iYpysW1XEL948SPnuekpyksk/YynyxRp5D8Ioa1IyRfYgtCw7UjXoNA0CQZu+gEWcyzHBIxOR6cQ6XoX/jSfACmIuvAbH1bde2B8qzggIx/OPHLavi8AHr2Md3gHYEJeAc8WnMOddhWFqn0EREZEzKSAUEZkA4YCwtbsPw4D5s1L4ZEkm83JTLmqJcHF2MmsWZPPOgRP8busRvnP7klGHRo1tPo42N1A4I2bQm7TuEbsYR88SXcuyTy+Xjju3i3E0VeD5+gJYdujrH+ty0NbdR3ePXwGhRI3HH3+cqqoq5syZw3333Re5vba2lkcffRSAr3/96+Tn50/UEOU8rJO1+F9/HAL+UGfhVbdf8M9QY6CjMMFAaB9AV8yYjtEOBgjufZfgjrfB3w+mA8eiVTiuvAEjNm5MX0tERGSqUEAoIjIBls1J59jJLnLSElhRnHHersejceuVs6k80cGJNh8vfVDNulVF531MW3cfP3vjAL6+AF+9cR7zZ6VG7vP1Dg7VzhRNexD6+gPYA6GaY6BixOU0iXGa9Acsev3ByJLvya5zYP/BxDgXMS4zFBD2+klP0htemfyqqqro7e3lgQce4NFHH+XIkSPMnTsXgKeeeor169djmia//OUv+bu/+7sJHu3UF9i1BbuxGufKz0B6+qgeY51qwP/qr8Dfjzl3Gc7Vd158x9+YOOjpDi0zHqOA0LZtrOoDBP74CnS2AmDmz8dxzacxk0d3jiIiItNVdLwjEhGZYpLdMdx7w7wxfU6nw+RLq+fyk1f28uGRU8yflcri/OE3Xg8ELX67pTIS8r2z/0QkIPQHLfoCFg7TIHaI6rSEKAoITy8vHvwrLyHORX93H97eQNQEhOHlxYnxLlxOc9Bt0SZoWRw50cmczERinKqAnA4qKytZsmQJAIsXL6aioiISEHq9XtIHQiqv1zvk48vLyykvLwfgoYceihwvF6f5VC19NQfxrLgRp9N53q+nv6mB5tceg/5e4kqXk/bZv8AwL/7aPRmfQKCnm5SEeFxjMJf+pno6Nv0XgepDADjTc0i+6QvEFS685OeejEYzZzJ5aL6ij+Ys+mjOLl10vCMSEZFRyUp18+nl+bz4QTXPvl9FXrqH5IShKzNe+biW2uZuUhJi6O0PcqSxk4ZWL7lpCaf3H4x1Drl0LD7GiQH09AcJWvaYdU4eD2d3MA7zxDpp6+7D2+cnneiowAs3KEmMd+F0hALCaNtHMezjo808s62Km5fNGrPGOjK5eb1eMjMzAXC73dTX10fus237vI8vKyujrOx0I4zm5uaxH+Q0EnAnA9BRe5T4kmUjfj3tnm76n3kEerox80qxrv0sLa1tl/T6QUfoZ/Kp53+BWbAQM28eRlrWBS9Xtnu8BD7ahHVwO9g2xLpxXnUT5oIVdJsOuqfo90l6erqugSii+Yo+mrPoozkbvZycoZuCKSAUEZliVpVmcqihjcMNHTz13lG+euO8SJgUtru6hXcPNuIwDf78umION/p4c8cx3tl/grtXzx2xgzGAaRrExTjo6Q/S0x84J3ybTIYLCBOisJPx6YAwJhLKdkfR+M/U1NEDQHNn73mOlKnC7Xbj8/kA6Onpwe12D3lctOwJGu2MlJkA2O2nznusVXsIeroxZs7GedOfhfYQvERm4WKCzcexm+oINtUR/OB1SEjCnD0PM28eZu5cjJjh/3hjB4ME979P8OPy0DJlw8Sx6Bocy8sw4ob+3hIREZHhKSAUEZliDMNg3aoiHn5xD5UnOnjouV2sXZTNiuKZxDgdNHX08Mx7RwG4/ap88jISmZ2Tyaadx9h1rIXbrsyLhGpDdTAOS4hz0dMfxNsbrQFh9HUyPrOCMNzhOlqXGHcOnEv4nGTqKykpoby8nJUrV7J3717Wrl0buc/j8dDS0oJhGMTHx0/cIKcRIyUDGF1AaHeFqgXN3LkYzrH5ee9cdh2O+SuwGo5g1R7GqjsM3k6sQx9iHfoQTBMjq2AgMCzFSJ0ZCY+DtYcJvv9yZOzGrGKcKz+DmZo5JmMTERGZjhQQiohMQUnxMXzlhnn8/v0qTrb38OIHNZTvbmD1gmx2HWumL2CxtCCNlaWhN1MZyW4W56Wxp6aVbYcbyUwJVV94huhgHHa6UYkfuPA39A0tXuJjHKQlju/y3u6eUIWdJ/6sgHDg3LqjYB/FsK5wk5J4V+SNcneUBmxdvtC5dEVpwCkXrrCwEJfLxYYNGygoKCA9PZ3nnnuOO++8k3Xr1vHII48A8LWvfW1iBzpNnA4Im867xDscEBqJqSMed8FjiI3HUbgYR+FibNvGbjmOVVuBVXcI+2Qt9vEqgserCG5/DTwpmLPnQXd7KEwEjOT0UAOSvFJVnoqIiFwiBYQiIlPUnJmJ/M2fLOFAXRtv72mgrsXL6zvrAMhIiuPzK4sGvaFavSCbPTWtvH/4JNctDO1LMdwSYzjdqMR7EQFb5YkOHt10EHesk//1p0tHfJ1L1TVFKwjDoreCcCAgHPi/TA/33XffoM/vvPNOAPLz89m4ceNEDGn6cieCKxb6erB83SMeane3A2MfEJ7JMAyM9FzM9Fy48nrsXh9WfSVW3WGsuopQMHhwe+jgmFgcy8twLLxmTJY7i4iIiAJCEZEpzTQMFuWlsXB2KkcaO3l7TwMtXb18eW0JcWd1Jy6YmUhehofaU91sO9QIjLzE2H2RnYw7vP08+U4lth3a/+8PH9XwxWvnXuCZjd6wS4xjo3sPwnDFT9QGhL7QuH29gUnf6EZkKjIMAyMlA/tUPYHWRogfPvwLVxAyjgHh2Yw4N465S3HMXYptW9jNx7FqD4NthYLBeM9lG4uIiMh0oIBQRGQaMAyD4uxkirOTRzxuzYJsfrulMrI/XLhKcCgXExAGLYvfbKnA2xsgP8NDQ4uXj482s7wo47xju1iRgPDsJcbhCsK+6AnYwtWQiXEurIGAMBqX6PYHgvT6gwDYhKo4k9xDd9sWkfETCQibT8DsocM/2wpCd0foeE/KZRzdaYZhYmTMwsxQx3MREZHxYp7/EBERmS4W5aWRmnA6qBmp+Ui4Au9CAsJXPq6l5lQ3ye4Y7r1hHmVLQ2/2fv9+Ff6AdZGjHll4jz7PWdWQnijrYhwIWvj6AphGKJwNB5y+3gCWNfL+YZNNuHowTI1KRCZGuJNxoKVx+IO8nWBb4E7Scl4REZEpTAGhiIhEOEyDa+dnRz4fzRLj0e5BuKe6ha0HGjENg3uuK8YT5+K6hdlkpcTT0tXHpt31lzb4YQy/xNg56P7J7szzME0Dh2nijnVic+HLvCda51n7DkZjFaTIVBBuVOIfISA83aAk5XIMSURERCaIAkIRERlkRXEGsQP7EybFD7/sMxIQjiLcOdXRw9PbqgC4/RN5FMxMBMDpMPn8ykIMYMv+4xxv9V7i6Afr9wfpD1g4TeOcPRfDjVGiJVwbqkFJOPSMlpAz7OyKQTUqEZkY4YBwpApCu3t8OhiLiIjI5KKAUEREBomLcfKV60u4Y0UBGcnxwx6XcJ49CG3b5kSbjzd31fOLTQfp8wdZWpDGqtKsQcflZySysjQTy4Znt1WN6XLZ7r7T+w+e2bEZIC7GgWlArz9IIDg+y5vH0pkNSsLCy6ajLSDs9A0OBLu1xFhkQhjJM8AwCLafwg4O87M8XEHoUUAoIiIylWkjEREROcdoGpoM1aTEtm3qW7zsqWlhX00bzV29kfuyU918fmXROUEdwC1X5rGvto26Fi/vHWpk9YLsc465GKf3Hzx3L0XTMHDHuuju9ePtC5A8yZtkTKUKwvAS4/gYBz39Qe1BKDJBDIcTIzENu7MFu6MFIy3znGPsrvbQsaogFBERmdIUEIqIyEUJNynx9gXo8PWzo6qZj46coqmj5/QxcU4WzU5jUX4ac7OScDqGLlyPczn47NUFPP7fFbzycS1Zqe4x6WrcPdCAZLhmK544Zygg7PVHQUAYCtWmREA40KQkd0YCR050ag9CkQlkpGSEAsL2JhgqIOxuD30wQR2MRURE5PJQQCgiIhfFfcby1h89uwN7YGVwQpyTZQXpLMlPo2BmIqZ5bsXgUBbmpbF6QRZbDzTyxH9X8M1bFpCTljCqx55s9/Hbd45wTclMVp6xhHm4BiVhoX0IeyJB4mQ21Ll4BsLC7p7JP/4zhSsIc9MGAkJVEIpMCKuuAqv5OHBGEHgWw52IDdhtJyFv3uUbnIiIiFxWCghFROSiuBwmCXFOvL0BTMNg/uxUPjE3g3m5yTjMi9vi9jNX5dPp62d3dSv/p/wQ37ptEame2BEf4w9Y/HZLJY3tPby2o44rC9OJixm8N58nfuhfd6f3UZz8AdWUWmIcriAcCIAVEIpcXnavj8D7L2NV7ADAlZWHUbh4yGPN/PlYlTuxag7C0jWXc5giIiJyGSkgFBGRi/aVtSWc6uxl4ezUSFfgS2EaBl+4di5dPQepOtnFL8sP8Ve3LozsdziUlz+qobE9tKy51x/kjxVNrF2UA5wOnkauICQqKgiHblISnQFheLl0uEI02sYvEq1s28Y6to/Auy9CTzc4nDiuuomMG+6gpbVtyMeYs0vAdGA3VmP3ejHiRlfZLSIiItFFXYxFROSizclMYkXxzDEJB8NcDpOvXD+PzJR4mjp6ePztw/iH6TK8v7aVbYdP4jANbrliNgBbD5yIdCU+/xLjUPDojdoKwujrYuwPWPT0B3GYBhlJcZhGqNFNNHSSFolmtreTwJu/JbDpSejpxsieg+vz63Euuw7DdAz7OCMmDiOnEGwbq/bQZRyxiIiIXE4KCEVEZNJxxzr5elkpye4YjjV18ctNBznZ7ht0TIe3n6e3VQFw65V53LA4h6yUeDp7/OysagbOHxB6wo1WoqKCcPgmJdG0RLfzjPMwTSNqqyBFooVt2wQPfUj/0w9jVe8HVyzO1Xfguv0bmCkZo3oOR/4CAKzqg+M5VBEREZlACghFRGRSSkmI5WtlpSTEOqk62cXDL+3hpQ+q6ekPYFk2v3v3CL6+ACU5yaxekIVhGJGlxZv3n8Cy7dNdjOPPU0F4keHU0cZOfrulkg5v/0U9frT6/EH6AhZOh0Gc63SlT/i8Lnb8E6HTF/paJQ10jQ6fQzSFnCLRwu5swf/K/yGw5ffQ34uZN4+Ydd/FseCTGMbo3waY+fOBUFMTO6BrVUREZCrSHoQiIjJpZae6+V93LOX1nXVsr2hi68FGdhxrpigziaONnXjiXHzx2iJMI9QpedmcGby+s46mjh4O1rXRPco9CL19F15B2O7t44nNFfj6AvgDFvfdOH7dPc/cf9AwTneFjnM5cJgGfQGL/kCQGOfwywQni86Bc0kaCAbDFZGqIBQZO7ZlEdz3HsEP34SAH+LcOFf+CebcpYN+hoyWkZiCMSMbu+UE9vEqDHUzFhERmXJUQSgiIpNaQpyLz11TyPrPLGbOzES8vQH21LQC8IVriwY17XCYJqvnZwPw9r7jkb0Fw3v1nfPcsRe3h59l2fxua6iCEeBAfRv7a1sv7MQuQHh8iWdVQhrG6SW60bBMGs6oIByYt2hcJi0ymVmtJ/G/+DOC778CAT/m3KXErPsbHMXLLiocDDMHlhkHaw6M1VBFRERkElFAKCIiUSF3RgLfvGUBX1o9l+xUN7deOZvS3JRzjru6ZCbxMQ5qT3Vj26H9DB3m0L/uEi4yXHtrbwNVJ7vwxLm4cUkuAC9+UE2/P3hhJzVKkQrCISoho20Pv/C5hJcYh4NCBYQil8YOBgh8XI7/9/+G3VQHCUk4P/VlXDfejRHvueTnNwtO70No2/YlP5+IiIhMLlpiLCIiUcMwDK4oTOeKwvRhj4l1OVg5L4u39jYAw1cPwukKQl+fH8u2I0uVR3KsqYtNu+sBuHt1EUVZyRyqb6Oh1Uf5ngZuW553Iac0KkM1KAnzxEdXJ+OOSAXh4CXGCghFLp7VVEdgy7PYrScBMOdfjfPqWzFi48bsNYz0HEhIAm8ndnMDRsasMXtuERERmXiqIBQRkSnn2vlZOM1Q2Dfc/oMATodJnMuBZUNv//mr/3x9Af7vO5XYNqxdlE1JTgoO0+DOT87BALbsP3FOt+WxcHoPwhEqCKMkYIuci/vsJcbj2+hFZCqy/f0E3n8Z/wv/id16EiNpBq7bv4FrzWfHNByE0B9oTHUzFhERmbLGNSB8/PHH2bBhA4899tg59/X39/ONb3yDPXv2jOcQRERkGvLEu7hqbkbo4xECQhh9J2Pbtnn2/Sravf3MTk/glitmR+7Ly0hkRclMLNvm+e3VY7787swmJWeLtiXGncNUEEbL+EUmC6vhCP3PPkJwz7sAOJauwfX59Zg5RWP+WrZtY7WfgoEqa0v7EIqIiEw547bEuKqqit7eXh544AEeffRRjhw5wty5cyP3v/XWW+Tljf0yLBEREYCbl82iP2DxyXmZIx6XEOuipauP7r4AGUPc7+31c6CujT01rRxqaCfW5eBLq4vP2dfwtivz2FfTytHGTnYea+HKEZZBX6hRVRBGS5OSgUrB8B6EWmIscmHsvh4Cf3wV69CHABhpWTjXfh5zDJf82paF3XICq/EY9oljWI010NM9aAwiIiIytYxbQFhZWcmSJUsAWLx4MRUVFZGAMBAIUFlZybx588br5UVEZJpLjI/h7tVzz3vcUBWEnb5+9tS0sq+2laqTnYQLAk3D4K6VhaQnnbt0zx3r5NNX5fH0e1X84cMaSrKT8QwR6I3Esm0CQeuc20fcgzCKKgj9AYue/iAO08A9sP9jopqUiIxasHo/ga0vgK8LTAeO5TfgWHodhuPS/klvB/xYJ44N/FeNfbIG/H2DD4r3YGbPwcgqwDFn4SW9noiIiEw+4xYQer1eMjNDVRtut5v6+vrIfZs3b2b16tVUVlYO+/jy8nLKy8sBeOihh0hPH7tKjIngdDqj/hymCs3F5KG5mDym81zMSPZAfTs9QQf7j/vYfriBQ7UthBcJO0yD0rx0lhdncUVRJime4ff1+tSMGeysbqeyoZWfvXmQ7965gqzU0XUPtSybR57/gGMnd3L/PauZkRQfuc/XHwoN83MySU92D3pcTpcFHKUvaEz6OTzVEdqfMTkhlpkZoXpN27ZxmAa9/iBJyanEuBwTOcRBpvN1IZOL7esi8N4fsKpCW/MYmXk4r/scZurIFdLDPl9/L3ZjTSgQbKzm+Kl6CJ5VhZyUhplVEAkFjeR0jFE0chIREZHoNG4BodvtxucLvRHo6enB7Q69oQkGg+zatYu//du/HTEgLCsro6ysLPJ5c3PzeA31skhPT4/6c5gqNBeTh+Zi8pjOc+Eg1Jzk6XdOb7rvMA1Kc1NYnJ/G/FmpkWq3QG83zb3dQz5P2BdXFvCrt/poaPWy8cl3ufeGecyZmXjecWzed5y91acAeH7rfu64ugAIBWjt3l4A/D3dNPsHN0Gx+kOft3V5J/0cVjd1AeCJdQ4aqyfORYevn+qGE6SNEMBeblPlusjJyZnoIchFsm0bq3IngW0vQ58PnC4cK27BsfAaDHP0W4nbvi6sxuqB5cLV2C0n4Ky9Uo20LIyBQNDMLsBISB7r0xEREZFJbNwCwpKSEsrLy1m5ciV79+5l7dq1AHR0dNDS0sKPfvQjGhsb2blzJ4WFhXg8o6uwEBERGUuZKaFKPcOAuVnJXDFnBovy04iPubhfkUnuGL55ywJ+u6WSQw3t/OKNA3xx9VyWFswY9jEn2ny8vrMu8vn2ypOULcnFE++ipz9I0LKJczlwOc8NBKKpi3GXb+il0onxoYCwu8c/qQJCkYlkd7Xj3/ocdl0FAMas4lB34sS0kR9n29DVhtUYWjJsn6jG7jgr6DZNjIzZoSAwq4CMhVfSOvCHCBEREZmexi0gLCwsxOVysWHDBgoKCkhPT+e5557jzjvv5MEHHwTg6aefprS0VOGgiIhMmCsLM0jzxDIzOX7ILsEXI9bl4N4b5vHC9mP8saKJ326ppLW7j7ULs89ZohcIWvxu6xGCls3VxTPpCxrsqjrJOwdOcNvyvBEblAAknNGkxLJtzEm8BPDsBiVh4XPrjIKQU2S82baFtX87gQ9eA38/xMbjvOYzmCVXDrnE17Yt7LamUHXgiWqsxmPg7Rx8kNOFkZk/sGS4AGNmHobr9HVoxntAAaGIiMi0Nm4BIcB999036PM777xz0Ofr1q0bz5cXERE5L4dpUJQ19kvpHKbBnZ+cw4zEOF75uJZXP67l2MlOPr+ykKQzgshNu+s50eYjzRPL7Z/Ip9eOYVfVSbYdPsn1i3NGbFAC4HKYxLkc9PqD9PYHI8uhR8uybDbtqSczOZ5lc8Z3v71OXygATBqighCio9GKyHiy2k8R2PJ77MZqAMzCxThX/QmG+/Q2BXYwiN3cEKoObKzGaqyGs7sKx7oxs/IxsudgZhVgpOdiOCbP/p4iIiIy+YxrQCgiIjKdGYbB2kU5pCXG8uy2Kg7Wt/MvL+7hc9fMYUn+DKqbuvjvfccxgC9eW0Ssy0Fueipzs5I40tjJewcbmZEYWnI7XEAIoWXGvf4g3b3+Cw4IN+8/TvnuBhymQU5aAjOT48//oIs0XAVheJm0OhnLdGUHgwT3vEPw47dCzULciThX/SmOwkXY/n6shiOnOww31ULgrGslIRkzuwAzaw5GdgFG6kwMY/R7FIqIiIgoIBQRERlnS/JnkJfu4en3qqg80cFvNldyRWEbtae6sG24flEOczKTIsffuCSXI42dbD3YyOr5WQAjLn/2xLto7uqlu8d/QQFffYuXN3bWAxC0bF78oJqvl5WOW6fS4SsIQ+emgFCmI+tUA4Etz4YahwBmwQLMgoXYJ2vp370Fu7kBLGvQY4yUjIGGIqGmInhS1WFYRERELokCQhERkcsgJSGWr99UyvuHT/LKR7XsrAo1DchOdXPzslmDji3KSiIv3UNtczfvHmoEzldBGPp1fiFLdP2B0N6Hlm1zZWE6B+vbqDjewf66NhbljdwE4WKdbw9CBYQyndgBP8GP3yK4+x2wBwJAw8CqPoBVfeD0gYaBkZ4bWiqcXRD6v/v8ndFFRERELoQCQhERkcvENAxWlWZRkp3M09uqaOro4YvXFuF0DF4KaBgGNy7J5bG3D+PtDQCQGDfyEmO4sIDw1R21NHX0MDM5js9dM4cPKj28+EE1f/iwhnk5KUN2TL5U4QAw6axqyMSLGL9INLNaTxJ48zfndhe2bXA4MTJmYYb3D8zKx4hRd28REREZXwoIRURELrOM5Hj+6taFBC0bhzn0ssDSWSlkpbppbPMB59+DEEYfsFUcb+fdg42YhsHdq+cS43RwzbxMtlc20djmY/P+49y0dNb5n+gC+IMWvr4ApmHgjhv8z4/TFYT9Y/qaIpNVcN+20+GgKxYjKx8za06ow3DGLAzn8Ne7iIiIyHhQQCgiIjJBhgsHIVRteOPiHJ585wgAnpH2IIwEhIHzvqavL8BT7x4F4OZls5g1wxMZyx0rCvjfbxzg7b0NXFWUQaondtTncj5ndmM2z9orzaMlxjLNOK+8ASszD2NGFkZaNoaphiIiIiIysfSvERERkUlqSf4MslPdxLkczEgcPqwLB2wjVRDats3xVi+/23qEzh4/+Rke1i7KGXRMUVYSywpmEAja/OGjmrE5iQGRBiXucyuj4lwOnA6D/oBFnz84pq8rMhkZnmQc85ZjpucqHBQREZFJQRWEIiIik5RpGnzzlgUEghbxMcP/yo40KTmrAi9o2VQ3dbKvto39ta20eUNVfDFOk7tXzx2ygvHTV+Wxv76NvTWtVBxvpyQn5YLG3N3j59UdtVxVlEFh1unOzJEGJUNUQhqGQWKcizZvP109fmJdjgt6TRERERERuTQKCEVERCaxkYLBsDP3IAwELSpPdLC3ppX9dW34+k4vO06Md7FgdirXzMtkRuLQTQ9SEmIpW5LLazvq+M3mSm5bnsfVJTPPWRY8FNu2eeb9Kg7UtXG0sZO/++xSHAPVUacrCIdeKp0YH0Obt5/uXj/pSWrIMNX09PTwk5/8BK/XS1lZGdddd92g+9evX09qaioAX//615k1a2z3wBQRERGRkSkgFBERiXLhgLClq4/7n/p40DLdjKQ4FuWlsTAvldnpnlEFfWsWZFPX7GVfbSvP/fEYO6ua+fzKQmYmx4/4uF3HWjhQ1wZAa3cfO6tauGpuBjB4D8Ihz0H7EE5pb731FqtWrWLVqlX88Ic/ZNWqVTidp/8ZmpSUxP333z9xAxQRERGZ5hQQioiIRLn4WCcxTjOyh19OmptFeWksyU8jM8V9wc/ndJh8eW0xe2taeX57Nceaunj4pT3ctHQWaxdlR6oCz9TZ088LH1QDMH9WCgfr23lrTwNXFKbjMA06fKGAMHnYCkJ1Mp7KKioq+NrXvoZpmuTn59PQ0EB+fn7k/u7ubn7wgx+Qm5vLvffeS0zMud8n5eXllJeXA/DQQw+Rnp5+2cY/1TmdTn09o4zmLLpovqKP5iz6aM4unQJCERGRKGcaBl9eW0JTRw/zZ6WOyRJdwzBYUjCDudnJvPxRDR8eOcXrO+vYX9vKn68tGdTh2LZtnnv/GL6+ACU5yXzl+nn8fy/sprmrl13HmllelBGpDByugjASEI7QaGUk2yuaeO9QI3+2ppjMlJErHeXy8/l8xMeH5sXtduP1egfdv3HjRjweD8899xzl5eXcdttt5zxHWVkZZWVlkc+bm5vHd9DTSHp6ur6eUUZzFl00X9FHcxZ9NGejl5OTM+TtCghFRESmgHm5KczLTRnz53XHOlm3qogrC9N5+r2j1LV4eeTlvfzZmmJKcpIB2F3dwv66NmJdDu5aWYjDNLhhSQ5Pv1cVqiKck07nQAXhsHsQxl38EuPGNh/Pbz9G0LJ5fvsx/sfN8zFGsZRaxl57ezuPPPLIoNtSUlJwu9309PQQExODz+cjISFh0DEejweAFStW8Morr1yu4YqIiIjIAAWEIiIicl5zs5P5zu1L+L9bKznc0MEvyw/yqWWz+URxBs9vrwbg9qvySEkIVRZeWZhO+e4GTnX2sru6hc6B4C9p2ArCUHB4difm8wlaFv/17hGClg3A0cZQ1+bF+WkXc5pyiVJSUobcS/Dll19m7969rFy5kpqaGnJzcyP3BQIBbNvG5XJx+PBhMjMzL+OIRURERAQUEIqIiMgouWOdfPXGUsp311O+u4HXd9bxzoET+PoCFGcns6J4ZuRYh2lyw+Jcnn2/ik276/H1BTANSIgb2yYlb+05TkOrj1RPLNeUzOTVHXW8/FENpbNScDnO3StRJsYNN9zAv/3bv/H6669TVlaG0+lk165dWJZFYWEhDz74IHFxcSQkJPDXf/3XEz1cERERkWlHAaGIiIiMmmkY3LxsNrPTPfxu6xF8fQFinSZ3rSw8Z1nv8qJ0yvfUc6qzFwhVCQ7XRTmyxPgC9iCsb/Hy1p4GANatLGROZhI7qpppbO9h64ET3LA49zzPIJeL2+3me9/73qDbli1bFvn4xz/+8WUekYiIiIicSX9aFxERkQs2f1Yq6z+zmKuKMrjnrKYlYU6HOSikG255MQzuYmzb9nlfPxC0eOrdI1i2zbXzs5ibnYzDNPiTFQUAvLWnIdI5WURERERERqaAUERERC7KjMQ4vnBtEaUjNEf5xNwMkgcakyQO06AEINblIMZpEgja9PmD533tN3fV09jeQ3pSHLdeOTtye3F2Mgtnp9IfsHhtR+3oT0ZEREREZBpTQCgiIiLjxukwuWlpqIowJ9U94rGJo9iHsLvXz/uHT7J5/3EMA76wqogYp2PQMZ+5Kh+HafDx0WZqT3Vd4hmIiIiIiEx92oNQRERExtXVJZnMmuFhZkr8iMd54ly0dPXR1eMnIzl0rG3bnOrsZX9dGwfq2qhp6iK8APm6hdkUzEw853nSk+JYsyCb/953nBc/qOEvb12Aw9TfREVEREREhqOAUERERMZd7oyE8x6TGB9agtzh6+fIiQ4O1LVxsL6d5q7eyDEO06AoK4nF+WmsmDtzuKfihiW5fHT0FLXN3fy/z+5k1fwsri6eOWwXZRERERGR6UwBoYiIiEwK4SXGv9t6hDPblLhjnZTmprBwdiolOcnExZz/ny9xLgf3rCnm9388RlNHD6/tqKN8dwPLi9K5dn42meepZhQRERERmU4UEIqIiMikMDO8rBjITI5nwexU5s9KIT8jEdM0Lvj5CrOS+H/+dAmVxzvYevAEhxs6+GNFE9srm7hjRQErS7PG+AxERERERKKTAkIRERGZFD5ZMpMZibHMTI5nRmLcmDynaRjMy01hXm4KJ9t72LL/OB8eOcXz26tp6erj01flYRoXHj6KiIiIiEwl2rFbREREJgWnw2T+rNQxCwfPlpkSz7pVRaxbVYhpGLxz4AS/2VxJfyA4Lq8nIiIiIhItFBCKiIjItPKJuTP5xk2lxLkc7Ktt5X+/cYCunv6JHpaIiIiIyIRRQCgiIiLTztzsZL5120JSE2Koa/by01f3c7LdN9HDEhERERGZEAoIRUREZFrKTHHz159exOwZCXT3+OnzWxM9JBERERGRCaEmJSIiIjJtJcbH8D9vWUBDq4+8DM9ED0dEREREZEKoglBERESmtRingzkzEyd6GCIiIiIiE0YBoYiIiIiIiIiIyDSmgFBERERERERERGQaU0AoIiIiIiIiIiIyjSkgFBERERERERERmcYUEIqIiIiIiIiIiExjCghFRERERERERESmMQWEIiIiIiIiIiIi05gCQhERERERERERkWlMAaGIiIiIiIiIiMg0poBQRERERERERERkGlNAKCIiIiIiIiIiMo0pIBQREREREREREZnGFBCKiIiIiIiIiIhMYwoIRUREREREREREpjEFhCIiIiIiIiIiItOYAkIREREREREREZFpTAGhiIiIiIiIiIjINKaAUEREREREREREZBpTQCgiIiIiIiIiIjKNKSAUERERERERERGZxhQQioiIiIiIiIiITGPOiR6AiIiIiExtO3fu5Ne//jWJiYls3LjxnPu3bt3KG2+8gcfj4dvf/jZut3sCRikiIiIyfamCUERERETGVXFxMf/8z/885H2BQIBNmzbxwx/+kDVr1lBeXn6ZRyciIiIiqiAUERERkXHl8XiGva+xsZG8vDwcDgeLFy/m5z//+ZDHlZeXR8LDhx56iPT09HEZ63TkdDr19YwymrPoovmKPpqz6KM5u3QKCEVERERkwni9XuLj4wFwu914vd4hjysrK6OsrCzyeXNz82UZ33SQnp6ur2eU0ZxFF81X9NGcRR/N2ejl5OQMebsCQhEREREZE+3t7TzyyCODbktJSeE73/nOsI9xu9309PQA0NPTQ0JCwjiOUERERESGooBQRERERMZESkoK999//wU9Jjs7m7q6OizLYs+ePRQXF4/P4ERERERkWGpSIiIiIiLj6ujRo2zcuJG6ujo2btxIf38/u3btYseOHTidTm688UY2bNjAli1buOmmmyZ6uCIiIiLTjioIRURERGRcFRUV8f3vf3/QbcuWLYt8vGbNGtasWXOZRyUiIiIiYYZt2/ZED0JEREREREREREQmhpYYXybf+973JnoIMkBzMXloLiYPzcXkobmYPDQXMl3oez36aM6ii+Yr+mjOoo/m7NIpIBQREREREREREZnGFBCKiIiIiIiIiIhMYwoIL5OysrKJHoIM0FxMHpqLyUNzMXloLiYPzYVMF/pejz6as+ii+Yo+mrPoozm7dGpSIiIiIiIiIiIiMo2pglBERERERERERGQaU0AoIiIiIiIiIiIyjTknegDTweOPP05VVRVz5szhvvvum+jhTAuVlZX8+te/xjAMioqKuPfee3nppZf48MMPycjI4C//8i9xOp1D3ibj4+WXX2b79u1s3LhxyGtC18nlsWXLFrZs2YJlWXz729/mpZde0lxMgL6+Ph5++GH6+vpwu91897vf5cknn9RcXEatra38+Mc/pr6+nieeeAKHwzHqn02aF5lK9P0cXZqamviHf/gHcnNzcTqd/OM//uNED0mGMNrfMTJ5nD1nLS0tutYmsdG+35cLowrCcVZVVUVvby8PPPAAgUCAI0eOTPSQpoWMjAw2bNjAxo0b6ezs5MCBA+zfv5+NGzeSl5fHhx9+SEdHxzm3yfjw+/1UV1cDQ18Tuk4uj9bWVg4cOMCGDRu4//77aW9v11xMkF27dlFcXMz999/P3LlzeeGFFzQXl5nH4+H73/8+xcXFwOh/NmleZCrR93N0Wrx4Mffff78Ci0lsNL9jZHI5e85A19pkNpr3+3LhFBCOs8rKSpYsWQKEfsBUVFRM8Iimh5SUFGJiYgBwOBzU1dWxYMECAJYsWUJFRQVHjx495zYZH2+//TZr164Fhr4mdJ1cHrt27cKyLB544AF+9atfUVFRobmYIJmZmfT29gLg9XoxDENzcZnFxMTg8Xgin4/2Z5PmRaYSfT9Hp/3797NhwwZefvnliR6KDGM0v2Nkcjl7zkDX2mQ2mvf7cuEUEI4zr9eL2+0GwO124/P5JnhE00tNTQ2dnZ0kJCQQHx8PhObB6/Xi8/nOuU3GXiAQYP/+/SxatAgY+prQdXJ5dHR0EAgE2LBhAzExMfh8Ps3FBMnOzqayspK/+Zu/oaqqCtM0NRcTbLQ/mzQvMpXo+zn6pKam8pOf/IQf/OAH7N27l5qamokekoyCrrXoo2stOoz0fl8unALCcXbmL4Cenp7ILwYZf93d3fzqV7/im9/8Jm63m56eHgB8Ph8JCQlD3iZj75133uHaa6+NfD7UNaHr5PJwu92Rv6yFA1vNxcTYsmULy5cv5+GHH+aKK64gGAxqLibYaH82aV5kKtH3c/RxuVzExcXhcDhYvnw5dXV1Ez0kGQVda9FH19rkd773+3LhFBCOs5KSEvbt2wfA3r17KSkpmeARTQ/BYJCf/vSn/Pmf/zkpKSkUFRVx4MABIDQPxcXFQ94mY+/48eNs2rSJH/3oR9TX19PV1XXONaHr5PKYN29e5K+f4T0hNRcTw7btyDKWpKQkQHMx0Yb6eo/2NpFope/n6BN+Awxw6NAhMjMzJ3A0Mlq61qKPrrXJbTTv9+XCGbZt2xM9iKnuscce49ixYxQUFPDVr351ooczLbz77rs89thjzJ49G4AvfelLHDhwgI8//pj09HT+6q/+CqfTyQsvvHDObTJ+vv/977Nx48YhrwldJ5fHE088QVVVFYmJiaxfv57f/OY3mosJ4PV6eeSRR/D7/TgcDr773e/yzDPPaC4uo0AgwIMPPhjpKHn33Xfz7rvvjmoONC8ylej7Obrs2LGDp556CpfLRWlpKffcc89ED0mGMNrfMTJ5nD1n8+fP56OPPtK1NkmN9v2+XBgFhCIiIiIiIiIiItOYlhiLiIiIiIiIiIhMYwoIRUREREREREREpjEFhCIiIiIiIiIiItOYAkIREREREREREZFpTAGhiIiIiIiIiIjINKaAUESmpKamJtatW8dDDz3Ejh07ePrpp2lqahrz16mvr+fpp59m//79kdv+4z/+g3Xr1nH06NExfz0RERERERGRseac6AGIiIyHpKQk1q9fT1paGtu2beONN95g4cKFzJw584KeJxgM4nA4hr2/vr6eZ599FoCFCxcCcPPNN7Ns2TIyMzMv/gRERERERERELhPDtm17ogchIjLWmpqa+Na3vkVsbCx9fX2D7nv66aepqKjg17/+NbW1taSlpXHXXXdx7bXXRh5XUlJCbGwstbW1/Mu//Av/9E//xIkTJwCYM2cO3/jGN4iNjeVb3/rWoOf+wQ9+wObNm9myZQsPPvggRUVFlJeX89JLL9HW1sasWbP4yle+QmlpKZs3b+Y///M/WblyJQ0NDTQ3N3PXXXdx2223cfz4cf793/+dmpoaYmJimD17Ng888MBl+/qJiIiIyOg8/PDDJCcnU11dTUtLC9/+9rfZtGkTR44cobS0lG9+85sTPUQRkfPSEmMRmdIWLFjA0qVLAfjc5z7H+vXr6e7u5qGHHsLn83HnnXeSkZHBT3/6U6qrqyOPq6ioYM6cOXzhC1/AMAxWrFjBfffdxx133EFNTQ2PP/44SUlJ3HbbbQBcffXVrF+/nlmzZg16/X379vGLX/yCpKQkvvzlL9Pc3MyPf/xjurq6Isfs37+fG2+8EYAnn3ySQCDAG2+8wdGjR7nnnnu4++67SU9PH+evlIiIiIhcjNraWjIzM9m4cSNlZWX87Gc/45577uHhhx9mx44d+P3+iR6iiMh5aYmxiExphmGQlZXF7t27WbRoEQsXLmTHjh10d3fT3d3N7373u8ix+/btY8WKFUCoSvCee+4BoLW1ld27d1NRUUG46Lq2tpa4uDhKS0t59dVXmT17NqtWrTrn9Xfs2AHAunXrWLJkCc3NzTz//PNUVlZGjrn++uu55ZZb+Pjjj9m9ezft7e1kZ2dj2zY7d+6kqKgoEkSKiIiIyOTR39+P1+uN/FvNMAxuuOEGUlNTATBNE6dTb7tFZPLTTyoRmfIMwxjy9jVr1rBmzZrI52fuTxj+Rx3Aa6+9xuHDh/n0pz/NFVdcwc9+9jN6enrGbCwejwcgstehZVnccsst5ObmcuDAAT766COee+45/vVf/5WcnJyLel0RERERGXv19fUUFhZimqHFeTU1Ndx8880AtLS0kJaWNuy/RUVEJhMtMRaRKS8hIQGAP/7xj+zYsYOSkhI8Hg+7d+/m+PHj1NXV8eKLL9La2jri83i9Xg4cOEBLS0vktnC4d+jQId577z36+/sHPebKK68E4JlnnmHTpk28/fbbJCQkUFxcPOJrvfnmm1RUVJCVlUVmZia2bdPe3n6hpy4iIiIi46i2tpb8/PzI5zU1NeTl5Z3zsYjIZKeAUESmvNWrV5Obm8ubb77JY489hsfj4Xvf+x5ZWVk8+eSTPPfcc8TExJCRkTHk42+99VaKiorYtm0bra2tzJ49O3JfaWkpixcv5uDBg/zkJz8ZtLcgwKJFi/iLv/gLOjo6eOKJJ5gxYwZ///d/T2Ji4ohjdrlcbN68mZ///OccPHiQT33qU5SWll76F0NERERExkxtbS0FBQVAaLlxf39/5A/INTU1g8JDEZHJTF2MRUREREREREREpjFVEIqIiIiIiIiIiExjCghFRERERERERESmMQWEIiIiIiIiIiIi05gCQhERERERERERkWlMAaGIiIiIiIiIiMg0poBQRERERERERERkGlNAKCIiIiIiIiIiMo39/8iKZ9lkYB+AAAAAAElFTkSuQmCC",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plot_all(cost_history, m, q, high=1000, step=10)"
]
},
{
"cell_type": "code",
"execution_count": 194,
"metadata": {},
"outputs": [],
"source": [
"#plot_1(cost_history, m, q, low, high, step)"
]
},
{
"cell_type": "code",
"execution_count": 196,
"metadata": {},
"outputs": [],
"source": [
"#plot_2(cost_history, m, q, low, high, step)"
]
},
{
"cell_type": "code",
"execution_count": 55,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"12835 passi e 12835 gradienti calcolati per arrivare a distanza minore o uguale di 0.1 dall'ottimo\n"
]
}
],
"source": [
"near_opt(m, min_dist=1e-1, ge_per_step=1)"
]
},
{
"cell_type": "code",
"execution_count": 56,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA7sAAAHzCAYAAADhDgreAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAABLJklEQVR4nO3df3RU9Z3/8dfNDIFkAkkmQ4L8+iqoBcEINFFraIEIyInV2pqlSsmettu1rp51bVePsG2llVKw6qnHimt7tLaN3bYuiB63szVNwbimtQZJGonFqq3SChiSECAJASZzv3+EDIT8ID9m7q95Ps7pkUxmyHvmk6Hzuvdz32/DNE1TAAAAAAB4SIrdBQAAAAAAEG+EXQAAAACA5xB2AQAAAACeQ9gFAAAAAHgOYRcAAAAA4DmEXQAAAACA5xB2AQAAAACeQ9gFAMBi559/vtLS0jR+/HhlZWXpqquu0uOPP65oNHrOx7733nsyDEORSCShNVr1cwAASBTCLgAANnjhhRd09OhRvf/++1qzZo3uv/9+/dM//ZPdZQEA4BmEXQAAbJSZmanrr79ev/zlL/WTn/xEu3fv1q9+9SvNnz9fEyZM0LRp0/TNb34zdv9PfOITkqSsrCxlZGTo97//vd59910VFxcrJydHoVBIn/vc59Ta2hp7zP33368pU6Zo/Pjx+shHPqLf/va3kqRoNKpNmzZp5syZysnJ0cqVK9XS0jLgzwEAwE0IuwAAOMDll1+uqVOn6v/+7/8UCAT005/+VK2trfrVr36l//zP/9Rzzz0nSXr55ZclSa2trWpra9PHPvYxmaaptWvXat++ffrTn/6kv/3tb7GA/NZbb+nRRx9VTU2Njh49qhdffFHnn3++JOn73/++nnvuOVVVVWnfvn3Kzs7W7bffPuDPAQDATQi7AAA4xOTJk9XS0qLFixfr0ksvVUpKivLz83XzzTerqqpqwMddeOGFWrZsmcaOHauJEyfqq1/9auz+Pp9Px48f15tvvqmTJ0/q/PPP18yZMyVJjz/+uDZs2KCpU6dq7Nix+uY3v6ktW7ZwnS4AwBMIuwAAOMQHH3ygYDCoP/zhD1qyZIkmTpyozMxMPf7442pqahrwcR9++KFuuukmTZkyRRMmTNDq1atj97/wwgv18MMP65vf/KZyc3N10003ad++fZKk999/X5/+9KeVlZWlrKwszZ49Wz6fTx9++KElzxcAgEQi7AIA4AA1NTX64IMPtHDhQq1atUrXX3+9/va3v+nw4cO69dZbZZqmJMkwjD6P/Y//+A8ZhqE33nhDR44c0dNPPx27vyStWrVKr7zyit5//30ZhqF77rlHkjRt2jT97//+r1pbW2P/6+zs1JQpU/r9OQAAuAlhFwAAGx05ckT/8z//o5tuukmrV6/WpZdeqqNHjyoYDGrcuHF67bXX9F//9V+x+0+cOFEpKSn6y1/+Ervt6NGjysjIUGZmpj744AM98MADse+99dZb2r59u44fP65x48YpLS1NKSnd//d/66236mtf+5ref/99SdLBgwf1/PPPD/hzAABwE8IuAAA2uO666zR+/HhNmzZNGzZs0Fe/+lU99dRTkqTHHntM9957r8aPH6/77rtPK1eujD0uPT1dX/va11RUVKSsrCy9+uqrWrdunXbt2qXMzExde+21+sxnPhO7//Hjx7VmzRqFQiFNmjRJjY2N2rhxoyTp3/7t33T99ddr+fLlGj9+vK688kr94Q9/GPDnAADgJoZ55j4nAAAAAAA8gDO7AAAAAADPIewCAAAAADyHsAsAAAAA8BzCLgAAAADAcwi7AAAAAADPIewCAAAAADzHb3cBVti3b5/dJThSKBRSU1OT3WXgLKyLM7EuzsS6OA9r4kysizOxLs7DmjjTYOsyefLkAR/HmV0AAAAAgOcQdgEAAAAAnkPYBQAAAAB4DmEXAAAAAOA5hF0AAAAAgOcQdgEAAAAAnkPYBQAAAAB4DmEXAAAAAOA5fqt/4GOPPaZdu3YpMzNTDz30kCTpmWee0W9/+1tNmDBBknTzzTdrwYIFfR5bV1enp556StFoVFdffbVuuOEGK0sHAAAAALiE5WF38eLFWrFihTZv3tzr9muvvVbXX3/9gI+LRqN68skn9fWvf105OTlau3atCgoKNHXq1ESXDAAAAABwGcu3MV9yySXKyMgY9uPeeecdTZo0SXl5efL7/brqqqtUU1OTgAoBAAAAAG5n+Zndgbz44ot6+eWXNWPGDP3jP/5jn0Dc0tKinJyc2Nc5OTl6++23rS4TAAAAAOACjgi7y5cvV2lpqSTpl7/8pX7605/qtttuG/HfV1lZqcrKSknSpk2bFAqF4lKn1/j9fl4bB2JdnIl1cSbWxXlYE2diXZyJdXEe1sSZRroujgi7WVlZsT9fffXVuv/++/vcJxgMqrm5OfZ1c3OzgsFgv3/f0qVLtXTp0tjXTU1N8SvWQ0KhEK+NA7EuzsS6OBPr4jysiTOxLs7EujgPa+JMg63L5MmTB3ycI0YPHTp0KPbn1157TdOmTetzn5kzZ2r//v1qbGxUJBLR7373OxUUFFhZJgAAAADAJSw/s/vwww/rzTff1NGjR3Xrrbdq5cqVamho0HvvvSfDMDRx4kTdcsstkrqv0/3BD36gtWvXyufz6Ytf/KI2bNigaDSqJUuW9BuKAQBA8mmoq9UbL4Y15libTqZl6NJrSjRn3ny7ywIA2MjysHvnnXf2ua24uLjf+waDQa1duzb29YIFC/qdvwsAAJJXQ12tDmwpV2luloz0dJlml6q2lEsSgRcAkpgjtjEDAACM1O6KsBblZskwDEmSYRhalJul3RVhmysDANiJsAsAAFzN39EWC7o9DMOQv6PdpooAAE5A2AUAAK4WSc+QaZq9bjNNU5H0gE0VAQCcgLALAABcbe7yElU1tsYCr2maqmps1dzlJTZXBgCwkyPm7AIAAIxUTxOqrRVh+TvaFUkPaG5pGc2pACDJEXYBAIDrzZk3n3ALAOiFbcwAAAAAAM8h7AIAAAAAPIewCwAAAADwHMIuAAAAAMBzCLsAAAAAAM8h7AIAAAAAPIewCwAAAADwHObsAgCAEWuoq9UbL4Y15libTqZl6OMrb9aUC2bYXRYAAJzZBQAAI9NQV6sDW8pVmtalG3LSVZrWpXd/+kM11NXaXRoAAIRdAAAwMrsrwlqUmyXDMCRJhmFocV6WdleEba4MAADCLgAAGCF/R1ss6PYwDEP+jnabKgIA4DTCLgAAGJFIeoZM0+x1m2maiqQHbKoIAIDTCLsAAGBE5i4vUVVjayzwmqaplz5s1dzlJTZXBgAA3ZgBAMAgzu62fOk1JZozb74kxf67tSIsf0e7IukBLfzHW+jGDABwBMIuAADoV6zbcm6WjPR0mWaXqraUS1KvwNvzZ0kKhUJqamqypV4vGewgAwBgaNjGDAAA+tVft+VFuXRbTrT+Rjod2FLOSCcAGCbCLgAA6Bfdlu3BQQYAiA/CLgAA6Bfdlu3BQQYAiA/CLgAA6Fd/3ZarGum2nGgcZACA+CDsAgCAfs2ZN1+TSsu0tdOn55qPaWunT5NKy2iUlGAcZACA+KAbMwAAGNDZ3ZaReP2NdJrLQQYAGDbCLgAAgMNwkAEARo9tzAAAAAAAzyHsAgAAAAA8h7ALAAAAAPAcwi4AAAAAwHNoUAUAAICEa6ir1RsvhjXmWJtOpmXo0mtKaMIFIKEIuwAAAEiohrpaHdhSrtLcLBnp6TLNLlVtKZckAi+AhGEbMwAAABJqd0VYi3KzZBiGJMkwDC3KzdLuirDNlQHwMsIuAAAAEsrf0RYLuj0Mw5C/o92migAkA8IuAAAAEiqSniHTNHvdZpqmIukBmyoCkAwIuwAAAEiouctLVNXYGgu8pmmqqrFVc5eX2FwZAC+jQRUAAAASqqcJ1daKsPwd7YqkBzS3tIzmVAASirALAACAhJszbz7hFoCl2MYMAAAAAPAcwi4AAAAAwHPYxgwAABBnDXW1euPFsMYca9PJtAxdek0JW3gBwGKEXQAAgDhqqKvVgS3lKs3NkpGeLtPsUtWWckki8LocBzEAdyHsAgAAxNHuirBuzM2SYRiSJMMwtCg3S1srwgSjfrglQHIQA3AfrtkFAACII39HWyzo9jAMQ/6Odpsqcq5YgEzr0g056SpN69KBLeVqqKu1u7Q+dleEtaifgxi7K8I2VwZgIJae2X3ssce0a9cuZWZm6qGHHpIklZeX6/XXX5ff71deXp5uu+02BQKBPo+9/fbbNW7cOKWkpMjn82nTpk1Wlg4AADAkkfQMmWZXr8BrmqYi6X0/3yQ7N50F93e0yUhL73UbBzEAZ7M07C5evFgrVqzQ5s2bY7fl5+dr1apV8vl8evrpp7Vt2zatXr2638evW7dOEyZMsKpcAACAYZu7vERVW8pjZwFN01RVY6vmlpbZXZrjuClAchADcB9Lw+4ll1yixsbGXrdddtllsT9ffPHFevXVV60sCQAAeJCd14H2/JytFWH5O9oVSQ9obmmZ485UOoGbAiQHMQD3cVSDqu3bt+uqq64a8PsbNmyQJC1btkxLly61qiwAAOAiTmgkNGfefMLtELgpQHIQA3AfwzRN08of2NjYqPvvvz92zW6PZ599Vu+++67uuuuuPk0dJKmlpUXBYFCHDx/Wt7/9bX3hC1/QJZdc0u/PqKysVGVlpSRp06ZNOnHiRPyfiAf4/X5FIhG7y8BZWBdnYl2ciXVxHiesyZP3rtWnU0/2OVu47cQY/dN9G22szD5OWJeB/LHmNe18YZt87W3qCmSo4LpP67LCy+0uyxJOXpdkxZo402DrkpqaOvDjElXQcLz00kt6/fXXde+99/YbdCUpGAxKkjIzM1VYWKh33nlnwLC7dOnSXmd+m5qa4l+0B4RCIV4bB2JdnIl1cSbWxXmcsCaRliadzEnv5/YjttdmFyesy0CmXDBDU+749163ObXWeHPyuiQr1sSZBluXyZMnD/g428NuXV2dnn/+eX3rW9/S2LFj+71PZ2enTNNUWlqaOjs7VV9fr9LSUosrBQAAbvD3tg798u0/KdXs0skUny6dPk2zJk105HWgAIDEsTTsPvzww3rzzTd19OhR3XrrrVq5cqW2bdumSCSi9evXS5Iuuugi3XLLLWppadEPfvADrV27VocPH9aDDz4oSerq6tLChQs1b948K0sHAAAu0FBXq/93ol1XZo5VaFyqZJrasfd97Wo5qo/e+m92lwcAsJClYffOO+/sc1txcXG/9w0Gg1q7dq0kKS8vTw888EAiSwMAAB6wuyKsGy+crvajR7T/YKNSuqL6SE6m3hmbTSMhAEgytm9jBgAkjp3jVwA79MxtzZiQqYwJmbHbc5uP2VgVAMAOhF0A8CgnjF8BrOamua0AgMQi7AKAR+2uCOvGU7MrJckwDC3KzdLWijBhF541mrmt7IQAAG8h7AKAR/Vs5zyTYRjyd7TbVBGQeD3hdGtFWP6OdkXSA5pbWnbO0MpOCADwHsIuAHgU2zmRrObMmz/sgMpOCADwnhS7CwAAJMbc5SWqamyVaZqSdHo75/ISmysDnMff0dbrwJDETggAcDvO7AKAR410OyeQjNgJAQDeQ9gFAA8byXZOIBmNprEVAMCZCLsAACQQHX7dgZ0QAOA9hF0AABKEDr/uwk4IAPAWGlQBAJAguyvCsW2x0ukOv7srwjZXBgCA9xF2AQBIEDr8AgBgH7YxAwCQIHT4hZcNdj0616oDcALCLgDA9c7+YJ1xwUy1/fVd2z9o0+EXXjXY9eiSuFYdgCMQdgEArnb2h+439+/Xm1te0Yr8SzQ+J8vWD9p0+IVX7a4I68Z+rkffeup69IG+x+8+ACsRdgEArnb2h+6GvX/XjVNydKDpoMZnZtn+QZsOv/Aif0ebjLT0Xredvh7dHOR7AGAdGlQBAFzt7CZQ/miXUgxDKV1dsdv4oA3EV/f16Gav23quRx/sewBgJcIuAMDVzv5gHUnxKWqaivp8sdv4oA3E19zlJapqbI2992LXoy8vGfR7AGAltjEDACyRqO6sZzeBmjN9qp59511dk3+JJNEUCkiAoVyPzrXqAOxG2AUAJNxgnVtH+wG4z4furPMUKF2oF997V/5mPmgDiTLY9ehcqw7ACQi7AICEG6xzazw+EPPBGgAAnI1rdgEACXd2EymJplEAACCxCLsAgISjOysAALAaYRcAkHB0ZwUAAFbjml0AQMINpXMrYJVEdQYHADgLYRcAYAk3NJEiBCWOU17bc3UGd0qdAIDRI+wCAKDEjkdKdk56bQfrDC7JMXUCAEaPa3YBAFB3CFrUTwjafSoEYeSc9NoO1hncSXUCAEaPsAsAgBiPlEhOem0H6wzupDoBAKNH2AUAQIxHSiQnvbaDdQZ3Up0AgNEj7AIAIMYjJZKTXts58+ZrUmmZtnb69FzzMW3t9GnSqc7gTqoTADB6NKgCAEDuHI/kls7BTnttB+oM7rQ6AQCjQ9gFAOAUN4xH6uGkDsdD4ZbX1uo63XLAAgDciG3MAAC4EJ2D3S92wCKtSzfkpKs0rUsHtpSroa7W7tIAwBMIuwAAuBCdg92PAxYAkFhsYwYAxBXbMq3R3Tm4q1fgpXOwu/g72mSkpfe6jQMWABA/nNkFAMQN2zKtQ+dg92PUEQAkFmEXABA3bMu0zmAjdOAOHLAAgMRiGzMAIG7Ylmktuzsc97dlfdHSZbbV4zaMOgKAxCLsAgDihutIk8dAo4/+mJmpKRfMsLs817D7gAUAeBlhFwAQN3OXl6hqS3lsK3NsW2Zpmd2lWcLK5lx2NwLbXRHWjf1sWf/VC9s05Y5/t6wOAAAGQtgFAMRNMm/LHOhMp6S4P38rf9ZABtqy7mtrs+TnA1az+wATgOEj7AIA4ipZt2UOdKZza0U47q+HlT9rIANtWe8KZFjy8wErOeEAE4DhoxszAABx4O9o6xX8pMQ157LyZw1koE7CBdd92rIaAKvQaR5wJ87sAgAQB1Y253JCI7CBtqxfVni5mpqaLKsDsAKd5gF3IuwCABAHVjbnckojsGTdso7k44QDTACGj7ALAEAcWNmcK5kbgQF2cMoBJgDDY3nYfeyxx7Rr1y5lZmbqoYcekiS1tbXpe9/7ng4ePKiJEyfqK1/5ijIy+ja4eOmll/Tss89Kkj7zmc9o8eLFVpYOAMCgrDzTyVlVwDocYALcyfKwu3jxYq1YsUKbN2+O3fbcc8/p0ksv1Q033KDnnntOzz33nFavXt3rcW1tbdqyZYs2bdokSVqzZo0KCgr6DcUAAABAPHGACXAfy7sxX3LJJX0Cak1NjRYtWiRJWrRokWpqavo8rq6uTvn5+crIyFBGRoby8/NVV1dnRckAAAAAAJdxxDW7hw8fVnZ2tiQpKytLhw8f7nOflpYW5eTkxL4OBoNqaWnp9++rrKxUZWWlJGnTpk0KhUIJqNr9/H4/r40DsS7OxLo4E+viPF5akz/WvKaaF7bJ335UkcB4FV73aV1WeLndZY2Il9bFS1gX52FNnGmk6+KIsHsmwzD6zA4crqVLl2rp0qWxrxmB0L9QKMRr40CsizOxLs7EujiPV9akoa5WB7aU65O5WTIyfDLNdlU9+ahaD7vzOk2vrIvXsC7Ow5o402DrMnny5AEfZ/k25v5kZmbq0KFDkqRDhw5pwoQJfe4TDAbV3Nwc+7qlpUXBYNCyGgEAQPLYXRGOdd6Vug/GL8rN0u6KsM2VAQCGyhFndgsKClRVVaUbbrhBVVVVKiws7HOfefPm6ec//7na2tokSX/84x+1atUqq0sFAAAWaKir1RsvhjXmWJtOpmXo0mtKLD2j6u9ok5GW3us2wzDk72i3rAYAwOhYHnYffvhhvfnmmzp69KhuvfVWrVy5UjfccIO+973vafv27bHRQ5L07rvv6je/+Y1uvfVWZWRk6MYbb9TatWslSaWlpXRiBgDAg3q2EJfmZslIT5dpdqlqS7kkWRZ4I+kZMs2uXpdWmaapSHrAkp8PABg9y8PunXfe2e/t9957b5/bZs6cqZkzZ8a+Li4uVnFxcaJKAwAADrC7Iqwb+9lCvLUibFnYnbu8RFVbymNbmU3TVFVjq+aWllny8wEAo+eIbcwAAAA9nLCFuCdUb60Iy9/Rrkh6QHNL3dmcKhHivc3c7m3rALyJsAsAccKHNSA+hrKF2Ir325x58/v8nbzP47/N3Anb1gF4kyO6MQOA28U+rKV16YacdJWmdenAlnI11NXaXRrgOnOXl6iqsVWmaUrS6S3Ey0sk2fd+433eLd6dqul8DSBRCLsAEAd8WAPiZ868+ZpUWqatnT4913xMWzt9mnTGFmK73m+8z7v5O9p6nXWXRrfNPN5/HwD0YBszAMSBE64xBLykvy3EPex6v/E+7xbvTtV0vgaQKJzZBYA46P6wZva6jQ9rQGLY9X7jfd7tXNvM7f77AKAHZ3YBIA4YUwJYJxHvt6E0nuJ93i1enarPfM0/PB7V7r3NmpoRoPM14ADHT0R0sKVDjS1tikSiujx/qt0ljQhhFwDigDElgHXi/X4bajdg3uenDbbNfCj6vObBNFU1tmrSDf+QlK8nYIdjnSfV2NKuxuZ2NTa36cNT/z3Y0q5DRzpj9wtmphF2ASDZjfbDH4Chi+f7bXdFWDf203hqa0W4z8/gfR4fw3nNAYxcW8cJNTa3nQq07fqwpS0Wbo+2nxjwcT6foVB2QHk5AeXmdF/CcXYjOTcg7AIAgKRG4ynr8ZoD8WGapo60HdeHp87Ifth8+kxtY3O7OjpPDvjYMf4U5Qa7w2xuzhn/DQYUzEyTz+f+9k6EXQAAkNToBmw9XnNg6KJRU61HjnUH2ZbTZ2m7tyC36fiJrgEfOzbVf+rs7Okwmxfs/m/m+HFKSXHf2drhIOwCgA2G0gwHzsBaeR+Np6zHaw701tUVVfPhY6e3HLe09/pzJBId8LGBtDHdQTZ4OtT2bD8eH0h15fbjeCHsAoDFhtoMB/ZjrYbmzAMCvmBIF32i2FWvD42nrMdrjmR0MtKlpkMdvbYZ94TapkMd6oqaAz52QsbY2Bbj2BnanAxNDAaUkZ5q4bNwF8IuAFiMxizuwVqd29kHBMaMOanfuPCAAI2nrMdrDi86c2TPmV2OD7a0q7m1Q+bAeVbZmWnKCwY08dS2457txhNzAkobO8a6J+EhhF0AsBiNWdyDtTo3DggASDZDHdlzNsOQQtnpyjt1ZnZi8HS344nBgFLH+Cx8FsmBsAsAFqMxi3uwVufGAQEAXhSXkT3Bni7H3f8LZQXk97u/w7GbEHYBwGI0ZnEP1urcOCAAwI0GGtnTcrhT+z48nPQje7yCsAsAFqMxi3uwVufGAQEATsXIHhB2AcAGNGZxD9ZqcGcfEPAH03UhBwQAWCTeI3sunjlFY32RpB/Z4xWEXQAAMCpnHhAIhUJqamoa1d/HbGMAZ7JyZE88/g2DcxB2AQCAYzDbGEhOjOxBIhB2AQCAYzDKCPAuRvbAaoRdAADgGIwyAtyNkT1wEsIuAABwDEYZAc420MienoDLyB44CWEXAAA4BqOMAPsxsgdeQdgFAACOwWxjwBrxHtnTcw0tI3vgJIRdAADgKMw2BuLDypE9XlBb36DtO3erqf24MnxRlSws1Pz8OXaXhVEg7AIAAAAuxcie+Kitb1B59R7l5S9S4ORJRU1T5dU1kkTgdTHCLgAAAOBgjOxJvHD1TmXPWtJr7Fn2rEKFq3cQdl2MsAsAADAEtfUNCr9So7auFLY4Iu4Y2WOvtoihwFnXGhuGofYI1x+7GWEXAADgHHq2OGbPLlbAMNjiiGHrb2TP4baI/ravmZE9DpDhNxU9a8+3aZoK+AfZBw7HI+wCAACcA1scMRSM7HGvkqIClVfXKC+/SFJ30D20p0ZlRQU2V4bRIOwCAACcA1sc0SOeI3tmnj9J6akmI3scoOeg1fbXq3S47bgCflNlRQUczHI5wi4AAMA59GxxPDOMsMXRu6wa2RMKhdTU1JTop4Mhmp8/R8uKF7EmHkLYBQDABRrqavXGi2GNOdamk2kZuvSaEmbRWqhni2P2rEIZhsEWRw9gZA/gfYRdAAAcrqGuVge2lKs0N0tGerpMs0tVW8olicBrkZ6tjOHqHWqPGGxxdAlG9gDJjbALAIDD7a4I68bcrF7NkRblZmlrRZiwa6H5+XMItw7EyB4AAyHsAgDgcP6ONhlp6b1uMwxD/o52myoCrNPfyJ4zr6VlZA+AgRB2AQBwuEh6hkyzq09zpEh6wMaqgPhhZA+ARCDsAgDgcHOXl6hqS7kWndrKbJqmqhpbNbe0zO7SgCGL58ie3JyM2DW0jOwBMBDCLgAADtdzXe7WirD8He2KpAc0t7SM63XhOFaN7AGAoSDsAgDgAnPmzSfcwhGSaWRPbX2Dwq/UqK0rRRm+qEoWFtKkDHARwi4AAAB6YWRPd9Atr96j7NnFChiGoqap8uoaSSLwAi5B2AUAAEhCjOwZXLh6p7JnLek18it7VqHC1TsIu4BLEHYBAAA86MyRPX/8c4veff8AI3uGoS1iKHBW4yvDMNQeoRkW4BaEXQAAAJdiZE/iZPhNRU2zz8ivgH+Qi5IBOIojwu6+ffv0ve99L/Z1Y2OjVq5cqWuvvTZ2W0NDg7773e8qNzdXknTFFVeotLTU8loBAACsNJqRPeNSUxQ4cVgXpZsKpXRqou+4PjjSrJnXXaeCKz7KyJ5BlBQVqLy6RtmzCmMjvw7tqVFZUYHdpQEYIkeE3cmTJ+uBBx6QJEWjUX35y1/W5Zdf3ud+s2fP1po1a6wuDwAAIKESNbLnV48+oBuDXRo7dqxOnOi+DtdM82nryy+q8EpC22B6rssNV+9Qe8RQwG+qrKiA63UBF3FE2D3TG2+8oUmTJmnixIl2lwIAABA3dozs8Xe0yUhL73WbYRjyd7TH62l52vz8OYRbwMUcF3arq6tVVFTU7/f+/Oc/6+6771Z2drbKyso0bdq0fu9XWVmpyspKSdKmTZsUCoUSVq+b+f1+XhsHYl2ciXVxJtbFeZJ9TTqOndD+g0e0v/HIqf8e1v7GIzpw8KiaWwcOmCmGodxQhs6bOEHn5U7QpFP/nZw7QXmhCRqbOrKPbP5gSGPGnFSKYSg1NVVS93Wn/mB6Uq+TUyT7+8WJWBNnGum6GKY52HFEa0UiEX35y1/WQw89pKysrF7f6+joUEpKisaNG6ddu3bpxz/+sR555JEh/b379u1LQLXuFwqF1NTUZHcZOAvr4kysizOxLs6TDGvippE9DXW1OrClXMum5urkyZMyTVNVja2aVFqmOfPmx/3nYXiS4f3iNqyJMw22LpMnTx7wcY46s1tbW6sLLrigT9CVpPT001twFixYoCeffFJHjhzRhAkTLKwQAAB43Zkjew62tHd3OnbpyJ6eQLvt5e2KtBxRJD2guQRdAEnCUWF3sC3Mra2tyszMlGEYeueddxSNRjV+/HiLKwQAAF6QTCN75sybr0VLl3G2CkDScUzY7ezsVH19vW655ZbYbRUVFZKk5cuX69VXX1VFRYV8Pp9SU1N155130i4fAAAMaDQjewJpY7qDbPB0qM079d/xgVQ+gwCACzgm7I4bN04/+tGPet22fPny2J9XrFihFStWWF0WAOAsDXW1euPFsMYca9PJtAxdek0JWyJhm0SN7MlIT7XwWQAAEsExYRcA4Hw9zW5Kc7NkpKfLNLtUtaVckgi8SBg7RvYAANyPsAsAGLLdFWHdmJsV28JpGIYW5WZpa0WYsItROdZ58tQZ2dNhtvFUg6hDRzoHfJxhSKHsdOWdOjM7MRiIbTeeGAwodYyv1/1r6xtU/txv1NaVogxfVCULC5mjCgAeRdgFAAyZv6NNRlp6r9sMw5C/Y+D5oUAPu0f21NY3qLx6j7JnFytgGIqapsqraySJwAsAHkTYBQAMWSQ9Q6bZ1as5j2maiqQHbKwKTmGapg4d7tCf32ty5MiecPVOZc9a0mtnQvasQoWrdxB2AcCDCLsAgCGbu7xEVVvKtejUVmbTNFXV2Kq5pWV2lwaLuHlkT1vEUOCsLsqGYag94uzOyrX1DQq/UsPWawAYJsIugITjg5p39FyXu7UiLH9HuyLpAc0tLeN6XY8Zzcie8YGxCmWnO3JkT4bfVNQ0++xMCPgH6XBlM7ZeA8DIEXYBJBQf1Lxnzrz5hFsPSNTInvOnT1ZTU9OAj7Xz4FdJUYHKq2uUPaswtjPh0J4alRUVWPLzR4Kt1wAwcoRdAAnFBzXAPk4b2WP3wa+enxGu3qH2iKGA31RZUYGj/y1y69ZrAHACwi6AhOKDGpBYVo3siQcnHPyanz/H0eH2bG7ceg0ATkHYBZBQfFADRsc0TbUfO3G6EZQNI3vihYNfw+fGrdcA4BSEXQAJxQc14NxM09SRtuP68NQZWaeN7IkXDn4Nnxu3XgOAUxB2ASQUH9SAbm4e2RMvHPwaGbdtvQYApyDsAkg4PqjBjRrqavXGi2GNOdamk2kZuvSaknN2oR7NyJ5A2pjuIOvAkT3xwsEvAICVCLsAAJyloa5WB7aUqzQ3S0Z6ukyzS1VbyiVJF8/NT8jInoz0VKuenq04+AUAsAphFwCAs/zxxf9VUXae6o6PVWMkVY1dY9Xov0Dvb/mzOv/7PctH9gCAG9g5RxvoD2EXAJCUBh/ZM1uVAzzu7JE9Z56pTdTIHgBwOrvnaAP9IewCADxpNCN7DJnK9Z1Qrv+Ecn3HNdF/QhN9J1Qbiegf7/53y0f2AIDTOWGONnA2wi4AwLVM09Tho51xH9lz4L231Pjs01qUnRXrGlzV2KorSssIugDQD+Zow4kIuwAARxtsZM/BlnZ1Ho8M+NiRjuyZGFyghhRDWyvC8ne0K5Ie0NzSsnN2YwaAZMUcbTgRYRcAYDsnjuyZM28+4RYAhog52nAiwi4AwBInI11xH9kz66JpOn6szcJnAQDoD3O04USEXQBA3Bw/EdHBlo4ztht3dzk+2NKu5taOuI/sGR8YR9i12dmjRm7+5FLNmD7V7rIA2IA52nAawi4AYFgGH9nTOeDjGNnjPf2NGvlhRa0+e/lhPvA6FHNQASQTwi4AJIGGulq98WJYY4616WRahi69pmTA61FHM7LH5zMUyg50XzMbPCPU5gQUygrQydhj+h01MrtQ4eoXCVAOxBxUAMmGsAsAHtdQV6sDW8pVmpslIz1dptmll/67XO3HIso674K4juwJZqbJ5yPQJgtGjbgLc1ABJBvCLgB4VM/InqpfvaTZGRfo2aNj1diVqsZIqg4qVcdf+Lukv/f72JGO7EFyYdSIu3BwAkCyIewCgIsNbWTP+drZz2PHKKKpUyfGfWQPkke/o0b+VKPPJmDUCNeajh4HJwAkG8IuADjcaEf2pBw7pNljjivXf0IT/SeU6zuhib7j+vUJ6bO3/YOFzwRe09+okVuuvTru3Zi51jQ+mIMKINkMKexGo1HV1NTIMAwVFBQoJaX7eqzf//73+tjHPpbQAgEgGSRyZE/PNbuLsrJiH3CrGls1t7TMuicIzzp71EgoFFJTU1NcfwbXmsYHc1ABJJshhd1HH31UoVBIfr9fL7zwgm6//XZNmjRJFRUVhF0AGCK7Rvb0dF3eWhGWv6NdkfSA5paWDdiNGXAarjWNH+agAkgmQwq7LS0tuuOOOyRJS5Ys0aOPPqp/+Ae2vgHAmZw8smfOvPmEWxtxvenocK3p6NTWN2j7zt1qaj/O7x+ApDKksBuJRHTy5EmNGTNGEydO1Jo1a/Twww9r7969ia4PABzFNE0daTuuD0+dkWVkD86F601Hj2tNR67n9y8vf5ECJ0/y+wcgqQwadru6uuTz+fT5z39e7e3tysrKkiSlpaXpnnvu0SuvvGJFjQBgqZ6RPR82t8euoT3cFtHf9reosblNx090DfhYRvbgbFxvOnpcazpy/P4BSGaDht3vfOc7uvvuu3XhhRf2+V5KSoo+8YlPJKwwAEikoY3s6V8gbUx3kGVkD4aA603jg2tNR4bfPwDJbNCwe/755+sb3/iG1q5dq2AwKEl688039Ytf/EL33XefJQUCwEiNdmTPmY2gZp4/SemppiYGA8pIT7XwWcDtuN4Udur5/TsTv38AksWgYbesrEwVFRX6xje+oVWrVmn79u3au3evrr/+eqvqA4BBJXJkz5kSMU4FyYHrTWGnnt+/vPwiSeL3D0BSOWeDqosvvljp6el65JFHtGjRIt1zzz1KTeWsBgDr2DWyB4gHrjeFnXp+z7a/XqXDbcf5/TsHOqcD3jJo2H3ggQf05ptv6tprr9XKlSv1xBNPaPfu3VqwYIFV9QFIAk4e2QPEA9ebwk7z8+doWfEidqecA53TAe8ZNOyed955+pd/+RdlZGRIkvLy8nT//fersbFRK1assKRAAN7AyB4AgJPRuRrwnkHD7urVq3t9PX36dK1fv14bN24k7ALoo7+RPWc2hWJkDwDAqehcDXjPOa/ZPVswGKQTM5DEGNkDAPAiOqcD3jPssCtJaWlp8a4DgIPEc2RPbk5AeacaQjGyBwDgVHROB7xnRGEXgPtZNbIHAAA3oHM64D2EXcDDGNkDAMDQ0Tkd8BbCLuBijOwBAAAA+kfYBRyOkT0AAADA8Dkq7N5+++0aN26cUlJS5PP5tGnTpl7fN01TTz31lGprazV27FjddtttmjFjhk3VAvFz5siejj816S/vH2BkDwAAZ6itb1D4lRq1daUowxdVycJCT2059vrzA+zgqLArSevWrdOECRP6/V5tba0OHDigRx55RG+//baeeOIJfec737G4QmBkGNkDAHA7uwJZbX2Dyqv3KHt2sQKGoahpqry6RpI8EQi9/vwAuzgu7A5m586d+sQnPiHDMHTxxRervb1dhw4dUnZ2tt2lAZLiM7Jn2uQcZQb8jOwBADiKnYEsXL1T2bOWxA7uGoah7FmFClfv8EQY9PrzA+ziuLC7YcMGSdKyZcu0dOnSXt9raWlRKBSKfZ2Tk6OWlpY+YbeyslKVlZWSpE2bNvV6DE7z+/28NiNw/HhEB5qOaH/jEe0/eET7Gw/H/tzU0q7oIDN7QtkBnTdxgiblTtB5EyfovNwJOi83U5Mmjlf6uO5A6/f7FYlErHo6GCLeL87EujgPa+JM8ViX7a/vVl7+ol67ifLyi7T99SotK1402hIHddI3Tuljx/a5/ZhvnKt/33rWxavPz434N8yZRroujgq769evVzAY1OHDh/Xtb39bkydP1iWXXDLsv2fp0qW9gnJTU1M8y/SMUCjEazMAa0f2mOpoO6KOtu6vWBdnYl2ciXVxHtbEmeKxLk1txxU42bcp4uG24wlf8zFdnTp+/HivoG2apvxdna7+fetZF68+Pzfi3zBnGmxdJk+ePODjHBV2g8GgJCkzM1OFhYV65513eoXdYDDY60k2NzfHHgMMByN7AAAYngy/qahp9glkAf/AO5ripaSoQOXVNcqeVSjDMGSapg7tqVFZUUHCf7YVvP78ALs4Jux2dnbKNE2lpaWps7NT9fX1Ki0t7XWfgoIC/frXv1ZRUZHefvttpaenc70uBsTIHgBeRddW2MHOQNbz+x2u3qH2iKGA31RZUYFnfu+9/vwAuzgm7B4+fFgPPvigJKmrq0sLFy7UvHnzVFFRIUlavny55s+fr127dumOO+5QamqqbrvtNjtLhgOcObKnMXZmlpE9ALyLrq2wi92BbH7+HE//jnv9+QF2cEzYzcvL0wMPPNDn9uXLl8f+bBiGvvSlL1lZFhyAkT2AtThr6Gx0bYWdCGQA3MQxYRfJLR4je87cdszIHmBkOGvofG0RQ4GzDtQZhqH2CAfvAAA4E2EXljl+IqKDLR1nbDfu7nJ8sKVdza0dGmRij7Iz05QXDGjiqW3HPduNJ+YElDZ2jHVPAvA4zho6n51NggAAcBPCLuLK2pE9AOKNs4bOR9dWAACGhrCLYWFkD+BtnDV0PrubBAEA4BaEXfTByB4geXHW0B1oEgQAwLkRdpNUNGrqYEub9rx7kJE9AGKS4awh3aYBAEgOhF0PY2QPgJHw8llDuk0DAJA8CLsuN5qRPVkT0hTKTmNkD4CkQbdpAACSB2HXBRI1smfalPPU1NRk3RMBAJvRbRoAgORB2HUIRvYAQOLRbRoAgORB2LXRM/+7W2+/38zIHgCwCN2mAQBIHoRdG/3twGG9u7dFEiN7AMAKPdfl/vT5rfrLwcPqOnlcM3OzJM2ytS4AABB/hF0bfap4lj656COM7AEAixmh6SpYePrsLh2ZAQDwHk4X2ujC/5ejj8wIKTszjaALABbp7shc2E9H5p02VwYAAOKJM7sAgKTi5o7MtfUNCr9So7auFGX4oipZWMjZaAAABkDYBQAkFbd2ZK6tb1B59R5lzy5WwDAUZfs1AACDYhszACCplBQV6NCeGpmnhpT3dGQucXhHZrZfAwAwPJzZBQAknWjT+9q5bbeiJzo1Y1K2Pv+Zax1/dtTN268BALADYRcAkDR6tgLnLCxV6Iw5u27g1u3XAADYhW3MAICk4eatwG7dfg0AgF04swsASBpu3grcs806XL1D7RFDAb+psqICx2+/BgDALoRdAEDScPtW4Pn5cwi3AAAMEduYAQBJg63AAAAkD87sAgCSBluBAQBIHoRdAEBSYSuwN9XWNyj8So3aulKU4YuqZGEh6wwASY6wCwAAXK1npFT27GIFDENR01R5dfdIKQIvACQvrtkFAACu5uaRUgCAxCHsAgAAV2uLGL06bEvuGSkFAEgcwi4AAHC1DL8Z67Ddw00jpQAAicE1uwAAOAzNloanpKhA5dU1sa3MPSOlyhgpBQBJjbALAICD0Gxp+BgpBbc4+0DWzZ9cqhnTp9pdFuBZhF0AAByku9nSkn6aLe0gvA2CkVJwuv4OZP2wolafvfwwv7tAghB2AQBwkLaIoQDNluAwbK0fvX4PZM0uVLj6RV5LIEEIuwAAOEiG31TUNHt1F6bZEuzE1vr44EAWYD26MQMA4CAlRQU6tKcm1l24p9lSCc2WYBPmGMcHXcMB63FmFwAAB6HZEpyGM5Lx0W/X8D/V6LMcyAIShrALAIDD0GwJTsLW+vjo70DWLddeTTdmIIEIuwAAABgQc4zj5+wDWaFQSE1NTTZWBHgbYRcAAEii4y76x9Z6AG5F2AUAAHTcxaDYWg/AjejGDAAA6LgLAPAcwi4AAFBbxOjVgEii4y4AwN3YxgwAAIbdcZfrewEATkfYBZA0+HAODGw4HXcHu753WfEiq0v3JP69AoDRI+wCSAo03wEGN5yOu93X9y7p5/reHYTdOODfKwCID8IugKQw2IdzPjwC3YbacbctYijA9b3nNNKzs/x7BQDx4Yiw29TUpM2bN6u1tVWGYWjp0qUqKSnpdZ+GhgZ997vfVW5uriTpiiuuUGlpqR3lAnAhPpwD8TPc63uT0WjOzvLvFQDEhyPCrs/nU1lZmWbMmKFjx45pzZo1ys/P19SpU3vdb/bs2VqzZo1NVQJwMz6cA/EznOt7k9Vozs7y7xUAxIcjRg9lZ2drxowZkqS0tDRNmTJFLS0tNlcFwEtKigp0aE+NTLP7w2LPh/MSPpwDwzY/f47KimYpZc8OdbyxQyl7dqisaBZbbM8wmlFO/HsFAPHhiDO7Z2psbNRf//pXXXjhhX2+9+c//1l33323srOzVVZWpmnTptlQIQA3Gk7zHQDnNtTre5PVaM7O8u8VAMSHYfYcNnSAzs5OrVu3Tp/5zGd0xRVX9PpeR0eHUlJSNG7cOO3atUs//vGP9cgjj/T791RWVqqyslKStGnTJp04cSLhtbuR3+9XJBKxuwychXVxJtbFmVgX52FNur22q04/rKhV9uwztnr/qUa3LJ+vyxfMs7we1sWZWBfnYU2cabB1SU1NHfBxjgm7kUhE999/vy677DJ98pOfPOf9b7/9dm3cuFETJkw453337dsXjxI9JxQKqampye4ycBbWxZlYF2diXZyHNTmttr5B4eqdsbOzJTaenWVdnIl1cR7WxJkGW5fJkycP+DhHbGM2TVOPP/64pkyZMmDQbW1tVWZmpgzD0DvvvKNoNKrx48dbXCkAAMDQsNUbAOzliLD71ltv6eWXX9b06dN19913S5JuvvnmWHpfvny5Xn31VVVUVMjn8yk1NVV33nlnn8YPAAAAAABIDgm7s2bN0jPPPDPofVasWKEVK1ZYVBEAAABGq7a+QeFXatTWlaIMX1QlCws52w3AMo4IuwAAAPCW2voGlVfvUfbsYgUMQ1HTVHl1jSQReAFYwhFzdgEAAOAt4eqdyp5VGLvszDAMZc8qVLh6p82VAUgWhF0AAADEXVvE6NNfxTAMtUfouQLAGmxjBgAAOIVrTOMnw28qapq9Aq9pmgr4HTH1EkAS4MwuAACATl9jGp1drMClSxSdXazy6j2qrW+wuzRXKikq0KE9NTLN7nBrmqYO7alRSVGBzZUBSBac2QUAAFDPNaZL+rnGdAdnd0eg5zULV+9Qe8RQwG+qrKiA1xKAZQi7AAAA6r7GNMA1pnE1P38O4RaAbdjGDAAAoO5rTHu23PbgGlMAcC/CLgAAgLjGFAC8hm3MAABHoAsu7MY1pgDgLYRdAIDterrgZs8uVsAwFDVNlVfXSBJBA5biGlMA8A62MQMAbNfdBbewny64O22uDAAAuBVndgEAtqMLLjByXAIAAP0j7AIAbJfhNxU1zdiZXYkuuMBQcAkAAAyMbcwAANvRBRcYGS4BAICBcWYXAGA7uuACI8MlAAAwMMIuAMAR6IILDB+XAADAwNjGDAAA4FJcAgAAA+PMLgAAgEtxCQAADIywCwAA4GJcAgAA/SPsAgAwTMw1BQDA+Qi7AAAMA3NNAQBwBxpUAQAwDMw1BQDAHQi7AAAMQ1vE6DXmRWKuKQAATkTYBQBgGDL8ZmzMSw/mmgIA4DyEXQAAhoG5pgAAuAMNqgAAGAbmmsYPXa0BAIlE2AUAYJiYazp6dLUGACQa25gBAIDl6GoNAEg0wi4AALAcXa0BAIlG2AUAAJajqzUAINEIuwAAwHJ0tQYAJBoNqgAAgOXoag0ASDTCLgAAsAVdrQEAicQ2ZgAAAACA53BmFwAAAH3U1jco/EqN2rpSlOGLqmRhIWfiAbgKYRcAMCR88AWSR219g8qr9yh7drEChqGoaaq8ukaSeN8DcA3CLgDgnPjg6z0cvMBgwtU7lT1rSWwWsmEYyp5VqHD1Dn5PALgGYRcAcE588PUWDl7gXNoihgKn3u89DMNQe8QY4BEA4Dw0qAIAnFNbxIgF3R588HWv7oMXhf0cvNhpc2Vwigy/GZuB3MM0TQX85gCPAADnIewCAM6JD77ewsELnEtJUYEO7amJve9N09ShPTUqKSqwuTIAGDq2MQMAzqmkqEDl1TWxs4E9H3zL+ODrShl+U1HT7BV4OXiBM/VsZw9X71B7xFDAb6qsqIBt7gBchbALADgnPvh6CwcvMBTz8+fwHgfgaoRdAMCQ8MHXOzh4AQBIBoRdAJ7FaBVgYBy8AAB4HWEXgCcxWgVwFg4+AQCs5qiwW1dXp6eeekrRaFRXX321brjhhl7fP3nypB599FH95S9/0fjx43XnnXcqNzfXnmIBOBpzYQHn4OATAMAOjgm70WhUTz75pL7+9a8rJydHa9euVUFBgaZOnRq7z/bt2xUIBPT9739f1dXV+tnPfqavfOUrNlYNwKnaIoYCHhutwpkxuBUHnwAAdnDMnN133nlHkyZNUl5envx+v6666irV1NT0us/OnTu1ePFiSdKVV16p3bt395n7CACS9+bC9pwZi84uVuDSJYrOLlZ59R7V1jfYXRpwTsz1BQDYwTFht6WlRTk5ObGvc3Jy1NLSMuB9fD6f0tPTdfToUUvrBOAOJUUFOrSnJhZ4e0arlLh0tEr3mbHCfs6M7bS5MuDcvHbwCQDgDo7ZxhxPlZWVqqyslCRt2rRJoVDI5oqcye/389o4EOsSH8uKFykzK1PbfluttpNSxhjpc9cW6fIF80b099m9Lid945Q+dmyf24/5xiX174vd64K++luTm6+9Wj+sqFX27DPm+v6pRrdcezXrZxHeK87EujgPa+JMI10Xx4TdYDCo5ubm2NfNzc0KBoP93icnJ0ddXV3q6OjQ+PHj+/xdS5cu1dKlS2NfNzU1Ja5wFwuFQrw2DsS6xM+M6VP171/4bK/bRvra2r0uY7o6dfz48V5bQU3TlL+rM6l/X+xeF/TV35rMmD5Vn738sMLVL8bm+n62qEAzpk9l/SzCe8WZWBfnYU2cabB1mTx58oCPc0zYnTlzpvbv36/GxkYFg0H97ne/0x133NHrPh/96Ef10ksv6eKLL9arr76qOXPm9LkGCAC8qKSoQOXVNbGtzD3bsstcui0byYe5vgAAqzkm7Pp8Pn3xi1/Uhg0bFI1GtWTJEk2bNk2//OUvNXPmTBUUFKi4uFiPPvqo/vVf/1UZGRm688477S4bACzRExLC1TtiZ8bKigoIDwAAAANwTNiVpAULFmjBggW9bvvsZ09vQUxNTdVXv/pVq8sCAEfgzBgAAMDQOaYbMwAAAAAA8ULYBQAAAAB4DmEXAAAAAOA5hF0AAAAAgOc4qkEVAOC02voGhV+pUVtXijJ8UZUsLKRBFQAAwBARdgHAgWrrG1RevUfZs4sVMAxFTVPl1TWSROAFAAAYArYxA4ADhat3KntWoQzDkCQZhqHsWYUKV++0uTIAAAB3IOwCgAO1RYxY0O1hGIbaI8YAjwAAAMCZ2MYMAA6U4TcVNc1egdc0TQX8po1VAaPDdegAACtxZhcAHKikqECH9tTINLvDrWmaOrSnRiVFBTZXBoxMz3Xo0dnFCly6RNHZxSqv3qPa+ga7SwMAeBRndgHAgXrOdoWrd6g9YijgN1VWVMBZMLhW93XoS/q5Dn0Hv9cAgIQg7AKAQ83Pn0MIgGe0RQwFuA4dAGAhtjEDAICEy/CbsW35PbgOHQCQSIRdAACQcFyHDgCwGtuYAQBAwnEdOgDAaoRdAABgCa5DBwBYiW3MAAAAAADPIewCAAAAADyHsAsAAAAA8BzCLgAAAADAcwi7AAAAAADPIewCAAAAADyHsAsAAAAA8BzCLgAAAADAc/x2FwAAgJ1q6xsUfqVGbV0pyvBFVbKwUPPz59hdFgAAGCXCLgAgadXWN6i8eo+yZxcrYBiKmqbKq2skicALAIDLsY0ZAJC0wtU7lT2rUIZhSJIMw1D2rEKFq3faXBkAABgtzuzCEdhGCMAObRFDgVNBt4dhGGqPGAM8AgAAuAVhF7ZjGyEAu2T4TUVNM3ZmV5JM01TAb9pYFQAAiAfCLmzXvY1wST/bCHcQdgEkVElRgcqra2JbmU3T1KE9NSorKrC7tCFhVwwAAAMj7MJ2bCMEYLUzQ2K0tUlNVe8qkDNJAb+psqICVwRGdsUAADA4wi5sxzZCAFY6OySmnzqb+w9Fs1wVEtkVAwDA4OjGDNuVFBXo0J4amWZ3uO3ZRljikm2EANzFKx2Y2yJGr4OEErtiAAA4E2d2YbueMxDh6h1qjxiu2kYIwH28cukEu2IAABgcYReOMD9/DuEWgCW8EhLd3lwLAIBEI+wCAJKKV0Iiu2IAABgcYRcAkFS8FBLZFQMAwMAIuwCApENIBADA++jGDAAAAADwHMIuAAAAAMBz2MYMAMAw1dY3KPxKjdq6UpThi6pkYSHbogEAcBjCLgAAw1Bb36Dy6j3Knl2sgGEoapoqr66RJAIvAAAOwjZmAACGIVy9Mza2SJIMw1D2rEKFq3faXBkAADgTYRcAgGFoixixoNvDMAy1R4wBHgEAAOxA2AUAYBgy/KZM0+x1m2maCvjNAR4BAADswDW7AIBzoiHTaSVFBSqvroltZTZNU4f21KisqMDu0gAAwBlsD7vl5eV6/fXX5ff7lZeXp9tuu02BQKDP/W6//XaNGzdOKSkp8vl82rRpkw3VAkDyoSFTbz3POVy9Q+0RQwG/qbKigqR8LQAAcDLbw25+fr5WrVoln8+np59+Wtu2bdPq1av7ve+6des0YcIEiysEgOTW3ZBpST8NmXYkbcCbnz8naZ87AABuYfs1u5dddpl8Pp8k6eKLL1ZLS4vNFQEAzkRDJgAA4Ea2n9k90/bt23XVVVcN+P0NGzZIkpYtW6alS5daVRYAJLUMv6moafYKvDRkAgAATmeYZ7eUTID169ertbW1z+033XSTCgsLJUnPPvus3n33Xd111119ziBIUktLi4LBoA4fPqxvf/vb+sIXvqBLLrmk359XWVmpyspKSdKmTZt04sSJ+D0ZD/H7/YpEInaXgbOwLs6UzOvy2q46/bCiVtmzz2jI9Kca3bJ8vi5fMM/W2pJ5XZyKNXEm1sWZWBfnYU2cabB1SU1NHfBxloTdc3nppZf0m9/8Rvfee6/Gjh17zvs/88wzGjdunK6//voh/f379u0bbYmeFAqF1NTUZHcZOAvr4kzJvi619Q0KV++MNWQqcUhDpmRfFydiTZyJdXEm1sV5WBNnGmxdJk+ePODjbN/GXFdXp+eff17f+ta3Bgy6nZ2dMk1TaWlp6uzsVH19vUpLSy2uFACSFw2ZAACA29gedp988klFIhGtX79eknTRRRfplltuUUtLi37wgx9o7dq1Onz4sB588EFJUldXlxYuXKh58+bZWDUAAAAAwMlsD7vf//73+709GAxq7dq1kqS8vDw98MADVpYFAAAAAHAx20cPAQAAAAAQb4RdAAAAAIDnEHYBAAAAAJ5D2AUAAAAAeA5hFwAAAADgOYRdAAAAAIDnEHYBAAAAAJ5j+5xdAADOVlvfoPArNWrrSlGGL6qShYWanz/H7rIAAICLEHYBAI5SW9+g8uo9yp5drIBhKGqaKq+ukSQCLwAAGDK2MQMAHCVcvVPZswplGIYkyTAMZc8qVLh6p82VAQAANyHsAgAcpS1ixIJuD8Mw1B4xBngEAABAX4RdAICjZPhNmabZ6zbTNBXwmwM8AgAAoC/CLgDAUUqKCnRoT00s8JqmqUN7alRSVGBzZQAAwE1oUAUAcJSeJlTh6h1qjxgK+E2VFRXQnAoAAAwLYRcA4Djz8+cQbgEAwKiwjRkAAAAA4DmEXQAAAACA5xB2AQAAAACeQ9gFAAAAAHgOYRcAAAAA4DmEXQAAAACA5xB2AQAAAACeQ9gFAAAAAHgOYRcAAAAA4DmEXQAAAACA5xB2AQAAAACeQ9gFAAAAAHgOYRcAAAAA4DmEXQAAAACA5xB2AQAAAACeY5imadpdBAAAAAAA8cSZ3SS2Zs0au0tAP1gXZ2JdnIl1cR7WxJlYF2diXZyHNXGmka4LYRcAAAAA4DmEXQAAAACA5xB2k9jSpUvtLgH9YF2ciXVxJtbFeVgTZ2JdnIl1cR7WxJlGui40qAIAAAAAeA5ndgEAAAAAnuO3uwA4wwsvvKDy8nI98cQTmjBhgt3lJL1f/OIX2rlzpwzDUGZmpm677TYFg0G7y0p65eXlev311+X3+5WXl6fbbrtNgUDA7rKS2u9//3v993//tz744AN95zvf0cyZM+0uKanV1dXpqaeeUjQa1dVXX60bbrjB7pKS3mOPPaZdu3YpMzNTDz30kN3lQFJTU5M2b96s1tZWGYahpUuXqqSkxO6ykt6JEye0bt06RSIRdXV16corr9TKlSvtLguSotGo1qxZo2AwOOyuzIRdqKmpSfX19QqFQnaXglOuv/563XTTTZKkcDisLVu26JZbbrG5KuTn52vVqlXy+Xx6+umntW3bNq1evdruspLatGnTdNddd+mHP/yh3aUkvWg0qieffFJf//rXlZOTo7Vr16qgoEBTp061u7SktnjxYq1YsUKbN2+2uxSc4vP5VFZWphkzZujYsWNas2aN8vPzea/YbMyYMVq3bp3GjRunSCSie++9V/PmzdPFF19sd2lJLxwOa8qUKTp27NiwH8s2ZugnP/mJPve5z8kwDLtLwSnp6emxPx8/fpy1cYjLLrtMPp9PknTxxRerpaXF5oowdepUTZ482e4yIOmdd97RpEmTlJeXJ7/fr6uuuko1NTV2l5X0LrnkEmVkZNhdBs6QnZ2tGTNmSJLS0tI0ZcoU/v/EAQzD0Lhx4yRJXV1d6urq4vOXAzQ3N2vXrl26+uqrR/R4zuwmuZqaGgWDQZ1//vl2l4Kz/PznP9fLL7+s9PR0rVu3zu5ycJbt27frqquusrsMwDFaWlqUk5MT+zonJ0dvv/22jRUBztfY2Ki//vWvuvDCC+0uBereoXLPPffowIEDuuaaa3TRRRfZXVLS+/GPf6zVq1eP6KyuRNhNCuvXr1dra2uf22+66SZt27ZNX//6160vCoOuS2FhoW6++WbdfPPN2rZtm379619z3YhFzrUukvTss8/K5/Pp4x//uMXVJaehrAkAuE1nZ6ceeughff7zn++1owv2SUlJ0QMPPKD29nY9+OCD2rt3r6ZPn253WUnr9ddfV2ZmpmbMmKGGhoYR/R2E3STwjW98o9/b9+7dq8bGRt19992SurcJ3HPPPdq4caOysrIsrDA5DbQuZ/v4xz+ujRs3EnYtcq51eemll/T666/r3nvvZXuTRYb6XoG9gsGgmpubY183NzfTWA8YQCQS0UMPPaSPf/zjuuKKK+wuB2cJBAKaM2eO6urqCLs2euutt7Rz507V1tbqxIkTOnbsmB555BHdcccdQ/47CLtJbPr06XriiSdiX99+++3auHEj3ZgdYP/+/TrvvPMkdW8155pEZ6irq9Pzzz+vb33rWxo7dqzd5QCOMnPmTO3fv1+NjY0KBoP63e9+N6wPJECyME1Tjz/+uKZMmaJPfvKTdpeDU44cOSKfz6dAIKATJ06ovr5en/rUp+wuK6mtWrVKq1atkiQ1NDTohRdeGPb/rxB2AQf62c9+pv3798swDIVCIToxO8STTz6pSCSi9evXS5Iuuugi1sZmr732mn70ox/pyJEj2rRpk84//3x97Wtfs7uspOTz+fTFL35RGzZsUDQa1ZIlSzRt2jS7y0p6Dz/8sN58800dPXpUt956q1auXKni4mK7y0pqb731ll5++WVNnz49trvu5ptv1oIFC2yuLLkdOnRImzdvVjQalWma+tjHPqaPfvSjdpeFUTJM0zTtLgIAAAAAgHhi9BAAAAAAwHMIuwAAAAAAzyHsAgAAAAA8h7ALAAAAAPAcwi4AAAAAwHMIuwAAAAAAzyHsAgDgUk8//bS++93vxr4uLy/Xfffdp0gkYmNVAAA4A2EXAACX+tSnPqWGhgb99a9/VUVFherq6nTXXXfJ7/fbXRoAALYzTNM07S4CAACMzDPPPKPXXntNHR0duu+++xQKhdTR0aH169fr73//uzZs2KDp06fbXSYAAJbjzC4AAC52wQUXaO/evVq1apVCoZAkKTU1VWvXrtWVV15pc3UAANiHsAsAgEvt3btXTzzxhBYtWqQdO3bEbvf7/ZowYYKNlQEAYD/CLgAALtTS0qL7779f//zP/6wvfelL2rt3rxoaGuwuCwAAxyDsAgDgMh0dHdq4caOuvfZaFRQUaOzYsbruuuv0i1/8wu7SAABwDBpUAQDgUZs3b9Z1111HgyoAQFIi7AIA4EEbN27Ue++9p1AopGXLlmnx4sV2lwQAgKUIuwAAAAAAz+GaXQAAAACA5xB2AQAAAACeQ9gFAAAAAHgOYRcAAAAA4DmEXQAAAACA5xB2AQAAAACeQ9gFAAAAAHgOYRcAAAAA4DmEXQAAAACA5/x/aaMPfyD1EYMAAAAASUVORK5CYII=",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plot_ds(data,m[-1],q[-1])"
]
},
{
"cell_type": "code",
"execution_count": 64,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Valore della funzione loss per la soluzione: 0.0943\n"
]
}
],
"source": [
"print(f'Valore della funzione loss per la soluzione: {cost_history[-1][0]:.4f}')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Come si può vedere dalla figura seguente, considerando i valori di costo e dei coefficienti soltanto alla fine delle varie epoche risulta una andamento uniforme dei valori stessi."
]
},
{
"cell_type": "code",
"execution_count": 60,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABQgAAAGoCAYAAAAKMwiTAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAABqxklEQVR4nO3deXQc9YHu/aeqF0mt1mKptcuW5EXebWxjA7YBA2YPhBgCl4Rkhpkkc8kk4SYzNzfn3BuGQHJCzkxImCzzhkwIyWSZADEJSwggjNlsDHjfJVu2Vsvat9bW3VXvH20LG2wj2Zaq1f39nKNjqVotPaqS5NbTv8WwbdsWAAAAAAAAgIRkOh0AAAAAAAAAgHMoCAEAAAAAAIAERkEIAAAAAAAAJDAKQgAAAAAAACCBURACAAAAAAAACYyCEAAAAAAAAEhgbqcDjFRjY6PTEc5ZIBBQa2ur0zEgrkWs4XrEDq5FbOF6xI54uRaFhYVORzhr8fBY8HTi5ftrvHC+RofzNTqcr9HhfI0O52t0OF+jM9LzdbrHg4wgBAAAAAAAABIYBSEAAAAAAACQwCgIAQAAAAAAgARGQQgAAAAAAAAkMApCAAAAAAAAIIFREAIAAAAAAAAJjIIQAAAAAAAASGAUhAAAAAAAAEACoyAEAAAAAAAAEhgFIQAAAAAAAJDAKAgBAAAAAACABEZBCAAAAAAAACQwCkIAAAAAAAAggVEQAgAAAAAAAAmMghAAAAAAAABIYBSEAAAAAAAAQAKjIAQAAAAAAAASGAUhAAAAAAAAkMAoCAEAAAAAAIAERkEIAAAAAAAAJDAKQgAAAAAAACCBURACAAAAAAAACYyCEAAAAAAAAEhgFIQAAAAAAABAAqMgBAAAAAAAABIYBSEAAAAAAACQwCgIAQAAAAAAgARGQQgAAAAAAAAkMArCcWLbtiKW5XQMAAAAAAAA4CRupwMkgk2Vzfrr1jpdvbhMy2dkOR0HAAAAAAAAGMYIwnHgdZvqHQipprnL6SgAAAAAAADASRhBOA6KslMlSTVHux1OAgAAMH4ef/xxVVdXq6ysTHfffffw8Y0bN+qZZ56RYRj6xCc+oaVLlzqYEgAAAIwgHAeBtGR53KbaevoVHAg5HQcAAGDMVVdXa2BgQA888IDC4bAOHDgwfNvzzz+v+++/X/fff7+ee+45B1MCAABAYgThuDBNQ4WTfKpp6VVDe5/KCzOcjgQAADCmqqqqtGDBAknS/PnzVVlZqenTp0uS8vLyNDg4KElKSUk55f0rKipUUVEhSXrooYcUCATGIbUz3G53XH995xvna3Q4X6PD+RodztfocL5Gh/M1Oud6vigIx0lxduqxgjBIQQgAAOJeMBhUXl6eJMnn86m+vn74tmXLlunrX/+6bNvWF7/4xVPef/Xq1Vq9evXw262trWMb2EGBQCCuv77zjfM1Opyv0eF8jQ7na3Q4X6PD+RqdkZ6vwsLCUx6nIBwnRVnRdQgb2oIOJwEAABh7Pp9PfX19kqT+/n75fL7h25566ik9/PDDkqTvfve7WrhwoSMZAQAAEDWmBeHpFqbu7e3Vo48+qp6eHs2fP19r1qwZyxgx4fhGJQ3tFIQAACD+lZeXq6KiQsuXL9fOnTu1atWq4ds8Ho+SkpJkGIbC4bBzIQEAACBpDAvCExem/vnPf64DBw4Mrzvz5JNP6o477lBRUdFYffqYk5eZIrfLVGv3gAaGwkr2MngTAADEr6lTp8rj8ei+++5TaWmpAoGA1q5dqzVr1uiaa67RN7/5TUk6aRoxAAAAnDFmLdWZFqauq6vT008/rba2Nt15550qLy//0P3jcWHqyTnpOtTUqT7Lo+JAttNxEhqLncYWrkfs4FrEFq5H7OBanJ0TZ5BIGp41smrVqpNGFAIAAMBZY1YQnmlh6v379+t73/ue/H6/vv/97+vBBx/80P3jcWHqKccKwt3VjcpKtp2Ok9BY7DS2cD1iB9citnA9Yke8XIvTLUoNAACAxDZmBeGZFqYuLCxUcXGxJMk0zbGKEHNK8jKknaxDCAAAAAAAgNgxZu1ceXm5du3aJUnauXPnSdOICwoK1NHRoYGBAUUikbGKEHNKctMlsZMxAAAAAAAAYseYjSA808LUt99+ux555BENDQ3ptttuG6sIMac4kC7TkJq7+hUKW/K4E2f0JAAAAAAAAGLTmG6le7qFqYuLi3X//feP5aeOSV6PS7kZKWrq7NeRjj5NyfE7HQkAAAAAAAAJjiFs46woO1US6xACAAAAAAAgNlAQjrOirGMFIesQAgAAAAAAIAZQEI4zRhACAAAAAAAgllAQjrPCST5J0pGOPkUsy+E0AAAAAAAASHQUhOMs2etWID1ZEcvW0c5+p+MAAAAAAAAgwVEQOoB1CAEAAAAAABArKAgdwDqEAAAAAAAAiBVupwMkouMjCOsZQQgAAAAAAOKUbdtSaFAaGpAdGpTCISkSlqyIZNvRdzJMyXRJbo/k8crwJElJKc4GT0AUhA4oyopuVNLY0SfLsmWahsOJAAAAAAAARs62bWkgKLurTXZ3m+yeDtm9HbKD3VKwW3Z/rzTQJ9lnt0FroydJdnKqDF+ajNQMGf5MGelZ0ZfMHMmfIcNgYuz5QkHogNRkjzJTveoMDqm1Z0C5GTTjAAAAAAAgNtnhkOy2I7LbGmW1HZHdflR2R7M02PfRd3Z7JW+yDG9S9HWXKzpi0Dg2WMqyoiMKI2HZoSFpaEAa6o+OOAwNyu5pl32aj2tk5cnILpAZKJKRUywjK1+Gy3U+v/SEQUHokKKsVHUGh9TQFqQgBAAAAAAAMcPu6ZTVdFjW0RrZR2tktzdFi7wP8iTJyAjIyMiWkZYlIy1TSs2IjvrzpUnJqTJco6+ebNtWdlqqWhtqo6MRg12yezpl97RFRyx2tkj9vbKb62Q312k4mdsjI3eyzPwymYVTZeRNkeH2nMupSBgUhA4pyk7V7roO1bcFtWhqwOk4AAAAAAAgQdl9PbLqD8hqOCDrSLXU0/GB9zBkTMqTESiMjtjLLpAxKVfypcswzv+yaYZhyEz2ycwISBmn7kzs/qDs9iZZbY2yWxqiZWF3m+zGakUaqxXZ8kq0MMwvkzllplxTZsnIyD7vWeMFBaFDitnJGAAAAAAAOMC2LNnNtbJq9smq2y+77cjJ7+BNlplfKiO/RGbelOj0XU+SM2FPw0hJlVE0TWbRtOFjdn+vrKYa2UeqZTUclN3eJLu+UpH6SkU2PCtjUp7Msrkyp86PTkceg3JzoqIgdMjxnYwb2oKybZtvSgAAAAAAMGbscEhWfZWsQ7tk1ew7ef1At0dGQZnM4hnRqblZBTLMibcBiJHil6tsrlQ2V9LxkZFVsmqPFaEdRxXpOKrIlnUyMnNkTr9ArhmLZKRnOZzceRSEDkn3eZWW4lFPf0jtvYPKTkt2OhIAAAAAAIgjdiQsq65S1sHtsmr2SqGh929Mz5arZJbMKbNkFJSd1VqBsc7wpclVvliu8sWyI+Ho9ONDu2Qd2i27s0WR915W5L2XZRSUyTXrQpll82V4vE7HdkT8Xf0JpCgrVfsaOtXQFqQgBAAAAAAA58y2bdlHDilStUVW9a7orsDHGIGi6BTbsrkyMnMTajaj4XLLmFwuc3K57BUfj663WLVV1uHdso8cUvjIIemtZ+UqXyxz7iUyM3OcjjyuKAgdVJR9rCBsD2pBKQtlAgAAAACAs2P3tCuyf4silVuknvbh40ZWfnQq7bQFTKU9xnC55JoyU64pM2UPDcg6uEORve/IbqlXZNcGRXZtkFFcLvf8FdrW49fLGw6qNzgkf6pX16ycrkWzC53+Es47CkIHHV+HsL6NjUoAAAAAAMDo2JGIrNq90XKrrkqSHb0hNV2uGYtlli+SOSnP0YyxzvAmyzV7mVyzl8lqbVBk99uyDmyTXV+pd/c363ed09UTdg2/f2Nzr7RGcVcSUhA66MSdjNmoBAAAAAAAjIQd7FZkz9uK7HtX6uuJHnS5ZZbNk2vmEhmF0ybkJiNOMwNFMi+/VfZF1yuy7x2te67+pHJQknqCg3rpzQMUhDh/MlO98iW5FRwIq6tvSJmpsbVlOAAAAAAAiA22bcs+WqPIrg2yDu2SLEuSZGTmypy9TK7yRTKSUx1OGR+MZJ/cF6xS3/qK9wvYE/T2DZ3iXhMbBaGDDMNQUVaqqo50qb4tSEEIAAAAAABOYkcisg7tVGT7G7JbG6IHDVPm1Plyzb0kugMxMxLHhD/11Dsa+33xt9MxBaHDirJ9qjrSpYb2oOZNYbFQAAAAAAAg2UODiux7R5Gdb0m9ndGDyanR9fLmXCzDn+FovkRwzcrpamzuVU9wcPhYWmqSrlk53cFUY4OC0GHHNyppYKMSAAAAAAASnt0fVGTnm4rs3igNDUiSjMwcuRZcKnPGIhluj8MJE8ei2YXSGumlNw+ot29Ifh+7GGOMFGVTEAIAAAAAkOjsYLciO15XZM8mKRySJBn5pXItvExmySwZBpuOOGHR7MK4LAQ/iILQYdlpyUryuNTdH1J3/5DSU+JvHjsAAAAAADg1u7dT4a3rZe17V7IikiRzyky5Fl0pM7/E4XRIFBSEDjMNQ0VZPlUf7VFjW1DpxRSEAAAAAADEOzvYrfDWV2Xtfef9YrBsnlyLrpCZU+RwOiQaCsIYUJSdquqjPWpo79Os4klOxwEAAAAAAGPE7u9VZOt6Rfa8LUXCkgyZ0xbKtfhKmVl5TsdDgqIgjAHHNyqpZx1CAAAAAADikjXQp/A7Lyqy883hNQbNsrlyXXi1zKx8h9Mh0VEQxoDi4xuVtFMQAgAAAAAQT+xIWJHdG9W0bb3s/ujf/eaUWXItvVpmgKnEiA0UhDEgJz1FHpepjt5B9Q2G5UvisgAAAAAAMJHZtiWrarvC774o9XZKkoyCMrkvul5m3hRnwwEfQBMVA0zTUGGWTzUtvWpoD2pGQYbTkQAAAAAAwFmy6qsUfvsvstuOSJKMrDxlrb5DPZkFMgzD4XTAh1EQxoiirNRoQdhGQQgAAAAAwERkdbYosvF5WbX7ogdSM+ReerXMGYuVnJur3tZWZwMCp0FBGCOKstmoBAAAAACAicge7FNk8yuK7N4oWZbkSZJr8RVyzVshw+1xOh7wkSgIY0QRG5UAAAAAADCh2JGIrL2bFH6vQhrsk2TInLVM7qVXy/ClOR0PGDEKwhiRl5Eil2motXtAA0NhJXu5NAAAAAAAxCqr4YDCbz4ju7NZkmQUTpX7ko/JDBQ6nAwYPVqoGOF2mSqY5FN9W1CN7X2amp/udCQAAAAAAPABdm+Xwhufl1W9I3ogPVvuS26QWTKHDUgwYVEQxpCirFTVtwVV3xakIAQAAAAAIIbYkbAiO99SZPMrUnhIcnvkWnSFXAsvk+GiXsHExndwDCkOpGpTlVTX1ut0FAAAAAAAcIxVX6XwW8/I7myRJJllc+W+5GMy0iY5nAw4PygIY0hJTnQB05rmHoeTAAAAAAAAO9it8IbnhqcTGxkBuVfcLHNyucPJgPOLgjCG5GWkKNnjUkdwSF3BIWWkep2OBAAAAABAwrEtK7o78Tt/lYYGo9OJF18l14KVTCdGXOK7OoaYpqEpOX5VNnappqVHC1KznY4EAAAAAEBCsdoaFX79adnNdZIks2S23Cs+LiMt09lgwBiiIIwxJTlpqmzs0uGWHi0opSAEAAAAAGA82KEhRTZXKLLjTcm2JF96dDpx2Vx2J0bcoyCMMSU5fklSTQsblQAAAAAAMB4itfsVfvNPUk+HJEOuecvlWnqNDG+y09GAcUFBGGOm5PhlSGpoCyoUseRxmU5HAgAAAAAgLtn9vQq/9Yysg8c2IckukPuyNTJzJzucDBhfFIQxJsXrVt4kn5o6+lTfFlRZbprTkQAAAAAAiCu2bcs6sF3hDc9IA33RTUguvFqu+StkmC6n4wHjjoIwBpXm+NXU0aea5h4KQgAAAAAAziM72KXw60/Lqt0nSTKKpstz2RoZ6VkOJwOcQ0EYg0py0/R2ZbMON/c4HQUAAAAAgLhg27asfe8q/Pbz0tCg5E2S+5KPyZx5IZuQIOFREMagEzcqsW2bX1QAAAAAAJwDu7tdodfXym44IEkyS2bLfektMlIzHE4GxAYKwhgUSEtWapJbvQMhtfcOKjuNXZMAAAAAABgt27IU2b1BkXdelMIhKdkn94qbZU5byGAc4AQUhDHIMAyV5KZpT12HDjf3UBACAAAAADBKdlebQuuflN10WJJkTlsg94qbZaT4nQ0GxCAKwhhVmuPXnroO1bT0asm0HKfjAAAAAAAwIdi2LWvPpuhag+GQlOKX+9JPyFU21+loQMyiIIxRJcd2L2ajEgAAAAAARsbu6VTotafeX2tw2kK5V94sIznV4WRAbKMgjFGTs/0yDUNNnX0aCEWU7HE5HQkAAAAAgJhk27asys0Kb3g2ukNxsk/ulbfINW2B09GACYGCMEZ53KaKsnyqawuqrrVXMwrYWQkAAAAAgA+y+3oUfn2trJq9ko7tUHzZGhm+NIeTARMHBWEMK8lNU11bUIebeygIAQAAAAD4gMiB7Qq/+WdpsE/yJsu94iaZMxazQzEwShSEMaw0N01v7m1STQvrEAIAAAAAcJw9EFT4jT/Lqt4hSTKKZ8hz+W0y/AyuAc4GBWEMK8mJbr1e09wry7Zl8gwIAAAAACDBWXWVCq1/UurrkdxeuS+5UebsZYwaBM4BBWEMy0xNUobPq66+ITV39it/ks/pSAAAAAAAOMIOhxTZ9IIiuzZIkoz8EnmuuF1GerbDyYCJj4IwxpXm+rX9cLtqWnooCAEAAAAACclqbVB43R9kdzRLpinXkqvluuByGabpdDQgLvCTFONKc6O7LlUfZR1CAAAAAEBisS1L4W2vKfT0T2V3NMvIzJHnli/KvfgKykHgPGIEYYybnh9dYPXAkS7Zts2aCgAAYMJ4/PHHVV1drbKyMt19993Dx3t7e/Xoo4+qp6dH8+fP15o1axxMCQCIVXZPh0KvPiH7yCFJkjnnYrkvvkGGx+twMiD+UBDGuLzMFKUmu9XdH1JL94ByM1KcjgQAAPCRqqurNTAwoAceeEA///nPdeDAAU2fPl2S9OSTT+qOO+5QUVGRwykBALHItm1ZB7Yp/OafpKFBKcUv96rb5Joyy+loQNwa04LwdM8a/+QnP1FDQ4O8Xq9Wr16tlStXjmWMCc0wDE3Pz9D2w206cKSLghAAAEwIVVVVWrBggSRp/vz5qqysHC4I6+rq9PTTT6utrU133nmnysvLP3T/iooKVVRUSJIeeughBQKB8Qs/ztxud1x/fecb52t0OF+jw/kanbE4X1Z/UJ1//Y2G9rwrSUouv0CZN/yNXKlp5/XzOIHvr9HhfI3OuZ6vMSsIz/SssSR95StfUX5+/lh9+rgyoyA9WhA2dWv5LM4ZAACIfcFgUHl5eZIkn8+n+vr64dv279+v733ve/L7/fr+97+vBx988EP3X716tVavXj38dmtr69iHdkggEIjrr+9843yNDudrdDhfo3O+z5fVeFChdU9IwS7J7ZV7xU2yZl6ojv5BqX/wvH0ep/D9NTqcr9EZ6fkqLCw85fExKwjP9KyxYRj68Y9/LL/fr7//+79XTk7Oh+4fj88an22bu9Sdoqc2HlL10R5lZWfLZB3Cc8YzEbGF6xE7uBaxhesRO7gWo+fz+dTX1ydJ6u/vl8/nG76tsLBQxcXFkiSTBeYBIOHZkYgimysU2bpeki0jd4o8V94uI4P/e4HxMmYF4ZmeNf7sZz8rv9+vffv26de//rX+6Z/+6UP3j8dnjc+2/TZsW5mpXnUGh7SzslZF2aljkC6x8ExEbOF6xA6uRWzhesSOeLkWp3vGeCyUl5eroqJCy5cv186dO7Vq1arh2woKCtTR0aGUlBRFIpFxywQAiD12V5tC6/5bdnOdZBhyLbpKriVXyjBdTkcDEsqYPWV7pmeN/X6/JGnWrFnq7OwcqwhxwzAMzSg4tptxU5fDaQAAAD7a1KlT5fF4dN9998k0TQUCAa1du1aSdPvtt+uRRx7RAw88wA7GAJDAIpVbNfTHf4+Wg/4MeW76gtxLr6YcBBwwZiMIz/SscV9fn3w+nxobG5Waymi4kZiWn653D7TowJFuXT53/J79BwAAOFsnblInabgMLC4u1v333+9AIgBALLCHBhR+40+yDmyTJJlT58t92SdkJPnOfEcAY2bMCsITnzUuLS0dftZ4zZo1+vd//3cFg0EZhqHPfe5zYxUhrkw/NoKw+mi3IpYlF+v1AAAAAAAmGOtorUKv/LfU0y65PXKvuFnmzAtlsNY+4KgxKwil0z9r/I1vfGMsP21cyvB5lZuRrOauAdW1BlWaO/G3eAcAAAAAJAbbshTZtl6R9yok25IRKJT7qjtlZn5401IA429MC0KcX9PyM9TcNaCqI10UhAAAAACACcHu7VLo1T/IbqyWJLkWXCrXsmtluKgkgFjBPNUJZHpBuiTpYFO3w0kAAAAAAPhokepdGnrqh9FyMMUvzw1/J/clN1IOAjGGn8gJZFpeugxJh5t7FApb8rjpdwEAAAAAsccODSm88XlZezdJkswpM+Ve9UkZKX6HkwE4FQrCCSQ12aPCLJ8a2vt0qLlH5YUZTkcCAAAAAOAkVvtRhSt+J7vjqGS65Lr4BrnmLWcjEiCGURBOMNPyM9TQ3qeDTV0UhAAAAACAmGHbtqx97yq84VkpHJKRmSP36jtlZhc6HQ3AR6AgnGBmFKTr9T1HdOAI6xACAAAAAGKDPTig8BtrZR3cIUkyy5fIvfLjMjxeh5MBGAkKwgmmNC9dpmGorq1X/UNhpXi5hAAAAAAA51jNdQq98nupu13yeOVe+Qm5yhc5HQvAKNAuTTDJHpcmB1JV09KrQ0d7NGfyJKcjAQAAAAASkG1bCm9/XZF3/ipZloxAUXRKcUbA6WgARomCcAKaUZChmpZe7W/opCAEAAAAAIw7u79XbX/4rSIHd0qSXPOWy3XxDTJc1AzARGQ6HQCjN6s4U5K0t6FTtm07GwYAAAAAkFCshoMaeuoRDR7cKSX55L72s3KvuJlyEJjA+OmdgCZn+5Wa7FZH76Cau/qVl+lzOhIAAAAAIM7ZVkSRzesU2bJOki3v5BnSZbfK8Gc6HQ3AOWIE4QRkmoZmFWVKkvbUdzqaBQAAAAAQ/+zeLoWe/bkiW16RJLkWX6nAXf9MOQjECQrCCWp2cXTtwb11HQ4nAQAAAADEs8jhPRp66hHZTYclX5o8H/uc3EuvkWG6nI4G4DxhivEEVV6YIdMwdLilR32DYfmSuJQAAAAAgPPHjoQV2fSCIjvfkiSZk2fKfcUnZaT4HU4G4HxjBOEEleJ1a2pemmxb2t/Q6XQcAAAAAEAcsbvbFPrz/xctB01TrotvkPv6v6EcBOIUBeEENjzNuJ5pxgAAAACA8yNSvVNDf/x32S31UtokeT5+j9wLL5NhUCEA8Yp5qRPY7MmZeva9Gu1r6FTEsuUyDacjAQAAAAAmKDscUnjj87L2vC1JMsvmyn35bTKSUhxOBmCsURBOYDnpKQqkJ6u1e0A1LT2ampfudCQAAAAAwARkdbYoXPE72W1HJNMl9yU3ypx7iQyDgShAImB88AQ3uzhTkrSvvtPRHAAAAACAiSlStU2htT+KloPp2fLc8kW55i2nHAQSCAXhBDfn2DqEe1iHEAAAAAAwCnZoSKHXnlJ43X9LoSGZ0xbIe+uXZeYUOR0NwDhjivEEV5qbpmSPS0c7+9XeM6CstGSnIwEAAAAAYpzVcVThl38nu+Oo5HLLvfwmmbOXMWoQSFCMIJzg3C5T5YUZkqS9TDMGAAAAAHyEyP73FFr7Y9kdR2Vk5sjziX+Ua85FlINAAqMgjAOzJzPNGAAAAABwZnZoUKF1f1B4/VNSOCRzxiJ51nxJZnaB09EAOIwpxnFgVlGmDEkHm7o1GIooyeNyOhIAAAAAIIZYbUeiuxR3tkhuj9wrPi5z5hJGDQKQREEYF/zJHk3O8au2pVdVR7o0b0qW05EAAAAAADHAtm1Ze99ReMOzUiQsY1Ke3Fd/SuakPKejAYghFIRxYk7xJNW29GpXbTsFIQAAAABA9tCAwq+vlXVwhyTJnHWh3MtvluHxOpwMQKyhIIwTC0qy9Netddpd26FwxJLbxfKSAAAAAJCorJYGhSp+J3W3SW6v3Jd9Qq4Zi5yOBSBGURDGiZyMFBVm+dTY3qfKxi7NObZxCQAAAAAgcdi2LWv3RoU3Pi9ZERnZBXKv/pTMzBynowGIYRSEcWRhabYa2/u0/XAbBSEAAAAAJBh7sF/h1/4o69AuSZI552K5L7lRhtvjcDIAsY6CMI4sKMnWC1vqtLuuQ6GIJQ/TjAEAAAAgIVjNdQpV/F7qaZc8SXJffqtc0xY4HQvABEFBGEcC6ckqzk5VfVtQ+xs62awEAAAAAOKcbduK7HxLkU0vRKcUB4rkWf0pGRnZTkcDMIFQEMaZBaXZqm8LavvhNgpCAAAAAIhj9kCfwuuflFWzV5LkmrdcrotvkOHiT30Ao8NvjTizsCRLf9lcqz11HQqFLXncTDMGAAAAgHhjNdUo9Mrvpd5OyZss96rb5Cqb53QsABMUBWGcyUpL1uTsVNW1BbWvoVPzSxhFCAAAAADxwrYtRba/oci7L0qWJSN3sjyr75SRxt9+AM4eBWEcWlCarbpj04wpCAEAAAAgPtj9QYXXPyGrdr8kybXgUrmWXcuUYgDnjPmncWhhaXQx2j31HRoKRxxOAwAAAAA4V9aRQxr64yPRcjDJJ/e1n5X7khspBwGcF/wmiUOT/EmaEvCrtrVX++o7taCU3asAAAAAYCKybUuRra8p8t7Lkm3JyCuR56o7ZaRlOh0NQByhIIxTC0qzVdvaq+2H2ygIAQAAAGACsvt7FVr3B9n1VZIk1wWr5Lrwahkul8PJAMQbphjHqQXH1h7cW9+pwRDTjAEAAABgIrEaDmroqUei5WByqjzX3y33RddRDgIYE4wgjFOT/EkqyfGrpqVXe+s7dEFZwOlIAAAAAICPYFuWIlvWKbLlFcm2ZRSUyXPV/5CRmuF0NABxjBGEcex4KfjewRaHkwAAAAAAPood7Fbo+V8osrlCsiXX4ivl+djnKAcBjDkKwji2qCxbLtNQZWOXuoJDTscBAAAAAJyGVVcZnVLceFBK8ctz49/JvfQaGSZTigGMPQrCOJaa7NHcyZNk29LmakYRAgAAAECssSMRhd9+QaG/PCYNBGUUTZf3tntlFs9wOhqABEJBGOcunJ4jSXq3qkW2bTucBgAAAABwnN3TrtAzP1Nk+2uSYcq19Fp5bvg7Gb40p6MBSDBsUhLnygszlZ7iUWvPgA4396gsL93pSAAAAACQ8CLVOxV+7Y/S0IDkz5DnyjtlFpQ6HQtAgmIEYZxzmYaWTDs2ivAA04wBAAAAwEl2OKTQG39S+OXfSkMDMkvnyHvrvZSDABxFQZgAlh6bZrzjcJsGQxGH0wAAAABAYrI6mhV6+iey9rwtmS65V9wk9zWfkZHsczoagATHFOMEkJORopIcv2paerWjpk1Lp+c6HQkAAAAAEoZt27IqNyv85p+lcEhGerbcqz8lM6fI6WgAIIkRhAnjeCn4HtOMAQAAAGDc2EODCr/6hMLrn5LCIZnTL5Dn1q9QDgKIKRSECWJhaZY8blPVR3vU2j3gdBwAAAAAiHtWa4NCa38kq2qr5PbIveo2ua+8Q4Y3yeloAHASCsIEkex1a0FJliRGEQIAAADAWLJtW5Fdbyn09E9ld7XKyMqXZ82X5Zp5oQzDcDoeAHwIBWECOb5ZyXsHW2RZtsNpAAAAACD+2AN9Cr/0Xwq/9axkRWTOuVieT/yjzEmsBQ8gdrFJSQIpy0tXlj9J7b2DqjrSpZlFmU5HAgAAAIC4YTUdVuiV30u9XZI3We7Lb5Vr6nynYwHAR2IEYQIxDWN4FOGG/UcdTgMAAAAA8cG2LYW3vKrQM49KvV0ycifLe9tXKAcBTBgUhAnmovJcuUxDe+s61N7DZiUAAAAAcC7svh6Fnn9MkXdflGxLroWXy3Pz/5SRluV0NAAYMQrCBJOW4tXC0mzZkt7axyhCAAAAADhbVl2lhp56RHbDASk5VZ7r75b74utluFxORwOAUaEgTEArZ+dLkt490KyhUMThNAAAAAAwsdiRiMKb/qrQXx6T+ntlFE6T97Z7ZU6Z6XQ0ADgrbFKSgCYH/JqS41dtS682V7fqkpl5TkcCAAAAgAnB7ulQ6JXfyz5aKxmGXBeuluuCK2SYjL8BMHHxGyxBrZwVHUX41r4m2bbtcBoAAAAAiH2R6p3RKcVHa6XUDHlu+oLci6+iHAQw4TGCMEHNL8lS2nseHe3s18Gmbk0vyHA6EgAAAADEJDs0pPCGZ2Tte0+SZJbMlnvVbTKSUx1OBgDnB09zJCi3y9TF5dGpxW/ubXI4DQAAAADEJqulXqE//nu0HHS55V7xcbmv/SzlIIC4MqYF4eOPP6777rtPv/zlLz9029DQkD7/+c9rx44dYxkBZ3DxzFy5TEN76jvU3jvgdBwAAAAAiBm2bSm87TWF/vQfsrtaZWTlybPmS3LNu0SGYTgdDwDOqzErCKurqzUwMKAHHnhA4XBYBw4cOOn2V155RVOmTBmrT48RSE/xakFptmxb2rDvqNNxAABAnOHJYgATlR3sVuj5xxTZ9IJkRWTOvUSeT3xJZla+09EAYEyMWUFYVVWlBQsWSJLmz5+vysrK4dvC4bCqqqo0cyZbwDtt5azoNON3qpo1FI44nAYAAMQLniwGMFFFDu/R0FM/lN1wQEpOlfu6v5Fn5cdluD1ORwOAMTNmm5QEg0Hl5UXLJ5/Pp/r6+uHb1q9fr0svvVRVVVWnvX9FRYUqKiokSQ899JACgcBYRR03brc75r6OQCCgqVsaVN3Uqf1HB3TFwhKnI42LWLwWiYzrETu4FrGF6xE7uBajd6oni6dPny6JJ4sBxCY7NKTOF36j8Jb1kiSjeIY8V9wuw5fmbDAAGAdjVhD6fD719fVJkvr7++Xz+SRJkUhE27Zt0z//8z+fsSBcvXq1Vq9ePfx2a2vrWEUdN4FAICa/jkvKA6pu6tRzb1dqToFPLjP+19OI1WuRqLgesYNrEVu4HrEjXq5FYWHhuH0uniweOQro0eF8jQ7na2RCR+vU/szPFWxtlFxuZVyxRqnLVssw2NfzTPj+Gh3O1+hwvkbnXM/XiArCO+64Q/fee6+WL18uSdqyZYt+9atf6ZFHHjntfcrLy1VRUaHly5dr586dWrVqlSSpq6tLbW1t+s53vqOmpiZt3bpVU6dOld/vP+svAudmQUm2XkyrV2vPgLYfbtPiqfwAAgCAc8OTxSMXLwX0eOF8jQ7n68xs21Zk11uKvB1da9CdnS9j1e0aCBRqoK3d6Xgxj++v0eF8jQ7na3RGer5O94TxGQvC1tZWNTc3S5Lq6+u1Z88eSdK2bdt09OiZN7WYOnWqPB6P7rvvPpWWlioQCGjt2rVas2aNvvvd70qSnnjiCc2aNYty0GGmaeiK+YV6ckO11u1s0AVl2TLZlQsAAJwDniwGEOvsvh6F1j8puy66Xr45+yLl3PRZtXf1OJwMAMbfGQvCV199VU899ZQk6Y9//KP++Mc/Dt9WVFT0kR/87rvvPuntNWvWnPT27bffPuKgGFuLpwb00rZ6He3s1566Ds2bkuV0JAAAMIHxZDGAWBap3afw+qek/l4pySf35bfKVTZXpidJEgUhgMRzxoJw+vTpuuaaa/TSSy9pwYIFKigokCT5/X6tXLlyXAJifLhdplbNK9Cf36nRuh0Nmjt5kgxGEQIAgHPAk8UAYo0dDimy6QVFdm2QJBmF0+S58nYZqRkOJwMAZ52xIFy0aJEWLVqkadOmae7cucrJyZEkWZYl02Sx1nizbEauKnY0qK4tqKoj3Sov5D9JAAAAAPHBaj+q8Cu/l93eJJmmXEuvlWvhpWxEAgCSRvSbsK6uTq+++qra29t1zz336DOf+YzWrVs31tkwzrxuly6bEx0lum5ng8NpAAAAAODc2batyO6NCq39kez2Jhnp2fLc8kW5L7icchAAjhnRb8M333xTqampeuuttxQOh1VQUKC1a9eOdTY44JKZeUr2uHSwqVuHm1l7AwAAAMDEZfcHFX7x1wq/+WcpEpY580J5bvuKzJxip6MBQEw54xTj43p7e5WWlqZt27bpsssuU0lJiX72s5+NdTY4IMXr1vJZeVq3s1Hrdjbo766a5XQkAADgkC9/+cuaPHmySktLNWXKFJWWlio/P9/pWAAwIlZ9lUKvPiH19UjeZLkvWyPXtAVOxwKAmDSigjAQCOj3v/+9ent7dc8996izs5Pd5uLYpXMK9MaeJu2t71Rje1CFWalORwIAAA5YunSpwuGwMjMztWPHDv34xz9WWlqasrKyVFJSoi984QtORwSAD7EjYUXeeUmRHa9Lkoz8Unmu/B8y0jKdDQYAMWxEBeGnP/1pPfnkk5oxY4aWLVum3/3ud7rooovGOhsc4k/26OLyXL2xt0kvbq3X3VfNdDoSAABwwI4dO/Rv//Zvw29fccUVeuedd3TdddeppqbGwWQAcGpWZ0t0I5LWRskw5brwKrkuuEIGm2wCwBmNqCBctmyZlixZoiNHjqipqUl33XUXuxjHuSvnF2lTVbP21HfoUHOPynLTnI4EAADGWVpamg4fPqzS0lJJ0owZM/Too4/q05/+tLKzs50NBwAnsG1b1r53Fd7wrBQOSWlZ8lz1P2TmTXE6GgBMCCMqCOvr6/Wv//qvampqkiTl5+fr61//uoqKisY0HJzjT/HosrkFqtjeoBc21+qe6+bIMAynYwEAgHH0D//wD/rxj3+s4uJilZaWqqGhQV6v1+lYAHASe6BP4df/KOvQbkmSOWOR3Cs/LsOb7HAyAJg4RjQM8Be/+IU6Ojq0YsUKrVixQp2dnXrsscfGOhscdvmcAvmS3DrU3KN9DZ1OxwEAAOMsPz9fDzzwgBYtWqTOzk7l5+frG9/4htOxAGCY1XhQQ0/9MFoOepLkvvIOea68g3IQAEZpRCMIq6ur9alPfUrXXXedJOmvf/2rfv/7349pMDgv2evWVfOL9Ox7NXphS51mFmXKZBQhAAAJxTRNXXTRRaw/DSCm2JGwIu++rMj21yXZMvKmRDciSc9yOhoATEgjGkHo9/u1Y8cOHT16VEePHtWOHTvYxThBXDIrT5mpXh3p6NP2Q21OxwEAAACQ4KzWRoXW/kiR7a9JhuRafKU8N/8D5SAAnIMRjSC88sor9cQTT2jz5s3Dx+64444xC4XY4XGZumZhsZ7YUK2/bq3T/JIsuV1sUAMAAABgfNlWRJFtrymyuUKyLBkZAblXfVJmfonT0QBgwhtRQXjZZZcpIyNDO3bskCQtXLhQCxYsGNNgiB2Lp+Vo/e4jau7q1ztVzVo+K9/pSAAAAAASiNXZovCrT8hurpMkmXMvkfui62V42DgJAM6HEQ0Fe/DBB9Xa2qqvfe1r+trXvqaWlhZ9+9vfHutsiBEu09B1iyZLkl7e3qChUMThRAAAAAASgW1bCu98S6E//nu0HEzNkOfGv5dn5ccpBwHgPBrRCML29nbl5uYOv52Tk6O2NtajSyTzpkzS5ECq6lqDenVXo649VhgCAAAAwFiwezoVWv+k7MaDkiSzfLHcy2+SkZTicDIAiD8jKgjz8vL07LPPKisrS7Zt67nnnlNeXt5YZ0MMMQxDNy0t1U9f2K31uxq1dHqOstKSnY4FAAAAIM7Yti2rcrPCG56Vhgal5FS5L1sjV9lcp6MBQNwaUUH48Y9/XD/5yU/03e9+d/jYl770pTELhdhUlpumRVMD2lrdqmferdHfXjnT6UgAAAAA4ojd16Pw62tl1eyVJJmlc+W+7BMyUvwOJwOA+DbiTUoCgYC2bNkiSVq8eLHmzJkzpsEQm25cMkW7a9u1u65D+xs6NbMo0+lIAAAAAOJApHqnwm/8SRoISt4kuVfcLHPGYhmG4XQ0AIh7IyoIJWnOnDmUglCGz6vVC4r0ly11eubdw/pq/gK5XSPa6wYAAAAAPsQe7Ff4rWdkVW2VJBlF0+VZdZsMf6azwQAggYy4IASOu3ROgd450KLmrgG9ta9Jl88tdDoSAAAAgAnIqqtU6LWnpGC35PbIfdENMudeJMNgEAIAjCd+62LU3C5TNy8tkSS9vL1B3f1DDicCAAAAMJHYoSGF3viTQn95TAp2y8idIs+tX5Fr3iWUgwDgAH7z4qzMLp6k2cWZGgxF9JfNtU7HAQAAADBBWE01Cj31iKw9b0umS65l18rz8X+QmZnjdDQASFhMMcZZu3lpqSobt2vzwVZdVJ6nstw0pyMBAAAAiFF2JKzIexWKbH9Nsm0ZWflyX3m7zGyWLAIApzGCEGctkJ6sVcfWH3xqQ7XCEcvhRAAAAABikdXWqNDaHyuybb0kyXXBKnnWfIlyEABiBCMIcU6uWlikHTVtau7q1ys7GnTtoslORwIAAAAQI2wrosj21xV5r0KyIlJ6tjxX3C4zv8TpaACAEzCCEOfE4zL1yeVTJUnrdjaqsT3ocCIAAAAAscDqalXozz9T5J0XJSsic87F8t52L+UgAMQgCkKcs7K8dC2fmSfLtvXkhmpFLNvpSAAAAAAcYtuWIrs2KPTUI7Kba6XUdHlu+Dt5Lr1FhsfrdDwAwCkwxRjnxfVLpmhPfYfq24J6c+8RXT6XtUQAAACARGP3diq0/inZDQckSeaMRXKvuElGks/hZACAM2EEIc6LZI9Lt15cJkl6cWu9WrsHHE4EAAAAYLzYtq1I5WYNPfnDaDmYnCr31XfJc+UdlIMAMAFQEOK8mVU8SYunBhSKWHpqY7Vsm6nGAAAAQLyz+3sVfum/FH71SWloQGbpHHk/+b/kmjrP6WgAgBFiijHOq5uXlmh/Y6cONnVrw76jWjE73+lIAAAAAMZI5NAuhV9/WhoISt4kuZffJLN8iQzDcDoaAGAUGEGI8yo12aNbL47uavzc5ho1dfQ5nAgAAADA+WYP9iv06hMKv/QbaSAoo3CavLd9Va6ZF1IOAsAEREGI825+SZaWTs9ROGLrd28cUDhiOR0JAAAAwHli1Vdp6MkfyqrcIrnccq+4SZ6P/b2MtEynowEAzhJTjDEmPr6sVIeO9uhIR59e2FKnm5aWOB0JAAAAwDmwQ0MKb3pB1u6NkiQjd7LcV9wuMzPH4WQAgHPFCEKMiSSPS3deOl2mIb2+54gqGzudjgQAAADgLFm1+zX0xMPRctA05Vp6jTwf/5+UgwAQJygIMWam5Ph1zQWTJUl/ePOgggMhhxMBAAAAGA27v1ehV/5boRd+KfV2yggUyvOJf5R78ZUyTJfT8QAA5wlTjDGmrphXqP0NnTrU3KOnNlbrs6vKWbQYAAAAiHG2bcuq3KLwxuelwT7J7ZFryWq5FqykGASAOMQIQowp0zR056XTlexxaVdthzbsO+p0JAAAAABnYHe1KfT8LxRe/6Q02CejaLq8t/0vuS+4nHIQAOIUIwgx5ib5k3Tb8qn6zWtVeva9GhVlp6o0N83pWAAAAABOYFsRRXa8qcjmCikckpJ8ci+/UeaMxcwCAoA4xwhCjIuFpdm6dHa+Ipat37xWpd5+1iMEAAAAYoXVUq/Q0z9RZNMLUjgkc/oF8t7xNbnKl1AOAkACYAQhxs2NF05RfVtQh5p79JvXq/T5q2fLZfJgAwAAAHCKHRpS5L2XFdn5pmTbkj9Tnks/IXPKTKejAQDGESMIMW5cpqlPXz5D/mSPDjZ168WtdU5HAgAAABKWVVepoSd/oMiONyRJrgUr5b39a5SDAJCAGEGIcZXh8+quy2fo0Zf26NVdjZqS49e8KVlOxwIAAAASht3fq/DG52VVbZUkGdkFcl9+q8ycYoeTAQCcQkGIcTctP13XL56i5zfX6g9vHlTujSnKzUhxOhYAAAAQ12zbllW1VeGNz0kDfZLLLdeFV8s1f6UMF7sTA0AioyCEIy6fW6C61l7tqGnXY6/s05dvmKfUZI/TsQAAAIC4ZHe3KfTGn2TXV0mSjKLp8lz6CRkZ2Q4nAwDEAgpCOMIwDN2xYpraegbU0N6nX6+v1Oevni23i2UxAQAAgPPFtiIKb39dkfdelsIhKckn9yU3yixfzO7EAIBhtDFwjNfj0t1XzlJ6ikfVR3u09u1Dsm3b6VgAAABAXLBaGtTyy+8o8vZfpHBI5vQL5L3ja3LNXEI5CAA4CSMI4aiMVK/uvmqmfvrCHr17oEU5GSm6Yl6h07EAAACACcsODSnyXoUiO9+UbEvyZ8p96SfkYndiAMBpUBDCccXZft156XT9en2lXthcq0BasuaXsLMxAAAAMFpWfZVCrz8t9bRLhqHUZVcrNG+lDE+S09EAADGMKcaICfNLsnT94smyJf3+jQOqbelxOhIAAAAwYdj9QYXW/UGh538h9bTLyC6Q55YvKvPqOygHAQAfiRGEiBlXzCtUa/eA3j3Qol+8sl9fvG6u8jJTnI4FAAAAxCzbtmVVbVV443PSQJ/kcst14Wq55l8qw+VyOh4AYIKgIETMMAxDt15Spt6BkPbWd+rnL+/VP14/V5P8POMJAAAAfJDd3a7QG0/Lrq+SJBmF0+S57BMyMgIOJwMATDRMMUZMcZmm7rp8hspy09TVN6T/rNir4EDI6VgAAABAzLCtiMLbX9fQkz+IloNJKXKvuk2ej32OchAAcFYoCBFzvG6X/vbKmcqf5FNz14B+8co+DYYiTscCAAAAHGe1NCj09E8VefsvUjgkc/pCee/4J7lmXijDMJyOBwCYoCgIEZN8SW59bvUsTfInqa41qF+9WqlwxHI6FgAAAOAIOzSk8Ma/KPT0T2S3Nkj+TLmv/1t5rrpTRorf6XgAgAmOghAxK8Pn1eevniV/skdVR7r06/WUhAAAAEg8Vn2Vhp78oSI7XpdkyzV/hby3f1WuKbOcjgYAiBMUhIhpOekp+vzVs+RLcmtvfaf+67UqSkIAAAAkBLs/qNCrTyj0/C+knnYZWfny3PJFuZffJMPDRn4AgPOHghAxrzArVV+4ZrZSvC7tqevQbygJAQAAEMds21akaquGnnhYVuUWyeWWa9l18qz5sszcyU7HAwDEIQpCTAhFWan6wjVzlOJ1aXddh377epUiFiUhAAAA4ovd067QX36p8Lo/SANBGYVT5fnk/5J70SoZLpfT8QAAcYqCEBNGcfb7Iwl31Xbot68foCQEAABAXLCtiMI73tDQEz+QXV8pJaXIfflt8nzs8zIzAk7HAwDEOQpCTCjF2X59/urZSva4tLOmXb96tVKhMCUhAAAAJi6rtVGhp3+qyMbnpXBI5rSF8t7+NblmXSjDMJyOBwBIAO6x/OCPP/64qqurVVZWprvvvnv4+C9/+UsdPnxYoVBIn/3sZzVrFrtvYeQmB/z6wjWz9Z8V+7S3vlP/WbFXd185U8neMf12BgAAAM4rOzSkyOZXFNnxhmRbkj9D7pWfkKuEv48AAONrzEYQVldXa2BgQA888IDC4bAOHDgwfNtnPvMZfetb39JXv/pVPf3002MVAXFscsCvL143R+kpHlUf7dHPXtqr4EDI6VgAAADAiERq92voqR8qsv01ybblmrdc3k9+jXIQAOCIMSsIq6qqtGDBAknS/PnzVVlZOXyb2x0d6TUwMKCSkpKxioA4l5fp0z9eP1dZ/iTVtwX107/uUVdwyOlYAAAAwGlZHc3RTUhe+KXU3S4jK1+eW+6Re8XNMrxJTscDACSoMZuTGQwGlZeXJ0ny+Xyqr68/6fZ//dd/1YEDB/TlL3/5lPevqKhQRUWFJOmhhx5SIDDxF+Z1u91x8XXEkkBA+uanA/q3pzapoa1H/99Le/W1Wy9SQZb/jPfjWsQWrkfs4FrEFq5H7OBaADhX9kCfIpsrFNn9dnQ6sTdJrsVXyTVvBbsTAwAcN2YFoc/nU19fnySpv79fPp/vpNv/9//+32pra9PDDz+s73znOx+6/+rVq7V69erht1tbW8cq6rgJBAJx8XXEos+vLtcvXtmnutagvv27N/U3V5Rral76ad+faxFbuB6xg2sRW7gesSNerkVhYeG4fr7TrUf96KOPqq6uTpL0uc99jhkliGu2FZG15x2F33tZGuyTDEPm7IvkXnq1jJQzP6kNAMB4GbMpxuXl5dq1a5ckaefOnSovLx++LRSKrhWXnJyspCSG0ePcpSZ79D+vmaM5xZPUNxjWoy/t1bZDE/8POQAAJqozrUd9yy236MEHH9QXv/hFPfnkkw6mBMaWVVep0FOPKPzWn6XBPhmFU+W59SvyXPYJykEAQEwZsxGEU6dOlcfj0X333afS0lIFAgGtXbtWa9as0Q9+8AP19fXJsix96lOfGqsISDBej0t/c0W5/vzOYW3Yf1S/ff2AOnoHtWpeoQzDcDoeAAAJ5VTrUU+fPl2SlJubK0lyuVwyzTF7vhpwjNXZosjG52XV7oseSM+S++IbZJbO5XEpACAmjVlBKOmkqSSStGbNGknS17/+9bH8tEhgpmnolotKlZWWpOfeq9VfttSpvXdQt1xUKhd/gAAAMG4+aj1qSfrd736nG2644ZT3j8f1qE+HNS5HJ5bPlzXQp+43nlXwvXWSFZHhTVbayhvlX7pahtvjSKZYPl+xiPM1Opyv0eF8jQ7na3TO9XyNaUEIOMEwDF0+t1CZqUn67zcO6O3KZrV0D+gzl89QarIzD8wAAEg0H7Ue9fPPP6/i4mLNmjXrlPePx/WoTyde1rgcL7F4vmwrImvfuwq/+7I0EJRkyJy1VO6l12jQl6bBzi7HssXi+YplnK/R4XyNDudrdDhfozPS83W6NakZUoW4tbA0W/9w7Rz5kz062NStR57fpSMdfU7HAgAgIZxpPert27dr//79uvXWW52KB5w3Vv0Bhf747wq/8SdpICijoEyeW78kz+W3yvClOR0PAIARoSBEXCvNTdO9H5un4uxUdfQO6sd/2aUdNW1OxwIAIO6duB61aZrD61FL0mOPPaaWlhZ961vf0qOPPupwUuDs2F2tCv31Vwo9/5+y249KaZPkvvrT8tz0BZmBIqfjAQAwKkwxRtzLTE3SF6+bq6c2VmtLdav+a32VugakFeVZMlkkGgCAMXO69agfeeQRJ+IA54U9OKDIlnWK7HpLsiKSxyvXoivkmr/SsXUGAQA4VxSESAget6n/sXKaCrN8en5zrZ55u0r7ajN056XT5WddQgAAAHwE27KOrTP40vvrDM5cIvfSa2WkpjsdDwCAc0JBiIRxfPOSgkk+/f7NalU2dumHz+7UXZfPUGku68MAAADg1KzGgwpveE522xFJkpFfIvfym2TmFDucDACA84M1CJFwygsz9a3PXKqSHL+6+ob0H3/do9d3H5Ft205HAwAAQAyxu9sUevG/FHr259Fy0J8p9+pPyXPz/6QcBADEFUYQIiFlpaXonuvm6C+b6/T6niN69r0aHWru1ieXT5MviR8LAACARGYPDSiy9VVFdrwZXWfQ7ZFr0Sq5FlzGOoMAgLhEE4KE5TJN3bS0RKW5aXrirYPaVduhutYduvPSaZqWn+F0PAAAAIwz27JkVW5W+J0Xpf5eSZJZvljuZdexziAAIK5RECLhzS/JUmGWT79744BqW3r1sxf3atW8Ql1zQbHcLmbhAwAAJAKrsVrhjc/Jbm2UJBl5U6LrDOZOdjgZAABjj4IQkJSdlqwvXjdXFTvq9cqOBr26q1FVR7r0qcumKyc9xel4AAAAGCN2T7vCb78gq3pn9EBqhtwXXy9z2kIZhuFsOAAAxgkFIXCMyzR07QWTVV6Qod+/cUD1bUH94NmdunHxFF0yK08mDxABAADihh0aVGTrekV2vCFFwtF1Bi+4PLrOoMfrdDwAAMYVBSHwAWV56frqzQv09KbD2lrdqj+9c1g7a9t1+/KpykpLdjoeAAAAzoFtW7Iqt0TXGezrkSSZ0y+Q+6LrZfhZhxoAkJgoCIFTSPG69alLp2v+lCz98e1qHWzq1vef2aGPXViii8tzmW4CAAAwAVlNhxXe8JzslnpJkpE7ObrOYN4Uh5MBAOAsCkLgDOaXZKksL01/2nRI2w+3a+3bh7Sjpk23XjxVgXRGEwIAAEwEdk+nwptekHVwe/RAarrcy66XOWOhDINN6QAAoCAEPoI/2aO7Li/X/JI2rX37kA4c6db3n9muaxYW67K5BXKZPKgEAACIRXZoSJFt6xXZ/np0nUGXW66Fl8t1weWsMwgAwAkoCIERWliarWn56Xr23RptqW7VX7bUaeuhNt12yVRNyfE7HQ8AAADH2LYlq2qbwpv+KvV1S5LMaQuj6wymZTobDgCAGERBCIyCP9mjOy+drsVTA1r79iEd6ejTj/+yS8tn5evaRcVK8fIjBQAA4CTraK3CG56V3VwnSTJyiuVe/jGZ+aXOBgMAIIbRZgBnYWZRpv7p4wv08vZ6vb77iN7a16Tth9t045IpWjwtIJNNTAAAAMaV3dup8Ka/yjqwLXrAlyb3sutkli9inUEAAD4CBSFwlrxul25cUqJFZQH9adNhHWru0R/eOqi3K4/qExeVqSg71emIAAAAcc8ODSmy/XVFtr8mhUPRdQYXXCrXolUyPElOxwMAYEKgIATOUWFWqu65bo62VLfqufdqVdPSq0ee36mLy/N07QXFSk32OB0RAAAg7ti2LevAdoU3vSAFuyRJ5tT5cl98vYy0LIfTAQAwsVAQAueBYRhaMi1HcyZP0svb6vXWviZt3H9UW6tbddWCIq2cnS+3i6ktAAAA54PVXKfwW8/Kbq6VJBmBQrkv+ZjMwqkOJwMAYGKiIATOoxSvWzcvK9WyGbl69r0aVTZ26fnNtdq4/6huvHCK5k/JksH6hAAAAGfFDnapfcOfFdq5MXogxS/3smtlli+RYfJkLAAAZ4uCEBgD+ZN8+vzVs7WvvkPPvler5q5+/df6KpXlpumGJVNUmpvmdEQAAIAJww6HousMblsfXWfQdB1bZ/AKGV7WGQQA4FxREAJjaFbxJM0ozNSmyqN6cVu9DjX36Ccv7NbcyZN0/eLJysv0OR0RAAAgZtm2Levgjug6g72dkqTkmYtlLb5KRnq2s+EAAIgjFITAGHOZhpbPyteiqQG9tuuIXt97RLvrOrSnvkNLpubomguKNcnPM98AAAAnslrqFd7wnOymw5IkI7tA7uUfU/aCi9Ta2upsOAAA4gwFITBOUrxuXbd4spbPylPFjgZtqmzWewdbtPVQqy6akasr5xcpI9XrdEwAAABH2cFuhd95UVblFkm2lJwaXWdw5oWsMwgAwBihIATGWbrPqzUXl+myOQV6cWudth9u04b9R/VOVbMunpmnK+YXKj2FohAAACQWOxJWZOebimxZJ4WGousMzl8h16IrZSQlOx0PAIC4RkEIOCSQnqxPXz5DVy0o0svb67Wjpl1v7m3SpspmXTwzV5fPLVSGj6IQAADEN9u2ZdXuU2TDc7K72yRJZslsuS+5UUZGwOF0AAAkBgpCwGH5k3z6zKpyNbYH9dK2eu2u69Abe5q0Yd9RLZuRq1XzCpTl51lzAAAQf6zOFoU3PCu7rlKSZGTmyr38YzInlzucDACAxEJBCMSIwqxU/e2VM9XQFtQrOxu0s6ZdG/cf1abKZi2eGtAV8wuVm5HidEwAAIBzZg8OKLLlFUV2vSVZluRNlmvJarnmXiLD5XI6HgAACYeCEIgxRdmp+uyqch3t7NO6nY3aeqhV7x1s0eaDLZozeZJWzStUaW6a0zEBAABGzbYtWfs3K/zOi1J/ryRD5qxlci+7RkaK3+l4AAAkLApCIEblZfp056XTdfXCYq3f1aj3DrZod12Hdtd1qDQ3TZfPLdCcyZNkGobTUQEAAD6SdbRW4beekd1SL0ky8krkXnGTzJxih5MBAAAKQiDGBdKTddvyqbpmUbHe2tukjfuP6nBzjw439ygnPVkrZ+drybQcJXmYjgMAAGKPHexWeNMLsqq2Rg/40uW++AaZ0xfK4IlOAABiAgUhMEGkp3h1/eIpumJ+kd6pbNYbe4+opXtAT286rL9urdOyGblaMStfk/xJTkcFAACQHQkrsvNNRbask0JDkumSa+Flci1aJcPD4xUAAGIJBSEwwSR7XLpsboFWzM7TrtoOvbHniGpaevXa7iN6Y88RzZ2SpeUz8zQtP51n5QEAwLizbVtW7T5FNjwnu7tNkmSWzpH7khtlpGc7nA4AAJwKBSEwQblMUwtLs7WwNFu1LT16Y2+Tdhxu186a6EteRooumZWnJVMDSvbyow4AAMae1dmi8IZnZddVSpKMzNzoOoPFMxxOBgAAzoTWAIgDU3LS9OmcNH1syZDerjqqTZXNOtrVrz9tOqwXNtdq0dSALp6Zp6KsVKejAgCAOGQPDiiy5RVFdr0lWZbkTZbrwtVyzblEhot1kgEAiHUUhEAcyUj16toLJmv1giLtqu3Qhn1Nqj7ao7crm/V2ZbMmZ6fqovI8XVCWzaYmAADgnNm2JWv/ZoXfeVHq75VkyJy1TO5l18hI8TsdDwAAjBAFIRCHTpx+3NTRp01Vzdp8sEV1bUHVbazWs+/V6IKybC2bnqPJAT9rFQIAgFGzjtYq/NYzslvqJUlGXoncK26WmVPkcDIAADBaFIRAnMuf5NPHl5Xq+sWTtaOmXZsqm3W4uUebKpu1qbJZuRkpWjo9R0umBZSW4nU6LgAAiHF2sFvhTS/IqtoaPeBLl/viG2ROX8iTjgAATFAUhECC8LpdunBaji6clqOjnX1690CLNh9sVXNXv57fXKsXttRqVtEkLZkW0OzJk+RxmU5HBgAAMcSOhBXZ+aYiW9ZJoSHJdMm18DK5Fq2S4UlyOh4AADgHFIRAAsrL9OljF5bo+sWTtbe+U+8eaNG++g7tOfaS4nVpQWm2lkzLUWkOU5ABAEhktm3LqtmryMbnZXe3SZLM0jlyX3KjjPRsh9MBAIDzgYIQSGAu09S8KVmaNyVLPf1D2naoTZsPtqihvW94CnKWP0kXlGVrUVlA+ZN8TkcGAADjyOpoVnjjc7LrKiVJRmau3Ctuklk8w+FkAADgfKIgBCBJSkvx6tI5Bbp0ToGaOvq0ubpFW6vb1N47qHU7G7VuZ6PyJ/m0qCxbF5RmKyst2enIAABgjNiDA4psqVBk1wbJsiRvslwXrpZrziUyXC6n4wEAgPOMghDAh+RP8unGJSW6ftEUHWru1tbqNu2oaVNTR59e6OjTC1vqNDk7VQuO7ZQ8yc+6QwAAxAPbtmTt36zwOy9K/b2SDJmzlsm97BoZKX6n4wEAgDFCQQjgtEzT0LT8DE3Lz9AtF5WqsrFLW6tbtae+Q3VtQdW1BfX85lpNyfFrQUmW5k/JYmQhAAATlNVUo/CGZ2W31EuSjPwSuZffLDOnyOFkAABgrFEQAhgRt8vUnMmTNGfyJA2FI9rX0Kkdh9u0p75TtS29qm3p1XPv1aooK1XzS7I0vyRLuRkpTscGAAAfwQ52K7zpBVlVW6MHUtPlvugGmdMXslEZAAAJgoIQwKh53S4tKMnWgpJsDYUi2tvQqZ017dpX36GG9qAa2oP669Y65WYka+7kLM2bMknFAb9M/sgAACBm2JGwIjvfVGTLOik0JLncci24VK5Fq2R4WD4EAIBEQkEI4Jx4PS4tPLYWYShiqaqxSztq2rSnrkPNXQNq7mrUq7salZ7i0ezJkzR38iRNz8+Qx206HR0AgIRk27asmr2KbHxednebJMksnSP3JTfKSM92OB0AAHACBSGA88ZzwjTkiGXp0NEe7art0O66dnUGh7SpslmbKpvlcZuaUZChOcWTNLs4UwGngwMAkCCsjmaFNz4nu65SkmRMypV7+U0yi2c4nAwAADiJghDAmHCZpqYXZGh6QYY+vqxEje192l3Xrj11nWpoD2pPXYf21HVIkkpyD2p6vl+zijI1JeCXaTIVGQCA88keHFBkS4UiuzZIliV5k+W6cLVccy6R4XI5HQ8AADiMghDAmDMMQ0XZqSrKTtU1F0xWV3BIexs6tLeuU1VHulTTHH15ZUeDfElulRdmaGZRpsoLM5Se4nU6PgAAE5ZtW7L2b1b4nRel/l5JhsxZy+Redo2MFL/T8QAAQIygIAQw7jJSvbq4PE8Xl+cpFLbU2i9t2lOrvfUdau8d1LZDbdp2KLomUmGWTzMLo2VhaW6a3C7WLgQAYCSsphqFNzwru6VekmTkl8i9/GaZOUUOJwMAALGGghCAozxuU/PLAipIM/XxZSVq7R7QvoZO7W/sVHVTjxrb+9TY3qdXdzXK4zY1LS9d0wsyVF6YofzMFBnsjAwAwEnsYLfCm16QVbU1eiA1Xe6LbpA5fSH/bwIAgFOiIAQQMwzDUE5GinIyUnTpnAKFIpYOHe3W/oYuVTZ2qqmzX/saOrWvoVOS5E/2aEZBtDCcnp+urLRkZ78AAAAcZEfCiux4U5Et66TwkORyy7XgUrkWrZLhSXI6HgAAiGEUhABilsdlqrwwU+WFmZJK1N03pKojXdGXxi5194e09VCbth6bjjzJn6Tp+emaduwlM5U/hgAA8c+2bVk1exXe+LzUHf0/0SydI/clN8pIz3Y4HQAAmAgoCAFMGOk+r5ZMy9GSaTmybVvNXf06cKRbB5q6dLCpWx29g3r3QIvePdAiSQqkJWvqsbJwal4ahSEAIO5YHc0Kb3hOdn2lJMmYlCv38ptkFs9wOBkAAJhIKAgBTEiGYSgv06e8TJ9WzM6XZdlq7OjTgSNdqj7areqjPWrtGVBrz4DeqWqWFB1hODUvTVPz0lWWm6ZAejJrMQEAJiR7cECRLRWK7NogWZbkTZbrwtVyzblEhsvldDwAADDBUBACiAumaag4O1XF2alaNa9QEctWY3tQB5u6dbCpW4ebe9TRO6jNvYPafLBVUnQNw9LcNJXlpqksL02FWT65THZJBgDELtu2ZO3frPA7L0r9vZIMmbOXyb30GhkpfqfjAQCACYqCEEBccpmGJgf8mhzwa9W8QlmWrSOdfTp0bHRh9dFu9Q6EtKu2Xbtq2yVFd1SeEvCrNCdNJbl+leSkyZfEr0kAQGywmmoU3vCs7JZ6SZKRXyL38ptl5hQ5nAwAAEx0/OULICGYpqGirFQVZaVq5ewC2bat1p4BHT7ao0PNPTrc3KOW7oHhEYfH5WakqCTHr5Icv6bkpCkvI0WmybRkAMD4sYPdCm96QVbV1uiB1HS5L75B5rSFLJUBAADOizEtCB9//HFVV1errKxMd9999/DxRx99VHV1dZKkz33ucyopKRnLGADwIYZhKCc9RTnpKVo6I1eS1Nsf0uGWHtW09KimuVd1rb1q7upXc1f/8MYnSW5TkwN+TcmJjk6cEvAr3ed18ksBAMQpOxJWZMebimxZJ4WHJJdbrgWXyrXoChke/u8BAADnz5gVhNXV1RoYGNADDzygn//85zpw4ICmT58uSbrllluUm5urI0eO6Le//a3++Z//eaxiAMCI+VM8mjclS/OmZEmSwhFLje1B1bT0qralVzUtPeoIDulAU7cOnDDKMMPnjRaG2amaHPCrKDtVKV4GaAMAzo5t27Jq9iq88Xmpu02SZJbOkfuSG2WkZzucDgAAxKMx+wu2qqpKCxYskCTNnz9flZWVwwVhbm50tI7L5ZLJhgAAYpTbZWpKTpqm5KQNH+vuG1Jta3R0YW1Lr+ragurqG9LOmnbtrGkffr+c9GQVB6KlYVF2dGpzkoddJQEAZ2Z1NCu84TnZ9ZWSJGNSrtzLb5JZPMPhZAAAIJ6NWUEYDAaVl5cnSfL5fKqvr//Q+/zud7/TDTfccMr7V1RUqKKiQpL00EMPKRAIjFXUceN2u+Pi64gHXIvYMpGuR0DS1Cnvv23Ztprae1V9pFOHmjp16Gin6lqi6xm2dA9oa3V0x2RDUkGWXyV5GdGX3AxNyU2XL8njyNdxOhPpWiQCrkfs4FpgrNmDA4psqVBk1wbJsiRvslwXrpZrziUyXDzBBAAAxtaYFYQ+n099fX2SpP7+fvl8vpNuf/7551VcXKxZs2ad8v6rV6/W6tWrh99ubW0dq6jjJhAIxMXXEQ+4FrFlol8Pr6RZ+SmalZ8iqUDhiKWmzj7VtQZV3xZUfVuvmjr61djeq8b2Xm3c2zB830BasgqzfCrKTlVhVqoKs3xKT3FuXamJfi3iDdcjdsTLtSgsLHQ6Aj7Ati0Ft72hoXV/lPp7JRkyZy+Te+k1MlL8TscDAAAJYswKwvLyclVUVGj58uXauXOnVq1aNXzb9u3btX//fn31q18dq08PAI5xu0wVZ/tVnP3+H3ahiKWmjj7Vtfaqsb1PDe1BHenoU2vPgFp7BrTjhOnJaSkeFWb5VDgpVQWTfCrM8imQniIXuycDQFyxmmoUfusZdbZGnzgy8kvkXn6zzJwih5MBAIBEM2YF4dSpU+XxeHTfffeptLRUgUBAa9eu1Zo1a/TYY4/J5/PpW9/6lgoLC/WFL3xhrGIAQEzwuKK7H08OvF8ahiOWmrv61dAWVGNHnxrbg2ps71NPf0j7G7q0v6Fr+H3dLkP5mT4VTHr/JX+ST/7k2JqiDAD4aHawW+FNL8iq2ipJMtMmyVx2rcxpC2UYPBkEAADG35hus3n33Xef9PaaNWskSY888shYfloAmBDcLvPYtOLU4WOWbaujd1CN7X1q7AjqSHu0OOwIDh2brhw86WP4kz3HysIUFWRGS8O8zBR53axXBcB5jz/+uKqrq1VWVnbS48La2lr9/Oc/lyR97nOfU0lJiVMRx5UdCSuy401FtqyTwkOSyy3XgkuVu/o2tXf3OB0PAAAksDEtCAEAo2MahrLTkpWdlqz5JVnDx/uHwjrS3qcjnX060hF9OdrRp96BkKqOdKnqyPujDQ1Jk/xJys+MloXHS8Pc9BR53OwcD2B8VFdXa2BgQA888IB+/vOf68CBA5o+fbok6Q9/+IPuvfdemaap//zP/9TXv/51h9OOLdu2ZdXsVXjj81J3myTJLJ0r9yU3yEjPlulNkkRBCAAAnENBCAATQIrXran56Zqanz587Phow6aOPjV19h/7t0/NXQNq7x1Ue++g9tR3DL+/YUjZ/mTlZqYoLyMlWhpmRF+SPIw4BHB+VVVVacGCBZKk+fPnq7KycrggDAaDw7tCB4PB036MuBEOKfzG01Jfj4xJuXIvv0lm8QynUwEAAAyjIASACerE0YZzp7x/PByx1No9oKNd/Wrq7FNTR7+Odvap7diGKK09A9pT13HSx8pM9So3I0Wl+Vnye3WsOEyWP9nDelgAzkowGFReXp4kyefzqb6+fvg227Y/8v4VFRWqqKiQJD300EPDheJE1Xftp2QFu5S6eJUM18kPwd1u94T/+sYT52t0OF+jw/kaHc7X6HC+RofzNTrner4oCAEgzrhdpvKPbWKyUNnDx48Xh02dfTra1a/mzn4d7epXa/eAOoND6gwOqbKx66SPleJ1KScjRTnpycrNSFFOerQ4zE5LltvFdGUAp+fz+dTX1ydJ6u/vl8/nO+X7ne5JiNWrV2v16tXDb7e2tp7/kOMpt0ySNNDR+aGbAoHAxP/6xhHna3Q4X6PD+RodztfocL5Gh/M1OiM9X4WFhac8TkEIAAnixOLwRBHLVntPdMRhMGTq8JE2NXdHC8T+oYhqW3pV29J70n0MQ5qUmqScjGTlpKcokJ6sQFqycjKSlelLkmky6hBIdOXl5aqoqNDy5cu1c+dOrVq1avg2v9+vtrY2GYahlJQU50ICAABAEgUhACQ8l2lERwlmpBx71ilTUnQKYM9ASC1d/WruGlBLd79ajv17fI3D9t5B7W/o+tDHy05LHi4NA+nvv56R6pXJlGUgIUydOlUej0f33XefSktLFQgEtHbtWq1Zs0a33367fvjDH0qS/v7v/97ZoAAAAKAgBACcmmEYSk/xKj3Fq2n5GSfdFo5YausZVEt3dIry8X9buwfU3R9Sc1e/mrv6P/Qx3aahrLRkZaclKXBs/cTstCRlpyVrkj+JactAnLn77rtPenvNmjWSpJKSEj344INORAIAAMApUBACAEbN7TKVlxndCfmDBkOR6GYoxwrDtuOv9wyo5wzloWFImT7vsQLx/eIwyx/9N8XrYsMUAAAAABgDFIQAgPMqyeNSUVaqirJSP3TbQCii9mM7Kbf1DKqtZ0Btx0rEzr4hdQSjLwebuj9032SPS1lpScryJynLHy0OJ/mPv50kr8c1Hl8eAAAAAMQdCkIAwLhJ9rhUmJWqwlOUh+GIpY7g4HBx2N4zqPbeaJHY3juogVBEje19amzvO+XHTk12D5eFk/xJmpT6foE4KZUCEQAAAABOh4IQABAT3C5TOekpykn/8LRl27bVNxh+f3OUngG19Q6qvWdQHcFBdfQOKjgQVnAgrLrW4Ck/vi/Jfaw09A6Xh5mpx8tEr3xJbqYwAwAAAEhIFIQAgJhnGIZSkz1KTfZocsD/odst21ZPX0jtwWh52BkcUntvtDjsCA6qs3dQfYNh9Q2G1dB+6gLR4zY1KdWrDF+0RMxMTVKmz6tMf/TfjFSvvG5GIQIAAACIPxSEAIAJzzQMZaRGS7yy3LQP3W7Ztnr7Q8OjDTuDQ++Xh8EhdQYH1T8UUXPXgJq7Bk77eXxJbmWmepXhO1YgDr8eLRYzUr3ysBMzAAAAgAmGghAAEPdMw1C6z6t0n1clOR8uECVpYCisjmNlYecp/u3qGxoehXi6dRAlKTXJrfTh0jD6OTNOfEn1KtnDjswAAAAAYgcFIQAAkpK9bhV43SqY5Dvl7ZZtq3cgpK7g0LHC8FhxGBxSZ1+0SOzuCyk4GFZwMKwjHacvET1uc7gwTPd5lZ7ief91n1cZKR6l+bxj9aUCAAAAwEkoCAEAGAHTMJSe4lV6ileTA6d+nxNLxK6+off/7RtSd9/7rw+FLbV2D6i1+/TTmSUpNdmjtOToiMS0YyViWopX6T7PsSzRIpFpzQAAAADOBQUhAADnyUkl4mnex7ZtDYQi6u4LnVQcdvcNqbt/aPh4T/+QggMhBQdCaursP+PnTfG6osXhscIwLdmjdJ9HaSnRYjEt2aO0FA87NQMAAAA4JQpCAADGkWEYSvG6leJ1Ky8z5bTvZ9m2knzpOtzQFC0P+0LHCsQh9fRHX+/pD6mnP6T+oYj6h/rV3HXmItFlGvIfKwujL97h8tB/rEj0H7uNdRIBAACAxEFBCABADIruzJykoqxUFWWlnvb9LNtW/2BY3f0h9fQPRf/te788PLFIHAhFhqc5fxS3acif4hkuFE/894Ov+5LcMk3KRAAAAGCioiAEAGACMw1DqckepSZ7TrvBynGhsKWegfcLw/dfhtQ78P7bwYGQBsPWsV2cP7pMNAwpNckjf7JbqcnvF4epye7h10+8LdnrksnoRAAAACBmUBACAJAgPG5TWf5kZfmTP/J9h0KRaGl4rDjsHQip99i/w28PhNU7EFLfYPjY2yFJZ57mLB0vNY8VhknHi8Pov6knvp0ULRl9SR65GKEIAAAAjBkKQgAA8CFej0tZHpey0j66TIxYloKD4WMFYljBgdBwYXi8SDx+LDgQ1kAoMjxacaRSvK73C8Th4vD9UvHE11OToms8Mu0ZAAAAGBkKQgAAcE5cpjm8e/NIhCLWsR2awwoORv/tPeHt44Xi8dv6BsPHNmKJqHWEmQxJKcfKQt8JL6lJnhNe//BtHrd51ucBAAAAmKgoCAEAwLjyuExlpiYpMzVpRO9vWbb6h8IKDh4vDqOl4fHXj09z7ht8/336hyLDx0abzZfk1p2XTtO0/Iyz+fIAAACACYeCEAAAxDTTfH8jFmWkjOg+kWOlYt8HSsUTi8S+wdAJr0dfQhFLXX1DMk1GEgIAACBxUBACAIC44zKN4R2UR1oq2ratobClvsGw/CmeMU4IAAAAxA4KQgAAAEmGYSjJ41KSx+V0FAAAAGBcMX8GAAAAAAAASGAUhAAAAAAAAEACoyAEAAAAAAAAEhgFIQAAAAAAAJDAKAgBAAAAAACABEZBCAAAAAAAACQwCkIAAAAAAAAggVEQAgAAAAAAAAmMghAAAAAAAABIYBSEAAAAAAAAQAKjIAQAAAAAAAASGAUhAAAAAAAAkMAoCAEAAAAAAIAERkEIAAAAAAAAJDAKQgAAAAAAACCBURACAAAAAAAACYyCEAAAAAAAAEhgFIQAAAAAAABAAqMgBAAAAAAAABIYBSEAAAAAAACQwCgIAQAAAAAAgARGQQgAAAAAAAAkMApCAAAAAAAAIIFREAIAAAAAAAAJjIIQAAAAAAAASGAUhAAAAAAAAEACoyAEAAAAAAAAEhgFIQAAAAAAAJDAKAgBAAAAAACABGbYtm07HQIAAAAAAACAMxhBOI6+8Y1vOB0Bx3AtYgvXI3ZwLWIL1yN2cC0wlvj+Gh3O1+hwvkaH8zU6nK/R4XyNDudrdM71fFEQAgAAAAAAAAmMghAAAAAAAABIYBSE42j16tVOR8AxXIvYwvWIHVyL2ML1iB1cC4wlvr9Gh/M1Opyv0eF8jQ7na3Q4X6PD+Rqdcz1fbFICAAAAAAAAJDBGEAIAAAAAAAAJjIIQAAAAAAAASGBupwMkiscff1zV1dUqKyvT3Xff7XScuFZVVaVf/epXMgxD06ZN09/+7d/qmWee0bvvvqucnBx98YtflNvtHvExnLvnnntOmzZt0oMPPnjKn4WRHsO5e+211/Taa6/Jsix95Stf0TPPPMP1cMDg4KAefvhhDQ4Oyufz6atf/ap++9vfci3GWXt7u773ve+pvr5ev/71r+Vyuc7pdxTXBmeD75uRO9XPLE7vVI+JcXq1tbV69NFHZZqm8vPzdc8998gwDKdjxbQTH+PjzJqbm/V//+//VVFRkdxut/7f//t/TkeKeR/8uyUrK8vpSDFr27Zt+tOf/iRJamxs1Oc+9zktW7Zs1B+HEYTjoLq6WgMDA3rggQcUDod14MABpyPFtZycHN1333168MEH1d3drT179mj37t168MEHNWXKFL377rvq6uoa0TGcu1AopMOHD0s69c/CSI/h3LW3t2vPnj267777dP/996uzs5Pr4ZBt27ZpxowZuv/++zV9+nT96U9/4lo4wO/365vf/KZmzJgh6dx+R3FtcDb4vhmdD/7M4sw++Ji4trbW6UgxrbCwUN/+9rf1wAMPSJIOHjzocKLYduJjfIzM/Pnzdf/991MOjsAH/26hHDyzCy64QPfff7/uv/9+BQIBLViw4Kw+DgXhOKiqqhq+QPPnz1dlZaXDieJbZmamvF6vJMnlcqmurk5z5syRJC1YsECVlZU6ePDgiI7h3K1bt06rVq2SdOqfhZEew7nbtm2bLMvSAw88oMcee0yVlZVcD4fk5eVpYGBAkhQMBmUYBtfCAV6vV36/f/jtc/kdxbXB2eD7ZnQ++DOLM/vgY2LT5E+/Mzlx5pDb7VYgEHAwTew78TE+Rmb37t2677779NxzzzkdJeZ98O8Wy7KcjjQhHD16VBkZGUpOTj6r+/O/xDgIBoPy+XySJJ/Pp76+PocTJYaamhp1d3crNTVVKSkpkqLnPxgMqq+vb0THcG7C4bB2796tefPmSTr1z8JIj+HcdXV1KRwO67777pPX61VfXx/XwyEFBQWqqqrS1772NVVXV8s0Ta5FDDiX31FcG5wNvm8wHo4/Ji4uLnY6Ssx777339E//9E/q6uqijD6DDz7Gx0ebNGmSHnnkEf3Lv/yLdu7cqZqaGqcjxbQP/t3C7L6R2bRp01lNLT6OgnAcnPiAr7+/f/iBIMZOb2+vHnvsMd1zzz3y+Xzq7++XJPX19Sk1NXXEx3BuXn/9da1cuXL47VP9LIz0GM6dz+cbHiV7/AEd18MZr732mpYsWaKHH35YixYtUiQS4VrEgHP5HcW1wdng+wZj7cTHxPhoF154ob7//e8rOztbW7ZscTpOzPrgY3x8NI/Ho+TkZLlcLi1ZskR1dXVOR4ppH/y7paGhweFEE8PmzZt14YUXnvX9KQjHQXl5uXbt2iVJ2rlzp8rLyx1OFN8ikYh+9KMf6TOf+YwyMzM1bdo07dmzR1L0/M+YMWPEx3BuGhsb9fLLL+s73/mO6uvr1dPT86GfhVP9fPAzMzZmzpw5/Gzl8TVjuB7OsG17eGRCenq6JK5FLBjpOefa4Hzh+wZj6YOPiXFmoVBo+PWUlJTh6dn4sA8+xn/hhRecjhTzjg9EkaR9+/YpLy/PwTSx74N/t+Tm5jqcKPZ1dnbK7XYrLS3trD8GW7SOg6lTp8rj8ei+++5TaWmppk+f7nSkuLZx40YdOHBAv/nNbyRJn/rUpzR79mx985vfVCAQ0I033ii32z2iYzg3d9111/Dr3/zmN/XJT35Sv/zlLz/0s3Cqnw9+Zs6/0tJSeb1e3X///UpLS9O9996r//qv/+J6OGDlypX64Q9/qNdff10ul0tf/epX9eSTT3Itxlk4HNZ3v/td1dTU6Dvf+Y7uvPPOEZ9zrg3OBx4jjs6pfmZ5Qvf0TvWYmBL69LZt2za8NlxBQcFZL/KfCD74GP/66693MM3EsHfvXv3hD3+Qx+PRrFmz+N31ET74d8vHPvYxpyPFvHfffVdLly49p49h2LZtn6c8AAAAAAAAACYYphgDAAAAAAAACYyCEAAAAAAAAEhgFIQAAAAAAABAAqMgBAAAAAAAABIYBSEAAAAAAACQwCgIAcS15uZm3X777XrooYe0ZcsWPfHEE2pubj7vn6e+vl5PPPGEdu/ePXzsJz/5iW6//XYdPHjwvH8+AAAAAADOF7fTAQBgLKWnp+vee+9VVlaWNmzYoBdffFFz585Vbm7uqD5OJBKRy+U67e319fV66qmnJElz586VJF1zzTW64IILlJeXd/ZfAAAAAAAAY8ywbdt2OgQAjJXm5mZ96UtfUlJSkgYHB0+67YknnlBlZaV+9atfqba2VllZWfrkJz+plStXDt+vvLxcSUlJqq2t1fe//319+9vf1pEjRyRJZWVl+vznP6+kpCR96UtfOulj/8u//IvWr1+v1157Td/97nc1bdo0VVRU6JlnnlFHR4eKi4v1N3/zN5o1a5bWr1+vn/70p1q+fLkaGhrU2tqqT37yk7rhhhvU2NioH//4x6qpqZHX69XkyZP1wAMPjNv5AwAAwKk9/PDDysjI0OHDh9XW1qavfOUrevnll3XgwAHNmjVL99xzj9MRAWDEmGIMICHMmTNHCxculCTdeuutuvfee9Xb26uHHnpIfX19WrNmjXJycvSjH/1Ihw8fHr5fZWWlysrKdMcdd8gwDC1btkx33323brnlFtXU1Ojxxx9Xenq6brjhBknSRRddpHvvvVfFxcUnff5du3bp0UcfVXp6uj772c+qtbVV3/ve99TT0zP8Prt379ZVV10lSfrtb3+rcDisF198UQcPHtRdd92lO++8U4FAYIzPFAAAAEaitrZWeXl5evDBB7V69Wr9x3/8h+666y49/PDD2rJli0KhkNMRAWDEmGIMICEYhqH8/Hxt375d8+bN09y5c7Vlyxb19vaqt7dXv//974ffd9euXVq2bJmk6CjBu+66S5LU3t6u7du3q7KyUscHX9fW1io5OVmzZs3SX/7yF02ePFkrVqz40OffsmWLJOn222/XggUL1NraqqefflpVVVXD73PFFVfouuuu0+bNm7V9+3Z1dnaqoKBAtm1r69atmjZt2nARCQAAAOcMDQ0pGAwOPzYzDENXXnmlJk2aJEkyTVNuN39uA5g4+I0FIGEYhnHK45dddpkuu+yy4bdPXJ/w+IM8SXrhhRe0f/9+3XjjjVq0aJH+4z/+Q/39/ecti9/vl6ThtQ4ty9J1112noqIi7dmzR++9957Wrl2rH/zgByosLDyrzwsAAIBzV19fr6lTp8o0o5PyampqdM0110iS2tralJWVddrHngAQi5hiDCBhpKamSpLefvttbdmyReXl5fL7/dq+fbsaGxtVV1enP//5z2pvbz/jxwkGg9qzZ4/a2tqGjx0v9/bt26e33npLQ0NDJ91n8eLFkqQnn3xSL7/8statW6fU1FTNmDHjjJ/rpZdeUmVlpfLz85WXlyfbttXZ2TnaLx0AAADnUW1trUpKSobfrqmp0ZQpUz70OgBMFBSEABLGpZdeqqKiIr300kv65S9/Kb/fr2984xvKz8/Xb3/7W61du1Zer1c5OTmnvP/111+vadOmacOGDWpvb9fkyZOHb5s1a5bmz5+vvXv36pFHHjlpbUFJmjdvnr7whS+oq6tLv/71r5Wdna3/83/+j9LS0s6Y2ePxaP369frZz36mvXv36tprr9WsWbPO/WQAAADgrNXW1qq0tFRSdLrx0NDQ8BPGNTU1J5WHADARsIsxAAAAAAAAkMAYQQgAAAAAAAAkMApCAAAAAAAAIIFREAIAAAAAAAAJjIIQAAAAAAAASGAUhAAAAAAAAEACoyAEAAAAAAAAEhgFIQAAAAAAAJDA/n9YvS2uqFeD/QAAAABJRU5ErkJggg==",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"high, step = 100*n, n\n",
"plot_all(cost_history, m, q, high=high, step=step)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Mini-batch gradient descent\n",
"\n",
"Questo approccio si pone in posizione intermedia rispetto ai due precedenti, generalizzando l'impostazione di SGD di considerare un solo elemento per iterazione a considerare sottoinsiemi diversi del dataset. L'algoritmo opera quindi partizionando, all'inizio di ogni epoca, il dataset in $\\lceil n/s\\rceil$ sottoinsiemi (*mini-batch*) di dimensione prefissata $s$, ed effettuando poi $\\lceil n/s\\rceil$ iterazioni all'interno di ognuna delle quali l'aggiornamento di $\\theta$ viene effettuato valutando il gradiente sugli $s$ elementi del mini-batch attuale.\n",
"\n",
"La discesa del gradiente con mini-batch è l'algoritmo tipicamente utilizzato per l'addestramento di reti neurali, in particolare in presenza di reti *deep*.\n",
"\n",
"Se indichiamo con $X_i\\subset X$ il mini-batch attualmente considerato, l'aggiornamento a ogni iterazione è il seguente\n",
"$$\n",
"\\theta^{(k+1)}=\\theta^{(k)}-\\eta J'(\\theta^{(k)};\\mathbf{x})=\\theta^{(k)}-\\frac{\\eta}{s}\\sum_{\\mathbf{x}\\in X_i}J'(\\theta^{(k)};\\mathbf{x})\n",
"$$\n",
"o anche\n",
"$$\n",
"\\theta_j^{(k+1)}=\\theta_j^{(k)}-\\frac{\\eta}{s}\\sum_{\\mathbf{x}\\in X_i}\\frac{\\partial J(\\theta;\\mathbf{x})}{\\partial\\theta_j}\\LARGE\\vert_{\\small\\theta=\\theta^{(k)}}\n",
"$$\n",
"In questo modo, la varianza degli aggiornamenti dei coefficienti viene diminuita. Inoltre, è possibile fare uso, in pratica, di implementazioni molto efficienti del calcolo del gradiente rispetto a un mini-batch disponibili nelle più recenti librerie per il *deep learning*. La dimensione dei mini-batch varia tra $50$ e $256$.\n",
"\n",
"```python\n",
"for i in range(n_epochs):\n",
" for batch in get_batches(dataset, batch_size):\n",
" g = 0\n",
" for x in batch:\n",
" g = g+evaluate_gradient(loss_function, theta, batch)\n",
" theta = theta-eta*g\n",
"```\n",
"Ne risulta un andamento oscillante sia della funzione di costo che dei valori stimati dei coefficienti. Chiaramente, l'oscillazione sarà tanto più marcata quanto minore è la dimensione dei mini-batch, e quindi quanto più si tende a SGD.\n",
"\n",
"Gli aggiornamenti nel caso della logistic regression derivano immediatamente da quanto sopra \n",
"\n",
"\n",
"\\begin{align*} \n",
"\\theta_j^{(k+1)}&=\\theta_j^{(k)}+\\frac{\\eta}{s}\\sum_{\\mathbf{x}\\in X_i}(t-f(\\mathbf{x};\\theta^{(k)}))x_{ij}\\hspace{1cm}j=1,\\ldots,d\\\\ \n",
"\\theta_0^{(k+1)}&=\\theta_0^{(k)}+\\frac{\\eta}{s}\\sum_{\\mathbf{x}\\in X_i}(t-f(\\mathbf{x};\\theta^{(k)})) \n",
"\\end{align*}\n"
]
},
{
"cell_type": "code",
"execution_count": 122,
"metadata": {},
"outputs": [],
"source": [
"def mb_gd(X, t, eta = 0.01, epochs = 1000, minibatch_size = 5):\n",
" mb = int(np.ceil(float(n)/minibatch_size))\n",
" theta = np.zeros(nfeatures+1).reshape(-1,1)\n",
" theta_history = []\n",
" cost_history = []\n",
"\n",
" for j in range(epochs):\n",
" for k in range(mb-1):\n",
" delta = - eta * gradient(theta,X[k*minibatch_size:(k+1)*minibatch_size,:],t[k*minibatch_size:(k+1)*minibatch_size])\n",
" theta = theta + delta\n",
" theta_history.append(theta)\n",
" cost_history.append(cost(theta, X, t))\n",
" theta_history = np.array(theta_history).reshape(-1,3)\n",
" cost_history = np.array(cost_history).reshape(-1,1)\n",
" m = -theta_history[:,1]/theta_history[:,2]\n",
" q = -theta_history[:,0]/theta_history[:,2]\n",
" return cost_history, m, q, minibatch_size"
]
},
{
"cell_type": "code",
"execution_count": 123,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"tempo di esecuzione: 6.574 secondi\n",
"190000 passi\n",
"950000 gradienti calcolati\n"
]
}
],
"source": [
"start_time = time.time()\n",
"cost_history, m, q, mbs = mb_gd(X, t, eta = 0.01, epochs = 10000, minibatch_size = 5)\n",
"print(f\"tempo di esecuzione: {time.time()-start_time: 4.3f} secondi\")\n",
"print(f\"{len(m)} passi\")\n",
"print(f\"{len(m)*mbs} gradienti calcolati\")"
]
},
{
"cell_type": "code",
"execution_count": 124,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABQgAAAGoCAYAAAAKMwiTAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAABuRElEQVR4nO3deXyU5b3///d9z5KVPRAIWwgQUQQEFRU30NS1Lo27dSmt1WNPW097ao89VmpRj/Tnqa3f054etVVqq1ZUrPsWUVxxYwchCZEl7EkgkHXmXn5/DEwYEzDAzNyTzOv5ePhw5r7vua7P3LkzJO9c130Zruu6AgAAAAAAAJCWTK8LAAAAAAAAAOAdAkIAAAAAAAAgjREQAgAAAAAAAGmMgBAAAAAAAABIYwSEAAAAAAAAQBojIAQAAAAAAADSmN/rAjpr06ZNXpdw2PLy8lRTU+N1GUgBXAvYi2sBEtcB2iT6WigoKEhY24nWlX4W5Hs6FucjFucjFucjFucjFuejDeciFucj1sGcj/39PMgIQgAAAAAAACCNERACAAAAAAAAaYyAEAAAAAAAAEhjBIQAAAAAAABAGiMgBAAAAAAAANIYASEAAAAAAACQxggIAQAAAAAAgDRGQAgAAAAAAACkMQJCAAAAAAAAII0REAIAAAAAAABpjIAQAAAAAAAASGMEhAAAAAAAAEAaIyAEAAAAAAAA0hgBIQAAAAAAAJDGCAgBAAAAAACANEZACAAAAAAAAKQxAkIAAAAAAAAgjREQAgAAAAAAAGmMgBAAAAAAAABIYwSEAAAAAAAAQBojIAQAAAAAAADSGAEhAAAAAAAAkMb8XhcAAACA7qmurk6/+c1vVF1drccee0w+ny+6b/369Xr44YclSTfccIOGDx/uVZkAAABpjxGEAAAASIjc3FzdcccdGj16dLt9Tz31lG655Rb95Cc/0VNPPeVBdQAAANiLEYQAAABIiGAwqGAw2OG+xsZG5eXlRR9/VVlZmcrKyiRJs2bNih7bFfj9/i5Vb6JxPmJxPmJxPmJxPmJxPtpwLmJxPmLF43wQEAIAACDpXNc94P6SkhKVlJREn9fU1CS6pLjJy8vrUvUmGucjFucjFucjFucjFuejDeciFucj1sGcj4KCgg63JzQgnD17tqqqqjRixAhNnz49ur2hoUEPPfSQdu/erXHjxqm0tDSRZQAAACCFGYbhdQkAAABpLWEBYVVVlVpaWjRz5kw9/PDDqqys1KhRoyRJTz/9tK644goNHjw4Ud0DAAAgheXm5qq2tlaGYSgrK8vrcgAAANJawgLCiooKjR8/XpI0btw4lZeXRwPCDRs26LnnnlNtba2uuuoqFRcXJ6oMAAAAeMSyLN17771at26d7rnnHl166aVatWqVSktLdfnll+v3v/+9JOl73/uet4UCAACkuYQFhI2NjcrPz5ckZWdnq7q6Orpv9erV+s1vfqPc3Fz99re/1V133dXu9V35xtRftbmuQQ+9skiXnXaUjhrWdd8H4ocbqmIvrgVIXAdo092uBb/frzvuuCNm21FHHSVJGj58eIc/AwIAACD5EhYQZmdnq6mpSZLU3Nys7Ozs6L6CggINGTJEkmSaZoev78o3pv6qB19ZrnXbG3Tf0x/pvutP9LocpABuqIq9uBYgcR2gTaKvhf3dlBoAAADpreN0Lg6Ki4u1fPlySdKyZctiphEPGjRIO3bsUEtLi2zbTlQJKSNsO16XAAAAAAAAAHQoYSMIi4qKFAgENGPGDBUWFiovL09z586N3nPmgQceUCgU0qWXXpqoElKGIVbmAwAAAAAAQGpKWEAoSdOnT495XlpaKkkaMmSI7rzzzkR2nVKOHNJbG+saNXxAL69LAQAAAAAAAGIkbIox2vTtkSFJGtK/h8eVAAAAAAAAALEICJPAMCJTjF3X9bgSAAAAAAAAIBYBYRLsvQOhQz4IAAAAAACAFENAmASMIAQAAAAAAECqIiBMgugaxuSDAAAAAAAASDEEhEmwZwChHEYQAgAAAAAAIMUQECZBdIqxx3UAAAAAAAAAX0VAmAR7pxg3tYQ9rQMAAAAAAAD4KgLCJKjcskuStHJ9jceVAAAAAAAAALEICJNgaL8cr0sAAAAAAAAAOkRAmAQ5mQFJ0oSiAR5XAgAAAAAAAMQiIEyC6CrGDsuUAAAAAAAAILUQECZBY6slSVq2drvHlQAAAAAAAACxCAiTwGXkIAAAAAAAAFIUAWES9MnNkCQdMaSvx5UAAAAAAAAAsQgIk8DccxNCBhICAAAAAAAg1RAQJoFhRgJC1yUhBAAAAAAAQGrxe11AOtiziLEcAkIAAAAAABBnrmNLVlhqbZLb2iLZlmSFJMOQTJ/k88vIyJIysiR/hmSaMgzj6xtG2iAgTILoFGPmGAMAAAAAgIPghlvVuqFCVvkyORvK5W6sTEg/Rq88+SZNk1k4VkYwMyF9IHURECaBuWciNyMIAQAAAABAR1zXkVuzWc66L2Sv/lRqqI/uq0lG//U1st5+WtLTMdv9p35L5pjjZJi+JFQBrxAQJoGhvfcg9LgQAAAAAADgOdd1pcZ62V+ukLPiI7n1yYgAD4313nPSe89Fnwe+9a8yBwz1sCIkAgFhEuyd1s8IQgAAAAAA0pNbXyO7arnsT1/v0iOIws/9Mfo4cOFNMgeN8LAaxAsBYRLsvQehyz0IAQAAAABIC264Vc6mKtkLXpW7c5vX5SRE+IUHo4+D37tLhj/gYTU4HASESWCaexYp6cJ/IQAAAAAAAAfm7qqVve4L2R++5HUpSRf6yx2SpMBF/yJzYKG3xeCgERAmwd6FwwkIAQAAAADoXpwdW+VULpG9cJ7XpaSE8PP/J0nyn36JfGOO97gadBYBYRIYBouUAAAAAADQXTg7t8tZu1L2x696XUrKsuY/K2v+s/J/49vyFY3zuhx8DQLCJDDNyP+31zd5WwgAAAAAADgkbjgkp3KxrHfnel1Kl2K9+bgsScFv/0JGbi+vy8F+EBAmQWOL5XUJAAAAAADgILmuG5k+vPQ9uTUbvS6nSws9fq8kKeOmWR5Xgo4QECZBc4iAEAAAAACArsINtcj64AU55Qu9LqXbaX3wNvkmTpN/8tlel4J9EBAmQU4Gy3wDAAAAAJDK3FCrnOpyWR+8IDXt9rqcbs1e9LbsRW8reOO90XUb4C0CwiTo2yPD6xIAAAAAAEAH3F21sj5/i9GCHgg99Av5p10uX/Ekr0tJewSESbA3C88M+DytAwAAAAAARDib1ij85hNSS6PXpaQ16+05st6ew70JPUZAmAR7h8s6rseFAAAAAACQxlzXlbPyY1nv/9PrUvAVrQ/expRjDxEQJoG55+J2RUIIAAAAAECyuVZY1ocvyvniE69LwQGEHvqFApf9m8y+A70uJe0QECbB3vA7bDneFgIAAAAAQBpxG3cp/Npf5dZs9LoUdFL46d/LHD1RgTOu8LqUtEJACAAAAAAAuhVn2waFX/6LFGrxuhQcAqdikVorFnFfwiQiIEwC02ybP287rnwm8+kBAAAAAIg3u2qZrLeflqyQ16UgDlofvI2QMElMrwtIB+Y+N9gMWbaHlQAAAAAA0L24ji171acKPfdHWW8+TjjYzbQ+eJvXJaQFAsIkc1jKGAAAAACAw+ZaYTk1GxV64jey5j8rd9sGr0tCghASJh5TjJOM6cUAAAAAABweZ+t6hf/5v16XgSRiunFiERAmSWbAp5awLcYPAgAAAABwaOzVn8t652mvy4gLc+gRMgqKZPYbJOX2lpGVIwUyZfh87Y7Ny8vT9q1bpJYmuY31cuu2yNlYKadyiQeVe4eQMHEICJNk720ImWIMAAAAAEDnubYlZ/Xnsld9Knd7tdfldIpv3CkyRx8jo98gGWb7wO9QGD6/lNNTRk5PacBQ+cYcL515VYfHuuGQnNWfyvrgxbj0nUpaH7xNuv3PXpfR7RAQJsnehUqIBwEAAAAA6By3oV6huf8jNTd4XUqHfONOke/oKVKPPjKM1LmlmBEIynf0yfIdfXJ0m+u6cjdWKvzyXzysLD423nMDIwnjjIAwSfZ+UDguESEAAAAAAAfibF6rjSm2MIU5coL8J5wjo0cfr0s5JIZhyBgyOiZYc7ZtUPi5P3pY1aFrffh2ZXz/Hq/L6DYICJNk79ok5IMAAAAAALTnuq7c6grZX66Q88XHXpcj3/FnyTfhtMjU3m7KHDA0Ghi6tqXQn3/pcUUHwbFlVy6Rb9QEryvpFrrvVZ5i9o4gdEkIAQAAAACI4YZDsub9Q87alZ7VYBaNl3/aZTL8Ac9q8JLh8+8TFtoK/fl2jyv6etZbT8occXSHC7vg4BAQJkl0kRICQgAAAAAAJEnu7jqFy/4hd9t6T/oPXHSzzIHDPek7lRk+X1tYuKtWoSfv87ii/Qv9+XbuRxgHBIRJsrMxJElqbLHUN9fjYgAAAAAA8Ji9frWsVx9Ner/B78yQkZGd9H67KqNnP2XcNEuu6yr00C+8LqdDrQ/eRkh4mAgIk2zrzmYNzSMhBAAA3d/s2bNVVVWlESNGaPr06dHtH330kV544QUZhqFvfetbOv744z2sEgCQTK7ryF40X/anrye13+AN9zAN9TAZhhEN4awFr8he8q7HFcUiJDw8BIRJVtCXv1IAAIDur6qqSi0tLZo5c6YefvhhVVZWatSoUZKkl19+WXfeeacMw9A999xDQAgAacB1XamlUeE3/i53y9qk9BmcfqeMYGZS+ko3/hPPk//E82SXL5T19hyvy4myyxfKVzzJ6zK6JALCJCnom61NdU1yuAUhAABIAxUVFRo/frwkady4cSovL48GhPn5+WptbZUkZWVleVYjACA5nB3bFJ5zf1L68p9ykXxjT0pKX5B8xZPkK54ke/kHsj540etyZL09h4DwEBEQJonJKsYAACCNNDY2Kj8/X5KUnZ2t6urq6L7Jkyfr5z//uVzX1Q9+8IMOX19WVqaysjJJ0qxZs5SXl5f4ouPE7/d3qXoTjfMRi/MRi/MRq7udD9cKq7l8sXY892DC+yr4jz9169WHU/7amHqRNPUibXvkboU3r/W0lNYHb9Pg2//saQ3JFo/rg4AwSVjFGAAApJPs7Gw1NTVJkpqbm5Wd3XablWeeeUb33x8ZSXLvvfdqwoQJ7V5fUlKikpKS6POampoEVxw/eXl5XareRON8xOJ8xOJ8xOou58N1bNkfvyZ76XsJ7cd/ysXyjT1RklS7sz6hfXmtq1wb5oX/ogxFQjovbbznhrS6H+HBXB8FBQUdbjfjWRD2b+8IQqYYAwCAdFBcXKzly5dLkpYtW6bi4uLovkAgoIyMDGVmZsqyLK9KBAAkgNvcoPAzDyQ0HAxeeasybpoVDQeRejJumqXg9+7ytIbWJ+/ztP+uhhGEScIUYwAAkE6KiooUCAQ0Y8YMFRYWKi8vT3PnzlVpaanOOuss3XHHHZIUM0oQANB1OdurFZ77h4T2EfzuTBmBYEL7QPwY/oAybpql8Lyn5FQsSn4Bu2rlWuFuPfU8nhIaEM6ePVtVVVUaMWKEpk+fHt3+xz/+URs3blQwGFRJSYlOOeWURJaREvZOMSYgBAAA6WLfn/8kqbS0VJI0depUTZ061YOKAACJYK/6VNb8ZxPStpE3WIFv/asMkwmQXVXgjCukM67wZNpx6C93pNVU48ORsICwqqpKLS0tmjlzph5++GFVVlZGV66TpB//+McaOHBgorpPOQZTjAEAAAAA3YRrW7I/fUP2kncT0r5v3MkaeOH0LnHfPXROxk2zZH36huyF85Lab+uDtxESdkLCIviKigqNHz9ekjRu3DiVl5dH9xmGoT/84Q+aNWuWtm/fnqgSUkr0HoQkhAAAAACALsxtqFfoz79MSDjoP/ViZdw0S/4pF8S9bXjPf/xZnoR1Xi+a0hUkbARhY2Oj8vPzJUVWsauuro7uu+6665Sbm6tVq1bpscce07//+7+3e31ZWZnKysokSbNmzUrt5bw7oWJzZEWl7Y22Tu7i7wWHL+WXqEfScC1A4jpAG64FAEAqc3Zsk7tlrax358a9bd+J58k/4bS4t4vUlHHTrKSHdq7rRmd3or2EBYTZ2dlqamqSJDU3Nys7Ozu6Lzc3V5I0ZswYPf744x2+vqSkJOam1d1lWPHrn1XplOJ+XpcBj3WVJeqReFwLkLgO0CbR10JBQUHC2gYAdF+u68peNE/2p2/GvW0jf5gCF9wow8caqukm46ZZcpt2K/S3e5LSX+ihXzDV+AASNsW4uLhYy5cvlyQtW7ZMxcXF0X17g8NNmzYpJycnUSWkpFbL9roEAAAAAAA6xQ2HFPrHffEPBw1DwRvuVvDiHxAOpjEju0dSQzumGu9fwr4Li4qKFAgENGPGDBUWFiovL09z585VaWmp/t//+39qbGyUYRi64YYbElVCSmIRYwAAAABAqnPqaxT+x38npO3gDXcTCiJGMqccu6FWGcGMpPTVlST0O3L69Okxz0tLSyVJt91GYgsAAAAAQCqyV30ma/4zcW83ePXPZfToG/d20T1k3DRL1ievy170dkL7CT36K6YadyBhU4wBAAAAAEDX4bY0qfXB2+IeDvq/cY0ybppFOIiv5Z98toLfuyvh/TDVuD3G9AIAAAAAkMYStVCE/8yr5Bs1Ie7tonsz/IGkTDl2HUeGybi5vTgTAAAAAACkKbt8YdzDQbNonILX30E4iMOS6GnAoYf/M6HtdzUEhAAAAAAApBn7i08i04nfnhPXdoPX3q7AN74tIzMnru0iPSU6JGSqcRumGAMAAAAAkCZcK6zQX+6Ie7vBq26V0bNf3NsFkrnCcTpjBCEAAAAAAN2c2xpZgCTe4aA56hgFv/9fhINIqESOJCR8jGAEIQAAAAAA3Zi9dqWs1x+La5tG/nAFLrhRhs8X13aB/UnkSEK3uUFGVm5C2u4qGEEIAAAAAEA35GxZG7nPYJzDwcB531Xw4psJB5F0iRpJGHrs7oS025UQEAIAAAAA0I24VlitD96m8PP/F9d2/WdeqYybZskcWhzXdoGDkaiQMN2nGhMQAgAAAADQDbiOI2dTVWIWIbn2dvlGHRP3doFDMfj2P3tdQrfDPQgBAAAAAOji7PKFst6eE/d2g1feKqMXC5Ag9STinoStD96W0AVRUhkjCAEAAAAA6KJc21Lrk/fFPRw0hhYr+P17CAeR0tI1zEsEAkIAAAAAALoYNxxS619nKvTnX0q7auPXsD+g4HdnKnjed2WYLEKC1BfvkDBd70VIQAgAAAAAQBfibNug0CMzpJamuLbrP61UGd+7S0YgGNd2gURjJOHhIyAEAAAAAKALcHfXKfz6Ywo/98e4tmuOnqjg9+6S78jJcW0XSKZ4hoTpOIqQRUoAAAAAAEhhrmMr9Ld74j5iUJICl/xYZl5B3NsFvJCIhUvSBSMIAQAAAABIUU59jUIP3x73cNAoKFLwhrsJB9HtxGskYboFjYwgBAAAAAAgxTibqhR+bbYUDsW97eD1d8jIzIl7uwC6LkYQAgAAAACQIlzXVfjtOQq/+FDcw0HzqBMVvPFewkF0e4wiPHiMIAQAAAAAIAXYDfUKPfSL+Ddsmgp+d6YMHxEA0gf3Izw4fDokid80ZDmu12UAAAAAAFKMu3unQk/M0pYEtO2fdpl8xccmoGUg9RESdh5TjJMkGPB5XQIAAAAAIMXYqz5V6In4TIf8quB1vyQcRNrzf+Oaw3p9ugSMjCBMkqDfVFOr11UAAAAAAFKBG25V+J9/klsX/3GDgYv+RebAwri3C3RFvqKjZXldRBdAQJgkLrOLAQAAACDtuVZYob/ckbD2g9+7S4Y/kLD2ga7ocKcau7bV7e/hyRTjJKlviv/S9AAAAACArsPZtiFh4aD/9EuUcdMswkFgP4I3/tchvzb051/GsZLU1L3jTwAAAAAAPOY6juzPy2QvnJeQ9oPf/y8ZJuN/gAMxDL5HDoSzkyTXTyv2ugQAAAAAQBK5rqtw2ZMKPfyfCQkH/SVXR0YNEg4CnZJxU2IWBOoO+BRJkt45GZKkgr7ZHlcCAAAAAEg0t3GXQg/9Qs6aJQlpP/idO+UbOT4hbQNor7uvZkxAmCSmEfl/2HK8LQQAAAAAkFD2l8sV+vuh3+/sQALnTo+MGszITEj7QHfHKMKOcQ/CJGkJ25Kk7btaPK4EAAAAAJAIztb1sj55Te6mqoS0zwrFQHz4Jpwme8m7XpeRUggIk2TzjiavSwAAAAAAJIBrWwld5dQ3/hT5T/pmwtoH0o3/xPPaBYSLG3tr3u5BarD9yvVZOrPHZk3I2elNgR4gIEySgj7cexAAAAAAuhunbovCT/8+Ye0Hb7hbho9f3YG48/kl25IUCQefqBuh3U4wss+StoQzJX2ZNiEh9yBMkn49uT8EAAAAAHQXruvIWvpewsJB88jJkXsNEg4CCZFxw93Rx/N2D2oLB/fY7QT11u5B0efBa29PWm1e4JMmSUwjskpJdganHAAAAAC6svBb/5BTuThh7Qe/fZuM3N4Jax9ArAa746ym0fanzaImjCBMkr0Boeu6HlcCAAAAADgUbmuLWh+8LWHhoK93/8ioQcJBICn2hn+5PqvD/T2GDk1mOZ5iOFuSmGYkIHQcAkIAAAAA6GqcTVUKv/hQwtoPXPYTDSgeq5qamoT1AaC9jJtm6ZwvNmnL3MXa3dga3d4jJ0NnnTLKw8qSi4AwSXx7RhC2Wo7HlQAAAAAAOsu1LdmfvtFuxdN4Ct54r4w9vzMCSL6JRxZIpdIb71eqoSmk3OygzjplVGR7miAgTJJ9P+vDlqOAn9ndAAAAAJCqXNdVeM7v5O7clrA+/CdfJN/RJyWsfQCdN/HIgrQKBL+KgDBJfGZbQhiybAJCAAAAAEhRbtNuhf52T0L7CN5wNysUA0gZfBolyb7DxVvCtnIyAx5WAwAAAADoiL12pazXH0tY+8aAYQp+6wcJax8ADgUBoQdawrbXJQAAAAAA9uGGWmV99KKcVZ8lrI/g1T+X0aNvwtoHgENFQOiBlhABIQAAAACkAtd1FHr011K49esPPlRZucq47peJax8ADhMBoQdaQpbXJQAAAABA2nMb6xX6+70J7cN3bIn8x5UktA8AOFwEhB5gijEAAAAAeMuuXCLrrScT2kfwO7+SkZGV0D4AIB4ICD3AFGMAAAAA8Ibb2izr/eflVC5OXCfZPZVx7X8mrn0AiDMCQg8wghAAAAAAkst1HYXn/lFuzcaE9hO48mcye+UltA8AiDcCQg+0hLkHIQAA6P5mz56tqqoqjRgxQtOnT49ub2ho0EMPPaTdu3dr3LhxKi0t9bBKAOkgGfcalKTgjffKMIyE9wMA8UZA6AGmGAMAgO6uqqpKLS0tmjlzph5++GFVVlZq1KhRkqSnn35aV1xxhQYPHuxxlQDSgb1mqayyJxLahzlqggJnXpXQPgAgkQgIPbCxrtHrEgAAABKqoqJC48ePlySNGzdO5eXl0YBww4YNeu6551RbW6urrrpKxcXFXpYKoJtyW5tlffCCnIpFCe0ncOG/yBxUmNA+ACDRCAg9sKGGgBAAAHRvjY2Nys/PlyRlZ2eruro6um/16tX6zW9+o9zcXP32t7/VXXfd1e71ZWVlKisrkyTNmjVLeXld535efr+/S9WbaJyPWJyPWIk6H82rF6n+jSfl7KqLe9v7KvjFQzJMM27tcX3E4ny04VzE4nzEisf5ICAEAABA3GVnZ6upqUmS1NzcrOzs7Oi+goICDRkyRJJk7ucX65KSEpWUlESf19TUJLDa+MrLy+tS9SYa5yMW5yNWvM+H29yg0GN3x629/fGXXC3fyPGqrYtvAMn1EYvz0YZzEYvzEetgzkdBQUGH2+P3pw502rVTR3tdAgAAQEIVFxdr+fLlkqRly5bFTCMeNGiQduzYoZaWFtk292YGEB/2ulVJCQeD350p38jxCe8HAJKJEYRJVNAvV5tqGxS2HK9LAQAASKiioiIFAgHNmDFDhYWFysvL09y5c1VaWqrLL79cDzzwgEKhkC699FKvSwXQxbnhkKwFL8tZ+XFC+zFHTlCghIVIAHRPBIRJtKm2QZL06sINOnZkf4+rAQAASKzp06fHPC8tLZUkDRkyRHfeeacHFQHobpyt62XNe0rurtqE9mMOO4JwEEC3RkDogfqmkNclAAAAAECX5YZaZc37h5z1qyTXTWhfgSv+XWZvBngA6N4Seg/C2bNna8aMGXr00Ufb7QuFQvr+97+vpUuXJrKElJKbFZQknTGu4xtCAgAAAAAOzNm0RqFHfyVn3RcJDQeN3v0VvPG/CAcBpIWEBYRVVVVqaWnRzJkzZVmWKisrY/a/9dZbGjZsWKK6T0mTiwdJknruCQoBAAAAAJ3j2rasj19T+MWHE95XoPSHCl7x7zIM1vUEkB4SNsW4oqJC48dHVnYaN26cysvLNWrUKEmSZVmqqKjQEUcckajuU5JpGpIkJ8FD4AEAAACgO3F2bpf11j/k1mxMeF/BG+6W4eNuXADSS8I+9RobG5Wfny9Jys7OVnV1dXTfO++8o1NPPVUVFRX7fX1ZWZnKysokSbNmzVJeXl6iSk2aXU3rJUkNIXWL94ND5/f7uQYgiWsBEVwH2ItrAQBiua4rZ8UCWR+9KDlOQvvyHVsi/3ElCe0DAFJVwgLC7OxsNTU1SZKam5uVnZ0tSbJtW4sXL9bPfvazAwaEJSUlKilp+3CuqalJVKlJ88nqTZKkeUvW6dxjBnlcDbyUl5fXLa5pHD6uBUhcB2iT6GuhoID7IAPoOtzdOxSe/6zcjZVff/BhMgqKCAcBpLWEBYTFxcUqKyvTlClTtGzZMk2dOlWSVF9fr9raWt1zzz3asmWLFi1apKKiIuXm5iaqFAAAAABAF+G6ruwPX5K9/IOk9Be45Mcy8/gDCoD0lrCAsKioSIFAQDNmzFBhYaHy8vI0d+5clZaW6t5775UkzZkzR2PGjCEcBAAAAADIbWlS+JVH5G6v/vqDD5PRd6ACl/xYhslCJACQ0DuvTp8+PeZ5aWlpzPPLL788kd0DAAAAALoIZ0O5wq88KinxizoGLrpZ5sDhCe8HALoKlmYCAAAAAHjGDYdkLXhFzsoFie8smKngtbfL8AcS3xcAdCEEhAAAAAAAT4Q2Vin83ENy6xO/WJf/rGvlGzE24f0AQFdEQAgAAAAASCrXcWTN+4e2r1malP7MI08gHASAAyAgBAAAAAAkjburTuG3n5K7ZV1S+vOffol8Y45PSl8A0FUREAIAAAAAEs51XTmrP5P14YtSOJSUPoPTfy0jmJGUvgCgKyMgBAAAAAAklNvcIOvduXLWrkxKf4waBICDY3pdQDr5+WUnel0CAAAAACSVvXaFQnN+l7RwMHjdLwkHAeAgMYIwiTbU7PK6BAAAAABICte2ZL3/TzmrPktKf76Tzpdv3CkyDCMp/QFAd0JAmETbdzZ5XQIAAAAAJJyzc7vCT/02af0Fr7xVRq9+SesPALobphgn0ZSjhnhdAgAAAAAkjOs6spd/mNRw0DflAsJBADhMjCBMotysoCSpT07Q40oAAAAAIL7chnqF33la7sbKpPXpP/ta+QrHJq0/AOiuCAiTyGdG7oWxozHkcSUAAAAAEB+u68qpXCzrveekcJJ+18nppeBVt8rw8SstAMQDn6ZJ1Bq2vS4BAAAAAOLGbWmU9d4/5VQtS1qf/nOnyzfsiKT1BwDpgIAwiQJ+bvkIAAAAoHtwtqxV+M3HpabdyemwZz8FL/mRjGBmcvoDgDRCQJhEvbIzoo8d15VpGB5WAwAAAAAHz3VdubWbFS57MmnhoP+sa+QbcXRS+gKAdERAmER+X9sIwoaWsHpmsVgJAAAAgK7Dbdota/6zctavSk6Hub0ULP2RjKzc5PQHAGmKgDCJjH1GDG6vbyYgBAAAANBl2FXLIguRtDQlrc/g1f8hw+BWTQCQaASEHtl3ujEAAAAApCq3tVnWBy/IqViU1H79J19EOAgASUJA6JGWsOV1CQAAAABwQE51hcLvPCM11ie13+B3fiUjIyupfQJAOiMg9EjFpnoN6cd9NAAAAACkHtcKy/74VdnLP0xqv/7TL5FvzPFJ7RMAIHVqvPYVV1yhDz9s+4dh4cKFuuWWWxJWVDoY0Iu/hgEAAABITdZHLyc3HAxmKnj9HYSDAOCRA44grKmp0bZt2yRJ1dXVWrlypSRp8eLF2rp1a+Kr64bye2Vpa32zcrMCXpcCAAAAADGc2s1yt66X88UnSevTP+0ymaMnxSzqCABIrgMGhG+//baeeeYZSdKzzz6rZ599Nrpv8ODBia2sm9pa3yxJqm8KeVwJAAAAAES4tiX787dkL35Hct3kdJrbSwOn/1I7QnZy+gMA7NcBA8JRo0bprLPO0htvvKHx48dr0KBBkqTc3FydcsopSSmwu/rbOxW67/p+XpcBAAAAIM05tZtlvT1Hbu3mpPXpP+VimUedIF/PPlJNTdL6BQB07IAB4cSJEzVx4kSNHDlSY8eOVf/+/SVJjuPINFluHgAAAAC6KtdxZC99V/bHryW1X7PwKPnGnpjUPgEAB9aplG/Dhg16++23VVdXp5tvvlnXXnut5s2bl+jaAAAAAAAJ4NbXKPzCg0kPByXJd8K5Se8TAHBgnQoI33//feXk5OiDDz6QZVkaNGiQ5s6dm+jaAAAAAABxZq/+XKFnHpC7dV1S+zV691fwhntk9u6f1H4BAF/vgFOM92poaFCPHj20ePFinXbaaRo+fLgefPDBRNcGAAAAD/3oRz/S0KFDVVhYqGHDhqmwsFADBw70uiwAh8HdVStr/rOS6yS138AFN8osKEpqnwCAzutUQJiXl6cnn3xSDQ0Nuvnmm7Vz507l5uYmujYAAAB46Pjjj5dlWerdu7eWLl2qP/zhD+rRo4f69u2r4cOH68Ybb/S6RACd5LqO5DiyFr2T1HDQHH6k/CVXy/AHktYnAODgdSog/Pa3v62nn35ao0eP1uTJk/XEE0/ohBNOSHRtAAAA8NDSpUv13//939Hn06ZN0yeffKJzzjlH69Yld2oigEPnbKxUeP6z0u4d8WkwmCmFWr72sMBF/yJzYGF8+gQAJFSnAsLJkyfr2GOP1ebNm7VlyxZdc801rGJ8iIb2y9GG2kb1zOIvaAAAILX16NFDa9euVWFhoSRp9OjReuihh/Ttb39b/fr187Y4AF/LDYdkf/Ka7OUfxq1N86gT5Kz8+MDHFB8r/ykXyQgE49YvACCxOhUQVldX67777tOWLVskSQMHDtTPf/5zDR48OKHFdUcTRuRpQ22jBvfL8boUAACAA7rpppv0hz/8QUOGDFFhYaE2btyoYJBf+IGuwNmyTtY7T8utr4lfo8HMrw0HA+d/T+aQ0fHrEwCQFJ0aBviXv/xFO3bs0Mknn6yTTz5ZO3fu1COPPJLo2rqllz6LTMf5onqnt4UAAAB8jYEDB2rmzJmaOHGidu7cqYEDB+q2227zuiwAB+DalqyPX1P4hf+LbzgoHXBasTn8SAW/cyfhIAB0UZ0aQVhVVaWrr75a55xzjiTptdde05NPPpnQwgAAAOA90zR1wgkncP9poAtwajfJmveU3LqtSe/bHD1RRkZm0vsFAMRHpwLC3NxcLV26VBMnTpQUuWE1qxgDAAAAQGpwQ60Kv/QXqaXRk/7NwrGe9AsAiI9OBYRnnHGG5syZo88//zy67YorrkhYUQAAAACAzrNXLoiEg9k9pKbdh95Qbi+pob7Th/unXirfEccden8AgJTQqYDwtNNOU69evbR06VJJ0oQJEzR+/PiEFtZdjR/eV0vX1XldBgAAAIAuznVsqbVF8gdkL30vsvEwwkGj70C5dVs6d2yvPAUu+ZGMQMYh9wcASB2dWqTkrrvuUk1NjX7605/qpz/9qbZv366777470bV1S2OG9Pa6BAAAAABdnLN1vcJP/16hv/+X7E9ek5obDq/BrFyZw4/s1KGB876r4JU/IxwEgG6kUyMI6+rqNGDAgOjz/v37q7a2NmFFdWemYXhdAgAAAIAuyrUt2Z+VyV78TnSbvfzDw27XN3qS7EVvH/AYs3Cs/NMukxFkMRIA6G46FRDm5+frxRdfVN++feW6rl566SXl5+cnurZuqbigl9clAAAAAOiCnO0bZb0zJ+6rFBu9+8te+u4Bjwmc912ZQ4vj2i8AIHV0KiC86KKL9Mc//lH33ntvdNsPf/jDhBXVnfl9bbO6XdeVwYhCAAAAAAfg2rbsRfMiI/wcJ/7t79y+331m8bHyT/mmjIysuPcLAEgdnV6kJC8vTwsXLpQkTZo0SUcddVRCC+uu9g0IHdeVj4AQAAAAwH64u+sUfuPvcms2JbfjYIb8Z1wpXyfvSwgA6No6FRBK0lFHHUUoGAeBfQLC5pCt3MxOrRMDAAAAIA1Z7z0fCQdzekqNuw69IdMnOXanDw+cf4PMAUMPvT8AQJdCOuWhqq2H8Q88AAAAgG7NqdkkZ8NqyR9IajgoSfJ1eiwJAKAbICD00M6GkNclAAAAJMzs2bM1Y8YMPfroo+32hUIhff/739fSpUs9qAzoGqIrFVvhw2jFkNF/yEG9wn/mlTL7DTqMPgEAXQ0BoYd2NLZ6XQIAAEBCVFVVqaWlRTNnzpRlWaqsrIzZ/9Zbb2nYsGEeVQekJrdxl6yPXpGzfrWc+ho5VcsOu01z+Bi5W9d36lgjf7iCN9wt36hjDrtfAEDXwrhxD/XICnhdAgAAQEJUVFRo/PjxkqRx48apvLxco0aNkiRZlqWKigodccQR+319WVmZysrKJEmzZs1SXl5e4ouOE7/f36XqTTTOR6yOzofrumpevkA7XviLJMle+m5c+so68jg1f/FZp47t/91fKjioMC79Hgyuj1icj1icjzaci1icj1jxOB8EhB4Y1j9X67c3qF+PTK9LAQAASIjGxkbl5+dLkrKzs1VdXR3d98477+jUU09VRUXFfl9fUlKikpKS6POamprEFRtneXl5XareRON8xPrq+XAbd8l67zk5676Iaz9G/vDYcDCYKYVa2h3nG3+KfJPP1S6fT/Lg68T1EYvzEYvz0YZzEYvzEetgzkdBQUGH25li7IH8XlmSpNbwQd4oGAAAoIvIzs5WU1OTJKm5uVnZ2dmSJNu2tXjxYk2cONHL8gDPua4ru3yRQk//Lu7hoCS5W9e1PcnMaX8fw2CmApfeIv9J35Th88W9fwBA18IIQg9kBCL/ALeECAgBAED3VFxcrLKyMk2ZMkXLli3T1KlTJUn19fWqra3VPffcoy1btmjRokUqKipSbm6utwUDSeQ27Y6MGly7MjkdtjTGPPUdf7Z8E04jGAQARBEQeiBzT0DYahEQAgCA7qmoqEiBQEAzZsxQYWGh8vLyNHfuXJWWluree++VJM2ZM0djxowhHERacR1H4RcflrtzmxQISuFQ0vo28gbLP+0ymX0HJq1PAEDXQEDoAUYQAgCAdDB9+vSY56WlpTHPL7/88mSWA6SEltULI+Fgbu/IhiQFhL7J58g34VQZJqMGAQDtERB6IIMRhAAAAEDacV1Xuz98VZJkZGbLrdmUlH4Dl/9EZp/8pPQFAOiaWKTEA9EpxowgBAAAANKGu2mNwlsii4fEJRz0B2QWT5LMr/m1rrX96sUAAOyLgNADjCAEAAAAuj+3YafsLz6R29Iot6Fe4Xlz4tuBFZZTvlBynAMeZvQfHN9+AQDdTkKnGM+ePVtVVVUaMWJEzD1oHn30Ua1du1bhcFjXXXedxowZk8gyUg73IAQAAAC6L9d15az6VNa7cyMb9v7/cPn8km11/vCJ0+SffHZ8+gYAdGsJG0FYVVWllpYWzZw5U5ZlqbKyMrrv2muv1a9//Wv95Cc/0XPPPZeoElLW3inGLWECQgAAAKA7cXfXKfzyX9rCwcPl2zOmwx9sFw6aoyd2/JqsXAWvn0E4CADotISNIKyoqND48eMlSePGjVN5eblGjRoV6dQf6balpUXDhw9PVAkpKzrFmIAQAAAA6BZc15Gz8mNZH7/abmVic/iRctZ9cfCN7jti0Gpr0+jZT76J02RXLm73Ev+535FvWHrN0AIAHL6EBYSNjY3Kz4+slJWdna3q6uqY/ffdd58qKyv1ox/9qMPXl5WVqaysTJI0a9Ys5eXlJarUpPH7/crLy1Mwu1WSFLLdbvG+cPD2XgsA1wIkrgO04VoAuiZ3V63C85+Vu6mqw/37hoP+/oNlbd/YuYY7mE5sjpog+QKy5j8Tu/2IY+WfcqGMYEbnCwcAYI+EBYTZ2dlqamqSJDU3Nys7Oztm/6233qra2lrdf//9uueee9q9vqSkRCUlJdHnNTU1iSo1afLy8lRTU6OwFbmJcEtruFu8Lxy8vdcCwLUAiesAbRJ9LRQUFCSsbSBdueGQQs//n9S0W8rMkVoa939wIKPz4WBHgplyKpfEbsvIUuDs62QOGnHo7QIA0l7C7kFYXFys5cuXS5KWLVum4uLi6L5wOCxJyszMVEZG+v2Fy+8zZBqGLMeVZR94xTEAAAAAqctZ/bnUtFtGv0EyevU78MHh1sPrLNQS89R3zFQFr/lPwkEAwGFL2AjCoqIiBQIBzZgxQ4WFhcrLy9PcuXNVWlqq3/3ud2pqapLjOLr66qsTVULKMgxDGQFTzSFbrWFbfl/CcloAAAAACeI6jqxl70uSjF795VQtPew2fRNOk71mqYyeffc7ZdnoN0j+0y+R2X/IYfcHAICUwIBQkqZPnx7zvLS0VJL085//PJHddgmZAV80IMzJDHhdDgAAAICD5KxbKe2qjTyOQzhoFh4l3wnnyiwcq/Dzf+rgAJ98x54p34TTZfh8h90fAAB7JTQgxP7VN0WmWTeFbPX1uBYAAAAAB89e+l78GuvRV76J02S9+bicL5e3220MGCb/1Etk9smPX58AAOxBQOgRx3UlSW8v26hrpxZ/zdEAAAAAvORsqpK94iM5NZskx5Yadsa1fSM7NzJq0NnPPcqDGTJ6fs09DgEAOEQEhB5buq7O6xIAAAAA7Ifb2ixrwStyVn16yG0YvQfIf9L5cnfVyVy7XKGNa9r3s3X9geuorpBsW/LxKxwAIP5YHQMAAAAAOmCvXanQnN/FhINGQZHMovGxB2bmHLAd/9nXyhx2hIwBQxTeuqHDY8yhR8hfsv8FHAMX/ouMYEbniwcA4CDw5ycAAAAA2Ifb3CDrgxflrFnSfmfjLjn7ri4czJRaGg/YnuEPyN1dp/Brf5WsUOy+nv3kP/VbMvoXyF44r91rfceVyDfpTBmGcUjvBQCAziAgBAAAAIA97LUrZc1/dr+hn1tfE7sh1HLgBrN7SIGMyP0FmxtidvkmnCbfpDNlL/9Q9st/jtln5A1W4Pzvyvia0YkAAMQDASEAAAAAaM/IwbInJNuSUVAkd9+RgocoeOFNCr/1pNwd22K2+046XzJMhf52t2SFY/YFzv+ezCGjD7tvAAA6i4DQI31ygtrRGPr6AwEAAAAkhf3FJ5FwcGix3A3lh92e/7RSKbe33C1r2/e17H2poT5mm++Y0yPTiQPBw+4bAICDwSIlHumRzT/6AAAAQKpwbVv2igWRx5u/POz2zKFHyBxzvAyfX8FL/01GQVHsAfuEg0b/IQpc+mP5TziXcBAA4AlGEHpkxIAeWr+94esPBAAAAJBwzpfLpKZdkSdfmfJ7KPxnXinDMOS6rqyPXup4urI/IN/ks+UbO0WGydgNAIB3CAg9UlzQS/NXbPa6DAAAACBtua1NUiBDhumTveyDuLUbuPBfZGRkydlUpfCrs9utXCxJ5rAj5D/lYhk9+sStXwAADhUBoUcG9MqKPnYcV6ZpeFgNAAAAkF7s5R/I+uBFyTAk1z3o1wcu/oGcretkL31famybLuw79kzJ71fo5UfkVre/j6GZ00Pmid+UOXK8DIPfAQAAqYGA0CO99rkH4epNO3XkEP5yCAAAACSS29Ike+E8ubvr5OxdhOQgw0Gj/xAFvnmDjGCmlJEl+/O32nZmZMmt3azwvtv2YY45XvnnfVt1jS2H+hYAAEgIAkKP7PvXwk8qthMQAgAAAAniuq6cNUtlffii1Nx2H3CzeJLc5oZOr1hs9BmgwHnTZQQz5bY0yXrtr1Jon7CvtVnO2pWSzy8jp5fcXbWR1/XKk2/8KTJHT5KZlSsREAIAUgwBYQpYuWGH1yUAAAAA3ZLbsFPWe/+Us35V7I5ghpzqyraFSTohcM53ZGTmyLVthd98XG59TewBpilzzGT5J50hd8c2hec/E6mhvkbWe/+UuWWddPm/Hu5bAgAg7ggIU0BuJl8GAAAAIJ5cx5GzcoGsT16Twu0XCVGoNfLfwcjpGVmV+IPn5W5aE7PLHD1R/mNLZPTqJ9d15dZskhp2xh5TUHSQ7wIAgOQgmUoBu5rDXpcAAAAAdCvWO0/LqVgUt/b8Z18rw+eX/cUncr74JGZf4KKbZQ4cLtd1Za9dKev1x9q9PnDpLTL7DYpbPQAAxBMBIQAAAIBuxamviYSDPr/MonGHHRT6jiuRr3BspO2t62L2Bb71rzL6D5ZdtVzWgpel3bG3D/KfcYV8oyceVv8AACQaASEAAACAbsVZuUCSZOQPO+xw0CwcK9+kM6LP/RPPUGj155Ik3/Fnyd1VJ+udZ+Tu2Br7urEnyX/CuTICwcPqHwCAZCAgBAAAANBtuOGQ7D0Bnrup6rDb80+7XIZhRtpzHYU/eD66zylf2G6hEqP/EPmnXiqz78DD7hsAgGQhIPTQmMG9tWrjTq/LAAAAALoNZ80SqbU5Lm0FrvyZjGBG9Lm99H25G8qjz2PCwUCG/CdfILP4WBmGEZf+AQBIFgJCDxEQAgAAAIfHbW2WvfR9GT37yBw8SvaKBe2O8Z98kax9Rv59VfDKn0mZOQrN/nXba065WGavvEgftiXrw5eiU5e/yhwzWf4TzpaRmXOY7wYAAG8QEHqoML9H9LHtuPKZ/KURAAAAOBjW+8/LqVy83/3Bb/9C1ocvdrjPLBov/5lXyjBNORvXtO3o0Ue+sSfKtcJyVn0m6/M3pZamdq83+g6U/9RvyRw4/HDfBgAAniIg9NDA3tnRx9W1DRrev8cBjgYAAAAgSa7rRv6/sTISDvr8MvKHy920Jua44Ldvk1xHzrov2rVhDB4l/xmXyzBNuc2NCr/0cNvrLvs3WUvfl71kvtS0u30BgaB8x31DvqOnyDB9cX1vAAB4gYDQQ/uOGFy6to6AEAAAADgA17ZkL3lX9pL58o2dImfNUkmS78jJspd/GHNs8MqfyQ21KvzKXyTHlnr0kWxLatoto/8QBc66VobPL9exFXrsrujrzOJjFXryPqm5ocMazBFHyz/lAhm5vRL3RgEASDICwhTx7srNuuB4piYAAAAAHXE2Vcl6759yd26TJNmL3o7sMM324eB1v5RbX6vwa7Ol1mYZA4ZKtiW3drOMXnkKnPud6OIj1ttPx/ZTHlkB2eg/RL5JZ8heuSCyMEnPvvKffJF8w45I7BsFAMADBIQAAAAAUpbb3ChrwSvR4K4dx4l5Grz2djnbqmWVPS5ZYZnDj5SzsVKywpKkwPnflZGVK0myV3/e7v6FRv4w+SedKWNosQzDkJHbW27ROJmjjpHhD8T9/QEAkAoICAEAAACkJGf9aoXffqrDBUL2+5q1K2W9/7zkOpFwcN/7D+b2ltGjryTJbayX9c4+owd79FHgtEtkDB4pw2i7FZDRb5BkheU27JTRu/9hvycAAFIRASEAAACAlOM6tsLzn42Eg7m9pYadnXqd9d5zkQdZue0WJwlecGNb+427oo/NUccocOaVsf3blpyKxbKXvS+3bovUs68yrvr5Ib0XAABSHQEhAAAAgJTjbCiXmnZJ/mCnw8EYX1lkxH/ud2T03DN60HWj9zA0hoyW/4wrose5zQ2yVy6QvWJBWxv+oPwTpx3S+wAAoCsgIPTY2ccM0euLq70uAwAAAEgpzhefRB5YocNuyzfpDPmGjWlru2KxnLUrpWCGAqdfIsMw5OzYKnvp+3IqFkVWO97DHD1R/hPOkZHDqsUAgO6LgNBjRw/rGw0IW0KWMoN8SQAAAJDe3MZdctavbrc9cPlPZS94ucN9+2MMGS3fsSUxbVsfPC9J8p/0Tbk7tik8f67c6vLY1+UNlv/kC2QOLDy0NwEAQBdCGuWx/N5Z0ccVm3dp3PC+HlYDAAAAeMNtqJcys2X4A7LLP5fc2NWJfcdMleHz7z8czOklNdZLwQyZoyfJWfGRlNtLgTOulGGakT5cV9a7c6VQiyTJXvq+3B1bY9vJzJF/8tkyjzgu+joAALo7AkKP7btC2twFXxIQAgAAIO0461cr/NpsKStXvvGnyv7k9Zj9ZuFR8h1XIuvd5zp8vf+c78gcWKjQ7F9LodZIOGj6FPjGNTKycqLH2UvelbN+VfR5TDhomPKNPUm+486UkZEd1/cHAECqIyBMIQ0tYa9LAAAAAJLKtW1ZH70kua7UtFv2gldi9huDRshfcrXsz9+SU/65JMkcfmRkJKHryH/qt+QbPkbWBy9IcqOv80+5QOaAoZIkp26LrI9elltd0WENxuBRkeP75ifmTQIAkOIICAEAAAB4xln1idyd22X07Cdj4HA55QvbdmZkK3Ded2V9+JKclQsio/zGnSL7iwWS68h3zOnyHXWCnO0bZS//MPoyc/REmUdNlrN+taxl7+83GFSPPvKfdL7MwrExM3sAAEg3BIQAAAAAksZt2i031CKzd3+5rS2yPiuL7OjZNzYclBS8+j9kzX9WTuViyeeX/6TzZS16WwqHZI6cIN/ks+U6jqz32qYeGz37yeg/WOE5v5e7c1vHRfgD8k2cKt/402T4A4l5owAAdCEEhAAAAAASzrXCspe+K3vRO5LjKHjdHbIXvS21NEb27zvKL7eXgpfcIuutJyP3DAwE5T/jCtmfvik17opMO552mQzDlP3FArnbq9v62VUr+8OXIk9yeso3eqLsxfOj+82RE+Q/8VwZub2T8K4BAOgaCAhTwHVTi/XYO+WSJMd1ZTK9AQAAAN2IvW6VrA9flHbVRjb07Cu1NMpe9n6Hxwe/9UOF3/ib3M1fRqYZn3O9rM/elFu3RUbv/gqcda0Mn19uc4Os9/7Z7vVG3mD5xp8qs2ic1Lxb9oqPZPTsF7nPYEFRAt8pAABdEwFhCjhicK/o42Xr6jShsJ+H1QAAAADx4e7eqdp5/5BVsThmu3/iNFmfviE5doevC/3tnsiD7J4KnH2tws/9MbovcO50GZmRVYatmAVNjMhqx+NPkTGwsO2egrm9Fbz+VzJ8vni9LQAAuh0CwhQQ9Lf9sDJ3wZcEhAAAAOjyXNdV+NVH5O7YJgUyZOQVREYE5vaW0au/nPnPxhxvHnmCjKxc2QvfatuWPzQmHPSd9E0ZPftKkpxNVdF7FprFk+SfdKaMXh3/HE04CADAgREQppimVsvrEgAAAOJi9uzZqqqq0ogRIzR9+vTo9oceekgbNmyQJN1www0aPny4VyUigdyt6+Tu2CYzt5f8F/9A4VcelRQZPehsWhNzrFFQJN+4KdFj9nK+XNH2JJgp//hTIm3bVnRqse+4EvmPLUncGwEAIA2YXhcAAACA7qeqqkotLS2aOXOmLMtSZWVldN/FF1+su+66Sz/4wQ/09NNPe1glEskuXyRJchrqFZrzO7l1W6ScXjKPOFa+cSdL2jMFuEcf+UYdo/Cc30kNO/fbXvDbv2hre+n7cnduk9ErT75jpibuTQAAkCYICAEAABB3FRUVGj9+vCRp3LhxKi8vj+4bMGCAJMnn88k0+XG0O3JtS07l4rYNoRZJkv+Y02X4/ArP/YMkN7Jv9w5Z786NbcAwZfRsmy4cKP2hjGBGpO3dddFpyP5TLpLhi50U5YZDsisWK/TyX9T68O2yq5bF9b0BANAdMcU4RQzsk60tO5okSY7jyjRZyRgAAHRdjY2Nys/PlyRlZ2erurq63TFPPPGEzjvvvA5fX1ZWprKyMknSrFmzlJeXl7hi48zv93epehOhedXnqgu3xmwzc3ppwMnnqHHxe2qtr+nwdTmTTldg4HD5evdX3dw/SZJ6feMK5R55TPSY2nlPSlZYWUdNVt9jTpIUud9hqLpSTUs/VPPKT+XuCSRl+tSrX39lptDXg+sjFucjFucjFuejDeciFucjVjzOBwFhivjXc8fqjic+lSQtWVuriUVc6AAAoOvKzs5WU1Pkj5/Nzc3Kzs6O2f/yyy9ryJAhGjNmTIevLykpUUlJ233lamo6DpRSUV5eXpeqNx7c3TsUfvNxmYNGyHfCOQo9+6fYA0xT5mml2jr/Rdkfv9ru9ebICfKfcbks06ewYyv84sNyW5pkDhuj5hHHqGXP+bTXrpBVsUQKZsieVKLtX1bKrlgoZ/XncnfVfqXN8fIff7YaevVTQwp9PdLx+jgQzkcszkcszkcbzkUszkesgzkfBQUFHW4nIEwRmYG2ldWeeK+SgBAAAHRpxcXFKisr05QpU7Rs2TJNnTo1um/JkiVavXq1fvKTn3hXIOLKWviW3O3VsrdXy65c0m6/f9oVcrdvkP1ZmSRDvhPPlb3gFUmS0WeA/FMvlWFGfh62P58nd8taKbtHZLsRmVnjhkOyPngx8preAxR+e47cjWsUnaq8h1FQJP8J58ocMDRh7xcAgO6Gm74AAAAg7oqKihQIBDRjxgyZpqm8vDzNnRu5z9wjjzyi7du369e//rUeeughjyvF4XIbdsopXyTtCfLUtCtmf+9zr5VbuzkSDhqG/NMulbtja3S/75hpMvwBSZKzcY3shfMkGQqccaWMrNxIH66r8Ct/iS5i4m7bIHdjpfYNB42+A+U/d7oC3/w+4SAAAAeJEYQAAABIiOnTp8c8Ly0tlSQ98MADXpSDBLGXvCc5tozBo/aEdm18J5yrcO1m2YvfkQxT/jOukNu0S87qz6PHuLvrIv9vblR43lOSXPkmnSFz8Ei5u3fILl8o+7M3919Abi/5jztL5uiJMlj0BgCAQ0JACAAAAOCQuM0Nsld9Enn81XDwmKlyd9epceXHkumTv+RqGf6ArHn/kCSZhUfJWbsyMhrQdWW987TUtEtGXoGMHn0VevFhuZvW7L/zYKZ8E6fJd/SU6AhEAABwaPgTWwr5l7OPjD5es2XXAY4EAAAAksvZuV1OdWwIaC/7QLLC7Q/OypW7q07Oyo8ln1/+s6+V0WeAwmVPSG5khKAy9ixck5kje9kHctavkiS5NZtkzX8mEg76OhjP4PPLN+E0Ba/+ufzHnE44CABAHBAQppCRA3tFH//f6ys9rAQAAACIcJsbFH7vOYXn/E7hl/8stz6ySqLb2iJ7xYcxxxp9B0pZuVJzg5yqpZKkflfcIjN/mKzX/iqFWmQWjpU5coKc8s8lw5RZNK7dysZG/nD5T/2WgtfeLuX23rtVZvEkBa/4mfwnnicjI3ZlbAAAcOiYYgwAAACgHdcKy17+geyFb0vh1sjGjCwpJ/JHbfuLBVKoNXq80bu/AhfepPAL/ye3uSGy0fQpWDBC4Sd/L7e+Rka/QfKfcbmseU9JrivzyMkyghmSY0s5veQrniSzeJLM3v2j7ZpDj5BamyL3Jew3KGnvHwCAdEJACAAAACCG29qk8D//JHfn9sgG0yc5tsyRE9qm9DbtbnuBPyh/yVWy5j0lt65thWI5tjb/9w8jjzNzFDj7Orl1W+WsXSn5A/Ife6aMnJ4KXn+HFMzqcJGRwGnfStC7BAAAezHFOMUM7ZcTfWw7roeVAAAAIF05lUsi4WDPfvKf+x0pmClJ8h1xbPQYs2h89LH/5AtlLXg1ch/BzGz5p14m9ewX02bg7Gul3N6y9kwn9h19soycnpIkIzOHFYgBAPBQQkcQzp49W1VVVRoxYoSmT58e3f7QQw9pw4YNkqQbbrhBw4cPT2QZXcqNZx+lO574VJI054M1uurUUR5XBAAAgHRjVy2TJPmPLYlM/21plNEnX0b/IZIkt6VJ4beelBS576A1/5noa43c3rLeeUZS2x+7/adfInNgoez1q+Vu/lLKyJLvmNOT94YAAMABJezPdFVVVWppadHMmTNlWZYqK9tWPLv44ot111136Qc/+IGefvrpRJXQJWUGfNHHC6tqPKwEAAAA6chtbpC7qUqSZA4/Us7qzyOPjzhWhmFIkuxl70sNOyPH122JfX3NJu0bDva74hb5xhwv13Vkf/KaJMk3cZqMjKwEvxMAANBZCQsIKyoqNH58ZNrBuHHjVF5eHt03YMAASZLP55PJVAIAAAAgZVjvzo0+dnfVRKYNG6Z8oydGt5vDxsjIHxbzOqNnPxlDimWOOS6ykrEkc8zxyhw1TtKeacu1myOLkYw9KQnvBAAAdFbCphg3NjYqPz9fkpSdna3q6up2xzzxxBM677zzOnx9WVmZysrKJEmzZs1SXl5eokpNGr/ff9Dvo3efvvL7CFG7m0O5FtA9cS1A4jpAG64FeMFt2i3r0zflGzdFRq/+kQVE9gi/9lfJcSKrDWf3iG43+uZLVjjypGc/Bb95g4wefSRJ1udvSc0NUm5v+U86P9KHbcn69E1Jkv+4kraFTgAAQEpIWECYnZ2tpqYmSVJzc7Oys7Nj9r/88ssaMmSIxowZ0+HrS0pKVFJSEn1eU9P1p9vm5eV16n3cddVxuuPJzyRJtz86T7defEyCK0OydfZaQPfHtQCJ6wBtEn0tFBQUJKxtdF3WwnlyVn0id9u66GIkUU27ZRQUyX/yhdFNruvKevc5ubWbZfTKU+CC78vI6SVJcmo2yV74liQpMPVSGXvac774WNpdJ6P3AJnFkzqsw3VdybFl+BJ6m3QAANCBhA1NKy4u1vLlyyVJy5YtU3FxcXTfkiVLtHr1al1yySWJ6r5Lywy2/VC0rb7Fw0oAAADQnbm2JWfNksjjuq1yt6yL2W/0ylPgG9fEhHbOqk/lVC6W/AH5z742Gg66tiXr7TmREYdjT5I5OLLYntPaIuvzeZIk3+SzZZht99x2d9XJ/uIThcueVOhv9yj0yK/k7NiWyLcMAAA6kLA/zxUVFSkQCGjGjBkqLCxUXl6e5s6dq9LSUj3yyCPKzs7Wr3/9axUUFOjGG29MVBkAAAAA9sNZv0pqaZL8gbYpw/tw62sUfnW2AhffLMMw5NRslPXBC5Ik/6mlMvvkR4+1P38rsmBJz37yn3BudHvDx29EVkHOHyZz4HDZlUvkbFwjZ1OltKsutsOcXjICGYl5swAAYL8SOn5/+vTpMc9LS0slSQ888EAiu+0Wzhw3WG8t2yhJWr1xp44Y3NvbggAAANDtOOULIw86CAf3cretl1tfI2X1UPjNJyTbknnkZPmK2xYtcbZtkL34HUmGAtMukxEIRl67q06734sEiu7W9Qo9dnfHnfToI/8xp8ssPpb7EwIA4AFu8JGizpk0NBoQ/rlsle67/kSPKwIAAEB34jY3ylm/+sAHGYbkunLWr5a75UtpV62MfoPkn3JBWztWODK12HXlO3qK5LqyPntTzsY1cresPXDzfQbId8w0maPGx0w9BgAAyUVACAAAAKQhZ81iybGjz41BIxSYdoVCT8yKbvNP+aasD16U/dFLkQ3BDAW+8e2YUX72p6/L3bk98njlx7KXf/i1fRv9h8g3carMwqNkGAm7LToAAOgkAsIUlpsZUENLZLrHhpoGDc3L9bgiAAAAdBWu68jduEbKyJLZf0i7/XbV8rYnhqHA1EsVeumh2DZ274h57j/9Mhm98tr2NzfIXvpB2wGOLaPPAJmDR8kuXyiFYhfcMwqK5J84TcbgUTIM4zDeHQAAiCcCwhR2x+WT9B+PfSxJ+n8vL2eaMQAAAL6W6zpy1q6MLBpSu1nK7qGMa29vf6DjRB/6z/mOwq88Ku2qk5E3WL4Jp8p66x+yl38UPcboky9f0dGxbQSzZI45VnJcmYNHyRw8UkZOT7mN9TGvNYeNkW/iNJkDh8f9/QIAgMNHQJjCTP6qCgAAgIPgbNsg6925kWBwDyO7Z7vj3FCL3MZ6SZI59iTZH70st75GRr9BCpz/PRmZ2XI2VslZ9Un0NebQ0e3aMXw+BU6/tH0h/oCMQYUysnsqb9rFqvdlxeHdAQCAROGGHymuuKBX9PHrizZ4WAkAAABSmeu6Cr/1jz2jBnvKGDBUkqL/35f10ctSw04pt7fcjZVyd26T0TdfgfNvkIIZcq2w/CedL6NvftuLsnp0uhYjI1vBC29SoOQqBfLb9w8AAFILAWGK+/43jow+Llu60cNKAAAAkMrcndulXbVSZraCV90qIzsS6JlfCeicmk1yVn0aedKwU+7O7TJ65ck/7XLZyz9Q6O/3KvT3/5JcR/6Sb0eO8/nlO+LYZL4dAACQREwx7mLClqOAn1wXAAAAsZwN5ZIkc0ix5PPL2RaZfWIMGBZznBEISj6/ZFvRbW59jcJz/yi5e+5LmJUr+QNyVkbuh22OmiAjiwXzAADorkiauoCfXDAu+vg/H//kAEcCAAAgXTkbVkuSzKFHSLvqpKbdUkaWjF79Yg/MypXRZ0Dbc9+eMQPuPouWnHiuZNuyV38WOeToKQmtHQAAeIsRhF1AQd8cr0sAAABAinHqtspZu1y+sSfL+vR1udUVkiRz8EiF5z215/EoGUbbmAA33Krwq4/Krdkk5fZW8MKbpNze0u46WR+/LqdqqYyBhTJHT5KzYoEUbo08zxvsxVsEAABJwgjCLmLs0D7Rx7f+dYGHlQAAACAVhJ/7o+xP31Ro9p1yVnwkSTL6D5G9coHcTWukrFz5p1wQPd4NhxR+dbbcLeuknF4KXnCjjB59ZBiG3FCLnC+XSYYp/ykXS3Jlr/hQEqMHAQBIBwSEXcR3zjjC6xIAAACQIlzHkaxQh/vshfMkw1DgzCtl5PSMbrc+flXu5i+l7B4KXvB9GT37RtpyHVnvPS+5rnxHT5HZb6Dc6srIoic5vWQWjk3KewIAAN4hIOyi7n12kdclAAAAwCPuji0db99eLUnyHVcic/Co6HZnU1VklKFpKnDud2T0ymvbt/pzudvWS9k95DuuRJJkL/8g0s7YE2X4fIl6GwAAIEUQEHYh911/YvRxXUOrh5UAAADAS+6W9e22GXsDweye8k2c1nZsOKTw/GckSb6JZ8TcT9BtaZL18auSJP9J58sIZsqpr5GzfrXk88s3ZnIC3wUAAEgVBIRdGPciBAAASE/O1nUxz81Rxyhw9nVSMFNq2iV3+8boPvuT16RddTL6DZJv4tSY11mfvC61NMkoKJI5ckKk7eUfRds0slgsDwCAdEBA2MX8f9edEPPccVyPKgEAAIBXnIq2282YRxwXud9gIBgd8Wcvjyww4myqijw2TfmnXibD529rY9sGOV98Etl3ykV7Fitplb36M0mRxUlc15UbapXbWC9nxzY5W9fL2VAut74mie8WAAAkmv/rD0EqMQxD+b2ztHVnsyTpP/72cczUYwAAAHRvrutEHxu9+8s35ni5rivDMOQ7+kTZy96Ts2ap3ONKFJ7/rCTJd8w0mXkFbW04jqz3n5fkSpk9ZH/2lqxwi9wN5dFjwi8+JIVaI8d8lWEqOP1XMgIZiXqbAAAgiRhB2AX97KIJMc+Xr6/zqBIAAADEi9u4S/aKBbIWz48JAb/KWbOs7YlhKPz8n+SsWxl52qOvzOFHSY6t0PMPSrtqZfQdKN+kaTFtuLtqowuaqGmXnKqlMeGgJCnUog7DQX9QvnEnS/7AobxNAACQghhB2EXdfPZR+tPrkR8E//p2OaMIAQAAuij7y+WyF8+Xu21DdJuZP0zGoBHtjnVtK3LfwL3Pd2yTJDkVi+UrHCtJ8o2bImftCqlpl2SY8k+LnVosSUavPPlPv1RuS6OMYIYUzJS7dX10arIxeJTczV9Kjr3nBYaMwaPlGz1R5oixMgLBuJ4DAADgLQLCLqpoYM+Y57f+dQEhIQAAQBfjuo6sd+dKLU2Szy+ZphQOSbbV4fH2igXS7n1mjwQzpVCLnPWr5IZDMgJBGYOKZPQdKLdui3wTp8asWryXYRjyjTkuZlt4n/sauhsrI8f1GySzeJJ8IyfIyIn9+RMAAHQfTDHuwr4aCL7w6VpvCgEAAMAhcXfWRMLB7B4KXj9DRv+he/YY7Y91HNmL5rVt8PkVOPc7MgYMk6ywnA2rI680DPlLrpb/lIvkm3Rmp2txajdHHuT0lG/C6Qpc9m8KXnqL/ONPJRwEAKCbYwRhF3fVqaP05HuRv/C+t3KLzj5mqDICPo+rAgAAQGe4W9ZKksyBhZFpu3vvPWi2DwglNxIm7uE/8VyZAwtljhwne9t6OWuWyVc0LvLyPgOkPgMOqpbA+TdILY0y8ofLMBlHAABAOuFf/i5uUlFezPNfPvGpR5UAAADg67jhkMLvPy97xQK5ritnyzpJkpE/fM8BexcF6WAE4eYvY55byz6QvfzDtvsQrv9Cbjh0yLWZfQbIHDSCcBAAgDTEv/7dwFenGt/61wUeVQIAAIADsZe+K2fFR7Le/6ecikVyt0YCQnPgcLmuu2flYElG7I/pTt0Whd/4W+TY0RNl5A2WdtXJ+uAFOav2/IHYCsup/spKxAAAAJ1AQNhN/ObaE2KeExICAACkHre+NvrYqVomt75G8gdk9CuQ8+VyuXVbpGCmjL5t04PdxnqFX3lUCrXKLBon/7TLFPjm9+U7ekr7DsKtyXgbAACgmyEg7CZM09BPLxwfs42QEAAAILXsnQ4sScrKkSQZA4ZKVljWBy9IkvwnnCMjIztyfKglEg421ssYOFz+aZfLMEwZGZkyevWLvL53f8kfkCSZg0cn8d0AAIDugoCwGxnUJ1uXTSmK2UZICAAAkDrcmo3Rx86qzyRJ5vAjI6sTN+2WMWCYzCMnR461bYXffFxu3RYZvfsrcPZ1MvYEga4VlrXoHUmSUVAkWWEZ/Qax2jAAADgkBITdzOTRA3TkkN4x2wgJAQAAUpNZPEm+cSfL3bFVkuQbe5KMPfcftD97U251hZSVq8C502Vk5kRfZ3/xSSRQ7DdIhumLtDVsTPLfAAAA6BYICLuh7545RkX5PWK2ERICAAB4y929I+a5WTRe/tMviUwZ7lcQOWZPUOg27Za9/ANJUuCsa2T07NvWjhWWvfgdSZLvuBI561dH2ht2RKLfAgAA6KYICLupm88Zq8mj+8dsu/WvCxS2HY8qAgAASG/22hXRx2bhUfKfcUV09J8xYKgkydm2PnLsorclKyyz8CiZAwtj2/ni47bRg70HyN1VK2VkRdsAAAA4WASE3dhlU0bquqnFMdv+8++f6KPVWz2qCAAAIH05X0YCQrNonPwlV8vw+aL7zD3hnrt9o9zdOyNTiCX5jvtGTBuR0YPz9+wrkbNhz+jBIcXRsBEAAOBgERB2c+OG99WdVxwbs23ugi+ZcgwAAJBEbnOD3C1rJdMn/2mXyPD5Y/Yb2T2k3N5SuFXhd+ZItiWzaLzMfoNijrNX7hk9mFcgc/hR+0wv5v6DAADg0BEQpoGczID+v+tOaLf91r8u0M7GVg8qAgAASC/Oui8k15VRMFJGRmaHx0RHEW6qkgxDvuNKYva7Vlj2kj2jB8efJlnhyLEyZA4dndD6AQBA90ZAmCYMw9B915/Ybvs9zyxiNCEAAECC7Z1e7Bsxdr/H7HsPQXPUMTL7DIg9oKVRam6QJFnvPqvQU7+VHFvGgCEysnLjXzQAAEgbBIRp5r7rT9StF09ot/3Wvy7Qi5+u86AiAACA7s11HbkNOyUZMguP2u9xZv8hkQeGKd+xZ7bbb+T2VuD878kYMlqywlJjfaT9bRvkVFfIdd0EVA8AANKB/+sPQXczoFdWJCj8ysjBd1du1rsrN+tnF01Qfu8sj6oDAADoXgzDVODSW6RddZF7De7vuIHDZR5xnIx+g2T2yuvwGHPwKAUHj5JTt0Xhp38f3R5++S8y+ubLN+4UmaOOkeEPxPttAACAboyAMI3dd/2JamwJ686nPo/Z/t/PL5Ek/eclE9UnN8OL0gAAALoVwzCkXv0OfIzpU2DqpZ1tcW/D8h1bInvlArl1W2XNf1b6+DX5jjpBvvGnysjgj74AAODrMcU4zeVkBnTf9Sfq1CMHttv3X89G7k/45dZdHlQGAACA/XHWr4o8yMiSs6FcMoy2nS2NshfOk/Xhi94UBwAAuhxGEEKSdOHkQl04ubDDBUv+97WVkqSheTn68fnjkl0aAAAAvsLdsS3yoKVJbss+95EOZsjI7ill95Rv1DGe1AYAALoeAkLE2LvScUdB4Yaaxuj2/7pmsgI+BqACAID9mz17tqqqqjRixAhNnz49un39+vV6+OGHJUk33HCDhg8f7lWJXZb/+G/I6T9EysyWkd1DRk4kFDQCQa9LAwAAXRABITq0NyicPW+1VmzY0W7/f/79k3bHAgAA7FVVVaWWlhbNnDlTDz/8sCorKzVq1ChJ0lNPPaVbbrlFpmnqz3/+s37+8597XG3XY+T2lu/ok7wuAwAAdBMEhDig75xxhCRp+65m/X/PLenwmL2jCjMCPt199fFJqw0AAKSuiooKjR8/XpI0btw4lZeXRwPCxsZG5eXlRR8DAADAWwSE6JT+PbMOOP1YklrDdsy+WdeeIJ9pdHgsAADo3hobG5Wfny9Jys7OVnV1dXSf67pf+/qysjKVlZVJkmbNmhUNFLsCv9/fpepNNM5HLM5HLM5HLM5HLM5HG85FLM5HrHicDwJCHLS9QaHtOLrtb5/s97jb/vZx9HHJhME6+5ihCa8NAACkhuzsbDU1NUmSmpublZ2d3eFxhtHxHxNLSkpUUlISfV5TUxP/IhMkLy+vS9WbaJyPWJyPWJyPWJyPWJyPNpyLWJyPWAdzPgoKCjrcTkCIQ+YzzWhYGLYc/efj+w8Ly5ZsVNmSjdHnF00erlOOHJTwGgEAgDeKi4tVVlamKVOmaNmyZZo6dWp0X25urmpra2UYhrKysrwrEgAAAJIICBEnAb8Zs1jJ/qYh7/X8J+v0/CfrYrYxJRkAgO6jqKhIgUBAM2bMUGFhofLy8jR37lyVlpbq8ssv1+9//3tJ0ve+9z1vCwUAAAABIRJj37CwrqFF9z67+Gtfs++UZEnK65mpWy+aIJPQEACALmn69Okxz0tLSyVJw4cP11133eVFSQAAAOgAASESrm9uZkxguK2+Wff9s+MVkfdVs6tF//GV0FCSbjrrSI0a1CuuNQIAAAAAAKQrAkIk3YBeWTGBoeu6euCl5dpY19ip1z/4xhcdbj95zEBdOHm4zP3c7BwAAAAAAADtERDCc4Zh6N8uGBezzXVdPfTGF6rcsqvT7Xywaos+WLWlw319coL6yYXjlRXkkgcAAAAAANgXaQlSkmEYuunso9pt7+z05K/a0RjSjCc/O+Ax3z3zCI0Z3FsGIxABAAAAAEAaISBEl/LV6cl7WbajP766QtW1nZum3JFH3lrdqeN+dN5YDcnLZSozAAAAAADoFggI0S34faZu+ea4Dvc5rquPVm3VPz9ZG5e+/ueVFZ0+dsSAHio9cYTye2cxMhEAAAAAAKQkAkJ0e6Zh6OQjB+rkIwfu95i63S363YvL1BK249r3l9t267cvLD3o1+VmBnTxCYU6ckhvBXwm4SIAAAAAAEgYAkJAUt8embrr6uO/9rgtO5r0t/kV2lbfnNB6GlrC+vv8isNuZ3DfbE09ukBHDO6tzICPoBEAAAAAALST0IBw9uzZqqqq0ogRIzR9+vTo9rlz5+r111/XtGnTdOWVVyayBCCuBvbJ1q0XT+jUsY7j6sttu/SP99doZ2MowZV1bGNdkx5/tzIhbR81tI+OKeynovye6pEVkGkSPgIAAAAA0BUlLCCsqqpSS0uLZs6cqYcffliVlZUaNWqUJOmMM85QcXGxli9fnqjuAc+ZpqGRA3vp9ksntduXl5enmpqaDl/nuq7qGlr14aqtenfl5kSXechWbtihlRt2JL3foXk5Gj2ol4b376H83lnqnROUzzSTXgcAAAAAAN1FwgLCiooKjR8/XpI0btw4lZeXRwPC3r17a+PGjYnqGujSDMNQvx6ZuuD44brg+OGH3I7tONpU16TP12zXB6u2xrFCb22oadSGmkNfrTqZ/D5DQ/vlqqBvtgb0ylLfHpnqkxNUj6ygMgI+MegSAAAAAJAKEhYQNjY2Kj8/X5KUnZ2t6urqg3p9WVmZysrKJEmzZs1SXl5e3GtMNr/f3y3eBw5fsq6F/AHSxDGFuuH8+LXpuq7ClqMNNbu0fO12fbiyWtt2NsWvg27Esl19uW23vty22+tSUlKPrKD69MhU39ws9emRqd65meqdk6EeWUHlZAaUkxlURtCnzIBfAb9PPtOQaRjaeyvN7nRPTf59wF5cCwAAAPBCwgLC7OxsNTVFQoPm5mZlZ2cf1OtLSkpUUlISfb6/6ZhdyYGmlSK9dIdroVdAOnl0X508um9S+nNdV66kkOVoe32z1m1vUOXmeq2s3iHXTUoJiLPdzSHtbg5p/bZdXpeCbijgMxX0mwoGfJH/+0wF/JH/gn6fAnue790e9Pvk95kK+Iw9/49s9/tMmYahwX2zlZMZSHjdif73oaCgIGFtAwAAoOtKWEBYXFyssrIyTZkyRcuWLdPUqVMT1RWANGAYhgxJmQGfhublamherk45cqDXZR2Q67pyXak5ZKm+KaTa3a2q2dWsrfXN2ryjSZvrmkS2CSRG2HYUth01tlpxa/PH5x+toXm5cWsPAAAASBUJCwiLiooUCAQ0Y8YMFRYWKi8vT3PnzlVpaanmzZun119/XQ0NDWpoaNANN9yQqDIAwDPGnumwkemyARX0zWl3THcYTXoo9o4Idd3I/TJDlqPmkKWWkK3GlrB2NYfV0BLWrqaw6ptatbs5rPqmkHY3h2U7xKrwxtptuwkIAQAA0C0lLCCUpOnTp8c8Ly0tlRRZxfiMM85IZNcAgBS2d0SoDMln+hT0+5SbhOmbqSpdg+Jkcvfci8CNPo88c93IY8d1I/85rizHle04su3I4607mzQ0L1f9emR6VT4AAACQUAkNCAEAAFLB3kVtokvbGDHPDmhQn4O7jzIAAADQ1ZheFwAAAAAAAADAOwSEAAAAAAAAQBojIAQAAAAAAADSGAEhAAAAAAAAkMYICAEAAAAAAIA0RkAIAAAAAAAApDECQgAAAAAAACCNERACAAAAAAAAaYyAEAAAAAAAAEhjBIQAAAAAAABAGiMgBAAAAAAAANIYASEAAAAAAACQxggIAQAAAAAAgDRGQAgAAAAAAACkMQJCAAAAAAAAII0REAIAAAAAAABpjIAQAAAAAAAASGMEhAAAAAAAAEAaIyAEAAAAAAAA0hgBIQAAAAAAAJDGCAgBAAAAAACANEZACAAAAAAAAKQxAkIAAAAAAAAgjREQAgAAAAAAAGmMgBAAAAAAAABIYwSEAAAAAAAAQBojIAQAAAAAAADSGAEhAAAAAAAAkMYICAEAAAAAAIA0Zriu63pdBAAAAAAAAABvMIIwiW677TavS0CK4FrAXlwLkLgO0IZroXvg6xiL8xGL8xGL8xGL8xGL89GGcxGL8xErHueDgBAAAAAAAABIYwSEAAAAAAAAQBojIEyikpISr0tAiuBawF5cC5C4DtCGa6F74OsYi/MRi/MRi/MRi/MRi/PRhnMRi/MRKx7ng0VKAAAAAAAAgDTGCEIAAAAAAAAgjREQAgAAAAAAAGnM73UB3VVdXZ1+85vfqLq6Wo899ph8Pp9mz56tqqoqjRgxQtOnT/e6RMTRtm3bdPvtt2vw4MHy+/365S9/qRdeeEGffvqp+vfvrx/84Afy+/3ttknSr371K61fv1733XefBg4cKEkdvhapq7Pf753Z1lFb+3stUs9Xv361tbXtPhukjr/H+XzoXioqKvTXv/5VhmFo5MiR+s53vtOprzvXQtfH53Wb/f2blq46+lxIZ+vXr9dDDz0k0zQ1cOBA3XzzzTIMw+uyPPfSSy/p448/1l133eV1KZ7q6PerdDZ//nzNnz9fjuPoxz/+sfr27et1SZ5ZvHix/vnPf0qSNm3apBtuuEGTJ0/2tigPtba26v7771dra6uys7P1k5/8RIFA4JDaYgRhguTm5uqOO+7Q6NGjJUlVVVVqaWnRzJkzZVmWKisrPa4Q8TZu3Djdeeed+uUvf6n6+nqtWLFCd911l4YNG6ZPP/20w20+n0+33nqrTjzxxGg7HR2H1NaZ7/fObvtqW/trD6mpo6/fvp8NUsff43w+dD/9+/fXjBkzdNddd2nXrl1auXJlp77uXAtdG5/XsTr6TExnX/1cWL9+vdcleaqgoEB33323Zs6cKUlas2aNxxV5LxwOa+3atV6XkTK++jNUuqqrq9PKlSs1Y8YM3XnnnWkdDkrSMcccozvvvFN33nmn8vLyNH78eK9L8tTixYs1evRo3XnnnRo1apQWL158yG0RECZIMBhUbm5u9HlFRUX0wh03bpzKy8u9Kg0JsmLFCs2YMUMvvfSS1qxZo6OOOkqSNH78eJWXl3e4zTAM9e7dO6adjo5DauvM93tnt321rf21h9TU0ddv388GqePvcT4fup/evXsrGAxKknw+nzZs2NCprzvXQtfG53Wsjj4T09lXPxdMM71/Fdt31LPf71deXp6H1aSGefPmaerUqV6XkTK++jNUulq8eLEcx9HMmTP1yCOPyHEcr0tKCVu3blWvXr2UmZnpdSmeys/PV0tLiySpsbFRPXr0OOS20vtfpSRqbGxUdna2JCk7O1tNTU0eV4R46tOnjx544AH96le/0rJly1RVVaWsrCxJka93Y2Ojmpqa2m3rSGePQ+rq6Pu9s9s62x66hq9+Nqxbt67D73E+H7qvdevWadeuXcrJyenU151roWvj8xqdsfdzYciQIV6X4rnPPvtM//7v/676+vq0D5Mty9KKFSt09NFHe11KSujoZ6h0VV9fL8uyNGPGDAWDQWYN7PHxxx+n9dTivQYNGqSKigr99Kc/VVVVlYqLiw+5LQLCJNn3h8Tm5uboD4/oHgKBgDIzM+Xz+XTssccqPz9fzc3NkiK/xOXk5Cg7O7vdto509jikro6+3zu7rbPtoWv46mfDhg0bOvwe5/Ohe2poaNAjjzyim2++udNfd66Fro3Pa3ydfT8XIB133HH67W9/q379+mnhwoVel+Opd999V6eccorXZaSMjn6GSlfZ2dnRWQNHH320Nm7c6HFFqeHzzz/Xcccd53UZnps/f76OPfZY3X///Zo4caLee++9Q26LgDBJiouLtXz5cknSsmXLDivVRerZ+0uaJK1atUoDBw7UypUrJUW+3qNHj9bIkSPbbetIZ49D6uro+72z2zrbHrqGr3425Ofnd/g9zudD92Pbtv7nf/5H1157rXr37t3przvXQtfG5zUO5KufC+kuHA5HH2dlZUWnX6erTZs26c0339Q999yj6upqvfrqq16X5KmOfoZKV0cccUR0BOXatWs1YMAAjyvy3s6dO+X3+w9rOm134bpudAR2z549D2v2guG6rhuvwtDGsizde++90VXsrrrqKr3//vv68ssvVVhYqO9+97tel4g4WrhwoZ566ikFAgGNGTNG11xzjf75z3/q888/V15env71X/9Vfr+/w23333+/Vq9erQEDBujCCy/U8ccf3+FxSF2d/X5/9NFHv3ZbR22NHj26w9ci9Xz163fkkUfqs88+i/lskMTnQxp4//339eijj2ro0KGSpKuvvlorV67s1Neda6Fr4/O6zf7+TUtXHX0upHOI/Omnn0bvLTdo0CDdeOONaX9fxr3uuOOOtF/FuKPfr9LZY489pqqqKvXo0UO33HJL2v+b/+abb8q2bZ1zzjlel+K5xsZG/f73v1c4HJbP59NPfvKTQ75lAwEhAAAAAAAAkMb4Ew0AAAAAAACQxggIAQAAAAAAgDRGQAgAAAAAAACkMQJCAAAAAAAAII0REAIAAAAAAABpjIAQQLe2bds2XX755Zo1a5YWLlyoOXPmaNu2bXHvp7q6WnPmzNGKFSui2/74xz/q8ssv15o1a+LeHwAAAAAA8eL3ugAASKSePXvqlltuUd++ffXhhx/q9ddf19ixYzVgwICDase2bfl8vv3ur66u1jPPPCNJGjt2rCTprLPO0jHHHKP8/PxDfwMAAAAAACSY4bqu63URAJAo27Zt0w9/+ENlZGSotbU1Zt+cOXNUXl6uv/71r1q/fr369u2ryy67TKecckr0dcXFxcrIyND69ev129/+Vnfffbc2b94sSRoxYoS+//3vKyMjQz/84Q9j2v7Vr36ld955R/Pnz9e9996rkSNHqqysTC+88IJ27NihIUOG6Prrr9eYMWP0zjvv6H//9381ZcoUbdy4UTU1Nbrssst03nnnadOmTfrDH/6gdevWKRgMaujQoZo5c2bSzh8AAAA6dv/996tXr15au3atamtr9eMf/1hvvvmmKisrNWbMGN18881elwgAncYUYwBp4aijjtKECRMkSZdccoluueUWNTQ0aNasWWpqalJpaan69++v//mf/9HatWujrysvL9eIESN0xRVXyDAMTZ48WdOnT9fFF1+sdevWafbs2erZs6fOO+88SdIJJ5ygW265RUOGDInpf/ny5XrooYfUs2dPXXfddaqpqdFvfvMb7d69O3rMihUrdOaZZ0qSHn/8cVmWpddff11r1qzRNddco6uuukp5eXkJPlMAAADojPXr1ys/P1933XWXSkpK9Kc//UnXXHON7r//fi1cuFDhcNjrEgGg05hiDCAtGIahgQMHasmSJTr66KM1duxYLVy4UA0NDWpoaNCTTz4ZPXb58uWaPHmypMgowWuuuUaSVFdXpyVLlqi8vFx7B1+vX79emZmZGjNmjF555RUNHTpUJ598crv+Fy5cKEm6/PLLNX78eNXU1Oi5555TRUVF9Jhp06bpnHPO0eeff64lS5Zo586dGjRokFzX1aJFizRy5MhoEAkAAADvhEIhNTY2Rn82MwxDZ5xxhvr06SNJMk1Tfj+/bgPoOvjEApA2DMPocPtpp52m0047Lfp83/sT7v0hT5JeffVVrV69Wueff74mTpyoP/3pT2pubo5bLbm5uZIUvdeh4zg655xzNHjwYK1cuVKfffaZ5s6dq9/97ncqKCg4pH4BAABw+Kqrq1VUVCTTjEzKW7dunc466yxJUm1trfr27bvfnz0BIBUxxRhA2sjJyZEkLViwQAsXLlRxcbFyc3O1ZMkSbdq0SRs2bNDzzz+vurq6A7bT2NiolStXqra2Nrptb7i3atUqffDBBwqFQjGvmTRpkiTp6aef1ptvvql58+YpJydHo0ePPmBfb7zxhsrLyzVw4EDl5+fLdV3t3LnzYN86AAAA4mj9+vUaPnx49Pm6des0bNiwdo8BoKsgIASQNk499VQNHjxYb7zxhh599FHl5ubqtttu08CBA/X4449r7ty5CgaD6t+/f4evP/fcczVy5Eh9+OGHqqur09ChQ6P7xowZo3HjxumLL77QAw88EHNvQUk6+uijdeONN6q+vl6PPfaY+vXrp//4j/9Qjx49DlhzIBDQO++8owcffFBffPGFzj77bI0ZM+bwTwYAAAAO2fr161VYWCgpMt04FApF/2C8bt26mPAQALoCVjEGAAAAAAAA0hgjCAEAAAAAAIA0RkAIAAAAAAAApDECQgAAAAAAACCNERACAAAAAAAAaYyAEAAAAAAAAEhjBIQAAAAAAABAGiMgBAAAAAAAANLY/w/+t8DeZSd97AAAAABJRU5ErkJggg==",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"step = 10\n",
"plot_all(cost_history, m, q, step)"
]
},
{
"cell_type": "code",
"execution_count": 125,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"22901 passi e 114505 gradienti calcolati per arrivare a distanza minore o uguale di 0.1 dall'ottimo\n"
]
}
],
"source": [
"near_opt(m, min_dist=1e-1, ge_per_step=mbs)"
]
},
{
"cell_type": "code",
"execution_count": 126,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA7sAAAHzCAYAAADhDgreAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAABXsElEQVR4nO3df3Rb9Z3n/9e15B/64V+ybIf8+tIEmISEkFCHtpg2JISQY1qGlgyFFM9pO7MMC2cZplsOybaFtpQSSjnlUGBpDwydmtlpu6HQw9Y7uGlCWNwyOMSZENMwQFvoNBDHlu1Ykn9Jut8/ZMlWbDlOYuleSc/HORzHsm/8kT920Ot+3p/3xzBN0xQAAAAAAHmkyOoBAAAAAAAw1wi7AAAAAIC8Q9gFAAAAAOQdwi4AAAAAIO8QdgEAAAAAeYewCwAAAADIO4RdAAAAAEDeIewCAJBlZ599tlwul8rLy1VVVaVLLrlEjz/+uGKx2Emv/eMf/yjDMBSJRDI6xmx9HQAAMoWwCwCABZ5//nkNDg7q3Xff1bZt23T//ffrb/7mb6weFgAAeYOwCwCAhSorK3X11Vfrpz/9qf7pn/5Jhw4d0i9/+UutWbNGFRUVWrRokb7+9a8nP/8Tn/iEJKmqqkper1e//e1v9c4772jDhg2qqamR3+/X5z73OfX39yevuf/++7VgwQKVl5frL/7iL/TrX/9akhSLxbRjxw4tXbpUNTU1uu666xQIBNJ+HQAAcglhFwAAG7j44ou1cOFC/b//9//k8Xj04x//WP39/frlL3+p//k//6eee+45SdJLL70kServ71cwGNTHPvYxmaap7du368iRI/rd736nP/3pT8mA/Oabb+qRRx5RR0eHBgcH9cILL+jss8+WJH3/+9/Xc889p7179+rIkSOqrq7WrbfemvbrAACQSwi7AADYxPz58xUIBHTZZZfpggsuUFFRkVatWqUbbrhBe/fuTXvdOeecoyuuuEKlpaWqra3Vl770peTnOxwOjYyM6I033tDY2JjOPvtsLV26VJL0+OOP695779XChQtVWlqqr3/969q5cyf7dAEAeYGwCwCATfz5z3+Wz+fTv/3bv2n9+vWqra1VZWWlHn/8cfX09KS97ujRo7r++uu1YMECVVRU6MYbb0x+/jnnnKOHHnpIX//611VXV6frr79eR44ckSS9++67+vSnP62qqipVVVVp+fLlcjgcOnr0aFaeLwAAmUTYBQDABjo6OvTnP/9Zl156qbZu3aqrr75af/rTnzQwMKCbb75ZpmlKkgzDmHLt//gf/0OGYej111/X8ePH9fTTTyc/X5K2bt2ql19+We+++64Mw9Cdd94pSVq0aJH+7//9v+rv70/+Nzw8rAULFkz7dQAAyCWEXQAALHT8+HH9n//zf3T99dfrxhtv1AUXXKDBwUH5fD6VlZXp1Vdf1f/6X/8r+fm1tbUqKirS73//++Rjg4OD8nq9qqys1J///Gc98MADyY+9+eab2r17t0ZGRlRWViaXy6Wiovj//m+++WZ95Stf0bvvvitJOnbsmH7xi1+k/ToAAOQSwi4AABb41Kc+pfLyci1atEj33nuvvvSlL+mpp56SJD322GO66667VF5erm9+85u67rrrkte53W595StfUWNjo6qqqvTKK6/o7rvv1v79+1VZWamrrrpKn/nMZ5KfPzIyom3btsnv92vevHnq7u7WfffdJ0n6+7//e1199dXatGmTysvL9dGPflT/9m//lvbrAACQSwxzcp0TAAAAAAB5gJVdAAAAAEDeIewCAAAAAPIOYRcAAAAAkHcIuwAAAACAvEPYBQAAAADkHcIuAAAAACDvOK0eQDYcOXLE6iHYkt/vV09Pj9XDwAmYF3tiXuyJebEf5sSemBd7Yl7shzmxp5nmZf78+WmvY2UXAAAAAJB3CLsAAAAAgLxD2AUAAAAA5B3CLgAAAAAg7xB2AQAAAAB5h7ALAAAAAMg7hF0AAAAAQN4h7AIAAAAA8o4z21/wscce0/79+1VZWakHH3xQkvSzn/1Mv/71r1VRUSFJuuGGG3TRRRdNufbAgQN66qmnFIvFdPnll+uaa67J5tABAAAAADki62H3sssu0+bNm/Xoo4+mPH7VVVfp6quvTntdLBbTk08+qa9+9auqqanR9u3b1dDQoIULF2Z6yAAAAACAHJP1Mubzzz9fXq/3lK97++23NW/ePNXX18vpdOqSSy5RR0dHBkYIAAAAAMh1WV/ZTeeFF17QSy+9pCVLluiv//qvpwTiQCCgmpqa5Ps1NTV66623sj1MAAAAAEAOsEXY3bRpk7Zs2SJJ+ulPf6of//jHuuWWW07779u1a5d27dolSdqxY4f8fv+cjDPfOJ1Ovjc2xLzYE/NiT8yL/TAn9sS82BPzYj/MiT2d7rzYIuxWVVUl/3z55Zfr/vvvn/I5Pp9Pvb29yfd7e3vl8/mm/fs2btyojRs3Jt/v6emZu8HmEb/fz/fGhpgXe2Je7Il5sR/mxJ6YF3tiXuyHObGnmeZl/vz5aa+zxdFDfX19yT+/+uqrWrRo0ZTPWbp0qd5//311d3crEonoN7/5jRoaGrI5TAAAAABAjsj6yu5DDz2kN954Q4ODg7r55pt13XXXqaurS3/84x9lGIZqa2t10003SYrv0/3BD36g7du3y+Fw6Itf/KLuvfdexWIxrV+/ftpQDAAACk/XgU69/kKrioeCGnN5dcGVTVqxeo3VwwIAWCjrYff222+f8tiGDRum/Vyfz6ft27cn37/oooumPX8XAAAUrq4DnfpgZ4u21FXJcLtlmlHt3dkiSQReAChgtihjBgAAOF2H2lq1rq5KhmFIkgzD0Lq6Kh1qa7V4ZAAAKxF2AQBATnOGg8mgm2AYhpzhkEUjAgDYAWEXAADktIjbK9M0Ux4zTVMRt8eiEQEA7ICwCwAActrKTU3a292fDLymaWpvd79WbmqyeGQAACvZ4pxdAACA05VoQvVMW6uc4ZAibo9WbmmmORUAFDjCLgAAyHkrVq8h3AIAUlDGDAAAAADIO4RdAAAAAEDeIewCAAAAAPIOYRcAAAAAkHcIuwAAAACAvEPYBQAAAADkHcIuAAAAACDvcM4uAAA4bV0HOvX6C60qHgpqzOXVx6+7QQs+tMTqYQEAwMouAAA4PV0HOvXBzhZtcUV1TY1bW1xRvfPjH6rrQKfVQwMAgLALAABOz6G2Vq2rq5JhGJIkwzB0WX2VDrW1WjwyAAAIuwAA4DQ5w8Fk0E0wDEPOcMiiEQEAMIGwCwAATkvE7ZVpmimPmaapiNtj0YgAAJhA2AUAAKdl5aYm7e3uTwZe0zT14tF+rdzUZPHIAACgGzMAAJjBid2WL7iySStWr5Gk5Ntn2lrlDIcUcXt06V/fRDdmAIAtEHYBAMC0kt2W66pkuN0yzaj27myRpJTAm/izJPn9fvX09Fgy3nwy000GAMDsUMYMAACmNV235XV1dFvOtOmOdPpgZwtHOgHAKSLsAgCAadFt2RrcZACAuUHYBQAA06LbsjW4yQAAc4OwCwAApjVdt+W93XRbzjRuMgDA3CDsAgCAaa1YvUbztjTrmWGHnusd0jPDDs3b0kyjpAzjJgMAzA26MQMAgLRO7LaMzJvuSKeV3GQAgFNG2AUAALAZbjIAwJmjjBkAAAAAkHcIuwAAAACAvEPYBQAAAADkHcIuAAAAACDv0KAKAAAAGdd1oFOvv9Cq4qGgxlxeXXBlE024AGQUYRcAAAAZ1XWgUx/sbNGWuioZbrdMM6q9O1skicALIGMoYwYAAEBGHWpr1bq6KhmGIUkyDEPr6qp0qK3V4pEByGeEXQAAAGSUMxxMBt0EwzDkDIcsGhGAQkDYBQAAQEZF3F6ZppnymGmairg9Fo0IQCEg7AIAACCjVm5q0t7u/mTgNU1Te7v7tXJTk8UjA5DPaFAFAACAjEo0oXqmrVXOcEgRt0crtzTTnApARhF2AQAAkHErVq8h3ALIKsqYAQAAAAB5h7ALAAAAAMg7lDEDAADMsa4DnXr9hVYVDwU15vLqgiubKOEFgCwj7AIAAMyhrgOd+mBni7bUVclwu2WaUe3d2SJJBN4cx00MILcQdgEAAObQobZWXVtXJcMwJEmGYWhdXZWeaWslGE0jVwIkNzGA3MOeXQAAgDnkDAeTQTfBMAw5wyGLRmRfyQDpiuqaGre2uKL6YGeLug50Wj20KQ61tWrdNDcxDrW1WjwyAOlkdWX3scce0/79+1VZWakHH3xQktTS0qLXXntNTqdT9fX1uuWWW+TxeKZce+utt6qsrExFRUVyOBzasWNHNocOAAAwKxG3V6YZTQm8pmkq4p76+qbQ5dIquDMclOFypzzGTQzA3rIadi+77DJt3rxZjz76aPKxVatWaevWrXI4HHr66af17LPP6sYbb5z2+rvvvlsVFRXZGi4AAMApW7mpSXt3tiRXAU3T1N7ufq3c0mz10GwnlwIkNzGA3JPVsHv++eeru7s75bELL7ww+efzzjtPr7zySjaHBAAA8pCV+0ATX+eZtlY5wyFF3B6t3NJsu5VKO8ilAMlNDCD32KpB1e7du3XJJZek/fi9994rSbriiiu0cePGbA0LAADkEDs0Elqxeg3hdhZyKUByEwPIPYZpmmY2v2B3d7fuv//+5J7dhJ///Od655139OUvf3lKUwdJCgQC8vl8GhgY0Le+9S194Qtf0Pnnnz/t19i1a5d27dolSdqxY4dGR0fn/onkAafTqUgkYvUwcALmxZ6YF3tiXuzHDnPy5F3b9emSsSmrhc+OFutvvnmfhSOzjh3mJZ1/73hV+55/Vo5QUFGPVw2f+rQuXHux1cPKCjvPS6FiTuxppnkpKSlJf12mBnQqXnzxRb322mu66667pg26kuTz+SRJlZWVWrt2rd5+++20YXfjxo0pK789PT1zP+g84Pf7+d7YEPNiT8yLPTEv9mOHOYkEejRW457m8eOWj80qdpiXdBZ8aIkW3PbfUx6z61jnmp3npVAxJ/Y007zMnz8/7XWWh90DBw7oF7/4hb7xjW+otLR02s8ZHh6WaZpyuVwaHh7WwYMHtWXLliyPFAAA5IL/DIb107d+pxIzqrEihy5YvEjL5tXach8oACBzshp2H3roIb3xxhsaHBzUzTffrOuuu07PPvusIpGI7rnnHknSueeeq5tuukmBQEA/+MEPtH37dg0MDOi73/2uJCkajerSSy/V6tWrszl0AACQA7oOdOr/Gw3po5Wl8peVSKapPe+9q/2BQX345r+3engAgCzKati9/fbbpzy2YcOGaT/X5/Np+/btkqT6+no98MADmRwaAADIA4faWnXtOYsVGjyu9491qyga01/UVOrt0moaCQFAgbG8jBkAkDlWHr8CWCFxbqu3olLeisrk43W9QxaOCgBgBcIuAOQpOxy/AmRbLp3bCgDILMIuAOSpQ22tunb87EpJMgxD6+qq9ExbK2EXeetMzm2lEgIA8gthFwDyVKKcczLDMOQMhywaEZB5iXD6TFurnOGQIm6PVm5pPmlopRICAPIPYRcA8hTlnChUK1avOeWASiUEAOSfIqsHAADIjJWbmrS3u1+maUrSRDnnpiaLRwbYjzMcTLkxJFEJAQC5jpVdAMhTp1vOCRQiKiEAIP8QdgEgj51OOSdQiM6ksRUAwJ4IuwAAZBAdfnMDlRAAkH8IuwAAZAgdfnMLlRAAkF9oUAUAQIYcamtNlsVKEx1+D7W1WjwyAADyH2EXAIAMocMvAADWoYwZAIAMocMv8tlM+9HZqw7ADgi7AICcd+ILa++Hlir4h3csf6FNh1/kq5n2o0tirzoAWyDsAgBy2okvut94/329sfNlbV51vsprqix9oU2HX+SrQ22tunaa/ejPjO9HT/cxfvYBZBNhFwCQ00580d313n/q2gU1+qDnmMorqyx/oU2HX+QjZzgow+VOeWxiP7o5w8cAIHtoUAUAyGknNoFyxqIqMgwVRaPJx3ihDcyt+H50M+WxxH70mT4GANlE2AUA5LQTX1hHihyKmaZiDkfyMV5oA3Nr5aYm7e3uT/7uJfejb2qa8WMAkE2UMQMAsiJT3VlPbAK1YvFC/fztd3TlqvMliaZQQAbMZj86e9UBWI2wCwDIuJk6t57pC+ApL7qrzpJny6V64Y/vyNnLC20gU2baj85edQB2QNgFAGTcTJ1b5+IFMS+sAQDAidizCwDIuBObSEk0jQIAAJlF2AUAZBzdWQEAQLYRdgEAGUd3VgAAkG3s2QUAZNxsOrcC2ZKpzuAAAHsh7AIAsiIXmkgRgjLHLt/bk3UGt8s4AQBnjrALAIAyezxSobPT93amzuCSbDNOAMCZY88uAACKh6B104SgQ+MhCKfPTt/bmTqD22mcAIAzR9gFAEAcj5RJdvreztQZ3E7jBACcOcIuAADieKRMstP3dqbO4HYaJwDgzBF2AQAQxyNlkp2+tytWr9G8Lc16Ztih53qH9MywQ/PGO4PbaZwAgDNHgyoAAJSbxyPlSudgu31v03UGt9s4AQBnhrALAMC4XDgeKcFOHY5nI1e+t9keZ67csACAXEQZMwAAOYjOwbkvecPCFdU1NW5tcUX1wc4WdR3otHpoAJAXCLsAAOQgOgfnPm5YAEBmUcYMAJhTlGVmR7xzcDQl8NI5OLc4w0EZLnfKY9ywAIC5w8ouAGDOUJaZPXQOzn0cdQQAmUXYBQDMGcoys2emI3SQG7hhAQCZRRkzAGDOUJaZXVZ3OJ6uZH3dxissG0+u4agjAMgswi4AYM6wj7RwpDv66N8rK7XgQ0usHl7OsPqGBQDkM8IuAGDOrNzUpL07W5KlzMmyzC3NVg8tK7LZnMvqRmCH2lp17TQl6798/lktuO2/Z20cAACkQ9gFAMyZQi7LTLfSKWnOn382v1Y66UrWHcFgVr4+kG1W32ACcOoIuwCAOVWoZZnpVjqfaWud8+9HNr9WOulK1qMeb1a+PpBNdrjBBODU0Y0ZAIA54AwHU4KflLnmXNn8Wumk6yTc8KlPZ20MQLbQaR7ITazsAgAwB7LZnMsOjcDSlaxfuPZi9fT0ZG0cQDbQaR7ITYRdAADmQDabc9mlEVihlqyj8NjhBhOAU0fYBQBgDmSzOVchNwIDrGCXG0wATk3Ww+5jjz2m/fv3q7KyUg8++KAkKRgM6nvf+56OHTum2tpa/cM//IO83qkNLl588UX9/Oc/lyR95jOf0WWXXZbNoQMAMKNsrnSyqgpkDzeYgNyU9bB72WWXafPmzXr00UeTjz333HO64IILdM011+i5557Tc889pxtvvDHlumAwqJ07d2rHjh2SpG3btqmhoWHaUAwAAADMJW4wAbkn692Yzz///CkBtaOjQ+vWrZMkrVu3Th0dHVOuO3DggFatWiWv1yuv16tVq1bpwIED2RgyAAAAACDH2GLP7sDAgKqrqyVJVVVVGhgYmPI5gUBANTU1yfd9Pp8CgcC0f9+uXbu0a9cuSdKOHTvk9/szMOrc53Q6+d7YEPNiT8yLPTEv9pNPc/LvHa+q4/ln5QwNKuIp19pPfVoXrr3Y6mGdlnyal3zCvNgPc2JPpzsvtgi7kxmGMeXswFO1ceNGbdy4Mfk+RyBMz+/3872xIebFnpgXe2Je7Cdf5qTrQKc+2NmiT9ZVyfA6ZJoh7X3yEfUP5OY+zXyZl3zDvNgPc2JPM83L/Pnz016X9TLm6VRWVqqvr0+S1NfXp4qKiimf4/P51Nvbm3w/EAjI5/NlbYwAAKBwHGprTXbeleI349fVVelQW6vFIwMAzJYtVnYbGhq0d+9eXXPNNdq7d6/Wrl075XNWr16tf/mXf1EwGJQk/fu//7u2bt2a7aECAIAs6DrQqddfaFXxUFBjLq8uuLIpqyuqznBQhsud8phhGHKGQ1kbAwDgzGQ97D700EN64403NDg4qJtvvlnXXXedrrnmGn3ve9/T7t27k0cPSdI777yjX/3qV7r55pvl9Xp17bXXavv27ZKkLVu20IkZAIA8lCgh3lJXJcPtlmlGtXdniyRlLfBG3F6ZZjRla5Vpmoq4PVn5+gBgB0MjYwqGRlXry81/+7Iedm+//fZpH7/rrrumPLZ06VItXbo0+f6GDRu0YcOGTA0NAADYwKG2Vl07TQnxM22tWQu7Kzc1ae/OlmQps2ma2tvdr5VbmrPy9QEgW4aGx9TdG9LR3qCO9obU3RtUd29I3YGgBgZHNM/v1be/dIXVwzwttihjBgAASLBDCXEiVD/T1ipnOKSI26OVW3KzOVUmzHWZudVl60C+Cw2NJgPt5LfdvUENhkbTXud0Fqmk2CHTNM+4ibAVCLsAMEd4sQbMjdmUEGfj923F6jVT/k5+z+e+zNwOZetArjNNU6Gh0fGV2ZCO9gTVHZhYpQ2G0wfaYmeR6mq8qqvxqL7Go7oar+rH36+ucKmoKPdCbgJhFwDmAC/WgLlzshJiq37f+D2Pm+syczuUrQO5wDRNDYZG1X1CuXFilTY8PJb22pJix3iY9U55W1leltOBdiaEXQCYA7xYA+bOyUqIrfp94/c8bq7LzO1Qtg7YhWmaOh4cmabcOB5uh0Yiaa8tLXGq3u9Rnc87vkKbCLVeVZaX5mQZ8pki7ALAHODFGjC3pishTrDq943f87i57lRN52sUGtM01T84rO6ekI4GJvbOJlZrR0ajaa91lTpV5/dOWpmNlx3X+Tyq8BZmoJ0JYRcA5gAv1oDsser3jd/zuLnuVE3na+SjWMxU//GheIAdD7QT+2hDGh1LH2g9ruLxfbOeSXtp42+97hIC7Skg7ALAHODFGpA9mfh9m03jKX7P4+aqU/Xk7/nRkZgOvderhV4Pna+RM2IxU4GBoSl7aLt746F2LBJLe63XXTKlGVTd+Pted0kWn0V+I+wCwBzgmBIge+b69222jaf4PZ8wU5n5bEz5nvtc2tvdr3nX/FVBfj9hX9FoTL3jgfbEcuNjgbAi0fSBtsJTqjr/+Kqsz5PS8djtItBmA2EXAObImb74AzB7c/n7diqNp/g9nxs0+4KdRKIx9faH1d0bUujgB/r9u93qDsRDbU9fSNGomfbayvKyKc2g6mo8qvN55CorzuKzwHQIuwAAoKDReCr7+J4j2yKRmI71TXQ17u4N6WggpO6eoHr6w4rF0gfa6oqyKXtoE02hykqJU3bG7AAAgIJG46ns43uOTBgbi04KtKGU43t6+8My0+RZw5Bqqlyq83m1eEGNKjwO1fu9qvN5Vetzq7SEyJSrmDkAsMBsmuHAHpir/Efjqezje47TNToW1bHA5PNnJ/bQBgaGZgy0/mp3SmfjxOpsnc+j4mKHJMnv96unpyeLzwiZRNgFgCybbTMcWI+5mp3JNwQcPr/O/cSGnPr+0Hgq+/ieYyYjo5GUrsZHeybKjvsGhtJeV1RkqHY80J54ZI+/2q1ipyOLzwJ2QNgFgCyjMUvuYK5O7sQbAsXFY/pVDt4QoPFU9vE9L2xDI2M61htKrsoenRRu+48Pp73OUWSMr9Cmhtn6Gq9qqtxyOouy+Cxgd4RdAMgyGrPkDubq5LghACCd8PDYRDOoZKiNv388OJL2OqejSLU+96TOxuPNofxe1VS65HAQaDE7hF0AyDIas+QO5urkuCEAFLbQ0OhEM6iekI4GJvbSDoZG017ndBaNnz3rGe90PHEGra/SraIiI+21wGwRdgEgy2jMkjuYq5PjhgCQ30zTVGhoVEd7JpUbJ/fRBhUaGkt7bUmxQ7U+T8qRPfXjR/hUVbgItMg4wi4AZBmNWXIHc3Vy3BAAcp9pmhoMjSbD7OROx929IYWH0wfa0hLHRFfjZJiNB9vK8jICLSxF2AUAC9CYJXcwVzM78YaA0+fWOdwQAGzHNE0dD47oaE9QRwOhSXtp42+HRyJpry0rdU45sqfeF39bWV6aUtkB2AlhFwAAnJHJNwTm4oxKzjYGTk8sZmpgcHj8mJ7xMNsT73Dc3RvUyGg07bWusuITyo0T4darck8JgRY5ibALAABsg7ONgZnFYqb6jw9NLTcOhNTdG9LoWPpA63EVjzeD8qS8ravxyOsm0CL/EHYBAIBtcJQREA+0gYHw+HE9qUf2dAdCikRiaa/1uktU7x9fnfUlyo7jodbrLsniswCsR9gFAAC2wVFGKBTRaEwfHDuuw28fjXc6nnRkz7FAWJFo+kBb4S2d2EPr8yTDbZ3PI7eLQAskEHYBAIBtcJQR8kkkGlNvX3hSuXE81B7tCaqnL6xozEx7bWV52bTlxnU1HrlKi7P4LIDcRdgFAAC2wVFGyDWRSEzH+iaXG090Ou7pDys2Q6D1V3vkr3JNdDieFGpLS3iZDpwpfosAAIBtcLYx7GhsLKpjfaGUIJs4tqe3PywzTZ41DKmmyqU6n1f1/kmrsz6van1uLZg/74y7lwNIj7ALAABshbONYYWR0YiOBcLJvbNHe4LJsuPAwNCMgdZf7Z50Bu3EebS11R4VFzuy+0Rw2joPdmn3vkPqCY3I64ip6dK1WrNqhdXDwhkg7AIAAKAgjIxGkiuy3ZNWaY8GQuobGEp7XVGRodpqd0qQTazS+qvdKnYSaHNd58EutbQfVv2qdfKMjSlmmmpp75AkAm8OI+wCAAAgbwyNjE00g5q0h/Zob0gDg8Npr3MUGfEVWr9XdZOO7Kn3e1VT5ZbTUZTFZ4Fsa23fp+pl61OOPatetlat7XsIuzmMsAsAADALnQe71Ppyh4LRIkocLRYeHosH2J7x1dnAxGrt8eBI2uucjiLV+tzJVdnJq7Q1lS45CLQFKxgx5JnUBV6KB95QxEhzBXIBYRcAAOAkEiWO1cs3yGMYlDhmQWhodGLfbG9IRwNBdffEV2iD4dG01zmdRfGzZ08oN66v8cpX6VJREeEFU3mdpmInbMw2TVMeZ/pu2rA/wi4AAMBJUOI490zTVDA8Om25cXdvUKGhsbTXlhQ7xrsap4bZ+hqPqioItDh1TY0NamnvUP2qRknxn8++wx1qbmyweGQ4E4RdAACAk6DE8fSYpqnB0Oh4iXEiyE6E2qHh9IG2tMQRD7K++L7ZuhqP6sf30lZVlCVvPABzIXHTavdrezUQHJHHaaq5sYGbWTmOsAsAAHASiRLHyQGLEsc40zQ1MDgSD7CB0MRe2vEjfIZHImmvLSt1phzZUze+Oltf41WFt5RAi6xas2qFrtiwjrOP8whhFwCAHNB1oFOvv9Cq4qGgxlxeXXBlE2fRZlGixLF62VoZhlFwJY6xmKmBweHksT3Jo3vGw+3IaDTtta6yYtVPCrKT35Z7Sgi0ADKGsAsAgM11HejUBztbtKWuSobbLdOMau/OFkki8GZJopSxtX2PQhEjL0scYzFTfceHUs6hTbw9FghpdCx9oPW4isdLjcfLjhOh1u+Rx0WgBWANwi4AADZ3qK1V19ZVpTRHWldXpWfaWgm7WbRm1YqcD7exmKnAQDi+d7Znouw4sUobicTSXlvuKZlyZE99jVe1Po+87pIsPgsAmB3CLgAANucMB2W43CmPGYYhZzhk0YhgZ9FoTL394fGV2fje2f7BMf3pSEDH+kKKRtPvM67wlqYc2VM/aS+tu6w4i88CAM4cYRcAAJuLuL0yzeiU5kgRt8fCUcFKkWhMvX3hKeXG3b1B9fSFFY2lD7RVFWXJI3vqJ63S1tZ45Col0ALIH4RdAABsbuWmJu3d2aJ146XMpmlqb3e/Vm5ptnpoyKCxSFQ9kwLt5CN7evvDis0QaKsrXar3eVTnjwfapWefJVdxTHU1HpWW8PIPQGHgXzsAAGwusS/3mbZWOcMhRdwerdzSzH7dPDA2Fo13NJ7myJ7e/rDMNHnWMKSaKvf4vllPyl7aWp9HJcWOlM/3+/0cpwKg4BB2AQDIAStWryHc5qiR0YiOBRIrtJNWaQNBBQaGZgy0/mp3SjOoxHm0tdUeFZ8QaDH3Og92qfXlDgWjRfI6Ymq6dG3ONykDCglhFwAA4AwNj0SSq7OTy427e4PqOz6c9rqiIkO11e54ubFvohlUvd8jf5VHTmdRFp8FJus82KWW9sOqXr5BHsNQzDTV0t4hSQReIEcQdgEAAGZhaHhsPNCGUlZpj/aGNDCYPtA6igz5E2fP+uJBNlF2XFPlltNBoLWj1vZ9ql62PuXIr+pla9XavoewC+QIwi4AAMC48NDo+Irs+CptIKSjPfFQezw0kvY6p6NItT53yrE9idJjX6VLDgJtzglGDHkmdUCX4oE3FDHSXAHAbgi7AACgoATDo5NWZVPLjoPh0bTXFTuLkkf2pO6hjQfaoiJ7hqCuA51666XdigZ6NOby6oIrm9j/PQtep6mYaU458svjTN8FG4C92CLsHjlyRN/73veS73d3d+u6667TVVddlXysq6tL3/nOd1RXVydJ+shHPqItW7ZkfawAAMDeTNNUMDw67ZE93b1BhYbG0l5bUuyIB1ifR/X+8TDrix/fU1Vh30CbTteBTn2ws0WfWVinsRq3TDOqvTtbJInAexJNjQ1qae9Q9bK1ySO/+g53qLmxweqhAZglW4Td+fPn64EHHpAkxWIx/d3f/Z0uvvjiKZ+3fPlybdu2LdvDAwAANmOapo4HR1KP7OkN6uj4ntqh4fSBtrTEMW25cV2NR1XlZSkrebnuUFurrh0/n1mKl+Guq6vSM22thN2TSOzLbW3fo1DEkMdpqrmxgf26QA6xRdid7PXXX9e8efNUW1tr9VAAAICFTNPUwODI+KrsRDOoxDm0wyORtNeWlTqnPbKnvsarCm9pXgXamTjDQRkud8pjhmHIGQ5ZNKLcsmbVCsItkMNsF3bb29vV2Ng47cf+4z/+Q3fccYeqq6vV3NysRYsWTft5u3bt0q5duyRJO3bskN/vz9h4c5nT6eR7Y0PMiz0xL/bEvNjPqc5JLGYqMBDS+93H4/8dO64jRwf0/rH4+yOj6QOtx12i+XWVOquuQmfVVuisuork+xXe/FqhPV1On1/FxWMqMgyVlJRIit9EcPrc/O7YAP+G2Q9zYk+nOy+GaaY7yjz7IpGI/u7v/k4PPvigqqqqUj4WDodVVFSksrIy7d+/Xz/60Y/08MMPz+rvPXLkSAZGm/v8fr96enqsHgZOwLzYE/NiT8yL/Uw3J7GYqb7jQ/GV2Z6gugPBZMfjY4GQRseiaf8+r7tkotx40j7a+hqPPK4SAu1JJPbsXrGwTmNjYzJNU3u7+zVvSzNlzDbAv2H2w5zY00zzMn/+/LTX2Wplt7OzUx/60IemBF1JcrsnSnAuuugiPfnkkzp+/LgqKiqyOEIAADCdWMxUb39Yf+oe1tu/PxLfO9sTD7XH+kKKRGJpry33lKTdQ+txlWTxWeSfRKB99qXdigSOK+L2aCVBF0CBsFXYnamEub+/X5WVlTIMQ2+//bZisZjKy8uzPEIAAApXNBpTb384uXc2vo82vn/2WF9I0Wj6YrHK8lLV+SYCbf14oK2t8chdVpzFZ1F4Vqxeo3Ubr2C1CkDBsU3YHR4e1sGDB3XTTTclH2tra5Mkbdq0Sa+88ora2trkcDhUUlKi22+/ndIlAADmWCQaU09faKIZ1KTzaHv7worG0gfaqooyLaivkq+yNL46Ox5ua2s8cpUSaAEA2WWbsFtWVqZ//Md/THls06ZNyT9v3rxZmzdvzvawAAAn6DrQqddfaFXxUFBjLq8uuLKJksgcMxaJqicQ1tHxrsbxfbTxgNvbH1ZshkDrq3SlrM4m3tb6PCotcbLfDQBgG7YJuwAA+0s0u9lSVyXD7ZZpRrV3Z4skEXhtZmwsOnEG7XgzqMSRPb39YaVrT2kYUk2VO2XfbCLU1vo8Kil2ZPeJAABwmgi7AIBZO9TWqmvrqpLbSAzD0Lq6Kj3T1krYtcDIaETHAlPLjbt7Q+o7PjRjoPVXu+OdjX2elPNo/T63ip35G2g7D3ap9eUOBaNF8jpiarp0LeeoAkCeIuwCAGbNGQ7KcLlTHjMMQ85wyKIR5b/hkcikFdp4kO0eD7d9x4fTXldUZKjW546XGfs8qvMnyo498ld55HQWZfFZ2EPnwS61tB9W9fIN8hiGYqaplvYOSSLwAkAeIuwCAGYt4vbKNKMpDQJN01TE7bFwVLlvaHhsYlU2EWx74mXHA4Mjaa9zOAz5qz0pe2cTR/fUVLnldBReoJ1Ja/s+VS9bn1KZUL1srVrb9xB2ASAPEXYBALO2clOT9u5s0brxUmbTNLW3u18rtzRbPTTbCw+NJvfOTj6yp7s3pOOh9IHW6ShSrc+TXJWNlxzHA62v0iUHgXbWghFDnhNOcjAMQ6GIvU93oPQaAE4PYRdAxvFCLX8k9uU+09YqZzikiNujlVua2a87LhgenVRqPPH2aG9IwfBo2uuKnUWq842vzvo9KefR+ipdKiqydxjLFV6nqZhpTqlM8DjTd5+2GqXXAHD6CLsAMooXavlnxeo1BRtuTdPUYGg02dU49dieoEJDY2mvLSl2pHQ4nrxKW1VeVjCB1sqbX02NDWpp71D1srXJyoS+wx1qbmzIytc/HZReA8DpI+wCyCheqCHXmKap48ERdQfGg2xidXb8HNqh4fSBtrTEeUK58cQe2qryspQVxUJk9c2vxNdobd+jUMSQx2mqubHB1v8W5WrpNQDYAWEXQEbxQg12ZJqm+geHU8qNjybfhjQyGkl7ravUGe9s7JsIsokjfCq8pQUfaGdih5tfa1atsHW4PVEull4DgF0QdgFkFC/UYJVYLBFoU4/sSfx5dCya9lp3WXEywCbDbE18L225p4RAe5q4+XXqcrH0GgDsgrALIKN4oYZMisVM9fSFJ5pBBcaP7Bk/wmcsEkt7rdddknJUT3KVtsYrr7ski8+icHDz69TlYuk1ANgFYRdARvFCDWcqFjPV2x+e1Nl4oty4py+ssUj6FdoKT2myGVT8HNqJ5lAeF4E227j5dXpyrfQaAOyCsAsg43ihhpOJRmPq7Q+Pn0MbTHnb0xdSNJp+5a+yvFR1vvEje2ripceJUOsqKz7tMXUd6NTrL7SqeCioMZdXF1zZVLBdqOcKN78AANlE2AUAZEUkElNPfyi5Ktvdk+hwHFRvX1jRWPpAW11RNqnc2KN6n1d1fq+Wn7tYoeDAnI+160CnPtjZoi11VTLcbplmVHt3tkgSgfcMcfMLAJAthF0AwJwZi0TVEwhPKjUOJo/w6e0Py5xha6av0jXlyJ76Go9qfR6Vlkz/vytXWbFCwbl/HofaWnVtXVVK1+B1dVV6pq2VsAsAaVh5jjYwHcIuAOCUjI5FdSwwudx4osNxYCB9oDUMyV/tTnY1jgfbeKit9XlUUuzI7hOZgTMclOFypzxmGIac4ZBFIwIAe7P6HG1gOoRdAMAUI6MRHRtfke0OhJJ7aLt7Q+o7PjRjoK0dP66nzjdxZE+9zyu/z61ip30C7Uwibq9MMzqla3DE7bFwVABgX3Y4Rxs4EWEXAArU0MiYjiVWZgPjZcfj4bb/+HDa64qKDNX63FPKjetqPPJXeeR0FmXxWWTGyk1N2ruzRevGS5lN09Te7n6t3NJs9dAAwJY4Rxt2RNgFgDw2NDyWLDOevDrbHQhqYHAk7XUOh6Ha6tQjexKB1lflltOR+4F2Jol9uc+0tcoZDini9mjllmb26wJAGpyjDTsi7AJAjgsPjeropH2z3ZOaQw2GRtNe53QUqdbnSR7ZU+/zJDse11S5VVRU2HfjV6xeQ7gFgFniHG3YEWEXAGzONE2FxgNt9wnn0Hb3hhQMpw+0xc6iZICtH28MldhHW13hKvhACwCYG5yjDTsi7AKADZimqcHQ6JQgmzi2Jzw8lvbakmJHypE9k/fSVpWXEWiRUSceNXLDJzdqyeKFVg8LgAU4Rxt2Q9gFgCwxTVPHgyOTyo1TS4+HRiJpry0tccbLjX0Te2fjodaryvLSlD1SQLZMd9TID9s69dmLB3jBa1OcgwqgkBB2AWAOmaap/sHhKUE2/n5II6PpA62r1Kk6/8Te2cRe2jqfRxXeMwu0XQc69foLrSoeCmrM5dUFVzaxHxVnbNqjRpavVWv7CwQoG+IcVACFhrALAKcoFjPVf3woXm4cmLpKOzoWTXutx1U86aieRLlxfJXW6y7JyApt14FOfbCzRVvqqmS43TLNqPbubJEkAi/OCEeN5BbOQQVQaAi7ADCNWMxUYGAouSp7PPy23v3Pnvj7gZDGIrG013rdJSlhdvIeWq+7JIvPIu5QW6uuHT8vVoq/wF1XV6Vn2loJuzgjHDWSW7g5AaDQEHYBFKxoNKbAwNC0R/YcC4QViaYPtBWe0niQ9cfLjCd3PHa7sh9oZ+IMB2W43CmPGYYhZzhk0YiQL6Y9auR3HfpsBo4aYa/pmePmBIBCQ9gFkNci0Zh6+8MTR/b0xEuPj/aG1NMXUjSa/kVeZXlZshnU2Yvq5C0zkuHWVVacxWdxZiJur0wzOuUFbsTtsXBUyAfTHTVy01WXz3k3Zvaazg3OQQVQaGYVdmOxmDo6OmQYhhoaGlRUVCRJ+u1vf6uPfexjGR0gAJxMJBJTT38oHmQTq7OBkLp7gurpDysWSx9oqyvKptlDGw+0ZaUT/0T6/X719PRk4+nMuZWbmrR3Z4vWjZcym6apvd39Wrml2eqhIQ+ceNRIJn5X2Gs6NzgHFUChmVXYfeSRR+T3++V0OvX888/r1ltv1bx589TW1kbYBZAVY2NRHesLTWkGdbQ3qN7+sMw0edYwpJoql+p8E82g4uHWq1qfW6Ul+V/gktiX+0xbq5zhkCJuj1ZuaWa/LnIGe03nDuegAigks3qVFwgEdNttt0mS1q9fr0ceeUR/9Vd/ldGBASg8o2NRHQuMlxv3Tn4bUmBg5kDrr3bHg6wv9cieWp9HJcWO7D4RG1qxeg3h1kLsNz0z7DU9M50Hu7R73yH1hEb4+QNQUGYVdiORiMbGxlRcXKza2lpt27ZNDz30kN57771Mjw9AnhkZjUw0gwrEz57t7gnqaCCkvoGhtNcZhlTr80w9ssfnld/nVrGTQAt7Yr/pmWOv6elL/PzVr1onz9gYP38ACsqMYTcajcrhcOjzn/+8QqGQqqqqJEkul0t33nmnXn755WyMEUCOGRoZ07FJ5cZHJ4Xb/uPDaa9zFBnjK7TeSeXG8aN7aqrccjqLsvgsgLnBftMzx17T08fPH4BCNmPY/fa3v6077rhD55xzzpSPFRUV6ROf+ETGBgbA3sLDY5OO6kk9tud4cCTtdQ6Hodrq8SN7EmXH46u0NVVuORwEWuQX9pvODfaanh5+/gAUshnD7tlnn62vfe1r2r59u3w+nyTpjTfe0E9+8hN985vfzMoAAVgnNDQ6pRlUogR5MDSa9jqns2j87Nnx1VmfR3X+eKj1VbpVVMSLLBQO9pvCSomfv8n4+QNQKGYMu83NzWpra9PXvvY1bd26Vbt379Z7772nq6++OlvjA5BBpmkqNDSaPLLnaG9I3YkGUT1BhYbG0l5b7CxKlhvXn/C2usJFoAXGsd8UVkr8/NWvapQkfv4AFJSTNqg677zz5Ha79fDDD2vdunW68847VVJSko2xAZgDpmlqMDQ6TYfj+CpteDh9oC0tcSS7GifCbCLQVpaXEWiBWWC/KayU+Dnb/dpeDQRH+Pk7CTqnA/llxrD7wAMP6I033tBVV12l6667Tk888YQOHTqkiy66KFvjAzALpmnqeHAktRlUbyhZcjw0Ekl7bWmJM35Uz6Qje+p98beV5aUppZcATg/7TWGlNatW6IoN69TT02P1UGyNzulA/pkx7J511ln6r//1v8rr9UqS6uvrdf/996u7u1ubN2/OygABxJmmqf7jw/G9s4GJvbOJcDsyGk17ravUOb5nNlFunOh07FW5p4RACwAoeHSuBvLPjGH3xhtvTHl/8eLFuueee3TfffcRdoEMiMVMHQsEdfidYynNoOL7aEMaHUsfaD2u4uRRPZPf1tV45HUTaAEAmAmdq4H8c9I9uyfy+Xx0YgbOQCxmKjAwlBpmE52OAyFFIrG013rdJfEQ6/eq3pc4izYear1u9tIDAHC66JwO5J9TDruS5HK55nocQF6JRmPqHRhKDbLjwfZYIKxINH2grapwyV/tipcc+yafR+uR20WgBQAgE+icDuSf0wq7AKRINKbe/rCO9kxqBhWI76Ht6QspGk1/J7iyvGzacuM6n0eLFp5FExEAALKMzulA/iHsAjOIRGI61hea0gyquzeknv6wYrH0gba60jXe1diTch5trc+jslJ+9QAAsBs6pwP5hVfcKHhjY9FkoD066cieo71B9faHZabJs4Yh1VS5VDe+d3ai3NirWp9bpSX8egEAAABW4dU4CsLoWDRZZpxcpe2Jvx8YGJox0Pqr3ckje5KrtL54yXFxsSO7TwQAAADArNgq7N56660qKytTUVGRHA6HduzYkfJx0zT11FNPqbOzU6Wlpbrlllu0ZMkSi0YLuxkZjUxbbnw0EFLfwFDa64qKDNVWu5NBdvIeWn+1W8VOAi0AAFbrPNil1pc7FIwWyeuIqenStXlVcpzvzw+wgq3CriTdfffdqqiomPZjnZ2d+uCDD/Twww/rrbfe0hNPPKFvf/vbWR4hrDQ0MjbRDGpSqD3aG9LA4HDa6xxFRnyF1u9Nlh0n9tDWVLvldBRl8VkAAJCbrApknQe71NJ+WNXLN8hjGIqZplraOyQpLwJhvj8/wCq2C7sz2bdvnz7xiU/IMAydd955CoVC6uvrU3V1tdVDwxwKD49NOrInEWbj7x8PjqS9zukoUq3PPamzsVf1/vgqbU2lSw4CLQAAp83KQNbavk/Vy9Ynz8A1DEPVy9aqtX1PXoTBfH9+gFVsF3bvvfdeSdIVV1yhjRs3pnwsEAjI7/cn36+pqVEgEJgSdnft2qVdu3ZJknbs2JFyDSY4nU7LvjfB0IiOdA/o/e7jev/Ycb0//ucj3cd1PJh+hbbY6dC82nKdVVep+XUVOquuQmfVVuqsugr5fR45inI/0Fo5L0iPebEn5sV+mBN7mot52f3aIdWvWpcMZJJUv6pRu1/bqys2rDvTIc5ozFEmd2nplMeHHGU5/fOWmJd8fX65iH/D7Ol058VWYfeee+6Rz+fTwMCAvvWtb2n+/Pk6//zzT/nv2bhxY0pQ5szS6fn9/ox9b0zTVDA8Om25cXdvUKGhsbTXlhQ7kmfOTj6yp77Go6oKl4qKjGmuGlFfIP2qby7J5Lzg9DEv9sS82A9zYk9zMS89wRF5xqb+/3sgOJLxOS+ODmtkZCQlaJumKWd0OKd/3hLzkq/PLxfxb5g9zTQv8+fPT3udrcKuz+eTJFVWVmrt2rV6++23U8Kuz+dLeZK9vb3Ja5B9pmlqMDSaLDM+OmkvbXdvSOHh9IG2tMSR7GqcOLKnfnwvbWV5WZpACwAArOJ1moqZ5pRA5nGmP3N+rjQ1NqilvUPVy9bKMAyZpqm+wx1qbmzI+NfOhnx/foBVbBN2h4eHZZqmXC6XhoeHdfDgQW3ZsiXlcxoaGvSv//qvamxs1FtvvSW3281+3QwzTVMDgyPxQBuY1OF4/O3wSCTttWWlzuSqbLLT8Xi4rfCWpvzPEgAwe3RthRWsDGSJn+/W9j0KRQx5nKaaGxvy5uc+358fYBXbhN2BgQF997vflSRFo1FdeumlWr16tdra2iRJmzZt0po1a7R//37ddtttKikp0S233GLlkPNGLGZqYHA4GWITQbZ7PNyOjEbTXusqK045qqd+0tE95Z4SAi0AzDG6tsIqVgeyNatW5PXPeL4/P8AKtgm79fX1euCBB6Y8vmnTpuSfDcPQ3/7t32ZzWHkjFjPVf3xIRyetyvYHx/SnIwEdC4Q0OpY+0HpcxfFVWf942XFildbvkcdFoAXyDauG9kbXVliJQAYgl9gm7OLMxWKmAgPh5N7ZeKidWKWNRGJpry33lEyszvq8qvPHV2lrfR553SVZfBYArMSqof0FI4Y8J9xkNAxDoQg3HgEAmIywm2Oi0Zh6B4bU3TPeECoQTDaFOhYIKxJNH2grvKWT9tB6dc7Z8+QqianO55HbRaAFwKphLrCySRAAALmEsGtDkWhMvX3hZLlxcg9tb1A9fWFFY+lf0FRVlCWP7EmWG9d4VFvjkau0OOVzaa0O4ESsGtofXVsBAJgdwq6FjvYG9cGxYEqY7e4Nqac/rNgMgba60qV6nye+Sju+jzZRglxawpQCOH2sGtqf1U2CAADIFSQjC/3gJx3645/7pzxuGFJNlStldTZRflzr86ik2JH9wQIoCKwa5gaaBAEAcHKEXQude3aNPK6S8TNoJ86jra32qJhAC8AChbBqSLdpAAAKA2HXQjdctcrqIQDAFPm8aki3aQAACkeR1QMAACBb4t2m107TbXqfxSMDAABzjbALACgYwYiR0nxLots0AAD5irALACgYXqcp00ztLE23aQAA8hNhFwBQMJoaG9R3uCMZeBPdppvoNg0AQN6hQRUAoGAkmlD9+BfP6PfHBhQdG9HSuipJyywdFwAAmHuEXQBAwTH8i9Vw6cRZwnRkBgAg/1DGDAAoKHRkBgCgMLCyCwAoKMGIIU+OdmTuPNil1pc7FIwWyeuIqenStaxGAwCQBmEXAFBQvE5TMdNMOYIoFzoydx7sUkv7YVUv3yCPYShG+TUAADOijBkAUFBytSMz5dcAAJwaVnYBAAUn1vOu9j17SLHRYS2ZV63Pf+Yq26+O5nL5NQAAViDsAgAKRqIUuObSLfKPd2LuO9xh9bBmJVfLrwEAsAplzACAgpHLpcC5Wn4NAIBVWNkFABSMXC4FTpRZt7bvUShiyOM01dzYYPvyawAArELYBQAUjFwvBV6zagXhFgCAWaKMGQBQMCgFBgCgcLCyCwAoGJQCAwBQOAi7AICCQilwfuo82KXWlzsUjBbJ64ip6dK1zDMAFDjCLgAAyGmJI6Wql2+QxzAUM021tMePlCLwAkDhYs8uAADIabl8pBQAIHMIuwAAIKcFI0ZKh20pd46UAgBkDmEXAADkNK/TTHbYTsilI6UAAJnBnl0AAGyGZkunpqmxQS3tHclS5sSRUs0cKQUABY2wCwCAjdBs6dRxpBRyxYk3sm745EYtWbzQ6mEBeYuwCwCAjcSbLa2fptnSHsLbDDhSCnY33Y2sH7Z16rMXD/CzC2QIYRcAABsJRgx5aLYEm6G0/sxNeyNr+Vq1tr/A9xLIEMIuAAA24nWaiplmSndhmi3BSpTWzw1uZAHZRzdmAABspKmxQX2HO5LdhRPNlppotgSLcI7x3KBrOJB9rOwCAGAjNFuC3bAiOTem7Rr+uw59lhtZQMYQdgEAsBmaLcFOKK2fG9PdyLrpqsvpxgxkEGEXAAAAaXGO8dw58UaW3+9XT0+PhSMC8hthFwAASKLjLqZHaT2AXEXYBQAAdNzFjCitB5CL6MYMAADouAsAyDuEXQAAoGDESGlAJNFxFwCQ2yhjBgAAp9xxl/29AAC7I+wCKBi8OAfSO5WOuzPt771iw7psDz0v8e8VAJw5wi6AgkDzHWBmp9JxN76/d/00+3v3EHbnAP9eAcDcIOwCKAgzvTjnxSMQN9uOu8GIIQ/7e0/qdFdn+fcKAOaGLcJuT0+PHn30UfX398swDG3cuFFNTU0pn9PV1aXvfOc7qqurkyR95CMf0ZYtW6wYLoAcxItzYO6c6v7eQnQmq7P8ewUAc8MWYdfhcKi5uVlLlizR0NCQtm3bplWrVmnhwoUpn7d8+XJt27bNolECyGW8OAfmzqns7y1UZ7I6y79XADA3bHH0UHV1tZYsWSJJcrlcWrBggQKBgMWjApBPmhob1He4Q6YZf7GYeHHexItz4JStWbVCzY3LVHR4j8Kv71HR4T1qblxGie0kZ3KUE/9eAcDcsMXK7mTd3d36wx/+oHPOOWfKx/7jP/5Dd9xxh6qrq9Xc3KxFixZZMEIAuehUmu8AOLnZ7u8tVGeyOsu/VwAwNwwzcdvQBoaHh3X33XfrM5/5jD7ykY+kfCwcDquoqEhlZWXav3+/fvSjH+nhhx+e9u/ZtWuXdu3aJUnasWOHRkdHMz72XOR0OhWJRKweBk7AvNgT82JPzIv9MCdxr+4/oB+2dap6+aRS79916KZNa3TxRauzPh7mxZ6YF/thTuxppnkpKSlJe51twm4kEtH999+vCy+8UJ/85CdP+vm33nqr7rvvPlVUVJz0c48cOTIXQ8w7fr9fPT09Vg8DJ2Be7Il5sSfmxX6YkwmdB7vU2r4vuTrbZOHqLPNiT8yL/TAn9jTTvMyfPz/tdbYoYzZNU48//rgWLFiQNuj29/ersrJShmHo7bffViwWU3l5eZZHCgAAMDuUegOAtWwRdt9880299NJLWrx4se644w5J0g033JBM75s2bdIrr7yitrY2ORwOlZSU6Pbbb5/S+AEAAAAAAMkmYXfZsmX62c9+NuPnbN68WZs3b87SiAAAAHCmOg92qfXlDgWjRfI6Ymq6dC2r3QCyxhZhFwAAAPml82CXWtoPq3r5BnkMQzHTVEt7hyQReAFkhS3O2QUAAEB+aW3fp+pla5PbzgzDUPWytWpt32fxyAAUCsIuAAAA5lwwYkzpr2IYhkIReq4AyA7KmAEAAMaxx3TueJ2mYqaZEnhN05THaYtTLwEUAFZ2AQAANLHHNLZ8gzwXrFds+Qa1tB9W58Euq4eWk5oaG9R3uEOmGQ+3pmmq73CHmhobLB4ZgELByi4AAIASe0zXT7PHdA+ru6ch8T1rbd+jUMSQx2mqubGB7yWArCHsAgAAKL7H1MMe0zm1ZtUKwi0Ay1DGDAAAoPge00TJbQJ7TAEgdxF2AQAAxB5TAMg3lDEDAGyBLriwGntMASC/EHYBAJZLdMGtXr5BHsNQzDTV0t4hSQQNZBV7TAEgf1DGDACwXLwL7tppuuDus3hkAAAgV7GyCwCwHF1wgdPHFgAAmB5hFwBgOa/TVMw0kyu7El1wgdlgCwAApEcZMwDAcnTBBU4PWwAAID1WdgEAlqMLLnB62AIAAOkRdgEAtkAXXODUsQUAANKjjBkAACBHsQUAANJjZRcAACBHsQUAANIj7AIAAOQwtgAAwPQIuwAAnCLONQUAwP4IuwAAnALONQUAIDfQoAoAgFPAuaYAAOQGwi4AAKcgGDFSjnmRONcUAAA7IuwCAHAKvE4zecxLAueaAgBgP4RdAABOAeeaAgCQG2hQBQDAKeBc07lDV2sAQCYRdgEAOEWca3rm6GoNAMg0ypgBAEDW0dUaAJBphF0AAJB1dLUGAGQaYRcAAGQdXa0BAJlG2AUAAFlHV2sAQKbRoAoAAGQdXa0BAJlG2AUAAJagqzUAIJMoYwYAAAAA5B1WdgEAADBF58Eutb7coWC0SF5HTE2XrmUlHkBOIewCAGaFF75A4eg82KWW9sOqXr5BHsNQzDTV0t4hSfzeA8gZhF0AwEnxwjf/cPMCM2lt36fqZeuTZyEbhqHqZWvV2r6HnxMAOYOwCwA4KV745hduXuBkghFDnvHf9wTDMBSKGGmuAAD7oUEVAOCkghEjGXQTeOGbu+I3L9ZOc/Nin8Ujg114nWbyDOQE0zTlcZpprgAA+yHsAgBOihe++YWbFziZpsYG9R3uSP7em6apvsMdampssHhkADB7lDEDAE6qqbFBLe0dydXAxAvfZl745iSv01TMNFMCLzcvMFminL21fY9CEUMep6nmxgbK3AHkFMIuAOCkeOGbX7h5gdlYs2oFv+MAchphFwAwK7zwzR/cvAAAFALCLoC8xdEqQHrcvAAA5DvCLoC8xNEqgL1w8wkAkG22CrsHDhzQU089pVgspssvv1zXXHNNysfHxsb0yCOP6Pe//73Ky8t1++23q66uzprBArA1zoUF7IObTwAAK9gm7MZiMT355JP66le/qpqaGm3fvl0NDQ1auHBh8nN2794tj8ej73//+2pvb9c///M/6x/+4R8sHDUAuwpGDHny7GgVVsaQq7j5BACwgm3O2X377bc1b9481dfXy+l06pJLLlFHR0fK5+zbt0+XXXaZJOmjH/2oDh06NOXcRwCQ8u9c2MTKWGz5BnkuWK/Y8g1qaT+szoNdVg8NOCnO9QUAWME2YTcQCKimpib5fk1NjQKBQNrPcTgccrvdGhwczOo4AeSGpsYG9R3uSAbexNEqTTl6tEp8ZWztNCtj+yweGXBy+XbzCQCQG2xTxjyXdu3apV27dkmSduzYIb/fb/GI7MnpdPK9sSHmZW5csWGdKqsq9eyv2xUck7zF0ueuatTFF60+rb/P6nkZc5TJXVo65fEhR1lB/7xYPS+Yaro5ueGqy/XDtk5VL590ru/vOnTTVZczf1nC74o9MS/2w5zY0+nOi23Crs/nU29vb/L93t5e+Xy+aT+npqZG0WhU4XBY5eXlU/6ujRs3auPGjcn3e3p6MjfwHOb3+/ne2BDzMneWLF6o//6Fz6Y8drrfW6vnpTg6rJGRkZRSUNM05YwOF/TPi9Xzgqmmm5MlixfqsxcPqLX9heS5vp9tbNCSxQuZvyzhd8WemBf7YU7saaZ5mT9/ftrrbBN2ly5dqvfff1/d3d3y+Xz6zW9+o9tuuy3lcz784Q/rxRdf1HnnnadXXnlFK1asmLIHCADyUVNjg1raO5KlzImy7OYcLctG4eFcXwBAttkm7DocDn3xi1/Uvffeq1gspvXr12vRokX66U9/qqVLl6qhoUEbNmzQI488ov/23/6bvF6vbr/9dquHDQBZkQgJre17kitjzY0NhAcAAIA0bBN2Jemiiy7SRRddlPLYZz87UYJYUlKiL33pS9keFgDYAitjAAAAs2ebbswAAAAAAMwVwi4AAAAAIO8QdgEAAAAAeYewCwAAAADIO7ZqUAUAmNB5sEutL3coGC2S1xFT06VraVAFAAAwS4RdALChzoNdamk/rOrlG+QxDMVMUy3tHZJE4AUAAJgFypgBwIZa2/epetlaGYYhSTIMQ9XL1qq1fZ/FIwMAAMgNhF0AsKFgxEgG3QTDMBSKGGmuAAAAwGSUMQOADXmdpmKmmRJ4TdOUx2laOCrgzLAPHQCQTazsAoANNTU2qO9wh0wzHm5N01Tf4Q41NTZYPDLg9CT2oceWb5DngvWKLd+glvbD6jzYZfXQAAB5ipVdALChxGpXa/sehSKGPE5TzY0NrIIhZ8X3oa+fZh/6Hn6uAQAZQdgFAJtas2oFIQB5Ixgx5GEfOgAgiyhjBgAAGed1msmy/AT2oQMAMomwCwAAMo596ACAbKOMGQAAZBz70AEA2UbYBQAAWcE+dABANlHGDAAAAADIO4RdAAAAAEDeIewCAAAAAPIOYRcAAAAAkHcIuwAAAACAvEPYBQAAAADkHcIuAAAAACDvEHYBAAAAAHnHafUAAACwUufBLrW+3KFgtEheR0xNl67VmlUrrB4WAAA4Q4RdAEDB6jzYpZb2w6pevkEew1DMNNXS3iFJBF4AAHIcZcwAgILV2r5P1cvWyjAMSZJhGKpetlat7fssHhkAADhTrOzCFigjBGCFYMSQZzzoJhiGoVDESHMFAADIFYRdWI4yQgBW8TpNxUwzubIrSaZpyuM0LRwVAACYC4RdWC5eRrh+mjLCPYRdABnV1NiglvaOZCmzaZrqO9yh5sYGq4c2K1TFAACQHmEXlqOMEEC2TQ6Jsf4e9ex9R56aefI4TTU3NuREYKQqBgCAmRF2YTnKCAFk04kh0T2+mvtXjctyKiRSFQMAwMzoxgzLNTU2qO9wh0wzHm4TZYRNOVJGCCC35EsH5mDESLlJKFEVAwDAZKzswnKJFYjW9j0KRYycKiMEkHvyZesEVTEAAMyMsAtbWLNqBeEWQFbkS0jM9eZaAABkGmEXAFBQ8iUkUhUDAMDMCLsAgIKSTyGRqhgAANIj7AIACg4hEQCA/Ec3ZgAAAABA3iHsAgAAAADyDmXMAACcos6DXWp9uUPBaJG8jpiaLl1LWTQAADZD2AUA4BR0HuxSS/thVS/fII9hKGaaamnvkCQCLwAANkIZMwAAp6C1fV/y2CJJMgxD1cvWqrV9n8UjAwAAkxF2AQA4BcGIkQy6CYZhKBQx0lwBAACsQNgFAOAUeJ2mTNNMecw0TXmcZporAACAFdizCwA4KRoyTWhqbFBLe0eylNk0TfUd7lBzY4PVQwMAAJNYHnZbWlr02muvyel0qr6+Xrfccos8Hs+Uz7v11ltVVlamoqIiORwO7dixw4LRAkDhoSFTqsRzbm3fo1DEkMdpqrmxoSC/FwAA2JnlYXfVqlXaunWrHA6Hnn76aT377LO68cYbp/3cu+++WxUVFVkeIQAUtnhDpvXTNGTaU7ABb82qFQX73AEAyBWW79m98MIL5XA4JEnnnXeeAoGAxSMCAExGQyYAAJCLLF/ZnWz37t265JJL0n783nvvlSRdccUV2rhxY7aGBQAFzes0FTPNlMBLQyYAAGB3hnliS8kMuOeee9Tf3z/l8euvv15r166VJP385z/XO++8oy9/+ctTVhAkKRAIyOfzaWBgQN/61rf0hS98Qeeff/60X2/Xrl3atWuXJGnHjh0aHR2duyeTR5xOpyKRiNXDwAmYF3sq5Hl5df8B/bCtU9XLJzVk+l2Hbtq0RhdftNrSsRXyvNgVc2JPzIs9MS/2w5zY00zzUlJSkva6rITdk3nxxRf1q1/9SnfddZdKS0tP+vk/+9nPVFZWpquvvnpWf/+RI0fOdIh5ye/3q6enx+ph4ATMiz0V+rx0HuxSa/u+ZEOmJps0ZCr0ebEj5sSemBd7Yl7shzmxp5nmZf78+Wmvs7yM+cCBA/rFL36hb3zjG2mD7vDwsEzTlMvl0vDwsA4ePKgtW7ZkeaQAULhoyAQAAHKN5WH3ySefVCQS0T333CNJOvfcc3XTTTcpEAjoBz/4gbZv366BgQF997vflSRFo1FdeumlWr16tYWjBgAAAADYmeVh9/vf//60j/t8Pm3fvl2SVF9frwceeCCbwwIAAAAA5DDLjx4CAAAAAGCuEXYBAAAAAHmHsAsAAAAAyDuEXQAAAABA3iHsAgAAAADyDmEXAAAAAJB3CLsAAAAAgLxj+Tm7AACcqPNgl1pf7lAwWiSvI6amS9dqzaoVVg8LAADkEMIuAMBWOg92qaX9sKqXb5DHMBQzTbW0d0gSgRcAAMwaZcwAAFtpbd+n6mVrZRiGJMkwDFUvW6vW9n0WjwwAAOQSwi4AwFaCESMZdBMMw1AoYqS5AgAAYCrCLgDAVrxOU6ZppjxmmqY8TjPNFQAAAFMRdgEAttLU2KC+wx3JwGuapvoOd6ipscHikQEAgFxCgyoAgK0kmlC1tu9RKGLI4zTV3NhAcyoAAHBKCLsAANtZs2oF4RYAAJwRypgBAAAAAHmHsAsAAAAAyDuEXQAAAABA3iHsAgAAAADyDmEXAAAAAJB3CLsAAAAAgLxD2AUAAAAA5B3CLgAAAAAg7xB2AQAAAAB5h7ALAAAAAMg7hF0AAAAAQN4h7AIAAAAA8g5hFwAAAACQdwi7AAAAAIC8Q9gFAAAAAOQdwzRN0+pBAAAAAAAwl1jZLWDbtm2zegiYBvNiT8yLPTEv9sOc2BPzYk/Mi/0wJ/Z0uvNC2AUAAAAA5B3CLgAAAAAg7xB2C9jGjRutHgKmwbzYE/NiT8yL/TAn9sS82BPzYj/MiT2d7rzQoAoAAAAAkHdY2QUAAAAA5B2n1QOAPTz//PNqaWnRE088oYqKCquHU/B+8pOfaN++fTIMQ5WVlbrlllvk8/msHlbBa2lp0WuvvSan06n6+nrdcsst8ng8Vg+roP32t7/V//7f/1t//vOf9e1vf1tLly61ekgF7cCBA3rqqacUi8V0+eWX65prrrF6SAXvscce0/79+1VZWakHH3zQ6uFAUk9Pjx599FH19/fLMAxt3LhRTU1NVg+r4I2Ojuruu+9WJBJRNBrVRz/6UV133XVWDwuSYrGYtm3bJp/Pd8pdmQm7UE9Pjw4ePCi/32/1UDDu6quv1vXXXy9Jam1t1c6dO3XTTTdZPCqsWrVKW7dulcPh0NNPP61nn31WN954o9XDKmiLFi3Sl7/8Zf3whz+0eigFLxaL6cknn9RXv/pV1dTUaPv27WpoaNDChQutHlpBu+yyy7R582Y9+uijVg8F4xwOh5qbm7VkyRINDQ1p27ZtWrVqFb8rFisuLtbdd9+tsrIyRSIR3XXXXVq9erXOO+88q4dW8FpbW7VgwQINDQ2d8rWUMUP/9E//pM997nMyDMPqoWCc2+1O/nlkZIS5sYkLL7xQDodDknTeeecpEAhYPCIsXLhQ8+fPt3oYkPT2229r3rx5qq+vl9Pp1CWXXKKOjg6rh1Xwzj//fHm9XquHgUmqq6u1ZMkSSZLL5dKCBQv4/4kNGIahsrIySVI0GlU0GuX1lw309vZq//79uvzyy0/relZ2C1xHR4d8Pp/OPvtsq4eCE/zLv/yLXnrpJbndbt19991WDwcn2L17ty655BKrhwHYRiAQUE1NTfL9mpoavfXWWxaOCLC/7u5u/eEPf9A555xj9VCgeIXKnXfeqQ8++EBXXnmlzj33XKuHVPB+9KMf6cYbbzytVV2JsFsQ7rnnHvX39095/Prrr9ezzz6rr371q9kfFGacl7Vr1+qGG27QDTfcoGeffVb/+q//yr6RLDnZvEjSz3/+czkcDn384x/P8ugK02zmBAByzfDwsB588EF9/vOfT6nognWKior0wAMPKBQK6bvf/a7ee+89LV682OphFazXXntNlZWVWrJkibq6uk7r7yDsFoCvfe1r0z7+3nvvqbu7W3fccYekeJnAnXfeqfvuu09VVVVZHGFhSjcvJ/r4xz+u++67j7CbJSeblxdffFGvvfaa7rrrLsqbsmS2vyuwls/nU29vb/L93t5eGusBaUQiET344IP6+Mc/ro985CNWDwcn8Hg8WrFihQ4cOEDYtdCbb76pffv2qbOzU6OjoxoaGtLDDz+s2267bdZ/B2G3gC1evFhPPPFE8v1bb71V9913H92YbeD999/XWWedJSleas6eRHs4cOCAfvGLX+gb3/iGSktLrR4OYCtLly7V+++/r+7ubvl8Pv3mN785pRckQKEwTVOPP/64FixYoE9+8pNWDwfjjh8/LofDIY/Ho9HRUR08eFB/+Zd/afWwCtrWrVu1detWSVJXV5eef/75U/7/CmEXsKF//ud/1vvvvy/DMOT3++nEbBNPPvmkIpGI7rnnHknSueeey9xY7NVXX9U//uM/6vjx49qxY4fOPvtsfeUrX7F6WAXJ4XDoi1/8ou69917FYjGtX79eixYtsnpYBe+hhx7SG2+8ocHBQd1888267rrrtGHDBquHVdDefPNNvfTSS1q8eHGyuu6GG27QRRddZPHICltfX58effRRxWIxmaapj33sY/rwhz9s9bBwhgzTNE2rBwEAAAAAwFzi6CEAAAAAQN4h7AIAAAAA8g5hFwAAAACQdwi7AAAAAIC8Q9gFAAAAAOQdwi4AAAAAIO8QdgEAyFFPP/20vvOd7yTfb2lp0Te/+U1FIhELRwUAgD0QdgEAyFF/+Zd/qa6uLv3hD39QW1ubDhw4oC9/+ctyOp1WDw0AAMsZpmmaVg8CAACcnp/97Gd69dVXFQ6H9c1vflN+v1/hcFj33HOP/vM//1P33nuvFi9ebPUwAQDIOlZ2AQDIYR/60If03nvvaevWrfL7/ZKkkpISbd++XR/96EctHh0AANYh7AIAkKPee+89PfHEE1q3bp327NmTfNzpdKqiosLCkQEAYD3CLgAAOSgQCOj+++/Xf/kv/0V/+7d/q/fee09dXV1WDwsAANsg7AIAkGPC4bDuu+8+XXXVVWpoaFBpaak+9alP6Sc/+YnVQwMAwDZoUAUAQJ569NFH9alPfYoGVQCAgkTYBQAgD91333364x//KL/fryuuuEKXXXaZ1UMCACCrCLsAAAAAgLzDnl0AAAAAQN4h7AIAAAAA8g5hFwAAAACQdwi7AAAAAIC8Q9gFAAAAAOQdwi4AAAAAIO8QdgEAAAAAeYewCwAAAADIO4RdAAAAAEDe+f8BpjpGmHcpj5YAAAAASUVORK5CYII=",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plot_ds(data,m[-1],q[-1])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Criticità\n",
"\n",
"I metodi elementari di discesa del gradiente illustrati sopra non garantiscono in generale una elevata convergenza. Inoltre, il loro utilizzo pone un insieme di questioni\n",
"\n",
"- la scelta del valore del learning rate $\\eta$ può risultare difficile. Un valore troppo piccolo può comportare una convergenza eccessivamente lenta, mentre un valore troppo grande può portare ad oscillazioni intorno al minimo, o addirittura a divergenza\n",
"- per ovviare a questa problematica è possibile utilizzare dei metodi di aggiustamento di $\\eta$ nel tempo, ad esempio riducendolo secondo uno schema predefinito o quando il decremento della funzione di costo calcolata in due epoche successive risulti inferiore a una soglia data. Sia gli schemi che le soglie devono però essere predefiniti e non possono quindi adattarsi in dipendenza delle caratteristiche del dataset\n",
"- lo stesso learning rate si applica per l'aggiornamento di tutti i coefficienti\n",
"- in molti casi la funzione di costo, in particolare se si ha a che fare con reti neurali, risulta fortemente non convessa, caratterizzata quindi da numerosi minimi locali e da punti di sella. I metodi considerati possono avere difficoltà a uscire da situazioni di questo tipo, e in particolare dai punti di sella, spesso circondati da regioni a gradiente molto limitato.\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Momento\n",
"\n",
"I metodi precedenti risultano poco efficienti in situazioni in cui la funzione di costo varia in modo molto diverso al variare della direzione considerata (ad esempio se si hanno valli che discendono lentamente e con pareti laterali ripide). In questo caso, infatti, gli algoritmi precedenti procedono molto lentamente in direzione del minimo, oscillando in modo sostanziale nella direzione trasversale ad essa: questa situazione è illustrata a sinistra nella figura sottostante.\n",
"\n",
"Il *metodo del momento* fa riferimento ad una interpretazione fisica del metodo di ottimizzazione, in cui il processo di discesa del gradiente viene visto come lo spostamento di un corpo di massa $m=1$ che si muove sulla superficie della funzione di costo $J(\\theta)$ soggetto a una forza peso $F(\\theta)=-\\nabla U(\\theta)$, dove $U(\\theta)=\\eta h(\\theta)=\\eta J(\\theta)$ è l'energia potenziale del corpo nella posizione $\\theta$ (si assume quindi che la costante fisica $g$ relativa alla forza peso $F=-mgh$ sia pari a $\\eta$). In questo modello, il valore negativo del gradiente $-\\eta J'(\\theta)$ è quindi pari al vettore forza (e accelerazione, in quanto $a=\\frac{F}{m}$) del corpo nel punto $\\theta$. \n",
"\n",
"Nel metodo della discesa del gradiente, si assume che lo spostamento del corpo in un certo punto $\\theta$ sia determinato dalla accelerazione calcolata nello stesso punto, e quindi dal gradiente $J'(\\theta)$, in quanto vale la regola di aggiornamento $\\theta^{(k+1)}=\\theta^{(k)}-\\eta J'(\\theta^{(k)})$. \n",
"\n",
"Nel metodo del momento, si fa riferimento a un modello più consistente con la realtà fisica di un corpo che si muove su una superficie soggetto alla forza peso, modello che prevede di utilizzare il concetto di velocità $v(\\theta)$. In questo modello, lo spostamento del corpo a partire da un certo punto $\\theta$ è determinato dalla velocità calcolata nello stesso punto $\\theta^{(k+1)}=\\theta^{(k)}+v^{(k+1)}$, dove la variazione di velocità è data dalla accelerazione $v^{(k+1)}=v^{(k)}-\\eta J'(\\theta^{(k)})$. \n",
"\n",
"Come si può osservare, si ha che\n",
"\n",
"\\begin{align*}\n",
"v^{(k+1)}&=-\\eta J'(\\theta^{(k)})+v^{(k)}=-\\eta J'(\\theta^{(k)})-\\eta J'(\\theta^{(k-1)})+v^{(k-1)}=\\cdots=-\\eta\\sum_{i=0}^kJ'(\\theta^{(i)})+v^{(0)}\\\\\n",
"\\theta^{(k+1)}&=\\theta^{(k)}+v^{(k+1)}=\\theta^{(k)}-\\eta\\sum_{i=0}^kJ'(\\theta^{(i)})+v^{(0)}\n",
"\\end{align*}\n",
"\n",
"che corrisponde all'associare lo spostamento alla somma (integrale nel caso della fisica) delle accelerazioni passate.\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
" \n",
"\n",
"\n",
"Il riferimento a questo modello porta l'algoritmo a tendere ad ogni passo a mantenere, almeno in parte, la direzione del passo precedente (in quanto $v^{(k+1)}=-\\eta J'(\\theta^{(k)})+v^{(k)})$, premiando le direzioni che si manifestano con costanza in una sequenza di passi. Ne deriva il comportamento a destra della figura precedente, in cui l'inerzia nella direzione del minimo porta a una limitazione delle oscillazioni.\n",
"\n",
"Si noti che ciò non avviene nella discesa del gradiente, in cui si ha $v^{(k+1)}=-\\eta J'(\\theta^{(k)})$.\n",
"\n",
"Matematicamente, l'effetto di inerzia viene ottenuto sottraendo alla velocità (vettoriale) calcolata al passo precedente la valutazione del gradiente effettuata nella corrispondente posizione. Il gradiente viene sottratto in quanto, mantenendo la corrispondenza con la meccanica di corpo soggetto ad accelerazione di gravità, un gradiente positivo tende a ridurre la velocità.\n",
"\n",
"Il metodo del momento utilizza tipicamente un secondo parametro $\\gamma$, che determina la frazione di $v^{(k)}$ che permane nella definizione di $v^{(k+1)}$, e che svolge la funzione (fisicamente) di un coefficiente di attrito. Si ottiene quindi la formulazione:\n",
"\n",
"\\begin{align*}\n",
"v^{(k+1)}&=\\gamma v^{(k)} -\\eta\\sum_{i=1}^nJ'(\\theta^{(k)};x_i)\\\\\n",
"\\theta^{(k+1)}&=\\theta^{(k)}+v^{(k+1)}\n",
"\\end{align*}\n",
"Il metodo del momento ad ogni passo determina inizialmente il vettore di spostamento attuale, a partire da quello al passo precedente e dal gradiente di $\\theta$: il contributo relativo dei due termini è pesato dalla coppia di parametri $\\gamma$ e $\\eta$. Lo spostamento calcolato viene quindi applicato al valore attuale di $\\theta$ (il segno meno deriva come sempre dal fatto che stiamo assumendo di cercare un minimo locale).\n",
"\n",
"Se il gradiente è orientato nella stessa direzione della velocità attuale, tale velocità viene incrementata, per cui l'aggiornamento di $\\theta$ diviene maggiore, incrementandosi man mano che la direzione di spostamento rimane coerente con il gradiente nei punti attraversati.\n",
"\n",
"```python\n",
"v = 0\n",
"for i in range(n_epochs):\n",
" g = 0\n",
" for k in range(dataset_size):\n",
" g = g+evaluate_gradient(loss_function, theta, X[k])\n",
" v = gamma*v-eta*g\n",
" theta = theta+v\n",
"```"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n",
"Come si può vedere, mentre $\\theta^{(k)}=(\\theta_1^{(k)},\\ldots,\\theta_d^{(k)})^T$ è la valutazione della soluzione ottima al passo $k$, $v^{(k)}=(v_1^{(k)},\\ldots,v_d^{(k)})^T$ è l'aggiornamento applicato a tale valore per ottenere $\\theta^{(k+1)}$: possiamo vedere quindi $v$ come il vettore velocità di spostamento di $\\theta$ nello spazio delle soluzioni.\n",
"\n",
"Come già illustrato sopra, possiamo esprimere l'aggiornamento nel modo seguente, evidenziando come esso dipenda dal gradiente calcolato in tutte le posizioni precedentemente attraversate, con un effetto che va a diminuire esponenzialmente con $\\gamma$ man mano che si risale nel passato. Assumendo $v^{(0)}=0$:\n",
"\n",
"\\begin{align*}\n",
"\\theta^{(k+1)}&=\\theta^{(k+1)}+v^{(k+1)}= \\theta^{(k)}+\\gamma v^{(k)}-\\eta\\sum_{i=1}^nJ'(\\theta^{(k)};\\mathbf{x}_i)=\\theta^{(k)}+\\gamma^2 v^{(k-1)}-\\gamma\\eta\\sum_{i=1}^nJ'(\\theta^{(k-1)};\\mathbf{x}_i) -\\eta\\sum_{i=1}^nJ'(\\theta^{(k)};\\mathbf{x}_i)\\\\\n",
"&=\\theta^{(k)}+\\gamma^2 v^{(k-1)}-\\eta\\left(\\sum_{i=1}^nJ'(\\theta^{(k)};\\mathbf{x}_i)+\\gamma\\sum_{i=1}^nJ'(\\theta^{(k-1)};\\mathbf{x}_i)\\right)=\\cdots=\n",
"\\theta^{(k)}-\\eta\\left(\\sum_{j=0}^k\\gamma^j\\sum_{i=1}^nJ'(\\theta^{(k-j)};\\mathbf{x}_i)\\right)\n",
"\\end{align*}\n",
"\n",
"Gli aggiornamenti nel caso della logistic regression derivano immediatamente\n",
"\n",
"\\begin{align*} \n",
"v_j^{(k+1)}&=\\gamma v_j^{(k)}+\\frac{\\eta}{n}\\sum_{i=1}^n( t_i-f(\\mathbf{x}_i,\\theta))x_{ij}\\hspace{1cm}j=1,\\ldots,d\\\\ \n",
"v_0^{(k+1)}&=\\gamma v_0^{(k)}+\\frac{\\eta}{n}\\sum_{i=1}^n(t_i-y_i) \\\\\n",
"\\theta_j^{(k+1)}&=\\theta_j^{(k)}+v_j^{(k+1)}\\hspace{1cm}j=0,\\ldots,d\n",
"\\end{align*}"
]
},
{
"cell_type": "code",
"execution_count": 127,
"metadata": {},
"outputs": [],
"source": [
"def momentum_gd(X,t, eta = 0.1, gamma = 0.97, epochs = 1000):\n",
" theta = np.zeros(nfeatures+1).reshape(-1,1)\n",
" v = np.zeros(nfeatures+1).reshape(-1,1)\n",
" theta_history = []\n",
" cost_history = []\n",
" for k in range(epochs): \n",
" delta = - eta * gradient(theta,X,t)\n",
" v = gamma*v + delta\n",
" theta = theta + v\n",
" theta_history.append(theta)\n",
" cost_history.append(cost(theta, X, t))\n",
" theta_history = np.array(theta_history).reshape(-1,3)\n",
" cost_history = np.array(cost_history).reshape(-1,1)\n",
" m = -theta_history[:,1]/theta_history[:,2]\n",
" q = -theta_history[:,0]/theta_history[:,2]\n",
" return cost_history, m, q"
]
},
{
"cell_type": "code",
"execution_count": 128,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"tempo di esecuzione: 0.407 secondi\n",
"10000 passi totali\n",
"1000000 gradienti calcolati\n"
]
}
],
"source": [
"start_time = time.time()\n",
"cost_history, m, q = momentum_gd(X, t, eta = 0.1, gamma = 0.97, epochs = 10000)\n",
"print(f\"tempo di esecuzione: {time.time()-start_time: 4.3f} secondi\")\n",
"print(f\"{len(m)} passi totali\")\n",
"print(f\"{len(m)*n} gradienti calcolati\")"
]
},
{
"cell_type": "code",
"execution_count": 132,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABQgAAAGoCAYAAAAKMwiTAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAAB2wElEQVR4nOz9eXQU94Hu/z9V1d2SWitCuwSITQiBxGZ2jG0sb3hJhkzsOJNZmMnMvdnGN5ncOXPuOfFN8OSEfJN4kpnMzO/aWTyZSTy2E5x4X2Qw+74KBEhCbAIJIYlFu9RV9fujQQaDbbDVqpb6/ToHo67qVj/tKonWo099Pobruq4AAAAAAAAAxCTT6wAAAAAAAAAAvENBCAAAAAAAAMQwCkIAAAAAAAAghlEQAgAAAAAAADGMghAAAAAAAACIYRSEAAAAAAAAQAzzeR3gRp0+fdrrCJ9IRkaGmpubvY4BcSyiCccienAsogfHInoMl2ORl5fndYSIGMrvDYfLuYVPjnMBl3Eu4DLOBVwWqXPhg94bMoIQAAAAAAAAiGEUhAAAAAAAAEAMoyAEAAAAAAAAYhgFIQAAAAAAABDDKAgBAAAAAACAGEZBCAAAAAAAAMQwCkIAAAAAAAAghlEQAgAAAAAAADGMghAAAAAAAACIYRSEAAAAAAAAQAyjIAQAAAAAAABiGAUhAAAAAAAAEMMoCAEAAAAAAIAYRkEIAAAAAAAAxDAKQgAAAAAAACCGURACAAAAAAAAMYyCEAAAAAAAAIhhFIQAAAAAAABADKMgBAAAAAAAAGIYBSEAAAAAAAAQwygIAQAAAAAAgBhGQQgAAAAAAADEMApCAAAAAAAAIIZREAIAAAAAAAAxjIIQAAAAAAAAiGEUhAAAAAAAAEAMoyAEAAAAAAAAYpjP6wAAAAAY/lpbW/X9739f9fX1+tWvfiXLsvr3nThxQk8//bQk6Ytf/KLGjBnjVUwAAICYxAjCQdLe1et1BAAAAM8kJSXpW9/6liZOnHjNvueee06PPfaYvv71r+u5557zIB0AAEBsYwRhhLmuq99tOaqdR5r1jYdKlZmS4HUkAACAQRcIBBQIBK67r6OjQxkZGf0fAwAAYHBREEaYYRhyHFch29GaytN6eOF4ryMBAABEFdd1P/I+FRUVqqiokCStXLmyv1Acinw+35DOj4HDuYDLOBdwGecCLhvsc4GCcBAsKc3XjiNntfNIs8qn5Ss9Kd7rSAAAAFHJMIzrbi8vL1d5eXn/7ebm5sGKNOAyMjKGdH4MHM4FXMa5gMs4F3BZpM6FvLy8626PaEH4zDPPqK6uTmPHjtXy5cv7t7e3t+upp55SW1ubSktLtWzZskjG8FxGSrzmFedr88FTWlN5Wp+ZP87rSAAAAFEjKSlJLS0tMgxDCQlMxwIAADDYIrZISV1dnbq7u7VixQqFQiHV1tb273vhhRf0yCOP6P/+3/877MvByx6YO0GGpO21Z3WhgwVLAABAbAmFQnriiSd0/Phxffe731VVVZVWrVolSXr44Yf14x//WP/0T/+kRx55xOOkAAAAsSdiIwhrampUVlYmSSotLVV1dbUmTJggSTp58qRefPFFtbS06NFHH1VRUVGkYkSNvJHJKh2Trn3HW/XugdP61JxCryMBAAAMGp/Pp29961tXbSspKZEkjRkzRk888YQXsQAAAKAIFoQdHR3Kzs6WJAWDQdXX1/fvO3z4sL7//e8rKSlJP/rRj677hnA4TUQthd8U//FtU7XvV+u0taZJf3zbVKUmMhehF5j0NXpwLKIHxyJ6cCyiB8cCAAAAsSJiBWEwGFRnZ6ckqaurS8FgsH9fXl6eCgoKJEmmef2rnIfTRNRSeHLJBKNXU0aN0IGT5/Ti+gN64JYxXseKSUz6Gj04FtGDYxE9OBbRY7gciw+aiBoAAAC4LGJzEBYVFWn//v2SpMrKyqsuI87NzdW5c+fU3d0t27YjFSEqlU/LlyRtPnxGHd19HqcBAAAAAABArItYQThu3Dj5/X49/vjjMk1TGRkZV01E/ZOf/EQrVqyImUVKLisYmaTi/DT1hhytr2r0Og4AAAAAAABiXMQuMZak5cuXX3X7chlYUFCgb3/725F86qh2Z1m+Dp06r42HGnXb1FwlBCJ6GAAAAAAAAIAPFLERhPhghVnJmpCTou4+WxsOMooQAAAAAAAA3qEg9MjluQjXVzWouy+25mEEAAAAAABA9KAg9Mi47BSNzUpWV6+tzYcYRQgAAAAAAABvUBB6xDAM3VkWHkW4tqpBvYwiBAAAAAAAgAcoCD1UlJeqUSMT1dEd0pbqJq/jAAAAAAAAIAZREHrIMAyVTyuQJK09cFp9tuNxIgAAAAAAAMQaCkKPTS5IU156UBe7+rS9hlGEAAAAAAAAGFwUhB67ci7CNftPK8QoQgAAAAAAAAwiCsIoMHV0urJTE3S+o1c7jzR7HQcAAAAAAAAxhIIwCphXjCJcXXlKtuN6nAgAAAAAAACxgoIwSkwrHKmMlHi1tvdoz1FGEQIAAAAAAGBwUBBGCdM0tKQ0T5L0zr5TchhFCAAAAAAAcA23p1NuW6vXMYYVCsIoMnNchkYkxensxW7tO97idRwAAAAAAICo4XZcVGjTK+r9r++p979/JLezzetIwwYFYRSxTFN3TL1iFKHLKEIAAAAAABDb3Iut6lv3onp/833ZlRukUJ/MUUVSXNDraMOGz+sAuNrsCZl6Z98pNZ7vUtXJc5o6Ot3rSAAAAAAAAIPOOdcke/caObV7JdcJb0wZKd/8+2WOmSzDMLwNOIxQEEYZn2Xq9ql5+sO2Y6rYe0pTRo3ghAcAAAAAADHDaT4le9caOUcPSLp0daUvIGvmEllli2RY1FkDjf+jUWjuxCy9s++UTrV26NCp85pcMMLrSAAAAAAAABHlNB4LF4MnD1+13Zw4Q76598lITPEo2fBHQRiF/D5Tt03J1as7T6hi3ykV56cxihAAAAAAAAw7ruvKPVWr0K7VchuOXrXPyCyQb+FDMrNHe5QudlAQRqn5k7K1Zv9pnTjbrpqGiyrKS/U6EgAAAAAAwIBwXUfO8YOyd78rt+nk1TsTkuSbc6/MSTNlGKyvOxgoCKNUnN/S4pJcvbH7pN7ZV09BCAAAAAAAhjzXceTU7ZO9e43c1jNX7zQtWaULZc1cIiMQ703AGEVBGMUWFmdr7YHTqjvTprozFzUum2vtAQAAAADA0OPaITk1u8MjBi+2XLPfHD1J1vwHZKZlepAOFIRRLD7g08LJOarYe0oVe0/pb+6mIAQAAAAAAEOHG+qTc2ibQnvXSe0XrtlvpGbIWvCArNHFHqTDZRSEUe7Wyblaf6BBNQ0XdOJsm0ZnJnsdCQAAAAAA4EO5vd2yq7bI3rdB6mq/9g7+OFmz7pQ1dYEMi3rKaxyBKBeM82lBcY7W7D+tin2n9Jd30qgDAAAAAIDo5HZ3yt6/UXblRqm3+7r3MSfNkm/OvTKCDIKKFhSEQ8DiKbnacKhRB+vP61RLh/JHJnodCQAAAAAAoJ/b2SZ733rZVVukvt7wRtOSHLv/PkbWaPkWPigza5RHKfFBKAiHgKR4v+YXZWtdVYMq9p3Sn99R5HUkAAAAAAAAuW3nFdq7Vs6h7ZIdkiQZ6Tly+3qlttbwnYLJ8s1dKnPiNBmG6WFafBAKwiHitim52nSoUftPtKrxXKdyRgS9jgQAAAAAAGKUc/6s7D3vyqnZLTmOpPBKxPIF5Jw8HB5FaFqyym6VNfMOGf44jxPjw1AQDhEpwYDmTMzSpsNn9M6+U/qT2yZ6HQkAAAAAAMQYp6VB9u41cuoqJdeVDEPmhOky0nPkHNou92KLJMksLJFv3v0yUkd6nBg3goJwCLmjNE9ba5q091iL7ppeoKzUBK8jAQAAAACAGOCcOREuBo8fDG8wLZmTZsosLJG9f7OcbW9Ikoy0rPA8gwUMbBpKKAiHkLTEON0yPlNba5q0uvKUPrdogteRAAAAAADAMOW6rtzTdQrtXiP3VG14o88vq3i2zMlz5BzaodBb/xm+xDgQL+uWclkl82VYlrfBcdMoCIeYO0rztL22SbvrmnXXtAKNTI73OhIAAAAAABhGXNeVc+Kw7N2r5Z45Ed7oj5M1Zb6s0oVyjh9U38tPS90dkgyZk+fIN/tuGQlJnubGx0dBOMSMTI7XjHEZ2nmkWWsqT+uPF4zzOhIAAAAAABgGXMeRc3S/7N1r5LY0hDfGBWWVLpQ1db7cc03qe/0Zuc2nJElGTmH4cuKMfA9TYyBQEA5BS0rztetIs3YcOavyaflKS2QlIAAAAAAA8PG4ti2ndo/sPe/KPX82vDGYHF6BuGSu1NOt0IaX5NTuCe9LTJVv3lKZ48tkGIZnuTFwKAiHoKzUBE0rHKk9x1r07v7T+vTcsV5HAgAAAAAAQ4wb6pNTvVOhPWultnPhjUlp8k2/TeakWyRJ9r71snevkUJ9kuWTNW2xrOm3y/AHPEyOgUZBOETdWZavPcdatLW6SUtK85US5AsTAAAAAAB8NLevV/bBrbL3rpM62yRJRmqGrBm3y5wwQzJNOccOKLT5NamtVZJkjp0q3/ylMpLTPUyOSKEgHKJyRgQ1dfQI7T9xTmsPNOjB2WO8jgQAAAAAAKKY29Ml+8Am2ZUbpe5OSZIxMlfWjDtkjp0qwzTltJ5RaNPL/asWG+nZ8i14UGb+BC+jI8IoCIewO8sKtP/EOW2uPqM7SvOUFO/3OhIAAAAAAIgyble77H0bZFdtlnp7JElG1mhZM++QObpYhmHI7elUaEeF7ANbJNeR4hLku+VumSVzZJiWx68AkUZBOIQVjEzU5II0Haw/r/VVDbpv5mivIwEAAAAAgCjhtl+QvXed7EPbwnMISjLyxss38w4ZeePDxaDjyK7aqtCOt8KjCg1DZsk8+WbfJSM+0eNXgMFCQTjE3VmWr4P157Xx0BndNiVPwTgOKQAAAAAAscy90KLQnrVyqndKji1JMkcXy5q5RGb2e4OLnNN1Cm18SW5royTJyBsXvpx4ZK4nueEd2qQhbkxmsibmpqqm4YI2HGzQ3dNHeR0JAAAAAAB4wGk9I3v3GjlH9kquK8mQOa5M1szbZY7M67+f23ZOoS2vyamrDG9ISpNv/v3heQgNw5vw8BQF4TBQXpZ/qSBs1OKSXMUHOKwAAAAAAMQK52y97F1r5Bw7EN5gmjInzgyvSpyW2X8/t69X9t61svesleyQ5PPLmn6brGm3yfCxrkEso0kaBsblpGhcdrLqzrRp0+EzWlKa73UkAAAAAAAQYU7DUYV2rZFbXx3eYPlkTrpFvumLZSSn99/PdV05dZUKbXlNaj8vSTLHl8k3d6mM5LTBD46oQ0E4TNxZVqC6tw9q3YEGLSrOUcDPCkMAAAAAAAw3ruvKra9RaNdquY3Hwht9AVkl82SVLZKRmHLV/Z2WhvA8gw1HJUnGyNzwPIN54wY5OaIZBeEwMTE3RaMzk3TibLs2V4cXLAEAAAAAAMOD6zpyjh2UvXuN3LP14Y2BeFlTF8gqXXjNisNuV4dCO96Wc3BreD7C+KB8s++RWTxbhml68AoQzSgIhwnDMFRelq9fvHNY7+5v0IJJOfL7+IIHAAAAAGAocx1bzpHKcDF47kx4Y3yirLJbZU2ZJyMQf+39q7YotKNC6umSDFPW1PmybimXERf04BVgKKAgHEaK89OUn56oU60d2lrTpEWTc7yOBAAA0O+ZZ55RXV2dxo4dq+XLl/dv37x5s1566SUZhqE/+qM/0uzZsz1MCQBAdHDtkJzqXQrtWStdbAlvTEyVNW2xrOLZMvyBax7j1NcqtOnl/iLRyJ8Qvpw4PXswo2MIoiAcRgzD0J1l+frVu9V6d/9pzSvKks9iFCEAAPBeXV2duru7tWLFCj399NOqra3VhAkTJEmvvvqqvv3tb8swDH33u9+lIAQAxDS3r1f2oe2y966TOi6EN6aMlG/6bTKLZsqwrq1y3IutCm1+9b1VjJPT5Zt/v8zCEhmGMYjpMVRREA4zU0aPUE5aghrPd2nHkbOaV8RvCQAAgPdqampUVlYmSSotLVV1dXV/QZidna2enh5JUkJCgmcZAQDwktvbrbZNr6l385tSd4ckyRiRLWvGHTLHl8owr12M1O3rlb17jex96yU7FF6sZMYd4cVKfP7BfgkYwigIhxnz0ijCX6+r1erK05o9IVMWk48CAACPdXR0KDs7/IvLYDCo+vr6/n1z5szR3//938t1XX35y1++7uMrKipUUVEhSVq5cqUyMjIiHzpCfD7fkM6PgcO5gMs4F2Kb3dmuju0Vat+xWr3dnZIkf26hkhfer/iiaTKMa3+md11XXQe26cLq38ppOydJSpg6T6l3fEZWyohBzY/IGOzvCxSEw1DZmJF6K6VeZy92a1dds2ZPyPI6EgAAiHHBYFCdneEferq6uhQMvjdJ+m9/+1s9+eSTkqTvfe97mjZt2jWPLy8vV3l5ef/t5ubmCCeOnIyMjCGdHwOHcwGXcS7EJrfjoux962VXbZVCvZKkwOgiuVMXySiYqA7DUEdL6zWPc86eUmjTS3Ibj0uSjIx8+RY+JCdnjM712hLn0rAQqe8LeXl5191OQTgMmaahJWX5em7DEa2uPK1Z4zJlmsw5AAAAvFNUVKSKigotWLBAlZWVuv322/v3+f1+xcXFyTAMhUIh70ICADAI3LZWhfask3N4R/iyYEnGqCL5ZtyhzNLZH1gKuV3tCm17U86hHZJcKSFJvjn3yJw067qjDIGbQUE4TM0Ym6G399Sr+WK39h5r0YxxDFcHAADeGTdunPx+vx5//HEVFhYqIyNDq1at0rJly3T33XfrW9/6liRdNUoQAIDhxDl/VvbuNXJq90iOI0kyC6fImnmHzMyC9+53rklO9S65fT0ygikyEhLlHDsg58Th8B1MU9bURbJm3ikjLt6DV4LhiIJwmLJMQ0tK8/XbzXV6p/KUpo0dKZOViwAAgIeWL19+1e1ly5ZJkm6//farRhQCADCcOM2nw8Vg3X5JrmQYMidMDy8+kh6en9cN9cmp26+zr+1S38maj/iEjpxjVXLO1stITJURTJESU2Rc/nP59nVWOwY+CGfLMDZrfIYq9tXrzPku7T/RqrIxI72OBAAAAABATHAaj4eLwROHwhtMS2bRLPmm3yYjNfzzudN6Rs7BbbJrdkk9XeH7+QMyMkfJPX3k2k/qC0ihXrkXW6SLLXI/LEB88OryMJgiIzFVCiaHi8XEFCkhkcuTIYmCcFjzWaZun5qn3289pnf2nVLp6HQZjCIEAAAAACAiXNeVe/qIQrtWyz1dF97o88sqniNr2mIZSalyQ32yq3fKPritf6ERSTIyC5Q8bYHaG07KObgtvNEfkDXzTlmlC2VYPrmuK/X1yO24KHVclNt5QW5Hm9yOC5duXwzv62yTujvldndKrY0fXCSappSQ3D/6UJdKRCMxWUYwtb9clD+OPmGYi2hB+Mwzz6iurk5jx4696pKSf/3Xf9WpU6cUCARUXl6uRYsWRTJGTJszMUur953S6dZOHaw/r5JRLHcOAAAAAMBAcl1XzolDsnetkdt0IrwxECerZL6sskUyEpLktDbK3rhWdvUuqbc7fB9/nMyJ02UVz5Z77ozat7wpp/2CJIVHG869V0Ywuf95DMOQAvEyAvHSiKwPyeNIXR1yOy6Gy8POcInYXyBeKhPV3Sl1XAjv+7AX6AuEi8L+kYhXfhwuFJWYKsO0PuH/SXglYgVhXV2duru7tWLFCj399NOqra3VhAkT+vf/7d/+rXJyciL19LjEb5m6bUqeXt5xXBX76jW5II3WHwAAAACAAeA6jpyj+2XvXiO3pSG8MT4oq3ShrCkLJNOSU1cZHi145urRgtbkOTInTJN7rkmhDX+Q23QyvC9rlHwLH5KZNepj5zIMM3wpcTBZysz/4PyhvnB5eKk4vLI8vLJYVKhX7oVm6ULzBxaJRmqG/J/9X8x9OERF7KjV1NSorKxMklRaWqrq6ur+gtAwDP30pz9VUlKS/uqv/kqZmZnXPL6iokIVFRWSpJUrVyojY2ivwuvz+Tx7DfcvSNOaAw062dyhMx3S1MKh/f/yk/LyWOBqHIvowbGIHhyL6MGxAAAAH8S1bTm1u2XvWSv3/NnwxmCyrGmLZU2eI/fiOYW2vyWnZvf7RgvOkDV5tsyMfLmdbQpteElO9c7+x4+487PqyJ0waPMCGj6/lJIuIyX9A+/juq7U2yO389JlzFdeynz545YGuRea5bY0yPgExSa8E7GCsKOjQ9nZ4dV4gsGg6uvr+/f92Z/9mZKSknTo0CH96le/0t/93d9d8/jy8nKVl5f3325ubo5U1EGRkZHh6Wu4dXK2Xt91UqvWVyk7sSSmRxF6fSzwHo5F9OBYRA+ORfQYLsciLy/P6wgAAAwbbqhPzuEdCu1ZK7WfD29MHiHf9NtkjiuTc7xKfa/+XO6ZE/2PMbJGhUcLji+T4Y+Ta4cU2rNW9q7VUl+PZFqyyhbJmrFEwbx8dUbZ+w/DMKS4eBlx8dKI7Ovep2/NC3Kqd8o5c+ITjXyEdyJWEAaDQXV2dkqSurq6FAwG+/clJSVJkoqLi/XrX/86UhFwhQXFOXp3/2kdbWpT3ZmLGp+T6nUkAAAAAACGBLevR3bVVtn71ocXAJFkpGXKmnG7jBE5sg/vUGjr//feaMFAnMwJM8LFYMZ7v6yzjx+SvfmV8OW6kswxk+Wbf7+M1KF91YKZPUpO9c7+y6Qx9ESsICwqKlJFRYUWLFigyspK3X777f37Ojs7FQwGdfr0aSUmJkYqAq4Q77d0a0mu3tpTr4p9pygIAQAAAAD4CG5Pp+z9m2RXbpJ6woOgjJG5skoXSY4t+8CWq0oxI2v0FaMFA/3bnfNnZW96Rc7Jw+H7pWXKt+BBmaOKBvcFRcjly4odCsIhK2IF4bhx4+T3+/X444+rsLBQGRkZWrVqlZYtW6Z//ud/VkdHhwzD0Be/+MVIRcD7LJqco3UHGlTbcFHHmtpUmJX80Q8CAAAAACDGuF3tsvetl31gS/gyYElG9miZYybLbb+g0KaXpN7wdgXiL80tOEfmyNyrP09Pt+xdFbL3b5IcJ7yy8axyWVMWyLCGz4q/RnqO5PNLF1vkdnXISGAw2FAT0aVlli9fftXtZcuWSZL+4R/+IZJPiw+QEPBpQXG2Vlee1jv7Tumvyou9jgQAAAAAQNRw28/L3rtO9sFtkh2SFB4VaKSky73QLHvbm/33NbIvjRYcd/VoQUlyXUfO4Z0KbXtT6mqXZMgsni3fnHtkJCQN5ksaFIZpycjIl9t4TM7Zk7JG0zcMNaw9HWMWl+Rqw8FGHTp1Xieb2zUqY/h9YwIAAAAA4Ga4F5oV2vOunOrdkmOHNyalyohPknvujNymS4uOBOJlFc2UWTxH5sic634up/G4Qptelns2vFirkTMmfDlxZsFgvBTPmFmjZTcek3vmpERBOORQEMaYxHi/5k/K1toDDXpn3yn9xZJJXkcCAAAAAMATTmuj7N3vyjmyV3Ld93ZYPqn9gtz2C5IkI3uMrJI5MseWXjNa8DK346JCW1+XU7M7vCExRb65S2VOmBZeCXiYM7KZh3AooyCMQYun5GrjoUYdOHlOp1s7lJfO3AAAAAAAgNjhnK2XvWu1nGNV17+DHXpvtODkOTLTrz9aUJLcUJ/syg2yd62RQr2S5ZNVdqusGXd8YJk4HJmXFipxm07IdR0ZhulxItwMCsIYlJIQ0NyJ2dp4qFGrK0/pC7cNj1WTAAAAAAD4MM7pOoV2r5FbX/OB9zFyCi/NLVgqw+f/wPu5rivnWJVCW16VLrZKkszCKfLNXyojZeSAZ496ialSMFnqbJN7oUVGWqbXiXATKAhj1O1Tc7Wl+oz2HWvVmWldyk5L8DoSAAAAAAADznVduSerw8Vg47Hr3yku4b3RgiOyP/JzOufOKLTplf6i0RiRHZ5nsGDCACYfWgzDkJk1Ws6xA+E5GykIhxQKwhiVlhin2RMytaW6SasrT+nRW2P3mxgAAAAAYPhxXUfO0SrZu9fIbT513fuERwvOlTlu6oeOFuz/nD2dsndUyD6wRXIdKRAv3+y7ZJbMk2FaA/0Shhwje5R07ICcMydlFc3yOg5uAgVhDLujNE/bas5q99Fm3TWtQBkp8V5HAgAAAADgE3EdW07tPtl71sg913TtHeKCV4wWzLrBz+nIObRdoe1vSd0dkmHILJkr3y13y0hgXv/LzKxRsiW5LFQy5FAQxrD0pHjNGp+h7bVntWb/KX12wXivIwEAAAAA8LG4dkjO4Z0K7V3bPyfglYzcseHRgmOn3NBowcuchqMKbXxJbktD/+fxLXxQ5si8Acs+XBiZBZJhyG1tkBvqu6n/z/AWBWGMu6M0TzuOnNWO2maVlxVoRFKc15EAAAAAALhhbl+v7IPbZO9bJ3VcvHpnXFDWpJkyi298tGD/520/r9CW1+Qc2RfekJQq37z7w4uXGMYApR9eDH+cjBHZclsb5TaflpEzxutIuEEUhDEuMyVB0wtHavfRFq3Zf1rL5o31OhIAAAAAAB/J7emWfWCz7MoN4ct+r2DkjQuvRFx4c6MFJckN9cneu1b2nrVSqE+yfLKm3y5r2mIZ/sBAvoRhycgaJbe1UU7TCZkUhEMGBSF0Z1m+9hxt0baaJt1Zlq/UIN/wAAAAAADRye3qkF25QfaBzVJv93s74oOyimaF5xb8GCvouq4r5+h+hTa/KrWflySZ48rkm7dURnLawISPAWbWKDmHtss9wzyEQwkFIZSdFlTpmHTtO96qtftP66E5hV5HAgAAAADgKm7HRdn71smu2hoe2XdJeLTgpbkFrY9XczgtjQpteknu6brw5xyZK9+CB2XmjRuQ7LHEyB4tSXKaTnicBDeDghCSpCVl+dp3vFVbqpu0pDRfSQlMJAoAAAAAiA529S6F1v5OcuzwhvhEWZNmySye/bFGC17mdncotP1tOQe3Sq4rxQflm323zOI5MkxzgNLHFiMtS/IHpPbzcjvbZASTvY6EG0BBCElSfnqiSgpGqKr+nNZWndb9s5gnAAAAAAAQHdzWRsmxZeSND88t+AlGC0qS69hyqrYptONtqadTMkxZU+fLmlUuIz44gMljj2GaMjIL5J6uk9N0UlZhideRcAMoCNGvfFq+qurPadOhM7p9Sp4S4xlFCAAAAADwnjXnXlkzlsiIi//En8s5dUShTS+HS0dJRt54+RY+KDM95xN/boSZWaNln66T23RSoiAcEigI0W9URpKK8lJVffqCNhxs1D0zRnkdCQAAAACA8OW+n7AcdNtaFdr8mpyj+8MbkkfIN//+8ErHhjEAKXGZkRXuE5wmFioZKigIcZXyaQX9BeHiKblKCHCKAAAAAACGLrevV/aed2XvXSfZIcnnlzXjDlllt8rwceVcJJiXCkK36aRcx2E+xyGA9gdXGZuVrPE5KTrSeFEbDzaqfFqB15EAAAAAALhpruvKObJPoS2vSR0XJEnmhOnyzb1PRlKqx+mGNyMxRUpKldovyD1/VkZ6tteR8BEoCHGN8rJ8HWm8qPUHG7WoJFfxfsvrSAAAAAAA3DCn+ZRCG1+W23hMkmRk5IfnGcwp9DRXLDGzRstpr5TbdEKiIIx6FIS4xvicFI3JTNLxs+3acviMbp+a53UkAAAAAAA+ktvVrtD2t+Qc3C7JleIT5Ztzj8xJt3CZ6yAzskZJdZXhlYyLZ3sd52PbVXVab2+sVXtHr5ISA7p70QTNmDz8ehIKQlzDMAyVTyvQzysOae2BBi0ozlbAxyhCAAAAAEB0cm1bdtVm2TsqpN5uyTRlTVkoa9adMuISvI4Xk4zES5dx93R5G+QT2FV1Wv/x4h61dfT0bzvd1C4t07ArCSkIcV2T8lJVMDJR9S0d2lrdpFtLcr2OBAAAAADANZz6GoU2vSz3XJMkySgokm/BAzJHZHmcLMaFesN/+wLe5vgE3t5Ye1U5KEltHT16a0MtBSFig2EYurMsX/+xplrv7j+teZOy5bcYjg0AAAAAiA7uhRaFtrwq51hVeEPKSPnm3y9zzGQZhuFtOFxREA7dlaLb264/+rG9s3eQk0QeBSE+0JRRI5Q7IqiGc53aXtOkBcU5XkcCAAAAAMQ4t69H9q41svetlxxb8gdkzVwiq3SRDIuaI1q4oT5JkuEfmiMInQvNCnaelZR4zb6k4NB8TR+Grxx8oMujCP9rbY3W7D+tuUVZspjUFQAAAADgAdd15dTsUWjr61LnRUmSWTRTvjn3ykhM8TgdrtE3dC8xds6dUd8rP9OdQUuNvRPUFnpvXYbkxDjdvWiCh+kig4IQH6p0TLqyUhPUdKFLO480a85E5nAAAAAAAAwu52y9QhtfknvmhCTJyCyQb+FDMrNHe5wMH2iIXmLstDSo75WfSd0dmj5xnHyFc/X2lqNq7+xVUpBVjBGjTMPQktI8/feGI1pdeUqzxmfKMpnLAQAAAAAQeW5nm0Lb3pRzeKckV0pIkm/uvTKLZsowuMItmg3FS4yds6fU9+rPpZ5OGQVF8t/zp5rp82tm6Sivo0UcBSE+0vSxGXp7b71a2nq052izZo3P9DoSAAAAAGAYc+2Q7P2bZO98R+rrkUxLVulCWTOXyAjEex0PN6JvaI0gdBqPq+/1X0q93TJHF8t315/IGCLZBwIFIT6SZRpaUpqvFzbVaU3lac0cl8GKUAAAAACAiLBPHJK96RW5F5olSeboYlnz75eZxmCVIeXSCMJonoPQtW05x6tkV22Ve6pWkmSOnSLfnY/G3II3sfVq8bHNHJehN3ef1JkLXao+fUGT8tO8jgQAAAAAGEac82dlb35FzonDkiQjNUPWggdljZ7kcTJ8HO7lOQij8BJjt/2C7IPbZB/aJnW2hTf6/LImz5E1b6kM0/rwTzAMURDihvgsUwsn5+j1XSe1rqqBghAAAAAAMCDc3m7ZO1fL3r9RcmwpECdr5p2ypi6IuVFcw8qlS4yj5TJd13Xknjoi+8AWOccPSq4jSTLSMmWWzJNVNFNGXILHKb3DVxpu2LyibFXsO6Xq0xfUeK5TOSOCXkcCAAAAAAxRruvIqd6l0NY3pK52SYbM4lvkm32PjGCy1/HwSUXJJcZud4fswzvlVG2Ve7ElvNE0ZY4tlTVlnozccUyjJgpC3IRgnE+zx2dq0+EzWlfVoIcXjvc6EgAAAABgCHLOnFBo08tym05Kkozs0fItfEhmZoHHyTBgPLzE2HVduU0nZVdtkXNkn2SHwjuSUsOXEU+aLSMxZdBzRTMKQtyURSU52nz4jHbVNeu+maOUnBB9cwkAAAAAAKKT23FRoa2vy6nZHd4QTJFv3n0yJ0xnFNcwc3kOwsG8xNjt65VTu0d21Ra5zaf7txsFRbKmzJM5elJMzi94IygIcVMyUxJUMmqEDpw8p82Hz+ju6aO8jgQAAAAAiHKuHZK9b4Ps3avDc9OZlqxpi2XNuF2GP87reIiEQbzE2Dl3Rk7VVtnVO6XenvDG+KCsSbfImjxXRurIiGcY6igIcdMWl+TqwMlz2nT4jO6Ymi+/z/Q6EgAAAAAgCrmuK+f4QYU2vypdmv/NLCyRb/79MlIobYa1S4uURKogdO2QnKMHwqMFG472bzeyR8sqmS9z3NSoWSBlKKAgxE0bm52sgpGJqm/p0K66Zs0tyvI6EgAAAAAgyjjnmsLzDNbXSJKMtCz5Fj4os2Cix8kQaa7jvDfvn29gqye37bzsg1tlH9p+aXEbSb6AzIkzZE2ZK3Nk3oA+X6ygIMRNMwxDi0ty9Zv1tVpX1aA5EzOZKwIAAAAAIElye7pk76yQfWCz5DhSIF7WLeWySubLsJj/LSbYly8v9sswPvlVh67ryDlZI6dqi5wThyTXlSQZ6dmySubJnDhDRiD+Ez9PLKMgxMdSVpiuV3cG1HShS4dPX1BxfprXkQAAAAAAHnIdR87hHQpte1Pq7pBkyJw8V77Zd8lISPI6HgbT5cuL7ZB6X/25jKQ0GclpMpJGXPp4hJSY8pELhrhd7bIP75RdtVVqaw1vNC2Z46eGC+ecMQxYGiAUhPhYLNPUwsk5em3nCa070EBBCAAAAAAxzGk4ptCml/pXjjVyCuVb+JDMDC73jElxCVJSmtR+Xm59jdzr3ccwwyXhpcLQSEp7rzw0TNmHd8ipq5QcO3z/5BGyJs+VVXwLhXMEUBDiY5s7MUsVe+tV03BBDec6lTsi6HUkAAAQxZ555hnV1dVp7NixWr58ef/29vZ2PfXUU2pra1NpaamWLVvmYUoAwM1w2y8otPU1ObV7wxuSUuWbu1Tm+DJGdsUww/Ip8Mjfyb3YIrftvNR+Tm7beblX/K3OtnCB2H5ebuOxD/pMMkcXy5wyT2ZBkQyTRVIjhYIQH1swzqfZEzK18dAZra9q0MMLx3sdCQAARKm6ujp1d3drxYoVevrpp1VbW6sJEyZIkl544QU98sgjys/P9zglAOBGuaE+2fvWyd79rhTqkyyfrGm3yZp+mwx/ZFatxdBi+Pwy0nOk9Jzr7nftULggfF9x6Lafl7o7ZY4ullUyR0Zy+uAGj1EUhPhEFk3O1aZDZ7Srrln3zhyllAT+IQAAANeqqalRWVmZJKm0tFTV1dX9BeHJkyf14osvqqWlRY8++qiKioq8jAoA+BCu68o5ekChLa9KbeckSea4Uvnm3UeRg5tiWD4pNUNGaobXUSAKQnxCGSnxKhk1QgdOntPmQ2d0z4xRXkcCAABRqKOjQ9nZ2ZKkYDCo+vr6/n2HDx/W97//fSUlJelHP/qRnnjiiWseX1FRoYqKCknSypUrlZExdH+Y8Pl8Qzo/Bg7nAi4bKudCX9MpXXj7WYWOHZIk+bLylXbXo4orLPY42fAxVM4FRN5gnwsUhPjEFk/J1YGT57Tp8BktKc2X38ecAAAA4GrBYFCdnZ2SpK6uLgWD781dnJeXp4KCAkmS+QFzC5WXl6u8vLz/dnNzcwTTRlZGRsaQzo+Bw7mAy6L9XHC7OxXa8bacqq2S60hxQflm3yVz8hy1mZbaojj7UBPt5wIGT6TOhby86y8cRJODT2xsVrIKRiaqsyeknXVnvY4DAACiUFFRkfbv3y9JqqysvOoy4tzcXJ07d07d3d2ybduriACA93EdR/aBLep97odyDmyW5MqcMl+Bz31T1pT5MkzL64gABggjCPGJGYahxSW5+s36Wq2vatCciVkyWa0KAABcYdy4cfL7/Xr88cdVWFiojIwMrVq1SsuWLdPDDz+sn/zkJ+rt7dUf//Efex0VACDJOV2n0MaX5LY2SpKMvHHyLXhI5sjrLzgBYGijIMSAKCtM16s7A2q60K3Dp85rcsEIryMBAIAos3z58qtuL1u2TJJUUFCgb3/72x4kAgC8n9t2TqEtr8mpqwxvSEqTb/79MsdOlcFAEGDYoiDEgLBMU4sm5+jVnSe0rqqBghAAAAAAhhC3r1f23rWy96yV7JDk88uafrusaYtl+PxexwMQYRSEGDBzi7L09t561TZc1OnWDuWlJ3odCQAAAADwIVzXlVNXqdCWV6X2C5Ikc/w0+ebdJyMpzdtwAAYNBSEGTELApzkTs7ThYKPWVTXoc4smeB0JAAAAAPABnObTCm16WW7DUUmSMTJXvoUPycwd63EyAIONghADatHkHG082Kg9R1u0dOZopQQDXkcCAAAAAFzB7epQaPtbcg5tk1xXik+Ub/bdMotnyzBNr+MB8AAFIQbUyOR4TRmdrv0nWrXp8BndO2OU15EAAAAAAJJcx5ZTtUWh7W9Lvd2SYcqaukDWLXfKiAt6HQ+AhygIMeAWT8nV/hOt2nz4jJaU5ings7yOBAAAAAAxzamvDV9OfO6MJMkomCjfggdkjsj2OBmAaBDRgvCZZ55RXV2dxo4dq+XLl1+1r7e3V1/5ylf0ta99TWVlZZGMgUFWmJmkURmJOtncoZ1HmjV/Ev/gAAAAAIAX3IutCm1+Vc6xA+ENKenyzb9f5pgSGYbhbTgAUSNikwvU1dWpu7tbK1asUCgUUm1t7VX733nnHY0ePTpSTw8PGYahxSW5kqT1VQ1yXNfjRAAAAAAQW9y+HoW2vane558Ml4O+gKw59yrw8DdkFU6hHARwlYiNIKypqekfGVhaWqrq6mpNmBBe1TYUCqmmpkaTJk2K1NPDY6VjRiot8YTOXuzW4VPnNblghNeRAAAAAGDYc11XTu0ehba+LnVclCSZE2fIN/c+GYkpHqcDEK0iVhB2dHQoOzt8aWkwGFR9fX3/vnfffVe33nqrampqPvDxFRUVqqiokCStXLlSGRkZkYo6KHw+35B/DTfrnlvG67m1B7W5plm3Tp/odZx+sXgsohXHInpwLKIHxyJ6cCwAAEONc7ZeoY0vyz1zXJJkZBbIt+BBmTljPE4GINpFrCAMBoPq7OyUJHV1dSkYDK+IZNu29uzZo29+85sfWhCWl5ervLy8/3Zzc3Okog6KjIyMIf8abtaUvETF+UwdPNGivdXHlZ+e6HUkSbF5LKIVxyJ6cCyiB8ciegyXY5GXl+d1BABAhLld7Qpte0POoZ2SXCkhSb4598qcNFOGEbGZxQAMIxH7TlFUVKT9+/dLkiorK1VUVCRJunDhglpaWvTd735X69ev17PPPqv29vZIxYCHEgI+zZmYJSk8FyEAAAAAYOC4dkihfevV+98/kHNoh2QasspuVeCRb8oqvoVyEMANi9gIwnHjxsnv9+vxxx9XYWGhMjIytGrVKi1btkzf+973JEnPP/+8iouLlZSUFKkY8NiiyTnacKhRe4626L6Zo5UaDHgdCQAAAACGPOfEYYU2vyL3/FlJkjlqkqwFD8hMy/Q4GYChKGIFoSQtX778qtvLli276vbDDz8cyadHFEhPjtfU0emqPN6qTYcadd9MVq4GAAAAgI/LudAse9Mrck4ckiQZqRmyFjwga3Sxx8kADGURLQgBSVpckqvK463aUt2kO0vzFfBbXkcCAAAAgCHF7e2RvWu17MoNkmNL/jhZs+6UNXWBDIsf7QF8MnwXQcSNyUzS6IwknWhu144jZ7WgOMfrSAAAAAAwJLiuI6d6t0Lb3pA62yRJ5qRZ8s25V0Yw2eN0AIYLCkJEnGEYWjwlV/+1tkbrDzZq3qRsmYbhdSwAAAAAiGpO00mFNr4kt+mkJMnIGi3fwgdlZo3yOBmA4YaCEINi6uh0pSUG1HyxW4fqz6tk1AivIwEAAABAVHI7Liq07Q051bvCG4LJ8s29T+bE6axMDCAiKAgxKCzT0KLJuXplx3Gtq2qgIAQAAACA93HtkOzKjbJ3vSP19UqmJavsVlkz7pARiPM6HoBhjIIQg2bOxEy9vbdeRxovqr6lQwUjE72OBAAAAACec11X9vGDsje9IvdiiyTJHDNZvvn3y0jN8DgdgFhAQYhBkxDwac7ETK2vatT6qgY9eusEryMBAAAAgKecc01qefu/FKrbL0ky0rLkW/CAzFFFHicDEEsoCDGoFk3O0YaDjdpztEVLZ45WamLA60gAAAAAMOjcnm7Zuypk798kOY4UiJc1q1zWlPkyLMvreABiDAUhBlV6UrxKR6dr3/FWbTrcqPtmjvY6EgAAAAAMGtd15BzeqdC2N6WudkmGgtMXK1S2WEZCktfxAMQoCkIMusVTcrXveKs2Hz6jO0vzFfDz2zEAAAAAw5/TeFyhjS/JbT4lSTJyxsi34CGNmDxNzc3NHqcDEMsoCDHoxmQma0xmko6fbdeOI2e1oDjH60gAAAAAEDFuxwWFtrwup3ZPeENiinzzlsocP02GYXiaDQAkCkJ4ZHFJrv5zbY3WVzVq3qRsmfyjCAAAAGCYcUN9svdtkL17jRTqlSyfrGmLZU2/XYaf+dgBRA8KQnhiyuh0jUiKU3Nbtw6ePKcpo9O9jgQAAAAAA8J1XTnHqhTa8qp0sVWSZI6dIt+8+2Wk8LMPgOhDQQhPWKahWyfn6KXtx7WuqoGCEAAAAMCw4Jw7o9DGl+WeqpUkGenZ8i14UGb+BI+TAcAHoyCEZ2ZPyNRbe+pVd6ZN9S3tKhjJil0AAAAAhia3p1P2jgrZB7ZIriPFJch3y10yS+bKMFmYEUB0M2/kTo888og2bdrUf3vXrl167LHHIhYKsSE+4NOciVmSpHVVjR6nAQAAAICb5zqO7Kqt6v3vH8rev0mSK7NkngKf+6asqQsoBwEMCR86grC5uVlNTU2SpPr6elVVVUmS9uzZozNnzkQ+HYa9RZNztOFgg/YebdHSmaOUlhjndSQAAAAAuCHO6TqFNr0st6VBkmTkjQtfTjwy1+NkAHBzPrQgXLNmjX77299Kkn73u9/pd7/7Xf++/Pz8yCZDTBiRFKfSMenae6xVmw6d0dJZo72OBAAAAAAfym07r9CW1+TU7QtvSEqTb/79MsdOlWEY3oYDgI/hQwvCCRMm6O6779Zbb72lsrIy5eaGfwuSlJSkRYsWDUpADH+LS3K191irtlSf0Z1l+YrzMwQfAAAAQPRxQ32y96yVvXetFOqTfH5Z02+TNe02GT6/1/EA4GP70IJwxowZmjFjhsaPH68pU6YoMzNTkuQ4jkzzhqYvBD7S6MxkjclM0vGz7dpRe1YLJ+d4HQkAAAAA+rmuK6euUqEtr0nt5yVJ5rgy+eYtlZGc5mk2ABgIN9TynTx5UmvWrFFra6u+9KUv6U//9E+1evXqSGdDDFk8JTw6df3BBjmO63EaAAAAAAhzWhrU98rTClX8Rmo/L2NkrvwP/o38d32echDAsHFDBeGGDRuUmJiojRs3KhQKKTc3V6tWrYp0NsSQqaPSlZ4Up5a2HlXVn/M6DgAAAIAY53Z3qG/979X3u3+We7pOig/Kd+un5V/2NZl547yOBwAD6kMvMb6svb1dycnJ2rNnjxYvXqwxY8bo//2//xfpbIghpmlo0eQcvbT9uNYdaNDU0eleRwIAIOZ87Wtf06hRo1RYWKjRo0ersLBQOTlM/QEgtriOLadqq0I73pZ6uiTDlDV1vqxbymXEBb2OBwARcUMFYUZGhp599lm1t7frS1/6ks6fP6+kpKRIZ0OMmT0xS2/tqdfRpjadbG7XqAzOMQAABtPs2bMVCoWUlpamffv26ac//amSk5OVnp6uMWPG6G/+5m+8jggAEeWcqlVo08tyW89Ikoz8CfIteFBmerbHyQAgsm6oIPyTP/kTvfDCC5o4caLmzJmj3/zmN5o7d26ksyHGxPstzS3K0toDDVpf1aDPL57odSQAAGLKvn379MMf/rD/9h133KFt27bp3nvv1fHjxz1MBgCR5ba1KrT5VTlHD4Q3JKfLN/9+mYUlMgzD23AAMAhuqCCcM2eOZs2apYaGBjU2NuoLX/gCqxgjIhYW52h9VYP2HmvV0lk9SkuM8zoSAAAxIzk5WceOHVNhYaEkaeLEiXrqqaf0J3/yJxo5cqS34QAgAty+Xtl73pW9d51khySfX9aMJbLKFsnw+b2OBwCD5oYKwvr6ev3gBz9QY2OjJCknJ0d///d/r/z8/IiGQ+wZkRSnsjEjtedYizYeatT9s8Z4HQkAgJjxP/7H/9BPf/pTFRQUqLCwUKdOnVIgEPA6FgAMONd15RzZq9CW16WOC5Ikc8J0+ebdJyMx1eN0ADD4bmgY4M9//nOdO3dOCxcu1MKFC3X+/Hn94he/iHQ2xKhbS3IlSVsON6mnz/Y4DQAAsSMnJ0crVqzQjBkzdP78eeXk5Ogf/uEfvI4FAAPKaT6lvpf+n0Lv/LfUcUFGRr78n/qS/Hd+jnIQQMy6oRGEdXV1+vznP697771XkvTGG2/o2WefjWgwxK7RmUkam5Wso01t2l57Vosms3oiAACDxTRNzZ07l/mmAQw7ble7QtveknNouyRXSkiSb849MifNkmEwhRaA2HZDBWFSUpL27dunGTNmSApPYM0qxoikW0tydbSpTeurGrRgUrZMk4mBAQAAANw817ZlH9gse2eF1NstmaasqQtlzSyXERfvdTwAiAo3VBAuWbJEzz//vHbu3Nm/7ZFHHolYKGDKqBFKT4pTa3uPDpw8p9Ix6V5HAgAAADDEOCerFdr0itzzTZIkY1SRfPMfkDkiy+NkABBdbqggXLx4sVJTU7Vv3z5J0rRp01RWVhbRYIhtpmno1pJc/WHbMa2vaqAgBAAAAHDD3AstCm1+Rc7xg5IkI2WkrAUPyBxdLMPg6iQAeL8bmmjhiSeeUHNzs77xjW/oG9/4hs6ePat//Md/jHQ2xLjZEzIV77d0tKlNJ862ex0HAAAAQJRz+3oU2vqGep9/MlwO+gOy5t4n/8NflzVmMuUgAHyAGxpB2Nraqqys94ZgZ2ZmqqWlJWKhAEmK81uaNylL7+5v0PqqBv3JbRO9jgQAAAAgCrmuI6dmj0JbX5c62yRJZtFM+ebcKyMxxeN0ABD9bqggzM7O1ssvv6z09HS5rqtXXnlF2dnZkc4GaGFxjtYdaNS+4y1a2j5aI5LivI4EAAAAIIo4TScV2viy3KYTkiQja5R8Cx6UmT3a42QAMHTcUEH4qU99Sv/6r/+q733ve/3bvvrVr0YsFHBZWmKcphWma/fRFm081KgHbhnjdSQAAAAAUcDtbFNo2xtyDl9aTDOYLN+ce2UWzZBh3NBsWgCAS254kZKMjAzt2rVLkjRz5kyVlJRENBhw2a0ludp9tEVbq5tUPq1A8X7L60gAAOBjeOaZZ1RXV6exY8dq+fLlV+3r7e3VV77yFX3ta19jMTwAH8q1Q7L3b5K98x2pr0cyLVmli2TNXCIjwBVHAPBx3FBBKEklJSWUgvDEqIwkjc1K1tGmNm2vadKtJbleRwIAADeprq5O3d3dWrFihZ5++mnV1tZqwoQJ/fvfeecdjR7N5YAAPpx94pDsTa/IvdAsSTJHF4dXJ07N8DgZAAxtN1wQAl5aPCVXR5vatP5goxYW58g0WX0MAIChpKampn9kYGlpqaqrq/sLwlAopJqaGk2aNMnLiACimHP+rOzNr8g5cViSZKRlyjf/AZmj+b4BAAOBghBDQknBCI1MjlNLW4/2n2xV2ZiRXkcCAAA3oaOjo3+Ru2AwqPr6+v597777rm699VbV1NR84OMrKipUUVEhSVq5cqUyMobuaCGfzzek82PgcC58NKenS20bXlH7tgrJsWXEJSjl1geVeMsSGdbw+XGWcwGXcS7gssE+F4bPd1QMa6Zp6NbJufr9tmNad6CBghAAgCEmGAyqs7NTktTV1aVgMChJsm1be/bs0Te/+c0PLQjLy8tVXl7ef7u5uTmygSMoIyNjSOfHwOFc+GCu68g5vFOhbW9KXe2SDJnFs+Wbc4+6E5LUfe681xEHFOcCLuNcwGWROhfy8vKuu52lnTBk3DIhUwkBS8fPtuvE2Tav4wAAgJtQVFSk/fv3S5IqKytVVFQkSbpw4YJaWlr03e9+V+vXr9ezzz6r9vZ2L6MC8JjTeFx9L/6bQmt/J3W1y8geI/+yr8h/22dkJCR5HQ8AhiVGEGLIiPNbmleUrTX7T2tdVaO+cFuy15EAAMANGjdunPx+vx5//HEVFhYqIyNDq1at0rJly/S9731PkvT888+ruLhYSUkUAEAscjsuKrT1dTk1u8MbginyzbtP5oTpMgzmIAeASKIgxJCyoDhbaw80qPJ4i861j9aIpDivIwEAgBu0fPnyq24vW7bsqtsPP/zwYMYBECVcOyR73wbZu1ZLoV7J8skqu1XWjNtl+Hm/DwCDgYIQQ0paYpymjR2p3XXN2nCwUQ/OHuN1JAAAAAAfg+u6co4fVGjzq9LFFkmSWVgi3/z7ZaQw5zgADCYKQgw5i0tytLuuWdtqmnTXtHzFBziNAQAAgKHEOdek0KaX5daHFycyRmTLt+ABmQUTPU4GALGJZgVDTsHIJI3LTlbdmTZtrz2rW0tyvY4EAAAA4Aa4PV2yd1TIPrBZch0pEC/f7LtklsyTYVpexwOAmEVBiCFpcUmu6s60af3BRi0ozpFlMmkxAAAAEK1cx5FzaLtC29+Sujskw5BZMle+W+6WkZDodTwAiHkUhBiSJo8aoYzkeDW3devAiVaVFTJHCQAAABCNnIZjCm16SW7zaUmSkTtWvgUPyszI8zgZAOAyCkIMSaZh6NaSHL249ZjWVTVQEAIAAABRxm0/r9CW1+Uc2RvekJQq37z7ZY4rlWFwBRAARBMKQgxZt4zP1Bu7T+r42XYda2pTYVay15EAAACAmOeG+mTvXSd7z7tSqE+yfLKm3yZr2m0y/AGv4wEAroOCEENWwG9p/qRsra48rfVVDRSEAAAAgIdc15VzdL9CW16T2s5JksxxpfLNWyojeYTH6QAAH4aCEEPaguIcrT3QoMoTrWpt71Z6UrzXkQAAAICY47Q0hucZPF0nSTLSc+Rb+KDMvPEeJwMA3AgKQgxpqcGAphWO1K66Zm042KiHZhd6HQkAAACIGW53p0I73pZTtUVyXSkuKN/su2VOni3DtLyOBwC4QREtCJ955hnV1dVp7NixWr58ef/2X/7ylzp27Jj6+vr0Z3/2ZyouLo5kDAxzi0tytauuWdtqzuquaQVKCNB7AwAAAJHkOracg9sU2v621NMpGabMKfPku+UuGfFBr+MBAG6SGalPXFdXp+7ubq1YsUKhUEi1tbX9+/70T/9U3/nOd/T1r39dL774YqQiIEbkj0zU+JwU9fTZ2lZz1us4AAAAwLDmnD6ivt/9i0Ib/iD1dMrIGy//H/+t/Is+RTkIAENUxIZa1dTUqKysTJJUWlqq6upqTZgwIfykvvDTdnd3a8yYMZGKgBiyuCRXRxovasPBBi2anCPLNLyOBAAAAAwrbts5hba8JqeuMrwheYR88+6XOXaKDIP33wAwlEWsIOzo6FB2drYkKRgMqr6+/qr9P/jBD1RbW6uvfe1r1318RUWFKioqJEkrV65URkZGpKIOCp/PN+RfQzRbNHKkXttdrzPnOnT8XJ/mTMr7wPtyLKIHxyJ6cCyiB8cienAsACDM7euVvWet7L1rJTsk+fyyZtwuq2yxDJ/f63gAgAEQsYIwGAyqs7NTktTV1aVg8Oqh5v/7f/9vtbS06Mknn9R3v/vdax5fXl6u8vLy/tvNzc2RijooMjIyhvxriHYLijL14tYOvbqlWuNGBj7wfhyL6MGxiB4ci+jBsYgew+VY5OV98C/NAODDuK4r58g+hba+JrVfkCSZE6bJN3epjKRUj9MBAAZSxOYgLCoq0v79+yVJlZWVKioq6t/X19cnSYqPj1dcXFykIiDG3DI+U8E4n040t+tYU5vXcQAAAIAhy2k+rb6Xn1LonWel9gsyMvLkf+h/yn/no5SDADAMRWwE4bhx4+T3+/X444+rsLBQGRkZWrVqlZYtW6Z/+qd/UmdnpxzH0ec///lIRUCMCfgtzSvK0urK01pf1aDCrGSvIwEAAABDitvVodD2t+Qc2ia5rhSfKN+ce2ROukWGGbHxJQAAj0WsIJSk5cuXX3V72bJlkqS///u/j+TTIoYtKM7R2gMNqjzRqta2bqUnx3sdCQAAAIh6rm3Lrtoie8fbUm+3ZJqypi6QNatcRlyC1/EAABEW0YIQGGypwYCmjx2pnUeateFgox6aU+h1JAAAACCqOfU1Cm16We65JkmSUVAk34IHZI7I8jgZAGCwUBBi2Lm1JFc7jzRrW02T7ppeoIQApzkAAADwfu7FFoU2vyrnWFV4Q8pI+ebfL3PMZBmG4W04AMCgojnBsJOfnqgJOSmqbbyobTVNum0KqzcCAAAAl7l9PbJ3vyt77zrJsSVfQNbMJbLKFsmw+BERAGIR3/0xLC2ekqvaxovacLBRiybnyjL5DSgAAABim+u6cmr3KLTldanzoiTJnDhDvrn3yUhM8TgdAMBLFIQYliblpykzJV5nL3ar8niLpo/N8DoSAAAA4BnnbL1CG1+We+a4JMnILJBv4UMys0d7nAwAEA0oCDEsmYahW0tytWrLUa070KBphSOZRwUAAAAxx+1qV2jbG3IO7ZTkSglJ8s25V+akmTIM0+t4AIAoQUGIYWvW+Ay9sfukTrZ06NjZdo3NSvY6EgAAADAoXDsk+8Bm2TsrpN4eybRklS6UNXOJjEC81/EAAFGGghDDVsBnaf6kbL2z75TWHWigIAQAAEBMsE8clr35Fbnnz0qSzNHFsubfLzMt0+NkAIBoRUGIYW1Bcbbe3X9aB060qvlitzJS+G0pAAAAhifnQrPsTa/IOXFIkmSkZsha8KCs0ZM8TgYAiHYUhBjWUhICmjE2QzuOnNXGQ4361JxCryMBAAAAA8rt7Za9a7Xsyo2SY0v+OFmz7pQ1dYEMix/5AAAfjX8tMOzdWpKjHUfOaltNk+6eXuB1HAAAAGBAuK4jp3qXQtvelDrbJBkyJ90i35x7ZASZXgcAcOMoCDHs5aUnamJuqmoaLmhrdZNG5eV4HQkAAAD4RJwzJxTa9LLcppOSJCN7tHwLH5KZyS/EAQA3j4IQMWFxSY5qGi5ow8FGffrWqV7HAQAAAD4Wt+OiQtvekFO9K7whmCzf3KUyJ06XYRjehgMADFkUhIgJRflpykqNV9OFbu2obtCEzDivIwEAAAA3zLVDsis3yt71jtTXK5mWrLJbZc28Q4af97YAgE+GghAxwTQM3VqSq99tPqo3d9Zp/D3F/IYVAAAAUc91XTnHD8re/Krciy2SJLOwRL5598tIHelxOgDAcEFBiJgxa1ymXt91UsfOXNDOumbdMj7T60gAAADAB3LONSm06RW59dWSJCMtS76FD8osmOhxMgDAcENBiJjh95m6d8YordpyVC9srFNyvF+T8tO8jgUAAABcxe3plr2zQvaBTZLjSIF4WbeUyyqZL8OyvI4HABiGKAgRU+ZPylZXyNDrO+r0q3er9T/vKdGojCSvYwEAAAByHUfO4R0KbXtT6u6QZMicPEe+2XfLSOA9KwAgcigIEXP+ePFknWm9qF11zfr5O4f01fumKiMl3utYAAAAiGFO4zGFNr4st/mUJMnIKQxfTpyR73EyAEAsoCBEzDENQ59dME7t3X2qPn1BP6s4qK/cN0XJCQGvowEAACDGuO0XFNr6upzaPeENianyzVsqc3wZi+oBAAaN6XUAwAs+y9Sf3l6kgpGJamnr0S/eOazuPtvrWAAAAIgRbqhPbRteUe9zPwyXg5ZP1swlCjzyd7ImTKMcBAAMKgpCxKx4v6W/vHOSRibHqb6lQ//5brVCtuN1LAAAAAxjruvKPrpfvc//ky6u/b0U6pM5dqoCj3wjPNegn6taAACDj4IQMS05IaAvlk9WUrxf1acv6PlNdXJc1+tYAAAAGIac1jPqe/XnCr31X1Jbq3yZ+fI/8Nfy3/0FGcnpXscDAMQw5iBEzMtIiddflU/Sv79Rpd11zUpJ8OuBW8Z4HQsAAADDhNvTKXtHhewDWyTXkeKC8s2+S1m3LlVL6zmv4wEAQEEISFLByCT92e1F+sU7h7X2QINSEgJaPCXX61gAAAAYwlzHkXNom0Lb35K6OyXDkFkyT77Zd8mIT5RhWl5HBABAEgUh0G9SfpoeXjhO/73hiF7ecVwpQb+mj83wOhYAAACGIOd0nUKbXpbb0iBJMvLGybfgQZkj+SU0ACD6UBACV5g1PlNtXX16decJ/feGI0qM92tibqrXsQAAADBEuG3nFdrympy6feENSWnyzb9f5tiprEwMAIhaFITA+9w2JVcXu3q1vqpR/7GmWl+6p0T5IxO9jgUAAIAo5vb1yt67TvbetVKoT/L5ZU2/Tda022T4/F7HAwDgQ1EQAu9jGIYeuGWM2jr7tOdYi35WcUhfWzpF6cnxXkcDAABAlHFdV05dpUJbXpPaz0uSzPFl8s1dKiM5zdNsAADcKApC4DpMw9Aji8arvadPtQ0X9XTFIX3lvilKiue3vwAAAAhzWhoU2viS3IajkiRjZK58Cx+SmTvW42QAANwc0+sAQLTyWab+/PYi5aUH1XyxW7+oOKSePtvrWAAAAPCY29WhvvW/V9/v/jlcDsYnynfrH8m/7GuUgwCAIYmCEPgQ8QGf/qq8WOlJcTrZ0qH/Wlsj23G8jgUAAAAPuI4te/9G9T73QzlVWyQZsqYuVOBzfyerZK4Mkx+vAABDE/+CAR8hJSGgL5YXKzHOp0OnzuuFTXVyXdfrWAAAABhETn2t+n77zwptfFnq6ZJRMFH+zz4m38IHZcQFvY4HAMAnwhyEwA3ITE3QX95ZrP/fW1XaeaRZqcGA7ps52utYAAAMKc8884zq6uo0duxYLV++vH/7U089pZMnT0qSvvjFL2rMmDFeRQSu4V5sVWjzq3KOHQhvSEmXb/79MseUyDAMb8MBADBAGEEI3KDRmUn6s9smyjSk1ZWnteFgo9eRAAAYMurq6tTd3a0VK1YoFAqptra2f9+nP/1pPfHEE/ryl7+sF154wcOUwHvcvl6Ftr+l3uefDJeDvoCsOfco8NmvyyqcQjkIABhWGEEI3ITighH67ILxem7jEb207ZiSE/yaVjjS61gAAES9mpoalZWVSZJKS0tVXV2tCRMmSJKysrIkSZZlyfyAOdwqKipUUVEhSVq5cqUyMjIGIXVk+Hy+IZ1/uHNdV11V23Txnd/KbjsnSUqYOk+pd3xGVsqIAX0uzgVcxrmAyzgXcNlgnwsUhMBNumVCpi529er1XSf17PpaJcX7ND4n1etYAABEtY6ODmVnZ0uSgsGg6uvrr7nPb37zGy1duvS6jy8vL1d5eXn/7ebm5sgEHQQZGRlDOv9w5pw9pdCml+Q2HpckGRn58i18SE7OGJ3rtaUBPm6cC7iMcwGXcS7gskidC3l5edfdTkEIfAx3TM3Txc4+bTzUqGdWV+tL95YoLz3R61gAAEStYDCozs5OSVJXV5eCwasXdXj11VdVUFCg4uJiL+Ihxrld7Qpte1POoR2SXCkhSb4598icNEuGwaxMAIDhj3/tgI/BMAw9NHuMysakq7vP1s8rDulce4/XsQAAiFpFRUXav3+/JKmyslJFRUX9+/bu3avDhw/rM5/5jFfxEKNc21Zo33r1/vcP5RzaLpmGrLJbFXjkm7KKZ1MOAgBiBv/iAR+TaRr63K0TND4nRRe7+vT02wfV0d3ndSwAAKLSuHHj5Pf79fjjj8s0TWVkZGjVqlWSpF/84hc6e/asvvOd7+ipp57yOClihXOyWn2//bHsza9Kvd0yR02S/7Nfl2/+/TLi4r2OBwDAoOISY+AT8Fum/vyOIv37G1VqONepX6w+rP9x92QFfJbX0QAAiDrLly+/6vayZcskST/5yU+8iIMY5V5oVmjzq3KOH5QkGakZsuY/IGsMl7cDAGIXIwiBTygh4NNflRcrLTGgE2fb9V9ra2Q7rtexAAAAcAW3t0ehra+r9/l/CpeD/jhZc++T/7P/i3IQABDzKAiBAZAaDOiv75qsYJxPB+vPa9WWOrkuJSEAAIDXXNeRXb1Tvc/9UPaetZJjyyyapcDnvinf9NtkWFxUBQAA/xoCAyQrNUHLl0zSU28d1Laas0pJCOieGaO8jgUAABCznKaTCm18SW7TSUmSkTVKvoUPycziPRoAAFeiIAQGUGFWsr5w20T9x5rDqth3SskJfi0ozvE6FgAAQExxO9sU2vqGnOqd4Q3BZPnm3itz4gxWJgYA4DooCIEBVjJqhD4zf5xe2FSn3289puSEgErHpHsdCwAAYNhz7ZDsyo2yd62W+nok05JVtkjWjCUyAnFexwMAIGpREAIRMGdili529urNPfX6zboa/fXdkzUuO8XrWAAAAMOWffyQ7M2vyL3QLEkyx0yWb/79MlIzPE4GAED0oyAEIuTOsnxd7OrT5sNn9Mzqw/ryvVOUMyLodSwAAIBhxTl/VvamV+ScPCxJMtIy5VvwoMxRRR4nAwBg6KAgBCLEMAx9ek6h2rr6tP9Eq35WcUhfXTpFaYlc3gIAAPBJuT3dsne9I3v/RslxpECcrFnlsqYskGFZXscDAGBIYYZeIIJM09DnF0/Q2KxkXejs1dNvH1JnT8jrWAAAAEOW6zqyD21X73M/lL1vveS4MotnK/C5/y1f2a2UgwAAfAwUhECE+S1Tf7FkkrLTEtR0oUu/XH1YfSHH61gAAABDjtN4XH0v/ptCa38ndbXLyBkj/7KvyH/bZ2QkJHkdDwCAIYuCEBgEwTifvlherNRgQMea2vTrdTWyHdfrWAAAAEOC23FRfaufU98f/l3u2XopMUW+JZ+T/6H/KTOzwOt4AAAMeRSEwCBJS4zTX99VrISApQMnz+nFrUflupSEAAAAH8QN9Sm0e416//uHcmp2S5ZP1swlCjzyTVkTp8swDK8jAgAwLLBICTCIstOCWn5nsZ56q0pbq5uUGgzormn81hsAAOBKruvKOVal0JZXpYutkiRz7BT55t0vIyXd43QAAAw/FITAIBublaw/WTxRv3q3Wm/tqVdKgl9zi7K9jgUAABAVnHNnFNr0itz6GkmSMSJbvgUPyiyY4HEyAACGr4gWhM8884zq6uo0duxYLV++vH/7U089pZMnT0qSvvjFL2rMmDGRjAFEnamj0/VHc8dq1Zaj+t2Wo0qK92vKaH4bDgAAYpfb0yV7R4XsA5sl15HiEuS75S6ZJXNlmKxMDABAJEVsDsK6ujp1d3drxYoVCoVCqq2t7d/36U9/Wk888YS+/OUv64UXXohUBCCqzZ+Urbum5ct1pf9aV6NjTW1eRwIAABh0ruPIrtqq3v/+oez9GyW5MkvmhecZnLqAchAAgEEQsRGENTU1KisrkySVlpaqurpaEyaELwvIysqSJFmWJdO8fkdZUVGhiooKSdLKlSuVkZERqaiDwufzDfnXMFxE07F49M6R6nUsra08oWfWVOv/fG6B8kYmex1r0ETTsYh1HIvowbGIHhwLIPKchqMKbXpZbvNpSZKRO1a+hQ/KHJnncTIAAGJLxArCjo4OZWeH51ULBoOqr6+/5j6/+c1vtHTp0us+vry8XOXl5f23m5ubIxN0kGRkZAz51zBcRNuxuG96rs6eb1PVyXP6wQub9dX7pio1MeB1rEERbccilnEsogfHInoMl2ORl0fRgujjtp9XaMvrco7sDW9ISpVv3v0yx5WyMjEAAB6I2CXGwWBQnZ2dkqSuri4Fg8Gr9r/66qsqKChQcXFxpCIAQ4JlGvqTxRM0JjNJ5zt69bOKg+rqDXkdCwAAYMC5oT6Fdr6j3ud+FC4HLZ+sWeUKPPx3ssaXUQ4CAOCRiBWERUVF2r9/vySpsrJSRUVF/fv27t2rw4cP6zOf+Uyknh4YUgI+S395Z7GyUhPUeL5Lz6w+rD7b8ToWAADAgHBdV3ZdpXqf+5HsHW9LoT6Z48oUeOSb8t1SLsMfG1dPAAAQrSJWEI4bN05+v1+PP/64TNNURkaGVq1aJUn6xS9+obNnz+o73/mOnnrqqUhFAIaUYJxPXywvVkqCX3Vn2vTs+lo5jut1LAAAgE/EaWlU3ytPK/T2r6X28zJG5sr/4N/If9fnZSSneR0PAAAognMQStLy5cuvur1s2TJJ0k9+8pNIPi0wZI1IitMX75qsf3v9gCqPt+oP247p03MLudwGAAAMOW53h0Lb35ZzcKvkulJ8UL7Zd8ssniPjAxYqBAAA3ohoQQjg5uWOCOovlkzSz94+qE2HzyglGNCdZflexwIAALghrmPLqdqm0I63pZ5OyTBlTZ0va1a5jPjgR38CAAAw6CgIgSg0PidFjy6eoP96t0Zv7D6plAS/Zk/M8joWAADAh3JOHVFo08tyWxslSUb+BPkWPCAzPcfjZAAA4MNQEAJRqmzMSH16bp9e3HpMv91cp6QEvyYXjPA6FgAAwDXctlaFNr8m52h4kUIlp8s3f6nMwilMlQIAwBBAQQhEsQXFObrY2ad3Kk/pP9+t0f+8Z7JGZyZ7HQsAAECS5Pb1yt7zruy96yQ7JPn8smbcIavsVhk+v9fxAADADaIgBKLcPTMKdLGrV9trz+rn7xzWV+6boqzUBK9jAQCAGOa6rpwj+xTa8prUcUGSZE6YLt/c+2QkpXqcDgAA3CwKQiDKGYahz8wfp/buPh2sP6+fvX1QX1k6VanBgNfRAABADHKaTym08WW5jcckSUZGvnwLH5SZU+hpLgAA8PGZXgcA8NEs09AXFk/U6Iwknevo1c8rDqmrN+R1LAAAEEPcrnb1rVulvt/9NFwOxifKt3iZ/H/0FcpBAACGOEYQAkNEwG/pL++cpH99/YAaznXqp68d0KfnFmpiLpfxAACAyHFtW3bVZtk7KqTebsk0ZU1ZKGvWnTLimPYEAIDhgIIQGEIS4/364l3FevrtQ2q60KWn3jqosjHpeuCWMRqRFOd1PAAAMMw49TUKbXpZ7rkmSZJRUCTfggdkjsjyOBkAABhIFITAEJOeFK9vPFSmdQca9E7lKe073qqD9ee1pDRPt03Nk99i5gAAAPDJuBdaFNryqpxjVeENKSPlm3+/zDGTZRiGt+EAAMCAoyAEhiC/ZerOsnzNGp+hV3Yc195jrXpzT722157Vp+YUqmTUCK8jAgCAIcjt65G9a43sfeslx5b8AVkzl8gqXSTD4kcHAACGK/6VB4awtMQ4feG2Is0ruqDfbzumM+e79MvVh1Wcn6aH5oxRZgrzAgEAgI/muq6cmj0KbX1d6rwoSTKLZso3514ZiSkepwMAAJFGQQgMAxNyU/X1B0u16dAZvbWnXodOnVfNHy7otim5urM0XwG/5XVEAAAQpZyz9QptfEnumROSJCNrlHwLHpSZPdrjZAAAYLBQEALDhGWaurUkV9PHjtTru05qe+1Zra48rZ1HmvXALaM1rXAkcwYBAIB+bmebQtvelHN4pyRXCibLN+demUUzZBjMaQwAQCyhIASGmeSEgB5eOF5zi7L0+63HVN/SoV+vq9WW6iZ9ek6hckYEvY4IAAA85Noh2fs3yd71jtTbI5mWrNJFsmbeISMQ73U8AADgAQpCYJgak5msry2dqu21TXpt10kdabyof3p5nxYU5+ju6QVKCPDlDwBArLFPHJa9+RW5589KkszRxbIWPCAzNcPjZAAAwEs0BMAwZpqG5hZlq3TMSL25+6Q2V5/RhoON2nO0RUtnjtKsCZkyuewYAIBhz7nQLHvTK3JOHJIkGWmZ8s1/QOboSR4nAwAA0YCCEIgBwTif/mjeWM0pytIfth7T0aY2Pb+pLnzZ8dxCjcpI8joiAACIALe3W/au1bIrN0qOLQXiZM0qlzVlvgyLHwUAAEAY7wqAGJKfnqgv3Vui3Udb9OqO4zrR3K5/eXW/5kzM0n0zRykx3u91RAAAMABc15FTvUuhrW9IXe2SDJnFt8g3+x4ZwWSv4wEAgChDQQjEGMMwNHNchkpGjVDF3nqtr2rU1pom7TveontmjNK8omxZJpcdAwAwVDlnTii06WW5TSclSUb2aPkWPiQzs8DjZAAAIFpREAIxKt5v6YFbxmjOxPBqxzUNF/T7rce09dJlx+OyU7yOCAAAboLbcVGhra/Lqdkd3hBMkW/efTInTJfBnMMAAOBDUBACMS4rNUF/fVex9p84p5e3H1PDuU79+xtVmjEuQ/fPGq3UYMDriAAA4EO4dkj2vg2yd6+W+nol05I1bbGsGbfL8Md5HQ8AAAwBFIQAZBiGSseka1J+qt7df1prKk9rd12zqk60qnxagRZNzpHPMr2OCQAAruC6rpzjBxXa/Kp0sUWSZBaWyDf/fhkpIz1OBwAAhhIKQgD9Aj5Ld08fpVvGZ+ql7cd14OQ5vbrzhLbVNOlTcwo1KT/N64gAAECSc64pPM9gfY0kyRiRJd+CB2UWTPQ4GQAAGIooCAFcIz05Xn+xZJIOnzqvP2w7prMXu/WzikOaOnqEHpw9RulJ8V5HBAAgJrk9XbJ3viP7wCbJcaRAvKxb7pJVMk+GZXkdDwAADFEUhAA+0KT8NH3joTKtP9ioir312n/inA6dOq87pubrjql58vu47BgAgMHgOo6cwzsU2vam1N0hyZA5ea58s++SkZDkdTwAADDEURAC+FA+y9QdU/M0c2yGXt15XLuPtujtvfXaceSsHpo9RlNGjWBlRAAAIshpPKbQxpflNp+SJBk5hfItfEhmRp7HyQAAwHBBQQjghqQmBvT5xRM1ryhbv98WXu34P9ZUqygvVZ+aU6is1ASvIwIAMKy47RcU2vqanNq94Q1JqfLNXSpzfBm/nAMAAAOKghDATRmXk6LHHijVlsNn9Oaek6o+fUFPvrRPiybnqHxageL9zH8EALi+Z555RnV1dRo7dqyWL1/ev/3EiRN6+umnJUlf/OIXNWbMGK8iRgU31Cd73zrZu9+VQn2S5ZM17TZZ02+T4Q94HQ8AAAxDTCAG4KZZpqGFk3P09380XXMmZslxXK090KAfvLhHu+ua5bqu1xEBAFGmrq5O3d3dWrFihUKhkGpra/v3Pffcc3rsscf09a9/Xc8995yHKb3luq7suv3qff5J2dvflkJ9MseVKvDIN8JzDVIOAgCACGEEIYCPLSner88uGKd5RVl6cetRnWzu0G/W12rz4TP69NxC5aUneh0RABAlampqVFZWJkkqLS1VdXW1JkyYIEnq6OhQRkZG/8fXU1FRoYqKCknSypUr++8/FPl8vmvy9zWd0oW3n1Xo2KHwfbLylXbXo4orLPYiIgbJ9c4FxCbOBVzGuYDLBvtcoCAE8ImNykjSV5dO1Y7as3pt1wkdbWrTj1+p1PyibN0zY5SCcXyrAYBY19HRoezsbElSMBhUfX19/74bGXleXl6u8vLy/tvNzc0DH3KQZGRk9Od3uzsV2vG2nKqtkutIcUH5Zt8lc/IctZmW2obw68RHu/JcQGzjXMBlnAu4LFLnQl7e9Rc546d2AAPCNAzNmZil0jHpemtPvTYdatSmw2e091iL7ps5WrMnZspkQnUAiFnBYFCdnZ2SpK6uLgWDweveL1YW33AdR87BbQrteEvq7pQMQ+aU+fLdcpeM+Ov/vwEAAIgU5iAEMKASAj59ak6h/teDZRqXnayOnpB+u7lO//Lqfp042+Z1PACAR4qKirR//35JUmVlpYqKivr3JSUlqaWlRa2trUpISPAq4qDpOX5Yfb/7Z4U2/F7q7pSRN07+zzwm/6JPUQ4CAABPMIIQQETkjgjqf95Tor3HWvTKjhOqb+nQv7x2QLMnZGrpzNFKSvB7HREAMIjGjRsnv9+vxx9/XIWFhcrIyNCqVau0bNkyPfzww/rxj38sSfqrv/orb4NGmOs4Ov/Gr+W2NkpJafLNv1/m2KkxM3ISAABEJ8MdIsuNnj592usInwjzCEQPjsXg6+mz9c6+U1pX1SDbcRXvt3T39AI9tGiKzrW2eh0P4usimnAsosdwORYfNM/MUDeU3xsmtZ3V+ep9sqYtluHjF2axbLh8n8Enx7mAyzgXcBlzEAIYduL8lpbOGq3ZEzL10vbjOnTqvF7aflxbas4qPz2o7NQEZaUmKDstQSOT42WZjKIAAAxf8WMny5ec6XUMAACAfhSEAAZNZmqC/vLOSTpYf15/2HZMTec71XS+86r7WKahjJT4cGmYltBfHmamJshvMW0qAAAAAAADjYIQwKAyDEMlo0aoKC9VbSGfak406sz5LjVd6NKZC106196jM+e7dOZ8l3T8ysdJI5Pi+0caXv47MzVB8X7LuxcEAAAAAMAQR0EIwBM+y9TE7HSNiHOu2t7bZ6vpYrfOnO8Ml4aXysOWtm41X/pTVX/uqsekJQbCheH7Rh0mxjOvEwAAAAAAH4WCEEBUCfgtFYxMVMHIxKu2h2xHzRe7deZC11XF4dkLXTrf0avzHb2qPn3hqsckxfuVlRqv7LTgVSMPUxL8rBYJAAAAAMAlFIQAhgSfZSpnRFA5I4JXbXccV63tPe+NOLzQpabz4b/bu/vU3t2nujNtVz0m3m9dNdIw+9LHaUlxMikOAQAAAAAxhoIQwJBmXlrUJCMlXlOu2O66ri509r43v+EV8xx29oR04my7Tpxtv+pz+X2mslISrikPWVkZAAAAADCcURACGJYMw1BaYpzSEuM0KT+tf7vruuroDunMhc6rSsOm81262NWnU60dOtXacdXnYmVlAAAAAMBwRkEIIKYYhqGkBL+SElI1Pif1qn1dvaHrjjj8sJWV05PilBTvV8BnKc5vKuCzFPCZivNbH7jt8sdxPlMBv6U4nyWfZTAvIgAAAADAExSEAHBJQsCnwqxkFWYlX7X9w1ZWbmnrUUtbzyd+bsNQuFC8VBoGfKbifJYC/vDf/ku34y7tu7J8/LBtlknxCAAAAAD4cBSEAPARPmxl5Za2HnX1htTTZ6s35KgnZKv3qo8v/R1y1Ntnf+C2kO2qp89WT58tdfUNWHbTMK4zitF8X6loaWRai+JMWyOT4pWeHKeUhIBM5l0EAAAAgJhAQQgAH5PPMpWdljAgn8t2XPVeVRpeUSheue2qgtFWT5/T/7hwSfnetp4+R47rqqvXVlev/REJGq+6ZZmGRiTFKf3yn+R4jUyKU3pynNKT4hWM458PAAAAABgu+AkPAKKAZRpKCPiUEBjYzxuynavKw/c+fu/v3pAtx/SrvumcWtt71NrWo/buPjVf7Fbzxe7rft54v9VfFqZfKg5HXioSRyTFsXgLAAAAAAwhFIQAMIz5LFM+y/zIEX8ZGRlqbm7uv93bZ4fLwvYetbaH51rsv93Wre4+W6dbO3W6tfO6ny8lwa/05CvLw/c+TgkGZDIvIgAAAABEDQpCAMA1An5LOSOCyhkRvGaf67rq6Ampta27vzQMF4jdam3r0fmOHl3s6tPFrj4da2q75vFcvgwAAAAA0YWfwgAAN8UwDCXF+5UU79fozORr9tuOqwud4UuVw+Vh9xWjD2/+8uWRye8ViVy+DAAAAAADj4IQADCgLNO4VO7FX3f/QFy+PPJSWfj+y5eT4v3yUSACAAAAwE2hIAQADKqBunz56HUuX5Ykn2UoGPApPuBTQsAKL/4S51OC//LHl/6+cn/AUnzAp/iAxfyIAAAAAGJORAvCZ555RnV1dRo7dqyWL1/ev33VqlV68803dccdd+hzn/tcJCMAAIaQT3r5cmdPSCHb7S8Rb/r5JcX5rXCheEV5eLlQjA9Yl8pHS8G4cAkZvFQuJgQs+S1TBgUjAAAAgCEmYgVhXV2duru7tWLFCj399NOqra3VhAkTJElLlixRUVGR9u/fH6mnBwAMQx91+bLruuoLOerqtdXVG7r05zof91y7rbvXVnffe3/Ofcx8V5WKcZYS/B9UKF47gtEyB6ZcdF1XriTXlSRXrqtLt8MfOOE79d/HDd/x0v3ed//3b7/0sfrv8979nEufU66UELCUnnz94wQAAAAgukSsIKypqVFZWZkkqbS0VNXV1f0FYVpamk6dOhWppwYAxCjDMBTwWwr4LaUmBm768Y7jqrvvfeVhz/VLxu5eW529IXVfcb+Q46q9u0/t3Tc/elEKj16M8/vkOE5/ISddKvwuFXJy3UsF3wcXgdFgWuFIfeG2iV7HAAAAAHADIlYQdnR0KDs7W5IUDAZVX19/U4+vqKhQRUWFJGnlypXKyMgY8IyDyefzDfnXMFxwLKIHxyJ6cCwGRl/IVkd3nzp7+vr/7uwJqfOabZf+dIeu+LhPPX22evrsAcliXPrP5TkVDcOQYUiGLv1tGDKu2i7JMGReeqBphB//gfe/8valv8PPF35MfmbakD+n+LoAAABArIhYQRgMBtXZGV6BsqurS8HgtZPRf5jy8nKVl5f3325ubh7QfIMtIyNjyL+G4YJjET04FtGDYzGwApICcdKIOEuSJSnuIx/juK56+mwlp6Sp9VyrzHA7d1UpJ11ZyL1X3l2zPUrmQRzq59Rw+brIy8vzOgIAAACinBmpT3zlHIOVlZUqKiqK1FMBADDkmUZ4/sK0pHilJASUlBBerCUx3q9gnO+9hVL8luL8lgI+S36fKZ8V/mOZhkzTiJpyEAAAAMDQEbGCcNy4cfL7/Xr88cdlmqYyMjK0atUqSdLq1av1q1/9SuvXr9fPfvazSEUAAAAAAAAA8BEidomxJC1fvvyq28uWLZMUXsV4yZIlkXxqAAAAAAAAADcgYiMIAQAAAAAAAEQ/CkIAAAAAAAAghlEQAgAAAAAAADGMghAAAAAAAACIYRSEAAAAAAAAQAyjIAQAAAAAAABiGAUhAAAAAAAAEMMoCAEAAAAAAIAYRkEIAAAAAAAAxDAKQgAAAAAAACCGURACAAAAAAAAMYyCEAAAAAAAAIhhFIQAAAAAAABADKMgBAAAAAAAAGIYBSEAAAAAAAAQwygIAQAAAAAAgBhGQQgAAAAAAADEMApCAAAAAAAAIIZREAIAAAAAAAAxjIIQAAAAAAAAiGEUhAAAAAAAAEAMoyAEAAAAAAAAYhgFIQAAAAAAABDDKAgBAAAAAACAGObzOgAAAACGt66uLv3kJz9RR0eHysvLddttt1217wc/+IFs21ZCQoIee+wxJSQkeJgWAAAg9jCCEAAAABH1zjvvaOHChfrOd76j1atXKxQK9e+zLEtf+9rX9J3vfEe33HKL3n33Xe+CAgAAxCgKQgAAAERUdXW1ysrKZJqmxowZo1OnTvXvCwQCGjFihCTJ5/PJNHl7CgAAMNiGzCXGeXl5Xkf4xIbDaxguOBbRg2MRPTgW0YNjET04FgOjs7Oz/7LhYDCojo6Oa+7T3d2tt99+W//n//yf636OiooKVVRUSJJWrlw55I/NUM+PgcO5gMs4F3AZ5wIuG8xzgV/RDpJ/+Id/8DoCLuFYRA+ORfTgWEQPjkX04FjcvPPnz+vb3/72VX9+/OMfKxgMqqurS1K4LExMTLzqca7r6t/+7d/06KOPXrPvsvLycq1cuVIrV66M+OuINM4tXMa5gMs4F3AZ5wIuG+xzYciMIAQAAEB0S0tL07e//e1rtr/yyiuqrKzUggULdPz4ceXn51+1/7nnnlNxcbGmTp06SEkBAABwJQpCAAAARNSSJUv0z//8z3rjjTdUXl4un8+nPXv2yHEcFRYW6g9/+IMmTZqkbdu2acGCBbr77ru9jgwAABBTKAgHSXl5udcRcAnHInpwLKIHxyJ6cCyiB8di4ASDwWsuk5k+fXr/x88+++wgJ/IW5xYu41zAZZwLuIxzAZcN9rlguK7rDuozAgAAAAAAAIgaLFICAAAAAAAAxDAKQgAAAAAAACCGMQfhIHjmmWdUV1ensWPHavny5V7HiTk1NTX6j//4DxmGofHjx+sv/uIv9NJLL2n79u3KzMzUl7/8Zfl8fCkMpldeeUVbt27VE088wdeHh9auXau1a9fKcRz97d/+rV566SWOhQd6enr05JNPqqenR8FgUF//+tf161//mmMxSFpbW/X9739f9fX1+tWvfiXLsq77fYnvVRgonEuQrv/+FLHtyvfHiF3vf3+enp7udSR44Ho/H/j9/og/LyMII6yurk7d3d1asWKFQqGQamtrvY4UczIzM/X444/riSee0MWLF1VVVaUDBw7oiSee0OjRo7V9+3avI8aUvr4+HTt2TBJfH15qbW1VVVWVHn/8cX3729/W+fPnORYe2bNnjyZOnKhvf/vbmjBhgn7/+99zLAZRUlKSvvWtb2nixImSrv99ie9VGCicS7js/e9PT5w44XUkeOjK98eIXe9/f045GLve//PBnj17BuV5KQgjrKamRmVlZZKk0tJSVVdXe5wo9qSlpSkQCEiSLMvSyZMnVVJSIkkqKyvjmAyy1atX6/bbb5fE14eX9uzZI8dxtGLFCv3iF79QdXU1x8Ij2dnZ6u7uliR1dHTIMAyOxSAKBAJKSkrqv32970t8r8JA4VzCZe9/f2qa/FgWy658f4zY9f73547jeB0JHnn/zwfJycmD8rz8SxRhHR0dCgaDkqRgMKjOzk6PE8Wu48eP6+LFi0pMTFRCQoKk8DHp6OjwOFnsCIVCOnDggKZOnSqJrw8vXbhwQaFQSI8//rgCgYA6Ozs5Fh7Jzc1VTU2NvvGNb6iurk6maXIsPHS970t8r8JA4VzC+11+f1pQUOB1FHjk/e+PEbve//6cK91i1/t/PigqKhqU56UgjLAr3/x1dXX1vynE4Gpvb9cvfvELfelLX1IwGFRXV5ckqbOzU4mJiR6nix3r1q3TokWL+m/z9eGdYDDYP5L28htSjoU31q5dq1mzZunJJ5/UjBkzZNs2x8JD1/u+xPcqDBTOJVzpyveniF3vf3+M2PX+9+enTp3yOBG88v6fD9avXz8oz0tBGGFFRUXav3+/JKmysnLQml+8x7Zt/cu//Iv+9E//VGlpaRo/fryqqqokhY/J5XmnEHmnT5/W22+/re9+97uqr69XW1sbXx8emTRpko4fPy5J/XPecCy84bpu/yWuKSkpkjgWXrrev9v8W46BwrmEy97//hSx6/3vj19//XWvI8Ej739/npWV5XEieOX9Px8M1hUHhuu67qA8Uwz75S9/qaNHj6qwsFB/+Zd/6XWcmLNhwwb98pe/1KhRoyRJn//851VVVaWdO3cqIyNDX/nKV1jF2APf+ta39MQTT/D14aFf/epXqqurU3Jysh577DH953/+J8fCAx0dHfrxj3+svr4+WZalr3/963rhhRc4FoMkFArpe9/7Xv+qso8++qg2bNhwzf9/vldhoHAuQbr++1MKY1x+f4zY9f735/ycGpuu9/PBlXNmRwoFIQAAAAAAABDDuMQYAAAAAAAAiGEUhAAAAAAAAEAMoyAEAAAAAAAAYhgFIQAAAAAAABDDKAgBAAAAAACAGEZBCGBYampq0sMPP6yVK1dq165dev7559XU1DTgz1NfX6/nn39eBw4c6N/2r//6r3r44Yd15MiRAX8+AAAAAAAGms/rAAAQCSkpKXrssceUnp6uTZs26c0339SUKVOUlZV1U5/Htm1ZlvWB++vr6/Xb3/5WkjRlyhRJ0t13363p06crOzv7478AAAAAAAAGieG6rut1CAAYaE1NTfrqV7+quLg49fT0XLXv+eefV3V1tf7jP/5DJ06cUHp6uj772c9q0aJF/Y8rKipSXFycTpw4oR/96Ef6x3/8RzU0NEiSxo4dq7/+679WXFycvvrVr171uf/v//2/evfdd7V27Vp973vf0/jx41VRUaGXXnpJ586dU0FBgf78z/9cxcXFevfdd/Vv//ZvWrBggU6dOqXm5mZ99rOf1dKlS3X69Gn99Kc/1fHjxxUIBDRq1CitWLFi0P7/AQAA4MY8+eSTSk1N1bFjx9TS0qK//du/1dtvv63a2loVFxfrS1/6ktcRAeAjcYkxgGGtpKRE06ZNkyR95jOf0WOPPab29natXLlSnZ2dWrZsmTIzM/Uv//IvOnbsWP/jqqurNXbsWD3yyCMyDENz5szR8uXL9elPf1rHjx/XM888o5SUFC1dulSSNHfuXD322GMqKCi46vn379+vp556SikpKfqzP/szNTc36/vf/77a2tr673PgwAHdeeedkqRf//rXCoVCevPNN3XkyBF94Qtf0KOPPqqMjIwI/58CAADAx3HixAllZ2friSeeUHl5uf793/9dX/jCF/Tkk09q165d6uvr8zoiAHwkLjEGMKwZhqGcnBzt3btXU6dO1ZQpU7Rr1y61t7ervb1dzz77bP999+/frzlz5kgKjxL8whe+IElqbW3V3r17VV1drcuDrk+cOKH4+HgVFxfrtdde06hRo7Rw4cJrnn/Xrl2SpIcfflhlZWVqbm7Wiy+++P9v7+5ZGtkCOIw/CatNxkJFjAZfMCgptNDegBYa8Xv4FfRbiJVYCYKVELASIoiNYuELaRJfqolilxCLIExhtlg2rNy9wr3rQjDPr5q3M3NmiuHMf+ac4eHhobXNwsICuVyOq6srisUi9XqdoaEhms0mNzc3pNPpVhApSZKk9hFFEY1Go9VWi8ViLC4u0tvbC0A8HufbNx+7JbU/71SSvrxYLPbb5dlslmw225r/dXzCn406gKOjI+7u7lhdXWV2dpbt7W1eX18/rS5BEAC0xjp8e3sjl8uRSqUolUpcXl6Sz+fZ3NxkeHj4fx1XkiRJn+/p6YmJiQni8R+d88IwZGlpCYBqtUpfX9+/tkUlqZ3YxVjSl5dIJAC4uLjg+vqaqakpgiCgWCzy/PzM4+Mjh4eH1Gq1D/fTaDQolUpUq9XWsp/h3u3tLWdnZ0RR9K7M3NwcAAcHBxwfH3NyckIikWBycvLDYxUKBe7v70kmkwwODtJsNqnX6//11CVJkvQXVSoVxsbGWvNhGDI6OvqPaUlqdwaEkr68+fl5UqkUhUKB3d1dgiBgY2ODZDLJ/v4++Xye7u5uBgYGflt+ZWWFdDrN+fk5tVqNkZGR1rpMJsPMzAzlcpmtra13YwsCTE9Ps7a2xsvLC3t7e/T397O+vk5PT8+Hde7q6uL09JSdnR3K5TLLy8tkMpk/vxiSJEn6NJVKhfHxceBHd+MoilovkMMwfBceSlI78y/GkiRJkiRJUgfzC0JJkiRJkiSpgxkQSpIkSZIkSR3MgFCSJEmSJEnqYAaEkiRJkiRJUgczIJQkSZIkSZI6mAGhJEmSJEmS1MEMCCVJkiRJkqQO9h3w1xuQm3EioQAAAABJRU5ErkJggg==",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"low, high, step = 0, 100, 10\n",
"plot_all(cost_history, m, q, low, high, step)"
]
},
{
"cell_type": "code",
"execution_count": 133,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"56 passi e 5600 gradienti calcolati per arrivare a distanza minore o uguale di 0.1 dall'ottimo\n"
]
}
],
"source": [
"near_opt(m, min_dist=1e-1, ge_per_step=n)"
]
},
{
"cell_type": "code",
"execution_count": 134,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA7sAAAHzCAYAAADhDgreAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAABWBUlEQVR4nO3df3Rb9Z3n/9e15F+SYluy7KT59aUJMAkJIaEObXHakBBCjmkZWjwppHhO25llWDjLMN1ySLYttKWUUMophwJLe2Boa2an7YZCD1vv4KYJYXHL4BB7QkxDgVLoFKhjyz8l/5J0v384ki3bcn5ZuldXz8c5HGLFN/5IHzvR637en/fHME3TFAAAAAAADlJg9QAAAAAAAJhrhF0AAAAAgOMQdgEAAAAAjkPYBQAAAAA4DmEXAAAAAOA4hF0AAAAAgOMQdgEAAAAAjkPYBQAgy8466yyVlpZq3rx5qqio0MUXX6xHHnlE8Xj8hNf+8Y9/lGEYikajGR1jtr4OAACZQtgFAMACzzzzjAYGBvT2229r586duueee/R3f/d3Vg8LAADHIOwCAGCh8vJyXXnllfrpT3+qH/3oRzpy5Ih++ctfat26dSorK9OSJUv0ta99Lfn5H//4xyVJFRUV8vl8+u1vf6s333xTmzdvVmVlpYLBoD772c+qt7c3ec0999yjRYsWad68efqrv/or/frXv5YkxeNx7d69W8uXL1dlZaW2b9+uUCiU9usAAJBLCLsAANjARRddpMWLF+v//b//J6/Xqx//+Mfq7e3VL3/5S/3P//k/9fTTT0uSnn/+eUlSb2+vBgcH9dGPflSmaWrXrl1699139bvf/U5/+tOfkgH5tdde04MPPqjW1lYNDAzo2Wef1VlnnSVJ+t73vqenn35aBw4c0Lvvviu/36+bbrop7dcBACCXEHYBALCJhQsXKhQK6ZJLLtH555+vgoICrVmzRtdee60OHDiQ9rqzzz5bl112mYqLi1VVVaUvfvGLyc93uVwaGRnRq6++qrGxMZ111llavny5JOmRRx7RXXfdpcWLF6u4uFhf+9rXtGfPHvbpAgAcgbALAIBN/PnPf1YgENC///u/a9OmTaqqqlJ5ebkeeeQRdXV1pb3uL3/5i6655hotWrRIZWVluu6665Kff/bZZ+v+++/X1772NVVXV+uaa67Ru+++K0l6++239alPfUoVFRWqqKjQypUr5XK59Je//CUrzxcAgEwi7AIAYAOtra3685//rA0bNmjHjh268sor9ac//Ul9fX264YYbZJqmJMkwjGnX/o//8T9kGIZeeeUV9ff364knnkh+viTt2LFDL7zwgt5++20ZhqHbbrtNkrRkyRL93//7f9Xb25v8b3h4WIsWLZrx6wAAkEsIuwAAWKi/v1//5//8H11zzTW67rrrdP7552tgYECBQEAlJSV66aWX9L/+1/9Kfn5VVZUKCgr0hz/8IfnYwMCAfD6fysvL9ec//1n33ntv8vdee+017du3TyMjIyopKVFpaakKCsb/+b/hhhv05S9/WW+//bYk6dixY/rFL36R9usAAJBLCLsAAFjgk5/8pObNm6clS5borrvu0he/+EU9/vjjkqSHH35Yt99+u+bNm6dvfOMb2r59e/I6j8ejL3/5y6qtrVVFRYVefPFF3XHHHTp06JDKy8t1xRVX6NOf/nTy80dGRrRz504Fg0EtWLBAnZ2duvvuuyVJ//iP/6grr7xSW7du1bx58/SRj3xE//7v/5726wAAkEsMc3KdEwAAAAAADsDKLgAAAADAcQi7AAAAAADHIewCAAAAAByHsAsAAAAAcBzCLgAAAADAcQi7AAAAAADHcVs9gGx49913rR6CLQWDQXV1dVk9DEzBvNgT82JPzIv9MCf2xLzYE/NiP8yJPc02LwsXLkx7HSu7AAAAAADHIewCAAAAAByHsAsAAAAAcBzCLgAAAADAcQi7AAAAAADHIewCAAAAAByHsAsAAAAAcBzCLgAAAADAcdzZ/oIPP/ywDh06pPLyct13332SpJ/97Gf69a9/rbKyMknStddeqwsvvHDate3t7Xr88ccVj8d16aWX6qqrrsrm0AEAAAAAOSLrYfeSSy7Rtm3b9NBDD6U8fsUVV+jKK69Me108Htdjjz2mr3zlK6qsrNSuXbtUU1OjxYsXZ3rIAAAAAIAck/Uy5vPOO08+n++Ur3vjjTe0YMECzZ8/X263WxdffLFaW1szMEIAAAAAQK7L+spuOs8++6yef/55LVu2TH/7t387LRCHQiFVVlYmP66srNTrr7+e7WECAAAAAHKALcLu1q1bVV9fL0n66U9/qh//+Me68cYbT/vP27t3r/bu3StJ2r17t4LB4JyM02ncbjevjQ0xL/bEvNgT82I/zIk9MS/2xLzYD3NiT6c7L7YIuxUVFclfX3rppbrnnnumfU4gEFB3d3fy4+7ubgUCgRn/vC1btmjLli3Jj7u6uuZusA4SDAZ5bWyIebEn5sWemBf7YU7siXmxJ+bFfpgTe5ptXhYuXJj2OlscPdTT05P89UsvvaQlS5ZM+5zly5frvffeU2dnp6LRqH7zm9+opqYmm8MEAAAAAOSIrK/s3n///Xr11Vc1MDCgG264Qdu3b1dHR4f++Mc/yjAMVVVV6frrr5c0vk/3+9//vnbt2iWXy6UvfOELuuuuuxSPx7Vp06YZQzEAAMg/He1teuXZJhUODWqs1KfzL6/TqrXrrB4WAMBCWQ+7t9xyy7THNm/ePOPnBgIB7dq1K/nxhRdeOOP5uwAAIH91tLfp/T2Nqq+ukOHxyDRjOrCnUZIIvACQx2xRxgwAAHC6jjQ3aWN1hQzDkCQZhqGN1RU60txk8cgAAFYi7AIAgJzmjgwmg26CYRhyR8IWjQgAYAeEXQAAkNOiHp9M00x5zDRNRT1ei0YEALADwi4AAMhpq7fW6UBnbzLwmqapA529Wr21zuKRAQCsZItzdgEAAE5XognVk81NckfCinq8Wl3fQHMqAMhzhF0AAJDzVq1dR7gFAKSgjBkAAAAA4DiEXQAAAACA4xB2AQAAAACOQ9gFAAAAADgOYRcAAAAA4DiEXQAAAACA4xB2AQAAAACOwzm7AADgtHW0t+mVZ5tUODSosVKfPrb9Wi364DKrhwUAACu7AADg9HS0t+n9PY2qL43pqkqP6ktjevPHP1BHe5vVQwMAgLALAABOz5HmJm2srpBhGJIkwzB0yfwKHWlusnhkAAAQdgEAwGlyRwaTQTfBMAy5I2GLRgQAwATCLgAAOC1Rj0+maaY8Zpqmoh6vRSMCAGACYRcAAJyW1VvrdKCzNxl4TdPUc3/p1eqtdRaPDAAAujEDAIBZTO22fP7ldVq1dp0kJf//ZHOT3JGwoh6vNvzt9XRjBgDYAmEXAADMKNltubpChscj04zpwJ5GSUoJvIlfS1IwGFRXV5cl43WS2W4yAABODmXMAABgRjN1W95YTbflTJvpSKf39zRypBMAnCLCLgAAmBHdlq3BTQYAmBuEXQAAMCO6LVuDmwwAMDcIuwAAYEYzdVs+0Em35UzjJgMAzA3CLgAAmNGqteu0oL5BTw679HT3kJ4cdmlBfQONkjKMmwwAMDfoxgwAANKa2m0ZmTfTkU6ruckAAKeMsAsAAGAz3GQAgDNHGTMAAAAAwHEIuwAAAAAAxyHsAgAAAAAch7ALAAAAAHAcGlQBAAAg4zra2/TKs00qHBrUWKlP519eRxMuABlF2AUAAEBGdbS36f09jaqvrpDh8cg0Yzqwp1GSCLwAMoYyZgAAAGTUkeYmbayukGEYkiTDMLSxukJHmpssHhkAJyPsAgAAIKPckcFk0E0wDEPuSNiiEQHIB4RdAAAAZFTU45NpmimPmaapqMdr0YgA5APCLgAAADJq9dY6HejsTQZe0zR1oLNXq7fWWTwyAE5GgyoAAABkVKIJ1ZPNTXJHwop6vFpd30BzKgAZRdgFAABAxq1au45wCyCrKGMGAAAAADgOYRcAAAAA4DiUMQMAAMyxjvY2vfJskwqHBjVW6tP5l9dRwgsAWUbYBQAAmEMd7W16f0+j6qsrZHg8Ms2YDuxplCQCb47jJgaQWwi7AAAAc+hIc5Ourq6QYRiSJMMwtLG6Qk82NxGMZpArAZKbGEDuYc8uAADAHHJHBpNBN8EwDLkjYYtGZF/JAFka01WVHtWXxvT+nkZ1tLdZPbRpjjQ3aeMMNzGONDdZPDIA6WR1Zffhhx/WoUOHVF5ervvuu0+S1NjYqJdffllut1vz58/XjTfeKK/XO+3am266SSUlJSooKJDL5dLu3buzOXQAAICTEvX4ZJqxlMBrmqainunvb/JdLq2CuyODMko9KY9xEwOwt6yG3UsuuUTbtm3TQw89lHxszZo12rFjh1wul5544gk99dRTuu6662a8/o477lBZWVm2hgsAAHDKVm+t04E9jclVQNM0daCzV6vrG6wemu3kUoDkJgaQe7Iads877zx1dnamPHbBBRckf33uuefqxRdfzOaQAACAA1m5DzTxdZ5sbpI7ElbU49Xq+gbbrVTaQS4FSG5iALnHVg2q9u3bp4svvjjt7991112SpMsuu0xbtmzJ1rAAAEAOsUMjoVVr1xFuT0IuBUhuYgC5xzBN08zmF+zs7NQ999yT3LOb8POf/1xvvvmmvvSlL01r6iBJoVBIgUBAfX19+uY3v6nPf/7zOu+882b8Gnv37tXevXslSbt379bo6OjcPxEHcLvdikajVg8DUzAv9sS82BPzYj92mJPHbt+lTxWNTVstfGq0UH/3jbstHJl17DAv6fxH60s6+MxTcoUHFfP6VPPJT+mC9RdZPayssPO85CvmxJ5mm5eioqL012VqQKfiueee08svv6zbb799xqArSYFAQJJUXl6u9evX64033kgbdrds2ZKy8tvV1TX3g3aAYDDIa2NDzIs9MS/2xLzYjx3mJBrq0lilZ4bH+y0fm1XsMC/pLPrgMi26+b+nPGbXsc41O89LvmJO7Gm2eVm4cGHa6ywPu+3t7frFL36hr3/96youLp7xc4aHh2WapkpLSzU8PKzDhw+rvr4+yyMFAAC54D8HI/rp679TkRnTWIFL5y9dohULqmy5DxQAkDlZDbv333+/Xn31VQ0MDOiGG27Q9u3b9dRTTykajerOO++UJJ1zzjm6/vrrFQqF9P3vf1+7du1SX1+fvvOd70iSYrGYNmzYoLVr12Zz6AAAIAd0tLfp/xsN6yPlxQqWFEmmqf3vvK1DoQF96IZ/tHp4AIAsymrYveWWW6Y9tnnz5hk/NxAIaNeuXZKk+fPn6957783k0AAAgAMcaW7S1WcvVXigX+8d61RBLK6/qizXG8V+GgkBQJ6xvIwZAJA5Vh6/AlghcW6rr6xcvrLy5OPV3UMWjgoAYAXCLgA4lB2OXwGyLZfObQUAZBZhFwAc6khzk64+fnalJBmGoY3VFXqyuYmwC8c6k3NbqYQAAGch7AKAQyXKOSczDEPuSNiiEQGZlwinTzY3yR0JK+rxanV9wwlDK5UQAOA8hF0AcCjKOZGvVq1dd8oBlUoIAHCeAqsHAADIjNVb63Sgs1emaUrSRDnn1jqLRwbYjzsymHJjSKISAgByHSu7AOBQp1vOCeQjKiEAwHkIuwDgYKdTzgnkozNpbAUAsCfCLgAAGUSH39xAJQQAOA9hFwCADKHDb26hEgIAnIUGVQAAZMiR5qZkWaw00eH3SHOTxSMDAMD5CLsAAGQIHX4BALAOZcwAAGQIHX7hZLPtR2evOgA7IOwCAHLe1DfWvg8u1+Bbb1r+RpsOv3Cq2fajS2KvOgBbIOwCAHLa1Dfdr773nl7d84K2rTlP8yorLH2jTYdfONWR5iZdPcN+9CeP70dP93t87wPIJsIuACCnTX3T3fHOf+rqRZV6v+uY5pVXWP5Gmw6/cCJ3ZFBGqSflsYn96OYsvwcA2UODKgBATpvaBModj6nAMFQQiyUf4402MLfG96ObKY8l9qPP9nsAkE2EXQBATpv6xjpa4FLcNBV3uZKP8UYbmFurt9bpQGdv8mcvuR99a92svwcA2UQZMwAgKzLVnXVqE6hVSxfr52+8qcvXnCdJNIUCMuBk9qOzVx2A1Qi7AICMm61z65m+AZ72prviA/LWb9Czf3xT7m7eaAOZMtt+dPaqA7ADwi4AIONm69w6F2+IeWMNAACmYs8uACDjpjaRkmgaBQAAMouwCwDIOLqzAgCAbCPsAgAyju6sAAAg29izCwDIuJPp3ApkS6Y6gwMA7IWwCwDIilxoIkUIyhy7vLYn6gxul3ECAM4cYRcAAGX2eKR8Z6fXdrbO4JJsM04AwJljzy4AABoPQRtnCEFHjocgnD47vbazdQa30zgBAGeOsAsAgDgeKZPs9NrO1hncTuMEAJw5wi4AAOJ4pEyy02s7W2dwO40TAHDmCLsAAIjjkTLJTq/tqrXrtKC+QU8Ou/R095CeHHZpwfHO4HYaJwDgzNGgCgAA5ebxSLnSOdhur226zuB2GycA4MwQdgEAOC4XjkdKsFOH45ORK69ttseZKzcsACAXUcYMAEAOonNw7kvesCiN6apKj+pLY3p/T6M62tusHhoAOAJhFwCAHETn4NzHDQsAyCzKmAEAc4qyzOwY7xwcSwm8dA7OLe7IoIxST8pj3LAAgLnDyi4AYM5Qlpk9dA7OfRx1BACZRdgFAMwZyjKzZ7YjdJAbuGEBAJlFGTMAYM5QlpldVnc4nqlkfeOWyywbT67hqCMAyCzCLgBgzrCPNH+kO/roP8rLteiDy6weXs6w+oYFADgZYRcAMGdWb63TgT2NyVLmZFlmfYPVQ8uKbDbnsroR2JHmJl09Q8n6L595Sotu/u9ZGwcAAOkQdgEAcyafyzLTrXRKmvPnn82vlU66knXX4GBWvj6QbVbfYAJw6gi7AIA5la9lmelWOp9sbprz1yObXyuddCXrMa8vK18fyCY73GACcOroxgwAwBxwRwZTgp+UueZc2fxa6aTrJFzzyU9lbQxAttBpHshNrOwCADAHstmcyw6NwNKVrF+w/iJ1dXVlbRxANtBpHshNhF0AAOZANptz2aURWL6WrCP/2OEGE4BTR9gFAGAOZLM5Vz43AgOsYJcbTABOTdbD7sMPP6xDhw6pvLxc9913nyRpcHBQ3/3ud3Xs2DFVVVXpn/7pn+TzTW9w8dxzz+nnP/+5JOnTn/60LrnkkmwOHQCAWWVzpZNVVSB7uMEE5Kash91LLrlE27Zt00MPPZR87Omnn9b555+vq666Sk8//bSefvppXXfddSnXDQ4Oas+ePdq9e7ckaefOnaqpqZkxFAMAAABziRtMQO7Jejfm8847b1pAbW1t1caNGyVJGzduVGtr67Tr2tvbtWbNGvl8Pvl8Pq1Zs0bt7e3ZGDIAAAAAIMfYYs9uX1+f/H6/JKmiokJ9fX3TPicUCqmysjL5cSAQUCgUmvHP27t3r/bu3StJ2r17t4LBYAZGnfvcbjevjQ0xL/bEvNgT82I/TpqT/2h9Sa3PPCV3eEBR7zyt/+SndMH6i6we1mlx0rw4CfNiP8yJPZ3uvNgi7E5mGMa0swNP1ZYtW7Rly5bkxxyBMLNgMMhrY0PMiz0xL/bEvNiPU+ako71N7+9p1CeqK2T4XDLNsA489qB6+3Jzn6ZT5sVpmBf7YU7sabZ5WbhwYdrrsl7GPJPy8nL19PRIknp6elRWVjbtcwKBgLq7u5Mfh0IhBQKBrI0RAADkjyPNTcnOu9L4zfiN1RU60txk8cgAACfLFiu7NTU1OnDggK666iodOHBA69evn/Y5a9eu1b/+679qcHBQkvQf//Ef2rFjR7aHCgAAsqCjvU2vPNukwqFBjZX6dP7ldVldUXVHBmWUelIeMwxD7kg4a2MAAJyZrIfd+++/X6+++qoGBgZ0ww03aPv27brqqqv03e9+V/v27UsePSRJb775pn71q1/phhtukM/n09VXX61du3ZJkurr6+nEDACAAyVKiOurK2R4PDLNmA7saZSkrAXeqMcn04ylbK0yTVNRjzcrXx8AcOayHnZvueWWGR+//fbbpz22fPlyLV++PPnx5s2btXnz5kwNDQAA2MCR5iZdPUMJ8ZPNTVkLu6u31unAnsZkKbNpmjrQ2avV9Q1Z+foAgDNnizJmAACABDuUECdC9ZPNTXJHwop6vFpdn5vNqTJhrsvMrS5bBzBhMDKqY6GwOrvDOtYz/vfuJy75K4tHdXoIuwAwR3izBsyNkykhzsbP26q166b9mfycz32ZuR3K1oF8Eo+bCvUN6VgoPB5qE8H2+MeR4bGUzy/zFRN2ASCf8WYNmDsnKiG26ueNn/Nxc11mboeydcBpRkaj6uqJqDMU1rHu8UCbCLbdPRFFY/G01xYXuVQV8Ko64B3/f6VPpmme8fGwViDsAsAc4M0aMHdOVEJs1c8bP+fj5rrM3A5l60CuMU1TA+HRZIA9drzkuPN4sO0bGJ71+vJ5xarye1VVOR5qqwPjv67ye1XmK87JYDsTwi4AzAHerAFza6YS4gSrft74OR83152q6XwNzCwWi6u7b2g8yIZSV2ePhcIaHommvdZVYKjS75m0OutNWa0tLsqPGJgfzxIAMow3a0D2WPXzxs/5uLnuVE3na+Sz4ZFoMrwem7J3trs3oljcTHttabE7uTJbFZgIs9WVXvnLSuVyFWTxmdgTYRcA5gBv1oDsycTP28k0nuLnfNxcdaqe/Jr/ZSSuI+90a7HPS+drOIppmuofHJnWBCpRetwfHpn1en9ZSUqQnRxufZ4ix5QbZwphFwDmAMeUANkz1z9vJ9t4ip/zCbOVmZ+Maa95oFQHOnu14Kq/ycvXE7ktGo2ruzcyEWh7UptCjY7F0l7rdhUo6Peklhkf3ztbFfCqqNCVxWfiPIRdAJgjZ/rmD8DJm8uft1NpPMXP+dyg2RdyTWR4LGXv7OSmUN29EZnpq43lLS1MDbKBiaZQFWWlKihgdTZTCLsAACCv0Xgq+3jNYTfxuKnegWG9H3pPr7/1bsrK7LFQWIOR0bTXGoZUWVGaWm48qSmUt7Qoi88EkxF2AQBAXqPxVPbxmsMKY9GYukKRiZXZSU2hunrCGoumP3u20F0w477ZqoBXQb9HhW7Kje2IsAsAFjiZZjiwB+bK+Wg8lX285siUwcjoRFfjnommUJ2hsHr7h2YtN/Z5irRwfoUCZUXTmkKV+0ooN85BhF0AyLKTbYYD6zFXJ2fyDQFXIKhzPr45p14fGk9lH685Tlc8birUN5TS1XhyU6jI8FjaawsKDFVWlI6XF/unnz1bWlKoYDCorq6uLD4jZBJhFwCyjMYsuYO5OrGpNwQKC8f0qxy8IUDjqezjNUc6o2OxlON5OicF2+6eiKKx9OXGxUWu1DNnJzWFqqzwyM3Zs3mFsAsAWUZjltzBXJ0YNwQAnCrTNDUQHp0ItJP2znaGwuobGJ71+jJf8bS9s4n/l/mKOXsWSYRdAMgyGrPkDubqxLghAGAmsVhc3X1DKcf1TP7/8Eg07bWuAkOVfk9KE6jqScG2uIgIg5PDdwoAZBmNWXIHc3Vi3BAA8tfwSDQ1yE7aO9vdG1Esnr4bVGmxe7y8eMre2epKr/xlpXJRbow5QNgFgCyjMUvuYK5OjBsCgHOZpqn+wZGJJlCTV2e7w+oPj8x6vb+sZFpX48SvfZ4iyo2RcYRdALAAjVlyB3M1u6k3BNwBj87mhgCQM6LRuLp7I6llxpOaQo2OxdJe63YVKOj3JFdmJ++drQp4VVTI2bOwFmEXAACckck3BObi2A7ONgbmVmR4bHxV9niIndwUqrs3MuvZs97SwtQQWznR5biirJSzZ2FrhF0AAGAbnG0MnLp43FTfwPBEkJ3SFGowMpr2WsOQKitKVeWf0t34+Gqtt7Qoi88EmFuEXQAAYBscZQTMbCwaU1coMq2rcWd3WF09YY1F0589W+guSNk3O7nUOOj3qNBNuTGcibALAABsg6OMkM8GI6MpTaAmN4Xq6R+atdzY5ylKHs8TDEyUGldVelXuK6HcGHmJsAsAAGyDo4zgZPG4qZ7+oWSIHRj6g975c1ey9DgyPJb2WsPQRDOoKcf1VAW8Ki0pzOIzAXIDYRcAANgGRxkh142OxVK6GidXaUNhdfdEFI2lLzcuLnKldDWe3BSqssIjN2fPAqeEsAsAAGyDs41hd6ZpaiCcWm6c2Dt7rCes3v7hWa8v8xUny4vPWlwlb4mRDLVlvmLOngXmEGEXAADYCmcbw2qxWFyhvqFpZ84mwu3wSDTtta4CQ5V+T0oTqOpJTaGKiybefs/FUV2YO22HO7Tv4BF1hUfkc8VVt2G91q1ZZfWwcAYIuwAAAMg7wyPRlJXZyaXH3b0RxeLpu0GVFLunHdGTKD0OlJfKRblxzmk73KHGlqOav2ajvGNjipumGltaJYnAm8MIuwAAAHAc0zTVPzgyratxItD2h0dmvb6irGQi0E7aO1sd8MrnKaLc2GGaWg7Kv2JTyrFn/hXr1dSyn7Cbwwi7AAAAJ6HtcIeaXmjVYKyAEkebiEbj6u6NpDSBOnZ87+yxUFgjo7G017pdBSndjaeeP1tUyNmz+WQwasg75QaGYRgKR7mpkcsIuwAAACeQKHH0r9wsr2FQ4phFQ8NjKXtnJ5cdd/dGZj171ltamFJiPDnQ+stKOXsWST63qfiUbybTNOV1z/INBtsj7AIAAJwAJY6ZE4+b6hsYTg2yk5pCDUZG015rGFKgvHRakE3spfWWFmXxmSCX1dXWqLGlVfPX1EoaD7o9R1vVUFtj8chwJgi7AAAAJ0CJ45kZi8bUFYroWM/4/tnJx/V09YQ1Fk1/9myhuyBlZbbKP9EUKuj3qNBNuTHOXOKm1b6XD6hvcERet6mG2hpuZuU4wi4AAMAJJEocJzclosQxVXhoNNkIKtEUquv4r3v6h2YtN/Z5iqbtnU2s0pbPK6HcGFmxbs0qXbZ5I8dBOQhhFwCAHNDR3qZXnm1S4dCgxkp9Ov/yOs6izaJEiaN/xXoZhpGXJY7xuKme/qFpnY0T+2kjw2NprzUMKej3JFdopx7XU1pSmMVnAiBfEHYBALC5jvY2vb+nUfXVFTI8HplmTAf2NEoSgTdLEqWMTS37FY4aji1xHB2LTTuiJxFou3siisbSlxsXFbqSIbZ6SlOoygqP3Jw9CyDLCLsAANjckeYmXV1dkdIcaWN1hZ5sbiLsZtG6NatyPtyapqmB8Oj40TzdqZ2NO0Nh9fYPz3p9ma942t7ZRLAt8xVz9iwAWyHsAgBgc+7IoIxST8pjhmHIHQlbNCLYWSwWV6hvKGVltj8c1X++F1JnKKzhkWjaa10FhionlRsnuhpX+cd/XVLMW0cAuYO/sQAAsLmoxyfTjE1rjhT1eC0cFaw0PBKdKDWeUnbc3RtRLJ6+G1RJsTs1yE4qOQ6Ul8pFuTEAhyDsAgBgc6u31unAnkZtPF7KbJqmDnT2anV9g9VDQ4aYpqn+wZGUzsaTw23/4Mis11eUlaScObv8/1ugkqK4qgNe+TxFlBsDyAuEXQAAbC6xL/fJ5ia5I2FFPV6trm9gv26Oi8bi6u6NpDSBOjbpv5HRWNpr3a4CBf2eacf1JM6eLS5KfYsXDAY5TgVA3iHsAgCQA1atXUe4zUFDw2PJ8uJjPeMrtIlQ290bmfXsWW9poYKBSWfOTmoK5S8r5ezZLGg73KGmF1o1GCuQzxVX3Yb1Od+kDMgnhF0AAIDTFI+b6hsYTgbYyU2hjoXCGoyMpr3WMKRAeWkyyE4uO66u9MpbWpTFZ4Kp2g53qLHlqPwrN8trGIqbphpbWiWJwAvkCMIuAADALMaiMXX1RMbDbPf0cuOxaPqzZwvdBcnmT8lV2sqJcuNCtyuLzwSnoqnloPwrNqUc+eVfsV5NLfsJu0COIOwCAIC8Fx4andYEKrFC29M/NGu5sc9TNHFUz6QV2uqAV+XzSig3zlGDUUPeKY28DMNQOMp8ArmCsAsAABwvHjfV0z80Hmh7wqlNobrDigyPpb3WMKTgpLNnJzeFqgp45SkpzOIzOXUd7W16/fl9ioW6NFbq0/mX17H/+yT43KbipjntyC+ve5Y7HwBsxRZh991339V3v/vd5MednZ3avn27rrjiiuRjHR0d+va3v63q6mpJ0oc//GHV19dnfawAAMCeRsdi086cTazSdvVEFI2lLzcuKnRNO3M2sVJbWe6R252bZ892tLfp/T2N+vTiao1VemSaMR3Y0yhJBN4TqKutUWNLq/wr1ieP/Oo52qqG2hqrhwbgJNki7C5cuFD33nuvJCkej+sf/uEfdNFFF037vJUrV2rnzp3ZHh4AALAB0zQ1GBmdFmQT4ba3f3jW68t8xdOaQCU+LvMVO/Ls2SPNTbr6+PnM0ngZ7sbqCj3Z3ETYPYHEvtymlv0KRw153aYaamvYrwvkEFuE3cleeeUVLViwQFVVVVYPBQAAZFksFleob2jacT2JUDs0Ek17ravAUGWFZ3pn4+P/Lym23duejHNHBmWUelIeMwxD7kjYohHllnVrVhFugRxmu7/1W1paVFtbO+Pv/f73v9ett94qv9+vhoYGLVmyZMbP27t3r/bu3StJ2r17t4LBYMbGm8vcbjevjQ0xL/bEvNgT82I/JzMnQ8Njer+rX385NqD3jvXr/eP/vXdsQMe6BxSLp98TWVpSqAVVZfpAVZkWVM3TgmCZFlSVaUH1PFX5fXK5crPcOFPcgaAKC8dUYBgqKho/ysg0TbkDHn52bIC/w+yHObGn050XwzRn6y+YXdFoVP/wD/+g++67TxUVFSm/F4lEVFBQoJKSEh06dEg//OEP9cADD5zUn/vuu+9mYLS5LxgMqqury+phYArmxZ6YF3tiXuwnGAzq2LFj6h8cSZYXT16Z7QyF1T84MuufUVFWMn1l9nhTqHneIkeWG2dKYs/uZYurNTY2JtM0daCzVwvqGyhjtgH+DrMf5sSeZpuXhQsXpr3OViu7bW1t+uAHPzgt6EqSxzNRgnPhhRfqscceU39/v8rKyrI4QgAAIEnRWFzdvZGUvbOdobBCfSN6/1ifRkZjaa91uwpSuhtPLjsO+j0qLrLV25Oclgi0Tz2/T9FQv6Ier1YTdAHkCVv9azJbCXNvb6/Ky8tlGIbeeOMNxeNxzZs3L8sjBAAgfwwNj6U2gZoUbLt7I7OePespKUyG2KlNofxlpZw9m0Wr1q7Txi2XsVoFIO/YJuwODw/r8OHDuv7665OPNTc3S5K2bt2qF198Uc3NzXK5XCoqKtItt9xCGRMAAGcgHjfVNzA8UW48pSnUYGQ07bWGIQXKSydKjI+H2nOWLVKRa0ze0qIsPhMAAKazTdgtKSnRP//zP6c8tnXr1uSvt23bpm3btmV7WACAKTra2/TKs00qHBrUWKlP519eR0mkjY1FY+rqiSRXZo/1pB7bMxZNf/ZsobsguSKbPHv2+N7ZoN+jwkLXtGvY7wYAsAvbhF0AgP0lmt3UV1fI8HhkmjEd2NMoSQReC4WHRqc1gUoE2p7+oVnLjX2eohn3zlYHvCqfV0K5MQAgZxF2AQAn7Uhzk66urkhuIzEMQxurK/RkcxNhN4PicVM9/UPTgmxnKKyuUFjhobG01xqGUptBTe5uHPDKU1KYxWdivbbDHWp6oVWDsQL5XHHVbVjPOaoA4FCEXQDASXNHBmWUelIeMwxD7kjYohE5x+hYbNrKbGLvbFdPRNFY+nLjokLXeHnx5HLj44G2stwjt5uzZ6XxoNvYclT+lZvlNQzFTVONLa2SROAFAAci7AIATlrU45NpxlIaBJqmqajHa+GocoNpmhqMjE4E2VDqkT29/cOzXl/mK05dnZ3UFKrMV0zTxpPQ1HJQ/hWbUioT/CvWq6llP2EXAByIsAsAOGmrt9bpwJ5GbTxeymyapg509mp1fYPVQ7OFWCyuUN/QtON6Er8eGommvdZVYKiywpOyb3ZyuC0p5p/sMzUYNeSdclPAMAyFo/a+UUDpNQCcHv7lBJBxvFFzjsS+3Cebm+SOhBX1eLW6viGv9uuOjEYnjuqZ0hSquyeiWDx9N6iSYvf0IHs83AbKS+VyUW6cST63qbhpTqtM8Lpn6eBlMUqvAeD0EXYBZBRv1Jxn1dp1jg63pmmqf3AkNdBOOq6nf3Bk1usrykpU5U8tM06E23neorwvN7by5lddbY0aW1rlX7E+WZnQc7RVDbU1Wfn6p4PSawA4fYRdABnFGzXYUTQWV3dvJGXv7OTS45HRWNprXS5DQX9qE6hEqA36PSou4p/WdKy++ZX4Gk0t+xWOGvK6TTXU1tj676JcLb0GADvgX2QAGcUbNVhlaHhs2t7ZxMehviHFZyk39pQUTjtzNtEUyl9Wytmzp8kON7/WrVll63A7VS6WXgOAXRB2AWQUb9SQKfG4qe7esH7/VlfKmbOJ0uPByGjaaw1DCpSXTuydndIUyucpyuIzyR/c/Dp1uVh6DQB2QdgFkFG8UcOZGIvG1NUTmehqPGnv7LFQWGPR9GfPut0FM+6dTZQbFxa6svhMIHHz63TkYuk1ANgFYRdARvFGDScSHhqd1tU4EWh7+odkzpKD5nmLFfR7pu2drQ54VT6vhHJjm+Hm1+nJtdJrALALwi6AjOONWn6Lx0319g9NNIHqTm0GFR4aS3utYUhBvyflqJ7JwXbp4g+oq6srI+PuaG/TK882qXBoUGOlPp1/eZ2ju1BnAze/AADZRNgFAJyx0bFY6srspKZQXT0RRWPpy42LCl3TzpxNlBxXVnjkdmf/7NmO9ja9v6dR9dUVMjwemWZMB/Y0ShKB9wxx8wsAkC2EXQDACZmmqcHI6ESQnbI629M/POv1Zd7ilO7Gk5tClfmKbXf27JHmJl1dXZHSNXhjdYWebG4i7AJAGlaeow3MhLALAJAkxWJxhfqGUlZnJzeFGhqJpr3WVWCossIzPdAe/39JcW79c+OODMoo9aQ8ZhiG3JGwRSMCAHuz+hxtYCa59e4DAHBGRkajyTA7tSlUd09EsVnOni0pdk8Pssf3zlaWl8rlyn65caZEPT6ZZmxa1+Cox2vhqADAvuxwjjYwFWEXABzENE31D46krs5OKjvuHxyZ9fryeSXje2anHNdTFfBqnrfIduXGmbJ6a50O7GnUxuOlzKZp6kBnr1bXN1g9NACwJc7Rhh0RdgEgx0RjcXX3RlL2zk7ePzsyGkt7rctlKOhPbQKVKD0O+j0qLuKfBWmiCdWTzU1yR8KKerxaXd/Afl0ASINztGFHvKsBABsaGh6bce9sZ3dYob4hxWcpN/aUFI6XF/snmkAlGkL5y0o5e/YkrVq7jnALACeJc7RhR4RdALCAaZrqHRie1tU4sZd2MDKa9lrDkALlpdO6Gic+9nmKsvhMAADgHG3YE2EXADJkLBpTV08k9fzZ4+G2qyei0bH05cZud0FyZXby3tlEuXFhoSuLzwRIb+pRI9d+YouWLV1s9bAAWIBztGE3hF0AOAPhodGJMuMpe2dDfUMyZ9mq5PMUpTaBqpzYS1s+r4RyY9jeTEeN/KC5TZ+5qI83vDbFOagA8glhFwBmEY+b6u0f0nvd7+r1t97VsSmhNjw0lvZaw5CCfo+q/KlBNhFsPSWFWXseHe1teuXZJhUODWqs1KfzL69jPyrO2IxHjaxcr6aWZwlQNsQ5qADyDWEXQN4bHYslV2OnNoXq6okoGounvbao0JVy5uzkcuPKCo/cbuvPnu1ob9P7expVX10hw+ORacZ0YE+jJBF4cUY4aiS3cA4qgHxD2AXgeKZpajAyOlFiPKUpVE//8KzXl3mLtXB+ufxlxdOaQpX5im1/9uyR5iZdffy8WGn8De7G6go92dxE2MUZ4aiR3MLNCQD5hrALwBFisbh6+ofUOUN342PdYQ2NRNNeW1BgKFjhSQmyyWZQAY9KiwsVDAbV1dWVxWc0d9yRQRmlnpTHDMOQOxK2aERwihmPGvldqz6TgaNG2Gt65rg5ASDfEHYB5IyR0WjK8TyTA213T0SxWc6eLS5yp545O2nvbGV5qVwu68uNMyXq8ck0Y9Pe4EY9XgtHBSeY6aiR66+4dM67MbPXdG5wDiqAfHNSYTcej6u1tVWGYaimpkYFBeNvCn/729/qox/9aEYHCCB/mKap/sGR1DNnj6/MHusJq29gZNbry+eVjDeBqvSmNIWqCng1z1tk+3LjTFm9tU4H9jRq4/FSZtM0daCzV6vrG6weGhxg6lEjmaiCYK/p3OAcVAD55qTC7oMPPqhgMCi3261nnnlGN910kxYsWKDm5mbCLoBTEo3FFeqNpJw5O1F2HNHIaPpyY5fLUNA/ZXW2cuLs2eIiilVmktiX+2Rzk9yRsKIer1bXN7BfFzmDvaZzh3NQAeSTk3pnGAqFdPPNN0uSNm3apAcffFB/8zd/k9GBAchdQyNj05pAJUqPQ31Dis9SblxaUjgRZietzFYFvAqUl3L27GlatXYd4dZC7Dc9M+w1PTNthzu07+ARdYVH+P4DkFdOKuxGo1GNjY2psLBQVVVV2rlzp+6//3698847mR4fABsyTVO9A8PJ8uLOKWfPDoRH015rGJK/vDQl0Fb5J5pC+TxFWXwmQOax3/TMsdf09CW+/+av2Sjv2BjffwDyyqxhNxaLyeVy6XOf+5zC4bAqKiokSaWlpbrtttv0wgsvZGOMACwwFo2pqycyravxsVBYx3oiGh2Lpb3W7S6YCLCT9s4myo0LC11ZfCaAtdhveubYa3r6+P4DkM9mDbvf+ta3dOutt+rss8+e9nsFBQX6+Mc/nrGBAci8yNDojJ2Nj4XGy43NWSoEfZ6iiaN6AqnNoCrmlVBuDBzHftO5wV7T08P3H4B8NmvYPeuss/TVr35Vu3btUiAQkCS9+uqr+slPfqJvfOMbWRkggNMXj5vq7R9KbQI1aS9teGgs7bWGIVVWeFKC7OTjejwlhVl8JkDuYr8prJT4/puM7z8A+WLWsNvQ0KDm5mZ99atf1Y4dO7Rv3z698847uvLKK7M1PgAnMDoWO15aHJ7WFOpYT0TRaDzttUWFrpSV2UTpcXXAq8oKj9xu5549C2QL+01hpcT33/w1tZLE9x+AvHLCBlXnnnuuPB6PHnjgAW3cuFG33XabiopoIANki2maCg+NqrM7nHJcTyLQ9vQPz3p9mbd4PMhOWplNBNoyX3Henj0LZAv7TWGlxPfZvpcPqG9whO+/E6BzOuAss4bde++9V6+++qquuOIKbd++XY8++qiOHDmiCy+8MFvjA/JCPG4q1BdRZ3dYkVeP6a13/pLSFGpoJP3ZswUFhoIVnon9s5UTR/VUBTwqLabcGLAa+01hpXVrVumyzRvV1dVl9VBsjc7pgPPMGnY/8IEP6L/+1/8qn88nSZo/f77uuecedXZ2atu2bVkZIOAUI6PRlAZQk4/r6e6NKBZLv3+quMg97czZROlxZXmpXC7KjQEAOBN0rgacZ9awe91116V8vHTpUt155526++67CbvAFKZpqn9wJGXv7ORy476BkVmvL59XouqAV4sXBlTucad0N57nLaLcGACADKJzNeA8J9yzO1UgEKATM/JWNBZXqDcybe/s+P8jGhlNX27schkK+idWZSc3haoKeFRcNP7jGAwGKTUDACDL6JwOOM8ph11JKi0tnetxALYxNDI2rQlU4izaUN+Q4vH0/+iVlhSmNIGqCnhUHfCpKuBVoLyUs2cBALApOqcDznNaYRfIZaZpqndgWMe6x4/rmbx39lgorIHw6KzX+8tLp+2dTTSF8pYWUm4MAEAOonM64DyEXTjSWDSm7t7ItCA7HnAjGh2Lpb3W7S5IlhZXB3zJvbPVAa+Cfo8KC11ZfCYAACBb6JwOOAthFzkrMjSaLC8+FkoNtaG+IZmzbLHxeYqmdTWu9o//v2JeCeXGAAAAQI4j7MK24nFTvf1DqU2gJu2lDQ+Npb3WMKTKCs9EE6jjq7TVx8+e9ZQWZfGZAAAAAMg2W4Xdm266SSUlJSooKJDL5dLu3btTft80TT3++ONqa2tTcXGxbrzxRi1btsyi0WIujI3FxvfNTgmyx0Lj5cbRaDzttUWFromV2YBHVQFf8izaygqP3G7OngUAwCnaDneo6YVWDcYK5HPFVbdhvaNKjp3+/AAr2CrsStIdd9yhsrKyGX+vra1N77//vh544AG9/vrrevTRR/Wtb30ryyPEqTBNU+GhUXV2TwTayU2hevqHZ72+zFs8HmQrfZOaQo2v0pbPK6YZFAAAWWRVIGs73KHGlqPyr9wsr2EobppqbGmVJEcEQqc/P8Aqtgu7szl48KA+/vGPyzAMnXvuuQqHw+rp6ZHf77d6aHktHjcV6jveDGpad+OIhobTlxsXFBgT5caJrsb+8XBbFfCotLgwi88EAACkY2Uga2o5KP+KTcmb3IZhyL9ivZpa9jsiDDr9+QFWsV3YveuuuyRJl112mbZs2ZLye6FQSMFgMPlxZWWlQqHQtLC7d+9e7d27V5K0e/fulGswwe12n/RrMzwypr90Dei9Y/16/1i/3j82/uu/HOtXZ/egorH05calxYVaUDVPC6rKjv83/usPVJWpKuCTy0W58WSnMi/IHubFnpgX+2FO7Gku5mXfy0c0f83GlKqq+Wtqte/lA7ps88YzHeKsxlwl8hQXT3t8yFWS099viXlx6vPLRfwdZk+nOy+2Crt33nmnAoGA+vr69M1vflMLFy7Ueeedd8p/zpYtW1KCcldX11wO0zGCwWDytTFNUwPhUXWGBlP2zib+3zcwMuufVT6vJLl3dvJxPVUBr+Z5i9KUG4+qpyeUgWeW2ybPC+yDebEn5sV+mBN7mot56RockXdserVW3+BIxue8MDaskZGRlPcTpmnKHRvO6e+3xLw49fnlIv4Os6fZ5mXhwoVpr7NV2A0EApKk8vJyrV+/Xm+88UZK2A0EAilPsru7O3kNTiwaiyvUG0nunR0cflNv/+exZLnxyGg07bUul6FgxcTe2clNoaoCHhUX2epbCQAAzDGf21TcNKcFMq97lrP+5khdbY0aW1rlX7FehmHINE31HG1VQ21Nxr92Njj9+QFWsU1CGR4elmmaKi0t1fDwsA4fPqz6+vqUz6mpqdG//du/qba2Vq+//ro8Hg/7dacYGhkbbwIVmro6G1F3b0TxePp/kEpLClP3ziZWaQNeBcpLOXsWAGyCrq2wgpWBLPH93dSyX+GoIa/bVENtjWO+753+/ACr2Cbs9vX16Tvf+Y4kKRaLacOGDVq7dq2am5slSVu3btW6det06NAh3XzzzSoqKtKNN95o5ZAtYZqm+gZGxsuNQxPNoBKhdiA8Ouv1/vLS5KrsWYur5S0xjgdbr7ylhXQ3BgCbo2srrGJ1IFu3ZpWjv8ed/vwAK9gm7M6fP1/33nvvtMe3bt2a/LVhGPr7v//7bA7LEtFoXF2904Ps+LE9EY2OxdJe63YXqMo/095Zj6r8XhUWupKfy54EADNh1dDe6NoKKxHIAOQS24TdfPSn9/r0ftfgtKZQob4hmbNsf/GWFqq6cry8eGpTqIp5JZQbAzhtrBra32DUkHdKFY5hGApH+bsfAIDJCLsW+tHTbfrDn3qmPW4YmnT2rOf46qwv+bGntMiC0QLIB6wa2p+VTYIAAMglhF0LrVhWpTJf8fEQ60s2hQpWeOV2c/YsgOxj1dD+6NoKAMDJIexaqP5yVkkA2AurhvZndZMgAAByBWEXAJDEqmFuoEkQAAAnRtgFACTlw6oh3aYBAMgPhF0AQAonrxrSbRoAgPxBFyQAQN4Y7za9foZu0wctHhkAAJhrhF0AQN4YjBopzbckuk0DAOBUhF0AQN7wuU2ZZmpnabpNAwDgTIRdAEDeqKutUc/R1mTgTXSbrqPbNAAAjkODKgBA3kg0ofrxL57UH471KTY2ouXVFZJWWDouAAAw9wi7AIC8YwSXqmbDxFnCdGQGAMB5KGMGAOQVOjIDAJAfWNkFAOSVwaghb452ZG473KGmF1o1GCuQzxVX3Yb1rEYDAJAGYRcAkFd8blNx00w5gigXOjK3He5QY8tR+VdultcwFKf8GgCAWVHGDADIK7nakZnyawAATg0ruwCAvBPvelsHnzqi+Oiwli3w63OfvsL2q6O5XH4NAIAVCLsAgLyRKAWu3FCv4PFOzD1HW60e1knJ1fJrAACsQhkzACBv5HIpcK6WXwMAYBVWdgEAeSOXS4ETZdZNLfsVjhryuk011NbYvvwaAACrEHYBAHkj10uB161ZRbgFAOAkUcYMAMgblAIDAJA/WNkFAOQNSoEBAMgfhF0AQF6hFNiZ2g53qOmFVg3GCuRzxVW3YT3zDAB5jrALAAByWuJIKf/KzfIahuKmqcaW8SOlCLwAkL/YswsAAHJaLh8pBQDIHMIuAADIaYNRI6XDtpQ7R0oBADKHsAsAAHKaz20mO2wn5NKRUgCAzGDPLgAANkOzpVNTV1ujxpbWZClz4kipBo6UAoC8RtgFAMBGaLZ06jhSCrli6o2saz+xRcuWLrZ6WIBjEXYBALCR8WZLm2ZotrSf8DYLjpSC3c10I+sHzW36zEV9fO8CGULYBQDARgajhrw0W4LNUFp/5ma8kbVyvZpanuW1BDKEsAsAgI343KbippnSXZhmS7ASpfVzgxtZQPbRjRkAABupq61Rz9HWZHfhRLOlOpotwSKcYzw36BoOZB8ruwAA2AjNlmA3rEjOjRm7hv+uVZ/hRhaQMYRdAABshmZLsBNK6+fGTDeyrr/iUroxAxlE2AUAAEBanGM8d6beyAoGg+rq6rJwRICzEXYBAIAkOu5iZpTWA8hVhF0AAEDHXcyK0noAuYhuzAAAgI67AADHIewCAAANRo2UBkQSHXcBALmNMmYAAHDKHXfZ3wsAsDvCLoC8wZtzIL1T6bg72/7eyzZvzPbQHYm/rwDgzBF2AeQFmu8AszuVjrvj+3s3zbC/dz9hdw7w9xUAzA3CLoC8MNubc948AuNOtuPuYNSQl/29J3S6q7P8fQUAc8MWYberq0sPPfSQent7ZRiGtmzZorq6upTP6ejo0Le//W1VV1dLkj784Q+rvr7eiuECyEG8OQfmzqnu781HZ7I6y99XADA3bBF2XS6XGhoatGzZMg0NDWnnzp1as2aNFi9enPJ5K1eu1M6dOy0aJYBcxptzYO6cyv7efHUmq7P8fQUAc8MWRw/5/X4tW7ZMklRaWqpFixYpFApZPCoATlJXW6Oeo60yzfE3i4k353W8OQdO2bo1q9RQu0IFR/cr8sp+FRzdr4baFZTYTnImRznx9xUAzA1brOxO1tnZqbfeektnn332tN/7/e9/r1tvvVV+v18NDQ1asmSJBSMEkItOpfkOgBM72f29+epMVmf5+woA5oZhJm4b2sDw8LDuuOMOffrTn9aHP/zhlN+LRCIqKChQSUmJDh06pB/+8Id64IEHZvxz9u7dq71790qSdu/erdHR0YyPPRe53W5Fo1Grh4EpmBd7Yl7siXmxH+Zk3EuH2vWD5jb5V04q9f5dq67fuk4XXbg26+NhXuyJebEf5sSeZpuXoqKitNfZJuxGo1Hdc889uuCCC/SJT3zihJ9/00036e6771ZZWdkJP/fdd9+diyE6TjAYVFdXl9XDwBTMiz0xL/bEvNgPczKh7XCHmloOJldn6yxcnWVe7Il5sR/mxJ5mm5eFCxemvc4WZcymaeqRRx7RokWL0gbd3t5elZeXyzAMvfHGG4rH45o3b16WRwoAAHByKPUGAGvZIuy+9tprev7557V06VLdeuutkqRrr702md63bt2qF198Uc3NzXK5XCoqKtItt9wyrfEDAAAAAACSTcLuihUr9LOf/WzWz9m2bZu2bduWpREBAADgTLUd7lDTC60ajBXI54qrbsN6VrsBZI0twi4AAACcpe1whxpbjsq/crO8hqG4aaqxpVWSCLwAssIW5+wCAADAWZpaDsq/Yn1y25lhGPKvWK+mloMWjwxAviDsAgAAYM4NRo1p/VUMw1A4Ss8VANlBGTMAAMBx7DGdOz63qbhppgRe0zTlddvi1EsAeYCVXQAAAE3sMY2v3Czv+ZsUX7lZjS1H1Xa4w+qh5aS62hr1HG2VaY6HW9M01XO0VXW1NRaPDEC+YGUXAABAiT2mm2bYY7qf1d3TkHjNmlr2Kxw15HWbaqit4bUEkDWEXQAAAI3vMfWyx3ROrVuzinALwDKUMQMAAGh8j2mi5DaBPaYAkLsIuwAAAGKPKQA4DWXMAABboAsurMYeUwBwFsIuAMByiS64/pWb5TUMxU1TjS2tkkTQQFaxxxQAnIMyZgCA5ca74K6foQvuQYtHBgAAchUruwAAy9EFFzh9bAEAgJkRdgEAlvO5TcVNM7myK9EFFzgZbAEAgPQoYwYAWI4uuMDpYQsAAKTHyi4AwHJ0wQVOD1sAACA9wi4AwBboggucOrYAAEB6lDEDAADkKLYAAEB6rOwCAADkKLYAAEB6hF0AAIAcxhYAAJgZYRcAgFPEuaYAANgfYRcAgFPAuaYAAOQGGlQBAHAKONcUAIDcQNgFAOAUDEaNlGNeJM41BQDAjgi7AACcAp/bTB7zksC5pgAA2A9hFwCAU8C5pgAA5AYaVAEAcAo413Tu0NUaAJBJhF0AAE4R55qeObpaAwAyjTJmAACQdXS1BgBkGmEXAABkHV2tAQCZRtgFAABZR1drAECmEXYBAEDW0dUaAJBpNKgCAABZR1drAECmEXYBAIAl6GoNAMgkypgBAAAAAI7Dyi4AAACmaTvcoaYXWjUYK5DPFVfdhvWsxAPIKYRdAMBJ4Y0vkD/aDneoseWo/Cs3y2sYipumGltaJYmfewA5g7ALADgh3vg6DzcvMJumloPyr9iUPAvZMAz5V6xXU8t+vk8A5AzCLgDghHjj6yzcvMCJDEYNeY//vCcYhqFw1EhzBQDYDw2qAAAnNBg1kkE3gTe+uWv85sX6GW5eHLR4ZLALn9tMnoGcYJqmvG4zzRUAYD+EXQDACfHG11m4eYETqautUc/R1uTPvWma6jnaqrraGotHBgAnjzJmAMAJ1dXWqLGlNbkamHjj28Ab35zkc5uKm2ZK4OXmBSZLlLM3texXOGrI6zbVUFtDmTuAnELYBQCcEG98nYWbFzgZ69as4mccQE4j7AIATgpvfJ2DmxcAgHxA2AXgWBytAqTHzQsAgNMRdgE4EkerAPbCzScAQLbZKuy2t7fr8ccfVzwe16WXXqqrrroq5ffHxsb04IMP6g9/+IPmzZunW265RdXV1dYMFoCtcS4sYB/cfAIAWME2YTcej+uxxx7TV77yFVVWVmrXrl2qqanR4sWLk5+zb98+eb1efe9731NLS4v+5V/+Rf/0T/9k4agB2NVg1JDXYUersDKGXMXNJwCAFWxzzu4bb7yhBQsWaP78+XK73br44ovV2tqa8jkHDx7UJZdcIkn6yEc+oiNHjkw79xEAJOedC5tYGYuv3Czv+ZsUX7lZjS1H1Xa4w+qhASfEub4AACvYJuyGQiFVVlYmP66srFQoFEr7OS6XSx6PRwMDA1kdJ4DcUFdbo56jrcnAmzhapS5Hj1YZXxlbP8PK2EGLRwacmNNuPgEAcoNtypjn0t69e7V3715J0u7duxUMBi0ekT253W5eGxtiXubGZZs3qryiXE/9ukWDY5KvUPrsFbW66MK1p/XnWT0vY64SeYqLpz0+5CrJ6+8Xq+cF0800J9decal+0Nwm/8pJ5/r+rlXXX3Ep85cl/KzYE/NiP8yJPZ3uvNgm7AYCAXV3dyc/7u7uViAQmPFzKisrFYvFFIlENG/evGl/1pYtW7Rly5bkx11dXZkbeA4LBoO8NjbEvMydZUsX679//jMpj53ua2v1vBTGhjUyMpJSCmqaptyx4bz+frF6XjDdTHOybOlifeaiPjW1PJs81/cztTVatnQx85cl/KzYE/NiP8yJPc02LwsXLkx7nW3C7vLly/Xee++ps7NTgUBAv/nNb3TzzTenfM6HPvQhPffcczr33HP14osvatWqVdP2AAGAE9XV1qixpTVZypwoy27I0bJs5B/O9QUAZJttwq7L5dIXvvAF3XXXXYrH49q0aZOWLFmin/70p1q+fLlqamq0efNmPfjgg/pv/+2/yefz6ZZbbrF62ACQFYmQ0NSyP7ky1lBbQ3gAAABIwzZhV5IuvPBCXXjhhSmPfeYzEyWIRUVF+uIXv5jtYQGALbAyBgAAcPJs040ZAAAAAIC5QtgFAAAAADgOYRcAAAAA4DiEXQAAAACA49iqQRUAYELb4Q41vdCqwViBfK646jasp0EVAADASSLsAoANtR3uUGPLUflXbpbXMBQ3TTW2tEoSgRcAAOAkUMYMADbU1HJQ/hXrZRiGJMkwDPlXrFdTy0GLRwYAAJAbCLsAYEODUSMZdBMMw1A4aqS5AgAAAJNRxgwANuRzm4qbZkrgNU1TXrdp4aiAM8M+dABANrGyCwA2VFdbo56jrTLN8XBrmqZ6jraqrrbG4pEBpyexDz2+crO8529SfOVmNbYcVdvhDquHBgBwKFZ2AcCGEqtdTS37FY4a8rpNNdTWsAqGnDW+D33TDPvQ9/N9DQDICMIuANjUujWrCAFwjMGoIS/70AEAWUQZMwAAyDif20yW5SewDx0AkEmEXQAAkHHsQwcAZBtlzAAAIOPYhw4AyDbCLgAAyAr2oQMAsokyZgAAAACA4xB2AQAAAACOQ9gFAAAAADgOYRcAAAAA4DiEXQAAAACA4xB2AQAAAACOQ9gFAAAAADgOYRcAAAAA4DhuqwcAAICV2g53qOmFVg3GCuRzxVW3Yb3WrVll9bAAAMAZIuwCAPJW2+EONbYclX/lZnkNQ3HTVGNLqyQReAEAyHGUMQMA8lZTy0H5V6yXYRiSJMMw5F+xXk0tBy0eGQAAOFOs7MIWKCMEYIXBqCHv8aCbYBiGwlEjzRUAACBXEHZhOcoIAVjF5zYVN83kyq4kmaYpr9u0cFQAAGAuEHZhufEywk0zlBHuJ+wCyKi62ho1trQmS5lN01TP0VY11NZYPbSTQlUMAADpEXZhOcoIAWTb5JAY7+1S14E35a1cIK/bVENtTU4ERqpiAACYHWEXlqOMEEA2TQ2JnuOruX9TuyKnQiJVMQAAzI5uzLBcXW2Neo62yjTHw22ijLAuR8oIAeQWp3RgHowaKTcJJapiAACYjJVdWC6xAtHUsl/hqJFTZYQAco9Ttk5QFQMAwOwIu7CFdWtWEW4BZIVTQmKuN9cCACDTCLsAgLzilJBIVQwAALMj7AIA8oqTQiJVMQAApEfYBQDkHUIiAADORzdmAAAAAIDjEHYBAAAAAI5DGTMAAKeo7XCHml5o1WCsQD5XXHUb1lMWDQCAzRB2AQA4BW2HO9TYclT+lZvlNQzFTVONLa2SROAFAMBGKGMGAOAUNLUcTB5bJEmGYci/Yr2aWg5aPDIAADAZYRcAgFMwGDWSQTfBMAyFo0aaKwAAgBUIuwAAnAKf25RpmimPmaYpr9tMcwUAALACe3YBACdEQ6YJdbU1amxpTZYym6apnqOtaqitsXpoAABgEsvDbmNjo15++WW53W7Nnz9fN954o7xe77TPu+mmm1RSUqKCggK5XC7t3r3bgtECQP6hIVOqxHNuatmvcNSQ122qobYmL18LAADszPKwu2bNGu3YsUMul0tPPPGEnnrqKV133XUzfu4dd9yhsrKyLI8QAPLbeEOmTTM0ZNqftwFv3ZpVefvcAQDIFZbv2b3gggvkcrkkSeeee65CoZDFIwIATEZDJgAAkIssX9mdbN++fbr44ovT/v5dd90lSbrsssu0ZcuWbA0LAPKaz20qbpopgZeGTAAAwO4Mc2pLyQy488471dvbO+3xa665RuvXr5ck/fznP9ebb76pL33pS9NWECQpFAopEAior69P3/zmN/X5z39e55133oxfb+/evdq7d68kaffu3RodHZ27J+Mgbrdb0WjU6mFgCubFnvJ5Xl461K4fNLfJv3JSQ6bfter6ret00YVrLR1bPs+LXTEn9sS82BPzYj/MiT3NNi9FRUVpr8tK2D2R5557Tr/61a90++23q7i4+ISf/7Of/UwlJSW68sorT+rPf/fdd890iI4UDAbV1dVl9TAwBfNiT/k+L22HO9TUcjDZkKnOJg2Z8n1e7Ig5sSfmxZ6YF/thTuxptnlZuHBh2ussL2Nub2/XL37xC339619PG3SHh4dlmqZKS0s1PDysw4cPq76+PssjBYD8RUMmAACQaywPu4899pii0ajuvPNOSdI555yj66+/XqFQSN///ve1a9cu9fX16Tvf+Y4kKRaLacOGDVq7dq2FowYAAAAA2JnlYfd73/vejI8HAgHt2rVLkjR//nzde++92RwWAAAAACCHWX70EAAAAAAAc42wCwAAAABwHMIuAAAAAMBxCLsAAAAAAMch7AIAAAAAHIewCwAAAABwHMIuAAAAAMBxLD9nFwCAqdoOd6jphVYNxgrkc8VVt2G91q1ZZfWwAABADiHsAgBspe1whxpbjsq/crO8hqG4aaqxpVWSCLwAAOCkUcYMALCVppaD8q9YL8MwJEmGYci/Yr2aWg5aPDIAAJBLCLsAAFsZjBrJoJtgGIbCUSPNFQAAANMRdgEAtuJzmzJNM+Ux0zTldZtprgAAAJiOsAsAsJW62hr1HG1NBl7TNNVztFV1tTUWjwwAAOQSGlQBAGwl0YSqqWW/wlFDXrephtoamlMBAIBTQtgFANjOujWrCLcAAOCMUMYMAAAAAHAcwi4AAAAAwHEIuwAAAAAAxyHsAgAAAAAch7ALAAAAAHAcwi4AAAAAwHEIuwAAAAAAxyHsAgAAAAAch7ALAAAAAHAcwi4AAAAAwHEIuwAAAAAAxyHsAgAAAAAch7ALAAAAAHAcwi4AAAAAwHEIuwAAAAAAxzFM0zStHgQAAAAAAHOJld08tnPnTquHgBkwL/bEvNgT82I/zIk9MS/2xLzYD3NiT6c7L4RdAAAAAIDjEHYBAAAAAI5D2M1jW7ZssXoImAHzYk/Miz0xL/bDnNgT82JPzIv9MCf2dLrzQoMqAAAAAIDjsLILAAAAAHAct9UDgD0888wzamxs1KOPPqqysjKrh5P3fvKTn+jgwYMyDEPl5eW68cYbFQgErB5W3mtsbNTLL78st9ut+fPn68Ybb5TX67V6WHntt7/9rf73//7f+vOf/6xvfetbWr58udVDymvt7e16/PHHFY/Hdemll+qqq66yekh57+GHH9ahQ4dUXl6u++67z+rhQFJXV5ceeugh9fb2yjAMbdmyRXV1dVYPK++Njo7qjjvuUDQaVSwW00c+8hFt377d6mFBUjwe186dOxUIBE65KzNhF+rq6tLhw4cVDAatHgqOu/LKK3XNNddIkpqamrRnzx5df/31Fo8Ka9as0Y4dO+RyufTEE0/oqaee0nXXXWf1sPLakiVL9KUvfUk/+MEPrB5K3ovH43rsscf0la98RZWVldq1a5dqamq0ePFiq4eW1y655BJt27ZNDz30kNVDwXEul0sNDQ1atmyZhoaGtHPnTq1Zs4afFYsVFhbqjjvuUElJiaLRqG6//XatXbtW5557rtVDy3tNTU1atGiRhoaGTvlaypihH/3oR/rsZz8rwzCsHgqO83g8yV+PjIwwNzZxwQUXyOVySZLOPfdchUIhi0eExYsXa+HChVYPA5LeeOMNLViwQPPnz5fb7dbFF1+s1tZWq4eV98477zz5fD6rh4FJ/H6/li1bJkkqLS3VokWL+PfEBgzDUElJiSQpFospFovx/ssGuru7dejQIV166aWndT0ru3mutbVVgUBAZ511ltVDwRT/+q//queff14ej0d33HGH1cPBFPv27dPFF19s9TAA2wiFQqqsrEx+XFlZqddff93CEQH219nZqbfeektnn3221UOBxitUbrvtNr3//vu6/PLLdc4551g9pLz3wx/+UNddd91prepKhN28cOedd6q3t3fa49dcc42eeuopfeUrX8n+oDDrvKxfv17XXnutrr32Wj311FP6t3/7N/aNZMmJ5kWSfv7zn8vlculjH/tYlkeXn05mTgAg1wwPD+u+++7T5z73uZSKLlinoKBA9957r8LhsL7zne/onXfe0dKlS60eVt56+eWXVV5ermXLlqmjo+O0/gzCbh746le/OuPj77zzjjo7O3XrrbdKGi8TuO2223T33XeroqIiiyPMT+nmZaqPfexjuvvuuwm7WXKieXnuuef08ssv6/bbb6e8KUtO9mcF1goEAuru7k5+3N3dTWM9II1oNKr77rtPH/vYx/ThD3/Y6uFgCq/Xq1WrVqm9vZ2wa6HXXntNBw8eVFtbm0ZHRzU0NKQHHnhAN99880n/GYTdPLZ06VI9+uijyY9vuukm3X333XRjtoH33ntPH/jABySNl5qzJ9Ee2tvb9Ytf/EJf//rXVVxcbPVwAFtZvny53nvvPXV2dioQCOg3v/nNKb0hAfKFaZp65JFHtGjRIn3iE5+wejg4rr+/Xy6XS16vV6Ojozp8+LD++q//2uph5bUdO3Zox44dkqSOjg4988wzp/zvCmEXsKF/+Zd/0XvvvSfDMBQMBunEbBOPPfaYotGo7rzzTknSOeecw9xY7KWXXtI///M/q7+/X7t379ZZZ52lL3/5y1YPKy+5XC594Qtf0F133aV4PK5NmzZpyZIlVg8r791///169dVXNTAwoBtuuEHbt2/X5s2brR5WXnvttdf0/PPPa+nSpcnqumuvvVYXXnihxSPLbz09PXrooYcUj8dlmqY++tGP6kMf+pDVw8IZMkzTNK0eBAAAAAAAc4mjhwAAAAAAjkPYBQAAAAA4DmEXAAAAAOA4hF0AAAAAgOMQdgEAAAAAjkPYBQAAAAA4DmEXAIAc9cQTT+jb3/528uPGxkZ94xvfUDQatXBUAADYA2EXAIAc9dd//dfq6OjQW2+9pebmZrW3t+tLX/qS3G631UMDAMByhmmaptWDAAAAp+dnP/uZXnrpJUUiEX3jG99QMBhUJBLRnXfeqf/8z//UXXfdpaVLl1o9TAAAso6VXQAActgHP/hBvfPOO9qxY4eCwaAkqaioSLt27dJHPvIRi0cHAIB1CLsAAOSod955R48++qg2btyo/fv3Jx93u90qKyuzcGQAAFiPsAsAQA4KhUK655579F/+y3/R3//93+udd95RR0eH1cMCAMA2CLsAAOSYSCSiu+++W1dccYVqampUXFysT37yk/rJT35i9dAAALANGlQBAOBQDz30kD75yU/SoAoAkJcIuwAAONDdd9+tP/7xjwoGg7rssst0ySWXWD0kAACyirALAAAAAHAc9uwCAAAAAByHsAsAAAAAcBzCLgAAAADAcQi7AAAAAADHIewCAAAAAByHsAsAAAAAcBzCLgAAAADAcQi7AAAAAADHIewCAAAAABzn/wemdBeNT7h0aQAAAABJRU5ErkJggg==",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plot_ds(data,m[-1],q[-1])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Accelerazione del gradiente di Nesterov\n",
"Nel metodo del momento, la conoscenza al passo $k$ di $\\theta^{(k)}$ e di $v^{(k)}$ permette, senza calcolare il gradiente, di avere una valutazione approssimata $\\tilde{\\theta}^{(k+1)}=\\theta^{(k)}+\\gamma v^{(k)}$ di \n",
"$$\n",
"\\theta^{(k+1)}=\\theta^{(k)}+v^{(k+1)}=\\theta^{(k)}+\\gamma v^{(k)}-\\eta\\sum_{i=1}^nJ'(\\theta^{(k)};\\mathbf{x}_i)=\\tilde{\\theta}^{(k+1)}-\\eta\\sum_{i=1}^nJ'(\\theta^{(k)};\\mathbf{x}_i)\n",
"$$\n",
"Il metodo di Nesterov segue lo stesso approccio del metodo del momento, con la differenza che, ad ogni passo, la valutazione del gradiente viene effettuata, con un *look-ahead* approssimato, non nel punto attuale $\\theta^{(k)}$ dello spazio delle soluzioni visitato ma, più o meno, nel punto successivo $\\theta^{(k+1)}$ (approssimato da $\\tilde{\\theta}^{(k+1)}$). In questo modo, le variazioni di $v$ (e quindi di $\\theta$) vengono anticipate rispetto a quanto avviene nel metodo del momento.\n",
"\n",
"\\begin{align*}\n",
"v^{(k+1)}&=\\gamma v^{(k)} +\\eta\\sum_{i=1}^nJ'(\\tilde{\\theta}^{(k)};\\mathbf{x}_i)=\\gamma v^{(k)} +\\eta\\sum_{i=1}^nJ'(\\theta^{(k)}+\\gamma v^{(k)};\\mathbf{x}_i)\\\\\n",
"\\theta^{(k+1)}&=\\theta^{(k)}+v^{(k+1)}\n",
"\\end{align*}\n",
"\n",
"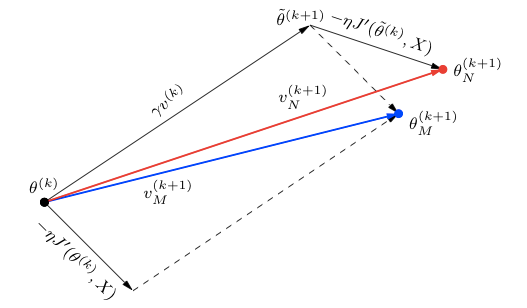\n",
"\n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"```python\n",
"v = 0\n",
"for i in range(n_epochs):\n",
" g = 0\n",
" theta_approx = theta+gamma*v\n",
" for k in range(dataset_size):\n",
" g = g+evaluate_gradient(loss_function, theta_approx, X[k])\n",
" v = gamma*v-eta*g\n",
" theta = theta+v\n",
"```"
]
},
{
"cell_type": "code",
"execution_count": 135,
"metadata": {},
"outputs": [],
"source": [
"def nesterov_gd(X,t, eta = 0.1, gamma = 0.97, epochs = 1000):\n",
" theta = np.zeros(nfeatures+1).reshape(-1,1)\n",
" v = np.zeros(nfeatures+1).reshape(-1,1)\n",
" theta_history = []\n",
" cost_history = []\n",
" for k in range(epochs): \n",
" delta = - eta * gradient(theta+gamma*v,X,t)\n",
" v = gamma*v +delta\n",
" theta = theta + v\n",
" theta_history.append(theta)\n",
" cost_history.append(cost(theta, X, t))\n",
" theta_history = np.array(theta_history).reshape(-1,3)\n",
" cost_history = np.array(cost_history).reshape(-1,1)\n",
" m = -theta_history[:,1]/theta_history[:,2]\n",
" q = -theta_history[:,0]/theta_history[:,2]\n",
" return cost_history, m, q"
]
},
{
"cell_type": "code",
"execution_count": 136,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"tempo di esecuzione: 0.407 secondi\n",
"10000 passi totali\n",
"1000000 gradienti valutati\n"
]
}
],
"source": [
"start_time = time.time()\n",
"cost_history, m, q = nesterov_gd(X, t, eta = 0.1, gamma = 0.97, epochs = 10000)\n",
"print(f\"tempo di esecuzione: {time.time()-start_time: 4.3f} secondi\")\n",
"print(f\"{len(m)} passi totali\")\n",
"print(f\"{len(m)*n} gradienti valutati\")"
]
},
{
"cell_type": "code",
"execution_count": 140,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABQgAAAGoCAYAAAAKMwiTAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAABaw0lEQVR4nO3deXiV9YH3/8+9nAQOYT8QCMgSICASBFFAFos2dbfaqDhtnc7kqtP5tVPr02mfPn1+MzIW6yX9zejUGfv0Gp2xtPPY1qW41y1VVDZB1rAmIbKEPQlbNpJ7+f1xyIlRpAFy7vvknPerl1c55+RwPvneSTh8+C6G7/u+AAAAAAAAAGQkM+wAAAAAAAAAAMJDQQgAAAAAAABkMApCAAAAAAAAIINREAIAAAAAAAAZjIIQAAAAAAAAyGAUhAAAAAAAAEAGs8MOAAAAgPRUV1enn/3sZ6qurtZvfvMbWZaVeGzPnj168sknJUn33HOPRo4cGVZMAACAjMcMQgAAACRFTk6O7r//fo0bN+4zjz3zzDO677779P3vf1/PPPNMCOkAAADQptvMINy/f3/YES5YLBZTTU1N2DEgrkWq4XqkDq5FauF6pI50uRZ5eXmBvl5WVpaysrLO+FhDQ4NisVji139Od38vmC5fQ12F8WjHWHTEeHTEeHTEeLRjLDpiPDo623h83vvBblMQAgAAIH34vn/Wx0tLS1VaWipJWrRoUaJM7K5s2+72n0NXYjzaMRYdMR4dMR4dMR7tGIuOGI+Ozmc8KAgBAAAQKsMwPnNfUVGRioqKEre7+6wAZjZ0xHi0Yyw6Yjw6Yjw6YjzaMRYdMR4dMYMQAAAA3UJOTo5qa2tlGIZ69uwZdhwAAICMRkEIAACApHAcRw8//LB2796thx56SHfccYe2b9+u4uJizZ8/Xz//+c8lSd/85jfDDQoAAJDhKAgBAACQFLZt6/777+9w38SJEyVJI0eO1IMPPhhGLAAAAHyKGXYAAAAAAAAAAOGhIAQAAAAAAAAyGAUhAAAAAAAAkMEoCAEAAAAAAIAMRkEIAAAAAAAAZDAKQgAAAAAAACCDURACAAAAAAAAGYyCEAAAAAAAAMhgFIQAAAAAAABABqMgBAAAAAAAADIYBSEAAAAAAACQwSgIAQAAAAAAgAxGQQgAAAAAAABkMApCAAAAAAAAIINREAIAAAAAAAAZjIIQAAAAAAAAyGAUhAAAAAAAAEAGoyAEAAAAAAAAMhgFIQAAAAAAAJDBKAgBAAAAAACADEZBCAAAAAAAAGQwCkIAAAAAAAAgg1EQAgAAAAAAABnMDjtAJjh0rFG7DtdrXLOpAT3CTgMAAAAAAAC0YwZhAHYePKHnV1Zp1fZ9YUcBAAAAAAAAOqAgDIBhGJIk3/dDTgIAAAAAAAB0REEYgNP9oOgHAQAAAAAAkGqSugfh4sWLVVVVpdGjR6ukpCRxf319vZ544gmdPHlShYWFKi4uTmaM0BmKN4QeDSEAAAAAAABSTNIKwqqqKjU3N2vhwoV68sknVVlZqbFjx0qSnnvuOd11110aNmxYsl4+pbTPIKQgBAAAAAAAQGpJ2hLjiooKTZ48WZJUWFio8vLyxGN79+7VCy+8oJ/85Ccd7k9XptE2gzDkIAAAAAAAAMCnJG0GYUNDg3JzcyVJ0WhU1dXVicd27Nihn/3sZ8rJydEjjzyiBx988DPPLy0tVWlpqSRp0aJFisViyYqadH0ON0uKzyTszp9HOrFtm2uRQrgeqYNrkVq4HqmDawEAAIB0lrSCMBqNqrGxUZLU1NSkaDSaeCwvL0/Dhw+XJJnmmScxFhUVqaioKHG7pqYmWVGTrr6+XpLkul63/jzSSSwW41qkEK5H6uBapBauR+pIl2uRl5cXdgQAAACkoKQtMS4oKNDmzZslSWVlZSooKEg8NnToUB09elTNzc1yXTdZEVLG6S0IOcUYAAAAAAAAKSdpMwjz8/MViUS0YMECjRo1SrFYTEuWLFFxcbHmz5+vxx57TC0tLbrjjjuSFSFltB1SwinGAAAAAAAASDVJKwglqaSkpMPt4uJiSdLw4cP1wAMPJPOlU4pxuiGkHgQAAAAAAECqSdoSY7Rrm0HoM4MQAAAAAAAAKYaCMADG6V0IKQgBAAAAAACQaigIA9C+B2G4OQAAAAAAAIBPoyAMgGkwgxAAAAAAAACpiYIwAO17EIabAwAAAAAAAPg0CsIAnO4HmUEIAAAAAACAlENBGADj9BRC9iAEAAAAAABAqqEgDED7EmMaQgAAAAAAAKQWCsIAtM0g9EVBCAAAAAAAgNRCQRiA9j0IQ40BAAAAAAAAfAYFYQASMwhpCAEAAAAAAJBi7LADZIK2PQg5pAQAAAAAACDO91z5J+rkHz18+r9D8o/XyLxovOwrvhR2vIxCQRgAZhACAAAAAIBM5buu/BO18QLwU2WgXOczH+8eqZYR7S3rkpkhpM1MFIQBaN+DkIIQAAAAAACkJ9915B+vaS8A28rA4zWS5575STn9ZPQfLLP/YBn9c+WfapK76o9ylr8so19M5rCxwX4SGYqCMADm6YaQfhAAAAAAAHR3vtMq//iRjrMBjx6Wf7xW8r0zP6n3gNMlYNt/uTL6DZaRlf3Zj21ukLvhPbW+/VtlfeXvZPQdmNxPCBSEQWhbYuzREAIAAAAAgG7Cb22JF4F1p0vAY6cLwRO1nzMLypDRZ2B7AdhWBvYbLCOS1enXta64Tn7dIXl7tqv1jV8r8pXvyMjq0XWfGD6DgjAA7YeUUBACAAAAAIDU4reekn/sSLwEPF0GescOSyeOSjpDl2EYMvrGPlECnv7/foNk2JELzmOYpuwv/oVaX/yl/KOH5Pzpd7Kv+ysZpnnBvzfOjIIwAO2HlIQcBAAAAAAA4DTv0B45y16UX7P/zB9gmjL6DJIx4PRy4MTS4JgMK7mVkpHVQ5Hrv6GWF34hb88OuavfkD3zxqS+ZiajIAwAh5QAAAAAAIBU4buO3I/elrvx/fhsJtOKl379cmUM+MSMwD4Dk14Eno3RZ6AiX/q6Wl/7L7kb35fRP1fW+Gmh5UlnFIQBMJlBCAAAAAAAUoB3pFrOu8/JP3pIMgxZl35B1uVFXbI0OBnMvDGyZ98q54MX5Ly/REbfmMwhI8OOlXYoCANgJE4xpiEEAAAAAADB811H7rp35a5/V/I9GX1jsufd2S3KNmviDHl1B+VtWanWt/5bWcXflZHTL+xYaYWCMACcYgwAADLR4sWLVVVVpdGjR6ukpCRx/8qVK/Xyyy/LMAx95Stf0RVXXBFiSgAA0p9Xe0DOu8/Krz0gSbImzZY1/bpzOlk4bPaVN6v12BH5+yrV+uZvFPny/9Ot8qc6jn8JQGIPwlBTAAAABKeqqkrNzc1auHChHMdRZWVl4rHXXntNDzzwgB544AG9+uqrIaYEACC9+Z4rZ907al3yeLwc7D1AkVu+JXv2Ld2uXDMsS5Gir8noM1B+zX45S5+T73thx0obFIQBaD/FmIoQAABkhoqKCk2ePFmSVFhYqPLy8sRjubm5OnXqlJqbm9WzZ8+wIgIAkNa8o4fV+uIv5a55S/JcmRNnKOvO+2Tm5Ycd7bwZPaKyr/8rKStbXlWZ3LXvhB0pbbDEOADtexCGmwMAACAoDQ0Nys3NlSRFo1FVV1cnHps+fbp+9KMfyfd9fec73znj80tLS1VaWipJWrRokWKxWPJDJ5Ft293+c+hKjEc7xqIjxqMjxqMjxqPd2cbC9zzVr35bJ5a+ILmOrD4D1O+mv1KP/EsCTpkksZiav/L/qPbZf5O7tlR9R42TPWQIXxufcD7fKxSEAWgrCNmDEAAAZIpoNKrGxkZJUlNTk6LRaOKx559/Xo8++qgk6eGHH9all176mecXFRWpqKgocbumpibJiZMrFot1+8+hKzEe7RiLjhiPjhiPjhiPdp83Ft7xmvgJxYd2S5LM8ZfLuvJm1Wf3UH06jV2/obJm3CB31R9V99J/yuo3SCfs6J9/XoY42/dKXl7eGe9niXEADLHEGAAAZJaCggJt3rxZklRWVqaCgoLEY5FIRNnZ2erRo4ccxwkrIgAAacP3PTlly9X6/GPxcjDaW/b1f63IvDtkZPcIO15SWJPnyiyYJjmtqnvucfmNJ8OO1K0xgzAALDEGAACZJj8/X5FIRAsWLNCoUaMUi8W0ZMkSFRcX69prr9X9998vSR1mCQIAgHPnn6hT63vPy99fJUkyx02VPesWGT3Se0adYRiyr/qKWo/XyD20W95b/63ILd+SYVF1nQ9GLQAcUgIAADJRSUlJh9vFxcWSpHnz5mnevHkhJAIAIH34vi9v22o5q16TWluknjmy594ma/SksKMFxrBsRa69W+5Lv5R7aI+c95fInndnoodB57HEOADtexCGmwMAAAAAAHR/zok6tf7xKTkfvCC1tsjML1TWnf8jo8rBNka0twbc+V3JjsgrXyd30wdhR+qWmEEYAJM9CAEAAAAAwAXyfV/ejrU6vOo1+aeapOyo7Dm3yhr72QO/MknWkBGyr54v5+2n5X74usyLxssckBt2rG6FgjAA7XsQUhACAAAAAIBz5zeckPP+Enl7tkuSzJEXy76qWEa0d8jJUoOVXyhvwnR521fL2/ahzNlfDjtSt0JBGIDEHoQh5wAAAAAAAN2L7/vyKjfKWf6SdKpJyuqh/td/XQ1DxrLX3qdYk2bK275abvk6WdOvlxHJCjtSt0FBGID2PQipCAEAAAAAQOf4TfVyPnhB3sdbJEnGRQWKfOF2RUeOUWNNTcjpUo85ME/G4IvkH94r7+MyWQXTwo7UbVAQBqCtz6cfBAAAAAAAneFWlcn54EWpuUGKZMu+8iaZE65g1uCfYV08Xc7hvXK3rqYgPAcUhAFILDGmIQQAAAAAAGfhNzfIWf6yvMqNkiQjb4wi8+6Q0bt/yMm6B3PMZGnFq/IP7ZZXd1DmgCFhR+oWzLADZAIOKQEAAAAAAH+Ou2urWp77ebwctCOyZ9+qyM3fpBw8B0YkW+a4KZIkb9vqcMN0I8wgDEDbDEKPfhAAAAAAAHyKf6pJzopX5JWvkyQZQ0bFZw32jYWcrHuyLp4hb+uH8cNKZtwgw46EHSnlURAGoH0PQhpCAAAAAADQzttbrtb3npcaTkiWLWv6dbImzZZhsujzfJmxPBmDhss/Ui2vqkxWwWVhR0p5FIQBaJ9BSEEIAAAAAAAkv+WUnJWvydseXwZrDL5I9rw7ZfYfHHKy9GBdPF3OkWq52z6kIOwECsIAmIk9CMPNAQAAAAAAwuft26nWpc9J9cck05J1+ZdkXTpXhmmFHS1tmGMvlVa+Kv/gbnl1h2QOyA07UkqjIAzAJ48g932fI8kBAAAAAMhAfmuLnA9fl7dlpSTJiA2TffWdnLSbBEYkW+bYqfK2fShv22qZs28JO1JKY0F7QAxmEQIAAAAAkLG8g7vU+vxj8XLQNGVdXqTIbd+hHEwi6+LpkiS3Yp18pzXkNKmNGYQBMWTIP/2/9mNLAAAAAABAOvOdVrlr3pK7aZkkX8aAIfFZg7FhYUdLe+agYZ84rGSzrIKpYUdKWRSEATEMST4zCAEAAAAAyBTeoT1ylj4n/9gRyTBkTbla1rQvyrCoY4LS8bASCsLPw1dkQFhiDAAAAABAZvBdR+5HpXI3vif5vox+g2RfPV/m4IvCjpZxzDFth5Xsknf0kMz+HFZyJuxBGJC2g0l8GkIAAAAAANKWV7NPrUsel7thqeRL1uS5itz+PcrBkBhZ2TLHTpEkedtWhxsmhTGDMCBtTawXagoAAAAAAJAMvuvKXf+u3PXvSJ4no8/A+F6DQ0aFHS3jWRdPl7dttdzydbKmXy/DjoQdKeVQEAaEGYQAAAAAAKQnr+6gnHefk1+zT5JkTZoVL6IiWSEngySZg4bLiA2TX7NP3sebZY1jL8JPoyAMCHsQAgAAAACQXnzPlbvxfbkflUqeK/Xur8gX7pA5bEzY0fAp1sXT5XzwgtxtqykIz4CCMCDMIAQAAAAAIH14Rw/HTyg+vFeSZF48XfbMm2RkZYecDGdijp0irXxN/oGP5R09LLP/4LAjpRQKwoCcnkAo6kEAAAAAALov3/Pkbl4ud/WbkutIvfrEZw1eVBB2NJxF/LCSyfK2fySvcoPMK64NO1JKoSAMCDMIAQAAAADo3vzjNWpd+rz8g7skSWbBNNmzbpaR3TPcYOgUa8yl8YKwqkz+5V9KdDVIckG4ePFiVVVVafTo0SopKUnc/4tf/EL79u1TVlaWioqKNGfOnGTGSAnsQQgAAAAAQPfk+568LavkfPi65LRK0d6y535F1qiJYUfDOTDy8qUeveQfOyK/7qCMgUPDjpQyklYQVlVVqbm5WQsXLtSTTz6pyspKjR07NvH49773PQ0ZMiRZL59yEkuMKQgBAAAAAOg2/JN1al36B/n7d0qK72Vnz75FRo9eISfDuTJMS+boS+RtWy2vqkwmBWGCmazfuKKiQpMnT5YkFRYWqry8PPGYYRh6/PHHtWjRIh05ciRZEVJKYokxuxACAAAAAJDyfN+Xu221Wp77ebwc7NFL9pe+rsgX/4JysBuz8uNdlbdzE9vAfULSZhA2NDQoNzdXkhSNRlVdXZ147Bvf+IZycnK0fft2/eY3v9EPfvCDzzy/tLRUpaWlkqRFixYpFoslK2ogbMuSJPXr31+xPtGQ08C27W7/NZVOuB6pg2uRWrgeqYNrAQBAZvHrj6v1/T/I3xuf7GSOniR77m0yeuaEnAwXysgbHV9mfLxGft0BGQPzwo6UEpJWEEajUTU2NkqSmpqaFI22l2I5OfFvqAkTJujpp58+4/OLiopUVFSUuF1TU5OsqIHwfE+SVFdbJ7U0hpwGsVis239NpROuR+rgWqQWrkfqSJdrkZfHG2AAAM7G9315FevkLH9FammWsnvKnnOrzDGXcqBFmjBMS2b+JHlbP5S3s0wmBaGkJC4xLigo0ObNmyVJZWVlKihoP+67rTjcv3+/evXKjGm5bT9GPGavAgAAAACQcvzGk3Le/I2cd5+TWppljpigrDu/L2vsFMrBNMMy489K2gzC/Px8RSIRLViwQKNGjVIsFtOSJUtUXFysf/u3f1NDQ4MMw9A999yTrAgpxWQPQgAAAAAAUo7v+/J2bpKz7CXpVKOUlS171i0yC6ZRDKYpY+hoqWeO/BO18msPyIgxizBpBaEklZSUdLhdXFwsSfrxj3+czJdNSW0/UyimAQAAAABIDX5TvZxlL8mrKpMkGcPHKfKF22Xk9As3GJLKME2ZoyfJ27pK3s5NMikIk1sQol17QUhDCAAAAABA2NyPN8t5/wWpuUGKZMmeeZPMi6czazBDWGMK5W1dJbeqTNb06zL+ulMQBsQ4vQsh/SAAAAAAAOHxmxvlLH9ZXuUGSZKRl6/IvDtk9B4QbjAEyhgSX2asE7Xya/bLGDQs7EihoiAMiGHGC0KPhhAAAAAAgFC4u7fLef8PUuNJyY7InnG9zEuulGEk7QxXpCjDNGXmF8rbslJe1SaZFIQIQttEVepBAAAAAACC5Z9qlrPyFXk71kqSjNyRsq++U2bfWMjJECbrdEHoVm6UdcV1MszMLYopCANickgJAAAAAACB8/aWq/W9P0gNxyXLlnXFtbIK52R0GYQ4Y8goqfcA6WSdvD3bZY2aGHak0PDdEJC2zS45pAQAAAAAgOTzW06p9f0X1PrHp6SG4zIGDVfk9u/JvvQqykFIii8ztiZdKUlyy5Yn7nd3blLLa/8l7+ihsKIFjhmEAUksMaYfBAAAAAAgqbz9O9W69Hnp5FHJtGRNK5I15SoZphV2NKQYa/zlcte8LX//Tnm1B2X0GSCn9LeSJHftOzKLvhpywmBQEAYkMYOQXQgBAAAAAEgKv7VF7uo35G5eIUkyBg6VffV8mQOHhpwMqcrI7ilz/LT4XoSbl8v8xDJjr7pCvu8nOp10RkEYEIM9CAEAAAAASBrv4G45S5+Tf7xGMk1ZU6+WNfVqGRbVB87OmjQrfppxxXr59cfaHzjVKDWckHL6hpYtKHyXBIQ9CAEAAAAA6Hq+0yr3o7flbvpA8n0Z/XPjswYHDQs7GroJs98gmReNl7d3h/zqCskwZPQZKP94jbza/bIyoCBkV86AsAchAAAAAABdyzu8V61/+He5G9+XJFlT5ily+72Ugzhn9tzbZI6YINkRmeMvlznyYkmSX7s/5GTBYAZhQBJLjNmDEAAAAACAC+K7jty1f5K74T3J92T0GyR73p0yc0eEHQ3dlNG7vyI3/HViz0G3fL0kyV3ztqxLv5D2S9XT+7NLIe1LjEMOAgAAAABAN+bV7Jfz7rPy6w5KMmQVzpE1/ToZdiTsaEgDbf2NEWs/2MbbuUlWwWVhRQoEBWFA2mYQehSEAAAAAACcM9915Kz9k9x1f5I8T+ozQJF5d8ocOjrsaEhDRr9BiV97h3anfUHIHoQBMcQhJQAAAAAAnA+v7pCOLH5Y7kdvS54nc+JMZd1xH+UgksYwLUW+8neSJG/39rTvc5hBGJD2PQgBAAAAAEBn+J4nd9MHcte8JXmulNNPkS/cIXP42LCjIQMYg4ZpgzNE7+zsr4ZH31TvPlFdO2espl6cF3a0LkdBGBDTYAYhAAAAAACd5R07Iufd5+Qf3iNJik6ZK2fqF2Vk9Qg5GTLF+m0H9dvDI3Sy1ZBONUm1Tdp/uF4qVtqVhBSEAUnMIKQfBAAAAADgc/m+J7dshdzVb0iuI0X7yP7C7ep/2WzV1NSEHQ8Z5O3llfFy8BNONpzSW8sqKQhxftiDEAAAAACAs/OP16p16XPyD+6SJJkFl8medbOM7Gi4wZCR6htaznx/45nv784oCAPCHoQAAAAAAJyZ73vytn4oZ9XrktMi9cyRfdVXZI26JOxoyGA5vbLOfH/0zPd3ZxSEAWGJMQAAAAAAn+WfPKbW956Xv69SkmSOmSx79q0yevYKORky3bVzxmr/4XqdbDiVuK93r2xdOyf9DsmhIAyIwSElAAAAAAAk+L4vb8dHcla8KrWeknpEZc+5TdaYyWFHAySdPoikWHprWaXqG1uUE83iFGNcmLYtLT0KQgAAAABAhvMbTsh5/w/y9uyQJJmjJsqe+xUZ0d4hJwM6mnpxXloWgp9GQRiQ9hmEIQcBAAAIyOLFi1VVVaXRo0erpKQkcX99fb2eeOIJnTx5UoWFhSouLg4xJQAgSL7vy6vYIGf5S1JLs5TVQ/acW2WOnZL4ezOA4FEQBsTkkBIAAJBBqqqq1NzcrIULF+rJJ59UZWWlxo6N79fz3HPP6a677tKwYcNCTgkACJLfeFLOBy/I27VVkmSOGC/7qttl9OoTcjIAFIQBYQ9CAACQSSoqKjR5cnwPqcLCQpWXlycKwr179+qFF15QbW2tvvrVr6qgoCDMqACAALg7N8lZ9qLU3ChFsmXPulnm+MuZNQikCArCgHCKMQAAyCQNDQ3Kzc2VJEWjUVVXVyce27Fjh372s58pJydHjzzyiB588MHPPL+0tFSlpaWSpEWLFikWiwUTPEls2+72n0NXYjzaMRYdMR4dpcN4uI0ndfyNp3Vq20eSpOzRF6vfTX8tu+/Ac/690mE8ugpj0RHj0dH5jAcFYUAMMYMQAABkjmg0qsbGRklSU1OTotFo4rG8vDwNHz5ckmSa5hmfX1RUpKKiosTtmpqaJKZNvlgs1u0/h67EeLRjLDpiPDrq7uPh7toi5/0XpKZ6yc6SPfNG+RNn6FirL53H59Xdx6MrMRYdMR4dnW088vLOfODKmd+RocsZ7EEIAAAySEFBgTZv3ixJKisr67CMeOjQoTp69Kiam5vlum5YEQEASeKfalTrO8/IefO/paZ6GUNHK+vO+2RdMpMlxUCKYgZhQNiDEAAAZJL8/HxFIhEtWLBAo0aNUiwW05IlS1RcXKz58+frscceU0tLi+64446wowIAupC7Z4ec9/4gNZ6Q7Iis6dfJmjRLhsH8JCCVURAGpO0fSTz6QQAAkCFKSko63C4uLpYkDR8+XA888EAIiQAAyeK3NMtZ+aq87fG9Bo3cEbLn3Smz36CQkwHoDArCgLRNomYGIQAAAAAgnXjVlWp973mp/phkWrKuuFbW5LkyPmefWQCph4IwIIklxiHnAAAAAACgK/itp+Ssel3e1lWSJGPQcNlX3ymzf27IyQCcKwrCgJhth5TQEAIAAAAAujlvf1V81uCJuviswWnXyLp0ngzLCjsagPNAQRgQDikBAAAAAHR3vtMqd/UbcstWSPJlDBgi+5r5MgfmhR0NwAWgIAxI+x6EocYAAAAAAOC8eIf2yHn3WfnHayTDlDX1almXXSPDoloAuju+iwPSvgchDSEAAAAAoPvwW5rlfvS23M0rJN+X0W9wfK/BwReFHQ1AF6EgDIjBHoQAAAAAgG7E9315lRvlrHpNajwpGYasS6+SdfmXZNiRsOMB6EIUhAFpLwhpCAEAAAAAqc07ekjOspfk76+SJBmDR8iec6vMQcNCTgYgGSgIA2KobYkxAAAAAACpyW85JXftn+RuXiZ5ntSjl+wZ18scP02GYYYdD0CSUBAGhCXGAAAAAIBU5fu+vKoyOStflRpOSDJkTpwh+4rrZPSIhh0PQJJREAak7ZASj4YQAAAAAJBCvKOH5Sx/Wf6+SkmSMWh4fDkxh5AAGYOCMCDMIAQAAAAApBK/tUXuunfkbvpA8lwpu6fs6dfLnHCFDJPlxEAmoSAMSPsehDSEAAAAAIDw+L4v7+Mtcla+ItUflySZE66QPf16GT17hZwOQBgoCAPCDEIAAAAAQNi84zVylr0sv7pckmTEhsWXE+eOCDkZgDBREAbEPN0Q+jSEAAAAAICA+a0tcjcslbvhvfhy4qwesqdfJ/PiGSwnBkBBGBRmEAIAAAAAgub7vrzdW+Usf0WqPyZJMgumyZ55g4yeOeGGA5AyKAgDwinGAAAAAIAg+cdr5ax4Rd6e7ZIkY8AQ2XNvkzlkVLjBAKQcCsKAnJ5AyAxCAAAAAEBS+U5r+3Ji15GysmVdfq2sS2bKMK2w4wFIQRSEAWmbQcgpxgAAAACAZHF3b5ez4mXpRJ0kyRw3VfbMG2VEe4ecDEAqoyAMiMkehAAAAACAJPFP1slZ8aq8XVslSUb/3PjpxHn5IScD0B1QEAaEQ0oAAAAAAF3Ndx25G9+Tu+7d+HLiSJasy78k65JZMiyWEwPoHArCgBindyH0aQgBAAAAAF3A21suZ9lL8k/USpLMsZfKnnmTjF59Qk4GoLtJakG4ePFiVVVVafTo0SopKenwWEtLi/7u7/5O9957ryZPnpzMGCmhbQYhpxgDAAAAAC6Ef/KYnJWvyPt4iyTJ6DdY9pwvyxw2NuRkALorM1m/cVVVlZqbm7Vw4UI5jqPKysoOj//pT3/SiBEjkvXyKaf9kBIAAAAAAM6d7zpy1i9Vy7OPxMtBO0vWjBsUueN7lIMALkjSZhBWVFQkZgYWFhaqvLxcY8fGf2A5jqOKigqNHz8+WS+fcjikBAAAAABwvrzqCjnLX5Z/7IgkycwvlH3lzTJy+oacDEA6SFpB2NDQoNzcXElSNBpVdXV14rGlS5dq7ty5qqio+Nznl5aWqrS0VJK0aNEixWKxZEUNRO8DjZKkrKzsbv+5pAPbtrkOKYTrkTq4FqmF65E6uBYAgLD49cflrHxNXtUmSZLRNxY/nXj4uJCTAUgnSSsIo9GoGhvjpVhTU5Oi0agkyXVdbdiwQT/84Q/PWhAWFRWpqKgocbumpiZZUQPR0FAvSWpqbur2n0s6iMViXIcUwvVIHVyL1ML1SB3pci3y8vLCjgAA6CTfdXVy1Ztqee8lyWmR7Iisy66RNXmuDIvzRgF0raT9VCkoKFBpaalmzZqlsrIyzZs3T5J0/Phx1dbW6qGHHtLBgwe1fv165efnKycnJ1lRUkJiD0KWGAMAAAAAzsLbt1PO8pfUcvSwJMkcdYnsWTfL6N0/5GQA0lXSCsL8/HxFIhEtWLBAo0aNUiwW05IlS1RcXKyHH35YkvTss89qwoQJaV8OSpKZKAhpCAEAAAAAn+U3nJCz6jV5lRslSVb/QTJm3ixrRObs3w8gHEmdl1xSUtLhdnFxcYfb8+fPT+bLp5TTZ5QwgxAAAAAA0IHvuXI3r5D7UanUekqybFlTr1buF4tVe+x42PEAZAA2LgjI6QmE8mgIAQAAAACneQc+lrPsJfl1ByVJ5siLZc+6RUafATLsSMjpAGQKCsKAJJYYh5wDAAAAABA+v/GknA9fl1e+Ln5H7wGyZ98ia+TF4QYDkJEoCAPSdkiJ51ERAgAAAECm8j1X3tZVcta8JbWcXk586RdkTZ3HjEEAoaEgDEjbEmPqQQAAAADITN7B3XKWvSi/9oAkybxovOzZt8joGws5GYBMR0EYEE4xBgAAAIDM5DfVx5cT71gbvyOnn+zZt8gcOTGx2gwAwkRBGJDEDEL6QQAAAADICL7nydu2Ws7qN6SWZsm0ZF16laypV8uIZIUdDwASKAgDktiDkIYQAAAAANKed3ivnA9elF+zT5JkDB8ne/aXZfYbFHIyAPgsCsKAmMwgBAAAAIC05zc1yFn9prztayT5Uq++smfdLHP0JJYTA0hZFIQBYQYhAAAAAKQv3/fkbVsjZ/Wb0qlGyTRlTb5K1mXXyIhkhx0PAM6KgjAg7TMIKQgBAAAAIJ14R6rlLHtJ/uG9kiQjb4zsObfK7D845GQA0DkUhAEx1HaKcchBAAAAAABdwm9ulLPmTXlbV0vypWgf2VfeJHPMZJYTA+hWKAgDYpgsMQYAAACAdOD7nrwda+V8+IbU3BBfTjxprqxpX5SRxXJiAN0PBWFA2v7tiH4QAAAAALovr2ZffDnxoT2SJGPoaNlzbpM5IDfkZABw/igIA2IabUuMaQgBAAAAoLvxTzXJWfOWvK2r4jM/or1lz7xR5tgpLCcG0O1REAak7c8Lj34QAAAAALoN3/flVayTs+p1qaleMkxZhbNkTfuSjOweYccDgC5BQRiQxAxC0RACAAAAQHfg1R6Us+xF+Qd3SZKMISPjpxMPzAs3GAB0MQrCgLTNIGSFMQAAAACkNr+lWe5Hb8vdvFLyPalnjuyZN8gcdxnLiQGkJbMzH3TXXXdpxYoVidvr1q3Tfffdl7RQ6ahtBiGnGAMAAABAavJ9X27FBrU884jcsuWSfJmXXKmsu34gq2Aa5SCAtHXWGYQ1NTU6fPiwJKm6ulpbt26VJG3YsEGHDh1Kfro0wgxCAAAAAEhdXt2h+HLiAx9LkozBI2TPvVVmbFjIyQAg+c5aEL777rt6/vnnJUl/+MMf9Ic//CHx2LBh/JA8FwanGAMAAABAyvFbTsld+ye5m5dJnif16CV7xvUyx0+TYXRq0R0AdHtnLQjHjh2ra6+9Vm+99ZYmT56soUOHSpJycnI0Z86cQAKmC2YQAgAAAEDq8H1f3s5Ncla+JjWekGTInDhD9hXXyegRDTseAATqrAXh1KlTNXXqVI0ZM0aXXHKJBg0aJEnyPE+myb+knAv2IAQAAACA1OAdPSxn+cvy91VKkoxBw2XPvU3moOEhJwOAcHTqFOO9e/fq8OHDKioq0j/8wz/oxIkT+uY3v6lrrrkm2fnSRvsMQgpCAAAAAAiD39oid92f5G5aJnmulB2VPf06mRdfwXJiABmtUz8Bly1bpl69emn58uVyHEdDhw7VkiVLkp0trbTPIAw5CAAAAABkGN/35VaVqeXZR+RueE/yXJkTpsdPJ544g3IQQMbr1AzC+vp69e7dWxs2bNBVV12lkSNH6j/+4z+SnS2tGOKQEgAA0L3ce++9uuiiizRq1CiNGDFCo0aN0pAhQ8KOBQDnxDteI2fZy/KryyVJRmyY7Dm3yswdEXIyAEgdnSoIY7GYfve736m+vl7f/va3dezYMeXk5CQ7W1pp+wcpZhACAIDu4oorrpDjOOrXr582bdqkxx9/XL1799aAAQM0cuRIfetb3wo7IgB8Lr+1Re76d+VufD++nDirx+nlxDNksKc+AHTQqYLw61//up577jmNGzdO06dP129/+1vNmDEj2dnSitk2g1A0hAAAoHvYtGmT/uVf/iVx++qrr9bq1at1/fXXa/fu3X/2+YsXL1ZVVZVGjx6tkpKSDo+1tLTo7/7u73Tvvfdq8uTJXZ4dQObyfV/e7q1ylr8i1R+TJJnjp8mecYOMnkx0AYAz6VRBOH36dE2bNk0HDhzQwYMHdffdd3OK8TlqP6Qk3BwAAACd1bt3b+3atUujRo2SJI0bN05PPPGEvv71r2vgwIFnfW5VVZWam5u1cOFCPfnkk6qsrNTYsWMTj//pT3/SiBEs7wPQtfzjtXJWvCxvzw5JkjFwaHw58ZBR4QYDgBTXqYKwurpa//zP/6yDBw9KkoYMGaIf/ehHGjZsWFLDpRPDYA9CAADQvfzt3/6tHn/8cQ0fPlyjRo3Svn37lJWV1annVlRUJGYGFhYWqry8PFEQOo6jiooKjR8/PmnZAWQW32mVu2Fp/AAS15GysmVfca3MiTNlmFbY8QAg5XWqIPyv//ovHT16VLNnz5YkrV27Vk899ZTuv//+pIZLJ20zCNmDEAAAdBdDhgzRwoULtWbNGn388ccaMmSI5s+f36nnNjQ0KDc3V5IUjUZVXV2deGzp0qWaO3euKioqPvf5paWlKi0tlSQtWrRIsVjsAj6T8Nm23e0/h67EeLRjLDo6n/FortikY2/9Tu6xI5KknoVXqu81d8jK6ZuMiIHi66MjxqMdY9ER49HR+YxHpwrCqqoqfe1rX9P1118vSXrjjTf0u9/97twTZjCTGYQAAKAbMk1TM2bMOOf9p6PRqBobGyVJTU1NikajkiTXdbVhwwb98Ic/PGtBWFRUpKKiosTtmpqa80ifOmKxWLf/HLoS49GOsejoXMbDP1EnZ8Ur8nZvkyQZA3Jlz75VXl6+jja3Ss3df1z5+uiI8WjHWHTEeHR0tvHIy8s74/2dKghzcnK0adMmTZ06VVJ8w2pOMT437TMIKQgBAED6KygoUGlpqWbNmqWysjLNmzdPknT8+HHV1tbqoYce0sGDB7V+/Xrl5+fz3hJAp/lOq9xN78td9258OXEkW9blRbIumSXDYjkxAJyPThWE11xzjZ599lmtXbs2cd9dd92VtFDpqH0GYchBAAAAApCfn69IJKIFCxZo1KhRisViWrJkiYqLi/Xwww9Lkp599llNmDCBchBAp3l7dshZ/rL8E7WSJHPspbJn3iSjV5+QkwFA99apgvCqq65S3759tWnTJknSpZdemth0Gp3DKcYAACDTlJSUdLhdXFzc4XZn9zMEAP/kMTkrX5H38RZJktFvcPx04mFjQk4GAOmhUwXhgw8+qFmzZunv//7vJUm///3v9dOf/lSPPfZYUsOlE04xBgAAAIBz47uO3E3L5K77k+S0SnaWrGlflFU4W4bVqb/OAgA6oVM/Uevq6jR48ODE7UGDBqm2tjZpodLR6QmE8hUvCdsKQwAAAADAZ3nVFfHlxKdPJzbzJ8u+8iYZaXA6MQCkmk4VhLm5uXrllVc0YMAA+b6vV199Vbm5ucnOllYMw5BhxJcY+377kmMAAAAAQDu//ricla/Jq4pvcWX0jcWXEw8fF3IyAEhfnSoIb731Vv3iF79IbCgtSd/97neTFipdmYYh1/fly1f7nEIAAAAAgO86OrnyDbW8/7LktEh2RNZl18iaPJflxACQZJ0+pCQWi2ndunWSpMsuu0wTJ05MarB0FF9W7MvzJSvsMAAAAACQIrx9O+Use0ktxw5LkszRl8i+8hYZvfuFGwwAMkSn/xlm4sSJlIIXyEycZMxBJQAAAADgN5yQs+o1eZUbJUlW/0EyZ94sc8T4kJMBQGZhnnaAzNMbD3r0gwAAAAAymO+6creskPtRqdR6SrJsWZddrdxrilV77HjY8QAg41AQBqjt5GJmEAIAAADIVN6Bj+Use0l+3UFJkjnyYtmzbpHRZ4AMOxJyOgDITBSEATLNtoIw5CAAAAAAEDC/8aScVX+UV7E+fkfvAbJn3yJr5MXhBgMAUBAGqe3cYmYQAgAAAMgUvufK27pKzpq3pJbTy4mnfEHWlHnMGASAFEFBGKC2GYQeBSEAAACADOAd3C1n2Yvyaw9IkswR42XP+rKMvgNDTgYA+CQKwgC170EYchAAAAAASCK/qV7Oh6/L27E2fkdOP9mzb5E5cmLi70UAgNRBQRig9lOMaQgBAAAApB/f8+RtWy1n9RtSS7NkWrIuvUrW1KtlRLLCjgcA+BwUhAFq+4cy+kEAAAAA6cY7tCd+OnHNPkmSMXyc7NlfltlvUMjJAAB/DgVhgMzEEmMaQgAAAADpwW9qkLP6DXnb18Tv6NVX9qybZY6exHJiAOgmKAgDZCSWGIccBAAAAAAukO978ratkbP6TelUY3w58eS5si67huXEANDNUBAGqO0UY2YQAgAAAOjOvCPVcj54Uf6RakmSkTdG9pxbZfYfHHIyAMD5oCAMUNvkeupBAAAAAN2R39woZ82b8rauluRL0T7x5cT5hSwnBoBujIIwQOxBCAAAAKA78n1P3o61cj58Q2pukExT1qS5sqZ9UUZWdtjxAAAXKKkF4eLFi1VVVaXRo0erpKQkcf+vfvUr7dq1S62trfrGN76hCRMmJDNGyjBM9iAEAAAA0L14NfvipxMf2iNJMoaOlj3nNpkDckNOBgDoKkkrCKuqqtTc3KyFCxfqySefVGVlpcaOHStJ+su//EvZtq0jR47oP//zP/W///f/TlaMlHK6H2QGIQAAAICU559qkrPmLXlbV0m+L0V7y555k8yxl7KcGADSTNIKwoqKCk2ePFmSVFhYqPLy8kRBaNvxl21ubtbIkSOTFSHlcIoxAAAAgFTn+768inVyVr0uNdVLhimrcJasy78kI6tH2PEAAEmQtIKwoaFBubnxKefRaFTV1dUdHv/nf/5nVVZW6t577z3j80tLS1VaWipJWrRokWKxWLKiBsYyTUlS3759FYv1CzdMhrNtOy2+ptIF1yN1cC1SC9cjdXAtAGQKr/ZAfDnxwV2SJGPIqPjpxAOHhhsMAJBUSSsIo9GoGhsbJUlNTU2KRqMdHv+f//N/qra2Vo8++qgeeuihzzy/qKhIRUVFids1NTXJihqYtkn4R48eVW/bCTVLpovFYmnxNZUuuB6pg2uRWrgeqSNdrkVeXl7YEQCkKP9Us9y1b8vdvFLyPalnjuyZN8gcdxnLiQEgA5jJ+o0LCgq0efNmSVJZWZkKCgoSj7W2tkqSevTooezszDnxqu3PVZYYAwAAAEgFvu/LrVivlmcfkVu2XJIv85IrlXXXD2QVTKMcBIAMkbQZhPn5+YpEIlqwYIFGjRqlWCymJUuWqLi4WP/6r/+qxsZGeZ6nr33ta8mKkHLM03+4ckgJAAAAgLB5dYfkLHtR/oGPJUlG7oj4cuLYsJCTAQCClrSCUJJKSko63C4uLpYk/ehHP0rmy6YsI1EQhhwEAAAAQMbyW07JXVsqd/NyyfOkHr1kz7he5vhpMoykLTIDAKSwpBaE6Mg0204xpiEEAAAAECzf9+Xt3CRn5WtS4wlJhsyJM2Vfca2MHtE/+3wAQPqiIAxQ2/Yd1IMAAAAAguQdPSxn+cvy91VKkoxBw2XPvU3moOEhJwMApAIKwgC17UHocUoJAAAAgAD4rS1y1/1J7qZlkudK2dH4cuIJl7OcGACQQEEYoMQehCHnAAAAAJDefN+X9/FmOStfleqPSzJkTpgue/p1Mnr2CjseACDFUBAGiFOMAQAAACSbd+xIfDlxdYUkyYgNi59OnDsi5GQAgFRFQRigxB6E9IMAAAAAupjf2iJ3/btyN74fX06c1UP29OtlXjxdhslyYgDA56MgDFBiD0IaQgAAAABdxPd9ebu2ylnxilR/TJJkjp8me8YNMnrmhBsOANAtUBAGKLEHIf0gAAAAgC7gH6+Vs+JleXt2SJKMgUNlz7lN5pCRIScDAHQnFIQBMk32IAQAAABw4XynVe6GpXI3vCe5jpSVLfuKa2VOnCnDtMKOBwDoZigIA3R6C0KWGAMAAAA4b+7ubXKWvyKdrJMkmeOmyp55o4xo75CTAQC6KwrCALXPIAw5CAAAAIBuxz9RJ2fFK/J2b5MkGQNyZc++VWZefsjJAADdHQVhgAwOKQEAAABwjnynVe7G9+Wufze+nDiSLevyIlmXzJJhsZwYAHDhKAgD1HaKMfUgAAAAgM7w9uyQs/xl+SdqJUnm2Cnx5cS9+oScDACQTigIA3R6hbF8j4oQAAAAwOfzTx6Ts/IVeR9vkSQZ/QfLnnOrzLwxIScDAKQjCsIAGcwgBAAAAHAWvuvI3fSB3HXvSE6rZGfFlxNPms1yYgBA0lAQBshkD0IAAAAAn8OrrpCz7CX5x2skSWb+ZNlX3iQjp2/IyQAA6Y6CMECcYgwAAADg0/z643JWviqvqkySZPQbJHv2l2UOHxdyMgBApqAgDNDpLQiZQQgAAABAvuvo5Mo31PL+y5LTItkRWZd9UdbkOTIs/qoGAAgOf+oEKLEHIf0gAAAAkNG8fTvlLHtJLccOS5LM0ZNkX3mzjN79wg0GAMhIFIQBal9iTEMIAAAAZCK/4YScVa/Jq9woSbL6D5Y58yaZI8aHnAwAkMkoCAN0egKhPPpBAAAAIKP4rit3ywq5H70ttbZIli3rsquVe02xao8dDzseACDDURAGyDSYQQgAAABkGm9/lZzlL8mvOyRJMkdeLHv2LTJ6D5BhR0JOBwAABWGgDApCAAAAIGP4jSflrPqjvIr18Tt6D5A9+xZZIy8ONxgAAJ9CQRigthmELDEGAAAA0pfvuXK3rJL70VtSy6n4cuIp82RN+QIzBgEAKYmCMEBtexAygxAAAABIT97BXXKWvSS/9oAkyRwxXvasL8voOzDkZAAAfD4KwgAl9iAMOQcAAACAruU31ctZ9bq88rXxO3L6yZ59i8yRExNbDQEAkKooCANkJJYYUxECAAAA6cD3PHnbPpSz+k2ppVkyLVlTviBryjwZkayw4wEA0CkUhAEyzbZDSkIOAgAAAOCCeYf2xJcT1+yTJBnDC2TP+bLMvrGQkwEAcG4oCANksgchAAAA0O35TQ1yVr8hb/ua+B05fWVfeYvM0ZewnBgA0C1REAao7c0C/SAAAMgEixcvVlVVlUaPHq2SkpLE/U888YT27t0rSbrnnns0cuTIsCIC58T3PHnb18SXE59qjC8nnjxX1mXXsJwYANCtURAGyGQPQgAAkCGqqqrU3NyshQsX6sknn1RlZaXGjh0rSbrttts0ePBgHThwQE8//bR++MMfhpwW+PO8I9VyPnhR/pFqSZIxbKzs2V+W2X9wyMkAALhwFIQBMplBCAAAMkRFRYUmT54sSSosLFR5eXmiIBw8OF6oWJYl0zRDywh0ht/cKGfNm/K2rpbkS9E+smfdLDO/kOXEAIC0QUEYoLb3D8wgBAAA6a6hoUG5ubmSpGg0qurq6s98zG9/+1vdeOONZ3x+aWmpSktLJUmLFi1SLNa9D32wbbvbfw5dqTuMh+97aty4XCfe+YO8pnrJtJQzvUi959wiM7tHl71OdxiLIDEeHTEeHTEe7RiLjhiPjs5nPCgIA8QMQgAAkCmi0agaGxslSU1NTYpGox0ef+211zR8+HBNmDDhjM8vKipSUVFR4nZNTU3ywgYgFot1+8+hK6X6eHg1++R88JL8w3skSUZevuzZt6p1QK7qTtZLJ+u77LVSfSyCxnh0xHh0xHi0Yyw6Yjw6Ott45OXlnfF+1nQEyDx9jLHreSEnAQAASK6CggJt3rxZklRWVqaCgoLEYxs3btSOHTt0++23hxUPOCP/VJNal72k1iWPx8vBaG/Z1/yFIjf/jcwBuWHHAwAgaSgIA2Sd3mOHJcYAACDd5efnKxKJaMGCBTJNU7FYTEuWLJEkPfXUUzpy5Ih+8pOf6Iknngg5KSD5vi93x1q1/P5f5G1ZKcmQVThHWXf9QNa4Kew1CABIeywxDpBtxQtC16MgBAAA6a+kpKTD7eLiYknSY489FkYc4Iy82gNylr0k/+AuSZIxZJTsObfKHDg03GAAAASIgjBAtnV6ibFLQQgAAACEyT/VLPejt+VuWSn5ntQzR/bMG2WOm8qMQQBAxqEgDFDbEmOHGYQAAABAKHzfl1e5Qc6qP0qNJyXDkDVplqzLvyQju2fY8QAACAUFYYDalxhzSAkAAAAQNK/uYHw58YGPJUlG7gjZc26TGTvziY4AAGQKCsIAWW1LjJlBCAAAAATGbzkld22p3LLl8eXEPXrJnnGDzPGXyTA4txEAAArCALUtMaYgBAAAAJLP9315OzfJWfma1HhCkiFz4kzZV1wro0c07HgAAKQMCsIA2RSEAAAAQCC8o4fjy4n375QkGYMvip9OPGh4yMkAAEg9FIQBaj/FmD0IAQAAgGTwW0/JXfeO3E3LJM+VsqOyZ1wvc8LlLCcGAOBzUBAGKHFIic8MQgAAAKAr+b4v7+PNcla8KjUcl2TInDBd9ozrZPToFXY8AABSGgVhgBJ7ELoUhAAAAEBX8Y4dkbP8ZfnVFZIkIzYsvpw4d0TIyQAA6B4oCAPEKcYAAABA1/FbW+Suf1fuxvdPLyfuKXv6dTInTJdhspwYAIDOoiAMUNsSY8djD0IAAADgfPm+L2/XVjkrXpHqj0mSzPGXy55xvYyeOeGGAwCgG6IgDFDbEmOPGYQAAADAefGP18pZ8bK8PTskScbAobLn3CZzyMiQkwEA0H1REAbINttmEFIQAgAAAOfCd1rlrl8qd+N7kutIWT1kX3GtzIkzZJhW2PEAAOjWKAgDZLMHIQAAAHDO3N3b5Cx/RTpZJ0kyCy6TPeMGGdHeIScDACA9UBAGqG0PQtdlD0IAAADgz/FP1MlZ8Yq83dskScaAIfHTiYeODjkZAADphYIwQG17ELo+MwgBAACAz+M7rXI3vi93/bvx5cSRbFmXf0nWpCtZTgwAQBJQEAbINA0ZhuT78YNKTNMIOxIAAACQUrw9O+Qsf1n+iVpJkjl2iuyZN8ro1SfkZAAApK+kFoSLFy9WVVWVRo8erZKSksT9TzzxhPbu3StJuueeezRyZOacOGaZhhzXl0tBCAAAACT4J4/KWfGqvF1bJElG/8Hx5cR5Y0JOBgBA+ktaQVhVVaXm5mYtXLhQTz75pCorKzV27FhJ0m233abBgwfrwIEDevrpp/XDH/4wWTFSjmWaclxXjucpIjPsOAAAAECofNeRu/EDuevfkZxWyc6SdXmRrEmzZVgsJwYAIAhJKwgrKio0efJkSVJhYaHKy8sTBeHgwYMlSZZlyTQzqySzTs8a9DjJGAAAABnOq66Qs+wl+cdrJEnmmMmyZ94kI6dvyMkAAMgsSSsIGxoalJubK0mKRqOqrq7+zMf89re/1Y033njG55eWlqq0tFSStGjRIsVisWRFDYxt28qyLTWectSnX3/1z+kRdqSMZdt2WnxNpQuuR+rgWqQWrkfq4FoAXcs9UafWt5+WV1UmSTL6DZI9+8syh48LORkAAJkpaQVhNBpVY2OjJKmpqUnRaLTD46+99pqGDx+uCRMmnPH5RUVFKioqStyuqalJVtTAxGIxGYrPHDxSUyO3mYIwLLFYLC2+ptIF1yN1cC1SC9cjdaTLtcjLyws7AjKc7zpyy5br0Lp35LeekuyIrGlflFU4R4bF+YkAAIQlaet7CwoKtHnzZklSWVmZCgoKEo9t3LhRO3bs0O23356sl09Z1ukl1a7LEmMAAABkDm9fpVqf/ze5H74uv/WUzNGTlDX/B7KnzKMcBAAgZEkrCPPz8xWJRLRgwQKZpqlYLKYlS5ZIkp566ikdOXJEP/nJT/TEE08kK0JKatuD0GUPQgAAAGQAv+GEWkt/p9ZX/1P+scMy+gzUwL/4H4pce7eM3v3CjgcAAJTEJcaSVFJS0uF2cXGxJOmxxx5L5sumNMuiIAQAAED6811X7pYVcj96W2ptiS8nnnq1rEuvUo/cIapPg2X7AACkC+byB8wy2gpCL+QkAAAAQHJ4+6vkLH9Jft0hSZI5aqLsWTfL6D0g5GQAAOBMKAgDZlmn9yBkBiEAAADSjN94Us6qP8qrWB+/o88A2bO+LGvkmQ8mBAAAqYGCMGDsQQgAAIB043uu3C2r5H70ltRySrJsWVPmyZryBRl2JOx4AADgz6AgDFhbQehQEAIAACANeAd3yfngRfl1ByVJ5ogJsmffIqPPwJCTAQCAzqIgDFhiBqHLHoQAAADovvymejmrXpdXvjZ+R04/2bO/LHPkxTJO77sNAAC6BwrCgFnm6T0IfWYQAgAAoPvxPU/e1g/lrHlTammWTEvWlC/ImjJPRiQr7HgAAOA8UBAGzE7MIKQgBAAAQPfiHdojZ9mL8mv2S5KM4QWy53xZZt9YyMkAAMCFoCAMmMkhJQAAAOhm/KYGOavfkLd9TfyOnL6yr7xF5uhLWE4MAEAaoCAMmG21FYTsQQgAAIDU5nuevO1r5Kx+QzrVFF9OPHmurMuuYTkxAABphIIwYIk9CJlBCAAAgBTmHd4rZ9lL8o9US5KMYWPjh5D0HxxyMgAA0NUoCANmscQYAAAAKcxvbpCz+i1521ZL8qVoH9mzbpaZX8hyYgAA0hQFYcDaCkKHghAAAAApxPc9eTvWyvnwdam5UTJNWYVzZV32RRlZ2WHHAwAASURBGLDEDEKXPQgBAACQGrwj++LLiQ/vkSQZefmy59wqs39uyMkAAEAQKAgDltiD0GcGIQAAAMLln2qUs+ZteVtXSb4vRXvLvvImmWMuZTkxAAAZhIIwYO0zCCkIAQAAEA7f9+SVr5ez6o9Sc4NkmLIKZ8u6vEhGVo+w4wEAgIBREAaMQ0oAAAAQJq92f3w58cHdkiRjyCjZc26TOXBIyMkAAEBYKAgDZlunDylhD0IAAAAEyD/VLPejt+VuWRFfTtwzR/bMG2WOm8pyYgAAMhwFYcCybEuSdMpxQ04CAACATOD7vryKDXJWvSY11UuGIWvSLFmXf0lGds+w4wEAgBRAQRiw7MjpgrCVGYQAAABILq/uYHw58YGPJUlG7oj4cuJYXsjJAABAKqEgDFh7QcgMQgAAACSH33JK7tpSuWXLJd+TevSSPeMGmeMvk2GYYccDAAAphoIwYImCkCXGAAAA6GK+78vbuUnOytekxhOSDJkTZ8qefq2M7GjY8QAAQIqiIAxYth3/F1tmEAIAAKAreUcPx5cT798pSTIGXyR7zq0yBw0PORkAAEh1FIQB65HFEmMAAAB0Hb/1lNy178gt+0DyPKlHVPb062VOuJzlxAAAoFMoCAOWbVMQAgAA4ML5vi/v481yVrwqNRyXZMi8eLrs6dfJ6NEr7HgAAKAboSAM2CdPMfZ9X4ZhhJwIAAAA3Y137Iic5S/Lr66QJBmxYbLn3iZz8EUhJwMAAN0RBWHAbMuUZRpyPV+O5ytiURACAACgc/zWFrnr35W78X3Jc6XsnrKnXydzwnQZJsuJAQDA+aEgDEF2xFLjKUenWl1FLN7IAQAA4Ox835e3a6ucFa9I9cckSeb4y2XPuF5Gz5xwwwEAgG6PgjAEnywIc3pEwo4DAACAFOYfr5Gz/BV5e3dIkoyBQ2XPuU3mkJEhJwMAAOmCgjAE7fsQclAJAAAAzsx3WuWuXyp343uS60hZPWRfca3MiTNZTgwAALoUBWEIsu34GzoKQgAAAJyJu3ubnOWvSCfrJElmwWWyZ9wgI9o75GQAACAdURCGoG0GYTMFIQAASGOLFy9WVVWVRo8erZKSksT9e/bs0ZNPPilJuueeezRyJEtl2/gn6uSseEXe7m2SJGPAENlzbpU5dHTIyQAAQDpjbUIIerDEGAAApLmqqio1Nzdr4cKFchxHlZWViceeeeYZ3Xffffr+97+vZ555JsSUqcN3WuWsLVXLs4/Gy8FItqwrb1bk9nspBwEAQNIxgzAE7XsQeiEnAQAASI6KigpNnjxZklRYWKjy8nKNHTtWktTQ0KBYLJb4daZz9+yQs/xl6UStJMkcO0X2zBtl9OoTcjIAAJApKAhDwCElAAAg3TU0NCg3N1eSFI1GVV1dnXjM9/0/+/zS0lKVlpZKkhYtWpQoFLsr27Y/8zk4x2t1/K3fyylfH/+YWJ76Xf81ZY+cEEbEQJ1pPDIVY9ER49ER49ER49GOseiI8ejofMaDgjAEiYLQoSAEAADpKRqNqrGxUZLU1NSkaDR6xo8zDOOM9xcVFamoqChxu6amputDBigWiyU+B9915G78QO76dySnVYpkyZpWJHPSbJ20LJ3s5p9rZ3xyPDIdY9ER49ER49ER49GOseiI8ejobOORl5d3xvspCEPADEIAAJDuCgoKVFpaqlmzZqmsrEzz5s1LPJaTk6Pa2loZhqGePXuGFzIE3t5yOctfln88/qbdHDNZ9pU3yejVN+RkAAAgk1EQhiCaFR/2hmYn5CQAAADJkZ+fr0gkogULFmjUqFGKxWJasmSJiouLNX/+fP385z+XJH3zm98MN2hA3BN1an37aXlVZZIko98g2bNvlTl8bMjJAAAAKAhD0TcakSSdaGoJOQkAAEDylJSUdLhdXFwsSRo5cqQefPDBMCKFwm9t0eH//v/kNdZLdkTWtC/KKpwjw+KtOAAASA28KwlBn2iWJOl4IwUhAABAujMiWeo17Ro1VFfJnnWzjJx+YUcCAADogIIwBG0F4QkKQgAAgIzQe+7NaqmtCzsGAADAGZlhB8hEvbJtWaahphZXrY4XdhwAAAAkmWHwthsAAKQu3qmEwDAM9ekZ34eQZcYAAAAAAAAIEwVhSFhmDAAAAAAAgFRAQRiSvm0FIScZAwAAAAAAIEQUhCHhJGMAAAAAAACkAgrCkLTNIDzWQEEIAAAAAACA8FAQhiS3X09J0oGjjSEnAQAAAAAAQCajIAxJ3oBekqR9tQ3yfT/kNAAAAAAAAMhUFIQh6dMzopweETW3uqqrPxV2HAAAAAAAAGQoCsKQGIah4QPbZxECAAAAAAAAYaAgDFHegKgkaU9NfchJAAAAAAAAkKkoCEM0bmhfSdKWvUfZhxAAAAAAAAChoCAM0ejcPsrpEVHNiWbt5zRjAAAAAAAAhCCpBeHixYu1YMEC/epXv+pw/5IlS/S3f/u3+v3vf5/Ml095lmmocOQASdKaiiMhpwEAAAAAAEAmSlpBWFVVpebmZi1cuFCO46iysjLx2DXXXKN77703WS/drcwsGCxD0qryQ6o72Rx2HAAAAAAAAGSYpBWEFRUVmjx5siSpsLBQ5eXlicf69esnwzCS9dLdSt6AXrpsTEyu5+u3H1Sq1fHCjgQAAAAAAIAMYifrN25oaFBubq4kKRqNqrq6+pyeX1paqtLSUknSokWLFIvFujxj0GzbPuPn8Zdf6q2PD3+g3Ufq9V/vVOhvbpii3P69QkiYOT7vWiAcXI/UwbVILVyP1MG1AAAAQDpLWkEYjUbV2Bg/eKOpqUnRaPScnl9UVKSioqLE7Zqami7NF4ZYLPa5n0fJ1QX6z9Lt2nngqP7fXy1VQV5fTRoxQKMG5yjWp6cskxmXXels1wLB43qkDq5FauF6pI50uRZ5eXlhRwAAAEAKSlpBWFBQoNLSUs2aNUtlZWWaN29esl4qLQzpH9X/uKVQf1y7Rx/tPKLt+45p+75jkuKHmfSJZqlPz4h698xSzyxLWbal7Iip7IilbNtSlm3KtkxZphH/zzJlt/3aNGVZxunb8Y8xDMk0Pvn/Z7pPMgxDJsvBAQAAAAAA0lbSCsL8/HxFIhEtWLBAo0aNUiwW05IlS1RcXKx33nlHb775purr61VfX6977rknWTG6lZweEc2fPUY3XjZCW/bWaVv1MR042qi6+lM6evq/sJypNDQkmWb8/2VIp3+V+Hgj8euO95/+8MQNo8Nz2p9odHjOJz7WONvzP/GxZ+k1bduW4zid++Q/xznXpufRsxrn+qTkfvh56cx+oxHbVuvp60EdHS47EpHT2hp2DJzG9Ugdf33dVEWTtnMzAAAAEK6kFYSSVFJS0uF2cXGxpPgpxtdcc00yX7pby+kZ0YyCXM0oiO/h2OK4OtHYqhNNLTrZ1KpTrW77f46rU62eWhxXruvL8Xy5nifX89v/c73T97c/5nm+fEme78v3Jd/35SX+v+N9kuT7kuufviH/jLkBAEhXzS2tivYIOwUAAACQHEktCNE1smxLsT6WYn3C+ZvJJ8tD328rFTve58tvrw390xXi6fvbf5+2h/1Ex+if5f725/ifen78dT/xcu2v+amP/Tz9+vXTsWPHOjkCn/Xnfv8zPOPcX+NcPz6A3vbcP+3OPaNv3346fvwY1XMK6Ne3r44dPx52DJzG9Ugdwwf1UeNJrgUAAADSEwUh/izDMGR9YplvOojF+qnGvrAlxug6sdgA1fTwwo4BSbHYQNX0oKpNFVyP1BHNjqjxZNgpAAAAgORgNx0AAAAAAAAgg1EQAgAAAAAAABmMghAAAAAAAADIYBSEAAAAAAAAQAajIAQAAAAAAAAyGAUhAAAAAAAAkMEoCAEAAAAAAIAMRkEIAAAAAAAAZDAKQgAAAAAAACCDURACAAAAAAAAGYyCEAAAAAAAAMhgFIQAAAAAAABABqMgBAAAAAAAADIYBSEAAAAAAACQwSgIAQAAAAAAgAxGQQgAAAAAAABkMApCAAAAAAAAIINREAIAAAAAAAAZjIIQAAAAAAAAyGAUhAAAAAAAAEAGoyAEAAAAAAAAMhgFIQAAAAAAAJDBKAgBAAAAAACADEZBCAAAAAAAAGQwCkIAAAAAAAAgg1EQAgAAAAAAABmMghAAAAAAAADIYBSEAAAAAAAAQAajIAQAAAAAAAAymOH7vh92CAAAAAAAAADhYAZhgH784x+HHQGncS1SC9cjdXAtUgvXI3VwLXCh+BrqiPFox1h0xHh0xHh0xHi0Yyw6Yjw6Op/xoCAEAAAAAAAAMhgFIQAAAAAAAJDBKAgDVFRUFHYEnMa1SC1cj9TBtUgtXI/UwbXAheJrqCPGox1j0RHj0RHj0RHj0Y6x6Ijx6Oh8xoNDSgAAAAAAAIAMxgxCAAAAAAAAIIPZYQfIFIsXL1ZVVZVGjx6tkpKSsOOktbq6Ov3sZz9TdXW1fvOb38iyrDOOf2fvw/mrqKjQr3/9axmGoTFjxuiv//qv9fLLL2vNmjUaNGiQvvOd78i27U7fhwuzZ88ePfHEEzJNU0OGDNG3v/1t/frXv+Z7I0SvvvqqPvzwQz344IP8nArR4cOH9Q//8A8aNmyYbNvWP/7jP/KzCl2K79t2Z3qflsnO9F4pU53pfYphGGHHCt0n3ytksjP9WZ3J3nvvPb333nvyPE/f+973NGDAgLAjhWbDhg168cUXJUn79+/XPffco+nTp4cbKkSnTp3So48+qlOnTikajer73/++IpFIp57LDMIAVFVVqbm5WQsXLpTjOKqsrAw7UlrLycnR/fffr3Hjxkk68/h39j5cmEGDBmnBggV68MEHdeLECW3dulVbtmzRgw8+qBEjRmjNmjU6fvx4p+7DhcvLy9NPf/pTLVy4UJJUWVnJ90aIWltbtWvXLkn8nEoFhYWFeuCBB/SP//iPnf65xM8qdAbftx19+n1apvv0e6U9e/aEHSk0n36fsnPnzpAThe+T7xXQ8c/qTFZXV6etW7dqwYIFeuCBBzK6HJSkKVOm6IEHHtADDzygWCymyZMnhx0pVBs2bNC4ceP0wAMPaOzYsdqwYUOnn0tBGICKiorEF2lhYaHKy8tDTpTesrKylJOTk7h9pvHv7H24MP369VNWVpYkybIs7d27VxMnTpQkTZ48WeXl5dq5c2en7sOF++TMJtu2VVZWxvdGiN555x3NmzdPEj+nUsGWLVu0YMECvfrqq53+ucTPKnQG37cdffp9Wqb79Hsl08zcv559+n1KLBYLMU1q+OR7BXT8szqTbdiwQZ7naeHChXrqqafkeV7YkVLCoUOH1LdvX/Xo0SPsKKHKzc1Vc3OzJKmhoUG9e/fu9HMz90+gADU0NCgajUqSotGoGhsbQ06UWc40/p29D11j9+7dOnHihHr16qWePXtKio9xQ0ODGhsbO3UfusZHH32kH/zgBzp+/Lhc1+V7IySO42jLli2aNGmSJH5Oha1///567LHH9E//9E8qKytTVVUVP6vQZfi+RWe0vVcaPnx42FFC9cn3KZleJH/6vUKm+/Sf1bt37w47UmiOHz8ux3G0YMECZWVlsYLhtA8//DCjlxa3GTp0qCoqKvT3f//3qqqqUkFBQaefS0EYgE++GWxqakq8SUQwzjT+nb0PF66+vl5PPfWUvv3tbysajaqpqUmS1NjYqF69enX6PnSNyy+/XI888ogGDhwoy7L43gjJ+++/rzlz5iRu83MqXJFIRD169JBlWZo2bZpyc3P5WYUuw/ct/pxPvlfKdJ98n7Ju3bqw44Tq0+8VMt2n/6zeu3dv2JFCE41GEysYJk2apH379oWcKDWsXbtWl19+edgxQvfee+9p2rRpevTRRzV16lR98MEHnX4uBWEACgoKtHnzZklSWVnZOTW4uHBnGv/O3ocL47qu/v3f/11/+Zd/qX79+mnMmDHaunWrpPgYjxs3rtP34cK1trYmft0264nvjXDs379fb7/9th566CFVV1fr5MmTXIsQtZV8krR9+3YNGTKEn1XoMnzf4mw+/V4pk336fUrb0utM9en3Cq+//nrYkUL16T+rc3NzQ0wTrvHjxydmUO7atUuDBw8OOVH4jh07Jtu2z2k5bbryfT8xA7tPnz7ntHKBo/YCkJ+fr0gkogULFmjUqFEaO3Zs2JHSmuM4evjhh7V792499NBD+upXv3rG8e/sfTh/K1euVGVlpf7v//2/kqSvfe1ruvjii3X//fcrFovppptukm3bnboPF27Dhg2JPVuGDh2qb33rW/r1r3/N90YI7r777sSv77//ft1555361a9+xbUIybZt2/TMM88oEolowoQJGjduHD+r0GV4H9jRmd6nZXK5fqb3SplaIn/6fUqmHzTw6fcKN9xwQ4hpwnemP6sz1ahRo5SVlaUHHnhAvXv31s033xx2pNCtWbNGV1xxRdgxUsKcOXP085//XO+//74sy9L3v//9Tj/X8H3fT2I2AAAAAAAAACmMJcYAAAAAAABABqMgBAAAAAAAADIYBSEAAAAAAACQwSgIAQAAAAAAgAxGQQgAAAAAAABkMApCAGnt8OHDmj9/vhYtWqR169bp2Wef1eHDh7v8daqrq/Xss89qy5Ytift+8YtfaP78+dq5c2eXvx4AAAAAAF3FDjsAACRTnz59dN9992nAgAFasWKF3nzzTV1yySUaPHjwOf0+ruvKsqzPfby6ulrPP/+8JOmSSy6RJF177bWaMmWKcnNzz/8TAAAAAAAgyQzf9/2wQwBAshw+fFjf/e53lZ2drVOnTnV47Nlnn1V5ebl+/etfa8+ePRowYIDuvPNOzZkzJ/G8goICZWdna8+ePXrkkUf005/+VAcOHJAkjR49Wn/zN3+j7Oxsffe73+3we//TP/2Tli5dqvfee08PP/ywxowZo9LSUr388ss6evSohg8frr/6q7/ShAkTtHTpUv2f//N/NGvWLO3bt081NTW68847deONN2r//v16/PHHtXv3bmVlZemiiy7SwoULAxs/AAAAnNmjjz6qvn37ateuXaqtrdX3vvc9vf3226qsrNSECRP07W9/O+yIANBpLDEGkBEmTpyoSy+9VJJ0++2367777lN9fb0WLVqkxsZGFRcXa9CgQfr3f/937dq1K/G88vJyjR49WnfddZcMw9D06dNVUlKi2267Tbt379bixYvVp08f3XjjjZKkGTNm6L777tPw4cM7vP7mzZv1xBNPqE+fPvrGN76hmpoa/exnP9PJkycTH7NlyxZ98YtflCQ9/fTTchxHb775pnbu3Km7775bX/3qVxWLxZI8UgAAAOiMPXv2KDc3Vw8++KCKior0y1/+UnfffbceffRRrVu3Tq2trWFHBIBOY4kxgIxgGIaGDBmijRs3atKkSbrkkku0bt061dfXq76+Xr/73e8SH7t582ZNnz5dUnyW4N133y1Jqqur08aNG1VeXq62ydd79uxRjx49NGHCBP3xj3/URRddpNmzZ3/m9detWydJmj9/viZPnqyamhq98MILqqioSHzM1Vdfreuvv15r167Vxo0bdezYMQ0dOlS+72v9+vUaM2ZMoogEAABAeFpaWtTQ0JB4b2YYhq655hr1799fkmSapmybv24D6D74iQUgYxiGccb7r7rqKl111VWJ25/cn7DtTZ4kvf7669qxY4duuukmTZ06Vb/85S/V1NTUZVlycnIkKbHXoed5uv766zVs2DBt3bpVH330kZYsWaJ//dd/VV5e3nm9LgAAAC5cdXW18vPzZZrxRXm7d+/WtddeK0mqra3VgAEDPve9JwCkIpYYA8gYvXr1kiStWrVK69atU0FBgXJycrRx40bt379fe/fu1UsvvaS6urqz/j4NDQ3aunWramtrE/e1lXvbt2/X8uXL1dLS0uE5l112mSTpueee09tvv6133nlHvXr10rhx4876Wm+99ZbKy8s1ZMgQ5ebmyvd9HTt27Fw/dQAAAHShPXv2aOTIkYnbu3fv1ogRIz7zawDoLigIAWSMuXPnatiwYXrrrbf0q1/9Sjk5Ofrxj3+sIUOG6Omnn9aSJUuUlZWlQYMGnfH5N9xwg8aMGaMVK1aorq5OF110UeKxCRMmqLCwUNu2bdNjjz3WYW9BSZo0aZK+9a1v6fjx4/rNb36jgQMH6n/9r/+l3r17nzVzJBLR0qVL9R//8R/atm2brrvuOk2YMOHCBwMAAADnbc+ePRo1apSk+HLjlpaWxD8Y7969u0N5CADdAacYAwAAAAAAABmMGYQAAAAAAABABqMgBAAAAAAAADIYBSEAAAAAAACQwSgIAQAAAAAAgAxGQQgAAAAAAABkMApCAAAAAAAAIINREAIAAAAAAAAZjIIQAAAAAAAAyGD/P83itQ4cFmcRAAAAAElFTkSuQmCC",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"low, high, step = 0, 5000, 10\n",
"plot_all(cost_history, m, q, low, high, step)"
]
},
{
"cell_type": "code",
"execution_count": 141,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"57 passi e 5700 gradienti calcolati per arrivare a distanza minore o uguale di 0.1 dall'ottimo\n"
]
}
],
"source": [
"near_opt(m, min_dist=1e-1, ge_per_step=n)\n"
]
},
{
"cell_type": "code",
"execution_count": 142,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA7sAAAHzCAYAAADhDgreAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAABWBUlEQVR4nO3df3Rb9Z3n/9e15F+SYluy7KT59aUJMAkJIaEObXHakBBCjmkZWjwppHhO25llWDjLMN1ySLYttKWUUMophwJLe2Boa2an7YZCD1vv4KYJYXHL4BB7QkxDgVLoFKhjyz8l/5J0v384ki3bcn5ZuldXz8c5HGLFN/5IHzvR637en/fHME3TFAAAAAAADlJg9QAAAAAAAJhrhF0AAAAAgOMQdgEAAAAAjkPYBQAAAAA4DmEXAAAAAOA4hF0AAAAAgOMQdgEAAAAAjkPYBQAgy8466yyVlpZq3rx5qqio0MUXX6xHHnlE8Xj8hNf+8Y9/lGEYikajGR1jtr4OAACZQtgFAMACzzzzjAYGBvT2229r586duueee/R3f/d3Vg8LAADHIOwCAGCh8vJyXXnllfrpT3+qH/3oRzpy5Ih++ctfat26dSorK9OSJUv0ta99Lfn5H//4xyVJFRUV8vl8+u1vf6s333xTmzdvVmVlpYLBoD772c+qt7c3ec0999yjRYsWad68efqrv/or/frXv5YkxeNx7d69W8uXL1dlZaW2b9+uUCiU9usAAJBLCLsAANjARRddpMWLF+v//b//J6/Xqx//+Mfq7e3VL3/5S/3P//k/9fTTT0uSnn/+eUlSb2+vBgcH9dGPflSmaWrXrl1699139bvf/U5/+tOfkgH5tdde04MPPqjW1lYNDAzo2Wef1VlnnSVJ+t73vqenn35aBw4c0Lvvviu/36+bbrop7dcBACCXEHYBALCJhQsXKhQK6ZJLLtH555+vgoICrVmzRtdee60OHDiQ9rqzzz5bl112mYqLi1VVVaUvfvGLyc93uVwaGRnRq6++qrGxMZ111llavny5JOmRRx7RXXfdpcWLF6u4uFhf+9rXtGfPHvbpAgAcgbALAIBN/PnPf1YgENC///u/a9OmTaqqqlJ5ebkeeeQRdXV1pb3uL3/5i6655hotWrRIZWVluu6665Kff/bZZ+v+++/X1772NVVXV+uaa67Ru+++K0l6++239alPfUoVFRWqqKjQypUr5XK59Je//CUrzxcAgEwi7AIAYAOtra3685//rA0bNmjHjh268sor9ac//Ul9fX264YYbZJqmJMkwjGnX/o//8T9kGIZeeeUV9ff364knnkh+viTt2LFDL7zwgt5++20ZhqHbbrtNkrRkyRL93//7f9Xb25v8b3h4WIsWLZrx6wAAkEsIuwAAWKi/v1//5//8H11zzTW67rrrdP7552tgYECBQEAlJSV66aWX9L/+1/9Kfn5VVZUKCgr0hz/8IfnYwMCAfD6fysvL9ec//1n33ntv8vdee+017du3TyMjIyopKVFpaakKCsb/+b/hhhv05S9/WW+//bYk6dixY/rFL36R9usAAJBLCLsAAFjgk5/8pObNm6clS5borrvu0he/+EU9/vjjkqSHH35Yt99+u+bNm6dvfOMb2r59e/I6j8ejL3/5y6qtrVVFRYVefPFF3XHHHTp06JDKy8t1xRVX6NOf/nTy80dGRrRz504Fg0EtWLBAnZ2duvvuuyVJ//iP/6grr7xSW7du1bx58/SRj3xE//7v/5726wAAkEsMc3KdEwAAAAAADsDKLgAAAADAcQi7AAAAAADHIewCAAAAAByHsAsAAAAAcBzCLgAAAADAcQi7AAAAAADHcVs9gGx49913rR6CLQWDQXV1dVk9DEzBvNgT82JPzIv9MCf2xLzYE/NiP8yJPc02LwsXLkx7HSu7AAAAAADHIewCAAAAAByHsAsAAAAAcBzCLgAAAADAcQi7AAAAAADHIewCAAAAAByHsAsAAAAAcBzCLgAAAADAcdzZ/oIPP/ywDh06pPLyct13332SpJ/97Gf69a9/rbKyMknStddeqwsvvHDate3t7Xr88ccVj8d16aWX6qqrrsrm0AEAAAAAOSLrYfeSSy7Rtm3b9NBDD6U8fsUVV+jKK69Me108Htdjjz2mr3zlK6qsrNSuXbtUU1OjxYsXZ3rIAAAAAIAck/Uy5vPOO08+n++Ur3vjjTe0YMECzZ8/X263WxdffLFaW1szMEIAAAAAQK7L+spuOs8++6yef/55LVu2TH/7t387LRCHQiFVVlYmP66srNTrr7+e7WECAAAAAHKALcLu1q1bVV9fL0n66U9/qh//+Me68cYbT/vP27t3r/bu3StJ2r17t4LB4JyM02ncbjevjQ0xL/bEvNgT82I/zIk9MS/2xLzYD3NiT6c7L7YIuxUVFclfX3rppbrnnnumfU4gEFB3d3fy4+7ubgUCgRn/vC1btmjLli3Jj7u6uuZusA4SDAZ5bWyIebEn5sWemBf7YU7siXmxJ+bFfpgTe5ptXhYuXJj2OlscPdTT05P89UsvvaQlS5ZM+5zly5frvffeU2dnp6LRqH7zm9+opqYmm8MEAAAAAOSIrK/s3n///Xr11Vc1MDCgG264Qdu3b1dHR4f++Mc/yjAMVVVV6frrr5c0vk/3+9//vnbt2iWXy6UvfOELuuuuuxSPx7Vp06YZQzEAAMg/He1teuXZJhUODWqs1KfzL6/TqrXrrB4WAMBCWQ+7t9xyy7THNm/ePOPnBgIB7dq1K/nxhRdeOOP5uwAAIH91tLfp/T2Nqq+ukOHxyDRjOrCnUZIIvACQx2xRxgwAAHC6jjQ3aWN1hQzDkCQZhqGN1RU60txk8cgAAFYi7AIAgJzmjgwmg26CYRhyR8IWjQgAYAeEXQAAkNOiHp9M00x5zDRNRT1ei0YEALADwi4AAMhpq7fW6UBnbzLwmqapA529Wr21zuKRAQCsZItzdgEAAE5XognVk81NckfCinq8Wl3fQHMqAMhzhF0AAJDzVq1dR7gFAKSgjBkAAAAA4DiEXQAAAACA4xB2AQAAAACOQ9gFAAAAADgOYRcAAAAA4DiEXQAAAACA4xB2AQAAAACOwzm7AADgtHW0t+mVZ5tUODSosVKfPrb9Wi364DKrhwUAACu7AADg9HS0t+n9PY2qL43pqkqP6ktjevPHP1BHe5vVQwMAgLALAABOz5HmJm2srpBhGJIkwzB0yfwKHWlusnhkAAAQdgEAwGlyRwaTQTfBMAy5I2GLRgQAwATCLgAAOC1Rj0+maaY8Zpqmoh6vRSMCAGACYRcAAJyW1VvrdKCzNxl4TdPUc3/p1eqtdRaPDAAAujEDAIBZTO22fP7ldVq1dp0kJf//ZHOT3JGwoh6vNvzt9XRjBgDYAmEXAADMKNltubpChscj04zpwJ5GSUoJvIlfS1IwGFRXV5cl43WS2W4yAABODmXMAABgRjN1W95YTbflTJvpSKf39zRypBMAnCLCLgAAmBHdlq3BTQYAmBuEXQAAMCO6LVuDmwwAMDcIuwAAYEYzdVs+0Em35UzjJgMAzA3CLgAAmNGqteu0oL5BTw679HT3kJ4cdmlBfQONkjKMmwwAMDfoxgwAANKa2m0ZmTfTkU6ruckAAKeMsAsAAGAz3GQAgDNHGTMAAAAAwHEIuwAAAAAAxyHsAgAAAAAch7ALAAAAAHAcGlQBAAAg4zra2/TKs00qHBrUWKlP519eRxMuABlF2AUAAEBGdbS36f09jaqvrpDh8cg0Yzqwp1GSCLwAMoYyZgAAAGTUkeYmbayukGEYkiTDMLSxukJHmpssHhkAJyPsAgAAIKPckcFk0E0wDEPuSNiiEQHIB4RdAAAAZFTU45NpmimPmaapqMdr0YgA5APCLgAAADJq9dY6HejsTQZe0zR1oLNXq7fWWTwyAE5GgyoAAABkVKIJ1ZPNTXJHwop6vFpd30BzKgAZRdgFAABAxq1au45wCyCrKGMGAAAAADgOYRcAAAAA4DiUMQMAAMyxjvY2vfJskwqHBjVW6tP5l9dRwgsAWUbYBQAAmEMd7W16f0+j6qsrZHg8Ms2YDuxplCQCb47jJgaQWwi7AAAAc+hIc5Ourq6QYRiSJMMwtLG6Qk82NxGMZpArAZKbGEDuYc8uAADAHHJHBpNBN8EwDLkjYYtGZF/JAFka01WVHtWXxvT+nkZ1tLdZPbRpjjQ3aeMMNzGONDdZPDIA6WR1Zffhhx/WoUOHVF5ervvuu0+S1NjYqJdffllut1vz58/XjTfeKK/XO+3am266SSUlJSooKJDL5dLu3buzOXQAAICTEvX4ZJqxlMBrmqainunvb/JdLq2CuyODMko9KY9xEwOwt6yG3UsuuUTbtm3TQw89lHxszZo12rFjh1wul5544gk99dRTuu6662a8/o477lBZWVm2hgsAAHDKVm+t04E9jclVQNM0daCzV6vrG6wemu3kUoDkJgaQe7Iads877zx1dnamPHbBBRckf33uuefqxRdfzOaQAACAA1m5DzTxdZ5sbpI7ElbU49Xq+gbbrVTaQS4FSG5iALnHVg2q9u3bp4svvjjt7991112SpMsuu0xbtmzJ1rAAAEAOsUMjoVVr1xFuT0IuBUhuYgC5xzBN08zmF+zs7NQ999yT3LOb8POf/1xvvvmmvvSlL01r6iBJoVBIgUBAfX19+uY3v6nPf/7zOu+882b8Gnv37tXevXslSbt379bo6OjcPxEHcLvdikajVg8DUzAv9sS82BPzYj92mJPHbt+lTxWNTVstfGq0UH/3jbstHJl17DAv6fxH60s6+MxTcoUHFfP6VPPJT+mC9RdZPayssPO85CvmxJ5mm5eioqL012VqQKfiueee08svv6zbb799xqArSYFAQJJUXl6u9evX64033kgbdrds2ZKy8tvV1TX3g3aAYDDIa2NDzIs9MS/2xLzYjx3mJBrq0lilZ4bH+y0fm1XsMC/pLPrgMi26+b+nPGbXsc41O89LvmJO7Gm2eVm4cGHa6ywPu+3t7frFL36hr3/96youLp7xc4aHh2WapkpLSzU8PKzDhw+rvr4+yyMFAAC54D8HI/rp679TkRnTWIFL5y9dohULqmy5DxQAkDlZDbv333+/Xn31VQ0MDOiGG27Q9u3b9dRTTykajerOO++UJJ1zzjm6/vrrFQqF9P3vf1+7du1SX1+fvvOd70iSYrGYNmzYoLVr12Zz6AAAIAd0tLfp/xsN6yPlxQqWFEmmqf3vvK1DoQF96IZ/tHp4AIAsymrYveWWW6Y9tnnz5hk/NxAIaNeuXZKk+fPn6957783k0AAAgAMcaW7S1WcvVXigX+8d61RBLK6/qizXG8V+GgkBQJ6xvIwZAJA5Vh6/AlghcW6rr6xcvrLy5OPV3UMWjgoAYAXCLgA4lB2OXwGyLZfObQUAZBZhFwAc6khzk64+fnalJBmGoY3VFXqyuYmwC8c6k3NbqYQAAGch7AKAQyXKOSczDEPuSNiiEQGZlwinTzY3yR0JK+rxanV9wwlDK5UQAOA8hF0AcCjKOZGvVq1dd8oBlUoIAHCeAqsHAADIjNVb63Sgs1emaUrSRDnn1jqLRwbYjzsymHJjSKISAgByHSu7AOBQp1vOCeQjKiEAwHkIuwDgYKdTzgnkozNpbAUAsCfCLgAAGUSH39xAJQQAOA9hFwCADKHDb26hEgIAnIUGVQAAZMiR5qZkWaw00eH3SHOTxSMDAMD5CLsAAGQIHX4BALAOZcwAAGQIHX7hZLPtR2evOgA7IOwCAHLe1DfWvg8u1+Bbb1r+RpsOv3Cq2fajS2KvOgBbIOwCAHLa1Dfdr773nl7d84K2rTlP8yorLH2jTYdfONWR5iZdPcN+9CeP70dP93t87wPIJsIuACCnTX3T3fHOf+rqRZV6v+uY5pVXWP5Gmw6/cCJ3ZFBGqSflsYn96OYsvwcA2UODKgBATpvaBModj6nAMFQQiyUf4402MLfG96ObKY8l9qPP9nsAkE2EXQBATpv6xjpa4FLcNBV3uZKP8UYbmFurt9bpQGdv8mcvuR99a92svwcA2UQZMwAgKzLVnXVqE6hVSxfr52+8qcvXnCdJNIUCMuBk9qOzVx2A1Qi7AICMm61z65m+AZ72prviA/LWb9Czf3xT7m7eaAOZMtt+dPaqA7ADwi4AIONm69w6F2+IeWMNAACmYs8uACDjpjaRkmgaBQAAMouwCwDIOLqzAgCAbCPsAgAyju6sAAAg29izCwDIuJPp3ApkS6Y6gwMA7IWwCwDIilxoIkUIyhy7vLYn6gxul3ECAM4cYRcAAGX2eKR8Z6fXdrbO4JJsM04AwJljzy4AABoPQRtnCEFHjocgnD47vbazdQa30zgBAGeOsAsAgDgeKZPs9NrO1hncTuMEAJw5wi4AAOJ4pEyy02s7W2dwO40TAHDmCLsAAIjjkTLJTq/tqrXrtKC+QU8Ou/R095CeHHZpwfHO4HYaJwDgzNGgCgAA5ebxSLnSOdhur226zuB2GycA4MwQdgEAOC4XjkdKsFOH45ORK69ttseZKzcsACAXUcYMAEAOonNw7kvesCiN6apKj+pLY3p/T6M62tusHhoAOAJhFwCAHETn4NzHDQsAyCzKmAEAc4qyzOwY7xwcSwm8dA7OLe7IoIxST8pj3LAAgLnDyi4AYM5Qlpk9dA7OfRx1BACZRdgFAMwZyjKzZ7YjdJAbuGEBAJlFGTMAYM5QlpldVnc4nqlkfeOWyywbT67hqCMAyCzCLgBgzrCPNH+kO/roP8rLteiDy6weXs6w+oYFADgZYRcAMGdWb63TgT2NyVLmZFlmfYPVQ8uKbDbnsroR2JHmJl09Q8n6L595Sotu/u9ZGwcAAOkQdgEAcyafyzLTrXRKmvPnn82vlU66knXX4GBWvj6QbVbfYAJw6gi7AIA5la9lmelWOp9sbprz1yObXyuddCXrMa8vK18fyCY73GACcOroxgwAwBxwRwZTgp+UueZc2fxa6aTrJFzzyU9lbQxAttBpHshNrOwCADAHstmcyw6NwNKVrF+w/iJ1dXVlbRxANtBpHshNhF0AAOZANptz2aURWL6WrCP/2OEGE4BTR9gFAGAOZLM5Vz43AgOsYJcbTABOTdbD7sMPP6xDhw6pvLxc9913nyRpcHBQ3/3ud3Xs2DFVVVXpn/7pn+TzTW9w8dxzz+nnP/+5JOnTn/60LrnkkmwOHQCAWWVzpZNVVSB7uMEE5Kash91LLrlE27Zt00MPPZR87Omnn9b555+vq666Sk8//bSefvppXXfddSnXDQ4Oas+ePdq9e7ckaefOnaqpqZkxFAMAAABziRtMQO7Jejfm8847b1pAbW1t1caNGyVJGzduVGtr67Tr2tvbtWbNGvl8Pvl8Pq1Zs0bt7e3ZGDIAAAAAIMfYYs9uX1+f/H6/JKmiokJ9fX3TPicUCqmysjL5cSAQUCgUmvHP27t3r/bu3StJ2r17t4LBYAZGnfvcbjevjQ0xL/bEvNgT82I/TpqT/2h9Sa3PPCV3eEBR7zyt/+SndMH6i6we1mlx0rw4CfNiP8yJPZ3uvNgi7E5mGMa0swNP1ZYtW7Rly5bkxxyBMLNgMMhrY0PMiz0xL/bEvNiPU+ako71N7+9p1CeqK2T4XDLNsA489qB6+3Jzn6ZT5sVpmBf7YU7sabZ5WbhwYdrrsl7GPJPy8nL19PRIknp6elRWVjbtcwKBgLq7u5Mfh0IhBQKBrI0RAADkjyPNTcnOu9L4zfiN1RU60txk8cgAACfLFiu7NTU1OnDggK666iodOHBA69evn/Y5a9eu1b/+679qcHBQkvQf//Ef2rFjR7aHCgAAsqCjvU2vPNukwqFBjZX6dP7ldVldUXVHBmWUelIeMwxD7kg4a2MAAJyZrIfd+++/X6+++qoGBgZ0ww03aPv27brqqqv03e9+V/v27UsePSRJb775pn71q1/phhtukM/n09VXX61du3ZJkurr6+nEDACAAyVKiOurK2R4PDLNmA7saZSkrAXeqMcn04ylbK0yTVNRjzcrXx8AcOayHnZvueWWGR+//fbbpz22fPlyLV++PPnx5s2btXnz5kwNDQAA2MCR5iZdPUMJ8ZPNTVkLu6u31unAnsZkKbNpmjrQ2avV9Q1Z+foAgDNnizJmAACABDuUECdC9ZPNTXJHwop6vFpdn5vNqTJhrsvMrS5bBzBhMDKqY6GwOrvDOtYz/vfuJy75K4tHdXoIuwAwR3izBsyNkykhzsbP26q166b9mfycz32ZuR3K1oF8Eo+bCvUN6VgoPB5qE8H2+MeR4bGUzy/zFRN2ASCf8WYNmDsnKiG26ueNn/Nxc11mboeydcBpRkaj6uqJqDMU1rHu8UCbCLbdPRFFY/G01xYXuVQV8Ko64B3/f6VPpmme8fGwViDsAsAc4M0aMHdOVEJs1c8bP+fj5rrM3A5l60CuMU1TA+HRZIA9drzkuPN4sO0bGJ71+vJ5xarye1VVOR5qqwPjv67ye1XmK87JYDsTwi4AzAHerAFza6YS4gSrft74OR83152q6XwNzCwWi6u7b2g8yIZSV2ePhcIaHommvdZVYKjS75m0OutNWa0tLsqPGJgfzxIAMow3a0D2WPXzxs/5uLnuVE3na+Sz4ZFoMrwem7J3trs3oljcTHttabE7uTJbFZgIs9WVXvnLSuVyFWTxmdgTYRcA5gBv1oDsycTP28k0nuLnfNxcdaqe/Jr/ZSSuI+90a7HPS+drOIppmuofHJnWBCpRetwfHpn1en9ZSUqQnRxufZ4ix5QbZwphFwDmAMeUANkz1z9vJ9t4ip/zCbOVmZ+Maa95oFQHOnu14Kq/ycvXE7ktGo2ruzcyEWh7UptCjY7F0l7rdhUo6Peklhkf3ztbFfCqqNCVxWfiPIRdAJgjZ/rmD8DJm8uft1NpPMXP+dyg2RdyTWR4LGXv7OSmUN29EZnpq43lLS1MDbKBiaZQFWWlKihgdTZTCLsAACCv0Xgq+3jNYTfxuKnegWG9H3pPr7/1bsrK7LFQWIOR0bTXGoZUWVGaWm48qSmUt7Qoi88EkxF2AQBAXqPxVPbxmsMKY9GYukKRiZXZSU2hunrCGoumP3u20F0w477ZqoBXQb9HhW7Kje2IsAsAFjiZZjiwB+bK+Wg8lX285siUwcjoRFfjnommUJ2hsHr7h2YtN/Z5irRwfoUCZUXTmkKV+0ooN85BhF0AyLKTbYYD6zFXJ2fyDQFXIKhzPr45p14fGk9lH685Tlc8birUN5TS1XhyU6jI8FjaawsKDFVWlI6XF/unnz1bWlKoYDCorq6uLD4jZBJhFwCyjMYsuYO5OrGpNwQKC8f0qxy8IUDjqezjNUc6o2OxlON5OicF2+6eiKKx9OXGxUWu1DNnJzWFqqzwyM3Zs3mFsAsAWUZjltzBXJ0YNwQAnCrTNDUQHp0ItJP2znaGwuobGJ71+jJf8bS9s4n/l/mKOXsWSYRdAMgyGrPkDubqxLghAGAmsVhc3X1DKcf1TP7/8Eg07bWuAkOVfk9KE6jqScG2uIgIg5PDdwoAZBmNWXIHc3Vi3BAA8tfwSDQ1yE7aO9vdG1Esnr4bVGmxe7y8eMre2epKr/xlpXJRbow5QNgFgCyjMUvuYK5OjBsCgHOZpqn+wZGJJlCTV2e7w+oPj8x6vb+sZFpX48SvfZ4iyo2RcYRdALAAjVlyB3M1u6k3BNwBj87mhgCQM6LRuLp7I6llxpOaQo2OxdJe63YVKOj3JFdmJ++drQp4VVTI2bOwFmEXAACckck3BObi2A7ONgbmVmR4bHxV9niIndwUqrs3MuvZs97SwtQQWznR5biirJSzZ2FrhF0AAGAbnG0MnLp43FTfwPBEkJ3SFGowMpr2WsOQKitKVeWf0t34+Gqtt7Qoi88EmFuEXQAAYBscZQTMbCwaU1coMq2rcWd3WF09YY1F0589W+guSNk3O7nUOOj3qNBNuTGcibALAABsg6OMkM8GI6MpTaAmN4Xq6R+atdzY5ylKHs8TDEyUGldVelXuK6HcGHmJsAsAAGyDo4zgZPG4qZ7+oWSIHRj6g975c1ey9DgyPJb2WsPQRDOoKcf1VAW8Ki0pzOIzAXIDYRcAANgGRxkh142OxVK6GidXaUNhdfdEFI2lLzcuLnKldDWe3BSqssIjN2fPAqeEsAsAAGyDs41hd6ZpaiCcWm6c2Dt7rCes3v7hWa8v8xUny4vPWlwlb4mRDLVlvmLOngXmEGEXAADYCmcbw2qxWFyhvqFpZ84mwu3wSDTtta4CQ5V+T0oTqOpJTaGKiybefs/FUV2YO22HO7Tv4BF1hUfkc8VVt2G91q1ZZfWwcAYIuwAAAMg7wyPRlJXZyaXH3b0RxeLpu0GVFLunHdGTKD0OlJfKRblxzmk73KHGlqOav2ajvGNjipumGltaJYnAm8MIuwAAAHAc0zTVPzgyratxItD2h0dmvb6irGQi0E7aO1sd8MrnKaLc2GGaWg7Kv2JTyrFn/hXr1dSyn7Cbwwi7AAAAJ6HtcIeaXmjVYKyAEkebiEbj6u6NpDSBOnZ87+yxUFgjo7G017pdBSndjaeeP1tUyNmz+WQwasg75QaGYRgKR7mpkcsIuwAAACeQKHH0r9wsr2FQ4phFQ8NjKXtnJ5cdd/dGZj171ltamFJiPDnQ+stKOXsWST63qfiUbybTNOV1z/INBtsj7AIAAJwAJY6ZE4+b6hsYTg2yk5pCDUZG015rGFKgvHRakE3spfWWFmXxmSCX1dXWqLGlVfPX1EoaD7o9R1vVUFtj8chwJgi7AAAAJ0CJ45kZi8bUFYroWM/4/tnJx/V09YQ1Fk1/9myhuyBlZbbKP9EUKuj3qNBNuTHOXOKm1b6XD6hvcERet6mG2hpuZuU4wi4AAMAJJEocJzclosQxVXhoNNkIKtEUquv4r3v6h2YtN/Z5iqbtnU2s0pbPK6HcGFmxbs0qXbZ5I8dBOQhhFwCAHNDR3qZXnm1S4dCgxkp9Ov/yOs6izaJEiaN/xXoZhpGXJY7xuKme/qFpnY0T+2kjw2NprzUMKej3JFdopx7XU1pSmMVnAiBfEHYBALC5jvY2vb+nUfXVFTI8HplmTAf2NEoSgTdLEqWMTS37FY4aji1xHB2LTTuiJxFou3siisbSlxsXFbqSIbZ6SlOoygqP3Jw9CyDLCLsAANjckeYmXV1dkdIcaWN1hZ5sbiLsZtG6NatyPtyapqmB8Oj40TzdqZ2NO0Nh9fYPz3p9ma942t7ZRLAt8xVz9iwAWyHsAgBgc+7IoIxST8pjhmHIHQlbNCLYWSwWV6hvKGVltj8c1X++F1JnKKzhkWjaa10FhionlRsnuhpX+cd/XVLMW0cAuYO/sQAAsLmoxyfTjE1rjhT1eC0cFaw0PBKdKDWeUnbc3RtRLJ6+G1RJsTs1yE4qOQ6Ul8pFuTEAhyDsAgBgc6u31unAnkZtPF7KbJqmDnT2anV9g9VDQ4aYpqn+wZGUzsaTw23/4Mis11eUlaScObv8/1ugkqK4qgNe+TxFlBsDyAuEXQAAbC6xL/fJ5ia5I2FFPV6trm9gv26Oi8bi6u6NpDSBOjbpv5HRWNpr3a4CBf2eacf1JM6eLS5KfYsXDAY5TgVA3iHsAgCQA1atXUe4zUFDw2PJ8uJjPeMrtIlQ290bmfXsWW9poYKBSWfOTmoK5S8r5ezZLGg73KGmF1o1GCuQzxVX3Yb1Od+kDMgnhF0AAIDTFI+b6hsYTgbYyU2hjoXCGoyMpr3WMKRAeWkyyE4uO66u9MpbWpTFZ4Kp2g53qLHlqPwrN8trGIqbphpbWiWJwAvkCMIuAADALMaiMXX1RMbDbPf0cuOxaPqzZwvdBcnmT8lV2sqJcuNCtyuLzwSnoqnloPwrNqUc+eVfsV5NLfsJu0COIOwCAIC8Fx4andYEKrFC29M/NGu5sc9TNHFUz6QV2uqAV+XzSig3zlGDUUPeKY28DMNQOMp8ArmCsAsAABwvHjfV0z80Hmh7wqlNobrDigyPpb3WMKTgpLNnJzeFqgp45SkpzOIzOXUd7W16/fl9ioW6NFbq0/mX17H/+yT43KbipjntyC+ve5Y7HwBsxRZh991339V3v/vd5MednZ3avn27rrjiiuRjHR0d+va3v63q6mpJ0oc//GHV19dnfawAAMCeRsdi086cTazSdvVEFI2lLzcuKnRNO3M2sVJbWe6R252bZ892tLfp/T2N+vTiao1VemSaMR3Y0yhJBN4TqKutUWNLq/wr1ieP/Oo52qqG2hqrhwbgJNki7C5cuFD33nuvJCkej+sf/uEfdNFFF037vJUrV2rnzp3ZHh4AALAB0zQ1GBmdFmQT4ba3f3jW68t8xdOaQCU+LvMVO/Ls2SPNTbr6+PnM0ngZ7sbqCj3Z3ETYPYHEvtymlv0KRw153aYaamvYrwvkEFuE3cleeeUVLViwQFVVVVYPBQAAZFksFleob2jacT2JUDs0Ek17ravAUGWFZ3pn4+P/Lym23duejHNHBmWUelIeMwxD7kjYohHllnVrVhFugRxmu7/1W1paVFtbO+Pv/f73v9ett94qv9+vhoYGLVmyZMbP27t3r/bu3StJ2r17t4LBYMbGm8vcbjevjQ0xL/bEvNgT82I/JzMnQ8Njer+rX385NqD3jvXr/eP/vXdsQMe6BxSLp98TWVpSqAVVZfpAVZkWVM3TgmCZFlSVaUH1PFX5fXK5crPcOFPcgaAKC8dUYBgqKho/ysg0TbkDHn52bIC/w+yHObGn050XwzRn6y+YXdFoVP/wD/+g++67TxUVFSm/F4lEVFBQoJKSEh06dEg//OEP9cADD5zUn/vuu+9mYLS5LxgMqqury+phYArmxZ6YF3tiXuwnGAzq2LFj6h8cSZYXT16Z7QyF1T84MuufUVFWMn1l9nhTqHneIkeWG2dKYs/uZYurNTY2JtM0daCzVwvqGyhjtgH+DrMf5sSeZpuXhQsXpr3OViu7bW1t+uAHPzgt6EqSxzNRgnPhhRfqscceU39/v8rKyrI4QgAAIEnRWFzdvZGUvbOdobBCfSN6/1ifRkZjaa91uwpSuhtPLjsO+j0qLrLV25Oclgi0Tz2/T9FQv6Ier1YTdAHkCVv9azJbCXNvb6/Ky8tlGIbeeOMNxeNxzZs3L8sjBAAgfwwNj6U2gZoUbLt7I7OePespKUyG2KlNofxlpZw9m0Wr1q7Txi2XsVoFIO/YJuwODw/r8OHDuv7665OPNTc3S5K2bt2qF198Uc3NzXK5XCoqKtItt9xCGRMAAGcgHjfVNzA8UW48pSnUYGQ07bWGIQXKSydKjI+H2nOWLVKRa0ze0qIsPhMAAKazTdgtKSnRP//zP6c8tnXr1uSvt23bpm3btmV7WACAKTra2/TKs00qHBrUWKlP519eR0mkjY1FY+rqiSRXZo/1pB7bMxZNf/ZsobsguSKbPHv2+N7ZoN+jwkLXtGvY7wYAsAvbhF0AgP0lmt3UV1fI8HhkmjEd2NMoSQReC4WHRqc1gUoE2p7+oVnLjX2eohn3zlYHvCqfV0K5MQAgZxF2AQAn7Uhzk66urkhuIzEMQxurK/RkcxNhN4PicVM9/UPTgmxnKKyuUFjhobG01xqGUptBTe5uHPDKU1KYxWdivbbDHWp6oVWDsQL5XHHVbVjPOaoA4FCEXQDASXNHBmWUelIeMwxD7kjYohE5x+hYbNrKbGLvbFdPRNFY+nLjokLXeHnx5HLj44G2stwjt5uzZ6XxoNvYclT+lZvlNQzFTVONLa2SROAFAAci7AIATlrU45NpxlIaBJqmqajHa+GocoNpmhqMjE4E2VDqkT29/cOzXl/mK05dnZ3UFKrMV0zTxpPQ1HJQ/hWbUioT/CvWq6llP2EXAByIsAsAOGmrt9bpwJ5GbTxeymyapg509mp1fYPVQ7OFWCyuUN/QtON6Er8eGommvdZVYKiywpOyb3ZyuC0p5p/sMzUYNeSdclPAMAyFo/a+UUDpNQCcHv7lBJBxvFFzjsS+3Cebm+SOhBX1eLW6viGv9uuOjEYnjuqZ0hSquyeiWDx9N6iSYvf0IHs83AbKS+VyUW6cST63qbhpTqtM8Lpn6eBlMUqvAeD0EXYBZBRv1Jxn1dp1jg63pmmqf3AkNdBOOq6nf3Bk1usrykpU5U8tM06E23neorwvN7by5lddbY0aW1rlX7E+WZnQc7RVDbU1Wfn6p4PSawA4fYRdABnFGzXYUTQWV3dvJGXv7OTS45HRWNprXS5DQX9qE6hEqA36PSou4p/WdKy++ZX4Gk0t+xWOGvK6TTXU1tj676JcLb0GADvgX2QAGcUbNVhlaHhs2t7ZxMehviHFZyk39pQUTjtzNtEUyl9Wytmzp8kON7/WrVll63A7VS6WXgOAXRB2AWQUb9SQKfG4qe7esH7/VlfKmbOJ0uPByGjaaw1DCpSXTuydndIUyucpyuIzyR/c/Dp1uVh6DQB2QdgFkFG8UcOZGIvG1NUTmehqPGnv7LFQWGPR9GfPut0FM+6dTZQbFxa6svhMIHHz63TkYuk1ANgFYRdARvFGDScSHhqd1tU4EWh7+odkzpKD5nmLFfR7pu2drQ54VT6vhHJjm+Hm1+nJtdJrALALwi6AjOONWn6Lx0319g9NNIHqTm0GFR4aS3utYUhBvyflqJ7JwXbp4g+oq6srI+PuaG/TK882qXBoUGOlPp1/eZ2ju1BnAze/AADZRNgFAJyx0bFY6srspKZQXT0RRWPpy42LCl3TzpxNlBxXVnjkdmf/7NmO9ja9v6dR9dUVMjwemWZMB/Y0ShKB9wxx8wsAkC2EXQDACZmmqcHI6ESQnbI629M/POv1Zd7ilO7Gk5tClfmKbXf27JHmJl1dXZHSNXhjdYWebG4i7AJAGlaeow3MhLALAJAkxWJxhfqGUlZnJzeFGhqJpr3WVWCossIzPdAe/39JcW79c+OODMoo9aQ8ZhiG3JGwRSMCAHuz+hxtYCa59e4DAHBGRkajyTA7tSlUd09EsVnOni0pdk8Pssf3zlaWl8rlyn65caZEPT6ZZmxa1+Cox2vhqADAvuxwjjYwFWEXABzENE31D46krs5OKjvuHxyZ9fryeSXje2anHNdTFfBqnrfIduXGmbJ6a50O7GnUxuOlzKZp6kBnr1bXN1g9NACwJc7Rhh0RdgEgx0RjcXX3RlL2zk7ePzsyGkt7rctlKOhPbQKVKD0O+j0qLuKfBWmiCdWTzU1yR8KKerxaXd/Afl0ASINztGFHvKsBABsaGh6bce9sZ3dYob4hxWcpN/aUFI6XF/snmkAlGkL5y0o5e/YkrVq7jnALACeJc7RhR4RdALCAaZrqHRie1tU4sZd2MDKa9lrDkALlpdO6Gic+9nmKsvhMAADgHG3YE2EXADJkLBpTV08k9fzZ4+G2qyei0bH05cZud0FyZXby3tlEuXFhoSuLzwRIb+pRI9d+YouWLV1s9bAAWIBztGE3hF0AOAPhodGJMuMpe2dDfUMyZ9mq5PMUpTaBqpzYS1s+r4RyY9jeTEeN/KC5TZ+5qI83vDbFOagA8glhFwBmEY+b6u0f0nvd7+r1t97VsSmhNjw0lvZaw5CCfo+q/KlBNhFsPSWFWXseHe1teuXZJhUODWqs1KfzL69jPyrO2IxHjaxcr6aWZwlQNsQ5qADyDWEXQN4bHYslV2OnNoXq6okoGounvbao0JVy5uzkcuPKCo/cbuvPnu1ob9P7expVX10hw+ORacZ0YE+jJBF4cUY4aiS3cA4qgHxD2AXgeKZpajAyOlFiPKUpVE//8KzXl3mLtXB+ufxlxdOaQpX5im1/9uyR5iZdffy8WGn8De7G6go92dxE2MUZ4aiR3MLNCQD5hrALwBFisbh6+ofUOUN342PdYQ2NRNNeW1BgKFjhSQmyyWZQAY9KiwsVDAbV1dWVxWc0d9yRQRmlnpTHDMOQOxK2aERwihmPGvldqz6TgaNG2Gt65rg5ASDfEHYB5IyR0WjK8TyTA213T0SxWc6eLS5yp545O2nvbGV5qVwu68uNMyXq8ck0Y9Pe4EY9XgtHBSeY6aiR66+4dM67MbPXdG5wDiqAfHNSYTcej6u1tVWGYaimpkYFBeNvCn/729/qox/9aEYHCCB/mKap/sGR1DNnj6/MHusJq29gZNbry+eVjDeBqvSmNIWqCng1z1tk+3LjTFm9tU4H9jRq4/FSZtM0daCzV6vrG6weGhxg6lEjmaiCYK/p3OAcVAD55qTC7oMPPqhgMCi3261nnnlGN910kxYsWKDm5mbCLoBTEo3FFeqNpJw5O1F2HNHIaPpyY5fLUNA/ZXW2cuLs2eIiilVmktiX+2Rzk9yRsKIer1bXN7BfFzmDvaZzh3NQAeSTk3pnGAqFdPPNN0uSNm3apAcffFB/8zd/k9GBAchdQyNj05pAJUqPQ31Dis9SblxaUjgRZietzFYFvAqUl3L27GlatXYd4dZC7Dc9M+w1PTNthzu07+ARdYVH+P4DkFdOKuxGo1GNjY2psLBQVVVV2rlzp+6//3698847mR4fABsyTVO9A8PJ8uLOKWfPDoRH015rGJK/vDQl0Fb5J5pC+TxFWXwmQOax3/TMsdf09CW+/+av2Sjv2BjffwDyyqxhNxaLyeVy6XOf+5zC4bAqKiokSaWlpbrtttv0wgsvZGOMACwwFo2pqycyravxsVBYx3oiGh2Lpb3W7S6YCLCT9s4myo0LC11ZfCaAtdhveubYa3r6+P4DkM9mDbvf+ta3dOutt+rss8+e9nsFBQX6+Mc/nrGBAci8yNDojJ2Nj4XGy43NWSoEfZ6iiaN6AqnNoCrmlVBuDBzHftO5wV7T08P3H4B8NmvYPeuss/TVr35Vu3btUiAQkCS9+uqr+slPfqJvfOMbWRkggNMXj5vq7R9KbQI1aS9teGgs7bWGIVVWeFKC7OTjejwlhVl8JkDuYr8prJT4/puM7z8A+WLWsNvQ0KDm5mZ99atf1Y4dO7Rv3z698847uvLKK7M1PgAnMDoWO15aHJ7WFOpYT0TRaDzttUWFrpSV2UTpcXXAq8oKj9xu5549C2QL+01hpcT33/w1tZLE9x+AvHLCBlXnnnuuPB6PHnjgAW3cuFG33XabiopoIANki2maCg+NqrM7nHJcTyLQ9vQPz3p9mbd4PMhOWplNBNoyX3Henj0LZAv7TWGlxPfZvpcPqG9whO+/E6BzOuAss4bde++9V6+++qquuOIKbd++XY8++qiOHDmiCy+8MFvjA/JCPG4q1BdRZ3dYkVeP6a13/pLSFGpoJP3ZswUFhoIVnon9s5UTR/VUBTwqLabcGLAa+01hpXVrVumyzRvV1dVl9VBsjc7pgPPMGnY/8IEP6L/+1/8qn88nSZo/f77uuecedXZ2atu2bVkZIOAUI6PRlAZQk4/r6e6NKBZLv3+quMg97czZROlxZXmpXC7KjQEAOBN0rgacZ9awe91116V8vHTpUt155526++67CbvAFKZpqn9wJGXv7ORy476BkVmvL59XouqAV4sXBlTucad0N57nLaLcGACADKJzNeA8J9yzO1UgEKATM/JWNBZXqDcybe/s+P8jGhlNX27schkK+idWZSc3haoKeFRcNP7jGAwGKTUDACDL6JwOOM8ph11JKi0tnetxALYxNDI2rQlU4izaUN+Q4vH0/+iVlhSmNIGqCnhUHfCpKuBVoLyUs2cBALApOqcDznNaYRfIZaZpqndgWMe6x4/rmbx39lgorIHw6KzX+8tLp+2dTTSF8pYWUm4MAEAOonM64DyEXTjSWDSm7t7ItCA7HnAjGh2Lpb3W7S5IlhZXB3zJvbPVAa+Cfo8KC11ZfCYAACBb6JwOOAthFzkrMjSaLC8+FkoNtaG+IZmzbLHxeYqmdTWu9o//v2JeCeXGAAAAQI4j7MK24nFTvf1DqU2gJu2lDQ+Npb3WMKTKCs9EE6jjq7TVx8+e9ZQWZfGZAAAAAMg2W4Xdm266SSUlJSooKJDL5dLu3btTft80TT3++ONqa2tTcXGxbrzxRi1btsyi0WIujI3FxvfNTgmyx0Lj5cbRaDzttUWFromV2YBHVQFf8izaygqP3G7OngUAwCnaDneo6YVWDcYK5HPFVbdhvaNKjp3+/AAr2CrsStIdd9yhsrKyGX+vra1N77//vh544AG9/vrrevTRR/Wtb30ryyPEqTBNU+GhUXV2TwTayU2hevqHZ72+zFs8HmQrfZOaQo2v0pbPK6YZFAAAWWRVIGs73KHGlqPyr9wsr2EobppqbGmVJEcEQqc/P8Aqtgu7szl48KA+/vGPyzAMnXvuuQqHw+rp6ZHf77d6aHktHjcV6jveDGpad+OIhobTlxsXFBgT5caJrsb+8XBbFfCotLgwi88EAACkY2Uga2o5KP+KTcmb3IZhyL9ivZpa9jsiDDr9+QFWsV3YveuuuyRJl112mbZs2ZLye6FQSMFgMPlxZWWlQqHQtLC7d+9e7d27V5K0e/fulGswwe12n/RrMzwypr90Dei9Y/16/1i/3j82/uu/HOtXZ/egorH05calxYVaUDVPC6rKjv83/usPVJWpKuCTy0W58WSnMi/IHubFnpgX+2FO7Gku5mXfy0c0f83GlKqq+Wtqte/lA7ps88YzHeKsxlwl8hQXT3t8yFWS099viXlx6vPLRfwdZk+nOy+2Crt33nmnAoGA+vr69M1vflMLFy7Ueeedd8p/zpYtW1KCcldX11wO0zGCwWDytTFNUwPhUXWGBlP2zib+3zcwMuufVT6vJLl3dvJxPVUBr+Z5i9KUG4+qpyeUgWeW2ybPC+yDebEn5sV+mBN7mot56RockXdserVW3+BIxue8MDaskZGRlPcTpmnKHRvO6e+3xLw49fnlIv4Os6fZ5mXhwoVpr7NV2A0EApKk8vJyrV+/Xm+88UZK2A0EAilPsru7O3kNTiwaiyvUG0nunR0cflNv/+exZLnxyGg07bUul6FgxcTe2clNoaoCHhUX2epbCQAAzDGf21TcNKcFMq97lrP+5khdbY0aW1rlX7FehmHINE31HG1VQ21Nxr92Njj9+QFWsU1CGR4elmmaKi0t1fDwsA4fPqz6+vqUz6mpqdG//du/qba2Vq+//ro8Hg/7dacYGhkbbwIVmro6G1F3b0TxePp/kEpLClP3ziZWaQNeBcpLOXsWAGyCrq2wgpWBLPH93dSyX+GoIa/bVENtjWO+753+/ACr2Cbs9vX16Tvf+Y4kKRaLacOGDVq7dq2am5slSVu3btW6det06NAh3XzzzSoqKtKNN95o5ZAtYZqm+gZGxsuNQxPNoBKhdiA8Ouv1/vLS5KrsWYur5S0xjgdbr7ylhXQ3BgCbo2srrGJ1IFu3ZpWjv8ed/vwAK9gm7M6fP1/33nvvtMe3bt2a/LVhGPr7v//7bA7LEtFoXF2904Ps+LE9EY2OxdJe63YXqMo/095Zj6r8XhUWupKfy54EADNh1dDe6NoKKxHIAOQS24TdfPSn9/r0ftfgtKZQob4hmbNsf/GWFqq6cry8eGpTqIp5JZQbAzhtrBra32DUkHdKFY5hGApH+bsfAIDJCLsW+tHTbfrDn3qmPW4YmnT2rOf46qwv+bGntMiC0QLIB6wa2p+VTYIAAMglhF0LrVhWpTJf8fEQ60s2hQpWeOV2c/YsgOxj1dD+6NoKAMDJIexaqP5yVkkA2AurhvZndZMgAAByBWEXAJDEqmFuoEkQAAAnRtgFACTlw6oh3aYBAMgPhF0AQAonrxrSbRoAgPxBFyQAQN4Y7za9foZu0wctHhkAAJhrhF0AQN4YjBopzbckuk0DAOBUhF0AQN7wuU2ZZmpnabpNAwDgTIRdAEDeqKutUc/R1mTgTXSbrqPbNAAAjkODKgBA3kg0ofrxL57UH471KTY2ouXVFZJWWDouAAAw9wi7AIC8YwSXqmbDxFnCdGQGAMB5KGMGAOQVOjIDAJAfWNkFAOSVwaghb452ZG473KGmF1o1GCuQzxVX3Yb1rEYDAJAGYRcAkFd8blNx00w5gigXOjK3He5QY8tR+VdultcwFKf8GgCAWVHGDADIK7nakZnyawAATg0ruwCAvBPvelsHnzqi+Oiwli3w63OfvsL2q6O5XH4NAIAVCLsAgLyRKAWu3FCv4PFOzD1HW60e1knJ1fJrAACsQhkzACBv5HIpcK6WXwMAYBVWdgEAeSOXS4ETZdZNLfsVjhryuk011NbYvvwaAACrEHYBAHkj10uB161ZRbgFAOAkUcYMAMgblAIDAJA/WNkFAOQNSoEBAMgfhF0AQF6hFNiZ2g53qOmFVg3GCuRzxVW3YT3zDAB5jrALAAByWuJIKf/KzfIahuKmqcaW8SOlCLwAkL/YswsAAHJaLh8pBQDIHMIuAADIaYNRI6XDtpQ7R0oBADKHsAsAAHKaz20mO2wn5NKRUgCAzGDPLgAANkOzpVNTV1ujxpbWZClz4kipBo6UAoC8RtgFAMBGaLZ06jhSCrli6o2saz+xRcuWLrZ6WIBjEXYBALCR8WZLm2ZotrSf8DYLjpSC3c10I+sHzW36zEV9fO8CGULYBQDARgajhrw0W4LNUFp/5ma8kbVyvZpanuW1BDKEsAsAgI343KbippnSXZhmS7ASpfVzgxtZQPbRjRkAABupq61Rz9HWZHfhRLOlOpotwSKcYzw36BoOZB8ruwAA2AjNlmA3rEjOjRm7hv+uVZ/hRhaQMYRdAABshmZLsBNK6+fGTDeyrr/iUroxAxlE2AUAAEBanGM8d6beyAoGg+rq6rJwRICzEXYBAIAkOu5iZpTWA8hVhF0AAEDHXcyK0noAuYhuzAAAgI67AADHIewCAAANRo2UBkQSHXcBALmNMmYAAHDKHXfZ3wsAsDvCLoC8wZtzIL1T6bg72/7eyzZvzPbQHYm/rwDgzBF2AeQFmu8AszuVjrvj+3s3zbC/dz9hdw7w9xUAzA3CLoC8MNubc948AuNOtuPuYNSQl/29J3S6q7P8fQUAc8MWYberq0sPPfSQent7ZRiGtmzZorq6upTP6ejo0Le//W1VV1dLkj784Q+rvr7eiuECyEG8OQfmzqnu781HZ7I6y99XADA3bBF2XS6XGhoatGzZMg0NDWnnzp1as2aNFi9enPJ5K1eu1M6dOy0aJYBcxptzYO6cyv7efHUmq7P8fQUAc8MWRw/5/X4tW7ZMklRaWqpFixYpFApZPCoATlJXW6Oeo60yzfE3i4k353W8OQdO2bo1q9RQu0IFR/cr8sp+FRzdr4baFZTYTnImRznx9xUAzA1brOxO1tnZqbfeektnn332tN/7/e9/r1tvvVV+v18NDQ1asmSJBSMEkItOpfkOgBM72f29+epMVmf5+woA5oZhJm4b2sDw8LDuuOMOffrTn9aHP/zhlN+LRCIqKChQSUmJDh06pB/+8Id64IEHZvxz9u7dq71790qSdu/erdHR0YyPPRe53W5Fo1Grh4EpmBd7Yl7siXmxH+Zk3EuH2vWD5jb5V04q9f5dq67fuk4XXbg26+NhXuyJebEf5sSeZpuXoqKitNfZJuxGo1Hdc889uuCCC/SJT3zihJ9/00036e6771ZZWdkJP/fdd9+diyE6TjAYVFdXl9XDwBTMiz0xL/bEvNgPczKh7XCHmloOJldn6yxcnWVe7Il5sR/mxJ5mm5eFCxemvc4WZcymaeqRRx7RokWL0gbd3t5elZeXyzAMvfHGG4rH45o3b16WRwoAAHByKPUGAGvZIuy+9tprev7557V06VLdeuutkqRrr702md63bt2qF198Uc3NzXK5XCoqKtItt9wyrfEDAAAAAACSTcLuihUr9LOf/WzWz9m2bZu2bduWpREBAADgTLUd7lDTC60ajBXI54qrbsN6VrsBZI0twi4AAACcpe1whxpbjsq/crO8hqG4aaqxpVWSCLwAssIW5+wCAADAWZpaDsq/Yn1y25lhGPKvWK+mloMWjwxAviDsAgAAYM4NRo1p/VUMw1A4Ss8VANlBGTMAAMBx7DGdOz63qbhppgRe0zTlddvi1EsAeYCVXQAAAE3sMY2v3Czv+ZsUX7lZjS1H1Xa4w+qh5aS62hr1HG2VaY6HW9M01XO0VXW1NRaPDEC+YGUXAABAiT2mm2bYY7qf1d3TkHjNmlr2Kxw15HWbaqit4bUEkDWEXQAAAI3vMfWyx3ROrVuzinALwDKUMQMAAGh8j2mi5DaBPaYAkLsIuwAAAGKPKQA4DWXMAABboAsurMYeUwBwFsIuAMByiS64/pWb5TUMxU1TjS2tkkTQQFaxxxQAnIMyZgCA5ca74K6foQvuQYtHBgAAchUruwAAy9EFFzh9bAEAgJkRdgEAlvO5TcVNM7myK9EFFzgZbAEAgPQoYwYAWI4uuMDpYQsAAKTHyi4AwHJ0wQVOD1sAACA9wi4AwBboggucOrYAAEB6lDEDAADkKLYAAEB6rOwCAADkKLYAAEB6hF0AAIAcxhYAAJgZYRcAgFPEuaYAANgfYRcAgFPAuaYAAOQGGlQBAHAKONcUAIDcQNgFAOAUDEaNlGNeJM41BQDAjgi7AACcAp/bTB7zksC5pgAA2A9hFwCAU8C5pgAA5AYaVAEAcAo413Tu0NUaAJBJhF0AAE4R55qeObpaAwAyjTJmAACQdXS1BgBkGmEXAABkHV2tAQCZRtgFAABZR1drAECmEXYBAEDW0dUaAJBpNKgCAABZR1drAECmEXYBAIAl6GoNAMgkypgBAAAAAI7Dyi4AAACmaTvcoaYXWjUYK5DPFVfdhvWsxAPIKYRdAMBJ4Y0vkD/aDneoseWo/Cs3y2sYipumGltaJYmfewA5g7ALADgh3vg6DzcvMJumloPyr9iUPAvZMAz5V6xXU8t+vk8A5AzCLgDghHjj6yzcvMCJDEYNeY//vCcYhqFw1EhzBQDYDw2qAAAnNBg1kkE3gTe+uWv85sX6GW5eHLR4ZLALn9tMnoGcYJqmvG4zzRUAYD+EXQDACfHG11m4eYETqautUc/R1uTPvWma6jnaqrraGotHBgAnjzJmAMAJ1dXWqLGlNbkamHjj28Ab35zkc5uKm2ZK4OXmBSZLlLM3texXOGrI6zbVUFtDmTuAnELYBQCcEG98nYWbFzgZ69as4mccQE4j7AIATgpvfJ2DmxcAgHxA2AXgWBytAqTHzQsAgNMRdgE4EkerAPbCzScAQLbZKuy2t7fr8ccfVzwe16WXXqqrrroq5ffHxsb04IMP6g9/+IPmzZunW265RdXV1dYMFoCtcS4sYB/cfAIAWME2YTcej+uxxx7TV77yFVVWVmrXrl2qqanR4sWLk5+zb98+eb1efe9731NLS4v+5V/+Rf/0T/9k4agB2NVg1JDXYUersDKGXMXNJwCAFWxzzu4bb7yhBQsWaP78+XK73br44ovV2tqa8jkHDx7UJZdcIkn6yEc+oiNHjkw79xEAJOedC5tYGYuv3Czv+ZsUX7lZjS1H1Xa4w+qhASfEub4AACvYJuyGQiFVVlYmP66srFQoFEr7OS6XSx6PRwMDA1kdJ4DcUFdbo56jrcnAmzhapS5Hj1YZXxlbP8PK2EGLRwacmNNuPgEAcoNtypjn0t69e7V3715J0u7duxUMBi0ekT253W5eGxtiXubGZZs3qryiXE/9ukWDY5KvUPrsFbW66MK1p/XnWT0vY64SeYqLpz0+5CrJ6+8Xq+cF0800J9decal+0Nwm/8pJ5/r+rlXXX3Ep85cl/KzYE/NiP8yJPZ3uvNgm7AYCAXV3dyc/7u7uViAQmPFzKisrFYvFFIlENG/evGl/1pYtW7Rly5bkx11dXZkbeA4LBoO8NjbEvMydZUsX679//jMpj53ua2v1vBTGhjUyMpJSCmqaptyx4bz+frF6XjDdTHOybOlifeaiPjW1PJs81/cztTVatnQx85cl/KzYE/NiP8yJPc02LwsXLkx7nW3C7vLly/Xee++ps7NTgUBAv/nNb3TzzTenfM6HPvQhPffcczr33HP14osvatWqVdP2AAGAE9XV1qixpTVZypwoy27I0bJs5B/O9QUAZJttwq7L5dIXvvAF3XXXXYrH49q0aZOWLFmin/70p1q+fLlqamq0efNmPfjgg/pv/+2/yefz6ZZbbrF62ACQFYmQ0NSyP7ky1lBbQ3gAAABIwzZhV5IuvPBCXXjhhSmPfeYzEyWIRUVF+uIXv5jtYQGALbAyBgAAcPJs040ZAAAAAIC5QtgFAAAAADgOYRcAAAAA4DiEXQAAAACA49iqQRUAYELb4Q41vdCqwViBfK646jasp0EVAADASSLsAoANtR3uUGPLUflXbpbXMBQ3TTW2tEoSgRcAAOAkUMYMADbU1HJQ/hXrZRiGJMkwDPlXrFdTy0GLRwYAAJAbCLsAYEODUSMZdBMMw1A4aqS5AgAAAJNRxgwANuRzm4qbZkrgNU1TXrdp4aiAM8M+dABANrGyCwA2VFdbo56jrTLN8XBrmqZ6jraqrrbG4pEBpyexDz2+crO8529SfOVmNbYcVdvhDquHBgBwKFZ2AcCGEqtdTS37FY4a8rpNNdTWsAqGnDW+D33TDPvQ9/N9DQDICMIuANjUujWrCAFwjMGoIS/70AEAWUQZMwAAyDif20yW5SewDx0AkEmEXQAAkHHsQwcAZBtlzAAAIOPYhw4AyDbCLgAAyAr2oQMAsokyZgAAAACA4xB2AQAAAACOQ9gFAAAAADgOYRcAAAAA4DiEXQAAAACA4xB2AQAAAACOQ9gFAAAAADgOYRcAAAAA4DhuqwcAAICV2g53qOmFVg3GCuRzxVW3Yb3WrVll9bAAAMAZIuwCAPJW2+EONbYclX/lZnkNQ3HTVGNLqyQReAEAyHGUMQMA8lZTy0H5V6yXYRiSJMMw5F+xXk0tBy0eGQAAOFOs7MIWKCMEYIXBqCHv8aCbYBiGwlEjzRUAACBXEHZhOcoIAVjF5zYVN83kyq4kmaYpr9u0cFQAAGAuEHZhufEywk0zlBHuJ+wCyKi62ho1trQmS5lN01TP0VY11NZYPbSTQlUMAADpEXZhOcoIAWTb5JAY7+1S14E35a1cIK/bVENtTU4ERqpiAACYHWEXlqOMEEA2TQ2JnuOruX9TuyKnQiJVMQAAzI5uzLBcXW2Neo62yjTHw22ijLAuR8oIAeQWp3RgHowaKTcJJapiAACYjJVdWC6xAtHUsl/hqJFTZYQAco9Ttk5QFQMAwOwIu7CFdWtWEW4BZIVTQmKuN9cCACDTCLsAgLzilJBIVQwAALMj7AIA8oqTQiJVMQAApEfYBQDkHUIiAADORzdmAAAAAIDjEHYBAAAAAI5DGTMAAKeo7XCHml5o1WCsQD5XXHUb1lMWDQCAzRB2AQA4BW2HO9TYclT+lZvlNQzFTVONLa2SROAFAMBGKGMGAOAUNLUcTB5bJEmGYci/Yr2aWg5aPDIAADAZYRcAgFMwGDWSQTfBMAyFo0aaKwAAgBUIuwAAnAKf25RpmimPmaYpr9tMcwUAALACe3YBACdEQ6YJdbU1amxpTZYym6apnqOtaqitsXpoAABgEsvDbmNjo15++WW53W7Nnz9fN954o7xe77TPu+mmm1RSUqKCggK5XC7t3r3bgtECQP6hIVOqxHNuatmvcNSQ122qobYmL18LAADszPKwu2bNGu3YsUMul0tPPPGEnnrqKV133XUzfu4dd9yhsrKyLI8QAPLbeEOmTTM0ZNqftwFv3ZpVefvcAQDIFZbv2b3gggvkcrkkSeeee65CoZDFIwIATEZDJgAAkIssX9mdbN++fbr44ovT/v5dd90lSbrsssu0ZcuWbA0LAPKaz20qbpopgZeGTAAAwO4Mc2pLyQy488471dvbO+3xa665RuvXr5ck/fznP9ebb76pL33pS9NWECQpFAopEAior69P3/zmN/X5z39e55133oxfb+/evdq7d68kaffu3RodHZ27J+Mgbrdb0WjU6mFgCubFnvJ5Xl461K4fNLfJv3JSQ6bfter6ret00YVrLR1bPs+LXTEn9sS82BPzYj/MiT3NNi9FRUVpr8tK2D2R5557Tr/61a90++23q7i4+ISf/7Of/UwlJSW68sorT+rPf/fdd890iI4UDAbV1dVl9TAwBfNiT/k+L22HO9TUcjDZkKnOJg2Z8n1e7Ig5sSfmxZ6YF/thTuxptnlZuHBh2ussL2Nub2/XL37xC339619PG3SHh4dlmqZKS0s1PDysw4cPq76+PssjBYD8RUMmAACQaywPu4899pii0ajuvPNOSdI555yj66+/XqFQSN///ve1a9cu9fX16Tvf+Y4kKRaLacOGDVq7dq2FowYAAAAA2JnlYfd73/vejI8HAgHt2rVLkjR//nzde++92RwWAAAAACCHWX70EAAAAAAAc42wCwAAAABwHMIuAAAAAMBxCLsAAAAAAMch7AIAAAAAHIewCwAAAABwHMIuAAAAAMBxLD9nFwCAqdoOd6jphVYNxgrkc8VVt2G91q1ZZfWwAABADiHsAgBspe1whxpbjsq/crO8hqG4aaqxpVWSCLwAAOCkUcYMALCVppaD8q9YL8MwJEmGYci/Yr2aWg5aPDIAAJBLCLsAAFsZjBrJoJtgGIbCUSPNFQAAANMRdgEAtuJzmzJNM+Ux0zTldZtprgAAAJiOsAsAsJW62hr1HG1NBl7TNNVztFV1tTUWjwwAAOQSGlQBAGwl0YSqqWW/wlFDXrephtoamlMBAIBTQtgFANjOujWrCLcAAOCMUMYMAAAAAHAcwi4AAAAAwHEIuwAAAAAAxyHsAgAAAAAch7ALAAAAAHAcwi4AAAAAwHEIuwAAAAAAxyHsAgAAAAAch7ALAAAAAHAcwi4AAAAAwHEIuwAAAAAAxyHsAgAAAAAch7ALAAAAAHAcwi4AAAAAwHEIuwAAAAAAxzFM0zStHgQAAAAAAHOJld08tnPnTquHgBkwL/bEvNgT82I/zIk9MS/2xLzYD3NiT6c7L4RdAAAAAIDjEHYBAAAAAI5D2M1jW7ZssXoImAHzYk/Miz0xL/bDnNgT82JPzIv9MCf2dLrzQoMqAAAAAIDjsLILAAAAAHAct9UDgD0888wzamxs1KOPPqqysjKrh5P3fvKTn+jgwYMyDEPl5eW68cYbFQgErB5W3mtsbNTLL78st9ut+fPn68Ybb5TX67V6WHntt7/9rf73//7f+vOf/6xvfetbWr58udVDymvt7e16/PHHFY/Hdemll+qqq66yekh57+GHH9ahQ4dUXl6u++67z+rhQFJXV5ceeugh9fb2yjAMbdmyRXV1dVYPK++Njo7qjjvuUDQaVSwW00c+8hFt377d6mFBUjwe186dOxUIBE65KzNhF+rq6tLhw4cVDAatHgqOu/LKK3XNNddIkpqamrRnzx5df/31Fo8Ka9as0Y4dO+RyufTEE0/oqaee0nXXXWf1sPLakiVL9KUvfUk/+MEPrB5K3ovH43rsscf0la98RZWVldq1a5dqamq0ePFiq4eW1y655BJt27ZNDz30kNVDwXEul0sNDQ1atmyZhoaGtHPnTq1Zs4afFYsVFhbqjjvuUElJiaLRqG6//XatXbtW5557rtVDy3tNTU1atGiRhoaGTvlaypihH/3oR/rsZz8rwzCsHgqO83g8yV+PjIwwNzZxwQUXyOVySZLOPfdchUIhi0eExYsXa+HChVYPA5LeeOMNLViwQPPnz5fb7dbFF1+s1tZWq4eV98477zz5fD6rh4FJ/H6/li1bJkkqLS3VokWL+PfEBgzDUElJiSQpFospFovx/ssGuru7dejQIV166aWndT0ru3mutbVVgUBAZ511ltVDwRT/+q//queff14ej0d33HGH1cPBFPv27dPFF19s9TAA2wiFQqqsrEx+XFlZqddff93CEQH219nZqbfeektnn3221UOBxitUbrvtNr3//vu6/PLLdc4551g9pLz3wx/+UNddd91prepKhN28cOedd6q3t3fa49dcc42eeuopfeUrX8n+oDDrvKxfv17XXnutrr32Wj311FP6t3/7N/aNZMmJ5kWSfv7zn8vlculjH/tYlkeXn05mTgAg1wwPD+u+++7T5z73uZSKLlinoKBA9957r8LhsL7zne/onXfe0dKlS60eVt56+eWXVV5ermXLlqmjo+O0/gzCbh746le/OuPj77zzjjo7O3XrrbdKGi8TuO2223T33XeroqIiiyPMT+nmZaqPfexjuvvuuwm7WXKieXnuuef08ssv6/bbb6e8KUtO9mcF1goEAuru7k5+3N3dTWM9II1oNKr77rtPH/vYx/ThD3/Y6uFgCq/Xq1WrVqm9vZ2wa6HXXntNBw8eVFtbm0ZHRzU0NKQHHnhAN99880n/GYTdPLZ06VI9+uijyY9vuukm3X333XRjtoH33ntPH/jABySNl5qzJ9Ee2tvb9Ytf/EJf//rXVVxcbPVwAFtZvny53nvvPXV2dioQCOg3v/nNKb0hAfKFaZp65JFHtGjRIn3iE5+wejg4rr+/Xy6XS16vV6Ojozp8+LD++q//2uph5bUdO3Zox44dkqSOjg4988wzp/zvCmEXsKF/+Zd/0XvvvSfDMBQMBunEbBOPPfaYotGo7rzzTknSOeecw9xY7KWXXtI///M/q7+/X7t379ZZZ52lL3/5y1YPKy+5XC594Qtf0F133aV4PK5NmzZpyZIlVg8r791///169dVXNTAwoBtuuEHbt2/X5s2brR5WXnvttdf0/PPPa+nSpcnqumuvvVYXXnihxSPLbz09PXrooYcUj8dlmqY++tGP6kMf+pDVw8IZMkzTNK0eBAAAAAAAc4mjhwAAAAAAjkPYBQAAAAA4DmEXAAAAAOA4hF0AAAAAgOMQdgEAAAAAjkPYBQAAAAA4DmEXAIAc9cQTT+jb3/528uPGxkZ94xvfUDQatXBUAADYA2EXAIAc9dd//dfq6OjQW2+9pebmZrW3t+tLX/qS3G631UMDAMByhmmaptWDAAAAp+dnP/uZXnrpJUUiEX3jG99QMBhUJBLRnXfeqf/8z//UXXfdpaVLl1o9TAAAso6VXQAActgHP/hBvfPOO9qxY4eCwaAkqaioSLt27dJHPvIRi0cHAIB1CLsAAOSod955R48++qg2btyo/fv3Jx93u90qKyuzcGQAAFiPsAsAQA4KhUK655579F/+y3/R3//93+udd95RR0eH1cMCAMA2CLsAAOSYSCSiu+++W1dccYVqampUXFysT37yk/rJT35i9dAAALANGlQBAOBQDz30kD75yU/SoAoAkJcIuwAAONDdd9+tP/7xjwoGg7rssst0ySWXWD0kAACyirALAAAAAHAc9uwCAAAAAByHsAsAAAAAcBzCLgAAAADAcQi7AAAAAADHIewCAAAAAByHsAsAAAAAcBzCLgAAAADAcQi7AAAAAADHIewCAAAAABzn/wemdBeNT7h0aQAAAABJRU5ErkJggg==",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plot_ds(data,m[-1],q[-1])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Adagrad"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Adagrad introduce la possibilità di applicare learning rate diversi ai vari parametri da ottimizzare (dimensioni dello spazio di ricerca): in particolare, parametri per i quali si sono avuti nel corso dei passi precedenti valori elevati del gradiente avranno associati, tendenzialmente, learning rate più piccoli, in modo tale che l'aggiornamento dei prametri stessi sia limitato. Al contrario, in presenza di dimensioni (parametri) con valori del gradiente precedenti piccoli, e quindi poco modificate, il learning rate risulterà più grande, rendendo le modifiche delle componenti corrispondenti più sensibili ai valori del gradiente.\n",
"\n",
"Come visto, nella gradient descent \"base\" l'aggiornamento del coefficiente $k$-esimo è dato da\n",
"\n",
"$$\n",
"\\theta_j^{(k+1)}= \\theta_j^{(k)}-\\eta \\frac{\\partial J(\\theta, X)}{\\partial\\theta_j}\\Bigr\\vert_{\\small\\theta=\\theta^{(k)}}= \\theta_j^{(k)}-\\eta\\sum_{i=1}^n\\frac{\\partial J(\\theta;\\mathbf{x}_i)}{\\partial\\theta_j}\\Bigr\\vert_{\\small\\theta=\\theta^{(k)}}\n",
"$$\n",
"\n",
"dove $\\eta$ è lo stesso per tutti i coefficienti. In Adagrad, l'aggiornamento prevede un learning rate\n",
"$\\eta_{j}^{(k)}$, dipendente dal coefficiente e dal passo di applicazione del metodo, definito nel modo seguente\n",
"\n",
"$$\n",
"\\eta_{j}^{(k)} = \\frac{\\eta}{\\sqrt{G_{j,k}+\\varepsilon}}\n",
"$$\n",
"\n",
"dove $\\eta$ è una costante, $G_{j,k}=\\sum_{i=0}^{k}g_{j,i}^2$ è la somma dei valori $g_{j,i}=\\frac{\\partial J(\\theta, X)}{\\partial\\theta_j}\\Bigr\\vert_{\\small\\theta=\\theta^{(i)}}$ del gradiente relativo a $\\theta_j$ per tutte le iterazioni precedenti, mentre $\\varepsilon$ è una piccola costante di *smoothing* utilizzata per evitare denominatori nulli.\n",
"\n",
"Utilizzando il formalismo introdotto, l'aggiornamento di $\\theta_j$ alla $k+1$-esima iterazione è data da\n",
"\n",
"$$\n",
"\\theta_j^{(k+1)}= \\theta_j^{(k)}-\\frac{\\eta}{\\sqrt{G_{j,k}+\\varepsilon}}g_{j,k}\n",
"$$\n",
"\n",
"Come si può vedere, il learning rate diminuisce in modo monotono al procedere delle iterazioni per tutti i coefficienti. Al tempo stesso, coefficienti con elevati valori di gradiente nel passato (quindi soggetti a variazioni significative) avranno decrementi più elevati del learning rate, che quindi tenderà più rapidamente a $0$ e a modificare poco i valori di tali cofficienti, mentre coefficienti con valori limitati (che sono variati poco fino ad ora) manterrano un learning rate più alto.\n",
"\n",
"Dato che in ogni caso il denominatore cresce ad ogni iterazione, il learning rate continua a diminuire fino a raggiungere valori talmente piccoli da impedire un reale aggiornamento della soluzione."
]
},
{
"cell_type": "code",
"execution_count": 132,
"metadata": {},
"outputs": [],
"source": [
"def adagrad(X,t, eta = 0.1, G = 0, eps = 1e-8, epochs = 1000):\n",
" theta = np.zeros(nfeatures+1).reshape(-1,1)\n",
" theta_history = []\n",
" cost_history = []\n",
" for k in range(epochs): \n",
" g = gradient(theta,X,t)\n",
" G = G + g**2\n",
" theta = theta - eta * g / (np.sqrt(G) + eps)\n",
" theta_history.append(theta)\n",
" cost_history.append(cost(theta, X, t))\n",
" theta_history = np.array(theta_history).reshape(-1,3)\n",
" cost_history = np.array(cost_history).reshape(-1,1)\n",
" m = -theta_history[:,1]/theta_history[:,2]\n",
" q = -theta_history[:,0]/theta_history[:,2]\n",
" return cost_history, m, q"
]
},
{
"cell_type": "code",
"execution_count": 133,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"tempo di esecuzione: 0.562 secondi\n",
"10000 passi totali\n",
"1000000 gradienti calcolati\n"
]
}
],
"source": [
"start_time = time.time()\n",
"cost_history, m, q = adagrad(X, t, eta = 0.1, G = 0, eps = 1e-8, epochs = 10000)\n",
"print(f\"tempo di esecuzione: {time.time()-start_time: 4.3f} secondi\")\n",
"print(f\"{len(m)} passi totali\")\n",
"print(f\"{len(m)*n} gradienti calcolati\")\n"
]
},
{
"cell_type": "code",
"execution_count": 135,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABQgAAAGoCAYAAAAKMwiTAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAABfpUlEQVR4nO3deXQcd53u/6eqN6nVWt2yZFm2ZNmWl0ROnMWBbCRBZIPLzHiGMDCBGV8C9zIHyAXunck5d2KCDSfmx4UhDMwcwgWS3AEmCZgZJpBNCUkICXYSx1u8SLJiy7Ity5KsrbX0UvX7o6WW5CWRLXdXL+/XOTpdXdXLp6skdevR91sfw7ZtWwAAAAAAAABykul0AQAAAAAAAACcQ0AIAAAAAAAA5DACQgAAAAAAACCHERACAAAAAAAAOYyAEAAAAAAAAMhhBIQAAAAAAABADnM7XcBMHT161OkSZiUYDKq7u9vpMiCORTrhWKQPjkX64Fikj2w5FlVVVU6XkBR8NgT7cHbYf7PHPpwd9t/ssQ9nJ1f339k+GzKCEAAAAAAAAMhhBIQAAAAAAABADiMgBAAAAAAAAHIYASEAAAAAAACQwwgIAQAAAAAAgBxGQAgAAAAAAADkMAJCAAAAAAAAIIcREAIAAAAAAAA5jIAQAAAAAAAAyGEEhAAAAAAAAEAOIyAEAAAAAAAAchgBIQAAAAAAAJDDCAgBAAAAAACAHEZACAAAAAAAAOQwAkIAAAAAAAAghxEQAgAAAAAAADmMgBAAAAAAAADIYe5kPvhDDz2ktrY2LVq0SOvWrUusHxoa0oMPPqjBwUE1NDRo7dq1ySwDAAAAAAAAwFkkLSBsa2vT6OioNmzYoB/+8IdqbW3VkiVLJEmPP/64PvrRj2r+/PnJenoAAAAAAAAAM5C0gLClpUWrVq2SJDU0NKi5uTkREB4+fFi/+tWv1NPTo4997GOqr68/7f5NTU1qamqSJG3atEnBYDBZpaaE2+3O+NeQLTgW6YNjkT44FumDY5E+OBYAAADIFUkLCEOhkCoqKiRJfr9fHR0diW379+/XN77xDQUCAX3rW9/Sxo0bT7t/Y2OjGhsbE9e7u7uTVWpKBIPBjH8N2YJjkT44FumDY5E+OBbpI1uORVVVldMlAAAAIM0lLSD0+/0aHh6WJI2MjMjv9ye2VVVVqbq6WpJkmvRJAQAAAAAAAJyStHSuvr5eu3fvliTt2rVr2jTiefPm6eTJkxodHVUsFktWCQAAAAAAAADeRdJGENbV1cnj8Wj9+vWqra1VMBjU5s2btXbtWt1xxx164IEHFA6H9Rd/8RfJKgEAAAAAAADAu0haQChJ69atm3Z97dq1kqTq6mrdd999yXxqAAAAAAAAADPACQABAAAAAACAHEZACAAAAAAAAOQwAkIAAAAAAAAghxEQAgAAAAAAADksqU1KEPdvL7eqtfNNfeS9i7RsfonT5QAAAAAAAAAJjCBMgZFwTP2hMUViltOlAAAAAAAAANMwgjAFjPFL23a0DAAAAMf09vbqG9/4hjo6OvTII4/I5XIltrW3t+uHP/yhJOmuu+5STU2NU2UCAADkJEYQpoBpxiNCm4QQAADkqEAgoHvvvVdLly49bdujjz6qu+++W1/84hf16KOPOlAdAABAbmMEYQokRhA6WgUAAIBzvF6vvF7vGbeFQiEFg8HEMgAAAFKLgDAFDIMRhAAAAGczk89ITU1NampqkiRt2rQpEShmKrfbnfGvwWnsw9lh/80e+3B22H+zxz6cHfbfdASEKTCeD3IOQgAAgHcx8Y/VUzU2NqqxsTFxvbu7O1UlJUUwGMz41+A09uHssP9mj304O+y/2WMfzk6u7r+qqqozricgTIGJD7oWCSEAAMBpAoGAenp6ZBiG8vPznS4HAAAg5xAQpgDnIAQAALkuGo3q/vvv16FDh/T1r39df/EXf6F9+/Zp7dq1uuOOO/Sd73xHkvSpT33K2UIBAAByEAFhCkxOMSYiBAAAucntduvee++dtm7lypWSpJqaGm3cuNGJsgAAACDJdLqAXGAmmpQ4XAgAAAAAAABwCgLCFKBJCQAAAAAAANIVAWEKGKJJCQAAAAAAANITAWEKcA5CAAAAAAAApCsCwhQwJs5B6HAdAAAAAAAAwKkICFPA5ByEAAAAAAAASFMEhCmQGEFIQggAAAAAAIA0Q0CYAuMDCBlBCAAAAAAAgLRDQJgCk+cgJCEEAAAAAABAeiEgTAGDcxACAAAAAAAgTREQpsBkQEhCCAAAAAAAgPRCQJgChiamGAMAAAAAAADpxe10AblgYgShZRERAgAAAADgBNuypFhUsqKSZcW/7PEvy4rP+rMsyY5Jlp1Yn7iNpEQbUsMY/2N/yvVTL0235HLJMF2S6ZJc45cTy4aZ6FkAOI2AMAVMgxGEAAAAAACciW3b8eAuMiZFwrIj4fhyNCx7fF18fXzdtNvEolIsKnv8Mv4VkaJT10XGg0Hr3YtJKWMyNHR7JLdXhid+KY9PhtsjebyS2ze53uuT4c2XfPkaHaiQNRaR4YtflzdPhsFEUZwfAsIU4ByEAAAAAIBsZceiUnhUdnhUCo9KYyPx5YnL8KjssZFp245bEUWHh+LrIuEUdfU0JLd7chSfYUimKRmmZJrxcG3KdRlTl0/tPmqPjwKacjl1u21LVkyyYrJjsfioxVgssU6xWHxU4kSIGRnTlEc5bflMes70+rw+yeeXkeeXkR+Q8gPxS39ARn6hDH9Ayi+Mr/PlM4IRCQSEKTDxA0c+CAAAAABIZ3YkLI0Nyx4NSaPDskeHxy9D4+unbouvUyR8zs8TPXWFyz0+Ws4rw+OLL3t8MsbXJZZPXe/2SC63DJc7/hgut+TySO6p6zyJkXrpFIjZljUZFsYi8ZGR0TEpEpkyejIiRcfixyUalsJh2eFhaWxEbiumyFD/ePg6IoXH4oFreFT2YO+7z2I0XVKgREagWEagZNqXJpY93hTsCaQDAsIUmPj1Q0AIAAAAAEgl24pJIyHZI0PSyJDs4cHx5UHZw0Px5dFQPAgcG5aikXN/EsOUvHmSLy8+/dWbJ2PqdV/e+Lr8xLqSuZXqHxmN38/tk+FyXfgXn+YMc3x0otsjKS++7hzuHwwG1d3dnbhuW7HJUZqjw/FjO368py5PfB8oMiYN9Mge6Dl7mJgfkFE8R0ZRUEZxML48cenxne9LRxoiIEyBxAhCzkIIAAAAAJgl27bjod7wgOzQYDzsGxmSxgM/e3gwHgKNDEmjwzqnM+KbLimvQEaeX8rzy8griF/6/FPWxy+NPL/kK4ifF+8cR+Z5g0EZU8ItzJ4xfuyUVyCj+N1vb0fCsof6pKE+2ad8aag/fjn+fWR3Hjr9AfyFMkrKZZZVypj4Kq2Q4SU4zEQEhClw2qkKAAAAAAA4AzsSloYHZIfGv4YHpFD/KdcH4lNTZ8SIB0ZTzj03eU66iXWTwZ/c3rSahovkMTxeGaVzpdK5Z9xu25YUGpDd3y27v0d2/4nxy27ZA73xEYnDg4odbZt+x8LSydAwWCWzfIEUKOb7Ks0REKbAxA+BRUIIAAAAADnLjkZkh/qlwT7ZQycnR2yF4qGfHeqPTxGdCW+ejILi+Ciu/IAMf2F8Ouh4M4pEc4r8gvjIMuAcGYaZOBeh5i+Zts22LGmoT9bJLtm9nZNffSekwZOyBk9Kh/ZO3iE/ILN8voxgtYy51TLLq+Pfs0gbBIQpwDkIAQAAACC72bYdP/fbUDz801Cf7MFTpm0OD777A5mueOhXUCyjoEhGQZHkL0pcV0GRDH8RzSPgKMM0paIyuYrKpJrlifV2LCZ7oFt273HZPcdknTgi+0SHNDIkq32/1L5/8kEKS2VW1sqct0hGZa2MknJGGTqIgDAFOAchAAAAAGQ+OxKOd4cd6NHggTFFjh2WBnonQ8F36+ZrmlLBmTrGFsdDv4Ki+Pn+DDMlrwe40AyXS0ZphVRaIS1eJWk8PB88KetEh+wTHeOXRxIjDa2WN+N3ziuQWVkjY94imfMXyyibR2CYQgSEKWByDkIAAAAASHuJ5h8D8RAw/tWbuD51BODAmR7A45NROBH6lcYDwMKJILA0PjLQJPxDbjEMY3K04URoaFnxKcmdb8s6dlBW50FpeFDWwT3SwT2KSfFpydVLZVYvkTl/aTxAR9IQEKbAZJMSEkIAAAAAcJo9GpLdd2L8qzs+JXI8CFRk7Ox3NF0yCktlFM1RfsV8jXr8MopK4+sCpfHzAjLiCXhXhmnKCFZJwSq5Lr4mnpcM9MTDwmNtso60SqEBWS1vJkYYGmWVMqvrZdYsl1FZw7k1LzACwhSYbFLicCEAAAAAkCNsy4pPYew7Ibuva0ogeEIaDZ39jt48GUVzZBSVnXapguLECMCSYFDd3d0pejVAdjMMQyoOylUclGv5FbJtW3Zfl6zDLbKPtMg62ia7t1Ox3k7Fdr4k5fllLlwus3alzOp6zsl5ARAQpsBkkxISQgAAAAC4kOxoJB4A9nbFL/u7xwPBbsmKnflOHq+MkrnxpgglQRlFwfEgsEzy+RkFCDjMMAwZpRUySyukVdfKjkVldx6S1b5f1qE9svu7ZTVvk9W8TXK5Zc5fIrPuYpm1F8vw5TldfkYiIEyBySYlAAAAAIDzYdu2NHRSVk9n/NxlE5f93ZJtnflOBcXjIWC5zIlAsLQ83hWYEBDIGIbLLWP+YpnzF8t+z22y+07IOrhH1sE9srsOy2rfJ6t9n2T+SubCZTIXXyKzZgUjC88BAWEKmJyDEAAAAABmzI6EZfcck91zVNZEGHiyUwqf4fyAhjEe/FXIKJ2bCASN4nIZXl/qiweQVPHRhXNlls6VVt8ge7y5SezADtlH304Eh3J7ZdaukLlktcwFSzln4bsgIEwBczwhjHESQgAAAACYxo5F4yMBT3TI6uqQfaJD9smuM48KzA/EGxXMqZRRVimjbF48FHR7Ul84gLRg+AvlWnmVXCuvkh0aUKxtp6zWnbK72mW17pDVukPyF8lVf5nM5VfILA46XXJaIiBMAdf4SWwJCAEAAADkMtuy4o1CThyeDAN7jp1+rkDDjAeAwSoZc+bJLBsPBP2FzhQOICMYBUVyN1wrNVwre6BXsQM7ZO1/Q3Z/t2LbX1Bs+wsyKmvlWn6lrKIbnC43rRAQpoBrfAShRUAIAAAAIIfYoyFZnYdkdx6UdbxddvdRKRo+7XZGcVBGebWMudUyyxfImDOPc4cBmBWjqEzu1TfKvvQG2Z2HFNv/mqwDu2R3HlS086A6X31CZv3lcl30XhnFc5wu13EEhClgGkwxBgAAAJD97ME+WZ1vyzp2UHbnQdknj59+o0CJzEQYWC0jWE3XUQBJYxiGjHm1MufVyr76w7Ladiq29zXZXe2K7XpZsV1/kLlwWTwoXLBUhmE6XbIjCAhTIDGCkCYlAAAAALKIPTIk60irrI5WWUdapaG+6TdwuWXMXSCzslZGZU08EMwPOFIrABhen1zLr5Rr+ZUqioTU8/JvZR3YkeiCbBQH5Wq4RuayK3Lu3KYEhClAkxIAAAAA2cCOhOPThTtaZB1pjZ8/cCpvXjwMnFcrs3KRjPL5Mlz82Qkg/Xjn1chz40dkv+d2xfa9ptieV2X3dyv68n9IbzwnV8M1cq18j948cFLP/qFVQ6GwAgVe3XztEq1eUeV0+Rccv6lTwEVACAAAACBD2QO9ih3cI+vQXtmdB6c3FHG5ZcxbJHP+EpnVS+LnDszR6XkAMpORXyD36hvkuuQ6WW+/pdj2F2V3H1Fs69N64/fb9LPeOg1OOXXq0a4haa2yLiQkIEwBl0GTEgAAAACZwbYt2SeOyJoIBXs7p2w1ZJRXTwaCFTU5Nw0PQHYyTJdci1fJrGuQfaRV0e0v6vk3PNPCQUkaDI3pmZdbCQhx7hJTjDkHIQAAAIA0ZMeiso8cUOzQHlkH90rDA5MbPT6ZC5fJrFkpc8FSGXkFzhUKAElmGIaM6qXyVi9VaP+T0tjoabcZGj69G3umIyBMgUSTEkYQAgAAAEgTtm3J7jykWPObstp2SuEpfwQXFMusWSFX7UoZVXWcRxBATiosKpB6Tg8IA36vA9UkF7/lU4AmJQAAAADShdV3QgO7X1Z45x+kwZOJ9UZZpczalTJrV8oIzpcxfqokAMhVN1+7REe7hjQYGkusKyzw6eZrlzhYVXIQEKbAxDkICQgBAAAAOMEeGZJ1YKdiLW/K7jqsyMSGgmK5ll4qc+llMssqnCwRANLO6hVV0lrpmZdbNTQcVsBPF2PMAlOMAQAAAKSabVuy2ptl7d0i6/B+ybLiGzw++VdcocjCFfHpw3QdBoCzWr2iKisDwVMREKaAKzHF2HK4EgAAAADZzo6Mydq/TbHdf5Dd3x1faZjxRiNLL5NZs0Kl86rU3d3tbKEAgLRBQJgCE+cgZAAhAAAAgGSxB/sUe+sVxfZunWw4EiiR6+Kr5Vq6Woa/0NkCAQBpi4AwBWhSAgAAACBZrOPtiu18WdbbuyU7PmvJqKiRa9W18YYjpsvhCgEA6Y6AMAUmm5QwxRgAAADA7NmxmKy3dyu262XZXYfjK01T5uJL5Gq4VubcBc4WCADIKASEKUCTEgAAAAAXgm3FZO17XdE3n5eG+uMrfflyrbhKroveKyNQ7GyBAICMlNSA8KGHHlJbW5sWLVqkdevWJdZ///vf15EjR+T1etXY2Khrr702mWU4zmXGu4IxxRgAAADA+bBtW9ahvYpteVJ23wlJklFSLlfDNTKXXibD43W4QgBAJktaQNjW1qbR0VFt2LBBP/zhD9Xa2qolS5Yktn/hC19QZWVlsp4+rSTOQWgTEAIAAAA4N9bxdkX/+FvZnQfjK4rK5L7yFpmLG2QYpqO1AQCyQ9ICwpaWFq1atUqS1NDQoObm5kRAaBiGvve97ykQCOhTn/qUysvLk1VGWhjPB2XbkmXbMsfPSQgAAAAAZ2P3dyu69WlZbbviK/L8cl32frlWXiXDxdmiAAAXTtLeVUKhkCoqKiRJfr9fHR0diW2f/OQnFQgEtG/fPj3yyCP68pe/fNr9m5qa1NTUJEnatGmTgsFgskpNCZdpKGbZKiubI7eL//I5ye12Z/z3U7bgWKQPjkX64FikD44FAKfYI0OKvvGcrL1bJMuSXG65Gq6V69IbZPjynC4PAJCFkhYQ+v1+DQ8PS5JGRkbk9/sT2wKBgCRp+fLl+ulPf3rG+zc2NqqxsTFxvbu7O1mlpsREQNjVdUJej8vpcnJaMBjM+O+nbMGxSB8ci/TBsUgf2XIsqqqqnC4BwAzZkbBiu15WbPuLUmRMkiFz2eVyX3EzzUcAAEmVtICwvr5eTU1Nuvrqq7Vr1y7dcMMNiW3Dw8Py+/06evSoCgoKklVCWok3KrE4DyEAAACAaWzLktX8hqKvPSsND0iSzIXL5Fpzm8w5uXHedgCAs5IWENbV1cnj8Wj9+vWqra1VMBjU5s2btXbtWn33u99VKBSSYRi66667klVCWnFNNCqhkzEAAACAcVZ/t6LPPyq767AkyQjOl/s9t8mcv+Rd7gkAwIWT1DPbrlu3btr1tWvXSpLuueeeZD5tWnKNn3eQgBAAAACAbduy9m5V9NUnpGhEKiiOB4OLV9GZGACQcrS+SpGJxiSxmOVwJQAAAACcZA8PKvriL2W175MkmUsulfvaP5Hhy3e4MgBAriIgTBHPeEAYiTGCEAAAAMhVsYNvKfriZmk0JHnz5L7uz+RaconTZQEAchwBYYp43PHOxVGLEYQAAABArrHDY4q++p+y9r0uSTLmL5Hnho/QnRgAkBYICFPE446PIIwyxRgAAADIKVbnIUV+96g00Cu53HKtuVWuhqs51yAAIG0QEKbIxBRjAkIAAAAgN9ixmGLbnlPszd9Jti1jzjy5b/qozLJKp0sDAGAaAsIUcbvGpxhzDkIAAAAg61knuxR9/lHZ3UckGXJd+j65rviADBd/ggEA0g/vTikyMcU4wghCAAAAIGvZti3rrT8quuW3UjQiBUrkufEOmVV1TpcGAMBZERCmCFOMAQAAgOxmhwYUefEXsg83S5LM+svkvvrDMnx5DlcGAMA7IyBMkckmJUwxBgAAALKN1dupyG9+LA0PSD6/3Nf/mVx1DU6XBQDAjBAQpohn4hyEFiMIAQAAgGxidR5S5MmfSOFRGZW18jR+XEZBkdNlAQAwYwSEKTI5gpCAEAAAAMgWsfZ9ij77UykakVm7Uu73f0yG2+N0WQAAnBMCwhSZOAdhhCnGAAAgRz300ENqa2vTokWLtG7dusT673//+zpy5Ii8Xq8aGxt17bXXOlglMHOx5jcVffFxybJkLrtC7uv/TIbpcrosAADOGQFhirjd41OMGUEIAAByUFtbm0ZHR7Vhwwb98Ic/VGtrq5YsWZLY/oUvfEGVlZUOVgicm+jOlxV79QlJkuvS98m15lYZhuFwVQAAnB/T6QJyBV2MAQBALmtpadGqVaskSQ0NDWpubk5sMwxD3/ve97Rp0yadOHHCqRKBGbFtW9GtT0+Gg++5Xe6rbiMcBABkNEYQpghdjAEAQC4LhUKqqKiQJPn9fnV0dCS2ffKTn1QgENC+ffv0yCOP6Mtf/vJp929qalJTU5MkadOmTQoGg6kpPEncbnfGvwanObEPbctS31P/qvCbL0mGqZIP/bUKVl2T0houFL4HZ499ODvsv9ljH84O+286AsIUmehiHGEEIQAAyEF+v1/Dw8OSpJGREfn9/sS2QCAgSVq+fLl++tOfnvH+jY2NamxsTFzv7u5OYrXJFwwGM/41OC3V+9CORRV97t9kvb1bcrnlbvy4RqqWaSRDjyPfg7PHPpwd9t/ssQ9nJ1f3X1VV1RnXM8U4RSZGEMYsAkIAAJB76uvrtXv3bknSrl27VF9fn9g2ERwePXpUBQUFjtQHvBM7PKbIb38SDwe9efJ88FNy1a50uiwAAC4YRhCmiJsuxgAAIIfV1dXJ4/Fo/fr1qq2tVTAY1ObNm7V27Vp997vfVSgUkmEYuuuuu5wuFZjGHhlS5Lc/kd19RPIXynP7f5U5Z57TZQEAcEEREKbI5DkIGUEIAABy07p166ZdX7t2rSTpnnvucaIc4F3ZgycV+c2PZPd3S0Vz5P3gf5VRNMfpsgAAuOAICFPE6x4/B2GUgBAAAABId1bvcUV+8yNpeEDGnHny3P5fZfgLnS4LAICkICBMEZ8nHhCGozGHKwEAAADwTqzOQ4o89ZA0NiJj3iJ5bvlrGb48p8sCACBpCAhTxOuJ7+owIwgBAACAtBVr36/os/8qRSMya1bI3fhxGW6P02UBAJBUBIQpwghCAAAAIL3FWt5U9IXHJcuSuexyua9fK8N0OV0WAABJR0CYIpMBISMIAQAAgHQT27tV0Zc2S5Jcl7xPrqtulWEYDlcFAEBqEBCmiM/NFGMAAAAgHVlH2xR9+d8lSa6rbpP70vc5WxAAAClmOl1ArkiMIIwwxRgAAABIF/ZgnyLP/lSyLLlWXU84CADISQSEKeJxmzIkRS1blmU7XQ4AAACQ8+xoRJFn/p80GpJRvVSuq25xuiQAABxBQJgihmHI647vbhqVAAAAAM6ybVvRlzbL7j4iFZXJ8/6P0ZAEAJCzCAhTyOOmUQkAAACQDmK7XpbV8qbk9spz8ydl5PmdLgkAAMcQEKaQzzMxgpCAEAAAAHCK1dGi2B9/K0ly3/gRmXMqHa4IAABnERCmkHd8BOEYU4wBAAAAR9gDPYo0/VyybblW3yhXXYPTJQEA4DgCwhSaPAchIwgBAACAVLMjYUWe/n/S2LDMhcvluvIDTpcEAEBaICBMoYkRhOEIIwgBAACAVLJtW9EXHpfd2ymjpFzum/5ShsGfQwAASASEKcUIQgAAAMAZse0vymrbJXl8ct/8CRm+PKdLAgAgbRAQptBkQMgIQgAAACBVYu37FNv6tCTJfdNHZZbOdbgiAADSCwFhCiWmGDOCEAAAAEgJq++Eos/9myRbris+IFftSqdLAgAg7RAQphBTjAEAAIDUscOjij79/6TwqMxFF8l12Y1OlwQAQFoiIEwhr2diBCFTjAEAAIBksm1L0d89JruvS0Zphdw33EFTEgAAzoJ3yBTKGw8IR8MEhAAAAEAyxd54XtbBPZI3T55bPiHD63O6JAAA0hYBYQrleccDwkjU4UoAAACA7BV7+y3F3miSDEOexo/LKA46XRIAAGmNgDCFGEEIAAAAJJd18riiv3tUkuRac6vMBfUOVwQAQPojIEyhPK9bkjRCQAgAAABccPbYiKJPPSJFwjIXXyLXJdc7XRIAABmBgDCFEiMImWIMAAAAXFC2ZSn63L/JHuiRMWee3O/7cxmG4XRZAABkBALCFMr3MsUYAAAASIbYa8/IOrxfyiuINyXxeJ0uCQCAjEFAmEJ5nvgU49EIASEAAABwocQO7FRs+wuSYcabkhSWOV0SAAAZhYAwhfIYQQgAAABcUFbPUUVfeFyS5HrvB2XOX+xwRQAAZB4CwhTyuk2ZhhSJWYpZltPlAAAAABnNHg0p8vT/k6IRmfWXyXXx1U6XBABARiIgTCHDMOTzMIoQAAAAmC3biinS9HNp8KSM8mq5r/szmpIAAHCeCAhTLM8bPw/hCAEhAAAAcN76n/uF7COtUn5Anps/IcPtcbokAAAyltvpAnJN3sQIQhqVAAAAAOcl1rZLY1uflUyXPDffKSNQ7HRJAABkNEYQplh+olFJ1OFKAAAAgMxjR8KKvvqEJMn93ttlVtY6WxAAAFmAEYQplueJ73JGEAIAAADnLrbzJWmoX56KhTJWvtfpcgAAyAqMIEyxPC9NSgAAAIDzYQ/1K7b9RUlS8c1/KcPkzxkAAC4E3lFTzO+LjyAcHmOKMQAAAHAuolufkqIRmXUN8i2sd7ocAACyBgFhik0EhKGxiMOVAAAAAJnDOt4uq+VNyXTJfdVtTpcDAEBWISBMMUYQAgAAAOfGtm1FX4k3JnGtuk5GUZnDFQEAkF0ICFOsgIAQAAAAOCfWgR2yu9ql/IBcq290uhwAALIOAWGK+X0eSVKIgBAAAAB4V3YkrOgfn5QkudfcIsPrc7giAACyDwFhijGCEAAAAJi52M6XpFC/jGCVzPrLnS4HAICsRECYYokmJaM0KQEAAADeiT3Ur9j2FyVJ7vd+SIbJny8AACRDUt9hH3roIa1fv14/+clPTtsWDof16U9/Wjt37kxmCWmnIG9yBKFt2w5XAwAAAKSv6NanpGhEZl2DzKo6p8sBACBrJS0gbGtr0+joqDZs2KBoNKrW1tZp25977jktXLgwWU+ftrxul9wuQ1HLViRqOV0OAAAAkJas4+2yWt6UXG65r7rN6XIAAMhqSQsIW1patGrVKklSQ0ODmpubE9ui0ahaWlq0bNmyZD19WiugUQkAAABwVrZtK/rKE5IkV8O1MorKHK4IAIDs5k7WA4dCIVVUVEiS/H6/Ojo6EtteeOEFXXfddWppaTnr/ZuamtTU1CRJ2rRpk4LBYLJKTQm32514DUUFPvUPh+XNDygYLHa4stwz9VjAWRyL9MGxSB8ci/TBsQCcY7XukN3VLuUH5Fp9o9PlAACQ9ZIWEPr9fg0PD0uSRkZG5Pf7JUmxWEzbt2/X//yf//MdA8LGxkY1NjYmrnd3dyer1JQIBoOJ1+B1GZKkI8dPqMBFs5JUm3os4CyORfrgWKQPjkX6yJZjUVVV5XQJwDmxI2FFtzwpSXKvuUWG1+dwRQAAZL+kTTGur6/X7t27JUm7du1SfX29JKm/v189PT36+te/rt///vf6+c9/rqGhoWSVkZYKfJONSgAAAABMiu18SQr1ywhWyVx2udPlAACQE5I2grCurk4ej0fr169XbW2tgsGgNm/erLVr1+r++++XJD322GNavny5AoFAsspIS4G8+DkIh0YZPQgAAABMsIf6Fdv+oiTJ/d4PyTCSNp4BAABMkbSAUJLWrVs37fratWunXb/jjjuS+fRpqzA/HhAOjhAQAgAAABOiW5+SohGZdQ0yq+qcLgcAgJzBv+QcUJjvlURACAAAAEywjrfLanlTcrnlvuo2p8sBACCnEBA6gBGEAAAAwCTbthV95QlJkqvhWhlFZQ5XBABAbiEgdMBkQBh2uBIAAADAeVbrDtld7ZK/UK7VNzpdDgAAOYeA0AGMIAQAAADi7EhY0S1PSpLcV94iw+tzuCIAAHIPAaEDpnYxtmzb4WoAAAAA58R2vCSF+mUEq2Quu8zpcgAAyEkEhA5wu0z5fW5ZtjQ8FnW6HAAAAMAR9lC/YjtelCS5r/4vMgz+PAEAwAm8AzukMI9pxgAAAMht0a1PSdGIzLoGmfMWOV0OAAA5i4DQITQqAQAAQC6zjrfLanlTcrnlvuo2p8sBACCnERA6hEYlAAAAyFW2bSv6yn9KklwN18ooKnO4IgAAchsBoUMK872SpAECQgAAAOQYq3WH7K7Dkr9QrtU3Ol0OAAA5j4DQIcX+eEDYHxpzuBIAAAAgdexIWNEtT0qS3FfeIsPrc7giAABAQOiQkoJ4QNgX4hyEAAAAyB2xHS9JoX4Zwfkyl13mdDkAAEAEhI4hIAQAAECusYf6FdvxoiTJffWHZBj8OQIAQDrgHdkhxQXxqRR9w0wxBgAAQG6IbnlSikZk1jXInLfI6XIAAMA4AkKHFOZ5ZBqGQqNRRWKW0+UAAAAASWUdb5fVul1yueV+z21OlwMAAKYgIHSIaRoq9nskSf1MMwYAAEAWs21b0Vf+U5LkWnWdjMIyhysCAABTuZ0uIJeVFPh0MhRWX2hMwaI8p8sBAABIqoceekhtbW1atGiR1q1bl1jf3t6uH/7wh5Kku+66SzU1NU6ViCSxWrfL7jos+QvluvQGp8sBAACnYAShg4onGpUMM4IQAABkt7a2No2OjmrDhg2KRqNqbW1NbHv00Ud1991364tf/KIeffRRB6tEMtiRcPzcg5Lca26R4fU5XBEAADgVIwgdNNHJmCnGAAAg27W0tGjVqlWSpIaGBjU3N2vJkiWSpFAopGAwmFg+k6amJjU1NUmSNm3alLh9pnK73Rn/GmZq4KVfKxwakKdyocqvvvmCdS7OpX2YDOy/2WMfzg77b/bYh7PD/ptuRgHhRz/6Ud199926+uqrJUnbtm3Tww8/rAceeCCpxWW7Ev94J+MQnYwBAEB2C4VCqqiokCT5/X51dHQkttm2/a73b2xsVGNjY+J6d3f3hS8yhYLBYMa/hpmwh/oUfjU+elBrblNPT+8Fe+xc2YfJwv6bPfbh7LD/Zo99ODu5uv+qqqrOuP4dA8Lu7m51dXVJkjo6OrRnzx5J0vbt23X8+PELXGLuKQ3EA8LeIQJCAACQ3fx+v4aHhyVJIyMj8vv9Z7ydYRipLAtJFt3ylBSNyKxbJXPeIqfLAQAAZ/GOAeHvfvc7/eIXv5Ak/fKXv9Qvf/nLxLb58+cnt7IcMKcwHhD2DI46XAkAAEBy1dfXq6mpSVdffbV27dqlG264IbEtEAiop6dHhmEoPz/fuSJxQVnH22W1bpdcbrnfc6vT5QAAgHfwjgHhkiVLdPPNN+uZZ57RqlWrNG/ePEnxD3HXXnttSgrMZmWBeOfik0NhxSxbLpP/mAMAgOxUV1cnj8ej9evXq7a2VsFgUJs3b9batWt1xx136Dvf+Y4k6VOf+pSzheKCsG1L0Vf+U5LkWnWdjMIyhysCAADv5B0DwtWrV2v16tVavHixLrroIpWXl0uSLMuSadIAebY8blPFfq/6h8PqC41pTmGe0yUBAAAkzbp166ZdX7t2rSSppqZGGzdudKIkJInVukN212HJXyjX6hucLgcAALyLGaV8hw8f1u9+9zv19vbqs5/9rD7xiU/o+eefT3ZtOYFpxgAAAMgmdiSs6JZ4YxL3mltkeHwOVwQAAN7NjALCl19+WQUFBfrDH/6gaDSqefPmafPmzcmuLSdMjBrsGaRRCQAAADJfbMeLUmhARnC+zPrLnC4HAADMwDtOMZ4wNDSkwsJCbd++Xddff71qamr0gx/8INm15YTJgJARhAAAwFmf//zntWDBAtXW1mrhwoWqra1VZWWl02Uhg9hDfYrteEmS5L76v8gwOC0RAACZYEYBYTAY1M9//nMNDQ3ps5/9rPr6+hQIBJJdW06YnGLMCEIAAOCsK6+8UtFoVCUlJdq5c6e+973vqbCwUGVlZaqpqdFnPvMZp0tEmotueUqKRmTWrZI5r9bpcgAAwAzNKCD8q7/6Kz3++ONaunSp1qxZo5/97Ge66qqrkl1bTmAEIQAASBc7d+7U//k//ydx/cYbb9TWrVt166236tChQw5WhkxgHW+X1bpdcrnlfs+tTpcDAADOwYwCwjVr1ujyyy/XsWPH1NnZqTvvvJMuxhfI1IDQsm2ZhuFwRQAAIFcVFhbq4MGDqq2tlSQtXbpUDz74oP7qr/5Kc+bMcbY4pDXbthR95T8lSa5V18koLHO4IgAAcC5mFBB2dHTom9/8pjo7OyVJlZWV+ru/+zvNnz8/qcXlAr/PrUCeR0OjEfWHwioN0OUNAAA447/9t/+m733ve6qurlZtba2OHDkir9frdFnIAFbrDtldhyV/oVyrb3C6HAAAcI5mNAzwRz/6kU6ePKlrrrlG11xzjfr6+vTjH/842bXljLnF8VGEXf0jDlcCAAByWWVlpTZs2KDVq1err69PlZWVuueee5wuC2nOti3FXm+SJLnX3CLDwz+8AQDINDMaQdjW1qaPf/zjuvXW+LlEnnrqKf385z9PamG5ZG5xvtqOD6qrf0TL5pc4XQ4AAMhhpmnqqquu4nzTmDH7aJvsgR6poFjm0tVOlwMAAM7DjEYQBgIB7dy5U8ePH9fx48e1c+dOuhhfQBUl+ZKk432MIAQAAEBmie3ZKklyLb9ChulyuBoAAHA+ZjSC8KabbtJjjz2mN954I7Huox/9aNKKyjVzi+MBIVOMAQAAkEnskSFZB9+SDEOu5WucLgcAAJynGQWE119/vYqLi7Vz505J0iWXXKJVq1YltbBcMhEQHicgBAAAQAaJ7X9dsmIya1bICBQ7XQ4AADhPM5pivHHjRnV3d+tLX/qSvvSlL+nEiRP62te+luzackax3yufx6XhsaiGRiNOlwMAAAC8K9u2FNv7miTJXME5KwEAyGQzCgh7e3s1d+7cxPXy8nL19PQkrahcYxhGopMx5yEEAABAJrCPHJAGeqRAscwF9U6XAwAAZmFGU4wrKir0n//5nyorK5Nt23riiSdUUVGR7NpySmWJX4e7Q+o8OazFlUVOlwMAAAC8o9jeieYkV8owZzTuAAAApKkZBYR/8id/ou9///u6//77E+s+97nPJa2oXFRVViDphI6eDDldCgAAAPCO7OHBKc1JrnS6HAAAMEszblISDAa1bds2SdJll12mlStXJrWwXFNV5pckHe0ddrgSAAAA4J3F9r8hWVa8OUkBzUkAAMh0MwoIJWnlypWEgkk0rzQeEHaeHFbMsuRimgYAAADSkG1biu2LTy82V9KcBACAbEAKlSbyvW6VBXyKWrZO9I86XQ4AAABwRvHmJL1SoERmNc1JAADIBgSEaWT+nAJJ0pFezkMIAACA9BTbs0USzUkAAMgmvKOnkapSzkMIAACA9GUPD8o6tEcyTJqTAACQRQgI00i8k7F0lBGEAAAASEOxfa+PNydZLqOgyOlyAADABUJAmEaqx6cYH+4JybJsh6sBAAAAJk1tTuJaQXMSAACyCQFhGinye1VS4NVYJKau/hGnywEAAAAS7I5WafCkFCiRUb3U6XIAAMAFRECYZmrKA5Kk9u4hhysBAAAAJiWak6xYQ3MSAACyDO/saWZhsFCSdOgEASEAAADSgx0akHVob7w5ybIrnC4HAABcYASEaWYhIwgBAACQZmL7X5dsS2bNCpqTAACQhQgI08z8OQVymYaOnxzWaCTmdDkAAADIcbZlKbZ3vDnJSpqTAACQjQgI04zHZaqqzC9b0mFGEQIAAMBhdkeLNNQnFZbJqF7idDkAACAJCAjTUE15/DyEbx8fdLgSAAAA5LrY3onmJFfKMPjzAQCAbMQ7fBpaXBk/r0vb8QGHKwEAAEAuizcn2SeZNCcBACCbERCmobqKIhmSDnUNKhKznC4HAAAAOSq277Xx5iQrZfgLnS4HAAAkCQFhGvL73Kos9Stq2Wo/wTRjAAAApJ5tWfGAUDQnAQAg2xEQpqmJacYHOplmDAAAgNSzOprjzUmKymTMX+x0OQAAIIkICNMUASEAAACcZO0Zb06yfA3NSQAAyHK806epxHkITwwpHI05XQ4AAAByiB3ql9U+0ZzkcqfLAQAASeZO5oM/9NBDamtr06JFi7Ru3brE+p/85Cc6ePCgIpGIPvnJT2r58uXJLCMj+X1uzZ9ToI6ekNo6B7S8utTpkgAAAJAj4s1JbJmLLqY5CQAAOSBpIwjb2to0OjqqDRs2KBqNqrW1NbHtE5/4hL761a/qi1/8on71q18lq4SMt2x+iSRp35E+R+sAAABA7pjWnGTFGoerAQAAqZC0gLClpUWrVq2SJDU0NKi5uTmxze2OD1wcHR1VTU1NskrIeMsJCAEAAJBi1uFmaahfKppDcxIAAHJE0qYYh0IhVVRUSJL8fr86Ojqmbf/mN7+p1tZWff7znz/j/ZuamtTU1CRJ2rRpk4LBYLJKTQm3233Or6GsbI4KftesnsExRV15qiwNJKm63HI+xwLJwbFIHxyL9MGxSB8cC+Qqa+94c5IVNCcBACBXJC0g9Pv9Gh4eliSNjIzI7/dP2/6//tf/Uk9Pj7797W/r61//+mn3b2xsVGNjY+J6d3d3skpNiWAweF6vYem8Im1/u0ev7npb162cl4TKcs/5HgtceByL9MGxSB8ci/SRLceiqqrK6RKQQeyhvvHmJC6akwAAkEOS9i/B+vp67d69W5K0a9cu1dfXJ7ZFIhFJUl5ennw+X7JKyApMMwYAAECqJJqT1F4kI5/ZKwAA5IqkjSCsq6uTx+PR+vXrVVtbq2AwqM2bN2vt2rX6x3/8Rw0PD8uyLH384x9PVglZYdn8EhmGdKBzQCPhqPK9SW08DQAAgBxlWzHF9r0uSXKtpDkJAAC5JKlp07p166ZdX7t2rSTp7/7u75L5tFklkOdRXUWRDnQOaM/hk7p8cbnTJQEAACALWe37pVC/jKI5MqrqnC4HAACkEGcdzgANC8skSbsO9TpcCQAAALKVtXerJMmkOQkAADmHd/4McHFNPCDcf7RPY5GYw9UAAAAg29iDfbIO76c5CQAAOYqAMAMU+72qKQ8oGrNpVgIAAIALLtGcZBHNSQAAyEUEhBmioWaOJGnnwR6HKwEAAEA2iTcneU2S5FpxlcPVAAAAJxAQZohLastkSNpz+KRGwlGnywEAAECWsNr3ScMDMoqDNCcBACBHERBmiJICnxZXFilq2YwiBAAAwAUzvTmJ4XA1AADACQSEGeTyxeWSpDcOdDtcCQAAALKBPXhSVntzvDlJPc1JAADIVQSEGaShpkwet6m3uwbVPTDqdDkAAADIcPFzD9oy6y6WkV/gdDkAAMAhBIQZxOdxqWFhmSTpjbYTDlcDAACATEZzEgAAMIGAMMNcsSQ+zfj11hOKWbbD1QAAACBTWYf2ScODMkrKZcxb5HQ5AADAQQSEGWZxZZGChXnqC4W1t+Ok0+UAAAAgQ8X2bpFEcxIAAEBAmHFMw9B7llVIkl7df9zhagAAAJCJ7MFe2YdbJJdbrvrLnC4HAAA4jIAwA125pFxul6Hmo/00KwEAAMA5i+0db06y6GIZeTQnAQAg1xEQZiC/z63Vi4KSGEUIAACAc2PHYortf12S5FqxxuFqAABAOiAgzFDvHZ9mvLWlS6PhqMPVAAAAIFNYh/aONyeZS3MSAAAgiYAwYy0IBlRXUajRSEx/bO5yuhwAAABkiNjerZJoTgIAACYREGawGy6ukiT9fs8xRWOWw9UAAAAg3dkDvbI7aE4CAACmIyDMYMvnl6iyJF8DIxG92dbtdDkAAABIc/HRg7bMugYZeX6nywEAAGmCgDCDGYaRGEX4wltHZVm2wxUBAAAgXU1vTnKVw9UAAIB0QkCY4S5dNEelBV519Y9q+8Eep8sBAABAmrIO7ZFGhuLNSSprnC4HAACkEbfTBWB2XKapD1xSrcdeadMz2w/rktoyuUxyXwAAkD5GRkb0wAMPKBQKqbGxUe973/umbb/77rtVWloqSbrrrrtUXV3tRJlZL9GcZCXNSQAAwHQEhFngssXlen73UXUPjOr11m5dVT/X6ZIAAAASnnvuOV1zzTW65ppr9NWvflXXXHON3O7Jj6FFRUW67777nCswB9gDPTQnAQAAZ8VQsyzgMg3dfEn8P+1NOzvoaAwAANJKc3OzVq1aJdM0VVNToyNHjkzbPjQ0pK985St68MEHFQ6HHaoyu8X2viZJMhevkuGjOQkAAJiOEYRZ4pJFc/T8riPq7BvRH/Z16n0XVTldEgAAgCRpeHhY+fn5kiS/369QKDRt+8aNGxUIBLR582Y1NTXp9ttvP+0xmpqa1NTUJEnatGmTgsFg8gtPIrfbnbLXYMei6mx5Q5JU9p4PyJfh+25CKvdhNmL/zR77cHbYf7PHPpwd9t90BIRZwjQMffDyhfrRc/vVtOOILq8rVyDf43RZAAAgh/T19ek73/nOtHUlJSXy+/0aGRmR1+vV8PCwCgoKpt0mEAhIktasWaPf/OY3Z3zsxsZGNTY2Jq53d3df2OJTLBgMpuw1xA7slBUalFFaoYG8EhkZvu8mpHIfZiP23+yxD2eH/Td77MPZydX9V1V15gFlBIRZZHl1qZbPL9G+I316avth/cV765wuCQAA5JCSkpIznkvwiSee0K5du3T11Vfr0KFDmj9/fmJbNBqVbdvyeDzav3+/KioqUlhxbphoTuKiOQkAADgLAsIs81+urFHz0X5tbe7Se5dVaH5ZwbvfCQAAIIluuukmffe739VTTz2lxsZGud1ubd++XZZlqa6uTvfff7/y8vJUUFCgz3/+806Xm1Xs/m7ZR1oll1vm0tVOlwMAANIUAWGWmVucr2uWV+j3ezv1H1sO6r/fulIm/ykGAAAO8vv9uueee6atu/TSSxPL3/jGN1JcUe6gOQkAAJgJuhhnoQ9cWq1Ankdvdw1qa0uX0+UAAADAAXYsqtj+1yVJrhVXOVwNAABIZwSEWSjf69afXlUrSfrN6+3qHw47WxAAAABSzjq4RxoNySirkFGx0OlyAABAGiMgzFKrasq0srpUo5GY/n3L206XAwAAgBSL7dkiKT56kOYkAADgnRAQZinDMPRn76mVz21qd/tJ7TjY43RJAAAASBGrv1v20QOS20NzEgAA8K4ICLNYSYFPH7yiRpL0y1fb1Bcac7giAAAApIK1d6ukieYk+Q5XAwAA0h0BYZZ7T/1cragu0Ug4pkdfPiDLtp0uCQAAAEkUb07yhiSakwAAgJkhIMxyhmHoI1fXqSDPrdbOAb301jGnSwIAAEASWW+/Nd6cpFLG3AVOlwMAADIAAWEOKMz36o6rF0uSnnrzsNpPDDlcEQAAAJIltne8OclKmpMAAICZISDMESsXlOqa5ZWKWbYeeaFZQ6MRp0sCAADABWb1nZB9tC3enGQJzUkAAMDMEBDmkA9dsVA15QH1D4f10xdbFLM4HyEAAEA2mWxOcokMX57D1QAAgExBQJhD3C5Tn3hfvQJ5HrV2DuipN9udLgkAAAAXiB2LKtY83pxkJc1JAADAzBEQ5pjiAq/ufN9SmYb0wu5jeq21y+mSAAAAcAFYb++WRodlzJkno7za6XIAAEAGISDMQYsri/Qna2olSb945W21Hut3tiAAAADMWmzPeHOSFTQnAQAA54aAMEddvbxS16+cJ8u29fDvmnW8b9jpkgAAAHCerL4Tso+9Lbm9Mpde6nQ5AAAgwxAQ5rAPXrFQFy8s02gkph817VNfaMzpkgAAAHAerL3x0YPmkktkeGlOAgAAzg0BYQ4zDUMfu26xFpYHdDIU1oPP7NXQSMTpsgAAAHAO7GhEsf3bJEmuFWscrgYAAGQiAsIc53W79Kn3L9e8Ur9ODIzqwWf3angs6nRZAAAAmCHr7d3S2LCMYBXNSQAAwHkhIIT8Prc+/YHlKi/K07GTw/pR0z6NhAkJAQAAMkFs71ZJNCcBAADnj4AQkqTCfK8+c/MKlRZ41d49pAefYSQhAABAurNOdk02J1lyidPlAACADEVAiISSAp/++60rVRbwqaMnpH95eo8GR8JOlwUAAICzmGxOcinNSQAAwHkjIMQ0ZYE8/e2tF2lucZ46Tw7rX57aQ3djAACANGRHI4o1jzcnWUlzEgAAcP4ICHGa4gKvPnvLRYnGJd/77Vs62htyuiwAAABMYbXtlsZGZATny6Q5CQAAmAUCQpxRIN+j/37LSi2aW6j+4bD++ak92n+kz+myAAAAMC42Pr3YtYLRgwAAYHYICHFWfp9bn755hS6pnaOxSEw/fm6ftrZ0OV0WAABAzrNOHpfdeVDyeGUuudTpcgAAQIYjIMQ78rhMffz6Jbrx4ipZtvT4K236j60HFbMsp0sDAADIWdaerZIkc8lqGV6fw9UAAIBMR0CId2Uahm6/fKH+4r2L5DINvby3Uw8+s5cOxwAAAA6INyd5QxLTiwEAwIVBQIgZu6q+Qv/9lpUqyveo7figHnhit9pPDDpdFgAAQE6x2nZK4VEZ5dUyy+c7XQ4AAMgCBIQ4J7VzC3X3hxpUO6V5yQu7j8qybadLAwAAyAmxvfHpxYweBAAAFwoBIc5Zkd+r/3bzCl27olIxy9Zv3mjXj5r2aYApxwAAAEll9R6X3XlI8vhkLrnE6XIAAECWICDEeXG7TP3Jmlqtu2mZ/D63mo/269u/3qm9HSedLg0AACBrWXu3SJLMpZfK8NCcBAAAXBgEhJiVlQtK9aUPr9KSeUUKjUb14+f267E/HNDwWNTp0gAAALKKHQkr1rxNkuRacZXD1QAAgGxCQIhZK/Z79ekPrNAHL18ot2notdYT+tZ/7NBb7b1OlwYAAJA1rLZd8eYkcxfIDFY5XQ4AAMgiBIS4IEzD0A0XV+mLH16lmvKABkYieuh3zfrZSy0aGok4XR4AAEDGi41PL6Y5CQAAuNDcyXzwhx56SG1tbVq0aJHWrVuXWP/ggw/q8OHDkqS77rpLNTU1ySwDKTS3OF9/e+tF+sO+Tj257bDefLtH+4706ZbVC/Te+gqZpuF0iQAAABnH6umUfbxd8vpkLqY5CQAAuLCSNoKwra1No6Oj2rBhg6LRqFpbWxPb/vRP/1QbN27U3/7t3+rxxx9PVglwiGkaum7lPH3pw6tUX1WskXBM/77loL77m1062DXodHkAAAAZZ2L0oLlktQyP1+FqAABAtknaCMKWlhatWrVKktTQ0KDm5mYtWbJEkjR37lxJksvlkmmeOaNsampSU1OTJGnTpk0KBoPJKjUl3G53xr+GcxUMSvcsmq9trZ36+e/26EjvsL7/5Fu65qJq/fk1y1RamO9IXbl4LNIVxyJ9cCzSB8cifXAskC7sSFhWy5uSJNdKphcDAIALL2kBYSgUUkVFhSTJ7/ero6PjtNv87Gc/0+23337G+zc2NqqxsTFxvbu7OzmFpkgwGMz413C+ako9+tKHL9bzO4/qhbeO6g9vdWjrvqO6bmWlbri4SvnepM50P00uH4t0w7FIHxyL9MGxSB/ZciyqqmhmkemsAzsnm5PM4XgCAIALL2lTjP1+v4aHhyVJIyMj8vv907b/5je/UXV1tZYvX56sEpBGvG6Xbr1sgf7nn1yiVTVlisQsPb/rqDZt3q6X9x5TNGY5XSIAAEBaiu3dKklyrbjK4UoAAEC2SlpAWF9fr927d0uSdu3apfr6+sS2HTt2aP/+/frzP//zZD090lSwKE+fuKFen7v9Ii2aW6jhsaj+Y+sh/X//vkNbW7oUswgKAQAAJlg9x2R3tUvePJmLVzldDgAAyFJJCwjr6urk8Xi0fv16maapYDCozZs3S5J+/OMf68SJE/rqV7+qBx98MFklII3VlBfqs7eu1N/cWK+5xfk6OTSmx19p0zd+tUNbmrsYUQgAACAptme8OclSmpMAAIDkSerJ39atWzft+tq1ayVJDzzwQDKfFhnCMAxdtLBMK6pLteNgj5p2dqirf1S/eLVNz+3s0E2r5uvyxeXyuJKWYwMAAKQtOxKW1TrenITpxQAAIIlS2x0COAPTNLS6LqhLaueMB4VH1NU/ol+++raefrND166o1HuXVcjv49sVAADkDuvADik8JqNiocw5lU6XAwAAshiJC9LG1KBw56EePb/rqI6dHNZTbx7Wc7uOaM2SubpuZaXmFOY5XSoAAEDSTTYnWeNwJQAAINsRECLtmKahSxfFg8KWYwN68a2jaj7arz/s69Qr+zt10YIyXbO8Qosri2QYhtPlAgAAXHBW91HZXYfjzUnqaE4CAACSi4AQacswDNVXFau+qlhHe0N6ac8xbX+7R7vbe7W7vVflRXl677IKXbGkXPlevpUBAED2SIwerL+M5iQAACDpSFWQEarKCvSX1y7RbZct1NaWLv1x/3GdGBjVr187pCe3Hdbqujl6T32FqucUMKoQAABkNDsyJqsl3pzEZHoxAABIAQJCZJRiv1cfuKRaNzVUac/hPr26/7hajvVra8sJbW05ocqSfF2xpFyr64Iqyue/7QAAIPNYrTukyJiMihqZZTQnAQAAyUdAiIzkMk011JSpoaZMJ/pH9GrzcW070K3OvhE98Xq7fvtGu5bNL9EVS8q1srpUbpfpdMkAAAAzkphevJLRgwAAIDUICJHxyovz9eEra3X7ZQu170ifXm89ob0dfYkvv8+thpoyXVo7R3UVRU6XCwAAcFZW9xHZJzpoTgIAAFKKgBBZw+0ydfHCMl28sExDIxFta+vWawdOqPPksLY0d2lLc5cK8z1as2y+ls0rUE15QCbnKwQAAGkktmdKcxK3x+FqAABAriAgRFYK5Ht0/UXzdN3KSh07OawdB3u0/e0e9Q6N6bntB/Xc9vj5DC+pnaOGmjItDAZkmoSFAADAOXZkTFbreHOSlVc5XA0AAMglBITIaoZhqKqsQFVlBbp19QJ19IS0v3NYW/Z1qC8U1kt7jumlPccUyPNo5YISXbSgTEvnFcvj5pyFAAAgteLNScIyKmtlllY4XQ4AAMghBITIGYZhaEEwoNXLa3XTReVqPzGkHQd79Nbhkzo5NJbohOxxm1pWVayLFpRpRXWJCvKY3gMAAJIvtmeLJMm1guYkAAAgtQgIkZNMw1Dt3ELVzi3Uh6+s0bGTw3rr8Em91X5SR3pD2t1+UrvbT8owpAXBgJZVlWj5/GJVz2EqMgAAuPCsEx2yu49IvnyZdQ1OlwMAAHIMASFy3tRpyB+4pFp9obFEWNh2fEDtJ4bUfmJIz+7okN/nVv28Yi2bX6L6+cUqyvc6XT4AAMgCsb00JwEAAM4hIAROUVLg0zXLK3XN8kqNRWI60DmgfUf6tP9In3qHxrT9YI+2H+yRJM0r9WvJvCItqSzWoopC5Xv5kQIAAOfGDo/Jat0uSTJX0JwEAACkHmkG8A58HpdWLijVygWlsm1b3YOj2n+kX/uP9OlA54COnRzWsZPD+v2eThmGVF1WoMXzirS4sliL5hbK53E5/RIAAECas1q3T2lOMtfpcgAAQA4iIARmyDAMlRflq7woX9euqFQkZulQ16BaOwd0oDM+FflwT0iHe0J6YfcxmYahBcECLa4sUu3cQtWUF8rv40cOAABMl5hevJLRgwAAwBmkFcB58rhMLZlXrCXziiVJY5GYDnYN6kDngFo7+9XRE9KhE0M6dGIocZ+KkvxEc5Ta8kLNKfTJMGh6AgBArppsTuKXuehip8sBAAA5ioAQuEB8HpeWzS/RsvklkqTRcFRvjweGB7sG1dET0vG+ER3vG9GW5i5JUiDPkwgMa8oDml9WII/bdPBVAACAVIrt2SKJ5iQAAMBZBIRAkuR53VpRXaoV1aWSpEjMUkdPSAe7BnWwa1CHugY1NBrR7vZe7W7vlSSZhqHK0nwtmBPQgmBAC4IFqijxy2UyyhAAgGxjh0dlte6QJJkr1jhcDQAAyGUEhECKeFymFs0t1KK5hZIUb3oyMBoPDE8Mqr07pON9wzraG//a0tKVuF9VmV8LggEtDAZUPadAc4ryZDI1GQCAjGa1bpeiYRnzFtGcBAAAOIqAEHCIYRgqL85XeXG+rlwa/6MgHImpozekw90hdXQP6XDPkHoGx047l6HXbWpeqV9VZQWaXxa/rCzxMz0ZAIAMYdv25PTiFTQnAQAAziIgBNKI1+NSXUWR6iqKEutCoxF19IR0uDveJbmje0gDI5HTQkPDkOYW5atqPDCcuAzkcT4jAADSTeTYQdk9x6Q8v8w6mpMAAABnERACaa4gzzOt+YkkDY1Gxqcih3T0ZPzyRP+Ijo9/vfl2T+K2gTyPKkvyVVHiV0VJvipL/aosyVe+lx9/AACcEtr2oiTJVX+5DBfvyQAAwFl8GgEyUCDPo/qqYtVXFSfWRaKWOhPnMIwHh8d6Qxoajai1M6LWzoFpj1GU71Fl6XhoWBIPDeeW+JXncaX65QAAstybb76phx9+WIWFhdq4ceNp23//+9/r6aefViAQ0Be+8AX5/X4Hqkwde2xUI3u2SqI5CQAASA8EhECW8LjN8c7HgcQ6y7bVHwqrs29YnX0j6jw5rON9I+rqH9HASEQDI/1qPto/7XGK/V6VF+epvChfc8cvy4vzVFLgozEKAOC8LF26VN/85je1YcOG07ZFo1E9++yz+upXv6otW7aoqalJH/7whx2oMnWs1jdlR8IyqupklpQ7XQ4AAAABIZDNTMNQacCn0oBPK6pLE+sty1bv0Jg6++KB4cRlV/+I+ofD6h8Oq/XY9BGHbpehYFG+5hZNhoYTl0xXBgC8k0AgcNZtnZ2dWrhwoVwulxoaGvSDH/zgjLdrampSU1OTJGnTpk0KBoNJqTXZbNtWV/MbkqSSNY3yZ+jrSAdutztjvw/SAftv9tiHs8P+mz324eyw/6bjr3ogB5mmoWBRnoJFebp44eT6mGXr5NCYTgyMqKt/VCcGRnSif0QnBkY1OBJR58lhdZ4cPu3xAnkezSn0aU5h3pTL+HIgzyODkYcAgLMIhULKz8+XJPn9foVCoTPerrGxUY2NjYnr3d3dKanvQrNtW8bVH1ZB+x6Fggs1nKGvIx0Eg8GM/T5IB+y/2WMfzg77b/bYh7OTq/uvqqrqjOsJCAEkuKYEhyuqp28bCUfVPTCqrvHAcCI4PDEwoqHRiIZGI9O6Kk/wuk2VFeZpTuD0ALGk1ErRKwMApEJfX5++853vTFtXUlKi//E//sdZ7+P3+zUyMiJJGhkZUUFBQRIrdJ5hGDIqFqrkosty8o8SAACQnggIAcxIvtd92jkOpfh5DgeGw+oZHFXP4Nj45eTySDh21pGHprFDxQVelRZ4E1OhSwt8Kgv4VFLgU0mBV26XmaqXCACYpZKSEt13333ndJ958+bp8OHDsixLO3fu1NKlS5NTHAAAAM6KgBDArJiGMR7m+bS48vTtw2PR00LDieX+4bBODo3p5NCYdHzwtPsakor8XpWMB4gTweHksldeN12XASDdHThwQD/72c90+PBhbdy4UX//93+vPXv2yLIsXXbZZXr/+9+v9evXq6CgQHfffbfT5QIAAOQcAkIASeX3ueX3nT7yUJKKS0rVeuioTobGdHJoPCwMjSUuJxqm9A+Hzzh9WZIKfG4VF3hV7I9/lRT44stT1vk8hIgA4KTFixfr3nvvnbbu0ksvTSxff/31uv7661NcFQAAACYQEAJwjMftUnlxvsqL88+4PWZZ46MMTw8PTw6NqS8UVmgsqtBYVEd7T5/CPCHP40oEhiWJ4NCn4gKvSvxeFfm9yve6aKYCAAAAAMhJBIQA0pbLNFUWyFNZIO+M2y3bVmg0ov7hsPpC46MNQ5OjDvtCY+oPhTUaiWm0b0TH+0bO+lxul6HCfK+K8j2JyyK/V4X5nvg6f3xdQZ5HJkEiAAAAACCLEBACyFimEQ/1CvO9qp5z5tvYtq3hsaj6poaHobD6hsemBYrhqDV5PsR3fE4pkDc1PPSq0D9+mT95GcjzyOOmwQoAAAAAIP0REALIaoZhqCAvPvJvflnBWW83FolpYCSsweFI/HIkfjkwHEksD45ENDwW1cBIRAMjkXd9bp/bVEGeR4F8jwrz4qFhIM+jQL57cnl8u9/rlmkyMhEAAAAAkHoEhAAgyedxqdyTr/KiM58PcUI0Zp0SHk6EifHlgeGIhkbjX2NRS2NDY+p9l1GJkmQYUoHPo0CeOxEaTg0RC/LcKvC5VZDniTd+IVAEAAAAAFwgBIQAcA7cLlOlAZ9KA753vJ1t2xqNxDQ0MhEYRhPB4eBIRKHRySBxaDSq4bHJ7dLZz5U4wZCU73PL7xsPDn3xEDFxfTxIJFQEAAAAALwbAkIASALDMJTvdSvf6z5rl+apYpY1GSJOCxXDGhqJKjQWn94cGosqNBrRSDim4bF4sNg905oUDxULEsFiPFTM97oVLD0pOzomvy9+feplnsdFsAgAAAAAWYyAEADSgMs0Vez3qtjvndHtY5atkXBUodEp4eHZls8QKp7u2Fmfy5CU53VNCw7zva4zhon5Xld8ZKPXrXyfWz63KYOuzwAAAACQ1ggIASADuUwjcX5C6d1HKErTQ8Xhsch4cBjVcDgquTzq6RvUyFj8+shYTCPheJg4GolpJBz/msn5FKcyDUP5Ppf8XrfyvC7leeIhYp43PjIxsex1Kd8zZXn8toxeBAAAAIDkIyAEgBzxTqFiMBhUd/eZJytb48HixAjE+HJ0fHlyXeIyHEsEjZGoFR/NOHqmUYsz4/O4lOdxJUYxTgsW32E5z+uSz+OSz03ICAAAAADvhIAQAPCOTNNQQZ5HBXmec75vNGYlRiSORuKB4mh4clTiaDiq0XBMI5EzL49GYhob/+ofPv/X4HWbiaDRN+Ur75TL05dN+Txu+Tym8jwueT0umUyZBgAAAJBlCAgBAEnjdpkqyveqaGazoE9j2bbGIrF4cDgeLJ59eTyAHF8ei1gajcQUjsQUjloKRy0NjkRm/Zp842HjmQPFqQGkKa/blQgnve4zr3MxuhEAAACAwwgIAQBpy5zSDbpUvvN6DMu2FY5aiZGIY5HJkYlTRyiOhk9fd9r1qJX40gUIGyXJbRryelzyuePhYUG+T6asyXWe8UDR7Zq2zjceNE69r88Tv53bbTLSEQAAAMCMERACALKaaRjxcxJ6XLN+LMu2FY7EEqMTzxYohqPx28QvJ0Ywnr5uLBpT1LIVHYtqeKL/S//IrOuU4tOqJ0Yret2mPFOue1zxZc/4tvh2l7yuM9x2yu2nbmPkIwAAAJA9CAgBAJgh0zDGOy1LxRfg8WzbVjRmx0PDaEzhiKX8gkId7+5993Bx6raoFQ8uxx8jErMS06qTxWUa48Hh9LDR4zbldU0NEye3n3p7j2sygDx12T2+TBAJAAAAJB8BIQAADjEMQx63IY/bVIHiTWCCwVIVe2OzelzLshWOxUPEyHiIOBEaTlxPLMfGt0etROAYiU4NGadum1gfU8yyFbPiIyalCzPd+kxMw5gSHE4uu98hXPS4x7ef7TbvsM5lGjKYng0AAIAcQ0AIAECWMU1DeeaFmVZ9JrZtK2bZ0wPERAA5JXyMWorEJpvETAsnY1YiiJxYjsZOXz/RqGYsMrvQdKYMKTF60edx60v/5WLlefm4BAAAgOzGJ14AAHBODMOQ22XI7TLl9yXvo8REEDkRFkZPCRTPFDJGYnY8aDzTbd8hiJxYjll2fDlqaXgsKpfLTNrrAwAAANIFASEAAEhLU4PI/BQ9p2XZiQAxUFQia2woRc8MAAAAOId/iwMAAIwzTUNej0sFeR7NKcrnfIQAAADICQSEAAAAAAAAQA4jIAQAAAAAAAByGAEhAAAAAAAAkMMICAEAAAAAAIAcRkAIAAAAAAAA5DACQgAAAAAAACCHERACAAAAAAAAOYyAEAAAAAAAAMhh7mQ++EMPPaS2tjYtWrRI69atS6zfvHmznn76ad144436y7/8y2SWAAAAAAAAAOAdJG0EYVtbm0ZHR7VhwwZFo1G1trYmtt100036/Oc/n6ynBgAAAAAAADBDSQsIW1patGrVKklSQ0ODmpubE9tKSkpkGEaynhoAAAAAAADADCVtinEoFFJFRYUkye/3q6Oj45zu39TUpKamJknSpk2bFAwGL3iNqeR2uzP+NWQLjkX64FikD45F+uBYpA+OBQAAAHJF0gJCv9+v4eFhSdLIyIj8fv853b+xsVGNjY2J693d3Re0vlQLBoMZ/xqyBccifXAs0gfHIn1wLNJHthyLqqoqp0sAAABAmkvaFOP6+nrt3r1bkrRr1y7V19cn66kAAAAAAAAAnKekBYR1dXXyeDxav369TNNUMBjU5s2bJUnPP/+8HnnkEf3+97/X//2//zdZJQAAAAAAAAB4F0mbYixJ69atm3Z97dq1kuJdjG+66aZkPjUAAAAAAACAGUjaCEIAAAAAAAAA6Y+AEAAAAAAAAMhhBIQAAAAAAABADiMgBAAAAAAAAHIYASEAAAAAAACQwwgIAQAAAAAAgBxGQAgAAAAAAADkMAJCAAAAAAAAIIcREAIAAAAAAAA5jIAQAAAAAAAAyGEEhAAAAAAAAEAOIyAEAAAAAAAAchgBIQAAAAAAAJDDDNu2baeLAAAAAAAAAOAMRhCmyD333ON0CRjHsUgfHIv0wbFIHxyL9MGxQDLx/TV77MPZYf/NHvtwdth/s8c+nB3233QEhAAAAAAAAEAOIyAEAAAAAAAAchgBYYo0NjY6XQLGcSzSB8cifXAs0gfHIn1wLJBMfH/NHvtwdth/s8c+nB323+yxD2eH/TcdTUoAAAAAAACAHMYIQgAAAAAAACCHERACAAAAAAAAOcztdAG54KGHHlJbW5sWLVqkdevWOV1OVuvt7dU3vvENdXR06JFHHpHL5Trj/p/pOpy/lpYWPfzwwzIMQ4sXL9bf/M3f6Ne//rVee+01lZeX62//9m/ldrtnvA7nr729XQ8++KBM01RlZaU++9nP6uGHH+bnwkFPPPGEtmzZoo0bN/I7yiFdXV363//7f2v+/Plyu936h3/4B35HIWXO9HkFM3emzxiYuTN9LjAMw+myMtLU93PM3Jneg3HuXnzxRb344ouyLEtf+MIXVFZW5nRJGWP79u3693//d0nS0aNHddddd2nNmjXOFpUGGEGYZG1tbRodHdWGDRsUjUbV2trqdElZLRAI6N5779XSpUslnXn/z3QdZqe8vFzr16/Xxo0bNTAwoD179uitt97Sxo0btXDhQr322mvq7++f0TrMTlVVlb72ta9pw4YNkqTW1lZ+LhwUiUR08OBBSfyOclpDQ4Puu+8+/cM//MOMfx/xOwoXwqmfV3BuTv2M0d7e7nRJGeXUzwUHDhxwuKLMNPX9HOdu6nswzl1vb6/27Nmj9evX67777iMcPEeXXnqp7rvvPt13330KBoNatWqV0yWlBQLCJGtpaUl8szU0NKi5udnhirKb1+tVIBBIXD/T/p/pOsxOSUmJvF6vJMnlcunw4cNauXKlJGnVqlVqbm7WgQMHZrQOszN1dJPb7dauXbv4uXDQ888/rxtuuEESv6Oc9tZbb2n9+vV64oknZvz7iN9RuBBO/byCc3PqZwzT5E+ac3Hq54JgMOhgNZlr6vs5zt3U92Ccu+3bt8uyLG3YsEE//vGPZVmW0yVlpOPHj6u4uFh5eXlOl5IWeDdNslAoJL/fL0ny+/0aHh52uKLccqb9P9N1uDAOHTqkgYEBFRQUKD8/X1J8H4dCIQ0PD89oHWbv9ddf15e//GX19/crFovxc+GQaDSqt956SxdffLEkfkc5qbS0VA888IC+8pWvaNeuXWpra+N3FJBhJj5jVFdXO11Kxpn6uYCw+tyd+n6Oc3Pqe/ChQ4ecLinj9Pf3KxqNav369fJ6vcxoOE9btmxhavEUBIRJNvUPuZGRkcQfeEiNM+3/ma7D7A0NDenHP/6xPvvZz8rv92tkZESSNDw8rIKCghmvw+xdccUV+ta3vqU5c+bI5XLxc+GQl156Sddee23iOr+jnOPxeJSXlyeXy6XLL79cFRUV/I4CMsjUzxg4d1M/F2zbts3pcjLOqe/nODenvgcfPnzY6ZIyjt/vT8xouPjii3XkyBGHK8pMb7zxhq644gqny0gbBIRJVl9fr927d0uSdu3apfr6eocryi1n2v8zXYfZicVi+qd/+id94hOfUElJiRYvXqw9e/ZIiu/jpUuXzngdZicSiSSWJ0Y+8XPhjKNHj+rZZ5/V17/+dXV0dGhwcJBj4ZCJkE+S9u3bp8rKSn5HARni1M8YODenfi6YmK6NmTv1/fzJJ590uqSMcup7cEVFhYPVZKZly5YlRl4ePHhQc+fOdbiizNPX1ye3263CwkKnS0kbtN1Lsrq6Onk8Hq1fv161tbVasmSJ0yVltWg0qvvvv1+HDh3S17/+dX3sYx874/6f6Tqcv1dffVWtra3613/9V0nSxz/+ca1YsUL33nuvgsGgPvjBD8rtds9oHWZn+/btifO7zJs3T5/5zGf08MMP83PhgDvvvDOxfO+99+ojH/mIfvKTn3AsHLB37149+uij8ng8Wr58uZYuXcrvKKTMmT6vEDbP3Jk+Y/CPk5k79XMBJ+c/d6e+n992220OVpN5zvQejHNTW1srr9er++67T4WFhfrQhz7kdEkZ57XXXtOVV17pdBlpxbBt23a6CAAAAAAAAADOYIoxAAAAAAAAkMMICAEAAAAAAIAcRkAIAAAAAAAA5DACQgAAAAAAACCHERACAAAAAAAAOYyAEEBW6urq0h133KFNmzZp27Zteuyxx9TV1XXBn6ejo0OPPfaY3nrrrcS673//+7rjjjt04MCBC/58AAAAAABcaG6nCwCAZCgqKtLdd9+tsrIyvfLKK3r66ad10UUXae7cuef0OLFYTC6X66zbOzo69Itf/EKSdNFFF0mSbr75Zl166aWqqKg4/xcAAAAAAECKGLZt204XAQAXWldXlz73uc/J5/NpbGxs2rbHHntMzc3Nevjhh9Xe3q6ysjJ95CMf0bXXXpu4X319vXw+n9rb2/Wtb31LX/va13Ts2DFJ0qJFi/TpT39aPp9Pn/vc56Y99le+8hW98MILevHFF3X//fdr8eLFampq0q9//WudPHlS1dXV+uu//mstX75cL7zwgv75n/9ZV199tY4cOaLu7m595CMf0e23366jR4/qe9/7ng4dOiSv16sFCxZow4YNKdt/AAAAmJlvf/vbKi4u1sGDB9XT06MvfOELevbZZ9Xa2qrly5frs5/9rNMlAsC7YooxgKy2cuVKXXLJJZKkP//zP9fdd9+toaEhbdq0ScPDw1q7dq3Ky8v1T//0Tzp48GDifs3NzVq0aJE++tGPyjAMrVmzRuvWrdOf/umf6tChQ3rooYdUVFSk22+/XZJ01VVX6e6771Z1dfW059+9e7cefPBBFRUV6ZOf/KS6u7v1jW98Q4ODg4nbvPXWW3r/+98vSfrpT3+qaDSqp59+WgcOHNCdd96pj33sYwoGg0neUwAAADgf7e3tqqio0MaNG9XY2Kh/+Zd/0Z133qlvf/vb2rZtmyKRiNMlAsC7YooxgKxmGIYqKyu1Y8cOXXzxxbrooou0bds2DQ0NaWhoSD//+c8Tt929e7fWrFkjKT5K8M4775Qk9fb2aseOHWpubtbEoOv29nbl5eVp+fLl+u1vf6sFCxbommuuOe35t23bJkm64447tGrVKnV3d+tXv/qVWlpaEre58cYbdeutt+qNN97Qjh071NfXp3nz5sm2bb355ptavHhxIogEAABA+giHwwqFQonPaoZh6KabblJpaakkyTRNud382Q0g/fGbCkDWMwzjjOuvv/56XX/99YnrU89POPGhTpKefPJJ7d+/Xx/84Ae1evVq/cu//ItGRkYuWC2BQECSEuc6tCxLt956q+bPn689e/bo9ddf1+bNm/WP//iPqqqqOq/nBQAAwIXX0dGhuro6mWZ8ct6hQ4d08803S5J6enpUVlZ21s+iAJBOmGIMIOsVFBRIkv74xz9q27Ztqq+vVyAQ0I4dO3T06FEdPnxY//Ef/6He3t53fJxQKKQ9e/aop6cnsW4i3Nu3b5/+8Ic/KBwOT7vPZZddJkl6/PHH9eyzz+r5559XQUGBli5d+o7P9cwzz6i5uVmVlZWqqKiQbdvq6+s715cOAACAJGpvb1dNTU3i+qFDh7Rw4cLTlgEg3REQAsh61113nebPn69nnnlGP/nJTxQIBHTPPfeosrJSP/3pT7V582Z5vV6Vl5ef8f633XabFi9erFdeeUW9vb1asGBBYtvy5cvV0NCgvXv36oEHHph2bkFJuvjii/WZz3xG/f39euSRRzRnzhz9/d//vQoLC9+xZo/HoxdeeEE/+MEPtHfvXt1yyy1avnz57HcGAAAALpj29nbV1tZKik83DofDiX8gHzp0aFp4CADpjC7GAAAAAAAAQA5jBCEAAAAAAACQwwgIAQAAAAAAgBxGQAgAAAAAAADkMAJCAAAAAAAAIIcREAIAAAAAAAA5jIAQAAAAAAAAyGEEhAAAAAAAAEAO+/8BtyPMJDXbpoMAAAAASUVORK5CYII=",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"low, high, step = 0, 5000, 1\n",
"plot_all(cost_history, m, q, low, high, step)"
]
},
{
"cell_type": "code",
"execution_count": 137,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"8272 passi e 827200 gradienti calcolati per arrivare a distanza minore o uguale di 0.1 dall'ottimo\n"
]
}
],
"source": [
"near_opt(m, min_dist=1e-1, ge_per_step=n)"
]
},
{
"cell_type": "code",
"execution_count": 138,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA7sAAAHzCAYAAADhDgreAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAABRJElEQVR4nO3dfXjU9Z3v/9c3M0CSmZC7yY3cHQV1QRCBJrY1tAgi5cTWtTVLlZq92u4e16PXcd2eegmnrbZaKtZ61cuqx/bStdu4Z1sXvPm5zakpBfGY1jVIskgsVq2VrhByR0Im4SaT+f7+CDNkkkxuZ+Z7M8/HdXmRTGaST+aTxHl9P5/P+22YpmkKAAAAAAAXybB6AAAAAAAAJBphFwAAAADgOoRdAAAAAIDrEHYBAAAAAK5D2AUAAAAAuA5hFwAAAADgOoRdAAAAAIDrEHYBAEix888/X1lZWcrJyVFeXp6uuOIKPfHEEwqHw+M+9k9/+pMMw1AoFErqGFP1dQAASBbCLgAAFnjppZfU09OjDz/8UFu2bNEDDzygv/mbv7F6WAAAuAZhFwAAC+Xm5uraa6/VL37xC/3TP/2TDh48qF/+8pdauXKlZs+erfnz5+vb3/529P6f/vSnJUl5eXny+/363e9+p/fff1/r1q1TYWGhAoGAvvSlL6mrqyv6mAceeEBz585VTk6O/uIv/kK/+c1vJEnhcFjbt2/XokWLVFhYqE2bNqmzszPu1wEAwEkIuwAA2MDll1+uefPm6f/9v/8nn8+nn/3sZ+rq6tIvf/lL/e///b/1wgsvSJJeffVVSVJXV5eCwaA++clPyjRNbd26VUeOHNHvf/97/fnPf44G5HfeeUePPvqoGhoa1NPTo5dfflnnn3++JOlHP/qRXnjhBe3du1dHjhxRfn6+brvttrhfBwAAJyHsAgBgE3PmzFFnZ6euvPJKXXrppcrIyNDy5ct14403au/evXEfd+GFF+rqq6/WrFmzVFRUpK997WvR+3s8Hp0+fVpvv/22+vv7df7552vRokWSpCeeeELbtm3TvHnzNGvWLH3729/Wjh07OKcLAHAFwi4AADbx0UcfqaCgQP/+7/+utWvXqqioSLm5uXriiSfU3t4e93HHjh3TDTfcoLlz52r27Nm66aabove/8MIL9fDDD+vb3/62iouLdcMNN+jIkSOSpA8//FCf//znlZeXp7y8PC1ZskQej0fHjh1LyfcLAEAyEXYBALCBhoYGffTRR1q9erU2b96sa6+9Vn/+85/V3d2tW265RaZpSpIMwxjx2P/1v/6XDMPQW2+9pRMnTuiZZ56J3l+SNm/erNdee00ffvihDMPQXXfdJUmaP3++/u///b/q6uqK/nfq1CnNnTt31K8DAICTEHYBALDQiRMn9G//9m+64YYbdNNNN+nSSy9VT0+PCgoKlJmZqTfeeEP/5//8n+j9i4qKlJGRoT/+8Y/R23p6euT3+5Wbm6uPPvpIDz74YPRj77zzjnbv3q3Tp08rMzNTWVlZysgY/N//Lbfcom984xv68MMPJUltbW168cUX434dAACchLALAIAFPve5zyknJ0fz58/Xtm3b9LWvfU1PP/20JOnxxx/X3XffrZycHN17773atGlT9HHZ2dn6xje+oYqKCuXl5en111/XPffco/379ys3N1fXXHONvvCFL0Tvf/r0aW3ZskWBQEClpaVqbW3V/fffL0n6+7//e1177bXasGGDcnJy9IlPfEL//u//HvfrAADgJIY5dJ8TAAAAAAAuwMouAAAAAMB1CLsAAAAAANch7AIAAAAAXIewCwAAAABwHcIuAAAAAMB1CLsAAAAAANfxWj2AVDhy5IjVQ7ClQCCg9vZ2q4eBYZgXe2Je7Il5sR/mxJ6YF3tiXuyHObGnseZlzpw5cR/Hyi4AAAAAwHUIuwAAAAAA1yHsAgAAAABch7ALAAAAAHAdwi4AAAAAwHUIuwAAAAAA1yHsAgAAAABch7ALAAAAAHAdb6q/4OOPP679+/crNzdXDz30kCTp2Wef1W9+8xvNnj1bknTjjTdq1apVIx7b1NSkp59+WuFwWFdddZWuu+66VA4dAAAAAOAQKQ+7V155pTZu3KjHHnss5vZrrrlG1157bdzHhcNhPfXUU/rmN7+pwsJCbd26VWVlZZo3b16yhwwAAAAAcJiUb2O+5JJL5Pf7J/249957T6WlpSopKZHX69UVV1yhhoaGJIwQAAAAAOB0KV/Zjefll1/Wq6++qoULF+qv//qvRwTizs5OFRYWRt8vLCzUu+++m+phAgAAAAAcwBZhd8OGDaqqqpIk/eIXv9DPfvYz3XrrrVP+fLt27dKuXbskSdu3b1cgEEjION3G6/Xy3NgQ82JPzIs9MS/2w5zYE/NiT8yL/TAn9jTVebFF2M3Ly4u+fdVVV+mBBx4YcZ+CggJ1dHRE3+/o6FBBQcGon2/9+vVav3599P329vbEDdZFAoEAz40NMS/2xLzYE/NiP8yJPTEv9sS82A9zYk9jzcucOXPiPs4WrYeOHz8effuNN97Q/PnzR9xn0aJFOnr0qFpbWxUKhfTb3/5WZWVlqRwmAAAAAMAhUr6y+/DDD+vtt99WT0+PbrnlFm3atEnNzc3605/+JMMwVFRUpJtvvlnS4DndH//4x9q6das8Ho+++tWvatu2bQqHw1q7du2ooRgAAKSf5qZGvfVyrWacDKo/y69LP1OppStWWj0sAICFUh5277jjjhG3rVu3btT7FhQUaOvWrdH3V61aNWr/XQAAkL6amxrVsqNGVcV5MrKzZZoD2rujRpIIvACQxmyxjRkAAGCqDtbVak1xngzDkCQZhqE1xXk6WFdr8cgAAFYi7AIAAEfz9gWjQTfCMAx5+3otGhEAwA4IuwAAwNFC2X6Zphlzm2maCmX7LBoRAMAOCLsAAMDRlm2o1N7WrmjgNU1Te1u7tGxDpcUjAwBYyRZ9dgEAAKYqUoRqZ12tvH29CmX7tKyqmuJUAJDmCLsAAMDxlq5YSbgFAMRgGzMAAAAAwHUIuwAAAAAA1yHsAgAAAABch7ALAAAAAHAdwi4AAAAAwHUIuwAAAAAA1yHsAgAAAABchz67AABgypqbGvXWy7WacTKo/iy/PrXpRs29YKHVwwIAgJVdAAAwNc1NjWrZUaOqrAFdV5itqqwBvf+zn6i5qdHqoQEAQNgFAABTc7CuVmuK82QYhiTJMAxdWZKng3W1Fo8MAADCLgAAmCJvXzAadCMMw5C3r9eiEQEAcA5hFwAATEko2y/TNGNuM01ToWyfRSMCAOAcwi4AAJiSZRsqtbe1Kxp4TdPUK8e6tGxDpcUjAwCAaswAAGAMw6stX/qZSi1dsVKSov/urKuVt69XoWyfVv/1zVRjBgDYAmEXAACMKlptuThPRna2THNAe3fUSFJM4I28LUmBQEDt7e2WjNdNxrrIAACYGLYxAwCAUY1WbXlNMdWWk220lk4tO2po6QQAk0TYBQAAo6LasjW4yAAAiUHYBQAAo6LasjW4yAAAiUHYBQAAoxqt2vLeVqotJxsXGQAgMQi7AABgVEtXrFRpVbV2nvLohY6T2nnKo9KqagolJRkXGQAgMajGDAAA4hpebRnJN1pLp2VcZACASSPsAgAA2AwXGQBg+tjGDAAAAABwHcIuAAAAAMB1CLsAAAAAANch7AIAAAAAXIcCVQAAAEi65qZGvfVyrWacDKo/y69LP1NJES4ASUXYBQAAQFI1NzWqZUeNqorzZGRnyzQHtHdHjSQReAEkDduYAQAAkFQH62q1pjhPhmFIkgzD0JriPB2sq7V4ZADcjLALAACApPL2BaNBN8IwDHn7ei0aEYB0QNgFAABAUoWy/TJNM+Y20zQVyvZZNCIA6YCwCwAAgKRatqFSe1u7ooHXNE3tbe3Ssg2VFo8MgJtRoAoAAABJFSlCtbOuVt6+XoWyfVpWVU1xKgBJRdgFAABA0i1dsZJwCyCl2MYMAAAAAHAdwi4AAAAAwHXYxgwAAJBgzU2NeuvlWs04GVR/ll+XfqaSLbwAkGKEXQAAgARqbmpUy44aVRXnycjOlmkOaO+OGkki8DocFzEAZyHsAgAAJNDBulpdX5wnwzAkSYZhaE1xnnbW1RKMRuGUAMlFDMB5OLMLAACQQN6+YDToRhiGIW9fr0Ujsq9ogMwa0HWF2arKGlDLjho1NzVaPbQRDtbVas0oFzEO1tVaPDIA8aR0Zffxxx/X/v37lZubq4ceekiSVFNTozfffFNer1clJSW69dZb5fP5Rjz2tttuU2ZmpjIyMuTxeLR9+/ZUDh0AAGBCQtl+meZATOA1TVOh7JGvb9Kdk1bBvX1BGVnZMbdxEQOwt5SG3SuvvFIbN27UY489Fr1t+fLl2rx5szwej5555hk9//zzuummm0Z9/D333KPZs2enargAAACTtmxDpfbuqImuApqmqb2tXVpWVW310GzHSQGSixiA86Q07F5yySVqbW2Nue2yyy6Lvn3xxRfr9ddfT+WQAACAC1l5DjTydXbW1crb16tQtk/Lqqptt1JpB04KkFzEAJzHVgWqdu/erSuuuCLux7dt2yZJuvrqq7V+/fpUDQsAADiIHQoJLV2xknA7AU4KkFzEAJzHME3TTOUXbG1t1QMPPBA9sxvx3HPP6f3339fXv/71EUUdJKmzs1MFBQXq7u7Wd7/7XX3lK1/RJZdcMurX2LVrl3bt2iVJ2r59u86cOZP4b8QFvF6vQqGQ1cPAMMyLPTEv9sS82I8d5uSpu7fq8zP7R6wWPn9mhv7m3vstHJl17DAv8fxHwxva99Lz8vQGNeDzq+xzn9dl5ZdbPayUsPO8pCvmxJ7GmpeZM2fGf1yyBjQZr7zyit58803dfffdowZdSSooKJAk5ebmqry8XO+9917csLt+/fqYld/29vbED9oFAoEAz40NMS/2xLzYE/NiP3aYk1Bnu/oLs0e5/YTlY7OKHeYlnrkXLNTc2/9nzG12HWui2Xle0hVzYk9jzcucOXPiPs7ysNvU1KQXX3xR3/nOdzRr1qxR73Pq1CmZpqmsrCydOnVKBw4cUFVVVYpHCgAAnOA/g336xbu/10xzQP0ZHl26YL4WlxbZ8hwoACB5Uhp2H374Yb399tvq6enRLbfcok2bNun5559XKBTSfffdJ0m66KKLdPPNN6uzs1M//vGPtXXrVnV3d+sHP/iBJGlgYECrV6/WihUrUjl0AADgAM1NjfovZ3r1idxZCmTOlExTew5/qP2dPfrYLX9v9fAAACmU0rB7xx13jLht3bp1o963oKBAW7dulSSVlJTowQcfTObQAACACxysq9X1Fy5Qb88JHW1rVcZAWH9RmKv3ZuVTSAgA0ozl25gBAMljZfsVwAqRvq3+2bnyz86N3l7ccdLCUQEArEDYBQCXskP7FSDVnNS3FQCQXIRdAHCpg3W1uv5s70pJMgxDa4rztLOulrAL15pO31Z2QgCAuxB2AcClIts5hzIMQ96+XotGBCRfJJzurKuVt69XoWyfllVVjxta2QkBAO5D2AUAl2I7J9LV0hUrJx1Q2QkBAO6TYfUAAADJsWxDpfa2dsk0TUk6t51zQ6XFIwPsx9sXjLkwJLETAgCcjpVdAHCpqW7nBNIROyEAwH0IuwDgYlPZzgmko+kUtgIA2BNhFwCAJKLCrzOwEwIA3IewCwBAklDh11nYCQEA7kKBKgAAkuRgXW10W6x0rsLvwbpai0cGAID7EXYBAEgSKvwCAGAdtjEDAJAkVPiFm411Hp2z6gDsgLALAHC84S+s/RcsUvCD9y1/oU2FX7jVWOfRJXFWHYAtEHYBAI42/EX320eP6u0dr2nj8kuUU5hn6QttKvzCrQ7W1er6Uc6j7zx7Hj3ex/jZB5BKhF0AgKMNf9HdfPg/df3cQrW0tyknN8/yF9pU+IUbefuCMrKyY247dx7dHONjAJA6FKgCADja8CJQ3vCAMgxDGQMD0dt4oQ0k1uB5dDPmtsh59LE+BgCpRNgFADja8BfWoQyPwqapsMcTvY0X2kBiLdtQqb2tXdHfveh59A2VY34MAFKJbcwAgJRIVnXW4UWgli6Yp+fee1+fWX6JJFEUCkiCiZxH56w6AKsRdgEASTdW5dbpvgAe8aI77zz5qlbr5T+9L28HL7SBZBnrPDpn1QHYAWEXAJB0Y1VuTcQLYl5YAwCA4TizCwBIuuFFpCSKRgEAgOQi7AIAko7qrAAAINUIuwCApKM6KwAASDXO7AIAkm4ilVuBVElWZXAAgL0QdgEAKeGEIlKEoOSxy3M7XmVwu4wTADB9hF0AAJTc9kjpzk7P7ViVwSXZZpwAgOnjzC4AABoMQWtGCUEHz4YgTJ2dntuxKoPbaZwAgOkj7AIAINojJZOdntuxKoPbaZwAgOkj7AIAINojJZOdntuxKoPbaZwAgOkj7AIAINojJZOdntulK1aqtKpaO0959ELHSe085VHp2crgdhonAGD6KFAFAICc2R7JKZWD7fbcxqsMbrdxAgCmh7ALAMBZTmiPFGGnCscT4ZTnNtXjdMoFCwBwIrYxAwDgQFQOdr7oBYusAV1XmK2qrAG17KhRc1Oj1UMDAFcg7AIA4EBUDnY+LlgAQHKxjRkAkFBsy0yNwcrBAzGBl8rBzuLtC8rIyo65jQsWAJA4rOwCABKGbZmpQ+Vg56PVEQAkF2EXAJAwbMtMnbFa6MAZuGABAMnFNmYAQMKwLTO1rK5wPNqW9TXrr7ZsPE5DqyMASC7CLgAgYThHmj7itT76j9xczb1godXDcwyrL1gAgJsRdgEACbNsQ6X27qiJbmWObsusqrZ6aCmRyuJcVhcCO1hXq+tH2bL+y5ee19zb/2fKxgEAQDyEXQBAwqTztsx4K52SEv79p/JrxRNvy7onGEzJ1wdSzeoLTAAmj7ALAEiodN2WGW+lc2ddbcKfj1R+rXjibVkf8PlT8vWBVLLDBSYAk0c1ZgAAEsDbF4wJflLyinOl8mvFE6+ScNnnPp+yMQCpQqV5wJlY2QUAIAFSWZzLDoXA4m1Zv6z8crW3t6dsHEAqUGkecCbCLgAACZDK4lx2KQSWrlvWkX7scIEJwOQRdgEASIBUFudK50JggBXscoEJwOSkPOw+/vjj2r9/v3Jzc/XQQw9JkoLBoH74wx+qra1NRUVF+od/+Af5/SMLXLzyyit67rnnJElf+MIXdOWVV6Zy6AAAjCmVK52sqgKpwwUmwJlSHnavvPJKbdy4UY899lj0thdeeEGXXnqprrvuOr3wwgt64YUXdNNNN8U8LhgMaseOHdq+fbskacuWLSorKxs1FAMAAACJxAUmwHlSXo35kksuGRFQGxoatGbNGknSmjVr1NDQMOJxTU1NWr58ufx+v/x+v5YvX66mpqZUDBkAAAAA4DC2OLPb3d2t/Px8SVJeXp66u7tH3Kezs1OFhYXR9wsKCtTZ2Tnq59u1a5d27dolSdq+fbsCgUASRu18Xq+X58aGmBd7Yl7siXmxHzfNyX80vKGGl56Xt7dHIV+Oyj/3eV1WfrnVw5oSN82LmzAv9sOc2NNU58UWYXcowzBG9A6crPXr12v9+vXR92mBMLpAIMBzY0PMiz0xL/bEvNiPW+akualRLTtq9NniPBl+j0yzV3ufelRd3c48p+mWeXEb5sV+mBN7Gmte5syZE/dxKd/GPJrc3FwdP35cknT8+HHNnj17xH0KCgrU0dERfb+zs1MFBQUpGyMAAEgfB+tqo5V3pcGL8WuK83SwrtbikQEAJsoWK7tlZWXau3evrrvuOu3du1fl5eUj7rNixQr9y7/8i4LBoCTpP/7jP7R58+ZUDxUAAKRAc1Oj3nq5VjNOBtWf5deln6lM6Yqqty8oIys75jbDMOTt603ZGAAA05PysPvwww/r7bffVk9Pj2655RZt2rRJ1113nX74wx9q9+7d0dZDkvT+++/r17/+tW655Rb5/X5df/312rp1qySpqqqKSswAALhQZAtxVXGejOxsmeaA9u6okaSUBd5Qtl+mORBztMo0TYWyfSn5+gBghb5T/TrWHtSx9qBazv43w5uhv6n6mNVDm5KUh9077rhj1NvvvvvuEbctWrRIixYtir6/bt06rVu3LllDAwAANnCwrlbXj7KFeGddbcrC7rINldq7oya6ldk0Te1t7dKyquqUfH0ASJb+0IDaOntjAm3k7RPB0yPun505Q6ZpTruukhVssY0ZAAAgwg5biCOhemddrbx9vQpl+7SsypnFqZIh0dvMrd62DrhNOGzq+ImTamkbEmY7Bv9tP94r0xz9cTNneFRc6FNpwK+SgD/6r1MRdgEgQXixBiTGRLYQp+L3bemKlSM+J7/nid9mbodt64ATmaapYN+Z6Kps9N+zobY/FB71cYYhFRf4VDIs0J4X8CtvdpYyMpy3ghsPYRcAEoAXa0DijLeF2KrfN37PByV6m7kdtq0Ddnb6TEjHOnqHhNqeaLjtPdkf93G5ObNUUnguzJYW5ai00K+iAp+8Xls05Uk6wi4AJAAv1oDEGW8LsVW/b/yeD0r0NnM7bFsHrDYwEFZ7V9+5c7Rt57YeH+8+GfdxmbO8g0G20K/SoiErtYV+ZWXOSOF3YE+EXQBIAF6sAYk12hbiCKt+3/g9H5ToStVUvka6ME1T3T2ndaw9qKPtPTFVj9s6ezUQHv0grcdjqLjAP+IcbWnAr9n+WY4sHJUqhF0ASABerAGpY9XvG7/ngxJdqZrK13CbSPuemHO0Z/89fSYU93GFeVmD52gLYwNtYV62PJ702HacaIRdAEgAXqwBqZOM37eJFJ7i93xQoipVD33Oj50O6+DhDs3z+6h8DUfoDw2otaM3WgxqvPY9Ef7smbGrs4WD/xYX+jRrJtEs0XhGASABaFMCpE6if98mWniK3/NzxtpmPhEjnvOCLO1t7VLpdX+Vls8n7CkcNtXZfTI2zHYE1dLWo46uvkm17ykN5Kgk4JM/e1Zqv4k0R9gFgASZ7os/ABOXyN+3yRSe4vc8MSj2BbsY3r7nRN8H+uBwq1rag2rtmHj7nvOGBFu3te9xMsIuAABIaxSeSj2ec6RaTPueth61nN1+PJH2PYOrsrFbj9OpfY+TEXYBAEBao/BU6vGcIxki7XuibXvaJ96+p/RsmL1gQbFysjNo3+MShF0AsMBEiuHAHpgr96PwVOrxnGOqTNNUV8+pmDCbyPY9gUBA7e3tqfyWkESEXQBIsYkWw4H1mKuJGXpBwFMQ0EWfXueo54fCU6nHc47xJLR9T1GOCnOzaN+Thgi7AJBiFGZxDuZqfMMvCMyY0a9fO/CCAIWnUo/nHKO174lsQT7RO4n2PWf/KyqgfQ9i8dMAAClGYRbnYK7GxwUBAGMZ3r6npb0n+vZE2/fEFoiifQ8mjrALAClGYRbnYK7GxwUBAEPb9xwddo52Iu17SovOVTmmfQ8SibALAClGYRbnYK7GxwUBIH2cPhMaUeV4Yu17MkcWhqJ9D1KAsAsAKUZhFudgrsbHBQHAXUIDYXUc7xulMFSPjp84FfdxQ9v3lJz977xAjooDPmXNon0PrEHYBQALUJjFOZirsQ2/IOAtyNaFXBAAbG209j0tZ/9rn0z7nqJzW4+Htu8B7IKwCwAApmXoBYFE9KiktzGQGH0nz+hYR+/ZKsc9MVuPT58ZiPu4SPue2MJQftr3wHEIuwAAwDbobQxMTqR9z/BtxxNp3zPiHG3Ar+JCv2bO8KTwOwCSh7ALAABsg1ZGwEiD7XtGO0c7fvuekoBfJYX+YcGW9j1ID4RdAABgG7QyQroyTVM9vWd0rCN2dbalPahjHUGF4rTvycgwVFSQHVPlmPY9wCDCLgAAsA1aGcHthrbv6Tl5WH883KqWtsFg23dq4u17Im8X5dO+B4iHsAsAAGyDVkZwg5Hte3qib4/VvidrlndImD1XHIr2PcDUEHYBAIBt0NsYThHTvqftXJXjCbfvKfLrgvlFmu3z0L4HSBLCLgAAsBV6G8NO+k6eGVkYapz2PYYhFeadO0c7tOJxIC87eo42Ea26kDiNB5q1e99Btfeelt8TVuXqcq1cvtTqYWEaCLsAAABIa/39A2rtpH1POms80Kya+kMqWb5Gvv5+hU1TNfUNkkTgdTDCLgAAAFwv8e17/PJnz0ztN4Gkqa3fp/zFa2PanuUvLldt/R7CroMRdgEAACag8UCzal9rUHAggy2ONjVa+56Wtp7BVdrO3om37wnkRN/Oy8mkfU8aCIYM+YadlzYMQ70h5t7JCLsAAADjiGxxzF+yTj7DYIujxYa27xm+UjuR9j3DV2hp3wO/11R42PK+aZryeeMs+cMRCLsAAADjYItj6kXa9xxt74men51o+57SorNtewr9tO/BhFRWlKmmvkElyyskDQbd44caVF1RZvHIMB2EXQAAgHGwxTE5TNNU14lTI6ocj9e+x+vJUHGhL7YwFO17MA2Ri1a739yr7uBp+bymqivKuJjlcIRdAACAcUS2OA4NUWxxnLhR2/e0B3WsY/rte4BEWbl8qa5et4Z2UC5C2AUAwAGamxr11su1mnEyqP4svy79TCW9aFMossUxf3G5DMNgi+MoRrbv6Ym+3dN7Ju7jRm/fk6PiQh/tewBMC2EXAACba25qVMuOGlUV58nIzpZpDmjvjhpJIvCmSGQrY239HvWGjLTd4ji0fU9LW+zW48m07ykt8kffp30PgGQh7AIAYHMH62p1fXFeTHGkNcV52llXS9hNoZXLl6ZFuI2072k5Wxgqsjo7kfY9xQXZQ1Zoad8DwFqEXQAAbM7bF5SRlR1zm2EY8vb1WjQiuMGp0yEd6xjlHO047XvyZmdGi0HRvgeAnRF2AQCwuVC2X6Y5MKI4UijbZ+Go4AShgbDaj/fqgyO9+sMfj8T0pu2ifQ8AlyPsAgBgc8s2VGrvjhqtObuV2TRN7W3t0rKqaquHBhsYrX1PS9vgFuS2430KT6Z9z9niUDm+mbTvAeB4hF0AAGwuci53Z12tvH29CmX7tKyqmvO6aWZo+56jQ8/RTqB9z/zz8lWQO+tsmB0MtoW07wHgcoRdAAAcYOmKlYTbNBBt39PWE61yPJn2PZEqx4Nbj8+17wkEAvQOnYLGA82qfa1BwYEM+T1hVa4uT4siZYBbEHYBAABSKBw21dHVF1sYaoLteyKrskO3HtO+JzkaDzSrpv6Q8pesk88wFDZN1dQ3SBKBF3AIwi4AAECCJaN9T/7sTM7RplBt/T7lL14b0/Irf3G5auv3EHYBhyDsAgAATFG89j0t7UGdnGT7ntIivwL5Pnk9tO+xg2DIkG/YxQXDMNQb4oID4BSEXQAAgDFE2vdEw2zbua3Hk2nfEzlPW1yY2vY9zU2NevfV3RrobFd/ll+XfqaS898T4PeaCpvmiJZfPm+cfeYAbMcWYffIkSP64Q9/GH2/tbVVmzZt0jXXXBO9rbm5Wd///vdVXFwsSfr4xz+uqqqqlI8VAAC4z9D2PYOhticabifTvudcCx97tO9pbmpUy44afWFesfoLs2WaA9q7o0aSCLzjqKwoU019g/IXl0dbfh0/1KDqijKrhwZggmwRdufMmaMHH3xQkhQOh/V3f/d3uvzyy0fcb8mSJdqyZUuqhwcAAFyid0j7nqHnaFvagzrTP3b7ntIif3TrsVPa9xysq9X1Z/szS4PbcNcU52lnXS1hdxyRc7m19XvUGzLk85qqrijjvC7gILYIu0O99dZbKi0tVVFRkdVDAQAADtTfP6BjHb2Dq7NDztO2tAUV7IvfvifHNzMmyA5v3+NE3r6gjKzsmNsMw5C3r9eiETnLyuVLCbeAg9ku7NbX16uiomLUj/3hD3/QnXfeqfz8fFVXV2v+/Pmj3m/Xrl3atWuXJGn79u0KBAJJG6+Teb1enhsbYl7siXmxJ+bFflI1JwPhsNo6gzpyrFtHjnXro2Pd+qilW0dau9XWGYzbvmfWTK/mlORqbknu4L/Fg//OKZmtHF9m0sedat6CgGbM6FeGYWjmzMH2RKZpyluQze+ODfA3zH6YE3ua6rwYphnvfwepFwqF9Hd/93d66KGHlJeXF/Oxvr4+ZWRkKDMzU/v379dPf/pTPfLIIxP6vEeOHEnCaJ2PBvP2xLzYE/NiT8yL/SRyTkZr3xPZetza0avQQPz2PUX5I9v3lAb8ykuz9j2RM7tXzytWf3+/TNPU3tYulVZVs43ZBvgbZj/MiT2NNS9z5syJ+zhbrew2NjbqggsuGBF0JSk7+9wWnFWrVumpp57SiRMnNHv27BSOEAAAJFqkfc/QKsfHJtm+J1LpuDRA+56hIoH2+Vd3K9R5QqFsn5YRdAGkCVuF3bG2MHd1dSk3N1eGYei9995TOBxWTk5OikcIAACmIjQQVltn78jCUOO178mcMazK8dnetIV+Zc6y1csY21q6YqXWrL+a1SoAacc2/5c4deqUDhw4oJtvvjl6W11dnSRpw4YNev3111VXVyePx6OZM2fqjjvuSKttSAAA2J1pmmo/HtTv32+bdPuekrPte0ps2L4HAOBMtgm7mZmZ+sd//MeY2zZs2BB9e+PGjdq4cWOqhwUAGKa5qVFvvVyrGSeD6s/y69LPVLIlMs2M1r4n8u9Y7XsCkXO0DmvfAwBwJtuEXQCA/UWK3VQV58nIzpZpDmjvjhpJIvC6zJn+AbUOad8TPU/bPnb7ntycTBUVZMe07yktylFxgU8zHNq+BwDgTIRdAMCEHayr1fXFedFtpYZhaE1xnnbW1RJ2HSgcNtXR1adj7UEdHXqOtj2ozu6+uO17Zs7wxJyhjZ6jDfj1X+bPsfXZ0MYDzap9rUHBgQz5PWFVri6njyoAuBRhFwAwYd6+oIys7JjbDMOQt6/XohFhPKZp6kTw9IgqxxNp31NckK3SopwRW4+d2r6n8UCzauoPKX/JOvkMQ2HTVE19gyQReAHAhQi7AIAJC2X7ZZoDMUHHNE2Fsn0WjgqSdPJ0v1rbe8+doZ1g+5782ZmxVY5d3L6ntn6f8hevjdmZkL+4XLX1ewi7AOBChF0AwIQt21CpvTtqtObsVmbTNLW3tUvLqqqtHlpaCIXCajs+sn3P0fagunto3zOeYMiQb9iKtGEY6g3Ze5WardcAMDXp8384AJbhhZp7RM7l7qyrlbevV6Fsn5ZVVXNeN4HCYVNdPaeGBNrB9j0t7UG1j9W+x5uhkgLa94zF7zUVNs0ROxN83jiHk22ArdcAMHWEXQBJxQs191m6YiXhNgFi2ve0nQ22HVNo31M0GGwLcp3RvsfKi1+VFWWqqW9Q/uLy6M6E44caVF1RlpKvPxVsvQaAqSPsAkgqXqghnQ227xnZi3a89j05vpnRVdmhW4+d3r7H6otfka9RW79HvSFDPq+p6ooyW/8tcurWawCwA8IugKTihRrcLhw21X62fU/LJNr3zJrpGVHlOLIF2Zc1M7XfRIrY4eLXyuVLbR1uh3Pi1msAsAvCLoCk4oUa3CBe+56WtqDaOuO37/FkGAoU+s6tzrqgfc90cPFr8py49RoA7IKwCyCpeKEGJxnRvudscahj7UGdPB2K+7h0at8zHVz8mjwnbr0GALsg7AJIKl6owW6Gt+8Zeo52su17SgN+FadZ+57p4OLX1Dht6zUA2AX/dwaQdLxQQ6qFw6a6Tpw8F2SHbD2eaPseT7hXfR/+XrP7uzUry6NVGzdo2cpVKf5O3IWLXwCAVCLsAgAcq6f3lN4/3Blb7XiC7XtKR/SjPde+p7mpUS07ntWa4ryzK5AD2rvzGRmGQdulaeLiFwAgVQi7AABbm2r7ntm+WTHnZyfTvudgXa2uPxt0pcEiSmuK87SzrpawCwBxWNlHGxgNYRcAYLnR2ve0tPfoWHtQnd0n47bvyZzlVXGhb0T7ntKAX9nTaN/j7QvKyMqOuc0wDHn7eqf8OQHAzazuow2MhrALAEiJ4e17WtrOrdBOtn1PadHg2xdeME8dHR0JH2so2y/THBhRNTiU7Uv41wIAN7BDH21gOMIuACChTp7uj1mhHfr2RNv3lAZyom8X5mfHbd+TrD61yzZUau+OmiFndk3tbe3SsqrqpHw9AHA6+mjDjgi7AIBJC4XCauvsjalyPKn2PUX+mK3HdmvfEzmXu7OuVt6+XoWyfVpWVc15XQCIgz7asCP7vLIAANjKtNr3FJ47Pxs9S1voV45vZtJWYxNt6YqVhFsAmCD6aMOOCLsAkOaCfWdGrM62tPeotaN3Wu17AADpgz7asCPCLgCkgdHa90TeTlb7HqSH4a1Gbvzsei1cMM/qYQGwAH20YTeEXQBwiUj7npa2nnMrtWe3Hnd0nYz7uFkzPdEqxyUBv0qLcs5uO/ZNq30P3G+0ViM/qWvUFy/v5gWvTdEHFUA6IewCgINE2ve0tI8sDDVW+54MQ8o0Tstv9ilrRlgXX3qxVq5copKAX3k5mY45Rwt7GbXVyJJy1da/TICyIfqgAkg3hF0AsKGTp/p1rGNq7XuGtu0pCfjV03ZYJ3/1C60tzj3XRqfxbQ0sylH+QgowYepoNeIs9EEFkG4IuwBgkdHa97S09ehYR1DdPafjPi47c4ZKi/yxW4/HaN/zi//vKV1fkhvzAndNcZ521tVSbRjTQqsRZ+HiBIB0Q9gFgCQa3r7n6JCV2rbjvTLjZIJEtu/x9gVlZGXH3GYYhrx9vdP51oDRW438vkFfTEKrEc6aTh8XJwCkG8IuACRAsO+MWtp7RpyjnVr7nhwV5GYlrH1PKNsv0xwY8QI3lO1LyOdH+hqt1cjN11yV8GrMnDVNDPqgAkg3Ewq74XBYDQ0NMgxDZWVlysjIkCT97ne/0yc/+cmkDhAA7OL0mZBaO3oHg2xH7DnaibbvOe/s9uOSwtS171m2oVJ7d9RoTXHeuTO7rV1aVlWd9K8N9xveaiQQCKi9vT2hX4OzpolBH1QA6WZCYffRRx9VIBCQ1+vVSy+9pNtuu02lpaWqq6sj7AJwlYGBsDq6+mKrHXcE1dZ5Um2dwbiPi7bvCeTErtTaoH1P5Fzuzrpaeft6Fcr2aVlVNed14RicNU0c+qACSCcTCrudnZ26/fbbJUlr167Vo48+qr/6q79K6sAAIFnit+/pUWtnrwYGRj+/5skwVFTgG3mO1gHte5auWEm4tRDnTaeHs6bT03igWbv3HVR772l+/gCklQmF3VAopP7+fs2YMUNFRUXasmWLHn74YR0+fDjZ4wOAKRvevqel7dz241Njte/JzYqpclwS8GvJRfOVodPyejJS+B3ADThvOn2cNZ26yM9fyfI18vX38/MHIK2MGXYHBgbk8Xj05S9/Wb29vcrLy5MkZWVl6a677tJrr72WijECQFzR9j3tPSO2Hk+lfU9JwK9ZM0f+aQwEchN+DhHpgfOm08dZ06nj5w9AOhsz7H7ve9/TnXfeqQsvvHDExzIyMvTpT386aQMDgIhw2NTxIe17WqbYvqd0SKD1Z0+ufQ8wVZw3TQzOmk4NP38A0tmYYff888/Xt771LW3dulUFBQWSpLfffls///nPde+996ZkgADSR7BvtHO0E2zfU5QzYoU2ke17gKnivCmsFPn5G4qfPwDpYsywW11drbq6On3rW9/S5s2btXv3bh0+fFjXXnttqsYHwGXite9paetR78n+uI+b7Z81oh9tKtv3AFPFeVNYKfLzV7K8QpL4+QOQVsYtUHXxxRcrOztbjzzyiNasWaO77rpLM2da20YDgL2N1r4n8nZn98m4j5s10zsi0NqlfQ8wVZw3hZUiP2e739yr7uBpfv7GQeV0wF3GDLsPPvig3n77bV1zzTXatGmTnnzySR08eFCrVq1K1fgA2NTQ9j0t7T0xW4+n0r6nNJCj3JxZnKOFK3HeFFZauXyprl63hiJ746ByOuA+Y4bd8847T//9v/93+f1+SVJJSYkeeOABtba2auPGjSkZIABrnTzVP/Ic7RTa90QqHwfysuWhfQ8AwGaoXA24z5hh96abbop5f8GCBbrvvvt0//33E3YBF+kPDaits3dEYahJte8J5Aw5S+sbtX0PAAB2ReVqwH0m/Wq0oKCASsyAA8Vr39PSHlT7GO17ZngzosWghp+npX0PAMAtqJwOuM+Ull6ysrISPQ4ACTK8fU9L2+AK7bH2oPpD4VEfYxhSUYFvMMjSvgcAkIaonA64D/sMAQca2r7naHtQx4YUiJpS+55Cn2Z4ad8DAEhfVE4H3IewC9jUwEBY7V19I8/RTrV9T8Cv7MwZKfwOAABwFiqnA+5C2AUsZJqmuntOn61wPLg623miX38+0jGp9j2lRX6VFuaoJOCnfQ8AAAAgwi6QEtNt33Ou4jHtewAAAICJsFXYve2225SZmamMjAx5PB5t37495uOmaerpp59WY2OjZs2apVtvvVULFy60aLRArHjte1ragzoRjN++x5c149z52UCOLrrgPGXPMmnfAwDAEI0HmlX7WoOCAxnye8KqXF3uqi3Hbv/+ACvY7pX0Pffco9mzZ4/6scbGRrW0tOiRRx7Ru+++qyeffFLf+973UjxCpLOh7Xta2mJXaKfavifHNyvmvoFAQO3t7Sn4bgAAmByrAlnjgWbV1B9S/pJ18hmGwqapmvoGSXJFIHT79wdYxXZhdyz79u3Tpz/9aRmGoYsvvli9vb06fvy48vPzrR4aXCbYd1otbcMKQ02xfU9pkV/5s2nfAwBwNisDWW39PuUvXhutSWEYhvIXl6u2fo8rwqDbvz/AKrYLu9u2bZMkXX311Vq/fn3Mxzo7OxUIBKLvFxYWqrOzc0TY3bVrl3bt2iVJ2r59e8xjcI7X603r5+b06ZCOtHbro2PdOnKsWx+1Dv575Fi3enrjbzvOm52lOSW5mluSqznFuZpbOvh2aWC2ZsyYfvuedJ8Xu2Je7Il5sR/mxJ4SMS+73zyokuVrYoogliyv0O439+rqdWumO8Qx9XsylT1r1ojbT3oyHf3zFpkXt35/TsTfMHua6rzYKuzed999KigoUHd3t7773e9qzpw5uuSSSyb9edavXx8TlNkSOrp02C6bqPY9587UxmvfM6Du7uMJGXM6zIsTMS/2xLzYD3NiT4mYl/bgafn6R/Zy7w6eTvqczxg4pdOnT8cEbdM05R045eift8i8uPX7cyL+htnTWPMyZ86cuI+zVdgtKCiQJOXm5qq8vFzvvfdeTNgtKCiI+SY7Ojqij0H6Gq19T+RMbdvxCbTvKRpyjpb2PQAAjMrvNRU2zRGBzOeNU7AigSorylRT36D8xeUyDEOmaer4oQZVV5Ql/Wungtu/P8Aqtgm7p06dkmmaysrK0qlTp3TgwAFVVVXF3KesrEy/+tWvVFFRoXfffVfZ2dmc100jfaf6dWxYlePI26fPxG/fU5CbFVMQivY9AJyOqq2wgpWBLPLzXVu/R70hQz6vqeqKMtf83Lv9+wOsYpuw293drR/84AeSpIGBAa1evVorVqxQXV2dJGnDhg1auXKl9u/fr9tvv10zZ87UrbfeauWQkQT9oQG1dvRGi0ENDbSTad8TfZv2PQBchqqtsIrVgWzl8qWu/hl3+/cHWME2KaCkpEQPPvjgiNs3bNgQfdswDP3t3/5tKoeFJAiHTXV2n4wNs1No31NadG6l1p89sqgDgKlh1dDeqNoKKxHIADiJbcIu3MU0TQX7zowsDDWZ9j3Dth7TvgdIPlYN7S8YMuQbVlPAMAz1hvj7CADAUIRdTMvpMyEd6+gdEmp7ouG29+TIio0Rs/2zRoTZkoBfRQU+zfBOv30PgKlh1dD+rCwSBACAkxB2Ma7h7Xta2s5tPT4+XvueIr9KC2MDbfz2PQCsxqqh/VG1FQCAiSHsQtK59j0tQ1ZmI+G2rbNXA+E47Xs8hoqHbDumfQ/gbKwa2p/VRYIAAHAKwm6aibTvaWkPqqfvQ/3xcOuU2/eUBvwqpH0P4CqsGjoDRYIAABgfYdeFEtG+p7QoJ7r9uJj2PUDaSIdVQ6pNAwCQHkgwDhWvfU9LW486uvrGbd9TGvDrgvnFmu3LoH0PgBhuXjWk2jQAAOmDsGtjw9v3DF2hbe0Yu31P5Bzt8K3HQ9v3BAIBtbe3p/JbAgBLUW0aAID0Qdi1gUj7npa2nugK7bEJtO/JzZmlkkLa9wDARFFtGgCA9EHYtdBTO97U2++3jdm+J3OW92yF45GrtFm07wGASaHaNAAA6YOwa6Ge3tM63n1y9PY9gRyVBvya7ad9DwAkCtWmAQBIH4RdC236r8u0+bPLad8DACkSOZf7sxd36o9t3RroP61FxXmSFls6LgAAkHiEXQvNKZ5t9RAAIC0ZgQUqW31udZeKzAAAuA/LiQCAtDJYkbl8lIrM+yweGQAASCRWdgEAacXJFZkbDzSr9rUGBQcy5PeEVbm6nNVoAADiIOwCANKKUysyNx5oVk39IeUvWSefYSjM9msAAMbENmYAQFqprCjT8UMNMs3BcBupyFxp84rMbL8GAGByWNkFAKSdcPuH2vf8QYXPnNLC0nx9+QvX2H511MnbrwEAsAJhFwCQNiJbgQtXVykwpM+uEzh1+zUAAFZhGzMAIG04eSuwU7dfAwBgFVZ2AQBpw8lbgSPbrGvr96g3ZMjnNVVdUWb77dcAAFiFsAsASBtO3wq8cvlSwi0AABPENmYAQNpgKzAAAOmDlV0AQNpgKzAAAOmDsAsASCtsBXanxgPNqn2tQcGBDPk9YVWuLmeeASDNEXYBAICjRVpK5S9ZJ59hKGyaqqkfbClF4AWA9MWZXQAA4GhObikFAEgewi4AAHC0YMiIqbAtOaelFAAgeQi7AADA0fxeM1phO8JJLaUAAMnBmV0AAGyGYkuTU1lRppr6huhW5khLqWpaSgFAWiPsAgBgIxRbmjxaSsEphl/IuvGz67VwwTyrhwW4FmEXAAAbGSy2tHaUYkt7CG9joKUU7G60C1k/qWvUFy/v5mcXSBLCLgAANhIMGfJRbAk2w9b66Rv1QtaSctXWv8xzCSQJYRcAABvxe02FTTOmujDFlmAlttYnBheygNSjGjMAADZSWVGm44caotWFI8WWKim2BIvQxzgxqBoOpB4ruwAA2AjFlmA3rEgmxqhVw3/foC9yIQtIGsIuAAA2Q7El2Alb6xNjtAtZN19zFdWYgSQi7AIAACAu+hgnzvALWYFAQO3t7RaOCHA3wi4AAJBExV2Mjq31AJyKsAsAAKi4izGxtR6AE1GNGQAAUHEXAOA6hF0AAKBgyIgpQCRRcRcA4GxsYwYAAJOuuMv5XgCA3RF2AaQNXpwD8U2m4u5Y53uvXrcm1UN3Jf5eAcD0EXYBpAWK7wBjm0zF3cHzvWtHOd+7h7CbAPy9AoDEIOwCSAtjvTjnxSMwaKIVd4MhQz7O945rqquz/L0CgMSwRdhtb2/XY489pq6uLhmGofXr16uysjLmPs3Nzfr+97+v4uJiSdLHP/5xVVVVWTFcAA7Ei3MgcSZ7vjcdTWd1lr9XAJAYtgi7Ho9H1dXVWrhwoU6ePKktW7Zo+fLlmjdvXsz9lixZoi1btlg0SgBOxotzIHEmc743XU1ndZa/VwCQGLZoPZSfn6+FCxdKkrKysjR37lx1dnZaPCoAblJZUabjhxpkmoMvFiMvzit5cQ5M2srlS1VdsVgZh/ao7609yji0R9UVi9liO8R0Wjnx9woAEsMWK7tDtba26oMPPtCFF1444mN/+MMfdOeddyo/P1/V1dWaP3++BSME4ESTKb4DYHwTPd+brqazOsvfKwBIDMOMXDa0gVOnTumee+7RF77wBX384x+P+VhfX58yMjKUmZmp/fv366c//akeeeSRUT/Prl27tGvXLknS9u3bdebMmaSP3Ym8Xq9CoZDVw8AwzIs9MS/2xLzYD3My6I39TfpJXaPylwzZ6v37Bt28YaUuX7Ui5eNhXuyJebEf5sSexpqXmTNnxn2cbcJuKBTSAw88oMsuu0yf/exnx73/bbfdpvvvv1+zZ88e975HjhxJxBBdJxAIqL293ephYBjmxZ6YF3tiXuyHOTmn8UCzauv3RVdnKy1cnWVe7Il5sR/mxJ7Gmpc5c+bEfZwttjGbpqknnnhCc+fOjRt0u7q6lJubK8Mw9N577ykcDisnJyfFIwUAAJgYtnoDgLVsEXbfeecdvfrqq1qwYIHuvPNOSdKNN94YTe8bNmzQ66+/rrq6Onk8Hs2cOVN33HHHiMIPAAAAAABINgm7ixcv1rPPPjvmfTZu3KiNGzemaEQAAACYrsYDzap9rUHBgQz5PWFVri5ntRtAytgi7AIAAMBdGg80q6b+kPKXrJPPMBQ2TdXUN0gSgRdAStiizy4AAADcpbZ+n/IXl0ePnRmGofzF5aqt32fxyACkC8IuAAAAEi4YMkbUVzEMQ70haq4ASA22MQMAAJzFGdPE8XtNhU0zJvCapimf1xZdLwGkAVZ2AQAAdO6MaXjJOvkuXavwknWqqT+kxgPNVg/NkSorynT8UINMczDcmqap44caVFlRZvHIAKQLVnYBAAAUOWO6dpQzpntY3Z2CyHNWW79HvSFDPq+p6ooynksAKUPYBQAA0OAZUx9nTBNq5fKlhFsAlmEbMwAAgAbPmEa23EZwxhQAnIuwCwAAIM6YAoDbsI0ZAGALVMGF1ThjCgDuQtgFAFguUgU3f8k6+QxDYdNUTX2DJBE0kFKcMQUA92AbMwDAcoNVcMtHqYK7z+KRAQAAp2JlFwBgOargAlPHEQAAGB1hFwBgOb/XVNg0oyu7ElVwgYngCAAAxMc2ZgCA5aiCC0wNRwAAID5WdgEAlqMKLjA1HAEAgPgIuwAAW6AKLjB5HAEAgPjYxgwAAOBQHAEAgPhY2QUAAHAojgAAQHyEXQAAAAfjCAAAjI6wCwDAJNHXFAAA+yPsAgAwCfQ1BQDAGShQBQDAJNDXFAAAZyDsAgAwCcGQEdPmRaKvKQAAdkTYBQBgEvxeM9rmJYK+pgAA2A9hFwCASaCvKQAAzkCBKgAAJoG+polDVWsAQDIRdgEAmCT6mk4fVa0BAMnGNmYAAJByVLUGACQbYRcAAKQcVa0BAMlG2AUAAClHVWsAQLIRdgEAQMpR1RoAkGwUqAIAAClHVWsAQLIRdgEAgCWoag0ASCa2MQMAAAAAXIeVXQAAAIzQeKBZta81KDiQIb8nrMrV5azEA3AUwi4AYEJ44Qukj8YDzaqpP6T8JevkMwyFTVM19Q2SxO89AMcg7AIAxsULX/fh4gXGUlu/T/mL10Z7IRuGofzF5aqt38PPCQDHIOwCAMbFC1934eIFxhMMGfKd/X2PMAxDvSEjziMAwH4oUAUAGFcwZESDbgQvfJ1r8OJF+SgXL/ZZPDLYhd9rRnsgR5imKZ/XjPMIALAfwi4AYFy88HUXLl5gPJUVZTp+qCH6e2+apo4falBlRZnFIwOAiWMbMwBgXJUVZaqpb4iuBkZe+FbzwteR/F5TYdOMCbxcvMBQke3stfV71Bsy5POaqq4oY5s7AEch7AIAxsULX3fh4gUmYuXypfyOA3A0wi4AYEJ44eseXLwAAKQDwi4A16K1ChAfFy8AAG5H2AXgSrRWAeyFi08AgFSzVdhtamrS008/rXA4rKuuukrXXXddzMf7+/v16KOP6o9//KNycnJ0xx13qLi42JrBArA1+sIC9sHFJwCAFWwTdsPhsJ566il985vfVGFhobZu3aqysjLNmzcvep/du3fL5/PpRz/6kerr6/XP//zP+od/+AcLRw3AroIhQz6XtVZhZQxOxcUnAIAVbNNn97333lNpaalKSkrk9Xp1xRVXqKGhIeY++/bt05VXXilJ+sQnPqGDBw+O6PsIAJL7+sJGVsbCS9bJd+lahZesU039ITUeaLZ6aMC46OsLALCCbcJuZ2enCgsLo+8XFhaqs7Mz7n08Ho+ys7PV09OT0nECcIbKijIdP9QQDbyR1iqVDm2tMrgyVj7Kytg+i0cGjM9tF58AAM5gm23MibRr1y7t2rVLkrR9+3YFAgGLR2RPXq+X58aGmJfEuHrdGuXm5er539Qr2C/5Z0hfuqZCl69aMaXPZ/W89HsylT1r1ojbT3oy0/rnxep5wUijzcmN11yln9Q1Kn/JkL6+v2/QzddcxfylCL8r9sS82A9zYk9TnRfbhN2CggJ1dHRE3+/o6FBBQcGo9yksLNTAwID6+vqUk5Mz4nOtX79e69evj77f3t6evIE7WCAQ4LmxIeYlcRYumKf/+ZUvxtw21efW6nmZMXBKp0+fjtkKapqmvAOn0vrnxep5wUijzcnCBfP0xcu7VVv/crSv7xcryrRwwTzmL0X4XbEn5sV+mBN7Gmte5syZE/dxtgm7ixYt0tGjR9Xa2qqCggL99re/1e233x5zn4997GN65ZVXdPHFF+v111/X0qVLR5wBAgA3qqwoU019Q3Qrc2RbdrVDt2Uj/dDXFwCQarYJux6PR1/96le1bds2hcNhrV27VvPnz9cvfvELLVq0SGVlZVq3bp0effRR/Y//8T/k9/t1xx13WD1sAEiJSEiord8TXRmrrigjPAAAAMRhm7ArSatWrdKqVatibvviF89tQZw5c6a+9rWvpXpYAGALrIwBAABMnG2qMQMAAAAAkCiEXQAAAACA6xB2AQAAAACuQ9gFAAAAALiOrQpUAQDOaTzQrNrXGhQcyJDfE1bl6nIKVAEAAEwQYRcAbKjxQLNq6g8pf8k6+QxDYdNUTX2DJBF4AQAAJoBtzABgQ7X1+5S/uFyGYUiSDMNQ/uJy1dbvs3hkAAAAzkDYBQAbCoaMaNCNMAxDvSEjziMAAAAwFNuYAcCG/F5TYdOMCbymacrnNS0cFTA9nEMHAKQSK7sAYEOVFWU6fqhBpjkYbk3T1PFDDaqsKLN4ZMDURM6hh5esk+/StQovWaea+kNqPNBs9dAAAC7Fyi4A2FBktau2fo96Q4Z8XlPVFWWsgsGxBs+hrx3lHPoefq4BAElB2AUAm1q5fCkhAK4RDBnycQ4dAJBCbGMGAABJ5/ea0W35EZxDBwAkE2EXAAAkHefQAQCpxjZmAACQdJxDBwCkGmEXAACkBOfQAQCpxDZmAAAAAIDrEHYBAAAAAK5D2AUAAAAAuA5hFwAAAADgOoRdAAAAAIDrEHYBAAAAAK5D2AUAAAAAuA5hFwAAAADgOl6rBwAAgJUaDzSr9rUGBQcy5PeEVbm6XCuXL7V6WAAAYJoIuwCAtNV4oFk19YeUv2SdfIahsGmqpr5Bkgi8AAA4HNuYAQBpq7Z+n/IXl8swDEmSYRjKX1yu2vp9Fo8MAABMFyu7sAW2EQKwQjBkyHc26EYYhqHekBHnEQAAwCkIu7Ac2wgBWMXvNRU2zejKriSZpimf17RwVAAAIBEIu7Dc4DbCtaNsI9xD2AWQVJUVZaqpb4huZTZNU8cPNai6oszqoU0Iu2IAAIiPsAvLsY0QQKoNDYnhrna1731fvsJS+bymqivKHBEY2RUDAMDYCLuwHNsIAaTS8JCYfXY1968qFjsqJLIrBgCAsVGNGZarrCjT8UMNMs3BcBvZRljpkG2EAJzFLRWYgyEj5iKhxK4YAACGYmUXlousQNTW71FvyHDUNkIAzuOWoxPsigEAYGyEXdjCyuVLCbcAUsItIdHpxbUAAEg2wi4AIK24JSSyKwYAgLERdgEAacVNIZFdMQAAxEfYBQCkHUIiAADuRzVmAAAAAIDrEHYBAAAAAK7DNmYAACap8UCzal9rUHAgQ35PWJWry9kWDQCAzRB2AQCYhMYDzaqpP6T8JevkMwyFTVM19Q2SROAFAMBG2MYMAMAk1Nbvi7YtkiTDMJS/uFy19fssHhkAABiKsAsAwCQEQ0Y06EYYhqHekBHnEQAAwAqEXQAAJsHvNWWaZsxtpmnK5zXjPAIAAFiBM7sAgHFRkOmcyooy1dQ3RLcym6ap44caVF1RZvXQAADAEJaH3ZqaGr355pvyer0qKSnRrbfeKp/PN+J+t912mzIzM5WRkSGPx6Pt27dbMFoASD8UZIoV+Z5r6/eoN2TI5zVVXVGWls8FAAB2ZnnYXb58uTZv3iyPx6NnnnlGzz//vG666aZR73vPPfdo9uzZKR4hAKS3wYJMa0cpyLQnbQPeyuVL0/Z7BwDAKSw/s3vZZZfJ4/FIki6++GJ1dnZaPCIAwFAUZAIAAE5k+cruULt379YVV1wR9+Pbtm2TJF199dVav359qoYFAGnN7zUVNs2YwEtBJgAAYHeGObykZBLcd9996urqGnH7DTfcoPLycknSc889p/fff19f//rXR6wgSFJnZ6cKCgrU3d2t7373u/rKV76iSy65ZNSvt2vXLu3atUuStH37dp05cyZx34yLeL1ehUIhq4eBYZgXe0rneXljf5N+Uteo/CVDCjL9vkE3b1ipy1etsHRs6TwvdsWc2BPzYk/Mi/0wJ/Y01rzMnDkz7uNSEnbH88orr+jXv/617r77bs2aNWvc+z/77LPKzMzUtddeO6HPf+TIkekO0ZUCgYDa29utHgaGYV7sKd3npfFAs2rr90ULMlXapCBTus+LHTEn9sS82BPzYj/MiT2NNS9z5syJ+zjLtzE3NTXpxRdf1He+8524QffUqVMyTVNZWVk6deqUDhw4oKqqqhSPFADSFwWZAACA01gedp966imFQiHdd999kqSLLrpIN998szo7O/XjH/9YW7duVXd3t37wgx9IkgYGBrR69WqtWLHCwlEDAAAAAOzM8rD7ox/9aNTbCwoKtHXrVklSSUmJHnzwwVQOCwAAAADgYJa3HgIAAAAAINEIuwAAAAAA1yHsAgAAAABch7ALAAAAAHAdwi4AAAAAwHUIuwAAAAAA1yHsAgAAAABcx/I+uwAADNd4oFm1rzUoOJAhvyesytXlWrl8qdXDAgAADkLYBQDYSuOBZtXUH1L+knXyGYbCpqma+gZJIvACAIAJYxszAMBWauv3KX9xuQzDkCQZhqH8xeWqrd9n8cgAAICTEHYBALYSDBnRoBthGIZ6Q0acRwAAAIxE2AUA2Irfa8o0zZjbTNOUz2vGeQQAAMBIhF0AgK1UVpTp+KGGaOA1TVPHDzWosqLM4pEBAAAnoUAVAMBWIkWoauv3qDdkyOc1VV1RRnEqAAAwKYRdAIDtrFy+lHALAACmhW3MAAAAAADXIewCAAAAAFyHsAsAAAAAcB3CLgAAAADAdQi7AAAAAADXIewCAAAAAFyHsAsAAAAAcB3CLgAAAADAdQi7AAAAAADXIewCAAAAAFyHsAsAAAAAcB3CLgAAAADAdQi7AAAAAADXIewCAAAAAFyHsAsAAAAAcB3DNE3T6kEAAAAAAJBIrOymsS1btlg9BIyCebEn5sWemBf7YU7siXmxJ+bFfpgTe5rqvBB2AQAAAACuQ9gFAAAAALgOYTeNrV+/3uohYBTMiz0xL/bEvNgPc2JPzIs9MS/2w5zY01TnhQJVAAAAAADXYWUXAAAAAOA6XqsHAHt46aWXVFNToyeffFKzZ8+2ejhp7+c//7n27dsnwzCUm5urW2+9VQUFBVYPK+3V1NTozTfflNfrVUlJiW699Vb5fD6rh5XWfve73+lf//Vf9dFHH+l73/ueFi1aZPWQ0lpTU5OefvpphcNhXXXVVbruuuusHlLae/zxx7V//37l5ubqoYcesno4kNTe3q7HHntMXV1dMgxD69evV2VlpdXDSntnzpzRPffco1AopIGBAX3iE5/Qpk2brB4WJIXDYW3ZskUFBQWTrspM2IXa29t14MABBQIBq4eCs6699lrdcMMNkqTa2lrt2LFDN998s8WjwvLly7V582Z5PB4988wzev7553XTTTdZPay0Nn/+fH3961/XT37yE6uHkvbC4bCeeuopffOb31RhYaG2bt2qsrIyzZs3z+qhpbUrr7xSGzdu1GOPPWb1UHCWx+NRdXW1Fi5cqJMnT2rLli1avnw5vysWmzFjhu655x5lZmYqFArp7rvv1ooVK3TxxRdbPbS0V1tbq7lz5+rkyZOTfizbmKF/+qd/0pe+9CUZhmH1UHBWdnZ29O3Tp08zNzZx2WWXyePxSJIuvvhidXZ2WjwizJs3T3PmzLF6GJD03nvvqbS0VCUlJfJ6vbriiivU0NBg9bDS3iWXXCK/32/1MDBEfn6+Fi5cKEnKysrS3Llz+f+JDRiGoczMTEnSwMCABgYGeP1lAx0dHdq/f7+uuuqqKT2eld0019DQoIKCAp1//vlWDwXD/Mu//IteffVVZWdn65577rF6OBhm9+7duuKKK6weBmAbnZ2dKiwsjL5fWFiod99918IRAfbX2tqqDz74QBdeeKHVQ4EGd6jcddddamlp0Wc+8xlddNFFVg8p7f30pz/VTTfdNKVVXYmwmxbuu+8+dXV1jbj9hhtu0PPPP69vfvObqR8UxpyX8vJy3Xjjjbrxxhv1/PPP61e/+hXnRlJkvHmRpOeee04ej0ef+tSnUjy69DSROQEApzl16pQeeughffnLX47Z0QXrZGRk6MEHH1Rvb69+8IMf6PDhw1qwYIHVw0pbb775pnJzc7Vw4UI1NzdP6XMQdtPAt771rVFvP3z4sFpbW3XnnXdKGtwmcNddd+n+++9XXl5eCkeYnuLNy3Cf+tSndP/99xN2U2S8eXnllVf05ptv6u6772Z7U4pM9HcF1iooKFBHR0f0/Y6ODgrrAXGEQiE99NBD+tSnPqWPf/zjVg8Hw/h8Pi1dulRNTU2EXQu988472rdvnxobG3XmzBmdPHlSjzzyiG6//fYJfw7CbhpbsGCBnnzyyej7t912m+6//36qMdvA0aNHdd5550ka3GrOmUR7aGpq0osvvqjvfOc7mjVrltXDAWxl0aJFOnr0qFpbW1VQUKDf/va3k3pBAqQL0zT1xBNPaO7cufrsZz9r9XBw1okTJ+TxeOTz+XTmzBkdOHBAf/mXf2n1sNLa5s2btXnzZklSc3OzXnrppUn/f4WwC9jQP//zP+vo0aMyDEOBQIBKzDbx1FNPKRQK6b777pMkXXTRRcyNxd544w394z/+o06cOKHt27fr/PPP1ze+8Q2rh5WWPB6PvvrVr2rbtm0Kh8Nau3at5s+fb/Ww0t7DDz+st99+Wz09Pbrlllu0adMmrVu3zuphpbV33nlHr776qhYsWBDdXXfjjTdq1apVFo8svR0/flyPPfaYwuGwTNPUJz/5SX3sYx+zeliYJsM0TdPqQQAAAAAAkEi0HgIAAAAAuA5hFwAAAADgOoRdAAAAAIDrEHYBAAAAAK5D2AUAAAAAuA5hFwAAAADgOoRdAAAc6plnntH3v//96Ps1NTW69957FQqFLBwVAAD2QNgFAMCh/vIv/1LNzc364IMPVFdXp6amJn3961+X1+u1emgAAFjOME3TtHoQAABgap599lm98cYb6uvr07333qtAIKC+vj7dd999+s///E9t27ZNCxYssHqYAACkHCu7AAA42AUXXKDDhw9r8+bNCgQCkqSZM2dq69at+sQnPmHx6AAAsA5hFwAAhzp8+LCefPJJrVmzRnv27Ine7vV6NXv2bAtHBgCA9Qi7AAA4UGdnpx544AH9t//23/S3f/u3Onz4sJqbm60eFgAAtkHYBQDAYfr6+nT//ffrmmuuUVlZmWbNmqXPfe5z+vnPf2710AAAsA0KVAEA4FKPPfaYPve5z1GgCgCQlgi7AAC40P33368//elPCgQCuvrqq3XllVdaPSQAAFKKsAsAAAAAcB3O7AIAAAAAXIewCwAAAABwHcIuAAAAAMB1CLsAAAAAANch7AIAAAAAXIewCwAAAABwHcIuAAAAAMB1CLsAAAAAANch7AIAAAAAXOf/B0EpUq8N2UBiAAAAAElFTkSuQmCC",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plot_ds(data,m[-1],q[-1])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### RMSProp"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"RMSprop cerca di ridurre l'aggressività di Adagrad nel ridurre il learning rate in modo monotonicamente decrescente. \n",
"\t\n",
"La somma $G_{j,k}$ dei quadrati dei gradienti precedenti è sostituita da una sua versione $\\tilde G_{j,k}$ che decresce in modo geometrico per mezzo di un parametro di smorzamento $0<\\gamma<1$\n",
"\n",
"\\begin{align*}\n",
" \\tilde G_{j,k}&=\\gamma \\tilde G_{j,k-1}+(1-\\gamma)g_{j,k}^2\\\\\n",
" &=\\gamma (\\gamma \\tilde G_{j,k-2}+(1-\\gamma)g_{j,k-1}^2)+(1-\\gamma)g_{j,k}^2=\\gamma^2\\tilde G_{j,k-2}+(1-\\gamma)(\\gamma g_{j,k-1}^2+g_{j,k}^2)\\\\\n",
" &=\\cdots\\\\\n",
" &=(1-\\gamma)\\sum_{i=0}^k\\gamma^{k-i} g_{j,i}^2\n",
"\\end{align*}\n",
"\n",
"dato che assumiamo $\\tilde G_{j,k}=0$ if $k<0$.\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Ne deriva che alla $k+1$-esima iterazione vengono eseguite le azioni seguenti\n",
"\n",
"\\begin{align*}\n",
"g_{j, k} &= \\frac{\\partial J(\\theta)}{\\partial\\theta_j}\\Big\\rvert_{\\theta=\\theta^{(k)}}\\\\\n",
"\\tilde G_{j,k} & =\\gamma \\tilde G_{j,k-1}+(1-\\gamma)g_{j,k}^2\\\\\n",
"\\Delta_{j,k} &= - \\frac{\\eta}{\\sqrt{\\tilde G_{j,k}+\\varepsilon}} g_{j, k}\\\\\n",
"\\theta_j^{(k+1)} &= \\theta_j^{(k)} + \\Delta_{j,k}\n",
"\\end{align*}\n"
]
},
{
"cell_type": "code",
"execution_count": 139,
"metadata": {},
"outputs": [],
"source": [
"def RMSProp(X,t, eta = 0.1, G_tilde = 0, eps = 1e-8, gamma = 0.9, epochs = 10000):\n",
" theta = np.zeros(nfeatures+1).reshape(-1,1)\n",
" theta_history = []\n",
" cost_history = []\n",
" for k in range(epochs): \n",
" g = gradient(theta,X,t)\n",
" G_tilde = gamma * G_tilde + (1 - gamma) * g**2\n",
" theta = theta - eta * g / (np.sqrt(G_tilde) + eps)\n",
" theta_history.append(theta)\n",
" cost_history.append(cost(theta, X, t))\n",
" theta_history = np.array(theta_history).reshape(-1,3)\n",
" cost_history = np.array(cost_history).reshape(-1,1)\n",
" m = -theta_history[:,1]/theta_history[:,2]\n",
" q = -theta_history[:,0]/theta_history[:,2]\n",
" return cost_history, m, q"
]
},
{
"cell_type": "code",
"execution_count": 140,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"tempo di esecuzione: 0.547 secondi\n",
"10000 passi totali\n",
"1000000 gradienti calcolati\n"
]
}
],
"source": [
"start_time = time.time()\n",
"cost_history, m, q = RMSProp(X,t, eta = 0.1, G_tilde = 0, eps = 1e-8, gamma = 0.9, epochs = 10000)\n",
"print(f\"tempo di esecuzione: {time.time()-start_time: 4.3f} secondi\")\n",
"print(f\"{len(m)} passi totali\")\n",
"print(f\"{len(m)*n} gradienti calcolati\")"
]
},
{
"cell_type": "code",
"execution_count": 141,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA7sAAAHzCAYAAADhDgreAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAABYVElEQVR4nO3df3ib9X3v/9ctyb8k+Zek2Gl+8KUJsISEkDCHtjhtSAgpl2kZKxmFDO/auh3Gget0rKdcJKct0FJKKOUqFwUO7QWjq9lZ2xMKvTjzGV6WEA5uGQ5xFmIaBqwtW0OiyL9iSf4l6f7+YUu2bMtxEkv3Len5uK5etRXd8Uf+2EGv+/P+vD+GaZqmAAAAAAAoIA6rBwAAAAAAwHwj7AIAAAAACg5hFwAAAABQcAi7AAAAAICCQ9gFAAAAABQcwi4AAAAAoOAQdgEAAAAABYewCwBAjp1//vmqqKhQZWWlampqdMUVV+ipp55SIpE47bW/+c1vZBiGYrFYVseYq68DAEC2EHYBALDASy+9pIGBAf32t7/Vjh079NBDD+nP//zPrR4WAAAFg7ALAICFqqurdd111+knP/mJ/vZv/1ZHjhzRP/zDP2jdunWqqqrS0qVLdd9996We/6lPfUqSVFNTI6/Xq1/+8pd6//33tXnzZvn9fgUCAf3xH/+x+vr6Utc89NBDWrx4sSorK/V7v/d7+ud//mdJUiKR0K5du7R8+XL5/X7deOON6unpyfh1AADIJ4RdAABs4PLLL9eSJUv0//7f/5PH49GPfvQj9fX16R/+4R/0P//n/9SLL74oSXr11VclSX19fQqHw/rEJz4h0zS1c+dOHTt2TL/61a/0H//xH6mA/M477+jxxx9XR0eHBgYG9PLLL+v888+XJH3ve9/Tiy++qP379+vYsWOqra3VHXfckfHrAACQTwi7AADYxKJFi9TT06Mrr7xSl1xyiRwOh9asWaObb75Z+/fvz3jdBRdcoKuvvlplZWVasGCBvvSlL6We73Q6NTw8rLffflujo6M6//zztXz5cknSU089pQceeEBLlixRWVmZ7rvvPu3evZt9ugCAgkDYBQDAJn73u9/J5/PpX/7lX7Rp0yYtWLBA1dXVeuqppxQKhTJed+LECd10001avHixqqqqdMstt6Sef8EFF+jRRx/Vfffdp7q6Ot100006duyYJOm3v/2t/vAP/1A1NTWqqanRypUr5XQ6deLEiZy8XgAAsomwCwCADXR0dOh3v/udNmzYoO3bt+u6667Tf/zHf6i/v1+33XabTNOUJBmGMe3a//E//ocMw9Bbb72lU6dO6bnnnks9X5K2b9+u1157Tb/97W9lGIbuvvtuSdLSpUv1f//v/1VfX1/qf0NDQ1q8ePGMXwcAgHxC2AUAwEKnTp3S//k//0c33XSTbrnlFl1yySUaGBiQz+dTeXm53njjDf2v//W/Us9fsGCBHA6H/v3f/z312MDAgLxer6qrq/W73/1ODz/8cOrP3nnnHe3du1fDw8MqLy9XRUWFHI6x//zfdttt+spXvqLf/va3kqSTJ0/q5z//ecavAwBAPiHsAgBggc9+9rOqrKzU0qVL9cADD+hLX/qSnn32WUnSk08+qXvuuUeVlZX6xje+oRtvvDF1ndvt1le+8hU1NjaqpqZGr7/+uu69914dPHhQ1dXVuvbaa/W5z30u9fzh4WHt2LFDgUBACxcuVDAY1IMPPihJ+qu/+itdd9112rp1qyorK/Xxj39c//Iv/5Lx6wAAkE8Mc3KdEwAAAAAABYCVXQAAAABAwSHsAgAAAAAKDmEXAAAAAFBwCLsAAAAAgIJD2AUAAAAAFBzCLgAAAACg4LisHkAuHDt2zOoh2FIgEFAoFLJ6GJiCebEn5sWemBf7YU7siXmxJ+bFfpgTe5ptXhYtWpTxOlZ2AQAAAAAFh7ALAAAAACg4hF0AAAAAQMEh7AIAAAAACg5hFwAAAABQcAi7AAAAAICCQ9gFAAAAABQcwi4AAAAAoOC4cv0Fn3zySR08eFDV1dV65JFHJEk//elP9c///M+qqqqSJN1888267LLLpl176NAhPfvss0okErrqqqt0/fXX53LoAAAAAIA8kfOwe+WVV+qaa67RE088kfb4tddeq+uuuy7jdYlEQs8884y++tWvyu/3a+fOnWpoaNCSJUuyPWQAAAAAQJ7JeRnzxRdfLK/Xe8bXvffee1q4cKHq6+vlcrl0xRVXqKOjIwsjBAAAAADku5yv7Gby8ssv69VXX9WyZcv0J3/yJ9MCcU9Pj/x+f+pzv9+vd999N9fDBAAAAADkAVuE3a1bt2rbtm2SpJ/85Cf60Y9+pNtvv/2s/749e/Zoz549kqRdu3YpEAjMyzgLjcvl4ntjQ8yLPTEv9sS82A9zYk/Miz0xL/bDnNjT2c6LLcJuTU1N6uOrrrpKDz300LTn+Hw+dXd3pz7v7u6Wz+eb8e/bsmWLtmzZkvo8FArN32ALSCAQ4HtjQ8yLPTEv9sS82A9zYk/Miz0xL/bDnNjTbPOyaNGijNfZ4uih3t7e1MdvvPGGli5dOu05y5cv14cffqhgMKhYLKZf/OIXamhoyOUwAQAAAAB5Iucru48++qjefvttDQwM6LbbbtONN96orq4u/eY3v5FhGFqwYIFuvfVWSWP7dL///e9r586dcjqd+sIXvqAHHnhAiURCmzZtmjEUAwCA4tN1qFNvvdyqksGwRiu8uuTTTVq1dp3VwwIAWCjnYffOO++c9tjmzZtnfK7P59POnTtTn1922WUznr8LAACKV9ehTh3f3aJtdTUy3G6ZZlz7d7dIEoEXAIqYLcqYAQAAztaRtlZtrKuRYRiSJMMwtLGuRkfaWi0eGQDASoRdAACQ11zRcCroJhmGIVc0YtGIAAB2QNgFAAB5Leb2yjTNtMdM01TM7bFoRAAAOyDsAgCAvLZ6a5P2B/tSgdc0Te0P9mn11iaLRwYAsJItztkFAAA4W8kmVM+3tcoVjSjm9mj1tmaaUwFAkSPsAgCAvLdq7TrCLQAgDWXMAAAAAICCQ9gFAAAAABQcwi4AAAAAoOAQdgEAAAAABYewCwAAAAAoOIRdAAAAAEDBIewCAAAAAAoO5+wCAICz1nWoU2+93KqSwbBGK7z65I03a/FHl1k9LAAAWNkFAABnp+tQp47vbtG2iriu97u1rSKu93/0A3Ud6rR6aAAAEHYBAMDZOdLWqo11NTIMQ5JkGIaurK/RkbZWi0cGAABhFwAAnCVXNJwKukmGYcgVjVg0IgAAJhB2AQDAWYm5vTJNM+0x0zQVc3ssGhEAABMIuwAA4Kys3tqk/cG+VOA1TVOvnOjT6q1NFo8MAAC6MQMAgFlM7bZ8yaebtGrtOklK/f/zba1yRSOKuT3a8Ce30o0ZAGALhF0AADCjVLfluhoZbrdMM679u1skKS3wJj+WpEAgoFAoZMl4C8lsNxkAAHNDGTMAAJjRTN2WN9bRbTnbZjrS6fjuFo50AoAzRNgFAAAzotuyNbjJAADzg7ALAABmRLdla3CTAQDmB2EXAADMaKZuy/uDdFvONm4yAMD8IOwCAIAZrVq7Tgu3Nev5Iade7B7U80NOLdzWTKOkLOMmAwDMD7oxAwCAjKZ2W0b2zXSk02puMgDAGSPsAgAA2Aw3GQDg3FHGDAAAAAAoOIRdAAAAAEDBIewCAAAAAAoOYRcAAAAAUHBoUAUAAICs6zrUqbdeblXJYFijFV5d8ukmmnAByCrCLgAAALKq61Cnju9u0ba6Ghlut0wzrv27WySJwAsgayhjBgAAQFYdaWvVxroaGYYhSTIMQxvranSkrdXikQEoZIRdAAAAZJUrGk4F3STDMOSKRiwaEYBiQNgFAABAVsXcXpmmmfaYaZqKuT0WjQhAMSDsAgAAIKtWb23S/mBfKvCapqn9wT6t3tpk8cgAFDIaVAEAACCrkk2onm9rlSsaUczt0eptzTSnApBVhF0AAABk3aq16wi3AHKKMmYAAAAAQMEh7AIAAAAACg5lzAAAAPOs61Cn3nq5VSWDYY1WeHXJp5so4QWAHCPsAgAAzKOuQ506vrtF2+pqZLjdMs249u9ukSQCb57jJgaQXwi7AAAA8+hIW6tuqKuRYRiSJMMwtLGuRs+3tRKMZpAvAZKbGED+Yc8uAADAPHJFw6mgm2QYhlzRiEUjsq9UgKyI63q/W9sq4jq+u0VdhzqtHto0R9patXGGmxhH2lotHhmATHK6svvkk0/q4MGDqq6u1iOPPCJJamlp0ZtvvimXy6X6+nrdfvvt8ng806694447VF5eLofDIafTqV27duVy6AAAAHMSc3tlmvG0wGuapmLu6e9vil0+rYK7omEZFe60x7iJAdhbTsPulVdeqWuuuUZPPPFE6rE1a9Zo+/btcjqdeu655/TCCy/olltumfH6e++9V1VVVbkaLgAAwBlbvbVJ+3e3pFYBTdPU/mCfVm9rtnpotpNPAZKbGED+yWnYvfjiixUMBtMeu/TSS1MfX3TRRXr99ddzOSQAAFCArNwHmvw6z7e1yhWNKOb2aPW2ZtutVNpBPgVIbmIA+cdWDar27t2rK664IuOfP/DAA5Kkq6++Wlu2bMnVsAAAQB6xQyOhVWvXEW7nIJ8CJDcxgPxjmKZp5vILBoNBPfTQQ6k9u0k/+9nP9P777+vLX/7ytKYOktTT0yOfz6f+/n5985vf1J/92Z/p4osvnvFr7NmzR3v27JEk7dq1SyMjI/P/QgqAy+VSLBazehiYgnmxJ+bFnpgX+7HDnDxzz079YenotNXCF0ZK9OffeNDCkVnHDvOSyb92vKEDL70gZySsuMerhs/+oS5df7nVw8oJO89LsWJO7Gm2eSktLc18XbYGdCZeeeUVvfnmm7rnnntmDLqS5PP5JEnV1dVav3693nvvvYxhd8uWLWkrv6FQaP4HXQACgQDfGxtiXuyJebEn5sV+7DAnsZ6QRv3uGR4/ZfnYrGKHeclk8UeXafEX/3vaY3Yd63yz87wUK+bEnmabl0WLFmW8zvKwe+jQIf385z/X17/+dZWVlc34nKGhIZmmqYqKCg0NDenw4cPatm1bjkcKAADywX+Go/rJu79SqRnXqMOpS85bqhULF9hyHygAIHtyGnYfffRRvf322xoYGNBtt92mG2+8US+88IJisZjuv/9+SdKFF16oW2+9VT09Pfr+97+vnTt3qr+/X9/5znckSfF4XBs2bNDatWtzOXQAAJAHug516v8biejj1WUKlJdKpql9H/xWB3sG9Pu3/ZXVwwMA5FBOw+6dd9457bHNmzfP+Fyfz6edO3dKkurr6/Xwww9nc2gAAKAAHGlr1Q0XnKfIwCl9eDIoRzyh3/NX672yWhoJAUCRsbyMGQCQPVYevwJYIXluq7eqWt6q6tTjdd2DFo4KAGAFwi4AFCg7HL8C5Fo+ndsKAMguwi4AFKgjba26YfzsSkkyDEMb62r0fFsrYRcF61zObaUSAgAKC2EXAApUspxzMsMw5IpGLBoRkH3JcPp8W6tc0Yhibo9Wb2s+bWilEgIACg9hFwAKFOWcKFar1q4744BKJQQAFB6H1QMAAGTH6q1N2h/sk2makjRRzrm1yeKRAfbjiobTbgxJVEIAQL5jZRcACtTZlnMCxYhKCAAoPIRdAChgZ1POCRSjc2lsBQCwJ8IuAABZRIff/EAlBAAUHsIuAABZQoff/EIlBAAUFhpUAQCQJUfaWlNlsdJEh98jba0WjwwAgMJH2AUAIEvo8AsAgHUoYwYAIEvo8ItCNtt+dPaqA7ADwi4AIO9NfWPt/ehyhX/9vuVvtOnwi0I12350SexVB2ALhF0AQF6b+qb77Q8/1Nu7X9M1ay5Wpb/G0jfadPhFoTrS1qobZtiP/vz4fvRMf8bPPoBcIuwCAPLa1DfdXR/8p25Y7Nfx0ElVVtdY/kabDr8oRK5oWEaFO+2xif3o5ix/BgC5Q4MqAEBem9oEypWIy2EYcsTjqcd4ow3Mr7H96GbaY8n96LP9GQDkEmEXAJDXpr6xjjmcSpimEk5n6jHeaAPza/XWJu0P9qV+91L70bc2zfpnAJBLlDEDAHIiW91ZpzaBWnXeEv3svff16TUXSxJNoYAsmMt+dPaqA7AaYRcAkHWzdW491zfA095013xEnm0b9PJv3permzfaQLbMth+dveoA7ICwCwDIutk6t87HG2LeWAMAgKnYswsAyLqpTaQkmkYBAIDsIuwCALKO7qwAACDXCLsAgKyjOysAAMg19uwCALJuLp1bgVzJVmdwAIC9EHYBADmRD02kCEHZY5fv7ek6g9tlnACAc0fYBQBA2T0eqdjZ6Xs7W2dwSbYZJwDg3LFnFwAAjYWgjTOEoCPjIQhnz07f29k6g9tpnACAc0fYBQBAHI+UTXb63s7WGdxO4wQAnDvCLgAA4nikbLLT93a2zuB2GicA4NwRdgEAEMcjZZOdvrer1q7Twm3Nen7IqRe7B/X8kFMLxzuD22mcAIBzR4MqAACUn8cj5UvnYLt9bzN1BrfbOAEA54awCwDAuHw4HinJTh2O5yJfvre5Hme+3LAAgHxEGTMAAHmIzsH5L3XDoiKu6/1ubauI6/juFnUd6rR6aABQEAi7AADkIToH5z9uWABAdlHGDACYV5Rl5sZY5+B4WuClc3B+cUXDMircaY9xwwIA5g8ruwCAeUNZZu7QOTj/cdQRAGQXYRcAMG8oy8yd2Y7QQX7ghgUAZBdlzACAeUNZZm5Z3eF4ppL1jVuutmw8+YajjgAguwi7AIB5wz7S4pHp6KN/ra7W4o8us3p4ecPqGxYAUMgIuwCAebN6a5P2725JlTKnyjK3NVs9tJzIZXMuqxuBHWlr1Q0zlKz/w0svaPEX/3vOxgEAQCaEXQDAvCnmssxMK52S5v315/JrZZKpZN0ZDufk6wO5ZvUNJgBnjrALAJhXxVqWmWml8/m21nn/fuTya2WSqWQ97vHm5OsDuWSHG0wAzhzdmAEAmAeuaDgt+EnZa86Vy6+VSaZOwg2f/cOcjQHIFTrNA/mJlV0AAOZBLptz2aERWKaS9UvXX65QKJSzcQC5QKd5ID8RdgEAmAe5bM5ll0ZgxVqyjuJjhxtMAM4cYRcAgHmQy+ZcxdwIDLCCXW4wATgzOQ+7Tz75pA4ePKjq6mo98sgjkqRwOKzvfve7OnnypBYsWKC//uu/ltc7vcHFK6+8op/97GeSpM997nO68sorczl0AABmlcuVTlZVgdzhBhOQn3Iedq+88kpdc801euKJJ1KPvfjii7rkkkt0/fXX68UXX9SLL76oW265Je26cDis3bt3a9euXZKkHTt2qKGhYcZQDAAAAMwnbjChWMTjCYX6ojoRCutEd0SmaWpr4wVWD+us5DzsXnzxxQoGg2mPdXR06L777pMkbdy4Uffdd9+0sHvo0CGtWbMmFW7XrFmjQ4cOacOGDTkZNwAAAAAUgkTCVE9/VCdCEZ3oDo/9LzT2v1BvVPGEmXpudWU5Yfdc9Pf3q7a2VpJUU1Oj/v7+ac/p6emR3+9Pfe7z+dTT0zPj37dnzx7t2bNHkrRr1y4FAoEsjDr/uVwuvjc2xLzYE/NiT8yL/RTSnPxrxxvqeOkFuSIDinkqtf6zf6hL119u9bDOSiHNSyFhXuynkOZkLNBGdOzEKR0L9uvD4Cn97kS/Pgz268OTpxSLJTJeG6j1aFF9tRbVVWlRfbX8fv+0I+9y6WznxRZhdzLDMM75G7llyxZt2bIl9TlHIMwsEAjwvbEh5sWemBd7Yl7sp1DmpOtQp47vbtFn6mpkeJ0yzYj2P/O4+vrzc59mocxLoWFe7Cff5sQ0TZ0KD4+XHId1PBRWsHtstTbYHdHIaDzjtdWV5ar3e7Qw4FV9wKs6v1f1fq/q/B6VljjTntvd3Z3tlzKr2eZl0aJFGa+zRditrq5Wb2+vamtr1dvbq6qqqmnP8fl8evvtt1Of9/T06OKLL87lMAEAQJE40taqG8Y770pjN+M31tXo+bbWvAy7APKXaZoKR0cmlRpPlB4HuyMaGo5lvLbSU6r6wFiITf2/36M6v1flZbaIgllli1fY0NCg/fv36/rrr9f+/fu1fv36ac9Zu3at/v7v/17hcFiS9K//+q/avn17rocKAAByoOtQp956uVUlg2GNVnh1yaebchoyXdGwjAp32mOGYcgVjeRsDACKS2RwJNUU6kQorGD3xMfRodGM13kqSiYFWa/qAp5UuHWXl+TwFdhPzsPuo48+qrffflsDAwO67bbbdOONN+r666/Xd7/7Xe3duzd19JAkvf/++/qnf/on3XbbbfJ6vbrhhhu0c+dOSdK2bdvoxAwAQAFKlhBvq6uR4XbLNOPav7tFknIWeGNur0wznra1yjRNxdyenHx9AIVpcHhUweTK7HjpcTLQhqMjGa+rKHOpbtLK7MRqrUded1kOX0F+yXnYvfPOO2d8/J577pn22PLly7V8+fLU55s3b9bmzZuzNTQAAGADdighXr21Sft3t2jj+DhM09T+YJ9Wb2vOydcHkL+GR2KpfbNjoTYyvkobVv/AcMbrSkuc4yHWM75C6x3fU1upSk+ppQ2i8pUtypgBAACS7FBCnAzVz7e1yhWNKOb2aPW2/GxOlQ3zXWZuddk6cKZGY3EFuyNppcbJ1dreU0MZr3O5HKr3eSZWaQMeLfRXqi7gUU1lOYF2nhF2AWCe8GYNmB9zKSHOxe/bqrXrpv2d/J7Pf5m5HcrWgZnE4gmFeiMTDaFCEyu1Pf1RmebM1zmdhhbUjpcaTyk9rq2qkMNBoM0Vwi4AzAPerAHz53QlxFb9vvF7Pma+y8ztULaO4pVImAr1RRUcD7L9kX/Tb/4zpGAorFBfVInEzInW4TC0oNatuoBXC8dXaJOlx/7qCjmdjhy/EsyEsAsA84A3a8D8OV0JsVW/b/yej5nvMnM7lK2jsCUSpnpPDY4f25PeFOpkb0Tx+MyB1jCkQK07dfbs5KZQgVqPXARa2yPsAsA84M0aML9mKiFOsur3jd/zMfPdqZrO15gPpmmqb2AordT4RHdYwVBYwZ6IRmOJjNfWVlekmkIt+//q5S2X6vxe1fk8Kilx5vBVYL4RdgFgHvBmDcgdq37f+D0fM9+dqul8jbkyTVOnwsOpldngpFXaYHdYwyPxjNdWV5aNr9BOlBwnV2zLSiciUSAQUCgUysXLQQ4QdgFgHvBmDcidbPy+zaXxFL/nY+arU/Xk7/mJ4YSOfNCtJV4Pna+hcHR4SlOoiVXaweFYxuu87tK0o3uSZcd1AY8qykpy+ApgF4RdAJgHHFMC5M58/77NtfEUv+cTZiszn4tp33NfhfYH+7Tw+j8qyu9nMYoOjaZKjoPjwfZ4KKxgd1iRwdGM17nLS1KBtm480C4MjK3QeipKc/gKkA8IuwAwT871zR+AuZvP37czaTzF7/n8oNlXcRgajk2cQ5tcpR0PuAORkYzXlZW6JkqNJzWFqvd75XWXchYt5oywCwAAihqNp3KP73nhGBmNK5gsMx5fnU2WHvcPDGW8rrTEOdbhOBVoJz6u8pYRaDEvCLsAAKCo0Xgq9/ie55dYLKGTPemlxsk9tb2nBmXOfHKPXE7HpEA7XnY8HmhrKsvlcBBokV2EXQCwwFya4cAemKvCR+Op3ON7bj/xeEKhvuikUuOJ0uPuvmjGQOt0GAr4PWMrs8mS4/Fw66t2E2hhKcIuAOTYXJvhwHrM1dxMviHg9AV04ac259X3h8ZTucf33BqJhKnuvmj6ObTjgTbUG1U8MXOiNQxpgc+TKjWuS5YdB7wK1LjldDpy/EqAuSHsAkCO0ZglfzBXpzf1hkBJyaj+KQ9vCNB4Kvf4nmdHImGq79Tg2Mps6hzasXB7sieiWDwx43WGIflrKiaVGk+cRbvA55HLRaBF/iHsAkCO0ZglfzBXp8cNASD3TNNU/8DwpCAbVrA7ouOhsE72RDQyGs94bU1V+XiIHS87DkwE2tISZw5fBZB9hF0AyDEas+QP5ur0uCEAZIdpmhqIjIwf3TNRdpzcTzs8Est4bZWnTHXjK7MLx8NssvS4rJS3/yge/LQDQI7RmCV/MFenxw0B4NxEBkcmGkJNOof2RHdEg0OjGa/zVJSkrcxO7njsLi/J4SsA7IuwCwA5RmOW/MFcnR43BIDTGxweVTA0VmacLD0OhsIK9kQ1EBnOeF1FmWsizI6vzNaNf+51l+bwFQD5ibALABagMUv+YK5mN/WGgMvn1gXcEEARGh6JKThDU6gT3WGdCmcOtGWlzrEy48lNocYDbaWnNK1qAsCZIewCAIBzMvmGQCAQUCgUOqe/j7ONYVejo3EFe9L3zgbHw23vqaGM15W4HONdjtPPol1x0VIlRqMEWiBLCLsAAMA2ONsYVovFEjrZO34GbbIp1PgqbU9/VObMR9HK6TRU55t8Du1EuK2tqpDDMT3Q+ms8CoUGs/yKgOJF2AUAALbBUUbIhXg8oe6+6JSzaMc+7u6LKpGYOdE6HIYW+NxpDaGSK7X+GveMgRaAdQi7AADANjjKCPMlkTDV0z+YagaVDLTHQ2GFeiOKx2cOtIYhBWrd4/toPWNH9yQDba1bLqcjx68EwNki7AIAANvgKCOcCdM01XdqaFKp8URTqGBPRLFYIuO1tdUVqh8Ps3WTuh0v8HlU4nLm8FUAyBbCLgAAsA2OMsJUpmnqVHg4rSlUsvQ42B3RyGg847XVlWVp3Y2Te2gX+DwqK+VtMFDo+C0HAAC2wdnGxSscHdaJSWfRBpPBtjusoeFYxusqPaWpQDu543Gd36OKspIcvgIAdkPYBQAAtsLZxoUrOjgyY1OoYHdYkcHRjNd5KkrSSo3rJ33srijN4StAIes83KW9B44oFBmW15lQ04b1WrdmldXDwjkg7AIAAGDeDA3H0s+hTX0c1kBkJON15WWuVKlx6uiewNieWq+7LIevAMWo83CXWtqPqn7NRnlGR5UwTbW0d0gSgTePEXYBAABwRkZG45NCbGRSuA2rf2A443WlJU7VTVmZTe6nrfKWpTUmA3Kptf2AaldsSjv2rHbFerW27yPs5jHCLgAAwBx0Hu5S62sdCscdRVHiOBqL62RPJK3U+Ph4uO3tH8x4ncvlUJ3PM+0c2nq/VzVV5QRa2FI4Zsgz5WfTMAxFYvy85jPCLgAAwGkkSxxrV26WxzAKpsQxFk+ouzeaWpk9HhrrcHyiO6zuvqjMmY+ildNhKOAbP4N2fKU2WXrsq66Qw0FAQH7xukwlpvzAm6YpjyvDLwHyAmEXAADgNPK5xDGRMHU8dEpH3z2Rdg7tie6wQr1RJRIzv5k3DGmBzzNjUyh/jVtOpyPHrwTInqbGBrW0d6h+TaOksaDbe7RDzY0NFo8M54KwCwAAcBp2L3FMJEz1nRrUie6pR/eEdbInqlg8MeN1hiH5a9xj5cbjpcZ14x8vqPXI5SLQojgkb1rtfXO/+sPD8rhMNTc22P5mFmZH2AUAADiNZInj5P2muS5xNE1TfQNDCk5amZ3c8Xg0NnOglSR/jUcLaivGS40n9tHW+TwqKXHm7DUAdrZuzSpdvXmjQqGQ1UPBPCHsAgCQB7oOdeqtl1tVMhjWaIVXl3y6ibNocyhZ4li7Yr0Mw8haiaNpmhqIjKR1Nz4RGj++pzus4ZF4xmurvGUTTaH83lTZcZ3fo8WLFvIGHkDRIewCAGBzXYc6dXx3i7bV1chwu2Wace3f3SJJBN4cSZYytrbvUyRmnHOJYzg6MqnUODIRbLsjGhwazXid112afg6t36uF44G2orzkrMYCAIWKsAsAgM0daWvVDXU1ac2RNtbV6Pm2VsJuDq1bs+qMwu3g0GhqZTat7DgUVmQwc6CtKC9Jbwg1qfTYU1E6Hy8FAIoCYRcAAJtzRcMyKtxpjxmGIVc0YtGIkDQ8EhvbMzu+MjvRHCqiU5HhjNeVlTondTeeKD2u83tV6SnlLFoAmAeEXQAAbC7m9so049OaI8XcHgtHVTxGR+MK9kTSVmZPjJ9F23dqKON1JS6H6iaVGddPKj2uriwj0AJAlhF2AQCwudVbm7R/d4s2jpcym6ap/cE+rd7WbPXQCkYsltDJnsnlxmMfB7vD6ukflJmh6bLL6Rg/iza9KVS936Oaqgo5HARaALAKYRcAAJtL7st9vq1VrmhEMbdHq7c1s1/3DMXjCYX6ohPH9UxqChXqjWQMtE6HoYDPPd7ZOL3s2F/jJtACgE0RdgEAyAOr1q4j3M5BImGqpz86vSlUd0ShnojiiZkTrWFIgVr3pFJjT6o5lL/GLZfTkeNXAjvoPNyl1tc6FI475HUm1LRh/Vl34AaQe4RdAACQVxIJU30DQ6njeoKTy457IorFEhmv9VVXpFZmk/tp6/1eBXxulbicOXwVsLvOw11qaT+q2pWb5TEMJUxTLe0dkkTgBfIEYRcAANiOaZo6FR5OO392ItxGNDIaz3htdWV5amV24aTS4zq/R6UlBFrMTWv7AdWu2JR25FftivVqbd9H2AXyBGEXAABYwjRNhaMj6WfRTgq0Q8OxjNdWekqnnEM7Vnpc5/eqvIy3Nzh34Zghz5SO2YZhKBJjjzaQL/ivAQAAyKro4EhqZfZ4aLzsePzz6NBoxus8FSVpx/XUJTseB7xyl5fk8BXkt65DnXr31b2K94Q0WuHVJZ9uYv/3HHhdphKmOe3IL48rQyczALZji7B77Ngxffe73019HgwGdeONN+raa69NPdbV1aVvf/vbqqurkyR97GMf07Zt23I+VgAAMN3g8KiCoYh+9et+vffrD9NKj8PRkYzXVZS5VDe1KdT4nlqvuyyHr6AwdR3q1PHdLfrckjqN+t0yzbj2726RJALvaTQ1NqilvUO1K9anjvzqPdqh5sYGq4cGYI5sEXYXLVqkhx9+WJKUSCT0l3/5l7r88sunPW/lypXasWNHrocHAAAkDY/EFOxOP4s2OP5x/8BwxutKS5yps2fHVmgnPq7ylqWtnGF+HWlr1Q3j5zNLY2W4G+tq9HxbK2H3NJL7clvb9ykSM+RxmWpubGC/LpBHbBF2J3vrrbe0cOFCLViwwOqhAABQdEZjcQW7I2mlxslV2t7+wYzXuVwO1fs8WrrIp5rK0tQ5tPUBr2oqywm0FnFFwzIq3GmPGYYhVzRi0Yjyy7o1qwi3QB6zXdhtb29XY2PjjH/2b//2b7rrrrtUW1ur5uZmLV26dMbn7dmzR3v27JEk7dq1S4FAIGvjzWcul4vvjQ0xL/bEvNgT83J2YrGETnSf0rETp3Qs2K8Pg6d07ES/jgX7dbInLDPDlkSX06H6QKUW1VdrUV2VPlJXrcX11VpUVy1/rUcOhyGXy6VYLHNjKeSWyxdQScmoHIah0tJSSWP7Tl0+N787NsC/YfbDnNjT2c6LYZqZ/pOWe7FYTH/5l3+pRx55RDU1NWl/Fo1G5XA4VF5eroMHD+qHP/yhHnvssTn9vceOHcvCaPNfIBBQKBSyehiYgnmxJ+bFnpiXzBIJU6G+qIKhiZLj491hBUNhhfqiSiRm/s+/w2EoUONOlRonz6GtC3jlr66Q0+mY9esyJ/aS3LN79ZI6jY6OyjRN7Q/2aeG2ZsqYbYDfF/thTuxptnlZtGhRxutstbLb2dmpj370o9OCriS53RMlOJdddpmeeeYZnTp1SlVVVTkcIQAA9pFImOo9NTheajzp6J5QWCd7I4rHZw60hiH5a9xppcbJplCBGo9crtkDLfJHMtC+8OpexXpOKeb2aDVBF0CRsFXYna2Eua+vT9XV1TIMQ++9954SiYQqKytzPEIAAHLLNE31DQwpOH4O7fHkObShsII9EY3GEhmvra0qnxRkJ86hrfN5VFLizOGrgJVWrV2njVuuZrUKQNGxTdgdGhrS4cOHdeutt6Yea2trkyRt3bpVr7/+utra2uR0OlVaWqo777yTZhcAgIJgmqYGIiM6HhrQie7IROnxeKOo4ZF4xmurK8vGyozHV2ZTZ9L6PSortc1/5gEAyDnb/FewvLxcf/M3f5P22NatW1MfX3PNNbrmmmtyPSwAwBRdhzr11sutKhkMa7TCq0s+3URJ5ByFoyMT3Y0nlR4HQ2ENDmdu6uR1l6Yd3ZNcra3ze1RRXpLDVwAAQP6wTdgFANhfstnNtroaGW63TDOu/btbJInAOy46NJoKtMnS42S4jQyOZrzOXV6SVmqcCrcBrzwVpTl8BQAAFAbCLgBgzo60teqGuprUNhLDMLSxrkbPt7UWVdgdGo5NnEObWqUdC7enIsMZrysrdaWVGtcHPKlVWq+7lO05OdB5uEutr3UoHHfI60yoacN6zlEFgAJF2AUAzJkrGpZR4U57zDAMuaIRi0aUPSOjcQWTZcbjgfb4eOlx/8BQxutKS5yqGy83rpt0dE99wKsqbxmB1kKdh7vU0n5UtSs3y2MYSpimWto7JInACwAFiLALAJizmNsr04ynBTbTNBVzeywc1dmLxRI62TO51DiSWqXtPTWoTCfRu5wOLfB5VB8YC7N1/olAW1NZLoeDQGtHre0HVLtiU1plQu2K9Wpt30fYBYACRNgFAMzZ6q1N2r+7RRvHS5lN09T+YJ9Wb2u2emgZxeMJhfqiqfNnJ5ced/dFMwZap8NQwO9J7ZudXHrsq3YTaPNQOGbIM2Vl3TAMRWL2nktKrwHg7BB2AWQdb9QKR3Jf7vNtrXJFI4q5PVq9rdny/bqJhKme/uhYmXEovfQ41BtVPDFzojUMja3QJsuOJzWFCtS45XQ6cvxKkE1el6mEaU6rTPC4MtzxsAFKrwHg7BF2AWQVb9QKz6q16ywJt4mEqb6BoUkrtGH1DozqP4716GRPRLF4YsbrDEPy11RMKjWeaBC1wOeRy0WgzSUrb341NTaopb1DtSvWpyoTeo92qLmxISdf/2xQeg0AZ4+wCyCreKOGM2GapvoHhtOO65loEhXRyGg847U1VeXjIXZsZbbO79XCwFigLS1x5vBVIBOrb34lv0Zr+z5FYoY8LlPNjQ22/rcoX0uvAcAOCLsAsoo3apjKNE0NREbGj+6ZKDtOfjw8Est4bZWnTHXJldmAVxd+9COqKDVV7/eorJT/pNmdHW5+rVuzytbhdqp8LL0GALvgnQGArOKNWvGKDI5MNIQKje2hTR7dMzg0mvE6T0XJlIZQY6XHdX6v3OUlac8NBAIKhULZfimYJ9z8OnP5WHoNAHZB2AWQVbxRK2yDw6MKhia6G0/8f0Th6EjG6yrKXOPNoLzj59B6Up973aU5fAXIJW5+nbl8LL0GALsg7ALIKt6o5b/hkVhq3+xEoB37/FR4OON1ZaXOsQ7Hk5tCjQfaSk9pWuBBceDm19nJt9JrALALwi6ArOONmv2NjsYV7ImkrcwGkx2PTw1lvK7E5Rjvcpx+Fm1dwKOayvK8DrRdhzr11sutKhkMa7TCq0s+3WT5EUv5jptfAIBcIuwCQJGIxRI62Tve2XhKU6ie/qjMDJWkTqehOt/kc2gnwm1tVYUcjvwNtJl0HerU8d0t2lZXI8PtlmnGtX93iyQReM8RN78AALlC2AWAAhKPJ9TdF001hRoLtGOrtKG+qBKJmROtw2Fogc89qSnURNmxv8ZdkIF2NkfaWnVDXU1a1+CNdTV6vq2VsAsAGVh5jjYwE8IuAOSZRMJUT//g+ArtRKA9EQrrZG9E8fjMgdYwpECte3wf7djK7MLxlVp/rVsupyPHr8S+XNGwjAp32mOGYcgVjVg0IgCwN6vP0QZmQtgFABsyTVN9p4bSSo2T+2mDPRHFYomM19ZWV4yVGaeO7RkrO17g86jE5czhq8hfMbdXphmf1jU45vZYOCoAsC87nKMNTEXYBQCLmKapU+HhtFLj4+MrtcHuiEZG4xmvra4sS+tunNxDu8DnUVkp/7Sfq9Vbm7R/d4s2jpcym6ap/cE+rd7WbPXQAMCWOEcbdsQ7IgDIsnB0OLUyezyULD0e+3xoOJbxOq+7dKzMOOBN63hc5/eooqwkh6+g+CT35T7f1ipXNKKY26PV25rZrwsAGXCONuyIsAsA8yA6NDrWEGrKHtpgd1iRwdGM17nLS9JKjSdWaz1yV5Tm8BVgqlVr1xFuAWCOOEcbdkTYBYA5GhqOpZ9D2z0RbgciIxmvKy9zpUqNU0f3jHc79rpL8/osWgAAJM7Rhj0RdgFgkpHR+KQQO9EUKtQ7qJ7+aMbrSkucYx2O/dNXaau8ZQRaFKypR43c/JktWnbeEquHBcACnKMNuyHsAig6o7G4TvZE0kqNk3tqe/oHM17ncjlU5/OkVmbr/BNH99RUlRNoUXRmOmrkB22d+vzl/bzhtSnOQQVQTAi7AApSLJ5Qd280rew4+XF3X1Rmhn4ZToehgM+Taga10O9VXcCrlRculeJDcjjyM9B2HerUWy+3qmQwrNEKry75dBP7UXHOZjxqZOV6tba/TICyIc5BBVBsCLsA8lYiYaq7LzrtHNoT3WF190YVT8ycaA1DWjAp0E4uPfbXuOV0OqZdE/BXKhQazvZLyoquQ506vrtF2+pqZLjdMs249u9ukSQCL84JR43kF85BBVBsCLsAbC2RMNV3ajBVcny8O3l0T1gne6KKxRMzXmcYkr+mYtI5tF7VjTeFWlDrkcs1PdAWqiNtrbph/LxYaewN7sa6Gj3f1krYxTnhqJH8ws0JAMWGsAvAcqZpqn9gOG1ldnLH49HYzIFWkmqryseDrDdtpbbO51FJiTOHr8K+XNGwjAp32mOGYcgVjVg0IhSKGY8a+VWHPp+Fo0bYa3ruuDkBoNgQdgHkhGmaGoiMTAm048f3dEc0PBLLeG2VtyztuJ7J4baslH/GTifm9so049Pe4MbcHgtHhUIw01Ejt1571bx3Y2av6fzgHFQAxWZO7xITiYQ6OjpkGIYaGhrkcIyV//3yl7/UJz7xiawOEEB+CUfHAm0w2RQqGWy7IxocGs14ndddmn4O7aRwW1FeksNXUHhWb23S/t0t2jheymyapvYH+7R6W7PVQ0MBmHrUSCAQUCgUmtevwV7T+cE5qACKzZzC7uOPP65AICCXy6WXXnpJd9xxhxYuXKi2tjbCLlCEBodG05tCTQq34ehIxusqykvSzp9NlR0HvPJUlObwFRSX5L7c59ta5YpGFHN7tHpbM/t1kTfYazp/OAcVQDGZU9jt6enRF7/4RUnSpk2b9Pjjj+uP/uiPsjowANYaHomN7ZlNrcyOh9tQWKcimbsSl5U6x8qMx1dmk+fQ1vm9qvSUchatRVatXUe4tRD7Tc8Ne03PTefhLu09cEShyDA/fwCKypzCbiwW0+joqEpKSrRgwQLt2LFDjz76qD744INsjw9AFo2OxhXsiaSfRTsebvtODWW8rsTlGAuzk1Zmk6XH1ZVlBFpgEvabnjv2mp695M9f/ZqN8oyO8vMHoKjMGnbj8bicTqf+9E//VJFIRDU1NZKkiooK3X333XrttddyMUYA5yAWS+hkb2S81Dii4+NhNtgdVk//oMwMCyMup2PsLNpJTaGSpcc1VRVyOAi0wFyw3/Tcsdf07PHzB6CYzRp2v/Wtb+muu+7SBRdcMO3PHA6HPvWpT2VtYADmLh5PqLsvqhPdY2E2OKkpVKg3kjHQOh2GAj636gPjZceTmkL5a9wEWmAesN90frDX9Ozw8wegmM0ads8//3x97Wtf086dO+Xz+SRJb7/9tn784x/rG9/4Rk4GCGBMImGqpz+a1hQqWXoc6o0oHp850RqGFKh1Tyo1njiL1l/rlsvpyPErAYoL+01hpeTP32T8/AEoFrOG3ebmZrW1telrX/uatm/frr179+qDDz7Qddddl6vxAUXFNE2FesP61fsnU6XGyXAb7IkoFktkvNZXXZFama2bVHK8wOdRicuZw1cBYDL2m8JKyZ+/+jWNksTPH4CictoGVRdddJHcbrcee+wxbdy4UXfffbdKSzkiBDhbpmnqVHg47fzZE6l9tBGNjMYzXltdWZ62Mluf6nTsUWkJgRawI/abwkrJn7O9b+5Xf3iYn7/ToHM6UFhmDbsPP/yw3n77bV177bW68cYb9fTTT+vIkSO67LLLcjU+IC+ZpqlwdCTtLNrkObQnusMaGo5lvLa6slwLkmXHk0qP6/xelZfNqYE6AJthvymstG7NKl29eaNCoZDVQ7E1OqcDhWfWd84f+chH9F//63+V1+uVJNXX1+uhhx5SMBjUNddck5MBAnYWHRxJW5mdfHxPdGg043WeipJUqfFCv1d1yY7HAa/OW/IR3pAAAJBjdK4GCs+sYfeWW25J+/y8887T/fffrwcffJCwi6IxODyqYCrQRnQiNJAKtOHoSMbrystcMzaFqg945HWX5fAVAACA06FzNVB4zrgm0ufz0YkZBWd4JKaTPWMB9vh46XFwvONx/8BwxutKS5ypRlD1fq/qJn1c5S1L674KAADsi87pQOE5qw2AFRUV8z0OIOtGY3EFu5MhNpLWIKq3fzDjdS6XQ/U+z3iQnTiHtt7vVU1VOYEWAIACQOd0oPDQ7QYFJRZPKNQbmTiLNjTW4fhEd1jdfVGZGW7OOp2GFtR6Zlil9cpXXSGHg0ALAEAho3M6UHgIu8g7iYSpUF90vLvxRLfjE91hhXqjSiRmTrQOh6EFte60UuOFgbFQ66+ukNPpyPErAQAAdkLndKCwEHZhS4mEqd5TgxNNoVJH94QV7IkoHp850BqG5K9xT5QaTyo9DtR45HIRaAEAAIBiQNiFZUzTVN/AkIKTVmaPh8ZCbbAnotFYIuO1tVXlE2E2MHEObZ3Po5ISZw5fBQAAAAA7slXYveOOO1ReXi6HwyGn06ldu3al/blpmnr22WfV2dmpsrIy3X777Vq2bJlFo8VcmKapgcjIxBm0k5pCBbvDGh6JZ7y2yls2VmY8pSlUnd+jslJb/egCAIAs6zzcpdbXOhSOO+R1JtS0YX1BlRwX+usDrGC7xHDvvfeqqqpqxj/r7OzU8ePH9dhjj+ndd9/V008/rW9961s5HiFmEo5ODbQTpceDw7GM13ndpWlNoZJlx3V+jyrKS3L4CgAAwOlYFcg6D3eppf2oaldulscwlDBNtbR3SFJBBMJCf32AVWwXdmdz4MABfepTn5JhGLrooosUiUTU29ur2tpaq4dWFKJDo6mV2cmlxydCYUUGRzNe5y4vSSs1ToXbgFeeitIcvgIAAHC2rAxkre0HVLtiU+q4P8MwVLtivVrb9xVEGCz01wdYxXZh94EHHpAkXX311dqyZUvan/X09CgQCKQ+9/v96unpmRZ29+zZoz179kiSdu3alXYNJrhcrmnfm6HhUR0LntKxE/06FuzXh6mPT6l/IPNZtBVlJfpIXZUW1VdrUV2VPlJXrUX11VpcV61Kbxln0Z6BmeYF1mNe7Il5sR/mxJ7mY172vnlE9Ws2pv03vX5No/a+uV9Xb954rkOc1aizXO6ysmmPDzrL8/rnLTkvhfr68hH/htnT2c6LrcLu/fffL5/Pp/7+fn3zm9/UokWLdPHFF5/x37Nly5a0oBwKheZzmHlvZDSuYHdEg6OG3vv1h2llx32nhjJeV1riVF3yDNrxldmF4yu1VRkC7chwWN3D4Wy+nIITCAT4mbUh5sWemBf7YU7saT7mJRQelmd0eiVXf3g463NeEh/S8PBw2nsN0zTlig/l9c9bcl4K9fXlI/4Ns6fZ5mXRokUZr7NV2PX5fJKk6upqrV+/Xu+9915a2PX5fGkvsru7O3UN0sViCZ3smVxqHEmVHPeeGpQ588k9cjkdWuDzzHB0j1c1leVyOFihBQCgGHldphKmOS2QeVwZ3lTMo6bGBrW0d6h2xXoZhiHTNNV7tEPNjQ1Z/9q5UOivD7CKbcLu0NCQTNNURUWFhoaGdPjwYW3bti3tOQ0NDfrHf/xHNTY26t1335Xb7S7q/brxeEKhvmhqZTYYCuv4eKDt7otmDLROh6GAz62lH/Gptro01eW4PuCRr9pNoAUAm6NrK6xgZSBL/ny3tu9TJGbI4zLV3NhQMD/3hf76AKvYJuz29/frO9/5jiQpHo9rw4YNWrt2rdra2iRJW7du1bp163Tw4EF98YtfVGlpqW6//XYrh5wTiYSpnv5oamX2eCis4HigDfVGFU/MnGgNQwrUurUw2d14UlOoQI1bTqeDMg0AyEN0bYVVrA5k69asKuif8UJ/fYAVbBN26+vr9fDDD097fOvWramPDcPQX/zFX+RyWDmRSJjqGxiacg7tWOnxyZ6IYvFExmv9NRVjHY6nnEUb8LlV4nLm8FUAKBSsGtobXVthJQIZgHxim7BbjP7upX/VO78OKdgd0choPOPzaqrKx0Ps2MpsMtzW+T0qLSHQApg/rBraXzhmyDOlIaBhGIrE2IICAMBkhF0LnQiF9Z/HT0mSqjxlqpvaFGr8XNryMqYJQG6wamh/VjYJAgAgn5CiLPS5rRfrc1svVp3fK3d5idXDAQBWDfMAXVsBAJgbwq6Fzl9cvJ2kAdgTq4b2Z3WTIAAA8gVhFwCQwqphfqBJEAAAp0fYBQCkFMOqId2mAQAoDoRdAECaQl41pNs0AADFw2H1AAAAyJWxbtPrZ+g2fcDikQEAgPlG2AUAFI1wzEhrviXRbRoAgEJF2AUAFA2vy5RppneWpts0AACFibALACgaTY0N6j3akQq8yW7TTXSbBgCg4NCgCgBQNJJNqH708+f17yf7FR8d1vK6GkkrLB0XAACYf4RdAEDRMQLnqWHDxFnCdGQGAKDwUMYMACgqdGQGAKA4sLILACgq4ZghT552ZO483KXW1zoUjjvkdSbUtGE9q9EAAGRA2AUAFBWvy1TCNNOOIMqHjsydh7vU0n5UtSs3y2MYSlB+DQDArChjBgAUlXztyEz5NQAAZ4aVXQBA0UmEfqsDLxxRYmRIyxbW6k8/d63tV0fzufwaAAArEHYBAEUjWQrs37BNgfFOzL1HO6we1pzka/k1AABWoYwZAFA08rkUOF/LrwEAsAoruwCAopHPpcDJMuvW9n2KxAx5XKaaGxtsX34NAIBVCLsAgKKR76XA69asItwCADBHlDEDAIoGpcAAABQPVnYBAEWDUmAAAIoHYRcAUFQoBS5MnYe71Ppah8Jxh7zOhJo2rGeeAaDIEXYBAEBeSx4pVbtyszyGoYRpqqV97EgpAi8AFC/27AIAgLyWz0dKAQCyh7ALAADyWjhmpHXYlvLnSCkAQPYQdgEAQF7zusxUh+2kfDpSCgCQHezZBQDAZmi2dGaaGhvU0t6RKmVOHinVzJFSAFDUCLsAANgIzZbOHEdKIV9MvZF182e2aNl5S6weFlCwCLsAANjIWLOlTTM0W9pHeJsFR0rB7ma6kfWDtk59/vJ+fnaBLCHsAgBgI+GYIQ/NlmAzlNafuxlvZK1cr9b2l/leAllC2AUAwEa8LlMJ00zrLkyzJViJ0vr5wY0sIPfoxgwAgI00NTao92hHqrtwstlSE82WYBHOMZ4fdA0Hco+VXQAAbIRmS7AbViTnx4xdw3/Voc9zIwvIGsIuAAA2Q7Ml2Aml9fNjphtZt157Fd2YgSwi7AIAACAjzjGeP1NvZAUCAYVCIQtHBBQ2wi4AAJBEx13MjNJ6APmKsAsAAOi4i1lRWg8gH9GNGQAA0HEXAFBwCLsAAEDhmJHWgEii4y4AIL9RxgwAAM644y77ewEAdkfYBVA0eHMOZHYmHXdn29979eaNuR56QeLfKwA4d4RdAEWB5jvA7M6k4+7Y/t5NM+zv3UfYnQf8ewUA84OwC6AozPbmnDePwJi5dtwNxwx52N97Wme7Osu/VwAwP2wRdkOhkJ544gn19fXJMAxt2bJFTU1Nac/p6urSt7/9bdXV1UmSPvaxj2nbtm1WDBdAHuLNOTB/znR/bzE6l9VZ/r0CgPlhi7DrdDrV3NysZcuWaXBwUDt27NCaNWu0ZMmStOetXLlSO3bssGiUAPIZb86B+XMm+3uL1bmszvLvFQDMD1scPVRbW6tly5ZJkioqKrR48WL19PRYPCoAhaSpsUG9RztkmmNvFpNvzpt4cw6csXVrVqm5cYUcR/cp+tY+OY7uU3PjCkpsJzmXo5z49woA5octVnYnCwaD+vWvf60LLrhg2p/927/9m+666y7V1taqublZS5cutWCEAPLRmTTfAXB6c93fW6zOZXWWf68AYH4YZvK2oQ0MDQ3p3nvv1ec+9zl97GMfS/uzaDQqh8Oh8vJyHTx4UD/84Q/12GOPzfj37NmzR3v27JEk7dq1SyMjI1kfez5yuVyKxWJWDwNTMC/2xLzYE/NiP8zJmDcOHtIP2jpVu3JSqfevOnTr1nW6/LK1OR8P82JPzIv9MCf2NNu8lJaWZrzONmE3FovpoYce0qWXXqrPfOYzp33+HXfcoQcffFBVVVWnfe6xY8fmY4gFJxAIKBQKWT0MTMG82BPzYk/Mi/0wJxM6D3eptf1AanW2ycLVWebFnpgX+2FO7Gm2eVm0aFHG62xRxmyapp566iktXrw4Y9Dt6+tTdXW1DMPQe++9p0QiocrKyhyPFAAAYG4o9QYAa9ki7L7zzjt69dVXdd555+muu+6SJN18882p9L5161a9/vrramtrk9PpVGlpqe68885pjR8AAAAAAJBsEnZXrFihn/70p7M+55prrtE111yToxEBAADgXHUe7lLrax0Kxx3yOhNq2rCe1W4AOWOLsAsAAIDC0nm4Sy3tR1W7crM8hqGEaaqlvUOSCLwAcsIW5+wCAACgsLS2H1DtivWpbWeGYah2xXq1th+weGQAigVhFwAAAPMuHDOm9VcxDEORGD1XAOQGZcwAAADj2GM6f7wuUwnTTAu8pmnK47LFqZcAigAruwAAAJrYY5pYuVmeSzYpsXKzWtqPqvNwl9VDy0tNjQ3qPdoh0xwLt6Zpqvdoh5oaGyweGYBiwcouAACAkntMN82wx3Qfq7tnIfk9a23fp0jMkMdlqrmxge8lgJwh7AIAAGhsj6mHPabzat2aVYRbAJahjBkAAEBje0yTJbdJ7DEFgPxF2AUAABB7TAGg0FDGDACwBbrgwmrsMQWAwkLYBQBYLtkFt3blZnkMQwnTVEt7hyQRNJBT7DEFgMJBGTMAwHJjXXDXz9AF94DFIwMAAPmKlV0AgOXoggucPbYAAMDMCLsAAMt5XaYSppla2ZXoggvMBVsAACAzypgBAJajCy5wdtgCAACZsbILALAcXXCBs8MWAADIjLALALAFuuACZ44tAACQGWXMAAAAeYotAACQGSu7AAAAeYotAACQGWEXAAAgj7EFAABmRtgFAOAMca4pAAD2R9gFAOAMcK4pAAD5gQZVAACcAc41BQAgPxB2AQA4A+GYkXbMi8S5pgAA2BFhFwCAM+B1maljXpI41xQAAPsh7AIAcAY41xQAgPxAgyoAAM4A55rOH7paAwCyibALAMAZ4lzTc0dXawBAtlHGDAAAco6u1gCAbCPsAgCAnKOrNQAg2wi7AAAg5+hqDQDINsIuAADIObpaAwCyjQZVAAAg5+hqDQDINsIuAACwBF2tAQDZRBkzAAAAAKDgsLILAACAaToPd6n1tQ6F4w55nQk1bVjPSjyAvELYBQDMCW98geLRebhLLe1HVbtyszyGoYRpqqW9Q5L4vQeQNwi7AIDT4o1v4eHmBWbT2n5AtSs2pc5CNgxDtSvWq7V9Hz8nAPIGYRcAcFq88S0s3LzA6YRjhjzjv+9JhmEoEjMyXAEA9kODKgDAaYVjRiroJvHGN3+N3bxYP8PNiwMWjwx24XWZqTOQk0zTlMdlZrgCAOyHsAsAOC3e+BYWbl7gdJoaG9R7tCP1e2+apnqPdqipscHikQHA3FHGDAA4rabGBrW0d6RWA5NvfJt545uXvC5TCdNMC7zcvMBkyXL21vZ9isQMeVymmhsbKHMHkFcIuwCA0+KNb2Hh5gXmYt2aVfyOA8hrhF0AwJzwxrdwcPMCAFAMCLsAChZHqwCZcfMCAFDoCLsAChJHqwD2ws0nAECu2SrsHjp0SM8++6wSiYSuuuoqXX/99Wl/Pjo6qscff1z//u//rsrKSt15552qq6uzZrAAbI1zYQH74OYTAMAKtgm7iURCzzzzjL761a/K7/dr586damho0JIlS1LP2bt3rzwej773ve+pvb1df/d3f6e//uu/tnDUAOwqHDPkKbCjVVgZQ77i5hMAwAq2OWf3vffe08KFC1VfXy+Xy6UrrrhCHR0dac85cOCArrzySknSxz/+cR05cmTauY8AIBXeubDJlbHEys3yXLJJiZWb1dJ+VJ2Hu6weGnBanOsLALCCbcJuT0+P/H5/6nO/36+enp6Mz3E6nXK73RoYGMjpOAHkh6bGBvUe7UgF3uTRKk15erTK2MrY+hlWxg5YPDLg9Art5hMAID/Ypox5Pu3Zs0d79uyRJO3atUuBQMDiEdmTy+Xie2NDzMv8uHrzRlXXVOuFf25XeFTylkh/fG2jLr9s7Vn9fVbPy6izXO6ysmmPDzrLi/rnxep5wXQzzcnN116lH7R1qnblpHN9f9WhW6+9ivnLEX5X7Il5sR/mxJ7Odl5sE3Z9Pp+6u7tTn3d3d8vn8834HL/fr3g8rmg0qsrKyml/15YtW7Rly5bU56FQKHsDz2OBQIDvjQ0xL/Nn2XlL9N//7PNpj53t99bqeSmJD2l4eDitFNQ0TbniQ0X982L1vGC6meZk2XlL9PnL+9Xa/nLqXN/PNzZo2XlLmL8c4XfFnpgX+2FO7Gm2eVm0aFHG62wTdpcvX64PP/xQwWBQPp9Pv/jFL/TFL34x7Tm///u/r1deeUUXXXSRXn/9da1atWraHiAAKERNjQ1qae9IlTIny7Kb87QsG8WHc30BALlmm7DrdDr1hS98QQ888IASiYQ2bdqkpUuX6ic/+YmWL1+uhoYGbd68WY8//rj+23/7b/J6vbrzzjutHjYA5EQyJLS270utjDU3NhAeAAAAMrBN2JWkyy67TJdddlnaY5///EQJYmlpqb70pS/lelgAYAusjAEAAMydbboxAwAAAAAwXwi7AAAAAICCQ9gFAAAAABQcwi4AAAAAoODYqkEVAGBC5+Eutb7WoXDcIa8zoaYN62lQBQAAMEeEXQCwoc7DXWppP6ralZvlMQwlTFMt7R2SROAFAACYA8qYAcCGWtsPqHbFehmGIUkyDEO1K9artf2AxSMDAADID4RdALChcMxIBd0kwzAUiRkZrgAAAMBklDEDgA15XaYSppkWeE3TlMdlWjgq4NywDx0AkEus7AKADTU1Nqj3aIdMcyzcmqap3qMdampssHhkwNlJ7kNPrNwszyWblFi5WS3tR9V5uMvqoQEAChQruwBgQ8nVrtb2fYrEDHlcppobG1gFQ94a24e+aYZ96Pv4uQYAZAVhFwBsat2aVYQAFIxwzJCHfegAgByijBkAAGSd12WmyvKT2IcOAMgmwi4AAMg69qEDAHKNMmYAAJB17EMHAOQaYRcAAOQE+9ABALlEGTMAAAAAoOAQdgEAAAAABYewCwAAAAAoOIRdAAAAAEDBIewCAAAAAAoOYRcAAAAAUHAIuwAAAACAgkPYBQAAAAAUHJfVAwAAwEqdh7vU+lqHwnGHvM6Emjas17o1q6weFgAAOEeEXQBA0eo83KWW9qOqXblZHsNQwjTV0t4hSQReAADyHGXMAICi1dp+QLUr1sswDEmSYRiqXbFere0HLB4ZAAA4V6zswhYoIwRghXDMkGc86CYZhqFIzMhwBQAAyBeEXViOMkIAVvG6TCVMM7WyK0mmacrjMi0cFQAAmA+EXVhurIxw0wxlhPsIuwCyqqmxQS3tHalSZtM01Xu0Q82NDVYPbU6oigEAIDPCLixHGSGAXJscEhN9IYX2vy+Pf6E8LlPNjQ15ERipigEAYHaEXViOMkIAuTQ1JLrHV3P/qHFFXoVEqmIAAJgd3ZhhuabGBvUe7ZBpjoXbZBlhU56UEQLIL4XSgTkcM9JuEkpUxQAAMBkru7BccgWitX2fIjEjr8oIAeSfQtk6QVUMAACzI+zCFtatWUW4BZAThRIS8725FgAA2UbYBQAUlUIJiVTFAAAwO8IuAKCoFFJIpCoGAIDMCLsAgKJDSAQAoPDRjRkAAAAAUHAIuwAAAACAgkMZMwAAZ6jzcJdaX+tQOO6Q15lQ04b1lEUDAGAzhF0AAM5A5+EutbQfVe3KzfIYhhKmqZb2Dkki8AIAYCOUMQMAcAZa2w+kji2SJMMwVLtivVrbD1g8MgAAMBlhFwCAMxCOGamgm2QYhiIxI8MVAADACoRdAADOgNdlyjTNtMdM05THZWa4AgAAWIE9uwCA06Ih04Smxga1tHekSplN01Tv0Q41NzZYPTQAADCJ5WG3paVFb775plwul+rr63X77bfL4/FMe94dd9yh8vJyORwOOZ1O7dq1y4LRAkDxoSFTuuRrbm3fp0jMkMdlqrmxoSi/FwAA2JnlYXfNmjXavn27nE6nnnvuOb3wwgu65ZZbZnzuvffeq6qqqhyPEACK21hDpk0zNGTaV7QBb92aVUX72gEAyBeW79m99NJL5XQ6JUkXXXSRenp6LB4RAGAyGjIBAIB8ZPnK7mR79+7VFVdckfHPH3jgAUnS1VdfrS1btuRqWABQ1LwuUwnTTAu8NGQCAAB2Z5hTW0pmwf3336++vr5pj990001av369JOlnP/uZ3n//fX35y1+etoIgST09PfL5fOrv79c3v/lN/dmf/ZkuvvjiGb/enj17tGfPHknSrl27NDIyMn8vpoC4XC7FYjGrh4EpmBd7KuZ5eePgIf2grVO1Kyc1ZPpVh27duk6XX7bW0rEV87zYFXNiT8yLPTEv9sOc2NNs81JaWprxupyE3dN55ZVX9E//9E+65557VFZWdtrn//SnP1V5ebmuu+66Of39x44dO9chFqRAIKBQKGT1MDAF82JPxT4vnYe71Np+INWQqckmDZmKfV7siDmxJ+bFnpgX+2FO7Gm2eVm0aFHG6ywvYz506JB+/vOf6+tf/3rGoDs0NCTTNFVRUaGhoSEdPnxY27Zty/FIAaB40ZAJAADkG8vD7jPPPKNYLKb7779fknThhRfq1ltvVU9Pj77//e9r586d6u/v13e+8x1JUjwe14YNG7R27VoLRw0AAAAAsDPLw+73vve9GR/3+XzauXOnJKm+vl4PP/xwLocFAAAAAMhjlh89BAAAAADAfCPsAgAAAAAKDmEXAAAAAFBwCLsAAAAAgIJD2AUAAAAAFBzCLgAAAACg4BB2AQAAAAAFx/JzdgEAmKrzcJdaX+tQOO6Q15lQ04b1WrdmldXDAgAAeYSwCwCwlc7DXWppP6ralZvlMQwlTFMt7R2SROAFAABzRhkzAMBWWtsPqHbFehmGIUkyDEO1K9artf2AxSMDAAD5hLALALCVcMxIBd0kwzAUiRkZrgAAAJiOsAsAsBWvy5RpmmmPmaYpj8vMcAUAAMB0hF0AgK00NTao92hHKvCapqneox1qamyweGQAACCf0KAKAGArySZUre37FIkZ8rhMNTc20JwKAACcEcIuAMB21q1ZRbgFAADnhDJmAAAAAEDBIewCAAAAAAoOYRcAAAAAUHAIuwAAAACAgkPYBQAAAAAUHMIuAAAAAKDgEHYBAAAAAAWHsAsAAAAAKDiEXQAAAABAwSHsAgAAAAAKDmEXAAAAAFBwCLsAAAAAgIJD2AUAAAAAFBzCLgAAAACg4BB2AQAAAAAFxzBN07R6EAAAAAAAzCdWdovYjh07rB4CZsC82BPzYk/Mi/0wJ/bEvNgT82I/zIk9ne28EHYBAAAAAAWHsAsAAAAAKDiE3SK2ZcsWq4eAGTAv9sS82BPzYj/MiT0xL/bEvNgPc2JPZzsvNKgCAAAAABQcVnYBAAAAAAXHZfUAYA8vvfSSWlpa9PTTT6uqqsrq4RS9H//4xzpw4IAMw1B1dbVuv/12+Xw+q4dV9FpaWvTmm2/K5XKpvr5et99+uzwej9XDKmq//OUv9b//9//W7373O33rW9/S8uXLrR5SUTt06JCeffZZJRIJXXXVVbr++uutHlLRe/LJJ3Xw4EFVV1frkUcesXo4kBQKhfTEE0+or69PhmFoy5YtampqsnpYRW9kZET33nuvYrGY4vG4Pv7xj+vGG2+0eliQlEgktGPHDvl8vjPuykzYhUKhkA4fPqxAIGD1UDDuuuuu00033SRJam1t1e7du3XrrbdaPCqsWbNG27dvl9Pp1HPPPacXXnhBt9xyi9XDKmpLly7Vl7/8Zf3gBz+weihFL5FI6JlnntFXv/pV+f1+7dy5Uw0NDVqyZInVQytqV155pa655ho98cQTVg8F45xOp5qbm7Vs2TINDg5qx44dWrNmDb8rFispKdG9996r8vJyxWIx3XPPPVq7dq0uuugiq4dW9FpbW7V48WINDg6e8bWUMUN/+7d/qz/+4z+WYRhWDwXj3G536uPh4WHmxiYuvfRSOZ1OSdJFF12knp4ei0eEJUuWaNGiRVYPA5Lee+89LVy4UPX19XK5XLriiivU0dFh9bCK3sUXXyyv12v1MDBJbW2tli1bJkmqqKjQ4sWL+e+JDRiGofLycklSPB5XPB7n/ZcNdHd36+DBg7rqqqvO6npWdotcR0eHfD6fzj//fKuHgin+/u//Xq+++qrcbrfuvfdeq4eDKfbu3asrrrjC6mEAttHT0yO/35/63O/3691337VwRID9BYNB/frXv9YFF1xg9VCgsQqVu+++W8ePH9enP/1pXXjhhVYPqej98Ic/1C233HJWq7oSYbco3H///err65v2+E033aQXXnhBX/3qV3M/KMw6L+vXr9fNN9+sm2++WS+88IL+8R//kX0jOXK6eZGkn/3sZ3I6nfrkJz+Z49EVp7nMCQDkm6GhIT3yyCP60z/907SKLljH4XDo4YcfViQS0Xe+8x198MEHOu+886weVtF68803VV1drWXLlqmrq+us/g7CbhH42te+NuPjH3zwgYLBoO666y5JY2UCd999tx588EHV1NTkcITFKdO8TPXJT35SDz74IGE3R043L6+88orefPNN3XPPPZQ35chcf1dgLZ/Pp+7u7tTn3d3dNNYDMojFYnrkkUf0yU9+Uh/72MesHg6m8Hg8WrVqlQ4dOkTYtdA777yjAwcOqLOzUyMjIxocHNRjjz2mL37xi3P+Owi7Rey8887T008/nfr8jjvu0IMPPkg3Zhv48MMP9ZGPfETSWKk5exLt4dChQ/r5z3+ur3/96yorK7N6OICtLF++XB9++KGCwaB8Pp9+8YtfnNEbEqBYmKapp556SosXL9ZnPvMZq4eDcadOnZLT6ZTH49HIyIgOHz6sP/iDP7B6WEVt+/bt2r59uySpq6tLL7300hn/d4WwC9jQ3/3d3+nDDz+UYRgKBAJ0YraJZ555RrFYTPfff78k6cILL2RuLPbGG2/ob/7mb3Tq1Cnt2rVL559/vr7yla9YPayi5HQ69YUvfEEPPPCAEomENm3apKVLl1o9rKL36KOP6u2339bAwIBuu+023Xjjjdq8ebPVwypq77zzjl599VWdd955qeq6m2++WZdddpnFIytuvb29euKJJ5RIJGSapj7xiU/o93//960eFs6RYZqmafUgAAAAAACYTxw9BAAAAAAoOIRdAAAAAEDBIewCAAAAAAoOYRcAAAAAUHAIuwAAAACAgkPYBQAAAAAUHMIuAAB56rnnntO3v/3t1OctLS36xje+oVgsZuGoAACwB8IuAAB56g/+4A/U1dWlX//612pra9OhQ4f05S9/WS6Xy+qhAQBgOcM0TdPqQQAAgLPz05/+VG+88Yai0ai+8Y1vKBAIKBqN6v7779d//ud/6oEHHtB5551n9TABAMg5VnYBAMhjH/3oR/XBBx9o+/btCgQCkqTS0lLt3LlTH//4xy0eHQAA1iHsAgCQpz744AM9/fTT2rhxo/bt25d63OVyqaqqysKRAQBgPcIuAAB5qKenRw899JD+y3/5L/qLv/gLffDBB+rq6rJ6WAAA2AZhFwCAPBONRvXggw/q2muvVUNDg8rKyvTZz35WP/7xj60eGgAAtkGDKgAACtQTTzyhz372szSoAgAUJcIuAAAF6MEHH9RvfvMbBQIBXX311bryyiutHhIAADlF2AUAAAAAFBz27AIAAAAACg5hFwAAAABQcAi7AAAAAICCQ9gFAAAAABQcwi4AAAAAoOAQdgEAAAAABYewCwAAAAAoOIRdAAAAAEDBIewCAAAAAArO/w+MSVjGtDxTvAAAAABJRU5ErkJggg==",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plot_ds(data,m[-1],q[-1])"
]
},
{
"cell_type": "code",
"execution_count": 449,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"57 passi e 5700 gradienti calcolati per arrivare a distanza minore o uguale di 0.3 dall'ottimo\n"
]
}
],
"source": [
"near_opt(m, min_dist=3e-1, ge_per_step=n)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Adadelta"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Adadelta è una estensione di RMSprop in cui non è presente un valore $\\eta$ arbitrariamente definito: questo parametro è sostituito da una somma smorzata, mediante un coefficiente $0<\\gamma<1$, dei quadrati degli aggiornamenti precedenti. Inoltre, al fine di limitare una eccessiva diminuzione del learning rate, non vengono accumulati tutti i gradienti passati attraverso la somma dei loro quadrati, ma viene invece applicato anche qui uno smorzamento con lo stesso coefficiente $0<\\gamma<1$.\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"L'aggiornamento alla $k+1$-esima iterazione è quindi definito come:\n",
"\n",
"\\begin{align*}\n",
"g_{j, k} &= \\frac{\\partial J(\\theta)}{\\partial\\theta_j}\\Big\\rvert_{\\theta^{(k)}}\\\\\n",
"\\tilde G_{j,k} & =\\gamma \\tilde G_{j,k-1}+(1-\\gamma)g_{j,k}^2\\\\\n",
"\\Delta_{j,k} &= - \\frac{\\sqrt{\\overline G_{j,k-1}+\\varepsilon}}{\\sqrt{\\tilde G_{j,k}+\\varepsilon}} g_{j, k}\\\\\n",
"\\overline G_{j,k} & =\\gamma \\overline G_{j,k-1}+(1-\\gamma)\\Delta_{j,k}^2\\\\\n",
"\\theta_j^{(k+1)} &= \\theta_j^{(k)} + \\Delta_{j,k}\n",
"\\end{align*}"
]
},
{
"cell_type": "code",
"execution_count": 420,
"metadata": {},
"outputs": [],
"source": [
"def adadelta(X,t, G_tilde = 0, G_over = 0, eps = 1e-8, gamma = 0.9, epochs = 10000):\n",
" theta = np.zeros(nfeatures+1).reshape(-1,1)\n",
" theta_history = []\n",
" cost_history = []\n",
" for k in range(epochs): \n",
" g = gradient(theta,X,t)\n",
" G_tilde = gamma * G_tilde + (1 - gamma)*g**2\n",
" delta = - np.sqrt(G_over + eps) / np.sqrt(G_tilde + eps) * g\n",
" G_over = gamma * G_over + (1 - gamma) * delta**2\n",
" theta = theta + delta\n",
" theta_history.append(theta)\n",
" cost_history.append(cost(theta, X, t))\n",
" theta_history = np.array(theta_history).reshape(-1,3)\n",
" cost_history = np.array(cost_history).reshape(-1,1)\n",
" m = -theta_history[:,1]/theta_history[:,2]\n",
" q = -theta_history[:,0]/theta_history[:,2]\n",
" return cost_history, m, q"
]
},
{
"cell_type": "code",
"execution_count": 421,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"tempo di esecuzione: 0.449 secondi\n",
"10000 passi totali\n",
"1000000 gradienti valutati\n"
]
}
],
"source": [
"start_time = time.time()\n",
"cost_history, m, q = adadelta(X,t, G_tilde = 0, G_over = 0, eps = 1e-8, gamma = 0.9, epochs = 10000)\n",
"print(f\"tempo di esecuzione: {time.time()-start_time: 4.3f} secondi\")\n",
"print(f\"{len(m)} passi totali\")\n",
"print(f\"{len(m)*n} gradienti valutati\")"
]
},
{
"cell_type": "code",
"execution_count": 254,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABQgAAAGoCAYAAAAKMwiTAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAABnyElEQVR4nO39d3xc92Hne3/OzKCDaARYwF7ETonqvVf3OI6PEzvNyUbZzWbXu9l9tmXv5t5nH9/Nfe7ddXY3VXESp9nOySZ2bNmWLVlWl6xKsffeAYLoAAHMnPvHDCmKoiSKxOAMMJ/36zWvOXPOzOA755CYmS9+55wgjmMkSZIkSZIkladU0gEkSZIkSZIkJceCUJIkSZIkSSpjFoSSJEmSJElSGbMglCRJkiRJksqYBaEkSZIkSZJUxjJJB7hInmpZkiTp0gVJBxhnfjaUJEm6dO/4bDhZCkKOHDmSdITL0traSmdnZ9IxhNuilLgtSofbonS4LUrHVNkW7e3tSUcoCj8bClyP48X1OD5cj+PD9Tg+XI/jYyqux3f7bOguxpIkSZIkSVIZsyCUJEmSJEmSypgFoSRJkiRJklTGLAglSZIkSZKkMmZBKEmSJEmSJJUxC0JJkiRJkiSpjFkQSpIkSZIkSWXMglCSJEmSJEkqYxaEkiRJkiRJUhmzIJQkSZIkSZLKmAWhJEmSJEmSVMYsCCVJkiRJkqQyZkEoSZIkSZIklTELQkmSJEmSJKmMWRBKkiRJkiRJZcyCUJIkSZIkSSpjFoSSJEmSJElSGbMglCRJkiRJksqYBaEkSZIkSZJUxiwIJUmSJEmSpDJmQShJkiRJkiSVMQtCSZIkSZIkqYxZEEqSJEmSJEllLFPMJw/D8EvAdcDrURR94Zz5XwdmAVVATRRF64qZQ5IkSZIkSdKFFW0EYRiG1wD1URTdDlSGYXj9mWVRFP10FEV3Af9/4NFiZZAkSZIkSZL03oq5i/FNwOOF6SeAmy9wn08Cf1/EDJIkSZIkSZLeQzF3MW4C9hSme4DV5y4Mw7ACWBtF0esXenAYhg8DDwNEUURra2vxkk6ATCYz6V/DVOG2KB1ui9LhtigdbovS4baQJElSuShmQdgDNBSmG4Du85bfBTz1bg+OougR4JHCzbizs3N8002w1tZWJvtrmCrcFqXDbVE63Balw21ROqbKtmhvb086giRJkkpcMXcxfhG4tzB9H/DSecs/CXyjiD+/pJwezRLHcdIxJEmSJEmSpLcpWkFY2HV4OAzDZ4EscCAMw98ECMMwIH9MwueK9fNLyd88t5t/9vvf53j3UNJRJEmSJEmSpLcp5i7GRFH0hfNmfbEwPwauLubPLjWjYzm2HDrFrObapKNIkiRJkiRJZxVzF2MVrJrXDMCWg6cSTiJJkiRJkiS9XVFHECrvivZGMukUBzr6GRgepa66IulIkiRJEyoMw3bgUWAVUB9F0dg5y9YAfwgEwD+JomhDMiklSZLKkyMIJ0B1RZrlc6cTA1sPdycdR5IkKQld5E9gd/6J6wD+M/AzQFiYliRJ0gSyIJwg6xbPAGCruxlLkqQyFEXRcBRF7/ZBqDmKooNRFB0GmiYwliRJknAX4wlz1ZKZ/PWPNrP9SA9j2RyZtN2sJElSwbkfjIIL3SEMw4eBhwGiKKK1tXUichVNJpOZ9K+hFLgex4frcXy4HseH63F8uB7HRzmtRwvCCdLWWMvMphqOdw+x90QfV8xuTDqSJElSqYjPmc5d6A5RFD0CPHLm/p2dnUUPVUytra1M9tdQClyP48P1OD5cj+PD9Tg+XI/jYyqux/b29gvOtyCcQKvmNnO8e4gtB09ZEEqSJL2lKwzDueTLwd6kw0iSJJUb93OdQCvnNQOw5eAp4jh+n3tLkiRNHWEYVoRh+ARwFfD9MAzvDMPwNwuLfwv4G+Bvgf+UVEZJkqRy5QjCCbSgtZ7aqgxd/afp6B1mRmNN0pEkSZImRBRFo8B9581+urBsA3DrhIeSJEkS4AjCCZVKBayY0wTkRxFKkiRJkiRJSbMgnGCrCrsZbz1kQShJkiRJkqTkWRBOsGXtjaSCgH0n+hg8PZZ0HEmSJEmSJJU5C8IJVlOZYfHMaeRi2H64O+k4kiRJkiRJKnMWhAlYdc7ZjCVJkiRJkqQkWRAmYOXcfEG4/Ug32Vwu4TSSJEmSJEkqZxaECWhtqGZGYzVDI1n2nehPOo4kSZIkSZLKmAVhQs6MInQ3Y0mSJEmSJCXJgjAhZwrCrYcsCCVJkiRJkpQcC8KELJwxjZrKNB29w3T0DCUdR5IkSZIkSWXKgjAh6VTAisIowk3uZixJkiRJkqSEZJIOUM7Wzm/hjT2dbNx/krvXtCcdR5IkSZKkSSGOc5DN5i+5McjmL3EuB3EOzr3O5SDOQpCG6hoggDgGYogpXF/oNm+/DgJIpSAoXFIpCAKCs9OpC98nnSZIpRNYS9LFsyBM0PI5jVSkUxzsHKB74DRNdVVJR5IkSZIk6ZLFcQyjIzAyRDwyDCOnYWyEeGwERkffMc3YCPE5050BjAwNni38yGWJz0xns4V5Y/nSbzIJUpDOQCYDqfx1kM5AuiI/P50hyGQK0xVQUUVQUQkVVVBZRVBRlZ8+M7/yzHQVVNXkn0u6DP4LSlBlJs3yOU1sOtDFpgNd3LZydtKRJEmSJEllLo7jfGE3PEA8NEA8PAjD/fnr00PEp4dgZBhGhgslYOH69BCMnn5r1N0lOP1B7pxKny3XSKchlSFIp88Z3Ve4PjOdzcLImXMABBCcuQ4Ks85cp867HZxZMYXLOSMU4/itUYuF25x7O5eDXDZ/XShBzzh/LV36WgMyFVBVS1BdC1U1nGxoZpT02dtBdS1U1xLUTCOonQY19QSZisv5iZpiLAgTduWCFjYd6GLjfgtCSZIkSVLxxKMjMNhLPNBLXLhmoJd4qJ94eCBfCA4PwNBAfqTepcpUQGUNQWV1fqRbpoIgUwkVlZCpzI+Ay1Tm71dRmV+WqYSKChqnt9E7MPjO0i9dGHl3dn6a4ExxNwnEucLu0NnR/LodGyuMjLzA7bFRGB0hHj2dL1xHTr81fc78uLCMkaH8Y8Z6iAd6ABg+chGhKqvzZWHttEJxWJ+frp1GUN9EUN8MdQ2OTiwTbuWErZjbRDoVsPdEH/1Do9TX2OBLkiRJkj6YOM7BYD9xXxdxb1f+uu9UoQTsyV+PDF/8E6YzUFNHUF0H1fnroLoOqmqgqrpQ/lUTVNYUrquhqhoqqvOF3iWqbm2lv7Pzkh9fqoJUvtSkovKteeP03Gd36z49SHx6EIaHmFaVobfjGPHw0FvzhwbyZfBgHwz1vTXys7vjPUYvBvnSsL6JYFpToThsgmnNBA3TCRpaLBCnCLdiwmoqM1wxu5Fth7vZfLCLG5fNTDqSJEmSJKkExdlsvvjrPkHcc5K4twv6Tp0tA9931F8qnS976hoJ6hoIahvyI8Rq66G6nqC6lqCmDqrr86P+JtEIvXIWBEF+pGZlFcG0ZgBqWlsZaHv3ojWOc/ndxQf7YbCPeKgvXxwO9hMP9hD3dxP3d8NAb37U6WAv8YkDF/rhUN9M0DidoLH1nOtWgmnNnpxlErEgLAFrF7Sw7XA3Gw9YEEqSJElSuYtHR4hPHc8Xgac68tfdHcS9J9/75BzVdflSZloLQUP+mvpzysDqOks/AeTPvHxmVGjLu/cQcTabLwj7u4n7us8Wh3FfF3FPJ/R1Q19hxOqhnW9/cDpD0DyDoHkmQcssgpaZpFpmQV2j/w5LkAVhCVg9r5m/C2DX0V6GRsaoqXSzSJIkSdJUF8cxDPSQO3mU+NxLz0ne9ZQV05oJmtpINbbCOUVgMK2FoLJqQvNr6gvS6fy/uWnNcIHTJsTZsfwu7T2dhcvJs9MM9BB3HiHuPO+AiJVVBM2zCFrbSbXNIWidS9Dc5mjDhNlElYC66goWz2xg17Fethw8xbVL2pKOJEmSJEkaZ/FgH7kTB4lPHMxfdx6B04PvvGMqRdBUGHnV1JafbmrL77Z5zjHspKQFhVGCNM94x7L49HB+JGzXMXJdx85OMzxIfHw/8fH9nB0Pm6kgmF4oDNvm5i9NbY40nEAWhCVizYIWdh3rZeP+LgtCSZIkSZrk4tER4o5D+SKw4xC5Ewegv+edd6yuJWiZTWr6LILps/OX5pme+EGTXlBVTTBrAcxawJmxgXEcw1B/vjTsPEzccZhcx6H8sTSP7yd7fP9bT1BdS2rmAoJZC0nNWkjQNsf/F0Xkmi0Ra+a38M0f72P7kW5Oj2apqnBorSRJkiRNFrnTw+QO7iB3ZA+5Y3uJTxyCXPbtd6qoImibS2rGPIIZ80i1zc2fJMRRUioTQVA4K3LtNFJzrzg7Px4eKJSFh98q1Af7yO3fCvu3koX8MQ3b5pKatZDUnCUEsxYSZCoSey1TjQVhiWisrWRBWz37O/rZeugU6xa1Jh1JkiRJkvQu4pHT5I7sJj66j9zRPRztPALxuScQCfKjAWfOP1sI5neZTCWWWSpVQXUdwbxlpOYtAwojDftOkTu2j9yx/cTH9uV3UT62j+yxfWTXP5UvDGctJDVnKam5SwmmtxOk/P91qSwIS8i6RdPZ39HP+r0nLQglSZIkqYTEcY745FFyB3eSO7id+Pj+t59ROEjlRwXOXkQwe1F+l8iqmuQCS5NYEATQ0EK6oYX0smsAiIcHyR3fT3x0L7nDu/InQDm8i+zhXWRfBqpqSc1ZQmreclILVhDU1Cf7IiYZC8IScuWC6Xzr5f1sO9zt2YwlSZIkKWHx0AC5wzvzuw4f3AFD/W8tDIL86MD2JaRmL6J11TV09fW/+5NJuixBdS3pBSthwUqg8P/zyG5yh3aRO7wzP+Jwz0ZyezYCQb6wX7CS1IKVBC0z3ZX/fdhAlZCG2koWz2pg97FeNh84xXVLPVmJJEmSJE2kuOck2X2bye3dTHz8ABC/tbCugdS8ZfkRSnOWEFTVnl2UqqoGC0JpwgQ1daSXXEl6yZUAxL0nyR3cQXb/VuLDu4lPHCB74gDZV74P05pJL1hJasmVBDPnu6v/BVgQlpirF01n97Fe3tjbaUEoSZIkSUUWxzFx13FyezeR27uJuOvYWwtT6fzuwoVSMGie4SgkqUQFDdNJr76Z9OqbiUdPkzu0k9z+reQObIe+U2Q3vUB20wtQ10B68VpSi68kmDnPsrDAgrDErJnfwt+/tI9dR3voHx6lvtoz8kiSJEnSeIrjmPjEQXJ7N5Hduxl6T761sKKK1IIVpBatITVvGUFFVXJBJV2SoKKK9KI1pBetyR8/9MQhcns2kd2zAfq7yW58nuzG56G+MV8WXnF1/iQnZfwHAAvCElNXXcGy9ka2He5m4/4ubl4+M+lIkiRJkjQl5E6dILdrPdld66G3660F1XWkFq7Kl4JzlhCk/aosTRVBkMofL3TmfNI3fSj/x4E9G8ju3gj9PWQ3PEd2w3MELbNILb+W9NJ1BLXTko494fytV4LWLZrOtsPdrN/baUEoSZIkSZchHuglu2s9uV3riTuPvLWgdlp+5NCiNQSzFhKk3M1QmuqCMycXmjmf9E0fJj5+sPD74U3irmNkX/wO2Ze+lz+swPJriZtu4/UtR3j8+V30D4xQX1fJA7ct5eqV7Um/lHFnQViCVs9rJpMO2Hu8j56BERrrKpOOJEmSJEmTRpwdI3dgG7ltr5I7uB3iwolGKqtJLVpD+op1BLMXWwpKZSwIUgSzFpCatYD45o+Q27+N3I7XyB3Ynv/9cWAbjz32JH91Yj59I2897siJfvhJplxJaEFYgqorM6yc28zG/V28ue8kd6yenXQkSZIkSSp5ua7j5La/QnbHGzA8kJ+ZSuePKXjF1aTmLyfIeJx3SW8XpDOkF68hvXgN8WBfflTh9ld5YkvT28pBgL6B0/zguV0WhJoY6xZOZ+P+Ltbv67QglCRJkqR3EWfH8icf2PIi8bH9Z+cHzTNJrbiO9BVXE9TUJ5hQ0mQS1E4jc+XtxGtvY/h3HoeOgXfcp39w5AKPnNwsCEvUirlNVGVSHOwcoLN3mNaG6qQjSZIkSVLJiPu6yW79Mdltr8BQf35mRRWppetIr7iOoG1uWZ+RVNLlCYKAxuYGDl6gIKyvnXqHgrMgLFGVmTSr57fw+p5OXt/TyQPr5iYdSZIkSZISFccx8dE9ZDc+T27/1rPHFgxaZpFefTOpK9YRVFQlnFLSVPGJ+9ay/3AXfQOnz86bVlfFA7ctTTBVcVgQlrBrl7QVCsIO7r9qjn/9kiRJklSW4myW3N6NZN98lrjzcH5mKk1q8RrSq28mmLXA70uSxt2N6xbwi33r+MFzu+gfHKG+1rMYKwFLZzXQUFPByb7T7O/oZ+GMaUlHkiRJkqQJE48Mk932CtmNz0N/d35mdR3p1TeTXnUjQa3fkSQV19Ur26dkIXg+C8ISlkoFXLOklac2HeW13R0WhJIkSZLKQjzUT3bDc2S3vAgj+V37gqY20lfeTuqKqz0TsSSNMwvCEnft4jae2nSUN/ed5BM3LCSTTiUdSZIkSZKKIh7sI/vmM2S3vARjowAEsxeRvuoOUvOXEwR+H5KkYrAgLHGzmmuZ01LL4a5Bthw6xZULpicdSZIkSZLGVTzQQ3b902S3vgzZMQBS81eQvuYeUjPnJ5xOkqa+ohaEYRh+CbgOeD2Koi+cM78F+EOgFfhhFEVfLGaOye6axW0c7trP67s7LQglSZIkTRnxYB9jrz9JbuvLkMsCkFq4Ol8Mts1JOJ0klY+iFYRhGF4D1EdRdHsYhn8QhuH1URS9Ulj8W8B/iqJoW7F+/lSybvF0Hn1tP1sPdTMwPEpdtcfbkCRJkjR5xaeHyb75NNmNzxV2JQ5ILb6S9DV3k5o+O+l4klR2ijmC8Cbg8cL0E8DNwJmCcA3wH8IwnAf8hyiKXixijkmvoaaS5e1NbDvczfp9J7l1xaykI0mSJEnSBxaPjZLd/CLZN56C04MApBauIn39g6RaZiYbTpLKWDELwiZgT2G6B1h9zrJbgGuALuDvgNvOf3AYhg8DDwNEUURra2sRoxZfJpO5rNdw51WL2Hb4DTbs7+YTt60Zx2Tl53K3hcaP26J0uC1Kh9uidLgtJGn8xLkcue2vMvbaEzDQC+RPPpK58UMeY1CSSkAxC8IeoKEw3QB0n7NsRxRFWwHCMMxd6MFRFD0CPFK4GXd2dhYp5sRobW3lcl7D/OYMVRVp9hzrZvOug8xsqhnHdOXlcreFxo/bonS4LUqH26J0TJVt0d7ennQESWUud2Q3Y89/m7jrGADB9NlkbvwQwdwrCIIg4XSSJChuQfgi8KtABNwHfOWcZTvCMJwN9BY5w5RRmUlz1cLpvLzzBK/sOsFHr1uQdCRJkiRJeldxXxdjL32P3J6N+Rn1TWRufIjUkisJglSy4SRJb1O038pRFL0ODIdh+CyQBQ6EYfibhcW/BXwNeBL4/xUrw1RzwxVtALy2u5Ns7oIDLyVJkiQpUfHoCGOv/ICRv/lv+XIwU0H6+vup/My/Ir10neWgJJWgoo7ei6LoC+fN+mJh/hbgrmL+7Klofms9MxtrON4zxNZD3ayZ35J0JEmSJEkCII5jcrs3MPbSd2GgB4DU0nX53YnrGxNOJ0l6L+7eO4kEQcD1V8zg0Vf38/LOExaEkiRJkkpC3NvF6HPfJD64A4CgdQ6ZWz9GatbCZINJki6KBeEkc+3iVr772gG2He6mZ3CExtrKpCNJkiRJKlNxLkt24/NkX30cxkahsprMTR8mteI6dyWWpEnEgnCSqa+pYNW8ZjYd6OK13R3cs3ZO0pEkSZIklaFcxyHGnvl74s4jAKSWXEXmlo8S1E5LOJkk6YOyIJyEbriijU0HunhlZwd3r2knCIKkI0mSJEkqE/HoabKvPE520/MQx/mzE9/+E6Tnr0g6miTpElkQTkLL25torK2ks2+Yvcf7WDyrIelIkiRJkspA7tg+Rp+MoK8LgoD0lbeRvu5+goqqpKNJki6DBeEklEoFXLekjR9uPMzLu05YEEqSJEkqqjg7RvbVJ8i++TTEMUHLLDJ3/RSptrlJR5MkjQOPGjtJXbe0DYAN+7oYGhlLOI0kSZKkqSrXdYzRb/we2fVPAZBedxcVP/nrloOSNIU4gnCSam2oZumsBnYd6+X13Z3cunJW0pEkSZIkTSFxnMufofjHj0EuCw0tVNwdkpq1MOlokqRxZkE4id28fCa7jvXy4vbj3LJipicrkSRJkjQu4r5uRp+KiI/sASC14gYyN3+EoNJjDUrSVGRBOImtnt/MtJoKjvcMsfdEH4tneixCSZIkSZcnu38bYz+K4PQg1NSTueMnSS9clXQsSVIReQzCSSydSnHD0hkAvLT9eMJpJEmSJE1mcS7L2I8fY+yxr8DpQVLzl1P56X9hOShJZcCCcJK7cdkMggA27O+if3g06TiSJEmSJqF4oJfRR7+cPxFJEJC+4SEyD/0CQU190tEkSRPAgnCSa66vYsWcJrK5mFd2dSQdR5IkSdIkc3rfNkb+7n8QH90LtdOo+OivkLn6LoLAr4uSVC78jT8F3Lx8JpDfzTgXxwmnkSRJkjQZxHGOsdefpPOr/xWG+gnaF1P5qX9Oqn1x0tEkSRPMk5RMAcvbm2iuq6Sr/zQ7j/SwfE5T0pEkSZIklbD49DBjT36d3IFtAKSvvpv0dfcTpBxDIknlyN/+U0AqFXDjsvwowhc9WYkkSZKk95Dr7mD0m7+XLwerapn+mS+QueFBy0FJKmO+A0wR11/RRioI2HLoFKf6TycdR5IkSVIJyh3cweg3fo+4u4OgZSaVP/nrVC9dm3QsSVLC3MV4imioqeTKhS2s33uSF7cf58PXzk86kiRJ0tuEYfgl4Drg9SiKvnDO/K8AK4Eh4JEoir6aTEJpastuep6xFx6FOCa1cBWZuz9DUFmVdCxJUglwBOEUctvKWQD8eOcJRsdyCaeRJEl6SxiG1wD1URTdDlSGYXj9eXf5XBRFd1kOSuMvzuUYe/7bjD3/bYhj0tfcQ+aBn7UclCSd5QjCKWR+az3zptdx8OQAb+zt5IYrZiQdSZIk6YybgMcL008ANwOvFG7HwF+EYXgS+PUoivaf/+AwDB8GHgaIoojW1tbiJy6iTCYz6V9DKXA9vr/cyGlOffOPGdm5HtIZmj/yC9Suvflt93E9jg/X4/hwPY4P1+P4KKf1aEE4hQRBwK0rZ/H153bz3NZjXL+0jSAIko4lSZIE0ATsKUz3AKvPWfavoijqCsPwNuC/Aj91/oOjKHoEeKRwM+7s7Cxi1OJrbW1lsr+GUuB6fG/xYB+jj/05ccchqKqh4oGfY3D2YgbPW2eux/Hhehwfrsfx4XocH1NxPba3t19wvrsYTzFXLZxOfXUFR08Nsud4X9JxJEmSzugBGgrTDUD3mQVRFHUVrp8DZk14MmkKintPMvIPf5gvBxtaqPiJXyPVvjjpWJKkEmVBOMVk0iluXp7ftfi5rccSTiNJknTWi8C9hen7gJfOLAjDsKFwvZxzikNJlybXeYSRb/4B9J4kaJ1D5Sf+CammtqRjSZJKmAXhFHTTspmkUwGbD3bR1T+cdBxJkiSiKHodGA7D8FkgCxwIw/A3C4v/OgzD54AvA/8uqYzSVJA7spvRb/8RDPUTzFlKxcd+haB2WtKxJEklzmMQTkENtZVcuXA6b+zp5IVtx/nodQuSjiRJkkQURV84b9YXC/M/lkAcacrJ7t/G2ON/BdkxUouvJHNPSJD2K58k6f05gnCKum1F/vA9L+88wenRbMJpJEmSJBVTds9Gxn7wl/lycNWNZO79actBSdJFsyCcoua31bOgrZ6hkSyv7OpIOo4kSZKkIsnufIOxJ74GuSzpK28nc9tPEKT8qidJuni+a0xhd67On7r62S1HyebihNNIkiRJGm/Zba8w9mQEcY70NfeQvunDBEGQdCxJ0iRjQTiFrZ7XTOu0arr6T7PpQFfScSRJkiSNo+y2Vxh7+u+AmPQND5K5/gHLQUnSJbEgnMJSqYDbV+WPRfj0piPEsaMIJUmSpKkgu+M1xp7+ewDSN32YzNV3J5xIkjSZWRBOcdctbaOuKsPBkwPsOd6XdBxJkiRJlym7cz1jT/0v8iMHHyJz1R1JR5IkTXIWhFNcZSbNLStmAvD05iMJp5EkSZJ0ObK7NzD2o7+BOCZ9/f1krr4r6UiSpCnAgrAM3LJiFpl0wNZD3RzvHko6jiRJkqRLkD2wnbEnv54vB6+5l8w19yYdSZI0RVgQloH66gquW9IGwDNbHEUoSZIkTTa5Y/sYe/yvIJcjfeUdpK+7L+lIkqQpxIKwTNyxejYB8NruTnqHRpKOI0mSJOki5U4eZfR7X4GxUVLLryN904c8W7EkaVxZEJaJtoYaVs9vJpuLeX7rsaTjSJIkSboIcc9JRr/zJzAyTGrhajJ3fNJyUJI07iwIy8idq9sBeHH7cYZHxhJOI0mSJOm9xEP9jHz3T2Gon6B9CZl7f5oglU46liRpCrIgLCMLZ0xj8cxpDI1keXH78aTjSJIkSXoX8egIo4/9OfSeJGidQ8WDP0+QqUg6liRpirIgLDP3rJ0DwNNbjjIylk04jSRJkqTzxbkcY0/+DfGJg1DfRMVDv0BQWZV0LEnSFGZBWGaWtTcyb3odA8NjvLzzRNJxJEmSJJ0n+9J3yO3bDJXVVHzo8wR1DUlHkiRNcRaEZSYIAu69Mj+K8KlNRxnL5hJOJEmSJOmM7KbnyW58HlJpKh74OVItM5OOJEkqAxaEZWjlvGZmNdfSMzjCq7s7ko4jSZIkCcgd3MHYC48CkLnzU6TmLEk4kSSpXFgQlqFUEHDv2vwZjX+08QjZXJxwIkmSJKm85bo7GH3iqxDHpK+5h/Sya5KOJEkqIxaEZerKBdNpa6imq/806/d2Jh1HkiRJKlvx6WHGvv8XMDJMauEq0tfdl3QkSVKZsSAsU6lUcPaMxk9uPEzOUYSSJEnShMufsfhrxN0dBC0zydzzGYLAr2mSpInlO08Zu3rxdJrrqzjRM8zGA11Jx5EkSZLKTvbl75M7sB2qa6l48BcIKqqSjiRJKkMWhGUsnUpx95r8sQh/uOEwudhRhJIkSdJEye7ZRPbNpyGVouL+zxE0tCQdSZJUpiwIy9x1S9torK3k6KlBNu53FKEkSZI0EXI9nYw9/bcApG/8MKl2z1gsSUqOBWGZq0inuPfK/LEIf7D+kMcilCRJkoosHh1h7Ad/BSOnSS1eS3rtrUlHkiSVuUwxnzwMwy8B1wGvR1H0hXPmfwVYCQwBj0RR9NVi5tB7u35pGz/adIQTPUOs33eSaxa3Jh1JkiRJmrLGnv8H4q5jBI2tZO78FEEQJB1JklTmijaCMAzDa4D6KIpuByrDMLz+vLt8LoqiuywHk5dJp7ivMIrw8fWHyDqKUJIkSSqK7LZXyG1/DTIVZO7/WYLK6qQjSZJU1F2MbwIeL0w/Adx8zrIY+IswDL8dhuGCImbQRbp2SRut06rp7Bvmtd0dSceRJEmSppzcyWOMPfcPAGRu/wlS02clnEiSpLxi7mLcBOwpTPcAq89Z9q+iKOoKw/A24L8CP3X+g8MwfBh4GCCKIlpbJ/dur5lMpuRfw0/evoJHvrueJzcd5YEbVpBJT81DVE6GbVEu3Balw21ROtwWpcNtIWk8xWOjjP3wa5AdI7XiOtLLrk06kiRJZxWzIOwBGgrTDUD3mQVRFHUVrp8Lw/C3L/TgKIoeAR4p3Iw7OzuLl3QCtLa2UuqvYcn0KmY21nC8Z4jvvbSVm5fPTDpSUUyGbVEu3Balw21ROtwWpWOqbIv29vakI0gCxl76LvGp4wRNbWRu+XjScSRJeptiDhF7Ebi3MH0f8NKZBWEYNhSul3NOcahkpVIB96+bC8APNxxmNJtLOJEkSZI0+WX3byW3+UVIpcnc+9MEFZVJR5Ik6W2KVhBGUfQ6MByG4bNAFjgQhuFvFhb/dRiGzwFfBv5dsTLog1u7oIXZzbX0DI7w0vbjSceRJEmSJrV4oJexp/4XAOkbHiTVOifhRJIkvVMxdzEmiqIvnDfri4X5Hyvmz9WlSwUBD66by1d+tIMfbjzM9VfMoLoinXQsSZIkadKJ4xyjT/0tDA8QzL2C9JW3JR1JkqQLmppnodBlWTWvmQVt9QwMj/H05iNJx5EkSZImpeymF4gP7YTqOiru+jRB4NcvSVJp8h1K7xAEAR+5dj4Az2w+Su/QSMKJJEmSpMkl191B9uXvA5C581MEdQ3v8whJkpJjQagLWjSzgVXzmhkZy/H4+kNJx5EkSZImjTiXyx93cGyU1LJrSC9clXQkSZLekwWh3tWHr5lHEMDLO09womco6TiSJEnSpJDd+Bzx8f1Q20Dmlo8mHUeSpPdlQah3NbOpluuXziAXw/deP5h0HEmSJKnk5U6dIPvKDwDI3PGTBFW1CSeSJOn9WRDqPT2wbi4V6RSbDnSx70Rf0nEkSZKkknV21+LsGKll15JesCLpSJIkXRQLQr2nxtpKbl81C4DvvnaAOI4TTiRJkiSVpuyGZ4lPHIA6dy2WJE0uFoR6X3etaae2KsPeE31sOXgq6TiSJElSyYl7T5J99XHgzK7FNQknkiTp4lkQ6n3VVGa478o5AHzntQNkc7mEE0mSJEmlI45jRp/9h/yuxUvXkZ7vrsWSpMnFglAX5eblM2ltqKajd5gXth1POo4kSZJUMnK7NxAf2gFVNe5aLEmalCwIdVEy6RQfu24BAI+/eYiB4dGEE0mSJEnJi08PMfbCtwHI3Pghgpr6hBNJkvTBWRDqoq2c28QVsxsZGsny/fWHko4jSZIkJW7s5cdgqJ9g1kJSK65LOo4kSZfEglAXLQgCPn79AlIBvLTjOEdPDSYdSZIkSUpM7th+clt+DKkUmds/SRD49UqSNDn5DqYPZFZzLTcvn0kcw7de2Uccx0lHkiRJkiZcnM0y9uzfA5C+6k5SLTMTTiRJ0qWzINQHdv9Vc6mpTLPraC+bD55KOo4kSZI04bKbXyDuOg4NLaSvuSfpOJIkXRYLQn1gddUVPLBuHgCPvrqfsWwu4USSJEnSxImH+sm+9gQAmVs+TpCpSDiRJEmXx4JQl+Tm5TOY0VjDyb7TPLv1WNJxJEmSpAkz9vL3YeQ0qXnLSS9YkXQcSZIumwWhLkk6leLj1y8A4Ik3D9E9cDrhRJIkSVLx5ToOkdv2KqRSpG/5aNJxJEkaFxaEumTL5zSxZn4LI2M5vv3K/qTjSJIkSUUVxzFjL3wbiEmvuZVUU1vSkSRJGhcWhLosn7hhAZWZFBv2d7H9cHfScSRJkqSiye16k/jYfqipJ33NvUnHkSRp3FgQ6rI01VVx/1VzAfjmj/cx6glLJEmSNAXFoyOM/fi7AGRueJCgqjrhRJIkjR8LQl2221fNYmZjDZ19wzy16UjScSRJkqRxl13/FAz0ErTNJbX82qTjSJI0riwIddnSqRSfvGkRAE9uOExn73DCiSRJkqTxEw/0kN3wLACZWz5GEPg1SpI0tfjOpnGxZFYD1yxuZSwX8w8v7yOO46QjSZIkSeNi7NXHYWyU1OK1pGYtSDqOJEnjzoJQ4+aj182nuiLNtsPdbDpwKuk4kiRJ0mXLnTpObvtrkEqRvuHBpONIklQUFoQaN9NqKnnomnkAfPPHexkaGUs4kSRJknR5sj9+DOKY1IobSDW2Jh1HkqSisCDUuLp52Uzmt9bTOzTKd187kHQcSZIk6ZLlju4lt38rZCrJXHtv0nEkSSoaC0KNq1Qq4NO3LCadCnhpxwl2H+tNOpIkSZL0gcVxzNhL3wMgfdXtBLXTEk4kSVLxWBBq3M1qruWete0A/K8X9zCazSWcSJIkSfpgcns3E584ADX1pK+8I+k4kiQVlQWhiuKetXOY2VhDZ+8wT7x5KOk4kiRJ0kWLs1myLz8GQObaewkqqxJOJElScVkQqigy6RQ/dctiAuCpTUc43DWQdCRJkiTpouR2vEbc00nQ2EpqxQ1Jx5EkqegsCFU0C2dM49aVs8jF8LfP7yGbi5OOJEmSJL2nODvG2OtPApC+7n6CdDrhRJIkFV8m6QCa2h66eh6bDnRxuGuAZ7Yc5e417UlHkiRJCQnD8EvAdcDrURR94Zz5a4A/BALgn0RRtCGhiBK57a9CfzdB80xSS9YmHUeSpAnhCEIVVVVFmp+6eTEA33/jIMdODSacSJIkJSEMw2uA+iiKbgcqwzC8/pzF/xn4GSAsTEuJiMdGGXv9RwCkr7uPIPDrkiSpPPiOp6JbPqeJG6+YQTYX8/XndpPNeVZjSZLK0E3A44XpJ4Cbz1nWHEXRwSiKDgNNEx1MOiO37RUY6CFomUVq0eqk40iSNGEuahfjMAyzwM9EURQVbn8Y+J0oipYVM5ymjo9ev4AdR3s43DXADzcc5oF185KOJEmSJlYTsKcw3QOc276c+0fr4EIPDsPwYeBhgCiKaG1tLULEiZPJZCb9aygF47ke49ERjr35NADN93yKmrYZ4/K8k4H/HseH63F8uB7Hh+txfJTTenzPgjAMw/nAQvIf1FaFYXhHYdGHgMXFjaappLoizWduXcIffn8LP9xwmFXzmpk7vT7pWJIkaeL0AA2F6Qag+5xl557J7IK7GkRR9AjwyJn7d3Z2jne+CdXa2spkfw2lYDzX49jG58j19xC0ttPfMpeBMto+/nscH67H8eF6HB+ux/ExFddje/uFzw3xfrsYfx74EfkPbf9bYfpHwD8Fto9jPpWBJbMauL1wVuOvP7ub0ay7GkuSVEZeBO4tTN8HvHTOsq4wDOeGYdgO9E54MpW9eHSE7BtPAZC+9j6C4IIDWSVJmrLeryB8GfgD8iMIHwd+H/g98geP/mRxo2kq+tA182lrqOZ4zxDff+Ng0nEkSdIEiaLodWA4DMNngSxwIAzD3yws/i3gb4C/Bf5TQhFVxrJbXoKhfoK2uaQWrEw6jiRJE+49dzGOouh7wPfCMHwFeCqKov0AYRimoihy+Jc+sIpMip++bSm/+71NPLP5KKvmNbN4ZsP7P1CSJE16URR94bxZXyzM3wDcOvGJpMLowfX5Yw/mz1zs6EFJUvm52LMYrwE+H4ZhexiGB4CBMAx/qYi5NIXNb6vnnjVziIGvPbuLoZGxpCNJkiSpTGW3vQLDA/nRg/OWJx1HkqREXGxB+FnyB5L+GaAS2An8xyJlUhm4f90c5k2vo3tghL97cQ9xHL//gyRJkqRxFGfHyL75DADpq+929KAkqWy95y7G55gOnAQeBP4S2AD8cbFCaepLp1J89o4r+J1vb+DNfV0sa+/ghitmJB1LkqSyFobhLmAT8Cb5z3tvRlG0K9lUUvHkdq6HgR6C5hmkFnrsQUlS+brYEYQHyB8j5ieAV4Fm8oWhdMlaG6r5iZsWAfDNl/dxomco4USSJJW9b5L/3HcMuB/YEIbhgTAMXwzD8I8STSaNsziXI7v+KQDS6+4mCC72q5EkSVPPxY4g/DfA/wG8BHwD+C/A3xUrlMrHtYtb2XG4mzf2nuSrz+zk1z+8hkzaD2eSJCXkgSiKrjxzIwzDPwM+CfwucFViqaQiyO3bTNzTCdOaSS298v0fIEnSFHZRTUwURd8ErgV+C1gC/Jsoiv55EXOpTARBwE/etIiW+ioOdw3yvdcPJh1JkqRydjIMw7NFYBRFPwY+FEXRoSiKvpNgLmlcxXFM9o0fAZC56k6CVDrhRJIkJeuiRhCGYbiK/C4nSwqzdoVh+IkoirYVK5jKR3Vlhs/esZTf/95mntlylCvaG1kxpynpWJIklaNfAf4iDMPNwHpgJeAxQDTlxAd3EHcegZp6UsuvTTqOJEmJu9h9OX8XmA18rXCZXZgnjYsFbdN4YN08AL727C66B04nnEiSpPJTOCHJbcD3gFnALuAjiYaSimDszLEHr7ydIFORbBhJkkrAxR6D8Drg30dR9LsAYRj+OvB/Fi2VytLda9vZc7yXHUd6+Mund/JPHlzl8QglSZpgURTlgL8vXKQpJ3d0H/HRvVBZTXrVTUnHkSSpJFxsQdgF3BeG4XcLt+/nIs5iHIbhl8iXi69HUfSF85bVAHuBn42i6ImLj6ypKhUEfPb2pfzOoxs50NHPd147wCduWJh0LEmSJE0hZ89cvOYWgsqqZMNIklQiLnZ41peBjwM7C5ePAX/8Xg8Iw/AaoD6KotuByjAMrz/vLv8I2PjB4mqqq6uu4GfvvIJ0KuC5rcd4c9/79tCSJEnSRcmdOkHuwDbIVJBec2vScSRJKhkXWxD+JfCPeWt3k4eBv36fx9wEPF6YfgK4+cyCMAwrC8uf/yBhVR4WtE3jo9ctAOBvX9hDR4/HRpckSdLly254FoDUsmsIauoSTiNJUum42F2MnwC+HkXRpwHCMPzP5Mu/Ze/xmCZgT2G6B1h9zrJfBP4KuPHdHhyG4cPki0iiKKK1tfUio5amTCYz6V/DRPrEbdM50n2aV3Yc5avP7eE/fvY2qirS4/LcbovS4bYoHW6L0uG2KB1uC2lqiQf7yO18AwhIr70t6TiSJJWUiy0I5wD7zrm9H5j7Po/pARoK0w1AN0AYhhngwSiKPhWG4bsWhFEUPQI8UrgZd3Z2XmTU0tTa2spkfw0T7ePXzWXfsVMc6uzjD7/9Mp+9fSlBEFz287otSofbonS4LUqH26J0TJVt0d7ennQEqSRkN78E2TFSC1eRampLOo4kSSXlYncx3gP86zAMHwrD8EPAv+Kt0YHv5kXg3sL0fcBLhemZwPwwDB8Dfhb4L2EYNn+w2CoH1RVpfv6uZVRmUqzfe5KnNx9NOpIkSZImoXhslOyW/NeR9JW3J5xGkqTSc7EF4f8FLAe+AzxamP4v7/WAKIpeB4bDMHwWyAIHwjD8zSiKDkdRdH0URQ+R383430dRdOqSX4GmtFnNtfz0bUsB+O5rB9h2uDvZQJIkSZp0cjteh+EBgra5BLMWJh1HkqSSc1G7GEdR9JdhGO4HPlqY9WgURc9cxOO+cN6sL563/H+/mJ+v8rZ2QQv3XzWXx988xF8/vZN//pE1tDXWJB1LkiRJk0Ac586enCR95e3jcsgaSZKmmos9BiGFQvB9S0GpGO67ag5HTw2w6cApvvKj7fyzD6+huvKi//lKkiSpTOX2byPu6YT6JlKL1yQdR5KkknSxuxhLiUoFAZ+5bSmzmmo40TPMV5/dRS6Ok44lSZKkEnd29ODaWwlS6YTTSJJUmiwINWlUV6T5xXuWU1uVYeuhbr73+oGkI0mSJKmE5ToOER/dC5VVpFdcn3QcSZJKlgWhJpXp06r5uTuvIBUEPLXpKC/tOJ50JEmSJJWo7IbnAEivuJGgsjrhNJIklS4LQk06S2c38qmbFwHwjZf2st0zG0uSJOk88UAvuT0bIEiRXnNL0nEkSSppFoSalG64Ygb3rG0nF8NfPr2TI10DSUeSJElSCclueQlyOVKLVhNMa0o6jiRJJc2CUJPWg1fPY93C6ZwezfKnP9xOz+BI0pEkSZJUAuLsGNktPwZw9KAkSRfBglCTVioICG9bwoK2enoGR/izH27j9Gg26ViSJElKWG7XmzA8QNDaTjBrYdJxJEkqeRaEmtQq0ik+f89ypk+r4nDXIH/x1A7GsrmkY0mSJCkhcRyT3fQ8kB89GARBwokkSSp9FoSa9OqqK/jl+1ZQV51hx5Ee/ua53eTiOOlYkiRJSkB8fD9x5xGoriO15Kqk40iSNClYEGpKaGuo4R/dt5KqijTr953kWy/vI7YklCRJKjvZjYXRgytvIMhUJJxGkqTJwYJQU8bc6XX84t3LSKcCnt92nB9uOJx0JEmSJE2guL+b3N7NkEqRXn1T0nEkSZo0LAg1pSyd3chn71hKAHx//SFe3H486UiSJEmaINnNL0GcI7VoLUFdY9JxJEmaNCwINeVcuWA6n7xpEQDfeGkv6/d2JpxIkiRJxRaPjZLd9jKQPzmJJEm6eBaEmpJuXj6Th66eRwx87dldbNzflXQkSZIkFVFu13oYHiRom0swc37ScSRJmlQsCDVl3bO2nXvWtpOL4a+f2cmWg6eSjiRJkqQiiOP4rZOTrLmFIAgSTiRJ0uRiQagpKwgCHrp6Hnesmk02F/MXT+1g++HupGNJkiRpnMVH9xJ3HYOaelJLrkw6jiRJk04m6QBSMQVBwEevm89YNscL24/zlR9tZ3pLE601SSeTJEnSeMluegGA9MobCNJ+xZEk6YNyBKGmvCAI+MSNC7nhihmMZWN+5xuvsPtYb9KxJEmSNA7i/m5y+7ZAKkV61U1Jx5EkaVKyIFRZSAUBn7p5EdcuaeX0aJY/eWIbO4/2JB1LkiRJlym7+SWIc6QWrSWoa0g6jiRJk5IFocpGKggIb1nCbavnMprN8ac/3MY2j0koSZI0acWjI2S3vQzkT04iSZIujQWhykoqFfD5B6/ipmX53Y2/8uR2z24sSZI0SQ1ueRmGBwla5xDMnJ90HEmSJi0LQpWdVBDwkzct4tYVs8jmYv78RzvYuL8r6ViSJEn6AOI4ZuCVHwL50YNBECScSJKkycuCUGUpCAI+ccMC7lw9m1wc81dP7+DV3R1Jx5IkSdJFio/tZ/T4QaiuI7XkyqTjSJI0qVkQqmwFQcBHrp3PvVfOIRfD3zy3m6c3H0k6liRJki5CdtPzAKRX3kCQqUg4jSRJk5sFocpaEAQ8dPU8Pn79AgAeffUA333tAHEcJ5xMkiRJ7ybu7yG3dzMEKdKrb0o6jiRJk54FoQTcvmo2P33bElJBwI82HeFvX9hDNmdJKEmSVIqyW16COEfNimsI6hqTjiNJ0qRnQSgVXLukjV+8ZxkV6RSv7OrgL5/awehYLulYkiRJOkc8Nkp268sA1F1/b8JpJEmaGiwIpXOsnNvMww+spKYyzeaDp/jyE1sZPD2WdCxJkiQV5HZvgOEBgtZ2KucuTTqOJElTggWhdJ6FM6bxaw+tpqGmgj3H+/jd726is3c46ViSJEllL45jspteACC9+haCIEg4kSRJU4MFoXQBs5pr+fUPr2FWcy0dvcP87nc3se9EX9KxJEmSylp8/ABx52GoriO19Kqk40iSNGVYEErvorm+in/60CqWtTcycHqMP/r+Ftbv7Uw6liRJUtnKbnoegPSK6wkyFQmnkSRp6rAglN5DdWWGX7p3BTctm8FYLuavn9nFDzccJo49w7EkSdJEigd6yO3dBEGK9Oqbko4jSdKUYkEovY90KuAnb1rER69bQAA89sZBouf3MJb1DMeSJEkTJbvlx5DLkVq0mqC+Kek4kiRNKRaE0kUIgoA7V8/m5+9eRkU6xau7O/iD72+hZ3Ak6WiSJElTXpwdyxeEQHr1zQmnkSRp6rEglD6ANfNb+LUPraaprpIDHf38j0c3sr/Dk5dIkiQVU273mzA8QDB9NsHsRUnHkSRpyrEglD6gudPr+MJH1rJ45jR6h0b5g8e28PLOE0nHkiRJmpLiOCa78QUA0mtuIQiChBNJkjT1WBBKl6C+poKHH1jJrStmks3F/O0Le/j7l/Z6XEJJkqRxFh8/QNx5GKpqSS1dl3QcSZKmJAtC6RKlUyl+4sZFfPqWxaRTAS9uP84jP9jqcQklSZLGUXZzYfTgyusJMhUJp5EkaWqyIJQu0w1XzODXHlpFQ00Fe0/08aVvb2DHkZ6kY0mSJE16cW8Xud0bIUiRXnVT0nEkSZqyLAilcTC/bRr/4mNrWTq7gYHhMb78+FZ+sP4QuVycdDRJkqRJa+zNZyDOkVp6FcG05qTjSJI0ZVkQSuNkWk0lv3LfSu6/ag4Aj795iC8/sY3+odGEk0mSJE0+8UAvue2vApC++q5Es0iSNNVZEErjKJUKeGDdPP7R/Suoq86w82gPX/r2BvYc6006miRJ0qSS3fAsZMdILVxNqnlm0nEkSZrSLAilIljW3sS//OiVLJoxjd6hUf7wB1v4/hsHybrLsSRJ0vuKhwfIbvkxAOlr7k44jSRJU58FoVQkjXWV/OqDq7hnbTvE8MSGw/z+Y5s52TecdDRJkqSSlt34AoyNEMxdRqptbtJxJEma8iwIpSJKpwI+dM18fvXBlTTWVnKgo58vfXsjr+3uII4dTShJknS+eGSY7KbnAcg4elCSpAlhQShNgCWzGvmNj1/JlQtaOD2a5evP7earz+5iaGQs6WiSJEklJbvlxzAyTDBrIanZi5KOI0lSWcgkHUAqF7VVGX72zit4ZVcH//DyPtbvPcm+E318+pbFLGtvSjqeJElFE4bhNOCrQAvwR1EU/cV5y7cDRws3fy2Koi0THFElIh4bzZ+cBMhc7ehBSZImigWhNIGCIOCGK2awaOY0vvbMLg6eHOCPH9/GTctm8JHrFlBdkU46oiRJxfArwNcLlx+FYfj1KIpGzlneEUXRXYkkU0nJbXsFhvoJWucQzFuWdBxJkspGUQvCMAy/BFwHvB5F0RfOmf/fgXVANfAbURQ9X8wcUqlpa6jhn354DU9tOsLjbx7ipR0n2H6kh/CWxSyd3Zh0PEmSxttNwK9HUZQNw/BNYAWw4ZzlLWEYPgNsBb4QRZFn9CpDcXaMsTefBiB99V0EQZBsIEmSykjRCsIwDK8B6qMouj0Mwz8Iw/D6KIpeKSz+11EUjYZhuAD4feAjxcohlap0KuDeK+ewal4zf/PcLg53DfJHP9jKrStm8uFr5lPpaEJJ0tTRBPQWpnsKt891WxRFXWEY/gfgYeB/nP8EYRg+XFhGFEW0trYWLexEyGQyk/41jLe+l77PSH8PmdbZzLj+ToLg/Q+X7nocH67H8eF6HB+ux/Hhehwf5bQeizmC8Cbg8cL0E8DNwCsAURSNFubXA28WMYNU8mY31/LPPrKGJzce4Yk3D/P8tuNsPdTNZ25dwuJZDUnHkyTpooVhOIv8bsTnOka+FGwAhgvX3efeIYqirsLkN4B/eaHnjqLoEeCRws24s7NzfEInpLW1lcn+GsZTPNDLyDP/kL9x/UOcPNn13g8ocD2OD9fj+HA9jg/X4/hwPY6Pqbge29vbLzi/mAVhE7CnMN0DrD53YRiG3wBuAH7uQg/2r8QqllLdFj9z7wxuXbuILz+2noMdffzB97dwx9p5hHespK66Mul4RVGq26IcuS1Kh9uidLgtPrgoio4Bd50/PwzD3wDuDcMwIn+YmW3nLKsEgiiKTgO3ArsnJKxKythL34XREVILV5GevzzpOJIklZ1iFoRn/lIMF/5L8SfDMJwL/C/yow05b7l/JVZRlPK2qE3Brz24kic3HubJjUd4ZuNBXt95jE/csICrFk6fcsfiKeVtUW7cFqXDbVE6psq2eLe/Ek+wL5M/i/E/Ax6JomgkDMOHgDTwKvC9MAz7gVPAzyYXU0nIHdlDbtd6SGfI3PzRpONIklSWilkQvgj8KhAB9wFfObMgDMOqwl+J+4GBImaQJp1MOsUD6+Zx1cJW/u7FPew90cdfP7OL13Z38smbFtJSX510REmSPpAoinqBj54377Fzbl4zsYlUKuJclrHnvwVAet1dBA0tCSeSJKk8vf+Rfy9RFEWvA8NhGD4LZIEDYRj+ZmHx34Rh+BTwbeC3ipVBmsxmNtXwjx9axU/dvIiayjTbDnfz//zDBp7efIRsLk46niRJ0mXLbn6JuOsYTGshve7OpONIklS2ijmCkCiKvnDerC8W5v9EMX+uNFWkgoAbl81k5bxmvvXyft7cd5JHXz2QH01440IWzfQkJpIkaXKKB/vIvvoDADK3fJQgU5FwIkmSylfRRhBKGj8NNZX87J1X8Ev3Lqe5rpKjpwb5/ce28LVnd9E7OJJ0PEmSpA9s7MePwchpUvOXk1qwMuk4kiSVtaKOIJQ0vlbObWbJTzTw1KYj/GjjEV7f08nmA13cv24ut62cRTpl5y9Jkkpf7th+cjteg1SazC0fm3InYpMkabKxTZAmmcpMmgfWzeNf/8RVrJrXzOmxHI++eoD/9q2N7DjSk3Q8SZKk9xSPDDP2owiA9FV3EDS2JpxIkiRZEEqT1PRp1Xz+nuX80r3LaZ1WzYmeIf748a185cntdPQOJR1PkiTpHeI4ZuyZbxD3niRomUX6mnuSjiRJknAXY2nSWzm3mStmN/LMlqM8seEwmw+eYuuhbm5ZMZP7rpxDXbUH/JYkSaUht+0VcrvfhEwlmfs/54lJJEkqERaE0hSQSae4Z+0crl3SxvffOMiruzp4busxXtvdwb1XzuHWFbPIpB0wLEmSkpM7eZSx578FQOaOT5Jqaks4kSRJOsPGQJpCGmsrCW9dwr/42FqumN3I0EiWR189wP/9zTd5c99J4jhOOqIkSSpD8ehpxp74KmTHSK24jvQVVycdSZIkncMRhNIU1N5Sx6/cv4Jth7v5zqsHON4zxF89vZMFbfV85Nr5LJrZkHRESZJURsae+wfi7g6C5plkbvl40nEkSdJ5LAilKSoIAlbObWZZexMv7zzBD9YfYn9HP7//2BZWzGnioavnMWd6XdIxJUnSFJfd/iq5Ha9DpoLM/Z8lqKhMOpIkSTqPBaE0xaVTATcvn8nVi6bz9OajPLvlKNsOd7PtcDdXLWzhgXXzmNFYk3RMSZI0BeU6DjP23D8AkLn1E6SaZyacSJIkXYgFoVQmqiszPHj1PG5dOYsfbTzCC9uO8ea+Ljbs7+K6JW3cf9Vcmuurko4pSZKmiLi/m9HHvgJjo6SWX0tq+bVJR5IkSe/CglAqM/XVFXzs+gXcvmoWT2w4zCs7T/DKrg5e39PJzctncveadhpq3fVHkiRdunjkNKPf+woM9hHMXkTm9k8SBEHSsSRJ0ruwIJTKVFNdFT9182LuXD2bx9cfYv3ekzy39Rgv7TjOTctmctfqdhrrLAolSdIHE+eyjD3xVeKuYwSNrVQ88HMEab92SJJUynynlspcW0MNn73jCu5a084P1h9i88FTPLf1GC9uP84NV8zg7jXt7nosSZIuShzHjD3/bXIHt0N1HRUf+jxBdW3SsSRJ0vuwIJQEQHtLHb94z3KOdA3www2H2bi/ixe3H+flnSe4bmkb96xtp6W+OumYkiSphGU3Pk9uy0uQSlPx4M8RNE5POpIkSboIFoSS3qa9pY6fu2sZx04N8sONh3lz70l+vOMEr+zs4Lqlrdy1up02z3osSZLOk927meyL3wEgc/enSc1amGwgSZJ00SwIJV3QrOZaPnfHFdx/1Vx+uOEwb+zt5OWdHbyys4PV81u4e00789vqk44pSZJKQO7IbsZ++DUgJn39A6SXrks6kiRJ+gAsCCW9pxmNNfzM7Uu576o5PLXpCK/t7mTTgS42Hehi8cxp3L2mneVzmjwzoSRJZSp34iCjj/05ZMdIrbqR9NV3Jx1JkiR9QBaEki5KW0MNn75lCQ+sm8fzhZOY7Dnex57j25nVXMtdq2ezbtF00qlU0lElSdIEyXUdZ/S7fwajI6SWriNz2yf8o6EkSZOQBaGkD6SxtpIPXzufe9a289KOEzy75SjHTg3y9ed289gbB7lj1WyuX9pGdaW/XiRJmsri3pOMfufLcHqQ1PwVZO76NEHgHwolSZqM/AYv6ZJUV2a4a007t62cxRt7Onlq8xFO9AzzrVf28/31h7h+aRu3rphFa4NnPpYkaaqJB3oZefRPYLCPoH0xmfs/R5BOJx1LkiRdIgtCSZclk05x/RUzuHZpG1sOnuLZLUfZc7yP57Ye4/mtx1g5r5nbV85iyawGdzmSJGkKiIcH8iMH+7oI2uZS8eAvEGQqko4lSZIugwWhpHGRCgLWzG9hzfwWDp8c4Lmtx3hjbydbDp5iy8FTzGqu5faVs7h6USsVGXc/kiRpMoqHBxh99MvEp04QNM+k4sOfJ6isSjqWJEm6TBaEksbdnOl1fOa2JXzk2vm8uOM4L24/zrFTg/ztC3v4zmsHuGnZDG5aNpPW1qSTSpKki3W2HDx5lKCxlYqP/DJBdV3SsSRJ0jiwIJRUNPU1Fdx/1VzuXtPOm/tO8tzWYxw6OcCTG4/wo01HuGrREa5Z1MTy9iZSKXc/liSpVMXDg4x+50/eKgc/9jBBXUPSsSRJ0jixIJRUdJl0imuXtHHN4lb2dfTz4rZjbNjfxfo9x1m/5zjN9VXctGwGNyydQX2NxzCSJKmU5MvBLxN3HimUg79iOShJ0hRjQShpwgRBwKIZ01g0YxofHxpl89EBnnxjL139p/ne6wf5wfpDrJ3fws3LZ7Jo5jRPaiJJUsIuXA42Jh1LkiSNMwtCSYmor6ngIzcs5fpFjew43M2LO06w9dAp1u87yfp9J5nRWMMNV7Rx7eI2RxVKkpSAs7sVdx4haJhuOShJ0hRmQSgpUakgYMXcZlbMbeZU/2l+vPMEL+88wYmeIR599QDffe0gq+Y1ccMVM1jW3kTaYxVKklR08VB//oQkXccK5eDDloOSJE1hFoSSSkZzfRUPXT2P+6+aw9ZD3byys4Nth0+x6UD+0lBTwXVL27huaRttDTVJx5UkaUqKB3ry5WB3B0FTGxUf/UeWg5IkTXEWhJJKTjqVYs38FtbMb6FncITXd3fw8q4OOnuHeXLjEZ7ceITFM6dx/dIZXLmghcqKdNKRJUmaEuK+LkYe/TL0dhG0zKLiI79MUDst6ViSJKnILAgllbTG2kruXjuHu9a0s/dEH6/s7ODN/SfZc7yPPcf7+OaP97JmQQvXLmljycwGUu6CLEnSJcl1dzD66JdhoIegbS4VH/4lgurapGNJkqQJYEEoaVIIgoDFMxtYPLOBT9ywgDf3dfHyrhMc6Ojntd2dvLa7k8baStYtms41i1tpb6lLOrIkSZNGrutYvhwc6ieYtYCKhz5PUFWddCxJkjRBLAglTTrVlRluXDaDG5fNoKNniNf3dvL67k66+k/z9OajPL35KLOba7lmcStXL2qlsa4y6ciSJJWsXMchRr/7pzA8SDBnKRUP/jxBhe+dkiSVEwtCSZNaW2MND66bxwNXzWV/Rz+v7e7gzX0nOXpqkO+8doDvvnaApbMbuXrxdNbMb6Gm0l97kiSdkTu8i9Hv/wWMjpCav4LM/Z8jyFQkHUuSJE0wvylLmhKCIGDhjGksnDGNT9ywkG2Hu3ltdydbD51i59Eedh7t4e9e3Mvy9iauWjSdVfOaqfbkJpKkMpbdu4mxJ74GuSyppevI3PVpgrTvjZIklSMLQklTTib91lmQB0+PsWH/SdbvPcme471sOXSKLYdOkUkHrJjTzLpF01k5t4nKjF+IJEnlI7vtFcae+XuIY1KrbyZz68cIglTSsSRJUkIsCCVNabVVGW5aNpObls2kd2iEjfu6eHPfSfae6GPTgS42HeiiIpNi1dxmrlo4nRVzm6hI+wVJkjR1jb35DNmXvgtA+tp7SV97H0EQJJxKkiQlyYJQUtloqKnk1pWzuHXlLLoHTrOhUBYe6OznzX0neXPfSaoq0qya18za+S0sb2+k0t2QJUlTRBzHZF9+jOz6pwFI3/IxMmtvTTiVJEkqBRaEkspSU10Vd6yezR2rZ9PVN3y2IDzcNcgbezp5Y08nFekUy+c0smZ+CyvnNlNb5a9MSdLkFOeyjD3zDXLbX4UgRebuT5O+4uqkY0mSpBLht11JZa9lWjV3r53D3Wvn0NE7xKb9XWw6cIoDnf1sOnCKTQdOkQoCls5uYM38FlbPb6ahpjLp2JIkXZR4dISxJ75K7sA2yFSQue+zpBesTDqWJEkqIRaEknSOtoaas2Vh98BpNh84xaYDXew53suOIz3sONLDN17ay4IZ0/Jl4bxmWhuqk44tSdIFxUMDjD72FeITB6GqlooP/SKpmfOTjiVJkkqMBaEkvYumuqqzxywcGB5ly8H8aMIdR7rZd6KPfSf6ePTV/cxorGHVvCZWzW1mfts00ikP9C5JSl7c28Xod/+UuKcT6puo+PAvkWqekXQsSZJUgiwIJeki1FVXcP0VM7j+ihkMj2bZfribTfu72Ha4mxM9Q5zoGeKpTUeprcqwYk4Tq+Y1s6y9kZpKf81KkiZervMIo9/7MxjsI5g+m4oPfZ6griHpWJIkqUT5zVWSPqDqijRXLZzOVQunk83l2Hu8jy2HTrH1YDedfcO8vqeT1/d0kgoCFs+axqq5zayc667IkqSJkTu0i9Ef/CWMniZoX0zFAz9PUOV7kCRJencWhJJ0GdKpFEtnN7J0diMfuy6mo3eYLQdPseXgKfZ19LHraC+7jvbyrVfyuyKvmNPE8jlNLJ45jUw6lXR8SdIUk93xGmNP/x3kcqSWXEnm7pAg7Ud+SZL03vy0IEnjJAgCZjTWMKOxhrvWtDMwPMr2Iz1sOXiK7efsivzMlqNUZFIsndXA8vZ8YejoQknS5YjjmOzrPyT76hMApK+8jfRNHyYI/GOUJEl6fxaEklQkddUVXLO4lWsWt57dFXn7kW62H+7h6KlBth7qZuuhbgCmT6s6WxYumdVAVUU62fCSpEkjzmYZe+bvye14DYKAzC0fI73mlqRjSZKkScSCUJImwLm7In/kWugZHGHH4W62H+lmx5EeTvad5oXtx3lh+3HSqYBFM6edLQxnNdUQBJ4ZWZL0TvHpYUYf/yviw7sgU0Hm3p8hvXBV0rEkSdIkU9SCMAzDLwHXAa9HUfSFc+b/EbAGiIFfi6JoQzFzSFKpaaytPHtW5Gwu5mBnf74sPNzDwc7+s8cu/M5rB5hWU8HSWQ0snd3IFbMbaa6vSjq+JKkExP09jH7vz4i7jkFNPRUP/QKpGfOSjiVJkiahohWEYRheA9RHUXR7GIZ/EIbh9VEUvVJY/NtRFO0Nw/AK4LeBTxUrhySVunQqYOGMaSycMY0H181jYHiUnUd72HY4P7qwb2iUN/ae5I29JwFonVbN0tkNXDG7kSWzGqirrkj4FUiSJlqu4zCjj/05DPYSNLVR8aHPEzS0JB1LkiRNUsUcQXgT8Hhh+gngZuAVgCiK9hbmjwLZImaQpEmnrrqCdYtaWbeolTiOOdEzxM6jPew82sueY7109g3T2TfMSztOEADtLXVnC8NFM6dRmfH4hZI0lWX3bmbsya/D2CjB7EVUPPBzBNW1SceSJEmTWDELwiZgT2G6B1h9gfv8F+B/XOjBYRg+DDwMEEURra2tRYg4cTKZzKR/DVOF26J0uC0uTlsbrF6an87mcuw71sOWA51sOdDJriOnONw1wOGuAZ7efJRMOsWS2U2smDed5XOns2R2M5UXccITt0XpcFuUDreFSk0cx2Q3PEv2pe8BMall15C54ycJ0h5WXJIkXZ5ifproARoK0w1A97kLwzD8F8CWKIqeu9CDoyh6BHikcDPu7OwsTsoJ0traymR/DVOF26J0uC0uTWMl3Ly0mZuXNjMylmXfiT52He1l59EeDp8cYPuhLrYf6gJ2kk4FzG+tZ/HMBhbPmsbCtmkXLAzdFqXDbVE6psq2aG9vTzqCxkGczTL23DfJbcsfsSd9w4Ok193lSawkSdK4KGZB+CLwq0AE3Ad85cyCMAwfAG4BPlPEny9JU15lJs2y9iaWtTcBMHh6jD3H87si7z7ey9GuQfae6GPviT5+uBFSQcDc1jqWzGxg8cz8cQ+rKx15IkmlLD49yOgP/pr4yG5IZ8jc8xnSi9cmHUuSJE0hRftWGEXR62EYDodh+CywHjgQhuFvRlH0ReB/Ar3Aj8Iw3B5F0a8WK4cklZPaqgxr5rewZn7+QPWDp8fYd6KP3cd62XO8l8NdAxzo6OdARz8/2gRBAHNa6li9cCbtjRUsaKv3pCeSVEJyPZ2MPfbnxN0dUDuNigd/3jMVS5KkcVfUYSNRFH3hvFlfLMxfXsyfK0nKq63KsGpeM6vmNQMwPJIvDPcc72P38V4OdfZz6OQAh07uOfuYGY3V+bMqt+VHGLY2VLsLmyQlIHdoJ6OP/zWMDBO0zKLioV8kmNaUdCxJkjQFuV+ZJJWR6soMK+Y2s2JuvjA8PZo/huGxvjE27z3OwZP9nOgZ5kTPMC/v7ACgrirDghn5snDhjGnMnV5HRTqV5MuQpCktjmOym14g++J3IM6RWriKzN2fIaisSjqaJEmaoiwIJamMVVWkWT6niVtbW7lzRStj2RxHugbYe6KffSf62Heij/7hUbYcPMWWg6cASKcC5k6vO1sYLpwxjXp3S5akcRFnxwonI3kVgPTVd5O+/n6CwD/MSJKk4rEglCSdlUmnmN82jflt07hz9WziOOZk32n2dfSdLQyPdw+xv6Of/R39PL35KACt06qZ11bP/Nb8pb2lloyjDCXpA4mH+hn9wV8RH9uXPxnJXZ8mvfSqpGNJkqQyYEEoSXpXQRDQ2lBNa0M11y1pA/InPjnQ0ce+E/3s6+jjQEc/nX3DdPYN88aeTiA/ynBOSx3zC6XhvNZ6pk+r8liGkvQucp1HGP3+X0B/N9Q15E9G0jY36ViSJKlMWBBKkj6Q2qq3H8cwm8tx9NQQBzr6ONDZz8HO/HEMD3T2c6Cz/+zj6qoyzGutf1tpWFvl25AkZXe8wdgzfwfZMYIZ86l48OcIaqclHUuSJJURv5lJki5LOpVi7vQ65k6v45bCvKGRMQ529nOgo/9sUTgwPMa2w91sO9x99rFtDdXMba1n3vQ65kyvY05LHVUV6URehyRNtDibJfvSd8huegGA1IrryNz6CYKMx3WVJEkTy4JQkjTuaiozLGtvYll7E5A/I+epgdNvFYYd/RzuGqCjd5iO3rd2TQ6Atsaas4WjpaE0NYRh+CHgS0BnFEW3XWD554B/CnQBn42iqHeCI064bH8Po4/+cf54g6k0mVs/TnrVjUnHkiRJZcqCUJJUdEEQ0FJfTUt9NesWtQJndk0e5GDnAIdPDnDoZD9HTw1xoid/ef1dSsO50+totzSUJpuXgKuAH56/IAzDCuAfA3cAnwJ+Ffi/JzTdBMsd28+JH36VuL8nf7zB+3+W1Mz5SceSJEllzIJQkpSI/K7J9cydXn923lg2XxoeOjnAoZMDHH6P0nBGY83ZEYbtLbW0t9R5TEOpREVRdAogDMMLLb4C2BhF0VgYhk8Af3yhO4Vh+DDwcOH5aG1tLVLa4opzWY5H/5Vcfw+V85fR8slfJV3fmHSsSSuTyUzafwulxPU4PlyP48P1OD5cj+OjnNaj36QkSSUjk04xr3ACkzNGszmOnRrkYGd+t+RDJwc4dmqI4z35y5nSEKCprpL25rcKw/aWWprrq0h59mSplDUBZ3Yp7incfocoih4BHincjDs7Oy90t0khdfdnqDm8g5G1d3JqeBSGJ+9rSVprayuT+d9CqXA9jg/X4/hwPY4P1+P4mIrrsb29/YLzLQglSSWt4l1Kw6Ndgxw62c+RU4Mc6cqXht0DI3QPjLDl0Kmz962uSDO7ufZtpeHMploq0qkkXo40pYVhOAv4+nmzj0VR9NPv8bAeoKEw3QB0FyFaSUm1zaVx5bop94VDkiRNXhaEkqRJpyKdYn5bPfPb3ioNc7mYzr5hjnQNcKRrkCOn8td9Q6PsPdHH3hN9Z++bCvLHNWxvqaO9uZbZzbXMaqqlobaCwNGG0iWLougYcNcHfNgOYE0YhmngPvLHK5QkSdIEsiCUJE0JqVTAjMYaZjTWsG7RW/N7h0Y42jV4dqThka5BOnqHON6dv7xxznPUVKaZ1VTLrOZaZjXVFK5rPbahdJnCMLwO+G3yReATwEfJF4npKIq+E4bhHwPPAqeAzyYWVJIkqUz5jUeSNKU11FTSMKeS5XOazs4bGctyvHuII10DHO4a5Hj3IEdPDTI0kn3HaEOAxtpKZjbVnB1pOKu5hpmNtVRk3E1ZuhhRFL1KfnTguR47Z/lfAn85oaEkSZJ0lgWhJKnsVGbS7ziuYRzH9A6NcuzUIMe6hwrXgxzvHqJncISewRF2HOk5e/8ggOnTqt820nBmYw2tDdVkPL6hJEmSpEnEglCSJCAIAhprK2msfftow1wupqv/NMcKowyPdw9y7NQQHb1DdPYO09k7zKYDb50UJVUoDs/s7jyjqYaZjTW0NdZQXZFO4JVJkiRJ0nuzIJQk6T2kUgGtDdW0NlSzZn7L2flj2RwnevLHMTxaGG14omeIrv7TdPQO09E7zOaDp972XE11lW8Vh4354nBGUw311RUT/bIkSZIk6SwLQkmSLkEmncqfBbmljqvPmT+azdHRM8SJwuV4d/66o3eY7oERugfevqsyQF1V5uxow8XtvdSks7Q11NBcX0U65VmVJUmSJBWXBaEkSeOo4pzi8FzZXExX/zAnCoXh8Z6hs9MDp8fOnhzlxztOnH1MOhUwfVoVrQ01tDVUFy41tDZWM626giCwPJQkSZJ0+SwIJUmaAOlUQFtDDW0NNaw+Z34cx/QMjpwdcdh7Gg6eOEVnYcThiZ5hTvQMv+P5qirStBV2fW47UyA2VtM6rZrqSt/eJUmSJF08v0FIkpSgIAhoqquiqa6KZe1NtLa20tnZCcDIaJbOvvzxDDt7h+noHaKjJ389NJLl0MkBDp0ceMdzNtRUFI6bWMP0aVVMn5YvDqdPq7I8lCRJkvQOfkuQJKlEVVakL7i7chzHDJ4eK5wM5UxpOExn4czKvUOj9A6Nsud43zues646w/Rp1YXSsOqc6WrqqjPutixJkiSVIQtCSZImmSAIqKuuoK66goUzpr1tWS4X0z14mo6eYU72DdPZN8zJvtOc7MvfHhgeY2C4nwMd/e943qpMiukN1YXSsKow6jB/aaytJOUJUyRJkqQpyYJQkqQpJJUKaKmvpqW++h3LcnFM3+DoOcXh28vDoZEsR7oGOdI1+I7HplMBLfVVNNdX0VK45KeraZlWRV2Vow8lSZKkycqCUJKkMpEKAhrrKmmsq2TxrIZ3LB88PUZn7/DbCsSuvtN09g3TNzRa2KX5nSdMAajMpM4rD6vPTrdMq6LGYx9KkiRJJctP65IkCYDaqgzz2+qZ31b/jmUjo1m6+k/T1X+aU4Xrrv7hs9NDI1mOdw9xvHvogs9dXZGmZdp5Iw/rq2iqq6S5vorqirQjECVJkqSEWBBKkqT3VVmRZlZzLbOaay+4fGhkLF8a9l24QBwefffdlwGqKtL5srAuXxo2Fa6b66poqq+ksbaSdCpVzJcoSZIklS0LQkmSdNlqKjPMackw57wzLkP+rMsDp8feKg77hs+ORuweGKF74DSnR997BGIANNRWvrM8rKukqb6K5roqaiodhShJkiRdCgtCSZJUVEEQUF9dQX11BfNa37n7chzHDI1kOTVwmu5CaXhq4K3ysHtghN7BEXoKl/0XOAMz5I+D2HR2BGJ+1GFjbRWNtRU01lXRWFtpiShJkiRdgAWhJElKVBAE1FZlqK268AhEgGwuR8/gCN397ywPzxSLp8dynOgZ4kTPhUchAlRkUjTVFsrDsyXimdtVNNVWUludIWWJKEmSpDJiQShJkkpeOpUqnNik+oLL4zhmeDTLqcIIxDOjDXvOTp+mZ2CE02O59zwbc/5nBTTUVvIbn7qRC/80SZIkaWqxIJQkSZNeEATUVGaoacnQ/i6jEAGGR8byIxEvWCLmL4OF4yXWVFYQj4xM4KuQJEmSkmFBKEmSykZ1ZYbqygwzmy58NmaAkbEsPYMjNNdX09U1MIHpJEmSpGSkkg4gSZJUSiozadoaakilPA6hJEmSyoMFoSRJkiRJklTGLAglSZIkSZKkMmZBKEmSJEmSJJUxC0JJkiRJkiSpjFkQSpIkSZIkSWXMglCSJEmSJEkqYxaEkiRJkiRJUhmzIJQkSZIkSZLKmAWhJEmSJEmSVMYsCCVJkiRJkqQyZkEoSZIkSZIklTELQkmSJEmSJKmMWRBKkiRJkiRJZcyCUJIkSZIkSSpjFoSSJEmSJElSGcsU88nDMPwScB3wehRFXzhn/m8C/xT40yiK/mMxM0iSJEmSJEl6d0UbQRiG4TVAfRRFtwOVYRhef87iLwOfK9bPliRJkiRJknRxijmC8Cbg8cL0E8DNwCsAURQdD8Nw5Xs9OAzDh4GHC/entbW1iFGLL5PJTPrXMFW4LUqH26J0uC1Kh9uidLgtJEmSVC6KWRA2AXsK0z3A6g/y4CiKHgEeKdyMOzs7xy9ZAlpbW5nsr2GqcFuUDrdF6XBblA63RemYKtuivb096QiSJEkqccU8SUkP0FCYbgC6i/izJEmSJEmSJF2CYhaELwL3FqbvA14q4s+SJEmSJEmSdAmKVhBGUfQ6MByG4bNAFjhQOHsxYRj+MvBfgc+FYfh7xcogSZIkSZIk6b0V8xiERFH0hfNmfbEw/0+APynmz5YkSZIkSZL0/oq5i7EkSZIkSZKkEmdBKEmSJEmSJJUxC0JJkiRJkiSpjFkQSpIkSZIkSWXMglCSJEmSJEkqYxaEkiRJkiRJUhkL4jhOOsPFmBQhJUmSSlSQdIBx5mdDSZKkS/eOz4aTZQRhMNkvYRi+lnQGL26LUru4LUrn4rYonYvbonQuU2xbTDVJr0//fZXIxfXoeiyli+vR9VhKF9ej6/F9Lu8wWQpCSZIkSZIkSUVgQShJkiRJkiSVMQvCifNI0gF0ltuidLgtSofbonS4LUqH20LF5L+v8eF6HB+ux/Hhehwfrsfx4XocH2WzHifLSUokSZIkSZIkFYEjCCVJkiRJkqQyZkEoSZIkSZIklbFM0gHKQRiGXwKuA16PougLSeeZysIwbAceBVYB9VEUjV1o/V/sPF26MAxvBL4E5IBXoij6l2EY/n+ATwD7gV+Momj0Yucl8yqmhjAM15A/dkYW2AX8EvDf8P9FYsIw/JfAp6Ious3fUckIw3Ah8GNgKzASRdED/o7SRLnQ55WEI006F/qckXCkSelCnxGiKPIYVJfo3Pf3pLNMRhd6b0420eQVhuHPA78ApIHPRVF0OOFIk04Yhg8B/65wcznwT6Io+mZyiYrPEYRFFobhNeQ/+N0OVIZheH3Smaa4LuBe4CW48Pq/2HlJvYApZD9wT+ED0owwDO8E7i7c3gD8RBiGMy5mXjLxp5TtURTdUvj3DXAD/r9ITBiGVcC6wrS/o5L1eBRFdxXKwYv6feTvKI2Tt31e0SU5/3PG2qQDTVLnf0a4LtE0k9i57++6LGffm5MOMlmFYTgHuDOKonsL69Jy8BJEUfRYYf3dBRwAnkg4UtE5grD4bgIeL0w/AdwMvJJcnKktiqJhYDgMwzOzLrT+xy5yntvpMkRRdOycm6PAauCpwu0ngM8BAxc572+LGnaKO29002nyX0r9f5GcXwb+HPj/4u+opN0dhuGzwN8D2/F3lCbIBT6v6AO6wOeMbFJZJrMLfEY4mFSWKeDc93ddurPvzVEUfSnpMJPUg0A6DMMfAluAfxFFkb8jL1EYhouB41EU9SedpdgcQVh8TUBvYbqncFsTp4l3rv+LnadxEIbhlUAb0I3bIjFhGH48DMNNwEygArdFIsIwrADuiqLoycKsJtwWSTkKLAPuBu4jP2rGbSFNMmc+Z0RRtCXpLJPVeZ8RTiadZzK6wPu7Ls3b3psL/7/1wc0EKqMouhcYJH9YFF26nwS+kXSIieAIwuLrARoK0w3kSxJNnAut/+xFztNlCsOwBfhdIASuBeYWFp1Zxz0XOU+XKYqibwHfCsPwf5Ifjeb/i2T8HPDVc277OyohURSdJj9ahjAMHyVf+s0pLPZ3lDQJnPc5Q5fovM8IH6VMvgiPs/Pf33UJLvDevIb84Tz0wfQATxemn8RDB1yuj5EvCac8RxAW34vkd+eD/AgFjzUzsS60/i92ni5DGIYZ4K+Af13YDegV4M7C4jPr+GLn6TIUjolzRi8Q4/+LpCwH/kkYho+R3+2+FbdFIsIwnHbOzVvJH5zf31HSJHGBzxm6BBf4jDCUVJZJ7m3v72EY/rOkA01GF3hv3p1UlknuBeDM6Mt1wN7kokxuYRjOIn/CnLIYXR3EsSepKrYwDP87cA2wPooi3yyKqDC8/3vkR6u9DvwH4LOct/4vtE3cTuMrDMOfAf4HsLkw698Dd5D/C8wB8mf+HAnD8N9ezLwJfwFTSBiGnwB+o3BzJ/Aw+TM/+v8iQWEYPlc4i/FFrXe3xfgKw/DDwH8mP1Lh2SiK/u3F/j7yd5Qu14U+r0RR9ONkU00uF/qcEUXRiwlGmpQu9BkhiqJcgpEmvTPv70nnmIwu9N6ccKRJKwzD/4f8yMFO4LN+Vrk0YRj+KlARRdHvJp1lIlgQSpIkSZIkSWXMXYwlSZIkSZKkMmZBKEmSJEmSJJUxC0JJkiRJkiSpjFkQSpIkSZIkSWXMglCSJEmSJEkqY5mkA0hSMYRhuBDYC3wH+H3gBuArURTtG+efswoIgaeiKHqqMO8rwC8A10dR9Op4/jxJkiRJksabIwglTVUdwM8A/xfwYeC3gIUf9EnCMHy/P6SsKjz3XefM+4PCz979QX+eJEmSJEkTLYjjOOkMkjTuzhlBOADUnbssiqIgDMObgf8GrAWOAL8VRdHXznnci8BgYfka4AfAFYWneAP4x4Xn3nvej74b+EXOGUEYhuGvAP8GaAc2A78RRdFzYRj+IvBnwNfJF43zgf89iqL/HobhcuAvgCuBYWBTFEW3X/aKkSRJ0rgKw/BvgePAOmAe8DngV4EbgWejKPrl5NJJ0sVxBKGkqe5p8uUewH8GfiYMwxbgUaAJ+CKwD/irMAzXnfO4m4HXgP8NyAF/D3wB+G3gKuB3yI9S/J3C/f+O/KjBLef+8DAM7wEeKdz3N8iXgN8Kw3D6OXe7u3CfGPjtMAwrgV8DridfLP57YP8lvn5JkiQV11pgTxRFtwF/BPwJ+c9wq4CPhGFYlWQ4SboYFoSSproY2FmYfjKKoq+TL/9agBXA/wncT/734T3nPO6NKIr+bRRFjwBVwEPAH5MvGacBa6MoGgCeL9x/UxRFX4+i6MR5P//DhevfiqLozAfGZuCmc+7zp1EU/R7wMlANzCxkDgqPbwf++6WvAkmSJBVDGIbV5P/o/DuFWTHwJ1EUHY2iaAzIAiPJpJOki2dBKKkcvNuxFP6CfDl45vKtc5YdOWf6nwO3kP/g9wBwiHyR917P/W4ZLnT/rsL1WOE6HUXR7wL3Aa8AnwBeKux2LEmSpNKxGng9iqJc4fZVwI8BwjCcCxyJosjjekkqeZ7FWFI5OFW4/qkwDOvIH1+wi/yowFfI/y78KPnRge+1K28zcAcwF+g577lvD8Pwp4F/OO8x3wX+FfB/hGG4BPjlwmNeAj72bj8oDMN/DLQCuwqXK8mPLNz+Pq9VkiRJE2ct8OY5t68ENhSmrzpnWpJKmiMIJZWDvwa2kT+u33+PoqiLfCG4i/wxBX+T/AlJ9r3L4/8n+SLxM8AcYNM5y54DfgjcDnwNOPfYgkRR9CTwMDCD/ElRDgEfj6Lo5PtkPg18nvxuzXcCv1f4WZIkSSoda4H1cHZ345oois78AfncslCSSppnMZYkSZIkSZLKmCMIJUmSJEmSpDJmQShJkiRJkiSVMQtCSZIkSZIkqYxZEEqSJEmSJEllzIJQkiRJkiRJKmMWhJIkSZIkSVIZsyCUJEmSJEmSytj/C8A8IXxoWHSQAAAAAElFTkSuQmCC",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"low, high, step = 0, 5000, 10\n",
"plot_all(cost_history, m, q, low, high, step)"
]
},
{
"cell_type": "code",
"execution_count": 422,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"8247 passi e 824700 gradienti calcolati per arrivare a distanza minore o uguale di 0.1 dall'ottimo\n"
]
}
],
"source": [
"near_opt(m, min_dist=1e-1, ge_per_step=n)"
]
},
{
"cell_type": "code",
"execution_count": 423,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA7sAAAHzCAYAAADhDgreAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAABSUUlEQVR4nO3de3Sb2X3e++clQVIEIIkXiJrRjB17YjeSpVFGiTRJl6aRR/ZobNqJnVjZjtsqcZKeqdO4l7XcJnV8VuLj1D3OcU5SrzqXTmMf28zF2UfKJE6CZjitVU2Hp24om7JGjNXE447jGXlE8SYJAG8A9vkDFwIUQVEigPfFi+9nLS0SIF5yA5ug3ufde/+255wTAAAAAABh0uF3AwAAAAAAqDfCLgAAAAAgdAi7AAAAAIDQIewCAAAAAEKHsAsAAAAACB3CLgAAAAAgdAi7AAAAAIDQIewCANBknue96Hnegud5Nz3Pm/c87//zPO99nufd9v9lz/Ne43me8zwv0uA2NuXnAADQKIRdAAD88YPOue2SvkPSxyT9vKRP+dskAADCg7ALAICPnHPXnXNfkPRuST/hed4Bz/Pe5nnehOd5NzzP+5bneR+uOOTZ4sd5z/NSnuf9Xc/zvtPzvC96njfjed6053m/53leX+kAz/N+3vO8l4sjyf/T87w3Fe/v8DzvX3ue90LxWOt53kCtn9PYVwIAgPoi7AIAEADOub+U9JKkvycpLenHJfVJepukn/E8753Fh/5A8WOfcy7unPvvkjxJ/6ekPZL2SXqVpA9Lkud53yXp/ZKOFEeSH5f0YvF7/FNJ75R0rHjsnKTf2ODnAADQMgi7AAAExxVJA865/+qce945l3fOXZT0ByoE0nU5577unHvGObfknLsm6dcqHp+T1CPpDZ7ndTnnXnTOvVD82vskfcg595JzbkmFgHySdboAgDAg7AIAEBz3SZr1PO/7PM8763neNc/zrqsQShO1DvI8b7fneZ8vTlW+Iel3S493zn1d0r9QIchOFR+3p3jod0h6qlgka17S11QIx7sb8/QAAGgewi4AAAHged4RFcLuc5J+X9IXJL3KObdT0m+rMFVZktw6h//b4v0POud2SPqHFY+Xc+73nXOPqBBunaRfKX7pW5Le6pzrq/i3zTn3co2fAwBAyyDsAgDgI8/zdnie93ZJn5f0u8655yVtlzTrnFv0PO9hSX+/4pBrkvKSHqi4b7uklKTrnufdJ+lfVXz/7/I877jneT2SFiUtFI+XCiH6o57nfUfxsbs8z3vHBj8HAICWQdgFAMAff+p53k0VRlc/pMI6258sfu2fSPpI8eu/KMmWDnLOZSR9VNJYcfrx90v6PyR9j6Trkv5c0h9V/JweFbY2mpb0iqQhSR8sfu0TKowgjxZ/1pckfd8GPwcAgJbhOccsJQAAAABAuDCyCwAAAAAIHcIuAAAAACB0CLsAAAAAgNAh7AIAAAAAQoewCwAAAAAInYjfDWgCyk0DAAAAQHh5693ZDmFXV65c8bsJgZRIJDQ9Pe13M7AG/RJM9Esw0S/BQ58EE/0STPRL8NAnwbRRv+zZs6fmcUxjBgAAAACEDmEXAAAAABA6hF0AAAAAQOgQdgEAAAAAoUPYBQAAAACEDmEXAAAAABA6hF0AAAAAQOgQdgEAAAAAoRNp9g80xnxa0tslTVlrDxTv+7Ck/03SteLDfsFam1zn2LdI+oSkTkm/Y639WFMaDQAAAABoKU0Pu5I+I+mTkj635v5ft9b+aq2DjDGdkn5D0mOSXpI0boz5grX2rxrVUAAAAABAa2r6NGZr7bOSZu/i0Iclfd1a+w1r7bKkz0t6R10bBwAAAAAIBT9Gdmt5vzHmxyWdl/QBa+3cmq/fJ+lbFbdfkvR9zWocAAAAAKB1BCXs/pakX5bkih//b0k/dbffzBjzhKQnJMlaq0QiUY82hk4kEuG1CSD6JZjol2CiX4KHPgkm+iWY6JfgoU+C6W77JRBh11p7tfS5MeY/SvqzdR72sqRXVdy+v3jfet/vSUlPFm+66enpOrU0XBKJhHhtgod+CSb6JZjol+ChT4KJfgkm+iV46JNg2qhf9uzZU/O4QGw9ZIy5t+LmD0u6tM7DxiW93hjzWmNMt6Qfk/SFZrQPAAAAANBa/Nh66A8kvVFSwhjzkqRfkvRGY8xDKkxjflHSPy4+do8KWwwNW2uzxpj3S3paha2HPm2tnWx2+wEAQPBMXpjQ808n1bWQ0kpvXA8+Pqz9Dx3yu1kAAB81Pexaa9+zzt2fqvHYK5KGK24nJd2y/y4AAGhfkxcm9MrpEZ0c6pMXjcq5nM6dHpEkAi8AtLFATGMGAAC4W5dGkzo21CfP8yRJnufp2FCfLo1yfRwA2hlhFwAAtLRIJlUOuiWe5ymSSfvUIgBAEBB2AQBAS8tG43LOVd3nnFM2GvOpRQCAICDsAgCAlnbgxLDOTc2XA69zTuem5nXgxPBtjgQAhFkg9tkFAAC4W6UiVGdGk4pk0spGYzpw8hTFqQCgzRF2AQBAy9v/0CHCLQCgCtOYAQAAAAChQ9gFAAAAAIQOYRcAAAAAEDqEXQAAAABA6BB2AQAAAAChQ9gFAAAAAIQOYRcAAAAAEDrsswsAAO7a5IUJPf90Ul0LKa30xvX3zHt032sf8LtZAAAwsgsAAO7O5IUJvXJ6RCd7c3rnYFQne3N64XNPavLChN9NAwCAsAsAAO7OpdGkjg31yfM8SZLneXrj7j5dGk363DIAAAi7AADgLkUyqXLQLfE8T5FM2qcWAQCwirALAADuSjYal3Ou6j7nnLLRmE8tAgBgFWEXAADclQMnhnVuar4ceJ1z+q9X53XgxLDPLQMAgGrMAABgA2urLT/4+LD2P3RIksofz4wmFcmklY3G9MiPP0E1ZgBAIBB2AQDAusrVlof65EWjci6nc6dHJKkq8JY+l6REIqHp6Wlf2hsmG11kAABsDtOYAQDAutartnxsiGrLjbbelk6vnB5hSycAuEOEXQAAsC6qLfuDiwwAUB+EXQAAsC6qLfuDiwwAUB+EXQAAsK71qi2fm6LacqNxkQEA6oOwCwAA1rX/oUO65+QpnVns1B/PLOjMYqfuOXmKQkkNxkUGAKgPqjEDAICa1lZbRuOtt6XTAS4yAMAdI+wCAAAEDBcZAGDrmMYMAAAAAAgdwi4AAAAAIHQIuwAAAACA0CHsAgAAAABChwJVAAAAaLjJCxN6/umkuhZSWumN68HHhynCBaChCLsAAABoqMkLE3rl9IhODvXJi0blXE7nTo9IEoEXQMMwjRkAAAANdWk0qWNDffI8T5LkeZ6ODfXp0mjS55YBCDPCLgAAABoqkkmVg26J53mKZNI+tQhAOyDsAgAAoKGy0bicc1X3OeeUjcZ8ahGAdkDYBQAAQEMdODGsc1Pz5cDrnNO5qXkdODHsc8sAhBkFqgAAANBQpSJUZ0aTimTSykZjOnDyFMWpADQUYRcAAAANt/+hQ4RbAE3FNGYAAAAAQOgQdgEAAAAAocM0ZgAAgDqbvDCh559OqmshpZXeuB58fJgpvADQZIRdAACAOpq8MKFXTo/o5FCfvGhUzuV07vSIJBF4WxwXMYDWQtgFAACoo0ujSb1rqE+e50mSPM/TsaE+nRlNEozW0SoBkosYQOthzS4AAEAdRTKpctAt8TxPkUzapxYFVzlA9ub0zsGoTvbm9MrpEU1emPC7abe4NJrUsXUuYlwaTfrcMgC1NHVk1xjzaUlvlzRlrT1QvO/jkn5Q0rKkFyT9pLV2fp1jX5R0U1JOUtZae7hJzQYAANi0bDQu53JVgdc5p2w05mOrgqmVRsEjmZS83mjVfVzEAIKt2SO7n5H0ljX3PSPpgLX2oKS/lvTBDY5/1Fr7EEEXAAAE1YETwzo3NS/nnKRC0D03Na8DJ4Z9blnwtNIoeOEihqu6j4sYQLA1dWTXWvusMeY1a+4brbj5JUknm9kmAAAQPn6uAy39nDOjSUUyaWWjMR04eSpwI5VB0Eqj4AdODOvc6ZHyVObyRYyTp/xuGoAaglag6qck/WGNrzlJo8YYJ+k/WGufbF6zAABAqwhCIaH9Dx0i3G5CKwVILmIArScwYdcY8yFJWUm/V+Mhj1hrXzbGDEl6xhhz2Vr7bI3v9YSkJyTJWqtEItGQNre6SCTCaxNA9Esw0S/BRL8ETxD65OvPflE/fP9Q1WjhY/cP6alnv6hjb37Mx5b5Jwj9sp5jb35MX925U3/+p0+pM5VSLhbX4Z/+h/ruIw/73bR1HXvzY3X9HQpqv7Qz+iSY7rZfAhF2jTHvVaFw1ZustW69x1hrXy5+nDLGPCXpYUnrht3iqG9p5NdNT0/Xvc1hkEgkxGsTPPRLMNEvwUS/BE8Q+iQ7O62Vweg699/wvW1+CUK/1HLfax/Qff/sA1X3BbWt9RbkfmlX9EkwbdQve/bsqXmc72HXGPMWST8n6Zi1NlPjMTFJHdbam8XPT0j6SBObCQAAWsRLqYz+8G++pm6X00pHpx589au0955dgVwHCgBonGZvPfQHkt4oKWGMeUnSL6lQfblHhanJkvQla+37jDF7JP2OtXZY0m5JTxW/HpH0+9bav2hm2wEAQPBNXpjQdyyn9f07e5TY1i05p7N/+019Zfamvvd9/9zv5gEAmqjZ1Zjfs87dn6rx2CuShouff0PSdzewaQAAIAQujSb1rte9WumbN/Tta1PqyOX1XYM79fWefgoJAUCb8X0aMwCgcfzcfgXwQySTktcbVXzHTsV37CzfPzSz4GOrAAB+IOwCQEgFYfsVoNlaad9WAEBjEXYBIKQujSb1ruLelZLkeZ6ODfXpzGiSsIvQ2sq+rcyEAIBwIewCQEiVpnNW8jxPkUzapxYBjVcKp2dGk4pk0spGYzpw8tRtQyszIQAgfAi7ABBSTOdEu9r/0KE7DqjMhACA8OnwuwEAgMY4cGJY56bm5ZyTpNXpnCeGfW4ZEDyRTKrqwpDETAgAaHWM7AJASN3tdE6gHTETAgDCh7ALACF2N9M5gXa0lcJWAIBgIuwCANBAVPhtDcyEAIDwIewCANAgVPhtLcyEAIBwoUAVAAANcmk0WZ4WK61W+L00mvS5ZQAAhB9hFwCABqHCLwAA/mEaMwAADUKFX4TZRuvRWasOIAgIuwCAlrf2xDr+2u9U6n+94PuJNhV+EVYbrUeXxFp1AIFA2AUAtLS1J91/9e1v669OP6e3HHyDtg/2+XqiTYVfhNWl0aTetc569DPF9ei1vsbvPoBmIuwCAFra2pPuyb99Se+6b1CvTF/T9p19vp9oU+EXYRTJpOT1RqvuW12P7jb4GgA0DwWqAAAtbW0RqEg+pw7PU0cuV76PE22gvgrr0V3VfaX16Bt9DQCaibALAGhpa0+ssx2dyjunfGdn+T5OtIH6OnBiWOem5svvvfJ69BPDG34NAJqJacwAgKZoVHXWtUWg9r/6fv3R11/Q4wffIEkUhQIaYDPr0VmrDsBvhF0AQMNtVLl1qyfAt5x0992r2MlH9PSLLygyw4k20CgbrUdnrTqAICDsAgAabqPKrfU4IebEGgAArMWaXQBAw60tIiVRNAoAADQWYRcA0HBUZwUAAM1G2AUANBzVWQEAQLOxZhcA0HCbqdwKNEujKoMDAIKFsAsAaIpWKCJFCGqcoLy2t6sMHpR2AgC2jrALAIAauz1SuwvSa7tRZXBJgWknAGDrWLMLAIAKIejYOiHoUjEE4e4F6bXdqDJ4kNoJANg6wi4AAGJ7pEYK0mu7UWXwILUTALB1hF0AAMT2SI0UpNd2o8rgQWonAGDrCLsAAIjtkRopSK/t/ocO6Z6Tp3RmsVN/PLOgM4uduqdYGTxI7QQAbB0FqgAAUGtuj9QqlYOD9trWqgwetHYCALaGsAsAQFErbI9UEqQKx5vRKq9ts9vZKhcsAKAVMY0ZAIAWROXg1le+YNGb0zsHozrZm9Mrp0c0eWHC76YBQCgQdgEAaEFUDm59XLAAgMZiGjMAoK6YltkchcrBuarAS+Xg1hLJpOT1Rqvu44IFANQPI7sAgLphWmbzUDm49bHVEQA0FmEXAFA3TMtsno220EFr4IIFADQW05gBAHXDtMzm8rvC8XpT1o+9+THf2tNq2OoIABqLsAsAqBvWkbaPWlsffXXnTt332gf8bl7L8PuCBQCEGWEXAFA3B04M69zpkfJU5vK0zJOn/G5aUzSzOJffhcAujSb1rnWmrP/5nz6l+/7ZB5rWDgAAaiHsAgDqpp2nZdYa6ZRU9+ffzJ9VS60p652pVFN+PtBsfl9gAnDnCLsAgLpq12mZtUY6z4wm6/56NPNn1VJrynouFm/KzweaKQgXmADcOaoxAwBQB5FMqir4SY0rztXMn1VLrUrCh3/wh5vWBqBZqDQPtCZGdgEAqINmFucKQiGwWlPWv/vIw5qenm5aO4BmoNI80JoIuwAA1EEzi3MFpRBYu05ZR/sJwgUmAHeOsAsAQB00szhXOxcCA/wQlAtMAO5M08OuMebTkt4uacpae6B434CkP5T0GkkvSjLW2rl1jv0JSf978ea/sdZ+thltBgBgM5o50smoKtA8XGACWpMfI7ufkfRJSZ+ruO9fS/ov1tqPGWP+dfH2z1ceVAzEvyTpsCQn6cvGmC+sF4oBAACAeuICE9B6ml6N2Vr7rKTZNXe/Q1JplPazkt65zqGPS3rGWjtbDLjPSHpLo9oJAAAAAGhdQVmzu9ta++3i569I2r3OY+6T9K2K2y8V77uFMeYJSU9IkrVWiUSijk0Nj0gkwmsTQPRLMNEvwUS/BE+Y+uSr43+p8T99SpH0TWVj23XkB39Y333kYb+bdVfC1C9hQr8ED30STHfbL0EJu2XWWmeMcVv8Hk9KerJ407EFwvoSiQTbQwQQ/RJM9Esw0S/BE5Y+mbwwoVdOj+jtQ33y4p1yLq1zn/qk5q+35jrNsPRL2NAvwUOfBNNG/bJnz56axzV9GnMNV40x90pS8ePUOo95WdKrKm7fX7wPAACgri6NJsuVd6XCnqrHhvp0aTTpc8sAAJsVlJHdL0j6CUkfK378k3Ue87Skf2uM6S/ePiHpg81pHgAAaKbJCxN6/umkuhZSWumN68HHh5s6ohrJpOT1Rqvu8zxPkUy6aW0AAGyNH1sP/YGkN0pKGGNeUqHC8sckWWPMT0v6piRTfOxhSe+z1v4ja+2sMeaXJY0Xv9VHrLVrC10BAIAWV5pCfHKoT140KudyOnd6RJKaFniz0bicy5VHdiXJOadsNNaUnw8A2Lqmh11r7XtqfOlN6zz2vKR/VHH705I+3aCmAQCAALg0mtS71plCfGY02bSwe+DEsM6dHilPZXbO6dzUvA6cPNWUnw8AzZbPO83fXNTUTEpTM2ldLX7sinToiXcf8bt5dyUo05gBAAAkBWMKcSlUnxlNKpJJKxuN6cDJ1ixO1Qj1nmbu97R1oF3k806z1xfKgXZqNqWr0+nC7dm0VrL5W46JbuuSc65qpkurIOwCQJ1wsgbUx2amEDfj/bb/oUO3fE/e5/WfZh6EaetAmORyec1UBtqKkdprsxllc7cG2pIdsR4NDcaK/+IaGoxp92C8ia2vL8IuANQBJ2tA/dxuCrFf7zfe5wX1nmYehGnrQKvJ5vKamcuUpxqvjtKmND2XUS5feyfXndu3aXdloB0oBNqhwZh6t3U18Vk0HmEXAOqAkzWgfm43hdiv9xvv84J6TzMPwrR1IIhWsjlNz2Z0dbYi0BbD7fR8RvkNAm3/zl7tHqgeoS0F22097RMB2+eZAkADcbIG1Nd6U4hL/Hq/8T4vqHelaipfo52trOQ0NVsIsVcrRminZtKamc/I1ciznicN9vVqaDBeHKUtBtqBuHYNRNXTTcyTCLsAUBecrAHN49f7jfd5Qb0rVVP5GmG3tJzVtdm0rk4XikBdrRihnbuxsGGgTfRHy1OMd5dHaGPa1R9TV1dnc59ICyLsAkAdcLIGNE8j3m+bKTzF+7ygXpWqK1/zq0t5XfrbGd0fj1H5Gi1pYWlF12ZWg2w50M6mNX9jseZxHR2edg1Eq0ZoS+tpE30xRSIdTXwW4UPYBYA6YJsSoHnq/X7bbOEp3uerNppmvhm3vOYDvTo3Na973vmjbfl6ojVkFldWKxuXR2kLt2+klmoe19npaVf/6vrZ3RWBdqAvqkgngbZRCLsAUCdbPfkDsHn1fL/dSeEp3uf1QbEvBNXN9KK+8a3ZckGoQpgtjNSmMss1j4tEOjQ0UB1oC1OPYxrYGVVHR+vtURsGhF0AANDWKDzVfLzm8ItzTjfTy+UiUFNrph2nF1ZqHtvd1VksAlW9B+3uwZj6dvQSaAOIsAsAANoahaeaj9ccjeSc043UUvUetBWBdmEpW/PY3p6u4hraikA7ENdQIqa+7duqfmcRfIRdAPDBZorhIBjoq/Cj8FTz8Zpjq/J5p+s3FwtTjcujtMX1tDNpLS1vFGgjGkrEi/vQrlY43j0Y1wOvuU8zMzNNfCZoJMIuADTZZovhwH/01eZUXhDoHEjo9T9wvKVeHwpPNR+vOTYjn3eau7FQsXZ2tcLx1Exayyu5msfGertu3YO2uA/t9lh3zRFaRm7DhbALAE1GYZbWQV/d3toLAl1dK3qmBS8IUHiq+XjNIRUC7ez1jK5OF6caz66O0E7NppXN5mseG492F8JsIl6Yajy4WiAqHu1u4rNAUBF2AaDJKMzSOuir2+OCAIDbyeXympnP3LoH7Uxa1+bSyuVczWN3xHvKU4wr96AdGogp2kugxcYIuwDQZBRmaR301e1xQQCAJGWzeU3Pp8trZqemV0dpZ+YyyuVrB9q+HdvKFY53J2LlUdpdgzH19nQ18VkgbAi7ANBkFGZpHfTV7XFBAGgfKys5XZtLr9mDtvBxZj4jVzvPamBnb8UetKsfdw3E1NNNJEFj8JsFAE1GYZbWQV/dHhcEgHBZWs7q2mymYh/aVGE97WxKs9cXagZaz5MS/dFyEajC1ONCqN01EFN3V2dznwggwi4A+ILCLK2DvtrY2gsCkYGoXscFASDQFpeyxYrGa7fsSWnuxmLN4zo6PO3qr96DtrSeNtEfVVeEQItgIewCAIAtqbwgkEgkND09vaXvx97GwNYtLK6sTjWerQ60128u1Tyus8NTYqA4KjtQHWgH+6OKdHY08VkAW0PYBQAAgcHexsDmpReWb92Dtrie9ka6dqCNdHZoVynQVo3SxjW4s1edBFqEBGEXAAAEBlsZAaucc0ovLK/uQVvce7YUalOZ5ZrHdkU6ChWOE/E1o7RxDezsVUeHV/NYICwIuwAAIDDYygjtxjmnm+nlYpgt7UG7Gmgziys1j+3u6qzYg3b149BgXH3btxFo0fYIuwAAIDDYyghh5JzT9ZtL5UBb2ot29vqirkxd1+JStuax23oi5QrHuxPFLXuKe9Lu3N5T9V4BUI2wCwAAAoOtjNCq8nmn+ZuLVYWgKj8ur+RqHtu7rau8TU9phLZ0e3usm0AL3CXCLgAACAz2NkaQ5fNOs9cXVgtBzabK62mnZtNayeZrHhuPdq8WgxqIaXcirr/zwH3qiawo1kugBRqBsAsAAAKFvY3hp1wur5nKQFsxQnttNqNsrnag3RHrKW/VM7RmHW2st/uWx9djqy7Uz8TFSX3x/CVNp5cU78xr+JEjOnRwv9/NwhYQdgEAANBWsrm8ZuYyFVv2lEZpU5qeyyiXdzWP3bl9W/WWPQOrgbZ3W1cTnwXqaeLipEbGLmv3wWOKrawo75xGxsYlicDbwgi7AAAACJ2VbE7Tsxldna0ItMVwOz2fUX6DQNu/s7dYBKp6D9qhgZi29XD6HEbJsfPq3/to1bZn/XuPKDl2lrDbwni3AgAAbMLExUklnxtXKtfBFMeAWFnJlfedvVoxQjs1k9bMfEauRp71PGmwr7dQ2bgy0A7EtWsgqp5uTpHbTSrrKbZm3bTneUpnWUvdyngnAwAA3EZpimP/vuOKeR5THJtoaTmra7NpXZ0uFIG6WjFCO3djYcNAm+iPrrMHbUy7+mPq6ups7hNBoMUjTvk1v0zOOcUitWcAIPgIuwAAALfBFMfGWlha0bWZ1SBbDrSzac3fWKx5XEeHp10D0aoR2tJ62kRfTJFIRxOfBVrZ8NHDGhkb1+6DRyUVgu7c5XGdOnrY55ZhKwi7AAAAt8EUx63LLK6sVjYuj9IWbt9ILdU8rrPT067+1fWzuysC7UBfVJFOAi22rnTR6otfPqfrqSXFIk6njh7mYlaLI+wCAADcRmmKY+VeqExxvFUqs1yxZU8pzBZGalOZ5ZrHRSIdGqooCLV7IKahRCHUDuyMqqODiwpovEMH9+ux48fYDipECLsAALSAyQsTev7ppLoWUlrpjevBx4fZi7aJSlMc+/ceked5bTvF0Tmnm+nlchGoqTXTjtMLKzWP7e7qLBaBqt6DdvdgTH07egm0AOqOsAsAQMBNXpjQK6dHdHKoT140KudyOnd6RJIIvE1SmsqYHDurdNYL9RRH55xupJaq96CdSenqbOHzhcXagbanu7OiEFQx0A7ENZSIqW/7tqqRcQBoNMIuAAABd2k0qXcN9VUVRzo21Kczo0nCbhMdOrg/NOHWOaf5G4uFqcblUdrietqZtJaWszWP7e2JFKYYD1TuQVsYpd0R7yHQAggMwi4AAAEXyaTk9Uar7vM8T5FM2qcWoRXk805zNxY0NZNW+q+u6RvfvFqucDw1k9bySq7msbHerlv3oC3uQ7s91k2gBdASCLsAAARcNhqXc7lbiiNlozEfW4UgyOedZq9ndHW6cqpxcaR2Nq1sNl/z2Hi0uxBmE/HCVOPB1QJR8Wh3E58FADQGYRcAgIA7cGJY506P6FhxKrNzTuem5nXg5Cm/m4YmyOXympnPlKsbX62YcnxtLq1crnZF6B3xHg0NxvTqPYPaGe8qb9kzNBBTtJdACyDcCLsAAARcaV3umdGkIpm0stGYDpw8xXrdEMlm85qeT5fXzE5Nr47SzsxllMvXDrR9O7aVKxzvTsTKo7S7BmPq7emSJCUSCbZTAdB2CLsAALSA/Q8dIty2uJWVnK7NpdfsQVv4ODOfkdtgy96Bnb2re9BWfNw1EFNPN6dzjTJxcVLJ58aVynUo3pnX8CNHQlOkDGgH/HUEAACok6XlrK7NZir2oU0V1tPOpjR7faFmoPU8KdEfLReBKlQ3LoTaXQMxdXd1NveJQBMXJzUydln9+44r5nnKO6eRsXFJIvACLYKwCwAAcAcWl7LFisZrt+xJae7GYs3jOjo87SoF2jVb9iT6o+qKEGiDJDl2Xv17H63a8qt/7xElx84SdoEWQdgFAABYY2FxZXWq8Wx1oL1+c6nmcZ0dnhIDxVHZgepAO9gfVaSzo4nPAluRynqKrdliyfM8pbNsuwS0CsIuAABoS+mF5aq1s6sjtWndSNcOtJHODu0qBdqqUdq4Bnf2qjNggXbywoT+5tkvKjc7rZXeuB58fJj135sQjzjlnbtly69YZIPF1QACJRBh1xjzXZL+sOKuByT9orX231U85o2S/kTS/yre9UfW2o80q40AAKC1OOeUXlhe3YO2uPdsKdSmMss1j+2KdBQqHCfia0Zp4xrY2auOjtYY3Zu8MKFXTo/oR+4f0spgVM7ldO70iCQReG9j+OhhjYyNq3/vkfKWX3OXx3Xq6GG/mwZgkwIRdq21/1PSQ5JkjOmU9LKkp9Z56H+z1r69iU0DAAAB5pzTzfRyMcyW9qBdDbSZxZWax3Z3dZanGFd+HBqMq2/7tpYJtBu5NJrUu4r7M0uFabjHhvp0ZjRJ2L2N0rrc5NhZpbOeYhGnU0cPs14XaCGBCLtrvEnSC9bab/rdEAAA4D/nnK7fXCoH2vJetMWKx4tL2ZrHbuuJlCsc704Ut+wp7km7c3tP1RTVMIpkUvJ6o1X3eZ6nSCbtU4tay6GD+wm3QAsLYtj9MUl/UONrf9cY81VJVyT9S2vt5HoPMsY8IekJSbLWKpFINKShrS4SifDaBBD9Ekz0SzDRL8Fzt32SzzvNXk/r21M39O2pG7oydb3w+bXC7aXl2oE21tute4d26N6hnbp3aIf2lD7ftUM7t28LfaDdSGQgoa6uFXV4nrq7uyUVLh5EBqK8dwKAv2HBQ58E0932S6DCrjGmW9IPSfrgOl/+iqTvsNamjDHDkv5Y0uvX+z7W2iclPVm86aanpxvQ2taXSCTEaxM89Esw0S/BRL8Ez0Z9Ugi0C6uFoGZT5fW0U7NprWTzNb9vPNq9WgxqIKbdidW9aGO93esG2uxyWjMz7T2C+bofOK5nTo/osfuHtLKyIueczk3N63UnT/HeCQD+hgUPfRJMG/XLnj17ah4XqLAr6a2SvmKtvbr2C9baGxWfJ40xv2mMSVhr+W0EACAgcrl8zT1or81mlM3VDrQ7Yj3lrXqG1qyjjfV2N/FZhEdpXe5Tz35R2dkbykZjOnDyFOt1AbSFoIXd96jGFGZjzD2SrlprnTHmYUkdkmaa2TgAACBlc3nNzGUqtuwpjdKmND2XUS5fe2uWndu3VW/ZM7AaaHu3dTXxWbSP/Q8d0rE3P8ZoFYC2E5iwa4yJSXpM0j+uuO99kmSt/W1JJyX9jDEmK2lB0o9Za9noDACABljJ5jQ9m9HV2YpAWwy30/MZ5TcItP07e4tFoKr3oB0aiGlbT2BOPQAAIec5F/q86K5cueJ3GwKJNQnBRL8EE/2yavLChJ5/OqmuhZRWeuN68PFh36ZE0i9bs7KSK085vloxQjs1k9bMfEa1ThE8TxrY2VuobFwZaAfi2vf6V+vmzfmmPg/cHu+VYKJfgoc+CaZNrNldtxIhl1cBAJs2eWFCr5we0cmhPnnRqJzL6dzpEUliDWBALS1ndW02ravThSJQVytGaOduLGwYaBP90XX2oI1pV39MXV2d6x7X0xPRzZsNfEIAAGwSYRcAsGmXRpN611BfufKt53k6NtSnM6NJwq6PFpZWdK04Mnu1PEpbCLfzNxZrHtfR4WnXQHR179lEvLyeNtEXUyTS0cRn0RwTFyeVfG5cqVyH4p15DT9yhH1UASCkCLsAgE2LZFLyeqNV93mep0imvbd3aYbM4kpFZePS1OPC7RuppZrHdXZ62tW/un529+BqoB3oiyrSGb5AW8vExUmNjF1W/77jinme8s5pZGxckgi8ABBChF0AwKZlo3E5l6va09Q5p2w05mOrwiOVWa7YsiddDLOFkdpUZrnmcZFIh4YqCkJVjtIO7Iyqo2PdpUxtJzl2Xv17H62amdC/94iSY2cJuwAQQoRdAMCmHTgxrHOnR3SsOJXZOadzU/M6cPKU301rCc453Uwvl4tATc1UFodKKb2wUvPY7q7OYhGo6j1odw/G1Lejl0C7Camsp5hX/Tp5nqd0NtivHVOvAeDuEHYBNBwnauFRWpd7ZjSpSCatbDSmAydPsV63gnNON1JL1XvQzqR0dbbw+cJi7UDb091ZUQiqGGgH4hpKxNS3fVvViDruXDzilHfulpkJsUhwd6Zg6jUA3D3CLoCG4kQtfPY/dKjtw61zTvM3FgtTjcujtKvraZeWszWP7e2JFKYYD1TuQVsYpd0R7wl9oPXz4tfw0cMaGRtX/94j5ZkJc5fHdero4ab8/LvB1GsAuHuEXQANxYkaWlU+7zR3Y6Fi7exqheOpmbSWV3I1j431dt26B21xH9rtse7QB9pa/L74VfoZybGzSmc9xSJOp44eDvTfoladeg0AQUDYBdBQnKghyPJ5p9nrGV2drpxqXAy2s2lls/max8aj3YUwm4gXphoPrhaIike7m/gsWkcQLn4dOrg/0OF2rVaceg0AQUHYBdBQnKjBb7lcXjPzmVv3oJ1J69pcWrlc7d/FHfGe8hTjoYote4YGYor2EmjvFBe/7lwrTr0GgKAg7AJoKE7U0AzZbF7T8+nVPWinV0dpZ+YyyuVrB9q+HdvKFY53J2LlUdpdgzH19nQ18VmEHxe/7lwrTr0GgKAg7AJoKE7UUC8rKzldm0tX7UE7d2NZL70yp5n5jNwGeWlgZ+/qHrQVH3cNxNTTzX+FzcLFr7vTalOvASAo+B8eQMNxoobNWlrO6tpspmIf2lRhPe1sSrPXF2oGWs+TEv3RchGowtTjQqjdNRBTd1fnHbdl8sKEnn86qa6FlFZ643rw8eG2r0K9VVz8AgA0E2EXANBUi0vZYkXjtVv2pDR3Y7HmcR0dnnaVAm2xwvHrX3uvtnXlleiPqity54G2lskLE3rl9IhODvXJi0blXE7nTo9IEoF3i7j4BQBoFsIuAKDuFhZXVrfsma0OtNdvLtU8rrPDU2KgOCo7UL0H7WB/VJHOjqrHJxIJTU9P1739l0aTetdQX1XV4GNDfTozmiTsAkANfu6jDayHsAsAuCvpheVb96Atrqe9ka4daCOdHdpVCrRV+9DGNbizV51rAq0fIpmUvN5o1X2e5ymSSfvUIgAINr/30QbWQ9gFAKzLOaf0wvLqHrTFvWdLoTaVWa55bFeko1DhOBFfM0ob18DOXnV0BHurmWw0Ludyt1QNzkZjPrYKAIIrCPtoA2sRdgGgjTnndDO9XAyzpT1oVwNtZnGl5rHdXZ0Ve9CufhwajKtv+7bAB9qNHDgxrHOnR3SsOJXZOadzU/M6cPKU300DgEBiH20EEWEXAELOOafrN5fKgba8F22x4vHiUrbmsdt6IuUKx7sHiyO1xT1pd27vqRr5DJPSutwzo0lFMmllozEdOHmK9boAUAP7aCOICLsAEAL5vNP8zcWqQlCVH5dXcjWP7d3WVd6mpzRCW7q9PdYd2kB7O/sfOkS4BYBNYh9tBBFhFwBaRD7vNHt9YbUQ1GyqvJ52ajatlWy+5rHxaPdqMahScajietpYb/sGWgBAfbCPNoKIsAsAAZLL5TVTGWgrRmivzWaUzdUOtDtiPeWteobWrKON9XY38VmgnazdauQ9b3+zHnj1/X43C4AP2EcbQUPYBYAmy+bympnLVGzZUxylnUlrei6tXK72+qad27dVb9kzsBpoe7d1NfFZAOtvNfLk6ITe/fB1TngDin1QAbQTwi4ANMBKNqfp2YyuzlYE2mK4nZ7PKJ+vHWj7d/YWi0BV70E7NBDTtp67+7M9eWFCzz+dVNdCSiu9cT34+DDrUbFl6241su+IkmNPE6ACiH1QAbQbwi4A3KWVlVx539mrFSO0UzNpzcxn5GrkWc+TBvt6NVRRCKpU8XjXQFQ93fX90zx5YUKvnB7RyaE+edGonMvp3OkRSSLwYkvYaqS1sA8qgHZD2AWADSwtZ3VtNq2//tubeuHFbxdDbSHQzt1Y2DDQJvqj6+xBG9Ou/pi6ujqb9hwujSb1ruJ+sYW2eTo21Kczo0nCLraErUZaCxcnALQbwi6AtrewtKJrxZHZq+VR2kKF4/kbizWP6+jwtGsgWhihHVitbjw0GFOiL6ZIpKOJz6K2SCYlrzdadZ/neYpk0j61CGGx7lYjXxvXuxuw1QhrTbeOixMA2g1hF0BbyCyuVFQ2Lk09Lty+kVqqeVxnp6dd/THdf2+/+rZ3V+xBG9NAX1SRzmAE2o1ko3E5l7vlBDcbjfnYKoTBeluNPPG2N9W9GjNrTeuDfVABtJtNhV1jTKekd0jKS/pTa22ueP+PWmv/3wa2DwA2LZVZrtiyJ10Ms4WR2lRmueZxkUiHhioKQlWO0g7sjKqjw1MikdD09HQTn039HDgxrHOnR3SsOJXZOadzU/M6cPKU301DCKzdaqQR7xXWmtYH+6ACaDebHdn9nKRvSlqW9K+MMT9hrf26pJ+RRNgF0BTOOd1ML5eLQE3NVBaHSim9sFLz2O6uzmIRqOo9aHcPxtS3o1cdHeFds1Zal3tmNKlIJq1sNKYDJ0+xXhctg7Wm9cM+qADayWbD7n3W2n8gScaY/0fS54wxH25YqwC0LeecbqSWqvegnUnp6mzh84XF2oG2p7uzohBUMdAOxDWUiKlv+7aqabztZv9Dhwi3PmK96daw1nRrJi5O6ovnL2k6vcTvH4C2stmw222M6bHWLllrv2mMebukz0t6sIFtAxBSzjnN31gsTDUuj9KurqddWs7WPLa3J1KYYjxQuQdtYZR2R7ynrQMtgon1plvHWtO7V/r9233wmGIrK/z+AWgrG4ZdY0zEWpuV9M8l9Um6KknW2pvGmB+S9J6GtxBAS8rnneZuLFSsnV2tcDw1k9bySq7msbHerlv3oC3uQ7s91k2gRUthvenWsdb07vH7B6Cd3W5k9z8ZY37YWju+9gvFIlW/25hmAWgF+bzT7PWMrk5XTjUuBtvZtLLZfM1j49HuQphNxAtTjQdXC0TFo91NfBZAY7HetD5Ya3p3+P0D0M5uF3YvSBozxrzVWntFkowxPyDpo9bav9foxgHwXy6X18x85tY9aGfSujaXVi5Xe83cjnhPeYrxUMWWPUMDMUV7CbRoD6w3hZ9Kv3+V+P0D0C42DLvW2n9ljHlBhcD7QUk/rcI63Y83o3EAmiObzWt6Pr26B+306ijtzFxGuXztk6K+HdvKFY53J2LlUdpdgzH19nQ18VkAwcR6U/ip9Pu3++BRSeL3D0Bb2UyBqv8u6Yak35P0WUk/ZK1daGirANTdykpO1+bSa/agLXycmc/IbXCRf2Bn7+oetBUfdw3E1NO92Tp3QHtivSn8VPo9++KXz+l6aonfv9ugcjoQLrcrUPWUpDdK+nVJvyjpNyUdl/TnDW8ZgDu2tJzVtdlMxT60qcJ62tmUZq8v1Ay0nicl+qPlIlCFqceFULtrIKburs7mPhEgZFhvCj8dOrhfjx0/punpab+bEmhUTgfC53ZDMn8t6aettbOSZIz5hqQvGGNeY639jYa3DsAtFpeyxYrGa7fsSWnuxmLN4zo6PO0qBdo1W/Yk+qPqihBoAQDti8rVQPjcbs3uz6+5/bwx5hEVRnYJu0CDLCyurE41nq0OtNdvLtU8rrPDU2KgOCo7UB1oB/ujinR2NPFZAADQOqhcDYTPHS+2s9a+bIyhEjOwRemF5Vv3oJ1J69rcgq7frL0sPtLZoV2lQFs1ShvX4M5edRJoAQC4Y1ROB8LnrirLWGtv1rshQNg455ReWF7dg7a492wp1KYyyzWP7Yp0FCocJ+JrRmnjGtjZq44OrjIDAFBPVE4HwocyqsAWOOd0M71cDLOlPWhXA21mcaXmsd1dnRV70K5+3Pv6Vym/skCgBQCgiaicDoQPYRe4Deecrt9cKgTa2eIetDPpcsXjxaVszWO39UTKFY53DxZHaot70u7c3lM1Vaok0R/X9HTtQlMAAKAxqJwOhAthF5CUzzvN31ysKgRV+XF5JVfz2N5tXeVtekojtKXb22Pd6wZaAAAAAI1F2EXbyOedZq8vrG7ZM5sqr6edmk1rJZuveWw82r1aDKpUHKq4njbWS6AFAAAAgiZQYdcY86Kkm5JykrLW2sNrvu5J+oSkYUkZSe+11n6l2e1EcOVyec1UBtqKEdprsxllc7UD7Y5YT3mrnqE162hjvd1NfBYAAGCtiYuTSj43rlSuQ/HOvIYfORKqKcdhf36AHwIVdosetdZO1/jaWyW9vvjv+yT9VvEj2kg2l9fMXKZiy57iKO1MWtNzaeVytbcI2Ll9W/WWPQOrgbZ3W1cTnwUAAK3Hr0A2cXFSI2OX1b/vuGKep7xzGhkbl6RQBMKwPz/AL0EMuxt5h6TPWWudpC8ZY/qMMfdaa7/td8NQXyvZnKZnM7o6WxFoi+F2ej6jfL52oO3f2VssAlW9B+3QQEzbelrtVx4AgGDwM5Alx86rf++j5WVDnuepf+8RJcfOhiIMhv35AX4J2pm/kzRqjHGS/oO19sk1X79P0rcqbr9UvK8q7BpjnpD0hCRZa5VIJBrX4hYWiUR8fW2WV7J65doNXZm6oW9P3dC3rxU/Tl3X9Gxaebd+oPU8addAXHuGdujeoR26d2in7t1V+PyexA71tHig9btfsD76JZjol+ChT4KpHv3yxS9f0u6Dx6rqVOw+eFRf/PI5PXb82FabuKGVzm2K9vTccv9C57aW/n0r9UtYn18r4m9YMN1tvwQtFTxirX3ZGDMk6RljzGVr7bN3+k2KIbkUlN30dK1Z0e0tkUio0a/N0nJW12bTujpdKAJ1tWKEdu7GgmrkWXmelOiP3rIH7dBgTLv6Y+rq6lznqLxu3pzXzZsNfUoN14x+wZ2jX4KJfgke+iSY6tEv06klxVZu3T/+emqp4X3elVvU0tJSVdB2zimSW2zp37dSv4T1+bUi/oYF00b9smfPnprHBSrsWmtfLn6cMsY8JelhSZVh92VJr6q4fX/xPvhoYWlF14pTja/OpFYD7Wxa8zdq7xfb0eFp10BUQ4PFvWcT8fJ62kRfTJFIRxOfBQAA2Eg84pR37pZAFovUXlpUL8NHD2tkbFz9e4/I8zw55zR3eVynjh6+/cEtIOzPD/BLYMKuMSYmqcNae7P4+QlJH1nzsC9Ier8x5vMqFKa6znrd5sgsrlRUNi6E2VKBqBuppZrHdXZ62tW/un52dQ/amAb6oop0EmgB4E5RtRV+8DOQlX6/k2Nnlc56ikWcTh09HJrf+7A/P8AvgQm7knZLesoYIxXa9fvW2r8wxrxPkqy1vy0pqcK2Q19XYeuhn/SpraGUyixXbNmTLobZwkhtKrNc87hIpENDFQWhKkdpB3ZG1dHBHrQAUC9UbYVf/A5khw7uD/XveNifH+AHz9VaNBke7sqVK363IRCcc7qZXtZUscJxasHpxW9NlUdq0wu3rsMp6e7qLITZgeo9aHcPxtS3o5dAW0esFQmmduqXVho1bKd+Kfnob31W+YqqrVLh73vH5bP60M/8hI8tK2jHPmkF9Esw0S/BQ58E0ybW7K4bRoI0sos6cM7pRmqpeg/amZSuzhY+X1isHWh7ujsrCkEVA+1AXEOJmPq2b6s6sQIQTowaBl8q6ym25u+x53lKZ/kbDQBAJcJuC3LOaf7GYmGqcXkf2tX1tEvL2ZrH9vZEClOMB2J6zat2Kd7bUR6l3RHvIdACbY69HoPPzyJBAAC0EsJuQOXzTnM3FirWzq5WOJ6aSWt5JVfz2FhvV7EY1OoIbWEKclzbY93lEySmaQBYi1HD4KNqKwAAm0PY9VE+7zR7PaOr05VTjYvBdjatbDZf89h4tLsQZhPxwlTjwdUCUfFodxOfBYAwYdQw+PwuEgQAQKsg7Prol3/zv+qbV+Zrfn1HvKc8xXioYsueoYGYor0EWgD1x6hha6BqKwAAt0fY9VGiP6rrqcVyhePd5WAb067BmHp7uvxuIoA20w6jhq1UbRoAANw9wq6PfuY9D7NlD4DACfOoIdWmAQBoHx1+N6CdEXQBoLkK1aaPrFNt+rzPLQMAAPVG2AUAtI1U1rtlizWqTQMAEE6EXQBA24hHnJyrrixNtWkAAMKJsAsAaBvDRw9r7vJ4OfCWqk0PU20aAIDQoUAVAKBtlIpQfe5Pzugb164rt7Kk7xzqk7TX13YBAID6I+wCANqOl3i1Dj+yupcwFZkBAAgfpjEDANoKFZkBAGgPjOwCANpKKusp1qIVmScuTir53LhSuQ7FO/MafuQIo9EAANRA2AUAtJV4xCnvXNUWRK1QkXni4qRGxi6rf99xxTxPeaZfAwCwIaYxAwDaSqtWZGb6NQAAd4aRXQBA28lPf1Pnn7qk/PKiHrinX+/9kbcFfnS0ladfAwDgB8IuAKBtlKYCDz5yUoliJea5y+N+N2tTWnX6NQAAfmEaMwCgbbTyVOBWnX4NAIBfGNkFALSNVp4KXJpmnRw7q3TWUyzidOro4cBPvwYAwC+EXQBA22j1qcCHDu4n3AIAsElMYwYAtA2mAgMA0D4Y2QUAtA2mAgMA0D4IuwCAtsJU4HCauDip5HPjSuU6FO/Ma/iRI/QzALQ5wi4AAGhppS2l+vcdV8zzlHdOI2OFLaUIvADQvlizCwAAWlorbykFAGgcwi4AAGhpqaxXVWFbap0tpQAAjUPYBQAALS0eceUK2yWttKUUAKAxWLMLAEDAUGzpzgwfPayRsfHyVObSllKn2FIKANoaYRcAgACh2NKdY0sptIq1F7Le8/Y364FX3+93s4DQIuwCABAghWJLj65TbOks4W0DbCmFoFvvQtaToxN698PX+d0FGoSwCwBAgKSynmIUW0LAMLV+69a9kLXviJJjT/NaAg1C2AUAIEDiEae8c1XVhSm2BD8xtb4+uJAFNB/VmAEACJDho4c1d3m8XF24VGxpmGJL8An7GNcHVcOB5mNkFwCAAKHYEoKGEcn6WLdq+NfG9W4uZAENQ9gFACBgKLaEIGFqfX2sdyHribe9iWrMQAMRdgEAAFAT+xjXz9oLWYlEQtPT0z62CAg3wi4AAJBExV2sj6n1AFoVYRcAAFBxFxtiaj2AVkQ1ZgAAQMVdAEDoEHYBAIBSWa+qAJFExV0AQGtjGjMAALjjirus7wUABB1hF0Db4OQcqO1OKu5utL73sePHmt30UOLvFQBsHWEXQFug+A6wsTupuFtY3/voOut7zxJ264C/VwBQH4RdAG1ho5NzTh6Bgs1W3E1lPcVY33tbdzs6y98rAKiPQIRdY8yrJH1O0m5JTtKT1tpPrHnMGyX9iaT/Vbzrj6y1H2lmOwG0Lk7Ogfq50/W97Wgro7P8vQKA+ghKNeaspA9Ya98g6fsl/awx5g3rPO6/WWsfKv4j6ALYtHjEybnqE3FOzoG7M3z0sOYuj5ffU6X1vcPrrO9tV1vZyom/VwBQH4EIu9bab1trv1L8/Kakr0m6z99WAQgTTs6B+jl0cL9OHd2rjstnlXn+rDoun9Wpo3uZYlthK1s58fcKAOojENOYKxljXiPpkKT/sc6X/64x5quSrkj6l9bayWa2DUDrupPiOwBub7Pre9vVVqZ68/cKAOrDWztNxk/GmLikc5I+aq39ozVf2yEpb61NGWOGJX3CWvv6Gt/nCUlPSJK19nuXl5cb3PLWFIlElM1m/W4G1qBfgol+CSb6JXjok4K//MoFPTk6of59FVs5fW1cT5w4pIe/56Gmt4d+CSb6JXjok2DaqF+6u7slad1pM4EJu8aYLkl/Julpa+2vbeLxL0o6bK2dvs1D3ZUrV+rQwvBJJBKanr7dy4dmo1+CiX4JJvoleOiTVRMXJ5UcO18enR32cXSWfgkm+iV46JNg2qhf9uzZI9UIu4GYxmyM8SR9StLXagVdY8w9kq5aa50x5mEV1hvPNLGZAAAAm8ZUbwDwVyDCrqSjkk5Jet4Yc6F43y9IerUkWWt/W9JJST9jjMlKWpD0Y9baYAxLAwAAAAACJRBh11r7nGoMPVc85pOSPtmcFgEAAGCrJi5OKvncuFK5DsU78xp+5Aij3QCaJhBhFwAAAOEycXFSI2OX1b/vuGKep7xzGhkblyQCL4CmCMQ+uwAAAAiX5Nh59e89Ut5+yfM89e89ouTYeZ9bBqBdEHYBAABQd6msV7XPsFQIvOnshivXAKBumMYMAABQxBrT+olHnPLOVQVe55xiEeqLAmgORnYBAAC0usY0v++4Yg8+qvy+4xoZu6yJi5N+N60lDR89rLnL43KuEG6dc5q7PK7ho4d9bhmAdsHILgAAgEprTB9dZ43pWUZ370LpNUuOnVU66ykWcTp19DCvJYCmIewCAACosMY0xhrTujp0cD/hFoBvmMYMAACgwhrT0pTbEtaYAkDrIuwCAACINaYAEDZMYwYABAJVcOE31pgCQLgQdgEAvitVwe3fd1wxz1PeOY2MjUsSQQNNxRpTAAgPpjEDAHxXqIJ7ZJ0quOd9bhkAAGhVjOwCAHxHFVzg7rEEAADWR9gFAPguHnHKO1ce2ZWoggtsBksAAKA2pjEDAHxHFVzg7rAEAABqY2QXAOA7quACd4clAABQG2EXABAIVMEF7hxLAACgNqYxAwAAtCiWAABAbYzsAgAAtCiWAABAbYRdAACAFsYSAABYH2EXAIA7xL6mAAAEH2EXAIA7wL6mAAC0BgpUAQBwB9jXFACA1kDYBQDgDqSyXtU2LxL7mgIAEESEXQAA7kA84srbvJSwrykAAMFD2AUA4A6wrykAAK2BAlUAANwB9jWtH6paAwAaibALAMAdYl/TraOqNQCg0ZjGDAAAmo6q1gCARiPsAgCApqOqNQCg0Qi7AACg6ahqDQBoNMIuAABoOqpaAwAajQJVAACg6ahqDQBoNMIuAADwBVWtAQCNxDRmAAAAAEDoMLILAACAW0xcnFTyuXGlch2Kd+Y1/MgRRuIBtBTCLgBgUzjxBdrHxMVJjYxdVv++44p5nvLOaWRsXJJ43wNoGYRdAMBtceIbPly8wEaSY+fVv/fR8l7Inuepf+8RJcfO8nsCoGUQdgEAt8WJb7hw8QK3k8p6ihXf7yWe5ymd9WocAQDBQ4EqAMBtpbJeOeiWcOLbugoXL46sc/HivM8tQ1DEI668B3KJc06xiKtxBAAED2EXAHBbnPiGCxcvcDvDRw9r7vJ4+X3vnNPc5XENHz3sc8sAYPOYxgwAuK3ho4c1MjZeHg0snfie4sS3JcUjTnnnqgIvFy9QqTSdPTl2Vumsp1jE6dTRw0xzB9BSCLsAgNvixDdcuHiBzTh0cD/vcQAtjbALANgUTnzDg4sXAIB2QNgFEFpsrQLUxsULAEDYEXYBhBJbqwDBwsUnAECzBSrsGmPeIukTkjol/Y619mNrvt4j6XOSvlfSjKR3W2tfbHY7AQQf+8ICwcHFJwCAHwKz9ZAxplPSb0h6q6Q3SHqPMeYNax7205LmrLWvk/Trkn6lua0E0CrCuLXKxMVJffQ3P6MP/vvP6aO/+RlNXJz0u0nAprCvLwDAD4EJu5IelvR1a+03rLXLkj4v6R1rHvMOSZ8tfn5a0puMMa175gqgYcK2L2xpZCy/77hiDz6q/L7jGhm7TOBFSwjjxScAQPAFKezeJ+lbFbdfKt637mOstVlJ1yUNNqV1AFrK8NHDmrs8Xg68pa1Vhlt0axVGxtDKwnbxCQDQGgK1ZrdejDFPSHpCkqy1SiQSPrcomCKRCK9NANEv9fHY8WPa2bdTT/2XMaVWpHiX9A/edlQPf89Dd/X9/O6Xlc5tivb03HL/Que2tv598btfcKv1+uQ9b3uTnhydUP++in19vzauJ972JvqvSXivBBP9Ejz0STDdbb8EKey+LOlVFbfvL9633mNeMsZEJO1UoVBVFWvtk5KeLN5009PT9W9tCCQSCfHaBA/9Uj8PvPp+feAn3111392+tn73S1duUUtLS1VTQZ1ziuQW2/r3xe9+wa3W65MHXn2/3v3wdSXHni7v6/vuo4f1wKvvp/+ahPdKMNEvwUOfBNNG/bJnz56axwUp7I5Ler0x5rUqhNofk/T31zzmC5J+QtJ/l3RS0hettcyBAhB6w0cPa2RsvDyVuTQt+1SLTstG+2FfXwBAswUm7Fprs8aY90t6WoWthz5trZ00xnxE0nlr7RckfUrSiDHm65JmVQjEABB6pZCQHDtbHhk7dfQw4QEAAKAGb23BiBByV65c8bsNgcQ0jWCiX4KJfgkm+iV46JNgol+CiX4JHvokmDYxjXnd8v5BqsYMAAAAAEBdEHYBAAAAAKFD2AUAAAAAhA5hFwAAAAAQOoGpxgwAqDZxcVLJ58aVynUo3pnX8CNHqL4MAACwSYRdAAigiYuTGhm7rP59xxXzPOWd08jYuCQReAEAADaBacwAEEDJsfPq33tEnleopO95nvr3HlFy7LzPLQMAAGgNhF0ACKBU1isH3RLP85TOrruNHAAAANZgGjMABFA84pR3rirwOucUizgfWwVsDevQAQDNxMguAATQ8NHDmrs8LucK4dY5p7nL4xo+etjnlgF3p7QOPb/vuGIPPqr8vuMaGbusiYuTfjcNABBSjOwCQACVRruSY2eVznqKRZxOHT3MKBhaVmEd+qPrrEM/y+81AKAhCLsAEFCHDu4nBCA0UllPMdahAwCaiGnMAACg4eIRV56WX8I6dABAIxF2AQBAw7EOHQDQbExjBgAADcc6dABAsxF2AQBAU7AOHQDQTExjBgAAAACEDmEXAAAAABA6hF0AAAAAQOgQdgEAAAAAoUPYBQAAAACEDmEXAAAAABA6hF0AAAAAQOgQdgEAAAAAoRPxuwEAAPhp4uKkks+NK5XrULwzr+FHjujQwf1+NwsAAGwRYRcA0LYmLk5qZOyy+vcdV8zzlHdOI2PjkkTgBQCgxTGNGQDQtpJj59W/94g8z5MkeZ6n/r1HlBw773PLAADAVjGyi0BgGiEAP6SynmLFoFvieZ7SWa/GEQAAoFUQduE7phEC8Es84pR3rjyyK0nOOcUizsdWAQCAeiDswneFaYSPrjON8CxhF0BDDR89rJGx8fJUZuec5i6P69TRw343bVOYFQMAQG2EXfiOaYQAmq0yJObnpzV97gXFBu9RLOJ06ujhlgiMzIoBAGBjhF34jmmEAJppbUiMFkdzf/To3pYKicyKAQBgY1Rjhu+Gjx7W3OVxOVcIt6VphMMtMo0QQGsJSwXmVNarukgoMSsGAIBKjOzCd6URiOTYWaWzXktNIwTQesKydIJZMQAAbIywi0A4dHA/4RZAU4QlJLZ6cS0AABqNsAsAaCthCYnMigEAYGOEXQBAWwlTSGRWDAAAtRF2AQBth5AIAED4UY0ZAAAAABA6hF0AAAAAQOgwjRkAgDs0cXFSyefGlcp1KN6Z1/AjR5gWDQBAwBB2AQC4AxMXJzUydln9+44r5nnKO6eRsXFJIvACABAgTGMGAOAOJMfOl7ctkiTP89S/94iSY+d9bhkAAKhE2AUA4A6ksl456JZ4nqd01qtxBAAA8ANhFwCAOxCPODnnqu5zzikWcTWOAAAAfmDNLgDgtijItGr46GGNjI2XpzI75zR3eVynjh72u2kAAKCC72HXGPNxST8oaVnSC5J+0lo7v87jXpR0U1JOUtZay1kFADQBBZmqlZ5zcuys0llPsYjTqaOH2/K1AAAgyHwPu5KekfRBa23WGPMrkj4o6edrPPZRa+1085oGACgUZHp0nYJMZ9s24B06uL9tnzsAAK3C97BrrR2tuPklSSf9agsA4FaprKcYBZkAAECLCVqBqp+S9J9qfM1JGjXGfNkY80QT2wQAbY2CTAAAoBV5a09gGsEY858l3bPOlz5krf2T4mM+JOmwpB+x1t7SKGPMfdbal40xQypMff6n1tpna/y8JyQ9IUnW2u9dXl6u0zMJl0gkomw263czsAb9Ekzt3C9/+ZULenJ0Qv37KgoyfW1cT5w4pIe/5yFf29bO/RJU9Ekw0S/BRL8ED30STBv1S3d3tyStO92sKWH3dowx75X0jyW9yVqb2cTjPywpZa391U18e3flypWtNTCkEomEpqdZAh009EswtXu/TFycVHLsfLkg03BACjK1e78EEX0STPRLMNEvwUOfBNNG/bJnzx6pRtj1fc2uMeYtkn5O0rFaQdcYE5PUYa29Wfz8hKSPNLGZANDWKMgEAABaTRDW7H5S0nZJzxhjLhhjfluSjDF7jDHJ4mN2S3rOGPNVSX8p6c+ttX/hT3MBAAAAAEHn+8iutfZ1Ne6/Imm4+Pk3JH13M9sFAAAAAGhdQRjZBQAAAACgrgi7AAAAAIDQIewCAAAAAEKHsAsAAAAACB3CLgAAAAAgdAi7AAAAAIDQIewCAAAAAELH9312AQBYa+LipJLPjSuV61C8M6/hR47o0MH9fjcLAAC0EMIuACBQJi5OamTssvr3HVfM85R3TiNj45JE4AUAAJvGNGYAQKAkx86rf+8ReZ4nSfI8T/17jyg5dt7nlgEAgFZC2AUABEoq65WDbonneUpnvRpHAAAA3IqwCwAIlHjEyTlXdZ9zTrGIq3EEAADArQi7AIBAGT56WHOXx8uB1zmnucvjGj562OeWAQCAVkKBKgBAoJSKUCXHziqd9RSLOJ06epjiVAAA4I4QdgEAgXPo4H7CLQAA2BKmMQMAAAAAQoewCwAAAAAIHcIuAAAAACB0CLsAAAAAgNAh7AIAAAAAQoewCwAAAAAIHcIuAAAAACB0CLsAAAAAgNAh7AIAAAAAQoewCwAAAAAIHcIuAAAAACB0CLsAAAAAgNAh7AIAAAAAQoewCwAAAAAIHcIuAAAAACB0POec321otNA/QQAAAABoY956d7bDyK7Hv/X/GWO+7Hcb+Ee/tMo/+iWY/+iX4P2jT4L5j34J5j/6JXj/6JNg/ttEv6yrHcIuAAAAAKDNEHYBAAAAAKFD2G1vT/rdAKyLfgkm+iWY6JfgoU+CiX4JJvoleOiTYLqrfmmHAlUAAAAAgDbDyC4AAAAAIHQifjcAwWCM+YCkX5W0y1o77Xd72p0x5pclvUNSXtKUpPdaa6/42yoYYz4u6QclLUt6QdJPWmvnfW1UmzPG/KikD0vaJ+lha+15f1vU3owxb5H0CUmdkn7HWvsxn5vU9owxn5b0dklT1toDfrcHkjHmVZI+J2m3CltkPmmt/YS/rYIxZpukZyX1qJCRTltrf8nfVkGSjDGdks5Letla+/Y7OZaRXZT+6J6Q9Ld+twVlH7fWHrTWPiTpzyT9os/tQcEzkg5Yaw9K+mtJH/S5PZAuSfoRFU5Q4KPiychvSHqrpDdIeo8x5g3+tgqSPiPpLX43AlWykj5grX2DpO+X9LO8VwJhSdJxa+13S3pI0luMMd/vb5NQ9M8lfe1uDiTsQpJ+XdLPqXB1EQFgrb1RcTMm+iYQrLWj1tps8eaXJN3vZ3sgWWu/Zq39n363A5KkhyV93Vr7DWvtsqTPqzBDBT6y1j4radbvdmCVtfbb1tqvFD+/qcJJ/H3+tgrWWmetTRVvdhX/cf7lM2PM/ZLeJul37uZ4pjG3OWPMO1SYEvBVY4zfzUEFY8xHJf24pOuSHvW5ObjVT0n6Q78bAQTIfZK+VXH7JUnf51NbgJZgjHmNpEOS/ofPTYHKM1S+LOl1kn7DWku/+O/fqTAot/1uDibstgFjzH+WdM86X/qQpF9QYQozmmyjfrHW/om19kOSPmSM+aCk90ti3UgT3K5fio/5kArT0H6vmW1rV5vpEwBoNcaYuKQzkv7Fmhld8Im1NifpIWNMn6SnjDEHrLWXfG5W2zLGlOoNfNkY88a7+R6E3TZgrX3zevcbYx6U9FpJpVHd+yV9xRjzsLX2lSY2sS3V6pd1/J6kpAi7TXG7fjHGvFeFYi9vstYyvakJ7uC9An+9LOlVFbfvL94HYA1jTJcKQff3rLV/5Hd7UM1aO2+MOavCenfCrn+OSvohY8ywpG2Sdhhjftda+w83+w0Iu23MWvu8pKHSbWPMi5IOU43Zf8aY11tr/6Z48x2SLvvZHhQUK83+nKRj1tqM3+0BAmZc0uuNMa9VIeT+mKS/72+TgOAxxniSPiXpa9baX/O7PSgwxuyStFIMur2SHpP0Kz43q61Zaz+oYjHQ4sjuv7yToCsRdoGg+pgx5rtU2Hrom5Le53N7UPBJFbYkeKY4G+JL1lr6xkfGmB+W9O8l7ZL058aYC9bax31uVluy1maNMe+X9LQKWw992lo76XOz2p4x5g8kvVFSwhjzkqRfstZ+yt9Wtb2jkk5Jet4Yc6F43y9Ya5P+NQmS7pX02eK63Q5J1lr7Zz63CVvkOccsPAAAAABAuLD1EAAAAAAgdAi7AAAAAIDQIewCAAAAAEKHsAsAAAAACB3CLgAAAAAgdAi7AAAAAIDQYZ9dAABalDHm/5L0d6y17yze/rik75H0Vmvtsp9tAwDAb+yzCwBAizLGDEr6hqQ3Svo+ST8r6RFr7XU/2wUAQBAQdgEAaGHGmA9L+hFJO1UIut8yxuyU9IykN0j6fmvtJR+bCACAL1izCwBAa5uQ9KCkD1prv1W8LyPpbZJO+9YqAAB8RtgFAKBFGWMelPRbkj4r6adK91trV6y113xrGAAAAUDYBQCgBRlj7pP0p5LeJ+mfSHrQGPNGXxsFAECAEHYBAGgxxpgdkpKSfs1a+wVrbUbSxyV91N+WAQAQHBSoAgAgpIwxn5H0qxSoAgC0I0Z2AQAIIWNMUtIJSf/RGPNen5sDAEDTMbILAAAAAAgdRnYBAAAAAKFD2AUAAAAAhA5hFwAAAAAQOoRdAAAAAEDoEHYBAAAAAKFD2AUAAAAAhA5hFwAAAAAQOoRdAAAAAEDoEHYBAAAAAKHz/wO/jQwD+x3qeQAAAABJRU5ErkJggg==",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"plot_ds(data,m[-1],q[-1])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Adam"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Oltre a memorizzare la somma smorzata $\\tilde G_{j,k}$ dei quadrati dei gradienti precedenti, come in Adadelta e RMSprop, Adam mantiene anche una somma smorzata $\\tilde H_{j,k}$ dei gradienti precedenti $g_{j,k}$, utilizzata in sostituzione del gradiente $g_{j,k}$ nell'aggiornamento effettuato ad gni iterazione.\n",
"\n",
"\\begin{align*}\n",
"\\tilde G_{j,k} &= \\gamma \\tilde G_{j,k-1} + (1 - \\gamma) g_{j,k}^2\\\\\n",
"\\tilde H_{j,k} &= \\beta \\tilde H_{j,k-1} + (1 - \\beta) g_{j,k}\n",
"\\end{align*}\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Dato che si assume che $\\tilde H_{j,k}=\\tilde G_{j,k}=0$ se $k<0$ e i valori $\\gamma, \\beta$ sono normalmente prossimi a $1$, il metodo manifesta la tendenza (bias) a fornire valori piccoli di $\\tilde H_{j,k}$ e $\\tilde G_{j,k}$, soprattutto nelle iterazioni iniziali. \n",
"\n",
"Per correggere questo comportamento viene applicata una correzione del bias:\n",
"\n",
"\\begin{align*}\n",
"\\hat{G}_{j,k} &= \\frac{\\tilde G_{j,k}}{1 - \\gamma^k}\\\\\n",
"\\hat{H}_{j,k} &= \\frac{\\tilde H_{j,k}}{1 - \\beta^k}\n",
"\\end{align*}"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"I parametri sono aggiornati come visto in Adadelta e RMSprop, per cui risulta ad ogni iterazione:\n",
"\n",
"\\begin{align*}\n",
"g_{j, k} &= \\frac{\\partial J(\\theta)}{\\partial\\theta_j}\\Big\\rvert_{\\theta=\\theta^{(k)}}\\\\\n",
"\\tilde G_{j,k} & =\\gamma \\tilde G_{j,k-1}+(1-\\gamma)g_{j,k}^2\\\\\n",
"\\tilde H_{j,k} & =\\beta \\tilde H_{j,k-1}+(1-\\beta)g_{j,k}\\\\\n",
"\\hat{G}_{j,k} &= \\frac{\\tilde G_{j,k}}{1 - \\gamma^k}\\\\\n",
"\\hat{H}_{j,k} &= \\frac{\\tilde H_{j,k}}{1 - \\beta^k}\\\\\n",
"\\Delta_{j,k} &= - \\frac{\\eta}{\\sqrt{\\hat G_{j,k}+\\varepsilon}} \\hat H_{j, k}\\\\\n",
"\\theta_j^{(k+1)} &= \\theta_j^{(k)} + \\Delta_{j,k}\n",
"\\end{align*}\t"
]
},
{
"cell_type": "code",
"execution_count": 142,
"metadata": {},
"outputs": [],
"source": [
"def Adam(X,t, eta = 0.1, gamma = 0.999, beta = 0.9, eps = 1e-8, epochs = 10000):\n",
" theta = np.zeros(nfeatures+1).reshape(-1,1)\n",
" G_tilde = np.zeros(nfeatures+1).reshape(-1,1)\n",
" H_tilde = np.zeros(nfeatures+1).reshape(-1,1)\n",
" theta_history = []\n",
" cost_history = []\n",
" for k in range(epochs): \n",
" g = gradient(theta,X,t)\n",
" G_tilde = gamma * G_tilde + (1 - gamma)*g**2\n",
" H_tilde = beta * H_tilde + (1 - beta)*g\n",
" G_hat = G_tilde/(1 - gamma**(k+1))\n",
" H_hat = H_tilde/(1 - beta**(k+1))\n",
" delta = - eta * H_hat/(np.sqrt(G_hat)+ eps)\n",
" theta = theta + delta\n",
" theta_history.append(theta)\n",
" cost_history.append(cost(theta, X, t))\n",
" theta_history = np.array(theta_history).reshape(-1,3)\n",
" cost_history = np.array(cost_history).reshape(-1,1)\n",
" m = -theta_history[:,1]/theta_history[:,2]\n",
" q = -theta_history[:,0]/theta_history[:,2]\n",
" return cost_history, m, q"
]
},
{
"cell_type": "code",
"execution_count": 143,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"tempo di esecuzione: 0.666 secondi\n",
"10000 passi totali\n",
"1000000 gradienti valutati\n"
]
}
],
"source": [
"start_time = time.time()\n",
"cost_history, m, q = Adam(X,t, eta = 0.1, gamma = 0.999, beta = 0.9, eps = 1e-8, epochs = 10000)\n",
"print(f\"tempo di esecuzione: {time.time()-start_time: 4.3f} secondi\")\n",
"print(f\"{len(m)} passi totali\")\n",
"print(f\"{len(m)*n} gradienti valutati\")"
]
},
{
"cell_type": "code",
"execution_count": 144,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABQgAAAGoCAYAAAAKMwiTAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAABi4ElEQVR4nO3deXiU9aH3/8+9zCSZhC0MJIQtbBHZFEWxgqgQFbWtivsuv9qeYxc9bZ/nHJ/rOXIs1Et69XSx1fapnrZAXapW3CtLxH1FEdlkCZFA2JOwZSNzL78/QoIgYoDM3LO8X9fFRWbLfOZ7Qyb55Pu9v4bv+74AAAAAAAAAZCQz6AAAAAAAAAAAgkNBCAAAAAAAAGQwCkIAAAAAAAAgg1EQAgAAAAAAABmMghAAAAAAAADIYBSEAAAAAAAAQAazgw7QXlu2bAk6wgmJRqOqrq4OOgbEsUgmHIvkwbFIDhyH5JEOx6KoqCjoCHHD94WZiXE7dozZ8WHcjh1jdnwYt2PHmB2f9nxfyAxCAAAAAAAAIINREAIAAAAAAAAZjIIQAAAAAAAAyGAUhAAAAAAAAEAGoyAEAAAAAAAAMhgFIQAAAAAAAJDBKAgBAAAAAACADEZBCAAAAAAAAGQwCkIAAAAAAAAgg1EQAgAAAAAAABmMghAAAAAAAADIYBSEAAAAAAAAQAajIAQAAAAAAAAyGAUhAAAAAAAAkMEoCAEAAAAAAIAMRkEIAAAAAAAAZDAKQgAAAAAAACCD2fH85LNmzVJFRYUGDBigqVOntl1fV1enhx9+WPv27dPIkSM1ZcqUeMYAAAAAAAAA8BXiVhBWVFSoqalJ06dP1yOPPKLy8nINHjxYkvT000/r2muvVe/eveP19AAAAAAAAADaIW5LjNetW6dRo0ZJkkaOHKm1a9e23bZp0yY9++yz+tnPfnbI9QAAAAAAAAASK24zCOvr61VQUCBJikQiqqqqarttzZo1+sUvfqG8vDz96le/0owZM770+LKyMpWVlUmSZs6cqWg0Gq+oCWHbdsq/hnTBsUgeHIvkwbFIDhyH5MGxAAAAQCaJW0EYiUTU0NAgSWpsbFQkEmm7raioSH369JEkmeaRJzGWlpaqtLS07XJ1dXW8oiZENBpN+deQLjgWyYNjkTw4FsmB45A80uFYFBUVBR0BAAAAKSJuS4xLSkq0YsUKSdLy5ctVUlLSdluvXr20a9cuNTU1yXXdeEUAAAAAAAAA8DXiNoNw4MCBCoVCmjZtmoqLixWNRjV37lxNmTJF11xzjR544AE1NzfrqquuilcEAAAAAAAAAF8jbgWhJE2dOvWQy1OmTJEk9enTR/fee288nxoAAAAAAABAO8RtiTEAAAAAAACA5EdBCAAAAAAAAGQwCkIAAAAAAAAgg1EQAgAAAAAAABksrpuUoMWfy1Zry65G/X8TS9S7e27QcQAAAAAAAIA2zCBMgPr9Me1t2C/X84KOAgAAAAAAAByCgjABDMOQJHl+wEEAAAAAAACAw1AQJoB5oCD0fRpCAAAAAAAAJBcKwgQwDvzNDEIAAAAAAAAkGwrCBDBNZhACAAAAAAAgOVEQJgAzCAEAAAAAAJCsKAgTwOAchAAAAAAAAEhSFIQJcKAfpCAEAAAAAABA0rGDDpAJ2nYxDjgHAABAEGpra/WLX/xCVVVVmjNnjizLarvtoYce0ubNmxUOh1VaWqrx48cHmBQAACAzURAmQOsMQo+TEAIAgAyUl5ene+65R//93/99xNvvvPNOFRYWJjgVAAAAWlEQJgAzCAEAQCYLh8MKh8NHvM0wDD344IPKy8vTd77zHfXo0SPB6QAAAEBBmABtMwg5ByEAAMAhbrnlFuXl5Wn16tWaM2eOfvrTn37pPmVlZSorK5MkzZw5U9FoNNExO5Rt2yn/GoLAuB07xuz4MG7HjjE7PozbsWPM4oeCMAHaZhDSDwIAABwiLy9PkjR06FA99thjR7xPaWmpSktL2y5XV1cnJFu8RKPRlH8NQWDcjh1jdnwYt2PHmB0fxu3YMWbHp6io6Gvvwy7GCcAuxgAAAEfW0NAgSdqyZYtyc3MDTgMAAJCZmEGYAAYzCAEAQAZzHEf333+/Kisrdd999+mqq67S6tWrNWXKFP3ud79TfX29DMPQ7bffHnRUAACAjERBmACtBSHnIAQAAJnItm3dc889h1w3bNgwSdLdd98dRCQAAAB8AUuME8BsW2IcbA4AAAAAAADgcBSECWCIGYQAAAAAAABIThSECWAeGGX6QQAAAAAAACQbCsIEYAYhAAAAAAAAkhUFYQIYbecgpCAEAAAAAABAcqEgTIDWXYzpBwEAAAAAmcz3fXm7d8r3vKCjAPgCO+gAmcBsLQhFQwgAAAAAyEy+68h581l5az+WWTxc9oU3tU2oARAsZhAmQOvXO35BAgAAAADIRH5jvWIv/1ne2o8lSd6GlXJXvBtwKgCtKAgTgBmEAAAAAIBM5e3aoebn/iB/6+dSpJOsMy6QJLnv/1Pezs0BpwMgURAmRNsMQvpBAAAAAEAG8arWKfbcH6S9NTKiRQpf8UPZp02SOfwbkufKKXtcfvP+oGMCGY+CMAHaZhCySwkAAAAAIEO4q95X7J9/lZqbZBYPU+jb/yojr4skyT7rEhnde8nfWyPnrWf5eRkIGAVhArTOIOTrHQAAAAAg3fmeK+edF+S89Zzke7JOPa9lQ5JQuO0+hh2SXXqDZIfllS+Vt+aj4AIDoCBMhNZdmTwaQgAAAABAGvObm+TMm9OyAYlpyT7vKtljJ8swvlw/mF17yD7nMkmS884L8nZtT3RcAAdQECbAwRmEFIQAAAAAgPTk761V7Lk/ytu0RsqOKHTpd2SdNOaoj7FKTpdZcprkxFrOR+jEEpQWwBdRECaAodZzEAYcBAAAAACAOPC2Var52Yfk79ouo2sPhS//gcyige16rD3+Mhlde8iv3S7n3RfjnBTAkVAQJoDZtosxDSEAAAAAIL00rHhfsRcflprqZfQZotDl35fRpXu7H2+EsmSXXi9ZtrzPPpS7flkc0wI4EgrCBDAMZhACAAAAANKL73tyFi/Qruf/R/JcmcPOUuji22Rk5Rzz5zK7F8n+xqWSJOfNZ+TvrenouACOgoIwAZhBCAAAAABIJ36sWU7ZE3KXLJIMQ/a4byt0zuUyTOu4P6c57CyZA0ZIzfsVK3tCvut0YGIAR0NBmADMIAQAAAAApAu/fq9iLz4sr2K5FMpS92vvkjXi7BP+vIZhyD73Simvq/ydVXI/nNcBaQG0BwVhArQVhKIhBAAAAACkLq96c8tmJDurpE7dFLr8+8oeNKLDPr+RlaNQ6Q2Sacpd9rbcytUd9rkBfDUKwgRoXWLMDEIAAAAAQKpyP1+p2PP/T6rfI6Owv8JX/EBmfkGHP49Z0E/WGRdJkpzXn5Jft6fDnwPAoSgIE+DgEmMaQgAAAABAavF9X87SN+QseFRyYjKHjFbom9+VkZMXt+e0TjlHRp8SqalBsUV/l++5cXsuABSECWG0bVISbA4AAAAAAI6F7zpy3viH3A9ekeTLOuNC2edfI8Oy4/q8hmEqNPEaKdJJ/tbP5X68KK7PB2Q6CsIEMJlBCAAAAABIMX5jvWIv/1nemo8lOyT7ghtlnzaxbZVcvBk5eQpNvFaSIXfJInmb1yfkeYFMREGYAMwgBAAAAACkEm/XDjU/9wf5Wz+XIp0U+va/yBo4MuE5zN6DZZ12viS/ZalxY13CMwCZgIIwAZhBCAAAAABIFV7VOsWe+4O0t0ZG914KX/FDmT36BJbHOn2SjMJiqWGfnNeelu97gWUB0hUFYQK0Tr72KAgBAAAAAEnMXfW+Yv/8q9TcJLN4mEKX/auMvC6BZjJMS6FJ10tZEXmb1shd9nageYB0REGYAIbZOoMw4CAAAAAAAByB73ly3nlRzlvPSb4n69RzZV94k4xQVtDRJElGXhfZ510lSXI/nCdv+8aAEwHphYIwAVpnELLEGAAAAACQbPzmJjnzZ8td8Y5kWrLPu0r22ItlGMlVGVjFw2SNHCd5nmKvPiF/f2PQkYC0kVz/29PUwXMQBhwEAAAAAIAv8PfVKvb8H+VtXCNlRRS69DuyThoTdKyvZI29WEa0t7Rvl5w35zIRB+ggFIQJcHAXY75wAQAAAACSg7etUs1zH5Jfu11G1x4KX/EDmUUDg451VIZlK1R6gxTKklexXN5nHwQdCUgLFIQJ0DaDMOAcAAAAAABIkrvuE8VefFhqqpfRZ4hCl39fRpfuQcdqF6NLd9kTpkiSnHdfklezNeBEQOqjIEwA40BB6HlUhAAAAACA4Pi+J2fxAjmLnpQ8V+awsxSafJuMrJygox0Ta/ApMoeeIbmOnLLH5ceag44EpDQKwgRoXWJMPQgAAAAACIofa5ZT9oTcJYskw5A97luyx18mw7KCjnZc7LO/JaNbgfzdO+W8/XzQcYCURkGYAAc3KaEiBAAAAAAknl+/V7EXH5ZXsVwKZcmefJusEePaVrylIiMUll16g2SH5K39WO7aT4KOBKQsCsIEaJtBSD8IAAAAAEgwr3qLmp99SP7OKqlTN4Uuv0NWv5OCjtUhzPwC2Wd/S5LkvPWsvN07A04EpCY7np981qxZqqio0IABAzR16tS26x966CFt3rxZ4XBYpaWlGj9+fDxjBK7tHIQ0hAAAAACABHI3rJTz6pOS0yyjoL9CF90sIycv6Fgdyhx6hszN6+Wt/1RO2eMtG67YoaBjASklbgVhRUWFmpqaNH36dD3yyCMqLy/X4MGD226/8847VVhYGK+nTyomMwgBAAAAAAnk+77cT9+U+8E8Sb7MIaNlT5iSlsWZYRiyJ1yh5p2b5NdslfP+PxUaf1nQsYCUErclxuvWrdOoUaMkSSNHjtTatWvbbjMMQw8++KBmzpypnTvTf/ovMwgBAAAAAIniu46cN56R+8ErknxZZ1wo+/xr0rIcbGWEsxUqvUEyLXkr35P7+YqgIwEpJW4zCOvr61VQUCBJikQiqqqqarvtlltuUV5enlavXq05c+bopz/96ZceX1ZWprKyMknSzJkzFY1G4xU17qobW/62bTulX0e64DgkD45F8uBYJAeOQ/LgWAAAUpXfVK/Ygkflb/1cskOyz79G1sCRQcdKCLNHH1ljJ8t972U5r/9DZrS3jE7dgo4FpIS4FYSRSEQNDQ2SpMbGRkUikbbb8vJazncwdOhQPfbYY0d8fGlpqUpLS9suV1dXxytq3O3ds1eS1NwcS+nXkS6i0SjHIUlwLJIHxyI5cBySRzoci6KioqAjAAASzNu1Q7F5s6W9NVKkk0KTb5XZo0/QsRLKGjle/ub18jauVuzVJxT61r/IsKygYwFJL25LjEtKSrRiRcuU3uXLl6ukpKTtttbicMuWLcrNzY1XhKRhmCwxBgAAAADEj1e1TrHn/iDtrZHRvZfCV/ww48pB6cD5CM+7WsrtLH/7RrkfLQw6EpAS4jaDcODAgQqFQpo2bZqKi4sVjUY1d+5cTZkyRb/73e9UX18vwzB0++23xytC0jiwRwmblAAAAAAAOpy76n05b78g+Z7M4mGyJ14rI5QVdKzAGDm5Ck26XrEXH5a79HWZRQNl9i35+gcCGSxuBaEkTZ069ZDLU6ZMkSTdfffd8XzapGMe2KTEpyEEAAAAAHQQ3/Pkvvey3BXvSJKsU86VNfYiGUbcFgumDLPXAFmnl8r9aKFirz2l8FV3yYh0CjoWkLT4qpEAB/pBefSDAAAAAIAO4Dc3yZk/u6UcNC3Z514l+6yLKQe/wBp9voyiQVJjnWKLnpTve0FHApIWXzkSoG0GoWgIAQAAAAAnxt9Xq9jzf5S3cY2UFVHo0u/IGjom6FhJxzBNhSZeK2Xnyt9cLveTN4KOBCQtCsIEYAYhAAAAAKAjeNsq1Tz3Ifm122V07aHwFd+XWTQw6FhJy8jtrND510iS3I8Wytu2IdhAQJKiIEwAzkEIAAAAADhR7rqlir30iNRUL6P3YIUuv0NGl2jQsZKe2e8kWaecK/meYq8+Ib+pIehIQNKhIEyA1hmEFIQAAAAAgGPl+56cxQvkLPq75Doyh41V6OKpMrIiQUdLGdYZF8ro2U+q2yPn9af5+Rw4DAVhAhhtMwgDDgIAABCA2tpa/cd//IduvPFGua57yG0bN27UPffco3vuuUeVlZUBJQSA5OU7MTllf5e7ZJFkGLLO/pbs8ZfLsKygo6UUw7IUKr1OCmfLq/xM7op3g44EJBUKwgQ4eA5CGkIAAJB58vLydM8992jIkCFfuu3JJ5/UXXfdpR//+Md68sknA0gHAMnLr9+r2IsPy6tYJoWyZE++TfbIcW2TUHBsjE75ss+9SpLkvv9PeTs3B5wISB4UhAlgMoMQAABksHA4rLy8vCPeVl9fr2g0qvz8fNXX1yc4GQAkL696i5qffUj+jk1SXleFLr9DVr+Tgo6V8qyBI2QOO0vyXDllj8tv3h90JCAp2EEHyATMIAQAADiy9pwDqqysTGVlZZKkmTNnKhpN7RPy27ad8q8hCIzbsWPMjk8yjFvj2qXa9cIjUmy/wn0GKf+qH8jK7RxopqNJhjE7Fv63btWO6io5O6pkffhPdbvs9kBmZabauCUDxix+KAgTgBmEAAAAX++rfjgrLS1VaWlp2+Xq6upERYqLaDSa8q8hCIzbsWPMjk+Q4+b7vtxlb8l9/xVJvszBp0rnXqldjc1SY/Iey1T8t2acd4009/dqXPmBYtE+soaekfAMqThuQWPMjk9RUdHX3oclxglgqLUgpCEEAAD4ory8PNXU1Ki2tlY5OTlBxwGAwPiuI+fNZ+S+/09JvqwzLpA98VoZdijoaGnJ7NZT9vjLJUnOOy/I27U92EBAwCgIE8A4MMoe/SAAAMhAjuNoxowZqqys1H333adVq1Zp7ty5kqRrrrlGv/3tb/Wb3/xG1157bcBJASAYflO9Yi//Wd7qjyTLll16g+zTJrEZSZxZJ50uc8hoyYm1nI/QiQUdCQgMS4wTwGQGIQAAyGC2beuee+455Lphw4ZJkvr3768ZM2YEEQsAkoK3e6ecV2bJ31sjRTopdNEtMnv2DTpWxrDPuVyxHZvk126X8+6LCk2YEnQkIBDMIEyA1l/6UA8CAAAAAFp5VeWKPfuQ/L01Mrr3UviKH1AOJpgRypJdeoNk2fI++1Du+mVBRwICQUGYAK3Twj3WGAMAAAAAJLmrPlDsn3+RmptkFg9T6LJ/lZHXNehYGcmMFsk+61JJkvPmMy2zOYEMQ0GYACYzCAEAAAAAknzPk/Pui3LeelbyPVmnnCv7wptkhLKCjpbRzOFnySweLjXvV6zsCfmuE3QkIKEoCBOgbQYh5yAEAAAAgIzlNzfJmT9H7vJ3JNOSfe5Vss+6WIbBj+ZBMwxD9nlXSnld5e+skvvhvKAjAQnFV6EEMA02KQEAAACATObvq1Xs+T/K27hayooodOl3ZA0dE3QsfIGRFVFo0vWSYcpd9rbcytVHvb/fWCfn0zflbauU73sJSgnEB7sYJ0DbJiX0gwAAAACQcbxtlYot+JvUWCejaw+FJt8qo0s06Fg4ArOwv6wzL5T7wTw5rz8l86q7ZOR2OeJ93VUfyP1ooVxJyu0ia8AImYNGyijox6xQpBwKwgQwmEEIAAAAABnJXbdUzhv/kFxHRu/BCl1wg4ysSNCxcBTWKRPkba6QX7VWsVf/rtA3vyvD/HLhZ+QXHLxQv0fuinfkrnhHyu3cUhYOHCWjkLIQqYGCMAFaZxCyiTEAAAAAZAbf9+R+VCZ3ySJJknnyWNnjvi3DsgJOhq9jGKZCE69R8z8ekL/1c7lLXpU95oIv3c8sGiQdKP9Cl0yVt2mt3IrlUt1uuSvelbviXSnSWdbAETIHjpRR2J+yEEmLgjABWs9BKLXMIjS+cBkAAAAAkF58JybntaflVSyTDEPWNy6VNWIcPwumECMnT6Hzr1Xs5T/LXbJIZtHAlkLwi/fJypHRs6/87ZXynZjsb1wq66xL5O+skrd+udyKZYeVhZ1kDhgha+BIGYXFwbww4CtQECaIYbScg9DzJYv3BAAAAABIS37DPsXmz5G/Y5MUypJder2sfkODjoXjYPYZLGv0eXI/eU2xV/+u8FV3ycjJO+w+Q+Rur5RXtU5W8TAZhiGjZ1+ZPfvKOuvilrKwYnnLzMJ9u+StfE/eyvekSCftPnmMvKLBMgoHHHEJM5BIFIQJYhqGXN8/cB5CGkIAAAAASDdezRbF5s2W6vZIeV0VmnybzO6FQcfCCbDGlMrb+rn8bRvkvPa07ItvPWSZsNlniNyPy+RXrfvSYw8pC8deLL9684GZhculfbWq//g16ePXpJy8gzMLe1EWIhgUhAnSMpXcZydjAAAAAEhD7oZVcl79u+Q0yyjop9BFt3xpthlSj2FaCk26Ts3/+J28TWvkLntb9ikTDt7es48Uzpa/p1r+vloZnfKP/HkMQ0aPPjJ79JE1drL86i3K2lauuhUfSntr5K16X96q9w+UhcO/UBYm7zkrfd+Xv2OT3DUfSfsbZU+YIiMrJ+hYOE4UhAlispMxAAAAAKQd3/flLntL7vuvSPJlDj5V9rlXyrBDQUdDBzHyuso+7yo58+fI/XCezMJimQX9Wm4zLZm9B8n7fKW8qnJZJ5/59Z/PMGT06K0uJ5+i5hET5Ndskbd+ubyK5fL31shb9YG8VR9I2bkHZhaOkFE0MGnKQr9hn9x1n8hb85H8XTvarndCWQqdd1WAyXAiKAgTxGzbyZiCEAAAAADSge86ct5+Tt7qjyRJ1hkXyBo9kc1I0pBVPEz+iHFyV7yj2KtPKHzlnW2z5cw+JQcKwnXtKgi/yDAMGdHeMqO95Z95kfyarfIqDpSFe6rlffaBvM8OlIXFw2UNGhlIWeh7rryNa+St+UjextWS57XckJMnc+BIeZ992HLb4FNk9hmS0GzoGBSECWIcaAipBwEAAAAg9flNDYotfFT+lgrJsmWff42sQaOCjoU4ss66WN62DfKrN8t5c67s0htkGEZbIeZVrZPvecd9DsGWsrBIZrRI/hkXyq/denBm4Z5qeas/lLf6Qyk70lIWDhwpo2iQDCt+ZaG3e6e8NR/JXbtEath3IKgps//JMk8aI7PfUBmWJSfSWe7i+Yq9OVfhq38sIxSOWybEBwVhgrQuMfY8KkIAAAAASGXe7p1y5s2Wv6dainRS6KJbZPbsG3QsxJlh2QqVXq/mZ37fMsvvsw9kDTtLRud8GZ27y99bI39nlYwDy49P6LkMQ0b3IpndW8vC7fIqlrWUhbt3ylu9WN7qxVJWROaAYbIGjuqwstCP7Ze3fpncNR/J31Z5MFOXqMyhZ8gaMlpGbudDHmOdMkFexTL5NVvllD0ue+K1nI8wxVAQJkjrFHPqQQAAAABIXV5VuWILH5Wam2R076XQ5Ftl5HUNOhYSxOgSlT3hCjmv/l3Ouy/JKOgvs3svGX2GyF9VI69qXdv5CTvsOQ1DRvdCmd0L5Y+5QP6u7QdnFu7eIW/1Ry3L3LMiMouHyRw4UmbvQTKs9lc+vu/L314pd/VH8tYvk5zmlhvssMxBo2QNHSOjoP9XLp83LEv2+Vcr9sLD8jauVvPcBxW64EaZ0aKOGAIkAAVhgnAOQgAAAABIbe6qD+S887zkeTL7nyx70nUyQllBx0KCWYNPlbe5XN7qj+SUPa7QlB/J7DOkZSfiqnXS6ZPi9tyGYcjIL5SZXyidcYG8L84s3LWj5TyAaz6SsnJk9h8mc9BImb0Hf2VZ6NfvlbtuibzVH7XMiG19nsJiWSeNkTloZLv/jZvdixSe8qOWpfc1WxV77g+yx18ma+gZX/kY33Olxnop0olzdwaMgjBBDu5iHHAQAAAAAMAx8T1P7vv/lLv8bUktyymtMycf97nmkPrss7+t2PaN8nftkPP287LP/pZkmPK3b5Tf3CQjnJ2QHGZ+gcz8C6QxF8j74szCXdvlrf1Y3tqPpXD2gZmFo2T2GSzJkLdx9YENR9ZI/oENRyKdZJWc1nJuwa49jiuP0aW7Qpd/X847L8hbvVjOG8/I21Ype/xlkmVLdbvk7aiSv2Njy9/VmyUnJqN7L1nDxsocPFpGmNI9CBSECdK2xJiGEAAAAABSht+8X86rT7Ts3Gqass+54qgzopAZjFBYdukNis19sKWI6z1YRkFf+dsq5W1ZL6t4eMIzmd0KZI4pkMaUytu14+DMwtrt8tYukbd2iRTOlkxLaqo/8CBTZv/hMoeOkdm3pEN2RzbskELnXim3sL+ct56Tt+YjNW9ZLzkxqbHuyw+wQy3nLnzrOen9f8ocMlrWsLNkdu91wlnQfhSECcIMQgAAAABILf6+XYrNmy2/dpuUFVHowhtlFg0KOhaShJlfKHvct+W8OVfOW8/KLB4mX5XyNq0LpCA8JFu3njJPL5VOP1AWfr5c3vrlLf+WJRndeso8aYysktNk5OTFJYN10hgZ0SI5Cx6Tv7em5crsiMwefWX07COjZz+ZPfpI4Sx5n6+Qu/J9+ds2yFv1gbxVH8go6NdSFA4Ywa7ICUBBmCAG5yAEAAAAgJThbd+o2Pw5UmOdjK49WjYj6RINOhaSjDn0DJmby+WtXybv8xWSJL9qXcCpDmV26ymz2yTptEny9lS3LOnNL0zIOf/M7kUKXXWn/O0bZXTOlzrlH/F5rcGntpzbsXa7vM8+kLv2Y/nbN8rZvlF64xkZBf1k9h6k2Knj5JvZnK8wDigIE8RgBiEAAAAApAS3fKmc1/8huY6M3oMVuuAGGVmRoGMhCRmGIfucKWreWSXtrZUk+Xtr5O+tbSnEkowZQMlthLJk9BnSrvua+QUyx31b1pmT5a3/VO5ni+Xv2CR/6+dyt36uHR+Vyejao2Wn5kGjWjZrQYegIEwQ88A2xswgBAAAAIDk5Pu+9r7xvJy3X5QkmSePlT3u2zKsEz8vG9KXkZWt0KTrFXv+/0meK0nyqtbJGjY24GSpywiFZQ09Q9bQM+Tvb5C3pULeprVS5Sp5u3fKXbJI7pJFLUulB45qKQu79Qw6dkqjIEyQ1smv9IMAAAAAkHx8Jybn9afVvH6ZZBiyvnGprBHjWMqIdjF79pU1drLc916WREHYkYysiKwBI2QNGKHu+d/RzmUfyl2/XN6GFfJ37ZD7cZncj8tk5BfIHHSqrJLRMvK6Bh075VAQJkjrDEJ2MQYAAACA5OI37FNs/hz5OzbJCGfJmni9rP5Dg46FFGONHC9/83p5G1fL21wu33M7ZFdgHGSYlsw+Q2T2GSJ//GXyt6yXW7FM3ucr5ddul1s7X+7iBTJ6D5JVchobnBwDCsIEaf2tE0uMAQAAACB5eDVbFJs3W6rbI+V1VY/r/017zOygYyEFGYYh+7yr1Tz3d1JjPUsI48ywLBl9S2T2LZE//nJ5m8vlrV0ib8Mq+ZvL5Wwul959UdZJY2QNO0tGl+5BR05qFIQJYrZuUhJwDgAAAABAC3fDKjmv/l1ymmX07KfQRTcr1LOPVF0ddDSkKCMnV+Grfyztb5BhUbkkimHZsvoNldVvaMs5C9cvl7t6sfydVXKXvSV32dsy+50kc/g3ZPYdIsMwg46cdPjXmiCtBaHnURECAAAAQJB835e7/G257/1Tki9z8Cmyz71Khh0KOhrSgBHOlsLMQg2KkRWRNWysrGFj5e3YJHfle/LWL2tZ+r1xtYyuPWSNPk/moFPZgOgLKAgTxDxQTnMOQgAAAAAIju86ct5+Xt7qxZIka8wFsk6byGYkQBoye/aV2bOv/LMulbtmsdyV78nfvVPOa09LH5XJPuVcmSedzi8HREGYMOaB6atMIAQAAACAYPhNDYotfFT+lgrJsmWff42sQaOCjgUgzoycXNmnnidr5DnyypfKXfp6S1H49nPS0tdlj50sc9ApGf2LAgrCBLFMlhgDAAAAQFC83TvlzJstf0+1lJOn0ORbZfbsG3QsAAlkWJask06XOWS0vA0r5X5cJr92u5xX/y5j+Tuyx307Y78uUBAmiGmyizEAAAAABMHbXK7Ywsek/Y0yuvdS6KJbZXTqGnQsAAExTFPWwJEyi4fLW/uxnMUL5O/YpNhzf5B1yrmyxpRm3CYzmfVqA9S6SYnLDEIAAAAASBj3sw9blhF6nsz+J8uedJ2MUFbQsQAkAcM0ZQ09Q+agUXI/frVlx+Olr8vbtEahybfKyOsadMSEoSBMkNYlxmxSAgAAAADx53ue3A/+KXfZ25Ika9QEWWMny2jdQRIADjBCWbLPukRm8XA5rz0lv2arPpwzW69puOqbpbzcsC4cP1ijTy4KOmrcUBAmyMElxgEHAQAAAIA05zfvl/PqE/I2rpZMU/Y5V8gaekbQsQAkObOwv0JX/ECLn3xKj6/L0T5vX9ttW3bUSVOUtiUhvzpJEJYYAwAAAED8+ft2Kfb8H1vKwayIQpd+h3IQQLsZ2REt2j9Q+7zwIdfvq9+vBW+XB5Qq/phBmCAsMQYAAACA+PK2b1Rs/hypsU5Gl6jsi2+T2SUadCwAKaa+ofmI19d9xfXpgIIwQcwD57lgF2MAAAAA6Hhu+adyXn9ach0ZRYMUuvBGGVmRoGMBSEF5ueEjXx858vXpgIIwQQ5MIGSJMQAAAAB0IN/35X5cJvfjVyVJ5slnyh53mQzLCjgZgFR14fjB2rKjTvvq97dd1yk3SxeOHxxgqviiIEwQZhACAAAAQMfynZic1/8hb/2nkmHIOutSWSPHyThwDngAOB6jTy6SpkgL3i5XXUOz8iLsYowOcvAchAEHAQAAAIA04DfsU2z+HPk7NkmhsOxJN8jqPzToWADSxOiTi9K6EDwcBWGCmCa7GAMAAABAR/Bqtio2b5ZUt0fK66rQ5Ntkdi8MOhYApCwznp981qxZmjZtmv76179+6bbm5mZ997vf1bJly+IZIWmYB6a4s8QYAAAAAI6fu2GVYs/9UarbI6NnP4Wv+AHlIACcoLgVhBUVFWpqatL06dPlOI7Ky8sPuf3VV19Vv3794vX0SefgEmMKQgAAAAA4Vr7vy1n2lpz5f5OcZpmDT1HoW9+VEekUdDQASHlxKwjXrVunUaNGSZJGjhyptWvXtt3mOI7WrVunk046KV5Pn3QOLjEOOAgAAAAApBjfdeS8OVfuey9L8mWNuUD2xOtk2KGgowFAWojbOQjr6+tVUFAgSYpEIqqqqmq77fXXX9c555yjdevWfeXjy8rKVFZWJkmaOXOmotFovKImhG1VS5JycnJS/rWkOtu2OQZJgmORPDgWyYHjkDw4FgCQPPymBsUWPip/S4Vk2bLPu1rW4FOCjgUAaSVuBWEkElFDQ4MkqbGxUZFIRJLkuq6WLl2q//W//tdRC8LS0lKVlpa2Xa6uro5X1ARpWVq8r64+DV5LaotGoxyDJMGxSB4ci+TAcUge6XAsiooyZ9c9AOnL271TzrzZ8vdUSzl5Cl10i8yCzDlVFQAkStyWGJeUlGjFihWSpOXLl6ukpESStGfPHtXU1Oi+++7TW2+9pSeeeEJ1dXXxipE0LLNlqNmkBAAAAAC+nrd5vWLP/UH+nmoZ+YUKX/FDykEAiJO4zSAcOHCgQqGQpk2bpuLiYkWjUc2dO1dTpkzR/fffL0l66qmnNHToUOXl5cUrRtJgF2MAAJDJZs2apYqKCg0YMEBTp05tu/6hhx7S5s2bFQ6HVVpaqvHjxweYEkCycD/7UM7bz0meJ7P/yS3nGwxnBR0LANJW3ApCSYd88ydJU6ZMOeTyNddcE8+nTyqtm5R4HgUhAADILBUVFWpqatL06dP1yCOPqLy8XIMHD267/c4771RhYWGACQEkC9/z5H7witxlb0mSrFHnyBp7sQwzbovfAACKc0GIg6wDMwiZQAgAADLNunXrNGrUKEnSyJEjtXbt2raC0DAMPfjgg8rLy9N3vvMd9ejR40uPT7vN69gE57gwbscu1cbM29+kXc89rObyZZJpqevkG5U7ekLCc6TauCUDxuz4MG7HjjGLHwrCBGmdQegygxAAAGSY+vp6FRQUSGrZyK6qqqrttltuuUV5eXlavXq15syZo5/+9Kdfeny6bV6XDpvgBIFxO3apNGb+vt2KzZslv3ablJWj0AU3qbH3IDUGkD+Vxi1ZMGbHh3E7dozZ8WnP5nXM006QtiXGTCEEAAAZJhKJqKGhQZLU2NioSCTSdlvruaiHDh2q3bt3BxEPQMC87RvV/OyD8mu3yegSVeiKH8jsPSjoWACQUSgIE6R1iTHnIAQAAJmmpKREK1askCQtX75cJSUlbbe1FodbtmxRbm5uIPkABMct/1SxFx+WGutkFA1S6Irvy+zC8kEASDSWGCcIMwgBAECmGjhwoEKhkKZNm6bi4mJFo1HNnTtXU6ZM0e9+9zvV19fLMAzdfvvtQUcFkCC+78v9+FW5H7ecX9Q8+UzZ4y6TYVkBJwOAzERBmCBWW0EYcBAAAIAATJ069ZDLU6ZMkSTdfffdQcQBECDficl54x/yyj+VZMj6xiWyRo6XcWDVFQAg8SgIE8RgiTEAAACADOc37FNs/hz5OzZJobDsSdfL6n9y0LEAIONRECaIZbac7pElxgAAAAAykVezVbF5s6W63VJeV4Um3yqze6+gYwEAREGYMJyDEAAAAECmcis/k/PqE1KsWUbPfgpddLOMSKegYwEADqAgTBCTJcYAAAAAMozv+3KXvy33vX9K8mUOPkX2uVfJsENBRwMAfAEFYYJYzCAEAAAAkEF815Xz9vPyVn8oSbLGlMo6bRKbkQBAEqIgTBCTXYwBAAAAZAi/qUGxhY/J37JesmzZ510ta/ApQccCAHwFCsIEaZtBSEMIAAAAII15u3fKmTdb/p5qKSdPoYtukVnQL+hYAICjoCBMkLZzELLEGAAAAECa8javV2zho9L+Rhn5hQpNvk1Gp65BxwIAfA0KwgRhF2MAAAAA6cz97EM5bz8neZ7M/ifLnnidjHBW0LEAAO1AQZggLDEGAAAAkI58z5P7wStyl70lSbJGnSNr7MUyTDPgZACA9qIgTJCDS4wDDgIAAAAAHcSP7Zfz6t/lVX4mmabs8ZfLOvnMoGMBAI4RBWGCmAd+e8YMQgAAAADpwN+3W7H5s+XXbJWychS64CaZvQcFHQsAcBwoCBOEcxACAAAASBfe9o2KzZ8jNdbJ6BKVPflWmV17BB0LAHCcKAgTxGIXYwAAAABpwC3/VM7rT0uuI6NooEIX3CQjOxJ0LADACaAgTBCTTUoAAAAApDDf9+UueVXuR2WSJHPombLHXybDsgJOBgA4URSECXJwiXHAQQAAAADgGPlOTM4b/5BX/qkkQ9Y3LpE1cryMAyulAACpjYIwQVhiDAAAACAV+Q37FJv/N/k7NkqhsOyJ18kqHhZ0LABAB6IgTBCWGAMAAABINV7NNsXmzZLqdkt5XRWafKvM7r2CjgUA6GAUhAnCLsYAAAAAUolbuVrOq49LsWYZPfsqdNEtMiKdgo4FAIgDCsIEaVtizAxCAAAAAEnM9325y9+W+/4/Jd+XOegU2eddJcMOBR0NABAnZnvudO211+rdd99tu7xkyRLdddddcQuVjkyzZajpBwEAAAAkK9915bz1rNz3XpZ8X9bppbInXUc5CABp7qgzCKurq7Vjxw5JUlVVlVatWiVJWrp0qbZv3x7/dGnEZJMSAAAAAEnM39+g2ILH5G9ZL1m27POuljX4lKBjAQAS4KgF4WuvvaZ//OMfkqRnnnlGzzzzTNttvXv3jm+yNGOxSQkAAACAJOXtqZbzyiz5e6qlnDyFLrpFZkG/oGMBABLkqAXh4MGDdeGFF2rBggUaNWqUevVq2a0qLy9P48ePT0jAdMEmJQAAAACSkbdlvWILHpX2N8rIL1Ro8m0yOnUNOhYAIIGOWhCOHj1ao0eP1qBBgzR8+HD16NFDkuR5Xts59dA+JpuUAAAAAEgy7mcfynn7OcnzZPYbKnvS9TLCWUHHAgAkWLtavk2bNum1115TbW2t7rjjDt18881atGhRvLOlFWYQAgAAAEgWvufJee9lOW/OlTxP1qhzZF90C+UgAGSodhWEb7/9tnJzc/XOO+/IcRz16tVLc+fOjXe2tHKwIJR8SkIAAAAAAfFj++Us+JvcZW9Jpil7whTZ37hUBqvEACBjHXWJcau6ujp16tRJS5cu1YQJE9S/f3/96U9/ine2tGIahgxD8v2WPwdWHAMAACSFH/3oR+rbt6+Ki4vVr18/FRcXq7CwMOhYADqYv2+3YvNny6/ZKmXlKHTBTTJ7Dwo6FgAgYO0qCKPRqJ544gnV1dXpjjvu0O7du5WXlxfvbGnHNAy5vi/P92WKhhAAACSPM844Q47jqGvXrlq2bJkefPBBderUSfn5+erfv7++973vBR0RwAnydmxSbN5sqbFORpeo7Mm3yuzaI+hYAIAk0K6C8MYbb9TTTz+tIUOG6Mwzz9Tjjz+usWPHxjtb2jENQ658zkMIAACSzrJly/Tf//3fbZfPP/98ffjhh5o8ebIqKysDTAagI7jrl8l57SnJdWQUDVTogptkZEeCjgUASBLtKgjPPPNMnX766dq6dau2bdumm266iV2Mj4NpGpLLTsYAACD5dOrUSRs2bFBxcbEkaciQIXr44Yd14403qnv37sGGA3DcfN+Xu2SR3I8WSpLMoWfIHn+5DMsKOBkAIJm0qyCsqqrSL3/5S23btk2SVFhYqH//939X79694xou3RzYp0T0gwAAINn8y7/8ix588EH16dNHxcXF2rx5s8LhcNCxAJwA34nJWfSkvPKlkgxZ37hE1sjxMjghOgDgMO2aBvjnP/9Zu3bt0rhx4zRu3Djt3r1bf/nLX+KdLe2YB96ImUEIAACSTWFhoaZPn67Ro0dr9+7dKiws1N133x10LADHyW/Yp+pH/7ulHLTDsi+6WfaocygHAQBH1K4ZhBUVFbrhhhs0efJkSdK8efP0xBNPxDVYOjIPTCHkHIQAACAZmaapsWPHcq5pIMV5NdsUmzdLqtst5XVRaPKtMrsXBR0LAJDE2lUQ5uXladmyZRo9erSklpNYs4vxsWubQUhBCAAAACAO3MrVcl59XIo1K1Q0QMakG2REOgUdCwCQ5NpVEE6cOFFPPfWUPv7447brrr322riFSldt5yBkiTEAAACADuT7vtzl78h9/2XJ92UOGqUeV/6ravbsDToaACAFtKsgnDBhgrp06aJly5ZJkk455RSNGjUqrsHS0cElxgEHAQAAAJA2fNeV884L8j77QJJknT5J1umlMkJsNAQAaJ92bVIyY8YMVVdX6yc/+Yl+8pOfaOfOnfr5z38e72xphyXGAAAAADqSv79BsVf+2lIOWrbsSdfJHnMBm5EAAI5Ju2YQ1tbWqmfPnm2Xe/TooZqamriFSlfsYgwAAACgo3h7quW8Mkv+nmopJ0+hi26RWdAv6FgAgBTUroKwoKBAL774ovLz8+X7vl566SUVFBTEO1vaaV1i7FIQAgAAADgB3pb1ii14VNrfKCO/UKHJt8ro1C3oWACAFNWugvCyyy7TQw89pPvvv7/tuh/+8IdxC5WuLApCAAAAACfIXb1YzlvPSp4ns99Q2ZOulxHOCjoWACCFtXuTkmg0qiVLlkiSTjvtNA0bNiyuwdKRbbWc8tHxvICTAAAAAEg1vufJ/WCe3GVvSpKsUeNljb1EhtmuU8sDAPCV2lUQStKwYcMoBU+QfWAGoeMygxAAAABA+/mx/XJe/bu8ys8k05Q9/nJZJ58ZdCwAQJpod0GIE9c6g9BlBiEAAACAdvLrdis2b7b8mq1SOFuhC2+S2Xtw0LEAAGmEgjCBLGYQAgAAADgG3o5Nis2fIzXsk9ElKnvyrTK79gg6FgAgzVAQJpBttW5SwgxCAAAAAEfnrl8m57WnJNeRUTRQoQtukpEdCToWACANURAmkHXg5MHMIAQAAADwVXzfl7tkkdyPFkqSzKFnyB5/mQyLH98AAPHBO0wCMYMQAAAAwNH4TkzOG8/IK18qyZD1jUtkjRwvwzCCjgYASGMUhAnEDEIAAJCpZs2apYqKCg0YMEBTp05tu37jxo165JFHJEm33367+vfvH1REIHB+Y51i8+fI375RssOyJ10nq3hY0LEAABnADDpAJmmdQegwgxAAAGSQiooKNTU1afr06XIcR+Xl5W23Pfnkk7rrrrv04x//WE8++WSAKYFgebXb1Dz3wZZyMK+LQpf/K+UgACBhmEGYQPaBGYSuxwxCAACQOdatW6dRo0ZJkkaOHKm1a9dq8ODBkqT6+npFo9G2j4FM5G5cLafsCSm2X0bPvgpddIuMSKegYwEAMkhcC8KvWkry17/+VRs2bFAsFtMtt9yioUOHxjNG0rBaZxC6zCAEAACZo76+XgUFBZKkSCSiqqqqttt8/+t/cVpWVqaysjJJ0syZM9sKxVRl23bKv4YgpOO4+b6v+sWvak/Zk5LvK+fkMer2rf9PRijcIZ8/HccsERi3Y8eYHR/G7dgxZvETt4Lwi0tJHnnkEZWXl7f9pvjmm2+WbdvauXOn/ud//kf/5//8n3jFSCo25yAEAAAZKBKJqKGhQZLU2NioSCRyxPt91SYMpaWlKi0tbbtcXV3d8SETKBqNpvxrCEK6jZvvunLefUHeqg8kSdZpk+SOmaSaPXs77DnSbcwShXE7dozZ8WHcjh1jdnyKioq+9j5xOwfhkZaStLLtll6yqakpo05EbZmtuxhTEAIAgMxRUlKiFStWSJKWL1+ukpKSttvy8vJUU1Oj2tpa5eTkBBURSCh/f4Nir/y1pRy0bNkTr5N9xgUyDE4RDwAIRtxmEB5tKYkk/fKXv1R5ebl+9KMfHfHx6biUpGvnlvOI2OFwyr+eVMaU5OTBsUgeHIvkwHFIHhyLjjVw4ECFQiFNmzZNxcXFikajmjt3rqZMmaJrrrlGv/3tbyVJ3/nOd4INCiSAv6dasXmz5e/eKeXkKXThzTILM2fSBAAgOcWtIPy6pST/+3//b9XU1OjXv/617rvvvi89Ph2XkjQ1tYxHXX1jyr+eVMaU5OTBsUgeHIvkwHFIHulwLNqzlCSRvng+akmaMmWKJKl///6aMWNGEJGAhPO2VCi24FFpf4OM/AKFJt8mo1O3oGMBABC/JcZHW0oSi8UkSdnZ2crKyopXhKRz8ByEbFICAAAAZBJ39WLFXv6ztL9BZr+hCl32fcpBAEDSiNsMwqMtJfnNb36jhoYGeZ6nG264IV4Rkg7nIAQAAAAyi+95cj+cJ/fTNyVJ1sjxss66RIbJ+QYBAMkjbgWh9NVLSf793/89nk+btGyLGYQAAABApvBj++UselLehlWSacoed5msYWODjgUAwJfEtSDEoWyLGYQAAABAJvDrdrdsRlKzVQpnK3TBTTL7DA46FgAAR0RBmECtS4wdjxmEAAAAQLrydmxSbP4cqWGfjM7dZV98m8yuPYKOBQDAV6IgTKDWTUpclxmEAAAAQDpy1y+T89pTkuvIKBqo0AU3ysjODToWAABHRUGYQK1LjDkHIQAAAJBefN+X+8kiuYsXSpLMoWNkj79chsWPXACA5Me7VQJZB2YQOpyDEAAAAEgbvhOT88Yz8sqXSjJknXWxrFHnyDCMoKMBANAuFIQJdHCTEmYQAgAAAOnAb6xTbP4c+ds3SnZY9qTrZBUPCzoWAADHhIIwgdpmEHIOQgAAACDlebXbFHtlllS3W8rrotDkW2V2Lwo6FgAAx4yCMIE4ByEAAACQHtyNq+WUPSHF9svo2Vehi26REekUdCwAAI4LBWECte1izDkIAQAAgJTk+77cFe/Kfe8lyfdlDhwl+/yrZdihoKMBAHDcKAgTyGqdQUhBCAAAAKQc33XlvPuCvFUfSJKs0ybJGjNJhmEGnAwAgBNDQZhAttV6DkKWGAMAAACpxN/fqNjCx+RvLpcsW/a5V8kacmrQsQAA6BAUhAlkma27GPvyfV+GYQScCAAAAMDX8fdUKzZvtvzdO6WcPIUuvFlmYf+gYwEA0GEoCBPINAyZhiHP9+V6ftumJQAAAACSk7elQrEFj0r7G2TkFyg0+TYZnboFHQsAgA5FQZhgtmWo2fHleL5sK+g0AAAAAL6Ku/ojOW89K3muzH4nyZ50vYxwdtCxAADocBSECda2zNj1pBANIQAAAJBsfN+T+8F8uZ++IUmyRo6TddalMkw2IwEApCcKwgRr2ajEZSdjAAAAIAn5sf1yFj0pb8MqyTBlj79M1rCxQccCACCuKAgTzP7iDEIAAAAAScOv26PYvFnya7ZK4WyFLrhRZp8hQccCACDuKAgTzLJaliUwgxAAAABIHt6OTYrNnyM17JPRubvsi2+T2bVH0LEAAEgICsIEsw8UhDFmEAIAAABJwV2/TM5rT0muI6PXAIUuvElGdm7QsQAASBgKwgQLtxaEDgUhAAAAECTf9+V+skju4oWSJPOkMbLPuVyGxY9JAIDMwjtfgoXtloKwmYIQAAAACIzvxOS88Yy88qWSDFlnXSxr1DkyDCPoaAAAJBwFYYKF7NYZhG7ASQAAAIDM5DfWKTb/b/K3V0p2WPak62QVDws6FgAAgaEgTLCwbUliBiEAAAAQBK92m2LzZkv7dkm5XRSafKvMaFHQsQAACBQFYYK1LjFmkxIAAAAgsdyNa+SUPS7F9svo0Uehi26Rkds56FgAAASOgjDBQhbnIAQAAAASyfd9uSvelfveS5Lvyxw4Svb5V8uwQ0FHAwAgKVAQJlg41FoQcg5CAAAAIN5815Xz7gvyVn0gSbJOmyRrzCQZhhlwMgAAkgcFYYKFrJZzEMaYQQgAAADElb+/UbGyx+VXrZMsW/a5V8oaMjroWAAAJB0KwgRrPQchS4wBAACA+PH31Cg2b5b83TulnDyFLrxZZmH/oGMBAJCUKAgT7GBByBJjAAAAIB68LRWKLXxUamqQkV+g0ORbZXTKDzoWAABJi4IwwcL2gSXG7GIMAAAAdDh3zUdy3nxW8lyZ/U6SPel6GeHsoGMBAJDUKAgTLMQSYwAAAKDD+b4n98P5cpe+IUmyRo6TddalMkw2IwEA4OtQECZY6xJjNikBAAAAOoYfa5az6O/yNqySDFP2+MtkDRsbdCwAAFIGBWGCcQ5CAAAAoOP4dXsUmz9bfvUWKZyt0AU3yuwzJOhYAACkFArCBAtZLecgZIkxAAAAcGK8nVWKzZstNeyTOndXaPKtMrv1DDoWAAAph4IwwcKcgxAAAAA4YW7FcjmvPSU5MRm9Bih04U0ysnODjgUAQEqiIEywg+cgZIkxAAAAcKx835f7yWtyFy+QJJknjZF9zuUyLH60AQDgePEummBh+8ASY5cZhAAAAMCx8F1HzhvPyFv3iSRD1tjJsk6ZIMMwgo4GAEBKoyBMsBBLjAEAAIBj5tbvVezFR+Rvr5TskOxJ18kqHh50LAAA0gIFYYKF2pYYe/J9n992AgAAAF/Dq92unQv+Jn9PtZTbRaHJt8iM9g46FgAAaYOCMMFMw5BtGXJcXzHXa1tyDAAAAODLvI1rFCt7XIrtl9Gjj0IX3SIjt3PQsQAASCsUhAEI25Yc11HMoSAEAAAAjsT3fXkr35Xz7kuS7yvn5DFyv/FtGaFw0NEAAEg7ZtABMlGY8xACAAAAX8l3XTlvPy/nnRcl35d12kR1u+J7lIMAAMQJMwgDcLAgdANOAgAAACQXf3+jYmWPy69aJ5mW7POukjVktAyDuQ0AAMQLBWEAskMtw97YTEEIAAAAtPL31Cg2b5b83Tul7FyFLrpFZmH/oGMBAJD2KAgDkJPVct7BxmYn4CQAAABAcvC2VCi28FGpqUFGtwKFLr5VRqf8oGMBAJARKAgDkBNmBiEAAADQyl3zkZw3n5U8V2bfk2SXXi8jnB10LAAAMgYFYQDaCsL9zCAEAADprbGxUQ888IDq6+tVWlqqc88995Db77rrLnXr1k2SdPvtt6tPnz5BxERAfN+T++ECuUtflyRZI8bJ+sYlMkwr2GAAAGQYCsIA5IRZYgwAADLDq6++qnHjxmncuHH62c9+pnHjxsm2D34L2rlzZ917773BBURg/FiznEVPytuwUjJM2eO/LWvYWUHHAgAgI7EVWABYYgwAADLF2rVrNWrUKJmmqf79+2vz5s2H3F5XV6f/+q//0sMPP6zm5uaAUiLR/Po9ir3w/1rKwXC2QpdMpRwEACBAzCAMwMGCkBmEAAAgvTU0NCgnJ0eSFIlEVF9ff8jtM2bMUF5enubOnauysjJdcsklX/ocZWVlKisrkyTNnDlT0Wg0/sHjyLbtlH8NJ6J5ywbVPPcH+XV7ZHXroe7X3KlQtNfXPi7Tx+14MGbHh3E7dozZ8WHcjh1jFj8UhAFgF2MAAJBudu/erd/+9reHXNe1a1dFIhE1NjYqHA6roaFBubm5h9wnLy9PknTmmWfq5ZdfPuLnLi0tVWlpadvl6urqjg2fYNFoNOVfw/FyK5bLee0pyYnJ6DVA1oU3aY9CUjvGI5PH7XgxZseHcTt2jNnxYdyOHWN2fIqKir72PhSEAWCJMQAASDddu3Y94rkEX3rpJS1fvlxnn322Kisr1bt377bbHMeR7/sKhUJas2aNCgoKEpgYieT7vtxPXpe7eL4kyTxpjOxzLpdh8eMIAADJgHfkALQWhA3sYgwAANLcxIkT9bvf/U7z5s1TaWmpbNvW0qVL5XmeBg4cqPvvv1/Z2dnKzc3Vj370o6DjIg5815HzxjPy1n0iyZA1drKsUybIMIygowEAgAMoCAPQuotxE0uMAQBAmotEIrr77rsPue7UU09t+/gXv/hFghMhkfzGOsUW/E3+tkrJDsmeeJ2sAcODjgUAAA5DQRgAlhgDAAAg3Xm12xWbN1vaVyvldlZo8q0yo72//oEAACDhKAgDkB22ZEhqirnyPF+myfIKAAAApA9v4xrFXn1cat4vo0cfhS66RUZu56BjAQCArxDXgnDWrFmqqKjQgAEDNHXq1LbrH374YW3atEmSdPvtt6t///7xjJF0TMNQVshSU8xVU8xVJIueFgAAAOnBXfGunHdflHxf5sCRss+7WkYoHHQsAABwFGa8PnFFRYWampo0ffp0OY6j8vLyttsuv/xyzZgxQ9///vf19NNPxytCUsvJYqMSAAAApA/fcxV76zk577wg+b6s0ybKLr2echAAgBQQt4Jw3bp1GjVqlCRp5MiRWrt2bdttPXv2lCRZliXTjFuEpJZ3oCCsa4oFnAQAAAA4Mf7+RsVemSVv1fuSack+/1rZZ1wow8jM7/UBAEg1cVvbWl9fr4KCAkktu9dVVVV96T6PP/64LrnkkiM+vqysTGVlZZKkmTNnKhqNxitqQti2fchryO+Sq0019TJC2Sn/2lLN4ccCweFYJA+ORXLgOCQPjgXQfv6eGsXmzZK/e6eUnavQRTfLLCwOOhYAADgGcSsII5GIGhoaJEmNjY2KRCKH3P7yyy+rT58+Gjp06BEfX1paqtLS0rbL1dXV8YqaENFo9JDXkGW1/L1lR636dwsFlCozHX4sEByORfLgWCQHjkPySIdjUVRUFHQEZABv6+eKLfib1NQgo1uBQhffKqNTftCxAADAMYrbnP+SkhKtWLFCkrR8+XKVlJS03fbpp59qzZo1uvLKK+P19EmvU3ZLKbivkSXGAAAASD3umo8Ue+l/pKYGmX1PUujyOygHAQBIUXErCAcOHKhQKKRp06bJNE1Fo1HNnTtXkvSXv/xFO3fu1M9+9jM9/PDD8YqQ1DrltBaEzQEnAQAAANrP9z05H8yT8/o/JM+VNeJs2ZNvkRHODjoaAAA4TnFbYixJU6dOPeTylClTJEkPPPBAPJ82JeQdKAjZpAQAAACpwo81y1n0pLwNKyXDlD3u27KGnxV0LAAAcILiWhDiq7HEGAAAAKnEr9+j2LzZ8qu3SOFshS64UWafIUHHAgAAHYCCMCAHlxhTEAIAACC5eTurFJs3R2rYK3XurtDkW2V26xl0LAAA0EEoCAPCEmMAAACkArdihZzXnpScmIxeAxS68CYZ2blBxwIAAB2IgjAg2SFLtmWo2fG0P+YqK2QFHQkAAABo4/u+3KWvy/1wviTJPOl02edcIcPiRwgAANIN7+4BMQxDnXLC2lW3X3sbm9UjlBN0JAAAAECS5LuOnDfnylu7RJIha+xkWadMkGEYQUcDAABxQEEYoG65LQXh7vpm9ehMQQgAAIDg+Y11ii14VP62DZIdkj3xOlkDhgcdCwAAxBEFYYC65mZJ2qdddfuDjgIAAADI27VdsVdmS/tqpdzOLZuRRHsHHQsAAMQZBWGA8vOyJImCEAAAAIHzNq1VrOwxqXm/jB59FLroFhm5nYOOBQAAEoCCMEDdDhSEtRSEAAAACJC74l05774o+b7MgSNln3e1jFA46FgAACBBKAgDxAxCAAAABMn3XDnvviRv5XuSJOu0ibLGlMowzICTAQCARKIgDFDrDMJd9RSEAAAASCx/f5NiZY/Jr1onmZbsc6+UVXJa0LEAAEAAKAgD1CUSlmFIexqa5biebIvf1AIAACD+/L01ir0yW/7uHVJ2rkIX3SyzsDjoWAAAICAUhAGyLVNdImHtrm/W7vpmRTtnBx0JAAAAac7b+rliC/4mNTXI6NZTocm3yeicH3QsAAAQIArCgEU7Z2t3fbN27GmkIAQAAEBcuWs+lvPmXMlzZfQtUWjSDTKy+B4UAIBMx5rWgBV0yZEk7djTGHASAAAApCvf9+R8ME/O609LnitrxNkKTb6VchAAAEhiBmHgelIQAgAAII78WLOc156U9/lKyTBlj/uWrOHfCDoWAABIIhSEAaMgBAAAQLz49XsUmzdHfvVmKZyt0AU3yuwzJOhYAAAgyVAQBuyLBaHv+zIMI+BEAAAASAfezirF5s2RGvZKnfMVmnybzG49g44FAACSEAVhwDrlhJQdstTY7GpfU0ydc8JBRwIAAECKcytWyHntScmJySgsVujCm2Xk5AYdCwAAJCk2KQmYYRjq1S0iSdpSUx9wGgAAAKQy3/flfPKanIWPSk5MZsnpCn3zdspBAABwVBSESaBP95Zv2DbXNgScBAAAAKnKdx05rz8t98P5kgxZYy+Wfd5VMiwWDQEAgKPju4Uk0PtAQVhVUxdwEgAAAKQiv7FesQV/k79tg2SHZE+8VtaAEUHHAgAAKYKCMAn0aSsIWWIMAACAY+Pt2q7YK7OlfbVSbmeFJt8qM9o76FgAACCFUBAmgR6dcxS2Te2ub1ZdU0x52aGgIwEAACAFeJvWKlb2mNS8X0a0t0KTb5WR2znoWAAAIMVwDsIkYJqG+kbzJEkbduwLOA0AAABSgbviPcVemSU175c5cKRC3/4XykEAAHBcKAiTxICenSRJn2+nIAQAAMBX8z1Xsbefl/PO85LvyRp9vuzS62WEwkFHAwAAKYolxkliQEFnSZv1+fa9QUcBAABAkvL3NylW9rj8qrWSack+90pZJacFHQsAAKQ4CsIk0b9HnkxD2lxbr6aYq+yQFXQkAAAAJBF/b41i82bL37VDys5V6KKbZRYWBx0LAACkAZYYJ4mskKW+0Tx5vrR+656g4wAAACCJeFs3qPnZP8jftUNGt54KX/EDykEAANBhKAiTyEm9u0qSVm/eHWgOAAAAJA937ceKvfSI1FQvo2+JQpd9X0bn/KBjAQCANEJBmESGHigI12zZI9/3gw0DAACAQPm+J+eDeXJee1ryXFkjzlZo8q0ysrKDjgYAANIM5yBMIr275yo329auuv3auqtBRfm5QUcCAABAAPxYs5zXnpT3+UrJMGWP+5as4d8IOhYAAEhTzCBMIqZhaES/luUiyytrA04DAACAIPj1exR74U8t5WA4S6GLb6McBAAAcUVBmGRG9W8pCJdV1rDMGAAAIMN4Ozeree5D8qs3S53zFbr8+zL7lgQdCwAApDmWGCeZQYWdFcmytWNPkzbX1qtP97ygIwEAACAB3IoVcl57UnJiMgqLFbrwZhk5nHIGAADEHzMIk4xlmjptYFSStHjdzoDTAAAAIN5835fzyetyFj4qOTGZJacp9M3bKQcBAEDCUBAmoTMG95AkffJ5tZodN+A0AAAAiBffdeS8/rTcD+dJkqyxk2Wfd7UMi4U+AAAgcSgIk1BRfq76RnPV2OxqcTmzCAEAANKR31iv2Ev/I2/tEskOyb7wJtmnnifDMIKOBgAAMgwFYZI6b0SRJOnNlVvlemxWAgAAkE68XTvU/NxD8rdtkCKdFfr2v8oaMCLoWAAAIEOxdiFJjeibr2jnbFXvbdLyyhqdOiAadCQAAIBj9sknn2j27Nnq1KmTZsyY8aXb33rrLc2fP195eXm68847FYlEAkiZWE0VKxV77o9Sc5OMaG+FJt8iI7dL0LEAAEAGYwZhkjJNQ+cO7yVJem3FFnk+swgBAEDqGTJkiH75y18e8TbHcbRw4UL97Gc/04QJE1RWVpbgdInnrnxPNX9/QGpukjlghELf/hfKQQAAEDhmECax0wf10MKlVdpS26BPKqp1+qAeQUcCAAA4Jnl5eV9527Zt29SvXz9ZlqWRI0fqT3/60xHvV1ZW1lYezpw5U9Foaq6siNVs0453XpR8T3lnX6LO510uw+D39e1l23bKHvugMGbHh3E7dozZ8WHcjh1jFj8UhEksZJm6+LR+evKd9Xr5440a3i9f2SEr6FgAAAAdor6+Xjk5OZKkSCSi+vr6I96vtLRUpaWlbZerq6sTkq/j2bLHX6ZO3fLV0GuIampqgw6UUqLRaAof+2AwZseHcTt2jNnxYdyOHWN2fIqKir72PhSESe60QVG9t3a7Nu6sU9mnVfrmmP5BRwIAAPiS3bt367e//e0h13Xt2lX/9m//9pWPiUQiamxslCQ1NjYqNzc3jgmTgzVsrCLRqBr44QYAACQRCsIkZxqGLj+zWL9/eYXeWrVVI/vnq3+PTkHHAgAAOETXrl117733HtNjevXqpU2bNsnzPC1btkxDhgyJTzgAAAAcFSc9SQF9o3k6Z1gveb70+Jvlamx2go4EAADQLuvXr9eMGTO0adMmzZgxQ83NzVq6dKmWLFki27Y1adIkTZs2TW+88YYuuOCCoOMCAABkJGYQpoiLT+ur9dv2anNtvZ55r0I3ThgiwzCCjgUAAHBUgwYN0j333HPIdaeeemrbxxMmTNCECRMSnAoAAABfxAzCFGFbpm6cMFhh29SnG2o1f2lV0JEAAAAAAACQBigIU0iPLjm66dwhMgzp1WWb9d6a7UFHAgAAAAAAQIqjIEwxJ/fppivPGiBJmvv+53p39baAEwEAAAAAACCVURCmoLElBfrmmH6SpGc/2KCyT6vk+37AqQAAAAAAAJCKKAhT1LnDi3TlNwbIkDR/aZUefWOd9sfcoGMBAAAAAAAgxVAQprCzSgp06/klygpZWlZZqwdeWq6NO/cFHQsAAAAAAAAphIIwxQ3vl687Lx2hgi452rm3SQ++slIvLq5UY7MTdDQAAAAAAACkAArCNNCzS47u+tZInTu8l+RLb67aqplzl+qdz7bJ9byg4wEAAAAAACCJURCmiZBl6ptj+utHl47QwIJOatjv6LkPN+gXz36qt1ZtVRPnJwQAAAAAAMAR2EEHQMfqG83Tv140TCs37dI/P96onXub9MLiSi1YWqUxg3vo9EE91Ds/IsMwgo4KAAAAAACAJBDXgnDWrFmqqKjQgAEDNHXq1Lbr586dq/nz5+v888/XddddF88IGckwDI3ol69hfbtp1aZdenPlVn2+Y5/e/myb3v5smwq65mhU/+4a1rerivJzZVIWAgAAAAAAZKy4FYQVFRVqamrS9OnT9cgjj6i8vFyDBw+WJE2cOFElJSVasWJFvJ4ekswDReGIfvmqqqnXx+t36pOKam3f3aiFu6u08NMqdcoJaWjvrhrcq4uKe+apW24WswsBAAAAAAAySNwKwnXr1mnUqFGSpJEjR2rt2rVtBWHXrl21efPmeD01jqBP91z16Z6rb47pp7Vb9mjVpl1avXm3dtc3a3H5Ti0u3ylJ6pwTUnHPTurdPVe9ukVU2DWirrlhSkMAAAAAAIA0FbeCsL6+XgUFBZKkSCSiqqqqY3p8WVmZysrKJEkzZ85UNBrt8IyJZNt20ryGgp49dc6pku/7qqrep+Wf79DazbUq37JLextjWlZZq2WVtW33z8my1ad7JxV0y1W0S0Q9DvyJdomoS25Wyi1RTqZjkek4FsmDY5EcOA7Jg2MBAACATBK3gjASiaihoUGS1NjYqEgkckyPLy0tVWlpadvl6urqDs2XaNFoNClfQ44hnTmwq84c2FWe72vnniZV7tynrbsatG1Xg7bualD9fkfrtuzSui27vvR42zTUKSekTjlh5eWE1Ck7pE45obaPc7Js5YQtZYcO/B22ZZnBForJeiwyEccieXAskgPHIXmkw7EoKioKOgIAAABSRNwKwpKSEpWVlenss8/W8uXLdd5558XrqdBBTMNQQdccFXTNabvO933ta4pp265G1dY1qXbfftXW7VftvibV1u1X/X5Hu+qbtau+ud3PE7ZN5YRtZYcshWxTYdtUyDYVsqy2j8PWgb9tS7ZlyjKNI/w57HrLlGUYsixDlmHINA2ZhiHDUMsftXxsZzdpX2OzDMOQIck0W/42Dty37TFqfWxqzZAEAAAAAAA4FnErCAcOHKhQKKRp06apuLhY0WhUc+fO1ZQpU7Ro0SLNnz9fdXV1qqur0+233x6vGDhBhmGoc05YnXPCkrp86fbmmKu9jTHVNcW0rzGmfY3N2tcUU11jy+WmmKumZkeNza4amx01xVw1O56anWbtSfzLOW4tkx5bisLD+0LjsA+Mgx986T4H72scfpcjf+7DrvjK50pRpmnK87ygY2ScI3XeHIvkkGzHIbW/wpyYn992ftARAAAAgISJW0EoSVOnTj3k8pQpUyS17GI8ceLEeD41EiQcshQNWYp2zm7X/X3f137HU1Ozo6ZmVzHXU7PjKea4am77+OB1Mbflsuv5cn1frtv694Hr2v4cftmX5/vyfV++3/K83oG/DdOU63oHrjtwu3ToZV/y1fKxJHm+1HKvg38d5VUe32ACAJKGz9dyAAAAZJC4FoTA4QzDUHbIUnbIknKDyXCs55VqLRoltRWGrfzDPvAPKxH9I97X/9JtR/zch13xVc+Vyj/Cds/PV01t7dffER3nK/7B5Ofnq5ZjEbhkOg6p/LWlI+Rlh1XbEHQKAAAAIDEoCIGvYbaexBAdrktutmKN4aBjQFLXvGw5TRyLoHEckocZ8IZaAAAAQCKZQQcAAAAAAAAAEBwKQgAAAAAAACCDURACAAAAAAAAGYyCEAAAAAAAAMhgFIQAAAAAAABABqMgBAAAAAAAADIYBSEAAAAAAACQwSgIAQAAAAAAgAxGQQgAAAAAAABkMApCAAAAAAAAIINREAIAAAAAAAAZjIIQAAAAAAAAyGAUhAAAAAAAAEAGoyAEAAAAAAAAMhgFIQAAAAAAAJDBKAgBAAAAAACADEZBCAAAAAAAAGQwCkIAAAAAAAAgg1EQAgAAAAAAABmMghAAAAAAAADIYBSEAAAAAAAAQAajIAQAAAAAAAAyGAUhAAAAAAAAkMEoCAEAAAAAAIAMRkEIAAAAAAAAZDAKQgAAAAAAACCDURACAAAAAAAAGYyCEAAAAAAAAMhgFIQAAAAAAABABjN83/eDDgEAAAAAAAAgGMwgTJC777476Ag4gGORPDgWyYNjkRw4DsmDY4F44t/X8WHcjh1jdnwYt2PHmB0fxu3YMWbHpz3jRkEIAAAAAAAAZDAKQgAAAAAAACCDURAmSGlpadARcADHInlwLJIHxyI5cBySB8cC8cS/r+PDuB07xuz4MG7HjjE7PozbsWPMjk97xo1NSgAAAAAAAIAMxgxCAAAAAAAAIINREAIAAAAAAAAZzA46QCaYNWuWKioqNGDAAE2dOjXoOGmttrZWv/jFL1RVVaU5c+bIsqwjjn97r8PxWbdunWbPni3DMDRo0CDddttteuGFF7R48WL16NFD3//+92Xbdruvw/HbuHGjHn74YZmmqcLCQt1xxx2aPXs2/ycC9NJLL+mDDz7QjBkz+PoUkB07duj//t//q969e8u2bf3nf/4nX6OQEEf6PgVf70jfV+DojvT+bxhG0LFSxhffq3F0R3pPRfu88cYbeuONN+R5nu68807l5+cHHSnpLV26VM8995wkacuWLbr99tt15plnBhsqye3fv1+//vWvtX//fkUiEf34xz9WKBQ64n2ZQRhnFRUVampq0vTp0+U4jsrLy4OOlNby8vJ0zz33aMiQIZKOPP7tvQ7Hr0ePHpo2bZpmzJihvXv3atWqVVq5cqVmzJihfv36afHixdqzZ0+7rsOJKSoq0s9//nNNnz5dklReXs7/iQDFYjFt2LBBEl+fgjZy5Ejde++9+s///M92fz3iaxRO1OHfp6B9Dv++YuPGjUFHSnqHv/+vX78+4ESp44vv1WifL76non1qa2u1atUqTZs2Tffeey/lYDudeuqpuvfee3XvvfcqGo1q1KhRQUdKekuXLtWQIUN07733avDgwVq6dOlX3peCMM7WrVvX9o925MiRWrt2bcCJ0ls4HFZeXl7b5SONf3uvw/Hr2rWrwuGwJMmyLG3atEnDhg2TJI0aNUpr167V+vXr23UdTswXZzfZtq3ly5fzfyJAixYt0nnnnSeJr09BW7lypaZNm6aXXnqp3V+P+BqFE3X49ylon8O/rzBNfoT5Ooe//0ej0QDTpJYvvlejfb74nor2Wbp0qTzP0/Tp0/WXv/xFnucFHSmlbN++XV26dFF2dnbQUZJeQUGBmpqaJEn19fXq1KnTV96Xd9c4q6+vVyQSkSRFIhE1NDQEnCizHGn823sdTlxlZaX27t2r3Nxc5eTkSGoZ3/r6ejU0NLTrOpy4jz76SD/96U+1Z88eua7L/4mAOI6jlStXasSIEZL4+hSkbt266YEHHtB//dd/afny5aqoqOBrFJACWr+v6NOnT9BRUsIX3/8pptvn8PdqfL3D31MrKyuDjpQS9uzZI8dxNG3aNIXDYVYlHKMPPviApcXt1KtXL61bt04/+clPVFFRoZKSkq+8LwVhnH3xh7nGxsa2H/KQGEca//ZehxNTV1env/zlL7rjjjsUiUTU2NgoSWpoaFBubm67r8OJGzNmjH71q1+pe/fusiyL/xMBefPNNzV+/Pi2y3x9Ck4oFFJ2drYsy9Lpp5+ugoICvkYBSe6L31egfb74/r9kyZKg46SEw9+r8fUOf0/dtGlT0JFSQiQSaVuVMGLECG3evDngRKnl448/1pgxY4KOkRLeeOMNnX766fr1r3+t0aNH66233vrK+1IQxllJSYlWrFghSVq+fPlR21p0vCONf3uvw/FzXVe///3vdfPNN6tr164aNGiQVq1aJallfIcMGdLu63BiYrFY28etM5/4PxGMLVu2aOHChbrvvvtUVVWlffv2cSwC0lrySdLq1atVWFjI1yggiR3+fQW+3uHv/61LtHF0h79Xv/LKK0FHSnqHv6cWFBQEmCZ1nHTSSW2zLTds2KCePXsGnCh17N69W7ZtH3WpLA7yfb9tFnnnzp2PuhqJrffibODAgQqFQpo2bZqKi4s1ePDgoCOlNcdxdP/996uyslL33Xefrr/++iOOf3uvw/F57733VF5erkcffVSSdMMNN+jkk0/WPffco2g0qksvvVS2bbfrOpyYpUuXtp0PplevXvre976n2bNn838iADfddFPbx/fcc4+uvvpq/fWvf+VYBOCzzz7Tk08+qVAopKFDh2rIkCF8jUJCHOn7FIrmr3ek7yv4ZcnRHf7+z4n82+fw9+qLL744wDSp4Ujvqfh6xcXFCofDuvfee9WpUyd985vfDDpSyli8eLHOOOOMoGOkjPHjx+u3v/2t3nzzTVmWpR//+MdfeV/D930/gdkAAAAAAAAAJBGWGAMAAAAAAAAZjIIQAAAAAAAAyGAUhAAAAAAAAEAGoyAEAAAAAAAAMhgFIQAAAAAAAJDBKAgBpKUdO3bommuu0cyZM7VkyRI99dRT2rFjR4c/T1VVlZ566imtXLmy7bqHHnpI11xzjdavX9/hzwcAAAAAQEezgw4AAPHQuXNn3XXXXcrPz9e7776r+fPna/jw4erZs+cxfR7XdWVZ1lfeXlVVpX/84x+SpOHDh0uSLrzwQp166qkqKCg4/hcAAAAAAECCGL7v+0GHAICOtmPHDv3whz9UVlaW9u/ff8htTz31lNauXavZs2dr48aNys/P19VXX63x48e3Pa6kpERZWVnauHGjfvWrX+nnP/+5tm7dKkkaMGCAvvvd7yorK0s//OEPD/nc//Vf/6XXX39db7zxhu6//34NGjRIZWVleuGFF7Rr1y716dNHt956q4YOHarXX39df/jDH3T22Wdr8+bNqq6u1tVXX61LLrlEW7Zs0YMPPqjKykqFw2H17dtX06dPT9j4AQAA4Oh+/etfq0uXLtqwYYNqamp05513auHChSovL9fQoUN1xx13BB0RANqNJcYA0tqwYcN0yimnSJKuvPJK3XXXXaqrq9PMmTPV0NCgKVOmqEePHvr973+vDRs2tD1u7dq1GjBggK699loZhqEzzzxTU6dO1eWXX67KykrNmjVLnTt31iWXXCJJGjt2rO666y716dPnkOdfsWKFHn74YXXu3Fm33HKLqqur9Ytf/EL79u1ru8/KlSs1adIkSdJjjz0mx3E0f/58rV+/XjfddJOuv/56RaPROI8UAAAAjsXGjRtVUFCgGTNmqLS0VH/84x9100036de//rWWLFmiWCwWdEQAaDeWGANIa4ZhqLCwUJ9++qlGjBih4cOHa8mSJaqrq1NdXZ2eeOKJtvuuWLFCZ555pqSWWYI33XSTJKm2tlaffvqp1q5dq9ZJ1xs3blR2draGDh2qf/7zn+rbt6/GjRv3pedfsmSJJOmaa67RqFGjVF1drWeffVbr1q1ru8/555+vyZMn6+OPP9ann36q3bt3q1evXvJ9X5988okGDRrUVkQCAAAgeM3Nzaqvr2/7Hs0wDE2cOFHdunWTJJmmKdvmx20AqYOvWADSnmEYR7x+woQJmjBhQtvlL56fsPWbO0l65ZVXtGbNGl166aUaPXq0/vjHP6qxsbHDsuTl5UlS27kOPc/T5MmT1bt3b61atUofffSR5s6dq9/85jcqKio6rucFAABAx6mqqtLAgQNlmi2L8iorK3XhhRdKkmpqapSfn/+V34MCQDJiiTGAtJebmytJev/997VkyRKVlJQoLy9Pn376qbZs2aJNmzbp+eefV21t7VE/T319vVatWqWampq261rLvdWrV+udd95Rc3PzIY857bTTJElPP/20Fi5cqEWLFik3N1dDhgw56nMtWLBAa9euVWFhoQoKCuT7vnbv3n2sLx0AAABxsHHjRvXv37/tcmVlpfr16/eljwEgVVAQAkh755xzjnr37q0FCxbor3/9q/Ly8nT33XersLBQjz32mObOnatwOKwePXoc8fEXX3yxBg0apHfffVe1tbXq27dv221Dhw7VyJEj9dlnn+mBBx445NyCkjRixAh973vf0549ezRnzhx1795d//Ef/6FOnTodNXMoFNLrr7+uP/3pT/rss8900UUXaejQoSc+GAAAADhhGzduVHFxsaSW5cbNzc1tvziurKw8pDwEgFTALsYAAAAAAABABmMGIQAAAAAAAJDBKAgBAAAAAACADEZBCAAAAAAAAGQwCkIAAAAAAAAgg1EQAgAAAAAAABmMghAAAAAAAADIYBSEAAAAAAAAQAb7/wGYLpwJtbOSUwAAAABJRU5ErkJggg==",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"low, high, step = 0, 5000, 10\n",
"plot_all(cost_history, m, q, low, high, step)"
]
},
{
"cell_type": "code",
"execution_count": 145,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"254 passi e 25400 gradienti calcolati per arrivare a distanza minore o uguale di 0.1 dall'ottimo\n"
]
}
],
"source": [
"near_opt(m, min_dist=1e-1, ge_per_step=n)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Metodi del secondo ordine"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"La ricerca di un punto di massimo (o minimo) può anche essere effettuata in termini di ricerca di punti in cui la derivata prima (o il gradiente, in generale) si annullano, applicando uno dei metodi iterativi standard per la ricerca degli zeri di una funzione.\n",
"\n",
"Un tipico metodo utilizzato in questo ambito è quello di Newton-Raphson, in cui (considerando una funzione univariata) viene applicato, ad ogni iterazione, l'aggiornamento\n",
"\n",
"$$\n",
"x_{i+1}=x_{i}-\\frac{f(x_{i})}{f'(x_{i})}\n",
"$$\n",
"\n",
"A ogni iterazione, l'algoritmo approssima $f$ per mezzo di una retta tangente a $f$ in $(x_i,f(x_{i}))$, e definisce $x_{i+1}$ come il valore in cui tale retta interseca l'asse $x$.\n",
"\n",
"\n",
"\n",
"\n",
"Nel caso in cui si cercano punti di massimo o minimo, l'iterazione evidentemente diviene\n",
"\n",
"$$\n",
"x_{i+1}=x_{i}-\\frac{f'(x_{i})}{f''(x_{i})}\n",
"$$"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Nel caso di funzioni a più variabili, la derivata prima è sostituita dal gradiente \n",
"$\\nabla f$, mentre la derivata seconda corrisponde alla matrice *Hessiana* $H$, definita come\n",
"\n",
"$$\n",
"H_{ij}(f)=\\frac{\\partial^{2}f}{\\partial x_{i}\\partial x_{j}}\n",
"$$\n",
"\n",
"L'aggiornamento ad ogni iterazione diviene quindi\n",
"\n",
"$$\n",
"\\mathbf{x}^{(i+1)}=\\mathbf{x}^{(i)}-\\big(H(f)^{-1}\\nabla f\\big)\\big|_{ \\mathbf{x}_{(i)}}\n",
"$$\n"
]
},
{
"cell_type": "code",
"execution_count": 216,
"metadata": {},
"outputs": [],
"source": [
"theta = theta_history[1]\n",
"c1 = sigma(theta,X)\n",
"h = np.zeros([3,3])\n",
"for i in range(t.shape[0]):\n",
" m=X[i,:].reshape(1,-1)\n",
" h = h+np.dot(m.T,m)*c1[i]*(1-c1[i])\n",
"h = h/t.shape[0]\n",
"g=gradient(theta,X,t)"
]
},
{
"cell_type": "code",
"execution_count": 217,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(3, 1)"
]
},
"execution_count": 217,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"g.shape"
]
},
{
"cell_type": "code",
"execution_count": 219,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([[-2.81931877],\n",
" [-0.44421613],\n",
" [ 0.31414362]])"
]
},
"execution_count": 219,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"np.dot(np.linalg.inv(h),g)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"def gradient(theta, X, t):\n",
" return -np.dot(X.T, (t-sigma(theta, X))) / len(X)"
]
},
{
"cell_type": "code",
"execution_count": 222,
"metadata": {},
"outputs": [],
"source": [
"def newton(X,t, epochs = 100):\n",
" theta = np.zeros(nfeatures+1).reshape(-1,1)\n",
" theta_history = []\n",
" cost_history = []\n",
" for k in range(epochs): \n",
" g = gradient(theta,X,t)\n",
" c1 = sigma(theta,X)\n",
" h = np.zeros([nfeatures+1,nfeatures+1])\n",
" for i in range(t.shape[0]):\n",
" m=X[i,:].reshape(1,-1)\n",
" h = h+np.dot(m.T,m)*c1[i]*(1-c1[i])\n",
" h = h/t.shape[0]\n",
" theta = theta - np.dot(np.linalg.inv(h),g)\n",
" theta_history.append(theta)\n",
" cost_history.append(cost(theta, X, t))\n",
" theta_history = np.array(theta_history).reshape(-1,3)\n",
" cost_history = np.array(cost_history).reshape(-1,1)\n",
" m = -theta_history[:,1]/theta_history[:,2]\n",
" q = -theta_history[:,0]/theta_history[:,2]\n",
" return cost_history, m, q"
]
},
{
"cell_type": "code",
"execution_count": 323,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"tempo di esecuzione: 0.021 secondi\n",
"100 passi totali\n",
"10000 gradienti valutati\n"
]
}
],
"source": [
"start_time = time.time()\n",
"cost_history, m, q = newton(X,t, epochs = 100)\n",
"print(f\"tempo di esecuzione: {time.time()-start_time: 4.3f} secondi\")\n",
"print(f\"{len(m)} passi totali\")\n",
"print(f\"{len(m)*n} gradienti valutati\")"
]
},
{
"cell_type": "code",
"execution_count": 324,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABQgAAAGoCAYAAAAKMwiTAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAABshUlEQVR4nO3de3yU9Z33//d1XTNJmITzQCCckhBCOCTI2QOiQjyU2qpR0a7a3VSW3Xa72oPr7X3/tthCu6XtXVeqXe+VrWVdsStqtFZdkRTRonI+BQMkMQIJRwMi5EQy13X9/ggZjIKiMrmuybyej0cfda6ZDJ+ZDwnJO5/v92u4rusKAAAAAAAAQEIyvS4AAAAAAAAAgHcICAEAAAAAAIAERkAIAAAAAAAAJDACQgAAAAAAACCBERACAAAAAAAACYyAEAAAAAAAAEhgAa8LON/279/vdQlfSjgcVl1dnddlJDz64B/0wh/ogz/QB3/oKn3IyMjwuoTzKt6/B/SrrvL3PZ7RA+/RA2/x/nuPHnjvfPbgbN8DMkEIAAAAAAAAJDACQgAAAAAAACCBERACAAAAAAAACYyAEAAAAAAAAEhgBIQAAAAAAABAAiMgBAAAAAAAABIYASEAAAAAAACQwAgIAQAAAAAAgARGQAgAAAAAAAAkMAJCAAAAAAAAIIEREAIAAAAAAAAJjIAQAAAAAAAASGAEhAAAAAAAAEACIyAEAAAAAAAAEhgBIQAAAAAAAJDACAgBAAAAAACABBaI5ZMvWbJE1dXVysrKUnFxcfT6o48+qpqaGknSnDlzNGzYMC1ZskS7d++WJO3Zs0e///3vtWrVKj333HPq3bu3cnJydPvtt8eyXAAAAAAAACDhxCwgrK6uVnNzs+bPn6/FixerqqpKOTk5kqTrr79e/fv314EDB7R06VLdc889+pu/+RtJ0nvvvac//elP0ef5+te/rpkzZ8aqTAAAAAAAACChxWyJcWVlpQoKCiRJ+fn5qqioiN7Xv39/SZJlWTLNjiWsW7dOU6dOjd5++eWXdf/996usrCxWpQIAAAAAAAAJK2YThA0NDUpPT5ckhUIh1dbWfuIxTz75pGbNmtXh2pYtW3T99ddLkiZPnqzp06ervr5eP/3pT7Vw4cJPBIqlpaUqLS2VJC1cuFDhcDgGr6bzBAKBuH8NXQF98A964Q/0wR/ogz/QBwAAAHQ1MQsIQ6GQGhsbJUlNTU0KhUId7n/ppZc0ePBg5eXlRa8dOHBAffr0UXJysiQpNTVVktSjRw8NHDhQx44dU58+fTo8T2FhoQoLC6O36+rqYvJ6Oks4HI7719AV0Af/oBf+QB/8gT74Q1fpQ0ZGhtclAAAAwCditsQ4NzdX27dvlySVlZUpNzc3et/WrVu1a9cu3XjjjR0+Zt26dZoyZUr0dnvA2NLSooMHD6pHjx6xKhcAAAAAAABISDGbIMzOzlYwGNS8efOUmZmpcDiskpISFRUV6bHHHlMoFNJPfvITZWRkaO7cuZKkTZs26Z/+6Z+iz/HSSy9py5Ytcl1X1113nQKBmB66DAAAAAAAACQcw3Vd1+sizqf9+/d7XcKX0lWWLcU7+uAf9MIf6IM/0Ad/6Cp96OwlxkuWLFF1dbWysrJUXFwcvb5t2zY99dRTSkpK0pw5czRo0CAtW7ZM69evV2pqqiZNmqRrr732M58/3r8H9Kuu8vc9ntED79EDb/H+e48eeO989uBs3wMykgcAAICYqq6uVnNzs+bPn6/FixerqqpKOTk5kqRnnnlGP/rRj9TU1KQlS5bo+9//viTpjjvuUEFBgZdlAwAAJIyY7UEIAAAASFJlZWU07MvPz1dFRUWH+1NSUtS7d28dOnQoem3p0qVasGCBdu/e3ZmlAgAAJCQmCAEAABBTDQ0NSk9PlySFQiHV1tZ2uP/YsWNqaGjQvn37JEmzZs3S7NmzdeDAAT3yyCOaP3/+J56ztLRUpaWlkqSFCxcqHA7H+FUkpkAgwHvrMXrgPXrgLd5/79ED73VGDwgIAQAAEFOhUEiNjY2SpKamJoVCoeh9t99+uxYtWqRwOKyRI0dKktLS0iRJAwcOPOtzFhYWqrCwMHqbvZFig32nvEcPvEcPvMX77z164L3O2IOQJcYAAACIqdzcXG3fvl2SVFZWptzc3A733X///SoqKtKgQYMkKRomHj9+XLZtd37BAAAACYYJQh9ZvGKHDh5r0t8W5mlA79BnfwAAAEAcyM7OVjAY1Lx585SZmalwOKySkhIVFRWppKREZWVlSktL09y5cyVJTzzxhGpqauQ4jm677TaPqwcAAOj6CAh9pPFkRMcbW9QScbwuBQAA4LwqLi7ucLuoqCj6/+3/3a49KAQAAEDnYImxjwSstnZEHAJCAAAAAAAAdA4CQh8JmIYkKWK7HlcCAAAAAACAREFA6CPtE4Q2E4QAAAAAAADoJASEPmIxQQgAAAAAAIBORkDoI9E9CG0mCAEAAAAAANA5CAh9JGCdmiBkiTEAAAAAAAA6CQGhjwTM9glClhgDAAAAAACgcxAQ+kj7BCGHlAAAAAAAAKCzEBD6iMUEIQAAAAAAADoZAaGPRPcg5JASAAAAAAAAdBICQh+JnmLsMEEIAAAAAACAzkFA6CMBkwlCAAAAAAAAdC4CQh9pnyC0mSAEAAAAAABAJyEg9BGLCUIAAAAAAAB0MgJCH4nuQcgpxgAAAAAAAOgkBIQ+cvqQEiYIAQAAAAAA0DkICH3k9CElTBACAAAAAACgcxAQ+sjpQ0qYIAQAAAAAAEDnICD0EYsJQgAAAAAAAHQyAkIfOX1ICROEAAAAAAAA6BwBrwvAaQHr1AQhS4wBAAAShnNwjyRXRvowGYbhdTkAACABERD6SMBsnyBkiTEAAECiiKxfLnd/tYw+6bJGXShzxHgZySlelwUAABIIAaGPtO9ByCElAAAAicF1HZnpw2R/cFju0UOKvPlHae3LMnPGyRp9ocx+g70uEQAAJAACQh85vQchE4QAAACJwDBMBaZcLWviTDm7y2WXr5W7/105OzfI2blBRniQrNFTZeZcICOY5HW5AACgiyIg9JHoHoQcUgIAAJBQDCsga3iBrOEFco69L2fHWtm7Nsmt26fIGyXSmpdkjpgga9RUmX0HeF0uAADoYggIfSS6B6HDBCEAAECiMnv1k3nRtbImXy2nervsHWvkHtwj55235bzztoz0YW1Thdn5MgJBr8sFAABdAAGhj1inJghtJggBAAASnhEIysodLyt3vJwjB2XvWCunYpPcQ3sUObRHeutFWSMnyBw1VWavfl6XCwAA4hgBoY9E9yBkghAAAAAfYfYdIHPadXKnXiOnamvbXoV1+2RvWy1722oZGcPbpgozR8uw+BYfAAB8Pnz34COnTzF25biuTMPwuCIAAAD4iRFMljVqiqxRU+S8Xyu7fK2cqi1y97+ryP53pW5pskZOkjVqiowefbwuFwAAxAkCQh8xDUOWach2XNmOK9MiIAQAAMCZmf0Gy7xssNwLvyqncnPbXoVHD8neskr2ltdlDsmVOXqqzKEjZZiW1+UCAAAfi2lAuGTJElVXVysrK0vFxcXR648++qhqamokSXPmzNGwYcO0bNkyrV+/XqmpqZo0aZKuvfZaNTU1adGiRWpoaFBhYaEuu+yyWJbrC0HLlO3YitiOgqeWHAMAAABnYySnyBp7kcwxF8o9tKdtqrC6TE7NLjk1u6TUnrJGTZaVN1lGak+vywUAAD4Us4Cwurpazc3Nmj9/vhYvXqyqqirl5ORIkq6//nr1799fBw4c0NKlS3XPPfdIku644w4VFBREn+PPf/6zLrnkEl1yySX6yU9+oksuuUSBQNceegxYptRqy7bZhxAAAADnzjAMGQMyZQ7IlHvxtbIrNskpXyv3wzrZG0plb1wpc1ierNEXyhicI8Pgl9EAAKBNzL4rqKysjIZ9+fn5qqioiN7Xv39/SZJlWTLN0yUsXbpUCxYs0O7duyVJFRUVKigokGmaGjZsmPbt2xercn0jEGg/qISTjAEAAPDFGCmpChRcquAtP1Tw2jkys/MlQ3J2l6v15cfU8t//V5Etq+Q21XtdKgAA8IGYjeM1NDQoPT1dkhQKhVRbW/uJxzz55JOaNWuWJGnWrFmaPXu2Dhw4oEceeUTz589XY2OjunXrFn2OhoaGTzxHaWmpSktLJUkLFy5UOByO1UvqFEGrbX+Y7j16Kdw71eNqElcgEIj7v0tdBb3wB/rgD/TBH+gD4olhGDIG5cgclCO38YTsnRtk71grHT8qe+0rstevkJk1VtboqTIGZsngkDwAABJSzALCUCikxsZGSVJTU5NCoVCH+1966SUNHjxYeXl5kqS0tDRJ0sCBAzs8R1NTk5KSktTY2KjU1E8GZoWFhSosLIzerqurO++vpTMFTu07+H7dEVl2k8fVJK5wOBz3f5e6CnrhD/TBH+iDP3SVPmRkZHhdAjqZEequwIQrZF1wmZzaSjnla+Ts3Snn3a1y3t0qo1c/maOmysqdICMl9NlPCAAAuoyYLTHOzc3V9u3bJUllZWXKzc2N3rd161bt2rVLN954Y/Rae5h4/Phx2bYdfY6ysjI5jqM9e/Zo0KBBsSrXN9oDwojDHoQAAAA4/wzTlDV0pILX/LWS/up/yZowUwp1l3vsfdlvv6iWJ/5Fra8tk3Nor1yX70kBAEgEMZsgzM7OVjAY1Lx585SZmalwOKySkhIVFRXpscceUygU0k9+8hNlZGRo7ty5euKJJ1RTUyPHcXTbbbdJkmbMmKHf/OY3euWVV1RYWNjlDyiRFD25OGKzByEAAABiy0jrpcDkK2VNmCFn7w7Z5Wvl1lbKqdgkp2KT3n9riNyRE2XmjJeRlOx1uQAAIEZimrgVFxd3uF1UVCRJWrRo0SceO3fu3E9cC4VCuu+++2JTnE+1TxDaHFICAACATmJYlqyssbKyxsr98Ijsnetk79yg1sM10uEa6e2XZY64QNboqTLDXX9VDwAAiabrj+TFmegSY5vlHAAAoOtYsmSJqqurlZWV1eGXyNu2bdNTTz2lpKQkzZkzR4MGDdLRo0f10EMPqbW1VbNnz1ZBQYGHlSceo2dfBaZ+RdakK5Vat1fH1q6Qe+A9OTvWydmxTkb/IbJGTZU5vEBGMMnrcgEAwHkQsz0I8cUEAywxBgAAXUt1dbWam5s1f/58RSIRVVVVRe975pln9KMf/Uh33XWXli1bJkl6/vnndcstt+if//mfVVJS4lXZCc+wAgqNmaKkr/+dgrN/IGvsJVJSitzDNYq8/oxanvgXRd58Qc4Hh7wuFQAAfElMEPoMh5QAAICuprKyMjoFmJ+fr4qKCuXk5ETvT0lJUUpKig4daguaampqNHLkSBmGoZSUFDU2NioU4lRdL5m9+8u85Guyplwtp7qsba/Cw3tlb39L9va3ZAzIlDX6QpnZY2VY/IgBAEC84V9vnwlwSAkAAOhiGhoalJ6eLqltj+na2toO9x87dkwNDQ3at2+fJMlxHBmGEX38mQLC0tJSlZaWSpIWLlyocDgc65eRkAKBwCff24EZ0iVXq+XgXjVufl2N29fIPbhbkYO7Za5JU6jgEqWOn65An3Rviu5iztgDdCp64C3ef+/RA+91Rg8ICH0mGD2khAlCAADQNbSHfJLU1NTUIey7/fbbtWjRIoXDYY0cOVKSouHgmR7frrCwUIWFhdHbdXV1sSo/oYXD4bO/t4GQNPkrCo6bIadqi+zyNXKOHFD9muWqX7NcxuARskZNkTlstAzL6tzCu5BP7QE6BT3wFu+/9+iB985nDzIyMs54nYDQZ5ggBAAAXU1ubq5KS0t18cUXq6ysTJdffnmH++6//34dOHBAr7zyiiRp6NChqqio0NChQ88aEMI/jKTkttONR02R+35tW1D47ja5tZWK1FZKoe6y8ibLypsio3svr8sFAABnQEDoM5xiDAAAuprs7GwFg0HNmzdPmZmZCofDKikpUVFRkUpKSlRWVqa0tDTNnTtXknTdddfp4YcfVktLi2bPnu1x9ThXhmHI6D9EZv8hci/6quyKzXLK18o9dlj2ppWyN78mc8hImaMvlDkkV4bJeYkAAPgFAaHPBKOHlDBBCAAAuo7i4uIOt4uKiqL/3/7f7fr27av777+/02rD+WckhxTIv0Tu2IvlHnhP9o61cqq3y9m7U87enVJaL1mjpsgaOUlGag+vywUAIOEREPpMINC2PwsThAAAAIh3hmHIyMiWmZEt9+J62bs2yt6xTjp+RPb6V2VvLJU5bLSs0VNlDBouw2CqEAAALxAQ+kwgekgJE4QAAADoOoxuaQpccJmscZfK3fdu216Fu3fIeW+7nPe2y+jRV+boqbJyJ8rolup1uQAAJBQCQp8JsgchAAAAujDDMGUMHiFz8Ai5Dcdl71wve+c6ucePyF7zsux1y2Vm57dNFQ7I7HCqNQAAiA0CQp/hFGMAAAAkCiO1hwITZ8oaf4Wcml1yytfK2btLTtUWOVVbZPTu33ZC8ogJMpK7eV0uAABdFgGhz0QDQocJQgAAACQGwzRlDRsla9gouSc+kL1jneyd6+V+cFiRN/8krX1F5vACWaMvlNFvMFOFAACcZwSEPhNkghAAAAAJzOjeW4EpV8uaWChnT7ns8rVy91XJ2bVRzq6NMsIZskZNlTniAhnBZK/LBQCgSyAg9BkOKQEAAAAkw7JkZefLys6X82GdnPJ1sis2yK3br8hfnpPWvCxzxHhZo6fI7JvhdbkAAMQ1AkKfCQQ4pAQAAAD4KLNnWOZFs2RNvlLOe9vbpgoP7pZTvkZO+RoZ/Ye27VU4vEBGIOh1uQAAxB0CQp+JLjFmghAAAADowAgEZY0YL2vEeDlHD8nZsVZ2xUa5h/cqcniv9PaLsnInyBw1VWbv/l6XCwBA3CAg9JnoEmMmCAEAAICzMvuky7zk67KmXCPn3a1tU4Xv18oue1N22ZsyMrLb9irMGiPD4sceAAA+Df9S+kyQU4wBAACAc2YEk2TlTZaVN1nO+7Wyy9fJqdoid3+1IvurpZRUWXmTZI2aIqNHX6/LBQDAlwgIfSbAKcYAAADAF2L2GyzzssFyL5olp3KL7PI1co8elL3lddlbXpcxOLdtr8JheTJMy+tyAQDwDQJCnwlYbd+oMEEIAAAAfDFGUoqsMRfKHD1V7qG9sneslfPuNrm1FYrUVkihHrJGTZaVN0VGWk+vywUAwHMEhD4TjO5ByAQhAAAA8GUYhiFjwDCZA4bJveha2RUb5ZSvlfthneyNf5a9aaXMoXkyR18oc/AIGabpdckAAHiCgNBnAgGWGAMAAADnm5ESUqDgUrn50+QeqJZdvlbOe+/I2bNDzp4dUvfeskZNkTVykoxQd6/LBQCgUxEQ+kyAQ0oAAACAmDEMQ0bGcJkZw+U2npC9a6PsHWulEx/IXrdc9oYVMjPHyho9VUZGtgzD8LpkAABijoDQZ4IcUgIAAAB0CiPUXYHxl8u6YLrcmsq2vQr37JBTvU1O9TYZPcMyR0+VlTtBRkqq1+UCABAzBIQ+wwQhAAAA0LkMw5QxdKTMoSPl1n8oe+d62TvXte1V+PZLstctl5mdL2v0hTLShzJVCADocggIfSbAISUAAACAZ4y0ngpMKpQ14Qo5e3fKLl8rt6ZSTuVmOZWbZfQZIGv0VJk542Ukp3hdLgAA5wUBoc9YpiFDkuNKjuPKNPntJAAAANDZDNOSlTlGVuYYucePyN6xXvbO9XKPHlRk9R+lNS/LzLmgLSzsN9jrcgEA+FIICH3GMAxZlqGI7SriOEoyLa9LAgAAABKa0aOvAlOvkTWpUM7uctnla+Tur5azc72cnetl9BvcFhQOHycjmOR1uQAAfG4EhD4UME1FbFsR21USHQIAAAB8wbACsoYXyBpeIOeDw3J2rJNdsVHu+7WKvF4rvf2izBET2sLCPgO8LhcAgHNG/ORDAcuUWm1FHPYhBAAAAPzI7N1f5sXXyppytZzqbW17FR7aK+edt+W887aMAcNkjbpQZvZYGYGg1+UCAPCpCAh9KGC17Tto25xkDAAAAPiZEQjKyp0oK3einCMHZJevlVO5We7BPYoc3CO99SdZIyfKHDVFZq9+XpcLAMAZERD6UMBsO8k4wknGAAAAQNww+w6Ueen1ci/8ipyqrW17Fdbtl73tL7K3/UXGoBxZo6bIzBwtw+JHMQCAf/Cvkg9ZpyYIIw4ThAAAAEC8MYLJbUFg3mS579fK3rFWTtVWufuqFNlXJXVLk5U3WdaoyTK69/G6XAAACAj9iAlCAAAAIP4ZhiGj/xCZ/YfIvfCrcio3t+1V+MEh2Ztfk715lcyhuTJHTZU5NE/GqZ8DAADobASEPhRgghAAAADoUozkbrLGXixzzEVyD+5pmyp8d5ucvbvk7N0lpfVsmyrMmywjtafX5QIAEgwBoQ8FrLbfHNpMEAIAAABdimEYMgZmyhyYKfeia2VXbJRTvlbu8SOyN5TK3rhS5rBRskZPlTE4x+tyAQAJIqYB4ZIlS1RdXa2srCwVFxdHrz/66KOqqamRJM2ZM0fDhg3T008/rS1btkiSbr31VuXn52vVqlV67rnn1Lt3b+Xk5Oj222+PZbm+YZmnJggJCAEAAIAuy+iWqsC46XILpsndV902Vbj7nej/1KOPTky6Qu7gUTK6pXldLgCgC4tZQFhdXa3m5mbNnz9fixcvVlVVlXJy2n4Ddv3116t///46cOCAli5dqnvuuUeXXXaZbr75ZjU0NOiXv/yl8vPzJUlf//rXNXPmzFiV6UvtE4QsMQYAAAC6PsMwZQzOkTk4R27jCdk7N8jesVY6flTHVz4rmZbMrLFtU4UDs2QYhtclAwC6mJgFhJWVlSooKJAk5efnq6KiIhoQ9u/fX5JkWZbMUxvxtl8LBoMdnufll1/WG2+8oZtuuikaGnZ1ASYIAQAAgIRkhLorMOEKWRdcJqe2QoGqzWqu2ibn3a1y3t0qo1c/maOnysqdICM55HW5AIAuImYBYUNDg9LT0yVJoVBItbW1n3jMk08+qVmzZnW4tmzZMl155ZWSpMmTJ2v69Omqr6/XT3/6Uy1cuDAaKLYrLS1VaWmpJGnhwoUKh8OxeDmdJhAIKDXUTZLULZQW968nXgUCAd57n6AX/kAf/IE++AN9ANAZDNOUNTRPfSdM0/vvVcneuU72zvVyj70v+60XZa99RebwcW1Thf2HMFUIAPhSYhYQhkIhNTY2SpKampoUCnX87dZLL72kwYMHKy8vL3pt3bp1qq+v17Rp0yRJqampkqQePXpo4MCBOnbsmPr06dPheQoLC1VYWBi9XVdXF5PX01nC4bDsSIsk6diHH6quLsXjihJTOByO+79LXQW98Af64A/0wR+6Sh8yMjK8LgHAOTK691Jg8lWyJsyUs2eH7B1r5dZWyqnYKKdio4y+A2WNniozZ7yMpGSvywUAxCHzsx/yxeTm5mr79u2SpLKyMuXm5kbv27p1q3bt2qUbb7wxem3Pnj1avny57rzzzui19oCxpaVFBw8eVI8ePWJVrq9Yp6YkIzZ7EAIAAABoY1iWrOyxSvrqnUq69R5Z4y6TUlLlHjmgyF+eV8sTP1PrG8/JqdvvdakAgDgTswnC7OxsBYNBzZs3T5mZmQqHwyopKVFRUZEee+wxhUIh/eQnP1FGRobmzp2rJ554QseOHdPPfvYzhUIh3XvvvXrppZe0ZcsWua6r6667ToFATA9d9o2AdWoPQoc9CAEAAAB8ktEzrMCFX5E1+Uo5722XXb5W7oH35OxYK2fHWhn9h7RNFWYXyAgmeV0uAMDnYpq4FRcXd7hdVFQkSVq0aNEnHvv//X//3yeu3Xzzzbr55ptjU5yPBZggBAAAAHAODCsgK+cCWTkXyPngkJzydbIrNso9XKPI4RrprRdl5U6QOXqqzN7pXpcLAPCpxBjJizNMEAIAAAD4vMze6TIv+ZqsKVfLqd7WNlV4uEb29rdkb39LxsCstqnCrLEyLH4UBACcxr8KPhSw2iYIbSYIAQBAF7FkyRJVV1crKyurwyqTt99+Wy+88IIMw9ANN9ygyZMn67e//a327dunpKQkFRYWRg+wA3BujGCSrJGTZI2cJKdun+zydXKqNss98J4iB96TUlLb7h81RUbPvl6XCwDwAQJCHzp9SAkThAAAIP5VV1erublZ8+fP1+LFi1VVVaWcnBxJ0ksvvaQf//jHMgxDP/vZzzR58mRJ0l133aUBAwZ4WTbQJZjhQTKn3yD3wllyqrbILl8j98gB2Vtfl731dRmDR8gaNVXmsFEyLMvrcgEAHiEg9KHTS4yZIAQAAPGvsrJSBQUFkqT8/HxVVFREA8L09HSdPHlSktStWzdJkmEYevjhh5WWlqY777xT/fr186ZwoAsxkpLblhePmtK27Lh8rZx3t8qtrVSktlIKdZeVN1lW3hQZ3Xt5XS4AoJMREPpQgAlCAADQhTQ0NCg9ve1whFAopNra2uh9U6ZM0b333ivXdfWd73xHkvTNb35TaWlp2rlzpx5//HH98Ic//MRzlpaWqrS0VJK0cOFChcPhTngliScQCPDeeiwmPejXTxozQU5TgxrL3lbDplWKHDkoe9NK2ZtfU0pOgVInXKbk7LEyTv1sksj4PPAW77/36IH3OqMHBIQ+xAQhAADoSkKhkBobGyVJTU1NCoVC0fueeeYZPfDAA5Kkn//85xo3bpzS0tIkSXl5eVq6dOkZn7OwsFCFhYXR23V1dbEqP6GFw2HeW4/FvAfZF8jMGqfggfdk71grp3q7miu3qrlyq5TWS9aoKbLyJssIdY9dDT7H54G3eP+9Rw+8dz57kJGRccbr/DrIh04fUsIEIQAAiH+5ubnavn27JKmsrEy5ubnR+4LBoJKTk5WSkqJIJCJJ0TBx//79Sk1N7fyCgQRjGIbMjGwFZ35DSbf/b1lTvyL16CPVH5O9/lW1LP25WlcslVNbJdflZxQA6IqYIPQhyzw1QcgpxgAAoAvIzs5WMBjUvHnzlJmZqXA4rJKSEhUVFemqq67Sj370I0mKTgT+5je/UUNDgwzD0Jw5c7wsHUg4Rrc0BS64TNa4S+XWVrXtVbhnh5zqMjnVZTJ6hmWOmiIrd6KMbgT4ANBVEBD6UPsEYcTht3MAAKBrKC4u7nC7qKhIknT55Zfr8ssv73Dffffd11llATgLwzBlDMmVOSRXbsNx2TvXy96xTu6HdbLXvCx73XKZ2fmyRl8oY8AwGYbhdckAgC+BgNCHAtEJQgJCAAAAAN4yUnsoMHGmrPGXy9m7S86OtXL2Vsip2iKnaouM3ultJySPmCAjOcXrcgEAXwABoQ+dniBkiTEAAAAAfzBMS1bmaFmZo+WeOCp7x3rZO9fL/eCQIm++IK39H5k542SNvlBmv8FelwsA+BwICH2o/RRjDikBAAAA4EdG9z4KTLla1sSZcvbskF2+Vu6+Kjk7N8jZuUFGeFDbVGHOOBnBZK/LBQB8BgJCHwqYpyYIOaQEAAAAgI8ZVkBWdr6s7Hw5x96Xs2Od7F0b5dbtU+SNEuntl2SOGN8WFvYd6HW5AICzICD0IevUBCGHlAAAAACIF2avfjIv+qqsyVfJqd4ue8cauQf3yClfI6d8jYz0YW1BYXa+jEDQ63IBAB9BQOhDTBACAAAAiFdGICgrd7ys3PFyjh6UXb5WTuUmuYf2KHJoj/TWn2TlTpQ5eqrMXv28LhcAIAJCXwowQQgAAACgCzD7DJA57Tq5U78i592tbXsVvl8ru2y17LLVMjKy2w41yRwtw+LHUwDwCl+Bfaj9FGObCUIAAAAAXYARTJKVN1lW3mQ579e2TRVWbZG7v1qR/dVStzRZIyfJGjVFRo8+XpcLAAmHgNCHTi8xZoIQAAAAQNdi9hss87LBci/8qpyqzbLL18g9ekj2llWyt7wuY8iItr0Kh+bJMC2vywWAhEBA6EOnDylx5bquDMPwuCIAAAAAOL+M5BRZYy6SOfpCuYf2yi5fI6e6TG5NhSI1FVJqj1NTh1NkpPX0ulwA6NIICH3INAyZhiHHdWU7bnRPQgAAAADoagzDkDFgmMwBw+RefK3sik1yytfK/bBO9sY/y960UuawUbJGTZUxZIQMw/S6ZADocggIfSpgGWqJuIo4rgJM1QMAAABIAEZKqgIFl8rNnyZ3f3XbXoW7t8vZXS5nd7nUvY+sUVNkjZwoI9Td63IBoMsgIPSpgGWqJeLIth0pSEIIAAAAIHEYhiFj0HCZg4bLbTwhe9cG2TvWSSeOyl73iuwNK2RmjpE1eqqMjGy2ZQKAL4mA0KcC5ql9CDnJGAAAAEACM0LdFRh/haxxl8mprZSzY62cPTvkVG+TU71NRq9+MkdNkZU7UUZKyOtyASAuERD6lGWdOsnY4SRjAAAAADBMU9bQkbKGjpRbf0z2zvWyd6yXe+x92W+/JHvdcpnDC9r2KkwfylQhAHwOBIQ+xQQhAAAAAJyZkdZLgUlXypowQ86enbLL18qtrZBTsUlOxSYZfQbIGj1V5ojxMpJSvC4XAHyPgNCnAkwQAgAAAMCnMkxLVtYYWVlj5B4/InvHetk718s9elCR1X+U1r8qa9x0WWMvlhFM9rpcAPAtAkKfap8gtG0CQgAAAAD4LEaPvgpMvUbWpEI5770j+5235R7cLXvdctnbVssaf7ms0RfKCAS9LhUAfIeA0KeiE4QsMQYAAACAc2ZYAVk542QOL5C7711F1r8q9/Detn0Kt/5FgQkzZOZNkmHx4zAAtOMrok9Z1qk9CFliDAAAAACfm2EYMgbnKDhouJy9u2RveFVu3X5FVj8vbVmlwMSZMnMnyDAtr0sFAM8REPpUwGSCEAAAAAC+LMMwZA3Lkzk0V8575W1B4QeHFXn9WRlbXpc1sVDm8AIZp34GA4BEREDoUwEmCAEAAADgvDEMU1b2WJmZo+W8u032hhVyP6xTZOV/y9j8mqxJV8rMGiPDMLwuFQA6HQGhT7VPENpMEAIAAADAeWOYpqwRF8gcni+nYrMiG0vlfnBIkRVPyAhnyJp0lcyhIwkKASQUAkKfiu5ByCnGAAAAAHDeGaYlK2+SzBEXyNm5QZFNK9v2KHxliYz+QxWYfKWMQTlelwkAnYKA0Keipxg7TBACAAAAQKwYVkDWmAtljpwou3yN7M2r5B7eq9aXfidjYJZOXjlb6tbb6zIBIKYICH3q9CElTBACAAAAQKwZgaACBZfKGjVF9va3ZG99Q+6B91T3+C9kDM5VYPKVMvsP8bpMAIgJAkKfOn1ICROEAAAAANBZjGCyAuOvkDX6Itllf5FT9qbc2gq11lbIzBzddphJ34FelwkA5xUBoU8xQQgAAAAA3jGSUxSYdKV6T/+a3n/tOdnb35Kzu1zO7nKZ2QWyJhXK7N3f6zIB4LyIaUC4ZMkSVVdXKysrS8XFxdHrjz76qGpqaiRJc+bM0bBhw3T06FE99NBDam1t1ezZs1VQUHDGa4mi/ZASTjEGAAAAAO9YoTQFpn5FVv402VtWyS5fK6d6m5z3ymSOGK/AhJkyevb1ukwA+FLMWD1xdXW1mpubNX/+fEUiEVVVVUXvu/7667VgwQJ95zvf0dNPPy1Jev7553XLLbfon//5n1VSUnLWa4ni9CElTBACAAAAgNeMUHcFLv6akm79J5mjp0qGIadik1qW/Vqtr5fIPXHM6xIB4AuLWUBYWVkZnfjLz89XRUVF9L7+/dvGsC3LknlqKW1NTY1GjhyplJQUpaSkqLGx8YzXEkXAPLUHIROEAAAAAOAbRlpPBS+9QUm33CNz5ETJdeXsXKeW//6VIm++ILfhuNclAsDnFrMlxg0NDUpPT5ckhUIh1dbWfuIxTz75pGbNmiVJchxHhmFEH9/Y2HjGa6FQqMNzlJaWqrS0VJK0cOFChcPhWL2kThEIBBQOh9WrZ0Pb7aSkuH9N8ai9D/AevfAH+uAP9MEf6AMAQJKMHn0UvPxmORdcLntjqZyqbW2nH+9cL2vMRbLGXSajW6rXZQLAOYlZQNge6ElSU1PTJ4K9l156SYMHD1ZeXp4kRYPAjz7+TNc+rrCwUIWFhdHbdXV15/V1dLZwOKy6ujo1N7YFhPUNjXH/muJRex/gPXrhD/TBH+iDP3SVPmRkZHhdAgB0CWavfjJnfkPOBVfI3rBCzu53ZG99Q3b5Gln502QVXCojuZvXZQLAp4rZEuPc3Fxt375dklRWVqbc3NzofVu3btWuXbt04403Rq8NHTpUFRUVam5ujoaBZ7qWKNr3IOSQEgAAAADwP7PvAAWvvkPBou/KHDpSam2RvWmlWp78hSKbVsptOel1iQBwVjGbIMzOzlYwGNS8efOUmZmpcDiskpISFRUV6bHHHlMoFNJPfvITZWRkaO7cubruuuv08MMPq6WlRbNnz5akM15LFO2nGHNICQAAAADED7PfYJlfKZZzcI8i61+Vu/9d2etflV32pqwLLpM1+kIZwSSvywSADmIWEEpScXFxh9tFRUWSpEWLFn3isX379tX999//mdcSReDU4S0cUgIAAAAA8cccMExJX/tbOfvebQsKD+2RveZl2dv+osD4K2SOmiLDiumP5ABwzvhq5FMBJggBAAAAIO6Zg4YrmPH3cmsq2oLCun2KvPmCtPV1BSbMlJk7UYZleV0mgARHQOhT7ROE7EEIAAAAAPHNMAwZQ0cqOCRXzu5y2RtelXv0kCJvlEhbVikwsVBmzgUyzJgdEwAAn4qA0KeiE4Q2E4QAACD+LVmyRNXV1crKyuqwDc3bb7+tF154QYZh6IYbbtDkyZO1d+9eLV68WJI0Z84cDRs2zKuyAeC8MgxDVtYYmZmj5LxbJntjqdxj7yvy2jIZm1fJmlQoM3usDIOgEEDn4quOT1mnTjGOOEwQAgCA+FZdXa3m5mbNnz9fkUhEVVVV0fteeukl/fjHP9aPf/xjvfjii5Kkp556Snfffbe+//3v66mnnvKqbACIGcMwZeWMU/Dm7ylw+c1S9z5yjx1WpPRJtT77kOzd5XJdfhYE0HmYIPSp04eUMEEIAADiW2VlpQoKCiRJ+fn5qqioUE5OjiQpPT1dJ0+elCR169ZNktTQ0KBwOBz9bwDoqgzTkjVyosyccXJ2bVRk00q5Rw4osvxxGf0GKzD5KhmDR8gwDK9LBdDFERD61OlDSvitEQAAiG8NDQ1KT0+XJIVCIdXW1kbvmzJliu699165rqvvfOc7knROUzOlpaUqLS2VJC1cuDAaKOL8CgQCvLceowfe67QepH9V7sVXqWHz6zrx5sty3q9V68uPKWnICHW//AYlD82NfQ0+xOeA9+iB9zqjBwSEPnX6kBImCAEAQHwLhUJqbGyUJDU1NSkUCkXve+aZZ/TAAw9Ikn7+859r3LhxHT72bFMzhYWFKiwsjN6uq6s732VDUjgc5r31GD3wXqf3IOsCBQaPlv3O27K3vK6WmkrV/dcvZQzKUWDyVTLTh3ZeLT7A54D36IH3zmcPMjIyznidPQh9iglCAADQVeTm5mr79u2SpLKyMuXmnp6CCQaDSk5OVkpKiiKRiCQpLS1NR44c0dGjR6PLjgEgkRjBJAUuuExJf3WvrElXSknJcvdVqfX5f1Pr/yyRU7fP6xIBdDFMEPpU9JASJggBAECcy87OVjAY1Lx585SZmalwOKySkhIVFRXpqquu0o9+9CNJik4Ezp49Ww8++KAk6c477/SqbADwnJGUosDEmbLGXCR7219kl70pZ+9OOXt3yswaK2vSlTL7pHtdJoAugIDQpwLmqQlCmwlCAAAQ/4qLizvcLioqkiRdfvnluvzyyzvcN2zYMC1YsKCzSgMA3zNSQgpMuVpW/iWyt6yS/c4aOe9tl/PeOzJzxsmaVCizJ3vEAfjiCAh9yjoVEDquK8d1ZXJqFQAAAAAkNKNbmgIXXSurYLoim1+Ts2OdnKotct7dJnPkBAUmzJTRvbfXZQKIQwSEPmUYhgKmoYjjyrZdmQECQgAAAACAZKT2UHDadXLHTVdk05/l7NokZ+cGtVRslpk3WYEJM2Sk9vC6TABxhENKfCzQvg+hwz6EAAAAAICOjO69FbzsJiXd8gOZI8ZLjiOnfI1a/vBLRd5+UW5TvdclAogTBIQ+ZrWfZMxBJQAAAACAszB6hhWccYuCN39PZna+ZEdkb1utlid/qci65XKbG70uEYDPscTYxwJm+0nGHFQCAAAAAPh0Zp90mVfeJqdun+z1K+Ts3Sl782uy33lLVsGlsvKnyUhK8bpMAD5EQOhjgfYJQpYYAwAAAADOkRkeJPMrfyPn0F5FNqyQW1spe0Op7LK3ZF1wmawxF8kIJnldJgAfISD0sfYJQpsJQgAAAADA52SmD1XSV++Us79akfWvyj24W/ba/5G97S+yxl8ua9RUGYGg12UC8AH2IPQxJggBAAAAAF+WmZGt4Nf/TsFZ35LRf4jUVC/7rRfV8t+/kl2+Vq4d8bpEAB5jgtDHLIs9CAEAAAAAX55hGDKG5Co4eIScPTtkb1gh98gBRf7ynLTldQUmzpQ54gIZpuV1qQA8QEDoYwGTU4wBAAAAAOePYRiyMkfLHJYnp3p7W1B47H1FVj0tY/NrsiZdKXN4vgyDBYdAIiEg9LFA+wShwwQhAAAAAOD8MQxT1vACmVlj5VRtVWRjqdwP6xT58x9kbF4pa9JVMjNHyzAMr0sF0AnO6VcCt9xyi956663o7U2bNunuu++OWVFo035ICROEAAAAAIBYMExTVu54Jc3+gQLTi6S0nnKPHlLk1f9Sa8nDsvfukusytAJ0dZ86QVhXV6fDhw9Lkmpra1VeXi5J2rJliw4dOhT76hJc+yElNhOEAAAAAIAYMixL1qgpMnMnyNmxTpHNr8mt26fI//xeRvowBSZfJXPQcK/LBBAjnxoQvvbaa3rmmWckSc8++6yeffbZ6H2DBg2KbWX4yCElTBACAAAAAGLPsAKyxl4sc+Qk2eVrZG95Xe6hPWp9cbGMjOFtQeGAYV6XCeA8+9SAMCcnR1dddZVeffVVFRQUaODAgZKktLQ0TZs2rVMKTGSnDylhghAAAAAA0HmMYJIC46bLGjVV9vY3ZW99Q+7+d9X6x0dkDhkpa/KVMvsN9rpMAOfJpwaE48eP1/jx4zV8+HCNGTNG/fr1kyQ5jiPT5ESjWDt9SAkThAAAAACAzmckJSswYYasMRfJ3vYX2WWr5dTsklOzS2bmmLZTj/sO8LpMAF/SOaV8NTU1eu2113T06FF9+9vf1h133KGVK1fGuraExwQhAAAAAMAPjORuCky+Sknf+F+yxk2XAkE5u99R6zOL1PrnP8g59r7XJQL4Es4pIFy9erVSU1P15ptvKhKJaODAgSopKYl1bQmvfYLQZoIQAAAAAOADRrdUBS6cpaRb/0nW2Isl05RTtVWtyx5Q62tPyz1+1OsSAXwBn7rEuF19fb26d++uLVu2aPr06Ro2bJj+/d//Pda1JTzLap8gJCAEAADe+cd//EcNGTJEmZmZGjp0qDIzMzVgAMvJACCRGak9FLjk67LGTVdk00o5uzbIqdiolqrNMvMmKzB+hoy0nl6XCeAcnVNAGA6H9Yc//EH19fX69re/rWPHjiktLS3WtSW8gNl+ijFLjAEAgHcmT56sSCSiXr16adu2bXr44YfVvXt39enTR8OGDdPcuXO9LhEA4BEjrZeC04vkjrtMkU1/llO5WU75WrXs2ihr1FRZ4y+XEerudZkAPsM5BYS33Xabnn76aY0YMUJTpkzRk08+qalTp8a6toQXaJ8gZIkxAADw0LZt2/R//+//jd6+4oortG7dOl1zzTXas2ePh5UBAPzC6NlXwStmy7ngctkbSuVUb2s7/XjnOlljL5Y1brqMlFSvywRwFucUEE6ZMkUTJ07UgQMHdPDgQd1+++2cYtwJmCAEAAB+0L17d+3evVuZmZmSpBEjRujRRx/Vbbfdpr59+3pbHADAV8ze/WVe+VdyjpwKCneXy97yuux31sjKnyar4FIZySlelwngY84pIKytrdWvfvUrHTx4UJI0YMAA3XvvvRo0aFBMi0t07ROEHFICAAC89Hd/93d6+OGHNXjwYGVmZmrfvn1KSkryuiwAgI+ZfTNkXv1NOYdrFNmwQm5NhexNf5b9zluyxk2XNfZiGcFkr8sEcMo5jQH+7ne/0wcffKBLLrlEl1xyiY4dO6bHHnss1rUlPMtighAAAHhvwIABmj9/vsaPH69jx45pwIABuu+++7wuCwAQB8z+Q5Q061sKfv3vZQzMkk42yV63XC1P/lKRbX+RG2n1ukQAOscJwurqav3VX/2VrrnmGknSK6+8oj/84Q8xLQxSwOQUYwAA4A+maWrq1KnsQw0A+ELMgZkKfm2u3H3vKrL+VbmH98p++yXZW/+iwIQrZOZNlmGdU0QBIAbO6bMvLS1N27Zt0/jx4yW1bVTNKcaxF2ifIHSYIAQAAAAAxDfDMGQMzlFw0HA5e3fJ3vCq3Lr9iqz+o7TldQUmzpSZO0GGaXldKpBwzikgnDFjhpYtW6aNGzdGr91yyy0xKwptmCAEAAAAAHQ1hmHIGpYnc+hIOe+9I3vDCrkfHFLk9WdlbF4la1KhzOHjZHA4KtBpzikgnD59unr27Klt27ZJksaNG6eCgoKYFobTE4Q2E4QAAAAAgC7GMAxZ2WNlZo6W8+62tqDw+BFFVj4lY/NrsiZdKbfvZV6XCSSEcwoIFyxYoIsvvlg/+MEPJEn//d//rZ/+9KdatGjRp37ckiVLVF1draysLBUXF0evl5SUaPny5briiit06623SpIefPBBHTt2TK2trWppadGvfvUrLVu2TOvXr1dqaqomTZqka6+99ou+zrh0+pASJggBAAAAAF2TYZqyRlwgc3i+nIrNimwslfvBYUVWLNX72/4id/wMmUNHyjAMr0sFuqxzCgiPHj2q/v37R2/369dPR44c+dSPqa6uVnNzs+bPn6/FixerqqpKOTk5ktqWLOfm5mr79u3Rx3/ve9+TJK1bt07V1dXR63fccUfCTiueXmLMBCEAAAAAoGszTEtW3iSZIy6Qs3ODIptWqvXQXumVJTL6D1Fg8lUyBuUQFAIxcE4BYXp6uv70pz+pT58+cl1XL774otLT0z/1YyorK6PBXn5+vioqKqIBYa9evbRv374zfty6des0a9as6O2lS5fqj3/8o+644w5lZmZ+4vGlpaUqLS2VJC1cuFDhcPhcXpJvBQKB6GtocpPaLhpm3L+uePPRPsBb9MIf6IM/0Ad/oA8AAMSWYQVkjblQ5siJ6ranTB+ufknu4Rq1vvQ7GQOzFJh8lcyBWV6XCXQp5xQQXnfddfrtb3+rn//859Fr3/3udz/1YxoaGqIhYigUUm1t7Wf+OZFIRHv37lV2drYkadasWZo9e7YOHDigRx55RPPnz//ExxQWFqqwsDB6u66u7lxekm+Fw+Hoa6g/3iRJOtnSGvevK958tA/wFr3wB/rgD/TBH7pKHzIyMrwuAQCAT2UEgkqbepWaho6Rvf1t2Vtfl3vgPbW+8O8yBucqMPlKmf2HeF0m0CWc8yEl4XBYmzZtkiRNmDBBo0eP/tSPCYVCamxslCQ1NTUpFAp95p9TXl7e4XnT0tIkSQMHDjyXMruc9kNKIg57EAIAAAAAEpMRTFZg/OWyRl8ou+wvsretlltbodbaCpnDRsmafKXMvvziC/gyzikglKTRo0d/Zij4Ubm5uSotLdXFF1+ssrIyXX755Z/5MevWrdPFF18cvd3Y2KhQKKTjx4/Ltu1z/rO7CstiD0IAAAAAACTJSE5RYNKVssZeLHvrG7K3vyVnzw45e3bIzC6QNalQZu/+n/1EAD7hnAPCzys7O1vBYFDz5s1TZmamwuGwSkpKVFRUpJUrV2r58uWqr69XfX295syZI9d1VVFRoW9961vR53jiiSdUU1Mjx3F02223xapU3wqYnGIMAAAAAMBHGSmpCkz9iqz8abK3rJJdvlZO9TY575XJzLlAgYmFMnr29bpMIK7ELCCUpOLi4g63i4qKJLWdYjxjxowO9xmGoV/+8pcdrs2dOzeW5fle4NQEoe0wQQgAAAAAwEcZoe4KXPw1WQXTFdn8mpyd6+RUblZL1VaZIycpMGGGjO69vC4TiAsxDQjx5UQnCNmDEAAAAACAMzLSeip46fVyx01XZNOf5VRskrNznVoqNsoaPVXWBZfLSO3hdZmArxEQ+phpGjINyXHbpggt0/C6JAAAAAAAfMno0UfBy2+Wc8HlsjeWyqnaJnv7W7J3rpc1+iJZF0yX0S3N6zIBXyIg9DnLMuVEHNm2I8u0vC4HAADgC1myZImqq6uVlZXVYRuaBx98UMeOHVNra6taWlr0q1/9SsuWLdP69euVmpqqSZMm6dprr/WwcgBAvDF79ZM58xtyxl8he8MKOe+9I3vbG7J3rJGVP01WwaUykrt5XSbgKwSEPhcwDbVKijiukrwuBgAA4Auorq5Wc3Oz5s+fr8WLF6uqqko5OTmSpO9973uSpHXr1qm6ujr6MXfccYcKCgq8KBcA0EWYfQbIvOoOOe/XtgWFe3fJ3rRS9va3ZI27VNbYaTKSkr0uE/AF0+sC8OkCVluLWjnJGAAAxKnKyspo2Jefn6+KiopPPGbdunWaMmVK9PbSpUu1YMEC7d69u7PKBAB0UWa/wQp+pVjB674tI2O41NIse/0KtfzhF4psfUNua4vXJQKeY4LQ55ICbQFhS8T2uBIAAIAvpqGhQenp6ZKkUCik2traDvdHIhHt3btX2dnZkqRZs2Zp9uzZOnDggB555BHNnz//E89ZWlqq0tJSSdLChQsVDodj/CoSUyAQ4L31GD3wHj3w1nl9/8NhaexEndy9U8dff04tte/KXvOy3LI31f2SWUodP11GIHh+/qwuhM8B73VGDwgIfS4lGJB0Us0tBIQAACA+hUIhNTY2SpKampoUCoU63F9eXq7Ro0dHb6eltW0gP3DgwLM+Z2FhoQoLC6O36+rqzmfJOCUcDvPeeoweeI8eeCsm739aWJo1R8GaCkXWvyqnbp8+fPUP+vCtlxWYMFNm7kQZFmcAtONzwHvnswcZGRlnvM4SY59LSWr7otTcSkAIAADiU25urrZv3y5JKisrU25ubof7P768uD1MPH78uGyb74EAAOefYRgyh45UsOi7Clx9h4w+A6T6DxV5o0Qty34tu2KTXIetvpA4mCD0uZTgqYCQCUIAABCnsrOzFQwGNW/ePGVmZiocDqukpERFRUVyXVcVFRX61re+FX38E088oZqaGjmOo9tuu83DygEAXZ1hGLIyx8gcNkrOu2WyN5bKPfa+Iq8tk7H5NVmTrpSZPVaGwXwVujYCQp+LThC2RDyuBAAA4IsrLi7ucLuoqEhS2w9mv/zlLzvcN3fu3E6rCwAASTIMU1bOOJnZY+VUblFk45/bgsLSJ2X0GSBr8lUyh42SYRhelwrEBAGhz7XtQcgSYwAAAAAAYs0wLVkjJ8rMGSdn10ZFNq2Ue/SgIssfl9FvsAKTr5IxeARBIbocAkKfYw9CAAAAAAA6l2EFZI2eKjN3guwd62Rvfk3u+7VqffkxGQMyFZh8lcyMbK/LBM4bAkKfYw9CAAAAAAC8YQSCCuRfIitvsux33pa95XW5B3er9U+PyhiU0xYUpg/1ukzgSyMg9Llu0QlC9iAEAAAAAMALRjBJgQsukzV6quyyN2Vve0Puviq17quSOTRP1uQrZYYHeV0m8IUREPpcStKpPQiZIAQAAAAAwFNGUooCE2fKGnOR7G1/kV32ppy9O+Xs3Skza2zbqcd90r0uE/jcCAh9LvnUEuMmAkIAAAAAAHzBSAkpMOVqWfmXyN6ySvY7a+S8t13Oe+/IzBkna1KhzJ5hr8sEzhkBoc+170F4kkNKAAAAAADwFaNbmgIXXSurYLoim1+Ts2OdnKotct7dJnP0VAUmXy0jOcXrMoHPZHpdAD4dexACAAAAAOBvRmoPBaddp6Rb75GZN0mS5LzztlqWPSC7ukyu63pcIfDpCAh9LiXIHoQAAAAAAMQDo3tvBS+7ScEb75LRf6jUeFyRFUsVWf643PpjXpcHnBUBoc+lnJogbGKJMQAAAAAAccHsO0DB6/5egWnXSUnJcvbsUMtTDyiybbVcx/G6POATCAh9LilgyjCk1ogjmy8iAAAAAADEBcM0ZY25SEmzfygza6wUaZH99otqfe63ct7f53V5QAcEhD5nGEb0oBKWGQMAAAAAEF+M1B4KXnW7Ald/U0rrKbdun1qfe1iRt1+U23rS6/IASQSEcYGTjAEAAAAAiG9W5mglzf6BrPxLJEn2ttVqWfavsvfs9LgygIAwLqQktR1Uwj6EAAAAAADELyOYrMDFX1Pwhn+QER4k1R9T5JUlal2xVG7Dca/LQwIjIIwDLDEGAAAAAKDrMPsNVvCG78i66KtSIElOdZlalv1a9jtr5LqcP4DOR0AYB9pPMm5uiXhcCQAAAAAAOB8M01Kg4FIlzf6+zKF5UstJRVY/r9Y//j85Rw96XR4SDAFhHIhOELLEGAAAAACALsXo3luBa/5agStvk0Ld5R7aq9Znf6PI2lfkRlq9Lg8JgoAwDrTvQUhACAAAAABA12MYhqzsfCXN/qHM0RdKjit7yyq1PP2gnNpKr8tDAiAgjAPsQQgAAAAAQNdnJKcoeOn1Cl739zL6pEvHj6j1pd+pdeVTcpvqvS4PXRgBYRyI7kHYyh6EAAAAAAB0deaAYQoW3SVrytWSFZBTuVktTz0ge+cGua7rdXnogggI4wAThAAAAAAAJBbDshQYf4WSbv6+jMEjpJONirz+jFr/9KicY+97XR66GALCONCtfQ9CAkIAAAAAABKK0bOvgrO+pcCMW6SUVLkH3lPr0w8qsqFUrs1KQ5wfBIRxIJlTjAEAAAAASFiGYcgaMV5Jt/xA5shJkmPL3liq1mcWydlf7XV56AIICOPA6T0ICQgBAAAAAEhURkqqgpffpODX5sro1U/usffV+qdH1fr6M3KbG70uD3GMgDAOnN6DkNFhAAAAAAASnZmRreBNd8uaOFMyLTk7N6hl2QOyK7dwiAm+EALCOBDdg5AJQgAAAAAAIMmwAgpMulLBm+6WMTBLaqpXZOV/q/Xlx+QeP+J1eYgzBIRxILrEmENKAAAAAADAR5i9+yv4tb9V4LIbpeRucmsr1fL0g4psWSXXJkfAuQnE8smXLFmi6upqZWVlqbi4OHq9pKREy5cv1xVXXKFbb71VkvTb3/5W+/btU1JSkgoLCzVt2jQdPXpUDz30kFpbWzV79mwVFBTEslzfSg60BYQnW205rivTMDyuCAAAAAAA+IVhmLLyJsscNkqRt16UU7VF9tpX5FRuUWB6kcz0oV6XCJ+LWUBYXV2t5uZmzZ8/X4sXL1ZVVZVycnIkSTNmzFBubq62b9/e4WPuuusuDRgwIHr7+eef1y233KLMzEwtXLgwYQNC0zSUHDB1MuLoZKsdXXIMAAAAAADQzuiWpuDMW+XkTlDr6uflHj2o1ucfkTl6qgJTrpGRnOJ1ifCpmCVNlZWV0UAvPz9fFRUV0YCwV69e2rdvX4fHG4ahhx9+WGlpabrzzjvVr18/1dTUaOTIkTIMQykpKWpsbFQoFOrwcaWlpSotLZUkLVy4UOFwOFYvqVMEAoEzvoZQSpJO1jcrlNZTfXt086CyxHK2PqDz0Qt/oA/+QB/8gT4AAAC/M4fkKumm78netFL2tjfklK9Ry+5yBS75msyssTJYmYiPiVlA2NDQoPT0dElSKBRSbW3tpz7+m9/8ptLS0rRz5049/vjj+uEPfyjHcaJ/aUOh0BkDwsLCQhUWFkZv19XVnedX0rnC4fAZX0OS1fY+HDj0vtyW0Cfux/l1tj6g89ELf6AP/kAf/KGr9CEjI8PrEgAAQAwZwSQFpl4jM+cCRd4okXt4ryIrlsocNkqBadfJSOvldYnwkZgdUtIe6ElSU1PTJ4K9j0tLS5Mk5eXl6dixY5LUIdE+l+foytoPKmniJGMAAAAAAHCOzL4DFLzu7xWYdp2UlCxnzw61PPWAIttWy3Ucr8uDT8QsIPzoHoNlZWXKzc391Me3h4n79+9XamqqJGno0KGqqKhQc3MzAWH0JOOIx5UAAAAAAIB4YpimrDEXKWn2D2VmjZUiLbLfflGtz/1Wzvv7PvsJ0OXFbIlxdna2gsGg5s2bp8zMTIXDYZWUlKioqEgrV67U8uXLVV9fr/r6es2ZM0e/+c1v1NDQIMMwNGfOHEnSddddp4cfflgtLS2aPXt2rEqNCynB9oCQCUIAAAAAAPD5Gak9FLzqdtm7yxV5849y6/ap9bmHZeVfImvSlTKCyV6XCI/E9Djc4uLiDreLiooktZ1iPGPGjA733XfffZ/4+L59++r++++PXYFxJCXY1qpmlhgDAAAAAIAvwcocLXPQcNnrV8je/qbsbatlV29XYNr1sobleV0ePBCzJcY4v6JLjAkIAQAAAADAl2QEkxW4+FoFb/gHGeFBUv0xRV5ZotYVS+U2HPe6PHQyAsI4cXqJMXsQAgAAAACA88PsN1jBG74j66KvSoEkOdVlaln2a9nvrJHrcohJoiAgjBMpSaeWGLMHIQAAAAAAOI8M01Kg4FIlzf6+zKF5UstJRVY/r9Y//j+1HuYQk0RAQBgnohOELDEGAAAAAAAxYHTvrcA1f63AlbdJoe5yD+3V4d/NV2TtK3IjrV6XhxiK6SElOH+iexAyQQgAAOLQkiVLVF1draysrA4H2T344IM6duyYWltb1dLSol/96lc6evSoHnroIbW2tmr27NkqKCjwsHIAABKLYRiysvNlDhqhyLpX5JSvlb1llezqMgUvvV7m4BFel4gYICCME6cnCNmDEAAAxJfq6mo1Nzdr/vz5Wrx4saqqqpSTkyNJ+t73vidJWrdunaqrqyVJzz//vG655RZlZmZq4cKFBIQAAHjASE5R8NLr1X3yFTryp8fkHj2k1pd+J3PEeAUu+qqMbmlel4jziIAwTkT3IGSJMQAAiDOVlZXRkC8/P18VFRXRgLDdunXrNGvWLElSTU2NRo4cKcMwlJKSosbGRoVCoQ6PLy0tVWlpqSRp4cKFCofDnfBKEk8gEOC99Rg98B498Bbvv/cCgQFKmvsT1a95VcdX/0lO5Wa11lao58ybFSq4RIZheF1il9cZnwcEhHHi9CnGBIQAACC+NDQ0KD09XZIUCoVUW1vb4f5IJKK9e/cqOztbkuQ4TvSHjVAodMaAsLCwUIWFhdHbdXV1sXwJCSscDvPeeoweeI8eeIv333vhcFhHPjgmjZyipAHD1br6ebm1lTr24hJ9uPF1BaYXyezVz+syu7Tz+XmQkZFxxuscUhInuiVxSAkAAIhP7SGfJDU1NX0i7CsvL9fo0aOjtz86iXCmxwMAAG8YPfsqOOtbCsy4RUpJlXvgPbU+/aAiG0rl2myJFs8ICONEcnSCMCLXdT2uBgAA4Nzl5uZq+/btkqSysjLl5uZ2uH/dunWaMmVK9PbQoUNVUVGh5uZmAkIAAHzGMAxZI8Yr6ZYfyBw5SXJs2RtL1frMIjn7q70uD18QAWGcCFimApYhx5VaI47X5QAAAJyz7OxsBYNBzZs3T6ZpKhwOq6SkRJLkuq4qKiqUl5cXffx1112nP/zhD1qwYIFuuOEGr8oGAACfwkhJVfDymxT82lwZvfrJPfa+Wv/0qFpff0Zuc6PX5eFzYg/COJISDKjeblVzq62kUxOFAAAA8aC4uLjD7aKiIkltUwi//OUvO9zXt29f3X///Z1WGwAA+OLMjGwFb7pb9ubXZG9eJWfnBrXs2anARdfKzBnHISZxggnCOMI+hAAAAAAAwG8MK6DApCsVvOluGQOzpKZ6RVb+t1pffkzu8SNel4dzQEAYR1I+sg8hAAAAAACAn5i9+yv4tb9V4LIbpeRucmsr1fL0g4psWSXXZtjJzwgI40jyqQnCphY+qQAAAAAAgP8Yhikrb7KSbvmhzJwLpEir7LWvqLXkITmH9npdHs6CgDCOpATbtoxkiTEAAAAAAPAzo1uagjNvVXDWt6QefeQePajW5x9R61+el3uy2evy8DEEhHGkfQ/CkwSEAAAAAAAgDphDcpV00/dkXXC5ZBpyyteoZdkDsqvL5Lqu1+XhFALCONK+ByFLjAEAAAAAQLwwgkkKTL1GwaK7ZPQfKjUeV2TFUkWWPy73xDGvy4MICONKSvQUYw4pAQAAAAAA8cXsO0DB6/9egWnXSUnJcvbsUMuyBxTZtlqu43hdXkIjIIwjye17EDJBCAAAAAAA4pBhmLLGXKSk2T+UmTVWirTIfvtFtT73Wznv7/O6vIRFQBhH2vcgJCAEAAAAAADxzEjtoeBVtytw9TeltJ5y6/ap9bmHFXn7RbmtJ70uL+EQEMaR9j0IWWIMAAAAAAC6AitztJJm/0BW/jRJkr1ttVqW/avsPTs9riyxEBDGkdN7EDJBCAAAAAAAugYjmKzAxdcqeMM/yAgPkuqPKfLKErWuWCq34bjX5SUEAsI4ksIehAAAAAAAoIsy+w1W8IbvyLroq1IgSU51mVqW/Vr2O2vkuhxiEksEhHGECUIAAAAAANCVGaalQMGlSpr9fZlD86SWk4qsfl6tf/x/co4e9Lq8LouAMI5E9yBkghAAAAAAAHRhRvfeClzz1wpceZsU6i730F61Pvsb2bs2eF1alxTwugCcu+gEYQuHlAAAAAAAgK7NMAxZ2fkyB41QZN3/yClfq8iqZyVJ1shJHlfXtTBBGEeClinTMBRxXEVs1t4DAAAAAICuz0hOUfDSG2RNuVqSq8iqZ5kkPM8ICOOIYRjsQwgAAAAAABJSYPwVHwsJN3pdUpdBQBhn2IcQAAAAAAAkqo4h4TOEhOcJexDGmdMThOxDCAAAAAAAEk9g/BWSJHvdckVWPSNJskZO9LKkuMcEYZxhghAAAAAAACS6wPgrZE1mkvB8ISCMMylJbUOfTQSEAAAAAAAggQUmfCwkrCAk/KJYYhxn2icIT3JICQAAAAAASHCBCaeWG69frshrp5Yb57Lc+PMiIIwz3diDEAAAAAAAIIqQ8MtjiXGcSQmyxBgAAAAAAOCj2pYbXyXJVeQ1lht/XgSEcSY5iUNKAAAAAAAAPi4wYcbHQsJNXpcUN2K6xHjJkiWqrq5WVlaWiouLo9dLSkq0fPlyXXHFFbr11lslSY8++qhqamokSXPmzNGwYcO0bNkyrV+/XqmpqZo0aZKuvfbaWJYbF6KnGLMHIQAAAAAAQAeBCTMkSfb6VxV57WlJkpU7wcuS4kLMAsLq6mo1Nzdr/vz5Wrx4saqqqpSTkyNJmjFjhnJzc7V9+/bo46+//nr1799fBw4c0NKlS3XPPfdIku644w4VFBTEqsy4E92DsIU9CAEAAAAAAD6uLSR0Za9fQUh4jmK2xLiysjIa7OXn56uioiJ6X69evWQYRofH9+/fX5JkWZZM83RZS5cu1YIFC7R79+5YlRpXmCAEAAAAAAD4dIEJM2VNvlJty42fll2x2euSfC1mE4QNDQ1KT0+XJIVCIdXW1p7Txz355JOaNWuWJGnWrFmaPXu2Dhw4oEceeUTz58//xONLS0tVWloqSVq4cKHC4fB5egXeCAQCn/oa0k+2hae2a8T9a/Wzz+oDOg+98Af64A/0wR/oAwAAQHwITJgpSacmCZdJkqzc8V6W5FsxCwhDoZAaGxslSU1NTQqFQp/5MS+99JIGDx6svLw8SVJaWpokaeDAgWf9mMLCQhUWFkZv19XVfZmyPRcOhz/1NZw89Z6eaDwZ96/Vzz6rD+g89MIf6IM/0Ad/6Cp9yMjI8LoEAACAmCMkPDcxW2L80T0Gy8rKlJub+6mP37p1q3bt2qUbb7wxeq09YDx+/LhsmyW1kpTCHoQAAAAAAADnLDBhpqxJp5Ybr1rGcuMziNkEYXZ2toLBoObNm6fMzEyFw2GVlJSoqKhIK1eu1PLly1VfX6/6+nrNmTNHjz32mEKhkH7yk58oIyNDc+fO1RNPPKGamho5jqPbbrstVqXGFfYgBAAAAAAA+HwCE09NEm5YocgqJgk/LmYBoSQVFxd3uF1UVCSp7RTjGTNmdLhv0aJFn/j4uXPnxq64OJUUtGQYUkvEke04ssyYDYECAAAAAAB0GZ8ICQ3JGkFIKMVwiTFiwzQM9eiWJEn6sKHF42oAAAAAAADiR2DiTFmTCiXXVeS1ZbIrWW4sERDGpT5pyZKko/UnPa4EAAAAAAAgvgQmFhISfgwBYRzqTUAIAAAAAADwhRESdhTTPQgRG326nwoITxAQAgAAAAAAfBGBiYWSJHtDqSKvLZNkyBpxgac1eYWAMA6dXmLc7HElAAAAAAAA8SswsVByJXtjqSKvPSVJCRkSEhDGoT5pKZJYYgwAAOLHkiVLVF1draysLBUXF0ev19fX69FHH9WJEyeUn5+voqIi/fa3v9W+ffuUlJSkwsJCTZs2zcPKAQBAVxeYdGqSMIFDQgLCOMQhJQAAIJ5UV1erublZ8+fP1+LFi1VVVaWcnBxJ0tNPP61bbrlFgwYN6vAxd911lwYMGOBFuQAAIAElekhIQBiHeoaSZJmGTjS1qjXiKBjgrBkAAOBflZWVKigokCTl5+eroqIiGhDW1NToueee05EjR/SNb3xDubm5MgxDDz/8sNLS0nTnnXeqX79+n3jO0tJSlZaWSpIWLlyocDjceS8ogQQCAd5bj9ED79EDb/H+ey+henDNrToeCunEX15Q5LWn1L1Hd4XGTPW6qk7pAQFhHDJNQ71Sk3TkxEkdrT+p9F7dvC4JAADgrBoaGpSeni5JCoVCqq2tjd63a9cu/eIXv1BaWpp+/etfa8GCBfrmN7+ptLQ07dy5U48//rh++MMffuI5CwsLVVhYGL1dV1cX+xeSgMLhMO+tx+iB9+iBt3j/vZdwPRh9sazGBtkb/6wP/vgfOnHihKycCzwt6Xz2ICMj44zXGT2LU6f3IeSgEgAA4G+hUEiNjY2SpKamJoVCoeh9GRkZGjx4sHr16iXTbPvWNC0tTZKUl5enY8eOdXq9AAAgsQUmXSlr4kzJdRVZ+ZTsd7d5XVLMERDGKfYhBAAA8SI3N1fbt2+XJJWVlSk3Nzd638CBA/XBBx+oublZtm1LUjRM3L9/v1JTUzu/YAAAkPACk66UNaEtJLTXLfe6nJhjiXGc6tP9VEB4goAQAAD4W3Z2toLBoObNm6fMzEyFw2GVlJSoqKhIs2fP1qJFi9TS0qKbbrpJkvSb3/xGDQ0NMgxDc+bM8bh6AACQqKzxl8ve9Ge59R/IdR0ZRtedsyMgjFNMEAIAgHhSXFzc4XZRUZEkafDgwfrxj3/c4b777ruvs8oCAAA4KyMQlFJCUnOj1NQghbp7XVLMdN3os4trDwg/YA9CAAAAAACAmDBCPSRJbsOHHlcSWwSEcer0ISVMEAIAAAAAAMSCkdZTkuQ2HPe4ktgiIIxTqSkBBQOmmlpsNbVEvC4HAAAAAACg6wm1BYRighB+ZBjG6X0IOagEAAAAAADgvDPSTi0xricghE9xUAkAAAAAAEDsGKmnlhg3ssQYPtW3e/s+hBxUAgAAAAAAcL5FA0ImCOFXLDEGAAAAAACIoVMBoZgghF/1ZokxAAAAAABAzHx0gtB1XY+riR0CwjjGHoQAAAAAAAAxlJQsBZKkSIvU0nW3eCMgjGN9PrIHYVdOsQEAAAAAALxgGIaMtFNThA1dd5kxAWEcSwlaCiUHFLFdnWhq9bocAAAAAACArqd9H8KGrntQCQFhnGOZMQAAAAAAQOwYqT0kSS4BIfyKgBAAAAAAACB2okuL7Yi3hcRQwOsC8OX06X4qIDzRdTfKBAAAAAAA6EybyvdrxZtVOvFhvVIbgprZp58mDy/wuqyYISCMc33S2g8qYYIQAAAAAADgy9pUvl//+dwWnWhoz1p66ODRngq+96HGj0r1tLZYYYlxnGOJMQAAAAAAwPmz4s2qj4SDbU6cdPXq6iqPKoo9AsI4R0AIAAAAAABw/tQ3tJz5euOZr3cFBIRxrndasgxJHzaclO24XpcDAAAAAAAQ19JSk858PXTm610BAWGcC1imeoSS5LhtISEAAAAAAAC+uKum5ah7anKHa91Tk3XVtByPKoo9DinpAvqkJevDxhYdrT+pPt1TvC4HAAAAAAAgbo0flSEVSa+urlJ9Y4vSQkm6alpO2/UuioCwC+idlqz3Dp9gH0IAAAAAAIDzYPyojC4dCH4cS4y7gD7dTx1UcoKAEAAAAAAAAJ8PAWEXcPok42aPKwEAAAAAAEC8ISDsAvqmte07yBJjAAAAAAAAfF4x3YNwyZIlqq6uVlZWloqLi6PXS0pKtHz5cl1xxRW69dZbJUl79+7V4sWLJUlz5szRsGHDzngNn9S+xPj9481yHFemaXhcEQAAAAAAAOJFzCYIq6ur1dzcrPnz5ysSiaiqqip634wZM/SP//iPHR7/1FNP6e6779b3v/99PfXUU2e9hk/qGUpSn7RkNZ6MqGL/Ma/LAQAAAAAAQByJWUBYWVmpgoICSVJ+fr4qKiqi9/Xq1UuG0XHKraGhQeFwWH369FFDQ8NZr+GTDMPQ1Nz+kqS1lYc9rgYAAAAAAADxJGZLjBsaGpSeni5JCoVCqq2t/dTHu657Ttc+rrS0VKWlpZKkhQsXKhwOf4Fq/SMQCHyh13D1lDS9uqVW5TXHFEhJU69T+xLii/mifcD5Ry/8gT74A33wB/oAAACAriZmAWEoFFJjY6MkqampSaFQ6Jw/9uPThWe7JkmFhYUqLCyM3q6rq/uclfpLOBz+wq9h9JDeKttzVMvX7dLMgkHnubLE8mX6gPOLXvgDffAH+uAPXaUPGRkZXpcAAAAAn4jZEuPc3Fxt375dklRWVqbc3NxPfXxaWpqOHDmio0ePqlu3bme9hrObOuL0MmPnHKYvAQAAAAAAgJhNEGZnZysYDGrevHnKzMxUOBxWSUmJioqKtHLlSi1fvlz19fWqr6/XnDlzNHv2bD344IOSpDvvvFOSzngNZzcio6d6pyXrg/qTqtz/oUYO6uV1SQAAAAAAAPC5mAWEklRcXNzhdlFRkaS2U4xnzJjR4b5hw4ZpwYIFn3kNZ2cahqaO6K9XNtdobeVhAkIAAAAAAAB8ppgtMYY3JuX0k2lI7+z9QMebWrwuBwAAAAAAAD5HQNjF9AwladTg3nJcVxuq3ve6HAAAAAAAAPgcAWEXdGHuqcNKKjisBAAAAAAAAJ+OgLALys3opV6pSTpaf1JVB457XQ4AAAAAAAB8jICwCzJNQ1NGtE0Rvrxxr3bUfiDHYZIQAAAAAAAAnxTTU4zhnSkj+mv1joPad7RBj/15l3qGkjRxeFiTc/or3CPF6/IAAAAAAADgEwSEXVTPUJJ+8PUCbXz3fa2vfF91J5q1smy/VpbtVzBgyjQMmYZkGoaMU/+N00zTlOM4XpcB0Qu/oA/+QB+8cXHeAM0sGOR1GXFvyZIlqq6uVlZWloqLi6PX6+vr9eijj+rEiRPKz89XUVGR9u7dq8WLF0uS5syZo2HDhnlVNgAAQEIgIOzCeoaSNCN/kK4Ym6H3Dp/Q+sr3tXXPEbVG+OESAIBzdbLV9rqEuFddXa3m5mbNnz9fixcvVlVVlXJyciRJTz/9tG655RYNGnQ6hH3qqad09913yzRN/cd//Ifuvfder0oHAABICASECcAwDGWn91B2eg/ddHG2bNuR7bpyXclxXDmuK3Yo7KhPnz46evSo12VA9MIv6IM/0AdvJAfYsvnLqqysVEFBgSQpPz9fFRUV0YCwpqZGzz33nI4cOaJvfOMbys3NVUNDg8LhsCSpoaHhjM9ZWlqq0tJSSdLChQujj8f5FQgEeG89Rg+8Rw+8xfvvPXrgvc7oAQFhgrFMQ5ZpeV2G7/VOS5HdnOR1GRC98Av64A/0AfGqoaFB6enpkqRQKKTa2trofbt27dIvfvELpaWl6de//rUWLFgg1/3sX10WFhaqsLAweruuru78Fw6Fw2HeW4/RA+/RA2/x/nuPHnjvfPYgIyPjjNcJCAEAABBToVBIjY2NkqSmpiaFQqHofRkZGRo8eLCktn02P84w2CgZAAAg1lgzAwAAgJjKzc3V9u3bJUllZWXKzc2N3jdw4EB98MEHam5ulm237feYlpamI0eO6OjRo+rWrZsnNQMAACQSJggBAAAQU9nZ2QoGg5o3b54yMzMVDodVUlKioqIizZ49W4sWLVJLS4tuuukmSdLs2bP14IMPSpLuvPNODysHAABIDASEAAAAiLni4uIOt4uKiiRJgwcP1o9//OMO9w0bNkwLFizorNIAAAASHkuMAQAAAAAAgARGQAgAAAAAAAAkMAJCAAAAAAAAIIEREAIAAAAAAAAJjIAQAAAAAAAASGAEhAAAAAAAAEACIyAEAAAAAAAAEhgBIQAAAAAAAJDACAgBAAAAAACABEZACAAAAAAAACQwAkIAAAAAAAAggREQAgAAAAAAAAmMgBAAAAAAAABIYASEAAAAAAAAQAIjIAQAAAAAAAASGAEhAAAAAAAAkMAICAEAAAAAAIAERkAIAAAAAAAAJDACQgAAAAAAACCBERACAAAAAAAACYyAEAAAAAAAAEhgBIQAAAAAAABAAiMgBAAAAAAAABIYASEAAAAAAACQwAgIAQAAAAAAgARmuK7rel0EAAAAAAAAAG8wQegz9913n9clQPTBT+iFP9AHf6AP/kAfkEj4++49euA9euAt3n/v0QPvdUYPCAgBAAAAAACABEZACAAAAAAAACQwAkKfKSws9LoEiD74Cb3wB/rgD/TBH+gDEgl/371HD7xHD7zF++89euC9zugBh5QAAAAAAAAACYwJQgAAAAAAACCBERACAAAAAAAACSzgdQE4bcmSJaqurlZWVpaKi4u9LiehVFZW6j//8z9lGIaGDx+uv/mbv9ELL7yg9evXq1+/fvrOd76jQIBPl87y4osvau3atVqwYAGfFx55/fXX9frrr8txHN1111164YUX6IMHTp48qQceeEAnT55UKBTS97//fS1dupRedJKjR4/qF7/4hWpra/X444/Lsqwzfk3i6xS6io9/7e/Tp48kadu2bXrqqaeUlJSkOXPmaNCgQR5X2jVt2bJFzz//vCRp//79mjNnjqZMmSKp7evRQw89pNbWVs2ePVsFBQUeVtp1fVoPVq5cqWeffVYjR47UXXfd5WGVXdun9eDpp5/Wli1bJEm33nqr8vPzPaqy6/q09//555/X5s2b1dLSohtuuCF6HefXp/VAklzX1b333qtrrrlGM2fOPL9/uAtfePfdd91HHnnEdV3XffTRR93KykqPK0osH3zwgXvy5EnXdV130aJF7jvvvOP+y7/8i+u6rvvcc8+5b731lpflJZSWlhb3oYcecv/5n/+ZzwuPHDlyxP23f/u36G364J01a9a4Tz/9tOu6rvvss8+6y5Ytoxed6OTJk+6JEyfc+++/341EImf8XODzA13Fx7/2f9SPfvQjt6mpyT169Kj7wAMPdHJliel//+//7TY1NUVv/+53v3N37NjhNjU1uffff793hSWQj/fgww8/dA8cOOAuWrTIw6oSy8d7cOjQIdd1Xbe+vt6dN2+eV2UljI+//62tra7rum5TU5P7f/7P//GqrITy8R64ruuuX7/enT9/vltaWnre/zyWGPtEZWVl9DeB+fn5qqio8LiixNKrVy8lJSVJkizLUk1NjUaPHi1JKigooB+daOXKlbr88ssl8XnhlS1btshxHM2fP1+PPfaYKioq6INH0tPT1dzcLElqaGiQYRj0ohMlJSUpLS0tevtMX5P4OoWu4uNf+x3H6XB/SkqKevfurUOHDnlUYeI4dOiQevbsqZSUlOi1mpoajRw5UikpKUpJSVFjY6OHFXZ9Z+pBjx49ZJr8+NxZztSD/v37S5KCwaBXZSWMM73/7SvqWlpaNGTIEK9KSxhn6oEkrV69WpdccklM/ky+wvlEQ0ODQqGQJCkUCvGPvkf27Nmj48ePKzU1Vd26dZPU1o+GhgaPK0sMkUhE77zzjsaOHSuJzwuvfPjhh4pEIpo3b56SkpLU2NhIHzwycOBAVVZW6gc/+IGqq6tlmia98NCZvibxdQpdxce/9q9fv77D/ceOHdO+ffu0b98+jypMHGvXrv3E0j3HcWQYhiS+1nSGM/UAnevTerBs2TJdeeWVnVxRYjnb+/8f//Efuueee6I/ryF2ztSDrVu3avTo0TH7ZQUBoU989B/6pqam6A8b6Dz19fV67LHH9O1vf1uhUEhNTU2SpMbGRqWmpnpcXWJ44403NG3atOhtPi+8EQqFohO07f/40wdvvP7665o4caIeeOABjR8/XrZt0wsPnelrEl+n0FV8/Gv/R4PA22+/XYsWLdLzzz+vkSNHelViwti4caMmTZrU4Vp7OCjxtaYznKkH6Fxn68G6detUX1/f4WcGnH9ne//nzJmjBx98UCUlJR5UlVjO1IM///nP0dV2sUBA6BO5ubnavn27JKmsrEy5ubkeV5RYbNvWQw89pDvuuEO9evXS8OHDVV5eLqmtHyNGjPC4wsSwf/9+rVixQj/72c9UW1urEydO8HnhgZEjR2rPnj2SpN27d0sSffCI67rRJa49evSQRC+8dKZ/q/n3G13Fx7/2ty/lk9r+7t9///0qKirigJIYO3bsmAKBgLp3797h+tChQ1VRUaHm5mYCwhg7Ww/Qec7Wgz179mj58uW68847PaosMZzt/W9tbZXUtgVL+2o7xMbZenDgwAH96le/0p/+9Ce9/PLL532q33Bd1z2vz4gv7Pe//73ee+89ZWZm6lvf+pbX5SSU1atX6/e//310L4W/+qu/Unl5uTZu3KhwOKx/+Id/4BTjTvajH/1ICxYs4PPCI48//riqq6vVvXt33X333fqv//ov+uCBhoYGPfjgg2ptbZVlWfr+97+vp59+ml50kkgkop///OfRE4q/8Y1vaPXq1Z94//k6ha7io1/7//qv/1pvvPGGioqKVFJSorKyMqWlpWnu3LkEJzG0YsUK2bata665RpL02GOP6Vvf+paOHDmihx9+WC0tLZo9e7bGjRvncaVd19l6sHHjRj3//PM6dOiQcnNzdc8993hcadd1th787Gc/09GjR9W9e3eFQiHde++9HlfaNZ3t/X/00Ue1f/9+RSIRfe1rX9PUqVM9rrTrOlsP2q1atUq2bZ/3U4wJCAEAAAAAAIAExhJjAAAAAAAAIIEREAIAAAAAAAAJjIAQAAAAAAAASGAEhAAAAAAAAEACIyAEAAAAAAAAEhgBIYCEdPjwYc2ePVsLFy7Upk2btGzZMh0+fPi8/zm1tbVatmyZ3nnnnei13/72t5o9e7befffd8/7nAQAAAADweQW8LgAAvNCjRw/dfffd6tOnj9566y0tX75cY8aMUf/+/T/X89i2Lcuyznp/bW2tnnnmGUnSmDFjJElXXXWVLrjgAqWnp3/xFwAAAAAAwHliuK7rel0EAHS2w4cP67vf/a6Sk5N18uTJDvctW7ZMFRUV+s///E/t3btXffr00c0336xp06ZFPy43N1fJycnau3evfv3rX+unP/2pDhw4IEnKysrS3/7t3yo5OVnf/e53Ozz3/fffr1WrVun111/Xz3/+cw0fPlylpaV64YUX9MEHH2jw4MH667/+a+Xl5WnVqlX6t3/7N1188cXat2+f6urqdPPNN2vWrFnav3+/Hn74Ye3Zs0dJSUkaMmSI5s+f32nvHwAAADp64IEH1LNnT+3evVtHjhzRXXfdpRUrVqiqqkp5eXn69re/7XWJAHBWLDEGkNBGjx6tcePGSZJuvPFG3X333aqvr9fChQvV2NiooqIi9evXTw899JB2794d/biKigplZWXplltukWEYmjJlioqLi3X99ddrz549WrJkiXr06KFZs2ZJkqZOnaq7775bgwcP7vDnb9++XY8++qh69Oihb37zm6qrq9MvfvELnThxIvqYd955RzNnzpQkLV26VJFIRMuXL9e7776r22+/Xd/4xjcUDodj/E4BAADg0+zdu1fp6elasGCBCgsL9cgjj+j222/XAw88oE2bNqm1tdXrEgHgrFhiDCChGYahAQMGaOvWrRo7dqzGjBmjTZs2qb6+XvX19frDH/4Qfez27ds1ZcoUSW1Tgrfffrsk6ejRo9q6dasqKirUPpS9d+9epaSkKC8vTy+//LKGDBmiSy655BN//qZNmyRJs2fPVkFBgerq6vTcc8+psrIy+pgrrrhC11xzjTZu3KitW7fq2LFjGjhwoFzX1ebNmzV8+PBoEAkAAIDO19LSooaGhuj3ZIZhaMaMGerdu7ckyTRNBQL8+A3Av/gKBSDhGYZxxuvTp0/X9OnTo7c/uj9h+zd7kvQ///M/2rVrl7761a9q/PjxeuSRR9TU1HTeaklLS5Ok6F6HjuPommuu0aBBg1ReXq4NGzaopKRE//qv/6qMjIwv9OcCAADgi6utrVV2drZMs22R3p49e3TVVVdJko4cOaI+ffqc9XtOAPADlhgDSHipqamSpDVr1mjTpk3Kzc1VWlqatm7dqv3796umpkZ//OMfdfTo0U99noaGBpWXl+vIkSPRa+3h3s6dO/Xmm2+qpaWlw8dMmDBBkvT0009rxYoVWrlypVJTUzVixIhP/bNeffVVVVRUaMCAAUpPT5frujp27NjnfekAAAA4D/bu3athw4ZFb+/Zs0dDhw79xH8DgF8REAJIeJdeeqkGDRqkV199Vb///e+Vlpam++67TwMGDNDSpUtVUlKipKQk9evX74wf/5WvfEXDhw/XW2+9paNHj2rIkCHR+/Ly8pSfn68dO3Zo0aJFHfYWlKSxY8dq7ty5+vDDD/X444+rb9+++l//63+pe/fun1pzMBjUqlWr9O///u/asWOHrr76auXl5X35NwMAAACf2969e5WZmSmpbblxS0tL9BfFe/bs6RAeAoAfcYoxAAAAAAAAkMCYIAQAAAAAAAASGAEhAAAAAAAAkMAICAEAAAAAAIAERkAIAAAAAAAAJDACQgAAAAAAACCBERACAAAAAAAACYyAEAAAAAAAAEhg/z9iUMn6CUl1SQAAAABJRU5ErkJggg==",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"\n",
"plot_all(cost_history, m, q)"
]
},
{
"cell_type": "code",
"execution_count": 325,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"3 passi e 300 gradienti calcolati per arrivare a distanza minore o uguale di 0.1 dall'ottimo\n"
]
}
],
"source": [
"near_opt(m, min_dist=1e-1, ge_per_step=n)"
]
},
{
"cell_type": "code",
"execution_count": 322,
"metadata": {},
"outputs": [],
"source": [
"def newton(X,t, epochs = 100):\n",
" theta = np.zeros(nfeatures+1).reshape(-1,1)\n",
" theta_history = []\n",
" cost_history = []\n",
" for k in range(epochs): \n",
" g = gradient(theta,X,t)\n",
" c1 = sigma(theta,X)\n",
" c2 = c1*(1-c1)\n",
" h0=np.einsum('ij,ik->ijk',X,X)\n",
" h=np.einsum('ijk, iq-> jk',h0,c2)/t.shape[0]\n",
" theta = theta - np.dot(np.linalg.inv(h),g)\n",
" theta_history.append(theta)\n",
" cost_history.append(cost(theta, X, t))\n",
" theta_history = np.array(theta_history).reshape(-1,3)\n",
" cost_history = np.array(cost_history).reshape(-1,1)\n",
" m = -theta_history[:,1]/theta_history[:,2]\n",
" q = -theta_history[:,0]/theta_history[:,2]\n",
" return cost_history, m, q"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3.8",
"language": "python",
"name": "python3.8"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.8.0"
},
"vscode": {
"interpreter": {
"hash": "ce48646bb6368aff8c12a2b8eeb9d1b908c9dd0a6e2925fc70e8d8f5f2053bd1"
}
}
},
"nbformat": 4,
"nbformat_minor": 2
}
"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [],
"source": [
"%matplotlib inline\n",
"import matplotlib as mpl\n",
"import matplotlib.pyplot as plt\n",
"import numpy as np\n",
"import scipy as scipy\n",
"import scipy.special as sp\n",
"import pandas as pd\n",
"\n",
"import time"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [],
"source": [
"colors = [\"xkcd:dusty blue\", \"xkcd:dark peach\", \"xkcd:dark seafoam green\", \n",
" \"xkcd:dusty purple\",\"xkcd:watermelon\", \"xkcd:dusky blue\", \"xkcd:amber\", \n",
" \"xkcd:purplish\", \"xkcd:dark teal\", \"xkcd:orange\", \"xkcd:slate\"]\n",
"\n",
"plt.style.use('ggplot')\n",
"plt.rcParams['font.family'] = 'sans-serif'\n",
"plt.rcParams['font.serif'] = 'Ubuntu'\n",
"plt.rcParams['font.monospace'] = 'Ubuntu Mono'\n",
"plt.rcParams['font.size'] = 10\n",
"plt.rcParams['axes.labelsize'] = 10\n",
"plt.rcParams['axes.labelweight'] = 'bold'\n",
"plt.rcParams['axes.titlesize'] = 10\n",
"plt.rcParams['xtick.labelsize'] = 8\n",
"plt.rcParams['ytick.labelsize'] = 8\n",
"plt.rcParams['legend.fontsize'] = 10\n",
"plt.rcParams['figure.titlesize'] = 12\n",
"plt.rcParams['image.cmap'] = 'jet'\n",
"plt.rcParams['image.interpolation'] = 'none'\n",
"plt.rcParams['figure.figsize'] = (16, 8)\n",
"plt.rcParams['lines.linewidth'] = 2\n",
"plt.rcParams['lines.markersize'] = 8"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [],
"source": [
"import urllib.request\n",
"\n",
"filepath = \"../dataset/\"\n",
"url = \"https://tvml.github.io/ml2425/dataset/\"\n",
"\n",
"def get_file(filename, local):\n",
" #IS_COLAB = ('google.colab' in str(get_ipython()))\n",
" if local:\n",
" urllib.request.urlretrieve (url+filename, filename)\n",
" return filename\n",
" else:\n",
" return filepath+filename"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [],
"source": [
"def plot_ds(data,m=None,q=None):\n",
" fig = plt.figure(figsize=(16,8))\n",
" minx, maxx = min(data.x1), max(data.x1)\n",
" deltax = .1*(maxx-minx)\n",
" x = np.linspace(minx-deltax,maxx+deltax,1000)\n",
" ax = fig.gca()\n",
" ax.scatter(data[data.t==0].x1, data[data.t==0].x2, s=40, edgecolor='k', alpha=.7)\n",
" ax.scatter(data[data.t==1].x1, data[data.t==1].x2, s=40, edgecolor='k', alpha=.7)\n",
" if m:\n",
" ax.plot(x, m*x+q, lw=2, color=colors[5])\n",
" plt.xlabel('$x_1$', fontsize=12)\n",
" plt.ylabel('$x_2$', fontsize=12)\n",
" plt.xticks(fontsize=10)\n",
" plt.yticks(fontsize=10)\n",
" plt.title('Dataset', fontsize=12)\n",
" plt.show()"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [],
"source": [
"def plot_1(cost_history, m, q, low=0, high=None, step=1):\n",
" if high is None:\n",
" high = m.shape[0]\n",
" idx = range(low,high,step)\n",
" ch = cost_history[idx]\n",
" th1 = m[idx]\n",
" th0 = q[idx]\n",
" fig = plt.figure(figsize=(12,6))\n",
" ax = fig.add_subplot(1,1,1)\n",
" minx, maxx, miny, maxy = 0, len(ch), ch.min(), ch.max()\n",
" deltay, deltax = .1*(maxy-miny), .1*(maxx-minx)\n",
" miny, maxy, minx, maxx = miny - deltay, maxy + deltay, minx - deltax, maxx + deltax\n",
" ax.plot(range(len(ch)), ch, alpha=1, color=colors[0], linewidth=2)\n",
" plt.xlabel('iterations')\n",
" plt.ylabel('cost')\n",
" plt.xlim(minx,maxx)\n",
" plt.ylim(miny,maxy)\n",
" ax.xaxis.set_major_formatter(mpl.ticker.FuncFormatter(lambda x, pos: '{:0.0f}'.format(x*step+low)))\n",
" plt.xticks(fontsize=8)\n",
" plt.yticks(fontsize=8)\n",
" ax.set_yticklabels([]) \n",
" plt.tight_layout()\n",
" plt.show()"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [],
"source": [
"def plot_2(cost_history, m, q, low=0, high=None, step=1):\n",
" if high is None:\n",
" high = m.shape[0]\n",
" idx = range(low, high ,step)\n",
" ch = cost_history[idx]\n",
" th1 = m[idx]\n",
" th0 = q[idx]\n",
" fig = plt.figure(figsize=(12,6))\n",
" ax = fig.add_subplot(1,1,1)\n",
" minx, maxx, miny, maxy = th0.min(), th0.max(), th1.min(), th1.max()\n",
" deltay, deltax = .1*(maxy-miny), .1*(maxx-minx)\n",
" miny, maxy = miny - deltay, maxy + deltay\n",
" miny, maxy, minx, maxx = miny - deltay, maxy + deltay, minx - deltax, maxx + deltax\n",
" ax.plot(th0, th1, alpha=1, color=colors[1], linewidth=2, zorder=1)\n",
" ax.scatter(th0[-1],th1[-1], color=colors[5], marker='o', s=40, zorder=2)\n",
" plt.xlabel(r'$x_1$')\n",
" plt.ylabel(r'$x_2$')\n",
" plt.xlim(minx,maxx)\n",
" plt.ylim(miny,maxy)\n",
" plt.xticks(fontsize=8)\n",
" plt.yticks(fontsize=8)\n",
" ax.grid(True)\n",
" ax.set_xticklabels([]) \n",
" ax.set_yticklabels([]) \n",
" plt.tight_layout()\n",
" plt.show()"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [],
"source": [
"def plot_all(cost_history, m, q, low=0, high=None, step=1):\n",
" if high is None:\n",
" high = m.shape[0]\n",
" idx = range(low,high,step)\n",
" ch = cost_history[idx]\n",
" th1 = m[idx]\n",
" th0 = q[idx]\n",
" fig = plt.figure(figsize=(18,6))\n",
" ax = fig.add_subplot(1,2,1)\n",
" minx, maxx, miny, maxy = 0, len(ch), ch.min(), ch.max()\n",
" deltay, deltax = .1*(maxy-miny), .1*(maxx-minx)\n",
" miny, maxy, minx, maxx = miny - deltay, maxy + deltay, minx - deltax, maxx + deltax\n",
" ax.plot(range(len(ch)), ch, alpha=1, color=colors[0], linewidth=2)\n",
" plt.xlabel('iterations')\n",
" plt.ylabel('cost')\n",
" plt.xlim(minx,maxx)\n",
" plt.ylim(miny,maxy)\n",
" ax.xaxis.set_major_formatter(mpl.ticker.FuncFormatter(lambda x, pos: '{:0.0f}'.format(x*step+low)))\n",
" plt.xticks(fontsize=8)\n",
" plt.yticks(fontsize=8)\n",
" ax = fig.add_subplot(1,2,2)\n",
" minx, maxx, miny, maxy = th0.min(), th0.max(), th1.min(), th1.max()\n",
" deltay, deltax = .1*(maxy-miny), .1*(maxx-minx)\n",
" miny, maxy = miny - deltay, maxy + deltay\n",
" miny, maxy, minx, maxx = miny - deltay, maxy + deltay, minx - deltax, maxx + deltax\n",
" ax.plot(th0, th1, alpha=1, color=colors[1], linewidth=2, zorder=1)\n",
" ax.scatter(th0[-1],th1[-1], color=colors[5], marker='o', s=40, zorder=2)\n",
" plt.xlabel(r'$m$')\n",
" plt.ylabel(r'$q$')\n",
" plt.xlim(minx,maxx)\n",
" plt.ylim(miny,maxy)\n",
" plt.xticks(fontsize=8)\n",
" plt.yticks(fontsize=8)\n",
" plt.tight_layout()\n",
" plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Rischio e minimizzazione\n",
"Dato un qualunque algoritmo che fornisce per ogni valore di input $x$ una previsione $f(x)$, la qualità delle previsioni fornite dall'algoritmo può essere definita per mezzo di una *funzione di costo* (loss function) $L(x_1, x_2)$, dove $x_1$ è il valore predetto dal modello e $x_2$ è il valore corretto associato a $x$ . Sostanzialmente, il valore della funzione di costo $L(f(x),y)$ misura quindi quanto \"costa\" (secondo il modello di costo indotto dalla funzione stessa) prevedere, dato $x$, il valore $f(x)$ invece del valore corretto $y$.\n",
"\n",
"Dato che evidentemente il costo è dipendente dalla coppia di valori $x,y$, una valutazione complessiva della qualità delle predizioni dell'algoritmo potrà essere fornita considerando il valore atteso della funzione di costo al variare di $x$ e $y$, nell'ipotesi di una (densità di) distribuzione di probabilità congiunta di tali valori $p(x,y)$. La distribuzione $p(x,y)$ ci fornisce quindi la probabilità che il prossimo punto su cui effettuare la predizione sia $x$ e che il valore corretto da predire sia $y$. Si noti che non si fa l'ipotesi che due diverse occorrenze di $x$ siano associate allo stesso valore di $y$: non si assume quindi una relazione funzionale, seppure sconosciuta, tra $x$ e $y$, ma solo una relazione in probabilità $p(y\\mid x)$. \n",
"Questo permette di considerare la presenza di rumore nelle osservazioni effettuate.\n",
"\n",
"Da quanto detto, indicando con $D_x$ e $D_y$ i domini di definizione di $x$ e $y$, e assunta una distribuzione $p(x,y)$ che fornisce un modello statistico del contesto in cui si intende effettuare le predizioni, la qualità di un algoritmo di previsione che calcola la funzione $f(x)$ sarà data dal *rischio*\n",
"$$\n",
"\\mathcal{R}(f)=\\mathbb{E}_p[L(f(x),y)]=\\int_{D_x}\\int_{D_y} L(f(x),y)p(x,y)dxdy\n",
"$$\n",
"\n",
"Il rischio di dice quindi quanto ci aspettiamo che ci costi prevedere $f(x)$, assumendo che:\n",
"\n",
"1. $x$ sia estratto a caso dalla distribuzione marginale\n",
" $$\n",
" p(x)=\\int_{D_y} p(x,y)dy\n",
" $$\n",
"\n",
"2. il relativo valore corretto da predire sia estratto a caso dalla distribuzione condizionata \n",
"$$\n",
"p(y\\mid x)=\\frac{p(x,y)}{p(x)}\n",
"$$\n",
"\n",
"3. il costo sia rappresentato dalla funzione $L(x_1,x_2)$"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### Esempio\n",
"\n",
"Consideriamo il caso in cui vogliamo effettuare previsioni sulla possibilità di pioggia in giornata, date le condizioni del cielo al mattino, assumendo che le possibili osservazioni siano \"sereno\" (S), \"nuvoloso\" (N), \"coperto\" (C), e che le previsioni siano \"pioggia\" (T) e \"non pioggia\" (F). La funzione di costo, sarà allora del tipo $L:\\{T,F\\}^2\\mapsto\\mathbb{R}$\n",
"\n",
"La definizione di una particolare funzione di costo è legata alla valutazione delle priorità dell'utente. Nel caso specifico, se si valuta allo stesso modo \"sgradevole\" uscire con l'ombrello (per una previsione T) senza poi doverlo usare che bagnarsi per la pioggia non avendo preso l'ombrello (per una previsione F) allora la funzione di costo risulta $L_1(y,t)$, definita dalla tabella seguente\n",
"\n",
"| $x_1$/$x_2$ | T | F |\n",
"| :---------: | :--: | :--: |\n",
"| T | 0 | 1 |\n",
"| F | 1 | 0 |\n",
"\n",
"Se invece reputiamo molto più sgradevole bagnarci per non aver preso l'ombrello rispetto a prendere l'ombrello stesso inutilmente, allora la funzione di costo $L_2(y,t)$, potrà essere definita come\n",
"\n",
"| $x_1$/$x_2$ | T | F |\n",
"| :---------: | :--: | :--: |\n",
"| T | 0 | 1 |\n",
"| F | 25 | 0 |\n",
"\n",
"Se facciamo l'ipotesi che la distribuzione congiunta su $\\{S,N,C\\}\\times\\{T,F\\}$ sia \n",
"\n",
"| $x$/$y$ | T | F |\n",
"| :-----: | :--: | :--: |\n",
"| S | .05 | .2 |\n",
"| N | .25 | .25 |\n",
"| C | .2 | .05 |\n",
"\n",
"e consideriamo due possibili funzioni predittive $f_1(x)$ e $f_2(x)$\n",
"\n",
"\n",
"| $x$ | $f_1(x)$ | $f_2(x)$ |\n",
"| :--: | :--------------------: | :------: |\n",
"| S | F | F |\n",
"| N | F | T |\n",
"| C | T | T |\n",
"\n",
"\n",
"possiamo verificare che nel caso in cui la funzione di costo sia $L_1$ allora il rischio nei due casi è $\\mathcal{R}(f_1)=0.65$ e $\\mathcal{R}(f_2)=0.4$ per cui $f_2$ è preferibile a $f_1$. Al contrario, se la funzione di costo è $L_2$, allora risulta $\\mathcal{R}(f_1)=1.55$ e $\\mathcal{R}(f_2)=7.55$, per cui, al contrario, $f_1$ è preferibile a $f_2$.\n",
"\n",
"Come si vede, quindi, la scelta tra $f_1(x)$ e $f_2(x)$ è dipendente dalla funzione di costo adottata e dalla distribuzione $p(x,y)$ che invece è data e, tra l'altro, sconosciuta. Quindi, una diversa distribuzione potrebbe portare a conclusioni diverse anche considerando una stessa funzione di costo: se ad esempio si fa riferimento alla funzione di costo $L_1$, allora la distribuzione congiunta\n",
"\n",
"| $x$/$y$ | T | F |\n",
"| :-----: | :--: | :--: |\n",
"| S | .05 | .05 |\n",
"| N | .05 | .4 |\n",
"| C | .05 | .4 |\n",
"\n",
"determina dei valori di rischio $\\mathcal{R}(f_1)=0.6$ e $\\mathcal{R}(f_2)=0.9$, rendendo ora $f_1$ preferibile a $f_2$.\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Rischio empirico\n",
"Dato che la distribuzione reale $p(x,y)$ è sconosciuta per ipotesi (se così non fosse potremmo sempre effettuare predizioni utilizzando la distribuzione condizionata reale $p(y\\mid x)$) il calcolo del rischio reale è impossibile ed è necessario effettuare delle approssimazioni, sulla base dei dati disponibili. In particolare, possiamo applicare il metodo standard di utilizzando la media aritmetica su un campione come stimatore del valore atteso, e considerare il *rischio empirico* (empirical risk) calcolato effettuando l'operazione di media sul campione offerto dai dati disponibili nel training set $X=\\{(x_1,y_1),\\ldots,(x_n,y_n)\\}$\n",
"\n",
"$$\n",
"\\overline{\\mathcal{R}}(f; X)=\\overline{L}(f(x), y; X)=\\frac{1}{n}\\sum_{i=1}^nL(f(x_i),y_i)\n",
"$$\n",
"\n",
"La funzione utilizzata per le predizioni sarà allora quella che, nell'insieme di funzioni considerato, minimizza il rischio empirico\n",
"\n",
"$$\n",
"f^*=\\underset{f\\in F}{\\mathrm{argmin}}\\;\\overline{\\mathcal{R}}(f;X)\n",
"$$\n",
"\n",
"Si noti che, in effetti, il rischio empirico dipende sia dai dati in $X$ che dalla funzione $f$: in questo senso è una funzione rispetto a $X$ e un funzionale rispetto a $f$. La ricerca di $f^*$ comporta quindi una minimizzazione funzionale del rischio empirico. In generale, tale situazione viene semplificata limitando la ricerca all'interno di classi di funzioni definite da coefficienti: in questo modo, il rischio empirico può essere espresso come funzione dei coefficienti della funzione (oltre che di $X$) e la minimizzazione è una normale minimizzazione di funzione. \n",
"\n",
"Chiaramente, la speranza è che minimizzare il rischio empirico dia risultati simili a quelli che si otterrebbero minimizzando il rischio reale. Ciò dipende, in generale, da quattro fattori:\n",
"\n",
"- La dimensione del training set $X$. Al crescere della quantità di dati, $\\overline{\\mathcal{R}}(f; X)$ tende a $\\mathcal{R}(f)$ per ogni funzione $f$\n",
"- La distribuzione reale $p(x,y)$. Maggiore è la sua complessità, maggiore è la quantità di dati necessari per averne una buona approssimazione.\n",
"- La funzione di costo $L$, che può creare problemi se assegna costi molto elevati in situazioni particolari e poco probabili\n",
"- L'insieme $F$ delle funzioni considerate. Se la sua dimensione è elevata, e le funzioni hanno una struttura complessa, una maggior quantità di dati risulta necessaria per avere una buona approssimazione.\n",
"Al tempo stesso, considerare un insieme piccolo di funzioni semplici rende sì la minimizzazione del rischio implicito su $F$ una buona approssimazione del minimo rischio reale su $F$ stesso, ma al tempo stesso comporta che tale minimo possa essere molto peggiore di quello ottenibile considerando classi più ampie di funzioni.#### Rischio empirico\n",
"Dato che la distribuzione reale $p(\\mathbf{x},t)$ è sconosciuta per ipotesi (se così non fosse potremmo sempre effettuare predizioni utilizzando la distribuzione condizionata reale $p(t\\mid \\mathbf{x})$) il calcolo del rischio reale è impossibile ed è necessario effettuare delle approssimazioni, sulla base dei dati disponibili. In particolare, possiamo applicare il metodo standard di utilizzando la media aritmetica su un campione come stimatore del valore atteso, e considerare il *rischio empirico* (empirical risk) calcolato effettuando l'operazione di media sul campione offerto dai dati disponibili nel training set $X=\\{(\\mathbf{x}_1,t_1),\\ldots,(\\mathbf{x}_n,t_n)\\}$\n",
"\n",
"$$\n",
"\\overline{\\mathcal{R}}(f; X)=\\frac{1}{n}\\sum_{i=1}^nL(f(x_i),y_i)\n",
"$$\n",
"\n",
"La funzione utilizzata per le predizioni sarà allora quella che, nell'insieme di funzioni considerato, minimizza il rischio empirico\n",
"\n",
"$$\n",
"f^*=\\underset{f\\in F}{\\mathrm{argmin}}\\;\\overline{\\mathcal{R}}(f;X)\n",
"$$\n",
"\n",
"Si noti che, in effetti, il rischio empirico dipende sia dai dati in $X$ che dalla funzione $f$: in questo senso è una funzione rispetto a $X$ e un funzionale rispetto a $f$. La ricerca di $f^*$ comporta quindi una minimizzazione funzionale del rischio empirico. In generale, tale situazione viene semplificata limitando la ricerca all'interno di classi di funzioni definite da coefficienti: in questo modo, il rischio empirico può essere espresso come funzione dei coefficienti della funzione (oltre che di $X$) e la minimizzazione è una normale minimizzazione di funzione. \n",
"\n",
"Chiaramente, la speranza è che minimizzare il rischio empirico dia risultati simili a quelli che si otterrebbero minimizzando il rischio reale. Ciò dipende, in generale, da quattro fattori:\n",
"\n",
"- La dimensione del training set $X$. Al crescere della quantità di dati, $\\overline{\\mathcal{R}}(f; X)$ tende a $\\mathcal{R}(f)$ per ogni funzione $f$\n",
"- La distribuzione reale $p(\\mathbf{x},t)$. Maggiore è la sua complessità, maggiore è la quantità di dati necessari per averne una buona approssimazione.\n",
"- La funzione di costo $L$, che può creare problemi se assegna costi molto elevati in situazioni particolari e poco probabili\n",
"- L'insieme $F$ delle funzioni considerate. Se la sua dimensione è elevata, e le funzioni hanno una struttura complessa, una maggior quantità di dati risulta necessaria per avere una buona approssimazione.\n",
"Al tempo stesso, considerare un insieme piccolo di funzioni semplici rende sì la minimizzazione del rischio implicito su $F$ una buona approssimazione del minimo rischio reale su $F$ stesso, ma al tempo stesso comporta che tale minimo possa essere molto peggiore di quello ottenibile considerando classi più ampie di funzioni."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Minimizzazione della funzione di rischio\n",
"\n",
"In generale, l'insieme $F$ delle funzioni è definito in modo parametrico $F=\\{f(\\mathbf{x};\\theta)\\}$ dove $\\theta\\in D_\\theta$ è un coefficiente (tipicamente multidimensionale) che determina, all'interno della classe $F$ (definita tipicamente in termini ''strutturali'', con la definizione di $f$) la particolare funzione utilizzata. Un esempio tipico è offerto dalla *regressione lineare*, in cui si vuole prevedere il valore di un attributo $y$ con dominio $R$ sulla base dei valori di altri $m$ attributi $\\mathbf{x}=(x_1,\\ldots, x_m)$ (che assumiamo per semplicità in $R$ anch'essi): nella regressione lineare, l'insieme delle possibili funzioni $f:R^m\\mapsto R$ è limitato alle sole funzioni lineari $f_\\mathbf{w}(\\mathbf{x})=w_0+w_1x_1+\\ldots+w_mx_m$, e il parametro $\\theta$ corrisponde al vettore $\\mathbf{w}=(w_0,\\ldots,w_m)$ dei coefficienti.\n",
"\n",
"In questo caso, il rischio empirico, fissata la famiglia $F$ di funzioni, può essere ora inteso come funzione di $\\theta$\n",
"$$\n",
"\\overline{\\mathcal{R}}(\\theta; X)=\\frac{1}{n}\\sum_{i=1}^nL(f(\\mathbf{x}_i;\\theta),t_i)\\hspace{2cm}f\\in F\n",
"$$\n",
"e la minimizzazione del rischio empirico può essere effettuata rispetto a $\\theta$\n",
"$$\n",
"\\theta^*=\\underset{\\theta\\in D_\\theta}{\\mathrm{argmin}}\\;\\overline{\\mathcal{R}}(\\theta;X)\n",
"$$\n",
"da cui deriva la funzione ottima (nella famiglia $F$) $f^*=f(\\mathbf{x};\\theta^*)$\n",
"\n",
"la minimizzazione della funzione di rischio avrà luogo nel dominio di definizione $D_\\theta$ di $\\theta$, e potrà essere effettuata in modi diversi, in dipendenza della situazione e di considerazioni di efficienza di calcolo e di qualità delle soluzioni derivate."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Ricerca analitica dell'ottimo\n",
"Se il problema si pone in termini di minimizzazione *senza vincoli*, e quindi all'interno di $R^m$, un primo approccio è quello standard dell'analisi di funzioni, consistente nella ricerca di valori $\\overline\\theta$ di $\\theta$ per i quali si annullano tutte le derivate parziali $\\frac{\\partial \\overline{\\mathcal{R}}(\\theta; X)}{\\partial \\theta_i}$, tale cioè che, se indichiamo con $m$ la dimensione (numero delle componenti) di $\\theta$, il sistema su $m$ incognite definito dalle $m$ equazioni \n",
"$$\n",
"\\frac{\\partial \\overline{\\mathcal{R}}(\\theta; X)}{\\partial \\theta_i}\\Bigr|_{\\theta=\\overline\\theta}=0\\hspace{2cm} i=1,\\ldots,m\n",
"$$\n",
"risulta soddisfatto. La soluzione analitica di questo sistema risulta tipicamente ardua o impossibile, per cui vengono spesso adottate tecniche di tipo numerico.\n",
"\n",
"La stessa condizione può essere espressa, in modo vettoriale, ponendo il *gradiente* pari a $0$.\n",
"$$\n",
"\\nabla_\\theta\\overline{\\mathcal{R}}(\\theta; X)=0\n",
"$$\n",
"Si ricorda che, data una funzione $f(x_1,x_2,\\ldots,x_d)$, il gradiente $\\nabla f$ di $f$ è il vettore $d$-dimensionale delle derivate di $f$ rispetto alle variabili $x_1,\\ldots, x_d$: il vettore cioè tale che $[\\nabla f]_i=\\frac{\\partial f}{\\partial x_i}$.\n",
"\n",
"Come si può osservare, in questo modo il metodo consente di raggiungere un valore di $\\theta$ per il quale il gradiente risulta nullo, e quindi un ottimo locale o un punto di sella della funzione di costo. Tipicamente, il rischio di ottenere un valore di $\\theta$ che non corrisponde a un minimo (in particolare globale) viene limitato mediante vari accorgimenti (scelta della funzione $\\overline{\\mathcal{R}}$, scelta del metodo di calcolo)."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### Gradient descent\n",
"\n",
"La discesa del gradiente (*gradient descent*) è una delle tecniche di ottimizzazione più popolari, in particolare nel settore del Machine Learning e delle Reti Neurali. La tecnica consiste nel minimizzare una funzione obiettivo $J(\\theta)$ definita sui parametri $\\theta\\in\\mathbb{R}^d$ del modello mediante aggiornamenti successivi del valore di $\\theta$ (a partire da un valore iniziale $\\theta^{(0)}$) nella direzione opposta a quella del valore attuale del gradiente $J'(\\theta)=\\nabla J(\\theta)$. Un parametro $\\eta$, detto *learning rate* determina la scala degli aggiornamenti effettuati, e quindi la dimensione dei passi effettuati nella direzione di un minimo locale.\n",
"\n",
"Possiamo interpretare la tecnica come il muoversi sulla superficie della funzione $J(\\theta)$ seguendo sempre la direzione di massima pendenza verso il basso, fino a raggiungere un punto da cui è impossibile scendere ulteriormente. Il metodo è detto del *primo ordine* in quanto richiede il calcolo delle derivate prime della funzione da ottimizzare."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### Varianti di discesa del gradiente\n",
"In molti casi, e sempre nell'ambito del ML, la funzione obiettivo corrisponde all'applicazione di una funzione di costo (*loss function*), predefinita e dipendente dal modello adottato, su un insieme dato di elementi di un dataset $X=(\\mathbf{x}_1,\\ldots, \\mathbf{x}_n)$ (che nel caso di apprendimento supervisionato è un insieme di coppie $X=((\\mathbf{x}_1,t_1),\\ldots,(\\mathbf{x}_n,t_n))$): indichiamo tale funzione come $J(\\theta; X)$: si noti che, fissata la funzione di costo $J$ e il dataset $X$, il risultato è funzione dei parametri $\\theta$. \n",
"\n",
"Questo corrisponde all'approssimazione del *rischio* \n",
"\n",
"$$\n",
"\\mathcal{R}(\\theta)=\\int J(\\theta,\\mathbf{x})p(\\mathbf{x})d\\mathbf{x}=E_{p}[\\theta]\n",
"$$\n",
"\n",
"In generale, la funzione di costo è definita in modo additivo rispetto agli elementi di $X$ (il costo relativo all'insieme $X$ è pari alla somma dei costi relativi ai suoi elementi), per cui il valore risulta $J(\\theta;X)=\\sum_{i=1}^nJ(\\theta;\\mathbf{x}_i)$, o preferibilmente, per evitare una eccessiva dipendenza dal numero di elementi, come media \n",
"$$\n",
"J(\\theta;X)=\\frac{1}{n}\\sum_{i=1}^nJ(\\theta;\\mathbf{x}_i)\n",
"$$ \n",
"Si noti che, per le proprietà dell'operazione di derivazione, da questa ipotesi deriva l'additività anche del gradiente, per cui \n",
"$$\n",
"J'(\\theta; X)=\\sum_{i=1}^nJ'(\\theta;\\mathbf{x}_i)\n",
"$$ \n",
"o \n",
"$$\n",
"J'(\\theta;X)=\\frac{1}{n}\\sum_{i=1}^nJ'(\\theta;\\mathbf{x}_i)\n",
"$$\n",
"\n",
"Possiamo allora identificare tre varianti del metodo, che differiscono tra loro per la quantità di elementi di $X$ utilizzati, ad ogni passo, per calcolare il gradiente della funzione obiettivo. Una quantità maggiore di dati utilizzati aumenta l'accuratezza dell'aggiornamento, ma anche il tempo necessario per effettuare l'aggiornamento stesso (in particolare, per valutare il gradiente per il valore attuale di $\\theta$)."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### Batch gradient descent\n",
"\n",
"In questo caso, il gradiente è valutato, ogni volta, considerando tutti gli elementi nel training set $X$. Quindi si ha che al passo $k$-esimo viene eseguito l'aggiornamento\n",
"\n",
"$$\n",
"\\theta^{(k+1)}=\\theta^{(k)}-\\eta\\sum_{i=1}^nJ'(\\theta^{(k)};\\mathbf{x}_i)\n",
"$$\n",
"\n",
" o anche, per i singoli coefficienti\n",
"\n",
"$$\n",
"\\theta_j^{(k+1)}=\\theta_j^{(k)}-\\eta\\sum_{i=1}^n\\frac{\\partial J(\\theta;\\mathbf{x}_i)}{\\partial\\theta_j}\\Bigr\\vert_{\\small\\theta=\\theta^{(k)}}\n",
"$$\n",
"\n",
"Dato che si richiede quindi, ad ogni iterazione, la valutazione del gradiente (con il valore attuale $\\theta^{(k)}$ di tutti i coefficienti) su tutti gli elementi di $X$, questa soluzione tende ad essere molto lenta, soprattutto in presenza di dataset di dimensioni molto estese, come nel caso di reti neurali complesse e deep learning. Inoltre, l'approccio diventa del tutto impraticabile se il dataset è talmente esteso da non entrare neanche in memoria.\n",
"\n",
"In termini di codice, il metodo batch gradient descent si presenta come:\n",
"\n",
"```python\n",
"for i in range(n_epochs):\n",
" g = 0\n",
" for k in range(dataset_size):\n",
" g = g+evaluate_gradient(loss_function, theta, X[k])\n",
" theta = theta-eta*g\n",
"```\n",
"Il ciclo viene eseguito un numero di volte pari al numero di epoche, dove per *epoca* si intende una iterazione su tutti gli\n",
"elementi di $X$. Di conseguenza, la valutazione di $\\theta$ viene aggiornata un numero di volte pari al numero di epoche. Il\n",
"metodo batch gradient descent converge certamente al minimo globale se la funzione $J(\\theta)$ è convessa, mentre altrimenti\n",
"converge a un minimo locale.\n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"##### Esempio\n",
"Applichiamo le considerazioni a un semplice problema di classificazione su un dataset bidimensionale, riportato graficamente di seguito.\n"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA7sAAAHzCAYAAADhDgreAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAABEK0lEQVR4nO3de3TUd53H/9c3M0AyM5ArgQ2XU6FluRe6SVsJNUAD5Qy2i23EUsn+1N3FLj1qde2vsFXQIpZeOO2vlm71qFXTXW0Xejmuszam0HQbrR1KYkowWry0WlpjCKEkIchkvr8/YmYJSSAhM/O9PR/neI6ZzJA3+ZB0Xt/v+/P+GKZpmgIAAAAAwEUyrC4AAAAAAIBkI+wCAAAAAFyHsAsAAAAAcB3CLgAAAADAdQi7AAAAAADXIewCAAAAAFyHsAsAAAAAcB3CLgAAaXbJJZcoKytL48ePV05OjpYsWaLHHntM8Xj8gq/9/e9/L8MwFIvFUlpjur4OAACpQtgFAMACP/zhD3Xy5Em9+eab2rx5s+6991794z/+o9VlAQDgGoRdAAAslJ2drRtuuEFPPvmkvvvd7+rQoUP60Y9+pMWLF2vChAmaNm2avvSlLyWe/4EPfECSlJOTo1AopJ/97Gf6zW9+oxUrVig/P18FBQX66Ec/qvb29sRr7r33Xk2ZMkXjx4/X3/7t3+qFF16QJMXjce3cuVMzZ85Ufn6+1q1bp7a2tiG/DgAATkLYBQDABq688kpNnTpV//u//6tgMKjvfe97am9v149+9CP9+7//u5599llJ0ksvvSRJam9vV0dHh97//vfLNE1t2bJFR48e1S9/+Uv94Q9/SATkX/3qV3rkkUcUjUZ18uRJPf/887rkkkskSV/72tf07LPPqra2VkePHlVubq5uu+22Ib8OAABOQtgFAMAmioqK1NbWpmXLlmnBggXKyMjQwoULtX79etXW1g75uksvvVQrV67UuHHjNHHiRH3uc59LPN/n8+n06dM6fPiwzpw5o0suuUQzZ86UJD322GPasWOHpk6dqnHjxulLX/qS9uzZwz5dAIArEHYBALCJt99+W3l5efr5z3+u5cuXa+LEicrOztZjjz2m1tbWIV/3pz/9STfffLOmTJmiCRMmaMOGDYnnX3rppXrooYf0pS99SYWFhbr55pt19OhRSdKbb76pD33oQ8rJyVFOTo7mzJkjn8+nP/3pT2n5+wIAkEqEXQAAbCAajertt9/W0qVLdcstt+iGG27QH/7wB504cUK33nqrTNOUJBmGMeC1//Zv/ybDMPT666/rvffe0xNPPJF4viTdcsstevnll/Xmm2/KMAzdeeedkqRp06bpf/7nf9Te3p74X3d3t6ZMmTLo1wEAwEkIuwAAWOi9997Tf//3f+vmm2/Whg0btGDBAp08eVJ5eXnKzMzUq6++qv/8z/9MPH/ixInKyMjQb3/728RjJ0+eVCgUUnZ2tt5++23df//9ic/96le/0r59+3T69GllZmYqKytLGRm9//m/9dZbddddd+nNN9+UJP35z3/Wc889N+TXAQDASQi7AABY4Prrr9f48eM1bdo07dixQ5/73Of0+OOPS5IeffRRbd26VePHj9fdd9+tdevWJV4XCAR01113qbS0VDk5OXrllVe0bds2HTx4UNnZ2VqzZo1uvPHGxPNPnz6tzZs3q6CgQJMnT1ZLS4vuueceSdJnPvMZ3XDDDVq1apXGjx+vq6++Wj//+c+H/DoAADiJYZ7d5wQAAAAAgAtwZxcAAAAA4DqEXQAAAACA6xB2AQAAAACuQ9gFAAAAALgOYRcAAAAA4DqEXQAAAACA6/itLiAdjh49anUJSIGCggK1trZaXQZSjHX2BtbZG1hnb2CdvYF19gYnrHNRUdGQn+POLgAAAADAdQi7AAAAAADXIewCAAAAAFyHsAsAAAAAcB3CLgAAAADAdQi7AAAAAADXIewCAAAAAFyHsAsAAAAAcB1/ur/go48+qoMHDyo7O1u7du2SJD311FN64YUXNGHCBEnS+vXrdcUVVwx4bUNDgx5//HHF43Fde+21Wrt2bTpLBwAAAAA4RNrD7rJly7R69Wrt3r273+Nr1qzRDTfcMOTr4vG4vvWtb+kLX/iC8vPztWXLFhUXF2vq1KmpLhkAAAAA4DBpb2OeO3euQqHQiF935MgRTZ48WZMmTZLf79eSJUsUjUZTUCEAAAAAwOnSfmd3KM8//7xeeuklzZgxQ//wD/8wIBC3tbUpPz8/8XF+fr7eeOONdJcJAAAAAHAAW4TdVatWqaKiQpL05JNP6nvf+542bdp00X9eTU2NampqJEk7d+5UQUFBUuqEvfj9ftbWA1hnb2CdvYF19gbW2RtYZ29w+jrbIuzm5OQk/v+1116re++9d8Bz8vLydOzYscTHx44dU15e3qB/Xnl5ucrLyxMft7a2Jq9Y2EZBQQFr6wGsszewzt7AOnsD6+wNrLM3OGGdi4qKhvycLY4eOn78eOL/v/rqq5o2bdqA58ycOVPvvPOOWlpaFIvF9NOf/lTFxcXpLBMAAAAA4BBpv7P70EMP6fDhwzp58qRuvfVWrVu3Tk1NTfr9738vwzA0ceJEbdy4UVLvPt2vf/3r2rJli3w+nz7xiU9ox44disfjWr58+aChGAAAYDiaGur1+vMRjTnVoTNZIS24Lqx5ixZbXRYAIEkM0zRNq4tItaNHj1pdAlLACW0VGD3W2RtYZ2+w0zo3NdTr3T1VKivMkWEYMk1TtS3tmlxRSeAdJTutM1KHdfYGJ6yz7duYAQAA0ulQdSQRdCXJMAyVFeboUHXE4soAAMlC2AUAAJ7j7+pIBN0+hmHI39VpUUUAgGQj7AIAAM+JBUI6dyeXaZqKBYIWVQQASDbCLgAA8Jz5q8KqbWlPBN6+PbvzV4UtrgwAkCy2OGcXAAAgnfqGUO2tjsjf1alYIKj5DKcCAFch7AIAAE+at2gx4RYAXIw2ZgAAAACA6xB2AQAAAACuQ9gFAAAAALgOYRcAAAAA4DqEXQAAAACA6xB2AQAAAACuQ9gFAAAAALgO5+wCAICka2qo1+vPRzTmVIfOZIW04LqwyspXWl0WAMBDCLsAACCpmhrq9e6eKlUU5sgIBGSaPardU6VfZGdryvtmWF0eAMAjaGMGAABJdag6orLCHBmGIUkyDENlhTk68MNnLK4MAOAlhF0AAJBU/q6ORNDtYxiGfJ0dFlUEAPAiwi4AAEiqWCAk0zT7PWaapnqCIYsqAgB4EWEXAAAk1fxVYdW2tCcCr2maqm1pV/H1H7K4MgCAlzCgCgAADNtgU5bnLVrc7zl9H++tjsjf1alYIKj5FZW6vORKtba2WlE2AMCDCLsAAGBYhpqyLGnQwHvuY7CH4VywAAA3oI0ZAAAMy1BTlg9VRyyuDMOVuGCR1aO1+QFVZPXo3T1Vamqot7o0AEg6wi4AABiWoaYs+7s6LaoII8UFCwBeQtgFAADDMtSU5VggaFFFGCkuWADwEsIuAAAYlqGmLM9fFba4MgwXFywAeAlhFwAADMu8RYs1uaJSe7t9evbYKe3t9mlyRSXDjRyECxYAvIRpzAAAYNiYsuxsQx0LxZoCcCPCLgAAgIdwwQKAV9DGDAAAAABwHcIuAAAAAMB1CLsAAAAAANch7AIAAAAAXIcBVQAAAPCMpoZ6vf58RGNOdehMVkgLrgszsAtwKcIuAAAAPKGpoV7v7qlSRWGOjEBAptmj2j1VkkTgBVyINmYAAAB4wqHqiMoKc2QYhiTJMAyVFeboUHXE4soApAJhFwAAAJ7g7+pIBN0+hmHI39VpUUUAUomwCwAAAE+IBUIyTbPfY6ZpKhYIWlQRgFQi7AIAAMAT5q8Kq7alPRF4TdNUbUu75q8KW1wZgFRgQBUAAAA8oW8I1d7qiPxdnYoFgppfUclwKsClCLsAAADwjHmLFhNuAY+gjRkAAAAA4DqEXQAAAACA69DGDAAAYHNNDfV6/fmIxpzq0JmskBZcF6YVFwAugLALAABgY00N9Xp3T5UqCnNkBAIyzR7V7qmSJAIvhsQFEoCwCwAAYGuHqiO6qTBHhmFIkgzDUFlhjvZWRwgvSeSmcMgFEqAXe3YBAABszN/VkQi6fQzDkL+r06KK3CcRDrN6tDY/oIqsHr27p0pNDfVWl3ZRDlVHVDbIBZJD1RGLKwPSK613dh999FEdPHhQ2dnZ2rVrlySpqqpKr732mvx+vyZNmqRNmzYpGAwOeO1tt92mzMxMZWRkyOfzaefOneksHQAAwBKxQEim2dMv8JqmqVhg4PslXBy33T33d3XIyAr0e4wLJPCitIbdZcuWafXq1dq9e3fisYULF+qWW26Rz+fTE088oWeeeUYbNmwY9PXbtm3ThAkT0lUuAACA5eavCqt2T1XiTp1pmqptadf8ikqrS3MNt4VDLpAAvdIadufOnauWlpZ+j11++eWJ/z9r1iy98sor6SwJAAAgwY77Nvu+/t7qiPxdnYoFgppfUWl5XW7itnDIBRKgl60GVO3bt09LliwZ8vM7duyQJK1cuVLl5eXpKgsAAHiAnYf6zFu02PIa3Mxt4ZALJEAv24Tdp59+Wj6fT9dcc82gn9++fbvy8vJ04sQJfeUrX1FRUZHmzp076HNrampUU1MjSdq5c6cKCgpSVjes4/f7WVsPYJ29gXX2Bruv85GX9ulDUwv73d1bObVQz7y0T2XlKy2szFnsvs6DKStfqV9kZ+tHP3xGvo4O9QRDKv7HDbq85EqrS7toZeUrU/rv1onrjJFz+jrbIuy++OKLeu2117R169YB0wb75OXlSZKys7NVUlKiI0eODBl2y8vL+935bW1tTX7RsFxBQQFr6wGsszewzt5g93WOtbXqTH5gkMffs3XddmP3dR7KlPfN0JRP/2u/x5z490gXp64zRsYJ61xUVDTk5ywPuw0NDXruuef05S9/WePGjRv0Od3d3TJNU1lZWeru7lZjY6MqKirSXCkAAHCrpoZ6Hf5ls+K+mGIZPi2YPk1z/qbQ0fs2AcDr0hp2H3roIR0+fFgnT57UrbfeqnXr1umZZ55RLBbT9u3bJUmXXXaZNm7cqLa2Nn3961/Xli1bdOLECT3wwAOSpJ6eHi1dulSLFi1KZ+kAAMCl+vbqfmrBDJ1+523ljfWr9q03ZcpUS8ZYx+7bBACvM0zTNK0uItWOHj1qdQlIASe0VWD0WGdvYJ29wa7r/OR9O3RTZu8k3o73Tui9P7fIiMX0ndZT+tDmrQz1GSG7rjOSi3X2Biess63bmAHAq+x4xAngRWefsRqakK3QhGxJ0pyCU/xMAoCDEXYBwAJ2PuIE8Bq3nbEKAOhF2AUACxyqjuimv57nKEmGYaisMEd7qyOEXSDNknXGKt0aAGAvhF0AsMDZbZN9DMOQv6vToooA7+oLpHurI/J3dSoWCGp+ReWIgirdGgBgP4RdALAAbZOAvcxbtHhUoZRuDQCwnwyrCwAAL5q/Kqzalnb1DcRPtE2uCltcGYCL4e/q6HfxSqJbAwCsxp1dALBAMtomAdgH3RoAYD+EXQCwyGjbJgHYR7KGXAEAkoewCwBAEjCJ19vo1gAA+yHsAgAwSkzihUS3BgDYDQOqAAAYpUPVkUT7qvR/k3gPVUcsrgwAAO8i7AIAMEpM4gUAwH5oYwYAYJSYxAuk13D2yLOPHgBhFwBgK4O9QZVk6zetTOIF0mc4e+TZRw9AIuwCAGxksDeo//nY/6cJY/2quHS6bd+0MokXSJ9D1RHdNMge+b3VkcTP3HCeA8D9CLsAANsY7A3qmJPtuqJgvO3ftDKJF0gPf1eHjKxAv8fO3SM/nOcAcD8GVAEAbGOwQU9jzB754vF+j/GmFfCu3j3yZr/Hzt0jP5znAHA/wi4AwDYGe4N6xvCpJ6P/f6540wp41/xVYdW2tCd+VyT2yK8Kj+g5ANyPNmYAwHmlc6LpYIOezozP0UHTryLTZPgTgGHtkWcfPQCJsAsAOI90TzQd7A3q3936mQGP8aYV8Lbh7JFnHz0Awi4AYEhWTDQd6g0qb1oBAMBIsGcXADCkwQZGMRwKAAA4AWEXADAkJpoCAACnIuwCAIbERFMAAOBU7NkFAAyJiaZAf+mcTg4AGB3CLgDgvNww0ZSAYn9OWKPhTid3wt8FALyAsAsAcLV0H5+EkXPKGg1nOrlT/i4A4AXs2QUAuNqh6ojKBgkoh6ojFleGPk5Zo+FMJ3fK3wUAvICwCwBwNY5Psj+nrNFwppM75e8CAF5A2AUAuBrHJ9mfU9ZoONPJnfJ3AQAvIOwCAFyN45PszylrNG/RYk2uqNTebp+ePXZKe7t9mnzOdHKn/F0AwAsYUAUAcDU3H5/klqm/TlqjC00nd9LfBQDcjrALAHA9NxyfdC63Tf110xrZ4e/ilgshADAatDEDAOBATP3FUBIXQrJ6tDY/oIqsHr27p0pNDfVWlwYAaUXYBQDAgZj6i6FwIQQAetHGDACQRNuj0/RO/e3pF3iZ+gvprxdCsgL9HuNCCAAv4s4uAIC2Rwdi6i+GwvFHANCLsAsAoO3RgYZzDA68iQshANCLNmYAAG2PDmWHqb+DoSXeWhx/BAC9CLsAAPZ/ImnOdyRSWflKi6vzDrteCAGAdCLsAgB62x73VCVamRNtjxWVVpdmS1bfubT665/PoeqIbhqkJX5vdYSwCwBIK8IuAIC2xxE4353LdHy/rP76F0JLPGAPdr4oBqQLYRcAIIm2x+E6353LdHz/rP76F0JLPGA9u18UA9KFacwAAIyAv6ujX5CT0nvn0uqvfyFMAgasx4R9oBd3dgEAGAGr71xa/fUvhJZ4wHpsJwB6EXYBABgBq4d5Wf31h4OWeMBadr8oBqQLYRcAgBGw+s6l1V8fgP054aIYkA5pD7uPPvqoDh48qOzsbO3atUuS1NHRoQcffFB//vOfNXHiRH32s59VKBQa8NoXX3xRTz/9tCTpxhtv1LJly9JZOgAAkqy/c2n11wdgb1wUA3qlPewuW7ZMq1ev1u7duxOPPfvss1qwYIHWrl2rZ599Vs8++6w2bNjQ73UdHR3as2ePdu7cKUnavHmziouLBw3FAAAAgJdxUQywYBrz3LlzBwTUaDSqsrIySVJZWZmi0eiA1zU0NGjhwoUKhUIKhUJauHChGhoa0lEyAAAAAMBhbLFn98SJE8rNzZUk5eTk6MSJEwOe09bWpvz8/MTHeXl5amtrG/TPq6mpUU1NjSRp586dKigoSEHVsJrf72dtPYB19gbW2Ru8uM6/iL6q6A+fkb/zpGLB8Sq5/kO6vORKq8tKKS+usxexzt7g9HW2Rdg9m2EYA84PHKny8nKVl5cnPm5tbR1tWbChgoIC1tYDWGdvYJ29wWvr3NRQr3f3VOmDhTkyQj6ZZqdqv/WI2k+4e++k19bZq1hnb3DCOhcVFQ35ubS3MQ8mOztbx48flyQdP35cEyZMGPCcvLw8HTt2LPFxW1ub8vLy0lYjAADASByqjiSm4Uq9F/TLCnN0qDpicWUA4A22uLNbXFys2tparV27VrW1tSopKRnwnEWLFun73/++Ojo6JEm/+MUvdMstt6S7VAAAYDNNDfV6/fmIxpzq0JmskBZcF7bFnVN/V4eMrEC/xwzDkL+r06KKAMBb0h52H3roIR0+fFgnT57UrbfeqnXr1mnt2rV68MEHtW/fvsTRQ5L0m9/8Rj/5yU906623KhQK6aabbtKWLVskSRUVFUxiBgDA4/pahSsKc2QEAjLNHtXuqZIkywNvLBCSafb0255lmqZigaCFVQGAdximaZpWF5FqR48etboEpIAT9hBg9Fhnb2CdvSEV6/zkfTt0U+bAQLm326eP/L93JfVrjVRfEO9rZTZNU7Ut7Zrs8vNO+Xn2BtbZG5ywzufbs2uLNmYAAICLYedW4b5Au7c6In9Xp2KBoOa7POimQ6rb1u3aFg9g5Ai7AFyDNyiA9wy3Vdiq3w/zFi0e9Ovw++ripLpt3c5t8QBGzhbTmAFgtBJvULJ6tDY/oIqsHr27p0pNDfVWlwYgheavCqu2pV19u7L6WoXnrwonnmO33w92q8dJUj3hmgnagLsQdgG4Am9QAG+at2ixJldUam+3T88eO6W93b4Be2Lt9vvBbvU4ib+ro99dfCm5beup/vMBpBdtzABcwc779gCk1lCtwn3s9vvBbvU4SaonXDNBG3AX7uwCcIXeNyj9h8vzBgWAZL/fD3arx0mG07Zu5z8fQHpxZxeAK8xfFVbtIEd8zK+otLo0ABZLx++HkQyc4vfVxUvVhOuz1+9Pp+M69NYxTQ0FmaANOBxhF4ArcMQHgKGk+vfDSCf48vtqdC7Utj5SA9YvL6v3POS1H2ZNAIcj7AJwjWS/AQLgHqn8/XCoOqKbBhk4tbc6MuTX5PeVfVzM+gFwBvbsAgAAjAITfJ2N9QPci7ALAAAwCgyccjbWD3Av2pgBeNpIhsrAfVh/JAMDp5yN9QPci7ALwLNGOlQG7sL6p8fZFxR8eQW67AMrXPf9ZeCUs7F+gHsRdgF4FkNJvI31T71zLyiMGXNGP3HpBQUGTjkb6we4E3t2AXgWQ0m8jfVPvUPVkURrqPR/FxQOVUcsrgwA4AWEXQCexVASb2P9U48LCgAAKxF2AXjW/FVh1ba0JwJPYijJqrDFlSEdWP/U44ICAMBK7NkF4FkMJfE21j/1mHILALASYReApzGUxNtY/9Q694KCPy+gS7mgAABIE8IuAABImbMvKBQUFKi1tTVpfzbnJAMAzoewCwAAHIdzkgEAF8KAKgAA4DgcawQAuBDCLgAAcByONQIAXAhhFwAAOA7HGgEALoSwCwAAHIdzkgEAF8KAKgAA4DickwwAuBDCLgAAcCTOSQaA1KlvbNK+A4fU2nlaIV9c4aUlWrxwntVljQhhFwAAAACQUN/YpKq6Zk1aWKbgmTOKm6aq6qKS5KjAy55dAAAAAEBCpO6AcmeX9DveLXd2iSJ1ByyubGS4swsAAJBG9Y1NirwcVUdPhmNbAwG4W0fMUHCQ4906Y8YQr7Anwi4AAECa9LUG5s5ZoaBhOLY1EIC7hfym4oMc7xb0m0O8wp5oYwYAAEgTt7QGAnC3cGmxjjdH+x3vdrw5qnBpscWVjQx3dgEAANLELa2BANytr9Nk32u1OtFxWkG/qcrSYsd1oBB2AQAA0qSvNdA4K/A6sTUQgPstXjhPK1eUqbW11epSLhphFwAAG2tqqNfrz0c05lSHzmSFtOC6MGfLOli4tFhVddFEK3Nfa2Clw1oDAcAJCLsAANhUU0O93t1TpYrCHBmBgEyzR7V7qiSJwOtQfS2Akbr96owZjm0NBAAnIOwCAGBTh6ojuqkwp98wo7LCHO2tjhB2HWzxwnmEWwBIA6YxAwBgU/6ujn57O6XewOvv6rSoIgAAnIOwCwCATcUCocSxD31M01QsELSoIgAAnIOwCwCATc1fFVZtS3u/cw5rW9o1f1XY4soAALA/9uwCAGBTffty91ZH5O/qVCwQ1PyKSvbrAgAwDIRdAABsbN6ixYRbABdU39ikyMtRdfRkKOSLK7y0hEFo8DzCLgAAAOBg9Y1NqqprVu6cFQoahuKmqaq6qCQReOFp7NkFAAAAHCxSd0C5s0v6HVOWO7tEkboDFlcGWIuwCwAAADhYR8wY9JiyzpgxxCsAb6CNGQAAAEnzi+ir+t+nvq8xpzp0JiukBdeF2XeeYiG/qbhp9gu8pmkq6DfP8yrA/WwRdo8ePaoHH3ww8XFLS4vWrVunNWvWJB5ramrSfffdp8LCQknSVVddpYqKirTXCgAAgME1NdTr2HNPqiI3ICMQkGn2qHZPlSQReFMoXFqsqrpoopXZNE0db46qsrTY6tIAS9ki7BYVFen++++XJMXjcX3yk5/UlVdeOeB5c+bM0ebNm9NdHgAAAIbhUHVE6yfl6MyZM5J6W2nLCnO0tzpC2E2hviFUkbr96owZCvpNVZYWM5wKnmeLsHu2119/XZMnT9bEiROtLgUAAAAj4O/qkJGd0+8xwzDk7+q0piAPWbxwHuEWOIftwm5dXZ1KS0sH/dyvf/1r3XHHHcrNzVVlZaWmTZs26PNqampUU1MjSdq5c6cKCgpSVi+s4/f7WVsPYJ29gXX2BtbZ/fx5BTIU09ixYxOPmaYpf16AtXcZfp69wenrbJimaZud67FYTJ/85Ce1a9cu5eTk9PtcV1eXMjIylJmZqYMHD+o73/mOHn744WH9uUePHk1BtbBaQUGBWltbrS4DKcY6ewPr7A2ss/v17dldkhtI7B2tbWnX5IpK2phdhp9nb3DCOhcVFQ35OVsdPVRfX6/3ve99A4KuJAUCAWVmZkqSrrjiCvX09Oi9995Lc4UAAAAYyrxFizXzHzZqb7dPzx47pb3dPoIuAMvYqo35fC3M7e3tys7OlmEYOnLkiOLxuMaPH5/mCgEAAHA+l5dcqSnvm2F1GQBgn7Db3d2txsZGbdy4MfFYdXW1JGnVqlV65ZVXVF1dLZ/Pp7Fjx+r2228fcHg2AAAAAACSjcJuZmamvv3tb/d7bNWqVYn/v3r1aq1evTrdZQGAozU11Ov15yMac6pDZ7JCWnBdmHZCAADgCbYJuwCA5GpqqNe7e6pUUZgjIxCQafaodk+VJBF4AQCA6xF2AcClDlVHdFNhTmLLh2EYKivM0d7qCGEXGKH6xiZFXo6qoydDIV9c4aUlnGkKADZH2AUAl/J3dcjICvR7zDAM+bs6LaoIcKb6xiZV1TUrd84KBQ1DcdNUVV1Ukgi8AGBjtjp6CACQPLFASOcepW6apmKBoEUVAc4UqTug3Nkl/bokcmeXKFJ3wOLKAADnw51dAHCp+avCqt1TpbK/tjKbpqnalnbNr6i0ujTAUTpihoLnnABhGIY6Y84/FYL2bABuRtgFHIg3JxiOvn25e6sj8nd1KhYIan5FJft1gREK+U3FTbPfkYemaSroN8/zKvujPRuA2xF2AYfhzQlGYt6ixYRbOI7dLuiFS4tVVRdNtDKbpqnjzVFVlhZbVlMy9LZnLx+kPXs//z0B4AqEXcBheHMCwM3seEGv7+tG6varM2Yo6DdVWVrs+N+5bm7PBgCJsAs4Dm9OALiZXS/oLV44z/Hh9lxubc8GgD5MYwYcJuQ3B52wy5sTAG7QETP6hS+JC3qpEi4t1vHmaOK/KX3t2WGHt2cDQB/u7AIO49a9YwAgcbcxndzang0AfQi7gMPw5gSAm3FBL73c2J4NAH0Iu4AD8eYEGJ2mhnq9/nxEY0516ExWSAuuCzO12ia4oAcASBbCLgDAU5oa6vXunipVFObICARkmj2q3VMlSQRem+CCHgAgGQi7AABPOVQd0U2FOf2m/ZYV5mhvdYSwCwA4L7udA47zI+wCADzF39UhIyvQ7zHDMOTv6rSoIgCAE9jxHHCcH0cPAQA8JRYIDXp8VywQtKgiAIAT9J4DXjLIOeAHLK4MQyHsAgA8Zf6qsGpb2vudLVrb0q75q8IWVwYAsDPOAXce2pgBAJ7Sty93b3VE/q5OxQJBza+oZL8uAOC8OAfceQi7AADPmbdoMeEWADAinAPuPIRdAAAAALgAzgF3HsIuAABIusGO51i5oszqsgBgVDgH3FkIuwAAIKmGOp4jOydbM6ZPtbo8pBFnkgKwEmEXACzW1FCv15+PaMypDp3JCmnBdWH2k8LReo/nWD7geI5nXqjTv378IxZXh3ThTFIAVuPoIQCwUFNDvd7dU6WKrB6tzQ+oIqtH7+6pUlNDvdWlARdtqOM5Os5YVBAswZmkAKxG2AUACx2qjqisMKffm8Gywhwdqo5YXBlw8UJ+M3GOcR/TNBUaY1FBsARnkgKwGm3MAGAhf1eHjKxAv8cMw5C/q9OiioDRG+p4jo+uKU3L12efqD1wJikAqxF2AcBCsUBIptkz4M1gLBC0sCpgdIY6nuPKKxaptbU1pV+bfaL2wZmkAKw2rLAbj8cVjUZlGIaKi4uVkdHb/fyzn/1M73//+1NaIAC42fxVYdXuqUq0MpumqdqWds2vqLS6NGBUrDqeY6jhWJG6/YTdNONMUgBWG1bYfeSRR1RQUCC/368f/vCHuu222zR58mRVV1cTdgFgFPqmLu+tjsjf1alYIKj5FZVMYwYuUkfMUJB9orbBmaQArDSssNvW1qZPf/rTkqTly5frkUce0Yc//OGUFgYAXjFv0WLCrUuwV9R67BO1Vn1jk/YdOKTWztP8DACw3LDCbiwW05kzZzRmzBhNnDhRmzdv1kMPPaS33nor1fUBAOAI7BW1B/aJWqfvZ2DSwjIFz5zhZwCA5c4bdnt6euTz+fSxj31MnZ2dysnJkSRlZWXpzjvv1Msvv5yOGgEAsD32itoD+0Stw88AALs5b9j96le/qjvuuEOXXnrpgM9lZGToAx/4QMoKAwDASdgrah/sE7UGPwMA7CbjfJ+85JJL9MUvflFtbW2Jxw4fPqytW7emvDAAAJwk5Ddlmv33hbJXFF7CzwAAuzlv2K2srNTKlSv1xS9+UXV1ddq+fbsefPBBlZSUpKs+AAAcIVxarOPN0cSb/b69omH2isIj+BkAYDcXHFA1a9YsBQIBPfzwwyorK9Odd96psWPHpqM2AAAcg72i8Lq+f+v7XqvViY7T/AykEJPfgeE5b9i9//77dfjwYa1Zs0br1q3TN7/5TR06dEhXXHFFuuoDAMAx2CsKr1u8cJ5WrihTa2ur1aW4FpPfgeE7b9j9m7/5G/3Lv/yLQqGQJGnSpEm699571dLSotWrV6elQAAAAAC9mHoNDN959+xu2LAhEXQlafr06dq+fbteeOGFlBcGAAAAoL+OmJEIun2Yeg0M7rxhdzB5eXm6++67U1ELAAAAgPNg6jUwfCMOu5KUlZWV7DoAAAAAXABTr4Hhu+A0ZgAAAAD2wOR3YPgIuwAAAICDMPkdGJ6LamMGAAAAAMDOCLsAAAAAANexVRvzbbfdpszMTGVkZMjn82nnzp39Pm+aph5//HHV19dr3Lhx2rRpk2bMmGFRtQAAAPC6+sYmRV6OqqMnQyFfXOGlJZ5tMeZ7AbuxVdiVpG3btmnChAmDfq6+vl7vvvuuHn74Yb3xxhv65je/qa9+9atprhAAAADpZscgVd/YpKq6ZuXOWaGgYShumqqqi0qS5bWlG98L2JGj2pgPHDigD3zgAzIMQ7NmzVJnZ6eOHz9udVkAAABIob4gFZ+zQsEFyxWfs0JVdc2qb2yytK5I3QHlzi6RYRiSJMMwlDu7RJG6A5bWZQW+F7Aj293Z3bFjhyRp5cqVKi8v7/e5trY2FRQUJD7Oz89XW1ubcnNz+z2vpqZGNTU1kqSdO3f2ew3cw+/3s7YewDp7A+vsDayzN6Rinfe9dkiTFpYlgpQkTVpYqn2v1WrlirKkfq2ROOPLVGDcuAGPn/Jluv7f+rnr7OXvhZs5/fe2rcLu9u3blZeXpxMnTugrX/mKioqKNHfu3BH/OeXl5f2CcmtrazLLhE0UFBSwth7AOnsD6+wNrLM3pGKdWztOK3jmzIDHT3SctvTf1Jiebp0+fbpfCDdNU/6ebtf/Wz93nb38vXAzJ/zeLioqGvJztmpjzsvLkyRlZ2erpKRER44cGfD5s7/Zx44dS7wGAAAA7hTymzJNs99jpmkq6DeHeEV6hEuLdbw5mqjNNE0db44qXFpsaV1W4HsBO7LNnd3u7m6ZpqmsrCx1d3ersbFRFRUV/Z5TXFysH//4xyotLdUbb7yhQCAwoIUZAAA3s+OQHiDVwqXFqqqLJvaE9gWpSouDVN/PXqRuvzpjhoJ+U5WlxZ78meR7ATuyTdg9ceKEHnjgAUlST0+Pli5dqkWLFqm6ulqStGrVKi1evFgHDx7Upz/9aY0dO1abNm2ysmQAANKKaafwKjsHqcUL59miDjvgewG7Mcxze0Jc6OjRo1aXgBRwwh4CjB7rPDQ33eFjnYdnx79/V/HZywfsicto3q+7/uX/sbCy4WGdvYF19gbW2RucsM7n27Nrmzu7AIDh4w6fN3XEDAXPCrpS7/EenTFjiFcAAOBdthpQBQAYHs4z9Ca7DukBAMCOCLsA4EAdMaNfK6vEHT4vYNopAADDRxszADhQyG8qbpoD9m5yh8/d7DykBwAAuyHsAoAD2fUYDqQe004BABgewi4AOBB3+Ppz02RqAACQHIRdAHAo7vD1YjI1AAAYDAOqAACOxmRqAAAwGMIuAMDRmEwNAAAGQ9gFADgaZ88CAIDBEHYBAI7G2bMAAGAwDKgCADha3xCq7z23V7/98wn1nDmtmYU5kmZbWhcAALAWYRcA4ApGwXQVL/2/c4eZyAwAgLfRxgwAcDwmMgMAgHNxZxcA4HgdMUNBF09krm9sUuTlqDp6MhTyxRVeWsIdawAALoCwCwBwvJDfVNw0+x1B5JaJzPWNTaqqa1bunBUKGobitGgDADAstDEDABzPzROZadEGAODicGcXAOAK8dY3deCZQ4r/pVszJufqYzeuccWdT7e3aAMAkCqEXQCAo/W1+eYvrVDBXycxH2+OWl1W0ri5RRsAgFSijRkA4Ghub/N1c4s2AACpxJ1dAICjub3Nt68VO1K3X50xQ0G/qcrSYle0aAMAkEqEXQCAo3mhzXfxwnmEWwAARog2ZgCAo9HmCwAABsOdXQCAo9HmCwAABkPYBQA4Hm2+uBj1jU2KvBxVR0+GQr64wktL+HcEAC5C2AUAAJ7Td2RV7pwVChqG4qapqrreI6sIvADgDuzZBQAAnuP2I6sAAIRdAADgQR0xo98Eb8ldR1YBAAi7AADAg0J+MzHBu4/bjqwCAK9jzy4AADbAsKT0CpcWq6oummhl7juyqpIjqwDANQi7AABYjGFJ6ceRVcDInHtBbv0HyzVj+lSrywLOi7ALAIDFeoclLR9kWNJ+wlcKcWQVMDyDXZD7RnW9PnLlCX6GYGuEXQAALNYRMxRkWBIwAO399jDoBbk5JYrUPc96wNYIuwAAWCzkNxU3zX7TgRmWBK+jvd8+uCAHp2IaMwAAFguXFut4czQxHbhvWFKYYUnwMM5Ctg+ml8OpuLMLAIDFGJYEDMTdRPsYdHr5L6P6CBfkYHOEXQAAbIBhSUB/tPfbx2AX5DauuZZpzLA9wi4AAABsh7OQ7eXcC3IFBQVqbW21sCLgwgi7AABgUEzChZVo7wcwWoRdAAAwAJNwYQe09wMYDaYxAwCAAZiECwBwOsIuAAAYoCNm9BsMJDEJFwDgLLQxAwCAAS52Ei77fAEAdkHYBZASvOEFnO1iJuGyz9c5+B0NwAsIuwCSjje8gPNdzCTc3n2+ywfZ57ufn30b4Xc0AK8g7AJIOt7wAu4w0km4HTFDQfb5pkyy7sbyOxqAV9gi7La2tmr37t1qb2+XYRgqLy9XOBzu95ympibdd999KiwslCRdddVVqqiosKJcABfAG17Amy52ny8uLJl3Y/kdDcArbBF2fT6fKisrNWPGDJ06dUqbN2/WwoULNXXq1H7PmzNnjjZv3mxRlQCGize8gDddzD5fDE8y78byOxqAV9ji6KHc3FzNmDFDkpSVlaUpU6aora3N4qoAXKxwabGON0dlmr1vnPre8IZ5wwu42uKF81RZOlsZzfvV9fp+ZTTvV2XpbFpjkyCZR0HxOxqAV9jizu7ZWlpa9Lvf/U6XXnrpgM/9+te/1h133KHc3FxVVlZq2rRpFlQI4EIuZrANAHcY6T5fDE8y78byOxqAVxhm32U9G+ju7ta2bdt044036qqrrur3ua6uLmVkZCgzM1MHDx7Ud77zHT388MOD/jk1NTWqqamRJO3cuVN/+ctfUl470s/v9ysWi1ldBlKMdfYG1tkbWOeL9+rBBn2jul65c85qEf9lVBtXLdaVVyyyurx+WGdvYJ29wQnrPHbs2CE/Z5uwG4vFdO+99+ryyy/XBz/4wQs+/7bbbtM999yjCRMmXPC5R48eTUaJsJmCggK1trZaXQZSjHX2BtbZG1jn0alvbFKk7kDibmzYpndjWWdvYJ29wQnrXFRUNOTnbNHGbJqmHnvsMU2ZMmXIoNve3q7s7GwZhqEjR44oHo9r/Pjxaa4UAADAGrSIA8DI2CLs/upXv9JLL72k6dOn64477pAkrV+/PnEVYdWqVXrllVdUXV0tn8+nsWPH6vbbbx8wqAEAAAAAAMkmYXf27Nl66qmnzvuc1atXa/Xq1WmqCAAAAG5R39ikyMtRdfRkKOSLK7y0hLvkgAfYIuwCAAAAqVDf2KSqumblzlmhoGEobpqqqotKEoEXcDlbnLMLAAAApEKk7oByZ5cktr8ZhqHc2SWK1B2wuDIAqUbYBQAAgGt1xIwBc14Mw1BnjNkvgNvRxgwAAJAk7A21n5DfVNw0+wVe0zQV9Nvi9E0AKcSdXQAAgCTo2xsan7NCwQXLFZ+zQlV1zapvbLK6NE8LlxbreHNUptkbbk3T1PHmqMKlxRZXBiDVuLMLAACQBL17Q5cPsjd0P3d3LdT3vY/U7VdnzFDQb6qytJg1ATyAsAsAAJAEHTFDQfaG2tLihfMIt4AH0cYMAACQBCG/mWiV7cPeUACwDmEXAAAgCdgbCgD2QhszACApmEILr2NvKADYC2EXADBqfVNoc+esUNAwFDdNVdVFJYk3+vAU9oYCgH3QxgwAGLXeKbQlg0yhPWBxZQAAwKu4swsAGDWm0ALuxjYFAE5E2AUAjFrIbypumok7uxJTaAG3YJsCAKeijRkAMGpMoQXci20KAJyKO7sAgFFjCi3gXmxTAOBUhF0AQFIwhRZwJ7YpAHAq2pgBAAAwJLYpAHAq7uwCAABgSGxTAOBUhF0AAACcF9sUADgRYRcAgEFwrigAAM5G2AUA4BycKwoAgPMxoAoAgHNwrigAAM5H2AUA4BwdMaPfMSsS54oCAOA0hF0AAM4R8puJY1b6cK4oAADOQtgFAOAcnCsKAIDzMaAKAIBzcK6ofTAVGwBwsQi7AAAMgnNFrcdUbADAaNDGDAAAbImp2ACA0SDsAgAAW2IqNgBgNAi7AADAlpiKDQAYDcIuAACwJaZiAwBGgwFVAADAlpiKDQAYDcIuAACwLaZiAwAuFm3MAAAAAADX4c4uAAAAbKO+sUmRl6Pq6MlQyBdXeGkJd/cBXBTCLgC4EG8WAThRfWOTquqalTtnhYKGobhpqqouKkn8DgMwYoRdAHAZ3ixipLg4AruI1B1Q7uzlifOVDcNQ7uwSRer2828SwIgRdgHAZXiziJHg4gjspCNmKPjX3119DMNQZ8wY4hUAMDQGVAGAy3TEjETQ7cObRQyl9+JIySAXRw5YXBm8KOQ3E+cq9zFNU0G/OcQrAGBohF0AcBneLGIkuDgCOwmXFut4czTxO8w0TR1vjipcWmxxZQCciDZmAHCZcGmxquqiibt1fW8WK3mziEGE/Kbiptkv8HJxBFbpa52P1O1XZ8xQ0G+qsrSYlnoAF4WwCwAuw5tFjAQXR2A3ixfO4/cVgKQg7AKAC/FmEcPFxREAgFsRdgGMGseWAM7GxREAgBsRdgGMCseWAEgGLpoBAJLNVmG3oaFBjz/+uOLxuK699lqtXbu23+fPnDmjRx55RL/97W81fvx43X777SosLLSmWACSONMVwOhx0QwAkAq2CbvxeFzf+ta39IUvfEH5+fnasmWLiouLNXXq1MRz9u3bp2AwqK997Wuqq6vTf/zHf+izn/2shVUD6IgZCnr02BLuRAHJwUUzAEAq2Oac3SNHjmjy5MmaNGmS/H6/lixZomg02u85Bw4c0LJlyyRJV199tQ4dOjTgLEkA6eXVM1377kTF56xQcMFyxeesUFVds+obm6wuDXAczvoFAKSCbcJuW1ub8vPzEx/n5+erra1tyOf4fD4FAgGdPHkyrXUC6C9cWqzjzdFE4O07tiTs8mNLeu9ElQxyJ+qAxZUBzuPVi2YAgNSyTRtzMtXU1KimpkaStHPnThUUFFhcEVLB7/eztjawckWZsnOy9cwLdeo4I4XGSB9dU6orr1iUlD/frut8xpepwLhxAx4/5cu0Zb12Z9d1RnINtc7r11yrb1TXK3fOWWf9/jKqjWuu5d+FA/Hz7A2sszc4fZ1tE3bz8vJ07NixxMfHjh1TXl7eoM/Jz89XT0+Purq6NH78+AF/Vnl5ucrLyxMft7a2pq5wWKagoIC1tYkZ06fqXz/+kX6PJWtt7LrOY3q6dfr06X6tl6Zpyt/Tbct67c6u64zkGmqdZ0yfqo9ceUKRuucTZ/1+pLRYM6ZP5d+FA/Hz7A2sszc4YZ2LioqG/Jxtwu7MmTP1zjvvqKWlRXl5efrpT3+qT3/60/2e83d/93d68cUXNWvWLL3yyiuaN2/egD0+AJAO4dJiVdVFE63Mfe3blS5v3wZShbN+AQDJZpuw6/P59IlPfEI7duxQPB7X8uXLNW3aND355JOaOXOmiouLtWLFCj3yyCP61Kc+pVAopNtvv93qsgF4VN+b8kjd/sSdqMrSYt6sAwAA2IRhemCc8dGjR60uASnghLYKjB7r7A2sszewzt7AOnsD6+wNTljn87Ux22YaMwAAAAAAyULYBQAAAAC4DmEXAAAAAOA6hF0AAAAAgOvYZhozANhdfWOTIi9H1dGToZAvrvDSEqYvAwAA2BRhFwCGob6xSVV1zcqds0JBw1DcNFVVF5UkAi8AAIAN0cYMAMMQqTug3NklMgxDkmQYhnJnlyhSd8DiygAAADAYwi4ADENHzEgE3T6GYagzZgzxCgAAAFiJNmYAGIaQ31TcNPsFXtM0FfSbFlYFuA974wEAycKdXQAYhnBpsY43R2WaveHWNE0db44qXFpscWWAe/TtjY/PWaHgguWKz1mhqrpm1Tc2WV0aAMCBuLMLAMPQd2cpUrdfnTFDQb+pytJi7jgBSdS7N375IHvj9/OzBgAYMcIuAAzT4oXzeMMNpFBHzFCQvfEAgCShjRkAANhCyG8mtgr0YW88AOBiEXYBAIAtsDceAJBMtDEDAABbYG88ACCZCLsAAMA22BsPAEgW2pgBAAAAAK5D2AUAAAAAuA5hFwAAAADgOoRdAAAAAIDrEHYBAAAAAK5D2AUAAAAAuA5hFwAAAADgOoRdAAAAAIDr+K0uAACAVKhvbFLk5ag6ejIU8sUVXlqixQvnWV0WAABIE8IuAMB16hubVFXXrNw5KxQ0DMVNU1V1UUki8AIA4BG0MQMAXCdSd0C5s0tkGIYkyTAM5c4uUaTugMWVAQCAdOHOrkVorwOA1OmIGQr+Nej2MQxDnTFjiFcAAAC3IexagPY6AEitkN9U3DQTd3YlyTRNBf2mhVUBAIB0IuxaoLe9bvkg7XX7CbsAkATh0mJV1UUTrcymaep4c1SVpcVWl5Y0dAgBAHB+hF0L0F4HAKlxdgCMt7eqtfY3CuZPVtBvqrK02DVhkA4hAAAujLBrAdrrACD5zg2Agb/ezf1w6WzXBUA6hAAAuDCmMVsgXFqs481RmWZvuO1rrwu7qL0OANLNSxOYO2JGvwumEh1CAACcizu7Fui76h6p26/OmOG69joAsIKXtojQIQQAwIURdi2yeOE8wi0AJJGXAqAXBnABADBahF0AgCt4KQDSIQQAwIURdgEAruC1AEiHEAAA50fYBQC4BgEQAAD0YRozAAAAAMB1CLsAAAAAANehjRkAgHPUNzYp8nJUHT0ZCvniCi8toT0aAACHIewCAHCW+sYmVdU1K3fOCgUNQ3HTVFVdVJIIvAAAOAhtzAAAnCVSdyBxfJEkGYah3NklitQdsLgyAAAwEoRdAADO0hEzEkG3j2EY6owZQ7wCAADYEWEXAICzhPymTNPs95hpmgr6zSFeAQAA7Ig9uwDgMgxXGp1wabGq6qKJVmbTNHW8OarK0mKrSwMAACNgeditqqrSa6+9Jr/fr0mTJmnTpk0KBoMDnnfbbbcpMzNTGRkZ8vl82rlzpwXVAoC9MVxp9Pq+T5G6/eqMGQr6TVWWFvP9AwDAYSwPuwsXLtQtt9win8+nJ554Qs8884w2bNgw6HO3bdumCRMmpLlCAHCO3uFKywcZrrSfsDYCixfO4/sFAIDDWb5n9/LLL5fP55MkzZo1S21tbRZXBADOxXAlAACAXpbf2T3bvn37tGTJkiE/v2PHDknSypUrVV5enq6yAMAxQn5TcdPsF3gZrgQAALzIMM8dOZkC27dvV3t7+4DHb775ZpWUlEiSnn76af3mN7/R5z//+QF3JSSpra1NeXl5OnHihL7yla/o4x//uObOnTvo16upqVFNTY0kaefOnfrLX/6SvL8MbMPv9ysWi1ldBlKMdR6ZVw826BvV9cqdc9ZwpV9GtXHVYl15xSKryxsS6+wNrLM3sM7ewDp7gxPWeezYsUN+Li1h90JefPFF/eQnP9HWrVs1bty4Cz7/qaeeUmZmpm644YZh/flHjx4dbYmwoYKCArW2tlpdBlKMdR65+sYmReoOJIYrhR0wXIl19gbW2RtYZ29gnb3BCetcVFQ05Ocsb2NuaGjQc889py9/+ctDBt3u7m6ZpqmsrCx1d3ersbFRFRUVaa4UAJyB4UoAAAA2CLvf+ta3FIvFtH37dknSZZddpo0bN6qtrU1f//rXtWXLFp04cUIPPPCAJKmnp0dLly7VokWLLKwaAAAAAGBntmhjTjXamN3JCW0VGD3W2RtYZ29gnb2BdfYG1tkbnLDO52tjtvzoIQAAAAAAko2wCwAAAABwHcIuAAAAAMB1CLsAAAAAANch7AIAAAAAXIewCwAAAABwHcIuAAAAAMB1/FYXAABwn/rGJkVejqqjJ0MhX1zhpSVavHCe1WUBAAAPIewCAJKqvrFJVXXNyp2zQkHDUNw0VVUXlSQCLwAASBvamAEASRWpO6Dc2SUyDEOSZBiGcmeXKFJ3wOLKAACAlxB2AQBJ1REzEkG3j2EY6owZQ7wCAAAg+Qi7AICkCvlNmabZ7zHTNBX0m0O8AgAAIPkIuwCApAqXFut4czQReE3T1PHmqMKlxRZXBgAAvIQBVQCApOobQhWp26/OmKGg31RlaTHDqQAAQFoRdgEASbd44TzCLQAAsBRtzAAAAAAA1yHsAgAAAABch7ALAAAAAHAdwi4AAAAAwHUIuwAAAAAA1yHsAgAAAABch7ALAAAAAHAdwi4AAAAAwHUIuwAAAAAA1yHsAgAAAABch7ALAAAAAHAdwi4AAAAAwHUIuwAAAAAA1yHsAgAAAABch7ALAAAAAHAdwzRN0+oiAAAAAABIJu7swrE2b95sdQlIA9bZG1hnb2CdvYF19gbW2Rucvs6EXQAAAACA6xB2AQAAAACuQ9iFY5WXl1tdAtKAdfYG1tkbWGdvYJ29gXX2BqevMwOqAAAAAACuw51dAAAAAIDr+K0uALhYP/jBD3TgwAEZhqHs7Gxt2rRJeXl5VpeFJKuqqtJrr70mv9+vSZMmadOmTQoGg1aXhST72c9+pv/6r//S22+/ra9+9auaOXOm1SUhiRoaGvT4448rHo/r2muv1dq1a60uCSnw6KOP6uDBg8rOztauXbusLgcp0Nraqt27d6u9vV2GYai8vFzhcNjqspBkf/nLX7Rt2zbFYjH19PTo6quv1rp166wu66LQxgzH6urqUiAQkCRFIhH98Y9/1MaNGy2uCsn2i1/8QvPnz5fP59MTTzwhSdqwYYPFVSHZ/vjHPyojI0Pf+MY3VFlZSdh1kXg8rs985jP6whe+oPz8fG3ZskWf+cxnNHXqVKtLQ5IdPnxYmZmZ2r17N2HXpY4fP67jx49rxowZOnXqlDZv3qw77riDn2eXMU1Tp0+fVmZmpmKxmLZu3aqPfexjmjVrltWljRhtzHCsvqArSadPn5ZhGBZWg1S5/PLL5fP5JEmzZs1SW1ubxRUhFaZOnaqioiKry0AKHDlyRJMnT9akSZPk9/u1ZMkSRaNRq8tCCsydO1ehUMjqMpBCubm5mjFjhiQpKytLU6ZM4b/LLmQYhjIzMyVJPT096unpcez7bNqY4Wjf//739dJLLykQCGjbtm1Wl4MU27dvn5YsWWJ1GQBGoK2tTfn5+YmP8/Pz9cYbb1hYEYBkaGlp0e9+9ztdeumlVpeCFIjH47rzzjv17rvv6rrrrtNll11mdUkXhbALW9u+fbva29sHPH7zzTerpKRE69ev1/r16/XMM8/oxz/+sWP3E3jdhdZZkp5++mn5fD5dc801aa4OyTKcdQYA2F93d7d27dqlj33sY/067eAeGRkZuv/++9XZ2akHHnhAb731lqZPn251WSNG2IWtffGLXxzW86655hrdc889hF2HutA6v/jii3rttde0detWx7bRYPg/z3CXvLw8HTt2LPHxsWPHGCYIOFgsFtOuXbt0zTXX6KqrrrK6HKRYMBjUvHnz1NDQ4Miwy55dONY777yT+P/RaJT9fi7V0NCg5557TnfeeafGjRtndTkARmjmzJl655131NLSolgspp/+9KcqLi62uiwAF8E0TT322GOaMmWKPvjBD1pdDlLkvffeU2dnp6TeycyNjY2aMmWKxVVdHKYxw7EeeOABvfPOOzIMQwUFBdq4cSN3C1zoU5/6lGKxWGLoyWWXXcbUbRd69dVX9e1vf1vvvfeegsGgLrnkEt11111Wl4UkOXjwoL773e8qHo9r+fLluvHGG60uCSnw0EMP6fDhwzp58qSys7O1bt06rVixwuqykETNzc3aunWrpk+fnui0Wr9+va644gqLK0Myvfnmm9q9e7fi8bhM09T73/9+VVRUWF3WRSHsAgAAAABchzZmAAAAAIDrEHYBAAAAAK5D2AUAAAAAuA5hFwAAAADgOoRdAAAAAIDrEHYBAAAAAK5D2AUAwKGeeOIJ3XfffYmPq6qqdPfddysWi1lYFQAA9kDYBQDAof7+7/9eTU1N+t3vfqfq6mo1NDTo85//vPx+v9WlAQBgOcM0TdPqIgAAwMV56qmn9Oqrr6qrq0t33323CgoK1NXVpe3bt+uPf/yjduzYoenTp1tdJgAAacedXQAAHOx973uf3nrrLd1yyy0qKCiQJI0dO1ZbtmzR1VdfbXF1AABYh7ALAIBDvfXWW/rmN7+psrIy7d+/P/G43+/XhAkTLKwMAADrEXYBAHCgtrY23Xvvvfrnf/5n/dM//ZPeeustNTU1WV0WAAC2QdgFAMBhurq6dM8992jNmjUqLi7WuHHjdP311+sHP/iB1aUBAGAbDKgCAMCldu/ereuvv54BVQAATyLsAgDgQvfcc49+//vfq6CgQCtXrtSyZcusLgkAgLQi7AIAAAAAXIc9uwAAAAAA1yHsAgAAAABch7ALAAAAAHAdwi4AAAAAwHUIuwAAAAAA1yHsAgAAAABch7ALAAAAAHAdwi4AAAAAwHUIuwAAAAAA1/n/AUlQYQ7XtAxKAAAAAElFTkSuQmCC",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"data = pd.read_csv(get_file(\"testSet.txt\", local=False), \\\n",
" delim_whitespace=True, header=None, names=['x1','x2','t'])\n",
"plot_ds(data)"
]
},
{
"cell_type": "code",
"execution_count": 29,
"metadata": {},
"outputs": [],
"source": [
"n = len(data)\n",
"nfeatures = len(data.columns)-1\n",
"\n",
"X = np.array(data[['x1','x2']])\n",
"t = np.array(data['t']).reshape(-1,1)\n",
"X = np.column_stack((np.ones(n), X))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n",
"Il metodo considerato per la classificazione è la *logistic regression*, che determina un iperpiano (retta, in questo caso) di separazione minimizzando rispetto al vettore $\\theta$ dei coefficienti dell'equazione dell'iperpiano (3 in questo caso) il rischio empirico sul dataset associato alla funzione di costo *cross-entropy*, per la quale il costo associato a un singolo elemento $\\mathbf{x}=(x_1,\\ldots,x_d)$ è\n",
"\n",
"$$ J(\\theta, \\mathbf{x})=-\\left(t\\log y + (1-t)\\log (1-y)\\right) $$\n",
"dove $t$ è il valore *target* è il valore $0/1$ della classe dell'elemento e $y\\in (0,1)$ è il valore predetto dal modello, definito come \n",
"$$\n",
"y = f(\\mathbf{x}; \\theta) = \\sigma\\left(\\sum_{i=1}^d\\theta_ix_i+\\theta_0\\right) = \\frac{1}{1+e^{-(\\sum_{i=1}^d\\theta_ix_i+\\theta_0)}}\n",
"$$"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {},
"outputs": [],
"source": [
"def f(theta, X):\n",
" return sp.expit(np.dot(X, theta)).reshape(-1,1)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Il rischio empirico associato all'intero dataset può essere allora definito come la corrispondente media\n",
"$$\n",
"J(\\theta, X)=\\frac{1}{n}\\sum_{i=1}^n \\left(t_i\\log f(\\mathbf{x}_i;\\theta) -(1-t_i)\\log (1-f(\\mathbf{x}_i;\\theta))\\right)\n",
"$$"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {},
"outputs": [],
"source": [
"def approx_zero(v):\n",
" eps = 1e-50\n",
" v[v"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plot_all(cost_history, m, q)"
]
},
{
"cell_type": "code",
"execution_count": 30,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA1gAAAGoCAYAAABbkkSYAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAAAvLklEQVR4nO3deYzd90Hv/c9ZZh+Pl4zjJc7qxEmT1E1abkpJGjZT0gIFwdNWQFiqR6BbVJGH6hEgoYaoARF0H0AIChfupbS9VBWhLbRUQFPTNpSmlLQhq5M6S+PEcWJ7PN5mX855/pjF4yWeSXI8Z5nXS7LmzO9sX0++neTd7+98f4VqtVoNAAAAr1mx3gMAAABoFQILAACgRgQWAABAjQgsAACAGhFYAAAANSKwAAAAaqRcjzfdt29fPd62YfX392dgYKDew6CBmSOcjfnBYswRFmOOsBhz5HSbN28+43ErWAAAADUisAAAAGpEYAEAANSIwAIAAKgRgQUAAFAjAgsAAKBGBBYAAECNCCwAAIAaEVgAAAA1IrAAAABqRGABAADUiMACAACoEYEFAABQIwILAACgRgQWAABAjQgsAACAGhFYAAAANSKwAAAAakRgAQAA1IjAAgAAqBGBBQAAUCMCCwAAoEYEFgAAQI0ILAAAgBoRWAAAADUisAAAAGpEYAEAANSIwAIAAKgRgQUAAFAj5XoPYCV7ZM9g/v4b38l3bducd1y3qd7DAQAAXiMrWHU0NV3J8dHJjIxN1nsoAABADQisOioWC0mS6Wq1ziMBAABqQWDVUWGmr1KpCCwAAGgFAquOirOFVbGCBQAALUFg1dFcYFUFFgAAtIRl2UVw586d2blzZ5LkrrvuSn9//3K8bcNbfWw6SVKtxs+EsyqXy+YIL8v8YDHmCIsxR1iMObJ0yxJYO3bsyI4dO+a/HxgYWI63bXhDx48nmdlN0M+Es+nv7zdHeFnmB4sxR1iMOcJizJHTbd68+YzHnSJYR3O7CPoMFgAAtAaBVUezfeUzWAAA0CIEVh0V5nYRtE07AAC0BIFVR7ZpBwCA1iKw6khgAQBAaxFYdVSc/elPO0UQAABagsCqo4ILDQMAQEsRWHU0f4pgpc4DAQAAakJg1dHcNu0+gwUAAK1BYNXR3ArWtCUsAABoCQKrjkql2cCatoIFAACtQGDVUbk08+OfnJ6u80gAAIBaEFh11DYfWE4RBACAViCw6qg8eyGsySmBBQAArUBg1dHcZ7CmpiuuhQUAAC1AYNVRsVBIaXav9qmKwAIAgGYnsOpsbqOLKZ/DAgCApiew6qy84DRBAACguQmsOmubX8FyiiAAADQ7gVVnczsJWsECAIDmJ7DqbO4UQdfCAgCA5iew6qzsFEEAAGgZAqvO5gOrYgULAACancCqM7sIAgBA6xBYdWYXQQAAaB0Cq85KdhEEAICWIbDqrM0uggAA0DIEVp3ZRRAAAFqHwKozuwgCAEDrEFh1ZhdBAABoHQKrzuwiCAAArUNg1ZldBAEAoHUIrDqziyAAALQOgVVndhEEAIDWIbDqzC6CAADQOgRWndlFEAAAWofAqrMTuwgKLAAAaHYCq85O7CLoM1gAANDsBFad2UUQAABah8Cqs7JTBAEAoGUIrDo7sYugUwQBAKDZCaw6s4IFAACtQ2DVWZtt2gEAoGUIrDqziyAAALQOgVVnroMFAACtQ2DVWdk27QAA0DIEVp2dWMFyiiAAADQ7gVVn5fLMP4LJ6UqqVZEFAADNTGDVWbFQWLBVu8ACAIBmJrAaQEdbKUkyMTVd55EAAACvhcBqAG0LThMEAACal8BqAO3lmRWsySmBBQAAzUxgNYC5UwStYAEAQHMTWA2grTz3GSyBBQAAzUxgNYD5UwStYAEAQFMTWA1g/hRBK1gAANDUBFYDaLOCBQAALUFgNQC7CAIAQGsQWA2gffY6WC40DAAAzU1gNYB227QDAEBLKC/Hm+zcuTM7d+5Mktx1113p7+9fjrdtGp3tg0mSto4uPxvOqFwumxu8LPODxZgjLMYcYTHmyNItS2Dt2LEjO3bsmP9+YGBgOd62aZSLhSTJ0WPH/Ww4o/7+fnODl2V+sBhzhMWYIyzGHDnd5s2bz3jcKYINYO4UQRcaBgCA5iawGoALDQMAQGsQWA3ANu0AANAaBFYDaG+b+cdgBQsAAJqbwGoAVrAAAKA1CKwGMBdYLjQMAADNTWA1ABcaBgCA1iCwGoBTBAEAoDUIrAZgm3YAAGgNAqsBzJ8iaAULAACamsBqAO3lmX8MEwILAACamsBqAE4RBACA1iCwGkC5VEyhkExXqqlUqvUeDgAA8CoJrAZQKBTSVpo7TdC1sAAAoFkJrAZx4mLDThMEAIBmJbAaREebjS4AAKDZCawGMbeCNe4UQQAAaFoCq0F0zF4La2JSYAEAQLMSWA1i7lpY404RBACApiWwGoQVLAAAaH4Cq0GcWMESWAAA0KwEVoPomNumfdIpggAA0KwEVoNob7OCBQAAzU5gNYh2K1gAAND0BFaD6HAdLAAAaHoCq0F0zJ4iOCGwAACgaQmsBjF3iuC4UwQBAKBpCawGMX8dLCtYAADQtARWg5i/DpYLDQMAQNMSWA3ixAqWUwQBAKBZCawGceIzWFawAACgWQmsBnFiF0ErWAAA0KwEVoOYv9CwTS4AAKBpCawGcWKTi0qq1WqdRwMAALwaAqtBlEvFlIqFVKrVTFcEFgAANCOB1UBs1Q4AAM1NYDWQua3ax30OCwAAmpLAaiAd81u120kQAACakcBqIJ3tM4E1NjFV55EAAACvhsBqIHOnCI75DBYAADQlgdVAuuZXsAQWAAA0I4HVQDrbykmsYAEAQLMSWA3EKYIAANDcBFYDsckFAAA0N4HVQHwGCwAAmpvAaiBOEQQAgOYmsBqITS4AAKC5CawGMneK4LjAAgCApiSwGsj8KYI2uQAAgKYksBrI3C6Coza5AACApiSwGkhnm1MEAQCgmQmsBtLZfmKTi2q1WufRAAAAr5TAaiBtpWJKxUKmK9VMVQQWAAA0G4HVYDptdAEAAE1LYDWYuY0uxmx0AQAATUdgNRgXGwYAgOYlsBrM/AqWwAIAgKYjsBrM3GewRn0GCwAAmo7AajDdHTOnCI6OW8ECAIBmI7AazFxgjVjBAgCAplNejjfZuXNndu7cmSS566670t/fvxxv2zTK5fL8z6R/7ZEkLybFNj8n5i2cI3Aq84PFmCMsxhxhMebI0i1LYO3YsSM7duyY/35gYGA53rZp9Pf3z/9MqlPjSZJDR477OTFv4RyBU5kfLMYcYTHmCIsxR063efPmMx53imCDcYogAAA0L4HVYOYDa1xgAQBAsxFYDaarXWABAECzElgNprvDdbAAAKBZCawG090+dx0sgQUAAM1GYDWYjrZSioVkfKqSqelKvYcDAAC8AgKrwRQKhXTNbnThNEEAAGguAqsBdc9vdDFd55EAAACvhMBqQK6FBQAAzUlgNaC5wLLRBQAANBeB1YBcCwsAAJqTwGpAcytYwwILAACaisBqQPOfwRqfrPNIAACAV0JgNaDezrYkydCYFSwAAGgmAqsBzQXW8JgVLAAAaCYCqwH1ds6cIjgksAAAoKkIrAZ04hRBgQUAAM1EYDWgnvlTBH0GCwAAmonAakBd7aUUC4WMTU5narpS7+EAAABLtKTAes973pP77rtv/vsHHnggt9122zkb1EpXKBR8DgsAAJpQ+Wx3DgwM5MCBA0mSvXv3ZteuXUmSBx98MPv37z/3o1vBejrbcmx0MkNjU1nT01Hv4QAAAEtw1sD68pe/nE996lNJkk9/+tP59Kc/PX/fBRdccG5HtsLZqh0AAJrPWQPr8ssvz9ve9rbcc8892b59ezZt2pQk6e3tzU033bQsA1ypnCIIAADN56yBdf311+f666/P1q1bc80112T9+vVJkkqlkmLR/hjnUo+t2gEAoOksqZKef/75fPnLX87g4GDe97735ed+7ufypS996VyPbUXrtVU7AAA0nSUF1r//+7+np6cnX/va1zI1NZVNmzblM5/5zLke24rmFEEAAGg+SwqsoaGhrFq1Kt/5zndy8803553vfGcOHz58rse2os2dInh8VGABAECzWFJg9ff355Of/GTuv//+bN26NUNDQ+nt7T3XY1vRVne3J0mOj07UeSQAAMBSLSmwfvZnfza9vb25/vrrc8MNN2RgYCBvfvObz/XYVrS+rpnAOjpiBQsAAJrFWXcRnHPDDTfkTW96U1588cW89NJLufXWW+0ieI71drWlkJnrYE1XqikVC/UeEgAAsIglBdbevXvzP/7H/8hLL72UJNm4cWN+/dd/3cWGz6FSsZDerrYcH53M0OhkVve013tIAADAIpa0DPVXf/VXOXz4cG688cbceOONOXLkSD7ykY+c67GteHOnCR7zOSwAAGgKS1rBeuaZZ/IzP/MzueWWW5Ik//Iv/5JPfvKT53RgJH3dbXlhMDk6MpEL6z0YAABgUUtawert7c3DDz+c/fv3Z//+/Xn44YftIrgM+mZ3Ejw2YgULAACawZJWsH7gB34gd999d771rW/NH3vPe95zzgbFjBOnCNpJEAAAmsGSAuvmm2/O6tWr8/DDDydJ3vCGN2T79u3ndGAkq7tnLjZsBQsAAJrDkk4RvPPOOzMwMJAPfOAD+cAHPpCDBw/md37nd8712Fa8+VMEbXIBAABNYUmBNTg4mPPPP3/++/Xr1+fQoUPnbFDMmD9F0MWGAQCgKSzpFMENGzbkH//xH7Nu3bpUq9V8/vOfz4YNG8712Fa8PqcIAgBAU1lSYP34j/94PvzhD+f3fu/35o+9//3vP2eDYkZPZ1uKhUKGx6cyOVVJW3lJC44AAECdLHmTi/7+/jzwwANJkje+8Y25+uqrz+nASIqFQlb3tOfw0HiODI9n/equeg8JAAA4iyUFVpJcffXVoqoO1s4G1mGBBQAADc85Zw1ubW9HkuTwkM9hAQBAoxNYDW5tz2xgDY/XeSQAAMBiBFaDO7GCJbAAAKDRCawGt2Z2BeuIFSwAAGh4AqvBre2dudiwFSwAAGh8AqvBza1gHR2ZyHSlWufRAAAAZyOwGlxbqZhVXW2pVJNjI3YSBACARiawmsBan8MCAICmILCawNxOgoM+hwUAAA1NYDWB81bNBNah42N1HgkAAHA2AqsJ9K/qTJIMHBNYAADQyARWE+jvE1gAANAMBFYTmA+s42OpVm3VDgAAjUpgNYHezrZ0tJUyOjGdkfGpeg8HAAB4GQKrCRQKhfnPYR10miAAADQsgdUk+vtmdhIcsJMgAAA0LIHVJPpXdSVJDlnBAgCAhiWwmoSdBAEAoPGVl+NNdu7cmZ07dyZJ7rrrrvT39y/H2zaNcrm86M9k63gxydM5PDLl57cCLWWOsHKZHyzGHGEx5giLMUeWblkCa8eOHdmxY8f89wMDA8vxtk2jv79/0Z9JR2Z2D9x36HgOHDyYYqGwHEOjQSxljrBymR8sxhxhMeYIizFHTrd58+YzHneKYJPo7iinr6stk9OVDB4fr/dwAACAMxBYTWTDmu4kyf4jI3UeCQAAcCYCq4lsXDOzk+BLR0brPBIAAOBMBFYT2bjWChYAADQygdVENljBAgCAhiawmsiG1TOBdeDoaKYr1TqPBgAAOJXAaiKd7eWs6WnPdKWaQ8ddcBgAABqNwGoyG2d3EnzpsM9hAQBAoxFYTWbzupnA2ntouM4jAQAATiWwmsyW83qTJC8MCiwAAGg0AqvJbDmvJ8nMCla1aqMLAABoJAKryazpaU93Rzkj41M5MjxR7+EAAAALCKwmUygUTlrFAgAAGofAakInAmuoziMBAAAWElhN6AIrWAAA0JAEVhOy0QUAADQmgdWE1vZ0ZFVXW0bGp3Lw2Fi9hwMAAMwSWE2oUCjkkvNXJUmePXC8zqMBAADmCKwmdanAAgCAhiOwmpQVLAAAaDwCq0ltXtedtnIxB4+NZWhsst7DAQAAIrCaVqlYzEX9vUmsYgEAQKMQWE3skvUzpwl+Z7/AAgCARiCwmtjlm/qSJE++eLTOIwEAABKB1dQuPn9VyqVCXjw8kuOjE/UeDgAArHgCq4m1lYq5bMPMKtZTLx6r82gAAACB1eSu2LQ6idMEAQCgEQisJnfF5pnA2r3vaKrVap1HAwAAK5vAanKb1nanp7OcoyMTOXhsrN7DAQCAFU1gNblioZBtm9ckSXY9f7i+gwEAgBVOYLWAay5cm0RgAQBAvQmsFnDl5tUpFQt59uDxDI1N1ns4AACwYgmsFtDZXs7WjX2pVpPHrWIBAEDdCKwWMXea4GMCCwAA6kZgtYirZwNr976jmZicrvNoAABgZRJYLWJNT0cuXt+byemKVSwAAKgTgdVCrr+0P0nyX98ZqPNIAABgZRJYLWT7JetSLCTffuFohu0mCAAAy05gtZBVXe25fNPqVKrVPLxnsN7DAQCAFUdgtZjrL5s9TfAZpwkCAMByE1gt5tqL1qW9XMx3DhzPgaOj9R4OAACsKAKrxXS2lXLd7GYX39h9oM6jAQCAlUVgtaDv3nZ+kuSbTx/M5HSlzqMBAICVQ2C1oC3n9eSCdd0ZGZ/Koza7AACAZSOwWlChUMibt21Iktz37f11Hg0AAKwcAqtFXX9ZfzrbSnn2wPE8d/B4vYcDAAArgsBqUZ1tpbzlyplVrHsfe7HOowEAgJVBYLWwG6/amFKxkEeeG8yh42P1Hg4AALQ8gdXCVve057pLz0u1mnx1l1UsAAA41wRWi/veazYnmbkm1tHhiTqPBgAAWpvAanGb1nZn+8XrMlWp5l8feaHewwEAgJYmsFaAt123JYUk//nkgRweGq/3cAAAoGUJrBVgw5ruXHdZf6Yr1Xzxob31Hg4AALQsgbVC/NAbLkixkHzz6YPZNzhc7+EAAEBLElgrxPq+rnzPVRtTrSafu39PqtVqvYcEAAAtR2CtID/0hi3p7ijn6ZeO5dHnDtd7OAAA0HIE1grS3VHOD1+3JUny+W/uycTUdJ1HBAAArUVgrTBv3rYhG9d2Z3BoPPc8aMMLAACoJYG1wpSKhbzrLZelUEj+bdeLeX5gqN5DAgCAliGwVqCL1vfmra/blGo1ufu+ZzI1Xan3kAAAoCUUqsuwndzOnTuzc+fOJMldd92ViYmJc/2WTaVcLmdqampZ33N8cjof/Ni9OXh0JD/65svzUzddtazvzytTjzlC8zA/WIw5wmLMERZjjpyuvb39jMeXJbBOtW/fvuV+y4bW39+fgYGBZX/fZ146lv95z66kmvzy216XyzetXvYxsDT1miM0B/ODxZgjLMYcYTHmyOk2b958xuNOEVzBLtvYlx/cfkGqST751acyPDZZ7yEBAEBTE1gr3I7tW3LJ+atybHQyf/u1p1NxAWIAAHjVBNYKVyoW8jNvvTxd7aU8vvdI7vkvW7cDAMCrJbDI2t6O3Pq9V6RQSP71kRfy0LOH6j0kAABoSgKLJMm2zWvyY991cZLkb//96ew9NFznEQEAQPMRWMy76XUb811b12dyupK/2vlEBo6N1XtIAADQVAQW8wqFQn7qLZfmik2rMzQ2mf/1xcdzbNQ1ywAAYKkEFicpl4r5+e/fli3n9WRwaDz/+4tPZGTcReUAAGApBBan6Wwr5f/ecVXW93XmxcMj+ct7drlGFgAALIHA4ox6O9vyy297XfpXdeaFwZH8xT2PZ0hkAQDAWQksXtaano7891uunl/J+p9f2JUjw+P1HhYAADQsgcVZre5uz3+/5epsWN2V/UdG86f/9FhePDxS72EBAEBDElgsqq+rPe+75epccv6qHB2ZyJ/982N56sWj9R4WAAA0HIHFkvTMfiZr+8XrMjY5nf+984nc98RLqVar9R4aAAA0DIHFkrWVivnZ770iN1+9KdOVav7+G8/m7q89k8mpSr2HBgAADUFg8YoUC4X82H+7OD/z1svTVirmm08fzIf/+bEcOj5W76EBAEDdCSxelesv68/733FN1vV25IXB4fzR5x7O/U8dcMogAAArmsDiVdu8rie3/ejrs/3idRmfquTurz2Tv7n3yYyMT9V7aAAAUBcCi9eku6OcW7/3irznxq3pKBfz8J7B/MFnH8rDew5ZzQIAYMURWLxmhUIh33X5+vw/P7Y9F6/vzbHRyfyfrzyZj315twsTAwCwoggsaqa/rzO/css1+Yk3X5KOtlIee/5w/r/PPpyv7nox0xU7DQIA0PoEFjVVLBZy41Ub8//++PZcc+HajE9O53P378kffPbh7Hr+sNMGAQBoaQKLc2JNT0d+8QeuzHt/4Mqs7+vMwWNj+esvfTv/64tPZN/gcL2HBwAA50S53gOgtV194dps27w6X//2/nzxob158sWj+aN/fCTbL16Xt123JRvWdNd7iAAAUDMCi3OuXCrmrVdvyhsv68/Oh1/If3x7fx7eM5hH9gzmukvPy443bMn5q7vqPUwAAHjNBBbLpqezLT9+wyX5vms2518feSH/+eSB/Nd3DuXB7xzKNRetzfdeszmXnL+q3sMEAIBXTWCx7Fb3tOcnv/vSfP+1M6H1zacO5tHnDufR5w7n4vW9+d5rNueaC9emWCzUe6gAAPCKCCzqZm1vR/6vt1yWt123JV97/KV8/dv7s+fgUD7+ld1Z29uR7952fv7b5euzqqu93kMFAIAlEVjUXV9Xe97+xovyA6+/IPc/dSBf3fVSBofG888PPJ97Htybay9al7dcuSGXbViVQsGqFgAAjUtg0TA62kq56XWb8j1XbszufUfy9d0H8vjew3no2UN56NlD6V/VmTdu7c8bL+vPeas66z1cAAA4jcCi4RSLhVy1ZW2u2rI2R4bH843dB/KfTx7IwPGx3PPg3tzz4N5ccv6qvPGy/rzhkvPS3WEaAwDQGPyXKQ1tTU9Hfvj6C/NDb9iSJ188mgeeGcgjzw3m2QPH8+yB4/nsfz6byzf15fUXnZdrLlqb3s62eg8ZAIAVTGDRFIrFQq68YE2uvGBNfnJyOo8+N5hvPT2Qp146mm+/MPPn0/+RXLahL6+/aF2uvWhdVvfYHAMAgOUlsGg6HW2lvGnr+rxp6/oMjU3msecO55HnDuWpF4/l6Zdm/vzDfz6bzeu6c9UFa3LVBWty0fpVKdn2HQCAc0xg0dR6O9vy5m3n583bzs/oxFR2PX84j+wZzO59R7NvcCT7BkfypUf2pau9lG2bV+fKC9Zk2+Y1Wd1tdQsAgNoTWLSMrvby/MrW5HQlz7x0LE+8cCRPvHAkA8fG8tCzg3no2cEkyfq+zmzd2JfLN63O1g196e3y2S0AAF47gUVLaisV5z+z9eNJBo6N5YkXjuTbLxzJM/uP5eCxsRw8Npb/2H0gSbJhTVcu39iXyzb05eLzV1nhAgDgVRFYrAj9fZ25qW9jbnrdxkxXKnl+YHj+81rPHjie/UdGs//IaL72xP4kyZqe9lyyflUuPr83F69flc3rulMqFuv8twAAoNEJLFacUrGYS85flUvOX5Uf3H5BpqYreW5gKE+/dCzf2X88zw8M5cjwRB4cPpQHnz2UZGZF7ML+nlzY35st5/XkgvN6ct6qzhQLNs4AAOAEgcWKVy4Vc9mGmdMDk6RSqWb/0dHsOThzra3nDg7l4LGxPLP/eJ7Zf3z+eZ1tpWxe150t552Irv4+0QUAsJIJLDhFsVjIprXd2bS2O9+9bUOSZHhsMnsODmXvoaHsPTScFw4N59jo5GnR1VEuZsPa7mxa052Na7uycU13Nq7tdgFkAIAVQmDBEvR0tuXqC9fm6gvXzh87NjKRFwaH54Nr76HhHB2ZyHMHh/LcwaGTnt/b2TYfXJvWdmfDmq6s7+tKd4f/CQIAtBL/dQevUl93e/q62/O6LSeia2hsMi8dHslLR0by4uHRvHRkJPsPj2RobDJPvTiZp148dtJr9HSWc35fV9av7sz6vq6s7+vM+tVdOW9Vh001AACakMCCGurtbMvlm1bn8k2r549VqtUcGR7PS7PB9dLhkew/OpqDx8YyPDaV74wdz3cOHD/pdYqFZN2qzqzv60z/qs5ctPF4OopTWdfbmXW9HWkriy8AgEYksOAcKxYKs2HUedIphpVqNcdGJnLg6FgOHhvNwbmvx8ZyZGg8A8fGMnBsbObBj7900mv2dbXlvFWdWbeqI+t6O7JuVWfOm/26qqvNRhsAAHUisKBOioVC1vR0ZE1PR7ZtXn3SfZNTlQwcH8vBo6M5NDSekcnkhYNHMzg0lsNDEzk2Opljo5OnrXwlSalYSF93e9b2tGd1T8fM1+722fea+drVXkpBhAEA1JzAggbUVi7O72SYJP39/RkYGEiSTFeqOToynsHj4zl0fDyDQ2Mzt2e/Do9P5fDQeA4PjSc5PcCSmd0OVy8Irr7utvR1taevq23ms2Vd7entakupKMIAAF4JgQVNplQ8ccrh5ZtOv39iajpHhydyZGQiR4bGZ74OT+TI8Pj81/GpSg4cHc2Bo6Mv+z6FzOyeOB9f3W1ZdVKEzXzf29WWtpLPhAEAJAILWk57uZT1q7uyfnXXGe+vVqsZnZjOkeHxHB2ZyOGh8Rwfncyx0YkcGznxdXhsMkOzf/Zl5Kzv2dFWSm9nOb2dbfN/ehZ+3zV3vJzuDitjAEDrEliwwhQKhXR3lNPdUc7mdT0v+7jpSjVD8+E187mv46dE2PHRiQyPT2V8cjrjk9M5dHx88fdP0tVRPim4ujvK6Zkd08I/PR3ldHWU091eTtkqGQDQBAQWcEalYiGre9qzuqf9rI+rVqsZm5zO0OjcitfU/MrX0Ohkhsdnj83ePzI+Nf/nwNGlj6ejrZTu9tJJQda1IMy6Osrpaiulq72czvaZr13tpbS3leyqCAAsG4EFvCaFQmE2Zsove1riQtOVakbGT4TYwuAaGZ/K8Pjpx0YmTqySHR6eeIXjSzrbSumcDa6u9nI6204EWOf81zMcayuno63oos8AwJIJLGBZlYqFrOpqz6qus6+MLVSpVjM+OZ3hsamMTkxl+KQAmw2yiemMTUxlbGI6oxNTGZ39fnyqktGJ6YxOTOfwqxxzuVhIR3spHeWZEOsol9LRVkpn28zXhX9mjhVPun/h45zqCACtTWABDa+4YJXslZquVGfCa3J6PrpGT4mwmfumTrt/btVsqlLN1NhUhjP1mv8upWJhPrbay8W0l4vpKJfSXp79vq144vaCrx0nHZ+9PXts1eR0qtWqa5sBQAMQWEBLKxUL6elsS09n26t6frVazeR0ZTa2Khmbja65Py/7/dR0xiamMz5VyfjsStrYxPTsKZIzq2+1VMjM9dNOhNrJMdZWmrldLhXTVirOPnbmdrl04nbbqV9POVYuFX2mDQDOQmABnEWhUJiNllJWLf4Rs7OqVquZqlTnY2xiqpKJqZmv45PTmTzl+5n7Txyb/7rgueNTlUxOV2afO/PnXCuXCrPBNhNu5XIxbaXCie9LJ8dbuVSYD7tyqZBy8fTjpWLhjI8vzb5XuThzW9wB0OgEFsAyKRQKaZsNht5XuaJ2Jv39/Tlw4GAmpmcjbPL0KJucC7HpBbdP+ToxVcnU9Nzt6UxOVzM1NXd75vjUdHX2z8wpl8utVCzMR9hceM0FWfmUgGs7w/HS3NdiYf61Tr1dLhZSmr8995xCSrPPK5dmbs88bib6nJ4JwByBBdACisVCOoszG2rkNa60nU2lWp2JsLPG2Yn7pqZn/1Sqs7ers6G28NhcuM1G3BmOzz1+ulLNdGU645Pn7u/4ShUyE36lUwKtPBtupdkIPPX2XLydHG6FlArFFOefOxNwpWLhpGPz38/fV3zZ+0rFQoodozk+OpFSccFrF2YeB0BtCSwAlqy44JTJ5VapzgTWmaJsurIg3OairLIg2mYfMzVdzXSlMvt15vbca05XqrMRt+D++bBb+JyF31dSqWbmvSrLv6L3WhWSk2PupDArvux9p8decT7YioXMh2HxlK+l2fsLhcIZHpMFjznTc3Pa8dLs6mGxmAXvf/pj5l7bSiOwHAQWAE2hWCikOHtqYCOpVKqZrp6ItOm5iFsQbtOnRNpUpTL7uBO3pyonHlupnIi5ubCce42Xu29uHCfdP/ucaqGQyanp0+6rJvPfrwSFQk4Jr9kQK+Rl4uz0qJt/jcKJ24W51ygUUiguuL3g+KLPLZ7yOqeM65U892zjmLs9F6Zzx9qGxzM8Nvmy4xCnsHSFarV6zn+r7ty5Mzt37kyS3HXXXZmYeGUXCm115XI5U1O13VGM1mKOcDbmB4t5uTkyF2BTs6t1C1f1Fn6/2P1zq4DV6pljrzL7mEr15PBb+LiF9y3l8ScdX/jcU19nweN59eZWOwuFE1FamIu/BfedHH8nf3+m22d8TLGQQgonR2AW3HfKexaX9B4nQrEwF7zJyZF66nuc7fmz95/08zjl+NxrFRf8XQoL/y6zj8nc83Pq3yHzjz3T321u/Kc9p1A46b7igucvvO+V8u+a07W3n/manssSWKfat2/fcr9lQ+vv78/AwEC9h0EDM0c4G/ODxZgjM7t4Vqszp5qeGnaVyolTUCsLj1dzUrRVqyeOV+cfl/nj869/ynstfMySn1s55fFzt89w/OWfu/C+E8890ziTwnzEnnrf8v+XIsvh5IA7JcySk8KukJnPlv7aj177qi970oo2b958xuNOEQQAWt78/8ufQrL8HyFseGeL8OopsTUfdsmC46c8JjPhWs3cc0593sLXOuU98jLHqwtf7/QxVXPqGM/8uqc9b8HrnvH5p73u3HNmovX058693ynfL3zeKeM+8fX0MZ358S93+2yPO/F6mbsvCw6cuMFrJLAAAHhZJ8UpLeG0iJuLx5k7T4u9SqpZu3ZdJkeP13nkzUFgAQDACjIXzXkF0by2tzMDY0PnbEytpLG2YgIAAGhiAgsAAKBGBBYAAECNCCwAAIAaEVgAAAA1IrAAAABqRGABAADUiMACAACoEYEFAABQIwILAACgRgQWAABAjQgsAACAGhFYAAAANSKwAAAAakRgAQAA1IjAAgAAqBGBBQAAUCMCCwAAoEYEFgAAQI0ILAAAgBoRWAAAADUisAAAAGpEYAEAANSIwAIAAKgRgQUAAFAjAgsAAKBGBBYAAECNCCwAAIAaEVgAAAA1UqhWq9V6DwIAAKAVWMFqAL/5m79Z7yHQ4MwRzsb8YDHmCIsxR1iMObJ0AgsAAKBGBBYAAECNCKwGsGPHjnoPgQZnjnA25geLMUdYjDnCYsyRpbPJBQAAQI1YwQIAAKgRgQUAAFAj5XoPYKX76Ec/mmeeeSaXXnpp3vve99Z7OCyzJ598Mh/72MdSKBSydevW/OIv/mI+97nP5f7778/69evzK7/yKymXy0s+Ruv6/Oc/n2984xu58847z/h7Y6nHaE333ntv7r333lQqlfzqr/5qPve5z5kjzBsfH88f/uEfZnx8PN3d3fm1X/u1fOITnzBHVrjBwcH8/u//fvbu3ZuPf/zjKZVKr+nfL+bKCVaw6uiZZ57J2NhYPvShD2VqaipPPfVUvYfEMlu/fn1uv/323HnnnTl27Fh27dqVxx57LHfeeWcuuuii3H///Tl69OiSjtG6Jicn8+yzzyY58++NpR6jNQ0ODmbXrl25/fbbc8cdd+TIkSPmCCd58MEHc8UVV+SOO+7I5Zdfnn/4h38wR0hvb28++MEP5oorrkjy2v79Yq6czP/lXUdPPvlktm/fniR5/etfn927d+fyyy+v86hYTmvWrJm/XSqV8vzzz+fqq69Okmzfvj1f/epX09HRsaRjb3nLW5Z9/CyPL33pS/m+7/u+/O3f/u0Zf2+USqUlHfP7pTU9+OCDqVQq+dCHPpQtW7Zk8+bN5ggn2bBhQ5588skkyfDwcLq6uswR0t7envb29vnvX8u/X8yVk1nBqqPh4eF0d3cnSbq7uzMyMlLnEVEve/bsybFjx9LT05Ourq4kM3NieHg4IyMjSzpGa5qamspjjz2Wa6+9NsmZf28s9Rit6ejRo5mamsrtt9+e9vb2jIyMmCOcZNOmTXnyySfzgQ98IM8880yKxaI5wmley79fzJWTCaw6WjgBR0dH5ycmK8vQ0FA+8pGP5H3ve1+6u7szOjqaJBkZGUlPT8+Sj9Ga/u3f/i033XTT/Pdn+r2x1GO0pu7u7vkV7bkQN0dY6N57782b3vSm/OEf/mGuv/76TE9PmyOc5rX8+8VcOZnAqqNt27bl0UcfTZI88sgj2bZtW51HxHKbnp7On/zJn+Tnfu7nsmbNmmzdujW7du1KMjMnrrjiiiUfozXt27cvX/ziF/O7v/u72bt3b44fP37a740z/S7x+2XluPLKK7Nnz54kmf+snjnCQtVqNb29vUmSvr6+JOYIp1vqHDBXFiew6uiyyy5LW1tbbr/99hSLxRV9rupK9fWvfz1PPfVU/uZv/iZ33HFH9u/fn9e97nX54Ac/mGeffTY33HBDVq9evaRjtKZbb701v/Vbv5Xf+q3fypYtW/Kud73rtN8bZ/pd4vfLynHJJZekvb09d9xxR55++um8853vNEc4yU033ZSvf/3rueOOO/LVr341b3/7280RMjU1lTvvvDN79uzJ7/7u72Z6evpVzwtz5WSFarVarfcgAAAAWoEVLAAAgBoRWAAAADUisAAAAGpEYAEAANSIwAIAAKgRgQXAsjhw4EDe/e5356677soDDzyQu+++OwcOHKj5++zduzd33313HnvssfljH/7wh/Pud787Tz/9dM3fDwAWKtd7AACsDH19fbntttuybt263HffffnCF76Qa665Jueff/4rep3p6emUSqWXvX/v3r351Kc+lSS55pprkiRve9vbct1112XDhg2v/i8AAEvgOlgALIsDBw7k/e9/fzo6OjI+Pn7SfXfffXd2796dj33sY3nuueeybt26vOtd78pNN900/7xt27alo6Mjzz33XP7gD/4gv/M7v5MXX3wxSXLppZfml37pl9LR0ZH3v//9J732b//2b+crX/lK7r333vze7/1etm7dmp07d+Zzn/tcDh8+nC1btuQXfuEXctVVV+UrX/lK/uzP/izf8z3fkxdeeCEDAwN517velXe84x3Zt29f/vRP/zR79uxJe3t7LrzwwnzoQx9atp8fAM3BKYIALKurr746b3jDG5IkP/VTP5XbbrstQ0NDueuuuzIyMpKf/MmfzPr16/Mnf/InefbZZ+eft3v37lx66aV5z3vek0KhkBtuuCHvfe978xM/8RPZs2dPPvrRj6avry/veMc7kiRvfvObc9ttt2XLli0nvf+jjz6av/zLv0xfX19+/ud/PgMDA/n93//9HD9+fP4xjz32WH7wB38wSfKJT3wiU1NT+cIXvpCnn346t956a376p386/f395/gnBUAzcoogAMuqUChk48aNeeihh3LttdfmmmuuyQMPPJChoaEMDQ3lk5/85PxjH3300dxwww1JZlapbr311iTJ4OBgHnrooezevTtzJ2I899xz6ezszFVXXZV/+qd/yoUXXpgbb7zxtPd/4IEHkiTvfve7s3379gwMDOTv//7v8+STT84/5vu///tzyy235Fvf+lYeeuihHDlyJJs2bUq1Ws1//dd/ZevWrfMhBwALCSwAll2hUDjj8Ztvvjk333zz/PcLP5+1du3a+dv//M//nG9/+9v5kR/5kVx//fX58z//84yOjtZsLL29vUky/1mvSqWSW265JRdccEF27dqVb37zm/nMZz6TP/qjP8rmzZtf1fsC0JqcIgjAsuvp6UmS/Md//EceeOCBbNu2Lb29vXnooYeyb9++PP/88/nsZz+bwcHBs77O8PBwdu3alUOHDs0fm4ujJ554Il/72tcyMTFx0nPe+MY3Jkn+7u/+Ll/84hfzpS99KT09PbniiivO+l733HNPdu/enY0bN2bDhg2pVqs5cuTIK/2rA9DiBBYAy+6tb31rLrjggtxzzz3567/+6/T29uY3f/M3s3HjxnziE5/IZz7zmbS3t2f9+vVnfP7b3/72bN26Nffdd18GBwdz4YUXzt931VVX5fWvf30ef/zx/PEf//FJn61KkmuvvTa//Mu/nKNHj+bjH/94zjvvvPzGb/xGVq1addYxt7W15Stf+Ur+4i/+Io8//nh++Id/OFddddVr/2EA0FLsIggAAFAjVrAAAABqRGABAADUiMACAACoEYEFAABQIwILAACgRgQWAABAjQgsAACAGvn/AfMp6izwDZjFAAAAAElFTkSuQmCC",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plot_1(cost_history, m, q)"
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA1gAAAGoCAYAAABbkkSYAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAAA0YElEQVR4nO3daXBe133n+d+592IlwBXcwA3cSZAE90WkdlISJfeM23ZlkrF7lIx7UtOemu7Jm1RSmcpWlRdKVVyZSnd1eronTlV3x84kbU+nY2uFKImkuC8gQHDfF3ADSIIAQSz33DMvLkVKNCVxuXjOg+f5fqpYoo8gPX8fySS+fu5zjnHOOQEAAAAAnlrgewAAAAAAKBQEFgAAAABkhMACAAAAgIwQWAAAAACQEQILAAAAADJCYAEAAABARiKfL97W1ubz5fNGTU2N2tvbfY9RVNhzP9j33GPP/WDf/WDfc48994N99+PBfa+trX3o1/EOFgAAAABkhMACAAAAgIwQWAAAAACQEQILAAAAADJCYAEAAABARggsAAAAAMgIgQUAAAAAGSGwAAAAACAjBBYAAAAAZITAAgAAAICMEFgAAAAAkBECCwAAAAAyQmABAAAAQEYILAAAAADICIEFAAAAABkhsAAAAAAgIwQWAAAAAGSEwAIAAACAjBBYAAAAAJARAgsAAAAAMkJgAQAAAEBGCCwAAAAAyAiBBQAAAAAZIbAAAAAAICMEFgAAAABkhMACAAAAgIwQWAAAAACQEQILAAAAADJCYAEAAABARggsAAAAAMgIgQUAAAAAGSGwAAAAACAjBBYAAAAAZITAAgAAAICMEFgAAAAAkBECCwAAAAAyQmABAAAAQEYILAAAAADICIEFAAAAABkhsAAAAAAgIwQWAAAAAGSEwAIAAACAjBBYAAAAAJARAgsAAAAAMkJgAQAAAEBGCCwAAAAAyAiBBQAAAAAZIbAAAAAAICMEFgAAAABkhMACAAAAgIwY55zL1Ys1NjaqsbFRkvTWW2+pv78/Vy+d16IoUhzHvscoKuy5H+x77rHnfrDvfrDvucee+8G++/HgvpeWlj7063IaWA9qa2vz9dJ5paamRu3t7b7HKCrsuR/se+6x536w736w77nHnvvBvvvx4L7X1tY+9OuiXA0EAAAAPC3nEimOpbhfigfk4oH055+9Z2DM3a80UhTJlJRJJaVSSZlMEHqbG8WDwAIAAIB3Lkmkni657htyXXd/3L4l3emW670t3bmd/rG3R9ITPoAVRlJ5pUzlcJmKKqlyuExltczw0TIjxsiMqJHKh8ncizTg8RFYAAAAyBk30Cd346rczavpHz/70X1TSuyj/U2ikns/TFSa/twE99/Fkkt/bmO5gT5poF8a6JNsLN2+JXf71pcnWkmZzMixMmNqFdTUytTUyoyeIFPy8M/bAA8isAAAADAoXF+P3LWLSq5dlLt2QUn7Ranrxpf/BRVVMtWjZKpGylSPkoaNkKmokqkYJpV/9sfKJ3rUzzknxQNS7225ni65nq70HbPbnXK3rsvd6pDrbJf6e+WuXUjn/ewvNkZmzEQFE+pkJk5XMHF6+g4Y8BAEFgAAAJ6ac4nc9Styl84ouXxGybXz0q3rv/yFQSgzskZm5HiZUePu/6gePajvEhlj7n4WqzSNt4f+d3BpgN24oqT9klxHm1x7W/oOW3ubbHubdHBb+vcbNU7BlLkKps6TmTBNJuTbaqT4NwEAAACPzSVW/RdPKj7cJHfptJLLZ6T+3i9+URilj9jVTFIwdrLM2Enp43d5etiEMSZ9F62iSkHtzHvrbqBf7up5JZdPK7l0Ru7KWbkbV2VvXJVt3iKVlCmYPFvBjIUKps1PD9ZA0SKwAAAA8EjcretKLhxTcv64krYTutbf98UvqBqpYEJd+gjd+Ckyo8bnbUw9DlNSKjNppoJJaXQ5a+WunFVy7oiSc0fTd7xOH1Ry+qAUlSiYNl/BzMUKpsyRiUo8T49cI7AAAADwUC4eUHLhuJILx+XOH5O71fGFPx+NHq9k/DQFE6YrmFj3pY/eFRoThjK1MxTUzpDWvCHXdV3J2cOyJ5rT8DrZrORks1RWqXDOUgXzVysYNc732MgRAgsAAAD3uDu3lZw7rOTMISUXjqcHQ3ymtDx9FO7uj7HTZ3PhrSRTPVrhwnUKF66T67ohe7JZyYkmuY5Lsi2fyrZ8KjOhTuH81QpmLuLzWgWOf7oAAABFznV2yJ49pOR0q9yVs5877lwyYycrmDovfdxt7KSCeORvMJnqUYqWvCAteUHJtQuyh3elsXX5jOLLZ6Sd7yhctFbh/NUyZRW+x8UgILAAAACKkOu6KXvygJKTzXLtF+//iSCUmTRTYV29grr5MsNG+BtyiAvGTlYwdrLcmm8oOdEk27pN7voV2Z3vyu7bpHDeKoUNz8lUsceFhMACAAAoEq6nS8mp5nufFbqnpCx9l6quXsGUuTJl5f6GLECmtExh/WoF81fJnT+muHmL3MUTsi1bZQ/tUDh/lcKlL8lUVvseFRkgsAAAAAqY6+9VcqpF9niT3KVT9x//i0oUTJ2vYFZDGlWcdjfojDEyU+eqdOpcJe0XZfd/kgbvwW2yR3YrrH9G4ZLnucR4iCOwAAAACoxzidzFU7LH9qZHh392UEUQKpg6R8GsxdzX5FlQM0nBK99V0vGS7J4PlJw5JNu8WfbIToVLX1a4aB2HYQxR/FMDAAAoEElnu5Kje2WP75O6O++tm4nTFc5ZpmD6Qg5WyDPBmIkKXntTybULine/L3f+mOzOd2QP71S05g0FdQvSC5AxZBBYAAAAQ5gb6E8fMzuyW+7y5z5XVT1K4ZxlCucskxk+xt+AeCTB2MkqfeP7Ss4fU7z953I3rip+/z/L1M5Q9Ow3FYwa73tEPCICCwAAYAhKblxRcmin7LF9Un9vuhiVKpixUOHc5TITp8uYwO+QeGzBlDkqmfR/KDm8S/GeD+TaTmngv/yFwiUvpAdh8Fm5vEdgAQAADBHOxkpOHZQ9tEPu8pl762bs5PSUupkNfK6qAJggVLjgGQWzFive+Z6Swztl921ScrJZ0XPfkmpqfI+Ir0BgAQAA5Lmks13JoV2yx/ZIvT3pYkmpgllLFdavUlAzye+AGBSmrFIlz39Lyeylirf8TO7GVQ38/D/oxoWjcsvWE9N5isACAADIQ84lcuePKz74qdz5Y/fWzZiJCuvXKJi1RKaUb7CLQTCxTiXf+VeyBz6R3btJPU2bpVMHVfLS/6BgQp3v8fAAAgsAACCPuIE+JUf3ybZuk7t5LV0MIwWzFiusXyMzdjKnyhUhE0aKlq1XULdA+uSnGrh6XgP/7f9WuPgFhSs2cKR7HuGfBAAAQB5wtzpkW7fLHtlz/9CKYSMULnhG4fyVMuXD/A6IvBCMnqAx3/8/deXdv03f0Wr6WMn5oyp55XsyI/hsVj4gsAAAADxxzsm1nZI9+KmSM4clOUmSmTBN4cJ1CqYvkAlCv0Mi75gwUrR6o4Jp8zXw0f8r13FJ/T/914pe+I7CmQ2+xyt6BBYAAECOucSmpwEe+ESuvS1dDEIFMxsULlqnYOxkvwNiSAgmTFPpt/+V4s0/VXKqRXHjj5VcOq3omW/wyKBH7DwAAECOuIF+2SO7ZVu2Sl030sWKKoX1axTWr5aprPY7IIYcU1auaMN3lbRuU7z9bSWt2zVw9bxKXv1nMlUjfY9XlAgsAACAQebudMse3Cbbul3quyNJMiNqFDY8p2DOMi6PxVMxxihcuE5m3FQNNP5Y7toF9f/s36jk1f9JwYRpvscrOgQWAADAIEk622UPbFFybK9kY0mSGT9V4eLnFUyrlwkCzxOikATjpqj02/+7Bj74sVzbSQ38479X9Py3FM5d4Xu0okJgAQAAZCy5ej493e30IX12cEUwbb7CJS9wbxEGlSkfppI3vq94+8+VtG5X/PF/kbt+WeHqNwj6HCGwAAAAMuCck7t0WvG+TXIXT6SLQahgzlKFDc8rGDXO74AoGiYMVfLsN2VHT1D86T/INm+Vu3VD0fpf43HUHCCwAAAAnoJzTu78McX7P5K7fCZdLClTuGBN+rmYYcO9zofiFdavlhlZo4H3/pOSM60a+MVfqWTjmzJllb5HK2gEFgAAwBNwLlFy5rDsvk1y7RfTxbIKhYvWKVy4lm9ikReC2pkq+ea/0MDbP5K7fEYD//DvVPLG9zlhcBARWAAAAI/BJYmSU82y+z6Su3ElXayoUtjwnML6NTKlZX4HBB4QjJ6g0n/6v6WRdeOq+v/rv1XJN/4XHlsdJAQWAADAI3DWKjm+T7bpE7nO9nRx2AhFS55XMG8Vn21BXjNVI9N3st79j+k7Wf/471XyT35TwejxvkcrOAQWAADAV/gsrOJ9m+5fDjx8jKIlL6R3WIV8O4WhwZRVquSN72vgvf8od/HE3cj65wrG1PoeraDwKwIAAMBDuMQqObZf8f5N0q3rkiQzcqzCZS8rmNkgE4SeJwQenykpVcnGX9fA+/9J7vwxDfzj/6OSb/xzBWMn+R6tYBBYAAAAn+MSq+R4U/qO1a0OSZ+F1fq7YcVdQhjaTFSiktfeVPzB3yg5ezg9XfC//195XDAjBBYAAIDuhtWJA+mpgHc/Y2VG1KRhNWsxYYWCYsJI0SvfU/z+f1Zy7ogGfvFXKv3mv5AZPtr3aEMegQUAAIqaSxIlJw/I7v3w/uEVw8coWv6ygllLeBQQBeuzyBp4+0dyl06r/7PIqqz2PdqQRmABAICidO+49b0fyt28li5Wj1a07GUFc5YSVigKJipJP5P1j/9Brv1i+rjgN3/AdQNPgcACAABFxTmn5Eyr7O4P7t9jVT0qDavZy2RCwgrFxZSWq+SN/1kD//Dv5K5fVvzhTxS99iaPxT4hAgsAABQF55zcxROKd70nd+1Culg18u47Vhy3juJmKqpU8vpvqP//+7dKzh2R3fm2omf+ie+xhiR+JQEAAAUvuXxW8e735NpOpQsVVWlYzV9FWAF3mRE1Knn1n2ngF38l27xVZtR4hfNW+h5ryOFXFAAAULCSjjbZXe8rOXckXSirULjkBYUL1sqUlPodDshDQe0MRc/9U8Wf/FTx1n+QqZmkoIaLiB8HgQUAAApOcvOa7J5GJScPpAtRqcKGZxU2PCdTVuF3OCDPhfNWKrl6XsnhXYobf6ySb/9LDr14DAQWAAAoGK77puK9Hyo5uldyiRSEChesUbj0JZmKKt/jAUNGtPa/08CVc9p/vleb/q+fq6d0hKqGlerVZ2dp6Xze0foqBBYAABjy3J1u3fygUf17PpISK5lAwbyVipatl6ke6Xs8YMgxUYla6jbqxwea1ZUEkrokSW1Xu6Vvi8j6CgQWAAAYslx/r+yBzbLNW9Uf90uSgpmLFa7YoGDkWM/TAUNbY9NVdSUlX1jrut2n97eeILC+AoEFAACGHGdj2UM7ZPd9JPXeliSVz2qQXfwiH8gHMtJ9u//h6z0PX0eKwAIAAEOGc4mSE82Kd78vdV2XJJkJdYpWv64xC5ervb3d84RA4aga9vCTNqsqOYHzqxBYAABgSEjOH1O88x25jkuSJDNqnMJVGxVMmy9jjOfpgMLz6rOz1Ha1W123++6tVQ8r06vPzvI4Vf4jsAAAQF5Lrl1QvPNduYsn0oVhIxSteEXBnGUyQeB3OKCALZ1fK31ben/rCXX39KuqklMEHwWBBQAA8pLr7FC8+/37d1mVlitc+pLChWtlopKv/osBZGLp/FqC6jERWAAAIK+4O92y+zbJHtqZHrkeRgoXrlW45EWZ8krf4wHAVyKwAABAXnADfbLNW2QPbJYG+iUZBXOXK1rxikzVSN/jAcAjIbAAAIBXzlolR3Yr3tso3emWJAVT5ylcvVHB6AmepwOAx0NgAQAAL5xzSk61yO56T+5WhyTJjJuqaPVGBbUzPE8HAE+GwAIAADmXtJ1Kj1y/el6SZEbUpEeuT1/AkesAhjQCCwAA5Exy85rszneUnDmULlRWK1q+QcG8FTJB6Hc4AMgAgQUAAAadu3Nbdt+Hsod2SEkiRaUKl7ygsOE5mZJS3+MBQGYILAAAMGicjWUPbpPdt0nq75WMUTBvlaIVG2SGDfc9HgBkjsACAACZc84pOdmseNe7UtcNSZKZPEfRmjcUjOFkQACFi8ACAACZSi6fVbz9F3JXz0mSzOjxitZ8Q8GUOZ4nA4DBR2ABAIBMuM4OxbveVXKqJV2oqFK08lUFc1fIBIHf4QAgRwgsAADwVFxfj+y+TbIHt0uJlaIShQ3PKVz8gkxpme/xACCnCCwAAPBEnI1lD+2Q3btJ6uuRZBTMWaZo5WsyVSN8jwcAXhBYAADgsTjnlJxpld3xjtytDkmSqZ2h6JlvKKiZ5Hk6APCLwAIAAI8suXo+PcDi8hlJkhk5VuGaNxRMnSdjjN/hACAPGOecy9WLNTY2qrGxUZL01ltvqb+/P1cvndeiKFIcx77HKCrsuR/se+6x534U4r7HnR269dHPdKd1pyQpqKxS9XPf1LClz8mE+fH/1xbivuc79twP9t2PB/e9tPThl6TnNLAe1NbW5uul80pNTY3a29t9j1FU2HM/2PfcY8/9KKR9d329sk0fy7ZslWwshZHCResULnlJpqzc93hfUEj7PlSw536w7348uO+1tbUP/br8+L+cAABAXnGJVXJ4t+I9H0i9tyVJwazFila9JlM92vN0AJC/CCwAAHCPc07JuSOyO96Wu3lNkmQm1KUHWIyb4nk6AMh/BBYAAJAkJe1t6QEWbSclSWb4GIWrX1cwfQEHWADAIyKwAAAocu52p+Jd7ys5tk+Sk8oqFC5br3DBmrw5wAIAhgp+1QQAoEi5gT7Zpk9km7dI8YAUhAoXPKNw2csy5ZW+xwOAIYnAAgCgyLgkUXJ0T3qARU+XJCmYsUjRqo0yI8Z4ng4AhjYCCwCAIpKcP6Z4x9ty1y9Lksy4KekBFhPq/A4GAAWCwAIAoAgk1y+nYXX+WLpQPUrRqo0KZjZwgAUAZIjAAgCggLmeLsW7P1BydLfknFRapnDpywoXrpWJSnyPBwAFh8ACAKAAuYF+2ZYtsk2fSAP9kgkULFijaPkGmYphvscDgIJFYAEAUECcS5Qc269493vS7VuSpGDafIVr3lAwcqzn6QCg8BFYAAAUiOTiScU7fiHX3iZJMjWTFD3zhoLamZ4nA4DiQWABADDEJTeuyu58R8nZw+nCsBGKVr2mYPYSGRP4HQ4AigyBBQDAEOXudCve+6GSQzsll0glpQqXvKhw0bMyJaW+xwOAokRgAQAwxLh4QPbgp7L7P5L6+yRjFMxfpWjFKzKV1b7HA4CiRmABADBEOOeUnDygeOe7UvdNSVIwZW56gMXo8X6HAwBIIrAAABgSkktn0gMsrp6XJJnRExQ98w0Fk2d7ngwA8HkEFgAAecx1tive+Y6S063pQmW1opWvKpizXCbgAAsAyDcEFgAAecj19sju+1C2dYeUWCkqUdjwvMIlz8uUlPkeDwDwJQgsAADyiLOxbOt22X2bpL47koyCucsVrXxVZtgI3+MBAL4GgQUAQB5wzik5fTA9wOJWhyTJTJqlaM0bCmpqPU8HAHhUBBYAAJ4lV86lB1hcPitJMiPHpScDTp0rY4zn6QAAj4PAAgDAE9d1XfHO95ScPJAulA9TtPIVBfNWygSh3+EAAE+EwAIAIMdcX6/s/o9kD34q2VgKI4WLnlW49EWZ0nLf4wEAngKBBQBAjjhrlRzepXhvo9R7W5IUzFqiaNVGmeqRfocDAGSCwAIAYJA555ScPSy78x25m9ckSWZCXXpR8LgpnqcDAGSJwAIAYBAl1y4o3vG2XNspSZIZUaNw9esK6uo5wAIAChCBBQDAIHBdNxXvfk/J8f3pQlmlwuXrFdavlgn57RcAChW/wgMAkCHX36vOj36m/p3vpwdYBKHCResULn1JpqzC93gAgEFGYAEAkAFnrZIjuxTvaVT/ZwdYzFysaPVrMtWjPU8HAMgVAgsAgKfwsAMsSqfMllv+ioLxUz1PBwDINQILAIAn9EsHWAwfo3D166pZ+YI6Ojo8TwcA8IHAAgDgMbnum4p3ffkBFpwOCADFi8ACAOARuf5e2f0fy7Zs5QALAMBDEVgAAHwNl1glh3cr3vOB9PkDLFa9JjOcAywAAPcRWAAAfImHHWBhJkxTtOYbHGABAHgoAgsAgIdIrl1UvOMXv3SARTB9AZ+xAgB8KQILAIDPefgBFi8rrF8jE/LbJgDgq/E7BQAAunuARdMnss1b7h9gsXCdwmUvypRV+h4PADBEEFgAgKLmEqvkyG7FexqlO92SpGBmw90DLMZ4ng4AMNQQWACAouScU3LuiOyOtznAAgCQGQILAFB0kvaLirffP8BCw8coWr1RwfSFHGABAHgqBBYAoGi47puKd7+v5Nh+SY4DLAAAmeN3EwBAwXN9vbJNH8u2bP3cARZrFS57iQMsAACZIrAAAAXL2Vj20E7ZfR9KvT2SpGBGg6LVHGABABgcBBYAoOA455ScalG8613p1nVJkpk4XdHq1znAAgAwqAgsAEBBSdpOKd7xtty1C5IkM3KcwtUbFUybzwEWAIBBR2ABAApCcv2K7M53lJw7ki5UVita8YqCuctlgtDvcACAokFgAQCGNHf7luI9Hyg5ukdyTiopVbj4BYUNz8mUlPoeDwBQZAgsAMCQ5Pp7ZQ9slm3eIsUDkgkU1K9WtHy9TGW17/EAAEWKwAIADCnOWiWHdyne2yj13pYkBdMXKFy1UcHIsZ6nAwAUOwILADAkOOeUnD4ou+s9uc52SZIZP03RmjcUTJjmeToAAFIEFgAg7yWXz6QnA145J0kyI2oUrn5dQV09JwMCAPIKgQUAyFvJzWuyO99VcqY1XaioUrR8g4J5K2VCTgYEAOQfAgsAkHdcT5fivR8qObxLcokUlShseF7h4udlSst8jwcAwJcisAAAecMN9Mk2b5Ft2izF/ZIxCuavUrR8g8yw4b7HAwDgaxFYAADvXGKVHNmTngzY0yVJCqbNTz9nNWqc5+kAAHh0BBYAwJt7JwPufl/u5jVJkhk3RdHq1xXUzvA8HQAAj4/AAgB4kbSdVLzzXbmr5yVJZvgYhateUzBjEScDAgCGLAILAJBTSUeb7M73lJw/mi5wMiAAoIAQWACAnHC3rive84GS402SnFRSpnDJ8woXPStTwsmAAIDCQGABAAaVu9Mtu2+T7KGdUmKlIFS4YI3CpS/JVFT5Hg8AgEwRWACAQZEeub5V9sBmaaBPklEwe6mila/IVI/2PR4AAIOCwAIAZMrZWMnh3Yr3fSjd6ZYkBVPnKly1UcGYiZ6nAwBgcBFYAIBMOJcoOdmiePf70q0OSRy5DgAoPgQWAOCpJReOp0eut1+UJJmRY9Mj1+sWcOQ6AKCoEFgAgCeWXLuQhtXFE+lC5XBFKzYomLtcJuDIdQBA8THOOZerF2tsbFRjY6Mk6a233lJ/f3+uXjqvRVGkOI59j1FU2HM/2PfcG6w9j69f0a1P/qvuHNotSTJlFape+4aGrXxZAUeu8++6J+x77rHnfrDvfjy476WlpQ/9ukcOrObmZm3btk0bN25UXV2dGhsbtWHDhqcasq2t7an++kJRU1Oj9vZ232MUFfbcD/Y997Lec9fTpXjvh0qO7JKSRAojhQvXKlzyokx5ZWavM9Tx77of7Hvused+sO9+PLjvtbW1D/26R35EcNOmTfrN3/xN/fSnP1V3d7fOnDnz1EMCAIYG198re2CzbPNWKe6XjFEwd4WiFRtkqkb6Hg8AgLzxyIFVUVGhYcOG6c0339Tf/M3f6OTJk4M5FwAgD7h4QLZ1u2zTx1JvjyQpqKtPD7AYNd7vcAAA5KFHDqxly5bd+/n3vvc9vfPOO4MyEADAP2etkqN70rusbt+SJJkJdYpWb1Qwoc7vcAAA5LGvDay//uu/1m/8xm9o5cqVX1h//fXXB20oAIAfn91lZfd8INeZPmduxkxMLwmeMocj1wEA+BrB131BRUWF/vRP/1R9fX2SpKamJv3+7//+oA8GAMgd55zsuSMa+Om/VvzhT+Q622VG1Cha/z+q5Dv/UuHUucQVAACP4Gvfwfq1X/s1bd26VX/0R3+kKIpUXl6u7373u7mYDQCQA8mlM4p3vSt3+Uy6MGy4ouUbFMxZLhNylxUAAI/jawOrpaVFH374ocrKynTjxg394Ac/+NIjCQEAQ0fS3ia76z0l54+mC+WVCpe+pLB+jUxU4nc4AACGqK8NrJ/97Gf61V/9Vc2bN0/nzp3Tn//5n+vXf/3XtXDhwlzMBwDIWHLzmuyeD5ScbE4XSkoVNjynsOE5mdJyv8MBADDEfW1g/eEf/uG9n0+dOlW/93u/px/+8If6kz/5k0EdDACQLdfdqXhvo5KjeyV395Lg+jUKl74oU1HlezwAAArCIx/T/plRo0bpD/7gDwZjFgDAIHB3bss2fSTbukOysWQCBfNWKlq+nkuCAQDI2GMHliSVlpZmPQcAIGOuv0+3Nv839e94TxpIT4INZjQoXPmKgpFjPU8HAEBheqLAAgDkLxcPyB7aIbv/Y/X33pYkmSlzFK18TcHYSZ6nAwCgsBFYAFAgnLVKju1VvPdD6XanJKl08ky5pesV1M7wPB0AAMWBwAKAIc4liZITBxTvbZRudUiSzOgJCldtVM2ydero6PA8IQAAxYPAAoAhyrlEyamDsnsa5W5elSSZETUKV2xQMLNBxgQyxnieEgCA4kJgAcAQ45xTcu6I7O735ToupYvVoxQtX69g9lKZIPQ7IAAARYzAAoAhwjknd/GE4t3vy109ny5WDle0/GUFc1fIhPySDgCAb/xuDABDQHLpdBpWl06nCxVVCpe8qLB+tUxU4nc4AABwD4EFAHksuXpe8e4P5C4cSxfKKhQufkHhwmdkSsr8DgcAAH4JgQUAeSjpuCS75wMlZw6lCyVlChueVbjoOZmycr/DAQCAL0VgAUAeSW5cld3bqORkc7oQlShcuFbh4udlyof5HQ4AAHwtAgsA8oC71aF474dKju+XnJOCUGH9GoVLX5SprPY9HgAAeEQEFgB45Lo7Fe/bpOTobilJpCBQMG+VomUvyVSN9D0eAAB4TAQWAHjgerpk938se3inZGPJGAVzlilavl5m+Bjf4wEAgCdEYAFADrne27IHNsse3CbFA5KkYEaDwhUbFIwa53k6AADwtAgsAMgB19cj27xVtuVTaaBPkhRMm69w5SsKxtR6ng4AAGSFwAKAQeT6emVbtsq2bJX6eyVJZvJsRStfVTBuiufpAABA1ggsABgErr9XtuVT2eYt98OqdqaiFa8omFjndzgAADBoCCwAyJDr75M9uC0Nq74eSZKpnaFo+QYFtTM8TwcAAAYbgQUAGXADfbKt22UPbJZ674bVhLr0HatJMz1PBwAAcoXAAoCn4Ab6ZQ/tkG36ROq9LUky46cpWvGKzKSZMsZ4nhAAAOQSgQUAT8AN9Mse3pmG1Z1uSZIZN1XRig0yk2cTVgAAFCkCCwAeg4sH7odVT5ckyYydrHDFKwqmzCGsAAAocgQWADwCFw8oObJL8f6P74dVzaQ0rKbOJawAAIAkAgsAvpKzsZIjuxXv/0i6fUuSZGpqFS7foGDafMIKAAB8AYEFAA/hbKzk6J40rLo7JUlm9IT0Hau6esIKAAA8FIEFAJ/j4oG7YfWxdPuzsBqfvmM1fYGMCfwOCAAA8hqBBQD63Gesmj65/yjg6PEKl61XMGMhYQUAAB4JgQWgqD30VMDRExQuX887VgAA4LERWACK0kPvsRozMQ2runrCCgAAPBECC0BRcQP9sq3bZZu33A+rmklpWHEqIAAAeEoEFoCi4Ab60rA6sEXqvS3p7gXByzdwjxUAAMgMgQWgoLn+XtmD22Vbtki9PZIkM25KGlZT5hBWAAAgUwQWgILk+nplD34q27JV6rsjSTLjpylavl5m8mzCCgAADAoCC0BBcX13ZFvuhlV/ryTJTKhTtHyDzKSZhBUAABhUBBaAguB6e2Rbtsoe/FTq75MkmYnT07CqnUFYAQCAnCCwAAxprve2bPNW2YPbpIG7YVU7U9Hy9QpqZ3ieDgAAFBsCC8CQ5Hq6ZA9skT20Q4r7JUlm0ixFyzcomFjndzgAAFC0CCwAQ4rruqn4wCdKjuyWbCxJMlPmKFq2XsGEaZ6nAwAAxY7AAjAkuM4OxU0fKzm2T0qsJCmoW6Bw2UsKxk72PB0AAECKwAKQ15IbV2T3faTk5AHJOckYBbMWK1z6koLRE3yPBwAA8AUEFoC8lLRfTMPq9MF0IQgUzFmucOmLCkbUeJ0NAADgyxBYAPJKcvms7P5NSs4dTRfCSMHcFYqWvCBTPcrvcAAAAF+DwALgnXNOru2U4n2b5NpOpotRicL61QobnpcZNtzvgAAAAI+IwALgjXNOyfmjsvs2yV05ly6WlilcsFbhomdlKob5HRAAAOAxEVgAcs65RMnpQ7L7N8m1t6WL5ZUKF61TuGCtTFmF3wEBAACeEIEFIGdcYmWP75fd/5HcjavpYkWVwsXPK6xfLVNS5ndAAACAp0RgARh0zsZKju/XlebNsjeupYtVIxQtflHBvBUyUYnfAQEAADJCYAEYNC4eUHJkj+IDH0vdneni8DGKlr6oYPZSmZBfggAAQGHhuxsAmXN9vbKHdsi2bJXudEuSzKhxGvn8N3V7XJ1MEHqeEAAAYHAQWAAy43q6ZFs+lT20XervkySZmkkKl76kYHq9KseOU097u+cpAQAABg+BBeCpua7rips2Kzm6R7KxJMnUzlC05EWZybNljPE8IQAAQG4QWACeWHL9smzTJ0pOHJBcIkkK6uoVLnlRwfipnqcDAADIPQILwGNLLp+VbfpYydnD6YIJFMxemobV6PF+hwMAAPCIwALwSJxzcheOK97/kdyl0+liGCmYt1LR4udkqkf7HRAAACAPEFgAvpJLEiWnD8o2fSzX3pYulpYrXPCMwkXrZCqq/A4IAACQRwgsAA/lbKzk2D7ZA5vlOu+e/FdRpbDhWYXz18iUlfsdEAAAIA8Z55zL1Ys1NjaqsbFRkvTWW2+pv78/Vy+d16IoUhzHvscoKuz5l0v6e3V7/2Z173hfSfdNSVI4skbVazaqcvE6majkif/e7Hvused+sO9+sO+5x577wb778eC+l5aWPvTrchpYD2pra/P10nmlpqZG7dwNlFPs+S9zvbdlW7bJtm6T+u5IkszoCenBFTMXZXI5MPuee+y5H+y7H+x77rHnfrDvfjy477W1tQ/9Oh4RBIqc674p27xF9vAuKR6QJJnx0xQufVHB1HncYQUAAPAYCCygSCU3r6VHrR9vkhIrSQqmzE3DauJ0r7MBAAAMVQQWUGSSaxdk93+s5HSrJCcZo2BmQ/ooYM3D3+oGAADAoyGwgCJw7w6rA5vlLp5IF4NQwdzlihY/LzOixu+AAAAABYLAAgqYS6ySky2yBz6R67iULpaUKpy/RmHDszLDhvsdEAAAoMAQWEABcgP9So7uVnxgi3T3qHVVVClc9KzC+tUyZRVe5wMAAChUBBZQQNydbtmD22Vbt0t9PZIkM6JG4eLnFcxe+lR3WAEAAODrEVhAAXCdHYqbtyg5ukey6QV4ZtxUhUteUFA3X8YEnicEAAAoDgQWMIQl1y7INm1WcrpFuntneDB1nsIlL8pMmMYdVgAAADlGYAFDzL0TAZs+kWs7mS4GoYLZS9JHAUeP9zsgAABAESOwgCHCWavkVLNs0ydy1y+niyVlCuevVrhonUzVCL8DAgAAgMAC8p0b6JM9slu2eev9EwErqxUuWqdwPicCAgAA5BMCC8hTrqdLtvWzEwHvSJLMyLH3TwQM+Z8vAABAvuE7NCDPJDeuyDZvUXJsv5RYSZIZf/dEwGmcCAgAAJDPCCwgDzjn5C6dkj2wRcm5I3dXjYK6eoUNzyuYWOdzPAAAADwiAgvwyFmr5HSL7IEtcu0X08UwUjB3ucJFzyoYOdbvgAAAAHgsBBbggevvkz2yS7bl0/sHV5QPU7jwGYX1a2QqqrzOBwAAgCdDYAE55Lo7ZQ9+Knt4l9TfK0kyI2oUNjynYM4ymajE84QAAAB4GgQWkANJR1v6+aqTB6QkkSSZidPTsJo2j4MrAAAACgSBBQwS55zcheOKm7fIXTieLhqjYEaDwsXPKRg3xe+AAAAAyByBBWTM2VjJiQOyzVvkrl9OF6NShfNWKFz0rMzw0X4HBAAAwKAhsICMuL47sod3yrZsk3pupYuV1QoXrlNYv0qmrNLvgAAAABh0BBbwlNytDtmWT2WP7pEG+iVJZtT49DHAWUtkQv5nBgAAUCz4zg94As45uctnZZu3KDlzSJKTJJlJsxQ1PCczZY6MMX6HBAAAQM4RWMBjuHcxcPNWuWsX0sUgVDBrcXoxcE2t3wEBAADgFYEFPALX1yN7eLfswW3S7c50sbxSYf2a9GLgYcP9DggAAIC8QGABX8F1titu+VTJ0b1SfPfzVSPHpu9WzV4qU1LqeUIAAADkEwILeIBzTu7SadmWrUrOHNbnP18VNjynYMpsLgYGAADAQxFYwF3OxkpOtsi2bJVrv5guBqGC2UvTd6zGTPA7IAAAAPIegYWi53p70vurDm6/f39V+TCFC+5+vqqy2u+AAAAAGDIILBSt5OY12ZZPlRzbK8UDkiQzalz6GOCsJTJRiecJAQAAMNQQWCgqzjm5tlPq+PDHGjjRfG/dTJ6jqOFZmcmzub8KAAAAT4zAQlFIP191IL2/quOSBiQpjBTMXqawYZ2CUeN9jwgAAIACQGChoLmeLtlDO2QP7ZTudKeLFVWqXrlefXWLZCqq/A4IAACAgkJgoSAl1y6kn6862SwlVpJkRk9Q2PCsgllLNHz8BLW3t3ueEgAAAIWGwELBcIlVcrpV9uA2uctn7q4aBXX1Chetk5k4g89XAQAAYFARWBjyXG+P7JFdsq3bpe7OdLG0XOG8FQoXrJUZPtrvgAAAACgaBBaGrOTGFdmWbUqO77t/zPqIGoUL1ymYu0ympMzzhAAAACg2BBaGFOcSJeeOyR78VO7C8XvrZvIchYvWKZgyW8YEHicEAABAMSOwMCS4/j4lx/bItmyTu9WRLkYlCuYsV7hwrYJR4/wOCAAAAIjAQp5znR2yrdtkj+6R+vvSxaqRCheuVThvhUxZpd8BAQAAgM8hsJB3nHNybSfTY9bPHpHkJElm4vT081V182WC0O+QAAAAwEMQWMgbLh5Qcnx/+vmq61fSxSBUMGuJwkVrFdRM8jsgAAAA8DUILHjnujtlW7fLHtkl9faki5XVCuvXKKxfLVNR5XdAAAAA4BERWPDCOSd36bRs63Ylp1sll0iSzNjJ6WOAMxfJhPzrCQAAgKGF72CRU26gT8nxJtnWbfcfAzSBghkNChetkxk/VcYYv0MCAAAAT4jAQk4kN68pad0he+xzpwFWVCmcv1ph/SqZYSP8DggAAABkgMDCoHFJouT8UdmD2+UuHLu3biZMU7jgGQXTF/IYIAAAAAoK390ic663R/boHtnWHVLX9XQxjBTMXpKGFacBAgAAoEARWMhM0n5R9uB2JSeaJBuni9WjFS5Yo3DuCplyLgUGAABAYSOw8FScjZWcPpg+Bnjl7L11M2WOwgVrFUyZIxMEHicEAAAAcofAwhNxtztlD+2SPbxTutOdLpaWK5y7XEH9GgUjx/odEAAAAPCAwMIj+9K7q0aPT9+tmr1EpqTM85QAAACAPwQWvpYb6FdyfL9s63a565fTRRMomLFI4YJnZCZO5+4qAAAAQAQWvoLrbJdt3SF7dI/U35suVlQpnL9K4fzVMlXcXQUAAAB8HoGFL3AuUXLumGzrNrnzn7u7avzU9DHAGdxdBQAAAHwZvlOGpM/dXXVoh3Trc3dXzVqc3l01drLfAQEAAIAhgMAqckl7m2zrNiUnDkjxQLpYPUph/RqF81bIlA/zOyAAAAAwhBBYRSi9u6o1fQzw8ufurpo8O323auo87q4CAAAAngCBVUTc7Vuyh3fKHt4l9XSli6VlCuesULCAu6sAAACAp0VgFTjnnNzls+ljgKcPSsndu6tGjVe48BkFs5dydxUAAACQEQKrQLmBfiUnmmQPbvvi3VXTFypc+IzMxBncXQUAAABkjMAqMK6zXfbQDtkjD9xdNW+lwvrVMlUjvc4HAAAAFDICqwA4lyg5f1xJ6zYl545JcpIkM25q+hjgjEXcXQUAAADkAN91D2Gur0f26F7Z1h3SrY50MYwUzFychhV3VwEAAAA5RWANQUlHm+zBHUpO7L9/d1XVSIULnlE4d4VMBXdXAQAAAD4QWEOEs1bJmdb00IrLZ+6tc3cVAAAAkD+Mc87l6sUaGxvV2NgoSXrrrbfU39+fq5fOa1EUKY7jh/4523VTt/dv1u39nyjp7pQkmdJyVTas1bDlL6mkZmIuRy0YX7XnGDzse+6x536w736w77nHnvvBvvvx4L6XlpY+9OtyGlgPamtr8/XSeaWmpkbt7e33/rNzTu7KWdmD25Wcbrl/d9XIcXfvrlomU8rdVU/jwT1HbrDvucee+8G++8G+5x577gf77seD+15bW/vQr+MRwTxy7+6q1u1yHZfSRWMUTF+gcMFamVrurgIAAADyGYGVB+IbVxVvf0f26B6p7066WD5M4fxVCuevlqke6XU+AAAAAI+GwPLMOaeOv/s3su3p45Jm3JT00IoZi2SiEs/TAQAAAHgcBJZnxhhVrVyvWydb07AaN8X3SAAAAACeEIGVB4Yte0F3pi7wPQYAAACAp8TFSQAAAACQEQILAAAAADJCYAEAAABARggsAAAAAMgIgQUAAAAAGSGwAAAAACAjBBYAAAAAZITAAgAAAICMEFgAAAAAkBECCwAAAAAyQmABAAAAQEYILAAAAADICIEFAAAAABkhsAAAAAAgIwQWAAAAAGSEwAIAAACAjBBYAAAAAJARAgsAAAAAMkJgAQAAAEBGCCwAAAAAyAiBBQAAAAAZIbAAAAAAICMEFgAAAABkhMACAAAAgIwQWAAAAACQEQILAAAAADJCYAEAAABARggsAAAAAMgIgQUAAAAAGSGwAAAAACAjBBYAAAAAZITAAgAAAICMEFgAAAAAkBECCwAAAAAyQmABAAAAQEYILAAAAADICIEFAAAAABkhsAAAAAAgIwQWAAAAAGSEwAIAAACAjBBYAAAAAJARAgsAAAAAMkJgAQAAAEBGCCwAAAAAyAiBBQAAAAAZIbAAAAAAICMEFgAAAABkhMACAAAAgIwQWAAAAACQEQILAAAAADJCYAEAAABARggsAAAAAMgIgQUAAAAAGTHOOed7CAAAAAAoBLyDlQd+93d/1/cIRYc994N9zz323A/23Q/2PffYcz/Ydz8edd8JLAAAAADICIEFAAAAABkhsPLAhg0bfI9QdNhzP9j33GPP/WDf/WDfc48994N99+NR951DLgAAAAAgI7yDBQAAAAAZIbAAAAAAICMEFgAAAABkhMACAAAAgIwQWAAAAACQEQILAAAAADJCYAEAAABARggsAAAAAMgIgQUAKAh//Md/rObmZknS3/7t3+pHP/qR54kAAMUo8j0AAABZ+JVf+RX93d/9nTo7O3X69Gn9zu/8ju+RAABFiHewAAAFob6+Xs45/fznP9dv/dZvKQgCXblyRX/5l3+pH/7wh77HAwAUCQILAFAQzp07p5s3byqKIlVUVEiSxo8frx/84AeeJwMAFBMCCwAw5N24cUN/8Rd/od/+7d9WeXm5mpqafI8EAChSBBYAYEjr6+vTn/3Zn+nNN9/U5MmT9Z3vfEd///d/73ssAECRMs4553sIAAAGQ1dXl37yk5+opaVFL7/8sr71rW/5HgkAUOAILAAAAADICI8IAgAAAEBGCCwAAAAAyAiBBQAAAAAZIbAAAAAAICMEFgAAAABkhMACAAAAgIwQWAAAAACQEQILAAAAADLy/wPfRPZeTks5IgAAAABJRU5ErkJggg==",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plot_2(cost_history, m, q)"
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {},
"outputs": [],
"source": [
"#m_star = 0.62595499\n",
"#q_star = 7.3662299\n",
"d = lambda i: np.sqrt((m_star-m[i])**2+(q_star-q[i])**2)"
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {},
"outputs": [],
"source": [
"def near_opt(m, min_dist=1e-1, ge_per_step=1):\n",
" dist = np.array([d(i) for i in range(len(m))])\n",
" near = np.where(dist0:\n",
" ll = np.min(near[0])\n",
" print(f\"{ll} passi e {ll*ge_per_step} gradienti calcolati per arrivare a distanza minore o uguale di {min_dist} dall'ottimo\")\n",
" else:\n",
" print(f\"in {len(m)} passi e {(len(m))*ge_per_step} gradienti calcolati non raggiunge un punto a distanza minore o uguale di {min_dist} dall'ottimo\")"
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"3767 passi e 376700 gradienti calcolati per arrivare a distanza minore o uguale di 0.1 dall'ottimo\n"
]
}
],
"source": [
"near_opt(m, min_dist=1e-1, ge_per_step=n)"
]
},
{
"cell_type": "code",
"execution_count": 31,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA7sAAAHzCAYAAADhDgreAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAABS30lEQVR4nO3de3Rb5Z3v/8+2FMeWFF9kxQ65HZoAk5AQEmpTitOGhBCyTMvQ4kkhxbPazgzDgXUYpqcsktMW2tKUUMqvLAoM7YKhUzNn2p5wW5zqDG6aEAa3DA6xJ8Q0lNAWWgIxsmwn8iWxpP37w5Zi+e7Y0t7aer/WYimWpfixHjvos5/v830M0zRNAQAAAADgIHlWDwAAAAAAgJlG2AUAAAAAOA5hFwAAAADgOIRdAAAAAIDjEHYBAAAAAI5D2AUAAAAAOA5hFwAAAADgOIRdAAAy7Oyzz1ZhYaHmzJmjkpISXXrppXr00UcVj8cnfO4f//hHGYahaDSa1jFm6usAAJAuhF0AACzw/PPP68SJE3rnnXe0bds23Xvvvfqbv/kbq4cFAIBjEHYBALBQcXGxrr76av3sZz/Tv/zLv+jQoUP6xS9+oTVr1qioqEiLFi3SN77xjeTjP/nJT0qSSkpK5PP59Jvf/EZvv/22NmzYoLKyMgUCAX3+859XZ2dn8jn33nuvFixYoDlz5ugv/uIv9Ktf/UqSFI/HtXPnTi1dulRlZWXasmWLwuHwmF8HAIBsQtgFAMAGLr74Yi1cuFD/8R//Ia/Xq5/85Cfq7OzUL37xC/3TP/2Tnn32WUnSSy+9JEnq7OxUJBLRxz/+cZmmqe3bt+vo0aP67W9/qz/96U/JgPzmm2/qoYceUlNTk06cOKEXXnhBZ599tiTpBz/4gZ599lnt27dPR48eVWlpqW655ZYxvw4AANmEsAsAgE3Mnz9f4XBYl112mS644ALl5eVp1apVuv7667Vv374xn3fOOefoiiuu0OzZszV37lx9+ctfTj7e5XLp5MmTeuONN9Tf36+zzz5bS5culSQ9+uij2rFjhxYuXKjZs2frG9/4hnbt2sU+XQCAIxB2AQCwiffee09+v1//+Z//qfXr12vu3LkqLi7Wo48+qlAoNObzjh07puuuu04LFixQUVGRbrjhhuTjzznnHD3wwAP6xje+ofLycl133XU6evSoJOmdd97RZz7zGZWUlKikpETLly+Xy+XSsWPHMvL9AgCQToRdAABsoKmpSe+9957Wrl2rrVu36uqrr9af/vQndXV16aabbpJpmpIkwzBGPPd//a//JcMw9Prrr+v48eN68sknk4+XpK1bt+rll1/WO++8I8MwdMcdd0iSFi1apP/3//6fOjs7k//19fVpwYIFo34dAACyCWEXAAALHT9+XP/3//5fXXfddbrhhht0wQUX6MSJE/L7/SooKNCrr76q//2//3fy8XPnzlVeXp5+//vfJ+87ceKEfD6fiouL9d577+m+++5Lfu7NN9/Unj17dPLkSRUUFKiwsFB5eQP/+7/pppv01a9+Ve+8844k6cMPP9Rzzz035tcBACCbEHYBALDApz/9ac2ZM0eLFi3Sjh079OUvf1lPPPGEJOmRRx7RnXfeqTlz5uhb3/qWtmzZknyex+PRV7/6VVVXV6ukpESvvPKK7rrrLh04cEDFxcW66qqr9NnPfjb5+JMnT2rbtm0KBAKaN2+e2tradM8990iS/uEf/kFXX321Nm3apDlz5uiSSy7Rf/7nf475dQAAyCaGObTOCQAAAAAAB2BlFwAAAADgOIRdAAAAAIDjEHYBAAAAAI5D2AUAAAAAOA5hFwAAAADgOIRdAAAAAIDjuK0eQCYcPXrU6iHYUiAQUCgUsnoYGIZ5sSfmxZ6YF/thTuyJebEn5sV+mBN7Gm9e5s+fP+bzWNkFAAAAADgOYRcAAAAA4DiEXQAAAACA4xB2AQAAAACOQ9gFAAAAADgOYRcAAAAA4DiEXQAAAACA4xB2AQAAAACO4870F3zkkUd04MABFRcX6/7775ck/fznP9evfvUrFRUVSZKuv/56XXTRRSOe29LSoieeeELxeFyXX365rrnmmkwOHQAAAACQJTIedi+77DJt3rxZDz/8cMr9V111la6++uoxnxePx/X444/ra1/7msrKyrR9+3ZVVlZq4cKF6R4yAAAAACDLZLyM+fzzz5fP55vy844cOaJ58+apoqJCbrdbl156qZqamtIwQgAAAABAtsv4yu5YXnjhBb300ktasmSJ/vqv/3pEIA6HwyorK0t+XFZWprfeeivTwwQAAAAAZAFbhN1NmzaptrZWkvSzn/1MP/nJT3TzzTef8d+3e/du7d69W5K0c+dOBQKBGRmn07jdbl4bG2Je7Il5sSfmxX6YE3tiXuyJebEf5sSeznRebBF2S0pKkn++/PLLde+99454jN/vV3t7e/Lj9vZ2+f3+Uf++jRs3auPGjcmPQ6HQzA3WQQKBAK+NDTEv9sS82BPzYj/MiT0xL/bEvNgPc2JP483L/Pnzx3yeLY4e6ujoSP751Vdf1aJFi0Y8ZunSpXr//ffV1tamaDSqX//616qsrMzkMAEAAAAAWSLjK7sPPPCA3njjDZ04cUI33XSTtmzZotbWVv3xj3+UYRiaO3eubrzxRkkD+3R/+MMfavv27XK5XPrSl76kHTt2KB6Pa/369aOGYgAAkHtaW5r1+gtBzeqNqL/QpwuurNGK1WusHhYAwEIZD7u33XbbiPs2bNgw6mP9fr+2b9+e/Piiiy4a9fxdAACQu1pbmvXBrnrVlpfI8HhkmjHt21UvSQReAMhhtihjBgAAOFOHGoJaV14iwzAkSYZhaF15iQ41BC0eGQDASoRdAACQ1dw9kWTQTTAMQ+6ebotGBACwA8IuAADIalGPT6ZpptxnmqaiHq9FIwIA2AFhFwAAZLWVm2q0r60zGXhN09S+tk6t3FRj8cgAAFayxTm7AAAAZyrRhOqphqDcPd2KerxaWVtHcyoAyHGEXQAAkPVWrF5DuAUApKCMGQAAAADgOIRdAAAAAIDjEHYBAAAAAI5D2AUAAAAAOA5hFwAAAADgOIRdAAAAAIDjEHYBAAAAAI7DObsAAOCMtbY06/UXgprVG1F/oU+f2HK9FnxkidXDAgCAlV0AAHBmWlua9cGuetUWxnRNmUe1hTG9/ZMfqbWl2eqhAQBA2AUAAGfmUENQ68pLZBiGJMkwDF1WUaJDDUGLRwYAAGEXAACcIXdPJBl0EwzDkLun26IRAQBwGmEXAACckajHJ9M0U+4zTVNRj9eiEQEAcBphFwAAnJGVm2q0r60zGXhN09SLxzq1clONxSMDAIBuzAAAYBzDuy1fcGWNVqxeI0nJ26cagnL3dCvq8WrtX99IN2YAgC0QdgEAwKiS3ZbLS2R4PDLNmPbtqpeklMCb+LMkBQIBhUIhS8brJONdZAAATA5lzAAAYFSjdVteV0635XQb7UinD3bVc6QTAEwRYRcAAIyKbsvW4CIDAMwMwi4AABgV3ZatwUUGAJgZhF0AADCq0bot72uj23K6cZEBAGYGYRcAAIxqxeo1mldbp6f6XHq2vVdP9bk0r7aORklpxkUGAJgZdGMGAABjGt5tGek32pFOK7nIAABTRtgFAACwGS4yAMD0UcYMAAAAAHAcwi4AAAAAwHEIuwAAAAAAxyHsAgAAAAAchwZVAAAASLvWlma9/kJQs3oj6i/06YIra2jCBSCtCLsAAABIq9aWZn2wq1615SUyPB6ZZkz7dtVLEoEXQNpQxgwAAIC0OtQQ1LryEhmGIUkyDEPrykt0qCFo8cgAOBlhFwAAAGnl7okkg26CYRhy93RbNCIAuYCwCwAAgLSKenwyTTPlPtM0FfV4LRoRgFxA2AUAAEBardxUo31tncnAa5qm9rV1auWmGotHBsDJaFAFAACAtEo0oXqqISh3T7eiHq9W1tbRnApAWhF2AQAAkHYrVq8h3ALIKMqYAQAAAACOQ9gFAAAAADgOZcwAAAAzrLWlWa+/ENSs3oj6C3264MoaSngBIMMIuwAAADOotaVZH+yqV215iQyPR6YZ075d9ZJE4M1yXMQAsgthFwAAYAYdagjq2vISGYYhSTIMQ+vKS/RUQ5BgNIpsCZBcxACyD3t2AQAAZpC7J5IMugmGYcjd023RiOwrGSALY7qmzKPawpg+2FWv1pZmq4c2wqGGoNaNchHjUEPQ4pEBGEtGV3YfeeQRHThwQMXFxbr//vslSfX19XrttdfkdrtVUVGhm2++WV6vd8Rzb7nlFhUUFCgvL08ul0s7d+7M5NABAAAmJerxyTRjKYHXNE1FPSPf3+S6bFoFd/dEZBR6Uu7jIgZgbxkNu5dddpk2b96shx9+OHnfqlWrtHXrVrlcLj355JN65plndMMNN4z6/LvuuktFRUWZGi4AAMCUrdxUo3276pOrgKZpal9bp1bW1lk9NNvJpgDJRQwg+2Q07J5//vlqa2tLue/CCy9M/vm8887TK6+8kskhAQAAB7JyH2ji6zzVEJS7p1tRj1cra+tst1JpB9kUILmIAWQfWzWo2rNnjy699NIxP79jxw5J0hVXXKGNGzdmalgAACCL2KGR0IrVawi3k5BNAZKLGED2MUzTNDP5Bdva2nTvvfcm9+wmPP3003r77bf1la98ZURTB0kKh8Py+/3q6urSt7/9bX3xi1/U+eefP+rX2L17t3bv3i1J2rlzp06dOjXz34gDuN1uRaNRq4eBYZgXe2Je7Il5sR87zMnjd27XZ/L7R6wWPnNqlv7mW/dYODLr2GFexvJfTa9q//PPyNUdUczrU+WnP6MLqy62elgZYed5yVXMiT2NNy/5+fljPy9dA5qKF198Ua+99pruvPPOUYOuJPn9fklScXGxqqqqdOTIkTHD7saNG1NWfkOh0MwP2gECgQCvjQ0xL/bEvNgT82I/dpiTaDik/jLPKPcft3xsVrHDvIxlwUeWaMGt/zPlPruOdabZeV5yFXNiT+PNy/z588d8nuVht6WlRc8995y++c1vavbs2aM+pq+vT6ZpqrCwUH19fTp48KBqa2szPFIAAJAN/hzp0c/e+q3yzZj681y6YPEiLZs315b7QAEA6ZPRsPvAAw/ojTfe0IkTJ3TTTTdpy5YteuaZZxSNRnX33XdLks4991zdeOONCofD+uEPf6jt27erq6tL3/ve9yRJsVhMa9eu1erVqzM5dAAAkAVaW5r1305165Li2QoU5Eumqb3vvqMD4RP66E3/YPXwAAAZlNGwe9ttt424b8OGDaM+1u/3a/v27ZKkiooK3XfffekcGgAAcIBDDUFde85idZ84rvc/bFNeLK6/KCvWkdmlNBICgBxjeRkzACB9rDx+BbBC4txWX1GxfEXFyfvL23stHBUAwAqEXQBwKDscvwJkWjad2woASC/CLgA41KGGoK4dPLtSkgzD0LryEj3VECTswrGmc24rlRAA4CyEXQBwqEQ551CGYcjd023RiID0S4TTpxqCcvd0K+rxamVt3YShlUoIAHAewi4AOBTlnMhVK1avmXJApRICAJwnz+oBAADSY+WmGu1r65RpmpJ0upxzU43FIwPsx90TSbkwJFEJAQDZjpVdAHCoMy3nBHIRlRAA4DyEXQBwsDMp5wRy0XQaWwEA7ImwCwBAGtHhNztQCQEAzkPYBQAgTejwm12ohAAAZ6FBFQAAaXKoIZgsi5VOd/g91BC0eGQAADgfYRcAgDShwy8AANahjBkAgDShwy+cbLz96OxVB2AHhF0AQNYb/sba95GlivzhbcvfaNPhF0413n50SexVB2ALhF0AQFYb/qb7jfff1xu7XtbmVedrTlmJpW+06fALpzrUENS1o+xHf2pwP/pYn+NnH0AmEXYBAFlt+Jvu1nf/rGsXlOmD0IeaU1xi+RttOvzCidw9ERmFnpT7Tu9HN8f5HABkDg2qAABZbXgTKHc8pjzDUF4slryPN9rAzBrYj26m3JfYjz7e5wAgkwi7AICsNvyNdTTPpbhpKu5yJe/jjTYws1ZuqtG+ts7k715yP/qmmnE/BwCZRBkzACAj0tWddXgTqBWLF+rpI2/rylXnSxJNoYA0mMx+dPaqA7AaYRcAkHbjdW6d7hvgEW+6S86St3atXvjj23K380YbSJfx9qOzVx2AHRB2AQBpN17n1pl4Q8wbawAAMBx7dgEAaTe8iZRE0ygAAJBehF0AQNrRnRUAAGQaYRcAkHZ0ZwUAAJnGnl0AQNpNpnMrkCnp6gwOALAXwi4AICOyoYkUISh97PLaTtQZ3C7jBABMH2EXAACl93ikXGen13a8zuCSbDNOAMD0sWcXAAANhKB1o4SgQ4MhCGfOTq/teJ3B7TROAMD0EXYBABDHI6WTnV7b8TqD22mcAIDpI+wCACCOR0onO72243UGt9M4AQDTR9gFAEAcj5ROdnptV6xeo3m1dXqqz6Vn23v1VJ9L8wY7g9tpnACA6aNBFQAAys7jkbKlc7DdXtuxOoPbbZwAgOkh7AIAMCgbjkdKsFOH48nIltc20+PMlgsWAJCNKGMGACAL0Tk4+yUvWBTGdE2ZR7WFMX2wq16tLc1WDw0AHIGwCwBAFqJzcPbjggUApBdlzACAGUVZZmYMdA6OpQReOgdnF3dPREahJ+U+LlgAwMxhZRcAMGMoy8wcOgdnP446AoD0IuwCAGYMZZmZM94ROsgOXLAAgPSijBkAMGMoy8wsqzscj1ayvm7jFZaNJ9tw1BEApBdhFwAwY9hHmjvGOvrov4qLteAjS6weXtaw+oIFADgZYRcAMGNWbqrRvl31yVLmZFlmbZ3VQ8uITDbnsroR2KGGoK4dpWT9F88/owW3/s+MjQMAgLEQdgEAMyaXyzLHWumUNOPffya/1ljGKll3RSIZ+fpApll9gQnA1BF2AQAzKlfLMsda6XyqITjjr0cmv9ZYxipZj3l9Gfn6QCbZ4QITgKmjGzMAADPA3RNJCX5S+ppzZfJrjWWsTsKVn/5MxsYAZAqd5oHsxMouAAAzIJPNuezQCGyskvULqy5WKBTK2DiATKDTPJCdCLsAAMyATDbnsksjsFwtWUfuscMFJgBTR9gFAGAGZLI5Vy43AgOsYJcLTACmJuNh95FHHtGBAwdUXFys+++/X5IUiUT0/e9/Xx9++KHmzp2rf/zHf5TPN7LBxYsvvqinn35akvTZz35Wl112WSaHDgDAuDK50smqKpA5XGACslPGw+5ll12mzZs36+GHH07e9+yzz+qCCy7QNddco2effVbPPvusbrjhhpTnRSIR7dq1Szt37pQkbdu2TZWVlaOGYgAAAGAmcYEJyD4Z78Z8/vnnjwioTU1NWrdunSRp3bp1ampqGvG8lpYWrVq1Sj6fTz6fT6tWrVJLS0smhgwAAAAAyDK22LPb1dWl0tJSSVJJSYm6urpGPCYcDqusrCz5sd/vVzgcHvXv2717t3bv3i1J2rlzpwKBQBpGnf3cbjevjQ0xL/bEvNgT82I/TpqT/2p6VU3PPyN39wlFvXNU9enP6MKqi60e1hlx0rw4CfNiP8yJPZ3pvNgi7A5lGMaIswOnauPGjdq4cWPyY45AGF0gEOC1sSHmxZ6YF3tiXuzHKXPS2tKsD3bV61PlJTJ8Lplmt/Y9/pA6u7Jzn6ZT5sVpmBf7YU7sabx5mT9//pjPy3gZ82iKi4vV0dEhSero6FBRUdGIx/j9frW3tyc/DofD8vv9GRsjAADIHYcagsnOu9LAxfh15SU61BC0eGQAgMmyxcpuZWWl9u3bp2uuuUb79u1TVVXViMesXr1a//Zv/6ZIJCJJ+q//+i9t3bo100MFAAAZ0NrSrNdfCGpWb0T9hT5dcGVNRldU3T0RGYWelPsMw5C7pztjYwAATE/Gw+4DDzygN954QydOnNBNN92kLVu26JprrtH3v/997dmzJ3n0kCS9/fbb+uUvf6mbbrpJPp9P1157rbZv3y5Jqq2tpRMzAAAOlCghri0vkeHxyDRj2rerXpIyFnijHp9MM5aytco0TUU93ox8fQCwC9M0p73N1CoZD7u33XbbqPffeeedI+5bunSpli5dmvx4w4YN2rBhQ7qGBgAAbOBQQ1DXjlJC/FRDMGNhd+WmGu3bVZ8sZTZNU/vaOrWyti4jXx8AMikeN9Xe2aO29m4da4/oWHtk4M+hiAoLZunrN19m9RDPiC3KmAEAABLsUEKcCNVPNQTl7ulW1OPVytrsbE6VDjNdZm512TqQC+JxU6HOHrW1R3Qs1K228OlA+2FHt2Ixc9Tnzc53Z+3qLmEXAGYIb9aAmTGZEuJM/L6tWL1mxN/J7/nMl5nboWwdcIpYLK72rl61hSI6NrhK29Y+8OfQOIFWkkqKClRR5lN5mXfEbTYGXYmwCwAzgjdrwMyZqITYqt83fs8HzHSZuR3K1oFsEovFh5Ucd0860JYWFai8zKeKMm/KbXmZV7PznRcNnfcdAYAFeLMGzJyJSoit+n3j93zATJeZ26FsHbCbRKBNBtnBsuNjoYhCHT2KxccPtMmV2YBP5f6B27l+Zwba8eTWdwsAacKbNWBmjVZCnGDV7xu/5wNmulM1na+Rq2Kx+OAe2oF9s21Dyo4nDLTFharwe1UeSF2lzcVAOx5eCQCYAbxZAzLHqt83fs8HzHSnajpfw8miiRXalDA7cNs+mUA7rNy4osynuX4PgXaSeJUAYAbwZg3InHT8vk2m8RS/5wNmqlP10Nf82Mm4Dr3broU+L52vkXWisbjaO3pG7J9tm0Sg9RcXpjaECvhU7h/4c/4sVwa/C2ci7ALADOCYEiBzZvr3bbKNp/g9P228MvPJGPGa+wu1r61T8675q5x8PWF/IwJtKKJj4YHbUGeP4hME2pQwOxhu5/oJtOlG2AWAGTLdN38AJm8mf9+m0niK3/OZQbMv2FE0Ftd7xzr15pEPRpQdjxdoDUMqKykctcsxgdZahF0AAJDTaDyVebzmsEo0Gleos3ugu/GwsuP2qQbawU7H5X6vZhFobYmwCwAAchqNpzKP1xzpFI3G9WFH94iGUG2D59CaY1QcG4ZUXuZToLRQ5X6fKgKDZ9ASaLMWYRcALDCZZjiwB+bK+Wg8lXm85piuRKBNhtlQRG3hgdv2zp5xA22g1JPaFGrwdq7fq7PmVSgUCmX2m0HaEHYBIMMm2wwH1mOuJmfoBQGXP6BzP7khq14fGk9lHq85JqM/GlMo3KNj4YjaQsOO7ZlEoB0eZivKfAr4PZrlZoU2VxB2ASDDaMySPZiriQ2/IDBrVr9+mYUXBGg8lXm85pAGAu2H4YGS4xHn0E410Aa8qvATaHEaYRcAMozGLNmDuZoYFwQATCQRaJPNoELdagsP3Ia7JhFoBxtBDT22J1BKoMXECLsAkGE0ZskezNXEuCAAQJL6+2NqC3cn980OXaWdKNDO9XtH30Nb6pXbnZfZbwSOQtgFgAyjMUv2YK4mxgUBIHckA+2wI3va2iMKd/VOGGiHn0FbEfAqUEKgRfoQdgEgw2jMkj2Yq4lxQQBwllED7WDZ8XiBNi/P0NzhXY4Hy44JtLAKYRcALEBjluzBXI1v+AUBt9+jc7ggANjaqf7EHtohx/YMlh13HJ9EoA34VOH3DtwOhtuyEg+BFrZD2AUAANMy9IJAIBCY9hmVnG0MTN+p/thAh+NwZMQe2gkDrd+TWm6cCLSlHrldBFpkD8IuAACwDc42BiYvEWgHQmzqPtqOrt4xn5cItCPOoQ0MrtASaOEQhF0AAGAbHGUEpDp5Kpp6bE97t9pCER0Ljx9oXXmGAqWJFdrUPbQEWuQKwi4AALANjjJCLkoG2lBkxNE9Hcf7xnxeItAOnEM70N04UXZcVuKRi0CLHEfYBQAAtsFRRnCqk6eiA3tohx7Xc/yU3vugY+JAO+zYnsRKLYEWGB9hFwAA2AZHGSGbJQJtssvxkNvO8QKty9DcUu/pUuMhq7RlxYUEWuAMEXYBAIBtcLYx7O7kqeiQ/bNDju4Jd08q0Cb2zVaU+XTuR+arYFZMfgItkBaEXQAAYCucbQyr9Z2Mqi2caAQV0bHQ6fLjrhPjB9pyv3fYsT2nS47z8oyUx8/EUV2YOc0HW7Vn/yGFuk/K54qrZm2V1qxaYfWwMA2EXQAAAOScvpNRtQ0pMx66Wtt14uSYz3O78kY5tmeg7NhfPDLQIjs0H2xVfeNhVaxaJ29/v+KmqfrGJkki8GYxwi4AAAAcqfdkvz5s7x5ZdjypQDvYFCrgU4V/8LaMQOtUwcb9Kl22PuXYs9JlVQo27iXsZjHCLgAAwCQ0H2xV8OUmRWJ5lDjaSO/J/pR9s0OP7TkemUSgDaSWG1eU+eQvLiTQ5phI1JDXSJ1zwzDUHeXnIJsRdgEAACaQKHEsXb5BXsOgxDHDevv6Ry03bmvvHj/QuvMG99AOKTce3EtLoMVQPrepuGmm3Geaprxuc4xnIBsQdgEAACZAiWP6jRloQ9063j1xoE3dQzvQ9bi0iECLyamprlR9Y5MqVlVLGgi6HYebVFddafHIMB2EXQAAgAlQ4jgzevv6RxzXkyg7Hi/Qzkqu0A6eP+v3JY/wIdBiJiQuWu15bZ+6IifldZuqq67kYlaWI+wCAABMIFHiaAwJvJQ4jq6nr39gVTY0sinUie5TYz4vGWgDqcf2VJR5VUKgRQasWbVCV2xYx3FQDkLYBQAgC7S2NOv1F4Ka1RtRf6FPF1xZw1m0GZQocSxdViXDMHK+xLGnrz+lEVTbkNLjCQPt8HJjAi2ANCHsAgBgc60tzfpgV71qy0tkeDwyzZj27aqXJAJvhiRKGYONe9UdNXKixLGn95SOJcNsd0r5caRn4kCbXJ0dUnZcMqeAQAsgYwi7AADY3KGGoK4tL0lpjrSuvERPNQQJuxm0ZtUKx4XblEAb6taxcERtoYFV2vECbf4sl8rLvAONoQK+lG7HBFoAdkHYBQDA5tw9ERmFnpT7DMOQu6fbohEhm3T3nlLHHz/Um0f+PKLseDKBdkSX4zKfSooKUvYvA4AdEXYBALC5qMcn04yNaI4U9XgtHBXspLv31LA9tKdvpxpoE38m0ALIdoRdAABsbuWmGu3bVa91g6XMpmlqX1unVtbWWT00ZFCk51RKI6jkbSii7t7+MZ+XP8ulBRXF8hcXDCs59qpkDoEWgHMRdgEAsLnEvtynGoJy93Qr6vFqZW0d+3UdKNJzaoxzaMcPtLPzXalNoYYc3VM8Z7bmzp3LcSoAcg5hFwCALLBi9RrCrUNEek4OrMqGRq7SThRoR9s/Wz4YaFmhnXnNB1sVfLlJkViefK64atZWOa5JGeBkhF0AAIAZZJrmYMlx94hV2okDrTt1dTbgU8Vgx+MiH4E2k5oPtqq+8bBKl2+Q1zAUN03VNzZJEoEXyBKEXQAAgClKBNqUMDsk3Pb0TRBok2fPng62FWUEWjsJNu5X6bL1KUd+lS6rUrBxL2EXyBKEXQAAgFGYpqkT3afUFo7oWCi13HiygXa0smMCbXaIRA15h82TYRjqjjJ3QLYg7AIAgJyVDLSDQXb4sT294wTagtnukWE24FO532urQNva0qy3XtqjWDik/kKfLriyhv3fk+Bzm4qb5ogjv7xu08JRAZgKW4Tdo0eP6vvf/37y47a2Nm3ZskVXXXVV8r7W1lZ997vfVXl5uSTpYx/7mGprazM+VgAAkF1SA23kdHOocPekA21yH23gdJfjOd582wTasbS2NOuDXfX67MJy9Zd5ZJox7dtVL0kE3gnUVFeqvrFJpcuqkkd+dRxuUl11pdVDAzBJtgi78+fP13333SdJisfj+vu//3tdfPHFIx63fPlybdu2LdPDAwAANpcItAMrsiPLjntPRsd8buFsd7IRVHng9P7Z8iwJtOM51BDUtYPnM0sDZbjrykv0VEOQsDuBxL7cYONedUcNed2m6qor2a8LZBFbhN2hXn/9dc2bN09z5861eigAAMBGTNPU8cjJIWfPni43nnSgHVJ2nFitzfZAOx53T0RGoSflPsMw5O7ptmhE2WXNqhWEWyCL2S7sNjY2qrq6etTP/e53v9Ptt9+u0tJS1dXVadGiRaM+bvfu3dq9e7ckaefOnQoEAmkbbzZzu928NjbEvNgT82JPzIv9THdOTNNU54levX/suN7/8LiOHutKuR2v5NhbmK+zyot0Vnmx5pcX6azyIs0vL9ZZ5UUq8hU4NtCOx+0PaNasfuUZhvLz8yUNvMZuv4ffHRvg3zD7YU7s6UznxTBN0za77KPRqP7+7/9e999/v0pKSlI+19PTo7y8PBUUFOjAgQP68Y9/rAcffHBSf+/Ro0fTMNrsFwgEFAqFrB4GhmFe7Il5sSfmxX4mMyeJFdpjQ8qMj4W61RYeWKXtG2+FtmDWkDLjwYZQgx/7PM5doT1TiT27VywsV39/v0zT1L62Ts2rraOM2Qb4N8x+mBN7Gm9e5s+fP+bzbLWy29zcrI985CMjgq4keTynS3AuuugiPf744zp+/LiKiooyOEIAADAZyUCbaAQVGhJs27t18tTYgdZTMCvZ1XhomC0v8xJopygRaJ95aY+i4eOKerxaSdAFkCNsFXbHK2Hu7OxUcXGxDMPQkSNHFI/HNWfOnAyPEAAAJJimqa4TJ5Ndjtvau9Vxol9/fj88YaD1Fs4a7GrsPX072BzK55mdwe/C+VasXqN1G69gtQpAzrFN2O3r69PBgwd14403Ju9raGiQJG3atEmvvPKKGhoa5HK5lJ+fr9tuu40ruwAApFki0Ca7HLendjk+eSo25nOTgXaUVVqfJz+D3wUAIBfZJuwWFBTon//5n1Pu27RpU/LPmzdv1ubNmzM9LADAMK0tzXr9haBm9UbUX+jTBVfWUBKZ5QaaQvWldDc+FoqoLTy5QDsQYgdWZZeefZY8+XGVE2gBABazTdgFANhfotlNbXmJDI9HphnTvl31kkTgtblkoA1161g4MuLonlP9Ywdanyc/Zd9s4na0QEtzFwCAXRB2AQCTdqghqGvLS5LbSAzD0LryEj3VECTs2oBpmuo8fnqFNrlKO8lAe3r/bGqnY2+hc1Zomw+2KvhykyKxPPlccdWsreIcVQBwKMIuAGDS3D0RGYWelPsMw5C7p9uiEeWeeDxRchwZpeR4koE24FOF36fywOlVWicF2rE0H2xVfeNhlS7fIK9hKG6aqm9skiQCLwA4EGEXADBpUY9PphlLaRBomqaiHq+Fo3KeRKAdCLGDZ9AONoX6MDyJQDvsuJ5cCrTjCTbuV+my9SmVCaXLqhRs3EvYBQAHIuwCACZt5aYa7dtVr3WDpcymaWpfW6dW1tZZPbSsE4+b6jzeq2NDm0IN3k4UaOd484cd25MItV55cjzQjicSNeQddpKDYRjqjtr7dAdKrwHgzBB2AaQdb9ScI7Ev96mGoNw93Yp6vFpZW8d+3TGMDLSDR/YMlh33R+NjPneON3/YyqxPFQGvyv0E2jPlc5uKm+aIygSv27RwVOOj9BoAzhxhF0Ba8UbNeVasXkO4HSIeN9VxvHfI3tnTZccTBdoi7+zTjaCGnENbXuaTp2BWBr+LzLHy4ldNdaXqG5tUuqwqWZnQcbhJddWVGfn6Z4LSawA4c4RdAGnFGzU4QSLQDj+u59hgoI1OFGgDQ1ZnB1dq55Z5HRtox2L1xa/E1wg27lV31JDXbaquutLW/xZla+k1ANgBYRdAWvFGDdkiHjcV7uo9XWo8pNvxhIHWNzu13HhIU6jCHAu047HDxa81q1bYOtwOl42l1wBgF4RdAGnFGzXYSSLQpjaEGig7/rBj4kCbcv6s//QtgXZyuPg1ddlYeg0AdkHYBZBWvFFDpg0E2p5kI6hj4cHbwS7H0djYgbZ4zmyV+wcbQQ3pclxe5lXhbALtdHHxa+qysfQaAOyCsAsgrXijhnRIBNo/tfXpyO+PpqzUfhjumTDQjuhyXObVXAJt2nHx68xkW+k1ANgFYRdA2vFGDWciHjfV3tmTWm48uJd24kBbcPoM2oBXFX6fygdLjgtmT+5/fa0tzXr9haBm9UbUX+jTBVfW0IV6mrj4BQDIJMIuAMAyiUCbuod24AifDzu6FYuNXd5aUlSgBRUl8henNoeaSqAdS2tLsz7YVa/a8hIZHo9MM6Z9u+olicA7TVz8AgBkCmEXAJBWsVhc7Ykux6HuwXNoB0LtZAJtasnx6dvZ+W4FAgGFQqEZH/OhhqCuLS9J6Rq8rrxETzUECbsAMAYrz9EGRkPYBQBMWywWTyk5Pn10T7dCEwTa0qKC5L7ZobeJQGsFd09ERqEn5T7DMOTu6bZkPABgd1afow2MhrALAJiUEYF2yCptqKNHsfj4gXa0Y3vm+q0LtOOJenwyzdiIrsFRj9fCUQGAfdnhHG1gOPu9wwAAWCYWiyuUCLSDpcaTDrTFharwe1UeSF2ltWugHc/KTTXat6te6wZLmU3T1L62Tq2srbN6aABgS5yjDTvKrncfAIBpiw6u0CbC7NDmUO2TCbTDyo0rynya6/dkXaAdT2Jf7lMNQbl7uhX1eLWyto79ugAwBs7Rhh05550JACApGourvaNnxP7ZtkkEWn9xYWpDqIBP5f6BP+fPcmXwu7DWitVrCLcAMEmcow07IuwCQJYaEWhDER0LD9yGOnsUnyDQpoTZwXA7159bgRYAMDM4Rxt2RNgFABuLxuIKdXSn7KFNlB2PF2gNQyorKVS536eKQGrZMYEWM2n4USPXf2qjlixeaPWwAFiAc7RhN4RdALBYNBpXqLN7oLvxsLLj9skE2tGO7fF7NYtAizQb7aiRHzU063MXd/GG16Y4BxVALiHsAkAGRKNxfZhYoW1PXaGdONB6RtlD651SoG1tadbrLwQ1qzei/kKfLriyhv2omLZRjxpZXqVg4wsEKBviHFQAuYawCwAzJBFok2E2FFFbeOC2vbNH5hhbaBOBtiLgHVF2PLd0+iu0rS3N+mBXvWrLS2R4PDLNmPbtqpckAi+mhaNGsgvnoALINYRdAJiCaDSuD8PdOhaOqC007NieCQJtoNRzenV28LZ88BzaWe70lRwfagjq2sHzYgfGYmhdeYmeaggSdjEtHDWSXbg4ASDXEHYBYJj+aEyhcE9KkO04fkp//qBj6oE24FWF36eA35PWQDsed09ERqFn2FgNuXu6LRkPnGPUo0Z+26TPpeGoEfaaTh8XJwDkGsIugJzUH43pw/DYe2gnDLSD+2aTx/ZYHGjHE/X4ZJqxEW9wox6vhaOCE4x21MiNV10+492Y2Ws6MzgHFUCumVTYjcfjampqkmEYqqysVF5eniTpN7/5jT7+8Y+ndYAAcKb6+2ODe2gHuxuHutUWHrgNd40faOf6vSnlxud+ZL4KZsU0t9Qrtzsvs9/INK3cVKN9u+q1brCU2TRN7Wvr1MraOquHBgcYftRIIBBQKBSa0a/BXtOZwTmoAHLNpMLuQw89pEAgILfbreeff1633HKL5s2bp4aGBsIuAEv198fUFu5ONoIaukI7mUA7/MieioBXgZKRgTYdb+AzJbEv96mGoNw93Yp6vFpZW8d+XWQN9prOHM5BBZBLJhV2w+Gwbr31VknS+vXr9dBDD+mv/uqv0jowAEhIBtphZ9C2tUcU7uodM9Dm5RmaWzrKsT1lowdaJ1uxeg3h1kLsN50e9ppOT/PBVu3Zf0ih7pP8/AHIKZMKu9FoVP39/Zo1a5bmzp2rbdu26YEHHtC7776b7vEByBGn+gf20KYc25NsDjWJQBvwqcLvHbgdDLdlJZ6cCrSwJ/abTh97Tc9c4uevYtU6efv7+fkDkFPGDbuxWEwul0tf+MIX1N3drZKSEklSYWGh7rjjDr388suZGCMAhzjVH1Nbe2LfbGrJ8YSB1u9JLTdOBNpSj9wuAi3si/2m08de0zPHzx+AXDZu2P3Od76j22+/Xeecc86Iz+Xl5emTn/xk2gYGIDslAu1AiE0tO+7o6h3zeYlAO/wc2orA4AotgRZZiv2mM4O9pmeGnz8AuWzcsHv22Wfr61//urZv3y6/3y9JeuONN/TTn/5U3/rWtzIyQAD2c/JUdLDkeMj+2VBEx8LjB1pXnqFAaWKFNnUPLYEWTsV+U1gp8fM3FD9/AHLFuGG3rq5ODQ0N+vrXv66tW7dqz549evfdd3X11VdnanwALJIMtKHIiE7HHcf7xnxeItAOnEM70N04UXbsJ9AiB7HfFFZK/PxVrKqWJH7+AOSUCRtUnXfeefJ4PHrwwQe1bt063XHHHcrPz8/E2ACk2clT0YE9tKN0OZ4w0A47tiexUltW4pGLQAsksd8UVkr8nO15bZ+6Iif5+ZsAndMBZxk37N5333164403dNVVV2nLli167LHHdOjQIV100UWZGh+AaUoE2mSX4yG3neMFWpehQOnQQDvYHCrgU1lxIYEWmAL2m8JKa1at0BUb1mXtWeGZQud0wHnGDbtnnXWW/vt//+/y+XySpIqKCt17771qa2vT5s2bMzJAABM7eSo6ZGV2yNE94e4JA+3cUu/pvbNDyo4JtACAXELnasB5xg27N9xwQ8rHixcv1t1336177rmHsAtkWN/JqNrCiUZQER0LnS477joxcaBNNIIa2u3YT6AFAEASnasBJ5pwz+5wfr+fTsxAmvSdjOr3f2rX7468p2PD9tGOF2jdrryUY3uGdjsuK/EoL4//UQMAMB46pwPOM+WwK0mFhYUzPQ4gZ/Se7NeH7d0jy47bI+o6cXLM5w0EWm9y32yFf/C2zCt/MYEWAIDpoHM64DxnFHYBjK/3ZP9gl+NEQ6jBsuPwxIH2rPIilZUUpJ5FO1hyTKAFACA96JwOOA9hFzhDiUA72jm0xyPjBFp3nsr93iH7Z33Jjsf+4kKVl8+lYyYAABagczrgLIRdYBy9ff3JAJtSdhzq1vHuiQPt0JXZRMfj0iJWaAEAAIB0I+wi500n0Fb4B5tBBbyDx/YMhFoCLQAAAGAtW4XdW265RQUFBcrLy5PL5dLOnTtTPm+app544gk1Nzdr9uzZuvnmm7VkyRKLRots0tPXf3rf7LCmUCe6T435vFmJkuPA6VLjisGy4xICLQAAGdN8sFXBl5sUieXJ54qrZm2Vo0qOnf79AVawVdiVpLvuuktFRUWjfq65uVkffPCBHnzwQb311lt67LHH9J3vfCfDI4Rd9fT1p+ybbRuyUjthoB1ebkygBQBgBKsCWfPBVtU3Hlbp8g3yGobipqn6xiZJckQgdPr3B1jFdmF3PPv379cnP/lJGYah8847T93d3ero6FBpaanVQ0OG9PSe0rFkmB1yG4oo0jNxoE2uzg4pOy6ZU0CgBQBgAlYGsmDjfpUuW588A9cwDJUuq1Kwca8jwqDTvz/AKrYLuzt27JAkXXHFFdq4cWPK58LhsAKBQPLjsrIyhcPhEWF39+7d2r17tyRp586dKc/BaW6325avTaTnpN5vO66jbV16v+243m/r0tG243q/7biOR/rGfF7+LJfOKi/WWeVFml9epLPKiwdvi+Qv9mZNoLXrvOQ65sWemBf7YU7saSbmZc9rh1Sxal0ykElSxapq7Xltn67YsG66QxxXv6tAntmzR9zf6yrI6p+3xLw49fvLRvwbZk9nOi+2Crt33323/H6/urq69O1vf1vz58/X+eefP+W/Z+PGjSlBmWNcRhcIBCx7bbp7T50+tmdY2fF4K7T5s1wjyo0Tt8VjrdDG+hQOjx2S7cbKecHYmBd7Yl7shzmxp5mYl1DkpLz9/SPu74qcTPucz4r16eTJkylB2zRNuWN9Wf3zlpgXp35/2Yh/w+xpvHmZP3/+mM+zVdj1+/2SpOLiYlVVVenIkSMpYdfv96d8k+3t7cnnwH66e08NC7Onb6caaBN/LikqSPkfAQAAyAyf21TcNEcEMq/bTPvXrqmuVH1jk0qXVckwDJmmqY7DTaqrrkz7184Ep39/gFVsE3b7+vpkmqYKCwvV19engwcPqra2NuUxlZWV+vd//3dVV1frrbfeksfjYb+uxSI9p1IaQSVvQxF19468+pswItAGfKrw+1Qe8KpkDoEWAMZD11ZYwcpAlvj5DjbuVXfUkNdtqq660jE/907//gCr2CbsdnV16Xvf+54kKRaLae3atVq9erUaGhokSZs2bdKaNWt04MAB3XrrrcrPz9fNN99s5ZBzRqTnVEojqLZwovx4/EA7O9810OXY702eP5tcoSXQAsAZoWsrrGJ1IFuzaoWjf8ad/v0BVrBN2K2oqNB999034v5NmzYl/2wYhv72b/82k8PKGZGekwOrsqGRq7STCbSnz6A9fRZt8ZzZBFogC7FqaG90bYWVCGQAsoltwi7SyzTNwT20p4NsV6Rf7x4NTyrQjtYQqpxACzgOq4b2F4ka8g77d9cwDHVH+bcYAIChCLsOYprm4B7a7lHLjnv6xgu07iFnz55epa0o86nIR6AFcgWrhvZnZZMgAACyCWE3yyQCbUqYHRJuJxNoE6uz55x9lgrz4wRaAEmsGtofXVsBAJgcwq4NmaapE92n1BaOpJQdJ257xwm0BbPdI0uOAwNNooYHWs4RAzAcq4b2Z3WTIAAAsgVh10LHIyeTAXb4ObSTCbTJZlCB002h5njzWaEFcMZYNcwONAkCAGBihF0L/X8/btS7R7tG/VzhbLfKAz5V+L0Dt0OaQhFoAaRLLqwa0m0aAIDcQNi10H+bXyLDMFLKjhOrtQRaAFZx8qoh3aYBAMgdhF0LffGzF1k9BADIKXSbBgAgd+RZPQAAADIlEjVGVM3QbRoAAGci7AIAcobPbco0UztL020aAABnIuwCAHJGTXWlOg43JQNvott0Dd2mAQBwHPbsAgByRmJf7k+ee0q//7BLsf6TWlpeImmZpeMCAAAzj7ALAMg5RmCxKteePkuYjswAADgPZcwAgJwy0JG5apSOzPstHhkAAJhJrOwCAHJKJGrIm6UdmZsPtir4cpMisTz5XHHVrK1iNRoAgDEQdgEAOcXnNhU3zZQjiLKhI3PzwVbVNx5W6fIN8hqG4pRfAwAwLsqYAQA5JVs7MlN+DQDA1LCyCwDIOfHQO9r/zCHFT/VpybxSfeGzV9l+dTSby68BALACYRcAkDMSpcBla2sVGOzE3HG4yephTUq2ll8DAGAVypgBADkjm0uBs7X8GgAAq7CyCwDIGdlcCpwosw427lV31JDXbaquutL25dcAAFiFsAsAyBnZXgq8ZtUKwi0AAJNEGTMAIGdQCgwAQO5gZRcAkDMoBQYAIHcQdgEAOYVSYGdqPtiq4MtNisTy5HPFVbO2inkGgBxH2AUAAFktcaRU6fIN8hqG4qap+saBI6UIvACQu9izCwAAslo2HykFAEgfwi4AAMhqkaiR0mFbyp4jpQAA6UPYBQAAWc3nNpMdthOy6UgpAEB6sGcXAACbodnS1NRUV6q+sSlZypw4UqqOI6UAIKcRdgEAsBGaLU0dR0ohWwy/kHX9pzZqyeKFVg8LcCzCLgAANjLQbGn9KM2W9hLexsGRUrC70S5k/aihWZ+7uIufXSBNCLsAANhIJGrIS7Ml2Ayl9dM36oWs5VUKNr7AawmkCWEXAAAb8blNxU0zpbswzZZgJUrrZwYXsoDMoxszAAA2UlNdqY7DTcnuwolmSzU0W4JFOMd4ZtA1HMg8VnYBALARmi3BbliRnBmjdg3/bZM+x4UsIG0IuwAA2AzNlmAnlNbPjNEuZN141eV0YwbSiLALAACAMXGO8cwZfiErEAgoFApZOCLA2Qi7AABAEh13MTpK6wFkK8IuAACg4y7GRWk9gGxEN2YAAEDHXQCA4xB2AQCAIlEjpQGRRMddAEB2o4wZAABMueMu+3sBAHZH2AWQM3hzDoxtKh13x9vfe8WGdZkeuiPx7xUATB9hF0BOoPkOML6pdNwd2N+7fpT9vXsJuzOAf68AYGYQdgHkhPHenPPmERgw2Y67kaghL/t7J3Smq7P8ewUAM8MWYTcUCunhhx9WZ2enDMPQxo0bVVNTk/KY1tZWffe731V5ebkk6WMf+5hqa2utGC6ALMSbc2DmTHV/by6azuos/14BwMywRdh1uVyqq6vTkiVL1Nvbq23btmnVqlVauHBhyuOWL1+ubdu2WTRKANmMN+fAzJnK/t5cNZ3VWf69AoCZYYujh0pLS7VkyRJJUmFhoRYsWKBwOGzxqAA4SU11pToON8k0B94sJt6c1/DmHJiyNatWqK56mfIO71XP63uVd3iv6qqXUWI7xHSOcuLfKwCYGbZY2R2qra1Nf/jDH3TOOeeM+Nzvfvc73X777SotLVVdXZ0WLVpkwQgBZKOpNN8BMLHJ7u/NVdNZneXfKwCYGYaZuGxoA319fbrrrrv02c9+Vh/72MdSPtfT06O8vDwVFBTowIED+vGPf6wHH3xw1L9n9+7d2r17tyRp586dOnXqVNrHno3cbrei0ajVw8AwzIs9MS/2xLzYD3My4NUDLfpRQ7NKlw8p9f5tk27ctEYXX7Q64+NhXuyJebEf5sSexpuX/Pz8MZ9nm7AbjUZ177336sILL9SnPvWpCR9/yy236J577lFRUdGEjz169OhMDNFxAoGAQqGQ1cPAMMyLPTEv9sS82A9zclrzwVYFG/cnV2drLFydZV7siXmxH+bEnsabl/nz54/5PFuUMZumqUcffVQLFiwYM+h2dnaquLhYhmHoyJEjisfjmjNnToZHCgAAMDmUegOAtWwRdt9880299NJLWrx4sW6//XZJ0vXXX59M75s2bdIrr7yihoYGuVwu5efn67bbbhvR+AEAAAAAAMkmYXfZsmX6+c9/Pu5jNm/erM2bN2doRAAAAJiu5oOtCr7cpEgsTz5XXDVrq1jtBpAxtgi7AAAAcJbmg62qbzys0uUb5DUMxU1T9Y1NkkTgBZARtjhnFwAAAM4SbNyv0mVVyW1nhmGodFmVgo37LR4ZgFxB2AUAAMCMi0SNEf1VDMNQd5SeKwAygzJmAACAQewxnTk+t6m4aaYEXtM05XXb4tRLADmAlV0AAACd3mMaX75B3gvWK758g+obD6v5YKvVQ8tKNdWV6jjcJNMcCLemaarjcJNqqistHhmAXMHKLgAAgBJ7TNePssd0L6u7ZyDxmgUb96o7asjrNlVXXclrCSBjCLsAAAAa2GPqZY/pjFqzagXhFoBlKGMGAADQwB7TRMltAntMASB7EXYBAADEHlMAcBrKmAEAtkAXXFiNPaYA4CyEXQCA5RJdcEuXb5DXMBQ3TdU3NkkSQQMZxR5TAHAOypgBAJYb6IJbNUoX3P0WjwwAAGQrVnYBAJajCy5w5tgCAACjI+wCACznc5uKm2ZyZVeiCy4wGWwBAICxUcYMALAcXXCBM8MWAAAYGyu7AADL0QUXODNsAQCAsRF2AQC2QBdcYOrYAgAAY6OMGQAAIEuxBQAAxsbKLgAAQJZiCwAAjI2wCwAAkMXYAgAAoyPsAgAwRZxrCgCA/RF2AQCYAs41BQAgO9CgCgCAKeBcUwAAsgNhFwCAKYhEjZRjXiTONQUAwI4IuwAATIHPbSaPeUngXFMAAOyHsAsAwBRwrikAANmBBlUAAEwB55rOHLpaAwDSibALAMAUca7p9NHVGgCQbpQxAwCAjKOrNQAg3Qi7AAAg4+hqDQBIN8IuAADIOLpaAwDSjbALAAAyjq7WAIB0o0EVAADIOLpaAwDSjbALAAAsQVdrAEA6UcYMAAAAAHAcVnYBAAAwQvPBVgVfblIkliefK66atVWsxAPIKoRdAMCk8MYXyB3NB1tV33hYpcs3yGsYipum6hubJInfewBZg7ALAJgQb3ydh4sXGE+wcb9Kl61PnoVsGIZKl1Up2LiXnxMAWYOwCwCYEG98nYWLF5hIJGrIO/j7nmAYhrqjxhjPAAD7oUEVAGBCkaiRDLoJvPHNXgMXL6pGuXix3+KRwS58bjN5BnKCaZryus0xngEA9kPYBQBMiDe+zsLFC0ykprpSHYebkr/3pmmq43CTaqorLR4ZAEweZcwAgAnVVFeqvrEpuRqYeONbxxvfrORzm4qbZkrg5eIFhkqUswcb96o7asjrNlVXXUmZO4CsQtgFAEyIN77OwsULTMaaVSv4HQeQ1Qi7AIBJ4Y2vc3DxAgCQCwi7AByLo1WAsXHxAgDgdIRdAI7E0SqAvXDxCQCQabYKuy0tLXriiScUj8d1+eWX65prrkn5fH9/vx566CH9/ve/15w5c3TbbbepvLzcmsECsDXOhQXsg4tPAAAr2CbsxuNxPf744/ra176msrIybd++XZWVlVq4cGHyMXv27JHX69UPfvADNTY26l//9V/1j//4jxaOGoBdRaKGvA47WoWVMWQrLj4BAKxgm3N2jxw5onnz5qmiokJut1uXXnqpmpqaUh6zf/9+XXbZZZKkSy65RIcOHRpx7iMASM47FzaxMhZfvkHeC9YrvnyD6hsPq/lgq9VDAybEub4AACvYJuyGw2GVlZUlPy4rK1M4HB7zMS6XSx6PRydOnMjoOAFkh5rqSnUcbkoG3sTRKjVZerTKwMpY1SgrY/stHhkwMaddfAIAZAfblDHPpN27d2v37t2SpJ07dyoQCFg8Intyu928NjbEvMyMKzasU3FJsZ75VaMi/ZJvlvT5q6p18UWrz+jvs3pe+l0F8syePeL+XldBTv+8WD0vGGm0Obn+qsv1o4ZmlS4fcq7vb5t041WXM38Zwu+KPTEv9sOc2NOZzottwq7f71d7e3vy4/b2dvn9/lEfU1ZWplgspp6eHs2ZM2fE37Vx40Zt3Lgx+XEoFErfwLNYIBDgtbEh5mXmLFm8UP/zi59Lue9MX1ur52VWrE8nT55MKQU1TVPuWF9O/7xYPS8YabQ5WbJ4oT53cZeCjS8kz/X9XHWllixeyPxlCL8r9sS82A9zYk/jzcv8+fPHfJ5twu7SpUv1/vvvq62tTX6/X7/+9a916623pjzmox/9qF588UWdd955euWVV7RixYoRe4AAwIlqqitV39iULGVOlGXXZWlZNnIP5/oCADLNNmHX5XLpS1/6knbs2KF4PK7169dr0aJF+tnPfqalS5eqsrJSGzZs0EMPPaT/8T/+h3w+n2677Tarhw0AGZEICcHGvcmVsbrqSsIDAADAGGwTdiXpoosu0kUXXZRy3+c+d7oEMT8/X1/+8pczPSwAsAVWxgAAACbPNt2YAQAAAACYKYRdAAAAAIDjEHYBAAAAAI5D2AUAAAAAOI6tGlQBAE5rPtiq4MtNisTy5HPFVbO2igZVAAAAk0TYBQAbaj7YqvrGwypdvkFew1DcNFXf2CRJBF4AAIBJoIwZAGwo2LhfpcuqZBiGJMkwDJUuq1Kwcb/FIwMAAMgOhF0AsKFI1EgG3QTDMNQdNcZ4BgAAAIaijBkAbMjnNhU3zZTAa5qmvG7TwlEB08M+dABAJrGyCwA2VFNdqY7DTTLNgXBrmqY6DjepprrS4pEBZyaxDz2+fIO8F6xXfPkG1TceVvPBVquHBgBwKFZ2AcCGEqtdwca96o4a8rpN1VVXsgqGrDWwD339KPvQ9/JzDQBIC8IuANjUmlUrCAFwjEjUkJd96ACADKKMGQAApJ3PbSbL8hPYhw4ASCfCLgAASDv2oQMAMo0yZgAAkHbsQwcAZBphFwAAZAT70AEAmUQZMwAAAADAcQi7AAAAAADHIewCAAAAAByHsAsAAAAAcBzCLgAAAADAcQi7AAAAAADHIewCAAAAAByHsAsAAAAAcBy31QMAAMBKzQdbFXy5SZFYnnyuuGrWVmnNqhVWDwsAAEwTYRcAkLOaD7aqvvGwSpdvkNcwFDdN1Tc2SRKBFwCALEcZMwAgZwUb96t0WZUMw5AkGYah0mVVCjbut3hkAABguljZhS1QRgjACpGoIe9g0E0wDEPdUWOMZwAAgGxB2IXlKCMEYBWf21TcNJMru5Jkmqa8btPCUQEAgJlA2IXlBsoI149SRriXsAsgrWqqK1Xf2JQsZTZNUx2Hm1RXXWn10CaFqhgAAMZG2IXlKCMEkGlDQ2K8M6TQvrflLZsnr9tUXXVlVgRGqmIAABgfYReWo4wQQCYND4mewdXcv6pellUhkaoYAADGRzdmWK6mulIdh5tkmgPhNlFGWJMlZYQAsotTOjBHokbKRUKJqhgAAIZiZReWS6xABBv3qjtqZFUZIYDs45StE1TFAAAwPsIubGHNqhWEWwAZ4ZSQmO3NtQAASDfCLgAgpzglJFIVAwDA+Ai7AICc4qSQSFUMAABjI+wCAHIOIREAAOejGzMAAAAAwHEIuwAAAAAAx6GMGQCAKWo+2Krgy02KxPLkc8VVs7aKsmgAAGyGsAsAwBQ0H2xVfeNhlS7fIK9hKG6aqm9skiQCLwAANkIZMwAAUxBs3J88tkiSDMNQ6bIqBRv3WzwyAAAwFGEXAIApiESNZNBNMAxD3VFjjGcAAAArEHYBAJgCn9uUaZop95mmKa/bHOMZAADACuzZBQBMiIZMp9VUV6q+sSlZymyapjoON6muutLqoQEAgCEsD7v19fV67bXX5Ha7VVFRoZtvvller3fE42655RYVFBQoLy9PLpdLO3futGC0AJB7aMiUKvE9Bxv3qjtqyOs2VVddmZOvBQAAdmZ52F21apW2bt0ql8ulJ598Us8884xuuOGGUR971113qaioKMMjBIDcNtCQaf0oDZn25mzAW7NqRc5+7wAAZAvL9+xeeOGFcrlckqTzzjtP4XDY4hEBAIaiIRMAAMhGlq/sDrVnzx5deumlY35+x44dkqQrrrhCGzduzNSwACCn+dym4qaZEnhpyAQAAOzOMIe3lEyDu+++W52dnSPuv+6661RVVSVJevrpp/X222/rK1/5yogVBEkKh8Py+/3q6urSt7/9bX3xi1/U+eefP+rX2717t3bv3i1J2rlzp06dOjVz34yDuN1uRaNRq4eBYZgXe8rleXn1QIt+1NCs0uVDGjL9tkk3blqjiy9abenYcnle7Io5sSfmxZ6YF/thTuxpvHnJz88f83kZCbsTefHFF/XLX/5Sd955p2bPnj3h43/+85+roKBAV1999aT+/qNHj053iI4UCAQUCoWsHgaGYV7sKdfnpflgq4KN+5MNmWps0pAp1+fFjpgTe2Je7Il5sR/mxJ7Gm5f58+eP+TzLy5hbWlr03HPP6Zvf/OaYQbevr0+maaqwsFB9fX06ePCgamtrMzxSAMhdNGQCAADZxvKw+/jjjysajeruu++WJJ177rm68cYbFQ6H9cMf/lDbt29XV1eXvve970mSYrGY1q5dq9WrV1s4agAAAACAnVkedn/wgx+Mer/f79f27dslSRUVFbrvvvsyOSwAAAAAQBaz/OghAAAAAABmGmEXAAAAAOA4hF0AAAAAgOMQdgEAAAAAjkPYBQAAAAA4DmEXAAAAAOA4hF0AAAAAgONYfs4uAADDNR9sVfDlJkViefK54qpZW6U1q1ZYPSwAAJBFCLsAAFtpPtiq+sbDKl2+QV7DUNw0Vd/YJEkEXgAAMGmUMQMAbCXYuF+ly6pkGIYkyTAMlS6rUrBxv8UjAwAA2YSwCwCwlUjUSAbdBMMw1B01xngGAADASIRdAICt+NymTNNMuc80TXnd5hjPAAAAGImwCwCwlZrqSnUcbkoGXtM01XG4STXVlRaPDAAAZBMaVAEAbCXRhCrYuFfdUUNet6m66kqaUwEAgCkh7AIAbGfNqhWEWwAAMC2UMQMAAAAAHIewCwAAAABwHMIuAAAAAMBxCLsAAAAAAMch7AIAAAAAHIewCwAAAABwHMIuAAAAAMBxCLsAAAAAAMch7AIAAAAAHIewCwAAAABwHMIuAAAAAMBxCLsAAAAAAMch7AIAAAAAHIewCwAAAABwHMIuAAAAAMBxDNM0TasHAQAAAADATGJlN4dt27bN6iFgFMyLPTEv9sS82A9zYk/Miz0xL/bDnNjTmc4LYRcAAAAA4DiEXQAAAACA4xB2c9jGjRutHgJGwbzYE/NiT8yL/TAn9sS82BPzYj/MiT2d6bzQoAoAAAAA4Dis7AIAAAAAHMdt9QBgD88//7zq6+v12GOPqaioyOrh5Lyf/vSn2r9/vwzDUHFxsW6++Wb5/X6rh5Xz6uvr9dprr8ntdquiokI333yzvF6v1cPKab/5zW/0f/7P/9F7772n73znO1q6dKnVQ8ppLS0teuKJJxSPx3X55ZfrmmuusXpIOe+RRx7RgQMHVFxcrPvvv9/q4UBSKBTSww8/rM7OThmGoY0bN6qmpsbqYeW8U6dO6a677lI0GlUsFtMll1yiLVu2WD0sSIrH49q2bZv8fv+UuzITdqFQKKSDBw8qEAhYPRQMuvrqq3XddddJkoLBoHbt2qUbb7zR4lFh1apV2rp1q1wul5588kk988wzuuGGG6weVk5btGiRvvKVr+hHP/qR1UPJefF4XI8//ri+9rWvqaysTNu3b1dlZaUWLlxo9dBy2mWXXabNmzfr4YcftnooGORyuVRXV6clS5aot7dX27Zt06pVq/hdsdisWbN01113qaCgQNFoVHfeeadWr16t8847z+qh5bxgMKgFCxaot7d3ys+ljBn6l3/5F33+85+XYRhWDwWDPB5P8s8nT55kbmziwgsvlMvlkiSdd955CofDFo8ICxcu1Pz5860eBiQdOXJE8+bNU0VFhdxuty699FI1NTVZPaycd/7558vn81k9DAxRWlqqJUuWSJIKCwu1YMEC/n9iA4ZhqKCgQJIUi8UUi8V4/2UD7e3tOnDggC6//PIzej4ruzmuqalJfr9fZ599ttVDwTD/9m//ppdeekkej0d33XWX1cPBMHv27NGll15q9TAA2wiHwyorK0t+XFZWprfeesvCEQH219bWpj/84Q8655xzrB4KNFChcscdd+iDDz7QlVdeqXPPPdfqIeW8H//4x7rhhhvOaFVXIuzmhLvvvludnZ0j7r/uuuv0zDPP6Gtf+1rmB4Vx56WqqkrXX3+9rr/+ej3zzDP693//d/aNZMhE8yJJTz/9tFwulz7xiU9keHS5aTJzAgDZpq+vT/fff7++8IUvpFR0wTp5eXm677771N3dre9973t69913tXjxYquHlbNee+01FRcXa8mSJWptbT2jv4OwmwO+/vWvj3r/u+++q7a2Nt1+++2SBsoE7rjjDt1zzz0qKSnJ4Ahz01jzMtwnPvEJ3XPPPYTdDJloXl588UW99tpruvPOOylvypDJ/q7AWn6/X+3t7cmP29vbaawHjCEajer+++/XJz7xCX3sYx+zejgYxuv1asWKFWppaSHsWujNN9/U/v371dzcrFOnTqm3t1cPPvigbr311kn/HYTdHLZ48WI99thjyY9vueUW3XPPPXRjtoH3339fZ511lqSBUnP2JNpDS0uLnnvuOX3zm9/U7NmzrR4OYCtLly7V+++/r7a2Nvn9fv3617+e0hsSIFeYpqlHH31UCxYs0Kc+9Smrh4NBx48fl8vlktfr1alTp3Tw4EH95V/+pdXDymlbt27V1q1bJUmtra16/vnnp/z/FcIuYEP/+q//qvfff1+GYSgQCNCJ2SYef/xxRaNR3X333ZKkc889l7mx2Kuvvqp//ud/1vHjx7Vz506dffbZ+upXv2r1sHKSy+XSl770Je3YsUPxeFzr16/XokWLrB5WznvggQf0xhtv6MSJE7rpppu0ZcsWbdiwweph5bQ333xTL730khYvXpysrrv++ut10UUXWTyy3NbR0aGHH35Y8Xhcpmnq4x//uD760Y9aPSxMk2Gapmn1IAAAAAAAmEkcPQQAAAAAcBzCLgAAAADAcQi7AAAAAADHIewCAAAAAByHsAsAAAAAcBzCLgAAAADAcQi7AABkqSeffFLf/e53kx/X19frW9/6lqLRqIWjAgDAHgi7AABkqb/8y79Ua2ur/vCHP6ihoUEtLS36yle+IrfbbfXQAACwnGGapmn1IAAAwJn5+c9/rldffVU9PT361re+pUAgoJ6eHt19993685//rB07dmjx4sVWDxMAgIxjZRcAgCz2kY98RO+++662bt2qQCAgScrPz9f27dt1ySWXWDw6AACsQ9gFACBLvfvuu3rssce0bt067d27N3m/2+1WUVGRhSMDAMB6hF0AALJQOBzWvffeq7/7u7/T3/7t3+rdd99Va2ur1cMCAMA2CLsAAGSZnp4e3XPPPbrqqqtUWVmp2bNn69Of/rR++tOfWj00AABsgwZVAAA41MMPP6xPf/rTNKgCAOQkwi4AAA50zz336I9//KMCgYCuuOIKXXbZZVYPCQCAjCLsAgAAAAAchz27AAAAAADHIewCAAAAAByHsAsAAAAAcBzCLgAAAADAcQi7AAAAAADHIewCAAAAAByHsAsAAAAAcBzCLgAAAADAcQi7AAAAAADH+f8BegkpDTe4mNwAAAAASUVORK5CYII=",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plot_ds(data,m_star,q_star)"
]
},
{
"cell_type": "code",
"execution_count": 32,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Valore della funzione loss per la soluzione: 0.0974\n"
]
}
],
"source": [
"print(f'Valore della funzione loss per la soluzione: {cost_history[-1][0]:.4f}')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Stochastic gradient descent\n",
"\n",
"Nella stochastic gradient descent, a differenza del caso precedente, la valutazione del gradiente effettuata ad ogni iterazione fa riferimento a un solo elemento $\\mathbf{x}_i$ del training set. Quindi si ha \n",
"\n",
"$$\n",
"\\theta^{(k+1)}=\\theta^{(k)}-\\eta J'(\\theta^{(k)};\\mathbf{x}_i)\n",
"$$\n",
"\n",
"e, per i singoli coefficienti,\n",
"\n",
"$$\n",
"\\theta_j^{(k+1)}=\\theta_j^{(k)}-\\eta\\frac{\\partial J(\\theta;\\mathbf{x}_i)}{\\partial\\theta_j}\\LARGE\\vert_{\\small\\theta=\\theta^{(k)}}\n",
"$$\n",
"\n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"La discesa del gradiente batch valuta il gradiente per tutti gli elementi, anche quelli simili tra loro, a ogni iterazione,\n",
"eseguendo così un insieme ridondante di operazioni. SGD risolve questo problema effettuando una sola valutazione, e quindi\n",
"operando in modo più veloce.\n",
"\n",
"Al tempo stesso, però, mentre i valori della funzione di costo nel caso di BGD decrescono con regolarità verso il minimo locale,\n",
"applicando SGD si riscontra un andamento molto più irregolare, con fluttuazione della funzione di costo intorno a un trend\n",
"complessivo di decrescita, ma con incrementi locali anche significativi. Questo da un lato può non risultare negativo, in quanto\n",
"le oscillazioni locali posso consentire di uscire dall'intorno di un minimo locale, proseguendo la ricerca di nuovi minimi. Al\n",
"tempo stesso, l'oscillazione locale rende difficile la convergenza finale verso il minimo.\n",
"\n",
"Questa oscillazione si riscontra anche nell'andamento dei valori dei coefficienti. Si noti comunque che, considerando la sequenza dei valori della funzione di costo assunti al termine di ogni *epoca* (sequenza\n",
"delle iterazioni che considerano tutti gli elementi del dataset), emerge la tendenza di decrescita di fondo. \n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"In termini di codice, il metodo stochastic gradient descent si presenta come:\n",
"\n",
"```python\n",
"for i in range(n_epochs):\n",
" np.random.shuffle(data)\n",
" for k in range(dataset_size):\n",
" g = evaluate_gradient(loss_function, theta, X[k])\n",
" theta = theta-eta*g\n",
"```\n",
"\n",
"\n",
"Nel caso della logistic regression, l'aggiornamento a ogni iterazione risulta quindi\n",
"\n",
"\\begin{align*}\n",
"\\theta_j^{(k+1)}&=\\theta_j^{(k)}+\\eta(t_i-f(\\mathbf{x}_i;\\theta^{(k)}))x_{ij}\\hspace{1cm}j=1,\\ldots,d\\\\\n",
"\\theta_0^{(k+1)}&=\\theta_0^{(k)}+\\eta(t_i-f(\\mathbf{x}_i;\\theta^{(k)}))\n",
"\\end{align*}"
]
},
{
"cell_type": "code",
"execution_count": 52,
"metadata": {},
"outputs": [],
"source": [
"def stochastic_gd(X, t, eta = 0.01, epochs = 1000):\n",
" theta = np.zeros(nfeatures+1).reshape(-1,1)\n",
" theta_history = []\n",
" cost_history = []\n",
" for j in range(epochs):\n",
" for i in range(n):\n",
" delta = - eta * gradient(theta,X[i,:].reshape(1,-1),t[i])\n",
" theta = theta + delta\n",
" #e = (t[i] - f(theta, X[i,:]))[0]\n",
" #theta = theta + eta * e * X[i,:].reshape(-1,1)\n",
" theta_history.append(theta)\n",
" cost_history.append(cost(theta, X, t))\n",
" theta_history = np.array(theta_history).reshape(-1,3)\n",
" cost_history = np.array(cost_history).reshape(-1,1)\n",
" m = -theta_history[:,1]/theta_history[:,2]\n",
" q = -theta_history[:,0]/theta_history[:,2]\n",
" return cost_history, theta_history, m, q"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Applicando il metodo è necessario ancora specificare il valore di $\\theta$ e il numero di epoche. Per la struttura dell'algoritmo, si avranno allora un numero di iterazioni pari al numero di epoche moltiplicato per la dimensione $n$ del dataset."
]
},
{
"cell_type": "code",
"execution_count": 53,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"tempo di esecuzione: 1.720 secondi\n",
"50000 passi\n",
"50000 gradienti calcolati\n"
]
}
],
"source": [
"start_time = time.time()\n",
"cost_history, theta_history, m, q = stochastic_gd(X, t, eta = 0.01, epochs = 500)\n",
"print(f\"tempo di esecuzione: {time.time()-start_time: 4.3f} secondi\")\n",
"print(f\"{len(m)} passi\")\n",
"print(f\"{len(m)} gradienti calcolati\")"
]
},
{
"cell_type": "code",
"execution_count": 54,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABQgAAAGoCAYAAAAKMwiTAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAAC7sElEQVR4nOz9d3Rc933n/z9vmUElCJIgCYINbGAnxV7VoUKJsh3GKyf22mvZXudkN5usk/PN8W/3a+/32Mk3ysb5buKyWVuOYyvuRY6sRomQqMLexN4J9g6C6MDM3PL742IGAAGQIAlw5gKvxzk+Ju69M3hfXIHlhffn8zZ83/cRERERERERERGRAclMdwEiIiIiIiIiIiKSPgoIRUREREREREREBjAFhCIiIiIiIiIiIgOYAkIREREREREREZEBTAGhiIiIiIiIiIjIAKaAUEREREREREREZACz011AT124cCHdJdyVoqIiqqqq0l2GoGeRSfQsMoeeRebQs8gc/eVZlJSUpLuEPhH2vxtmkv7y3/pAomcWLnpe4aNnFj56Zj3X3d8N1UEoIiIiIiIiIiIygCkgFBERERERERERGcAUEIqIiIiIiIiIiAxgCghFREREREREREQGMAWEIiIiIiIiIiIiA5gCQhERERERERERkQFMAaGIiIiIiIiIiMgApoBQRERERERERERkAFNAKCIiIiIiIiIiMoApIBQRERERERERERnAFBCKiIiIiIiIiIgMYAoIRUREREREREREBjAFhCIiIiIiIiIiIgOYAkIREREREREREZEBTAGhiIiIiIiIiIjIAKaAUEREREREREREZABTQCgiIiIiIiIiIjKAKSAUEREREREREREZwBQQioiIiIiIiIiIDGAKCEVERERERERERAYwBYQiIiIiIiIiIiIDmAJCERERERERERGRAUwBoYiIiIiIiIiIyACmgFBERERERERERGQAU0AoIiIiIiIiIiIygCkgFBERERERERERGcAUEIqIiIiIiIiIiAxgdroLEBEREZH+78yZM3zve9/DNE2Ki4v54z/+YwzDSJ174YUXAPjCF77A+PHj01mqiIiIyICjDkIRERER6XMlJSX81V/9FV/72tcAOHHiROrcL37xC/7sz/6ML33pS/ziF79IV4kiIiIiA5YCwgzy/oGL/O83DpBwvHSXIiIiItKrbNvu8OuioqLUx42NjRQVFTF06FAaGxvTUZ6IiIjIgKYlxhlkx4mrXLzexIXrjYwfPijd5YiIiIj0qh07dvCzn/2M4uJi8vPzU8d937/laysqKqioqADg+eef7xAwyt25MbCVzKdnFi56XuGjZxY+emZ3TwFhBok7LoA6CEVERKRfWrhwIQsXLuQHP/gBu3btYvHixZ2uSe5LeKPy8nLKy8tTH1dVVfVZnQNNUVGRvp4ho2cWLnpe4aNnFj56Zj1XUlLS5XEFhBkk3hoMxhUQioiISD+TSCSIRCIA5OTkEI1GU+fy8/O5du0ahmGQk5OTrhJFREREBiwFhBkknmjtIHQVEIqIiEj/snv3bl599VUARo0axbhx43jppZdYs2YNzz77LP/wD/8AwOc///k0VikiIiIyMCkgzBC+76c6B7XEWERERPqbRYsWsWjRog7H1qxZA8D48eP5+te/no6yRERERARNMc4YjuuT3J47uRehiIiIiIiIiIhIX1NAmCHah4JaYiwiIiIiIiIiIveKAsIM0X4wiYaUiIiIiIiIiIjIvaKAMEPEEu06CBUQioiIiIiIiIjIPaKAMEO07xrUEmMREREREREREblXFBBmiPZ7EGqJsYiIiIiIiIiI3CsKCDNEhw5CTTEWEREREREREZF7RAFhhlAHoYiIiIiIiIiIpIMCwgyhPQhFRERERERERCQdFBBmiPYdhJpiLCIiIiIiIiIi94oCwgyhDkIREREREREREUkHBYQZIp5oCwW1B6GIiIiIiIiIiNwrCggzRKzDEmNNMRYRERERERERkXtDAWGGaN81GNcSYxERERERERERuUcUEGYIDSkREREREREREZF0UECYIToMKXE8fN9PYzUiIiIiIiIiIjJQKCDMEPFEWwehDzieAkIRERERERERkXTzWxrxG2rTXUafstNdgARunFyccDwilvJbEREREREREZF08GPNuLvfw92/EYDoZ/8HhtU/o7T+eVchFL9hcnHC8SArTcWIiIiIiIiIiAxQvpPAPbgFd9d6iDUBYJbNB7P/NnIpIMwQyQ5C0wDPh7jr3uIVIiIiIiIiIiLSW3zPwzv+Ic72ddBQA4AxtBh7+TOYoyelt7g+poAwQyQDwtysCA0tCU0yFhERERERERG5B3zfxzt7BHfrWvzqS8HB7DzsRY9jTluE0Y87B5MUEGaIWOsS4/xsm4aWRKc9CUVEREREREREpHd5l8/gbH0D/+LJ4IBpYs1ajjX/UYysnPQWdw8pIMwAnu+nOgZzs4JHknAVEIqIiIiIiIiI9AWv5irutjfxTu5PHTPHTcNa9jRm4fA0VpYeCggzgNMaDkYsk6yIBaAlxiIiIiIiIiIivcxvrMPZ+Tbe4e3gB9mLUTgCe/lqzLFlaa4ufRQQZoDkcuJoxCRima3HNKRERERERERERKQ3+LEW3D3v4e7bAE4iOBjNxlr4GNaMpRiWld4C00wBYQZI7j8YtS0idhAQqoNQREREREREROTu+K6De2AL7ofvQEtTcNAwMGcsxV5YjpGdl94CM4QCwgyQ6iC0TaJ26xJj7UEoIiIiIiIiInJHfN/DO7YHZ8dbUH89ddwYPTlYTjy0OI3VZR4FhBkgnuogbL/EWAGhiIiIiIiIiMjt8H0f/+xRnG1r8a9dTB03CoYFA0jGT8cwjDRWmJkUEGaAtg5Ci2hyibE6CEVEREREREREesy7chZn6xv4FyrbDkaysOY/gjV7BYalGKw7ffqV+eEPf0hlZSUTJkzgueeeSx3/h3/4B2pqakgkEsTjcf7u7/6uL8vIePFE0EGYpT0IRURERERERERui1N9mcS6X+BV7m131MCcthB70eMYuYPSVltY9FlAWFlZSUtLC1/72td44YUXOH78OJMnTwbgv/7X/wrAtm3bqKysvMm7DAzt9yDUEmMRERERERERkVvzm+pxdr7N5cPbwXNTx43iUuwVz2AWjU5jdeHSZwHhsWPHmDNnDgCzZ8/m6NGjqYAwadu2bTz11FNdvr6iooKKigoAnn/+eYqKivqq1HvCtu1u7yF6oRGAQfm5DC0sAMC0I6G/50x1s2ch95aeRebQs8gcehaZQ89CREREJDP58RbcPR/g7v0AnHjbifxC7KVPYU6crX0Gb1OfBYSNjY2MHDkSgNzcXM6dO9fhvOM4nDlzhokTJ3b5+vLycsrLy1MfV1VV9VWp90RRUVG391BdUweA7yaItTQDUN/YFPp7zlQ3exZyb+lZZA49i8yhZ5E5+suzKCkpSXcJIiIiIr3Cdx28Q1txdr4DLY2p40Ykinnfg1hzHsCwI2msMLz6LCDMzc2lqakJgObmZnJzczucP3jwIDNmzOirTx8qXS0x1h6EIiIiIiIiIiLg+x7eib0429+CuuoO58wp8xjx5Ce5Hne7ebX0hNlXb1xWVsb+/fsB2LdvH2VlZR3Ob9u2jcWLF/fVpw+VWOuQkvZTjLUHoYiIiIiIiIgMdN65YyRe+jbO2z/vEA4aI8YS+dh/IvLIJ7AKhqSxwv6hzzoIJ06cSCQS4atf/SqlpaUUFRXx0ksvsWbNGnzf5+jRo3zuc5/rq08fKh06CFsDQsdVQCgiIiL9x7Fjx/jRj36EYRhMmjSJz372s6lzv/zlL9m+fTt5eXksXLiQ1atXp69QERERyQje1XM4W9finz/e8URuAfaSVZhT5mIYfdb3NuD0WUAI8Nxzz3X4eM2aNQAYhsH//J//sy8/dajEHXUQioiISP82fPhwvvrVrxKNRvnmN7/JmTNnGDduXOr8pz/96dSAOxERERm4/NprONvfwjuxp+MJy8aa+wDWfQ9iRLLSU1w/1qcBofRMxz0ILQASrtbOi4iISP9RWFiY+rVlWZhmx5/4/+QnP+Hll1/m05/+NKWlpfe2OBEREUk7v7kBZ+fbeIe2gtexacqcOBt76SqMQUPTVF3/p4AwAyQ7CLMiFhHbaD2mDkIRERHpf06fPk1dXR1jxoxJHXvqqad49tlnuXjxIv/0T//E1772tU6vq6iooKKiAoDnn3+eoqKie1Zzf2fbtr6eIaNnFi56XuGjZ3ZvebEWGra+RcPWN/HjsQ7nIiPHMfjxPyBrXFk3rw7omd09BYQZoH0HYTTZQaiAUERERPqZhoYGfvCDH/ClL32pw/H8/HwARo0a1e1ry8vLKS8vT31cVVXVN0UOQEVFRfp6hoyeWbjoeYWPntm94bsO3qHtOLvehuaGjidz8rEXP4FRtoB606T+Fs9Dz6znSkpKujyugDADxFNTjNuGlMQ1pERERET6Edd1+da3vsWnP/3pDsuNAZqamsjNzaWurg5X26yIiIj0a77v4Z3Yh7P9Lai71vGkaWHNXoE1/xGMaHZ6ChygFBBmgLYOQouIFQSECcfD930Mw0hnaSIiIiK9YvPmzRw/fpwf//jHAHzyk59kw4YNfO5zn+PHP/4xZ8+exfM8PvWpT6W5UhEREekr3vnjwWTiq+c6nTNLZ2AvfQpjsJYKp4MCwgyQmmIcMTFNA9s0cDwfx/VTexKKiIiIhNnKlStZuXJlh2NlZcF+Ql/84hfTUZKIiIjcI17VhSAYPHe00zljyEjs5asxx0xJQ2WSpIAwA8TadRACRGwTJ+4Sd9zUkmMRERERERERkTDx66pxtr+Fd3x355NZudiLHsOcvhjDtO55bdKRAsIMkOogbA0Do7ZFc9wloX0IRURERERERCRk/OYG3F3rcQ9uAe+G/YUNE2vmUqwF5RjZuekpUDpRQJhmXutSYgNS+w8muwY1yVhEREREREREwsJPxHH3fYC7+31IxDqdN8aUBcuJh4xIQ3VyMwoI0yw5rThim6mBJMmgUJOMRURERERERCTT+a6Ld2Q7zs63oam+03ljcBHWstWY46ZqGGuGUkCYZm3Li9vW26uDUEREREREREQyne/7eCf34257E7+2qvMF0WysBY9izVyGYSmCymR6OmkWTyQHlLQNI4kmOwgVEIqIiIiIiIhIBvIunAgmE1852/mkYWBOW4y96DGMnPx7X5zcNgWEaZbqIIx01UHodvkaEREREREREZF08K5dxN26Fu/skS7PGyUTsZc/gzls1D2uTO6GAsI0S3YJduggTAaE2oNQRERERERERDKAX1+Ns30d3rHdgN/5gkFDsZc+hTlhpvYZDCEFhGmW7CDMar8HoWW1nlNAKCIiIiIiIiLp4zc34n64HvfAZvC6WOloR7HmP4w1eyWGHbn3BUqvUECYZrEu9iDUkBIRERERERERSSc/EcfdtxF3z7sQj3V5jVm2AHvxExh5Bfe2OOl1CgjTrG2KceclxnEtMRYRERERERGRe8j3XLwjO3F2rIOm+uCgHQHHIbm02Bg5Hnv5aswRY9NXqPQqBYRp1rYHYVdDSsIXEMYSLr/bfpoFE4uYWKyfIIiIiIiIiIiEge/7eKcO4G57E7/manAwOw/woaUp+DhvMPbSVZiT5mqfwX5GAWGadTWkJGIlh5SEb4rx0Qu1bDt2hYaWhAJCERERERERkRDwLlTibF2Lf+VMcCB3EEYkC7+hBlwH7AjW3Aew5j6IEYmmtVbpGwoI0yy1xDjS1kEYDXEHYUvc6fD/IiIiIiIiIpKZvOpLuFvX4p05HBzIzsMoGIZfdw2/tgoAc/Jc7CWrMPIL01eo9DkFhGnW1R6EYZ5iHGu9nzDWLiIiIiIiIjIQ+PU1ODvW4R3dBfgQiWIWT8BvqEl1ERpFo7FXPINZXJrWWuXeUECYZvFE5z0Iw91BGASEsUT4lkeLiIiIiIiI9Gd+SxPuh+/iHtgULB02TcxxM/CdON7ZI8FFuYOwFz+BWTYfwzBv/obSbyggTLMu9yAM8RTjZAehAkIRERERERGRzOA7Cdz9G3E/fBfiLQCYpTMgmoNXuRecBJgW1pz7seY9jBHNSm/Bcs8pIEyz5BLjrHZ7EKaGlIS4g1BLjEVERERERETSy/dcvKO7cHasg8Y6AIzRkzGHj8Y9vgcaagAwJ8zEXvoURsGwNFYr6aSAMM266iBM/joZHoZJrPV+Yo6L7/saey4iIiIiIiJyj/m+j3f6IO7WN/FrrgBgFJVgTpqLd+Yw7u73gmNDi7GXP4M5elI6y5UMoIAwzbocUtK6H2EijEuMWzsIfT+ov/3eiiIiIiIiIiLSt7xLp3C2vIF/+XRwYNBQrFnL8a8HE4vBh+w87EWPY05bhGFqn0FRQJh2bR2E/WNISaxd12Ms4SogFBEREREREbkHvOuXcbeuxTt9KDiQnYd134Pgurg71kEiBqaJNWsF1vxHMbJy0luwZBQFhGnWZQdhcg/CEHYQJvcgBIglPAbp9xsRERERERGRPuM31OLsWId3dGewnM+OYs1ZiVE4HHdHBX7dNQDMcdOwlj2NWTg8zRVLJlJAmGZddRCmphiHvYMwhHsoioiIiIiIiISBH2vC3f0e7r6N4DpgmpjTl2BNmIWz+138Xe8AYBSOwF6+GnNsWZorlkymgDDNYonOHYTRfjDFGCCeUEAoIiIiIiIi0pt8J4F7YDPuh+sh1gyAOXE21pz7cY99SOL1H4DvQTQba+FjWDOWYlja/ktuTgFhmqU6CCNt36y23bbE2PN9zBBNAr5xD0IRERERERERuXu+5+Ed24WzYx001AJglEzEXvQE3tVzJN74lyAwNAzMmcuwF5ZjZOeluWoJCwWEaeR6Pq7nYxhgm20hoGkY2JaB4/o4IZoE7Hp+h67HWAg7IEVEREREREQyie/7eGcO425di3/9MgDG0GLsJavAMHDe+w1+zZXg+OjJwXLiocXpLFlCSAFhGiUHlGTZFsYNXYJR28JxHRJOeALC+A17DqqDUEREREREROTOeZdO42x9A//SqeBAfiH2oicwho/G3fI63pnDwfGCYdjLnsIcP6NTviDSEwoI0yieSA4oMTudS04yjjseYWkIbr//IHQODEVERERERETk1rzrV3C3vYl36kBwIDsXa94jWFPuw939Ls57vwLPg0gW1vxHsGavwLAU8cid0389aZQM0LrqEIy224cwLG7sGIwlwlO7iIiIiIiISLr5jbU4O97GO7IdfB/sCNbslVhz7ser3Ef8l/8LWhoBA3PawqCbMHdQusuWfkABYRolB5REuuogtMM3ybilU0CoDkIRERERERGRW/Fjzbi738PdvxGcBBgm5vTF2Asexa+9SuLVF/CvXQTAKC7FXv4M5vDRaa5a+hMFhGnU1kF4kyXGoe4gVEAoIiIiIiIi0h3fSeAe3IK7az3EmgAwJ8zCWvwEhmnibHwZ72TrMuP8QuylT2FOnK19BqXXKSBMo2QHYVak8xLjtg7C8IRsnQLCENUuIiIiIiIicq/4nod3/EOc7eugoQYAY9QE7CWrMIaMxP1wPe7eD8Bzg2XG8x7CmvMAhh1Ja93SfykgTKPYTToIo1YQGsZDtMQ4GRBGbZO444WqdhEREREREZG+5vs+3tkjuFvX4ldfAsAYOhJrySrMsWV4R3eReOtfoakeAHPKPOwlT2LkDU5n2TIAKCBMo2SA1tWQkjDuQZgMPAtyo1TVtWiJsYiIiIiIiEgr7/IZnK1v4F88GRzIL8Re9Bjm5Hn4V86S+O3/xr96DgBjxNhgn8GR49JYsQwkCgjTKJ64SQdhCKcYt8RbA8KciAJCEREREREREcCruYq7/S28yn3BgaxcrPkPY81YCi2NOOt/gXd8T3AutwB7ySrMKXMxjM5ZgUhfUUCYRjftIEwOKQljB2FOtPXj8NQuIiIifevYsWP86Ec/wjAMJk2axGc/+9nUuerqar71rW+RSCR49tlnmTNnTvoKFRER6SV+Yx3OrrfxDm0H3wPLxpq9Euu+B8G0gqnFe94LphZbNtbcB7DuexAjkpXu0mUAUkCYRqkpxpEuphiHcEhJqoMwNwgI4+ogFBERkVbDhw/nq1/9KtFolG9+85ucOXOGceOCZVP/9m//xic+8QlKS0t5/vnnFRCKiEio+fEW3D3vB0NGnAQYBua0RdgLyyG3AO/EXpytr0NDLQDmxNnYS1dhDBqa5splIFNAmEY36yBMLjGOh2iJcbJjsCA3mKqkJcYiIiKSVFhYmPq1ZVmYZtsPSM+ePcvUqVMxDIPs7GyamprIzc1NQ5UiIiJ3zncd3INbcHeth5ZGAMzSGViLn8QcMgLv6jmcip/iXzoNgFFUgr1sNWbJxHSWLQIoIEyrtoCwiw5CK4RDSuI3LjFWQCgiIiIdnT59mrq6OsaMGZM65nkehmEAkJub22VAWFFRQUVFBQDPP/88RUVF967ofs62bX09Q0bPLFz0vMLndp+Z73s0H9hG3bv/hltbBUB07BQKHvl9ssZMxm2opW79S8T2bgJ8zLxBFDy0htw5KzBM7TPYG/R9dvcUEKZRaolxVwFha1dhqALC1vsZlBPBMMBxfVzPxzKNNFcmIiIimaChoYEf/OAHfOlLX+pwPBkOAjQ3N3fZPVheXk55eXnq46qqqr4rdIApKirS1zNk9MzCRc8rfHr6zHzfxz93LJhMfO0iAMaQEViLn4Tx06lzHdx1v8b98B1IxMG0sGavwJr/CM3RbJqrq/v6VgYMfZ/1XElJSZfHFRCmUbKDMOsmS4zDOMU4K2KRZVu0JFzijktOVP+ZiYiIDHSu6/Ktb32LT3/60x2WGwOMGzeOo0ePMm7cuG4DQhERkUziXT2Hs+UN/AsnggN5g7EXPoZZNh8MA+/UAZzNr0N9EAKapTOwlz6FMVhdbpKZlNykUXKPvpstMQ7jFOPsiEXUNmlJuMQSCghFREQENm/ezPHjx/nxj38MwCc/+Uk2bNjA5z73OT760Y/y7W9/m3g8zrPPPpvmSkVERLrn11bhbHsLr3JvcCCajTXvYaxZyzHsCN61izibXsG/UAmAMWQk9vLVmGOmpLFqkVtTcpNGiZsMKWmbYhyegLBDB2HEguYEsUR46hcREZG+s3LlSlauXNnhWFlZGQDDhg3jf/yP/5GOskRERHrEb6rH2fk23uFt4Hlg2VizVmDNexAjKxe/uYHEpleD874PWbnYix7DnL4Yw+z8b36RTKOAMI1SexBGOncQtk0xDs+gj/YdhFmR4DdATTIWERERERGRsPLjMdw97+Pu/QCcOBgG5tSF2AvLMfIL8V0HZ+8HuDvfhngLGCbWrGVYC8oxsrVlhoSHAsI0it+0gzBcQ0pczyfheBhG0P2YDAjjmmQsIiIiIiIiIeO7Dt6hrTg734GWRgDM8dOxFj+JOXQkAO6Zw7ibXsVvnVxsjCnDXv405pCRaatb5E4pIEyjm+1BGA3ZHoTJIDDLtjAMI3VPLeogFBERERERkZDwfY+mA9uIv/NrqAsGjBgjx2MvWYU5qhQA7/oVnM2v4p89GpwfXIS1bDXmuKkYhpGu0kXuigLCNLp5B2G4phi333+w/f+HJeAUERERERGRgc07dwxn61quV50HwCgcjrXkSczxMzAMAz/WhLujAvfAFvC9YEDJgkexZi7DsBSvSLjpv+A0agsIu59iHJYlxsluyOxkQGhrD0IRERERERHJfN7V8zjb1uKfOwaAmV+IOf8RzKkLMEwL33NxD27D2bEOWpqCfQinL8Fe9BhGTn6aqxfpHQoI08RxPTzfxzQMbKv7ISWh6SBMdN1BGNaA0PN84o5LdlTfIiIiIiIiIv2RX3cNZ/tbeMf3BAei2Vj3PcSIh56hurYeaO0q3PwqfvVlAIySidjLV2MOK0lX2SJ9QulHmiS7B7O6mGAMbUuMwzLkI3ZDQJiczByW+m/0r+8d49iFGv7bx+eTm6VvExERERERkf7Cb27A3fUO7sGt4LlgWlizlmPNewgjOw8zkoVfexJny+t4pw4GLxo0FHvpU5gTZmqfQemXlHykSTI462r/QSDVVei4fqrTMJPdGBC2LTEORwfkjc5fayDmeFyrbyE3Sy3jIiIiIiIiYecnYrh7P8Dd8z4k4oCBWTYfe+FjGIOGBNfEW6h9+1fEt1UE4aEdxZr/MNbslRh2JL03INKHFBCmyc32HwQwDYOIZZJwPRzHIxrpOkjMFJ32IEwuMQ5pB2FyybSmMIuIiIiIiISb77p4h7fh7HwbmhsAMMdNw1r8JOaw4uAaz8M7uhNn25vEk9eULcBe/ARGXkHaahe5VxQQpklbB2HXASEEy4wTrkfczfyAsD/tQej7fqru5HRmERERERERCRff9/Eq9+FuexO/7hoAxoix2EtWYZZMTF3nXTyJs+kV/KoLAETHTMJf9CTmiLFpqVskHRQQpkk8kewg7D74i9omTbFwTDK+sYMwGXzGQ7jEOO54eH7w67B2QIqIiIiIiAxk3vnjOFvX4l89B4AxuCjoGGy3h6Bffx1nyxt4lXuDF+UNxl66iqIlj3Lt2rV0lS6SFgoI0yTVQdjNkBKAiJUc9JH5IVtbB6HZ+v/hXWLcvmswpg5CERERERGR0PCqLgTB4LmjwYHcQdgLyjGnLcQwg3+n+ok47u53g70IXQfsCNbcB7DmPogRiWoIiQxICgjTJOb0rIMQIOFmfkjV/ZCSzK/9Ru33HdQehCIiIiIiIpnPr6vG2f4W3vHdwYFoFtbch7Bmr8CIRINrfA/v2B6cbW9AYx0A5uS52EtWYeQXpqdwkQyhgDBNerIHYXKScZiWGLftQWh2OB4mLQkn9esw1i8iIiIiIjJQ+M2NuLvewT24JZg6bFpYM5dhzXsYIycvdZ135SzOxlfwr5wBwCgajb3iGczi0jRVLpJZFBCmSbxHHYRWh2szWax1r8Ebh5SEofYbtV9irA5CERERERGRzOMn4rj7NuDufg8SMcDAnDIPe9FjGIOGtl3XWIuzdS3esQ+DA7mDsBc/gVk2H8PovmFHZKBRQJgmbQHhzacYAyTczA/Zkl13bUNK+scS4zDWLyIiIiIi0l/5rot3ZAfOzgpoqgfAHDsVa8kTmMNK2q5zErh7P8D9cD04iaCzcM79QWdhNCtd5YtkLAWE94jv+x0+jieSS4xv0kEYqiXGN3YQti4xdlx83w/VJq8t8bYlxuogFBERERERST/f9/FO7sfd9iZ+bRUAxvAx2EtWYY6e1PG6yn04W16HhhoAzAkzsZc+hVEwLB2li4SCAsJ7YP+ZaravP87vLxlHQW6wOertdBCGYZluclpxsoPQMk1s08DxfBKud9MgNNOog1BERERERCRzeBcqcba+gX/lLABGwTCsxU9gTpzdoRnFqzqPs+lV/Isng+uGFmMvf6ZDgCgiXVNA2Mc8z+eNXWe4UtvCmSu1/MHKSUwdXdijISVhmmKc3Lcv2UGY/LUTc4gnQhYQxhUQioiIiIiIpJt37SLutrV4Z44EB3LysReUY05bhGG1/RvTb6oPJhgf3gH4kJ2Hvejx4DpT+wyK9IQCwj5mmgZ/9PgMfrP1DAfPVPH9isM8PKskFUJFI90HZ2HuIITg3hpjDi0Jl/ycSLpKu23tOwi1xFhEREREROTe8uuv4+xYh3f0Q8CHSBRr7oNYc1ZiRNr2D/RdB3f/JtydbweDSkwTa+YKrAWPYmTlpO8GREJIAeE9UJAb5S9+fwm/encvb+4+y/r9F1Lnsm7SWRdp/YlIpu9B6Ho+CcfDMNpCTWg/yThcIVtzuz0I1UEoIiIiIiJyb/gtjbgfrsfdvxk8NxgsMmMJ1vxHMHLy267zfbzTh3A3v4Zfdw0Ac9xUrGWrMQuHp6t8kVBTQHiPmKbBo3NGM3HkIH7y/nFqm+JA/9iDMBkAZtlWh/0fsuzkoJLMrv9GMXUQioiIiIiI3DN+Io67fyPu7nchHgPAnHwf9qLHOg0W8aovBfsMnj8OgFE4HHvZasxxU+912SL9igLCe2zCyAK+9MxsXtpyktNXGygZmtvttakpxm5mB2xd7T/Y/uOwdeG134Mw4Xi4no9lhmcKs4iIiIiISBj4not3ZCfOjgpoqgPAGDMFe8mTmEWjO17b0oizowLv4FbwPYhmYy18DGvG0g77EYrInVFAmAZ52RE+/VAZvu936Li7UbKDMNOXGCcDwOwbAsLkYJJ42ALCG+qNOy45UX2riIiIiIiI9Abf9/FOHcDd9iZ+zVUAjKLRQTA4ZkrHa10X9+AW3J0VEGsGw8CcsRR74WMYOXnpKF+kX1LqkUY3CwchPFOMk4Fa5w7C1iXGYQsI426njxUQioiIiIiI3D3v4kmcLW/gXzkTHCgYir3oCcxJszGMjltweWePBsuJa64AYIyejL18NebQ4ntdtki/p9Qjg0WscOxBGOsuIGztIAzbHoTNiWBISW6WTVPMCV3AKSIiIiIikmm86ku4W9finTkcHMjOw15Qjjl9EYbVMZrwaq7ibn6t7dqCYdjLnsIcP+OWjTYicmf6NCD84Q9/SGVlJRMmTOC5555LHW9oaOB73/se9fX1zJ49mzVr1vRlGaEVscMxxbjbgDCkexDGWjsIB+dGaYo5GlQiIiIiIiJyh/yGGpwd6/CO7gLfBzuKNfcBrDn3Y0SzOl4ba8bd9Tbu/k3geRDJwpr/CNbsFZ1CRBHpXX32HVZZWUlLSwtf+9rXeOGFFzh+/DiTJ08G4Fe/+hWf+MQnGD169C3eZWBLLjGOZ/iQku72IEwGhMkpx2HguB6O52MaBvnZESB8AaeIiIiIiEi6+S1NuLvfDcI+1wHTDPYOnP8IRu6gjtd6Ht7h7Tjb34KWRsDAnLYQe9ETna4Vkb7RZwHhsWPHmDNnDgCzZ8/m6NGjqYDw7Nmz/Pa3v+XatWv84R/+IWVlZZ1eX1FRQUVFBQDPP/88RUVFfVXqPWHb9m3fQ5MXBFQ+Rkbfv3UmmDZVWJDXoc6hhfUAGFY0o+q/2bOoa4oBwfLigvwcoJZodm5G1d+f3Mn3hfQNPYvMoWeROfQsREREbp/vJHD3b8T98F2ItwBgTpqDvehxjMGd/1z1LpwI9hm8dhEAo7gUe/kzmMPVUCRyL/VZQNjY2MjIkSMByM3N5dy5c6lzR44c4W//9m/Jz8/n7//+7/n617/e6fXl5eWUl5enPq6qquqrUu+JoqKi276HxvpmAJpbEhl9/9XXg4DQdzrWmYgF9dfWN2ZU/Td7FlfrgpqjtonhBZ2DV6trqKqK3rP6BpI7+b6QvqFnkTn0LDJHf3kWJSUl6S5BREQGAN9z8Y7uwtmxDhqDfyMaJZOwl67CHD6m8/V11ThbXsc7uT84kF+IvfQpzImztc+gSBr0WUCYm5tLU1MTAM3NzeTm5qbOlZSUMGZM8BuEaZpdvl4gklxifIdLdOua4hgGDMrp23CrbYpxx2eZ2oMwREuMkxOMc6IW2dFw7qEoIiIiIiJyr/i+j3f6EO62tfjXW6cNDxuFvWQVxpgpncI+Px7D/XA97r4NwdJjO4I17yGsOQ9g2JE03IGIQB8GhGVlZVRUVLB8+XL27dvHQw89lDo3atQorl+/Tk5ODq6r8KU7ySnGidvcg7Al4fL23nN8cPAStmnw2UemMnnU4L4oEbjZFGOzw/kwaH8vySnMGlIiIiIiIiLSmXfpFM7WN/AvnQ4ODBqKvehxzMlzMIyODSS+7+Ed/RBn21poCrajMqfMw17yJEZe3/17VUR6ps8CwokTJxKJRPjqV79KaWkpRUVFvPTSS6xZs4Znn32Wf/zHfyQej/Pxj3+8r0oIvehtTjH2fJ8PK6t4becZ6psTALiez/crDvOpB6Ywe/zQPqmzu4AwGsIpxs2tHYTZUZssdRCKiIiIiIh04l2/jLvtTbxTB4MD2XnBtOEZS7qcNuxdOo2z6RX8q8HWY8aIscE+gyPH3cuyReQm+nRO+HPPPdfh4zVr1gAwZswY/p//5//py0/dL9hW0IrteD6e52OaXe/D4LgelZfreWv3WU5fbQBgXFE+H108nl2VVWw8fJl/fe8ov790IkvKRvR6nbFEEGB2P8U4s6cwt9eScIDgXpL3ow5CERERERER8BtqcXauwzuyE3w/WB48536suQ9gRLO7uL4GZ+tavOO7gwO5BdhLnsSccl+nDkMRSa8+DQjl7hiGQcQ2STgeCdcjywwCK9fzOXetgROX6jh+sY6TV+pwXB+A/OwITy8Yx/xJRZiGwdiifHKzIqzbc45fb66kKZbgoVklvbrpazJU67zEOHwdeO33IEztoRgPT/0iIiIiIiK9zY814e5+D3ffxmDfQMPEnLEEe8GjGLmDOl+fiOPueR93z3vgJMCygyBx3kMYkax7fwMicksKCDNc1AoCwvPVjVysbuLoxVoqL9V16morHpLLzLFDeGjmKLKjbY/VMAwev28Medk2L289xeu7zhJ3PJ6YN7bXakx1EEZv7CBs3YMwTENKWr+u2RFbHYQiIiK9qLq6mr/927/l3LlzvPjii1hW298bvvOd73D+/Hmi0Sjl5eWsXLkyjZWKiEiS7yRwD2zG/XA9xJoBMCfOxlr0OGbh8M7X+z7eib04W1+HhtrU9fbSVRiD+mbLKxHpHQoIM1zENiEG/7T2YIfjRQXZTC4uYPKowUwqLiA/++bTnlZMKyY3avOzDcd5Z995Hpg5ipxo7zz+1B6Edv/pIMxq30EYovpFREQyVX5+Pl/5ylf4xje+0eX5P/3TP6W4uPgeVyUiIl3xPQ/v2C6cHetSQZ9RMhF7ySrMEV03m3hXzwX7DLYOLDGGjQr2GSyZeM/qFpE7p4Aww40szKGmMU5ets2UUYMpGzWYyaMGMyT/9tuy500sYsvRy1RerufohVrmlg7rlRpbuhlSErFNDMBxfVzPx+pmD8VM0tZBqD0IRUREelM0GiUajXZ5zjAMvv3tb5Ofn8/nP/95hg/v3JUiIiJ9z/d9vDOHcbeuxb9+GQBjaDH2klUYY8u63KrKb6rH2bYW78guwIec/GCS8dSFGKb2GRQJCwWEGe4zD5ZR2xxn2KBszF7YN3Da6EIqL9dz+FxNrwWEsXahWnuGYRCNWMQSLnHH7bWOxb7UEg/2U8zpBx2Enudz8Nx1JowYRN4tOkxFRETS6TOf+Qz5+fkcPnyYF198kb/4i7/odE1FRQUVFRUAPP/88xQVFd3rMvst27b19QwZPbNwCcvzip8/Qe07v8E5cxQAa/AwCh78GDmzlnQ5UMR3EjRsW0f9xtfw4zEwLfIXlzNoxdOY2bn3uvxeFZZnJm30zO5e5ic2A1w0YjE8ktNr7zd9zBBe33WWw+dr8Hz/rkNH1/NJuB6G0boc+gZZtkks4RJLhCQg7KKDMKwB4ZELNfxo/VGWlI3g48vU1i8iIpkrPz8fgGnTpvGTn/yky2vKy8spLy9PfVxVVXVPahsIioqK9PUMGT2zcMn05+Vdv4K77U28UweCA9m5WPMewZq5lCbLpuladYfrfd/HO3UAZ/PrUB+cM8dPx1r2NInBRVQ3NEFD072+jV6V6c9MOtMz67mSkpIuj2d+YiO9amRhDoV5UWoa45y/1sjYovy7er/2+w921W6eFbGgOUHc8e7q89wrqeXSUZusaLiXGNc0xgGobf1/ERGRTNXU1ERubi4XLlwgLy8v3eWIiAwIfmMdzo4KvCM7wPfAjmDNXok190GMrOwuX+NduxjsM3ihEgBjyEjs5asxx0y5l6WLSB9QQDjAGIbBtNGFbDl6hcPna3ovILxheXFS2JbpJoeU5EQsbNPANAxcz8dxPWwrXPtnNLcul07+v4iISDo5jsPf/M3fcPr0af76r/+aj3/84xw+fJg1a9bwzW9+k8bGRgzD4Atf+EK6SxUR6df8WAvunvdw920AJwGGiTl9MfaCcoy8gq5f09yAs30d3uFt4PuQlYu98DHMGYsxzK7/LSgi4aKAcACaPmZIEBCeq+GxuWPu6r26238wKdq67Dg8AWEQpmVHg47I7KhFU8whlnBDGxCGtQNSRET6F9u2+cpXvtLh2IwZMwD48pe/nI6SREQGFN91cA9sxt21HmLBEmBzwkysRU9gDhlx89fsfBviLWCYWLOWYS0oxwj5PoMi0pECwgFocnEBlmlwtqqBhpYE+XcxwKK7CcZJoesgvCHwzIoEAWFLwg3doI/m1m7IsHztRURERESk9/meh3d8N872t6ChBgBj1ATsJaswR47r9nXumcO4m17Frw32dTPGlGEvfxpzyMh7UbaI3GMKCAegaMRiUnEBRy/UcuR8DQsmDb/j97rlEmM7OB6GPQg9zyfueBgEXyNou68wduEluyGTy6ZFRERERGTg8H0fd8/7uFvfSB0zho7EWrwKc9zULveQh2BoibP5VfyzwTRjY3AR1rLVN32NiISfAsIBatroQo5eqOXwuT4OCEMUsLXvhkxOdw7zJOP2HYS9MbFaRERERETCwa3ch7Ou41R4+6F/hzllHobZ9dZJfqwJd8fbuAc3g+dBNBtrwaNYM5dhWIoORPo7fZcPUNPHDOF3209z5EINrudjmXcWHt1yD8JI8IdP3Mn8gK0l0bb/YFK4A8LgfnyC+nOi+nYXEREREenPvEunSbz8T52ORz/zf2PkdD2g0vdcvEPbcHasg5YmMAzM6UuwFz3W7WtEpP9RYjBAFRVkU1SQTVVdC2eqGpgwYtAtX1NV10J+TqRDGNif9iBMLsVtf39ZrQFnGJfpNreruSWugFBEREREpL/ya68R//nfdToeWfUc5rip3b7OO3ccZ/Mr+NWXATBKJmIvX405rKTPahWRzKTEYACbNrqQDXWXOHzu+i0DwvcPXOSVHaeZMmowX3x8eur4rToIk3sQxhKZvwdhKiBsF6RlRYJfx0LQAXmjZAchhGOJt4iIiIiI3B6/pYn4L/4eWho7HLfmPYy18LHulxPXVuFseR3v1MHgwKCh2EufwpwwU/sMigxQCggHsGmjC9lw6BKHztWwan7X06s83+e1HWd4/+BFAI5drKWmMUZhXhbQvoOw6z94onZwPAwB240TjNv/OmwdhL7vd6i5pV1YKCIiIiIi4eY7CRKvfR//0ukOx40R44g8+ZnulxPHW3B3rcfdtwE8F+wo1vyHsWavxLAj96J0EclQCggHsEnFBURsk4vXm6htjDM4L9rhvON6/HLjCT48eQ3TMBg2KIurdS3sOVXNgzNHAT0fUhIPQQdbVwFhmJZIt5dwPVzPT32sDkIRERERkfDzfQ/n/ZfwDu/odC7y0T/GLB7f9es8D+/oTpxtb0JzAwBm2QLsxU9g5BX0ac0iEg4KCAcw2zKZMmowB89e5/D5GpaUjUida4k7vPjuMY5drCXLNvn0Q2W0JFx+/N4x9pysuu2AMBxLjDsPKQlrQNh8Q8dj2DogRURERESkje/7uLvfw922ttM5e8UzmDOWYphd/5vMu3gSZ9Or+FXnATBGjsNe/gzmiLF9WrOIhIsCwgFu2uhCDp69zjv7znPw7HXirkvC8ahpjFPbFCc/O8Lny6cxZlgeccclapucvdbItfoWhg3KTgV/3e5BmAzYwrTEuIspxmHrwLtxSXGzlhiLiIiIiISSe2IvTsVPOx03p8zDXvoURm7X+8n79ddxtryBV7k3OJA3GHvJKszJc7XPoIh0ooBwgJs+phDTMKhuiFHdEOtwrqggmy+UT2PYoGwAorbFjLFD2H3yGntOXeOR2aNpSQTBU7cdhMk9CEMQsLVNMW77tkiGhWGov72mGzsIQ1a/iIiIiMhA5106TeLlf+p03BhchP3gxzFHlXb5Oj8Rx939Lu6e98F1wI5gzX0Aa+6DGJFol68REVFAOMAV5mXxJ0/N5Fp9CxHLJGKbRGyLqGUysjAH2+o4fGRu6TB2n7zG7pNBQJjqIIzeYg/CMHUQtt+DsDXgDFvAdmMHoZYYi4iIiIiEg197jfjP/67Lc9byZ7Bmdr2c2Pc9vGN7cLa9AY11AJiT5mIvWYUxqLAvSxaRfkABoTC2KJ+xRV1PubrRtNGFZEcsLl5v4kptc9sehHbXAWHUDvkehNHgWyRsHYSd9iAMWf0iIiIiIgON39JI/Od/D7GmTudutZzYu3IWZ+Mr+FfOAGAUjQ72Jiwu7cuSRaQfUUAot8W2TGaOG8LOE1XsPnktFTxl3aKDMAwBW1cdhGHdgzC552BWxCKWcDt1FIqIiIiISGbwXYfEKy/gXz7d6ZwxtBh7xUcwSyZ2/drGWpyta/GOfRgcyB2EvegJzKnzMQyzy9eIiHRFAaHctvsmFLHzRBV7Tl1LBX/Z3XQQZkWCP5Tijovv+xm9GW5qD8Jo27dFsv4wBJztJe9lSF6USzXNoQs4RURERET6O9/3cN79Dd7RnZ1PRrKwFj6GNWtZ18uJnQTu3g9wP1wPTgJMC2vO/VjzHsaIZt2D6kWkv1FAKLdtyqgCcrNsrtQ2A2AYELG7/umUZZrYpoHj+TiuT8TO4ICwyynGYV1iHHQMDsnPCgJC7UEoIiIiIpIxnA/fxd22tstz5uT7guXEeQWdzvm+j1e5D2fL69BQE1xfOhN72VMYBcP6smQR6ed61HP8iU98gk2bNqU+3rVrF3/2Z3/WZ0VJZrNMk9njhqY+zrKtm3YGRpPLjDN8UElqD8L2Q0oibUNKfN9PS113IhkQFuYFPz1sDlnAKSIiIiLSH7nH9xD77pe7DAeNISOJPPNFIo/+QZfhoFd1nsQr38Op+Ck01GAMLSay+j8SeeLTCgdF5K7dtIOwqqqKK1euAHDu3DkOHjwIwO7du7l8+XLfVycZ674Jw9h6LPhvIyvS9fLipKyIRVPMIZZwyc+O3Ivy7khXexBapoltGTiuT8LxUmFnpksOKRmaHwSE2oNQRERERCR9vEunSLz8f7o+GYkGy4lnLsewulhO3FSPs/0tvMM7AB+y87AXPY45bRGGqX0GRaR33DQgXL9+Pb/+9a8B+M1vfsNvfvOb1LnRo0f3bWWS0SaOLCA/O0JDS6JDoNaVLDvz9/Hzfb/LJcYQLDNucBO0OG6IAsK2JcaAlhiLiIiIiPQx3/fxa65iFAzFsIJ/avu1VZz/7pe7fc1NlxO7Du7+Tbg734ZEDEwTa+YKrAWPYmTl9Nl9iMjAdNOAcPLkyTz++OO89dZbzJkzh1GjRgGQn5/PypUr70mBkplM02Bu6VA2Hr7cow5CgJjj3fbncT2fK7XNFBfm9OmAk5jj4fvBXorWDT+Fy45YNLQkiMVdCMmfw8lAsDAvCgThrOf7mBk8JEZEREREJKy8y2dwtryOf+kU1pwHsOY9SPxnfwfxli6vN4aMwF75UcySSZ3O+b6Pd/oQ7ubX8OuuAWCOm4q1bDVm4fA+vQ8RGbhuGhDOmzePefPmMWnSJGbOnMnw4cFvRp7nYaqVecBbOHkEW45eoXhI7k2vi7ZOOI7fZgdhVV0LP/3gGGerGpk/sYhPrJzUZwFXLN55eXFS+30IwyLZQZibZZNlm8Qcj3jC7TChWURERERE7o5fW4Wz7U28yn3BAcvG3fs+7t73u35BJIq1oBxr1ooulxN71ZdxNr+Kf+4YAEbhcOxlqzHHTe2rWxARAXo4xfjs2bNcuXKF8vJy/vt//+/U1dXx+c9/nkceeaSv65MMNmZYHl9ecx95t9hXMNVB2MOAzfd9dhy/yr9tO0W8tetwV2UVUdtkzdIJfdJJ2JLoPKAk6XbrzwTJPQhzojZZEYuY49GigFBEREREpFf4zQ04O9/GO7QVvHYrpdzu9/42J80Npg3nDe78fi2NODsq8A5uBd+DaHawL+GMpV0GiSIiva1HacGGDRv4yEc+wsaNG3Ech1GjRvHSSy8pIJTUlNybSXbg9WSKcVPM4TebK9l7uhqAuaVDmVtaxE/fP8aWo1fIilg8vWBcr4eEyUDtxv0HIdiDEMLTQej7foeJzNlRm7rmRLDsOC/NxYmIiIiIhJifiOPu24C7+71gX8AesIcVYyxbjTl6cuf3c128Q1twdlRArBkMA3PGUuyFj2Hk6C/vInLv9CggbGhoYNCgQezevZsHHniA8ePH893vfreva5N+IrnEOJboeg9Cx/U4fbWBYxdr2XH8KrVNcbJsk48tncCCiUUYhsFnHi7jh+8c5b0DF8mKWDw2d0yv1tg2wbjzt0RWNFwdhDHHw2vdT9G2zFTo2RyS+kVEJH3+y3/5L4wdO5bS0lLGjRtHaWkpxcXF6S5LRCTtfM/FO7ITZ8c6aKrv2YvsKNaCRxnx8Ee5dr2m02nv7FGcTa/i11wBwBg9GXv5asyh+n1XRO69HgWERUVF/OxnP6OhoYE//uM/pqamhvz8/L6uTfqJ5LLdeLsOwoaWBDtPVHHsYg2Vl+tJtBtgMm54Pn+4cjJFBdmpY9PHDOGTD0zmJ+8f463d58iyLR6YOarXakyGfzlddBCGYQpze8nuwdzW5cTJr3/yeNhsPHyJs1UNPLui7/agFBGRwKJFi3Ach8LCQvbu3cu3v/1tBg0axNChQxk/fjxf/OIX012iiEif8l0HEnGM7GCf9dTAkG1r8a9fufmLo1kQD7oKzYlzsJc9jZE/ODXROMmruYq7+TW8M4eDAwXDsJc9hTl+Rp8OZhQRuZkeBYSf+tSn+NWvfsWUKVNYvHgxP/3pT1myZElf1yb9RLRdwHatvoX3D1xk+/GrJNy2ULC4MIcpowYzpWQwZSWFWGbnPxjnlg4jnnD55aZKXtlxmhGFOUwbXdgrNSbDs64mMic78MKyxPjG5dLJ0DM52Ths1u+7QG1TnIdnjWZkYUjGSIuIhNTevXv5xje+kfr44YcfZtu2bTz55JOcPn06jZWJiPQt3/Pwju3C2fYWxJuJ/uFf4jfUBJOJL5686WuNwuH4NVchHguGiqz4COaYKZ0/R6wZd9fbuPs3g+dCJAtr/iNYs1d0ChFFRO61Hv0utHjxYhYsWMDFixe5dOkS//7f/3tNMZYeS4Zu245dZf3+C/h+cHz6mELum1DE5FEFFOREe/Rei6aMoLohRsXe82w9eqXXAsKe7EEYlg7C5ATjnFQHYbj2ULxRU+v9NIe0A1JEJEwGDRrEqVOnKC0tBWDKlCl873vf41Of+hTDhg1Lb3EiIn3EO3csCAKvXQwOZOfivP8S3ulDN32dMXoy/uUzQThoR7AWPIo1e2WnsM/3PNyDW3G2vwUtjYCBOW0h9qInMHIH9dFdiYjcnh4FhOfOnePv/u7vuHTpEgDFxcX85V/+JaNHj+7T4qR/SAaEDS0JLNNg3sQiHpw5iuIhuXf0fkvKRlCx9zyHz18PJvN20fV3u266B2EkbEuMOy6XTnVAhjBgc1wvtfw8jPWLiITNH/3RH/Htb3+bMWPGUFpayvnz54lGe/ZDPBGRTOe7Dt7Zo5gjx2Pk5OFVX8Ld8gbe2SMdL2xpvmk4aE6ei191Af/88eDjibNblxMXdrrWu3CCq7/9Ds6VswAYxaXYy5/BHK5/S4tIZulRQPjP//zPXL9+nRUrVgCwc+dOfvCDH/CVr3ylT4uT/mHKqMFMHDmIMcPyuX9GcY8mH99MYV4WE0YM4uSVeg6evc78iUV3XeONoVp7yYAzLB14yY677Bv3IAxJ/e01tQsFm0O6RFpEJEyKi4v52te+xvbt2zl58iTFxcU8++yz6S5LROSuBPsIHsTd8gZ+bRXm2KmQNxjvyHZSy5s6vqLL9zGnzAPXxTu+BwBjcFGwnHhsWed3qKvG2fI63sn9wYH8QuylT2FOnK19BkUkI/UoIKysrOSTn/wkTz75JABr167lZz/7WZ8WJv3HkPws/vjJmb36nnNLh3HySj17Tl3rnYAw0RqqdbUHYXKJbkgCqrYhJckOwqD+MAZszbH2AaE6CEVE7gXTNFmyZIn2mxaR0PJbGnF3vo135SzWvIdx937QYR/BTh2Dt2COm4YxqhR35zvgxIPlxPMfwZpzf+flxPEY7ofrcfdtANcBO8Kg5U8Rm7IQw470yv2JiPSFHgWE+fn57N27l3nz5gHBBtaaYizpNHv8UF7edooj52tojjup/fbuVDL8y+qyg7B1ibETjoCtbT/F1g7CkA1Zaa+pXagZxoBTRERERPqWX18Dvod7cj/uvo0YOfn4ddcg3gKA8+aLd/zexpARWEuewt3yemrisDlhJvayZzAGFXasw/fwjn6Is20tNNUH106Zh734SQpKJ1FVVXXHdYiI3As9SlUeeeQRfvnLX7Jz587UsU984hN9VpTIrRTkRplYXMCJS3UcOHOdhZOH39X73WwPwmRXYSwkAVXbkJLWDsJIePcgVAehiIiIiNzIb6wLlu8e393Fudq7/wSGSeT3/jPu3vdx1v4wOFQwLFhOPG5qp8u9S6dxNr2Cf/VccO2IscE+gyPH3X0tIiL3SI8CwgceeIDBgwezd+9eAObOncucOXP6tDCRW5lbOowTl+rYc+ra3QeEN92DMFxTgNvuxW79f6vD8TBpimkPQhEREREJ+E4Cd/d7uDsr+uxzRH7/T/HOHyfxynch0bqceN7DWHMf6LycuKEGZ+vatqAytwB7yZOYU+7DMMw+q1FEpC/0KCD8+te/zvLly/nzP/9zAH7+85/zV3/1V/zjP/5jnxYncjOzxw3lt1tPcvRCLU0xh9ysO19mHEt1EN5kiXFIAsLm1JCSZAdhuALO9tp3DYaxA1JERERE7p7v+3iV+3AqftpnnyPy9OfBNHHe+Tn+9SsAmKUzsJevxhg0tGM9iTjunvdx97wHTgIsG2vO/VjzHsKI3N1ARhGRdOlRolJdXc2IESNSHw8fPpxr1671WVEiPZGfE2Fy8WCOXaxl/5lqFk8ZcesXEfwF40bNrUNKutqDMLXEOCQBW/MNHYSpPQhDGLC17yBsCmH9IiIiInJ3vKrzJF77Z2hp6pP3tx/8OObYso5LlguGYa94BmvctA7X+r6Pd2IvztbXoSFYymxOnI29dFWnEFFEJGx6FBCOHDmSV155haFDh+L7Pq+++iojR47s69pEbmlu6TCOXaxl98lrtwwIHdfjV5sqOXJhJ3+yaiZFBdmpc6lluV3sQRhNBoSOh+f5mKbRi3fQ+9r2IGwNCCPhHVLSsYMwfPWLiEib6upq/vZv/5Zz587x4osvYlltP5Q7c+YML7zwAgBf+MIXGD9+fLrKFJEM4TfV43zwW7xTB/vk/a15D2MtKMc9sIn4L/4eErGgEzC5nPiGicPe1XPBPoOXTgNgDBsV7DNYMrFP6hMRudd6FBB+9KMf5Tvf+Q5/8zd/kzr2J3/yJ31WlEhPzRo3hJe2GJy4VEtDS4L87EiX1yVcj3999yiHztUAsPXYZZ5eMD51zvV8LNPAtjqHf6ZhkBWxiCVcYo571xOT+1rzDfsptp9i7Ps+hpHZAWd7TRpSIiLSb+Tn5/OVr3yFb3zjG53O/eIXv+DP/uzPME2T73//+/zlX/5lGioUkUzguw7unvdwt6/rk/c3x07FfvI/4F86ReKlb+JXXw6Oj5+OvfwZjIIblhM31eNsW4t3ZBfgQ04+9qLHMacuxDC1z6CI9B89HlJSVFTErl27AJg/fz4zZszo08JEeiIvO8KUkgKOnK9l3+lqlk3t3NkaT7j8cP1Rjl2sJWKbJByPXSeqWDVvHKZppJbeZkesbsOzLNsMAsJE5geELTd0EFqmmbrvmON1uc9ipmq/rFhDSkREwi0ajRKNRrs819jYSFFRUerXXamoqKCiIhhM8Pzzz6eul7tn27a+niHTH5+Z7/u0HPmQ6t/87z77HKP+8jv4sRZq3/4Vzfu3AGAVDmfw439AzpS5HetxEjRsq6B+46v48RiYFvmLyxm04mnM7Nzb+rz98Xn1d3pm4aNndvd6nHTMmDFDoaBkpLmlwzhyvpY9p651CghbEi4/qDjMySv15GdH+OLj0/nX945ztbaJ45fqKCsZnFp6m93F/oNJ2VGLuuZExu9D6Pl+ailuVrsgMCdikXA8WuJOqALC5ljb17s57oSuA1JERHqmq/2Bb1ReXk55eXnq46qqqr4saUApKirS1zNk+tsz865dJPH6D6Cpvk/eP/rv/xvk5HFlwxu4O9ZBvHU58X0PYd33II12hMbWr6fv+3inDuBseR3qqoGgu9Ba9jSJwUVUNzRBw+3th9jfntdAoGcWPnpmPVdSUtLl8cxuhRLpgZljh2KZJ6m8XMeGQxfJsi0itoltmazfd4EzVQ0Mzo3yxcenM2JwDstnjOblzcfYeeJqEBDGu59gnJQVkn38YgkXn6Beq91eiWEJOG/UvoPQ9wldB6SIiNw+/SBIZODwmxtwNryMV7mvT94/8sx/xCyZhHfxFM7rP8CvvgSAOW4a9opnMAqGdbjeu3Yx2GfwQiUAxpCR2MtXY46Z0if1iYhkEgWEEnq5WTZTSwo5eO46L2873en8kPws/ujx6QwbFAwlWT5jDC9vPsb+M9XEEm67DsLuvx2yQjLJuG1ASccQLbt1+ErYlukm9yC0TQPH82mOhasDUkREeiY/P59r165hGAY5OTnpLkdE+pjvOrj7NuBuXdsn72/Nexh78RP4TfUk1v8S72iwVRaDhmIvX41V2nFlnN/cgLNjHd6hbcFPpbNysRc+hjljMYapv3uKyMCggFD6hY8sHs/wwdnEEi4J1yPheCRcj9wsmyfnjaUwLyt17YjCPMYPz+f01Qb2n6kmarcO87hJ8BSWScBtA0o6fmu3H1QSFp7vpwLPIflZXK1roTnuMISsW7xSREQykeM4/M3f/A2nT5/mr//6r/n4xz/O4cOHWbNmDc8++yz/8A//AMDnP//59BYqIn3G932804dw3nyxbz7BoCFEn/1zME3c/Rtxtr/Vtpx47oNY8x7qMJ3Yd13cA5txd1ZAvAUME2vWMqwF5Ri3uc+giEjYKSCUfmHYoGxWLxzf4+sXTBrO6asN7DxRxbwJwdKCm+1BmOogzPAOvJZuOwitDufDIJZwgx/g2ib52RGu1rWkloOLiEj42LbNV77ylQ7Hkvtbjx8/nq9//evpKEtE7hGv+hKJN/4FGmr75P0jn/gLzMLheJdO4Wx4Gf/aRQDMcVOxl38EY3DH5cTumcO4m1/Dr7kKgDGmDHv505hDOg89FBEZCBQQyoA0t3QYL287xfGLtZQMDX462JMOwpiT2QFVsoPwxuXSyY/D1EGYWi6dZafC2+YQBZwiIiIiAn5zI86m3+Ed39Mn728/9O8wy+ZDSyOJ9b/CO7ozOJFfiL3iI5jjp3fY29S7fgVn86v4Z48CYAwuwlq2GnPcVO2BKiIDmgJCGZBys2xmjB3CvtPV7Dge/NQwuU9fV1JDSjK8g637PQjDUX97TbG25dLJJdNh20NRREREZKDyXRd3/0bcLa/3yfubU+ZhL38Gotl4B7bgbH8zWCZsWlj3PYh130MYkWhbPbEm3B1v4x7cDJ4H0SysBeVYM5dhWPpnsYiIfieUAWvBxCL2na6msXUQxs2WGIdlD8KWW+1BGKKALTmgJDerfUCoDkIRERGRTOeeOYzzxg/75s1z8ok8/u8xi0vxLp3G2fgyftUFAIyxZUHX4OCi1OW+5+Id2oazYx20NAEG5vTF2Isex8jJ75saRURCSAGhDFhTRxeSm2Wngqge7UGY4QFhUzcdhDmpISXhCdjauiHtVP3qIBQRERHJXN71KyTW/hDqqvvk/a0lq7Bmr4R4M4l3f413ZEdwIr8Qe/kzmKUzOi4nPnccZ/Mr+NWXATBKJmIvX405rKRP6hMRCTMFhDJg2ZbJvAnD2Hg4+AvDzfYgvJuA0Pd9dlZWkWVbzB4/9M6K7aFuOwgj4Vuiqw5CERERkXDwW5pwNr2Cd+zDPnl/c9w07JUfgbzCoBtw29q25cRzH8Ca93DH5cS1VThbXsc7dTA4MGgI9tKnMCfM0j6DIiLdUEAoA9r8icN7FBDe6RJjx/X41aZKdlVWAfCpByZz34SiW7zqziUDtBu7IVNLjDO8A7K95L3kZlntOggVEIqIiIhkCt9zcQ9sxt30at98gtwC7BXPYE6YhX/lLM5bP8GvOg+AMWZKsJy4cHhbPfEW3F3rcfdtAM8FO4o1/2Gs2Ssx7Ejf1Cgi0k8oIJQBbWxRHiMG53CltpmC3Gi3191JB2FjS4IX3z1K5eV6LNPA9Xx+sfEEQ/OzGDd80F3X3pXmbjsIk3sQhidgS3YQ5kTttinMIeqAbK+hJcGrO06zYloxY4u0142IiIjcG7sOXmDdxuM0NMbJz4vy+MrJzJve8+W1vu/jnTmMf+5YMPQjryB1zjt7lMTrP+iLssEwsGYux1r0GLgOzvu/wTucXE48GHvZM5gTZqa6AX3Pwzu6E2fbm9DcAIBZNh978ZMdahYRke4pIJQBzTAMPvtwGReuN1EyNK/b65IdeD0NCK/WNfODt49QVddCQU6Ezz06jc1HL7P16BX+5Z2j/OnTsxiSn9Ur99BeS3dTjJMBWyg7CG1ys8LdQXjgTDU7T1Th+/CH909OdzkiIiIyAOw6eIEf/XY39Y2x1LELVxpgDbcMCX3PxTuxF3f3u2379w0fjVW2AK/mKs6bL+LXXO2Tuo3hY7Dv/xjGsBK8w9uC0C/WHCwnnnM/1vxHOiwn9i6exNn0altn4chxwX6EI8b2SX0iIv2VAkIZ8IYPzmH44JybXpPVwyXGrudz9EINP99wgqaYQ8nQXD73yDQG50X5vSWlXKtv4fjFOv7lnSP8p1Uzb7qs+U4kOwizu+0gDE9A2BQLas1t10EYpj0U22toCYLNZFekiIiISF9bt/F4h3AQoL4xxlsbjncbEPpOAnf/Jtytb7QdbN3nzxw7reNgkN4WycJe/DjmjGX4VedJ/Nv/xr96DuhmOXH9dZwtb+BV7g0O5A3GXrIKc/Jc7TMoInIHFBCK9EB2aomx1+lcQ0uCI+drOHyuhiMXalIh1vQxhXzqgSmpcNEyTT79YBnffn0/F6838dP3j/HZh6dimr33F5hU190NAWFOiPcgzMmyQ78HYTIYbApp/SIiIhIufkMN9deud3muoSne+fpYC+6uCty9Gzqdi6z5E/yLp4i/+PVerzPJnDgbe/lqsGycD/4N7/B2wA9Cv+WrOwwX8RNx3N3v4u55H1wH7EgwqGTugx06C0VE5PYoIBTpgbYOwiDg8X2fI+dreO/gRU5crMNvd23RoGzmTyri0dmjO4V/uVk2n3t0Gt96fT+HztXw+q4zrF44vtfqbOsg7GZISdzB9/1Q/FQ1NcU42n6KcXgCzvYaYwkAmtVBKCIiIn3M2f0e7tY3yItNBzrvv5ffbt9tv7khmD58fE+n64yiEuzFT5L49T/2XbGDhmCv/Cjm2DK8Q9tblxM3gWlizXmgdTlxsC2P7/t4x3fjbH0DGusAMCfNxV6yCmNQYd/VKCIyQCggFOmBiGViGuC4PtuPXeH9Q5e4dL0JAMs0mFRcwLTRhUwbU8jwgpsvVy4qyOY/PFTGd986yAcHL/HAjFE3HZDSU67nE0u4GLQFmkmWaRKxTBKuR8LxiPby0ua+0NZBaJEVsTAI9oB0PR+rF7su74VUB6ECQhEREekDvpMg/s9f6XDs0UEXueTkUu+2/ZNvUF4Wj6+cjF9fTWL9r/Avnuzy/ezHPoW7s6LvhpC0CwD965dJ/LbdcuKSSUFoOGRE6nLvylmcja/gXzkTXFM0OphuXFzaN/WJiAxACghFesAwDLIiFs1xl19uqgSgICfCyhmjWFo2otPU4FuZWFzA9DFDOHD2OjtOXOWR2aPvusbkAJXsqIXZRYdgdtQi0ezRnHBDERC27yA0DYPsaPD1jyVccrPC9VtX8l6aQ9TBKSIiIpnPb27Eu3oO541/6XRu/oMLsXOms27jCRqa4uTnRnls7nBmfPhj4u9Xd/2Gpok5dSHOup/0Wc1G8Xjs+38PI3cQzubX8A5tA3zILQiWE0+c3bacuLEOZ9tavKO7ghfnDsJe9ATm1PkYhtlnNYqIDETh+le2SBoNzsuiOd7EiME5PDRzFPMmFmFbd/4Xk6VlIzhw9jpbj17hoVklXYZ6tyPZcXfjgJKk7IhFfXOClrjL4Ny7+lR9znE94o6HabR1Q2ZHbZrjLk0xJ7QBoecHQW53z0hERESkJ3zXIfa9/wZ+5/2xASIf/1PMYSXMB+bPGI136TSJl/8PfOh3eT2ANXsl7r4NrYFdL7LsYK/ArFzspaswyxbgHdlBYttaaGldTjz7fqz5j2JEW5cTOwncvR/gfvguOPG2CcbzHk5dIyIivUv/ShXpof/wUBk1jTEmFhfcdZgHUFZSyJC8KNUNMY5dqGXq6MK7er/k/ny50a67A1P7ECYyf5lranlx1E79BDk3anGdcNR/o8Z2S4ub4o4CQhEREblj3qVTXPju/+nynDluGvZjn8KwI8GefWeO4Kz94c3fMDsPWhpx93UeUHI3jIJh+HXXwHUwy+ZjL30Kv6GGxMv/hH/lbHBNycTW5cQjgdZ9Bk/ux9n8GjTUBPdUOhN72VMYBcN6tT4REelI/0oV6aGigmyKCrJ77f1M02DxlBG8ufscW49dueuAsOWWHYR263WZP+ijKdYadrbrFMwO6aASz/M7DCdpjrmQn8aCREREJHS82ioSP//GTa+JPPU5zLFl+J6He3Qnzvpf3fqNc/KhuaGXqgyY46bhnTmMX3cNo3A49v0fwxg6Cmf7W3gHtxIsJx6EvWw15qQ5qR8Ge1UXcDa9ktoX0RhajL38GczRk3q1PhER6ZoCQpE0WjRlBOv2nOPAmevUNccpyLnzYSVNqa67rjsIc1IdhJkfsLUNKGn7LSpZf9gmATfHnQ5TrpPPSURERKQnnF1v425f1/0FdoToJ78M0azUBOMe68Vw0Jw4G+/8Cbwzh8GyseY9jDX3Abzju0ms+ym0NAbLiWetxFpQ3racuLkBZ9tbeIe3Az5k52Evehxz2iIMU/sMiojcKwoIRdJocG60bVjJ8bsbVpLsDOxuYEpqiXEIAqr2A0qSckLaQXjj5GJNMhYREZGeCCYTfxXoft9Ae8VHMKcuwN2xDndv7y4R7imjuBQ8D69yX/Dx6MnY938M4jESr7zQNnl41ATslR/DHNq6nNh1cPdvwt31NsRjQXg4cwXWgkcxsnLSci8iIgOZAkKRNLvdYSXXG2L8enMls8cPZWnZyNTxtiEl3exBGAlPwNbUZQdhsv5wBWyNCghFRESkh7wzR0i88S8YQ0bgX79y02sjv/efcfd+gLPxd/eouhsZmJPm4J3cB54HOfnBFOKxZTjb1+Ed3AJ+63LipU9jTp6LYRjBPoOnD+Fufi3YoxAwx03FWvo05pARaboXERFRQCiSZmUlhRS2Dis5frGWspLCbq+ta4rzvbcOUVXfwtmqBhZMHE7EDpZeNPe0gzAMS4xTHYRtYWey/rAFhDcGgmGrX0RERPqe7/s4b/0r3qmDwcc3CQeN0ZOxfY/Eb79zr8rrxJwyD+/SKbwTewADc8YS7EVP4J0+SPznfx8sJzZMrNkrsBaWY0SDfby96ss4m1/FP3csuJfC4VjLVmONm5q2exERkYACQpE0Sw4reWv3ObYevdJtQNjQkkiFgxAEgvvPVDNvYhHQtnS424AwklxinPkBYVcdhLlaYiwiIiL9kN/cQPzFv+r59eePk+jDem7GGFMGnot37MPg46HF2A+sAcsmsfZH+JdPB8eLS4PlxMOKg5pbGnF2VARDSnwPotlYC8uxZizDsLpe/SIiIveWAkKRDLB48ggq9pxjfzfDSprjDt9fd4jLtc2MLMxhbukw3tp9jm3HrqQCwrYOwu6WGCc7CDM/oGpOTjGOtp9iHJ49FNtrjAV/hY/YJgnHUwehiIjIAOfHWiAaxTBM3BN7cSp+mu6Sbi2/ELNoNN7545CIgR3BWvgYVtkC3F1v4x7YHCwnzskPlhNPuS9YTuy6eIe24OyogFgzGAbmjKXYCx/DyMlL912JiEg7CghFMsDgvLZhJe/tv8jK6cUMzo1imgaxhMs/VxzmfHUTRYOy+eJj04nYJu/sO8/xS3Vcq29h2KDstsm/3S4xDo6HtYMw7ENKigZlc/F6E02xcNUvIiIivcP3POL/+lfQ0oQ5bRF+bRX+xZPpLuuWjLFl0FiLd+oAAOb46dgrPoJ3sZL4r/5XMAnZMLBmrcBa+BhGVuty4rNHcTa9il8TLJc2Rk/GXrY61VUoIiKZpU8Dwh/+8IdUVlYyYcIEnnvuudTx73znO5w/f55oNEp5eTkrV67syzJEQmFJ67CS9w9e5P2DF7FMg6H5Wfg+VNW3UJgX5YuPT6cgN+gunDN+GLsqq9h+7CpPzh+bCs66HVISyj0I2wWEWeEeUlJUEASEYatfRERE7p5fW0X8599Ifewd3p7GanrGGDICcgYF+wX6PuQNxl7xEYyCoSTe+QX+pVPBdcWl2Cs/ijlsFABezVXcza/hnTkcvFHBMOxlT2GOn4Fxi2F8IiKSPn0WEFZWVtLS0sLXvvY1XnjhBY4fP87kyZNT5//0T/+U4mL99EgkaeroQh6eVcLJK/Vcq2+hvjnB1bpgv8GCnAh/9PgMhuRnpa5fPGUEuyqr2HHiKo/fN+bWHYSR8CzRTXYQ5rbvIIwkh5RkfsDZXvsOwvYfi4iIyMDg7t+UxknDdyASxRg+Br/mKly/EnQHzl6JNfd+3N3v46z7SbCPYE4+9tKnMKfMC5YTx5qD5cb7N4PnQiQLa/4jWLNXYFhauCYikun67HfqY8eOMWfOHABmz57N0aNHUwGhYRh8+9vfJj8/n89//vMMHz680+srKiqoqKgA4Pnnn6eoqKivSr0nbNsO/T30F5n8LD7zRNv3QizhUFXbTHV9MxNHFZKX3XFfwmHDhvHS1lNcqWniYoNH3PEBGF08nKGDcjq9t2MFAVXcJWPuv7tnkbyXkpFFFA0bBICV1QxAzPEypv6eSHjBlL7SkiLYf4GWRGbWn8nfFwONnkXm0LMQkbvhOwkSv/0OfvWldJfSY8bQYjAM/AuVwccjxmLf/zH86svEf/OtdsuJl7cuJ87B9zzcQ9twtr8VTC/GwJy2EHvRExi5g9J7QyIi0mN9FhA2NjYycuRIAHJzczl37lzq3Gc+8xny8/M5fPgwL774In/xF3/R6fXl5eWUl5enPq6qquqrUu+JoqKi0N9DfxGmZ5EFjBpk0txQR3ND5/MLJg7jjV1NVOw8QWNLHIDmhjqqYo2drm1pDoZlNLbEM+b+u3sW9U0xAGJN9VT5wa/jTtA5mEn190RNQxBsZhtB52Cm1h+m74v+Ts8ic/SXZ1FSUpLuEkT6NT/WhH/9KsbIcakltF71ZRK/+l9pruw2ZOdhFAwNwkwnAdEs7MVPYhSPx9nwu7blxCPHB8uJi4LfV7wLJ4J9Bq9dDM4Xl2IvfwZz+Oh03YmIiNyhPgsIc3NzaWpqAqC5uZnc3NzUufz8fACmTZvGT37yk74qQaTfWzBpOG9+eJaDZ6/j+T6mAVHb7PLatinALr7vZ+weML7vd7lcOmKZWKaB4/okXI+I1fV9ZpqmliCYHZKfhWlA3PFwXA87JPWLiIhI97wLlSTe/hk01RP5vf8Mw8fg7t+Eu+mVdJfWY8bQYvx4M/6VswCYk+ZgLXwM7+BWnI2vBMuJs/OC5cRl8zAME7+uGmfL63gn9wdvkl8YnJ84O2P/jikiIjfXZwFhWVkZFRUVLF++nH379vHQQw+lzjU1NZGbm8uFCxfIy9N4e5E7NTg3yrTRQzh47joQTCru7i9ltmVimwaOFwRsUbvrYSbdaYo5HL1Qw8yxQ4l0E0L2hljCxfODoLN9iGYYBtlRi8YWh+a4QyQnepN3yQy+76f2HMzLtsnJsmlscWiKOxSEoP4b7T11jWsNMR6epW4kEREZ2Hzfw/1wPe6OCvB9jBFjMfIGk3j5/+BfPp3u8nomJx8jK7dtCXTBUCIrPoofayLxyvegqR4MA3PmMuxFjwXXJmI4H76Lu/cDcB2wI1j3PYQ19wEMO5Le+xERkbvSZwHhxIkTiUQifPWrX6W0tJSioiJeeukl1qxZwze/+U0aGxsxDIMvfOELfVWCyICwaMrwVECY080E46TsqE1DS4KWuHtbAWFdc5zvvnmIK7XNzB4/lE8/OKXPfjqcHELSfkBJUm40CNha4i4FnbdZzDhxx8PxfGzLIGpbqfqbY+Go/0YvbztFXXOC+ROKGJwXvoBTRESkN/jNDcEU33PBPsNm6UysGUuI//j/TXNlPWRakF8ILQ34NVfAtLDmPoA5YSbO5tfwL54EwBg5rnU58eggED2yE2fb2iA4BMwp84JlyPmD03gzIiLSW/p0nNRzzz3X4eM1a9YA8OUvf7kvP63IgDJ9TCH52REaWhLdTjBOyo5aQUCYcCno4fvXNcX57lsHuVIbTFTed7qaDw5e4oGZo+6y8q4lO+66upfkMunmEExihrZ7ycsKfqKe0xp6NoWk/vY836e+dbl0Q0tCAaGIiAxI7ZcUA1izVkA0i8TrP0hzZT2Ukw+GAXXXADBGTcBesgqvci+J3/7vtuXES1ZhTp2PYZh4l07jbHoF/2qwp7wxYmywz+DIcem8ExER6WWaNy8ScpZpsmjycNbvv5AK0LqTHUnuQ9izgKq2MQgHr9a1MGpILiumjeTXm0/y2s4zjB2ez4QRvT+ZLhmeddVBmAwNk12Gma4x1vFecpP1x8IXEDbHHPxguDSNsUR6ixEREbnHgiXF7+LuWAe+H0zynfsA3oWT+FfO9MnnNMdPx7t4EuItd/9mlg1ZOdDSBJ4L2bnYS54Cyybx1r+2Bp4G5oyl2Isex8jOxW+oJbH1Dbzju4P3yC3AXvIk5pT7MAztpSwi0t8oIBTpB1ZMK6bych0LJg2/6XVtHXi3DthqGmN8981DVNW3UDI0ly8+Np287AhXalt4/+BFfvzuUb70zBzyc3p3v5nmm3QQ5oQsYGtqDdLyWgPCMHcQNrb7mjeF5OsvIiLSE34ihhHJ6v78DUuKsSOYk+bi7n6vbwrKC5bseqcP9c77ZeUEoWByafDUBVhlC3B2VuBfqARauwJXfhRz+Bj8RBxnZ0Vwf04CLBtrzv1Y8x666ddJRETCTQGhSD8wOC/Knzw165bXZUeCb/mWRPcBYcLxOHaxlt9tP8W1+hijh+byH1vDQYCnFozlbFUDJ6/U85MPjvEfy6djmr23H2FbB2HnbsickC4x7g8dhI0tbV2DjSGsX0RE5Ea+6+Bs/B3eoe3Y5X+INWlOp2uCJcU/h6a64EA0G6NwON6RHX1XWGNt77yPaQWdg7FmAIzCEVhLn8K/UEnite+D57V2Eq7CnLoAMHCP78HZ+jo0BDWYE2djL12FMWho79QkIiIZSwGhyACSDNhabuggbGhJcOjcdQ6cuc7Ri7UkHA+AMcPy+I+PTe+w3NcyTT714BT+4ZV9HL9Yx1t7zvHkvLG9VmNPOghvFnBmkk5LjFtDzzB24DW0qINQRET6D7+pnsS6H+NfOg2miZHXcdBGpyXFbSfwr5y9x9XeAcsOAsBELOgAnP8oRv5gnPdfag07DcwZS7AXPYGRnYt39Vywz+ClYAKzMWxUsM9gycT03oeIiNwzCghFBpDUHoStAdvpq/W8f+Ai+85Ud/i775hhecwYO4SV04u7DOoG50b55AOTeWHdId7ee54powYzqbinY09u7uZ7EIYrYLtxSEnynsJSf3vt9x0MY/0ikhl++MMfUllZyYQJEzoMs/vOd77D+fPniUajlJeXs3LlyjRWKf2dd/UciTf/NejUM03s8k9iFo9Pne+0pLi9RKzX67FmrwDfx92/qXfe0DDADf6sNsaUYc1ajrv3A/wLJ4Jjw8dg3/+xYDlxUz2Jd3+Fd2QX4AcDShY/gTl1IYapfQZFRAYSBYQiA0hyD8KjF2rYd/oap682AGAaBlNKCpg5dggzxg6hMO/W+8tMGTWYR2aP5u2951m35xyTimf0So1NsSC87HqKcWsHYUiGlNy4xLhtyEr4ArbGdh2EWmIsIneisrKSlpYWvva1r/HCCy9w/PhxJk+enDr/p3/6pxQXF6exQhkI3GO7cd77dRCgGSb2o3+INaFtm5ZOS4r7mDl2Ku6+jb37pr4PuYOwFz2OX3MV560Xg27CrNxgyMi0heB5OLvfxd31DiTiYFpYs1ZgzX8EIyu7d+sREZFQUEAoMoAk9yA8eiHYVyYnarG0bCQrphUzOC962+/34MxRbDx0iROX6jh1pZ7SXphq3NyDDsKwBGzJfftys5NLjEM8pKT9HoQtmmIsIrfv2LFjzJkT7PE2e/Zsjh49mgoIDcPg29/+Nvn5+Xz+859n+PDOQ7cqKiqoqKgA4Pnnn6eoqOjeFd/P2bbd77+evudR9+5LxDavDQ4YJkPX/BE50xYE532Phk1vUPfev3VcUtwHcqYvpPlQsIehd/ZIL7+7Qd6Ch4iMHEvdB6/g1V8HDHLnPUDBQ2swc/JoOfIhtW//CrfmKgDZU+YyuPxZ7KEje7kWSRoI32P9jZ5Z+OiZ3T0FhCIDSPGQXACGDcri/hmjWDhpOFmRzsNAeionarN82kje2XeBd/ad53OPTrvrGpt6MsU4JB2Ejaklxh07CMO4RLdBU4xF5C41NjYycmQQQOTm5nLu3LnUuc985jPk5+dz+PBhXnzxRf7iL/6i0+vLy8spLy9PfVxVVdX3RQ8QRUVF/frr6ceacd7+eVsYZ5jYj/4BjUXjaayquvmS4j6QDAd7mzFsFNac+2k6ugt/5/rg2PAx2Cs/ijtiLNfOngz2GUxOLh4yAnv5M/hjplDjAf34v4F06+/fY/2Rnln46Jn1XElJSZfHFRCKDCBlJYP5yrPzyc+K9Nrk4funj+KDg5c4dK6GC9WNlAzNu6v3u3FZbnthW6LbdENAmLynsASc7bXvGlRAKCJ3Ijc3l6amJgCam5vJzc1NncvPzwdg2rRp/OQnP0lLfdI/edev4Lz5In5t6z8aW8PB5MTie72kmKxciDX17nvaUax5D0IshvPeb8BzISsHe/GTmNMWQayJxAe/xTu0LeiOzMrFXvgY5ozFGOad/6BYRET6FwWEIgNMQc7tLyW+mfycCEvKRrDh0CXW77/Apx6Y0uPX+l0s4WlbYtz5L6zdTWHOVG1hZ+uQkhB3EDZqirGI3KWysjIqKipYvnw5+/bt46GHHkqda2pqIjc3lwsXLpCXd3c/aJL+Ifl3BMO48x9ouqcP47zzM4i3DhYxDOxHPoE1aU4wpXj3e7jb37q7JcV2BJzb2Hqjl8NBs3QGxqiJuPs+gIZgCxlz2iLsxU9CNBt3/ybcnRUQbwHDxJq1DGtBOUZ27i3eWUREBhoFhCJy1x6cOYpNhy+z59Q1nrhvLEUFN9/c2vN9frnxBMcufsifrJrBkPy2oSjNPVhiHJY9/DoNKclq20PR833Mu/hHz73WfopxS8LF9TwsTTcUkdswceJEIpEIX/3qVyktLaWoqIiXXnqJNWvW8M1vfpPGxkYMw+ALX/hCukuVNPNbGkms/RH4PpGP/afbDgl93w/Cv21vAq3hn2FgP/IHWJPnti4p/iX+uaN3X+xNwsHIs1/CKBwBjXXEf/I3d/+52rEKhsKMpXjnjuFtfhUAo2g09sqPYo4ch3vmMO7m1/Bb9xk0xkzBXr4ac4j2GRQRka4pIBSRu1aYl8WCSUVsP36Vd/df4OPLJ970+ld3nGbniWCpz8bDl1i9cDwArucRczxMA7K72BsxO9VB6OD7/l11FfQ11/NoSbgYRlvdlmmSFbGIJVxiCbfLEDRTJTsII7ZJwvFoijkM6uVuVBHp/5577rkOH69ZswaAL3/5y+koRzKQH2sm8doP8KvOYxSOuP1wMBHHee83eCf2tB00DOyHP4E1ee49WVIcefrzmGOm4DsJ3L0fBJOCe4thYk5fTHZeHo3b3gyWE0ezg+XE0xfj11YRf/0H+GeD8NMYXIS17GnMcdMy+u9NIiKSfuH516mIZLSHZ5Ww4/hVdpy4ymNzx3Q7FfmDgxf54OAlDCNY0bP9+FWenDcW2zJpjgVLh3Oidpd/ibUtMxVQxR3vrgas9LVU92DU7tApmBMNAsLmmBOagDCecEm4HrZlUJgb5WpdiwJCERHpdX48RuL1f8GvOg+Aff/Hbu/19TUk3noRv+pC20HDwH74WczJc3A+XH/3S4p7wNmxDuPoLrwLJ6Dx1kGkff/v4R7ZgX/l7E2vM0aMwxw7BffIThobagAwpy0MlhObJu7m13APbgbPg2gW1oJyrJnLMKxw/H1DRETSS39aiEivGD44hzmlQ9lzqpr3Dl7gI4tKO12z9/Q1Xtl+GoA/WDmZDYevcPZqHXtPVzN/YlFq6XBOFwNKknIiFgnHoznuZHRAmOy4u3HYSm6WTU1jnKa4w9B0FHYHGlqXF+dnR1L3035PQhERkbvlJ+Ik3vgX/CtnADBnLMEsufmKhPa8iydJvPVjaGlsO2gY2A89izlmConXf3hHS4qNohLM4gkYQ4bjntibmgDcSTQ72OcP8C+fwb985pbvHf3Ul3EPb8fZ+LugE7DbC7Oxpi3Cq76Eu/NtACIjx8HSpzFGjME7tB1nx1vQ0gQYmNMXYy96HCMn/3ZvV0REBjAFhCLSax6eNZo9p6rZcvQKJUPzmDSyILW/4Mkr9fzs/eP4wKr5Y5k/sYhIVg4vVuxjy5HLQUDYruuuOzlZNnXNCZrjLoUZvI99d9OYwzioJBkG5mVFyGsduNIYovpFRCSz+U6CxJsv4l86FRzIH4y9ZFWPX+8e3Iqz8eWgcy7FwH7o32EMKiT+62/e0ZLi6Ce/DPmD8Q5tw/ngtze/ON4CpnlDDV2z5j2MX19N/DffbA31umeWzoDsPNz9m9qWEy96guEPPM3VvdtI/Oab+NWXATBKJgb7DA4r6fE9ioiIJCkgFJFeM3pYHtPHFHLoXA2/2HACgCF5USYWF3DoXA2O57O0bAQPzwr+4rp0+mh+8d5BTl6p5+L1ptQE45wuJhgnJZflNmf4oJJkgJYM1JKSgWFzSCYxAzS2BB2Eedk2ednhCzhFRCRz+a6Ds+7H+OePp45F7l+DEb35wLPUaze9indwS3DAMMH3CMLB38dvrMV599etx3rOGFsWdB2++8vuOwYBo3A4RvF4zKIxGEUl+DVXcXa9DXXVN31/98P1t66hYBjG2DK804cguZy4bAH20lUQj1H9m38icfTD4OJBQ7CXPoU5YZb2GRQRkTumgFBEetWnHpjClqNXqLxUx8krdVxvjKcGkkwfU8jHlkxI/eU1J2ozf2IRm49cZsuRy4wbHiyFuWkHYevAj+YMD6i66yDMCWEHYUMy7Gy3xLgp1v3UxkzXHA/P/o8iIv2Z77o4FT/DO3Mkdcwsm485buqtX9vcQGLdT/AvngTLxigYhn/9MmBgLXgU9/jeO55S7J89inv25q+Nfur/h5E/GADvwgmcjb/Dv3ru1m9u2RjDx7R1S97ItDAnzsZvqsc7sBkAY9go7JUfxRhajLtrPe6+DUE3oR3Fmv8w1uyVGHak6/cTERHpIf0LSUR6VVbE4sGZo3hw5ig8z+diTROVl+poijk8PKsEy+z4k+1lU0ey+chldlZWUZAbDL24MVRrL9VBmMjsDrxkgJbsuEtqC9jCExAmlxjnZ9ltexCGqP72jl2s5YW3DvGRxeNZOX1UussRERmwfM/DWf8LvFMH2g7m5GMvW33L13pVF0i8+WLQWZc7CLO4FK9yX3AybxDu7nfB7f0/p6xlT+Md34N/9RyJd36OvXw17vZ1eGcO3/R1xpARmGPKMMeW4cdbcDa/1vV1I8Zh5BcG95JaTvw45vTFeMc+DPZYbG4AIHfOcpw5D2HkFfT6fYqIyMCkgFBE+oxpGowemsfood1vFjhqSC6lIwZx6ko9W44Ge+jcrLsr2UHYcodLjK/UNhO1TQrzsu7o9T3V2F0HYVY4lki317bEOEJeCAPO9s5WNeADZ642wPR0VyMiMjD5vofz3q/xTuztcNxe+TGM7NybvtY9sRfn3V+Bk8AYMRazuBR37wdtF/RganAnrfv6eZdP4R3f0/l8wVCia/4LRlYO/qQ5xH/8N/gXT5L4zbe6fUtz3DTM0hmYY8owBhXiN9bhbHqlLchsLzsPs2Qi3tVzbUNayuZjL1mFX3uNxL/9U2qyszFyHPbyZxgyYx5VVVW3f68iIiLdUEAoImm3tGwEp67UU9MYB27eQZidWqJ7+x2EB89e54frj5AdsfjSM3NSA1T6QlNqD8J+MKSkXTdkbsiHlDQ0B/cS1vpFRMLO932cD/4N7+gusCPBvoGJGObE2VgTZ93kdR7u9nWp/fvMsvkYhSNwt63t0ee1n/gM5vAxxH/8/6aOGSPHESn/FH4ihvPur1PhXHuRpz+POWZKUEOsBffAlpt/nlWfxRw9BcOy2uo+uBVn6xupKcftGSUTwXVSwaExtDgISvMLg0AxGaLmBYNbzMlztc+giIj0CQWEIpJ2c0qH8bvtp1OhWU4PlhjfbgfhqSv1/Pi9Y/h+MCDk5xuO80ePz8A0++Yv2W17EHbcEyg5gCVMAWFDuynGYVwi3V59azdksitSRETuHd/3cTe9gndoG1g25sTZQVCYlYu94iPdvy7egvP2z4OlvIaJtewpqK/pUThoLV+NPXsl3rULJF77fnDQtLAWPY41ewXunvdxt7/V+YWGgbXoCdxTB3H3bsCvr8avqw6W/t7INIM9CXMHtdXcWId3+TTuvo1d7zdYMAxj0JDgnOtANAtr4eNYZQtw976Pu+f94LgdwZr7ANbcBzEi0Vver4iIyJ1SQCgiaRexTBZNHs57By4CPRxSchtTgC/XNPMv7xwh4XrMmzCM45fqqLxcz7sHLvDI7NF3V3w3ultinBuSKczttZ9i3NYBGc6AraH1XpKhp4iI3Bu+7+NufQN3/yYwLez7P4az6VUA7OWrO4Rr7Xm1VThrX8SvuQJZOUTKP4m7b+Mt9/0jK5fIk5/BGDkOZ+8HuFvXgudiDC7CWrIKv76a+Pf/75sV3KMAMvLsn2MUDsevuYp3+hDepVN4l051P8nYjmAUjcavv56a3GxOmYe9ZBXehRPEf/X/pZZJm5PmYi9ZhTGo8JZ1iIiI3C0FhCKSEZaWjUwFhD3pIOxpwFbbGOf7FYdoijnMGDOET6yczLGLtfxzxWHe/PAcU0YNZmxR/t3fwA1SQ0puDAiTHXi3EXCmWzLszM+OkB2xOhwLm2Qw2BhL4Pu+lmmJiNwj7o6KoCvONLEf+xTekR0Qb8EcNxVzyryuX3P6MM47P4d4C8aQkdgPfRznnV/g13bce88oHI4xejLesV0Qj0HuIOzlz+BXnSfx8v/pcK1fW4Xz1r/euuDsXKzJ9+G7Lt6hrZ1OW0tWBTVufQPv8mloaep4QSQKdjQ1VCSocwSYRqqj0Bg6EnvFR8GOkHjrx6klzkbRaOzlz2COKr11nSIiIr1EAaGIZISigmwWThrOkQs1FBfmdHtdWwfhrQOq5rjD9ysOUdMYZ/zwfD714GQs02Da6EJWTi9mw6FL/PSD43xp9WyircFXb+l2SEky4AxRwJbqIMyyyWr9OjXHnFAGbMk9CB3XJ+54qfsREZG+43y4HnfX22AY2I/8QbDn3qmDEMnCvv/3Ov1Z4jfW4mx6Da+ydf+9SBRj0BASv/1Oh+usWSswpy2CRIzE6z+ARCw40VSPU/HTHtdnjJmCPf8RjIJhuPs24u55DwwT98TeDgFf2ye2cbe+0fFY7iDM4gmYo8ZjDCvBq9yPe2BzcC4rFyOvIAg2XQciWVgLH8OaMAtnx1vBMmsIpjgvfhJz6nwMw+xx/SIiIr1BAaGIZIx/t2IiBtw0dGrrIOy+A6+6oYUDZ66z7dgVLtU0M2JwNs89MpWo3RYGPbVgHMcv1nKpppnfbT/Nx5dP7LX78H0/FQB2WmIcsj38XM+jOe5iGEFnp2kYZEUsYgmXloR704nTmcbz/NTAFQi6CBUQioj0LWfvB7jb3gQM7IeexSyZRPyX/x8A9tKnMPILU9f6rou7fyPuzgpIxNveJBHvsKTYKJlI5KnPYVjBn0GJDS+3hYNdsGYtxz1zBOqudThuls3HXvo0Rk5e27WzVwQBYVfBYJLrYAwZgVFcitn6PwYNwTAM3FMHSLzzc2ioBcOAgmEQb8GvvhR8zsn3YS96HPf47uDr4MSDPRHnrMSa9zBGNPsWX1EREZG+EZ5/2YlIv2f2oButuw7Cq7XN7D51jQNnqjlf3bbMpzAvyhfKp5OX3XFYSMQy+eQDU/jmq/vYeuwKU0cXMnv80F64C2hJuHg+ZEUsbKtjB0DUNrFMg4TrkXA9IlZmdwi074RMPp/cLJtYwqWxxQlVQNgUd/D9to8bWxyG9v7qchERaeUe2Iy7+TUA7AfXYJXNI/H2z6GlEaNkIub0RalrvQuVOO+/1Gn58I3sFR/FmrWs47GFj+GNngSNdTjb3wqmBZsW1tJVmENGpj5nSm4BkYf/XWo6MYDvOjgbfod3eFuXn9cYOR6zuBSjeDxm8XiM7LwO5/2GGhIbfxd0RgJk5YJtp0JJY8hI7JUfwW9pIv7K96ChBgCzdGYQlA4edtP7FhER6Wvh+ZediAht+xO2xF08z+fw+Ro2HLrEsYu1qWuybJNpYwqZNW4o08YMSe2bd6NRQ3J5asE4frf9NC9tOcmUUQVk90Lg1djSdfcgBN2ROVGbhpYEzTGHSG5mTyRM3kt+u2nMeVk21xtirfsshqfTIbm8OPWxJhmLiPQZ9/B2nA0vA62h3rRFuKcP4R3fDXaEyAO/j2GYeFXnSfzmW53fwLQwS2eC7+KdPND6Ph/pFA4CEM3Gr60KphF7XhDG3f97uEd3kWgdhJJkzX0Aa0F5aiKw73m4e95r7XLsyLrvIcxxUzGGj8GwI53OB693cfdvwt2+LtUNSDQ7CCljTRCJYi18DLO4FGfL6/gXTwJgDC3GXr4ac/Tknn5JRURE+pQCQhEJlayIhUHQpfe3v91NdUOwpChimcwtHcac0qFMHjW4x515K6YXs+fUNU5fbaBi73lWLxx/1zUmlw/fOKAkKTfLoqElQVPMoSDjA8K2CcZJyeAzbINKbgwEw1a/iEhYuMd247z3EgDWsqexZi3DjzXjvP/b4NjCx4LpxD//u06vNQYXYc5cijVlHl7lfpwPgtfYK57BmrW80/V+Qw2J9b/Ev1AZvPes5RijJpB4+6fBNGDTAi/YlsScPBd76VPB63wf7/hunHd+0fEN8wYT/b3/jJFXcMv79C6fwfngt/jXgiFr2FHAT3UrmpPnYs19EPfAFhKbXw/OZediL3occ9oiDFPbXIiISOZQQCgioWIaBtlRi+a4S3VDjKH5WSyfNpJFk0d02bHXk/f76OJSvvnafjYcusSSshEML+h+SEpPJCcYd1dPclluUw8nMadTMkRrv0Q7bPsoJnUKCNVBKCLS69zKfTjrfwn4WIuewJ5zPwDOltehqS64Zt+GILxrxygej71sddCtZxi4B7emwkFr+WqsWSs6f64Te3Hefyno1svJx176NN7ZI7jrfhK854ix2A99HEyLxM+/gXfyAH5LI371JRKvvNDp/SLP/jnmkBE3vT/f86C+GmfvBryDWwEfMMA0gw5CgmnF9vLVeNWXSLzy3WCysmlizVyOteBRjKzc2/mSioiI3BMKCEUkdO6fMYrz1xpZPGUE00YXYpp3N0l3bFE+CycNZ8eJq7y64wzPPTK1x6/1fL/T3ondTTBOSh4PwyTjhnYTjJPy+k1AGK76RUQynXvqIM7bPwPfw5r/CPb8h4MlvFtewzu8ve3CG8LB6B/+XxgFbXvwuYe2tYWDy1Zjz17Z4Xo/HsPZ+Du8ozsBMMdNwxxbhrP51aB7zzCDKcHJ5ci+hzF8DP7Vc8R/9PVOdUee+SJmScdhZb7r4Ndew6+5gn+99X81V/BrrgaTiDteHXQp2tEgACwYhrPhZfzW/QfNcVOxlj59y/BRREQknRQQikjoPDZ3TK+/56r5Y9l3+hoHz17n6IUaykoKb/mak1fq+Ze3D7N4yogOS5NvvcQ4RB2ELV11EAa/DtsS3YbmoN7BuVFqm+IdJhqLiMid830fL7nnoOdhzXkAa/pinB3rcPdvglhz6lpz3FS8C5XgJGDQUKIf+SOM/MGp8+6pg0FXIIBhBlON930Ang++1+V0Ye/M4Q5TjvE93O1v4m7vvK9ge/ajf4g5fjp+zVXcYx92DAJrrwWfryt5BcE9OW1/jpiT5mBNXYiz9wP8rW8E5RcOx1q2Gmtcz3/wKCIiki4KCEVEgILcKI/MGc0bu87yu+2n+dIzg7Fu0pl4vSHGi+uP0hx32XjoEg/NKiE/u2NwdsslxjG3l++i9yWX4eZn958OwpGFOUFAqA5CEZG75rc04rz3Et6pYJAIg4bi11wm/tO/pcPoeCD6B/8XiQ9+GwRreYOJrv5Ch3AQwL9+pd0HHtRfv/2iDBOM5LLfrn8YZIwpw9m2Ft7+OcEy4U5XQMFQzMIRGENa/1c4AiJR3B0VeCf3B1cVDg/2VLx4ksQbPwxqjmZjLSzHmrEMw9I+gyIiEg4KCEVEWt0/YxRbj17hck0zW45eZsW04i6vizsuP1p/hIaWBIYBjuez9egVHp0zGmgLznKzup54mFpiHIYOwlhyiXFXexCGqwOvvl1AePRCraYYi4jcJe/8CRLrf9FxyXB9NV59dTAcJC8fGmrBMIh89I9xNr2Cf/445OQTWf0FjIKhnd7Tuu9BrImz8T0XTBPDMPAbakms/yU01ABgjJ4MLY2p4SBGySQiD/4+DCrEMIIhZV7NVdxtb6aCPLJywY5AYy0A/rmjwXHTxCgY3hYCtgaBRuHwDpOLfdfB3bsBd9fbQehoR7HmPQy2HSyHjjWDYWDOWIq98DGMnLxe/mqLiIj0LQWEIiKtIpbJ6oXjefHdo7y1+xzzJhR16gL0fZ9fbqzkfHUTwwZl8eS8sfzk/eNsPnKZh2aNwjLNVHDW7RLjaHg68NqWGHcxxThkHXjJQLC4MNgcPmxLpEVEMoXvurjb3sTd+36nc8bgIszpi7EmzSHx2j/jA9ac+3H3vBcsA87OJbL6C5iFw7t8b8MwYPAwkj387tEPcTb8GyRikFtA5OF/h7N1bRAOZuViL1+NOWVe8DrAb6zD2fl2sOeh74EdwZq9Emvug2BZuB+uB8vCKBwZhIEFw27Z5eedO4az8XfB/oOAOXE25tgy3L0fpDoejdGTsZetxhzW9Q8XRUREMp0CQhGRdmaNG8Kk4gJOXKrjJ+8f45HZo5kwclBqEMn6/RfYc+oaWbbJZx+eysjCHNbtOceV2hb2n7nO3NJht15iHKYhJV1MMU6GhWEL2Bqag4BwxOBgSnWYpxiv23OOmsY4H182IfWPYhGRe8G7eo7ES9/ueNAwMCfNxZq+GGNU8PuSs3Utfs1VjMFF+HXVeCcPQDSbyNOfxxx66xDNjzXjbHgZ7/huAMwJM7EfWIORnQc73wbAvv9jWJPmtF7fgrvnvWBCspMIapq2GHthOUZeQep97UWP9/he/YZanM2v4lXuC25zcBHW7BV4Z47gvPeb4KKCYdjLnsIcP0O/H4uISKgpIBQRaccwDD6yaDzfen0/Ry/UcvRCLUPyosybWMSQ/CzW7jqLAfzh/ZMpHhJ0oq2YVsxvt55i46FLzC0d1jakJLu7DsKgUyEcQ0pa9yDscolx5tffXrKDcMTgHAwDmuMurudhmWaaK7s9vu/zzr7zOK7P4/eNYXBuNN0licgA4qz/ZYePrWVPY02Z32FJrXf1PO6e1u5C0wyW+UaiRJ76HGbR6Ft+Du/iSRLv/CJYUmxHsVc8gzl1YSqAM0dNwL10Cv/KOfzSGbgHtuB++A60NAXnS2diLX7ijqcG+66Du28j7s63wYkHXYizVoATx9n0ajCxOJKFNf8RrNkrMCz9k0pERMJPf5qJiNygZGgef/6ROew4fpVdlVVcb4zzzr4LqfNPzhvLzHFt+yYtmDScN3ad5eSVes5fa0wtve2ugzA3JB2Evu93s8Q4CAvDFBDGEy5xx8M2DXKiFrlRm8aYQ1PMYVBOuAK2loSL4wYb6je0JBQQisg9Zc1YhntwSxDAjZ/eqWvOdx2cd3+VmgDsX78CdoTIk5/FHDnupu/tuy7urreDZcC+jzF8DPajf4A5uKjDdWZxKS7g7n0ft3Jv296ExaXYS1ZhFo+/4/vzzh3H2fhy23Li0pkYQ0fiHtwKLY2AgTltIfaiJzByB93x5xEREck0CghFRLowvCCHVfPH8cS8sZy8XMeuyir2n7nOzLFDeGR2SYdrsyLW/7+9Ow+Pq7zv/v8+Z2a0jEarJWuzJVmyZHk3mJhgY2NAECChJSQ4IaUJZOnzpE3jpL8+ba6rjUNw84Nc/ZWSpm2ehDyBkPCkLGELuwW1MZiYxfsq2bJWW5a1SzNaZuac3x+jGVu2JMu2ZGmkz+u6uJBmzszcR7eO5Pnoe99fPjE3g60HG3nvUON5m5SElxhfbAXh0cYO3j/cxC1XzCY9Ke6inmM0ev1BLNsm1uXA6ThdZRfrNHGYBv6ghT9g4XJO/gq87oF9IT3xLgzDICHOhbcvgLc3+gLCrp7TS6O7e6J3mbSIRCfHomtwLLpm2PuDu7ZgtzaevsF04PrUlzFzCkd8XrujGf/bT2E31QEGjiuux7G87Jz9AW3bxvb3nb6hux0jLRPHilsw80ovepmv7e0gsO0VrKo9wMBeioWLsWoPRTo0G1kFOFfejplx/ipIERGRaKOAUERkBKZhUJSVTFFWMnetHP64laVZvHuwkR1VzQQtG4dpEDtMcHYpTUoa23w89tZh+gIWLV29fOu2RTjM8dnzKLwk9+xmK4ZhkBDrpLPHj7fPT4ozdlxefyx194S+1p6BvRTD5xSNnYwHBYRROH4RmbpsbyfBHW8Pus15059hzioe/jG2jXX4IwLv/SG0nNeTjOv6LwwZKFpNdQS2v4Z9vCpym1l8Bc61d2Fc5HYRQy0nNudeAb7OUCUjgCcF5ydvwyxcrH0GRURkylJAKCIyBtKT4iidlcLB+nYgtIx4uDcRcQMBYW9/qELPHOWbDW+vn8feDoWDBlDf4mXL/uPcsHh8KhmGWl4c5o4EhAFSEqIgIAzvpRgOCAf+H22NVgC6evojH3dHWSdpEZnibCu0P98ZAttexm44EqruyykctF+f3esj8M5zoT0KAbNoCc7Vn8WIjR/0HFZHM8EP3og0CyE2Hvp6ADASkqGnGzsYwA76IRCAYAACfuxgAIL+yOcEA6HbBj4m6MeqrcBuH+hEPKsYI96DVbkjdL/ThWPZWhxL12A4h14VICIiMlUoIBQRGSOrSrMGBYTDcZgGcS4Hvf4gvf3BEY8NC1oWv9lSSWt3H7NmJFC2JJfH/7uCN3fVs2BWaqRhyljynhWqnSnaGpWcHRB6wp2Yo7AC78wKwmgcv4hMXcFj+09/YpihIK+rleC+bQT3bQNnDOasYsz8UnC4CGx/Fbyd4IrFee2fYhZfMeiPa7avi8DHb2Ed+gAsCxxOHItX4Vh2HVbDUQKbniS4azPBXZsvbeBJMzBnzsI6XoXt6wLAnLsM59W3YniSL+25RUREooQCQhGRMVKck0xGUhynOnvPWZZ7Nnesk15/EF9fYFQB4Ysf1HC0sZPEeBf3Xj+P5IQYri6eyfbKJp567+i4LDUOV9clDLGXYrQ1KokEhPGhr3X4nKKzglBLjEVk8gke2E5w2x8AcK65E8f8FdiWhX2qHqvmIFbtIeyWE1jV+yN7+oU5134ec86iSDho9/cS3P0OwT1bQ9V+xkBjkOU3RQI7c1YxRloWdnc7OF3gcIaqEwc+Dn3uAqcTHGfcFr5/4Ha7sxW7sRrryG4AjJmzQ/sMnqehioiIyFSjgFBEZIyYhsGq+Vm8sL36vMtu42OcQB89o2hU8v7hk7x/+CRO0+De60tITgg11fjMVXkcPt4+bkuNw9VpQy0xDgeg0VLBFm7mcXqJcXSN/0wKCEVksglW7CCw9QUAHCtvxzF/BQCGaWJk5oXCthWfwu5ux6o9ROD9V0LB34DApifBnRRahpyYQnDvewMdg8EsWBDqmJyaOeg1jZg4Yu76zkWP2e7uILD9Nawju0I3uBNxXn3LQBXj5G++JSIiMtYUEIqIjKFrSjKJcZrMzRp5SdL5lujats3xVh97alrYvO8EAJ9fWUheRmLkmLgYJ3etLOTRTYfGZalxd2QPwuhfYtw1zB6E0biH35mhoLoYi8hECx7dQ2DzM4CN4+pbcC5eNeyxhicFx4JPYmTMwv/cvwNgzr8aq/YgeDtDS4nDx2bm4/zkrZhZBWM6XtvfT3DPOwR3bQmFlA4njiWrcVyxFsM1+ffUFRERGS8KCEVExpBpGnxi7szzHueOdQAMqiC0bZvqU93sq2llb20rbd19kfvWLspmeVHGOc9TkpMybkuNvX0DodoQS6CjLSA8p0lJuAKyL/oCtsFNSqJv/CIydQSrDxB4+7/AtnEsvxHnsrWjepwRExf6IDEN15rPYtt3hJYf1x7EbmvCLFqKmT9/TDsG27aNdXRPaN/D7g4AzMLFoX0Gk9LG7HVERESilQJCEZEJEB9zOmDr7vHz0dFTbK9oormrN3JMYryLRXlpLMlPoygradjnOnOp8dt7G7hp6awxGaN3hArCyBLdqAkIQ+P0xIeblAzsQRiFFYRnLjHu6vVj2/aYvokWERkNq74ytDTYsnAsXYNjednoHxwOCPtDv/MMw8BIz8FMzxmHkYJ1qp7Atj9gN9aEXm9GdmifwZzCcXk9ERGRaKSAUERkAoQr8LbsP8FLH9YQtGwAkt0xLC2YweL8NPIyPJijCH7iYpysW1XEL948SPnuekpyksk/YynyxRp5D8Ioa1IyRfYgtCw7UjXoNA0CQZu+gEWcyzHBIxOR6cQ6XoX/jSfACmIuvAbH1bde2B8qzggIx/OPHLavi8AHr2Md3gHYEJeAc8WnMOddhWFqn0EREZEzKSAUEZkA4YCwtbsPw4D5s1L4ZEkm83JTLmqJcHF2MmsWZPPOgRP8busRvnP7klGHRo1tPo42N1A4I2bQm7TuEbsYR88SXcuyTy+Xjju3i3E0VeD5+gJYdujrH+ty0NbdR3ePXwGhRI3HH3+cqqoq5syZw3333Re5vba2lkcffRSAr3/96+Tn50/UEOU8rJO1+F9/HAL+UGfhVbdf8M9QY6CjMMFAaB9AV8yYjtEOBgjufZfgjrfB3w+mA8eiVTiuvAEjNm5MX0tERGSqUEAoIjIBls1J59jJLnLSElhRnHHersejceuVs6k80cGJNh8vfVDNulVF531MW3cfP3vjAL6+AF+9cR7zZ6VG7vP1Dg7VzhRNexD6+gPYA6GaY6BixOU0iXGa9Acsev3ByJLvya5zYP/BxDgXMS4zFBD2+klP0htemfyqqqro7e3lgQce4NFHH+XIkSPMnTsXgKeeeor169djmia//OUv+bu/+7sJHu3UF9i1BbuxGufKz0B6+qgeY51qwP/qr8Dfjzl3Gc7Vd158x9+YOOjpDi0zHqOA0LZtrOoDBP74CnS2AmDmz8dxzacxk0d3jiIiItNVdLwjEhGZYpLdMdx7w7wxfU6nw+RLq+fyk1f28uGRU8yflcri/OE3Xg8ELX67pTIS8r2z/0QkIPQHLfoCFg7TIHaI6rSEKAoITy8vHvwrLyHORX93H97eQNQEhOHlxYnxLlxOc9Bt0SZoWRw50cmczERinKqAnA4qKytZsmQJAIsXL6aioiISEHq9XtIHQiqv1zvk48vLyykvLwfgoYceihwvF6f5VC19NQfxrLgRp9N53q+nv6mB5tceg/5e4kqXk/bZv8AwL/7aPRmfQKCnm5SEeFxjMJf+pno6Nv0XgepDADjTc0i+6QvEFS685OeejEYzZzJ5aL6ij+Ys+mjOLl10vCMSEZFRyUp18+nl+bz4QTXPvl9FXrqH5IShKzNe+biW2uZuUhJi6O0PcqSxk4ZWL7lpCaf3H4x1Drl0LD7GiQH09AcJWvaYdU4eD2d3MA7zxDpp6+7D2+cnneiowAs3KEmMd+F0hALCaNtHMezjo808s62Km5fNGrPGOjK5eb1eMjMzAXC73dTX10fus237vI8vKyujrOx0I4zm5uaxH+Q0EnAnA9BRe5T4kmUjfj3tnm76n3kEerox80qxrv0sLa1tl/T6QUfoZ/Kp53+BWbAQM28eRlrWBS9Xtnu8BD7ahHVwO9g2xLpxXnUT5oIVdJsOuqfo90l6erqugSii+Yo+mrPoozkbvZycoZuCKSAUEZliVpVmcqihjcMNHTz13lG+euO8SJgUtru6hXcPNuIwDf78umION/p4c8cx3tl/grtXzx2xgzGAaRrExTjo6Q/S0x84J3ybTIYLCBOisJPx6YAwJhLKdkfR+M/U1NEDQHNn73mOlKnC7Xbj8/kA6Onpwe12D3lctOwJGu2MlJkA2O2nznusVXsIeroxZs7GedOfhfYQvERm4WKCzcexm+oINtUR/OB1SEjCnD0PM28eZu5cjJjh/3hjB4ME979P8OPy0DJlw8Sx6Bocy8sw4ob+3hIREZHhKSAUEZliDMNg3aoiHn5xD5UnOnjouV2sXZTNiuKZxDgdNHX08Mx7RwG4/ap88jISmZ2Tyaadx9h1rIXbrsyLhGpDdTAOS4hz0dMfxNsbrQFh9HUyPrOCMNzhOlqXGHcOnEv4nGTqKykpoby8nJUrV7J3717Wrl0buc/j8dDS0oJhGMTHx0/cIKcRIyUDGF1AaHeFqgXN3LkYzrH5ee9cdh2O+SuwGo5g1R7GqjsM3k6sQx9iHfoQTBMjq2AgMCzFSJ0ZCY+DtYcJvv9yZOzGrGKcKz+DmZo5JmMTERGZjhQQiohMQUnxMXzlhnn8/v0qTrb38OIHNZTvbmD1gmx2HWumL2CxtCCNlaWhN1MZyW4W56Wxp6aVbYcbyUwJVV94huhgHHa6UYkfuPA39A0tXuJjHKQlju/y3u6eUIWdJ/6sgHDg3LqjYB/FsK5wk5J4V+SNcneUBmxdvtC5dEVpwCkXrrCwEJfLxYYNGygoKCA9PZ3nnnuOO++8k3Xr1vHII48A8LWvfW1iBzpNnA4Im867xDscEBqJqSMed8FjiI3HUbgYR+FibNvGbjmOVVuBVXcI+2Qt9vEqgserCG5/DTwpmLPnQXd7KEwEjOT0UAOSvFJVnoqIiFwiBYQiIlPUnJmJ/M2fLOFAXRtv72mgrsXL6zvrAMhIiuPzK4sGvaFavSCbPTWtvH/4JNctDO1LMdwSYzjdqMR7EQFb5YkOHt10EHesk//1p0tHfJ1L1TVFKwjDoreCcCAgHPi/TA/33XffoM/vvPNOAPLz89m4ceNEDGn6cieCKxb6erB83SMeane3A2MfEJ7JMAyM9FzM9Fy48nrsXh9WfSVW3WGsuopQMHhwe+jgmFgcy8twLLxmTJY7i4iIiAJCEZEpzTQMFuWlsXB2KkcaO3l7TwMtXb18eW0JcWd1Jy6YmUhehofaU91sO9QIjLzE2H2RnYw7vP08+U4lth3a/+8PH9XwxWvnXuCZjd6wS4xjo3sPwnDFT9QGhL7QuH29gUnf6EZkKjIMAyMlA/tUPYHWRogfPvwLVxAyjgHh2Yw4N465S3HMXYptW9jNx7FqD4NthYLBeM9lG4uIiMh0oIBQRGQaMAyD4uxkirOTRzxuzYJsfrulMrI/XLhKcCgXExAGLYvfbKnA2xsgP8NDQ4uXj482s7wo47xju1iRgPDsJcbhCsK+6AnYwtWQiXEurIGAMBqX6PYHgvT6gwDYhKo4k9xDd9sWkfETCQibT8DsocM/2wpCd0foeE/KZRzdaYZhYmTMwsxQx3MREZHxYp7/EBERmS4W5aWRmnA6qBmp+Ui4Au9CAsJXPq6l5lQ3ye4Y7r1hHmVLQ2/2fv9+Ff6AdZGjHll4jz7PWdWQnijrYhwIWvj6AphGKJwNB5y+3gCWNfL+YZNNuHowTI1KRCZGuJNxoKVx+IO8nWBb4E7Scl4REZEpTAGhiIhEOEyDa+dnRz4fzRLj0e5BuKe6ha0HGjENg3uuK8YT5+K6hdlkpcTT0tXHpt31lzb4YQy/xNg56P7J7szzME0Dh2nijnVic+HLvCda51n7DkZjFaTIVBBuVOIfISA83aAk5XIMSURERCaIAkIRERlkRXEGsQP7EybFD7/sMxIQjiLcOdXRw9PbqgC4/RN5FMxMBMDpMPn8ykIMYMv+4xxv9V7i6Afr9wfpD1g4TeOcPRfDjVGiJVwbqkFJOPSMlpAz7OyKQTUqEZkY4YBwpApCu3t8OhiLiIjI5KKAUEREBomLcfKV60u4Y0UBGcnxwx6XcJ49CG3b5kSbjzd31fOLTQfp8wdZWpDGqtKsQcflZySysjQTy4Znt1WN6XLZ7r7T+w+e2bEZIC7GgWlArz9IIDg+y5vH0pkNSsLCy6ajLSDs9A0OBLu1xFhkQhjJM8AwCLafwg4O87M8XEHoUUAoIiIylWkjEREROcdoGpoM1aTEtm3qW7zsqWlhX00bzV29kfuyU918fmXROUEdwC1X5rGvto26Fi/vHWpk9YLsc465GKf3Hzx3L0XTMHDHuuju9ePtC5A8yZtkTKUKwvAS4/gYBz39Qe1BKDJBDIcTIzENu7MFu6MFIy3znGPsrvbQsaogFBERmdIUEIqIyEUJNynx9gXo8PWzo6qZj46coqmj5/QxcU4WzU5jUX4ac7OScDqGLlyPczn47NUFPP7fFbzycS1Zqe4x6WrcPdCAZLhmK544Zygg7PVHQUAYCtWmREA40KQkd0YCR050ag9CkQlkpGSEAsL2JhgqIOxuD30wQR2MRURE5PJQQCgiIhfFfcby1h89uwN7YGVwQpyTZQXpLMlPo2BmIqZ5bsXgUBbmpbF6QRZbDzTyxH9X8M1bFpCTljCqx55s9/Hbd45wTclMVp6xhHm4BiVhoX0IeyJB4mQ21Ll4BsLC7p7JP/4zhSsIc9MGAkJVEIpMCKuuAqv5OHBGEHgWw52IDdhtJyFv3uUbnIiIiFxWCghFROSiuBwmCXFOvL0BTMNg/uxUPjE3g3m5yTjMi9vi9jNX5dPp62d3dSv/p/wQ37ptEame2BEf4w9Y/HZLJY3tPby2o44rC9OJixm8N58nfuhfd6f3UZz8AdWUWmIcriAcCIAVEIpcXnavj8D7L2NV7ADAlZWHUbh4yGPN/PlYlTuxag7C0jWXc5giIiJyGSkgFBGRi/aVtSWc6uxl4ezUSFfgS2EaBl+4di5dPQepOtnFL8sP8Ve3LozsdziUlz+qobE9tKy51x/kjxVNrF2UA5wOnkauICQqKgiHblISnQFheLl0uEI02sYvEq1s28Y6to/Auy9CTzc4nDiuuomMG+6gpbVtyMeYs0vAdGA3VmP3ejHiRlfZLSIiItFFXYxFROSizclMYkXxzDEJB8NcDpOvXD+PzJR4mjp6ePztw/iH6TK8v7aVbYdP4jANbrliNgBbD5yIdCU+/xLjUPDojdoKwujrYuwPWPT0B3GYBhlJcZhGqNFNNHSSFolmtreTwJu/JbDpSejpxsieg+vz63Euuw7DdAz7OCMmDiOnEGwbq/bQZRyxiIiIXE4KCEVEZNJxxzr5elkpye4YjjV18ctNBznZ7ht0TIe3n6e3VQFw65V53LA4h6yUeDp7/OysagbOHxB6wo1WoqKCcPgmJdG0RLfzjPMwTSNqqyBFooVt2wQPfUj/0w9jVe8HVyzO1Xfguv0bmCkZo3oOR/4CAKzqg+M5VBEREZlACghFRGRSSkmI5WtlpSTEOqk62cXDL+3hpQ+q6ekPYFk2v3v3CL6+ACU5yaxekIVhGJGlxZv3n8Cy7dNdjOPPU0F4keHU0cZOfrulkg5v/0U9frT6/EH6AhZOh0Gc63SlT/i8Lnb8E6HTF/paJQ10jQ6fQzSFnCLRwu5swf/K/yGw5ffQ34uZN4+Ydd/FseCTGMbo3waY+fOBUFMTO6BrVUREZCrSHoQiIjJpZae6+V93LOX1nXVsr2hi68FGdhxrpigziaONnXjiXHzx2iJMI9QpedmcGby+s46mjh4O1rXRPco9CL19F15B2O7t44nNFfj6AvgDFvfdOH7dPc/cf9AwTneFjnM5cJgGfQGL/kCQGOfwywQni86Bc0kaCAbDFZGqIBQZO7ZlEdz3HsEP34SAH+LcOFf+CebcpYN+hoyWkZiCMSMbu+UE9vEqDHUzFhERmXJUQSgiIpNaQpyLz11TyPrPLGbOzES8vQH21LQC8IVriwY17XCYJqvnZwPw9r7jkb0Fw3v1nfPcsRe3h59l2fxua6iCEeBAfRv7a1sv7MQuQHh8iWdVQhrG6SW60bBMGs6oIByYt2hcJi0ymVmtJ/G/+DOC778CAT/m3KXErPsbHMXLLiocDDMHlhkHaw6M1VBFRERkElFAKCIiUSF3RgLfvGUBX1o9l+xUN7deOZvS3JRzjru6ZCbxMQ5qT3Vj26H9DB3m0L/uEi4yXHtrbwNVJ7vwxLm4cUkuAC9+UE2/P3hhJzVKkQrCISoho20Pv/C5hJcYh4NCBYQil8YOBgh8XI7/9/+G3VQHCUk4P/VlXDfejRHvueTnNwtO70No2/YlP5+IiIhMLlpiLCIiUcMwDK4oTOeKwvRhj4l1OVg5L4u39jYAw1cPwukKQl+fH8u2I0uVR3KsqYtNu+sBuHt1EUVZyRyqb6Oh1Uf5ngZuW553Iac0KkM1KAnzxEdXJ+OOSAXh4CXGCghFLp7VVEdgy7PYrScBMOdfjfPqWzFi48bsNYz0HEhIAm8ndnMDRsasMXtuERERmXiqIBQRkSnn2vlZOM1Q2Dfc/oMATodJnMuBZUNv//mr/3x9Af7vO5XYNqxdlE1JTgoO0+DOT87BALbsP3FOt+WxcHoPwhEqCKMkYIuci/vsJcbj2+hFZCqy/f0E3n8Z/wv/id16EiNpBq7bv4FrzWfHNByE0B9oTHUzFhERmbLGNSB8/PHH2bBhA4899tg59/X39/ONb3yDPXv2jOcQRERkGvLEu7hqbkbo4xECQhh9J2Pbtnn2/Sravf3MTk/glitmR+7Ly0hkRclMLNvm+e3VY7787swmJWeLtiXGncNUEEbL+EUmC6vhCP3PPkJwz7sAOJauwfX59Zg5RWP+WrZtY7WfgoEqa0v7EIqIiEw547bEuKqqit7eXh544AEeffRRjhw5wty5cyP3v/XWW+Tljf0yLBEREYCbl82iP2DxyXmZIx6XEOuipauP7r4AGUPc7+31c6CujT01rRxqaCfW5eBLq4vP2dfwtivz2FfTytHGTnYea+HKEZZBX6hRVRBGS5OSgUrB8B6EWmIscmHsvh4Cf3wV69CHABhpWTjXfh5zDJf82paF3XICq/EY9oljWI010NM9aAwiIiIytYxbQFhZWcmSJUsAWLx4MRUVFZGAMBAIUFlZybx588br5UVEZJpLjI/h7tVzz3vcUBWEnb5+9tS0sq+2laqTnYQLAk3D4K6VhaQnnbt0zx3r5NNX5fH0e1X84cMaSrKT8QwR6I3Esm0CQeuc20fcgzCKKgj9AYue/iAO08A9sP9jopqUiIxasHo/ga0vgK8LTAeO5TfgWHodhuPS/klvB/xYJ44N/FeNfbIG/H2DD4r3YGbPwcgqwDFn4SW9noiIiEw+4xYQer1eMjNDVRtut5v6+vrIfZs3b2b16tVUVlYO+/jy8nLKy8sBeOihh0hPH7tKjIngdDqj/hymCs3F5KG5mDym81zMSPZAfTs9QQf7j/vYfriBQ7UthBcJO0yD0rx0lhdncUVRJime4ff1+tSMGeysbqeyoZWfvXmQ7965gqzU0XUPtSybR57/gGMnd3L/PauZkRQfuc/XHwoN83MySU92D3pcTpcFHKUvaEz6OTzVEdqfMTkhlpkZoXpN27ZxmAa9/iBJyanEuBwTOcRBpvN1IZOL7esi8N4fsKpCW/MYmXk4r/scZurIFdLDPl9/L3ZjTSgQbKzm+Kl6CJ5VhZyUhplVEAkFjeR0jFE0chIREZHoNG4BodvtxucLvRHo6enB7Q69oQkGg+zatYu//du/HTEgLCsro6ysLPJ5c3PzeA31skhPT4/6c5gqNBeTh+Zi8pjOc+Eg1Jzk6XdOb7rvMA1Kc1NYnJ/G/FmpkWq3QG83zb3dQz5P2BdXFvCrt/poaPWy8cl3ufeGecyZmXjecWzed5y91acAeH7rfu64ugAIBWjt3l4A/D3dNPsHN0Gx+kOft3V5J/0cVjd1AeCJdQ4aqyfORYevn+qGE6SNEMBeblPlusjJyZnoIchFsm0bq3IngW0vQ58PnC4cK27BsfAaDHP0W4nbvi6sxuqB5cLV2C0n4Ky9Uo20LIyBQNDMLsBISB7r0xEREZFJbNwCwpKSEsrLy1m5ciV79+5l7dq1AHR0dNDS0sKPfvQjGhsb2blzJ4WFhXg8o6uwEBERGUuZKaFKPcOAuVnJXDFnBovy04iPubhfkUnuGL55ywJ+u6WSQw3t/OKNA3xx9VyWFswY9jEn2ny8vrMu8vn2ypOULcnFE++ipz9I0LKJczlwOc8NBKKpi3GXb+il0onxoYCwu8c/qQJCkYlkd7Xj3/ocdl0FAMas4lB34sS0kR9n29DVhtUYWjJsn6jG7jgr6DZNjIzZoSAwq4CMhVfSOvCHCBEREZmexi0gLCwsxOVysWHDBgoKCkhPT+e5557jzjvv5MEHHwTg6aefprS0VOGgiIhMmCsLM0jzxDIzOX7ILsEXI9bl4N4b5vHC9mP8saKJ326ppLW7j7ULs89ZohcIWvxu6xGCls3VxTPpCxrsqjrJOwdOcNvyvBEblAAknNGkxLJtzEm8BPDsBiVh4XPrjIKQU2S82baFtX87gQ9eA38/xMbjvOYzmCVXDrnE17Yt7LamUHXgiWqsxmPg7Rx8kNOFkZk/sGS4AGNmHobr9HVoxntAAaGIiMi0Nm4BIcB999036PM777xz0Ofr1q0bz5cXERE5L4dpUJQ19kvpHKbBnZ+cw4zEOF75uJZXP67l2MlOPr+ykKQzgshNu+s50eYjzRPL7Z/Ip9eOYVfVSbYdPsn1i3NGbFAC4HKYxLkc9PqD9PYHI8uhR8uybDbtqSczOZ5lc8Z3v71OXygATBqighCio9GKyHiy2k8R2PJ77MZqAMzCxThX/QmG+/Q2BXYwiN3cEKoObKzGaqyGs7sKx7oxs/IxsudgZhVgpOdiOCbP/p4iIiIy+YxrQCgiIjKdGYbB2kU5pCXG8uy2Kg7Wt/MvL+7hc9fMYUn+DKqbuvjvfccxgC9eW0Ssy0Fueipzs5I40tjJewcbmZEYWnI7XEAIoWXGvf4g3b3+Cw4IN+8/TvnuBhymQU5aAjOT48//oIs0XAVheJm0OhnLdGUHgwT3vEPw47dCzULciThX/SmOwkXY/n6shiOnOww31ULgrGslIRkzuwAzaw5GdgFG6kwMY/R7FIqIiIgoIBQRERlnS/JnkJfu4en3qqg80cFvNldyRWEbtae6sG24flEOczKTIsffuCSXI42dbD3YyOr5WQAjLn/2xLto7uqlu8d/QQFffYuXN3bWAxC0bF78oJqvl5WOW6fS4SsIQ+emgFCmI+tUA4Etz4YahwBmwQLMgoXYJ2vp370Fu7kBLGvQY4yUjIGGIqGmInhS1WFYRERELokCQhERkcsgJSGWr99UyvuHT/LKR7XsrAo1DchOdXPzslmDji3KSiIv3UNtczfvHmoEzldBGPp1fiFLdP2B0N6Hlm1zZWE6B+vbqDjewf66NhbljdwE4WKdbw9CBYQyndgBP8GP3yK4+x2wBwJAw8CqPoBVfeD0gYaBkZ4bWiqcXRD6v/v8ndFFRERELoQCQhERkcvENAxWlWZRkp3M09uqaOro4YvXFuF0DF4KaBgGNy7J5bG3D+PtDQCQGDfyEmO4sIDw1R21NHX0MDM5js9dM4cPKj28+EE1f/iwhnk5KUN2TL5U4QAw6axqyMSLGL9INLNaTxJ48zfndhe2bXA4MTJmYYb3D8zKx4hRd28REREZXwoIRURELrOM5Hj+6taFBC0bhzn0ssDSWSlkpbppbPMB59+DEEYfsFUcb+fdg42YhsHdq+cS43RwzbxMtlc20djmY/P+49y0dNb5n+gC+IMWvr4ApmHgjhv8z4/TFYT9Y/qaIpNVcN+20+GgKxYjKx8za06ow3DGLAzn8Ne7iIiIyHhQQCgiIjJBhgsHIVRteOPiHJ585wgAnpH2IIwEhIHzvqavL8BT7x4F4OZls5g1wxMZyx0rCvjfbxzg7b0NXFWUQaondtTncj5ndmM2z9orzaMlxjLNOK+8ASszD2NGFkZaNoaphiIiIiIysfSvERERkUlqSf4MslPdxLkczEgcPqwLB2wjVRDats3xVi+/23qEzh4/+Rke1i7KGXRMUVYSywpmEAja/OGjmrE5iQGRBiXucyuj4lwOnA6D/oBFnz84pq8rMhkZnmQc85ZjpucqHBQREZFJQRWEIiIik5RpGnzzlgUEghbxMcP/yo40KTmrAi9o2VQ3dbKvto39ta20eUNVfDFOk7tXzx2ygvHTV+Wxv76NvTWtVBxvpyQn5YLG3N3j59UdtVxVlEFh1unOzJEGJUNUQhqGQWKcizZvP109fmJdjgt6TRERERERuTQKCEVERCaxkYLBsDP3IAwELSpPdLC3ppX9dW34+k4vO06Md7FgdirXzMtkRuLQTQ9SEmIpW5LLazvq+M3mSm5bnsfVJTPPWRY8FNu2eeb9Kg7UtXG0sZO/++xSHAPVUacrCIdeKp0YH0Obt5/uXj/pSWrIMNX09PTwk5/8BK/XS1lZGdddd92g+9evX09qaioAX//615k1a2z3wBQRERGRkSkgFBERiXLhgLClq4/7n/p40DLdjKQ4FuWlsTAvldnpnlEFfWsWZFPX7GVfbSvP/fEYO6ua+fzKQmYmx4/4uF3HWjhQ1wZAa3cfO6tauGpuBjB4D8Ihz0H7EE5pb731FqtWrWLVqlX88Ic/ZNWqVTidp/8ZmpSUxP333z9xAxQRERGZ5hQQioiIRLn4WCcxTjOyh19OmptFeWksyU8jM8V9wc/ndJh8eW0xe2taeX57Nceaunj4pT3ctHQWaxdlR6oCz9TZ088LH1QDMH9WCgfr23lrTwNXFKbjMA06fKGAMHnYCkJ1Mp7KKioq+NrXvoZpmuTn59PQ0EB+fn7k/u7ubn7wgx+Qm5vLvffeS0zMud8n5eXllJeXA/DQQw+Rnp5+2cY/1TmdTn09o4zmLLpovqKP5iz6aM4unQJCERGRKGcaBl9eW0JTRw/zZ6WOyRJdwzBYUjCDudnJvPxRDR8eOcXrO+vYX9vKn68tGdTh2LZtnnv/GL6+ACU5yXzl+nn8fy/sprmrl13HmllelBGpDByugjASEI7QaGUk2yuaeO9QI3+2ppjMlJErHeXy8/l8xMeH5sXtduP1egfdv3HjRjweD8899xzl5eXcdttt5zxHWVkZZWVlkc+bm5vHd9DTSHp6ur6eUUZzFl00X9FHcxZ9NGejl5OTM+TtCghFRESmgHm5KczLTRnz53XHOlm3qogrC9N5+r2j1LV4eeTlvfzZmmJKcpIB2F3dwv66NmJdDu5aWYjDNLhhSQ5Pv1cVqiKck07nQAXhsHsQxl38EuPGNh/Pbz9G0LJ5fvsx/sfN8zFGsZRaxl57ezuPPPLIoNtSUlJwu9309PQQExODz+cjISFh0DEejweAFStW8Morr1yu4YqIiIjIAAWEIiIicl5zs5P5zu1L+L9bKznc0MEvyw/yqWWz+URxBs9vrwbg9qvySEkIVRZeWZhO+e4GTnX2sru6hc6B4C9p2ArCUHB4difm8wlaFv/17hGClg3A0cZQ1+bF+WkXc5pyiVJSUobcS/Dll19m7969rFy5kpqaGnJzcyP3BQIBbNvG5XJx+PBhMjMzL+OIRURERAQUEIqIiMgouWOdfPXGUsp311O+u4HXd9bxzoET+PoCFGcns6J4ZuRYh2lyw+Jcnn2/ik276/H1BTANSIgb2yYlb+05TkOrj1RPLNeUzOTVHXW8/FENpbNScDnO3StRJsYNN9zAv/3bv/H6669TVlaG0+lk165dWJZFYWEhDz74IHFxcSQkJPDXf/3XEz1cERERkWlHAaGIiIiMmmkY3LxsNrPTPfxu6xF8fQFinSZ3rSw8Z1nv8qJ0yvfUc6qzFwhVCQ7XRTmyxPgC9iCsb/Hy1p4GANatLGROZhI7qpppbO9h64ET3LA49zzPIJeL2+3me9/73qDbli1bFvn4xz/+8WUekYiIiIicSX9aFxERkQs2f1Yq6z+zmKuKMrjnrKYlYU6HOSikG255MQzuYmzb9nlfPxC0eOrdI1i2zbXzs5ibnYzDNPiTFQUAvLWnIdI5WURERERERqaAUERERC7KjMQ4vnBtEaUjNEf5xNwMkgcakyQO06AEINblIMZpEgja9PmD533tN3fV09jeQ3pSHLdeOTtye3F2Mgtnp9IfsHhtR+3oT0ZEREREZBpTQCgiIiLjxukwuWlpqIowJ9U94rGJo9iHsLvXz/uHT7J5/3EMA76wqogYp2PQMZ+5Kh+HafDx0WZqT3Vd4hmIiIiIiEx92oNQRERExtXVJZnMmuFhZkr8iMd54ly0dPXR1eMnIzl0rG3bnOrsZX9dGwfq2qhp6iK8APm6hdkUzEw853nSk+JYsyCb/953nBc/qOEvb12Aw9TfREVEREREhqOAUERERMZd7oyE8x6TGB9agtzh6+fIiQ4O1LVxsL6d5q7eyDEO06AoK4nF+WmsmDtzuKfihiW5fHT0FLXN3fy/z+5k1fwsri6eOWwXZRERERGR6UwBoYiIiEwK4SXGv9t6hDPblLhjnZTmprBwdiolOcnExZz/ny9xLgf3rCnm9388RlNHD6/tqKN8dwPLi9K5dn42meepZhQRERERmU4UEIqIiMikMDO8rBjITI5nwexU5s9KIT8jEdM0Lvj5CrOS+H/+dAmVxzvYevAEhxs6+GNFE9srm7hjRQErS7PG+AxERERERKKTAkIRERGZFD5ZMpMZibHMTI5nRmLcmDynaRjMy01hXm4KJ9t72LL/OB8eOcXz26tp6erj01flYRoXHj6KiIiIiEwl2rFbREREJgWnw2T+rNQxCwfPlpkSz7pVRaxbVYhpGLxz4AS/2VxJfyA4Lq8nIiIiIhItFBCKiIjItPKJuTP5xk2lxLkc7Ktt5X+/cYCunv6JHpaIiIiIyIRRQCgiIiLTztzsZL5120JSE2Koa/by01f3c7LdN9HDEhERERGZEAoIRUREZFrKTHHz159exOwZCXT3+OnzWxM9JBERERGRCaEmJSIiIjJtJcbH8D9vWUBDq4+8DM9ED0dEREREZEKoglBERESmtRingzkzEyd6GCIiIiIiE0YBoYiIiIiIiIiIyDSmgFBERERERERERGQaU0AoIiIiIiIiIiIyjSkgFBERERERERERmcYUEIqIiIiIiIiIiExjCghFRERERERERESmMQWEIiIiIiIiIiIi05gCQhERERERERERkWlMAaGIiIiIiIiIiMg0poBQRERERERERERkGlNAKCIiIiIiIiIiMo0pIBQREREREREREZnGFBCKiIiIiIiIiIhMYwoIRUREREREREREpjEFhCIiIiIiIiIiItOYAkIREREREREREZFpTAGhiIiIiIiIiIjINKaAUEREREREREREZBpTQCgiIiIiIiIiIjKNKSAUERERERERERGZxhQQioiIiIiIiIiITGPOiR6AiIiIiExtO3fu5Ne//jWJiYls3LjxnPu3bt3KG2+8gcfj4dvf/jZut3sCRikiIiIyfamCUERERETGVXFxMf/8z/885H2BQIBNmzbxwx/+kDVr1lBeXn6ZRyciIiIiqiAUERERkXHl8XiGva+xsZG8vDwcDgeLFy/m5z//+ZDHlZeXR8LDhx56iPT09HEZ63TkdDr19YwymrPoovmKPpqz6KM5u3QKCEVERERkwni9XuLj4wFwu914vd4hjysrK6OsrCzyeXNz82UZ33SQnp6ur2eU0ZxFF81X9NGcRR/N2ejl5OQMebsCQhEREREZE+3t7TzyyCODbktJSeE73/nOsI9xu9309PQA0NPTQ0JCwjiOUERERESGooBQRERERMZESkoK999//wU9Jjs7m7q6OizLYs+ePRQXF4/P4ERERERkWGpSIiIiIiLj6ujRo2zcuJG6ujo2btxIf38/u3btYseOHTidTm688UY2bNjAli1buOmmmyZ6uCIiIiLTjioIRURERGRcFRUV8f3vf3/QbcuWLYt8vGbNGtasWXOZRyUiIiIiYYZt2/ZED0JEREREREREREQmhpYYXybf+973JnoIMkBzMXloLiYPzcXkobmYPDQXMl3oez36aM6ii+Yr+mjOoo/m7NIpIBQREREREREREZnGFBCKiIiIiIiIiIhMYwoIL5OysrKJHoIM0FxMHpqLyUNzMXloLiYPzYVMF/pejz6as+ii+Yo+mrPoozm7dGpSIiIiIiIiIiIiMo2pglBERERERERERGQaU0AoIiIiIiIiIiIyjTknegDTweOPP05VVRVz5szhvvvum+jhTAuVlZX8+te/xjAMioqKuPfee3nppZf48MMPycjI4C//8i9xOp1D3ibj4+WXX2b79u1s3LhxyGtC18nlsWXLFrZs2YJlWXz729/mpZde0lxMgL6+Ph5++GH6+vpwu91897vf5cknn9RcXEatra38+Mc/pr6+nieeeAKHwzHqn02aF5lK9P0cXZqamviHf/gHcnNzcTqd/OM//uNED0mGMNrfMTJ5nD1nLS0tutYmsdG+35cLowrCcVZVVUVvby8PPPAAgUCAI0eOTPSQpoWMjAw2bNjAxo0b6ezs5MCBA+zfv5+NGzeSl5fHhx9+SEdHxzm3yfjw+/1UV1cDQ18Tuk4uj9bWVg4cOMCGDRu4//77aW9v11xMkF27dlFcXMz999/P3LlzeeGFFzQXl5nH4+H73/8+xcXFwOh/NmleZCrR93N0Wrx4Mffff78Ci0lsNL9jZHI5e85A19pkNpr3+3LhFBCOs8rKSpYsWQKEfsBUVFRM8Iimh5SUFGJiYgBwOBzU1dWxYMECAJYsWUJFRQVHjx495zYZH2+//TZr164Fhr4mdJ1cHrt27cKyLB544AF+9atfUVFRobmYIJmZmfT29gLg9XoxDENzcZnFxMTg8Xgin4/2Z5PmRaYSfT9Hp/3797NhwwZefvnliR6KDGM0v2Nkcjl7zkDX2mQ2mvf7cuEUEI4zr9eL2+0GwO124/P5JnhE00tNTQ2dnZ0kJCQQHx8PhObB6/Xi8/nOuU3GXiAQYP/+/SxatAgY+prQdXJ5dHR0EAgE2LBhAzExMfh8Ps3FBMnOzqayspK/+Zu/oaqqCtM0NRcTbLQ/mzQvMpXo+zn6pKam8pOf/IQf/OAH7N27l5qamokekoyCrrXoo2stOoz0fl8unALCcXbmL4Cenp7ILwYZf93d3fzqV7/im9/8Jm63m56eHgB8Ph8JCQlD3iZj75133uHaa6+NfD7UNaHr5PJwu92Rv6yFA1vNxcTYsmULy5cv5+GHH+aKK64gGAxqLibYaH82aV5kKtH3c/RxuVzExcXhcDhYvnw5dXV1Ez0kGQVda9FH19rkd773+3LhFBCOs5KSEvbt2wfA3r17KSkpmeARTQ/BYJCf/vSn/Pmf/zkpKSkUFRVx4MABIDQPxcXFQ94mY+/48eNs2rSJH/3oR9TX19PV1XXONaHr5PKYN29e5K+f4T0hNRcTw7btyDKWpKQkQHMx0Yb6eo/2NpFope/n6BN+Awxw6NAhMjMzJ3A0Mlq61qKPrrXJbTTv9+XCGbZt2xM9iKnuscce49ixYxQUFPDVr351ooczLbz77rs89thjzJ49G4AvfelLHDhwgI8//pj09HT+6q/+CqfTyQsvvHDObTJ+vv/977Nx48YhrwldJ5fHE088QVVVFYmJiaxfv57f/OY3mosJ4PV6eeSRR/D7/TgcDr773e/yzDPPaC4uo0AgwIMPPhjpKHn33Xfz7rvvjmoONC8ylej7Obrs2LGDp556CpfLRWlpKffcc89ED0mGMNrfMTJ5nD1n8+fP56OPPtK1NkmN9v2+XBgFhCIiIiIiIiIiItOYlhiLiIiIiIiIiIhMYwoIRUREREREREREpjEFhCIiIiIiIiIiItOYAkIREREREREREZFpTAGhiIiIiIiIiIjINKaAUESmpKamJtatW8dDDz3Ejh07ePrpp2lqahrz16mvr+fpp59m//79kdv+4z/+g3Xr1nH06NExfz0RERERERGRseac6AGIiIyHpKQk1q9fT1paGtu2beONN95g4cKFzJw584KeJxgM4nA4hr2/vr6eZ599FoCFCxcCcPPNN7Ns2TIyMzMv/gRERERERERELhPDtm17ogchIjLWmpqa+Na3vkVsbCx9fX2D7nv66aepqKjg17/+NbW1taSlpXHXXXdx7bXXRh5XUlJCbGwstbW1/Mu//Av/9E//xIkTJwCYM2cO3/jGN4iNjeVb3/rWoOf+wQ9+wObNm9myZQsPPvggRUVFlJeX89JLL9HW1sasWbP4yle+QmlpKZs3b+Y///M/WblyJQ0NDTQ3N3PXXXdx2223cfz4cf793/+dmpoaYmJimD17Ng888MBl+/qJiIiIyOg8/PDDJCcnU11dTUtLC9/+9rfZtGkTR44cobS0lG9+85sTPUQRkfPSEmMRmdIWLFjA0qVLAfjc5z7H+vXr6e7u5qGHHsLn83HnnXeSkZHBT3/6U6qrqyOPq6ioYM6cOXzhC1/AMAxWrFjBfffdxx133EFNTQ2PP/44SUlJ3HbbbQBcffXVrF+/nlmzZg16/X379vGLX/yCpKQkvvzlL9Pc3MyPf/xjurq6Isfs37+fG2+8EYAnn3ySQCDAG2+8wdGjR7nnnnu4++67SU9PH+evlIiIiIhcjNraWjIzM9m4cSNlZWX87Gc/45577uHhhx9mx44d+P3+iR6iiMh5aYmxiExphmGQlZXF7t27WbRoEQsXLmTHjh10d3fT3d3N7373u8ix+/btY8WKFUCoSvCee+4BoLW1ld27d1NRUUG46Lq2tpa4uDhKS0t59dVXmT17NqtWrTrn9Xfs2AHAunXrWLJkCc3NzTz//PNUVlZGjrn++uu55ZZb+Pjjj9m9ezft7e1kZ2dj2zY7d+6kqKgoEkSKiIiIyOTR39+P1+uN/FvNMAxuuOEGUlNTATBNE6dTb7tFZPLTTyoRmfIMwxjy9jVr1rBmzZrI52fuTxj+Rx3Aa6+9xuHDh/n0pz/NFVdcwc9+9jN6enrGbCwejwcgstehZVnccsst5ObmcuDAAT766COee+45/vVf/5WcnJyLel0RERERGXv19fUUFhZimqHFeTU1Ndx8880AtLS0kJaWNuy/RUVEJhMtMRaRKS8hIQGAP/7xj+zYsYOSkhI8Hg+7d+/m+PHj1NXV8eKLL9La2jri83i9Xg4cOEBLS0vktnC4d+jQId577z36+/sHPebKK68E4JlnnmHTpk28/fbbJCQkUFxcPOJrvfnmm1RUVJCVlUVmZia2bdPe3n6hpy4iIiIi46i2tpb8/PzI5zU1NeTl5Z3zsYjIZKeAUESmvNWrV5Obm8ubb77JY489hsfj4Xvf+x5ZWVk8+eSTPPfcc8TExJCRkTHk42+99VaKiorYtm0bra2tzJ49O3JfaWkpixcv5uDBg/zkJz8ZtLcgwKJFi/iLv/gLOjo6eOKJJ5gxYwZ///d/T2Ji4ohjdrlcbN68mZ///OccPHiQT33qU5SWll76F0NERERExkxtbS0FBQVAaLlxf39/5A/INTU1g8JDEZHJTF2MRUREREREREREpjFVEIqIiIiIiIiIiExjCghFRERERERERESmMQWEIiIiIiIiIiIi05gCQhERERERERERkWlMAaGIiIiIiIiIiMg0poBQRERERERERERkGlNAKCIiIiIiIiIiMo39/8iKZ9lkYB+AAAAAAElFTkSuQmCC",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plot_all(cost_history, m, q, high=1000, step=10)"
]
},
{
"cell_type": "code",
"execution_count": 194,
"metadata": {},
"outputs": [],
"source": [
"#plot_1(cost_history, m, q, low, high, step)"
]
},
{
"cell_type": "code",
"execution_count": 196,
"metadata": {},
"outputs": [],
"source": [
"#plot_2(cost_history, m, q, low, high, step)"
]
},
{
"cell_type": "code",
"execution_count": 55,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"12835 passi e 12835 gradienti calcolati per arrivare a distanza minore o uguale di 0.1 dall'ottimo\n"
]
}
],
"source": [
"near_opt(m, min_dist=1e-1, ge_per_step=1)"
]
},
{
"cell_type": "code",
"execution_count": 56,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA7sAAAHzCAYAAADhDgreAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAABLJklEQVR4nO3df3RU9Z3/8dfNDIFkAkkmQ4L8+iqoBcEINFFraIEIyInV2pqlSsmettu1rp51bVePsG2llVKw6qnHimt7tLaN3bYuiB63szVNwbimtQZJGonFqq3SChiSECAJASZzv3+EDIT8ID9m7q95Ps7pkUxmyHvmk6Hzuvdz32/DNE1TAAAAAAB4SIrdBQAAAAAAEG+EXQAAAACA5xB2AQAAAACeQ9gFAAAAAHgOYRcAAAAA4DmEXQAAAACA5xB2AQAAAACeQ9gFAMBi559/vtLS0jR+/HhlZWXpqquu0uOPP65oNHrOx7733nsyDEORSCShNVr1cwAASBTCLgAANnjhhRd09OhRvf/++1qzZo3uv/9+/dM//ZPdZQEA4BmEXQAAbJSZmanrr79ev/zlL/WTn/xEu3fv1q9+9SvNnz9fEyZM0LRp0/TNb34zdv9PfOITkqSsrCxlZGTo97//vd59910VFxcrJydHoVBIn/vc59Ta2hp7zP33368pU6Zo/Pjx+shHPqLf/va3kqRoNKpNmzZp5syZysnJ0cqVK9XS0jLgzwEAwE0IuwAAOMDll1+uqVOn6v/+7/8UCAT005/+VK2trfrVr36l//zP/9Rzzz0nSXr55ZclSa2trWpra9PHPvYxmaaptWvXat++ffrTn/6kv/3tb7GA/NZbb+nRRx9VTU2Njh49qhdffFHnn3++JOn73/++nnvuOVVVVWnfvn3Kzs7W7bffPuDPAQDATQi7AAA4xOTJk9XS0qLFixfr0ksvVUpKivLz83XzzTerqqpqwMddeOGFWrZsmcaOHauJEyfqq1/9auz+Pp9Px48f15tvvqmTJ0/q/PPP18yZMyVJjz/+uDZs2KCpU6dq7Nix+uY3v6ktW7ZwnS4AwBMIuwAAOMQHH3ygYDCoP/zhD1qyZIkmTpyozMxMPf7442pqahrwcR9++KFuuukmTZkyRRMmTNDq1atj97/wwgv18MMP65vf/KZyc3N10003ad++fZKk999/X5/+9KeVlZWlrKwszZ49Wz6fTx9++KElzxcAgEQi7AIA4AA1NTX64IMPtHDhQq1atUrXX3+9/va3v+nw4cO69dZbZZqmJMkwjD6P/Y//+A8ZhqE33nhDR44c0dNPPx27vyStWrVKr7zyit5//30ZhqF77rlHkjRt2jT97//+r1pbW2P/6+zs1JQpU/r9OQAAuAlhFwAAGx05ckT/8z//o5tuukmrV6/WpZdeqqNHjyoYDGrcuHF67bXX9F//9V+x+0+cOFEpKSn6y1/+Ervt6NGjysjIUGZmpj744AM98MADse+99dZb2r59u44fP65x48YpLS1NKSnd//d/66236mtf+5ref/99SdLBgwf1/PPPD/hzAABwE8IuAAA2uO666zR+/HhNmzZNGzZs0Fe/+lU99dRTkqTHHntM9957r8aPH6/77rtPK1eujD0uPT1dX/va11RUVKSsrCy9+uqrWrdunXbt2qXMzExde+21+sxnPhO7//Hjx7VmzRqFQiFNmjRJjY2N2rhxoyTp3/7t33T99ddr+fLlGj9+vK688kr94Q9/GPDnAADgJoZ55j4nAAAAAAA8gDO7AAAAAADPIewCAAAAADyHsAsAAAAA8BzCLgAAAADAcwi7AAAAAADPIewCAAAAADzHb3cBVti3b5/dJThSKBRSU1OT3WXgLKyLM7EuzsS6OA9r4kysizOxLs7DmjjTYOsyefLkAR/HmV0AAAAAgOcQdgEAAAAAnkPYBQAAAAB4DmEXAAAAAOA5hF0AAAAAgOcQdgEAAAAAnkPYBQAAAAB4DmEXAAAAAOA5fqt/4GOPPaZdu3YpMzNTDz30kCTpmWee0W9/+1tNmDBBknTzzTdrwYIFfR5bV1enp556StFoVFdffbVuuOEGK0sHAAAAALiE5WF38eLFWrFihTZv3tzr9muvvVbXX3/9gI+LRqN68skn9fWvf105OTlau3atCgoKNHXq1ESXDAAAAABwGcu3MV9yySXKyMgY9uPeeecdTZo0SXl5efL7/brqqqtUU1OTgAoBAAAAAG5n+Zndgbz44ot6+eWXNWPGDP3jP/5jn0Dc0tKinJyc2Nc5OTl6++23rS4TAAAAAOACjgi7y5cvV2lpqSTpl7/8pX7605/qtttuG/HfV1lZqcrKSknSpk2bFAqF4lKn1/j9fl4bB2JdnIl1cSbWxXlYE2diXZyJdXEe1sSZRroujgi7WVlZsT9fffXVuv/++/vcJxgMqrm5OfZ1c3OzgsFgv3/f0qVLtXTp0tjXTU1N8SvWQ0KhEK+NA7EuzsS6OBPr4jysiTOxLs7EujgPa+JMg63L5MmTB3ycI0YPHTp0KPbn1157TdOmTetzn5kzZ2r//v1qbGxUJBLR7373OxUUFFhZJgAAAADAJSw/s/vwww/rzTff1NGjR3Xrrbdq5cqVamho0HvvvSfDMDRx4kTdcsstkrqv0/3BD36gtWvXyufz6Ytf/KI2bNigaDSqJUuW9BuKAQBA8mmoq9UbL4Y15libTqZl6NJrSjRn3ny7ywIA2MjysHvnnXf2ua24uLjf+waDQa1duzb29YIFC/qdvwsAAJJXQ12tDmwpV2luloz0dJlml6q2lEsSgRcAkpgjtjEDAACM1O6KsBblZskwDEmSYRhalJul3RVhmysDANiJsAsAAFzN39EWC7o9DMOQv6PdpooAAE5A2AUAAK4WSc+QaZq9bjNNU5H0gE0VAQCcgLALAABcbe7yElU1tsYCr2maqmps1dzlJTZXBgCwkyPm7AIAAIxUTxOqrRVh+TvaFUkPaG5pGc2pACDJEXYBAIDrzZk3n3ALAOiFbcwAAAAAAM8h7AIAAAAAPIewCwAAAADwHMIuAAAAAMBzCLsAAAAAAM8h7AIAAAAAPIewCwAAAADwHObsAgCAEWuoq9UbL4Y15libTqZl6OMrb9aUC2bYXRYAAJzZBQAAI9NQV6sDW8pVmtalG3LSVZrWpXd/+kM11NXaXRoAAIRdAAAwMrsrwlqUmyXDMCRJhmFocV6WdleEba4MAADCLgAAGCF/R1ss6PYwDEP+jnabKgIA4DTCLgAAGJFIeoZM0+x1m2maiqQHbKoIAIDTCLsAAGBE5i4vUVVjayzwmqaplz5s1dzlJTZXBgAA3ZgBAMAgzu62fOk1JZozb74kxf67tSIsf0e7IukBLfzHW+jGDABwBMIuAADoV6zbcm6WjPR0mWaXqraUS1KvwNvzZ0kKhUJqamqypV4vGewgAwBgaNjGDAAA+tVft+VFuXRbTrT+Rjod2FLOSCcAGCbCLgAA6Bfdlu3BQQYAiA/CLgAA6Bfdlu3BQQYAiA/CLgAA6Fd/3ZarGum2nGgcZACA+CDsAgCAfs2ZN1+TSsu0tdOn55qPaWunT5NKy2iUlGAcZACA+KAbMwAAGNDZ3ZaReP2NdJrLQQYAGDbCLgAAgMNwkAEARo9tzAAAAAAAzyHsAgAAAAA8h7ALAAAAAPAcwi4AAAAAwHNoUAUAAICEa6ir1RsvhjXmWJtOpmXo0mtKaMIFIKEIuwAAAEiohrpaHdhSrtLcLBnp6TLNLlVtKZckAi+AhGEbMwAAABJqd0VYi3KzZBiGJMkwDC3KzdLuirDNlQHwMsIuAAAAEsrf0RYLuj0Mw5C/o92migAkA8IuAAAAEiqSniHTNHvdZpqmIukBmyoCkAwIuwAAAEiouctLVNXYGgu8pmmqqrFVc5eX2FwZAC+jQRUAAAASqqcJ1daKsPwd7YqkBzS3tIzmVAASirALAACAhJszbz7hFoCl2MYMAAAAAPAcwi4AAAAAwHPYxgwAABBnDXW1euPFsMYca9PJtAxdek0JW3gBwGKEXQAAgDhqqKvVgS3lKs3NkpGeLtPsUtWWckki8LocBzEAdyHsAgAAxNHuirBuzM2SYRiSJMMwtCg3S1srwgSjfrglQHIQA3AfrtkFAACII39HWyzo9jAMQ/6Odpsqcq5YgEzr0g056SpN69KBLeVqqKu1u7Q+dleEtaifgxi7K8I2VwZgIJae2X3ssce0a9cuZWZm6qGHHpIklZeX6/XXX5ff71deXp5uu+02BQKBPo+9/fbbNW7cOKWkpMjn82nTpk1Wlg4AADAkkfQMmWZXr8BrmqYi6X0/3yQ7N50F93e0yUhL73UbBzEAZ7M07C5evFgrVqzQ5s2bY7fl5+dr1apV8vl8evrpp7Vt2zatXr2638evW7dOEyZMsKpcAACAYZu7vERVW8pjZwFN01RVY6vmlpbZXZrjuClAchADcB9Lw+4ll1yixsbGXrdddtllsT9ffPHFevXVV60sCQAAeJCd14H2/JytFWH5O9oVSQ9obmmZ485UOoGbAiQHMQD3cVSDqu3bt+uqq64a8PsbNmyQJC1btkxLly61qiwAAOAiTmgkNGfefMLtELgpQHIQA3AfwzRN08of2NjYqPvvvz92zW6PZ599Vu+++67uuuuuPk0dJKmlpUXBYFCHDx/Wt7/9bX3hC1/QJZdc0u/PqKysVGVlpSRp06ZNOnHiRPyfiAf4/X5FIhG7y8BZWBdnYl2ciXVxHiesyZP3rtWnU0/2OVu47cQY/dN9G22szD5OWJeB/LHmNe18YZt87W3qCmSo4LpP67LCy+0uyxJOXpdkxZo402DrkpqaOvDjElXQcLz00kt6/fXXde+99/YbdCUpGAxKkjIzM1VYWKh33nlnwLC7dOnSXmd+m5qa4l+0B4RCIV4bB2JdnIl1cSbWxXmcsCaRliadzEnv5/YjttdmFyesy0CmXDBDU+749163ObXWeHPyuiQr1sSZBluXyZMnD/g428NuXV2dnn/+eX3rW9/S2LFj+71PZ2enTNNUWlqaOjs7VV9fr9LSUosrBQAAbvD3tg798u0/KdXs0skUny6dPk2zJk105HWgAIDEsTTsPvzww3rzzTd19OhR3XrrrVq5cqW2bdumSCSi9evXS5Iuuugi3XLLLWppadEPfvADrV27VocPH9aDDz4oSerq6tLChQs1b948K0sHAAAu0FBXq/93ol1XZo5VaFyqZJrasfd97Wo5qo/e+m92lwcAsJClYffOO+/sc1txcXG/9w0Gg1q7dq0kKS8vTw888EAiSwMAAB6wuyKsGy+crvajR7T/YKNSuqL6SE6m3hmbTSMhAEgytm9jBgAkjp3jVwA79MxtzZiQqYwJmbHbc5uP2VgVAMAOhF0A8CgnjF8BrOamua0AgMQi7AKAR+2uCOvGU7MrJckwDC3KzdLWijBhF541mrmt7IQAAG8h7AKAR/Vs5zyTYRjyd7TbVBGQeD3hdGtFWP6OdkXSA5pbWnbO0MpOCADwHsIuAHgU2zmRrObMmz/sgMpOCADwnhS7CwAAJMbc5SWqamyVaZqSdHo75/ISmysDnMff0dbrwJDETggAcDvO7AKAR410OyeQjNgJAQDeQ9gFAA8byXZOIBmNprEVAMCZCLsAACQQHX7dgZ0QAOA9hF0AABKEDr/uwk4IAPAWGlQBAJAguyvCsW2x0ukOv7srwjZXBgCA9xF2AQBIEDr8AgBgH7YxAwCQIHT4hZcNdj0616oDcALCLgDA9c7+YJ1xwUy1/fVd2z9o0+EXXjXY9eiSuFYdgCMQdgEArnb2h+439+/Xm1te0Yr8SzQ+J8vWD9p0+IVX7a4I68Z+rkffeup69IG+x+8+ACsRdgEArnb2h+6GvX/XjVNydKDpoMZnZtn+QZsOv/Aif0ebjLT0Xredvh7dHOR7AGAdGlQBAFzt7CZQ/miXUgxDKV1dsdv4oA3EV/f16Gav23quRx/sewBgJcIuAMDVzv5gHUnxKWqaivp8sdv4oA3E19zlJapqbI2992LXoy8vGfR7AGAltjEDACyRqO6sZzeBmjN9qp59511dk3+JJNEUCkiAoVyPzrXqAOxG2AUAJNxgnVtH+wG4z4furPMUKF2oF997V/5mPmgDiTLY9ehcqw7ACQi7AICEG6xzazw+EPPBGgAAnI1rdgEACXd2EymJplEAACCxCLsAgISjOysAALAaYRcAkHB0ZwUAAFbjml0AQMINpXMrYJVEdQYHADgLYRcAYAk3NJEiBCWOU17bc3UGd0qdAIDRI+wCAKDEjkdKdk56bQfrDC7JMXUCAEaPa3YBAFB3CFrUTwjafSoEYeSc9NoO1hncSXUCAEaPsAsAgBiPlEhOem0H6wzupDoBAKNH2AUAQIxHSiQnvbaDdQZ3Up0AgNEj7AIAIMYjJZKTXts58+ZrUmmZtnb69FzzMW3t9GnSqc7gTqoTADB6NKgCAEDuHI/kls7BTnttB+oM7rQ6AQCjQ9gFAOAUN4xH6uGkDsdD4ZbX1uo63XLAAgDciG3MAAC4EJ2D3S92wCKtSzfkpKs0rUsHtpSroa7W7tIAwBMIuwAAuBCdg92PAxYAkFhsYwYAxBXbMq3R3Tm4q1fgpXOwu/g72mSkpfe6jQMWABA/nNkFAMQN2zKtQ+dg92PUEQAkFmEXABA3bMu0zmAjdOAOHLAAgMRiGzMAIG7Ylmktuzsc97dlfdHSZbbV4zaMOgKAxCLsAgDihutIk8dAo4/+mJmpKRfMsLs817D7gAUAeBlhFwAQN3OXl6hqS3lsK3NsW2Zpmd2lWcLK5lx2NwLbXRHWjf1sWf/VC9s05Y5/t6wOAAAGQtgFAMRNMm/LHOhMp6S4P38rf9ZABtqy7mtrs+TnA1az+wATgOEj7AIA4ipZt2UOdKZza0U47q+HlT9rIANtWe8KZFjy8wErOeEAE4DhoxszAABx4O9o6xX8pMQ157LyZw1koE7CBdd92rIaAKvQaR5wJ87sAgAQB1Y253JCI7CBtqxfVni5mpqaLKsDsAKd5gF3IuwCABAHVjbnckojsGTdso7k44QDTACGj7ALAEAcWNmcK5kbgQF2cMoBJgDDY3nYfeyxx7Rr1y5lZmbqoYcekiS1tbXpe9/7ng4ePKiJEyfqK1/5ijIy+ja4eOmll/Tss89Kkj7zmc9o8eLFVpYOAMCgrDzTyVlVwDocYALcyfKwu3jxYq1YsUKbN2+O3fbcc8/p0ksv1Q033KDnnntOzz33nFavXt3rcW1tbdqyZYs2bdokSVqzZo0KCgr6DcUAAABAPHGACXAfy7sxX3LJJX0Cak1NjRYtWiRJWrRokWpqavo8rq6uTvn5+crIyFBGRoby8/NVV1dnRckAAAAAAJdxxDW7hw8fVnZ2tiQpKytLhw8f7nOflpYW5eTkxL4OBoNqaWnp9++rrKxUZWWlJGnTpk0KhUIJqNr9/H4/r40DsS7OxLo4E+viPF5akz/WvKaaF7bJ335UkcB4FV73aV1WeLndZY2Il9bFS1gX52FNnGmk6+KIsHsmwzD6zA4crqVLl2rp0qWxrxmB0L9QKMRr40CsizOxLs7EujiPV9akoa5WB7aU65O5WTIyfDLNdlU9+ahaD7vzOk2vrIvXsC7Ow5o402DrMnny5AEfZ/k25v5kZmbq0KFDkqRDhw5pwoQJfe4TDAbV3Nwc+7qlpUXBYNCyGgEAQPLYXRGOdd6Vug/GL8rN0u6KsM2VAQCGyhFndgsKClRVVaUbbrhBVVVVKiws7HOfefPm6ec//7na2tokSX/84x+1atUqq0sFAAAWaKir1RsvhjXmWJtOpmXo0mtKLD2j6u9ok5GW3us2wzDk72i3rAYAwOhYHnYffvhhvfnmmzp69KhuvfVWrVy5UjfccIO+973vafv27bHRQ5L07rvv6je/+Y1uvfVWZWRk6MYbb9TatWslSaWlpXRiBgDAg3q2EJfmZslIT5dpdqlqS7kkWRZ4I+kZMs2uXpdWmaapSHrAkp8PABg9y8PunXfe2e/t9957b5/bZs6cqZkzZ8a+Li4uVnFxcaJKAwAADrC7Iqwb+9lCvLUibFnYnbu8RFVbymNbmU3TVFVjq+aWllny8wEAo+eIbcwAAAA9nLCFuCdUb60Iy9/Rrkh6QHNL3dmcKhHivc3c7m3rALyJsAsAccKHNSA+hrKF2Ir325x58/v8nbzP47/N3Anb1gF4kyO6MQOA28U+rKV16YacdJWmdenAlnI11NXaXRrgOnOXl6iqsVWmaUrS6S3Ey0sk2fd+433eLd6dqul8DSBRCLsAEAd8WAPiZ868+ZpUWqatnT4913xMWzt9mnTGFmK73m+8z7v5O9p6nXWXRrfNPN5/HwD0YBszAMSBE64xBLykvy3EPex6v/E+7xbvTtV0vgaQKJzZBYA46P6wZva6jQ9rQGLY9X7jfd7tXNvM7f77AKAHZ3YBIA4YUwJYJxHvt6E0nuJ93i1enarPfM0/PB7V7r3NmpoRoPM14ADHT0R0sKVDjS1tikSiujx/qt0ljQhhFwDigDElgHXi/X4bajdg3uenDbbNfCj6vObBNFU1tmrSDf+QlK8nYIdjnSfV2NKuxuZ2NTa36cNT/z3Y0q5DRzpj9wtmphF2ASDZjfbDH4Chi+f7bXdFWDf203hqa0W4z8/gfR4fw3nNAYxcW8cJNTa3nQq07fqwpS0Wbo+2nxjwcT6foVB2QHk5AeXmdF/CcXYjOTcg7AIAgKRG4ynr8ZoD8WGapo60HdeHp87Ifth8+kxtY3O7OjpPDvjYMf4U5Qa7w2xuzhn/DQYUzEyTz+f+9k6EXQAAkNToBmw9XnNg6KJRU61HjnUH2ZbTZ2m7tyC36fiJrgEfOzbVf+rs7Okwmxfs/m/m+HFKSXHf2drhIOwCgA2G0gwHzsBaeR+Np6zHaw701tUVVfPhY6e3HLe09/pzJBId8LGBtDHdQTZ4OtT2bD8eH0h15fbjeCHsAoDFhtoMB/ZjrYbmzAMCvmBIF32i2FWvD42nrMdrjmR0MtKlpkMdvbYZ94TapkMd6oqaAz52QsbY2Bbj2BnanAxNDAaUkZ5q4bNwF8IuAFiMxizuwVqd29kHBMaMOanfuPCAAI2nrMdrDi86c2TPmV2OD7a0q7m1Q+bAeVbZmWnKCwY08dS2457txhNzAkobO8a6J+EhhF0AsBiNWdyDtTo3DggASDZDHdlzNsOQQtnpyjt1ZnZi8HS344nBgFLH+Cx8FsmBsAsAFqMxi3uwVufGAQEAXhSXkT3Bni7H3f8LZQXk97u/w7GbEHYBwGI0ZnEP1urcOCAAwI0GGtnTcrhT+z48nPQje7yCsAsAFqMxi3uwVufGAQEATsXIHhB2AcAGNGZxD9ZqcGcfEPAH03UhBwQAWCTeI3sunjlFY32RpB/Z4xWEXQAAMCpnHhAIhUJqamoa1d/HbGMAZ7JyZE88/g2DcxB2AQCAYzDbGEhOjOxBIhB2AQCAYzDKCPAuRvbAaoRdAADgGIwyAtyNkT1wEsIuAABwDEYZAc420MienoDLyB44CWEXAAA4BqOMAPsxsgdeQdgFAACOwWxjwBrxHtnTcw0tI3vgJIRdAADgKMw2BuLDypE9XlBb36DtO3erqf24MnxRlSws1Pz8OXaXhVEg7AIAAAAuxcie+Kitb1B59R7l5S9S4ORJRU1T5dU1kkTgdTHCLgAAAOBgjOxJvHD1TmXPWtJr7Fn2rEKFq3cQdl2MsAsAADAEtfUNCr9So7auFLY4Iu4Y2WOvtoihwFnXGhuGofYI1x+7GWEXAADgHHq2OGbPLlbAMNjiiGHrb2TP4baI/ravmZE9DpDhNxU9a8+3aZoK+AfZBw7HI+wCAACcA1scMRSM7HGvkqIClVfXKC+/SFJ30D20p0ZlRQU2V4bRIOwCAACcA1sc0SOeI3tmnj9J6akmI3scoOeg1fbXq3S47bgCflNlRQUczHI5wi4AAMA59GxxPDOMsMXRu6wa2RMKhdTU1JTop4Mhmp8/R8uKF7EmHkLYBQDABRrqavXGi2GNOdamk2kZuvSaEmbRWqhni2P2rEIZhsEWRw9gZA/gfYRdAAAcrqGuVge2lKs0N0tGerpMs0tVW8olicBrkZ6tjOHqHWqPGGxxdAlG9gDJjbALAIDD7a4I68bcrF7NkRblZmlrRZiwa6H5+XMItw7EyB4AAyHsAgDgcP6ONhlp6b1uMwxD/o52myoCrNPfyJ4zr6VlZA+AgRB2AQBwuEh6hkyzq09zpEh6wMaqgPhhZA+ARCDsAgDgcHOXl6hqS7kWndrKbJqmqhpbNbe0zO7SgCGL58ie3JyM2DW0jOwBMBDCLgAADtdzXe7WirD8He2KpAc0t7SM63XhOFaN7AGAoSDsAgDgAnPmzSfcwhGSaWRPbX2Dwq/UqK0rRRm+qEoWFtKkDHARwi4AAAB6YWRPd9Atr96j7NnFChiGoqap8uoaSSLwAi5B2AUAAEhCjOwZXLh6p7JnLek18it7VqHC1TsIu4BLEHYBAAA86MyRPX/8c4veff8AI3uGoS1iKHBW4yvDMNQeoRkW4BaEXQAAAJdiZE/iZPhNRU2zz8ivgH+Qi5IBOIojwu6+ffv0ve99L/Z1Y2OjVq5cqWuvvTZ2W0NDg7773e8qNzdXknTFFVeotLTU8loBAACsNJqRPeNSUxQ4cVgXpZsKpXRqou+4PjjSrJnXXaeCKz7KyJ5BlBQVqLy6RtmzCmMjvw7tqVFZUYHdpQEYIkeE3cmTJ+uBBx6QJEWjUX35y1/W5Zdf3ud+s2fP1po1a6wuDwAAIKESNbLnV48+oBuDXRo7dqxOnOi+DtdM82nryy+q8EpC22B6rssNV+9Qe8RQwG+qrKiA63UBF3FE2D3TG2+8oUmTJmnixIl2lwIAABA3dozs8Xe0yUhL73WbYRjyd7TH62l52vz8OYRbwMUcF3arq6tVVFTU7/f+/Oc/6+6771Z2drbKyso0bdq0fu9XWVmpyspKSdKmTZsUCoUSVq+b+f1+XhsHYl2ciXVxJtbFeZJ9TTqOndD+g0e0v/HIqf8e1v7GIzpw8KiaWwcOmCmGodxQhs6bOEHn5U7QpFP/nZw7QXmhCRqbOrKPbP5gSGPGnFSKYSg1NVVS93Wn/mB6Uq+TUyT7+8WJWBNnGum6GKY52HFEa0UiEX35y1/WQw89pKysrF7f6+joUEpKisaNG6ddu3bpxz/+sR555JEh/b379u1LQLXuFwqF1NTUZHcZOAvr4kysizOxLs6TDGvippE9DXW1OrClXMum5urkyZMyTVNVja2aVFqmOfPmx/3nYXiS4f3iNqyJMw22LpMnTx7wcY46s1tbW6sLLrigT9CVpPT001twFixYoCeffFJHjhzRhAkTLKwQAAB43Zkjew62tHd3OnbpyJ6eQLvt5e2KtBxRJD2guQRdAEnCUWF3sC3Mra2tyszMlGEYeueddxSNRjV+/HiLKwQAAF6QTCN75sybr0VLl3G2CkDScUzY7ezsVH19vW655ZbYbRUVFZKk5cuX69VXX1VFRYV8Pp9SU1N155130i4fAAAMaDQjewJpY7qDbPB0qM079d/xgVQ+gwCACzgm7I4bN04/+tGPet22fPny2J9XrFihFStWWF0WAOAsDXW1euPFsMYca9PJtAxdek0JWyJhm0SN7MlIT7XwWQAAEsExYRcA4Hw9zW5Kc7NkpKfLNLtUtaVckgi8SBg7RvYAANyPsAsAGLLdFWHdmJsV28JpGIYW5WZpa0WYsItROdZ58tQZ2dNhtvFUg6hDRzoHfJxhSKHsdOWdOjM7MRiIbTeeGAwodYyv1/1r6xtU/txv1NaVogxfVCULC5mjCgAeRdgFAAyZv6NNRlp6r9sMw5C/Y+D5oUAPu0f21NY3qLx6j7JnFytgGIqapsqraySJwAsAHkTYBQAMWSQ9Q6bZ1as5j2maiqQHbKwKTmGapg4d7tCf32ty5MiecPVOZc9a0mtnQvasQoWrdxB2AcCDCLsAgCGbu7xEVVvKtejUVmbTNFXV2Kq5pWV2lwaLuHlkT1vEUOCsLsqGYag94uzOyrX1DQq/UsPWawAYJsIugITjg5p39FyXu7UiLH9HuyLpAc0tLeN6XY8Zzcie8YGxCmWnO3JkT4bfVNQ0++xMCPgH6XBlM7ZeA8DIEXYBJBQf1Lxnzrz5hFsPSNTInvOnT1ZTU9OAj7Xz4FdJUYHKq2uUPaswtjPh0J4alRUVWPLzR4Kt1wAwcoRdAAnFBzXAPk4b2WP3wa+enxGu3qH2iKGA31RZUYGj/y1y69ZrAHACwi6AhOKDGpBYVo3siQcnHPyanz/H0eH2bG7ceg0ATkHYBZBQfFADRsc0TbUfO3G6EZQNI3vihYNfw+fGrdcA4BSEXQAJxQc14NxM09SRtuP68NQZWaeN7IkXDn4Nnxu3XgOAUxB2ASQUH9SAbm4e2RMvHPwaGbdtvQYApyDsAkg4PqjBjRrqavXGi2GNOdamk2kZuvSaknN2oR7NyJ5A2pjuIOvAkT3xwsEvAICVCLsAAJyloa5WB7aUqzQ3S0Z6ukyzS1VbyiVJF8/NT8jInoz0VKuenq04+AUAsAphFwCAs/zxxf9VUXae6o6PVWMkVY1dY9Xov0Dvb/mzOv/7PctH9gCAG9g5RxvoD2EXAJCUBh/ZM1uVAzzu7JE9Z56pTdTIHgBwOrvnaAP9IewCADxpNCN7DJnK9Z1Qrv+Ecn3HNdF/QhN9J1Qbiegf7/53y0f2AIDTOWGONnA2wi4AwLVM09Tho51xH9lz4L231Pjs01qUnRXrGlzV2KorSssIugDQD+Zow4kIuwAARxtsZM/BlnZ1Ho8M+NiRjuyZGFyghhRDWyvC8ne0K5Ie0NzSsnN2YwaAZMUcbTgRYRcAYDsnjuyZM28+4RYAhog52nAiwi4AwBInI11xH9kz66JpOn6szcJnAQDoD3O04USEXQBA3Bw/EdHBlo4ztht3dzk+2NKu5taOuI/sGR8YR9i12dmjRm7+5FLNmD7V7rIA2IA52nAawi4AYFgGH9nTOeDjGNnjPf2NGvlhRa0+e/lhPvA6FHNQASQTwi4AJIGGulq98WJYY4616WRahi69pmTA61FHM7LH5zMUyg50XzMbPCPU5gQUygrQydhj+h01MrtQ4eoXCVAOxBxUAMmGsAsAHtdQV6sDW8pVmpslIz1dptmll/67XO3HIso674K4juwJZqbJ5yPQJgtGjbgLc1ABJBvCLgB4VM/InqpfvaTZGRfo2aNj1diVqsZIqg4qVcdf+Lukv/f72JGO7EFyYdSIu3BwAkCyIewCgIsNbWTP+drZz2PHKKKpUyfGfWQPkke/o0b+VKPPJmDUCNeajh4HJwAkG8IuADjcaEf2pBw7pNljjivXf0IT/SeU6zuhib7j+vUJ6bO3/YOFzwRe09+okVuuvTru3Zi51jQ+mIMKINkMKexGo1HV1NTIMAwVFBQoJaX7eqzf//73+tjHPpbQAgEgGSRyZE/PNbuLsrJiH3CrGls1t7TMuicIzzp71EgoFFJTU1NcfwbXmsYHc1ABJJshhd1HH31UoVBIfr9fL7zwgm6//XZNmjRJFRUVhF0AGCK7Rvb0dF3eWhGWv6NdkfSA5paWDdiNGXAarjWNH+agAkgmQwq7LS0tuuOOOyRJS5Ys0aOPPqp/+Ae2vgHAmZw8smfOvPmEWxtxvenocK3p6NTWN2j7zt1qaj/O7x+ApDKksBuJRHTy5EmNGTNGEydO1Jo1a/Twww9r7969ia4PABzFNE0daTuuD0+dkWVkD86F601Hj2tNR67n9y8vf5ECJ0/y+wcgqQwadru6uuTz+fT5z39e7e3tysrKkiSlpaXpnnvu0SuvvGJFjQBgqZ6RPR82t8euoT3cFtHf9reosblNx090DfhYRvbgbFxvOnpcazpy/P4BSGaDht3vfOc7uvvuu3XhhRf2+V5KSoo+8YlPJKwwAEikoY3s6V8gbUx3kGVkD4aA603jg2tNR4bfPwDJbNCwe/755+sb3/iG1q5dq2AwKEl688039Ytf/EL33XefJQUCwEiNdmTPmY2gZp4/SemppiYGA8pIT7XwWcDtuN4Udur5/TsTv38AksWgYbesrEwVFRX6xje+oVWrVmn79u3au3evrr/+eqvqA4BBJXJkz5kSMU4FyYHrTWGnnt+/vPwiSeL3D0BSOWeDqosvvljp6el65JFHtGjRIt1zzz1KTeWsBgDr2DWyB4gHrjeFnXp+z7a/XqXDbcf5/TsHOqcD3jJo2H3ggQf05ptv6tprr9XKlSv1xBNPaPfu3VqwYIFV9QFIAk4e2QPEA9ebwk7z8+doWfEidqecA53TAe8ZNOyed955+pd/+RdlZGRIkvLy8nT//fersbFRK1assKRAAN7AyB4AgJPRuRrwnkHD7urVq3t9PX36dK1fv14bN24k7ALoo7+RPWc2hWJkDwDAqehcDXjPOa/ZPVswGKQTM5DEGNkDAPAiOqcD3jPssCtJaWlp8a4DgIPEc2RPbk5AeacaQjGyBwDgVHROB7xnRGEXgPtZNbIHAAA3oHM64D2EXcDDGNkDAMDQ0Tkd8BbCLuBijOwBAAAA+kfYBRyOkT0AAADA8Dkq7N5+++0aN26cUlJS5PP5tGnTpl7fN01TTz31lGprazV27FjddtttmjFjhk3VAvFz5siejj816S/vH2BkDwAAZ6itb1D4lRq1daUowxdVycJCT2059vrzA+zgqLArSevWrdOECRP6/V5tba0OHDigRx55RG+//baeeOIJfec737G4QmBkGNkDAHA7uwJZbX2Dyqv3KHt2sQKGoahpqry6RpI8EQi9/vwAuzgu7A5m586d+sQnPiHDMHTxxRervb1dhw4dUnZ2tt2lAZLiM7Jn2uQcZQb8jOwBADiKnYEsXL1T2bOWxA7uGoah7FmFClfv8EQY9PrzA+ziuLC7YcMGSdKyZcu0dOnSXt9raWlRKBSKfZ2Tk6OWlpY+YbeyslKVlZWSpE2bNvV6DE7z+/28NiNw/HhEB5qOaH/jEe0/eET7Gw/H/tzU0q7oIDN7QtkBnTdxgiblTtB5EyfovNwJOi83U5Mmjlf6uO5A6/f7FYlErHo6GCLeL87EujgPa+JM8ViX7a/vVl7+ol67ifLyi7T99SotK1402hIHddI3Tuljx/a5/ZhvnKt/33rWxavPz434N8yZRroujgq769evVzAY1OHDh/Xtb39bkydP1iWXXDLsv2fp0qW9gnJTU1M8y/SMUCjEazMAa0f2mOpoO6KOtu6vWBdnYl2ciXVxHtbEmeKxLk1txxU42bcp4uG24wlf8zFdnTp+/HivoG2apvxdna7+fetZF68+Pzfi3zBnGmxdJk+ePODjHBV2g8GgJCkzM1OFhYV65513eoXdYDDY60k2NzfHHgMMByN7AAAYngy/qahp9glkAf/AO5ripaSoQOXVNcqeVSjDMGSapg7tqVFZUUHCf7YVvP78ALs4Jux2dnbKNE2lpaWps7NT9fX1Ki0t7XWfgoIC/frXv1ZRUZHefvttpaenc70uBsTIHgBeRddW2MHOQNbz+x2u3qH2iKGA31RZUYFnfu+9/vwAuzgm7B4+fFgPPvigJKmrq0sLFy7UvHnzVFFRIUlavny55s+fr127dumOO+5QamqqbrvtNjtLhgOcObKnMXZmlpE9ALyLrq2wi92BbH7+HE//jnv9+QF2cEzYzcvL0wMPPNDn9uXLl8f+bBiGvvSlL1lZFhyAkT2AtThr6Gx0bYWdCGQA3MQxYRfJLR4je87cdszIHmBkOGvofG0RQ4GzDtQZhqH2CAfvAAA4E2EXljl+IqKDLR1nbDfu7nJ8sKVdza0dGmRij7Iz05QXDGjiqW3HPduNJ+YElDZ2jHVPAvA4zho6n51NggAAcBPCLuLK2pE9AOKNs4bOR9dWAACGhrCLYWFkD+BtnDV0PrubBAEA4BaEXfTByB4geXHW0B1oEgQAwLkRdpNUNGrqYEub9rx7kJE9AGKS4awh3aYBAEgOhF0PY2QPgJHw8llDuk0DAJA8CLsuN5qRPVkT0hTKTmNkD4CkQbdpAACSB2HXBRI1smfalPPU1NRk3RMBAJvRbRoAgORB2HUIRvYAQOLRbRoAgORB2LXRM/+7W2+/38zIHgCwCN2mAQBIHoRdG/3twGG9u7dFEiN7AMAKPdfl/vT5rfrLwcPqOnlcM3OzJM2ytS4AABB/hF0bfap4lj656COM7AEAixmh6SpYePrsLh2ZAQDwHk4X2ujC/5ejj8wIKTszjaALABbp7shc2E9H5p02VwYAAOKJM7sAgKTi5o7MtfUNCr9So7auFGX4oipZWMjZaAAABkDYBQAkFbd2ZK6tb1B59R5lzy5WwDAUZfs1AACDYhszACCplBQV6NCeGpmnhpT3dGQucXhHZrZfAwAwPJzZBQAknWjT+9q5bbeiJzo1Y1K2Pv+Zax1/dtTN268BALADYRcAkDR6tgLnLCxV6Iw5u27g1u3XAADYhW3MAICk4eatwG7dfg0AgF04swsASBpu3grcs806XL1D7RFDAb+psqICx2+/BgDALoRdAEDScPtW4Pn5cwi3AAAMEduYAQBJg63AAAAkD87sAgCSBluBAQBIHoRdAEBSYSuwN9XWNyj8So3aulKU4YuqZGEh6wwASY6wCwAAXK1npFT27GIFDENR01R5dfdIKQIvACQvrtkFAACu5uaRUgCAxCHsAgAAV2uLGL06bEvuGSkFAEgcwi4AAHC1DL8Z67Ddw00jpQAAicE1uwAAOAzNloanpKhA5dU1sa3MPSOlyhgpBQBJjbALAICD0Gxp+BgpBbc4+0DWzZ9cqhnTp9pdFuBZhF0AAByku9nSkn6aLe0gvA2CkVJwuv4OZP2wolafvfwwv7tAghB2AQBwkLaIoQDNluAwbK0fvX4PZM0uVLj6RV5LIEEIuwAAOEiG31TUNHt1F6bZEuzE1vr44EAWYD26MQMA4CAlRQU6tKcm1l24p9lSCc2WYBPmGMcHXcMB63FmFwAAB6HZEpyGM5Lx0W/X8D/V6LMcyAIShrALAIDD0GwJTsLW+vjo70DWLddeTTdmIIEIuwAAABgQc4zj5+wDWaFQSE1NTTZWBHgbYRcAAEii4y76x9Z6AG5F2AUAAHTcxaDYWg/AjejGDAAA6LgLAPAcwi4AAFBbxOjVgEii4y4AwN3YxgwAAIbdcZfrewEATkfYBZA0+HAODGw4HXcHu753WfEiq0v3JP69AoDRI+wCSAo03wEGN5yOu93X9y7p5/reHYTdOODfKwCID8IugKQw2IdzPjwC3YbacbctYijA9b3nNNKzs/x7BQDx4Yiw29TUpM2bN6u1tVWGYWjp0qUqKSnpdZ+GhgZ997vfVW5uriTpiiuuUGlpqR3lAnAhPpwD8TPc63uT0WjOzvLvFQDEhyPCrs/nU1lZmWbMmKFjx45pzZo1ys/P19SpU3vdb/bs2VqzZo1NVQJwMz6cA/EznOt7k9Vozs7y7xUAxIcjRg9lZ2drxowZkqS0tDRNmTJFLS0tNlcFwEtKigp0aE+NTLP7w2LPh/MSPpwDwzY/f47KimYpZc8OdbyxQyl7dqisaBZbbM8wmlFO/HsFAPHhiDO7Z2psbNRf//pXXXjhhX2+9+c//1l33323srOzVVZWpmnTptlQIQA3Gk7zHQDnNtTre5PVaM7O8u8VAMSHYfYcNnSAzs5OrVu3Tp/5zGd0xRVX9PpeR0eHUlJSNG7cOO3atUs//vGP9cgjj/T791RWVqqyslKStGnTJp04cSLhtbuR3+9XJBKxuwychXVxJtbFmVgX52FNur22q04/rKhV9uwztnr/qUa3LJ+vyxfMs7we1sWZWBfnYU2cabB1SU1NHfBxjgm7kUhE999/vy677DJ98pOfPOf9b7/9dm3cuFETJkw453337dsXjxI9JxQKqampye4ycBbWxZlYF2diXZyHNTmttr5B4eqdsbOzJTaenWVdnIl1cR7WxJkGW5fJkycP+DhHbGM2TVOPP/64pkyZMmDQbW1tVWZmpgzD0DvvvKNoNKrx48dbXCkAAMDQsNUbAOzliLD71ltv6eWXX9b06dN19913S5JuvvnmWHpfvny5Xn31VVVUVMjn8yk1NVV33nlnn8YPAAAAAABIDgm7s2bN0jPPPDPofVasWKEVK1ZYVBEAAABGq7a+QeFXatTWlaIMX1QlCws52w3AMo4IuwAAAPCW2voGlVfvUfbsYgUMQ1HTVHl1jSQReAFYwhFzdgEAAOAt4eqdyp5VGLvszDAMZc8qVLh6p82VAUgWhF0AAADEXVvE6NNfxTAMtUfouQLAGmxjBgAAOIVrTOMnw28qapq9Aq9pmgr4HTH1EkAS4MwuAACATl9jGp1drMClSxSdXazy6j2qrW+wuzRXKikq0KE9NTLN7nBrmqYO7alRSVGBzZUBSBac2QUAAFDPNaZL+rnGdAdnd0eg5zULV+9Qe8RQwG+qrKiA1xKAZQi7AAAA6r7GNMA1pnE1P38O4RaAbdjGDAAAoO5rTHu23PbgGlMAcC/CLgAAgLjGFAC8hm3MAABHoAsu7MY1pgDgLYRdAIDterrgZs8uVsAwFDVNlVfXSBJBA5biGlMA8A62MQMAbNfdBbewny64O22uDAAAuBVndgEAtqMLLjByXAIAAP0j7AIAbJfhNxU1zdiZXYkuuMBQcAkAAAyMbcwAANvRBRcYGS4BAICBcWYXAGA7uuACI8MlAAAwMMIuAMAR6IILDB+XAADAwNjGDAAA4FJcAgAAA+PMLgAAgEtxCQAADIywCwAA4GJcAgAA/SPsAgAwTMw1BQDA+Qi7AAAMA3NNAQBwBxpUAQAwDMw1BQDAHQi7AAAMQ1vE6DXmRWKuKQAATkTYBQBgGDL8ZmzMSw/mmgIA4DyEXQAAhoG5pgAAuAMNqgAAGAbmmsYPXa0BAIlE2AUAYJiYazp6dLUGACQa25gBAIDl6GoNAEg0wi4AALAcXa0BAIlG2AUAAJajqzUAINEIuwAAwHJ0tQYAJBoNqgAAgOXoag0ASDTCLgAAsAVdrQEAicQ2ZgAAAACA53BmFwAAAH3U1jco/EqN2rpSlOGLqmRhIWfiAbgKYRcAMCR88AWSR219g8qr9yh7drEChqGoaaq8ukaSeN8DcA3CLgDgnPjg6z0cvMBgwtU7lT1rSWwWsmEYyp5VqHD1Dn5PALgGYRcAcE588PUWDl7gXNoihgKn3u89DMNQe8QY4BEA4Dw0qAIAnFNbxIgF3R588HWv7oMXhf0cvNhpc2Vwigy/GZuB3MM0TQX85gCPAADnIewCAM6JD77ewsELnEtJUYEO7amJve9N09ShPTUqKSqwuTIAGDq2MQMAzqmkqEDl1TWxs4E9H3zL+ODrShl+U1HT7BV4OXiBM/VsZw9X71B7xFDAb6qsqIBt7gBchbALADgnPvh6CwcvMBTz8+fwHgfgaoRdAMCQ8MHXOzh4AQBIBoRdAJ7FaBVgYBy8AAB4HWEXgCcxWgVwFg4+AQCs5qiwW1dXp6eeekrRaFRXX321brjhhl7fP3nypB599FH95S9/0fjx43XnnXcqNzfXnmIBOBpzYQHn4OATAMAOjgm70WhUTz75pL7+9a8rJydHa9euVUFBgaZOnRq7z/bt2xUIBPT9739f1dXV+tnPfqavfOUrNlYNwKnaIoYCHhutwpkxuBUHnwAAdnDMnN133nlHkyZNUl5envx+v6666irV1NT0us/OnTu1ePFiSdKVV16p3bt395n7CACS9+bC9pwZi84uVuDSJYrOLlZ59R7V1jfYXRpwTsz1BQDYwTFht6WlRTk5ObGvc3Jy1NLSMuB9fD6f0tPTdfToUUvrBOAOJUUFOrSnJhZ4e0arlLh0tEr3mbHCfs6M7bS5MuDcvHbwCQDgDo7ZxhxPlZWVqqyslCRt2rRJoVDI5oqcye/389o4EOsSH8uKFykzK1PbfluttpNSxhjpc9cW6fIF80b099m9Lid945Q+dmyf24/5xiX174vd64K++luTm6+9Wj+sqFX27DPm+v6pRrdcezXrZxHeK87EujgPa+JMI10Xx4TdYDCo5ubm2NfNzc0KBoP93icnJ0ddXV3q6OjQ+PHj+/xdS5cu1dKlS2NfNzU1Ja5wFwuFQrw2DsS6xM+M6VP171/4bK/bRvra2r0uY7o6dfz48V5bQU3TlL+rM6l/X+xeF/TV35rMmD5Vn738sMLVL8bm+n62qEAzpk9l/SzCe8WZWBfnYU2cabB1mTx58oCPc0zYnTlzpvbv36/GxkYFg0H97ne/0x133NHrPh/96Ef10ksv6eKLL9arr76qOXPm9LkGCAC8qKSoQOXVNbGtzD3bsstcui0byYe5vgAAqzkm7Pp8Pn3xi1/Uhg0bFI1GtWTJEk2bNk2//OUvNXPmTBUUFKi4uFiPPvqo/vVf/1UZGRm688477S4bACzRExLC1TtiZ8bKigoIDwAAAANwTNiVpAULFmjBggW9bvvsZ09vQUxNTdVXv/pVq8sCAEfgzBgAAMDQOaYbMwAAAAAA8ULYBQAAAAB4DmEXAAAAAOA5hF0AAAAAgOc4qkEVAOC02voGhV+pUVtXijJ8UZUsLKRBFQAAwBARdgHAgWrrG1RevUfZs4sVMAxFTVPl1TWSROAFAAAYArYxA4ADhat3KntWoQzDkCQZhqHsWYUKV++0uTIAAAB3IOwCgAO1RYxY0O1hGIbaI8YAjwAAAMCZ2MYMAA6U4TcVNc1egdc0TQX8po1VAaPDdegAACtxZhcAHKikqECH9tTINLvDrWmaOrSnRiVFBTZXBoxMz3Xo0dnFCly6RNHZxSqv3qPa+ga7SwMAeBRndgHAgXrOdoWrd6g9YijgN1VWVMBZMLhW93XoS/q5Dn0Hv9cAgIQg7AKAQ83Pn0MIgGe0RQwFuA4dAGAhtjEDAICEy/CbsW35PbgOHQCQSIRdAACQcFyHDgCwGtuYAQBAwnEdOgDAaoRdAABgCa5DBwBYiW3MAAAAAADPIewCAAAAADyHsAsAAAAA8BzCLgAAAADAcwi7AAAAAADPIewCAAAAADyHsAsAAAAA8BzCLgAAAADAc/x2FwAAgJ1q6xsUfqVGbV0pyvBFVbKwUPPz59hdFgAAGCXCLgAgadXWN6i8eo+yZxcrYBiKmqbKq2skicALAIDLsY0ZAJC0wtU7lT2rUIZhSJIMw1D2rEKFq3faXBkAABgtzuzCEdhGCMAObRFDgVNBt4dhGGqPGAM8AgAAuAVhF7ZjGyEAu2T4TUVNM3ZmV5JM01TAb9pYFQAAiAfCLmzXvY1wST/bCHcQdgEkVElRgcqra2JbmU3T1KE9NSorKrC7tCFhVwwAAAMj7MJ2bCMEYLUzQ2K0tUlNVe8qkDNJAb+psqICVwRGdsUAADA4wi5sxzZCAFY6OySmnzqb+w9Fs1wVEtkVAwDA4OjGDNuVFBXo0J4amWZ3uO3ZRljikm2EANzFKx2Y2yJGr4OEErtiAAA4E2d2YbueMxDh6h1qjxiu2kYIwH28cukEu2IAABgcYReOMD9/DuEWgCW8EhLd3lwLAIBEI+wCAJKKV0Iiu2IAABgcYRcAkFS8FBLZFQMAwMAIuwCApENIBADA++jGDAAAAADwHMIuAAAAAMBz2MYMAMAw1dY3KPxKjdq6UpThi6pkYSHbogEAcBjCLgAAw1Bb36Dy6j3Knl2sgGEoapoqr66RJAIvAAAOwjZmAACGIVy9Mza2SJIMw1D2rEKFq3faXBkAADgTYRcAgGFoixixoNvDMAy1R4wBHgEAAOxA2AUAYBgy/KZM0+x1m2maCvjNAR4BAADswDW7AIBzoiHTaSVFBSqvroltZTZNU4f21KisqMDu0gAAwBlsD7vl5eV6/fXX5ff7lZeXp9tuu02BQKDP/W6//XaNGzdOKSkp8vl82rRpkw3VAkDyoSFTbz3POVy9Q+0RQwG/qbKigqR8LQAAcDLbw25+fr5WrVoln8+np59+Wtu2bdPq1av7ve+6des0YcIEiysEgOTW3ZBpST8NmXYkbcCbnz8naZ87AABuYfs1u5dddpl8Pp8k6eKLL1ZLS4vNFQEAzkRDJgAA4Ea2n9k90/bt23XVVVcN+P0NGzZIkpYtW6alS5daVRYAJLUMv6moafYKvDRkAgAATmeYZ7eUTID169ertbW1z+033XSTCgsLJUnPPvus3n33Xd111119ziBIUktLi4LBoA4fPqxvf/vb+sIXvqBLLrmk359XWVmpyspKSdKmTZt04sSJ+D0ZD/H7/YpEInaXgbOwLs6UzOvy2q46/bCiVtmzz2jI9Kca3bJ8vi5fMM/W2pJ5XZyKNXEm1sWZWBfnYU2cabB1SU1NHfBxloTdc3nppZf0m9/8Rvfee6/Gjh17zvs/88wzGjdunK6//voh/f379u0bbYmeFAqF1NTUZHcZOAvr4kzJvi619Q0KV++MNWQqcUhDpmRfFydiTZyJdXEm1sV5WBNnGmxdJk+ePODjbN/GXFdXp+eff17f+ta3Bgy6nZ2dMk1TaWlp6uzsVH19vUpLSy2uFACSFw2ZAACA29gedp988klFIhGtX79eknTRRRfplltuUUtLi37wgx9o7dq1Onz4sB588EFJUldXlxYuXKh58+bZWDUAAAAAwMlsD7vf//73+709GAxq7dq1kqS8vDw98MADVpYFAAAAAHAx20cPAQAAAAAQb4RdAAAAAIDnEHYBAAAAAJ5D2AUAAAAAeA5hFwAAAADgOYRdAAAAAIDnEHYBAAAAAJ5j+5xdAADOVlvfoPArNWrrSlGGL6qShYWanz/H7rIAAICLEHYBAI5SW9+g8uo9yp5drIBhKGqaKq+ukSQCLwAAGDK2MQMAHCVcvVPZswplGIYkyTAMZc8qVLh6p82VAQAANyHsAgAcpS1ixIJuD8Mw1B4xBngEAABAX4RdAICjZPhNmabZ6zbTNBXwmwM8AgAAoC/CLgDAUUqKCnRoT00s8JqmqUN7alRSVGBzZQAAwE1oUAUAcJSeJlTh6h1qjxgK+E2VFRXQnAoAAAwLYRcA4Djz8+cQbgEAwKiwjRkAAAAA4DmEXQAAAACA5xB2AQAAAACeQ9gFAAAAAHgOYRcAAAAA4DmEXQAAAACA5xB2AQAAAACeQ9gFAAAAAHgOYRcAAAAA4DmEXQAAAACA5xB2AQAAAACeQ9gFAAAAAHgOYRcAAAAA4DmEXQAAAACA5xB2AQAAAACeY5imadpdBAAAAAAA8cSZ3SS2Zs0au0tAP1gXZ2JdnIl1cR7WxJlYF2diXZyHNXGmka4LYRcAAAAA4DmEXQAAAACA5xB2k9jSpUvtLgH9YF2ciXVxJtbFeVgTZ2JdnIl1cR7WxJlGui40qAIAAAAAeA5ndgEAAAAAnuO3uwA4wwsvvKDy8nI98cQTmjBhgt3lJL1f/OIX2rlzpwzDUGZmpm677TYFg0G7y0p65eXlev311+X3+5WXl6fbbrtNgUDA7rKS2u9//3v993//tz744AN95zvf0cyZM+0uKanV1dXpqaeeUjQa1dVXX60bbrjB7pKS3mOPPaZdu3YpMzNTDz30kN3lQFJTU5M2b96s1tZWGYahpUuXqqSkxO6ykt6JEye0bt06RSIRdXV16corr9TKlSvtLguSotGo1qxZo2AwOOyuzIRdqKmpSfX19QqFQnaXglOuv/563XTTTZKkcDisLVu26JZbbrG5KuTn52vVqlXy+Xx6+umntW3bNq1evdruspLatGnTdNddd+mHP/yh3aUkvWg0qieffFJf//rXlZOTo7Vr16qgoEBTp061u7SktnjxYq1YsUKbN2+2uxSc4vP5VFZWphkzZujYsWNas2aN8vPzea/YbMyYMVq3bp3GjRunSCSie++9V/PmzdPFF19sd2lJLxwOa8qUKTp27NiwH8s2ZugnP/mJPve5z8kwDLtLwSnp6emxPx8/fpy1cYjLLrtMPp9PknTxxRerpaXF5oowdepUTZ482e4yIOmdd97RpEmTlJeXJ7/fr6uuuko1NTV2l5X0LrnkEmVkZNhdBs6QnZ2tGTNmSJLS0tI0ZcoU/v/EAQzD0Lhx4yRJXV1d6urq4vOXAzQ3N2vXrl26+uqrR/R4zuwmuZqaGgWDQZ1//vl2l4Kz/PznP9fLL7+s9PR0rVu3zu5ycJbt27frqquusrsMwDFaWlqUk5MT+zonJ0dvv/22jRUBztfY2Ki//vWvuvDCC+0uBereoXLPPffowIEDuuaaa3TRRRfZXVLS+/GPf6zVq1eP6KyuRNhNCuvXr1dra2uf22+66SZt27ZNX//6160vCoOuS2FhoW6++WbdfPPN2rZtm379619z3YhFzrUukvTss8/K5/Pp4x//uMXVJaehrAkAuE1nZ6ceeughff7zn++1owv2SUlJ0QMPPKD29nY9+OCD2rt3r6ZPn253WUnr9ddfV2ZmpmbMmKGGhoYR/R2E3STwjW98o9/b9+7dq8bGRt19992SurcJ3HPPPdq4caOysrIsrDA5DbQuZ/v4xz+ujRs3EnYtcq51eemll/T666/r3nvvZXuTRYb6XoG9gsGgmpubY183NzfTWA8YQCQS0UMPPaSPf/zjuuKKK+wuB2cJBAKaM2eO6urqCLs2euutt7Rz507V1tbqxIkTOnbsmB555BHdcccdQ/47CLtJbPr06XriiSdiX99+++3auHEj3ZgdYP/+/TrvvPMkdW8155pEZ6irq9Pzzz+vb33rWxo7dqzd5QCOMnPmTO3fv1+NjY0KBoP63e9+N6wPJECyME1Tjz/+uKZMmaJPfvKTdpeDU44cOSKfz6dAIKATJ06ovr5en/rUp+wuK6mtWrVKq1atkiQ1NDTohRdeGPb/rxB2AQf62c9+pv3798swDIVCIToxO8STTz6pSCSi9evXS5Iuuugi1sZmr732mn70ox/pyJEj2rRpk84//3x97Wtfs7uspOTz+fTFL35RGzZsUDQa1ZIlSzRt2jS7y0p6Dz/8sN58800dPXpUt956q1auXKni4mK7y0pqb731ll5++WVNnz49trvu5ptv1oIFC2yuLLkdOnRImzdvVjQalWma+tjHPqaPfvSjdpeFUTJM0zTtLgIAAAAAgHhi9BAAAAAAwHMIuwAAAAAAzyHsAgAAAAA8h7ALAAAAAPAcwi4AAAAAwHMIuwAAAAAAzyHsAgDgUk8//bS++93vxr4uLy/Xfffdp0gkYmNVAAA4A2EXAACX+tSnPqWGhgb99a9/VUVFherq6nTXXXfJ7/fbXRoAALYzTNM07S4CAACMzDPPPKPXXntNHR0duu+++xQKhdTR0aH169fr73//uzZs2KDp06fbXSYAAJbjzC4AAC52wQUXaO/evVq1apVCoZAkKTU1VWvXrtWVV15pc3UAANiHsAsAgEvt3btXTzzxhBYtWqQdO3bEbvf7/ZowYYKNlQEAYD/CLgAALtTS0qL7779f//zP/6wvfelL2rt3rxoaGuwuCwAAxyDsAgDgMh0dHdq4caOuvfZaFRQUaOzYsbruuuv0i1/8wu7SAABwDBpUAQDgUZs3b9Z1111HgyoAQFIi7AIA4EEbN27Ue++9p1AopGXLlmnx4sV2lwQAgKUIuwAAAAAAz+GaXQAAAACA5xB2AQAAAACeQ9gFAAAAAHgOYRcAAAAA4DmEXQAAAACA5xB2AQAAAACeQ9gFAAAAAHgOYRcAAAAA4DmEXQAAAACA5/x/aaMPfyD1EYMAAAAASUVORK5CYII=",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plot_ds(data,m[-1],q[-1])"
]
},
{
"cell_type": "code",
"execution_count": 64,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Valore della funzione loss per la soluzione: 0.0943\n"
]
}
],
"source": [
"print(f'Valore della funzione loss per la soluzione: {cost_history[-1][0]:.4f}')"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Come si può vedere dalla figura seguente, considerando i valori di costo e dei coefficienti soltanto alla fine delle varie epoche risulta una andamento uniforme dei valori stessi."
]
},
{
"cell_type": "code",
"execution_count": 60,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABQgAAAGoCAYAAAAKMwiTAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAABqxklEQVR4nO3deXQc9YHu/aeqF0mt1mKptcuW5EXebWxjA7YBA2YPhBgCl4Rkhpkkc8kk4SYzNzfn3BuGQHJCzkxImCzzhkwIyWSZADEJSwggjNlsDHjfJVu2Vsvat9bW3VXvH20LG2wj2Zaq1f39nKNjqVotPaqS5NbTv8WwbdsWAAAAAAAAgIRkOh0AAAAAAAAAgHMoCAEAAAAAAIAERkEIAAAAAAAAJDAKQgAAAAAAACCBURACAAAAAAAACYyCEAAAAAAAAEhgbqcDjFRjY6PTEc5ZIBBQa2ur0zEgrkWs4XrEDq5FbOF6xI54uRaFhYVORzhr8fBY8HTi5ftrvHC+RofzNTqcr9HhfI0O52t0OF+jM9LzdbrHg4wgBAAAAAAAABIYBSEAAAAAAACQwCgIAQAAAAAAgARGQQgAAAAAAAAkMApCAAAAAAAAIIFREAIAAAAAAAAJjIIQAAAAAAAASGAUhAAAAAAAAEACoyAEAAAAAAAAEhgFIQAAAAAAAJDAKAgBAAAAAACABEZBCAAAAAAAACQwCkIAAAAAAAAggVEQAgAAAAAAAAmMghAAAAAAAABIYBSEAAAAAAAAQAKjIAQAAAAAAAASGAUhAAAAAAAAkMAoCAEAAAAAAIAERkEIAAAAAAAAJDAKQgAAAAAAACCBURACAAAAAAAACYyCEAAAAAAAAEhgFIQAAAAAAABAAqMgBAAAAAAAABIYBSEAAAAAAACQwCgIAQAAAAAAgARGQQgAAAAAAAAkMArCcWLbtiKW5XQMAAAAAAAA4CRupwMkgk2Vzfrr1jpdvbhMy2dkOR0HAAAAAAAAGMYIwnHgdZvqHQipprnL6SgAAAAAAADASRhBOA6KslMlSTVHux1OAgAAMH4ef/xxVVdXq6ysTHfffffw8Y0bN+qZZ56RYRj6xCc+oaVLlzqYEgAAAIwgHAeBtGR53KbaevoVHAg5HQcAAGDMVVdXa2BgQA888IDC4bAOHDgwfNvzzz+v+++/X/fff7+ee+45B1MCAABAYgThuDBNQ4WTfKpp6VVDe5/KCzOcjgQAADCmqqqqtGDBAknS/PnzVVlZqenTp0uS8vLyNDg4KElKSUk55f0rKipUUVEhSXrooYcUCATGIbUz3G53XH995xvna3Q4X6PD+RodztfocL5Gh/M1Oud6vigIx0lxduqxgjBIQQgAAOJeMBhUXl6eJMnn86m+vn74tmXLlunrX/+6bNvWF7/4xVPef/Xq1Vq9evXw262trWMb2EGBQCCuv77zjfM1Opyv0eF8jQ7na3Q4X6PD+RqdkZ6vwsLCUx6nIBwnRVnRdQgb2oIOJwEAABh7Pp9PfX19kqT+/n75fL7h25566ik9/PDDkqTvfve7WrhwoSMZAQAAEDWmBeHpFqbu7e3Vo48+qp6eHs2fP19r1qwZyxgx4fhGJQ3tFIQAACD+lZeXq6KiQsuXL9fOnTu1atWq4ds8Ho+SkpJkGIbC4bBzIQEAACBpDAvCExem/vnPf64DBw4Mrzvz5JNP6o477lBRUdFYffqYk5eZIrfLVGv3gAaGwkr2MngTAADEr6lTp8rj8ei+++5TaWmpAoGA1q5dqzVr1uiaa67RN7/5TUk6aRoxAAAAnDFmLdWZFqauq6vT008/rba2Nt15550qLy//0P3jcWHqyTnpOtTUqT7Lo+JAttNxEhqLncYWrkfs4FrEFq5H7OBanJ0TZ5BIGp41smrVqpNGFAIAAMBZY1YQnmlh6v379+t73/ue/H6/vv/97+vBBx/80P3jcWHqKccKwt3VjcpKtp2Ok9BY7DS2cD1iB9citnA9Yke8XIvTLUoNAACAxDZmBeGZFqYuLCxUcXGxJMk0zbGKEHNK8jKknaxDCAAAAAAAgNgxZu1ceXm5du3aJUnauXPnSdOICwoK1NHRoYGBAUUikbGKEHNKctMlsZMxAAAAAAAAYseYjSA808LUt99+ux555BENDQ3ptttuG6sIMac4kC7TkJq7+hUKW/K4E2f0JAAAAAAAAGLTmG6le7qFqYuLi3X//feP5aeOSV6PS7kZKWrq7NeRjj5NyfE7HQkAAAAAAAAJjiFs46woO1US6xACAAAAAAAgNlAQjrOirGMFIesQAgAAAAAAIAZQEI4zRhACAAAAAAAgllAQjrPCST5J0pGOPkUsy+E0AAAAAAAASHQUhOMs2etWID1ZEcvW0c5+p+MAAAAAAAAgwVEQOoB1CAEAAAAAABArKAgdwDqEAAAAAAAAiBVupwMkouMjCOsZQQgAAAAAAOKUbdtSaFAaGpAdGpTCISkSlqyIZNvRdzJMyXRJbo/k8crwJElJKc4GT0AUhA4oyopuVNLY0SfLsmWahsOJAAAAAAAARs62bWkgKLurTXZ3m+yeDtm9HbKD3VKwW3Z/rzTQJ9lnt0FroydJdnKqDF+ajNQMGf5MGelZ0ZfMHMmfIcNgYuz5QkHogNRkjzJTveoMDqm1Z0C5GTTjAAAAAAAgNtnhkOy2I7LbGmW1HZHdflR2R7M02PfRd3Z7JW+yDG9S9HWXKzpi0Dg2WMqyoiMKI2HZoSFpaEAa6o+OOAwNyu5pl32aj2tk5cnILpAZKJKRUywjK1+Gy3U+v/SEQUHokKKsVHUGh9TQFqQgBAAAAAAAMcPu6ZTVdFjW0RrZR2tktzdFi7wP8iTJyAjIyMiWkZYlIy1TSs2IjvrzpUnJqTJco6+ebNtWdlqqWhtqo6MRg12yezpl97RFRyx2tkj9vbKb62Q312k4mdsjI3eyzPwymYVTZeRNkeH2nMupSBgUhA4pyk7V7roO1bcFtWhqwOk4AAAAAAAgQdl9PbLqD8hqOCDrSLXU0/GB9zBkTMqTESiMjtjLLpAxKVfypcswzv+yaYZhyEz2ycwISBmn7kzs/qDs9iZZbY2yWxqiZWF3m+zGakUaqxXZ8kq0MMwvkzllplxTZsnIyD7vWeMFBaFDitnJGAAAAAAAOMC2LNnNtbJq9smq2y+77cjJ7+BNlplfKiO/RGbelOj0XU+SM2FPw0hJlVE0TWbRtOFjdn+vrKYa2UeqZTUclN3eJLu+UpH6SkU2PCtjUp7Msrkyp86PTkceg3JzoqIgdMjxnYwb2oKybZtvSgAAAAAAMGbscEhWfZWsQ7tk1ew7ef1At0dGQZnM4hnRqblZBTLMibcBiJHil6tsrlQ2V9LxkZFVsmqPFaEdRxXpOKrIlnUyMnNkTr9ArhmLZKRnOZzceRSEDkn3eZWW4lFPf0jtvYPKTkt2OhIAAAAAAIgjdiQsq65S1sHtsmr2SqGh929Mz5arZJbMKbNkFJSd1VqBsc7wpclVvliu8sWyI+Ho9ONDu2Qd2i27s0WR915W5L2XZRSUyTXrQpll82V4vE7HdkT8Xf0JpCgrVfsaOtXQFqQgBAAAAAAA58y2bdlHDilStUVW9a7orsDHGIGi6BTbsrkyMnMTajaj4XLLmFwuc3K57BUfj663WLVV1uHdso8cUvjIIemtZ+UqXyxz7iUyM3OcjjyuKAgdVJR9rCBsD2pBKQtlAgAAAACAs2P3tCuyf4silVuknvbh40ZWfnQq7bQFTKU9xnC55JoyU64pM2UPDcg6uEORve/IbqlXZNcGRXZtkFFcLvf8FdrW49fLGw6qNzgkf6pX16ycrkWzC53+Es47CkIHHV+HsL6NjUoAAAAAAMDo2JGIrNq90XKrrkqSHb0hNV2uGYtlli+SOSnP0YyxzvAmyzV7mVyzl8lqbVBk99uyDmyTXV+pd/c363ed09UTdg2/f2Nzr7RGcVcSUhA66MSdjNmoBAAAAAAAjIQd7FZkz9uK7HtX6uuJHnS5ZZbNk2vmEhmF0ybkJiNOMwNFMi+/VfZF1yuy7x2te67+pHJQknqCg3rpzQMUhDh/MlO98iW5FRwIq6tvSJmpsbVlOAAAAAAAiA22bcs+WqPIrg2yDu2SLEuSZGTmypy9TK7yRTKSUx1OGR+MZJ/cF6xS3/qK9wvYE/T2DZ3iXhMbBaGDDMNQUVaqqo50qb4tSEEIAAAAAABOYkcisg7tVGT7G7JbG6IHDVPm1Plyzb0kugMxMxLHhD/11Dsa+33xt9MxBaHDirJ9qjrSpYb2oOZNYbFQAAAAAAAg2UODiux7R5Gdb0m9ndGDyanR9fLmXCzDn+FovkRwzcrpamzuVU9wcPhYWmqSrlk53cFUY4OC0GHHNyppYKMSAAAAAAASnt0fVGTnm4rs3igNDUiSjMwcuRZcKnPGIhluj8MJE8ei2YXSGumlNw+ot29Ifh+7GGOMFGVTEAIAAAAAkOjsYLciO15XZM8mKRySJBn5pXItvExmySwZBpuOOGHR7MK4LAQ/iILQYdlpyUryuNTdH1J3/5DSU+JvHjsAAAAAADg1u7dT4a3rZe17V7IikiRzyky5Fl0pM7/E4XRIFBSEDjMNQ0VZPlUf7VFjW1DpxRSEAAAAAADEOzvYrfDWV2Xtfef9YrBsnlyLrpCZU+RwOiQaCsIYUJSdquqjPWpo79Os4klOxwEAAAAAAGPE7u9VZOt6Rfa8LUXCkgyZ0xbKtfhKmVl5TsdDgqIgjAHHNyqpZx1CAAAAAADikjXQp/A7Lyqy883hNQbNsrlyXXi1zKx8h9Mh0VEQxoDi4xuVtFMQAgAAAAAQT+xIWJHdG9W0bb3s/ujf/eaUWXItvVpmgKnEiA0UhDEgJz1FHpepjt5B9Q2G5UvisgAAAAAAMJHZtiWrarvC774o9XZKkoyCMrkvul5m3hRnwwEfQBMVA0zTUGGWTzUtvWpoD2pGQYbTkQAAAAAAwFmy6qsUfvsvstuOSJKMrDxlrb5DPZkFMgzD4XTAh1EQxoiirNRoQdhGQQgAAAAAwERkdbYosvF5WbX7ogdSM+ReerXMGYuVnJur3tZWZwMCp0FBGCOKstmoBAAAAACAicge7FNk8yuK7N4oWZbkSZJr8RVyzVshw+1xOh7wkSgIY0QRG5UAAAAAADCh2JGIrL2bFH6vQhrsk2TInLVM7qVXy/ClOR0PGDEKwhiRl5Eil2motXtAA0NhJXu5NAAAAAAAxCqr4YDCbz4ju7NZkmQUTpX7ko/JDBQ6nAwYPVqoGOF2mSqY5FN9W1CN7X2amp/udCQAAAAAAPABdm+Xwhufl1W9I3ogPVvuS26QWTKHDUgwYVEQxpCirFTVtwVV3xakIAQAAAAAIIbYkbAiO99SZPMrUnhIcnvkWnSFXAsvk+GiXsHExndwDCkOpGpTlVTX1ut0FAAAAAAAcIxVX6XwW8/I7myRJJllc+W+5GMy0iY5nAw4PygIY0hJTnQB05rmHoeTAAAAAAAAO9it8IbnhqcTGxkBuVfcLHNyucPJgPOLgjCG5GWkKNnjUkdwSF3BIWWkep2OBAAAAABAwrEtK7o78Tt/lYYGo9OJF18l14KVTCdGXOK7OoaYpqEpOX5VNnappqVHC1KznY4EAAAAAEBCsdoaFX79adnNdZIks2S23Cs+LiMt09lgwBiiIIwxJTlpqmzs0uGWHi0opSAEAAAAAGA82KEhRTZXKLLjTcm2JF96dDpx2Vx2J0bcoyCMMSU5fklSTQsblQAAAAAAMB4itfsVfvNPUk+HJEOuecvlWnqNDG+y09GAcUFBGGOm5PhlSGpoCyoUseRxmU5HAgAAAAAgLtn9vQq/9Yysg8c2IckukPuyNTJzJzucDBhfFIQxJsXrVt4kn5o6+lTfFlRZbprTkQAAAAAAiCu2bcs6sF3hDc9IA33RTUguvFqu+StkmC6n4wHjjoIwBpXm+NXU0aea5h4KQgAAAAAAziM72KXw60/Lqt0nSTKKpstz2RoZ6VkOJwOcQ0EYg0py0/R2ZbMON/c4HQUAAAAAgLhg27asfe8q/Pbz0tCg5E2S+5KPyZx5IZuQIOFREMagEzcqsW2bX1QAAAAAAJwDu7tdodfXym44IEkyS2bLfektMlIzHE4GxAYKwhgUSEtWapJbvQMhtfcOKjuNXZMAAAAAABgt27IU2b1BkXdelMIhKdkn94qbZU5byGAc4AQUhDHIMAyV5KZpT12HDjf3UBACAAAAADBKdlebQuuflN10WJJkTlsg94qbZaT4nQ0GxCAKwhhVmuPXnroO1bT0asm0HKfjAAAAAAAwIdi2LWvPpuhag+GQlOKX+9JPyFU21+loQMyiIIxRJcd2L2ajEgAAAAAARsbu6VTotafeX2tw2kK5V94sIznV4WRAbKMgjFGTs/0yDUNNnX0aCEWU7HE5HQkAAAAAgJhk27asys0Kb3g2ukNxsk/ulbfINW2B09GACYGCMEZ53KaKsnyqawuqrrVXMwrYWQkAAAAAgA+y+3oUfn2trJq9ko7tUHzZGhm+NIeTARMHBWEMK8lNU11bUIebeygIAQAAAAD4gMiB7Qq/+WdpsE/yJsu94iaZMxazQzEwShSEMaw0N01v7m1STQvrEAIAAAAAcJw9EFT4jT/Lqt4hSTKKZ8hz+W0y/AyuAc4GBWEMK8mJbr1e09wry7Zl8gwIAAAAACDBWXWVCq1/UurrkdxeuS+5UebsZYwaBM4BBWEMy0xNUobPq66+ITV39it/ks/pSAAAAAAAOMIOhxTZ9IIiuzZIkoz8EnmuuF1GerbDyYCJj4IwxpXm+rX9cLtqWnooCAEAAAAACclqbVB43R9kdzRLpinXkqvluuByGabpdDQgLvCTFONKc6O7LlUfZR1CAAAAAEBisS1L4W2vKfT0T2V3NMvIzJHnli/KvfgKykHgPGIEYYybnh9dYPXAkS7Zts2aCgAAYMJ4/PHHVV1drbKyMt19993Dx3t7e/Xoo4+qp6dH8+fP15o1axxMCQCIVXZPh0KvPiH7yCFJkjnnYrkvvkGGx+twMiD+UBDGuLzMFKUmu9XdH1JL94ByM1KcjgQAAPCRqqurNTAwoAceeEA///nPdeDAAU2fPl2S9OSTT+qOO+5QUVGRwykBALHItm1ZB7Yp/OafpKFBKcUv96rb5Joyy+loQNwa04LwdM8a/+QnP1FDQ4O8Xq9Wr16tlStXjmWMCc0wDE3Pz9D2w206cKSLghAAAEwIVVVVWrBggSRp/vz5qqysHC4I6+rq9PTTT6utrU133nmnysvLP3T/iooKVVRUSJIeeughBQKB8Qs/ztxud1x/fecb52t0OF+jw/kanbE4X1Z/UJ1//Y2G9rwrSUouv0CZN/yNXKlp5/XzOIHvr9HhfI3OuZ6vMSsIz/SssSR95StfUX5+/lh9+rgyoyA9WhA2dWv5LM4ZAACIfcFgUHl5eZIkn8+n+vr64dv279+v733ve/L7/fr+97+vBx988EP3X716tVavXj38dmtr69iHdkggEIjrr+9843yNDudrdDhfo3O+z5fVeFChdU9IwS7J7ZV7xU2yZl6ojv5BqX/wvH0ep/D9NTqcr9EZ6fkqLCw85fExKwjP9KyxYRj68Y9/LL/fr7//+79XTk7Oh+4fj88an22bu9Sdoqc2HlL10R5lZWfLZB3Cc8YzEbGF6xE7uBaxhesRO7gWo+fz+dTX1ydJ6u/vl8/nG76tsLBQxcXFkiSTBeYBIOHZkYgimysU2bpeki0jd4o8V94uI4P/e4HxMmYF4ZmeNf7sZz8rv9+vffv26de//rX+6Z/+6UP3j8dnjc+2/TZsW5mpXnUGh7SzslZF2aljkC6x8ExEbOF6xA6uRWzhesSOeLkWp3vGeCyUl5eroqJCy5cv186dO7Vq1arh2woKCtTR0aGUlBRFIpFxywQAiD12V5tC6/5bdnOdZBhyLbpKriVXyjBdTkcDEsqYPWV7pmeN/X6/JGnWrFnq7OwcqwhxwzAMzSg4tptxU5fDaQAAAD7a1KlT5fF4dN9998k0TQUCAa1du1aSdPvtt+uRRx7RAw88wA7GAJDAIpVbNfTHf4+Wg/4MeW76gtxLr6YcBBwwZiMIz/SscV9fn3w+nxobG5Waymi4kZiWn653D7TowJFuXT53/J79BwAAOFsnblInabgMLC4u1v333+9AIgBALLCHBhR+40+yDmyTJJlT58t92SdkJPnOfEcAY2bMCsITnzUuLS0dftZ4zZo1+vd//3cFg0EZhqHPfe5zYxUhrkw/NoKw+mi3IpYlF+v1AAAAAAAmGOtorUKv/LfU0y65PXKvuFnmzAtlsNY+4KgxKwil0z9r/I1vfGMsP21cyvB5lZuRrOauAdW1BlWaO/G3eAcAAAAAJAbbshTZtl6R9yok25IRKJT7qjtlZn5401IA429MC0KcX9PyM9TcNaCqI10UhAAAAACACcHu7VLo1T/IbqyWJLkWXCrXsmtluKgkgFjBPNUJZHpBuiTpYFO3w0kAAAAAAPhokepdGnrqh9FyMMUvzw1/J/clN1IOAjGGn8gJZFpeugxJh5t7FApb8rjpdwEAAAAAsccODSm88XlZezdJkswpM+Ve9UkZKX6HkwE4FQrCCSQ12aPCLJ8a2vt0qLlH5YUZTkcCAAAAAOAkVvtRhSt+J7vjqGS65Lr4BrnmLWcjEiCGURBOMNPyM9TQ3qeDTV0UhAAAAACAmGHbtqx97yq84VkpHJKRmSP36jtlZhc6HQ3AR6AgnGBmFKTr9T1HdOAI6xACAAAAAGKDPTig8BtrZR3cIUkyy5fIvfLjMjxeh5MBGAkKwgmmNC9dpmGorq1X/UNhpXi5hAAAAAAA51jNdQq98nupu13yeOVe+Qm5yhc5HQvAKNAuTTDJHpcmB1JV09KrQ0d7NGfyJKcjAQAAAAASkG1bCm9/XZF3/ipZloxAUXRKcUbA6WgARomCcAKaUZChmpZe7W/opCAEAAAAAIw7u79XbX/4rSIHd0qSXPOWy3XxDTJc1AzARGQ6HQCjN6s4U5K0t6FTtm07GwYAAAAAkFCshoMaeuoRDR7cKSX55L72s3KvuJlyEJjA+OmdgCZn+5Wa7FZH76Cau/qVl+lzOhIAAAAAIM7ZVkSRzesU2bJOki3v5BnSZbfK8Gc6HQ3AOWIE4QRkmoZmFWVKkvbUdzqaBQAAAAAQ/+zeLoWe/bkiW16RJLkWX6nAXf9MOQjECQrCCWp2cXTtwb11HQ4nAQAAAADEs8jhPRp66hHZTYclX5o8H/uc3EuvkWG6nI4G4DxhivEEVV6YIdMwdLilR32DYfmSuJQAAAAAgPPHjoQV2fSCIjvfkiSZk2fKfcUnZaT4HU4G4HxjBOEEleJ1a2pemmxb2t/Q6XQcAAAAAEAcsbvbFPrz/xctB01TrotvkPv6v6EcBOIUBeEENjzNuJ5pxgAAAACA8yNSvVNDf/x32S31UtokeT5+j9wLL5NhUCEA8Yp5qRPY7MmZeva9Gu1r6FTEsuUyDacjAQAAAAAmKDscUnjj87L2vC1JMsvmyn35bTKSUhxOBmCsURBOYDnpKQqkJ6u1e0A1LT2ampfudCQAAAAAwARkdbYoXPE72W1HJNMl9yU3ypx7iQyDgShAImB88AQ3uzhTkrSvvtPRHAAAAACAiSlStU2htT+KloPp2fLc8kW55i2nHAQSCAXhBDfn2DqEe1iHEAAAAAAwCnZoSKHXnlJ43X9LoSGZ0xbIe+uXZeYUOR0NwDhjivEEV5qbpmSPS0c7+9XeM6CstGSnIwEAAAAAYpzVcVThl38nu+Oo5HLLvfwmmbOXMWoQSFCMIJzg3C5T5YUZkqS9TDMGAAAAAHyEyP73FFr7Y9kdR2Vk5sjziX+Ua85FlINAAqMgjAOzJzPNGAAAAABwZnZoUKF1f1B4/VNSOCRzxiJ51nxJZnaB09EAOIwpxnFgVlGmDEkHm7o1GIooyeNyOhIAAAAAIIZYbUeiuxR3tkhuj9wrPi5z5hJGDQKQREEYF/zJHk3O8au2pVdVR7o0b0qW05EAAAAAADHAtm1Ze99ReMOzUiQsY1Ke3Fd/SuakPKejAYghFIRxYk7xJNW29GpXbTsFIQAAAABA9tCAwq+vlXVwhyTJnHWh3MtvluHxOpwMQKyhIIwTC0qy9Netddpd26FwxJLbxfKSAAAAAJCorJYGhSp+J3W3SW6v3Jd9Qq4Zi5yOBSBGURDGiZyMFBVm+dTY3qfKxi7NObZxCQAAAAAgcdi2LWv3RoU3Pi9ZERnZBXKv/pTMzBynowGIYRSEcWRhabYa2/u0/XAbBSEAAAAAJBh7sF/h1/4o69AuSZI552K5L7lRhtvjcDIAsY6CMI4sKMnWC1vqtLuuQ6GIJQ/TjAEAAAAgIVjNdQpV/F7qaZc8SXJffqtc0xY4HQvABEFBGEcC6ckqzk5VfVtQ+xs62awEAAAAAOKcbduK7HxLkU0vRKcUB4rkWf0pGRnZTkcDMIFQEMaZBaXZqm8LavvhNgpCAAAAAIhj9kCfwuuflFWzV5LkmrdcrotvkOHiT30Ao8NvjTizsCRLf9lcqz11HQqFLXncTDMGAAAAgHhjNdUo9Mrvpd5OyZss96rb5Cqb53QsABMUBWGcyUpL1uTsVNW1BbWvoVPzSxhFCAAAAADxwrYtRba/oci7L0qWJSN3sjyr75SRxt9+AM4eBWEcWlCarbpj04wpCAEAAAAgPtj9QYXXPyGrdr8kybXgUrmWXcuUYgDnjPmncWhhaXQx2j31HRoKRxxOAwAAAAA4V9aRQxr64yPRcjDJJ/e1n5X7khspBwGcF/wmiUOT/EmaEvCrtrVX++o7taCU3asAAAAAYCKybUuRra8p8t7Lkm3JyCuR56o7ZaRlOh0NQByhIIxTC0qzVdvaq+2H2ygIAQAAAGACsvt7FVr3B9n1VZIk1wWr5Lrwahkul8PJAMQbphjHqQXH1h7cW9+pwRDTjAEAAABgIrEaDmroqUei5WByqjzX3y33RddRDgIYE4wgjFOT/EkqyfGrpqVXe+s7dEFZwOlIAAAAAICPYFuWIlvWKbLlFcm2ZRSUyXPV/5CRmuF0NABxjBGEcex4KfjewRaHkwAAAAAAPood7Fbo+V8osrlCsiXX4ivl+djnKAcBjDkKwji2qCxbLtNQZWOXuoJDTscBAAAAAJyGVVcZnVLceFBK8ctz49/JvfQaGSZTigGMPQrCOJaa7NHcyZNk29LmakYRAgAAAECssSMRhd9+QaG/PCYNBGUUTZf3tntlFs9wOhqABEJBGOcunJ4jSXq3qkW2bTucBgAAAABwnN3TrtAzP1Nk+2uSYcq19Fp5bvg7Gb40p6MBSDBsUhLnygszlZ7iUWvPgA4396gsL93pSAAAAACQ8CLVOxV+7Y/S0IDkz5DnyjtlFpQ6HQtAgmIEYZxzmYaWTDs2ivAA04wBAAAAwEl2OKTQG39S+OXfSkMDMkvnyHvrvZSDABxFQZgAlh6bZrzjcJsGQxGH0wAAAABAYrI6mhV6+iey9rwtmS65V9wk9zWfkZHsczoagATHFOMEkJORopIcv2paerWjpk1Lp+c6HQkAAAAAEoZt27IqNyv85p+lcEhGerbcqz8lM6fI6WgAIIkRhAnjeCn4HtOMAQAAAGDc2EODCr/6hMLrn5LCIZnTL5Dn1q9QDgKIKRSECWJhaZY8blPVR3vU2j3gdBwAAAAAiHtWa4NCa38kq2qr5PbIveo2ua+8Q4Y3yeloAHASCsIEkex1a0FJliRGEQIAAADAWLJtW5Fdbyn09E9ld7XKyMqXZ82X5Zp5oQzDcDoeAHwIBWECOb5ZyXsHW2RZtsNpAAAAACD+2AN9Cr/0Xwq/9axkRWTOuVieT/yjzEmsBQ8gdrFJSQIpy0tXlj9J7b2DqjrSpZlFmU5HAgAAAIC4YTUdVuiV30u9XZI3We7Lb5Vr6nynYwHAR2IEYQIxDWN4FOGG/UcdTgMAAAAA8cG2LYW3vKrQM49KvV0ycifLe9tXKAcBTBgUhAnmovJcuUxDe+s61N7DZiUAAAAAcC7svh6Fnn9MkXdflGxLroWXy3Pz/5SRluV0NAAYMQrCBJOW4tXC0mzZkt7axyhCAAAAADhbVl2lhp56RHbDASk5VZ7r75b74utluFxORwOAUaEgTEArZ+dLkt490KyhUMThNAAAAAAwsdiRiMKb/qrQXx6T+ntlFE6T97Z7ZU6Z6XQ0ADgrbFKSgCYH/JqS41dtS682V7fqkpl5TkcCAAAAgAnB7ulQ6JXfyz5aKxmGXBeuluuCK2SYjL8BMHHxGyxBrZwVHUX41r4m2bbtcBoAAAAAiH2R6p3RKcVHa6XUDHlu+oLci6+iHAQw4TGCMEHNL8lS2nseHe3s18Gmbk0vyHA6EgAAAADEJDs0pPCGZ2Tte0+SZJbMlnvVbTKSUx1OBgDnB09zJCi3y9TF5dGpxW/ubXI4DQAAAADEJqulXqE//nu0HHS55V7xcbmv/SzlIIC4MqYF4eOPP6777rtPv/zlLz9029DQkD7/+c9rx44dYxkBZ3DxzFy5TEN76jvU3jvgdBwAAAAAiBm2bSm87TWF/vQfsrtaZWTlybPmS3LNu0SGYTgdDwDOqzErCKurqzUwMKAHHnhA4XBYBw4cOOn2V155RVOmTBmrT48RSE/xakFptmxb2rDvqNNxAABAnOHJYgATlR3sVuj5xxTZ9IJkRWTOvUSeT3xJZla+09EAYEyMWUFYVVWlBQsWSJLmz5+vysrK4dvC4bCqqqo0cyZbwDtt5azoNON3qpo1FI44nAYAAMQLniwGMFFFDu/R0FM/lN1wQEpOlfu6v5Fn5cdluD1ORwOAMTNmm5QEg0Hl5UXLJ5/Pp/r6+uHb1q9fr0svvVRVVVWnvX9FRYUqKiokSQ899JACgcBYRR03brc75r6OQCCgqVsaVN3Uqf1HB3TFwhKnI42LWLwWiYzrETu4FrGF6xE7uBajd6oni6dPny6JJ4sBxCY7NKTOF36j8Jb1kiSjeIY8V9wuw5fmbDAAGAdjVhD6fD719fVJkvr7++Xz+SRJkUhE27Zt0z//8z+fsSBcvXq1Vq9ePfx2a2vrWEUdN4FAICa/jkvKA6pu6tRzb1dqToFPLjP+19OI1WuRqLgesYNrEVu4HrEjXq5FYWHhuH0uniweOQro0eF8jQ7na2RCR+vU/szPFWxtlFxuZVyxRqnLVssw2NfzTPj+Gh3O1+hwvkbnXM/XiArCO+64Q/fee6+WL18uSdqyZYt+9atf6ZFHHjntfcrLy1VRUaHly5dr586dWrVqlSSpq6tLbW1t+s53vqOmpiZt3bpVU6dOld/vP+svAudmQUm2XkyrV2vPgLYfbtPiqfwAAgCAc8OTxSMXLwX0eOF8jQ7n68xs21Zk11uKvB1da9CdnS9j1e0aCBRqoK3d6Xgxj++v0eF8jQ7na3RGer5O94TxGQvC1tZWNTc3S5Lq6+u1Z88eSdK2bdt09OiZN7WYOnWqPB6P7rvvPpWWlioQCGjt2rVas2aNvvvd70qSnnjiCc2aNYty0GGmaeiK+YV6ckO11u1s0AVl2TLZlQsAAJwDniwGEOvsvh6F1j8puy66Xr45+yLl3PRZtXf1OJwMAMbfGQvCV199VU899ZQk6Y9//KP++Mc/Dt9WVFT0kR/87rvvPuntNWvWnPT27bffPuKgGFuLpwb00rZ6He3s1566Ds2bkuV0JAAAMIHxZDGAWBap3afw+qek/l4pySf35bfKVTZXpidJEgUhgMRzxoJw+vTpuuaaa/TSSy9pwYIFKigokCT5/X6tXLlyXAJifLhdplbNK9Cf36nRuh0Nmjt5kgxGEQIAgHPAk8UAYo0dDimy6QVFdm2QJBmF0+S58nYZqRkOJwMAZ52xIFy0aJEWLVqkadOmae7cucrJyZEkWZYl02Sx1nizbEauKnY0qK4tqKoj3Sov5D9JAAAAAPHBaj+q8Cu/l93eJJmmXEuvlWvhpWxEAgCSRvSbsK6uTq+++qra29t1zz336DOf+YzWrVs31tkwzrxuly6bEx0lum5ng8NpAAAAAODc2batyO6NCq39kez2Jhnp2fLc8kW5L7icchAAjhnRb8M333xTqampeuuttxQOh1VQUKC1a9eOdTY44JKZeUr2uHSwqVuHm1l7AwAAAMDEZfcHFX7x1wq/+WcpEpY580J5bvuKzJxip6MBQEw54xTj43p7e5WWlqZt27bpsssuU0lJiX72s5+NdTY4IMXr1vJZeVq3s1Hrdjbo766a5XQkAADgkC9/+cuaPHmySktLNWXKFJWWlio/P9/pWAAwIlZ9lUKvPiH19UjeZLkvWyPXtAVOxwKAmDSigjAQCOj3v/+9ent7dc8996izs5Pd5uLYpXMK9MaeJu2t71Rje1CFWalORwIAAA5YunSpwuGwMjMztWPHDv34xz9WWlqasrKyVFJSoi984QtORwSAD7EjYUXeeUmRHa9Lkoz8Unmu/B8y0jKdDQYAMWxEBeGnP/1pPfnkk5oxY4aWLVum3/3ud7rooovGOhsc4k/26OLyXL2xt0kvbq3X3VfNdDoSAABwwI4dO/Rv//Zvw29fccUVeuedd3TdddeppqbGwWQAcGpWZ0t0I5LWRskw5brwKrkuuEIGm2wCwBmNqCBctmyZlixZoiNHjqipqUl33XUXuxjHuSvnF2lTVbP21HfoUHOPynLTnI4EAADGWVpamg4fPqzS0lJJ0owZM/Too4/q05/+tLKzs50NBwAnsG1b1r53Fd7wrBQOSWlZ8lz1P2TmTXE6GgBMCCMqCOvr6/Wv//qvampqkiTl5+fr61//uoqKisY0HJzjT/HosrkFqtjeoBc21+qe6+bIMAynYwEAgHH0D//wD/rxj3+s4uJilZaWqqGhQV6v1+lYAHASe6BP4df/KOvQbkmSOWOR3Cs/LsOb7HAyAJg4RjQM8Be/+IU6Ojq0YsUKrVixQp2dnXrsscfGOhscdvmcAvmS3DrU3KN9DZ1OxwEAAOMsPz9fDzzwgBYtWqTOzk7l5+frG9/4htOxAGCY1XhQQ0/9MFoOepLkvvIOea68g3IQAEZpRCMIq6ur9alPfUrXXXedJOmvf/2rfv/7349pMDgv2evWVfOL9Ox7NXphS51mFmXKZBQhAAAJxTRNXXTRRaw/DSCm2JGwIu++rMj21yXZMvKmRDciSc9yOhoATEgjGkHo9/u1Y8cOHT16VEePHtWOHTvYxThBXDIrT5mpXh3p6NP2Q21OxwEAAACQ4KzWRoXW/kiR7a9JhuRafKU8N/8D5SAAnIMRjSC88sor9cQTT2jz5s3Dx+64444xC4XY4XGZumZhsZ7YUK2/bq3T/JIsuV1sUAMAAABgfNlWRJFtrymyuUKyLBkZAblXfVJmfonT0QBgwhtRQXjZZZcpIyNDO3bskCQtXLhQCxYsGNNgiB2Lp+Vo/e4jau7q1ztVzVo+K9/pSAAAAAASiNXZovCrT8hurpMkmXMvkfui62V42DgJAM6HEQ0Fe/DBB9Xa2qqvfe1r+trXvqaWlhZ9+9vfHutsiBEu09B1iyZLkl7e3qChUMThRAAAAAASgW1bCu98S6E//nu0HEzNkOfGv5dn5ccpBwHgPBrRCML29nbl5uYOv52Tk6O2NtajSyTzpkzS5ECq6lqDenVXo649VhgCAAAAwFiwezoVWv+k7MaDkiSzfLHcy2+SkZTicDIAiD8jKgjz8vL07LPPKisrS7Zt67nnnlNeXt5YZ0MMMQxDNy0t1U9f2K31uxq1dHqOstKSnY4FAAAAIM7Yti2rcrPCG56Vhgal5FS5L1sjV9lcp6MBQNwaUUH48Y9/XD/5yU/03e9+d/jYl770pTELhdhUlpumRVMD2lrdqmferdHfXjnT6UgAAAAA4ojd16Pw62tl1eyVJJmlc+W+7BMyUvwOJwOA+DbiTUoCgYC2bNkiSVq8eLHmzJkzpsEQm25cMkW7a9u1u65D+xs6NbMo0+lIAAAAAOJApHqnwm/8SRoISt4kuVfcLHPGYhmG4XQ0AIh7IyoIJWnOnDmUglCGz6vVC4r0ly11eubdw/pq/gK5XSPa6wYAAAAAPsQe7Ff4rWdkVW2VJBlF0+VZdZsMf6azwQAggYy4IASOu3ROgd450KLmrgG9ta9Jl88tdDoSAAAAgAnIqqtU6LWnpGC35PbIfdENMudeJMNgEAIAjCd+62LU3C5TNy8tkSS9vL1B3f1DDicCAAAAMJHYoSGF3viTQn95TAp2y8idIs+tX5Fr3iWUgwDgAH7z4qzMLp6k2cWZGgxF9JfNtU7HAQAAADBBWE01Cj31iKw9b0umS65l18rz8X+QmZnjdDQASFhMMcZZu3lpqSobt2vzwVZdVJ6nstw0pyMBAAAAiFF2JKzIexWKbH9Nsm0ZWflyX3m7zGyWLAIApzGCEGctkJ6sVcfWH3xqQ7XCEcvhRAAAAABikdXWqNDaHyuybb0kyXXBKnnWfIlyEABiBCMIcU6uWlikHTVtau7q1ys7GnTtoslORwIAAAAQI2wrosj21xV5r0KyIlJ6tjxX3C4zv8TpaACAEzCCEOfE4zL1yeVTJUnrdjaqsT3ocCIAAAAAscDqalXozz9T5J0XJSsic87F8t52L+UgAMQgCkKcs7K8dC2fmSfLtvXkhmpFLNvpSAAAAAAcYtuWIrs2KPTUI7Kba6XUdHlu+Dt5Lr1FhsfrdDwAwCkwxRjnxfVLpmhPfYfq24J6c+8RXT6XtUQAAACARGP3diq0/inZDQckSeaMRXKvuElGks/hZACAM2EEIc6LZI9Lt15cJkl6cWu9WrsHHE4EAAAAYLzYtq1I5WYNPfnDaDmYnCr31XfJc+UdlIMAMAFQEOK8mVU8SYunBhSKWHpqY7Vsm6nGAAAAQLyz+3sVfum/FH71SWloQGbpHHk/+b/kmjrP6WgAgBFiijHOq5uXlmh/Y6cONnVrw76jWjE73+lIAAAAAMZI5NAuhV9/WhoISt4kuZffJLN8iQzDcDoaAGAUGEGI8yo12aNbL47uavzc5ho1dfQ5nAgAAADA+WYP9iv06hMKv/QbaSAoo3CavLd9Va6ZF1IOAsAEREGI825+SZaWTs9ROGLrd28cUDhiOR0JAAAAwHli1Vdp6MkfyqrcIrnccq+4SZ6P/b2MtEynowEAzhJTjDEmPr6sVIeO9uhIR59e2FKnm5aWOB0JAAAAwDmwQ0MKb3pB1u6NkiQjd7LcV9wuMzPH4WQAgHPFCEKMiSSPS3deOl2mIb2+54gqGzudjgQAAADgLFm1+zX0xMPRctA05Vp6jTwf/5+UgwAQJygIMWam5Ph1zQWTJUl/ePOgggMhhxMBAAAAGA27v1ehV/5boRd+KfV2yggUyvOJf5R78ZUyTJfT8QAA5wlTjDGmrphXqP0NnTrU3KOnNlbrs6vKWbQYAAAAiHG2bcuq3KLwxuelwT7J7ZFryWq5FqykGASAOMQIQowp0zR056XTlexxaVdthzbsO+p0JAAAAABnYHe1KfT8LxRe/6Q02CejaLq8t/0vuS+4nHIQAOIUIwgx5ib5k3Tb8qn6zWtVeva9GhVlp6o0N83pWAAAAABOYFsRRXa8qcjmCikckpJ8ci+/UeaMxcwCAoA4xwhCjIuFpdm6dHa+Ipat37xWpd5+1iMEAAAAYoXVUq/Q0z9RZNMLUjgkc/oF8t7xNbnKl1AOAkACYAQhxs2NF05RfVtQh5p79JvXq/T5q2fLZfJgAwAAAHCKHRpS5L2XFdn5pmTbkj9Tnks/IXPKTKejAQDGESMIMW5cpqlPXz5D/mSPDjZ168WtdU5HAgAAABKWVVepoSd/oMiONyRJrgUr5b39a5SDAJCAGEGIcZXh8+quy2fo0Zf26NVdjZqS49e8KVlOxwIAAAASht3fq/DG52VVbZUkGdkFcl9+q8ycYoeTAQCcQkGIcTctP13XL56i5zfX6g9vHlTujSnKzUhxOhYAAAAQ12zbllW1VeGNz0kDfZLLLdeFV8s1f6UMF7sTA0AioyCEIy6fW6C61l7tqGnXY6/s05dvmKfUZI/TsQAAAIC4ZHe3KfTGn2TXV0mSjKLp8lz6CRkZ2Q4nAwDEAgpCOMIwDN2xYpraegbU0N6nX6+v1Oevni23i2UxAQAAgPPFtiIKb39dkfdelsIhKckn9yU3yixfzO7EAIBhtDFwjNfj0t1XzlJ6ikfVR3u09u1Dsm3b6VgAAABAXLBaGtTyy+8o8vZfpHBI5vQL5L3ja3LNXEI5CAA4CSMI4aiMVK/uvmqmfvrCHr17oEU5GSm6Yl6h07EAAACACcsODSnyXoUiO9+UbEvyZ8p96SfkYndiAMBpUBDCccXZft156XT9en2lXthcq0BasuaXsLMxAAAAMFpWfZVCrz8t9bRLhqHUZVcrNG+lDE+S09EAADGMKcaICfNLsnT94smyJf3+jQOqbelxOhIAAAAwYdj9QYXW/UGh538h9bTLyC6Q55YvKvPqOygHAQAfiRGEiBlXzCtUa/eA3j3Qol+8sl9fvG6u8jJTnI4FAAAAxCzbtmVVbVV443PSQJ/kcst14Wq55l8qw+VyOh4AYIKgIETMMAxDt15Spt6BkPbWd+rnL+/VP14/V5P8POMJAAAAfJDd3a7QG0/Lrq+SJBmF0+S57BMyMgIOJwMATDRMMUZMcZmm7rp8hspy09TVN6T/rNir4EDI6VgAAABAzLCtiMLbX9fQkz+IloNJKXKvuk2ej32OchAAcFYoCBFzvG6X/vbKmcqf5FNz14B+8co+DYYiTscCAAAAHGe1NCj09E8VefsvUjgkc/pCee/4J7lmXijDMJyOBwCYoCgIEZN8SW59bvUsTfInqa41qF+9WqlwxHI6FgAAAOAIOzSk8Ma/KPT0T2S3Nkj+TLmv/1t5rrpTRorf6XgAgAmOghAxK8Pn1eevniV/skdVR7r06/WUhAAAAEg8Vn2Vhp78oSI7XpdkyzV/hby3f1WuKbOcjgYAiBMUhIhpOekp+vzVs+RLcmtvfaf+67UqSkIAAAAkBLs/qNCrTyj0/C+knnYZWfny3PJFuZffJMPDRn4AgPOHghAxrzArVV+4ZrZSvC7tqevQbygJAQAAEMds21akaquGnnhYVuUWyeWWa9l18qz5sszcyU7HAwDEIQpCTAhFWan6wjVzlOJ1aXddh377epUiFiUhAAAA4ovd067QX36p8Lo/SANBGYVT5fnk/5J70SoZLpfT8QAAcYqCEBNGcfb7Iwl31Xbot68foCQEAABAXLCtiMI73tDQEz+QXV8pJaXIfflt8nzs8zIzAk7HAwDEOQpCTCjF2X59/urZSva4tLOmXb96tVKhMCUhAAAAJi6rtVGhp3+qyMbnpXBI5rSF8t7+NblmXSjDMJyOBwBIAO6x/OCPP/64qqurVVZWprvvvnv4+C9/+UsdPnxYoVBIn/3sZzVrFrtvYeQmB/z6wjWz9Z8V+7S3vlP/WbFXd185U8neMf12BgAAAM4rOzSkyOZXFNnxhmRbkj9D7pWfkKuEv48AAONrzEYQVldXa2BgQA888IDC4bAOHDgwfNtnPvMZfetb39JXv/pVPf3002MVAXFscsCvL143R+kpHlUf7dHPXtqr4EDI6VgAAADAiERq92voqR8qsv01ybblmrdc3k9+jXIQAOCIMSsIq6qqtGDBAknS/PnzVVlZOXyb2x0d6TUwMKCSkpKxioA4l5fp0z9eP1dZ/iTVtwX107/uUVdwyOlYAAAAwGlZHc3RTUhe+KXU3S4jK1+eW+6Re8XNMrxJTscDACSoMZuTGQwGlZeXJ0ny+Xyqr68/6fZ//dd/1YEDB/TlL3/5lPevqKhQRUWFJOmhhx5SIDDxF+Z1u91x8XXEkkBA+uanA/q3pzapoa1H/99Le/W1Wy9SQZb/jPfjWsQWrkfs4FrEFq5H7OBaADhX9kCfIpsrFNn9dnQ6sTdJrsVXyTVvBbsTAwAcN2YFoc/nU19fnySpv79fPp/vpNv/9//+32pra9PDDz+s73znOx+6/+rVq7V69erht1tbW8cq6rgJBAJx8XXEos+vLtcvXtmnutagvv27N/U3V5Rral76ad+faxFbuB6xg2sRW7gesSNerkVhYeG4fr7TrUf96KOPqq6uTpL0uc99jhkliGu2FZG15x2F33tZGuyTDEPm7IvkXnq1jJQzP6kNAMB4GbMpxuXl5dq1a5ckaefOnSovLx++LRSKrhWXnJyspCSG0ePcpSZ79D+vmaM5xZPUNxjWoy/t1bZDE/8POQAAJqozrUd9yy236MEHH9QXv/hFPfnkkw6mBMaWVVep0FOPKPzWn6XBPhmFU+W59SvyXPYJykEAQEwZsxGEU6dOlcfj0X333afS0lIFAgGtXbtWa9as0Q9+8AP19fXJsix96lOfGqsISDBej0t/c0W5/vzOYW3Yf1S/ff2AOnoHtWpeoQzDcDoeAAAJ5VTrUU+fPl2SlJubK0lyuVwyzTF7vhpwjNXZosjG52XV7oseSM+S++IbZJbO5XEpACAmjVlBKOmkqSSStGbNGknS17/+9bH8tEhgpmnolotKlZWWpOfeq9VfttSpvXdQt1xUKhd/gAAAMG4+aj1qSfrd736nG2644ZT3j8f1qE+HNS5HJ5bPlzXQp+43nlXwvXWSFZHhTVbayhvlX7pahtvjSKZYPl+xiPM1Opyv0eF8jQ7na3TO9XyNaUEIOMEwDF0+t1CZqUn67zcO6O3KZrV0D+gzl89QarIzD8wAAEg0H7Ue9fPPP6/i4mLNmjXrlPePx/WoTyde1rgcL7F4vmwrImvfuwq/+7I0EJRkyJy1VO6l12jQl6bBzi7HssXi+YplnK/R4XyNDudrdDhfozPS83W6NakZUoW4tbA0W/9w7Rz5kz062NStR57fpSMdfU7HAgAgIZxpPert27dr//79uvXWW52KB5w3Vv0Bhf747wq/8SdpICijoEyeW78kz+W3yvClOR0PAIARoSBEXCvNTdO9H5un4uxUdfQO6sd/2aUdNW1OxwIAIO6duB61aZrD61FL0mOPPaaWlhZ961vf0qOPPupwUuDs2F2tCv31Vwo9/5+y249KaZPkvvrT8tz0BZmBIqfjAQAwKkwxRtzLTE3SF6+bq6c2VmtLdav+a32VugakFeVZMlkkGgCAMXO69agfeeQRJ+IA54U9OKDIlnWK7HpLsiKSxyvXoivkmr/SsXUGAQA4VxSESAget6n/sXKaCrN8en5zrZ55u0r7ajN056XT5WddQgAAAHwE27KOrTP40vvrDM5cIvfSa2WkpjsdDwCAc0JBiIRxfPOSgkk+/f7NalU2dumHz+7UXZfPUGku68MAAADg1KzGgwpveE522xFJkpFfIvfym2TmFDucDACA84M1CJFwygsz9a3PXKqSHL+6+ob0H3/do9d3H5Ft205HAwAAQAyxu9sUevG/FHr259Fy0J8p9+pPyXPz/6QcBADEFUYQIiFlpaXonuvm6C+b6/T6niN69r0aHWru1ieXT5MviR8LAACARGYPDSiy9VVFdrwZXWfQ7ZFr0Sq5FlzGOoMAgLhEE4KE5TJN3bS0RKW5aXrirYPaVduhutYduvPSaZqWn+F0PAAAAIwz27JkVW5W+J0Xpf5eSZJZvljuZdexziAAIK5RECLhzS/JUmGWT79744BqW3r1sxf3atW8Ql1zQbHcLmbhAwAAJAKrsVrhjc/Jbm2UJBl5U6LrDOZOdjgZAABjj4IQkJSdlqwvXjdXFTvq9cqOBr26q1FVR7r0qcumKyc9xel4AAAAGCN2T7vCb78gq3pn9EBqhtwXXy9z2kIZhuFsOAAAxgkFIXCMyzR07QWTVV6Qod+/cUD1bUH94NmdunHxFF0yK08mDxABAADihh0aVGTrekV2vCFFwtF1Bi+4PLrOoMfrdDwAAMYVBSHwAWV56frqzQv09KbD2lrdqj+9c1g7a9t1+/KpykpLdjoeAAAAzoFtW7Iqt0TXGezrkSSZ0y+Q+6LrZfhZhxoAkJgoCIFTSPG69alLp2v+lCz98e1qHWzq1vef2aGPXViii8tzmW4CAAAwAVlNhxXe8JzslnpJkpE7ObrOYN4Uh5MBAOAsCkLgDOaXZKksL01/2nRI2w+3a+3bh7Sjpk23XjxVgXRGEwIAAEwEdk+nwptekHVwe/RAarrcy66XOWOhDINN6QAAoCAEPoI/2aO7Li/X/JI2rX37kA4c6db3n9muaxYW67K5BXKZPKgEAACIRXZoSJFt6xXZ/np0nUGXW66Fl8t1weWsMwgAwAkoCIERWliarWn56Xr23RptqW7VX7bUaeuhNt12yVRNyfE7HQ8AAADH2LYlq2qbwpv+KvV1S5LMaQuj6wymZTobDgCAGERBCIyCP9mjOy+drsVTA1r79iEd6ejTj/+yS8tn5evaRcVK8fIjBQAA4CTraK3CG56V3VwnSTJyiuVe/jGZ+aXOBgMAIIbRZgBnYWZRpv7p4wv08vZ6vb77iN7a16Tth9t045IpWjwtIJNNTAAAAMaV3dup8Ka/yjqwLXrAlyb3sutkli9inUEAAD4CBSFwlrxul25cUqJFZQH9adNhHWru0R/eOqi3K4/qExeVqSg71emIAAAAcc8ODSmy/XVFtr8mhUPRdQYXXCrXolUyPElOxwMAYEKgIATOUWFWqu65bo62VLfqufdqVdPSq0ee36mLy/N07QXFSk32OB0RAAAg7ti2LevAdoU3vSAFuyRJ5tT5cl98vYy0LIfTAQAwsVAQAueBYRhaMi1HcyZP0svb6vXWviZt3H9UW6tbddWCIq2cnS+3i6ktAAAA54PVXKfwW8/Kbq6VJBmBQrkv+ZjMwqkOJwMAYGKiIATOoxSvWzcvK9WyGbl69r0aVTZ26fnNtdq4/6huvHCK5k/JksH6hAAAAGfFDnapfcOfFdq5MXogxS/3smtlli+RYfJkLAAAZ4uCEBgD+ZN8+vzVs7WvvkPPvler5q5+/df6KpXlpumGJVNUmpvmdEQAAIAJww6HousMblsfXWfQdB1bZ/AKGV7WGQQA4FxREAJjaFbxJM0ozNSmyqN6cVu9DjX36Ccv7NbcyZN0/eLJysv0OR0RAAAgZtm2Levgjug6g72dkqTkmYtlLb5KRnq2s+EAAIgjFITAGHOZhpbPyteiqQG9tuuIXt97RLvrOrSnvkNLpubomguKNcnPM98AAAAnslrqFd7wnOymw5IkI7tA7uUfU/aCi9Ta2upsOAAA4gwFITBOUrxuXbd4spbPylPFjgZtqmzWewdbtPVQqy6akasr5xcpI9XrdEwAAABH2cFuhd95UVblFkm2lJwaXWdw5oWsMwgAwBihIATGWbrPqzUXl+myOQV6cWudth9u04b9R/VOVbMunpmnK+YXKj2FohAAACQWOxJWZOebimxZJ4WGousMzl8h16IrZSQlOx0PAIC4RkEIOCSQnqxPXz5DVy0o0svb67Wjpl1v7m3SpspmXTwzV5fPLVSGj6IQAADEN9u2ZdXuU2TDc7K72yRJZslsuS+5UUZGwOF0AAAkBgpCwGH5k3z6zKpyNbYH9dK2eu2u69Abe5q0Yd9RLZuRq1XzCpTl51lzAAAQf6zOFoU3PCu7rlKSZGTmyr38YzInlzucDACAxEJBCMSIwqxU/e2VM9XQFtQrOxu0s6ZdG/cf1abKZi2eGtAV8wuVm5HidEwAAIBzZg8OKLLlFUV2vSVZluRNlmvJarnmXiLD5XI6HgAACYeCEIgxRdmp+uyqch3t7NO6nY3aeqhV7x1s0eaDLZozeZJWzStUaW6a0zEBAABGzbYtWfs3K/zOi1J/ryRD5qxlci+7RkaK3+l4AAAkLApCIEblZfp056XTdfXCYq3f1aj3DrZod12Hdtd1qDQ3TZfPLdCcyZNkGobTUQEAAD6SdbRW4beekd1SL0ky8krkXnGTzJxih5MBAAAKQiDGBdKTddvyqbpmUbHe2tukjfuP6nBzjw439ygnPVkrZ+drybQcJXmYjgMAAGKPHexWeNMLsqq2Rg/40uW++AaZ0xfK4IlOAABiAgUhMEGkp3h1/eIpumJ+kd6pbNYbe4+opXtAT286rL9urdOyGblaMStfk/xJTkcFAACQHQkrsvNNRbask0JDkumSa+Flci1aJcPD4xUAAGIJBSEwwSR7XLpsboFWzM7TrtoOvbHniGpaevXa7iN6Y88RzZ2SpeUz8zQtP51n5QEAwLizbVtW7T5FNjwnu7tNkmSWzpH7khtlpGc7nA4AAJwKBSEwQblMUwtLs7WwNFu1LT16Y2+Tdhxu186a6EteRooumZWnJVMDSvbyow4AAMae1dmi8IZnZddVSpKMzNzoOoPFMxxOBgAAzoTWAIgDU3LS9OmcNH1syZDerjqqTZXNOtrVrz9tOqwXNtdq0dSALp6Zp6KsVKejAgCAOGQPDiiy5RVFdr0lWZbkTZbrwtVyzblEhot1kgEAiHUUhEAcyUj16toLJmv1giLtqu3Qhn1Nqj7ao7crm/V2ZbMmZ6fqovI8XVCWzaYmAADgnNm2JWv/ZoXfeVHq75VkyJy1TO5l18hI8TsdDwAAjBAFIRCHTpx+3NTRp01Vzdp8sEV1bUHVbazWs+/V6IKybC2bnqPJAT9rFQIAgFGzjtYq/NYzslvqJUlGXoncK26WmVPkcDIAADBaFIRAnMuf5NPHl5Xq+sWTtaOmXZsqm3W4uUebKpu1qbJZuRkpWjo9R0umBZSW4nU6LgAAiHF2sFvhTS/IqtoaPeBLl/viG2ROX8iTjgAATFAUhECC8LpdunBaji6clqOjnX1690CLNh9sVXNXv57fXKsXttRqVtEkLZkW0OzJk+RxmU5HBgAAMcSOhBXZ+aYiW9ZJoSHJdMm18DK5Fq2S4UlyOh4AADgHFIRAAsrL9OljF5bo+sWTtbe+U+8eaNG++g7tOfaS4nVpQWm2lkzLUWkOU5ABAEhktm3LqtmryMbnZXe3SZLM0jlyX3KjjPRsh9MBAIDzgYIQSGAu09S8KVmaNyVLPf1D2naoTZsPtqihvW94CnKWP0kXlGVrUVlA+ZN8TkcGAADjyOpoVnjjc7LrKiVJRmau3Ctuklk8w+FkAADgfKIgBCBJSkvx6tI5Bbp0ToGaOvq0ubpFW6vb1N47qHU7G7VuZ6PyJ/m0qCxbF5RmKyst2enIAABgjNiDA4psqVBk1wbJsiRvslwXrpZrziUyXC6n4wEAgPOMghDAh+RP8unGJSW6ftEUHWru1tbqNu2oaVNTR59e6OjTC1vqNDk7VQuO7ZQ8yc+6QwAAxAPbtmTt36zwOy9K/b2SDJmzlsm97BoZKX6n4wEAgDFCQQjgtEzT0LT8DE3Lz9AtF5WqsrFLW6tbtae+Q3VtQdW1BfX85lpNyfFrQUmW5k/JYmQhAAATlNVUo/CGZ2W31EuSjPwSuZffLDOnyOFkAABgrFEQAhgRt8vUnMmTNGfyJA2FI9rX0Kkdh9u0p75TtS29qm3p1XPv1aooK1XzS7I0vyRLuRkpTscGAAAfwQ52K7zpBVlVW6MHUtPlvugGmdMXslEZAAAJgoIQwKh53S4tKMnWgpJsDYUi2tvQqZ017dpX36GG9qAa2oP669Y65WYka+7kLM2bMknFAb9M/sgAACBm2JGwIjvfVGTLOik0JLncci24VK5Fq2R4WD4EAIBEQkEI4Jx4PS4tPLYWYShiqaqxSztq2rSnrkPNXQNq7mrUq7salZ7i0ezJkzR38iRNz8+Qx206HR0AgIRk27asmr2KbHxednebJMksnSP3JTfKSM92OB0AAHACBSGA88ZzwjTkiGXp0NEe7art0O66dnUGh7SpslmbKpvlcZuaUZChOcWTNLs4UwGngwMAkCCsjmaFNz4nu65SkmRMypV7+U0yi2c4nAwAADiJghDAmHCZpqYXZGh6QYY+vqxEje192l3Xrj11nWpoD2pPXYf21HVIkkpyD2p6vl+zijI1JeCXaTIVGQCA88keHFBkS4UiuzZIliV5k+W6cLVccy6R4XI5HQ8AADiMghDAmDMMQ0XZqSrKTtU1F0xWV3BIexs6tLeuU1VHulTTHH15ZUeDfElulRdmaGZRpsoLM5Se4nU6PgAAE5ZtW7L2b1b4nRel/l5JhsxZy+Redo2MFL/T8QAAQIygIAQw7jJSvbq4PE8Xl+cpFLbU2i9t2lOrvfUdau8d1LZDbdp2KLomUmGWTzMLo2VhaW6a3C7WLgQAYCSsphqFNzwru6VekmTkl8i9/GaZOUUOJwMAALGGghCAozxuU/PLAipIM/XxZSVq7R7QvoZO7W/sVHVTjxrb+9TY3qdXdzXK4zY1LS9d0wsyVF6YofzMFBnsjAwAwEnsYLfCm16QVbU1eiA1Xe6LbpA5fSH/bwIAgFOiIAQQMwzDUE5GinIyUnTpnAKFIpYOHe3W/oYuVTZ2qqmzX/saOrWvoVOS5E/2aEZBtDCcnp+urLRkZ78AAAAcZEfCiux4U5Et66TwkORyy7XgUrkWrZLhSXI6HgAAiGEUhABilsdlqrwwU+WFmZJK1N03pKojXdGXxi5194e09VCbth6bjjzJn6Tp+emaduwlM5U/hgAA8c+2bVk1exXe+LzUHf0/0SydI/clN8pIz3Y4HQAAmAgoCAFMGOk+r5ZMy9GSaTmybVvNXf06cKRbB5q6dLCpWx29g3r3QIvePdAiSQqkJWvqsbJwal4ahSEAIO5YHc0Kb3hOdn2lJMmYlCv38ptkFs9wOBkAAJhIKAgBTEiGYSgv06e8TJ9WzM6XZdlq7OjTgSNdqj7areqjPWrtGVBrz4DeqWqWFB1hODUvTVPz0lWWm6ZAejJrMQEAJiR7cECRLRWK7NogWZbkTZbrwtVyzblEhsvldDwAADDBUBACiAumaag4O1XF2alaNa9QEctWY3tQB5u6dbCpW4ebe9TRO6jNvYPafLBVUnQNw9LcNJXlpqksL02FWT65THZJBgDELtu2ZO3frPA7L0r9vZIMmbOXyb30GhkpfqfjAQCACYqCEEBccpmGJgf8mhzwa9W8QlmWrSOdfTp0bHRh9dFu9Q6EtKu2Xbtq2yVFd1SeEvCrNCdNJbl+leSkyZfEr0kAQGywmmoU3vCs7JZ6SZKRXyL38ptl5hQ5nAwAAEx0/OULICGYpqGirFQVZaVq5ewC2bat1p4BHT7ao0PNPTrc3KOW7oHhEYfH5WakqCTHr5Icv6bkpCkvI0WmybRkAMD4sYPdCm96QVbV1uiB1HS5L75B5rSFLJUBAADOizEtCB9//HFVV1errKxMd9999/DxRx99VHV1dZKkz33ucyopKRnLGADwIYZhKCc9RTnpKVo6I1eS1Nsf0uGWHtW09KimuVd1rb1q7upXc1f/8MYnSW5TkwN+TcmJjk6cEvAr3ed18ksBAMQpOxJWZMebimxZJ4WHJJdbrgWXyrXoChke/u8BAADnz5gVhNXV1RoYGNADDzygn//85zpw4ICmT58uSbrllluUm5urI0eO6Le//a3++Z//eaxiAMCI+VM8mjclS/OmZEmSwhFLje1B1bT0qralVzUtPeoIDulAU7cOnDDKMMPnjRaG2amaHPCrKDtVKV4GaAMAzo5t27Jq9iq88Xmpu02SZJbOkfuSG2WkZzucDgAAxKMx+wu2qqpKCxYskCTNnz9flZWVwwVhbm50tI7L5ZLJhgAAYpTbZWpKTpqm5KQNH+vuG1Jta3R0YW1Lr+ragurqG9LOmnbtrGkffr+c9GQVB6KlYVF2dGpzkoddJQEAZ2Z1NCu84TnZ9ZWSJGNSrtzLb5JZPMPhZAAAIJ6NWUEYDAaVl5cnSfL5fKqvr//Q+/zud7/TDTfccMr7V1RUqKKiQpL00EMPKRAIjFXUceN2u+Pi64gHXIvYMpGuR0DS1Cnvv23Ztprae1V9pFOHmjp16Gin6lqi6xm2dA9oa3V0x2RDUkGWXyV5GdGX3AxNyU2XL8njyNdxOhPpWiQCrkfs4FpgrNmDA4psqVBk1wbJsiRvslwXrpZrziUyXDzBBAAAxtaYFYQ+n099fX2SpP7+fvl8vpNuf/7551VcXKxZs2ad8v6rV6/W6tWrh99ubW0dq6jjJhAIxMXXEQ+4FrFlol8Pr6RZ+SmalZ8iqUDhiKWmzj7VtQZV3xZUfVuvmjr61djeq8b2Xm3c2zB830BasgqzfCrKTlVhVqoKs3xKT3FuXamJfi3iDdcjdsTLtSgsLHQ6Aj7Ati0Ft72hoXV/lPp7JRkyZy+Te+k1MlL8TscDAAAJYswKwvLyclVUVGj58uXauXOnVq1aNXzb9u3btX//fn31q18dq08PAI5xu0wVZ/tVnP3+H3ahiKWmjj7Vtfaqsb1PDe1BHenoU2vPgFp7BrTjhOnJaSkeFWb5VDgpVQWTfCrM8imQniIXuycDQFyxmmoUfusZdbZGnzgy8kvkXn6zzJwih5MBAIBEM2YF4dSpU+XxeHTfffeptLRUgUBAa9eu1Zo1a/TYY4/J5/PpW9/6lgoLC/WFL3xhrGIAQEzwuKK7H08OvF8ahiOWmrv61dAWVGNHnxrbg2ps71NPf0j7G7q0v6Fr+H3dLkP5mT4VTHr/JX+ST/7k2JqiDAD4aHawW+FNL8iq2ipJMtMmyVx2rcxpC2UYPBkEAADG35hus3n33Xef9PaaNWskSY888shYfloAmBDcLvPYtOLU4WOWbaujd1CN7X1q7AjqSHu0OOwIDh2brhw86WP4kz3HysIUFWRGS8O8zBR53axXBcB5jz/+uKqrq1VWVnbS48La2lr9/Oc/lyR97nOfU0lJiVMRx5UdCSuy401FtqyTwkOSyy3XgkuVu/o2tXf3OB0PAAAksDEtCAEAo2MahrLTkpWdlqz5JVnDx/uHwjrS3qcjnX060hF9OdrRp96BkKqOdKnqyPujDQ1Jk/xJys+MloXHS8Pc9BR53OwcD2B8VFdXa2BgQA888IB+/vOf68CBA5o+fbok6Q9/+IPuvfdemaap//zP/9TXv/51h9OOLdu2ZdXsVXjj81J3myTJLJ0r9yU3yEjPlulNkkRBCAAAnENBCAATQIrXran56Zqanz587Phow6aOPjV19h/7t0/NXQNq7x1Ue++g9tR3DL+/YUjZ/mTlZqYoLyMlWhpmRF+SPIw4BHB+VVVVacGCBZKk+fPnq7KycrggDAaDw7tCB4PB036MuBEOKfzG01Jfj4xJuXIvv0lm8QynUwEAAAyjIASACerE0YZzp7x/PByx1No9oKNd/Wrq7FNTR7+Odvap7diGKK09A9pT13HSx8pM9So3I0Wl+Vnye3WsOEyWP9nDelgAzkowGFReXp4kyefzqb6+fvg227Y/8v4VFRWqqKiQJD300EPDheJE1Xftp2QFu5S6eJUM18kPwd1u94T/+sYT52t0OF+jw/kaHc7X6HC+RofzNTrner4oCAEgzrhdpvKPbWKyUNnDx48Xh02dfTra1a/mzn4d7epXa/eAOoND6gwOqbKx66SPleJ1KScjRTnpycrNSFFOerQ4zE5LltvFdGUAp+fz+dTX1ydJ6u/vl8/nO+X7ne5JiNWrV2v16tXDb7e2tp7/kOMpt0ySNNDR+aGbAoHAxP/6xhHna3Q4X6PD+RodztfocL5Gh/M1OiM9X4WFhac8TkEIAAnixOLwRBHLVntPdMRhMGTq8JE2NXdHC8T+oYhqW3pV29J70n0MQ5qUmqScjGTlpKcokJ6sQFqycjKSlelLkmky6hBIdOXl5aqoqNDy5cu1c+dOrVq1avg2v9+vtrY2GYahlJQU50ICAABAEgUhACQ8l2lERwlmpBx71ilTUnQKYM9ASC1d/WruGlBLd79ajv17fI3D9t5B7W/o+tDHy05LHi4NA+nvv56R6pXJlGUgIUydOlUej0f33XefSktLFQgEtHbtWq1Zs0a33367fvjDH0qS/v7v/97ZoAAAAKAgBACcmmEYSk/xKj3Fq2n5GSfdFo5YausZVEt3dIry8X9buwfU3R9Sc1e/mrv6P/Qx3aahrLRkZaclKXBs/cTstCRlpyVrkj+JactAnLn77rtPenvNmjWSpJKSEj344INORAIAAMApUBACAEbN7TKVlxndCfmDBkOR6GYoxwrDtuOv9wyo5wzloWFImT7vsQLx/eIwyx/9N8XrYsMUAAAAABgDFIQAgPMqyeNSUVaqirJSP3TbQCii9mM7Kbf1DKqtZ0Btx0rEzr4hdQSjLwebuj9032SPS1lpScryJynLHy0OJ/mPv50kr8c1Hl8eAAAAAMQdCkIAwLhJ9rhUmJWqwlOUh+GIpY7g4HBx2N4zqPbeaJHY3juogVBEje19amzvO+XHTk12D5eFk/xJmpT6foE4KZUCEQAAAABOh4IQABAT3C5TOekpykn/8LRl27bVNxh+f3OUngG19Q6qvWdQHcFBdfQOKjgQVnAgrLrW4Ck/vi/Jfaw09A6Xh5mpx8tEr3xJbqYwAwAAAEhIFIQAgJhnGIZSkz1KTfZocsD/odst21ZPX0jtwWh52BkcUntvtDjsCA6qs3dQfYNh9Q2G1dB+6gLR4zY1KdWrDF+0RMxMTVKmz6tMf/TfjFSvvG5GIQIAAACIPxSEAIAJzzQMZaRGS7yy3LQP3W7Ztnr7Q8OjDTuDQ++Xh8EhdQYH1T8UUXPXgJq7Bk77eXxJbmWmepXhO1YgDr8eLRYzUr3ysBMzAAAAgAmGghAAEPdMw1C6z6t0n1clOR8uECVpYCisjmNlYecp/u3qGxoehXi6dRAlKTXJrfTh0jD6OTNOfEn1KtnDjswAAAAAYgcFIQAAkpK9bhV43SqY5Dvl7ZZtq3cgpK7g0LHC8FhxGBxSZ1+0SOzuCyk4GFZwMKwjHacvET1uc7gwTPd5lZ7ief91n1cZKR6l+bxj9aUCAAAAwEkoCAEAGAHTMJSe4lV6ileTA6d+nxNLxK6+off/7RtSd9/7rw+FLbV2D6i1+/TTmSUpNdmjtOToiMS0YyViWopX6T7PsSzRIpFpzQAAAADOBQUhAADnyUkl4mnex7ZtDYQi6u4LnVQcdvcNqbt/aPh4T/+QggMhBQdCaursP+PnTfG6osXhscIwLdmjdJ9HaSnRYjEt2aO0FA87NQMAAAA4JQpCAADGkWEYSvG6leJ1Ky8z5bTvZ9m2knzpOtzQFC0P+0LHCsQh9fRHX+/pD6mnP6T+oYj6h/rV3HXmItFlGvIfKwujL97h8tB/rEj0H7uNdRIBAACAxEFBCABADIruzJykoqxUFWWlnvb9LNtW/2BY3f0h9fQPRf/te788PLFIHAhFhqc5fxS3acif4hkuFE/894Ov+5LcMk3KRAAAAGCioiAEAGACMw1DqckepSZ7TrvBynGhsKWegfcLw/dfhtQ78P7bwYGQBsPWsV2cP7pMNAwpNckjf7JbqcnvF4epye7h10+8LdnrksnoRAAAACBmUBACAJAgPG5TWf5kZfmTP/J9h0KRaGl4rDjsHQip99i/w28PhNU7EFLfYPjY2yFJZ57mLB0vNY8VhknHi8Pov6knvp0ULRl9SR65GKEIAAAAjBkKQgAA8CFej0tZHpey0j66TIxYloKD4WMFYljBgdBwYXi8SDx+LDgQ1kAoMjxacaRSvK73C8Th4vD9UvHE11OToms8Mu0ZAAAAGBkKQgAAcE5cpjm8e/NIhCLWsR2awwoORv/tPeHt44Xi8dv6BsPHNmKJqHWEmQxJKcfKQt8JL6lJnhNe//BtHrd51ucBAAAAmKgoCAEAwLjyuExlpiYpMzVpRO9vWbb6h8IKDh4vDqOl4fHXj09z7ht8/336hyLDx0abzZfk1p2XTtO0/Iyz+fIAAACACYeCEAAAxDTTfH8jFmWkjOg+kWOlYt8HSsUTi8S+wdAJr0dfQhFLXX1DMk1GEgIAACBxUBACAIC44zKN4R2UR1oq2ratobClvsGw/CmeMU4IAAAAxA4KQgAAAEmGYSjJ41KSx+V0FAAAAGBcMX8GAAAAAAAASGAUhAAAAAAAAEACoyAEAAAAAAAAEhgFIQAAAAAAAJDAKAgBAAAAAACABEZBCAAAAAAAACQwCkIAAAAAAAAggVEQAgAAAAAAAAmMghAAAAAAAABIYBSEAAAAAAAAQAKjIAQAAAAAAAASGAUhAAAAAAAAkMAoCAEAAAAAAIAERkEIAAAAAAAAJDAKQgAAAAAAACCBURACAAAAAAAACYyCEAAAAAAAAEhgFIQAAAAAAABAAqMgBAAAAAAAABIYBSEAAAAAAACQwCgIAQAAAAAAgARGQQgAAAAAAAAkMApCAAAAAAAAIIFREAIAAAAAAAAJjIIQAAAAAAAASGAUhAAAAAAAAEACoyAEAAAAAAAAEhgFIQAAAAAAAJDAKAgBAAAAAACABGbYtm07HQIAAAAAAACAMxhBOI6+8Y1vOB0Bx3AtYgvXI3ZwLWIL1yN2cC0wlvj+Gh3O1+hwvkaH8zU6nK/R4XyNDudrdM71fFEQAgAAAAAAAAmMghAAAAAAAABIYBSE42j16tVOR8AxXIvYwvWIHVyL2ML1iB1cC4wlvr9Gh/M1Opyv0eF8jQ7na3Q4X6PD+Rqdcz1fbFICAAAAAAAAJDBGEAIAAAAAAAAJjIIQAAAAAAAASGBupwMkiscff1zV1dUqKyvT3Xff7XScuFZVVaVf/epXMgxD06ZN09/+7d/qmWee0bvvvqucnBx98YtflNvtHvExnLvnnntOmzZt0oMPPnjKn4WRHsO5e+211/Taa6/Jsix95Stf0TPPPMP1cMDg4KAefvhhDQ4Oyufz6atf/ap++9vfci3GWXt7u773ve+pvr5ev/71r+Vyuc7pdxTXBmeD75uRO9XPLE7vVI+JcXq1tbV69NFHZZqm8vPzdc8998gwDKdjxbQTH+PjzJqbm/V//+//VVFRkdxut/7f//t/TkeKeR/8uyUrK8vpSDFr27Zt+tOf/iRJamxs1Oc+9zktW7Zs1B+HEYTjoLq6WgMDA3rggQcUDod14MABpyPFtZycHN1333168MEH1d3drT179mj37t168MEHNWXKFL377rvq6uoa0TGcu1AopMOHD0s69c/CSI/h3LW3t2vPnj267777dP/996uzs5Pr4ZBt27ZpxowZuv/++zV9+nT96U9/4lo4wO/365vf/KZmzJgh6dx+R3FtcDb4vhmdD/7M4sw++Ji4trbW6UgxrbCwUN/+9rf1wAMPSJIOHjzocKLYduJjfIzM/Pnzdf/991MOjsAH/26hHDyzCy64QPfff7/uv/9+BQIBLViw4Kw+DgXhOKiqqhq+QPPnz1dlZaXDieJbZmamvF6vJMnlcqmurk5z5syRJC1YsECVlZU6ePDgiI7h3K1bt06rVq2SdOqfhZEew7nbtm2bLMvSAw88oMcee0yVlZVcD4fk5eVpYGBAkhQMBmUYBtfCAV6vV36/f/jtc/kdxbXB2eD7ZnQ++DOLM/vgY2LT5E+/Mzlx5pDb7VYgEHAwTew78TE+Rmb37t2677779NxzzzkdJeZ98O8Wy7KcjjQhHD16VBkZGUpOTj6r+/O/xDgIBoPy+XySJJ/Pp76+PocTJYaamhp1d3crNTVVKSkpkqLnPxgMqq+vb0THcG7C4bB2796tefPmSTr1z8JIj+HcdXV1KRwO67777pPX61VfXx/XwyEFBQWqqqrS1772NVVXV8s0Ta5FDDiX31FcG5wNvm8wHo4/Ji4uLnY6Ssx777339E//9E/q6uqijD6DDz7Gx0ebNGmSHnnkEf3Lv/yLdu7cqZqaGqcjxbQP/t3C7L6R2bRp01lNLT6OgnAcnPiAr7+/f/iBIMZOb2+vHnvsMd1zzz3y+Xzq7++XJPX19Sk1NXXEx3BuXn/9da1cuXL47VP9LIz0GM6dz+cbHiV7/AEd18MZr732mpYsWaKHH35YixYtUiQS4VrEgHP5HcW1wdng+wZj7cTHxPhoF154ob7//e8rOztbW7ZscTpOzPrgY3x8NI/Ho+TkZLlcLi1ZskR1dXVOR4ppH/y7paGhweFEE8PmzZt14YUXnvX9KQjHQXl5uXbt2iVJ2rlzp8rLyx1OFN8ikYh+9KMf6TOf+YwyMzM1bdo07dmzR1L0/M+YMWPEx3BuGhsb9fLLL+s73/mO6uvr1dPT86GfhVP9fPAzMzZmzpw5/Gzl8TVjuB7OsG17eGRCenq6JK5FLBjpOefa4Hzh+wZj6YOPiXFmoVBo+PWUlJTh6dn4sA8+xn/hhRecjhTzjg9EkaR9+/YpLy/PwTSx74N/t+Tm5jqcKPZ1dnbK7XYrLS3trD8GW7SOg6lTp8rj8ei+++5TaWmppk+f7nSkuLZx40YdOHBAv/nNbyRJn/rUpzR79mx985vfVCAQ0I033ii32z2iYzg3d9111/Dr3/zmN/XJT35Sv/zlLz/0s3Cqnw9+Zs6/0tJSeb1e3X///UpLS9O9996r//qv/+J6OGDlypX64Q9/qNdff10ul0tf/epX9eSTT3Itxlk4HNZ3v/td1dTU6Dvf+Y7uvPPOEZ9zrg3OBx4jjs6pfmZ5Qvf0TvWYmBL69LZt2za8NlxBQcFZL/KfCD74GP/66693MM3EsHfvXv3hD3+Qx+PRrFmz+N31ET74d8vHPvYxpyPFvHfffVdLly49p49h2LZtn6c8AAAAAAAAACYYphgDAAAAAAAACYyCEAAAAAAAAEhgFIQAAAAAAABAAqMgBAAAAAAAABIYBSEAAAAAAACQwCgIAcS15uZm3X777XrooYe0ZcsWPfHEE2pubj7vn6e+vl5PPPGEdu/ePXzsJz/5iW6//XYdPHjwvH8+AAAAAADOF7fTAQBgLKWnp+vee+9VVlaWNmzYoBdffFFz585Vbm7uqD5OJBKRy+U67e319fV66qmnJElz586VJF1zzTW64IILlJeXd/ZfAAAAAAAAY8ywbdt2OgQAjJXm5mZ96UtfUlJSkgYHB0+67YknnlBlZaV+9atfqba2VllZWfrkJz+plStXDt+vvLxcSUlJqq2t1fe//319+9vf1pEjRyRJZWVl+vznP6+kpCR96UtfOulj/8u//IvWr1+v1157Td/97nc1bdo0VVRU6JlnnlFHR4eKi4v1N3/zN5o1a5bWr1+vn/70p1q+fLkaGhrU2tqqT37yk7rhhhvU2NioH//4x6qpqZHX69XkyZP1wAMPjNv5AwAAwKk9/PDDysjI0OHDh9XW1qavfOUrevnll3XgwAHNmjVL99xzj9MRAWDEmGIMICHMmTNHCxculCTdeuutuvfee9Xb26uHHnpIfX19WrNmjXJycvSjH/1Ihw8fHr5fZWWlysrKdMcdd8gwDC1btkx33323brnlFtXU1Ojxxx9Xenq6brjhBknSRRddpHvvvVfFxcUnff5du3bp0UcfVXp6uj772c+qtbVV3/ve99TT0zP8Prt379ZVV10lSfrtb3+rcDisF198UQcPHtRdd92lO++8U4FAYIzPFAAAAEaitrZWeXl5evDBB7V69Wr9x3/8h+666y49/PDD2rJli0KhkNMRAWDEmGIMICEYhqH8/Hxt375d8+bN09y5c7Vlyxb19vaqt7dXv//974ffd9euXVq2bJmk6CjBu+66S5LU3t6u7du3q7KyUscHX9fW1io5OVmzZs3SX/7yF02ePFkrVqz40OffsmWLJOn222/XggUL1NraqqefflpVVVXD73PFFVfouuuu0+bNm7V9+3Z1dnaqoKBAtm1r69atmjZt2nARCQAAAOcMDQ0pGAwOPzYzDENXXnmlJk2aJEkyTVNuN39uA5g4+I0FIGEYhnHK45dddpkuu+yy4bdPXJ/w+IM8SXrhhRe0f/9+3XjjjVq0aJH+4z/+Q/39/ecti9/vl6ThtQ4ty9J1112noqIi7dmzR++9957Wrl2rH/zgByosLDyrzwsAAIBzV19fr6lTp8o0o5PyampqdM0110iS2tralJWVddrHngAQi5hiDCBhpKamSpLefvttbdmyReXl5fL7/dq+fbsaGxtVV1enP//5z2pvbz/jxwkGg9qzZ4/a2tqGjx0v9/bt26e33npLQ0NDJ91n8eLFkqQnn3xSL7/8statW6fU1FTNmDHjjJ/rpZdeUmVlpfLz85WXlyfbttXZ2TnaLx0AAADnUW1trUpKSobfrqmp0ZQpUz70OgBMFBSEABLGpZdeqqKiIr300kv65S9/Kb/fr2984xvKz8/Xb3/7W61du1Zer1c5OTmnvP/111+vadOmacOGDWpvb9fkyZOHb5s1a5bmz5+vvXv36pFHHjlpbUFJmjdvnr7whS+oq6tLv/71r5Wdna3/83/+j9LS0s6Y2ePxaP369frZz36mvXv36tprr9WsWbPO/WQAAADgrNXW1qq0tFRSdLrx0NDQ8BPGNTU1J5WHADARsIsxAAAAAAAAkMAYQQgAAAAAAAAkMApCAAAAAAAAIIFREAIAAAAAAAAJjIIQAAAAAAAASGAUhAAAAAAAAEACoyAEAAAAAAAAEhgFIQAAAAAAAJDA/n9YvS2uqFeD/QAAAABJRU5ErkJggg==",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"high, step = 100*n, n\n",
"plot_all(cost_history, m, q, high=high, step=step)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Mini-batch gradient descent\n",
"\n",
"Questo approccio si pone in posizione intermedia rispetto ai due precedenti, generalizzando l'impostazione di SGD di considerare un solo elemento per iterazione a considerare sottoinsiemi diversi del dataset. L'algoritmo opera quindi partizionando, all'inizio di ogni epoca, il dataset in $\\lceil n/s\\rceil$ sottoinsiemi (*mini-batch*) di dimensione prefissata $s$, ed effettuando poi $\\lceil n/s\\rceil$ iterazioni all'interno di ognuna delle quali l'aggiornamento di $\\theta$ viene effettuato valutando il gradiente sugli $s$ elementi del mini-batch attuale.\n",
"\n",
"La discesa del gradiente con mini-batch è l'algoritmo tipicamente utilizzato per l'addestramento di reti neurali, in particolare in presenza di reti *deep*.\n",
"\n",
"Se indichiamo con $X_i\\subset X$ il mini-batch attualmente considerato, l'aggiornamento a ogni iterazione è il seguente\n",
"$$\n",
"\\theta^{(k+1)}=\\theta^{(k)}-\\eta J'(\\theta^{(k)};\\mathbf{x})=\\theta^{(k)}-\\frac{\\eta}{s}\\sum_{\\mathbf{x}\\in X_i}J'(\\theta^{(k)};\\mathbf{x})\n",
"$$\n",
"o anche\n",
"$$\n",
"\\theta_j^{(k+1)}=\\theta_j^{(k)}-\\frac{\\eta}{s}\\sum_{\\mathbf{x}\\in X_i}\\frac{\\partial J(\\theta;\\mathbf{x})}{\\partial\\theta_j}\\LARGE\\vert_{\\small\\theta=\\theta^{(k)}}\n",
"$$\n",
"In questo modo, la varianza degli aggiornamenti dei coefficienti viene diminuita. Inoltre, è possibile fare uso, in pratica, di implementazioni molto efficienti del calcolo del gradiente rispetto a un mini-batch disponibili nelle più recenti librerie per il *deep learning*. La dimensione dei mini-batch varia tra $50$ e $256$.\n",
"\n",
"```python\n",
"for i in range(n_epochs):\n",
" for batch in get_batches(dataset, batch_size):\n",
" g = 0\n",
" for x in batch:\n",
" g = g+evaluate_gradient(loss_function, theta, batch)\n",
" theta = theta-eta*g\n",
"```\n",
"Ne risulta un andamento oscillante sia della funzione di costo che dei valori stimati dei coefficienti. Chiaramente, l'oscillazione sarà tanto più marcata quanto minore è la dimensione dei mini-batch, e quindi quanto più si tende a SGD.\n",
"\n",
"Gli aggiornamenti nel caso della logistic regression derivano immediatamente da quanto sopra \n",
"\n",
"\n",
"\\begin{align*} \n",
"\\theta_j^{(k+1)}&=\\theta_j^{(k)}+\\frac{\\eta}{s}\\sum_{\\mathbf{x}\\in X_i}(t-f(\\mathbf{x};\\theta^{(k)}))x_{ij}\\hspace{1cm}j=1,\\ldots,d\\\\ \n",
"\\theta_0^{(k+1)}&=\\theta_0^{(k)}+\\frac{\\eta}{s}\\sum_{\\mathbf{x}\\in X_i}(t-f(\\mathbf{x};\\theta^{(k)})) \n",
"\\end{align*}\n"
]
},
{
"cell_type": "code",
"execution_count": 122,
"metadata": {},
"outputs": [],
"source": [
"def mb_gd(X, t, eta = 0.01, epochs = 1000, minibatch_size = 5):\n",
" mb = int(np.ceil(float(n)/minibatch_size))\n",
" theta = np.zeros(nfeatures+1).reshape(-1,1)\n",
" theta_history = []\n",
" cost_history = []\n",
"\n",
" for j in range(epochs):\n",
" for k in range(mb-1):\n",
" delta = - eta * gradient(theta,X[k*minibatch_size:(k+1)*minibatch_size,:],t[k*minibatch_size:(k+1)*minibatch_size])\n",
" theta = theta + delta\n",
" theta_history.append(theta)\n",
" cost_history.append(cost(theta, X, t))\n",
" theta_history = np.array(theta_history).reshape(-1,3)\n",
" cost_history = np.array(cost_history).reshape(-1,1)\n",
" m = -theta_history[:,1]/theta_history[:,2]\n",
" q = -theta_history[:,0]/theta_history[:,2]\n",
" return cost_history, m, q, minibatch_size"
]
},
{
"cell_type": "code",
"execution_count": 123,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"tempo di esecuzione: 6.574 secondi\n",
"190000 passi\n",
"950000 gradienti calcolati\n"
]
}
],
"source": [
"start_time = time.time()\n",
"cost_history, m, q, mbs = mb_gd(X, t, eta = 0.01, epochs = 10000, minibatch_size = 5)\n",
"print(f\"tempo di esecuzione: {time.time()-start_time: 4.3f} secondi\")\n",
"print(f\"{len(m)} passi\")\n",
"print(f\"{len(m)*mbs} gradienti calcolati\")"
]
},
{
"cell_type": "code",
"execution_count": 124,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABQgAAAGoCAYAAAAKMwiTAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAABuRElEQVR4nO3deXyU5b3///d9z5KVPRAIWwgQUQQEFRU30NS1Lo27dSmt1WNPW097ao89VmpRj/Tnqa3f054etVVqq1ZUrPsWUVxxYwchCZEl7EkgkHXmXn5/DEwYEzDAzNyTzOv5ePhw5r7vua7P3LkzJO9c130Zruu6AgAAAAAAAJCWTK8LAAAAAAAAAOAdAkIAAAAAAAAgjREQAgAAAAAAAGmMgBAAAAAAAABIYwSEAAAAAAAAQBojIAQAAAAAAADSmN/rAjpr06ZNXpdw2PLy8lRTU+N1GUgBXAvYi2sBEtcB2iT6WigoKEhY24nWlX4W5Hs6FucjFucjFucjFucjFuejDeciFucj1sGcj/39PMgIQgAAAAAAACCNERACAAAAAAAAaYyAEAAAAAAAAEhjBIQAAAAAAABAGiMgBAAAAAAAANIYASEAAAAAAACQxggIAQAAAAAAgDRGQAgAAAAAAACkMQJCAAAAAAAAII0REAIAAAAAAABpjIAQAAAAAAAASGMEhAAAAAAAAEAaIyAEAAAAAAAA0hgBIQAAAAAAAJDGCAgBAAAAAACANEZACAAAAAAAAKQxAkIAAAAAAAAgjREQAgAAAAAAAGmMgBAAAAAAAABIYwSEAAAAAAAAQBojIAQAAAAAAADSGAEhAAAAAAAAkMb8XhcAAACA7qmurk6/+c1vVF1drccee0w+ny+6b/369Xr44YclSTfccIOGDx/uVZkAAABpjxGEAAAASIjc3FzdcccdGj16dLt9Tz31lG655Rb95Cc/0VNPPeVBdQAAANiLEYQAAABIiGAwqGAw2OG+xsZG5eXlRR9/VVlZmcrKyiRJs2bNih7bFfj9/i5Vb6JxPmJxPmJxPmJxPmJxPtpwLmJxPmLF43wQEAIAACDpXNc94P6SkhKVlJREn9fU1CS6pLjJy8vrUvUmGucjFucjFucjFucjFuejDeciFucj1sGcj4KCgg63JzQgnD17tqqqqjRixAhNnz49ur2hoUEPPfSQdu/erXHjxqm0tDSRZQAAACCFGYbhdQkAAABpLWEBYVVVlVpaWjRz5kw9/PDDqqys1KhRoyRJTz/9tK644goNHjw4Ud0DAAAgheXm5qq2tlaGYSgrK8vrcgAAANJawgLCiooKjR8/XpI0btw4lZeXRwPCDRs26LnnnlNtba2uuuoqFRcXJ6oMAAAAeMSyLN17771at26d7rnnHl166aVatWqVSktLdfnll+v3v/+9JOl73/uet4UCAACkuYQFhI2NjcrPz5ckZWdnq7q6Orpv9erV+s1vfqPc3Fz99re/1V133dXu9V35xtRftbmuQQ+9skiXnXaUjhrWdd8H4ocbqmIvrgVIXAdo092uBb/frzvuuCNm21FHHSVJGj58eIc/AwIAACD5EhYQZmdnq6mpSZLU3Nys7Ozs6L6CggINGTJEkmSaZoev78o3pv6qB19ZrnXbG3Tf0x/pvutP9LocpABuqIq9uBYgcR2gTaKvhf3dlBoAAADpreN0Lg6Ki4u1fPlySdKyZctiphEPGjRIO3bsUEtLi2zbTlQJKSNsO16XAAAAAAAAAHQoYSMIi4qKFAgENGPGDBUWFiovL09z586N3nPmgQceUCgU0qWXXpqoElKGIVbmAwAAAAAAQGpKWEAoSdOnT495XlpaKkkaMmSI7rzzzkR2nVKOHNJbG+saNXxAL69LAQAAAAAAAGIkbIox2vTtkSFJGtK/h8eVAAAAAAAAALEICJPAMCJTjF3X9bgSAAAAAAAAIBYBYRLsvQOhQz4IAAAAAACAFENAmASMIAQAAAAAAECqIiBMgugaxuSDAAAAAAAASDEEhEmwZwChHEYQAgAAAAAAIMUQECZBdIqxx3UAAAAAAAAAX0VAmAR7pxg3tYQ9rQMAAAAAAAD4KgLCJKjcskuStHJ9jceVAAAAAAAAALEICJNgaL8cr0sAAAAAAAAAOkRAmAQ5mQFJ0oSiAR5XAgAAAAAAAMQiIEyC6CrGDsuUAAAAAAAAILUQECZBY6slSVq2drvHlQAAAAAAAACxCAiTwGXkIAAAAAAAAFIUAWES9MnNkCQdMaSvx5UAAAAAAAAAsQgIk8DccxNCBhICAAAAAAAg1RAQJoFhRgJC1yUhBAAAAAAAQGrxe11AOtiziLEcAkIAAAAAABBnrmNLVlhqbZLb2iLZlmSFJMOQTJ/k88vIyJIysiR/hmSaMgzj6xtG2iAgTILoFGPmGAMAAAAAgIPghlvVuqFCVvkyORvK5W6sTEg/Rq88+SZNk1k4VkYwMyF9IHURECaBuWciNyMIAQAAAABAR1zXkVuzWc66L2Sv/lRqqI/uq0lG//U1st5+WtLTMdv9p35L5pjjZJi+JFQBrxAQJoGhvfcg9LgQAAAAAADgOdd1pcZ62V+ukLPiI7n1yYgAD4313nPSe89Fnwe+9a8yBwz1sCIkAgFhEuyd1s8IQgAAAAAA0pNbXyO7arnsT1/v0iOIws/9Mfo4cOFNMgeN8LAaxAsBYRLsvQehyz0IAQAAAABIC264Vc6mKtkLXpW7c5vX5SRE+IUHo4+D37tLhj/gYTU4HASESWCaexYp6cJ/IQAAAAAAAAfm7qqVve4L2R++5HUpSRf6yx2SpMBF/yJzYKG3xeCgERAmwd6FwwkIAQAAAADoXpwdW+VULpG9cJ7XpaSE8PP/J0nyn36JfGOO97gadBYBYRIYBouUAAAAAADQXTg7t8tZu1L2x696XUrKsuY/K2v+s/J/49vyFY3zuhx8DQLCJDDNyP+31zd5WwgAAAAAADgkbjgkp3KxrHfnel1Kl2K9+bgsScFv/0JGbi+vy8F+EBAmQWOL5XUJAAAAAADgILmuG5k+vPQ9uTUbvS6nSws9fq8kKeOmWR5Xgo4QECZBc4iAEAAAAACArsINtcj64AU55Qu9LqXbaX3wNvkmTpN/8tlel4J9EBAmQU4Gy3wDAAAAAJDK3FCrnOpyWR+8IDXt9rqcbs1e9LbsRW8reOO90XUb4C0CwiTo2yPD6xIAAAAAAEAH3F21sj5/i9GCHgg99Av5p10uX/Ekr0tJewSESbA3C88M+DytAwAAAAAARDib1ij85hNSS6PXpaQ16+05st6ew70JPUZAmAR7h8s6rseFAAAAAACQxlzXlbPyY1nv/9PrUvAVrQ/expRjDxEQJoG55+J2RUIIAAAAAECyuVZY1ocvyvniE69LwQGEHvqFApf9m8y+A70uJe0QECbB3vA7bDneFgIAAAAAQBpxG3cp/Npf5dZs9LoUdFL46d/LHD1RgTOu8LqUtEJACAAAAAAAuhVn2waFX/6LFGrxuhQcAqdikVorFnFfwiQiIEwC02ybP287rnwm8+kBAAAAAIg3u2qZrLeflqyQ16UgDlofvI2QMElMrwtIB+Y+N9gMWbaHlQAAAAAA0L24ji171acKPfdHWW8+TjjYzbQ+eJvXJaQFAsIkc1jKGAAAAACAw+ZaYTk1GxV64jey5j8rd9sGr0tCghASJh5TjJOM6cUAAAAAABweZ+t6hf/5v16XgSRiunFiERAmSWbAp5awLcYPAgAAAABwaOzVn8t652mvy4gLc+gRMgqKZPYbJOX2lpGVIwUyZfh87Y7Ny8vT9q1bpJYmuY31cuu2yNlYKadyiQeVe4eQMHEICJNk720ImWIMAAAAAEDnubYlZ/Xnsld9Knd7tdfldIpv3CkyRx8jo98gGWb7wO9QGD6/lNNTRk5PacBQ+cYcL515VYfHuuGQnNWfyvrgxbj0nUpaH7xNuv3PXpfR7RAQJsnehUqIBwEAAAAA6By3oV6huf8jNTd4XUqHfONOke/oKVKPPjKM1LmlmBEIynf0yfIdfXJ0m+u6cjdWKvzyXzysLD423nMDIwnjjIAwSfZ+UDguESEAAAAAAAfibF6rjSm2MIU5coL8J5wjo0cfr0s5JIZhyBgyOiZYc7ZtUPi5P3pY1aFrffh2ZXz/Hq/L6DYICJNk79ok5IMAAAAAALTnuq7c6grZX66Q88XHXpcj3/FnyTfhtMjU3m7KHDA0Ghi6tqXQn3/pcUUHwbFlVy6Rb9QEryvpFrrvVZ5i9o4gdEkIAQAAAACI4YZDsub9Q87alZ7VYBaNl3/aZTL8Ac9q8JLh8+8TFtoK/fl2jyv6etZbT8occXSHC7vg4BAQJkl0kRICQgAAAAAAJEnu7jqFy/4hd9t6T/oPXHSzzIHDPek7lRk+X1tYuKtWoSfv87ii/Qv9+XbuRxgHBIRJsrMxJElqbLHUN9fjYgAAAAAA8Ji9frWsVx9Ner/B78yQkZGd9H67KqNnP2XcNEuu6yr00C+8LqdDrQ/eRkh4mAgIk2zrzmYNzSMhBAAA3d/s2bNVVVWlESNGaPr06dHtH330kV544QUZhqFvfetbOv744z2sEgCQTK7ryF40X/anrye13+AN9zAN9TAZhhEN4awFr8he8q7HFcUiJDw8BIRJVtCXv1IAAIDur6qqSi0tLZo5c6YefvhhVVZWatSoUZKkl19+WXfeeacMw9A999xDQAgAacB1XamlUeE3/i53y9qk9BmcfqeMYGZS+ko3/hPPk//E82SXL5T19hyvy4myyxfKVzzJ6zK6JALCJCnom61NdU1yuAUhAABIAxUVFRo/frwkady4cSovL48GhPn5+WptbZUkZWVleVYjACA5nB3bFJ5zf1L68p9ykXxjT0pKX5B8xZPkK54ke/kHsj540etyZL09h4DwEBEQJonJKsYAACCNNDY2Kj8/X5KUnZ2t6urq6L7Jkyfr5z//uVzX1Q9+8IMOX19WVqaysjJJ0qxZs5SXl5f4ouPE7/d3qXoTjfMRi/MRi/MRq7udD9cKq7l8sXY892DC+yr4jz9169WHU/7amHqRNPUibXvkboU3r/W0lNYHb9Pg2//saQ3JFo/rg4AwSVjFGAAApJPs7Gw1NTVJkpqbm5Wd3XablWeeeUb33x8ZSXLvvfdqwoQJ7V5fUlKikpKS6POampoEVxw/eXl5XareRON8xOJ8xOJ8xOou58N1bNkfvyZ76XsJ7cd/ysXyjT1RklS7sz6hfXmtq1wb5oX/ogxFQjovbbznhrS6H+HBXB8FBQUdbjfjWRD2b+8IQqYYAwCAdFBcXKzly5dLkpYtW6bi4uLovkAgoIyMDGVmZsqyLK9KBAAkgNvcoPAzDyQ0HAxeeasybpoVDQeRejJumqXg9+7ytIbWJ+/ztP+uhhGEScIUYwAAkE6KiooUCAQ0Y8YMFRYWKi8vT3PnzlVpaanOOuss3XHHHZIUM0oQANB1OdurFZ77h4T2EfzuTBmBYEL7QPwY/oAybpql8Lyn5FQsSn4Bu2rlWuFuPfU8nhIaEM6ePVtVVVUaMWKEpk+fHt3+xz/+URs3blQwGFRJSYlOOeWURJaREvZOMSYgBAAA6WLfn/8kqbS0VJI0depUTZ061YOKAACJYK/6VNb8ZxPStpE3WIFv/asMkwmQXVXgjCukM67wZNpx6C93pNVU48ORsICwqqpKLS0tmjlzph5++GFVVlZGV66TpB//+McaOHBgorpPOQZTjAEAAAAA3YRrW7I/fUP2kncT0r5v3MkaeOH0LnHfPXROxk2zZH36huyF85Lab+uDtxESdkLCIviKigqNHz9ekjRu3DiVl5dH9xmGoT/84Q+aNWuWtm/fnqgSUkr0HoQkhAAAAACALsxtqFfoz79MSDjoP/ViZdw0S/4pF8S9bXjPf/xZnoR1Xi+a0hUkbARhY2Oj8vPzJUVWsauuro7uu+6665Sbm6tVq1bpscce07//+7+3e31ZWZnKysokSbNmzUrt5bw7oWJzZEWl7Y22Tu7i7wWHL+WXqEfScC1A4jpAG64FAEAqc3Zsk7tlrax358a9bd+J58k/4bS4t4vUlHHTrKSHdq7rRmd3or2EBYTZ2dlqamqSJDU3Nys7Ozu6Lzc3V5I0ZswYPf744x2+vqSkJOam1d1lWPHrn1XplOJ+XpcBj3WVJeqReFwLkLgO0CbR10JBQUHC2gYAdF+u68peNE/2p2/GvW0jf5gCF9wow8caqukm46ZZcpt2K/S3e5LSX+ihXzDV+AASNsW4uLhYy5cvlyQtW7ZMxcXF0X17g8NNmzYpJycnUSWkpFbL9roEAAAAAAA6xQ2HFPrHffEPBw1DwRvuVvDiHxAOpjEju0dSQzumGu9fwr4Li4qKFAgENGPGDBUWFiovL09z585VaWmp/t//+39qbGyUYRi64YYbElVCSmIRYwAAAABAqnPqaxT+x38npO3gDXcTCiJGMqccu6FWGcGMpPTVlST0O3L69Okxz0tLSyVJt91GYgsAAAAAQCqyV30ma/4zcW83ePXPZfToG/d20T1k3DRL1ievy170dkL7CT36K6YadyBhU4wBAAAAAEDX4bY0qfXB2+IeDvq/cY0ybppFOIiv5Z98toLfuyvh/TDVuD3G9AIAAAAAkMYStVCE/8yr5Bs1Ie7tonsz/IGkTDl2HUeGybi5vTgTAAAAAACkKbt8YdzDQbNonILX30E4iMOS6GnAoYf/M6HtdzUEhAAAAAAApBn7i08i04nfnhPXdoPX3q7AN74tIzMnru0iPSU6JGSqcRumGAMAAAAAkCZcK6zQX+6Ie7vBq26V0bNf3NsFkrnCcTpjBCEAAAAAAN2c2xpZgCTe4aA56hgFv/9fhINIqESOJCR8jGAEIQAAAAAA3Zi9dqWs1x+La5tG/nAFLrhRhs8X13aB/UnkSEK3uUFGVm5C2u4qGEEIAAAAAEA35GxZG7nPYJzDwcB531Xw4psJB5F0iRpJGHrs7oS025UQEAIAAAAA0I24VlitD96m8PP/F9d2/WdeqYybZskcWhzXdoGDkaiQMN2nGhMQAgAAAADQDbiOI2dTVWIWIbn2dvlGHRP3doFDMfj2P3tdQrfDPQgBAAAAAOji7PKFst6eE/d2g1feKqMXC5Ag9STinoStD96W0AVRUhkjCAEAAAAA6KJc21Lrk/fFPRw0hhYr+P17CAeR0tI1zEsEAkIAAAAAALoYNxxS619nKvTnX0q7auPXsD+g4HdnKnjed2WYLEKC1BfvkDBd70VIQAgAAAAAQBfibNug0CMzpJamuLbrP61UGd+7S0YgGNd2gURjJOHhIyAEAAAAAKALcHfXKfz6Ywo/98e4tmuOnqjg9+6S78jJcW0XSKZ4hoTpOIqQRUoAAAAAAEhhrmMr9Ld74j5iUJICl/xYZl5B3NsFvJCIhUvSBSMIAQAAAABIUU59jUIP3x73cNAoKFLwhrsJB9HtxGskYboFjYwgBAAAAAAgxTibqhR+bbYUDsW97eD1d8jIzIl7uwC6LkYQAgAAAACQIlzXVfjtOQq/+FDcw0HzqBMVvPFewkF0e4wiPHiMIAQAAAAAIAXYDfUKPfSL+Ddsmgp+d6YMHxEA0gf3Izw4fDokid80ZDmu12UAAAAAAFKMu3unQk/M0pYEtO2fdpl8xccmoGUg9RESdh5TjJMkGPB5XQIAAAAAIMXYqz5V6In4TIf8quB1vyQcRNrzf+Oaw3p9ugSMjCBMkqDfVFOr11UAAAAAAFKBG25V+J9/klsX/3GDgYv+RebAwri3C3RFvqKjZXldRBdAQJgkLrOLAQAAACDtuVZYob/ckbD2g9+7S4Y/kLD2ga7ocKcau7bV7e/hyRTjJKlviv/S9AAAAACArsPZtiFh4aD/9EuUcdMswkFgP4I3/tchvzb051/GsZLU1L3jTwAAAAAAPOY6juzPy2QvnJeQ9oPf/y8ZJuN/gAMxDL5HDoSzkyTXTyv2ugQAAAAAQBK5rqtw2ZMKPfyfCQkH/SVXR0YNEg4CnZJxU2IWBOoO+BRJkt45GZKkgr7ZHlcCAAAAAEg0t3GXQg/9Qs6aJQlpP/idO+UbOT4hbQNor7uvZkxAmCSmEfl/2HK8LQQAAAAAkFD2l8sV+vuh3+/sQALnTo+MGszITEj7QHfHKMKOcQ/CJGkJ25Kk7btaPK4EAAAAAJAIztb1sj55Te6mqoS0zwrFQHz4Jpwme8m7XpeRUggIk2TzjiavSwAAAAAAJIBrWwld5dQ3/hT5T/pmwtoH0o3/xPPaBYSLG3tr3u5BarD9yvVZOrPHZk3I2elNgR4gIEySgj7cexAAAAAAuhunbovCT/8+Ye0Hb7hbho9f3YG48/kl25IUCQefqBuh3U4wss+StoQzJX2ZNiEh9yBMkn49uT8EAAAAAHQXruvIWvpewsJB88jJkXsNEg4CCZFxw93Rx/N2D2oLB/fY7QT11u5B0efBa29PWm1e4JMmSUwjskpJdganHAAAAAC6svBb/5BTuThh7Qe/fZuM3N4Jax9ArAa746ym0fanzaImjCBMkr0Boeu6HlcCAAAAADgUbmuLWh+8LWHhoK93/8ioQcJBICn2hn+5PqvD/T2GDk1mOZ5iOFuSmGYkIHQcAkIAAAAA6GqcTVUKv/hQwtoPXPYTDSgeq5qamoT1AaC9jJtm6ZwvNmnL3MXa3dga3d4jJ0NnnTLKw8qSi4AwSXx7RhC2Wo7HlQAAAAAAOsu1LdmfvtFuxdN4Ct54r4w9vzMCSL6JRxZIpdIb71eqoSmk3OygzjplVGR7miAgTJJ9P+vDlqOAn9ndAAAAAJCqXNdVeM7v5O7clrA+/CdfJN/RJyWsfQCdN/HIgrQKBL+KgDBJfGZbQhiybAJCAAAAAEhRbtNuhf52T0L7CN5wNysUA0gZfBolyb7DxVvCtnIyAx5WAwAAAADoiL12pazXH0tY+8aAYQp+6wcJax8ADgUBoQdawrbXJQAAAAAA9uGGWmV99KKcVZ8lrI/g1T+X0aNvwtoHgENFQOiBlhABIQAAAACkAtd1FHr011K49esPPlRZucq47peJax8ADhMBoQdaQpbXJQAAAABA2nMb6xX6+70J7cN3bIn8x5UktA8AOFwEhB5gijEAAAAAeMuuXCLrrScT2kfwO7+SkZGV0D4AIB4ICD3AFGMAAAAA8Ibb2izr/eflVC5OXCfZPZVx7X8mrn0AiDMCQg8wghAAAAAAkst1HYXn/lFuzcaE9hO48mcye+UltA8AiDcCQg+0hLkHIQAA6P5mz56tqqoqjRgxQtOnT49ub2ho0EMPPaTdu3dr3LhxKi0t9bBKAOkgGfcalKTgjffKMIyE9wMA8UZA6AGmGAMAgO6uqqpKLS0tmjlzph5++GFVVlZq1KhRkqSnn35aV1xxhQYPHuxxlQDSgb1mqayyJxLahzlqggJnXpXQPgAgkQgIPbCxrtHrEgAAABKqoqJC48ePlySNGzdO5eXl0YBww4YNeu6551RbW6urrrpKxcXFXpYKoJtyW5tlffCCnIpFCe0ncOG/yBxUmNA+ACDRCAg9sKGGgBAAAHRvjY2Nys/PlyRlZ2eruro6um/16tX6zW9+o9zcXP32t7/VXXfd1e71ZWVlKisrkyTNmjVLeXld535efr+/S9WbaJyPWJyPWIk6H82rF6n+jSfl7KqLe9v7KvjFQzJMM27tcX3E4ny04VzE4nzEisf5ICAEAABA3GVnZ6upqUmS1NzcrOzs7Oi+goICDRkyRJJk7ucX65KSEpWUlESf19TUJLDa+MrLy+tS9SYa5yMW5yNWvM+H29yg0GN3x629/fGXXC3fyPGqrYtvAMn1EYvz0YZzEYvzEetgzkdBQUGH2+P3pw502rVTR3tdAgAAQEIVFxdr+fLlkqRly5bFTCMeNGiQduzYoZaWFtk292YGEB/2ulVJCQeD350p38jxCe8HAJKJEYRJVNAvV5tqGxS2HK9LAQAASKiioiIFAgHNmDFDhYWFysvL09y5c1VaWqrLL79cDzzwgEKhkC699FKvSwXQxbnhkKwFL8tZ+XFC+zFHTlCghIVIAHRPBIRJtKm2QZL06sINOnZkf4+rAQAASKzp06fHPC8tLZUkDRkyRHfeeacHFQHobpyt62XNe0rurtqE9mMOO4JwEEC3RkDogfqmkNclAAAAAECX5YZaZc37h5z1qyTXTWhfgSv+XWZvBngA6N4Seg/C2bNna8aMGXr00Ufb7QuFQvr+97+vpUuXJrKElJKbFZQknTGu4xtCAgAAAAAOzNm0RqFHfyVn3RcJDQeN3v0VvPG/CAcBpIWEBYRVVVVqaWnRzJkzZVmWKisrY/a/9dZbGjZsWKK6T0mTiwdJknruCQoBAAAAAJ3j2rasj19T+MWHE95XoPSHCl7x7zIM1vUEkB4SNsW4oqJC48dHVnYaN26cysvLNWrUKEmSZVmqqKjQEUcckajuU5JpGpIkJ8FD4AEAAACgO3F2bpf11j/k1mxMeF/BG+6W4eNuXADSS8I+9RobG5Wfny9Jys7OVnV1dXTfO++8o1NPPVUVFRX7fX1ZWZnKysokSbNmzVJeXl6iSk2aXU3rJUkNIXWL94ND5/f7uQYgiWsBEVwH2ItrAQBiua4rZ8UCWR+9KDlOQvvyHVsi/3ElCe0DAFJVwgLC7OxsNTU1SZKam5uVnZ0tSbJtW4sXL9bPfvazAwaEJSUlKilp+3CuqalJVKlJ88nqTZKkeUvW6dxjBnlcDbyUl5fXLa5pHD6uBUhcB2iT6GuhoID7IAPoOtzdOxSe/6zcjZVff/BhMgqKCAcBpLWEBYTFxcUqKyvTlClTtGzZMk2dOlWSVF9fr9raWt1zzz3asmWLFi1apKKiIuXm5iaqFAAAAABAF+G6ruwPX5K9/IOk9Be45Mcy8/gDCoD0lrCAsKioSIFAQDNmzFBhYaHy8vI0d+5clZaW6t5775UkzZkzR2PGjCEcBAAAAADIbWlS+JVH5G6v/vqDD5PRd6ACl/xYhslCJACQ0DuvTp8+PeZ5aWlpzPPLL788kd0DAAAAALoIZ0O5wq88KinxizoGLrpZ5sDhCe8HALoKlmYCAAAAAHjGDYdkLXhFzsoFie8smKngtbfL8AcS3xcAdCEEhAAAAAAAT4Q2Vin83ENy6xO/WJf/rGvlGzE24f0AQFdEQAgAAAAASCrXcWTN+4e2r1malP7MI08gHASAAyAgBAAAAAAkjburTuG3n5K7ZV1S+vOffol8Y45PSl8A0FUREAIAAAAAEs51XTmrP5P14YtSOJSUPoPTfy0jmJGUvgCgKyMgBAAAAAAklNvcIOvduXLWrkxKf4waBICDY3pdQDr5+WUnel0CAAAAACSVvXaFQnN+l7RwMHjdLwkHAeAgMYIwiTbU7PK6BAAAAABICte2ZL3/TzmrPktKf76Tzpdv3CkyDCMp/QFAd0JAmETbdzZ5XQIAAAAAJJyzc7vCT/02af0Fr7xVRq9+SesPALobphgn0ZSjhnhdAgAAAAAkjOs6spd/mNRw0DflAsJBADhMjCBMotysoCSpT07Q40oAAAAAIL7chnqF33la7sbKpPXpP/ta+QrHJq0/AOiuCAiTyGdG7oWxozHkcSUAAAAAEB+u68qpXCzrveekcJJ+18nppeBVt8rw8SstAMQDn6ZJ1Bq2vS4BAAAAAOLGbWmU9d4/5VQtS1qf/nOnyzfsiKT1BwDpgIAwiQJ+bvkIAAAAoHtwtqxV+M3HpabdyemwZz8FL/mRjGBmcvoDgDRCQJhEvbIzoo8d15VpGB5WAwAAAAAHz3VdubWbFS57MmnhoP+sa+QbcXRS+gKAdERAmER+X9sIwoaWsHpmsVgJAAAAgK7Dbdota/6zctavSk6Hub0ULP2RjKzc5PQHAGmKgDCJjH1GDG6vbyYgBAAAANBl2FXLIguRtDQlrc/g1f8hw+BWTQCQaASEHtl3ujEAAAAApCq3tVnWBy/IqViU1H79J19EOAgASUJA6JGWsOV1CQAAAABwQE51hcLvPCM11ie13+B3fiUjIyupfQJAOiMg9EjFpnoN6cd9NAAAAACkHtcKy/74VdnLP0xqv/7TL5FvzPFJ7RMAIHVqvPYVV1yhDz9s+4dh4cKFuuWWWxJWVDoY0Iu/hgEAAABITdZHLyc3HAxmKnj9HYSDAOCRA44grKmp0bZt2yRJ1dXVWrlypSRp8eLF2rp1a+Kr64bye2Vpa32zcrMCXpcCAAAAADGc2s1yt66X88UnSevTP+0ymaMnxSzqCABIrgMGhG+//baeeeYZSdKzzz6rZ599Nrpv8ODBia2sm9pa3yxJqm8KeVwJAAAAAES4tiX787dkL35Hct3kdJrbSwOn/1I7QnZy+gMA7NcBA8JRo0bprLPO0htvvKHx48dr0KBBkqTc3FydcsopSSmwu/rbOxW67/p+XpcBAAAAIM05tZtlvT1Hbu3mpPXpP+VimUedIF/PPlJNTdL6BQB07IAB4cSJEzVx4kSNHDlSY8eOVf/+/SVJjuPINFluHgAAAAC6KtdxZC99V/bHryW1X7PwKPnGnpjUPgEAB9aplG/Dhg16++23VVdXp5tvvlnXXnut5s2bl+jaAAAAAAAJ4NbXKPzCg0kPByXJd8K5Se8TAHBgnQoI33//feXk5OiDDz6QZVkaNGiQ5s6dm+jaAAAAAABxZq/+XKFnHpC7dV1S+zV691fwhntk9u6f1H4BAF/vgFOM92poaFCPHj20ePFinXbaaRo+fLgefPDBRNcGAAAAD/3oRz/S0KFDVVhYqGHDhqmwsFADBw70uiwAh8HdVStr/rOS6yS138AFN8osKEpqnwCAzutUQJiXl6cnn3xSDQ0Nuvnmm7Vz507l5uYmujYAAAB46Pjjj5dlWerdu7eWLl2qP/zhD+rRo4f69u2r4cOH68Ybb/S6RACd5LqO5DiyFr2T1HDQHH6k/CVXy/AHktYnAODgdSog/Pa3v62nn35ao0eP1uTJk/XEE0/ohBNOSHRtAAAA8NDSpUv13//939Hn06ZN0yeffKJzzjlH69Yld2oigEPnbKxUeP6z0u4d8WkwmCmFWr72sMBF/yJzYGF8+gQAJFSnAsLJkyfr2GOP1ebNm7VlyxZdc801rGJ8iIb2y9GG2kb1zOIvaAAAILX16NFDa9euVWFhoSRp9OjReuihh/Ttb39b/fr187Y4AF/LDYdkf/Ka7OUfxq1N86gT5Kz8+MDHFB8r/ykXyQgE49YvACCxOhUQVldX67777tOWLVskSQMHDtTPf/5zDR48OKHFdUcTRuRpQ22jBvfL8boUAACAA7rpppv0hz/8QUOGDFFhYaE2btyoYJBf+IGuwNmyTtY7T8utr4lfo8HMrw0HA+d/T+aQ0fHrEwCQFJ0aBviXv/xFO3bs0Mknn6yTTz5ZO3fu1COPPJLo2rqllz6LTMf5onqnt4UAAAB8jYEDB2rmzJmaOHGidu7cqYEDB+q2227zuiwAB+DalqyPX1P4hf+LbzgoHXBasTn8SAW/cyfhIAB0UZ0aQVhVVaWrr75a55xzjiTptdde05NPPpnQwgAAAOA90zR1wgkncP9poAtwajfJmveU3LqtSe/bHD1RRkZm0vsFAMRHpwLC3NxcLV26VBMnTpQUuWE1qxgDAAAAQGpwQ60Kv/QXqaXRk/7NwrGe9AsAiI9OBYRnnHGG5syZo88//zy67YorrkhYUQAAAACAzrNXLoiEg9k9pKbdh95Qbi+pob7Th/unXirfEccden8AgJTQqYDwtNNOU69evbR06VJJ0oQJEzR+/PiEFtZdjR/eV0vX1XldBgAAAIAuznVsqbVF8gdkL30vsvEwwkGj70C5dVs6d2yvPAUu+ZGMQMYh9wcASB2dWqTkrrvuUk1NjX7605/qpz/9qbZv366777470bV1S2OG9Pa6BAAAAABdnLN1vcJP/16hv/+X7E9ek5obDq/BrFyZw4/s1KGB876r4JU/IxwEgG6kUyMI6+rqNGDAgOjz/v37q7a2NmFFdWemYXhdAgAAAIAuyrUt2Z+VyV78TnSbvfzDw27XN3qS7EVvH/AYs3Cs/NMukxFkMRIA6G46FRDm5+frxRdfVN++feW6rl566SXl5+cnurZuqbigl9clAAAAAOiCnO0bZb0zJ+6rFBu9+8te+u4Bjwmc912ZQ4vj2i8AIHV0KiC86KKL9Mc//lH33ntvdNsPf/jDhBXVnfl9bbO6XdeVwYhCAAAAAAfg2rbsRfMiI/wcJ/7t79y+331m8bHyT/mmjIysuPcLAEgdnV6kJC8vTwsXLpQkTZo0SUcddVRCC+uu9g0IHdeVj4AQAAAAwH64u+sUfuPvcms2JbfjYIb8Z1wpXyfvSwgA6No6FRBK0lFHHUUoGAeBfQLC5pCt3MxOrRMDAAAAIA1Z7z0fCQdzekqNuw69IdMnOXanDw+cf4PMAUMPvT8AQJdCOuWhqq2H8Q88AAAAgG7NqdkkZ8NqyR9IajgoSfJ1eiwJAKAbICD00M6GkNclAAAAJMzs2bM1Y8YMPfroo+32hUIhff/739fSpUs9qAzoGqIrFVvhw2jFkNF/yEG9wn/mlTL7DTqMPgEAXQ0BoYd2NLZ6XQIAAEBCVFVVqaWlRTNnzpRlWaqsrIzZ/9Zbb2nYsGEeVQekJrdxl6yPXpGzfrWc+ho5VcsOu01z+Bi5W9d36lgjf7iCN9wt36hjDrtfAEDXwrhxD/XICnhdAgAAQEJUVFRo/PjxkqRx48apvLxco0aNkiRZlqWKigodccQR+319WVmZysrKJEmzZs1SXl5e4ouOE7/f36XqTTTOR6yOzofrumpevkA7XviLJMle+m5c+so68jg1f/FZp47t/91fKjioMC79Hgyuj1icj1icjzaci1icj1jxOB8EhB4Y1j9X67c3qF+PTK9LAQAASIjGxkbl5+dLkrKzs1VdXR3d98477+jUU09VRUXFfl9fUlKikpKS6POamprEFRtneXl5XareRON8xPrq+XAbd8l67zk5676Iaz9G/vDYcDCYKYVa2h3nG3+KfJPP1S6fT/Lg68T1EYvzEYvz0YZzEYvzEetgzkdBQUGH25li7IH8XlmSpNbwQd4oGAAAoIvIzs5WU1OTJKm5uVnZ2dmSJNu2tXjxYk2cONHL8gDPua4ru3yRQk//Lu7hoCS5W9e1PcnMaX8fw2CmApfeIv9J35Th88W9fwBA18IIQg9kBCL/ALeECAgBAED3VFxcrLKyMk2ZMkXLli3T1KlTJUn19fWqra3VPffcoy1btmjRokUqKipSbm6utwUDSeQ27Y6MGly7MjkdtjTGPPUdf7Z8E04jGAQARBEQeiBzT0DYahEQAgCA7qmoqEiBQEAzZsxQYWGh8vLyNHfuXJWWluree++VJM2ZM0djxowhHERacR1H4RcflrtzmxQISuFQ0vo28gbLP+0ymX0HJq1PAEDXQEDoAUYQAgCAdDB9+vSY56WlpTHPL7/88mSWA6SEltULI+Fgbu/IhiQFhL7J58g34VQZJqMGAQDtERB6IIMRhAAAAEDacV1Xuz98VZJkZGbLrdmUlH4Dl/9EZp/8pPQFAOiaWKTEA9EpxowgBAAAANKGu2mNwlsii4fEJRz0B2QWT5LMr/m1rrX96sUAAOyLgNADjCAEAAAAuj+3YafsLz6R29Iot6Fe4Xlz4tuBFZZTvlBynAMeZvQfHN9+AQDdTkKnGM+ePVtVVVUaMWJEzD1oHn30Ua1du1bhcFjXXXedxowZk8gyUg73IAQAAAC6L9d15az6VNa7cyMb9v7/cPn8km11/vCJ0+SffHZ8+gYAdGsJG0FYVVWllpYWzZw5U5ZlqbKyMrrv2muv1a9//Wv95Cc/0XPPPZeoElLW3inGLWECQgAAAKA7cXfXKfzyX9rCwcPl2zOmwx9sFw6aoyd2/JqsXAWvn0E4CADotISNIKyoqND48eMlSePGjVN5eblGjRoV6dQf6balpUXDhw9PVAkpKzrFmIAQAAAA6BZc15Gz8mNZH7/abmVic/iRctZ9cfCN7jti0Gpr0+jZT76J02RXLm73Ev+535FvWHrN0AIAHL6EBYSNjY3Kz4+slJWdna3q6uqY/ffdd58qKyv1ox/9qMPXl5WVqaysTJI0a9Ys5eXlJarUpPH7/crLy1Mwu1WSFLLdbvG+cPD2XgsA1wIkrgO04VoAuiZ3V63C85+Vu6mqw/37hoP+/oNlbd/YuYY7mE5sjpog+QKy5j8Tu/2IY+WfcqGMYEbnCwcAYI+EBYTZ2dlqamqSJDU3Nys7Oztm/6233qra2lrdf//9uueee9q9vqSkRCUlJdHnNTU1iSo1afLy8lRTU6OwFbmJcEtruFu8Lxy8vdcCwLUAiesAbRJ9LRQUFCSsbSBdueGQQs//n9S0W8rMkVoa939wIKPz4WBHgplyKpfEbsvIUuDs62QOGnHo7QIA0l7C7kFYXFys5cuXS5KWLVum4uLi6L5wOCxJyszMVEZG+v2Fy+8zZBqGLMeVZR94xTEAAAAAqctZ/bnUtFtGv0EyevU78MHh1sPrLNQS89R3zFQFr/lPwkEAwGFL2AjCoqIiBQIBzZgxQ4WFhcrLy9PcuXNVWlqq3/3ud2pqapLjOLr66qsTVULKMgxDGQFTzSFbrWFbfl/CcloAAAAACeI6jqxl70uSjF795VQtPew2fRNOk71mqYyeffc7ZdnoN0j+0y+R2X/IYfcHAICUwIBQkqZPnx7zvLS0VJL085//PJHddgmZAV80IMzJDHhdDgAAAICD5KxbKe2qjTyOQzhoFh4l3wnnyiwcq/Dzf+rgAJ98x54p34TTZfh8h90fAAB7JTQgxP7VN0WmWTeFbPX1uBYAAAAAB89e+l78GuvRV76J02S9+bicL5e3220MGCb/1Etk9smPX58AAOxBQOgRx3UlSW8v26hrpxZ/zdEAAAAAvORsqpK94iM5NZskx5Yadsa1fSM7NzJq0NnPPcqDGTJ6fs09DgEAOEQEhB5buq7O6xIAAAAA7Ifb2ixrwStyVn16yG0YvQfIf9L5cnfVyVy7XKGNa9r3s3X9geuorpBsW/LxKxwAIP5YHQMAAAAAOmCvXanQnN/FhINGQZHMovGxB2bmHLAd/9nXyhx2hIwBQxTeuqHDY8yhR8hfsv8FHAMX/ouMYEbniwcA4CDw5ycAAAAA2Ifb3CDrgxflrFnSfmfjLjn7ri4czJRaGg/YnuEPyN1dp/Brf5WsUOy+nv3kP/VbMvoXyF44r91rfceVyDfpTBmGcUjvBQCAziAgBAAAAIA97LUrZc1/dr+hn1tfE7sh1HLgBrN7SIGMyP0FmxtidvkmnCbfpDNlL/9Q9st/jtln5A1W4Pzvyvia0YkAAMQDASEAAAAAaM/IwbInJNuSUVAkd9+RgocoeOFNCr/1pNwd22K2+046XzJMhf52t2SFY/YFzv+ezCGjD7tvAAA6i4DQI31ygtrRGPr6AwEAAAAkhf3FJ5FwcGix3A3lh92e/7RSKbe33C1r2/e17H2poT5mm++Y0yPTiQPBw+4bAICDwSIlHumRzT/6AAAAQKpwbVv2igWRx5u/POz2zKFHyBxzvAyfX8FL/01GQVHsAfuEg0b/IQpc+mP5TziXcBAA4AlGEHpkxIAeWr+94esPBAAAAJBwzpfLpKZdkSdfmfJ7KPxnXinDMOS6rqyPXup4urI/IN/ks+UbO0WGydgNAIB3CAg9UlzQS/NXbPa6DAAAACBtua1NUiBDhumTveyDuLUbuPBfZGRkydlUpfCrs9utXCxJ5rAj5D/lYhk9+sStXwAADhUBoUcG9MqKPnYcV6ZpeFgNAAAAkF7s5R/I+uBFyTAk1z3o1wcu/oGcretkL31famybLuw79kzJ71fo5UfkVre/j6GZ00Pmid+UOXK8DIPfAQAAqYGA0CO99rkH4epNO3XkEP5yCAAAACSS29Ike+E8ubvr5OxdhOQgw0Gj/xAFvnmDjGCmlJEl+/O32nZmZMmt3azwvtv2YY45XvnnfVt1jS2H+hYAAEgIAkKP7PvXwk8qthMQAgAAAAniuq6cNUtlffii1Nx2H3CzeJLc5oZOr1hs9BmgwHnTZQQz5bY0yXrtr1Jon7CvtVnO2pWSzy8jp5fcXbWR1/XKk2/8KTJHT5KZlSsREAIAUgwBYQpYuWGH1yUAAAAA3ZLbsFPWe/+Us35V7I5ghpzqyraFSTohcM53ZGTmyLVthd98XG59TewBpilzzGT5J50hd8c2hec/E6mhvkbWe/+UuWWddPm/Hu5bAgAg7ggIU0BuJl8GAAAAIJ5cx5GzcoGsT16Twu0XCVGoNfLfwcjpGVmV+IPn5W5aE7PLHD1R/mNLZPTqJ9d15dZskhp2xh5TUHSQ7wIAgOQgmUoBu5rDXpcAAAAAdCvWO0/LqVgUt/b8Z18rw+eX/cUncr74JGZf4KKbZQ4cLtd1Za9dKev1x9q9PnDpLTL7DYpbPQAAxBMBIQAAAIBuxamviYSDPr/MonGHHRT6jiuRr3BspO2t62L2Bb71rzL6D5ZdtVzWgpel3bG3D/KfcYV8oyceVv8AACQaASEAAACAbsVZuUCSZOQPO+xw0CwcK9+kM6LP/RPPUGj155Ik3/Fnyd1VJ+udZ+Tu2Br7urEnyX/CuTICwcPqHwCAZCAgBAAAANBtuOGQ7D0Bnrup6rDb80+7XIZhRtpzHYU/eD66zylf2G6hEqP/EPmnXiqz78DD7hsAgGQhIPTQmMG9tWrjTq/LAAAAALoNZ80SqbU5Lm0FrvyZjGBG9Lm99H25G8qjz2PCwUCG/CdfILP4WBmGEZf+AQBIFgJCDxEQAgAAAIfHbW2WvfR9GT37yBw8SvaKBe2O8Z98kax9Rv59VfDKn0mZOQrN/nXba065WGavvEgftiXrw5eiU5e/yhwzWf4TzpaRmXOY7wYAAG8QEHqoML9H9LHtuPKZ/KURAAAAOBjW+8/LqVy83/3Bb/9C1ocvdrjPLBov/5lXyjBNORvXtO3o0Ue+sSfKtcJyVn0m6/M3pZamdq83+g6U/9RvyRw4/HDfBgAAniIg9NDA3tnRx9W1DRrev8cBjgYAAAAgSa7rRv6/sTISDvr8MvKHy920Jua44Ldvk1xHzrov2rVhDB4l/xmXyzBNuc2NCr/0cNvrLvs3WUvfl71kvtS0u30BgaB8x31DvqOnyDB9cX1vAAB4gYDQQ/uOGFy6to6AEAAAADgA17ZkL3lX9pL58o2dImfNUkmS78jJspd/GHNs8MqfyQ21KvzKXyTHlnr0kWxLatoto/8QBc66VobPL9exFXrsrujrzOJjFXryPqm5ocMazBFHyz/lAhm5vRL3RgEASDICwhTx7srNuuB4piYAAAAAHXE2Vcl6759yd26TJNmL3o7sMM324eB1v5RbX6vwa7Ol1mYZA4ZKtiW3drOMXnkKnPud6OIj1ttPx/ZTHlkB2eg/RL5JZ8heuSCyMEnPvvKffJF8w45I7BsFAMADBIQAAAAAUpbb3ChrwSvR4K4dx4l5Grz2djnbqmWVPS5ZYZnDj5SzsVKywpKkwPnflZGVK0myV3/e7v6FRv4w+SedKWNosQzDkJHbW27ROJmjjpHhD8T9/QEAkAoICAEAAACkJGf9aoXffqrDBUL2+5q1K2W9/7zkOpFwcN/7D+b2ltGjryTJbayX9c4+owd79FHgtEtkDB4pw2i7FZDRb5BkheU27JTRu/9hvycAAFIRASEAAACAlOM6tsLzn42Eg7m9pYadnXqd9d5zkQdZue0WJwlecGNb+427oo/NUccocOaVsf3blpyKxbKXvS+3bovUs68yrvr5Ib0XAABSHQEhAAAAgJTjbCiXmnZJ/mCnw8EYX1lkxH/ud2T03DN60HWj9zA0hoyW/4wrose5zQ2yVy6QvWJBWxv+oPwTpx3S+wAAoCsgIPTY2ccM0euLq70uAwAAAEgpzhefRB5YocNuyzfpDPmGjWlru2KxnLUrpWCGAqdfIsMw5OzYKnvp+3IqFkVWO97DHD1R/hPOkZHDqsUAgO6LgNBjRw/rGw0IW0KWMoN8SQAAAJDe3MZdctavbrc9cPlPZS94ucN9+2MMGS3fsSUxbVsfPC9J8p/0Tbk7tik8f67c6vLY1+UNlv/kC2QOLDy0NwEAQBdCGuWx/N5Z0ccVm3dp3PC+HlYDAAAAeMNtqJcys2X4A7LLP5fc2NWJfcdMleHz7z8czOklNdZLwQyZoyfJWfGRlNtLgTOulGGakT5cV9a7c6VQiyTJXvq+3B1bY9vJzJF/8tkyjzgu+joAALo7AkKP7btC2twFXxIQAgAAIO0461cr/NpsKStXvvGnyv7k9Zj9ZuFR8h1XIuvd5zp8vf+c78gcWKjQ7F9LodZIOGj6FPjGNTKycqLH2UvelbN+VfR5TDhomPKNPUm+486UkZEd1/cHAECqIyBMIQ0tYa9LAAAAAJLKtW1ZH70kua7UtFv2gldi9huDRshfcrXsz9+SU/65JMkcfmRkJKHryH/qt+QbPkbWBy9IcqOv80+5QOaAoZIkp26LrI9elltd0WENxuBRkeP75ifmTQIAkOIICAEAAAB4xln1idyd22X07Cdj4HA55QvbdmZkK3Ded2V9+JKclQsio/zGnSL7iwWS68h3zOnyHXWCnO0bZS//MPoyc/REmUdNlrN+taxl7+83GFSPPvKfdL7MwrExM3sAAEg3BIQAAAAAksZt2i031CKzd3+5rS2yPiuL7OjZNzYclBS8+j9kzX9WTuViyeeX/6TzZS16WwqHZI6cIN/ks+U6jqz32qYeGz37yeg/WOE5v5e7c1vHRfgD8k2cKt/402T4A4l5owAAdCEEhAAAAAASzrXCspe+K3vRO5LjKHjdHbIXvS21NEb27zvKL7eXgpfcIuutJyP3DAwE5T/jCtmfvik17opMO552mQzDlP3FArnbq9v62VUr+8OXIk9yeso3eqLsxfOj+82RE+Q/8VwZub2T8K4BAOgaCAhTwHVTi/XYO+WSJMd1ZTK9AQAAAN2IvW6VrA9flHbVRjb07Cu1NMpe9n6Hxwe/9UOF3/ib3M1fRqYZn3O9rM/elFu3RUbv/gqcda0Mn19uc4Os9/7Z7vVG3mD5xp8qs2ic1Lxb9oqPZPTsF7nPYEFRAt8pAABdEwFhCjhicK/o42Xr6jShsJ+H1QAAAADx4e7eqdp5/5BVsThmu3/iNFmfviE5doevC/3tnsiD7J4KnH2tws/9MbovcO50GZmRVYatmAVNjMhqx+NPkTGwsO2egrm9Fbz+VzJ8vni9LQAAuh0CwhQQ9Lf9sDJ3wZcEhAAAAOjyXNdV+NVH5O7YJgUyZOQVREYE5vaW0au/nPnPxhxvHnmCjKxc2QvfatuWPzQmHPSd9E0ZPftKkpxNVdF7FprFk+SfdKaMXh3/HE04CADAgREQppimVsvrEgAAAOJi9uzZqqqq0ogRIzR9+vTo9oceekgbNmyQJN1www0aPny4VyUigdyt6+Tu2CYzt5f8F/9A4VcelRQZPehsWhNzrFFQJN+4KdFj9nK+XNH2JJgp//hTIm3bVnRqse+4EvmPLUncGwEAIA2YXhcAAACA7qeqqkotLS2aOXOmLMtSZWVldN/FF1+su+66Sz/4wQ/09NNPe1glEskuXyRJchrqFZrzO7l1W6ScXjKPOFa+cSdL2jMFuEcf+UYdo/Cc30kNO/fbXvDbv2hre+n7cnduk9ErT75jpibuTQAAkCYICAEAABB3FRUVGj9+vCRp3LhxKi8vj+4bMGCAJMnn88k0+XG0O3JtS07l4rYNoRZJkv+Y02X4/ArP/YMkN7Jv9w5Z786NbcAwZfRsmy4cKP2hjGBGpO3dddFpyP5TLpLhi50U5YZDsisWK/TyX9T68O2yq5bF9b0BANAdMcU4RQzsk60tO5okSY7jyjRZyRgAAHRdjY2Nys/PlyRlZ2erurq63TFPPPGEzjvvvA5fX1ZWprKyMknSrFmzlJeXl7hi48zv93epehOhedXnqgu3xmwzc3ppwMnnqHHxe2qtr+nwdTmTTldg4HD5evdX3dw/SZJ6feMK5R55TPSY2nlPSlZYWUdNVt9jTpIUud9hqLpSTUs/VPPKT+XuCSRl+tSrX39lptDXg+sjFucjFucjFuejDeciFucjVjzOBwFhivjXc8fqjic+lSQtWVuriUVc6AAAoOvKzs5WU1Pkj5/Nzc3Kzs6O2f/yyy9ryJAhGjNmTIevLykpUUlJ233lamo6DpRSUV5eXpeqNx7c3TsUfvNxmYNGyHfCOQo9+6fYA0xT5mml2jr/Rdkfv9ru9ebICfKfcbks06ewYyv84sNyW5pkDhuj5hHHqGXP+bTXrpBVsUQKZsieVKLtX1bKrlgoZ/XncnfVfqXN8fIff7YaevVTQwp9PdLx+jgQzkcszkcszkcbzkUszkesgzkfBQUFHW4nIEwRmYG2ldWeeK+SgBAAAHRpxcXFKisr05QpU7Rs2TJNnTo1um/JkiVavXq1fvKTn3hXIOLKWviW3O3VsrdXy65c0m6/f9oVcrdvkP1ZmSRDvhPPlb3gFUmS0WeA/FMvlWFGfh62P58nd8taKbtHZLsRmVnjhkOyPngx8preAxR+e47cjWsUnaq8h1FQJP8J58ocMDRh7xcAgO6Gm74AAAAg7oqKihQIBDRjxgyZpqm8vDzNnRu5z9wjjzyi7du369e//rUeeughjyvF4XIbdsopXyTtCfLUtCtmf+9zr5VbuzkSDhqG/NMulbtja3S/75hpMvwBSZKzcY3shfMkGQqccaWMrNxIH66r8Ct/iS5i4m7bIHdjpfYNB42+A+U/d7oC3/w+4SAAAAeJEYQAAABIiOnTp8c8Ly0tlSQ98MADXpSDBLGXvCc5tozBo/aEdm18J5yrcO1m2YvfkQxT/jOukNu0S87qz6PHuLvrIv9vblR43lOSXPkmnSFz8Ei5u3fILl8o+7M3919Abi/5jztL5uiJMlj0BgCAQ0JACAAAAOCQuM0Nsld9Enn81XDwmKlyd9epceXHkumTv+RqGf6ArHn/kCSZhUfJWbsyMhrQdWW987TUtEtGXoGMHn0VevFhuZvW7L/zYKZ8E6fJd/SU6AhEAABwaPgTWwr5l7OPjD5es2XXAY4EAAAAksvZuV1OdWwIaC/7QLLC7Q/OypW7q07Oyo8ln1/+s6+V0WeAwmVPSG5khKAy9ixck5kje9kHctavkiS5NZtkzX8mEg76OhjP4PPLN+E0Ba/+ufzHnE44CABAHBAQppCRA3tFH//f6ys9rAQAAACIcJsbFH7vOYXn/E7hl/8stz6ySqLb2iJ7xYcxxxp9B0pZuVJzg5yqpZKkflfcIjN/mKzX/iqFWmQWjpU5coKc8s8lw5RZNK7dysZG/nD5T/2WgtfeLuX23rtVZvEkBa/4mfwnnicjI3ZlbAAAcOiYYgwAAACgHdcKy17+geyFb0vh1sjGjCwpJ/JHbfuLBVKoNXq80bu/AhfepPAL/ye3uSGy0fQpWDBC4Sd/L7e+Rka/QfKfcbmseU9JrivzyMkyghmSY0s5veQrniSzeJLM3v2j7ZpDj5BamyL3Jew3KGnvHwCAdEJACAAAACCG29qk8D//JHfn9sgG0yc5tsyRE9qm9DbtbnuBPyh/yVWy5j0lt65thWI5tjb/9w8jjzNzFDj7Orl1W+WsXSn5A/Ife6aMnJ4KXn+HFMzqcJGRwGnfStC7BAAAezHFOMUM7ZcTfWw7roeVAAAAIF05lUsi4WDPfvKf+x0pmClJ8h1xbPQYs2h89LH/5AtlLXg1ch/BzGz5p14m9ewX02bg7Gul3N6y9kwn9h19soycnpIkIzOHFYgBAPBQQkcQzp49W1VVVRoxYoSmT58e3f7QQw9pw4YNkqQbbrhBw4cPT2QZXcqNZx+lO574VJI054M1uurUUR5XBAAAgHRjVy2TJPmPLYlM/21plNEnX0b/IZIkt6VJ4beelBS576A1/5noa43c3rLeeUZS2x+7/adfInNgoez1q+Vu/lLKyJLvmNOT94YAAMABJezPdFVVVWppadHMmTNlWZYqK9tWPLv44ot111136Qc/+IGefvrpRJXQJWUGfNHHC6tqPKwEAAAA6chtbpC7qUqSZA4/Us7qzyOPjzhWhmFIkuxl70sNOyPH122JfX3NJu0bDva74hb5xhwv13Vkf/KaJMk3cZqMjKwEvxMAANBZCQsIKyoqNH58ZNrBuHHjVF5eHt03YMAASZLP55PJVAIAAAAgZVjvzo0+dnfVRKYNG6Z8oydGt5vDxsjIHxbzOqNnPxlDimWOOS6ykrEkc8zxyhw1TtKeacu1myOLkYw9KQnvBAAAdFbCphg3NjYqPz9fkpSdna3q6up2xzzxxBM677zzOnx9WVmZysrKJEmzZs1SXl5eokpNGr/ff9Dvo3efvvL7CFG7m0O5FtA9cS1A4jpAG64FeMFt2i3r0zflGzdFRq/+kQVE9gi/9lfJcSKrDWf3iG43+uZLVjjypGc/Bb95g4wefSRJ1udvSc0NUm5v+U86P9KHbcn69E1Jkv+4kraFTgAAQEpIWECYnZ2tpqYmSVJzc7Oys7Nj9r/88ssaMmSIxowZ0+HrS0pKVFJSEn1eU9P1p9vm5eV16n3cddVxuuPJzyRJtz86T7defEyCK0OydfZaQPfHtQCJ6wBtEn0tFBQUJKxtdF3WwnlyVn0id9u66GIkUU27ZRQUyX/yhdFNruvKevc5ubWbZfTKU+CC78vI6SVJcmo2yV74liQpMPVSGXvac774WNpdJ6P3AJnFkzqsw3VdybFl+BJ6m3QAANCBhA1NKy4u1vLlyyVJy5YtU3FxcXTfkiVLtHr1al1yySWJ6r5Lywy2/VC0rb7Fw0oAAADQnbm2JWfNksjjuq1yt6yL2W/0ylPgG9fEhHbOqk/lVC6W/AH5z742Gg66tiXr7TmREYdjT5I5OLLYntPaIuvzeZIk3+SzZZht99x2d9XJ/uIThcueVOhv9yj0yK/k7NiWyLcMAAA6kLA/zxUVFSkQCGjGjBkqLCxUXl6e5s6dq9LSUj3yyCPKzs7Wr3/9axUUFOjGG29MVBkAAAAA9sNZv0pqaZL8gbYpw/tw62sUfnW2AhffLMMw5NRslPXBC5Ik/6mlMvvkR4+1P38rsmBJz37yn3BudHvDx29EVkHOHyZz4HDZlUvkbFwjZ1OltKsutsOcXjICGYl5swAAYL8SOn5/+vTpMc9LS0slSQ888EAiu+0Wzhw3WG8t2yhJWr1xp44Y3NvbggAAANDtOOULIw86CAf3cretl1tfI2X1UPjNJyTbknnkZPmK2xYtcbZtkL34HUmGAtMukxEIRl67q06734sEiu7W9Qo9dnfHnfToI/8xp8ssPpb7EwIA4AFu8JGizpk0NBoQ/rlsle67/kSPKwIAAEB34jY3ylm/+sAHGYbkunLWr5a75UtpV62MfoPkn3JBWztWODK12HXlO3qK5LqyPntTzsY1cresPXDzfQbId8w0maPGx0w9BgAAyUVACAAAAKQhZ81iybGjz41BIxSYdoVCT8yKbvNP+aasD16U/dFLkQ3BDAW+8e2YUX72p6/L3bk98njlx7KXf/i1fRv9h8g3carMwqNkGAm7LToAAOgkAsIUlpsZUENLZLrHhpoGDc3L9bgiAAAAdBWu68jduEbKyJLZf0i7/XbV8rYnhqHA1EsVeumh2DZ274h57j/9Mhm98tr2NzfIXvpB2wGOLaPPAJmDR8kuXyiFYhfcMwqK5J84TcbgUTIM4zDeHQAAiCcCwhR2x+WT9B+PfSxJ+n8vL2eaMQAAAL6W6zpy1q6MLBpSu1nK7qGMa29vf6DjRB/6z/mOwq88Ku2qk5E3WL4Jp8p66x+yl38UPcboky9f0dGxbQSzZI45VnJcmYNHyRw8UkZOT7mN9TGvNYeNkW/iNJkDh8f9/QIAgMNHQJjCTP6qCgAAgIPgbNsg6925kWBwDyO7Z7vj3FCL3MZ6SZI59iTZH70st75GRr9BCpz/PRmZ2XI2VslZ9Un0NebQ0e3aMXw+BU6/tH0h/oCMQYUysnsqb9rFqvdlxeHdAQCAROGGHymuuKBX9PHrizZ4WAkAAABSmeu6Cr/1jz2jBnvKGDBUkqL/35f10ctSw04pt7fcjZVyd26T0TdfgfNvkIIZcq2w/CedL6NvftuLsnp0uhYjI1vBC29SoOQqBfLb9w8AAFILAWGK+/43jow+Llu60cNKAAAAkMrcndulXbVSZraCV90qIzsS6JlfCeicmk1yVn0aedKwU+7O7TJ65ck/7XLZyz9Q6O/3KvT3/5JcR/6Sb0eO8/nlO+LYZL4dAACQREwx7mLClqOAn1wXAAAAsZwN5ZIkc0ix5PPL2RaZfWIMGBZznBEISj6/ZFvRbW59jcJz/yi5e+5LmJUr+QNyVkbuh22OmiAjiwXzAADorkiauoCfXDAu+vg/H//kAEcCAAAgXTkbVkuSzKFHSLvqpKbdUkaWjF79Yg/MypXRZ0Dbc9+eMQPuPouWnHiuZNuyV38WOeToKQmtHQAAeIsRhF1AQd8cr0sAAABAinHqtspZu1y+sSfL+vR1udUVkiRz8EiF5z215/EoGUbbmAA33Krwq4/Krdkk5fZW8MKbpNze0u46WR+/LqdqqYyBhTJHT5KzYoEUbo08zxvsxVsEAABJwgjCLmLs0D7Rx7f+dYGHlQAAACAVhJ/7o+xP31Ro9p1yVnwkSTL6D5G9coHcTWukrFz5p1wQPd4NhxR+dbbcLeuknF4KXnCjjB59ZBiG3FCLnC+XSYYp/ykXS3Jlr/hQEqMHAQBIBwSEXcR3zjjC6xIAAACQIlzHkaxQh/vshfMkw1DgzCtl5PSMbrc+flXu5i+l7B4KXvB9GT37RtpyHVnvPS+5rnxHT5HZb6Dc6srIoic5vWQWjk3KewIAAN4hIOyi7n12kdclAAAAwCPuji0db99eLUnyHVcic/Co6HZnU1VklKFpKnDud2T0ymvbt/pzudvWS9k95DuuRJJkL/8g0s7YE2X4fIl6GwAAIEUQEHYh911/YvRxXUOrh5UAAADAS+6W9e22GXsDweye8k2c1nZsOKTw/GckSb6JZ8TcT9BtaZL18auSJP9J58sIZsqpr5GzfrXk88s3ZnIC3wUAAEgVBIRdGPciBAAASE/O1nUxz81Rxyhw9nVSMFNq2iV3+8boPvuT16RddTL6DZJv4tSY11mfvC61NMkoKJI5ckKk7eUfRds0slgsDwCAdEBA2MX8f9edEPPccVyPKgEAAIBXnIq2282YRxwXud9gIBgd8Wcvjyww4myqijw2TfmnXibD529rY9sGOV98Etl3ykV7Fitplb36M0mRxUlc15UbapXbWC9nxzY5W9fL2VAut74mie8WAAAkmv/rD0EqMQxD+b2ztHVnsyTpP/72cczUYwAAAHRvrutEHxu9+8s35ni5rivDMOQ7+kTZy96Ts2ap3ONKFJ7/rCTJd8w0mXkFbW04jqz3n5fkSpk9ZH/2lqxwi9wN5dFjwi8+JIVaI8d8lWEqOP1XMgIZiXqbAAAgiRhB2AX97KIJMc+Xr6/zqBIAAADEi9u4S/aKBbIWz48JAb/KWbOs7YlhKPz8n+SsWxl52qOvzOFHSY6t0PMPSrtqZfQdKN+kaTFtuLtqowuaqGmXnKqlMeGgJCnUog7DQX9QvnEnS/7AobxNAACQghhB2EXdfPZR+tPrkR8E//p2OaMIAQAAuij7y+WyF8+Xu21DdJuZP0zGoBHtjnVtK3LfwL3Pd2yTJDkVi+UrHCtJ8o2bImftCqlpl2SY8k+LnVosSUavPPlPv1RuS6OMYIYUzJS7dX10arIxeJTczV9Kjr3nBYaMwaPlGz1R5oixMgLBuJ4DAADgLQLCLqpoYM+Y57f+dQEhIQAAQBfjuo6sd+dKLU2Szy+ZphQOSbbV4fH2igXS7n1mjwQzpVCLnPWr5IZDMgJBGYOKZPQdKLdui3wTp8asWryXYRjyjTkuZlt4n/sauhsrI8f1GySzeJJ8IyfIyIn9+RMAAHQfTDHuwr4aCL7w6VpvCgEAAMAhcXfWRMLB7B4KXj9DRv+he/YY7Y91HNmL5rVt8PkVOPc7MgYMk6ywnA2rI680DPlLrpb/lIvkm3Rmp2txajdHHuT0lG/C6Qpc9m8KXnqL/ONPJRwEAKCbYwRhF3fVqaP05HuRv/C+t3KLzj5mqDICPo+rAgAAQGe4W9ZKksyBhZFpu3vvPWi2DwglNxIm7uE/8VyZAwtljhwne9t6OWuWyVc0LvLyPgOkPgMOqpbA+TdILY0y8ofLMBlHAABAOuFf/i5uUlFezPNfPvGpR5UAAADg67jhkMLvPy97xQK5ritnyzpJkpE/fM8BexcF6WAE4eYvY55byz6QvfzDtvsQrv9Cbjh0yLWZfQbIHDSCcBAAgDTEv/7dwFenGt/61wUeVQIAAIADsZe+K2fFR7Le/6ecikVyt0YCQnPgcLmuu2flYElG7I/pTt0Whd/4W+TY0RNl5A2WdtXJ+uAFOav2/IHYCsup/spKxAAAAJ1AQNhN/ObaE2KeExICAACkHre+NvrYqVomt75G8gdk9CuQ8+VyuXVbpGCmjL5t04PdxnqFX3lUCrXKLBon/7TLFPjm9+U7ekr7DsKtyXgbAACgmyEg7CZM09BPLxwfs42QEAAAILXsnQ4sScrKkSQZA4ZKVljWBy9IkvwnnCMjIztyfKglEg421ssYOFz+aZfLMEwZGZkyevWLvL53f8kfkCSZg0cn8d0AAIDugoCwGxnUJ1uXTSmK2UZICAAAkDrcmo3Rx86qzyRJ5vAjI6sTN+2WMWCYzCMnR461bYXffFxu3RYZvfsrcPZ1MvYEga4VlrXoHUmSUVAkWWEZ/Qax2jAAADgkBITdzOTRA3TkkN4x2wgJAQAAUpNZPEm+cSfL3bFVkuQbe5KMPfcftD97U251hZSVq8C502Vk5kRfZ3/xSSRQ7DdIhumLtDVsTPLfAAAA6BYICLuh7545RkX5PWK2ERICAAB4y929I+a5WTRe/tMviUwZ7lcQOWZPUOg27Za9/ANJUuCsa2T07NvWjhWWvfgdSZLvuBI561dH2ht2RKLfAgAA6KYICLupm88Zq8mj+8dsu/WvCxS2HY8qAgAASG/22hXRx2bhUfKfcUV09J8xYKgkydm2PnLsorclKyyz8CiZAwtj2/ni47bRg70HyN1VK2VkRdsAAAA4WASE3dhlU0bquqnFMdv+8++f6KPVWz2qCAAAIH05X0YCQrNonPwlV8vw+aL7zD3hnrt9o9zdOyNTiCX5jvtGTBuR0YPz9+wrkbNhz+jBIcXRsBEAAOBgERB2c+OG99WdVxwbs23ugi+ZcgwAAJBEbnOD3C1rJdMn/2mXyPD5Y/Yb2T2k3N5SuFXhd+ZItiWzaLzMfoNijrNX7hk9mFcgc/hR+0wv5v6DAADg0BEQpoGczID+v+tOaLf91r8u0M7GVg8qAgAASC/Oui8k15VRMFJGRmaHx0RHEW6qkgxDvuNKYva7Vlj2kj2jB8efJlnhyLEyZA4dndD6AQBA90ZAmCYMw9B915/Ybvs9zyxiNCEAAECC7Z1e7Bsxdr/H7HsPQXPUMTL7DIg9oKVRam6QJFnvPqvQU7+VHFvGgCEysnLjXzQAAEgbBIRp5r7rT9StF09ot/3Wvy7Qi5+u86AiAACA7s11HbkNOyUZMguP2u9xZv8hkQeGKd+xZ7bbb+T2VuD878kYMlqywlJjfaT9bRvkVFfIdd0EVA8AANKB/+sPQXczoFdWJCj8ysjBd1du1rsrN+tnF01Qfu8sj6oDAADoXgzDVODSW6RddZF7De7vuIHDZR5xnIx+g2T2yuvwGHPwKAUHj5JTt0Xhp38f3R5++S8y+ubLN+4UmaOOkeEPxPttAACAboyAMI3dd/2JamwJ686nPo/Z/t/PL5Ek/eclE9UnN8OL0gAAALoVwzCkXv0OfIzpU2DqpZ1tcW/D8h1bInvlArl1W2XNf1b6+DX5jjpBvvGnysjgj74AAODrMcU4zeVkBnTf9Sfq1CMHttv3X89G7k/45dZdHlQGAACA/XHWr4o8yMiSs6FcMoy2nS2NshfOk/Xhi94UBwAAuhxGEEKSdOHkQl04ubDDBUv+97WVkqSheTn68fnjkl0aAAAAvsLdsS3yoKVJbss+95EOZsjI7ill95Rv1DGe1AYAALoeAkLE2LvScUdB4Yaaxuj2/7pmsgI+BqACAID9mz17tqqqqjRixAhNnz49un39+vV6+OGHJUk33HCDhg8f7lWJXZb/+G/I6T9EysyWkd1DRk4kFDQCQa9LAwAAXRABITq0NyicPW+1VmzY0W7/f/79k3bHAgAA7FVVVaWWlhbNnDlTDz/8sCorKzVq1ChJ0lNPPaVbbrlFpmnqz3/+s37+8597XG3XY+T2lu/ok7wuAwAAdBMEhDig75xxhCRp+65m/X/PLenwmL2jCjMCPt199fFJqw0AAKSuiooKjR8/XpI0btw4lZeXRwPCxsZG5eXlRR8DAADAWwSE6JT+PbMOOP1YklrDdsy+WdeeIJ9pdHgsAADo3hobG5Wfny9Jys7OVnV1dXSf67pf+/qysjKVlZVJkmbNmhUNFLsCv9/fpepNNM5HLM5HLM5HLM5HLM5HG85FLM5HrHicDwJCHLS9QaHtOLrtb5/s97jb/vZx9HHJhME6+5ihCa8NAACkhuzsbDU1NUmSmpublZ2d3eFxhtHxHxNLSkpUUlISfV5TUxP/IhMkLy+vS9WbaJyPWJyPWJyPWJyPWJyPNpyLWJyPWAdzPgoKCjrcTkCIQ+YzzWhYGLYc/efj+w8Ly5ZsVNmSjdHnF00erlOOHJTwGgEAgDeKi4tVVlamKVOmaNmyZZo6dWp0X25urmpra2UYhrKysrwrEgAAAJIICBEnAb8Zs1jJ/qYh7/X8J+v0/CfrYrYxJRkAgO6jqKhIgUBAM2bMUGFhofLy8jR37lyVlpbq8ssv1+9//3tJ0ve+9z1vCwUAAAABIRJj37CwrqFF9z67+Gtfs++UZEnK65mpWy+aIJPQEACALmn69Okxz0tLSyVJw4cP11133eVFSQAAAOgAASESrm9uZkxguK2+Wff9s+MVkfdVs6tF//GV0FCSbjrrSI0a1CuuNQIAAAAAAKQrAkIk3YBeWTGBoeu6euCl5dpY19ip1z/4xhcdbj95zEBdOHm4zP3c7BwAAAAAAADtERDCc4Zh6N8uGBezzXVdPfTGF6rcsqvT7Xywaos+WLWlw319coL6yYXjlRXkkgcAAAAAANgXaQlSkmEYuunso9pt7+z05K/a0RjSjCc/O+Ax3z3zCI0Z3FsGIxABAAAAAEAaISBEl/LV6cl7WbajP766QtW1nZum3JFH3lrdqeN+dN5YDcnLZSozAAAAAADoFggI0S34faZu+ea4Dvc5rquPVm3VPz9ZG5e+/ueVFZ0+dsSAHio9cYTye2cxMhEAAAAAAKQkAkJ0e6Zh6OQjB+rkIwfu95i63S363YvL1BK249r3l9t267cvLD3o1+VmBnTxCYU6ckhvBXwm4SIAAAAAAEgYAkJAUt8embrr6uO/9rgtO5r0t/kV2lbfnNB6GlrC+vv8isNuZ3DfbE09ukBHDO6tzICPoBEAAAAAALST0IBw9uzZqqqq0ogRIzR9+vTo9rlz5+r111/XtGnTdOWVVyayBCCuBvbJ1q0XT+jUsY7j6sttu/SP99doZ2MowZV1bGNdkx5/tzIhbR81tI+OKeynovye6pEVkGkSPgIAAAAA0BUlLCCsqqpSS0uLZs6cqYcffliVlZUaNWqUJOmMM85QcXGxli9fnqjuAc+ZpqGRA3vp9ksntduXl5enmpqaDl/nuq7qGlr14aqtenfl5kSXechWbtihlRt2JL3foXk5Gj2ol4b376H83lnqnROUzzSTXgcAAAAAAN1FwgLCiooKjR8/XpI0btw4lZeXRwPC3r17a+PGjYnqGujSDMNQvx6ZuuD44brg+OGH3I7tONpU16TP12zXB6u2xrFCb22oadSGmkNfrTqZ/D5DQ/vlqqBvtgb0ylLfHpnqkxNUj6ygMgI+MegSAAAAAJAKEhYQNjY2Kj8/X5KUnZ2t6urqg3p9WVmZysrKJEmzZs1SXl5e3GtMNr/f3y3eBw5fsq6F/AHSxDGFuuH8+LXpuq7ClqMNNbu0fO12fbiyWtt2NsWvg27Esl19uW23vty22+tSUlKPrKD69MhU39ws9emRqd65meqdk6EeWUHlZAaUkxlURtCnzIBfAb9PPtOQaRjaeyvN7nRPTf59wF5cCwAAAPBCwgLC7OxsNTVFQoPm5mZlZ2cf1OtLSkpUUlISfb6/6ZhdyYGmlSK9dIdroVdAOnl0X508um9S+nNdV66kkOVoe32z1m1vUOXmeq2s3iHXTUoJiLPdzSHtbg5p/bZdXpeCbijgMxX0mwoGfJH/+0wF/JH/gn6fAnue790e9Pvk95kK+Iw9/49s9/tMmYahwX2zlZMZSHjdif73oaCgIGFtAwAAoOtKWEBYXFyssrIyTZkyRcuWLdPUqVMT1RWANGAYhgxJmQGfhublamherk45cqDXZR2Q67pyXak5ZKm+KaTa3a2q2dWsrfXN2ryjSZvrmkS2CSRG2HYUth01tlpxa/PH5x+toXm5cWsPAAAASBUJCwiLiooUCAQ0Y8YMFRYWKi8vT3PnzlVpaanmzZun119/XQ0NDWpoaNANN9yQqDIAwDPGnumwkemyARX0zWl3THcYTXoo9o4Idd3I/TJDlqPmkKWWkK3GlrB2NYfV0BLWrqaw6ptatbs5rPqmkHY3h2U7xKrwxtptuwkIAQAA0C0lLCCUpOnTp8c8Ly0tlRRZxfiMM85IZNcAgBS2d0SoDMln+hT0+5SbhOmbqSpdg+Jkcvfci8CNPo88c93IY8d1I/85rizHle04su3I4607mzQ0L1f9emR6VT4AAACQUAkNCAEAAFLB3kVtokvbGDHPDmhQn4O7jzIAAADQ1ZheFwAAAAAAAADAOwSEAAAAAAAAQBojIAQAAAAAAADSGAEhAAAAAAAAkMYICAEAAAAAAIA0RkAIAAAAAAAApDECQgAAAAAAACCNERACAAAAAAAAaYyAEAAAAAAAAEhjBIQAAAAAAABAGiMgBAAAAAAAANIYASEAAAAAAACQxggIAQAAAAAAgDRGQAgAAAAAAACkMQJCAAAAAAAAII0REAIAAAAAAABpjIAQAAAAAAAASGMEhAAAAAAAAEAaIyAEAAAAAAAA0hgBIQAAAAAAAJDGCAgBAAAAAACANEZACAAAAAAAAKQxAkIAAAAAAAAgjREQAgAAAAAAAGmMgBAAAAAAAABIYwSEAAAAAAAAQBojIAQAAAAAAADSGAEhAAAAAAAAkMYICAEAAAAAAIA0Zriu63pdBAAAAAAAAABvMIIwiW677TavS0CK4FrAXlwLkLgO0IZroXvg6xiL8xGL8xGL8xGL8xGL89GGcxGL8xErHueDgBAAAAAAAABIYwSEAAAAAAAAQBojIEyikpISr0tAiuBawF5cC5C4DtCGa6F74OsYi/MRi/MRi/MRi/MRi/PRhnMRi/MRKx7ng0VKAAAAAAAAgDTGCEIAAAAAAAAgjREQAgAAAAAAAGnM73UB3VVdXZ1+85vfqLq6Wo899ph8Pp9mz56tqqoqjRgxQtOnT/e6RMTRtm3bdPvtt2vw4MHy+/365S9/qRdeeEGffvqp+vfvrx/84Afy+/3ttknSr371K61fv1733XefBg4cKEkdvhapq7Pf753Z1lFb+3stUs9Xv361tbXtPhukjr/H+XzoXioqKvTXv/5VhmFo5MiR+s53vtOprzvXQtfH53Wb/f2blq46+lxIZ+vXr9dDDz0k0zQ1cOBA3XzzzTIMw+uyPPfSSy/p448/1l133eV1KZ7q6PerdDZ//nzNnz9fjuPoxz/+sfr27et1SZ5ZvHix/vnPf0qSNm3apBtuuEGTJ0/2tigPtba26v7771dra6uys7P1k5/8RIFA4JDaYgRhguTm5uqOO+7Q6NGjJUlVVVVqaWnRzJkzZVmWKisrPa4Q8TZu3Djdeeed+uUvf6n6+nqtWLFCd911l4YNG6ZPP/20w20+n0+33nqrTjzxxGg7HR2H1NaZ7/fObvtqW/trD6mpo6/fvp8NUsff43w+dD/9+/fXjBkzdNddd2nXrl1auXJlp77uXAtdG5/XsTr6TExnX/1cWL9+vdcleaqgoEB33323Zs6cKUlas2aNxxV5LxwOa+3atV6XkTK++jNUuqqrq9PKlSs1Y8YM3XnnnWkdDkrSMcccozvvvFN33nmn8vLyNH78eK9L8tTixYs1evRo3XnnnRo1apQWL158yG0RECZIMBhUbm5u9HlFRUX0wh03bpzKy8u9Kg0JsmLFCs2YMUMvvfSS1qxZo6OOOkqSNH78eJWXl3e4zTAM9e7dO6adjo5DauvM93tnt321rf21h9TU0ddv388GqePvcT4fup/evXsrGAxKknw+nzZs2NCprzvXQtfG53Wsjj4T09lXPxdMM71/Fdt31LPf71deXp6H1aSGefPmaerUqV6XkTK++jNUulq8eLEcx9HMmTP1yCOPyHEcr0tKCVu3blWvXr2UmZnpdSmeys/PV0tLiySpsbFRPXr0OOS20vtfpSRqbGxUdna2JCk7O1tNTU0eV4R46tOnjx544AH96le/0rJly1RVVaWsrCxJka93Y2Ojmpqa2m3rSGePQ+rq6Pu9s9s62x66hq9+Nqxbt67D73E+H7qvdevWadeuXcrJyenU151roWvj8xqdsfdzYciQIV6X4rnPPvtM//7v/676+vq0D5Mty9KKFSt09NFHe11KSujoZ6h0VV9fL8uyNGPGDAWDQWYN7PHxxx+n9dTivQYNGqSKigr99Kc/VVVVlYqLiw+5LQLCJNn3h8Tm5uboD4/oHgKBgDIzM+Xz+XTssccqPz9fzc3NkiK/xOXk5Cg7O7vdto509jikro6+3zu7rbPtoWv46mfDhg0bOvwe5/Ohe2poaNAjjzyim2++udNfd66Fro3Pa3ydfT8XIB133HH67W9/q379+mnhwoVel+Opd999V6eccorXZaSMjn6GSlfZ2dnRWQNHH320Nm7c6HFFqeHzzz/Xcccd53UZnps/f76OPfZY3X///Zo4caLee++9Q26LgDBJiouLtXz5cknSsmXLDivVRerZ+0uaJK1atUoDBw7UypUrJUW+3qNHj9bIkSPbbetIZ49D6uro+72z2zrbHrqGr3425Ofnd/g9zudD92Pbtv7nf/5H1157rXr37t3przvXQtfG5zUO5KufC+kuHA5HH2dlZUWnX6erTZs26c0339Q999yj6upqvfrqq16X5KmOfoZKV0cccUR0BOXatWs1YMAAjyvy3s6dO+X3+w9rOm134bpudAR2z549D2v2guG6rhuvwtDGsizde++90VXsrrrqKr3//vv68ssvVVhYqO9+97tel4g4WrhwoZ566ikFAgGNGTNG11xzjf75z3/q888/V15env71X/9Vfr+/w23333+/Vq9erQEDBujCCy/U8ccf3+FxSF2d/X5/9NFHv3ZbR22NHj26w9ci9Xz163fkkUfqs88+i/lskMTnQxp4//339eijj2ro0KGSpKuvvlorV67s1Neda6Fr4/O6zf7+TUtXHX0upHOI/Omnn0bvLTdo0CDdeOONaX9fxr3uuOOOtF/FuKPfr9LZY489pqqqKvXo0UO33HJL2v+b/+abb8q2bZ1zzjlel+K5xsZG/f73v1c4HJbP59NPfvKTQ75lAwEhAAAAAAAAkMb4Ew0AAAAAAACQxggIAQAAAAAAgDRGQAgAAAAAAACkMQJCAAAAAAAAII0REAIAAAAAAABpjIAQQLe2bds2XX755Zo1a5YWLlyoOXPmaNu2bXHvp7q6WnPmzNGKFSui2/74xz/q8ssv15o1a+LeHwAAAAAA8eL3ugAASKSePXvqlltuUd++ffXhhx/q9ddf19ixYzVgwICDase2bfl8vv3ur66u1jPPPCNJGjt2rCTprLPO0jHHHKP8/PxDfwMAAAAAACSY4bqu63URAJAo27Zt0w9/+ENlZGSotbU1Zt+cOXNUXl6uv/71r1q/fr369u2ryy67TKecckr0dcXFxcrIyND69ev129/+Vnfffbc2b94sSRoxYoS+//3vKyMjQz/84Q9j2v7Vr36ld955R/Pnz9e9996rkSNHqqysTC+88IJ27NihIUOG6Prrr9eYMWP0zjvv6H//9381ZcoUbdy4UTU1Nbrssst03nnnadOmTfrDH/6gdevWKRgMaujQoZo5c2bSzh8AAAA6dv/996tXr15au3atamtr9eMf/1hvvvmmKisrNWbMGN18881elwgAncYUYwBp4aijjtKECRMkSZdccoluueUWNTQ0aNasWWpqalJpaan69++v//mf/9HatWujrysvL9eIESN0xRVXyDAMTZ48WdOnT9fFF1+sdevWafbs2erZs6fOO+88SdIJJ5ygW265RUOGDInpf/ny5XrooYfUs2dPXXfddaqpqdFvfvMb7d69O3rMihUrdOaZZ0qSHn/8cVmWpddff11r1qzRNddco6uuukp5eXkJPlMAAADojPXr1ys/P1933XWXSkpK9Kc//UnXXHON7r//fi1cuFDhcNjrEgGg05hiDCAtGIahgQMHasmSJTr66KM1duxYLVy4UA0NDWpoaNCTTz4ZPXb58uWaPHmypMgowWuuuUaSVFdXpyVLlqi8vFx7B1+vX79emZmZGjNmjF555RUNHTpUJ598crv+Fy5cKEm6/PLLNX78eNXU1Oi5555TRUVF9Jhp06bpnHPO0eeff64lS5Zo586dGjRokFzX1aJFizRy5MhoEAkAAADvhEIhNTY2Rn82MwxDZ5xxhvr06SNJMk1Tfj+/bgPoOvjEApA2DMPocPtpp52m0047Lfp83/sT7v0hT5JeffVVrV69Wueff74mTpyoP/3pT2pubo5bLbm5uZIUvdeh4zg655xzNHjwYK1cuVKfffaZ5s6dq9/97ncqKCg4pH4BAABw+Kqrq1VUVCTTjEzKW7dunc466yxJUm1trfr27bvfnz0BIBUxxRhA2sjJyZEkLViwQAsXLlRxcbFyc3O1ZMkSbdq0SRs2bNDzzz+vurq6A7bT2NiolStXqra2Nrptb7i3atUqffDBBwqFQjGvmTRpkiTp6aef1ptvvql58+YpJydHo0ePPmBfb7zxhsrLyzVw4EDl5+fLdV3t3LnzYN86AAAA4mj9+vUaPnx49Pm6des0bNiwdo8BoKsgIASQNk499VQNHjxYb7zxhh599FHl5ubqtttu08CBA/X4449r7ty5CgaD6t+/f4evP/fcczVy5Eh9+OGHqqur09ChQ6P7xowZo3HjxumLL77QAw88EHNvQUk6+uijdeONN6q+vl6PPfaY+vXrp//4j/9Qjx49DlhzIBDQO++8owcffFBffPGFzj77bI0ZM+bwTwYAAAAO2fr161VYWCgpMt04FApF/2C8bt26mPAQALoCVjEGAAAAAAAA0hgjCAEAAAAAAIA0RkAIAAAAAAAApDECQgAAAAAAACCNERACAAAAAAAAaYyAEAAAAAAAAEhjBIQAAAAAAABAGiMgBAAAAAAAANLY/w/+t8DeZSd97AAAAABJRU5ErkJggg==",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"step = 10\n",
"plot_all(cost_history, m, q, step)"
]
},
{
"cell_type": "code",
"execution_count": 125,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"22901 passi e 114505 gradienti calcolati per arrivare a distanza minore o uguale di 0.1 dall'ottimo\n"
]
}
],
"source": [
"near_opt(m, min_dist=1e-1, ge_per_step=mbs)"
]
},
{
"cell_type": "code",
"execution_count": 126,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA7sAAAHzCAYAAADhDgreAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAABXsElEQVR4nO3df3Rb9Z3n/9e15B/64V+ybIf8+tIEmISEkFCHtpg2JISQY1qGlgyFFM9pO7MMC2cZplsOybaFtpQSSjnlUGBpDwydmtlpu6HQw9Y7uGlCWNwyOMSZENMwQFvoNBDHlu1Ykn9Jut8/ZMlWbDlOYuleSc/HORzHsm/8kT920Ot+3p/3xzBN0xQAAAAAAHmkyOoBAAAAAAAw1wi7AAAAAIC8Q9gFAAAAAOQdwi4AAAAAIO8QdgEAAAAAeYewCwAAAADIO4RdAAAAAEDeIewCAJBlZ599tlwul8rLy1VVVaVLLrlEjz/+uGKx2Emv/eMf/yjDMBSJRDI6xmx9HQAAMoWwCwCABZ5//nkNDg7q3Xff1bZt23T//ffrb/7mb6weFgAAeYOwCwCAhSorK3X11Vfrpz/9qf7pn/5Jhw4d0i9/+UutWbNGFRUVWrRokb7+9a8nP/8Tn/iEJKmqqkper1e//e1v9c4772jDhg2qqamR3+/X5z73OfX39yevuf/++7VgwQKVl5frL/7iL/TrX/9akhSLxbRjxw4tXbpUNTU1uu666xQIBNJ+HQAAcglhFwAAG7j44ou1cOFC/b//9//k8Xj04x//WP39/frlL3+p//k//6eee+45SdJLL70kServ71cwGNTHPvYxmaap7du368iRI/rd736nP/3pT8mA/Oabb+qRRx5RR0eHBgcH9cILL+jss8+WJH3/+9/Xc889p7179+rIkSOqrq7WrbfemvbrAACQSwi7AADYxPz58xUIBHTZZZfpggsuUFFRkVatWqUbbrhBe/fuTXvdOeecoyuuuEKlpaWqra3Vl770peTnOxwOjYyM6I033tDY2JjOPvtsLV26VJL0+OOP695779XChQtVWlqqr3/969q5cyf7dAEAeYGwCwCATfz5z3+Wz+fTv/3bv2n9+vWqra1VZWWlHn/8cfX09KS97ujRo7r++uu1YMECVVRU6MYbb0x+/jnnnKOHHnpIX//611VXV6frr79eR44ckSS9++67+vSnP62qqipVVVVp+fLlcjgcOnr0aFaeLwAAmUTYBQDABjo6OvTnP/9Zl156qbZu3aqrr75af/rTnzQwMKCbb75ZpmlKkgzDmHLt//gf/0OGYej111/X8ePH9fTTTyc/X5K2bt2ql19+We+++64Mw9Cdd94pSVq0aJH+7//9v+rv70/+Nzw8rAULFkz7dQAAyCWEXQAALHT8+HH9n//zf3T99dfrxhtv1AUXXKDBwUH5fD6VlZXp1Vdf1f/6X/8r+fm1tbUqKirS73//++Rjg4OD8nq9qqys1J///Gc98MADyY+9+eab2r17t0ZGRlRWViaXy6Wiovj//m+++WZ95Stf0bvvvitJOnbsmH7xi1+k/ToAAOQSwi4AABb41Kc+pfLyci1atEj33nuvvvSlL+mpp56SJD322GO66667VF5erm9+85u67rrrkte53W595StfUWNjo6qqqvTKK6/o7rvv1v79+1VZWamrrrpKn/nMZ5KfPzIyom3btsnv92vevHnq7u7WfffdJ0n6+7//e1199dXatGmTysvL9dGPflT/9m//lvbrAACQSwxzcp0TAAAAAAB5gJVdAAAAAEDeIewCAAAAAPIOYRcAAAAAkHcIuwAAAACAvEPYBQAAAADkHcIuAAAAACDvOK0eQDYcOXLE6iHYkt/vV09Pj9XDwAmYF3tiXuyJebEf5sSemBd7Yl7shzmxp5nmZf78+WmvY2UXAAAAAJB3CLsAAAAAgLxD2AUAAAAA5B3CLgAAAAAg7xB2AQAAAAB5h7ALAAAAAMg7hF0AAAAAQN4h7AIAAAAA8o4z21/wscce0/79+1VZWakHH3xQkvSzn/1Mv/71r1VRUSFJuuGGG3TRRRdNufbAgQN66qmnFIvFdPnll+uaa67J5tABAAAAADki62H3sssu0+bNm/Xoo4+mPH7VVVfp6quvTntdLBbTk08+qa9+9auqqanR9u3b1dDQoIULF2Z6yAAAAACAHJP1Mubzzz9fXq/3lK97++23NW/ePNXX18vpdOqSSy5RR0dHBkYIAAAAAMh1WV/ZTeeFF17QSy+9pCVLluiv//qvpwTiQCCgmpqa5Ps1NTV66623sj1MAAAAAEAOsEXY3bRpk7Zs2SJJ+ulPf6of//jHuuWWW07779u1a5d27dolSdqxY4f8fv+cjDPfOJ1Ovjc2xLzYE/NiT8yL/TAn9sS82BPzYj/MiT2d7rzYIuxWVVUl/3z55Zfr/vvvn/I5Pp9Pvb29yfd7e3vl8/mm/fs2btyojRs3Jt/v6emZu8HmEb/fz/fGhpgXe2Je7Il5sR/mxJ6YF3tiXuyHObGnmeZl/vz5aa+zxdFDfX19yT+/+uqrWrRo0ZTPWbp0qd5//311d3crEonoN7/5jRoaGrI5TAAAAABAjsj6yu5DDz2kN954Q4ODg7r55pt13XXXqaurS3/84x9lGIZqa2t10003SYrv0/3BD36g7du3y+Fw6Itf/KLuvfdexWIxrV+/ftpQDAAACk/XgU69/kKrioeCGnN5dcGVTVqxeo3VwwIAWCjrYff222+f8tiGDRum/Vyfz6ft27cn37/oooumPX8XAAAUrq4DnfpgZ4u21FXJcLtlmlHt3dkiSQReAChgtihjBgAAOF2H2lq1rq5KhmFIkgzD0Lq6Kh1qa7V4ZAAAKxF2AQBATnOGg8mgm2AYhpzhkEUjAgDYAWEXAADktIjbK9M0Ux4zTVMRt8eiEQEA7ICwCwAActrKTU3a292fDLymaWpvd79WbmqyeGQAACvZ4pxdAACA05VoQvVMW6uc4ZAibo9WbmmmORUAFDjCLgAAyHkrVq8h3AIAUlDGDAAAAADIO4RdAAAAAEDeIewCAAAAAPIOYRcAAAAAkHcIuwAAAACAvEPYBQAAAADkHcIuAAAAACDvcM4uAAA4bV0HOvX6C60qHgpqzOXVx6+7QQs+tMTqYQEAwMouAAA4PV0HOvXBzhZtcUV1TY1bW1xRvfPjH6rrQKfVQwMAgLALAABOz6G2Vq2rq5JhGJIkwzB0WX2VDrW1WjwyAAAIuwAA4DQ5w8Fk0E0wDEPOcMiiEQEAMIGwCwAATkvE7ZVpmimPmaapiNtj0YgAAJhA2AUAAKdl5aYm7e3uTwZe0zT14tF+rdzUZPHIAACgGzMAAJjBid2WL7iySStWr5Gk5Ntn2lrlDIcUcXt06V/fRDdmAIAtEHYBAMC0kt2W66pkuN0yzaj27myRpJTAm/izJPn9fvX09Fgy3nwy000GAMDsUMYMAACmNV235XV1dFvOtOmOdPpgZwtHOgHAKSLsAgCAadFt2RrcZACAuUHYBQAA06LbsjW4yQAAc4OwCwAApjVdt+W93XRbzjRuMgDA3CDsAgCAaa1YvUbztjTrmWGHnusd0jPDDs3b0kyjpAzjJgMAzA26MQMAgLRO7LaMzJvuSKeV3GQAgFNG2AUAALAZbjIAwJmjjBkAAAAAkHcIuwAAAACAvEPYBQAAAADkHcIuAAAAACDv0KAKAAAAGdd1oFOvv9Cq4qGgxlxeXXBlE024AGQUYRcAAAAZ1XWgUx/sbNGWuioZbrdMM6q9O1skicALIGMoYwYAAEBGHWpr1bq6KhmGIUkyDEPr6qp0qK3V4pEByGeEXQAAAGSUMxxMBt0EwzDkDIcsGhGAQkDYBQAAQEZF3F6ZppnymGmairg9Fo0IQCEg7AIAACCjVm5q0t7u/mTgNU1Te7v7tXJTk8UjA5DPaFAFAACAjEo0oXqmrVXOcEgRt0crtzTTnApARhF2AQAAkHErVq8h3ALIKsqYAQAAAAB5h7ALAAAAAMg7lDEDAADMsa4DnXr9hVYVDwU15vLqgiubKOEFgCwj7AIAAMyhrgOd+mBni7bUVclwu2WaUe3d2SJJBN4cx00MILcQdgEAAObQobZWXVtXJcMwJEmGYWhdXZWeaWslGE0jVwIkNzGA3MOeXQAAgDnkDAeTQTfBMAw5wyGLRmRfyQDpiuqaGre2uKL6YGeLug50Wj20KQ61tWrdNDcxDrW1WjwyAOlkdWX3scce0/79+1VZWakHH3xQktTS0qLXXntNTqdT9fX1uuWWW+TxeKZce+utt6qsrExFRUVyOBzasWNHNocOAAAwKxG3V6YZTQm8pmkq4p76+qbQ5dIquDMclOFypzzGTQzA3rIadi+77DJt3rxZjz76aPKxVatWaevWrXI4HHr66af17LPP6sYbb5z2+rvvvlsVFRXZGi4AAMApW7mpSXt3tiRXAU3T1N7ufq3c0mz10GwnlwIkNzGA3JPVsHv++eeru7s75bELL7ww+efzzjtPr7zySjaHBAAA8pCV+0ATX+eZtlY5wyFF3B6t3NJsu5VKO8ilAMlNDCD32KpB1e7du3XJJZek/fi9994rSbriiiu0cePGbA0LAADkEDs0Elqxeg3hdhZyKUByEwPIPYZpmmY2v2B3d7fuv//+5J7dhJ///Od655139OUvf3lKUwdJCgQC8vl8GhgY0Le+9S194Qtf0Pnnnz/t19i1a5d27dolSdqxY4dGR0fn/onkAafTqUgkYvUwcALmxZ6YF3tiXuzHDnPy5F3b9emSsSmrhc+OFutvvnmfhSOzjh3mJZ1/73hV+55/Vo5QUFGPVw2f+rQuXHux1cPKCjvPS6FiTuxppnkpKSlJf12mBnQqXnzxRb322mu66667pg26kuTz+SRJlZWVWrt2rd5+++20YXfjxo0pK789PT1zP+g84Pf7+d7YEPNiT8yLPTEv9mOHOYkEejRW457m8eOWj80qdpiXdBZ8aIkW3PbfUx6z61jnmp3npVAxJ/Y007zMnz8/7XWWh90DBw7oF7/4hb7xjW+otLR02s8ZHh6WaZpyuVwaHh7WwYMHtWXLliyPFAAA5IL/DIb107d+pxIzqrEihy5YvEjL5tXach8oACBzshp2H3roIb3xxhsaHBzUzTffrOuuu07PPvusIpGI7rnnHknSueeeq5tuukmBQEA/+MEPtH37dg0MDOi73/2uJCkajerSSy/V6tWrszl0AACQA7oOdOr/Gw3po5Wl8peVSKapPe+9q/2BQX345r+3engAgCzKati9/fbbpzy2YcOGaT/X5/Np+/btkqT6+no98MADmRwaAADIA4faWnXtOYsVGjyu9491qyga01/UVOrt0moaCQFAgbG8jBkAkDlWHr8CWCFxbqu3olLeisrk43W9QxaOCgBgBcIuAOQpOxy/AmRbLp3bCgDILMIuAOSpQ22tunb87EpJMgxD6+qq9ExbK2EXeetMzm2lEgIA8gthFwDyVKKcczLDMOQMhywaEZB5iXD6TFurnOGQIm6PVm5pPmlopRICAPIPYRcA8hTlnChUK1avOeWASiUEAOSfIqsHAADIjJWbmrS3u1+maUrSRDnnpiaLRwbYjzMcTLkxJFEJAQC5jpVdAMhTp1vOCRQiKiEAIP8QdgEgj51OOSdQiM6ksRUAwJ4IuwAAZBAdfnMDlRAAkH8IuwAAZAgdfnMLlRAAkF9oUAUAQIYcamtNlsVKEx1+D7W1WjwyAADyH2EXAIAMocMvAADWoYwZAIAMocMv8tlM+9HZqw7ADgi7AICcd+ILa++Hlir4h3csf6FNh1/kq5n2o0tirzoAWyDsAgBy2okvut94/329sfNlbV51vsprqix9oU2HX+SrQ22tunaa/ejPjO9HT/cxfvYBZBNhFwCQ00580d313n/q2gU1+qDnmMorqyx/oU2HX+QjZzgow+VOeWxiP7o5w8cAIHtoUAUAyGknNoFyxqIqMgwVRaPJx3ihDcyt+H50M+WxxH70mT4GANlE2AUA5LQTX1hHihyKmaZiDkfyMV5oA3Nr5aYm7e3uT/7uJfejb2qa8WMAkE2UMQMAsiJT3VlPbAK1YvFC/fztd3TlqvMliaZQQAbMZj86e9UBWI2wCwDIuJk6t57pC+ApL7qrzpJny6V64Y/vyNnLC20gU2baj85edQB2QNgFAGTcTJ1b5+IFMS+sAQDAidizCwDIuBObSEk0jQIAAJlF2AUAZBzdWQEAQLYRdgEAGUd3VgAAkG3s2QUAZNxsOrcC2ZKpzuAAAHsh7AIAsiIXmkgRgjLHLt/bk3UGt8s4AQBnjrALAIAyezxSobPT93amzuCSbDNOAMCZY88uAACKh6B104SgQ+MhCKfPTt/bmTqD22mcAIAzR9gFAEAcj5RJdvreztQZ3E7jBACcOcIuAADieKRMstP3dqbO4HYaJwDgzBF2AQAQxyNlkp2+tytWr9G8Lc16Ztih53qH9MywQ/PGO4PbaZwAgDNHgyoAAJSbxyPlSudgu31v03UGt9s4AQBnhrALAMC4XDgeKcFOHY5nI1e+t9keZ67csACAXEQZMwAAOYjOwbkvecPCFdU1NW5tcUX1wc4WdR3otHpoAJAXCLsAAOQgOgfnPm5YAEBmUcYMAJhTlGVmR7xzcDQl8NI5OLc4w0EZLnfKY9ywAIC5w8ouAGDOUJaZPXQOzn0cdQQAmUXYBQDMGcoys2emI3SQG7hhAQCZRRkzAGDOUJaZXVZ3OJ6uZH3dxissG0+u4agjAMgswi4AYM6wj7RwpDv66N8rK7XgQ0usHl7OsPqGBQDkM8IuAGDOrNzUpL07W5KlzMmyzC3NVg8tK7LZnMvqRmCH2lp17TQl6798/lktuO2/Z20cAACkQ9gFAMyZQi7LTLfSKWnOn382v1Y66UrWHcFgVr4+kG1W32ACcOoIuwCAOVWoZZnpVjqfaWud8+9HNr9WOulK1qMeb1a+PpBNdrjBBODU0Y0ZAIA54AwHU4KflLnmXNn8Wumk6yTc8KlPZ20MQLbQaR7ITazsAgAwB7LZnMsOjcDSlaxfuPZi9fT0ZG0cQDbQaR7ITYRdAADmQDabc9mlEVihlqyj8NjhBhOAU0fYBQBgDmSzOVchNwIDrGCXG0wATk3Ww+5jjz2m/fv3q7KyUg8++KAkKRgM6nvf+56OHTum2tpa/cM//IO83qkNLl588UX9/Oc/lyR95jOf0WWXXZbNoQMAMKNsrnSyqgpkDzeYgNyU9bB72WWXafPmzXr00UeTjz333HO64IILdM011+i5557Tc889pxtvvDHlumAwqJ07d2rHjh2SpG3btqmhoWHaUAwAAADMJW4wAbkn692Yzz///CkBtaOjQ+vWrZMkrVu3Th0dHVOuO3DggFatWiWv1yuv16tVq1bpwIED2RgyAAAAACDH2GLP7sDAgKqrqyVJVVVVGhgYmPI5gUBANTU1yfd9Pp8CgcC0f9+uXbu0a9cuSdKOHTvk9/szMOrc53Q6+d7YEPNiT8yLPTEv9pNPc/LvHa+q4/ln5QwNKuIp19pPfVoXrr3Y6mGdlnyal3zCvNgPc2JPpzsvtgi7kxmGMeXswFO1ceNGbdy4Mfk+RyBMz+/3872xIebFnpgXe2Je7Cdf5qTrQKc+2NmiT9ZVyfA6ZJoh7X3yEfUP5OY+zXyZl3zDvNgPc2JPM83L/Pnz016X9TLm6VRWVqqvr0+S1NfXp4qKiimf4/P51Nvbm3w/EAjI5/NlbYwAAKBwHGprTXbeleI349fVVelQW6vFIwMAzJYtVnYbGhq0d+9eXXPNNdq7d6/Wrl075XNWr16tf/mXf1EwGJQk/fu//7u2bt2a7aECAIAs6DrQqddfaFXxUFBjLq8uuLIpqyuqznBQhsud8phhGHKGQ1kbAwDgzGQ97D700EN64403NDg4qJtvvlnXXXedrrnmGn3ve9/T7t27k0cPSdI777yjX/3qV7r55pvl9Xp17bXXavv27ZKkLVu20IkZAIA8lCgh3lJXJcPtlmlGtXdniyRlLfBG3F6ZZjRla5Vpmoq4PVn5+gBgB0MjYwqGRlXry81/+7Iedm+//fZpH7/rrrumPLZ06VItXbo0+f6GDRu0YcOGTA0NAADYwKG2Vl07TQnxM22tWQu7Kzc1ae/OlmQps2ma2tvdr5VbmrPy9QEgW4aGx9TdG9LR3qCO9obU3RtUd29I3YGgBgZHNM/v1be/dIXVwzwttihjBgAASLBDCXEiVD/T1ipnOKSI26OVW3KzOVUmzHWZudVl60C+Cw2NJgPt5LfdvUENhkbTXud0Fqmk2CHTNM+4ibAVCLsAMEd4sQbMjdmUEGfj923F6jVT/k5+z+e+zNwOZetArjNNU6Gh0fGV2ZCO9gTVHZhYpQ2G0wfaYmeR6mq8qqvxqL7Go7oar+rH36+ucKmoKPdCbgJhFwDmAC/WgLlzshJiq37f+D2Pm+syczuUrQO5wDRNDYZG1X1CuXFilTY8PJb22pJix3iY9U55W1leltOBdiaEXQCYA7xYA+bOyUqIrfp94/c8bq7LzO1Qtg7YhWmaOh4cmabcOB5uh0Yiaa8tLXGq3u9Rnc87vkKbCLVeVZaX5mQZ8pki7ALAHODFGjC3pishTrDq943f87i57lRN52sUGtM01T84rO6ekI4GJvbOJlZrR0ajaa91lTpV5/dOWpmNlx3X+Tyq8BZmoJ0JYRcA5gAv1oDsser3jd/zuLnuVE3na+SjWMxU//GheIAdD7QT+2hDGh1LH2g9ruLxfbOeSXtp42+97hIC7Skg7ALAHODFGpA9mfh9m03jKX7P4+aqU/Xk7/nRkZgOvderhV4Pna+RM2IxU4GBoSl7aLt746F2LBJLe63XXTKlGVTd+Pted0kWn0V+I+wCwBzgmBIge+b69222jaf4PZ8wU5n5bEz5nvtc2tvdr3nX/FVBfj9hX9FoTL3jgfbEcuNjgbAi0fSBtsJTqjr/+Kqsz5PS8djtItBmA2EXAObImb74AzB7c/n7diqNp/g9nxs0+4KdRKIx9faH1d0bUujgB/r9u93qDsRDbU9fSNGomfbayvKyKc2g6mo8qvN55CorzuKzwHQIuwAAoKDReCr7+J4j2yKRmI71TXQ17u4N6WggpO6eoHr6w4rF0gfa6oqyKXtoE02hykqJU3bG7AAAgIJG46ns43uOTBgbi04KtKGU43t6+8My0+RZw5Bqqlyq83m1eEGNKjwO1fu9qvN5Vetzq7SEyJSrmDkAsMBsmuHAHpir/Efjqezje47TNToW1bHA5PNnJ/bQBgaGZgy0/mp3SmfjxOpsnc+j4mKHJMnv96unpyeLzwiZRNgFgCybbTMcWI+5mp3JNwQcPr/O/cSGnPr+0Hgq+/ieYyYjo5GUrsZHeybKjvsGhtJeV1RkqHY80J54ZI+/2q1ipyOLzwJ2QNgFgCyjMUvuYK5O7sQbAsXFY/pVDt4QoPFU9vE9L2xDI2M61htKrsoenRRu+48Pp73OUWSMr9Cmhtn6Gq9qqtxyOouy+Cxgd4RdAMgyGrPkDubq5LghACCd8PDYRDOoZKiNv388OJL2OqejSLU+96TOxuPNofxe1VS65HAQaDE7hF0AyDIas+QO5urkuCEAFLbQ0OhEM6iekI4GJvbSDoZG017ndBaNnz3rGe90PHEGra/SraIiI+21wGwRdgEgy2jMkjuYq5PjhgCQ30zTVGhoVEd7JpUbJ/fRBhUaGkt7bUmxQ7U+T8qRPfXjR/hUVbgItMg4wi4AZBmNWXIHc3Vy3BAAcp9pmhoMjSbD7OROx929IYWH0wfa0hLHRFfjZJiNB9vK8jICLSxF2AUAC9CYJXcwVzM78YaA0+fWOdwQAGzHNE0dD47oaE9QRwOhSXtp42+HRyJpry0rdU45sqfeF39bWV6aUtkB2AlhFwAAnJHJNwTm4oxKzjYGTk8sZmpgcHj8mJ7xMNsT73Dc3RvUyGg07bWusuITyo0T4darck8JgRY5ibALAABsg7ONgZnFYqb6jw9NLTcOhNTdG9LoWPpA63EVjzeD8qS8ravxyOsm0CL/EHYBAIBtcJQREA+0gYHw+HE9qUf2dAdCikRiaa/1uktU7x9fnfUlyo7jodbrLsniswCsR9gFAAC2wVFGKBTRaEwfHDuuw28fjXc6nnRkz7FAWJFo+kBb4S2d2EPr8yTDbZ3PI7eLQAskEHYBAIBtcJQR8kkkGlNvX3hSuXE81B7tCaqnL6xozEx7bWV52bTlxnU1HrlKi7P4LIDcRdgFAAC2wVFGyDWRSEzH+iaXG090Ou7pDys2Q6D1V3vkr3JNdDieFGpLS3iZDpwpfosAAIBtcLYx7GhsLKpjfaGUIJs4tqe3PywzTZ41DKmmyqU6n1f1/kmrsz6van1uLZg/74y7lwNIj7ALAABshbONYYWR0YiOBcLJvbNHe4LJsuPAwNCMgdZf7Z50Bu3EebS11R4VFzuy+0Rw2joPdmn3vkPqCY3I64ip6dK1WrNqhdXDwhkg7AIAAKAgjIxGkiuy3ZNWaY8GQuobGEp7XVGRodpqd0qQTazS+qvdKnYSaHNd58EutbQfVv2qdfKMjSlmmmpp75AkAm8OI+wCAAAgbwyNjE00g5q0h/Zob0gDg8Npr3MUGfEVWr9XdZOO7Kn3e1VT5ZbTUZTFZ4Fsa23fp+pl61OOPatetlat7XsIuzmMsAsAADALnQe71Ppyh4LRIkocLRYeHosH2J7x1dnAxGrt8eBI2uucjiLV+tzJVdnJq7Q1lS45CLQFKxgx5JnUBV6KB95QxEhzBXIBYRcAAOAkEiWO1cs3yGMYlDhmQWhodGLfbG9IRwNBdffEV2iD4dG01zmdRfGzZ08oN66v8cpX6VJREeEFU3mdpmInbMw2TVMeZ/pu2rA/wi4AAMBJUOI490zTVDA8Om25cXdvUKGhsbTXlhQ7xrsap4bZ+hqPqioItDh1TY0NamnvUP2qRknxn8++wx1qbmyweGQ4E4RdAACAk6DE8fSYpqnB0Oh4iXEiyE6E2qHh9IG2tMQRD7K++L7ZuhqP6sf30lZVlCVvPABzIXHTavdrezUQHJHHaaq5sYGbWTmOsAsAAHASiRLHyQGLEsc40zQ1MDgSD7CB0MRe2vEjfIZHImmvLSt1phzZUze+Oltf41WFt5RAi6xas2qFrtiwjrOP8whhFwCAHNB1oFOvv9Cq4qGgxlxeXXBlE2fRZlGixLF62VoZhlFwJY6xmKmBweHksT3Jo3vGw+3IaDTtta6yYtVPCrKT35Z7Sgi0ADKGsAsAgM11HejUBztbtKWuSobbLdOMau/OFkki8GZJopSxtX2PQhEjL0scYzFTfceHUs6hTbw9FghpdCx9oPW4isdLjcfLjhOh1u+Rx0WgBWANwi4AADZ3qK1V19ZVpTRHWldXpWfaWgm7WbRm1YqcD7exmKnAQDi+d7Znouw4sUobicTSXlvuKZlyZE99jVe1Po+87pIsPgsAmB3CLgAANucMB2W43CmPGYYhZzhk0YhgZ9FoTL394fGV2fje2f7BMf3pSEDH+kKKRtPvM67wlqYc2VM/aS+tu6w4i88CAM4cYRcAAJuLuL0yzeiU5kgRt8fCUcFKkWhMvX3hKeXG3b1B9fSFFY2lD7RVFWXJI3vqJ63S1tZ45Col0ALIH4RdAABsbuWmJu3d2aJ146XMpmlqb3e/Vm5ptnpoyKCxSFQ9kwLt5CN7evvDis0QaKsrXar3eVTnjwfapWefJVdxTHU1HpWW8PIPQGHgXzsAAGwusS/3mbZWOcMhRdwerdzSzH7dPDA2Fo13NJ7myJ7e/rDMNHnWMKSaKvf4vllPyl7aWp9HJcWOlM/3+/0cpwKg4BB2AQDIAStWryHc5qiR0YiOBRIrtJNWaQNBBQaGZgy0/mp3SjOoxHm0tdUeFZ8QaDH3Og92qfXlDgWjRfI6Ymq6dG3ONykDCglhFwAA4AwNj0SSq7OTy427e4PqOz6c9rqiIkO11e54ubFvohlUvd8jf5VHTmdRFp8FJus82KWW9sOqXr5BHsNQzDTV0t4hSQReIEcQdgEAAGZhaHhsPNCGUlZpj/aGNDCYPtA6igz5E2fP+uJBNlF2XFPlltNBoLWj1vZ9ql62PuXIr+pla9XavoewC+QIwi4AAMC48NDo+Irs+CptIKSjPfFQezw0kvY6p6NItT53yrE9idJjX6VLDgJtzglGDHkmdUCX4oE3FDHSXAHAbgi7AACgoATDo5NWZVPLjoPh0bTXFTuLkkf2pO6hjQfaoiJ7hqCuA51666XdigZ6NOby6oIrm9j/PQtep6mYaU458svjTN8FG4C92CLsHjlyRN/73veS73d3d+u6667TVVddlXysq6tL3/nOd1RXVydJ+shHPqItW7ZkfawAAMDeTNNUMDw67ZE93b1BhYbG0l5bUuyIB1ifR/X+8TDrix/fU1Vh30CbTteBTn2ws0WfWVinsRq3TDOqvTtbJInAexJNjQ1qae9Q9bK1ySO/+g53qLmxweqhAZglW4Td+fPn64EHHpAkxWIx/d3f/Z0uvvjiKZ+3fPlybdu2LdvDAwAANmOapo4HR1KP7OkN6uj4ntqh4fSBtrTEMW25cV2NR1XlZSkrebnuUFurrh0/n1mKl+Guq6vSM22thN2TSOzLbW3fo1DEkMdpqrmxgf26QA6xRdid7PXXX9e8efNUW1tr9VAAAICFTNPUwODI+KrsRDOoxDm0wyORtNeWlTqnPbKnvsarCm9pXgXamTjDQRkud8pjhmHIGQ5ZNKLcsmbVCsItkMNsF3bb29vV2Ng47cf+4z/+Q3fccYeqq6vV3NysRYsWTft5u3bt0q5duyRJO3bskN/vz9h4c5nT6eR7Y0PMiz0xL/bEvNjPqc5JLGYqMBDS+93H4/8dO64jRwf0/rH4+yOj6QOtx12i+XWVOquuQmfVVuisuork+xXe/FqhPV1On1/FxWMqMgyVlJRIit9EcPrc/O7YAP+G2Q9zYk+nOy+GaaY7yjz7IpGI/u7v/k4PPvigqqqqUj4WDodVVFSksrIy7d+/Xz/60Y/08MMPz+rvPXLkSAZGm/v8fr96enqsHgZOwLzYE/NiT8yL/Uw3J7GYqb7jQ/GV2Z6gugPBZMfjY4GQRseiaf8+r7tkotx40j7a+hqPPK4SAu1JJPbsXrGwTmNjYzJNU3u7+zVvSzNlzDbAv2H2w5zY00zzMn/+/LTX2Wplt7OzUx/60IemBF1JcrsnSnAuuugiPfnkkzp+/LgqKiqyOEIAADCdWMxUb39Yf+oe1tu/PxLfO9sTD7XH+kKKRGJpry33lKTdQ+txlWTxWeSfRKB99qXdigSOK+L2aCVBF0CBsFXYnamEub+/X5WVlTIMQ2+//bZisZjKy8uzPEIAAApXNBpTb384uXc2vo82vn/2WF9I0Wj6YrHK8lLV+SYCbf14oK2t8chdVpzFZ1F4Vqxeo3Ubr2C1CkDBsU3YHR4e1sGDB3XTTTclH2tra5Mkbdq0Sa+88ora2trkcDhUUlKi22+/ndIlAADmWCQaU09faKIZ1KTzaHv7worG0gfaqooyLaivkq+yNL46Ox5ua2s8cpUSaAEA2WWbsFtWVqZ//Md/THls06ZNyT9v3rxZmzdvzvawAAAn6DrQqddfaFXxUFBjLq8uuLKJksgcMxaJqicQ1tHxrsbxfbTxgNvbH1ZshkDrq3SlrM4m3tb6PCotcbLfDQBgG7YJuwAA+0s0u9lSVyXD7ZZpRrV3Z4skEXhtZmwsOnEG7XgzqMSRPb39YaVrT2kYUk2VO2XfbCLU1vo8Kil2ZPeJAABwmgi7AIBZO9TWqmvrqpLbSAzD0Lq6Kj3T1krYtcDIaETHAlPLjbt7Q+o7PjRjoPVXu+OdjX2elPNo/T63ip35G2g7D3ap9eUOBaNF8jpiarp0LeeoAkCeIuwCAGbNGQ7KcLlTHjMMQ85wyKIR5b/hkcikFdp4kO0eD7d9x4fTXldUZKjW546XGfs8qvMnyo498ld55HQWZfFZ2EPnwS61tB9W9fIN8hiGYqaplvYOSSLwAkAeIuwCAGYt4vbKNKMpDQJN01TE7bFwVLlvaHhsYlU2EWx74mXHA4Mjaa9zOAz5qz0pe2cTR/fUVLnldBReoJ1Ja/s+VS9bn1KZUL1srVrb9xB2ASAPEXYBALO2clOT9u5s0brxUmbTNLW3u18rtzRbPTTbCw+NJvfOTj6yp7s3pOOh9IHW6ShSrc+TXJWNlxzHA62v0iUHgXbWghFDnhNOcjAMQ6GIvU93oPQaAE4PYRdAxvFCLX8k9uU+09YqZzikiNujlVua2a87LhgenVRqPPH2aG9IwfBo2uuKnUWq842vzvo9KefR+ipdKiqydxjLFV6nqZhpTqlM8DjTd5+2GqXXAHD6CLsAMooXavlnxeo1BRtuTdPUYGg02dU49dieoEJDY2mvLSl2pHQ4nrxKW1VeVjCB1sqbX02NDWpp71D1srXJyoS+wx1qbmzIytc/HZReA8DpI+wCyCheqCHXmKap48ERdQfGg2xidXb8HNqh4fSBtrTEeUK58cQe2qryspQVxUJk9c2vxNdobd+jUMSQx2mqubHB1v8W5WrpNQDYAWEXQEbxQg12ZJqm+geHU8qNjybfhjQyGkl7ravUGe9s7JsIsokjfCq8pQUfaGdih5tfa1atsHW4PVEull4DgF0QdgFkFC/UYJVYLBFoU4/sSfx5dCya9lp3WXEywCbDbE18L225p4RAe5q4+XXqcrH0GgDsgrALIKN4oYZMisVM9fSFJ5pBBcaP7Bk/wmcsEkt7rdddknJUT3KVtsYrr7ski8+icHDz69TlYuk1ANgFYRdARvFCDWcqFjPV2x+e1Nl4oty4py+ssUj6FdoKT2myGVT8HNqJ5lAeF4E227j5dXpyrfQaAOyCsAsg43ihhpOJRmPq7Q+Pn0MbTHnb0xdSNJp+5a+yvFR1vvEje2ripceJUOsqKz7tMXUd6NTrL7SqeCioMZdXF1zZVLBdqOcKN78AANlE2AUAZEUkElNPfyi5Ktvdk+hwHFRvX1jRWPpAW11RNqnc2KN6n1d1fq+Wn7tYoeDAnI+160CnPtjZoi11VTLcbplmVHt3tkgSgfcMcfMLAJAthF0AwJwZi0TVEwhPKjUOJo/w6e0Py5xha6av0jXlyJ76Go9qfR6Vlkz/vytXWbFCwbl/HofaWnVtXVVK1+B1dVV6pq2VsAsAaVh5jjYwHcIuAOCUjI5FdSwwudx4osNxYCB9oDUMyV/tTnY1jgfbeKit9XlUUuzI7hOZgTMclOFypzxmGIac4ZBFIwIAe7P6HG1gOoRdAMAUI6MRHRtfke0OhJJ7aLt7Q+o7PjRjoK0dP66nzjdxZE+9zyu/z61ip30C7Uwibq9MMzqla3DE7bFwVABgX3Y4Rxs4EWEXAArU0MiYjiVWZgPjZcfj4bb/+HDa64qKDNX63FPKjetqPPJXeeR0FmXxWWTGyk1N2ruzRevGS5lN09Te7n6t3NJs9dAAwJY4Rxt2RNgFgDw2NDyWLDOevDrbHQhqYHAk7XUOh6Ha6tQjexKB1lflltOR+4F2Jol9uc+0tcoZDini9mjllmb26wJAGpyjDTsi7AJAjgsPjeropH2z3ZOaQw2GRtNe53QUqdbnSR7ZU+/zJDse11S5VVRU2HfjV6xeQ7gFgFniHG3YEWEXAGzONE2FxgNt9wnn0Hb3hhQMpw+0xc6iZICtH28MldhHW13hKvhACwCYG5yjDTsi7AKADZimqcHQ6JQgmzi2Jzw8lvbakmJHypE9k/fSVpWXEWiRUSceNXLDJzdqyeKFVg8LgAU4Rxt2Q9gFgCwxTVPHgyOTyo1TS4+HRiJpry0tccbLjX0Te2fjodaryvLSlD1SQLZMd9TID9s69dmLB3jBa1OcgwqgkBB2AWAOmaap/sHhKUE2/n5II6PpA62r1Kk6/8Te2cRe2jqfRxXeMwu0XQc69foLrSoeCmrM5dUFVzaxHxVnbNqjRpavVWv7CwQoG+IcVACFhrALAKcoFjPVf3woXm4cmLpKOzoWTXutx1U86aieRLlxfJXW6y7JyApt14FOfbCzRVvqqmS43TLNqPbubJEkAi/OCEeN5BbOQQVQaAi7ADCNWMxUYGAouSp7PPy23v3Pnvj7gZDGIrG013rdJSlhdvIeWq+7JIvPIu5QW6uuHT8vVoq/wF1XV6Vn2loJuzgjHDWSW7g5AaDQEHYBFKxoNKbAwNC0R/YcC4QViaYPtBWe0niQ9cfLjCd3PHa7sh9oZ+IMB2W43CmPGYYhZzhk0YiQL6Y9auR3HfpsBo4aYa/pmePmBIBCQ9gFkNci0Zh6+8MTR/b0xEuPj/aG1NMXUjSa/kVeZXlZshnU2Yvq5C0zkuHWVVacxWdxZiJur0wzOuUFbsTtsXBUyAfTHTVy01WXz3k3Zvaazg3OQQVQaGYVdmOxmDo6OmQYhhoaGlRUVCRJ+u1vf6uPfexjGR0gAJxMJBJTT38oHmQTq7OBkLp7gurpDysWSx9oqyvKptlDGw+0ZaUT/0T6/X719PRk4+nMuZWbmrR3Z4vWjZcym6apvd39Wrml2eqhIQ+ceNRIJn5X2Gs6NzgHFUChmVXYfeSRR+T3++V0OvX888/r1ltv1bx589TW1kbYBZAVY2NRHesLTWkGdbQ3qN7+sMw0edYwpJoql+p8E82g4uHWq1qfW6Ul+V/gktiX+0xbq5zhkCJuj1ZuaWa/LnIGe03nDuegAigks3qVFwgEdNttt0mS1q9fr0ceeUR/9Vd/ldGBASg8o2NRHQuMlxv3Tn4bUmBg5kDrr3bHg6wv9cieWp9HJcWO7D4RG1qxeg3h1kLsNz0z7DU9M50Hu7R73yH1hEb4+QNQUGYVdiORiMbGxlRcXKza2lpt27ZNDz30kN57771Mjw9AnhkZjUw0gwrEz57t7gnqaCCkvoGhtNcZhlTr80w9ssfnld/nVrGTQAt7Yr/pmWOv6elL/PzVr1onz9gYP38ACsqMYTcajcrhcOjzn/+8QqGQqqqqJEkul0t33nmnXn755WyMEUCOGRoZ07FJ5cZHJ4Xb/uPDaa9zFBnjK7TeSeXG8aN7aqrccjqLsvgsgLnBftMzx17T08fPH4BCNmPY/fa3v6077rhD55xzzpSPFRUV6ROf+ETGBgbA3sLDY5OO6kk9tud4cCTtdQ6Hodrq8SN7EmXH46u0NVVuORwEWuQX9pvODfaanh5+/gAUshnD7tlnn62vfe1r2r59u3w+nyTpjTfe0E9+8hN985vfzMoAAVgnNDQ6pRlUogR5MDSa9jqns2j87Nnx1VmfR3X+eKj1VbpVVMSLLBQO9pvCSomfv8n4+QNQKGYMu83NzWpra9PXvvY1bd26Vbt379Z7772nq6++OlvjA5BBpmkqNDSaPLLnaG9I3YkGUT1BhYbG0l5b7CxKlhvXn/C2usJFoAXGsd8UVkr8/NWvapQkfv4AFJSTNqg677zz5Ha79fDDD2vdunW68847VVJSko2xAZgDpmlqMDQ6TYfj+CpteDh9oC0tcSS7GifCbCLQVpaXEWiBWWC/KayU+Dnb/dpeDQRH+Pk7CTqnA/llxrD7wAMP6I033tBVV12l6667Tk888YQOHTqkiy66KFvjAzALpmnqeHAktRlUbyhZcjw0Ekl7bWmJM35Uz6Qje+p98beV5aUppZcATg/7TWGlNatW6IoN69TT02P1UGyNzulA/pkx7J511ln6r//1v8rr9UqS6uvrdf/996u7u1ubN2/OygABxJmmqf7jw/G9s4GJvbOJcDsyGk17ravUOb5nNlFunOh07FW5p4RACwAoeHSuBvLPjGH3xhtvTHl/8eLFuueee3TfffcRdoEMiMVMHQsEdfidYynNoOL7aEMaHUsfaD2u4uRRPZPf1tV45HUTaAEAmAmdq4H8c9I9uyfy+Xx0YgbOQCxmKjAwlBpmE52OAyFFIrG013rdJfEQ6/eq3pc4izYear1u9tIDAHC66JwO5J9TDruS5HK55nocQF6JRmPqHRhKDbLjwfZYIKxINH2grapwyV/tipcc+yafR+uR20WgBQAgE+icDuSf0wq7AKRINKbe/rCO9kxqBhWI76Ht6QspGk1/J7iyvGzacuM6n0eLFp5FExEAALKMzulA/iHsAjOIRGI61hea0gyquzeknv6wYrH0gba60jXe1diTch5trc+jslJ+9QAAsBs6pwP5hVfcKHhjY9FkoD066cieo71B9faHZabJs4Yh1VS5VDe+d3ai3NirWp9bpSX8egEAAABW4dU4CsLoWDRZZpxcpe2Jvx8YGJox0Pqr3ckje5KrtL54yXFxsSO7TwQAAADArNgq7N56660qKytTUVGRHA6HduzYkfJx0zT11FNPqbOzU6Wlpbrlllu0ZMkSi0YLuxkZjUxbbnw0EFLfwFDa64qKDNVWu5NBdvIeWn+1W8VOAi0AAFbrPNil1pc7FIwWyeuIqenStXlVcpzvzw+wgq3CriTdfffdqqiomPZjnZ2d+uCDD/Twww/rrbfe0hNPPKFvf/vbWR4hrDQ0MjbRDGpSqD3aG9LA4HDa6xxFRnyF1u9Nlh0n9tDWVLvldBRl8VkAAJCbrApknQe71NJ+WNXLN8hjGIqZplraOyQpLwJhvj8/wCq2C7sz2bdvnz7xiU/IMAydd955CoVC6uvrU3V1tdVDwxwKD49NOrInEWbj7x8PjqS9zukoUq3PPamzsVf1/vgqbU2lSw4CLQAAp83KQNbavk/Vy9Ynz8A1DEPVy9aqtX1PXoTBfH9+gFVsF3bvvfdeSdIVV1yhjRs3pnwsEAjI7/cn36+pqVEgEJgSdnft2qVdu3ZJknbs2JFyDSY4nU7LvjfB0IiOdA/o/e7jev/Ycb0//ucj3cd1PJh+hbbY6dC82nKdVVep+XUVOquuQmfVVuqsugr5fR45inI/0Fo5L0iPebEn5sV+mBN7mot52f3aIdWvWpcMZJJUv6pRu1/bqys2rDvTIc5ozFEmd2nplMeHHGU5/fOWmJd8fX65iH/D7Ol058VWYfeee+6Rz+fTwMCAvvWtb2n+/Pk6//zzT/nv2bhxY0pQ5szS6fn9/ox9b0zTVDA8Om25cXdvUKGhsbTXlhQ7kmfOTj6yp77Go6oKl4qKjGmuGlFfIP2qby7J5Lzg9DEv9sS82A9zYk9zMS89wRF5xqb+/3sgOJLxOS+ODmtkZCQlaJumKWd0OKd/3hLzkq/PLxfxb5g9zTQv8+fPT3udrcKuz+eTJFVWVmrt2rV6++23U8Kuz+dLeZK9vb3Ja5B9pmlqMDSaLDM+OmkvbXdvSOHh9IG2tMSR7GqcOLKnfnwvbWV5WZpACwAArOJ1moqZ5pRA5nGmP3N+rjQ1NqilvUPVy9bKMAyZpqm+wx1qbmzI+NfOhnx/foBVbBN2h4eHZZqmXC6XhoeHdfDgQW3ZsiXlcxoaGvSv//qvamxs1FtvvSW3281+3QwzTVMDgyPxQBuY1OF4/O3wSCTttWWlzuSqbLLT8Xi4rfCWpvzPEgAwe3RthRWsDGSJn+/W9j0KRQx5nKaaGxvy5uc+358fYBXbhN2BgQF997vflSRFo1FdeumlWr16tdra2iRJmzZt0po1a7R//37ddtttKikp0S233GLlkPNGLGZqYHA4GWITQbZ7PNyOjEbTXusqK045qqd+0tE95Z4SAi0AzDG6tsIqVgeyNatW5PXPeL4/P8AKtgm79fX1euCBB6Y8vmnTpuSfDcPQ3/7t32ZzWHkjFjPVf3xIRyetyvYHx/SnIwEdC4Q0OpY+0HpcxfFVWf942XFildbvkcdFoAXyDauG9kbXVliJQAYgl9gm7OLMxWKmAgPh5N7ZeKidWKWNRGJpry33lEyszvq8qvPHV2lrfR553SVZfBYArMSqof0FI4Y8J9xkNAxDoQg3HgEAmIywm2Oi0Zh6B4bU3TPeECoQTDaFOhYIKxJNH2grvKWT9tB6dc7Z8+QqianO55HbRaAFwKphLrCySRAAALmEsGtDkWhMvX3hZLlxcg9tb1A9fWFFY+lf0FRVlCWP7EmWG9d4VFvjkau0OOVzaa0O4ESsGtofXVsBAJgdwq6FjvYG9cGxYEqY7e4Nqac/rNgMgba60qV6nye+Sju+jzZRglxawpQCOH2sGtqf1U2CAADIFSQjC/3gJx3645/7pzxuGFJNlStldTZRflzr86ik2JH9wQIoCKwa5gaaBAEAcHKEXQude3aNPK6S8TNoJ86jra32qJhAC8AChbBqSLdpAAAKA2HXQjdctcrqIQDAFPm8aki3aQAACkeR1QMAACBb4t2m107TbXqfxSMDAABzjbALACgYwYiR0nxLots0AAD5irALACgYXqcp00ztLE23aQAA8hNhFwBQMJoaG9R3uCMZeBPdppvoNg0AQN6hQRUAoGAkmlD9+BfP6PfHBhQdG9HSuipJyywdFwAAmHuEXQBAwTH8i9Vw6cRZwnRkBgAg/1DGDAAoKHRkBgCgMLCyCwAoKMGIIU+OdmTuPNil1pc7FIwWyeuIqenStaxGAwCQBmEXAFBQvE5TMdNMOYIoFzoydx7sUkv7YVUv3yCPYShG+TUAADOijBkAUFBytSMz5dcAAJwaVnYBAAUn1vOu9j17SLHRYS2ZV63Pf+Yq26+O5nL5NQAAViDsAgAKRqIUuObSLfKPd2LuO9xh9bBmJVfLrwEAsAplzACAgpHLpcC5Wn4NAIBVWNkFABSMXC4FTpRZt7bvUShiyOM01dzYYPvyawAArELYBQAUjFwvBV6zagXhFgCAWaKMGQBQMCgFBgCgcLCyCwAoGJQCAwBQOAi7AICCQilwfuo82KXWlzsUjBbJ64ip6dK1zDMAFDjCLgAAyGmJI6Wql2+QxzAUM021tMePlCLwAkDhYs8uAADIabl8pBQAIHMIuwAAIKcFI0ZKh20pd46UAgBkDmEXAADkNK/TTHbYTsilI6UAAJnBnl0AAGyGZkunpqmxQS3tHclS5sSRUs0cKQUABY2wCwCAjdBs6dRxpBRyxYk3sm745EYtWbzQ6mEBeYuwCwCAjcSbLa2fptnSHsLbDDhSCnY33Y2sH7Z16rMXD/CzC2QIYRcAABsJRgx5aLYEm6G0/sxNeyNr+Vq1tr/A9xLIEMIuAAA24nWaiplmSndhmi3BSpTWzw1uZAHZRzdmAABspKmxQX2HO5LdhRPNlppotgSLcI7x3KBrOJB9rOwCAGAjNFuC3bAiOTem7Rr+uw59lhtZQMYQdgEAsBmaLcFOKK2fG9PdyLrpqsvpxgxkEGEXAAAAaXGO8dw58UaW3+9XT0+PhSMC8hthFwAASKLjLqZHaT2AXEXYBQAAdNzFjCitB5CL6MYMAADouAsAyDuEXQAAoGDESGlAJNFxFwCQ2yhjBgAAp9xxl/29AAC7I+wCKBi8OAfSO5WOuzPt771iw7psDz0v8e8VAJw5wi6AgkDzHWBmp9JxN76/d/00+3v3EHbnAP9eAcDcIOwCKAgzvTjnxSMQN9uOu8GIIQ/7e0/qdFdn+fcKAOaGLcJuT0+PHn30UfX398swDG3cuFFNTU0pn9PV1aXvfOc7qqurkyR95CMf0ZYtW6wYLoAcxItzYO6c6v7eQnQmq7P8ewUAc8MWYdfhcKi5uVlLlizR0NCQtm3bplWrVmnhwoUpn7d8+XJt27bNolECyGW8OAfmzqns7y1UZ7I6y79XADA3bHH0UHV1tZYsWSJJcrlcWrBggQKBgMWjApBPmhob1He4Q6YZf7GYeHHexItz4JStWbVCzY3LVHR4j8Kv71HR4T1qblxGie0kZ3KUE/9eAcDcsMXK7mTd3d36wx/+oHPOOWfKx/7jP/5Dd9xxh6qrq9Xc3KxFixZZMEIAuehUmu8AOLnZ7u8tVGeyOsu/VwAwNwwzcdvQBoaHh3X33XfrM5/5jD7ykY+kfCwcDquoqEhlZWXav3+/fvSjH+nhhx+e9u/ZtWuXdu3aJUnasWOHRkdHMz72XOR0OhWJRKweBk7AvNgT82JPzIv9MCdxr+4/oB+2dap6+aRS79916KZNa3TxRauzPh7mxZ6YF/thTuxppnkpKSlJe51twm4kEtH999+vCy+8UJ/85CdP+vm33nqr7rvvPlVUVJz0c48cOTIXQ8w7fr9fPT09Vg8DJ2Be7Il5sSfmxX6YkwmdB7vU2r4vuTrbZOHqLPNiT8yL/TAn9jTTvMyfPz/tdbYoYzZNU48//rgWLFiQNuj29/ersrJShmHo7bffViwWU3l5eZZHCgAAMDuUegOAtWwRdt9880299NJLWrx4se644w5J0g033JBM75s2bdIrr7yitrY2ORwOlZSU6Pbbb5/S+AEAAAAAAMkmYXfZsmX62c9+NuPnbN68WZs3b87SiAAAAHCmOg92qfXlDgWjRfI6Ymq6dC2r3QCyxhZhFwAAAPml82CXWtoPq3r5BnkMQzHTVEt7hyQReAFkhS3O2QUAAEB+aW3fp+pla5PbzgzDUPWytWpt32fxyAAUCsIuAAAA5lwwYkzpr2IYhkIReq4AyA7KmAEAAMaxx3TueJ2mYqaZEnhN05THaYtTLwEUAFZ2AQAANLHHNLZ8gzwXrFds+Qa1tB9W58Euq4eWk5oaG9R3uEOmGQ+3pmmq73CHmhobLB4ZgELByi4AAIASe0zXT7PHdA+ru6ch8T1rbd+jUMSQx2mqubGB7yWArCHsAgAAKL7H1MMe0zm1ZtUKwi0Ay1DGDAAAoPge00TJbQJ7TAEgdxF2AQAAxB5TAMg3lDEDAGyBLriwGntMASC/EHYBAJZLdMGtXr5BHsNQzDTV0t4hSQQNZBV7TAEgf1DGDACwXLwL7tppuuDus3hkAAAgV7GyCwCwHF1wgdPHFgAAmB5hFwBgOa/TVMw0kyu7El1wgdlgCwAApEcZMwDAcnTBBU4PWwAAID1WdgEAlqMLLnB62AIAAOkRdgEAtkAXXODUsQUAANKjjBkAACBHsQUAANJjZRcAACBHsQUAANIj7AIAAOQwtgAAwPQIuwAAnCLONQUAwP4IuwAAnALONQUAIDfQoAoAgFPAuaYAAOQGwi4AAKcgGDFSjnmRONcUAAA7IuwCAHAKvE4zecxLAueaAgBgP4RdAABOAeeaAgCQG2hQBQDAKeBc07lDV2sAQCYRdgEAOEWca3rm6GoNAMg0ypgBAEDW0dUaAJBphF0AAJB1dLUGAGQaYRcAAGQdXa0BAJlG2AUAAFlHV2sAQKbRoAoAAGQdXa0BAJlG2AUAAJagqzUAIJMoYwYAAAAA5B1WdgEAADBF58Eutb7coWC0SF5HTE2XrmUlHkBOIewCAGaFF75A4eg82KWW9sOqXr5BHsNQzDTV0t4hSfzeA8gZhF0AwEnxwjf/cPMCM2lt36fqZeuTZyEbhqHqZWvV2r6HnxMAOYOwCwA4KV745hduXuBkghFDnvHf9wTDMBSKGGmuAAD7oUEVAOCkghEjGXQTeOGbu+I3L9ZOc/Nin8Ujg114nWbyDOQE0zTlcZpprgAA+yHsAgBOihe++YWbFziZpsYG9R3uSP7em6apvsMdampssHhkADB7lDEDAE6qqbFBLe0dydXAxAvfZl745iSv01TMNFMCLzcvMFminL21fY9CEUMep6nmxgbK3AHkFMIuAOCkeOGbX7h5gdlYs2oFv+MAchphFwAwK7zwzR/cvAAAFALCLoC8xdEqQHrcvAAA5DvCLoC8xNEqgL1w8wkAkG22CrsHDhzQU089pVgspssvv1zXXHNNysfHxsb0yCOP6Pe//73Ky8t1++23q66uzprBArA1zoUF7IObTwAAK9gm7MZiMT355JP66le/qpqaGm3fvl0NDQ1auHBh8nN2794tj8ej73//+2pvb9c///M/6x/+4R8sHDUAuwpGDHny7GgVVsaQq7j5BACwgm3O2X377bc1b9481dfXy+l06pJLLlFHR0fK5+zbt0+XXXaZJOmjH/2oDh06NOXcRwCQ8u9c2MTKWGz5BnkuWK/Y8g1qaT+szoNdVg8NOCnO9QUAWME2YTcQCKimpib5fk1NjQKBQNrPcTgccrvdGhwczOo4AeSGpsYG9R3uSAbexNEqTTl6tEp8ZWztNCtj+yweGXBy+XbzCQCQG2xTxjyXdu3apV27dkmSduzYIb/fb/GI7MnpdPK9sSHmZW5csWGdKqsq9eyv2xUck7zF0ueuatTFF60+rb/P6nkZc5TJXVo65fEhR1lB/7xYPS+Yaro5ueGqy/XDtk5VL590ru/vOnTTVZczf1nC74o9MS/2w5zY0+nOi23Crs/nU29vb/L93t5e+Xy+aT+npqZG0WhU4XBY5eXlU/6ujRs3auPGjcn3e3p6MjfwHOb3+/ne2BDzMneWLF6o//6Fz6Y8drrfW6vnpTg6rJGRkZRSUNM05YwOF/TPi9Xzgqmmm5MlixfqsxcPqLX9heS5vp9tbNCSxQuZvyzhd8WemBf7YU7saaZ5mT9/ftrrbBN2ly5dqvfff1/d3d3y+Xz6zW9+o9tuuy3lcz784Q/rxRdf1HnnnadXXnlFK1asmLIHCADyUVNjg1raO5KlzImy7OYcLctG4eFcXwBAttkm7DocDn3xi1/Uvffeq1gspvXr12vRokX66U9/qqVLl6qhoUEbNmzQI488ov/23/6bvF6vbr/9dquHDQBZkQgJre17kitjzY0NhAcAAIA0bBN2Jemiiy7SRRddlPLYZz87UYJYUlKiL33pS9keFgDYAitjAAAAs2ebbswAAAAAAMwVwi4AAAAAIO8QdgEAAAAAeYewCwAAAADIO7ZqUAUAmNB5sEutL3coGC2S1xFT06VraVAFAAAwS4RdALChzoNdamk/rOrlG+QxDMVMUy3tHZJE4AUAAJgFypgBwIZa2/epetlaGYYhSTIMQ9XL1qq1fZ/FIwMAAMgNhF0AsKFgxEgG3QTDMBSKGGmuAAAAwGSUMQOADXmdpmKmmRJ4TdOUx2laOCrgzLAPHQCQTazsAoANNTU2qO9wh0wzHm5N01Tf4Q41NTZYPDLg9CT2oceWb5DngvWKLd+glvbD6jzYZfXQAAB5ipVdALChxGpXa/sehSKGPE5TzY0NrIIhZ8X3oa+fZh/6Hn6uAQAZQdgFAJtas2oFIQB5Ixgx5GEfOgAgiyhjBgAAGed1msmy/AT2oQMAMomwCwAAMo596ACAbKOMGQAAZBz70AEA2UbYBQAAWcE+dABANlHGDAAAAADIO4RdAAAAAEDeIewCAAAAAPIOYRcAAAAAkHcIuwAAAACAvEPYBQAAAADkHcIuAAAAACDvEHYBAAAAAHnHafUAAACwUufBLrW+3KFgtEheR0xNl67VmlUrrB4WAAA4Q4RdAEDB6jzYpZb2w6pevkEew1DMNNXS3iFJBF4AAHIcZcwAgILV2r5P1cvWyjAMSZJhGKpetlat7fssHhkAADhTrOzCFigjBGCFYMSQZzzoJhiGoVDESHMFAADIFYRdWI4yQgBW8TpNxUwzubIrSaZpyuM0LRwVAACYC4RdWC5eRrh+mjLCPYRdABnV1NiglvaOZCmzaZrqO9yh5sYGq4c2K1TFAACQHmEXlqOMEEC2TQ6Jsf4e9ex9R56aefI4TTU3NuREYKQqBgCAmRF2YTnKCAFk04kh0T2+mvtXjctyKiRSFQMAwMzoxgzLNTU2qO9wh0wzHm4TZYRNOVJGCCC35EsH5mDESLlJKFEVAwDAZKzswnKJFYjW9j0KRYycKiMEkHvyZesEVTEAAMyMsAtbWLNqBeEWQFbkS0jM9eZaAABkGmEXAFBQ8iUkUhUDAMDMCLsAgIKSTyGRqhgAANIj7AIACg4hEQCA/Ec3ZgAAAABA3iHsAgAAAADyDmXMAACcos6DXWp9uUPBaJG8jpiaLl1LWTQAADZD2AUA4BR0HuxSS/thVS/fII9hKGaaamnvkCQCLwAANkIZMwAAp6C1fV/y2CJJMgxD1cvWqrV9n8UjAwAAkxF2AQA4BcGIkQy6CYZhKBQx0lwBAACsQNgFAOAUeJ2mTNNMecw0TXmcZporAACAFdizCwA4KRoyTWhqbFBLe0eylNk0TfUd7lBzY4PVQwMAAJNYHnZbWlr02muvyel0qr6+Xrfccos8Hs+Uz7v11ltVVlamoqIiORwO7dixw4LRAkDhoSFTqsRzbm3fo1DEkMdpqrmxoSC/FwAA2JnlYXfVqlXaunWrHA6Hnn76aT377LO68cYbp/3cu+++WxUVFVkeIQAUtnhDpvXTNGTaU7ABb82qFQX73AEAyBWW79m98MIL5XA4JEnnnXeeAoGAxSMCAExGQyYAAJCLLF/ZnWz37t265JJL0n783nvvlSRdccUV2rhxY7aGBQAFzes0FTPNlMBLQyYAAGB3hnliS8kMuOeee9Tf3z/l8euvv15r166VJP385z/XO++8oy9/+ctTVhAkKRAIyOfzaWBgQN/61rf0hS98Qeeff/60X2/Xrl3atWuXJGnHjh0aHR2duyeTR5xOpyKRiNXDwAmYF3sq5Hl5df8B/bCtU9XLJzVk+l2Hbtq0RhdftNrSsRXyvNgVc2JPzIs9MS/2w5zY00zzUlJSkva6rITdk3nxxRf1q1/9SnfddZdKS0tP+vk/+9nPVFZWpquvvnpWf/+RI0fOdIh5ye/3q6enx+ph4ATMiz0V+rx0HuxSa/u+ZEOmJps0ZCr0ebEj5sSemBd7Yl7shzmxp5nmZf78+Wmvs7yM+cCBA/rFL36hb3zjG2mD7vDwsEzTlMvl0vDwsA4ePKgtW7ZkeaQAULhoyAQAAHKN5WH3ySefVCQS0T333CNJOvfcc3XTTTcpEAjoBz/4gbZv366BgQF997vflSRFo1FdeumlWr16tYWjBgAAAADYmeVh9/vf//60j/t8Pm3fvl2SVF9frwceeCCbwwIAAAAA5DDLjx4CAAAAAGCuEXYBAAAAAHmHsAsAAAAAyDuEXQAAAABA3iHsAgAAAADyDmEXAAAAAJB3CLsAAAAAgLxj+Tm7AACcqPNgl1pf7lAwWiSvI6amS9dqzaoVVg8LAADkEMIuAMBWOg92qaX9sKqXb5DHMBQzTbW0d0gSgRcAAMwaZcwAAFtpbd+n6mVrZRiGJMkwDFUvW6vW9n0WjwwAAOQSwi4AwFaCESMZdBMMw1AoYqS5AgAAYCrCLgDAVrxOU6ZppjxmmqY8TjPNFQAAAFMRdgEAttLU2KC+wx3JwGuapvoOd6ipscHikQEAgFxCgyoAgK0kmlC1tu9RKGLI4zTV3NhAcyoAAHBKCLsAANtZs2oF4RYAAJwRypgBAAAAAHmHsAsAAAAAyDuEXQAAAABA3iHsAgAAAADyDmEXAAAAAJB3CLsAAAAAgLxD2AUAAAAA5B3CLgAAAAAg7xB2AQAAAAB5h7ALAAAAAMg7hF0AAAAAQN4h7AIAAAAA8g5hFwAAAACQdwi7AAAAAIC8Q9gFAAAAAOQdwzRN0+pBAAAAAAAwl1jZLWDbtm2zegiYBvNiT8yLPTEv9sOc2BPzYk/Mi/0wJ/Z0uvNC2AUAAAAA5B3CLgAAAAAg7xB2C9jGjRutHgKmwbzYE/NiT8yL/TAn9sS82BPzYj/MiT2d7rzQoAoAAAAAkHdY2QUAAAAA5B2n1QOAPTz//PNqaWnRE088oYqKCquHU/B+8pOfaN++fTIMQ5WVlbrlllvk8/msHlbBa2lp0WuvvSan06n6+nrdcsst8ng8Vg+roP32t7/V//7f/1t//vOf9e1vf1tLly61ekgF7cCBA3rqqacUi8V0+eWX65prrrF6SAXvscce0/79+1VZWakHH3zQ6uFAUk9Pjx599FH19/fLMAxt3LhRTU1NVg+r4I2Ojuruu+9WJBJRNBrVRz/6UV133XVWDwuSYrGYtm3bJp/Pd8pdmQm7UE9Pjw4ePCi/32/1UDDu6quv1vXXXy9Jam1t1c6dO3XTTTdZPCqsWrVKW7dulcPh0NNPP61nn31WN954o9XDKmiLFi3Sl7/8Zf3whz+0eigFLxaL6cknn9RXv/pV1dTUaPv27WpoaNDChQutHlpBu+yyy7R582Y9+uijVg8F4xwOh5qbm7VkyRINDQ1p27ZtWrVqFb8rFisuLtbdd9+tsrIyRSIR3XXXXVq9erXOO+88q4dW8FpbW7VgwQINDQ2d8rWUMUP/9E//pM997nMyDMPqoWCc2+1O/nlkZIS5sYkLL7xQDodDknTeeecpEAhYPCIsXLhQ8+fPt3oYkPT2229r3rx5qq+vl9Pp1CWXXKKOjg6rh1Xwzj//fHm9XquHgUmqq6u1ZMkSSZLL5dKCBQv4/4kNGIahsrIySVI0GlU0GuX1lw309vZq//79uvzyy0/relZ2C1xHR4d8Pp/OPvtsq4eCE/zLv/yLXnrpJbndbt19991WDwcn2L17ty655BKrhwHYRiAQUE1NTfL9mpoavfXWWxaOCLC/7u5u/eEPf9A555xj9VCgeIXKnXfeqQ8++EBXXnmlzj33XKuHVPB+9KMf6cYbbzytVV2JsFsQ7rnnHvX39095/Prrr9ezzz6rr371q9kfFGacl7Vr1+qGG27QDTfcoGeffVb/+q//yr6RLDnZvEjSz3/+czkcDn384x/P8ugK02zmBAByzfDwsB588EF9/vOfT6nognWKior0wAMPKBQK6bvf/a7ee+89LV682OphFazXXntNlZWVWrJkibq6uk7r7yDsFoCvfe1r0z7+3nvvqbu7W3fccYekeJnAnXfeqfvuu09VVVVZHGFhSjcvJ/r4xz+u++67j7CbJSeblxdffFGvvfaa7rrrLsqbsmS2vyuwls/nU29vb/L93t5eGusBaUQiET344IP6+Mc/ro985CNWDwcn8Hg8WrFihQ4cOEDYtdCbb76pffv2qbOzU6OjoxoaGtLDDz+s2267bdZ/B2G3gC1evFhPPPFE8v1bb71V9913H92YbeD999/XWWedJSleas6eRHs4cOCAfvGLX+gb3/iGSktLrR4OYCtLly7V+++/r+7ubvl8Pv3mN785pRckQKEwTVOPP/64FixYoE9+8pNWDwfjjh8/LofDIY/Ho9HRUR08eFB/+Zd/afWwCtrWrVu1detWSVJXV5eef/75U/7/CmEXsKF//ud/1vvvvy/DMOT3++nEbBNPPvmkIpGI7rnnHknSueeey9xY7NVXX9U//uM/6vjx49qxY4fOPvtsfeUrX7F6WAXJ4XDoi1/8ou69917FYjGtX79eixYtsnpYBe+hhx7SG2+8ocHBQd1888267rrrtGHDBquHVdDefPNNvfTSS1q8eHGyuu6GG27QRRddZPHICltfX58effRRxWIxmaapj33sY/rwhz9s9bBwhgzTNE2rBwEAAAAAwFzi6CEAAAAAQN4h7AIAAAAA8g5hFwAAAACQdwi7AAAAAIC8Q9gFAAAAAOQdwi4AAAAAIO8QdgEAyFFPP/20vvOd7yTfb2lp0Te/+U1FIhELRwUAgD0QdgEAyFF/+Zd/qa6uLv3hD39QW1ubDhw4oC9/+ctyOp1WDw0AAMsZpmmaVg8CAACcnp/97Gd69dVXFQ6H9c1vflN+v1/hcFj33HOP/vM//1P33nuvFi9ebPUwAQDIOlZ2AQDIYR/60If03nvvaevWrfL7/ZKkkpISbd++XR/96EctHh0AANYh7AIAkKPee+89PfHEE1q3bp327NmTfNzpdKqiosLCkQEAYD3CLgAAOSgQCOj+++/Xf/kv/0V/+7d/q/fee09dXV1WDwsAANsg7AIAkGPC4bDuu+8+XXXVVWpoaFBpaak+9alP6Sc/+YnVQwMAwDZoUAUAQJ569NFH9alPfYoGVQCAgkTYBQAgD91333364x//KL/fryuuuEKXXXaZ1UMCACCrCLsAAAAAgLzDnl0AAAAAQN4h7AIAAAAA8g5hFwAAAACQdwi7AAAAAIC8Q9gFAAAAAOQdwi4AAAAAIO8QdgEAAAAAeYewCwAAAADIO4RdAAAAAEDe+f8BpjpGmHcpj5YAAAAASUVORK5CYII=",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plot_ds(data,m[-1],q[-1])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Criticità\n",
"\n",
"I metodi elementari di discesa del gradiente illustrati sopra non garantiscono in generale una elevata convergenza. Inoltre, il loro utilizzo pone un insieme di questioni\n",
"\n",
"- la scelta del valore del learning rate $\\eta$ può risultare difficile. Un valore troppo piccolo può comportare una convergenza eccessivamente lenta, mentre un valore troppo grande può portare ad oscillazioni intorno al minimo, o addirittura a divergenza\n",
"- per ovviare a questa problematica è possibile utilizzare dei metodi di aggiustamento di $\\eta$ nel tempo, ad esempio riducendolo secondo uno schema predefinito o quando il decremento della funzione di costo calcolata in due epoche successive risulti inferiore a una soglia data. Sia gli schemi che le soglie devono però essere predefiniti e non possono quindi adattarsi in dipendenza delle caratteristiche del dataset\n",
"- lo stesso learning rate si applica per l'aggiornamento di tutti i coefficienti\n",
"- in molti casi la funzione di costo, in particolare se si ha a che fare con reti neurali, risulta fortemente non convessa, caratterizzata quindi da numerosi minimi locali e da punti di sella. I metodi considerati possono avere difficoltà a uscire da situazioni di questo tipo, e in particolare dai punti di sella, spesso circondati da regioni a gradiente molto limitato.\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Momento\n",
"\n",
"I metodi precedenti risultano poco efficienti in situazioni in cui la funzione di costo varia in modo molto diverso al variare della direzione considerata (ad esempio se si hanno valli che discendono lentamente e con pareti laterali ripide). In questo caso, infatti, gli algoritmi precedenti procedono molto lentamente in direzione del minimo, oscillando in modo sostanziale nella direzione trasversale ad essa: questa situazione è illustrata a sinistra nella figura sottostante.\n",
"\n",
"Il *metodo del momento* fa riferimento ad una interpretazione fisica del metodo di ottimizzazione, in cui il processo di discesa del gradiente viene visto come lo spostamento di un corpo di massa $m=1$ che si muove sulla superficie della funzione di costo $J(\\theta)$ soggetto a una forza peso $F(\\theta)=-\\nabla U(\\theta)$, dove $U(\\theta)=\\eta h(\\theta)=\\eta J(\\theta)$ è l'energia potenziale del corpo nella posizione $\\theta$ (si assume quindi che la costante fisica $g$ relativa alla forza peso $F=-mgh$ sia pari a $\\eta$). In questo modello, il valore negativo del gradiente $-\\eta J'(\\theta)$ è quindi pari al vettore forza (e accelerazione, in quanto $a=\\frac{F}{m}$) del corpo nel punto $\\theta$. \n",
"\n",
"Nel metodo della discesa del gradiente, si assume che lo spostamento del corpo in un certo punto $\\theta$ sia determinato dalla accelerazione calcolata nello stesso punto, e quindi dal gradiente $J'(\\theta)$, in quanto vale la regola di aggiornamento $\\theta^{(k+1)}=\\theta^{(k)}-\\eta J'(\\theta^{(k)})$. \n",
"\n",
"Nel metodo del momento, si fa riferimento a un modello più consistente con la realtà fisica di un corpo che si muove su una superficie soggetto alla forza peso, modello che prevede di utilizzare il concetto di velocità $v(\\theta)$. In questo modello, lo spostamento del corpo a partire da un certo punto $\\theta$ è determinato dalla velocità calcolata nello stesso punto $\\theta^{(k+1)}=\\theta^{(k)}+v^{(k+1)}$, dove la variazione di velocità è data dalla accelerazione $v^{(k+1)}=v^{(k)}-\\eta J'(\\theta^{(k)})$. \n",
"\n",
"Come si può osservare, si ha che\n",
"\n",
"\\begin{align*}\n",
"v^{(k+1)}&=-\\eta J'(\\theta^{(k)})+v^{(k)}=-\\eta J'(\\theta^{(k)})-\\eta J'(\\theta^{(k-1)})+v^{(k-1)}=\\cdots=-\\eta\\sum_{i=0}^kJ'(\\theta^{(i)})+v^{(0)}\\\\\n",
"\\theta^{(k+1)}&=\\theta^{(k)}+v^{(k+1)}=\\theta^{(k)}-\\eta\\sum_{i=0}^kJ'(\\theta^{(i)})+v^{(0)}\n",
"\\end{align*}\n",
"\n",
"che corrisponde all'associare lo spostamento alla somma (integrale nel caso della fisica) delle accelerazioni passate.\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
" \n",
"\n",
"\n",
"Il riferimento a questo modello porta l'algoritmo a tendere ad ogni passo a mantenere, almeno in parte, la direzione del passo precedente (in quanto $v^{(k+1)}=-\\eta J'(\\theta^{(k)})+v^{(k)})$, premiando le direzioni che si manifestano con costanza in una sequenza di passi. Ne deriva il comportamento a destra della figura precedente, in cui l'inerzia nella direzione del minimo porta a una limitazione delle oscillazioni.\n",
"\n",
"Si noti che ciò non avviene nella discesa del gradiente, in cui si ha $v^{(k+1)}=-\\eta J'(\\theta^{(k)})$.\n",
"\n",
"Matematicamente, l'effetto di inerzia viene ottenuto sottraendo alla velocità (vettoriale) calcolata al passo precedente la valutazione del gradiente effettuata nella corrispondente posizione. Il gradiente viene sottratto in quanto, mantenendo la corrispondenza con la meccanica di corpo soggetto ad accelerazione di gravità, un gradiente positivo tende a ridurre la velocità.\n",
"\n",
"Il metodo del momento utilizza tipicamente un secondo parametro $\\gamma$, che determina la frazione di $v^{(k)}$ che permane nella definizione di $v^{(k+1)}$, e che svolge la funzione (fisicamente) di un coefficiente di attrito. Si ottiene quindi la formulazione:\n",
"\n",
"\\begin{align*}\n",
"v^{(k+1)}&=\\gamma v^{(k)} -\\eta\\sum_{i=1}^nJ'(\\theta^{(k)};x_i)\\\\\n",
"\\theta^{(k+1)}&=\\theta^{(k)}+v^{(k+1)}\n",
"\\end{align*}\n",
"Il metodo del momento ad ogni passo determina inizialmente il vettore di spostamento attuale, a partire da quello al passo precedente e dal gradiente di $\\theta$: il contributo relativo dei due termini è pesato dalla coppia di parametri $\\gamma$ e $\\eta$. Lo spostamento calcolato viene quindi applicato al valore attuale di $\\theta$ (il segno meno deriva come sempre dal fatto che stiamo assumendo di cercare un minimo locale).\n",
"\n",
"Se il gradiente è orientato nella stessa direzione della velocità attuale, tale velocità viene incrementata, per cui l'aggiornamento di $\\theta$ diviene maggiore, incrementandosi man mano che la direzione di spostamento rimane coerente con il gradiente nei punti attraversati.\n",
"\n",
"```python\n",
"v = 0\n",
"for i in range(n_epochs):\n",
" g = 0\n",
" for k in range(dataset_size):\n",
" g = g+evaluate_gradient(loss_function, theta, X[k])\n",
" v = gamma*v-eta*g\n",
" theta = theta+v\n",
"```"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n",
"Come si può vedere, mentre $\\theta^{(k)}=(\\theta_1^{(k)},\\ldots,\\theta_d^{(k)})^T$ è la valutazione della soluzione ottima al passo $k$, $v^{(k)}=(v_1^{(k)},\\ldots,v_d^{(k)})^T$ è l'aggiornamento applicato a tale valore per ottenere $\\theta^{(k+1)}$: possiamo vedere quindi $v$ come il vettore velocità di spostamento di $\\theta$ nello spazio delle soluzioni.\n",
"\n",
"Come già illustrato sopra, possiamo esprimere l'aggiornamento nel modo seguente, evidenziando come esso dipenda dal gradiente calcolato in tutte le posizioni precedentemente attraversate, con un effetto che va a diminuire esponenzialmente con $\\gamma$ man mano che si risale nel passato. Assumendo $v^{(0)}=0$:\n",
"\n",
"\\begin{align*}\n",
"\\theta^{(k+1)}&=\\theta^{(k+1)}+v^{(k+1)}= \\theta^{(k)}+\\gamma v^{(k)}-\\eta\\sum_{i=1}^nJ'(\\theta^{(k)};\\mathbf{x}_i)=\\theta^{(k)}+\\gamma^2 v^{(k-1)}-\\gamma\\eta\\sum_{i=1}^nJ'(\\theta^{(k-1)};\\mathbf{x}_i) -\\eta\\sum_{i=1}^nJ'(\\theta^{(k)};\\mathbf{x}_i)\\\\\n",
"&=\\theta^{(k)}+\\gamma^2 v^{(k-1)}-\\eta\\left(\\sum_{i=1}^nJ'(\\theta^{(k)};\\mathbf{x}_i)+\\gamma\\sum_{i=1}^nJ'(\\theta^{(k-1)};\\mathbf{x}_i)\\right)=\\cdots=\n",
"\\theta^{(k)}-\\eta\\left(\\sum_{j=0}^k\\gamma^j\\sum_{i=1}^nJ'(\\theta^{(k-j)};\\mathbf{x}_i)\\right)\n",
"\\end{align*}\n",
"\n",
"Gli aggiornamenti nel caso della logistic regression derivano immediatamente\n",
"\n",
"\\begin{align*} \n",
"v_j^{(k+1)}&=\\gamma v_j^{(k)}+\\frac{\\eta}{n}\\sum_{i=1}^n( t_i-f(\\mathbf{x}_i,\\theta))x_{ij}\\hspace{1cm}j=1,\\ldots,d\\\\ \n",
"v_0^{(k+1)}&=\\gamma v_0^{(k)}+\\frac{\\eta}{n}\\sum_{i=1}^n(t_i-y_i) \\\\\n",
"\\theta_j^{(k+1)}&=\\theta_j^{(k)}+v_j^{(k+1)}\\hspace{1cm}j=0,\\ldots,d\n",
"\\end{align*}"
]
},
{
"cell_type": "code",
"execution_count": 127,
"metadata": {},
"outputs": [],
"source": [
"def momentum_gd(X,t, eta = 0.1, gamma = 0.97, epochs = 1000):\n",
" theta = np.zeros(nfeatures+1).reshape(-1,1)\n",
" v = np.zeros(nfeatures+1).reshape(-1,1)\n",
" theta_history = []\n",
" cost_history = []\n",
" for k in range(epochs): \n",
" delta = - eta * gradient(theta,X,t)\n",
" v = gamma*v + delta\n",
" theta = theta + v\n",
" theta_history.append(theta)\n",
" cost_history.append(cost(theta, X, t))\n",
" theta_history = np.array(theta_history).reshape(-1,3)\n",
" cost_history = np.array(cost_history).reshape(-1,1)\n",
" m = -theta_history[:,1]/theta_history[:,2]\n",
" q = -theta_history[:,0]/theta_history[:,2]\n",
" return cost_history, m, q"
]
},
{
"cell_type": "code",
"execution_count": 128,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"tempo di esecuzione: 0.407 secondi\n",
"10000 passi totali\n",
"1000000 gradienti calcolati\n"
]
}
],
"source": [
"start_time = time.time()\n",
"cost_history, m, q = momentum_gd(X, t, eta = 0.1, gamma = 0.97, epochs = 10000)\n",
"print(f\"tempo di esecuzione: {time.time()-start_time: 4.3f} secondi\")\n",
"print(f\"{len(m)} passi totali\")\n",
"print(f\"{len(m)*n} gradienti calcolati\")"
]
},
{
"cell_type": "code",
"execution_count": 132,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABQgAAAGoCAYAAAAKMwiTAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAAB2wElEQVR4nOz9eXQU94Hu/z9V1d2SWitCuwSITQiBxGZ2jG0sb3hJhkzsOJNZmMnMvdnGN5ncOXPuOfFN8OSEfJN4kpnMzO/aWTyZSTy2E5x4X2Qw+74KBEhCbAIJIYlFu9RV9fujQQaDbbDVqpb6/ToHo67qVj/tKonWo099Pobruq4AAAAAAAAAxCTT6wAAAAAAAAAAvENBCAAAAAAAAMQwCkIAAAAAAAAghlEQAgAAAAAAADGMghAAAAAAAACIYRSEAAAAAAAAQAzzeR3gRp0+fdrrCJ9IRkaGmpubvY4BcSyiCccienAsogfHInoMl2ORl5fndYSIGMrvDYfLuYVPjnMBl3Eu4DLOBVwWqXPhg94bMoIQAAAAAAAAiGEUhAAAAAAAAEAMoyAEAAAAAAAAYhgFIQAAAAAAABDDKAgBAAAAAACAGEZBCAAAAAAAAMQwCkIAAAAAAAAghlEQAgAAAAAAADGMghAAAAAAAACIYRSEAAAAAAAAQAyjIAQAAAAAAABiGAUhAAAAAAAAEMMoCAEAAAAAAIAYRkEIAAAAAAAAxDAKQgAAAAAAACCGURACAAAAAAAAMYyCEAAAAAAAAIhhFIQAAAAAAABADKMgBAAAAAAAAGIYBSEAAAAAAAAQwygIAQAAAAAAgBhGQQgAAAAAAADEMApCAAAAAAAAIIZREAIAAAAAAAAxjIIQAAAAAAAAiGEUhAAAAAAAAEAMoyAEAAAAAAAAYpjP6wAAAAAY/lpbW/X9739f9fX1+tWvfiXLsvr3nThxQk8//bQk6Ytf/KLGjBnjVUwAAICYxAjCQdLe1et1BAAAAM8kJSXpW9/6liZOnHjNvueee06PPfaYvv71r+u5557zIB0AAEBsYwRhhLmuq99tOaqdR5r1jYdKlZmS4HUkAACAQRcIBBQIBK67r6OjQxkZGf0fAwAAYHBREEaYYRhyHFch29GaytN6eOF4ryMBAABEFdd1P/I+FRUVqqiokCStXLmyv1Acinw+35DOj4HDuYDLOBdwGecCLhvsc4GCcBAsKc3XjiNntfNIs8qn5Ss9Kd7rSAAAAFHJMIzrbi8vL1d5eXn/7ebm5sGKNOAyMjKGdH4MHM4FXMa5gMs4F3BZpM6FvLy8626PaEH4zDPPqK6uTmPHjtXy5cv7t7e3t+upp55SW1ubSktLtWzZskjG8FxGSrzmFedr88FTWlN5Wp+ZP87rSAAAAFEjKSlJLS0tMgxDCQlMxwIAADDYIrZISV1dnbq7u7VixQqFQiHV1tb273vhhRf0yCOP6P/+3/877MvByx6YO0GGpO21Z3WhgwVLAABAbAmFQnriiSd0/Phxffe731VVVZVWrVolSXr44Yf14x//WP/0T/+kRx55xOOkAAAAsSdiIwhrampUVlYmSSotLVV1dbUmTJggSTp58qRefPFFtbS06NFHH1VRUVGkYkSNvJHJKh2Trn3HW/XugdP61JxCryMBAAAMGp/Pp29961tXbSspKZEkjRkzRk888YQXsQAAAKAIFoQdHR3Kzs6WJAWDQdXX1/fvO3z4sL7//e8rKSlJP/rRj677hnA4TUQthd8U//FtU7XvV+u0taZJf3zbVKUmMhehF5j0NXpwLKIHxyJ6cCyiB8cCAAAAsSJiBWEwGFRnZ6ckqaurS8FgsH9fXl6eCgoKJEmmef2rnIfTRNRSeHLJBKNXU0aN0IGT5/Ti+gN64JYxXseKSUz6Gj04FtGDYxE9OBbRY7gciw+aiBoAAAC4LGJzEBYVFWn//v2SpMrKyqsuI87NzdW5c+fU3d0t27YjFSEqlU/LlyRtPnxGHd19HqcBAAAAAABArItYQThu3Dj5/X49/vjjMk1TGRkZV01E/ZOf/EQrVqyImUVKLisYmaTi/DT1hhytr2r0Og4AAAAAAABiXMQuMZak5cuXX3X7chlYUFCgb3/725F86qh2Z1m+Dp06r42HGnXb1FwlBCJ6GAAAAAAAAIAPFLERhPhghVnJmpCTou4+WxsOMooQAAAAAAAA3qEg9MjluQjXVzWouy+25mEEAAAAAABA9KAg9Mi47BSNzUpWV6+tzYcYRQgAAAAAAABvUBB6xDAM3VkWHkW4tqpBvYwiBAAAAAAAgAcoCD1UlJeqUSMT1dEd0pbqJq/jAAAAAAAAIAZREHrIMAyVTyuQJK09cFp9tuNxIgAAAAAAAMQaCkKPTS5IU156UBe7+rS9hlGEAAAAAAAAGFwUhB67ci7CNftPK8QoQgAAAAAAAAwiCsIoMHV0urJTE3S+o1c7jzR7HQcAAAAAAAAxhIIwCphXjCJcXXlKtuN6nAgAAAAAAACxgoIwSkwrHKmMlHi1tvdoz1FGEQIAAAAAAGBwUBBGCdM0tKQ0T5L0zr5TchhFCAAAAAAAcA23p1NuW6vXMYYVCsIoMnNchkYkxensxW7tO97idRwAAAAAAICo4XZcVGjTK+r9r++p979/JLezzetIwwYFYRSxTFN3TL1iFKHLKEIAAAAAABDb3Iut6lv3onp/833ZlRukUJ/MUUVSXNDraMOGz+sAuNrsCZl6Z98pNZ7vUtXJc5o6Ot3rSAAAAAAAAIPOOdcke/caObV7JdcJb0wZKd/8+2WOmSzDMLwNOIxQEEYZn2Xq9ql5+sO2Y6rYe0pTRo3ghAcAAAAAADHDaT4le9caOUcPSLp0daUvIGvmEllli2RY1FkDjf+jUWjuxCy9s++UTrV26NCp85pcMMLrSAAAAAAAABHlNB4LF4MnD1+13Zw4Q76598lITPEo2fBHQRiF/D5Tt03J1as7T6hi3ykV56cxihAAAAAAAAw7ruvKPVWr0K7VchuOXrXPyCyQb+FDMrNHe5QudlAQRqn5k7K1Zv9pnTjbrpqGiyrKS/U6EgAAAAAAwIBwXUfO8YOyd78rt+nk1TsTkuSbc6/MSTNlGKyvOxgoCKNUnN/S4pJcvbH7pN7ZV09BCAAAAAAAhjzXceTU7ZO9e43c1jNX7zQtWaULZc1cIiMQ703AGEVBGMUWFmdr7YHTqjvTprozFzUum2vtAQAAAADA0OPaITk1u8MjBi+2XLPfHD1J1vwHZKZlepAOFIRRLD7g08LJOarYe0oVe0/pb+6mIAQAAAAAAEOHG+qTc2ibQnvXSe0XrtlvpGbIWvCArNHFHqTDZRSEUe7Wyblaf6BBNQ0XdOJsm0ZnJnsdCQAAAAAA4EO5vd2yq7bI3rdB6mq/9g7+OFmz7pQ1dYEMi3rKaxyBKBeM82lBcY7W7D+tin2n9Jd30qgDAAAAAIDo5HZ3yt6/UXblRqm3+7r3MSfNkm/OvTKCDIKKFhSEQ8DiKbnacKhRB+vP61RLh/JHJnodCQAAAAAAoJ/b2SZ733rZVVukvt7wRtOSHLv/PkbWaPkWPigza5RHKfFBKAiHgKR4v+YXZWtdVYMq9p3Sn99R5HUkAAAAAAAAuW3nFdq7Vs6h7ZIdkiQZ6Tly+3qlttbwnYLJ8s1dKnPiNBmG6WFafBAKwiHitim52nSoUftPtKrxXKdyRgS9jgQAAAAAAGKUc/6s7D3vyqnZLTmOpPBKxPIF5Jw8HB5FaFqyym6VNfMOGf44jxPjw1AQDhEpwYDmTMzSpsNn9M6+U/qT2yZ6HQkAAAAAAMQYp6VB9u41cuoqJdeVDEPmhOky0nPkHNou92KLJMksLJFv3v0yUkd6nBg3goJwCLmjNE9ba5q091iL7ppeoKzUBK8jAQAAAACAGOCcOREuBo8fDG8wLZmTZsosLJG9f7OcbW9Ikoy0rPA8gwUMbBpKKAiHkLTEON0yPlNba5q0uvKUPrdogteRAAAAAADAMOW6rtzTdQrtXiP3VG14o88vq3i2zMlz5BzaodBb/xm+xDgQL+uWclkl82VYlrfBcdMoCIeYO0rztL22SbvrmnXXtAKNTI73OhIAAAAAABhGXNeVc+Kw7N2r5Z45Ed7oj5M1Zb6s0oVyjh9U38tPS90dkgyZk+fIN/tuGQlJnubGx0dBOMSMTI7XjHEZ2nmkWWsqT+uPF4zzOhIAAAAAABgGXMeRc3S/7N1r5LY0hDfGBWWVLpQ1db7cc03qe/0Zuc2nJElGTmH4cuKMfA9TYyBQEA5BS0rztetIs3YcOavyaflKS2QlIAAAAAAA8PG4ti2ndo/sPe/KPX82vDGYHF6BuGSu1NOt0IaX5NTuCe9LTJVv3lKZ48tkGIZnuTFwKAiHoKzUBE0rHKk9x1r07v7T+vTcsV5HAgAAAAAAQ4wb6pNTvVOhPWultnPhjUlp8k2/TeakWyRJ9r71snevkUJ9kuWTNW2xrOm3y/AHPEyOgUZBOETdWZavPcdatLW6SUtK85US5AsTAAAAAAB8NLevV/bBrbL3rpM62yRJRmqGrBm3y5wwQzJNOccOKLT5NamtVZJkjp0q3/ylMpLTPUyOSKEgHKJyRgQ1dfQI7T9xTmsPNOjB2WO8jgQAAAAAAKKY29Ml+8Am2ZUbpe5OSZIxMlfWjDtkjp0qwzTltJ5RaNPL/asWG+nZ8i14UGb+BC+jI8IoCIewO8sKtP/EOW2uPqM7SvOUFO/3OhIAAAAAAIgyble77H0bZFdtlnp7JElG1mhZM++QObpYhmHI7elUaEeF7ANbJNeR4hLku+VumSVzZJiWx68AkUZBOIQVjEzU5II0Haw/r/VVDbpv5mivIwEAAAAAgCjhtl+QvXed7EPbwnMISjLyxss38w4ZeePDxaDjyK7aqtCOt8KjCg1DZsk8+WbfJSM+0eNXgMFCQTjE3VmWr4P157Xx0BndNiVPwTgOKQAAAAAAscy90KLQnrVyqndKji1JMkcXy5q5RGb2e4OLnNN1Cm18SW5royTJyBsXvpx4ZK4nueEd2qQhbkxmsibmpqqm4YI2HGzQ3dNHeR0JAAAAAAB4wGk9I3v3GjlH9kquK8mQOa5M1szbZY7M67+f23ZOoS2vyamrDG9ISpNv/v3heQgNw5vw8BQF4TBQXpZ/qSBs1OKSXMUHOKwAAAAAAMQK52y97F1r5Bw7EN5gmjInzgyvSpyW2X8/t69X9t61svesleyQ5PPLmn6brGm3yfCxrkEso0kaBsblpGhcdrLqzrRp0+EzWlKa73UkAAAAAAAQYU7DUYV2rZFbXx3eYPlkTrpFvumLZSSn99/PdV05dZUKbXlNaj8vSTLHl8k3d6mM5LTBD46oQ0E4TNxZVqC6tw9q3YEGLSrOUcDPCkMAAAAAAAw3ruvKra9RaNdquY3Hwht9AVkl82SVLZKRmHLV/Z2WhvA8gw1HJUnGyNzwPIN54wY5OaIZBeEwMTE3RaMzk3TibLs2V4cXLAEAAAAAAMOD6zpyjh2UvXuN3LP14Y2BeFlTF8gqXXjNisNuV4dCO96Wc3BreD7C+KB8s++RWTxbhml68AoQzSgIhwnDMFRelq9fvHNY7+5v0IJJOfL7+IIHAAAAAGAocx1bzpHKcDF47kx4Y3yirLJbZU2ZJyMQf+39q7YotKNC6umSDFPW1PmybimXERf04BVgKKAgHEaK89OUn56oU60d2lrTpEWTc7yOBAAA0O+ZZ55RXV2dxo4dq+XLl/dv37x5s1566SUZhqE/+qM/0uzZsz1MCQBAdHDtkJzqXQrtWStdbAlvTEyVNW2xrOLZMvyBax7j1NcqtOnl/iLRyJ8Qvpw4PXswo2MIoiAcRgzD0J1l+frVu9V6d/9pzSvKks9iFCEAAPBeXV2duru7tWLFCj399NOqra3VhAkTJEmvvvqqvv3tb8swDH33u9+lIAQAxDS3r1f2oe2y966TOi6EN6aMlG/6bTKLZsqwrq1y3IutCm1+9b1VjJPT5Zt/v8zCEhmGMYjpMVRREA4zU0aPUE5aghrPd2nHkbOaV8RvCQAAgPdqampUVlYmSSotLVV1dXV/QZidna2enh5JUkJCgmcZAQDwktvbrbZNr6l385tSd4ckyRiRLWvGHTLHl8owr12M1O3rlb17jex96yU7FF6sZMYd4cVKfP7BfgkYwigIhxnz0ijCX6+r1erK05o9IVMWk48CAACPdXR0KDs7/IvLYDCo+vr6/n1z5szR3//938t1XX35y1++7uMrKipUUVEhSVq5cqUyMjIiHzpCfD7fkM6PgcO5gMs4F2Kb3dmuju0Vat+xWr3dnZIkf26hkhfer/iiaTKMa3+md11XXQe26cLq38ppOydJSpg6T6l3fEZWyohBzY/IGOzvCxSEw1DZmJF6K6VeZy92a1dds2ZPyPI6EgAAiHHBYFCdneEferq6uhQMvjdJ+m9/+1s9+eSTkqTvfe97mjZt2jWPLy8vV3l5ef/t5ubmCCeOnIyMjCGdHwOHcwGXcS7EJrfjoux962VXbZVCvZKkwOgiuVMXySiYqA7DUEdL6zWPc86eUmjTS3Ibj0uSjIx8+RY+JCdnjM712hLn0rAQqe8LeXl5191OQTgMmaahJWX5em7DEa2uPK1Z4zJlmsw5AAAAvFNUVKSKigotWLBAlZWVuv322/v3+f1+xcXFyTAMhUIh70ICADAI3LZWhfask3N4R/iyYEnGqCL5ZtyhzNLZH1gKuV3tCm17U86hHZJcKSFJvjn3yJw067qjDIGbQUE4TM0Ym6G399Sr+WK39h5r0YxxDFcHAADeGTdunPx+vx5//HEVFhYqIyNDq1at0rJly3T33XfrW9/6liRdNUoQAIDhxDl/VvbuNXJq90iOI0kyC6fImnmHzMyC9+53rklO9S65fT0ygikyEhLlHDsg58Th8B1MU9bURbJm3ikjLt6DV4LhiIJwmLJMQ0tK8/XbzXV6p/KUpo0dKZOViwAAgIeWL19+1e1ly5ZJkm6//farRhQCADCcOM2nw8Vg3X5JrmQYMidMDy8+kh6en9cN9cmp26+zr+1S38maj/iEjpxjVXLO1stITJURTJESU2Rc/nP59nVWOwY+CGfLMDZrfIYq9tXrzPku7T/RqrIxI72OBAAAAABATHAaj4eLwROHwhtMS2bRLPmm3yYjNfzzudN6Rs7BbbJrdkk9XeH7+QMyMkfJPX3k2k/qC0ihXrkXW6SLLXI/LEB88OryMJgiIzFVCiaHi8XEFCkhkcuTIYmCcFjzWaZun5qn3289pnf2nVLp6HQZjCIEAAAAACAiXNeVe/qIQrtWyz1dF97o88sqniNr2mIZSalyQ32yq3fKPritf6ERSTIyC5Q8bYHaG07KObgtvNEfkDXzTlmlC2VYPrmuK/X1yO24KHVclNt5QW5Hm9yOC5duXwzv62yTujvldndKrY0fXCSappSQ3D/6UJdKRCMxWUYwtb9clD+OPmGYi2hB+Mwzz6iurk5jx4696pKSf/3Xf9WpU6cUCARUXl6uRYsWRTJGTJszMUur953S6dZOHaw/r5JRLHcOAAAAAMBAcl1XzolDsnetkdt0IrwxECerZL6sskUyEpLktDbK3rhWdvUuqbc7fB9/nMyJ02UVz5Z77ozat7wpp/2CJIVHG869V0Ywuf95DMOQAvEyAvHSiKwPyeNIXR1yOy6Gy8POcInYXyBeKhPV3Sl1XAjv+7AX6AuEi8L+kYhXfhwuFJWYKsO0PuH/SXglYgVhXV2duru7tWLFCj399NOqra3VhAkT+vf/7d/+rXJyciL19LjEb5m6bUqeXt5xXBX76jW5II3WHwAAAACAAeA6jpyj+2XvXiO3pSG8MT4oq3ShrCkLJNOSU1cZHi145urRgtbkOTInTJN7rkmhDX+Q23QyvC9rlHwLH5KZNepj5zIMM3wpcTBZysz/4PyhvnB5eKk4vLI8vLJYVKhX7oVm6ULzBxaJRmqG/J/9X8x9OERF7KjV1NSorKxMklRaWqrq6ur+gtAwDP30pz9VUlKS/uqv/kqZmZnXPL6iokIVFRWSpJUrVyojY2ivwuvz+Tx7DfcvSNOaAw062dyhMx3S1MKh/f/yk/LyWOBqHIvowbGIHhyL6MGxAAAAH8S1bTm1u2XvWSv3/NnwxmCyrGmLZU2eI/fiOYW2vyWnZvf7RgvOkDV5tsyMfLmdbQpteElO9c7+x4+487PqyJ0waPMCGj6/lJIuIyX9A+/juq7U2yO389JlzFdeynz545YGuRea5bY0yPgExSa8E7GCsKOjQ9nZ4dV4gsGg6uvr+/f92Z/9mZKSknTo0CH96le/0t/93d9d8/jy8nKVl5f3325ubo5U1EGRkZHh6Wu4dXK2Xt91UqvWVyk7sSSmRxF6fSzwHo5F9OBYRA+ORfQYLsciLy/P6wgAAAwbbqhPzuEdCu1ZK7WfD29MHiHf9NtkjiuTc7xKfa/+XO6ZE/2PMbJGhUcLji+T4Y+Ta4cU2rNW9q7VUl+PZFqyyhbJmrFEwbx8dUbZ+w/DMKS4eBlx8dKI7Ovep2/NC3Kqd8o5c+ITjXyEdyJWEAaDQXV2dkqSurq6FAwG+/clJSVJkoqLi/XrX/86UhFwhQXFOXp3/2kdbWpT3ZmLGp+T6nUkAAAAAACGBLevR3bVVtn71ocXAJFkpGXKmnG7jBE5sg/vUGjr//feaMFAnMwJM8LFYMZ7v6yzjx+SvfmV8OW6kswxk+Wbf7+M1KF91YKZPUpO9c7+y6Qx9ESsICwqKlJFRYUWLFigyspK3X777f37Ojs7FQwGdfr0aSUmJkYqAq4Q77d0a0mu3tpTr4p9pygIAQAAAAD4CG5Pp+z9m2RXbpJ6woOgjJG5skoXSY4t+8CWq0oxI2v0FaMFA/3bnfNnZW96Rc7Jw+H7pWXKt+BBmaOKBvcFRcjly4odCsIhK2IF4bhx4+T3+/X444+rsLBQGRkZWrVqlZYtW6Z//ud/VkdHhwzD0Be/+MVIRcD7LJqco3UHGlTbcFHHmtpUmJX80Q8CAAAAACDGuF3tsvetl31gS/gyYElG9miZYybLbb+g0KaXpN7wdgXiL80tOEfmyNyrP09Pt+xdFbL3b5IcJ7yy8axyWVMWyLCGz4q/RnqO5PNLF1vkdnXISGAw2FAT0aVlli9fftXtZcuWSZL+4R/+IZJPiw+QEPBpQXG2Vlee1jv7Tumvyou9jgQAAAAAQNRw28/L3rtO9sFtkh2SFB4VaKSky73QLHvbm/33NbIvjRYcd/VoQUlyXUfO4Z0KbXtT6mqXZMgsni3fnHtkJCQN5ksaFIZpycjIl9t4TM7Zk7JG0zcMNaw9HWMWl+Rqw8FGHTp1Xieb2zUqY/h9YwIAAAAA4Ga4F5oV2vOunOrdkmOHNyalyohPknvujNymS4uOBOJlFc2UWTxH5sic634up/G4Qptelns2vFirkTMmfDlxZsFgvBTPmFmjZTcek3vmpERBOORQEMaYxHi/5k/K1toDDXpn3yn9xZJJXkcCAAAAAMATTmuj7N3vyjmyV3Ld93ZYPqn9gtz2C5IkI3uMrJI5MseWXjNa8DK346JCW1+XU7M7vCExRb65S2VOmBZeCXiYM7KZh3AooyCMQYun5GrjoUYdOHlOp1s7lJfO3AAAAAAAgNjhnK2XvWu1nGNV17+DHXpvtODkOTLTrz9aUJLcUJ/syg2yd62RQr2S5ZNVdqusGXd8YJk4HJmXFipxm07IdR0ZhulxItwMCsIYlJIQ0NyJ2dp4qFGrK0/pC7cNj1WTAAAAAAD4MM7pOoV2r5FbX/OB9zFyCi/NLVgqw+f/wPu5rivnWJVCW16VLrZKkszCKfLNXyojZeSAZ496ialSMFnqbJN7oUVGWqbXiXATKAhj1O1Tc7Wl+oz2HWvVmWldyk5L8DoSAAAAAAADznVduSerw8Vg47Hr3yku4b3RgiOyP/JzOufOKLTplf6i0RiRHZ5nsGDCACYfWgzDkJk1Ws6xA+E5GykIhxQKwhiVlhin2RMytaW6SasrT+nRW2P3mxgAAAAAYPhxXUfO0SrZu9fIbT513fuERwvOlTlu6oeOFuz/nD2dsndUyD6wRXIdKRAv3+y7ZJbMk2FaA/0Shhwje5R07ICcMydlFc3yOg5uAgVhDLujNE/bas5q99Fm3TWtQBkp8V5HAgAAAADgE3EdW07tPtl71sg913TtHeKCV4wWzLrBz+nIObRdoe1vSd0dkmHILJkr3y13y0hgXv/LzKxRsiW5LFQy5FAQxrD0pHjNGp+h7bVntWb/KX12wXivIwEAAAAA8LG4dkjO4Z0K7V3bPyfglYzcseHRgmOn3NBowcuchqMKbXxJbktD/+fxLXxQ5si8Acs+XBiZBZJhyG1tkBvqu6n/z/AWBWGMu6M0TzuOnNWO2maVlxVoRFKc15EAAAAAALhhbl+v7IPbZO9bJ3VcvHpnXFDWpJkyi298tGD/520/r9CW1+Qc2RfekJQq37z7w4uXGMYApR9eDH+cjBHZclsb5TaflpEzxutIuEEUhDEuMyVB0wtHavfRFq3Zf1rL5o31OhIAAAAAAB/J7emWfWCz7MoN4ct+r2DkjQuvRFx4c6MFJckN9cneu1b2nrVSqE+yfLKm3y5r2mIZ/sBAvoRhycgaJbe1UU7TCZkUhEMGBSF0Z1m+9hxt0baaJt1Zlq/UIN/wAAAAAADRye3qkF25QfaBzVJv93s74oOyimaF5xb8GCvouq4r5+h+hTa/KrWflySZ48rkm7dURnLawISPAWbWKDmHtss9wzyEQwkFIZSdFlTpmHTtO96qtftP66E5hV5HAgAAAADgKm7HRdn71smu2hoe2XdJeLTgpbkFrY9XczgtjQpteknu6brw5xyZK9+CB2XmjRuQ7LHEyB4tSXKaTnicBDeDghCSpCVl+dp3vFVbqpu0pDRfSQlMJAoAAAAAiA529S6F1v5OcuzwhvhEWZNmySye/bFGC17mdncotP1tOQe3Sq4rxQflm323zOI5MkxzgNLHFiMtS/IHpPbzcjvbZASTvY6EG0BBCElSfnqiSgpGqKr+nNZWndb9s5gnAAAAAAAQHdzWRsmxZeSND88t+AlGC0qS69hyqrYptONtqadTMkxZU+fLmlUuIz44gMljj2GaMjIL5J6uk9N0UlZhideRcAMoCNGvfFq+qurPadOhM7p9Sp4S4xlFCAAAAADwnjXnXlkzlsiIi//En8s5dUShTS+HS0dJRt54+RY+KDM95xN/boSZWaNln66T23RSoiAcEigI0W9URpKK8lJVffqCNhxs1D0zRnkdCQAAAACA8OW+n7AcdNtaFdr8mpyj+8MbkkfIN//+8ErHhjEAKXGZkRXuE5wmFioZKigIcZXyaQX9BeHiKblKCHCKAAAAAACGLrevV/aed2XvXSfZIcnnlzXjDlllt8rwceVcJJiXCkK36aRcx2E+xyGA9gdXGZuVrPE5KTrSeFEbDzaqfFqB15EAAAAAALhpruvKObJPoS2vSR0XJEnmhOnyzb1PRlKqx+mGNyMxRUpKldovyD1/VkZ6tteR8BEoCHGN8rJ8HWm8qPUHG7WoJFfxfsvrSAAAAAAA3DCn+ZRCG1+W23hMkmRk5IfnGcwp9DRXLDGzRstpr5TbdEKiIIx6FIS4xvicFI3JTNLxs+3acviMbp+a53UkAAAAAAA+ktvVrtD2t+Qc3C7JleIT5Ztzj8xJt3CZ6yAzskZJdZXhlYyLZ3sd52PbVXVab2+sVXtHr5ISA7p70QTNmDz8ehIKQlzDMAyVTyvQzysOae2BBi0ozlbAxyhCAAAAAEB0cm1bdtVm2TsqpN5uyTRlTVkoa9adMuISvI4Xk4zES5dx93R5G+QT2FV1Wv/x4h61dfT0bzvd1C4t07ArCSkIcV2T8lJVMDJR9S0d2lrdpFtLcr2OBAAAAADANZz6GoU2vSz3XJMkySgokm/BAzJHZHmcLMaFesN/+wLe5vgE3t5Ye1U5KEltHT16a0MtBSFig2EYurMsX/+xplrv7j+teZOy5bcYjg0AAAAAiA7uhRaFtrwq51hVeEPKSPnm3y9zzGQZhuFtOFxREA7dlaLb264/+rG9s3eQk0QeBSE+0JRRI5Q7IqiGc53aXtOkBcU5XkcCAAAAAMQ4t69H9q41svetlxxb8gdkzVwiq3SRDIuaI1q4oT5JkuEfmiMInQvNCnaelZR4zb6k4NB8TR+Grxx8oMujCP9rbY3W7D+tuUVZspjUFQAAAADgAdd15dTsUWjr61LnRUmSWTRTvjn3ykhM8TgdrtE3dC8xds6dUd8rP9OdQUuNvRPUFnpvXYbkxDjdvWiCh+kig4IQH6p0TLqyUhPUdKFLO480a85E5nAAAAAAAAwu52y9QhtfknvmhCTJyCyQb+FDMrNHe5wMH2iIXmLstDSo75WfSd0dmj5xnHyFc/X2lqNq7+xVUpBVjBGjTMPQktI8/feGI1pdeUqzxmfKMpnLAQAAAAAQeW5nm0Lb3pRzeKckV0pIkm/uvTKLZsowuMItmg3FS4yds6fU9+rPpZ5OGQVF8t/zp5rp82tm6Sivo0UcBSE+0vSxGXp7b71a2nq052izZo3P9DoSAAAAAGAYc+2Q7P2bZO98R+rrkUxLVulCWTOXyAjEex0PN6JvaI0gdBqPq+/1X0q93TJHF8t315/IGCLZBwIFIT6SZRpaUpqvFzbVaU3lac0cl8GKUAAAAACAiLBPHJK96RW5F5olSeboYlnz75eZxmCVIeXSCMJonoPQtW05x6tkV22Ve6pWkmSOnSLfnY/G3II3sfVq8bHNHJehN3ef1JkLXao+fUGT8tO8jgQAAAAAGEac82dlb35FzonDkiQjNUPWggdljZ7kcTJ8HO7lOQij8BJjt/2C7IPbZB/aJnW2hTf6/LImz5E1b6kM0/rwTzAMURDihvgsUwsn5+j1XSe1rqqBghAAAAAAMCDc3m7ZO1fL3r9RcmwpECdr5p2ypi6IuVFcw8qlS4yj5TJd13Xknjoi+8AWOccPSq4jSTLSMmWWzJNVNFNGXILHKb3DVxpu2LyibFXsO6Xq0xfUeK5TOSOCXkcCAAAAAAxRruvIqd6l0NY3pK52SYbM4lvkm32PjGCy1/HwSUXJJcZud4fswzvlVG2Ve7ElvNE0ZY4tlTVlnozccUyjJgpC3IRgnE+zx2dq0+EzWlfVoIcXjvc6EgAAAABgCHLOnFBo08tym05Kkozs0fItfEhmZoHHyTBgPLzE2HVduU0nZVdtkXNkn2SHwjuSUsOXEU+aLSMxZdBzRTMKQtyURSU52nz4jHbVNeu+maOUnBB9cwkAAAAAAKKT23FRoa2vy6nZHd4QTJFv3n0yJ0xnFNcwc3kOwsG8xNjt65VTu0d21Ra5zaf7txsFRbKmzJM5elJMzi94IygIcVMyUxJUMmqEDpw8p82Hz+ju6aO8jgQAAAAAiHKuHZK9b4Ps3avDc9OZlqxpi2XNuF2GP87reIiEQbzE2Dl3Rk7VVtnVO6XenvDG+KCsSbfImjxXRurIiGcY6igIcdMWl+TqwMlz2nT4jO6Ymi+/z/Q6EgAAAAAgCrmuK+f4QYU2vypdmv/NLCyRb/79MlIobYa1S4uURKogdO2QnKMHwqMFG472bzeyR8sqmS9z3NSoWSBlKKAgxE0bm52sgpGJqm/p0K66Zs0tyvI6EgAAAAAgyjjnmsLzDNbXSJKMtCz5Fj4os2Cix8kQaa7jvDfvn29gqye37bzsg1tlH9p+aXEbSb6AzIkzZE2ZK3Nk3oA+X6ygIMRNMwxDi0ty9Zv1tVpX1aA5EzOZKwIAAAAAIElye7pk76yQfWCz5DhSIF7WLeWySubLsJj/LSbYly8v9sswPvlVh67ryDlZI6dqi5wThyTXlSQZ6dmySubJnDhDRiD+Ez9PLKMgxMdSVpiuV3cG1HShS4dPX1BxfprXkQAAAAAAHnIdR87hHQpte1Pq7pBkyJw8V77Zd8lISPI6HgbT5cuL7ZB6X/25jKQ0GclpMpJGXPp4hJSY8pELhrhd7bIP75RdtVVqaw1vNC2Z46eGC+ecMQxYGiAUhPhYLNPUwsk5em3nCa070EBBCAAAAAAxzGk4ptCml/pXjjVyCuVb+JDMDC73jElxCVJSmtR+Xm59jdzr3ccwwyXhpcLQSEp7rzw0TNmHd8ipq5QcO3z/5BGyJs+VVXwLhXMEUBDiY5s7MUsVe+tV03BBDec6lTsi6HUkAAAQxZ555hnV1dVp7NixWr58ef/29vZ2PfXUU2pra1NpaamWLVvmYUoAwM1w2y8otPU1ObV7wxuSUuWbu1Tm+DJGdsUww/Ip8Mjfyb3YIrftvNR+Tm7beblX/K3OtnCB2H5ebuOxD/pMMkcXy5wyT2ZBkQyTRVIjhYIQH1swzqfZEzK18dAZra9q0MMLx3sdCQAARKm6ujp1d3drxYoVevrpp1VbW6sJEyZIkl544QU98sgjys/P9zglAOBGuaE+2fvWyd79rhTqkyyfrGm3yZp+mwx/ZFatxdBi+Pwy0nOk9Jzr7nftULggfF9x6Lafl7o7ZY4ullUyR0Zy+uAGj1EUhPhEFk3O1aZDZ7Srrln3zhyllAT+IQAAANeqqalRWVmZJKm0tFTV1dX9BeHJkyf14osvqqWlRY8++qiKioq8jAoA+BCu68o5ekChLa9KbeckSea4Uvnm3UeRg5tiWD4pNUNGaobXUSAKQnxCGSnxKhk1QgdOntPmQ2d0z4xRXkcCAABRqKOjQ9nZ2ZKkYDCo+vr6/n2HDx/W97//fSUlJelHP/qRnnjiiWseX1FRoYqKCknSypUrlZExdH+Y8Pl8Qzo/Bg7nAi4bKudCX9MpXXj7WYWOHZIk+bLylXbXo4orLPY42fAxVM4FRN5gnwsUhPjEFk/J1YGT57Tp8BktKc2X38ecAAAA4GrBYFCdnZ2SpK6uLgWD781dnJeXp4KCAkmS+QFzC5WXl6u8vLz/dnNzcwTTRlZGRsaQzo+Bw7mAy6L9XHC7OxXa8bacqq2S60hxQflm3yVz8hy1mZbaojj7UBPt5wIGT6TOhby86y8cRJODT2xsVrIKRiaqsyeknXVnvY4DAACiUFFRkfbv3y9JqqysvOoy4tzcXJ07d07d3d2ybduriACA93EdR/aBLep97odyDmyW5MqcMl+Bz31T1pT5MkzL64gABggjCPGJGYahxSW5+s36Wq2vatCciVkyWa0KAABcYdy4cfL7/Xr88cdVWFiojIwMrVq1SsuWLdPDDz+sn/zkJ+rt7dUf//Efex0VACDJOV2n0MaX5LY2SpKMvHHyLXhI5sjrLzgBYGijIMSAKCtM16s7A2q60K3Dp85rcsEIryMBAIAos3z58qtuL1u2TJJUUFCgb3/72x4kAgC8n9t2TqEtr8mpqwxvSEqTb/79MsdOlcFAEGDYoiDEgLBMU4sm5+jVnSe0rqqBghAAAAAAhhC3r1f23rWy96yV7JDk88uafrusaYtl+PxexwMQYRSEGDBzi7L09t561TZc1OnWDuWlJ3odCQAAAADwIVzXlVNXqdCWV6X2C5Ikc/w0+ebdJyMpzdtwAAYNBSEGTELApzkTs7ThYKPWVTXoc4smeB0JAAAAAPABnObTCm16WW7DUUmSMTJXvoUPycwd63EyAIONghADatHkHG082Kg9R1u0dOZopQQDXkcCAAAAAFzB7epQaPtbcg5tk1xXik+Ub/bdMotnyzBNr+MB8AAFIQbUyOR4TRmdrv0nWrXp8BndO2OU15EAAAAAAJJcx5ZTtUWh7W9Lvd2SYcqaukDWLXfKiAt6HQ+AhygIMeAWT8nV/hOt2nz4jJaU5ings7yOBAAAAAAxzamvDV9OfO6MJMkomCjfggdkjsj2OBmAaBDRgvCZZ55RXV2dxo4dq+XLl1+1r7e3V1/5ylf0ta99TWVlZZGMgUFWmJmkURmJOtncoZ1HmjV/Ev/gAAAAAIAX3IutCm1+Vc6xA+ENKenyzb9f5pgSGYbhbTgAUSNikwvU1dWpu7tbK1asUCgUUm1t7VX733nnHY0ePTpSTw8PGYahxSW5kqT1VQ1yXNfjRAAAAAAQW9y+HoW2vane558Ml4O+gKw59yrw8DdkFU6hHARwlYiNIKypqekfGVhaWqrq6mpNmBBe1TYUCqmmpkaTJk2K1NPDY6VjRiot8YTOXuzW4VPnNblghNeRAAAAAGDYc11XTu0ehba+LnVclCSZE2fIN/c+GYkpHqcDEK0iVhB2dHQoOzt8aWkwGFR9fX3/vnfffVe33nqrampqPvDxFRUVqqiokCStXLlSGRkZkYo6KHw+35B/DTfrnlvG67m1B7W5plm3Tp/odZx+sXgsohXHInpwLKIHxyJ6cCwAAEONc7ZeoY0vyz1zXJJkZBbIt+BBmTljPE4GINpFrCAMBoPq7OyUJHV1dSkYDK+IZNu29uzZo29+85sfWhCWl5ervLy8/3Zzc3Okog6KjIyMIf8abtaUvETF+UwdPNGivdXHlZ+e6HUkSbF5LKIVxyJ6cCyiB8ciegyXY5GXl+d1BABAhLld7Qpte0POoZ2SXCkhSb4598qcNFOGEbGZxQAMIxH7TlFUVKT9+/dLkiorK1VUVCRJunDhglpaWvTd735X69ev17PPPqv29vZIxYCHEgI+zZmYJSk8FyEAAAAAYOC4dkihfevV+98/kHNoh2QasspuVeCRb8oqvoVyEMANi9gIwnHjxsnv9+vxxx9XYWGhMjIytGrVKi1btkzf+973JEnPP/+8iouLlZSUFKkY8NiiyTnacKhRe4626L6Zo5UaDHgdCQAAAACGPOfEYYU2vyL3/FlJkjlqkqwFD8hMy/Q4GYChKGIFoSQtX778qtvLli276vbDDz8cyadHFEhPjtfU0emqPN6qTYcadd9MVq4GAAAAgI/LudAse9Mrck4ckiQZqRmyFjwga3Sxx8kADGURLQgBSVpckqvK463aUt2kO0vzFfBbXkcCAAAAgCHF7e2RvWu17MoNkmNL/jhZs+6UNXWBDIsf7QF8MnwXQcSNyUzS6IwknWhu144jZ7WgOMfrSAAAAAAwJLiuI6d6t0Lb3pA62yRJ5qRZ8s25V0Yw2eN0AIYLCkJEnGEYWjwlV/+1tkbrDzZq3qRsmYbhdSwAAAAAiGpO00mFNr4kt+mkJMnIGi3fwgdlZo3yOBmA4YaCEINi6uh0pSUG1HyxW4fqz6tk1AivIwEAAABAVHI7Liq07Q051bvCG4LJ8s29T+bE6axMDCAiKAgxKCzT0KLJuXplx3Gtq2qgIAQAAACA93HtkOzKjbJ3vSP19UqmJavsVlkz7pARiPM6HoBhjIIQg2bOxEy9vbdeRxovqr6lQwUjE72OBAAAAACec11X9vGDsje9IvdiiyTJHDNZvvn3y0jN8DgdgFhAQYhBkxDwac7ETK2vatT6qgY9eusEryMBAAAAgKecc01qefu/FKrbL0ky0rLkW/CAzFFFHicDEEsoCDGoFk3O0YaDjdpztEVLZ45WamLA60gAAAAAMOjcnm7Zuypk798kOY4UiJc1q1zWlPkyLMvreABiDAUhBlV6UrxKR6dr3/FWbTrcqPtmjvY6EgAAAAAMGtd15BzeqdC2N6WudkmGgtMXK1S2WEZCktfxAMQoCkIMusVTcrXveKs2Hz6jO0vzFfDz2zEAAAAAw5/TeFyhjS/JbT4lSTJyxsi34CGNmDxNzc3NHqcDEMsoCDHoxmQma0xmko6fbdeOI2e1oDjH60gAAAAAEDFuxwWFtrwup3ZPeENiinzzlsocP02GYXiaDQAkCkJ4ZHFJrv5zbY3WVzVq3qRsmfyjCAAAAGCYcUN9svdtkL17jRTqlSyfrGmLZU2/XYaf+dgBRA8KQnhiyuh0jUiKU3Nbtw6ePKcpo9O9jgQAAAAAA8J1XTnHqhTa8qp0sVWSZI6dIt+8+2Wk8LMPgOhDQQhPWKahWyfn6KXtx7WuqoGCEAAAAMCw4Jw7o9DGl+WeqpUkGenZ8i14UGb+BI+TAcAHoyCEZ2ZPyNRbe+pVd6ZN9S3tKhjJil0AAAAAhia3p1P2jgrZB7ZIriPFJch3y10yS+bKMFmYEUB0M2/kTo888og2bdrUf3vXrl167LHHIhYKsSE+4NOciVmSpHVVjR6nAQAAAICb5zqO7Kqt6v3vH8rev0mSK7NkngKf+6asqQsoBwEMCR86grC5uVlNTU2SpPr6elVVVUmS9uzZozNnzkQ+HYa9RZNztOFgg/YebdHSmaOUlhjndSQAAAAAuCHO6TqFNr0st6VBkmTkjQtfTjwy1+NkAHBzPrQgXLNmjX77299Kkn73u9/pd7/7Xf++/Pz8yCZDTBiRFKfSMenae6xVmw6d0dJZo72OBAAAAAAfym07r9CW1+TU7QtvSEqTb/79MsdOlWEY3oYDgI/hQwvCCRMm6O6779Zbb72lsrIy5eaGfwuSlJSkRYsWDUpADH+LS3K191irtlSf0Z1l+YrzMwQfAAAAQPRxQ32y96yVvXetFOqTfH5Z02+TNe02GT6/1/EA4GP70IJwxowZmjFjhsaPH68pU6YoMzNTkuQ4jkzzhqYvBD7S6MxkjclM0vGz7dpRe1YLJ+d4HQkAAAAA+rmuK6euUqEtr0nt5yVJ5rgy+eYtlZGc5mk2ABgIN9TynTx5UmvWrFFra6u+9KUv6U//9E+1evXqSGdDDFk8JTw6df3BBjmO63EaAAAAAAhzWhrU98rTClX8Rmo/L2NkrvwP/o38d32echDAsHFDBeGGDRuUmJiojRs3KhQKKTc3V6tWrYp0NsSQqaPSlZ4Up5a2HlXVn/M6DgAAAIAY53Z3qG/979X3u3+We7pOig/Kd+un5V/2NZl547yOBwAD6kMvMb6svb1dycnJ2rNnjxYvXqwxY8bo//2//xfpbIghpmlo0eQcvbT9uNYdaNDU0eleRwIAIOZ87Wtf06hRo1RYWKjRo0ersLBQOTlM/QEgtriOLadqq0I73pZ6uiTDlDV1vqxbymXEBb2OBwARcUMFYUZGhp599lm1t7frS1/6ks6fP6+kpKRIZ0OMmT0xS2/tqdfRpjadbG7XqAzOMQAABtPs2bMVCoWUlpamffv26ac//amSk5OVnp6uMWPG6G/+5m+8jggAEeWcqlVo08tyW89Ikoz8CfIteFBmerbHyQAgsm6oIPyTP/kTvfDCC5o4caLmzJmj3/zmN5o7d26ksyHGxPstzS3K0toDDVpf1aDPL57odSQAAGLKvn379MMf/rD/9h133KFt27bp3nvv1fHjxz1MBgCR5ba1KrT5VTlHD4Q3JKfLN/9+mYUlMgzD23AAMAhuqCCcM2eOZs2apYaGBjU2NuoLX/gCqxgjIhYW52h9VYP2HmvV0lk9SkuM8zoSAAAxIzk5WceOHVNhYaEkaeLEiXrqqaf0J3/yJxo5cqS34QAgAty+Xtl73pW9d51khySfX9aMJbLKFsnw+b2OBwCD5oYKwvr6ev3gBz9QY2OjJCknJ0d///d/r/z8/IiGQ+wZkRSnsjEjtedYizYeatT9s8Z4HQkAgJjxP/7H/9BPf/pTFRQUqLCwUKdOnVIgEPA6FgAMONd15RzZq9CW16WOC5Ikc8J0+ebdJyMx1eN0ADD4bmgY4M9//nOdO3dOCxcu1MKFC3X+/Hn94he/iHQ2xKhbS3IlSVsON6mnz/Y4DQAAsSMnJ0crVqzQjBkzdP78eeXk5Ogf/uEfvI4FAAPKaT6lvpf+n0Lv/LfUcUFGRr78n/qS/Hd+jnIQQMy6oRGEdXV1+vznP697771XkvTGG2/o2WefjWgwxK7RmUkam5Wso01t2l57Vosms3oiAACDxTRNzZ07l/mmAQw7ble7QtveknNouyRXSkiSb849MifNkmEwhRaA2HZDBWFSUpL27dunGTNmSApPYM0qxoikW0tydbSpTeurGrRgUrZMk4mBAQAAANw817ZlH9gse2eF1NstmaasqQtlzSyXERfvdTwAiAo3VBAuWbJEzz//vHbu3Nm/7ZFHHolYKGDKqBFKT4pTa3uPDpw8p9Ix6V5HAgAAADDEOCerFdr0itzzTZIkY1SRfPMfkDkiy+NkABBdbqggXLx4sVJTU7Vv3z5J0rRp01RWVhbRYIhtpmno1pJc/WHbMa2vaqAgBAAAAHDD3AstCm1+Rc7xg5IkI2WkrAUPyBxdLMPg6iQAeL8bmmjhiSeeUHNzs77xjW/oG9/4hs6ePat//Md/jHQ2xLjZEzIV77d0tKlNJ862ex0HAAAAQJRz+3oU2vqGep9/MlwO+gOy5t4n/8NflzVmMuUgAHyAGxpB2Nraqqys94ZgZ2ZmqqWlJWKhAEmK81uaNylL7+5v0PqqBv3JbRO9jgQAAAAgCrmuI6dmj0JbX5c62yRJZtFM+ebcKyMxxeN0ABD9bqggzM7O1ssvv6z09HS5rqtXXnlF2dnZkc4GaGFxjtYdaNS+4y1a2j5aI5LivI4EAAAAIIo4TScV2viy3KYTkiQja5R8Cx6UmT3a42QAMHTcUEH4qU99Sv/6r/+q733ve/3bvvrVr0YsFHBZWmKcphWma/fRFm081KgHbhnjdSQAAAAAUcDtbFNo2xtyDl9aTDOYLN+ce2UWzZBh3NBsWgCAS254kZKMjAzt2rVLkjRz5kyVlJRENBhw2a0ludp9tEVbq5tUPq1A8X7L60gAAOBjeOaZZ1RXV6exY8dq+fLlV+3r7e3VV77yFX3ta19jMTwAH8q1Q7L3b5K98x2pr0cyLVmli2TNXCIjwBVHAPBx3FBBKEklJSWUgvDEqIwkjc1K1tGmNm2vadKtJbleRwIAADeprq5O3d3dWrFihZ5++mnV1tZqwoQJ/fvfeecdjR7N5YAAPpx94pDsTa/IvdAsSTJHF4dXJ07N8DgZAAxtN1wQAl5aPCVXR5vatP5goxYW58g0WX0MAIChpKampn9kYGlpqaqrq/sLwlAopJqaGk2aNMnLiACimHP+rOzNr8g5cViSZKRlyjf/AZmj+b4BAAOBghBDQknBCI1MjlNLW4/2n2xV2ZiRXkcCAAA3oaOjo3+Ru2AwqPr6+v597777rm699VbV1NR84OMrKipUUVEhSVq5cqUyMobuaCGfzzek82PgcC58NKenS20bXlH7tgrJsWXEJSjl1geVeMsSGdbw+XGWcwGXcS7gssE+F4bPd1QMa6Zp6NbJufr9tmNad6CBghAAgCEmGAyqs7NTktTV1aVgMChJsm1be/bs0Te/+c0PLQjLy8tVXl7ef7u5uTmygSMoIyNjSOfHwOFc+GCu68g5vFOhbW9KXe2SDJnFs+Wbc4+6E5LUfe681xEHFOcCLuNcwGWROhfy8vKuu52lnTBk3DIhUwkBS8fPtuvE2Tav4wAAgJtQVFSk/fv3S5IqKytVVFQkSbpw4YJaWlr03e9+V+vXr9ezzz6r9vZ2L6MC8JjTeFx9L/6bQmt/J3W1y8geI/+yr8h/22dkJCR5HQ8AhiVGEGLIiPNbmleUrTX7T2tdVaO+cFuy15EAAMANGjdunPx+vx5//HEVFhYqIyNDq1at0rJly/S9731PkvT888+ruLhYSUkUAEAscjsuKrT1dTk1u8MbginyzbtP5oTpMgzmIAeASKIgxJCyoDhbaw80qPJ4i861j9aIpDivIwEAgBu0fPnyq24vW7bsqtsPP/zwYMYBECVcOyR73wbZu1ZLoV7J8skqu1XWjNtl+Hm/DwCDgYIQQ0paYpymjR2p3XXN2nCwUQ/OHuN1JAAAAAAfg+u6co4fVGjzq9LFFkmSWVgi3/z7ZaQw5zgADCYKQgw5i0tytLuuWdtqmnTXtHzFBziNAQAAgKHEOdek0KaX5daHFycyRmTLt+ABmQUTPU4GALGJZgVDTsHIJI3LTlbdmTZtrz2rW0tyvY4EAAAA4Aa4PV2yd1TIPrBZch0pEC/f7LtklsyTYVpexwOAmEVBiCFpcUmu6s60af3BRi0ozpFlMmkxAAAAEK1cx5FzaLtC29+Sujskw5BZMle+W+6WkZDodTwAiHkUhBiSJo8aoYzkeDW3devAiVaVFTJHCQAAABCNnIZjCm16SW7zaUmSkTtWvgUPyszI8zgZAOAyCkIMSaZh6NaSHL249ZjWVTVQEAIAAABRxm0/r9CW1+Uc2RvekJQq37z7ZY4rlWFwBRAARBMKQgxZt4zP1Bu7T+r42XYda2pTYVay15EAAACAmOeG+mTvXSd7z7tSqE+yfLKm3yZr2m0y/AGv4wEAroOCEENWwG9p/qRsra48rfVVDRSEAAAAgIdc15VzdL9CW16T2s5JksxxpfLNWyojeYTH6QAAH4aCEEPaguIcrT3QoMoTrWpt71Z6UrzXkQAAAICY47Q0hucZPF0nSTLSc+Rb+KDMvPEeJwMA3AgKQgxpqcGAphWO1K66Zm042KiHZhd6HQkAAACIGW53p0I73pZTtUVyXSkuKN/su2VOni3DtLyOBwC4QREtCJ955hnV1dVp7NixWr58ef/2X/7ylzp27Jj6+vr0Z3/2ZyouLo5kDAxzi0tytauuWdtqzuquaQVKCNB7AwAAAJHkOracg9sU2v621NMpGabMKfPku+UuGfFBr+MBAG6SGalPXFdXp+7ubq1YsUKhUEi1tbX9+/70T/9U3/nOd/T1r39dL774YqQiIEbkj0zU+JwU9fTZ2lZz1us4AAAAwLDmnD6ivt/9i0Ib/iD1dMrIGy//H/+t/Is+RTkIAENUxIZa1dTUqKysTJJUWlqq6upqTZgwIfykvvDTdnd3a8yYMZGKgBiyuCRXRxovasPBBi2anCPLNLyOBAAAAAwrbts5hba8JqeuMrwheYR88+6XOXaKDIP33wAwlEWsIOzo6FB2drYkKRgMqr6+/qr9P/jBD1RbW6uvfe1r1318RUWFKioqJEkrV65URkZGpKIOCp/PN+RfQzRbNHKkXttdrzPnOnT8XJ/mTMr7wPtyLKIHxyJ6cCyiB8cienAsACDM7euVvWet7L1rJTsk+fyyZtwuq2yxDJ/f63gAgAEQsYIwGAyqs7NTktTV1aVg8Oqh5v/7f/9vtbS06Mknn9R3v/vdax5fXl6u8vLy/tvNzc2RijooMjIyhvxriHYLijL14tYOvbqlWuNGBj7wfhyL6MGxiB4ci+jBsYgew+VY5OV98C/NAODDuK4r58g+hba+JrVfkCSZE6bJN3epjKRUj9MBAAZSxOYgLCoq0v79+yVJlZWVKioq6t/X19cnSYqPj1dcXFykIiDG3DI+U8E4n040t+tYU5vXcQAAAIAhy2k+rb6Xn1LonWel9gsyMvLkf+h/yn/no5SDADAMRWwE4bhx4+T3+/X444+rsLBQGRkZWrVqlZYtW6Z/+qd/UmdnpxzH0ec///lIRUCMCfgtzSvK0urK01pf1aDCrGSvIwEAAABDitvVodD2t+Qc2ia5rhSfKN+ce2ROukWGGbHxJQAAj0WsIJSk5cuXX3V72bJlkqS///u/j+TTIoYtKM7R2gMNqjzRqta2bqUnx3sdCQAAAIh6rm3Lrtoie8fbUm+3ZJqypi6QNatcRlyC1/EAABEW0YIQGGypwYCmjx2pnUeateFgox6aU+h1JAAAACCqOfU1Cm16We65JkmSUVAk34IHZI7I8jgZAGCwUBBi2Lm1JFc7jzRrW02T7ppeoIQApzkAAADwfu7FFoU2vyrnWFV4Q8pI+ebfL3PMZBmG4W04AMCgojnBsJOfnqgJOSmqbbyobTVNum0KqzcCAAAAl7l9PbJ3vyt77zrJsSVfQNbMJbLKFsmw+BERAGIR3/0xLC2ekqvaxovacLBRiybnyjL5DSgAAABim+u6cmr3KLTldanzoiTJnDhDvrn3yUhM8TgdAMBLFIQYliblpykzJV5nL3ar8niLpo/N8DoSAAAA4BnnbL1CG1+We+a4JMnILJBv4UMys0d7nAwAEA0oCDEsmYahW0tytWrLUa070KBphSOZRwUAAAAxx+1qV2jbG3IO7ZTkSglJ8s25V+akmTIM0+t4AIAoQUGIYWvW+Ay9sfukTrZ06NjZdo3NSvY6EgAAADAoXDsk+8Bm2TsrpN4eybRklS6UNXOJjEC81/EAAFGGghDDVsBnaf6kbL2z75TWHWigIAQAAEBMsE8clr35Fbnnz0qSzNHFsubfLzMt0+NkAIBoRUGIYW1Bcbbe3X9aB060qvlitzJS+G0pAAAAhifnQrPsTa/IOXFIkmSkZsha8KCs0ZM8TgYAiHYUhBjWUhICmjE2QzuOnNXGQ4361JxCryMBAAAAA8rt7Za9a7Xsyo2SY0v+OFmz7pQ1dYEMix/5AAAfjX8tMOzdWpKjHUfOaltNk+6eXuB1HAAAAGBAuK4jp3qXQtvelDrbJBkyJ90i35x7ZASZXgcAcOMoCDHs5aUnamJuqmoaLmhrdZNG5eV4HQkAAAD4RJwzJxTa9LLcppOSJCN7tHwLH5KZyS/EAQA3j4IQMWFxSY5qGi5ow8FGffrWqV7HAQAAAD4Wt+OiQtvekFO9K7whmCzf3KUyJ06XYRjehgMADFkUhIgJRflpykqNV9OFbu2obtCEzDivIwEAAAA3zLVDsis3yt71jtTXK5mWrLJbZc28Q4af97YAgE+GghAxwTQM3VqSq99tPqo3d9Zp/D3F/IYVAAAAUc91XTnHD8re/Krciy2SJLOwRL5598tIHelxOgDAcEFBiJgxa1ymXt91UsfOXNDOumbdMj7T60gAAADAB3LONSm06RW59dWSJCMtS76FD8osmOhxMgDAcENBiJjh95m6d8YordpyVC9srFNyvF+T8tO8jgUAAABcxe3plr2zQvaBTZLjSIF4WbeUyyqZL8OyvI4HABiGKAgRU+ZPylZXyNDrO+r0q3er9T/vKdGojCSvYwEAAAByHUfO4R0KbXtT6u6QZMicPEe+2XfLSOA9KwAgcigIEXP+ePFknWm9qF11zfr5O4f01fumKiMl3utYAAAAiGFO4zGFNr4st/mUJMnIKQxfTpyR73EyAEAsoCBEzDENQ59dME7t3X2qPn1BP6s4qK/cN0XJCQGvowEAACDGuO0XFNr6upzaPeENianyzVsqc3wZi+oBAAaN6XUAwAs+y9Sf3l6kgpGJamnr0S/eOazuPtvrWAAAAIgRbqhPbRteUe9zPwyXg5ZP1swlCjzyd7ImTKMcBAAMKgpCxKx4v6W/vHOSRibHqb6lQ//5brVCtuN1LAAAAAxjruvKPrpfvc//ky6u/b0U6pM5dqoCj3wjPNegn6taAACDj4IQMS05IaAvlk9WUrxf1acv6PlNdXJc1+tYAAAAGIac1jPqe/XnCr31X1Jbq3yZ+fI/8Nfy3/0FGcnpXscDAMQw5iBEzMtIiddflU/Sv79Rpd11zUpJ8OuBW8Z4HQsAAADDhNvTKXtHhewDWyTXkeKC8s2+S1m3LlVL6zmv4wEAQEEISFLByCT92e1F+sU7h7X2QINSEgJaPCXX61gAAAAYwlzHkXNom0Lb35K6OyXDkFkyT77Zd8mIT5RhWl5HBABAEgUh0G9SfpoeXjhO/73hiF7ecVwpQb+mj83wOhYAAACGIOd0nUKbXpbb0iBJMvLGybfgQZkj+SU0ACD6UBACV5g1PlNtXX16decJ/feGI0qM92tibqrXsQAAADBEuG3nFdrympy6feENSWnyzb9f5tiprEwMAIhaFITA+9w2JVcXu3q1vqpR/7GmWl+6p0T5IxO9jgUAAIAo5vb1yt67TvbetVKoT/L5ZU2/Tda022T4/F7HAwDgQ1EQAu9jGIYeuGWM2jr7tOdYi35WcUhfWzpF6cnxXkcDAABAlHFdV05dpUJbXpPaz0uSzPFl8s1dKiM5zdNsAADcKApC4DpMw9Aji8arvadPtQ0X9XTFIX3lvilKiue3vwAAAAhzWhoU2viS3IajkiRjZK58Cx+SmTvW42QAANwc0+sAQLTyWab+/PYi5aUH1XyxW7+oOKSePtvrWAAAAPCY29WhvvW/V9/v/jlcDsYnynfrH8m/7GuUgwCAIYmCEPgQ8QGf/qq8WOlJcTrZ0qH/Wlsj23G8jgUAAAAPuI4te/9G9T73QzlVWyQZsqYuVOBzfyerZK4Mkx+vAABDE/+CAR8hJSGgL5YXKzHOp0OnzuuFTXVyXdfrWAAAABhETn2t+n77zwptfFnq6ZJRMFH+zz4m38IHZcQFvY4HAMAnwhyEwA3ITE3QX95ZrP/fW1XaeaRZqcGA7ps52utYAAAMKc8884zq6uo0duxYLV++vH/7U089pZMnT0qSvvjFL2rMmDFeRQSu4V5sVWjzq3KOHQhvSEmXb/79MseUyDAMb8MBADBAGEEI3KDRmUn6s9smyjSk1ZWnteFgo9eRAAAYMurq6tTd3a0VK1YoFAqptra2f9+nP/1pPfHEE/ryl7+sF154wcOUwHvcvl6Ftr+l3uefDJeDvoCsOfco8NmvyyqcQjkIABhWGEEI3ITighH67ILxem7jEb207ZiSE/yaVjjS61gAAES9mpoalZWVSZJKS0tVXV2tCRMmSJKysrIkSZZlyfyAOdwqKipUUVEhSVq5cqUyMjIGIXVk+Hy+IZ1/uHNdV11V23Txnd/KbjsnSUqYOk+pd3xGVsqIAX0uzgVcxrmAyzgXcNlgnwsUhMBNumVCpi529er1XSf17PpaJcX7ND4n1etYAABEtY6ODmVnZ0uSgsGg6uvrr7nPb37zGy1duvS6jy8vL1d5eXn/7ebm5sgEHQQZGRlDOv9w5pw9pdCml+Q2HpckGRn58i18SE7OGJ3rtaUBPm6cC7iMcwGXcS7gskidC3l5edfdTkEIfAx3TM3Txc4+bTzUqGdWV+tL95YoLz3R61gAAEStYDCozs5OSVJXV5eCwasXdXj11VdVUFCg4uJiL+Ihxrld7Qpte1POoR2SXCkhSb4598icNEuGwaxMAIDhj3/tgI/BMAw9NHuMysakq7vP1s8rDulce4/XsQAAiFpFRUXav3+/JKmyslJFRUX9+/bu3avDhw/rM5/5jFfxEKNc21Zo33r1/vcP5RzaLpmGrLJbFXjkm7KKZ1MOAgBiBv/iAR+TaRr63K0TND4nRRe7+vT02wfV0d3ndSwAAKLSuHHj5Pf79fjjj8s0TWVkZGjVqlWSpF/84hc6e/asvvOd7+ipp57yOClihXOyWn2//bHsza9Kvd0yR02S/7Nfl2/+/TLi4r2OBwDAoOISY+AT8Fum/vyOIv37G1VqONepX6w+rP9x92QFfJbX0QAAiDrLly+/6vayZcskST/5yU+8iIMY5V5oVmjzq3KOH5QkGakZsuY/IGsMl7cDAGIXIwiBTygh4NNflRcrLTGgE2fb9V9ra2Q7rtexAAAAcAW3t0ehra+r9/l/CpeD/jhZc++T/7P/i3IQABDzKAiBAZAaDOiv75qsYJxPB+vPa9WWOrkuJSEAAIDXXNeRXb1Tvc/9UPaetZJjyyyapcDnvinf9NtkWFxUBQAA/xoCAyQrNUHLl0zSU28d1Laas0pJCOieGaO8jgUAABCznKaTCm18SW7TSUmSkTVKvoUPycziPRoAAFeiIAQGUGFWsr5w20T9x5rDqth3SskJfi0ozvE6FgAAQExxO9sU2vqGnOqd4Q3BZPnm3itz4gxWJgYA4DooCIEBVjJqhD4zf5xe2FSn3289puSEgErHpHsdCwAAYNhz7ZDsyo2yd62W+nok05JVtkjWjCUyAnFexwMAIGpREAIRMGdili529urNPfX6zboa/fXdkzUuO8XrWAAAAMOWffyQ7M2vyL3QLEkyx0yWb/79MlIzPE4GAED0oyAEIuTOsnxd7OrT5sNn9Mzqw/ryvVOUMyLodSwAAIBhxTl/VvamV+ScPCxJMtIy5VvwoMxRRR4nAwBg6KAgBCLEMAx9ek6h2rr6tP9Eq35WcUhfXTpFaYlc3gIAAPBJuT3dsne9I3v/RslxpECcrFnlsqYskGFZXscDAGBIYYZeIIJM09DnF0/Q2KxkXejs1dNvH1JnT8jrWAAAAEOW6zqyD21X73M/lL1vveS4MotnK/C5/y1f2a2UgwAAfAwUhECE+S1Tf7FkkrLTEtR0oUu/XH1YfSHH61gAAABDjtN4XH0v/ptCa38ndbXLyBkj/7KvyH/bZ2QkJHkdDwCAIYuCEBgEwTifvlherNRgQMea2vTrdTWyHdfrWAAAAEOC23FRfaufU98f/l3u2XopMUW+JZ+T/6H/KTOzwOt4AAAMeRSEwCBJS4zTX99VrISApQMnz+nFrUflupSEAAAAH8QN9Sm0e416//uHcmp2S5ZP1swlCjzyTVkTp8swDK8jAgAwLLBICTCIstOCWn5nsZ56q0pbq5uUGgzormn81hsAAOBKruvKOVal0JZXpYutkiRz7BT55t0vIyXd43QAAAw/FITAIBublaw/WTxRv3q3Wm/tqVdKgl9zi7K9jgUAABAVnHNnFNr0itz6GkmSMSJbvgUPyiyY4HEyAACGr4gWhM8884zq6uo0duxYLV++vH/7U089pZMnT0qSvvjFL2rMmDGRjAFEnamj0/VHc8dq1Zaj+t2Wo0qK92vKaH4bDgAAYpfb0yV7R4XsA5sl15HiEuS75S6ZJXNlmKxMDABAJEVsDsK6ujp1d3drxYoVCoVCqq2t7d/36U9/Wk888YS+/OUv64UXXohUBCCqzZ+Urbum5ct1pf9aV6NjTW1eRwIAABh0ruPIrtqq3v/+oez9GyW5MkvmhecZnLqAchAAgEEQsRGENTU1KisrkySVlpaqurpaEyaELwvIysqSJFmWJdO8fkdZUVGhiooKSdLKlSuVkZERqaiDwufzDfnXMFxE07F49M6R6nUsra08oWfWVOv/fG6B8kYmex1r0ETTsYh1HIvowbGIHhwLIPKchqMKbXpZbvNpSZKRO1a+hQ/KHJnncTIAAGJLxArCjo4OZWeH51ULBoOqr6+/5j6/+c1vtHTp0us+vry8XOXl5f23m5ubIxN0kGRkZAz51zBcRNuxuG96rs6eb1PVyXP6wQub9dX7pio1MeB1rEERbccilnEsogfHInoMl2ORl0fRgujjtp9XaMvrco7sDW9ISpVv3v0yx5WyMjEAAB6I2CXGwWBQnZ2dkqSuri4Fg8Gr9r/66qsqKChQcXFxpCIAQ4JlGvqTxRM0JjNJ5zt69bOKg+rqDXkdCwAAYMC5oT6Fdr6j3ud+FC4HLZ+sWeUKPPx3ssaXUQ4CAOCRiBWERUVF2r9/vySpsrJSRUVF/fv27t2rw4cP6zOf+Uyknh4YUgI+S395Z7GyUhPUeL5Lz6w+rD7b8ToWAADAgHBdV3ZdpXqf+5HsHW9LoT6Z48oUeOSb8t1SLsMfG1dPAAAQrSJWEI4bN05+v1+PP/64TNNURkaGVq1aJUn6xS9+obNnz+o73/mOnnrqqUhFAIaUYJxPXywvVkqCX3Vn2vTs+lo5jut1LAAAgE/EaWlU3ytPK/T2r6X28zJG5sr/4N/If9fnZSSneR0PAAAognMQStLy5cuvur1s2TJJ0k9+8pNIPi0wZI1IitMX75qsf3v9gCqPt+oP247p03MLudwGAAAMOW53h0Lb35ZzcKvkulJ8UL7Zd8ssniPjAxYqBAAA3ohoQQjg5uWOCOovlkzSz94+qE2HzyglGNCdZflexwIAALghrmPLqdqm0I63pZ5OyTBlTZ0va1a5jPjgR38CAAAw6CgIgSg0PidFjy6eoP96t0Zv7D6plAS/Zk/M8joWAADAh3JOHVFo08tyWxslSUb+BPkWPCAzPcfjZAAA4MNQEAJRqmzMSH16bp9e3HpMv91cp6QEvyYXjPA6FgAAwDXctlaFNr8m52h4kUIlp8s3f6nMwilMlQIAwBBAQQhEsQXFObrY2ad3Kk/pP9+t0f+8Z7JGZyZ7HQsAAECS5Pb1yt7zruy96yQ7JPn8smbcIavsVhk+v9fxAADADaIgBKLcPTMKdLGrV9trz+rn7xzWV+6boqzUBK9jAQCAGOa6rpwj+xTa8prUcUGSZE6YLt/c+2QkpXqcDgAA3CwKQiDKGYahz8wfp/buPh2sP6+fvX1QX1k6VanBgNfRAABADHKaTym08WW5jcckSUZGvnwLH5SZU+hpLgAA8PGZXgcA8NEs09AXFk/U6Iwknevo1c8rDqmrN+R1LAAAEEPcrnb1rVulvt/9NFwOxifKt3iZ/H/0FcpBAACGOEYQAkNEwG/pL++cpH99/YAaznXqp68d0KfnFmpiLpfxAACAyHFtW3bVZtk7KqTebsk0ZU1ZKGvWnTLimPYEAIDhgIIQGEIS4/364l3FevrtQ2q60KWn3jqosjHpeuCWMRqRFOd1PAAAMMw49TUKbXpZ7rkmSZJRUCTfggdkjsjyOBkAABhIFITAEJOeFK9vPFSmdQca9E7lKe073qqD9ee1pDRPt03Nk99i5gAAAPDJuBdaFNryqpxjVeENKSPlm3+/zDGTZRiGt+EAAMCAoyAEhiC/ZerOsnzNGp+hV3Yc195jrXpzT722157Vp+YUqmTUCK8jAgCAIcjt65G9a43sfeslx5b8AVkzl8gqXSTD4kcHAACGK/6VB4awtMQ4feG2Is0ruqDfbzumM+e79MvVh1Wcn6aH5oxRZgrzAgEAgI/muq6cmj0KbX1d6rwoSTKLZso3514ZiSkepwMAAJFGQQgMAxNyU/X1B0u16dAZvbWnXodOnVfNHy7otim5urM0XwG/5XVEAAAQpZyz9QptfEnumROSJCNrlHwLHpSZPdrjZAAAYLBQEALDhGWaurUkV9PHjtTru05qe+1Zra48rZ1HmvXALaM1rXAkcwYBAIB+bmebQtvelHN4pyRXCibLN+demUUzZBjMaQwAQCyhIASGmeSEgB5eOF5zi7L0+63HVN/SoV+vq9WW6iZ9ek6hckYEvY4IAAA85Noh2fs3yd71jtTbI5mWrNJFsmbeISMQ73U8AADgAQpCYJgak5msry2dqu21TXpt10kdabyof3p5nxYU5+ju6QVKCPDlDwBArLFPHJa9+RW5589KkszRxbIWPCAzNcPjZAAAwEs0BMAwZpqG5hZlq3TMSL25+6Q2V5/RhoON2nO0RUtnjtKsCZkyuewYAIBhz7nQLHvTK3JOHJIkGWmZ8s1/QOboSR4nAwAA0YCCEIgBwTif/mjeWM0pytIfth7T0aY2Pb+pLnzZ8dxCjcpI8joiAACIALe3W/au1bIrN0qOLQXiZM0qlzVlvgyLHwUAAEAY7wqAGJKfnqgv3Vui3Udb9OqO4zrR3K5/eXW/5kzM0n0zRykx3u91RAAAMABc15FTvUuhrW9IXe2SDJnFt8g3+x4ZwWSv4wEAgChDQQjEGMMwNHNchkpGjVDF3nqtr2rU1pom7TveontmjNK8omxZJpcdAwAwVDlnTii06WW5TSclSUb2aPkWPiQzs8DjZAAAIFpREAIxKt5v6YFbxmjOxPBqxzUNF/T7rce09dJlx+OyU7yOCAAAboLbcVGhra/Lqdkd3hBMkW/efTInTJfBnMMAAOBDUBACMS4rNUF/fVex9p84p5e3H1PDuU79+xtVmjEuQ/fPGq3UYMDriAAA4EO4dkj2vg2yd6+W+nol05I1bbGsGbfL8Md5HQ8AAAwBFIQAZBiGSseka1J+qt7df1prKk9rd12zqk60qnxagRZNzpHPMr2OCQAAruC6rpzjBxXa/Kp0sUWSZBaWyDf/fhkpIz1OBwAAhhIKQgD9Aj5Ld08fpVvGZ+ql7cd14OQ5vbrzhLbVNOlTcwo1KT/N64gAAECSc64pPM9gfY0kyRiRJd+CB2UWTPQ4GQAAGIooCAFcIz05Xn+xZJIOnzqvP2w7prMXu/WzikOaOnqEHpw9RulJ8V5HBAAgJrk9XbJ3viP7wCbJcaRAvKxb7pJVMk+GZXkdDwAADFEUhAA+0KT8NH3joTKtP9ioir312n/inA6dOq87pubrjql58vu47BgAgMHgOo6cwzsU2vam1N0hyZA5ea58s++SkZDkdTwAADDEURAC+FA+y9QdU/M0c2yGXt15XLuPtujtvfXaceSsHpo9RlNGjWBlRAAAIshpPKbQxpflNp+SJBk5hfItfEhmRp7HyQAAwHBBQQjghqQmBvT5xRM1ryhbv98WXu34P9ZUqygvVZ+aU6is1ASvIwIAMKy47RcU2vqanNq94Q1JqfLNXSpzfBm/nAMAAAOKghDATRmXk6LHHijVlsNn9Oaek6o+fUFPvrRPiybnqHxageL9zH8EALi+Z555RnV1dRo7dqyWL1/ev/3EiRN6+umnJUlf/OIXNWbMGK8iRgU31Cd73zrZu9+VQn2S5ZM17TZZ02+T4Q94HQ8AAAxDTCAG4KZZpqGFk3P09380XXMmZslxXK090KAfvLhHu+ua5bqu1xEBAFGmrq5O3d3dWrFihUKhkGpra/v3Pffcc3rsscf09a9/Xc8995yHKb3luq7suv3qff5J2dvflkJ9MseVKvDIN8JzDVIOAgCACGEEIYCPLSner88uGKd5RVl6cetRnWzu0G/W12rz4TP69NxC5aUneh0RABAlampqVFZWJkkqLS1VdXW1JkyYIEnq6OhQRkZG/8fXU1FRoYqKCknSypUr++8/FPl8vmvy9zWd0oW3n1Xo2KHwfbLylXbXo4orLPYiIgbJ9c4FxCbOBVzGuYDLBvtcoCAE8ImNykjSV5dO1Y7as3pt1wkdbWrTj1+p1PyibN0zY5SCcXyrAYBY19HRoezsbElSMBhUfX19/74bGXleXl6u8vLy/tvNzc0DH3KQZGRk9Od3uzsV2vG2nKqtkutIcUH5Zt8lc/IctZmW2obw68RHu/JcQGzjXMBlnAu4LFLnQl7e9Rc546d2AAPCNAzNmZil0jHpemtPvTYdatSmw2e091iL7ps5WrMnZspkQnUAiFnBYFCdnZ2SpK6uLgWDweveL1YW33AdR87BbQrteEvq7pQMQ+aU+fLdcpeM+Ov/vwEAAIgU5iAEMKASAj59ak6h/teDZRqXnayOnpB+u7lO//Lqfp042+Z1PACAR4qKirR//35JUmVlpYqKivr3JSUlqaWlRa2trUpISPAq4qDpOX5Yfb/7Z4U2/F7q7pSRN07+zzwm/6JPUQ4CAABPMIIQQETkjgjqf95Tor3HWvTKjhOqb+nQv7x2QLMnZGrpzNFKSvB7HREAMIjGjRsnv9+vxx9/XIWFhcrIyNCqVau0bNkyPfzww/rxj38sSfqrv/orb4NGmOs4Ov/Gr+W2NkpJafLNv1/m2KkxM3ISAABEJ8MdIsuNnj592usInwjzCEQPjsXg6+mz9c6+U1pX1SDbcRXvt3T39AI9tGiKzrW2eh0P4usimnAsosdwORYfNM/MUDeU3xsmtZ3V+ep9sqYtluHjF2axbLh8n8Enx7mAyzgXcBlzEAIYduL8lpbOGq3ZEzL10vbjOnTqvF7aflxbas4qPz2o7NQEZaUmKDstQSOT42WZjKIAAAxf8WMny5ec6XUMAACAfhSEAAZNZmqC/vLOSTpYf15/2HZMTec71XS+86r7WKahjJT4cGmYltBfHmamJshvMW0qAAAAAAADjYIQwKAyDEMlo0aoKC9VbSGfak406sz5LjVd6NKZC106196jM+e7dOZ8l3T8ysdJI5Pi+0caXv47MzVB8X7LuxcEAAAAAMAQR0EIwBM+y9TE7HSNiHOu2t7bZ6vpYrfOnO8Ml4aXysOWtm41X/pTVX/uqsekJQbCheH7Rh0mxjOvEwAAAAAAH4WCEEBUCfgtFYxMVMHIxKu2h2xHzRe7deZC11XF4dkLXTrf0avzHb2qPn3hqsckxfuVlRqv7LTgVSMPUxL8rBYJAAAAAMAlFIQAhgSfZSpnRFA5I4JXbXccV63tPe+NOLzQpabz4b/bu/vU3t2nujNtVz0m3m9dNdIw+9LHaUlxMikOAQAAAAAxhoIQwJBmXlrUJCMlXlOu2O66ri509r43v+EV8xx29oR04my7Tpxtv+pz+X2mslISrikPWVkZAAAAADCcURACGJYMw1BaYpzSEuM0KT+tf7vruuroDunMhc6rSsOm81262NWnU60dOtXacdXnYmVlAAAAAMBwRkEIIKYYhqGkBL+SElI1Pif1qn1dvaHrjjj8sJWV05PilBTvV8BnKc5vKuCzFPCZivNbH7jt8sdxPlMBv6U4nyWfZTAvIgAAAADAExSEAHBJQsCnwqxkFWYlX7X9w1ZWbmnrUUtbzyd+bsNQuFC8VBoGfKbifJYC/vDf/ku34y7tu7J8/LBtlknxCAAAAAD4cBSEAPARPmxl5Za2HnX1htTTZ6s35KgnZKv3qo8v/R1y1Ntnf+C2kO2qp89WT58tdfUNWHbTMK4zitF8X6loaWRai+JMWyOT4pWeHKeUhIBM5l0EAAAAgJhAQQgAH5PPMpWdljAgn8t2XPVeVRpeUSheue2qgtFWT5/T/7hwSfnetp4+R47rqqvXVlev/REJGq+6ZZmGRiTFKf3yn+R4jUyKU3pynNKT4hWM458PAAAAABgu+AkPAKKAZRpKCPiUEBjYzxuynavKw/c+fu/v3pAtx/SrvumcWtt71NrWo/buPjVf7Fbzxe7rft54v9VfFqZfKg5HXioSRyTFsXgLAAAAAAwhFIQAMIz5LFM+y/zIEX8ZGRlqbm7uv93bZ4fLwvYetbaH51rsv93Wre4+W6dbO3W6tfO6ny8lwa/05CvLw/c+TgkGZDIvIgAAAABEDQpCAMA1An5LOSOCyhkRvGaf67rq6Ampta27vzQMF4jdam3r0fmOHl3s6tPFrj4da2q75vFcvgwAAAAA0YWfwgAAN8UwDCXF+5UU79fozORr9tuOqwud4UuVw+Vh9xWjD2/+8uWRye8ViVy+DAAAAAADj4IQADCgLNO4VO7FX3f/QFy+PPJSWfj+y5eT4v3yUSACAAAAwE2hIAQADKqBunz56HUuX5Ykn2UoGPApPuBTQsAKL/4S51OC//LHl/6+cn/AUnzAp/iAxfyIAAAAAGJORAvCZ555RnV1dRo7dqyWL1/ev33VqlV68803dccdd+hzn/tcJCMAAIaQT3r5cmdPSCHb7S8Rb/r5JcX5rXCheEV5eLlQjA9Yl8pHS8G4cAkZvFQuJgQs+S1TBgUjAAAAgCEmYgVhXV2duru7tWLFCj399NOqra3VhAkTJElLlixRUVGR9u/fH6mnBwAMQx91+bLruuoLOerqtdXVG7r05zof91y7rbvXVnffe3/Ofcx8V5WKcZYS/B9UKF47gtEyB6ZcdF1XriTXlSRXrqtLt8MfOOE79d/HDd/x0v3ed//3b7/0sfrv8979nEufU66UELCUnnz94wQAAAAgukSsIKypqVFZWZkkqbS0VNXV1f0FYVpamk6dOhWppwYAxCjDMBTwWwr4LaUmBm768Y7jqrvvfeVhz/VLxu5eW529IXVfcb+Q46q9u0/t3Tc/elEKj16M8/vkOE5/ISddKvwuFXJy3UsF3wcXgdFgWuFIfeG2iV7HAAAAAHADIlYQdnR0KDs7W5IUDAZVX19/U4+vqKhQRUWFJGnlypXKyMgY8IyDyefzDfnXMFxwLKIHxyJ6cCwGRl/IVkd3nzp7+vr/7uwJqfOabZf+dIeu+LhPPX22evrsAcliXPrP5TkVDcOQYUiGLv1tGDKu2i7JMGReeqBphB//gfe/8valv8PPF35MfmbakD+n+LoAAABArIhYQRgMBtXZGV6BsqurS8HgtZPRf5jy8nKVl5f3325ubh7QfIMtIyNjyL+G4YJjET04FtGDYzGwApICcdKIOEuSJSnuIx/juK56+mwlp6Sp9VyrzHA7d1UpJ11ZyL1X3l2zPUrmQRzq59Rw+brIy8vzOgIAAACinBmpT3zlHIOVlZUqKiqK1FMBADDkmUZ4/sK0pHilJASUlBBerCUx3q9gnO+9hVL8luL8lgI+S36fKZ8V/mOZhkzTiJpyEAAAAMDQEbGCcNy4cfL7/Xr88cdlmqYyMjK0atUqSdLq1av1q1/9SuvXr9fPfvazSEUAAAAAAAAA8BEidomxJC1fvvyq28uWLZMUXsV4yZIlkXxqAAAAAAAAADcgYiMIAQAAAAAAAEQ/CkIAAAAAAAAghlEQAgAAAAAAADGMghAAAAAAAACIYRSEAAAAAAAAQAyjIAQAAAAAAABiGAUhAAAAAAAAEMMoCAEAAAAAAIAYRkEIAAAAAAAAxDAKQgAAAAAAACCGURACAAAAAAAAMYyCEAAAAAAAAIhhFIQAAAAAAABADKMgBAAAAAAAAGIYBSEAAAAAAAAQwygIAQAAAAAAgBhGQQgAAAAAAADEMApCAAAAAAAAIIZREAIAAAAAAAAxjIIQAAAAAAAAiGEUhAAAAAAAAEAMoyAEAAAAAAAAYhgFIQAAAAAAABDDKAgBAAAAAACAGObzOgAAAACGt66uLv3kJz9RR0eHysvLddttt1217wc/+IFs21ZCQoIee+wxJSQkeJgWAAAg9jCCEAAAABH1zjvvaOHChfrOd76j1atXKxQK9e+zLEtf+9rX9J3vfEe33HKL3n33Xe+CAgAAxCgKQgAAAERUdXW1ysrKZJqmxowZo1OnTvXvCwQCGjFihCTJ5/PJNHl7CgAAMNiGzCXGeXl5Xkf4xIbDaxguOBbRg2MRPTgW0YNjET04FgOjs7Oz/7LhYDCojo6Oa+7T3d2tt99+W//n//yf636OiooKVVRUSJJWrlw55I/NUM+PgcO5gMs4F3AZ5wIuG8xzgV/RDpJ/+Id/8DoCLuFYRA+ORfTgWEQPjkX04FjcvPPnz+vb3/72VX9+/OMfKxgMqqurS1K4LExMTLzqca7r6t/+7d/06KOPXrPvsvLycq1cuVIrV66M+OuINM4tXMa5gMs4F3AZ5wIuG+xzYciMIAQAAEB0S0tL07e//e1rtr/yyiuqrKzUggULdPz4ceXn51+1/7nnnlNxcbGmTp06SEkBAABwJQpCAAAARNSSJUv0z//8z3rjjTdUXl4un8+nPXv2yHEcFRYW6g9/+IMmTZqkbdu2acGCBbr77ru9jgwAABBTKAgHSXl5udcRcAnHInpwLKIHxyJ6cCyiB8di4ASDwWsuk5k+fXr/x88+++wgJ/IW5xYu41zAZZwLuIxzAZcN9rlguK7rDuozAgAAAAAAAIgaLFICAAAAAAAAxDAKQgAAAAAAACCGMQfhIHjmmWdUV1ensWPHavny5V7HiTk1NTX6j//4DxmGofHjx+sv/uIv9NJLL2n79u3KzMzUl7/8Zfl8fCkMpldeeUVbt27VE088wdeHh9auXau1a9fKcRz97d/+rV566SWOhQd6enr05JNPqqenR8FgUF//+tf161//mmMxSFpbW/X9739f9fX1+tWvfiXLsq77fYnvVRgonEuQrv/+FLHtyvfHiF3vf3+enp7udSR44Ho/H/j9/og/LyMII6yurk7d3d1asWKFQqGQamtrvY4UczIzM/X444/riSee0MWLF1VVVaUDBw7oiSee0OjRo7V9+3avI8aUvr4+HTt2TBJfH15qbW1VVVWVHn/8cX3729/W+fPnORYe2bNnjyZOnKhvf/vbmjBhgn7/+99zLAZRUlKSvvWtb2nixImSrv99ie9VGCicS7js/e9PT5w44XUkeOjK98eIXe9/f045GLve//PBnj17BuV5KQgjrKamRmVlZZKk0tJSVVdXe5wo9qSlpSkQCEiSLMvSyZMnVVJSIkkqKyvjmAyy1atX6/bbb5fE14eX9uzZI8dxtGLFCv3iF79QdXU1x8Ij2dnZ6u7uliR1dHTIMAyOxSAKBAJKSkrqv32970t8r8JA4VzCZe9/f2qa/FgWy658f4zY9f73547jeB0JHnn/zwfJycmD8rz8SxRhHR0dCgaDkqRgMKjOzk6PE8Wu48eP6+LFi0pMTFRCQoKk8DHp6OjwOFnsCIVCOnDggKZOnSqJrw8vXbhwQaFQSI8//rgCgYA6Ozs5Fh7Jzc1VTU2NvvGNb6iurk6maXIsPHS970t8r8JA4VzC+11+f1pQUOB1FHjk/e+PEbve//6cK91i1/t/PigqKhqU56UgjLAr3/x1dXX1vynE4Gpvb9cvfvELfelLX1IwGFRXV5ckqbOzU4mJiR6nix3r1q3TokWL+m/z9eGdYDDYP5L28htSjoU31q5dq1mzZunJJ5/UjBkzZNs2x8JD1/u+xPcqDBTOJVzpyveniF3vf3+M2PX+9+enTp3yOBG88v6fD9avXz8oz0tBGGFFRUXav3+/JKmysnLQml+8x7Zt/cu//Iv+9E//VGlpaRo/fryqqqokhY/J5XmnEHmnT5/W22+/re9+97uqr69XW1sbXx8emTRpko4fPy5J/XPecCy84bpu/yWuKSkpkjgWXrrev9v8W46BwrmEy97//hSx6/3vj19//XWvI8Ej739/npWV5XEieOX9Px8M1hUHhuu67qA8Uwz75S9/qaNHj6qwsFB/+Zd/6XWcmLNhwwb98pe/1KhRoyRJn//851VVVaWdO3cqIyNDX/nKV1jF2APf+ta39MQTT/D14aFf/epXqqurU3Jysh577DH953/+J8fCAx0dHfrxj3+svr4+WZalr3/963rhhRc4FoMkFArpe9/7Xv+qso8++qg2bNhwzf9/vldhoHAuQbr++1MKY1x+f4zY9f735/ycGpuu9/PBlXNmRwoFIQAAAAAAABDDuMQYAAAAAAAAiGEUhAAAAAAAAEAMoyAEAAAAAAAAYhgFIQAAAAAAABDDKAgBAAAAAACAGEZBCGBYampq0sMPP6yVK1dq165dev7559XU1DTgz1NfX6/nn39eBw4c6N/2r//6r3r44Yd15MiRAX8+AAAAAAAGms/rAAAQCSkpKXrssceUnp6uTZs26c0339SUKVOUlZV1U5/Htm1ZlvWB++vr6/Xb3/5WkjRlyhRJ0t13363p06crOzv7478AAAAAAAAGieG6rut1CAAYaE1NTfrqV7+quLg49fT0XLXv+eefV3V1tf7jP/5DJ06cUHp6uj772c9q0aJF/Y8rKipSXFycTpw4oR/96Ef6x3/8RzU0NEiSxo4dq7/+679WXFycvvrVr171uf/v//2/evfdd7V27Vp973vf0/jx41VRUaGXXnpJ586dU0FBgf78z/9cxcXFevfdd/Vv//ZvWrBggU6dOqXm5mZ99rOf1dKlS3X69Gn99Kc/1fHjxxUIBDRq1CitWLFi0P7/AQAA4MY8+eSTSk1N1bFjx9TS0qK//du/1dtvv63a2loVFxfrS1/6ktcRAeAjcYkxgGGtpKRE06ZNkyR95jOf0WOPPab29natXLlSnZ2dWrZsmTIzM/Uv//IvOnbsWP/jqqurNXbsWD3yyCMyDENz5szR8uXL9elPf1rHjx/XM888o5SUFC1dulSSNHfuXD322GMqKCi46vn379+vp556SikpKfqzP/szNTc36/vf/77a2tr673PgwAHdeeedkqRf//rXCoVCevPNN3XkyBF94Qtf0KOPPqqMjIwI/58CAADAx3HixAllZ2friSeeUHl5uf793/9dX/jCF/Tkk09q165d6uvr8zoiAHwkLjEGMKwZhqGcnBzt3btXU6dO1ZQpU7Rr1y61t7ervb1dzz77bP999+/frzlz5kgKjxL8whe+IElqbW3V3r17VV1drcuDrk+cOKH4+HgVFxfrtdde06hRo7Rw4cJrnn/Xrl2SpIcfflhlZWVqbm7Wiy+++P9v7+5ZGtkCOIw/CatNxkJFjAZfMCgptNDegBYa8Xv4FfRbiJVYCYKVELASIoiNYuELaRJfqolilxCLIExhtlg2rNy9wr3rQjDPr5q3M3NmiuHMf+ac4eHhobXNwsICuVyOq6srisUi9XqdoaEhms0mNzc3pNPpVhApSZKk9hFFEY1Go9VWi8ViLC4u0tvbC0A8HufbNx+7JbU/71SSvrxYLPbb5dlslmw225r/dXzCn406gKOjI+7u7lhdXWV2dpbt7W1eX18/rS5BEAC0xjp8e3sjl8uRSqUolUpcXl6Sz+fZ3NxkeHj4fx1XkiRJn+/p6YmJiQni8R+d88IwZGlpCYBqtUpfX9+/tkUlqZ3YxVjSl5dIJAC4uLjg+vqaqakpgiCgWCzy/PzM4+Mjh4eH1Gq1D/fTaDQolUpUq9XWsp/h3u3tLWdnZ0RR9K7M3NwcAAcHBxwfH3NyckIikWBycvLDYxUKBe7v70kmkwwODtJsNqnX6//11CVJkvQXVSoVxsbGWvNhGDI6OvqPaUlqdwaEkr68+fl5UqkUhUKB3d1dgiBgY2ODZDLJ/v4++Xye7u5uBgYGflt+ZWWFdDrN+fk5tVqNkZGR1rpMJsPMzAzlcpmtra13YwsCTE9Ps7a2xsvLC3t7e/T397O+vk5PT8+Hde7q6uL09JSdnR3K5TLLy8tkMpk/vxiSJEn6NJVKhfHxceBHd+MoilovkMMwfBceSlI78y/GkiRJkiRJUgfzC0JJkiRJkiSpgxkQSpIkSZIkSR3MgFCSJEmSJEnqYAaEkiRJkiRJUgczIJQkSZIkSZI6mAGhJEmSJEmS1MEMCCVJkiRJkqQO9h3w1xuQm3EioQAAAABJRU5ErkJggg==",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"low, high, step = 0, 100, 10\n",
"plot_all(cost_history, m, q, low, high, step)"
]
},
{
"cell_type": "code",
"execution_count": 133,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"56 passi e 5600 gradienti calcolati per arrivare a distanza minore o uguale di 0.1 dall'ottimo\n"
]
}
],
"source": [
"near_opt(m, min_dist=1e-1, ge_per_step=n)"
]
},
{
"cell_type": "code",
"execution_count": 134,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA7sAAAHzCAYAAADhDgreAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAABWBUlEQVR4nO3df3Rb9Z3n/9e15F+SYluy7KT59aUJMAkJIaEObXHakBBCjmkZWjwppHhO25llWDjLMN1ySLYttKWUUMophwJLe2Boa2an7YZCD1vv4KYJYXHL4BB7QkxDgVLoFKhjyz8l/5J0v384ki3bcn5ZuldXz8c5HGLFN/5IHzvR637en/fHME3TFAAAAAAADlJg9QAAAAAAAJhrhF0AAAAAgOMQdgEAAAAAjkPYBQAAAAA4DmEXAAAAAOA4hF0AAAAAgOMQdgEAAAAAjkPYBQAgy8466yyVlpZq3rx5qqio0MUXX6xHHnlE8Xj8hNf+8Y9/lGEYikajGR1jtr4OAACZQtgFAMACzzzzjAYGBvT2229r586duueee/R3f/d3Vg8LAADHIOwCAGCh8vJyXXnllfrpT3+qH/3oRzpy5Ih++ctfat26dSorK9OSJUv0ta99Lfn5H//4xyVJFRUV8vl8+u1vf6s333xTmzdvVmVlpYLBoD772c+qt7c3ec0999yjRYsWad68efqrv/or/frXv5YkxeNx7d69W8uXL1dlZaW2b9+uUCiU9usAAJBLCLsAANjARRddpMWLF+v//b//J6/Xqx//+Mfq7e3VL3/5S/3P//k/9fTTT0uSnn/+eUlSb2+vBgcH9dGPflSmaWrXrl1699139bvf/U5/+tOfkgH5tdde04MPPqjW1lYNDAzo2Wef1VlnnSVJ+t73vqenn35aBw4c0Lvvviu/36+bbrop7dcBACCXEHYBALCJhQsXKhQK6ZJLLtH555+vgoICrVmzRtdee60OHDiQ9rqzzz5bl112mYqLi1VVVaUvfvGLyc93uVwaGRnRq6++qrGxMZ111llavny5JOmRRx7RXXfdpcWLF6u4uFhf+9rXtGfPHvbpAgAcgbALAIBN/PnPf1YgENC///u/a9OmTaqqqlJ5ebkeeeQRdXV1pb3uL3/5i6655hotWrRIZWVluu6665Kff/bZZ+v+++/X1772NVVXV+uaa67Ru+++K0l6++239alPfUoVFRWqqKjQypUr5XK59Je//CUrzxcAgEwi7AIAYAOtra3685//rA0bNmjHjh268sor9ac//Ul9fX264YYbZJqmJMkwjGnX/o//8T9kGIZeeeUV9ff364knnkh+viTt2LFDL7zwgt5++20ZhqHbbrtNkrRkyRL93//7f9Xb25v8b3h4WIsWLZrx6wAAkEsIuwAAWKi/v1//5//8H11zzTW67rrrdP7552tgYECBQEAlJSV66aWX9L/+1/9Kfn5VVZUKCgr0hz/8IfnYwMCAfD6fysvL9ec//1n33ntv8vdee+017du3TyMjIyopKVFpaakKCsb/+b/hhhv05S9/WW+//bYk6dixY/rFL36R9usAAJBLCLsAAFjgk5/8pObNm6clS5borrvu0he/+EU9/vjjkqSHH35Yt99+u+bNm6dvfOMb2r59e/I6j8ejL3/5y6qtrVVFRYVefPFF3XHHHTp06JDKy8t1xRVX6NOf/nTy80dGRrRz504Fg0EtWLBAnZ2duvvuuyVJ//iP/6grr7xSW7du1bx58/SRj3xE//7v/5726wAAkEsMc3KdEwAAAAAADsDKLgAAAADAcQi7AAAAAADHIewCAAAAAByHsAsAAAAAcBzCLgAAAADAcQi7AAAAAADHcVs9gGx49913rR6CLQWDQXV1dVk9DEzBvNgT82JPzIv9MCf2xLzYE/NiP8yJPc02LwsXLkx7HSu7AAAAAADHIewCAAAAAByHsAsAAAAAcBzCLgAAAADAcQi7AAAAAADHIewCAAAAAByHsAsAAAAAcBzCLgAAAADAcdzZ/oIPP/ywDh06pPLyct13332SpJ/97Gf69a9/rbKyMknStddeqwsvvHDate3t7Xr88ccVj8d16aWX6qqrrsrm0AEAAAAAOSLrYfeSSy7Rtm3b9NBDD6U8fsUVV+jKK69Me108Htdjjz2mr3zlK6qsrNSuXbtUU1OjxYsXZ3rIAAAAAIAck/Uy5vPOO08+n++Ur3vjjTe0YMECzZ8/X263WxdffLFaW1szMEIAAAAAQK7L+spuOs8++6yef/55LVu2TH/7t387LRCHQiFVVlYmP66srNTrr7+e7WECAAAAAHKALcLu1q1bVV9fL0n66U9/qh//+Me68cYbT/vP27t3r/bu3StJ2r17t4LB4JyM02ncbjevjQ0xL/bEvNgT82I/zIk9MS/2xLzYD3NiT6c7L7YIuxUVFclfX3rppbrnnnumfU4gEFB3d3fy4+7ubgUCgRn/vC1btmjLli3Jj7u6uuZusA4SDAZ5bWyIebEn5sWemBf7YU7siXmxJ+bFfpgTe5ptXhYuXJj2OlscPdTT05P89UsvvaQlS5ZM+5zly5frvffeU2dnp6LRqH7zm9+opqYmm8MEAAAAAOSIrK/s3n///Xr11Vc1MDCgG264Qdu3b1dHR4f++Mc/yjAMVVVV6frrr5c0vk/3+9//vnbt2iWXy6UvfOELuuuuuxSPx7Vp06YZQzEAAMg/He1teuXZJhUODWqs1KfzL6/TqrXrrB4WAMBCWQ+7t9xyy7THNm/ePOPnBgIB7dq1K/nxhRdeOOP5uwAAIH91tLfp/T2Nqq+ukOHxyDRjOrCnUZIIvACQx2xRxgwAAHC6jjQ3aWN1hQzDkCQZhqGN1RU60txk8cgAAFYi7AIAgJzmjgwmg26CYRhyR8IWjQgAYAeEXQAAkNOiHp9M00x5zDRNRT1ei0YEALADwi4AAMhpq7fW6UBnbzLwmqapA529Wr21zuKRAQCsZItzdgEAAE5XognVk81NckfCinq8Wl3fQHMqAMhzhF0AAJDzVq1dR7gFAKSgjBkAAAAA4DiEXQAAAACA4xB2AQAAAACOQ9gFAAAAADgOYRcAAAAA4DiEXQAAAACA4xB2AQAAAACOwzm7AADgtHW0t+mVZ5tUODSosVKfPrb9Wi364DKrhwUAACu7AADg9HS0t+n9PY2qL43pqkqP6ktjevPHP1BHe5vVQwMAgLALAABOz5HmJm2srpBhGJIkwzB0yfwKHWlusnhkAAAQdgEAwGlyRwaTQTfBMAy5I2GLRgQAwATCLgAAOC1Rj0+maaY8Zpqmoh6vRSMCAGACYRcAAJyW1VvrdKCzNxl4TdPUc3/p1eqtdRaPDAAAujEDAIBZTO22fP7ldVq1dp0kJf//ZHOT3JGwoh6vNvzt9XRjBgDYAmEXAADMKNltubpChscj04zpwJ5GSUoJvIlfS1IwGFRXV5cl43WS2W4yAABODmXMAABgRjN1W95YTbflTJvpSKf39zRypBMAnCLCLgAAmBHdlq3BTQYAmBuEXQAAMCO6LVuDmwwAMDcIuwAAYEYzdVs+0Em35UzjJgMAzA3CLgAAmNGqteu0oL5BTw679HT3kJ4cdmlBfQONkjKMmwwAMDfoxgwAANKa2m0ZmTfTkU6ruckAAKeMsAsAAGAz3GQAgDNHGTMAAAAAwHEIuwAAAAAAxyHsAgAAAAAch7ALAAAAAHAcGlQBAAAg4zra2/TKs00qHBrUWKlP519eRxMuABlF2AUAAEBGdbS36f09jaqvrpDh8cg0Yzqwp1GSCLwAMoYyZgAAAGTUkeYmbayukGEYkiTDMLSxukJHmpssHhkAJyPsAgAAIKPckcFk0E0wDEPuSNiiEQHIB4RdAAAAZFTU45NpmimPmaapqMdr0YgA5APCLgAAADJq9dY6HejsTQZe0zR1oLNXq7fWWTwyAE5GgyoAAABkVKIJ1ZPNTXJHwop6vFpd30BzKgAZRdgFAABAxq1au45wCyCrKGMGAAAAADgOYRcAAAAA4DiUMQMAAMyxjvY2vfJskwqHBjVW6tP5l9dRwgsAWUbYBQAAmEMd7W16f0+j6qsrZHg8Ms2YDuxplCQCb47jJgaQWwi7AAAAc+hIc5Ourq6QYRiSJMMwtLG6Qk82NxGMZpArAZKbGEDuYc8uAADAHHJHBpNBN8EwDLkjYYtGZF/JAFka01WVHtWXxvT+nkZ1tLdZPbRpjjQ3aeMMNzGONDdZPDIA6WR1Zffhhx/WoUOHVF5ervvuu0+S1NjYqJdffllut1vz58/XjTfeKK/XO+3am266SSUlJSooKJDL5dLu3buzOXQAAICTEvX4ZJqxlMBrmqainunvb/JdLq2CuyODMko9KY9xEwOwt6yG3UsuuUTbtm3TQw89lHxszZo12rFjh1wul5544gk99dRTuu6662a8/o477lBZWVm2hgsAAHDKVm+t04E9jclVQNM0daCzV6vrG6wemu3kUoDkJgaQe7Iads877zx1dnamPHbBBRckf33uuefqxRdfzOaQAACAA1m5DzTxdZ5sbpI7ElbU49Xq+gbbrVTaQS4FSG5iALnHVg2q9u3bp4svvjjt7991112SpMsuu0xbtmzJ1rAAAEAOsUMjoVVr1xFuT0IuBUhuYgC5xzBN08zmF+zs7NQ999yT3LOb8POf/1xvvvmmvvSlL01r6iBJoVBIgUBAfX19+uY3v6nPf/7zOu+882b8Gnv37tXevXslSbt379bo6OjcPxEHcLvdikajVg8DUzAv9sS82BPzYj92mJPHbt+lTxWNTVstfGq0UH/3jbstHJl17DAv6fxH60s6+MxTcoUHFfP6VPPJT+mC9RdZPayssPO85CvmxJ5mm5eioqL012VqQKfiueee08svv6zbb799xqArSYFAQJJUXl6u9evX64033kgbdrds2ZKy8tvV1TX3g3aAYDDIa2NDzIs9MS/2xLzYjx3mJBrq0lilZ4bH+y0fm1XsMC/pLPrgMi26+b+nPGbXsc41O89LvmJO7Gm2eVm4cGHa6ywPu+3t7frFL36hr3/96youLp7xc4aHh2WapkpLSzU8PKzDhw+rvr4+yyMFAAC54D8HI/rp679TkRnTWIFL5y9dohULqmy5DxQAkDlZDbv333+/Xn31VQ0MDOiGG27Q9u3b9dRTTykajerOO++UJJ1zzjm6/vrrFQqF9P3vf1+7du1SX1+fvvOd70iSYrGYNmzYoLVr12Zz6AAAIAd0tLfp/xsN6yPlxQqWFEmmqf3vvK1DoQF96IZ/tHp4AIAsymrYveWWW6Y9tnnz5hk/NxAIaNeuXZKk+fPn6957783k0AAAgAMcaW7S1WcvVXigX+8d61RBLK6/qizXG8V+GgkBQJ6xvIwZAJA5Vh6/AlghcW6rr6xcvrLy5OPV3UMWjgoAYAXCLgA4lB2OXwGyLZfObQUAZBZhFwAc6khzk64+fnalJBmGoY3VFXqyuYmwC8c6k3NbqYQAAGch7AKAQyXKOSczDEPuSNiiEQGZlwinTzY3yR0JK+rxanV9wwlDK5UQAOA8hF0AcCjKOZGvVq1dd8oBlUoIAHCeAqsHAADIjNVb63Sgs1emaUrSRDnn1jqLRwbYjzsymHJjSKISAgByHSu7AOBQp1vOCeQjKiEAwHkIuwDgYKdTzgnkozNpbAUAsCfCLgAAGUSH39xAJQQAOA9hFwCADKHDb26hEgIAnIUGVQAAZMiR5qZkWaw00eH3SHOTxSMDAMD5CLsAAGQIHX4BALAOZcwAAGQIHX7hZLPtR2evOgA7IOwCAHLe1DfWvg8u1+Bbb1r+RpsOv3Cq2fajS2KvOgBbIOwCAHLa1Dfdr773nl7d84K2rTlP8yorLH2jTYdfONWR5iZdPcN+9CeP70dP93t87wPIJsIuACCnTX3T3fHOf+rqRZV6v+uY5pVXWP5Gmw6/cCJ3ZFBGqSflsYn96OYsvwcA2UODKgBATpvaBModj6nAMFQQiyUf4402MLfG96ObKY8l9qPP9nsAkE2EXQBATpv6xjpa4FLcNBV3uZKP8UYbmFurt9bpQGdv8mcvuR99a92svwcA2UQZMwAgKzLVnXVqE6hVSxfr52+8qcvXnCdJNIUCMuBk9qOzVx2A1Qi7AICMm61z65m+AZ72prviA/LWb9Czf3xT7m7eaAOZMtt+dPaqA7ADwi4AIONm69w6F2+IeWMNAACmYs8uACDjpjaRkmgaBQAAMouwCwDIOLqzAgCAbCPsAgAyju6sAAAg29izCwDIuJPp3ApkS6Y6gwMA7IWwCwDIilxoIkUIyhy7vLYn6gxul3ECAM4cYRcAAGX2eKR8Z6fXdrbO4JJsM04AwJljzy4AABoPQRtnCEFHjocgnD47vbazdQa30zgBAGeOsAsAgDgeKZPs9NrO1hncTuMEAJw5wi4AAOJ4pEyy02s7W2dwO40TAHDmCLsAAIjjkTLJTq/tqrXrtKC+QU8Ou/R095CeHHZpwfHO4HYaJwDgzNGgCgAA5ebxSLnSOdhur226zuB2GycA4MwQdgEAOC4XjkdKsFOH45ORK69ttseZKzcsACAXUcYMAEAOonNw7kvesCiN6apKj+pLY3p/T6M62tusHhoAOAJhFwCAHETn4NzHDQsAyCzKmAEAc4qyzOwY7xwcSwm8dA7OLe7IoIxST8pj3LAAgLnDyi4AYM5Qlpk9dA7OfRx1BACZRdgFAMwZyjKzZ7YjdJAbuGEBAJlFGTMAYM5QlpldVnc4nqlkfeOWyywbT67hqCMAyCzCLgBgzrCPNH+kO/roP8rLteiDy6weXs6w+oYFADgZYRcAMGdWb63TgT2NyVLmZFlmfYPVQ8uKbDbnsroR2JHmJl09Q8n6L595Sotu/u9ZGwcAAOkQdgEAcyafyzLTrXRKmvPnn82vlU66knXX4GBWvj6QbVbfYAJw6gi7AIA5la9lmelWOp9sbprz1yObXyuddCXrMa8vK18fyCY73GACcOroxgwAwBxwRwZTgp+UueZc2fxa6aTrJFzzyU9lbQxAttBpHshNrOwCADAHstmcyw6NwNKVrF+w/iJ1dXVlbRxANtBpHshNhF0AAOZANptz2aURWL6WrCP/2OEGE4BTR9gFAGAOZLM5Vz43AgOsYJcbTABOTdbD7sMPP6xDhw6pvLxc9913nyRpcHBQ3/3ud3Xs2DFVVVXpn/7pn+TzTW9w8dxzz+nnP/+5JOnTn/60LrnkkmwOHQCAWWVzpZNVVSB7uMEE5Kash91LLrlE27Zt00MPPZR87Omnn9b555+vq666Sk8//bSefvppXXfddSnXDQ4Oas+ePdq9e7ckaefOnaqpqZkxFAMAAABziRtMQO7Jejfm8847b1pAbW1t1caNGyVJGzduVGtr67Tr2tvbtWbNGvl8Pvl8Pq1Zs0bt7e3ZGDIAAAAAIMfYYs9uX1+f/H6/JKmiokJ9fX3TPicUCqmysjL5cSAQUCgUmvHP27t3r/bu3StJ2r17t4LBYAZGnfvcbjevjQ0xL/bEvNgT82I/TpqT/2h9Sa3PPCV3eEBR7zyt/+SndMH6i6we1mlx0rw4CfNiP8yJPZ3uvNgi7E5mGMa0swNP1ZYtW7Rly5bkxxyBMLNgMMhrY0PMiz0xL/bEvNiPU+ako71N7+9p1CeqK2T4XDLNsA489qB6+3Jzn6ZT5sVpmBf7YU7sabZ5WbhwYdrrsl7GPJPy8nL19PRIknp6elRWVjbtcwKBgLq7u5Mfh0IhBQKBrI0RAADkjyPNTcnOu9L4zfiN1RU60txk8cgAACfLFiu7NTU1OnDggK666iodOHBA69evn/Y5a9eu1b/+679qcHBQkvQf//Ef2rFjR7aHCgAAsqCjvU2vPNukwqFBjZX6dP7ldVldUXVHBmWUelIeMwxD7kg4a2MAAJyZrIfd+++/X6+++qoGBgZ0ww03aPv27brqqqv03e9+V/v27UsePSRJb775pn71q1/phhtukM/n09VXX61du3ZJkurr6+nEDACAAyVKiOurK2R4PDLNmA7saZSkrAXeqMcn04ylbK0yTVNRjzcrXx8AcOayHnZvueWWGR+//fbbpz22fPlyLV++PPnx5s2btXnz5kwNDQAA2MCR5iZdPUMJ8ZPNTVkLu6u31unAnsZkKbNpmjrQ2avV9Q1Z+foAgDNnizJmAACABDuUECdC9ZPNTXJHwop6vFpdn5vNqTJhrsvMrS5bBzBhMDKqY6GwOrvDOtYz/vfuJy75K4tHdXoIuwAwR3izBsyNkykhzsbP26q166b9mfycz32ZuR3K1oF8Eo+bCvUN6VgoPB5qE8H2+MeR4bGUzy/zFRN2ASCf8WYNmDsnKiG26ueNn/Nxc11mboeydcBpRkaj6uqJqDMU1rHu8UCbCLbdPRFFY/G01xYXuVQV8Ko64B3/f6VPpmme8fGwViDsAsAc4M0aMHdOVEJs1c8bP+fj5rrM3A5l60CuMU1TA+HRZIA9drzkuPN4sO0bGJ71+vJ5xarye1VVOR5qqwPjv67ye1XmK87JYDsTwi4AzAHerAFza6YS4gSrft74OR83152q6XwNzCwWi6u7b2g8yIZSV2ePhcIaHommvdZVYKjS75m0OutNWa0tLsqPGJgfzxIAMow3a0D2WPXzxs/5uLnuVE3na+Sz4ZFoMrwem7J3trs3oljcTHttabE7uTJbFZgIs9WVXvnLSuVyFWTxmdgTYRcA5gBv1oDsycTP28k0nuLnfNxcdaqe/Jr/ZSSuI+90a7HPS+drOIppmuofHJnWBCpRetwfHpn1en9ZSUqQnRxufZ4ix5QbZwphFwDmAMeUANkz1z9vJ9t4ip/zCbOVmZ+Maa95oFQHOnu14Kq/ycvXE7ktGo2ruzcyEWh7UptCjY7F0l7rdhUo6Peklhkf3ztbFfCqqNCVxWfiPIRdAJgjZ/rmD8DJm8uft1NpPMXP+dyg2RdyTWR4LGXv7OSmUN29EZnpq43lLS1MDbKBiaZQFWWlKihgdTZTCLsAACCv0Xgq+3jNYTfxuKnegWG9H3pPr7/1bsrK7LFQWIOR0bTXGoZUWVGaWm48qSmUt7Qoi88EkxF2AQBAXqPxVPbxmsMKY9GYukKRiZXZSU2hunrCGoumP3u20F0w477ZqoBXQb9HhW7Kje2IsAsAFjiZZjiwB+bK+Wg8lX285siUwcjoRFfjnommUJ2hsHr7h2YtN/Z5irRwfoUCZUXTmkKV+0ooN85BhF0AyLKTbYYD6zFXJ2fyDQFXIKhzPr45p14fGk9lH685Tlc8birUN5TS1XhyU6jI8FjaawsKDFVWlI6XF/unnz1bWlKoYDCorq6uLD4jZBJhFwCyjMYsuYO5OrGpNwQKC8f0qxy8IUDjqezjNUc6o2OxlON5OicF2+6eiKKx9OXGxUWu1DNnJzWFqqzwyM3Zs3mFsAsAWUZjltzBXJ0YNwQAnCrTNDUQHp0ItJP2znaGwuobGJ71+jJf8bS9s4n/l/mKOXsWSYRdAMgyGrPkDubqxLghAGAmsVhc3X1DKcf1TP7/8Eg07bWuAkOVfk9KE6jqScG2uIgIg5PDdwoAZBmNWXIHc3Vi3BAA8tfwSDQ1yE7aO9vdG1Esnr4bVGmxe7y8eMre2epKr/xlpXJRbow5QNgFgCyjMUvuYK5OjBsCgHOZpqn+wZGJJlCTV2e7w+oPj8x6vb+sZFpX48SvfZ4iyo2RcYRdALAAjVlyB3M1u6k3BNwBj87mhgCQM6LRuLp7I6llxpOaQo2OxdJe63YVKOj3JFdmJ++drQp4VVTI2bOwFmEXAACckck3BObi2A7ONgbmVmR4bHxV9niIndwUqrs3MuvZs97SwtQQWznR5biirJSzZ2FrhF0AAGAbnG0MnLp43FTfwPBEkJ3SFGowMpr2WsOQKitKVeWf0t34+Gqtt7Qoi88EmFuEXQAAYBscZQTMbCwaU1coMq2rcWd3WF09YY1F0589W+guSNk3O7nUOOj3qNBNuTGcibALAABsg6OMkM8GI6MpTaAmN4Xq6R+atdzY5ylKHs8TDEyUGldVelXuK6HcGHmJsAsAAGyDo4zgZPG4qZ7+oWSIHRj6g975c1ey9DgyPJb2WsPQRDOoKcf1VAW8Ki0pzOIzAXIDYRcAANgGRxkh142OxVK6GidXaUNhdfdEFI2lLzcuLnKldDWe3BSqssIjN2fPAqeEsAsAAGyDs41hd6ZpaiCcWm6c2Dt7rCes3v7hWa8v8xUny4vPWlwlb4mRDLVlvmLOngXmEGEXAADYCmcbw2qxWFyhvqFpZ84mwu3wSDTtta4CQ5V+T0oTqOpJTaGKiybefs/FUV2YO22HO7Tv4BF1hUfkc8VVt2G91q1ZZfWwcAYIuwAAAMg7wyPRlJXZyaXH3b0RxeLpu0GVFLunHdGTKD0OlJfKRblxzmk73KHGlqOav2ajvGNjipumGltaJYnAm8MIuwAAAHAc0zTVPzgyratxItD2h0dmvb6irGQi0E7aO1sd8MrnKaLc2GGaWg7Kv2JTyrFn/hXr1dSyn7Cbwwi7AAAAJ6HtcIeaXmjVYKyAEkebiEbj6u6NpDSBOnZ87+yxUFgjo7G017pdBSndjaeeP1tUyNmz+WQwasg75QaGYRgKR7mpkcsIuwAAACeQKHH0r9wsr2FQ4phFQ8NjKXtnJ5cdd/dGZj171ltamFJiPDnQ+stKOXsWST63qfiUbybTNOV1z/INBtsj7AIAAJwAJY6ZE4+b6hsYTg2yk5pCDUZG015rGFKgvHRakE3spfWWFmXxmSCX1dXWqLGlVfPX1EoaD7o9R1vVUFtj8chwJgi7AAAAJ0CJ45kZi8bUFYroWM/4/tnJx/V09YQ1Fk1/9myhuyBlZbbKP9EUKuj3qNBNuTHOXOKm1b6XD6hvcERet6mG2hpuZuU4wi4AAMAJJEocJzclosQxVXhoNNkIKtEUquv4r3v6h2YtN/Z5iqbtnU2s0pbPK6HcGFmxbs0qXbZ5I8dBOQhhFwCAHNDR3qZXnm1S4dCgxkp9Ov/yOs6izaJEiaN/xXoZhpGXJY7xuKme/qFpnY0T+2kjw2NprzUMKej3JFdopx7XU1pSmMVnAiBfEHYBALC5jvY2vb+nUfXVFTI8HplmTAf2NEoSgTdLEqWMTS37FY4aji1xHB2LTTuiJxFou3siisbSlxsXFbqSIbZ6SlOoygqP3Jw9CyDLCLsAANjckeYmXV1dkdIcaWN1hZ5sbiLsZtG6NatyPtyapqmB8Oj40TzdqZ2NO0Nh9fYPz3p9ma942t7ZRLAt8xVz9iwAWyHsAgBgc+7IoIxST8pjhmHIHQlbNCLYWSwWV6hvKGVltj8c1X++F1JnKKzhkWjaa10FhionlRsnuhpX+cd/XVLMW0cAuYO/sQAAsLmoxyfTjE1rjhT1eC0cFaw0PBKdKDWeUnbc3RtRLJ6+G1RJsTs1yE4qOQ6Ul8pFuTEAhyDsAgBgc6u31unAnkZtPF7KbJqmDnT2anV9g9VDQ4aYpqn+wZGUzsaTw23/4Mis11eUlaScObv8/1ugkqK4qgNe+TxFlBsDyAuEXQAAbC6xL/fJ5ia5I2FFPV6trm9gv26Oi8bi6u6NpDSBOjbpv5HRWNpr3a4CBf2eacf1JM6eLS5KfYsXDAY5TgVA3iHsAgCQA1atXUe4zUFDw2PJ8uJjPeMrtIlQ290bmfXsWW9poYKBSWfOTmoK5S8r5ezZLGg73KGmF1o1GCuQzxVX3Yb1Od+kDMgnhF0AAIDTFI+b6hsYTgbYyU2hjoXCGoyMpr3WMKRAeWkyyE4uO66u9MpbWpTFZ4Kp2g53qLHlqPwrN8trGIqbphpbWiWJwAvkCMIuAADALMaiMXX1RMbDbPf0cuOxaPqzZwvdBcnmT8lV2sqJcuNCtyuLzwSnoqnloPwrNqUc+eVfsV5NLfsJu0COIOwCAIC8Fx4andYEKrFC29M/NGu5sc9TNHFUz6QV2uqAV+XzSig3zlGDUUPeKY28DMNQOMp8ArmCsAsAABwvHjfV0z80Hmh7wqlNobrDigyPpb3WMKTgpLNnJzeFqgp45SkpzOIzOXUd7W16/fl9ioW6NFbq0/mX17H/+yT43KbipjntyC+ve5Y7HwBsxRZh991339V3v/vd5MednZ3avn27rrjiiuRjHR0d+va3v63q6mpJ0oc//GHV19dnfawAAMCeRsdi086cTazSdvVEFI2lLzcuKnRNO3M2sVJbWe6R252bZ892tLfp/T2N+vTiao1VemSaMR3Y0yhJBN4TqKutUWNLq/wr1ieP/Oo52qqG2hqrhwbgJNki7C5cuFD33nuvJCkej+sf/uEfdNFFF037vJUrV2rnzp3ZHh4AALAB0zQ1GBmdFmQT4ba3f3jW68t8xdOaQCU+LvMVO/Ls2SPNTbr6+PnM0ngZ7sbqCj3Z3ETYPYHEvtymlv0KRw153aYaamvYrwvkEFuE3cleeeUVLViwQFVVVVYPBQAAZFksFleob2jacT2JUDs0Ek17ravAUGWFZ3pn4+P/Lym23duejHNHBmWUelIeMwxD7kjYohHllnVrVhFugRxmu7/1W1paVFtbO+Pv/f73v9ett94qv9+vhoYGLVmyZMbP27t3r/bu3StJ2r17t4LBYMbGm8vcbjevjQ0xL/bEvNgT82I/JzMnQ8Njer+rX385NqD3jvXr/eP/vXdsQMe6BxSLp98TWVpSqAVVZfpAVZkWVM3TgmCZFlSVaUH1PFX5fXK5crPcOFPcgaAKC8dUYBgqKho/ysg0TbkDHn52bIC/w+yHObGn050XwzRn6y+YXdFoVP/wD/+g++67TxUVFSm/F4lEVFBQoJKSEh06dEg//OEP9cADD5zUn/vuu+9mYLS5LxgMqqury+phYArmxZ6YF3tiXuwnGAzq2LFj6h8cSZYXT16Z7QyF1T84MuufUVFWMn1l9nhTqHneIkeWG2dKYs/uZYurNTY2JtM0daCzVwvqGyhjtgH+DrMf5sSeZpuXhQsXpr3OViu7bW1t+uAHPzgt6EqSxzNRgnPhhRfqscceU39/v8rKyrI4QgAAIEnRWFzdvZGUvbOdobBCfSN6/1ifRkZjaa91uwpSuhtPLjsO+j0qLrLV25Oclgi0Tz2/T9FQv6Ier1YTdAHkCVv9azJbCXNvb6/Ky8tlGIbeeOMNxeNxzZs3L8sjBAAgfwwNj6U2gZoUbLt7I7OePespKUyG2KlNofxlpZw9m0Wr1q7Txi2XsVoFIO/YJuwODw/r8OHDuv7665OPNTc3S5K2bt2qF198Uc3NzXK5XCoqKtItt9xCGRMAAGcgHjfVNzA8UW48pSnUYGQ07bWGIQXKSydKjI+H2nOWLVKRa0ze0qIsPhMAAKazTdgtKSnRP//zP6c8tnXr1uSvt23bpm3btmV7WACAKTra2/TKs00qHBrUWKlP519eR0mkjY1FY+rqiSRXZo/1pB7bMxZNf/ZsobsguSKbPHv2+N7ZoN+jwkLXtGvY7wYAsAvbhF0AgP0lmt3UV1fI8HhkmjEd2NMoSQReC4WHRqc1gUoE2p7+oVnLjX2eohn3zlYHvCqfV0K5MQAgZxF2AQAn7Uhzk66urkhuIzEMQxurK/RkcxNhN4PicVM9/UPTgmxnKKyuUFjhobG01xqGUptBTe5uHPDKU1KYxWdivbbDHWp6oVWDsQL5XHHVbVjPOaoA4FCEXQDASXNHBmWUelIeMwxD7kjYohE5x+hYbNrKbGLvbFdPRNFY+nLjokLXeHnx5HLj44G2stwjt5uzZ6XxoNvYclT+lZvlNQzFTVONLa2SROAFAAci7AIATlrU45NpxlIaBJqmqajHa+GocoNpmhqMjE4E2VDqkT29/cOzXl/mK05dnZ3UFKrMV0zTxpPQ1HJQ/hWbUioT/CvWq6llP2EXAByIsAsAOGmrt9bpwJ5GbTxeymyapg509mp1fYPVQ7OFWCyuUN/QtON6Er8eGommvdZVYKiywpOyb3ZyuC0p5p/sMzUYNeSdclPAMAyFo/a+UUDpNQCcHv7lBJBxvFFzjsS+3Cebm+SOhBX1eLW6viGv9uuOjEYnjuqZ0hSquyeiWDx9N6iSYvf0IHs83AbKS+VyUW6cST63qbhpTqtM8Lpn6eBlMUqvAeD0EXYBZBRv1Jxn1dp1jg63pmmqf3AkNdBOOq6nf3Bk1usrykpU5U8tM06E23neorwvN7by5lddbY0aW1rlX7E+WZnQc7RVDbU1Wfn6p4PSawA4fYRdABnFGzXYUTQWV3dvJGXv7OTS45HRWNprXS5DQX9qE6hEqA36PSou4p/WdKy++ZX4Gk0t+xWOGvK6TTXU1tj676JcLb0GADvgX2QAGcUbNVhlaHhs2t7ZxMehviHFZyk39pQUTjtzNtEUyl9Wytmzp8kON7/WrVll63A7VS6WXgOAXRB2AWQUb9SQKfG4qe7esH7/VlfKmbOJ0uPByGjaaw1DCpSXTuydndIUyucpyuIzyR/c/Dp1uVh6DQB2QdgFkFG8UcOZGIvG1NUTmehqPGnv7LFQWGPR9GfPut0FM+6dTZQbFxa6svhMIHHz63TkYuk1ANgFYRdARvFGDScSHhqd1tU4EWh7+odkzpKD5nmLFfR7pu2drQ54VT6vhHJjm+Hm1+nJtdJrALALwi6AjOONWn6Lx0319g9NNIHqTm0GFR4aS3utYUhBvyflqJ7JwXbp4g+oq6srI+PuaG/TK882qXBoUGOlPp1/eZ2ju1BnAze/AADZRNgFAJyx0bFY6srspKZQXT0RRWPpy42LCl3TzpxNlBxXVnjkdmf/7NmO9ja9v6dR9dUVMjwemWZMB/Y0ShKB9wxx8wsAkC2EXQDACZmmqcHI6ESQnbI629M/POv1Zd7ilO7Gk5tClfmKbXf27JHmJl1dXZHSNXhjdYWebG4i7AJAGlaeow3MhLALAJAkxWJxhfqGUlZnJzeFGhqJpr3WVWCossIzPdAe/39JcW79c+OODMoo9aQ8ZhiG3JGwRSMCAHuz+hxtYCa59e4DAHBGRkajyTA7tSlUd09EsVnOni0pdk8Pssf3zlaWl8rlyn65caZEPT6ZZmxa1+Cox2vhqADAvuxwjjYwFWEXABzENE31D46krs5OKjvuHxyZ9fryeSXje2anHNdTFfBqnrfIduXGmbJ6a50O7GnUxuOlzKZp6kBnr1bXN1g9NACwJc7Rhh0RdgEgx0RjcXX3RlL2zk7ePzsyGkt7rctlKOhPbQKVKD0O+j0qLuKfBWmiCdWTzU1yR8KKerxaXd/Afl0ASINztGFHvKsBABsaGh6bce9sZ3dYob4hxWcpN/aUFI6XF/snmkAlGkL5y0o5e/YkrVq7jnALACeJc7RhR4RdALCAaZrqHRie1tU4sZd2MDKa9lrDkALlpdO6Gic+9nmKsvhMAADgHG3YE2EXADJkLBpTV08k9fzZ4+G2qyei0bH05cZud0FyZXby3tlEuXFhoSuLzwRIb+pRI9d+YouWLV1s9bAAWIBztGE3hF0AOAPhodGJMuMpe2dDfUMyZ9mq5PMUpTaBqpzYS1s+r4RyY9jeTEeN/KC5TZ+5qI83vDbFOagA8glhFwBmEY+b6u0f0nvd7+r1t97VsSmhNjw0lvZaw5CCfo+q/KlBNhFsPSWFWXseHe1teuXZJhUODWqs1KfzL69jPyrO2IxHjaxcr6aWZwlQNsQ5qADyDWEXQN4bHYslV2OnNoXq6okoGounvbao0JVy5uzkcuPKCo/cbuvPnu1ob9P7expVX10hw+ORacZ0YE+jJBF4cUY4aiS3cA4qgHxD2AXgeKZpajAyOlFiPKUpVE//8KzXl3mLtXB+ufxlxdOaQpX5im1/9uyR5iZdffy8WGn8De7G6go92dxE2MUZ4aiR3MLNCQD5hrALwBFisbh6+ofUOUN342PdYQ2NRNNeW1BgKFjhSQmyyWZQAY9KiwsVDAbV1dWVxWc0d9yRQRmlnpTHDMOQOxK2aERwihmPGvldqz6TgaNG2Gt65rg5ASDfEHYB5IyR0WjK8TyTA213T0SxWc6eLS5yp545O2nvbGV5qVwu68uNMyXq8ck0Y9Pe4EY9XgtHBSeY6aiR66+4dM67MbPXdG5wDiqAfHNSYTcej6u1tVWGYaimpkYFBeNvCn/729/qox/9aEYHCCB/mKap/sGR1DNnj6/MHusJq29gZNbry+eVjDeBqvSmNIWqCng1z1tk+3LjTFm9tU4H9jRq4/FSZtM0daCzV6vrG6weGhxg6lEjmaiCYK/p3OAcVAD55qTC7oMPPqhgMCi3261nnnlGN910kxYsWKDm5mbCLoBTEo3FFeqNpJw5O1F2HNHIaPpyY5fLUNA/ZXW2cuLs2eIiilVmktiX+2Rzk9yRsKIer1bXN7BfFzmDvaZzh3NQAeSTk3pnGAqFdPPNN0uSNm3apAcffFB/8zd/k9GBAchdQyNj05pAJUqPQ31Dis9SblxaUjgRZietzFYFvAqUl3L27GlatXYd4dZC7Dc9M+w1PTNthzu07+ARdYVH+P4DkFdOKuxGo1GNjY2psLBQVVVV2rlzp+6//3698847mR4fABsyTVO9A8PJ8uLOKWfPDoRH015rGJK/vDQl0Fb5J5pC+TxFWXwmQOax3/TMsdf09CW+/+av2Sjv2BjffwDyyqxhNxaLyeVy6XOf+5zC4bAqKiokSaWlpbrtttv0wgsvZGOMACwwFo2pqycyravxsVBYx3oiGh2Lpb3W7S6YCLCT9s4myo0LC11ZfCaAtdhveubYa3r6+P4DkM9mDbvf+ta3dOutt+rss8+e9nsFBQX6+Mc/nrGBAci8yNDojJ2Nj4XGy43NWSoEfZ6iiaN6AqnNoCrmlVBuDBzHftO5wV7T08P3H4B8NmvYPeuss/TVr35Vu3btUiAQkCS9+uqr+slPfqJvfOMbWRkggNMXj5vq7R9KbQI1aS9teGgs7bWGIVVWeFKC7OTjejwlhVl8JkDuYr8prJT4/puM7z8A+WLWsNvQ0KDm5mZ99atf1Y4dO7Rv3z698847uvLKK7M1PgAnMDoWO15aHJ7WFOpYT0TRaDzttUWFrpSV2UTpcXXAq8oKj9xu5549C2QL+01hpcT33/w1tZLE9x+AvHLCBlXnnnuuPB6PHnjgAW3cuFG33XabiopoIANki2maCg+NqrM7nHJcTyLQ9vQPz3p9mbd4PMhOWplNBNoyX3Henj0LZAv7TWGlxPfZvpcPqG9whO+/E6BzOuAss4bde++9V6+++qquuOIKbd++XY8++qiOHDmiCy+8MFvjA/JCPG4q1BdRZ3dYkVeP6a13/pLSFGpoJP3ZswUFhoIVnon9s5UTR/VUBTwqLabcGLAa+01hpXVrVumyzRvV1dVl9VBsjc7pgPPMGnY/8IEP6L/+1/8qn88nSZo/f77uuecedXZ2atu2bVkZIOAUI6PRlAZQk4/r6e6NKBZLv3+quMg97czZROlxZXmpXC7KjQEAOBN0rgacZ9awe91116V8vHTpUt155526++67CbvAFKZpqn9wJGXv7ORy476BkVmvL59XouqAV4sXBlTucad0N57nLaLcGACADKJzNeA8J9yzO1UgEKATM/JWNBZXqDcybe/s+P8jGhlNX27schkK+idWZSc3haoKeFRcNP7jGAwGKTUDACDL6JwOOM8ph11JKi0tnetxALYxNDI2rQlU4izaUN+Q4vH0/+iVlhSmNIGqCnhUHfCpKuBVoLyUs2cBALApOqcDznNaYRfIZaZpqndgWMe6x4/rmbx39lgorIHw6KzX+8tLp+2dTTSF8pYWUm4MAEAOonM64DyEXTjSWDSm7t7ItCA7HnAjGh2Lpb3W7S5IlhZXB3zJvbPVAa+Cfo8KC11ZfCYAACBb6JwOOAthFzkrMjSaLC8+FkoNtaG+IZmzbLHxeYqmdTWu9o//v2JeCeXGAAAAQI4j7MK24nFTvf1DqU2gJu2lDQ+Npb3WMKTKCs9EE6jjq7TVx8+e9ZQWZfGZAAAAAMg2W4Xdm266SSUlJSooKJDL5dLu3btTft80TT3++ONqa2tTcXGxbrzxRi1btsyi0WIujI3FxvfNTgmyx0Lj5cbRaDzttUWFromV2YBHVQFf8izaygqP3G7OngUAwCnaDneo6YVWDcYK5HPFVbdhvaNKjp3+/AAr2CrsStIdd9yhsrKyGX+vra1N77//vh544AG9/vrrevTRR/Wtb30ryyPEqTBNU+GhUXV2TwTayU2hevqHZ72+zFs8HmQrfZOaQo2v0pbPK6YZFAAAWWRVIGs73KHGlqPyr9wsr2EobppqbGmVJEcEQqc/P8Aqtgu7szl48KA+/vGPyzAMnXvuuQqHw+rp6ZHf77d6aHktHjcV6jveDGpad+OIhobTlxsXFBgT5caJrsb+8XBbFfCotLgwi88EAACkY2Uga2o5KP+KTcmb3IZhyL9ivZpa9jsiDDr9+QFWsV3YveuuuyRJl112mbZs2ZLye6FQSMFgMPlxZWWlQqHQtLC7d+9e7d27V5K0e/fulGswwe12n/RrMzwypr90Dei9Y/16/1i/3j82/uu/HOtXZ/egorH05calxYVaUDVPC6rKjv83/usPVJWpKuCTy0W58WSnMi/IHubFnpgX+2FO7Gku5mXfy0c0f83GlKqq+Wtqte/lA7ps88YzHeKsxlwl8hQXT3t8yFWS099viXlx6vPLRfwdZk+nOy+2Crt33nmnAoGA+vr69M1vflMLFy7Ueeedd8p/zpYtW1KCcldX11wO0zGCwWDytTFNUwPhUXWGBlP2zib+3zcwMuufVT6vJLl3dvJxPVUBr+Z5i9KUG4+qpyeUgWeW2ybPC+yDebEn5sV+mBN7mot56RockXdserVW3+BIxue8MDaskZGRlPcTpmnKHRvO6e+3xLw49fnlIv4Os6fZ5mXhwoVpr7NV2A0EApKk8vJyrV+/Xm+88UZK2A0EAilPsru7O3kNTiwaiyvUG0nunR0cflNv/+exZLnxyGg07bUul6FgxcTe2clNoaoCHhUX2epbCQAAzDGf21TcNKcFMq97lrP+5khdbY0aW1rlX7FehmHINE31HG1VQ21Nxr92Njj9+QFWsU1CGR4elmmaKi0t1fDwsA4fPqz6+vqUz6mpqdG//du/qba2Vq+//ro8Hg/7dacYGhkbbwIVmro6G1F3b0TxePp/kEpLClP3ziZWaQNeBcpLOXsWAGyCrq2wgpWBLPH93dSyX+GoIa/bVENtjWO+753+/ACr2Cbs9vX16Tvf+Y4kKRaLacOGDVq7dq2am5slSVu3btW6det06NAh3XzzzSoqKtKNN95o5ZAtYZqm+gZGxsuNQxPNoBKhdiA8Ouv1/vLS5KrsWYur5S0xjgdbr7ylhXQ3BgCbo2srrGJ1IFu3ZpWjv8ed/vwAK9gm7M6fP1/33nvvtMe3bt2a/LVhGPr7v//7bA7LEtFoXF2904Ps+LE9EY2OxdJe63YXqMo/095Zj6r8XhUWupKfy54EADNh1dDe6NoKKxHIAOQS24TdfPSn9/r0ftfgtKZQob4hmbNsf/GWFqq6cry8eGpTqIp5JZQbAzhtrBra32DUkHdKFY5hGApH+bsfAIDJCLsW+tHTbfrDn3qmPW4YmnT2rOf46qwv+bGntMiC0QLIB6wa2p+VTYIAAMglhF0LrVhWpTJf8fEQ60s2hQpWeOV2c/YsgOxj1dD+6NoKAMDJIexaqP5yVkkA2AurhvZndZMgAAByBWEXAJDEqmFuoEkQAAAnRtgFACTlw6oh3aYBAMgPhF0AQAonrxrSbRoAgPxBFyQAQN4Y7za9foZu0wctHhkAAJhrhF0AQN4YjBopzbckuk0DAOBUhF0AQN7wuU2ZZmpnabpNAwDgTIRdAEDeqKutUc/R1mTgTXSbrqPbNAAAjkODKgBA3kg0ofrxL57UH471KTY2ouXVFZJWWDouAAAw9wi7AIC8YwSXqmbDxFnCdGQGAMB5KGMGAOQVOjIDAJAfWNkFAOSVwaghb452ZG473KGmF1o1GCuQzxVX3Yb1rEYDAJAGYRcAkFd8blNx00w5gigXOjK3He5QY8tR+VdultcwFKf8GgCAWVHGDADIK7nakZnyawAATg0ruwCAvBPvelsHnzqi+Oiwli3w63OfvsL2q6O5XH4NAIAVCLsAgLyRKAWu3FCv4PFOzD1HW60e1knJ1fJrAACsQhkzACBv5HIpcK6WXwMAYBVWdgEAeSOXS4ETZdZNLfsVjhryuk011NbYvvwaAACrEHYBAHkj10uB161ZRbgFAOAkUcYMAMgblAIDAJA/WNkFAOQNSoEBAMgfhF0AQF6hFNiZ2g53qOmFVg3GCuRzxVW3YT3zDAB5jrALAAByWuJIKf/KzfIahuKmqcaW8SOlCLwAkL/YswsAAHJaLh8pBQDIHMIuAADIaYNRI6XDtpQ7R0oBADKHsAsAAHKaz20mO2wn5NKRUgCAzGDPLgAANkOzpVNTV1ujxpbWZClz4kipBo6UAoC8RtgFAMBGaLZ06jhSCrli6o2saz+xRcuWLrZ6WIBjEXYBALCR8WZLm2ZotrSf8DYLjpSC3c10I+sHzW36zEV9fO8CGULYBQDARgajhrw0W4LNUFp/5ma8kbVyvZpanuW1BDKEsAsAgI343KbippnSXZhmS7ASpfVzgxtZQPbRjRkAABupq61Rz9HWZHfhRLOlOpotwSKcYzw36BoOZB8ruwAA2AjNlmA3rEjOjRm7hv+uVZ/hRhaQMYRdAABshmZLsBNK6+fGTDeyrr/iUroxAxlE2AUAAEBanGM8d6beyAoGg+rq6rJwRICzEXYBAIAkOu5iZpTWA8hVhF0AAEDHXcyK0noAuYhuzAAAgI67AADHIewCAAANRo2UBkQSHXcBALmNMmYAAHDKHXfZ3wsAsDvCLoC8wZtzIL1T6bg72/7eyzZvzPbQHYm/rwDgzBF2AeQFmu8AszuVjrvj+3s3zbC/dz9hdw7w9xUAzA3CLoC8MNubc948AuNOtuPuYNSQl/29J3S6q7P8fQUAc8MWYberq0sPPfSQent7ZRiGtmzZorq6upTP6ejo0Le//W1VV1dLkj784Q+rvr7eiuECyEG8OQfmzqnu781HZ7I6y99XADA3bBF2XS6XGhoatGzZMg0NDWnnzp1as2aNFi9enPJ5K1eu1M6dOy0aJYBcxptzYO6cyv7efHUmq7P8fQUAc8MWRw/5/X4tW7ZMklRaWqpFixYpFApZPCoATlJXW6Oeo60yzfE3i4k353W8OQdO2bo1q9RQu0IFR/cr8sp+FRzdr4baFZTYTnImRznx9xUAzA1brOxO1tnZqbfeektnn332tN/7/e9/r1tvvVV+v18NDQ1asmSJBSMEkItOpfkOgBM72f29+epMVmf5+woA5oZhJm4b2sDw8LDuuOMOffrTn9aHP/zhlN+LRCIqKChQSUmJDh06pB/+8Id64IEHZvxz9u7dq71790qSdu/erdHR0YyPPRe53W5Fo1Grh4EpmBd7Yl7siXmxH+Zk3EuH2vWD5jb5V04q9f5dq67fuk4XXbg26+NhXuyJebEf5sSeZpuXoqKitNfZJuxGo1Hdc889uuCCC/SJT3zihJ9/00036e6771ZZWdkJP/fdd9+diyE6TjAYVFdXl9XDwBTMiz0xL/bEvNgPczKh7XCHmloOJldn6yxcnWVe7Il5sR/mxJ5mm5eFCxemvc4WZcymaeqRRx7RokWL0gbd3t5elZeXyzAMvfHGG4rH45o3b16WRwoAAHByKPUGAGvZIuy+9tprev7557V06VLdeuutkqRrr702md63bt2qF198Uc3NzXK5XCoqKtItt9wyrfEDAAAAAACSTcLuihUr9LOf/WzWz9m2bZu2bduWpREBAADgTLUd7lDTC60ajBXI54qrbsN6VrsBZI0twi4AAACcpe1whxpbjsq/crO8hqG4aaqxpVWSCLwAssIW5+wCAADAWZpaDsq/Yn1y25lhGPKvWK+mloMWjwxAviDsAgAAYM4NRo1p/VUMw1A4Ss8VANlBGTMAAMBx7DGdOz63qbhppgRe0zTlddvi1EsAeYCVXQAAAE3sMY2v3Czv+ZsUX7lZjS1H1Xa4w+qh5aS62hr1HG2VaY6HW9M01XO0VXW1NRaPDEC+YGUXAABAiT2mm2bYY7qf1d3TkHjNmlr2Kxw15HWbaqit4bUEkDWEXQAAAI3vMfWyx3ROrVuzinALwDKUMQMAAGh8j2mi5DaBPaYAkLsIuwAAAGKPKQA4DWXMAABboAsurMYeUwBwFsIuAMByiS64/pWb5TUMxU1TjS2tkkTQQFaxxxQAnIMyZgCA5ca74K6foQvuQYtHBgAAchUruwAAy9EFFzh9bAEAgJkRdgEAlvO5TcVNM7myK9EFFzgZbAEAgPQoYwYAWI4uuMDpYQsAAKTHyi4AwHJ0wQVOD1sAACA9wi4AwBboggucOrYAAEB6lDEDAADkKLYAAEB6rOwCAADkKLYAAEB6hF0AAIAcxhYAAJgZYRcAgFPEuaYAANgfYRcAgFPAuaYAAOQGGlQBAHAKONcUAIDcQNgFAOAUDEaNlGNeJM41BQDAjgi7AACcAp/bTB7zksC5pgAA2A9hFwCAU8C5pgAA5AYaVAEAcAo413Tu0NUaAJBJhF0AAE4R55qeObpaAwAyjTJmAACQdXS1BgBkGmEXAABkHV2tAQCZRtgFAABZR1drAECmEXYBAEDW0dUaAJBpNKgCAABZR1drAECmEXYBAIAl6GoNAMgkypgBAAAAAI7Dyi4AAACmaTvcoaYXWjUYK5DPFVfdhvWsxAPIKYRdAMBJ4Y0vkD/aDneoseWo/Cs3y2sYipumGltaJYmfewA5g7ALADgh3vg6DzcvMJumloPyr9iUPAvZMAz5V6xXU8t+vk8A5AzCLgDghHjj6yzcvMCJDEYNeY//vCcYhqFw1EhzBQDYDw2qAAAnNBg1kkE3gTe+uWv85sX6GW5eHLR4ZLALn9tMnoGcYJqmvG4zzRUAYD+EXQDACfHG11m4eYETqautUc/R1uTPvWma6jnaqrraGotHBgAnjzJmAMAJ1dXWqLGlNbkamHjj28Ab35zkc5uKm2ZK4OXmBSZLlLM3texXOGrI6zbVUFtDmTuAnELYBQCcEG98nYWbFzgZ69as4mccQE4j7AIATgpvfJ2DmxcAgHxA2AXgWBytAqTHzQsAgNMRdgE4EkerAPbCzScAQLbZKuy2t7fr8ccfVzwe16WXXqqrrroq5ffHxsb04IMP6g9/+IPmzZunW265RdXV1dYMFoCtcS4sYB/cfAIAWME2YTcej+uxxx7TV77yFVVWVmrXrl2qqanR4sWLk5+zb98+eb1efe9731NLS4v+5V/+Rf/0T/9k4agB2NVg1JDXYUersDKGXMXNJwCAFWxzzu4bb7yhBQsWaP78+XK73br44ovV2tqa8jkHDx7UJZdcIkn6yEc+oiNHjkw79xEAJOedC5tYGYuv3Czv+ZsUX7lZjS1H1Xa4w+qhASfEub4AACvYJuyGQiFVVlYmP66srFQoFEr7OS6XSx6PRwMDA1kdJ4DcUFdbo56jrcnAmzhapS5Hj1YZXxlbP8PK2EGLRwacmNNuPgEAcoNtypjn0t69e7V3715J0u7duxUMBi0ekT253W5eGxtiXubGZZs3qryiXE/9ukWDY5KvUPrsFbW66MK1p/XnWT0vY64SeYqLpz0+5CrJ6+8Xq+cF0800J9decal+0Nwm/8pJ5/r+rlXXX3Ep85cl/KzYE/NiP8yJPZ3uvNgm7AYCAXV3dyc/7u7uViAQmPFzKisrFYvFFIlENG/evGl/1pYtW7Rly5bkx11dXZkbeA4LBoO8NjbEvMydZUsX679//jMpj53ua2v1vBTGhjUyMpJSCmqaptyx4bz+frF6XjDdTHOybOlifeaiPjW1PJs81/cztTVatnQx85cl/KzYE/NiP8yJPc02LwsXLkx7nW3C7vLly/Xee++ps7NTgUBAv/nNb3TzzTenfM6HPvQhPffcczr33HP14osvatWqVdP2AAGAE9XV1qixpTVZypwoy27I0bJs5B/O9QUAZJttwq7L5dIXvvAF3XXXXYrH49q0aZOWLFmin/70p1q+fLlqamq0efNmPfjgg/pv/+2/yefz6ZZbbrF62ACQFYmQ0NSyP7ky1lBbQ3gAAABIwzZhV5IuvPBCXXjhhSmPfeYzEyWIRUVF+uIXv5jtYQGALbAyBgAAcPJs040ZAAAAAIC5QtgFAAAAADgOYRcAAAAA4DiEXQAAAACA49iqQRUAYELb4Q41vdCqwViBfK646jasp0EVAADASSLsAoANtR3uUGPLUflXbpbXMBQ3TTW2tEoSgRcAAOAkUMYMADbU1HJQ/hXrZRiGJMkwDPlXrFdTy0GLRwYAAJAbCLsAYEODUSMZdBMMw1A4aqS5AgAAAJNRxgwANuRzm4qbZkrgNU1TXrdp4aiAM8M+dABANrGyCwA2VFdbo56jrTLN8XBrmqZ6jraqrrbG4pEBpyexDz2+crO8529SfOVmNbYcVdvhDquHBgBwKFZ2AcCGEqtdTS37FY4a8rpNNdTWsAqGnDW+D33TDPvQ9/N9DQDICMIuANjUujWrCAFwjMGoIS/70AEAWUQZMwAAyDif20yW5SewDx0AkEmEXQAAkHHsQwcAZBtlzAAAIOPYhw4AyDbCLgAAyAr2oQMAsokyZgAAAACA4xB2AQAAAACOQ9gFAAAAADgOYRcAAAAA4DiEXQAAAACA4xB2AQAAAACOQ9gFAAAAADgOYRcAAAAA4DhuqwcAAICV2g53qOmFVg3GCuRzxVW3Yb3WrVll9bAAAMAZIuwCAPJW2+EONbYclX/lZnkNQ3HTVGNLqyQReAEAyHGUMQMA8lZTy0H5V6yXYRiSJMMw5F+xXk0tBy0eGQAAOFOs7MIWKCMEYIXBqCHv8aCbYBiGwlEjzRUAACBXEHZhOcoIAVjF5zYVN83kyq4kmaYpr9u0cFQAAGAuEHZhufEywk0zlBHuJ+wCyKi62ho1trQmS5lN01TP0VY11NZYPbSTQlUMAADpEXZhOcoIAWTb5JAY7+1S14E35a1cIK/bVENtTU4ERqpiAACYHWEXlqOMEEA2TQ2JnuOruX9TuyKnQiJVMQAAzI5uzLBcXW2Neo62yjTHw22ijLAuR8oIAeQWp3RgHowaKTcJJapiAACYjJVdWC6xAtHUsl/hqJFTZYQAco9Ttk5QFQMAwOwIu7CFdWtWEW4BZIVTQmKuN9cCACDTCLsAgLzilJBIVQwAALMj7AIA8oqTQiJVMQAApEfYBQDkHUIiAADORzdmAAAAAIDjEHYBAAAAAI5DGTMAAKeo7XCHml5o1WCsQD5XXHUb1lMWDQCAzRB2AQA4BW2HO9TYclT+lZvlNQzFTVONLa2SROAFAMBGKGMGAOAUNLUcTB5bJEmGYci/Yr2aWg5aPDIAADAZYRcAgFMwGDWSQTfBMAyFo0aaKwAAgBUIuwAAnAKf25RpmimPmaYpr9tMcwUAALACe3YBACdEQ6YJdbU1amxpTZYym6apnqOtaqitsXpoAABgEsvDbmNjo15++WW53W7Nnz9fN954o7xe77TPu+mmm1RSUqKCggK5XC7t3r3bgtECQP6hIVOqxHNuatmvcNSQ122qobYmL18LAADszPKwu2bNGu3YsUMul0tPPPGEnnrqKV133XUzfu4dd9yhsrKyLI8QAPLbeEOmTTM0ZNqftwFv3ZpVefvcAQDIFZbv2b3gggvkcrkkSeeee65CoZDFIwIATEZDJgAAkIssX9mdbN++fbr44ovT/v5dd90lSbrsssu0ZcuWbA0LAPKaz20qbpopgZeGTAAAwO4Mc2pLyQy488471dvbO+3xa665RuvXr5ck/fznP9ebb76pL33pS9NWECQpFAopEAior69P3/zmN/X5z39e55133oxfb+/evdq7d68kaffu3RodHZ27J+Mgbrdb0WjU6mFgCubFnvJ5Xl461K4fNLfJv3JSQ6bfter6ret00YVrLR1bPs+LXTEn9sS82BPzYj/MiT3NNi9FRUVpr8tK2D2R5557Tr/61a90++23q7i4+ISf/7Of/UwlJSW68sorT+rPf/fdd890iI4UDAbV1dVl9TAwBfNiT/k+L22HO9TUcjDZkKnOJg2Z8n1e7Ig5sSfmxZ6YF/thTuxptnlZuHBh2ussL2Nub2/XL37xC339619PG3SHh4dlmqZKS0s1PDysw4cPq76+PssjBYD8RUMmAACQaywPu4899pii0ajuvPNOSdI555yj66+/XqFQSN///ve1a9cu9fX16Tvf+Y4kKRaLacOGDVq7dq2FowYAAAAA2JnlYfd73/vejI8HAgHt2rVLkjR//nzde++92RwWAAAAACCHWX70EAAAAAAAc42wCwAAAABwHMIuAAAAAMBxCLsAAAAAAMch7AIAAAAAHIewCwAAAABwHMIuAAAAAMBxLD9nFwCAqdoOd6jphVYNxgrkc8VVt2G91q1ZZfWwAABADiHsAgBspe1whxpbjsq/crO8hqG4aaqxpVWSCLwAAOCkUcYMALCVppaD8q9YL8MwJEmGYci/Yr2aWg5aPDIAAJBLCLsAAFsZjBrJoJtgGIbCUSPNFQAAANMRdgEAtuJzmzJNM+Ux0zTldZtprgAAAJiOsAsAsJW62hr1HG1NBl7TNNVztFV1tTUWjwwAAOQSGlQBAGwl0YSqqWW/wlFDXrephtoamlMBAIBTQtgFANjOujWrCLcAAOCMUMYMAAAAAHAcwi4AAAAAwHEIuwAAAAAAxyHsAgAAAAAch7ALAAAAAHAcwi4AAAAAwHEIuwAAAAAAxyHsAgAAAAAch7ALAAAAAHAcwi4AAAAAwHEIuwAAAAAAxyHsAgAAAAAch7ALAAAAAHAcwi4AAAAAwHEIuwAAAAAAxzFM0zStHgQAAAAAAHOJld08tnPnTquHgBkwL/bEvNgT82I/zIk9MS/2xLzYD3NiT6c7L4RdAAAAAIDjEHYBAAAAAI5D2M1jW7ZssXoImAHzYk/Miz0xL/bDnNgT82JPzIv9MCf2dLrzQoMqAAAAAIDjsLILAAAAAHAct9UDgD0888wzamxs1KOPPqqysjKrh5P3fvKTn+jgwYMyDEPl5eW68cYbFQgErB5W3mtsbNTLL78st9ut+fPn68Ybb5TX67V6WHntt7/9rf73//7f+vOf/6xvfetbWr58udVDymvt7e16/PHHFY/Hdemll+qqq66yekh57+GHH9ahQ4dUXl6u++67z+rhQFJXV5ceeugh9fb2yjAMbdmyRXV1dVYPK++Njo7qjjvuUDQaVSwW00c+8hFt377d6mFBUjwe186dOxUIBE65KzNhF+rq6tLhw4cVDAatHgqOu/LKK3XNNddIkpqamrRnzx5df/31Fo8Ka9as0Y4dO+RyufTEE0/oqaee0nXXXWf1sPLakiVL9KUvfUk/+MEPrB5K3ovH43rsscf0la98RZWVldq1a5dqamq0ePFiq4eW1y655BJt27ZNDz30kNVDwXEul0sNDQ1atmyZhoaGtHPnTq1Zs4afFYsVFhbqjjvuUElJiaLRqG6//XatXbtW5557rtVDy3tNTU1atGiRhoaGTvlaypihH/3oR/rsZz8rwzCsHgqO83g8yV+PjIwwNzZxwQUXyOVySZLOPfdchUIhi0eExYsXa+HChVYPA5LeeOMNLViwQPPnz5fb7dbFF1+s1tZWq4eV98477zz5fD6rh4FJ/H6/li1bJkkqLS3VokWL+PfEBgzDUElJiSQpFospFovx/ssGuru7dejQIV166aWndT0ru3mutbVVgUBAZ511ltVDwRT/+q//queff14ej0d33HGH1cPBFPv27dPFF19s9TAA2wiFQqqsrEx+XFlZqddff93CEQH219nZqbfeektnn3221UOBxitUbrvtNr3//vu6/PLLdc4551g9pLz3wx/+UNddd91prepKhN28cOedd6q3t3fa49dcc42eeuopfeUrX8n+oDDrvKxfv17XXnutrr32Wj311FP6t3/7N/aNZMmJ5kWSfv7zn8vlculjH/tYlkeXn05mTgAg1wwPD+u+++7T5z73uZSKLlinoKBA9957r8LhsL7zne/onXfe0dKlS60eVt56+eWXVV5ermXLlqmjo+O0/gzCbh746le/OuPj77zzjjo7O3XrrbdKGi8TuO2223T33XeroqIiiyPMT+nmZaqPfexjuvvuuwm7WXKieXnuuef08ssv6/bbb6e8KUtO9mcF1goEAuru7k5+3N3dTWM9II1oNKr77rtPH/vYx/ThD3/Y6uFgCq/Xq1WrVqm9vZ2wa6HXXntNBw8eVFtbm0ZHRzU0NKQHHnhAN99880n/GYTdPLZ06VI9+uijyY9vuukm3X333XRjtoH33ntPH/jABySNl5qzJ9Ee2tvb9Ytf/EJf//rXVVxcbPVwAFtZvny53nvvPXV2dioQCOg3v/nNKb0hAfKFaZp65JFHtGjRIn3iE5+wejg4rr+/Xy6XS16vV6Ojozp8+LD++q//2uph5bUdO3Zox44dkqSOjg4988wzp/zvCmEXsKF/+Zd/0XvvvSfDMBQMBunEbBOPPfaYotGo7rzzTknSOeecw9xY7KWXXtI///M/q7+/X7t379ZZZ52lL3/5y1YPKy+5XC594Qtf0F133aV4PK5NmzZpyZIlVg8r791///169dVXNTAwoBtuuEHbt2/X5s2brR5WXnvttdf0/PPPa+nSpcnqumuvvVYXXnihxSPLbz09PXrooYcUj8dlmqY++tGP6kMf+pDVw8IZMkzTNK0eBAAAAAAAc4mjhwAAAAAAjkPYBQAAAAA4DmEXAAAAAOA4hF0AAAAAgOMQdgEAAAAAjkPYBQAAAAA4DmEXAIAc9cQTT+jb3/528uPGxkZ94xvfUDQatXBUAADYA2EXAIAc9dd//dfq6OjQW2+9pebmZrW3t+tLX/qS3G631UMDAMByhmmaptWDAAAAp+dnP/uZXnrpJUUiEX3jG99QMBhUJBLRnXfeqf/8z//UXXfdpaVLl1o9TAAAso6VXQAActgHP/hBvfPOO9qxY4eCwaAkqaioSLt27dJHPvIRi0cHAIB1CLsAAOSod955R48++qg2btyo/fv3Jx93u90qKyuzcGQAAFiPsAsAQA4KhUK655579F/+y3/R3//93+udd95RR0eH1cMCAMA2CLsAAOSYSCSiu+++W1dccYVqampUXFysT37yk/rJT35i9dAAALANGlQBAOBQDz30kD75yU/SoAoAkJcIuwAAONDdd9+tP/7xjwoGg7rssst0ySWXWD0kAACyirALAAAAAHAc9uwCAAAAAByHsAsAAAAAcBzCLgAAAADAcQi7AAAAAADHIewCAAAAAByHsAsAAAAAcBzCLgAAAADAcQi7AAAAAADHIewCAAAAABzn/wemdBeNT7h0aQAAAABJRU5ErkJggg==",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plot_ds(data,m[-1],q[-1])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Accelerazione del gradiente di Nesterov\n",
"Nel metodo del momento, la conoscenza al passo $k$ di $\\theta^{(k)}$ e di $v^{(k)}$ permette, senza calcolare il gradiente, di avere una valutazione approssimata $\\tilde{\\theta}^{(k+1)}=\\theta^{(k)}+\\gamma v^{(k)}$ di \n",
"$$\n",
"\\theta^{(k+1)}=\\theta^{(k)}+v^{(k+1)}=\\theta^{(k)}+\\gamma v^{(k)}-\\eta\\sum_{i=1}^nJ'(\\theta^{(k)};\\mathbf{x}_i)=\\tilde{\\theta}^{(k+1)}-\\eta\\sum_{i=1}^nJ'(\\theta^{(k)};\\mathbf{x}_i)\n",
"$$\n",
"Il metodo di Nesterov segue lo stesso approccio del metodo del momento, con la differenza che, ad ogni passo, la valutazione del gradiente viene effettuata, con un *look-ahead* approssimato, non nel punto attuale $\\theta^{(k)}$ dello spazio delle soluzioni visitato ma, più o meno, nel punto successivo $\\theta^{(k+1)}$ (approssimato da $\\tilde{\\theta}^{(k+1)}$). In questo modo, le variazioni di $v$ (e quindi di $\\theta$) vengono anticipate rispetto a quanto avviene nel metodo del momento.\n",
"\n",
"\\begin{align*}\n",
"v^{(k+1)}&=\\gamma v^{(k)} +\\eta\\sum_{i=1}^nJ'(\\tilde{\\theta}^{(k)};\\mathbf{x}_i)=\\gamma v^{(k)} +\\eta\\sum_{i=1}^nJ'(\\theta^{(k)}+\\gamma v^{(k)};\\mathbf{x}_i)\\\\\n",
"\\theta^{(k+1)}&=\\theta^{(k)}+v^{(k+1)}\n",
"\\end{align*}\n",
"\n",
"\n",
"\n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"```python\n",
"v = 0\n",
"for i in range(n_epochs):\n",
" g = 0\n",
" theta_approx = theta+gamma*v\n",
" for k in range(dataset_size):\n",
" g = g+evaluate_gradient(loss_function, theta_approx, X[k])\n",
" v = gamma*v-eta*g\n",
" theta = theta+v\n",
"```"
]
},
{
"cell_type": "code",
"execution_count": 135,
"metadata": {},
"outputs": [],
"source": [
"def nesterov_gd(X,t, eta = 0.1, gamma = 0.97, epochs = 1000):\n",
" theta = np.zeros(nfeatures+1).reshape(-1,1)\n",
" v = np.zeros(nfeatures+1).reshape(-1,1)\n",
" theta_history = []\n",
" cost_history = []\n",
" for k in range(epochs): \n",
" delta = - eta * gradient(theta+gamma*v,X,t)\n",
" v = gamma*v +delta\n",
" theta = theta + v\n",
" theta_history.append(theta)\n",
" cost_history.append(cost(theta, X, t))\n",
" theta_history = np.array(theta_history).reshape(-1,3)\n",
" cost_history = np.array(cost_history).reshape(-1,1)\n",
" m = -theta_history[:,1]/theta_history[:,2]\n",
" q = -theta_history[:,0]/theta_history[:,2]\n",
" return cost_history, m, q"
]
},
{
"cell_type": "code",
"execution_count": 136,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"tempo di esecuzione: 0.407 secondi\n",
"10000 passi totali\n",
"1000000 gradienti valutati\n"
]
}
],
"source": [
"start_time = time.time()\n",
"cost_history, m, q = nesterov_gd(X, t, eta = 0.1, gamma = 0.97, epochs = 10000)\n",
"print(f\"tempo di esecuzione: {time.time()-start_time: 4.3f} secondi\")\n",
"print(f\"{len(m)} passi totali\")\n",
"print(f\"{len(m)*n} gradienti valutati\")"
]
},
{
"cell_type": "code",
"execution_count": 140,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABQgAAAGoCAYAAAAKMwiTAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAABaw0lEQVR4nO3deXiV9YH3/8+9nAQOYT8QCMgSICASBFFAFos2dbfaqDhtnc7kqtP5tVPr02mfPn1+MzIW6yX9zejUGfv0Gp2xtPPY1qW41y1VVDZB1rAmIbKEPQlbNpJ7+f1xyIlRpAFy7vvknPerl1c55+RwPvneSTh8+C6G7/u+AAAAAAAAAGQkM+wAAAAAAAAAAMJDQQgAAAAAAABkMApCAAAAAAAAIINREAIAAAAAAAAZjIIQAAAAAAAAyGAUhAAAAAAAAEAGs8MOAAAAgPRUV1enn/3sZ6qurtZvfvMbWZaVeGzPnj168sknJUn33HOPRo4cGVZMAACAjMcMQgAAACRFTk6O7r//fo0bN+4zjz3zzDO677779P3vf1/PPPNMCOkAAADQptvMINy/f3/YES5YLBZTTU1N2DEgrkWq4XqkDq5FauF6pI50uRZ5eXmBvl5WVpaysrLO+FhDQ4NisVji139Od38vmC5fQ12F8WjHWHTEeHTEeHTEeLRjLDpiPDo623h83vvBblMQAgAAIH34vn/Wx0tLS1VaWipJWrRoUaJM7K5s2+72n0NXYjzaMRYdMR4dMR4dMR7tGIuOGI+Ozmc8KAgBAAAQKsMwPnNfUVGRioqKEre7+6wAZjZ0xHi0Yyw6Yjw6Yjw6YjzaMRYdMR4dMYMQAAAA3UJOTo5qa2tlGIZ69uwZdhwAAICMRkEIAACApHAcRw8//LB2796thx56SHfccYe2b9+u4uJizZ8/Xz//+c8lSd/85jfDDQoAAJDhKAgBAACQFLZt6/777+9w38SJEyVJI0eO1IMPPhhGLAAAAHyKGXYAAAAAAAAAAOGhIAQAAAAAAAAyGAUhAAAAAAAAkMEoCAEAAAAAAIAMRkEIAAAAAAAAZDAKQgAAAAAAACCDURACAAAAAAAAGYyCEAAAAAAAAMhgFIQAAAAAAABABqMgBAAAAAAAADIYBSEAAAAAAACQwSgIAQAAAAAAgAxGQQgAAAAAAABkMApCAAAAAAAAIINREAIAAAAAAAAZjIIQAAAAAAAAyGAUhAAAAAAAAEAGoyAEAAAAAAAAMhgFIQAAAAAAAJDBKAgBAAAAAACADEZBCAAAAAAAAGQwCkIAAAAAAAAgg1EQAgAAAAAAABnMDjtAJjh0rFG7DtdrXLOpAT3CTgMAAAAAAAC0YwZhAHYePKHnV1Zp1fZ9YUcBAAAAAAAAOqAgDIBhGJIk3/dDTgIAAAAAAAB0REEYgNP9oOgHAQAAAAAAkGqSugfh4sWLVVVVpdGjR6ukpCRxf319vZ544gmdPHlShYWFKi4uTmaM0BmKN4QeDSEAAAAAAABSTNIKwqqqKjU3N2vhwoV68sknVVlZqbFjx0qSnnvuOd11110aNmxYsl4+pbTPIKQgBAAAAAAAQGpJ2hLjiooKTZ48WZJUWFio8vLyxGN79+7VCy+8oJ/85Ccd7k9XptE2gzDkIAAAAAAAAMCnJG0GYUNDg3JzcyVJ0WhU1dXVicd27Nihn/3sZ8rJydEjjzyiBx988DPPLy0tVWlpqSRp0aJFisViyYqadH0ON0uKzyTszp9HOrFtm2uRQrgeqYNrkVq4HqmDawEAAIB0lrSCMBqNqrGxUZLU1NSkaDSaeCwvL0/Dhw+XJJnmmScxFhUVqaioKHG7pqYmWVGTrr6+XpLkul63/jzSSSwW41qkEK5H6uBapBauR+pIl2uRl5cXdgQAAACkoKQtMS4oKNDmzZslSWVlZSooKEg8NnToUB09elTNzc1yXTdZEVLG6S0IOcUYAAAAAAAAKSdpMwjz8/MViUS0YMECjRo1SrFYTEuWLFFxcbHmz5+vxx57TC0tLbrjjjuSFSFltB1SwinGAAAAAAAASDVJKwglqaSkpMPt4uJiSdLw4cP1wAMPJPOlU4pxuiGkHgQAAAAAAECqSdoSY7Rrm0HoM4MQAAAAAAAAKYaCMADG6V0IKQgBAAAAAACQaigIA9C+B2G4OQAAAAAAAIBPoyAMgGkwgxAAAAAAAACpiYIwAO17EIabAwAAAAAAAPg0CsIAnO4HmUEIAAAAAACAlENBGADj9BRC9iAEAAAAAABAqqEgDED7EmMaQgAAAAAAAKQWCsIAtM0g9EVBCAAAAAAAgNRCQRiA9j0IQ40BAAAAAAAAfAYFYQASMwhpCAEAAAAAAJBi7LADZIK2PQg5pAQAAAAAACDO91z5J+rkHz18+r9D8o/XyLxovOwrvhR2vIxCQRgAZhACAAAAAIBM5buu/BO18QLwU2WgXOczH+8eqZYR7S3rkpkhpM1MFIQBaN+DkIIQAAAAAACkJ9915B+vaS8A28rA4zWS5575STn9ZPQfLLP/YBn9c+WfapK76o9ylr8so19M5rCxwX4SGYqCMADm6YaQfhAAAAAAAHR3vtMq//iRjrMBjx6Wf7xW8r0zP6n3gNMlYNt/uTL6DZaRlf3Zj21ukLvhPbW+/VtlfeXvZPQdmNxPCBSEQWhbYuzREAIAAAAAgG7Cb22JF4F1p0vAY6cLwRO1nzMLypDRZ2B7AdhWBvYbLCOS1enXta64Tn7dIXl7tqv1jV8r8pXvyMjq0XWfGD6DgjAA7YeUUBACAAAAAIDU4reekn/sSLwEPF0GescOSyeOSjpDl2EYMvrGPlECnv7/foNk2JELzmOYpuwv/oVaX/yl/KOH5Pzpd7Kv+ysZpnnBvzfOjIIwAO2HlIQcBAAAAAAA4DTv0B45y16UX7P/zB9gmjL6DJIx4PRy4MTS4JgMK7mVkpHVQ5Hrv6GWF34hb88OuavfkD3zxqS+ZiajIAwAh5QAAAAAAIBU4buO3I/elrvx/fhsJtOKl379cmUM+MSMwD4Dk14Eno3RZ6AiX/q6Wl/7L7kb35fRP1fW+Gmh5UlnFIQBMJlBCAAAAAAAUoB3pFrOu8/JP3pIMgxZl35B1uVFXbI0OBnMvDGyZ98q54MX5Ly/REbfmMwhI8OOlXYoCANgJE4xpiEEAAAAAADB811H7rp35a5/V/I9GX1jsufd2S3KNmviDHl1B+VtWanWt/5bWcXflZHTL+xYaYWCMACcYgwAADLR4sWLVVVVpdGjR6ukpCRx/8qVK/Xyyy/LMAx95Stf0RVXXBFiSgAA0p9Xe0DOu8/Krz0gSbImzZY1/bpzOlk4bPaVN6v12BH5+yrV+uZvFPny/9Ot8qc6jn8JQGIPwlBTAAAABKeqqkrNzc1auHChHMdRZWVl4rHXXntNDzzwgB544AG9+uqrIaYEACC9+Z4rZ907al3yeLwc7D1AkVu+JXv2Ld2uXDMsS5Gir8noM1B+zX45S5+T73thx0obFIQBaD/FmIoQAABkhoqKCk2ePFmSVFhYqPLy8sRjubm5OnXqlJqbm9WzZ8+wIgIAkNa8o4fV+uIv5a55S/JcmRNnKOvO+2Tm5Ycd7bwZPaKyr/8rKStbXlWZ3LXvhB0pbbDEOADtexCGmwMAACAoDQ0Nys3NlSRFo1FVV1cnHps+fbp+9KMfyfd9fec73znj80tLS1VaWipJWrRokWKxWPJDJ5Ft293+c+hKjEc7xqIjxqMjxqMjxqPd2cbC9zzVr35bJ5a+ILmOrD4D1O+mv1KP/EsCTpkksZiav/L/qPbZf5O7tlR9R42TPWQIXxufcD7fKxSEAWgrCNmDEAAAZIpoNKrGxkZJUlNTk6LRaOKx559/Xo8++qgk6eGHH9all176mecXFRWpqKgocbumpibJiZMrFot1+8+hKzEe7RiLjhiPjhiPjhiPdp83Ft7xmvgJxYd2S5LM8ZfLuvJm1Wf3UH06jV2/obJm3CB31R9V99J/yuo3SCfs6J9/XoY42/dKXl7eGe9niXEADLHEGAAAZJaCggJt3rxZklRWVqaCgoLEY5FIRNnZ2erRo4ccxwkrIgAAacP3PTlly9X6/GPxcjDaW/b1f63IvDtkZPcIO15SWJPnyiyYJjmtqnvucfmNJ8OO1K0xgzAALDEGAACZJj8/X5FIRAsWLNCoUaMUi8W0ZMkSFRcX69prr9X9998vSR1mCQIAgHPnn6hT63vPy99fJUkyx02VPesWGT3Se0adYRiyr/qKWo/XyD20W95b/63ILd+SYVF1nQ9GLQAcUgIAADJRSUlJh9vFxcWSpHnz5mnevHkhJAIAIH34vi9v22o5q16TWluknjmy594ma/SksKMFxrBsRa69W+5Lv5R7aI+c95fInndnoodB57HEOADtexCGmwMAAAAAAHR/zok6tf7xKTkfvCC1tsjML1TWnf8jo8rBNka0twbc+V3JjsgrXyd30wdhR+qWmEEYAJM9CAEAAAAAwAXyfV/ejrU6vOo1+aeapOyo7Dm3yhr72QO/MknWkBGyr54v5+2n5X74usyLxssckBt2rG6FgjAA7XsQUhACAAAAAIBz5zeckPP+Enl7tkuSzJEXy76qWEa0d8jJUoOVXyhvwnR521fL2/ahzNlfDjtSt0JBGIDEHoQh5wAAAAAAAN2L7/vyKjfKWf6SdKpJyuqh/td/XQ1DxrLX3qdYk2bK275abvk6WdOvlxHJCjtSt0FBGID2PQipCAEAAAAAQOf4TfVyPnhB3sdbJEnGRQWKfOF2RUeOUWNNTcjpUo85ME/G4IvkH94r7+MyWQXTwo7UbVAQBqCtz6cfBAAAAAAAneFWlcn54EWpuUGKZMu+8iaZE65g1uCfYV08Xc7hvXK3rqYgPAcUhAFILDGmIQQAAAAAAGfhNzfIWf6yvMqNkiQjb4wi8+6Q0bt/yMm6B3PMZGnFq/IP7ZZXd1DmgCFhR+oWzLADZAIOKQEAAAAAAH+Ou2urWp77ebwctCOyZ9+qyM3fpBw8B0YkW+a4KZIkb9vqcMN0I8wgDEDbDEKPfhAAAAAAAHyKf6pJzopX5JWvkyQZQ0bFZw32jYWcrHuyLp4hb+uH8cNKZtwgw46EHSnlURAGoH0PQhpCAAAAAADQzttbrtb3npcaTkiWLWv6dbImzZZhsujzfJmxPBmDhss/Ui2vqkxWwWVhR0p5FIQBaJ9BSEEIAAAAAAAkv+WUnJWvydseXwZrDL5I9rw7ZfYfHHKy9GBdPF3OkWq52z6kIOwECsIAmIk9CMPNAQAAAAAAwuft26nWpc9J9cck05J1+ZdkXTpXhmmFHS1tmGMvlVa+Kv/gbnl1h2QOyA07UkqjIAzAJ48g932fI8kBAAAAAMhAfmuLnA9fl7dlpSTJiA2TffWdnLSbBEYkW+bYqfK2fShv22qZs28JO1JKY0F7QAxmEQIAAAAAkLG8g7vU+vxj8XLQNGVdXqTIbd+hHEwi6+LpkiS3Yp18pzXkNKmNGYQBMWTIP/2/9mNLAAAAAABAOvOdVrlr3pK7aZkkX8aAIfFZg7FhYUdLe+agYZ84rGSzrIKpYUdKWRSEATEMST4zCAEAAAAAyBTeoT1ylj4n/9gRyTBkTbla1rQvyrCoY4LS8bASCsLPw1dkQFhiDAAAAABAZvBdR+5HpXI3vif5vox+g2RfPV/m4IvCjpZxzDFth5Xsknf0kMz+HFZyJuxBGJC2g0l8GkIAAAAAANKWV7NPrUsel7thqeRL1uS5itz+PcrBkBhZ2TLHTpEkedtWhxsmhTGDMCBtTawXagoAAAAAAJAMvuvKXf+u3PXvSJ4no8/A+F6DQ0aFHS3jWRdPl7dttdzydbKmXy/DjoQdKeVQEAaEGYQAAAAAAKQnr+6gnHefk1+zT5JkTZoVL6IiWSEngySZg4bLiA2TX7NP3sebZY1jL8JPoyAMCHsQAgAAAACQXnzPlbvxfbkflUqeK/Xur8gX7pA5bEzY0fAp1sXT5XzwgtxtqykIz4CCMCDMIAQAAAAAIH14Rw/HTyg+vFeSZF48XfbMm2RkZYecDGdijp0irXxN/oGP5R09LLP/4LAjpRQKwoCcnkAo6kEAAAAAALov3/Pkbl4ud/WbkutIvfrEZw1eVBB2NJxF/LCSyfK2fySvcoPMK64NO1JKoSAMCDMIAQAAAADo3vzjNWpd+rz8g7skSWbBNNmzbpaR3TPcYOgUa8yl8YKwqkz+5V9KdDVIckG4ePFiVVVVafTo0SopKUnc/4tf/EL79u1TVlaWioqKNGfOnGTGSAnsQQgAAAAAQPfk+568LavkfPi65LRK0d6y535F1qiJYUfDOTDy8qUeveQfOyK/7qCMgUPDjpQyklYQVlVVqbm5WQsXLtSTTz6pyspKjR07NvH49773PQ0ZMiRZL59yEkuMKQgBAAAAAOg2/JN1al36B/n7d0qK72Vnz75FRo9eISfDuTJMS+boS+RtWy2vqkwmBWGCmazfuKKiQpMnT5YkFRYWqry8PPGYYRh6/PHHtWjRIh05ciRZEVJKYokxuxACAAAAAJDyfN+Xu221Wp77ebwc7NFL9pe+rsgX/4JysBuz8uNdlbdzE9vAfULSZhA2NDQoNzdXkhSNRlVdXZ147Bvf+IZycnK0fft2/eY3v9EPfvCDzzy/tLRUpaWlkqRFixYpFoslK2ogbMuSJPXr31+xPtGQ08C27W7/NZVOuB6pg2uRWrgeqYNrAQBAZvHrj6v1/T/I3xuf7GSOniR77m0yeuaEnAwXysgbHV9mfLxGft0BGQPzwo6UEpJWEEajUTU2NkqSmpqaFI22l2I5OfFvqAkTJujpp58+4/OLiopUVFSUuF1TU5OsqIHwfE+SVFdbJ7U0hpwGsVis239NpROuR+rgWqQWrkfqSJdrkZfHG2AAAM7G9315FevkLH9FammWsnvKnnOrzDGXcqBFmjBMS2b+JHlbP5S3s0wmBaGkJC4xLigo0ObNmyVJZWVlKihoP+67rTjcv3+/evXKjGm5bT9GPGavAgAAAACQcvzGk3Le/I2cd5+TWppljpigrDu/L2vsFMrBNMMy489K2gzC/Px8RSIRLViwQKNGjVIsFtOSJUtUXFysf/u3f1NDQ4MMw9A999yTrAgpxWQPQgAAAAAAUo7v+/J2bpKz7CXpVKOUlS171i0yC6ZRDKYpY+hoqWeO/BO18msPyIgxizBpBaEklZSUdLhdXFwsSfrxj3+czJdNSW0/UyimAQAAAABIDX5TvZxlL8mrKpMkGcPHKfKF22Xk9As3GJLKME2ZoyfJ27pK3s5NMikIk1sQol17QUhDCAAAAABA2NyPN8t5/wWpuUGKZMmeeZPMi6czazBDWGMK5W1dJbeqTNb06zL+ulMQBsQ4vQsh/SAAAAAAAOHxmxvlLH9ZXuUGSZKRl6/IvDtk9B4QbjAEyhgSX2asE7Xya/bLGDQs7EihoiAMiGHGC0KPhhAAAAAAgFC4u7fLef8PUuNJyY7InnG9zEuulGEk7QxXpCjDNGXmF8rbslJe1SaZFIQIQttEVepBAAAAAACC5Z9qlrPyFXk71kqSjNyRsq++U2bfWMjJECbrdEHoVm6UdcV1MszMLYopCANickgJAAAAAACB8/aWq/W9P0gNxyXLlnXFtbIK52R0GYQ4Y8goqfcA6WSdvD3bZY2aGHak0PDdEJC2zS45pAQAAAAAgOTzW06p9f0X1PrHp6SG4zIGDVfk9u/JvvQqykFIii8ztiZdKUlyy5Yn7nd3blLLa/8l7+ihsKIFjhmEAUksMaYfBAAAAAAgqbz9O9W69Hnp5FHJtGRNK5I15SoZphV2NKQYa/zlcte8LX//Tnm1B2X0GSCn9LeSJHftOzKLvhpywmBQEAYkMYOQXQgBAAAAAEgKv7VF7uo35G5eIUkyBg6VffV8mQOHhpwMqcrI7ilz/LT4XoSbl8v8xDJjr7pCvu8nOp10RkEYEIM9CAEAAAAASBrv4G45S5+Tf7xGMk1ZU6+WNfVqGRbVB87OmjQrfppxxXr59cfaHzjVKDWckHL6hpYtKHyXBIQ9CAEAAAAA6Hq+0yr3o7flbvpA8n0Z/XPjswYHDQs7GroJs98gmReNl7d3h/zqCskwZPQZKP94jbza/bIyoCBkV86AsAchAAAAAABdyzu8V61/+He5G9+XJFlT5ily+72Ugzhn9tzbZI6YINkRmeMvlznyYkmSX7s/5GTBYAZhQBJLjNmDEAAAAACAC+K7jty1f5K74T3J92T0GyR73p0yc0eEHQ3dlNG7vyI3/HViz0G3fL0kyV3ztqxLv5D2S9XT+7NLIe1LjEMOAgAAAABAN+bV7Jfz7rPy6w5KMmQVzpE1/ToZdiTsaEgDbf2NEWs/2MbbuUlWwWVhRQoEBWFA2mYQehSEAAAAAACcM9915Kz9k9x1f5I8T+ozQJF5d8ocOjrsaEhDRr9BiV97h3anfUHIHoQBMcQhJQAAAAAAnA+v7pCOLH5Y7kdvS54nc+JMZd1xH+UgksYwLUW+8neSJG/39rTvc5hBGJD2PQgBAAAAAEBn+J4nd9MHcte8JXmulNNPkS/cIXP42LCjIQMYg4ZpgzNE7+zsr4ZH31TvPlFdO2espl6cF3a0LkdBGBDTYAYhAAAAAACd5R07Iufd5+Qf3iNJik6ZK2fqF2Vk9Qg5GTLF+m0H9dvDI3Sy1ZBONUm1Tdp/uF4qVtqVhBSEAUnMIKQfBAAAAADgc/m+J7dshdzVb0iuI0X7yP7C7ep/2WzV1NSEHQ8Z5O3llfFy8BNONpzSW8sqKQhxftiDEAAAAACAs/OP16p16XPyD+6SJJkFl8medbOM7Gi4wZCR6htaznx/45nv784oCAPCHoQAAAAAAJyZ73vytn4oZ9XrktMi9cyRfdVXZI26JOxoyGA5vbLOfH/0zPd3ZxSEAWGJMQAAAAAAn+WfPKbW956Xv69SkmSOmSx79q0yevYKORky3bVzxmr/4XqdbDiVuK93r2xdOyf9DsmhIAyIwSElAAAAAAAk+L4vb8dHcla8KrWeknpEZc+5TdaYyWFHAySdPoikWHprWaXqG1uUE83iFGNcmLYtLT0KQgAAAABAhvMbTsh5/w/y9uyQJJmjJsqe+xUZ0d4hJwM6mnpxXloWgp9GQRiQ9hmEIQcBAAAIyOLFi1VVVaXRo0erpKQkcX99fb2eeOIJnTx5UoWFhSouLg4xJQAgSL7vy6vYIGf5S1JLs5TVQ/acW2WOnZL4ezOA4FEQBsTkkBIAAJBBqqqq1NzcrIULF+rJJ59UZWWlxo6N79fz3HPP6a677tKwYcNCTgkACJLfeFLOBy/I27VVkmSOGC/7qttl9OoTcjIAFIQBYQ9CAACQSSoqKjR5cnwPqcLCQpWXlycKwr179+qFF15QbW2tvvrVr6qgoCDMqACAALg7N8lZ9qLU3ChFsmXPulnm+MuZNQikCArCgHCKMQAAyCQNDQ3Kzc2VJEWjUVVXVyce27Fjh372s58pJydHjzzyiB588MHPPL+0tFSlpaWSpEWLFikWiwUTPEls2+72n0NXYjzaMRYdMR4dpcN4uI0ndfyNp3Vq20eSpOzRF6vfTX8tu+/Ac/690mE8ugpj0RHj0dH5jAcFYUAMMYMQAABkjmg0qsbGRklSU1OTotFo4rG8vDwNHz5ckmSa5hmfX1RUpKKiosTtmpqaJKZNvlgs1u0/h67EeLRjLDpiPDrq7uPh7toi5/0XpKZ6yc6SPfNG+RNn6FirL53H59Xdx6MrMRYdMR4dnW088vLOfODKmd+RocsZ7EEIAAAySEFBgTZv3ixJKisr67CMeOjQoTp69Kiam5vlum5YEQEASeKfalTrO8/IefO/paZ6GUNHK+vO+2RdMpMlxUCKYgZhQNiDEAAAZJL8/HxFIhEtWLBAo0aNUiwW05IlS1RcXKz58+frscceU0tLi+64446wowIAupC7Z4ec9/4gNZ6Q7Iis6dfJmjRLhsH8JCCVURAGpO0fSTz6QQAAkCFKSko63C4uLpYkDR8+XA888EAIiQAAyeK3NMtZ+aq87fG9Bo3cEbLn3Smz36CQkwHoDArCgLRNomYGIQAAAAAgnXjVlWp973mp/phkWrKuuFbW5LkyPmefWQCph4IwIIklxiHnAAAAAACgK/itp+Ssel3e1lWSJGPQcNlX3ymzf27IyQCcKwrCgJhth5TQEAIAAAAAujlvf1V81uCJuviswWnXyLp0ngzLCjsagPNAQRgQDikBAAAAAHR3vtMqd/UbcstWSPJlDBgi+5r5MgfmhR0NwAWgIAxI+x6EocYAAAAAAOC8eIf2yHn3WfnHayTDlDX1almXXSPDoloAuju+iwPSvgchDSEAAAAAoPvwW5rlfvS23M0rJN+X0W9wfK/BwReFHQ1AF6EgDIjBHoQAAAAAgG7E9315lRvlrHpNajwpGYasS6+SdfmXZNiRsOMB6EIUhAFpLwhpCAEAAAAAqc07ekjOspfk76+SJBmDR8iec6vMQcNCTgYgGSgIA2KobYkxAAAAAACpyW85JXftn+RuXiZ5ntSjl+wZ18scP02GYYYdD0CSUBAGhCXGAAAAAIBU5fu+vKoyOStflRpOSDJkTpwh+4rrZPSIhh0PQJJREAak7ZASj4YQAAAAAJBCvKOH5Sx/Wf6+SkmSMWh4fDkxh5AAGYOCMCDMIAQAAAAApBK/tUXuunfkbvpA8lwpu6fs6dfLnHCFDJPlxEAmoSAMSPsehDSEAAAAAIDw+L4v7+Mtcla+ItUflySZE66QPf16GT17hZwOQBgoCAPCDEIAAAAAQNi84zVylr0sv7pckmTEhsWXE+eOCDkZgDBREAbEPN0Q+jSEAAAAAICA+a0tcjcslbvhvfhy4qwesqdfJ/PiGSwnBkBBGBRmEAIAAAAAgub7vrzdW+Usf0WqPyZJMgumyZ55g4yeOeGGA5AyKAgDwinGAAAAAIAg+cdr5ax4Rd6e7ZIkY8AQ2XNvkzlkVLjBAKQcCsKAnJ5AyAxCAAAAAEBS+U5r+3Ji15GysmVdfq2sS2bKMK2w4wFIQRSEAWmbQcgpxgAAAACAZHF3b5ez4mXpRJ0kyRw3VfbMG2VEe4ecDEAqoyAMiMkehAAAAACAJPFP1slZ8aq8XVslSUb/3PjpxHn5IScD0B1QEAaEQ0oAAAAAAF3Ndx25G9+Tu+7d+HLiSJasy78k65JZMiyWEwPoHArCgBindyH0aQgBAAAAAF3A21suZ9lL8k/USpLMsZfKnnmTjF59Qk4GoLtJakG4ePFiVVVVafTo0SopKenwWEtLi/7u7/5O9957ryZPnpzMGCmhbQYhpxgDAAAAAC6Ef/KYnJWvyPt4iyTJ6DdY9pwvyxw2NuRkALorM1m/cVVVlZqbm7Vw4UI5jqPKysoOj//pT3/SiBEjkvXyKaf9kBIAAAAAAM6d7zpy1i9Vy7OPxMtBO0vWjBsUueN7lIMALkjSZhBWVFQkZgYWFhaqvLxcY8fGf2A5jqOKigqNHz8+WS+fcjikBAAAAABwvrzqCjnLX5Z/7IgkycwvlH3lzTJy+oacDEA6SFpB2NDQoNzcXElSNBpVdXV14rGlS5dq7ty5qqio+Nznl5aWqrS0VJK0aNEixWKxZEUNRO8DjZKkrKzsbv+5pAPbtrkOKYTrkTq4FqmF65E6uBYAgLD49cflrHxNXtUmSZLRNxY/nXj4uJCTAUgnSSsIo9GoGhvjpVhTU5Oi0agkyXVdbdiwQT/84Q/PWhAWFRWpqKgocbumpiZZUQPR0FAvSWpqbur2n0s6iMViXIcUwvVIHVyL1ML1SB3pci3y8vLCjgAA6CTfdXVy1Ztqee8lyWmR7Iisy66RNXmuDIvzRgF0raT9VCkoKFBpaalmzZqlsrIyzZs3T5J0/Phx1dbW6qGHHtLBgwe1fv165efnKycnJ1lRUkJiD0KWGAMAAAAAzsLbt1PO8pfUcvSwJMkcdYnsWTfL6N0/5GQA0lXSCsL8/HxFIhEtWLBAo0aNUiwW05IlS1RcXKyHH35YkvTss89qwoQJaV8OSpKZKAhpCAEAAAAAn+U3nJCz6jV5lRslSVb/QTJm3ixrRObs3w8gHEmdl1xSUtLhdnFxcYfb8+fPT+bLp5TTZ5QwgxAAAAAA0IHvuXI3r5D7UanUekqybFlTr1buF4tVe+x42PEAZAA2LgjI6QmE8mgIAQAAAACneQc+lrPsJfl1ByVJ5siLZc+6RUafATLsSMjpAGQKCsKAJJYYh5wDAAAAABA+v/GknA9fl1e+Ln5H7wGyZ98ia+TF4QYDkJEoCAPSdkiJ51ERAgAAAECm8j1X3tZVcta8JbWcXk586RdkTZ3HjEEAoaEgDEjbEmPqQQAAAADITN7B3XKWvSi/9oAkybxovOzZt8joGws5GYBMR0EYEE4xBgAAAIDM5DfVx5cT71gbvyOnn+zZt8gcOTGx2gwAwkRBGJDEDEL6QQAAAADICL7nydu2Ws7qN6SWZsm0ZF16laypV8uIZIUdDwASKAgDktiDkIYQAAAAANKed3ivnA9elF+zT5JkDB8ne/aXZfYbFHIyAPgsCsKAmMwgBAAAAIC05zc1yFn9prztayT5Uq++smfdLHP0JJYTA0hZFIQBYQYhAAAAAKQv3/fkbVsjZ/Wb0qlGyTRlTb5K1mXXyIhkhx0PAM6KgjAg7TMIKQgBAAAAIJ14R6rlLHtJ/uG9kiQjb4zsObfK7D845GQA0DkUhAEx1HaKcchBAAAAAABdwm9ulLPmTXlbV0vypWgf2VfeJHPMZJYTA+hWKAgDYpgsMQYAAACAdOD7nrwda+V8+IbU3BBfTjxprqxpX5SRxXJiAN0PBWFA2v7tiH4QAAAAALovr2ZffDnxoT2SJGPoaNlzbpM5IDfkZABw/igIA2IabUuMaQgBAAAAoLvxTzXJWfOWvK2r4jM/or1lz7xR5tgpLCcG0O1REAak7c8Lj34QAAAAALoN3/flVayTs+p1qaleMkxZhbNkTfuSjOweYccDgC5BQRiQxAxC0RACAAAAQHfg1R6Us+xF+Qd3SZKMISPjpxMPzAs3GAB0MQrCgLTNIGSFMQAAAACkNr+lWe5Hb8vdvFLyPalnjuyZN8gcdxnLiQGkJbMzH3TXXXdpxYoVidvr1q3Tfffdl7RQ6ahtBiGnGAMAAABAavJ9X27FBrU884jcsuWSfJmXXKmsu34gq2Aa5SCAtHXWGYQ1NTU6fPiwJKm6ulpbt26VJG3YsEGHDh1Kfro0wgxCAAAAAEhdXt2h+HLiAx9LkozBI2TPvVVmbFjIyQAg+c5aEL777rt6/vnnJUl/+MMf9Ic//CHx2LBh/JA8FwanGAMAAABAyvFbTsld+ye5m5dJnif16CV7xvUyx0+TYXRq0R0AdHtnLQjHjh2ra6+9Vm+99ZYmT56soUOHSpJycnI0Z86cQAKmC2YQAgAAAEDq8H1f3s5Ncla+JjWekGTInDhD9hXXyegRDTseAATqrAXh1KlTNXXqVI0ZM0aXXHKJBg0aJEnyPE+myb+knAv2IAQAAACA1OAdPSxn+cvy91VKkoxBw2XPvU3moOEhJwOAcHTqFOO9e/fq8OHDKioq0j/8wz/oxIkT+uY3v6lrrrkm2fnSRvsMQgpCAAAAAAiD39oid92f5G5aJnmulB2VPf06mRdfwXJiABmtUz8Bly1bpl69emn58uVyHEdDhw7VkiVLkp0trbTPIAw5CAAAAABkGN/35VaVqeXZR+RueE/yXJkTpsdPJ544g3IQQMbr1AzC+vp69e7dWxs2bNBVV12lkSNH6j/+4z+SnS2tGOKQEgAA0L3ce++9uuiiizRq1CiNGDFCo0aN0pAhQ8KOBQDnxDteI2fZy/KryyVJRmyY7Dm3yswdEXIyAEgdnSoIY7GYfve736m+vl7f/va3dezYMeXk5CQ7W1pp+wcpZhACAIDu4oorrpDjOOrXr582bdqkxx9/XL1799aAAQM0cuRIfetb3wo7IgB8Lr+1Re76d+VufD++nDirx+nlxDNksKc+AHTQqYLw61//up577jmNGzdO06dP129/+1vNmDEj2dnSitk2g1A0hAAAoHvYtGmT/uVf/iVx++qrr9bq1at1/fXXa/fu3X/2+YsXL1ZVVZVGjx6tkpKSDo+1tLTo7/7u73Tvvfdq8uTJXZ4dQObyfV/e7q1ylr8i1R+TJJnjp8mecYOMnkx0AYAz6VRBOH36dE2bNk0HDhzQwYMHdffdd3OK8TlqP6Qk3BwAAACd1bt3b+3atUujRo2SJI0bN05PPPGEvv71r2vgwIFnfW5VVZWam5u1cOFCPfnkk6qsrNTYsWMTj//pT3/SiBEs7wPQtfzjtXJWvCxvzw5JkjFwaHw58ZBR4QYDgBTXqYKwurpa//zP/6yDBw9KkoYMGaIf/ehHGjZsWFLDpRPDYA9CAADQvfzt3/6tHn/8cQ0fPlyjRo3Svn37lJWV1annVlRUJGYGFhYWqry8PFEQOo6jiooKjR8/PmnZAWQW32mVu2Fp/AAS15GysmVfca3MiTNlmFbY8QAg5XWqIPyv//ovHT16VLNnz5YkrV27Vk899ZTuv//+pIZLJ20zCNmDEAAAdBdDhgzRwoULtWbNGn388ccaMmSI5s+f36nnNjQ0KDc3V5IUjUZVXV2deGzp0qWaO3euKioqPvf5paWlKi0tlSQtWrRIsVjsAj6T8Nm23e0/h67EeLRjLDo6n/FortikY2/9Tu6xI5KknoVXqu81d8jK6ZuMiIHi66MjxqMdY9ER49HR+YxHpwrCqqoqfe1rX9P1118vSXrjjTf0u9/97twTZjCTGYQAAKAbMk1TM2bMOOf9p6PRqBobGyVJTU1NikajkiTXdbVhwwb98Ic/PGtBWFRUpKKiosTtmpqa80ifOmKxWLf/HLoS49GOsejoXMbDP1EnZ8Ur8nZvkyQZA3Jlz75VXl6+jja3Ss3df1z5+uiI8WjHWHTEeHR0tvHIy8s74/2dKghzcnK0adMmTZ06VVJ8w2pOMT437TMIKQgBAED6KygoUGlpqWbNmqWysjLNmzdPknT8+HHV1tbqoYce0sGDB7V+/Xrl5+fz3hJAp/lOq9xN78td9258OXEkW9blRbIumSXDYjkxAJyPThWE11xzjZ599lmtXbs2cd9dd92VtFDpqH0GYchBAAAAApCfn69IJKIFCxZo1KhRisViWrJkiYqLi/Xwww9Lkp599llNmDCBchBAp3l7dshZ/rL8E7WSJHPspbJn3iSjV5+QkwFA99apgvCqq65S3759tWnTJknSpZdemth0Gp3DKcYAACDTlJSUdLhdXFzc4XZn9zMEAP/kMTkrX5H38RZJktFvcPx04mFjQk4GAOmhUwXhgw8+qFmzZunv//7vJUm///3v9dOf/lSPPfZYUsOlE04xBgAAAIBz47uO3E3L5K77k+S0SnaWrGlflFU4W4bVqb/OAgA6oVM/Uevq6jR48ODE7UGDBqm2tjZpodLR6QmE8hUvCdsKQwAAAADAZ3nVFfHlxKdPJzbzJ8u+8iYZaXA6MQCkmk4VhLm5uXrllVc0YMAA+b6vV199Vbm5ucnOllYMw5BhxJcY+377kmMAAAAAQDu//ricla/Jq4pvcWX0jcWXEw8fF3IyAEhfnSoIb731Vv3iF79IbCgtSd/97neTFipdmYYh1/fly1f7nEIAAAAAgO86OrnyDbW8/7LktEh2RNZl18iaPJflxACQZJ0+pCQWi2ndunWSpMsuu0wTJ05MarB0FF9W7MvzJSvsMAAAAACQIrx9O+Use0ktxw5LkszRl8i+8hYZvfuFGwwAMkSn/xlm4sSJlIIXyEycZMxBJQAAAADgN5yQs+o1eZUbJUlW/0EyZ94sc8T4kJMBQGZhnnaAzNMbD3r0gwAAAAAymO+6creskPtRqdR6SrJsWZddrdxrilV77HjY8QAg41AQBqjt5GJmEAIAAADIVN6Bj+Use0l+3UFJkjnyYtmzbpHRZ4AMOxJyOgDITBSEATLNtoIw5CAAAAAAEDC/8aScVX+UV7E+fkfvAbJn3yJr5MXhBgMAUBAGqe3cYmYQAgAAAMgUvufK27pKzpq3pJbTy4mnfEHWlHnMGASAFEFBGKC2GYQeBSEAAACADOAd3C1n2Yvyaw9IkswR42XP+rKMvgNDTgYA+CQKwgC170EYchAAAAAASCK/qV7Oh6/L27E2fkdOP9mzb5E5cmLi70UAgNRBQRig9lOMaQgBAAAApB/f8+RtWy1n9RtSS7NkWrIuvUrW1KtlRLLCjgcA+BwUhAFq+4cy+kEAAAAA6cY7tCd+OnHNPkmSMXyc7NlfltlvUMjJAAB/DgVhgMzEEmMaQgAAAADpwW9qkLP6DXnb18Tv6NVX9qybZY6exHJiAOgmKAgDZCSWGIccBAAAAAAukO978ratkbP6TelUY3w58eS5si67huXEANDNUBAGqO0UY2YQAgAAAOjOvCPVcj54Uf6RakmSkTdG9pxbZfYfHHIyAMD5oCAMUNvkeupBAAAAAN2R39woZ82b8rauluRL0T7x5cT5hSwnBoBujIIwQOxBCAAAAKA78n1P3o61cj58Q2pukExT1qS5sqZ9UUZWdtjxAAAXKKkF4eLFi1VVVaXRo0erpKQkcf+vfvUr7dq1S62trfrGN76hCRMmJDNGyjBM9iAEAAAA0L14NfvipxMf2iNJMoaOlj3nNpkDckNOBgDoKkkrCKuqqtTc3KyFCxfqySefVGVlpcaOHStJ+su//EvZtq0jR47oP//zP/W///f/TlaMlHK6H2QGIQAAAICU559qkrPmLXlbV0m+L0V7y555k8yxl7KcGADSTNIKwoqKCk2ePFmSVFhYqPLy8kRBaNvxl21ubtbIkSOTFSHlcIoxAAAAgFTn+768inVyVr0uNdVLhimrcJasy78kI6tH2PEAAEmQtIKwoaFBubnxKefRaFTV1dUdHv/nf/5nVVZW6t577z3j80tLS1VaWipJWrRokWKxWLKiBsYyTUlS3759FYv1CzdMhrNtOy2+ptIF1yN1cC1SC9cjdXAtAGQKr/ZAfDnxwV2SJGPIqPjpxAOHhhsMAJBUSSsIo9GoGhsbJUlNTU2KRqMdHv+f//N/qra2Vo8++qgeeuihzzy/qKhIRUVFids1NTXJihqYtkn4R48eVW/bCTVLpovFYmnxNZUuuB6pg2uRWrgeqSNdrkVeXl7YEQCkKP9Us9y1b8vdvFLyPalnjuyZN8gcdxnLiQEgA5jJ+o0LCgq0efNmSVJZWZkKCgoSj7W2tkqSevTooezszDnxqu3PVZYYAwAAAEgFvu/LrVivlmcfkVu2XJIv85IrlXXXD2QVTKMcBIAMkbQZhPn5+YpEIlqwYIFGjRqlWCymJUuWqLi4WP/6r/+qxsZGeZ6nr33ta8mKkHLM03+4ckgJAAAAgLB5dYfkLHtR/oGPJUlG7oj4cuLYsJCTAQCClrSCUJJKSko63C4uLpYk/ehHP0rmy6YsI1EQhhwEAAAAQMbyW07JXVsqd/NyyfOkHr1kz7he5vhpMoykLTIDAKSwpBaE6Mg0204xpiEEAAAAECzf9+Xt3CRn5WtS4wlJhsyJM2Vfca2MHtE/+3wAQPqiIAxQ2/Yd1IMAAAAAguQdPSxn+cvy91VKkoxBw2XPvU3moOEhJwMApAIKwgC17UHocUoJAAAAgAD4rS1y1/1J7qZlkudK2dH4cuIJl7OcGACQQEEYoMQehCHnAAAAAJDefN+X9/FmOStfleqPSzJkTpgue/p1Mnr2CjseACDFUBAGiFOMAQAAACSbd+xIfDlxdYUkyYgNi59OnDsi5GQAgFRFQRigxB6E9IMAAAAAupjf2iJ3/btyN74fX06c1UP29OtlXjxdhslyYgDA56MgDFBiD0IaQgAAAABdxPd9ebu2ylnxilR/TJJkjp8me8YNMnrmhBsOANAtUBAGKLEHIf0gAAAAgC7gH6+Vs+JleXt2SJKMgUNlz7lN5pCRIScDAHQnFIQBMk32IAQAAABw4XynVe6GpXI3vCe5jpSVLfuKa2VOnCnDtMKOBwDoZigIA3R6C0KWGAMAAAA4b+7ubXKWvyKdrJMkmeOmyp55o4xo75CTAQC6KwrCALXPIAw5CAAAAIBuxz9RJ2fFK/J2b5MkGQNyZc++VWZefsjJAADdHQVhgAwOKQEAAABwjnynVe7G9+Wufze+nDiSLevyIlmXzJJhsZwYAHDhKAgD1HaKMfUgAAAAgM7w9uyQs/xl+SdqJUnm2Cnx5cS9+oScDACQTigIA3R6hbF8j4oQAAAAwOfzTx6Ts/IVeR9vkSQZ/QfLnnOrzLwxIScDAKQjCsIAGcwgBAAAAHAWvuvI3fSB3HXvSE6rZGfFlxNPms1yYgBA0lAQBshkD0IAAAAAn8OrrpCz7CX5x2skSWb+ZNlX3iQjp2/IyQAA6Y6CMECcYgwAAADg0/z643JWviqvqkySZPQbJHv2l2UOHxdyMgBApqAgDNDpLQiZQQgAAABAvuvo5Mo31PL+y5LTItkRWZd9UdbkOTIs/qoGAAgOf+oEKLEHIf0gAAAAkNG8fTvlLHtJLccOS5LM0ZNkX3mzjN79wg0GAMhIFIQBal9iTEMIAAAAZCK/4YScVa/Jq9woSbL6D5Y58yaZI8aHnAwAkMkoCAN0egKhPPpBAAAAIKP4rit3ywq5H70ttbZIli3rsquVe02xao8dDzseACDDURAGyDSYQQgAAABkGm9/lZzlL8mvOyRJMkdeLHv2LTJ6D5BhR0JOBwAABWGgDApCAAAAIGP4jSflrPqjvIr18Tt6D5A9+xZZIy8ONxgAAJ9CQRigthmELDEGAAAA0pfvuXK3rJL70VtSy6n4cuIp82RN+QIzBgEAKYmCMEBtexAygxAAAABIT97BXXKWvSS/9oAkyRwxXvasL8voOzDkZAAAfD4KwgAl9iAMOQcAAACAruU31ctZ9bq88rXxO3L6yZ59i8yRExNbDQEAkKooCANkJJYYUxECAAAA6cD3PHnbPpSz+k2ppVkyLVlTviBryjwZkayw4wEA0CkUhAEyzbZDSkIOAgAAAOCCeYf2xJcT1+yTJBnDC2TP+bLMvrGQkwEAcG4oCANksgchAAAA0O35TQ1yVr8hb/ua+B05fWVfeYvM0ZewnBgA0C1REAao7c0C/SAAAMgEixcvVlVVlUaPHq2SkpLE/U888YT27t0rSbrnnns0cuTIsCIC58T3PHnb18SXE59qjC8nnjxX1mXXsJwYANCtURAGyGQPQgAAkCGqqqrU3NyshQsX6sknn1RlZaXGjh0rSbrttts0ePBgHThwQE8//bR++MMfhpwW+PO8I9VyPnhR/pFqSZIxbKzs2V+W2X9wyMkAALhwFIQBMplBCAAAMkRFRYUmT54sSSosLFR5eXmiIBw8OF6oWJYl0zRDywh0ht/cKGfNm/K2rpbkS9E+smfdLDO/kOXEAIC0QUEYoLb3D8wgBAAA6a6hoUG5ubmSpGg0qurq6s98zG9/+1vdeOONZ3x+aWmpSktLJUmLFi1SLNa9D32wbbvbfw5dqTuMh+97aty4XCfe+YO8pnrJtJQzvUi959wiM7tHl71OdxiLIDEeHTEeHTEe7RiLjhiPjs5nPCgIA8QMQgAAkCmi0agaGxslSU1NTYpGox0ef+211zR8+HBNmDDhjM8vKipSUVFR4nZNTU3ywgYgFot1+8+hK6X6eHg1++R88JL8w3skSUZevuzZt6p1QK7qTtZLJ+u77LVSfSyCxnh0xHh0xHi0Yyw6Yjw6Ott45OXlnfF+1nQEyDx9jLHreSEnAQAASK6CggJt3rxZklRWVqaCgoLEYxs3btSOHTt0++23hxUPOCP/VJNal72k1iWPx8vBaG/Z1/yFIjf/jcwBuWHHAwAgaSgIA2Sd3mOHJcYAACDd5efnKxKJaMGCBTJNU7FYTEuWLJEkPfXUUzpy5Ih+8pOf6Iknngg5KSD5vi93x1q1/P5f5G1ZKcmQVThHWXf9QNa4Kew1CABIeywxDpBtxQtC16MgBAAA6a+kpKTD7eLiYknSY489FkYc4Iy82gNylr0k/+AuSZIxZJTsObfKHDg03GAAAASIgjBAtnV6ibFLQQgAAACEyT/VLPejt+VuWSn5ntQzR/bMG2WOm8qMQQBAxqEgDFDbEmOHGYQAAABAKHzfl1e5Qc6qP0qNJyXDkDVplqzLvyQju2fY8QAACAUFYYDalxhzSAkAAAAQNK/uYHw58YGPJUlG7gjZc26TGTvziY4AAGQKCsIAWW1LjJlBCAAAAATGbzkld22p3LLl8eXEPXrJnnGDzPGXyTA4txEAAArCALUtMaYgBAAAAJLP9315OzfJWfma1HhCkiFz4kzZV1wro0c07HgAAKQMCsIA2RSEAAAAQCC8o4fjy4n375QkGYMvip9OPGh4yMkAAEg9FIQBaj/FmD0IAQAAgGTwW0/JXfeO3E3LJM+VsqOyZ1wvc8LlLCcGAOBzUBAGKHFIic8MQgAAAKAr+b4v7+PNcla8KjUcl2TInDBd9ozrZPToFXY8AABSGgVhgBJ7ELoUhAAAAEBX8Y4dkbP8ZfnVFZIkIzYsvpw4d0TIyQAA6B4oCAPEKcYAAABA1/FbW+Suf1fuxvdPLyfuKXv6dTInTJdhspwYAIDOoiAMUNsSY8djD0IAAADgfPm+L2/XVjkrXpHqj0mSzPGXy55xvYyeOeGGAwCgG6IgDFDbEmOPGYQAAADAefGP18pZ8bK8PTskScbAobLn3CZzyMiQkwEA0H1REAbINttmEFIQAgAAAOfCd1rlrl8qd+N7kutIWT1kX3GtzIkzZJhW2PEAAOjWKAgDZLMHIQAAAHDO3N3b5Cx/RTpZJ0kyCy6TPeMGGdHeIScDACA9UBAGqG0PQtdlD0IAAADgz/FP1MlZ8Yq83dskScaAIfHTiYeODjkZAADphYIwQG17ELo+MwgBAACAz+M7rXI3vi93/bvx5cSRbFmXf0nWpCtZTgwAQBJQEAbINA0ZhuT78YNKTNMIOxIAAACQUrw9O+Qsf1n+iVpJkjl2iuyZN8ro1SfkZAAApK+kFoSLFy9WVVWVRo8erZKSksT9TzzxhPbu3StJuueeezRyZOacOGaZhhzXl0tBCAAAACT4J4/KWfGqvF1bJElG/8Hx5cR5Y0JOBgBA+ktaQVhVVaXm5mYtXLhQTz75pCorKzV27FhJ0m233abBgwfrwIEDevrpp/XDH/4wWTFSjmWaclxXjucpIjPsOAAAAECofNeRu/EDuevfkZxWyc6SdXmRrEmzZVgsJwYAIAhJKwgrKio0efJkSVJhYaHKy8sTBeHgwYMlSZZlyTQzqySzTs8a9DjJGAAAABnOq66Qs+wl+cdrJEnmmMmyZ94kI6dvyMkAAMgsSSsIGxoalJubK0mKRqOqrq7+zMf89re/1Y033njG55eWlqq0tFSStGjRIsVisWRFDYxt28qyLTWectSnX3/1z+kRdqSMZdt2WnxNpQuuR+rgWqQWrkfq4FoAXcs9UafWt5+WV1UmSTL6DZI9+8syh48LORkAAJkpaQVhNBpVY2OjJKmpqUnRaLTD46+99pqGDx+uCRMmnPH5RUVFKioqStyuqalJVtTAxGIxGYrPHDxSUyO3mYIwLLFYLC2+ptIF1yN1cC1SC9cjdaTLtcjLyws7AjKc7zpyy5br0Lp35LeekuyIrGlflFU4R4bF+YkAAIQlaet7CwoKtHnzZklSWVmZCgoKEo9t3LhRO3bs0O23356sl09Z1ukl1a7LEmMAAABkDm9fpVqf/ze5H74uv/WUzNGTlDX/B7KnzKMcBAAgZEkrCPPz8xWJRLRgwQKZpqlYLKYlS5ZIkp566ikdOXJEP/nJT/TEE08kK0JKatuD0GUPQgAAAGQAv+GEWkt/p9ZX/1P+scMy+gzUwL/4H4pce7eM3v3CjgcAAJTEJcaSVFJS0uF2cXGxJOmxxx5L5sumNMuiIAQAAED6811X7pYVcj96W2ptiS8nnnq1rEuvUo/cIapPg2X7AACkC+byB8wy2gpCL+QkAAAAQHJ4+6vkLH9Jft0hSZI5aqLsWTfL6D0g5GQAAOBMKAgDZlmn9yBkBiEAAADSjN94Us6qP8qrWB+/o88A2bO+LGvkmQ8mBAAAqYGCMGDsQQgAAIB043uu3C2r5H70ltRySrJsWVPmyZryBRl2JOx4AADgz6AgDFhbQehQEAIAACANeAd3yfngRfl1ByVJ5ogJsmffIqPPwJCTAQCAzqIgDFhiBqHLHoQAAADovvymejmrXpdXvjZ+R04/2bO/LHPkxTJO77sNAAC6BwrCgFnm6T0IfWYQAgAAoPvxPU/e1g/lrHlTammWTEvWlC/ImjJPRiQr7HgAAOA8UBAGzE7MIKQgBAAAQPfiHdojZ9mL8mv2S5KM4QWy53xZZt9YyMkAAMCFoCAMmMkhJQAAAOhm/KYGOavfkLd9TfyOnL6yr7xF5uhLWE4MAEAaoCAMmG21FYTsQQgAAIDU5nuevO1r5Kx+QzrVFF9OPHmurMuuYTkxAABphIIwYIk9CJlBCAAAgBTmHd4rZ9lL8o9US5KMYWPjh5D0HxxyMgAA0NUoCANmscQYAAAAKcxvbpCz+i1521ZL8qVoH9mzbpaZX8hyYgAA0hQFYcDaCkKHghAAAAApxPc9eTvWyvnwdam5UTJNWYVzZV32RRlZ2WHHAwAASURBGLDEDEKXPQgBAACQGrwj++LLiQ/vkSQZefmy59wqs39uyMkAAEAQKAgDltiD0GcGIQAAAMLln2qUs+ZteVtXSb4vRXvLvvImmWMuZTkxAAAZhIIwYO0zCCkIAQAAEA7f9+SVr5ez6o9Sc4NkmLIKZ8u6vEhGVo+w4wEAgIBREAaMQ0oAAAAQJq92f3w58cHdkiRjyCjZc26TOXBIyMkAAEBYKAgDZlunDylhD0IAAAAEyD/VLPejt+VuWRFfTtwzR/bMG2WOm8pyYgAAMhwFYcCybEuSdMpxQ04CAACATOD7vryKDXJWvSY11UuGIWvSLFmXf0lGds+w4wEAgBRAQRiw7MjpgrCVGYQAAABILq/uYHw58YGPJUlG7oj4cuJYXsjJAABAKqEgDFh7QcgMQgAAACSH33JK7tpSuWXLJd+TevSSPeMGmeMvk2GYYccDAAAphoIwYImCkCXGAAAA6GK+78vbuUnOytekxhOSDJkTZ8qefq2M7GjY8QAAQIqiIAxYth3/F1tmEAIAAKAreUcPx5cT798pSTIGXyR7zq0yBw0PORkAAEh1FIQB65HFEmMAAAB0Hb/1lNy178gt+0DyPKlHVPb062VOuJzlxAAAoFMoCAOWbVMQAgAA4ML5vi/v481yVrwqNRyXZMi8eLrs6dfJ6NEr7HgAAKAboSAM2CdPMfZ9X4ZhhJwIAAAA3Y137Iic5S/Lr66QJBmxYbLn3iZz8EUhJwMAAN0RBWHAbMuUZRpyPV+O5ytiURACAACgc/zWFrnr35W78X3Jc6XsnrKnXydzwnQZJsuJAQDA+aEgDEF2xFLjKUenWl1FLN7IAQAA4Ox835e3a6ucFa9I9cckSeb4y2XPuF5Gz5xwwwEAgG6PgjAEnywIc3pEwo4DAACAFOYfr5Gz/BV5e3dIkoyBQ2XPuU3mkJEhJwMAAOmCgjAE7fsQclAJAAAAzsx3WuWuXyp343uS60hZPWRfca3MiTNZTgwAALoUBWEIsu34GzoKQgAAAJyJu3ubnOWvSCfrJElmwWWyZ9wgI9o75GQAACAdURCGoG0GYTMFIQAASGOLFy9WVVWVRo8erZKSksT9e/bs0ZNPPilJuueeezRyJEtl2/gn6uSseEXe7m2SJGPAENlzbpU5dHTIyQAAQDpjbUIIerDEGAAApLmqqio1Nzdr4cKFchxHlZWViceeeeYZ3Xffffr+97+vZ555JsSUqcN3WuWsLVXLs4/Gy8FItqwrb1bk9nspBwEAQNIxgzAE7XsQeiEnAQAASI6KigpNnjxZklRYWKjy8nKNHTtWktTQ0KBYLJb4daZz9+yQs/xl6UStJMkcO0X2zBtl9OoTcjIAAJApKAhDwCElAAAg3TU0NCg3N1eSFI1GVV1dnXjM9/0/+/zS0lKVlpZKkhYtWpQoFLsr27Y/8zk4x2t1/K3fyylfH/+YWJ76Xf81ZY+cEEbEQJ1pPDIVY9ER49ER49ER49GOseiI8ejofMaDgjAEiYLQoSAEAADpKRqNqrGxUZLU1NSkaDR6xo8zDOOM9xcVFamoqChxu6amputDBigWiyU+B9915G78QO76dySnVYpkyZpWJHPSbJ20LJ3s5p9rZ3xyPDIdY9ER49ER49ER49GOseiI8ejobOORl5d3xvspCEPADEIAAJDuCgoKVFpaqlmzZqmsrEzz5s1LPJaTk6Pa2loZhqGePXuGFzIE3t5yOctfln88/qbdHDNZ9pU3yejVN+RkAAAgk1EQhiCaFR/2hmYn5CQAAADJkZ+fr0gkogULFmjUqFGKxWJasmSJiouLNX/+fP385z+XJH3zm98MN2hA3BN1an37aXlVZZIko98g2bNvlTl8bMjJAAAAKAhD0TcakSSdaGoJOQkAAEDylJSUdLhdXFwsSRo5cqQefPDBMCKFwm9t0eH//v/kNdZLdkTWtC/KKpwjw+KtOAAASA28KwlBn2iWJOl4IwUhAABAujMiWeo17Ro1VFfJnnWzjJx+YUcCAADogIIwBG0F4QkKQgAAgIzQe+7NaqmtCzsGAADAGZlhB8hEvbJtWaahphZXrY4XdhwAAAAkmWHwthsAAKQu3qmEwDAM9ekZ34eQZcYAAAAAAAAIEwVhSFhmDAAAAAAAgFRAQRiSvm0FIScZAwAAAAAAIEQUhCHhJGMAAAAAAACkAgrCkLTNIDzWQEEIAAAAAACA8FAQhiS3X09J0oGjjSEnAQAAAAAAQCajIAxJ3oBekqR9tQ3yfT/kNAAAAAAAAMhUFIQh6dMzopweETW3uqqrPxV2HAAAAAAAAGQoCsKQGIah4QPbZxECAAAAAAAAYaAgDFHegKgkaU9NfchJAAAAAAAAkKkoCEM0bmhfSdKWvUfZhxAAAAAAAAChoCAM0ejcPsrpEVHNiWbt5zRjAAAAAAAAhCCpBeHixYu1YMEC/epXv+pw/5IlS/S3f/u3+v3vf5/Ml095lmmocOQASdKaiiMhpwEAAAAAAEAmSlpBWFVVpebmZi1cuFCO46iysjLx2DXXXKN77703WS/drcwsGCxD0qryQ6o72Rx2HAAAAAAAAGSYpBWEFRUVmjx5siSpsLBQ5eXlicf69esnwzCS9dLdSt6AXrpsTEyu5+u3H1Sq1fHCjgQAAAAAAIAMYifrN25oaFBubq4kKRqNqrq6+pyeX1paqtLSUknSokWLFIvFujxj0GzbPuPn8Zdf6q2PD3+g3Ufq9V/vVOhvbpii3P69QkiYOT7vWiAcXI/UwbVILVyP1MG1AAAAQDpLWkEYjUbV2Bg/eKOpqUnRaPScnl9UVKSioqLE7Zqami7NF4ZYLPa5n0fJ1QX6z9Lt2nngqP7fXy1VQV5fTRoxQKMG5yjWp6cskxmXXels1wLB43qkDq5FauF6pI50uRZ5eXlhRwAAAEAKSlpBWFBQoNLSUs2aNUtlZWWaN29esl4qLQzpH9X/uKVQf1y7Rx/tPKLt+45p+75jkuKHmfSJZqlPz4h698xSzyxLWbal7Iip7IilbNtSlm3KtkxZphH/zzJlt/3aNGVZxunb8Y8xDMk0Pvn/Z7pPMgxDJsvBAQAAAAAA0lbSCsL8/HxFIhEtWLBAo0aNUiwW05IlS1RcXKx33nlHb775purr61VfX6977rknWTG6lZweEc2fPUY3XjZCW/bWaVv1MR042qi6+lM6evq/sJypNDQkmWb8/2VIp3+V+Hgj8euO95/+8MQNo8Nz2p9odHjOJz7WONvzP/GxZ+k1bduW4zid++Q/xznXpufRsxrn+qTkfvh56cx+oxHbVuvp60EdHS47EpHT2hp2DJzG9Ugdf33dVEWTtnMzAAAAEK6kFYSSVFJS0uF2cXGxpPgpxtdcc00yX7pby+kZ0YyCXM0oiO/h2OK4OtHYqhNNLTrZ1KpTrW77f46rU62eWhxXruvL8Xy5nifX89v/c73T97c/5nm+fEme78v3Jd/35SX+v+N9kuT7kuufviH/jLkBAEhXzS2tivYIOwUAAACQHEktCNE1smxLsT6WYn3C+ZvJJ8tD328rFTve58tvrw390xXi6fvbf5+2h/1Ex+if5f725/ifen78dT/xcu2v+amP/Tz9+vXTsWPHOjkCn/Xnfv8zPOPcX+NcPz6A3vbcP+3OPaNv3346fvwY1XMK6Ne3r44dPx52DJzG9Ugdwwf1UeNJrgUAAADSEwUh/izDMGR9YplvOojF+qnGvrAlxug6sdgA1fTwwo4BSbHYQNX0oKpNFVyP1BHNjqjxZNgpAAAAgORgNx0AAAAAAAAgg1EQAgAAAAAAABmMghAAAAAAAADIYBSEAAAAAAAAQAajIAQAAAAAAAAyGAUhAAAAAAAAkMEoCAEAAAAAAIAMRkEIAAAAAAAAZDAKQgAAAAAAACCDURACAAAAAAAAGYyCEAAAAAAAAMhgFIQAAAAAAABABqMgBAAAAAAAADIYBSEAAAAAAACQwSgIAQAAAAAAgAxGQQgAAAAAAABkMApCAAAAAAAAIINREAIAAAAAAAAZjIIQAAAAAAAAyGAUhAAAAAAAAEAGoyAEAAAAAAAAMhgFIQAAAAAAAJDBKAgBAAAAAACADEZBCAAAAAAAAGQwCkIAAAAAAAAgg1EQAgAAAAAAABmMghAAAAAAAADIYBSEAAAAAAAAQAajIAQAAAAAAAAymOH7vh92CAAAAAAAAADhYAZhgH784x+HHQGncS1SC9cjdXAtUgvXI3VwLXCh+BrqiPFox1h0xHh0xHh0xHi0Yyw6Yjw6Op/xoCAEAAAAAAAAMhgFIQAAAAAAAJDBKAgDVFRUFHYEnMa1SC1cj9TBtUgtXI/UwbXAheJrqCPGox1j0RHj0RHj0RHj0Y6x6Ijx6Oh8xoNDSgAAAAAAAIAMxgxCAAAAAAAAIIPZYQfIFIsXL1ZVVZVGjx6tkpKSsOOktbq6Ov3sZz9TdXW1fvOb38iyrDOOf2fvw/mrqKjQr3/9axmGoTFjxuiv//qv9fLLL2vNmjUaNGiQvvOd78i27U7fhwuzZ88ePfHEEzJNU0OGDNG3v/1t/frXv+Z7I0SvvvqqPvzwQz344IP8nArR4cOH9Q//8A8aNmyYbNvWP/7jP/KzCl2K79t2Z3qflsnO9F4pU53pfYphGGHHCt0n3ytksjP9WZ3J3nvvPb333nvyPE/f+973NGDAgLAjhWbDhg168cUXJUn79+/XPffco+nTp4cbKkSnTp3So48+qlOnTikajer73/++IpFIp57LDMIAVFVVqbm5WQsXLpTjOKqsrAw7UlrLycnR/fffr3Hjxkk68/h39j5cmEGDBmnBggV68MEHdeLECW3dulVbtmzRgw8+qBEjRmjNmjU6fvx4p+7DhcvLy9NPf/pTLVy4UJJUWVnJ90aIWltbtWvXLkn8nEoFhYWFeuCBB/SP//iPnf65xM8qdAbftx19+n1apvv0e6U9e/aEHSk0n36fsnPnzpAThe+T7xXQ8c/qTFZXV6etW7dqwYIFeuCBBzK6HJSkKVOm6IEHHtADDzygWCymyZMnhx0pVBs2bNC4ceP0wAMPaOzYsdqwYUOnn0tBGICKiorEF2lhYaHKy8tDTpTesrKylJOTk7h9pvHv7H24MP369VNWVpYkybIs7d27VxMnTpQkTZ48WeXl5dq5c2en7sOF++TMJtu2VVZWxvdGiN555x3NmzdPEj+nUsGWLVu0YMECvfrqq53+ucTPKnQG37cdffp9Wqb79Hsl08zcv559+n1KLBYLMU1q+OR7BXT8szqTbdiwQZ7naeHChXrqqafkeV7YkVLCoUOH1LdvX/Xo0SPsKKHKzc1Vc3OzJKmhoUG9e/fu9HMz90+gADU0NCgajUqSotGoGhsbQ06UWc40/p29D11j9+7dOnHihHr16qWePXtKio9xQ0ODGhsbO3UfusZHH32kH/zgBzp+/Lhc1+V7IySO42jLli2aNGmSJH5Oha1///567LHH9E//9E8qKytTVVUVP6vQZfi+RWe0vVcaPnx42FFC9cn3KZleJH/6vUKm+/Sf1bt37w47UmiOHz8ux3G0YMECZWVlsYLhtA8//DCjlxa3GTp0qCoqKvT3f//3qqqqUkFBQaefS0EYgE++GWxqakq8SUQwzjT+nb0PF66+vl5PPfWUvv3tbysajaqpqUmS1NjYqF69enX6PnSNyy+/XI888ogGDhwoy7L43gjJ+++/rzlz5iRu83MqXJFIRD169JBlWZo2bZpyc3P5WYUuw/ct/pxPvlfKdJ98n7Ju3bqw44Tq0+8VMt2n/6zeu3dv2JFCE41GEysYJk2apH379oWcKDWsXbtWl19+edgxQvfee+9p2rRpevTRRzV16lR98MEHnX4uBWEACgoKtHnzZklSWVnZOTW4uHBnGv/O3ocL47qu/v3f/11/+Zd/qX79+mnMmDHaunWrpPgYjxs3rtP34cK1trYmft0264nvjXDs379fb7/9th566CFVV1fr5MmTXIsQtZV8krR9+3YNGTKEn1XoMnzf4mw+/V4pk336fUrb0utM9en3Cq+//nrYkUL16T+rc3NzQ0wTrvHjxydmUO7atUuDBw8OOVH4jh07Jtu2z2k5bbryfT8xA7tPnz7ntHKBo/YCkJ+fr0gkogULFmjUqFEaO3Zs2JHSmuM4evjhh7V792499NBD+upXv3rG8e/sfTh/K1euVGVlpf7v//2/kqSvfe1ruvjii3X//fcrFovppptukm3bnboPF27Dhg2JPVuGDh2qb33rW/r1r3/N90YI7r777sSv77//ft1555361a9+xbUIybZt2/TMM88oEolowoQJGjduHD+r0GV4H9jRmd6nZXK5fqb3SplaIn/6fUqmHzTw6fcKN9xwQ4hpwnemP6sz1ahRo5SVlaUHHnhAvXv31s033xx2pNCtWbNGV1xxRdgxUsKcOXP085//XO+//74sy9L3v//9Tj/X8H3fT2I2AAAAAAAAACmMJcYAAAAAAABABqMgBAAAAAAAADIYBSEAAAAAAACQwSgIAQAAAAAAgAxGQQgAAAAAAABkMApCAGnt8OHDmj9/vhYtWqR169bp2Wef1eHDh7v8daqrq/Xss89qy5Ytift+8YtfaP78+dq5c2eXvx4AAAAAAF3FDjsAACRTnz59dN9992nAgAFasWKF3nzzTV1yySUaPHjwOf0+ruvKsqzPfby6ulrPP/+8JOmSSy6RJF177bWaMmWKcnNzz/8TAAAAAAAgyQzf9/2wQwBAshw+fFjf/e53lZ2drVOnTnV47Nlnn1V5ebl+/etfa8+ePRowYIDuvPNOzZkzJ/G8goICZWdna8+ePXrkkUf005/+VAcOHJAkjR49Wn/zN3+j7Oxsffe73+3we//TP/2Tli5dqvfee08PP/ywxowZo9LSUr388ss6evSohg8frr/6q7/ShAkTtHTpUv2f//N/NGvWLO3bt081NTW68847deONN2r//v16/PHHtXv3bmVlZemiiy7SwoULAxs/AAAAnNmjjz6qvn37ateuXaqtrdX3vvc9vf3226qsrNSECRP07W9/O+yIANBpLDEGkBEmTpyoSy+9VJJ0++2367777lN9fb0WLVqkxsZGFRcXa9CgQfr3f/937dq1K/G88vJyjR49WnfddZcMw9D06dNVUlKi2267Tbt379bixYvVp08f3XjjjZKkGTNm6L777tPw4cM7vP7mzZv1xBNPqE+fPvrGN76hmpoa/exnP9PJkycTH7NlyxZ98YtflCQ9/fTTchxHb775pnbu3Km7775bX/3qVxWLxZI8UgAAAOiMPXv2KDc3Vw8++KCKior0y1/+UnfffbceffRRrVu3Tq2trWFHBIBOY4kxgIxgGIaGDBmijRs3atKkSbrkkku0bt061dfXq76+Xr/73e8SH7t582ZNnz5dUnyW4N133y1Jqqur08aNG1VeXq62ydd79uxRjx49NGHCBP3xj3/URRddpNmzZ3/m9detWydJmj9/viZPnqyamhq98MILqqioSHzM1Vdfreuvv15r167Vxo0bdezYMQ0dOlS+72v9+vUaM2ZMoogEAABAeFpaWtTQ0JB4b2YYhq655hr1799fkmSapmybv24D6D74iQUgYxiGccb7r7rqKl111VWJ25/cn7DtTZ4kvf7669qxY4duuukmTZ06Vb/85S/V1NTUZVlycnIkKbHXoed5uv766zVs2DBt3bpVH330kZYsWaJ//dd/VV5e3nm9LgAAAC5cdXW18vPzZZrxRXm7d+/WtddeK0mqra3VgAEDPve9JwCkIpYYA8gYvXr1kiStWrVK69atU0FBgXJycrRx40bt379fe/fu1UsvvaS6urqz/j4NDQ3aunWramtrE/e1lXvbt2/X8uXL1dLS0uE5l112mSTpueee09tvv6133nlHvXr10rhx4876Wm+99ZbKy8s1ZMgQ5ebmyvd9HTt27Fw/dQAAAHShPXv2aOTIkYnbu3fv1ogRIz7zawDoLigIAWSMuXPnatiwYXrrrbf0q1/9Sjk5Ofrxj3+sIUOG6Omnn9aSJUuUlZWlQYMGnfH5N9xwg8aMGaMVK1aorq5OF110UeKxCRMmqLCwUNu2bdNjjz3WYW9BSZo0aZK+9a1v6fjx4/rNb36jgQMH6n/9r/+l3r17nzVzJBLR0qVL9R//8R/atm2brrvuOk2YMOHCBwMAAADnbc+ePRo1apSk+HLjlpaWxD8Y7969u0N5CADdAacYAwAAAAAAABmMGYQAAAAAAABABqMgBAAAAAAAADIYBSEAAAAAAACQwSgIAQAAAAAAgAxGQQgAAAAAAABkMApCAAAAAAAAIINREAIAAAAAAAAZjIIQAAAAAAAAyGD/P83itQ4cFmcRAAAAAElFTkSuQmCC",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"low, high, step = 0, 5000, 10\n",
"plot_all(cost_history, m, q, low, high, step)"
]
},
{
"cell_type": "code",
"execution_count": 141,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"57 passi e 5700 gradienti calcolati per arrivare a distanza minore o uguale di 0.1 dall'ottimo\n"
]
}
],
"source": [
"near_opt(m, min_dist=1e-1, ge_per_step=n)\n"
]
},
{
"cell_type": "code",
"execution_count": 142,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA7sAAAHzCAYAAADhDgreAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAABWBUlEQVR4nO3df3Rb9Z3n/9e15F+SYluy7KT59aUJMAkJIaEObXHakBBCjmkZWjwppHhO25llWDjLMN1ySLYttKWUUMophwJLe2Boa2an7YZCD1vv4KYJYXHL4BB7QkxDgVLoFKhjyz8l/5J0v384ki3bcn5ZuldXz8c5HGLFN/5IHzvR637en/fHME3TFAAAAAAADlJg9QAAAAAAAJhrhF0AAAAAgOMQdgEAAAAAjkPYBQAAAAA4DmEXAAAAAOA4hF0AAAAAgOMQdgEAAAAAjkPYBQAgy8466yyVlpZq3rx5qqio0MUXX6xHHnlE8Xj8hNf+8Y9/lGEYikajGR1jtr4OAACZQtgFAMACzzzzjAYGBvT2229r586duueee/R3f/d3Vg8LAADHIOwCAGCh8vJyXXnllfrpT3+qH/3oRzpy5Ih++ctfat26dSorK9OSJUv0ta99Lfn5H//4xyVJFRUV8vl8+u1vf6s333xTmzdvVmVlpYLBoD772c+qt7c3ec0999yjRYsWad68efqrv/or/frXv5YkxeNx7d69W8uXL1dlZaW2b9+uUCiU9usAAJBLCLsAANjARRddpMWLF+v//b//J6/Xqx//+Mfq7e3VL3/5S/3P//k/9fTTT0uSnn/+eUlSb2+vBgcH9dGPflSmaWrXrl1699139bvf/U5/+tOfkgH5tdde04MPPqjW1lYNDAzo2Wef1VlnnSVJ+t73vqenn35aBw4c0Lvvviu/36+bbrop7dcBACCXEHYBALCJhQsXKhQK6ZJLLtH555+vgoICrVmzRtdee60OHDiQ9rqzzz5bl112mYqLi1VVVaUvfvGLyc93uVwaGRnRq6++qrGxMZ111llavny5JOmRRx7RXXfdpcWLF6u4uFhf+9rXtGfPHvbpAgAcgbALAIBN/PnPf1YgENC///u/a9OmTaqqqlJ5ebkeeeQRdXV1pb3uL3/5i6655hotWrRIZWVluu6665Kff/bZZ+v+++/X1772NVVXV+uaa67Ru+++K0l6++239alPfUoVFRWqqKjQypUr5XK59Je//CUrzxcAgEwi7AIAYAOtra3685//rA0bNmjHjh268sor9ac//Ul9fX264YYbZJqmJMkwjGnX/o//8T9kGIZeeeUV9ff364knnkh+viTt2LFDL7zwgt5++20ZhqHbbrtNkrRkyRL93//7f9Xb25v8b3h4WIsWLZrx6wAAkEsIuwAAWKi/v1//5//8H11zzTW67rrrdP7552tgYECBQEAlJSV66aWX9L/+1/9Kfn5VVZUKCgr0hz/8IfnYwMCAfD6fysvL9ec//1n33ntv8vdee+017du3TyMjIyopKVFpaakKCsb/+b/hhhv05S9/WW+//bYk6dixY/rFL36R9usAAJBLCLsAAFjgk5/8pObNm6clS5borrvu0he/+EU9/vjjkqSHH35Yt99+u+bNm6dvfOMb2r59e/I6j8ejL3/5y6qtrVVFRYVefPFF3XHHHTp06JDKy8t1xRVX6NOf/nTy80dGRrRz504Fg0EtWLBAnZ2duvvuuyVJ//iP/6grr7xSW7du1bx58/SRj3xE//7v/5726wAAkEsMc3KdEwAAAAAADsDKLgAAAADAcQi7AAAAAADHIewCAAAAAByHsAsAAAAAcBzCLgAAAADAcQi7AAAAAADHcVs9gGx49913rR6CLQWDQXV1dVk9DEzBvNgT82JPzIv9MCf2xLzYE/NiP8yJPc02LwsXLkx7HSu7AAAAAADHIewCAAAAAByHsAsAAAAAcBzCLgAAAADAcQi7AAAAAADHIewCAAAAAByHsAsAAAAAcBzCLgAAAADAcdzZ/oIPP/ywDh06pPLyct13332SpJ/97Gf69a9/rbKyMknStddeqwsvvHDate3t7Xr88ccVj8d16aWX6qqrrsrm0AEAAAAAOSLrYfeSSy7Rtm3b9NBDD6U8fsUVV+jKK69Me108Htdjjz2mr3zlK6qsrNSuXbtUU1OjxYsXZ3rIAAAAAIAck/Uy5vPOO08+n++Ur3vjjTe0YMECzZ8/X263WxdffLFaW1szMEIAAAAAQK7L+spuOs8++6yef/55LVu2TH/7t387LRCHQiFVVlYmP66srNTrr7+e7WECAAAAAHKALcLu1q1bVV9fL0n66U9/qh//+Me68cYbT/vP27t3r/bu3StJ2r17t4LB4JyM02ncbjevjQ0xL/bEvNgT82I/zIk9MS/2xLzYD3NiT6c7L7YIuxUVFclfX3rppbrnnnumfU4gEFB3d3fy4+7ubgUCgRn/vC1btmjLli3Jj7u6uuZusA4SDAZ5bWyIebEn5sWemBf7YU7siXmxJ+bFfpgTe5ptXhYuXJj2OlscPdTT05P89UsvvaQlS5ZM+5zly5frvffeU2dnp6LRqH7zm9+opqYmm8MEAAAAAOSIrK/s3n///Xr11Vc1MDCgG264Qdu3b1dHR4f++Mc/yjAMVVVV6frrr5c0vk/3+9//vnbt2iWXy6UvfOELuuuuuxSPx7Vp06YZQzEAAMg/He1teuXZJhUODWqs1KfzL6/TqrXrrB4WAMBCWQ+7t9xyy7THNm/ePOPnBgIB7dq1K/nxhRdeOOP5uwAAIH91tLfp/T2Nqq+ukOHxyDRjOrCnUZIIvACQx2xRxgwAAHC6jjQ3aWN1hQzDkCQZhqGN1RU60txk8cgAAFYi7AIAgJzmjgwmg26CYRhyR8IWjQgAYAeEXQAAkNOiHp9M00x5zDRNRT1ei0YEALADwi4AAMhpq7fW6UBnbzLwmqapA529Wr21zuKRAQCsZItzdgEAAE5XognVk81NckfCinq8Wl3fQHMqAMhzhF0AAJDzVq1dR7gFAKSgjBkAAAAA4DiEXQAAAACA4xB2AQAAAACOQ9gFAAAAADgOYRcAAAAA4DiEXQAAAACA4xB2AQAAAACOwzm7AADgtHW0t+mVZ5tUODSosVKfPrb9Wi364DKrhwUAACu7AADg9HS0t+n9PY2qL43pqkqP6ktjevPHP1BHe5vVQwMAgLALAABOz5HmJm2srpBhGJIkwzB0yfwKHWlusnhkAAAQdgEAwGlyRwaTQTfBMAy5I2GLRgQAwATCLgAAOC1Rj0+maaY8Zpqmoh6vRSMCAGACYRcAAJyW1VvrdKCzNxl4TdPUc3/p1eqtdRaPDAAAujEDAIBZTO22fP7ldVq1dp0kJf//ZHOT3JGwoh6vNvzt9XRjBgDYAmEXAADMKNltubpChscj04zpwJ5GSUoJvIlfS1IwGFRXV5cl43WS2W4yAABODmXMAABgRjN1W95YTbflTJvpSKf39zRypBMAnCLCLgAAmBHdlq3BTQYAmBuEXQAAMCO6LVuDmwwAMDcIuwAAYEYzdVs+0Em35UzjJgMAzA3CLgAAmNGqteu0oL5BTw679HT3kJ4cdmlBfQONkjKMmwwAMDfoxgwAANKa2m0ZmTfTkU6ruckAAKeMsAsAAGAz3GQAgDNHGTMAAAAAwHEIuwAAAAAAxyHsAgAAAAAch7ALAAAAAHAcGlQBAAAg4zra2/TKs00qHBrUWKlP519eRxMuABlF2AUAAEBGdbS36f09jaqvrpDh8cg0Yzqwp1GSCLwAMoYyZgAAAGTUkeYmbayukGEYkiTDMLSxukJHmpssHhkAJyPsAgAAIKPckcFk0E0wDEPuSNiiEQHIB4RdAAAAZFTU45NpmimPmaapqMdr0YgA5APCLgAAADJq9dY6HejsTQZe0zR1oLNXq7fWWTwyAE5GgyoAAABkVKIJ1ZPNTXJHwop6vFpd30BzKgAZRdgFAABAxq1au45wCyCrKGMGAAAAADgOYRcAAAAA4DiUMQMAAMyxjvY2vfJskwqHBjVW6tP5l9dRwgsAWUbYBQAAmEMd7W16f0+j6qsrZHg8Ms2YDuxplCQCb47jJgaQWwi7AAAAc+hIc5Ourq6QYRiSJMMwtLG6Qk82NxGMZpArAZKbGEDuYc8uAADAHHJHBpNBN8EwDLkjYYtGZF/JAFka01WVHtWXxvT+nkZ1tLdZPbRpjjQ3aeMMNzGONDdZPDIA6WR1Zffhhx/WoUOHVF5ervvuu0+S1NjYqJdffllut1vz58/XjTfeKK/XO+3am266SSUlJSooKJDL5dLu3buzOXQAAICTEvX4ZJqxlMBrmqainunvb/JdLq2CuyODMko9KY9xEwOwt6yG3UsuuUTbtm3TQw89lHxszZo12rFjh1wul5544gk99dRTuu6662a8/o477lBZWVm2hgsAAHDKVm+t04E9jclVQNM0daCzV6vrG6wemu3kUoDkJgaQe7Iads877zx1dnamPHbBBRckf33uuefqxRdfzOaQAACAA1m5DzTxdZ5sbpI7ElbU49Xq+gbbrVTaQS4FSG5iALnHVg2q9u3bp4svvjjt7991112SpMsuu0xbtmzJ1rAAAEAOsUMjoVVr1xFuT0IuBUhuYgC5xzBN08zmF+zs7NQ999yT3LOb8POf/1xvvvmmvvSlL01r6iBJoVBIgUBAfX19+uY3v6nPf/7zOu+882b8Gnv37tXevXslSbt379bo6OjcPxEHcLvdikajVg8DUzAv9sS82BPzYj92mJPHbt+lTxWNTVstfGq0UH/3jbstHJl17DAv6fxH60s6+MxTcoUHFfP6VPPJT+mC9RdZPayssPO85CvmxJ5mm5eioqL012VqQKfiueee08svv6zbb799xqArSYFAQJJUXl6u9evX64033kgbdrds2ZKy8tvV1TX3g3aAYDDIa2NDzIs9MS/2xLzYjx3mJBrq0lilZ4bH+y0fm1XsMC/pLPrgMi26+b+nPGbXsc41O89LvmJO7Gm2eVm4cGHa6ywPu+3t7frFL36hr3/96youLp7xc4aHh2WapkpLSzU8PKzDhw+rvr4+yyMFAAC54D8HI/rp679TkRnTWIFL5y9dohULqmy5DxQAkDlZDbv333+/Xn31VQ0MDOiGG27Q9u3b9dRTTykajerOO++UJJ1zzjm6/vrrFQqF9P3vf1+7du1SX1+fvvOd70iSYrGYNmzYoLVr12Zz6AAAIAd0tLfp/xsN6yPlxQqWFEmmqf3vvK1DoQF96IZ/tHp4AIAsymrYveWWW6Y9tnnz5hk/NxAIaNeuXZKk+fPn6957783k0AAAgAMcaW7S1WcvVXigX+8d61RBLK6/qizXG8V+GgkBQJ6xvIwZAJA5Vh6/AlghcW6rr6xcvrLy5OPV3UMWjgoAYAXCLgA4lB2OXwGyLZfObQUAZBZhFwAc6khzk64+fnalJBmGoY3VFXqyuYmwC8c6k3NbqYQAAGch7AKAQyXKOSczDEPuSNiiEQGZlwinTzY3yR0JK+rxanV9wwlDK5UQAOA8hF0AcCjKOZGvVq1dd8oBlUoIAHCeAqsHAADIjNVb63Sgs1emaUrSRDnn1jqLRwbYjzsymHJjSKISAgByHSu7AOBQp1vOCeQjKiEAwHkIuwDgYKdTzgnkozNpbAUAsCfCLgAAGUSH39xAJQQAOA9hFwCADKHDb26hEgIAnIUGVQAAZMiR5qZkWaw00eH3SHOTxSMDAMD5CLsAAGQIHX4BALAOZcwAAGQIHX7hZLPtR2evOgA7IOwCAHLe1DfWvg8u1+Bbb1r+RpsOv3Cq2fajS2KvOgBbIOwCAHLa1Dfdr773nl7d84K2rTlP8yorLH2jTYdfONWR5iZdPcN+9CeP70dP93t87wPIJsIuACCnTX3T3fHOf+rqRZV6v+uY5pVXWP5Gmw6/cCJ3ZFBGqSflsYn96OYsvwcA2UODKgBATpvaBModj6nAMFQQiyUf4402MLfG96ObKY8l9qPP9nsAkE2EXQBATpv6xjpa4FLcNBV3uZKP8UYbmFurt9bpQGdv8mcvuR99a92svwcA2UQZMwAgKzLVnXVqE6hVSxfr52+8qcvXnCdJNIUCMuBk9qOzVx2A1Qi7AICMm61z65m+AZ72prviA/LWb9Czf3xT7m7eaAOZMtt+dPaqA7ADwi4AIONm69w6F2+IeWMNAACmYs8uACDjpjaRkmgaBQAAMouwCwDIOLqzAgCAbCPsAgAyju6sAAAg29izCwDIuJPp3ApkS6Y6gwMA7IWwCwDIilxoIkUIyhy7vLYn6gxul3ECAM4cYRcAAGX2eKR8Z6fXdrbO4JJsM04AwJljzy4AABoPQRtnCEFHjocgnD47vbazdQa30zgBAGeOsAsAgDgeKZPs9NrO1hncTuMEAJw5wi4AAOJ4pEyy02s7W2dwO40TAHDmCLsAAIjjkTLJTq/tqrXrtKC+QU8Ou/R095CeHHZpwfHO4HYaJwDgzNGgCgAA5ebxSLnSOdhur226zuB2GycA4MwQdgEAOC4XjkdKsFOH45ORK69ttseZKzcsACAXUcYMAEAOonNw7kvesCiN6apKj+pLY3p/T6M62tusHhoAOAJhFwCAHETn4NzHDQsAyCzKmAEAc4qyzOwY7xwcSwm8dA7OLe7IoIxST8pj3LAAgLnDyi4AYM5Qlpk9dA7OfRx1BACZRdgFAMwZyjKzZ7YjdJAbuGEBAJlFGTMAYM5QlpldVnc4nqlkfeOWyywbT67hqCMAyCzCLgBgzrCPNH+kO/roP8rLteiDy6weXs6w+oYFADgZYRcAMGdWb63TgT2NyVLmZFlmfYPVQ8uKbDbnsroR2JHmJl09Q8n6L595Sotu/u9ZGwcAAOkQdgEAcyafyzLTrXRKmvPnn82vlU66knXX4GBWvj6QbVbfYAJw6gi7AIA5la9lmelWOp9sbprz1yObXyuddCXrMa8vK18fyCY73GACcOroxgwAwBxwRwZTgp+UueZc2fxa6aTrJFzzyU9lbQxAttBpHshNrOwCADAHstmcyw6NwNKVrF+w/iJ1dXVlbRxANtBpHshNhF0AAOZANptz2aURWL6WrCP/2OEGE4BTR9gFAGAOZLM5Vz43AgOsYJcbTABOTdbD7sMPP6xDhw6pvLxc9913nyRpcHBQ3/3ud3Xs2DFVVVXpn/7pn+TzTW9w8dxzz+nnP/+5JOnTn/60LrnkkmwOHQCAWWVzpZNVVSB7uMEE5Kash91LLrlE27Zt00MPPZR87Omnn9b555+vq666Sk8//bSefvppXXfddSnXDQ4Oas+ePdq9e7ckaefOnaqpqZkxFAMAAABziRtMQO7Jejfm8847b1pAbW1t1caNGyVJGzduVGtr67Tr2tvbtWbNGvl8Pvl8Pq1Zs0bt7e3ZGDIAAAAAIMfYYs9uX1+f/H6/JKmiokJ9fX3TPicUCqmysjL5cSAQUCgUmvHP27t3r/bu3StJ2r17t4LBYAZGnfvcbjevjQ0xL/bEvNgT82I/TpqT/2h9Sa3PPCV3eEBR7zyt/+SndMH6i6we1mlx0rw4CfNiP8yJPZ3uvNgi7E5mGMa0swNP1ZYtW7Rly5bkxxyBMLNgMMhrY0PMiz0xL/bEvNiPU+ako71N7+9p1CeqK2T4XDLNsA489qB6+3Jzn6ZT5sVpmBf7YU7sabZ5WbhwYdrrsl7GPJPy8nL19PRIknp6elRWVjbtcwKBgLq7u5Mfh0IhBQKBrI0RAADkjyPNTcnOu9L4zfiN1RU60txk8cgAACfLFiu7NTU1OnDggK666iodOHBA69evn/Y5a9eu1b/+679qcHBQkvQf//Ef2rFjR7aHCgAAsqCjvU2vPNukwqFBjZX6dP7ldVldUXVHBmWUelIeMwxD7kg4a2MAAJyZrIfd+++/X6+++qoGBgZ0ww03aPv27brqqqv03e9+V/v27UsePSRJb775pn71q1/phhtukM/n09VXX61du3ZJkurr6+nEDACAAyVKiOurK2R4PDLNmA7saZSkrAXeqMcn04ylbK0yTVNRjzcrXx8AcOayHnZvueWWGR+//fbbpz22fPlyLV++PPnx5s2btXnz5kwNDQAA2MCR5iZdPUMJ8ZPNTVkLu6u31unAnsZkKbNpmjrQ2avV9Q1Z+foAgDNnizJmAACABDuUECdC9ZPNTXJHwop6vFpdn5vNqTJhrsvMrS5bBzBhMDKqY6GwOrvDOtYz/vfuJy75K4tHdXoIuwAwR3izBsyNkykhzsbP26q166b9mfycz32ZuR3K1oF8Eo+bCvUN6VgoPB5qE8H2+MeR4bGUzy/zFRN2ASCf8WYNmDsnKiG26ueNn/Nxc11mboeydcBpRkaj6uqJqDMU1rHu8UCbCLbdPRFFY/G01xYXuVQV8Ko64B3/f6VPpmme8fGwViDsAsAc4M0aMHdOVEJs1c8bP+fj5rrM3A5l60CuMU1TA+HRZIA9drzkuPN4sO0bGJ71+vJ5xarye1VVOR5qqwPjv67ye1XmK87JYDsTwi4AzAHerAFza6YS4gSrft74OR83152q6XwNzCwWi6u7b2g8yIZSV2ePhcIaHommvdZVYKjS75m0OutNWa0tLsqPGJgfzxIAMow3a0D2WPXzxs/5uLnuVE3na+Sz4ZFoMrwem7J3trs3oljcTHttabE7uTJbFZgIs9WVXvnLSuVyFWTxmdgTYRcA5gBv1oDsycTP28k0nuLnfNxcdaqe/Jr/ZSSuI+90a7HPS+drOIppmuofHJnWBCpRetwfHpn1en9ZSUqQnRxufZ4ix5QbZwphFwDmAMeUANkz1z9vJ9t4ip/zCbOVmZ+Maa95oFQHOnu14Kq/ycvXE7ktGo2ruzcyEWh7UptCjY7F0l7rdhUo6Peklhkf3ztbFfCqqNCVxWfiPIRdAJgjZ/rmD8DJm8uft1NpPMXP+dyg2RdyTWR4LGXv7OSmUN29EZnpq43lLS1MDbKBiaZQFWWlKihgdTZTCLsAACCv0Xgq+3jNYTfxuKnegWG9H3pPr7/1bsrK7LFQWIOR0bTXGoZUWVGaWm48qSmUt7Qoi88EkxF2AQBAXqPxVPbxmsMKY9GYukKRiZXZSU2hunrCGoumP3u20F0w477ZqoBXQb9HhW7Kje2IsAsAFjiZZjiwB+bK+Wg8lX285siUwcjoRFfjnommUJ2hsHr7h2YtN/Z5irRwfoUCZUXTmkKV+0ooN85BhF0AyLKTbYYD6zFXJ2fyDQFXIKhzPr45p14fGk9lH685Tlc8birUN5TS1XhyU6jI8FjaawsKDFVWlI6XF/unnz1bWlKoYDCorq6uLD4jZBJhFwCyjMYsuYO5OrGpNwQKC8f0qxy8IUDjqezjNUc6o2OxlON5OicF2+6eiKKx9OXGxUWu1DNnJzWFqqzwyM3Zs3mFsAsAWUZjltzBXJ0YNwQAnCrTNDUQHp0ItJP2znaGwuobGJ71+jJf8bS9s4n/l/mKOXsWSYRdAMgyGrPkDubqxLghAGAmsVhc3X1DKcf1TP7/8Eg07bWuAkOVfk9KE6jqScG2uIgIg5PDdwoAZBmNWXIHc3Vi3BAA8tfwSDQ1yE7aO9vdG1Esnr4bVGmxe7y8eMre2epKr/xlpXJRbow5QNgFgCyjMUvuYK5OjBsCgHOZpqn+wZGJJlCTV2e7w+oPj8x6vb+sZFpX48SvfZ4iyo2RcYRdALAAjVlyB3M1u6k3BNwBj87mhgCQM6LRuLp7I6llxpOaQo2OxdJe63YVKOj3JFdmJ++drQp4VVTI2bOwFmEXAACckck3BObi2A7ONgbmVmR4bHxV9niIndwUqrs3MuvZs97SwtQQWznR5biirJSzZ2FrhF0AAGAbnG0MnLp43FTfwPBEkJ3SFGowMpr2WsOQKitKVeWf0t34+Gqtt7Qoi88EmFuEXQAAYBscZQTMbCwaU1coMq2rcWd3WF09YY1F0589W+guSNk3O7nUOOj3qNBNuTGcibALAABsg6OMkM8GI6MpTaAmN4Xq6R+atdzY5ylKHs8TDEyUGldVelXuK6HcGHmJsAsAAGyDo4zgZPG4qZ7+oWSIHRj6g975c1ey9DgyPJb2WsPQRDOoKcf1VAW8Ki0pzOIzAXIDYRcAANgGRxkh142OxVK6GidXaUNhdfdEFI2lLzcuLnKldDWe3BSqssIjN2fPAqeEsAsAAGyDs41hd6ZpaiCcWm6c2Dt7rCes3v7hWa8v8xUny4vPWlwlb4mRDLVlvmLOngXmEGEXAADYCmcbw2qxWFyhvqFpZ84mwu3wSDTtta4CQ5V+T0oTqOpJTaGKiybefs/FUV2YO22HO7Tv4BF1hUfkc8VVt2G91q1ZZfWwcAYIuwAAAMg7wyPRlJXZyaXH3b0RxeLpu0GVFLunHdGTKD0OlJfKRblxzmk73KHGlqOav2ajvGNjipumGltaJYnAm8MIuwAAAHAc0zTVPzgyratxItD2h0dmvb6irGQi0E7aO1sd8MrnKaLc2GGaWg7Kv2JTyrFn/hXr1dSyn7Cbwwi7AAAAJ6HtcIeaXmjVYKyAEkebiEbj6u6NpDSBOnZ87+yxUFgjo7G017pdBSndjaeeP1tUyNmz+WQwasg75QaGYRgKR7mpkcsIuwAAACeQKHH0r9wsr2FQ4phFQ8NjKXtnJ5cdd/dGZj171ltamFJiPDnQ+stKOXsWST63qfiUbybTNOV1z/INBtsj7AIAAJwAJY6ZE4+b6hsYTg2yk5pCDUZG015rGFKgvHRakE3spfWWFmXxmSCX1dXWqLGlVfPX1EoaD7o9R1vVUFtj8chwJgi7AAAAJ0CJ45kZi8bUFYroWM/4/tnJx/V09YQ1Fk1/9myhuyBlZbbKP9EUKuj3qNBNuTHOXOKm1b6XD6hvcERet6mG2hpuZuU4wi4AAMAJJEocJzclosQxVXhoNNkIKtEUquv4r3v6h2YtN/Z5iqbtnU2s0pbPK6HcGFmxbs0qXbZ5I8dBOQhhFwCAHNDR3qZXnm1S4dCgxkp9Ov/yOs6izaJEiaN/xXoZhpGXJY7xuKme/qFpnY0T+2kjw2NprzUMKej3JFdopx7XU1pSmMVnAiBfEHYBALC5jvY2vb+nUfXVFTI8HplmTAf2NEoSgTdLEqWMTS37FY4aji1xHB2LTTuiJxFou3siisbSlxsXFbqSIbZ6SlOoygqP3Jw9CyDLCLsAANjckeYmXV1dkdIcaWN1hZ5sbiLsZtG6NatyPtyapqmB8Oj40TzdqZ2NO0Nh9fYPz3p9ma942t7ZRLAt8xVz9iwAWyHsAgBgc+7IoIxST8pjhmHIHQlbNCLYWSwWV6hvKGVltj8c1X++F1JnKKzhkWjaa10FhionlRsnuhpX+cd/XVLMW0cAuYO/sQAAsLmoxyfTjE1rjhT1eC0cFaw0PBKdKDWeUnbc3RtRLJ6+G1RJsTs1yE4qOQ6Ul8pFuTEAhyDsAgBgc6u31unAnkZtPF7KbJqmDnT2anV9g9VDQ4aYpqn+wZGUzsaTw23/4Mis11eUlaScObv8/1ugkqK4qgNe+TxFlBsDyAuEXQAAbC6xL/fJ5ia5I2FFPV6trm9gv26Oi8bi6u6NpDSBOjbpv5HRWNpr3a4CBf2eacf1JM6eLS5KfYsXDAY5TgVA3iHsAgCQA1atXUe4zUFDw2PJ8uJjPeMrtIlQ290bmfXsWW9poYKBSWfOTmoK5S8r5ezZLGg73KGmF1o1GCuQzxVX3Yb1Od+kDMgnhF0AAIDTFI+b6hsYTgbYyU2hjoXCGoyMpr3WMKRAeWkyyE4uO66u9MpbWpTFZ4Kp2g53qLHlqPwrN8trGIqbphpbWiWJwAvkCMIuAADALMaiMXX1RMbDbPf0cuOxaPqzZwvdBcnmT8lV2sqJcuNCtyuLzwSnoqnloPwrNqUc+eVfsV5NLfsJu0COIOwCAIC8Fx4andYEKrFC29M/NGu5sc9TNHFUz6QV2uqAV+XzSig3zlGDUUPeKY28DMNQOMp8ArmCsAsAABwvHjfV0z80Hmh7wqlNobrDigyPpb3WMKTgpLNnJzeFqgp45SkpzOIzOXUd7W16/fl9ioW6NFbq0/mX17H/+yT43KbipjntyC+ve5Y7HwBsxRZh991339V3v/vd5MednZ3avn27rrjiiuRjHR0d+va3v63q6mpJ0oc//GHV19dnfawAAMCeRsdi086cTazSdvVEFI2lLzcuKnRNO3M2sVJbWe6R252bZ892tLfp/T2N+vTiao1VemSaMR3Y0yhJBN4TqKutUWNLq/wr1ieP/Oo52qqG2hqrhwbgJNki7C5cuFD33nuvJCkej+sf/uEfdNFFF037vJUrV2rnzp3ZHh4AALAB0zQ1GBmdFmQT4ba3f3jW68t8xdOaQCU+LvMVO/Ls2SPNTbr6+PnM0ngZ7sbqCj3Z3ETYPYHEvtymlv0KRw153aYaamvYrwvkEFuE3cleeeUVLViwQFVVVVYPBQAAZFksFleob2jacT2JUDs0Ek17ravAUGWFZ3pn4+P/Lym23duejHNHBmWUelIeMwxD7kjYohHllnVrVhFugRxmu7/1W1paVFtbO+Pv/f73v9ett94qv9+vhoYGLVmyZMbP27t3r/bu3StJ2r17t4LBYMbGm8vcbjevjQ0xL/bEvNgT82I/JzMnQ8Njer+rX385NqD3jvXr/eP/vXdsQMe6BxSLp98TWVpSqAVVZfpAVZkWVM3TgmCZFlSVaUH1PFX5fXK5crPcOFPcgaAKC8dUYBgqKho/ysg0TbkDHn52bIC/w+yHObGn050XwzRn6y+YXdFoVP/wD/+g++67TxUVFSm/F4lEVFBQoJKSEh06dEg//OEP9cADD5zUn/vuu+9mYLS5LxgMqqury+phYArmxZ6YF3tiXuwnGAzq2LFj6h8cSZYXT16Z7QyF1T84MuufUVFWMn1l9nhTqHneIkeWG2dKYs/uZYurNTY2JtM0daCzVwvqGyhjtgH+DrMf5sSeZpuXhQsXpr3OViu7bW1t+uAHPzgt6EqSxzNRgnPhhRfqscceU39/v8rKyrI4QgAAIEnRWFzdvZGUvbOdobBCfSN6/1ifRkZjaa91uwpSuhtPLjsO+j0qLrLV25Oclgi0Tz2/T9FQv6Ier1YTdAHkCVv9azJbCXNvb6/Ky8tlGIbeeOMNxeNxzZs3L8sjBAAgfwwNj6U2gZoUbLt7I7OePespKUyG2KlNofxlpZw9m0Wr1q7Txi2XsVoFIO/YJuwODw/r8OHDuv7665OPNTc3S5K2bt2qF198Uc3NzXK5XCoqKtItt9xCGRMAAGcgHjfVNzA8UW48pSnUYGQ07bWGIQXKSydKjI+H2nOWLVKRa0ze0qIsPhMAAKazTdgtKSnRP//zP6c8tnXr1uSvt23bpm3btmV7WACAKTra2/TKs00qHBrUWKlP519eR0mkjY1FY+rqiSRXZo/1pB7bMxZNf/ZsobsguSKbPHv2+N7ZoN+jwkLXtGvY7wYAsAvbhF0AgP0lmt3UV1fI8HhkmjEd2NMoSQReC4WHRqc1gUoE2p7+oVnLjX2eohn3zlYHvCqfV0K5MQAgZxF2AQAn7Uhzk66urkhuIzEMQxurK/RkcxNhN4PicVM9/UPTgmxnKKyuUFjhobG01xqGUptBTe5uHPDKU1KYxWdivbbDHWp6oVWDsQL5XHHVbVjPOaoA4FCEXQDASXNHBmWUelIeMwxD7kjYohE5x+hYbNrKbGLvbFdPRNFY+nLjokLXeHnx5HLj44G2stwjt5uzZ6XxoNvYclT+lZvlNQzFTVONLa2SROAFAAci7AIATlrU45NpxlIaBJqmqajHa+GocoNpmhqMjE4E2VDqkT29/cOzXl/mK05dnZ3UFKrMV0zTxpPQ1HJQ/hWbUioT/CvWq6llP2EXAByIsAsAOGmrt9bpwJ5GbTxeymyapg509mp1fYPVQ7OFWCyuUN/QtON6Er8eGommvdZVYKiywpOyb3ZyuC0p5p/sMzUYNeSdclPAMAyFo/a+UUDpNQCcHv7lBJBxvFFzjsS+3Cebm+SOhBX1eLW6viGv9uuOjEYnjuqZ0hSquyeiWDx9N6iSYvf0IHs83AbKS+VyUW6cST63qbhpTqtM8Lpn6eBlMUqvAeD0EXYBZBRv1Jxn1dp1jg63pmmqf3AkNdBOOq6nf3Bk1usrykpU5U8tM06E23neorwvN7by5lddbY0aW1rlX7E+WZnQc7RVDbU1Wfn6p4PSawA4fYRdABnFGzXYUTQWV3dvJGXv7OTS45HRWNprXS5DQX9qE6hEqA36PSou4p/WdKy++ZX4Gk0t+xWOGvK6TTXU1tj676JcLb0GADvgX2QAGcUbNVhlaHhs2t7ZxMehviHFZyk39pQUTjtzNtEUyl9Wytmzp8kON7/WrVll63A7VS6WXgOAXRB2AWQUb9SQKfG4qe7esH7/VlfKmbOJ0uPByGjaaw1DCpSXTuydndIUyucpyuIzyR/c/Dp1uVh6DQB2QdgFkFG8UcOZGIvG1NUTmehqPGnv7LFQWGPR9GfPut0FM+6dTZQbFxa6svhMIHHz63TkYuk1ANgFYRdARvFGDScSHhqd1tU4EWh7+odkzpKD5nmLFfR7pu2drQ54VT6vhHJjm+Hm1+nJtdJrALALwi6AjOONWn6Lx0319g9NNIHqTm0GFR4aS3utYUhBvyflqJ7JwXbp4g+oq6srI+PuaG/TK882qXBoUGOlPp1/eZ2ju1BnAze/AADZRNgFAJyx0bFY6srspKZQXT0RRWPpy42LCl3TzpxNlBxXVnjkdmf/7NmO9ja9v6dR9dUVMjwemWZMB/Y0ShKB9wxx8wsAkC2EXQDACZmmqcHI6ESQnbI629M/POv1Zd7ilO7Gk5tClfmKbXf27JHmJl1dXZHSNXhjdYWebG4i7AJAGlaeow3MhLALAJAkxWJxhfqGUlZnJzeFGhqJpr3WVWCossIzPdAe/39JcW79c+OODMoo9aQ8ZhiG3JGwRSMCAHuz+hxtYCa59e4DAHBGRkajyTA7tSlUd09EsVnOni0pdk8Pssf3zlaWl8rlyn65caZEPT6ZZmxa1+Cox2vhqADAvuxwjjYwFWEXABzENE31D46krs5OKjvuHxyZ9fryeSXje2anHNdTFfBqnrfIduXGmbJ6a50O7GnUxuOlzKZp6kBnr1bXN1g9NACwJc7Rhh0RdgEgx0RjcXX3RlL2zk7ePzsyGkt7rctlKOhPbQKVKD0O+j0qLuKfBWmiCdWTzU1yR8KKerxaXd/Afl0ASINztGFHvKsBABsaGh6bce9sZ3dYob4hxWcpN/aUFI6XF/snmkAlGkL5y0o5e/YkrVq7jnALACeJc7RhR4RdALCAaZrqHRie1tU4sZd2MDKa9lrDkALlpdO6Gic+9nmKsvhMAADgHG3YE2EXADJkLBpTV08k9fzZ4+G2qyei0bH05cZud0FyZXby3tlEuXFhoSuLzwRIb+pRI9d+YouWLV1s9bAAWIBztGE3hF0AOAPhodGJMuMpe2dDfUMyZ9mq5PMUpTaBqpzYS1s+r4RyY9jeTEeN/KC5TZ+5qI83vDbFOagA8glhFwBmEY+b6u0f0nvd7+r1t97VsSmhNjw0lvZaw5CCfo+q/KlBNhFsPSWFWXseHe1teuXZJhUODWqs1KfzL69jPyrO2IxHjaxcr6aWZwlQNsQ5qADyDWEXQN4bHYslV2OnNoXq6okoGounvbao0JVy5uzkcuPKCo/cbuvPnu1ob9P7expVX10hw+ORacZ0YE+jJBF4cUY4aiS3cA4qgHxD2AXgeKZpajAyOlFiPKUpVE//8KzXl3mLtXB+ufxlxdOaQpX5im1/9uyR5iZdffy8WGn8De7G6go92dxE2MUZ4aiR3MLNCQD5hrALwBFisbh6+ofUOUN342PdYQ2NRNNeW1BgKFjhSQmyyWZQAY9KiwsVDAbV1dWVxWc0d9yRQRmlnpTHDMOQOxK2aERwihmPGvldqz6TgaNG2Gt65rg5ASDfEHYB5IyR0WjK8TyTA213T0SxWc6eLS5yp545O2nvbGV5qVwu68uNMyXq8ck0Y9Pe4EY9XgtHBSeY6aiR66+4dM67MbPXdG5wDiqAfHNSYTcej6u1tVWGYaimpkYFBeNvCn/729/qox/9aEYHCCB/mKap/sGR1DNnj6/MHusJq29gZNbry+eVjDeBqvSmNIWqCng1z1tk+3LjTFm9tU4H9jRq4/FSZtM0daCzV6vrG6weGhxg6lEjmaiCYK/p3OAcVAD55qTC7oMPPqhgMCi3261nnnlGN910kxYsWKDm5mbCLoBTEo3FFeqNpJw5O1F2HNHIaPpyY5fLUNA/ZXW2cuLs2eIiilVmktiX+2Rzk9yRsKIer1bXN7BfFzmDvaZzh3NQAeSTk3pnGAqFdPPNN0uSNm3apAcffFB/8zd/k9GBAchdQyNj05pAJUqPQ31Dis9SblxaUjgRZietzFYFvAqUl3L27GlatXYd4dZC7Dc9M+w1PTNthzu07+ARdYVH+P4DkFdOKuxGo1GNjY2psLBQVVVV2rlzp+6//3698847mR4fABsyTVO9A8PJ8uLOKWfPDoRH015rGJK/vDQl0Fb5J5pC+TxFWXwmQOax3/TMsdf09CW+/+av2Sjv2BjffwDyyqxhNxaLyeVy6XOf+5zC4bAqKiokSaWlpbrtttv0wgsvZGOMACwwFo2pqycyravxsVBYx3oiGh2Lpb3W7S6YCLCT9s4myo0LC11ZfCaAtdhveubYa3r6+P4DkM9mDbvf+ta3dOutt+rss8+e9nsFBQX6+Mc/nrGBAci8yNDojJ2Nj4XGy43NWSoEfZ6iiaN6AqnNoCrmlVBuDBzHftO5wV7T08P3H4B8NmvYPeuss/TVr35Vu3btUiAQkCS9+uqr+slPfqJvfOMbWRkggNMXj5vq7R9KbQI1aS9teGgs7bWGIVVWeFKC7OTjejwlhVl8JkDuYr8prJT4/puM7z8A+WLWsNvQ0KDm5mZ99atf1Y4dO7Rv3z698847uvLKK7M1PgAnMDoWO15aHJ7WFOpYT0TRaDzttUWFrpSV2UTpcXXAq8oKj9xu5549C2QL+01hpcT33/w1tZLE9x+AvHLCBlXnnnuuPB6PHnjgAW3cuFG33XabiopoIANki2maCg+NqrM7nHJcTyLQ9vQPz3p9mbd4PMhOWplNBNoyX3Henj0LZAv7TWGlxPfZvpcPqG9whO+/E6BzOuAss4bde++9V6+++qquuOIKbd++XY8++qiOHDmiCy+8MFvjA/JCPG4q1BdRZ3dYkVeP6a13/pLSFGpoJP3ZswUFhoIVnon9s5UTR/VUBTwqLabcGLAa+01hpXVrVumyzRvV1dVl9VBsjc7pgPPMGnY/8IEP6L/+1/8qn88nSZo/f77uuecedXZ2atu2bVkZIOAUI6PRlAZQk4/r6e6NKBZLv3+quMg97czZROlxZXmpXC7KjQEAOBN0rgacZ9awe91116V8vHTpUt155526++67CbvAFKZpqn9wJGXv7ORy476BkVmvL59XouqAV4sXBlTucad0N57nLaLcGACADKJzNeA8J9yzO1UgEKATM/JWNBZXqDcybe/s+P8jGhlNX27schkK+idWZSc3haoKeFRcNP7jGAwGKTUDACDL6JwOOM8ph11JKi0tnetxALYxNDI2rQlU4izaUN+Q4vH0/+iVlhSmNIGqCnhUHfCpKuBVoLyUs2cBALApOqcDznNaYRfIZaZpqndgWMe6x4/rmbx39lgorIHw6KzX+8tLp+2dTTSF8pYWUm4MAEAOonM64DyEXTjSWDSm7t7ItCA7HnAjGh2Lpb3W7S5IlhZXB3zJvbPVAa+Cfo8KC11ZfCYAACBb6JwOOAthFzkrMjSaLC8+FkoNtaG+IZmzbLHxeYqmdTWu9o//v2JeCeXGAAAAQI4j7MK24nFTvf1DqU2gJu2lDQ+Npb3WMKTKCs9EE6jjq7TVx8+e9ZQWZfGZAAAAAMg2W4Xdm266SSUlJSooKJDL5dLu3btTft80TT3++ONqa2tTcXGxbrzxRi1btsyi0WIujI3FxvfNTgmyx0Lj5cbRaDzttUWFromV2YBHVQFf8izaygqP3G7OngUAwCnaDneo6YVWDcYK5HPFVbdhvaNKjp3+/AAr2CrsStIdd9yhsrKyGX+vra1N77//vh544AG9/vrrevTRR/Wtb30ryyPEqTBNU+GhUXV2TwTayU2hevqHZ72+zFs8HmQrfZOaQo2v0pbPK6YZFAAAWWRVIGs73KHGlqPyr9wsr2EobppqbGmVJEcEQqc/P8Aqtgu7szl48KA+/vGPyzAMnXvuuQqHw+rp6ZHf77d6aHktHjcV6jveDGpad+OIhobTlxsXFBgT5caJrsb+8XBbFfCotLgwi88EAACkY2Uga2o5KP+KTcmb3IZhyL9ivZpa9jsiDDr9+QFWsV3YveuuuyRJl112mbZs2ZLye6FQSMFgMPlxZWWlQqHQtLC7d+9e7d27V5K0e/fulGswwe12n/RrMzwypr90Dei9Y/16/1i/3j82/uu/HOtXZ/egorH05calxYVaUDVPC6rKjv83/usPVJWpKuCTy0W58WSnMi/IHubFnpgX+2FO7Gku5mXfy0c0f83GlKqq+Wtqte/lA7ps88YzHeKsxlwl8hQXT3t8yFWS099viXlx6vPLRfwdZk+nOy+2Crt33nmnAoGA+vr69M1vflMLFy7Ueeedd8p/zpYtW1KCcldX11wO0zGCwWDytTFNUwPhUXWGBlP2zib+3zcwMuufVT6vJLl3dvJxPVUBr+Z5i9KUG4+qpyeUgWeW2ybPC+yDebEn5sV+mBN7mot56RockXdserVW3+BIxue8MDaskZGRlPcTpmnKHRvO6e+3xLw49fnlIv4Os6fZ5mXhwoVpr7NV2A0EApKk8vJyrV+/Xm+88UZK2A0EAilPsru7O3kNTiwaiyvUG0nunR0cflNv/+exZLnxyGg07bUul6FgxcTe2clNoaoCHhUX2epbCQAAzDGf21TcNKcFMq97lrP+5khdbY0aW1rlX7FehmHINE31HG1VQ21Nxr92Njj9+QFWsU1CGR4elmmaKi0t1fDwsA4fPqz6+vqUz6mpqdG//du/qba2Vq+//ro8Hg/7dacYGhkbbwIVmro6G1F3b0TxePp/kEpLClP3ziZWaQNeBcpLOXsWAGyCrq2wgpWBLPH93dSyX+GoIa/bVENtjWO+753+/ACr2Cbs9vX16Tvf+Y4kKRaLacOGDVq7dq2am5slSVu3btW6det06NAh3XzzzSoqKtKNN95o5ZAtYZqm+gZGxsuNQxPNoBKhdiA8Ouv1/vLS5KrsWYur5S0xjgdbr7ylhXQ3BgCbo2srrGJ1IFu3ZpWjv8ed/vwAK9gm7M6fP1/33nvvtMe3bt2a/LVhGPr7v//7bA7LEtFoXF2904Ps+LE9EY2OxdJe63YXqMo/095Zj6r8XhUWupKfy54EADNh1dDe6NoKKxHIAOQS24TdfPSn9/r0ftfgtKZQob4hmbNsf/GWFqq6cry8eGpTqIp5JZQbAzhtrBra32DUkHdKFY5hGApH+bsfAIDJCLsW+tHTbfrDn3qmPW4YmnT2rOf46qwv+bGntMiC0QLIB6wa2p+VTYIAAMglhF0LrVhWpTJf8fEQ60s2hQpWeOV2c/YsgOxj1dD+6NoKAMDJIexaqP5yVkkA2AurhvZndZMgAAByBWEXAJDEqmFuoEkQAAAnRtgFACTlw6oh3aYBAMgPhF0AQAonrxrSbRoAgPxBFyQAQN4Y7za9foZu0wctHhkAAJhrhF0AQN4YjBopzbckuk0DAOBUhF0AQN7wuU2ZZmpnabpNAwDgTIRdAEDeqKutUc/R1mTgTXSbrqPbNAAAjkODKgBA3kg0ofrxL57UH471KTY2ouXVFZJWWDouAAAw9wi7AIC8YwSXqmbDxFnCdGQGAMB5KGMGAOQVOjIDAJAfWNkFAOSVwaghb452ZG473KGmF1o1GCuQzxVX3Yb1rEYDAJAGYRcAkFd8blNx00w5gigXOjK3He5QY8tR+VdultcwFKf8GgCAWVHGDADIK7nakZnyawAATg0ruwCAvBPvelsHnzqi+Oiwli3w63OfvsL2q6O5XH4NAIAVCLsAgLyRKAWu3FCv4PFOzD1HW60e1knJ1fJrAACsQhkzACBv5HIpcK6WXwMAYBVWdgEAeSOXS4ETZdZNLfsVjhryuk011NbYvvwaAACrEHYBAHkj10uB161ZRbgFAOAkUcYMAMgblAIDAJA/WNkFAOQNSoEBAMgfhF0AQF6hFNiZ2g53qOmFVg3GCuRzxVW3YT3zDAB5jrALAAByWuJIKf/KzfIahuKmqcaW8SOlCLwAkL/YswsAAHJaLh8pBQDIHMIuAADIaYNRI6XDtpQ7R0oBADKHsAsAAHKaz20mO2wn5NKRUgCAzGDPLgAANkOzpVNTV1ujxpbWZClz4kipBo6UAoC8RtgFAMBGaLZ06jhSCrli6o2saz+xRcuWLrZ6WIBjEXYBALCR8WZLm2ZotrSf8DYLjpSC3c10I+sHzW36zEV9fO8CGULYBQDARgajhrw0W4LNUFp/5ma8kbVyvZpanuW1BDKEsAsAgI343KbippnSXZhmS7ASpfVzgxtZQPbRjRkAABupq61Rz9HWZHfhRLOlOpotwSKcYzw36BoOZB8ruwAA2AjNlmA3rEjOjRm7hv+uVZ/hRhaQMYRdAABshmZLsBNK6+fGTDeyrr/iUroxAxlE2AUAAEBanGM8d6beyAoGg+rq6rJwRICzEXYBAIAkOu5iZpTWA8hVhF0AAEDHXcyK0noAuYhuzAAAgI67AADHIewCAAANRo2UBkQSHXcBALmNMmYAAHDKHXfZ3wsAsDvCLoC8wZtzIL1T6bg72/7eyzZvzPbQHYm/rwDgzBF2AeQFmu8AszuVjrvj+3s3zbC/dz9hdw7w9xUAzA3CLoC8MNubc948AuNOtuPuYNSQl/29J3S6q7P8fQUAc8MWYberq0sPPfSQent7ZRiGtmzZorq6upTP6ejo0Le//W1VV1dLkj784Q+rvr7eiuECyEG8OQfmzqnu781HZ7I6y99XADA3bBF2XS6XGhoatGzZMg0NDWnnzp1as2aNFi9enPJ5K1eu1M6dOy0aJYBcxptzYO6cyv7efHUmq7P8fQUAc8MWRw/5/X4tW7ZMklRaWqpFixYpFApZPCoATlJXW6Oeo60yzfE3i4k353W8OQdO2bo1q9RQu0IFR/cr8sp+FRzdr4baFZTYTnImRznx9xUAzA1brOxO1tnZqbfeektnn332tN/7/e9/r1tvvVV+v18NDQ1asmSJBSMEkItOpfkOgBM72f29+epMVmf5+woA5oZhJm4b2sDw8LDuuOMOffrTn9aHP/zhlN+LRCIqKChQSUmJDh06pB/+8Id64IEHZvxz9u7dq71790qSdu/erdHR0YyPPRe53W5Fo1Grh4EpmBd7Yl7siXmxH+Zk3EuH2vWD5jb5V04q9f5dq67fuk4XXbg26+NhXuyJebEf5sSeZpuXoqKitNfZJuxGo1Hdc889uuCCC/SJT3zihJ9/00036e6771ZZWdkJP/fdd9+diyE6TjAYVFdXl9XDwBTMiz0xL/bEvNgPczKh7XCHmloOJldn6yxcnWVe7Il5sR/mxJ5mm5eFCxemvc4WZcymaeqRRx7RokWL0gbd3t5elZeXyzAMvfHGG4rH45o3b16WRwoAAHByKPUGAGvZIuy+9tprev7557V06VLdeuutkqRrr702md63bt2qF198Uc3NzXK5XCoqKtItt9wyrfEDAAAAAACSTcLuihUr9LOf/WzWz9m2bZu2bduWpREBAADgTLUd7lDTC60ajBXI54qrbsN6VrsBZI0twi4AAACcpe1whxpbjsq/crO8hqG4aaqxpVWSCLwAssIW5+wCAADAWZpaDsq/Yn1y25lhGPKvWK+mloMWjwxAviDsAgAAYM4NRo1p/VUMw1A4Ss8VANlBGTMAAMBx7DGdOz63qbhppgRe0zTlddvi1EsAeYCVXQAAAE3sMY2v3Czv+ZsUX7lZjS1H1Xa4w+qh5aS62hr1HG2VaY6HW9M01XO0VXW1NRaPDEC+YGUXAABAiT2mm2bYY7qf1d3TkHjNmlr2Kxw15HWbaqit4bUEkDWEXQAAAI3vMfWyx3ROrVuzinALwDKUMQMAAGh8j2mi5DaBPaYAkLsIuwAAAGKPKQA4DWXMAABboAsurMYeUwBwFsIuAMByiS64/pWb5TUMxU1TjS2tkkTQQFaxxxQAnIMyZgCA5ca74K6foQvuQYtHBgAAchUruwAAy9EFFzh9bAEAgJkRdgEAlvO5TcVNM7myK9EFFzgZbAEAgPQoYwYAWI4uuMDpYQsAAKTHyi4AwHJ0wQVOD1sAACA9wi4AwBboggucOrYAAEB6lDEDAADkKLYAAEB6rOwCAADkKLYAAEB6hF0AAIAcxhYAAJgZYRcAgFPEuaYAANgfYRcAgFPAuaYAAOQGGlQBAHAKONcUAIDcQNgFAOAUDEaNlGNeJM41BQDAjgi7AACcAp/bTB7zksC5pgAA2A9hFwCAU8C5pgAA5AYaVAEAcAo413Tu0NUaAJBJhF0AAE4R55qeObpaAwAyjTJmAACQdXS1BgBkGmEXAABkHV2tAQCZRtgFAABZR1drAECmEXYBAEDW0dUaAJBpNKgCAABZR1drAECmEXYBAIAl6GoNAMgkypgBAAAAAI7Dyi4AAACmaTvcoaYXWjUYK5DPFVfdhvWsxAPIKYRdAMBJ4Y0vkD/aDneoseWo/Cs3y2sYipumGltaJYmfewA5g7ALADgh3vg6DzcvMJumloPyr9iUPAvZMAz5V6xXU8t+vk8A5AzCLgDghHjj6yzcvMCJDEYNeY//vCcYhqFw1EhzBQDYDw2qAAAnNBg1kkE3gTe+uWv85sX6GW5eHLR4ZLALn9tMnoGcYJqmvG4zzRUAYD+EXQDACfHG11m4eYETqautUc/R1uTPvWma6jnaqrraGotHBgAnjzJmAMAJ1dXWqLGlNbkamHjj28Ab35zkc5uKm2ZK4OXmBSZLlLM3texXOGrI6zbVUFtDmTuAnELYBQCcEG98nYWbFzgZ69as4mccQE4j7AIATgpvfJ2DmxcAgHxA2AXgWBytAqTHzQsAgNMRdgE4EkerAPbCzScAQLbZKuy2t7fr8ccfVzwe16WXXqqrrroq5ffHxsb04IMP6g9/+IPmzZunW265RdXV1dYMFoCtcS4sYB/cfAIAWME2YTcej+uxxx7TV77yFVVWVmrXrl2qqanR4sWLk5+zb98+eb1efe9731NLS4v+5V/+Rf/0T/9k4agB2NVg1JDXYUersDKGXMXNJwCAFWxzzu4bb7yhBQsWaP78+XK73br44ovV2tqa8jkHDx7UJZdcIkn6yEc+oiNHjkw79xEAJOedC5tYGYuv3Czv+ZsUX7lZjS1H1Xa4w+qhASfEub4AACvYJuyGQiFVVlYmP66srFQoFEr7OS6XSx6PRwMDA1kdJ4DcUFdbo56jrcnAmzhapS5Hj1YZXxlbP8PK2EGLRwacmNNuPgEAcoNtypjn0t69e7V3715J0u7duxUMBi0ekT253W5eGxtiXubGZZs3qryiXE/9ukWDY5KvUPrsFbW66MK1p/XnWT0vY64SeYqLpz0+5CrJ6+8Xq+cF0800J9decal+0Nwm/8pJ5/r+rlXXX3Ep85cl/KzYE/NiP8yJPZ3uvNgm7AYCAXV3dyc/7u7uViAQmPFzKisrFYvFFIlENG/evGl/1pYtW7Rly5bkx11dXZkbeA4LBoO8NjbEvMydZUsX679//jMpj53ua2v1vBTGhjUyMpJSCmqaptyx4bz+frF6XjDdTHOybOlifeaiPjW1PJs81/cztTVatnQx85cl/KzYE/NiP8yJPc02LwsXLkx7nW3C7vLly/Xee++ps7NTgUBAv/nNb3TzzTenfM6HPvQhPffcczr33HP14osvatWqVdP2AAGAE9XV1qixpTVZypwoy27I0bJs5B/O9QUAZJttwq7L5dIXvvAF3XXXXYrH49q0aZOWLFmin/70p1q+fLlqamq0efNmPfjgg/pv/+2/yefz6ZZbbrF62ACQFYmQ0NSyP7ky1lBbQ3gAAABIwzZhV5IuvPBCXXjhhSmPfeYzEyWIRUVF+uIXv5jtYQGALbAyBgAAcPJs040ZAAAAAIC5QtgFAAAAADgOYRcAAAAA4DiEXQAAAACA49iqQRUAYELb4Q41vdCqwViBfK646jasp0EVAADASSLsAoANtR3uUGPLUflXbpbXMBQ3TTW2tEoSgRcAAOAkUMYMADbU1HJQ/hXrZRiGJMkwDPlXrFdTy0GLRwYAAJAbCLsAYEODUSMZdBMMw1A4aqS5AgAAAJNRxgwANuRzm4qbZkrgNU1TXrdp4aiAM8M+dABANrGyCwA2VFdbo56jrTLN8XBrmqZ6jraqrrbG4pEBpyexDz2+crO8529SfOVmNbYcVdvhDquHBgBwKFZ2AcCGEqtdTS37FY4a8rpNNdTWsAqGnDW+D33TDPvQ9/N9DQDICMIuANjUujWrCAFwjMGoIS/70AEAWUQZMwAAyDif20yW5SewDx0AkEmEXQAAkHHsQwcAZBtlzAAAIOPYhw4AyDbCLgAAyAr2oQMAsokyZgAAAACA4xB2AQAAAACOQ9gFAAAAADgOYRcAAAAA4DiEXQAAAACA4xB2AQAAAACOQ9gFAAAAADgOYRcAAAAA4DhuqwcAAICV2g53qOmFVg3GCuRzxVW3Yb3WrVll9bAAAMAZIuwCAPJW2+EONbYclX/lZnkNQ3HTVGNLqyQReAEAyHGUMQMA8lZTy0H5V6yXYRiSJMMw5F+xXk0tBy0eGQAAOFOs7MIWKCMEYIXBqCHv8aCbYBiGwlEjzRUAACBXEHZhOcoIAVjF5zYVN83kyq4kmaYpr9u0cFQAAGAuEHZhufEywk0zlBHuJ+wCyKi62ho1trQmS5lN01TP0VY11NZYPbSTQlUMAADpEXZhOcoIAWTb5JAY7+1S14E35a1cIK/bVENtTU4ERqpiAACYHWEXlqOMEEA2TQ2JnuOruX9TuyKnQiJVMQAAzI5uzLBcXW2Neo62yjTHw22ijLAuR8oIAeQWp3RgHowaKTcJJapiAACYjJVdWC6xAtHUsl/hqJFTZYQAco9Ttk5QFQMAwOwIu7CFdWtWEW4BZIVTQmKuN9cCACDTCLsAgLzilJBIVQwAALMj7AIA8oqTQiJVMQAApEfYBQDkHUIiAADORzdmAAAAAIDjEHYBAAAAAI5DGTMAAKeo7XCHml5o1WCsQD5XXHUb1lMWDQCAzRB2AQA4BW2HO9TYclT+lZvlNQzFTVONLa2SROAFAMBGKGMGAOAUNLUcTB5bJEmGYci/Yr2aWg5aPDIAADAZYRcAgFMwGDWSQTfBMAyFo0aaKwAAgBUIuwAAnAKf25RpmimPmaYpr9tMcwUAALACe3YBACdEQ6YJdbU1amxpTZYym6apnqOtaqitsXpoAABgEsvDbmNjo15++WW53W7Nnz9fN954o7xe77TPu+mmm1RSUqKCggK5XC7t3r3bgtECQP6hIVOqxHNuatmvcNSQ122qobYmL18LAADszPKwu2bNGu3YsUMul0tPPPGEnnrqKV133XUzfu4dd9yhsrKyLI8QAPLbeEOmTTM0ZNqftwFv3ZpVefvcAQDIFZbv2b3gggvkcrkkSeeee65CoZDFIwIATEZDJgAAkIssX9mdbN++fbr44ovT/v5dd90lSbrsssu0ZcuWbA0LAPKaz20qbpopgZeGTAAAwO4Mc2pLyQy488471dvbO+3xa665RuvXr5ck/fznP9ebb76pL33pS9NWECQpFAopEAior69P3/zmN/X5z39e55133oxfb+/evdq7d68kaffu3RodHZ27J+Mgbrdb0WjU6mFgCubFnvJ5Xl461K4fNLfJv3JSQ6bfter6ret00YVrLR1bPs+LXTEn9sS82BPzYj/MiT3NNi9FRUVpr8tK2D2R5557Tr/61a90++23q7i4+ISf/7Of/UwlJSW68sorT+rPf/fdd890iI4UDAbV1dVl9TAwBfNiT/k+L22HO9TUcjDZkKnOJg2Z8n1e7Ig5sSfmxZ6YF/thTuxptnlZuHBh2ussL2Nub2/XL37xC339619PG3SHh4dlmqZKS0s1PDysw4cPq76+PssjBYD8RUMmAACQaywPu4899pii0ajuvPNOSdI555yj66+/XqFQSN///ve1a9cu9fX16Tvf+Y4kKRaLacOGDVq7dq2FowYAAAAA2JnlYfd73/vejI8HAgHt2rVLkjR//nzde++92RwWAAAAACCHWX70EAAAAAAAc42wCwAAAABwHMIuAAAAAMBxCLsAAAAAAMch7AIAAAAAHIewCwAAAABwHMIuAAAAAMBxLD9nFwCAqdoOd6jphVYNxgrkc8VVt2G91q1ZZfWwAABADiHsAgBspe1whxpbjsq/crO8hqG4aaqxpVWSCLwAAOCkUcYMALCVppaD8q9YL8MwJEmGYci/Yr2aWg5aPDIAAJBLCLsAAFsZjBrJoJtgGIbCUSPNFQAAANMRdgEAtuJzmzJNM+Ux0zTldZtprgAAAJiOsAsAsJW62hr1HG1NBl7TNNVztFV1tTUWjwwAAOQSGlQBAGwl0YSqqWW/wlFDXrephtoamlMBAIBTQtgFANjOujWrCLcAAOCMUMYMAAAAAHAcwi4AAAAAwHEIuwAAAAAAxyHsAgAAAAAch7ALAAAAAHAcwi4AAAAAwHEIuwAAAAAAxyHsAgAAAAAch7ALAAAAAHAcwi4AAAAAwHEIuwAAAAAAxyHsAgAAAAAch7ALAAAAAHAcwi4AAAAAwHEIuwAAAAAAxzFM0zStHgQAAAAAAHOJld08tnPnTquHgBkwL/bEvNgT82I/zIk9MS/2xLzYD3NiT6c7L4RdAAAAAIDjEHYBAAAAAI5D2M1jW7ZssXoImAHzYk/Miz0xL/bDnNgT82JPzIv9MCf2dLrzQoMqAAAAAIDjsLILAAAAAHAct9UDgD0888wzamxs1KOPPqqysjKrh5P3fvKTn+jgwYMyDEPl5eW68cYbFQgErB5W3mtsbNTLL78st9ut+fPn68Ybb5TX67V6WHntt7/9rf73//7f+vOf/6xvfetbWr58udVDymvt7e16/PHHFY/Hdemll+qqq66yekh57+GHH9ahQ4dUXl6u++67z+rhQFJXV5ceeugh9fb2yjAMbdmyRXV1dVYPK++Njo7qjjvuUDQaVSwW00c+8hFt377d6mFBUjwe186dOxUIBE65KzNhF+rq6tLhw4cVDAatHgqOu/LKK3XNNddIkpqamrRnzx5df/31Fo8Ka9as0Y4dO+RyufTEE0/oqaee0nXXXWf1sPLakiVL9KUvfUk/+MEPrB5K3ovH43rsscf0la98RZWVldq1a5dqamq0ePFiq4eW1y655BJt27ZNDz30kNVDwXEul0sNDQ1atmyZhoaGtHPnTq1Zs4afFYsVFhbqjjvuUElJiaLRqG6//XatXbtW5557rtVDy3tNTU1atGiRhoaGTvlaypihH/3oR/rsZz8rwzCsHgqO83g8yV+PjIwwNzZxwQUXyOVySZLOPfdchUIhi0eExYsXa+HChVYPA5LeeOMNLViwQPPnz5fb7dbFF1+s1tZWq4eV98477zz5fD6rh4FJ/H6/li1bJkkqLS3VokWL+PfEBgzDUElJiSQpFospFovx/ssGuru7dejQIV166aWndT0ru3mutbVVgUBAZ511ltVDwRT/+q//queff14ej0d33HGH1cPBFPv27dPFF19s9TAA2wiFQqqsrEx+XFlZqddff93CEQH219nZqbfeektnn3221UOBxitUbrvtNr3//vu6/PLLdc4551g9pLz3wx/+UNddd91prepKhN28cOedd6q3t3fa49dcc42eeuopfeUrX8n+oDDrvKxfv17XXnutrr32Wj311FP6t3/7N/aNZMmJ5kWSfv7zn8vlculjH/tYlkeXn05mTgAg1wwPD+u+++7T5z73uZSKLlinoKBA9957r8LhsL7zne/onXfe0dKlS60eVt56+eWXVV5ermXLlqmjo+O0/gzCbh746le/OuPj77zzjjo7O3XrrbdKGi8TuO2223T33XeroqIiiyPMT+nmZaqPfexjuvvuuwm7WXKieXnuuef08ssv6/bbb6e8KUtO9mcF1goEAuru7k5+3N3dTWM9II1oNKr77rtPH/vYx/ThD3/Y6uFgCq/Xq1WrVqm9vZ2wa6HXXntNBw8eVFtbm0ZHRzU0NKQHHnhAN99880n/GYTdPLZ06VI9+uijyY9vuukm3X333XRjtoH33ntPH/jABySNl5qzJ9Ee2tvb9Ytf/EJf//rXVVxcbPVwAFtZvny53nvvPXV2dioQCOg3v/nNKb0hAfKFaZp65JFHtGjRIn3iE5+wejg4rr+/Xy6XS16vV6Ojozp8+LD++q//2uph5bUdO3Zox44dkqSOjg4988wzp/zvCmEXsKF/+Zd/0XvvvSfDMBQMBunEbBOPPfaYotGo7rzzTknSOeecw9xY7KWXXtI///M/q7+/X7t379ZZZ52lL3/5y1YPKy+5XC594Qtf0F133aV4PK5NmzZpyZIlVg8r791///169dVXNTAwoBtuuEHbt2/X5s2brR5WXnvttdf0/PPPa+nSpcnqumuvvVYXXnihxSPLbz09PXrooYcUj8dlmqY++tGP6kMf+pDVw8IZMkzTNK0eBAAAAAAAc4mjhwAAAAAAjkPYBQAAAAA4DmEXAAAAAOA4hF0AAAAAgOMQdgEAAAAAjkPYBQAAAAA4DmEXAIAc9cQTT+jb3/528uPGxkZ94xvfUDQatXBUAADYA2EXAIAc9dd//dfq6OjQW2+9pebmZrW3t+tLX/qS3G631UMDAMByhmmaptWDAAAAp+dnP/uZXnrpJUUiEX3jG99QMBhUJBLRnXfeqf/8z//UXXfdpaVLl1o9TAAAso6VXQAActgHP/hBvfPOO9qxY4eCwaAkqaioSLt27dJHPvIRi0cHAIB1CLsAAOSod955R48++qg2btyo/fv3Jx93u90qKyuzcGQAAFiPsAsAQA4KhUK655579F/+y3/R3//93+udd95RR0eH1cMCAMA2CLsAAOSYSCSiu+++W1dccYVqampUXFysT37yk/rJT35i9dAAALANGlQBAOBQDz30kD75yU/SoAoAkJcIuwAAONDdd9+tP/7xjwoGg7rssst0ySWXWD0kAACyirALAAAAAHAc9uwCAAAAAByHsAsAAAAAcBzCLgAAAADAcQi7AAAAAADHIewCAAAAAByHsAsAAAAAcBzCLgAAAADAcQi7AAAAAADHIewCAAAAABzn/wemdBeNT7h0aQAAAABJRU5ErkJggg==",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plot_ds(data,m[-1],q[-1])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Adagrad"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Adagrad introduce la possibilità di applicare learning rate diversi ai vari parametri da ottimizzare (dimensioni dello spazio di ricerca): in particolare, parametri per i quali si sono avuti nel corso dei passi precedenti valori elevati del gradiente avranno associati, tendenzialmente, learning rate più piccoli, in modo tale che l'aggiornamento dei prametri stessi sia limitato. Al contrario, in presenza di dimensioni (parametri) con valori del gradiente precedenti piccoli, e quindi poco modificate, il learning rate risulterà più grande, rendendo le modifiche delle componenti corrispondenti più sensibili ai valori del gradiente.\n",
"\n",
"Come visto, nella gradient descent \"base\" l'aggiornamento del coefficiente $k$-esimo è dato da\n",
"\n",
"$$\n",
"\\theta_j^{(k+1)}= \\theta_j^{(k)}-\\eta \\frac{\\partial J(\\theta, X)}{\\partial\\theta_j}\\Bigr\\vert_{\\small\\theta=\\theta^{(k)}}= \\theta_j^{(k)}-\\eta\\sum_{i=1}^n\\frac{\\partial J(\\theta;\\mathbf{x}_i)}{\\partial\\theta_j}\\Bigr\\vert_{\\small\\theta=\\theta^{(k)}}\n",
"$$\n",
"\n",
"dove $\\eta$ è lo stesso per tutti i coefficienti. In Adagrad, l'aggiornamento prevede un learning rate\n",
"$\\eta_{j}^{(k)}$, dipendente dal coefficiente e dal passo di applicazione del metodo, definito nel modo seguente\n",
"\n",
"$$\n",
"\\eta_{j}^{(k)} = \\frac{\\eta}{\\sqrt{G_{j,k}+\\varepsilon}}\n",
"$$\n",
"\n",
"dove $\\eta$ è una costante, $G_{j,k}=\\sum_{i=0}^{k}g_{j,i}^2$ è la somma dei valori $g_{j,i}=\\frac{\\partial J(\\theta, X)}{\\partial\\theta_j}\\Bigr\\vert_{\\small\\theta=\\theta^{(i)}}$ del gradiente relativo a $\\theta_j$ per tutte le iterazioni precedenti, mentre $\\varepsilon$ è una piccola costante di *smoothing* utilizzata per evitare denominatori nulli.\n",
"\n",
"Utilizzando il formalismo introdotto, l'aggiornamento di $\\theta_j$ alla $k+1$-esima iterazione è data da\n",
"\n",
"$$\n",
"\\theta_j^{(k+1)}= \\theta_j^{(k)}-\\frac{\\eta}{\\sqrt{G_{j,k}+\\varepsilon}}g_{j,k}\n",
"$$\n",
"\n",
"Come si può vedere, il learning rate diminuisce in modo monotono al procedere delle iterazioni per tutti i coefficienti. Al tempo stesso, coefficienti con elevati valori di gradiente nel passato (quindi soggetti a variazioni significative) avranno decrementi più elevati del learning rate, che quindi tenderà più rapidamente a $0$ e a modificare poco i valori di tali cofficienti, mentre coefficienti con valori limitati (che sono variati poco fino ad ora) manterrano un learning rate più alto.\n",
"\n",
"Dato che in ogni caso il denominatore cresce ad ogni iterazione, il learning rate continua a diminuire fino a raggiungere valori talmente piccoli da impedire un reale aggiornamento della soluzione."
]
},
{
"cell_type": "code",
"execution_count": 132,
"metadata": {},
"outputs": [],
"source": [
"def adagrad(X,t, eta = 0.1, G = 0, eps = 1e-8, epochs = 1000):\n",
" theta = np.zeros(nfeatures+1).reshape(-1,1)\n",
" theta_history = []\n",
" cost_history = []\n",
" for k in range(epochs): \n",
" g = gradient(theta,X,t)\n",
" G = G + g**2\n",
" theta = theta - eta * g / (np.sqrt(G) + eps)\n",
" theta_history.append(theta)\n",
" cost_history.append(cost(theta, X, t))\n",
" theta_history = np.array(theta_history).reshape(-1,3)\n",
" cost_history = np.array(cost_history).reshape(-1,1)\n",
" m = -theta_history[:,1]/theta_history[:,2]\n",
" q = -theta_history[:,0]/theta_history[:,2]\n",
" return cost_history, m, q"
]
},
{
"cell_type": "code",
"execution_count": 133,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"tempo di esecuzione: 0.562 secondi\n",
"10000 passi totali\n",
"1000000 gradienti calcolati\n"
]
}
],
"source": [
"start_time = time.time()\n",
"cost_history, m, q = adagrad(X, t, eta = 0.1, G = 0, eps = 1e-8, epochs = 10000)\n",
"print(f\"tempo di esecuzione: {time.time()-start_time: 4.3f} secondi\")\n",
"print(f\"{len(m)} passi totali\")\n",
"print(f\"{len(m)*n} gradienti calcolati\")\n"
]
},
{
"cell_type": "code",
"execution_count": 135,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABQgAAAGoCAYAAAAKMwiTAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAABfpUlEQVR4nO3deXQcd53u/6eqN6nVWt2yZFm2ZNmWl0ROnMWBbCRBZIPLzHiGMDCBGV8C9zIHyAXunck5d2KCDSfmx4UhDMwcwgWS3AEmCZgZJpBNCUkICXYSx1u8SLJiy7Ity5KsrbX0UvX7o6WW5CWRLXdXL+/XOTpdXdXLp6skdevR91sfw7ZtWwAAAAAAAABykul0AQAAAAAAAACcQ0AIAAAAAAAA5DACQgAAAAAAACCHERACAAAAAAAAOYyAEAAAAAAAAMhhBIQAAAAAAABADnM7XcBMHT161OkSZiUYDKq7u9vpMiCORTrhWKQPjkX64Fikj2w5FlVVVU6XkBR8NgT7cHbYf7PHPpwd9t/ssQ9nJ1f339k+GzKCEAAAAAAAAMhhBIQAAAAAAABADiMgBAAAAAAAAHIYASEAAAAAAACQwwgIAQAAAAAAgBxGQAgAAAAAAADkMAJCAAAAAAAAIIcREAIAAAAAAAA5jIAQAAAAAAAAyGEEhAAAAAAAAEAOIyAEAAAAAAAAchgBIQAAAAAAAJDDCAgBAAAAAACAHEZACAAAAAAAAOQwAkIAAAAAAAAghxEQAgAAAAAAADmMgBAAAAAAAADIYe5kPvhDDz2ktrY2LVq0SOvWrUusHxoa0oMPPqjBwUE1NDRo7dq1ySwDAAAAAAAAwFkkLSBsa2vT6OioNmzYoB/+8IdqbW3VkiVLJEmPP/64PvrRj2r+/PnJenoAAAAAAAAAM5C0gLClpUWrVq2SJDU0NKi5uTkREB4+fFi/+tWv1NPTo4997GOqr68/7f5NTU1qamqSJG3atEnBYDBZpaaE2+3O+NeQLTgW6YNjkT44FumDY5E+OBYAAADIFUkLCEOhkCoqKiRJfr9fHR0diW379+/XN77xDQUCAX3rW9/Sxo0bT7t/Y2OjGhsbE9e7u7uTVWpKBIPBjH8N2YJjkT44FumDY5E+OBbpI1uORVVVldMlAAAAIM0lLSD0+/0aHh6WJI2MjMjv9ye2VVVVqbq6WpJkmvRJAQAAAAAAAJyStHSuvr5eu3fvliTt2rVr2jTiefPm6eTJkxodHVUsFktWCQAAAAAAAADeRdJGENbV1cnj8Wj9+vWqra1VMBjU5s2btXbtWt1xxx164IEHFA6H9Rd/8RfJKgEAAAAAAADAu0haQChJ69atm3Z97dq1kqTq6mrdd999yXxqAAAAAAAAADPACQABAAAAAACAHEZACAAAAAAAAOQwAkIAAAAAAAAghxEQAgAAAAAAADksqU1KEPdvL7eqtfNNfeS9i7RsfonT5QAAAAAAAAAJjCBMgZFwTP2hMUViltOlAAAAAAAAANMwgjAFjPFL23a0DAAAAMf09vbqG9/4hjo6OvTII4/I5XIltrW3t+uHP/yhJOmuu+5STU2NU2UCAADkJEYQpoBpxiNCm4QQAADkqEAgoHvvvVdLly49bdujjz6qu+++W1/84hf16KOPOlAdAABAbmMEYQokRhA6WgUAAIBzvF6vvF7vGbeFQiEFg8HEMgAAAFKLgDAFDIMRhAAAAGczk89ITU1NampqkiRt2rQpEShmKrfbnfGvwWnsw9lh/80e+3B22H+zxz6cHfbfdASEKTCeD3IOQgAAgHcx8Y/VUzU2NqqxsTFxvbu7O1UlJUUwGMz41+A09uHssP9mj304O+y/2WMfzk6u7r+qqqozricgTIGJD7oWCSEAAMBpAoGAenp6ZBiG8vPznS4HAAAg5xAQpgDnIAQAALkuGo3q/vvv16FDh/T1r39df/EXf6F9+/Zp7dq1uuOOO/Sd73xHkvSpT33K2UIBAAByEAFhCkxOMSYiBAAAucntduvee++dtm7lypWSpJqaGm3cuNGJsgAAACDJdLqAXGAmmpQ4XAgAAAAAAABwCgLCFKBJCQAAAAAAANIVAWEKGKJJCQAAAAAAANITAWEKcA5CAAAAAAAApCsCwhQwJs5B6HAdAAAAAAAAwKkICFPA5ByEAAAAAAAASFMEhCmQGEFIQggAAAAAAIA0Q0CYAuMDCBlBCAAAAAAAgLRDQJgCk+cgJCEEAAAAAABAeiEgTAGDcxACAAAAAAAgTREQpsBkQEhCCAAAAAAAgPRCQJgChiamGAMAAAAAAADpxe10AblgYgShZRERAgAAAADgBNuypFhUsqKSZcW/7PEvy4rP+rMsyY5Jlp1Yn7iNpEQbUsMY/2N/yvVTL0235HLJMF2S6ZJc45cTy4aZ6FkAOI2AMAVMgxGEAAAAAACciW3b8eAuMiZFwrIj4fhyNCx7fF18fXzdtNvEolIsKnv8Mv4VkaJT10XGg0Hr3YtJKWMyNHR7JLdXhid+KY9PhtsjebyS2ze53uuT4c2XfPkaHaiQNRaR4YtflzdPhsFEUZwfAsIU4ByEAAAAAIBsZceiUnhUdnhUCo9KYyPx5YnL8KjssZFp245bEUWHh+LrIuEUdfU0JLd7chSfYUimKRmmZJrxcG3KdRlTl0/tPmqPjwKacjl1u21LVkyyYrJjsfioxVgssU6xWHxU4kSIGRnTlEc5bflMes70+rw+yeeXkeeXkR+Q8gPxS39ARn6hDH9Ayi+Mr/PlM4IRCQSEKTDxA0c+CAAAAABIZ3YkLI0Nyx4NSaPDskeHxy9D4+unbouvUyR8zs8TPXWFyz0+Ws4rw+OLL3t8MsbXJZZPXe/2SC63DJc7/hgut+TySO6p6zyJkXrpFIjZljUZFsYi8ZGR0TEpEpkyejIiRcfixyUalsJh2eFhaWxEbiumyFD/ePg6IoXH4oFreFT2YO+7z2I0XVKgREagWEagZNqXJpY93hTsCaQDAsIUmPj1Q0AIAAAAAEgl24pJIyHZI0PSyJDs4cHx5UHZw0Px5dFQPAgcG5aikXN/EsOUvHmSLy8+/dWbJ2PqdV/e+Lr8xLqSuZXqHxmN38/tk+FyXfgXn+YMc3x0otsjKS++7hzuHwwG1d3dnbhuW7HJUZqjw/FjO368py5PfB8oMiYN9Mge6Dl7mJgfkFE8R0ZRUEZxML48cenxne9LRxoiIEyBxAhCzkIIAAAAAJgl27bjod7wgOzQYDzsGxmSxgM/e3gwHgKNDEmjwzqnM+KbLimvQEaeX8rzy8griF/6/FPWxy+NPL/kK4ifF+8cR+Z5g0EZU8ItzJ4xfuyUVyCj+N1vb0fCsof6pKE+2ad8aag/fjn+fWR3Hjr9AfyFMkrKZZZVypj4Kq2Q4SU4zEQEhClw2qkKAAAAAAA4AzsSloYHZIfGv4YHpFD/KdcH4lNTZ8SIB0ZTzj03eU66iXWTwZ/c3rSahovkMTxeGaVzpdK5Z9xu25YUGpDd3y27v0d2/4nxy27ZA73xEYnDg4odbZt+x8LSydAwWCWzfIEUKOb7Ks0REKbAxA+BRUIIAAAAADnLjkZkh/qlwT7ZQycnR2yF4qGfHeqPTxGdCW+ejILi+Ciu/IAMf2F8Ouh4M4pEc4r8gvjIMuAcGYaZOBeh5i+Zts22LGmoT9bJLtm9nZNffSekwZOyBk9Kh/ZO3iE/ILN8voxgtYy51TLLq+Pfs0gbBIQpwDkIAQAAACC72bYdP/fbUDz801Cf7MFTpm0OD777A5mueOhXUCyjoEhGQZHkL0pcV0GRDH8RzSPgKMM0paIyuYrKpJrlifV2LCZ7oFt273HZPcdknTgi+0SHNDIkq32/1L5/8kEKS2VW1sqct0hGZa2MknJGGTqIgDAFOAchAAAAAGQ+OxKOd4cd6NHggTFFjh2WBnonQ8F36+ZrmlLBmTrGFsdDv4Ki+Pn+DDMlrwe40AyXS0ZphVRaIS1eJWk8PB88KetEh+wTHeOXRxIjDa2WN+N3ziuQWVkjY94imfMXyyibR2CYQgSEKWByDkIAAAAASHuJ5h8D8RAw/tWbuD51BODAmR7A45NROBH6lcYDwMKJILA0PjLQJPxDbjEMY3K04URoaFnxKcmdb8s6dlBW50FpeFDWwT3SwT2KSfFpydVLZVYvkTl/aTxAR9IQEKbAZJMSEkIAAAAAcJo9GpLdd2L8qzs+JXI8CFRk7Ox3NF0yCktlFM1RfsV8jXr8MopK4+sCpfHzAjLiCXhXhmnKCFZJwSq5Lr4mnpcM9MTDwmNtso60SqEBWS1vJkYYGmWVMqvrZdYsl1FZw7k1LzACwhSYbFLicCEAAAAAkCNsy4pPYew7Ibuva0ogeEIaDZ39jt48GUVzZBSVnXapguLECMCSYFDd3d0pejVAdjMMQyoOylUclGv5FbJtW3Zfl6zDLbKPtMg62ia7t1Ox3k7Fdr4k5fllLlwus3alzOp6zsl5ARAQpsBkkxISQgAAAAC4kOxoJB4A9nbFL/u7xwPBbsmKnflOHq+MkrnxpgglQRlFwfEgsEzy+RkFCDjMMAwZpRUySyukVdfKjkVldx6S1b5f1qE9svu7ZTVvk9W8TXK5Zc5fIrPuYpm1F8vw5TldfkYiIEyBySYlAAAAAIDzYdu2NHRSVk9n/NxlE5f93ZJtnflOBcXjIWC5zIlAsLQ83hWYEBDIGIbLLWP+YpnzF8t+z22y+07IOrhH1sE9srsOy2rfJ6t9n2T+SubCZTIXXyKzZgUjC88BAWEKmJyDEAAAAABmzI6EZfcck91zVNZEGHiyUwqf4fyAhjEe/FXIKJ2bCASN4nIZXl/qiweQVPHRhXNlls6VVt8ge7y5SezADtlH304Eh3J7ZdaukLlktcwFSzln4bsgIEwBczwhjHESQgAAAACYxo5F4yMBT3TI6uqQfaJD9smuM48KzA/EGxXMqZRRVimjbF48FHR7Ul84gLRg+AvlWnmVXCuvkh0aUKxtp6zWnbK72mW17pDVukPyF8lVf5nM5VfILA46XXJaIiBMAdf4SWwJCAEAAADkMtuy4o1CThyeDAN7jp1+rkDDjAeAwSoZc+bJLBsPBP2FzhQOICMYBUVyN1wrNVwre6BXsQM7ZO1/Q3Z/t2LbX1Bs+wsyKmvlWn6lrKIbnC43rRAQpoBrfAShRUAIAAAAIIfYoyFZnYdkdx6UdbxddvdRKRo+7XZGcVBGebWMudUyyxfImDOPc4cBmBWjqEzu1TfKvvQG2Z2HFNv/mqwDu2R3HlS086A6X31CZv3lcl30XhnFc5wu13EEhClgGkwxBgAAAJD97ME+WZ1vyzp2UHbnQdknj59+o0CJzEQYWC0jWE3XUQBJYxiGjHm1MufVyr76w7Ladiq29zXZXe2K7XpZsV1/kLlwWTwoXLBUhmE6XbIjCAhTIDGCkCYlAAAAALKIPTIk60irrI5WWUdapaG+6TdwuWXMXSCzslZGZU08EMwPOFIrABhen1zLr5Rr+ZUqioTU8/JvZR3YkeiCbBQH5Wq4RuayK3Lu3KYEhClAkxIAAAAA2cCOhOPThTtaZB1pjZ8/cCpvXjwMnFcrs3KRjPL5Mlz82Qkg/Xjn1chz40dkv+d2xfa9ptieV2X3dyv68n9IbzwnV8M1cq18j948cFLP/qFVQ6GwAgVe3XztEq1eUeV0+Rccv6lTwEVACAAAACBD2QO9ih3cI+vQXtmdB6c3FHG5ZcxbJHP+EpnVS+LnDszR6XkAMpORXyD36hvkuuQ6WW+/pdj2F2V3H1Fs69N64/fb9LPeOg1OOXXq0a4haa2yLiQkIEwBl0GTEgAAAACZwbYt2SeOyJoIBXs7p2w1ZJRXTwaCFTU5Nw0PQHYyTJdci1fJrGuQfaRV0e0v6vk3PNPCQUkaDI3pmZdbCQhx7hJTjDkHIQAAAIA0ZMeiso8cUOzQHlkH90rDA5MbPT6ZC5fJrFkpc8FSGXkFzhUKAElmGIaM6qXyVi9VaP+T0tjoabcZGj69G3umIyBMgUSTEkYQAgAAAEgTtm3J7jykWPObstp2SuEpfwQXFMusWSFX7UoZVXWcRxBATiosKpB6Tg8IA36vA9UkF7/lU4AmJQAAAADShdV3QgO7X1Z45x+kwZOJ9UZZpczalTJrV8oIzpcxfqokAMhVN1+7REe7hjQYGkusKyzw6eZrlzhYVXIQEKbAxDkICQgBAAAAOMEeGZJ1YKdiLW/K7jqsyMSGgmK5ll4qc+llMssqnCwRANLO6hVV0lrpmZdbNTQcVsBPF2PMAlOMAQAAAKSabVuy2ptl7d0i6/B+ybLiGzw++VdcocjCFfHpw3QdBoCzWr2iKisDwVMREKaAKzHF2HK4EgAAAADZzo6Mydq/TbHdf5Dd3x1faZjxRiNLL5NZs0Kl86rU3d3tbKEAgLRBQJgCE+cgZAAhAAAAgGSxB/sUe+sVxfZunWw4EiiR6+Kr5Vq6Woa/0NkCAQBpi4AwBWhSAgAAACBZrOPtiu18WdbbuyU7PmvJqKiRa9W18YYjpsvhCgEA6Y6AMAUmm5QwxRgAAADA7NmxmKy3dyu262XZXYfjK01T5uJL5Gq4VubcBc4WCADIKASEKUCTEgAAAAAXgm3FZO17XdE3n5eG+uMrfflyrbhKroveKyNQ7GyBAICMlNSA8KGHHlJbW5sWLVqkdevWJdZ///vf15EjR+T1etXY2Khrr702mWU4zmXGu4IxxRgAAADA+bBtW9ahvYpteVJ23wlJklFSLlfDNTKXXibD43W4QgBAJktaQNjW1qbR0VFt2LBBP/zhD9Xa2qolS5Yktn/hC19QZWVlsp4+rSTOQWgTEAIAAAA4N9bxdkX/+FvZnQfjK4rK5L7yFpmLG2QYpqO1AQCyQ9ICwpaWFq1atUqS1NDQoObm5kRAaBiGvve97ykQCOhTn/qUysvLk1VGWhjPB2XbkmXbMsfPSQgAAAAAZ2P3dyu69WlZbbviK/L8cl32frlWXiXDxdmiAAAXTtLeVUKhkCoqKiRJfr9fHR0diW2f/OQnFQgEtG/fPj3yyCP68pe/fNr9m5qa1NTUJEnatGmTgsFgskpNCZdpKGbZKiubI7eL//I5ye12Z/z3U7bgWKQPjkX64FikD44FAKfYI0OKvvGcrL1bJMuSXG65Gq6V69IbZPjynC4PAJCFkhYQ+v1+DQ8PS5JGRkbk9/sT2wKBgCRp+fLl+ulPf3rG+zc2NqqxsTFxvbu7O1mlpsREQNjVdUJej8vpcnJaMBjM+O+nbMGxSB8ci/TBsUgf2XIsqqqqnC4BwAzZkbBiu15WbPuLUmRMkiFz2eVyX3EzzUcAAEmVtICwvr5eTU1Nuvrqq7Vr1y7dcMMNiW3Dw8Py+/06evSoCgoKklVCWok3KrE4DyEAAACAaWzLktX8hqKvPSsND0iSzIXL5Fpzm8w5uXHedgCAs5IWENbV1cnj8Wj9+vWqra1VMBjU5s2btXbtWn33u99VKBSSYRi66667klVCWnFNNCqhkzEAAACAcVZ/t6LPPyq767AkyQjOl/s9t8mcv+Rd7gkAwIWT1DPbrlu3btr1tWvXSpLuueeeZD5tWnKNn3eQgBAAAACAbduy9m5V9NUnpGhEKiiOB4OLV9GZGACQcrS+SpGJxiSxmOVwJQAAAACcZA8PKvriL2W175MkmUsulfvaP5Hhy3e4MgBAriIgTBHPeEAYiTGCEAAAAMhVsYNvKfriZmk0JHnz5L7uz+RaconTZQEAchwBYYp43PHOxVGLEYQAAABArrHDY4q++p+y9r0uSTLmL5Hnho/QnRgAkBYICFPE446PIIwyxRgAAADIKVbnIUV+96g00Cu53HKtuVWuhqs51yAAIG0QEKbIxBRjAkIAAAAgN9ixmGLbnlPszd9Jti1jzjy5b/qozLJKp0sDAGAaAsIUcbvGpxhzDkIAAAAg61knuxR9/lHZ3UckGXJd+j65rviADBd/ggEA0g/vTikyMcU4wghCAAAAIGvZti3rrT8quuW3UjQiBUrkufEOmVV1TpcGAMBZERCmCFOMAQAAgOxmhwYUefEXsg83S5LM+svkvvrDMnx5DlcGAMA7IyBMkckmJUwxBgAAALKN1dupyG9+LA0PSD6/3Nf/mVx1DU6XBQDAjBAQpohn4hyEFiMIAQAAgGxidR5S5MmfSOFRGZW18jR+XEZBkdNlAQAwYwSEKTI5gpCAEAAAAMgWsfZ9ij77UykakVm7Uu73f0yG2+N0WQAAnBMCwhSZOAdhhCnGAAAgRz300ENqa2vTokWLtG7dusT673//+zpy5Ii8Xq8aGxt17bXXOlglMHOx5jcVffFxybJkLrtC7uv/TIbpcrosAADOGQFhirjd41OMGUEIAAByUFtbm0ZHR7Vhwwb98Ic/VGtrq5YsWZLY/oUvfEGVlZUOVgicm+jOlxV79QlJkuvS98m15lYZhuFwVQAAnB/T6QJyBV2MAQBALmtpadGqVaskSQ0NDWpubk5sMwxD3/ve97Rp0yadOHHCqRKBGbFtW9GtT0+Gg++5Xe6rbiMcBABkNEYQpghdjAEAQC4LhUKqqKiQJPn9fnV0dCS2ffKTn1QgENC+ffv0yCOP6Mtf/vJp929qalJTU5MkadOmTQoGg6kpPEncbnfGvwanObEPbctS31P/qvCbL0mGqZIP/bUKVl2T0houFL4HZ499ODvsv9ljH84O+286AsIUmehiHGEEIQAAyEF+v1/Dw8OSpJGREfn9/sS2QCAgSVq+fLl++tOfnvH+jY2NamxsTFzv7u5OYrXJFwwGM/41OC3V+9CORRV97t9kvb1bcrnlbvy4RqqWaSRDjyPfg7PHPpwd9t/ssQ9nJ1f3X1VV1RnXM8U4RSZGEMYsAkIAAJB76uvrtXv3bknSrl27VF9fn9g2ERwePXpUBQUFjtQHvBM7PKbIb38SDwe9efJ88FNy1a50uiwAAC4YRhCmiJsuxgAAIIfV1dXJ4/Fo/fr1qq2tVTAY1ObNm7V27Vp997vfVSgUkmEYuuuuu5wuFZjGHhlS5Lc/kd19RPIXynP7f5U5Z57TZQEAcEEREKbI5DkIGUEIAABy07p166ZdX7t2rSTpnnvucaIc4F3ZgycV+c2PZPd3S0Vz5P3gf5VRNMfpsgAAuOAICFPE6x4/B2GUgBAAAABId1bvcUV+8yNpeEDGnHny3P5fZfgLnS4LAICkICBMEZ8nHhCGozGHKwEAAADwTqzOQ4o89ZA0NiJj3iJ5bvlrGb48p8sCACBpCAhTxOuJ7+owIwgBAACAtBVr36/os/8qRSMya1bI3fhxGW6P02UBAJBUBIQpwghCAAAAIL3FWt5U9IXHJcuSuexyua9fK8N0OV0WAABJR0CYIpMBISMIAQAAgHQT27tV0Zc2S5Jcl7xPrqtulWEYDlcFAEBqEBCmiM/NFGMAAAAgHVlH2xR9+d8lSa6rbpP70vc5WxAAAClmOl1ArkiMIIwwxRgAAABIF/ZgnyLP/lSyLLlWXU84CADISQSEKeJxmzIkRS1blmU7XQ4AAACQ8+xoRJFn/p80GpJRvVSuq25xuiQAABxBQJgihmHI647vbhqVAAAAAM6ybVvRlzbL7j4iFZXJ8/6P0ZAEAJCzCAhTyOOmUQkAAACQDmK7XpbV8qbk9spz8ydl5PmdLgkAAMcQEKaQzzMxgpCAEAAAAHCK1dGi2B9/K0ly3/gRmXMqHa4IAABnERCmkHd8BOEYU4wBAAAAR9gDPYo0/VyybblW3yhXXYPTJQEA4DgCwhSaPAchIwgBAACAVLMjYUWe/n/S2LDMhcvluvIDTpcEAEBaICBMoYkRhOEIIwgBAACAVLJtW9EXHpfd2ymjpFzum/5ShsGfQwAASASEKcUIQgAAAMAZse0vymrbJXl8ct/8CRm+PKdLAgAgbRAQptBkQMgIQgAAACBVYu37FNv6tCTJfdNHZZbOdbgiAADSCwFhCiWmGDOCEAAAAEgJq++Eos/9myRbris+IFftSqdLAgAg7RAQphBTjAEAAIDUscOjij79/6TwqMxFF8l12Y1OlwQAQFoiIEwhr2diBCFTjAEAAIBksm1L0d89JruvS0Zphdw33EFTEgAAzoJ3yBTKGw8IR8MEhAAAAEAyxd54XtbBPZI3T55bPiHD63O6JAAA0hYBYQrleccDwkjU4UoAAACA7BV7+y3F3miSDEOexo/LKA46XRIAAGmNgDCFGEEIAAAAJJd18riiv3tUkuRac6vMBfUOVwQAQPojIEyhPK9bkjRCQAgAAABccPbYiKJPPSJFwjIXXyLXJdc7XRIAABmBgDCFEiMImWIMAAAAXFC2ZSn63L/JHuiRMWee3O/7cxmG4XRZAABkBALCFMr3MsUYAAAASIbYa8/IOrxfyiuINyXxeJ0uCQCAjEFAmEJ5nvgU49EIASEAAABwocQO7FRs+wuSYcabkhSWOV0SAAAZhYAwhfIYQQgAAABcUFbPUUVfeFyS5HrvB2XOX+xwRQAAZB4CwhTyuk2ZhhSJWYpZltPlAAAAABnNHg0p8vT/k6IRmfWXyXXx1U6XBABARiIgTCHDMOTzMIoQAAAAmC3biinS9HNp8KSM8mq5r/szmpIAAHCeCAhTLM8bPw/hCAEhAAAAcN76n/uF7COtUn5Anps/IcPtcbokAAAyltvpAnJN3sQIQhqVAAAAAOcl1rZLY1uflUyXPDffKSNQ7HRJAABkNEYQplh+olFJ1OFKAAAAgMxjR8KKvvqEJMn93ttlVtY6WxAAAFmAEYQplueJ73JGEAIAAADnLrbzJWmoX56KhTJWvtfpcgAAyAqMIEyxPC9NSgAAAIDzYQ/1K7b9RUlS8c1/KcPkzxkAAC4E3lFTzO+LjyAcHmOKMQAAAHAuolufkqIRmXUN8i2sd7ocAACyBgFhik0EhKGxiMOVAAAAAJnDOt4uq+VNyXTJfdVtTpcDAEBWISBMMUYQAgAAAOfGtm1FX4k3JnGtuk5GUZnDFQEAkF0ICFOsgIAQAAAAOCfWgR2yu9ql/IBcq290uhwAALIOAWGK+X0eSVKIgBAAAAB4V3YkrOgfn5QkudfcIsPrc7giAACyDwFhijGCEAAAAJi52M6XpFC/jGCVzPrLnS4HAICsRECYYokmJaM0KQEAAADeiT3Ur9j2FyVJ7vd+SIbJny8AACRDUt9hH3roIa1fv14/+clPTtsWDof16U9/Wjt37kxmCWmnIG9yBKFt2w5XAwAAAKSv6NanpGhEZl2DzKo6p8sBACBrJS0gbGtr0+joqDZs2KBoNKrW1tZp25977jktXLgwWU+ftrxul9wuQ1HLViRqOV0OAAAAkJas4+2yWt6UXG65r7rN6XIAAMhqSQsIW1patGrVKklSQ0ODmpubE9ui0ahaWlq0bNmyZD19WiugUQkAAABwVrZtK/rKE5IkV8O1MorKHK4IAIDs5k7WA4dCIVVUVEiS/H6/Ojo6EtteeOEFXXfddWppaTnr/ZuamtTU1CRJ2rRpk4LBYLJKTQm32514DUUFPvUPh+XNDygYLHa4stwz9VjAWRyL9MGxSB8ci/TBsQCcY7XukN3VLuUH5Fp9o9PlAACQ9ZIWEPr9fg0PD0uSRkZG5Pf7JUmxWEzbt2/X//yf//MdA8LGxkY1NjYmrnd3dyer1JQIBoOJ1+B1GZKkI8dPqMBFs5JUm3os4CyORfrgWKQPjkX6yJZjUVVV5XQJwDmxI2FFtzwpSXKvuUWG1+dwRQAAZL+kTTGur6/X7t27JUm7du1SfX29JKm/v189PT36+te/rt///vf6+c9/rqGhoWSVkZYKfJONSgAAAABMiu18SQr1ywhWyVx2udPlAACQE5I2grCurk4ej0fr169XbW2tgsGgNm/erLVr1+r++++XJD322GNavny5AoFAsspIS4G8+DkIh0YZPQgAAABMsIf6Fdv+oiTJ/d4PyTCSNp4BAABMkbSAUJLWrVs37fratWunXb/jjjuS+fRpqzA/HhAOjhAQAgAAABOiW5+SohGZdQ0yq+qcLgcAgJzBv+QcUJjvlURACAAAAEywjrfLanlTcrnlvuo2p8sBACCnEBA6gBGEAAAAwCTbthV95QlJkqvhWhlFZQ5XBABAbiEgdMBkQBh2uBIAAADAeVbrDtld7ZK/UK7VNzpdDgAAOYeA0AGMIAQAAADi7EhY0S1PSpLcV94iw+tzuCIAAHIPAaEDpnYxtmzb4WoAAAAA58R2vCSF+mUEq2Quu8zpcgAAyEkEhA5wu0z5fW5ZtjQ8FnW6HAAAAMAR9lC/YjtelCS5r/4vMgz+PAEAwAm8AzukMI9pxgAAAMht0a1PSdGIzLoGmfMWOV0OAAA5i4DQITQqAQAAQC6zjrfLanlTcrnlvuo2p8sBACCnERA6hEYlAAAAyFW2bSv6yn9KklwN18ooKnO4IgAAchsBoUMK872SpAECQgAAAOQYq3WH7K7Dkr9QrtU3Ol0OAAA5j4DQIcX+eEDYHxpzuBIAAAAgdexIWNEtT0qS3FfeIsPrc7giAABAQOiQkoJ4QNgX4hyEAAAAyB2xHS9JoX4Zwfkyl13mdDkAAEAEhI4hIAQAAECusYf6FdvxoiTJffWHZBj8OQIAQDrgHdkhxQXxqRR9w0wxBgAAQG6IbnlSikZk1jXInLfI6XIAAMA4AkKHFOZ5ZBqGQqNRRWKW0+UAAAAASWUdb5fVul1yueV+z21OlwMAAKYgIHSIaRoq9nskSf1MMwYAAEAWs21b0Vf+U5LkWnWdjMIyhysCAABTuZ0uIJeVFPh0MhRWX2hMwaI8p8sBAABIqoceekhtbW1atGiR1q1bl1jf3t6uH/7wh5Kku+66SzU1NU6ViCSxWrfL7jos+QvluvQGp8sBAACnYAShg4onGpUMM4IQAABkt7a2No2OjmrDhg2KRqNqbW1NbHv00Ud1991364tf/KIeffRRB6tEMtiRcPzcg5Lca26R4fU5XBEAADgVIwgdNNHJmCnGAAAg27W0tGjVqlWSpIaGBjU3N2vJkiWSpFAopGAwmFg+k6amJjU1NUmSNm3alLh9pnK73Rn/GmZq4KVfKxwakKdyocqvvvmCdS7OpX2YDOy/2WMfzg77b/bYh7PD/ptuRgHhRz/6Ud199926+uqrJUnbtm3Tww8/rAceeCCpxWW7Ev94J+MQnYwBAEB2C4VCqqiokCT5/X51dHQkttm2/a73b2xsVGNjY+J6d3f3hS8yhYLBYMa/hpmwh/oUfjU+elBrblNPT+8Fe+xc2YfJwv6bPfbh7LD/Zo99ODu5uv+qqqrOuP4dA8Lu7m51dXVJkjo6OrRnzx5J0vbt23X8+PELXGLuKQ3EA8LeIQJCAACQ3fx+v4aHhyVJIyMj8vv9Z7ydYRipLAtJFt3ylBSNyKxbJXPeIqfLAQAAZ/GOAeHvfvc7/eIXv5Ak/fKXv9Qvf/nLxLb58+cnt7IcMKcwHhD2DI46XAkAAEBy1dfXq6mpSVdffbV27dqlG264IbEtEAiop6dHhmEoPz/fuSJxQVnH22W1bpdcbrnfc6vT5QAAgHfwjgHhkiVLdPPNN+uZZ57RqlWrNG/ePEnxD3HXXnttSgrMZmWBeOfik0NhxSxbLpP/mAMAgOxUV1cnj8ej9evXq7a2VsFgUJs3b9batWt1xx136Dvf+Y4k6VOf+pSzheKCsG1L0Vf+U5LkWnWdjMIyhysCAADv5B0DwtWrV2v16tVavHixLrroIpWXl0uSLMuSadIAebY8blPFfq/6h8PqC41pTmGe0yUBAAAkzbp166ZdX7t2rSSppqZGGzdudKIkJInVukN212HJXyjX6hucLgcAALyLGaV8hw8f1u9+9zv19vbqs5/9rD7xiU/o+eefT3ZtOYFpxgAAAMgmdiSs6JZ4YxL3mltkeHwOVwQAAN7NjALCl19+WQUFBfrDH/6gaDSqefPmafPmzcmuLSdMjBrsGaRRCQAAADJfbMeLUmhARnC+zPrLnC4HAADMwDtOMZ4wNDSkwsJCbd++Xddff71qamr0gx/8INm15YTJgJARhAAAwFmf//zntWDBAtXW1mrhwoWqra1VZWWl02Uhg9hDfYrteEmS5L76v8gwOC0RAACZYEYBYTAY1M9//nMNDQ3ps5/9rPr6+hQIBJJdW06YnGLMCEIAAOCsK6+8UtFoVCUlJdq5c6e+973vqbCwUGVlZaqpqdFnPvMZp0tEmotueUqKRmTWrZI5r9bpcgAAwAzNKCD8q7/6Kz3++ONaunSp1qxZo5/97Ge66qqrkl1bTmAEIQAASBc7d+7U//k//ydx/cYbb9TWrVt166236tChQw5WhkxgHW+X1bpdcrnlfs+tTpcDAADOwYwCwjVr1ujyyy/XsWPH1NnZqTvvvJMuxhfI1IDQsm2ZhuFwRQAAIFcVFhbq4MGDqq2tlSQtXbpUDz74oP7qr/5Kc+bMcbY4pDXbthR95T8lSa5V18koLHO4IgAAcC5mFBB2dHTom9/8pjo7OyVJlZWV+ru/+zvNnz8/qcXlAr/PrUCeR0OjEfWHwioN0OUNAAA447/9t/+m733ve6qurlZtba2OHDkir9frdFnIAFbrDtldhyV/oVyrb3C6HAAAcI5mNAzwRz/6kU6ePKlrrrlG11xzjfr6+vTjH/842bXljLnF8VGEXf0jDlcCAAByWWVlpTZs2KDVq1err69PlZWVuueee5wuC2nOti3FXm+SJLnX3CLDwz+8AQDINDMaQdjW1qaPf/zjuvXW+LlEnnrqKf385z9PamG5ZG5xvtqOD6qrf0TL5pc4XQ4AAMhhpmnqqquu4nzTmDH7aJvsgR6poFjm0tVOlwMAAM7DjEYQBgIB7dy5U8ePH9fx48e1c+dOuhhfQBUl+ZKk432MIAQAAEBmie3ZKklyLb9ChulyuBoAAHA+ZjSC8KabbtJjjz2mN954I7Huox/9aNKKyjVzi+MBIVOMAQAAkEnskSFZB9+SDEOu5WucLgcAAJynGQWE119/vYqLi7Vz505J0iWXXKJVq1YltbBcMhEQHicgBAAAQAaJ7X9dsmIya1bICBQ7XQ4AADhPM5pivHHjRnV3d+tLX/qSvvSlL+nEiRP62te+luzackax3yufx6XhsaiGRiNOlwMAAAC8K9u2FNv7miTJXME5KwEAyGQzCgh7e3s1d+7cxPXy8nL19PQkrahcYxhGopMx5yEEAABAJrCPHJAGeqRAscwF9U6XAwAAZmFGU4wrKir0n//5nyorK5Nt23riiSdUUVGR7NpySmWJX4e7Q+o8OazFlUVOlwMAAAC8o9jeieYkV8owZzTuAAAApKkZBYR/8id/ou9///u6//77E+s+97nPJa2oXFRVViDphI6eDDldCgAAAPCO7OHBKc1JrnS6HAAAMEszblISDAa1bds2SdJll12mlStXJrWwXFNV5pckHe0ddrgSAAAA4J3F9r8hWVa8OUkBzUkAAMh0MwoIJWnlypWEgkk0rzQeEHaeHFbMsuRimgYAAADSkG1biu2LTy82V9KcBACAbEAKlSbyvW6VBXyKWrZO9I86XQ4AAABwRvHmJL1SoERmNc1JAADIBgSEaWT+nAJJ0pFezkMIAACA9BTbs0USzUkAAMgmvKOnkapSzkMIAACA9GUPD8o6tEcyTJqTAACQRQgI00i8k7F0lBGEAAAASEOxfa+PNydZLqOgyOlyAADABUJAmEaqx6cYH+4JybJsh6sBAAAAJk1tTuJaQXMSAACyCQFhGinye1VS4NVYJKau/hGnywEAAAAS7I5WafCkFCiRUb3U6XIAAMAFRECYZmrKA5Kk9u4hhysBAAAAJiWak6xYQ3MSAACyDO/saWZhsFCSdOgEASEAAADSgx0akHVob7w5ybIrnC4HAABcYASEaWYhIwgBAACQZmL7X5dsS2bNCpqTAACQhQgI08z8OQVymYaOnxzWaCTmdDkAAADIcbZlKbZ3vDnJSpqTAACQjQgI04zHZaqqzC9b0mFGEQIAAMBhdkeLNNQnFZbJqF7idDkAACAJCAjTUE15/DyEbx8fdLgSAAAA5LrY3onmJFfKMPjzAQCAbMQ7fBpaXBk/r0vb8QGHKwEAAEAuizcn2SeZNCcBACCbERCmobqKIhmSDnUNKhKznC4HAAAAOSq277Xx5iQrZfgLnS4HAAAkCQFhGvL73Kos9Stq2Wo/wTRjAAAApJ5tWfGAUDQnAQAg2xEQpqmJacYHOplmDAAAgNSzOprjzUmKymTMX+x0OQAAIIkICNMUASEAAACcZO0Zb06yfA3NSQAAyHK806epxHkITwwpHI05XQ4AAAByiB3ql9U+0ZzkcqfLAQAASeZO5oM/9NBDamtr06JFi7Ru3brE+p/85Cc6ePCgIpGIPvnJT2r58uXJLCMj+X1uzZ9ToI6ekNo6B7S8utTpkgAAAJAj4s1JbJmLLqY5CQAAOSBpIwjb2to0OjqqDRs2KBqNqrW1NbHtE5/4hL761a/qi1/8on71q18lq4SMt2x+iSRp35E+R+sAAABA7pjWnGTFGoerAQAAqZC0gLClpUWrVq2SJDU0NKi5uTmxze2OD1wcHR1VTU1NskrIeMsJCAEAAJBi1uFmaahfKppDcxIAAHJE0qYYh0IhVVRUSJL8fr86Ojqmbf/mN7+p1tZWff7znz/j/ZuamtTU1CRJ2rRpk4LBYLJKTQm3233Or6GsbI4KftesnsExRV15qiwNJKm63HI+xwLJwbFIHxyL9MGxSB8cC+Qqa+94c5IVNCcBACBXJC0g9Pv9Gh4eliSNjIzI7/dP2/6//tf/Uk9Pj7797W/r61//+mn3b2xsVGNjY+J6d3d3skpNiWAweF6vYem8Im1/u0ev7npb162cl4TKcs/5HgtceByL9MGxSB8ci/SRLceiqqrK6RKQQeyhvvHmJC6akwAAkEOS9i/B+vp67d69W5K0a9cu1dfXJ7ZFIhFJUl5ennw+X7JKyApMMwYAAECqJJqT1F4kI5/ZKwAA5IqkjSCsq6uTx+PR+vXrVVtbq2AwqM2bN2vt2rX6x3/8Rw0PD8uyLH384x9PVglZYdn8EhmGdKBzQCPhqPK9SW08DQAAgBxlWzHF9r0uSXKtpDkJAAC5JKlp07p166ZdX7t2rSTp7/7u75L5tFklkOdRXUWRDnQOaM/hk7p8cbnTJQEAACALWe37pVC/jKI5MqrqnC4HAACkEGcdzgANC8skSbsO9TpcCQAAALKVtXerJMmkOQkAADmHd/4McHFNPCDcf7RPY5GYw9UAAAAg29iDfbIO76c5CQAAOYqAMAMU+72qKQ8oGrNpVgIAAIALLtGcZBHNSQAAyEUEhBmioWaOJGnnwR6HKwEAAEA2iTcneU2S5FpxlcPVAAAAJxAQZohLastkSNpz+KRGwlGnywEAAECWsNr3ScMDMoqDNCcBACBHERBmiJICnxZXFilq2YwiBAAAwAUzvTmJ4XA1AADACQSEGeTyxeWSpDcOdDtcCQAAALKBPXhSVntzvDlJPc1JAADIVQSEGaShpkwet6m3uwbVPTDqdDkAAADIcPFzD9oy6y6WkV/gdDkAAMAhBIQZxOdxqWFhmSTpjbYTDlcDAACATEZzEgAAMIGAMMNcsSQ+zfj11hOKWbbD1QAAACBTWYf2ScODMkrKZcxb5HQ5AADAQQSEGWZxZZGChXnqC4W1t+Ok0+UAAAAgQ8X2bpFEcxIAAEBAmHFMw9B7llVIkl7df9zhagAAAJCJ7MFe2YdbJJdbrvrLnC4HAAA4jIAwA125pFxul6Hmo/00KwEAAMA5i+0db06y6GIZeTQnAQAg1xEQZiC/z63Vi4KSGEUIAACAc2PHYortf12S5FqxxuFqAABAOiAgzFDvHZ9mvLWlS6PhqMPVAAAAIFNYh/aONyeZS3MSAAAgiYAwYy0IBlRXUajRSEx/bO5yuhwAAABkiNjerZJoTgIAACYREGawGy6ukiT9fs8xRWOWw9UAAAAg3dkDvbI7aE4CAACmIyDMYMvnl6iyJF8DIxG92dbtdDkAAABIc/HRg7bMugYZeX6nywEAAGmCgDCDGYaRGEX4wltHZVm2wxUBAAAgXU1vTnKVw9UAAIB0QkCY4S5dNEelBV519Y9q+8Eep8sBAABAmrIO7ZFGhuLNSSprnC4HAACkEbfTBWB2XKapD1xSrcdeadMz2w/rktoyuUxyXwAAkD5GRkb0wAMPKBQKqbGxUe973/umbb/77rtVWloqSbrrrrtUXV3tRJlZL9GcZCXNSQAAwHQEhFngssXlen73UXUPjOr11m5dVT/X6ZIAAAASnnvuOV1zzTW65ppr9NWvflXXXHON3O7Jj6FFRUW67777nCswB9gDPTQnAQAAZ8VQsyzgMg3dfEn8P+1NOzvoaAwAANJKc3OzVq1aJdM0VVNToyNHjkzbPjQ0pK985St68MEHFQ6HHaoyu8X2viZJMhevkuGjOQkAAJiOEYRZ4pJFc/T8riPq7BvRH/Z16n0XVTldEgAAgCRpeHhY+fn5kiS/369QKDRt+8aNGxUIBLR582Y1NTXp9ttvP+0xmpqa1NTUJEnatGmTgsFg8gtPIrfbnbLXYMei6mx5Q5JU9p4PyJfh+25CKvdhNmL/zR77cHbYf7PHPpwd9t90BIRZwjQMffDyhfrRc/vVtOOILq8rVyDf43RZAAAgh/T19ek73/nOtHUlJSXy+/0aGRmR1+vV8PCwCgoKpt0mEAhIktasWaPf/OY3Z3zsxsZGNTY2Jq53d3df2OJTLBgMpuw1xA7slBUalFFaoYG8EhkZvu8mpHIfZiP23+yxD2eH/Td77MPZydX9V1V15gFlBIRZZHl1qZbPL9G+I316avth/cV765wuCQAA5JCSkpIznkvwiSee0K5du3T11Vfr0KFDmj9/fmJbNBqVbdvyeDzav3+/KioqUlhxbphoTuKiOQkAADgLAsIs81+urFHz0X5tbe7Se5dVaH5ZwbvfCQAAIIluuukmffe739VTTz2lxsZGud1ubd++XZZlqa6uTvfff7/y8vJUUFCgz3/+806Xm1Xs/m7ZR1oll1vm0tVOlwMAANIUAWGWmVucr2uWV+j3ezv1H1sO6r/fulIm/ykGAAAO8vv9uueee6atu/TSSxPL3/jGN1JcUe6gOQkAAJgJuhhnoQ9cWq1Ankdvdw1qa0uX0+UAAADAAXYsqtj+1yVJrhVXOVwNAABIZwSEWSjf69afXlUrSfrN6+3qHw47WxAAAABSzjq4RxoNySirkFGx0OlyAABAGiMgzFKrasq0srpUo5GY/n3L206XAwAAgBSL7dkiKT56kOYkAADgnRAQZinDMPRn76mVz21qd/tJ7TjY43RJAAAASBGrv1v20QOS20NzEgAA8K4ICLNYSYFPH7yiRpL0y1fb1Bcac7giAAAApIK1d6ukieYk+Q5XAwAA0h0BYZZ7T/1cragu0Ug4pkdfPiDLtp0uCQAAAEkUb07yhiSakwAAgJkhIMxyhmHoI1fXqSDPrdbOAb301jGnSwIAAEASWW+/Nd6cpFLG3AVOlwMAADIAAWEOKMz36o6rF0uSnnrzsNpPDDlcEQAAAJIltne8OclKmpMAAICZISDMESsXlOqa5ZWKWbYeeaFZQ6MRp0sCAADABWb1nZB9tC3enGQJzUkAAMDMEBDmkA9dsVA15QH1D4f10xdbFLM4HyEAAEA2mWxOcokMX57D1QAAgExBQJhD3C5Tn3hfvQJ5HrV2DuipN9udLgkAAAAXiB2LKtY83pxkJc1JAADAzBEQ5pjiAq/ufN9SmYb0wu5jeq21y+mSAAAAcAFYb++WRodlzJkno7za6XIAAEAGISDMQYsri/Qna2olSb945W21Hut3tiAAAADMWmzPeHOSFTQnAQAA54aAMEddvbxS16+cJ8u29fDvmnW8b9jpkgAAAHCerL4Tso+9Lbm9Mpde6nQ5AAAgwxAQ5rAPXrFQFy8s02gkph817VNfaMzpkgAAAHAerL3x0YPmkktkeGlOAgAAzg0BYQ4zDUMfu26xFpYHdDIU1oPP7NXQSMTpsgAAAHAO7GhEsf3bJEmuFWscrgYAAGQiAsIc53W79Kn3L9e8Ur9ODIzqwWf3angs6nRZAAAAmCHr7d3S2LCMYBXNSQAAwHkhIIT8Prc+/YHlKi/K07GTw/pR0z6NhAkJAQAAMkFs71ZJNCcBAADnj4AQkqTCfK8+c/MKlRZ41d49pAefYSQhAABAurNOdk02J1lyidPlAACADEVAiISSAp/++60rVRbwqaMnpH95eo8GR8JOlwUAAICzmGxOcinNSQAAwHkjIMQ0ZYE8/e2tF2lucZ46Tw7rX57aQ3djAACANGRHI4o1jzcnWUlzEgAAcP4ICHGa4gKvPnvLRYnGJd/77Vs62htyuiwAAABMYbXtlsZGZATny6Q5CQAAmAUCQpxRIN+j/37LSi2aW6j+4bD++ak92n+kz+myAAAAMC42Pr3YtYLRgwAAYHYICHFWfp9bn755hS6pnaOxSEw/fm6ftrZ0OV0WAABAzrNOHpfdeVDyeGUuudTpcgAAQIYjIMQ78rhMffz6Jbrx4ipZtvT4K236j60HFbMsp0sDAADIWdaerZIkc8lqGV6fw9UAAIBMR0CId2Uahm6/fKH+4r2L5DINvby3Uw8+s5cOxwAAAA6INyd5QxLTiwEAwIVBQIgZu6q+Qv/9lpUqyveo7figHnhit9pPDDpdFgAAQE6x2nZK4VEZ5dUyy+c7XQ4AAMgCBIQ4J7VzC3X3hxpUO6V5yQu7j8qybadLAwAAyAmxvfHpxYweBAAAFwoBIc5Zkd+r/3bzCl27olIxy9Zv3mjXj5r2aYApxwAAAEll9R6X3XlI8vhkLrnE6XIAAECWICDEeXG7TP3Jmlqtu2mZ/D63mo/269u/3qm9HSedLg0AACBrWXu3SJLMpZfK8NCcBAAAXBgEhJiVlQtK9aUPr9KSeUUKjUb14+f267E/HNDwWNTp0gAAALKKHQkr1rxNkuRacZXD1QAAgGxCQIhZK/Z79ekPrNAHL18ot2notdYT+tZ/7NBb7b1OlwYAAJA1rLZd8eYkcxfIDFY5XQ4AAMgiBIS4IEzD0A0XV+mLH16lmvKABkYieuh3zfrZSy0aGok4XR4AAEDGi41PL6Y5CQAAuNDcyXzwhx56SG1tbVq0aJHWrVuXWP/ggw/q8OHDkqS77rpLNTU1ySwDKTS3OF9/e+tF+sO+Tj257bDefLtH+4706ZbVC/Te+gqZpuF0iQAAABnH6umUfbxd8vpkLqY5CQAAuLCSNoKwra1No6Oj2rBhg6LRqFpbWxPb/vRP/1QbN27U3/7t3+rxxx9PVglwiGkaum7lPH3pw6tUX1WskXBM/77loL77m1062DXodHkAAAAZZ2L0oLlktQyP1+FqAABAtknaCMKWlhatWrVKktTQ0KDm5mYtWbJEkjR37lxJksvlkmmeOaNsampSU1OTJGnTpk0KBoPJKjUl3G53xr+GcxUMSvcsmq9trZ36+e/26EjvsL7/5Fu65qJq/fk1y1RamO9IXbl4LNIVxyJ9cCzSB8cifXAskC7sSFhWy5uSJNdKphcDAIALL2kBYSgUUkVFhSTJ7/ero6PjtNv87Gc/0+23337G+zc2NqqxsTFxvbu7OzmFpkgwGMz413C+ako9+tKHL9bzO4/qhbeO6g9vdWjrvqO6bmWlbri4SvnepM50P00uH4t0w7FIHxyL9MGxSB/ZciyqqmhmkemsAzsnm5PM4XgCAIALL2lTjP1+v4aHhyVJIyMj8vv907b/5je/UXV1tZYvX56sEpBGvG6Xbr1sgf7nn1yiVTVlisQsPb/rqDZt3q6X9x5TNGY5XSIAAEBaiu3dKklyrbjK4UoAAEC2SlpAWF9fr927d0uSdu3apfr6+sS2HTt2aP/+/frzP//zZD090lSwKE+fuKFen7v9Ii2aW6jhsaj+Y+sh/X//vkNbW7oUswgKAQAAJlg9x2R3tUvePJmLVzldDgAAyFJJCwjr6urk8Xi0fv16maapYDCozZs3S5J+/OMf68SJE/rqV7+qBx98MFklII3VlBfqs7eu1N/cWK+5xfk6OTSmx19p0zd+tUNbmrsYUQgAACAptme8OclSmpMAAIDkSerJ39atWzft+tq1ayVJDzzwQDKfFhnCMAxdtLBMK6pLteNgj5p2dqirf1S/eLVNz+3s0E2r5uvyxeXyuJKWYwMAAKQtOxKW1TrenITpxQAAIIlS2x0COAPTNLS6LqhLaueMB4VH1NU/ol+++raefrND166o1HuXVcjv49sVAADkDuvADik8JqNiocw5lU6XAwAAshiJC9LG1KBw56EePb/rqI6dHNZTbx7Wc7uOaM2SubpuZaXmFOY5XSoAAEDSTTYnWeNwJQAAINsRECLtmKahSxfFg8KWYwN68a2jaj7arz/s69Qr+zt10YIyXbO8Qosri2QYhtPlAgAAXHBW91HZXYfjzUnqaE4CAACSi4AQacswDNVXFau+qlhHe0N6ac8xbX+7R7vbe7W7vVflRXl677IKXbGkXPlevpUBAED2SIwerL+M5iQAACDpSFWQEarKCvSX1y7RbZct1NaWLv1x/3GdGBjVr187pCe3Hdbqujl6T32FqucUMKoQAABkNDsyJqsl3pzEZHoxAABIAQJCZJRiv1cfuKRaNzVUac/hPr26/7hajvVra8sJbW05ocqSfF2xpFyr64Iqyue/7QAAIPNYrTukyJiMihqZZTQnAQAAyUdAiIzkMk011JSpoaZMJ/pH9GrzcW070K3OvhE98Xq7fvtGu5bNL9EVS8q1srpUbpfpdMkAAAAzkphevJLRgwAAIDUICJHxyovz9eEra3X7ZQu170ifXm89ob0dfYkvv8+thpoyXVo7R3UVRU6XCwAAcFZW9xHZJzpoTgIAAFKKgBBZw+0ydfHCMl28sExDIxFta+vWawdOqPPksLY0d2lLc5cK8z1as2y+ls0rUE15QCbnKwQAAGkktmdKcxK3x+FqAABAriAgRFYK5Ht0/UXzdN3KSh07OawdB3u0/e0e9Q6N6bntB/Xc9vj5DC+pnaOGmjItDAZkmoSFAADAOXZkTFbreHOSlVc5XA0AAMglBITIaoZhqKqsQFVlBbp19QJ19IS0v3NYW/Z1qC8U1kt7jumlPccUyPNo5YISXbSgTEvnFcvj5pyFAAAgteLNScIyKmtlllY4XQ4AAMghBITIGYZhaEEwoNXLa3XTReVqPzGkHQd79Nbhkzo5NJbohOxxm1pWVayLFpRpRXWJCvKY3gMAAJIvtmeLJMm1guYkAAAgtQgIkZNMw1Dt3ELVzi3Uh6+s0bGTw3rr8Em91X5SR3pD2t1+UrvbT8owpAXBgJZVlWj5/GJVz2EqMgAAuPCsEx2yu49IvnyZdQ1OlwMAAHIMASFy3tRpyB+4pFp9obFEWNh2fEDtJ4bUfmJIz+7okN/nVv28Yi2bX6L6+cUqyvc6XT4AAMgCsb00JwEAAM4hIAROUVLg0zXLK3XN8kqNRWI60DmgfUf6tP9In3qHxrT9YI+2H+yRJM0r9WvJvCItqSzWoopC5Xv5kQIAAOfGDo/Jat0uSTJX0JwEAACkHmkG8A58HpdWLijVygWlsm1b3YOj2n+kX/uP9OlA54COnRzWsZPD+v2eThmGVF1WoMXzirS4sliL5hbK53E5/RIAAECas1q3T2lOMtfpcgAAQA4iIARmyDAMlRflq7woX9euqFQkZulQ16BaOwd0oDM+FflwT0iHe0J6YfcxmYahBcECLa4sUu3cQtWUF8rv40cOAABMl5hevJLRgwAAwBmkFcB58rhMLZlXrCXziiVJY5GYDnYN6kDngFo7+9XRE9KhE0M6dGIocZ+KkvxEc5Ta8kLNKfTJMGh6AgBArppsTuKXuehip8sBAAA5ioAQuEB8HpeWzS/RsvklkqTRcFRvjweGB7sG1dET0vG+ER3vG9GW5i5JUiDPkwgMa8oDml9WII/bdPBVAACAVIrt2SKJ5iQAAMBZBIRAkuR53VpRXaoV1aWSpEjMUkdPSAe7BnWwa1CHugY1NBrR7vZe7W7vlSSZhqHK0nwtmBPQgmBAC4IFqijxy2UyyhAAgGxjh0dlte6QJJkr1jhcDQAAyGUEhECKeFymFs0t1KK5hZIUb3oyMBoPDE8Mqr07pON9wzraG//a0tKVuF9VmV8LggEtDAZUPadAc4ryZDI1GQCAjGa1bpeiYRnzFtGcBAAAOIqAEHCIYRgqL85XeXG+rlwa/6MgHImpozekw90hdXQP6XDPkHoGx047l6HXbWpeqV9VZQWaXxa/rCzxMz0ZAIAMYdv25PTiFTQnAQAAziIgBNKI1+NSXUWR6iqKEutCoxF19IR0uDveJbmje0gDI5HTQkPDkOYW5atqPDCcuAzkcT4jAADSTeTYQdk9x6Q8v8w6mpMAAABnERACaa4gzzOt+YkkDY1Gxqcih3T0ZPzyRP+Ijo9/vfl2T+K2gTyPKkvyVVHiV0VJvipL/aosyVe+lx9/AACcEtr2oiTJVX+5DBfvyQAAwFl8GgEyUCDPo/qqYtVXFSfWRaKWOhPnMIwHh8d6Qxoajai1M6LWzoFpj1GU71Fl6XhoWBIPDeeW+JXncaX65QAAstybb76phx9+WIWFhdq4ceNp23//+9/r6aefViAQ0Be+8AX5/X4Hqkwde2xUI3u2SqI5CQAASA8EhECW8LjN8c7HgcQ6y7bVHwqrs29YnX0j6jw5rON9I+rqH9HASEQDI/1qPto/7XGK/V6VF+epvChfc8cvy4vzVFLgozEKAOC8LF26VN/85je1YcOG07ZFo1E9++yz+upXv6otW7aoqalJH/7whx2oMnWs1jdlR8IyqupklpQ7XQ4AAAABIZDNTMNQacCn0oBPK6pLE+sty1bv0Jg6++KB4cRlV/+I+ofD6h8Oq/XY9BGHbpehYFG+5hZNhoYTl0xXBgC8k0AgcNZtnZ2dWrhwoVwulxoaGvSDH/zgjLdrampSU1OTJGnTpk0KBoNJqTXZbNtWV/MbkqSSNY3yZ+jrSAdutztjvw/SAftv9tiHs8P+mz324eyw/6bjr3ogB5mmoWBRnoJFebp44eT6mGXr5NCYTgyMqKt/VCcGRnSif0QnBkY1OBJR58lhdZ4cPu3xAnkezSn0aU5h3pTL+HIgzyODkYcAgLMIhULKz8+XJPn9foVCoTPerrGxUY2NjYnr3d3dKanvQrNtW8bVH1ZB+x6Fggs1nKGvIx0Eg8GM/T5IB+y/2WMfzg77b/bYh7OTq/uvqqrqjOsJCAEkuKYEhyuqp28bCUfVPTCqrvHAcCI4PDEwoqHRiIZGI9O6Kk/wuk2VFeZpTuD0ALGk1ErRKwMApEJfX5++853vTFtXUlKi//E//sdZ7+P3+zUyMiJJGhkZUUFBQRIrdJ5hGDIqFqrkosty8o8SAACQnggIAcxIvtd92jkOpfh5DgeGw+oZHFXP4Nj45eTySDh21pGHprFDxQVelRZ4E1OhSwt8Kgv4VFLgU0mBV26XmaqXCACYpZKSEt13333ndJ958+bp8OHDsixLO3fu1NKlS5NTHAAAAM6KgBDArJiGMR7m+bS48vTtw2PR00LDieX+4bBODo3p5NCYdHzwtPsakor8XpWMB4gTweHksldeN12XASDdHThwQD/72c90+PBhbdy4UX//93+vPXv2yLIsXXbZZXr/+9+v9evXq6CgQHfffbfT5QIAAOQcAkIASeX3ueX3nT7yUJKKS0rVeuioTobGdHJoPCwMjSUuJxqm9A+Hzzh9WZIKfG4VF3hV7I9/lRT44stT1vk8hIgA4KTFixfr3nvvnbbu0ksvTSxff/31uv7661NcFQAAACYQEAJwjMftUnlxvsqL88+4PWZZ46MMTw8PTw6NqS8UVmgsqtBYVEd7T5/CPCHP40oEhiWJ4NCn4gKvSvxeFfm9yve6aKYCAAAAAMhJBIQA0pbLNFUWyFNZIO+M2y3bVmg0ov7hsPpC46MNQ5OjDvtCY+oPhTUaiWm0b0TH+0bO+lxul6HCfK+K8j2JyyK/V4X5nvg6f3xdQZ5HJkEiAAAAACCLEBACyFimEQ/1CvO9qp5z5tvYtq3hsaj6poaHobD6hsemBYrhqDV5PsR3fE4pkDc1PPSq0D9+mT95GcjzyOOmwQoAAAAAIP0REALIaoZhqCAvPvJvflnBWW83FolpYCSsweFI/HIkfjkwHEksD45ENDwW1cBIRAMjkXd9bp/bVEGeR4F8jwrz4qFhIM+jQL57cnl8u9/rlmkyMhEAAAAAkHoEhAAgyedxqdyTr/KiM58PcUI0Zp0SHk6EifHlgeGIhkbjX2NRS2NDY+p9l1GJkmQYUoHPo0CeOxEaTg0RC/LcKvC5VZDniTd+IVAEAAAAAFwgBIQAcA7cLlOlAZ9KA753vJ1t2xqNxDQ0MhEYRhPB4eBIRKHRySBxaDSq4bHJ7dLZz5U4wZCU73PL7xsPDn3xEDFxfTxIJFQEAAAAALwbAkIASALDMJTvdSvf6z5rl+apYpY1GSJOCxXDGhqJKjQWn94cGosqNBrRSDim4bF4sNg905oUDxULEsFiPFTM97oVLD0pOzomvy9+feplnsdFsAgAAAAAWYyAEADSgMs0Vez3qtjvndHtY5atkXBUodEp4eHZls8QKp7u2Fmfy5CU53VNCw7zva4zhon5Xld8ZKPXrXyfWz63KYOuzwAAAACQ1ggIASADuUwjcX5C6d1HKErTQ8Xhsch4cBjVcDgquTzq6RvUyFj8+shYTCPheJg4GolpJBz/msn5FKcyDUP5Ppf8XrfyvC7leeIhYp43PjIxsex1Kd8zZXn8toxeBAAAAIDkIyAEgBzxTqFiMBhUd/eZJytb48HixAjE+HJ0fHlyXeIyHEsEjZGoFR/NOHqmUYsz4/O4lOdxJUYxTgsW32E5z+uSz+OSz03ICAAAAADvhIAQAPCOTNNQQZ5HBXmec75vNGYlRiSORuKB4mh4clTiaDiq0XBMI5EzL49GYhob/+ofPv/X4HWbiaDRN+Ur75TL05dN+Txu+Tym8jwueT0umUyZBgAAAJBlCAgBAEnjdpkqyveqaGazoE9j2bbGIrF4cDgeLJ59eTyAHF8ei1gajcQUjsQUjloKRy0NjkRm/Zp842HjmQPFqQGkKa/blQgnve4zr3MxuhEAAACAwwgIAQBpy5zSDbpUvvN6DMu2FY5aiZGIY5HJkYlTRyiOhk9fd9r1qJX40gUIGyXJbRryelzyuePhYUG+T6asyXWe8UDR7Zq2zjceNE69r88Tv53bbTLSEQAAAMCMERACALKaaRjxcxJ6XLN+LMu2FY7EEqMTzxYohqPx28QvJ0Ywnr5uLBpT1LIVHYtqeKL/S//IrOuU4tOqJ0Yret2mPFOue1zxZc/4tvh2l7yuM9x2yu2nbmPkIwAAAJA9CAgBAJgh0zDGOy1LxRfg8WzbVjRmx0PDaEzhiKX8gkId7+5993Bx6raoFQ8uxx8jErMS06qTxWUa48Hh9LDR4zbldU0NEye3n3p7j2sygDx12T2+TBAJAAAAJB8BIQAADjEMQx63IY/bVIHiTWCCwVIVe2OzelzLshWOxUPEyHiIOBEaTlxPLMfGt0etROAYiU4NGadum1gfU8yyFbPiIyalCzPd+kxMw5gSHE4uu98hXPS4x7ef7TbvsM5lGjKYng0AAIAcQ0AIAECWMU1DeeaFmVZ9JrZtK2bZ0wPERAA5JXyMWorEJpvETAsnY1YiiJxYjsZOXz/RqGYsMrvQdKYMKTF60edx60v/5WLlefm4BAAAgOzGJ14AAHBODMOQ22XI7TLl9yXvo8REEDkRFkZPCRTPFDJGYnY8aDzTbd8hiJxYjll2fDlqaXgsKpfLTNrrAwAAANIFASEAAEhLU4PI/BQ9p2XZiQAxUFQia2woRc8MAAAAOId/iwMAAIwzTUNej0sFeR7NKcrnfIQAAADICQSEAAAAAAAAQA4jIAQAAAAAAAByGAEhAAAAAAAAkMMICAEAAAAAAIAcRkAIAAAAAAAA5DACQgAAAAAAACCHERACAAAAAAAAOYyAEAAAAAAAAMhh7mQ++EMPPaS2tjYtWrRI69atS6zfvHmznn76ad144436y7/8y2SWAAAAAAAAAOAdJG0EYVtbm0ZHR7VhwwZFo1G1trYmtt100036/Oc/n6ynBgAAAAAAADBDSQsIW1patGrVKklSQ0ODmpubE9tKSkpkGEaynhoAAAAAAADADCVtinEoFFJFRYUkye/3q6Oj45zu39TUpKamJknSpk2bFAwGL3iNqeR2uzP+NWQLjkX64FikD45F+uBYpA+OBQAAAHJF0gJCv9+v4eFhSdLIyIj8fv853b+xsVGNjY2J693d3Re0vlQLBoMZ/xqyBccifXAs0gfHIn1wLNJHthyLqqoqp0sAAABAmkvaFOP6+nrt3r1bkrRr1y7V19cn66kAAAAAAAAAnKekBYR1dXXyeDxav369TNNUMBjU5s2bJUnPP/+8HnnkEf3+97/X//2//zdZJQAAAAAAAAB4F0mbYixJ69atm3Z97dq1kuJdjG+66aZkPjUAAAAAAACAGUjaCEIAAAAAAAAA6Y+AEAAAAAAAAMhhBIQAAAAAAABADiMgBAAAAAAAAHIYASEAAAAAAACQwwgIAQAAAAAAgBxGQAgAAAAAAADkMAJCAAAAAAAAIIcREAIAAAAAAAA5jIAQAAAAAAAAyGEEhAAAAAAAAEAOIyAEAAAAAAAAchgBIQAAAAAAAJDDDNu2baeLAAAAAAAAAOAMRhCmyD333ON0CRjHsUgfHIv0wbFIHxyL9MGxQDLx/TV77MPZYf/NHvtwdth/s8c+nB3233QEhAAAAAAAAEAOIyAEAAAAAAAAchgBYYo0NjY6XQLGcSzSB8cifXAs0gfHIn1wLJBMfH/NHvtwdth/s8c+nB323+yxD2eH/TcdTUoAAAAAAACAHMYIQgAAAAAAACCHERACAAAAAAAAOcztdAG54KGHHlJbW5sWLVqkdevWOV1OVuvt7dU3vvENdXR06JFHHpHL5Trj/p/pOpy/lpYWPfzwwzIMQ4sXL9bf/M3f6Ne//rVee+01lZeX62//9m/ldrtnvA7nr729XQ8++KBM01RlZaU++9nP6uGHH+bnwkFPPPGEtmzZoo0bN/I7yiFdXV363//7f2v+/Plyu936h3/4B35HIWXO9HkFM3emzxiYuTN9LjAMw+myMtLU93PM3Jneg3HuXnzxRb344ouyLEtf+MIXVFZW5nRJGWP79u3693//d0nS0aNHddddd2nNmjXOFpUGGEGYZG1tbRodHdWGDRsUjUbV2trqdElZLRAI6N5779XSpUslnXn/z3QdZqe8vFzr16/Xxo0bNTAwoD179uitt97Sxo0btXDhQr322mvq7++f0TrMTlVVlb72ta9pw4YNkqTW1lZ+LhwUiUR08OBBSfyOclpDQ4Puu+8+/cM//MOMfx/xOwoXwqmfV3BuTv2M0d7e7nRJGeXUzwUHDhxwuKLMNPX9HOdu6nswzl1vb6/27Nmj9evX67777iMcPEeXXnqp7rvvPt13330KBoNatWqV0yWlBQLCJGtpaUl8szU0NKi5udnhirKb1+tVIBBIXD/T/p/pOsxOSUmJvF6vJMnlcunw4cNauXKlJGnVqlVqbm7WgQMHZrQOszN1dJPb7dauXbv4uXDQ888/rxtuuEESv6Oc9tZbb2n9+vV64oknZvz7iN9RuBBO/byCc3PqZwzT5E+ac3Hq54JgMOhgNZlr6vs5zt3U92Ccu+3bt8uyLG3YsEE//vGPZVmW0yVlpOPHj6u4uFh5eXlOl5IWeDdNslAoJL/fL0ny+/0aHh52uKLccqb9P9N1uDAOHTqkgYEBFRQUKD8/X1J8H4dCIQ0PD89oHWbv9ddf15e//GX19/crFovxc+GQaDSqt956SxdffLEkfkc5qbS0VA888IC+8pWvaNeuXWpra+N3FJBhJj5jVFdXO11Kxpn6uYCw+tyd+n6Oc3Pqe/ChQ4ecLinj9Pf3KxqNav369fJ6vcxoOE9btmxhavEUBIRJNvUPuZGRkcQfeEiNM+3/ma7D7A0NDenHP/6xPvvZz8rv92tkZESSNDw8rIKCghmvw+xdccUV+ta3vqU5c+bI5XLxc+GQl156Sddee23iOr+jnOPxeJSXlyeXy6XLL79cFRUV/I4CMsjUzxg4d1M/F2zbts3pcjLOqe/nODenvgcfPnzY6ZIyjt/vT8xouPjii3XkyBGHK8pMb7zxhq644gqny0gbBIRJVl9fr927d0uSdu3apfr6eocryi1n2v8zXYfZicVi+qd/+id94hOfUElJiRYvXqw9e/ZIiu/jpUuXzngdZicSiSSWJ0Y+8XPhjKNHj+rZZ5/V17/+dXV0dGhwcJBj4ZCJkE+S9u3bp8rKSn5HARni1M8YODenfi6YmK6NmTv1/fzJJ590uqSMcup7cEVFhYPVZKZly5YlRl4ePHhQc+fOdbiizNPX1ye3263CwkKnS0kbtN1Lsrq6Onk8Hq1fv161tbVasmSJ0yVltWg0qvvvv1+HDh3S17/+dX3sYx874/6f6Tqcv1dffVWtra3613/9V0nSxz/+ca1YsUL33nuvgsGgPvjBD8rtds9oHWZn+/btifO7zJs3T5/5zGf08MMP83PhgDvvvDOxfO+99+ojH/mIfvKTn3AsHLB37149+uij8ng8Wr58uZYuXcrvKKTMmT6vEDbP3Jk+Y/CPk5k79XMBJ+c/d6e+n992220OVpN5zvQejHNTW1srr9er++67T4WFhfrQhz7kdEkZ57XXXtOVV17pdBlpxbBt23a6CAAAAAAAAADOYIoxAAAAAAAAkMMICAEAAAAAAIAcRkAIAAAAAAAA5DACQgAAAAAAACCHERACAAAAAAAAOYyAEEBW6urq0h133KFNmzZp27Zteuyxx9TV1XXBn6ejo0OPPfaY3nrrrcS673//+7rjjjt04MCBC/58AAAAAABcaG6nCwCAZCgqKtLdd9+tsrIyvfLKK3r66ad10UUXae7cuef0OLFYTC6X66zbOzo69Itf/EKSdNFFF0mSbr75Zl166aWqqKg4/xcAAAAAAECKGLZt204XAQAXWldXlz73uc/J5/NpbGxs2rbHHntMzc3Nevjhh9Xe3q6ysjJ95CMf0bXXXpu4X319vXw+n9rb2/Wtb31LX/va13Ts2DFJ0qJFi/TpT39aPp9Pn/vc56Y99le+8hW98MILevHFF3X//fdr8eLFampq0q9//WudPHlS1dXV+uu//mstX75cL7zwgv75n/9ZV199tY4cOaLu7m595CMf0e23366jR4/qe9/7ng4dOiSv16sFCxZow4YNKdt/AAAAmJlvf/vbKi4u1sGDB9XT06MvfOELevbZZ9Xa2qrly5frs5/9rNMlAsC7YooxgKy2cuVKXXLJJZKkP//zP9fdd9+toaEhbdq0ScPDw1q7dq3Ky8v1T//0Tzp48GDifs3NzVq0aJE++tGPyjAMrVmzRuvWrdOf/umf6tChQ3rooYdUVFSk22+/XZJ01VVX6e6771Z1dfW059+9e7cefPBBFRUV6ZOf/KS6u7v1jW98Q4ODg4nbvPXWW3r/+98vSfrpT3+qaDSqp59+WgcOHNCdd96pj33sYwoGg0neUwAAADgf7e3tqqio0MaNG9XY2Kh/+Zd/0Z133qlvf/vb2rZtmyKRiNMlAsC7YooxgKxmGIYqKyu1Y8cOXXzxxbrooou0bds2DQ0NaWhoSD//+c8Tt929e7fWrFkjKT5K8M4775Qk9fb2aseOHWpubtbEoOv29nbl5eVp+fLl+u1vf6sFCxbommuuOe35t23bJkm64447tGrVKnV3d+tXv/qVWlpaEre58cYbdeutt+qNN97Qjh071NfXp3nz5sm2bb355ptavHhxIogEAABA+giHwwqFQonPaoZh6KabblJpaakkyTRNud382Q0g/fGbCkDWMwzjjOuvv/56XX/99YnrU89POPGhTpKefPJJ7d+/Xx/84Ae1evVq/cu//ItGRkYuWC2BQECSEuc6tCxLt956q+bPn689e/bo9ddf1+bNm/WP//iPqqqqOq/nBQAAwIXX0dGhuro6mWZ8ct6hQ4d08803S5J6enpUVlZ21s+iAJBOmGIMIOsVFBRIkv74xz9q27Ztqq+vVyAQ0I4dO3T06FEdPnxY//Ef/6He3t53fJxQKKQ9e/aop6cnsW4i3Nu3b5/+8Ic/KBwOT7vPZZddJkl6/PHH9eyzz+r5559XQUGBli5d+o7P9cwzz6i5uVmVlZWqqKiQbdvq6+s715cOAACAJGpvb1dNTU3i+qFDh7Rw4cLTlgEg3REQAsh61113nebPn69nnnlGP/nJTxQIBHTPPfeosrJSP/3pT7V582Z5vV6Vl5ef8f633XabFi9erFdeeUW9vb1asGBBYtvy5cvV0NCgvXv36oEHHph2bkFJuvjii/WZz3xG/f39euSRRzRnzhz9/d//vQoLC9+xZo/HoxdeeEE/+MEPtHfvXt1yyy1avnz57HcGAAAALpj29nbV1tZKik83DofDiX8gHzp0aFp4CADpjC7GAAAAAAAAQA5jBCEAAAAAAACQwwgIAQAAAAAAgBxGQAgAAAAAAADkMAJCAAAAAAAAIIcREAIAAAAAAAA5jIAQAAAAAAAAyGEEhAAAAAAAAEAO+/8BtyPMJDXbpoMAAAAASUVORK5CYII=",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"low, high, step = 0, 5000, 1\n",
"plot_all(cost_history, m, q, low, high, step)"
]
},
{
"cell_type": "code",
"execution_count": 137,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"8272 passi e 827200 gradienti calcolati per arrivare a distanza minore o uguale di 0.1 dall'ottimo\n"
]
}
],
"source": [
"near_opt(m, min_dist=1e-1, ge_per_step=n)"
]
},
{
"cell_type": "code",
"execution_count": 138,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA7sAAAHzCAYAAADhDgreAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAABRJElEQVR4nO3dfXjU9Z3v/9c3M0CSmZC7yY3cHQV1QRCBJrY1tAgi5cTWtTVLlZq92u4e16PXcd2eegmnrbZaKtZ61cuqx/bStdu4Z1sXvPm5zakpBfGY1jVIskgsVq2VrhByR0Im4SaT+f7+CDNkkkxuZ+Z7M8/HdXmRTGaST+aTxHl9P5/P+22YpmkKAAAAAAAXybB6AAAAAAAAJBphFwAAAADgOoRdAAAAAIDrEHYBAAAAAK5D2AUAAAAAuA5hFwAAAADgOoRdAAAAAIDrEHYBAEix888/X1lZWcrJyVFeXp6uuOIKPfHEEwqHw+M+9k9/+pMMw1AoFErqGFP1dQAASBbCLgAAFnjppZfU09OjDz/8UFu2bNEDDzygv/mbv7F6WAAAuAZhFwAAC+Xm5uraa6/VL37xC/3TP/2TDh48qF/+8pdauXKlZs+erfnz5+vb3/529P6f/vSnJUl5eXny+/363e9+p/fff1/r1q1TYWGhAoGAvvSlL6mrqyv6mAceeEBz585VTk6O/uIv/kK/+c1vJEnhcFjbt2/XokWLVFhYqE2bNqmzszPu1wEAwEkIuwAA2MDll1+uefPm6f/9v/8nn8+nn/3sZ+rq6tIvf/lL/e///b/1wgsvSJJeffVVSVJXV5eCwaA++clPyjRNbd26VUeOHNHvf/97/fnPf44G5HfeeUePPvqoGhoa1NPTo5dfflnnn3++JOlHP/qRXnjhBe3du1dHjhxRfn6+brvttrhfBwAAJyHsAgBgE3PmzFFnZ6euvPJKXXrppcrIyNDy5ct14403au/evXEfd+GFF+rqq6/WrFmzVFRUpK997WvR+3s8Hp0+fVpvv/22+vv7df7552vRokWSpCeeeELbtm3TvHnzNGvWLH3729/Wjh07OKcLAHAFwi4AADbx0UcfqaCgQP/+7/+utWvXqqioSLm5uXriiSfU3t4e93HHjh3TDTfcoLlz52r27Nm66aabove/8MIL9fDDD+vb3/62iouLdcMNN+jIkSOSpA8//FCf//znlZeXp7y8PC1ZskQej0fHjh1LyfcLAEAyEXYBALCBhoYGffTRR1q9erU2b96sa6+9Vn/+85/V3d2tW265RaZpSpIMwxjx2P/1v/6XDMPQW2+9pRMnTuiZZ56J3l+SNm/erNdee00ffvihDMPQXXfdJUmaP3++/u///b/q6uqK/nfq1CnNnTt31K8DAICTEHYBALDQiRMn9G//9m+64YYbdNNNN+nSSy9VT0+PCgoKlJmZqTfeeEP/5//8n+j9i4qKlJGRoT/+8Y/R23p6euT3+5Wbm6uPPvpIDz74YPRj77zzjnbv3q3Tp08rMzNTWVlZysgY/N//Lbfcom984xv68MMPJUltbW168cUX434dAACchLALAIAFPve5zyknJ0fz58/Xtm3b9LWvfU1PP/20JOnxxx/X3XffrZycHN17773atGlT9HHZ2dn6xje+oYqKCuXl5en111/XPffco/379ys3N1fXXHONvvCFL0Tvf/r0aW3ZskWBQEClpaVqbW3V/fffL0n6+7//e1177bXasGGDcnJy9IlPfEL//u//HvfrAADgJIY5dJ8TAAAAAAAuwMouAAAAAMB1CLsAAAAAANch7AIAAAAAXIewCwAAAABwHcIuAAAAAMB1CLsAAAAAANfxWj2AVDhy5IjVQ7ClQCCg9vZ2q4eBYZgXe2Je7Il5sR/mxJ6YF3tiXuyHObGnseZlzpw5cR/Hyi4AAAAAwHUIuwAAAAAA1yHsAgAAAABch7ALAAAAAHAdwi4AAAAAwHUIuwAAAAAA1yHsAgAAAABch7ALAAAAAHAdb6q/4OOPP679+/crNzdXDz30kCTp2Wef1W9+8xvNnj1bknTjjTdq1apVIx7b1NSkp59+WuFwWFdddZWuu+66VA4dAAAAAOAQKQ+7V155pTZu3KjHHnss5vZrrrlG1157bdzHhcNhPfXUU/rmN7+pwsJCbd26VWVlZZo3b16yhwwAAAAAcJiUb2O+5JJL5Pf7J/249957T6WlpSopKZHX69UVV1yhhoaGJIwQAAAAAOB0KV/Zjefll1/Wq6++qoULF+qv//qvRwTizs5OFRYWRt8vLCzUu+++m+phAgAAAAAcwBZhd8OGDaqqqpIk/eIXv9DPfvYz3XrrrVP+fLt27dKuXbskSdu3b1cgEEjION3G6/Xy3NgQ82JPzIs9MS/2w5zYE/NiT8yL/TAn9jTVebFF2M3Ly4u+fdVVV+mBBx4YcZ+CggJ1dHRE3+/o6FBBQcGon2/9+vVav3599P329vbEDdZFAoEAz40NMS/2xLzYE/NiP8yJPTEv9sS82A9zYk9jzcucOXPiPs4WrYeOHz8effuNN97Q/PnzR9xn0aJFOnr0qFpbWxUKhfTb3/5WZWVlqRwmAAAAAMAhUr6y+/DDD+vtt99WT0+PbrnlFm3atEnNzc3605/+JMMwVFRUpJtvvlnS4DndH//4x9q6das8Ho+++tWvatu2bQqHw1q7du2ooRgAAKSf5qZGvfVyrWacDKo/y69LP1OppStWWj0sAICFUh5277jjjhG3rVu3btT7FhQUaOvWrdH3V61aNWr/XQAAkL6amxrVsqNGVcV5MrKzZZoD2rujRpIIvACQxmyxjRkAAGCqDtbVak1xngzDkCQZhqE1xXk6WFdr8cgAAFYi7AIAAEfz9gWjQTfCMAx5+3otGhEAwA4IuwAAwNFC2X6Zphlzm2maCmX7LBoRAMAOCLsAAMDRlm2o1N7WrmjgNU1Te1u7tGxDpcUjAwBYyRZ9dgEAAKYqUoRqZ12tvH29CmX7tKyqmuJUAJDmCLsAAMDxlq5YSbgFAMRgGzMAAAAAwHUIuwAAAAAA1yHsAgAAAABch7ALAAAAAHAdwi4AAAAAwHUIuwAAAAAA1yHsAgAAAABchz67AABgypqbGvXWy7WacTKo/iy/PrXpRs29YKHVwwIAgJVdAAAwNc1NjWrZUaOqrAFdV5itqqwBvf+zn6i5qdHqoQEAQNgFAABTc7CuVmuK82QYhiTJMAxdWZKng3W1Fo8MAADCLgAAmCJvXzAadCMMw5C3r9eiEQEAcA5hFwAATEko2y/TNGNuM01ToWyfRSMCAOAcwi4AAJiSZRsqtbe1Kxp4TdPUK8e6tGxDpcUjAwCAaswAAGAMw6stX/qZSi1dsVKSov/urKuVt69XoWyfVv/1zVRjBgDYAmEXAACMKlptuThPRna2THNAe3fUSFJM4I28LUmBQEDt7e2WjNdNxrrIAACYGLYxAwCAUY1WbXlNMdWWk220lk4tO2po6QQAk0TYBQAAo6LasjW4yAAAiUHYBQAAo6LasjW4yAAAiUHYBQAAoxqt2vLeVqotJxsXGQAgMQi7AABgVEtXrFRpVbV2nvLohY6T2nnKo9KqagolJRkXGQAgMajGDAAA4hpebRnJN1pLp2VcZACASSPsAgAA2AwXGQBg+tjGDAAAAABwHcIuAAAAAMB1CLsAAAAAANch7AIAAAAAXIcCVQAAAEi65qZGvfVyrWacDKo/y69LP1NJES4ASUXYBQAAQFI1NzWqZUeNqorzZGRnyzQHtHdHjSQReAEkDduYAQAAkFQH62q1pjhPhmFIkgzD0JriPB2sq7V4ZADcjLALAACApPL2BaNBN8IwDHn7ei0aEYB0QNgFAABAUoWy/TJNM+Y20zQVyvZZNCIA6YCwCwAAgKRatqFSe1u7ooHXNE3tbe3Ssg2VFo8MgJtRoAoAAABJFSlCtbOuVt6+XoWyfVpWVU1xKgBJRdgFAABA0i1dsZJwCyCl2MYMAAAAAHAdwi4AAAAAwHXYxgwAAJBgzU2NeuvlWs04GVR/ll+XfqaSLbwAkGKEXQAAgARqbmpUy44aVRXnycjOlmkOaO+OGkki8DocFzEAZyHsAgAAJNDBulpdX5wnwzAkSYZhaE1xnnbW1RKMRuGUAMlFDMB5OLMLAACQQN6+YDToRhiGIW9fr0Ujsq9ogMwa0HWF2arKGlDLjho1NzVaPbQRDtbVas0oFzEO1tVaPDIA8aR0Zffxxx/X/v37lZubq4ceekiSVFNTozfffFNer1clJSW69dZb5fP5Rjz2tttuU2ZmpjIyMuTxeLR9+/ZUDh0AAGBCQtl+meZATOA1TVOh7JGvb9Kdk1bBvX1BGVnZMbdxEQOwt5SG3SuvvFIbN27UY489Fr1t+fLl2rx5szwej5555hk9//zzuummm0Z9/D333KPZs2enargAAACTtmxDpfbuqImuApqmqb2tXVpWVW310GzHSQGSixiA86Q07F5yySVqbW2Nue2yyy6Lvn3xxRfr9ddfT+WQAACAC1l5DjTydXbW1crb16tQtk/Lqqptt1JpB04KkFzEAJzHVgWqdu/erSuuuCLux7dt2yZJuvrqq7V+/fpUDQsAADiIHQoJLV2xknA7AU4KkFzEAJzHME3TTOUXbG1t1QMPPBA9sxvx3HPP6f3339fXv/71EUUdJKmzs1MFBQXq7u7Wd7/7XX3lK1/RJZdcMurX2LVrl3bt2iVJ2r59u86cOZP4b8QFvF6vQqGQ1cPAMMyLPTEv9sS82I8d5uSpu7fq8zP7R6wWPn9mhv7m3vstHJl17DAv8fxHwxva99Lz8vQGNeDzq+xzn9dl5ZdbPayUsPO8pCvmxJ7GmpeZM2fGf1yyBjQZr7zyit58803dfffdowZdSSooKJAk5ebmqry8XO+9917csLt+/fqYld/29vbED9oFAoEAz40NMS/2xLzYE/NiP3aYk1Bnu/oLs0e5/YTlY7OKHeYlnrkXLNTc2/9nzG12HWui2Xle0hVzYk9jzcucOXPiPs7ysNvU1KQXX3xR3/nOdzRr1qxR73Pq1CmZpqmsrCydOnVKBw4cUFVVVYpHCgAAnOA/g336xbu/10xzQP0ZHl26YL4WlxbZ8hwoACB5Uhp2H374Yb399tvq6enRLbfcok2bNun5559XKBTSfffdJ0m66KKLdPPNN6uzs1M//vGPtXXrVnV3d+sHP/iBJGlgYECrV6/WihUrUjl0AADgAM1NjfovZ3r1idxZCmTOlExTew5/qP2dPfrYLX9v9fAAACmU0rB7xx13jLht3bp1o963oKBAW7dulSSVlJTowQcfTObQAACACxysq9X1Fy5Qb88JHW1rVcZAWH9RmKv3ZuVTSAgA0ozl25gBAMljZfsVwAqRvq3+2bnyz86N3l7ccdLCUQEArEDYBQCXskP7FSDVnNS3FQCQXIRdAHCpg3W1uv5s70pJMgxDa4rztLOulrAL15pO31Z2QgCAuxB2AcClIts5hzIMQ96+XotGBCRfJJzurKuVt69XoWyfllVVjxta2QkBAO5D2AUAl2I7J9LV0hUrJx1Q2QkBAO6TYfUAAADJsWxDpfa2dsk0TUk6t51zQ6XFIwPsx9sXjLkwJLETAgCcjpVdAHCpqW7nBNIROyEAwH0IuwDgYlPZzgmko+kUtgIA2BNhFwCAJKLCrzOwEwIA3IewCwBAklDh11nYCQEA7kKBKgAAkuRgXW10W6x0rsLvwbpai0cGAID7EXYBAEgSKvwCAGAdtjEDAJAkVPiFm411Hp2z6gDsgLALAHC84S+s/RcsUvCD9y1/oU2FX7jVWOfRJXFWHYAtEHYBAI42/EX320eP6u0dr2nj8kuUU5hn6QttKvzCrQ7W1er6Uc6j7zx7Hj3ex/jZB5BKhF0AgKMNf9HdfPg/df3cQrW0tyknN8/yF9pU+IUbefuCMrKyY247dx7dHONjAJA6FKgCADja8CJQ3vCAMgxDGQMD0dt4oQ0k1uB5dDPmtsh59LE+BgCpRNgFADja8BfWoQyPwqapsMcTvY0X2kBiLdtQqb2tXdHfveh59A2VY34MAFKJbcwAgJRIVnXW4UWgli6Yp+fee1+fWX6JJFEUCkiCiZxH56w6AKsRdgEASTdW5dbpvgAe8aI77zz5qlbr5T+9L28HL7SBZBnrPDpn1QHYAWEXAJB0Y1VuTcQLYl5YAwCA4TizCwBIuuFFpCSKRgEAgOQi7AIAko7qrAAAINUIuwCApKM6KwAASDXO7AIAkm4ilVuBVElWZXAAgL0QdgEAKeGEIlKEoOSxy3M7XmVwu4wTADB9hF0AAJTc9kjpzk7P7ViVwSXZZpwAgOnjzC4AABoMQWtGCUEHz4YgTJ2dntuxKoPbaZwAgOkj7AIAINojJZOdntuxKoPbaZwAgOkj7AIAINojJZOdntuxKoPbaZwAgOkj7AIAINojJZOdntulK1aqtKpaO0959ELHSe085VHp2crgdhonAGD6KFAFAICc2R7JKZWD7fbcxqsMbrdxAgCmh7ALAMBZTmiPFGGnCscT4ZTnNtXjdMoFCwBwIrYxAwDgQFQOdr7oBYusAV1XmK2qrAG17KhRc1Oj1UMDAFcg7AIA4EBUDnY+LlgAQHKxjRkAkFBsy0yNwcrBAzGBl8rBzuLtC8rIyo65jQsWAJA4rOwCABKGbZmpQ+Vg56PVEQAkF2EXAJAwbMtMnbFa6MAZuGABAMnFNmYAQMKwLTO1rK5wPNqW9TXrr7ZsPE5DqyMASC7CLgAgYThHmj7itT76j9xczb1godXDcwyrL1gAgJsRdgEACbNsQ6X27qiJbmWObsusqrZ6aCmRyuJcVhcCO1hXq+tH2bL+y5ee19zb/2fKxgEAQDyEXQBAwqTztsx4K52SEv79p/JrxRNvy7onGEzJ1wdSzeoLTAAmj7ALAEiodN2WGW+lc2ddbcKfj1R+rXjibVkf8PlT8vWBVLLDBSYAk0c1ZgAAEsDbF4wJflLyinOl8mvFE6+ScNnnPp+yMQCpQqV5wJlY2QUAIAFSWZzLDoXA4m1Zv6z8crW3t6dsHEAqUGkecCbCLgAACZDK4lx2KQSWrlvWkX7scIEJwOQRdgEASIBUFudK50JggBXscoEJwOSkPOw+/vjj2r9/v3Jzc/XQQw9JkoLBoH74wx+qra1NRUVF+od/+Af5/SMLXLzyyit67rnnJElf+MIXdOWVV6Zy6AAAjCmVK52sqgKpwwUmwJlSHnavvPJKbdy4UY899lj0thdeeEGXXnqprrvuOr3wwgt64YUXdNNNN8U8LhgMaseOHdq+fbskacuWLSorKxs1FAMAAACJxAUmwHlSXo35kksuGRFQGxoatGbNGknSmjVr1NDQMOJxTU1NWr58ufx+v/x+v5YvX66mpqZUDBkAAAAA4DC2OLPb3d2t/Px8SVJeXp66u7tH3Kezs1OFhYXR9wsKCtTZ2Tnq59u1a5d27dolSdq+fbsCgUASRu18Xq+X58aGmBd7Yl7siXmxHzfNyX80vKGGl56Xt7dHIV+Oyj/3eV1WfrnVw5oSN82LmzAv9sOc2NNU58UWYXcowzBG9A6crPXr12v9+vXR92mBMLpAIMBzY0PMiz0xL/bEvNiPW+akualRLTtq9NniPBl+j0yzV3ufelRd3c48p+mWeXEb5sV+mBN7Gmte5syZE/dxKd/GPJrc3FwdP35cknT8+HHNnj17xH0KCgrU0dERfb+zs1MFBQUpGyMAAEgfB+tqo5V3pcGL8WuK83SwrtbikQEAJsoWK7tlZWXau3evrrvuOu3du1fl5eUj7rNixQr9y7/8i4LBoCTpP/7jP7R58+ZUDxUAAKRAc1Oj3nq5VjNOBtWf5deln6lM6Yqqty8oIys75jbDMOTt603ZGAAA05PysPvwww/r7bffVk9Pj2655RZt2rRJ1113nX74wx9q9+7d0dZDkvT+++/r17/+tW655Rb5/X5df/312rp1qySpqqqKSswAALhQZAtxVXGejOxsmeaA9u6okaSUBd5Qtl+mORBztMo0TYWyfSn5+gBghb5T/TrWHtSx9qBazv43w5uhv6n6mNVDm5KUh9077rhj1NvvvvvuEbctWrRIixYtir6/bt06rVu3LllDAwAANnCwrlbXj7KFeGddbcrC7rINldq7oya6ldk0Te1t7dKyquqUfH0ASJb+0IDaOntjAm3k7RPB0yPun505Q6ZpTruukhVssY0ZAAAgwg5biCOhemddrbx9vQpl+7SsypnFqZIh0dvMrd62DrhNOGzq+ImTamkbEmY7Bv9tP94r0xz9cTNneFRc6FNpwK+SgD/6r1MRdgEgQXixBiTGRLYQp+L3bemKlSM+J7/nid9mbodt64ATmaapYN+Z6Kps9N+zobY/FB71cYYhFRf4VDIs0J4X8CtvdpYyMpy3ghsPYRcAEoAXa0DijLeF2KrfN37PByV6m7kdtq0Ddnb6TEjHOnqHhNqeaLjtPdkf93G5ObNUUnguzJYW5ai00K+iAp+8Xls05Uk6wi4AJAAv1oDEGW8LsVW/b/yeD0r0NnM7bFsHrDYwEFZ7V9+5c7Rt57YeH+8+GfdxmbO8g0G20K/SoiErtYV+ZWXOSOF3YE+EXQBIAF6sAYk12hbiCKt+3/g9H5ToStVUvka6ME1T3T2ndaw9qKPtPTFVj9s6ezUQHv0grcdjqLjAP+IcbWnAr9n+WY4sHJUqhF0ASABerAGpY9XvG7/ngxJdqZrK13CbSPuemHO0Z/89fSYU93GFeVmD52gLYwNtYV62PJ702HacaIRdAEgAXqwBqZOM37eJFJ7i93xQoipVD33Oj50O6+DhDs3z+6h8DUfoDw2otaM3WgxqvPY9Ef7smbGrs4WD/xYX+jRrJtEs0XhGASABaFMCpE6if98mWniK3/NzxtpmPhEjnvOCLO1t7VLpdX+Vls8n7CkcNtXZfTI2zHYE1dLWo46uvkm17ykN5Kgk4JM/e1Zqv4k0R9gFgASZ7os/ABOXyN+3yRSe4vc8MSj2BbsY3r7nRN8H+uBwq1rag2rtmHj7nvOGBFu3te9xMsIuAABIaxSeSj2ec6RaTPueth61nN1+PJH2PYOrsrFbj9OpfY+TEXYBAEBao/BU6vGcIxki7XuibXvaJ96+p/RsmL1gQbFysjNo3+MShF0AsMBEiuHAHpgr96PwVOrxnGOqTNNUV8+pmDCbyPY9gUBA7e3tqfyWkESEXQBIsYkWw4H1mKuJGXpBwFMQ0EWfXueo54fCU6nHc47xJLR9T1GOCnOzaN+Thgi7AJBiFGZxDuZqfMMvCMyY0a9fO/CCAIWnUo/nHKO174lsQT7RO4n2PWf/KyqgfQ9i8dMAAClGYRbnYK7GxwUBAGMZ3r6npb0n+vZE2/fEFoiifQ8mjrALAClGYRbnYK7GxwUBAEPb9xwddo52Iu17SovOVTmmfQ8SibALAClGYRbnYK7GxwUBIH2cPhMaUeV4Yu17MkcWhqJ9D1KAsAsAKUZhFudgrsbHBQHAXUIDYXUc7xulMFSPjp84FfdxQ9v3lJz977xAjooDPmXNon0PrEHYBQALUJjFOZirsQ2/IOAtyNaFXBAAbG209j0tZ/9rn0z7nqJzW4+Htu8B7IKwCwAApmXoBYFE9KiktzGQGH0nz+hYR+/ZKsc9MVuPT58ZiPu4SPue2MJQftr3wHEIuwAAwDbobQxMTqR9z/BtxxNp3zPiHG3Ar+JCv2bO8KTwOwCSh7ALAABsg1ZGwEiD7XtGO0c7fvuekoBfJYX+YcGW9j1ID4RdAABgG7QyQroyTVM9vWd0rCN2dbalPahjHUGF4rTvycgwVFSQHVPlmPY9wCDCLgAAsA1aGcHthrbv6Tl5WH883KqWtsFg23dq4u17Im8X5dO+B4iHsAsAAGyDVkZwg5Hte3qib4/VvidrlndImD1XHIr2PcDUEHYBAIBt0NsYThHTvqftXJXjCbfvKfLrgvlFmu3z0L4HSBLCLgAAsBV6G8NO+k6eGVkYapz2PYYhFeadO0c7tOJxIC87eo42Ea26kDiNB5q1e99Btfeelt8TVuXqcq1cvtTqYWEaCLsAAABIa/39A2rtpH1POms80Kya+kMqWb5Gvv5+hU1TNfUNkkTgdTDCLgAAAFwv8e17/PJnz0ztN4Gkqa3fp/zFa2PanuUvLldt/R7CroMRdgEAACag8UCzal9rUHAggy2ONjVa+56Wtp7BVdrO3om37wnkRN/Oy8mkfU8aCIYM+YadlzYMQ70h5t7JCLsAAADjiGxxzF+yTj7DYIujxYa27xm+UjuR9j3DV2hp3wO/11R42PK+aZryeeMs+cMRCLsAAADjYItj6kXa9xxt74men51o+57SorNtewr9tO/BhFRWlKmmvkElyyskDQbd44caVF1RZvHIMB2EXQAAgHGwxTE5TNNU14lTI6ocj9e+x+vJUHGhL7YwFO17MA2Ri1a739yr7uBp+bymqivKuJjlcIRdAACAcUS2OA4NUWxxnLhR2/e0B3WsY/rte4BEWbl8qa5et4Z2UC5C2AUAwAGamxr11su1mnEyqP4svy79TCW9aFMossUxf3G5DMNgi+MoRrbv6Ym+3dN7Ju7jRm/fk6PiQh/tewBMC2EXAACba25qVMuOGlUV58nIzpZpDmjvjhpJIvCmSGQrY239HvWGjLTd4ji0fU9LW+zW48m07ykt8kffp30PgGQh7AIAYHMH62p1fXFeTHGkNcV52llXS9hNoZXLl6ZFuI2072k5Wxgqsjo7kfY9xQXZQ1Zoad8DwFqEXQAAbM7bF5SRlR1zm2EY8vb1WjQiuMGp0yEd6xjlHO047XvyZmdGi0HRvgeAnRF2AQCwuVC2X6Y5MKI4UijbZ+Go4AShgbDaj/fqgyO9+sMfj8T0pu2ifQ8AlyPsAgBgc8s2VGrvjhqtObuV2TRN7W3t0rKqaquHBhsYrX1PS9vgFuS2430KT6Z9z9niUDm+mbTvAeB4hF0AAGwuci53Z12tvH29CmX7tKyqmvO6aWZo+56jQ8/RTqB9z/zz8lWQO+tsmB0MtoW07wHgcoRdAAAcYOmKlYTbNBBt39PWE61yPJn2PZEqx4Nbj8+17wkEAvQOnYLGA82qfa1BwYEM+T1hVa4uT4siZYBbEHYBAABSKBw21dHVF1sYaoLteyKrskO3HtO+JzkaDzSrpv6Q8pesk88wFDZN1dQ3SBKBF3AIwi4AAECCJaN9T/7sTM7RplBt/T7lL14b0/Irf3G5auv3EHYBhyDsAgAATFG89j0t7UGdnGT7ntIivwL5Pnk9tO+xg2DIkG/YxQXDMNQb4oID4BSEXQAAgDFE2vdEw2zbua3Hk2nfEzlPW1yY2vY9zU2NevfV3RrobFd/ll+XfqaS898T4PeaCpvmiJZfPm+cfeYAbMcWYffIkSP64Q9/GH2/tbVVmzZt0jXXXBO9rbm5Wd///vdVXFwsSfr4xz+uqqqqlI8VAAC4z9D2PYOhticabifTvudcCx97tO9pbmpUy44afWFesfoLs2WaA9q7o0aSCLzjqKwoU019g/IXl0dbfh0/1KDqijKrhwZggmwRdufMmaMHH3xQkhQOh/V3f/d3uvzyy0fcb8mSJdqyZUuqhwcAAFyid0j7nqHnaFvagzrTP3b7ntIif3TrsVPa9xysq9X1Z/szS4PbcNcU52lnXS1hdxyRc7m19XvUGzLk85qqrijjvC7gILYIu0O99dZbKi0tVVFRkdVDAQAADtTfP6BjHb2Dq7NDztO2tAUV7IvfvifHNzMmyA5v3+NE3r6gjKzsmNsMw5C3r9eiETnLyuVLCbeAg9ku7NbX16uiomLUj/3hD3/QnXfeqfz8fFVXV2v+/Pmj3m/Xrl3atWuXJGn79u0KBAJJG6+Teb1enhsbYl7siXmxJ+bFflI1JwPhsNo6gzpyrFtHjnXro2Pd+qilW0dau9XWGYzbvmfWTK/mlORqbknu4L/Fg//OKZmtHF9m0sedat6CgGbM6FeGYWjmzMH2RKZpyluQze+ODfA3zH6YE3ua6rwYphnvfwepFwqF9Hd/93d66KGHlJeXF/Oxvr4+ZWRkKDMzU/v379dPf/pTPfLIIxP6vEeOHEnCaJ2PBvP2xLzYE/NiT8yL/SRyTkZr3xPZetza0avQQPz2PUX5I9v3lAb8ykuz9j2RM7tXzytWf3+/TNPU3tYulVZVs43ZBvgbZj/MiT2NNS9z5syJ+zhbrew2NjbqggsuGBF0JSk7+9wWnFWrVumpp57SiRMnNHv27BSOEAAAJFqkfc/QKsfHJtm+J1LpuDRA+56hIoH2+Vd3K9R5QqFsn5YRdAGkCVuF3bG2MHd1dSk3N1eGYei9995TOBxWTk5OikcIAACmIjQQVltn78jCUOO178mcMazK8dnetIV+Zc6y1csY21q6YqXWrL+a1SoAacc2/5c4deqUDhw4oJtvvjl6W11dnSRpw4YNev3111VXVyePx6OZM2fqjjvuSKttSAAA2J1pmmo/HtTv32+bdPuekrPte0ps2L4HAOBMtgm7mZmZ+sd//MeY2zZs2BB9e+PGjdq4cWOqhwUAGKa5qVFvvVyrGSeD6s/y69LPVLIlMs2M1r4n8u9Y7XsCkXO0DmvfAwBwJtuEXQCA/UWK3VQV58nIzpZpDmjvjhpJIvC6zJn+AbUOad8TPU/bPnb7ntycTBUVZMe07yktylFxgU8zHNq+BwDgTIRdAMCEHayr1fXFedFtpYZhaE1xnnbW1RJ2HSgcNtXR1adj7UEdHXqOtj2ozu6+uO17Zs7wxJyhjZ6jDfj1X+bPsfXZ0MYDzap9rUHBgQz5PWFVri6njyoAuBRhFwAwYd6+oIys7JjbDMOQt6/XohFhPKZp6kTw9IgqxxNp31NckK3SopwRW4+d2r6n8UCzauoPKX/JOvkMQ2HTVE19gyQReAHAhQi7AIAJC2X7ZZoDMUHHNE2Fsn0WjgqSdPJ0v1rbe8+doZ1g+5782ZmxVY5d3L6ntn6f8hevjdmZkL+4XLX1ewi7AOBChF0AwIQt21CpvTtqtObsVmbTNLW3tUvLqqqtHlpaCIXCajs+sn3P0fagunto3zOeYMiQb9iKtGEY6g3Ze5WardcAMDXp8384AJbhhZp7RM7l7qyrlbevV6Fsn5ZVVXNeN4HCYVNdPaeGBNrB9j0t7UG1j9W+x5uhkgLa94zF7zUVNs0ROxN83jiHk22ArdcAMHWEXQBJxQs191m6YiXhNgFi2ve0nQ22HVNo31M0GGwLcp3RvsfKi1+VFWWqqW9Q/uLy6M6E44caVF1RlpKvPxVsvQaAqSPsAkgqXqghnQ227xnZi3a89j05vpnRVdmhW4+d3r7H6otfka9RW79HvSFDPq+p6ooyW/8tcurWawCwA8IugKTihRrcLhw21X62fU/LJNr3zJrpGVHlOLIF2Zc1M7XfRIrY4eLXyuVLbR1uh3Pi1msAsAvCLoCk4oUa3CBe+56WtqDaOuO37/FkGAoU+s6tzrqgfc90cPFr8py49RoA7IKwCyCpeKEGJxnRvudscahj7UGdPB2K+7h0at8zHVz8mjwnbr0GALsg7AJIKl6owW6Gt+8Zeo52su17SgN+FadZ+57p4OLX1Dht6zUA2AX/dwaQdLxQQ6qFw6a6Tpw8F2SHbD2eaPseT7hXfR/+XrP7uzUry6NVGzdo2cpVKf5O3IWLXwCAVCLsAgAcq6f3lN4/3Blb7XiC7XtKR/SjPde+p7mpUS07ntWa4ryzK5AD2rvzGRmGQdulaeLiFwAgVQi7AABbm2r7ntm+WTHnZyfTvudgXa2uPxt0pcEiSmuK87SzrpawCwBxWNlHGxgNYRcAYLnR2ve0tPfoWHtQnd0n47bvyZzlVXGhb0T7ntKAX9nTaN/j7QvKyMqOuc0wDHn7eqf8OQHAzazuow2MhrALAEiJ4e17WtrOrdBOtn1PadHg2xdeME8dHR0JH2so2y/THBhRNTiU7Uv41wIAN7BDH21gOMIuACChTp7uj1mhHfr2RNv3lAZyom8X5mfHbd+TrD61yzZUau+OmiFndk3tbe3SsqrqpHw9AHA6+mjDjgi7AIBJC4XCauvsjalyPKn2PUX+mK3HdmvfEzmXu7OuVt6+XoWyfVpWVc15XQCIgz7asCP7vLIAANjKtNr3FJ47Pxs9S1voV45vZtJWYxNt6YqVhFsAmCD6aMOOCLsAkOaCfWdGrM62tPeotaN3Wu17AADpgz7asCPCLgCkgdHa90TeTlb7HqSH4a1Gbvzsei1cMM/qYQGwAH20YTeEXQBwiUj7npa2nnMrtWe3Hnd0nYz7uFkzPdEqxyUBv0qLcs5uO/ZNq30P3G+0ViM/qWvUFy/v5gWvTdEHFUA6IewCgINE2ve0tI8sDDVW+54MQ8o0Tstv9ilrRlgXX3qxVq5copKAX3k5mY45Rwt7GbXVyJJy1da/TICyIfqgAkg3hF0AsKGTp/p1rGNq7XuGtu0pCfjV03ZYJ3/1C60tzj3XRqfxbQ0sylH+QgowYepoNeIs9EEFkG4IuwBgkdHa97S09ehYR1DdPafjPi47c4ZKi/yxW4/HaN/zi//vKV1fkhvzAndNcZ521tVSbRjTQqsRZ+HiBIB0Q9gFgCQa3r7n6JCV2rbjvTLjZIJEtu/x9gVlZGXH3GYYhrx9vdP51oDRW438vkFfTEKrEc6aTh8XJwCkG8IuACRAsO+MWtp7RpyjnVr7nhwV5GYlrH1PKNsv0xwY8QI3lO1LyOdH+hqt1cjN11yV8GrMnDVNDPqgAkg3Ewq74XBYDQ0NMgxDZWVlysjIkCT97ne/0yc/+cmkDhAA7OL0mZBaO3oHg2xH7DnaibbvOe/s9uOSwtS171m2oVJ7d9RoTXHeuTO7rV1aVlWd9K8N9xveaiQQCKi9vT2hX4OzpolBH1QA6WZCYffRRx9VIBCQ1+vVSy+9pNtuu02lpaWqq6sj7AJwlYGBsDq6+mKrHXcE1dZ5Um2dwbiPi7bvCeTErtTaoH1P5Fzuzrpaeft6Fcr2aVlVNed14RicNU0c+qACSCcTCrudnZ26/fbbJUlr167Vo48+qr/6q79K6sAAIFnit+/pUWtnrwYGRj+/5skwVFTgG3mO1gHte5auWEm4tRDnTaeHs6bT03igWbv3HVR772l+/gCklQmF3VAopP7+fs2YMUNFRUXasmWLHn74YR0+fDjZ4wOAKRvevqel7dz241Njte/JzYqpclwS8GvJRfOVodPyejJS+B3ADThvOn2cNZ26yM9fyfI18vX38/MHIK2MGXYHBgbk8Xj05S9/Wb29vcrLy5MkZWVl6a677tJrr72WijECQFzR9j3tPSO2Hk+lfU9JwK9ZM0f+aQwEchN+DhHpgfOm08dZ06nj5w9AOhsz7H7ve9/TnXfeqQsvvHDExzIyMvTpT386aQMDgIhw2NTxIe17WqbYvqd0SKD1Z0+ufQ8wVZw3TQzOmk4NP38A0tmYYff888/Xt771LW3dulUFBQWSpLfffls///nPde+996ZkgADSR7BvtHO0E2zfU5QzYoU2ke17gKnivCmsFPn5G4qfPwDpYsywW11drbq6On3rW9/S5s2btXv3bh0+fFjXXnttqsYHwGXite9paetR78n+uI+b7Z81oh9tKtv3AFPFeVNYKfLzV7K8QpL4+QOQVsYtUHXxxRcrOztbjzzyiNasWaO77rpLM2da20YDgL2N1r4n8nZn98m4j5s10zsi0NqlfQ8wVZw3hZUiP2e739yr7uBpfv7GQeV0wF3GDLsPPvig3n77bV1zzTXatGmTnnzySR08eFCrVq1K1fgA2NTQ9j0t7T0xW4+n0r6nNJCj3JxZnKOFK3HeFFZauXyprl63hiJ746ByOuA+Y4bd8847T//9v/93+f1+SVJJSYkeeOABtba2auPGjSkZIABrnTzVP/Ic7RTa90QqHwfysuWhfQ8AwGaoXA24z5hh96abbop5f8GCBbrvvvt0//33E3YBF+kPDaits3dEYahJte8J5Aw5S+sbtX0PAAB2ReVqwH0m/Wq0oKCASsyAA8Vr39PSHlT7GO17ZngzosWghp+npX0PAMAtqJwOuM+Ull6ysrISPQ4ACTK8fU9L2+AK7bH2oPpD4VEfYxhSUYFvMMjSvgcAkIaonA64D/sMAQca2r7naHtQx4YUiJpS+55Cn2Z4ad8DAEhfVE4H3IewC9jUwEBY7V19I8/RTrV9T8Cv7MwZKfwOAABwFiqnA+5C2AUsZJqmuntOn61wPLg623miX38+0jGp9j2lRX6VFuaoJOCnfQ8AAAAgwi6QEtNt33Ou4jHtewAAAICJsFXYve2225SZmamMjAx5PB5t37495uOmaerpp59WY2OjZs2apVtvvVULFy60aLRArHjte1ragzoRjN++x5c149z52UCOLrrgPGXPMmnfAwDAEI0HmlX7WoOCAxnye8KqXF3uqi3Hbv/+ACvY7pX0Pffco9mzZ4/6scbGRrW0tOiRRx7Ru+++qyeffFLf+973UjxCpLOh7Xta2mJXaKfavifHNyvmvoFAQO3t7Sn4bgAAmByrAlnjgWbV1B9S/pJ18hmGwqapmvoGSXJFIHT79wdYxXZhdyz79u3Tpz/9aRmGoYsvvli9vb06fvy48vPzrR4aXCbYd1otbcMKQ02xfU9pkV/5s2nfAwBwNisDWW39PuUvXhutSWEYhvIXl6u2fo8rwqDbvz/AKrYLu9u2bZMkXX311Vq/fn3Mxzo7OxUIBKLvFxYWqrOzc0TY3bVrl3bt2iVJ2r59e8xjcI7X603r5+b06ZCOtHbro2PdOnKsWx+1Dv575Fi3enrjbzvOm52lOSW5mluSqznFuZpbOvh2aWC2ZsyYfvuedJ8Xu2Je7Il5sR/mxJ4SMS+73zyokuVrYoogliyv0O439+rqdWumO8Qx9XsylT1r1ojbT3oyHf3zFpkXt35/TsTfMHua6rzYKuzed999KigoUHd3t7773e9qzpw5uuSSSyb9edavXx8TlNkSOrp02C6bqPY9587UxmvfM6Du7uMJGXM6zIsTMS/2xLzYD3NiT4mYl/bgafn6R/Zy7w6eTvqczxg4pdOnT8cEbdM05R045eift8i8uPX7cyL+htnTWPMyZ86cuI+zVdgtKCiQJOXm5qq8vFzvvfdeTNgtKCiI+SY7Ojqij0H6Gq19T+RMbdvxCbTvKRpyjpb2PQAAjMrvNRU2zRGBzOeNU7AigSorylRT36D8xeUyDEOmaer4oQZVV5Ql/Wungtu/P8Aqtgm7p06dkmmaysrK0qlTp3TgwAFVVVXF3KesrEy/+tWvVFFRoXfffVfZ2dmc100jfaf6dWxYlePI26fPxG/fU5CbFVMQivY9AJyOqq2wgpWBLPLzXVu/R70hQz6vqeqKMtf83Lv9+wOsYpuw293drR/84AeSpIGBAa1evVorVqxQXV2dJGnDhg1auXKl9u/fr9tvv10zZ87UrbfeauWQkQT9oQG1dvRGi0ENDbSTad8TfZv2PQBchqqtsIrVgWzl8qWu/hl3+/cHWME2KaCkpEQPPvjgiNs3bNgQfdswDP3t3/5tKoeFJAiHTXV2n4wNs1No31NadG6l1p89sqgDgKlh1dDeqNoKKxHIADiJbcIu3MU0TQX7zowsDDWZ9j3Dth7TvgdIPlYN7S8YMuQbVlPAMAz1hvj7CADAUIRdTMvpMyEd6+gdEmp7ouG29+TIio0Rs/2zRoTZkoBfRQU+zfBOv30PgKlh1dD+rCwSBACAkxB2Ma7h7Xta2s5tPT4+XvueIr9KC2MDbfz2PQCsxqqh/VG1FQCAiSHsQtK59j0tQ1ZmI+G2rbNXA+E47Xs8hoqHbDumfQ/gbKwa2p/VRYIAAHAKwm6aibTvaWkPqqfvQ/3xcOuU2/eUBvwqpH0P4CqsGjoDRYIAABgfYdeFEtG+p7QoJ7r9uJj2PUDaSIdVQ6pNAwCQHkgwDhWvfU9LW486uvrGbd9TGvDrgvnFmu3LoH0PgBhuXjWk2jQAAOmDsGtjw9v3DF2hbe0Yu31P5Bzt8K3HQ9v3BAIBtbe3p/JbAgBLUW0aAID0Qdi1gUj7npa2nugK7bEJtO/JzZmlkkLa9wDARFFtGgCA9EHYtdBTO97U2++3jdm+J3OW92yF45GrtFm07wGASaHaNAAA6YOwa6Ge3tM63n1y9PY9gRyVBvya7ad9DwAkCtWmAQBIH4RdC236r8u0+bPLad8DACkSOZf7sxd36o9t3RroP61FxXmSFls6LgAAkHiEXQvNKZ5t9RAAIC0ZgQUqW31udZeKzAAAuA/LiQCAtDJYkbl8lIrM+yweGQAASCRWdgEAacXJFZkbDzSr9rUGBQcy5PeEVbm6nNVoAADiIOwCANKKUysyNx5oVk39IeUvWSefYSjM9msAAMbENmYAQFqprCjT8UMNMs3BcBupyFxp84rMbL8GAGByWNkFAKSdcPuH2vf8QYXPnNLC0nx9+QvX2H511MnbrwEAsAJhFwCQNiJbgQtXVykwpM+uEzh1+zUAAFZhGzMAIG04eSuwU7dfAwBgFVZ2AQBpw8lbgSPbrGvr96g3ZMjnNVVdUWb77dcAAFiFsAsASBtO3wq8cvlSwi0AABPENmYAQNpgKzAAAOmDlV0AQNpgKzAAAOmDsAsASCtsBXanxgPNqn2tQcGBDPk9YVWuLmeeASDNEXYBAICjRVpK5S9ZJ59hKGyaqqkfbClF4AWA9MWZXQAA4GhObikFAEgewi4AAHC0YMiIqbAtOaelFAAgeQi7AADA0fxeM1phO8JJLaUAAMnBmV0AAGyGYkuTU1lRppr6huhW5khLqWpaSgFAWiPsAgBgIxRbmjxaSsEphl/IuvGz67VwwTyrhwW4FmEXAAAbGSy2tHaUYkt7CG9joKUU7G60C1k/qWvUFy/v5mcXSBLCLgAANhIMGfJRbAk2w9b66Rv1QtaSctXWv8xzCSQJYRcAABvxe02FTTOmujDFlmAlttYnBheygNSjGjMAADZSWVGm44caotWFI8WWKim2BIvQxzgxqBoOpB4ruwAA2AjFlmA3rEgmxqhVw3/foC9yIQtIGsIuAAA2Q7El2Alb6xNjtAtZN19zFdWYgSQi7AIAACAu+hgnzvALWYFAQO3t7RaOCHA3wi4AAJBExV2Mjq31AJyKsAsAAKi4izGxtR6AE1GNGQAAUHEXAOA6hF0AAKBgyIgpQCRRcRcA4GxsYwYAAJOuuMv5XgCA3RF2AaQNXpwD8U2m4u5Y53uvXrcm1UN3Jf5eAcD0EXYBpAWK7wBjm0zF3cHzvWtHOd+7h7CbAPy9AoDEIOwCSAtjvTjnxSMwaKIVd4MhQz7O945rqquz/L0CgMSwRdhtb2/XY489pq6uLhmGofXr16uysjLmPs3Nzfr+97+v4uJiSdLHP/5xVVVVWTFcAA7Ei3MgcSZ7vjcdTWd1lr9XAJAYtgi7Ho9H1dXVWrhwoU6ePKktW7Zo+fLlmjdvXsz9lixZoi1btlg0SgBOxotzIHEmc743XU1ndZa/VwCQGLZoPZSfn6+FCxdKkrKysjR37lx1dnZaPCoAblJZUabjhxpkmoMvFiMvzit5cQ5M2srlS1VdsVgZh/ao7609yji0R9UVi9liO8R0Wjnx9woAEsMWK7tDtba26oMPPtCFF1444mN/+MMfdOeddyo/P1/V1dWaP3++BSME4ESTKb4DYHwTPd+brqazOsvfKwBIDMOMXDa0gVOnTumee+7RF77wBX384x+P+VhfX58yMjKUmZmp/fv366c//akeeeSRUT/Prl27tGvXLknS9u3bdebMmaSP3Ym8Xq9CoZDVw8AwzIs9MS/2xLzYD3My6I39TfpJXaPylwzZ6v37Bt28YaUuX7Ui5eNhXuyJebEf5sSexpqXmTNnxn2cbcJuKBTSAw88oMsuu0yf/exnx73/bbfdpvvvv1+zZ88e975HjhxJxBBdJxAIqL293ephYBjmxZ6YF3tiXuyHOTmn8UCzauv3RVdnKy1cnWVe7Il5sR/mxJ7Gmpc5c+bEfZwttjGbpqknnnhCc+fOjRt0u7q6lJubK8Mw9N577ykcDisnJyfFIwUAAJgYtnoDgLVsEXbfeecdvfrqq1qwYIHuvPNOSdKNN94YTe8bNmzQ66+/rrq6Onk8Hs2cOVN33HHHiMIPAAAAAABINgm7ixcv1rPPPjvmfTZu3KiNGzemaEQAAACYrsYDzap9rUHBgQz5PWFVri5ntRtAytgi7AIAAMBdGg80q6b+kPKXrJPPMBQ2TdXUN0gSgRdAStiizy4AAADcpbZ+n/IXl0ePnRmGofzF5aqt32fxyACkC8IuAAAAEi4YMkbUVzEMQ70haq4ASA22MQMAAJzFGdPE8XtNhU0zJvCapimf1xZdLwGkAVZ2AQAAdO6MaXjJOvkuXavwknWqqT+kxgPNVg/NkSorynT8UINMczDcmqap44caVFlRZvHIAKQLVnYBAAAUOWO6dpQzpntY3Z2CyHNWW79HvSFDPq+p6ooynksAKUPYBQAA0OAZUx9nTBNq5fKlhFsAlmEbMwAAgAbPmEa23EZwxhQAnIuwCwAAIM6YAoDbsI0ZAGALVMGF1ThjCgDuQtgFAFguUgU3f8k6+QxDYdNUTX2DJBE0kFKcMQUA92AbMwDAcoNVcMtHqYK7z+KRAQAAp2JlFwBgOargAlPHEQAAGB1hFwBgOb/XVNg0oyu7ElVwgYngCAAAxMc2ZgCA5aiCC0wNRwAAID5WdgEAlqMKLjA1HAEAgPgIuwAAW6AKLjB5HAEAgPjYxgwAAOBQHAEAgPhY2QUAAHAojgAAQHyEXQAAAAfjCAAAjI6wCwDAJNHXFAAA+yPsAgAwCfQ1BQDAGShQBQDAJNDXFAAAZyDsAgAwCcGQEdPmRaKvKQAAdkTYBQBgEvxeM9rmJYK+pgAA2A9hFwCASaCvKQAAzkCBKgAAJoG+polDVWsAQDIRdgEAmCT6mk4fVa0BAMnGNmYAAJByVLUGACQbYRcAAKQcVa0BAMlG2AUAAClHVWsAQLIRdgEAQMpR1RoAkGwUqAIAAClHVWsAQLIRdgEAgCWoag0ASCa2MQMAAAAAXIeVXQAAAIzQeKBZta81KDiQIb8nrMrV5azEA3AUwi4AYEJ44Qukj8YDzaqpP6T8JevkMwyFTVM19Q2SxO89AMcg7AIAxsULX/fh4gXGUlu/T/mL10Z7IRuGofzF5aqt38PPCQDHIOwCAMbFC1934eIFxhMMGfKd/X2PMAxDvSEjziMAwH4oUAUAGFcwZESDbgQvfJ1r8OJF+SgXL/ZZPDLYhd9rRnsgR5imKZ/XjPMIALAfwi4AYFy88HUXLl5gPJUVZTp+qCH6e2+apo4falBlRZnFIwOAiWMbMwBgXJUVZaqpb4iuBkZe+FbzwteR/F5TYdOMCbxcvMBQke3stfV71Bsy5POaqq4oY5s7AEch7AIAxsULX3fh4gUmYuXypfyOA3A0wi4AYEJ44eseXLwAAKQDwi4A16K1ChAfFy8AAG5H2AXgSrRWAeyFi08AgFSzVdhtamrS008/rXA4rKuuukrXXXddzMf7+/v16KOP6o9//KNycnJ0xx13qLi42JrBArA1+sIC9sHFJwCAFWwTdsPhsJ566il985vfVGFhobZu3aqysjLNmzcvep/du3fL5/PpRz/6kerr6/XP//zP+od/+AcLRw3AroIhQz6XtVZhZQxOxcUnAIAVbNNn97333lNpaalKSkrk9Xp1xRVXqKGhIeY++/bt05VXXilJ+sQnPqGDBw+O6PsIAJL7+sJGVsbCS9bJd+lahZesU039ITUeaLZ6aMC46OsLALCCbcJuZ2enCgsLo+8XFhaqs7Mz7n08Ho+ys7PV09OT0nECcIbKijIdP9QQDbyR1iqVDm2tMrgyVj7Kytg+i0cGjM9tF58AAM5gm23MibRr1y7t2rVLkrR9+3YFAgGLR2RPXq+X58aGmJfEuHrdGuXm5er539Qr2C/5Z0hfuqZCl69aMaXPZ/W89HsylT1r1ojbT3oy0/rnxep5wUijzcmN11yln9Q1Kn/JkL6+v2/QzddcxfylCL8r9sS82A9zYk9TnRfbhN2CggJ1dHRE3+/o6FBBQcGo9yksLNTAwID6+vqUk5Mz4nOtX79e69evj77f3t6evIE7WCAQ4LmxIeYlcRYumKf/+ZUvxtw21efW6nmZMXBKp0+fjtkKapqmvAOn0vrnxep5wUijzcnCBfP0xcu7VVv/crSv7xcryrRwwTzmL0X4XbEn5sV+mBN7Gmte5syZE/dxtgm7ixYt0tGjR9Xa2qqCggL99re/1e233x5zn4997GN65ZVXdPHFF+v111/X0qVLR5wBAgA3qqwoU019Q3Qrc2RbdrVDt2Uj/dDXFwCQarYJux6PR1/96le1bds2hcNhrV27VvPnz9cvfvELLVq0SGVlZVq3bp0effRR/Y//8T/k9/t1xx13WD1sAEiJSEiord8TXRmrrigjPAAAAMRhm7ArSatWrdKqVatibvviF89tQZw5c6a+9rWvpXpYAGALrIwBAABMnG2qMQMAAAAAkCiEXQAAAACA6xB2AQAAAACuQ9gFAAAAALiOrQpUAQDOaTzQrNrXGhQcyJDfE1bl6nIKVAEAAEwQYRcAbKjxQLNq6g8pf8k6+QxDYdNUTX2DJBF4AQAAJoBtzABgQ7X1+5S/uFyGYUiSDMNQ/uJy1dbvs3hkAAAAzkDYBQAbCoaMaNCNMAxDvSEjziMAAAAwFNuYAcCG/F5TYdOMCbymacrnNS0cFTA9nEMHAKQSK7sAYEOVFWU6fqhBpjkYbk3T1PFDDaqsKLN4ZMDURM6hh5esk+/StQovWaea+kNqPNBs9dAAAC7Fyi4A2FBktau2fo96Q4Z8XlPVFWWsgsGxBs+hrx3lHPoefq4BAElB2AUAm1q5fCkhAK4RDBnycQ4dAJBCbGMGAABJ5/ea0W35EZxDBwAkE2EXAAAkHefQAQCpxjZmAACQdJxDBwCkGmEXAACkBOfQAQCpxDZmAAAAAIDrEHYBAAAAAK5D2AUAAAAAuA5hFwAAAADgOoRdAAAAAIDrEHYBAAAAAK5D2AUAAAAAuA5hFwAAAADgOl6rBwAAgJUaDzSr9rUGBQcy5PeEVbm6XCuXL7V6WAAAYJoIuwCAtNV4oFk19YeUv2SdfIahsGmqpr5Bkgi8AAA4HNuYAQBpq7Z+n/IXl8swDEmSYRjKX1yu2vp9Fo8MAABMFyu7sAW2EQKwQjBkyHc26EYYhqHekBHnEQAAwCkIu7Ac2wgBWMXvNRU2zejKriSZpimf17RwVAAAIBEIu7Dc4DbCtaNsI9xD2AWQVJUVZaqpb4huZTZNU8cPNai6oszqoU0Iu2IAAIiPsAvLsY0QQKoNDYnhrna1731fvsJS+bymqivKHBEY2RUDAMDYCLuwHNsIAaTS8JCYfXY1968qFjsqJLIrBgCAsVGNGZarrCjT8UMNMs3BcBvZRljpkG2EAJzFLRWYgyEj5iKhxK4YAACGYmUXlousQNTW71FvyHDUNkIAzuOWoxPsigEAYGyEXdjCyuVLCbcAUsItIdHpxbUAAEg2wi4AIK24JSSyKwYAgLERdgEAacVNIZFdMQAAxEfYBQCkHUIiAADuRzVmAAAAAIDrEHYBAAAAAK7DNmYAACap8UCzal9rUHAgQ35PWJWry9kWDQCAzRB2AQCYhMYDzaqpP6T8JevkMwyFTVM19Q2SROAFAMBG2MYMAMAk1Nbvi7YtkiTDMJS/uFy19fssHhkAABiKsAsAwCQEQ0Y06EYYhqHekBHnEQAAwAqEXQAAJsHvNWWaZsxtpmnK5zXjPAIAAFiBM7sAgHFRkOmcyooy1dQ3RLcym6ap44caVF1RZvXQAADAEJaH3ZqaGr355pvyer0qKSnRrbfeKp/PN+J+t912mzIzM5WRkSGPx6Pt27dbMFoASD8UZIoV+Z5r6/eoN2TI5zVVXVGWls8FAAB2ZnnYXb58uTZv3iyPx6NnnnlGzz//vG666aZR73vPPfdo9uzZKR4hAKS3wYJMa0cpyLQnbQPeyuVL0/Z7BwDAKSw/s3vZZZfJ4/FIki6++GJ1dnZaPCIAwFAUZAIAAE5k+cruULt379YVV1wR9+Pbtm2TJF199dVav359qoYFAGnN7zUVNs2YwEtBJgAAYHeGObykZBLcd9996urqGnH7DTfcoPLycknSc889p/fff19f//rXR6wgSFJnZ6cKCgrU3d2t7373u/rKV76iSy65ZNSvt2vXLu3atUuStH37dp05cyZx34yLeL1ehUIhq4eBYZgXe0rneXljf5N+Uteo/CVDCjL9vkE3b1ipy1etsHRs6TwvdsWc2BPzYk/Mi/0wJ/Y01rzMnDkz7uNSEnbH88orr+jXv/617r77bs2aNWvc+z/77LPKzMzUtddeO6HPf+TIkekO0ZUCgYDa29utHgaGYV7sKd3npfFAs2rr90ULMlXapCBTus+LHTEn9sS82BPzYj/MiT2NNS9z5syJ+zjLtzE3NTXpxRdf1He+8524QffUqVMyTVNZWVk6deqUDhw4oKqqqhSPFADSFwWZAACA01gedp966imFQiHdd999kqSLLrpIN998szo7O/XjH/9YW7duVXd3t37wgx9IkgYGBrR69WqtWLHCwlEDAAAAAOzM8rD7ox/9aNTbCwoKtHXrVklSSUmJHnzwwVQOCwAAAADgYJa3HgIAAAAAINEIuwAAAAAA1yHsAgAAAABch7ALAAAAAHAdwi4AAAAAwHUIuwAAAAAA1yHsAgAAAABcx/I+uwAADNd4oFm1rzUoOJAhvyesytXlWrl8qdXDAgAADkLYBQDYSuOBZtXUH1L+knXyGYbCpqma+gZJIvACAIAJYxszAMBWauv3KX9xuQzDkCQZhqH8xeWqrd9n8cgAAICTEHYBALYSDBnRoBthGIZ6Q0acRwAAAIxE2AUA2Irfa8o0zZjbTNOUz2vGeQQAAMBIhF0AgK1UVpTp+KGGaOA1TVPHDzWosqLM4pEBAAAnoUAVAMBWIkWoauv3qDdkyOc1VV1RRnEqAAAwKYRdAIDtrFy+lHALAACmhW3MAAAAAADXIewCAAAAAFyHsAsAAAAAcB3CLgAAAADAdQi7AAAAAADXIewCAAAAAFyHsAsAAAAAcB3CLgAAAADAdQi7AAAAAADXIewCAAAAAFyHsAsAAAAAcB3CLgAAAADAdQi7AAAAAADXIewCAAAAAFyHsAsAAAAAcB3DNE3T6kEAAAAAAJBIrOymsS1btlg9BIyCebEn5sWemBf7YU7siXmxJ+bFfpgTe5rqvBB2AQAAAACuQ9gFAAAAALgOYTeNrV+/3uohYBTMiz0xL/bEvNgPc2JPzIs9MS/2w5zY01TnhQJVAAAAAADXYWUXAAAAAOA6XqsHAHt46aWXVFNToyeffFKzZ8+2ejhp7+c//7n27dsnwzCUm5urW2+9VQUFBVYPK+3V1NTozTfflNfrVUlJiW699Vb5fD6rh5XWfve73+lf//Vf9dFHH+l73/ueFi1aZPWQ0lpTU5OefvpphcNhXXXVVbruuuusHlLae/zxx7V//37l5ubqoYcesno4kNTe3q7HHntMXV1dMgxD69evV2VlpdXDSntnzpzRPffco1AopIGBAX3iE5/Qpk2brB4WJIXDYW3ZskUFBQWTrspM2IXa29t14MABBQIBq4eCs6699lrdcMMNkqTa2lrt2LFDN998s8WjwvLly7V582Z5PB4988wzev7553XTTTdZPay0Nn/+fH3961/XT37yE6uHkvbC4bCeeuopffOb31RhYaG2bt2qsrIyzZs3z+qhpbUrr7xSGzdu1GOPPWb1UHCWx+NRdXW1Fi5cqJMnT2rLli1avnw5vysWmzFjhu655x5lZmYqFArp7rvv1ooVK3TxxRdbPbS0V1tbq7lz5+rkyZOTfizbmKF/+qd/0pe+9CUZhmH1UHBWdnZ29O3Tp08zNzZx2WWXyePxSJIuvvhidXZ2WjwizJs3T3PmzLF6GJD03nvvqbS0VCUlJfJ6vbriiivU0NBg9bDS3iWXXCK/32/1MDBEfn6+Fi5cKEnKysrS3Llz+f+JDRiGoczMTEnSwMCABgYGeP1lAx0dHdq/f7+uuuqqKT2eld0019DQoIKCAp1//vlWDwXD/Mu//IteffVVZWdn65577rF6OBhm9+7duuKKK6weBmAbnZ2dKiwsjL5fWFiod99918IRAfbX2tqqDz74QBdeeKHVQ4EGd6jcddddamlp0Wc+8xlddNFFVg8p7f30pz/VTTfdNKVVXYmwmxbuu+8+dXV1jbj9hhtu0PPPP69vfvObqR8UxpyX8vJy3Xjjjbrxxhv1/PPP61e/+hXnRlJkvHmRpOeee04ej0ef+tSnUjy69DSROQEApzl16pQeeughffnLX47Z0QXrZGRk6MEHH1Rvb69+8IMf6PDhw1qwYIHVw0pbb775pnJzc7Vw4UI1NzdP6XMQdtPAt771rVFvP3z4sFpbW3XnnXdKGtwmcNddd+n+++9XXl5eCkeYnuLNy3Cf+tSndP/99xN2U2S8eXnllVf05ptv6u6772Z7U4pM9HcF1iooKFBHR0f0/Y6ODgrrAXGEQiE99NBD+tSnPqWPf/zjVg8Hw/h8Pi1dulRNTU2EXQu988472rdvnxobG3XmzBmdPHlSjzzyiG6//fYJfw7CbhpbsGCBnnzyyej7t912m+6//36qMdvA0aNHdd5550ka3GrOmUR7aGpq0osvvqjvfOc7mjVrltXDAWxl0aJFOnr0qFpbW1VQUKDf/va3k3pBAqQL0zT1xBNPaO7cufrsZz9r9XBw1okTJ+TxeOTz+XTmzBkdOHBAf/mXf2n1sNLa5s2btXnzZklSc3OzXnrppUn/f4WwC9jQP//zP+vo0aMyDEOBQIBKzDbx1FNPKRQK6b777pMkXXTRRcyNxd544w394z/+o06cOKHt27fr/PPP1ze+8Q2rh5WWPB6PvvrVr2rbtm0Kh8Nau3at5s+fb/Ww0t7DDz+st99+Wz09Pbrlllu0adMmrVu3zuphpbV33nlHr776qhYsWBDdXXfjjTdq1apVFo8svR0/flyPPfaYwuGwTNPUJz/5SX3sYx+zeliYJsM0TdPqQQAAAAAAkEi0HgIAAAAAuA5hFwAAAADgOoRdAAAAAIDrEHYBAAAAAK5D2AUAAAAAuA5hFwAAAADgOoRdAAAc6plnntH3v//96Ps1NTW69957FQqFLBwVAAD2QNgFAMCh/vIv/1LNzc364IMPVFdXp6amJn3961+X1+u1emgAAFjOME3TtHoQAABgap599lm98cYb6uvr07333qtAIKC+vj7dd999+s///E9t27ZNCxYssHqYAACkHCu7AAA42AUXXKDDhw9r8+bNCgQCkqSZM2dq69at+sQnPmHx6AAAsA5hFwAAhzp8+LCefPJJrVmzRnv27Ine7vV6NXv2bAtHBgCA9Qi7AAA4UGdnpx544AH9t//23/S3f/u3Onz4sJqbm60eFgAAtkHYBQDAYfr6+nT//ffrmmuuUVlZmWbNmqXPfe5z+vnPf2710AAAsA0KVAEA4FKPPfaYPve5z1GgCgCQlgi7AAC40P33368//elPCgQCuvrqq3XllVdaPSQAAFKKsAsAAAAAcB3O7AIAAAAAXIewCwAAAABwHcIuAAAAAMB1CLsAAAAAANch7AIAAAAAXIewCwAAAABwHcIuAAAAAMB1CLsAAAAAANch7AIAAAAAXOf/B0EpUq8N2UBiAAAAAElFTkSuQmCC",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plot_ds(data,m[-1],q[-1])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### RMSProp"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"RMSprop cerca di ridurre l'aggressività di Adagrad nel ridurre il learning rate in modo monotonicamente decrescente. \n",
"\t\n",
"La somma $G_{j,k}$ dei quadrati dei gradienti precedenti è sostituita da una sua versione $\\tilde G_{j,k}$ che decresce in modo geometrico per mezzo di un parametro di smorzamento $0<\\gamma<1$\n",
"\n",
"\\begin{align*}\n",
" \\tilde G_{j,k}&=\\gamma \\tilde G_{j,k-1}+(1-\\gamma)g_{j,k}^2\\\\\n",
" &=\\gamma (\\gamma \\tilde G_{j,k-2}+(1-\\gamma)g_{j,k-1}^2)+(1-\\gamma)g_{j,k}^2=\\gamma^2\\tilde G_{j,k-2}+(1-\\gamma)(\\gamma g_{j,k-1}^2+g_{j,k}^2)\\\\\n",
" &=\\cdots\\\\\n",
" &=(1-\\gamma)\\sum_{i=0}^k\\gamma^{k-i} g_{j,i}^2\n",
"\\end{align*}\n",
"\n",
"dato che assumiamo $\\tilde G_{j,k}=0$ if $k<0$.\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Ne deriva che alla $k+1$-esima iterazione vengono eseguite le azioni seguenti\n",
"\n",
"\\begin{align*}\n",
"g_{j, k} &= \\frac{\\partial J(\\theta)}{\\partial\\theta_j}\\Big\\rvert_{\\theta=\\theta^{(k)}}\\\\\n",
"\\tilde G_{j,k} & =\\gamma \\tilde G_{j,k-1}+(1-\\gamma)g_{j,k}^2\\\\\n",
"\\Delta_{j,k} &= - \\frac{\\eta}{\\sqrt{\\tilde G_{j,k}+\\varepsilon}} g_{j, k}\\\\\n",
"\\theta_j^{(k+1)} &= \\theta_j^{(k)} + \\Delta_{j,k}\n",
"\\end{align*}\n"
]
},
{
"cell_type": "code",
"execution_count": 139,
"metadata": {},
"outputs": [],
"source": [
"def RMSProp(X,t, eta = 0.1, G_tilde = 0, eps = 1e-8, gamma = 0.9, epochs = 10000):\n",
" theta = np.zeros(nfeatures+1).reshape(-1,1)\n",
" theta_history = []\n",
" cost_history = []\n",
" for k in range(epochs): \n",
" g = gradient(theta,X,t)\n",
" G_tilde = gamma * G_tilde + (1 - gamma) * g**2\n",
" theta = theta - eta * g / (np.sqrt(G_tilde) + eps)\n",
" theta_history.append(theta)\n",
" cost_history.append(cost(theta, X, t))\n",
" theta_history = np.array(theta_history).reshape(-1,3)\n",
" cost_history = np.array(cost_history).reshape(-1,1)\n",
" m = -theta_history[:,1]/theta_history[:,2]\n",
" q = -theta_history[:,0]/theta_history[:,2]\n",
" return cost_history, m, q"
]
},
{
"cell_type": "code",
"execution_count": 140,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"tempo di esecuzione: 0.547 secondi\n",
"10000 passi totali\n",
"1000000 gradienti calcolati\n"
]
}
],
"source": [
"start_time = time.time()\n",
"cost_history, m, q = RMSProp(X,t, eta = 0.1, G_tilde = 0, eps = 1e-8, gamma = 0.9, epochs = 10000)\n",
"print(f\"tempo di esecuzione: {time.time()-start_time: 4.3f} secondi\")\n",
"print(f\"{len(m)} passi totali\")\n",
"print(f\"{len(m)*n} gradienti calcolati\")"
]
},
{
"cell_type": "code",
"execution_count": 141,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA7sAAAHzCAYAAADhDgreAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAABYVElEQVR4nO3df3ib9X3v/9ctyb8k+Zek2Gl+8KUJsISEkDCHtjhtSAgpl2kZKxmFDO/auh3Gget0rKdcJKct0FJKKOUqFwUO7QWjq9lZ2xMKvTjzGV6WEA5uGQ5xFmIaBqwtW0OiyL9iSf4l6f7+YUu2bMtxEkv3Len5uK5etRXd8Uf+2EGv+/P+vD+GaZqmAAAAAAAoIA6rBwAAAAAAwHwj7AIAAAAACg5hFwAAAABQcAi7AAAAAICCQ9gFAAAAABQcwi4AAAAAoOAQdgEAAAAABYewCwBAjp1//vmqqKhQZWWlampqdMUVV+ipp55SIpE47bW/+c1vZBiGYrFYVseYq68DAEC2EHYBALDASy+9pIGBAf32t7/Vjh079NBDD+nP//zPrR4WAAAFg7ALAICFqqurdd111+knP/mJ/vZv/1ZHjhzRP/zDP2jdunWqqqrS0qVLdd9996We/6lPfUqSVFNTI6/Xq1/+8pd6//33tXnzZvn9fgUCAf3xH/+x+vr6Utc89NBDWrx4sSorK/V7v/d7+ud//mdJUiKR0K5du7R8+XL5/X7deOON6unpyfh1AADIJ4RdAABs4PLLL9eSJUv0//7f/5PH49GPfvQj9fX16R/+4R/0P//n/9SLL74oSXr11VclSX19fQqHw/rEJz4h0zS1c+dOHTt2TL/61a/0H//xH6mA/M477+jxxx9XR0eHBgYG9PLLL+v888+XJH3ve9/Tiy++qP379+vYsWOqra3VHXfckfHrAACQTwi7AADYxKJFi9TT06Mrr7xSl1xyiRwOh9asWaObb75Z+/fvz3jdBRdcoKuvvlplZWVasGCBvvSlL6We73Q6NTw8rLffflujo6M6//zztXz5cknSU089pQceeEBLlixRWVmZ7rvvPu3evZt9ugCAgkDYBQDAJn73u9/J5/PpX/7lX7Rp0yYtWLBA1dXVeuqppxQKhTJed+LECd10001avHixqqqqdMstt6Sef8EFF+jRRx/Vfffdp7q6Ot100006duyYJOm3v/2t/vAP/1A1NTWqqanRypUr5XQ6deLEiZy8XgAAsomwCwCADXR0dOh3v/udNmzYoO3bt+u6667Tf/zHf6i/v1+33XabTNOUJBmGMe3a//E//ocMw9Bbb72lU6dO6bnnnks9X5K2b9+u1157Tb/97W9lGIbuvvtuSdLSpUv1f//v/1VfX1/qf0NDQ1q8ePGMXwcAgHxC2AUAwEKnTp3S//k//0c33XSTbrnlFl1yySUaGBiQz+dTeXm53njjDf2v//W/Us9fsGCBHA6H/v3f/z312MDAgLxer6qrq/W73/1ODz/8cOrP3nnnHe3du1fDw8MqLy9XRUWFHI6x//zfdttt+spXvqLf/va3kqSTJ0/q5z//ecavAwBAPiHsAgBggc9+9rOqrKzU0qVL9cADD+hLX/qSnn32WUnSk08+qXvuuUeVlZX6xje+oRtvvDF1ndvt1le+8hU1NjaqpqZGr7/+uu69914dPHhQ1dXVuvbaa/W5z30u9fzh4WHt2LFDgUBACxcuVDAY1IMPPihJ+qu/+itdd9112rp1qyorK/Xxj39c//Iv/5Lx6wAAkE8Mc3KdEwAAAAAABYCVXQAAAABAwSHsAgAAAAAKDmEXAAAAAFBwCLsAAAAAgIJD2AUAAAAAFBzCLgAAAACg4LisHkAuHDt2zOoh2FIgEFAoFLJ6GJiCebEn5sWemBf7YU7siXmxJ+bFfpgTe5ptXhYtWpTxOlZ2AQAAAAAFh7ALAAAAACg4hF0AAAAAQMEh7AIAAAAACg5hFwAAAABQcAi7AAAAAICCQ9gFAAAAABQcwi4AAAAAoOC4cv0Fn3zySR08eFDV1dV65JFHJEk//elP9c///M+qqqqSJN1888267LLLpl176NAhPfvss0okErrqqqt0/fXX53LoAAAAAIA8kfOwe+WVV+qaa67RE088kfb4tddeq+uuuy7jdYlEQs8884y++tWvyu/3a+fOnWpoaNCSJUuyPWQAAAAAQJ7JeRnzxRdfLK/Xe8bXvffee1q4cKHq6+vlcrl0xRVXqKOjIwsjBAAAAADku5yv7Gby8ssv69VXX9WyZcv0J3/yJ9MCcU9Pj/x+f+pzv9+vd999N9fDBAAAAADkAVuE3a1bt2rbtm2SpJ/85Cf60Y9+pNtvv/2s/749e/Zoz549kqRdu3YpEAjMyzgLjcvl4ntjQ8yLPTEv9sS82A9zYk/Miz0xL/bDnNjT2c6LLcJuTU1N6uOrrrpKDz300LTn+Hw+dXd3pz7v7u6Wz+eb8e/bsmWLtmzZkvo8FArN32ALSCAQ4HtjQ8yLPTEv9sS82A9zYk/Miz0xL/bDnNjTbPOyaNGijNfZ4uih3t7e1MdvvPGGli5dOu05y5cv14cffqhgMKhYLKZf/OIXamhoyOUwAQAAAAB5Iucru48++qjefvttDQwM6LbbbtONN96orq4u/eY3v5FhGFqwYIFuvfVWSWP7dL///e9r586dcjqd+sIXvqAHHnhAiURCmzZtmjEUAwCA4tN1qFNvvdyqksGwRiu8uuTTTVq1dp3VwwIAWCjnYffOO++c9tjmzZtnfK7P59POnTtTn1922WUznr8LAACKV9ehTh3f3aJtdTUy3G6ZZlz7d7dIEoEXAIqYLcqYAQAAztaRtlZtrKuRYRiSJMMwtLGuRkfaWi0eGQDASoRdAACQ11zRcCroJhmGIVc0YtGIAAB2QNgFAAB5Leb2yjTNtMdM01TM7bFoRAAAOyDsAgCAvLZ6a5P2B/tSgdc0Te0P9mn11iaLRwYAsJItztkFAAA4W8kmVM+3tcoVjSjm9mj1tmaaUwFAkSPsAgCAvLdq7TrCLQAgDWXMAAAAAICCQ9gFAAAAABQcwi4AAAAAoOAQdgEAAAAABYewCwAAAAAoOIRdAAAAAEDBIewCAAAAAAoO5+wCAICz1nWoU2+93KqSwbBGK7z65I03a/FHl1k9LAAAWNkFAABnp+tQp47vbtG2iriu97u1rSKu93/0A3Ud6rR6aAAAEHYBAMDZOdLWqo11NTIMQ5JkGIaurK/RkbZWi0cGAABhFwAAnCVXNJwKukmGYcgVjVg0IgAAJhB2AQDAWYm5vTJNM+0x0zQVc3ssGhEAABMIuwAA4Kys3tqk/cG+VOA1TVOvnOjT6q1NFo8MAAC6MQMAgFlM7bZ8yaebtGrtOklK/f/zba1yRSOKuT3a8Ce30o0ZAGALhF0AADCjVLfluhoZbrdMM679u1skKS3wJj+WpEAgoFAoZMl4C8lsNxkAAHNDGTMAAJjRTN2WN9bRbTnbZjrS6fjuFo50AoAzRNgFAAAzotuyNbjJAADzg7ALAABmRLdla3CTAQDmB2EXAADMaKZuy/uDdFvONm4yAMD8IOwCAIAZrVq7Tgu3Nev5Iade7B7U80NOLdzWTKOkLOMmAwDMD7oxAwCAjKZ2W0b2zXSk02puMgDAGSPsAgAA2Aw3GQDg3FHGDAAAAAAoOIRdAAAAAEDBIewCAAAAAAoOYRcAAAAAUHBoUAUAAICs6zrUqbdeblXJYFijFV5d8ukmmnAByCrCLgAAALKq61Cnju9u0ba6Ghlut0wzrv27WySJwAsgayhjBgAAQFYdaWvVxroaGYYhSTIMQxvranSkrdXikQEoZIRdAAAAZJUrGk4F3STDMOSKRiwaEYBiQNgFAABAVsXcXpmmmfaYaZqKuT0WjQhAMSDsAgAAIKtWb23S/mBfKvCapqn9wT6t3tpk8cgAFDIaVAEAACCrkk2onm9rlSsaUczt0eptzTSnApBVhF0AAABk3aq16wi3AHKKMmYAAAAAQMEh7AIAAAAACg5lzAAAAPOs61Cn3nq5VSWDYY1WeHXJp5so4QWAHCPsAgAAzKOuQ506vrtF2+pqZLjdMs249u9ukSQCb57jJgaQXwi7AAAA8+hIW6tuqKuRYRiSJMMwtLGuRs+3tRKMZpAvAZKbGED+Yc8uAADAPHJFw6mgm2QYhlzRiEUjsq9UgKyI63q/W9sq4jq+u0VdhzqtHto0R9patXGGmxhH2lotHhmATHK6svvkk0/q4MGDqq6u1iOPPCJJamlp0ZtvvimXy6X6+nrdfvvt8ng806694447VF5eLofDIafTqV27duVy6AAAAHMSc3tlmvG0wGuapmLu6e9vil0+rYK7omEZFe60x7iJAdhbTsPulVdeqWuuuUZPPPFE6rE1a9Zo+/btcjqdeu655/TCCy/olltumfH6e++9V1VVVbkaLgAAwBlbvbVJ+3e3pFYBTdPU/mCfVm9rtnpotpNPAZKbGED+yWnYvfjiixUMBtMeu/TSS1MfX3TRRXr99ddzOSQAAFCArNwHmvw6z7e1yhWNKOb2aPW2ZtutVNpBPgVIbmIA+cdWDar27t2rK664IuOfP/DAA5Kkq6++Wlu2bMnVsAAAQB6xQyOhVWvXEW7nIJ8CJDcxgPxjmKZp5vILBoNBPfTQQ6k9u0k/+9nP9P777+vLX/7ytKYOktTT0yOfz6f+/n5985vf1J/92Z/p4osvnvFr7NmzR3v27JEk7dq1SyMjI/P/QgqAy+VSLBazehiYgnmxJ+bFnpgX+7HDnDxzz079YenotNXCF0ZK9OffeNDCkVnHDvOSyb92vKEDL70gZySsuMerhs/+oS5df7nVw8oJO89LsWJO7Gm2eSktLc18XbYGdCZeeeUVvfnmm7rnnntmDLqS5PP5JEnV1dVav3693nvvvYxhd8uWLWkrv6FQaP4HXQACgQDfGxtiXuyJebEn5sV+7DAnsZ6QRv3uGR4/ZfnYrGKHeclk8UeXafEX/3vaY3Yd63yz87wUK+bEnmabl0WLFmW8zvKwe+jQIf385z/X17/+dZWVlc34nKGhIZmmqYqKCg0NDenw4cPatm1bjkcKAADywX+Go/rJu79SqRnXqMOpS85bqhULF9hyHygAIHtyGnYfffRRvf322xoYGNBtt92mG2+8US+88IJisZjuv/9+SdKFF16oW2+9VT09Pfr+97+vnTt3qr+/X9/5znckSfF4XBs2bNDatWtzOXQAAJAHug516v8biejj1WUKlJdKpql9H/xWB3sG9Pu3/ZXVwwMA5FBOw+6dd9457bHNmzfP+Fyfz6edO3dKkurr6/Xwww9nc2gAAKAAHGlr1Q0XnKfIwCl9eDIoRzyh3/NX672yWhoJAUCRsbyMGQCQPVYevwJYIXluq7eqWt6q6tTjdd2DFo4KAGAFwi4AFCg7HL8C5Fo+ndsKAMguwi4AFKgjba26YfzsSkkyDEMb62r0fFsrYRcF61zObaUSAgAKC2EXAApUspxzMsMw5IpGLBoRkH3JcPp8W6tc0Yhibo9Wb2s+bWilEgIACg9hFwAKFOWcKFar1q4744BKJQQAFB6H1QMAAGTH6q1N2h/sk2makjRRzrm1yeKRAfbjiobTbgxJVEIAQL5jZRcACtTZlnMCxYhKCAAoPIRdAChgZ1POCRSjc2lsBQCwJ8IuAABZRIff/EAlBAAUHsIuAABZQoff/EIlBAAUFhpUAQCQJUfaWlNlsdJEh98jba0WjwwAgMJH2AUAIEvo8AsAgHUoYwYAIEvo8ItCNtt+dPaqA7ADwi4AIO9NfWPt/ehyhX/9vuVvtOnwi0I12350SexVB2ALhF0AQF6b+qb77Q8/1Nu7X9M1ay5Wpb/G0jfadPhFoTrS1qobZtiP/vz4fvRMf8bPPoBcIuwCAPLa1DfdXR/8p25Y7Nfx0ElVVtdY/kabDr8oRK5oWEaFO+2xif3o5ix/BgC5Q4MqAEBem9oEypWIy2EYcsTjqcd4ow3Mr7H96GbaY8n96LP9GQDkEmEXAJDXpr6xjjmcSpimEk5n6jHeaAPza/XWJu0P9qV+91L70bc2zfpnAJBLlDEDAHIiW91ZpzaBWnXeEv3svff16TUXSxJNoYAsmMt+dPaqA7AaYRcAkHWzdW491zfA095013xEnm0b9PJv3permzfaQLbMth+dveoA7ICwCwDIutk6t87HG2LeWAMAgKnYswsAyLqpTaQkmkYBAIDsIuwCALKO7qwAACDXCLsAgKyjOysAAMg19uwCALJuLp1bgVzJVmdwAIC9EHYBADmRD02kCEHZY5fv7ek6g9tlnACAc0fYBQBA2T0eqdjZ6Xs7W2dwSbYZJwDg3LFnFwAAjYWgjTOEoCPjIQhnz07f29k6g9tpnACAc0fYBQBAHI+UTXb63s7WGdxO4wQAnDvCLgAA4nikbLLT93a2zuB2GicA4NwRdgEAEMcjZZOdvrer1q7Twm3Nen7IqRe7B/X8kFMLxzuD22mcAIBzR4MqAACUn8cj5UvnYLt9bzN1BrfbOAEA54awCwDAuHw4HinJTh2O5yJfvre5Hme+3LAAgHxEGTMAAHmIzsH5L3XDoiKu6/1ubauI6/juFnUd6rR6aABQEAi7AADkIToH5z9uWABAdlHGDACYV5Rl5sZY5+B4WuClc3B+cUXDMircaY9xwwIA5g8ruwCAeUNZZu7QOTj/cdQRAGQXYRcAMG8oy8yd2Y7QQX7ghgUAZBdlzACAeUNZZm5Z3eF4ppL1jVuutmw8+YajjgAguwi7AIB5wz7S4pHp6KN/ra7W4o8us3p4ecPqGxYAUMgIuwCAebN6a5P2725JlTKnyjK3NVs9tJzIZXMuqxuBHWlr1Q0zlKz/w0svaPEX/3vOxgEAQCaEXQDAvCnmssxMK52S5v315/JrZZKpZN0ZDufk6wO5ZvUNJgBnjrALAJhXxVqWmWml8/m21nn/fuTya2WSqWQ97vHm5OsDuWSHG0wAzhzdmAEAmAeuaDgt+EnZa86Vy6+VSaZOwg2f/cOcjQHIFTrNA/mJlV0AAOZBLptz2aERWKaS9UvXX65QKJSzcQC5QKd5ID8RdgEAmAe5bM5ll0ZgxVqyjuJjhxtMAM4cYRcAgHmQy+ZcxdwIDLCCXW4wATgzOQ+7Tz75pA4ePKjq6mo98sgjkqRwOKzvfve7OnnypBYsWKC//uu/ltc7vcHFK6+8op/97GeSpM997nO68sorczl0AABmlcuVTlZVgdzhBhOQn3Iedq+88kpdc801euKJJ1KPvfjii7rkkkt0/fXX68UXX9SLL76oW265Je26cDis3bt3a9euXZKkHTt2qKGhYcZQDAAAAMwnbjChWMTjCYX6ojoRCutEd0SmaWpr4wVWD+us5DzsXnzxxQoGg2mPdXR06L777pMkbdy4Uffdd9+0sHvo0CGtWbMmFW7XrFmjQ4cOacOGDTkZNwAAAAAUgkTCVE9/VCdCEZ3oDo/9LzT2v1BvVPGEmXpudWU5Yfdc9Pf3q7a2VpJUU1Oj/v7+ac/p6emR3+9Pfe7z+dTT0zPj37dnzx7t2bNHkrRr1y4FAoEsjDr/uVwuvjc2xLzYE/NiT8yL/RTSnPxrxxvqeOkFuSIDinkqtf6zf6hL119u9bDOSiHNSyFhXuynkOZkLNBGdOzEKR0L9uvD4Cn97kS/Pgz268OTpxSLJTJeG6j1aFF9tRbVVWlRfbX8fv+0I+9y6WznxRZhdzLDMM75G7llyxZt2bIl9TlHIMwsEAjwvbEh5sWemBd7Yl7sp1DmpOtQp47vbtFn6mpkeJ0yzYj2P/O4+vrzc59mocxLoWFe7Cff5sQ0TZ0KD4+XHId1PBRWsHtstTbYHdHIaDzjtdWV5ar3e7Qw4FV9wKs6v1f1fq/q/B6VljjTntvd3Z3tlzKr2eZl0aJFGa+zRditrq5Wb2+vamtr1dvbq6qqqmnP8fl8evvtt1Of9/T06OKLL87lMAEAQJE40taqG8Y770pjN+M31tXo+bbWvAy7APKXaZoKR0cmlRpPlB4HuyMaGo5lvLbSU6r6wFiITf2/36M6v1flZbaIgllli1fY0NCg/fv36/rrr9f+/fu1fv36ac9Zu3at/v7v/17hcFiS9K//+q/avn17rocKAAByoOtQp956uVUlg2GNVnh1yaebchoyXdGwjAp32mOGYcgVjeRsDACKS2RwJNUU6kQorGD3xMfRodGM13kqSiYFWa/qAp5UuHWXl+TwFdhPzsPuo48+qrffflsDAwO67bbbdOONN+r666/Xd7/7Xe3duzd19JAkvf/++/qnf/on3XbbbfJ6vbrhhhu0c+dOSdK2bdvoxAwAQAFKlhBvq6uR4XbLNOPav7tFknIWeGNur0wznra1yjRNxdyenHx9AIVpcHhUweTK7HjpcTLQhqMjGa+rKHOpbtLK7MRqrUded1kOX0F+yXnYvfPOO2d8/J577pn22PLly7V8+fLU55s3b9bmzZuzNTQAAGADdighXr21Sft3t2jj+DhM09T+YJ9Wb2vOydcHkL+GR2KpfbNjoTYyvkobVv/AcMbrSkuc4yHWM75C6x3fU1upSk+ppQ2i8pUtypgBAACS7FBCnAzVz7e1yhWNKOb2aPW2/GxOlQ3zXWZuddk6cKZGY3EFuyNppcbJ1dreU0MZr3O5HKr3eSZWaQMeLfRXqi7gUU1lOYF2nhF2AWCe8GYNmB9zKSHOxe/bqrXrpv2d/J7Pf5m5HcrWgZnE4gmFeiMTDaFCEyu1Pf1RmebM1zmdhhbUjpcaTyk9rq2qkMNBoM0Vwi4AzAPerAHz53QlxFb9vvF7Pma+y8ztULaO4pVImAr1RRUcD7L9kX/Tb/4zpGAorFBfVInEzInW4TC0oNatuoBXC8dXaJOlx/7qCjmdjhy/EsyEsAsA84A3a8D8OV0JsVW/b/yej5nvMnM7lK2jsCUSpnpPDY4f25PeFOpkb0Tx+MyB1jCkQK07dfbs5KZQgVqPXARa2yPsAsA84M0aML9mKiFOsur3jd/zMfPdqZrO15gPpmmqb2AordT4RHdYwVBYwZ6IRmOJjNfWVlekmkIt+//q5S2X6vxe1fk8Kilx5vBVYL4RdgFgHvBmDcgdq37f+D0fM9+dqul8jbkyTVOnwsOpldngpFXaYHdYwyPxjNdWV5aNr9BOlBwnV2zLSiciUSAQUCgUysXLQQ4QdgFgHvBmDcidbPy+zaXxFL/nY+arU/Xk7/mJ4YSOfNCtJV4Pna+hcHR4SlOoiVXaweFYxuu87tK0o3uSZcd1AY8qykpy+ApgF4RdAJgHHFMC5M58/77NtfEUv+cTZiszn4tp33NfhfYH+7Tw+j8qyu9nMYoOjaZKjoPjwfZ4KKxgd1iRwdGM17nLS1KBtm480C4MjK3QeipKc/gKkA8IuwAwT871zR+AuZvP37czaTzF7/n8oNlXcRgajk2cQ5tcpR0PuAORkYzXlZW6JkqNJzWFqvd75XWXchYt5oywCwAAihqNp3KP73nhGBmNK5gsMx5fnU2WHvcPDGW8rrTEOdbhOBVoJz6u8pYRaDEvCLsAAKCo0Xgq9/ie55dYLKGTPemlxsk9tb2nBmXOfHKPXE7HpEA7XnY8HmhrKsvlcBBokV2EXQCwwFya4cAemKvCR+Op3ON7bj/xeEKhvuikUuOJ0uPuvmjGQOt0GAr4PWMrs8mS4/Fw66t2E2hhKcIuAOTYXJvhwHrM1dxMviHg9AV04ac259X3h8ZTucf33BqJhKnuvmj6ObTjgTbUG1U8MXOiNQxpgc+TKjWuS5YdB7wK1LjldDpy/EqAuSHsAkCO0ZglfzBXpzf1hkBJyaj+KQ9vCNB4Kvf4nmdHImGq79Tg2Mps6hzasXB7sieiWDwx43WGIflrKiaVGk+cRbvA55HLRaBF/iHsAkCO0ZglfzBXp8cNASD3TNNU/8DwpCAbVrA7ouOhsE72RDQyGs94bU1V+XiIHS87DkwE2tISZw5fBZB9hF0AyDEas+QP5ur0uCEAZIdpmhqIjIwf3TNRdpzcTzs8Est4bZWnTHXjK7MLx8NssvS4rJS3/yge/LQDQI7RmCV/MFenxw0B4NxEBkcmGkJNOof2RHdEg0OjGa/zVJSkrcxO7njsLi/J4SsA7IuwCwA5RmOW/MFcnR43BIDTGxweVTA0VmacLD0OhsIK9kQ1EBnOeF1FmWsizI6vzNaNf+51l+bwFQD5ibALABagMUv+YK5mN/WGgMvn1gXcEEARGh6JKThDU6gT3WGdCmcOtGWlzrEy48lNocYDbaWnNK1qAsCZIewCAIBzMvmGQCAQUCgUOqe/j7ONYVejo3EFe9L3zgbHw23vqaGM15W4HONdjtPPol1x0VIlRqMEWiBLCLsAAMA2ONsYVovFEjrZO34GbbIp1PgqbU9/VObMR9HK6TRU55t8Du1EuK2tqpDDMT3Q+ms8CoUGs/yKgOJF2AUAALbBUUbIhXg8oe6+6JSzaMc+7u6LKpGYOdE6HIYW+NxpDaGSK7X+GveMgRaAdQi7AADANjjKCPMlkTDV0z+YagaVDLTHQ2GFeiOKx2cOtIYhBWrd4/toPWNH9yQDba1bLqcjx68EwNki7AIAANvgKCOcCdM01XdqaFKp8URTqGBPRLFYIuO1tdUVqh8Ps3WTuh0v8HlU4nLm8FUAyBbCLgAAsA2OMsJUpmnqVHg4rSlUsvQ42B3RyGg847XVlWVp3Y2Te2gX+DwqK+VtMFDo+C0HAAC2wdnGxSscHdaJSWfRBpPBtjusoeFYxusqPaWpQDu543Gd36OKspIcvgIAdkPYBQAAtsLZxoUrOjgyY1OoYHdYkcHRjNd5KkrSSo3rJ33srijN4StAIes83KW9B44oFBmW15lQ04b1WrdmldXDwjkg7AIAAGDeDA3H0s+hTX0c1kBkJON15WWuVKlx6uiewNieWq+7LIevAMWo83CXWtqPqn7NRnlGR5UwTbW0d0gSgTePEXYBAABwRkZG45NCbGRSuA2rf2A443WlJU7VTVmZTe6nrfKWpTUmA3Kptf2AaldsSjv2rHbFerW27yPs5jHCLgAAwBx0Hu5S62sdCscdRVHiOBqL62RPJK3U+Ph4uO3tH8x4ncvlUJ3PM+0c2nq/VzVV5QRa2FI4Zsgz5WfTMAxFYvy85jPCLgAAwGkkSxxrV26WxzAKpsQxFk+ouzeaWpk9HhrrcHyiO6zuvqjMmY+ildNhKOAbP4N2fKU2WXrsq66Qw0FAQH7xukwlpvzAm6YpjyvDLwHyAmEXAADgNPK5xDGRMHU8dEpH3z2Rdg7tie6wQr1RJRIzv5k3DGmBzzNjUyh/jVtOpyPHrwTInqbGBrW0d6h+TaOksaDbe7RDzY0NFo8M54KwCwAAcBp2L3FMJEz1nRrUie6pR/eEdbInqlg8MeN1hiH5a9xj5cbjpcZ14x8vqPXI5SLQojgkb1rtfXO/+sPD8rhMNTc22P5mFmZH2AUAADiNZInj5P2muS5xNE1TfQNDCk5amZ3c8Xg0NnOglSR/jUcLaivGS40n9tHW+TwqKXHm7DUAdrZuzSpdvXmjQqGQ1UPBPCHsAgCQB7oOdeqtl1tVMhjWaIVXl3y6ibNocyhZ4li7Yr0Mw8haiaNpmhqIjKR1Nz4RGj++pzus4ZF4xmurvGUTTaH83lTZcZ3fo8WLFvIGHkDRIewCAGBzXYc6dXx3i7bV1chwu2Wace3f3SJJBN4cSZYytrbvUyRmnHOJYzg6MqnUODIRbLsjGhwazXid112afg6t36uF44G2orzkrMYCAIWKsAsAgM0daWvVDXU1ac2RNtbV6Pm2VsJuDq1bs+qMwu3g0GhqZTat7DgUVmQwc6CtKC9Jbwg1qfTYU1E6Hy8FAIoCYRcAAJtzRcMyKtxpjxmGIVc0YtGIkDQ8EhvbMzu+MjvRHCqiU5HhjNeVlTondTeeKD2u83tV6SnlLFoAmAeEXQAAbC7m9so049OaI8XcHgtHVTxGR+MK9kTSVmZPjJ9F23dqKON1JS6H6iaVGddPKj2uriwj0AJAlhF2AQCwudVbm7R/d4s2jpcym6ap/cE+rd7WbPXQCkYsltDJnsnlxmMfB7vD6ukflJmh6bLL6Rg/iza9KVS936Oaqgo5HARaALAKYRcAAJtL7st9vq1VrmhEMbdHq7c1s1/3DMXjCYX6ohPH9UxqChXqjWQMtE6HoYDPPd7ZOL3s2F/jJtACgE0RdgEAyAOr1q4j3M5BImGqpz86vSlUd0ShnojiiZkTrWFIgVr3pFJjT6o5lL/GLZfTkeNXAjvoPNyl1tc6FI475HUm1LRh/Vl34AaQe4RdAACQVxIJU30DQ6njeoKTy457IorFEhmv9VVXpFZmk/tp6/1eBXxulbicOXwVsLvOw11qaT+q2pWb5TEMJUxTLe0dkkTgBfIEYRcAANiOaZo6FR5OO392ItxGNDIaz3htdWV5amV24aTS4zq/R6UlBFrMTWv7AdWu2JR25FftivVqbd9H2AXyBGEXAABYwjRNhaMj6WfRTgq0Q8OxjNdWekqnnEM7Vnpc5/eqvIy3Nzh34Zghz5SO2YZhKBJjjzaQL/ivAQAAyKro4EhqZfZ4aLzsePzz6NBoxus8FSVpx/XUJTseB7xyl5fk8BXkt65DnXr31b2K94Q0WuHVJZ9uYv/3HHhdphKmOe3IL48rQyczALZji7B77Ngxffe73019HgwGdeONN+raa69NPdbV1aVvf/vbqqurkyR97GMf07Zt23I+VgAAMN3g8KiCoYh+9et+vffrD9NKj8PRkYzXVZS5VDe1KdT4nlqvuyyHr6AwdR3q1PHdLfrckjqN+t0yzbj2726RJALvaTQ1NqilvUO1K9anjvzqPdqh5sYGq4cGYI5sEXYXLVqkhx9+WJKUSCT0l3/5l7r88sunPW/lypXasWNHrocHAAAkDY/EFOxOP4s2OP5x/8BwxutKS5yps2fHVmgnPq7ylqWtnGF+HWlr1Q3j5zNLY2W4G+tq9HxbK2H3NJL7clvb9ykSM+RxmWpubGC/LpBHbBF2J3vrrbe0cOFCLViwwOqhAABQdEZjcQW7I2mlxslV2t7+wYzXuVwO1fs8WrrIp5rK0tQ5tPUBr2oqywm0FnFFwzIq3GmPGYYhVzRi0Yjyy7o1qwi3QB6zXdhtb29XY2PjjH/2b//2b7rrrrtUW1ur5uZmLV26dMbn7dmzR3v27JEk7dq1S4FAIGvjzWcul4vvjQ0xL/bEvNgT83J2YrGETnSf0rETp3Qs2K8Pg6d07ES/jgX7dbInLDPDlkSX06H6QKUW1VdrUV2VPlJXrcX11VpUVy1/rUcOhyGXy6VYLHNjKeSWyxdQScmoHIah0tJSSWP7Tl0+N787NsC/YfbDnNjT2c6LYZqZ/pOWe7FYTH/5l3+pRx55RDU1NWl/Fo1G5XA4VF5eroMHD+qHP/yhHnvssTn9vceOHcvCaPNfIBBQKBSyehiYgnmxJ+bFnpiXzBIJU6G+qIKhiZLj491hBUNhhfqiSiRm/s+/w2EoUONOlRonz6GtC3jlr66Q0+mY9esyJ/aS3LN79ZI6jY6OyjRN7Q/2aeG2ZsqYbYDfF/thTuxptnlZtGhRxutstbLb2dmpj370o9OCriS53RMlOJdddpmeeeYZnTp1SlVVVTkcIQAA9pFImOo9NTheajzp6J5QWCd7I4rHZw60hiH5a9xppcbJplCBGo9crtkDLfJHMtC+8OpexXpOKeb2aDVBF0CRsFXYna2Eua+vT9XV1TIMQ++9954SiYQqKytzPEIAAHLLNE31DQwpOH4O7fHkObShsII9EY3GEhmvra0qnxRkJ86hrfN5VFLizOGrgJVWrV2njVuuZrUKQNGxTdgdGhrS4cOHdeutt6Yea2trkyRt3bpVr7/+utra2uR0OlVaWqo777yTZhcAgIJgmqYGIiM6HhrQie7IROnxeKOo4ZF4xmurK8vGyozHV2ZTZ9L6PSortc1/5gEAyDnb/FewvLxcf/M3f5P22NatW1MfX3PNNbrmmmtyPSwAwBRdhzr11sutKhkMa7TCq0s+3URJ5ByFoyMT3Y0nlR4HQ2ENDmdu6uR1l6Yd3ZNcra3ze1RRXpLDVwAAQP6wTdgFANhfstnNtroaGW63TDOu/btbJInAOy46NJoKtMnS42S4jQyOZrzOXV6SVmqcCrcBrzwVpTl8BQAAFAbCLgBgzo60teqGuprUNhLDMLSxrkbPt7UWVdgdGo5NnEObWqUdC7enIsMZrysrdaWVGtcHPKlVWq+7lO05OdB5uEutr3UoHHfI60yoacN6zlEFgAJF2AUAzJkrGpZR4U57zDAMuaIRi0aUPSOjcQWTZcbjgfb4eOlx/8BQxutKS5yqGy83rpt0dE99wKsqbxmB1kKdh7vU0n5UtSs3y2MYSpimWto7JInACwAFiLALAJizmNsr04ynBTbTNBVzeywc1dmLxRI62TO51DiSWqXtPTWoTCfRu5wOLfB5VB8YC7N1/olAW1NZLoeDQGtHre0HVLtiU1plQu2K9Wpt30fYBYACRNgFAMzZ6q1N2r+7RRvHS5lN09T+YJ9Wb2u2emgZxeMJhfqiqfNnJ5ced/dFMwZap8NQwO9J7ZudXHrsq3YTaPNQOGbIM2Vl3TAMRWL2nktKrwHg7BB2AWQdb9QKR3Jf7vNtrXJFI4q5PVq9rdny/bqJhKme/uhYmXEovfQ41BtVPDFzojUMja3QJsuOJzWFCtS45XQ6cvxKkE1el6mEaU6rTPC4MtzxsAFKrwHg7BF2AWQVb9QKz6q16ywJt4mEqb6BoUkrtGH1DozqP4716GRPRLF4YsbrDEPy11RMKjWeaBC1wOeRy0WgzSUrb341NTaopb1DtSvWpyoTeo92qLmxISdf/2xQeg0AZ4+wCyCreKOGM2GapvoHhtOO65loEhXRyGg847U1VeXjIXZsZbbO79XCwFigLS1x5vBVIBOrb34lv0Zr+z5FYoY8LlPNjQ22/rcoX0uvAcAOCLsAsoo3apjKNE0NREbGj+6ZKDtOfjw8Est4bZWnTHXJldmAVxd+9COqKDVV7/eorJT/pNmdHW5+rVuzytbhdqp8LL0GALvgnQGArOKNWvGKDI5MNIQKje2hTR7dMzg0mvE6T0XJlIZQY6XHdX6v3OUlac8NBAIKhULZfimYJ9z8OnP5WHoNAHZB2AWQVbxRK2yDw6MKhia6G0/8f0Th6EjG6yrKXOPNoLzj59B6Up973aU5fAXIJW5+nbl8LL0GALsg7ALIKt6o5b/hkVhq3+xEoB37/FR4OON1ZaXOsQ7Hk5tCjQfaSk9pWuBBceDm19nJt9JrALALwi6ArOONmv2NjsYV7ImkrcwGkx2PTw1lvK7E5Rjvcpx+Fm1dwKOayvK8DrRdhzr11sutKhkMa7TCq0s+3WT5EUv5jptfAIBcIuwCQJGIxRI62Tve2XhKU6ie/qjMDJWkTqehOt/kc2gnwm1tVYUcjvwNtJl0HerU8d0t2lZXI8PtlmnGtX93iyQReM8RN78AALlC2AWAAhKPJ9TdF001hRoLtGOrtKG+qBKJmROtw2Fogc89qSnURNmxv8ZdkIF2NkfaWnVDXU1a1+CNdTV6vq2VsAsAGVh5jjYwE8IuAOSZRMJUT//g+ArtRKA9EQrrZG9E8fjMgdYwpECte3wf7djK7MLxlVp/rVsupyPHr8S+XNGwjAp32mOGYcgVjVg0IgCwN6vP0QZmQtgFABsyTVN9p4bSSo2T+2mDPRHFYomM19ZWV4yVGaeO7RkrO17g86jE5czhq8hfMbdXphmf1jU45vZYOCoAsC87nKMNTEXYBQCLmKapU+HhtFLj4+MrtcHuiEZG4xmvra4sS+tunNxDu8DnUVkp/7Sfq9Vbm7R/d4s2jpcym6ap/cE+rd7WbPXQAMCWOEcbdsQ7IgDIsnB0OLUyezyULD0e+3xoOJbxOq+7dKzMOOBN63hc5/eooqwkh6+g+CT35T7f1ipXNKKY26PV25rZrwsAGXCONuyIsAsA8yA6NDrWEGrKHtpgd1iRwdGM17nLS9JKjSdWaz1yV5Tm8BVgqlVr1xFuAWCOOEcbdkTYBYA5GhqOpZ9D2z0RbgciIxmvKy9zpUqNU0f3jHc79rpL8/osWgAAJM7Rhj0RdgFgkpHR+KQQO9EUKtQ7qJ7+aMbrSkucYx2O/dNXaau8ZQRaFKypR43c/JktWnbeEquHBcACnKMNuyHsAig6o7G4TvZE0kqNk3tqe/oHM17ncjlU5/OkVmbr/BNH99RUlRNoUXRmOmrkB22d+vzl/bzhtSnOQQVQTAi7AApSLJ5Qd280rew4+XF3X1Rmhn4ZToehgM+Taga10O9VXcCrlRculeJDcjjyM9B2HerUWy+3qmQwrNEKry75dBP7UXHOZjxqZOV6tba/TICyIc5BBVBsCLsA8lYiYaq7LzrtHNoT3WF190YVT8ycaA1DWjAp0E4uPfbXuOV0OqZdE/BXKhQazvZLyoquQ506vrtF2+pqZLjdMs249u9ukSQCL84JR43kF85BBVBsCLsAbC2RMNV3ajBVcny8O3l0T1gne6KKxRMzXmcYkr+mYtI5tF7VjTeFWlDrkcs1PdAWqiNtrbph/LxYaewN7sa6Gj3f1krYxTnhqJH8ws0JAMWGsAvAcqZpqn9gOG1ldnLH49HYzIFWkmqryseDrDdtpbbO51FJiTOHr8K+XNGwjAp32mOGYcgVjVg0IhSKGY8a+VWHPp+Fo0bYa3ruuDkBoNgQdgHkhGmaGoiMTAm048f3dEc0PBLLeG2VtyztuJ7J4baslH/GTifm9so049Pe4MbcHgtHhUIw01Ejt1571bx3Y2av6fzgHFQAxWZO7xITiYQ6OjpkGIYaGhrkcIyV//3yl7/UJz7xiawOEEB+CUfHAm0w2RQqGWy7IxocGs14ndddmn4O7aRwW1FeksNXUHhWb23S/t0t2jheymyapvYH+7R6W7PVQ0MBmHrUSCAQUCgUmtevwV7T+cE5qACKzZzC7uOPP65AICCXy6WXXnpJd9xxhxYuXKi2tjbCLlCEBodG05tCTQq34ehIxusqykvSzp9NlR0HvPJUlObwFRSX5L7c59ta5YpGFHN7tHpbM/t1kTfYazp/OAcVQDGZU9jt6enRF7/4RUnSpk2b9Pjjj+uP/uiPsjowANYaHomN7ZlNrcyOh9tQWKcimbsSl5U6x8qMx1dmk+fQ1vm9qvSUchatRVatXUe4tRD7Tc8Ne03PTefhLu09cEShyDA/fwCKypzCbiwW0+joqEpKSrRgwQLt2LFDjz76qD744INsjw9AFo2OxhXsiaSfRTsebvtODWW8rsTlGAuzk1Zmk6XH1ZVlBFpgEvabnjv2mp695M9f/ZqN8oyO8vMHoKjMGnbj8bicTqf+9E//VJFIRDU1NZKkiooK3X333XrttddyMUYA5yAWS+hkb2S81Dii4+NhNtgdVk//oMwMCyMup2PsLNpJTaGSpcc1VRVyOAi0wFyw3/Tcsdf07PHzB6CYzRp2v/Wtb+muu+7SBRdcMO3PHA6HPvWpT2VtYADmLh5PqLsvqhPdY2E2OKkpVKg3kjHQOh2GAj636gPjZceTmkL5a9wEWmAesN90frDX9Ozw8wegmM0ads8//3x97Wtf086dO+Xz+SRJb7/9tn784x/rG9/4Rk4GCGBMImGqpz+a1hQqWXoc6o0oHp850RqGFKh1Tyo1njiL1l/rlsvpyPErAYoL+01hpeTP32T8/AEoFrOG3ebmZrW1telrX/uatm/frr179+qDDz7Qddddl6vxAUXFNE2FesP61fsnU6XGyXAb7IkoFktkvNZXXZFama2bVHK8wOdRicuZw1cBYDL2m8JKyZ+/+jWNksTPH4CictoGVRdddJHcbrcee+wxbdy4UXfffbdKSzkiBDhbpmnqVHg47fzZE6l9tBGNjMYzXltdWZ62Mluf6nTsUWkJgRawI/abwkrJn7O9b+5Xf3iYn7/ToHM6UFhmDbsPP/yw3n77bV177bW68cYb9fTTT+vIkSO67LLLcjU+IC+ZpqlwdCTtLNrkObQnusMaGo5lvLa6slwLkmXHk0qP6/xelZfNqYE6AJthvymstG7NKl29eaNCoZDVQ7E1OqcDhWfWd84f+chH9F//63+V1+uVJNXX1+uhhx5SMBjUNddck5MBAnYWHRxJW5mdfHxPdGg043WeipJUqfFCv1d1yY7HAa/OW/IR3pAAAJBjdK4GCs+sYfeWW25J+/y8887T/fffrwcffJCwi6IxODyqYCrQRnQiNJAKtOHoSMbrystcMzaFqg945HWX5fAVAACA06FzNVB4zrgm0ufz0YkZBWd4JKaTPWMB9vh46XFwvONx/8BwxutKS5ypRlD1fq/qJn1c5S1L674KAADsi87pQOE5qw2AFRUV8z0OIOtGY3EFu5MhNpLWIKq3fzDjdS6XQ/U+z3iQnTiHtt7vVU1VOYEWAIACQOd0oPDQ7QYFJRZPKNQbmTiLNjTW4fhEd1jdfVGZGW7OOp2GFtR6Zlil9cpXXSGHg0ALAEAho3M6UHgIu8g7iYSpUF90vLvxRLfjE91hhXqjSiRmTrQOh6EFte60UuOFgbFQ66+ukNPpyPErAQAAdkLndKCwEHZhS4mEqd5TgxNNoVJH94QV7IkoHp850BqG5K9xT5QaTyo9DtR45HIRaAEAAIBiQNiFZUzTVN/AkIKTVmaPh8ZCbbAnotFYIuO1tVXlE2E2MHEObZ3Po5ISZw5fBQAAAAA7slXYveOOO1ReXi6HwyGn06ldu3al/blpmnr22WfV2dmpsrIy3X777Vq2bJlFo8VcmKapgcjIxBm0k5pCBbvDGh6JZ7y2yls2VmY8pSlUnd+jslJb/egCAIAs6zzcpdbXOhSOO+R1JtS0YX1BlRwX+usDrGC7xHDvvfeqqqpqxj/r7OzU8ePH9dhjj+ndd9/V008/rW9961s5HiFmEo5ODbQTpceDw7GM13ndpWlNoZJlx3V+jyrKS3L4CgAAwOlYFcg6D3eppf2oaldulscwlDBNtbR3SFJBBMJCf32AVWwXdmdz4MABfepTn5JhGLrooosUiUTU29ur2tpaq4dWFKJDo6mV2cmlxydCYUUGRzNe5y4vSSs1ToXbgFeeitIcvgIAAHC2rAxkre0HVLtiU+q4P8MwVLtivVrb9xVEGCz01wdYxXZh94EHHpAkXX311dqyZUvan/X09CgQCKQ+9/v96unpmRZ29+zZoz179kiSdu3alXYNJrhcrmnfm6HhUR0LntKxE/06FuzXh6mPT6l/IPNZtBVlJfpIXZUW1VdrUV2VPlJXrUX11VpcV61Kbxln0Z6BmeYF1mNe7Il5sR/mxJ7mY172vnlE9Ws2pv03vX5No/a+uV9Xb954rkOc1aizXO6ysmmPDzrL8/rnLTkvhfr68hH/htnT2c6LrcLu/fffL5/Pp/7+fn3zm9/UokWLdPHFF5/x37Nly5a0oBwKheZzmHlvZDSuYHdEg6OG3vv1h2llx32nhjJeV1riVF3yDNrxldmF4yu1VRkC7chwWN3D4Wy+nIITCAT4mbUh5sWemBf7YU7saT7mJRQelmd0eiVXf3g463NeEh/S8PBw2nsN0zTlig/l9c9bcl4K9fXlI/4Ns6fZ5mXRokUZr7NV2PX5fJKk6upqrV+/Xu+9915a2PX5fGkvsru7O3UN0sViCZ3smVxqHEmVHPeeGpQ588k9cjkdWuDzzHB0j1c1leVyOFihBQCgGHldphKmOS2QeVwZ3lTMo6bGBrW0d6h2xXoZhiHTNNV7tEPNjQ1Z/9q5UOivD7CKbcLu0NCQTNNURUWFhoaGdPjwYW3bti3tOQ0NDfrHf/xHNTY26t1335Xb7S7q/brxeEKhvmhqZTYYCuv4eKDt7otmDLROh6GAz62lH/Gptro01eW4PuCRr9pNoAUAm6NrK6xgZSBL/ny3tu9TJGbI4zLV3NhQMD/3hf76AKvYJuz29/frO9/5jiQpHo9rw4YNWrt2rdra2iRJW7du1bp163Tw4EF98YtfVGlpqW6//XYrh5wTiYSpnv5oamX2eCis4HigDfVGFU/MnGgNQwrUurUw2d14UlOoQI1bTqeDMg0AyEN0bYVVrA5k69asKuif8UJ/fYAVbBN26+vr9fDDD097fOvWramPDcPQX/zFX+RyWDmRSJjqGxiacg7tWOnxyZ6IYvFExmv9NRVjHY6nnEUb8LlV4nLm8FUAKBSsGtobXVthJQIZgHxim7BbjP7upX/VO78OKdgd0choPOPzaqrKx0Ps2MpsMtzW+T0qLSHQApg/rBraXzhmyDOlIaBhGIrE2IICAMBkhF0LnQiF9Z/HT0mSqjxlqpvaFGr8XNryMqYJQG6wamh/VjYJAgAgn5CiLPS5rRfrc1svVp3fK3d5idXDAQBWDfMAXVsBAJgbwq6Fzl9cvJ2kAdgTq4b2Z3WTIAAA8gVhFwCQwqphfqBJEAAAp0fYBQCkFMOqId2mAQAoDoRdAECaQl41pNs0AADFw2H1AAAAyJWxbtPrZ+g2fcDikQEAgPlG2AUAFI1wzEhrviXRbRoAgEJF2AUAFA2vy5RppneWpts0AACFibALACgaTY0N6j3akQq8yW7TTXSbBgCg4NCgCgBQNJJNqH708+f17yf7FR8d1vK6GkkrLB0XAACYf4RdAEDRMQLnqWHDxFnCdGQGAKDwUMYMACgqdGQGAKA4sLILACgq4ZghT552ZO483KXW1zoUjjvkdSbUtGE9q9EAAGRA2AUAFBWvy1TCNNOOIMqHjsydh7vU0n5UtSs3y2MYSlB+DQDArChjBgAUlXztyEz5NQAAZ4aVXQBA0UmEfqsDLxxRYmRIyxbW6k8/d63tV0fzufwaAAArEHYBAEUjWQrs37BNgfFOzL1HO6we1pzka/k1AABWoYwZAFA08rkUOF/LrwEAsAoruwCAopHPpcDJMuvW9n2KxAx5XKaaGxtsX34NAIBVCLsAgKKR76XA69asItwCADBHlDEDAIoGpcAAABQPVnYBAEWDUmAAAIoHYRcAUFQoBS5MnYe71Ppah8Jxh7zOhJo2rGeeAaDIEXYBAEBeSx4pVbtyszyGoYRpqqV97EgpAi8AFC/27AIAgLyWz0dKAQCyh7ALAADyWjhmpHXYlvLnSCkAQPYQdgEAQF7zusxUh+2kfDpSCgCQHezZBQDAZmi2dGaaGhvU0t6RKmVOHinVzJFSAFDUCLsAANgIzZbOHEdKIV9MvZF182e2aNl5S6weFlCwCLsAANjIWLOlTTM0W9pHeJsFR0rB7ma6kfWDtk59/vJ+fnaBLCHsAgBgI+GYIQ/NlmAzlNafuxlvZK1cr9b2l/leAllC2AUAwEa8LlMJ00zrLkyzJViJ0vr5wY0sIPfoxgwAgI00NTao92hHqrtwstlSE82WYBHOMZ4fdA0Hco+VXQAAbIRmS7AbViTnx4xdw3/Voc9zIwvIGsIuAAA2Q7Ml2Aml9fNjphtZt157Fd2YgSwi7AIAACAjzjGeP1NvZAUCAYVCIQtHBBQ2wi4AAJBEx13MjNJ6APmKsAsAAOi4i1lRWg8gH9GNGQAA0HEXAFBwCLsAAEDhmJHWgEii4y4AIL9RxgwAAM644y77ewEAdkfYBVA0eHMOZHYmHXdn29979eaNuR56QeLfKwA4d4RdAEWB5jvA7M6k4+7Y/t5NM+zv3UfYnQf8ewUA84OwC6AozPbmnDePwJi5dtwNxwx52N97Wme7Osu/VwAwP2wRdkOhkJ544gn19fXJMAxt2bJFTU1Nac/p6urSt7/9bdXV1UmSPvaxj2nbtm1WDBdAHuLNOTB/znR/bzE6l9VZ/r0CgPlhi7DrdDrV3NysZcuWaXBwUDt27NCaNWu0ZMmStOetXLlSO3bssGiUAPIZb86B+XMm+3uL1bmszvLvFQDMD1scPVRbW6tly5ZJkioqKrR48WL19PRYPCoAhaSpsUG9RztkmmNvFpNvzpt4cw6csXVrVqm5cYUcR/cp+tY+OY7uU3PjCkpsJzmXo5z49woA5octVnYnCwaD+vWvf60LLrhg2p/927/9m+666y7V1taqublZS5cutWCEAPLRmTTfAXB6c93fW6zOZXWWf68AYH4YZvK2oQ0MDQ3p3nvv1ec+9zl97GMfS/uzaDQqh8Oh8vJyHTx4UD/84Q/12GOPzfj37NmzR3v27JEk7dq1SyMjI1kfez5yuVyKxWJWDwNTMC/2xLzYE/NiP8zJmDcOHtIP2jpVu3JSqfevOnTr1nW6/LK1OR8P82JPzIv9MCf2NNu8lJaWZrzONmE3FovpoYce0qWXXqrPfOYzp33+HXfcoQcffFBVVVWnfe6xY8fmY4gFJxAIKBQKWT0MTMG82BPzYk/Mi/0wJxM6D3eptf1AanW2ycLVWebFnpgX+2FO7Gm2eVm0aFHG62xRxmyapp566iktXrw4Y9Dt6+tTdXW1DMPQe++9p0QiocrKyhyPFAAAYG4o9QYAa9ki7L7zzjt69dVXdd555+muu+6SJN18882p9L5161a9/vrramtrk9PpVGlpqe68885pjR8AAAAAAJBsEnZXrFihn/70p7M+55prrtE111yToxEBAADgXHUe7lLrax0Kxx3yOhNq2rCe1W4AOWOLsAsAAIDC0nm4Sy3tR1W7crM8hqGEaaqlvUOSCLwAcsIW5+wCAACgsLS2H1DtivWpbWeGYah2xXq1th+weGQAigVhFwAAAPMuHDOm9VcxDEORGD1XAOQGZcwAAADj2GM6f7wuUwnTTAu8pmnK47LFqZcAigAruwAAAJrYY5pYuVmeSzYpsXKzWtqPqvNwl9VDy0tNjQ3qPdoh0xwLt6Zpqvdoh5oaGyweGYBiwcouAACAkntMN82wx3Qfq7tnIfk9a23fp0jMkMdlqrmxge8lgJwh7AIAAGhsj6mHPabzat2aVYRbAJahjBkAAEBje0yTJbdJ7DEFgPxF2AUAABB7TAGg0FDGDACwBbrgwmrsMQWAwkLYBQBYLtkFt3blZnkMQwnTVEt7hyQRNJBT7DEFgMJBGTMAwHJjXXDXz9AF94DFIwMAAPmKlV0AgOXoggucPbYAAMDMCLsAAMt5XaYSppla2ZXoggvMBVsAACAzypgBAJajCy5wdtgCAACZsbILALAcXXCBs8MWAADIjLALALAFuuACZ44tAACQGWXMAAAAeYotAACQGSu7AAAAeYotAACQGWEXAAAgj7EFAABmRtgFAOAMca4pAAD2R9gFAOAMcK4pAAD5gQZVAACcAc41BQAgPxB2AQA4A+GYkXbMi8S5pgAA2BFhFwCAM+B1maljXpI41xQAAPsh7AIAcAY41xQAgPxAgyoAAM4A55rOH7paAwCyibALAMAZ4lzTc0dXawBAtlHGDAAAco6u1gCAbCPsAgCAnKOrNQAg2wi7AAAg5+hqDQDINsIuAADIObpaAwCyjQZVAAAg5+hqDQDINsIuAACwBF2tAQDZRBkzAAAAAKDgsLILAACAaToPd6n1tQ6F4w55nQk1bVjPSjyAvELYBQDMCW98geLRebhLLe1HVbtyszyGoYRpqqW9Q5L4vQeQNwi7AIDT4o1v4eHmBWbT2n5AtSs2pc5CNgxDtSvWq7V9Hz8nAPIGYRcAcFq88S0s3LzA6YRjhjzjv+9JhmEoEjMyXAEA9kODKgDAaYVjRiroJvHGN3+N3bxYP8PNiwMWjwx24XWZqTOQk0zTlMdlZrgCAOyHsAsAOC3e+BYWbl7gdJoaG9R7tCP1e2+apnqPdqipscHikQHA3FHGDAA4rabGBrW0d6RWA5NvfJt545uXvC5TCdNMC7zcvMBkyXL21vZ9isQMeVymmhsbKHMHkFcIuwCA0+KNb2Hh5gXmYt2aVfyOA8hrhF0AwJzwxrdwcPMCAFAMCLsAChZHqwCZcfMCAFDoCLsAChJHqwD2ws0nAECu2SrsHjp0SM8++6wSiYSuuuoqXX/99Wl/Pjo6qscff1z//u//rsrKSt15552qq6uzZrAAbI1zYQH74OYTAMAKtgm7iURCzzzzjL761a/K7/dr586damho0JIlS1LP2bt3rzwej773ve+pvb1df/d3f6e//uu/tnDUAOwqHDPkKbCjVVgZQ77i5hMAwAq2OWf3vffe08KFC1VfXy+Xy6UrrrhCHR0dac85cOCArrzySknSxz/+cR05cmTauY8AIBXeubDJlbHEys3yXLJJiZWb1dJ+VJ2Hu6weGnBanOsLALCCbcJuT0+P/H5/6nO/36+enp6Mz3E6nXK73RoYGMjpOAHkh6bGBvUe7UgF3uTRKk15erTK2MrY+hlWxg5YPDLg9Art5hMAID/Ypox5Pu3Zs0d79uyRJO3atUuBQMDiEdmTy+Xie2NDzMv8uHrzRlXXVOuFf25XeFTylkh/fG2jLr9s7Vn9fVbPy6izXO6ysmmPDzrLi/rnxep5wXQzzcnN116lH7R1qnblpHN9f9WhW6+9ivnLEX5X7Il5sR/mxJ7Odl5sE3Z9Pp+6u7tTn3d3d8vn8834HL/fr3g8rmg0qsrKyml/15YtW7Rly5bU56FQKHsDz2OBQIDvjQ0xL/Nn2XlL9N//7PNpj53t99bqeSmJD2l4eDitFNQ0TbniQ0X982L1vGC6meZk2XlL9PnL+9Xa/nLqXN/PNzZo2XlLmL8c4XfFnpgX+2FO7Gm2eVm0aFHG62wTdpcvX64PP/xQwWBQPp9Pv/jFL/TFL34x7Tm///u/r1deeUUXXXSRXn/9da1atWraHiAAKERNjQ1qae9IlTIny7Kb87QsG8WHc30BALlmm7DrdDr1hS98QQ888IASiYQ2bdqkpUuX6ic/+YmWL1+uhoYGbd68WY8//rj+23/7b/J6vbrzzjutHjYA5EQyJLS270utjDU3NhAeAAAAMrBN2JWkyy67TJdddlnaY5///EQJYmlpqb70pS/lelgAYAusjAEAAMydbboxAwAAAAAwXwi7AAAAAICCQ9gFAAAAABQcwi4AAAAAoODYqkEVAGBC5+Eutb7WoXDcIa8zoaYN62lQBQAAMEeEXQCwoc7DXWppP6ralZvlMQwlTFMt7R2SROAFAACYA8qYAcCGWtsPqHbFehmGIUkyDEO1K9artf2AxSMDAADID4RdALChcMxIBd0kwzAUiRkZrgAAAMBklDEDgA15XaYSppkWeE3TlMdlWjgq4NywDx0AkEus7AKADTU1Nqj3aIdMcyzcmqap3qMdampssHhkwNlJ7kNPrNwszyWblFi5WS3tR9V5uMvqoQEAChQruwBgQ8nVrtb2fYrEDHlcppobG1gFQ94a24e+aYZ96Pv4uQYAZAVhFwBsat2aVYQAFIxwzJCHfegAgByijBkAAGSd12WmyvKT2IcOAMgmwi4AAMg69qEDAHKNMmYAAJB17EMHAOQaYRcAAOQE+9ABALlEGTMAAAAAoOAQdgEAAAAABYewCwAAAAAoOIRdAAAAAEDBIewCAAAAAAoOYRcAAAAAUHAIuwAAAACAgkPYBQAAAAAUHJfVAwAAwEqdh7vU+lqHwnGHvM6Emjas17o1q6weFgAAOEeEXQBA0eo83KWW9qOqXblZHsNQwjTV0t4hSQReAADyHGXMAICi1dp+QLUr1sswDEmSYRiqXbFere0HLB4ZAAA4V6zswhYoIwRghXDMkGc86CYZhqFIzMhwBQAAyBeEXViOMkIAVvG6TCVMM7WyK0mmacrjMi0cFQAAmA+EXVhurIxw0wxlhPsIuwCyqqmxQS3tHalSZtM01Xu0Q82NDVYPbU6oigEAIDPCLixHGSGAXJscEhN9IYX2vy+Pf6E8LlPNjQ15ERipigEAYHaEXViOMkIAuTQ1JLrHV3P/qHFFXoVEqmIAAJgd3ZhhuabGBvUe7ZBpjoXbZBlhU56UEQLIL4XSgTkcM9JuEkpUxQAAMBkru7BccgWitX2fIjEjr8oIAeSfQtk6QVUMAACzI+zCFtatWUW4BZAThRIS8725FgAA2UbYBQAUlUIJiVTFAAAwO8IuAKCoFFJIpCoGAIDMCLsAgKJDSAQAoPDRjRkAAAAAUHAIuwAAAACAgkMZMwAAZ6jzcJdaX+tQOO6Q15lQ04b1lEUDAGAzhF0AAM5A5+EutbQfVe3KzfIYhhKmqZb2Dkki8AIAYCOUMQMAcAZa2w+kji2SJMMwVLtivVrbD1g8MgAAMBlhFwCAMxCOGamgm2QYhiIxI8MVAADACoRdAADOgNdlyjTNtMdM05THZWa4AgAAWIE9uwCA06Ih04Smxga1tHekSplN01Tv0Q41NzZYPTQAADCJ5WG3paVFb775plwul+rr63X77bfL4/FMe94dd9yh8vJyORwOOZ1O7dq1y4LRAkDxoSFTuuRrbm3fp0jMkMdlqrmxoSi/FwAA2JnlYXfNmjXavn27nE6nnnvuOb3wwgu65ZZbZnzuvffeq6qqqhyPEACK21hDpk0zNGTaV7QBb92aVUX72gEAyBeW79m99NJL5XQ6JUkXXXSRenp6LB4RAGAyGjIBAIB8ZPnK7mR79+7VFVdckfHPH3jgAUnS1VdfrS1btuRqWABQ1LwuUwnTTAu8NGQCAAB2Z5hTW0pmwf3336++vr5pj990001av369JOlnP/uZ3n//fX35y1+etoIgST09PfL5fOrv79c3v/lN/dmf/ZkuvvjiGb/enj17tGfPHknSrl27NDIyMn8vpoC4XC7FYjGrh4EpmBd7KuZ5eePgIf2grVO1Kyc1ZPpVh27duk6XX7bW0rEV87zYFXNiT8yLPTEv9sOc2NNs81JaWprxupyE3dN55ZVX9E//9E+65557VFZWdtrn//SnP1V5ebmuu+66Of39x44dO9chFqRAIKBQKGT1MDAF82JPxT4vnYe71Np+INWQqckmDZmKfV7siDmxJ+bFnpgX+2FO7Gm2eVm0aFHG6ywvYz506JB+/vOf6+tf/3rGoDs0NCTTNFVRUaGhoSEdPnxY27Zty/FIAaB40ZAJAADkG8vD7jPPPKNYLKb7779fknThhRfq1ltvVU9Pj77//e9r586d6u/v13e+8x1JUjwe14YNG7R27VoLRw0AAAAAsDPLw+73vve9GR/3+XzauXOnJKm+vl4PP/xwLocFAAAAAMhjlh89BAAAAADAfCPsAgAAAAAKDmEXAAAAAFBwCLsAAAAAgIJD2AUAAAAAFBzCLgAAAACg4BB2AQAAAAAFx/JzdgEAmKrzcJdaX+tQOO6Q15lQ04b1WrdmldXDAgAAeYSwCwCwlc7DXWppP6ralZvlMQwlTFMt7R2SROAFAABzRhkzAMBWWtsPqHbFehmGIUkyDEO1K9artf2AxSMDAAD5hLALALCVcMxIBd0kwzAUiRkZrgAAAJiOsAsAsBWvy5RpmmmPmaYpj8vMcAUAAMB0hF0AgK00NTao92hHKvCapqneox1qamyweGQAACCf0KAKAGArySZUre37FIkZ8rhMNTc20JwKAACcEcIuAMB21q1ZRbgFAADnhDJmAAAAAEDBIewCAAAAAAoOYRcAAAAAUHAIuwAAAACAgkPYBQAAAAAUHMIuAAAAAKDgEHYBAAAAAAWHsAsAAAAAKDiEXQAAAABAwSHsAgAAAAAKDmEXAAAAAFBwCLsAAAAAgIJD2AUAAAAAFBzCLgAAAACg4BB2AQAAAAAFxzBN07R6EAAAAAAAzCdWdovYjh07rB4CZsC82BPzYk/Mi/0wJ/bEvNgT82I/zIk9ne28EHYBAAAAAAWHsAsAAAAAKDiE3SK2ZcsWq4eAGTAv9sS82BPzYj/MiT0xL/bEvNgPc2JPZzsvNKgCAAAAABQcVnYBAAAAAAXHZfUAYA8vvfSSWlpa9PTTT6uqqsrq4RS9H//4xzpw4IAMw1B1dbVuv/12+Xw+q4dV9FpaWvTmm2/K5XKpvr5et99+uzwej9XDKmq//OUv9b//9//W7373O33rW9/S8uXLrR5SUTt06JCeffZZJRIJXXXVVbr++uutHlLRe/LJJ3Xw4EFVV1frkUcesXo4kBQKhfTEE0+or69PhmFoy5YtampqsnpYRW9kZET33nuvYrGY4vG4Pv7xj+vGG2+0eliQlEgktGPHDvl8vjPuykzYhUKhkA4fPqxAIGD1UDDuuuuu00033SRJam1t1e7du3XrrbdaPCqsWbNG27dvl9Pp1HPPPacXXnhBt9xyi9XDKmpLly7Vl7/8Zf3gBz+weihFL5FI6JlnntFXv/pV+f1+7dy5Uw0NDVqyZInVQytqV155pa655ho98cQTVg8F45xOp5qbm7Vs2TINDg5qx44dWrNmDb8rFispKdG9996r8vJyxWIx3XPPPVq7dq0uuugiq4dW9FpbW7V48WINDg6e8bWUMUN/+7d/qz/+4z+WYRhWDwXj3G536uPh4WHmxiYuvfRSOZ1OSdJFF12knp4ei0eEJUuWaNGiRVYPA5Lee+89LVy4UPX19XK5XLriiivU0dFh9bCK3sUXXyyv12v1MDBJbW2tli1bJkmqqKjQ4sWL+e+JDRiGofLycklSPB5XPB7n/ZcNdHd36+DBg7rqqqvO6npWdotcR0eHfD6fzj//fKuHgin+/u//Xq+++qrcbrfuvfdeq4eDKfbu3asrrrjC6mEAttHT0yO/35/63O/3691337VwRID9BYNB/frXv9YFF1xg9VCgsQqVu+++W8ePH9enP/1pXXjhhVYPqej98Ic/1C233HJWq7oSYbco3H///err65v2+E033aQXXnhBX/3qV3M/KMw6L+vXr9fNN9+sm2++WS+88IL+8R//kX0jOXK6eZGkn/3sZ3I6nfrkJz+Z49EVp7nMCQDkm6GhIT3yyCP60z/907SKLljH4XDo4YcfViQS0Xe+8x198MEHOu+886weVtF68803VV1drWXLlqmrq+us/g7CbhH42te+NuPjH3zwgYLBoO666y5JY2UCd999tx588EHV1NTkcITFKdO8TPXJT35SDz74IGE3R043L6+88orefPNN3XPPPZQ35chcf1dgLZ/Pp+7u7tTn3d3dNNYDMojFYnrkkUf0yU9+Uh/72MesHg6m8Hg8WrVqlQ4dOkTYtdA777yjAwcOqLOzUyMjIxocHNRjjz2mL37xi3P+Owi7Rey8887T008/nfr8jjvu0IMPPkg3Zhv48MMP9ZGPfETSWKk5exLt4dChQ/r5z3+ur3/96yorK7N6OICtLF++XB9++KGCwaB8Pp9+8YtfnNEbEqBYmKapp556SosXL9ZnPvMZq4eDcadOnZLT6ZTH49HIyIgOHz6sP/iDP7B6WEVt+/bt2r59uySpq6tLL7300hn/d4WwC9jQ3/3d3+nDDz+UYRgKBAJ0YraJZ555RrFYTPfff78k6cILL2RuLPbGG2/ob/7mb3Tq1Cnt2rVL559/vr7yla9YPayi5HQ69YUvfEEPPPCAEomENm3apKVLl1o9rKL36KOP6u2339bAwIBuu+023Xjjjdq8ebPVwypq77zzjl599VWdd955qeq6m2++WZdddpnFIytuvb29euKJJ5RIJGSapj7xiU/o93//960eFs6RYZqmafUgAAAAAACYTxw9BAAAAAAoOIRdAAAAAEDBIewCAAAAAAoOYRcAAAAAUHAIuwAAAACAgkPYBQAAAAAUHMIuAAB56rnnntO3v/3t1OctLS36xje+oVgsZuGoAACwB8IuAAB56g/+4A/U1dWlX//612pra9OhQ4f05S9/WS6Xy+qhAQBgOcM0TdPqQQAAgLPz05/+VG+88Yai0ai+8Y1vKBAIKBqN6v7779d//ud/6oEHHtB5551n9TABAMg5VnYBAMhjH/3oR/XBBx9o+/btCgQCkqTS0lLt3LlTH//4xy0eHQAA1iHsAgCQpz744AM9/fTT2rhxo/bt25d63OVyqaqqysKRAQBgPcIuAAB5qKenRw899JD+y3/5L/qLv/gLffDBB+rq6rJ6WAAA2AZhFwCAPBONRvXggw/q2muvVUNDg8rKyvTZz35WP/7xj60eGgAAtkGDKgAACtQTTzyhz372szSoAgAUJcIuAAAF6MEHH9RvfvMbBQIBXX311bryyiutHhIAADlF2AUAAAAAFBz27AIAAAAACg5hFwAAAABQcAi7AAAAAICCQ9gFAAAAABQcwi4AAAAAoOAQdgEAAAAABYewCwAAAAAoOIRdAAAAAEDBIewCAAAAAArO/w+MSVjGtDxTvAAAAABJRU5ErkJggg==",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plot_ds(data,m[-1],q[-1])"
]
},
{
"cell_type": "code",
"execution_count": 449,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"57 passi e 5700 gradienti calcolati per arrivare a distanza minore o uguale di 0.3 dall'ottimo\n"
]
}
],
"source": [
"near_opt(m, min_dist=3e-1, ge_per_step=n)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Adadelta"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Adadelta è una estensione di RMSprop in cui non è presente un valore $\\eta$ arbitrariamente definito: questo parametro è sostituito da una somma smorzata, mediante un coefficiente $0<\\gamma<1$, dei quadrati degli aggiornamenti precedenti. Inoltre, al fine di limitare una eccessiva diminuzione del learning rate, non vengono accumulati tutti i gradienti passati attraverso la somma dei loro quadrati, ma viene invece applicato anche qui uno smorzamento con lo stesso coefficiente $0<\\gamma<1$.\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"L'aggiornamento alla $k+1$-esima iterazione è quindi definito come:\n",
"\n",
"\\begin{align*}\n",
"g_{j, k} &= \\frac{\\partial J(\\theta)}{\\partial\\theta_j}\\Big\\rvert_{\\theta^{(k)}}\\\\\n",
"\\tilde G_{j,k} & =\\gamma \\tilde G_{j,k-1}+(1-\\gamma)g_{j,k}^2\\\\\n",
"\\Delta_{j,k} &= - \\frac{\\sqrt{\\overline G_{j,k-1}+\\varepsilon}}{\\sqrt{\\tilde G_{j,k}+\\varepsilon}} g_{j, k}\\\\\n",
"\\overline G_{j,k} & =\\gamma \\overline G_{j,k-1}+(1-\\gamma)\\Delta_{j,k}^2\\\\\n",
"\\theta_j^{(k+1)} &= \\theta_j^{(k)} + \\Delta_{j,k}\n",
"\\end{align*}"
]
},
{
"cell_type": "code",
"execution_count": 420,
"metadata": {},
"outputs": [],
"source": [
"def adadelta(X,t, G_tilde = 0, G_over = 0, eps = 1e-8, gamma = 0.9, epochs = 10000):\n",
" theta = np.zeros(nfeatures+1).reshape(-1,1)\n",
" theta_history = []\n",
" cost_history = []\n",
" for k in range(epochs): \n",
" g = gradient(theta,X,t)\n",
" G_tilde = gamma * G_tilde + (1 - gamma)*g**2\n",
" delta = - np.sqrt(G_over + eps) / np.sqrt(G_tilde + eps) * g\n",
" G_over = gamma * G_over + (1 - gamma) * delta**2\n",
" theta = theta + delta\n",
" theta_history.append(theta)\n",
" cost_history.append(cost(theta, X, t))\n",
" theta_history = np.array(theta_history).reshape(-1,3)\n",
" cost_history = np.array(cost_history).reshape(-1,1)\n",
" m = -theta_history[:,1]/theta_history[:,2]\n",
" q = -theta_history[:,0]/theta_history[:,2]\n",
" return cost_history, m, q"
]
},
{
"cell_type": "code",
"execution_count": 421,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"tempo di esecuzione: 0.449 secondi\n",
"10000 passi totali\n",
"1000000 gradienti valutati\n"
]
}
],
"source": [
"start_time = time.time()\n",
"cost_history, m, q = adadelta(X,t, G_tilde = 0, G_over = 0, eps = 1e-8, gamma = 0.9, epochs = 10000)\n",
"print(f\"tempo di esecuzione: {time.time()-start_time: 4.3f} secondi\")\n",
"print(f\"{len(m)} passi totali\")\n",
"print(f\"{len(m)*n} gradienti valutati\")"
]
},
{
"cell_type": "code",
"execution_count": 254,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABQgAAAGoCAYAAAAKMwiTAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAABnyElEQVR4nO39d3xc92Hne3/OzKCDaARYwF7ETonqvVf3OI6PEzvNyUbZzWbXu9l9tmXv5t5nH9/Nfe7ddXY3VXESp9nOySZ2bNmWLVlWl6xKsffeAYLoAAHMnPvHDCmKoiSKxOAMMJ/36zWvOXPOzOA755CYmS9+55wgjmMkSZIkSZIkladU0gEkSZIkSZIkJceCUJIkSZIkSSpjFoSSJEmSJElSGbMglCRJkiRJksqYBaEkSZIkSZJUxjJJB7hInmpZkiTp0gVJBxhnfjaUJEm6dO/4bDhZCkKOHDmSdITL0traSmdnZ9IxhNuilLgtSofbonS4LUrHVNkW7e3tSUcoCj8bClyP48X1OD5cj+PD9Tg+XI/jYyqux3f7bOguxpIkSZIkSVIZsyCUJEmSJEmSypgFoSRJkiRJklTGLAglSZIkSZKkMmZBKEmSJEmSJJUxC0JJkiRJkiSpjFkQSpIkSZIkSWXMglCSJEmSJEkqYxaEkiRJkiRJUhmzIJQkSZIkSZLKmAWhJEmSJEmSVMYsCCVJkiRJkqQyZkEoSZIkSZIklTELQkmSJEmSJKmMWRBKkiRJkiRJZcyCUJIkSZIkSSpjFoSSJEmSJElSGbMglCRJkiRJksqYBaEkSZIkSZJUxiwIJUmSJEmSpDJmQShJkiRJkiSVMQtCSZIkSZIkqYxZEEqSJEmSJEllLFPMJw/D8EvAdcDrURR94Zz5XwdmAVVATRRF64qZQ5IkSZIkSdKFFW0EYRiG1wD1URTdDlSGYXj9mWVRFP10FEV3Af9/4NFiZZAkSZIkSZL03oq5i/FNwOOF6SeAmy9wn08Cf1/EDJIkSZIkSZLeQzF3MW4C9hSme4DV5y4Mw7ACWBtF0esXenAYhg8DDwNEUURra2vxkk6ATCYz6V/DVOG2KB1ui9LhtigdbovS4baQJElSuShmQdgDNBSmG4Du85bfBTz1bg+OougR4JHCzbizs3N8002w1tZWJvtrmCrcFqXDbVE63Balw21ROqbKtmhvb086giRJkkpcMXcxfhG4tzB9H/DSecs/CXyjiD+/pJwezRLHcdIxJEmSJEmSpLcpWkFY2HV4OAzDZ4EscCAMw98ECMMwIH9MwueK9fNLyd88t5t/9vvf53j3UNJRJEmSJEmSpLcp5i7GRFH0hfNmfbEwPwauLubPLjWjYzm2HDrFrObapKNIkiRJkiRJZxVzF2MVrJrXDMCWg6cSTiJJkiRJkiS9XVFHECrvivZGMukUBzr6GRgepa66IulIkiRJEyoMw3bgUWAVUB9F0dg5y9YAfwgEwD+JomhDMiklSZLKkyMIJ0B1RZrlc6cTA1sPdycdR5IkKQld5E9gd/6J6wD+M/AzQFiYliRJ0gSyIJwg6xbPAGCruxlLkqQyFEXRcBRF7/ZBqDmKooNRFB0GmiYwliRJknAX4wlz1ZKZ/PWPNrP9SA9j2RyZtN2sJElSwbkfjIIL3SEMw4eBhwGiKKK1tXUichVNJpOZ9K+hFLgex4frcXy4HseH63F8uB7HRzmtRwvCCdLWWMvMphqOdw+x90QfV8xuTDqSJElSqYjPmc5d6A5RFD0CPHLm/p2dnUUPVUytra1M9tdQClyP48P1OD5cj+PD9Tg+XI/jYyqux/b29gvOtyCcQKvmNnO8e4gtB09ZEEqSJL2lKwzDueTLwd6kw0iSJJUb93OdQCvnNQOw5eAp4jh+n3tLkiRNHWEYVoRh+ARwFfD9MAzvDMPwNwuLfwv4G+Bvgf+UVEZJkqRy5QjCCbSgtZ7aqgxd/afp6B1mRmNN0pEkSZImRBRFo8B9581+urBsA3DrhIeSJEkS4AjCCZVKBayY0wTkRxFKkiRJkiRJSbMgnGCrCrsZbz1kQShJkiRJkqTkWRBOsGXtjaSCgH0n+hg8PZZ0HEmSJEmSJJU5C8IJVlOZYfHMaeRi2H64O+k4kiRJkiRJKnMWhAlYdc7ZjCVJkiRJkqQkWRAmYOXcfEG4/Ug32Vwu4TSSJEmSJEkqZxaECWhtqGZGYzVDI1n2nehPOo4kSZIkSZLKmAVhQs6MInQ3Y0mSJEmSJCXJgjAhZwrCrYcsCCVJkiRJkpQcC8KELJwxjZrKNB29w3T0DCUdR5IkSZIkSWXKgjAh6VTAisIowk3uZixJkiRJkqSEZJIOUM7Wzm/hjT2dbNx/krvXtCcdR5IkSZKkSSGOc5DN5i+5McjmL3EuB3EOzr3O5SDOQpCG6hoggDgGYogpXF/oNm+/DgJIpSAoXFIpCAKCs9OpC98nnSZIpRNYS9LFsyBM0PI5jVSkUxzsHKB74DRNdVVJR5IkSZIk6ZLFcQyjIzAyRDwyDCOnYWyEeGwERkffMc3YCPE5050BjAwNni38yGWJz0xns4V5Y/nSbzIJUpDOQCYDqfx1kM5AuiI/P50hyGQK0xVQUUVQUQkVVVBZRVBRlZ8+M7/yzHQVVNXkn0u6DP4LSlBlJs3yOU1sOtDFpgNd3LZydtKRJEmSJEllLo7jfGE3PEA8NEA8PAjD/fnr00PEp4dgZBhGhgslYOH69BCMnn5r1N0lOP1B7pxKny3XSKchlSFIp88Z3Ve4PjOdzcLImXMABBCcuQ4Ks85cp867HZxZMYXLOSMU4/itUYuF25x7O5eDXDZ/XShBzzh/LV36WgMyFVBVS1BdC1U1nGxoZpT02dtBdS1U1xLUTCOonQY19QSZisv5iZpiLAgTduWCFjYd6GLjfgtCSZIkSVLxxKMjMNhLPNBLXLhmoJd4qJ94eCBfCA4PwNBAfqTepcpUQGUNQWV1fqRbpoIgUwkVlZCpzI+Ay1Tm71dRmV+WqYSKChqnt9E7MPjO0i9dGHl3dn6a4ExxNwnEucLu0NnR/LodGyuMjLzA7bFRGB0hHj2dL1xHTr81fc78uLCMkaH8Y8Z6iAd6ABg+chGhKqvzZWHttEJxWJ+frp1GUN9EUN8MdQ2OTiwTbuWErZjbRDoVsPdEH/1Do9TX2OBLkiRJkj6YOM7BYD9xXxdxb1f+uu9UoQTsyV+PDF/8E6YzUFNHUF0H1fnroLoOqmqgqrpQ/lUTVNYUrquhqhoqqvOF3iWqbm2lv7Pzkh9fqoJUvtSkovKteeP03Gd36z49SHx6EIaHmFaVobfjGPHw0FvzhwbyZfBgHwz1vTXys7vjPUYvBvnSsL6JYFpToThsgmnNBA3TCRpaLBCnCLdiwmoqM1wxu5Fth7vZfLCLG5fNTDqSJEmSJKkExdlsvvjrPkHcc5K4twv6Tp0tA9931F8qnS976hoJ6hoIahvyI8Rq66G6nqC6lqCmDqrr86P+JtEIvXIWBEF+pGZlFcG0ZgBqWlsZaHv3ojWOc/ndxQf7YbCPeKgvXxwO9hMP9hD3dxP3d8NAb37U6WAv8YkDF/rhUN9M0DidoLH1nOtWgmnNnpxlErEgLAFrF7Sw7XA3Gw9YEEqSJElSuYtHR4hPHc8Xgac68tfdHcS9J9/75BzVdflSZloLQUP+mvpzysDqOks/AeTPvHxmVGjLu/cQcTabLwj7u4n7us8Wh3FfF3FPJ/R1Q19hxOqhnW9/cDpD0DyDoHkmQcssgpaZpFpmQV2j/w5LkAVhCVg9r5m/C2DX0V6GRsaoqXSzSJIkSdJUF8cxDPSQO3mU+NxLz0ne9ZQV05oJmtpINbbCOUVgMK2FoLJqQvNr6gvS6fy/uWnNcIHTJsTZsfwu7T2dhcvJs9MM9BB3HiHuPO+AiJVVBM2zCFrbSbXNIWidS9Dc5mjDhNlElYC66goWz2xg17Fethw8xbVL2pKOJEmSJEkaZ/FgH7kTB4lPHMxfdx6B04PvvGMqRdBUGHnV1JafbmrL77Z5zjHspKQFhVGCNM94x7L49HB+JGzXMXJdx85OMzxIfHw/8fH9nB0Pm6kgmF4oDNvm5i9NbY40nEAWhCVizYIWdh3rZeP+LgtCSZIkSZrk4tER4o5D+SKw4xC5Ewegv+edd6yuJWiZTWr6LILps/OX5pme+EGTXlBVTTBrAcxawJmxgXEcw1B/vjTsPEzccZhcx6H8sTSP7yd7fP9bT1BdS2rmAoJZC0nNWkjQNsf/F0Xkmi0Ra+a38M0f72P7kW5Oj2apqnBorSRJkiRNFrnTw+QO7iB3ZA+5Y3uJTxyCXPbtd6qoImibS2rGPIIZ80i1zc2fJMRRUioTQVA4K3LtNFJzrzg7Px4eKJSFh98q1Af7yO3fCvu3koX8MQ3b5pKatZDUnCUEsxYSZCoSey1TjQVhiWisrWRBWz37O/rZeugU6xa1Jh1JkiRJkvQu4pHT5I7sJj66j9zRPRztPALxuScQCfKjAWfOP1sI5neZTCWWWSpVQXUdwbxlpOYtAwojDftOkTu2j9yx/cTH9uV3UT62j+yxfWTXP5UvDGctJDVnKam5SwmmtxOk/P91qSwIS8i6RdPZ39HP+r0nLQglSZIkqYTEcY745FFyB3eSO7id+Pj+t59ROEjlRwXOXkQwe1F+l8iqmuQCS5NYEATQ0EK6oYX0smsAiIcHyR3fT3x0L7nDu/InQDm8i+zhXWRfBqpqSc1ZQmreclILVhDU1Cf7IiYZC8IScuWC6Xzr5f1sO9zt2YwlSZIkKWHx0AC5wzvzuw4f3AFD/W8tDIL86MD2JaRmL6J11TV09fW/+5NJuixBdS3pBSthwUqg8P/zyG5yh3aRO7wzP+Jwz0ZyezYCQb6wX7CS1IKVBC0z3ZX/fdhAlZCG2koWz2pg97FeNh84xXVLPVmJJEmSJE2kuOck2X2bye3dTHz8ABC/tbCugdS8ZfkRSnOWEFTVnl2UqqoGC0JpwgQ1daSXXEl6yZUAxL0nyR3cQXb/VuLDu4lPHCB74gDZV74P05pJL1hJasmVBDPnu6v/BVgQlpirF01n97Fe3tjbaUEoSZIkSUUWxzFx13FyezeR27uJuOvYWwtT6fzuwoVSMGie4SgkqUQFDdNJr76Z9OqbiUdPkzu0k9z+reQObIe+U2Q3vUB20wtQ10B68VpSi68kmDnPsrDAgrDErJnfwt+/tI9dR3voHx6lvtoz8kiSJEnSeIrjmPjEQXJ7N5Hduxl6T761sKKK1IIVpBatITVvGUFFVXJBJV2SoKKK9KI1pBetyR8/9MQhcns2kd2zAfq7yW58nuzG56G+MV8WXnF1/iQnZfwHAAvCElNXXcGy9ka2He5m4/4ubl4+M+lIkiRJkjQl5E6dILdrPdld66G3660F1XWkFq7Kl4JzlhCk/aosTRVBkMofL3TmfNI3fSj/x4E9G8ju3gj9PWQ3PEd2w3MELbNILb+W9NJ1BLXTko494fytV4LWLZrOtsPdrN/baUEoSZIkSZchHuglu2s9uV3riTuPvLWgdlp+5NCiNQSzFhKk3M1QmuqCMycXmjmf9E0fJj5+sPD74U3irmNkX/wO2Ze+lz+swPJriZtu4/UtR3j8+V30D4xQX1fJA7ct5eqV7Um/lHFnQViCVs9rJpMO2Hu8j56BERrrKpOOJEmSJEmTRpwdI3dgG7ltr5I7uB3iwolGKqtJLVpD+op1BLMXWwpKZSwIUgSzFpCatYD45o+Q27+N3I7XyB3Ynv/9cWAbjz32JH91Yj59I2897siJfvhJplxJaEFYgqorM6yc28zG/V28ue8kd6yenXQkSZIkSSp5ua7j5La/QnbHGzA8kJ+ZSuePKXjF1aTmLyfIeJx3SW8XpDOkF68hvXgN8WBfflTh9ld5YkvT28pBgL6B0/zguV0WhJoY6xZOZ+P+Ltbv67QglCRJkqR3EWfH8icf2PIi8bH9Z+cHzTNJrbiO9BVXE9TUJ5hQ0mQS1E4jc+XtxGtvY/h3HoeOgXfcp39w5AKPnNwsCEvUirlNVGVSHOwcoLN3mNaG6qQjSZIkSVLJiPu6yW79Mdltr8BQf35mRRWppetIr7iOoG1uWZ+RVNLlCYKAxuYGDl6gIKyvnXqHgrMgLFGVmTSr57fw+p5OXt/TyQPr5iYdSZIkSZISFccx8dE9ZDc+T27/1rPHFgxaZpFefTOpK9YRVFQlnFLSVPGJ+9ay/3AXfQOnz86bVlfFA7ctTTBVcVgQlrBrl7QVCsIO7r9qjn/9kiRJklSW4myW3N6NZN98lrjzcH5mKk1q8RrSq28mmLXA70uSxt2N6xbwi33r+MFzu+gfHKG+1rMYKwFLZzXQUFPByb7T7O/oZ+GMaUlHkiRJkqQJE48Mk932CtmNz0N/d35mdR3p1TeTXnUjQa3fkSQV19Ur26dkIXg+C8ISlkoFXLOklac2HeW13R0WhJIkSZLKQjzUT3bDc2S3vAgj+V37gqY20lfeTuqKqz0TsSSNMwvCEnft4jae2nSUN/ed5BM3LCSTTiUdSZIkSZKKIh7sI/vmM2S3vARjowAEsxeRvuoOUvOXEwR+H5KkYrAgLHGzmmuZ01LL4a5Bthw6xZULpicdSZIkSZLGVTzQQ3b902S3vgzZMQBS81eQvuYeUjPnJ5xOkqa+ohaEYRh+CbgOeD2Koi+cM78F+EOgFfhhFEVfLGaOye6axW0c7trP67s7LQglSZIkTRnxYB9jrz9JbuvLkMsCkFq4Ol8Mts1JOJ0klY+iFYRhGF4D1EdRdHsYhn8QhuH1URS9Ulj8W8B/iqJoW7F+/lSybvF0Hn1tP1sPdTMwPEpdtcfbkCRJkjR5xaeHyb75NNmNzxV2JQ5ILb6S9DV3k5o+O+l4klR2ijmC8Cbg8cL0E8DNwJmCcA3wH8IwnAf8hyiKXixijkmvoaaS5e1NbDvczfp9J7l1xaykI0mSJEnSBxaPjZLd/CLZN56C04MApBauIn39g6RaZiYbTpLKWDELwiZgT2G6B1h9zrJbgGuALuDvgNvOf3AYhg8DDwNEUURra2sRoxZfJpO5rNdw51WL2Hb4DTbs7+YTt60Zx2Tl53K3hcaP26J0uC1Kh9uidLgtJGn8xLkcue2vMvbaEzDQC+RPPpK58UMeY1CSSkAxC8IeoKEw3QB0n7NsRxRFWwHCMMxd6MFRFD0CPFK4GXd2dhYp5sRobW3lcl7D/OYMVRVp9hzrZvOug8xsqhnHdOXlcreFxo/bonS4LUqH26J0TJVt0d7ennQESWUud2Q3Y89/m7jrGADB9NlkbvwQwdwrCIIg4XSSJChuQfgi8KtABNwHfOWcZTvCMJwN9BY5w5RRmUlz1cLpvLzzBK/sOsFHr1uQdCRJkiRJeldxXxdjL32P3J6N+Rn1TWRufIjUkisJglSy4SRJb1O038pRFL0ODIdh+CyQBQ6EYfibhcW/BXwNeBL4/xUrw1RzwxVtALy2u5Ns7oIDLyVJkiQpUfHoCGOv/ICRv/lv+XIwU0H6+vup/My/Ir10neWgJJWgoo7ei6LoC+fN+mJh/hbgrmL+7Klofms9MxtrON4zxNZD3ayZ35J0JEmSJEkCII5jcrs3MPbSd2GgB4DU0nX53YnrGxNOJ0l6L+7eO4kEQcD1V8zg0Vf38/LOExaEkiRJkkpC3NvF6HPfJD64A4CgdQ6ZWz9GatbCZINJki6KBeEkc+3iVr772gG2He6mZ3CExtrKpCNJkiRJKlNxLkt24/NkX30cxkahsprMTR8mteI6dyWWpEnEgnCSqa+pYNW8ZjYd6OK13R3cs3ZO0pEkSZIklaFcxyHGnvl74s4jAKSWXEXmlo8S1E5LOJkk6YOyIJyEbriijU0HunhlZwd3r2knCIKkI0mSJEkqE/HoabKvPE520/MQx/mzE9/+E6Tnr0g6miTpElkQTkLL25torK2ks2+Yvcf7WDyrIelIkiRJkspA7tg+Rp+MoK8LgoD0lbeRvu5+goqqpKNJki6DBeEklEoFXLekjR9uPMzLu05YEEqSJEkqqjg7RvbVJ8i++TTEMUHLLDJ3/RSptrlJR5MkjQOPGjtJXbe0DYAN+7oYGhlLOI0kSZKkqSrXdYzRb/we2fVPAZBedxcVP/nrloOSNIU4gnCSam2oZumsBnYd6+X13Z3cunJW0pEkSZIkTSFxnMufofjHj0EuCw0tVNwdkpq1MOlokqRxZkE4id28fCa7jvXy4vbj3LJipicrkSRJkjQu4r5uRp+KiI/sASC14gYyN3+EoNJjDUrSVGRBOImtnt/MtJoKjvcMsfdEH4tneixCSZIkSZcnu38bYz+K4PQg1NSTueMnSS9clXQsSVIReQzCSSydSnHD0hkAvLT9eMJpJEmSJE1mcS7L2I8fY+yxr8DpQVLzl1P56X9hOShJZcCCcJK7cdkMggA27O+if3g06TiSJEmSJqF4oJfRR7+cPxFJEJC+4SEyD/0CQU190tEkSRPAgnCSa66vYsWcJrK5mFd2dSQdR5IkSdIkc3rfNkb+7n8QH90LtdOo+OivkLn6LoLAr4uSVC78jT8F3Lx8JpDfzTgXxwmnkSRJkjQZxHGOsdefpPOr/xWG+gnaF1P5qX9Oqn1x0tEkSRPMk5RMAcvbm2iuq6Sr/zQ7j/SwfE5T0pEkSZIklbD49DBjT36d3IFtAKSvvpv0dfcTpBxDIknlyN/+U0AqFXDjsvwowhc9WYkkSZKk95Dr7mD0m7+XLwerapn+mS+QueFBy0FJKmO+A0wR11/RRioI2HLoFKf6TycdR5IkSVIJyh3cweg3fo+4u4OgZSaVP/nrVC9dm3QsSVLC3MV4imioqeTKhS2s33uSF7cf58PXzk86kiRJ0tuEYfgl4Drg9SiKvnDO/K8AK4Eh4JEoir6aTEJpastuep6xFx6FOCa1cBWZuz9DUFmVdCxJUglwBOEUctvKWQD8eOcJRsdyCaeRJEl6SxiG1wD1URTdDlSGYXj9eXf5XBRFd1kOSuMvzuUYe/7bjD3/bYhj0tfcQ+aBn7UclCSd5QjCKWR+az3zptdx8OQAb+zt5IYrZiQdSZIk6YybgMcL008ANwOvFG7HwF+EYXgS+PUoivaf/+AwDB8GHgaIoojW1tbiJy6iTCYz6V9DKXA9vr/cyGlOffOPGdm5HtIZmj/yC9Suvflt93E9jg/X4/hwPY4P1+P4KKf1aEE4hQRBwK0rZ/H153bz3NZjXL+0jSAIko4lSZIE0ATsKUz3AKvPWfavoijqCsPwNuC/Aj91/oOjKHoEeKRwM+7s7Cxi1OJrbW1lsr+GUuB6fG/xYB+jj/05ccchqKqh4oGfY3D2YgbPW2eux/Hhehwfrsfx4XocH1NxPba3t19wvrsYTzFXLZxOfXUFR08Nsud4X9JxJEmSzugBGgrTDUD3mQVRFHUVrp8DZk14MmkKintPMvIPf5gvBxtaqPiJXyPVvjjpWJKkEmVBOMVk0iluXp7ftfi5rccSTiNJknTWi8C9hen7gJfOLAjDsKFwvZxzikNJlybXeYSRb/4B9J4kaJ1D5Sf+CammtqRjSZJKmAXhFHTTspmkUwGbD3bR1T+cdBxJkiSiKHodGA7D8FkgCxwIw/A3C4v/OgzD54AvA/8uqYzSVJA7spvRb/8RDPUTzFlKxcd+haB2WtKxJEklzmMQTkENtZVcuXA6b+zp5IVtx/nodQuSjiRJkkQURV84b9YXC/M/lkAcacrJ7t/G2ON/BdkxUouvJHNPSJD2K58k6f05gnCKum1F/vA9L+88wenRbMJpJEmSJBVTds9Gxn7wl/lycNWNZO79actBSdJFsyCcoua31bOgrZ6hkSyv7OpIOo4kSZKkIsnufIOxJ74GuSzpK28nc9tPEKT8qidJuni+a0xhd67On7r62S1HyebihNNIkiRJGm/Zba8w9mQEcY70NfeQvunDBEGQdCxJ0iRjQTiFrZ7XTOu0arr6T7PpQFfScSRJkiSNo+y2Vxh7+u+AmPQND5K5/gHLQUnSJbEgnMJSqYDbV+WPRfj0piPEsaMIJUmSpKkgu+M1xp7+ewDSN32YzNV3J5xIkjSZWRBOcdctbaOuKsPBkwPsOd6XdBxJkiRJlym7cz1jT/0v8iMHHyJz1R1JR5IkTXIWhFNcZSbNLStmAvD05iMJp5EkSZJ0ObK7NzD2o7+BOCZ9/f1krr4r6UiSpCnAgrAM3LJiFpl0wNZD3RzvHko6jiRJkqRLkD2wnbEnv54vB6+5l8w19yYdSZI0RVgQloH66gquW9IGwDNbHEUoSZIkTTa5Y/sYe/yvIJcjfeUdpK+7L+lIkqQpxIKwTNyxejYB8NruTnqHRpKOI0mSJOki5U4eZfR7X4GxUVLLryN904c8W7EkaVxZEJaJtoYaVs9vJpuLeX7rsaTjSJIkSboIcc9JRr/zJzAyTGrhajJ3fNJyUJI07iwIy8idq9sBeHH7cYZHxhJOI0mSJOm9xEP9jHz3T2Gon6B9CZl7f5oglU46liRpCrIgLCMLZ0xj8cxpDI1keXH78aTjSJIkSXoX8egIo4/9OfSeJGidQ8WDP0+QqUg6liRpirIgLDP3rJ0DwNNbjjIylk04jSRJkqTzxbkcY0/+DfGJg1DfRMVDv0BQWZV0LEnSFGZBWGaWtTcyb3odA8NjvLzzRNJxJEmSJJ0n+9J3yO3bDJXVVHzo8wR1DUlHkiRNcRaEZSYIAu69Mj+K8KlNRxnL5hJOJEmSJOmM7KbnyW58HlJpKh74OVItM5OOJEkqAxaEZWjlvGZmNdfSMzjCq7s7ko4jSZIkCcgd3MHYC48CkLnzU6TmLEk4kSSpXFgQlqFUEHDv2vwZjX+08QjZXJxwIkmSJKm85bo7GH3iqxDHpK+5h/Sya5KOJEkqIxaEZerKBdNpa6imq/806/d2Jh1HkiRJKlvx6WHGvv8XMDJMauEq0tfdl3QkSVKZsSAsU6lUcPaMxk9uPEzOUYSSJEnShMufsfhrxN0dBC0zydzzGYLAr2mSpInlO08Zu3rxdJrrqzjRM8zGA11Jx5EkSZLKTvbl75M7sB2qa6l48BcIKqqSjiRJKkMWhGUsnUpx95r8sQh/uOEwudhRhJIkSdJEye7ZRPbNpyGVouL+zxE0tCQdSZJUpiwIy9x1S9torK3k6KlBNu53FKEkSZI0EXI9nYw9/bcApG/8MKl2z1gsSUqOBWGZq0inuPfK/LEIf7D+kMcilCRJkoosHh1h7Ad/BSOnSS1eS3rtrUlHkiSVuUwxnzwMwy8B1wGvR1H0hXPmfwVYCQwBj0RR9NVi5tB7u35pGz/adIQTPUOs33eSaxa3Jh1JkiRJmrLGnv8H4q5jBI2tZO78FEEQJB1JklTmijaCMAzDa4D6KIpuByrDMLz+vLt8LoqiuywHk5dJp7ivMIrw8fWHyDqKUJIkSSqK7LZXyG1/DTIVZO7/WYLK6qQjSZJU1F2MbwIeL0w/Adx8zrIY+IswDL8dhuGCImbQRbp2SRut06rp7Bvmtd0dSceRJEmSppzcyWOMPfcPAGRu/wlS02clnEiSpLxi7mLcBOwpTPcAq89Z9q+iKOoKw/A24L8CP3X+g8MwfBh4GCCKIlpbJ/dur5lMpuRfw0/evoJHvrueJzcd5YEbVpBJT81DVE6GbVEu3Balw21ROtwWpcNtIWk8xWOjjP3wa5AdI7XiOtLLrk06kiRJZxWzIOwBGgrTDUD3mQVRFHUVrp8Lw/C3L/TgKIoeAR4p3Iw7OzuLl3QCtLa2UuqvYcn0KmY21nC8Z4jvvbSVm5fPTDpSUUyGbVEu3Balw21ROtwWpWOqbIv29vakI0gCxl76LvGp4wRNbWRu+XjScSRJeptiDhF7Ebi3MH0f8NKZBWEYNhSul3NOcahkpVIB96+bC8APNxxmNJtLOJEkSZI0+WX3byW3+UVIpcnc+9MEFZVJR5Ik6W2KVhBGUfQ6MByG4bNAFjgQhuFvFhb/dRiGzwFfBv5dsTLog1u7oIXZzbX0DI7w0vbjSceRJEmSJrV4oJexp/4XAOkbHiTVOifhRJIkvVMxdzEmiqIvnDfri4X5Hyvmz9WlSwUBD66by1d+tIMfbjzM9VfMoLoinXQsSZIkadKJ4xyjT/0tDA8QzL2C9JW3JR1JkqQLmppnodBlWTWvmQVt9QwMj/H05iNJx5EkSZImpeymF4gP7YTqOiru+jRB4NcvSVJp8h1K7xAEAR+5dj4Az2w+Su/QSMKJJEmSpMkl191B9uXvA5C581MEdQ3v8whJkpJjQagLWjSzgVXzmhkZy/H4+kNJx5EkSZImjTiXyx93cGyU1LJrSC9clXQkSZLekwWh3tWHr5lHEMDLO09womco6TiSJEnSpJDd+Bzx8f1Q20Dmlo8mHUeSpPdlQah3NbOpluuXziAXw/deP5h0HEmSJKnk5U6dIPvKDwDI3PGTBFW1CSeSJOn9WRDqPT2wbi4V6RSbDnSx70Rf0nEkSZKkknV21+LsGKll15JesCLpSJIkXRQLQr2nxtpKbl81C4DvvnaAOI4TTiRJkiSVpuyGZ4lPHIA6dy2WJE0uFoR6X3etaae2KsPeE31sOXgq6TiSJElSyYl7T5J99XHgzK7FNQknkiTp4lkQ6n3VVGa478o5AHzntQNkc7mEE0mSJEmlI45jRp/9h/yuxUvXkZ7vrsWSpMnFglAX5eblM2ltqKajd5gXth1POo4kSZJUMnK7NxAf2gFVNe5aLEmalCwIdVEy6RQfu24BAI+/eYiB4dGEE0mSJEnJi08PMfbCtwHI3Pghgpr6hBNJkvTBWRDqoq2c28QVsxsZGsny/fWHko4jSZIkJW7s5cdgqJ9g1kJSK65LOo4kSZfEglAXLQgCPn79AlIBvLTjOEdPDSYdSZIkSUpM7th+clt+DKkUmds/SRD49UqSNDn5DqYPZFZzLTcvn0kcw7de2Uccx0lHkiRJkiZcnM0y9uzfA5C+6k5SLTMTTiRJ0qWzINQHdv9Vc6mpTLPraC+bD55KOo4kSZI04bKbXyDuOg4NLaSvuSfpOJIkXRYLQn1gddUVPLBuHgCPvrqfsWwu4USSJEnSxImH+sm+9gQAmVs+TpCpSDiRJEmXx4JQl+Tm5TOY0VjDyb7TPLv1WNJxJEmSpAkz9vL3YeQ0qXnLSS9YkXQcSZIumwWhLkk6leLj1y8A4Ik3D9E9cDrhRJIkSVLx5ToOkdv2KqRSpG/5aNJxJEkaFxaEumTL5zSxZn4LI2M5vv3K/qTjSJIkSUUVxzFjL3wbiEmvuZVUU1vSkSRJGhcWhLosn7hhAZWZFBv2d7H9cHfScSRJkqSiye16k/jYfqipJ33NvUnHkSRp3FgQ6rI01VVx/1VzAfjmj/cx6glLJEmSNAXFoyOM/fi7AGRueJCgqjrhRJIkjR8LQl2221fNYmZjDZ19wzy16UjScSRJkqRxl13/FAz0ErTNJbX82qTjSJI0riwIddnSqRSfvGkRAE9uOExn73DCiSRJkqTxEw/0kN3wLACZWz5GEPg1SpI0tfjOpnGxZFYD1yxuZSwX8w8v7yOO46QjSZIkSeNi7NXHYWyU1OK1pGYtSDqOJEnjzoJQ4+aj182nuiLNtsPdbDpwKuk4kiRJ0mXLnTpObvtrkEqRvuHBpONIklQUFoQaN9NqKnnomnkAfPPHexkaGUs4kSRJknR5sj9+DOKY1IobSDW2Jh1HkqSisCDUuLp52Uzmt9bTOzTKd187kHQcSZIk6ZLlju4lt38rZCrJXHtv0nEkSSoaC0KNq1Qq4NO3LCadCnhpxwl2H+tNOpIkSZL0gcVxzNhL3wMgfdXtBLXTEk4kSVLxWBBq3M1qruWete0A/K8X9zCazSWcSJIkSfpgcns3E584ADX1pK+8I+k4kiQVlQWhiuKetXOY2VhDZ+8wT7x5KOk4kiRJ0kWLs1myLz8GQObaewkqqxJOJElScVkQqigy6RQ/dctiAuCpTUc43DWQdCRJkiTpouR2vEbc00nQ2EpqxQ1Jx5EkqegsCFU0C2dM49aVs8jF8LfP7yGbi5OOJEmSJL2nODvG2OtPApC+7n6CdDrhRJIkFV8m6QCa2h66eh6bDnRxuGuAZ7Yc5e417UlHkiRJCQnD8EvAdcDrURR94Zz5a4A/BALgn0RRtCGhiBK57a9CfzdB80xSS9YmHUeSpAnhCEIVVVVFmp+6eTEA33/jIMdODSacSJIkJSEMw2uA+iiKbgcqwzC8/pzF/xn4GSAsTEuJiMdGGXv9RwCkr7uPIPDrkiSpPPiOp6JbPqeJG6+YQTYX8/XndpPNeVZjSZLK0E3A44XpJ4Cbz1nWHEXRwSiKDgNNEx1MOiO37RUY6CFomUVq0eqk40iSNGEuahfjMAyzwM9EURQVbn8Y+J0oipYVM5ymjo9ev4AdR3s43DXADzcc5oF185KOJEmSJlYTsKcw3QOc276c+0fr4EIPDsPwYeBhgCiKaG1tLULEiZPJZCb9aygF47ke49ERjr35NADN93yKmrYZ4/K8k4H/HseH63F8uB7Hh+txfJTTenzPgjAMw/nAQvIf1FaFYXhHYdGHgMXFjaappLoizWduXcIffn8LP9xwmFXzmpk7vT7pWJIkaeL0AA2F6Qag+5xl557J7IK7GkRR9AjwyJn7d3Z2jne+CdXa2spkfw2lYDzX49jG58j19xC0ttPfMpeBMto+/nscH67H8eF6HB+ux/ExFddje/uFzw3xfrsYfx74EfkPbf9bYfpHwD8Fto9jPpWBJbMauL1wVuOvP7ub0ay7GkuSVEZeBO4tTN8HvHTOsq4wDOeGYdgO9E54MpW9eHSE7BtPAZC+9j6C4IIDWSVJmrLeryB8GfgD8iMIHwd+H/g98geP/mRxo2kq+tA182lrqOZ4zxDff+Ng0nEkSdIEiaLodWA4DMNngSxwIAzD3yws/i3gb4C/Bf5TQhFVxrJbXoKhfoK2uaQWrEw6jiRJE+49dzGOouh7wPfCMHwFeCqKov0AYRimoihy+Jc+sIpMip++bSm/+71NPLP5KKvmNbN4ZsP7P1CSJE16URR94bxZXyzM3wDcOvGJpMLowfX5Yw/mz1zs6EFJUvm52LMYrwE+H4ZhexiGB4CBMAx/qYi5NIXNb6vnnjVziIGvPbuLoZGxpCNJkiSpTGW3vQLDA/nRg/OWJx1HkqREXGxB+FnyB5L+GaAS2An8xyJlUhm4f90c5k2vo3tghL97cQ9xHL//gyRJkqRxFGfHyL75DADpq+929KAkqWy95y7G55gOnAQeBP4S2AD8cbFCaepLp1J89o4r+J1vb+DNfV0sa+/ghitmJB1LkqSyFobhLmAT8Cb5z3tvRlG0K9lUUvHkdq6HgR6C5hmkFnrsQUlS+brYEYQHyB8j5ieAV4Fm8oWhdMlaG6r5iZsWAfDNl/dxomco4USSJJW9b5L/3HcMuB/YEIbhgTAMXwzD8I8STSaNsziXI7v+KQDS6+4mCC72q5EkSVPPxY4g/DfA/wG8BHwD+C/A3xUrlMrHtYtb2XG4mzf2nuSrz+zk1z+8hkzaD2eSJCXkgSiKrjxzIwzDPwM+CfwucFViqaQiyO3bTNzTCdOaSS298v0fIEnSFHZRTUwURd8ErgV+C1gC/Jsoiv55EXOpTARBwE/etIiW+ioOdw3yvdcPJh1JkqRydjIMw7NFYBRFPwY+FEXRoSiKvpNgLmlcxXFM9o0fAZC56k6CVDrhRJIkJeuiRhCGYbiK/C4nSwqzdoVh+IkoirYVK5jKR3Vlhs/esZTf/95mntlylCvaG1kxpynpWJIklaNfAf4iDMPNwHpgJeAxQDTlxAd3EHcegZp6UsuvTTqOJEmJu9h9OX8XmA18rXCZXZgnjYsFbdN4YN08AL727C66B04nnEiSpPJTOCHJbcD3gFnALuAjiYaSimDszLEHr7ydIFORbBhJkkrAxR6D8Drg30dR9LsAYRj+OvB/Fi2VytLda9vZc7yXHUd6+Mund/JPHlzl8QglSZpgURTlgL8vXKQpJ3d0H/HRvVBZTXrVTUnHkSSpJFxsQdgF3BeG4XcLt+/nIs5iHIbhl8iXi69HUfSF85bVAHuBn42i6ImLj6ypKhUEfPb2pfzOoxs50NHPd147wCduWJh0LEmSJE0hZ89cvOYWgsqqZMNIklQiLnZ41peBjwM7C5ePAX/8Xg8Iw/AaoD6KotuByjAMrz/vLv8I2PjB4mqqq6uu4GfvvIJ0KuC5rcd4c9/79tCSJEnSRcmdOkHuwDbIVJBec2vScSRJKhkXWxD+JfCPeWt3k4eBv36fx9wEPF6YfgK4+cyCMAwrC8uf/yBhVR4WtE3jo9ctAOBvX9hDR4/HRpckSdLly254FoDUsmsIauoSTiNJUum42F2MnwC+HkXRpwHCMPzP5Mu/Ze/xmCZgT2G6B1h9zrJfBP4KuPHdHhyG4cPki0iiKKK1tfUio5amTCYz6V/DRPrEbdM50n2aV3Yc5avP7eE/fvY2qirS4/LcbovS4bYoHW6L0uG2KB1uC2lqiQf7yO18AwhIr70t6TiSJJWUiy0I5wD7zrm9H5j7Po/pARoK0w1AN0AYhhngwSiKPhWG4bsWhFEUPQI8UrgZd3Z2XmTU0tTa2spkfw0T7ePXzWXfsVMc6uzjD7/9Mp+9fSlBEFz287otSofbonS4LUqH26J0TJVt0d7ennQEqSRkN78E2TFSC1eRampLOo4kSSXlYncx3gP86zAMHwrD8EPAv+Kt0YHv5kXg3sL0fcBLhemZwPwwDB8Dfhb4L2EYNn+w2CoH1RVpfv6uZVRmUqzfe5KnNx9NOpIkSZImoXhslOyW/NeR9JW3J5xGkqTSc7EF4f8FLAe+AzxamP4v7/WAKIpeB4bDMHwWyAIHwjD8zSiKDkdRdH0URQ+R383430dRdOqSX4GmtFnNtfz0bUsB+O5rB9h2uDvZQJIkSZp0cjteh+EBgra5BLMWJh1HkqSSc1G7GEdR9JdhGO4HPlqY9WgURc9cxOO+cN6sL563/H+/mJ+v8rZ2QQv3XzWXx988xF8/vZN//pE1tDXWJB1LkiRJk0Ac586enCR95e3jcsgaSZKmmos9BiGFQvB9S0GpGO67ag5HTw2w6cApvvKj7fyzD6+huvKi//lKkiSpTOX2byPu6YT6JlKL1yQdR5KkknSxuxhLiUoFAZ+5bSmzmmo40TPMV5/dRS6Ok44lSZKkEnd29ODaWwlS6YTTSJJUmiwINWlUV6T5xXuWU1uVYeuhbr73+oGkI0mSJKmE5ToOER/dC5VVpFdcn3QcSZJKlgWhJpXp06r5uTuvIBUEPLXpKC/tOJ50JEmSJJWo7IbnAEivuJGgsjrhNJIklS4LQk06S2c38qmbFwHwjZf2st0zG0uSJOk88UAvuT0bIEiRXnNL0nEkSSppFoSalG64Ygb3rG0nF8NfPr2TI10DSUeSJElSCclueQlyOVKLVhNMa0o6jiRJJc2CUJPWg1fPY93C6ZwezfKnP9xOz+BI0pEkSZJUAuLsGNktPwZw9KAkSRfBglCTVioICG9bwoK2enoGR/izH27j9Gg26ViSJElKWG7XmzA8QNDaTjBrYdJxJEkqeRaEmtQq0ik+f89ypk+r4nDXIH/x1A7GsrmkY0mSJCkhcRyT3fQ8kB89GARBwokkSSp9FoSa9OqqK/jl+1ZQV51hx5Ee/ua53eTiOOlYkiRJSkB8fD9x5xGoriO15Kqk40iSNClYEGpKaGuo4R/dt5KqijTr953kWy/vI7YklCRJKjvZjYXRgytvIMhUJJxGkqTJwYJQU8bc6XX84t3LSKcCnt92nB9uOJx0JEmSJE2guL+b3N7NkEqRXn1T0nEkSZo0LAg1pSyd3chn71hKAHx//SFe3H486UiSJEmaINnNL0GcI7VoLUFdY9JxJEmaNCwINeVcuWA6n7xpEQDfeGkv6/d2JpxIkiRJxRaPjZLd9jKQPzmJJEm6eBaEmpJuXj6Th66eRwx87dldbNzflXQkSZIkFVFu13oYHiRom0swc37ScSRJmlQsCDVl3bO2nXvWtpOL4a+f2cmWg6eSjiRJkqQiiOP4rZOTrLmFIAgSTiRJ0uRiQagpKwgCHrp6Hnesmk02F/MXT+1g++HupGNJkiRpnMVH9xJ3HYOaelJLrkw6jiRJk04m6QBSMQVBwEevm89YNscL24/zlR9tZ3pLE601SSeTJEnSeMluegGA9MobCNJ+xZEk6YNyBKGmvCAI+MSNC7nhihmMZWN+5xuvsPtYb9KxJEmSNA7i/m5y+7ZAKkV61U1Jx5EkaVKyIFRZSAUBn7p5EdcuaeX0aJY/eWIbO4/2JB1LkiRJlym7+SWIc6QWrSWoa0g6jiRJk5IFocpGKggIb1nCbavnMprN8ac/3MY2j0koSZI0acWjI2S3vQzkT04iSZIujQWhykoqFfD5B6/ipmX53Y2/8uR2z24sSZI0SQ1ueRmGBwla5xDMnJ90HEmSJi0LQpWdVBDwkzct4tYVs8jmYv78RzvYuL8r6ViSJEn6AOI4ZuCVHwL50YNBECScSJKkycuCUGUpCAI+ccMC7lw9m1wc81dP7+DV3R1Jx5IkSdJFio/tZ/T4QaiuI7XkyqTjSJI0qVkQqmwFQcBHrp3PvVfOIRfD3zy3m6c3H0k6liRJki5CdtPzAKRX3kCQqUg4jSRJk5sFocpaEAQ8dPU8Pn79AgAeffUA333tAHEcJ5xMkiRJ7ybu7yG3dzMEKdKrb0o6jiRJk54FoQTcvmo2P33bElJBwI82HeFvX9hDNmdJKEmSVIqyW16COEfNimsI6hqTjiNJ0qRnQSgVXLukjV+8ZxkV6RSv7OrgL5/awehYLulYkiRJOkc8Nkp268sA1F1/b8JpJEmaGiwIpXOsnNvMww+spKYyzeaDp/jyE1sZPD2WdCxJkiQV5HZvgOEBgtZ2KucuTTqOJElTggWhdJ6FM6bxaw+tpqGmgj3H+/jd726is3c46ViSJEllL45jspteACC9+haCIEg4kSRJU4MFoXQBs5pr+fUPr2FWcy0dvcP87nc3se9EX9KxJEmSylp8/ABx52GoriO19Kqk40iSNGVYEErvorm+in/60CqWtTcycHqMP/r+Ftbv7Uw6liRJUtnKbnoegPSK6wkyFQmnkSRp6rAglN5DdWWGX7p3BTctm8FYLuavn9nFDzccJo49w7EkSdJEigd6yO3dBEGK9Oqbko4jSdKUYkEovY90KuAnb1rER69bQAA89sZBouf3MJb1DMeSJEkTJbvlx5DLkVq0mqC+Kek4kiRNKRaE0kUIgoA7V8/m5+9eRkU6xau7O/iD72+hZ3Ak6WiSJElTXpwdyxeEQHr1zQmnkSRp6rEglD6ANfNb+LUPraaprpIDHf38j0c3sr/Dk5dIkiQVU273mzA8QDB9NsHsRUnHkSRpyrEglD6gudPr+MJH1rJ45jR6h0b5g8e28PLOE0nHkiRJmpLiOCa78QUA0mtuIQiChBNJkjT1WBBKl6C+poKHH1jJrStmks3F/O0Le/j7l/Z6XEJJkqRxFh8/QNx5GKpqSS1dl3QcSZKmJAtC6RKlUyl+4sZFfPqWxaRTAS9uP84jP9jqcQklSZLGUXZzYfTgyusJMhUJp5EkaWqyIJQu0w1XzODXHlpFQ00Fe0/08aVvb2DHkZ6kY0mSJE16cW8Xud0bIUiRXnVT0nEkSZqyLAilcTC/bRr/4mNrWTq7gYHhMb78+FZ+sP4QuVycdDRJkqRJa+zNZyDOkVp6FcG05qTjSJI0ZVkQSuNkWk0lv3LfSu6/ag4Aj795iC8/sY3+odGEk0mSJE0+8UAvue2vApC++q5Es0iSNNVZEErjKJUKeGDdPP7R/Suoq86w82gPX/r2BvYc6006miRJ0qSS3fAsZMdILVxNqnlm0nEkSZrSLAilIljW3sS//OiVLJoxjd6hUf7wB1v4/hsHybrLsSRJ0vuKhwfIbvkxAOlr7k44jSRJU58FoVQkjXWV/OqDq7hnbTvE8MSGw/z+Y5s52TecdDRJkqSSlt34AoyNEMxdRqptbtJxJEma8iwIpSJKpwI+dM18fvXBlTTWVnKgo58vfXsjr+3uII4dTShJknS+eGSY7KbnAcg4elCSpAlhQShNgCWzGvmNj1/JlQtaOD2a5evP7earz+5iaGQs6WiSJEklJbvlxzAyTDBrIanZi5KOI0lSWcgkHUAqF7VVGX72zit4ZVcH//DyPtbvPcm+E318+pbFLGtvSjqeJElFE4bhNOCrQAvwR1EU/cV5y7cDRws3fy2Koi0THFElIh4bzZ+cBMhc7ehBSZImigWhNIGCIOCGK2awaOY0vvbMLg6eHOCPH9/GTctm8JHrFlBdkU46oiRJxfArwNcLlx+FYfj1KIpGzlneEUXRXYkkU0nJbXsFhvoJWucQzFuWdBxJkspGUQvCMAy/BFwHvB5F0RfOmf/fgXVANfAbURQ9X8wcUqlpa6jhn354DU9tOsLjbx7ipR0n2H6kh/CWxSyd3Zh0PEmSxttNwK9HUZQNw/BNYAWw4ZzlLWEYPgNsBb4QRZFn9CpDcXaMsTefBiB99V0EQZBsIEmSykjRCsIwDK8B6qMouj0Mwz8Iw/D6KIpeKSz+11EUjYZhuAD4feAjxcohlap0KuDeK+ewal4zf/PcLg53DfJHP9jKrStm8uFr5lPpaEJJ0tTRBPQWpnsKt891WxRFXWEY/gfgYeB/nP8EYRg+XFhGFEW0trYWLexEyGQyk/41jLe+l77PSH8PmdbZzLj+ToLg/Q+X7nocH67H8eF6HB+ux/Hhehwf5bQeizmC8Cbg8cL0E8DNwCsAURSNFubXA28WMYNU8mY31/LPPrKGJzce4Yk3D/P8tuNsPdTNZ25dwuJZDUnHkyTpooVhOIv8bsTnOka+FGwAhgvX3efeIYqirsLkN4B/eaHnjqLoEeCRws24s7NzfEInpLW1lcn+GsZTPNDLyDP/kL9x/UOcPNn13g8ocD2OD9fj+HA9jg/X4/hwPY6Pqbge29vbLzi/mAVhE7CnMN0DrD53YRiG3wBuAH7uQg/2r8QqllLdFj9z7wxuXbuILz+2noMdffzB97dwx9p5hHespK66Mul4RVGq26IcuS1Kh9uidLgtPrgoio4Bd50/PwzD3wDuDcMwIn+YmW3nLKsEgiiKTgO3ArsnJKxKythL34XREVILV5GevzzpOJIklZ1iFoRn/lIMF/5L8SfDMJwL/C/yow05b7l/JVZRlPK2qE3Brz24kic3HubJjUd4ZuNBXt95jE/csICrFk6fcsfiKeVtUW7cFqXDbVE6psq2eLe/Ek+wL5M/i/E/Ax6JomgkDMOHgDTwKvC9MAz7gVPAzyYXU0nIHdlDbtd6SGfI3PzRpONIklSWilkQvgj8KhAB9wFfObMgDMOqwl+J+4GBImaQJp1MOsUD6+Zx1cJW/u7FPew90cdfP7OL13Z38smbFtJSX510REmSPpAoinqBj54377Fzbl4zsYlUKuJclrHnvwVAet1dBA0tCSeSJKk8vf+Rfy9RFEWvA8NhGD4LZIEDYRj+ZmHx34Rh+BTwbeC3ipVBmsxmNtXwjx9axU/dvIiayjTbDnfz//zDBp7efIRsLk46niRJ0mXLbn6JuOsYTGshve7OpONIklS2ijmCkCiKvnDerC8W5v9EMX+uNFWkgoAbl81k5bxmvvXyft7cd5JHXz2QH01440IWzfQkJpIkaXKKB/vIvvoDADK3fJQgU5FwIkmSylfRRhBKGj8NNZX87J1X8Ev3Lqe5rpKjpwb5/ce28LVnd9E7OJJ0PEmSpA9s7MePwchpUvOXk1qwMuk4kiSVtaKOIJQ0vlbObWbJTzTw1KYj/GjjEV7f08nmA13cv24ut62cRTpl5y9Jkkpf7th+cjteg1SazC0fm3InYpMkabKxTZAmmcpMmgfWzeNf/8RVrJrXzOmxHI++eoD/9q2N7DjSk3Q8SZKk9xSPDDP2owiA9FV3EDS2JpxIkiRZEEqT1PRp1Xz+nuX80r3LaZ1WzYmeIf748a185cntdPQOJR1PkiTpHeI4ZuyZbxD3niRomUX6mnuSjiRJknAXY2nSWzm3mStmN/LMlqM8seEwmw+eYuuhbm5ZMZP7rpxDXbUH/JYkSaUht+0VcrvfhEwlmfs/54lJJEkqERaE0hSQSae4Z+0crl3SxvffOMiruzp4busxXtvdwb1XzuHWFbPIpB0wLEmSkpM7eZSx578FQOaOT5Jqaks4kSRJOsPGQJpCGmsrCW9dwr/42FqumN3I0EiWR189wP/9zTd5c99J4jhOOqIkSSpD8ehpxp74KmTHSK24jvQVVycdSZIkncMRhNIU1N5Sx6/cv4Jth7v5zqsHON4zxF89vZMFbfV85Nr5LJrZkHRESZJURsae+wfi7g6C5plkbvl40nEkSdJ5LAilKSoIAlbObWZZexMv7zzBD9YfYn9HP7//2BZWzGnioavnMWd6XdIxJUnSFJfd/iq5Ha9DpoLM/Z8lqKhMOpIkSTqPBaE0xaVTATcvn8nVi6bz9OajPLvlKNsOd7PtcDdXLWzhgXXzmNFYk3RMSZI0BeU6DjP23D8AkLn1E6SaZyacSJIkXYgFoVQmqiszPHj1PG5dOYsfbTzCC9uO8ea+Ljbs7+K6JW3cf9Vcmuurko4pSZKmiLi/m9HHvgJjo6SWX0tq+bVJR5IkSe/CglAqM/XVFXzs+gXcvmoWT2w4zCs7T/DKrg5e39PJzctncveadhpq3fVHkiRdunjkNKPf+woM9hHMXkTm9k8SBEHSsSRJ0ruwIJTKVFNdFT9182LuXD2bx9cfYv3ekzy39Rgv7TjOTctmctfqdhrrLAolSdIHE+eyjD3xVeKuYwSNrVQ88HMEab92SJJUynynlspcW0MNn73jCu5a084P1h9i88FTPLf1GC9uP84NV8zg7jXt7nosSZIuShzHjD3/bXIHt0N1HRUf+jxBdW3SsSRJ0vuwIJQEQHtLHb94z3KOdA3www2H2bi/ixe3H+flnSe4bmkb96xtp6W+OumYkiSphGU3Pk9uy0uQSlPx4M8RNE5POpIkSboIFoSS3qa9pY6fu2sZx04N8sONh3lz70l+vOMEr+zs4Lqlrdy1up02z3osSZLOk927meyL3wEgc/enSc1amGwgSZJ00SwIJV3QrOZaPnfHFdx/1Vx+uOEwb+zt5OWdHbyys4PV81u4e00789vqk44pSZJKQO7IbsZ++DUgJn39A6SXrks6kiRJ+gAsCCW9pxmNNfzM7Uu576o5PLXpCK/t7mTTgS42Hehi8cxp3L2mneVzmjwzoSRJZSp34iCjj/05ZMdIrbqR9NV3Jx1JkiR9QBaEki5KW0MNn75lCQ+sm8fzhZOY7Dnex57j25nVXMtdq2ezbtF00qlU0lElSdIEyXUdZ/S7fwajI6SWriNz2yf8o6EkSZOQBaGkD6SxtpIPXzufe9a289KOEzy75SjHTg3y9ed289gbB7lj1WyuX9pGdaW/XiRJmsri3pOMfufLcHqQ1PwVZO76NEHgHwolSZqM/AYv6ZJUV2a4a007t62cxRt7Onlq8xFO9AzzrVf28/31h7h+aRu3rphFa4NnPpYkaaqJB3oZefRPYLCPoH0xmfs/R5BOJx1LkiRdIgtCSZclk05x/RUzuHZpG1sOnuLZLUfZc7yP57Ye4/mtx1g5r5nbV85iyawGdzmSJGkKiIcH8iMH+7oI2uZS8eAvEGQqko4lSZIugwWhpHGRCgLWzG9hzfwWDp8c4Lmtx3hjbydbDp5iy8FTzGqu5faVs7h6USsVGXc/kiRpMoqHBxh99MvEp04QNM+k4sOfJ6isSjqWJEm6TBaEksbdnOl1fOa2JXzk2vm8uOM4L24/zrFTg/ztC3v4zmsHuGnZDG5aNpPW1qSTSpKki3W2HDx5lKCxlYqP/DJBdV3SsSRJ0jiwIJRUNPU1Fdx/1VzuXtPOm/tO8tzWYxw6OcCTG4/wo01HuGrREa5Z1MTy9iZSKXc/liSpVMXDg4x+50/eKgc/9jBBXUPSsSRJ0jixIJRUdJl0imuXtHHN4lb2dfTz4rZjbNjfxfo9x1m/5zjN9VXctGwGNyydQX2NxzCSJKmU5MvBLxN3HimUg79iOShJ0hRjQShpwgRBwKIZ01g0YxofHxpl89EBnnxjL139p/ne6wf5wfpDrJ3fws3LZ7Jo5jRPaiJJUsIuXA42Jh1LkiSNMwtCSYmor6ngIzcs5fpFjew43M2LO06w9dAp1u87yfp9J5nRWMMNV7Rx7eI2RxVKkpSAs7sVdx4haJhuOShJ0hRmQSgpUakgYMXcZlbMbeZU/2l+vPMEL+88wYmeIR599QDffe0gq+Y1ccMVM1jW3kTaYxVKklR08VB//oQkXccK5eDDloOSJE1hFoSSSkZzfRUPXT2P+6+aw9ZD3byys4Nth0+x6UD+0lBTwXVL27huaRttDTVJx5UkaUqKB3ry5WB3B0FTGxUf/UeWg5IkTXEWhJJKTjqVYs38FtbMb6FncITXd3fw8q4OOnuHeXLjEZ7ceITFM6dx/dIZXLmghcqKdNKRJUmaEuK+LkYe/TL0dhG0zKLiI79MUDst6ViSJKnILAgllbTG2kruXjuHu9a0s/dEH6/s7ODN/SfZc7yPPcf7+OaP97JmQQvXLmljycwGUu6CLEnSJcl1dzD66JdhoIegbS4VH/4lgurapGNJkqQJYEEoaVIIgoDFMxtYPLOBT9ywgDf3dfHyrhMc6Ojntd2dvLa7k8baStYtms41i1tpb6lLOrIkSZNGrutYvhwc6ieYtYCKhz5PUFWddCxJkjRBLAglTTrVlRluXDaDG5fNoKNniNf3dvL67k66+k/z9OajPL35KLOba7lmcStXL2qlsa4y6ciSJJWsXMchRr/7pzA8SDBnKRUP/jxBhe+dkiSVEwtCSZNaW2MND66bxwNXzWV/Rz+v7e7gzX0nOXpqkO+8doDvvnaApbMbuXrxdNbMb6Gm0l97kiSdkTu8i9Hv/wWMjpCav4LM/Z8jyFQkHUuSJE0wvylLmhKCIGDhjGksnDGNT9ywkG2Hu3ltdydbD51i59Eedh7t4e9e3Mvy9iauWjSdVfOaqfbkJpKkMpbdu4mxJ74GuSyppevI3PVpgrTvjZIklSMLQklTTib91lmQB0+PsWH/SdbvPcme471sOXSKLYdOkUkHrJjTzLpF01k5t4nKjF+IJEnlI7vtFcae+XuIY1KrbyZz68cIglTSsSRJUkIsCCVNabVVGW5aNpObls2kd2iEjfu6eHPfSfae6GPTgS42HeiiIpNi1dxmrlo4nRVzm6hI+wVJkjR1jb35DNmXvgtA+tp7SV97H0EQJJxKkiQlyYJQUtloqKnk1pWzuHXlLLoHTrOhUBYe6OznzX0neXPfSaoq0qya18za+S0sb2+k0t2QJUlTRBzHZF9+jOz6pwFI3/IxMmtvTTiVJEkqBRaEkspSU10Vd6yezR2rZ9PVN3y2IDzcNcgbezp5Y08nFekUy+c0smZ+CyvnNlNb5a9MSdLkFOeyjD3zDXLbX4UgRebuT5O+4uqkY0mSpBLht11JZa9lWjV3r53D3Wvn0NE7xKb9XWw6cIoDnf1sOnCKTQdOkQoCls5uYM38FlbPb6ahpjLp2JIkXZR4dISxJ75K7sA2yFSQue+zpBesTDqWJEkqIRaEknSOtoaas2Vh98BpNh84xaYDXew53suOIz3sONLDN17ay4IZ0/Jl4bxmWhuqk44tSdIFxUMDjD72FeITB6GqlooP/SKpmfOTjiVJkkqMBaEkvYumuqqzxywcGB5ly8H8aMIdR7rZd6KPfSf6ePTV/cxorGHVvCZWzW1mfts00ikP9C5JSl7c28Xod/+UuKcT6puo+PAvkWqekXQsSZJUgiwIJeki1FVXcP0VM7j+ihkMj2bZfribTfu72Ha4mxM9Q5zoGeKpTUeprcqwYk4Tq+Y1s6y9kZpKf81KkiZervMIo9/7MxjsI5g+m4oPfZ6griHpWJIkqUT5zVWSPqDqijRXLZzOVQunk83l2Hu8jy2HTrH1YDedfcO8vqeT1/d0kgoCFs+axqq5zayc667IkqSJkTu0i9Ef/CWMniZoX0zFAz9PUOV7kCRJencWhJJ0GdKpFEtnN7J0diMfuy6mo3eYLQdPseXgKfZ19LHraC+7jvbyrVfyuyKvmNPE8jlNLJ45jUw6lXR8SdIUk93xGmNP/x3kcqSWXEnm7pAg7Ud+SZL03vy0IEnjJAgCZjTWMKOxhrvWtDMwPMr2Iz1sOXiK7efsivzMlqNUZFIsndXA8vZ8YejoQknS5YjjmOzrPyT76hMApK+8jfRNHyYI/GOUJEl6fxaEklQkddUVXLO4lWsWt57dFXn7kW62H+7h6KlBth7qZuuhbgCmT6s6WxYumdVAVUU62fCSpEkjzmYZe+bvye14DYKAzC0fI73mlqRjSZKkScSCUJImwLm7In/kWugZHGHH4W62H+lmx5EeTvad5oXtx3lh+3HSqYBFM6edLQxnNdUQBJ4ZWZL0TvHpYUYf/yviw7sgU0Hm3p8hvXBV0rEkSdIkU9SCMAzDLwHXAa9HUfSFc+b/EbAGiIFfi6JoQzFzSFKpaaytPHtW5Gwu5mBnf74sPNzDwc7+s8cu/M5rB5hWU8HSWQ0snd3IFbMbaa6vSjq+JKkExP09jH7vz4i7jkFNPRUP/QKpGfOSjiVJkiahohWEYRheA9RHUXR7GIZ/EIbh9VEUvVJY/NtRFO0Nw/AK4LeBTxUrhySVunQqYOGMaSycMY0H181jYHiUnUd72HY4P7qwb2iUN/ae5I29JwFonVbN0tkNXDG7kSWzGqirrkj4FUiSJlqu4zCjj/05DPYSNLVR8aHPEzS0JB1LkiRNUsUcQXgT8Hhh+gngZuAVgCiK9hbmjwLZImaQpEmnrrqCdYtaWbeolTiOOdEzxM6jPew82sueY7109g3T2TfMSztOEADtLXVnC8NFM6dRmfH4hZI0lWX3bmbsya/D2CjB7EVUPPBzBNW1SceSJEmTWDELwiZgT2G6B1h9gfv8F+B/XOjBYRg+DDwMEEURra2tRYg4cTKZzKR/DVOF26J0uC0uTlsbrF6an87mcuw71sOWA51sOdDJriOnONw1wOGuAZ7efJRMOsWS2U2smDed5XOns2R2M5UXccITt0XpcFuUDreFSk0cx2Q3PEv2pe8BMall15C54ycJ0h5WXJIkXZ5ifproARoK0w1A97kLwzD8F8CWKIqeu9CDoyh6BHikcDPu7OwsTsoJ0traymR/DVOF26J0uC0uTWMl3Ly0mZuXNjMylmXfiT52He1l59EeDp8cYPuhLrYf6gJ2kk4FzG+tZ/HMBhbPmsbCtmkXLAzdFqXDbVE6psq2aG9vTzqCxkGczTL23DfJbcsfsSd9w4Ok193lSawkSdK4KGZB+CLwq0AE3Ad85cyCMAwfAG4BPlPEny9JU15lJs2y9iaWtTcBMHh6jD3H87si7z7ey9GuQfae6GPviT5+uBFSQcDc1jqWzGxg8cz8cQ+rKx15IkmlLD49yOgP/pr4yG5IZ8jc8xnSi9cmHUuSJE0hRftWGEXR62EYDodh+CywHjgQhuFvRlH0ReB/Ar3Aj8Iw3B5F0a8WK4cklZPaqgxr5rewZn7+QPWDp8fYd6KP3cd62XO8l8NdAxzo6OdARz8/2gRBAHNa6li9cCbtjRUsaKv3pCeSVEJyPZ2MPfbnxN0dUDuNigd/3jMVS5KkcVfUYSNRFH3hvFlfLMxfXsyfK0nKq63KsGpeM6vmNQMwPJIvDPcc72P38V4OdfZz6OQAh07uOfuYGY3V+bMqt+VHGLY2VLsLmyQlIHdoJ6OP/zWMDBO0zKLioV8kmNaUdCxJkjQFuV+ZJJWR6soMK+Y2s2JuvjA8PZo/huGxvjE27z3OwZP9nOgZ5kTPMC/v7ACgrirDghn5snDhjGnMnV5HRTqV5MuQpCktjmOym14g++J3IM6RWriKzN2fIaisSjqaJEmaoiwIJamMVVWkWT6niVtbW7lzRStj2RxHugbYe6KffSf62Heij/7hUbYcPMWWg6cASKcC5k6vO1sYLpwxjXp3S5akcRFnxwonI3kVgPTVd5O+/n6CwD/MSJKk4rEglCSdlUmnmN82jflt07hz9WziOOZk32n2dfSdLQyPdw+xv6Of/R39PL35KACt06qZ11bP/Nb8pb2lloyjDCXpA4mH+hn9wV8RH9uXPxnJXZ8mvfSqpGNJkqQyYEEoSXpXQRDQ2lBNa0M11y1pA/InPjnQ0ce+E/3s6+jjQEc/nX3DdPYN88aeTiA/ynBOSx3zC6XhvNZ6pk+r8liGkvQucp1HGP3+X0B/N9Q15E9G0jY36ViSJKlMWBBKkj6Q2qq3H8cwm8tx9NQQBzr6ONDZz8HO/HEMD3T2c6Cz/+zj6qoyzGutf1tpWFvl25AkZXe8wdgzfwfZMYIZ86l48OcIaqclHUuSJJURv5lJki5LOpVi7vQ65k6v45bCvKGRMQ529nOgo/9sUTgwPMa2w91sO9x99rFtDdXMba1n3vQ65kyvY05LHVUV6URehyRNtDibJfvSd8huegGA1IrryNz6CYKMx3WVJEkTy4JQkjTuaiozLGtvYll7E5A/I+epgdNvFYYd/RzuGqCjd5iO3rd2TQ6Atsaas4WjpaE0NYRh+CHgS0BnFEW3XWD554B/CnQBn42iqHeCI064bH8Po4/+cf54g6k0mVs/TnrVjUnHkiRJZcqCUJJUdEEQ0FJfTUt9NesWtQJndk0e5GDnAIdPDnDoZD9HTw1xoid/ef1dSsO50+totzSUJpuXgKuAH56/IAzDCuAfA3cAnwJ+Ffi/JzTdBMsd28+JH36VuL8nf7zB+3+W1Mz5SceSJEllzIJQkpSI/K7J9cydXn923lg2XxoeOjnAoZMDHH6P0nBGY83ZEYbtLbW0t9R5TEOpREVRdAogDMMLLb4C2BhF0VgYhk8Af3yhO4Vh+DDwcOH5aG1tLVLa4opzWY5H/5Vcfw+V85fR8slfJV3fmHSsSSuTyUzafwulxPU4PlyP48P1OD5cj+OjnNaj36QkSSUjk04xr3ACkzNGszmOnRrkYGd+t+RDJwc4dmqI4z35y5nSEKCprpL25rcKw/aWWprrq0h59mSplDUBZ3Yp7incfocoih4BHincjDs7Oy90t0khdfdnqDm8g5G1d3JqeBSGJ+9rSVprayuT+d9CqXA9jg/X4/hwPY4P1+P4mIrrsb29/YLzLQglSSWt4l1Kw6Ndgxw62c+RU4Mc6cqXht0DI3QPjLDl0Kmz962uSDO7ufZtpeHMploq0qkkXo40pYVhOAv4+nmzj0VR9NPv8bAeoKEw3QB0FyFaSUm1zaVx5bop94VDkiRNXhaEkqRJpyKdYn5bPfPb3ioNc7mYzr5hjnQNcKRrkCOn8td9Q6PsPdHH3hN9Z++bCvLHNWxvqaO9uZbZzbXMaqqlobaCwNGG0iWLougYcNcHfNgOYE0YhmngPvLHK5QkSdIEsiCUJE0JqVTAjMYaZjTWsG7RW/N7h0Y42jV4dqThka5BOnqHON6dv7xxznPUVKaZ1VTLrOZaZjXVFK5rPbahdJnCMLwO+G3yReATwEfJF4npKIq+E4bhHwPPAqeAzyYWVJIkqUz5jUeSNKU11FTSMKeS5XOazs4bGctyvHuII10DHO4a5Hj3IEdPDTI0kn3HaEOAxtpKZjbVnB1pOKu5hpmNtVRk3E1ZuhhRFL1KfnTguR47Z/lfAn85oaEkSZJ0lgWhJKnsVGbS7ziuYRzH9A6NcuzUIMe6hwrXgxzvHqJncISewRF2HOk5e/8ggOnTqt820nBmYw2tDdVkPL6hJEmSpEnEglCSJCAIAhprK2msfftow1wupqv/NMcKowyPdw9y7NQQHb1DdPYO09k7zKYDb50UJVUoDs/s7jyjqYaZjTW0NdZQXZFO4JVJkiRJ0nuzIJQk6T2kUgGtDdW0NlSzZn7L2flj2RwnevLHMTxaGG14omeIrv7TdPQO09E7zOaDp972XE11lW8Vh4354nBGUw311RUT/bIkSZIk6SwLQkmSLkEmncqfBbmljqvPmT+azdHRM8SJwuV4d/66o3eY7oERugfevqsyQF1V5uxow8XtvdSks7Q11NBcX0U65VmVJUmSJBWXBaEkSeOo4pzi8FzZXExX/zAnCoXh8Z6hs9MDp8fOnhzlxztOnH1MOhUwfVoVrQ01tDVUFy41tDZWM626giCwPJQkSZJ0+SwIJUmaAOlUQFtDDW0NNaw+Z34cx/QMjpwdcdh7Gg6eOEVnYcThiZ5hTvQMv+P5qirStBV2fW47UyA2VtM6rZrqSt/eJUmSJF08v0FIkpSgIAhoqquiqa6KZe1NtLa20tnZCcDIaJbOvvzxDDt7h+noHaKjJ389NJLl0MkBDp0ceMdzNtRUFI6bWMP0aVVMn5YvDqdPq7I8lCRJkvQOfkuQJKlEVVakL7i7chzHDJ4eK5wM5UxpOExn4czKvUOj9A6Nsud43zues646w/Rp1YXSsOqc6WrqqjPutixJkiSVIQtCSZImmSAIqKuuoK66goUzpr1tWS4X0z14mo6eYU72DdPZN8zJvtOc7MvfHhgeY2C4nwMd/e943qpMiukN1YXSsKow6jB/aaytJOUJUyRJkqQpyYJQkqQpJJUKaKmvpqW++h3LcnFM3+DoOcXh28vDoZEsR7oGOdI1+I7HplMBLfVVNNdX0VK45KeraZlWRV2Vow8lSZKkycqCUJKkMpEKAhrrKmmsq2TxrIZ3LB88PUZn7/DbCsSuvtN09g3TNzRa2KX5nSdMAajMpM4rD6vPTrdMq6LGYx9KkiRJJctP65IkCYDaqgzz2+qZ31b/jmUjo1m6+k/T1X+aU4Xrrv7hs9NDI1mOdw9xvHvogs9dXZGmZdp5Iw/rq2iqq6S5vorqirQjECVJkqSEWBBKkqT3VVmRZlZzLbOaay+4fGhkLF8a9l24QBwefffdlwGqKtL5srAuXxo2Fa6b66poqq+ksbaSdCpVzJcoSZIklS0LQkmSdNlqKjPMackw57wzLkP+rMsDp8feKg77hs+ORuweGKF74DSnR997BGIANNRWvrM8rKukqb6K5roqaiodhShJkiRdCgtCSZJUVEEQUF9dQX11BfNa37n7chzHDI1kOTVwmu5CaXhq4K3ysHtghN7BEXoKl/0XOAMz5I+D2HR2BGJ+1GFjbRWNtRU01lXRWFtpiShJkiRdgAWhJElKVBAE1FZlqK268AhEgGwuR8/gCN397ywPzxSLp8dynOgZ4kTPhUchAlRkUjTVFsrDsyXimdtVNNVWUludIWWJKEmSpDJiQShJkkpeOpUqnNik+oLL4zhmeDTLqcIIxDOjDXvOTp+mZ2CE02O59zwbc/5nBTTUVvIbn7qRC/80SZIkaWqxIJQkSZNeEATUVGaoacnQ/i6jEAGGR8byIxEvWCLmL4OF4yXWVFYQj4xM4KuQJEmSkmFBKEmSykZ1ZYbqygwzmy58NmaAkbEsPYMjNNdX09U1MIHpJEmSpGSkkg4gSZJUSiozadoaakilPA6hJEmSyoMFoSRJkiRJklTGLAglSZIkSZKkMmZBKEmSJEmSJJUxC0JJkiRJkiSpjFkQSpIkSZIkSWXMglCSJEmSJEkqYxaEkiRJkiRJUhmzIJQkSZIkSZLKmAWhJEmSJEmSVMYsCCVJkiRJkqQyZkEoSZIkSZIklTELQkmSJEmSJKmMWRBKkiRJkiRJZcyCUJIkSZIkSSpjFoSSJEmSJElSGcsU88nDMPwScB3wehRFXzhn/m8C/xT40yiK/mMxM0iSJEmSJEl6d0UbQRiG4TVAfRRFtwOVYRhef87iLwOfK9bPliRJkiRJknRxijmC8Cbg8cL0E8DNwCsAURQdD8Nw5Xs9OAzDh4GHC/entbW1iFGLL5PJTPrXMFW4LUqH26J0uC1Kh9uidLgtJEmSVC6KWRA2AXsK0z3A6g/y4CiKHgEeKdyMOzs7xy9ZAlpbW5nsr2GqcFuUDrdF6XBblA63RemYKtuivb096QiSJEkqccU8SUkP0FCYbgC6i/izJEmSJEmSJF2CYhaELwL3FqbvA14q4s+SJEmSJEmSdAmKVhBGUfQ6MByG4bNAFjhQOHsxYRj+MvBfgc+FYfh7xcogSZIkSZIk6b0V8xiERFH0hfNmfbEw/0+APynmz5YkSZIkSZL0/oq5i7EkSZIkSZKkEmdBKEmSJEmSJJUxC0JJkiRJkiSpjFkQSpIkSZIkSWXMglCSJEmSJEkqYxaEkiRJkiRJUhkL4jhOOsPFmBQhJUmSSlSQdIBx5mdDSZKkS/eOz4aTZQRhMNkvYRi+lnQGL26LUru4LUrn4rYonYvbonQuU2xbTDVJr0//fZXIxfXoeiyli+vR9VhKF9ej6/F9Lu8wWQpCSZIkSZIkSUVgQShJkiRJkiSVMQvCifNI0gF0ltuidLgtSofbonS4LUqH20LF5L+v8eF6HB+ux/Hhehwfrsfx4XocH2WzHifLSUokSZIkSZIkFYEjCCVJkiRJkqQyZkEoSZIkSZIklbFM0gHKQRiGXwKuA16PougLSeeZysIwbAceBVYB9VEUjV1o/V/sPF26MAxvBL4E5IBXoij6l2EY/n+ATwD7gV+Momj0Yucl8yqmhjAM15A/dkYW2AX8EvDf8P9FYsIw/JfAp6Ious3fUckIw3Ah8GNgKzASRdED/o7SRLnQ55WEI006F/qckXCkSelCnxGiKPIYVJfo3Pf3pLNMRhd6b0420eQVhuHPA78ApIHPRVF0OOFIk04Yhg8B/65wcznwT6Io+mZyiYrPEYRFFobhNeQ/+N0OVIZheH3Smaa4LuBe4CW48Pq/2HlJvYApZD9wT+ED0owwDO8E7i7c3gD8RBiGMy5mXjLxp5TtURTdUvj3DXAD/r9ITBiGVcC6wrS/o5L1eBRFdxXKwYv6feTvKI2Tt31e0SU5/3PG2qQDTVLnf0a4LtE0k9i57++6LGffm5MOMlmFYTgHuDOKonsL69Jy8BJEUfRYYf3dBRwAnkg4UtE5grD4bgIeL0w/AdwMvJJcnKktiqJhYDgMwzOzLrT+xy5yntvpMkRRdOycm6PAauCpwu0ngM8BAxc572+LGnaKO29002nyX0r9f5GcXwb+HPj/4u+opN0dhuGzwN8D2/F3lCbIBT6v6AO6wOeMbFJZJrMLfEY4mFSWKeDc93ddurPvzVEUfSnpMJPUg0A6DMMfAluAfxFFkb8jL1EYhouB41EU9SedpdgcQVh8TUBvYbqncFsTp4l3rv+LnadxEIbhlUAb0I3bIjFhGH48DMNNwEygArdFIsIwrADuiqLoycKsJtwWSTkKLAPuBu4jP2rGbSFNMmc+Z0RRtCXpLJPVeZ8RTiadZzK6wPu7Ls3b3psL/7/1wc0EKqMouhcYJH9YFF26nwS+kXSIieAIwuLrARoK0w3kSxJNnAut/+xFztNlCsOwBfhdIASuBeYWFp1Zxz0XOU+XKYqibwHfCsPwf5Ifjeb/i2T8HPDVc277OyohURSdJj9ahjAMHyVf+s0pLPZ3lDQJnPc5Q5fovM8IH6VMvgiPs/Pf33UJLvDevIb84Tz0wfQATxemn8RDB1yuj5EvCac8RxAW34vkd+eD/AgFjzUzsS60/i92ni5DGIYZ4K+Af13YDegV4M7C4jPr+GLn6TIUjolzRi8Q4/+LpCwH/kkYho+R3+2+FbdFIsIwnHbOzVvJH5zf31HSJHGBzxm6BBf4jDCUVJZJ7m3v72EY/rOkA01GF3hv3p1UlknuBeDM6Mt1wN7kokxuYRjOIn/CnLIYXR3EsSepKrYwDP87cA2wPooi3yyKqDC8/3vkR6u9DvwH4LOct/4vtE3cTuMrDMOfAf4HsLkw698Dd5D/C8wB8mf+HAnD8N9ezLwJfwFTSBiGnwB+o3BzJ/Aw+TM/+v8iQWEYPlc4i/FFrXe3xfgKw/DDwH8mP1Lh2SiK/u3F/j7yd5Qu14U+r0RR9ONkU00uF/qcEUXRiwlGmpQu9BkhiqJcgpEmvTPv70nnmIwu9N6ccKRJKwzD/4f8yMFO4LN+Vrk0YRj+KlARRdHvJp1lIlgQSpIkSZIkSWXMXYwlSZIkSZKkMmZBKEmSJEmSJJUxC0JJkiRJkiSpjFkQSpIkSZIkSWXMglCSJEmSJEkqY5mkA0hSMYRhuBDYC3wH+H3gBuArURTtG+efswoIgaeiKHqqMO8rwC8A10dR9Op4/jxJkiRJksabIwglTVUdwM8A/xfwYeC3gIUf9EnCMHy/P6SsKjz3XefM+4PCz979QX+eJEmSJEkTLYjjOOkMkjTuzhlBOADUnbssiqIgDMObgf8GrAWOAL8VRdHXznnci8BgYfka4AfAFYWneAP4x4Xn3nvej74b+EXOGUEYhuGvAP8GaAc2A78RRdFzYRj+IvBnwNfJF43zgf89iqL/HobhcuAvgCuBYWBTFEW3X/aKkSRJ0rgKw/BvgePAOmAe8DngV4EbgWejKPrl5NJJ0sVxBKGkqe5p8uUewH8GfiYMwxbgUaAJ+CKwD/irMAzXnfO4m4HXgP8NyAF/D3wB+G3gKuB3yI9S/J3C/f+O/KjBLef+8DAM7wEeKdz3N8iXgN8Kw3D6OXe7u3CfGPjtMAwrgV8DridfLP57YP8lvn5JkiQV11pgTxRFtwF/BPwJ+c9wq4CPhGFYlWQ4SboYFoSSproY2FmYfjKKoq+TL/9agBXA/wncT/734T3nPO6NKIr+bRRFjwBVwEPAH5MvGacBa6MoGgCeL9x/UxRFX4+i6MR5P//DhevfiqLozAfGZuCmc+7zp1EU/R7wMlANzCxkDgqPbwf++6WvAkmSJBVDGIbV5P/o/DuFWTHwJ1EUHY2iaAzIAiPJpJOki2dBKKkcvNuxFP6CfDl45vKtc5YdOWf6nwO3kP/g9wBwiHyR917P/W4ZLnT/rsL1WOE6HUXR7wL3Aa8AnwBeKux2LEmSpNKxGng9iqJc4fZVwI8BwjCcCxyJosjjekkqeZ7FWFI5OFW4/qkwDOvIH1+wi/yowFfI/y78KPnRge+1K28zcAcwF+g577lvD8Pwp4F/OO8x3wX+FfB/hGG4BPjlwmNeAj72bj8oDMN/DLQCuwqXK8mPLNz+Pq9VkiRJE2ct8OY5t68ENhSmrzpnWpJKmiMIJZWDvwa2kT+u33+PoqiLfCG4i/wxBX+T/AlJ9r3L4/8n+SLxM8AcYNM5y54DfgjcDnwNOPfYgkRR9CTwMDCD/ElRDgEfj6Lo5PtkPg18nvxuzXcCv1f4WZIkSSoda4H1cHZ345oois78AfncslCSSppnMZYkSZIkSZLKmCMIJUmSJEmSpDJmQShJkiRJkiSVMQtCSZIkSZIkqYxZEEqSJEmSJEllzIJQkiRJkiRJKmMWhJIkSZIkSVIZsyCUJEmSJEmSytj/C8A8IXxoWHSQAAAAAElFTkSuQmCC",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"low, high, step = 0, 5000, 10\n",
"plot_all(cost_history, m, q, low, high, step)"
]
},
{
"cell_type": "code",
"execution_count": 422,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"8247 passi e 824700 gradienti calcolati per arrivare a distanza minore o uguale di 0.1 dall'ottimo\n"
]
}
],
"source": [
"near_opt(m, min_dist=1e-1, ge_per_step=n)"
]
},
{
"cell_type": "code",
"execution_count": 423,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA7sAAAHzCAYAAADhDgreAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAABSUUlEQVR4nO3de3Sb2X3e++clQVIEIIkXiJrRjB17YjeSpVFGiTRJl6aRR/ZobNqJnVjZjtsqcZKeqdO4l7XcJnV8VuLj1D3OcU5SrzqXTmMf28zF2UfKJE6CZjitVU2Hp24om7JGjNXE447jGXlE8SYJAG8A9vkDFwIUQVEigPfFi+9nLS0SIF5yA5ug3ufde/+255wTAAAAAABh0uF3AwAAAAAAqDfCLgAAAAAgdAi7AAAAAIDQIewCAAAAAEKHsAsAAAAACB3CLgAAAAAgdAi7AAAAAIDQIewCANBknue96Hnegud5Nz3Pm/c87//zPO99nufd9v9lz/Ne43me8zwv0uA2NuXnAADQKIRdAAD88YPOue2SvkPSxyT9vKRP+dskAADCg7ALAICPnHPXnXNfkPRuST/hed4Bz/Pe5nnehOd5NzzP+5bneR+uOOTZ4sd5z/NSnuf9Xc/zvtPzvC96njfjed6053m/53leX+kAz/N+3vO8l4sjyf/T87w3Fe/v8DzvX3ue90LxWOt53kCtn9PYVwIAgPoi7AIAEADOub+U9JKkvycpLenHJfVJepukn/E8753Fh/5A8WOfcy7unPvvkjxJ/6ekPZL2SXqVpA9Lkud53yXp/ZKOFEeSH5f0YvF7/FNJ75R0rHjsnKTf2ODnAADQMgi7AAAExxVJA865/+qce945l3fOXZT0ByoE0nU5577unHvGObfknLsm6dcqHp+T1CPpDZ7ndTnnXnTOvVD82vskfcg595JzbkmFgHySdboAgDAg7AIAEBz3SZr1PO/7PM8763neNc/zrqsQShO1DvI8b7fneZ8vTlW+Iel3S493zn1d0r9QIchOFR+3p3jod0h6qlgka17S11QIx7sb8/QAAGgewi4AAAHged4RFcLuc5J+X9IXJL3KObdT0m+rMFVZktw6h//b4v0POud2SPqHFY+Xc+73nXOPqBBunaRfKX7pW5Le6pzrq/i3zTn3co2fAwBAyyDsAgDgI8/zdnie93ZJn5f0u8655yVtlzTrnFv0PO9hSX+/4pBrkvKSHqi4b7uklKTrnufdJ+lfVXz/7/I877jneT2SFiUtFI+XCiH6o57nfUfxsbs8z3vHBj8HAICWQdgFAMAff+p53k0VRlc/pMI6258sfu2fSPpI8eu/KMmWDnLOZSR9VNJYcfrx90v6PyR9j6Trkv5c0h9V/JweFbY2mpb0iqQhSR8sfu0TKowgjxZ/1pckfd8GPwcAgJbhOccsJQAAAABAuDCyCwAAAAAIHcIuAAAAACB0CLsAAAAAgNAh7AIAAAAAQoewCwAAAAAInYjfDWgCyk0DAAAAQHh5693ZDmFXV65c8bsJgZRIJDQ9Pe13M7AG/RJM9Esw0S/BQ58EE/0STPRL8NAnwbRRv+zZs6fmcUxjBgAAAACEDmEXAAAAABA6hF0AAAAAQOgQdgEAAAAAoUPYBQAAAACEDmEXAAAAABA6hF0AAAAAQOgQdgEAAAAAoRNp9g80xnxa0tslTVlrDxTv+7Ck/03SteLDfsFam1zn2LdI+oSkTkm/Y639WFMaDQAAAABoKU0Pu5I+I+mTkj635v5ft9b+aq2DjDGdkn5D0mOSXpI0boz5grX2rxrVUAAAAABAa2r6NGZr7bOSZu/i0Iclfd1a+w1r7bKkz0t6R10bBwAAAAAIBT9Gdmt5vzHmxyWdl/QBa+3cmq/fJ+lbFbdfkvR9zWocAAAAAKB1BCXs/pakX5bkih//b0k/dbffzBjzhKQnJMlaq0QiUY82hk4kEuG1CSD6JZjol2CiX4KHPgkm+iWY6JfgoU+C6W77JRBh11p7tfS5MeY/SvqzdR72sqRXVdy+v3jfet/vSUlPFm+66enpOrU0XBKJhHhtgod+CSb6JZjol+ChT4KJfgkm+iV46JNg2qhf9uzZU/O4QGw9ZIy5t+LmD0u6tM7DxiW93hjzWmNMt6Qfk/SFZrQPAAAAANBa/Nh66A8kvVFSwhjzkqRfkvRGY8xDKkxjflHSPy4+do8KWwwNW2uzxpj3S3paha2HPm2tnWx2+wEAQPBMXpjQ808n1bWQ0kpvXA8+Pqz9Dx3yu1kAAB81Pexaa9+zzt2fqvHYK5KGK24nJd2y/y4AAGhfkxcm9MrpEZ0c6pMXjcq5nM6dHpEkAi8AtLFATGMGAAC4W5dGkzo21CfP8yRJnufp2FCfLo1yfRwA2hlhFwAAtLRIJlUOuiWe5ymSSfvUIgBAEBB2AQBAS8tG43LOVd3nnFM2GvOpRQCAICDsAgCAlnbgxLDOTc2XA69zTuem5nXgxPBtjgQAhFkg9tkFAAC4W6UiVGdGk4pk0spGYzpw8hTFqQCgzRF2AQBAy9v/0CHCLQCgCtOYAQAAAAChQ9gFAAAAAIQOYRcAAAAAEDqEXQAAAABA6BB2AQAAAAChQ9gFAAAAAIQOYRcAAAAAEDrsswsAAO7a5IUJPf90Ul0LKa30xvX3zHt032sf8LtZAAAwsgsAAO7O5IUJvXJ6RCd7c3rnYFQne3N64XNPavLChN9NAwCAsAsAAO7OpdGkjg31yfM8SZLneXrj7j5dGk363DIAAAi7AADgLkUyqXLQLfE8T5FM2qcWAQCwirALAADuSjYal3Ou6j7nnLLRmE8tAgBgFWEXAADclQMnhnVuar4ceJ1z+q9X53XgxLDPLQMAgGrMAABgA2urLT/4+LD2P3RIksofz4wmFcmklY3G9MiPP0E1ZgBAIBB2AQDAusrVlof65EWjci6nc6dHJKkq8JY+l6REIqHp6Wlf2hsmG11kAABsDtOYAQDAutartnxsiGrLjbbelk6vnB5hSycAuEOEXQAAsC6qLfuDiwwAUB+EXQAAsC6qLfuDiwwAUB+EXQAAsK71qi2fm6LacqNxkQEA6oOwCwAA1rX/oUO65+QpnVns1B/PLOjMYqfuOXmKQkkNxkUGAKgPqjEDAICa1lZbRuOtt6XTAS4yAMAdI+wCAAAEDBcZAGDrmMYMAAAAAAgdwi4AAAAAIHQIuwAAAACA0CHsAgAAAABChwJVAAAAaLjJCxN6/umkuhZSWumN68HHhynCBaChCLsAAABoqMkLE3rl9IhODvXJi0blXE7nTo9IEoEXQMMwjRkAAAANdWk0qWNDffI8T5LkeZ6ODfXp0mjS55YBCDPCLgAAABoqkkmVg26J53mKZNI+tQhAOyDsAgAAoKGy0bicc1X3OeeUjcZ8ahGAdkDYBQAAQEMdODGsc1Pz5cDrnNO5qXkdODHsc8sAhBkFqgAAANBQpSJUZ0aTimTSykZjOnDyFMWpADQUYRcAAAANt/+hQ4RbAE3FNGYAAAAAQOgQdgEAAAAAocM0ZgAAgDqbvDCh559OqmshpZXeuB58fJgpvADQZIRdAACAOpq8MKFXTo/o5FCfvGhUzuV07vSIJBF4WxwXMYDWQtgFAACoo0ujSb1rqE+e50mSPM/TsaE+nRlNEozW0SoBkosYQOthzS4AAEAdRTKpctAt8TxPkUzapxYFVzlA9ub0zsGoTvbm9MrpEU1emPC7abe4NJrUsXUuYlwaTfrcMgC1NHVk1xjzaUlvlzRlrT1QvO/jkn5Q0rKkFyT9pLV2fp1jX5R0U1JOUtZae7hJzQYAANi0bDQu53JVgdc5p2w05mOrgqmVRsEjmZS83mjVfVzEAIKt2SO7n5H0ljX3PSPpgLX2oKS/lvTBDY5/1Fr7EEEXAAAE1YETwzo3NS/nnKRC0D03Na8DJ4Z9blnwtNIoeOEihqu6j4sYQLA1dWTXWvusMeY1a+4brbj5JUknm9kmAAAQPn6uAy39nDOjSUUyaWWjMR04eSpwI5VB0Eqj4AdODOvc6ZHyVObyRYyTp/xuGoAaglag6qck/WGNrzlJo8YYJ+k/WGufbF6zAABAqwhCIaH9Dx0i3G5CKwVILmIArScwYdcY8yFJWUm/V+Mhj1hrXzbGDEl6xhhz2Vr7bI3v9YSkJyTJWqtEItGQNre6SCTCaxNA9Esw0S/BRL8ETxD65OvPflE/fP9Q1WjhY/cP6alnv6hjb37Mx5b5Jwj9sp5jb35MX925U3/+p0+pM5VSLhbX4Z/+h/ruIw/73bR1HXvzY3X9HQpqv7Qz+iSY7rZfAhF2jTHvVaFw1ZustW69x1hrXy5+nDLGPCXpYUnrht3iqG9p5NdNT0/Xvc1hkEgkxGsTPPRLMNEvwUS/BE8Q+iQ7O62Vweg699/wvW1+CUK/1HLfax/Qff/sA1X3BbWt9RbkfmlX9EkwbdQve/bsqXmc72HXGPMWST8n6Zi1NlPjMTFJHdbam8XPT0j6SBObCQAAWsRLqYz+8G++pm6X00pHpx589au0955dgVwHCgBonGZvPfQHkt4oKWGMeUnSL6lQfblHhanJkvQla+37jDF7JP2OtXZY0m5JTxW/HpH0+9bav2hm2wEAQPBNXpjQdyyn9f07e5TY1i05p7N/+019Zfamvvd9/9zv5gEAmqjZ1Zjfs87dn6rx2CuShouff0PSdzewaQAAIAQujSb1rte9WumbN/Tta1PqyOX1XYM79fWefgoJAUCb8X0aMwCgcfzcfgXwQySTktcbVXzHTsV37CzfPzSz4GOrAAB+IOwCQEgFYfsVoNlaad9WAEBjEXYBIKQujSb1ruLelZLkeZ6ODfXpzGiSsIvQ2sq+rcyEAIBwIewCQEiVpnNW8jxPkUzapxYBjVcKp2dGk4pk0spGYzpw8tRtQyszIQAgfAi7ABBSTOdEu9r/0KE7DqjMhACA8OnwuwEAgMY4cGJY56bm5ZyTpNXpnCeGfW4ZEDyRTKrqwpDETAgAaHWM7AJASN3tdE6gHTETAgDCh7ALACF2N9M5gXa0lcJWAIBgIuwCANBAVPhtDcyEAIDwIewCANAgVPhtLcyEAIBwoUAVAAANcmk0WZ4WK61W+L00mvS5ZQAAhB9hFwCABqHCLwAA/mEaMwAADUKFX4TZRuvRWasOIAgIuwCAlrf2xDr+2u9U6n+94PuJNhV+EVYbrUeXxFp1AIFA2AUAtLS1J91/9e1v669OP6e3HHyDtg/2+XqiTYVfhNWl0aTetc569DPF9ei1vsbvPoBmIuwCAFra2pPuyb99Se+6b1CvTF/T9p19vp9oU+EXYRTJpOT1RqvuW12P7jb4GgA0DwWqAAAtbW0RqEg+pw7PU0cuV76PE22gvgrr0V3VfaX16Bt9DQCaibALAGhpa0+ssx2dyjunfGdn+T5OtIH6OnBiWOem5svvvfJ69BPDG34NAJqJacwAgKZoVHXWtUWg9r/6fv3R11/Q4wffIEkUhQIaYDPr0VmrDsBvhF0AQMNtVLl1qyfAt5x0992r2MlH9PSLLygyw4k20CgbrUdnrTqAICDsAgAabqPKrfU4IebEGgAArMWaXQBAw60tIiVRNAoAADQWYRcA0HBUZwUAAM1G2AUANBzVWQEAQLOxZhcA0HCbqdwKNEujKoMDAIKFsAsAaIpWKCJFCGqcoLy2t6sMHpR2AgC2jrALAIAauz1SuwvSa7tRZXBJgWknAGDrWLMLAIAKIejYOiHoUjEE4e4F6bXdqDJ4kNoJANg6wi4AAGJ7pEYK0mu7UWXwILUTALB1hF0AAMT2SI0UpNd2o8rgQWonAGDrCLsAAIjtkRopSK/t/ocO6Z6Tp3RmsVN/PLOgM4uduqdYGTxI7QQAbB0FqgAAUGtuj9QqlYOD9trWqgwetHYCALaGsAsAQFErbI9UEqQKx5vRKq9ts9vZKhcsAKAVMY0ZAIAWROXg1le+YNGb0zsHozrZm9Mrp0c0eWHC76YBQCgQdgEAaEFUDm59XLAAgMZiGjMAoK6YltkchcrBuarAS+Xg1hLJpOT1Rqvu44IFANQPI7sAgLphWmbzUDm49bHVEQA0FmEXAFA3TMtsno220EFr4IIFADQW05gBAHXDtMzm8rvC8XpT1o+9+THf2tNq2OoIABqLsAsAqBvWkbaPWlsffXXnTt332gf8bl7L8PuCBQCEGWEXAFA3B04M69zpkfJU5vK0zJOn/G5aUzSzOJffhcAujSb1rnWmrP/5nz6l+/7ZB5rWDgAAaiHsAgDqpp2nZdYa6ZRU9+ffzJ9VS60p652pVFN+PtBsfl9gAnDnCLsAgLpq12mZtUY6z4wm6/56NPNn1VJrynouFm/KzweaKQgXmADcOaoxAwBQB5FMqir4SY0rztXMn1VLrUrCh3/wh5vWBqBZqDQPtCZGdgEAqINmFucKQiGwWlPWv/vIw5qenm5aO4BmoNI80JoIuwAA1EEzi3MFpRBYu05ZR/sJwgUmAHeOsAsAQB00szhXOxcCA/wQlAtMAO5M08OuMebTkt4uacpae6B434CkP5T0GkkvSjLW2rl1jv0JSf978ea/sdZ+thltBgBgM5o50smoKtA8XGACWpMfI7ufkfRJSZ+ruO9fS/ov1tqPGWP+dfH2z1ceVAzEvyTpsCQn6cvGmC+sF4oBAACAeuICE9B6ml6N2Vr7rKTZNXe/Q1JplPazkt65zqGPS3rGWjtbDLjPSHpLo9oJAAAAAGhdQVmzu9ta++3i569I2r3OY+6T9K2K2y8V77uFMeYJSU9IkrVWiUSijk0Nj0gkwmsTQPRLMNEvwUS/BE+Y+uSr43+p8T99SpH0TWVj23XkB39Y333kYb+bdVfC1C9hQr8ED30STHfbL0EJu2XWWmeMcVv8Hk9KerJ407EFwvoSiQTbQwQQ/RJM9Esw0S/BE5Y+mbwwoVdOj+jtQ33y4p1yLq1zn/qk5q+35jrNsPRL2NAvwUOfBNNG/bJnz56axzV9GnMNV40x90pS8ePUOo95WdKrKm7fX7wPAACgri6NJsuVd6XCnqrHhvp0aTTpc8sAAJsVlJHdL0j6CUkfK378k3Ue87Skf2uM6S/ePiHpg81pHgAAaKbJCxN6/umkuhZSWumN68HHh5s6ohrJpOT1Rqvu8zxPkUy6aW0AAGyNH1sP/YGkN0pKGGNeUqHC8sckWWPMT0v6piRTfOxhSe+z1v4ja+2sMeaXJY0Xv9VHrLVrC10BAIAWV5pCfHKoT140KudyOnd6RJKaFniz0bicy5VHdiXJOadsNNaUnw8A2Lqmh11r7XtqfOlN6zz2vKR/VHH705I+3aCmAQCAALg0mtS71plCfGY02bSwe+DEsM6dHilPZXbO6dzUvA6cPNWUnw8AzZbPO83fXNTUTEpTM2ldLX7sinToiXcf8bt5dyUo05gBAAAkBWMKcSlUnxlNKpJJKxuN6cDJ1ixO1Qj1nmbu97R1oF3k806z1xfKgXZqNqWr0+nC7dm0VrL5W46JbuuSc65qpkurIOwCQJ1wsgbUx2amEDfj/bb/oUO3fE/e5/WfZh6EaetAmORyec1UBtqKkdprsxllc7cG2pIdsR4NDcaK/+IaGoxp92C8ia2vL8IuANQBJ2tA/dxuCrFf7zfe5wX1nmYehGnrQKvJ5vKamcuUpxqvjtKmND2XUS5feyfXndu3aXdloB0oBNqhwZh6t3U18Vk0HmEXAOqAkzWgfm43hdiv9xvv84J6TzMPwrR1IIhWsjlNz2Z0dbYi0BbD7fR8RvkNAm3/zl7tHqgeoS0F22097RMB2+eZAkADcbIG1Nd6U4hL/Hq/8T4vqHelaipfo52trOQ0NVsIsVcrRminZtKamc/I1ciznicN9vVqaDBeHKUtBtqBuHYNRNXTTcyTCLsAUBecrAHN49f7jfd5Qb0rVVP5GmG3tJzVtdm0rk4XikBdrRihnbuxsGGgTfRHy1OMd5dHaGPa1R9TV1dnc59ICyLsAkAdcLIGNE8j3m+bKTzF+7ygXpWqK1/zq0t5XfrbGd0fj1H5Gi1pYWlF12ZWg2w50M6mNX9jseZxHR2edg1Eq0ZoS+tpE30xRSIdTXwW4UPYBYA6YJsSoHnq/X7bbOEp3uerNppmvhm3vOYDvTo3Na973vmjbfl6ojVkFldWKxuXR2kLt2+klmoe19npaVf/6vrZ3RWBdqAvqkgngbZRCLsAUCdbPfkDsHn1fL/dSeEp3uf1QbEvBNXN9KK+8a3ZckGoQpgtjNSmMss1j4tEOjQ0UB1oC1OPYxrYGVVHR+vtURsGhF0AANDWKDzVfLzm8ItzTjfTy+UiUFNrph2nF1ZqHtvd1VksAlW9B+3uwZj6dvQSaAOIsAsAANoahaeaj9ccjeSc043UUvUetBWBdmEpW/PY3p6u4hraikA7ENdQIqa+7duqfmcRfIRdAPDBZorhIBjoq/Cj8FTz8Zpjq/J5p+s3FwtTjcujtMX1tDNpLS1vFGgjGkrEi/vQrlY43j0Y1wOvuU8zMzNNfCZoJMIuADTZZovhwH/01eZUXhDoHEjo9T9wvKVeHwpPNR+vOTYjn3eau7FQsXZ2tcLx1Exayyu5msfGertu3YO2uA/t9lh3zRFaRm7DhbALAE1GYZbWQV/d3toLAl1dK3qmBS8IUHiq+XjNIRUC7ez1jK5OF6caz66O0E7NppXN5mseG492F8JsIl6Yajy4WiAqHu1u4rNAUBF2AaDJKMzSOuir2+OCAIDbyeXympnP3LoH7Uxa1+bSyuVczWN3xHvKU4wr96AdGogp2kugxcYIuwDQZBRmaR301e1xQQCAJGWzeU3Pp8trZqemV0dpZ+YyyuVrB9q+HdvKFY53J2LlUdpdgzH19nQ18VkgbAi7ANBkFGZpHfTV7XFBAGgfKys5XZtLr9mDtvBxZj4jVzvPamBnb8UetKsfdw3E1NNNJEFj8JsFAE1GYZbWQV/dHhcEgHBZWs7q2mymYh/aVGE97WxKs9cXagZaz5MS/dFyEajC1ONCqN01EFN3V2dznwggwi4A+ILCLK2DvtrY2gsCkYGoXscFASDQFpeyxYrGa7fsSWnuxmLN4zo6PO3qr96DtrSeNtEfVVeEQItgIewCAIAtqbwgkEgkND09vaXvx97GwNYtLK6sTjWerQ60128u1Tyus8NTYqA4KjtQHWgH+6OKdHY08VkAW0PYBQAAgcHexsDmpReWb92Dtrie9ka6dqCNdHZoVynQVo3SxjW4s1edBFqEBGEXAAAEBlsZAaucc0ovLK/uQVvce7YUalOZ5ZrHdkU6ChWOE/E1o7RxDezsVUeHV/NYICwIuwAAIDDYygjtxjmnm+nlYpgt7UG7Gmgziys1j+3u6qzYg3b149BgXH3btxFo0fYIuwAAIDDYyghh5JzT9ZtL5UBb2ot29vqirkxd1+JStuax23oi5QrHuxPFLXuKe9Lu3N5T9V4BUI2wCwAAAoOtjNCq8nmn+ZuLVYWgKj8ur+RqHtu7rau8TU9phLZ0e3usm0AL3CXCLgAACAz2NkaQ5fNOs9cXVgtBzabK62mnZtNayeZrHhuPdq8WgxqIaXcirr/zwH3qiawo1kugBRqBsAsAAAKFvY3hp1wur5nKQFsxQnttNqNsrnag3RHrKW/VM7RmHW2st/uWx9djqy7Uz8TFSX3x/CVNp5cU78xr+JEjOnRwv9/NwhYQdgEAANBWsrm8ZuYyFVv2lEZpU5qeyyiXdzWP3bl9W/WWPQOrgbZ3W1cTnwXqaeLipEbGLmv3wWOKrawo75xGxsYlicDbwgi7AAAACJ2VbE7Tsxldna0ItMVwOz2fUX6DQNu/s7dYBKp6D9qhgZi29XD6HEbJsfPq3/to1bZn/XuPKDl2lrDbwni3AgAAbMLExUklnxtXKtfBFMeAWFnJlfedvVoxQjs1k9bMfEauRp71PGmwr7dQ2bgy0A7EtWsgqp5uTpHbTSrrKbZm3bTneUpnWUvdyngnAwAA3EZpimP/vuOKeR5THJtoaTmra7NpXZ0uFIG6WjFCO3djYcNAm+iPrrMHbUy7+mPq6ups7hNBoMUjTvk1v0zOOcUitWcAIPgIuwAAALfBFMfGWlha0bWZ1SBbDrSzac3fWKx5XEeHp10D0aoR2tJ62kRfTJFIRxOfBVrZ8NHDGhkb1+6DRyUVgu7c5XGdOnrY55ZhKwi7AAAAt8EUx63LLK6sVjYuj9IWbt9ILdU8rrPT067+1fWzuysC7UBfVJFOAi22rnTR6otfPqfrqSXFIk6njh7mYlaLI+wCAADcRmmKY+VeqExxvFUqs1yxZU8pzBZGalOZ5ZrHRSIdGqooCLV7IKahRCHUDuyMqqODiwpovEMH9+ux48fYDipECLsAALSAyQsTev7ppLoWUlrpjevBx4fZi7aJSlMc+/ceked5bTvF0Tmnm+nlchGoqTXTjtMLKzWP7e7qLBaBqt6DdvdgTH07egm0AOqOsAsAQMBNXpjQK6dHdHKoT140KudyOnd6RJIIvE1SmsqYHDurdNYL9RRH55xupJaq96CdSenqbOHzhcXagbanu7OiEFQx0A7ENZSIqW/7tqqRcQBoNMIuAAABd2k0qXcN9VUVRzo21Kczo0nCbhMdOrg/NOHWOaf5G4uFqcblUdrietqZtJaWszWP7e2JFKYYD1TuQVsYpd0R7yHQAggMwi4AAAEXyaTk9Uar7vM8T5FM2qcWoRXk805zNxY0NZNW+q+u6RvfvFqucDw1k9bySq7msbHerlv3oC3uQ7s91k2gBdASCLsAAARcNhqXc7lbiiNlozEfW4UgyOedZq9ndHW6cqpxcaR2Nq1sNl/z2Hi0uxBmE/HCVOPB1QJR8Wh3E58FADQGYRcAgIA7cGJY506P6FhxKrNzTuem5nXg5Cm/m4YmyOXympnPlKsbX62YcnxtLq1crnZF6B3xHg0NxvTqPYPaGe8qb9kzNBBTtJdACyDcCLsAAARcaV3umdGkIpm0stGYDpw8xXrdEMlm85qeT5fXzE5Nr47SzsxllMvXDrR9O7aVKxzvTsTKo7S7BmPq7emSJCUSCbZTAdB2CLsAALSA/Q8dIty2uJWVnK7NpdfsQVv4ODOfkdtgy96Bnb2re9BWfNw1EFNPN6dzjTJxcVLJ58aVynUo3pnX8CNHQlOkDGgH/HUEAACok6XlrK7NZir2oU0V1tPOpjR7faFmoPU8KdEfLReBKlQ3LoTaXQMxdXd1NveJQBMXJzUydln9+44r5nnKO6eRsXFJIvACLYKwCwAAcAcWl7LFisZrt+xJae7GYs3jOjo87SoF2jVb9iT6o+qKEGiDJDl2Xv17H63a8qt/7xElx84SdoEWQdgFAABYY2FxZXWq8Wx1oL1+c6nmcZ0dnhIDxVHZgepAO9gfVaSzo4nPAluRynqKrdliyfM8pbNsuwS0CsIuAABoS+mF5aq1s6sjtWndSNcOtJHODu0qBdqqUdq4Bnf2qjNggXbywoT+5tkvKjc7rZXeuB58fJj135sQjzjlnbtly69YZIPF1QACJRBh1xjzXZL+sOKuByT9orX231U85o2S/kTS/yre9UfW2o80q40AAKC1OOeUXlhe3YO2uPdsKdSmMss1j+2KdBQqHCfia0Zp4xrY2auOjtYY3Zu8MKFXTo/oR+4f0spgVM7ldO70iCQReG9j+OhhjYyNq3/vkfKWX3OXx3Xq6GG/mwZgkwIRdq21/1PSQ5JkjOmU9LKkp9Z56H+z1r69iU0DAAAB5pzTzfRyMcyW9qBdDbSZxZWax3Z3dZanGFd+HBqMq2/7tpYJtBu5NJrUu4r7M0uFabjHhvp0ZjRJ2L2N0rrc5NhZpbOeYhGnU0cPs14XaCGBCLtrvEnSC9bab/rdEAAA4D/nnK7fXCoH2vJetMWKx4tL2ZrHbuuJlCsc704Ut+wp7km7c3tP1RTVMIpkUvJ6o1X3eZ6nSCbtU4tay6GD+wm3QAsLYtj9MUl/UONrf9cY81VJVyT9S2vt5HoPMsY8IekJSbLWKpFINKShrS4SifDaBBD9Ekz0SzDRL8Fzt32SzzvNXk/r21M39O2pG7oydb3w+bXC7aXl2oE21tute4d26N6hnbp3aIf2lD7ftUM7t28LfaDdSGQgoa6uFXV4nrq7uyUVLh5EBqK8dwKAv2HBQ58E0932S6DCrjGmW9IPSfrgOl/+iqTvsNamjDHDkv5Y0uvX+z7W2iclPVm86aanpxvQ2taXSCTEaxM89Esw0S/BRL8Ez0Z9Ugi0C6uFoGZT5fW0U7NprWTzNb9vPNq9WgxqIKbdidW9aGO93esG2uxyWjMz7T2C+bofOK5nTo/osfuHtLKyIueczk3N63UnT/HeCQD+hgUPfRJMG/XLnj17ah4XqLAr6a2SvmKtvbr2C9baGxWfJ40xv2mMSVhr+W0EACAgcrl8zT1or81mlM3VDrQ7Yj3lrXqG1qyjjfV2N/FZhEdpXe5Tz35R2dkbykZjOnDyFOt1AbSFoIXd96jGFGZjzD2SrlprnTHmYUkdkmaa2TgAACBlc3nNzGUqtuwpjdKmND2XUS5fe2uWndu3VW/ZM7AaaHu3dTXxWbSP/Q8d0rE3P8ZoFYC2E5iwa4yJSXpM0j+uuO99kmSt/W1JJyX9jDEmK2lB0o9Za9noDACABljJ5jQ9m9HV2YpAWwy30/MZ5TcItP07e4tFoKr3oB0aiGlbT2BOPQAAIec5F/q86K5cueJ3GwKJNQnBRL8EE/2yavLChJ5/OqmuhZRWeuN68PFh36ZE0i9bs7KSK085vloxQjs1k9bMfEa1ThE8TxrY2VuobFwZaAfi2vf6V+vmzfmmPg/cHu+VYKJfgoc+CaZNrNldtxIhl1cBAJs2eWFCr5we0cmhPnnRqJzL6dzpEUliDWBALS1ndW02ravThSJQVytGaOduLGwYaBP90XX2oI1pV39MXV2d6x7X0xPRzZsNfEIAAGwSYRcAsGmXRpN611BfufKt53k6NtSnM6NJwq6PFpZWdK04Mnu1PEpbCLfzNxZrHtfR4WnXQHR179lEvLyeNtEXUyTS0cRn0RwTFyeVfG5cqVyH4p15DT9yhH1UASCkCLsAgE2LZFLyeqNV93mep0imvbd3aYbM4kpFZePS1OPC7RuppZrHdXZ62tW/un529+BqoB3oiyrSGb5AW8vExUmNjF1W/77jinme8s5pZGxckgi8ABBChF0AwKZlo3E5l6va09Q5p2w05mOrwiOVWa7YsiddDLOFkdpUZrnmcZFIh4YqCkJVjtIO7Iyqo2PdpUxtJzl2Xv17H62amdC/94iSY2cJuwAQQoRdAMCmHTgxrHOnR3SsOJXZOadzU/M6cPKU301rCc453Uwvl4tATc1UFodKKb2wUvPY7q7OYhGo6j1odw/G1Lejl0C7Camsp5hX/Tp5nqd0NtivHVOvAeDuEHYBNBwnauFRWpd7ZjSpSCatbDSmAydPsV63gnNON1JL1XvQzqR0dbbw+cJi7UDb091ZUQiqGGgH4hpKxNS3fVvViDruXDzilHfulpkJsUhwd6Zg6jUA3D3CLoCG4kQtfPY/dKjtw61zTvM3FgtTjcujtKvraZeWszWP7e2JFKYYD1TuQVsYpd0R7wl9oPXz4tfw0cMaGRtX/94j5ZkJc5fHdero4ab8/LvB1GsAuHuEXQANxYkaWlU+7zR3Y6Fi7exqheOpmbSWV3I1j431dt26B21xH9rtse7QB9pa/L74VfoZybGzSmc9xSJOp44eDvTfoladeg0AQUDYBdBQnKghyPJ5p9nrGV2drpxqXAy2s2lls/max8aj3YUwm4gXphoPrhaIike7m/gsWkcQLn4dOrg/0OF2rVaceg0AQUHYBdBQnKjBb7lcXjPzmVv3oJ1J69pcWrlc7d/FHfGe8hTjoYote4YGYor2EmjvFBe/7lwrTr0GgKAg7AJoKE7U0AzZbF7T8+nVPWinV0dpZ+YyyuVrB9q+HdvKFY53J2LlUdpdgzH19nQ18VmEHxe/7lwrTr0GgKAg7AJoKE7UUC8rKzldm0tX7UE7d2NZL70yp5n5jNwGeWlgZ+/qHrQVH3cNxNTTzX+FzcLFr7vTalOvASAo+B8eQMNxoobNWlrO6tpspmIf2lRhPe1sSrPXF2oGWs+TEv3RchGowtTjQqjdNRBTd1fnHbdl8sKEnn86qa6FlFZ643rw8eG2r0K9VVz8AgA0E2EXANBUi0vZYkXjtVv2pDR3Y7HmcR0dnnaVAm2xwvHrX3uvtnXlleiPqity54G2lskLE3rl9IhODvXJi0blXE7nTo9IEoF3i7j4BQBoFsIuAKDuFhZXVrfsma0OtNdvLtU8rrPDU2KgOCo7UL0H7WB/VJHOjqrHJxIJTU9P1739l0aTetdQX1XV4GNDfTozmiTsAkANfu6jDayHsAsAuCvpheVb96Atrqe9ka4daCOdHdpVCrRV+9DGNbizV51rAq0fIpmUvN5o1X2e5ymSSfvUIgAINr/30QbWQ9gFAKzLOaf0wvLqHrTFvWdLoTaVWa55bFeko1DhOBFfM0ob18DOXnV0BHurmWw0Ludyt1QNzkZjPrYKAIIrCPtoA2sRdgGgjTnndDO9XAyzpT1oVwNtZnGl5rHdXZ0Ve9CufhwajKtv+7bAB9qNHDgxrHOnR3SsOJXZOadzU/M6cPKU300DgEBiH20EEWEXAELOOafrN5fKgba8F22x4vHiUrbmsdt6IuUKx7sHiyO1xT1pd27vqRr5DJPSutwzo0lFMmllozEdOHmK9boAUAP7aCOICLsAEAL5vNP8zcWqQlCVH5dXcjWP7d3WVd6mpzRCW7q9PdYd2kB7O/sfOkS4BYBNYh9tBBFhFwBaRD7vNHt9YbUQ1GyqvJ52ajatlWy+5rHxaPdqMahScajietpYb/sGWgBAfbCPNoKIsAsAAZLL5TVTGWgrRmivzWaUzdUOtDtiPeWteobWrKON9XY38VmgnazdauQ9b3+zHnj1/X43C4AP2EcbQUPYBYAmy+bympnLVGzZUxylnUlrei6tXK72+qad27dVb9kzsBpoe7d1NfFZAOtvNfLk6ITe/fB1TngDin1QAbQTwi4ANMBKNqfp2YyuzlYE2mK4nZ7PKJ+vHWj7d/YWi0BV70E7NBDTtp67+7M9eWFCzz+dVNdCSiu9cT34+DDrUbFl6241su+IkmNPE6ACiH1QAbQbwi4A3KWVlVx539mrFSO0UzNpzcxn5GrkWc+TBvt6NVRRCKpU8XjXQFQ93fX90zx5YUKvnB7RyaE+edGonMvp3OkRSSLwYkvYaqS1sA8qgHZD2AWADSwtZ3VtNq2//tubeuHFbxdDbSHQzt1Y2DDQJvqj6+xBG9Ou/pi6ujqb9hwujSb1ruJ+sYW2eTo21Kczo0nCLraErUZaCxcnALQbwi6AtrewtKJrxZHZq+VR2kKF4/kbizWP6+jwtGsgWhihHVitbjw0GFOiL6ZIpKOJz6K2SCYlrzdadZ/neYpk0j61CGGx7lYjXxvXuxuw1QhrTbeOixMA2g1hF0BbyCyuVFQ2Lk09Lty+kVqqeVxnp6dd/THdf2+/+rZ3V+xBG9NAX1SRzmAE2o1ko3E5l7vlBDcbjfnYKoTBeluNPPG2N9W9GjNrTeuDfVABtJtNhV1jTKekd0jKS/pTa22ueP+PWmv/3wa2DwA2LZVZrtiyJ10Ms4WR2lRmueZxkUiHhioKQlWO0g7sjKqjw1MikdD09HQTn039HDgxrHOnR3SsOJXZOadzU/M6cPKU301DCKzdaqQR7xXWmtYH+6ACaDebHdn9nKRvSlqW9K+MMT9hrf26pJ+RRNgF0BTOOd1ML5eLQE3NVBaHSim9sFLz2O6uzmIRqOo9aHcPxtS3o1cdHeFds1Zal3tmNKlIJq1sNKYDJ0+xXhctg7Wm9cM+qADayWbD7n3W2n8gScaY/0fS54wxH25YqwC0LeecbqSWqvegnUnp6mzh84XF2oG2p7uzohBUMdAOxDWUiKlv+7aqabztZv9Dhwi3PmK96daw1nRrJi5O6ovnL2k6vcTvH4C2stmw222M6bHWLllrv2mMebukz0t6sIFtAxBSzjnN31gsTDUuj9KurqddWs7WPLa3J1KYYjxQuQdtYZR2R7ynrQMtgon1plvHWtO7V/r9233wmGIrK/z+AWgrG4ZdY0zEWpuV9M8l9Um6KknW2pvGmB+S9J6GtxBAS8rnneZuLFSsnV2tcDw1k9bySq7msbHerlv3oC3uQ7s91k2gRUthvenWsdb07vH7B6Cd3W5k9z8ZY37YWju+9gvFIlW/25hmAWgF+bzT7PWMrk5XTjUuBtvZtLLZfM1j49HuQphNxAtTjQdXC0TFo91NfBZAY7HetD5Ya3p3+P0D0M5uF3YvSBozxrzVWntFkowxPyDpo9bav9foxgHwXy6X18x85tY9aGfSujaXVi5Xe83cjnhPeYrxUMWWPUMDMUV7CbRoD6w3hZ9Kv3+V+P0D0C42DLvW2n9ljHlBhcD7QUk/rcI63Y83o3EAmiObzWt6Pr26B+306ijtzFxGuXztk6K+HdvKFY53J2LlUdpdgzH19nQ18VkAwcR6U/ip9Pu3++BRSeL3D0Bb2UyBqv8u6Yak35P0WUk/ZK1daGirANTdykpO1+bSa/agLXycmc/IbXCRf2Bn7+oetBUfdw3E1NO92Tp3QHtivSn8VPo9++KXz+l6aonfv9ugcjoQLrcrUPWUpDdK+nVJvyjpNyUdl/TnDW8ZgDu2tJzVtdlMxT60qcJ62tmUZq8v1Ay0nicl+qPlIlCFqceFULtrIKburs7mPhEgZFhvCj8dOrhfjx0/punpab+bEmhUTgfC53ZDMn8t6aettbOSZIz5hqQvGGNeY639jYa3DsAtFpeyxYrGa7fsSWnuxmLN4zo6PO0qBdo1W/Yk+qPqihBoAQDti8rVQPjcbs3uz6+5/bwx5hEVRnYJu0CDLCyurE41nq0OtNdvLtU8rrPDU2KgOCo7UB1oB/ujinR2NPFZAADQOqhcDYTPHS+2s9a+bIyhEjOwRemF5Vv3oJ1J69rcgq7frL0sPtLZoV2lQFs1ShvX4M5edRJoAQC4Y1ROB8LnrirLWGtv1rshQNg455ReWF7dg7a492wp1KYyyzWP7Yp0FCocJ+JrRmnjGtjZq44OrjIDAFBPVE4HwocyqsAWOOd0M71cDLOlPWhXA21mcaXmsd1dnRV70K5+3Pv6Vym/skCgBQCgiaicDoQPYRe4Deecrt9cKgTa2eIetDPpcsXjxaVszWO39UTKFY53DxZHaot70u7c3lM1Vaok0R/X9HTtQlMAAKAxqJwOhAthF5CUzzvN31ysKgRV+XF5JVfz2N5tXeVtekojtKXb22Pd6wZaAAAAAI1F2EXbyOedZq8vrG7ZM5sqr6edmk1rJZuveWw82r1aDKpUHKq4njbWS6AFAAAAgiZQYdcY86Kkm5JykrLW2sNrvu5J+oSkYUkZSe+11n6l2e1EcOVyec1UBtqKEdprsxllc7UD7Y5YT3mrnqE162hjvd1NfBYAAGCtiYuTSj43rlSuQ/HOvIYfORKqKcdhf36AHwIVdosetdZO1/jaWyW9vvjv+yT9VvEj2kg2l9fMXKZiy57iKO1MWtNzaeVytbcI2Ll9W/WWPQOrgbZ3W1cTnwUAAK3Hr0A2cXFSI2OX1b/vuGKep7xzGhkbl6RQBMKwPz/AL0EMuxt5h6TPWWudpC8ZY/qMMfdaa7/td8NQXyvZnKZnM7o6WxFoi+F2ej6jfL52oO3f2VssAlW9B+3QQEzbelrtVx4AgGDwM5Alx86rf++j5WVDnuepf+8RJcfOhiIMhv35AX4J2pm/kzRqjHGS/oO19sk1X79P0rcqbr9UvK8q7BpjnpD0hCRZa5VIJBrX4hYWiUR8fW2WV7J65doNXZm6oW9P3dC3rxU/Tl3X9Gxaebd+oPU8addAXHuGdujeoR26d2in7t1V+PyexA71tHig9btfsD76JZjol+ChT4KpHv3yxS9f0u6Dx6rqVOw+eFRf/PI5PXb82FabuKGVzm2K9vTccv9C57aW/n0r9UtYn18r4m9YMN1tvwQtFTxirX3ZGDMk6RljzGVr7bN3+k2KIbkUlN30dK1Z0e0tkUio0a/N0nJW12bTujpdKAJ1tWKEdu7GgmrkWXmelOiP3rIH7dBgTLv6Y+rq6lznqLxu3pzXzZsNfUoN14x+wZ2jX4KJfgke+iSY6tEv06klxVZu3T/+emqp4X3elVvU0tJSVdB2zimSW2zp37dSv4T1+bUi/oYF00b9smfPnprHBSrsWmtfLn6cMsY8JelhSZVh92VJr6q4fX/xPvhoYWlF14pTja/OpFYD7Wxa8zdq7xfb0eFp10BUQ4PFvWcT8fJ62kRfTJFIRxOfBQAA2Eg84pR37pZAFovUXlpUL8NHD2tkbFz9e4/I8zw55zR3eVynjh6+/cEtIOzPD/BLYMKuMSYmqcNae7P4+QlJH1nzsC9Ier8x5vMqFKa6znrd5sgsrlRUNi6E2VKBqBuppZrHdXZ62tW/un52dQ/amAb6oop0EmgB4E5RtRV+8DOQlX6/k2Nnlc56ikWcTh09HJrf+7A/P8AvgQm7knZLesoYIxXa9fvW2r8wxrxPkqy1vy0pqcK2Q19XYeuhn/SpraGUyixXbNmTLobZwkhtKrNc87hIpENDFQWhKkdpB3ZG1dHBHrQAUC9UbYVf/A5khw7uD/XveNifH+AHz9VaNBke7sqVK363IRCcc7qZXtZUscJxasHpxW9NlUdq0wu3rsMp6e7qLITZgeo9aHcPxtS3o5dAW0esFQmmduqXVho1bKd+Kfnob31W+YqqrVLh73vH5bP60M/8hI8tK2jHPmkF9Esw0S/BQ58E0ybW7K4bRoI0sos6cM7pRmqpeg/amZSuzhY+X1isHWh7ujsrCkEVA+1AXEOJmPq2b6s6sQIQTowaBl8q6ym25u+x53lKZ/kbDQBAJcJuC3LOaf7GYmGqcXkf2tX1tEvL2ZrH9vZEClOMB2J6zat2Kd7bUR6l3RHvIdACbY69HoPPzyJBAAC0EsJuQOXzTnM3FirWzq5WOJ6aSWt5JVfz2FhvV7EY1OoIbWEKclzbY93lEySmaQBYi1HD4KNqKwAAm0PY9VE+7zR7PaOr05VTjYvBdjatbDZf89h4tLsQZhPxwlTjwdUCUfFodxOfBYAwYdQw+PwuEgQAQKsg7Prol3/zv+qbV+Zrfn1HvKc8xXioYsueoYGYor0EWgD1x6hha6BqKwAAt0fY9VGiP6rrqcVyhePd5WAb067BmHp7uvxuIoA20w6jhq1UbRoAANw9wq6PfuY9D7NlD4DACfOoIdWmAQBoHx1+N6CdEXQBoLkK1aaPrFNt+rzPLQMAAPVG2AUAtI1U1rtlizWqTQMAEE6EXQBA24hHnJyrrixNtWkAAMKJsAsAaBvDRw9r7vJ4OfCWqk0PU20aAIDQoUAVAKBtlIpQfe5Pzugb164rt7Kk7xzqk7TX13YBAID6I+wCANqOl3i1Dj+yupcwFZkBAAgfpjEDANoKFZkBAGgPjOwCANpKKusp1qIVmScuTir53LhSuQ7FO/MafuQIo9EAANRA2AUAtJV4xCnvXNUWRK1QkXni4qRGxi6rf99xxTxPeaZfAwCwIaYxAwDaSqtWZGb6NQAAd4aRXQBA28lPf1Pnn7qk/PKiHrinX+/9kbcFfnS0ladfAwDgB8IuAKBtlKYCDz5yUoliJea5y+N+N2tTWnX6NQAAfmEaMwCgbbTyVOBWnX4NAIBfGNkFALSNVp4KXJpmnRw7q3TWUyzidOro4cBPvwYAwC+EXQBA22j1qcCHDu4n3AIAsElMYwYAtA2mAgMA0D4Y2QUAtA2mAgMA0D4IuwCAtsJU4HCauDip5HPjSuU6FO/Ma/iRI/QzALQ5wi4AAGhppS2l+vcdV8zzlHdOI2OFLaUIvADQvlizCwAAWlorbykFAGgcwi4AAGhpqaxXVWFbap0tpQAAjUPYBQAALS0eceUK2yWttKUUAKAxWLMLAEDAUGzpzgwfPayRsfHyVObSllKn2FIKANoaYRcAgACh2NKdY0sptIq1F7Le8/Y364FX3+93s4DQIuwCABAghWJLj65TbOks4W0DbCmFoFvvQtaToxN698PX+d0FGoSwCwBAgKSynmIUW0LAMLV+69a9kLXviJJjT/NaAg1C2AUAIEDiEae8c1XVhSm2BD8xtb4+uJAFNB/VmAEACJDho4c1d3m8XF24VGxpmGJL8An7GNcHVcOB5mNkFwCAAKHYEoKGEcn6WLdq+NfG9W4uZAENQ9gFACBgKLaEIGFqfX2sdyHribe9iWrMQAMRdgEAAFAT+xjXz9oLWYlEQtPT0z62CAg3wi4AAJBExV2sj6n1AFoVYRcAAFBxFxtiaj2AVkQ1ZgAAQMVdAEDoEHYBAIBSWa+qAJFExV0AQGtjGjMAALjjirus7wUABB1hF0Db4OQcqO1OKu5utL73sePHmt30UOLvFQBsHWEXQFug+A6wsTupuFtY3/voOut7zxJ264C/VwBQH4RdAG1ho5NzTh6Bgs1W3E1lPcVY33tbdzs6y98rAKiPQIRdY8yrJH1O0m5JTtKT1tpPrHnMGyX9iaT/Vbzrj6y1H2lmOwG0Lk7Ogfq50/W97Wgro7P8vQKA+ghKNeaspA9Ya98g6fsl/awx5g3rPO6/WWsfKv4j6ALYtHjEybnqE3FOzoG7M3z0sOYuj5ffU6X1vcPrrO9tV1vZyom/VwBQH4EIu9bab1trv1L8/Kakr0m6z99WAQgTTs6B+jl0cL9OHd2rjstnlXn+rDoun9Wpo3uZYlthK1s58fcKAOojENOYKxljXiPpkKT/sc6X/64x5quSrkj6l9bayWa2DUDrupPiOwBub7Pre9vVVqZ68/cKAOrDWztNxk/GmLikc5I+aq39ozVf2yEpb61NGWOGJX3CWvv6Gt/nCUlPSJK19nuXl5cb3PLWFIlElM1m/W4G1qBfgol+CSb6JXjok4K//MoFPTk6of59FVs5fW1cT5w4pIe/56Gmt4d+CSb6JXjok2DaqF+6u7slad1pM4EJu8aYLkl/Julpa+2vbeLxL0o6bK2dvs1D3ZUrV+rQwvBJJBKanr7dy4dmo1+CiX4JJvoleOiTVRMXJ5UcO18enR32cXSWfgkm+iV46JNg2qhf9uzZI9UIu4GYxmyM8SR9StLXagVdY8w9kq5aa50x5mEV1hvPNLGZAAAAm8ZUbwDwVyDCrqSjkk5Jet4Yc6F43y9IerUkWWt/W9JJST9jjMlKWpD0Y9baYAxLAwAAAAACJRBh11r7nGoMPVc85pOSPtmcFgEAAGCrJi5OKvncuFK5DsU78xp+5Aij3QCaJhBhFwAAAOEycXFSI2OX1b/vuGKep7xzGhkblyQCL4CmCMQ+uwAAAAiX5Nh59e89Ut5+yfM89e89ouTYeZ9bBqBdEHYBAABQd6msV7XPsFQIvOnshivXAKBumMYMAABQxBrT+olHnPLOVQVe55xiEeqLAmgORnYBAAC0usY0v++4Yg8+qvy+4xoZu6yJi5N+N60lDR89rLnL43KuEG6dc5q7PK7ho4d9bhmAdsHILgAAgEprTB9dZ43pWUZ370LpNUuOnVU66ykWcTp19DCvJYCmIewCAACosMY0xhrTujp0cD/hFoBvmMYMAACgwhrT0pTbEtaYAkDrIuwCAACINaYAEDZMYwYABAJVcOE31pgCQLgQdgEAvitVwe3fd1wxz1PeOY2MjUsSQQNNxRpTAAgPpjEDAHxXqIJ7ZJ0quOd9bhkAAGhVjOwCAHxHFVzg7rEEAADWR9gFAPguHnHKO1ce2ZWoggtsBksAAKA2pjEDAHxHFVzg7rAEAABqY2QXAOA7quACd4clAABQG2EXABAIVMEF7hxLAACgNqYxAwAAtCiWAABAbYzsAgAAtCiWAABAbYRdAACAFsYSAABYH2EXAIA7xL6mAAAEH2EXAIA7wL6mAAC0BgpUAQBwB9jXFACA1kDYBQDgDqSyXtU2LxL7mgIAEESEXQAA7kA84srbvJSwrykAAMFD2AUA4A6wrykAAK2BAlUAANwB9jWtH6paAwAaibALAMAdYl/TraOqNQCg0ZjGDAAAmo6q1gCARiPsAgCApqOqNQCg0Qi7AACg6ahqDQBoNMIuAABoOqpaAwAajQJVAACg6ahqDQBoNMIuAADwBVWtAQCNxDRmAAAAAEDoMLILAACAW0xcnFTyuXGlch2Kd+Y1/MgRRuIBtBTCLgBgUzjxBdrHxMVJjYxdVv++44p5nvLOaWRsXJJ43wNoGYRdAMBtceIbPly8wEaSY+fVv/fR8l7Inuepf+8RJcfO8nsCoGUQdgEAt8WJb7hw8QK3k8p6ihXf7yWe5ymd9WocAQDBQ4EqAMBtpbJeOeiWcOLbugoXL46sc/HivM8tQ1DEI668B3KJc06xiKtxBAAED2EXAHBbnPiGCxcvcDvDRw9r7vJ4+X3vnNPc5XENHz3sc8sAYPOYxgwAuK3ho4c1MjZeHg0snfie4sS3JcUjTnnnqgIvFy9QqTSdPTl2Vumsp1jE6dTRw0xzB9BSCLsAgNvixDdcuHiBzTh0cD/vcQAtjbALANgUTnzDg4sXAIB2QNgFEFpsrQLUxsULAEDYEXYBhBJbqwDBwsUnAECzBSrsGmPeIukTkjol/Y619mNrvt4j6XOSvlfSjKR3W2tfbHY7AQQf+8ICwcHFJwCAHwKz9ZAxplPSb0h6q6Q3SHqPMeYNax7205LmrLWvk/Trkn6lua0E0CrCuLXKxMVJffQ3P6MP/vvP6aO/+RlNXJz0u0nAprCvLwDAD4EJu5IelvR1a+03rLXLkj4v6R1rHvMOSZ8tfn5a0puMMa175gqgYcK2L2xpZCy/77hiDz6q/L7jGhm7TOBFSwjjxScAQPAFKezeJ+lbFbdfKt637mOstVlJ1yUNNqV1AFrK8NHDmrs8Xg68pa1Vhlt0axVGxtDKwnbxCQDQGgK1ZrdejDFPSHpCkqy1SiQSPrcomCKRCK9NANEv9fHY8WPa2bdTT/2XMaVWpHiX9A/edlQPf89Dd/X9/O6Xlc5tivb03HL/Que2tv598btfcKv1+uQ9b3uTnhydUP++in19vzauJ972JvqvSXivBBP9Ejz0STDdbb8EKey+LOlVFbfvL9633mNeMsZEJO1UoVBVFWvtk5KeLN5009PT9W9tCCQSCfHaBA/9Uj8PvPp+feAn3111392+tn73S1duUUtLS1VTQZ1ziuQW2/r3xe9+wa3W65MHXn2/3v3wdSXHni7v6/vuo4f1wKvvp/+ahPdKMNEvwUOfBNNG/bJnz56axwUp7I5Ler0x5rUqhNofk/T31zzmC5J+QtJ/l3RS0hettcyBAhB6w0cPa2RsvDyVuTQt+1SLTstG+2FfXwBAswUm7Fprs8aY90t6WoWthz5trZ00xnxE0nlr7RckfUrSiDHm65JmVQjEABB6pZCQHDtbHhk7dfQw4QEAAKAGb23BiBByV65c8bsNgcQ0jWCiX4KJfgkm+iV46JNgol+CiX4JHvokmDYxjXnd8v5BqsYMAAAAAEBdEHYBAAAAAKFD2AUAAAAAhA5hFwAAAAAQOoGpxgwAqDZxcVLJ58aVynUo3pnX8CNHqL4MAACwSYRdAAigiYuTGhm7rP59xxXzPOWd08jYuCQReAEAADaBacwAEEDJsfPq33tEnleopO95nvr3HlFy7LzPLQMAAGgNhF0ACKBU1isH3RLP85TOrruNHAAAANZgGjMABFA84pR3rirwOucUizgfWwVsDevQAQDNxMguAATQ8NHDmrs8LucK4dY5p7nL4xo+etjnlgF3p7QOPb/vuGIPPqr8vuMaGbusiYuTfjcNABBSjOwCQACVRruSY2eVznqKRZxOHT3MKBhaVmEd+qPrrEM/y+81AKAhCLsAEFCHDu4nBCA0UllPMdahAwCaiGnMAACg4eIRV56WX8I6dABAIxF2AQBAw7EOHQDQbExjBgAADcc6dABAsxF2AQBAU7AOHQDQTExjBgAAAACEDmEXAAAAABA6hF0AAAAAQOgQdgEAAAAAoUPYBQAAAACEDmEXAAAAABA6hF0AAAAAQOgQdgEAAAAAoRPxuwEAAPhp4uKkks+NK5XrULwzr+FHjujQwf1+NwsAAGwRYRcA0LYmLk5qZOyy+vcdV8zzlHdOI2PjkkTgBQCgxTGNGQDQtpJj59W/94g8z5MkeZ6n/r1HlBw773PLAADAVjGyi0BgGiEAP6SynmLFoFvieZ7SWa/GEQAAoFUQduE7phEC8Es84pR3rjyyK0nOOcUizsdWAQCAeiDswneFaYSPrjON8CxhF0BDDR89rJGx8fJUZuec5i6P69TRw343bVOYFQMAQG2EXfiOaYQAmq0yJObnpzV97gXFBu9RLOJ06ujhlgiMzIoBAGBjhF34jmmEAJppbUiMFkdzf/To3pYKicyKAQBgY1Rjhu+Gjx7W3OVxOVcIt6VphMMtMo0QQGsJSwXmVNarukgoMSsGAIBKjOzCd6URiOTYWaWzXktNIwTQesKydIJZMQAAbIywi0A4dHA/4RZAU4QlJLZ6cS0AABqNsAsAaCthCYnMigEAYGOEXQBAWwlTSGRWDAAAtRF2AQBth5AIAED4UY0ZAAAAABA6hF0AAAAAQOgwjRkAgDs0cXFSyefGlcp1KN6Z1/AjR5gWDQBAwBB2AQC4AxMXJzUydln9+44r5nnKO6eRsXFJIvACABAgTGMGAOAOJMfOl7ctkiTP89S/94iSY+d9bhkAAKhE2AUA4A6ksl456JZ4nqd01qtxBAAA8ANhFwCAOxCPODnnqu5zzikWcTWOAAAAfmDNLgDgtijItGr46GGNjI2XpzI75zR3eVynjh72u2kAAKCC72HXGPNxST8oaVnSC5J+0lo7v87jXpR0U1JOUtZay1kFADQBBZmqlZ5zcuys0llPsYjTqaOH2/K1AAAgyHwPu5KekfRBa23WGPMrkj4o6edrPPZRa+1085oGACgUZHp0nYJMZ9s24B06uL9tnzsAAK3C97BrrR2tuPklSSf9agsA4FaprKcYBZkAAECLCVqBqp+S9J9qfM1JGjXGfNkY80QT2wQAbY2CTAAAoBV5a09gGsEY858l3bPOlz5krf2T4mM+JOmwpB+x1t7SKGPMfdbal40xQypMff6n1tpna/y8JyQ9IUnW2u9dXl6u0zMJl0gkomw263czsAb9Ekzt3C9/+ZULenJ0Qv37KgoyfW1cT5w4pIe/5yFf29bO/RJU9Ekw0S/BRL8ED30STBv1S3d3tyStO92sKWH3dowx75X0jyW9yVqb2cTjPywpZa391U18e3flypWtNTCkEomEpqdZAh009EswtXu/TFycVHLsfLkg03BACjK1e78EEX0STPRLMNEvwUOfBNNG/bJnzx6pRtj1fc2uMeYtkn5O0rFaQdcYE5PUYa29Wfz8hKSPNLGZANDWKMgEAABaTRDW7H5S0nZJzxhjLhhjfluSjDF7jDHJ4mN2S3rOGPNVSX8p6c+ttX/hT3MBAAAAAEHn+8iutfZ1Ne6/Imm4+Pk3JH13M9sFAAAAAGhdQRjZBQAAAACgrgi7AAAAAIDQIewCAAAAAEKHsAsAAAAACB3CLgAAAAAgdAi7AAAAAIDQIewCAAAAAELH9312AQBYa+LipJLPjSuV61C8M6/hR47o0MH9fjcLAAC0EMIuACBQJi5OamTssvr3HVfM85R3TiNj45JE4AUAAJvGNGYAQKAkx86rf+8ReZ4nSfI8T/17jyg5dt7nlgEAgFZC2AUABEoq65WDbonneUpnvRpHAAAA3IqwCwAIlHjEyTlXdZ9zTrGIq3EEAADArQi7AIBAGT56WHOXx8uB1zmnucvjGj562OeWAQCAVkKBKgBAoJSKUCXHziqd9RSLOJ06epjiVAAA4I4QdgEAgXPo4H7CLQAA2BKmMQMAAAAAQoewCwAAAAAIHcIuAAAAACB0CLsAAAAAgNAh7AIAAAAAQoewCwAAAAAIHcIuAAAAACB0CLsAAAAAgNAh7AIAAAAAQoewCwAAAAAIHcIuAAAAACB0CLsAAAAAgNAh7AIAAAAAQoewCwAAAAAIHcIuAAAAACB0POec321otNA/QQAAAABoY956d7bDyK7Hv/X/GWO+7Hcb+Ee/tMo/+iWY/+iX4P2jT4L5j34J5j/6JXj/6JNg/ttEv6yrHcIuAAAAAKDNEHYBAAAAAKFD2G1vT/rdAKyLfgkm+iWY6JfgoU+CiX4JJvoleOiTYLqrfmmHAlUAAAAAgDbDyC4AAAAAIHQifjcAwWCM+YCkX5W0y1o77Xd72p0x5pclvUNSXtKUpPdaa6/42yoYYz4u6QclLUt6QdJPWmvnfW1UmzPG/KikD0vaJ+lha+15f1vU3owxb5H0CUmdkn7HWvsxn5vU9owxn5b0dklT1toDfrcHkjHmVZI+J2m3CltkPmmt/YS/rYIxZpukZyX1qJCRTltrf8nfVkGSjDGdks5Letla+/Y7OZaRXZT+6J6Q9Ld+twVlH7fWHrTWPiTpzyT9os/tQcEzkg5Yaw9K+mtJH/S5PZAuSfoRFU5Q4KPiychvSHqrpDdIeo8x5g3+tgqSPiPpLX43AlWykj5grX2DpO+X9LO8VwJhSdJxa+13S3pI0luMMd/vb5NQ9M8lfe1uDiTsQpJ+XdLPqXB1EQFgrb1RcTMm+iYQrLWj1tps8eaXJN3vZ3sgWWu/Zq39n363A5KkhyV93Vr7DWvtsqTPqzBDBT6y1j4radbvdmCVtfbb1tqvFD+/qcJJ/H3+tgrWWmetTRVvdhX/cf7lM2PM/ZLeJul37uZ4pjG3OWPMO1SYEvBVY4zfzUEFY8xHJf24pOuSHvW5ObjVT0n6Q78bAQTIfZK+VXH7JUnf51NbgJZgjHmNpEOS/ofPTYHKM1S+LOl1kn7DWku/+O/fqTAot/1uDibstgFjzH+WdM86X/qQpF9QYQozmmyjfrHW/om19kOSPmSM+aCk90ti3UgT3K5fio/5kArT0H6vmW1rV5vpEwBoNcaYuKQzkv7Fmhld8Im1NifpIWNMn6SnjDEHrLWXfG5W2zLGlOoNfNkY88a7+R6E3TZgrX3zevcbYx6U9FpJpVHd+yV9xRjzsLX2lSY2sS3V6pd1/J6kpAi7TXG7fjHGvFeFYi9vstYyvakJ7uC9An+9LOlVFbfvL94HYA1jTJcKQff3rLV/5Hd7UM1aO2+MOavCenfCrn+OSvohY8ywpG2Sdhhjftda+w83+w0Iu23MWvu8pKHSbWPMi5IOU43Zf8aY11tr/6Z48x2SLvvZHhQUK83+nKRj1tqM3+0BAmZc0uuNMa9VIeT+mKS/72+TgOAxxniSPiXpa9baX/O7PSgwxuyStFIMur2SHpP0Kz43q61Zaz+oYjHQ4sjuv7yToCsRdoGg+pgx5rtU2Hrom5Le53N7UPBJFbYkeKY4G+JL1lr6xkfGmB+W9O8l7ZL058aYC9bax31uVluy1maNMe+X9LQKWw992lo76XOz2p4x5g8kvVFSwhjzkqRfstZ+yt9Wtb2jkk5Jet4Yc6F43y9Ya5P+NQmS7pX02eK63Q5J1lr7Zz63CVvkOccsPAAAAABAuLD1EAAAAAAgdAi7AAAAAIDQIewCAAAAAEKHsAsAAAAACB3CLgAAAAAgdAi7AAAAAIDQYZ9dAABalDHm/5L0d6y17yze/rik75H0Vmvtsp9tAwDAb+yzCwBAizLGDEr6hqQ3Svo+ST8r6RFr7XU/2wUAQBAQdgEAaGHGmA9L+hFJO1UIut8yxuyU9IykN0j6fmvtJR+bCACAL1izCwBAa5uQ9KCkD1prv1W8LyPpbZJO+9YqAAB8RtgFAKBFGWMelPRbkj4r6adK91trV6y113xrGAAAAUDYBQCgBRlj7pP0p5LeJ+mfSHrQGPNGXxsFAECAEHYBAGgxxpgdkpKSfs1a+wVrbUbSxyV91N+WAQAQHBSoAgAgpIwxn5H0qxSoAgC0I0Z2AQAIIWNMUtIJSf/RGPNen5sDAEDTMbILAAAAAAgdRnYBAAAAAKFD2AUAAAAAhA5hFwAAAAAQOoRdAAAAAEDoEHYBAAAAAKFD2AUAAAAAhA5hFwAAAAAQOoRdAAAAAEDoEHYBAAAAAKHz/wO/jQwD+x3qeQAAAABJRU5ErkJggg==",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"plot_ds(data,m[-1],q[-1])"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Adam"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Oltre a memorizzare la somma smorzata $\\tilde G_{j,k}$ dei quadrati dei gradienti precedenti, come in Adadelta e RMSprop, Adam mantiene anche una somma smorzata $\\tilde H_{j,k}$ dei gradienti precedenti $g_{j,k}$, utilizzata in sostituzione del gradiente $g_{j,k}$ nell'aggiornamento effettuato ad gni iterazione.\n",
"\n",
"\\begin{align*}\n",
"\\tilde G_{j,k} &= \\gamma \\tilde G_{j,k-1} + (1 - \\gamma) g_{j,k}^2\\\\\n",
"\\tilde H_{j,k} &= \\beta \\tilde H_{j,k-1} + (1 - \\beta) g_{j,k}\n",
"\\end{align*}\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Dato che si assume che $\\tilde H_{j,k}=\\tilde G_{j,k}=0$ se $k<0$ e i valori $\\gamma, \\beta$ sono normalmente prossimi a $1$, il metodo manifesta la tendenza (bias) a fornire valori piccoli di $\\tilde H_{j,k}$ e $\\tilde G_{j,k}$, soprattutto nelle iterazioni iniziali. \n",
"\n",
"Per correggere questo comportamento viene applicata una correzione del bias:\n",
"\n",
"\\begin{align*}\n",
"\\hat{G}_{j,k} &= \\frac{\\tilde G_{j,k}}{1 - \\gamma^k}\\\\\n",
"\\hat{H}_{j,k} &= \\frac{\\tilde H_{j,k}}{1 - \\beta^k}\n",
"\\end{align*}"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"I parametri sono aggiornati come visto in Adadelta e RMSprop, per cui risulta ad ogni iterazione:\n",
"\n",
"\\begin{align*}\n",
"g_{j, k} &= \\frac{\\partial J(\\theta)}{\\partial\\theta_j}\\Big\\rvert_{\\theta=\\theta^{(k)}}\\\\\n",
"\\tilde G_{j,k} & =\\gamma \\tilde G_{j,k-1}+(1-\\gamma)g_{j,k}^2\\\\\n",
"\\tilde H_{j,k} & =\\beta \\tilde H_{j,k-1}+(1-\\beta)g_{j,k}\\\\\n",
"\\hat{G}_{j,k} &= \\frac{\\tilde G_{j,k}}{1 - \\gamma^k}\\\\\n",
"\\hat{H}_{j,k} &= \\frac{\\tilde H_{j,k}}{1 - \\beta^k}\\\\\n",
"\\Delta_{j,k} &= - \\frac{\\eta}{\\sqrt{\\hat G_{j,k}+\\varepsilon}} \\hat H_{j, k}\\\\\n",
"\\theta_j^{(k+1)} &= \\theta_j^{(k)} + \\Delta_{j,k}\n",
"\\end{align*}\t"
]
},
{
"cell_type": "code",
"execution_count": 142,
"metadata": {},
"outputs": [],
"source": [
"def Adam(X,t, eta = 0.1, gamma = 0.999, beta = 0.9, eps = 1e-8, epochs = 10000):\n",
" theta = np.zeros(nfeatures+1).reshape(-1,1)\n",
" G_tilde = np.zeros(nfeatures+1).reshape(-1,1)\n",
" H_tilde = np.zeros(nfeatures+1).reshape(-1,1)\n",
" theta_history = []\n",
" cost_history = []\n",
" for k in range(epochs): \n",
" g = gradient(theta,X,t)\n",
" G_tilde = gamma * G_tilde + (1 - gamma)*g**2\n",
" H_tilde = beta * H_tilde + (1 - beta)*g\n",
" G_hat = G_tilde/(1 - gamma**(k+1))\n",
" H_hat = H_tilde/(1 - beta**(k+1))\n",
" delta = - eta * H_hat/(np.sqrt(G_hat)+ eps)\n",
" theta = theta + delta\n",
" theta_history.append(theta)\n",
" cost_history.append(cost(theta, X, t))\n",
" theta_history = np.array(theta_history).reshape(-1,3)\n",
" cost_history = np.array(cost_history).reshape(-1,1)\n",
" m = -theta_history[:,1]/theta_history[:,2]\n",
" q = -theta_history[:,0]/theta_history[:,2]\n",
" return cost_history, m, q"
]
},
{
"cell_type": "code",
"execution_count": 143,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"tempo di esecuzione: 0.666 secondi\n",
"10000 passi totali\n",
"1000000 gradienti valutati\n"
]
}
],
"source": [
"start_time = time.time()\n",
"cost_history, m, q = Adam(X,t, eta = 0.1, gamma = 0.999, beta = 0.9, eps = 1e-8, epochs = 10000)\n",
"print(f\"tempo di esecuzione: {time.time()-start_time: 4.3f} secondi\")\n",
"print(f\"{len(m)} passi totali\")\n",
"print(f\"{len(m)*n} gradienti valutati\")"
]
},
{
"cell_type": "code",
"execution_count": 144,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABQgAAAGoCAYAAAAKMwiTAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAABi4ElEQVR4nO3deXiU9aH3/8+9zCSZhC0MJIQtbBHZFEWxgqgQFbWtivsuv9qeYxc9bZ/nHJ/rOXIs1Et69XSx1fapnrZAXapW3CtLxH1FEdlkCZFA2JOwZSNzL78/QoIgYoDM3LO8X9fFRWbLfOZ7Qyb55Pu9v4bv+74AAAAAAAAAZCQz6AAAAAAAAAAAgkNBCAAAAAAAAGQwCkIAAAAAAAAgg1EQAgAAAAAAABmMghAAAAAAAADIYBSEAAAAAAAAQAazgw7QXlu2bAk6wgmJRqOqrq4OOgbEsUgmHIvkwbFIDhyH5JEOx6KoqCjoCHHD94WZiXE7dozZ8WHcjh1jdnwYt2PHmB2f9nxfyAxCAAAAAAAAIINREAIAAAAAAAAZjIIQAAAAAAAAyGAUhAAAAAAAAEAGoyAEAAAAAAAAMhgFIQAAAAAAAJDBKAgBAAAAAACADEZBCAAAAAAAAGQwCkIAAAAAAAAgg1EQAgAAAAAAABmMghAAAAAAAADIYBSEAAAAAAAAQAajIAQAAAAAAAAyGAUhAAAAAAAAkMEoCAEAAAAAAIAMRkEIAAAAAAAAZDAKQgAAAAAAACCD2fH85LNmzVJFRYUGDBigqVOntl1fV1enhx9+WPv27dPIkSM1ZcqUeMYAAAAAAAAA8BXiVhBWVFSoqalJ06dP1yOPPKLy8nINHjxYkvT000/r2muvVe/eveP19AAAAAAAAADaIW5LjNetW6dRo0ZJkkaOHKm1a9e23bZp0yY9++yz+tnPfnbI9QAAAAAAAAASK24zCOvr61VQUCBJikQiqqqqarttzZo1+sUvfqG8vDz96le/0owZM770+LKyMpWVlUmSZs6cqWg0Gq+oCWHbdsq/hnTBsUgeHIvkwbFIDhyH5MGxAAAAQCaJW0EYiUTU0NAgSWpsbFQkEmm7raioSH369JEkmeaRJzGWlpaqtLS07XJ1dXW8oiZENBpN+deQLjgWyYNjkTw4FsmB45A80uFYFBUVBR0BAAAAKSJuS4xLSkq0YsUKSdLy5ctVUlLSdluvXr20a9cuNTU1yXXdeEUAAAAAAAAA8DXiNoNw4MCBCoVCmjZtmoqLixWNRjV37lxNmTJF11xzjR544AE1NzfrqquuilcEAAAAAAAAAF8jbgWhJE2dOvWQy1OmTJEk9enTR/fee288nxoAAAAAAABAO8RtiTEAAAAAAACA5EdBCAAAAAAAAGQwCkIAAAAAAAAgg1EQAgAAAAAAABksrpuUoMWfy1Zry65G/X8TS9S7e27QcQAAAAAAAIA2zCBMgPr9Me1t2C/X84KOAgAAAAAAAByCgjABDMOQJHl+wEEAAAAAAACAw1AQJoB5oCD0fRpCAAAAAAAAJBcKwgQwDvzNDEIAAAAAAAAkGwrCBDBNZhACAAAAAAAgOVEQJgAzCAEAAAAAAJCsKAgTwOAchAAAAAAAAEhSFIQJcKAfpCAEAAAAAABA0rGDDpAJ2nYxDjgHAABAEGpra/WLX/xCVVVVmjNnjizLarvtoYce0ubNmxUOh1VaWqrx48cHmBQAACAzURAmQOsMQo+TEAIAgAyUl5ene+65R//93/99xNvvvPNOFRYWJjgVAAAAWlEQJgAzCAEAQCYLh8MKh8NHvM0wDD344IPKy8vTd77zHfXo0SPB6QAAAEBBmABtMwg5ByEAAMAhbrnlFuXl5Wn16tWaM2eOfvrTn37pPmVlZSorK5MkzZw5U9FoNNExO5Rt2yn/GoLAuB07xuz4MG7HjjE7PozbsWPM4oeCMAHaZhDSDwIAABwiLy9PkjR06FA99thjR7xPaWmpSktL2y5XV1cnJFu8RKPRlH8NQWDcjh1jdnwYt2PHmB0fxu3YMWbHp6io6Gvvwy7GCcAuxgAAAEfW0NAgSdqyZYtyc3MDTgMAAJCZmEGYAAYzCAEAQAZzHEf333+/Kisrdd999+mqq67S6tWrNWXKFP3ud79TfX29DMPQ7bffHnRUAACAjERBmACtBSHnIAQAAJnItm3dc889h1w3bNgwSdLdd98dRCQAAAB8AUuME8BsW2IcbA4AAAAAAADgcBSECWCIGYQAAAAAAABIThSECWAeGGX6QQAAAAAAACQbCsIEYAYhAAAAAAAAkhUFYQIYbecgpCAEAAAAAABAcqEgTIDWXYzpBwEAAAAAmcz3fXm7d8r3vKCjAPgCO+gAmcBsLQhFQwgAAAAAyEy+68h581l5az+WWTxc9oU3tU2oARAsZhAmQOvXO35BAgAAAADIRH5jvWIv/1ne2o8lSd6GlXJXvBtwKgCtKAgTgBmEAAAAAIBM5e3aoebn/iB/6+dSpJOsMy6QJLnv/1Pezs0BpwMgURAmRNsMQvpBAAAAAEAG8arWKfbcH6S9NTKiRQpf8UPZp02SOfwbkufKKXtcfvP+oGMCGY+CMAHaZhCySwkAAAAAIEO4q95X7J9/lZqbZBYPU+jb/yojr4skyT7rEhnde8nfWyPnrWf5eRkIGAVhArTOIOTrHQAAAAAg3fmeK+edF+S89Zzke7JOPa9lQ5JQuO0+hh2SXXqDZIfllS+Vt+aj4AIDoCBMhNZdmTwaQgAAAABAGvObm+TMm9OyAYlpyT7vKtljJ8swvlw/mF17yD7nMkmS884L8nZtT3RcAAdQECbAwRmEFIQAAAAAgPTk761V7Lk/ytu0RsqOKHTpd2SdNOaoj7FKTpdZcprkxFrOR+jEEpQWwBdRECaAodZzEAYcBAAAAACAOPC2Var52Yfk79ouo2sPhS//gcyige16rD3+Mhlde8iv3S7n3RfjnBTAkVAQJoDZtosxDSEAAAAAIL00rHhfsRcflprqZfQZotDl35fRpXu7H2+EsmSXXi9ZtrzPPpS7flkc0wI4EgrCBDAMZhACAAAAANKL73tyFi/Qruf/R/JcmcPOUuji22Rk5Rzz5zK7F8n+xqWSJOfNZ+TvrenouACOgoIwAZhBCAAAAABIJ36sWU7ZE3KXLJIMQ/a4byt0zuUyTOu4P6c57CyZA0ZIzfsVK3tCvut0YGIAR0NBmADMIAQAAAAApAu/fq9iLz4sr2K5FMpS92vvkjXi7BP+vIZhyD73Simvq/ydVXI/nNcBaQG0BwVhArQVhKIhBAAAAACkLq96c8tmJDurpE7dFLr8+8oeNKLDPr+RlaNQ6Q2Sacpd9rbcytUd9rkBfDUKwgRoXWLMDEIAAAAAQKpyP1+p2PP/T6rfI6Owv8JX/EBmfkGHP49Z0E/WGRdJkpzXn5Jft6fDnwPAoSgIE+DgEmMaQgAAAABAavF9X87SN+QseFRyYjKHjFbom9+VkZMXt+e0TjlHRp8SqalBsUV/l++5cXsuABSECWG0bVISbA4AAAAAAI6F7zpy3viH3A9ekeTLOuNC2edfI8Oy4/q8hmEqNPEaKdJJ/tbP5X68KK7PB2Q6CsIEMJlBCAAAAABIMX5jvWIv/1nemo8lOyT7ghtlnzaxbZVcvBk5eQpNvFaSIXfJInmb1yfkeYFMREGYAMwgBAAAAACkEm/XDjU/9wf5Wz+XIp0U+va/yBo4MuE5zN6DZZ12viS/ZalxY13CMwCZgIIwAZhBCAAAAABIFV7VOsWe+4O0t0ZG914KX/FDmT36BJbHOn2SjMJiqWGfnNeelu97gWUB0hUFYQK0Tr72KAgBAAAAAEnMXfW+Yv/8q9TcJLN4mEKX/auMvC6BZjJMS6FJ10tZEXmb1shd9nageYB0REGYAIbZOoMw4CAAAAAAAByB73ly3nlRzlvPSb4n69RzZV94k4xQVtDRJElGXhfZ510lSXI/nCdv+8aAEwHphYIwAVpnELLEGAAAAACQbPzmJjnzZ8td8Y5kWrLPu0r22ItlGMlVGVjFw2SNHCd5nmKvPiF/f2PQkYC0kVz/29PUwXMQBhwEAAAAAIAv8PfVKvb8H+VtXCNlRRS69DuyThoTdKyvZI29WEa0t7Rvl5w35zIRB+ggFIQJcHAXY75wAQAAAACSg7etUs1zH5Jfu11G1x4KX/EDmUUDg451VIZlK1R6gxTKklexXN5nHwQdCUgLFIQJ0DaDMOAcAAAAAABIkrvuE8VefFhqqpfRZ4hCl39fRpfuQcdqF6NLd9kTpkiSnHdfklezNeBEQOqjIEwA40BB6HlUhAAAAACA4Pi+J2fxAjmLnpQ8V+awsxSafJuMrJygox0Ta/ApMoeeIbmOnLLH5ceag44EpDQKwgRoXWJMPQgAAAAACIofa5ZT9oTcJYskw5A97luyx18mw7KCjnZc7LO/JaNbgfzdO+W8/XzQcYCURkGYAAc3KaEiBAAAAAAknl+/V7EXH5ZXsVwKZcmefJusEePaVrylIiMUll16g2SH5K39WO7aT4KOBKQsCsIEaJtBSD8IAAAAAEgwr3qLmp99SP7OKqlTN4Uuv0NWv5OCjtUhzPwC2Wd/S5LkvPWsvN07A04EpCY7np981qxZqqio0IABAzR16tS26x966CFt3rxZ4XBYpaWlGj9+fDxjBK7tHIQ0hAAAAACABHI3rJTz6pOS0yyjoL9CF90sIycv6Fgdyhx6hszN6+Wt/1RO2eMtG67YoaBjASklbgVhRUWFmpqaNH36dD3yyCMqLy/X4MGD226/8847VVhYGK+nTyomMwgBAAAAAAnk+77cT9+U+8E8Sb7MIaNlT5iSlsWZYRiyJ1yh5p2b5NdslfP+PxUaf1nQsYCUErclxuvWrdOoUaMkSSNHjtTatWvbbjMMQw8++KBmzpypnTvTf/ovMwgBAAAAAIniu46cN56R+8ErknxZZ1wo+/xr0rIcbGWEsxUqvUEyLXkr35P7+YqgIwEpJW4zCOvr61VQUCBJikQiqqqqarvtlltuUV5enlavXq05c+bopz/96ZceX1ZWprKyMknSzJkzFY1G4xU17qobW/62bTulX0e64DgkD45F8uBYJAeOQ/LgWAAAUpXfVK/Ygkflb/1cskOyz79G1sCRQcdKCLNHH1ljJ8t972U5r/9DZrS3jE7dgo4FpIS4FYSRSEQNDQ2SpMbGRkUikbbb8vJazncwdOhQPfbYY0d8fGlpqUpLS9suV1dXxytq3O3ds1eS1NwcS+nXkS6i0SjHIUlwLJIHxyI5cBySRzoci6KioqAjAAASzNu1Q7F5s6W9NVKkk0KTb5XZo0/QsRLKGjle/ub18jauVuzVJxT61r/IsKygYwFJL25LjEtKSrRiRcuU3uXLl6ukpKTtttbicMuWLcrNzY1XhKRhmCwxBgAAAADEj1e1TrHn/iDtrZHRvZfCV/ww48pB6cD5CM+7WsrtLH/7RrkfLQw6EpAS4jaDcODAgQqFQpo2bZqKi4sVjUY1d+5cTZkyRb/73e9UX18vwzB0++23xytC0jiwRwmblAAAAAAAOpy76n05b78g+Z7M4mGyJ14rI5QVdKzAGDm5Ck26XrEXH5a79HWZRQNl9i35+gcCGSxuBaEkTZ069ZDLU6ZMkSTdfffd8XzapGMe2KTEpyEEAAAAAHQQ3/Pkvvey3BXvSJKsU86VNfYiGUbcFgumDLPXAFmnl8r9aKFirz2l8FV3yYh0CjoWkLT4qpEAB/pBefSDAAAAAIAO4Dc3yZk/u6UcNC3Z514l+6yLKQe/wBp9voyiQVJjnWKLnpTve0FHApIWXzkSoG0GoWgIAQAAAAAnxt9Xq9jzf5S3cY2UFVHo0u/IGjom6FhJxzBNhSZeK2Xnyt9cLveTN4KOBCQtCsIEYAYhAAAAAKAjeNsq1Tz3Ifm122V07aHwFd+XWTQw6FhJy8jtrND510iS3I8Wytu2IdhAQJKiIEwAzkEIAAAAADhR7rqlir30iNRUL6P3YIUuv0NGl2jQsZKe2e8kWaecK/meYq8+Ib+pIehIQNKhIEyA1hmEFIQAAAAAgGPl+56cxQvkLPq75Doyh41V6OKpMrIiQUdLGdYZF8ro2U+q2yPn9af5+Rw4DAVhAhhtMwgDDgIAABCA2tpa/cd//IduvPFGua57yG0bN27UPffco3vuuUeVlZUBJQSA5OU7MTllf5e7ZJFkGLLO/pbs8ZfLsKygo6UUw7IUKr1OCmfLq/xM7op3g44EJBUKwgQ4eA5CGkIAAJB58vLydM8992jIkCFfuu3JJ5/UXXfdpR//+Md68sknA0gHAMnLr9+r2IsPy6tYJoWyZE++TfbIcW2TUHBsjE75ss+9SpLkvv9PeTs3B5wISB4UhAlgMoMQAABksHA4rLy8vCPeVl9fr2g0qvz8fNXX1yc4GQAkL696i5qffUj+jk1SXleFLr9DVr+Tgo6V8qyBI2QOO0vyXDllj8tv3h90JCAp2EEHyATMIAQAADiy9pwDqqysTGVlZZKkmTNnKhpN7RPy27ad8q8hCIzbsWPMjk8yjFvj2qXa9cIjUmy/wn0GKf+qH8jK7RxopqNJhjE7Fv63btWO6io5O6pkffhPdbvs9kBmZabauCUDxix+KAgTgBmEAAAAX++rfjgrLS1VaWlp2+Xq6upERYqLaDSa8q8hCIzbsWPMjk+Q4+b7vtxlb8l9/xVJvszBp0rnXqldjc1SY/Iey1T8t2acd4009/dqXPmBYtE+soaekfAMqThuQWPMjk9RUdHX3oclxglgqLUgpCEEAAD4ory8PNXU1Ki2tlY5OTlBxwGAwPiuI+fNZ+S+/09JvqwzLpA98VoZdijoaGnJ7NZT9vjLJUnOOy/I27U92EBAwCgIE8A4MMoe/SAAAMhAjuNoxowZqqys1H333adVq1Zp7ty5kqRrrrlGv/3tb/Wb3/xG1157bcBJASAYflO9Yi//Wd7qjyTLll16g+zTJrEZSZxZJ50uc8hoyYm1nI/QiQUdCQgMS4wTwGQGIQAAyGC2beuee+455Lphw4ZJkvr3768ZM2YEEQsAkoK3e6ecV2bJ31sjRTopdNEtMnv2DTpWxrDPuVyxHZvk126X8+6LCk2YEnQkIBDMIEyA1l/6UA8CAAAAAFp5VeWKPfuQ/L01Mrr3UviKH1AOJpgRypJdeoNk2fI++1Du+mVBRwICQUGYAK3Twj3WGAMAAAAAJLmrPlDsn3+RmptkFg9T6LJ/lZHXNehYGcmMFsk+61JJkvPmMy2zOYEMQ0GYACYzCAEAAAAAknzPk/Pui3LeelbyPVmnnCv7wptkhLKCjpbRzOFnySweLjXvV6zsCfmuE3QkIKEoCBOgbQYh5yAEAAAAgIzlNzfJmT9H7vJ3JNOSfe5Vss+6WIbBj+ZBMwxD9nlXSnld5e+skvvhvKAjAQnFV6EEMA02KQEAAACATObvq1Xs+T/K27hayooodOl3ZA0dE3QsfIGRFVFo0vWSYcpd9rbcytVHvb/fWCfn0zflbauU73sJSgnEB7sYJ0DbJiX0gwAAAACQcbxtlYot+JvUWCejaw+FJt8qo0s06Fg4ArOwv6wzL5T7wTw5rz8l86q7ZOR2OeJ93VUfyP1ooVxJyu0ia8AImYNGyijox6xQpBwKwgQwmEEIAAAAABnJXbdUzhv/kFxHRu/BCl1wg4ysSNCxcBTWKRPkba6QX7VWsVf/rtA3vyvD/HLhZ+QXHLxQv0fuinfkrnhHyu3cUhYOHCWjkLIQqYGCMAFaZxCyiTEAAAAAZAbf9+R+VCZ3ySJJknnyWNnjvi3DsgJOhq9jGKZCE69R8z8ekL/1c7lLXpU95oIv3c8sGiQdKP9Cl0yVt2mt3IrlUt1uuSvelbviXSnSWdbAETIHjpRR2J+yEEmLgjABWs9BKLXMIjS+cBkAAAAAkF58JybntaflVSyTDEPWNy6VNWIcPwumECMnT6Hzr1Xs5T/LXbJIZtHAlkLwi/fJypHRs6/87ZXynZjsb1wq66xL5O+skrd+udyKZYeVhZ1kDhgha+BIGYXFwbww4CtQECaIYbScg9DzJYv3BAAAAABIS37DPsXmz5G/Y5MUypJder2sfkODjoXjYPYZLGv0eXI/eU2xV/+u8FV3ycjJO+w+Q+Rur5RXtU5W8TAZhiGjZ1+ZPfvKOuvilrKwYnnLzMJ9u+StfE/eyvekSCftPnmMvKLBMgoHHHEJM5BIFIQJYhqGXN8/cB5CGkIAAAAASDdezRbF5s2W6vZIeV0VmnybzO6FQcfCCbDGlMrb+rn8bRvkvPa07ItvPWSZsNlniNyPy+RXrfvSYw8pC8deLL9684GZhculfbWq//g16ePXpJy8gzMLe1EWIhgUhAnSMpXcZydjAAAAAEhD7oZVcl79u+Q0yyjop9BFt3xpthlSj2FaCk26Ts3/+J28TWvkLntb9ikTDt7es48Uzpa/p1r+vloZnfKP/HkMQ0aPPjJ79JE1drL86i3K2lauuhUfSntr5K16X96q9w+UhcO/UBYm7zkrfd+Xv2OT3DUfSfsbZU+YIiMrJ+hYOE4UhAlispMxAAAAAKQd3/flLntL7vuvSPJlDj5V9rlXyrBDQUdDBzHyuso+7yo58+fI/XCezMJimQX9Wm4zLZm9B8n7fKW8qnJZJ5/59Z/PMGT06K0uJ5+i5hET5Ndskbd+ubyK5fL31shb9YG8VR9I2bkHZhaOkFE0MGnKQr9hn9x1n8hb85H8XTvarndCWQqdd1WAyXAiKAgTxGzbyZiCEAAAAADSge86ct5+Tt7qjyRJ1hkXyBo9kc1I0pBVPEz+iHFyV7yj2KtPKHzlnW2z5cw+JQcKwnXtKgi/yDAMGdHeMqO95Z95kfyarfIqDpSFe6rlffaBvM8OlIXFw2UNGhlIWeh7rryNa+St+UjextWS57XckJMnc+BIeZ992HLb4FNk9hmS0GzoGBSECWIcaAipBwEAAAAg9flNDYotfFT+lgrJsmWff42sQaOCjoU4ss66WN62DfKrN8t5c67s0htkGEZbIeZVrZPvecd9DsGWsrBIZrRI/hkXyq/denBm4Z5qeas/lLf6Qyk70lIWDhwpo2iQDCt+ZaG3e6e8NR/JXbtEath3IKgps//JMk8aI7PfUBmWJSfSWe7i+Yq9OVfhq38sIxSOWybEBwVhgrQuMfY8KkIAAAAASGXe7p1y5s2Wv6dainRS6KJbZPbsG3QsxJlh2QqVXq/mZ37fMsvvsw9kDTtLRud8GZ27y99bI39nlYwDy49P6LkMQ0b3IpndW8vC7fIqlrWUhbt3ylu9WN7qxVJWROaAYbIGjuqwstCP7Ze3fpncNR/J31Z5MFOXqMyhZ8gaMlpGbudDHmOdMkFexTL5NVvllD0ue+K1nI8wxVAQJkjrFHPqQQAAAABIXV5VuWILH5Wam2R076XQ5Ftl5HUNOhYSxOgSlT3hCjmv/l3Ouy/JKOgvs3svGX2GyF9VI69qXdv5CTvsOQ1DRvdCmd0L5Y+5QP6u7QdnFu7eIW/1Ry3L3LMiMouHyRw4UmbvQTKs9lc+vu/L314pd/VH8tYvk5zmlhvssMxBo2QNHSOjoP9XLp83LEv2+Vcr9sLD8jauVvPcBxW64EaZ0aKOGAIkAAVhgnAOQgAAAABIbe6qD+S887zkeTL7nyx70nUyQllBx0KCWYNPlbe5XN7qj+SUPa7QlB/J7DOkZSfiqnXS6ZPi9tyGYcjIL5SZXyidcYG8L84s3LWj5TyAaz6SsnJk9h8mc9BImb0Hf2VZ6NfvlbtuibzVH7XMiG19nsJiWSeNkTloZLv/jZvdixSe8qOWpfc1WxV77g+yx18ma+gZX/kY33Olxnop0olzdwaMgjBBDu5iHHAQAAAAAMAx8T1P7vv/lLv8bUktyymtMycf97nmkPrss7+t2PaN8nftkPP287LP/pZkmPK3b5Tf3CQjnJ2QHGZ+gcz8C6QxF8j74szCXdvlrf1Y3tqPpXD2gZmFo2T2GSzJkLdx9YENR9ZI/oENRyKdZJWc1nJuwa49jiuP0aW7Qpd/X847L8hbvVjOG8/I21Ype/xlkmVLdbvk7aiSv2Njy9/VmyUnJqN7L1nDxsocPFpGmNI9CBSECdK2xJiGEAAAAABSht+8X86rT7Ts3Gqass+54qgzopAZjFBYdukNis19sKWI6z1YRkFf+dsq5W1ZL6t4eMIzmd0KZI4pkMaUytu14+DMwtrt8tYukbd2iRTOlkxLaqo/8CBTZv/hMoeOkdm3pEN2RzbskELnXim3sL+ct56Tt+YjNW9ZLzkxqbHuyw+wQy3nLnzrOen9f8ocMlrWsLNkdu91wlnQfhSECcIMQgAAAABILf6+XYrNmy2/dpuUFVHowhtlFg0KOhaShJlfKHvct+W8OVfOW8/KLB4mX5XyNq0LpCA8JFu3njJPL5VOP1AWfr5c3vrlLf+WJRndeso8aYysktNk5OTFJYN10hgZ0SI5Cx6Tv7em5crsiMwefWX07COjZz+ZPfpI4Sx5n6+Qu/J9+ds2yFv1gbxVH8go6NdSFA4Ywa7ICUBBmCAG5yAEAAAAgJThbd+o2Pw5UmOdjK49WjYj6RINOhaSjDn0DJmby+WtXybv8xWSJL9qXcCpDmV26ymz2yTptEny9lS3LOnNL0zIOf/M7kUKXXWn/O0bZXTOlzrlH/F5rcGntpzbsXa7vM8+kLv2Y/nbN8rZvlF64xkZBf1k9h6k2Knj5JvZnK8wDigIE8RgBiEAAAAApAS3fKmc1/8huY6M3oMVuuAGGVmRoGMhCRmGIfucKWreWSXtrZUk+Xtr5O+tbSnEkowZQMlthLJk9BnSrvua+QUyx31b1pmT5a3/VO5ni+Xv2CR/6+dyt36uHR+Vyejao2Wn5kGjWjZrQYegIEwQ88A2xswgBAAAAIDk5Pu+9r7xvJy3X5QkmSePlT3u2zKsEz8vG9KXkZWt0KTrFXv+/0meK0nyqtbJGjY24GSpywiFZQ09Q9bQM+Tvb5C3pULeprVS5Sp5u3fKXbJI7pJFLUulB45qKQu79Qw6dkqjIEyQ1smv9IMAAAAAkHx8Jybn9afVvH6ZZBiyvnGprBHjWMqIdjF79pU1drLc916WREHYkYysiKwBI2QNGKHu+d/RzmUfyl2/XN6GFfJ37ZD7cZncj8tk5BfIHHSqrJLRMvK6Bh075VAQJkjrDEJ2MQYAAACA5OI37FNs/hz5OzbJCGfJmni9rP5Dg46FFGONHC9/83p5G1fL21wu33M7ZFdgHGSYlsw+Q2T2GSJ//GXyt6yXW7FM3ucr5ddul1s7X+7iBTJ6D5JVchobnBwDCsIEaf2tE0uMAQAAACB5eDVbFJs3W6rbI+V1VY/r/017zOygYyEFGYYh+7yr1Tz3d1JjPUsI48ywLBl9S2T2LZE//nJ5m8vlrV0ib8Mq+ZvL5Wwul959UdZJY2QNO0tGl+5BR05qFIQJYrZuUhJwDgAAAABAC3fDKjmv/l1ymmX07KfQRTcr1LOPVF0ddDSkKCMnV+Grfyztb5BhUbkkimHZsvoNldVvaMs5C9cvl7t6sfydVXKXvSV32dsy+50kc/g3ZPYdIsMwg46cdPjXmiCtBaHnURECAAAAQJB835e7/G257/1Tki9z8Cmyz71Khh0KOhrSgBHOlsLMQg2KkRWRNWysrGFj5e3YJHfle/LWL2tZ+r1xtYyuPWSNPk/moFPZgOgLKAgTxDxQTnMOQgAAAAAIju86ct5+Xt7qxZIka8wFsk6byGYkQBoye/aV2bOv/LMulbtmsdyV78nfvVPOa09LH5XJPuVcmSedzi8HREGYMOaB6atMIAQAAACAYPhNDYotfFT+lgrJsmWff42sQaOCjgUgzoycXNmnnidr5DnyypfKXfp6S1H49nPS0tdlj50sc9ApGf2LAgrCBLFMlhgDAAAAQFC83TvlzJstf0+1lJOn0ORbZfbsG3QsAAlkWJask06XOWS0vA0r5X5cJr92u5xX/y5j+Tuyx307Y78uUBAmiGmyizEAAAAABMHbXK7Ywsek/Y0yuvdS6KJbZXTqGnQsAAExTFPWwJEyi4fLW/uxnMUL5O/YpNhzf5B1yrmyxpRm3CYzmfVqA9S6SYnLDEIAAAAASBj3sw9blhF6nsz+J8uedJ2MUFbQsQAkAcM0ZQ09Q+agUXI/frVlx+Olr8vbtEahybfKyOsadMSEoSBMkNYlxmxSAgAAAADx53ue3A/+KXfZ25Ika9QEWWMny2jdQRIADjBCWbLPukRm8XA5rz0lv2arPpwzW69puOqbpbzcsC4cP1ijTy4KOmrcUBAmyMElxgEHAQAAAIA05zfvl/PqE/I2rpZMU/Y5V8gaekbQsQAkObOwv0JX/ECLn3xKj6/L0T5vX9ttW3bUSVOUtiUhvzpJEJYYAwAAAED8+ft2Kfb8H1vKwayIQpd+h3IQQLsZ2REt2j9Q+7zwIdfvq9+vBW+XB5Qq/phBmCAsMQYAAACA+PK2b1Rs/hypsU5Gl6jsi2+T2SUadCwAKaa+ofmI19d9xfXpgIIwQcwD57lgF2MAAAAA6Hhu+adyXn9ach0ZRYMUuvBGGVmRoGMBSEF5ueEjXx858vXpgIIwQQ5MIGSJMQAAAAB0IN/35X5cJvfjVyVJ5slnyh53mQzLCjgZgFR14fjB2rKjTvvq97dd1yk3SxeOHxxgqviiIEwQZhACAAAAQMfynZic1/8hb/2nkmHIOutSWSPHyThwDngAOB6jTy6SpkgL3i5XXUOz8iLsYowOcvAchAEHAQAAAIA04DfsU2z+HPk7NkmhsOxJN8jqPzToWADSxOiTi9K6EDwcBWGCmCa7GAMAAABAR/Bqtio2b5ZUt0fK66rQ5Ntkdi8MOhYApCwznp981qxZmjZtmv76179+6bbm5mZ997vf1bJly+IZIWmYB6a4s8QYAAAAAI6fu2GVYs/9UarbI6NnP4Wv+AHlIACcoLgVhBUVFWpqatL06dPlOI7Ky8sPuf3VV19Vv3794vX0SefgEmMKQgAAAAA4Vr7vy1n2lpz5f5OcZpmDT1HoW9+VEekUdDQASHlxKwjXrVunUaNGSZJGjhyptWvXtt3mOI7WrVunk046KV5Pn3QOLjEOOAgAAAAApBjfdeS8OVfuey9L8mWNuUD2xOtk2KGgowFAWojbOQjr6+tVUFAgSYpEIqqqqmq77fXXX9c555yjdevWfeXjy8rKVFZWJkmaOXOmotFovKImhG1VS5JycnJS/rWkOtu2OQZJgmORPDgWyYHjkDw4FgCQPPymBsUWPip/S4Vk2bLPu1rW4FOCjgUAaSVuBWEkElFDQ4MkqbGxUZFIRJLkuq6WLl2q//W//tdRC8LS0lKVlpa2Xa6uro5X1ARpWVq8r64+DV5LaotGoxyDJMGxSB4ci+TAcUge6XAsiooyZ9c9AOnL271TzrzZ8vdUSzl5Cl10i8yCzDlVFQAkStyWGJeUlGjFihWSpOXLl6ukpESStGfPHtXU1Oi+++7TW2+9pSeeeEJ1dXXxipE0LLNlqNmkBAAAAAC+nrd5vWLP/UH+nmoZ+YUKX/FDykEAiJO4zSAcOHCgQqGQpk2bpuLiYkWjUc2dO1dTpkzR/fffL0l66qmnNHToUOXl5cUrRtJgF2MAAJDJZs2apYqKCg0YMEBTp05tu/6hhx7S5s2bFQ6HVVpaqvHjxweYEkCycD/7UM7bz0meJ7P/yS3nGwxnBR0LANJW3ApCSYd88ydJU6ZMOeTyNddcE8+nTyqtm5R4HgUhAADILBUVFWpqatL06dP1yCOPqLy8XIMHD267/c4771RhYWGACQEkC9/z5H7witxlb0mSrFHnyBp7sQwzbovfAACKc0GIg6wDMwiZQAgAADLNunXrNGrUKEnSyJEjtXbt2raC0DAMPfjgg8rLy9N3vvMd9ejR40uPT7vN69gE57gwbscu1cbM29+kXc89rObyZZJpqevkG5U7ekLCc6TauCUDxuz4MG7HjjGLHwrCBGmdQegygxAAAGSY+vp6FRQUSGrZyK6qqqrttltuuUV5eXlavXq15syZo5/+9Kdfeny6bV6XDpvgBIFxO3apNGb+vt2KzZslv3ablJWj0AU3qbH3IDUGkD+Vxi1ZMGbHh3E7dozZ8WnP5nXM006QtiXGTCEEAAAZJhKJqKGhQZLU2NioSCTSdlvruaiHDh2q3bt3BxEPQMC87RvV/OyD8mu3yegSVeiKH8jsPSjoWACQUSgIE6R1iTHnIAQAAJmmpKREK1askCQtX75cJSUlbbe1FodbtmxRbm5uIPkABMct/1SxFx+WGutkFA1S6Irvy+zC8kEASDSWGCcIMwgBAECmGjhwoEKhkKZNm6bi4mJFo1HNnTtXU6ZM0e9+9zvV19fLMAzdfvvtQUcFkCC+78v9+FW5H7ecX9Q8+UzZ4y6TYVkBJwOAzERBmCBWW0EYcBAAAIAATJ069ZDLU6ZMkSTdfffdQcQBECDficl54x/yyj+VZMj6xiWyRo6XcWDVFQAg8SgIE8RgiTEAAACADOc37FNs/hz5OzZJobDsSdfL6n9y0LEAIONRECaIZbac7pElxgAAAAAykVezVbF5s6W63VJeV4Um3yqze6+gYwEAREGYMJyDEAAAAECmcis/k/PqE1KsWUbPfgpddLOMSKegYwEADqAgTBCTJcYAAAAAMozv+3KXvy33vX9K8mUOPkX2uVfJsENBRwMAfAEFYYJYzCAEAAAAkEF815Xz9vPyVn8oSbLGlMo6bRKbkQBAEqIgTBCTXYwBAAAAZAi/qUGxhY/J37JesmzZ510ta/ApQccCAHwFCsIEaZtBSEMIAAAAII15u3fKmTdb/p5qKSdPoYtukVnQL+hYAICjoCBMkLZzELLEGAAAAECa8javV2zho9L+Rhn5hQpNvk1Gp65BxwIAfA0KwgRhF2MAAAAA6cz97EM5bz8neZ7M/ifLnnidjHBW0LEAAO1AQZggLDEGAAAAkI58z5P7wStyl70lSbJGnSNr7MUyTDPgZACA9qIgTJCDS4wDDgIAAAAAHcSP7Zfz6t/lVX4mmabs8ZfLOvnMoGMBAI4RBWGCmAd+e8YMQgAAAADpwN+3W7H5s+XXbJWychS64CaZvQcFHQsAcBwoCBOEcxACAAAASBfe9o2KzZ8jNdbJ6BKVPflWmV17BB0LAHCcKAgTxGIXYwAAAABpwC3/VM7rT0uuI6NooEIX3CQjOxJ0LADACaAgTBCTTUoAAAAApDDf9+UueVXuR2WSJHPombLHXybDsgJOBgA4URSECXJwiXHAQQAAAADgGPlOTM4b/5BX/qkkQ9Y3LpE1cryMAyulAACpjYIwQVhiDAAAACAV+Q37FJv/N/k7NkqhsOyJ18kqHhZ0LABAB6IgTBCWGAMAAABINV7NNsXmzZLqdkt5XRWafKvM7r2CjgUA6GAUhAnCLsYAAAAAUolbuVrOq49LsWYZPfsqdNEtMiKdgo4FAIgDCsIEaVtizAxCAAAAAEnM9325y9+W+/4/Jd+XOegU2eddJcMOBR0NABAnZnvudO211+rdd99tu7xkyRLdddddcQuVjkyzZajpBwEAAAAkK9915bz1rNz3XpZ8X9bppbInXUc5CABp7qgzCKurq7Vjxw5JUlVVlVatWiVJWrp0qbZv3x7/dGnEZJMSAAAAAEnM39+g2ILH5G9ZL1m27POuljX4lKBjAQAS4KgF4WuvvaZ//OMfkqRnnnlGzzzzTNttvXv3jm+yNGOxSQkAAACAJOXtqZbzyiz5e6qlnDyFLrpFZkG/oGMBABLkqAXh4MGDdeGFF2rBggUaNWqUevVq2a0qLy9P48ePT0jAdMEmJQAAAACSkbdlvWILHpX2N8rIL1Ro8m0yOnUNOhYAIIGOWhCOHj1ao0eP1qBBgzR8+HD16NFDkuR5Xts59dA+JpuUAAAAAEgy7mcfynn7OcnzZPYbKnvS9TLCWUHHAgAkWLtavk2bNum1115TbW2t7rjjDt18881atGhRvLOlFWYQAgAAAEgWvufJee9lOW/OlTxP1qhzZF90C+UgAGSodhWEb7/9tnJzc/XOO+/IcRz16tVLc+fOjXe2tHKwIJR8SkIAAAAAAfFj++Us+JvcZW9Jpil7whTZ37hUBqvEACBjHXWJcau6ujp16tRJS5cu1YQJE9S/f3/96U9/ine2tGIahgxD8v2WPwdWHAMAACSFH/3oR+rbt6+Ki4vVr18/FRcXq7CwMOhYADqYv2+3YvNny6/ZKmXlKHTBTTJ7Dwo6FgAgYO0qCKPRqJ544gnV1dXpjjvu0O7du5WXlxfvbGnHNAy5vi/P92WKhhAAACSPM844Q47jqGvXrlq2bJkefPBBderUSfn5+erfv7++973vBR0RwAnydmxSbN5sqbFORpeo7Mm3yuzaI+hYAIAk0K6C8MYbb9TTTz+tIUOG6Mwzz9Tjjz+usWPHxjtb2jENQ658zkMIAACSzrJly/Tf//3fbZfPP/98ffjhh5o8ebIqKysDTAagI7jrl8l57SnJdWQUDVTogptkZEeCjgUASBLtKgjPPPNMnX766dq6dau2bdumm266iV2Mj4NpGpLLTsYAACD5dOrUSRs2bFBxcbEkaciQIXr44Yd14403qnv37sGGA3DcfN+Xu2SR3I8WSpLMoWfIHn+5DMsKOBkAIJm0qyCsqqrSL3/5S23btk2SVFhYqH//939X79694xou3RzYp0T0gwAAINn8y7/8ix588EH16dNHxcXF2rx5s8LhcNCxAJwA34nJWfSkvPKlkgxZ37hE1sjxMjghOgDgMO2aBvjnP/9Zu3bt0rhx4zRu3Djt3r1bf/nLX+KdLe2YB96ImUEIAACSTWFhoaZPn67Ro0dr9+7dKiws1N133x10LADHyW/Yp+pH/7ulHLTDsi+6WfaocygHAQBH1K4ZhBUVFbrhhhs0efJkSdK8efP0xBNPxDVYOjIPTCHkHIQAACAZmaapsWPHcq5pIMV5NdsUmzdLqtst5XVRaPKtMrsXBR0LAJDE2lUQ5uXladmyZRo9erSklpNYs4vxsWubQUhBCAAAACAO3MrVcl59XIo1K1Q0QMakG2REOgUdCwCQ5NpVEE6cOFFPPfWUPv7447brrr322riFSldt5yBkiTEAAACADuT7vtzl78h9/2XJ92UOGqUeV/6ravbsDToaACAFtKsgnDBhgrp06aJly5ZJkk455RSNGjUqrsHS0cElxgEHAQAAAJA2fNeV884L8j77QJJknT5J1umlMkJsNAQAaJ92bVIyY8YMVVdX6yc/+Yl+8pOfaOfOnfr5z38e72xphyXGAAAAADqSv79BsVf+2lIOWrbsSdfJHnMBm5EAAI5Ju2YQ1tbWqmfPnm2Xe/TooZqamriFSlfsYgwAAACgo3h7quW8Mkv+nmopJ0+hi26RWdAv6FgAgBTUroKwoKBAL774ovLz8+X7vl566SUVFBTEO1vaaV1i7FIQAgAAADgB3pb1ii14VNrfKCO/UKHJt8ro1C3oWACAFNWugvCyyy7TQw89pPvvv7/tuh/+8IdxC5WuLApCAAAAACfIXb1YzlvPSp4ns99Q2ZOulxHOCjoWACCFtXuTkmg0qiVLlkiSTjvtNA0bNiyuwdKRbbWc8tHxvICTAAAAAEg1vufJ/WCe3GVvSpKsUeNljb1EhtmuU8sDAPCV2lUQStKwYcMoBU+QfWAGoeMygxAAAABA+/mx/XJe/bu8ys8k05Q9/nJZJ58ZdCwAQJpod0GIE9c6g9BlBiEAAACAdvLrdis2b7b8mq1SOFuhC2+S2Xtw0LEAAGmEgjCBLGYQAgAAADgG3o5Nis2fIzXsk9ElKnvyrTK79gg6FgAgzVAQJpBttW5SwgxCAAAAAEfnrl8m57WnJNeRUTRQoQtukpEdCToWACANURAmkHXg5MHMIAQAAADwVXzfl7tkkdyPFkqSzKFnyB5/mQyLH98AAPHBO0wCMYMQAAAAwNH4TkzOG8/IK18qyZD1jUtkjRwvwzCCjgYASGMUhAnEDEIAAJCpZs2apYqKCg0YMEBTp05tu37jxo165JFHJEm33367+vfvH1REIHB+Y51i8+fI375RssOyJ10nq3hY0LEAABnADDpAJmmdQegwgxAAAGSQiooKNTU1afr06XIcR+Xl5W23Pfnkk7rrrrv04x//WE8++WSAKYFgebXb1Dz3wZZyMK+LQpf/K+UgACBhmEGYQPaBGYSuxwxCAACQOdatW6dRo0ZJkkaOHKm1a9dq8ODBkqT6+npFo9G2j4FM5G5cLafsCSm2X0bPvgpddIuMSKegYwEAMkhcC8KvWkry17/+VRs2bFAsFtMtt9yioUOHxjNG0rBaZxC6zCAEAACZo76+XgUFBZKkSCSiqqqqttt8/+t/cVpWVqaysjJJ0syZM9sKxVRl23bKv4YgpOO4+b6v+sWvak/Zk5LvK+fkMer2rf9PRijcIZ8/HccsERi3Y8eYHR/G7dgxZvETt4Lwi0tJHnnkEZWXl7f9pvjmm2+WbdvauXOn/ud//kf/5//8n3jFSCo25yAEAAAZKBKJqKGhQZLU2NioSCRyxPt91SYMpaWlKi0tbbtcXV3d8SETKBqNpvxrCEK6jZvvunLefUHeqg8kSdZpk+SOmaSaPXs77DnSbcwShXE7dozZ8WHcjh1jdnyKioq+9j5xOwfhkZaStLLtll6yqakpo05EbZmtuxhTEAIAgMxRUlKiFStWSJKWL1+ukpKSttvy8vJUU1Oj2tpa5eTkBBURSCh/f4Nir/y1pRy0bNkTr5N9xgUyDE4RDwAIRtxmEB5tKYkk/fKXv1R5ebl+9KMfHfHx6biUpGvnlvOI2OFwyr+eVMaU5OTBsUgeHIvkwHFIHhyLjjVw4ECFQiFNmzZNxcXFikajmjt3rqZMmaJrrrlGv/3tbyVJ3/nOd4INCiSAv6dasXmz5e/eKeXkKXThzTILM2fSBAAgOcWtIPy6pST/+3//b9XU1OjXv/617rvvvi89Ph2XkjQ1tYxHXX1jyr+eVMaU5OTBsUgeHIvkwHFIHulwLNqzlCSRvng+akmaMmWKJKl///6aMWNGEJGAhPO2VCi24FFpf4OM/AKFJt8mo1O3oGMBABC/JcZHW0oSi8UkSdnZ2crKyopXhKRz8ByEbFICAAAAZBJ39WLFXv6ztL9BZr+hCl32fcpBAEDSiNsMwqMtJfnNb36jhoYGeZ6nG264IV4Rkg7nIAQAAAAyi+95cj+cJ/fTNyVJ1sjxss66RIbJ+QYBAMkjbgWh9NVLSf793/89nk+btGyLGYQAAABApvBj++UselLehlWSacoed5msYWODjgUAwJfEtSDEoWyLGYQAAABAJvDrdrdsRlKzVQpnK3TBTTL7DA46FgAAR0RBmECtS4wdjxmEAAAAQLrydmxSbP4cqWGfjM7dZV98m8yuPYKOBQDAV6IgTKDWTUpclxmEAAAAQDpy1y+T89pTkuvIKBqo0AU3ysjODToWAABHRUGYQK1LjDkHIQAAAJBefN+X+8kiuYsXSpLMoWNkj79chsWPXACA5Me7VQJZB2YQOpyDEAAAAEgbvhOT88Yz8sqXSjJknXWxrFHnyDCMoKMBANAuFIQJdHCTEmYQAgAAAOnAb6xTbP4c+ds3SnZY9qTrZBUPCzoWAADHhIIwgdpmEHIOQgAAACDlebXbFHtlllS3W8rrotDkW2V2Lwo6FgAAx4yCMIE4ByEAAACQHtyNq+WUPSHF9svo2Vehi26REekUdCwAAI4LBWECte1izDkIAQAAgJTk+77cFe/Kfe8lyfdlDhwl+/yrZdihoKMBAHDcKAgTyGqdQUhBCAAAAKQc33XlvPuCvFUfSJKs0ybJGjNJhmEGnAwAgBNDQZhAttV6DkKWGAMAAACpxN/fqNjCx+RvLpcsW/a5V8kacmrQsQAA6BAUhAlkma27GPvyfV+GYQScCAAAAMDX8fdUKzZvtvzdO6WcPIUuvFlmYf+gYwEA0GEoCBPINAyZhiHP9+V6ftumJQAAAACSk7elQrEFj0r7G2TkFyg0+TYZnboFHQsAgA5FQZhgtmWo2fHleL5sK+g0AAAAAL6Ku/ojOW89K3muzH4nyZ50vYxwdtCxAADocBSECda2zNj1pBANIQAAAJBsfN+T+8F8uZ++IUmyRo6TddalMkw2IwEApCcKwgRr2ajEZSdjAAAAIAn5sf1yFj0pb8MqyTBlj79M1rCxQccCACCuKAgTzP7iDEIAAAAAScOv26PYvFnya7ZK4WyFLrhRZp8hQccCACDuKAgTzLJaliUwgxAAAABIHt6OTYrNnyM17JPRubvsi2+T2bVH0LEAAEgICsIEsw8UhDFmEAIAAABJwV2/TM5rT0muI6PXAIUuvElGdm7QsQAASBgKwgQLtxaEDgUhAAAAECTf9+V+skju4oWSJPOkMbLPuVyGxY9JAIDMwjtfgoXtloKwmYIQAAAACIzvxOS88Yy88qWSDFlnXSxr1DkyDCPoaAAAJBwFYYKF7NYZhG7ASQAAAIDM5DfWKTb/b/K3V0p2WPak62QVDws6FgAAgaEgTLCwbUliBiEAAAAQBK92m2LzZkv7dkm5XRSafKvMaFHQsQAACBQFYYK1LjFmkxIAAAAgsdyNa+SUPS7F9svo0Uehi26Rkds56FgAAASOgjDBQhbnIAQAAAASyfd9uSvelfveS5Lvyxw4Svb5V8uwQ0FHAwAgKVAQJlg41FoQcg5CAAAAIN5815Xz7gvyVn0gSbJOmyRrzCQZhhlwMgAAkgcFYYKFrJZzEMaYQQgAAADElb+/UbGyx+VXrZMsW/a5V8oaMjroWAAAJB0KwgRrPQchS4wBAACA+PH31Cg2b5b83TulnDyFLrxZZmH/oGMBAJCUKAgT7GBByBJjAAAAIB68LRWKLXxUamqQkV+g0ORbZXTKDzoWAABJi4IwwcL2gSXG7GIMAAAAdDh3zUdy3nxW8lyZ/U6SPel6GeHsoGMBAJDUKAgTLMQSYwAAAKDD+b4n98P5cpe+IUmyRo6TddalMkw2IwEA4OtQECZY6xJjNikBAAAAOoYfa5az6O/yNqySDFP2+MtkDRsbdCwAAFIGBWGCcQ5CAAAAoOP4dXsUmz9bfvUWKZyt0AU3yuwzJOhYAACkFArCBAtZLecgZIkxAAAAcGK8nVWKzZstNeyTOndXaPKtMrv1DDoWAAAph4IwwcKcgxAAAAA4YW7FcjmvPSU5MRm9Bih04U0ysnODjgUAQEqiIEywg+cgZIkxAAAAcKx835f7yWtyFy+QJJknjZF9zuUyLH60AQDgePEummBh+8ASY5cZhAAAAMCx8F1HzhvPyFv3iSRD1tjJsk6ZIMMwgo4GAEBKoyBMsBBLjAEAAIBj5tbvVezFR+Rvr5TskOxJ18kqHh50LAAA0gIFYYKF2pYYe/J9n992AgAAAF/Dq92unQv+Jn9PtZTbRaHJt8iM9g46FgAAaYOCMMFMw5BtGXJcXzHXa1tyDAAAAODLvI1rFCt7XIrtl9Gjj0IX3SIjt3PQsQAASCsUhAEI25Yc11HMoSAEAAAAjsT3fXkr35Xz7kuS7yvn5DFyv/FtGaFw0NEAAEg7ZtABMlGY8xACAAAAX8l3XTlvPy/nnRcl35d12kR1u+J7lIMAAMQJMwgDcLAgdANOAgAAACQXf3+jYmWPy69aJ5mW7POukjVktAyDuQ0AAMQLBWEAskMtw97YTEEIAAAAtPL31Cg2b5b83Tul7FyFLrpFZmH/oGMBAJD2KAgDkJPVct7BxmYn4CQAAABAcvC2VCi28FGpqUFGtwKFLr5VRqf8oGMBAJARKAgDkBNmBiEAAADQyl3zkZw3n5U8V2bfk2SXXi8jnB10LAAAMgYFYQDaCsL9zCAEAADprbGxUQ888IDq6+tVWlqqc88995Db77rrLnXr1k2SdPvtt6tPnz5BxERAfN+T++ECuUtflyRZI8bJ+sYlMkwr2GAAAGQYCsIA5IRZYgwAADLDq6++qnHjxmncuHH62c9+pnHjxsm2D34L2rlzZ917773BBURg/FiznEVPytuwUjJM2eO/LWvYWUHHAgAgI7EVWABYYgwAADLF2rVrNWrUKJmmqf79+2vz5s2H3F5XV6f/+q//0sMPP6zm5uaAUiLR/Po9ir3w/1rKwXC2QpdMpRwEACBAzCAMwMGCkBmEAAAgvTU0NCgnJ0eSFIlEVF9ff8jtM2bMUF5enubOnauysjJdcsklX/ocZWVlKisrkyTNnDlT0Wg0/sHjyLbtlH8NJ6J5ywbVPPcH+XV7ZHXroe7X3KlQtNfXPi7Tx+14MGbHh3E7dozZ8WHcjh1jFj8UhAFgF2MAAJBudu/erd/+9reHXNe1a1dFIhE1NjYqHA6roaFBubm5h9wnLy9PknTmmWfq5ZdfPuLnLi0tVWlpadvl6urqjg2fYNFoNOVfw/FyK5bLee0pyYnJ6DVA1oU3aY9CUjvGI5PH7XgxZseHcTt2jNnxYdyOHWN2fIqKir72PhSEAWCJMQAASDddu3Y94rkEX3rpJS1fvlxnn322Kisr1bt377bbHMeR7/sKhUJas2aNCgoKEpgYieT7vtxPXpe7eL4kyTxpjOxzLpdh8eMIAADJgHfkALQWhA3sYgwAANLcxIkT9bvf/U7z5s1TaWmpbNvW0qVL5XmeBg4cqPvvv1/Z2dnKzc3Vj370o6DjIg5815HzxjPy1n0iyZA1drKsUybIMIygowEAgAMoCAPQuotxE0uMAQBAmotEIrr77rsPue7UU09t+/gXv/hFghMhkfzGOsUW/E3+tkrJDsmeeJ2sAcODjgUAAA5DQRgAlhgDAAAg3Xm12xWbN1vaVyvldlZo8q0yo72//oEAACDhKAgDkB22ZEhqirnyPF+myfIKAAAApA9v4xrFXn1cat4vo0cfhS66RUZu56BjAQCArxDXgnDWrFmqqKjQgAEDNHXq1LbrH374YW3atEmSdPvtt6t///7xjJF0TMNQVshSU8xVU8xVJIueFgAAAOnBXfGunHdflHxf5sCRss+7WkYoHHQsAABwFGa8PnFFRYWampo0ffp0OY6j8vLyttsuv/xyzZgxQ9///vf19NNPxytCUsvJYqMSAAAApA/fcxV76zk577wg+b6s0ybKLr2echAAgBQQt4Jw3bp1GjVqlCRp5MiRWrt2bdttPXv2lCRZliXTjFuEpJZ3oCCsa4oFnAQAAAA4Mf7+RsVemSVv1fuSack+/1rZZ1wow8jM7/UBAEg1cVvbWl9fr4KCAkktu9dVVVV96T6PP/64LrnkkiM+vqysTGVlZZKkmTNnKhqNxitqQti2fchryO+Sq0019TJC2Sn/2lLN4ccCweFYJA+ORXLgOCQPjgXQfv6eGsXmzZK/e6eUnavQRTfLLCwOOhYAADgGcSsII5GIGhoaJEmNjY2KRCKH3P7yyy+rT58+Gjp06BEfX1paqtLS0rbL1dXV8YqaENFo9JDXkGW1/L1lR636dwsFlCozHX4sEByORfLgWCQHjkPySIdjUVRUFHQEZABv6+eKLfib1NQgo1uBQhffKqNTftCxAADAMYrbnP+SkhKtWLFCkrR8+XKVlJS03fbpp59qzZo1uvLKK+P19EmvU3ZLKbivkSXGAAAASD3umo8Ue+l/pKYGmX1PUujyOygHAQBIUXErCAcOHKhQKKRp06bJNE1Fo1HNnTtXkvSXv/xFO3fu1M9+9jM9/PDD8YqQ1DrltBaEzQEnAQAAANrP9z05H8yT8/o/JM+VNeJs2ZNvkRHODjoaAAA4TnFbYixJU6dOPeTylClTJEkPPPBAPJ82JeQdKAjZpAQAAACpwo81y1n0pLwNKyXDlD3u27KGnxV0LAAAcILiWhDiq7HEGAAAAKnEr9+j2LzZ8qu3SOFshS64UWafIUHHAgAAHYCCMCAHlxhTEAIAACC5eTurFJs3R2rYK3XurtDkW2V26xl0LAAA0EEoCAPCEmMAAACkArdihZzXnpScmIxeAxS68CYZ2blBxwIAAB2IgjAg2SFLtmWo2fG0P+YqK2QFHQkAAABo4/u+3KWvy/1wviTJPOl02edcIcPiRwgAANIN7+4BMQxDnXLC2lW3X3sbm9UjlBN0JAAAAECS5LuOnDfnylu7RJIha+xkWadMkGEYQUcDAABxQEEYoG65LQXh7vpm9ehMQQgAAIDg+Y11ii14VP62DZIdkj3xOlkDhgcdCwAAxBEFYYC65mZJ2qdddfuDjgIAAADI27VdsVdmS/tqpdzOLZuRRHsHHQsAAMQZBWGA8vOyJImCEAAAAIHzNq1VrOwxqXm/jB59FLroFhm5nYOOBQAAEoCCMEDdDhSEtRSEAAAACJC74l05774o+b7MgSNln3e1jFA46FgAACBBKAgDxAxCAAAABMn3XDnvviRv5XuSJOu0ibLGlMowzICTAQCARKIgDFDrDMJd9RSEAAAASCx/f5NiZY/Jr1onmZbsc6+UVXJa0LEAAEAAKAgD1CUSlmFIexqa5biebIvf1AIAACD+/L01ir0yW/7uHVJ2rkIX3SyzsDjoWAAAICAUhAGyLVNdImHtrm/W7vpmRTtnBx0JAAAAac7b+rliC/4mNTXI6NZTocm3yeicH3QsAAAQIArCgEU7Z2t3fbN27GmkIAQAAEBcuWs+lvPmXMlzZfQtUWjSDTKy+B4UAIBMx5rWgBV0yZEk7djTGHASAAAApCvf9+R8ME/O609LnitrxNkKTb6VchAAAEhiBmHgelIQAgAAII78WLOc156U9/lKyTBlj/uWrOHfCDoWAABIIhSEAaMgBAAAQLz49XsUmzdHfvVmKZyt0AU3yuwzJOhYAAAgyVAQBuyLBaHv+zIMI+BEAAAASAfezirF5s2RGvZKnfMVmnybzG49g44FAACSEAVhwDrlhJQdstTY7GpfU0ydc8JBRwIAAECKcytWyHntScmJySgsVujCm2Xk5AYdCwAAJCk2KQmYYRjq1S0iSdpSUx9wGgAAAKQy3/flfPKanIWPSk5MZsnpCn3zdspBAABwVBSESaBP95Zv2DbXNgScBAAAAKnKdx05rz8t98P5kgxZYy+Wfd5VMiwWDQEAgKPju4Uk0PtAQVhVUxdwEgAAAKQiv7FesQV/k79tg2SHZE+8VtaAEUHHAgAAKYKCMAn0aSsIWWIMAACAY+Pt2q7YK7OlfbVSbmeFJt8qM9o76FgAACCFUBAmgR6dcxS2Te2ub1ZdU0x52aGgIwEAACAFeJvWKlb2mNS8X0a0t0KTb5WR2znoWAAAIMVwDsIkYJqG+kbzJEkbduwLOA0AAABSgbviPcVemSU175c5cKRC3/4XykEAAHBcKAiTxICenSRJn2+nIAQAAMBX8z1Xsbefl/PO85LvyRp9vuzS62WEwkFHAwAAKYolxkliQEFnSZv1+fa9QUcBAABAkvL3NylW9rj8qrWSack+90pZJacFHQsAAKQ4CsIk0b9HnkxD2lxbr6aYq+yQFXQkAAAAJBF/b41i82bL37VDys5V6KKbZRYWBx0LAACkAZYYJ4mskKW+0Tx5vrR+656g4wAAACCJeFs3qPnZP8jftUNGt54KX/EDykEAANBhKAiTyEm9u0qSVm/eHWgOAAAAJA937ceKvfSI1FQvo2+JQpd9X0bn/KBjAQCANEJBmESGHigI12zZI9/3gw0DAACAQPm+J+eDeXJee1ryXFkjzlZo8q0ysrKDjgYAANIM5yBMIr275yo329auuv3auqtBRfm5QUcCAABAAPxYs5zXnpT3+UrJMGWP+5as4d8IOhYAAEhTzCBMIqZhaES/luUiyytrA04DAACAIPj1exR74U8t5WA4S6GLb6McBAAAcUVBmGRG9W8pCJdV1rDMGAAAIMN4Ozeree5D8qs3S53zFbr8+zL7lgQdCwAApDmWGCeZQYWdFcmytWNPkzbX1qtP97ygIwEAACAB3IoVcl57UnJiMgqLFbrwZhk5nHIGAADEHzMIk4xlmjptYFSStHjdzoDTAAAAIN5835fzyetyFj4qOTGZJacp9M3bKQcBAEDCUBAmoTMG95AkffJ5tZodN+A0AAAAiBffdeS8/rTcD+dJkqyxk2Wfd7UMi4U+AAAgcSgIk1BRfq76RnPV2OxqcTmzCAEAANKR31iv2Ev/I2/tEskOyb7wJtmnnifDMIKOBgAAMgwFYZI6b0SRJOnNlVvlemxWAgAAkE68XTvU/NxD8rdtkCKdFfr2v8oaMCLoWAAAIEOxdiFJjeibr2jnbFXvbdLyyhqdOiAadCQAAIBj9sknn2j27Nnq1KmTZsyY8aXb33rrLc2fP195eXm68847FYlEAkiZWE0VKxV77o9Sc5OMaG+FJt8iI7dL0LEAAEAGYwZhkjJNQ+cO7yVJem3FFnk+swgBAEDqGTJkiH75y18e8TbHcbRw4UL97Gc/04QJE1RWVpbgdInnrnxPNX9/QGpukjlghELf/hfKQQAAEDhmECax0wf10MKlVdpS26BPKqp1+qAeQUcCAAA4Jnl5eV9527Zt29SvXz9ZlqWRI0fqT3/60xHvV1ZW1lYezpw5U9Foaq6siNVs0453XpR8T3lnX6LO510uw+D39e1l23bKHvugMGbHh3E7dozZ8WHcjh1jFj8UhEksZJm6+LR+evKd9Xr5440a3i9f2SEr6FgAAAAdor6+Xjk5OZKkSCSi+vr6I96vtLRUpaWlbZerq6sTkq/j2bLHX6ZO3fLV0GuIampqgw6UUqLRaAof+2AwZseHcTt2jNnxYdyOHWN2fIqKir72PhSESe60QVG9t3a7Nu6sU9mnVfrmmP5BRwIAAPiS3bt367e//e0h13Xt2lX/9m//9pWPiUQiamxslCQ1NjYqNzc3jgmTgzVsrCLRqBr44QYAACQRCsIkZxqGLj+zWL9/eYXeWrVVI/vnq3+PTkHHAgAAOETXrl117733HtNjevXqpU2bNsnzPC1btkxDhgyJTzgAAAAcFSc9SQF9o3k6Z1gveb70+Jvlamx2go4EAADQLuvXr9eMGTO0adMmzZgxQ83NzVq6dKmWLFki27Y1adIkTZs2TW+88YYuuOCCoOMCAABkJGYQpoiLT+ur9dv2anNtvZ55r0I3ThgiwzCCjgUAAHBUgwYN0j333HPIdaeeemrbxxMmTNCECRMSnAoAAABfxAzCFGFbpm6cMFhh29SnG2o1f2lV0JEAAAAAAACQBigIU0iPLjm66dwhMgzp1WWb9d6a7UFHAgAAAAAAQIqjIEwxJ/fppivPGiBJmvv+53p39baAEwEAAAAAACCVURCmoLElBfrmmH6SpGc/2KCyT6vk+37AqQAAAAAAAJCKKAhT1LnDi3TlNwbIkDR/aZUefWOd9sfcoGMBAAAAAAAgxVAQprCzSgp06/klygpZWlZZqwdeWq6NO/cFHQsAAAAAAAAphIIwxQ3vl687Lx2hgi452rm3SQ++slIvLq5UY7MTdDQAAAAAAACkAArCNNCzS47u+tZInTu8l+RLb67aqplzl+qdz7bJ9byg4wEAAAAAACCJURCmiZBl6ptj+utHl47QwIJOatjv6LkPN+gXz36qt1ZtVRPnJwQAAAAAAMAR2EEHQMfqG83Tv140TCs37dI/P96onXub9MLiSi1YWqUxg3vo9EE91Ds/IsMwgo4KAAAAAACAJBDXgnDWrFmqqKjQgAEDNHXq1Lbr586dq/nz5+v888/XddddF88IGckwDI3ol69hfbtp1aZdenPlVn2+Y5/e/myb3v5smwq65mhU/+4a1rerivJzZVIWAgAAAAAAZKy4FYQVFRVqamrS9OnT9cgjj6i8vFyDBw+WJE2cOFElJSVasWJFvJ4ekswDReGIfvmqqqnXx+t36pOKam3f3aiFu6u08NMqdcoJaWjvrhrcq4uKe+apW24WswsBAAAAAAAySNwKwnXr1mnUqFGSpJEjR2rt2rVtBWHXrl21efPmeD01jqBP91z16Z6rb47pp7Vb9mjVpl1avXm3dtc3a3H5Ti0u3ylJ6pwTUnHPTurdPVe9ukVU2DWirrlhSkMAAAAAAIA0FbeCsL6+XgUFBZKkSCSiqqqqY3p8WVmZysrKJEkzZ85UNBrt8IyJZNt20ryGgp49dc6pku/7qqrep+Wf79DazbUq37JLextjWlZZq2WVtW33z8my1ad7JxV0y1W0S0Q9DvyJdomoS25Wyi1RTqZjkek4FsmDY5EcOA7Jg2MBAACATBK3gjASiaihoUGS1NjYqEgkckyPLy0tVWlpadvl6urqDs2XaNFoNClfQ44hnTmwq84c2FWe72vnniZV7tynrbsatG1Xg7bualD9fkfrtuzSui27vvR42zTUKSekTjlh5eWE1Ck7pE45obaPc7Js5YQtZYcO/B22ZZnBForJeiwyEccieXAskgPHIXmkw7EoKioKOgIAAABSRNwKwpKSEpWVlenss8/W8uXLdd5558XrqdBBTMNQQdccFXTNabvO933ta4pp265G1dY1qXbfftXW7VftvibV1u1X/X5Hu+qbtau+ud3PE7ZN5YRtZYcshWxTYdtUyDYVsqy2j8PWgb9tS7ZlyjKNI/w57HrLlGUYsixDlmHINA2ZhiHDUMsftXxsZzdpX2OzDMOQIck0W/42Dty37TFqfWxqzZAEAAAAAAA4FnErCAcOHKhQKKRp06apuLhY0WhUc+fO1ZQpU7Ro0SLNnz9fdXV1qqur0+233x6vGDhBhmGoc05YnXPCkrp86fbmmKu9jTHVNcW0rzGmfY3N2tcUU11jy+WmmKumZkeNza4amx01xVw1O56anWbtSfzLOW4tkx5bisLD+0LjsA+Mgx986T4H72scfpcjf+7DrvjK50pRpmnK87ygY2ScI3XeHIvkkGzHIbW/wpyYn992ftARAAAAgISJW0EoSVOnTj3k8pQpUyS17GI8ceLEeD41EiQcshQNWYp2zm7X/X3f137HU1Ozo6ZmVzHXU7PjKea4am77+OB1Mbflsuv5cn1frtv694Hr2v4cftmX5/vyfV++3/K83oG/DdOU63oHrjtwu3ToZV/y1fKxJHm+1HKvg38d5VUe32ACAJKGz9dyAAAAZJC4FoTA4QzDUHbIUnbIknKDyXCs55VqLRoltRWGrfzDPvAPKxH9I97X/9JtR/zch13xVc+Vyj/Cds/PV01t7dffER3nK/7B5Ofnq5ZjEbhkOg6p/LWlI+Rlh1XbEHQKAAAAIDEoCIGvYbaexBAdrktutmKN4aBjQFLXvGw5TRyLoHEckocZ8IZaAAAAQCKZQQcAAAAAAAAAEBwKQgAAAAAAACCDURACAAAAAAAAGYyCEAAAAAAAAMhgFIQAAAAAAABABqMgBAAAAAAAADIYBSEAAAAAAACQwSgIAQAAAAAAgAxGQQgAAAAAAABkMApCAAAAAAAAIINREAIAAAAAAAAZjIIQAAAAAAAAyGAUhAAAAAAAAEAGoyAEAAAAAAAAMhgFIQAAAAAAAJDBKAgBAAAAAACADEZBCAAAAAAAAGQwCkIAAAAAAAAgg1EQAgAAAAAAABmMghAAAAAAAADIYBSEAAAAAAAAQAajIAQAAAAAAAAyGAUhAAAAAAAAkMEoCAEAAAAAAIAMRkEIAAAAAAAAZDAKQgAAAAAAACCDURACAAAAAAAAGYyCEAAAAAAAAMhgFIQAAAAAAABABjN83/eDDgEAAAAAAAAgGMwgTJC777476Ag4gGORPDgWyYNjkRw4DsmDY4F44t/X8WHcjh1jdnwYt2PHmB0fxu3YMWbHpz3jRkEIAAAAAAAAZDAKQgAAAAAAACCDURAmSGlpadARcADHInlwLJIHxyI5cBySB8cC8cS/r+PDuB07xuz4MG7HjjE7PozbsWPMjk97xo1NSgAAAAAAAIAMxgxCAAAAAAAAIINREAIAAAAAAAAZzA46QCaYNWuWKioqNGDAAE2dOjXoOGmttrZWv/jFL1RVVaU5c+bIsqwjjn97r8PxWbdunWbPni3DMDRo0CDddttteuGFF7R48WL16NFD3//+92Xbdruvw/HbuHGjHn74YZmmqcLCQt1xxx2aPXs2/ycC9NJLL+mDDz7QjBkz+PoUkB07duj//t//q969e8u2bf3nf/4nX6OQEEf6PgVf70jfV+DojvT+bxhG0LFSxhffq3F0R3pPRfu88cYbeuONN+R5nu68807l5+cHHSnpLV26VM8995wkacuWLbr99tt15plnBhsqye3fv1+//vWvtX//fkUiEf34xz9WKBQ64n2ZQRhnFRUVampq0vTp0+U4jsrLy4OOlNby8vJ0zz33aMiQIZKOPP7tvQ7Hr0ePHpo2bZpmzJihvXv3atWqVVq5cqVmzJihfv36afHixdqzZ0+7rsOJKSoq0s9//nNNnz5dklReXs7/iQDFYjFt2LBBEl+fgjZy5Ejde++9+s///M92fz3iaxRO1OHfp6B9Dv++YuPGjUFHSnqHv/+vX78+4ESp44vv1WifL76non1qa2u1atUqTZs2Tffeey/lYDudeuqpuvfee3XvvfcqGo1q1KhRQUdKekuXLtWQIUN07733avDgwVq6dOlX3peCMM7WrVvX9o925MiRWrt2bcCJ0ls4HFZeXl7b5SONf3uvw/Hr2rWrwuGwJMmyLG3atEnDhg2TJI0aNUpr167V+vXr23UdTswXZzfZtq3ly5fzfyJAixYt0nnnnSeJr09BW7lypaZNm6aXXnqp3V+P+BqFE3X49ylon8O/rzBNfoT5Ooe//0ej0QDTpJYvvlejfb74nor2Wbp0qTzP0/Tp0/WXv/xFnucFHSmlbN++XV26dFF2dnbQUZJeQUGBmpqaJEn19fXq1KnTV96Xd9c4q6+vVyQSkSRFIhE1NDQEnCizHGn823sdTlxlZaX27t2r3Nxc5eTkSGoZ3/r6ejU0NLTrOpy4jz76SD/96U+1Z88eua7L/4mAOI6jlStXasSIEZL4+hSkbt266YEHHtB//dd/afny5aqoqOBrFJACWr+v6NOnT9BRUsIX3/8pptvn8PdqfL3D31MrKyuDjpQS9uzZI8dxNG3aNIXDYVYlHKMPPviApcXt1KtXL61bt04/+clPVFFRoZKSkq+8LwVhnH3xh7nGxsa2H/KQGEca//ZehxNTV1env/zlL7rjjjsUiUTU2NgoSWpoaFBubm67r8OJGzNmjH71q1+pe/fusiyL/xMBefPNNzV+/Pi2y3x9Ck4oFFJ2drYsy9Lpp5+ugoICvkYBSe6L31egfb74/r9kyZKg46SEw9+r8fUOf0/dtGlT0JFSQiQSaVuVMGLECG3evDngRKnl448/1pgxY4KOkRLeeOMNnX766fr1r3+t0aNH66233vrK+1IQxllJSYlWrFghSVq+fPlR21p0vCONf3uvw/FzXVe///3vdfPNN6tr164aNGiQVq1aJallfIcMGdLu63BiYrFY28etM5/4PxGMLVu2aOHChbrvvvtUVVWlffv2cSwC0lrySdLq1atVWFjI1yggiR3+fQW+3uHv/61LtHF0h79Xv/LKK0FHSnqHv6cWFBQEmCZ1nHTSSW2zLTds2KCePXsGnCh17N69W7ZtH3WpLA7yfb9tFnnnzp2PuhqJrffibODAgQqFQpo2bZqKi4s1ePDgoCOlNcdxdP/996uyslL33Xefrr/++iOOf3uvw/F57733VF5erkcffVSSdMMNN+jkk0/WPffco2g0qksvvVS2bbfrOpyYpUuXtp0PplevXvre976n2bNn838iADfddFPbx/fcc4+uvvpq/fWvf+VYBOCzzz7Tk08+qVAopKFDh2rIkCF8jUJCHOn7FIrmr3ek7yv4ZcnRHf7+z4n82+fw9+qLL744wDSp4Ujvqfh6xcXFCofDuvfee9WpUyd985vfDDpSyli8eLHOOOOMoGOkjPHjx+u3v/2t3nzzTVmWpR//+MdfeV/D930/gdkAAAAAAAAAJBGWGAMAAAAAAAAZjIIQAAAAAAAAyGAUhAAAAAAAAEAGoyAEAAAAAAAAMhgFIQAAAAAAAJDBKAgBpKUdO3bommuu0cyZM7VkyRI99dRT2rFjR4c/T1VVlZ566imtXLmy7bqHHnpI11xzjdavX9/hzwcAAAAAQEezgw4AAPHQuXNn3XXXXcrPz9e7776r+fPna/jw4erZs+cxfR7XdWVZ1lfeXlVVpX/84x+SpOHDh0uSLrzwQp166qkqKCg4/hcAAAAAAECCGL7v+0GHAICOtmPHDv3whz9UVlaW9u/ff8htTz31lNauXavZs2dr48aNys/P19VXX63x48e3Pa6kpERZWVnauHGjfvWrX+nnP/+5tm7dKkkaMGCAvvvd7yorK0s//OEPD/nc//Vf/6XXX39db7zxhu6//34NGjRIZWVleuGFF7Rr1y716dNHt956q4YOHarXX39df/jDH3T22Wdr8+bNqq6u1tVXX61LLrlEW7Zs0YMPPqjKykqFw2H17dtX06dPT9j4AQAA4Oh+/etfq0uXLtqwYYNqamp05513auHChSovL9fQoUN1xx13BB0RANqNJcYA0tqwYcN0yimnSJKuvPJK3XXXXaqrq9PMmTPV0NCgKVOmqEePHvr973+vDRs2tD1u7dq1GjBggK699loZhqEzzzxTU6dO1eWXX67KykrNmjVLnTt31iWXXCJJGjt2rO666y716dPnkOdfsWKFHn74YXXu3Fm33HKLqqur9Ytf/EL79u1ru8/KlSs1adIkSdJjjz0mx3E0f/58rV+/XjfddJOuv/56RaPROI8UAAAAjsXGjRtVUFCgGTNmqLS0VH/84x9100036de//rWWLFmiWCwWdEQAaDeWGANIa4ZhqLCwUJ9++qlGjBih4cOHa8mSJaqrq1NdXZ2eeOKJtvuuWLFCZ555pqSWWYI33XSTJKm2tlaffvqp1q5dq9ZJ1xs3blR2draGDh2qf/7zn+rbt6/GjRv3pedfsmSJJOmaa67RqFGjVF1drWeffVbr1q1ru8/555+vyZMn6+OPP9ann36q3bt3q1evXvJ9X5988okGDRrUVkQCAAAgeM3Nzaqvr2/7Hs0wDE2cOFHdunWTJJmmKdvmx20AqYOvWADSnmEYR7x+woQJmjBhQtvlL56fsPWbO0l65ZVXtGbNGl166aUaPXq0/vjHP6qxsbHDsuTl5UlS27kOPc/T5MmT1bt3b61atUofffSR5s6dq9/85jcqKio6rucFAABAx6mqqtLAgQNlmi2L8iorK3XhhRdKkmpqapSfn/+V34MCQDJiiTGAtJebmytJev/997VkyRKVlJQoLy9Pn376qbZs2aJNmzbp+eefV21t7VE/T319vVatWqWampq261rLvdWrV+udd95Rc3PzIY857bTTJElPP/20Fi5cqEWLFik3N1dDhgw56nMtWLBAa9euVWFhoQoKCuT7vnbv3n2sLx0AAABxsHHjRvXv37/tcmVlpfr16/eljwEgVVAQAkh755xzjnr37q0FCxbor3/9q/Ly8nT33XersLBQjz32mObOnatwOKwePXoc8fEXX3yxBg0apHfffVe1tbXq27dv221Dhw7VyJEj9dlnn+mBBx445NyCkjRixAh973vf0549ezRnzhx1795d//Ef/6FOnTodNXMoFNLrr7+uP/3pT/rss8900UUXaejQoSc+GAAAADhhGzduVHFxsaSW5cbNzc1tvziurKw8pDwEgFTALsYAAAAAAABABmMGIQAAAAAAAJDBKAgBAAAAAACADEZBCAAAAAAAAGQwCkIAAAAAAAAgg1EQAgAAAAAAABmMghAAAAAAAADIYBSEAAAAAAAAQAb7/wGYLpwJtbOSUwAAAABJRU5ErkJggg==",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"low, high, step = 0, 5000, 10\n",
"plot_all(cost_history, m, q, low, high, step)"
]
},
{
"cell_type": "code",
"execution_count": 145,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"254 passi e 25400 gradienti calcolati per arrivare a distanza minore o uguale di 0.1 dall'ottimo\n"
]
}
],
"source": [
"near_opt(m, min_dist=1e-1, ge_per_step=n)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Metodi del secondo ordine"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"La ricerca di un punto di massimo (o minimo) può anche essere effettuata in termini di ricerca di punti in cui la derivata prima (o il gradiente, in generale) si annullano, applicando uno dei metodi iterativi standard per la ricerca degli zeri di una funzione.\n",
"\n",
"Un tipico metodo utilizzato in questo ambito è quello di Newton-Raphson, in cui (considerando una funzione univariata) viene applicato, ad ogni iterazione, l'aggiornamento\n",
"\n",
"$$\n",
"x_{i+1}=x_{i}-\\frac{f(x_{i})}{f'(x_{i})}\n",
"$$\n",
"\n",
"A ogni iterazione, l'algoritmo approssima $f$ per mezzo di una retta tangente a $f$ in $(x_i,f(x_{i}))$, e definisce $x_{i+1}$ come il valore in cui tale retta interseca l'asse $x$.\n",
"\n",
"\n",
"\n",
"\n",
"Nel caso in cui si cercano punti di massimo o minimo, l'iterazione evidentemente diviene\n",
"\n",
"$$\n",
"x_{i+1}=x_{i}-\\frac{f'(x_{i})}{f''(x_{i})}\n",
"$$"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Nel caso di funzioni a più variabili, la derivata prima è sostituita dal gradiente \n",
"$\\nabla f$, mentre la derivata seconda corrisponde alla matrice *Hessiana* $H$, definita come\n",
"\n",
"$$\n",
"H_{ij}(f)=\\frac{\\partial^{2}f}{\\partial x_{i}\\partial x_{j}}\n",
"$$\n",
"\n",
"L'aggiornamento ad ogni iterazione diviene quindi\n",
"\n",
"$$\n",
"\\mathbf{x}^{(i+1)}=\\mathbf{x}^{(i)}-\\big(H(f)^{-1}\\nabla f\\big)\\big|_{ \\mathbf{x}_{(i)}}\n",
"$$\n"
]
},
{
"cell_type": "code",
"execution_count": 216,
"metadata": {},
"outputs": [],
"source": [
"theta = theta_history[1]\n",
"c1 = sigma(theta,X)\n",
"h = np.zeros([3,3])\n",
"for i in range(t.shape[0]):\n",
" m=X[i,:].reshape(1,-1)\n",
" h = h+np.dot(m.T,m)*c1[i]*(1-c1[i])\n",
"h = h/t.shape[0]\n",
"g=gradient(theta,X,t)"
]
},
{
"cell_type": "code",
"execution_count": 217,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"(3, 1)"
]
},
"execution_count": 217,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"g.shape"
]
},
{
"cell_type": "code",
"execution_count": 219,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([[-2.81931877],\n",
" [-0.44421613],\n",
" [ 0.31414362]])"
]
},
"execution_count": 219,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"np.dot(np.linalg.inv(h),g)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"def gradient(theta, X, t):\n",
" return -np.dot(X.T, (t-sigma(theta, X))) / len(X)"
]
},
{
"cell_type": "code",
"execution_count": 222,
"metadata": {},
"outputs": [],
"source": [
"def newton(X,t, epochs = 100):\n",
" theta = np.zeros(nfeatures+1).reshape(-1,1)\n",
" theta_history = []\n",
" cost_history = []\n",
" for k in range(epochs): \n",
" g = gradient(theta,X,t)\n",
" c1 = sigma(theta,X)\n",
" h = np.zeros([nfeatures+1,nfeatures+1])\n",
" for i in range(t.shape[0]):\n",
" m=X[i,:].reshape(1,-1)\n",
" h = h+np.dot(m.T,m)*c1[i]*(1-c1[i])\n",
" h = h/t.shape[0]\n",
" theta = theta - np.dot(np.linalg.inv(h),g)\n",
" theta_history.append(theta)\n",
" cost_history.append(cost(theta, X, t))\n",
" theta_history = np.array(theta_history).reshape(-1,3)\n",
" cost_history = np.array(cost_history).reshape(-1,1)\n",
" m = -theta_history[:,1]/theta_history[:,2]\n",
" q = -theta_history[:,0]/theta_history[:,2]\n",
" return cost_history, m, q"
]
},
{
"cell_type": "code",
"execution_count": 323,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"tempo di esecuzione: 0.021 secondi\n",
"100 passi totali\n",
"10000 gradienti valutati\n"
]
}
],
"source": [
"start_time = time.time()\n",
"cost_history, m, q = newton(X,t, epochs = 100)\n",
"print(f\"tempo di esecuzione: {time.time()-start_time: 4.3f} secondi\")\n",
"print(f\"{len(m)} passi totali\")\n",
"print(f\"{len(m)*n} gradienti valutati\")"
]
},
{
"cell_type": "code",
"execution_count": 324,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABQgAAAGoCAYAAAAKMwiTAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAABshUlEQVR4nO3de3yU9Z33//d1XTNJmITzQCCckhBCOCTI2QOiQjyU2qpR0a7a3VSW3Xa72oPr7X3/tthCu6XtXVeqXe+VrWVdsStqtFZdkRTRonI+BQMkMQIJRwMi5EQy13X9/ggZjIKiMrmuybyej0cfda6ZDJ+ZDwnJO5/v92u4rusKAAAAAAAAQEIyvS4AAAAAAAAAgHcICAEAAAAAAIAERkAIAAAAAAAAJDACQgAAAAAAACCBERACAAAAAAAACYyAEAAAAAAAAEhgAa8LON/279/vdQlfSjgcVl1dnddlJDz64B/0wh/ogz/QB3/oKn3IyMjwuoTzKt6/B/SrrvL3PZ7RA+/RA2/x/nuPHnjvfPbgbN8DMkEIAAAAAAAAJDACQgAAAAAAACCBERACAAAAAAAACYyAEAAAAAAAAEhgBIQAAAAAAABAAiMgBAAAAAAAABIYASEAAAAAAACQwAgIAQAAAAAAgARGQAgAAAAAAAAkMAJCAAAAAAAAIIEREAIAAAAAAAAJjIAQAAAAAAAASGAEhAAAAAAAAEACIyAEAAAAAAAAEhgBIQAAAAAAAJDACAgBAAAAAACABBaI5ZMvWbJE1dXVysrKUnFxcfT6o48+qpqaGknSnDlzNGzYMC1ZskS7d++WJO3Zs0e///3vtWrVKj333HPq3bu3cnJydPvtt8eyXAAAAAAAACDhxCwgrK6uVnNzs+bPn6/FixerqqpKOTk5kqTrr79e/fv314EDB7R06VLdc889+pu/+RtJ0nvvvac//elP0ef5+te/rpkzZ8aqTAAAAAAAACChxWyJcWVlpQoKCiRJ+fn5qqioiN7Xv39/SZJlWTLNjiWsW7dOU6dOjd5++eWXdf/996usrCxWpQIAAAAAAAAJK2YThA0NDUpPT5ckhUIh1dbWfuIxTz75pGbNmtXh2pYtW3T99ddLkiZPnqzp06ervr5eP/3pT7Vw4cJPBIqlpaUqLS2VJC1cuFDhcDgGr6bzBAKBuH8NXQF98A964Q/0wR/ogz/QBwAAAHQ1MQsIQ6GQGhsbJUlNTU0KhUId7n/ppZc0ePBg5eXlRa8dOHBAffr0UXJysiQpNTVVktSjRw8NHDhQx44dU58+fTo8T2FhoQoLC6O36+rqYvJ6Oks4HI7719AV0Af/oBf+QB/8gT74Q1fpQ0ZGhtclAAAAwCditsQ4NzdX27dvlySVlZUpNzc3et/WrVu1a9cu3XjjjR0+Zt26dZoyZUr0dnvA2NLSooMHD6pHjx6xKhcAAAAAAABISDGbIMzOzlYwGNS8efOUmZmpcDiskpISFRUV6bHHHlMoFNJPfvITZWRkaO7cuZKkTZs26Z/+6Z+iz/HSSy9py5Ytcl1X1113nQKBmB66DAAAAAAAACQcw3Vd1+sizqf9+/d7XcKX0lWWLcU7+uAf9MIf6IM/0Ad/6Cp96OwlxkuWLFF1dbWysrJUXFwcvb5t2zY99dRTSkpK0pw5czRo0CAtW7ZM69evV2pqqiZNmqRrr732M58/3r8H9Kuu8vc9ntED79EDb/H+e48eeO989uBs3wMykgcAAICYqq6uVnNzs+bPn6/FixerqqpKOTk5kqRnnnlGP/rRj9TU1KQlS5bo+9//viTpjjvuUEFBgZdlAwAAJIyY7UEIAAAASFJlZWU07MvPz1dFRUWH+1NSUtS7d28dOnQoem3p0qVasGCBdu/e3ZmlAgAAJCQmCAEAABBTDQ0NSk9PlySFQiHV1tZ2uP/YsWNqaGjQvn37JEmzZs3S7NmzdeDAAT3yyCOaP3/+J56ztLRUpaWlkqSFCxcqHA7H+FUkpkAgwHvrMXrgPXrgLd5/79ED73VGDwgIAQAAEFOhUEiNjY2SpKamJoVCoeh9t99+uxYtWqRwOKyRI0dKktLS0iRJAwcOPOtzFhYWqrCwMHqbvZFig32nvEcPvEcPvMX77z164L3O2IOQJcYAAACIqdzcXG3fvl2SVFZWptzc3A733X///SoqKtKgQYMkKRomHj9+XLZtd37BAAAACYYJQh9ZvGKHDh5r0t8W5mlA79BnfwAAAEAcyM7OVjAY1Lx585SZmalwOKySkhIVFRWppKREZWVlSktL09y5cyVJTzzxhGpqauQ4jm677TaPqwcAAOj6CAh9pPFkRMcbW9QScbwuBQAA4LwqLi7ucLuoqCj6/+3/3a49KAQAAEDnYImxjwSstnZEHAJCAAAAAAAAdA4CQh8JmIYkKWK7HlcCAAAAAACAREFA6CPtE4Q2E4QAAAAAAADoJASEPmIxQQgAAAAAAIBORkDoI9E9CG0mCAEAAAAAANA5CAh9JGCdmiBkiTEAAAAAAAA6CQGhjwTM9glClhgDAAAAAACgcxAQ+kj7BCGHlAAAAAAAAKCzEBD6iMUEIQAAAAAAADoZAaGPRPcg5JASAAAAAAAAdBICQh+JnmLsMEEIAAAAAACAzkFA6CMBkwlCAAAAAAAAdC4CQh9pnyC0mSAEAAAAAABAJyEg9BGLCUIAAAAAAAB0MgJCH4nuQcgpxgAAAAAAAOgkBIQ+cvqQEiYIAQAAAAAA0DkICH3k9CElTBACAAAAAACgcxAQ+sjpQ0qYIAQAAAAAAEDnICD0EYsJQgAAAAAAAHQyAkIfOX1ICROEAAAAAAAA6BwBrwvAaQHr1AQhS4wBAAAShnNwjyRXRvowGYbhdTkAACABERD6SMBsnyBkiTEAAECiiKxfLnd/tYw+6bJGXShzxHgZySlelwUAABIIAaGPtO9ByCElAAAAicF1HZnpw2R/cFju0UOKvPlHae3LMnPGyRp9ocx+g70uEQAAJAACQh85vQchE4QAAACJwDBMBaZcLWviTDm7y2WXr5W7/105OzfI2blBRniQrNFTZeZcICOY5HW5AACgiyIg9JHoHoQcUgIAAJBQDCsga3iBrOEFco69L2fHWtm7Nsmt26fIGyXSmpdkjpgga9RUmX0HeF0uAADoYggIfSS6B6HDBCEAAECiMnv1k3nRtbImXy2nervsHWvkHtwj55235bzztoz0YW1Thdn5MgJBr8sFAABdAAGhj1inJghtJggBAAASnhEIysodLyt3vJwjB2XvWCunYpPcQ3sUObRHeutFWSMnyBw1VWavfl6XCwAA4hgBoY9E9yBkghAAAAAfYfYdIHPadXKnXiOnamvbXoV1+2RvWy1722oZGcPbpgozR8uw+BYfAAB8Pnz34COnTzF25biuTMPwuCIAAAD4iRFMljVqiqxRU+S8Xyu7fK2cqi1y97+ryP53pW5pskZOkjVqiowefbwuFwAAxAkCQh8xDUOWach2XNmOK9MiIAQAAMCZmf0Gy7xssNwLvyqncnPbXoVHD8neskr2ltdlDsmVOXqqzKEjZZiW1+UCAAAfi2lAuGTJElVXVysrK0vFxcXR648++qhqamokSXPmzNGwYcO0bNkyrV+/XqmpqZo0aZKuvfZaNTU1adGiRWpoaFBhYaEuu+yyWJbrC0HLlO3YitiOgqeWHAMAAABnYySnyBp7kcwxF8o9tKdtqrC6TE7NLjk1u6TUnrJGTZaVN1lGak+vywUAAD4Us4Cwurpazc3Nmj9/vhYvXqyqqirl5ORIkq6//nr1799fBw4c0NKlS3XPPfdIku644w4VFBREn+PPf/6zLrnkEl1yySX6yU9+oksuuUSBQNceegxYptRqy7bZhxAAAADnzjAMGQMyZQ7IlHvxtbIrNskpXyv3wzrZG0plb1wpc1ierNEXyhicI8Pgl9EAAKBNzL4rqKysjIZ9+fn5qqioiN7Xv39/SZJlWTLN0yUsXbpUCxYs0O7duyVJFRUVKigokGmaGjZsmPbt2xercn0jEGg/qISTjAEAAPDFGCmpChRcquAtP1Tw2jkys/MlQ3J2l6v15cfU8t//V5Etq+Q21XtdKgAA8IGYjeM1NDQoPT1dkhQKhVRbW/uJxzz55JOaNWuWJGnWrFmaPXu2Dhw4oEceeUTz589XY2OjunXrFn2OhoaGTzxHaWmpSktLJUkLFy5UOByO1UvqFEGrbX+Y7j16Kdw71eNqElcgEIj7v0tdBb3wB/rgD/TBH+gD4olhGDIG5cgclCO38YTsnRtk71grHT8qe+0rstevkJk1VtboqTIGZsngkDwAABJSzALCUCikxsZGSVJTU5NCoVCH+1966SUNHjxYeXl5kqS0tDRJ0sCBAzs8R1NTk5KSktTY2KjU1E8GZoWFhSosLIzerqurO++vpTMFTu07+H7dEVl2k8fVJK5wOBz3f5e6CnrhD/TBH+iDP3SVPmRkZHhdAjqZEequwIQrZF1wmZzaSjnla+Ts3Snn3a1y3t0qo1c/maOmysqdICMl9NlPCAAAuoyYLTHOzc3V9u3bJUllZWXKzc2N3rd161bt2rVLN954Y/Rae5h4/Phx2bYdfY6ysjI5jqM9e/Zo0KBBsSrXN9oDwojDHoQAAAA4/wzTlDV0pILX/LWS/up/yZowUwp1l3vsfdlvv6iWJ/5Fra8tk3Nor1yX70kBAEgEMZsgzM7OVjAY1Lx585SZmalwOKySkhIVFRXpscceUygU0k9+8hNlZGRo7ty5euKJJ1RTUyPHcXTbbbdJkmbMmKHf/OY3euWVV1RYWNjlDyiRFD25OGKzByEAAABiy0jrpcDkK2VNmCFn7w7Z5Wvl1lbKqdgkp2KT3n9riNyRE2XmjJeRlOx1uQAAIEZimrgVFxd3uF1UVCRJWrRo0SceO3fu3E9cC4VCuu+++2JTnE+1TxDaHFICAACATmJYlqyssbKyxsr98Ijsnetk79yg1sM10uEa6e2XZY64QNboqTLDXX9VDwAAiabrj+TFmegSY5vlHAAAoOtYsmSJqqurlZWV1eGXyNu2bdNTTz2lpKQkzZkzR4MGDdLRo0f10EMPqbW1VbNnz1ZBQYGHlSceo2dfBaZ+RdakK5Vat1fH1q6Qe+A9OTvWydmxTkb/IbJGTZU5vEBGMMnrcgEAwHkQsz0I8cUEAywxBgAAXUt1dbWam5s1f/58RSIRVVVVRe975pln9KMf/Uh33XWXli1bJkl6/vnndcstt+if//mfVVJS4lXZCc+wAgqNmaKkr/+dgrN/IGvsJVJSitzDNYq8/oxanvgXRd58Qc4Hh7wuFQAAfElMEPoMh5QAAICuprKyMjoFmJ+fr4qKCuXk5ETvT0lJUUpKig4daguaampqNHLkSBmGoZSUFDU2NioU4lRdL5m9+8u85Guyplwtp7qsba/Cw3tlb39L9va3ZAzIlDX6QpnZY2VY/IgBAEC84V9vnwlwSAkAAOhiGhoalJ6eLqltj+na2toO9x87dkwNDQ3at2+fJMlxHBmGEX38mQLC0tJSlZaWSpIWLlyocDgc65eRkAKBwCff24EZ0iVXq+XgXjVufl2N29fIPbhbkYO7Za5JU6jgEqWOn65An3Rviu5iztgDdCp64C3ef+/RA+91Rg8ICH0mGD2khAlCAADQNbSHfJLU1NTUIey7/fbbtWjRIoXDYY0cOVKSouHgmR7frrCwUIWFhdHbdXV1sSo/oYXD4bO/t4GQNPkrCo6bIadqi+zyNXKOHFD9muWqX7NcxuARskZNkTlstAzL6tzCu5BP7QE6BT3wFu+/9+iB985nDzIyMs54nYDQZ5ggBAAAXU1ubq5KS0t18cUXq6ysTJdffnmH++6//34dOHBAr7zyiiRp6NChqqio0NChQ88aEMI/jKTkttONR02R+35tW1D47ja5tZWK1FZKoe6y8ibLypsio3svr8sFAABnQEDoM5xiDAAAuprs7GwFg0HNmzdPmZmZCofDKikpUVFRkUpKSlRWVqa0tDTNnTtXknTdddfp4YcfVktLi2bPnu1x9ThXhmHI6D9EZv8hci/6quyKzXLK18o9dlj2ppWyN78mc8hImaMvlDkkV4bJeYkAAPgFAaHPBKOHlDBBCAAAuo7i4uIOt4uKiqL/3/7f7fr27av777+/02rD+WckhxTIv0Tu2IvlHnhP9o61cqq3y9m7U87enVJaL1mjpsgaOUlGag+vywUAIOEREPpMINC2PwsThAAAAIh3hmHIyMiWmZEt9+J62bs2yt6xTjp+RPb6V2VvLJU5bLSs0VNlDBouw2CqEAAALxAQ+kwgekgJE4QAAADoOoxuaQpccJmscZfK3fdu216Fu3fIeW+7nPe2y+jRV+boqbJyJ8rolup1uQAAJBQCQp8JsgchAAAAujDDMGUMHiFz8Ai5Dcdl71wve+c6ucePyF7zsux1y2Vm57dNFQ7I7HCqNQAAiA0CQp/hFGMAAAAkCiO1hwITZ8oaf4Wcml1yytfK2btLTtUWOVVbZPTu33ZC8ogJMpK7eV0uAABdFgGhz0QDQocJQgAAACQGwzRlDRsla9gouSc+kL1jneyd6+V+cFiRN/8krX1F5vACWaMvlNFvMFOFAACcZwSEPhNkghAAAAAJzOjeW4EpV8uaWChnT7ns8rVy91XJ2bVRzq6NMsIZskZNlTniAhnBZK/LBQCgSyAg9BkOKQEAAAAkw7JkZefLys6X82GdnPJ1sis2yK3br8hfnpPWvCxzxHhZo6fI7JvhdbkAAMQ1AkKfCQQ4pAQAAAD4KLNnWOZFs2RNvlLOe9vbpgoP7pZTvkZO+RoZ/Ye27VU4vEBGIOh1uQAAxB0CQp+JLjFmghAAAADowAgEZY0YL2vEeDlHD8nZsVZ2xUa5h/cqcniv9PaLsnInyBw1VWbv/l6XCwBA3CAg9JnoEmMmCAEAAICzMvuky7zk67KmXCPn3a1tU4Xv18oue1N22ZsyMrLb9irMGiPD4sceAAA+Df9S+kyQU4wBAACAc2YEk2TlTZaVN1nO+7Wyy9fJqdoid3+1IvurpZRUWXmTZI2aIqNHX6/LBQDAlwgIfSbAKcYAAADAF2L2GyzzssFyL5olp3KL7PI1co8elL3lddlbXpcxOLdtr8JheTJMy+tyAQDwDQJCnwlYbd+oMEEIAAAAfDFGUoqsMRfKHD1V7qG9sneslfPuNrm1FYrUVkihHrJGTZaVN0VGWk+vywUAwHMEhD4TjO5ByAQhAAAA8GUYhiFjwDCZA4bJveha2RUb5ZSvlfthneyNf5a9aaXMoXkyR18oc/AIGabpdckAAHiCgNBnAgGWGAMAAADnm5ESUqDgUrn50+QeqJZdvlbOe+/I2bNDzp4dUvfeskZNkTVykoxQd6/LBQCgUxEQ+kyAQ0oAAACAmDEMQ0bGcJkZw+U2npC9a6PsHWulEx/IXrdc9oYVMjPHyho9VUZGtgzD8LpkAABijoDQZ4IcUgIAAAB0CiPUXYHxl8u6YLrcmsq2vQr37JBTvU1O9TYZPcMyR0+VlTtBRkqq1+UCABAzBIQ+wwQhAAAA0LkMw5QxdKTMoSPl1n8oe+d62TvXte1V+PZLstctl5mdL2v0hTLShzJVCADocggIfSbAISUAAACAZ4y0ngpMKpQ14Qo5e3fKLl8rt6ZSTuVmOZWbZfQZIGv0VJk542Ukp3hdLgAA5wUBoc9YpiFDkuNKjuPKNPntJAAAANDZDNOSlTlGVuYYucePyN6xXvbO9XKPHlRk9R+lNS/LzLmgLSzsN9jrcgEA+FIICH3GMAxZlqGI7SriOEoyLa9LAgAAABKa0aOvAlOvkTWpUM7uctnla+Tur5azc72cnetl9BvcFhQOHycjmOR1uQAAfG4EhD4UME1FbFsR21USHQIAAAB8wbACsoYXyBpeIOeDw3J2rJNdsVHu+7WKvF4rvf2izBET2sLCPgO8LhcAgHNG/ORDAcuUWm1FHPYhBAAAAPzI7N1f5sXXyppytZzqbW17FR7aK+edt+W887aMAcNkjbpQZvZYGYGg1+UCAPCpCAh9KGC17Tto25xkDAAAAPiZEQjKyp0oK3einCMHZJevlVO5We7BPYoc3CO99SdZIyfKHDVFZq9+XpcLAMAZERD6UMBsO8k4wknGAAAAQNww+w6Ueen1ci/8ipyqrW17Fdbtl73tL7K3/UXGoBxZo6bIzBwtw+JHMQCAf/Cvkg9ZpyYIIw4ThAAAAEC8MYLJbUFg3mS579fK3rFWTtVWufuqFNlXJXVLk5U3WdaoyTK69/G6XAAACAj9iAlCAAAAIP4ZhiGj/xCZ/YfIvfCrcio3t+1V+MEh2Ztfk715lcyhuTJHTZU5NE/GqZ8DAADobASEPhRgghAAAADoUozkbrLGXixzzEVyD+5pmyp8d5ucvbvk7N0lpfVsmyrMmywjtafX5QIAEgwBoQ8FrLbfHNpMEAIAAABdimEYMgZmyhyYKfeia2VXbJRTvlbu8SOyN5TK3rhS5rBRskZPlTE4x+tyAQAJIqYB4ZIlS1RdXa2srCwVFxdHrz/66KOqqamRJM2ZM0fDhg3T008/rS1btkiSbr31VuXn52vVqlV67rnn1Lt3b+Xk5Oj222+PZbm+YZmnJggJCAEAAIAuy+iWqsC46XILpsndV902Vbj7nej/1KOPTky6Qu7gUTK6pXldLgCgC4tZQFhdXa3m5mbNnz9fixcvVlVVlXJy2n4Ddv3116t///46cOCAli5dqnvuuUeXXXaZbr75ZjU0NOiXv/yl8vPzJUlf//rXNXPmzFiV6UvtE4QsMQYAAAC6PsMwZQzOkTk4R27jCdk7N8jesVY6flTHVz4rmZbMrLFtU4UDs2QYhtclAwC6mJgFhJWVlSooKJAk5efnq6KiIhoQ9u/fX5JkWZbMUxvxtl8LBoMdnufll1/WG2+8oZtuuikaGnZ1ASYIAQAAgIRkhLorMOEKWRdcJqe2QoGqzWqu2ibn3a1y3t0qo1c/maOnysqdICM55HW5AIAuImYBYUNDg9LT0yVJoVBItbW1n3jMk08+qVmzZnW4tmzZMl155ZWSpMmTJ2v69Omqr6/XT3/6Uy1cuDAaKLYrLS1VaWmpJGnhwoUKh8OxeDmdJhAIKDXUTZLULZQW968nXgUCAd57n6AX/kAf/IE++AN9ANAZDNOUNTRPfSdM0/vvVcneuU72zvVyj70v+60XZa99RebwcW1Thf2HMFUIAPhSYhYQhkIhNTY2SpKampoUCnX87dZLL72kwYMHKy8vL3pt3bp1qq+v17Rp0yRJqampkqQePXpo4MCBOnbsmPr06dPheQoLC1VYWBi9XVdXF5PX01nC4bDsSIsk6diHH6quLsXjihJTOByO+79LXQW98Af64A/0wR+6Sh8yMjK8LgHAOTK691Jg8lWyJsyUs2eH7B1r5dZWyqnYKKdio4y+A2WNniozZ7yMpGSvywUAxCHzsx/yxeTm5mr79u2SpLKyMuXm5kbv27p1q3bt2qUbb7wxem3Pnj1avny57rzzzui19oCxpaVFBw8eVI8ePWJVrq9Yp6YkIzZ7EAIAAABoY1iWrOyxSvrqnUq69R5Z4y6TUlLlHjmgyF+eV8sTP1PrG8/JqdvvdakAgDgTswnC7OxsBYNBzZs3T5mZmQqHwyopKVFRUZEee+wxhUIh/eQnP1FGRobmzp2rJ554QseOHdPPfvYzhUIh3XvvvXrppZe0ZcsWua6r6667ToFATA9d9o2AdWoPQoc9CAEAAAB8ktEzrMCFX5E1+Uo5722XXb5W7oH35OxYK2fHWhn9h7RNFWYXyAgmeV0uAMDnYpq4FRcXd7hdVFQkSVq0aNEnHvv//X//3yeu3Xzzzbr55ptjU5yPBZggBAAAAHAODCsgK+cCWTkXyPngkJzydbIrNso9XKPI4RrprRdl5U6QOXqqzN7pXpcLAPCpxBjJizNMEAIAAAD4vMze6TIv+ZqsKVfLqd7WNlV4uEb29rdkb39LxsCstqnCrLEyLH4UBACcxr8KPhSw2iYIbSYIAQBAF7FkyRJVV1crKyurwyqTt99+Wy+88IIMw9ANN9ygyZMn67e//a327dunpKQkFRYWRg+wA3BujGCSrJGTZI2cJKdun+zydXKqNss98J4iB96TUlLb7h81RUbPvl6XCwDwAQJCHzp9SAkThAAAIP5VV1erublZ8+fP1+LFi1VVVaWcnBxJ0ksvvaQf//jHMgxDP/vZzzR58mRJ0l133aUBAwZ4WTbQJZjhQTKn3yD3wllyqrbILl8j98gB2Vtfl731dRmDR8gaNVXmsFEyLMvrcgEAHiEg9KHTS4yZIAQAAPGvsrJSBQUFkqT8/HxVVFREA8L09HSdPHlSktStWzdJkmEYevjhh5WWlqY777xT/fr186ZwoAsxkpLblhePmtK27Lh8rZx3t8qtrVSktlIKdZeVN1lW3hQZ3Xt5XS4AoJMREPpQgAlCAADQhTQ0NCg9ve1whFAopNra2uh9U6ZM0b333ivXdfWd73xHkvTNb35TaWlp2rlzpx5//HH98Ic//MRzlpaWqrS0VJK0cOFChcPhTngliScQCPDeeiwmPejXTxozQU5TgxrL3lbDplWKHDkoe9NK2ZtfU0pOgVInXKbk7LEyTv1sksj4PPAW77/36IH3OqMHBIQ+xAQhAADoSkKhkBobGyVJTU1NCoVC0fueeeYZPfDAA5Kkn//85xo3bpzS0tIkSXl5eVq6dOkZn7OwsFCFhYXR23V1dbEqP6GFw2HeW4/FvAfZF8jMGqfggfdk71grp3q7miu3qrlyq5TWS9aoKbLyJssIdY9dDT7H54G3eP+9Rw+8dz57kJGRccbr/DrIh04fUsIEIQAAiH+5ubnavn27JKmsrEy5ubnR+4LBoJKTk5WSkqJIJCJJ0TBx//79Sk1N7fyCgQRjGIbMjGwFZ35DSbf/b1lTvyL16CPVH5O9/lW1LP25WlcslVNbJdflZxQA6IqYIPQhyzw1QcgpxgAAoAvIzs5WMBjUvHnzlJmZqXA4rJKSEhUVFemqq67Sj370I0mKTgT+5je/UUNDgwzD0Jw5c7wsHUg4Rrc0BS64TNa4S+XWVrXtVbhnh5zqMjnVZTJ6hmWOmiIrd6KMbgT4ANBVEBD6UPsEYcTht3MAAKBrKC4u7nC7qKhIknT55Zfr8ssv73Dffffd11llATgLwzBlDMmVOSRXbsNx2TvXy96xTu6HdbLXvCx73XKZ2fmyRl8oY8AwGYbhdckAgC+BgNCHAtEJQgJCAAAAAN4yUnsoMHGmrPGXy9m7S86OtXL2Vsip2iKnaouM3ultJySPmCAjOcXrcgEAXwABoQ+dniBkiTEAAAAAfzBMS1bmaFmZo+WeOCp7x3rZO9fL/eCQIm++IK39H5k542SNvlBmv8FelwsA+BwICH2o/RRjDikBAAAA4EdG9z4KTLla1sSZcvbskF2+Vu6+Kjk7N8jZuUFGeFDbVGHOOBnBZK/LBQB8BgJCHwqYpyYIOaQEAAAAgI8ZVkBWdr6s7Hw5x96Xs2Od7F0b5dbtU+SNEuntl2SOGN8WFvYd6HW5AICzICD0IevUBCGHlAAAAACIF2avfjIv+qqsyVfJqd4ue8cauQf3yClfI6d8jYz0YW1BYXa+jEDQ63IBAB9BQOhDTBACAAAAiFdGICgrd7ys3PFyjh6UXb5WTuUmuYf2KHJoj/TWn2TlTpQ5eqrMXv28LhcAIAJCXwowQQgAAACgCzD7DJA57Tq5U78i592tbXsVvl8ru2y17LLVMjKy2w41yRwtw+LHUwDwCl+Bfaj9FGObCUIAAAAAXYARTJKVN1lW3mQ579e2TRVWbZG7v1qR/dVStzRZIyfJGjVFRo8+XpcLAAmHgNCHTi8xZoIQAAAAQNdi9hss87LBci/8qpyqzbLL18g9ekj2llWyt7wuY8iItr0Kh+bJMC2vywWAhEBA6EOnDylx5bquDMPwuCIAAAAAOL+M5BRZYy6SOfpCuYf2yi5fI6e6TG5NhSI1FVJqj1NTh1NkpPX0ulwA6NIICH3INAyZhiHHdWU7bnRPQgAAAADoagzDkDFgmMwBw+RefK3sik1yytfK/bBO9sY/y960UuawUbJGTZUxZIQMw/S6ZADocggIfSpgGWqJuIo4rgJM1QMAAABIAEZKqgIFl8rNnyZ3f3XbXoW7t8vZXS5nd7nUvY+sUVNkjZwoI9Td63IBoMsgIPSpgGWqJeLIth0pSEIIAAAAIHEYhiFj0HCZg4bLbTwhe9cG2TvWSSeOyl73iuwNK2RmjpE1eqqMjGy2ZQKAL4mA0KcC5ql9CDnJGAAAAEACM0LdFRh/haxxl8mprZSzY62cPTvkVG+TU71NRq9+MkdNkZU7UUZKyOtyASAuERD6lGWdOsnY4SRjAAAAADBMU9bQkbKGjpRbf0z2zvWyd6yXe+x92W+/JHvdcpnDC9r2KkwfylQhAHwOBIQ+xQQhAAAAAJyZkdZLgUlXypowQ86enbLL18qtrZBTsUlOxSYZfQbIGj1V5ojxMpJSvC4XAHyPgNCnAkwQAgAAAMCnMkxLVtYYWVlj5B4/InvHetk718s9elCR1X+U1r8qa9x0WWMvlhFM9rpcAPAtAkKfap8gtG0CQgAAAAD4LEaPvgpMvUbWpEI5770j+5235R7cLXvdctnbVssaf7ms0RfKCAS9LhUAfIeA0KeiE4QsMQYAAACAc2ZYAVk542QOL5C7711F1r8q9/Detn0Kt/5FgQkzZOZNkmHx4zAAtOMrok9Z1qk9CFliDAAAAACfm2EYMgbnKDhouJy9u2RveFVu3X5FVj8vbVmlwMSZMnMnyDAtr0sFAM8REPpUwGSCEAAAAAC+LMMwZA3Lkzk0V8575W1B4QeHFXn9WRlbXpc1sVDm8AIZp34GA4BEREDoUwEmCAEAAADgvDEMU1b2WJmZo+W8u032hhVyP6xTZOV/y9j8mqxJV8rMGiPDMLwuFQA6HQGhT7VPENpMEAIAAADAeWOYpqwRF8gcni+nYrMiG0vlfnBIkRVPyAhnyJp0lcyhIwkKASQUAkKfiu5ByCnGAAAAAHDeGaYlK2+SzBEXyNm5QZFNK9v2KHxliYz+QxWYfKWMQTlelwkAnYKA0Keipxg7TBACAAAAQKwYVkDWmAtljpwou3yN7M2r5B7eq9aXfidjYJZOXjlb6tbb6zIBIKYICH3q9CElTBACAAAAQKwZgaACBZfKGjVF9va3ZG99Q+6B91T3+C9kDM5VYPKVMvsP8bpMAIgJAkKfOn1ICROEAAAAANBZjGCyAuOvkDX6Itllf5FT9qbc2gq11lbIzBzddphJ34FelwkA5xUBoU8xQQgAAAAA3jGSUxSYdKV6T/+a3n/tOdnb35Kzu1zO7nKZ2QWyJhXK7N3f6zIB4LyIaUC4ZMkSVVdXKysrS8XFxdHrjz76qGpqaiRJc+bM0bBhw3T06FE99NBDam1t1ezZs1VQUHDGa4mi/ZASTjEGAAAAAO9YoTQFpn5FVv402VtWyS5fK6d6m5z3ymSOGK/AhJkyevb1ukwA+FLMWD1xdXW1mpubNX/+fEUiEVVVVUXvu/7667VgwQJ95zvf0dNPPy1Jev7553XLLbfon//5n1VSUnLWa4ni9CElTBACAAAAgNeMUHcFLv6akm79J5mjp0qGIadik1qW/Vqtr5fIPXHM6xIB4AuLWUBYWVkZnfjLz89XRUVF9L7+/dvGsC3LknlqKW1NTY1GjhyplJQUpaSkqLGx8YzXEkXAPLUHIROEAAAAAOAbRlpPBS+9QUm33CNz5ETJdeXsXKeW//6VIm++ILfhuNclAsDnFrMlxg0NDUpPT5ckhUIh1dbWfuIxTz75pGbNmiVJchxHhmFEH9/Y2HjGa6FQqMNzlJaWqrS0VJK0cOFChcPhWL2kThEIBBQOh9WrZ0Pb7aSkuH9N8ai9D/AevfAH+uAP9MEf6AMAQJKMHn0UvPxmORdcLntjqZyqbW2nH+9cL2vMRbLGXSajW6rXZQLAOYlZQNge6ElSU1PTJ4K9l156SYMHD1ZeXp4kRYPAjz7+TNc+rrCwUIWFhdHbdXV15/V1dLZwOKy6ujo1N7YFhPUNjXH/muJRex/gPXrhD/TBH+iDP3SVPmRkZHhdAgB0CWavfjJnfkPOBVfI3rBCzu53ZG99Q3b5Gln502QVXCojuZvXZQLAp4rZEuPc3Fxt375dklRWVqbc3NzofVu3btWuXbt04403Rq8NHTpUFRUVam5ujoaBZ7qWKNr3IOSQEgAAAADwP7PvAAWvvkPBou/KHDpSam2RvWmlWp78hSKbVsptOel1iQBwVjGbIMzOzlYwGNS8efOUmZmpcDiskpISFRUV6bHHHlMoFNJPfvITZWRkaO7cubruuuv08MMPq6WlRbNnz5akM15LFO2nGHNICQAAAADED7PfYJlfKZZzcI8i61+Vu/9d2etflV32pqwLLpM1+kIZwSSvywSADmIWEEpScXFxh9tFRUWSpEWLFn3isX379tX999//mdcSReDU4S0cUgIAAAAA8cccMExJX/tbOfvebQsKD+2RveZl2dv+osD4K2SOmiLDiumP5ABwzvhq5FMBJggBAAAAIO6Zg4YrmPH3cmsq2oLCun2KvPmCtPV1BSbMlJk7UYZleV0mgARHQOhT7ROE7EEIAAAAAPHNMAwZQ0cqOCRXzu5y2RtelXv0kCJvlEhbVikwsVBmzgUyzJgdEwAAn4qA0KeiE4Q2E4QAACD+LVmyRNXV1crKyuqwDc3bb7+tF154QYZh6IYbbtDkyZO1d+9eLV68WJI0Z84cDRs2zKuyAeC8MgxDVtYYmZmj5LxbJntjqdxj7yvy2jIZm1fJmlQoM3usDIOgEEDn4quOT1mnTjGOOEwQAgCA+FZdXa3m5mbNnz9fkUhEVVVV0fteeukl/fjHP9aPf/xjvfjii5Kkp556Snfffbe+//3v66mnnvKqbACIGcMwZeWMU/Dm7ylw+c1S9z5yjx1WpPRJtT77kOzd5XJdfhYE0HmYIPSp04eUMEEIAADiW2VlpQoKCiRJ+fn5qqioUE5OjiQpPT1dJ0+elCR169ZNktTQ0KBwOBz9bwDoqgzTkjVyosyccXJ2bVRk00q5Rw4osvxxGf0GKzD5KhmDR8gwDK9LBdDFERD61OlDSvitEQAAiG8NDQ1KT0+XJIVCIdXW1kbvmzJliu699165rqvvfOc7knROUzOlpaUqLS2VJC1cuDAaKOL8CgQCvLceowfe67QepH9V7sVXqWHz6zrx5sty3q9V68uPKWnICHW//AYlD82NfQ0+xOeA9+iB9zqjBwSEPnX6kBImCAEAQHwLhUJqbGyUJDU1NSkUCkXve+aZZ/TAAw9Ikn7+859r3LhxHT72bFMzhYWFKiwsjN6uq6s732VDUjgc5r31GD3wXqf3IOsCBQaPlv3O27K3vK6WmkrV/dcvZQzKUWDyVTLTh3ZeLT7A54D36IH3zmcPMjIyznidPQh9iglCAADQVeTm5mr79u2SpLKyMuXmnp6CCQaDSk5OVkpKiiKRiCQpLS1NR44c0dGjR6PLjgEgkRjBJAUuuExJf3WvrElXSknJcvdVqfX5f1Pr/yyRU7fP6xIBdDFMEPpU9JASJggBAECcy87OVjAY1Lx585SZmalwOKySkhIVFRXpqquu0o9+9CNJik4Ezp49Ww8++KAk6c477/SqbADwnJGUosDEmbLGXCR7219kl70pZ+9OOXt3yswaK2vSlTL7pHtdJoAugIDQpwLmqQlCmwlCAAAQ/4qLizvcLioqkiRdfvnluvzyyzvcN2zYMC1YsKCzSgMA3zNSQgpMuVpW/iWyt6yS/c4aOe9tl/PeOzJzxsmaVCizJ3vEAfjiCAh9yjoVEDquK8d1ZXJqFQAAAAAkNKNbmgIXXSurYLoim1+Ts2OdnKotct7dJnPkBAUmzJTRvbfXZQKIQwSEPmUYhgKmoYjjyrZdmQECQgAAAACAZKT2UHDadXLHTVdk05/l7NokZ+cGtVRslpk3WYEJM2Sk9vC6TABxhENKfCzQvg+hwz6EAAAAAICOjO69FbzsJiXd8gOZI8ZLjiOnfI1a/vBLRd5+UW5TvdclAogTBIQ+ZrWfZMxBJQAAAACAszB6hhWccYuCN39PZna+ZEdkb1utlid/qci65XKbG70uEYDPscTYxwJm+0nGHFQCAAAAAPh0Zp90mVfeJqdun+z1K+Ts3Sl782uy33lLVsGlsvKnyUhK8bpMAD5EQOhjgfYJQpYYAwAAAADOkRkeJPMrfyPn0F5FNqyQW1spe0Op7LK3ZF1wmawxF8kIJnldJgAfISD0sfYJQpsJQgAAAADA52SmD1XSV++Us79akfWvyj24W/ba/5G97S+yxl8ua9RUGYGg12UC8AH2IPQxJggBAAAAAF+WmZGt4Nf/TsFZ35LRf4jUVC/7rRfV8t+/kl2+Vq4d8bpEAB5jgtDHLIs9CAEAAAAAX55hGDKG5Co4eIScPTtkb1gh98gBRf7ynLTldQUmzpQ54gIZpuV1qQA8QEDoYwGTU4wBAAAAAOePYRiyMkfLHJYnp3p7W1B47H1FVj0tY/NrsiZdKXN4vgyDBYdAIiEg9LFA+wShwwQhAAAAAOD8MQxT1vACmVlj5VRtVWRjqdwP6xT58x9kbF4pa9JVMjNHyzAMr0sF0AnO6VcCt9xyi956663o7U2bNunuu++OWVFo035ICROEAAAAAIBYMExTVu54Jc3+gQLTi6S0nnKPHlLk1f9Sa8nDsvfukusytAJ0dZ86QVhXV6fDhw9Lkmpra1VeXi5J2rJliw4dOhT76hJc+yElNhOEAAAAAIAYMixL1qgpMnMnyNmxTpHNr8mt26fI//xeRvowBSZfJXPQcK/LBBAjnxoQvvbaa3rmmWckSc8++6yeffbZ6H2DBg2KbWX4yCElTBACAAAAAGLPsAKyxl4sc+Qk2eVrZG95Xe6hPWp9cbGMjOFtQeGAYV6XCeA8+9SAMCcnR1dddZVeffVVFRQUaODAgZKktLQ0TZs2rVMKTGSnDylhghAAAAAA0HmMYJIC46bLGjVV9vY3ZW99Q+7+d9X6x0dkDhkpa/KVMvsN9rpMAOfJpwaE48eP1/jx4zV8+HCNGTNG/fr1kyQ5jiPT5ESjWDt9SAkThAAAAACAzmckJSswYYasMRfJ3vYX2WWr5dTsklOzS2bmmLZTj/sO8LpMAF/SOaV8NTU1eu2113T06FF9+9vf1h133KGVK1fGuraExwQhAAAAAMAPjORuCky+Sknf+F+yxk2XAkE5u99R6zOL1PrnP8g59r7XJQL4Es4pIFy9erVSU1P15ptvKhKJaODAgSopKYl1bQmvfYLQZoIQAAAAAOADRrdUBS6cpaRb/0nW2Isl05RTtVWtyx5Q62tPyz1+1OsSAXwBn7rEuF19fb26d++uLVu2aPr06Ro2bJj+/d//Pda1JTzLap8gJCAEAADe+cd//EcNGTJEmZmZGjp0qDIzMzVgAMvJACCRGak9FLjk67LGTVdk00o5uzbIqdiolqrNMvMmKzB+hoy0nl6XCeAcnVNAGA6H9Yc//EH19fX69re/rWPHjiktLS3WtSW8gNl+ijFLjAEAgHcmT56sSCSiXr16adu2bXr44YfVvXt39enTR8OGDdPcuXO9LhEA4BEjrZeC04vkjrtMkU1/llO5WU75WrXs2ihr1FRZ4y+XEerudZkAPsM5BYS33Xabnn76aY0YMUJTpkzRk08+qalTp8a6toQXaJ8gZIkxAADw0LZt2/R//+//jd6+4oortG7dOl1zzTXas2ePh5UBAPzC6NlXwStmy7ngctkbSuVUb2s7/XjnOlljL5Y1brqMlFSvywRwFucUEE6ZMkUTJ07UgQMHdPDgQd1+++2cYtwJmCAEAAB+0L17d+3evVuZmZmSpBEjRujRRx/Vbbfdpr59+3pbHADAV8ze/WVe+VdyjpwKCneXy97yuux31sjKnyar4FIZySlelwngY84pIKytrdWvfvUrHTx4UJI0YMAA3XvvvRo0aFBMi0t07ROEHFICAAC89Hd/93d6+OGHNXjwYGVmZmrfvn1KSkryuiwAgI+ZfTNkXv1NOYdrFNmwQm5NhexNf5b9zluyxk2XNfZiGcFkr8sEcMo5jQH+7ne/0wcffKBLLrlEl1xyiY4dO6bHHnss1rUlPMtighAAAHhvwIABmj9/vsaPH69jx45pwIABuu+++7wuCwAQB8z+Q5Q061sKfv3vZQzMkk42yV63XC1P/lKRbX+RG2n1ukQAOscJwurqav3VX/2VrrnmGknSK6+8oj/84Q8xLQxSwOQUYwAA4A+maWrq1KnsQw0A+ELMgZkKfm2u3H3vKrL+VbmH98p++yXZW/+iwIQrZOZNlmGdU0QBIAbO6bMvLS1N27Zt0/jx4yW1bVTNKcaxF2ifIHSYIAQAAAAAxDfDMGQMzlFw0HA5e3fJ3vCq3Lr9iqz+o7TldQUmzpSZO0GGaXldKpBwzikgnDFjhpYtW6aNGzdGr91yyy0xKwptmCAEAAAAAHQ1hmHIGpYnc+hIOe+9I3vDCrkfHFLk9WdlbF4la1KhzOHjZHA4KtBpzikgnD59unr27Klt27ZJksaNG6eCgoKYFobTE4Q2E4QAAAAAgC7GMAxZ2WNlZo6W8+62tqDw+BFFVj4lY/NrsiZdKbfvZV6XCSSEcwoIFyxYoIsvvlg/+MEPJEn//d//rZ/+9KdatGjRp37ckiVLVF1draysLBUXF0evl5SUaPny5briiit06623SpIefPBBHTt2TK2trWppadGvfvUrLVu2TOvXr1dqaqomTZqka6+99ou+zrh0+pASJggBAAAAAF2TYZqyRlwgc3i+nIrNimwslfvBYUVWLNX72/4id/wMmUNHyjAMr0sFuqxzCgiPHj2q/v37R2/369dPR44c+dSPqa6uVnNzs+bPn6/FixerqqpKOTk5ktqWLOfm5mr79u3Rx3/ve9+TJK1bt07V1dXR63fccUfCTiueXmLMBCEAAAAAoGszTEtW3iSZIy6Qs3ODIptWqvXQXumVJTL6D1Fg8lUyBuUQFAIxcE4BYXp6uv70pz+pT58+cl1XL774otLT0z/1YyorK6PBXn5+vioqKqIBYa9evbRv374zfty6des0a9as6O2lS5fqj3/8o+644w5lZmZ+4vGlpaUqLS2VJC1cuFDhcPhcXpJvBQKB6GtocpPaLhpm3L+uePPRPsBb9MIf6IM/0Ad/oA8AAMSWYQVkjblQ5siJ6ranTB+ufknu4Rq1vvQ7GQOzFJh8lcyBWV6XCXQp5xQQXnfddfrtb3+rn//859Fr3/3udz/1YxoaGqIhYigUUm1t7Wf+OZFIRHv37lV2drYkadasWZo9e7YOHDigRx55RPPnz//ExxQWFqqwsDB6u66u7lxekm+Fw+Hoa6g/3iRJOtnSGvevK958tA/wFr3wB/rgD/TBH7pKHzIyMrwuAQCAT2UEgkqbepWaho6Rvf1t2Vtfl3vgPbW+8O8yBucqMPlKmf2HeF0m0CWc8yEl4XBYmzZtkiRNmDBBo0eP/tSPCYVCamxslCQ1NTUpFAp95p9TXl7e4XnT0tIkSQMHDjyXMruc9kNKIg57EAIAAAAAEpMRTFZg/OWyRl8ou+wvsretlltbodbaCpnDRsmafKXMvvziC/gyzikglKTRo0d/Zij4Ubm5uSotLdXFF1+ssrIyXX755Z/5MevWrdPFF18cvd3Y2KhQKKTjx4/Ltu1z/rO7CstiD0IAAAAAACTJSE5RYNKVssZeLHvrG7K3vyVnzw45e3bIzC6QNalQZu/+n/1EAD7hnAPCzys7O1vBYFDz5s1TZmamwuGwSkpKVFRUpJUrV2r58uWqr69XfX295syZI9d1VVFRoW9961vR53jiiSdUU1Mjx3F02223xapU3wqYnGIMAAAAAMBHGSmpCkz9iqz8abK3rJJdvlZO9TY575XJzLlAgYmFMnr29bpMIK7ELCCUpOLi4g63i4qKJLWdYjxjxowO9xmGoV/+8pcdrs2dOzeW5fle4NQEoe0wQQgAAAAAwEcZoe4KXPw1WQXTFdn8mpyd6+RUblZL1VaZIycpMGGGjO69vC4TiAsxDQjx5UQnCNmDEAAAAACAMzLSeip46fVyx01XZNOf5VRskrNznVoqNsoaPVXWBZfLSO3hdZmArxEQ+phpGjINyXHbpggt0/C6JAAAAAAAfMno0UfBy2+Wc8HlsjeWyqnaJnv7W7J3rpc1+iJZF0yX0S3N6zIBXyIg9DnLMuVEHNm2I8u0vC4HAADgC1myZImqq6uVlZXVYRuaBx98UMeOHVNra6taWlr0q1/9SsuWLdP69euVmpqqSZMm6dprr/WwcgBAvDF79ZM58xtyxl8he8MKOe+9I3vbG7J3rJGVP01WwaUykrt5XSbgKwSEPhcwDbVKijiukrwuBgAA4Auorq5Wc3Oz5s+fr8WLF6uqqko5OTmSpO9973uSpHXr1qm6ujr6MXfccYcKCgq8KBcA0EWYfQbIvOoOOe/XtgWFe3fJ3rRS9va3ZI27VNbYaTKSkr0uE/AF0+sC8OkCVluLWjnJGAAAxKnKyspo2Jefn6+KiopPPGbdunWaMmVK9PbSpUu1YMEC7d69u7PKBAB0UWa/wQp+pVjB674tI2O41NIse/0KtfzhF4psfUNua4vXJQKeY4LQ55ICbQFhS8T2uBIAAIAvpqGhQenp6ZKkUCik2traDvdHIhHt3btX2dnZkqRZs2Zp9uzZOnDggB555BHNnz//E89ZWlqq0tJSSdLChQsVDodj/CoSUyAQ4L31GD3wHj3w1nl9/8NhaexEndy9U8dff04tte/KXvOy3LI31f2SWUodP11GIHh+/qwuhM8B73VGDwgIfS4lGJB0Us0tBIQAACA+hUIhNTY2SpKampoUCoU63F9eXq7Ro0dHb6eltW0gP3DgwLM+Z2FhoQoLC6O36+rqzmfJOCUcDvPeeoweeI8eeCsm739aWJo1R8GaCkXWvyqnbp8+fPUP+vCtlxWYMFNm7kQZFmcAtONzwHvnswcZGRlnvM4SY59LSWr7otTcSkAIAADiU25urrZv3y5JKisrU25ubof7P768uD1MPH78uGyb74EAAOefYRgyh45UsOi7Clx9h4w+A6T6DxV5o0Qty34tu2KTXIetvpA4mCD0uZTgqYCQCUIAABCnsrOzFQwGNW/ePGVmZiocDqukpERFRUVyXVcVFRX61re+FX38E088oZqaGjmOo9tuu83DygEAXZ1hGLIyx8gcNkrOu2WyN5bKPfa+Iq8tk7H5NVmTrpSZPVaGwXwVujYCQp+LThC2RDyuBAAA4IsrLi7ucLuoqEhS2w9mv/zlLzvcN3fu3E6rCwAASTIMU1bOOJnZY+VUblFk45/bgsLSJ2X0GSBr8lUyh42SYRhelwrEBAGhz7XtQcgSYwAAAAAAYs0wLVkjJ8rMGSdn10ZFNq2Ue/SgIssfl9FvsAKTr5IxeARBIbocAkKfYw9CAAAAAAA6l2EFZI2eKjN3guwd62Rvfk3u+7VqffkxGQMyFZh8lcyMbK/LBM4bAkKfYw9CAAAAAAC8YQSCCuRfIitvsux33pa95XW5B3er9U+PyhiU0xYUpg/1ukzgSyMg9Llu0QlC9iAEAAAAAMALRjBJgQsukzV6quyyN2Vve0Puviq17quSOTRP1uQrZYYHeV0m8IUREPpcStKpPQiZIAQAAAAAwFNGUooCE2fKGnOR7G1/kV32ppy9O+Xs3Skza2zbqcd90r0uE/jcCAh9LvnUEuMmAkIAAAAAAHzBSAkpMOVqWfmXyN6ySvY7a+S8t13Oe+/IzBkna1KhzJ5hr8sEzhkBoc+170F4kkNKAAAAAADwFaNbmgIXXSurYLoim1+Ts2OdnKotct7dJnP0VAUmXy0jOcXrMoHPZHpdAD4dexACAAAAAOBvRmoPBaddp6Rb75GZN0mS5LzztlqWPSC7ukyu63pcIfDpCAh9LiXIHoQAAAAAAMQDo3tvBS+7ScEb75LRf6jUeFyRFUsVWf643PpjXpcHnBUBoc+lnJogbGKJMQAAAAAAccHsO0DB6/5egWnXSUnJcvbsUMtTDyiybbVcx/G6POATCAh9LilgyjCk1ogjmy8iAAAAAADEBcM0ZY25SEmzfygza6wUaZH99otqfe63ct7f53V5QAcEhD5nGEb0oBKWGQMAAAAAEF+M1B4KXnW7Ald/U0rrKbdun1qfe1iRt1+U23rS6/IASQSEcYGTjAEAAAAAiG9W5mglzf6BrPxLJEn2ttVqWfavsvfs9LgygIAwLqQktR1Uwj6EAAAAAADELyOYrMDFX1Pwhn+QER4k1R9T5JUlal2xVG7Dca/LQwIjIIwDLDEGAAAAAKDrMPsNVvCG78i66KtSIElOdZlalv1a9jtr5LqcP4DOR0AYB9pPMm5uiXhcCQAAAAAAOB8M01Kg4FIlzf6+zKF5UstJRVY/r9Y//j85Rw96XR4SDAFhHIhOELLEGAAAAACALsXo3luBa/5agStvk0Ld5R7aq9Znf6PI2lfkRlq9Lg8JgoAwDrTvQUhACAAAAABA12MYhqzsfCXN/qHM0RdKjit7yyq1PP2gnNpKr8tDAiAgjAPsQQgAAAAAQNdnJKcoeOn1Cl739zL6pEvHj6j1pd+pdeVTcpvqvS4PXRgBYRyI7kHYyh6EAAAAAAB0deaAYQoW3SVrytWSFZBTuVktTz0ge+cGua7rdXnogggI4wAThAAAAAAAJBbDshQYf4WSbv6+jMEjpJONirz+jFr/9KicY+97XR66GALCONCtfQ9CAkIAAAAAABKK0bOvgrO+pcCMW6SUVLkH3lPr0w8qsqFUrs1KQ5wfBIRxIJlTjAEAAAAASFiGYcgaMV5Jt/xA5shJkmPL3liq1mcWydlf7XV56AIICOPA6T0ICQgBAAAAAEhURkqqgpffpODX5sro1U/usffV+qdH1fr6M3KbG70uD3GMgDAOnN6DkNFhAAAAAAASnZmRreBNd8uaOFMyLTk7N6hl2QOyK7dwiAm+EALCOBDdg5AJQgAAAAAAIMmwAgpMulLBm+6WMTBLaqpXZOV/q/Xlx+QeP+J1eYgzBIRxILrEmENKAAAAAADAR5i9+yv4tb9V4LIbpeRucmsr1fL0g4psWSXXJkfAuQnE8smXLFmi6upqZWVlqbi4OHq9pKREy5cv1xVXXKFbb71VkvTb3/5W+/btU1JSkgoLCzVt2jQdPXpUDz30kFpbWzV79mwVFBTEslzfSg60BYQnW205rivTMDyuCAAAAAAA+IVhmLLyJsscNkqRt16UU7VF9tpX5FRuUWB6kcz0oV6XCJ+LWUBYXV2t5uZmzZ8/X4sXL1ZVVZVycnIkSTNmzFBubq62b9/e4WPuuusuDRgwIHr7+eef1y233KLMzEwtXLgwYQNC0zSUHDB1MuLoZKsdXXIMAAAAAADQzuiWpuDMW+XkTlDr6uflHj2o1ucfkTl6qgJTrpGRnOJ1ifCpmCVNlZWV0UAvPz9fFRUV0YCwV69e2rdvX4fHG4ahhx9+WGlpabrzzjvVr18/1dTUaOTIkTIMQykpKWpsbFQoFOrwcaWlpSotLZUkLVy4UOFwOFYvqVMEAoEzvoZQSpJO1jcrlNZTfXt086CyxHK2PqDz0Qt/oA/+QB/8gT4AAAC/M4fkKumm78netFL2tjfklK9Ry+5yBS75msyssTJYmYiPiVlA2NDQoPT0dElSKBRSbW3tpz7+m9/8ptLS0rRz5049/vjj+uEPfyjHcaJ/aUOh0BkDwsLCQhUWFkZv19XVnedX0rnC4fAZX0OS1fY+HDj0vtyW0Cfux/l1tj6g89ELf6AP/kAf/KGr9CEjI8PrEgAAQAwZwSQFpl4jM+cCRd4okXt4ryIrlsocNkqBadfJSOvldYnwkZgdUtIe6ElSU1PTJ4K9j0tLS5Mk5eXl6dixY5LUIdE+l+foytoPKmniJGMAAAAAAHCOzL4DFLzu7xWYdp2UlCxnzw61PPWAIttWy3Ucr8uDT8QsIPzoHoNlZWXKzc391Me3h4n79+9XamqqJGno0KGqqKhQc3MzAWH0JOOIx5UAAAAAAIB4YpimrDEXKWn2D2VmjZUiLbLfflGtz/1Wzvv7PvsJ0OXFbIlxdna2gsGg5s2bp8zMTIXDYZWUlKioqEgrV67U8uXLVV9fr/r6es2ZM0e/+c1v1NDQIMMwNGfOHEnSddddp4cfflgtLS2aPXt2rEqNCynB9oCQCUIAAAAAAPD5Gak9FLzqdtm7yxV5849y6/ap9bmHZeVfImvSlTKCyV6XCI/E9Djc4uLiDreLiooktZ1iPGPGjA733XfffZ/4+L59++r++++PXYFxJCXY1qpmlhgDAAAAAIAvwcocLXPQcNnrV8je/qbsbatlV29XYNr1sobleV0ePBCzJcY4v6JLjAkIAQAAAADAl2QEkxW4+FoFb/gHGeFBUv0xRV5ZotYVS+U2HPe6PHQyAsI4cXqJMXsQAgAAAACA88PsN1jBG74j66KvSoEkOdVlaln2a9nvrJHrcohJoiAgjBMpSaeWGLMHIQAAAAAAOI8M01Kg4FIlzf6+zKF5UstJRVY/r9Y//j+1HuYQk0RAQBgnohOELDEGAAAAAAAxYHTvrcA1f63AlbdJoe5yD+3V4d/NV2TtK3IjrV6XhxiK6SElOH+iexAyQQgAAOLQkiVLVF1draysrA4H2T344IM6duyYWltb1dLSol/96lc6evSoHnroIbW2tmr27NkqKCjwsHIAABKLYRiysvNlDhqhyLpX5JSvlb1llezqMgUvvV7m4BFel4gYICCME6cnCNmDEAAAxJfq6mo1Nzdr/vz5Wrx4saqqqpSTkyNJ+t73vidJWrdunaqrqyVJzz//vG655RZlZmZq4cKFBIQAAHjASE5R8NLr1X3yFTryp8fkHj2k1pd+J3PEeAUu+qqMbmlel4jziIAwTkT3IGSJMQAAiDOVlZXRkC8/P18VFRXRgLDdunXrNGvWLElSTU2NRo4cKcMwlJKSosbGRoVCoQ6PLy0tVWlpqSRp4cKFCofDnfBKEk8gEOC99Rg98B498Bbvv/cCgQFKmvsT1a95VcdX/0lO5Wa11lao58ybFSq4RIZheF1il9cZnwcEhHHi9CnGBIQAACC+NDQ0KD09XZIUCoVUW1vb4f5IJKK9e/cqOztbkuQ4TvSHjVAodMaAsLCwUIWFhdHbdXV1sXwJCSscDvPeeoweeI8eeIv333vhcFhHPjgmjZyipAHD1br6ebm1lTr24hJ9uPF1BaYXyezVz+syu7Tz+XmQkZFxxuscUhInuiVxSAkAAIhP7SGfJDU1NX0i7CsvL9fo0aOjtz86iXCmxwMAAG8YPfsqOOtbCsy4RUpJlXvgPbU+/aAiG0rl2myJFs8ICONEcnSCMCLXdT2uBgAA4Nzl5uZq+/btkqSysjLl5uZ2uH/dunWaMmVK9PbQoUNVUVGh5uZmAkIAAHzGMAxZI8Yr6ZYfyBw5SXJs2RtL1frMIjn7q70uD18QAWGcCFimApYhx5VaI47X5QAAAJyz7OxsBYNBzZs3T6ZpKhwOq6SkRJLkuq4qKiqUl5cXffx1112nP/zhD1qwYIFuuOEGr8oGAACfwkhJVfDymxT82lwZvfrJPfa+Wv/0qFpff0Zuc6PX5eFzYg/COJISDKjeblVzq62kUxOFAAAA8aC4uLjD7aKiIkltUwi//OUvO9zXt29f3X///Z1WGwAA+OLMjGwFb7pb9ubXZG9eJWfnBrXs2anARdfKzBnHISZxggnCOMI+hAAAAAAAwG8MK6DApCsVvOluGQOzpKZ6RVb+t1pffkzu8SNel4dzQEAYR1I+sg8hAAAAAACAn5i9+yv4tb9V4LIbpeRucmsr1fL0g4psWSXXZtjJzwgI40jyqQnCphY+qQAAAAAAgP8Yhikrb7KSbvmhzJwLpEir7LWvqLXkITmH9npdHs6CgDCOpATbtoxkiTEAAAAAAPAzo1uagjNvVXDWt6QefeQePajW5x9R61+el3uy2evy8DEEhHGkfQ/CkwSEAAAAAAAgDphDcpV00/dkXXC5ZBpyyteoZdkDsqvL5Lqu1+XhFALCONK+ByFLjAEAAAAAQLwwgkkKTL1GwaK7ZPQfKjUeV2TFUkWWPy73xDGvy4MICONKSvQUYw4pAQAAAAAA8cXsO0DB6/9egWnXSUnJcvbsUMuyBxTZtlqu43hdXkIjIIwjye17EDJBCAAAAAAA4pBhmLLGXKSk2T+UmTVWirTIfvtFtT73Wznv7/O6vIRFQBhH2vcgJCAEAAAAAADxzEjtoeBVtytw9TeltJ5y6/ap9bmHFXn7RbmtJ70uL+EQEMaR9j0IWWIMAAAAAAC6AitztJJm/0BW/jRJkr1ttVqW/avsPTs9riyxEBDGkdN7EDJBCAAAAAAAugYjmKzAxdcqeMM/yAgPkuqPKfLKErWuWCq34bjX5SUEAsI4ksIehAAAAAAAoIsy+w1W8IbvyLroq1IgSU51mVqW/Vr2O2vkuhxiEksEhHGECUIAAAAAANCVGaalQMGlSpr9fZlD86SWk4qsfl6tf/x/co4e9Lq8LouAMI5E9yBkghAAAAAAAHRhRvfeClzz1wpceZsU6i730F61Pvsb2bs2eF1alxTwugCcu+gEYQuHlAAAAAAAgK7NMAxZ2fkyB41QZN3/yClfq8iqZyVJ1shJHlfXtTBBGEeClinTMBRxXEVs1t4DAAAAAICuz0hOUfDSG2RNuVqSq8iqZ5kkPM8ICOOIYRjsQwgAAAAAABJSYPwVHwsJN3pdUpdBQBhn2IcQAAAAAAAkqo4h4TOEhOcJexDGmdMThOxDCAAAAAAAEk9g/BWSJHvdckVWPSNJskZO9LKkuMcEYZxhghAAAAAAACS6wPgrZE1mkvB8ISCMMylJbUOfTQSEAAAAAAAggQUmfCwkrCAk/KJYYhxn2icIT3JICQAAAAAASHCBCaeWG69frshrp5Yb57Lc+PMiIIwz3diDEAAAAAAAIIqQ8MtjiXGcSQmyxBgAAAAAAOCj2pYbXyXJVeQ1lht/XgSEcSY5iUNKAAAAAAAAPi4wYcbHQsJNXpcUN2K6xHjJkiWqrq5WVlaWiouLo9dLSkq0fPlyXXHFFbr11lslSY8++qhqamokSXPmzNGwYcO0bNkyrV+/XqmpqZo0aZKuvfbaWJYbF6KnGLMHIQAAAAAAQAeBCTMkSfb6VxV57WlJkpU7wcuS4kLMAsLq6mo1Nzdr/vz5Wrx4saqqqpSTkyNJmjFjhnJzc7V9+/bo46+//nr1799fBw4c0NKlS3XPPfdIku644w4VFBTEqsy4E92DsIU9CAEAAAAAAD6uLSR0Za9fQUh4jmK2xLiysjIa7OXn56uioiJ6X69evWQYRofH9+/fX5JkWZZM83RZS5cu1YIFC7R79+5YlRpXmCAEAAAAAAD4dIEJM2VNvlJty42fll2x2euSfC1mE4QNDQ1KT0+XJIVCIdXW1p7Txz355JOaNWuWJGnWrFmaPXu2Dhw4oEceeUTz58//xONLS0tVWloqSVq4cKHC4fB5egXeCAQCn/oa0k+2hae2a8T9a/Wzz+oDOg+98Af64A/0wR/oAwAAQHwITJgpSacmCZdJkqzc8V6W5FsxCwhDoZAaGxslSU1NTQqFQp/5MS+99JIGDx6svLw8SVJaWpokaeDAgWf9mMLCQhUWFkZv19XVfZmyPRcOhz/1NZw89Z6eaDwZ96/Vzz6rD+g89MIf6IM/0Ad/6Cp9yMjI8LoEAACAmCMkPDcxW2L80T0Gy8rKlJub+6mP37p1q3bt2qUbb7wxeq09YDx+/LhsmyW1kpTCHoQAAAAAAADnLDBhpqxJp5Ybr1rGcuMziNkEYXZ2toLBoObNm6fMzEyFw2GVlJSoqKhIK1eu1PLly1VfX6/6+nrNmTNHjz32mEKhkH7yk58oIyNDc+fO1RNPPKGamho5jqPbbrstVqXGFfYgBAAAAAAA+HwCE09NEm5YocgqJgk/LmYBoSQVFxd3uF1UVCSp7RTjGTNmdLhv0aJFn/j4uXPnxq64OJUUtGQYUkvEke04ssyYDYECAAAAAAB0GZ8ICQ3JGkFIKMVwiTFiwzQM9eiWJEn6sKHF42oAAAAAAADiR2DiTFmTCiXXVeS1ZbIrWW4sERDGpT5pyZKko/UnPa4EAAAAAAAgvgQmFhISfgwBYRzqTUAIAAAAAADwhRESdhTTPQgRG326nwoITxAQAgAAAAAAfBGBiYWSJHtDqSKvLZNkyBpxgac1eYWAMA6dXmLc7HElAAAAAAAA8SswsVByJXtjqSKvPSVJCRkSEhDGoT5pKZJYYgwAAOLHkiVLVF1draysLBUXF0ev19fX69FHH9WJEyeUn5+voqIi/fa3v9W+ffuUlJSkwsJCTZs2zcPKAQBAVxeYdGqSMIFDQgLCOMQhJQAAIJ5UV1erublZ8+fP1+LFi1VVVaWcnBxJ0tNPP61bbrlFgwYN6vAxd911lwYMGOBFuQAAIAElekhIQBiHeoaSZJmGTjS1qjXiKBjgrBkAAOBflZWVKigokCTl5+eroqIiGhDW1NToueee05EjR/SNb3xDubm5MgxDDz/8sNLS0nTnnXeqX79+n3jO0tJSlZaWSpIWLlyocDjceS8ogQQCAd5bj9ED79EDb/H+ey+henDNrToeCunEX15Q5LWn1L1Hd4XGTPW6qk7pAQFhHDJNQ71Sk3TkxEkdrT+p9F7dvC4JAADgrBoaGpSeni5JCoVCqq2tjd63a9cu/eIXv1BaWpp+/etfa8GCBfrmN7+ptLQ07dy5U48//rh++MMffuI5CwsLVVhYGL1dV1cX+xeSgMLhMO+tx+iB9+iBt3j/vZdwPRh9sazGBtkb/6wP/vgfOnHihKycCzwt6Xz2ICMj44zXGT2LU6f3IeSgEgAA4G+hUEiNjY2SpKamJoVCoeh9GRkZGjx4sHr16iXTbPvWNC0tTZKUl5enY8eOdXq9AAAgsQUmXSlr4kzJdRVZ+ZTsd7d5XVLMERDGKfYhBAAA8SI3N1fbt2+XJJWVlSk3Nzd638CBA/XBBx+oublZtm1LUjRM3L9/v1JTUzu/YAAAkPACk66UNaEtJLTXLfe6nJhjiXGc6tP9VEB4goAQAAD4W3Z2toLBoObNm6fMzEyFw2GVlJSoqKhIs2fP1qJFi9TS0qKbbrpJkvSb3/xGDQ0NMgxDc+bM8bh6AACQqKzxl8ve9Ge59R/IdR0ZRtedsyMgjFNMEAIAgHhSXFzc4XZRUZEkafDgwfrxj3/c4b777ruvs8oCAAA4KyMQlFJCUnOj1NQghbp7XVLMdN3os4trDwg/YA9CAAAAAACAmDBCPSRJbsOHHlcSWwSEcer0ISVMEAIAAAAAAMSCkdZTkuQ2HPe4ktgiIIxTqSkBBQOmmlpsNbVEvC4HAAAAAACg6wm1BYRighB+ZBjG6X0IOagEAAAAAADgvDPSTi0xricghE9xUAkAAAAAAEDsGKmnlhg3ssQYPtW3e/s+hBxUAgAAAAAAcL5FA0ImCOFXLDEGAAAAAACIoVMBoZgghF/1ZokxAAAAAABAzHx0gtB1XY+riR0CwjjGHoQAAAAAAAAxlJQsBZKkSIvU0nW3eCMgjGN9PrIHYVdOsQEAAAAAALxgGIaMtFNThA1dd5kxAWEcSwlaCiUHFLFdnWhq9bocAAAAAACArqd9H8KGrntQCQFhnGOZMQAAAAAAQOwYqT0kSS4BIfyKgBAAAAAAACB2okuL7Yi3hcRQwOsC8OX06X4qIDzRdTfKBAAAAAAA6EybyvdrxZtVOvFhvVIbgprZp58mDy/wuqyYISCMc33S2g8qYYIQAAAAAADgy9pUvl//+dwWnWhoz1p66ODRngq+96HGj0r1tLZYYYlxnGOJMQAAAAAAwPmz4s2qj4SDbU6cdPXq6iqPKoo9AsI4R0AIAAAAAABw/tQ3tJz5euOZr3cFBIRxrndasgxJHzaclO24XpcDAAAAAAAQ19JSk858PXTm610BAWGcC1imeoSS5LhtISEAAAAAAAC+uKum5ah7anKHa91Tk3XVtByPKoo9DinpAvqkJevDxhYdrT+pPt1TvC4HAAAAAAAgbo0flSEVSa+urlJ9Y4vSQkm6alpO2/UuioCwC+idlqz3Dp9gH0IAAAAAAIDzYPyojC4dCH4cS4y7gD7dTx1UcoKAEAAAAAAAAJ8PAWEXcPok42aPKwEAAAAAAEC8ISDsAvqmte07yBJjAAAAAAAAfF4x3YNwyZIlqq6uVlZWloqLi6PXS0pKtHz5cl1xxRW69dZbJUl79+7V4sWLJUlz5szRsGHDzngNn9S+xPj9481yHFemaXhcEQAAAAAAAOJFzCYIq6ur1dzcrPnz5ysSiaiqqip634wZM/SP//iPHR7/1FNP6e6779b3v/99PfXUU2e9hk/qGUpSn7RkNZ6MqGL/Ma/LAQAAAAAAQByJWUBYWVmpgoICSVJ+fr4qKiqi9/Xq1UuG0XHKraGhQeFwWH369FFDQ8NZr+GTDMPQ1Nz+kqS1lYc9rgYAAAAAAADxJGZLjBsaGpSeni5JCoVCqq2t/dTHu657Ttc+rrS0VKWlpZKkhQsXKhwOf4Fq/SMQCHyh13D1lDS9uqVW5TXHFEhJU69T+xLii/mifcD5Ry/8gT74A33wB/oAAACAriZmAWEoFFJjY6MkqampSaFQ6Jw/9uPThWe7JkmFhYUqLCyM3q6rq/uclfpLOBz+wq9h9JDeKttzVMvX7dLMgkHnubLE8mX6gPOLXvgDffAH+uAPXaUPGRkZXpcAAAAAn4jZEuPc3Fxt375dklRWVqbc3NxPfXxaWpqOHDmio0ePqlu3bme9hrObOuL0MmPnHKYvAQAAAAAAgJhNEGZnZysYDGrevHnKzMxUOBxWSUmJioqKtHLlSi1fvlz19fWqr6/XnDlzNHv2bD344IOSpDvvvFOSzngNZzcio6d6pyXrg/qTqtz/oUYO6uV1SQAAAAAAAPC5mAWEklRcXNzhdlFRkaS2U4xnzJjR4b5hw4ZpwYIFn3kNZ2cahqaO6K9XNtdobeVhAkIAAAAAAAB8ppgtMYY3JuX0k2lI7+z9QMebWrwuBwAAAAAAAD5HQNjF9AwladTg3nJcVxuq3ve6HAAAAAAAAPgcAWEXdGHuqcNKKjisBAAAAAAAAJ+OgLALys3opV6pSTpaf1JVB457XQ4AAAAAAAB8jICwCzJNQ1NGtE0Rvrxxr3bUfiDHYZIQAAAAAAAAnxTTU4zhnSkj+mv1joPad7RBj/15l3qGkjRxeFiTc/or3CPF6/IAAAAAAADgEwSEXVTPUJJ+8PUCbXz3fa2vfF91J5q1smy/VpbtVzBgyjQMmYZkGoaMU/+N00zTlOM4XpcB0Qu/oA/+QB+8cXHeAM0sGOR1GXFvyZIlqq6uVlZWloqLi6PX6+vr9eijj+rEiRPKz89XUVGR9u7dq8WLF0uS5syZo2HDhnlVNgAAQEIgIOzCeoaSNCN/kK4Ym6H3Dp/Q+sr3tXXPEbVG+OESAIBzdbLV9rqEuFddXa3m5mbNnz9fixcvVlVVlXJyciRJTz/9tG655RYNGnQ6hH3qqad09913yzRN/cd//Ifuvfder0oHAABICASECcAwDGWn91B2eg/ddHG2bNuR7bpyXclxXDmuK3Yo7KhPnz46evSo12VA9MIv6IM/0AdvJAfYsvnLqqysVEFBgSQpPz9fFRUV0YCwpqZGzz33nI4cOaJvfOMbys3NVUNDg8LhsCSpoaHhjM9ZWlqq0tJSSdLChQujj8f5FQgEeG89Rg+8Rw+8xfvvPXrgvc7oAQFhgrFMQ5ZpeV2G7/VOS5HdnOR1GRC98Av64A/0AfGqoaFB6enpkqRQKKTa2trofbt27dIvfvELpaWl6de//rUWLFgg1/3sX10WFhaqsLAweruuru78Fw6Fw2HeW4/RA+/RA2/x/nuPHnjvfPYgIyPjjNcJCAEAABBToVBIjY2NkqSmpiaFQqHofRkZGRo8eLCktn02P84w2CgZAAAg1lgzAwAAgJjKzc3V9u3bJUllZWXKzc2N3jdw4EB98MEHam5ulm237feYlpamI0eO6OjRo+rWrZsnNQMAACQSJggBAAAQU9nZ2QoGg5o3b54yMzMVDodVUlKioqIizZ49W4sWLVJLS4tuuukmSdLs2bP14IMPSpLuvPNODysHAABIDASEAAAAiLni4uIOt4uKiiRJgwcP1o9//OMO9w0bNkwLFizorNIAAAASHkuMAQAAAAAAgARGQAgAAAAAAAAkMAJCAAAAAAAAIIEREAIAAAAAAAAJjIAQAAAAAAAASGAEhAAAAAAAAEACIyAEAAAAAAAAEhgBIQAAAAAAAJDACAgBAAAAAACABEZACAAAAAAAACQwAkIAAAAAAAAggREQAgAAAAAAAAmMgBAAAAAAAABIYASEAAAAAAAAQAIjIAQAAAAAAAASGAEhAAAAAAAAkMAICAEAAAAAAIAERkAIAAAAAAAAJDACQgAAAAAAACCBERACAAAAAAAACYyAEAAAAAAAAEhgBIQAAAAAAABAAiMgBAAAAAAAABIYASEAAAAAAACQwAgIAQAAAAAAgARmuK7rel0EAAAAAAAAAG8wQegz9913n9clQPTBT+iFP9AHf6AP/kAfkEj4++49euA9euAt3n/v0QPvdUYPCAgBAAAAAACABEZACAAAAAAAACQwAkKfKSws9LoEiD74Cb3wB/rgD/TBH+gDEgl/371HD7xHD7zF++89euC9zugBh5QAAAAAAAAACYwJQgAAAAAAACCBERACAAAAAAAACSzgdQE4bcmSJaqurlZWVpaKi4u9LiehVFZW6j//8z9lGIaGDx+uv/mbv9ELL7yg9evXq1+/fvrOd76jQIBPl87y4osvau3atVqwYAGfFx55/fXX9frrr8txHN1111164YUX6IMHTp48qQceeEAnT55UKBTS97//fS1dupRedJKjR4/qF7/4hWpra/X444/Lsqwzfk3i6xS6io9/7e/Tp48kadu2bXrqqaeUlJSkOXPmaNCgQR5X2jVt2bJFzz//vCRp//79mjNnjqZMmSKp7evRQw89pNbWVs2ePVsFBQUeVtp1fVoPVq5cqWeffVYjR47UXXfd5WGVXdun9eDpp5/Wli1bJEm33nqr8vPzPaqy6/q09//555/X5s2b1dLSohtuuCF6HefXp/VAklzX1b333qtrrrlGM2fOPL9/uAtfePfdd91HHnnEdV3XffTRR93KykqPK0osH3zwgXvy5EnXdV130aJF7jvvvOP+y7/8i+u6rvvcc8+5b731lpflJZSWlhb3oYcecv/5n/+ZzwuPHDlyxP23f/u36G364J01a9a4Tz/9tOu6rvvss8+6y5Ytoxed6OTJk+6JEyfc+++/341EImf8XODzA13Fx7/2f9SPfvQjt6mpyT169Kj7wAMPdHJliel//+//7TY1NUVv/+53v3N37NjhNjU1uffff793hSWQj/fgww8/dA8cOOAuWrTIw6oSy8d7cOjQIdd1Xbe+vt6dN2+eV2UljI+//62tra7rum5TU5P7f/7P//GqrITy8R64ruuuX7/enT9/vltaWnre/zyWGPtEZWVl9DeB+fn5qqio8LiixNKrVy8lJSVJkizLUk1NjUaPHi1JKigooB+daOXKlbr88ssl8XnhlS1btshxHM2fP1+PPfaYKioq6INH0tPT1dzcLElqaGiQYRj0ohMlJSUpLS0tevtMX5P4OoWu4uNf+x3H6XB/SkqKevfurUOHDnlUYeI4dOiQevbsqZSUlOi1mpoajRw5UikpKUpJSVFjY6OHFXZ9Z+pBjx49ZJr8+NxZztSD/v37S5KCwaBXZSWMM73/7SvqWlpaNGTIEK9KSxhn6oEkrV69WpdccklM/ky+wvlEQ0ODQqGQJCkUCvGPvkf27Nmj48ePKzU1Vd26dZPU1o+GhgaPK0sMkUhE77zzjsaOHSuJzwuvfPjhh4pEIpo3b56SkpLU2NhIHzwycOBAVVZW6gc/+IGqq6tlmia98NCZvibxdQpdxce/9q9fv77D/ceOHdO+ffu0b98+jypMHGvXrv3E0j3HcWQYhiS+1nSGM/UAnevTerBs2TJdeeWVnVxRYjnb+/8f//Efuueee6I/ryF2ztSDrVu3avTo0TH7ZQUBoU989B/6pqam6A8b6Dz19fV67LHH9O1vf1uhUEhNTU2SpMbGRqWmpnpcXWJ44403NG3atOhtPi+8EQqFohO07f/40wdvvP7665o4caIeeOABjR8/XrZt0wsPnelrEl+n0FV8/Gv/R4PA22+/XYsWLdLzzz+vkSNHelViwti4caMmTZrU4Vp7OCjxtaYznKkH6Fxn68G6detUX1/f4WcGnH9ne//nzJmjBx98UCUlJR5UlVjO1IM///nP0dV2sUBA6BO5ubnavn27JKmsrEy5ubkeV5RYbNvWQw89pDvuuEO9evXS8OHDVV5eLqmtHyNGjPC4wsSwf/9+rVixQj/72c9UW1urEydO8HnhgZEjR2rPnj2SpN27d0sSffCI67rRJa49evSQRC+8dKZ/q/n3G13Fx7/2ty/lk9r+7t9///0qKirigJIYO3bsmAKBgLp3797h+tChQ1VRUaHm5mYCwhg7Ww/Qec7Wgz179mj58uW68847PaosMZzt/W9tbZXUtgVL+2o7xMbZenDgwAH96le/0p/+9Ce9/PLL532q33Bd1z2vz4gv7Pe//73ee+89ZWZm6lvf+pbX5SSU1atX6/e//310L4W/+qu/Unl5uTZu3KhwOKx/+Id/4BTjTvajH/1ICxYs4PPCI48//riqq6vVvXt33X333fqv//ov+uCBhoYGPfjgg2ptbZVlWfr+97+vp59+ml50kkgkop///OfRE4q/8Y1vaPXq1Z94//k6ha7io1/7//qv/1pvvPGGioqKVFJSorKyMqWlpWnu3LkEJzG0YsUK2bata665RpL02GOP6Vvf+paOHDmihx9+WC0tLZo9e7bGjRvncaVd19l6sHHjRj3//PM6dOiQcnNzdc8993hcadd1th787Gc/09GjR9W9e3eFQiHde++9HlfaNZ3t/X/00Ue1f/9+RSIRfe1rX9PUqVM9rrTrOlsP2q1atUq2bZ/3U4wJCAEAAAAAAIAExhJjAAAAAAAAIIEREAIAAAAAAAAJjIAQAAAAAAAASGAEhAAAAAAAAEACIyAEAAAAAAAAEhgBIYCEdPjwYc2ePVsLFy7Upk2btGzZMh0+fPi8/zm1tbVatmyZ3nnnnei13/72t5o9e7befffd8/7nAQAAAADweQW8LgAAvNCjRw/dfffd6tOnj9566y0tX75cY8aMUf/+/T/X89i2Lcuyznp/bW2tnnnmGUnSmDFjJElXXXWVLrjgAqWnp3/xFwAAAAAAwHliuK7rel0EAHS2w4cP67vf/a6Sk5N18uTJDvctW7ZMFRUV+s///E/t3btXffr00c0336xp06ZFPy43N1fJycnau3evfv3rX+unP/2pDhw4IEnKysrS3/7t3yo5OVnf/e53Ozz3/fffr1WrVun111/Xz3/+cw0fPlylpaV64YUX9MEHH2jw4MH667/+a+Xl5WnVqlX6t3/7N1188cXat2+f6urqdPPNN2vWrFnav3+/Hn74Ye3Zs0dJSUkaMmSI5s+f32nvHwAAADp64IEH1LNnT+3evVtHjhzRXXfdpRUrVqiqqkp5eXn69re/7XWJAHBWLDEGkNBGjx6tcePGSZJuvPFG3X333aqvr9fChQvV2NiooqIi9evXTw899JB2794d/biKigplZWXplltukWEYmjJlioqLi3X99ddrz549WrJkiXr06KFZs2ZJkqZOnaq7775bgwcP7vDnb9++XY8++qh69Oihb37zm6qrq9MvfvELnThxIvqYd955RzNnzpQkLV26VJFIRMuXL9e7776r22+/Xd/4xjcUDodj/E4BAADg0+zdu1fp6elasGCBCgsL9cgjj+j222/XAw88oE2bNqm1tdXrEgHgrFhiDCChGYahAQMGaOvWrRo7dqzGjBmjTZs2qb6+XvX19frDH/4Qfez27ds1ZcoUSW1Tgrfffrsk6ejRo9q6dasqKirUPpS9d+9epaSkKC8vTy+//LKGDBmiSy655BN//qZNmyRJs2fPVkFBgerq6vTcc8+psrIy+pgrrrhC11xzjTZu3KitW7fq2LFjGjhwoFzX1ebNmzV8+PBoEAkAAIDO19LSooaGhuj3ZIZhaMaMGerdu7ckyTRNBQL8+A3Av/gKBSDhGYZxxuvTp0/X9OnTo7c/uj9h+zd7kvQ///M/2rVrl7761a9q/PjxeuSRR9TU1HTeaklLS5Ok6F6HjuPommuu0aBBg1ReXq4NGzaopKRE//qv/6qMjIwv9OcCAADgi6utrVV2drZMs22R3p49e3TVVVdJko4cOaI+ffqc9XtOAPADlhgDSHipqamSpDVr1mjTpk3Kzc1VWlqatm7dqv3796umpkZ//OMfdfTo0U99noaGBpWXl+vIkSPRa+3h3s6dO/Xmm2+qpaWlw8dMmDBBkvT0009rxYoVWrlypVJTUzVixIhP/bNeffVVVVRUaMCAAUpPT5frujp27NjnfekAAAA4D/bu3athw4ZFb+/Zs0dDhw79xH8DgF8REAJIeJdeeqkGDRqkV199Vb///e+Vlpam++67TwMGDNDSpUtVUlKipKQk9evX74wf/5WvfEXDhw/XW2+9paNHj2rIkCHR+/Ly8pSfn68dO3Zo0aJFHfYWlKSxY8dq7ty5+vDDD/X444+rb9+++l//63+pe/fun1pzMBjUqlWr9O///u/asWOHrr76auXl5X35NwMAAACf2969e5WZmSmpbblxS0tL9BfFe/bs6RAeAoAfcYoxAAAAAAAAkMCYIAQAAAAAAAASGAEhAAAAAAAAkMAICAEAAAAAAIAERkAIAAAAAAAAJDACQgAAAAAAACCBERACAAAAAAAACYyAEAAAAAAAAEhg/z9iUMn6CUl1SQAAAABJRU5ErkJggg==",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"\n",
"plot_all(cost_history, m, q)"
]
},
{
"cell_type": "code",
"execution_count": 325,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"3 passi e 300 gradienti calcolati per arrivare a distanza minore o uguale di 0.1 dall'ottimo\n"
]
}
],
"source": [
"near_opt(m, min_dist=1e-1, ge_per_step=n)"
]
},
{
"cell_type": "code",
"execution_count": 322,
"metadata": {},
"outputs": [],
"source": [
"def newton(X,t, epochs = 100):\n",
" theta = np.zeros(nfeatures+1).reshape(-1,1)\n",
" theta_history = []\n",
" cost_history = []\n",
" for k in range(epochs): \n",
" g = gradient(theta,X,t)\n",
" c1 = sigma(theta,X)\n",
" c2 = c1*(1-c1)\n",
" h0=np.einsum('ij,ik->ijk',X,X)\n",
" h=np.einsum('ijk, iq-> jk',h0,c2)/t.shape[0]\n",
" theta = theta - np.dot(np.linalg.inv(h),g)\n",
" theta_history.append(theta)\n",
" cost_history.append(cost(theta, X, t))\n",
" theta_history = np.array(theta_history).reshape(-1,3)\n",
" cost_history = np.array(cost_history).reshape(-1,1)\n",
" m = -theta_history[:,1]/theta_history[:,2]\n",
" q = -theta_history[:,0]/theta_history[:,2]\n",
" return cost_history, m, q"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3.8",
"language": "python",
"name": "python3.8"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.8.0"
},
"vscode": {
"interpreter": {
"hash": "ce48646bb6368aff8c12a2b8eeb9d1b908c9dd0a6e2925fc70e8d8f5f2053bd1"
}
}
},
"nbformat": 4,
"nbformat_minor": 2
}