{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#  "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Sequenza di plot della distribuzione a posteriori del parametro di una distribuzione di Bernoulli al crescere del numero di osservazioni (lanci di moneta)"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {},
"outputs": [],
"source": [
"#%matplotlib inline\n",
"import numpy as np\n",
"import scipy.stats as stats\n",
"import matplotlib.pyplot as plt"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {},
"outputs": [],
"source": [
"#!pip install xarray\n",
"import xarray"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {},
"outputs": [],
"source": [
"plt.style.use('ggplot')\n",
"\n",
"plt.rcParams['font.family'] = 'sans-serif'\n",
"plt.rcParams['font.serif'] = 'Ubuntu'\n",
"plt.rcParams['font.monospace'] = 'Ubuntu Mono'\n",
"plt.rcParams['font.size'] = 10\n",
"plt.rcParams['axes.labelsize'] = 10\n",
"plt.rcParams['axes.labelweight'] = 'bold'\n",
"plt.rcParams['axes.titlesize'] = 10\n",
"plt.rcParams['xtick.labelsize'] = 8\n",
"plt.rcParams['ytick.labelsize'] = 8\n",
"plt.rcParams['legend.fontsize'] = 10\n",
"plt.rcParams['figure.titlesize'] = 12\n",
"plt.rcParams['image.cmap'] = 'jet'\n",
"plt.rcParams['image.interpolation'] = 'none'\n",
"plt.rcParams['figure.figsize'] = (16, 8)\n",
"plt.rcParams['lines.linewidth'] = 2\n",
"\n",
"colors = ['#008fd5', '#fc4f30', '#e5ae38', '#6d904f', '#8b8b8b', '#810f7c', '#137e6d', '#be0119', '#3b638c', '#af6f09']"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Fissa la probabilità $\\theta$ di esito pari a $1$ e i numeri di osservazioni da considerare"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {},
"outputs": [],
"source": [
"theta_real = 0.26\n",
"n_trials = 1000"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Genera la sequenza casuale di risultati derivanti da lanci ripetuti con probabilità di $1$ pari a $\\theta$"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {},
"outputs": [],
"source": [
"data = stats.bernoulli.rvs(theta_real, size=n_trials)"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0])"
]
},
"execution_count": 18,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"data[:20]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
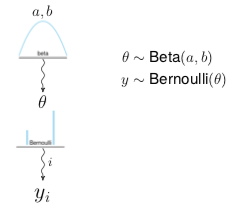
"Fissa la distribuzione a priori del parametro $\\theta$. Si utilizza un modello Beta-Bernoulli, per cui la prior (e di conseguenza la posterior) sono distribuzioni Beta. "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "code",
"execution_count": 34,
"metadata": {},
"outputs": [],
"source": [
"# dichiara la distribuzione prior\n",
"dist = stats.beta\n",
"# valori dei suoi parametri\n",
"alpha = 100\n",
"beta = 100\n",
"hyper = [alpha, beta]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Calcola i valori della densità di probabilità a priori su una griglia ($1$-dimensionale) di punti"
]
},
{
"cell_type": "code",
"execution_count": 35,
"metadata": {},
"outputs": [],
"source": [
"# fissa l'insieme dei valori sui quali calcolare la distribuzione\n",
"nv = 10000\n",
"x = np.linspace(0, 1, nv)\n",
"# calcola i valori di densità di probabilità per tutti i punti dell'insieme\n",
"yp = dist.pdf(x,*hyper)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Plot della distribuzione a priori di $\\theta$"
]
},
{
"cell_type": "code",
"execution_count": 36,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA6EAAAGTCAYAAADZdhSlAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAABFvElEQVR4nO3deXhddYH/8c85525Z7r3ZmtKNQAuyVRCBtsharaOjgrKIQp2BmQcYR0BGxdFBfoiOD+AUFJUBFCggMA5tEakgBQK0bC2UpXvTpk3SfUvTJdu9N/fe8/ujJNOQpM1yc793eb+eJ0BOTs755PJNTj4553yP5bquKwAAAAAA0sA2HQAAAAAAkD8ooQAAAACAtKGEAgAAAADShhIKAAAAAEgbSigAAAAAIG0ooQAAAACAtKGEAgAAAADShhIKAAAAAEgbSigAGPboo4/Ksqyut2AwqFNOOUX33nuv4vH4YT//tttuk2VZaUg6dN/97nf1la98pcfyrVu36sorr1RFRYWCwaC+8Y1vaO/evV0fv+eee/TJT35SyWRy2DM+9NBD3f5/2LatyspKXXTRRaqvrx/UNvfv36/bbrtNq1evHnSuj792mzdv1g033KAzzzxThYWFsixLDQ0NvX7upk2bdOmllyocDisUCuniiy/Wxo0bh7xuX4YjW3/XS+dYAQAMDiUUADLE7NmztXDhQj399NOaNGmSbrjhBv385z8/7OddffXVWrhwYRoSDs369ev1wAMP6Lbbbuu2vL6+XpMmTdL+/fv15JNP6v7779eLL76o66+/vmudf/mXf9GuXbv02GOPDXvODz/8UEVFRVq4cKEWLlyoBQsW6Oabb9bzzz+vf/zHfxzUNt977z397Gc/U0dHx6A+v7fXbt26dZo1a5ZKS0t1zjnn9Pm5bW1t+uxnP6uamho99thjevzxx1VbW6upU6eqtbV10OseSqqzDSRXOscKAGCQXACAUY888ogrya2tre22/Pzzz3dDoVCfnxeJRFKeZTi22en66693Tz/99G7LksmkO3nyZPfLX/6ym0wmu5b/v//3/1yfz+e2t7d3LfvhD3/onnjiicOWr9NnPvMZd8qUKT2Wf+UrX3GLiooGtc277rrL9fv9bkdHx6A+v7fXLpFIdP33gw8+6Epy6+vre3zuPffc49q23W181dXVuY7juHffffeg1z2UVGcbaK50jRUAwOBwJhQAMtQZZ5yh/fv3a+fOnV2X3K5YsUJf+MIXVFxcrMsuu0xS75fjzps3T2eeeaYKCgoUDof1ta99TWvWrOm2zqG2ORCTJ0/WZZddpltvvVUTJkxQIBDQySefrFdeeaVrnWg0qieeeEJXXHFFt8995pln9M477+hXv/pVt6/hyCOPVCwW09atW7uWffOb39SqVav09ttvDzhjf7muq2XLlunkk0/u8bGtW7fquOOO67H+ww8/rEmTJqmwsFBjx47V9773PbW3t3etc8IJJ+imm25SNBqV1+uVZVm65JJLJEkvv/yyvvKVr2jMmDEKBAIaN26cbrrppm5nTPt67Wy7f4fwuXPnasqUKTrmmGO6lh199NE666yz9Oyzzw563UNJdbaB5krHWAEADB4lFAAyVH19vRzHUXFxcdeyr371qzrvvPM0d+5cfe973+v18+bNm6cvf/nLKi4u1lNPPaX7779fK1as0Nlnn60tW7b0WL+3bTY0NMiyrB6Xzn5cPB7XsmXL9Pzzz+vNN9/UPffcoz/96U+Kx+O6+OKLtXv3bknSokWLtHfv3h6XZs6cOVNnnnmmxo8fr3g83vXW0tIiSfJ4PF3rfupTn1IwGNS8efP6zOO6brft9PWWSCR6/fza2lq1tLRo4sSJisfj6ujoUENDg7773e9q9erVuuuuu7qtf/XVV+u6667TtGnT9Oyzz+o//uM/NHPmTH3/+9/vWuePf/yjxo8frwsuuKDrEt9f/epXkqSlS5fqc5/7nB588EG9+OKL+v73v68HHnhAM2bM6Pr8vl67/lq5cqUmTpzYY/lJJ52kVatWDXrdVOjv/gaaqz9jBQBgjufwqwAA0iGRSCgej6u5uVmzZs3Sn//8Z11wwQUqLCzsWue73/2ubrzxxkNu55ZbbtH48eP1wgsvdJW4M888U5/4xCd09913dxWgQ23Tsiw5jnPYM1qrVq1SJBLRueeeq5dfflmO40iSysrKdP755+v111/XRRddpEWLFsmyrG5nGGOxmF577TW1tbXJ6/X22LbX69Xo0aO73rdtW6eccooWLVrUZ54FCxZo6tSph8wsSeedd57mz5/fY/mSJUskHXhNvvvd73YtHzVqlF5++WWdddZZXcv++Mc/aubMmXr66ad18cUXS5I+//nPKxKJ6Oabb9a9994rx3F0yimndE3UM2XKlG77u+mmm7r+O5FI6KyzztL8+fP11ltvdS3v7bUbiKamJpWWlvZYXlZWpj179gx63VTo7/4Gmqs/YwUAYA4lFAAyxPHHH9/137Zta/r06brnnnu6rXPRRRcdchutra364IMPdPPNN3c7i9h56eKCBQt6fE5v26yqqurXzLwffPCBJOn222/vKqAHfy2dZ0K3bt2qUCgkn8/Xtc6qVavU1tam//7v/9akSZO6bfeb3/ymSktLu30NkjRixAitXbu2zzynnXaaFi9efNjcwWCw1+VLliyRZVl688035fP5lEwm1dDQoFtuuUWXX365Vq5c2fW5v/jFL3Tuuefqwgsv7PZanXjiiV2XEo8bN04rV65ULBbTpz/96W77isfjeuKJJ/T73/9etbW1Xa+VpG6XRff22uHwDjdWAADmUEIBIEM888wzGjt2rILBoKqqqhQIBHqsM2rUqENuY8+ePXJdt9f1jjjiCG3YsGHA2zyU999/X6NHj+52hlBS172cY8eOlSRFIhH5/f5u63Q+suPss8/udpZvx44dqq+v1+WXX95jfwUFBd3ut/y44uJifepTnzps7r4eafPhhx9qwoQJ+sxnPtO1bNKkSfJ4PLrkkkv04osv6tJLL1V9fb1qa2tVW1vb61lcSQqHw5IOFHXLsnrkuuKKK/TCCy/o+uuv1y233KKKigpFIhFNnTq126Wnvb12A1FaWtrr2cLezi4OZN1U6O/+BpPrcGMFAGAOJRQAMsTEiRO7TbzSm8M9D7S0tFSWZWn79u09PrZ9+3aVlZUNeJuH8sEHH2jMmDE9lj/11FMqLCzsuo+xvLy823M/JXWdPTz4DKokPf7447IsS1dddVWP7TY1NamioqLPPKm4HPfgAtqp8w8CnaWm897aRx55pNd7FW3bVigUkvR/xbbz/c79zJ49W08++WS3CYfmzJkj13V16qmndi3r7bUbiJNOOkkrV67ssXzVqlU68cQTB71uKvR3f4PJdbixAgAwh4mJACCHFBUV6bTTTtPs2bO7Tb6zYcMGvf322zr//PNTtq9kMqmlS5dqw4YN3S5H3bp1q+677z5df/31KioqknTg8txYLKbNmzd3rXfUUUdJUrdysX37dv3yl7/UtddeqwkTJvTYZ319fY8Zag/WeTnu4d5+//vf9/jcHTt2aPv27b3eezlnzhzZtt1VUDuLt9/v1+mnn97j7eBLb3srShs3bpSkbl9La2urfvKTn0hSt8/v7bUbiAsvvFCLFi1SXV1d17KGhga99dZbuvDCCwe9bir0d3+DyXW4sQIAMMjoA2IAAH0+J/RgP/3pT11JvT5nsvNjnV544QXXtm33i1/8ojt37lz3f/7nf9xjjz3WraiocLds2dKvbTY0NLiO47g/+9nP+sy0cuVKV5I7btw4d/r06W51dbX76KOPuuPHj3fPOOOMbs/4rK+vdyW5Tz/9dNeyZDLpnnDCCe748ePdZ5991p01a5Z73HHHuVOmTHFbW1t77G/Pnj2uZVnugw8+2GemoXjhhRdcSe4vfvELd+HChe7ChQvdZ555xv3Wt77lSnL/4z/+o1v2qVOnuiNGjHDvuece97XXXnOff/55995773W/+tWvdntO5kUXXeRWVVW58+bNcxcuXOg2Nja6GzdudH0+nzt16lT3pZdecv/4xz+6EydOdI8++mi3srKyW67eXrtOs2fPdmfPnu1++9vfdiW59913nzt79mx3/vz5Xeu0tLS4EyZMcCdOnOj+5S9/cZ999ln35JNPdo8++mi3ubm52/b6u25npp/+9Kd9vp6pzDaQr8F1h3+sAACGhhIKAIaluoS67oFCNWXKFDcQCLihUMi98MIL3Zqamn5vsz8l4/HHH3clucuXL3e//OUvuwUFBW5lZaV7/fXXu/v37++x/qRJk9yrrrqq27Kamhr3nHPOcf1+vztmzBj3Rz/6kdvS0tLr/p544gnX7/e7jY2NfWYaijvuuMOV1PVmWZZbUlLifu5zn3PnzJnTY/3Gxkb3hhtucI8++mjX7/e7lZWV7rnnnuv+9re/7bbe8uXL3UmTJrmBQMCV5L7xxhuu6x4oaePHj3cDgYA7ZcoU929/+5v7+c9/3v3CF77QY1+9vXau63bLe/Dbeeed1229DRs2uBdffLEbDAbd4uJi96tf/apbX1/f6+vQn3VXrFjhSnLvv//+Pl/PVGcbyNcw3GMFADA0luu67jCfbAUA5KDvf//7mj17tjZt2tSv9R999FHdeOON2rZtW7fHzvTX3//936uiokKPP/74gD832w31tUu1P/zhD/rJT36iDRs2ZESej8vnsQIA2YB7QgEAg/L+++/rtNNO6/f63/rWtzR69Gjdd999A97XkiVL9Oqrr+qnP/3pgD83FwzltRsOCxYs0Pe+972MLKD5PlYAIBtQQgEAA+a6rpYsWTKgEurxePTII48Mqrhs375djz766GFnD85VQ3nthsOTTz6pm2++2XSMXuX7WAGAbMDluAAAAACAtOFMKAAAAAAgbSihAAAAAIC0oYQCAAAAANKGEgoAAAAASBtKKAAAAAAgbSihAAAAAIC0oYQCAAAAANKGEgoAAAAASBtKKAAAAAAgbSihAAAAAIC0oYQCAAAAANKGEgoAAAAASBtKKAAAAAAgbSihAAAAAIC0oYQCAAAAANKGEgoAAAAASBtKKAAAAAAgbSihAAAAAIC0oYQCAAAAANKGEgoAAAAASBtKKAAAAAAgbSihAAAAAIC0oYQCAAAAANKGEgoAAAAASBtKKAAAAAAgbSihAAAAAIC08Zja8datW03tul8qKirU2NhoOgbyHOMQmYKxiEzAOEQmYBwiU2T6WBw9enSfH+NMKAAAAAAgbSihAAAAAIC0oYQCAAAAANKGEgoAAAAASBtKKAAAAAAgbSihAAAAAIC0oYQCAAAAANKGEgoAAAAASBtKKAAAAAAgbSihAAAAAIC0oYQCAAAAANKGEgoAAAAASBuP6QAAAOSq9iUr1fhf9yu6okZWQUDhy7+m8uuukuXl8AsAyF+cCQUAYBjs/+vL2vadm2WHilVwziT5TvqE9j/zghq+9A9KtLWbjgcAgDGUUAAAUqztnQ/VeMe98p86UXawWE5xkbwjylUw+VQpmdTmy74t13VNxwQAwAhKKAAAKZRsadX2H/z8QAEtLJBlW10fsyxLgdM+qY5tO7Xrjt8ZTAkAgDmUUAAAUqjx7t/Ld8xRsn3ebgW0k2VZKvzMadr72Bx1bNluICEAAGZRQgEASJGOzdvU/LdXZQeLZfm8fa5nFxbIN+FIbfu3n6YxHQAAmYESCgBAijT++g8KfPJ4WQHfYdf1n3CsIktXKbK2Lg3JAADIHJRQAABSIL6zUW2vvyOrMCDLPvzh1fJ45DvmKO28dUYa0gEAkDkooQAApMDeJ/4s33ETZPn8/f4c/3HjFflgueJNe4YxGQAAmYUSCgDAELmxDu17aq7s0rAsp/+HVsvnk6dyhBrv+v0wpgMAILNQQgEAGKKW196Sd/QR/boM9+N8x41Xy4vzeW4oACBvUEIBABii/X9+Qc6IMtmB/l+K28kpL5XbHlHrawuHIRkAAJmHEgoAwBAk9jWr/b1lsnyHnxG3N5ZlyXv0OO2Z+acUJwMAIDNRQgEAGILm51+R75iqfj2WpS/eqrGKLFklNx5PYTIAADITJRQAgCFofr5anrJSWY4z6G04weID23quOlWxAADIWJRQAAAGKdHcomjNerlDKKCdvEeP1b7/nZuCVAAAZDZKKAAAg9S2YJG8VWNkD+FS3E7esaMUXV0rN5FIQTIAADIXJRQAgEFqfnGBnPKhXYrbyQkFlYxG1bbogxQkAwAgc1FCAQAYBLcjrra3F8v2D/0saCfvmFHa96dnU7Y9AAAyESUUAIBBaH9/mTyjRkopOAvayTt2lCJLVqRsewAAZCJKKAAAg9D2xjtyykplB/wp26Yzolzx7bvUsX1nyrYJAECmoYQCADAIra+/I7uoIKXbtBxbTmmJ9j3115RuFwCATEIJBQBggBL7mhXftlOyrZRv2zO6Um1vvpvy7QIAkCkooQAADFDbwvflGXuE7IJAyrftOaJSsXUNcpPJlG8bAIBMQAkFAGCADtwPWpKSR7N8nB0OKtnSqujaupRvGwCATEAJBQBggFrfeEdWYWrvB+1kWZacEWXaP/u5Ydk+AACmUUIBABiA+I5GKZ6QpdTfD9rJO2qk2t9bNmzbBwDAJEooAAAD0L54iZwjRsgqSN2jWT7OGVmhjvqNchOJYdsHAACmUEIBABiAtneXyAmHZNnDdwi1i4uUbIsoWls/bPsAAMAUSigAAAPQ/u6HsvzDdxZU+ui+0IpS7X/2pWHdDwAAJlBCAQDop2RLq+K7dmsYbwft4qmsUOSD5cO/IwAA0szTn5XmzZun+fPna+PGjTrrrLN03XXXdX1s+fLlevjhh9XY2Khjjz1W3/nOdzRixIhhCwwAgCntHyyXZ9RI2UXDMzPuwZwRZYour5HrurKsNLReAADSpF9nQktLS3XxxRdr6tSp3Zbv379fd911l77xjW9o5syZGj9+vO65557hyAkAgHHt7yyRZ5ieD/pxTlmJEk17Fd++c9j3BQBAOvWrhE6ePFmTJk1SMBjstvzdd9/VuHHjdOaZZ8rn8+nrX/+6GhoatGXLlmEJCwCASW2Llwzb80E/zrJt2cEitby4IC37AwAgXfp1OW5fNm3apKqqqq73A4GAjjjiCG3atEljxozptm51dbWqq6slSXfeeacqKiqGsuth5/F4Mj4jch/jEJmCsSi58bjq1jWoaOpZcgKBtOyzY/QRii9eqoqbvpOW/WU6xiEyAeMQmSKbx+KQSmgkElEoFOq2rLCwUJFIpMe606ZN07Rp07reb2xsHMquh11FRUXGZ0TuYxwiUzAWpcjKNbIryhSNd8ju5Tg3LErDalm5Ju9f+06MQ2QCxiEyRaaPxdGjR/f5sSHNjhsIBNTe3t5tWVtbmwJp+gsxAADpElmySnZJSJbfl7Z9OhWliu/YpWR7mkovAABpMKQSOm7cOG3YsKHr/Ugkoh07dmjcuHFDDgYAQCaJLFkpO1iU1plqbb9fbjKp9uWr07ZPAACGW79KaCKRUCwWUzKZVDKZVCwWUyKR0KRJk7Rx40YtWrRIsVhMc+bMUVVVVY/7QQEAyHbtH66Q5fWmfb9Oeala5s1P+34BABgu/bon9Omnn9acOXO63n/jjTd06aWX6rLLLtMPfvADzZw5U7/73e907LHH6sYbbxy2sAAAmJBsa1eiaY8sZ0La9+2pKFN01dq07xcAgOHSrxJ62WWX6bLLLuv1YyeffDLPBgUA5LTIijXyjKyUFUjf/aCdnPJSRWvWy3XdtF4KDADAcBnSPaEAAOSDyJIVckpCsjxDmlR+UJyyEiV2Nym5rznt+wYAYDhQQgEAOIzIkpWyigqM7NvyeGR5PGp790Mj+wcAINUooQAAHEZkySrZfr+x/TsVZWp99S1j+wcAIJUooQAAHEK8aa/cZFKuwQxOeZlia+sMJgAAIHUooQAAHEJ06Sp5KitkF5g7E+qpKFXHpq1yXZNVGACA1KCEAgBwCJGVa+SEimU5jrEMdklIiT37FG/aaywDAACpQgkFAOAQoivWSIGA0QyWbcvy+9X+zgdGcwAAkAqUUAAADiGyoka232s6hpzyErW98a7pGAAADBklFACAPiRbWpWMRI1OStTJKStRrLbBdAwAAIaMEgoAQB8iq2rlGVEu2/DluJLklIbVsWUbkxMBALIeJRQAgD5EV66REwrK8piblKiTUxpWYvceJfe3mI4CAMCQUEIBAOhDdMUaWUWFpmNIkiyvV7Ista+oMR0FAIAhoYQCANCHyIoaWT7zkxJ1cspK1Pba26ZjAAAwJJRQAAB64cY6FN++S7Iz51DplJUoVrPOdAwAAIYkc46sAABkkOi6ejmV5RnxeJZOTmlYsc3bTMcAAGBIKKEAAPQiumKNnHBI8mZQCS0rUWLXbiUjUdNRAAAYNEooAAC9iK5cKztYLMuyTEfpYhcE5EZjitZvNB0FAIBBo4QCANCLTJuUqJNdElLba2+ZjgEAwKBRQgEA+BjXdRVbv0GWx2M6Sg9OWYkiy3hMCwAge1FCAQD4mPjWHbLDQcnOnEtxOzklYXVs3GI6BgAAg0YJBQDgY6I16+SEQ7ICftNRenBKQorvbJTruqajAAAwKJRQAAA+JlqzTnawSFYGPSO0kx0KKrl3vxK795iOAgDAoGTe0RUAAMOiNetlFWTeWVBJshxblter9iUrTUcBAGBQKKEAAHxMtKZWls9nOkaf7NKw2t5cbDoGAACDQgkFAOAgbkdciV1NkjJvUqJOTmlYHesbTMcAAGBQKKEAABwkVr9RTnmJ7Ax8RmgnpySkji3bTccAAGBQKKEAABwkuma97FBQyvASGt+1W26sw3QUAAAGjBIKAMBBYjXrZBcXybIy93Jcq6hQblu7OrbtMB0FAIABo4QCAHCQyOp1svyZOymRJFmWJauoUG1vv2c6CgAAA0YJBQDgILHVtbIzeGbcTk5ZiSLvLzcdAwCAAaOEAgDwkWRbu5KxDrmZeyVuF6ckpNiGzaZjAAAwYJRQAAA+El1bJ09FqeyA33SUw3JKwopzTygAIAtRQgEA+EisZp3sUFCWx2M6ymHZJSEldu9Rsq3ddBQAAAaEEgoAwEeiNetkFxWajtEvtt8nN55QtGGj6SgAAAwIJRQAgI9E16yXlcHPB/04OxRU2+vvmo4BAMCAUEIBAPhIdG29lEUl1CkNKbpyjekYAAAMCCUUAABJ8d17ZPt9yoKJcbs44ZA6Nm01HQMAgAGhhAIAIClWs15OWYmsLJgZt5MdDiq+o9F0DAAABoQSCgCApGhtnexgkSzHMR2l35xwUMk9e5VsaTUdBQCAfqOEAgAgKVZbL7sgYDrGgFg+n9xEUtH6TaajAADQb5RQAAB04EyoPNkzKVEnO1Ss9jcXm44BAEC/UUIBAJAUW79B8mbPpbidnJKQIqvWmo4BAEC/eYa6gZ07d+rhhx/W2rVr5fF4NGXKFF111VVysuieGgBAfkvs2SfL45GVVXPjHuCUhNSxmRlyAQDZY8hnQh9++GGFQiH9/ve/14wZM7Rq1Sq9+OKLqcgGAEBaRNfVyyktkVWQPTPjdrJDIcW375LruqajAADQL0MuoTt37tSZZ54pn8+nkpISfepTn9LmzZtTkQ0AgLSI1TbIDmXXzLid7HBQyT37mCEXAJA1hnw57pe+9CW9/fbbOumkk9Ta2qolS5boG9/4Ro/1qqurVV1dLUm68847VVFRMdRdDyuPx5PxGZH7GIfIFLk+Fps3b1MgHJYvkF2z40qSAgG1JhIq2t+q4qOPMp1mWOX6OER2YBwiU2TzWBxyCT3hhBNUXV2tK6+8UslkUuedd57OOOOMHutNmzZN06ZN63q/sTGzH65dUVGR8RmR+xiHyBS5Phb3LlslOxBQMhIxHWVQrGCxtj73ssrGjDQdZVjl+jhEdmAcIlNk+lgcPXp0nx8b0uW4yWRSt99+uyZPnqzHH39cDz/8sFpbW/Xkk08OZbMAAKRVbG2d5M++x7N0YoZcAEA2GVIJbWlpUWNjo774xS/K6/UqGAzq/PPP14cffpiqfAAADKtka5vcRFKWlX0z43aywyF1bNpmOgYAAP0ypBIaCoVUWVmpl156SYlEQq2trVqwYIGOPPLIVOUDAGBYxdY1yFNWIiuQfTPjdnLCQcV37DQdAwCAfhnyPaE33XSTHn30UT377LOybVsnnXSSrrzyylRkAwBg2EVr62SHirNyZtxOdklQyaa9Sra1yy4sMB0HAIBDGnIJPeqoo3TbbbelIAoAAOkXq23I+uJm+/1yO+KKbdyswPHHmo4DAMAhDfk5oQAAZLPo2jrJO+S/yRpnB4vU9vb7pmMAAHBYlFAAQF6Lra2T5c/e+0E72SVhRZbXmI4BAMBhUUIBAHkrGYkq2dom2dk7M24npySkjo1bTMcAAOCwKKEAgLwVq9sop7xEdhbPjNvJCQeV2JG5Dy0HAKATJRQAkLdi6+plh4KyPDlwT2g4pETTXiUjUdNRAAA4JEooACBvxdbWyy4qNB0jJSy/T240po4t20xHAQDgkCihAIC8FV1XL8vnMx0jJSzLkh0sVNvCD0xHAQDgkCihAIC8FatZlzMlVPpohtwlq0zHAADgkCihAIC85MbjSuzZl1NHQiccUscmZsgFAGS2HDr0AgDQfx0bNsspK5Htz50zoU44qPj2naZjAABwSJRQAEBeiq6tlx0slrxe01FSxg4Hldi9R25H3HQUAAD6RAkFAOSl2Lp62cVFsizLdJSUsQoCctsj6uBsKAAgg1FCAQB5Kbq2XlYgdy7FlQ7MkGsVFijy3jLTUQAA6BMlFACQl2Jr62T5cudS3E5OaVjt7y01HQMAgD5RQgEAecdNJg9M4GM7pqOknBMOKdawyXQMAAD6RAkFAOSd+JbtssMhWV6P6SgpZ4eDim/jnlAAQOaihAIA8k50bZ2ccFBWDj2epZMTDire2CQ3mTQdBQCAXlFCAQB5J1ZbLzuYWzPjdrKKCuW2tim+e4/pKAAA9IoSCgDIO7HaelmBgOkYw8KyLFkBvyIfrDAdBQCAXlFCAQB5J7q2LifvB+3klITV/u4S0zEAAOgVJRQAkFdc11XHxi1SDpdQuySk2PoG0zEAAOgVJRQAkFcSOxplh4pz8n7QTk44qPjW7aZjAADQK0ooACCvRGvr5IRDsgJ+01GGjR0OKb5rt1zXNR0FAIAeKKEAgLxyYGbcYll27h4C7eJCJZtbldjXbDoKAAA95O4RGACAXkRr62UV5O5ZUEmybFuWz6voqrWmowAA0AMlFACQV2K19bK8XtMxhp0dDqn97fdNxwAAoAdKKAAgr8TqNki+3C+hTklI0TXrTMcAAKAHSigAIG/Em/bK8vtlJXN/wh4nHFLHFmbIBQBkHkooACBvxGrr5ZSV5PTMuJ3scFDxnY2mYwAA0AMlFACQN2K19bKLi2V5HNNRhp0dLFZy734l2yOmowAA0A0lFACQN2K19bKLAqZjpIXl2LI8HkXWrDcdBQCAbiihAIC8Ec2TmXE72aFitS9ihlwAQGahhAIA8kZsXZ6V0NKwostqTMcAAKAbSigAIC8kW1oP/IebNBskjZxwSB2bt5qOAQBAN5RQAEBeiK5rkFNeKsvnMx0lbZxwUPEdzJALAMgslFAAQF44MDNukeT1mI6SNnYoqMSefXI74qajAADQhRIKAMgLB0pooSzLMh0lbSyPI1mWYvWbTEcBAKALJRQAkBdi6+rz6lLcTnawSG2L3jMdAwCALpRQAEBeiK6pk5VHl+J2ckrDinywwnQMAAC6UEIBADkvGYkqGYlIrukk6eeUhNSxcYvpGAAAdKGEAgByXqxuozwVZZLHMR0l7exQUPHtu0zHAACgCyUUAJDzYuvqZRcXy/Ln3z2hTjio+O49cpP583xUAEBmo4QCAHJePs6M28nyeiXXVceWbaajAAAgSUrZDA1vvfWW5syZo8bGRpWUlOg73/mOTjjhhFRtHgCAQYvV1kt+v+kYxtjFhWpf9KF848aYjgIAQGpK6LJly/Tkk0/q3/7t33TMMcdo7969qdgsAAApEa2tl+/4CaZjGOOUhtX+/jKFv/4V01EAAEhNCZ01a5YuvfRSfeITn5AklZWVpWKzAAAMmRuPK7F7j5SHl+J2ckpCitVtNB0DAABJKSihyWRS69ev1+mnn64bbrhBHR0dOuOMM/QP//AP8h30UPDq6mpVV1dLku68805VVFQMddfDyuPxZHxG5D7GITJFNo/F9to6+UeOUCAQkBMImI5jhD2iQu0167L2/2GnbB6HyB2MQ2SKbB6LQy6he/fuVSKR0KJFi/Tzn/9cjuNoxowZevrpp3X55Zd3rTdt2jRNmzat6/3Gxsah7npYVVRUZHxG5D7GITJFNo/F5nc/kFtUoJglWZGI6ThGJAN+xXY0ateuXVk9OVM2j0PkDsYhMkWmj8XRo0f3+bEhz47bebbzi1/8okpLSxUKhfTlL39ZH3744VA3DQDAkMVq62UXFcqy83dCeNvvO3BZ8s7M/WUFAJA/hnxELi4uVnl5ebe/rGbzX1kBALklVlsvK08vwz2YXVSgtveWmY4BAEBqnhN6/vnna968edq3b59aWlr0/PPP69Of/nQqNg0AwJBE19ZJXsd0DOPskrDa3vnAdAwAAFIzO+4ll1yi5uZm3XjjjfJ6vTrzzDN18cUXp2LTAAAMmptMKr51h7wTqkxHMc4pDSu2rsF0DAAAUlNCPR6Prr76al199dWp2BwAACkR37ZTdmlY3CQiOeGgOho2m44BAEBqLscFACATxdbWyQkHuSdUkh0KKt7YJNd1TUcBAOQ5SigAIGdF19XLLi6S5XC4swJ+uZGoEnv3mY4CAMhzHJUBADkrtrZedgFnQaUDM9dbhQWKvL/cdBQAQJ6jhAIAcla0tl7ypGT6g5zglITUtpAZcgEAZlFCAQA5yXVddWzYJHl4PEsnuyR84JE1AAAYRAkFAOSkRGOT7MJCWUzE08UpCSq+dbvpGACAPEcJBQDkpOjaOjllYVncE9rFCYcU37XbdAwAQJ6jhAIAclJszXrZwWJZDpfjdrIKAnJb25XY32w6CgAgj1FCAQA5KbpmvayCAtMxMsqBGXIDal+60nQUAEAeo4QCAHJSdG2dLC8z436cEw6q/a33TMcAAOQxSigAIOe4rquO+k2S12s6SsaxS8KK1qw3HQMAkMcooQCAnBPfvkt2qFiWmzQdJeM4JSF1bGGGXACAOZRQAEDOia1ZL6e0RFbAbzpKxnHCQSWYIRcAYBAlFACQc6Jr18sOFjEzbi+sokIlm1uVaG4xHQUAkKcooQCAnBNds142zwftlWVZsgI+RZatNh0FAJCnKKEAgJwTW1Mni0mJ+uSEQ2pjhlwAgCGUUABATnGTSXVs2irX4RDXF7s0pOiadaZjAADyFEdoAEBOiW/ZLqesRFbSNR0lYznhkOLMkAsAMIQSCgDIKdG1dbLDIVncE9onOxxUfGejXJeiDgBIP0ooACCnRGvWfTQzLoe4vtjFRUrub1FiX7PpKACAPMQRGgCQU2Jr65gZ9zAs25bl9Sq6eq3pKACAPEQJBQDklGjNesnjMR0j49klIbW+8a7pGACAPEQJBQDkDDeRUHz7Tsnm8HY4TklIsTV1pmMAAPIQR2kAQM7o2LBFTnmpLMt0ksxnh4OKb9lmOgYAIA9RQgEAOSO6tk5OSUhWwG86SsZzSkKK79zNDLkAgLSjhAIAckZszTpZxYWyuBz3sOxgsZL7mxVv2ms6CgAgz3CUBgDkjOjaOll+zoL2h2Xbsvw+RT5YbjoKACDPUEIBADkjuqpWFjPj9ptTWqI2ZsgFAKQZJRQAkBOS0ZgSe/fLchzTUbKGUxZWbH2D6RgAgDxDCQUA5ITYunp5KiskD4e2/rJLwurYzAy5AID04kgNAMgJ0VW1ssPFsnw+01GyhlMSUqKxSW48bjoKACCPUEIBADkhurpWdnGRLB4S2m92QUBuNMbZUABAWlFCAQA5Ibq6lplxB8EOFav19XdMxwAA5BFKKAAg67muq+iaOlkeJiUaKKesRO3vLzMdAwCQRyihAICsl9i1W3ZhgdykazpK1nFKw+po2Gw6BgAgj1BCAQBZL7p6nZzyUtkBJiUaKKckrPi2HaZjAADyCCUUAJD1oqvWyg4Vy/J4TEfJOnY4qMSefUq2tJqOAgDIE5RQAEDWi66ulV0QMB0jK1mOIzmO2pevNh0FAJAnKKEAgKwXWVUreTkLOlhOaZgZcgEAaUMJBQBkNTfWocTuPZJ4PuhgOWUliq1eZzoGACBPUEIBAFktuq5BnspyWQ6HtMFySkLq2LTVdAwAQJ7giA0AyGrR1bWyQ0FZAb/pKFnLKQ0rvqtRbjxuOgoAIA+krIRu27ZN06dP129/+9tUbRIAgMOKrqqVXVwky+Jy3MGyCgvktkbUsXWn6SgAgDyQshL68MMPa8KECanaHAAA/RJdXSvL6zUdI6tZliU7VKS21xeZjgIAyAMpKaFvvfWWCgsLNXHixFRsDgCAfnFdV9E162T5mRl3qJyyUrW986HpGACAPDDkEtrW1qZZs2bpyiuvTEUeAAD6LbGjUXZhgZQ0nST7OeUlitVvNB0DAJAHhvyn46eeekpTp05VeXn5Iderrq5WdXW1JOnOO+9URUXFUHc9rDweT8ZnRO5jHCJTZOpYbHp3qQJHVKqgNCzLcUzHyWqeI0Zq/8L3VF5enrH312bqOER+YRwiU2TzWBxSCW1oaNDy5cv1X//1X4ddd9q0aZo2bVrX+42NjUPZ9bCrqKjI+IzIfYxDZIpMHYuNb72rZGFA0Y4OqaPDdJys5vq9iu/Zpx1ra+UpLzMdp1eZOg6RXxiHyBSZPhZHjx7d58eGVEJXrlypXbt26V//9V8lSZFIRMlkUj/60Y/0y1/+ciibBgDgsKIramQVFJiOkRMs25ZVEFDr2+8rfMHnTccBAOSwIZXQadOm6ayzzup6f+7cudq1a5euueaaIQcDAOBwIivWqGDSp0zHyBlOeana33yXEgoAGFZDKqF+v19+//89HDwQCMjr9SoUCg05GAAAhxJv2ivZtuS6pqPkDE95iaK19aZjAAByXErntL/ssstSuTkAAPoUXVEjT2WFLL/PdJSc4ZSWKLK8xnQMAECOS8lzQgEASLfI8hrZ4WJZHp4Rmip2SUiJ3XuUaG4xHQUAkMMooQCArBRdsUY2kxKllOU4snw+tX+wwnQUAEAOo4QCALJSZHmNLC9nQVPNKS9R66tvmo4BAMhhlFAAQNZJNLfIjcYk5iRKOae8VLGadaZjAAByGCUUAJB1oivXynNEhSy/13SUnOOUhhXbtM10DABADqOEAgCyTmRFjexQUJaXEppqTmlYicYmJVvbTEcBAOQoSigAIOtEl62WXcikRMPB8nol21b7kpWmowAAchQlFACQddqXrJR8nAUdLp6KUrW8tMB0DABAjqKEAgCySmJfs9xoTJYs01FyllNRruiqWtMxAAA5ihIKAMgqkWWr5Bk5QpbfZzpKznIqStWxcYvpGACAHEUJBQBklciSlXJKQjwjdBg5JSEldu9RfF+z6SgAgBxECQUAZJXIkpVMSjTMLMeRVRBQ29uLTUcBAOQgSigAIGu4rqvIstWS1zEdJec5FWVqfeVN0zEAADmIEgoAyBrxbTtlFRRIrukkuc9TUabYmjrTMQAAOYgSCgDIGpElK+UZUS4r4DcdJec5FaXq2LxVrkvjBwCkFiUUAJA1IktWyg4Xy3K4HHe42cFiJfe3Kr5tp+koAIAcQwkFAGSN9iUrZfk5C5oOlmXJDherpfoN01EAADmGEgoAyApuMqnY2jrJw1nQdHFGlKvtLWbIBQCkFiUUAJAVYusa5FSUyTIdJI94yksVW99gOgYAIMdQQgEAWaH9vWVyyktlFQRMR8kbTkWZ4lt3yI11mI4CAMghlFAAQFZof2/pgUmJLM6FpotdEJCbSKh9ZY3pKACAHEIJBQBkhfbFS2X5fKZj5B1PRbma575sOgYAIIdQQgEAGS/e2CQ3EZfFIyvTzjOyQtGlq03HAADkEEooACDjtb+3TN5RI2UFOBOabs6IcsUaNsl1+QsAACA1KKEAgIzX/t5S2SUhWR6P6Sh5xw4HldzfrPj2naajAAByBCUUAJDx2t9bKsvvNx0jL1mWJbskpObnqk1HAQDkCEooACCjJSNRdWzcKsvmkGWKZ2SFWt9cbDoGACBHcEQHAGS0yPLV8oweKXk4ZJniGVGhjvUNpmMAAHIER3QAQEZrX7xUTkmIx7MY5JSXKL6jUYnmFtNRAAA5gBIKAMho7YuXyC4qkmVZpqPkLcvjkRXwq+W1haajAAByACUUAJCx3ERCkSWrZPm8pqPkPc8RI9Qy7zXTMQAAOYASCgDIWNGVa+U5YoQknlFpmmfkCMVW15qOAQDIAZRQAEDGanv7PTnlpbIKAqaj5D1PZbk6tmxXoq3ddBQAQJajhAIAMlbbwvflhILcD5oBLK9Xlt+n1tfeNh0FAJDlKKEAgIzkxuOKLK+RPI7pKPiI54hKtTxXbToGACDLUUIBABkpsmKNPKMqJZf7QTOFZ9QIRVatNR0DAJDlKKEAgIzU9vZ7cspKuB80g3hGlCu+dQf3hQIAhoQSCgDISO0L35ddzPNBM4nl8cguCKjlxQWmowAAshglFACQcdyOuCIr10gOh6lM44weqZa/vWI6BgAgi3F0BwBknPb3l8k7ZpQsh0mJMo135AhFV/G8UADA4FFCAQAZp3XBQjkVZbIDftNR8DHOiDLFd+xSfFeT6SgAgCxFCQUAZJzW+YtkFRWajoFeWI4juzSsfXOeMx0FAJClKKEAgIwSb2xSYu8+WeLRLJnKO+YItb7ypukYAIAs5RnqBjo6OvTQQw9p+fLlamlp0ciRI3XFFVfo1FNPTUU+AECeaXv9HXmPHC3L7zMdBX3wjj5CrW++K9d1mb0YADBgQz4TmkgkVF5erttuu02PPvqovvnNb+rXv/61du7cmYp8AIA807pgoZySElmeIf+dFMPEDhbJjcXU/uEK01EAAFloyCU0EAjosssuU2VlpWzb1mmnnabKykrV1dWlIh8AII+4yaTa3n5Pls9rOgoOwztqpPb9z19MxwAAZKGU/5l579692rZtm8aNG9dteXV1taqrqyVJd955pyoqKlK965TyeDwZnxG5j3GITJGusdiydKV8Iyrk9/vkBALDvj8MnnX0kYouXZnWn1H8TEQmYBwiU2TzWLRc103ZzA/xeFx33HGHRo4cqWuvvfaQ627dujVVux0WFRUVamxsNB0DeY5xiEyRrrHYeM9Dav9guTxHjOBewwznxuNqnvuyJrz3NznhUFr2yc9EZALGITJFpo/F0aNH9/mxlM2Om0wmde+998rj8eif//mfU7VZAEAeaXlxgexwkAKaBSyPR3YoqH1P/dV0FABAlklJCXVdVw888ID27dunH/zgB/IwmQQAYIA6tu5QsrlF1M/s4a0ao+YXXjUdAwCQZVJSQh988EFt2bJFP/rRj+TzMaU+AGDgWl5+Xd6qsTyaJYt4x45SbPU6JTs6TEcBAGSRIZ+y3LVrl6qrq+X1enXNNdd0Lb/22mt1zjnnDHXzAIA80fLSAjklIVmOYzoK+skuCEg+r5pfmK/whZ83HQcAkCWGXEJHjBihWbNmpSILACBPJfa3KLZmvQJnnmY6CgbIWzVG+2fNpYQCAPotZRMTAQAwWK3z35b36CNle3k+aLbxjh2tyLLVSuFk+wCAHEcJBQAY1/xctZyyElleJrbLNk6oWIrH1fb2YtNRAABZghIKADAq2dKqyAcrZDGxXdbyHDlGex5+ynQMAECWoIQCAIxqeel1+SZUyfIyIVG28h01TpH3l3FJLgCgXyihAACj9s99SXZ5mSzuB81aTjgoN55Q66tvmY4CAMgClFAAgDGJPfsUXbVWcizTUTBE3qPHac/M/zUdAwCQBSihAABjmue9Ju+EKtk+zoJmO9/R4xT5cIWS8bjpKACADEcJBQAYs//pv8kpDcvyMCtutrMLC2R5vWp+Zp7pKACADEcJBQAYEavfpPjORslhQqJc4Z1Qpb1PPG06BgAgw1FCAQBG7Jv9V/mOOUp2wG86ClLEd9RYRVfXKr53n+koAIAMRgkFAKSdm0ho/59fkB0qlmVzKMoVltcrZ0SFdt/zsOkoAIAMxpEfAJB2ba+/I88RlVKS50rmGv9x49Xyt1dMxwAAZDBKKAAg7fY++Yw8I0fILgiYjoIUcyrKlGxpVeub75qOAgDIUJRQAEBadWzeduDZoH4ey5KLLMuSd8JR2v0bLskFAPSOEgoASKu9j82W74RjZPt8pqNgmPgnVCmydJXijU2mowAAMhAlFACQNsn2iPY/+6Ls4iJZDoegXGX5ffKOHqldt//OdBQAQAbiNwAAQNrsf2aefMccLVmmk2C4+U48Vi0vzlcyHjcdBQCQYSihAIC0cBMJ7fnDk3LKS2T7eTZornOCxbILC9V032OmowAAMgwlFACQFi0vvCanvFTiuaB5wz/xE9r7xzlKJpOmowAAMgi/CQAAhp3rutr924flGTNSdoCzoPnCU1khxRPa98SfTUcBAGQQSigAYNi1vvKmrMICcTNo/vGfcqJ2/3YmZ0MBAF0ooQCAYeUmk2q86wF5x46SXcBZ0HzjPWKElIhzNhQA0IUSCgAYVs1/OfBIFu4FzV/+U07U7nse4mwoAEASJRQAMIySkagaf/V7ecaMkl0QMB0HhnhHjpDlcbT7V38wHQUAkAEooQCAYbP30VnyHjVOkms6CgwLnH6y9j78JyX2N5uOAgAwjBIKABgWHVu3a88jT8kpK2FGXMgJFssZNVLbb/pP01EAAIZRQgEAw2LnrXer4LSTZXk9pqMgQxSccqJaFyxS+4crTEcBABhECQUApFzLSwvUsWWb5HFkeSihOMDyeRX49ERt/faP5TJJEQDkLUooACCl4o1N2vnTu+U79mhZXIaLj/EdOUayLe346d2mowAADKGEAgBSxnVdbb/pPxU4daIsx5FlWaYjIQMVTDpVzbP/qrb3lpmOAgAwgBIKAEiZvY/OUmLffsnrkeXzmo6DDGUH/Aqc8Slt/efvK9HcYjoOACDNKKEAgJRoe/s97Xn4f+UdN4bZcHFY3tEj5RlVqc3Tr5fr8ggfAMgnlFAAwJB1bNqq7T/4uQKnnyzLzxlQ9I//lBMV376Lx7YAQJ6hhAIAhiS+a7c2/8ONCpx+iizbkmVzaEH/WJalwnMmqfXl17X7vsdMxwEApAm/KQAABi2xd782f+sG+T95vCzHluXlLCgGxvJ4VHD+mWr670e157HZpuMAANKAEgoAGJT49l3a+PV/kXfCUQfOgPp9piMhSzkFARVOPUuN/3W/mmb+r+k4AIBhRgkFAAxYbH2DNl72L/KfcKxsr5fngWLInKICFU79jHb/+kHt+PmvmawIAHIYJRQAMCDNz7+iTdNvUOBTJ0m2JSvAGVCkhlNUoKJp56jl+Ve0efoNSra2mY4EABgGlFAAQL8kW9u04ye/VOOvH1TB5FNleT2yuQQXKWb7vCo8b4oSjU2qO+citS1eYjoSACDFKKEAgENyXVdNL7yqhi9coY6djfKfcKwsv0+Wx2M6GnKUZVkKnHqSAhOP15Z//oG2/eDnSuzdbzoWACBF+A0CANCn9veXa9cdv5PTEVfBpz8p17Y5+4m08YyqVFHFuYquXKu6cy5Sx03/Kt+lX5JdVGg6GgBgCCihAIBu3HhcLfPma8/D/6tEc4v8x0+Qv6BAMUuyLct0POQZ2+tR4JQT5D1qjHb96RlF7rpfJdMvUsm3LpF37CjT8QAAg0AJBQDI7Yir7d0P1fzXl9X6ypvyVo2VZ+woOXJlFQTkFBTIikRMx0Qec8IhFU3+tOydu9T6xrva979z5a0aq9BlX1Hx1LPkHT3SdEQAQD+lpIS2tLTo/vvv17JlyxQMBnXFFVfo7LPPTsWmAQDDILFnr6Kr16n9gxVqW/i+oqvWyjt2lDyjKlXwmdMlSTaPXUEGckJBOROPU/KEY5TYulP7nnxGu3/1B9nFRSo6d7IKTv2kAqdOlPeosbI4cw8AGSklJfShhx6Sx+PRgw8+qIaGBt1xxx2qqqrSuHHjUrF5AMAAuLEOJfbtV2JfsxK79yi+Zbs6tm5Xx+Zt6ti0VbHaeslx5Kkokx0Oyg4HVXj2JMm2KJ7IGrbjyB43St5xo+SeeKwSTfsUXVOn9g9XKrF7j5ItrfKMrJD/2KPlG3+UPKMq5RlZIWdEuTyVFXLKShjvAGDIkEtoJBLRO++8o7vvvluBQEDHH3+8Tj/9dL3++uuaPn16KjKmXeub76q9pk5tba2HXnEAD9Lu96oDeTh3f9cd0DZTvO8BbHRADybv99fe/00Oz+s5tK+9pbBQbW0fe05ev3dveiyl/v9Rv8eI6e+jVO9bkptMyo11yI1G5UYP/DsZi8mNROVGD/w72dIqtyMuObbswsIDM9j6fbKLCmUVBmR7vbKLC1Uw6dOSkrJ8Xlleb+q/LiDNLMeRZ0SZNKJM0oHvl2R7RG4kqkRLm9reWyo3Hj/wvdIekdvWrmR7REokJUuyCgKyi4sOvAX8B753vN6Pvkc8B75PfF5ZHo8s25ZsS7L+782yLMm2P3pfB9bRRx+3D17P7OvUb9kS1FDO9sKiw/+OCKRBxc/+3XSEQRtyCd22bZscx9Ho0aO7llVVVWnVqlXd1quurlZ1dbUk6c4771RFRcVQdz1sfJWV2jbrOUW37Ujxlvv5w3I4fqaaPqD0c/8DStnvlYfhax+eoD202JbcZC9FZTi+9mF5mYZjzBv8PkrV69ln93QP+pfbfT03KctxZFm2LNuSvF7J55cVDh/4JdnjOfDLs8c5sJ7PJzvgl10Q+OgX4qGxbFu+ZHLI2wGGIlXjMBmNKtkeUTIaU7IjLnXElYxG5cY+ej+ekJtISG1xyXXlJiXLTSrpfvR9aanrj0id/7QO+n51u30PH/RvpI7BlzNmWQP7wzkwTBI7G1VRmbmd6lBScia0oKCg27LCwkJFPjaBxbRp0zRt2rSu9xsbG4e66+HziaN03P/cl9kZkRcqKioYh8gIjEVkAsYhMgHjEJnCyfCxePBJyo8b8p/HA4GA2tvbuy1rb29XIBAY6qYBAAAAADlmyCV01KhRSiQS2rZtW9eyDRs2MCkRAAAAAKCHlJwJnTx5sp566ilFIhHV1NRo8eLFOvfcc1ORDwAAAACQQ4Y+W4Wkq6++WrFYTNdcc41+85vf6JprruFMKAAAAACgh5Q8J7S4uFj//u/ZO0UwAAAAACA9UnImFAAAAACA/qCEAgAAAADShhIKAAAAAEgbSigAAAAAIG0ooQAAAACAtKGEAgAAAADShhIKAAAAAEgbSigAAAAAIG0s13Vd0yEAAAAAAPmBM6F9+PGPf2w6AsA4RMZgLCITMA6RCRiHyBTZPBYpoQAAAACAtKGEAgAAAADShhLah2nTppmOADAOkTEYi8gEjENkAsYhMkU2j0UmJgIAAAAApA1nQgEAAAAAaUMJBQAAAACkDSUUAAAAAJA2HtMBTGlpadH999+vZcuWKRgM6oorrtDZZ5/dYz3XdfXkk0/q1VdflSR99rOf1fTp02VZVrojI0f1dyzOnTtXCxYs0K5duxQMBvWFL3xBF154oYHEyEX9HYed4vG4fvjDH6q9vV0PPPBAGpMilw1kHNbV1emxxx5TXV2dAoGALrroIn3pS19Kc2Lkov6Ow46ODj3yyCNavHix4vG4jjvuOF177bUqKyszkBq5Zt68eZo/f742btyos846S9ddd12f6z733HN69tlnFYvFNHnyZF1zzTXyer1pTDtweVtCH3roIXk8Hj344INqaGjQHXfcoaqqKo0bN67betXV1Vq8eLFmzJghy7L0n//5n6qsrNTf/d3fGUqOXNPfsei6rq677jpVVVVpx44d+sUvfqHy8nKdddZZhpIjl/R3HHaaO3euQqGQ2tvb05wUuay/43D//v26/fbbdeWVV2rKlCmKx+PavXu3odTINf0dh3/7299UW1urGTNmqLCwUH/4wx80c+ZM3XTTTYaSI5eUlpbq4osv1tKlSxWLxfpcb8mSJXr22Wd16623qrS0VHfddZdmzZql6dOnpzHtwOXl5biRSETvvPOOvvGNbygQCOj444/X6aefrtdff73HugsWLNAFF1yg8vJylZWV6YILLtCCBQsMpEYuGshY/OpXv6rx48fLcRyNHj1ap59+utasWWMgNXLNQMahJO3cuVNvvPGGvva1r6U3KHLaQMbhc889p1NOOUXnnHOOvF6vCgoKNHbsWAOpkWsGMg537typU045RSUlJfL5fPrMZz6jTZs2GUiNXDR58mRNmjRJwWDwkOstWLBAU6dO1bhx41RcXKxLLrlE8+fPT0/IIcjLErpt27auX+Q7VVVV9fqDY9OmTaqqqjrsesBgDGQsHsx1XdXU1PBLF1JioONw5syZuvzyy+Xz+dIVEXlgIOOwtrZWxcXFuuWWW3T11VfrzjvvVGNjYzrjIkcNZBx+9rOf1Zo1a9TU1KRoNKo33nhDp556ajrjAtq8ebOOOuqorverqqq0b98+NTc3mwvVD3lZQiORiAoKCrotKywsVCQS6XXdwsLCHuvxeFWkwkDG4sFmz54t13U1derU4YyHPDGQcfjuu+8qmUxq0qRJ6YqHPDGQcdjU1KQFCxboqquu0n333afKykr95je/SVdU5LCBjMNRo0apvLxc3/72t3XllVdqy5YtuvTSS9MVFZDUe1eRlPG3y+RlCQ0EAj3+x7S3tysQCBx23c71mJgIqTCQsdhp3rx5WrBggX784x9n/E3nyA79HYeRSERPPPGE/umf/imd8ZAnBvLz0OfzadKkSTrmmGPk8/n09a9/XWvWrFFbW1u64iJHDWQcPvTQQ+ro6NDMmTP1+OOPa9KkSbr99tvTFRWQdGDMHvyzr3P8fvyPKZkmL0voqFGjlEgktG3btq5lGzZs6HUCjnHjxqmhoaHr/YaGhj4n6gAGaiBjUZJeffVV/eUvf9Gtt96q8vLydMVEjuvvONy+fbt27dqlW2+9Vddcc43uuusu7dmzR9dcc4127tyZ7tjIMQP5eXjkkUd2e58/DCNVBjION2zYoPPPP1/FxcXyer36+7//e61bt0779+9PZ2TkubFjx2rDhg1d72/YsEHhcPiw95KalpclNBAIaPLkyXrqqacUiURUU1OjxYsX69xzz+2x7rnnnqvnn39eTU1Nampq0nPPPafzzjvPQGrkooGMxTfeeEN/+tOfdMstt2jkyJEG0iJX9Xccjhs3Tvfff79mzJihGTNm6Nvf/rZKSko0Y8YMVVRUGEqPXDGQn4dTp07V4sWL1dDQoHg8rjlz5uj444/vdkkaMBgDGYcTJkzQggUL1NbWpng8rhdffFGlpaUKhUIGkiPXJBIJxWIxJZNJJZNJxWIxJRKJHuudd955evXVV7V582a1trbq6aef1vnnn5/+wANkuXl6c2NLS4vuu+8+LV++XMXFxZo+fbrOPvtsrV69Wrfffrsef/xxSf/3nNBXXnlFkvS5z32O54Qipfo7Fq+77jo1NTXJ4/m/Jyudc845uvbaa01FRw7p7zg82MqVK/W73/2O54QiZQYyDl966SU9/fTTisViOu6443T11VfzxxCkRH/HYXNzsx555BEtW7ZM8Xhc48aN05VXXqljjjnG8FeAXDBr1izNmTOn27JLL71Un/3sZ/W9731Pv/71r7t+5mXjc0LztoQCAAAAANIvLy/HBQAAAACYQQkFAAAAAKQNJRQAAAAAkDaUUAAAAABA2lBCAQAAAABpQwkFAAAAAKQNJRQAAAAAkDaUUAAAAABA2vx/15lPvGmh2yIAAAAASUVORK5CYII=",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"fig, ax = plt.subplots(figsize=(16,6))\n",
"ax=plt.subplot(1,1,1)\n",
"ax.plot(x, yp, '-', c=colors[7], linewidth=0.9, alpha=1, label=\"prior\")\n",
"ax.fill_between(x, 0, yp, color=colors[7], alpha=0.6)\n",
"# testo sull'asse x\n",
"plt.xticks(fontsize=12)\n",
"plt.yticks(fontsize=12)\n",
"plt.tight_layout\n",
"# titolo della figura\n",
"plt.suptitle(r'Prior: $p(\\theta)=Beta({0:3d}, {1:3d})$'.format(alpha, beta), fontsize=16)\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Per ogni numero di osservazioni fissato, determina il numero di valori $1$ osservati, calcola i parametri della distribuzione a posteriori risultante e memorizza il valore della verosimiglianza e della densità di probabilità per tutti i punti della griglia."
]
},
{
"cell_type": "code",
"execution_count": 30,
"metadata": {},
"outputs": [],
"source": [
"n = 50"
]
},
{
"cell_type": "code",
"execution_count": 38,
"metadata": {},
"outputs": [],
"source": [
"# determina numero di esiti pari a 1\n",
"ones = data[:n].sum()\n",
"# modifica i parametri della distribuzione per tener conto degli esiti osservati\n",
"params = [sum(t) for t in zip(hyper, [ones, n-ones])]\n",
"# calcola elenco dei valori per la distribuzione a posteriori con i parametri calcolati\n",
"post = dist.pdf(x, *params)\n",
"# calcola il valore sulla griglia per cui la distribuzione a posteriori è massima\n",
"mp = x[np.argmax(post)]\n",
"# calcola elenco dei valori per la verosimiglianza con la probabilità considerata\n",
"lik = [p**ones*(1-p)**(n-ones) for p in x]\n",
"# calcola il valore sulla griglia per cui la verosimiglianza è massima\n",
"ml = x[np.argmax(lik)]\n",
"# calcola il valore dell'evidenza\n",
"ev = np.sum(list(map(lambda x,y:x*y/float(nv), lik, yp)))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Visualizza la distribuzione a priori, la verosimiglianza e la distribuzione a posteriori per il numero di osservazioni considerato"
]
},
{
"cell_type": "code",
"execution_count": 39,
"metadata": {},
"outputs": [],
"source": [
"def plot_dist():\n",
" fig, (ax1, ax2) = plt.subplots(2,1,sharex=True, figsize=(16,10))\n",
" ax1.plot(x, lik, '-', c=colors[1], linewidth=0.9, alpha=0.8)\n",
" # riempie la zona compresa tra la curva e l'asse x\n",
" ax1.fill_between(x, 0, lik, color=colors[1], alpha=0.3)\n",
" # testo sull'asse x\n",
" plt.xlabel(r\"$\\theta$\",fontsize=14)\n",
" plt.xticks(fontsize=12)\n",
" plt.yticks(fontsize=12)\n",
" ax1.set_title(r'Likelihood; $L(\\theta|X)=p(X|\\theta)=)\\theta^{%3d}(1-\\theta)^{%3d}\\qquad$ ML=%8.5f'%(ones, n-ones, ml), fontsize=14)\n",
" plt.tight_layout\n",
" # effettua il plot a partire dalla sequenza di ascisse in x e di ordinate calcolate e salvate \n",
" # nell'elemento attuale di ys\n",
" ax2.plot(x, post, '-', c=colors[3], linewidth=0.9, alpha=1)\n",
" # riempie la zona compresa tra la curva e l'asse x\n",
" ax2.fill_between(x, 0, post, color=colors[3], alpha=0.6)\n",
" # effettua il plot del prior a partire dalla sequenza di ascisse in x e di ordinate calcolate e salvate in yp\n",
" ax2.plot(x, yp, '-', c=colors[7], linewidth=0.9, alpha=1, label=\"prior\")\n",
" # riempie la zona compresa tra la curva e l'asse x\n",
" ax2.fill_between(x, 0, yp, color=colors[7], alpha=0.6)\n",
" plt.annotate(r'Evidence; $p(X)={0:10.3e}$'.format(ev), xy=(.05, .85), va='top', xycoords='axes fraction', \n",
" fontsize=10)\n",
" # testo sull'asse x\n",
" plt.xlabel(r'$\\theta$', fontsize=14)\n",
" plt.xticks(fontsize=12)\n",
" plt.yticks(fontsize=12)\n",
" plt.title(r'Posterior; $p(\\theta|X)=Beta({0:3d}, {1:3d})\\qquad$ MAP={2:8.5f}'.format(params[0],params[1],mp), fontsize=14)\n",
" plt.tight_layout\n",
" # titolo della figura\n",
" plt.suptitle(r'$\\theta={0:3.2f}\\qquad n={1:3d}\\qquad\\#1={2:3d}\\quad \\#0={3:3d}$'.format(theta_real, \n",
" n, ones, n-ones), fontsize=16)\n",
" plt.show()"
]
},
{
"cell_type": "code",
"execution_count": 40,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA6EAAAKcCAYAAAAZyLztAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAACveElEQVR4nOzdd3hUVf4G8PdOb6lMEgglBEKoiTQpohSJBRAVVGzrImtd1B+7iqIiWFDAXRQLuIiCKDYEEQsIEjrSIaEFQgkEQgmEkF6mnd8fWWYZ0ibJzNxJ8n6eJ4/OvXfufefOyWS+nHPPlYQQAkREREREREQ+oJA7ABERERERETUeLEKJiIiIiIjIZ1iEEhERERERkc+wCCUiIiIiIiKfYRFKREREREREPsMilIiIiIiIiHyGRSgRERERERH5DItQIqrXzp49i9GjR8NsNiMgIAD3338/cnJyvHa806dP495770VQUBACAwMxcuRInDp1qsrnLFmyBPfccw+ioqKg1+vRvn17vPLKK8jPz6/0OStWrED//v1hMpkQGBiInj17Yu3atZ5+OfXK+vXrIUlSuZ/g4OBy29bmfZLTwoUL0apVK+fjTp064ZNPPim3XUZGBp577jn07dsXBoMBkiTh5MmTXs1Wl2PefvvtkCQJr732mtfyuXvuAHnaxapVq3DzzTejadOm0Gq1aNGiBUaNGoWUlJQKt+fvPhE1BixCiajeOnHiBHr16oW8vDx88803+M9//oNVq1bh2Wef9crxioqKcPPNN+Pw4cP48ssvsXDhQhw9ehSDBg1CYWFhpc+bMWMGlEolpk6dipUrV+Lvf/87/vOf/+CWW26Bw+Eot/2nn36Ku+66Cz169MBPP/2ExYsX47777kNRUZFXXld989FHH2Hr1q3On8TERJf1tX2f5LR792706NEDAFBQUIDU1FTn46sdO3YMP/zwA0JCQnDTTTf5JFttj/ndd99h7969XkxWxt1zJ1e7yM7ORo8ePTBr1iz88ccfmDZtGg4ePIg+ffogPT3dZVv+7hNRoyGIiOohh8MhevfuLYYNGyYcDodz+aRJk4RGoxHFxcUeP+YHH3wgFAqFOHr0qHNZWlqaUCqV4r333qv0eRcuXCi37MsvvxQAxJo1a1yWnzhxQuh0OjFz5kyP5W4o1q1bJwCI1atXV7ldbd8nOd14441iypQpQgghNmzYIFQqVYVt2G63O///s88+EwDEiRMnvJqtNsfMzs4WERER4ttvvxUAxMSJE72Wz91z50/t4vDhwwKAmDFjhnMZf/eJqDFhTygR1Us//fQTtm/fjvfffx+SJDmXt2rVChaLBWfPnvX4MX/55Rf06dMHMTExzmXR0dHo168ffv7550qfFxYWVm7Z9ddfDwA4c+aMy/L58+dDoVDg6aef9lBq7+jSpQueeOIJLFy4EN26dYNer0enTp2wbt06uaPV+n2Si8PhQHJysrP3bteuXejUqRN0Ol25bRUK3//Zrs0xJ0yYgC5duuDBBx/0QqL/qcm586d20aRJEwCASqVyLqsvv/tERJ7AIpSI6qX58+ejb9++aNOmDWw2m/OnoKAAgOuXOwAQQrhsV9mP3W6v9JgHDx5Ely5dyi3v3Llzpdd3VWbDhg0AgI4dO7os37x5Mzp06IDvv/8ebdu2hUqlQkxMDGbPnl2j/XtTSUkJDh8+jMTERHz33XeYNGkSfvjhBzgcDvz1r3+t8DmeOP9XPPzww1AqlWjSpAkeeuihctf0efJ98qbWrVtDkiQolUoUFBRg6NChkCQJL7zwAvbt2+e85rWu13x68ty7Y/Pmzfjqq6+82mZrc+5q0y48ee7sdjssFguOHj2Kp556Ck2bNnUp0uvD7z4Rkaeoqt+EiMi/WCwWrFu3DkVFRVCr1eXWq9VqREZGuizbsGEDBg0aVO2+BwwYgPXr11e4Ljs7GyEhIeWWh4aG4vLly+6FR1nv5+TJk5GQkICePXu6rDt79izOnj2LF198EVOnTkXbtm2xePFiPPvss7DZbBg3bpzbx/GW/fv3w263o0ePHliyZIlz+enTp/HMM8+guLgYer3e5TmeOP9BQUF44YUXMGDAAAQGBiIpKQlTp05F3759kZSUhPDwcACee5+8bcWKFbBYLPjqq6+watUqfPPNNwCA/v37480333Ser2vbck154ty7y2Kx4KmnnsL48ePRvn37Ou2rKrU5d7VpF548d71798bu3bsBADExMVi7dq2zzQL143efiMhTWIQSUb2TkpKCoqIizJ49G7169XJZ98ADDyAkJKRcT2iPHj2wc+fOavcdEBDg0azXKigowF133QWVSoUvvvii3HqHw4H8/HwsWLAAI0eOBADcfPPNOHnyJKZNm4b/+7//cxl+LIekpCQAwFtvveWyPCsrC4GBgeUKUMAz579bt27o1q2b8/GAAQPQv39/9OrVCx999BHefvttd1+CX+jUqRMA4J133sHAgQPRtWtXHD16FPn5+bjvvvvQokULjxzHl23/X//6F4qLizFx4sQ676sq9fHcLVy4EHl5eUhLS8OMGTNwyy23YPPmzWjdujWA+vG7T0TkKSxCiajeuTLE7sYbb0R8fLxzeWZmJk6cOFHhdWgmkwldu3atdt9VfckLCQmpsMeksh6WaxUXF2P48OFIS0vDhg0bKvyi3KRJExw9ehS33HKLy/Jbb70VK1euxLlz5+rcM1ZXycnJaNGihbMQuCIpKcnl/biaJ85/Rbp3747Y2FiXQqGu75Mv2O12CCEAAH/++Sf+9a9/wWazYdOmTWjevDmaNm0Km80GpVJZ58LDW+f+WqdOncI777yDzz//HKWlpSgtLXWuKy0tRU5ODgICAqBUKut0nNqeu9q0C0+euytD73v37o0hQ4agdevWmD59OubMmQOgfvzuExF5Cq8JJaJ6x2azAUC5L7MLFy6EJEl49NFHyz1nw4YNUKvV1f4MHjy40uN27twZBw8eLLc8JSWlXEF2LavVinvvvRe7du3CihUrEBcXV+kxqiLHxDTXSkpKqvAWGElJSejevXuFz/HE+a/K1UVAXd4nXxk8eLDzNZ87dw6PPPII1Go1HnvsMZw5c8a57sq1w3Xh7XN/RVpaGkpKSvCXv/wFISEhzh+g7DZFISEh2L9/f51fT23PXW3ahbfOXXBwMGJiYnDs2DGXfFXxh999IiJPYU8oEdU7V4avHTx40PnF7fz583j33Xfx5JNPom3btuWe44lhdXfeeSfGjx+PtLQ0tGnTBkBZr+yff/6J6dOnV/o8h8OBhx9+GGvXrsVvv/2GPn36VLrtiBEjMG/ePKxatQr33nuvc/nKlSvRokULNG3atNrX4E0OhwP79+/HkCFDXJZfvnwZ6enpLsNlr+atIaG7du1Camqqy7mq7fvkS59++iny8/OxaNEiLFu2DN999x0AYOjQoRg3bhxuu+02APDIdZW+Go7btWvXCmdHHjRoEP7yl7/gsccec5mZtrZqe+5q0y68de4yMzNx+PBhPPzww85l/v67T0TkSZK4MqaFiKieEEKgc+fOKC0txcyZM1FaWopJkyYhJCQEa9asgcFg8MpxCwsLcd1110Gv1+Ptt9+GJEmYNGkS8vPzsW/fPphMJgBlvSeDBw/G/Pnz8de//hV///vfMWfOHEycOBF33HGHyz5btGjhMixXCIHBgwdj7969eOedd9CmTRssXrwYn3/+Ob744osKe3l96fDhw+jYsSN+++03DBs2zLl87dq1ztyVDcmtq4cffhjR0dHo3r07goODkZSUhGnTpsFgMGDPnj0wm80A3H+f/MFdd92F6OhofPDBB0hNTUXHjh1x9uzZKguOK5NBrVmzBnPmzMEnn3yCsLAwhIWFYcCAAV7JWZdjSpKEiRMnevya3ZqeO7naxYgRI9C9e3fEx8cjMDAQR44cwcyZM3H+/Hns2LEDsbGxAPz/d5+IyKNkuj8pEVGdHD58WNx0001Cq9WK5s2biwkTJoiCggKvHzc9PV2MHDlSBAQECJPJJO666y5x4sQJl23WrVsnAIgvvvhCCCFEVFSUAFDhz+uvv17uGLm5uWLs2LEiPDxcqNVqERcXJ7755huvvzZ3fPfddwKAOHv2rMvyGTNmCK1WK6xWq9eOPXXqVBEXFycCAwOFSqUSLVq0EE888US5LEK49z7JrbS0VBiNRvH7778LIYSYOXOm6N69e7XPq6wtDRgwwGtZ63JMAGLixIkezVPbcydHu5g+fbro3r27CAoKEnq9XsTGxoonn3yywuP68+8+EZEnsSeUiIiIiIiIfIZXuRMREREREZHPsAglIiIiIiIin2ERSkRERERERD7DIpSIiIiIiIh8hkUoERERERER+QyLUCIiIiIiIvIZFqFERERERETkMyxCiYiIiIiIyGdYhBIREREREZHPsAglIiIiIiIin2ERSkRERERERD7DIpSIiIiIiIh8hkUoERERERER+QyLUCIiIiIiIvIZFqFERERERETkMyxCiYiIiIiIyGdYhBIREREREZHPsAglIiIiIiIin2ERSkRERERERD7DIpSIiIiIiIh8hkUoERERERER+QyLUCIiIiIiIvIZFqFERERERETkMyxCiYiIiIiIyGdYhBIREREREZHPsAglIiIiIiIin2ERSkRERERERD7DIpSIiIiIiIh8hkUoERERERER+QyLUCIiIiIiIvIZFqFERERERETkMyxCiYiIiIiIyGdYhBIREREREZHPsAglIiIiIiIin2ERSkRERERERD7DIpSIiIiIiIh8hkUoERERERER+QyLUCIiIiIiIvIZFqFERET/NWLECISEhODee+8tt66oqAhRUVEYP368DMk8KycnBz179kTXrl3RpUsXfPbZZ851J06cwKBBg9CpUyfExcWhsLBQxqRERNQQSUIIIXcIIiIif7B+/Xrk5+fjyy+/xJIlS1zWTZw4EceOHUPLli0xY8YMmRJ6ht1uR2lpKQwGAwoLC9GlSxfs2rULTZo0wYABA/D222/jpptuQnZ2NgIDA6FSqeSOTEREDQh7QomowXr00Udxxx13OB8PHDgQzz77rEf36Y1j1NYdd9yBRx991OP7vXz5MiIiInD8+HGX5bNmzUJMTAz0ej1uv/12XLx40blu/fr1aN26dY2Pdd999+G9996ra+QqVZV74MCBCAgIKPeco0eP4vDhwxgyZEiF+6zsHPlSZa+ronOqVCphMBgAAKWlpRBCQAiBgwcPQq1W46abbgIAhIaGsgAlIiKPYxFKRPXatUXg1T788EN8/fXXXj2+L47hbYMHD8Zf//rXStdPnToVQ4cORdu2bZ3LJk6ciBkzZmDu3LnYvn070tLS8NJLL1W6DyEEunTpgueff95l+ebNm6HX6/Hpp58CACZPnox33nkHubm5dXxVFatp7ivGjx+PadOmVbq+onO0ceNG3HnnnWjevDkkScKCBQs88RIqVNXrquyc5uTk4LrrrkOLFi3w4osvwmw24+jRozCZTBg+fDi6d++OqVOnei1zTT366KOQJAmPPfZYuXUTJkyAJElV/gORN3zyySeIjo6GTqdDjx49sGnTpiq3nzZtGq6//noEBgYiLCwMw4cPx4EDB1y2sdvtmDRpknO/0dHReO2112Cz2Wp87Oq2mT17NuLj4xEYGIjAwED07dsXy5cvr+XZICJyH4tQImqwgoKCEBwcXO+P4W179uxBjx49KlxXVFSEzz//3OWL/65duzBt2jR8//33uPnmmxEfH49nn322yi+vkiRh4sSJ+PTTT5GVlQUASE1NxV133YXnn38eTz31FAAgLi4Obdq08UphX5vcAPDzzz8jNjYWsbGxFa6v6BwBQEFBAbp06YIPP/wQer3eY6/jWtW9rsrOaXBwMPbu3YsTJ07g22+/RWZmJmw2GzZt2oRPPvkEW7duxerVq7F69WqvZa+pli1b4ocffnC5TtVms+Grr75Cq1atfJpl0aJFGDduHF599VUkJSXhhhtuwJAhQ3Dq1KlKn7N+/XqMHTsWW7Zswdq1a6FSqZCQkIDs7GznNu+++y5mz56Njz76CIcPH8aHH36I2bNnu/wjiDvHdmebFi1a4N1338WePXuwa9cu3Hzzzbj77ruxb98+D58tIiJXLEKJqMGqridkzZo1CA4Oxpw5cwCU9db961//Qtu2baHX6xEXF1dtMVTRMRwOB1599VWYzWaEh4dj/PjxcDgczvWlpaX4xz/+gYiICOh0OvTp0webN292ez1QVvg8+uijMJlMiIiIqHWP1fHjx5GTk1NpEbpixQpIkoR+/fo5l82YMQP9+/dHnz59nMvCwsKcxWVl7r//fjRv3hzvv/8+MjMzMWTIEAwdOhTvvPOOy3Z33nknvvvuu1q9nqrUNve2bdvw/fffo3Xr1hg/fjw+++wzvPXWW871FZ0jABg6dCimTp2Ke++9FwqF9/7cuvO6qjqnERERuO6667Bp0yY0b94cPXv2RMuWLaHVajF06FAkJyd7LXtNxcfHo127dvjhhx+cy5YvXw6dToeBAwf6NMv777+PRx99FE888QQ6duyIjz/+GM2aNcN//vOfSp+zatUqjBkzBl26dEFcXBwWLlyIixcv4s8//3Rus2XLFgwfPhzDhw9H69atceedd+LOO+/E9u3ba3Rsd7a56667MGTIEMTExCA2NhbvvPMOAgICsHXrVg+fLSIiVyxCiahRWrJkCUaMGIG5c+fi6aefBgC89tprmDdvHmbPno2UlBS88soreOqpp2o8PO2bb76BSqXCli1bMGvWLHzwwQdYtGiRc/1LL72ERYsWYf78+UhKSkJcXBxuv/12nDt3zq31QNnw0NWrV+PHH3/EmjVrkJSUhI0bN7rkWLBgASRJwsmTJyvNunv3bigUCnTt2rXC9Zs2bUKPHj0gSRIAwGq14tdff8XIkSNdtisuLkZQUFCV50WhUODVV1/F7NmzMXToUERHR2PevHnltuvVqxd27NiB4uLicuumTp0Kk8lU5U9FwxLrknvatGk4ffo0Tp48iRkzZuCJJ57A5MmTneuvPUe+5O7ruvacZmZmIj8/HwCQm5uLjRs3on379rj++utx4cIFXL58GQ6HAxs3bkTHjh1994Lc8Nhjj2H+/PnOx/Pnz8eYMWNqfP5r25YAwGKxYPfu3bj11ltdlt96663YsmWL2xny8/PhcDgQEhLiXHbjjTdi3bp1OHz4MAAgJSUFa9euxdChQ90+dm3y2e12fP/99ygoKMANN9zg9msgIqoNzjZARI3O3Llz8eKLL2LJkiXOL2mFhYV4//338ccffzgnZYmOjsaOHTswe/ZsDBs2zO39d+rUydlTFhsbi88++wxr1qzBgw8+iMLCQvznP//B559/7tznnDlzsHbtWsyePRuvvPJKlevffvttFBQUYN68eZg/fz5uu+02AMAXX3yBFi1auOQICgpC+/btoVarK826e/duxMbGwmQyVbg+PT0dkZGRzsfJyckoKirChAkT8OqrrzqXW61WdOvWrdpz88ADD+C5555DXl4e1q5dC41GU26byMhIWK1WnD171uUaSwB4+umnMWrUqCqP0bx583LL3M2dkJCAvXv3orCwEC1atMDixYvRt2/fKo937TnyJXdf17XnND09HU8++aRzQqLnnnsOcXFxAMqKs/79+0MIgVtvvdXr11XW1EMPPYTx48fj6NGjCAgIwMqVK/Hxxx+7/MOAO2rblgAgKysLdrsdERERLssjIiKQmJjodoZx48aha9euLm1swoQJyM/PR6dOnaBUKmGz2TBx4kSMHTvW7WPXJN/+/fvRt29flJSUwGQy4aeffnK2BSIib2ERSkSNyrJly/Dpp59i48aNLl/8UlJSUFJSgttvv92lR8VqtdZ4ltf4+HiXx5GRkbhw4QKAsuGvVqvVZeimUqlE3759kZKSUu36K/uwWCwu+U0mU7kvjiNGjMCIESOqzFrV9aBAWY/a1V9kU1NTodFosH//fpftHnzwwXLDUSvy3HPPwWaz4dKlS5UOUb1y/WRFPaGhoaEIDQ2t9jjXcjd3dQVERbMPX3uOauO1114rNyz5WuvWrSs35NTd13XtOe3Vq1elw2yHDBlS6SzA/iAkJAQjRozA/PnzERwcjIEDB9bqetDatiVPef7557F582Zs3rwZSqXSuXzRokX46quv8O2336Jz585ITk7GuHHjEB0dXeGkTHXVvn17JCcnIzc3F0uWLMHo0aOxfv16dOnSxePHIiK6gkUoETUq1113Hfbv34958+ahT58+zoLzyjWbv/76a7kvtFX1JFbk2u0lSXK5JrQy1Q0n9MZwzz179uC1116rdL3ZbMbly5edj3Nzc2E2mxETE+NclpWVheTkZHz00UdVHuvNN9/Ejz/+iK1bt2L48OGYNWsWXnnllXLbXZmkJSwsrNy6qVOnVnv96++//+7szfZE7upce45q4x//+Af+8pe/VLlNRYWWu6+rqnNaH/3tb3/D6NGjYTKZXK7PrYnatiWg7D1XKpXIzMx0WZ6ZmYmmTZtWe+x//vOf+P7777Fu3Tq0adPGZd2LL76I8ePH44EHHgBQNrFUeno6pk2bhscee8ytY9ckn0ajcbafHj16YOfOnZg5c2aFQ+WJiDxFtiI0Ozsb7777LjIyMvDVV1+5/CugO5KSkvDll18iICAAU6ZMAVA269y6detgsVgwcOBA5zA1IqIroqOj8fHHH2PgwIF48sknMXfuXEiShE6dOkGr1SI9PR0333yz147ftm1baDQa/Pnnn86hpna7HVu3bsVDDz1U7for+1Cr1di2bZvzC2xhYSEOHDhQbvhqVU6cOIHs7Gx079690m26devmcmsRs9nsvI7tSk/mtGnT0Ldv3yqHrc6bNw/Tp0/HH3/8ga5du+Kll17ClClTMG7cOOf9Kq84cOAAmjdvXmHvYm2HUNY2tzuuPUe1YTabYTaba/U8d15XVee0Pho8eDA0Gg2ysrJw991312ofdRmOq9Fo0KNHD6xevRr33Xefc/nq1atxzz33VLnPcePGYdGiRVi3bh06dOhQbn1RUVG570RKpdL5D1nuHLsu+RwOB0pLS6vchoiormQrQk0mEyZNmoQZM2bU6vnt2rXDv//9b5d/Ab3xxhsxcOBAOBwOTJgwgUUoUSORl5dXbmhhVbdNadOmjXNo41NPPYVPP/0UAQEBGD9+PMaPHw8hBPr374+CggJs27YNCoUCTz75pEeyGo1G/P3vf8eECRNgNpsRHR2NmTNnIjMzE2PHjq12PVD2+fnYY49hwoQJCAsLQ2RkJN566y3Y7fYaZdm9ezeAsp7bq+9VqFQqnZPR3HbbbZgwYQIuXbqEJk2a4Oabb4bNZsM777yDRx55BEuWLMHChQtdZve81ooVKzB27Fh8/fXXzl6lJ554AlOnTsWnn36Kf/7zny7bb9q0qdLP79oOoaxNbndde46uKCgowLFjxwCUfbE/deoUkpOTERoa6rHbibj7uqo6p/WRJEnYt28fhBDQarWVblfZZ0Pr1q3rPBz3+eefxyOPPIJevXqhX79+mDNnDs6ePeuc6AwAZs2ahVmzZjknGXrmmWewcOFCLFu2DCEhITh//jwAOCdCAoDhw4dj+vTpiI6ORufOnZGUlIT333/f5V6+7hzbnW1efvllDBs2DC1btkR+fj6+/fZbrF+/nvcKJSLvEzJ7/fXXhc1mEw6HQ8ydO1e88cYbYurUqSI/P9+t57/22mvllpWWloqZM2d6OCkR+aPRo0cLAOV+7rnnHjF69GgxbNgw57YDBgwQzzzzjPPxsWPHRIsWLcQTTzwhHA6HcDgc4qOPPhIdO3YUGo1GmM1mkZCQIP744w+X4129z+qOUdE2JSUlYty4cSI8PFxoNBrRu3dvsWnTJrfXCyFEQUGBeOSRR4TRaBRhYWHirbfeEsOGDROjR492bvPFF18IAOLEiRMVnruXX365wnPXpUsXl+369OkjZs2a5Xy8ePFi0apVK6HX68Wtt94qUlJSyu173bp1IioqSuzYsUMYjUbx/vvvl9tmxowZIjIyUpSUlDiXFRcXi8DAQLF169YKM9eFO7lr69pzJETZOajo/F79HnlCda/Lm+fUl679PapufVWfDZ4ye/ZsERUVJTQajejevbvYsGGDy/rXX39dXP1Vq6I8AMTrr7/u3CYvL0+MGzdOtGrVSuh0OhEdHS1eeeUVUVxcXKNju7PN6NGjRatWrYRGoxFhYWFi8ODBYuXKlR44M0REVZOEEMI35W7F3njjDUyaNAlJSUk4ffo0RowYgaSkJJw8ebLaCTUAYNKkSc7huEDZbRcSExMxdOhQ3Hnnnd6MTkTk115//XUsWbIEe/fuhUpV+4EvK1euxLhx45CSkuL2pRPr16/Ho48+WuXtYSoye/Zs/Pzzz/jjjz9qkVQ+tTlHvlJfzykRETVcfjMx0ZkzZ7Blyxbs3bsXdrsdsbGxyMnJwQcffOCyXXBwMP7xj39Uup97770Xd911FyZPnoxBgwYhICDAu8GJiPzUihUrMHv27DoVoABw++2345lnnkFGRgaioqI8lK5iarUaH3/8sVeP4Q2+PEc1VV/PKRERNVx+U4RGRkaif//+GD58OADAZrNBpVLhjTfecHsfVqsVarUaKpUKWq22xjNaEhE1JDt37vTYvv7v//7PY/uqiqeuvZWDr85RTdXnc0pERA2TbMNxbTYbpk2bhrS0NERHR+PBBx/Epk2bcPr0aQDAsGHD0LNnz0qff/z4cXz77bc4fvw42rZtiwkTJmDZsmVISUmBzWZD//79nTehJyIi3zp58iSWLVtW5cgVIiIiapxkvyaUiIiIiIiIGg+F3AGIiIiIiIio8WARSkRERERERD4j28REZ8+elevQbjGbzcjKypI7BjVybIfkL9gWyR+wHZI/YDskf+HvbTEyMrLSdewJJSIiIiIiIp9hEUpEREREREQ+wyKUiIiIiIiIfIZFKBEREREREfkMi1AiIiIiIiLyGRahRERERERE5DMsQomIiIiIiMhnWIQSERERERGRz7AIJSL/JoTcCYiIiIjIg1RyByAiukIqzIfmyD6o0w5BmZkBRWnJf4tQAUdAMKytYmCN6QJrdAdAwX9DIyIiIqqPWIQSkewUOZeg/3MV1CcOw9a0BezBTWBt1gpQaSAkCZIQkIoLoLx8EYY1P0EqzEfJDbeipMdNgEotd3wiIiIiqgEWoUQkH7sN+q2rod27DZboDijuORBCpy/XyykACJ0ejpAwWNt0gpSXA03Kbui3rkbBHQ/DGtNFnvxEREREVGMsQolIForcbJiWLYDDYEJxt34QxkBAktx6rggMRmmP/rBeugDTr9/A0rodCu94BFCzV5SIiIjI3/GiKiLyOdWZkwj85iNYm0XBEt0BwhTkdgF6NUeTcBTefBcU+TkInvsOFLnZXkhLRERERJ7EIpSIfEp9PAXGnxegpFNP2MOaARpt3XYoSSjt2g+Wlm0Q9PlUKC6e9UxQIiIiIvIKFqFE5DOqk6kw/LEYpXHXwxFiBpRKj+3b1ro9Sjr3RtAX/4byXLrH9ktEREREnsUilIh8Qnn2JEwrvkNpp55wBDap1fDb6tgjW6Gke38EfvUBFBfPe3z/RERERFR3LEKJyOsUOZcQsOxLlHTqAUdQqFcK0Cvs4ZEoue4GBH35b0i5l712HCIiIiKqHRahRORdVgtMS+ehtF1nOIKalLv9ijfYI1uhNLYrghb8G7CUev14REREROQ+FqFE5D1CwPj797A3CYc9NMKj14BWx9Y6FjZzUwR8/wkghM+OS0RERERVYxFKRF6j3b8dypws2Jq1BtQanx/f0qUXFPk50K/5yefHJiIiIqKKsQglIq9QXM6CfvNKlLbtBKHTyxNCklDcJwG6PZuhPp4iTwYiIiIicsEilIg8z2GH6bevURrTGcIYJG8WtQbFvQbB9OPnkIoL5M1CRERERCxCicjzdDs3wKHRwhEa4ZOJiKrjCA2HNaodTIvnyh2FiIiIqNGT/9shETUoitxs6HZvhLVFWwiNVu44TpYO3aC8nAXtjnVyRyEiIiJq1FiEEpHnCAHDH0tgie4AYQyQO40rSUJxr5thXLsMUn6O3GmIiIiIGi0WoUTkMeoj+6AozIO9iX8Mw72WMAagNKYLAn6cJ3cUIiIiokbL/74lElH9ZLXCsO5nWNp0gtAZ5E5TKWu7OCguX4Rm71a5oxARERE1SixCicgjdLvWw25uCodJ5tlwqyNJKLl+IIwrfwBKiuROQ0RERNToqGqycXZ2Nt59911kZGTgq6++glKpdK6bO3cuTp8+DQB4/PHHERUV5dmkROS3pMJ86HZvQnH3GwFVjT5WZOEIDIEtMgrGlYtQePcYueMQERERNSo16gk1mUyYNGkS2rVrV27d3XffjSlTpmDs2LFYvHixxwISkf/Tb/4d1lYxEAY/m4yoCqWdekJ7KBmK8xlyRyEiIiJqVGpUhGo0GphMpgrXhYeHAwCUSiUUfjghCRF5h+JSJtRph2ALb+6XkxFVSq1GSZfrEfDzl3InISIiImpUPD5u7ttvv8XQoUPLLU9MTERiYiIAYPr06TCbzZ4+tEepVCq/z0gNX31oh9IfP0B07g51RFNAqkdFKAB06Q4pPRXmEynA9f3lTuPX6kNbpIaP7ZD8Adsh+Yv63BY9WoQuX74cLVq0QIcOHcqtS0hIQEJCgvNxVlaWJw/tcWaz2e8zUsPn7+1QefEcTGmHUdK9P0R+gdxxakUR3wf6H+fjcqtYQOn/17PKxd/bIjUObIfkD9gOyV/4e1uMjIysdJ3Hui327t2L1NRU3HPPPZ7aJRH5Of3m32FtHQuh1ckdpdYcwWbYA0Og27hC7ihEREREjUKNilCbzYYpU6YgPT0d77zzDlJSUrB06VIAwPz583Hx4kW8+eabmDt3rlfCEpH/UF44A2VmBuwhEYAkyR2nTkrjekO/fQ1QUix3FCIiIqIGTxJCCDkOfPbsWTkO6zZ/796mxsGf26Fp6Xw4jEbYmkbV+yIUALRJf8LRJByFd/xF7ih+yZ/bIjUebIfkD9gOyV/4e1v0yXBcImo8lBfPQXnhTIPoBb3C0qkHtPu3Q8rLkTsKERERUYPGIpSIaky3fQ2sUe3q9bWg1xJaHSzRnWBc+b3cUYiIiIgaNBahRFQjirzLUKcfhT00vMH0gl5hiY2H5ngKpOyLckchIiIiarBYhBJRjeh2roe1ZVsInUHuKJ6nUsES0wWmPxbLnYSIiIiowWIRSkRuk4qLoDmUBFtYswbXC3qFpW1nqE8chnTpgtxRiIiIiBokFqFE5DZt0mZYm0VB6IxyR/Ee9oYSEREReRWLUCJyj80KXfIW2Ju1BJRKudN4laVtZ6hPpkK6lCl3FCIiIqIGh0UoEblFcygJttBwOLQN8FrQazl7Q5fInYSIiIiowWERSkTVEwK63Rthj2gBqNVyp/EJZ29oNq8NJSIiIvIkFqFEVC3V2XTAboMjIEjuKL6jUsHSthOMiT/JnYSIiIioQWERSkTV0u7eCFtkNIRGJ3cUn7K07QzNsQOQ8nPljkJERETUYLAIJaIqSQV5UJ86BnuoWe4ovqfWwNqqHQzrfpY7CREREVGDwSKUiKqkS/4TtsjWEI1hQqIKWGLjoT24CygpljsKERERUYPAIpSIKme3QbtvO2wRzQFF4/y4EDo9rE1bwrBxudxRiIiIiBqExvmtkojcojmyH7ZgMxw6o9xRZGVp3xXapD8Bm0XuKERERET1HotQIqqUNnlLo7otS2WEKRD2YDO029bKHYWIiIio3mMRSkQVUlzOgiLnEhymQLmj+AVLx24wbF8LOBxyRyEiIiKq11iEElGFtHu3whYZBaFrnBMSXcsR3ARCrYZm/w65oxARERHVayxCiag8ux3alN2wm5sBkiR3Gr9R2qEb9Fv/kDsGERERUb3GIpSIylEfOwB7YAgcevaCXs0e0QKKvBwoTx2TOwoRERFRvcUilIjK0e3dCltES0DVuCckKkeSYGkXB8PG3+ROQkRERFRvsQglIheK3Gwoss7DERQidxS/ZI2KhfrUcUh52XJHISIiIqqXWIQSkQvtvu2wNYuC0OrljuKfVCpYo2JhWPer3EmIiIiI6iUWoUT0Pw4HtPt3wB7enBMSVcES0wXaQ3sAS6ncUYiIiIjqHRahROSkTj8CuykQDh17Qasi9AbYmkRAt3W13FGIiIiI6h0WoUTkpLnSC6rWyB3F71nad4V+9ybA4ZA7ChEREVG9UqMiNDs7GxMmTMDDDz8Mu93usu7UqVOYNGkSJk2ahPT0dI+GJCIfKC0p6wkNbiJ3knrBEdwEQqmE5tAeuaMQERER1Ss1KkJNJhMmTZqEdu3alVu3aNEijBs3Dv/85z+xaNEijwUkIt/QHk6CLaw5JySqAUtsPHRbE+WOQURERFSvqGqysUajgUZT8TC9wsJCmM1m5/9fKzExEYmJZV/Wpk+f7tzWX6lUKr/PSA2fL9uhdHQfRJt20IXw1ixuM8VBcWAnNLYSoGkLudN4FT8TyR+wHZI/YDskf1Gf22KNitCqCCGqXJ+QkICEhATn46ysLE8d2ivMZrPfZ6SGz1ftUJGThYCL51ES1R4iL8/rx2tINK3aAT9/jYJ7Hpc7ilfxM5H8Adsh+QO2Q/IX/t4WIyMjK13nlYmJJN7agahe0R7YCVuzVhAandxR6h1rmw7QHNkHWErkjkJERERUL3isCDWZTLh06RKys7Oh1/OaMqJ6w+GA5sAu2M3NeG/QWhBaPWzmptBtWyN3FCIiIqJ6oUZFqM1mw5QpU5Ceno533nkHKSkpWLp0KQBg1KhR+OCDDzBz5kzcf//9XglLRJ6nykiD0Onh0BvljlJvWdrFQ7fnT6CayxKIiIiIqIbXhKpUKkyaNMllWadOnQAAUVFRmDJliueSEZFPaA/sgC28Be8NWgeO0DBIdhvUR/fDGhsvdxwiIiIiv+aVa0KJqJ6wWqA+fgj2kPo5s5o/KY2Nh37LH3LHICIiIvJ7LEKJGjHN0QOwmZvx3qAeYGvRBqqz6ZByLskdhYiIiMivsQglasQ0h/bAbo4AVB67W1PjpVTCGhUL/aYVcichIiIi8mssQokaKamkGKqzJ+EIDJE7SoNhadsJ2oO7AZtV7ihEREREfotFKFEjpT66H7awSA7F9SBhMMERFArt7o1yRyEiIiLyWyxCiRopbcoeOJpEAAp+DHiSpV0X6HZtkjsGERERkd/it0+iRkgqKoDywhnYg0LljtLg2MMioSjMhTLjhNxRiIiIiPwSi1CiRkiTuhf2MM6K6xWSBEubTtD/uVLuJERERER+iUUoUSOkSdkDa1gzQJLkjtIgWVu3h+Z4ClBSJHcUIiIiIr/DIpSokZEKcqHMvgARwFlxvUajhS28OXTb1sqdhIiIiMjvsAglamQ0h/fCFt4cQquTO0qDZonpAl3yFkAIuaMQERER+RUWoUSNjDZlF+wciut1jhAzJLsVquMpckchIiIi8issQokaEUVuNhR5ObAHciiu10kSLG07Q791tdxJiIiIiPwKi1CiRkRzKAm2iOaARit3lEbB2ioG6lPHgII8uaMQERER+Q0WoUSNiObQHtjNkXLHaDxUalibR8Pw5yq5kxARERH5DRahRI2EIvsCpOJC2AOD5Y7SqFhjOkN7YAdgt8sdhYiIiMgvsAglaiQ0h5JgD28BqDVyR2lUHIEhEEoV1IeT5I5CRERE5BdYhBI1EtqDu2ALayp3jEbJ0i4O+u28ZygRERERwCKUqFFQXjwHOBxwBATLHaVRskW2hur8aUg5l+SOQkRERCQ7FqFEjYDm0B7YwpsDKrXcURonpRLWqFjoN/0udxIiIiIi2bEIJWrohIAmZTfs5gi5kzRqljYdoU3ZDdisckchIiIikhWLUKIGTnn+NKBQwmEKljtKoyaMAXCYAqHZt03uKERERESyYhFK1MBpDiX9dyiuSu4ojZ4lpgv0OzfIHYOIiIhIVixCiRoyhwPaQ3s4FNdP2Ju2hPLyRSgyz8odhYiIiEg2LEKJGjDV2XQIrQ4OY6DcUQgAJAmW6I4wbOYERURERNR4sQglasCcs+IqORTXX1ijO0BzdB9gscgdhYiIiEgWNfpmumDBAqSlpSE6OhpjxoxxLt+6dSt++eUXSJKEESNG4Prrr/d4UCKqIYcDmtS9KO7WT+4kdBWh08MWEgbtrvUoveFWueMQERER+ZzbPaFpaWkoKSnBW2+9BZvNhmPHjjnXLV++HG+88QbeeOMN/Pbbb14JSkQ1ozp9HA6DCcIQIHcUuoY1pgt0e/6UOwYRERGRLNzuCT169Cji4+MBAHFxcThy5AhiYmIAABERESgtLQUA6PX6Cp+fmJiIxMREAMD06dNhNpvrFNzbVCqV32ekhq8u7VDa+BtE6xhoQkI8nIrqLCAA0r6tMOdfAqLby53GLfxMJH/Adkj+gO2Q/EV9botuF6GFhYWIiCibYdNgMCAjI8O5rlevXnjppZcghMDYsWMrfH5CQgISEhKcj7Oysmqb2SfMZrPfZ6SGr9bt0G5HcPI2FF/fHyIvz/PBqM7UUbFQLP8e+Q88I3cUt/AzkfwB2yH5A7ZD8hf+3hYjIyMrXef2cFyDwYCioiIAQHFxMQwGg3PdkiVL8P7772PmzJlYsmRJHaISkSeoT6bCERQCoTPJHYUqYY2KhTrtMFBSJHcUIiIiIp9yuwiNjY3FgQMHAAD79+9HbGysc51arYZWq4VOp4PNZvN8SiKqkbJZcSMBpVLuKFQZtQa2pi2h37pa7iREREREPuV2EdqmTRuo1WpMnjwZCoUCZrMZS5cuBQDceuutmDRpEl577TWXIbdEJAObFeq0w7CHhMmdhKphiekCXdIWQAi5oxARERH5TI1u0XL1bVkAYOTIkQCAgQMHYuDAgR4LRUS1p047BHuIGUJnlDsKVcMR3ARCkqA6dgC2dnFyxyEiIiLyCbd7QomoftAeSoI9LBJQ8Ne7PrDEdIHhzz/kjkFERETkM/yWStSQWEqhSj8Ke3ATuZOQm2wt2kB19iSkvMtyRyEiIiLyCRahRA2I5thB2JuEQ+gM1W9M/kGphLVVO+g3r5Q7CREREZFPsAglakA0h/ZwKG49ZGnbCdoDOwC7Xe4oRERERF7Hb6pEDYRUUgzVmZOwB4bIHYVqSBgD4DAEQLN/u9xRiIiIiLyORShRA6E+uh+2sEgOxa2nLLHx0G9fK3cMIiIiIq9jEUrUQGgP7YEjLIJDcespe0QLKC5nQXHxnNxRiIiIiLyK31aJGgCpqADKzDOwB4bKHYVqS5JgbdMR+o3L5U5CRERE5FUsQokaAE3qXtgiWkBodHJHoTqwRneA5sg+wFoqdxQiIiIir2ERStQAaA4lwd6EQ3HrO6HVwW5uCu3O9XJHISIiIvIafmMlquekglwoL1+EwxQodxTyAEtMF+h3b5Y7BhEREZHXsAglquc0h/fCFtGcs+I2EI7QcEilxVClH5U7ChEREZFXsAglque0KbthMzcDJEnuKOQJklTWG7p5pdxJiIiIiLyCRShRPabIzYZUmAdhMMkdhTzI2ioG6vQjQGGB3FGIiIiIPI5FKFE9pjmUBHtECwitXu4o5EkqNazNW8Pw5+9yJyEiIiLyOBahRPWY5lASbOamHIrbAFljukC7dxvgcMgdhYiIiMijWIQS1VOK7AuQLCUcittAOQKCIfQGaPZtkzsKERERkUexCCWqp7SHkmCLaAGh1sodhbykNPY66LetkTsGERERkUexCCWqj4SAJmU3bE0iOBS3AbNHtIAi9xKUZ9PljkJERETkMSxCieoh5cWzEAoFoOe9QRs0SYKlXRwMG5fLnYSIiIjIY1iEEtVDmpQ9sIdzKG5jYI1qD3XaIaC4UO4oRERERB7BIpSovhECmsNJsIWGcyhuY6BWw9o8GvpNK+VOQkREROQRLEKJ6hnV2XQInRHQshe0sbC0i4Nu7xbAbpc7ChEREVGdsQglqmc0KbthC2sGodHJHYV8RJgC4TCYeLsWIiIiahBYhBLVJw4HNEf2wR4aLncS8jFL7HXQb0uUOwYRERFRnalqsvGCBQuQlpaG6OhojBkzxrm8oKAAc+fORX5+PuLi4jBy5EiPByUiQHXqGOyBIRAaDsVtbOzhkVAkbYby9HHYW7aVOw4RERFRrbndE5qWloaSkhK89dZbsNlsOHbsmHPd4sWLcf/99+P1119nAUrkRdpDe2APawaoNXJHIV+7cruWTSvkTkJERERUJ24XoUePHkV8fDwAIC4uDkeOHHGuO336NH766Se8+eabLsuJyIPsNqiPp8Ae1ETuJCQTa1Q7qE8egVSQJ3cUIiIiolpzezhuYWEhIiIiAAAGgwEZGRnOdampqXj33XdhMpnw3nvvYcqUKeWen5iYiMTEsuuZpk+fDrPZXNfsXqVSqfw+IzV8Lu3wcDKkZi2hamIGOBy30ZLadYZ551qI+x736XH5mUj+gO2Q/AHbIfmL+twW3S5CDQYDioqKAADFxcUwGAzOdZGRkWjRogUAQKGouHM1ISEBCQkJzsdZWVm1CuwrZrPZ7zNSw3d1OzRuXQcREAJbSSlQUipzMpKL1CoWhnW/4PKNQ306LJufieQP2A7JH7Adkr/w97YYGRlZ6Tq3h+PGxsbiwIEDAID9+/cjNjbWua5Zs2a4fPkySkpKYOd97Ig8z2qB+uQR2AND5E5CMhN6I+xNwqHbvkbuKERERES14nYR2qZNG6jVakyePBkKhQJmsxlLly4FAIwaNQoffvgh3nrrLU5MROQFmuMHYTM35b1BCQBgad8V+h3rAIdD7ihERERENVajW7RcfVsWAM6Cs0WLFnjjjTc8FoqIXGlS9sBubgaoavQrSw2UI7gJhEoN9cGdsMb1ljsOERERUY243RNKRPKQiougOpsOR2Cw3FHIj5R26AbD5lVyxyAiIiKqMRahRH5OczgJtogWHIpLLuwRLaAoyIUq/ajcUYiIiIhqhEUokZ/THtgJe3gkoFTKHYX8iSTB0v466Df8JncSIiIiohphEUrkz7IvQCrMg0NvlDsJ+SFryxioz5yAlH1R7ihEREREbmMRSuTHpKStsDWLgtDq5Y5C/kiphKVNJxjWLZM7CREREZHbWIQS+SshICVtgc0cAUiS3GnIT1nadoI2dR9QXCh3FCIiIiK3sAgl8lPKc6cgtDqAExJRVTRaWJtHw7D+V7mTEBEREbmFRSiRn9Ie2AnRrBVnxaVqWTp0hXbvVsBSIncUIiIiomqxCCXyR3Y7NEf2AxyKS24QeiPsYZHQ8b6hREREVA+wCCXyQ+oTh2APMXMoLrmttGM36HetB2xWuaMQERERVYlFKJEf0h7cDXt4M0CjlTsK1RPCFAR7YBPodqyVOwoRERFRlViEEvmb0hKoTh2DPTBE7iRUz1g694B+SyJgt8sdhYiIiKhSLEKJ/Iz2UBJsEc0hNLw3KNWMIygUDr0B2qQ/5Y5CREREVCkWoUR+Rrt/O+zhLQClUu4oVA+Vdu4J/aYVgBByRyEiIiKqEItQIj+iuJQJqbgQDr1B7ihUTzlCwwGlEpr9O+SOQkRERFQhFqFEfkS7bztsTVtB6FiEUu2VduoJw4bf2BtKREREfolFKJG/cNihPbQHNt4blOrIHtYMsNugPrhL7ihERERE5bAIJfIT6rRDsAeFQmg5IRHVkSShNK43jGt/Zm8oERER+R0WoUR+QrtvB2zhzQG1Ru4o1ADYw5oBwgH1gZ1yRyEiIiJywSKUyA9IRflQnTsJB+8NSh7E3lAiIiLyRyxCifyA9uBu2JpFQWh0ckehBsRubgpIgHrfdrmjEBERETmxCCWSmxBls+KGNeO9QcnjSuN6w7iOvaFERETkP1iEEslMef40BAChN8odhRoge5MIQKWCds9muaMQERERAWARSiQ7XdKfsEVyKC55T0mX3tBv+A2w2+WOQkRERMQilEhOUklx2a1ZQsLkjkINmCM0DEJngHbHOrmjEBEREbEIJZKT5uAu2Jq2hNCyF5S8qzS+DwybVgBWi9xRiIiIqJGrURG6YMECTJ48GV988UW5dRaLBU888QT27dvnsXBEDZoQ0CX/CXtEc0CpkjsNNXCOwGDYm0RAv3G53FGIiIiokXO7CE1LS0NJSQneeust2Gw2HDt2zGX9mjVr0KpVK48HJGqoVGdOQiiUcHBCIvKR0i7XQ79jPVBcKHcUIiIiasTcLkKPHj2K+Ph4AEBcXByOHDniXGez2XD06FG0b9/e8wmJGiht8p+wRkZBqLVyR6FGQuiNsLZsA+PqH+WOQkRERI2Y22MACwsLERERAQAwGAzIyMhwrlu/fj1uuukmHD16tNLnJyYmIjExEQAwffp0mM3m2mb2CZVK5fcZqR4rKoDizAk4brwVMAZWuplSqURgYOXriWqs1wAofv4KeuVfgRD3P+P4mUj+gO2Q/AHbIfmL+twW3S5CDQYDioqKAADFxcUwGAwAALvdjuTkZIwfP77KIjQhIQEJCQnOx1lZWbXN7BNms9nvM1L9pdu5HipzM1gsdsCeV+l2gYGByMurfD1Rbahbd4D09SwUPPis28/hZyL5A7ZD8gdsh+Qv/L0tRkZGVrrO7eG4sbGxOHDgAABg//79iI2NBQDk5ubi0qVLeOedd7Bp0yZ89913KCgoqGNkogbM4YA2eQtsYZGAUil3GmqErDFdoE4/BmXGCbmjEBERUSPkdhHapk0bqNVqTJ48GQqFAmazGUuXLkVoaCimTZuGiRMn4qabbsKDDz4Ik8nkzcxE9Zr6ZCocWj2Egb8nJBOlEqXX9YHp14WAEHKnISIiokamRveFGDNmjMvjkSNHujweNWpU3RMRNXC6XRthi4yC0HBCIpKPLbI1NEf2Q7N3Gyxd+8odh4iIiBqRGt0nlIjqRpF9AYrsC3AEhsgdhRo7SUJJ9xthXL0EsFrkTkNERESNCItQIh/S7d4Ea8u2EFq93FGI4AgKha1JU+jXLJM7ChERETUiLEKJfEQqKYYmdS/sTcIBSZI7DhEAoDSuF3RJmyHlXpI7ChERETUSLEKJfES7fztszVpBaNgLSn5Eq4OlXTxMvyyUOwkRERE1EixCiXzB4YB2z2bYwpsDqhrNB0bkddaYzlBlZkB9ZJ/cUYiIiKgRYBFK5APq4ylwGAPg0BvljkJUnkKB4u43wfTr14DNKncaIiIiauBYhBL5gH5bImzNowHeloX8lMPcFPbgJtAnLpU7ChERETVwLEKJvEyVkQZYLXCYAuWOQlSlkuv6Qp+8BYqL5+WOQkRERA0Yi1AiL9NtWwNbq7YQGp3cUYiqptGipFNPBPz0OSCE3GmIiIiogWIRSuRFyqxzUF7KhD0whLdloXrBFtUOUkkxtLs2yB2FiIiIGigWoURepNu2FtZW7SC0BrmjELlHklDccyCMa36ClJcjdxoiIiJqgFiEEnmJlJ8D1amjsIea2QtK9YowBaI0pgsCfvxM7ihERETUALEIJfIS/Y51sLVsy15Qqpes7eKgyM2GZvcmuaMQERFRA8MilMgLpIJcaFL3whYWCSj4a0b1kCShuPdgmFb/CCk/R+40RERE1IDw2zGRF+i3r4WlVQyEVi93FKJaE8aAsmG5Sz7jbLlERETkMSxCiTzsSi+ovUkzQKmUOw5RnVjbdYEiPwfY+LvcUYiIiKiBYBFK5GFlvaDtIHTsBaUG4L/DchW/L4Ii65zcaYiIiKgBYBFK5EH/6wVtyl5QajCE3ghHzwEI/HYWYLfJHYeIiIjqORahRB6k35oIa6u27AWlhqd1OzhMQTAs/1buJERERFTPsQgl8hBFThbUR/fDZo5kLyg1SCXd+kGbuhfqw8lyRyEiIqJ6jEUokYcYNiyHtU1HCB3vC0oNlFJVdtuWn7+ElJstdxoiIiKqp1iEEnmA8twpKDMzYA+N4H1BqUFzBDdBaYeuCPr6A14fSkRERLXCb8tEdSUEDOt/haVtRwitTu40RF5ni+4Ah94E489fyh2FiIiI6iEWoUR1pD5xGFJJMRwBIYAkyR2HyCdKut0IdfoRaHdtkDsKERER1TMsQonqwm6HYc0yWKLb81pQalyUShTfcBuMiUuhzDgpdxoiIiKqR1iEEtWBbvdG2IND4TAFyR2FyOeE3oji6wch8NuPOFERERERuU1Vk40XLFiAtLQ0REdHY8yYMc7lc+fOxenTpwEAjz/+OKKiojybksgPSQW50O1cj+JuNwIardxxiGRhD2uG0o7dEPTle8h5ehKg4XXRREREVDW3e0LT0tJQUlKCt956CzabDceOHXOuu/vuuzFlyhSMHTsWixcv9kpQIn9jWP8rLNEdIPRGuaMQycoWFQu7uRkCv50FOBxyxyEiIiI/53ZP6NGjRxEfHw8AiIuLw5EjRxATEwMACA8PBwAolUooKrk9RWJiIhITEwEA06dPh9lsrlNwb1OpVH6fkWR08gikS+chrh8AGExeO4xSqURgYKDX9k/krmrbYt+bIW1YjrA1SyAe+Dsn6SKv4N9m8gdsh+Qv6nNbdLsILSwsREREBADAYDAgIyOj3Dbffvsthg4dWuHzExISkJCQ4HyclZVV06w+ZTab/T4jycRmRdB3n8LSrgvsVjuQl+e1QwUGBiLPi/sncpdbbfG6fjBsWoHSHz5H8eARvglGjQr/NpM/YDskf+HvbTEyMrLSdW4PxzUYDCgqKgIAFBcXw2BwnQl0+fLlaNGiBTp06FDLmET1g35rImyhYbCbgtjbQ3Q1pRJF/W6Hdu826LauljsNERER+Sm3i9DY2FgcOHAAALB//37ExsY61+3duxepqam45557PJ+QyI8oL56D5sAO2CJbczIiooqo1SjqPwz6P1dBm7RF7jRERETkh9wuQtu0aQO1Wo3JkydDoVDAbDZj6dKlAID58+fj4sWLePPNNzF37lyvhSWSlcMB4+/fwRLblZMREVVFo0XRjUNgWL0Y6gM75E5DREREfqZGt2i5+rYsADBy5EgAwIcffui5RER+SrctEQ6tHo7gEKCSCbiIqIwwmFB00zCYVnyPQoeAJb633JGIiIjIT/CbNJEblGfTod23DdZW7SDUHIZL5A5hDEBR/2EwrvoBmr1b5Y5DREREfoJFKFF1LCUw/fY1LB26Q3jxdixEDdGVHlHjH0ug3bVR7jhERETkB1iEElXDmLgUtqYtYQ/gbLhEtSEMRhT1vwOGjb9Bv+5XQAi5IxEREZGMWIQSVUG7bxuUF87CFtESUGvkjkNUbwm9AYX9h0N7YAeMvy4EHA65IxEREZFMWIQSVUJ5/jR0m1fBEhsPoTdU/wQiqppGg6KbhkJ1/jQCvv0YsJTKnYiIiIhkwCKUqAJScSFMP38JS+fucBgC5I5D1HAoFCjuPRiAhOC570CRc0nuRERERORjLEKJrmW3wfTTF7C2ioE9gLdjIfI4SUJpfG9YWsci6LOpUJ04LHciIiIi8iF+uya6mhAwrvgODr0B9rBmgEotdyKiBsvWqh2Kew1CwJLPoNv0O68TJSIiaiRYhBJdRb/pd0j5ObA1bwOh0ckdh6jBc4SEoXDgndAe2InAr2ZCKsiTOxIRERF5GYtQov/S7tkE9bH9sEZ3gtDp5Y5D1HhodSi+4VbYTUEInjMF6mMH5E5EREREXqSSOwCRP9Amb4Fuz2aUdOoBYTTJHYeo8ZEkWGPjYA9rBuMvC2Ft2wlFt90HoePM1ERERA0Ne0Kp0dPs2w7dzvUo7dgDwhgodxyiRs0RYkbRoLugKMxD8CdvQn1kn9yRiIiIyMNYhFKjpt21EfptiSjt1AMOUyAgSXJHIiKlEqVdeqG4R38Yf/8epu8/4a1ciIiIGhAWodQ4CQH9xuXQ7t+O4i7Xw2EKYgFK5GccIWYUDbwTQqNF0OfToF/3C2AplTsWERER1RGLUGp8bFYYf/8OqtPHUdqxO8AClMh/SRKsMV1QOPBOqE4fR/Ds16Hdswmw2+VORkRERLXEiYmoUZHycxDw03zYA0NhaRfHSU+I6guNFqVdb4CUexnapD+h37wSxf3vQGl8L0ChlDsdERER1QCLUGo0VCdTYVrxPSztusAeGgah1sodiYhqSASFoOT6QZAuX4Ru53roNy1H8Q23oTS+N6DWyB2PiIiI3MAilBo+mxWGDb9BnXYIJZ17whEQDKjY9InqMxEShuLeN0O6nAXt/u0wrP8VJd1vQsn1/SFMQXLHIyIioirwmzg1aKqMNBhX/QBbkwiUxPWB0Bt4/SdRAyJCzCgJuQkoLIDm5GEEf/o2rC1jUNr9RljbdOBQXSIiIj/EIpQaJKkwH4Z1v0B1Nr1s+G1AMKDh8FuiBstogqVzT1g6dIPqTBoMa5dBWl6I0vg+sHTqAXt4JP8BioiIyE+wCKUGRSopgm7nBmj3bYMluj1KrutTNvkQv3wSNQ5KJWyt2sHWqh2kglyoM04gYMlcCCHKitSO3WCPaMHPBCIiIhmxCKUGQSrMhy7pT2j3boW1RTSKu99UVnwqORSPqLESpiBYOnSFpf11UORegjLzDExL50GylMLatjOsbTvBGt0eQm+UOyoREVGjwiKU6i8hoDx3Cro9m6FOPwJr89Yo7tYPQmfkxENE9D+SBEewGY5gM6ztrwMK86HOOgvdzvUwrlwER2AwrFGxsLVsA2vzNhABnNiIiIjIm/hNneodxaUL0B7aDc3B3RBqDWzNWqG4Z38IjZ49n0RUPWMArMb2sEa1B2w2KHIvQZGbDd2O9TDkLAEkBWwt2sDWtAXs4c1hi2gBYQqUOzUREVGDwSKU/J5UUgxVRhrUaYegTjsEoVTCHt4cJV2uBzRaCK1e7ohEVF+pVHA0iYCjSQRsAOBwQCrMhzL3ElQZJ6BJ3QtFfi5gt8Me3gx2czPYQ8PgCAmDPSQMjuBQzsBLRERUQyxCya9IxUVQXsqE8uJZqM6lQ3XmJKTSEthDzLCHhqM0vjeEWgOh0XFiESLyPIUCIiAItquH5NrtkEpLoCjIgVRUCPWJw1Ac3A2pKB+K4iIIrQ72oFA4gkLhCAyBIyAIjoAQOAKD4TCYyq45Vanle01ERER+pkZF6IIFC5CWlobo6GiMGTPGufzUqVP47LPPAACPP/44oqKiPJuS6j8hAGspFCXFkArzoSjIgyI/578/uWWThmRfhFAq4TAGQBgC4AgMQWnnnhAqNYRay6G2RCQPpRLCYITdcM0ERkIANiuk0mIoSoqB0mIocsomQJJKiyGVFEGyWiBZLIBwAGpN2eebMaCsONUZIDQ6CK0OQqP97391V/1XC6HSACoVhEoNKFX8xzciImoQ3C5C09LSUFJSgrfeegufffYZjh07hpiYGADAokWLMG7cOCgUCnz++ed46aWXvBbYF5RZ54C0A9Dm5ZV9yaiMyzpR4f+W3/Z/K6Wq9n31cyrartLn1uI5/10uVbCswhcjADjskOw2wGb773+tro+tVkiWEkglRVBYSsv2olJDqMsKSqHTQ2j0EDodHGotHM1bwxLTpawX4sqXLSIifyZJgFoDodbAbirrObVfu43d7vp5aS2FZCkt+4wsKYKiML9snd0GyXb1Z6kVks0K2B2QHPayYcIOO4QEAFLZsVUqCKW67DNTpYZQKsuGBisUZYXzlf9XKCAkhXM5JAWEQuHcVkiK/xW3knTN/yv+98dBUpR9lpfb9trnlP2/uPJ8t8+nG9sEBkKbl+/GvmQo1t06Jv8RoUEIDCz7jkgkt5tukTtBrbn9Tf/o0aOIj48HAMTFxeHIkSPOIrSwsBBms9n5/xVJTExEYmIiAGD69OnO7f1SUS6U+7YiMPdy2WPnH5YK/nhIFTyoaFmFi6SqlzkXVfRHq6LnVpWl6u0rLk8r2rH4Xybpv19o1FpAoS97rFD897/KsuFnGi2gUv5vmVJZNnMtr6Fyi1KhRGAQZ+ok+bEt+pgQZb2njv/+CAfgEGX/D1G23mEvK3Lttv8Wuw5A2AEHyrbHle3/+1iIso/wK/vFlX2L//1c+dgXuOZx2Xrp6nzODa/8R/zvvy7beOqcAAqFAoFXXlNVG7qxL89y55gePyjJxL12SOR9iut6whzWTO4YteJ2EVpYWIiIiAgAgMFgQEZGhnOdcOODNSEhAQkJCc7HWVlZNcnpW4YgmEc96d8ZqVEwm81sh+QX2BbJH7Adkj9gOyR/4e9tMTIystJ1bo+TMRgMKCoqAgAUFxfDYDBUuJ3E61WIiIiIiIioEm4XobGxsThw4AAAYP/+/YiNjXWuM5lMuHTpErKzs6HX83YZREREREREVDG3i9A2bdpArVZj8uTJUCgUMJvNWLp0KQBg1KhR+OCDDzBz5kzcf//9XgtLRERERERE9Zsk3Lmg0wvOnj0rx2Hd5u9jrKlxYDskf8G2SP6A7ZD8Adsh+Qt/b4seuSaUiIiIiIiIqK5YhBIREREREZHPsAglIiIiIiIin2ERSkRERERERD7DIpSIiIiIiIh8RrbZcYmIiIiIiKjxYU9oJV5++WW5IxCxHZLfYFskf8B2SP6A7ZD8RX1uiyxCiYiIiIiIyGdYhBIREREREZHPsAitREJCgtwRiNgOyW+wLZI/YDskf8B2SP6iPrdFTkxEREREREREPsOeUCIiIiIiIvIZFqFERERERETkMyxCiYiIiIiIyGdYhBIREREREZHPsAglIiIiIiIin2ERSkRERERERD7DIpSIiIiIiIh8hkUoERERERER+QyLUCIiIiIiIvIZFqFERERERETkMyxCiYiIiIiIyGdYhBIREREREZHPsAglIiIiIiIin2ERSkRERERERD7DIpSIiIiIiIh8hkUoERERERER+QyLUCIiIiIiIvIZFqFERERERETkMyxCiYiIiIiIyGdYhBIREREREZHPsAglIiIiIiIin2ERSkRERERERD7DIpSIiIiIiIh8hkUoERERERER+QyLUCIiIiIiIvIZFqFERERERETkMyxCiYiIiIiIyGdYhBIREREREZHPsAglIqqlRx99FHfccYfcMVxcvnwZEREROH78uMvyWbNmISYmBnq9HrfffjsuXrzoXLd+/Xq0bt26xse677778N5779U1st+q7Fw2Jg39PSYiInmwCCUiv/Hoo49CkiRIkgS1Wo02bdpg/PjxKCws9Mj+Bw4ciGeffdYj+wKADz/8EF9//bXH9ucJU6dOxdChQ9G2bVvnsokTJ2LGjBmYO3cutm/fjrS0NLz00ktV7kcIgS5duuD55593Wb5582bo9Xp8+umnmDx5Mt555x3k5uZ65bUMHjzY2R4kSUJISAiGDh2K06dP12g/L774Im677bYaH7+ic7lx40bceeedaN68OSRJwoIFC8o9z51trpg2bRokSapxu6zuGLNnz0Z8fDwCAwMRGBiIvn37Yvny5eX2c+7cOYwePRphYWHQ6XTo1KkTNmzY4Fzv7fe4Nq58Tjz22GPl1k2YMAGSJFX6j0N79uyBUqlEv379Kt2vtz5/rvjkk08QHR0NnU6HHj16YNOmTW4/t7L28sYbb7j8rkiShKZNm9Z4G6D6NuHufoiIqsIilIj8SkJCAs6dO4e0tDS8/fbb+OSTTzB+/Hi5Y7mwWCwAgKCgIAQHB9d5P55SVFSEzz//3OXL+a5duzBt2jR8//33uPnmmxEfH49nn322woLkapIkYeLEifj000+RlZUFAEhNTcVdd92F559/Hk899RTi4uLQpk0brxXie/bswdSpU3Hu3DmcOXMGS5cuxc6dO/Haa6/VaD87duxAr169avScis4lABQUFKBLly748MMPodfrK3yuO9sAwLZt2zB37lzEx8fXKJs7x2jRogXeffdd7NmzB7t27cLNN9+Mu+++G/v27XNuk5OTg379+kEIgeXLl+PQoUP4+OOPER4e7tzG2+9xbbVs2RI//PCDS4Fos9nw1VdfoVWrVpU+7/PPP8fYsWNx4MABHDp0qNx6b3/+LFq0COPGjcOrr76KpKQk3HDDDRgyZAhOnTpV7XOray/t27fHuXPnnD/79++v8TbutAl3j0VEVCVBROQnRo8eLYYNG+ay7PHHHxdNmzYVQghRUlIixo0bJ8LDw4VWqxW9e/cWmzZtctl+w4YNonfv3sJoNIrAwEBx/fXXi/3794vRo0cLAC4/J06cEA6HQ7z77ruiTZs2QqfTiS5duoiFCxe67HPAgAHi6aefFi+88IIwm82iZ8+eFeatLl9l+3HHxYsXBQDx/vvvi549ewqtVivatWsnVq1a5dxm8eLFIiQkRDgcDuey+++/XwwYMMBlX99++62QJMn5eN26dSIqKqrcMe12u2jXrp145ZVXxPnz50V0dLT4y1/+4rLNm2++Kfr16+f263DXsWPHBACxZcsWl+UDBw4U99xzj8uyjIwM8cgjj4jQ0FARFBQkRo4cKc6fPy9KS0uFWq12ec87duzofN6UKVNEXFycMBqNwmw2i9GjR4uioiIhRMXn8lpGo1F88cUXVb6OyrbJyckRbdq0EWvXrhUDBgwQzzzzTDVnpObHuFZISIiYM2eO8/Err7wibrjhhmqf5633uLau/N5169ZNzJ8/37l82bJlonXr1uKvf/1ruc8RIYQoKioSQUFBYt++feJvf/ubeOGFFyrc79Wu/vzxhF69eonHH3/cZVlMTIx4+eWXq3xede3l9ddfF507d65yH+5s406bcGc/RETVYU8oEfk1vV4Pq9UKAHjppZewaNEizJ8/H0lJSYiLi8Ptt9+Oc+fOASjrCbnrrrtw4403Yu/evdi+fTv+8Y9/QKlU4sMPP0Tfvn0xZswY57/et2zZEq+99hrmzZuH2bNnIyUlBa+88gqeeuqpcj2FX3/9NYQQ2LRpE7766qsKs1aXr7L9LFiwAJIk4eTJk5Weh+TkZABlPTnvvvsu9u3bh/j4eDz00EMoLi4GAGzatAk9evSAJEkAAKvVil9//RUjR4502VdxcTGCgoKqPfcKhQKvvvoqZs+ejaFDhyI6Ohrz5s1z2aZXr17YsWOHM8PVpk6dCpPJVOVPZUMRd+/eDZVKha5duzpfy7fffoudO3fimWeecW534sQJdO/eHc2bN8fmzZuxfv16ZGVl4emnn4ZKpcLWrVsBANu3b8e5c+fw559/Op9rs9nwn//8BwcPHsR3332H1atX44MPPqjwXHrak08+iXvvvReDBg3yyv6vZrfb8f3336OgoAA33HCDc/myZcvQu3dv3H///QgPD0fXrl0xa9YsCCFcnl/Veyynxx57DPPnz3c+nj9/PsaMGVPpe7ZkyRJERUUhLi4OjzzyCL766ivnZ0tlrv78AerWpi0WC3bv3o1bb73VZfmtt96KLVu2VJnDnfaSlpaGyMhIREdH44EHHkBaWlqNt3G3TbhzLCKiKslbAxMR/c+1PRHbt28XTZo0EaNGjRIFBQVCrVaLL7/80rneZrOJNm3aiIkTJwohhLh06ZIAINavX1/h/q/tQSgoKBA6nU5s3LjRZbtx48aJIUOGuDwvLi6uyrzu5KtsP0uXLhXt27cXGRkZlZ6bf//730KpVIrU1FTnsiu9hXv27BFCCHHXXXeJv/71r871O3bsEACETqcTRqPR+aPRaETv3r2d21XWEyqEEMXFxcJkMomYmBiRk5NTbv3evXsFAHHs2LFy6y5duiSOHj1a5c+VnsdrvfTSS0KSJGdmhUIhQkNDxR9//OGy3a233ipeeeUVl2WrV68WAQEBQgghfv31VxEQEFBlj+YVTzzxhPP8XXsuK1LbntC5c+eK7t27C4vFIoQo3y5rqrIc+/btE0ajUSiVShEUFCR+++03l/VarVZotVrx8ssviz179oj58+cLo9EoPv74Y5ftqnqP5XDl9y47O1vodDpx5MgRce7cOaHRaER6enqFPZpClJ3nf//730IIIRwOh4iKihKLFy8ut98rrv78uaIubfrMmTMCgNiwYYPL8jfffFPExsZW+nrdaS8rVqwQixYtEnv37hWrV68WAwYMEBERESIrK6tG27jTJtzZDxFRdVRyFsBERNdauXIlTCYTbDYbrFYr7rrrLnz88cc4fvw4rFary4QiSqUSffv2RUpKCgAgNDQUjz76KG677TYMHjwYgwcPxr333lvpNWIpKSkoKSnB7bff7tJ7YrVay80W26NHjypzu5Ovsv2MGDECI0aMqHL/ycnJGD58OGJjY53LAgMDXbYpLi5GRESE83Fqaio0Gk2567UefPDBCidmqchzzz0Hm82GS5cuQaEoP3jmyvWIFfWShYaGIjQ01K3jXGvPnj0YOXIkpk+fDgC4dOkSXn/9dTz55JM4dOgQdDod0tPT8ccff2DTpk346KOPnM+12+0wGAwAgKSkJFx33XXlesdOnz6Nf//731i3bh3OnDkDi8WC0tJS54RN155LT0lNTcWrr76KzZs3Q61We3z/V2vfvj2Sk5ORm5uLJUuWYPTo0Vi/fj26dOkCAHA4HOjZsyemTZsGAOjWrRuOHj2K2bNnu0x8U9V7LKeQkBCMGDEC8+fPR3BwMAYOHFjp7/qxY8ewefNmfPvttwDKrnl++OGHMW/ePNx7773O7Sr7/LmiLm26NtxtL0OGDHF53KdPH7Rp0wZffvmlc3Ixd7Zxp024sx8ioupwOC4R+ZX+/fsjOTkZqampKCkpwdKlS8tNinGtqwuML774Atu3b0f//v3xyy+/oH379li1alWFz3M4HACAX3/9FcnJyc6fgwcP4o8//nDZ1mg01vo1XZ2vtvtJTk5Gt27dXJZt2bIFOp0O7du3BwCYzWZcvnzZuT43NxdmsxkxMTHOn+DgYCQnJ7t88a7Mm2++iR9//BFbt26F0WjErFmzym2TnZ0NAAgLCyu3ri5DF/fs2YN+/fo5c/fu3Rsvv/wyTp486Szq9+7di8DAQOzbt8/l/du/fz+SkpIqPW+XLl3C9ddfj/Pnz2PGjBnYtGkTdu3aBZ1O5xz+e+259JStW7ciKysLnTt3hkqlgkqlwoYNG/DJJ59ApVKhtLTUY8fSaDSIiYlBjx49MG3aNHTt2hUzZ850rm/WrBk6derk8pyOHTuWmySnqvdYbn/729/w1VdfYf78+fjb3/5W6Xaff/457HY7WrVq5Tzv06dPxx9//OEy23J1nz91adNmsxlKpRKZmZkuyzMzMyudXba27cVkMqFz5844evRopeekom3cbRM1PRYR0bXYE0pEfsVgMCAmJqbc8rZt20Kj0eDPP/903jLDbrdj69ateOihh1y2ve6663DddddhwoQJGDJkCL788kvcdttt0Gg0sNvtzu06deoErVaL9PR03HzzzXXKXZN8NVVSUoLU1FRn0XzFe++9hwceeMDZ69etWzeXW3WYzWbk5+fD4XA4ezGnTZuGvn37om/fvlUec968ec4v6V27dsVLL72EKVOmYNy4cc7jAcCBAwfQvHnzCnsNn376aYwaNarK4zRv3rzcshMnTiA7O7tc8XjlurMrRYFarUZhYSGaNm0Kk8lU4f737t1brudm+fLlKCkpwaJFi5z/QPDll1+ioKDAWYReey495e6770bPnj1dlo0ZMwbt2rXDq6++Co1G4/FjXuFwOFyKln79+iE1NdVlmyNHjiAqKsplWVXvsdwGDx4MjUaDrKws3H333RVuY7PZ8OWXX2LatGnlbt3yyCOP4IsvvsDkyZMBVP75c0Vt2zRQ9o8CPXr0wOrVq3Hfffc5l69evRr33HNPhc+pbXspKSnB4cOHq7yGtKJt3G0TNT0WEdG1WIQSUb1gNBrx97//HRMmTIDZbEZ0dDRmzpyJzMxMjB07FkBZ8fLpp58675+YlpaGffv24e9//zsAoHXr1tixYwdOnjwJk8mE0NBQjB8/HuPHj4cQAv3790dBQQG2bdsGhUKBJ5980qP5auvAgQMQQuC7777D4MGDER4ejrfffhvHjh3DDz/84Nzutttuw4QJE3Dp0iU0adIEN998M2w2G9555x088sgjWLJkCRYuXOgyOU9FVqxYgbFjx+Lrr7/GTTfdBAB44oknMHXqVHz66af45z//6dx206ZNld6Ds7ZDF3fv3g0AaNq0Kc6fP4+ioiJs3boVL7/8Mh5++GG0aNECQNkwwJCQEDzyyCOYPHkyAgMDkZaWhmXLluHjjz+GQqGAzWbD4cOHcfbsWRgMBgQHB6NJkyYoKCjAsmXLEBcXh99//x1Tp05FQECAswC59lxeUVBQgGPHjgEoK+pOnTqF5ORkhIaGOoeCVrfNtbf1MRqNCA0NdQ6TdUd1x3j55ZcxbNgwtGzZEvn5+fj222+xfv16lwm3/vnPf+KGG27AO++8g/vvvx9JSUn46KOPMHXqVJdjVfUey02SJOzbtw9CCGi12gq3Wb58ObKysvDEE0+4vJcA8MADD2DOnDmYNGmSW8er63Dc559/Ho888gh69eqFfv36Yc6cOTh79iyefvpp5zazZs3CrFmzcPjwYQQHB7vVXsaPH4/hw4ejVatWuHDhAqZMmYLCwkKMHj26Rtu40ybc2Q8RUbVkviaViMipsglFrrj6FihXJte5+hYo58+fFyNGjBCRkZFCo9GIli1bihdffNE5oUdqaqro06eP0Ov1Lrdo+eijj0THjh2FRqMRZrNZJCQkuEyAU9nEMVXdoqWifJXt54svvnDmqchnn30mOnToIL777jvRvHlzodfrxbBhwyqcKKZPnz5i1qxZzseLFy8WrVq1Enq9Xtx6660iJSWl3HOunphox44dwmg0ivfff7/cdjNmzBCRkZGipKRECFE2aVFgYKDYunVrhblr6+WXX3a5rUpQUJDo0aOHmDNnjrBarS7b7ty5UwwaNEgEBQUJk8kk4uPjxdSpU53rv/76a9G8eXMhSZJ4+umnhRBlk9KMHTtWBAQEiLCwMPHcc8+JF154odxtSK49l0KUnStcc6sfAGL06NE12uZqFbWL6tpEdccYPXq0aNWqldBoNCIsLEwMHjxYrFy5stx+fvvtNxEfH++85c+HH37oMomTt97juqjuc+La9cOHDxe33HJLhdseP35cABCrVq2qdr+eMnv2bBEVFSU0Go3o3r17uYmKXn/9dVHV17OK2sv9998vmjVrJtRqtYiMjBQjR44UBw8erPE2QlTfJtzdDxFRVSQhrpl3m4iIfOr111/HkiVLsHfvXqhU5QeoPPvss7hw4YJLr2dlVq5ciXHjxiElJQVKpdKt469fvx6PPvpolbeIqcjs2bPx888/l7t+tqGozbn0lOrahK809PeYiIjkwYmJiIhktmLFCsyePbvSYiM5ORnx8fFu7ev222/HM888g4yMDE9GrJBarXaZObSh8eW5vFZ1bcJXGvp7TERE8mBPKBGRHxNCICgoCF9//TXuvPNOrxyjtj2hRERERLXBiYmIiPyYJEnIy8vz6jFat26Nf/zjH149BhEREdEV7AklIiIiIiIin+E1oUREREREROQzsg3HPXv2rFyHdovZbEZWVpbcMaiRYzskf8G2SP6A7ZD8Adsh+Qt/b4uRkZGVrmNPKBEREREREfkMi1AiIiIiIiLyGRahRERERERE5DMsQomIiIiIiMhnWIQSERERERGRz7AIJSIiIiIiIp9hEUpEREREREQ+wyKUiIiIiIiIfEYldwAiIiJPOpd9EukXjkCt0qBd5HUINITIHYmIiIiuwiKUiIgaBKvNghW7vsbF3DMI0Aej1FaKTQd/Q+/YBPTpcBskSZI7IhEREYFFKBERNQB2hw2LN38CjUqD8OAWUCs1kCQJIcYm2HV0PQpK8nBLt1FyxyQiIiLwmlAiImoA1u37CUqFClq1ARqV1tnrqVZp0aZZJxxM34F9J7bKnJKIiIgAFqFERFTPpV84gpOZh6HXGqFWacqtVypUiApvj8TkxSgozpUhIREREV2NRSgREdVbDocdick/wBwYCbWyfAF6hV5rRLDRjN92fOnDdERERFQRFqFERFRv7U/fBr3GBKVSWe3EQxEhLXEm+wTOXjrpm3BERERUIRahRERULzmEA9sPr4ZRF1hlL+gVSoUS4UGRSExe7IN0REREVBkWoUREVC+lZuyBQRcApaR0+zlNApriYu4ZZOWe82IyIiIiqgqLUCIiqpd2HV2PAH0wVCq1289RKJQIDYjA2n1LvZiMiIiIquLWfUJXrlyJ9evX49SpU+jXrx+eeeYZAMCRI0ewaNEipKWlQaFQoHPnzhgzZgxCQkK8GpqIiBq3i7lnUWIpRJCxSY2faw5shqNn98FiK4VGpfVCOiIiIqqKWz2hISEhGDlyJAYNGuSyvLCwEAkJCZg9ezY++eQT6HQ6fPLJJ14JSkREdEVy2maEmMLduhb0WmqVBlq1DttTE72QjIiIiKrjVhHau3dv9OrVCwEBAS7Lu3Xrhr59+8JgMECr1eL2229HamqqV4ISEREBgM1uReqZZKhV2mpnxK2MOTASh07t9HAyIiIicodbw3HddejQIbRs2bLCdYmJiUhMLPtX5+nTp8NsNnvy0B6nUqn8PiM1fGyH5C/8qS0eOLET5qCmMBqMUCndvx70alptU2RcOg67shQRIc09nJC8xZ/aITVebIfkL+pzW/RYEZqeno4lS5bgpZdeqnB9QkICEhISnI+zsrI8dWivMJvNfp+RGj62Q/IX/tQWd6Ssh1qhhc1qh81qr/V+AvXBWLntBwy7/hEPpiNv8qd2SI0X2yH5C39vi5GRkZWu88jsuOfPn8fUqVMxZswYdOzY0RO7JCIiKsdqtyD9QirUNZgRtzIhpnCcunAEQggPJCMiIiJ31bkIvXjxIqZMmYJ77rkH/fv390QmIiKiCqWdT0Gw0Qylou4DeYy6QBSV5uNi7hkPJCMiIiJ3uVWE2u12WCwWOBwOOBwOWCwW2O12ZGdn46233sJtt92GW2+91dtZiYiokUs9vQdGXaBHilBJkhBoCMWOI2s9kIyIiIjc5dZf8R9//BFLlixxPt60aRPuvfdeSJKEzMxMLF68GIsXL3auX7hwoeeTEhFRo+Zw2HHq4lG0DIv12D6DjWacuXTcY/sjIiKi6rlVhI4aNQqjRo2qcN19993n0UBEREQVOZN9AiZ9EJQKj0xnAAAw6gORfjEVeUWXEWgI8dh+iYiIqHKe+0tORETkRcfPHYBRG1Dr27JURCEpYNAGICltk8f2SURERFVjEUpERPXC8XMHoFFpPb7fIEMoTmYe9vh+iYiIqGIsQomIyO/lFV2G1WaBJCk9vu9AQygu5Z2HzW71+L6JiIioPBahRETk99LOH0SQsQnUKo3H961WaaCQFDh+br/H901ERETlsQglIiK/dyLzEHRqAyRJ8sr+Aw0hSDm12yv7JiIiIld1v9EaERGRFwnhwJmsNLTy4K1ZrhWgD8GF3DMe3acQAgUr1iLn6x9ReugYoFTA0LsbmvzfY9B2iPHosYiIiOoT9oQSEZFfu5h7Fnqt0Wu9oABg1AUgv/gyiksLPLI/e34Bzox5HtlzFkIRFAj9jb2g6x4PW2YWTt33FC5OmwUhhEeORUREVN+wCCUiIr+WfvEIDNpAj96a5VoKhRIalQ6HTu+p874cBYU4ff/fIamUUEe3hDIoAEqjHqrQIGhiWsOYcCPylq7AuWcnshAlIqJGiUUoERH5tfTMVGjUWq/2hAJAoD4Ex+o4OZGw2XD2769AHRkBhckIhV5XbhuFRgPDgD4o2roHF6d8UKfjERER1UcsQomIyG85hAPnsk9CpfBeL+gVAYZgZOWdq1PvZPZ/voLDYoVk0EPSVj6Tr6RUwti/N3K/XYaC9VtqfTwiIqL6iEVoDbVs2RK33HKL82fWrFlVbn/nnXdWuPy9997DnDlzvBHRI4qLi3HPPffAbrcDAL766iu8/PLLzvXvvvsunnvuOVgsFowcORI2m61Wxzlz5gzuvfdeDBw4EIMGDcLnn39e4XbPP/884uPjcfPNN5dbt27dOtx0003o16+fy/tR1XM8pbJj9O7dG4MHD8Ytt9yCIUOGeO34RA3dhZwMGHVBUCo8f3/Qaxm0JhSV5iO/OLdWzy9JOYKcb5dBFd6kwh7Qa0laDXR9uuPcc5PgKCmt1TGJiIjqIxahNaTT6bB69Wrnz7PPPlvl9r/88ouPknnWokWLMGTIECiVZV/87rvvPiQmJiI3NxerV6/GmjVr8K9//QsajQY33nhjrV+nSqXC66+/jvXr1+PXX3/FggULcOTIkXLbjRo1Ct9880255Xa7HRMnTsTXX3+NdevWYdmyZc7nV/YcT6rqGIsXL8bq1avx+++/ezUDUUOWfiEVBm0AlArvT+YuSQro1AYcPr2rxs8VQiDzlWnQd+sMSVd9AXqFOsIMZUgQzr/wVo2PSUREVF+xCPWAqVOnYsGCBc7HV/dytmvXzrn8ww8/xI033oi7774bx48fdy7/8ccfMWzYMNxyyy146aWXYLfbcfr0aQwYMAAvvvgiBg0ahAcffBDFxcUAyoqbhIQEJCQk4LnnnqtyPwDwyCOP4Pz58xVmHzt2LJ5++mkMGzYMvXr1QmJiIgBg6dKluO2225zb6fV63H333Xj33XcxefJkzJ07F3q9HgBw22234aeffqrVuYuIiEBcXBwAwGQyoV27dhVm7dOnD4KDg8stT0pKQuvWrREVFQWNRoO77roLq1atqvI5p06dwpgxYzBkyBAMGzYMx44dq1X2qo5BRJ5x6uJRaNU6r18PeoVJH4STF1Jr/Lz838o+O6HWQFLULKuuexwKVm9E6bGTNT4uERFRfcQitIZKSkpchuP+/PPPuPPOO/Hrr786t/n1118xfPhwl+ft27cPv/zyC1avXo2FCxdi7969AICjR4/il19+wbJly7B69WoolUosXboUAHDixAmMHj0a69atQ2BgIFasWIHU1FR8+OGH+OGHH5CYmIi33nqr2v0sXLgQTZs2rfD1pKSkICoqCsuXL8esWbMwc+ZMWCwWnDp1Ci1btnTZ9oEHHsCXX36JN998E61bt3Yu79ChA5KTk8vte8SIES7n6srPxo0bK8xy+vRpHDhwAN26daviHXB1/vx5REZGOh83a9as0oIbAKxWK8aPH4/XX38dv//+O55//nnMnj3b7eO5S5IkPPjgg7j99tvx9ddfe3z/RI2BEA6cv3zKOSLDF0y6IGTnZ9boOcJiRda7n0DdsjkUusqvA62MQquBJrYNMl96u8bPJSIiqo+8P76pgbkyHPdaWVlZOH/+PC5duoSgoCA0b97cZf327dtx++23O3sPb7nlFgDA5s2bsX//fgwdOhRAWZFrNpvRp08ftGzZEl26dAEAxMfH4/Tp08jNzcUdd9yB0NBQAEBISEiV+6lKSUkJLl26hH/+858Aynptc3JykJ2djcDAwHLbz5w5E02aNCl3/adSqYRGo0FBQQFMJpNzeU16RwsLC/HEE0/gzTffREBAgNvPq6mVK1fiyJEjeOKJJwCUDeft1atXue3uv/9+XLx4sdzyCRMmuPQQV+ann35Cs2bNkJWVhQceeAAxMTHo06dP3V8AUSOSnX8Beo0Rkg//vdSgNaGgJBdFpQUwaE3VPwFA3tIVUEVGAMra59S2b4v831ajeN8h6OM71no/RERE9QGLUA+54447sHz5cly4cKHSyYgqIoTAfffdh1deecVl+enTp6HVap2PlUolSkpKaryfqqSmpiI6Ohq6/16/tH//fnTq1Ak6nQ6lpa6TZMyZMwelpaWYM2cO3nvvPWexe0VpaalLXqCsJ7SgoPyN3ydNmoT+/fs7H1utVjzxxBMYMWJEuf1Wp2nTpjh79qzz8blz5yrt9QXKen4nTJiABx98sMr9Llq0qEY5rtWsWTMAgNlsxpAhQ5CcnMwilKiGMi4dh0Fr8ur9Qa+lUCihVmpw7Ox+xEf3rXZ7Ybcje85CaDq3h0KnrXb7ykgqJbQdYnBh8r8RtWx+rfdDRERUH3A4rofceeed+Pnnn7F8+XLccccd5db36dMHq1atQnFxMQoKCpy9qTfeeCN+++03ZGVlAQAuX76MjIyMSo/Tr18//Pbbb8jOznZuX91+Ro0ahXPnzpXbV0pKCs6cOYOSkhIUFRXhvffew5NPPong4GDY7XZn0bt582b88MMP+OCDD3DDDTcgPz8fBw4ccO4nOzsboaGhUKtdvyj+9NNPLpM4Xfm5ugAVQuCFF15ATEwMnnrqqWrOcnldu3bFiRMncOrUKVgsFvz888+49dZbK90+IiIC69evh8PhAAAcOnTI4zeLLyoqchbfRUVF2LBhA9q3b+/RYxA1Bmey0qBV6312PegVJn0Q0s4fdGvbgt/XQREcBElV9yHDmpjWKD14BJb0M3XeFxERkT9jEVpD114TOnXqVABA+/btUVhYiKZNmyIiIqLc8+Li4jB8+HDccsst+Mtf/oKuXbsCAGJjY/HSSy/hwQcfREJCAh588EFkZlZ+PVL79u3xf//3f7j33nuRkJCAN998s8r9OBwOnDx5ssLJc1JSUjB06FDccccdGDp0KP7617/i+uuvBwAMGDAAO3bswJkzZ/Diiy/i008/dQ61feyxx1xupbJlyxYMHjy4Vudz586d+PHHH7FlyxbnOV2zZg0A1wmVxo4dizvvvBPHjx9Hjx498N133wEom1337bffxkMPPYSBAwdi+PDhzoKvoufcf//9cDgcGDBgAG655RZ88skndfqCW9ExLl68iLvvvhsJCQkYNmwYBg8ejEGDBtX6GESNVUbWcSh9cH/Qa5l0QcjKK/8PdxXJ/uwbqJpH1KkX9ApJpYI6qgUuTJlZ530RERH5M0l4uhvITVcPofRHZrPZ2atYnx0+fBjff/893njjjXLr7rnnHrz77ruIiYkpt27//v2YO3cuPv7442qP8fjjj+OVV15B27ZtPRGZrtJQ2iHVf75ui8WlBfgicRpaNGkLjdr9W554gs1uxZEze/HcndOhVlY+0VBJyhGce2YitF06QGHwTEZHUTEKV29Cm92/Q2k0eGSfDQk/E8kfsB2Sv/D3tnj15KHXYk9oA9ehQ4cKC1AAOHnyJNq0aVPhuri4OPTr1895m5fKWCwW3HbbbSxAicijzlw6AZMuGGpVzWebrasr16CeyUqrcruchT9CHd0Skr7uvaBXKAx6KIIDcWnWAo/tk4iIyN+wCG3Edu/eDYWi8ibwwAMPVHtrBI1Gg/vuu8/T0YiokTtzKQ16rQGSJM+fKZMuEIczkipd7ygoROHqjVAYDB6/ZlUTG42CX/7w+PXqRERE/oJFKBER+Z2MrONQVTEU1tuMukBczK18gqC8ZaugjomGpPX8NauqiHDYsi6heM9+j++biIjIH7AIJSIiv2J32HEpPxMKqe4zztaWQRuA3MJLlfZG5v24AsomwZBUnr/TmaSQoI5uheyPv/D4vomIiPwBi1AiIvIrF3PPwKQPglIhXxGq0xhQYilCXvHlcussp87AduEi4MWhwtq2USjekQyH1eq1YxAREcmFRSgREfmVc9knodcYoVR4vpfRXZIkQaPW4diZ8kNi85ethLp1S4/NiFsRhckISa1C3tLfvXYMIiIiubhVhK5cuRIvv/wyHnroIcyePdtl3f79+/GPf/wDf/nLX/Dmm2/i4sWLXglKRESNw7nsdGhUWo9P+FNTRl0gTmUdcVkmhEDe0t+hDAr0ej51dEvkfv+LV49BREQkB7eK0JCQEIwcORKDBg1yWZ6Xl4cZM2bg/vvvx/z589GmTRt88MEH3shJRESNxNnsk1AqPD/hT00ZtQHIzr/gsqz0QCqgVgNK7w8kUrdqjtJDR2EvKvb6sYiIiHzJrb+ivXv3Rq9evRAQEOCyfMeOHWjZsiX69u3rvFXHyZMnceZM5TMKEhERVcZiK0WJpUj2XlAAMOgCkF90GTb7/67LzPt5FdQtmkLSe28o7hUKvQ4KvQ653/3s9WMRERH5Up0uuDl9+jSioqKcj3U6HZo2bYrTp0+jefPmLtsmJiYiMTERADB9+nSYzea6HNrrVCqV32ekho/tkPyFr9riiXOHEWQKhckYIOvERACggw52YYcVRWhqbgshBNJXb4KxZzxUer1PMjhi26B4+RqYJzzrk+P5O34mkj9gOyR/UZ/bYp2K0JKSEgQGBrosMxgMKCkpKbdtQkICEhISnI+zsrLqcmivM5vNfp+RGj62Q/IXvmqLh07shVqhhdVihRXyzwyr1xixI2UD9MoglB46BodKCYvFAluJjwrkZmEoXLEOmadOQ2nwTeHrz/iZSP6A7ZD8hb+3xcjIyErX1emiFp1Oh+Ji12tVioqKoNN5f5gSERE1POez06FWaeSO4WTUBeD85VMAgPyV66BqFu6TobhXKLRaKIx65C1Z7rNjEhEReVuditCWLVsiPT3d+bikpASZmZlo2bJlnYMREVHjczY7HUqF/xShBm0ALheUTU5U8Ps6KAJNPr9eVdWyOfJ/Xe3TYxIREXmTW0Wo3W6HxWKBw+GAw+GAxWKB3W5Hr169cOrUKWzbtg0WiwVLlixBVFRUuetBiYiIqlNsKYTdYYNC/jmJnAxaEwpL8lCQlgZHUTEkpe+vU9W0bIbSQ0chrDafH5uIiMgb3Lom9Mcff8SSJUucjzdt2oR7770Xo0aNwgsvvID58+fj448/Rrt27TBu3DivhSUioobrfHY6TPpAqPxoOK5SoYIkKXBu6U/QtYr06VDcKxQmI+AQKFj7JwJuG+Dz4xMREXmaW0XoqFGjMGrUqArXxcfH896gRERUZ+cup0OnNkIhef8enDVh0JpQtHoTDG06ynbrGFXLZshd9AuLUCIiahD86y89ERE1Wuey06FW+k8v6BUBNi2kc9mAUr4/meqWkSjdfwhCCNkyEBEReQqLUCIi8gvnL5+GUlmnO4d5RdiRXGRHm6DQaWXLoAwNhj03DyWpx2TLQERE5CksQomISHYFJblQKnw/6Y87Qvafx7kOAXBI8vVCSpIEVUQ4chculS0DERGRp7AIJSIi2V3IyYBBG+BX9wgFAAgBw97TuBwVgFxRJGsUdYumKN6ZLGsGIiIiT2ARSkREssu8fBoatc7vJiXSnLgIu1ELQwmQqS2UNYuqaRis6RmwF8pbDBMREdWVf/21JyKiRikzJ8MvJyXS7zkJe6gRAQVAtkne+3RKGg0krRb5vyXKmoOIiKiuWIQSEZHsMnNOQ6nwv0mJDLtPwGHQICBPIMck/8y06uZNUbBirdwxiIiI6oRFKBERyarUWgKrzQKFTPfgrIyioASqzFwIhQIBeQ7kB0qwO+TtDVU1b4rSlKO8VQsREdVrLEKJiEhWF3PPwKgLgMrPhuPq9p2CNSIIQquCyg5IDiBP5smJlKHBsOfkojQtXdYcREREdcEilIiIZJWZkwGt2gCFwr/+JOn3noI9QAcoy3IF5jlwXifv5ESSJEEZ1gR53/0saw4iIqK68K+/+ERE1Ohk5pz2v1uzoKwIheZ/16kG5AlkG+QdjguUXRdavG2P3DGIiIhqjUUoERHJ6vzlU1Aq1HLHcKG8mA8AEFddphqY50BOgPzXYqqahsFy4hSEVf6CmIiIqDZYhBIRkWzsDjvyi3L87v6g+n2nYGtigtD9rzj+3+REdhmTAQqDHrA7ULQzSdYcREREteVff/WJiKhRuZR3DkZdgN8Nx9XvTYfdqAWumrFXZSubnCgf8k5OBADKpmHI+/F3uWMQERHVCotQIiKSTWZOBnQaA5QKpdxR/kcI6A5mQGjKZwrIcyBTI+/kRACgbhaOkn2H5I5BRERUKyxCiYhINpk5GdCodHLHcKE+nQ2HXuucFfdqAfkC2UarDKlcKSPMsJ0+A0dxidxRiIiIaoxFKBERySYz5zRUClX1G/qQft8p2EIMEJryuQLyHMg1yT85kUKrBZRKFKzdIncUIiKiGmMRSkREshBC4FLeOSiV/lWE6vaeguOa60GvCMh3IM8kQQiHDMlcqZqFo2BFotwxiIiIaoxFKBERySK36BK0aj2U/tQTandAe/Q8hLria1Q1FsCuAors8g+DVTUNR+nBI3LHICIiqjEWoUREJIvMnAzoNUa/KkI1xzNhDzVWeD3oFaZ8gUxNgQ9TVUwV3gTWs5mw5eXLHYWIiKhGWIQSEZEsMi+fhkath1TBsFe56Pedhj3IUGlPKFB2XeglvcWHqSomqdWQdFoU/rFR7ihEREQ1wiKUiIhkcSEnA2qlWu4YLnQHM+DQqyu8HvSKgHwHck3yXxMK/Pe60FXr5Y5BRERUIyxCiYhIFpk5p6FU+FERandAk3YBQlH1n8aAPIHcgLKJleSmbhqO0sPH5I5BRERUIyxCiYjI54pKCyBBgqKags+XNCcvwh5iBFRVZ9IVC5TqJJTaS32UrHJKcwhs5y/ClsvrQomIqP7wn7/+RETUaFzIyYBBGwC1UiN3FCddyhnYA/UV3h/0ahIAQ6FAlqrQN8GqyqJSQdLrULh6g9xRiIiI3MYilIiIfC4z5zR0Gv+alEh34L/Xg7ohIF/gol7+27QAgKppGApWb5I7BhERkds8Mi/+hQsXMG/ePBw5cgQqlQp9+vTBo48+CqWy8tkFiYio8crMyYBK5T+9oBAC2tRzKO7S3K3NA/IcyAl0AMVezuUGVUQYLKnH5Y5BRETkNo/0hM6bNw+BgYH49NNP8e9//xspKSlYtWqVJ3ZNREQN0PnLp6Dyo0mJ1Gcuw2HUAir3/vHUlOdAXoD8ExMBgCoslPcLJSKiesUjReiFCxfQt29faDQaBAcHo2vXrsjIyPDEromIqIGx2iwotRZDkvznihDdwQzYg6u+P+jVjIUChUYJVruf3C9Uo0bR+m1yRyEiInKLR4bjDh06FFu2bEHnzp1RWFiI5ORk3H///S7bJCYmIjExEQAwffp0mM1mTxzaa1Qqld9npIaP7ZD8hSfbYnrmUQQaQxBgDIBC4R+XbRgPnwMC9FCq3PuzqASgLQUKtFY0UwV6N5wbLM2bwbJ+K8x/e1DuKF7Fz0TyB2yH5C/qc1v0SBHasWNHJCYmYvTo0XA4HBgwYACuv/56l20SEhKQkJDgfJyVleWJQ3uN2Wz2+4zU8LEdkr/wZFs8cvIA1AotLBYrAKtH9llX6n2nUNyhGYTd7vZzAvIUOKPIRUiJ0YvJ3CM1CUZ+8oEG/3nBz0TyB2yH5C/8vS1GRkZWuq7OY6EcDgemTp2K3r17Y+HChZg3bx4KCwvxzTff1HXXRETUAGXmnParW7OoLuRBqBTV3h/0WqZ8By4b3S9avUkZbob17Hk4ivxgpiQiIqJq1LkILSgoQFZWFm6//Xao1WoEBARg4MCBSEpK8kQ+IiJqYDIvn4ZK6T+TEmlTMmALMVZ7f9BrBeQJ5Jr8Y3IihVYDSaFA4Z875Y5CRERUrToXoYGBgQgPD8cff/wBu92OwsJCbNiwAa1atfJEPiIiakAcDjtyiy752aREZ8pmxq3hPUtN+Q4UBEiwO/ykNzQiDAXL18gdg4iIqFoeuSZ0/PjxWLBgAX7++WcoFAp07twZo0eP9sSuiYioAckuuACDNgAqpUf+/HiE7kAGLG3Cavw8lR2QHEA+ihCMAC8kqxl1RBhKUo7KHYOIiKhaHvkW0Lp1a7zxxhue2BURETVgmTkZ0GmMUCr8owhV5BRBstogFLXrmQ3IcyBTU4hgm/xFqDK8CUr2psBRaoFC6z/X3BIREV3Lf8ZDERFRg5d5+TS0Kh2kGg599RZdSgbsoSYIXe2K4oB8gWyDf8zwq9DrACFQvHuf3FGIiIiqxCKUiIh8JjMnA0p/Gop78AzsJl2Nrwe9IiDf4TeTEwGAMsKM/J9XyR2DiIioSixCiYjIJ4QQyMo76zdDcQFAdzADDm3t8wTkOZAfIEEIhwdT1Z4qwoySA6lyxyAiIqoSi1AiIvKJ/OLL0Ki0fjMUVyoshTK3qMb3B72axgLYVECRo8SDyWpPFW6GNT0DwmaTOwoREVGlWIQSEZFPZOZkwKAxQa30j0lzdIfOwBZqgtDW7Z6lpnyBTFWhh1LVjcJogLBYUXyQs+QSEZH/YhFKREQ+kZmTAa1a7zc9obqUM7AH6gFF3fIE5DtwyWDxUKq6U4U1Qf7PK+WOQUREVCkWoURE5BMXck5DpfKPXlCg7P6gQle3XlCg7LrQXJPdA4k8Q9U0DCVJB+SOQUREVCkWoURE5BOZORl+MymRVGqFKjMXQln3XtmAPIG8AMBf5shVhjeB9cRpCOEviYiIiFyxCCUiIq8rsRTB4XDAX0o17ZHzsDep+/WgAKArFijRSbDYSj2QrO4UASY4CgphOXFa7ihEREQVYhFKRERel5mTAZMu0H8mJTqYUXY9qLLufwYlAPpCgSw/mZxIkiQozSHIX/a73FGIiIgqxCKUiIi8LjPnNLRqPRQKpdxRAJRNSuTwwPWgVwTmC1zUFXtsf3WlahqOou3JcscgIiKqEItQIiLyusyc09Co/r+9O4+Oq7zvBv6928yd0cxoG622LAjGBuqUkBCThCWY+G2attkISROcHkqPTWg4nDSnS2hOSnPSvuC8hlJKCjS4kARcigMJGMwqE2zHLDEEYyPvlrWvo9FoRsts9z7vH7KEZUm2ZM3MczXz/ZyjI+vq+t6vrUdz72+e5z6PKTvGmLQFozkEoWeuIPZHbQz47Iwdb770yiBSTS2yYxAREU2LRSgREWVdz0CbYyYlch/rhVVWBOHKbBEa9TvjeVcAUIsDsAYGke7tkx2FiIhoChahRESUVWkrhdHkMByyPCjc+ztgFXuBDPaEeocFhosUpKxUxo45H4qqQC0JIPpsg+woREREU7AIJSKirOob7ITPLHbO86CN7bA9mXseFABUAbjjAmHVGZMTASeeC93+puwYREREU7AIJSKirOqJtMF0eZ0xHNcWcB/thjAyXxAHBgV6zJGMH/ds6VVBJI4clx2DiIhoChahRESUVeOTEikOGI9rtIZgBbyAmvnLnz9mY8BnZfy4Z0srLYHV1w8rGpMdhYiIaBIWoURElFU9A+3QNQf0ggIwGztglXgzOinROH/UxqCDJidSNBWqrwhDL22XHYWIiGgSFqFERJQ1trARGQ5BccjlxtzfAdvjQjZmSfLFBIZ8CtJ2OuPHPlt6dSWGXtkhOwYREdEkzrgrICKivDQQ60WR2w/IH4kLCAHzQAeEkZ1eWVUAroTAoOKw50IPHZMdg4iIaBIWoURElDVjkxIVwdBcsqNA746c6AXN3jn8UYFuB01OpAVLke7sgRVPyI5CREQ0gUUoERFlTU+kHW7DGZMSmY0dSJd6IczsPZ8aiNoIFzlnOK6i61A8JkZ2cKkWIiJyDhahRESUNT2RNuhaZtfkPFtmYwfsIjMrz4OO80dtDPrsrB3/bOhVQcS2bpMdg4iIaAKLUCIiygohBPoGO6GqmZ+J9myYje1ZmRX3ZL6YQMyvwLadU4jqVRVINB6WHYOIiGgCi1AiIsqK2GgELt2EEPILMi0Ug1AVKFmeIUmzAT3tsMmJKsqQauuEsJyzhikRERW2jD0Ys2vXLjz55JMIhUIoKSnBt7/9bVx44YWZOjwRES0wvZF2eN1+GLpbdhSY+ztglftgu7O/Xql/UKDbNYTSlC/r55oNxeWComsYeXsvii67RHYcIiKizBShe/fuxaZNm/A3f/M3WLp0KSKRSCYOS0REC1hPpA1uw4SqyB90Yza2w/KbgJr9CZL8MRthXwoYyPqpZk2vDCL2zIssQomIyBEycmewefNmXHfddVi2bBlUVUVZWRnKysoycWgiIlqgnDUpUTuEkZtnUwODAhFndIJO0KsrEH+3UXYMIiIiABnoCbVtG8eOHcOll16KW2+9FalUCh//+MfxF3/xF3C5PlgXrqGhAQ0NDQCA9evXIxgMzvfUWaXruuMzUv5jOySnOJu22BftxDlVy+B2mVlKNTtqZBhq0oKm6RBa9gvR4hEgFlDgcrmgqvJ7gQHAVbcI4b0HUV5e7ojlcs4WXxPJCdgOySkWclucdxEaiURgWRbefPNN/OhHP4KmadiwYQOeeuopfOMb35jYb/Xq1Vi9evXE16FQaL6nzqpgMOj4jJT/2A7JKebaFuPJEVjpNBKJBIQtt+jxvtuEVNCHtAYgB5PzKBagWDr64mEUqw7pElUAYVno2PEGzD9YJjvNWeNrIjkB2yE5hdPbYm1t7Yzfm/dbtOO9nX/8x3+M0tJSBAIB/Omf/inefffd+R6aiIgWqO5IG4o8xY4Yjms2dsDyewAtd72SgaiNbvdwzs43G1pFGaK/fkF2DCIiovkXoT6fb8rwnoU81IeIiOavO9wC0/A6Yo3QXKwPeip/VKDfm8rpOc9Er6nE6O49smMQERFlZmKiq6++Gi+++CIGBwcxNDSErVu34qMf/WgmDk1ERAtQ90ArXLrrzDtmmTKcgDY4AojcntcftTHol78+6sn0yiBSx9sgRI7/M4iIiE6RkSVavvKVryAWi+E73/kODMPAJz/5SVx77bWZODQRES1A3QOtqC07V3YMmAc7kaoMSOgJtRH1KxDChuKAJWoAQC3ywo4nkGzpgPucxbLjEBFRActIEarrOtauXYu1a9dm4nBERLSAjSaHYQsbItfdj9MwG9th+01Az20RaqTHPsfsEQQ0h0xOBEALliL26xfg/u462VGIiKiAOePtWSIiyhs9A23wO2ZSonYId0beb50zf9RGl8MmJ9KrKzGy623ZMYiIqMCxCCUioozqGmiB2/BCkzwpkZJIQe+JQkiaLC8wKNDvS0o590z0qiCSTc2yYxARUYFjEUpERBnVHW6FocmflMh9qAvpygBEjofijgsM2hjwyx+SfDLV74MdG0aqq1d2FCIiKmAsQomIKKO6B1qhaXKGwJ7M3N8By28ChqQiNGojGlBg286ZJVdRFGilxYg+/ZLsKEREVMBYhBIRUcaMJIYAwBHLgJjvt8M25T2XqlmAnhIYUJ31XKhWU4mRHW/KjkFERAWMRSgREWVM90ArfE6YlChlwWjrB1S5l7nAoEC3wyYnMiqDSB5tlh2DiIgKGItQIiLKmO6BVrgNj/RJidxHupGuCACanEmJxhUP2uj3paVmOJVaUgxrIIJ0aEB2FCIiKlAsQomIKGO6B1rg0uVPSuTZ2wor4IFwyX02NTBoI+J3zjOhAKCoCtTiAGLPvSI7ChERFSgWoURElDHdA61QVQdMSrSvDbZXfjFcNCQw5FOQtlOyo0yi11Rg+NVdsmMQEVGBYhFKREQZMRyPQVFUCCG3509JpGC0hwFJ64OeTBWAOSIQ0pz1XKheGUTiyHHZMYiIqECxCCUioozoHmhFkTsAQ3NLzeE+1IV0dbH050HHFUcFuj0jsmNMopWVwurrRzockR2FiIgKEItQIiLKiK5wM0yXF6rkGWk9e9tg+eU/DzouMGgj7LNkx5hE0VSoviLEnn9VdhQiIipALEKJiCgjOsPH4ZLcCwoA5r5WqeuDniowaCMSkJ1iKr2mEsMNO2XHICKiAsQilIiI5k0IgZ6BdiiSe0GV0ST03ijgjJG4AADPiEDcBOJWQnaUSfSaSiQOHpUdg4iIChCLUCIimreBoV543EXSaz/zQAfSVcUQutx1Sk+mAPDFbPQYMdlRJtHKS2GFwkj3hmRHISKiAsMilIiI5q0z3Ayv2wdDlzsc19zXBivgAQznFKEAEBgU6PE6qydUUVWoJcUY/NULsqMQEVGBYRFKRETz1tl/HKbhhSJ5WRTP3jbYDpmQ6GQlERvhYmdNTgQAem0lhl97XXYMIiIqMCxCiYho3jrDx6FpcicDUofi0AactR7nuEDERqRYkb6G6qmMmiokDx+HEEJ2FCIiKiAsQomIaF5SVhKx0UHZMWA2diBVGXDM0iwnM9KAZgkMKM5aL1Qt9sOODSHV0i47ChERFRAWoURENC89A20IeEqhqXKfwzT3tcL2m4DuzEtb8YCNDtNZkxMpigItWIbBJ7bIjkJERAXEmVdqIiJaMDrDzTDdRdBUuT2QnndbHLU+6KlKIgIhf1p2jCmMRVUYef0d2TGIiKiAsAglIqJ56ew/DpfmljopkdYXg2LZ0peIOZ3iiI2BYtkpptKrKpE81gJhO+t5VSIiyl8sQomIaF46w81QJQ/F9bzXgnRFALbbuT2hnhGBhBsYtZy1VIvq80KkUhjd0yg7ChERFQgWoUREdNZioxGoivxLiefdFlh+E1Cd2xeqAPAP2uh0R2VHmUKvrkB087OyYxARUYGQf+dAREQLVkeoCX5PCVy6S14IW8Dc3w7boRMSnawkItBb5KyeUGBsqZb479+XHYOIiAqE86/YRETkWG2hozBdXigSe0NdTb2wSn1QFsBSl8URG+Fi5wXVqoNItrTDGo3LjkJERAUgo3cNXV1dWLNmDf7jP/4jk4clIiKHag8dg65J7AUF4NnTgnSJF8J03vqgp/JHbUT9QNp21iy5qtsNxWVg+KXXZEchIqICkNEi9L//+79x3nnnZfKQRETkUIlUHMPxKCC5Y8/zbjNsrwFInJ13tjQbcMcFQuqQ7ChTGItrEN3ysuwYRERUADJWhO7atQterxcrVqzI1CGJiMjBOsPHUVxUDl2X1wOpjCZhdAw4ekKiU5UO2OgoGpYdYwq9tgqJ9w/JjkFERAUgI3cOIyMj2Lx5M26//XZs27Zt2n0aGhrQ0NAAAFi/fj2CwWAmTp01uq47PiPlP7ZDcorp2uI7TV0o9pWiyOuTlApwv9cOq7YUqssFaHKXiZmtskGgp1rAtEzZUSYRi2owuuMt+IZGYZ5TJzvOtPiaSE7AdkhOsZDbYkaK0CeeeAKrVq1CeXn5jPusXr0aq1evnvg6FApl4tRZEwwGHZ+R8h/bITnFdG3xcOteeN1+xOPyJrPxvnUY6SI3LBWAZUnLMReBEHBguYaR9mGoirMKZ62iDMfv24iKf7xVdpRp8TWRnIDtkJzC6W2xtrZ2xu/Nezhuc3Mz9u3bhz/7sz+b76GIiGiBsGwLoWiX1FlxIQS87xyH7THkZTgLugUYSWc+F6ovrsXwb3fLjkFERHlu3j2hjY2N6Ovrw1//9V8DAOLxOGzbxve+9z38+Mc/nndAIiJynp5IG/zeUigSJwMy2sIQbl36xEhnozRso907jMrhYtlRJtFrKjH00nbYyRRU18Iq7omIaOGYdxG6evVqXH755RNfb9myBX19fVi3bt18D01ERA7VHjoGj8sHXZNXqHjfbkK63L8glmY5VemAjd4aC3DY/ESq6Yai6xjathOBz10jOw4REeWpeY+jcrvdKCkpmfgwTROGYSAQCGQiHxEROVBb3xG4dLfUnlDP202witwLYmmWU5UM2BgoAWzhvOdY9cXViD71guwYRESUxzL+9vHXvva1TB+SiIgcxBY2OsPNqK9cLi2DOhSH0TOIdFDezLzzoacBPSXQrw6jQjjrTVtjUTUS+w5ACCH1TQYiIspfEmeUICKihag30g6fWQyZ5Ynn981I1ZRA6M6aXXYuyvpttHmdNzmRVlYKKxxBqqlVdhQiIspTLEKJiGhOWnoPwWv6oWsuaRm8bzfBCniABVyElg7Y6Ct23nBcRVWgV1ci/PPNsqMQEVGeYhFKRERz0tJ7GKbukTdU07Jh7muDvYALUOCD50It23mFqLGkFqNcqoWIiLKERSgREc2aZVvoGWiTuj6o+3AX0mW+Bf+8op4GXHGBXi0mO8oUenUlUm2dsCJR2VGIiCgPsQglIqJZ6wo3IyB5fdCiN4/CKvdBuBZ2TygAlPfbaPM7bJ0WAIquQSspxsBjv5IdhYiI8hCLUCIimrWW3sPwuiWuDyoEvG8ehW0aC3JpllOV99voKbVlx5iWXl+L4Zdekx2DiIjyEItQIiKatdbeQzAMeeuDuo73wfa4ACHl9BnnH7QR8wNJkZIdZQpjUQ0SR5pgJ5KyoxARUZ5hEUpERLOSspIIxbqhSLx0eN84gnTQD2FmfJlrKVQBFEdstLoHZUeZQjXdUN1uxJ59RXYUIiLKMyxCiYhoVtr6jqCkKAhNlVcAFr1xFHaRKy+G4o4r67fR6Y/LjjEtfckiDD65VXYMIiLKMyxCiYhoVpq69594HlROEWq0h8f+YOfJWNwTykM2+sqc+W9yLVmExL4DsFPOGy5MREQLF4tQIiKalaauRhiaW9r5vW8eRaoqAGFKmhQpSzyjAmkdGBQjsqNMofq8gKoi9sJrsqMQEVEeYRFKRERn1B/tgaIoEIq8HruiN47A9ubXUNxx5X0WjhdFZMeYlnFuHQY3cakWIiLKHBahRER0Roda30PAWwaX5pJyfr1rAMpIEkD+FaAAEOyz0VVmyY4xLVf94rEhuem07ChERJQnWIQSEdEZHWx9F27DC0WRc9nw7TiEVG0JhDs/ZsU9VWnYRqQYSArnFXqq1wPFMDhLLhERZQyLUCIiOq20lUJb71GosobBCoGinQdhF7kBNT97QseXamkxB2RHmZZxzmIM/s/TsmMQEVGeYBFKRESn1R46htJAJVRVk3J+1/E+CF3OuXMp2GejrTghO8a0jPrFSLx/EHaSs+QSEdH8sQglIqLTOtz5HvyeEuianFlpi3YcRLoikLdDcccF+yz0BgVsYcuOMoXqMaGYbgxu3iI7ChER5QEWoURENCMhBI517oPbMOUEsAWKdh3O21lxT2akAHdcoEuPyo4yLeO8czD4+DOyYxARUR5gEUpERDPqibTBdBVBSOqdM/e3wyr2AELe0jC5VNFrozkwJDvGtFxLFiF5uAnpgYjsKEREtMCxCCUiohkd7ngPfm8JXJJ6Qn3b9iMd9Of9UNxxlT0WOisFnFhyK4YOraIc4f/8mewoRES0wLEIJSKiGR3u2AOXZkKRMBRWGUnA814LhEvP+6G44zyjAqol0KM5c0iu+/xzEXv+N7JjEBHRAscilIiIpjUw1Ds2SY6k+s/320NI1pVD6IV1qarqsnG0OCY7xrS0qiCs/gGMvn9IdhQiIlrACuvKTkREs3aofQ+KveUwNJeU8/teeX/sedACWJ7lZJU9FroqbDhxUK6iKDDOWYz+f39IdhQiIlrAWIQSEdG09rfuhsdVJGUortEagjqahAPrsKzzxAW0tEC35szeUPfSczD6+tuwk0nZUYiIaIFiEUpERFOEol0n1quUUwX6X3kfqZpSCLMwJiQ6VVW3hWMOHZKr+oqgeD2IPLJZdhQiIlqg5n11T6VS2LhxI/bt24ehoSFUVVXh+uuvxyWXXJKJfEREJMGBtndQUhSEobtzfm4lnkLRrsMYXbG4YCYkOlVlt4Xfr7Rh99tQFee9X+xafh4im36Nsm99U3YUIiJagOZ9ZbMsC+Xl5fjhD3+In/3sZ/j617+Oe+65B729vZnIR0REOSaEwIG2d+A2PFKG4vq2HxibkEhzXvGVK2YC8AzbaHFHZEeZllFbjXRPH0b3HpAdhYiIFqB5X+FN08TXvvY1VFZWQlVVfOxjH0NlZSWampoykY+IiHKsJ9IGQzMghIShuEIgsHUPrBIvYBTWhESnqu2wcSQ4LDvGtBRVgWtpPUI/vl92FCIiWoAy/rBNJBJBV1cX6urqJm1vaGhAQ0MDAGD9+vUIBoOZPnVG6bru+IyU/9gOSYbfHtyCYEk1fJ7ARE+ooigwTTPr53btaQZMA5qqQWiFXYRWhYEjFypAWIUJOTMUn47rDy5A/5aXUWK4oBcHcnJOviaSE7AdklMs5LaoiAy+1Z1Op3HnnXeiqqoKN91002n37ezszNRpsyIYDCIUCsmOQQWO7ZByLW2l8F8v/DOWVJw/6XlQ0zQRj8ezfv7KO56B0DXYRa6CfR70ZAcv1FEx6sFHhqpkR5nWyOtvw3vlSlTf8Y85OR9fE8kJ2A7JKZzeFmtra2f8XsYeuLFtGz/5yU+g6zr+6q/+KlOHJSKiHDrcsQelvkooEibD0TsH4GoJQegKC9ATajssNFc5dykU94rliG15BXY6LTsKEREtIBm5yxBC4MEHH8Tg4CD+9m//FrpemFPqExEtdO8dfx0+MwBdM3J+7pKndiNxbgWEK/fndip/VCCtCnTrUdlRpqUF/FA9Hgw8+KjsKEREtIBkpAh96KGH0NHRge9973twuZz33AoREZ1ZZCiE6EhYysqgWigG870WCLcOqOwFHacAqGux0Bh0ZhEKAO4PL8fAzzbLmciKiIgWpHl3Wfb19aGhoQGGYWDdunUT22+66SZceeWV8z08ERHlyJ7jv0W5vxouCWuDFj/9DhLnVUHohT0Z0XSqui00na9jpCcFr3BeL7FeUQ6k0hj832dQ8o0vyY5DREQLwLyL0IqKCmzevDkTWYiISJJUOonGlt+hrmJZztcGVQdHUPTGYYyuqAMKeG3QmWg2UNVp4f3iEFZGamTHmZb74ovQf89DKP76F6WsLUtERAsLr/ZERIT3W95CMFADVUIBUfLk7070gvKSNJPFbRaO16RhCVt2lGnp1RUQyRQim34lOwoRES0AvOITERU4IWy8ffQ38Lr9OZ+QSOuLwvvGUdgeF3tBT8MTFwhEbBzw98uOMi1FUeD+yFhvqG07s1AmIiLn4BWfiKjANXUfgFv3SDl36f++gcT57AWdjXOOp3FwURxCytRRZ2ZUVQACGPjpJtlRiIjI4XjVJyIqYEIIvH7gBRQXlcPQczu7udHaD/P9dghDYy/oLPiGBMxhG4eLwrKjzMj86AqEf/II7HhCdhQiInIwXvWJiApYS+8hWLYFRcnx5UAIlG/8DRJLqyBcXFt6ts5tSqOxdsSxvaF6eSm00mL0/NMG2VGIiMjBWIQSERUoIQR+27gVpb4KGDl+FtT7+hEo8RSEpnJd0DkIRAWMuI1Dju4N/TBiW15Csr1LdhQiInIoFqFERAWqpfcQUlYSqqLmdFkNJZ5C2S92IlVTAuFmL+hcLT2cxt4lo7AUZ/aGqqYbrqXnouuW78uOQkREDsUilIioANnCxm/2/hrlgaqcz4hb+vjrSNaVA4oy9kFz4hsWKOlPY29xn+woM3JfdD6Sx1ow+ORW2VGIiMiBWIQSERWg91vegtvwQEFue0HdBzrh2d0Ey+uGcGk5O2+++dCxNA4tSmBUTcuOMi1FVeH55EfR+893wYoNyY5DREQOwyKUiKjAJNNx7Gp8Hn5PaU5nxFUSKQR/8jIS51cDbhag8+FOAItb0nijuld2lBnpZaXQa6rQ+a3bZEchIiKHYRFKRFRgdr7/HCqKa3M+ErbskR1I1ZZwGG6G1LVYCBel0e5xbk+j+ZGLEN97AJH/eVp2FCIichAWoUREBaQz3IxjXe/DbXhy+ixo0Y6DcB/shO1xcRhuhqgCuKAxhTfqB5B26CRFiqbBe+XH0feje5A43io7DhEROQSLUCKiApG2Unjh7U2oKa3PaQFqtIdR+uhvkawPcjbcDCuOCpT3pPHb6m7ZUWakBfxwr1iO9q9/G1Y8ITsOERE5AItQIqIC8dq+Z+D3lAI5XJJFjY6i8s4tiF9YC6GrHIabBecdtdBflMIxX1R2lBm5zquH4vWg45u3Qghn9toSEVHusAglIioARzr3oqXnIEyXF4aem15QJZFC1f99BokPVQKqCmi85GSDKoAV76Wwe8kgBl1J2XFm5Ln0YqRaO9Dz/fWyoxARkWS8IyAiynPhWC9eeXczKksWw8jVMNy0hYp/ewFWsQdQVT4HmmXeUYFl+5N45dxeJDVbdpxpKaoC75UrEdu6DaF7HpIdh4iIJGIRSkSUx0YTQ3hq14OoCy6Fqmq5GYabtlB51/NA2oLtMSC4HEtOVIQEqtuTeGVJNyynTlSk6yha9SkMPPy/6L//57LjEBGRJCxCiYjyVDIdx1O7/guVJYugKAo0NfvFoJJIofL/PQek0rB9bgh37iZAImBJiw13NImGJd2wHVqIqqYb3msuR/iBX6Dv7v+SHYeIiCRgEUpElIeS6Th+ufN+FHkCUBUtJ7PhqpFhVP/glxCKAttnsgCVQAGw7FAa6kgC25b0OLZHVDPdKPrM5Rjc9Gt0fud2CMuSHYmIiHKIRSgRUZ4ZSQzhiR0/gdfth6G5YOiurJ/TfagTtbc9gVR1CYRpcCkWiRQAyw+koQ7F8cKHupFw6DOiqtsN76pPIf72XrR84Uak+wdkRyIiohxhEUpElEdC0S489pu7Uewtg64Z2e8BtWwUP/k7VPzbC4gvqwY0lQWoA4z3iJZ2juK587swYKZkR5qWqmvwXH4poKk4vuqrGN7xpuxIRESUA7xTICLKA0II7G1+Hbv2v4DFwfOgKmrWC1DXkW4EH9wGy+vG6AW1gKEBKtcBdZIlbTaKhkbx8od78Ic9xbig3wcFzvoZKYoC88LzoZWXouvWf4LnsktQtf770MtKZEcjIqIsYRFKRLTARYZDaNjzJEbiMSwJng9VVaFmcRIivTeKks1vwt3YjsT51YCiAOz9dKzyAeBjb4zi0B/YOHb+MD7VXo6yUec9r2tUBqH9nyuR3H8Ux6+6FmXf+iZK114P1WPKjkZERBnGuwYiogVqJDGE3Ye3obF1NxaVn4sSXxC6nr3iwmgJIfDcu/DsaUFiaRUS51dDuHT2fi4A7pSCP9yTRG95CtsuSqNqxMRHuksQSDjrNkDVNJgfXg6jvhbRZ17GwMbHUbr2ehSv+TJ7RomI8ogihJAydV5nZ6eM085aMBhEKBSSHYMKHNshTScU7cKepl041P4uqkoWw214oKk6VDXzj/mrsVF4f9eE4m2NQHQEqUWlsE0DQtcAjdMKLEQ2gK5aFW3nuVAWd2N5vx+1UTdUhw3TBYB0JIp0SztSHd0oumIl6m76JtIrlkMxnFU8U2HhtZmcwultsba2dsbvsQidgdN/qFQY2A4JGHvesz/Wjabu/TjQ+jZSVhKlvgoYuglNVaGpGbwht2y4mvtgvt8O7zvHYXSEkVxUBpT6YNk2hKmPDb+lBc+GQKhcRc8SF4aKNdRFPaiLeFAdc0MXzvoZ24kk0u1dQCSKZG8I3qs+gaKrPwHvJz4GY3GN7HhUYHhtJqdwelvMehE6NDSEBx54AHv37oXf78f111+PK6644rR/h0Uo0ZmxHRYeIQTiqRH0DXage6AN3QOtaA8dg9sw4TNL4HF5AUWBobmgzKcYFALqcAJ6VwSulhBcrf1wNffBaAnBKvfBKvbA8pqACghDh+Y2YHEtx7yV0CyEKw2EqwxESlX4kjoqh90oH3GhJK4jENdh2PJ7vk3TxHCoH1YoDHtoBFZfP2ALuD+8HOaKC+C+aBlcS8+BsbiGz5JS1vDaTE7h9LZ4uiI0I2+fb9y4Ebqu46GHHkJzczPuvPNO1NfXo66uLhOHJyJaUIQQsIWFtJX64MNOI20lkbbSSKZGMZocHvtIDGMkOYSh0UFEhkIYig/C0F3wuvwwXV64dDcWl58HQMDQ3WOFpy2gpCwoyTSQtk782YKSSo/9OWVBHU1CHYpDHUpAG45DHU5AjcWh9Q9B74tCi8VhmwZsnxt2kQnb64JV5Eb6D5cACsaWWWGPZ8FwWxpqumzUdCVg2wIjXoFYmYGWYh0HK1UMFymACnhTOopSGjxJDd6UBpelwmUpMCwFhqXCZanQbQWqAFRbgSbG/qwJBYpARmbm1XxF0HxFAABh27CjMdgjcYy89S6Gt+2CFRuCHRsCAOjVldBrq6CXl0IrK4FWWgytrASq3wfVY0LxesY+e8yxz6Ybiq5D0TVA06BoGqBr83vDh4iIpph3T2g8HseNN96Iu+++e6Lave+++1BWVoY1a9bM+Pec3BPa+MC/I/2fv8SZ/2MElGwMZp71MWe7ozLLfccvsrPdN5PHnOt+mdz3bPY73b6z3W82+47/P093AzTdceez30znn81+mTjmqftmYr9sH/P0+8303ZNvxJWTDqeM/6gnfuQn9hNiaivVVAhVBTRl7LOqQKjK2F9RFAhNhdBVCF0b237iQ6gqbF09UV8qEIYGoZ+5h0vTNPaEFjAhBNKKjaSpIelVkfJoSHo0pA0FlqEirSuwDGXss65AqICtfvDZVgGhjH0o0/2qzfQyhw++P9ZkFWA2ty0CUCwb7mgSZiwFYyQN14h14nMaetyClrKgpgS0pAUtZUNL2tBSNhQhoNgCiiWg2IBiiw/OeSKjIgBxhsL0jK82p+zwwQhoFryON9tbIKIsW/7sI/Ccu0x2jBlltSe0q6sLmqZNOkl9fT32798/ab+GhgY0NDQAANavX49gMDjfU2fNFd//IQ6vWIHwKf+G6czpUpGhd1LHb2D5zmz+U1QVwrZlx1iwzvYeYdq3JcTJd8nixH5jRd+k+2dFPVEHqlAUBYqiQFXGelLGl06Z/JurnHIjfuImWxm7y1EUZayoxNj3FEWdKCihqmM9NqoK6DoUXQUMY2xbhl8fVE2FbbEt0ukJCNiWBVtYsG0btm3Bhg0hbAhbQGCsoB3/HRIQE2/ETBRm4uTjje+Pid8rIezZ/24vmrppym+GbQNpC0hbEJYFWPbYNtv+4M/iREDbHjvCSf+GiReAkz6LiW9Mc0ZxUlF78rbZ4rVfuvF2SCSb2+dzdE11OvMuQuPxODwez6RtXq8X8Xh80rbVq1dj9erVE187efwyAFz45a8jdKWzM1L+c/pYfyocbIvkBGyH5ARsh+QUTm+Lp+sJnfcsA6ZpYnR0dNK20dFRmCYnBCAiIiIiIqLJ5l2E1tTUwLIsdHV1TWxraWnhpEREREREREQ0RUZ6Qi+77DI88cQTiMfjOHjwIHbv3o2rrroqE/mIiIiIiIgoj2Rk0a+1a9cimUxi3bp1uPfee7Fu3Tr2hBIREREREdEUGVkn1Ofz4R/+4R8ycSgiIiIiIiLKYxnpCSUiIiIiIiKaDRahRERERERElDMsQomIiIiIiChnWIQSERERERFRzihCCCE7BBERERERERUG9oTO4LbbbpMdgYjtkByDbZGcgO2QnIDtkJxiIbdFFqFERERERESUMyxCiYiIiIiIKGdYhM5g9erVsiMQsR2SY7AtkhOwHZITsB2SUyzktsiJiYiIiIiIiChn2BNKREREREREOcMilIiIiIiIiHKGRSgRERERERHljC47gCxDQ0N44IEHsHfvXvj9flx//fW44oorpuwnhMCmTZvw6quvAgCuueYarFmzBoqi5Doy5anZtsUtW7Zg+/bt6Ovrg9/vx2c/+1l84QtfkJCY8tFs2+G4dDqNv//7v8fo6CgefPDBHCalfDaXdtjU1ISf//znaGpqgmma+PKXv4w/+ZM/yXFiylezbYupVAqPPPIIdu/ejXQ6jeXLl+Omm25CWVmZhNSUb1588UW89tpraG1txeWXX45bbrllxn2fe+45PPPMM0gmk7jsssuwbt06GIaRw7RzU7BF6MaNG6HrOh566CE0NzfjzjvvRH19Perq6ibt19DQgN27d2PDhg1QFAX/8i//gsrKSvzRH/2RpOSUb2bbFoUQuOWWW1BfX4+enh7867/+K8rLy3H55ZdLSk75ZLbtcNyWLVsQCAQwOjqa46SUz2bbDqPRKO644w7ccMMN+MQnPoF0Oo3+/n5JqSkfzbYtPv/88zhy5Ag2bNgAr9eLn/70p3j44Yfxd3/3d5KSUz4pLS3Ftddei/feew/JZHLG/fbs2YNnnnkGt99+O0pLS3HXXXdh8+bNWLNmTQ7Tzk1BDseNx+N466238Od//ucwTRMXXHABLr30UuzYsWPKvtu3b8fnP/95lJeXo6ysDJ///Oexfft2CakpH82lLX7xi1/Ehz70IWiahtraWlx66aU4dOiQhNSUb+bSDgGgt7cXO3fuxJe+9KXcBqW8Npd2+Nxzz+Hiiy/GlVdeCcMw4PF4sHjxYgmpKR/NpS329vbi4osvRklJCVwuFz71qU+hra1NQmrKR5dddhlWrlwJv99/2v22b9+OVatWoa6uDj6fD1/5ylfw2muv5SbkWSrIIrSrq2viRn5cfX39tC8abW1tqK+vP+N+RGdjLm3xZEIIHDx4kDddlBFzbYcPP/wwvvGNb8DlcuUqIhWAubTDI0eOwOfz4Qc/+AHWrl2L9evXIxQK5TIu5bG5tMVrrrkGhw4dQjgcRiKRwM6dO3HJJZfkMi4R2tvbcc4550x8XV9fj8HBQcRiMXmhzqAgi9B4PA6PxzNpm9frRTwen3Zfr9c7ZT8ur0qZMJe2eLJf/vKXEEJg1apV2YxHBWIu7fB3v/sdbNvGypUrcxWPCsRc2mE4HMb27dvxl3/5l7j//vtRWVmJe++9N1dRKc/NpS3W1NSgvLwcN998M2644QZ0dHTguuuuy1VUIgDT1ysAHP3ITEEWoaZpTvmhjI6OwjTNM+47vh8nJqJMmEtbHPfiiy9i+/btuO222xz9wDktHLNth/F4HI899hhuvPHGXMajAjGX10OXy4WVK1di6dKlcLlc+OpXv4pDhw5hZGQkV3Epj82lLW7cuBGpVAoPP/wwHn30UaxcuRJ33HFHrqISARhrsye//o2331PfTHGSgixCa2pqYFkWurq6Jra1tLRMOwFHXV0dmpubJ75ubm6ecaIOormaS1sEgFdffRVPP/00br/9dpSXl+cqJuW52bbD7u5u9PX14fbbb8e6detw1113YWBgAOvWrUNvb2+uY1Oemcvr4ZIlSyZ9zTeGKZPm0hZbWlpw9dVXw+fzwTAMfO5zn8PRo0cRjUZzGZkK3OLFi9HS0jLxdUtLC4qLi8/4LKlMBVmEmqaJyy67DE888QTi8TgOHjyI3bt346qrrpqy71VXXYWtW7ciHA4jHA7jueeew6c//WkJqSkfzaUt7ty5E48//jh+8IMfoKqqSkJaylezbYd1dXV44IEHsGHDBmzYsAE333wzSkpKsGHDBgSDQUnpKV/M5fVw1apV2L17N5qbm5FOp/Hkk0/iggsumDQcjehszaUtnnfeedi+fTtGRkaQTqfx0ksvobS0FIFAQEJyyjeWZSGZTMK2bdi2jWQyCcuypuz36U9/Gq+++ira29sxPDyMp556CldffXXuA8+BIgr04cahoSHcf//92LdvH3w+H9asWYMrrrgCBw4cwB133IFHH30UwAfrhG7btg0A8JnPfIbrhFJGzbYt3nLLLQiHw9D1D1ZWuvLKK3HTTTfJik55ZLbt8GSNjY247777uE4oZcxc2uHLL7+Mp556CslkEsuXL8fatWv5ZghlzGzbYiwWwyOPPIK9e/cinU6jrq4ON9xwA5YuXSr5X0D5YPPmzXjyyScnbbvuuutwzTXX4Lvf/S7uueeeide9hbZOaMEWoURERERERJR7BTkcl4iIiIiIiORgEUpEREREREQ5wyKUiIiIiIiIcoZFKBEREREREeUMi1AiIiIiIiLKGRahRERERERElDMsQomIiIiIiChn9DPvQkRERPPx4osvYuvWrQiHw7joootw6623IhAIyI5FREQkBXtCiYiIsujxxx/Hs88+i29961u444470Nvbi8cee0x2LCIiImlYhBIREWXJsWPH8PTTT+M73/kOVqxYgfr6enz2s5/F73//e9nRiIiIpGERSkRElCXPPvssLrzwQixbtmxiWyAQQCwWk5iKiIhILhahREREWZBOp/HOO+9g5cqVk7Ynk0l4vV5JqYiIiOTjxERERERZ0NzcjEQigU2bNuHxxx+f2G5ZFs4991yJyYiIiORiEUpERJQFnZ2d0HUdd99996Tt9957L5YvXy4pFRERkXwsQomIiLJgZGQEfr8f1dXVE9ui0Siam5tx4403SkxGREQkF58JJSIiyoJAIIB4PA7btie2Pf3001i2bNmkiYqIiIgKDYtQIiKiLFixYgUsy8KvfvUr9Pb2YsuWLdixYwduvvlm2dGIiIikUoQQQnYIIiKifPTmm2/iF7/4BaLRKC688ELccMMNWLx4sexYREREUrEIJSIiIiIiopzhcFwiIiIiIiLKGRahRERERERElDMsQomIiIiIiChnWIQSERERERFRzrAIJSIiIiIiopxhEUpEREREREQ5wyKUiIiIiIiIcoZFKBEREREREeXM/wdVZ/qAyoFKjQAAAABJRU5ErkJggg==",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plot_dist()"
]
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python 3.8",
"language": "python",
"name": "python3.8"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.8.0"
}
},
"nbformat": 4,
"nbformat_minor": 4
}
"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Sequenza di plot della distribuzione a posteriori del parametro di una distribuzione di Bernoulli al crescere del numero di osservazioni (lanci di moneta)"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {},
"outputs": [],
"source": [
"#%matplotlib inline\n",
"import numpy as np\n",
"import scipy.stats as stats\n",
"import matplotlib.pyplot as plt"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {},
"outputs": [],
"source": [
"#!pip install xarray\n",
"import xarray"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {},
"outputs": [],
"source": [
"plt.style.use('ggplot')\n",
"\n",
"plt.rcParams['font.family'] = 'sans-serif'\n",
"plt.rcParams['font.serif'] = 'Ubuntu'\n",
"plt.rcParams['font.monospace'] = 'Ubuntu Mono'\n",
"plt.rcParams['font.size'] = 10\n",
"plt.rcParams['axes.labelsize'] = 10\n",
"plt.rcParams['axes.labelweight'] = 'bold'\n",
"plt.rcParams['axes.titlesize'] = 10\n",
"plt.rcParams['xtick.labelsize'] = 8\n",
"plt.rcParams['ytick.labelsize'] = 8\n",
"plt.rcParams['legend.fontsize'] = 10\n",
"plt.rcParams['figure.titlesize'] = 12\n",
"plt.rcParams['image.cmap'] = 'jet'\n",
"plt.rcParams['image.interpolation'] = 'none'\n",
"plt.rcParams['figure.figsize'] = (16, 8)\n",
"plt.rcParams['lines.linewidth'] = 2\n",
"\n",
"colors = ['#008fd5', '#fc4f30', '#e5ae38', '#6d904f', '#8b8b8b', '#810f7c', '#137e6d', '#be0119', '#3b638c', '#af6f09']"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Fissa la probabilità $\\theta$ di esito pari a $1$ e i numeri di osservazioni da considerare"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {},
"outputs": [],
"source": [
"theta_real = 0.26\n",
"n_trials = 1000"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Genera la sequenza casuale di risultati derivanti da lanci ripetuti con probabilità di $1$ pari a $\\theta$"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {},
"outputs": [],
"source": [
"data = stats.bernoulli.rvs(theta_real, size=n_trials)"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"array([0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0])"
]
},
"execution_count": 18,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"data[:20]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Fissa la distribuzione a priori del parametro $\\theta$. Si utilizza un modello Beta-Bernoulli, per cui la prior (e di conseguenza la posterior) sono distribuzioni Beta. "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
""
]
},
{
"cell_type": "code",
"execution_count": 34,
"metadata": {},
"outputs": [],
"source": [
"# dichiara la distribuzione prior\n",
"dist = stats.beta\n",
"# valori dei suoi parametri\n",
"alpha = 100\n",
"beta = 100\n",
"hyper = [alpha, beta]"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Calcola i valori della densità di probabilità a priori su una griglia ($1$-dimensionale) di punti"
]
},
{
"cell_type": "code",
"execution_count": 35,
"metadata": {},
"outputs": [],
"source": [
"# fissa l'insieme dei valori sui quali calcolare la distribuzione\n",
"nv = 10000\n",
"x = np.linspace(0, 1, nv)\n",
"# calcola i valori di densità di probabilità per tutti i punti dell'insieme\n",
"yp = dist.pdf(x,*hyper)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Plot della distribuzione a priori di $\\theta$"
]
},
{
"cell_type": "code",
"execution_count": 36,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA6EAAAGTCAYAAADZdhSlAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAABFvElEQVR4nO3deXhddYH/8c85525Z7r3ZmtKNQAuyVRCBtsharaOjgrKIQp2BmQcYR0BGxdFBfoiOD+AUFJUBFCggMA5tEakgBQK0bC2UpXvTpk3SfUvTJdu9N/fe8/ujJNOQpM1yc793eb+eJ0BOTs755PJNTj4553yP5bquKwAAAAAA0sA2HQAAAAAAkD8ooQAAAACAtKGEAgAAAADShhIKAAAAAEgbSigAAAAAIG0ooQAAAACAtKGEAgAAAADShhIKAAAAAEgbSigAGPboo4/Ksqyut2AwqFNOOUX33nuv4vH4YT//tttuk2VZaUg6dN/97nf1la98pcfyrVu36sorr1RFRYWCwaC+8Y1vaO/evV0fv+eee/TJT35SyWRy2DM+9NBD3f5/2LatyspKXXTRRaqvrx/UNvfv36/bbrtNq1evHnSuj792mzdv1g033KAzzzxThYWFsixLDQ0NvX7upk2bdOmllyocDisUCuniiy/Wxo0bh7xuX4YjW3/XS+dYAQAMDiUUADLE7NmztXDhQj399NOaNGmSbrjhBv385z8/7OddffXVWrhwYRoSDs369ev1wAMP6Lbbbuu2vL6+XpMmTdL+/fv15JNP6v7779eLL76o66+/vmudf/mXf9GuXbv02GOPDXvODz/8UEVFRVq4cKEWLlyoBQsW6Oabb9bzzz+vf/zHfxzUNt977z397Gc/U0dHx6A+v7fXbt26dZo1a5ZKS0t1zjnn9Pm5bW1t+uxnP6uamho99thjevzxx1VbW6upU6eqtbV10OseSqqzDSRXOscKAGCQXACAUY888ogrya2tre22/Pzzz3dDoVCfnxeJRFKeZTi22en66693Tz/99G7LksmkO3nyZPfLX/6ym0wmu5b/v//3/1yfz+e2t7d3LfvhD3/onnjiicOWr9NnPvMZd8qUKT2Wf+UrX3GLiooGtc277rrL9fv9bkdHx6A+v7fXLpFIdP33gw8+6Epy6+vre3zuPffc49q23W181dXVuY7juHffffeg1z2UVGcbaK50jRUAwOBwJhQAMtQZZ5yh/fv3a+fOnV2X3K5YsUJf+MIXVFxcrMsuu0xS75fjzps3T2eeeaYKCgoUDof1ta99TWvWrOm2zqG2ORCTJ0/WZZddpltvvVUTJkxQIBDQySefrFdeeaVrnWg0qieeeEJXXHFFt8995pln9M477+hXv/pVt6/hyCOPVCwW09atW7uWffOb39SqVav09ttvDzhjf7muq2XLlunkk0/u8bGtW7fquOOO67H+ww8/rEmTJqmwsFBjx47V9773PbW3t3etc8IJJ+imm25SNBqV1+uVZVm65JJLJEkvv/yyvvKVr2jMmDEKBAIaN26cbrrppm5nTPt67Wy7f4fwuXPnasqUKTrmmGO6lh199NE666yz9Oyzzw563UNJdbaB5krHWAEADB4lFAAyVH19vRzHUXFxcdeyr371qzrvvPM0d+5cfe973+v18+bNm6cvf/nLKi4u1lNPPaX7779fK1as0Nlnn60tW7b0WL+3bTY0NMiyrB6Xzn5cPB7XsmXL9Pzzz+vNN9/UPffcoz/96U+Kx+O6+OKLtXv3bknSokWLtHfv3h6XZs6cOVNnnnmmxo8fr3g83vXW0tIiSfJ4PF3rfupTn1IwGNS8efP6zOO6brft9PWWSCR6/fza2lq1tLRo4sSJisfj6ujoUENDg7773e9q9erVuuuuu7qtf/XVV+u6667TtGnT9Oyzz+o//uM/NHPmTH3/+9/vWuePf/yjxo8frwsuuKDrEt9f/epXkqSlS5fqc5/7nB588EG9+OKL+v73v68HHnhAM2bM6Pr8vl67/lq5cqUmTpzYY/lJJ52kVatWDXrdVOjv/gaaqz9jBQBgjufwqwAA0iGRSCgej6u5uVmzZs3Sn//8Z11wwQUqLCzsWue73/2ubrzxxkNu55ZbbtH48eP1wgsvdJW4M888U5/4xCd09913dxWgQ23Tsiw5jnPYM1qrVq1SJBLRueeeq5dfflmO40iSysrKdP755+v111/XRRddpEWLFsmyrG5nGGOxmF577TW1tbXJ6/X22LbX69Xo0aO73rdtW6eccooWLVrUZ54FCxZo6tSph8wsSeedd57mz5/fY/mSJUskHXhNvvvd73YtHzVqlF5++WWdddZZXcv++Mc/aubMmXr66ad18cUXS5I+//nPKxKJ6Oabb9a9994rx3F0yimndE3UM2XKlG77u+mmm7r+O5FI6KyzztL8+fP11ltvdS3v7bUbiKamJpWWlvZYXlZWpj179gx63VTo7/4Gmqs/YwUAYA4lFAAyxPHHH9/137Zta/r06brnnnu6rXPRRRcdchutra364IMPdPPNN3c7i9h56eKCBQt6fE5v26yqqurXzLwffPCBJOn222/vKqAHfy2dZ0K3bt2qUCgkn8/Xtc6qVavU1tam//7v/9akSZO6bfeb3/ymSktLu30NkjRixAitXbu2zzynnXaaFi9efNjcwWCw1+VLliyRZVl688035fP5lEwm1dDQoFtuuUWXX365Vq5c2fW5v/jFL3Tuuefqwgsv7PZanXjiiV2XEo8bN04rV65ULBbTpz/96W77isfjeuKJJ/T73/9etbW1Xa+VpG6XRff22uHwDjdWAADmUEIBIEM888wzGjt2rILBoKqqqhQIBHqsM2rUqENuY8+ePXJdt9f1jjjiCG3YsGHA2zyU999/X6NHj+52hlBS172cY8eOlSRFIhH5/f5u63Q+suPss8/udpZvx44dqq+v1+WXX95jfwUFBd3ut/y44uJifepTnzps7r4eafPhhx9qwoQJ+sxnPtO1bNKkSfJ4PLrkkkv04osv6tJLL1V9fb1qa2tVW1vb61lcSQqHw5IOFHXLsnrkuuKKK/TCCy/o+uuv1y233KKKigpFIhFNnTq126Wnvb12A1FaWtrr2cLezi4OZN1U6O/+BpPrcGMFAGAOJRQAMsTEiRO7TbzSm8M9D7S0tFSWZWn79u09PrZ9+3aVlZUNeJuH8sEHH2jMmDE9lj/11FMqLCzsuo+xvLy823M/JXWdPTz4DKokPf7447IsS1dddVWP7TY1NamioqLPPKm4HPfgAtqp8w8CnaWm897aRx55pNd7FW3bVigUkvR/xbbz/c79zJ49W08++WS3CYfmzJkj13V16qmndi3r7bUbiJNOOkkrV67ssXzVqlU68cQTB71uKvR3f4PJdbixAgAwh4mJACCHFBUV6bTTTtPs2bO7Tb6zYcMGvf322zr//PNTtq9kMqmlS5dqw4YN3S5H3bp1q+677z5df/31KioqknTg8txYLKbNmzd3rXfUUUdJUrdysX37dv3yl7/UtddeqwkTJvTYZ319fY8Zag/WeTnu4d5+//vf9/jcHTt2aPv27b3eezlnzhzZtt1VUDuLt9/v1+mnn97j7eBLb3srShs3bpSkbl9La2urfvKTn0hSt8/v7bUbiAsvvFCLFi1SXV1d17KGhga99dZbuvDCCwe9bir0d3+DyXW4sQIAMMjoA2IAAH0+J/RgP/3pT11JvT5nsvNjnV544QXXtm33i1/8ojt37lz3f/7nf9xjjz3WraiocLds2dKvbTY0NLiO47g/+9nP+sy0cuVKV5I7btw4d/r06W51dbX76KOPuuPHj3fPOOOMbs/4rK+vdyW5Tz/9dNeyZDLpnnDCCe748ePdZ5991p01a5Z73HHHuVOmTHFbW1t77G/Pnj2uZVnugw8+2GemoXjhhRdcSe4vfvELd+HChe7ChQvdZ555xv3Wt77lSnL/4z/+o1v2qVOnuiNGjHDvuece97XXXnOff/55995773W/+tWvdntO5kUXXeRWVVW58+bNcxcuXOg2Nja6GzdudH0+nzt16lT3pZdecv/4xz+6EydOdI8++mi3srKyW67eXrtOs2fPdmfPnu1++9vfdiW59913nzt79mx3/vz5Xeu0tLS4EyZMcCdOnOj+5S9/cZ999ln35JNPdo8++mi3ubm52/b6u25npp/+9Kd9vp6pzDaQr8F1h3+sAACGhhIKAIaluoS67oFCNWXKFDcQCLihUMi98MIL3Zqamn5vsz8l4/HHH3clucuXL3e//OUvuwUFBW5lZaV7/fXXu/v37++x/qRJk9yrrrqq27Kamhr3nHPOcf1+vztmzBj3Rz/6kdvS0tLr/p544gnX7/e7jY2NfWYaijvuuMOV1PVmWZZbUlLifu5zn3PnzJnTY/3Gxkb3hhtucI8++mjX7/e7lZWV7rnnnuv+9re/7bbe8uXL3UmTJrmBQMCV5L7xxhuu6x4oaePHj3cDgYA7ZcoU929/+5v7+c9/3v3CF77QY1+9vXau63bLe/Dbeeed1229DRs2uBdffLEbDAbd4uJi96tf/apbX1/f6+vQn3VXrFjhSnLvv//+Pl/PVGcbyNcw3GMFADA0luu67jCfbAUA5KDvf//7mj17tjZt2tSv9R999FHdeOON2rZtW7fHzvTX3//936uiokKPP/74gD832w31tUu1P/zhD/rJT36iDRs2ZESej8vnsQIA2YB7QgEAg/L+++/rtNNO6/f63/rWtzR69Gjdd999A97XkiVL9Oqrr+qnP/3pgD83FwzltRsOCxYs0Pe+972MLKD5PlYAIBtQQgEAA+a6rpYsWTKgEurxePTII48Mqrhs375djz766GFnD85VQ3nthsOTTz6pm2++2XSMXuX7WAGAbMDluAAAAACAtOFMKAAAAAAgbSihAAAAAIC0oYQCAAAAANKGEgoAAAAASBtKKAAAAAAgbSihAAAAAIC0oYQCAAAAANKGEgoAAAAASBtKKAAAAAAgbSihAAAAAIC0oYQCAAAAANKGEgoAAAAASBtKKAAAAAAgbSihAAAAAIC0oYQCAAAAANKGEgoAAAAASBtKKAAAAAAgbSihAAAAAIC0oYQCAAAAANKGEgoAAAAASBtKKAAAAAAgbSihAAAAAIC0oYQCAAAAANKGEgoAAAAASBtKKAAAAAAgbSihAAAAAIC08Zja8datW03tul8qKirU2NhoOgbyHOMQmYKxiEzAOEQmYBwiU2T6WBw9enSfH+NMKAAAAAAgbSihAAAAAIC0oYQCAAAAANKGEgoAAAAASBtKKAAAAAAgbSihAAAAAIC0oYQCAAAAANKGEgoAAAAASBtKKAAAAAAgbSihAAAAAIC0oYQCAAAAANKGEgoAAAAASBuP6QAAAOSq9iUr1fhf9yu6okZWQUDhy7+m8uuukuXl8AsAyF+cCQUAYBjs/+vL2vadm2WHilVwziT5TvqE9j/zghq+9A9KtLWbjgcAgDGUUAAAUqztnQ/VeMe98p86UXawWE5xkbwjylUw+VQpmdTmy74t13VNxwQAwAhKKAAAKZRsadX2H/z8QAEtLJBlW10fsyxLgdM+qY5tO7Xrjt8ZTAkAgDmUUAAAUqjx7t/Ld8xRsn3ebgW0k2VZKvzMadr72Bx1bNluICEAAGZRQgEASJGOzdvU/LdXZQeLZfm8fa5nFxbIN+FIbfu3n6YxHQAAmYESCgBAijT++g8KfPJ4WQHfYdf1n3CsIktXKbK2Lg3JAADIHJRQAABSIL6zUW2vvyOrMCDLPvzh1fJ45DvmKO28dUYa0gEAkDkooQAApMDeJ/4s33ETZPn8/f4c/3HjFflgueJNe4YxGQAAmYUSCgDAELmxDu17aq7s0rAsp/+HVsvnk6dyhBrv+v0wpgMAILNQQgEAGKKW196Sd/QR/boM9+N8x41Xy4vzeW4oACBvUEIBABii/X9+Qc6IMtmB/l+K28kpL5XbHlHrawuHIRkAAJmHEgoAwBAk9jWr/b1lsnyHnxG3N5ZlyXv0OO2Z+acUJwMAIDNRQgEAGILm51+R75iqfj2WpS/eqrGKLFklNx5PYTIAADITJRQAgCFofr5anrJSWY4z6G04weID23quOlWxAADIWJRQAAAGKdHcomjNerlDKKCdvEeP1b7/nZuCVAAAZDZKKAAAg9S2YJG8VWNkD+FS3E7esaMUXV0rN5FIQTIAADIXJRQAgEFqfnGBnPKhXYrbyQkFlYxG1bbogxQkAwAgc1FCAQAYBLcjrra3F8v2D/0saCfvmFHa96dnU7Y9AAAyESUUAIBBaH9/mTyjRkopOAvayTt2lCJLVqRsewAAZCJKKAAAg9D2xjtyykplB/wp26Yzolzx7bvUsX1nyrYJAECmoYQCADAIra+/I7uoIKXbtBxbTmmJ9j3115RuFwCATEIJBQBggBL7mhXftlOyrZRv2zO6Um1vvpvy7QIAkCkooQAADFDbwvflGXuE7IJAyrftOaJSsXUNcpPJlG8bAIBMQAkFAGCADtwPWpKSR7N8nB0OKtnSqujaupRvGwCATEAJBQBggFrfeEdWYWrvB+1kWZacEWXaP/u5Ydk+AACmUUIBABiA+I5GKZ6QpdTfD9rJO2qk2t9bNmzbBwDAJEooAAAD0L54iZwjRsgqSN2jWT7OGVmhjvqNchOJYdsHAACmUEIBABiAtneXyAmHZNnDdwi1i4uUbIsoWls/bPsAAMAUSigAAAPQ/u6HsvzDdxZU+ui+0IpS7X/2pWHdDwAAJlBCAQDop2RLq+K7dmsYbwft4qmsUOSD5cO/IwAA0szTn5XmzZun+fPna+PGjTrrrLN03XXXdX1s+fLlevjhh9XY2Khjjz1W3/nOdzRixIhhCwwAgCntHyyXZ9RI2UXDMzPuwZwRZYour5HrurKsNLReAADSpF9nQktLS3XxxRdr6tSp3Zbv379fd911l77xjW9o5syZGj9+vO65557hyAkAgHHt7yyRZ5ieD/pxTlmJEk17Fd++c9j3BQBAOvWrhE6ePFmTJk1SMBjstvzdd9/VuHHjdOaZZ8rn8+nrX/+6GhoatGXLlmEJCwCASW2Llwzb80E/zrJt2cEitby4IC37AwAgXfp1OW5fNm3apKqqqq73A4GAjjjiCG3atEljxozptm51dbWqq6slSXfeeacqKiqGsuth5/F4Mj4jch/jEJmCsSi58bjq1jWoaOpZcgKBtOyzY/QRii9eqoqbvpOW/WU6xiEyAeMQmSKbx+KQSmgkElEoFOq2rLCwUJFIpMe606ZN07Rp07reb2xsHMquh11FRUXGZ0TuYxwiUzAWpcjKNbIryhSNd8ju5Tg3LErDalm5Ju9f+06MQ2QCxiEyRaaPxdGjR/f5sSHNjhsIBNTe3t5tWVtbmwJp+gsxAADpElmySnZJSJbfl7Z9OhWliu/YpWR7mkovAABpMKQSOm7cOG3YsKHr/Ugkoh07dmjcuHFDDgYAQCaJLFkpO1iU1plqbb9fbjKp9uWr07ZPAACGW79KaCKRUCwWUzKZVDKZVCwWUyKR0KRJk7Rx40YtWrRIsVhMc+bMUVVVVY/7QQEAyHbtH66Q5fWmfb9Oeala5s1P+34BABgu/bon9Omnn9acOXO63n/jjTd06aWX6rLLLtMPfvADzZw5U7/73e907LHH6sYbbxy2sAAAmJBsa1eiaY8sZ0La9+2pKFN01dq07xcAgOHSrxJ62WWX6bLLLuv1YyeffDLPBgUA5LTIijXyjKyUFUjf/aCdnPJSRWvWy3XdtF4KDADAcBnSPaEAAOSDyJIVckpCsjxDmlR+UJyyEiV2Nym5rznt+wYAYDhQQgEAOIzIkpWyigqM7NvyeGR5PGp790Mj+wcAINUooQAAHEZkySrZfr+x/TsVZWp99S1j+wcAIJUooQAAHEK8aa/cZFKuwQxOeZlia+sMJgAAIHUooQAAHEJ06Sp5KitkF5g7E+qpKFXHpq1yXZNVGACA1KCEAgBwCJGVa+SEimU5jrEMdklIiT37FG/aaywDAACpQgkFAOAQoivWSIGA0QyWbcvy+9X+zgdGcwAAkAqUUAAADiGyoka232s6hpzyErW98a7pGAAADBklFACAPiRbWpWMRI1OStTJKStRrLbBdAwAAIaMEgoAQB8iq2rlGVEu2/DluJLklIbVsWUbkxMBALIeJRQAgD5EV66REwrK8piblKiTUxpWYvceJfe3mI4CAMCQUEIBAOhDdMUaWUWFpmNIkiyvV7Ista+oMR0FAIAhoYQCANCHyIoaWT7zkxJ1cspK1Pba26ZjAAAwJJRQAAB64cY6FN++S7Iz51DplJUoVrPOdAwAAIYkc46sAABkkOi6ejmV5RnxeJZOTmlYsc3bTMcAAGBIKKEAAPQiumKNnHBI8mZQCS0rUWLXbiUjUdNRAAAYNEooAAC9iK5cKztYLMuyTEfpYhcE5EZjitZvNB0FAIBBo4QCANCLTJuUqJNdElLba2+ZjgEAwKBRQgEA+BjXdRVbv0GWx2M6Sg9OWYkiy3hMCwAge1FCAQD4mPjWHbLDQcnOnEtxOzklYXVs3GI6BgAAg0YJBQDgY6I16+SEQ7ICftNRenBKQorvbJTruqajAAAwKJRQAAA+JlqzTnawSFYGPSO0kx0KKrl3vxK795iOAgDAoGTe0RUAAMOiNetlFWTeWVBJshxblter9iUrTUcBAGBQKKEAAHxMtKZWls9nOkaf7NKw2t5cbDoGAACDQgkFAOAgbkdciV1NkjJvUqJOTmlYHesbTMcAAGBQKKEAABwkVr9RTnmJ7Ax8RmgnpySkji3bTccAAGBQKKEAABwkuma97FBQyvASGt+1W26sw3QUAAAGjBIKAMBBYjXrZBcXybIy93Jcq6hQblu7OrbtMB0FAIABo4QCAHCQyOp1svyZOymRJFmWJauoUG1vv2c6CgAAA0YJBQDgILHVtbIzeGbcTk5ZiSLvLzcdAwCAAaOEAgDwkWRbu5KxDrmZeyVuF6ckpNiGzaZjAAAwYJRQAAA+El1bJ09FqeyA33SUw3JKwopzTygAIAtRQgEA+EisZp3sUFCWx2M6ymHZJSEldu9Rsq3ddBQAAAaEEgoAwEeiNetkFxWajtEvtt8nN55QtGGj6SgAAAwIJRQAgI9E16yXlcHPB/04OxRU2+vvmo4BAMCAUEIBAPhIdG29lEUl1CkNKbpyjekYAAAMCCUUAABJ8d17ZPt9yoKJcbs44ZA6Nm01HQMAgAGhhAIAIClWs15OWYmsLJgZt5MdDiq+o9F0DAAABoQSCgCApGhtnexgkSzHMR2l35xwUMk9e5VsaTUdBQCAfqOEAgAgKVZbL7sgYDrGgFg+n9xEUtH6TaajAADQb5RQAAB04EyoPNkzKVEnO1Ss9jcXm44BAEC/UUIBAJAUW79B8mbPpbidnJKQIqvWmo4BAEC/eYa6gZ07d+rhhx/W2rVr5fF4NGXKFF111VVysuieGgBAfkvs2SfL45GVVXPjHuCUhNSxmRlyAQDZY8hnQh9++GGFQiH9/ve/14wZM7Rq1Sq9+OKLqcgGAEBaRNfVyyktkVWQPTPjdrJDIcW375LruqajAADQL0MuoTt37tSZZ54pn8+nkpISfepTn9LmzZtTkQ0AgLSI1TbIDmXXzLid7HBQyT37mCEXAJA1hnw57pe+9CW9/fbbOumkk9Ta2qolS5boG9/4Ro/1qqurVV1dLUm68847VVFRMdRdDyuPx5PxGZH7GIfIFLk+Fps3b1MgHJYvkF2z40qSAgG1JhIq2t+q4qOPMp1mWOX6OER2YBwiU2TzWBxyCT3hhBNUXV2tK6+8UslkUuedd57OOOOMHutNmzZN06ZN63q/sTGzH65dUVGR8RmR+xiHyBS5Phb3LlslOxBQMhIxHWVQrGCxtj73ssrGjDQdZVjl+jhEdmAcIlNk+lgcPXp0nx8b0uW4yWRSt99+uyZPnqzHH39cDz/8sFpbW/Xkk08OZbMAAKRVbG2d5M++x7N0YoZcAEA2GVIJbWlpUWNjo774xS/K6/UqGAzq/PPP14cffpiqfAAADKtka5vcRFKWlX0z43aywyF1bNpmOgYAAP0ypBIaCoVUWVmpl156SYlEQq2trVqwYIGOPPLIVOUDAGBYxdY1yFNWIiuQfTPjdnLCQcV37DQdAwCAfhnyPaE33XSTHn30UT377LOybVsnnXSSrrzyylRkAwBg2EVr62SHirNyZtxOdklQyaa9Sra1yy4sMB0HAIBDGnIJPeqoo3TbbbelIAoAAOkXq23I+uJm+/1yO+KKbdyswPHHmo4DAMAhDfk5oQAAZLPo2jrJO+S/yRpnB4vU9vb7pmMAAHBYlFAAQF6Lra2T5c/e+0E72SVhRZbXmI4BAMBhUUIBAHkrGYkq2dom2dk7M24npySkjo1bTMcAAOCwKKEAgLwVq9sop7xEdhbPjNvJCQeV2JG5Dy0HAKATJRQAkLdi6+plh4KyPDlwT2g4pETTXiUjUdNRAAA4JEooACBvxdbWyy4qNB0jJSy/T240po4t20xHAQDgkCihAIC8FV1XL8vnMx0jJSzLkh0sVNvCD0xHAQDgkCihAIC8FatZlzMlVPpohtwlq0zHAADgkCihAIC85MbjSuzZl1NHQiccUscmZsgFAGS2HDr0AgDQfx0bNsspK5Htz50zoU44qPj2naZjAABwSJRQAEBeiq6tlx0slrxe01FSxg4Hldi9R25H3HQUAAD6RAkFAOSl2Lp62cVFsizLdJSUsQoCctsj6uBsKAAgg1FCAQB5Kbq2XlYgdy7FlQ7MkGsVFijy3jLTUQAA6BMlFACQl2Jr62T5cudS3E5OaVjt7y01HQMAgD5RQgEAecdNJg9M4GM7pqOknBMOKdawyXQMAAD6RAkFAOSd+JbtssMhWV6P6SgpZ4eDim/jnlAAQOaihAIA8k50bZ2ccFBWDj2epZMTDire2CQ3mTQdBQCAXlFCAQB5J1ZbLzuYWzPjdrKKCuW2tim+e4/pKAAA9IoSCgDIO7HaelmBgOkYw8KyLFkBvyIfrDAdBQCAXlFCAQB5J7q2LifvB+3klITV/u4S0zEAAOgVJRQAkFdc11XHxi1SDpdQuySk2PoG0zEAAOgVJRQAkFcSOxplh4pz8n7QTk44qPjW7aZjAADQK0ooACCvRGvr5IRDsgJ+01GGjR0OKb5rt1zXNR0FAIAeKKEAgLxyYGbcYll27h4C7eJCJZtbldjXbDoKAAA95O4RGACAXkRr62UV5O5ZUEmybFuWz6voqrWmowAA0AMlFACQV2K19bK8XtMxhp0dDqn97fdNxwAAoAdKKAAgr8TqNki+3C+hTklI0TXrTMcAAKAHSigAIG/Em/bK8vtlJXN/wh4nHFLHFmbIBQBkHkooACBvxGrr5ZSV5PTMuJ3scFDxnY2mYwAA0AMlFACQN2K19bKLi2V5HNNRhp0dLFZy734l2yOmowAA0A0lFACQN2K19bKLAqZjpIXl2LI8HkXWrDcdBQCAbiihAIC8Ec2TmXE72aFitS9ihlwAQGahhAIA8kZsXZ6V0NKwostqTMcAAKAbSigAIC8kW1oP/IebNBskjZxwSB2bt5qOAQBAN5RQAEBeiK5rkFNeKsvnMx0lbZxwUPEdzJALAMgslFAAQF44MDNukeT1mI6SNnYoqMSefXI74qajAADQhRIKAMgLB0pooSzLMh0lbSyPI1mWYvWbTEcBAKALJRQAkBdi6+rz6lLcTnawSG2L3jMdAwCALpRQAEBeiK6pk5VHl+J2ckrDinywwnQMAAC6UEIBADkvGYkqGYlIrukk6eeUhNSxcYvpGAAAdKGEAgByXqxuozwVZZLHMR0l7exQUPHtu0zHAACgCyUUAJDzYuvqZRcXy/Ln3z2hTjio+O49cpP583xUAEBmo4QCAHJePs6M28nyeiXXVceWbaajAAAgSUrZDA1vvfWW5syZo8bGRpWUlOg73/mOTjjhhFRtHgCAQYvV1kt+v+kYxtjFhWpf9KF848aYjgIAQGpK6LJly/Tkk0/q3/7t33TMMcdo7969qdgsAAApEa2tl+/4CaZjGOOUhtX+/jKFv/4V01EAAEhNCZ01a5YuvfRSfeITn5AklZWVpWKzAAAMmRuPK7F7j5SHl+J2ckpCitVtNB0DAABJKSihyWRS69ev1+mnn64bbrhBHR0dOuOMM/QP//AP8h30UPDq6mpVV1dLku68805VVFQMddfDyuPxZHxG5D7GITJFNo/F9to6+UeOUCAQkBMImI5jhD2iQu0167L2/2GnbB6HyB2MQ2SKbB6LQy6he/fuVSKR0KJFi/Tzn/9cjuNoxowZevrpp3X55Zd3rTdt2jRNmzat6/3Gxsah7npYVVRUZHxG5D7GITJFNo/F5nc/kFtUoJglWZGI6ThGJAN+xXY0ateuXVk9OVM2j0PkDsYhMkWmj8XRo0f3+bEhz47bebbzi1/8okpLSxUKhfTlL39ZH3744VA3DQDAkMVq62UXFcqy83dCeNvvO3BZ8s7M/WUFAJA/hnxELi4uVnl5ebe/rGbzX1kBALklVlsvK08vwz2YXVSgtveWmY4BAEBqnhN6/vnna968edq3b59aWlr0/PPP69Of/nQqNg0AwJBE19ZJXsd0DOPskrDa3vnAdAwAAFIzO+4ll1yi5uZm3XjjjfJ6vTrzzDN18cUXp2LTAAAMmptMKr51h7wTqkxHMc4pDSu2rsF0DAAAUlNCPR6Prr76al199dWp2BwAACkR37ZTdmlY3CQiOeGgOho2m44BAEBqLscFACATxdbWyQkHuSdUkh0KKt7YJNd1TUcBAOQ5SigAIGdF19XLLi6S5XC4swJ+uZGoEnv3mY4CAMhzHJUBADkrtrZedgFnQaUDM9dbhQWKvL/cdBQAQJ6jhAIAcla0tl7ypGT6g5zglITUtpAZcgEAZlFCAQA5yXVddWzYJHl4PEsnuyR84JE1AAAYRAkFAOSkRGOT7MJCWUzE08UpCSq+dbvpGACAPEcJBQDkpOjaOjllYVncE9rFCYcU37XbdAwAQJ6jhAIAclJszXrZwWJZDpfjdrIKAnJb25XY32w6CgAgj1FCAQA5KbpmvayCAtMxMsqBGXIDal+60nQUAEAeo4QCAHJSdG2dLC8z436cEw6q/a33TMcAAOQxSigAIOe4rquO+k2S12s6SsaxS8KK1qw3HQMAkMcooQCAnBPfvkt2qFiWmzQdJeM4JSF1bGGGXACAOZRQAEDOia1ZL6e0RFbAbzpKxnHCQSWYIRcAYBAlFACQc6Jr18sOFjEzbi+sokIlm1uVaG4xHQUAkKcooQCAnBNds142zwftlWVZsgI+RZatNh0FAJCnKKEAgJwTW1Mni0mJ+uSEQ2pjhlwAgCGUUABATnGTSXVs2irX4RDXF7s0pOiadaZjAADyFEdoAEBOiW/ZLqesRFbSNR0lYznhkOLMkAsAMIQSCgDIKdG1dbLDIVncE9onOxxUfGejXJeiDgBIP0ooACCnRGvWfTQzLoe4vtjFRUrub1FiX7PpKACAPMQRGgCQU2Jr65gZ9zAs25bl9Sq6eq3pKACAPEQJBQDklGjNesnjMR0j49klIbW+8a7pGACAPEQJBQDkDDeRUHz7Tsnm8HY4TklIsTV1pmMAAPIQR2kAQM7o2LBFTnmpLMt0ksxnh4OKb9lmOgYAIA9RQgEAOSO6tk5OSUhWwG86SsZzSkKK79zNDLkAgLSjhAIAckZszTpZxYWyuBz3sOxgsZL7mxVv2ms6CgAgz3CUBgDkjOjaOll+zoL2h2Xbsvw+RT5YbjoKACDPUEIBADkjuqpWFjPj9ptTWqI2ZsgFAKQZJRQAkBOS0ZgSe/fLchzTUbKGUxZWbH2D6RgAgDxDCQUA5ITYunp5KiskD4e2/rJLwurYzAy5AID04kgNAMgJ0VW1ssPFsnw+01GyhlMSUqKxSW48bjoKACCPUEIBADkhurpWdnGRLB4S2m92QUBuNMbZUABAWlFCAQA5Ibq6lplxB8EOFav19XdMxwAA5BFKKAAg67muq+iaOlkeJiUaKKesRO3vLzMdAwCQRyihAICsl9i1W3ZhgdykazpK1nFKw+po2Gw6BgAgj1BCAQBZL7p6nZzyUtkBJiUaKKckrPi2HaZjAADyCCUUAJD1oqvWyg4Vy/J4TEfJOnY4qMSefUq2tJqOAgDIE5RQAEDWi66ulV0QMB0jK1mOIzmO2pevNh0FAJAnKKEAgKwXWVUreTkLOlhOaZgZcgEAaUMJBQBkNTfWocTuPZJ4PuhgOWUliq1eZzoGACBPUEIBAFktuq5BnspyWQ6HtMFySkLq2LTVdAwAQJ7giA0AyGrR1bWyQ0FZAb/pKFnLKQ0rvqtRbjxuOgoAIA+krIRu27ZN06dP129/+9tUbRIAgMOKrqqVXVwky+Jy3MGyCgvktkbUsXWn6SgAgDyQshL68MMPa8KECanaHAAA/RJdXSvL6zUdI6tZliU7VKS21xeZjgIAyAMpKaFvvfWWCgsLNXHixFRsDgCAfnFdV9E162T5mRl3qJyyUrW986HpGACAPDDkEtrW1qZZs2bpyiuvTEUeAAD6LbGjUXZhgZQ0nST7OeUlitVvNB0DAJAHhvyn46eeekpTp05VeXn5Iderrq5WdXW1JOnOO+9URUXFUHc9rDweT8ZnRO5jHCJTZOpYbHp3qQJHVKqgNCzLcUzHyWqeI0Zq/8L3VF5enrH312bqOER+YRwiU2TzWBxSCW1oaNDy5cv1X//1X4ddd9q0aZo2bVrX+42NjUPZ9bCrqKjI+IzIfYxDZIpMHYuNb72rZGFA0Y4OqaPDdJys5vq9iu/Zpx1ra+UpLzMdp1eZOg6RXxiHyBSZPhZHjx7d58eGVEJXrlypXbt26V//9V8lSZFIRMlkUj/60Y/0y1/+ciibBgDgsKIramQVFJiOkRMs25ZVEFDr2+8rfMHnTccBAOSwIZXQadOm6ayzzup6f+7cudq1a5euueaaIQcDAOBwIivWqGDSp0zHyBlOeana33yXEgoAGFZDKqF+v19+//89HDwQCMjr9SoUCg05GAAAhxJv2ivZtuS6pqPkDE95iaK19aZjAAByXErntL/ssstSuTkAAPoUXVEjT2WFLL/PdJSc4ZSWKLK8xnQMAECOS8lzQgEASLfI8hrZ4WJZHp4Rmip2SUiJ3XuUaG4xHQUAkMMooQCArBRdsUY2kxKllOU4snw+tX+wwnQUAEAOo4QCALJSZHmNLC9nQVPNKS9R66tvmo4BAMhhlFAAQNZJNLfIjcYk5iRKOae8VLGadaZjAAByGCUUAJB1oivXynNEhSy/13SUnOOUhhXbtM10DABADqOEAgCyTmRFjexQUJaXEppqTmlYicYmJVvbTEcBAOQoSigAIOtEl62WXcikRMPB8nol21b7kpWmowAAchQlFACQddqXrJR8nAUdLp6KUrW8tMB0DABAjqKEAgCySmJfs9xoTJYs01FyllNRruiqWtMxAAA5ihIKAMgqkWWr5Bk5QpbfZzpKznIqStWxcYvpGACAHEUJBQBklciSlXJKQjwjdBg5JSEldu9RfF+z6SgAgBxECQUAZJXIkpVMSjTMLMeRVRBQ29uLTUcBAOQgSigAIGu4rqvIstWS1zEdJec5FWVqfeVN0zEAADmIEgoAyBrxbTtlFRRIrukkuc9TUabYmjrTMQAAOYgSCgDIGpElK+UZUS4r4DcdJec5FaXq2LxVrkvjBwCkFiUUAJA1IktWyg4Xy3K4HHe42cFiJfe3Kr5tp+koAIAcQwkFAGSN9iUrZfk5C5oOlmXJDherpfoN01EAADmGEgoAyApuMqnY2jrJw1nQdHFGlKvtLWbIBQCkFiUUAJAVYusa5FSUyTIdJI94yksVW99gOgYAIMdQQgEAWaH9vWVyyktlFQRMR8kbTkWZ4lt3yI11mI4CAMghlFAAQFZof2/pgUmJLM6FpotdEJCbSKh9ZY3pKACAHEIJBQBkhfbFS2X5fKZj5B1PRbma575sOgYAIIdQQgEAGS/e2CQ3EZfFIyvTzjOyQtGlq03HAADkEEooACDjtb+3TN5RI2UFOBOabs6IcsUaNsl1+QsAACA1KKEAgIzX/t5S2SUhWR6P6Sh5xw4HldzfrPj2naajAAByBCUUAJDx2t9bKsvvNx0jL1mWJbskpObnqk1HAQDkCEooACCjJSNRdWzcKsvmkGWKZ2SFWt9cbDoGACBHcEQHAGS0yPLV8oweKXk4ZJniGVGhjvUNpmMAAHIER3QAQEZrX7xUTkmIx7MY5JSXKL6jUYnmFtNRAAA5gBIKAMho7YuXyC4qkmVZpqPkLcvjkRXwq+W1haajAAByACUUAJCx3ERCkSWrZPm8pqPkPc8RI9Qy7zXTMQAAOYASCgDIWNGVa+U5YoQknlFpmmfkCMVW15qOAQDIAZRQAEDGanv7PTnlpbIKAqaj5D1PZbk6tmxXoq3ddBQAQJajhAIAMlbbwvflhILcD5oBLK9Xlt+n1tfeNh0FAJDlKKEAgIzkxuOKLK+RPI7pKPiI54hKtTxXbToGACDLUUIBABkpsmKNPKMqJZf7QTOFZ9QIRVatNR0DAJDlKKEAgIzU9vZ7cspKuB80g3hGlCu+dQf3hQIAhoQSCgDISO0L35ddzPNBM4nl8cguCKjlxQWmowAAshglFACQcdyOuCIr10gOh6lM44weqZa/vWI6BgAgi3F0BwBknPb3l8k7ZpQsh0mJMo135AhFV/G8UADA4FFCAQAZp3XBQjkVZbIDftNR8DHOiDLFd+xSfFeT6SgAgCxFCQUAZJzW+YtkFRWajoFeWI4juzSsfXOeMx0FAJClKKEAgIwSb2xSYu8+WeLRLJnKO+YItb7ypukYAIAs5RnqBjo6OvTQQw9p+fLlamlp0ciRI3XFFVfo1FNPTUU+AECeaXv9HXmPHC3L7zMdBX3wjj5CrW++K9d1mb0YADBgQz4TmkgkVF5erttuu02PPvqovvnNb+rXv/61du7cmYp8AIA807pgoZySElmeIf+dFMPEDhbJjcXU/uEK01EAAFloyCU0EAjosssuU2VlpWzb1mmnnabKykrV1dWlIh8AII+4yaTa3n5Pls9rOgoOwztqpPb9z19MxwAAZKGU/5l579692rZtm8aNG9dteXV1taqrqyVJd955pyoqKlK965TyeDwZnxG5j3GITJGusdiydKV8Iyrk9/vkBALDvj8MnnX0kYouXZnWn1H8TEQmYBwiU2TzWLRc103ZzA/xeFx33HGHRo4cqWuvvfaQ627dujVVux0WFRUVamxsNB0DeY5xiEyRrrHYeM9Dav9guTxHjOBewwznxuNqnvuyJrz3NznhUFr2yc9EZALGITJFpo/F0aNH9/mxlM2Om0wmde+998rj8eif//mfU7VZAEAeaXlxgexwkAKaBSyPR3YoqH1P/dV0FABAlklJCXVdVw888ID27dunH/zgB/IwmQQAYIA6tu5QsrlF1M/s4a0ao+YXXjUdAwCQZVJSQh988EFt2bJFP/rRj+TzMaU+AGDgWl5+Xd6qsTyaJYt4x45SbPU6JTs6TEcBAGSRIZ+y3LVrl6qrq+X1enXNNdd0Lb/22mt1zjnnDHXzAIA80fLSAjklIVmOYzoK+skuCEg+r5pfmK/whZ83HQcAkCWGXEJHjBihWbNmpSILACBPJfa3KLZmvQJnnmY6CgbIWzVG+2fNpYQCAPotZRMTAQAwWK3z35b36CNle3k+aLbxjh2tyLLVSuFk+wCAHEcJBQAY1/xctZyyElleJrbLNk6oWIrH1fb2YtNRAABZghIKADAq2dKqyAcrZDGxXdbyHDlGex5+ynQMAECWoIQCAIxqeel1+SZUyfIyIVG28h01TpH3l3FJLgCgXyihAACj9s99SXZ5mSzuB81aTjgoN55Q66tvmY4CAMgClFAAgDGJPfsUXbVWcizTUTBE3qPHac/M/zUdAwCQBSihAABjmue9Ju+EKtk+zoJmO9/R4xT5cIWS8bjpKACADEcJBQAYs//pv8kpDcvyMCtutrMLC2R5vWp+Zp7pKACADEcJBQAYEavfpPjORslhQqJc4Z1Qpb1PPG06BgAgw1FCAQBG7Jv9V/mOOUp2wG86ClLEd9RYRVfXKr53n+koAIAMRgkFAKSdm0ho/59fkB0qlmVzKMoVltcrZ0SFdt/zsOkoAIAMxpEfAJB2ba+/I88RlVKS50rmGv9x49Xyt1dMxwAAZDBKKAAg7fY++Yw8I0fILgiYjoIUcyrKlGxpVeub75qOAgDIUJRQAEBadWzeduDZoH4ey5KLLMuSd8JR2v0bLskFAPSOEgoASKu9j82W74RjZPt8pqNgmPgnVCmydJXijU2mowAAMhAlFACQNsn2iPY/+6Ls4iJZDoegXGX5ffKOHqldt//OdBQAQAbiNwAAQNrsf2aefMccLVmmk2C4+U48Vi0vzlcyHjcdBQCQYSihAIC0cBMJ7fnDk3LKS2T7eTZornOCxbILC9V032OmowAAMgwlFACQFi0vvCanvFTiuaB5wz/xE9r7xzlKJpOmowAAMgi/CQAAhp3rutr924flGTNSdoCzoPnCU1khxRPa98SfTUcBAGQQSigAYNi1vvKmrMICcTNo/vGfcqJ2/3YmZ0MBAF0ooQCAYeUmk2q86wF5x46SXcBZ0HzjPWKElIhzNhQA0IUSCgAYVs1/OfBIFu4FzV/+U07U7nse4mwoAEASJRQAMIySkagaf/V7ecaMkl0QMB0HhnhHjpDlcbT7V38wHQUAkAEooQCAYbP30VnyHjVOkms6CgwLnH6y9j78JyX2N5uOAgAwjBIKABgWHVu3a88jT8kpK2FGXMgJFssZNVLbb/pP01EAAIZRQgEAw2LnrXer4LSTZXk9pqMgQxSccqJaFyxS+4crTEcBABhECQUApFzLSwvUsWWb5HFkeSihOMDyeRX49ERt/faP5TJJEQDkLUooACCl4o1N2vnTu+U79mhZXIaLj/EdOUayLe346d2mowAADKGEAgBSxnVdbb/pPxU4daIsx5FlWaYjIQMVTDpVzbP/qrb3lpmOAgAwgBIKAEiZvY/OUmLffsnrkeXzmo6DDGUH/Aqc8Slt/efvK9HcYjoOACDNKKEAgJRoe/s97Xn4f+UdN4bZcHFY3tEj5RlVqc3Tr5fr8ggfAMgnlFAAwJB1bNqq7T/4uQKnnyzLzxlQ9I//lBMV376Lx7YAQJ6hhAIAhiS+a7c2/8ONCpx+iizbkmVzaEH/WJalwnMmqfXl17X7vsdMxwEApAm/KQAABi2xd782f+sG+T95vCzHluXlLCgGxvJ4VHD+mWr670e157HZpuMAANKAEgoAGJT49l3a+PV/kXfCUQfOgPp9piMhSzkFARVOPUuN/3W/mmb+r+k4AIBhRgkFAAxYbH2DNl72L/KfcKxsr5fngWLInKICFU79jHb/+kHt+PmvmawIAHIYJRQAMCDNz7+iTdNvUOBTJ0m2JSvAGVCkhlNUoKJp56jl+Ve0efoNSra2mY4EABgGlFAAQL8kW9u04ye/VOOvH1TB5FNleT2yuQQXKWb7vCo8b4oSjU2qO+citS1eYjoSACDFKKEAgENyXVdNL7yqhi9coY6djfKfcKwsv0+Wx2M6GnKUZVkKnHqSAhOP15Z//oG2/eDnSuzdbzoWACBF+A0CANCn9veXa9cdv5PTEVfBpz8p17Y5+4m08YyqVFHFuYquXKu6cy5Sx03/Kt+lX5JdVGg6GgBgCCihAIBu3HhcLfPma8/D/6tEc4v8x0+Qv6BAMUuyLct0POQZ2+tR4JQT5D1qjHb96RlF7rpfJdMvUsm3LpF37CjT8QAAg0AJBQDI7Yir7d0P1fzXl9X6ypvyVo2VZ+woOXJlFQTkFBTIikRMx0Qec8IhFU3+tOydu9T6xrva979z5a0aq9BlX1Hx1LPkHT3SdEQAQD+lpIS2tLTo/vvv17JlyxQMBnXFFVfo7LPPTsWmAQDDILFnr6Kr16n9gxVqW/i+oqvWyjt2lDyjKlXwmdMlSTaPXUEGckJBOROPU/KEY5TYulP7nnxGu3/1B9nFRSo6d7IKTv2kAqdOlPeosbI4cw8AGSklJfShhx6Sx+PRgw8+qIaGBt1xxx2qqqrSuHHjUrF5AMAAuLEOJfbtV2JfsxK79yi+Zbs6tm5Xx+Zt6ti0VbHaeslx5Kkokx0Oyg4HVXj2JMm2KJ7IGrbjyB43St5xo+SeeKwSTfsUXVOn9g9XKrF7j5ItrfKMrJD/2KPlG3+UPKMq5RlZIWdEuTyVFXLKShjvAGDIkEtoJBLRO++8o7vvvluBQEDHH3+8Tj/9dL3++uuaPn16KjKmXeub76q9pk5tba2HXnEAD9Lu96oDeTh3f9cd0DZTvO8BbHRADybv99fe/00Oz+s5tK+9pbBQbW0fe05ev3dveiyl/v9Rv8eI6e+jVO9bkptMyo11yI1G5UYP/DsZi8mNROVGD/w72dIqtyMuObbswsIDM9j6fbKLCmUVBmR7vbKLC1Uw6dOSkrJ8Xlleb+q/LiDNLMeRZ0SZNKJM0oHvl2R7RG4kqkRLm9reWyo3Hj/wvdIekdvWrmR7REokJUuyCgKyi4sOvAX8B753vN6Pvkc8B75PfF5ZHo8s25ZsS7L+782yLMm2P3pfB9bRRx+3D17P7OvUb9kS1FDO9sKiw/+OCKRBxc/+3XSEQRtyCd22bZscx9Ho0aO7llVVVWnVqlXd1quurlZ1dbUk6c4771RFRcVQdz1sfJWV2jbrOUW37Ujxlvv5w3I4fqaaPqD0c/8DStnvlYfhax+eoD202JbcZC9FZTi+9mF5mYZjzBv8PkrV69ln93QP+pfbfT03KctxZFm2LNuSvF7J55cVDh/4JdnjOfDLs8c5sJ7PJzvgl10Q+OgX4qGxbFu+ZHLI2wGGIlXjMBmNKtkeUTIaU7IjLnXElYxG5cY+ej+ekJtISG1xyXXlJiXLTSrpfvR9aanrj0id/7QO+n51u30PH/RvpI7BlzNmWQP7wzkwTBI7G1VRmbmd6lBScia0oKCg27LCwkJFPjaBxbRp0zRt2rSu9xsbG4e66+HziaN03P/cl9kZkRcqKioYh8gIjEVkAsYhMgHjEJnCyfCxePBJyo8b8p/HA4GA2tvbuy1rb29XIBAY6qYBAAAAADlmyCV01KhRSiQS2rZtW9eyDRs2MCkRAAAAAKCHlJwJnTx5sp566ilFIhHV1NRo8eLFOvfcc1ORDwAAAACQQ4Y+W4Wkq6++WrFYTNdcc41+85vf6JprruFMKAAAAACgh5Q8J7S4uFj//u/ZO0UwAAAAACA9UnImFAAAAACA/qCEAgAAAADShhIKAAAAAEgbSigAAAAAIG0ooQAAAACAtKGEAgAAAADShhIKAAAAAEgbSigAAAAAIG0s13Vd0yEAAAAAAPmBM6F9+PGPf2w6AsA4RMZgLCITMA6RCRiHyBTZPBYpoQAAAACAtKGEAgAAAADShhLah2nTppmOADAOkTEYi8gEjENkAsYhMkU2j0UmJgIAAAAApA1nQgEAAAAAaUMJBQAAAACkDSUUAAAAAJA2HtMBTGlpadH999+vZcuWKRgM6oorrtDZZ5/dYz3XdfXkk0/q1VdflSR99rOf1fTp02VZVrojI0f1dyzOnTtXCxYs0K5duxQMBvWFL3xBF154oYHEyEX9HYed4vG4fvjDH6q9vV0PPPBAGpMilw1kHNbV1emxxx5TXV2dAoGALrroIn3pS19Kc2Lkov6Ow46ODj3yyCNavHix4vG4jjvuOF177bUqKyszkBq5Zt68eZo/f742btyos846S9ddd12f6z733HN69tlnFYvFNHnyZF1zzTXyer1pTDtweVtCH3roIXk8Hj344INqaGjQHXfcoaqqKo0bN67betXV1Vq8eLFmzJghy7L0n//5n6qsrNTf/d3fGUqOXNPfsei6rq677jpVVVVpx44d+sUvfqHy8nKdddZZhpIjl/R3HHaaO3euQqGQ2tvb05wUuay/43D//v26/fbbdeWVV2rKlCmKx+PavXu3odTINf0dh3/7299UW1urGTNmqLCwUH/4wx80c+ZM3XTTTYaSI5eUlpbq4osv1tKlSxWLxfpcb8mSJXr22Wd16623qrS0VHfddZdmzZql6dOnpzHtwOXl5biRSETvvPOOvvGNbygQCOj444/X6aefrtdff73HugsWLNAFF1yg8vJylZWV6YILLtCCBQsMpEYuGshY/OpXv6rx48fLcRyNHj1ap59+utasWWMgNXLNQMahJO3cuVNvvPGGvva1r6U3KHLaQMbhc889p1NOOUXnnHOOvF6vCgoKNHbsWAOpkWsGMg537typU045RSUlJfL5fPrMZz6jTZs2GUiNXDR58mRNmjRJwWDwkOstWLBAU6dO1bhx41RcXKxLLrlE8+fPT0/IIcjLErpt27auX+Q7VVVV9fqDY9OmTaqqqjrsesBgDGQsHsx1XdXU1PBLF1JioONw5syZuvzyy+Xz+dIVEXlgIOOwtrZWxcXFuuWWW3T11VfrzjvvVGNjYzrjIkcNZBx+9rOf1Zo1a9TU1KRoNKo33nhDp556ajrjAtq8ebOOOuqorverqqq0b98+NTc3mwvVD3lZQiORiAoKCrotKywsVCQS6XXdwsLCHuvxeFWkwkDG4sFmz54t13U1derU4YyHPDGQcfjuu+8qmUxq0qRJ6YqHPDGQcdjU1KQFCxboqquu0n333afKykr95je/SVdU5LCBjMNRo0apvLxc3/72t3XllVdqy5YtuvTSS9MVFZDUe1eRlPG3y+RlCQ0EAj3+x7S3tysQCBx23c71mJgIqTCQsdhp3rx5WrBggX784x9n/E3nyA79HYeRSERPPPGE/umf/imd8ZAnBvLz0OfzadKkSTrmmGPk8/n09a9/XWvWrFFbW1u64iJHDWQcPvTQQ+ro6NDMmTP1+OOPa9KkSbr99tvTFRWQdGDMHvyzr3P8fvyPKZkmL0voqFGjlEgktG3btq5lGzZs6HUCjnHjxqmhoaHr/YaGhj4n6gAGaiBjUZJeffVV/eUvf9Gtt96q8vLydMVEjuvvONy+fbt27dqlW2+9Vddcc43uuusu7dmzR9dcc4127tyZ7tjIMQP5eXjkkUd2e58/DCNVBjION2zYoPPPP1/FxcXyer36+7//e61bt0779+9PZ2TkubFjx2rDhg1d72/YsEHhcPiw95KalpclNBAIaPLkyXrqqacUiURUU1OjxYsX69xzz+2x7rnnnqvnn39eTU1Nampq0nPPPafzzjvPQGrkooGMxTfeeEN/+tOfdMstt2jkyJEG0iJX9Xccjhs3Tvfff79mzJihGTNm6Nvf/rZKSko0Y8YMVVRUGEqPXDGQn4dTp07V4sWL1dDQoHg8rjlz5uj444/vdkkaMBgDGYcTJkzQggUL1NbWpng8rhdffFGlpaUKhUIGkiPXJBIJxWIxJZNJJZNJxWIxJRKJHuudd955evXVV7V582a1trbq6aef1vnnn5/+wANkuXl6c2NLS4vuu+8+LV++XMXFxZo+fbrOPvtsrV69Wrfffrsef/xxSf/3nNBXXnlFkvS5z32O54Qipfo7Fq+77jo1NTXJ4/m/Jyudc845uvbaa01FRw7p7zg82MqVK/W73/2O54QiZQYyDl966SU9/fTTisViOu6443T11VfzxxCkRH/HYXNzsx555BEtW7ZM8Xhc48aN05VXXqljjjnG8FeAXDBr1izNmTOn27JLL71Un/3sZ/W9731Pv/71r7t+5mXjc0LztoQCAAAAANIvLy/HBQAAAACYQQkFAAAAAKQNJRQAAAAAkDaUUAAAAABA2lBCAQAAAABpQwkFAAAAAKQNJRQAAAAAkDaUUAAAAABA2vx/15lPvGmh2yIAAAAASUVORK5CYII=",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"fig, ax = plt.subplots(figsize=(16,6))\n",
"ax=plt.subplot(1,1,1)\n",
"ax.plot(x, yp, '-', c=colors[7], linewidth=0.9, alpha=1, label=\"prior\")\n",
"ax.fill_between(x, 0, yp, color=colors[7], alpha=0.6)\n",
"# testo sull'asse x\n",
"plt.xticks(fontsize=12)\n",
"plt.yticks(fontsize=12)\n",
"plt.tight_layout\n",
"# titolo della figura\n",
"plt.suptitle(r'Prior: $p(\\theta)=Beta({0:3d}, {1:3d})$'.format(alpha, beta), fontsize=16)\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Per ogni numero di osservazioni fissato, determina il numero di valori $1$ osservati, calcola i parametri della distribuzione a posteriori risultante e memorizza il valore della verosimiglianza e della densità di probabilità per tutti i punti della griglia."
]
},
{
"cell_type": "code",
"execution_count": 30,
"metadata": {},
"outputs": [],
"source": [
"n = 50"
]
},
{
"cell_type": "code",
"execution_count": 38,
"metadata": {},
"outputs": [],
"source": [
"# determina numero di esiti pari a 1\n",
"ones = data[:n].sum()\n",
"# modifica i parametri della distribuzione per tener conto degli esiti osservati\n",
"params = [sum(t) for t in zip(hyper, [ones, n-ones])]\n",
"# calcola elenco dei valori per la distribuzione a posteriori con i parametri calcolati\n",
"post = dist.pdf(x, *params)\n",
"# calcola il valore sulla griglia per cui la distribuzione a posteriori è massima\n",
"mp = x[np.argmax(post)]\n",
"# calcola elenco dei valori per la verosimiglianza con la probabilità considerata\n",
"lik = [p**ones*(1-p)**(n-ones) for p in x]\n",
"# calcola il valore sulla griglia per cui la verosimiglianza è massima\n",
"ml = x[np.argmax(lik)]\n",
"# calcola il valore dell'evidenza\n",
"ev = np.sum(list(map(lambda x,y:x*y/float(nv), lik, yp)))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Visualizza la distribuzione a priori, la verosimiglianza e la distribuzione a posteriori per il numero di osservazioni considerato"
]
},
{
"cell_type": "code",
"execution_count": 39,
"metadata": {},
"outputs": [],
"source": [
"def plot_dist():\n",
" fig, (ax1, ax2) = plt.subplots(2,1,sharex=True, figsize=(16,10))\n",
" ax1.plot(x, lik, '-', c=colors[1], linewidth=0.9, alpha=0.8)\n",
" # riempie la zona compresa tra la curva e l'asse x\n",
" ax1.fill_between(x, 0, lik, color=colors[1], alpha=0.3)\n",
" # testo sull'asse x\n",
" plt.xlabel(r\"$\\theta$\",fontsize=14)\n",
" plt.xticks(fontsize=12)\n",
" plt.yticks(fontsize=12)\n",
" ax1.set_title(r'Likelihood; $L(\\theta|X)=p(X|\\theta)=)\\theta^{%3d}(1-\\theta)^{%3d}\\qquad$ ML=%8.5f'%(ones, n-ones, ml), fontsize=14)\n",
" plt.tight_layout\n",
" # effettua il plot a partire dalla sequenza di ascisse in x e di ordinate calcolate e salvate \n",
" # nell'elemento attuale di ys\n",
" ax2.plot(x, post, '-', c=colors[3], linewidth=0.9, alpha=1)\n",
" # riempie la zona compresa tra la curva e l'asse x\n",
" ax2.fill_between(x, 0, post, color=colors[3], alpha=0.6)\n",
" # effettua il plot del prior a partire dalla sequenza di ascisse in x e di ordinate calcolate e salvate in yp\n",
" ax2.plot(x, yp, '-', c=colors[7], linewidth=0.9, alpha=1, label=\"prior\")\n",
" # riempie la zona compresa tra la curva e l'asse x\n",
" ax2.fill_between(x, 0, yp, color=colors[7], alpha=0.6)\n",
" plt.annotate(r'Evidence; $p(X)={0:10.3e}$'.format(ev), xy=(.05, .85), va='top', xycoords='axes fraction', \n",
" fontsize=10)\n",
" # testo sull'asse x\n",
" plt.xlabel(r'$\\theta$', fontsize=14)\n",
" plt.xticks(fontsize=12)\n",
" plt.yticks(fontsize=12)\n",
" plt.title(r'Posterior; $p(\\theta|X)=Beta({0:3d}, {1:3d})\\qquad$ MAP={2:8.5f}'.format(params[0],params[1],mp), fontsize=14)\n",
" plt.tight_layout\n",
" # titolo della figura\n",
" plt.suptitle(r'$\\theta={0:3.2f}\\qquad n={1:3d}\\qquad\\#1={2:3d}\\quad \\#0={3:3d}$'.format(theta_real, \n",
" n, ones, n-ones), fontsize=16)\n",
" plt.show()"
]
},
{
"cell_type": "code",
"execution_count": 40,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA6EAAAKcCAYAAAAZyLztAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/OQEPoAAAACXBIWXMAAAsTAAALEwEAmpwYAACveElEQVR4nOzdd3hUVf4G8PdOb6lMEgglBEKoiTQpohSJBRAVVGzrImtd1B+7iqIiWFDAXRQLuIiCKDYEEQsIEjrSIaEFQgkEQgmEkF6mnd8fWWYZ0ibJzNxJ8n6eJ4/OvXfufefOyWS+nHPPlYQQAkREREREREQ+oJA7ABERERERETUeLEKJiIiIiIjIZ1iEEhERERERkc+wCCUiIiIiIiKfYRFKREREREREPsMilIiIiIiIiHyGRSgRERERERH5DItQIqrXzp49i9GjR8NsNiMgIAD3338/cnJyvHa806dP495770VQUBACAwMxcuRInDp1qsrnLFmyBPfccw+ioqKg1+vRvn17vPLKK8jPz6/0OStWrED//v1hMpkQGBiInj17Yu3atZ5+OfXK+vXrIUlSuZ/g4OBy29bmfZLTwoUL0apVK+fjTp064ZNPPim3XUZGBp577jn07dsXBoMBkiTh5MmTXs1Wl2PefvvtkCQJr732mtfyuXvuAHnaxapVq3DzzTejadOm0Gq1aNGiBUaNGoWUlJQKt+fvPhE1BixCiajeOnHiBHr16oW8vDx88803+M9//oNVq1bh2Wef9crxioqKcPPNN+Pw4cP48ssvsXDhQhw9ehSDBg1CYWFhpc+bMWMGlEolpk6dipUrV+Lvf/87/vOf/+CWW26Bw+Eot/2nn36Ku+66Cz169MBPP/2ExYsX47777kNRUZFXXld989FHH2Hr1q3On8TERJf1tX2f5LR792706NEDAFBQUIDU1FTn46sdO3YMP/zwA0JCQnDTTTf5JFttj/ndd99h7969XkxWxt1zJ1e7yM7ORo8ePTBr1iz88ccfmDZtGg4ePIg+ffogPT3dZVv+7hNRoyGIiOohh8MhevfuLYYNGyYcDodz+aRJk4RGoxHFxcUeP+YHH3wgFAqFOHr0qHNZWlqaUCqV4r333qv0eRcuXCi37MsvvxQAxJo1a1yWnzhxQuh0OjFz5kyP5W4o1q1bJwCI1atXV7ldbd8nOd14441iypQpQgghNmzYIFQqVYVt2G63O///s88+EwDEiRMnvJqtNsfMzs4WERER4ttvvxUAxMSJE72Wz91z50/t4vDhwwKAmDFjhnMZf/eJqDFhTygR1Us//fQTtm/fjvfffx+SJDmXt2rVChaLBWfPnvX4MX/55Rf06dMHMTExzmXR0dHo168ffv7550qfFxYWVm7Z9ddfDwA4c+aMy/L58+dDoVDg6aef9lBq7+jSpQueeOIJLFy4EN26dYNer0enTp2wbt06uaPV+n2Si8PhQHJysrP3bteuXejUqRN0Ol25bRUK3//Zrs0xJ0yYgC5duuDBBx/0QqL/qcm586d20aRJEwCASqVyLqsvv/tERJ7AIpSI6qX58+ejb9++aNOmDWw2m/OnoKAAgOuXOwAQQrhsV9mP3W6v9JgHDx5Ely5dyi3v3Llzpdd3VWbDhg0AgI4dO7os37x5Mzp06IDvv/8ebdu2hUqlQkxMDGbPnl2j/XtTSUkJDh8+jMTERHz33XeYNGkSfvjhBzgcDvz1r3+t8DmeOP9XPPzww1AqlWjSpAkeeuihctf0efJ98qbWrVtDkiQolUoUFBRg6NChkCQJL7zwAvbt2+e85rWu13x68ty7Y/Pmzfjqq6+82mZrc+5q0y48ee7sdjssFguOHj2Kp556Ck2bNnUp0uvD7z4Rkaeoqt+EiMi/WCwWrFu3DkVFRVCr1eXWq9VqREZGuizbsGEDBg0aVO2+BwwYgPXr11e4Ljs7GyEhIeWWh4aG4vLly+6FR1nv5+TJk5GQkICePXu6rDt79izOnj2LF198EVOnTkXbtm2xePFiPPvss7DZbBg3bpzbx/GW/fv3w263o0ePHliyZIlz+enTp/HMM8+guLgYer3e5TmeOP9BQUF44YUXMGDAAAQGBiIpKQlTp05F3759kZSUhPDwcACee5+8bcWKFbBYLPjqq6+watUqfPPNNwCA/v37480333Ser2vbck154ty7y2Kx4KmnnsL48ePRvn37Ou2rKrU5d7VpF548d71798bu3bsBADExMVi7dq2zzQL143efiMhTWIQSUb2TkpKCoqIizJ49G7169XJZ98ADDyAkJKRcT2iPHj2wc+fOavcdEBDg0azXKigowF133QWVSoUvvvii3HqHw4H8/HwsWLAAI0eOBADcfPPNOHnyJKZNm4b/+7//cxl+LIekpCQAwFtvveWyPCsrC4GBgeUKUMAz579bt27o1q2b8/GAAQPQv39/9OrVCx999BHefvttd1+CX+jUqRMA4J133sHAgQPRtWtXHD16FPn5+bjvvvvQokULjxzHl23/X//6F4qLizFx4sQ676sq9fHcLVy4EHl5eUhLS8OMGTNwyy23YPPmzWjdujWA+vG7T0TkKSxCiajeuTLE7sYbb0R8fLxzeWZmJk6cOFHhdWgmkwldu3atdt9VfckLCQmpsMeksh6WaxUXF2P48OFIS0vDhg0bKvyi3KRJExw9ehS33HKLy/Jbb70VK1euxLlz5+rcM1ZXycnJaNGihbMQuCIpKcnl/biaJ85/Rbp3747Y2FiXQqGu75Mv2O12CCEAAH/++Sf+9a9/wWazYdOmTWjevDmaNm0Km80GpVJZ58LDW+f+WqdOncI777yDzz//HKWlpSgtLXWuKy0tRU5ODgICAqBUKut0nNqeu9q0C0+euytD73v37o0hQ4agdevWmD59OubMmQOgfvzuExF5Cq8JJaJ6x2azAUC5L7MLFy6EJEl49NFHyz1nw4YNUKvV1f4MHjy40uN27twZBw8eLLc8JSWlXEF2LavVinvvvRe7du3CihUrEBcXV+kxqiLHxDTXSkpKqvAWGElJSejevXuFz/HE+a/K1UVAXd4nXxk8eLDzNZ87dw6PPPII1Go1HnvsMZw5c8a57sq1w3Xh7XN/RVpaGkpKSvCXv/wFISEhzh+g7DZFISEh2L9/f51fT23PXW3ahbfOXXBwMGJiYnDs2DGXfFXxh999IiJPYU8oEdU7V4avHTx40PnF7fz583j33Xfx5JNPom3btuWe44lhdXfeeSfGjx+PtLQ0tGnTBkBZr+yff/6J6dOnV/o8h8OBhx9+GGvXrsVvv/2GPn36VLrtiBEjMG/ePKxatQr33nuvc/nKlSvRokULNG3atNrX4E0OhwP79+/HkCFDXJZfvnwZ6enpLsNlr+atIaG7du1Camqqy7mq7fvkS59++iny8/OxaNEiLFu2DN999x0AYOjQoRg3bhxuu+02APDIdZW+Go7btWvXCmdHHjRoEP7yl7/gsccec5mZtrZqe+5q0y68de4yMzNx+PBhPPzww85l/v67T0TkSZK4MqaFiKieEEKgc+fOKC0txcyZM1FaWopJkyYhJCQEa9asgcFg8MpxCwsLcd1110Gv1+Ptt9+GJEmYNGkS8vPzsW/fPphMJgBlvSeDBw/G/Pnz8de//hV///vfMWfOHEycOBF33HGHyz5btGjhMixXCIHBgwdj7969eOedd9CmTRssXrwYn3/+Ob744osKe3l96fDhw+jYsSN+++03DBs2zLl87dq1ztyVDcmtq4cffhjR0dHo3r07goODkZSUhGnTpsFgMGDPnj0wm80A3H+f/MFdd92F6OhofPDBB0hNTUXHjh1x9uzZKguOK5NBrVmzBnPmzMEnn3yCsLAwhIWFYcCAAV7JWZdjSpKEiRMnevya3ZqeO7naxYgRI9C9e3fEx8cjMDAQR44cwcyZM3H+/Hns2LEDsbGxAPz/d5+IyKNkuj8pEVGdHD58WNx0001Cq9WK5s2biwkTJoiCggKvHzc9PV2MHDlSBAQECJPJJO666y5x4sQJl23WrVsnAIgvvvhCCCFEVFSUAFDhz+uvv17uGLm5uWLs2LEiPDxcqNVqERcXJ7755huvvzZ3fPfddwKAOHv2rMvyGTNmCK1WK6xWq9eOPXXqVBEXFycCAwOFSqUSLVq0EE888US5LEK49z7JrbS0VBiNRvH7778LIYSYOXOm6N69e7XPq6wtDRgwwGtZ63JMAGLixIkezVPbcydHu5g+fbro3r27CAoKEnq9XsTGxoonn3yywuP68+8+EZEnsSeUiIiIiIiIfIZXuRMREREREZHPsAglIiIiIiIin2ERSkRERERERD7DIpSIiIiIiIh8hkUoERERERER+QyLUCIiIiIiIvIZFqFERERERETkMyxCiYiIiIiIyGdYhBIREREREZHPsAglIiIiIiIin2ERSkRERERERD7DIpSIiIiIiIh8hkUoERERERER+QyLUCIiIiIiIvIZFqFERERERETkMyxCiYiIiIiIyGdYhBIREREREZHPsAglIiIiIiIin2ERSkRERERERD7DIpSIiIiIiIh8hkUoERERERER+QyLUCIiIiIiIvIZFqFERERERETkMyxCiYiIiIiIyGdYhBIREREREZHPsAglIiIiIiIin2ERSkRERERERD7DIpSIiIiIiIh8hkUoERERERER+QyLUCIiIiIiIvIZFqFERERERETkMyxCiYiIiIiIyGdYhBIREREREZHPsAglIiIiIiIin2ERSkRERERERD7DIpSIiIiIiIh8hkUoERERERER+QyLUCIiIiIiIvIZFqFERET/NWLECISEhODee+8tt66oqAhRUVEYP368DMk8KycnBz179kTXrl3RpUsXfPbZZ851J06cwKBBg9CpUyfExcWhsLBQxqRERNQQSUIIIXcIIiIif7B+/Xrk5+fjyy+/xJIlS1zWTZw4EceOHUPLli0xY8YMmRJ6ht1uR2lpKQwGAwoLC9GlSxfs2rULTZo0wYABA/D222/jpptuQnZ2NgIDA6FSqeSOTEREDQh7QomowXr00Udxxx13OB8PHDgQzz77rEf36Y1j1NYdd9yBRx991OP7vXz5MiIiInD8+HGX5bNmzUJMTAz0ej1uv/12XLx40blu/fr1aN26dY2Pdd999+G9996ra+QqVZV74MCBCAgIKPeco0eP4vDhwxgyZEiF+6zsHPlSZa+ronOqVCphMBgAAKWlpRBCQAiBgwcPQq1W46abbgIAhIaGsgAlIiKPYxFKRPXatUXg1T788EN8/fXXXj2+L47hbYMHD8Zf//rXStdPnToVQ4cORdu2bZ3LJk6ciBkzZmDu3LnYvn070tLS8NJLL1W6DyEEunTpgueff95l+ebNm6HX6/Hpp58CACZPnox33nkHubm5dXxVFatp7ivGjx+PadOmVbq+onO0ceNG3HnnnWjevDkkScKCBQs88RIqVNXrquyc5uTk4LrrrkOLFi3w4osvwmw24+jRozCZTBg+fDi6d++OqVOnei1zTT366KOQJAmPPfZYuXUTJkyAJElV/gORN3zyySeIjo6GTqdDjx49sGnTpiq3nzZtGq6//noEBgYiLCwMw4cPx4EDB1y2sdvtmDRpknO/0dHReO2112Cz2Wp87Oq2mT17NuLj4xEYGIjAwED07dsXy5cvr+XZICJyH4tQImqwgoKCEBwcXO+P4W179uxBjx49KlxXVFSEzz//3OWL/65duzBt2jR8//33uPnmmxEfH49nn322yi+vkiRh4sSJ+PTTT5GVlQUASE1NxV133YXnn38eTz31FAAgLi4Obdq08UphX5vcAPDzzz8jNjYWsbGxFa6v6BwBQEFBAbp06YIPP/wQer3eY6/jWtW9rsrOaXBwMPbu3YsTJ07g22+/RWZmJmw2GzZt2oRPPvkEW7duxerVq7F69WqvZa+pli1b4ocffnC5TtVms+Grr75Cq1atfJpl0aJFGDduHF599VUkJSXhhhtuwJAhQ3Dq1KlKn7N+/XqMHTsWW7Zswdq1a6FSqZCQkIDs7GznNu+++y5mz56Njz76CIcPH8aHH36I2bNnu/wjiDvHdmebFi1a4N1338WePXuwa9cu3Hzzzbj77ruxb98+D58tIiJXLEKJqMGqridkzZo1CA4Oxpw5cwCU9db961//Qtu2baHX6xEXF1dtMVTRMRwOB1599VWYzWaEh4dj/PjxcDgczvWlpaX4xz/+gYiICOh0OvTp0webN292ez1QVvg8+uijMJlMiIiIqHWP1fHjx5GTk1NpEbpixQpIkoR+/fo5l82YMQP9+/dHnz59nMvCwsKcxWVl7r//fjRv3hzvv/8+MjMzMWTIEAwdOhTvvPOOy3Z33nknvvvuu1q9nqrUNve2bdvw/fffo3Xr1hg/fjw+++wzvPXWW871FZ0jABg6dCimTp2Ke++9FwqF9/7cuvO6qjqnERERuO6667Bp0yY0b94cPXv2RMuWLaHVajF06FAkJyd7LXtNxcfHo127dvjhhx+cy5YvXw6dToeBAwf6NMv777+PRx99FE888QQ6duyIjz/+GM2aNcN//vOfSp+zatUqjBkzBl26dEFcXBwWLlyIixcv4s8//3Rus2XLFgwfPhzDhw9H69atceedd+LOO+/E9u3ba3Rsd7a56667MGTIEMTExCA2NhbvvPMOAgICsHXrVg+fLSIiVyxCiahRWrJkCUaMGIG5c+fi6aefBgC89tprmDdvHmbPno2UlBS88soreOqpp2o8PO2bb76BSqXCli1bMGvWLHzwwQdYtGiRc/1LL72ERYsWYf78+UhKSkJcXBxuv/12nDt3zq31QNnw0NWrV+PHH3/EmjVrkJSUhI0bN7rkWLBgASRJwsmTJyvNunv3bigUCnTt2rXC9Zs2bUKPHj0gSRIAwGq14tdff8XIkSNdtisuLkZQUFCV50WhUODVV1/F7NmzMXToUERHR2PevHnltuvVqxd27NiB4uLicuumTp0Kk8lU5U9FwxLrknvatGk4ffo0Tp48iRkzZuCJJ57A5MmTneuvPUe+5O7ruvacZmZmIj8/HwCQm5uLjRs3on379rj++utx4cIFXL58GQ6HAxs3bkTHjh1994Lc8Nhjj2H+/PnOx/Pnz8eYMWNqfP5r25YAwGKxYPfu3bj11ltdlt96663YsmWL2xny8/PhcDgQEhLiXHbjjTdi3bp1OHz4MAAgJSUFa9euxdChQ90+dm3y2e12fP/99ygoKMANN9zg9msgIqoNzjZARI3O3Llz8eKLL2LJkiXOL2mFhYV4//338ccffzgnZYmOjsaOHTswe/ZsDBs2zO39d+rUydlTFhsbi88++wxr1qzBgw8+iMLCQvznP//B559/7tznnDlzsHbtWsyePRuvvPJKlevffvttFBQUYN68eZg/fz5uu+02AMAXX3yBFi1auOQICgpC+/btoVarK826e/duxMbGwmQyVbg+PT0dkZGRzsfJyckoKirChAkT8OqrrzqXW61WdOvWrdpz88ADD+C5555DXl4e1q5dC41GU26byMhIWK1WnD171uUaSwB4+umnMWrUqCqP0bx583LL3M2dkJCAvXv3orCwEC1atMDixYvRt2/fKo937TnyJXdf17XnND09HU8++aRzQqLnnnsOcXFxAMqKs/79+0MIgVtvvdXr11XW1EMPPYTx48fj6NGjCAgIwMqVK/Hxxx+7/MOAO2rblgAgKysLdrsdERERLssjIiKQmJjodoZx48aha9euLm1swoQJyM/PR6dOnaBUKmGz2TBx4kSMHTvW7WPXJN/+/fvRt29flJSUwGQy4aeffnK2BSIib2ERSkSNyrJly/Dpp59i48aNLl/8UlJSUFJSgttvv92lR8VqtdZ4ltf4+HiXx5GRkbhw4QKAsuGvVqvVZeimUqlE3759kZKSUu36K/uwWCwu+U0mU7kvjiNGjMCIESOqzFrV9aBAWY/a1V9kU1NTodFosH//fpftHnzwwXLDUSvy3HPPwWaz4dKlS5UOUb1y/WRFPaGhoaEIDQ2t9jjXcjd3dQVERbMPX3uOauO1114rNyz5WuvWrSs35NTd13XtOe3Vq1elw2yHDBlS6SzA/iAkJAQjRozA/PnzERwcjIEDB9bqetDatiVPef7557F582Zs3rwZSqXSuXzRokX46quv8O2336Jz585ITk7GuHHjEB0dXeGkTHXVvn17JCcnIzc3F0uWLMHo0aOxfv16dOnSxePHIiK6gkUoETUq1113Hfbv34958+ahT58+zoLzyjWbv/76a7kvtFX1JFbk2u0lSXK5JrQy1Q0n9MZwzz179uC1116rdL3ZbMbly5edj3Nzc2E2mxETE+NclpWVheTkZHz00UdVHuvNN9/Ejz/+iK1bt2L48OGYNWsWXnnllXLbXZmkJSwsrNy6qVOnVnv96++//+7szfZE7upce45q4x//+Af+8pe/VLlNRYWWu6+rqnNaH/3tb3/D6NGjYTKZXK7PrYnatiWg7D1XKpXIzMx0WZ6ZmYmmTZtWe+x//vOf+P7777Fu3Tq0adPGZd2LL76I8ePH44EHHgBQNrFUeno6pk2bhscee8ytY9ckn0ajcbafHj16YOfOnZg5c2aFQ+WJiDxFtiI0Ozsb7777LjIyMvDVV1+5/CugO5KSkvDll18iICAAU6ZMAVA269y6detgsVgwcOBA5zA1IqIroqOj8fHHH2PgwIF48sknMXfuXEiShE6dOkGr1SI9PR0333yz147ftm1baDQa/Pnnn86hpna7HVu3bsVDDz1U7for+1Cr1di2bZvzC2xhYSEOHDhQbvhqVU6cOIHs7Gx079690m26devmcmsRs9nsvI7tSk/mtGnT0Ldv3yqHrc6bNw/Tp0/HH3/8ga5du+Kll17ClClTMG7cOOf9Kq84cOAAmjdvXmHvYm2HUNY2tzuuPUe1YTabYTaba/U8d15XVee0Pho8eDA0Gg2ysrJw991312ofdRmOq9Fo0KNHD6xevRr33Xefc/nq1atxzz33VLnPcePGYdGiRVi3bh06dOhQbn1RUVG570RKpdL5D1nuHLsu+RwOB0pLS6vchoiormQrQk0mEyZNmoQZM2bU6vnt2rXDv//9b5d/Ab3xxhsxcOBAOBwOTJgwgUUoUSORl5dXbmhhVbdNadOmjXNo41NPPYVPP/0UAQEBGD9+PMaPHw8hBPr374+CggJs27YNCoUCTz75pEeyGo1G/P3vf8eECRNgNpsRHR2NmTNnIjMzE2PHjq12PVD2+fnYY49hwoQJCAsLQ2RkJN566y3Y7fYaZdm9ezeAsp7bq+9VqFQqnZPR3HbbbZgwYQIuXbqEJk2a4Oabb4bNZsM777yDRx55BEuWLMHChQtdZve81ooVKzB27Fh8/fXXzl6lJ554AlOnTsWnn36Kf/7zny7bb9q0qdLP79oOoaxNbndde46uKCgowLFjxwCUfbE/deoUkpOTERoa6rHbibj7uqo6p/WRJEnYt28fhBDQarWVblfZZ0Pr1q3rPBz3+eefxyOPPIJevXqhX79+mDNnDs6ePeuc6AwAZs2ahVmzZjknGXrmmWewcOFCLFu2DCEhITh//jwAOCdCAoDhw4dj+vTpiI6ORufOnZGUlIT333/f5V6+7hzbnW1efvllDBs2DC1btkR+fj6+/fZbrF+/nvcKJSLvEzJ7/fXXhc1mEw6HQ8ydO1e88cYbYurUqSI/P9+t57/22mvllpWWloqZM2d6OCkR+aPRo0cLAOV+7rnnHjF69GgxbNgw57YDBgwQzzzzjPPxsWPHRIsWLcQTTzwhHA6HcDgc4qOPPhIdO3YUGo1GmM1mkZCQIP744w+X4129z+qOUdE2JSUlYty4cSI8PFxoNBrRu3dvsWnTJrfXCyFEQUGBeOSRR4TRaBRhYWHirbfeEsOGDROjR492bvPFF18IAOLEiRMVnruXX365wnPXpUsXl+369OkjZs2a5Xy8ePFi0apVK6HX68Wtt94qUlJSyu173bp1IioqSuzYsUMYjUbx/vvvl9tmxowZIjIyUpSUlDiXFRcXi8DAQLF169YKM9eFO7lr69pzJETZOajo/F79HnlCda/Lm+fUl679PapufVWfDZ4ye/ZsERUVJTQajejevbvYsGGDy/rXX39dXP1Vq6I8AMTrr7/u3CYvL0+MGzdOtGrVSuh0OhEdHS1eeeUVUVxcXKNju7PN6NGjRatWrYRGoxFhYWFi8ODBYuXKlR44M0REVZOEEMI35W7F3njjDUyaNAlJSUk4ffo0RowYgaSkJJw8ebLaCTUAYNKkSc7huEDZbRcSExMxdOhQ3Hnnnd6MTkTk115//XUsWbIEe/fuhUpV+4EvK1euxLhx45CSkuL2pRPr16/Ho48+WuXtYSoye/Zs/Pzzz/jjjz9qkVQ+tTlHvlJfzykRETVcfjMx0ZkzZ7Blyxbs3bsXdrsdsbGxyMnJwQcffOCyXXBwMP7xj39Uup97770Xd911FyZPnoxBgwYhICDAu8GJiPzUihUrMHv27DoVoABw++2345lnnkFGRgaioqI8lK5iarUaH3/8sVeP4Q2+PEc1VV/PKRERNVx+U4RGRkaif//+GD58OADAZrNBpVLhjTfecHsfVqsVarUaKpUKWq22xjNaEhE1JDt37vTYvv7v//7PY/uqiqeuvZWDr85RTdXnc0pERA2TbMNxbTYbpk2bhrS0NERHR+PBBx/Epk2bcPr0aQDAsGHD0LNnz0qff/z4cXz77bc4fvw42rZtiwkTJmDZsmVISUmBzWZD//79nTehJyIi3zp58iSWLVtW5cgVIiIiapxkvyaUiIiIiIiIGg+F3AGIiIiIiIio8WARSkRERERERD4j28REZ8+elevQbjGbzcjKypI7BjVybIfkL9gWyR+wHZI/YDskf+HvbTEyMrLSdewJJSIiIiIiIp9hEUpEREREREQ+wyKUiIiIiIiIfIZFKBEREREREfkMi1AiIiIiIiLyGRahRERERERE5DMsQomIiIiIiMhnWIQSERERERGRz7AIJSL/JoTcCYiIiIjIg1RyByAiukIqzIfmyD6o0w5BmZkBRWnJf4tQAUdAMKytYmCN6QJrdAdAwX9DIyIiIqqPWIQSkewUOZeg/3MV1CcOw9a0BezBTWBt1gpQaSAkCZIQkIoLoLx8EYY1P0EqzEfJDbeipMdNgEotd3wiIiIiqgEWoUQkH7sN+q2rod27DZboDijuORBCpy/XyykACJ0ejpAwWNt0gpSXA03Kbui3rkbBHQ/DGtNFnvxEREREVGMsQolIForcbJiWLYDDYEJxt34QxkBAktx6rggMRmmP/rBeugDTr9/A0rodCu94BFCzV5SIiIjI3/GiKiLyOdWZkwj85iNYm0XBEt0BwhTkdgF6NUeTcBTefBcU+TkInvsOFLnZXkhLRERERJ7EIpSIfEp9PAXGnxegpFNP2MOaARpt3XYoSSjt2g+Wlm0Q9PlUKC6e9UxQIiIiIvIKFqFE5DOqk6kw/LEYpXHXwxFiBpRKj+3b1ro9Sjr3RtAX/4byXLrH9ktEREREnsUilIh8Qnn2JEwrvkNpp55wBDap1fDb6tgjW6Gke38EfvUBFBfPe3z/RERERFR3LEKJyOsUOZcQsOxLlHTqAUdQqFcK0Cvs4ZEoue4GBH35b0i5l712HCIiIiKqHRahRORdVgtMS+ehtF1nOIKalLv9ijfYI1uhNLYrghb8G7CUev14REREROQ+FqFE5D1CwPj797A3CYc9NMKj14BWx9Y6FjZzUwR8/wkghM+OS0RERERVYxFKRF6j3b8dypws2Jq1BtQanx/f0qUXFPk50K/5yefHJiIiIqKKsQglIq9QXM6CfvNKlLbtBKHTyxNCklDcJwG6PZuhPp4iTwYiIiIicsEilIg8z2GH6bevURrTGcIYJG8WtQbFvQbB9OPnkIoL5M1CRERERCxCicjzdDs3wKHRwhEa4ZOJiKrjCA2HNaodTIvnyh2FiIiIqNGT/9shETUoitxs6HZvhLVFWwiNVu44TpYO3aC8nAXtjnVyRyEiIiJq1FiEEpHnCAHDH0tgie4AYQyQO40rSUJxr5thXLsMUn6O3GmIiIiIGi0WoUTkMeoj+6AozIO9iX8Mw72WMAagNKYLAn6cJ3cUIiIiokbL/74lElH9ZLXCsO5nWNp0gtAZ5E5TKWu7OCguX4Rm71a5oxARERE1SixCicgjdLvWw25uCodJ5tlwqyNJKLl+IIwrfwBKiuROQ0RERNToqGqycXZ2Nt59911kZGTgq6++glKpdK6bO3cuTp8+DQB4/PHHERUV5dmkROS3pMJ86HZvQnH3GwFVjT5WZOEIDIEtMgrGlYtQePcYueMQERERNSo16gk1mUyYNGkS2rVrV27d3XffjSlTpmDs2LFYvHixxwISkf/Tb/4d1lYxEAY/m4yoCqWdekJ7KBmK8xlyRyEiIiJqVGpUhGo0GphMpgrXhYeHAwCUSiUUfjghCRF5h+JSJtRph2ALb+6XkxFVSq1GSZfrEfDzl3InISIiImpUPD5u7ttvv8XQoUPLLU9MTERiYiIAYPr06TCbzZ4+tEepVCq/z0gNX31oh9IfP0B07g51RFNAqkdFKAB06Q4pPRXmEynA9f3lTuPX6kNbpIaP7ZD8Adsh+Yv63BY9WoQuX74cLVq0QIcOHcqtS0hIQEJCgvNxVlaWJw/tcWaz2e8zUsPn7+1QefEcTGmHUdK9P0R+gdxxakUR3wf6H+fjcqtYQOn/17PKxd/bIjUObIfkD9gOyV/4e1uMjIysdJ3Hui327t2L1NRU3HPPPZ7aJRH5Of3m32FtHQuh1ckdpdYcwWbYA0Og27hC7ihEREREjUKNilCbzYYpU6YgPT0d77zzDlJSUrB06VIAwPz583Hx4kW8+eabmDt3rlfCEpH/UF44A2VmBuwhEYAkyR2nTkrjekO/fQ1QUix3FCIiIqIGTxJCCDkOfPbsWTkO6zZ/796mxsGf26Fp6Xw4jEbYmkbV+yIUALRJf8LRJByFd/xF7ih+yZ/bIjUebIfkD9gOyV/4e1v0yXBcImo8lBfPQXnhTIPoBb3C0qkHtPu3Q8rLkTsKERERUYPGIpSIaky3fQ2sUe3q9bWg1xJaHSzRnWBc+b3cUYiIiIgaNBahRFQjirzLUKcfhT00vMH0gl5hiY2H5ngKpOyLckchIiIiarBYhBJRjeh2roe1ZVsInUHuKJ6nUsES0wWmPxbLnYSIiIiowWIRSkRuk4qLoDmUBFtYswbXC3qFpW1nqE8chnTpgtxRiIiIiBokFqFE5DZt0mZYm0VB6IxyR/Ee9oYSEREReRWLUCJyj80KXfIW2Ju1BJRKudN4laVtZ6hPpkK6lCl3FCIiIqIGh0UoEblFcygJttBwOLQN8FrQazl7Q5fInYSIiIiowWERSkTVEwK63Rthj2gBqNVyp/EJZ29oNq8NJSIiIvIkFqFEVC3V2XTAboMjIEjuKL6jUsHSthOMiT/JnYSIiIioQWERSkTV0u7eCFtkNIRGJ3cUn7K07QzNsQOQ8nPljkJERETUYLAIJaIqSQV5UJ86BnuoWe4ovqfWwNqqHQzrfpY7CREREVGDwSKUiKqkS/4TtsjWEI1hQqIKWGLjoT24CygpljsKERERUYPAIpSIKme3QbtvO2wRzQFF4/y4EDo9rE1bwrBxudxRiIiIiBqExvmtkojcojmyH7ZgMxw6o9xRZGVp3xXapD8Bm0XuKERERET1HotQIqqUNnlLo7otS2WEKRD2YDO029bKHYWIiIio3mMRSkQVUlzOgiLnEhymQLmj+AVLx24wbF8LOBxyRyEiIiKq11iEElGFtHu3whYZBaFrnBMSXcsR3ARCrYZm/w65oxARERHVayxCiag8ux3alN2wm5sBkiR3Gr9R2qEb9Fv/kDsGERERUb3GIpSIylEfOwB7YAgcevaCXs0e0QKKvBwoTx2TOwoRERFRvcUilIjK0e3dCltES0DVuCckKkeSYGkXB8PG3+ROQkRERFRvsQglIheK3Gwoss7DERQidxS/ZI2KhfrUcUh52XJHISIiIqqXWIQSkQvtvu2wNYuC0OrljuKfVCpYo2JhWPer3EmIiIiI6iUWoUT0Pw4HtPt3wB7enBMSVcES0wXaQ3sAS6ncUYiIiIjqHRahROSkTj8CuykQDh17Qasi9AbYmkRAt3W13FGIiIiI6h0WoUTkpLnSC6rWyB3F71nad4V+9ybA4ZA7ChEREVG9UqMiNDs7GxMmTMDDDz8Mu93usu7UqVOYNGkSJk2ahPT0dI+GJCIfKC0p6wkNbiJ3knrBEdwEQqmE5tAeuaMQERER1Ss1KkJNJhMmTZqEdu3alVu3aNEijBs3Dv/85z+xaNEijwUkIt/QHk6CLaw5JySqAUtsPHRbE+WOQURERFSvqGqysUajgUZT8TC9wsJCmM1m5/9fKzExEYmJZV/Wpk+f7tzWX6lUKr/PSA2fL9uhdHQfRJt20IXw1ixuM8VBcWAnNLYSoGkLudN4FT8TyR+wHZI/YDskf1Gf22KNitCqCCGqXJ+QkICEhATn46ysLE8d2ivMZrPfZ6SGz1ftUJGThYCL51ES1R4iL8/rx2tINK3aAT9/jYJ7Hpc7ilfxM5H8Adsh+QO2Q/IX/t4WIyMjK13nlYmJJN7agahe0R7YCVuzVhAandxR6h1rmw7QHNkHWErkjkJERERUL3isCDWZTLh06RKys7Oh1/OaMqJ6w+GA5sAu2M3NeG/QWhBaPWzmptBtWyN3FCIiIqJ6oUZFqM1mw5QpU5Ceno533nkHKSkpWLp0KQBg1KhR+OCDDzBz5kzcf//9XglLRJ6nykiD0Onh0BvljlJvWdrFQ7fnT6CayxKIiIiIqIbXhKpUKkyaNMllWadOnQAAUVFRmDJliueSEZFPaA/sgC28Be8NWgeO0DBIdhvUR/fDGhsvdxwiIiIiv+aVa0KJqJ6wWqA+fgj2kPo5s5o/KY2Nh37LH3LHICIiIvJ7LEKJGjHN0QOwmZvx3qAeYGvRBqqz6ZByLskdhYiIiMivsQglasQ0h/bAbo4AVB67W1PjpVTCGhUL/aYVcichIiIi8mssQokaKamkGKqzJ+EIDJE7SoNhadsJ2oO7AZtV7ihEREREfotFKFEjpT66H7awSA7F9SBhMMERFArt7o1yRyEiIiLyWyxCiRopbcoeOJpEAAp+DHiSpV0X6HZtkjsGERERkd/it0+iRkgqKoDywhnYg0LljtLg2MMioSjMhTLjhNxRiIiIiPwSi1CiRkiTuhf2MM6K6xWSBEubTtD/uVLuJERERER+iUUoUSOkSdkDa1gzQJLkjtIgWVu3h+Z4ClBSJHcUIiIiIr/DIpSokZEKcqHMvgARwFlxvUajhS28OXTb1sqdhIiIiMjvsAglamQ0h/fCFt4cQquTO0qDZonpAl3yFkAIuaMQERER+RUWoUSNjDZlF+wciut1jhAzJLsVquMpckchIiIi8issQokaEUVuNhR5ObAHciiu10kSLG07Q791tdxJiIiIiPwKi1CiRkRzKAm2iOaARit3lEbB2ioG6lPHgII8uaMQERER+Q0WoUSNiObQHtjNkXLHaDxUalibR8Pw5yq5kxARERH5DRahRI2EIvsCpOJC2AOD5Y7SqFhjOkN7YAdgt8sdhYiIiMgvsAglaiQ0h5JgD28BqDVyR2lUHIEhEEoV1IeT5I5CRERE5BdYhBI1EtqDu2ALayp3jEbJ0i4O+u28ZygRERERwCKUqFFQXjwHOBxwBATLHaVRskW2hur8aUg5l+SOQkRERCQ7FqFEjYDm0B7YwpsDKrXcURonpRLWqFjoN/0udxIiIiIi2bEIJWrohIAmZTfs5gi5kzRqljYdoU3ZDdisckchIiIikhWLUKIGTnn+NKBQwmEKljtKoyaMAXCYAqHZt03uKERERESyYhFK1MBpDiX9dyiuSu4ojZ4lpgv0OzfIHYOIiIhIVixCiRoyhwPaQ3s4FNdP2Ju2hPLyRSgyz8odhYiIiEg2LEKJGjDV2XQIrQ4OY6DcUQgAJAmW6I4wbOYERURERNR4sQglasCcs+IqORTXX1ijO0BzdB9gscgdhYiIiEgWNfpmumDBAqSlpSE6OhpjxoxxLt+6dSt++eUXSJKEESNG4Prrr/d4UCKqIYcDmtS9KO7WT+4kdBWh08MWEgbtrvUoveFWueMQERER+ZzbPaFpaWkoKSnBW2+9BZvNhmPHjjnXLV++HG+88QbeeOMN/Pbbb14JSkQ1ozp9HA6DCcIQIHcUuoY1pgt0e/6UOwYRERGRLNzuCT169Cji4+MBAHFxcThy5AhiYmIAABERESgtLQUA6PX6Cp+fmJiIxMREAMD06dNhNpvrFNzbVCqV32ekhq8u7VDa+BtE6xhoQkI8nIrqLCAA0r6tMOdfAqLby53GLfxMJH/Adkj+gO2Q/EV9botuF6GFhYWIiCibYdNgMCAjI8O5rlevXnjppZcghMDYsWMrfH5CQgISEhKcj7Oysmqb2SfMZrPfZ6SGr9bt0G5HcPI2FF/fHyIvz/PBqM7UUbFQLP8e+Q88I3cUt/AzkfwB2yH5A7ZD8hf+3hYjIyMrXef2cFyDwYCioiIAQHFxMQwGg3PdkiVL8P7772PmzJlYsmRJHaISkSeoT6bCERQCoTPJHYUqYY2KhTrtMFBSJHcUIiIiIp9yuwiNjY3FgQMHAAD79+9HbGysc51arYZWq4VOp4PNZvN8SiKqkbJZcSMBpVLuKFQZtQa2pi2h37pa7iREREREPuV2EdqmTRuo1WpMnjwZCoUCZrMZS5cuBQDceuutmDRpEl577TWXIbdEJAObFeq0w7CHhMmdhKphiekCXdIWQAi5oxARERH5TI1u0XL1bVkAYOTIkQCAgQMHYuDAgR4LRUS1p047BHuIGUJnlDsKVcMR3ARCkqA6dgC2dnFyxyEiIiLyCbd7QomoftAeSoI9LBJQ8Ne7PrDEdIHhzz/kjkFERETkM/yWStSQWEqhSj8Ke3ATuZOQm2wt2kB19iSkvMtyRyEiIiLyCRahRA2I5thB2JuEQ+gM1W9M/kGphLVVO+g3r5Q7CREREZFPsAglakA0h/ZwKG49ZGnbCdoDOwC7Xe4oRERERF7Hb6pEDYRUUgzVmZOwB4bIHYVqSBgD4DAEQLN/u9xRiIiIiLyORShRA6E+uh+2sEgOxa2nLLHx0G9fK3cMIiIiIq9jEUrUQGgP7YEjLIJDcespe0QLKC5nQXHxnNxRiIiIiLyK31aJGgCpqADKzDOwB4bKHYVqS5JgbdMR+o3L5U5CRERE5FUsQokaAE3qXtgiWkBodHJHoTqwRneA5sg+wFoqdxQiIiIir2ERStQAaA4lwd6EQ3HrO6HVwW5uCu3O9XJHISIiIvIafmMlquekglwoL1+EwxQodxTyAEtMF+h3b5Y7BhEREZHXsAglquc0h/fCFtGcs+I2EI7QcEilxVClH5U7ChEREZFXsAglque0KbthMzcDJEnuKOQJklTWG7p5pdxJiIiIiLyCRShRPabIzYZUmAdhMMkdhTzI2ioG6vQjQGGB3FGIiIiIPI5FKFE9pjmUBHtECwitXu4o5EkqNazNW8Pw5+9yJyEiIiLyOBahRPWY5lASbOamHIrbAFljukC7dxvgcMgdhYiIiMijWIQS1VOK7AuQLCUcittAOQKCIfQGaPZtkzsKERERkUexCCWqp7SHkmCLaAGh1sodhbykNPY66LetkTsGERERkUexCCWqj4SAJmU3bE0iOBS3AbNHtIAi9xKUZ9PljkJERETkMSxCieoh5cWzEAoFoOe9QRs0SYKlXRwMG5fLnYSIiIjIY1iEEtVDmpQ9sIdzKG5jYI1qD3XaIaC4UO4oRERERB7BIpSovhECmsNJsIWGcyhuY6BWw9o8GvpNK+VOQkREROQRLEKJ6hnV2XQInRHQshe0sbC0i4Nu7xbAbpc7ChEREVGdsQglqmc0KbthC2sGodHJHYV8RJgC4TCYeLsWIiIiahBYhBLVJw4HNEf2wR4aLncS8jFL7HXQb0uUOwYRERFRnalqsvGCBQuQlpaG6OhojBkzxrm8oKAAc+fORX5+PuLi4jBy5EiPByUiQHXqGOyBIRAaDsVtbOzhkVAkbYby9HHYW7aVOw4RERFRrbndE5qWloaSkhK89dZbsNlsOHbsmHPd4sWLcf/99+P1119nAUrkRdpDe2APawaoNXJHIV+7cruWTSvkTkJERERUJ24XoUePHkV8fDwAIC4uDkeOHHGuO336NH766Se8+eabLsuJyIPsNqiPp8Ae1ETuJCQTa1Q7qE8egVSQJ3cUIiIiolpzezhuYWEhIiIiAAAGgwEZGRnOdampqXj33XdhMpnw3nvvYcqUKeWen5iYiMTEsuuZpk+fDrPZXNfsXqVSqfw+IzV8Lu3wcDKkZi2hamIGOBy30ZLadYZ551qI+x736XH5mUj+gO2Q/AHbIfmL+twW3S5CDQYDioqKAADFxcUwGAzOdZGRkWjRogUAQKGouHM1ISEBCQkJzsdZWVm1CuwrZrPZ7zNSw3d1OzRuXQcREAJbSSlQUipzMpKL1CoWhnW/4PKNQ306LJufieQP2A7JH7Adkr/w97YYGRlZ6Tq3h+PGxsbiwIEDAID9+/cjNjbWua5Zs2a4fPkySkpKYOd97Ig8z2qB+uQR2AND5E5CMhN6I+xNwqHbvkbuKERERES14nYR2qZNG6jVakyePBkKhQJmsxlLly4FAIwaNQoffvgh3nrrLU5MROQFmuMHYTM35b1BCQBgad8V+h3rAIdD7ihERERENVajW7RcfVsWAM6Cs0WLFnjjjTc8FoqIXGlS9sBubgaoavQrSw2UI7gJhEoN9cGdsMb1ljsOERERUY243RNKRPKQiougOpsOR2Cw3FHIj5R26AbD5lVyxyAiIiKqMRahRH5OczgJtogWHIpLLuwRLaAoyIUq/ajcUYiIiIhqhEUokZ/THtgJe3gkoFTKHYX8iSTB0v466Df8JncSIiIiohphEUrkz7IvQCrMg0NvlDsJ+SFryxioz5yAlH1R7ihEREREbmMRSuTHpKStsDWLgtDq5Y5C/kiphKVNJxjWLZM7CREREZHbWIQS+SshICVtgc0cAUiS3GnIT1nadoI2dR9QXCh3FCIiIiK3sAgl8lPKc6cgtDqAExJRVTRaWJtHw7D+V7mTEBEREbmFRSiRn9Ie2AnRrBVnxaVqWTp0hXbvVsBSIncUIiIiomqxCCXyR3Y7NEf2AxyKS24QeiPsYZHQ8b6hREREVA+wCCXyQ+oTh2APMXMoLrmttGM36HetB2xWuaMQERERVYlFKJEf0h7cDXt4M0CjlTsK1RPCFAR7YBPodqyVOwoRERFRlViEEvmb0hKoTh2DPTBE7iRUz1g694B+SyJgt8sdhYiIiKhSLEKJ/Iz2UBJsEc0hNLw3KNWMIygUDr0B2qQ/5Y5CREREVCkWoUR+Rrt/O+zhLQClUu4oVA+Vdu4J/aYVgBByRyEiIiKqEItQIj+iuJQJqbgQDr1B7ihUTzlCwwGlEpr9O+SOQkRERFQhFqFEfkS7bztsTVtB6FiEUu2VduoJw4bf2BtKREREfolFKJG/cNihPbQHNt4blOrIHtYMsNugPrhL7ihERERE5bAIJfIT6rRDsAeFQmg5IRHVkSShNK43jGt/Zm8oERER+R0WoUR+QrtvB2zhzQG1Ru4o1ADYw5oBwgH1gZ1yRyEiIiJywSKUyA9IRflQnTsJB+8NSh7E3lAiIiLyRyxCifyA9uBu2JpFQWh0ckehBsRubgpIgHrfdrmjEBERETmxCCWSmxBls+KGNeO9QcnjSuN6w7iOvaFERETkP1iEEslMef40BAChN8odhRoge5MIQKWCds9muaMQERERAWARSiQ7XdKfsEVyKC55T0mX3tBv+A2w2+WOQkRERMQilEhOUklx2a1ZQsLkjkINmCM0DEJngHbHOrmjEBEREbEIJZKT5uAu2Jq2hNCyF5S8qzS+DwybVgBWi9xRiIiIqJGrURG6YMECTJ48GV988UW5dRaLBU888QT27dvnsXBEDZoQ0CX/CXtEc0CpkjsNNXCOwGDYm0RAv3G53FGIiIiokXO7CE1LS0NJSQneeust2Gw2HDt2zGX9mjVr0KpVK48HJGqoVGdOQiiUcHBCIvKR0i7XQ79jPVBcKHcUIiIiasTcLkKPHj2K+Ph4AEBcXByOHDniXGez2XD06FG0b9/e8wmJGiht8p+wRkZBqLVyR6FGQuiNsLZsA+PqH+WOQkRERI2Y22MACwsLERERAQAwGAzIyMhwrlu/fj1uuukmHD16tNLnJyYmIjExEQAwffp0mM3m2mb2CZVK5fcZqR4rKoDizAk4brwVMAZWuplSqURgYOXriWqs1wAofv4KeuVfgRD3P+P4mUj+gO2Q/AHbIfmL+twW3S5CDQYDioqKAADFxcUwGAwAALvdjuTkZIwfP77KIjQhIQEJCQnOx1lZWbXN7BNms9nvM1L9pdu5HipzM1gsdsCeV+l2gYGByMurfD1Rbahbd4D09SwUPPis28/hZyL5A7ZD8gdsh+Qv/L0tRkZGVrrO7eG4sbGxOHDgAABg//79iI2NBQDk5ubi0qVLeOedd7Bp0yZ89913KCgoqGNkogbM4YA2eQtsYZGAUil3GmqErDFdoE4/BmXGCbmjEBERUSPkdhHapk0bqNVqTJ48GQqFAmazGUuXLkVoaCimTZuGiRMn4qabbsKDDz4Ik8nkzcxE9Zr6ZCocWj2Egb8nJBOlEqXX9YHp14WAEHKnISIiokamRveFGDNmjMvjkSNHujweNWpU3RMRNXC6XRthi4yC0HBCIpKPLbI1NEf2Q7N3Gyxd+8odh4iIiBqRGt0nlIjqRpF9AYrsC3AEhsgdhRo7SUJJ9xthXL0EsFrkTkNERESNCItQIh/S7d4Ea8u2EFq93FGI4AgKha1JU+jXLJM7ChERETUiLEKJfEQqKYYmdS/sTcIBSZI7DhEAoDSuF3RJmyHlXpI7ChERETUSLEKJfES7fztszVpBaNgLSn5Eq4OlXTxMvyyUOwkRERE1EixCiXzB4YB2z2bYwpsDqhrNB0bkddaYzlBlZkB9ZJ/cUYiIiKgRYBFK5APq4ylwGAPg0BvljkJUnkKB4u43wfTr14DNKncaIiIiauBYhBL5gH5bImzNowHeloX8lMPcFPbgJtAnLpU7ChERETVwLEKJvEyVkQZYLXCYAuWOQlSlkuv6Qp+8BYqL5+WOQkRERA0Yi1AiL9NtWwNbq7YQGp3cUYiqptGipFNPBPz0OSCE3GmIiIiogWIRSuRFyqxzUF7KhD0whLdloXrBFtUOUkkxtLs2yB2FiIiIGigWoURepNu2FtZW7SC0BrmjELlHklDccyCMa36ClJcjdxoiIiJqgFiEEnmJlJ8D1amjsIea2QtK9YowBaI0pgsCfvxM7ihERETUALEIJfIS/Y51sLVsy15Qqpes7eKgyM2GZvcmuaMQERFRA8MilMgLpIJcaFL3whYWCSj4a0b1kCShuPdgmFb/CCk/R+40RERE1IDw2zGRF+i3r4WlVQyEVi93FKJaE8aAsmG5Sz7jbLlERETkMSxCiTzsSi+ovUkzQKmUOw5RnVjbdYEiPwfY+LvcUYiIiKiBYBFK5GFlvaDtIHTsBaUG4L/DchW/L4Ii65zcaYiIiKgBYBFK5EH/6wVtyl5QajCE3ghHzwEI/HYWYLfJHYeIiIjqORahRB6k35oIa6u27AWlhqd1OzhMQTAs/1buJERERFTPsQgl8hBFThbUR/fDZo5kLyg1SCXd+kGbuhfqw8lyRyEiIqJ6jEUokYcYNiyHtU1HCB3vC0oNlFJVdtuWn7+ElJstdxoiIiKqp1iEEnmA8twpKDMzYA+N4H1BqUFzBDdBaYeuCPr6A14fSkRERLXCb8tEdSUEDOt/haVtRwitTu40RF5ni+4Ah94E489fyh2FiIiI6iEWoUR1pD5xGFJJMRwBIYAkyR2HyCdKut0IdfoRaHdtkDsKERER1TMsQonqwm6HYc0yWKLb81pQalyUShTfcBuMiUuhzDgpdxoiIiKqR1iEEtWBbvdG2IND4TAFyR2FyOeE3oji6wch8NuPOFERERERuU1Vk40XLFiAtLQ0REdHY8yYMc7lc+fOxenTpwEAjz/+OKKiojybksgPSQW50O1cj+JuNwIardxxiGRhD2uG0o7dEPTle8h5ehKg4XXRREREVDW3e0LT0tJQUlKCt956CzabDceOHXOuu/vuuzFlyhSMHTsWixcv9kpQIn9jWP8rLNEdIPRGuaMQycoWFQu7uRkCv50FOBxyxyEiIiI/53ZP6NGjRxEfHw8AiIuLw5EjRxATEwMACA8PBwAolUooKrk9RWJiIhITEwEA06dPh9lsrlNwb1OpVH6fkWR08gikS+chrh8AGExeO4xSqURgYKDX9k/krmrbYt+bIW1YjrA1SyAe+Dsn6SKv4N9m8gdsh+Qv6nNbdLsILSwsREREBADAYDAgIyOj3Dbffvsthg4dWuHzExISkJCQ4HyclZVV06w+ZTab/T4jycRmRdB3n8LSrgvsVjuQl+e1QwUGBiLPi/sncpdbbfG6fjBsWoHSHz5H8eARvglGjQr/NpM/YDskf+HvbTEyMrLSdW4PxzUYDCgqKgIAFBcXw2BwnQl0+fLlaNGiBTp06FDLmET1g35rImyhYbCbgtjbQ3Q1pRJF/W6Hdu826LauljsNERER+Sm3i9DY2FgcOHAAALB//37ExsY61+3duxepqam45557PJ+QyI8oL56D5sAO2CJbczIiooqo1SjqPwz6P1dBm7RF7jRERETkh9wuQtu0aQO1Wo3JkydDoVDAbDZj6dKlAID58+fj4sWLePPNNzF37lyvhSWSlcMB4+/fwRLblZMREVVFo0XRjUNgWL0Y6gM75E5DREREfqZGt2i5+rYsADBy5EgAwIcffui5RER+SrctEQ6tHo7gEKCSCbiIqIwwmFB00zCYVnyPQoeAJb633JGIiIjIT/CbNJEblGfTod23DdZW7SDUHIZL5A5hDEBR/2EwrvoBmr1b5Y5DREREfoJFKFF1LCUw/fY1LB26Q3jxdixEDdGVHlHjH0ug3bVR7jhERETkB1iEElXDmLgUtqYtYQ/gbLhEtSEMRhT1vwOGjb9Bv+5XQAi5IxEREZGMWIQSVUG7bxuUF87CFtESUGvkjkNUbwm9AYX9h0N7YAeMvy4EHA65IxEREZFMWIQSVUJ5/jR0m1fBEhsPoTdU/wQiqppGg6KbhkJ1/jQCvv0YsJTKnYiIiIhkwCKUqAJScSFMP38JS+fucBgC5I5D1HAoFCjuPRiAhOC570CRc0nuRERERORjLEKJrmW3wfTTF7C2ioE9gLdjIfI4SUJpfG9YWsci6LOpUJ04LHciIiIi8iF+uya6mhAwrvgODr0B9rBmgEotdyKiBsvWqh2Kew1CwJLPoNv0O68TJSIiaiRYhBJdRb/pd0j5ObA1bwOh0ckdh6jBc4SEoXDgndAe2InAr2ZCKsiTOxIRERF5GYtQov/S7tkE9bH9sEZ3gtDp5Y5D1HhodSi+4VbYTUEInjMF6mMH5E5EREREXqSSOwCRP9Amb4Fuz2aUdOoBYTTJHYeo8ZEkWGPjYA9rBuMvC2Ft2wlFt90HoePM1ERERA0Ne0Kp0dPs2w7dzvUo7dgDwhgodxyiRs0RYkbRoLugKMxD8CdvQn1kn9yRiIiIyMNYhFKjpt21EfptiSjt1AMOUyAgSXJHIiKlEqVdeqG4R38Yf/8epu8/4a1ciIiIGhAWodQ4CQH9xuXQ7t+O4i7Xw2EKYgFK5GccIWYUDbwTQqNF0OfToF/3C2AplTsWERER1RGLUGp8bFYYf/8OqtPHUdqxO8AClMh/SRKsMV1QOPBOqE4fR/Ds16Hdswmw2+VORkRERLXEiYmoUZHycxDw03zYA0NhaRfHSU+I6guNFqVdb4CUexnapD+h37wSxf3vQGl8L0ChlDsdERER1QCLUGo0VCdTYVrxPSztusAeGgah1sodiYhqSASFoOT6QZAuX4Ru53roNy1H8Q23oTS+N6DWyB2PiIiI3MAilBo+mxWGDb9BnXYIJZ17whEQDKjY9InqMxEShuLeN0O6nAXt/u0wrP8VJd1vQsn1/SFMQXLHIyIioirwmzg1aKqMNBhX/QBbkwiUxPWB0Bt4/SdRAyJCzCgJuQkoLIDm5GEEf/o2rC1jUNr9RljbdOBQXSIiIj/EIpQaJKkwH4Z1v0B1Nr1s+G1AMKDh8FuiBstogqVzT1g6dIPqTBoMa5dBWl6I0vg+sHTqAXt4JP8BioiIyE+wCKUGRSopgm7nBmj3bYMluj1KrutTNvkQv3wSNQ5KJWyt2sHWqh2kglyoM04gYMlcCCHKitSO3WCPaMHPBCIiIhmxCKUGQSrMhy7pT2j3boW1RTSKu99UVnwqORSPqLESpiBYOnSFpf11UORegjLzDExL50GylMLatjOsbTvBGt0eQm+UOyoREVGjwiKU6i8hoDx3Cro9m6FOPwJr89Yo7tYPQmfkxENE9D+SBEewGY5gM6ztrwMK86HOOgvdzvUwrlwER2AwrFGxsLVsA2vzNhABnNiIiIjIm/hNneodxaUL0B7aDc3B3RBqDWzNWqG4Z38IjZ49n0RUPWMArMb2sEa1B2w2KHIvQZGbDd2O9TDkLAEkBWwt2sDWtAXs4c1hi2gBYQqUOzUREVGDwSKU/J5UUgxVRhrUaYegTjsEoVTCHt4cJV2uBzRaCK1e7ohEVF+pVHA0iYCjSQRsAOBwQCrMhzL3ElQZJ6BJ3QtFfi5gt8Me3gx2czPYQ8PgCAmDPSQMjuBQzsBLRERUQyxCya9IxUVQXsqE8uJZqM6lQ3XmJKTSEthDzLCHhqM0vjeEWgOh0XFiESLyPIUCIiAItquH5NrtkEpLoCjIgVRUCPWJw1Ac3A2pKB+K4iIIrQ72oFA4gkLhCAyBIyAIjoAQOAKD4TCYyq45Vanle01ERER+pkZF6IIFC5CWlobo6GiMGTPGufzUqVP47LPPAACPP/44oqKiPJuS6j8hAGspFCXFkArzoSjIgyI/578/uWWThmRfhFAq4TAGQBgC4AgMQWnnnhAqNYRay6G2RCQPpRLCYITdcM0ERkIANiuk0mIoSoqB0mIocsomQJJKiyGVFEGyWiBZLIBwAGpN2eebMaCsONUZIDQ6CK0OQqP97391V/1XC6HSACoVhEoNKFX8xzciImoQ3C5C09LSUFJSgrfeegufffYZjh07hpiYGADAokWLMG7cOCgUCnz++ed46aWXvBbYF5RZ54C0A9Dm5ZV9yaiMyzpR4f+W3/Z/K6Wq9n31cyrartLn1uI5/10uVbCswhcjADjskOw2wGb773+tro+tVkiWEkglRVBYSsv2olJDqMsKSqHTQ2j0EDodHGotHM1bwxLTpawX4sqXLSIifyZJgFoDodbAbirrObVfu43d7vp5aS2FZCkt+4wsKYKiML9snd0GyXb1Z6kVks0K2B2QHPayYcIOO4QEAFLZsVUqCKW67DNTpYZQKsuGBisUZYXzlf9XKCAkhXM5JAWEQuHcVkiK/xW3knTN/yv+98dBUpR9lpfb9trnlP2/uPJ8t8+nG9sEBkKbl+/GvmQo1t06Jv8RoUEIDCz7jkgkt5tukTtBrbn9Tf/o0aOIj48HAMTFxeHIkSPOIrSwsBBms9n5/xVJTExEYmIiAGD69OnO7f1SUS6U+7YiMPdy2WPnH5YK/nhIFTyoaFmFi6SqlzkXVfRHq6LnVpWl6u0rLk8r2rH4Xybpv19o1FpAoS97rFD897/KsuFnGi2gUv5vmVJZNnMtr6Fyi1KhRGAQZ+ok+bEt+pgQZb2njv/+CAfgEGX/D1G23mEvK3Lttv8Wuw5A2AEHyrbHle3/+1iIso/wK/vFlX2L//1c+dgXuOZx2Xrp6nzODa/8R/zvvy7beOqcAAqFAoFXXlNVG7qxL89y55gePyjJxL12SOR9iut6whzWTO4YteJ2EVpYWIiIiAgAgMFgQEZGhnOdcOODNSEhAQkJCc7HWVlZNcnpW4YgmEc96d8ZqVEwm81sh+QX2BbJH7Adkj9gOyR/4e9tMTIystJ1bo+TMRgMKCoqAgAUFxfDYDBUuJ3E61WIiIiIiIioEm4XobGxsThw4AAAYP/+/YiNjXWuM5lMuHTpErKzs6HX83YZREREREREVDG3i9A2bdpArVZj8uTJUCgUMJvNWLp0KQBg1KhR+OCDDzBz5kzcf//9XgtLRERERERE9Zsk3Lmg0wvOnj0rx2Hd5u9jrKlxYDskf8G2SP6A7ZD8Adsh+Qt/b4seuSaUiIiIiIiIqK5YhBIREREREZHPsAglIiIiIiIin2ERSkRERERERD7DIpSIiIiIiIh8RrbZcYmIiIiIiKjxYU9oJV5++WW5IxCxHZLfYFskf8B2SP6A7ZD8RX1uiyxCiYiIiIiIyGdYhBIREREREZHPsAitREJCgtwRiNgOyW+wLZI/YDskf8B2SP6iPrdFTkxEREREREREPsOeUCIiIiIiIvIZFqFERERERETkMyxCiYiIiIiIyGdYhBIREREREZHPsAglIiIiIiIin2ERSkRERERERD7DIpSIiIiIiIh8hkUoERERERER+QyLUCIiIiIiIvIZFqFERERERETkMyxCiYiIiIiIyGdYhBIREREREZHPsAglIiIiIiIin2ERSkRERERERD7DIpSIiIiIiIh8hkUoERERERER+QyLUCIiIiIiIvIZFqFERERERETkMyxCiYiIiIiIyGdYhBIREREREZHPsAglIiIiIiIin2ERSkRERERERD7DIpSIiIiIiIh8hkUoERERERER+QyLUCIiIiIiIvIZFqFERERERETkMyxCiYiIiIiIyGdYhBIREREREZHPsAglIqqlRx99FHfccYfcMVxcvnwZEREROH78uMvyWbNmISYmBnq9HrfffjsuXrzoXLd+/Xq0bt26xse677778N5779U1st+q7Fw2Jg39PSYiInmwCCUiv/Hoo49CkiRIkgS1Wo02bdpg/PjxKCws9Mj+Bw4ciGeffdYj+wKADz/8EF9//bXH9ucJU6dOxdChQ9G2bVvnsokTJ2LGjBmYO3cutm/fjrS0NLz00ktV7kcIgS5duuD55593Wb5582bo9Xp8+umnmDx5Mt555x3k5uZ65bUMHjzY2R4kSUJISAiGDh2K06dP12g/L774Im677bYaH7+ic7lx40bceeedaN68OSRJwoIFC8o9z51trpg2bRokSapxu6zuGLNnz0Z8fDwCAwMRGBiIvn37Yvny5eX2c+7cOYwePRphYWHQ6XTo1KkTNmzY4Fzv7fe4Nq58Tjz22GPl1k2YMAGSJFX6j0N79uyBUqlEv379Kt2vtz5/rvjkk08QHR0NnU6HHj16YNOmTW4/t7L28sYbb7j8rkiShKZNm9Z4G6D6NuHufoiIqsIilIj8SkJCAs6dO4e0tDS8/fbb+OSTTzB+/Hi5Y7mwWCwAgKCgIAQHB9d5P55SVFSEzz//3OXL+a5duzBt2jR8//33uPnmmxEfH49nn322woLkapIkYeLEifj000+RlZUFAEhNTcVdd92F559/Hk899RTi4uLQpk0brxXie/bswdSpU3Hu3DmcOXMGS5cuxc6dO/Haa6/VaD87duxAr169avScis4lABQUFKBLly748MMPodfrK3yuO9sAwLZt2zB37lzEx8fXKJs7x2jRogXeffdd7NmzB7t27cLNN9+Mu+++G/v27XNuk5OTg379+kEIgeXLl+PQoUP4+OOPER4e7tzG2+9xbbVs2RI//PCDS4Fos9nw1VdfoVWrVpU+7/PPP8fYsWNx4MABHDp0qNx6b3/+LFq0COPGjcOrr76KpKQk3HDDDRgyZAhOnTpV7XOray/t27fHuXPnnD/79++v8TbutAl3j0VEVCVBROQnRo8eLYYNG+ay7PHHHxdNmzYVQghRUlIixo0bJ8LDw4VWqxW9e/cWmzZtctl+w4YNonfv3sJoNIrAwEBx/fXXi/3794vRo0cLAC4/J06cEA6HQ7z77ruiTZs2QqfTiS5duoiFCxe67HPAgAHi6aefFi+88IIwm82iZ8+eFeatLl9l+3HHxYsXBQDx/vvvi549ewqtVivatWsnVq1a5dxm8eLFIiQkRDgcDuey+++/XwwYMMBlX99++62QJMn5eN26dSIqKqrcMe12u2jXrp145ZVXxPnz50V0dLT4y1/+4rLNm2++Kfr16+f263DXsWPHBACxZcsWl+UDBw4U99xzj8uyjIwM8cgjj4jQ0FARFBQkRo4cKc6fPy9KS0uFWq12ec87duzofN6UKVNEXFycMBqNwmw2i9GjR4uioiIhRMXn8lpGo1F88cUXVb6OyrbJyckRbdq0EWvXrhUDBgwQzzzzTDVnpObHuFZISIiYM2eO8/Err7wibrjhhmqf5633uLau/N5169ZNzJ8/37l82bJlonXr1uKvf/1ruc8RIYQoKioSQUFBYt++feJvf/ubeOGFFyrc79Wu/vzxhF69eonHH3/cZVlMTIx4+eWXq3xede3l9ddfF507d65yH+5s406bcGc/RETVYU8oEfk1vV4Pq9UKAHjppZewaNEizJ8/H0lJSYiLi8Ptt9+Oc+fOASjrCbnrrrtw4403Yu/evdi+fTv+8Y9/QKlU4sMPP0Tfvn0xZswY57/et2zZEq+99hrmzZuH2bNnIyUlBa+88gqeeuqpcj2FX3/9NYQQ2LRpE7766qsKs1aXr7L9LFiwAJIk4eTJk5Weh+TkZABlPTnvvvsu9u3bh/j4eDz00EMoLi4GAGzatAk9evSAJEkAAKvVil9//RUjR4502VdxcTGCgoKqPfcKhQKvvvoqZs+ejaFDhyI6Ohrz5s1z2aZXr17YsWOHM8PVpk6dCpPJVOVPZUMRd+/eDZVKha5duzpfy7fffoudO3fimWeecW534sQJdO/eHc2bN8fmzZuxfv16ZGVl4emnn4ZKpcLWrVsBANu3b8e5c+fw559/Op9rs9nwn//8BwcPHsR3332H1atX44MPPqjwXHrak08+iXvvvReDBg3yyv6vZrfb8f3336OgoAA33HCDc/myZcvQu3dv3H///QgPD0fXrl0xa9YsCCFcnl/Veyynxx57DPPnz3c+nj9/PsaMGVPpe7ZkyRJERUUhLi4OjzzyCL766ivnZ0tlrv78AerWpi0WC3bv3o1bb73VZfmtt96KLVu2VJnDnfaSlpaGyMhIREdH44EHHkBaWlqNt3G3TbhzLCKiKslbAxMR/c+1PRHbt28XTZo0EaNGjRIFBQVCrVaLL7/80rneZrOJNm3aiIkTJwohhLh06ZIAINavX1/h/q/tQSgoKBA6nU5s3LjRZbtx48aJIUOGuDwvLi6uyrzu5KtsP0uXLhXt27cXGRkZlZ6bf//730KpVIrU1FTnsiu9hXv27BFCCHHXXXeJv/71r871O3bsEACETqcTRqPR+aPRaETv3r2d21XWEyqEEMXFxcJkMomYmBiRk5NTbv3evXsFAHHs2LFy6y5duiSOHj1a5c+VnsdrvfTSS0KSJGdmhUIhQkNDxR9//OGy3a233ipeeeUVl2WrV68WAQEBQgghfv31VxEQEFBlj+YVTzzxhPP8XXsuK1LbntC5c+eK7t27C4vFIoQo3y5rqrIc+/btE0ajUSiVShEUFCR+++03l/VarVZotVrx8ssviz179oj58+cLo9EoPv74Y5ftqnqP5XDl9y47O1vodDpx5MgRce7cOaHRaER6enqFPZpClJ3nf//730IIIRwOh4iKihKLFy8ut98rrv78uaIubfrMmTMCgNiwYYPL8jfffFPExsZW+nrdaS8rVqwQixYtEnv37hWrV68WAwYMEBERESIrK6tG27jTJtzZDxFRdVRyFsBERNdauXIlTCYTbDYbrFYr7rrrLnz88cc4fvw4rFary4QiSqUSffv2RUpKCgAgNDQUjz76KG677TYMHjwYgwcPxr333lvpNWIpKSkoKSnB7bff7tJ7YrVay80W26NHjypzu5Ovsv2MGDECI0aMqHL/ycnJGD58OGJjY53LAgMDXbYpLi5GRESE83Fqaio0Gk2567UefPDBCidmqchzzz0Hm82GS5cuQaEoP3jmyvWIFfWShYaGIjQ01K3jXGvPnj0YOXIkpk+fDgC4dOkSXn/9dTz55JM4dOgQdDod0tPT8ccff2DTpk346KOPnM+12+0wGAwAgKSkJFx33XXlesdOnz6Nf//731i3bh3OnDkDi8WC0tJS54RN155LT0lNTcWrr76KzZs3Q61We3z/V2vfvj2Sk5ORm5uLJUuWYPTo0Vi/fj26dOkCAHA4HOjZsyemTZsGAOjWrRuOHj2K2bNnu0x8U9V7LKeQkBCMGDEC8+fPR3BwMAYOHFjp7/qxY8ewefNmfPvttwDKrnl++OGHMW/ePNx7773O7Sr7/LmiLm26NtxtL0OGDHF53KdPH7Rp0wZffvmlc3Ixd7Zxp024sx8ioupwOC4R+ZX+/fsjOTkZqampKCkpwdKlS8tNinGtqwuML774Atu3b0f//v3xyy+/oH379li1alWFz3M4HACAX3/9FcnJyc6fgwcP4o8//nDZ1mg01vo1XZ2vtvtJTk5Gt27dXJZt2bIFOp0O7du3BwCYzWZcvnzZuT43NxdmsxkxMTHOn+DgYCQnJ7t88a7Mm2++iR9//BFbt26F0WjErFmzym2TnZ0NAAgLCyu3ri5DF/fs2YN+/fo5c/fu3Rsvv/wyTp486Szq9+7di8DAQOzbt8/l/du/fz+SkpIqPW+XLl3C9ddfj/Pnz2PGjBnYtGkTdu3aBZ1O5xz+e+259JStW7ciKysLnTt3hkqlgkqlwoYNG/DJJ59ApVKhtLTUY8fSaDSIiYlBjx49MG3aNHTt2hUzZ850rm/WrBk6derk8pyOHTuWmySnqvdYbn/729/w1VdfYf78+fjb3/5W6Xaff/457HY7WrVq5Tzv06dPxx9//OEy23J1nz91adNmsxlKpRKZmZkuyzMzMyudXba27cVkMqFz5844evRopeekom3cbRM1PRYR0bXYE0pEfsVgMCAmJqbc8rZt20Kj0eDPP/903jLDbrdj69ateOihh1y2ve6663DddddhwoQJGDJkCL788kvcdttt0Gg0sNvtzu06deoErVaL9PR03HzzzXXKXZN8NVVSUoLU1FRn0XzFe++9hwceeMDZ69etWzeXW3WYzWbk5+fD4XA4ezGnTZuGvn37om/fvlUec968ec4v6V27dsVLL72EKVOmYNy4cc7jAcCBAwfQvHnzCnsNn376aYwaNarK4zRv3rzcshMnTiA7O7tc8XjlurMrRYFarUZhYSGaNm0Kk8lU4f737t1brudm+fLlKCkpwaJFi5z/QPDll1+ioKDAWYReey495e6770bPnj1dlo0ZMwbt2rXDq6++Co1G4/FjXuFwOFyKln79+iE1NdVlmyNHjiAqKsplWVXvsdwGDx4MjUaDrKws3H333RVuY7PZ8OWXX2LatGnlbt3yyCOP4IsvvsDkyZMBVP75c0Vt2zRQ9o8CPXr0wOrVq3Hfffc5l69evRr33HNPhc+pbXspKSnB4cOHq7yGtKJt3G0TNT0WEdG1WIQSUb1gNBrx97//HRMmTIDZbEZ0dDRmzpyJzMxMjB07FkBZ8fLpp58675+YlpaGffv24e9//zsAoHXr1tixYwdOnjwJk8mE0NBQjB8/HuPHj4cQAv3790dBQQG2bdsGhUKBJ5980qP5auvAgQMQQuC7777D4MGDER4ejrfffhvHjh3DDz/84Nzutttuw4QJE3Dp0iU0adIEN998M2w2G9555x088sgjWLJkCRYuXOgyOU9FVqxYgbFjx+Lrr7/GTTfdBAB44oknMHXqVHz66af45z//6dx206ZNld6Ds7ZDF3fv3g0AaNq0Kc6fP4+ioiJs3boVL7/8Mh5++GG0aNECQNkwwJCQEDzyyCOYPHkyAgMDkZaWhmXLluHjjz+GQqGAzWbD4cOHcfbsWRgMBgQHB6NJkyYoKCjAsmXLEBcXh99//x1Tp05FQECAswC59lxeUVBQgGPHjgEoK+pOnTqF5ORkhIaGOoeCVrfNtbf1MRqNCA0NdQ6TdUd1x3j55ZcxbNgwtGzZEvn5+fj222+xfv16lwm3/vnPf+KGG27AO++8g/vvvx9JSUn46KOPMHXqVJdjVfUey02SJOzbtw9CCGi12gq3Wb58ObKysvDEE0+4vJcA8MADD2DOnDmYNGmSW8er63Dc559/Ho888gh69eqFfv36Yc6cOTh79iyefvpp5zazZs3CrFmzcPjwYQQHB7vVXsaPH4/hw4ejVatWuHDhAqZMmYLCwkKMHj26Rtu40ybc2Q8RUbVkviaViMipsglFrrj6FihXJte5+hYo58+fFyNGjBCRkZFCo9GIli1bihdffNE5oUdqaqro06eP0Ov1Lrdo+eijj0THjh2FRqMRZrNZJCQkuEyAU9nEMVXdoqWifJXt54svvnDmqchnn30mOnToIL777jvRvHlzodfrxbBhwyqcKKZPnz5i1qxZzseLFy8WrVq1Enq9Xtx6660iJSWl3HOunphox44dwmg0ivfff7/cdjNmzBCRkZGipKRECFE2aVFgYKDYunVrhblr6+WXX3a5rUpQUJDo0aOHmDNnjrBarS7b7ty5UwwaNEgEBQUJk8kk4uPjxdSpU53rv/76a9G8eXMhSZJ4+umnhRBlk9KMHTtWBAQEiLCwMPHcc8+JF154odxtSK49l0KUnStcc6sfAGL06NE12uZqFbWL6tpEdccYPXq0aNWqldBoNCIsLEwMHjxYrFy5stx+fvvtNxEfH++85c+HH37oMomTt97juqjuc+La9cOHDxe33HJLhdseP35cABCrVq2qdr+eMnv2bBEVFSU0Go3o3r17uYmKXn/9dVHV17OK2sv9998vmjVrJtRqtYiMjBQjR44UBw8erPE2QlTfJtzdDxFRVSQhrpl3m4iIfOr111/HkiVLsHfvXqhU5QeoPPvss7hw4YJLr2dlVq5ciXHjxiElJQVKpdKt469fvx6PPvpolbeIqcjs2bPx888/l7t+tqGozbn0lOrahK809PeYiIjkwYmJiIhktmLFCsyePbvSYiM5ORnx8fFu7ev222/HM888g4yMDE9GrJBarXaZObSh8eW5vFZ1bcJXGvp7TERE8mBPKBGRHxNCICgoCF9//TXuvPNOrxyjtj2hRERERLXBiYmIiPyYJEnIy8vz6jFat26Nf/zjH149BhEREdEV7AklIiIiIiIin+E1oUREREREROQzsg3HPXv2rFyHdovZbEZWVpbcMaiRYzskf8G2SP6A7ZD8Adsh+Qt/b4uRkZGVrmNPKBEREREREfkMi1AiIiIiIiLyGRahRERERERE5DMsQomIiIiIiMhnWIQSERERERGRz7AIJSIiIiIiIp9hEUpEREREREQ+wyKUiIiIiIiIfEYldwAiIiJPOpd9EukXjkCt0qBd5HUINITIHYmIiIiuwiKUiIgaBKvNghW7vsbF3DMI0Aej1FaKTQd/Q+/YBPTpcBskSZI7IhEREYFFKBERNQB2hw2LN38CjUqD8OAWUCs1kCQJIcYm2HV0PQpK8nBLt1FyxyQiIiLwmlAiImoA1u37CUqFClq1ARqV1tnrqVZp0aZZJxxM34F9J7bKnJKIiIgAFqFERFTPpV84gpOZh6HXGqFWacqtVypUiApvj8TkxSgozpUhIREREV2NRSgREdVbDocdick/wBwYCbWyfAF6hV5rRLDRjN92fOnDdERERFQRFqFERFRv7U/fBr3GBKVSWe3EQxEhLXEm+wTOXjrpm3BERERUIRahRERULzmEA9sPr4ZRF1hlL+gVSoUS4UGRSExe7IN0REREVBkWoUREVC+lZuyBQRcApaR0+zlNApriYu4ZZOWe82IyIiIiqgqLUCIiqpd2HV2PAH0wVCq1289RKJQIDYjA2n1LvZiMiIiIquLWfUJXrlyJ9evX49SpU+jXrx+eeeYZAMCRI0ewaNEipKWlQaFQoHPnzhgzZgxCQkK8GpqIiBq3i7lnUWIpRJCxSY2faw5shqNn98FiK4VGpfVCOiIiIqqKWz2hISEhGDlyJAYNGuSyvLCwEAkJCZg9ezY++eQT6HQ6fPLJJ14JSkREdEVy2maEmMLduhb0WmqVBlq1DttTE72QjIiIiKrjVhHau3dv9OrVCwEBAS7Lu3Xrhr59+8JgMECr1eL2229HamqqV4ISEREBgM1uReqZZKhV2mpnxK2MOTASh07t9HAyIiIicodbw3HddejQIbRs2bLCdYmJiUhMLPtX5+nTp8NsNnvy0B6nUqn8PiM1fGyH5C/8qS0eOLET5qCmMBqMUCndvx70alptU2RcOg67shQRIc09nJC8xZ/aITVebIfkL+pzW/RYEZqeno4lS5bgpZdeqnB9QkICEhISnI+zsrI8dWivMJvNfp+RGj62Q/IX/tQWd6Ssh1qhhc1qh81qr/V+AvXBWLntBwy7/hEPpiNv8qd2SI0X2yH5C39vi5GRkZWu88jsuOfPn8fUqVMxZswYdOzY0RO7JCIiKsdqtyD9QirUNZgRtzIhpnCcunAEQggPJCMiIiJ31bkIvXjxIqZMmYJ77rkH/fv390QmIiKiCqWdT0Gw0Qylou4DeYy6QBSV5uNi7hkPJCMiIiJ3uVWE2u12WCwWOBwOOBwOWCwW2O12ZGdn46233sJtt92GW2+91dtZiYiokUs9vQdGXaBHilBJkhBoCMWOI2s9kIyIiIjc5dZf8R9//BFLlixxPt60aRPuvfdeSJKEzMxMLF68GIsXL3auX7hwoeeTEhFRo+Zw2HHq4lG0DIv12D6DjWacuXTcY/sjIiKi6rlVhI4aNQqjRo2qcN19993n0UBEREQVOZN9AiZ9EJQKj0xnAAAw6gORfjEVeUWXEWgI8dh+iYiIqHKe+0tORETkRcfPHYBRG1Dr27JURCEpYNAGICltk8f2SURERFVjEUpERPXC8XMHoFFpPb7fIEMoTmYe9vh+iYiIqGIsQomIyO/lFV2G1WaBJCk9vu9AQygu5Z2HzW71+L6JiIioPBahRETk99LOH0SQsQnUKo3H961WaaCQFDh+br/H901ERETlsQglIiK/dyLzEHRqAyRJ8sr+Aw0hSDm12yv7JiIiIld1v9EaERGRFwnhwJmsNLTy4K1ZrhWgD8GF3DMe3acQAgUr1iLn6x9ReugYoFTA0LsbmvzfY9B2iPHosYiIiOoT9oQSEZFfu5h7Fnqt0Wu9oABg1AUgv/gyiksLPLI/e34Bzox5HtlzFkIRFAj9jb2g6x4PW2YWTt33FC5OmwUhhEeORUREVN+wCCUiIr+WfvEIDNpAj96a5VoKhRIalQ6HTu+p874cBYU4ff/fIamUUEe3hDIoAEqjHqrQIGhiWsOYcCPylq7AuWcnshAlIqJGiUUoERH5tfTMVGjUWq/2hAJAoD4Ex+o4OZGw2XD2769AHRkBhckIhV5XbhuFRgPDgD4o2roHF6d8UKfjERER1UcsQomIyG85hAPnsk9CpfBeL+gVAYZgZOWdq1PvZPZ/voLDYoVk0EPSVj6Tr6RUwti/N3K/XYaC9VtqfTwiIqL6iEVoDbVs2RK33HKL82fWrFlVbn/nnXdWuPy9997DnDlzvBHRI4qLi3HPPffAbrcDAL766iu8/PLLzvXvvvsunnvuOVgsFowcORI2m61Wxzlz5gzuvfdeDBw4EIMGDcLnn39e4XbPP/884uPjcfPNN5dbt27dOtx0003o16+fy/tR1XM8pbJj9O7dG4MHD8Ytt9yCIUOGeO34RA3dhZwMGHVBUCo8f3/Qaxm0JhSV5iO/OLdWzy9JOYKcb5dBFd6kwh7Qa0laDXR9uuPcc5PgKCmt1TGJiIjqIxahNaTT6bB69Wrnz7PPPlvl9r/88ouPknnWokWLMGTIECiVZV/87rvvPiQmJiI3NxerV6/GmjVr8K9//QsajQY33nhjrV+nSqXC66+/jvXr1+PXX3/FggULcOTIkXLbjRo1Ct9880255Xa7HRMnTsTXX3+NdevWYdmyZc7nV/YcT6rqGIsXL8bq1avx+++/ezUDUUOWfiEVBm0AlArvT+YuSQro1AYcPr2rxs8VQiDzlWnQd+sMSVd9AXqFOsIMZUgQzr/wVo2PSUREVF+xCPWAqVOnYsGCBc7HV/dytmvXzrn8ww8/xI033oi7774bx48fdy7/8ccfMWzYMNxyyy146aWXYLfbcfr0aQwYMAAvvvgiBg0ahAcffBDFxcUAyoqbhIQEJCQk4LnnnqtyPwDwyCOP4Pz58xVmHzt2LJ5++mkMGzYMvXr1QmJiIgBg6dKluO2225zb6fV63H333Xj33XcxefJkzJ07F3q9HgBw22234aeffqrVuYuIiEBcXBwAwGQyoV27dhVm7dOnD4KDg8stT0pKQuvWrREVFQWNRoO77roLq1atqvI5p06dwpgxYzBkyBAMGzYMx44dq1X2qo5BRJ5x6uJRaNU6r18PeoVJH4STF1Jr/Lz838o+O6HWQFLULKuuexwKVm9E6bGTNT4uERFRfcQitIZKSkpchuP+/PPPuPPOO/Hrr786t/n1118xfPhwl+ft27cPv/zyC1avXo2FCxdi7969AICjR4/il19+wbJly7B69WoolUosXboUAHDixAmMHj0a69atQ2BgIFasWIHU1FR8+OGH+OGHH5CYmIi33nqr2v0sXLgQTZs2rfD1pKSkICoqCsuXL8esWbMwc+ZMWCwWnDp1Ci1btnTZ9oEHHsCXX36JN998E61bt3Yu79ChA5KTk8vte8SIES7n6srPxo0bK8xy+vRpHDhwAN26daviHXB1/vx5REZGOh83a9as0oIbAKxWK8aPH4/XX38dv//+O55//nnMnj3b7eO5S5IkPPjgg7j99tvx9ddfe3z/RI2BEA6cv3zKOSLDF0y6IGTnZ9boOcJiRda7n0DdsjkUusqvA62MQquBJrYNMl96u8bPJSIiqo+8P76pgbkyHPdaWVlZOH/+PC5duoSgoCA0b97cZf327dtx++23O3sPb7nlFgDA5s2bsX//fgwdOhRAWZFrNpvRp08ftGzZEl26dAEAxMfH4/Tp08jNzcUdd9yB0NBQAEBISEiV+6lKSUkJLl26hH/+858Aynptc3JykJ2djcDAwHLbz5w5E02aNCl3/adSqYRGo0FBQQFMJpNzeU16RwsLC/HEE0/gzTffREBAgNvPq6mVK1fiyJEjeOKJJwCUDeft1atXue3uv/9+XLx4sdzyCRMmuPQQV+ann35Cs2bNkJWVhQceeAAxMTHo06dP3V8AUSOSnX8Beo0Rkg//vdSgNaGgJBdFpQUwaE3VPwFA3tIVUEVGAMra59S2b4v831ajeN8h6OM71no/RERE9QGLUA+54447sHz5cly4cKHSyYgqIoTAfffdh1deecVl+enTp6HVap2PlUolSkpKaryfqqSmpiI6Ohq6/16/tH//fnTq1Ak6nQ6lpa6TZMyZMwelpaWYM2cO3nvvPWexe0VpaalLXqCsJ7SgoPyN3ydNmoT+/fs7H1utVjzxxBMYMWJEuf1Wp2nTpjh79qzz8blz5yrt9QXKen4nTJiABx98sMr9Llq0qEY5rtWsWTMAgNlsxpAhQ5CcnMwilKiGMi4dh0Fr8ur9Qa+lUCihVmpw7Ox+xEf3rXZ7Ybcje85CaDq3h0KnrXb7ykgqJbQdYnBh8r8RtWx+rfdDRERUH3A4rofceeed+Pnnn7F8+XLccccd5db36dMHq1atQnFxMQoKCpy9qTfeeCN+++03ZGVlAQAuX76MjIyMSo/Tr18//Pbbb8jOznZuX91+Ro0ahXPnzpXbV0pKCs6cOYOSkhIUFRXhvffew5NPPong4GDY7XZn0bt582b88MMP+OCDD3DDDTcgPz8fBw4ccO4nOzsboaGhUKtdvyj+9NNPLpM4Xfm5ugAVQuCFF15ATEwMnnrqqWrOcnldu3bFiRMncOrUKVgsFvz888+49dZbK90+IiIC69evh8PhAAAcOnTI4zeLLyoqchbfRUVF2LBhA9q3b+/RYxA1Bmey0qBV6312PegVJn0Q0s4fdGvbgt/XQREcBElV9yHDmpjWKD14BJb0M3XeFxERkT9jEVpD114TOnXqVABA+/btUVhYiKZNmyIiIqLc8+Li4jB8+HDccsst+Mtf/oKuXbsCAGJjY/HSSy/hwQcfREJCAh588EFkZlZ+PVL79u3xf//3f7j33nuRkJCAN998s8r9OBwOnDx5ssLJc1JSUjB06FDccccdGDp0KP7617/i+uuvBwAMGDAAO3bswJkzZ/Diiy/i008/dQ61feyxx1xupbJlyxYMHjy4Vudz586d+PHHH7FlyxbnOV2zZg0A1wmVxo4dizvvvBPHjx9Hjx498N133wEom1337bffxkMPPYSBAwdi+PDhzoKvoufcf//9cDgcGDBgAG655RZ88skndfqCW9ExLl68iLvvvhsJCQkYNmwYBg8ejEGDBtX6GESNVUbWcSh9cH/Qa5l0QcjKK/8PdxXJ/uwbqJpH1KkX9ApJpYI6qgUuTJlZ530RERH5M0l4uhvITVcPofRHZrPZ2atYnx0+fBjff/893njjjXLr7rnnHrz77ruIiYkpt27//v2YO3cuPv7442qP8fjjj+OVV15B27ZtPRGZrtJQ2iHVf75ui8WlBfgicRpaNGkLjdr9W554gs1uxZEze/HcndOhVlY+0VBJyhGce2YitF06QGHwTEZHUTEKV29Cm92/Q2k0eGSfDQk/E8kfsB2Sv/D3tnj15KHXYk9oA9ehQ4cKC1AAOHnyJNq0aVPhuri4OPTr1895m5fKWCwW3HbbbSxAicijzlw6AZMuGGpVzWebrasr16CeyUqrcruchT9CHd0Skr7uvaBXKAx6KIIDcWnWAo/tk4iIyN+wCG3Edu/eDYWi8ibwwAMPVHtrBI1Gg/vuu8/T0YiokTtzKQ16rQGSJM+fKZMuEIczkipd7ygoROHqjVAYDB6/ZlUTG42CX/7w+PXqRERE/oJFKBER+Z2MrONQVTEU1tuMukBczK18gqC8ZaugjomGpPX8NauqiHDYsi6heM9+j++biIjIH7AIJSIiv2J32HEpPxMKqe4zztaWQRuA3MJLlfZG5v24AsomwZBUnr/TmaSQoI5uheyPv/D4vomIiPwBi1AiIvIrF3PPwKQPglIhXxGq0xhQYilCXvHlcussp87AduEi4MWhwtq2USjekQyH1eq1YxAREcmFRSgREfmVc9knodcYoVR4vpfRXZIkQaPW4diZ8kNi85ethLp1S4/NiFsRhckISa1C3tLfvXYMIiIiubhVhK5cuRIvv/wyHnroIcyePdtl3f79+/GPf/wDf/nLX/Dmm2/i4sWLXglKRESNw7nsdGhUWo9P+FNTRl0gTmUdcVkmhEDe0t+hDAr0ej51dEvkfv+LV49BREQkB7eK0JCQEIwcORKDBg1yWZ6Xl4cZM2bg/vvvx/z589GmTRt88MEH3shJRESNxNnsk1AqPD/hT00ZtQHIzr/gsqz0QCqgVgNK7w8kUrdqjtJDR2EvKvb6sYiIiHzJrb+ivXv3Rq9evRAQEOCyfMeOHWjZsiX69u3rvFXHyZMnceZM5TMKEhERVcZiK0WJpUj2XlAAMOgCkF90GTb7/67LzPt5FdQtmkLSe28o7hUKvQ4KvQ653/3s9WMRERH5Up0uuDl9+jSioqKcj3U6HZo2bYrTp0+jefPmLtsmJiYiMTERADB9+nSYzea6HNrrVCqV32ekho/tkPyFr9riiXOHEWQKhckYIOvERACggw52YYcVRWhqbgshBNJXb4KxZzxUer1PMjhi26B4+RqYJzzrk+P5O34mkj9gOyR/UZ/bYp2K0JKSEgQGBrosMxgMKCkpKbdtQkICEhISnI+zsrLqcmivM5vNfp+RGj62Q/IXvmqLh07shVqhhdVihRXyzwyr1xixI2UD9MoglB46BodKCYvFAluJjwrkZmEoXLEOmadOQ2nwTeHrz/iZSP6A7ZD8hb+3xcjIyErX1emiFp1Oh+Ji12tVioqKoNN5f5gSERE1POez06FWaeSO4WTUBeD85VMAgPyV66BqFu6TobhXKLRaKIx65C1Z7rNjEhEReVuditCWLVsiPT3d+bikpASZmZlo2bJlnYMREVHjczY7HUqF/xShBm0ALheUTU5U8Ps6KAJNPr9eVdWyOfJ/Xe3TYxIREXmTW0Wo3W6HxWKBw+GAw+GAxWKB3W5Hr169cOrUKWzbtg0WiwVLlixBVFRUuetBiYiIqlNsKYTdYYNC/jmJnAxaEwpL8lCQlgZHUTEkpe+vU9W0bIbSQ0chrDafH5uIiMgb3Lom9Mcff8SSJUucjzdt2oR7770Xo0aNwgsvvID58+fj448/Rrt27TBu3DivhSUioobrfHY6TPpAqPxoOK5SoYIkKXBu6U/QtYr06VDcKxQmI+AQKFj7JwJuG+Dz4xMREXmaW0XoqFGjMGrUqArXxcfH896gRERUZ+cup0OnNkIhef8enDVh0JpQtHoTDG06ynbrGFXLZshd9AuLUCIiahD86y89ERE1Wuey06FW+k8v6BUBNi2kc9mAUr4/meqWkSjdfwhCCNkyEBEReQqLUCIi8gvnL5+GUlmnO4d5RdiRXGRHm6DQaWXLoAwNhj03DyWpx2TLQERE5CksQomISHYFJblQKnw/6Y87Qvafx7kOAXBI8vVCSpIEVUQ4chculS0DERGRp7AIJSIi2V3IyYBBG+BX9wgFAAgBw97TuBwVgFxRJGsUdYumKN6ZLGsGIiIiT2ARSkREssu8fBoatc7vJiXSnLgIu1ELQwmQqS2UNYuqaRis6RmwF8pbDBMREdWVf/21JyKiRikzJ8MvJyXS7zkJe6gRAQVAtkne+3RKGg0krRb5vyXKmoOIiKiuWIQSEZHsMnNOQ6nwv0mJDLtPwGHQICBPIMck/8y06uZNUbBirdwxiIiI6oRFKBERyarUWgKrzQKFTPfgrIyioASqzFwIhQIBeQ7kB0qwO+TtDVU1b4rSlKO8VQsREdVrLEKJiEhWF3PPwKgLgMrPhuPq9p2CNSIIQquCyg5IDiBP5smJlKHBsOfkojQtXdYcREREdcEilIiIZJWZkwGt2gCFwr/+JOn3noI9QAcoy3IF5jlwXifv5ESSJEEZ1gR53/0saw4iIqK68K+/+ERE1Ohk5pz2v1uzoKwIheZ/16kG5AlkG+QdjguUXRdavG2P3DGIiIhqjUUoERHJ6vzlU1Aq1HLHcKG8mA8AEFddphqY50BOgPzXYqqahsFy4hSEVf6CmIiIqDZYhBIRkWzsDjvyi3L87v6g+n2nYGtigtD9rzj+3+REdhmTAQqDHrA7ULQzSdYcREREteVff/WJiKhRuZR3DkZdgN8Nx9XvTYfdqAWumrFXZSubnCgf8k5OBADKpmHI+/F3uWMQERHVCotQIiKSTWZOBnQaA5QKpdxR/kcI6A5mQGjKZwrIcyBTI+/kRACgbhaOkn2H5I5BRERUKyxCiYhINpk5GdCodHLHcKE+nQ2HXuucFfdqAfkC2UarDKlcKSPMsJ0+A0dxidxRiIiIaoxFKBERySYz5zRUClX1G/qQft8p2EIMEJryuQLyHMg1yT85kUKrBZRKFKzdIncUIiKiGmMRSkREshBC4FLeOSiV/lWE6vaeguOa60GvCMh3IM8kQQiHDMlcqZqFo2BFotwxiIiIaoxFKBERySK36BK0aj2U/tQTandAe/Q8hLria1Q1FsCuAors8g+DVTUNR+nBI3LHICIiqjEWoUREJIvMnAzoNUa/KkI1xzNhDzVWeD3oFaZ8gUxNgQ9TVUwV3gTWs5mw5eXLHYWIiKhGWIQSEZEsMi+fhkath1TBsFe56Pedhj3IUGlPKFB2XeglvcWHqSomqdWQdFoU/rFR7ihEREQ1wiKUiIhkcSEnA2qlWu4YLnQHM+DQqyu8HvSKgHwHck3yXxMK/Pe60FXr5Y5BRERUIyxCiYhIFpk5p6FU+FERandAk3YBQlH1n8aAPIHcgLKJleSmbhqO0sPH5I5BRERUIyxCiYjI54pKCyBBgqKags+XNCcvwh5iBFRVZ9IVC5TqJJTaS32UrHJKcwhs5y/ClsvrQomIqP7wn7/+RETUaFzIyYBBGwC1UiN3FCddyhnYA/UV3h/0ahIAQ6FAlqrQN8GqyqJSQdLrULh6g9xRiIiI3MYilIiIfC4z5zR0Gv+alEh34L/Xg7ohIF/gol7+27QAgKppGApWb5I7BhERkds8Mi/+hQsXMG/ePBw5cgQqlQp9+vTBo48+CqWy8tkFiYio8crMyYBK5T+9oBAC2tRzKO7S3K3NA/IcyAl0AMVezuUGVUQYLKnH5Y5BRETkNo/0hM6bNw+BgYH49NNP8e9//xspKSlYtWqVJ3ZNREQN0PnLp6Dyo0mJ1Gcuw2HUAir3/vHUlOdAXoD8ExMBgCoslPcLJSKiesUjReiFCxfQt29faDQaBAcHo2vXrsjIyPDEromIqIGx2iwotRZDkvznihDdwQzYg6u+P+jVjIUChUYJVruf3C9Uo0bR+m1yRyEiInKLR4bjDh06FFu2bEHnzp1RWFiI5ORk3H///S7bJCYmIjExEQAwffp0mM1mTxzaa1Qqld9npIaP7ZD8hSfbYnrmUQQaQxBgDIBC4R+XbRgPnwMC9FCq3PuzqASgLQUKtFY0UwV6N5wbLM2bwbJ+K8x/e1DuKF7Fz0TyB2yH5C/qc1v0SBHasWNHJCYmYvTo0XA4HBgwYACuv/56l20SEhKQkJDgfJyVleWJQ3uN2Wz2+4zU8LEdkr/wZFs8cvIA1AotLBYrAKtH9llX6n2nUNyhGYTd7vZzAvIUOKPIRUiJ0YvJ3CM1CUZ+8oEG/3nBz0TyB2yH5C/8vS1GRkZWuq7OY6EcDgemTp2K3r17Y+HChZg3bx4KCwvxzTff1HXXRETUAGXmnParW7OoLuRBqBTV3h/0WqZ8By4b3S9avUkZbob17Hk4ivxgpiQiIqJq1LkILSgoQFZWFm6//Xao1WoEBARg4MCBSEpK8kQ+IiJqYDIvn4ZK6T+TEmlTMmALMVZ7f9BrBeQJ5Jr8Y3IihVYDSaFA4Z875Y5CRERUrToXoYGBgQgPD8cff/wBu92OwsJCbNiwAa1atfJEPiIiakAcDjtyiy752aREZ8pmxq3hPUtN+Q4UBEiwO/ykNzQiDAXL18gdg4iIqFoeuSZ0/PjxWLBgAX7++WcoFAp07twZo0eP9sSuiYioAckuuACDNgAqpUf+/HiE7kAGLG3Cavw8lR2QHEA+ihCMAC8kqxl1RBhKUo7KHYOIiKhaHvkW0Lp1a7zxxhue2BURETVgmTkZ0GmMUCr8owhV5BRBstogFLXrmQ3IcyBTU4hgm/xFqDK8CUr2psBRaoFC6z/X3BIREV3Lf8ZDERFRg5d5+TS0Kh2kGg599RZdSgbsoSYIXe2K4oB8gWyDf8zwq9DrACFQvHuf3FGIiIiqxCKUiIh8JjMnA0p/Gop78AzsJl2Nrwe9IiDf4TeTEwGAMsKM/J9XyR2DiIioSixCiYjIJ4QQyMo76zdDcQFAdzADDm3t8wTkOZAfIEEIhwdT1Z4qwoySA6lyxyAiIqoSi1AiIvKJ/OLL0Ki0fjMUVyoshTK3qMb3B72axgLYVECRo8SDyWpPFW6GNT0DwmaTOwoREVGlWIQSEZFPZOZkwKAxQa30j0lzdIfOwBZqgtDW7Z6lpnyBTFWhh1LVjcJogLBYUXyQs+QSEZH/YhFKREQ+kZmTAa1a7zc9obqUM7AH6gFF3fIE5DtwyWDxUKq6U4U1Qf7PK+WOQUREVCkWoURE5BMXck5DpfKPXlCg7P6gQle3XlCg7LrQXJPdA4k8Q9U0DCVJB+SOQUREVCkWoURE5BOZORl+MymRVGqFKjMXQln3XtmAPIG8AMBf5shVhjeB9cRpCOEviYiIiFyxCCUiIq8rsRTB4XDAX0o17ZHzsDep+/WgAKArFijRSbDYSj2QrO4UASY4CgphOXFa7ihEREQVYhFKRERel5mTAZMu0H8mJTqYUXY9qLLufwYlAPpCgSw/mZxIkiQozSHIX/a73FGIiIgqxCKUiIi8LjPnNLRqPRQKpdxRAJRNSuTwwPWgVwTmC1zUFXtsf3WlahqOou3JcscgIiKqEItQIiLyusyc09Co/r+9O4+Oq7zvBv6928yd0cxoG622LAjGBuqUkBCThCWY+G2attkISROcHkqPTWg4nDSnS2hOSnPSvuC8hlJKCjS4kARcigMJGMwqE2zHLDEEYyPvlrWvo9FoRsts9z7vH7KEZUm2ZM3MczXz/ZyjI+vq+t6vrUdz72+e5z6PKTvGmLQFozkEoWeuIPZHbQz47Iwdb770yiBSTS2yYxAREU2LRSgREWVdz0CbYyYlch/rhVVWBOHKbBEa9TvjeVcAUIsDsAYGke7tkx2FiIhoChahRESUVWkrhdHkMByyPCjc+ztgFXuBDPaEeocFhosUpKxUxo45H4qqQC0JIPpsg+woREREU7AIJSKirOob7ITPLHbO86CN7bA9mXseFABUAbjjAmHVGZMTASeeC93+puwYREREU7AIJSKirOqJtMF0eZ0xHNcWcB/thjAyXxAHBgV6zJGMH/ds6VVBJI4clx2DiIhoChahRESUVeOTEikOGI9rtIZgBbyAmvnLnz9mY8BnZfy4Z0srLYHV1w8rGpMdhYiIaBIWoURElFU9A+3QNQf0ggIwGztglXgzOinROH/UxqCDJidSNBWqrwhDL22XHYWIiGgSFqFERJQ1trARGQ5BccjlxtzfAdvjQjZmSfLFBIZ8CtJ2OuPHPlt6dSWGXtkhOwYREdEkzrgrICKivDQQ60WR2w/IH4kLCAHzQAeEkZ1eWVUAroTAoOKw50IPHZMdg4iIaBIWoURElDVjkxIVwdBcsqNA746c6AXN3jn8UYFuB01OpAVLke7sgRVPyI5CREQ0gUUoERFlTU+kHW7DGZMSmY0dSJd6IczsPZ8aiNoIFzlnOK6i61A8JkZ2cKkWIiJyDhahRESUNT2RNuhaZtfkPFtmYwfsIjMrz4OO80dtDPrsrB3/bOhVQcS2bpMdg4iIaAKLUCIiygohBPoGO6GqmZ+J9myYje1ZmRX3ZL6YQMyvwLadU4jqVRVINB6WHYOIiGgCi1AiIsqK2GgELt2EEPILMi0Ug1AVKFmeIUmzAT3tsMmJKsqQauuEsJyzhikRERW2jD0Ys2vXLjz55JMIhUIoKSnBt7/9bVx44YWZOjwRES0wvZF2eN1+GLpbdhSY+ztglftgu7O/Xql/UKDbNYTSlC/r55oNxeWComsYeXsvii67RHYcIiKizBShe/fuxaZNm/A3f/M3WLp0KSKRSCYOS0REC1hPpA1uw4SqyB90Yza2w/KbgJr9CZL8MRthXwoYyPqpZk2vDCL2zIssQomIyBEycmewefNmXHfddVi2bBlUVUVZWRnKysoycWgiIlqgnDUpUTuEkZtnUwODAhFndIJO0KsrEH+3UXYMIiIiABnoCbVtG8eOHcOll16KW2+9FalUCh//+MfxF3/xF3C5PlgXrqGhAQ0NDQCA9evXIxgMzvfUWaXruuMzUv5jOySnOJu22BftxDlVy+B2mVlKNTtqZBhq0oKm6RBa9gvR4hEgFlDgcrmgqvJ7gQHAVbcI4b0HUV5e7ojlcs4WXxPJCdgOySkWclucdxEaiURgWRbefPNN/OhHP4KmadiwYQOeeuopfOMb35jYb/Xq1Vi9evXE16FQaL6nzqpgMOj4jJT/2A7JKebaFuPJEVjpNBKJBIQtt+jxvtuEVNCHtAYgB5PzKBagWDr64mEUqw7pElUAYVno2PEGzD9YJjvNWeNrIjkB2yE5hdPbYm1t7Yzfm/dbtOO9nX/8x3+M0tJSBAIB/Omf/inefffd+R6aiIgWqO5IG4o8xY4Yjms2dsDyewAtd72SgaiNbvdwzs43G1pFGaK/fkF2DCIiovkXoT6fb8rwnoU81IeIiOavO9wC0/A6Yo3QXKwPeip/VKDfm8rpOc9Er6nE6O49smMQERFlZmKiq6++Gi+++CIGBwcxNDSErVu34qMf/WgmDk1ERAtQ90ArXLrrzDtmmTKcgDY4AojcntcftTHol78+6sn0yiBSx9sgRI7/M4iIiE6RkSVavvKVryAWi+E73/kODMPAJz/5SVx77bWZODQRES1A3QOtqC07V3YMmAc7kaoMSOgJtRH1KxDChuKAJWoAQC3ywo4nkGzpgPucxbLjEBFRActIEarrOtauXYu1a9dm4nBERLSAjSaHYQsbItfdj9MwG9th+01Az20RaqTHPsfsEQQ0h0xOBEALliL26xfg/u462VGIiKiAOePtWSIiyhs9A23wO2ZSonYId0beb50zf9RGl8MmJ9KrKzGy623ZMYiIqMCxCCUioozqGmiB2/BCkzwpkZJIQe+JQkiaLC8wKNDvS0o590z0qiCSTc2yYxARUYFjEUpERBnVHW6FocmflMh9qAvpygBEjofijgsM2hjwyx+SfDLV74MdG0aqq1d2FCIiKmAsQomIKKO6B1qhaXKGwJ7M3N8By28ChqQiNGojGlBg286ZJVdRFGilxYg+/ZLsKEREVMBYhBIRUcaMJIYAwBHLgJjvt8M25T2XqlmAnhIYUJ31XKhWU4mRHW/KjkFERAWMRSgREWVM90ArfE6YlChlwWjrB1S5l7nAoEC3wyYnMiqDSB5tlh2DiIgKGItQIiLKmO6BVrgNj/RJidxHupGuCACanEmJxhUP2uj3paVmOJVaUgxrIIJ0aEB2FCIiKlAsQomIKGO6B1rg0uVPSuTZ2wor4IFwyX02NTBoI+J3zjOhAKCoCtTiAGLPvSI7ChERFSgWoURElDHdA61QVQdMSrSvDbZXfjFcNCQw5FOQtlOyo0yi11Rg+NVdsmMQEVGBYhFKREQZMRyPQVFUCCG3509JpGC0hwFJ64OeTBWAOSIQ0pz1XKheGUTiyHHZMYiIqECxCCUioozoHmhFkTsAQ3NLzeE+1IV0dbH050HHFUcFuj0jsmNMopWVwurrRzockR2FiIgKEItQIiLKiK5wM0yXF6rkGWk9e9tg+eU/DzouMGgj7LNkx5hE0VSoviLEnn9VdhQiIipALEKJiCgjOsPH4ZLcCwoA5r5WqeuDniowaCMSkJ1iKr2mEsMNO2XHICKiAsQilIiI5k0IgZ6BdiiSe0GV0ST03ijgjJG4AADPiEDcBOJWQnaUSfSaSiQOHpUdg4iIChCLUCIimreBoV543EXSaz/zQAfSVcUQutx1Sk+mAPDFbPQYMdlRJtHKS2GFwkj3hmRHISKiAsMilIiI5q0z3Ayv2wdDlzsc19zXBivgAQznFKEAEBgU6PE6qydUUVWoJcUY/NULsqMQEVGBYRFKRETz1tl/HKbhhSJ5WRTP3jbYDpmQ6GQlERvhYmdNTgQAem0lhl97XXYMIiIqMCxCiYho3jrDx6FpcicDUofi0AactR7nuEDERqRYkb6G6qmMmiokDx+HEEJ2FCIiKiAsQomIaF5SVhKx0UHZMWA2diBVGXDM0iwnM9KAZgkMKM5aL1Qt9sOODSHV0i47ChERFRAWoURENC89A20IeEqhqXKfwzT3tcL2m4DuzEtb8YCNDtNZkxMpigItWIbBJ7bIjkJERAXEmVdqIiJaMDrDzTDdRdBUuT2QnndbHLU+6KlKIgIhf1p2jCmMRVUYef0d2TGIiKiAsAglIqJ56ew/DpfmljopkdYXg2LZ0peIOZ3iiI2BYtkpptKrKpE81gJhO+t5VSIiyl8sQomIaF46w81QJQ/F9bzXgnRFALbbuT2hnhGBhBsYtZy1VIvq80KkUhjd0yg7ChERFQgWoUREdNZioxGoivxLiefdFlh+E1Cd2xeqAPAP2uh0R2VHmUKvrkB087OyYxARUYGQf+dAREQLVkeoCX5PCVy6S14IW8Dc3w7boRMSnawkItBb5KyeUGBsqZb479+XHYOIiAqE86/YRETkWG2hozBdXigSe0NdTb2wSn1QFsBSl8URG+Fi5wXVqoNItrTDGo3LjkJERAUgo3cNXV1dWLNmDf7jP/4jk4clIiKHag8dg65J7AUF4NnTgnSJF8J03vqgp/JHbUT9QNp21iy5qtsNxWVg+KXXZEchIqICkNEi9L//+79x3nnnZfKQRETkUIlUHMPxKCC5Y8/zbjNsrwFInJ13tjQbcMcFQuqQ7ChTGItrEN3ysuwYRERUADJWhO7atQterxcrVqzI1CGJiMjBOsPHUVxUDl2X1wOpjCZhdAw4ekKiU5UO2OgoGpYdYwq9tgqJ9w/JjkFERAUgI3cOIyMj2Lx5M26//XZs27Zt2n0aGhrQ0NAAAFi/fj2CwWAmTp01uq47PiPlP7ZDcorp2uI7TV0o9pWiyOuTlApwv9cOq7YUqssFaHKXiZmtskGgp1rAtEzZUSYRi2owuuMt+IZGYZ5TJzvOtPiaSE7AdkhOsZDbYkaK0CeeeAKrVq1CeXn5jPusXr0aq1evnvg6FApl4tRZEwwGHZ+R8h/bITnFdG3xcOteeN1+xOPyJrPxvnUY6SI3LBWAZUnLMReBEHBguYaR9mGoirMKZ62iDMfv24iKf7xVdpRp8TWRnIDtkJzC6W2xtrZ2xu/Nezhuc3Mz9u3bhz/7sz+b76GIiGiBsGwLoWiX1FlxIQS87xyH7THkZTgLugUYSWc+F6ovrsXwb3fLjkFERHlu3j2hjY2N6Ovrw1//9V8DAOLxOGzbxve+9z38+Mc/nndAIiJynp5IG/zeUigSJwMy2sIQbl36xEhnozRso907jMrhYtlRJtFrKjH00nbYyRRU18Iq7omIaOGYdxG6evVqXH755RNfb9myBX19fVi3bt18D01ERA7VHjoGj8sHXZNXqHjfbkK63L8glmY5VemAjd4aC3DY/ESq6Yai6xjathOBz10jOw4REeWpeY+jcrvdKCkpmfgwTROGYSAQCGQiHxEROVBb3xG4dLfUnlDP202witwLYmmWU5UM2BgoAWzhvOdY9cXViD71guwYRESUxzL+9vHXvva1TB+SiIgcxBY2OsPNqK9cLi2DOhSH0TOIdFDezLzzoacBPSXQrw6jQjjrTVtjUTUS+w5ACCH1TQYiIspfEmeUICKihag30g6fWQyZ5Ynn981I1ZRA6M6aXXYuyvpttHmdNzmRVlYKKxxBqqlVdhQiIspTLEKJiGhOWnoPwWv6oWsuaRm8bzfBCniABVyElg7Y6Ct23nBcRVWgV1ci/PPNsqMQEVGeYhFKRERz0tJ7GKbukTdU07Jh7muDvYALUOCD50It23mFqLGkFqNcqoWIiLKERSgREc2aZVvoGWiTuj6o+3AX0mW+Bf+8op4GXHGBXi0mO8oUenUlUm2dsCJR2VGIiCgPsQglIqJZ6wo3IyB5fdCiN4/CKvdBuBZ2TygAlPfbaPM7bJ0WAIquQSspxsBjv5IdhYiI8hCLUCIimrWW3sPwuiWuDyoEvG8ehW0aC3JpllOV99voKbVlx5iWXl+L4Zdekx2DiIjyEItQIiKatdbeQzAMeeuDuo73wfa4ACHl9BnnH7QR8wNJkZIdZQpjUQ0SR5pgJ5KyoxARUZ5hEUpERLOSspIIxbqhSLx0eN84gnTQD2FmfJlrKVQBFEdstLoHZUeZQjXdUN1uxJ59RXYUIiLKMyxCiYhoVtr6jqCkKAhNlVcAFr1xFHaRKy+G4o4r67fR6Y/LjjEtfckiDD65VXYMIiLKMyxCiYhoVpq69594HlROEWq0h8f+YOfJWNwTykM2+sqc+W9yLVmExL4DsFPOGy5MREQLF4tQIiKalaauRhiaW9r5vW8eRaoqAGFKmhQpSzyjAmkdGBQjsqNMofq8gKoi9sJrsqMQEVEeYRFKRERn1B/tgaIoEIq8HruiN47A9ubXUNxx5X0WjhdFZMeYlnFuHQY3cakWIiLKHBahRER0Roda30PAWwaX5pJyfr1rAMpIEkD+FaAAEOyz0VVmyY4xLVf94rEhuem07ChERJQnWIQSEdEZHWx9F27DC0WRc9nw7TiEVG0JhDs/ZsU9VWnYRqQYSArnFXqq1wPFMDhLLhERZQyLUCIiOq20lUJb71GosobBCoGinQdhF7kBNT97QseXamkxB2RHmZZxzmIM/s/TsmMQEVGeYBFKRESn1R46htJAJVRVk3J+1/E+CF3OuXMp2GejrTghO8a0jPrFSLx/EHaSs+QSEdH8sQglIqLTOtz5HvyeEuianFlpi3YcRLoikLdDcccF+yz0BgVsYcuOMoXqMaGYbgxu3iI7ChER5QEWoURENCMhBI517oPbMOUEsAWKdh3O21lxT2akAHdcoEuPyo4yLeO8czD4+DOyYxARUR5gEUpERDPqibTBdBVBSOqdM/e3wyr2AELe0jC5VNFrozkwJDvGtFxLFiF5uAnpgYjsKEREtMCxCCUiohkd7ngPfm8JXJJ6Qn3b9iMd9Of9UNxxlT0WOisFnFhyK4YOraIc4f/8mewoRES0wLEIJSKiGR3u2AOXZkKRMBRWGUnA814LhEvP+6G44zyjAqol0KM5c0iu+/xzEXv+N7JjEBHRAscilIiIpjUw1Ds2SY6k+s/320NI1pVD6IV1qarqsnG0OCY7xrS0qiCs/gGMvn9IdhQiIlrACuvKTkREs3aofQ+KveUwNJeU8/teeX/sedACWJ7lZJU9FroqbDhxUK6iKDDOWYz+f39IdhQiIlrAWIQSEdG09rfuhsdVJGUortEagjqahAPrsKzzxAW0tEC35szeUPfSczD6+tuwk0nZUYiIaIFiEUpERFOEol0n1quUUwX6X3kfqZpSCLMwJiQ6VVW3hWMOHZKr+oqgeD2IPLJZdhQiIlqg5n11T6VS2LhxI/bt24ehoSFUVVXh+uuvxyWXXJKJfEREJMGBtndQUhSEobtzfm4lnkLRrsMYXbG4YCYkOlVlt4Xfr7Rh99tQFee9X+xafh4im36Nsm99U3YUIiJagOZ9ZbMsC+Xl5fjhD3+In/3sZ/j617+Oe+65B729vZnIR0REOSaEwIG2d+A2PFKG4vq2HxibkEhzXvGVK2YC8AzbaHFHZEeZllFbjXRPH0b3HpAdhYiIFqB5X+FN08TXvvY1VFZWQlVVfOxjH0NlZSWampoykY+IiHKsJ9IGQzMghIShuEIgsHUPrBIvYBTWhESnqu2wcSQ4LDvGtBRVgWtpPUI/vl92FCIiWoAy/rBNJBJBV1cX6urqJm1vaGhAQ0MDAGD9+vUIBoOZPnVG6bru+IyU/9gOSYbfHtyCYEk1fJ7ARE+ooigwTTPr53btaQZMA5qqQWiFXYRWhYEjFypAWIUJOTMUn47rDy5A/5aXUWK4oBcHcnJOviaSE7AdklMs5LaoiAy+1Z1Op3HnnXeiqqoKN91002n37ezszNRpsyIYDCIUCsmOQQWO7ZByLW2l8F8v/DOWVJw/6XlQ0zQRj8ezfv7KO56B0DXYRa6CfR70ZAcv1FEx6sFHhqpkR5nWyOtvw3vlSlTf8Y85OR9fE8kJ2A7JKZzeFmtra2f8XsYeuLFtGz/5yU+g6zr+6q/+KlOHJSKiHDrcsQelvkooEibD0TsH4GoJQegKC9ATajssNFc5dykU94rliG15BXY6LTsKEREtIBm5yxBC4MEHH8Tg4CD+9m//FrpemFPqExEtdO8dfx0+MwBdM3J+7pKndiNxbgWEK/fndip/VCCtCnTrUdlRpqUF/FA9Hgw8+KjsKEREtIBkpAh96KGH0NHRge9973twuZz33AoREZ1ZZCiE6EhYysqgWigG870WCLcOqOwFHacAqGux0Bh0ZhEKAO4PL8fAzzbLmciKiIgWpHl3Wfb19aGhoQGGYWDdunUT22+66SZceeWV8z08ERHlyJ7jv0W5vxouCWuDFj/9DhLnVUHohT0Z0XSqui00na9jpCcFr3BeL7FeUQ6k0hj832dQ8o0vyY5DREQLwLyL0IqKCmzevDkTWYiISJJUOonGlt+hrmJZztcGVQdHUPTGYYyuqAMKeG3QmWg2UNVp4f3iEFZGamTHmZb74ovQf89DKP76F6WsLUtERAsLr/ZERIT3W95CMFADVUIBUfLk7070gvKSNJPFbRaO16RhCVt2lGnp1RUQyRQim34lOwoRES0AvOITERU4IWy8ffQ38Lr9OZ+QSOuLwvvGUdgeF3tBT8MTFwhEbBzw98uOMi1FUeD+yFhvqG07s1AmIiLn4BWfiKjANXUfgFv3SDl36f++gcT57AWdjXOOp3FwURxCytRRZ2ZUVQACGPjpJtlRiIjI4XjVJyIqYEIIvH7gBRQXlcPQczu7udHaD/P9dghDYy/oLPiGBMxhG4eLwrKjzMj86AqEf/II7HhCdhQiInIwXvWJiApYS+8hWLYFRcnx5UAIlG/8DRJLqyBcXFt6ts5tSqOxdsSxvaF6eSm00mL0/NMG2VGIiMjBWIQSERUoIQR+27gVpb4KGDl+FtT7+hEo8RSEpnJd0DkIRAWMuI1Dju4N/TBiW15Csr1LdhQiInIoFqFERAWqpfcQUlYSqqLmdFkNJZ5C2S92IlVTAuFmL+hcLT2cxt4lo7AUZ/aGqqYbrqXnouuW78uOQkREDsUilIioANnCxm/2/hrlgaqcz4hb+vjrSNaVA4oy9kFz4hsWKOlPY29xn+woM3JfdD6Sx1ow+ORW2VGIiMiBWIQSERWg91vegtvwQEFue0HdBzrh2d0Ey+uGcGk5O2+++dCxNA4tSmBUTcuOMi1FVeH55EfR+893wYoNyY5DREQOwyKUiKjAJNNx7Gp8Hn5PaU5nxFUSKQR/8jIS51cDbhag8+FOAItb0nijuld2lBnpZaXQa6rQ+a3bZEchIiKHYRFKRFRgdr7/HCqKa3M+ErbskR1I1ZZwGG6G1LVYCBel0e5xbk+j+ZGLEN97AJH/eVp2FCIichAWoUREBaQz3IxjXe/DbXhy+ixo0Y6DcB/shO1xcRhuhqgCuKAxhTfqB5B26CRFiqbBe+XH0feje5A43io7DhEROQSLUCKiApG2Unjh7U2oKa3PaQFqtIdR+uhvkawPcjbcDCuOCpT3pPHb6m7ZUWakBfxwr1iO9q9/G1Y8ITsOERE5AItQIqIC8dq+Z+D3lAI5XJJFjY6i8s4tiF9YC6GrHIabBecdtdBflMIxX1R2lBm5zquH4vWg45u3Qghn9toSEVHusAglIioARzr3oqXnIEyXF4aem15QJZFC1f99BokPVQKqCmi85GSDKoAV76Wwe8kgBl1J2XFm5Ln0YqRaO9Dz/fWyoxARkWS8IyAiynPhWC9eeXczKksWw8jVMNy0hYp/ewFWsQdQVT4HmmXeUYFl+5N45dxeJDVbdpxpKaoC75UrEdu6DaF7HpIdh4iIJGIRSkSUx0YTQ3hq14OoCy6Fqmq5GYabtlB51/NA2oLtMSC4HEtOVIQEqtuTeGVJNyynTlSk6yha9SkMPPy/6L//57LjEBGRJCxCiYjyVDIdx1O7/guVJYugKAo0NfvFoJJIofL/PQek0rB9bgh37iZAImBJiw13NImGJd2wHVqIqqYb3msuR/iBX6Dv7v+SHYeIiCRgEUpElIeS6Th+ufN+FHkCUBUtJ7PhqpFhVP/glxCKAttnsgCVQAGw7FAa6kgC25b0OLZHVDPdKPrM5Rjc9Gt0fud2CMuSHYmIiHKIRSgRUZ4ZSQzhiR0/gdfth6G5YOiurJ/TfagTtbc9gVR1CYRpcCkWiRQAyw+koQ7F8cKHupFw6DOiqtsN76pPIf72XrR84Uak+wdkRyIiohxhEUpElEdC0S489pu7Uewtg64Z2e8BtWwUP/k7VPzbC4gvqwY0lQWoA4z3iJZ2juK587swYKZkR5qWqmvwXH4poKk4vuqrGN7xpuxIRESUA7xTICLKA0II7G1+Hbv2v4DFwfOgKmrWC1DXkW4EH9wGy+vG6AW1gKEBKtcBdZIlbTaKhkbx8od78Ic9xbig3wcFzvoZKYoC88LzoZWXouvWf4LnsktQtf770MtKZEcjIqIsYRFKRLTARYZDaNjzJEbiMSwJng9VVaFmcRIivTeKks1vwt3YjsT51YCiAOz9dKzyAeBjb4zi0B/YOHb+MD7VXo6yUec9r2tUBqH9nyuR3H8Ux6+6FmXf+iZK114P1WPKjkZERBnGuwYiogVqJDGE3Ye3obF1NxaVn4sSXxC6nr3iwmgJIfDcu/DsaUFiaRUS51dDuHT2fi4A7pSCP9yTRG95CtsuSqNqxMRHuksQSDjrNkDVNJgfXg6jvhbRZ17GwMbHUbr2ehSv+TJ7RomI8ogihJAydV5nZ6eM085aMBhEKBSSHYMKHNshTScU7cKepl041P4uqkoWw214oKk6VDXzj/mrsVF4f9eE4m2NQHQEqUWlsE0DQtcAjdMKLEQ2gK5aFW3nuVAWd2N5vx+1UTdUhw3TBYB0JIp0SztSHd0oumIl6m76JtIrlkMxnFU8U2HhtZmcwultsba2dsbvsQidgdN/qFQY2A4JGHvesz/Wjabu/TjQ+jZSVhKlvgoYuglNVaGpGbwht2y4mvtgvt8O7zvHYXSEkVxUBpT6YNk2hKmPDb+lBc+GQKhcRc8SF4aKNdRFPaiLeFAdc0MXzvoZ24kk0u1dQCSKZG8I3qs+gaKrPwHvJz4GY3GN7HhUYHhtJqdwelvMehE6NDSEBx54AHv37oXf78f111+PK6644rR/h0Uo0ZmxHRYeIQTiqRH0DXage6AN3QOtaA8dg9sw4TNL4HF5AUWBobmgzKcYFALqcAJ6VwSulhBcrf1wNffBaAnBKvfBKvbA8pqACghDh+Y2YHEtx7yV0CyEKw2EqwxESlX4kjoqh90oH3GhJK4jENdh2PJ7vk3TxHCoH1YoDHtoBFZfP2ALuD+8HOaKC+C+aBlcS8+BsbiGz5JS1vDaTE7h9LZ4uiI0I2+fb9y4Ebqu46GHHkJzczPuvPNO1NfXo66uLhOHJyJaUIQQsIWFtJX64MNOI20lkbbSSKZGMZocHvtIDGMkOYSh0UFEhkIYig/C0F3wuvwwXV64dDcWl58HQMDQ3WOFpy2gpCwoyTSQtk782YKSSo/9OWVBHU1CHYpDHUpAG45DHU5AjcWh9Q9B74tCi8VhmwZsnxt2kQnb64JV5Eb6D5cACsaWWWGPZ8FwWxpqumzUdCVg2wIjXoFYmYGWYh0HK1UMFymACnhTOopSGjxJDd6UBpelwmUpMCwFhqXCZanQbQWqAFRbgSbG/qwJBYpARmbm1XxF0HxFAABh27CjMdgjcYy89S6Gt+2CFRuCHRsCAOjVldBrq6CXl0IrK4FWWgytrASq3wfVY0LxesY+e8yxz6Ybiq5D0TVA06BoGqBr83vDh4iIpph3T2g8HseNN96Iu+++e6Lave+++1BWVoY1a9bM+Pec3BPa+MC/I/2fv8SZ/2MElGwMZp71MWe7ozLLfccvsrPdN5PHnOt+mdz3bPY73b6z3W82+47/P093AzTdceez30znn81+mTjmqftmYr9sH/P0+8303ZNvxJWTDqeM/6gnfuQn9hNiaivVVAhVBTRl7LOqQKjK2F9RFAhNhdBVCF0b237iQ6gqbF09UV8qEIYGoZ+5h0vTNPaEFjAhBNKKjaSpIelVkfJoSHo0pA0FlqEirSuwDGXss65AqICtfvDZVgGhjH0o0/2qzfQyhw++P9ZkFWA2ty0CUCwb7mgSZiwFYyQN14h14nMaetyClrKgpgS0pAUtZUNL2tBSNhQhoNgCiiWg2IBiiw/OeSKjIgBxhsL0jK82p+zwwQhoFryON9tbIKIsW/7sI/Ccu0x2jBlltSe0q6sLmqZNOkl9fT32798/ab+GhgY0NDQAANavX49gMDjfU2fNFd//IQ6vWIHwKf+G6czpUpGhd1LHb2D5zmz+U1QVwrZlx1iwzvYeYdq3JcTJd8nixH5jRd+k+2dFPVEHqlAUBYqiQFXGelLGl06Z/JurnHIjfuImWxm7y1EUZayoxNj3FEWdKCihqmM9NqoK6DoUXQUMY2xbhl8fVE2FbbEt0ukJCNiWBVtYsG0btm3Bhg0hbAhbQGCsoB3/HRIQE2/ETBRm4uTjje+Pid8rIezZ/24vmrppym+GbQNpC0hbEJYFWPbYNtv+4M/iREDbHjvCSf+GiReAkz6LiW9Mc0ZxUlF78rbZ4rVfuvF2SCSb2+dzdE11OvMuQuPxODwez6RtXq8X8Xh80rbVq1dj9erVE187efwyAFz45a8jdKWzM1L+c/pYfyocbIvkBGyH5ARsh+QUTm+Lp+sJnfcsA6ZpYnR0dNK20dFRmCYnBCAiIiIiIqLJ5l2E1tTUwLIsdHV1TWxraWnhpEREREREREQ0RUZ6Qi+77DI88cQTiMfjOHjwIHbv3o2rrroqE/mIiIiIiIgoj2Rk0a+1a9cimUxi3bp1uPfee7Fu3Tr2hBIREREREdEUGVkn1Ofz4R/+4R8ycSgiIiIiIiLKYxnpCSUiIiIiIiKaDRahRERERERElDMsQomIiIiIiChnWIQSERERERFRzihCCCE7BBERERERERUG9oTO4LbbbpMdgYjtkByDbZGcgO2QnIDtkJxiIbdFFqFERERERESUMyxCiYiIiIiIKGdYhM5g9erVsiMQsR2SY7AtkhOwHZITsB2SUyzktsiJiYiIiIiIiChn2BNKREREREREOcMilIiIiIiIiHKGRSgRERERERHljC47gCxDQ0N44IEHsHfvXvj9flx//fW44oorpuwnhMCmTZvw6quvAgCuueYarFmzBoqi5Doy5anZtsUtW7Zg+/bt6Ovrg9/vx2c/+1l84QtfkJCY8tFs2+G4dDqNv//7v8fo6CgefPDBHCalfDaXdtjU1ISf//znaGpqgmma+PKXv4w/+ZM/yXFiylezbYupVAqPPPIIdu/ejXQ6jeXLl+Omm25CWVmZhNSUb1588UW89tpraG1txeWXX45bbrllxn2fe+45PPPMM0gmk7jsssuwbt06GIaRw7RzU7BF6MaNG6HrOh566CE0NzfjzjvvRH19Perq6ibt19DQgN27d2PDhg1QFAX/8i//gsrKSvzRH/2RpOSUb2bbFoUQuOWWW1BfX4+enh7867/+K8rLy3H55ZdLSk75ZLbtcNyWLVsQCAQwOjqa46SUz2bbDqPRKO644w7ccMMN+MQnPoF0Oo3+/n5JqSkfzbYtPv/88zhy5Ag2bNgAr9eLn/70p3j44Yfxd3/3d5KSUz4pLS3Ftddei/feew/JZHLG/fbs2YNnnnkGt99+O0pLS3HXXXdh8+bNWLNmTQ7Tzk1BDseNx+N466238Od//ucwTRMXXHABLr30UuzYsWPKvtu3b8fnP/95lJeXo6ysDJ///Oexfft2CakpH82lLX7xi1/Ehz70IWiahtraWlx66aU4dOiQhNSUb+bSDgGgt7cXO3fuxJe+9KXcBqW8Npd2+Nxzz+Hiiy/GlVdeCcMw4PF4sHjxYgmpKR/NpS329vbi4osvRklJCVwuFz71qU+hra1NQmrKR5dddhlWrlwJv99/2v22b9+OVatWoa6uDj6fD1/5ylfw2muv5SbkWSrIIrSrq2viRn5cfX39tC8abW1tqK+vP+N+RGdjLm3xZEIIHDx4kDddlBFzbYcPP/wwvvGNb8DlcuUqIhWAubTDI0eOwOfz4Qc/+AHWrl2L9evXIxQK5TIu5bG5tMVrrrkGhw4dQjgcRiKRwM6dO3HJJZfkMi4R2tvbcc4550x8XV9fj8HBQcRiMXmhzqAgi9B4PA6PxzNpm9frRTwen3Zfr9c7ZT8ur0qZMJe2eLJf/vKXEEJg1apV2YxHBWIu7fB3v/sdbNvGypUrcxWPCsRc2mE4HMb27dvxl3/5l7j//vtRWVmJe++9N1dRKc/NpS3W1NSgvLwcN998M2644QZ0dHTguuuuy1VUIgDT1ysAHP3ITEEWoaZpTvmhjI6OwjTNM+47vh8nJqJMmEtbHPfiiy9i+/btuO222xz9wDktHLNth/F4HI899hhuvPHGXMajAjGX10OXy4WVK1di6dKlcLlc+OpXv4pDhw5hZGQkV3Epj82lLW7cuBGpVAoPP/wwHn30UaxcuRJ33HFHrqISARhrsye//o2331PfTHGSgixCa2pqYFkWurq6Jra1tLRMOwFHXV0dmpubJ75ubm6ecaIOormaS1sEgFdffRVPP/00br/9dpSXl+cqJuW52bbD7u5u9PX14fbbb8e6detw1113YWBgAOvWrUNvb2+uY1Oemcvr4ZIlSyZ9zTeGKZPm0hZbWlpw9dVXw+fzwTAMfO5zn8PRo0cRjUZzGZkK3OLFi9HS0jLxdUtLC4qLi8/4LKlMBVmEmqaJyy67DE888QTi8TgOHjyI3bt346qrrpqy71VXXYWtW7ciHA4jHA7jueeew6c//WkJqSkfzaUt7ty5E48//jh+8IMfoKqqSkJaylezbYd1dXV44IEHsGHDBmzYsAE333wzSkpKsGHDBgSDQUnpKV/M5fVw1apV2L17N5qbm5FOp/Hkk0/iggsumDQcjehszaUtnnfeedi+fTtGRkaQTqfx0ksvobS0FIFAQEJyyjeWZSGZTMK2bdi2jWQyCcuypuz36U9/Gq+++ira29sxPDyMp556CldffXXuA8+BIgr04cahoSHcf//92LdvH3w+H9asWYMrrrgCBw4cwB133IFHH30UwAfrhG7btg0A8JnPfIbrhFJGzbYt3nLLLQiHw9D1D1ZWuvLKK3HTTTfJik55ZLbt8GSNjY247777uE4oZcxc2uHLL7+Mp556CslkEsuXL8fatWv5ZghlzGzbYiwWwyOPPIK9e/cinU6jrq4ON9xwA5YuXSr5X0D5YPPmzXjyyScnbbvuuutwzTXX4Lvf/S7uueeeide9hbZOaMEWoURERERERJR7BTkcl4iIiIiIiORgEUpEREREREQ5wyKUiIiIiIiIcoZFKBEREREREeUMi1AiIiIiIiLKGRahRERERERElDMsQomIiIiIiChn9DPvQkRERPPx4osvYuvWrQiHw7joootw6623IhAIyI5FREQkBXtCiYiIsujxxx/Hs88+i29961u444470Nvbi8cee0x2LCIiImlYhBIREWXJsWPH8PTTT+M73/kOVqxYgfr6enz2s5/F73//e9nRiIiIpGERSkRElCXPPvssLrzwQixbtmxiWyAQQCwWk5iKiIhILhahREREWZBOp/HOO+9g5cqVk7Ynk0l4vV5JqYiIiOTjxERERERZ0NzcjEQigU2bNuHxxx+f2G5ZFs4991yJyYiIiORiEUpERJQFnZ2d0HUdd99996Tt9957L5YvXy4pFRERkXwsQomIiLJgZGQEfr8f1dXVE9ui0Siam5tx4403SkxGREQkF58JJSIiyoJAIIB4PA7btie2Pf3001i2bNmkiYqIiIgKDYtQIiKiLFixYgUsy8KvfvUr9Pb2YsuWLdixYwduvvlm2dGIiIikUoQQQnYIIiKifPTmm2/iF7/4BaLRKC688ELccMMNWLx4sexYREREUrEIJSIiIiIiopzhcFwiIiIiIiLKGRahRERERERElDMsQomIiIiIiChnWIQSERERERFRzrAIJSIiIiIiopxhEUpEREREREQ5wyKUiIiIiIiIcoZFKBEREREREeXM/wdVZ/qAyoFKjQAAAABJRU5ErkJggg==",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plot_dist()"
]
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python 3.8",
"language": "python",
"name": "python3.8"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.8.0"
}
},
"nbformat": 4,
"nbformat_minor": 4
}